Формула момента рычага

Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

 = МОМЕНТ_РЫЧАГА * СИЛА

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

 = РАССТОЯНИЕ_ДО_ЦЕНТРА * СИЛА

[Править]Сила под углом

Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой

[Править]Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.

[Править]Момент силы как функция от времени

Момент силы — производная по времени от момента импульса,

 ,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

 ,

То есть, если I постоянная, то

 ,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

 = МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ

В системе СИ мощность   измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

 = МОМЕНТ_СИЛЫ * УГОЛ

В системе СИ работа   измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.

Обычно известна угловая скорость   в радианах в секунду и время действия МОМЕНТА  .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

 = МОМЕНТ_СИЛЫ *   * 

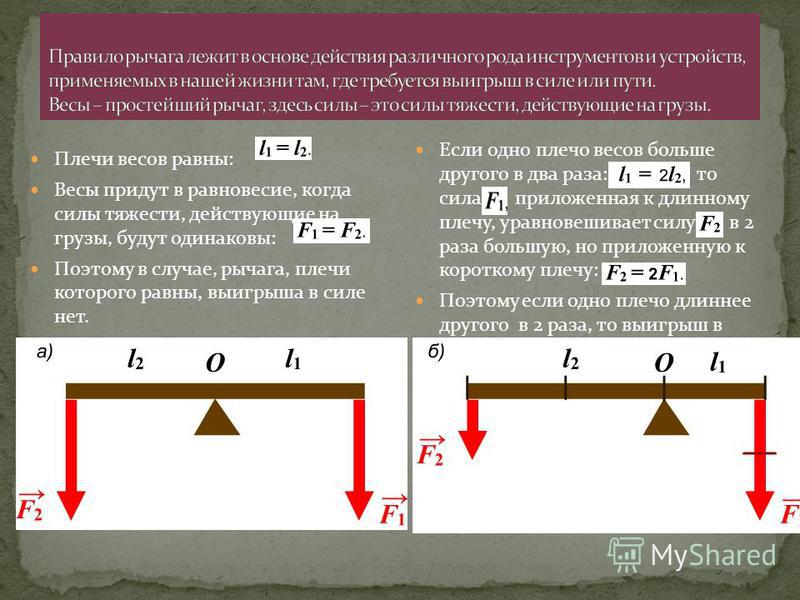
Если имеется материальная точка  , к которой приложена сила  , то момент силы относительно точки   равен векторному произведению радиус-вектора  , соединяющего точки   и  , на вектор силы  :

.

Существует несколько эквивалентных формулировок первого начала термодинамики

В любой изолированной системе запас энергии остаётся постоянным.^[2] Это — формулировка Дж. П. Джоуля (1842 г.).

Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил

Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики^[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.

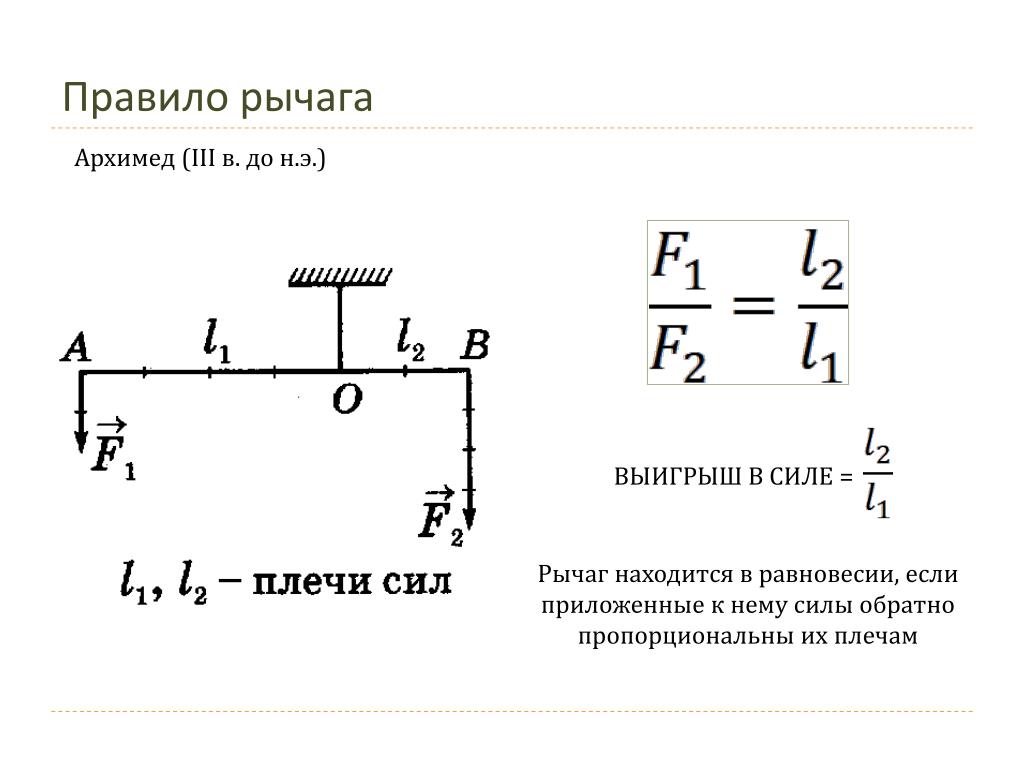
Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты  , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества   при химическом потенциале  , и работы ^[3], совершённой над системой внешними силами и полями, за вычетом работы  , совершённой самой системой против внешних сил

.

Для элементарного количества теплоты  , элементарной работы   и малого приращения   внутренней энергии первый закон термодинамики имеет вид:

.

Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.

Важно заметить, что   и   являются полными дифференциалами, а   и   — нет.

[править]Частные случаи

Рассмотрим несколько частных случаев:

1. Если  , то это означает, что тепло к системе подводится.

2. Если  , аналогично — тепло отводится.

3. Если  , то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.

Обобщая: в конечном процессе   элементарные количества теплоты могут быть любого знака. Общее количество теплоты, которое мы назвали просто   — это алгебраическая сумма количеств теплоты, сообщаемых на всех участках этого процесса.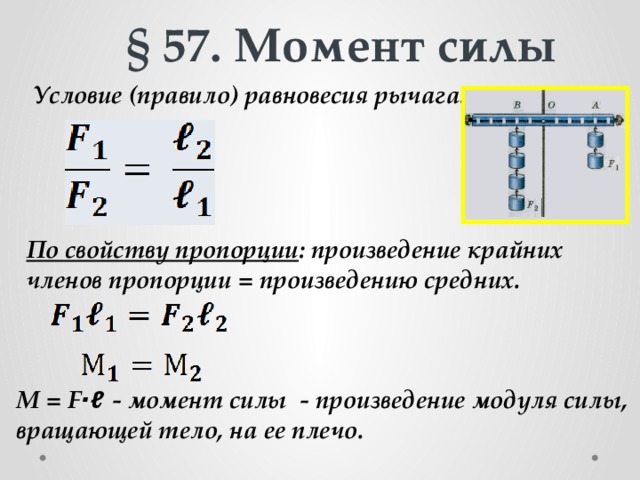

В ходе процесса теплота может поступать в систему или уходить из неё разными способами.

При отсутствии работы над системой и потоков энергии-вещества, когда  ,  ,  , выполнение системой работы   приводит к тому, что  , и энергия системы   убывает. Поскольку запас внутренней энергии   ограничен, то процесс, в котором система бесконечно долгое время выполняет работу без подвода энергии извне, невозможен, что запрещает существование вечных двигателей первого рода.

Первое начало термодинамики:

Здесь   — масса газа,   — молярная масса газа,   — молярная теплоёмкость при постоянном объёме,   — давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.

формула, примеры расчета с пояснениями / Справочник :: Бингоскул

Рассмотрим, как рассчитать выигрыш в силе при использовании простейших механизмов, которые люди тысячелетиями используют для перемещения тяжёлых предметов: рычаги, наклонные поверхности, блоки.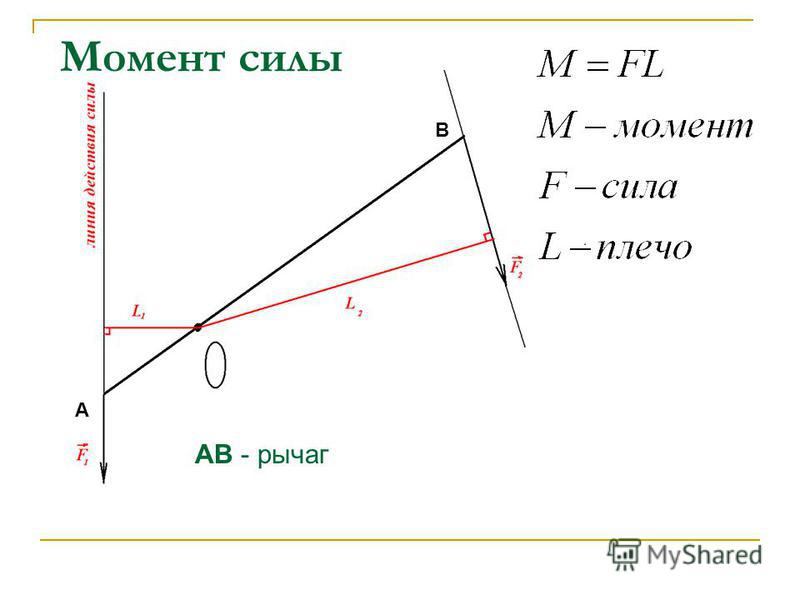 Первые применяются для перемещения массивных предметов с применением сил, которые имеют меньший за них вес; вторые – облегчают передвижение и подъём тел. 

О простейших механизмах

Тяжелые вещи люди издревле поднимали при помощи:

• рычагов – жёстких балок, способных вращаться вокруг точки опоры;


• блоков – колёс с желобами для скольжения верёвки, ремня, троса.

Части рычага до и после точки опоры называются плечами:

• коротким – плечо приложения усилия;


• длинным – плечо приложения силы.

 Механизм создаёт большее физическое усилие на коротком плече, чем сила, прилагаемая к длинному. На практике в его качестве применяются длинные (до нескольких метров) жёсткие деревянные балки, брус, металлические трубы.

Он же стал прообразом первых механических весов.

Рычаг будет находиться в равновесии до момента, пока вращающий его по часовой стрелке момент сил равняется силе, вращающей его в обратном направлении (по модулю).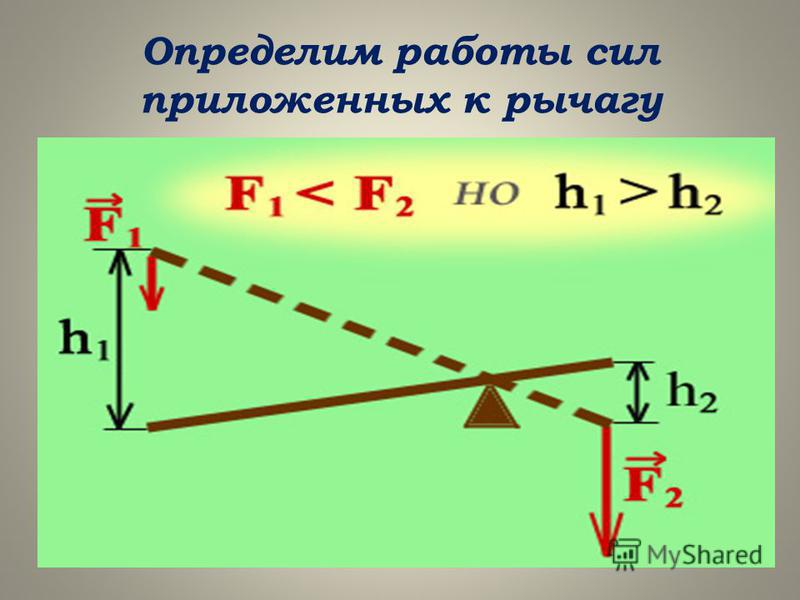 Если у механизма разные оси вращения – расстояние от точки опоры до места прикладывания усилия, такой рычаг даёт выигрыш в силе, расчёт которого проводится по формуле:

l₂ : l₁.

F₁ = F_{2 *} l₂ : l₁, здесь:

• F₁ и F₂ – величины усилий;
• l₁ и l₂ – длина первого и второго плеча.

В данном случае l₁ 2

Действительно, жёсткий рычаг с отличающейся в десятки раз длиной плеч сведёт к минимуму прикладываемую для передвижения либо подъёма предмета силу, но выигрыш в работе он не обеспечит. Во сколько раз легче будет подъем, ровно на столько вещь придётся переместить дальше, а значит выигрыша в работе не получить. Докажем это.

Выполняемая работа пропорциональна прикладываемой силе, пройденному телами расстоянию на угол поворота.

Отсюда выплывает, что энергия в системе ниоткуда не появляется и бесследно не исчезает, только переходит из одной формы в иную. Часть – уходит на нагрев тел вследствие их трения.

Примеры рычага: плоскогубцы, ножницы, клещи, ручной тормоз авто.

Какой выигрыш в силе дает подвижный блок

Различают неподвижные и подвижные блоки – колёса с продольными канавами для верёвки, крепящиеся на ось. Первые изменяют направление воздействия приложенной силы, не предоставляя преимуществ для перемещения вещей, вторые – прикладываемую силу. Подвижной блок перемещается с грузом, уменьшая прикладываемое для движения груза усилие.

Разберёмся, как найти выигрыш в силе в такой ситуации. Поднимая груз весом P посредством подвижного блока, нужно приложить вдвое меньшую силу, чем через неподвижный, ведь плечо OA (радиус) для силы P вдвое меньше OB (диаметра круга) для силы натяжения троса. Если тот вытягивается на длину l, груз поднимается только на половину этого расстояния l2:

 С учётом силы трения формула расчета выигрыша в силе приобретает вид:

K – коэффициент трения.

Задача

Рабочий посредством подвижного блока поднимает ведро песка на высоту 6 м. При этом прилагается сила, равная 160 Н. Трение повышает прикладываемую силу на 10%. Рассчитать совершаемую человеком работу?

A = kFs=1,1*160*6= 1056 Дж 1,056 кДж.

Ответ: 1056 Дж

Какой выигрыш в силе даcт использование показанной на рисунке схемы?

Механизм представлен парой неподвижных и тремя подвижными блоками. Каждый снижает прикладываемую силу вдвое, даёт выигрыш в шесть раз.

Рычаги и крутящий момент

Рычаги и крутящий момент

Рычаги и крутящий момент

Цели Рычаги Рассчитать крутящий момент Рассчитать механическое преимущество

Настройка Стержень метра Пружинные весы Строка А масса.

Теория

Рычаги используют крутящий момент, чтобы помочь нам поднимать или перемещать предметы.

Крутящий момент крест Произведение силы на расстояние силы от точки опоры (центральная точка вокруг которого вращается система). Перекрестное произведение принимает только компонент сила, действующая перпендикулярно расстоянию. С помощью тригонометрии определяется крутящий момент как:

Крутящий момент = Сила × Расстояние до точки опоры × грех (θ)

Помните, что работа была также силой, умноженной на расстояние, но это была точка произведения и использовали косинус угла между силой и расстоянием: сила × расстояние × соз (θ).

В этой лаборатории сила будет перпендикулярна (90°) расстоянию. синус 90° равен единице, поэтому крутящий момент будет:

Крутящий момент = Сила × Расстояние до точки опоры × sin (θ)
Крутящий момент = Сила × Расстояние до точки опоры × sin (90°)
Крутящий момент = Сила × Расстояние до точки опоры × 1
Крутящий момент = Сила × Расстояние до точки опоры

Процедура, сбор данных и расчеты

Рычаги класса I пробные один: d

_e = d _r

В рычаге первого класса точка опоры находится между силой сопротивления (F _r ) и сила усилия (F _e ).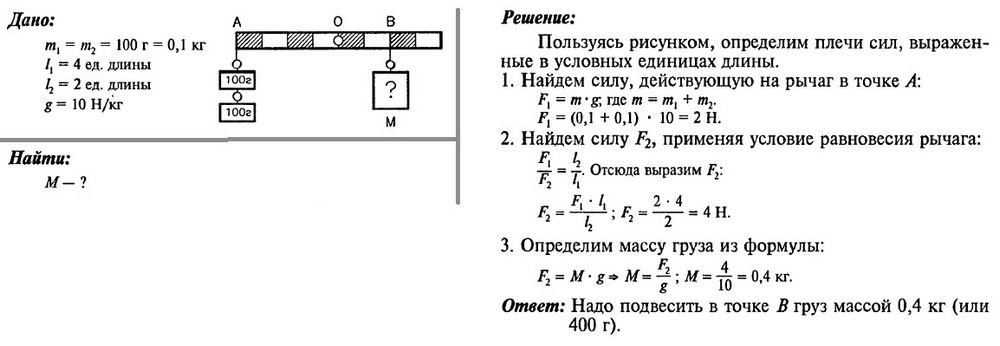

В классе один рычаг сила усилие (F _e ) умноженное на расстояние усилия от точки опоры (d _e ) равна силе сопротивления (F _r ), умноженной на расстояние сопротивление от точки опоры (d _r ). Усилие и сопротивление включены противоположные стороны точки опоры. Плоскогубцы являются примером рычага первого класса.

На схеме масса обеспечивает сопротивление, пружинная шкала измеряет наше усилия. Пружинная шкала откалибрована в граммах. грамм не является единицей сила сама по себе, но в этой лаборатории мы будем использовать термин «грамм-сила» как сила, действующая на один грамм на поверхности Земли за счет ускорения свободного падения. Один «грамм-сила» будет эквивалентна 980 см/сек

2 (дин).

Для диаграммы: F _e × d _e = F _r × d _r
Механическое преимущество = F _r /F _e

1. Подвесить груз 200 грамм на отметке 10 см, подвесить пружинные весы на отметке 90 см, подвесьте метровую рейку к отметке 50 см.
2. Найдите F _e , d _e , F _r , d _r в граммах силы. К определить грамм-силу массы (F _r ) с помощью весов балансира. д _д и d _r должна быть 40 см при правильной установке. Ф
   e можно прочитать из весенняя граммовая шкала напрямую.
3. Рассчитать F _e × d _e и F _r × d _r .
4. Укажите, является ли F _e × d _e = F _r × d _r .
5. Рассчитайте механическое преимущество F _r /F _e .

Ф и	д д	F e × d e	Ф р	д р	F R × D R	F e d e = F r d r ?	М. А.
________	________	________	________	________	________	Да | №	________

Класс I Рычаги пробные два: d

_е > д _р

Для диаграммы: F _E × D _E = F _R × D _R
Механическое преимущество = F _R /F _E

1. MASSES MASSE AT A 500 500 30038
   или MASS MASS MASS
2. . две гири по 200 грамм связаны вместе.
3. Поместите груз массой 500 грамм на отметку 10 см, а пружинные весы на отметку 90 см, подвесьте метровая палочка от отметки 30 см.
4. Найти F _e , d _e , F _r , d _r в граммах силы.
5. Рассчитать F _e × d _e и F _r × d _r .
6. Укажите, является ли F _e × d _e = F _r × d _r .
7. Рассчитайте механическое преимущество F _r /F _e .

Ф и	д д	F e × d e	Ф р	д р	F R × D R	F e d e = F r d r ?	М.А.
________	________	________	________	________	________	Да | №	________

Рычаги класса II

В рычаге второго класса сопротивление находится между силой усилия и точка опоры. В рычаге второго класса сила усилия, умноженная на расстояние усилие от точки опоры противоположно и равно силе сопротивления умножается на расстояние сопротивления от точки опоры. Усилия и сопротивления находятся по одну сторону от точки опоры, но направлены в противоположные стороны.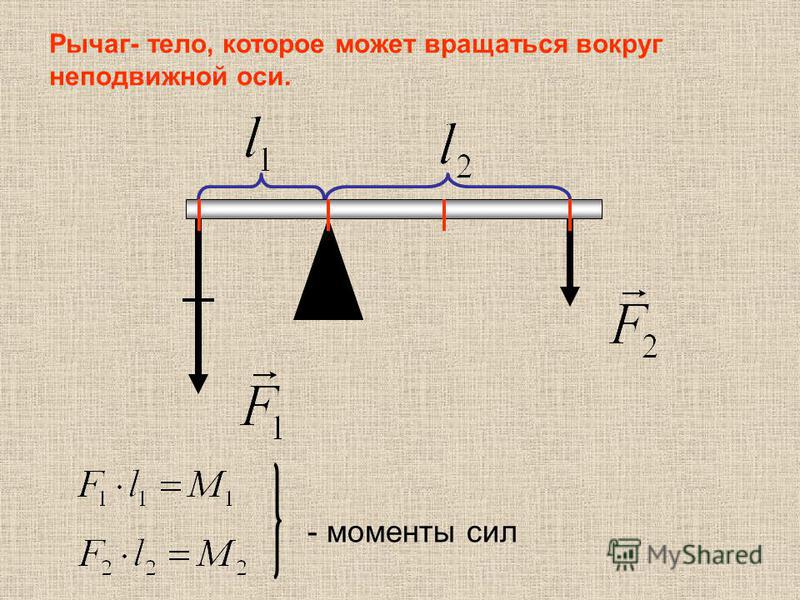

Расстояние усилия (также иногда называемое «плечом усилия») равно длиннее чем расстояние сопротивления.

Тачки и гигантские шесты для копания таро (когда мы нажимаем на шест) являются примерами рычаги второго класса.

Обратите внимание, что наш выбор дауна как положительного в первой части лаборатории означает, что up теперь отрицателен в этом разделе. Итак, F _e — отрицательная сила. Запишите F _e как отрицательное в таблице, а затем -F _e × d _e будет будь позитивным.

Для схемы: -F _e × d _e = F _r × d _r
Механическое преимущество = |F _r /F _e | где | означает «абсолютный значение.» Механическое преимущество всегда положительно.

1. Переместите 500 граммовую гирю (или две 200-граммовые гири) примерно на 30 см отметку и пружинную шкалу на отметке 90 см, подвешивают измерительную рейку к отметке 10 см. Возможно, вам придется отрегулировать положение груза в соответствии со способностями вашего тела. пружинная шкала для обеспечения точных показаний. Вы хотите избежать необходимости читать либо очень маленькое усилие в грамме или усилие в грамме слишком велико для вашей весовой шкалы. Если вы отрегулируете позиции, не забудьте измерить фактический d _e и d _r вы используете!
2. Найдите F _e , d _e , F _r , d _r в граммах силы.
3. Рассчитать F _e × d _e и F _r × d _r .
4. Укажите, является ли -F _e × d _e = F _r × d _r .
5. Рассчитайте механическое преимущество F _r /F _e .

F и	д д	-F e × d e	Ф р	д р	F R × D R	-F e d e = F r d r ?	М. А.
________	________	________	________	________	________	Да | №	________

Рычаги класса III

В рычаге третьего класса сопротивление находится между силой усилия и точка опоры. В рычаге третьего класса сила усилия, умноженная на расстояние усилие от точки опоры противоположно и равно силе сопротивления умножается на расстояние сопротивления от точки опоры. Усилия и сопротивления находятся по одну сторону от точки опоры, но направлены в противоположные стороны.

Расстояние усилия (также иногда называемое «плечом усилия») на короче чем расстояние сопротивления.

Для диаграммы: -F _e × d _e = F _r × d _r
Механическое преимущество = |F _r /F _e | где | означает «абсолютный значение.» Механическое преимущество всегда положительно.

1. Переключиться на массу 100 грамм.
2. Переместите 100-граммовую массу на отметку 90 см, а пружинную шкалу — примерно на 65 см. см до отметки 70 см, держа измерительную рейку подвешенной к отметке 10 см. Снова при необходимости отрегулируйте шкалу пружины и положения массы, чтобы получить точные показания Весенняя шкала.
3. Найдите F _e , d _e , F _r , d _r в граммах силы.
4. Рассчитать F _e × d _e и F _r × d _r .
5. Укажите, является ли -F _e × d _e = F _r × d _r .
6. Рассчитайте механическое преимущество F _r /F _e .

Ф и	д д	-F e × d e	Ф р	д р	F R × D R	-F e d e = F r d r ?	М. А.
________	________	________	________	________	________	Да | №	________

В рычаге класса III механическое преимущество можно назвать механическим недостаток. Почему? (Предложение: рассмотрите силу усилия, меньше силы сопротивления или больше силы сопротивления?)

Обратите внимание, что нижняя часть руки человека представляет собой рычаг третьего класса: бицепс, прикрепленный чуть ниже локоть, может использоваться для подъема веса, удерживаемого рукой в ​​конце нижнего рука.

Непрерывные рычаги: отвертки

Отвертка на самом деле представляет собой форму рычага, в котором рукоятка с большим радиусом обеспечивает механическое преимущество при повороте лезвия с меньшим радиусом. Все виды циркулярки. устройства используют эту форму механического преимущества. Круглые ручки водяного клапана, шина утюги, торцевые ключи, гаечные ключи и многие другие предметы используют это время круговой рычаг.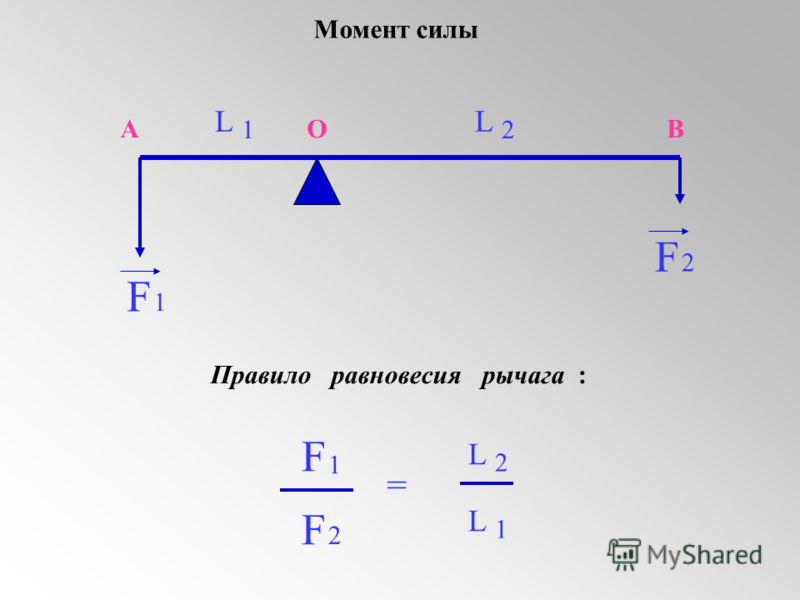

Измерьте радиус ручки отвертки, а затем измерьте радиус лезвие. Рассчитайте механическое преимущество по d _е / д _р .

Обратите внимание, что механическое преимущество круглого устройства de/dr, в то время как мех. нареч. для рычага было Fr/Fe. Обратите внимание, что кажущийся «триггер» дроби не ошибка.

Предположим, что F _e × d _e = F _r × d _r . Крест деление на F _e и d _r дает:

 д  е  = Ф  р 
-- -- = механическое преимущество
д  р  F  д  

Домашняя страница SC 130
Домашняя страница курсов Lee Ling
Домашняя страница COM-FSM

Калькулятор рычага

| Механическое преимущество

Создано Давиде Борчиа

Отзыв от Анны Щепанек, доктора философии, и Джека Боуотера

Последнее обновление: 13 февраля 2023 г.

Содержание:

• Что такое рычаг?
• Элементы рычага
• Уравнение рычага
• Механическое преимущество рычага и закон рычага
• Три типа рычагов
• Пример: рассчитать плечо рычага, чтобы поднять мир
• Как рассчитать механическое преимущество рычага с помощью нашего калькулятора рычагов
• FAQ

Архимед сказал: «Дайте мне рычаг достаточной длины » — используйте наш калькулятор рычагов, чтобы узнать, какой длины должен быть этот рычаг!

Здесь вы узнаете:

• Физика рычагов и уравнение рычага;
• Закон рычага Архимеда;
• Каково механическое преимущество рычага; и
• Несколько примеров рычагов в действии, как практичных, так и непрактичных!

Что такое рычаг?

Рычаг, вероятно, самый простой механизм, когда-либо изобретенный человечеством.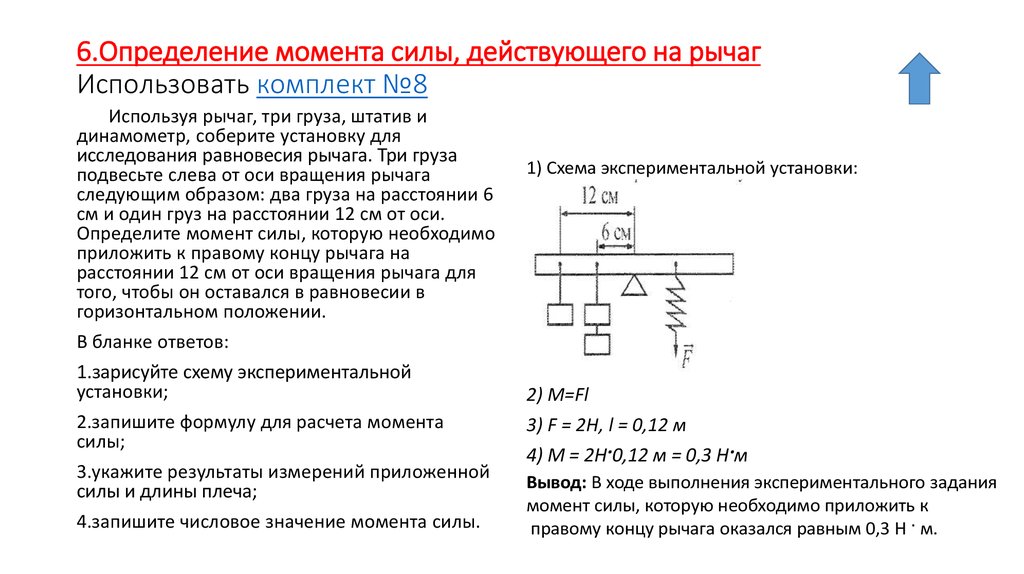 Возьмите деревянную доску (или любой другой жесткий материал), найдите место, куда ее положить, и все готово.

Несмотря на свою несложность, рычаги — чудесные механизмы в нашей повседневной жизни. Оглянитесь вокруг, где бы вы ни находились: ножницы, кусачки для ногтей, открывалки для бутылок и так далее — все это рычаги. Давайте узнаем о них больше.

🔎 Рычаги постоянно появляются в природе, в частности в царстве животных . Мышцы, суставы, челюсти: эволюция создала живое существо настолько совершенным, насколько это возможно.

Рычаг позволяет вам перемещать объект с особым преимуществом , то есть вы сможете перемещать его либо с уменьшенным усилием , либо с увеличенной скоростью или перемещением .

Рычаги работают благодаря приложению силы и эксплуатации крутящие моменты , которые вытекают из них. Это изменяет баланс, позволяя нам поднимать тяжелые грузы с минимальными усилиями.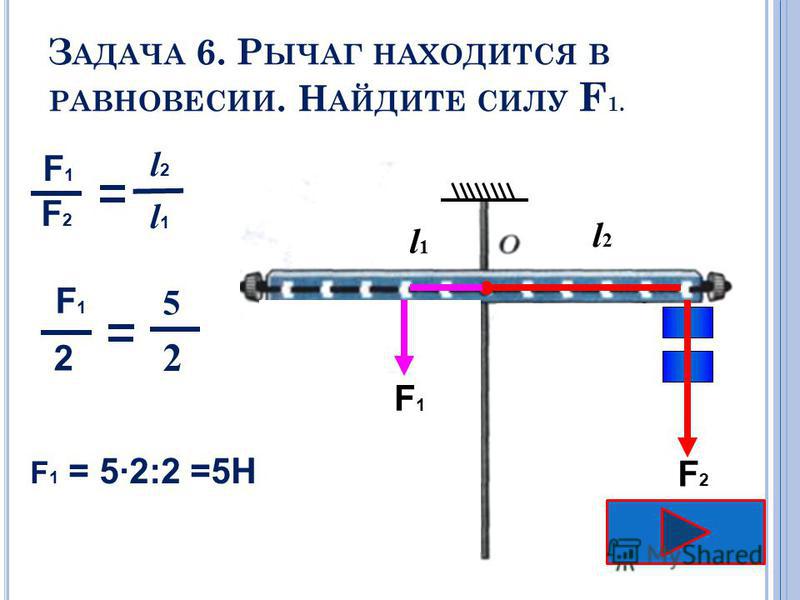

Элементы рычага

Мы можем описать рычаги с относительно небольшим количеством элементов:

• Точка опоры ;
• Усилие ; и
• Сопротивление .

Точка опоры находится там, где рычаг поворачивается . Точка опоры не обязательно должна находиться посередине рычага — на самом деле ее положение позволяет совершенно по-разному использовать эту простую машину. Вы можете узнать больше об этом с помощью нашего калькулятора точек опоры.

Сопротивление (или нагрузка ) — это сила , приложенная объектом , который вы хотите переместить, разрезать или сделать что-то еще, что делает ваш рычаг. Мы обозначаем сопротивление символом FbF_bFb​. Отрезок от точки опоры до точки приложения сопротивления обозначается как bbb.

Усилие — это усилие, которое вы прикладываете при работе с рычагом.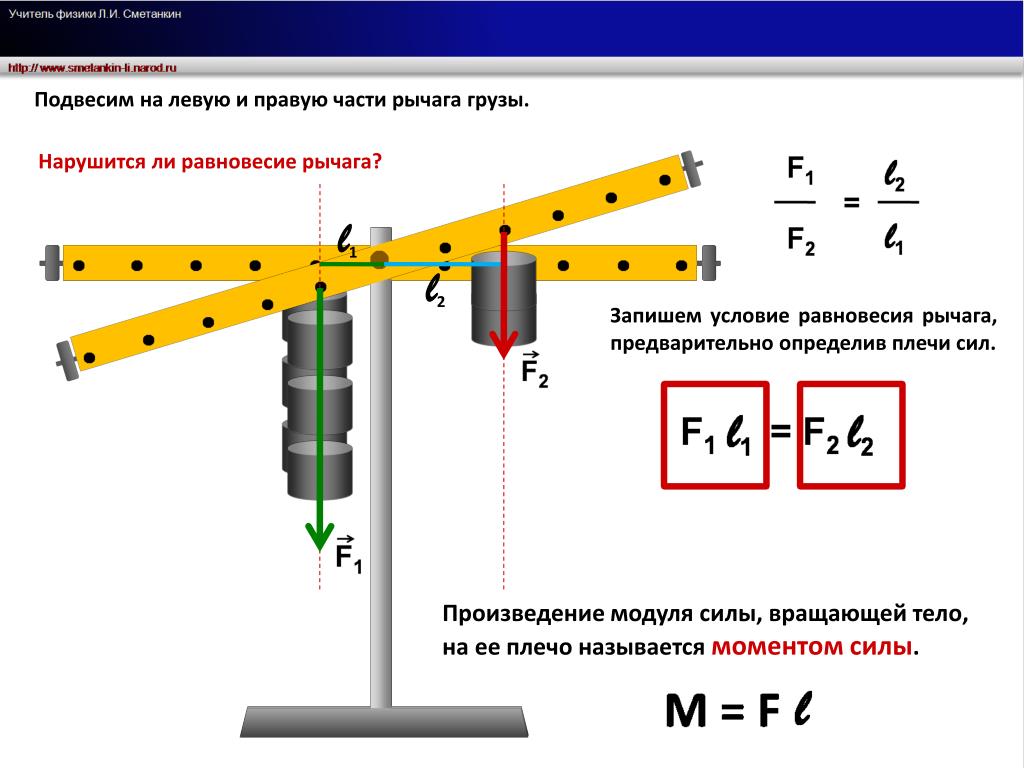 Расстояние от точки приложения до точки опоры равно aaa, а его значение равно FaF_aFa​.

Уравнение рычага

Принцип работы рычага прост. Мы можем определить ситуацию равновесия, когда рычаг неподвижен.

В этом состоянии крутящий момент , приложенный к рычагу обеими силами , равен друг другу .

Крутящий момент является вращательным аналогом линейной силы и, говоря простым языком, описывает действие силы FFF, приложенной на определенном расстоянии xxx ( плечо ) от оси:

τ=x×F=x×F×sin⁡θ\boldsymbol{\tau}= \mathbf{x}\times\mathbf{F}= x\times F\times sin{\theta}τ=x×F=x×F×sinθ

Величины выделены жирным шрифтом, потому что нам нужно рассматривать их как векторы: величина крутящего момента зависит от синуса угла между приложенной силой и плечом.

Хорошие новости! В рычаге угол θ\thetaθ обычно равен 90°90\градус90°, и мы можем спокойно его игнорировать, поскольку sin⁡90°=1\sin{90\градус}=1sin90°=1. Чтобы узнать больше о крутящем моменте, воспользуйтесь нашим калькулятором крутящего момента!

Вернуться к состоянию равновесия . Мы сказали, что моменты равны друг другу:

τa=a×Fa=b×Fb=τb\tau_a = a \times F_a = b \times F_b = \tau_bτa​=a×Fa​=b×Fb​=τb​

Это уравнение позволяет нам найти все необходимые величины в задаче с рычагами. Например, если известна длина плеча, можно рассчитать силу, необходимую для достижения равновесия при определенном сопротивлении.

Механическое преимущество рычага и закон рычага

Величина, которая измеряет «работу» рычага, называется механическим преимуществом. Он выводится из анализа крутящего момента, прикладываемого обеими силами к рычагу.

Знаменитый закон рычага гласит, что произведение силы в рычаге равно:

MA=FaFb=ab\text{MA} = \frac{F_a}{F_b} = \frac {a}{b}MA=Fb​Fa​=ba​

Взгляните на формулу и помните, что aaa соответствует стороне, на которую вы прикладываете усилие и bbb относятся к сопротивлению .

Во-первых: легче думать о руках, а не о силах: совершенно очевидно, что чем большую силу вы прикладываете, тем выше механическое преимущество. Но представьте теперь, что у вас действительно «неуравновешенный» рычаг с усилием, приложенным на расстоянии, намного превышающем сопротивление: a≫ba\gg ba≫b.

Механическое преимущество такого рычага было бы чрезвычайно велико, что выражается в необходимости приложения действительно большого усилия к одному из рычагов.

🔎 Архимед сказал: «Дайте мне достаточно длинный рычаг и точку опоры, на которую его можно поставить, и я переверну мир». Он имел в виду рычаг с особенно хорошим механическим преимуществом!

Значение механического преимущества говорит нам о том, как ведет себя рычаг . Чем выше механическое преимущество, тем меньше усилие, прикладываемое для уравновешивания того же сопротивления. В этом случае рычаг называется множителем силы .

Если механическое преимущество равно 111, рычаг не дает вам преимущества : это все равно, что прилагать усилие напрямую.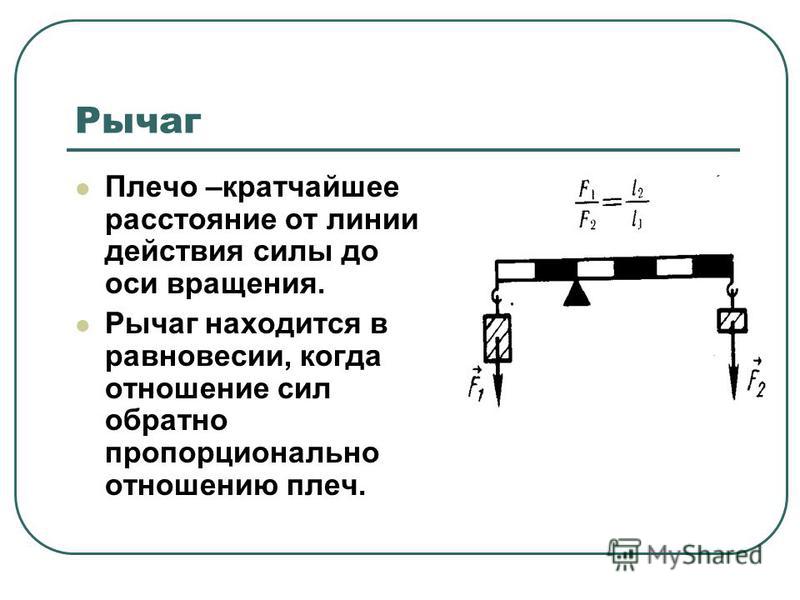 Наконец, если механическое преимущество меньше 111, рычаг является множителем скорости , что означает, что вы будете перемещать точку, где приложено сопротивление, быстрее, чем вы думаете для усилия (за то же время, следовательно, увеличивая скорость).

🙋 Мы посвятили целый калькулятор механическому преимуществу в различных простых машинах — проверьте его на нашем калькуляторе механического преимущества!

Три типа рычагов

То, как различные элементы рычага соотносятся друг с другом, позволяет нам определить три различных типа рычагов:

• Класс I рычаги – рычаги, которые мы представляем себе, когда кто-то спрашивает нас думать об одном. Точкой опоры является между сопротивлением и усилием.
• Рычаги класса II – Сопротивление и усилие расположены на одной стороне на одной стороне точки опоры, a>ba>ba>b.
• Рычаги класса III – Сопротивление и усилие расположены на одной стороне точки опоры, но на этот раз a

Три типа рычагов. Сверху: рычаг класса I , рычаг класса II и рычаг класса III .

Теперь мы знаем, как их охарактеризовать. Давайте посмотрим на возможные механические преимущества!

• Для рычага класса I aaa и bbb могут принимать все возможные значения больше 000 (и, конечно, ограничено длиной рычага). По соотношению aaa и bbb такой рычаг может быть мультипликатором силы.
• Для рычага класса II : a>ba\text{\textgreater}ba>b. Это означает, что механическое преимущество в раз больше, чем в 111, а рычаг всегда действует как множитель силы.
• Для рычага класса III верно обратное. Поскольку b>ab\text{\textgreater} ab>a, механическое преимущество равно 9.0037 всегда меньше, чем 111, поэтому рычаг всегда действует как множитель скорости.

Пример: расчет плеча рычага, способного поднять мир

Мы можем рассчитать характеристики рычага, способного поднять мир, используя уравнение рычага. Есть только условие: ты один делаешь подъем !

Предполагая, что вес 70 кг70\ \text{kg}70 кг и что вы стоите на своем конце рычага, мы можем вычислить усилие из: 99\ \text{м}148,81×109 м). Назвав длину lll и используя равенство a=l−ba = l-ba=l−b, мы можем записать уравнение рычага в виде:

l−b=Fb×bFal-b=\frac{F_b\ раз b}{F_a}l−b=Fa​Fb​×b​

Выделим bbb:

(l−b)×Fa=b×Fbl×Fa=(Fa+Fb)×bb=l×FaFa +Fb\begin{выравнивание*} (l-b)\times F_a &= b\times F_b\\\\ l\times F_a &= (F_a + F_b)\times b\\\\ b&=\frac{l\times F_a}{F_a+F_b} \end{align*}(l−b)×Fa​l×Fa​b​=b×Fb​=(Fa​+Fb​)×b=Fa​+Fb​l×Fa​​

Это Уравнение позволяет найти длину плеча рычага, связанного с сопротивлением, в нашем случае Земли. Подставляем числовые значения (пренебрегая FaF_aFa​ в знаменателе) и вычисляем плечо рычага: 9{-12}\ \text{м} \end{align*}b​=5,8587×1025 N1,481×1011 м×687,7 N=1,74×10−12 м​

Это один длинный рычаг: рука, на которой держится Земля, меньше атома водорода !

Наш Архимед пытается поднять мир, используя только рычаг.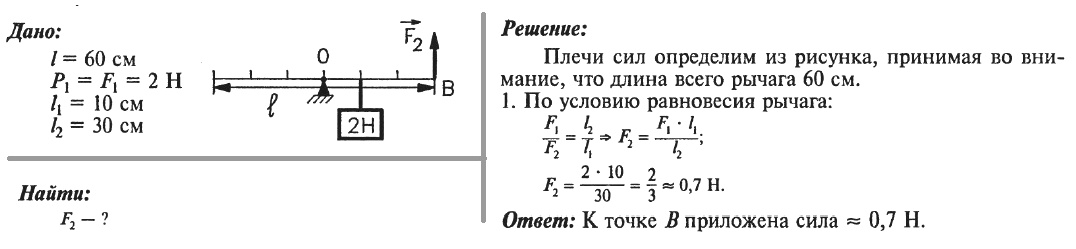 Удастся ли ему это сделать?

Вернемся к более практическим примерам, не связанным с подъемом планет. Допустим, вы на детской площадке, играете на качелях с одним из ваших друзей. К настоящему времени вы знаете, что качели — это рычаг класса I 9.0038 . Мы предполагаем, что ваш вес 75 кг75\ \text{kg}75 кг, а ваш друг, будучи худощавым, весит всего 60 кг60\ \text{kg}60 кг.

Качели длиной 4 м4\ \text{м}4 м. Где вы должны сидеть, чтобы уравновесить вашего друга? А в чем механическое преимущество созданного вами рычага?

Примените уравнение рычага, чтобы найти плечо рычага с вашей стороны. Обратите внимание, что в уравнении вы можете использовать массы вместо весов. Они отличаются только мультипликативной константой , ggg, стандартный гравитационный параметр , и мы можем его отменить.

а=г×60 кг×2 мг×75 кг=60 кг×2 м75 кг=1,6 м\footnotesize \начать{выравнивать*} a&=\frac{g\times 60\ \text{kg}\times 2\ \text{m}}{g\times 75\ \text{kg}}\\\\ &=\frac{60\ \text{кг}\times 2\ \text{м}}{75\ \text{кг}}=1,6\ \text{м} \end{align*}a​=g×75 kgg×60 kg×2 m​=75 kg60 kg×2 m​=1,6 m​

Вы должны сесть за 40 см40\ \text{cm}40 см до конец качелей, чтобы сравняться с сопротивлением вашего друга — теперь игра. .. сбалансирована!

Теперь мы можем рассчитать механическое преимущество рычага. Вычислить частное длин двух плеч

MA=ab=1,6 м2 m=0,8\text{MA}=\frac{a}{b}=\frac{1,6\ \text{m}}{2\ \ text{m}} = 0,8MA=ba​=2 m1,6 m​=0,8

Это меньше 111, потому что вы поднимаете меньший вес, чем ваш.

Как рассчитать механическое преимущество рычага с помощью нашего калькулятора рычага

Наш калькулятор рычага — это полезный инструмент, который позволяет вам рассчитать все, что вам нужно в вашей домашнее задание по физике — и не только: мы надеемся, что оно поможет вам и в решении ваших повседневных задач !

Используйте свое время и быстро найдите результаты: введите известные вам количества и найдите результаты. Вы можете подставить силы, действующие на рычаги, рычаги или механическое преимущество, и только одну из остальных величин, чтобы найти остальные!

Часто задаваемые вопросы

Что такое уравнение рычага?

Уравнение рычага определяет силы и физические свойства рычага в состоянии равновесия. Оно вытекает из сравнения крутящего момента, действующего на рычаг:

Fa × a = Fb × b

где:

• Fᵢ — силы, усилия или сопротивления; и
• lᵢ — это плечи рычага ( a и b ).

Поработайте с этим простым уравнением, чтобы выделить желаемое количество.

Какой длины должно быть плечо рычага, чтобы уравновесить автомобиль массой 1500 кг с моим весом?

Допустим, вы весите 70 кг . Уравновесить автомобиль массой 1500 кг , можно использовать рычаг, определяемый механическим преимуществом:

MA = (1500 × g)/(70 × g) = 21,43

, где г — стандартный гравитационный параметр, равный 9,81 м/с² . Плечо рычага с вашей стороны должно быть в 21,43 раз длиннее, чем со стороны автомобиля.

Как рассчитать механическое преимущество рычага?

Вы можете рассчитать механическое преимущество рычага, рассчитав отношение сил, действующих на рычаг, или, взаимозаменяемо, отношение плеч рычага:

MA = Fa/Fb = a/b

Механическое преимущество может быть меньше, больше или равно единице.