Как рассчитать индуктивность катушек с замкнутыми сердечниками?

Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

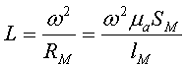
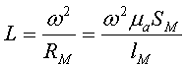
где ω – количество витков катушки,

R_M – сопротивление магнитной цепи,

μ_а – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

S_M – площадь поперечного сечения сердечника,

l_M – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l_e и эффективная площадь поперечного сечения S_e сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

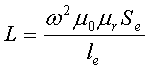
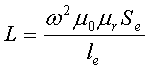
где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

S_e – эффективная площадь поперечного сечения сердечника,

l_e – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм^-1;

С₂ – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм^-3;

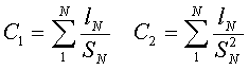
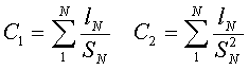
где N – количество разнородных участков сердечника,

l_N – длина N – го участка сердечника,

S_N – площадь N – го участка сердечника.

Тогда величины S_e и l_e определятся из следующих выражений

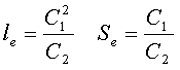
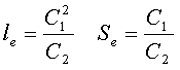
Кроме индуктивности с помощью постоянных С₁ и С­₂ определяют эффективный объём V_e, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С₁ по следующему выражению

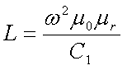
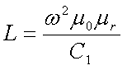
где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Расчёт катушки с тороидальным сердечником

Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.

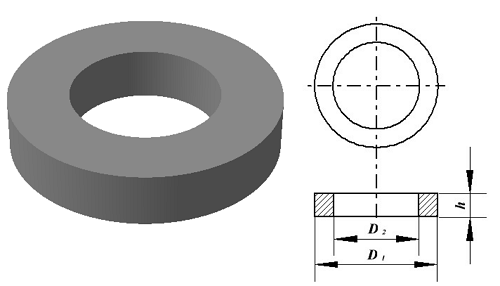
Тороидальный сердечник.

Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D₁ – внешний диаметр, D₂ – внутренний диаметр, h – высота сердечника.

Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С₁ и С₂, которые составляют

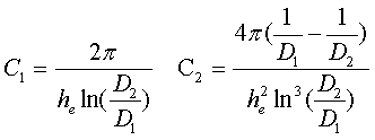
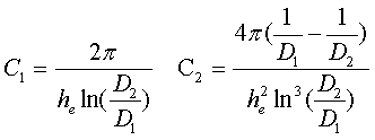
где h_e – эффективная высота сердечника,

D₁ – внешний диаметр сердечника,

D₂ – внутренний диаметр сердечника.

Расчёт эффективной высоты h_e сердечника зависит от конструктивных особенностей.

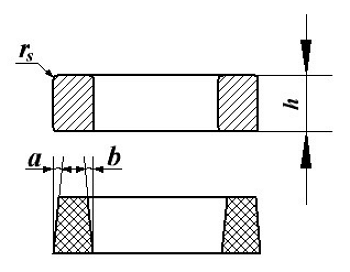
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).

Рассмотрим несколько случаев:

а) прямоугольное поперечное сечение с острыми кромками

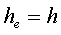
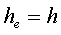
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления r_s

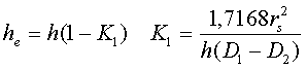
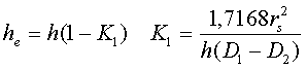
в) трапецеидальное поперечное сечение с острыми кромками

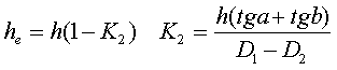
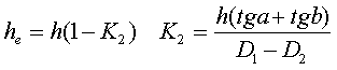
г) трапецеидальное поперечное сечение со скруглёнными кромками

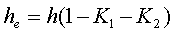
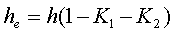
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D₁ = 20 мм, D₂ = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления r_s = 0,5 мм, относительная магнитная проницаемость материала сердечника μ_r = 1000.

Так как рассчитываем только индуктивность, то в расчёте коэффициента С₂ нет необходимости

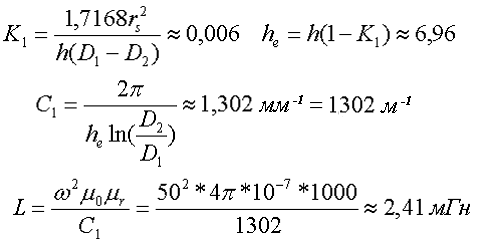
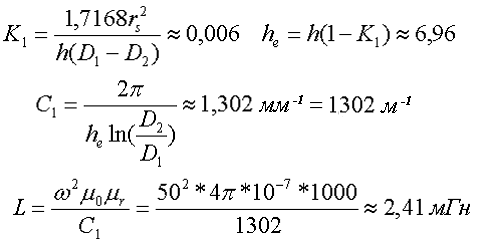
Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

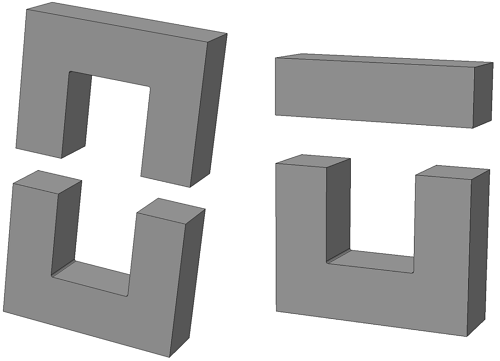
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

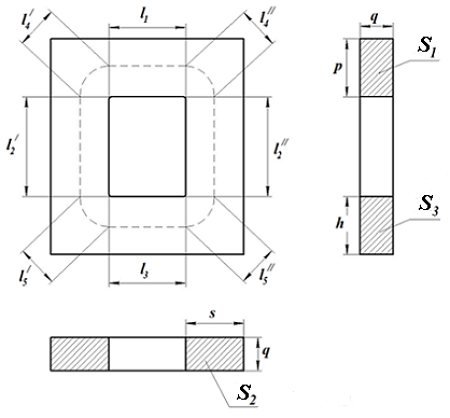
Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l₁, l₂, l₃, l₄, l₅ имеющих различное сечение S₁, S₂, S₃, S₄, S₅,. Тогда коэффициенты С₁ и С₂ составят

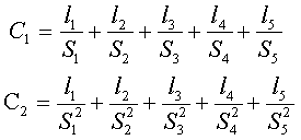
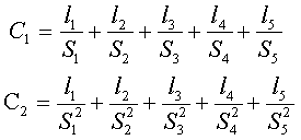
Неизвестные величины можно найти следующим образом

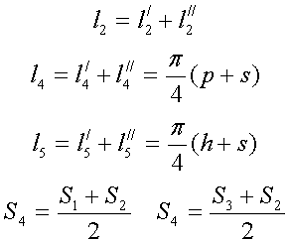
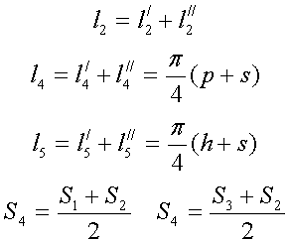
Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μ_r = 1950, количество витков ω = 150.

 

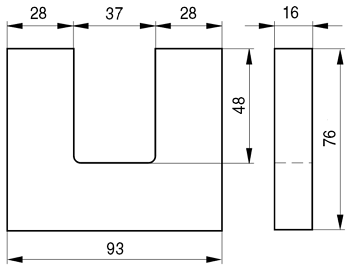
Сердечник Epcos U93/76/16.

Таким образом, расчётные параметры сердечника составят

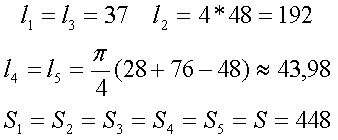
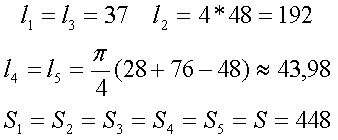
Таким образом коэффициент С1 и индуктивность L составят

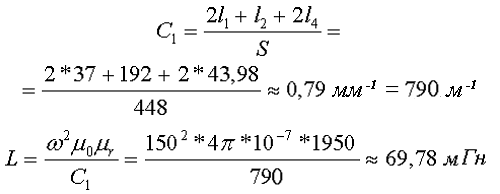
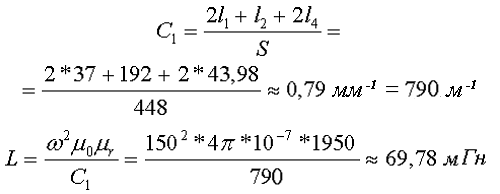
Расчёт катушки с П-образным сердечником круглого сечения

Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.

Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

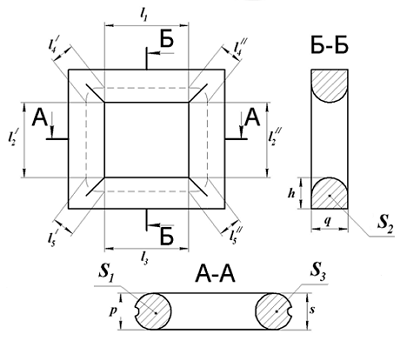
Сечение П-образного сердечника с круговым сечением.

Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь

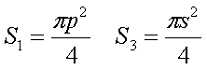
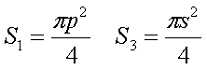
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μ_r = 2500), количество витков ω = 60.

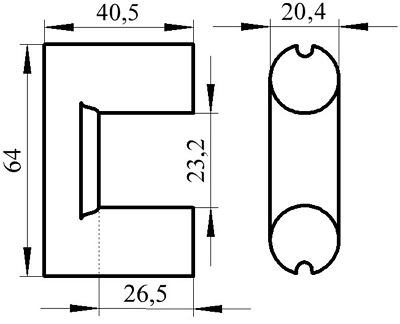
Сердечник типа SDMR 40 UY20.

Параметры сердечника для расчёта составят

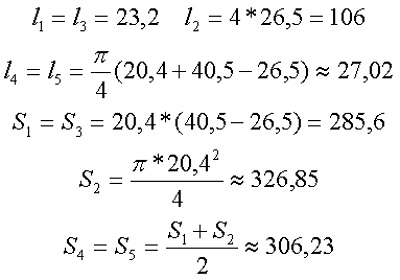
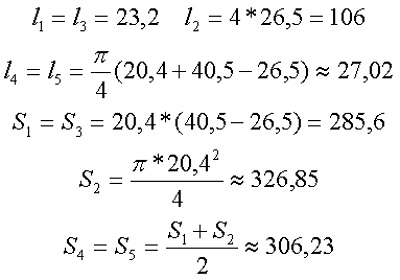
Таким образом коэффициент С1 и индуктивность L составят

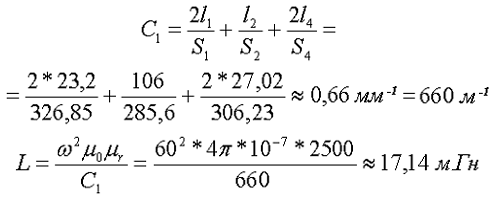
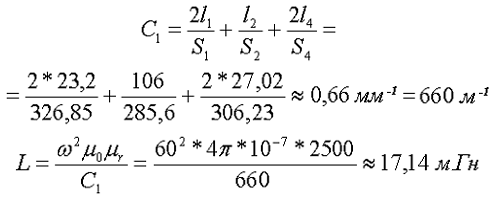
На сегодня всё. Продолжение смотри в следующей статье.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Калькулятор расчета индуктивности катушки с воздушным сердечником

Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр – индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:

где μ­­₀ – магнитная проницаемость вакуума,  μ – магнитная проницаемость сердечника (можно взять из таблицы 1), N – число витков, S – площадь сечения катушки, l – длина намотки. Такой способ является универсальным и может использоваться, как для полых катушек, так и для имеющих сердечник.

Таблица 1

Материал	— µ —  (Гн/м)
Воздух	1.25663753*10−6
Алюминий	1.256665*10−6
Аустенитная нержавеющая сталь	1.260*10−6  — 8.8*10−6
Вакуум (µ0)	4π*10−7
Вода	1.256627*10−6
Водород	1.2566371*10−6
Висмут	1.25643*10−6
Дерево	1.25663760*10−6
Железо (чистота 99.8%)	6.3*10−3
Железо (99.95% чистое Fe отожженное в водороде)	2.5*10−1
Железо-кобальтовые сплавы	2.3*10−2
Медь	1.256629*10−6
Никель-цинковый феррит — магнит	2.0*10−5 – 8.0*10−4
Мартенситная нержавеющая сталь (отожженная)	9.42*10−4 — 1.19*10−3
Мартенситная нержавеющая сталь (закаленная)	5.0*10−5 — 1.2*10−4
NANOPERM® — магнитомягкий нанокристаллический сплав	1.0*10−1
Неодимовый магнит	1.32*10−6
Никель	1.26*10−4 — 7.54*10−4
Пермаллой (сплав 80% никеля и 20% железа)	1.0*10−2
Платина	1.256970*10−6
Сарфир	1.2566368*10−6
Сверхпроводники	0
Углеродистая сталь	1.26*10−4
Ферритная нержавеющая сталь (отожженная)	1.26*10−3 — 2.26*10−3
Фторопласт 4, Ф-4,   Teflon	1.2567*10−6

Если рассматривать частный вариант – катушку с воздушным сердечником, то для расчета ее индуктивности можно использовать формулу:

Где D – диаметр катушки, n – количество витков, а l – длина ее намотки.

Такой способ расчета будет справедливым для катушек, имеющих однослойную структуру, набираемых в один уровень. В случае если катушка наматывается в несколько слоев, то их толщина вносит дополнительные изменения в расчет. При этом формула расчета преобразится к виду:

Где D – диаметр катушки, n – количество витков, h – высота самой катушки, g – толщина слоя намотки.

Для упрощения процесса расчета индуктивности катушки без сердечника можно воспользоваться онлайн калькулятором. Здесь вы указываете ее основные параметры – диаметр, длину и количество витков, после чего нажать кнопку «Рассчитать» и вы получите значение индуктивности без лишних вычислений и затрат времени.

Как рассчитать сердечник и витки самодельных катушек индуктивности

Катушки индуктивности предназначены для фильтрации токов высокой частоты. Они устанавливаются в колебательных контурах и используются для других целей в электрических и электронных схемах. Готовое устройство заводского изготовления надёжнее в работе, но дороже, чем изготовленное своими руками. Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками. В этом случае расчёт катушки  индуктивности и само устройство можно сделать самостоятельно.

Устройство катушки индуктивности

Конструкция катушки

Каркас устройства изготавливается из диэлектрика. Это может быть тонкий (нефольгированный) гетинакс, текстолит, а на тороидальных сердечниках –просто обмотка из лакоткани или аналогичного материала.

Обмотка выполняется из одножильного или многожильного изолированного провода.

Внутрь обмотки вставляется сердечник. Он изготавливается из железа, трансформаторной стали, феррита и других материалов. Он может быть замкнутым, тороидальным (бублик), квадратным или незамкнутым (стержень). Выбор материала зависит от условий работы: частоты, магнитного потока и других параметров.

Кроме того, есть приборы, в которых сердечник отсутствует. Они характеризуются большой линейностью импеданса, но при намотке тороидальной формы обладают паразитной ёмкостью.

Расчет параметров катушки индуктивности

Протекающий по проводу электрический ток создаёт вокруг него электромагнитное поле. Соотношение величины поля к силе тока называется индуктивностью. Если провод свернуть кольцом или намотать на каркас, то получится катушка индуктивности. Её параметры рассчитывают по определённым формулам.

Расчёт индуктивности прямого провода

Индуктивность прямого стержня – 1-2мкГн на метр. Она зависит от его диаметра. Точнее можно рассчитать по формуле:

L=0.2l(logl/d-1), где:

• d – диаметр провода,
• l – длина провода.

Эти величины нужно измерять в метрах (м). При этом результат будет иметь размерность микрогенри (мкГн). Вместо натурального логарифма ln допустимо использовать десятичный lg, который в 2,3 раза меньше.

Предположим, что какая-то деталь подключена проводами длиной 4 см и диаметром 0,4 мм. Произведя при помощи калькулятора расчет по выше приведённой формуле, получаем, что индуктивность каждого из этих проводов составит (округлённо) 0,03 мкГн, а двух – 0,06 мкГн.

Ёмкость монтажа составляет порядка 4,5пФ. При этом резонансная частота получившегося контура составит 300 МГц. Это диапазон УКВ.

Важно! Поэтому при монтаже устройств, работающих в частотах УКВ, длину выводов деталей нужно делать минимальной.

Расчёт однослойной намотки

Для увеличения индуктивности провод сворачивается кольцом. Величина магнитного потока внутри кольца выше примерно в три раза. Рассчитать её можно при помощи следующего выражения:

L = 0,27D(ln8D/d-2), где D – диаметр кольца, измеренный в метрах.

При увеличении количества витков индуктивность продолжает расти. При этом индукция отдельных витков влияет на соседние, поэтому получившиеся параметры пропорциональны не количеству витков N, а их квадрату.

Однослойная намотка

Дроссель с сердечником

Параметры обмотки, намотанной на каркас, диаметром намного меньше длины рассчитывается по формуле:

L=*0*N2*S.

Она справедлива для устройства большой длины или большого тора.

Размерность в ней дана в метрах (м) и генри (Гн). Здесь:

• 0 = 4•10-7 Гн/м – магнитная константа,
• S = D2/4 – площадь поперечного сечения обмотки, магнитная проницаемость магнитопровода, которая меньше проницаемости самого материала и учитывает длину сердечника; в разомкнутой конструкции она намного меньше, чем у материала.

Например, если стержень антенны изготовить из феррита с проницаемостью 600 (марки 600НН), то у получившегося изделия она будет равна 150. При отсутствии магнитного сердечника = 1.

Для того чтобы использовать это выражение для расчёта обмоток, намотанных на тороидальном сердечнике, его необходимо измерять по средней линии “бублика”. При расчёте обмоток, намотанных на железе Ш-образной формы без воздушного зазора, длину пути магнитного потока измеряют по средней линии сердечника.

Катушка с Ш-образным сердечником

В расчёте диаметр провода не учитывается, поэтому в низкочастотных конструкциях сечение провода выбирается по таблицам, исходя из допустимого нагрева проводника.

В высокочастотных устройствах, так же как и в остальных, стремятся свести омическое сопротивление к минимуму для достижения максимальной добротности прибора. Простое повышение сечения провода не помогает. Это приводит к необходимости наматывать обмотку в несколько слоёв. Но ток ВЧ идёт преимущественно по поверхности, что приводит к увеличению сопротивления. Добротность в высокочастотных элементах растёт вместе с увеличением всех размеров: длины и диаметров обмотки и провода.

Максимальная добротность получается в короткой обмотке большого диаметра, с соотношением диаметр/длина, равным 2,5. Параметры такого устройства вычисляются по формуле:

L=0.08D2N2/(3D+9b+10c).

В этой формуле все параметры измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

По этой формуле рассчитывается также плоская катушка. Диаметр “D” измеряется по среднему витку, а длина “l” по ширине:

l=Dmax-Dmin.

Плоская катушка

Многослойная намотка

Многослойная намотка без сердечника вычисляется по формуле:

L=0.08D2N2/(3D+9b+10c).

Размеры здесь измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

Добротность такого устройства зависит от способа намотки:

• обычная плотная намотка – самая плохая, не более 30-50;
• внавал и универсал;
• “сотовая”.

Многослойная катушка

Для увеличения добротности при частоте до 10 мГц вместо обычного, одножильного провода, можно взять литцендрат или посеребренный проводник.

Справка. Литцендрат – это провод, скрученный из большого количества тонких изолированных друг от друга жил.

Литцендрат имеет большую поверхность, по сравнению с одножильным проводником того же сечения, поэтому на высоких частотах его сопротивление ниже.

Использование сердечника в высокочастотных устройствах повышает индуктивность и добротность катушки. Особенно большой эффект даёт использование замкнутых сердечников. При этом добротность дросселя зависит не от активного сопротивления провода, а от проницаемости магнитопровода. Рассчитывается такой прибор по обычным формулам для низкочастотных устройств.

Сделать катушку или дроссель можно самостоятельно. Перед тем, как её изготавливать, необходимо рассчитать индуктивность катушки по формулам или при помощи онлайн-калькулятора.

Видео

Оцените статью:

Coil32 — Тороидальная однослойная катушка

Подробности

Опубликовано: 02 сентября 2013

Просмотров: 8718

Расчет тороидальной катушки

Тороидальные катушки без магнитного сердечника довольно редко используются. Магнитное поле такой катушки почти полностью сосредоточено внутри тороида, благодаря этому такая конструкция имеет малое поле рассеяния и, соответственно, такая катушка мало подвержена влиянию внешних полей даже без экрана. Для расчета индуктивности тороида круглого поперечного сечения можно за основу взять формулу расчета индуктивности соленоида [3].

S необходимо заменить на площадь поперечного сечения тора, а l — на среднюю длину окружности тора. Проделав эти манипуляции мы получим в итоге следующую формулу:

[1]

Обозначения понятны из рисунка, все размеры в метрах, индуктивность в генри, N — число витков катушки. Формула имеет не только академический интерес, но и может применяться для практических расчетов тороидальных катушек.

Однако в радиолюбительской практике мы чаще имеем дело с тороидами имеющими квадратное поперечное сечение, хотя при большом числе витков сечение такой катушки становится больше похожим на эллипс. Экспериментально было установлено, что расчет числа витков тороида с квадратным сечением лучше вести по эмпирическим формулам расчета катушки на ферритовом кольце, только магнитная проницаемость в этом случае принимается равной единице. Это и реализовано в программе Coil32.

 

Назад…      Вперед…

Добавить комментарий

Насыщение ферритового сердечника — торроидального и Ш-образного. Онлайн калькуляторы.

Итак, мы решили поразвлечься и всерьёз сваять что-нибудь стоящее своими руками, как то: индуктивный фильтр для блока питания, дроссель для усилительного каскада, выходной трансформатор для однотактного УНЧ, или фиг его знает — чего ещё похуже…

Что объединяет этих жертв нашего волеизъявления?
Каждое из перечисленных моточных изделий содержит магнитомягкий магнитопровод, и через каждое из них протекает постоянный ток. И если к переменному току, даже значительных величин, магнитопровод относится сдержанно-положительно, то к постоянке питает явную антипатию и может резко войти в насыщение от её переизбытка.
При насыщении сердечника его относительная магнитная проницаемость резко уменьшается, что влечёт за собой пропорциональное уменьшение индуктивности изделия.

На этой странице порассуждаем о тороидальных магнитопроводах из ферритов, распылённого железа, электротехнической стали и их способности противостоять постоянному току.

Для наглядности рассмотрим график зависимости B от H, называемый петлёй гистерезиса, для распространённого, где-то даже народного, феррита марки N87 фирмы EPCOS.

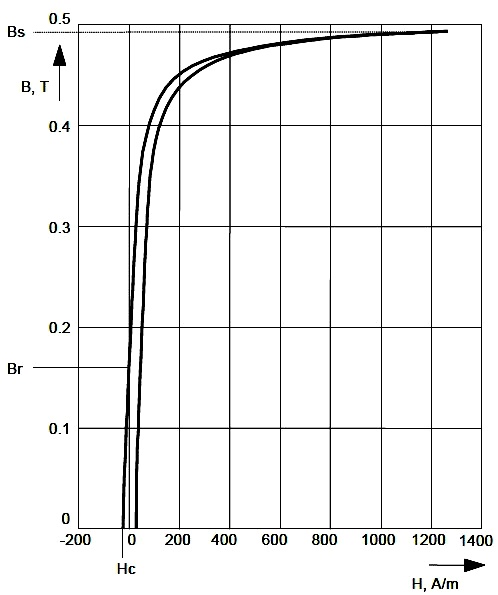Здесь:
H — напряжённость магнитного поля, а
B — магнитная индукция в сердечнике.

Зависимость приведена при температуре изделия +25 гр.С.

Интересующие нас параметры из datasheet-а производителя:

Начальная магнитная проницаемость —
µ = 2200,
Магнитная индукция насыщения при H=1200 А/м  —  Bнас = 0,490 Т.

Если внимательно присмотреться к графику, то легко заметить, что в области малых и средних индукций зависимость практически линейна и её наклон примерно равен µ. Именно на этот участок в большинстве случаев и должен приходиться диапазон рабочих индукций.
При дальнейшем повышении напря- жённости магнитного поля магнитная проницаемость начинает быстро падать, пока не наступает момент, при котором дальнейший рост магнитной индукции в сердечнике стопорится на определённой величине. В спецификациях это величина приводится, как значение магнитной индукции насыщения — Bнас, или Bs, т.е. величина, при которой значение магнитной проницаемости падает до неприлично малых значений.

Так что давайте без лишних прелюдий и телодвижений сделаем фундаментальный вывод — для нормальной работы катушки, намотанной на магнитопроводе, рабочие значения магнитной индукция в сердечнике не должны превышать величину 0,75 — 0,8 от значения справочной характеристики Bнас (Bs).

Переходим к незамысловатым формулам!

Магнитная индукция в сердечнике равна:
B = µ×µ₀×n×I/l, где:
µ — магнитная проницаемость сердечника,
µ₀ = 4π×10^-7 (Гн/м) — физическая константа, называемая магнитной постоянной,

n — количество витков обмотки,
I — ток в обмотке,
l — средняя длина магнитного контура.

Поскольку рабочий режим магнитопровода мы выбираем в линейной области петли гестерезиса, то в качестве значения µ можно использовать паспортную характеристику начальной магнитной проницаемости сердечника.

Теперь можно рисовать калькулятор для расчёта магнитной индукции в катушке с учетом выбранного типа сердечника и конкретного количества витков обмотки.

Для удобства восприятия, помещу сюда и значение индуктивности полученного моточного изделия. Формулы для вычислений этого параметра выглядят следующим образом:
L=0,0002×µ×h×n²×ln(D_внешн/D_внутр)   при соблюдении условия  D_внешн/D_внутр>1,75,
L=0,0004×µ×h×n²×(D_внешн-D_внутр)/(D_внешн+D_внутр)   при  D_внешн/D_внутр

ТАБЛИЦА РАСЧЁТА МАГНИТНОЙ ИНДУКЦИИ В КАТУШКЕ С ТОРОИДАЛЬНЫМ СЕРДЕЧНИКОМ.

Увы, но значительных токов через катушки на ферритовых кольцах, или торах из трансформаторной стали нам пропустить не удастся — нужны танцы с бубнами в виде немагнитных воздушных зазоров.
Другое дело — сердечники из распылённого железа, представляющие собой магнитопровод с немагнитными зазорами, технологически распределёнными по всему объёму магнитопровода. Их очевидный плюс — высокая индукция насыщения, минус — малые величины магнитной проницаемости.

В связи с этим, в некоторых случаях (в основном на низких частотах) предпочтительным является использование именно сердечников из ферритов (или железа) с пропилом для создания малого воздушного зазора. Данная мера позволяет в значительной мере увеличить величину допустимых токов через катушку без ввода магнитопровода в режим насыщения. Длина этого воздушного зазора позволяет регулировать как величину максимально-допустимой напряжённости магнитного поля в сердечнике, так и параметр изменившейся магнитной проницаемости, называемой эквивалентной магнитной проницаемостью сердечника с зазором — µ_эф. Значение этого параметра вычисляется по формуле:
µ_эф = µ/(1+l_з×µ/l), где:
µ — начальная магнитная проницаемость сердечника,
l — средняя длина магнитного контура,
l_з — длина воздушного зазора (толщина пропила).

Давайте посчитаем этот параметр.

РАСЧЁТ ЭКВИВАЛЕНТНОЙ МАГНИТНОЙ ПРОНИЦАЕМОСТИ СЕРДЕЧНИКА С ЗАЗОРОМ.

Таблица даёт приблизительную, но, в большинстве своём, приемлемую точность расчёта при величинах длины воздушного зазора 0,2-2 мм.

Для Ш-образных сердечников в качестве внутреннего и внешнего диаметров следует вводить справочную характеристику длины магнитного контура le.

Определив ниже магнитную проницаемость сердечника с зазором, следует ввести это значение в предыдущий калькулятор и заново произвести вычисления магнитной индукции и индуктивности катушки.

Для наглядности приведу два графика петли гистерезиса Ш-образного ферритового сердечника марки N87 без немагнитного воздушного зазора и с зазором около 1 мм. Феррит ETD 59/31/22, достаточно крупный, с средней длиной магнитного контура le = 139 мм.
Механизмы влияния зазора у Ш-образных и тороидальных сердечников абсолютно идентичны.

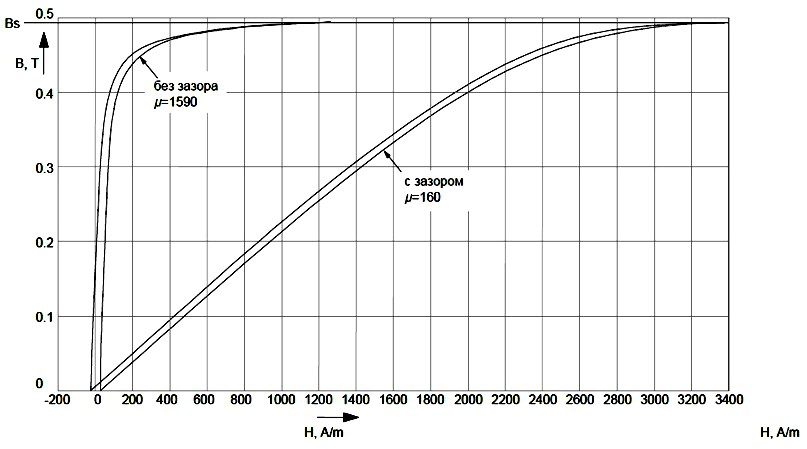
Эквивалентная магнитная проницаемость сердечника с зазором уменьшилась и составила величину 160 единиц. Соответственно, уменьшился и наклон петли, позволяя сердечнику работать при гораздо больших значениях напряжённости магнитного поля вдали от области магнитной индукции насыщения сердечника.
А учитывая то, что значение напряжённости H прямо пропорционально, протекающему через катушку току, можно с уверенностью сказать, что область безопасных индукций теперь соответствует более чем на порядок большим токам в обмотке.

Линейная область петли гистерезиса также заметно увеличилась, что позволяет увеличить максимальные рабочие значения магнитной индукция в сердечнике вплоть до 0,85-0,9 от значения справочной характеристики Bнас (Bs).

 

Как рассчитать индуктивность катушек с замкнутыми сердечниками? Часть 2.

Всем доброго времени суток. В первой части я рассказал, как рассчитать индуктивность катушек с замкнутыми сердечниками тороидального и П-образного типа. Данная статья продолжает тему индуктивности катушек с замкнутыми сердечниками, здесь я расскажу о расчёте катушек с Ш-образными и броневыми сердечниками.

Расчёт катушки с Ш – образным сердечником прямоугольного сечения

Ш-образные сердечники также как и П-образные выполняются разборными. Существует несколько видов таких сердечников, я рассмотрю два типа: с прямоугольным сечением и круговым сечением среднего керна.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Данные типы сердечников применяются в трансформаторах преобразователей с частотой работы до 100 кГц. Их применение обеспечивает наибольшее полное сопротивление при минимальном количестве витков в обмотке, что позволяет уменьшить потери и индуктивность рассеяния.

Вначале рассмотрим Ш-образные сердечники прямоугольного сечения, они могут состоять из двух Ш-образных половинок или из Ш-образной части с замыкающей пластиной.

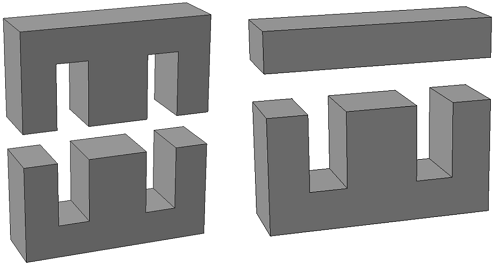
Ш – образный сердечник прямоугольного сечения: из двух Ш-образных половинок (слева) и Ш-образной части и замыкающей пластины (справа).

Для того чтобы рассчитать параметры такого сердечника рассмотрим его сечения.

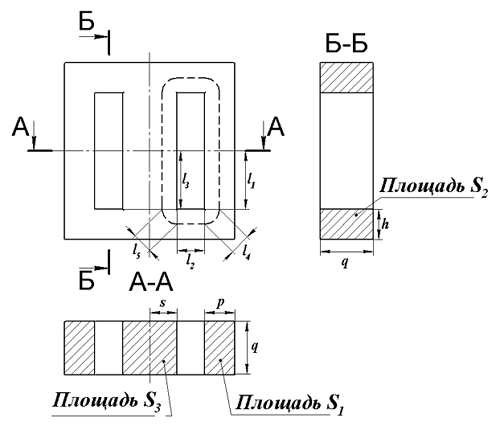
Расчёт параметров Ш – образного сердечника прямоугольного сечения.

Силовую линию магнитного поля в данном сердечнике можно разложить на несколько участков l₁, l₂, l₃, l₄, l₅ с различным сечением S₁, S₂, S₃, S₄, S₅. Исходя из этого постоянные сердечника можно рассчитать по следующим выражениям

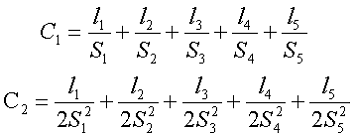
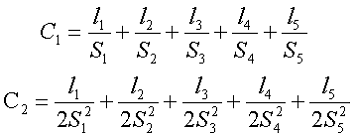
Некоторые величины можно найти измерением, а остальные по приведённым ниже выражениям. Так средняя длина магнитной линии и средняя площадь поперечного сечения на угловых участках составит

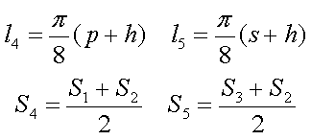
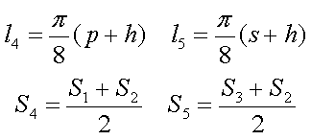
Пример. Рассчитаем индуктивность катушки намотанной на замкнутом Ш-образном сердечнике состоящего из двух половинок типа Ш20х28, выполненных из материала M2000НМ (μ_r = 2000), обмотка выполнена из ω = 200 витков.

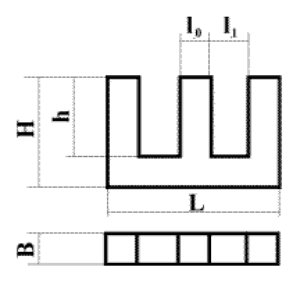
Сердечник типа Ш20х28, где L = 65, B = 28, H = 32,5, h = 22, l₀ = 20, l_l = 12.

Определим размеры и площади необходимых участков

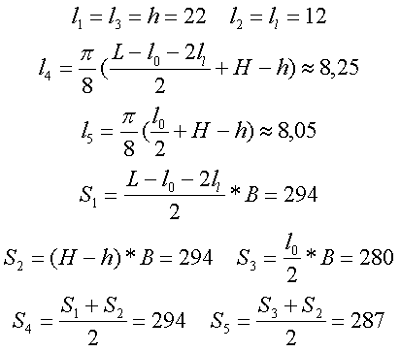
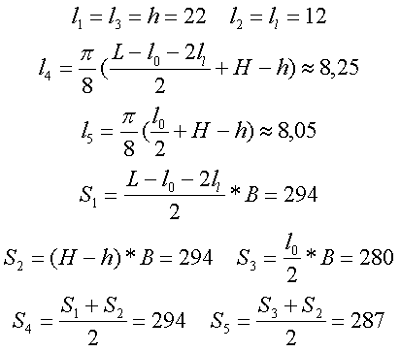
Из полученных значений вычислим коэффициент C1 и индуктивность L, полученной катушки

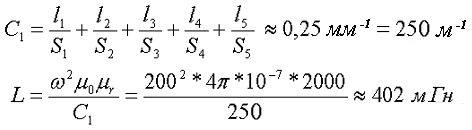
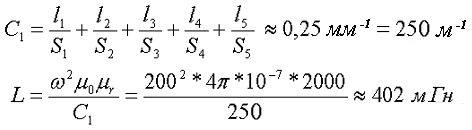
Расчёт катушки с Ш – образным сердечником круглого сечения

Теперь рассмотрим Ш-образные сердечники с круговым сечением центрального керна. Они также выполняются разборными, состоящими из двух одинаковых половинок.

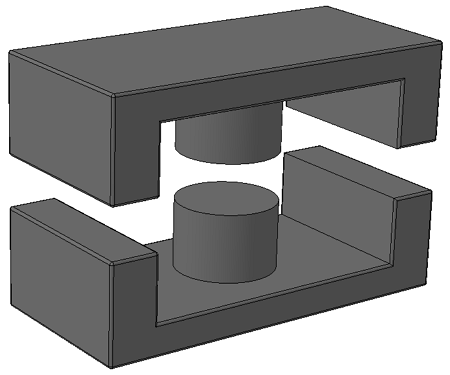
Ш – образный сердечник с центральным керном круглого сечения.

Для расчёта его параметров рассмотрим его сечение

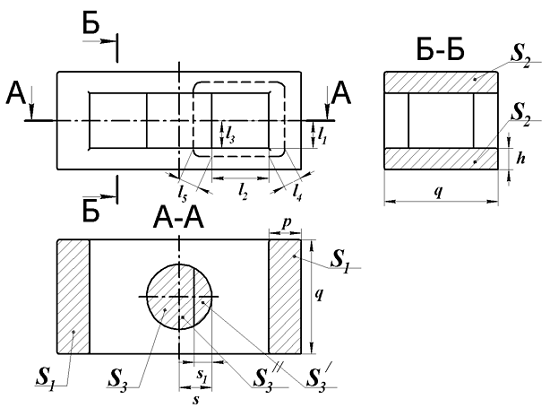
Расчёт параметров Ш – образного сердечника с центральным керном кругового сечения.

Аналогично предыдущим типам сердечников, разделим силовую линию магнитного поля на следующие части: линейные – l₁, l₂, l₃ и угловые – l₄, l₅, так же выделим соответствующие им поперечные сечения: S₁, S₂, S₃, S₄, S₅. Размеры линейных участков достаточно легко посчитать или измерить, а угловые размеры участков могут быть вычислены по следующим выражениям

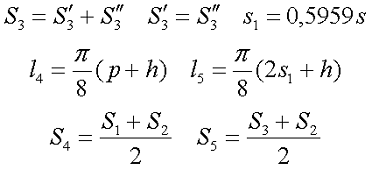
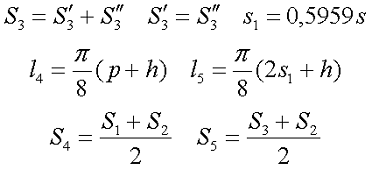
Исходя из этого, коэффициенты сердечника можно рассчитать по следующим выражениям

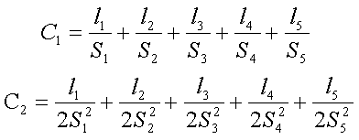
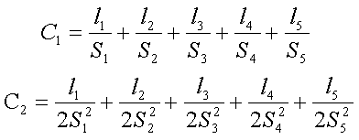
Пример. В качестве примера, рассчитаем индуктивность дросселя намотанного на сердечнике Epcos, состоящем из двух половинок ER 14.5/6 выполненных их материала N87 (μ_r = 2200), количество витков ω = 30

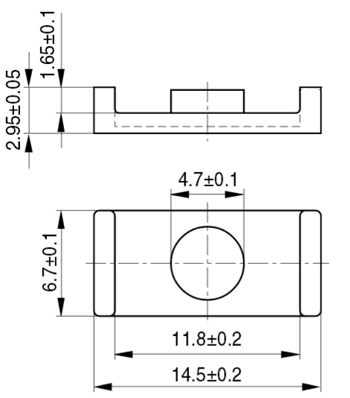
Сердечник Epcos типа ER 14.5/6.

Рассчитаем длину и сечение участков магнитной силовой линии

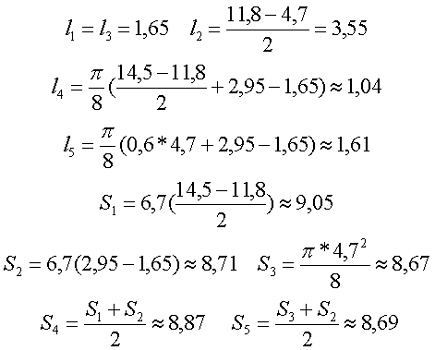
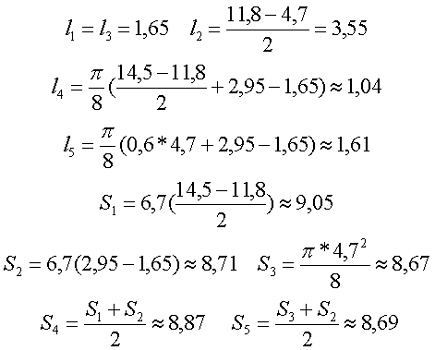
Таким образом, индуктивность данного дросселя составит

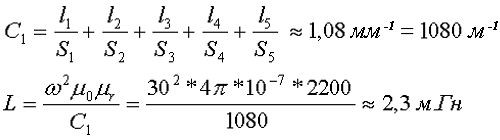
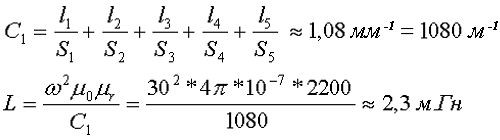
Существует большое количество различных типов Ш-образных сердечников, различающиеся теми или иными конструктивными особенностями, но расчёт их постоянных коэффициентов (С₁ и С₂) и эффективных параметров (l_e, S_e(A_e) и V_e) сводится к разделению полной длины магнитной силовой линии на простейшие линейные или угловые участки и вычисление постоянных коэффициентов.

Расчёт катушки с броневым сердечником

Броневые сердечники представляют собой сборную конструкцию, состоящую из двух чашеобразных частей. В центре каждой чашки имеется центральный керн, в большинстве случаев имеющий осевое отверстие, используемое для подстройки величины индуктивности.

Такие сердечники имеют универсальное применение благодаря высокой добротности в заданной полосе частот, низким искажениям, отсутствие полей рассеяния и небольшими габаритами.

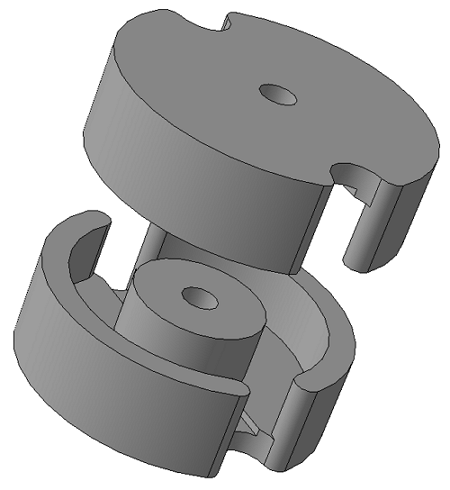
Броневой сердечник.

Расчёт постоянных С₁ и С₂ данного типа сердечника выполняется по аналогии с предыдущими типами, но в связи с формой броневого сердечника имеются свои особенности. Рассмотрим сечение броневого сердечника

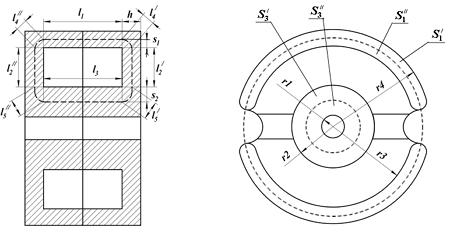
Расчёт параметров броневого сердечника.

Разделим данный сердечник на простейшие линейные и угловые участки с различным сечением: линейные – l₁, l₂, l₃ и угловые – l₄, l₅, так же выделим соответствующие им поперечные сечения: S₁, S₂, S₃, S₄, S₅. Длины линейных участков достаточно просто определить, для нахождения длины угловых участков и сечений на всех участках можно используя следующие выражения

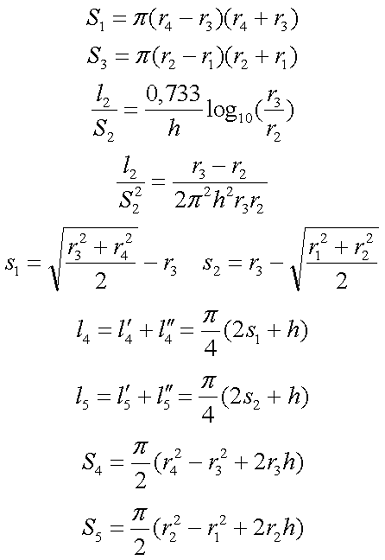
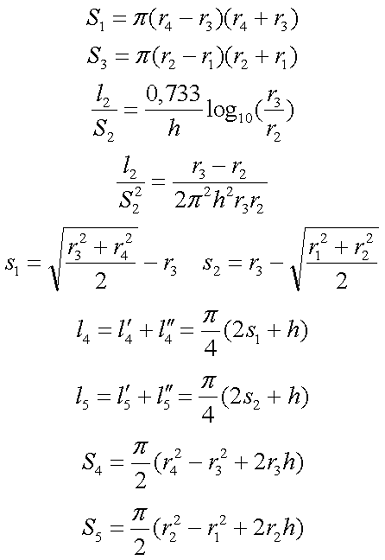
Таким образом, вычислив длину и площадь поперечного сечения отдельных участков, можно вычислить постоянные для данного типа сердечников

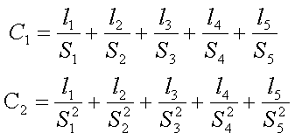
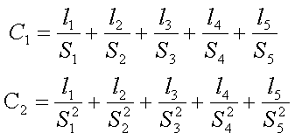
Данные выражения определяют параметры сердечника без технологических пазов и вырезов. При желании их учитывать необходимо, внести следующие поправки

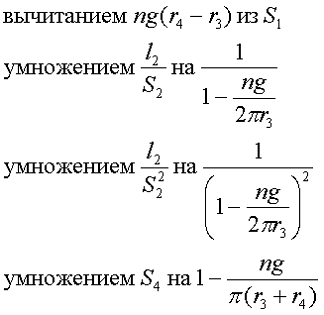
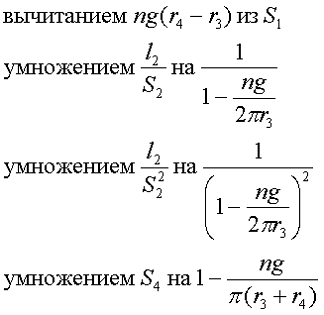
где n – число пазов,

g – ширина паза.

Пример. В качестве примера рассчитаем индуктивность дросселя выполненного на броневом сердечнике, состоящем из двух чашек типа Ч22 из феррита марки 50ВН (μ_r = 50), количество витков ω = 100.

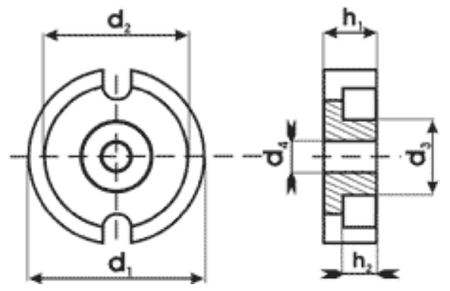
Сердечник типа Ч22: d₁ = 22, d₂ = 17,9, d₃ = 9,4, d₄ = 4,4, h₁ = 6,8, h₂ = 4,6.

С учётом конструктивных особенностей выразим величины заложенные в требуемые нам выражения:

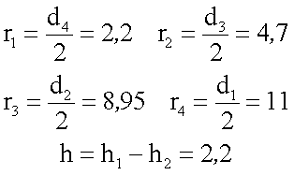
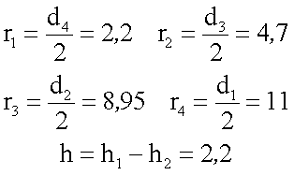
Найдем длины и сечение участков магнитопровода. Расчёт будем вести без учёта технологических пазов и вырезов.

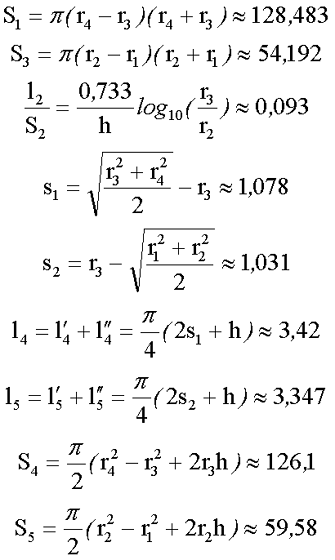
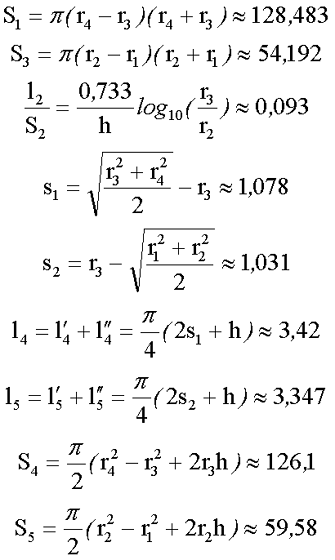
С учётом рассчитанных выше значений определим индуктивность исходного дросселя

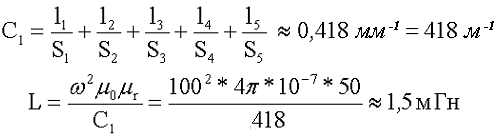
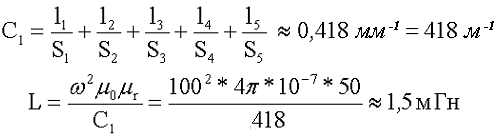
На этом можно и остановиться с расчётами индуктивных элементов с замкнутыми сердечниками. В следующей статье я рассмотрю индуктивные элементы на разомкнутых сердечниках.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Как рассчитать индуктивность катушек на разомкнутых сердечниках?

Всем доброго времени суток! В прошлой статье я рассказал о катушках индуктивности на сердечниках с малым магнитным зазором (длина зазора δ меньше любого линейного размера сердечника). Кроме сердечников с малым зазором существует сердечники, имеющие воздушный зазор сопоставимый с линейными размерами самого сердечника. Такие сердечники называются разомкнутыми. Данная статья описывает расчёт и параметры стержневых сердечников, являющихся разомкнутыми.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Факторы, влияющие на индуктивность катушки на разомкнутом сердечнике

В сердечниках с малым воздушным зазором магнитное поле практически всё сосредоточенно в сердечнике, и в воздушном зазоре рассеивание магнитного поля незначительно. Другая картина возникает, если магнитное поле возникает в сердечнике, имеющем воздушный зазор l_з сопоставимый с длиной магнитной силовой линии в сердечнике l_c.

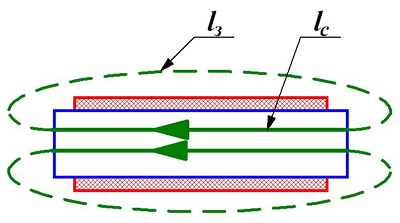
Магнитное поле в разомкнутом сердечнике.

Таким образом, магнитные сопротивления сердечника и воздушного зазора становятся соизмеримыми, что приводит к усложнению расчётных выражений для индуктивности катушек на таких сердечниках. В этом случае расчёт параметров ведут с учётом того, что в разомкнутых сердечниках на торцах сосредотачиваются противоположно ориентированные магнитные частицы, то есть частицы с положительным доменом смещаются в направлении внешнего поля, а отрицательные навстречу ему. В результате возникает размагничивающее поле, противоположное основному. Данное поле характеризуется размагничивающим фактором N или коэффициентом размагничивания. Данный фактор зависит от формы и размеров самого сердечника. Влияние размагничивающего фактора на магнитное поле сердечника описывается следующим выражением

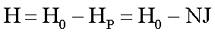
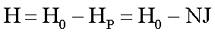
где Н – напряженность магнитного поля в сердечнике,

Н₀ – напряженность внешнего магнитного поля, то есть поля создаваемого катушкой, намотанной на разомкнутый сердечник,

Н_Р – размагничивающее поле сердечника,

N – размагничивающий фактор,

J – вектор намагничивания сердечника.

Точное значение размагничивающего фактора, возможно, рассчитать только для однородно намагниченных тел, например, эллипсоидов вращения, шаров, дисков. Для учёта размагничивающего фактора на магнитные свойства сердечника ввели понятие эффективной магнитной проницаемости сердечника μ_е, которая зависит от магнитной проницаемости вещества сердечника μ_r и размагничивающим фактором N. Значение эффективной магнитной проницаемости сердечника для однородно намагниченных тел определяется следующим выражением

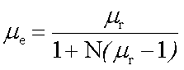
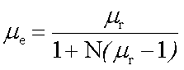
Однако в практике, используются неоднородно намагниченные тела – цилиндры, призмы, поэтому для расчёта эффективной магнитной проницаемости таких сердечников применяются эмпирически выведенные выражения.

Вследствие того, что значение размагничивающего фактора в неоднородно намагничиваемых телах различно по длине, то необходимо учитывать и расположение катушки индуктивности относительно сердечника и длину данной катушки относительно длины сердечника.

Таким образом, индуктивность катушки, выполненной на разомкнутом сердечнике можно определить по следующему выражению

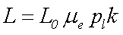
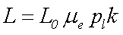
где L₀ – индуктивность катушки без сердечника, расчет смотреть (Часть 1, Часть 2, Часть 3),

μ_е – эквивалентная магнитная проницаемость разомкнутого сердечника,

k– коэффициент зависящий от отношения длины катушки к длине сердечника,

p_l – коэффициент зависящий от расположения катушки относительно середины длины сердечника.

Рассмотри более подробно зависимость индуктивности от различных факторов.

Расчёт размагничивающего фактора

Как я уже говорил, размагничивающий фактор N зависит от размеров сердечника

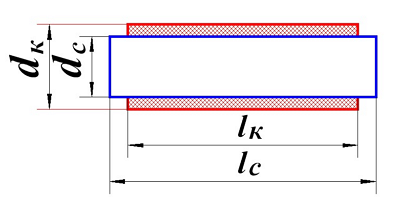
Катушка индуктивности с разомкнутым сердечником

Для его определения введём коэффициент λ, зависящий от отношения длины сердечника l_c к его диаметру d_c

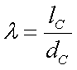
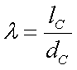
Тогда в интервале 2 ≤ λ ≤ 50 с точностью 10 % размагничивающий фактор данного сердечника можно определить по следующему выражению

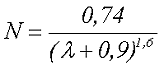
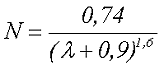
где λ – отношение длины сердечника к диаметру сердечника

Тогда эффективная магнитная проницаемость разомкнутого сердечника можно рассчитать по следующей формуле

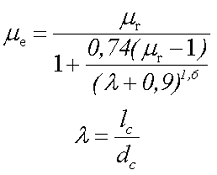
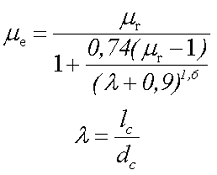
где μ_r – относительная магнитная проницаемость вещества сердечника,

l_c – длина сердечника,

d_c – диаметр сердечника.

Как влияет форма сердечника на магнитную проницаемость?

Эмпирическая формула вычисления эквивалентной магнитной проницаемости сердечников предполагает, что сечение сердечника представляет собой круг, но существует большое количество сердечников с не круглым сечением (прямоугольные, трубчатые).

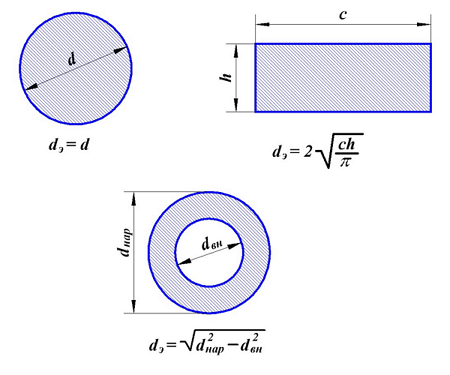
Вычисление эквивалентных диаметров сердечника.

Для упрощения расчётов все сердечники необходимо приводить к эквивалентному круговому сечению согласно следующим выражениям:

для прямоугольного сечения

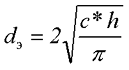
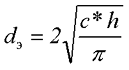
где с – ширина сердечника,

h – высота сердечника.

для трубчатого сечения

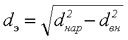
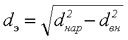
где d_нар – наружный диаметр сердечника,

d_вн – внутренний диаметр сердечника.

Влияние расположение катушки индуктивности относительно сердечника

Довольно часто стержневые сердечники используют для точной настройки индуктивности или подстройки в небольших пределах, также длинные стержневые сердечники используют в магнитных антеннах радиоприёмников на средне- и длинноволновом диапазоне. Их объединяет то, что катушка индуктивности зачастую расположена не на средине сердечника. Ниже представлена катушка индуктивности на разомкнутом сердечнике, используемая в качестве магнитной антенны

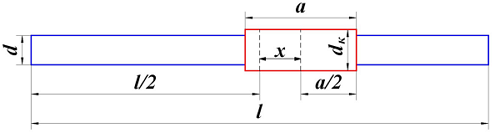
Расположение катушки индуктивности на сердечнике в магнитной антенне.

Как я уже говорил, размагничивающий фактор не равномерно распределён по длине разомкнутого сердечника. Его значение увеличивается от середины сердечника к его краям, а магнитная проницаемость, а соответственно уменьшается от центра сердечника к его краям. Чтобы не усложнять выражение для размагничивающего фактора введем корректирующий коэффициент p_l, зависящий от расположения катушки на сердечнике

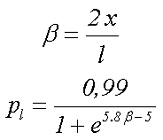
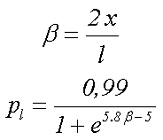
где х – расстояние от середины сердечника до середины катушки,

l – длина сердечника,

β – коэффициент, зависящий от расположения катушки на сердечнике.

Влияние размеров катушки относительно размеров сердечника

Как я писал выше, размагничивающий фактор неравномерен по длине сердечника, то необходимо учитывать любое различие в относительных размерах катушки индуктивности и сердечника.

Ещё одним существенным фактором при расчёте индуктивности является различие в длине катушки и длине сердечнике. Данное различие можно описать коэффициентом k, зависящем от отношения длины сердечника к длине катушки

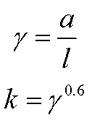
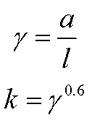
где а – длина катушки индуктивности,

l – длина сердечника,

γ – коэффициент, зависящий от отношения длины катушки к длине сердечника.

Пример расчёта индуктивности катушки на разомкнутом сердечнике

В качестве примера рассчитаем катушку индуктивности на разомкнутом сердечнике круглого сечения со следующими параметрами: диаметр сердечника d_c = 6 мм, длина сердечника l_c = 30 мм, катушка состоит из 30 витков провода диаметром d_p = 1 мм, намотанных плотно виток к витку в один ряд, магнитная проницаемость материала сердечника μ_r = 600.

1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит l_k = 30*1 = 30 мм, а диаметр катушки d_k = d_cp = 30,5 мм.

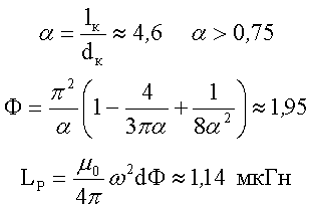
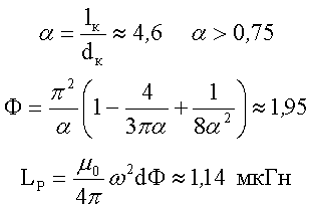
2.Вычислим эффективную магнитную проницаемость сердечника

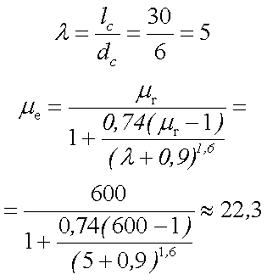
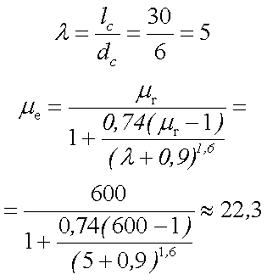
3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Так как длина катушки совпадает с длинной сердечника и смещение катушки относительно сердечника отсутствует, то поправочные коэффициенты будут равны 1, тогда индуктивность данной катушки составит

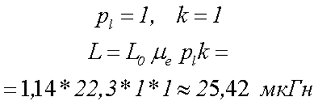
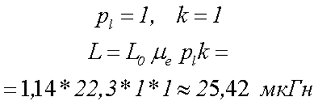
В качестве второго примера рассчитаем индуктивность магнитной антенны выполненной на сердечнике из феррита марки 600НН, размерами l_c = 160 мм, d_с = 8 мм, количество витков провода w = 60, диаметр провода d_р = 0,15 мм. Катушка смещена на 30 мм относительно середины сердечника.

1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит l_k = 60*0,15 = 9 мм, а диаметр катушки d_k = d_cp = 8,075 мм.

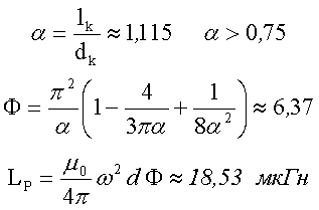
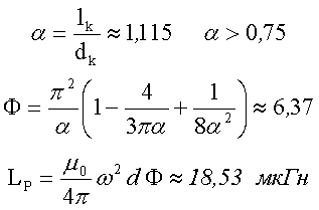
2.Вычислим эффективную магнитную проницаемость сердечника

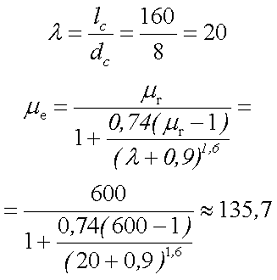
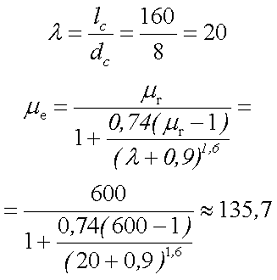
3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Коэффициент, учитывающий расположение катушки на сердечнике составит

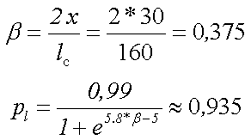
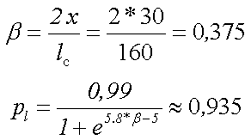
Коэффициент, учитывающий отношение длины катушки по отношению к длине сердечника составит

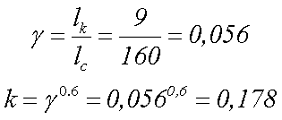
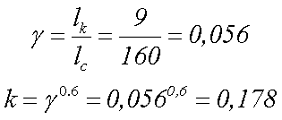
4.Рассчитаем индуктивность катушки индуктивности на разомкнутом сердечнике

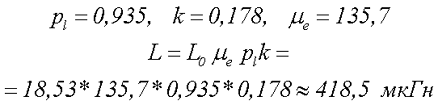
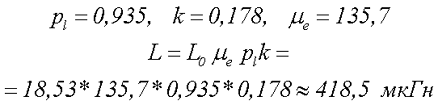
Данная статья заканчивает цикл расчётов индуктивности катушек с различными конструктивными параметрами.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.