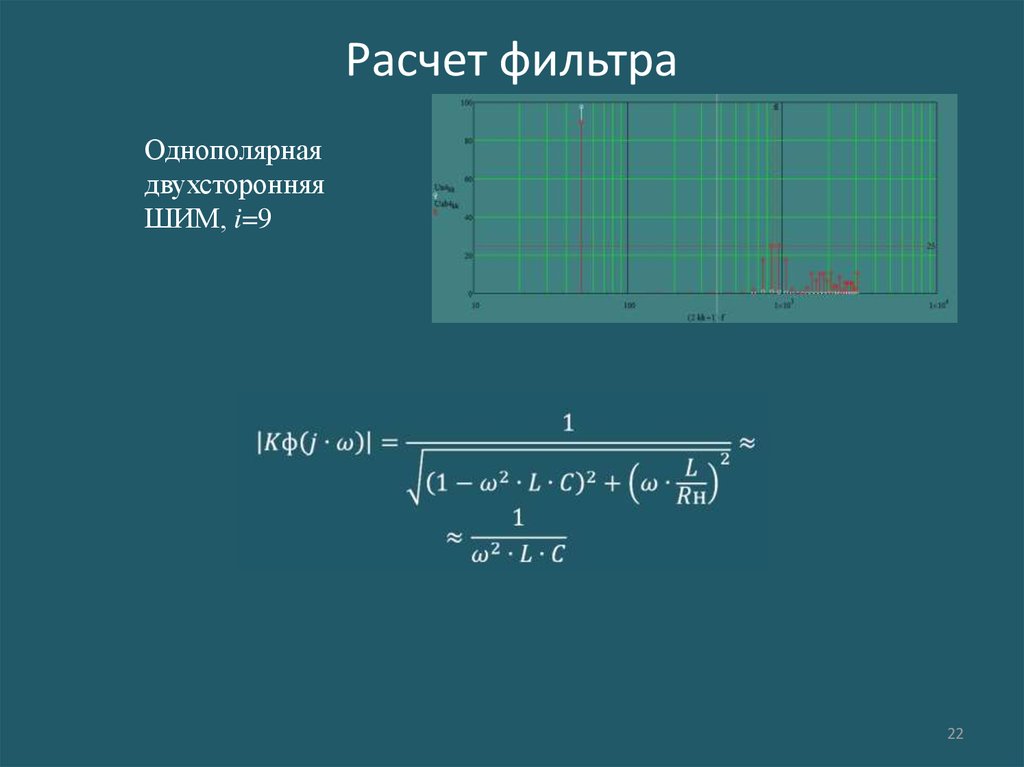
Практическая работа Фильтрация сточных вод. Расчет зернистых фильтров.
Цель работы: Приобретение знаний и навыков по расчету зернистых фильтров.
Вводная часть
Фильтрованием называют гидромеханический процесс, разделения жидких неоднородных систем с помощью пористых перегородок, задерживающих твердую фазу и пропускающих жидкость. Скорость фильтрации прямо пропорциональна разности давлений (движущей силе) на входе и выходе аппарата и обратно пропорциональна сопротивлению фильтра. По способу организации фильтры делятся на периодические и непрерывные. При этом, процессы фильтрования могут протекать при постоянных разности давлений ΔР и скорости фильтрации υ или при переменных ΔР и υ. По механизму фильтрования различают процесс с закупориванием пор или с образованием осадка. По способу выгрузки осадка различают процессы с механизированной и ручной выгрузкой.
Зернистые фильтры
относятся к периодическим фильтрам.
В
качестве фильтрующих веществ используют
различные зернистые элементы – кварцевый
песок, гранитный щебень, дробленные
антрацит и керамзит, шлак и др.
Конструктивная схема фильтра с восходящим потоком воды представлена на рисунке 1.1, высота слоев зависит от материала загрузки и размера зерен.
Подобные фильтры с насыпной загрузкой используются для окончательной очистки сточных вод. Исходная концентрация взвешенных частиц в сточных водах, поступающих в фильтры, должна быть: с=10-40 мг/л, а получаемая после фильтрации с≤3 мг/л.
При расчете фильтров
необходимо определить суммарную площадь
фильтров F∑,
м2,
число фильтров N, площадь одного фильтра
F, м2, расчетную скорость фильтрации υ
1.
Получить исходные
данные: Qр,
с, N (таблица 1). Назначить число промывок
фильтров в сутки n: n=2 при с>20 мг/л.
2. Рассчитать циркуляционный (промывочный) расход Qц в зависимости от числа промывок фильтров в сутки.
Qц=0,05Qр, при n=2 . (1.1)
3. Определить расчетную скорость фильтрования:
υр=υф (N-m)/N, м/ч, (1.2)
где υф — скорость фильтрования при форсированном режиме.
Принимается υф =12-14 м/ч,
m – число фильтров, находящихся в ремонте или на промывке.
Принимается m=2 при N<20 и m=3 при N≥20.
Определить
суммарную площадь фильтров:F∑=(Qр+Qц)/(24υр -nυрt), м2, (1.3)
где t — продолжительность простоя одного фильтра при промывке. Принимается t=0,5-0,6 ч.
5. Определить площадь одного фильтра:
F= F∑/N, м2. (1.4)
Из конструкционных соображений площадь одного фильтра должна быть не более 50 м2.
5. Определить диаметр одного фильтра:
, м. (1.5)
6. Высота фильтра:
H=h1+h2+h3,
м,
(1.
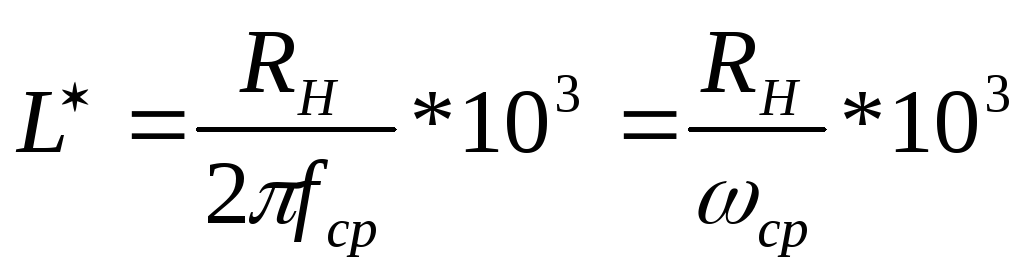6)
где h1,
h
Таблица 1.1 — Исходные данные для расчета.
Номер варианта | Qр, м3/сут | N, шт | с, мг/л | Размер зерен, мм | Высота слоя h1 h2, м | ||
гравия | песка | гравия | песка | ||||
8 | 38000 | 10 | 35 | 10-20 | 1-2 | 0,2-0,3 | 1,3-1,5 |
Теория и применение цифровой обработки сигналов
Теория и применение цифровой обработки сигналов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ 1.2. Обзор основных направлений цифровой обработки сигналов 1.  2.1. Введение 2.2. Последовательности 2.3. Представление произвольных последовательностей 2.4. Линейные системы с постоянными параметрами 2.5. Физическая реализуемость. Устойчивость 2.6. Разностные уравнения 2.7. Частотная характеристика 2.8. Частотная характеристика систем первого порядка 2.9. Частотная характеристика систем второго порядка 2.10. Дискретный ряд Фурье 2.11. Замечания о единицах измерения частоты 2.12. Соотношение между непрерывными и дискретными системами 2.13. z-преобразование 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности 2.15. Обратное z-преобразование 2.16. Свойства z-преобразования 2.18. Геометрическая интерпретация преобразования Фурье 2.19. Построение цифровых фильтров (структурные схемы фильтров) 2.20. Структурные схемы фильтров без полюсов 2. 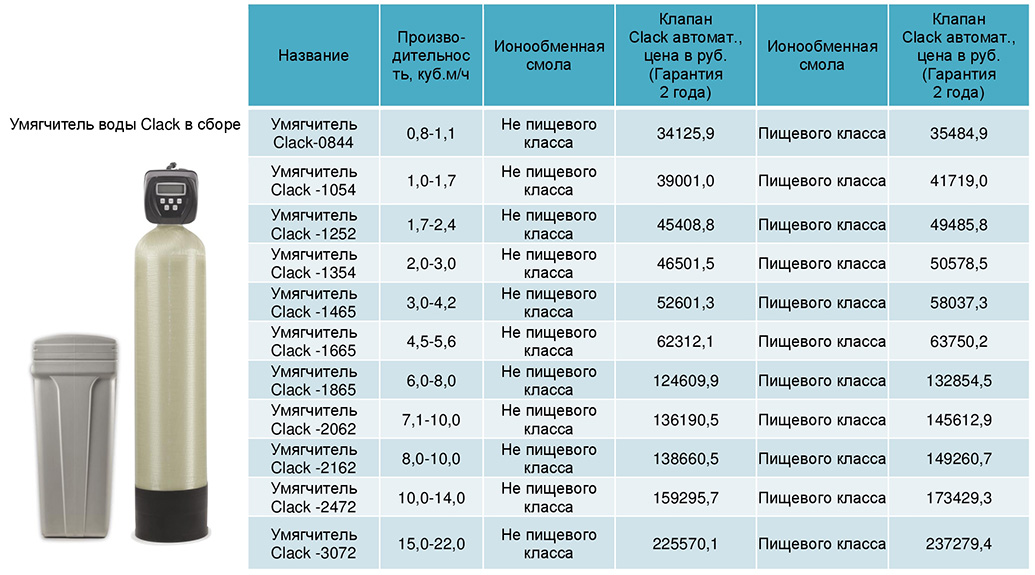 21. Дискретное преобразование Фурье2.22. Свойства ДПФ 2.23. Свертка последовательностей 2.24. Линейная свертка конечных последовательностей 2.25. Секционированные свертки 2.26. Дискретное преобразование Гильберта 2.27. Преобразование Гильберта действительных сигналов 3.2. Порядок расчета фильтров 3.3. Свойства КИХ-фильтров 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой 3.5. Частотная характеристика КИХ-фильтров с линейной фазой 3.6. Расположение нулей КИХ-фильтров с линейной фазой 3.7. Методы расчета КИХ-фильтров с линейными фазами 3.8. Первый метод расчета — метод взвешивания 3.9. Прямоугольное окно 3.10. «Обобщенное» окно Хэмминга 3.11. Окно Кайзера 3.12. Примеры фильтров нижних частот с различными окнами 3.13. Особенности использования метода взвешивания 3.14. Несколько практических приемов использования окон 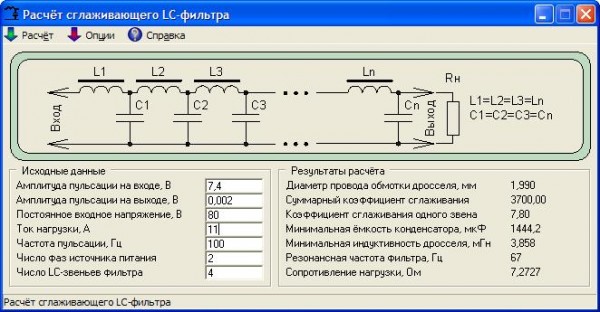 15. Дополнительные примеры фильтров рассчитанных методом взвешивания3.16. Общая характеристика окон 3.17. Второй метод проектирования — метод частотной выборки 3.18. Решение задачи оптимизации 3.19. Линейное программирование 3.20. Фильтры с частотной выборкой вида 1 и 2 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки 3.24. Заключение к описанию метода частотной выборки 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой 3.26. Аппроксимация по Чебышеву со взвешиванием 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров 3.  31. Расчет оптимальных КИХ-фильтров методами линейного программирования3.32. Характеристики оптимальных фильтров нижних частот вида 1 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1 3.34. Соотношения между параметрами оптимального фильтра нижних частот 3.35. Свойства оптимальных фильтров нижних частот вида 2 3.36. Характеристики оптимальных дифференциаторов 3.37. Характеристики оптимальных преобразователей Гильберта 3.38. Многополосные оптимальные КИХ-фильтры 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот Приложение Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки 4.3. Методы расчета коэффициентов БИХ-фильтра 4. 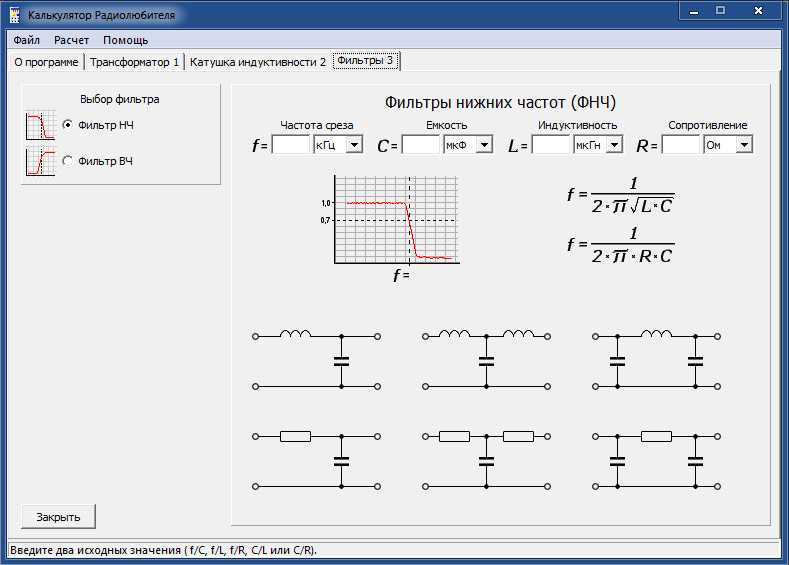 4. Расчет цифровых фильтров по фильтрам непрерывного времени4.5. Метод отображения дифференциалов 4.6. Метод инвариантного преобразования импульсной характеристики 4.7. Билинейное z-преобразование 4.8. Согласованное z-преобразование 4.9. Обзор методов расчета аналоговых фильтров нижних частот 4.10. Расчетные диаграммы фильтров нижних частот 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров 4.12. Частотные преобразования 4.13. Прямые методы расчета цифровых фильтров 4.14. Применение методов оптимизации для расчета БИХ-фильтров 4.15. Обзор методов расчета БИХ-фильтров 4.16. Сравнение КИХ- и БИХ-фильтров 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ 5.2. Аналого-цифровое преобразование 5.3. Цифро-аналоговое преобразование 5.  4. Системы счисления, применяемые в цифровых устройствах5.5. Система счисления с фиксированной запятой 5.6. Системы счисления с плавающей запятой 5.7. Система счисления с поблочно плавающей запятой 5.8. Виды квантования в цифровых фильтрах 5.9. Усечение 5.10. Округление 5.11. Шум округления в рекурсивных структурах с фиксированной запятой 5.12. Ограничение динамического диапазона в системах с фиксированной запятой 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления 5. 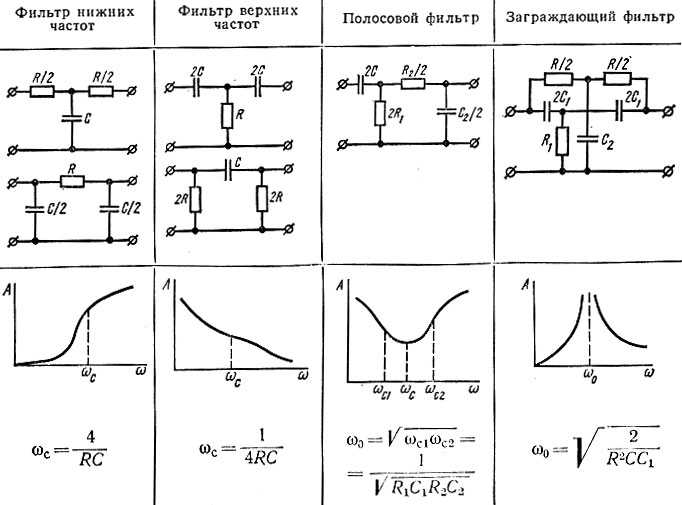 19. Шум округления в нерекурсивных структурах с фиксированной запятой5.20. Шум округления при построении нерекурсивных фильтров в прямой форме 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме 5.22. Шум округления в рекурсивных структурах с плавающей запятой 5.23. Квантование коэффициентов 5.24. Квантование коэффициентов в рекурсивных структурах 5.25. Квантование коэффициентов при построении фильтров в прямой форме 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов 5.27. Оптимальное квантование коэффициентов 5.28. Квантование коэффициентов в двухполюсном фильтре 5.29. Квантование коэффициентов в нерекурсивных структурах 5.30. Квантование коэффициентов при построении КИХ-фильтров 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме 5.32. Колебания предельного цикла Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ 6.2. Введение в алгоритмы БПФ с основанием 2 6.  3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени6.4. Перестановка данных и двоичная инверсия 6.5. Программа расчета БПФ на ФОРТРАНе 6.6. Алгоритм БПФ с прореживанием по частоте 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ 6.8. Единый подход к алгоритмам БПФ 6.9. Алгоритмы БПФ с основанием 2 6.10. Спектральный анализ в одной точке z-плоскости 6.11. Спектральный анализ с применением БПФ 6.12. Некоторые характеристики спектрального анализа 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров 6.14. Использование окон при спектральном анализе 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ 6.16. Алгоритм Блюстейна 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации 6.18. Энергетический спектр случайных сигналов 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ Глава 7.  ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ7.2. Двумерные сигналы 7.3. Двумерные системы 7.4. Физическая реализуемость. Разделимость. Устойчивость 7.5. Двумерные разностные уравнения 7.6. Частотные методы 7.7. Двумерное z-преобразование 7.8. Конечные последовательности 7.9. Свертка последовательностей 7.10. Двумерное ДПФ 7.11. Расчет двумерных фильтров 7.12. БИХ-фильтры 7.13. Устойчивость БИХ-фильтров 7.14. КИХ-фильтры 7.15. Двумерные весовые функции (окна) 7.16. Пример расчета фильтра нижних частот методом взвешивания 7.17. Фильтры с частотной выборкой 7.18. Двумерные фильтры нижних частот с частотной выборкой 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров 7.20. Частотное преобразование одномерных фильтров в двумерные 7.21. Примеры обработки изображений Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов 8.3. Булева алгебра.  Примеры простых логических цепей8.4. Основные типы интегральных логических схем 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства 8.6. Умножители 8.7. Делители и устройства с плавающей запятой 8.8. Пример: проектирование быстродействующего матричного умножителя 8.9. Заключение ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ 9.2. Аппаратурное построение КИХ-фильтра прямой формы 9.3. Параллелизм при построении КИХ-фильтров прямой формы 9.4. Каскадная форма КИХ-фильтра 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма 9.6. Прямая форма построения БИХ-фильтров 9.7. Каскадная форма БИХ-фильтров 9.8. Мультиплексирование 9.9. Цифровой приемник клавишно-тонального вызова 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах 9.  12. Специализированный цифровой синтезатор частот9.13. Методы генерации псевдослучайных чисел 9.14. Методы генерации гауссовых случайных чисел Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ 10.2. Обзор теоретических основ БПФ 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием 10.5. Эффекты квантования в алгоритмах БПФ 10.6. Особенности аппаратурной реализации БПФ с основанием 2 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2 10.9. Выполнение БПФ с использованием сверхоперативной памяти 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом 10.11. Общие вопросы построения поточных схем БПФ 10.12. Поточные схемы БПФ с основанием 2 10.13. Поточная схема БПФ с основанием 4 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4 10.15. Структуры БПФ с повышенным уровнем параллелизма 10.  16. Общие принципы построения специализированных процессоров БПФ10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом 10.19. Поточный свертыватель с тактовой частотой 10 МГц Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ 11.2. Специализированные и универсальные вычислительные машины 11.3. Способы описания вычислительных машин 11.4. Программа вычисления скользящей суммы 11.5. Особенности ввода — вывода при обработке в реальном времени 11.6. Методы увеличения быстродействия вычислительной машины 11.7. Сверхоперативные ЗУ 11.8. Распараллеливание арифметических операций 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории 11.11. Структурные схемы арифметических устройств 11.12. Синхронизация 11.13.  Обзор методов увеличения быстродействия, использованных в FDP11.14. Выполнение быстрого преобразования Фурье с помощью FDP 11.15. Подпрограммы для действий с плавающей запятой 11.16. Обзор особенностей FDP, связанных с распараллеливанием 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов 11.18. Лабораторная вычислительная система для цифровой обработки сигналов ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ 12.2. Модель образования речи 12.3. Кратковременный спектральный анализ 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе 12.5. Особенности анализа речи 12.6. Система анализа — синтеза 12.7. Полосный вокодер 12.8. Анализаторы вокодеров. Особенности обработки сигналов 12.9. Синтезаторы вокодеров. Особенности обработки сигналов 12.10. Другие схемы вокодеров 12.11. Выделение высоты основного тона и обнаружение тон — шум 12.12. Обнаружитель тон — шум 12.  13. Гомоморфная обработка речи12.14. Гомоморфный вокодер 12.15. Формантный синтез 12.16. Цепь возбуждения звонких фрикативных звуков 12.17. Генератор случайных чисел 12.18. Цифровая обработка в формантном синтезаторе 12.19. Линейное прогнозирование речи 12.20. Система речевого ответа для вычислительной машины 12.21. Заключение 13.1. Вводные замечания о принципах радиолокации и ее применениях 13.2. Состав и параметры радиолокационной системы 13.3. Выбор сигналов и функция неопределенности 13.4. Цифровые согласованные фильтры для радиолокационных сигналов 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений 13.6. Экспериментальный радиолокатор дальнего действия 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора 13.8. Заключение |
, Гоулд Б. Теория и применение цифровой обработки сигналов. М: Мир, 1978.
RC, RL, LC Калькулятор пассивного фильтра
Пассивный фильтр (также известный как фильтр с сосредоточенными элементами) используется для
ослабить сигнал выше или ниже определенной частоты.
Этот пассивный
Калькулятор фильтров позволяет выбрать композицию (RC –
Сопротивление/емкость, RL – сопротивление/индуктивность или LC –
Индуктивность/емкость) и введите свои значения для расчета порога/-3 дБ.
частота. В зависимости от конфигурации компонентов вы можете
построить фильтр нижних или верхних частот. Фильтр нижних частот пропускает
сигнал с минимальными искажениями вплоть до частоты среза, после чего
он заблокирует входной сигнал. Фильтр верхних частот заблокирует
частоты ниже частоты среза и пропускают те, что выше.
Сопутствующие инструменты
Описание пассивных фильтров
Фильтры с сосредоточенными элементами состоят из резисторов, катушек индуктивности и
Конденсаторы. Они позволяют частотам проходить выше или ниже
заданный уровень. Уровень, на котором частота ослабляется
-3 дБ (70,7%) называется частотой среза.
При построении фильтров с сосредоточенными элементами важно понимать влияние каждого элемента на сигнал. Резисторный элемент в основном не зависит от частоты. Катушка индуктивности увеличивает импеданс по мере того, как частота увеличивается, а сопротивление конденсатора уменьшается по мере частота становится быстрее. С этой разной динамикой следует обратить внимание на конфигурацию фильтра, чтобы для достижения желаемой частотной характеристики.
Фильтр первого порядка — это фильтр, содержащий только один активный элемент (индуктивность или
конденсатор) элемент. Фильтр второго порядка будет содержать два активных
элементов и имеет удвоенный спад частоты. RC-фильтры
обычно используется для фильтрации сигналов с меньшей мощностью, в то время как более
дорогой LC-фильтр лучше подходит для большей мощности.
Второй
LC-фильтр также более эффективен, чем RC-фильтры, так как в идеале
они не будут рассеивать энергию в виде тепла.
При построении фильтров с сосредоточенными элементами важно понимать влияние каждого элемента на сигнал. Резисторный элемент в основном не зависит от частоты. Катушка индуктивности увеличивает импеданс по мере того, как частота увеличивается, а сопротивление конденсатора уменьшается по мере частота увеличивается. С этой разной динамикой следует обратить внимание на конфигурацию фильтра, чтобы для достижения желаемой частотной характеристики.
Фильтр первого порядка — это фильтр, содержащий только один активный элемент (индуктивность или
конденсатор) элемент. Фильтр второго порядка будет содержать два активных
элементов и имеет удвоенный спад частоты. RC-фильтры
обычно используется для фильтрации сигналов с меньшей мощностью, в то время как более
дорогой LC-фильтр лучше подходит для более высоких мощностей.
Второй
LC-фильтр также более эффективен, чем RC-фильтры, так как в идеале
они не будут рассеивать энергию в виде тепла.
Сопутствующие инструменты
×
Функция ВЫЧИСЛЕНИЯ (DAX) — DAX
Редактировать
Твиттер LinkedIn Фейсбук Электронная почта
- Статья
- 4 минуты на чтение
Оценивает выражение в измененном контексте фильтра.
Примечание
Существует также функция РАСЧЕТНАЯ ТАБЛИЦА. Он выполняет точно такие же функции, за исключением того, что он изменяет контекст фильтра, примененный к выражению, которое возвращает объект таблицы .
Синтаксис
CALCULATE(<выражение>[ <фильтр1> [ <фильтр2> [ …]]])
Параметры
| Термин | Определение |
|---|---|
| выражение | Выражение, которое необходимо вычислить. |
| фильтр1, фильтр2,… | (Необязательно) Логические выражения или табличные выражения, определяющие фильтры, или функции-модификаторы фильтров. |
Выражение, используемое в качестве первого параметра, практически совпадает с мерой.
Фильтры могут быть:
- Логические выражения фильтра
- Выражения фильтра таблицы
- Функции модификации фильтра
При наличии нескольких фильтров их можно оценить с помощью логического оператора И (&&), что означает, что все условия должны быть ИСТИНА, или с помощью логического оператора ИЛИ (||), что означает, что любое условие может быть истинным.
Выражения логического фильтра
Фильтр логического выражения — это выражение, результатом которого является ИСТИНА или ЛОЖЬ.
Есть несколько правил, которые они должны соблюдать:
- Они могут ссылаться на столбцы из одной таблицы.
- Они не могут ссылаться на меры.
- Они не могут использовать вложенную функцию CALCULATE.
Начиная с выпуска Power BI Desktop за сентябрь 2021 г., также применяется следующее:
Выражение фильтра таблицы
Фильтр выражения таблицы применяет объект таблицы в качестве фильтра. Это может быть ссылка на модельную таблицу, но, скорее всего, это функция, которая возвращает объект таблицы. Вы можете использовать функцию ФИЛЬТР для применения сложных условий фильтрации, в том числе тех, которые не могут быть определены логическим выражением фильтра.
Функции модификатора фильтра
Функции модификатора фильтра позволяют делать больше, чем просто добавлять фильтры. Они предоставляют вам дополнительный контроль при изменении контекста фильтра.
| Функция | Назначение |
|---|---|
| УДАЛИТЬ ФИЛЬТРЫ | Удалить все фильтры или фильтры из одного или нескольких столбцов таблицы или из всех столбцов одной таблицы. |
| ВСЕ 1 , ALLEXCEPT, ALLNOBLANKROW | Удалить фильтры из одного или нескольких столбцов или из всех столбцов одной таблицы. |
| ФИЛЬТРЫ | Добавить фильтр, не удаляя существующие фильтры для тех же столбцов. |
| ОТНОШЕНИЯ С ПОЛЬЗОВАТЕЛЕМ | Задействуйте неактивную связь между связанными столбцами, и в этом случае активная связь автоматически станет неактивной. |
| ПЕРЕКРЕСТНЫЙ ФИЛЬТР | Изменить направление фильтра (с обоих на один или с одного на оба) или отключить взаимосвязь. |
1 Функция ALL и ее варианты ведут себя и как модификаторы фильтра, и как функции, возвращающие табличные объекты. Если функция REMOVEFILTERS поддерживается вашим инструментом, лучше использовать ее для удаления фильтров.
Возвращаемое значение
Значение, являющееся результатом выражения.
Если предоставлены выражения фильтра, функция ВЫЧИСЛИТЬ изменяет контекст фильтра для оценки выражения.
Для каждого выражения фильтра есть два возможных стандартных результата, если выражение фильтра не включено в функцию KEEPFILTERS:- Если столбцы (или таблицы) не входят в контекст фильтра, новые фильтры будут добавлены в контекст фильтра для оценки выражения.
- Если столбцы (или таблицы) уже находятся в контексте фильтра, существующие фильтры будут перезаписаны новыми фильтрами для оценки выражения CALCULATE.
Функция РАСЧЕТ, используемая без фильтров , удовлетворяет специфическим требованиям. Он переводит контекст строки в контекст фильтра. Это требуется, когда выражение (не мера модели), которое суммирует данные модели, должно быть оценено в контексте строки. Этот сценарий может произойти в формуле вычисляемого столбца или при вычислении выражения в функции итератора. Обратите внимание, что когда мера модели используется в контексте строки, переход контекста происходит автоматически.
Эта функция не поддерживается для использования в режиме DirectQuery при использовании в вычисляемых столбцах или правилах безопасности на уровне строк (RLS).
Для каждого выражения фильтра есть два возможных стандартных результата, если выражение фильтра не включено в функцию KEEPFILTERS:
Примеры
Следующее определение табличной меры Продажи дает результат дохода, но только для продуктов синего цвета.
Примеры в этой статье можно использовать с образцом модели Adventure Works DW 2020 Power BI Desktop. Чтобы получить модель, см. пример модели DAX.
Синий Доход =
ВЫЧИСЛИТЬ(
СУММ(Продажи[Сумма продаж]),
«Продукт» [Цвет] = «Синий»
)
| Категория | Сумма продаж | Голубой доход |
|---|---|---|
| Аксессуары | $1 272 057,89 | $165 406,62 |
| Велосипеды | $94 620 526,21 | $8 374 313,88 |
| Одежда | $2 117 613,45 | 259 488,37 $ |
| Компоненты | $11 799 076,66 | $803 642,10 |
| Итого | 109 809 274,20 $ | 9 602 850,97 $ |
Функция РАСЧЕТ оценивает сумму столбца Продажи таблицы Сумма продаж в измененном контексте фильтра.
В столбец Product table Color добавляется новый фильтр, или фильтр перезаписывает любой фильтр, уже примененный к столбцу.
Следующее определение табличной меры Продажи дает отношение продаж к продажам для всех каналов продаж.
| Канал | Сумма продаж | Доход, %, общий канал |
|---|---|---|
| Интернет | $29 358 677,22 | 26,74% |
| Реселлер | $80 450 596,98 | 73,26% |
| Итого | 109 809 долл. США,274,20 | 100,00% |
Доход % Общий канал =
РАЗДЕЛЯТЬ(
СУММ(Продажи[Сумма продаж]),
ВЫЧИСЛИТЬ(
СУММ(Продажи[Сумма продаж]),
REMOVEFILTERS('Заказ на продажу'[Канал])
)
)
Функция DIVIDE делит выражение, являющееся суммой значений столбца Sales Sales Amount (в контексте фильтра), на то же выражение в измененном контексте фильтра.
