Расчет частоты среза фильтра: Онлайн расчёт RC фильтров (ФНЧ и ФВЧ) – Частота среза фильтра — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Частота среза фильтра

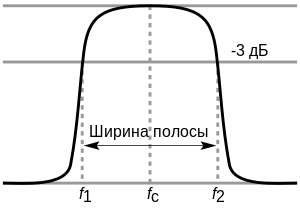
Частотой среза фильтра называют частоту, ослабление сигнала на которой достигает -3 дБ (по логарифмической шкале), или составляет 1/√2 (≈ 0.71) по линейной. Т.е амплитуда сигнала на частоте среза составляет 71% от входного значения.

Посмотреть вложение 7750

Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:

Xc=1/2пFС где:
Хс – реактивное сопротивление конденсатора;
п – оно и в Африке “пи”;
F – частота;
С – емкость конденсатора.

То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.

А реактивное сопротивление катушки индуктивности вот этой формулой:

XL=2пFL где:
XL — реактивное сопротивление катушки индуктивности;

п – оно и в России “пи”;
F – частота сигнала;
L – индуктивность катушки

Реальная частота среза и её слышимые последствия имеют следующий вид:

Для фильтра Низких частот:

Посмотреть вложение 7751

Для фильтра Высоких частот:

Посмотреть вложение 7752

Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ). Что это за показатель?

АЧХ фильтра — показывает как изменяется уровень амплитуду сигнала проходящего через этот фильтр в зависимости от частоты сигнала.
Т.е., на одной частоте входящего на фильтр сигнала уровень амплитуды такой-же как и на выходе, а для другой частоты, фильтр, оказывая сопротивление сигналу, ослабляет амплитуду входящего сигнала.

Суммарная АЧХ ФНЧ и ФВЧ

Посмотреть вложение 7758

Крутизна частотной характеристики фильтра – это показатель того, на сколько резко изменяется амплитуда входного сигнала на выходе при изменении его частоты. Чем быстрее происходит спад АЧХ тем лучше.

Посмотреть вложение 7753

Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах.

Частотные фильтры бывают нескольких типов:

одноэлементные;
Г- образные;
Т – образные;
П – образные;
многозвенные.

Одноэлементный фильтр

— фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот).

Г – образный фильтр

Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:

Посмотреть вложение 7754

С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.

Формулы для расчета параметров делителя напряжения:

Uвх=Uвых*(R1+R2)/R2
Uвых=Uвх*R2/(R1+R2)

Rобщ=R1+R2
R1=Uвх*R2/Uвых – R2
R2=Uвых*Rобщ/Uвх

К примеру, нам дано:
Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 В
Порядок расчета:
1. Определяем R2= 7*10000/10= 7000= 7 кОм
2. Определяем R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм
3. Проверяем Uвых=10*7000/(3000+7000)= 7 В
Что нам и требовалось.
Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже.

Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз.

Это правило также справедливо и при расчетах фильтров.

Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор.
Конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально.

Определимся, что понятия “верхние” и “нижние” частоты относятся к звукотехнике, а понятия “высокие” и “низкие” частоты – относятся к радиотехнике.

При замене сопротивления R1 на конденсатор (при этом на высоких частотах ток через него проходит беспрепятственно, а на низких ток через него не проходит) мы получим фильтр верхних частот.

А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот.

Посмотреть вложение 7755

Порядок расчета Г-образного фильтра верхней частоты

В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен. А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.

Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.

Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R1

, то реактивное сопротивление конденсатора Хс = R1.

2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы:Xc=1/2пFC=R1 —> C=1/2пFR1:
C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.
Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.

6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.
Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.
? Для справки:
? 1 мкФ = 10-6 Ф = 0,000 001 Ф
? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф
? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф
и так далее…

Порядок расчета Г-образного фильтра нижней частоты

Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.

Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.

Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.

5. Определяем емкость конденсатора, которую выводим из формулы:Xc=1/2пFC=R2 —> C=1/2пFR2:
C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.
Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.

6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.
Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.

Т – образный фильтр

Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:

Посмотреть вложение 7756

П – образный фильтр

П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных.

Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза. Посмотреть вложение 7757

Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.

Нажмите, чтобы раскрыть…

Частота среза — Википедия

Материал из Википедии — свободной энциклопедии

Частота́ сре́за (частота отсе́чки) fc{\displaystyle f_{c}} — частота, выше или ниже которой мощность выходного сигнала некоторого линейного частотно-зависимого объекта, например, электронной схемы уменьшается в два раза^[2] от мощности в полосе пропускания при воздействии на вход неизменного по амплитуде сигнала.

Амплитудно-частотная характеристика на частоте среза имеет спад до уровня −log10⁡2{\displaystyle -\log _{10}2} (приблизительно −3 дБ) относительно уровня в полосе пропускания.

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка[править | править код]

Фильтр нижних частот (ФНЧ) 1-го порядка имеет комплексную передаточную функцию H(s){\displaystyle H(s)} вида:

H(s)=11+αs,{\displaystyle H(s)={\frac {1}{1+\alpha s}},}

где s{\displaystyle s} — комплексная переменная преобразования Лапласа;

α{\displaystyle \alpha } — параметр фильтра, константа.

В случае подачи на вход фильтра гармонического сигнала с частотой ω{\displaystyle \omega } в установившемся режиме комплексная передаточная функция имеет вид:

H(jω)=11+αjω,{\displaystyle H(j\omega )={\frac {1}{1+\alpha j\omega }},}

где буквой j{\displaystyle j} обозначена мнимая единица;

ω{\displaystyle \omega } — угловая частота.

Эта функция имеет единственный полюс (частота, при которой знаменатель дроби обращается в 0) на частоте ωc=2πfc=1/α,{\displaystyle \omega _{c}=2\pi f_{c}=1/{\alpha },} fc{\displaystyle f_{c}} — частота среза.

Модуль коэффициента передачи этого ФНЧ в зависимости от частоты (эту функцию принято называть амплитудно-частотной характеристикой) имеет вид:

|H(jω)|=|11+αjω|=11+α2ω2.{\displaystyle \left|H(j\omega )\right|=\left|{\frac {1}{1+\alpha j\omega }}\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega ^{2}}}}.}

Модуль коэффициента передачи на частоте полюса:

|H(jωc)|=11+α2ωc2=12.{\displaystyle \left|H(j\omega _{\mathrm {c} })\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega _{\mathrm {c} }^{2}}}}={\frac {1}{\sqrt {2}}}.}

То есть, на частоте полюса коэффициент передачи уменьшается в 2.{\displaystyle {\sqrt {2}}.} В рассмотренном примере частота среза равна частоте полюса.

↑ Порядок фильтра равен порядку (степени алгебраического уравнения) знаменателя передаточной функции (ЛАФЧХ) фильтра. Как правило^{[уточнить]}, порядок фильтра равен количеству входящих в него сосредоточенных реактивных элементов.
↑ При этом амплитуда сигнала на частоте среза равна 12≈0,707{\displaystyle {\frac {1}{\sqrt {2}}}\approx 0,707} от амплитуды сигнала в полосе пропускания.

Онлайн расчёт полосовых LC — фильтров 3-го, 5-го и 7-го порядков.

Полосовой, он же полосно-пропускающий фильтр — это фильтр, пропускающий частоты в некоторой полосе частот, находящейся между нижней и верхней частотами среза, и может быть легко представлен в виде последовательности, состоящей из фильтра нижних частот и фильтра верхних частот.
Однако более рациональными с точки зрения оптимизации характеристик, являются фильтры, рассчитанные через ФНЧ-прототип. Преобразование фильтра низких частот в полосовой фильтр осуществляется заменой емкостей ФНЧ прототипа параллельными контурами, а индуктивностей — последовательными.

Примеры таких полосовых фильтров 3-го, 5-го и 7-го порядков приведены на Рис.1.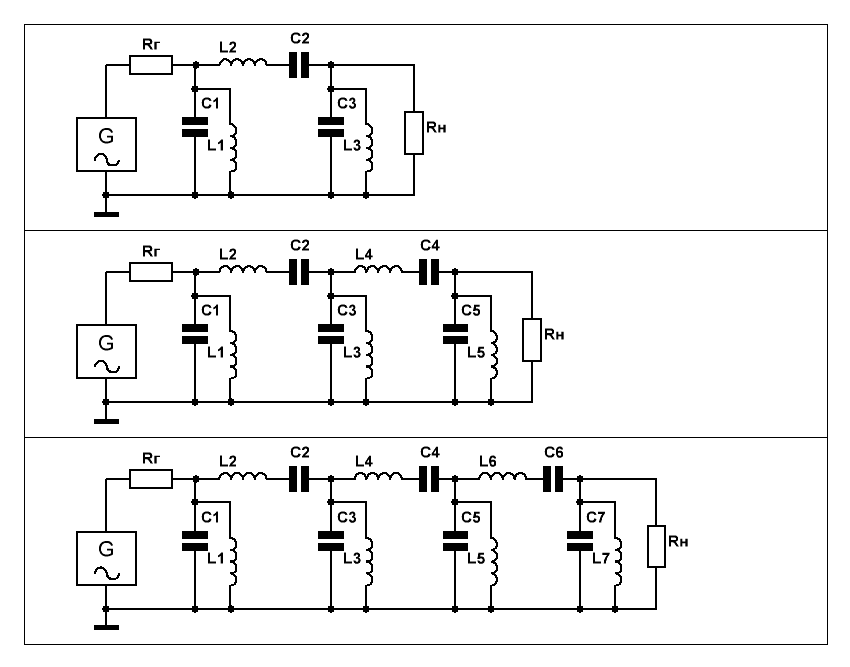

Рис.1

Расчёт поведём, используя прототипы фильтров нижних частот имени уважаемого Пафнутия Чебышева и таблицы не менее уважаемого господина Гранта Ханзела, приведённые в справочнике по расчёту фильтров.

ТАБЛИЦА РАСЧЁТА ПОЛОСОВЫХ LC ФИЛЬТРОВ.

На Рис.2 приведены амплитудно-частотные характеристики полосовых фильтров 3-го, 5-го и 7-го порядков с полосой пропускания 3-5 МГц.

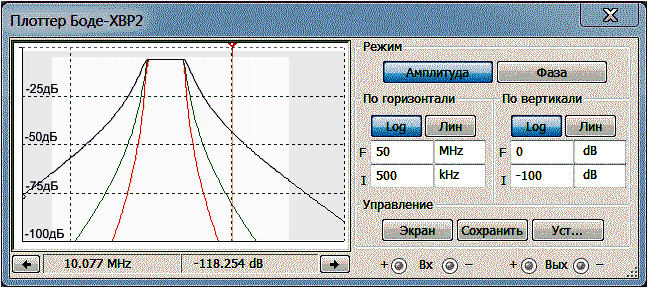
Рис.2

Характеристики затухания фильтров вне полосы пропускания симметричны и составляют величины: 38 дБ на октаву для фильтров 3-го порядка, 75 дБ — для фильтров 5-го порядка и 112 дБ — для фильтров 7-го порядка. Неравномерность в полосе пропускания — менее 0,5 дБ.

Приведённая таблица может стать хорошим подспорьем при расчёте входных диапазонных фильтров радиоприёмников и трансиверов, однако следует учитывать маленький, но ЖИРНЫЙ «НЮАНС»:
Фильтры Чебышева значительно лучше других справляются с подавлением внеполосных сигналов, но становятся крайне неудобными (с точки зрения критически малых значений номиналов некоторых элементов) при выборе узкой полосы прозрачности.
Поэтому наиболее выигрышно они будут смотреться в устройствах относительно широкополосных — с не менее, чем полуоктавной полосой пропускания.

порядок, расчет и построение схемы

В данной статье мы поговорим про фильтр Баттерворта, рассмотрим порядки фильтров, декады и октавы, подробно разберем фильтр низких частот Баттерворта третьего порядка с расчетом и схемой.

Введение

В устройствах, которые используют фильтры для формирования частотного спектра сигнала, например, в системах связи или управления, форма или ширина спада, также называемая «полосой перехода», для простого фильтра первого порядка может быть слишком длинной или необходимы широкие и активные фильтры, разработанные с более чем одним «заказом». Эти типы фильтров обычно известны как фильтры «высокого порядка» или «n- ^го порядка».

Порядок фильтров

Сложность или тип фильтра определяется «порядком» фильтров и зависит от количества реактивных компонентов, таких как конденсаторы или катушки индуктивности в его конструкции. Мы также знаем, что скорость спада и, следовательно, ширина полосы перехода зависит от порядкового номера фильтра и что для простого фильтра первого порядка он имеет стандартную скорость спада 20 дБ / декаду или 6 дБ / октава.

Тогда для фильтра, имеющего n- ^й порядковый номер, он будет иметь последующую скорость спада 20n дБ / декаду или 6n дБ / октаву. Таким образом:

фильтр первого порядка имеет скорость спада 20 дБ / декаду (6 дБ / октава)
фильтр второго порядка имеет скорость спада 40 дБ / декаду (12 дБ / октава)
фильтр четвертого порядка имеет частоту спада 80 дБ / декада (24 дБ / октава) и т. д.

Фильтры высокого порядка, такие как третий, четвертый и пятый, обычно формируются путем каскадного объединения одиночных фильтров первого и второго порядка.

Например, два фильтра нижних частот второго порядка могут быть соединены каскадно для получения фильтра нижних частот четвертого порядка и так далее. Несмотря на то, что порядок фильтра, который может быть сформирован, не ограничен, при увеличении порядка увеличиваются его размер и стоимость, а также снижается его точность.

Декады и октавы

Последний комментарий о Декадах и Октавах . По шкале частот декада — это десятикратное увеличение (умножение на 10) или десятикратное уменьшение (деление на 10). Например, от 2 до 20 Гц представляют одну декаду, тогда как от 50 до 5000 Гц представляют две декады (от 50 до 500 Гц, а затем от 500 до 5000 Гц).

Октава — это удвоение (умножить на 2) или уменьшение в два раза (деление на 2) по шкале частот. Например, от 10 до 20 Гц представляет одну октаву, а от 2 до 16 Гц — это три октавы (от 2 до 4, от 4 до 8 и, наконец, от 8 до 16 Гц), каждый раз удваивая частоту. В любом случае, логарифмические шкалы широко используются в частотной области для обозначения значения частоты при работе с усилителями и фильтрами, поэтому важно понимать их.

Логарифмическая шкала частот

Поскольку резисторы, определяющие частоту, все равны, как и конденсаторы, определяющие частоту, отсечка или угловая частота ( ƒ_C ) для первого, второго, третьего или даже для фильтра четвертого порядка также должны быть равны и найдены, используя знакомое уравнение:

Как и в случае фильтров первого и второго порядка, фильтры верхних частот третьего и четвертого порядка формируются простым взаимным обменом положений определяющих частоту компонентов (резисторов и конденсаторов) в эквивалентном фильтре нижних частот. Фильтры высокого порядка можно спроектировать, следуя процедурам, которые мы видели ранее в руководствах по фильтру нижних частот и фильтрам верхних частот. Однако общий коэффициент усиления фильтров высокого порядка является фиксированным, поскольку все компоненты, определяющие частоту, являются одинаковыми.

Аппроксимации фильтра

До сих пор мы рассматривали низкочастотные и высокочастотные схемы фильтра первого порядка, их результирующие частотные и фазовые характеристики. Идеальный фильтр дал бы нам спецификации максимального усиления полосы пропускания и плоскостности, минимального затухания полосы пропускания, а также очень крутой полосы пропускания, чтобы остановить спад полосы (полоса перехода), и поэтому очевидно, что большое количество сетевых откликов будет удовлетворять эти требования.

Неудивительно, что в линейном дизайне аналоговых фильтров есть ряд «аппроксимационных функций», в которых используется математический подход для наилучшего приближения передаточной функции, которая требуется нам для проектирования фильтров.

Такие конструкции известны как Эллиптический, Баттерворт, Чебышев, Бессель, Кауэр и многие другие. Из этих пяти «классических» функций аппроксимации линейного аналогового фильтра только фильтр Баттерворта и особенно конструкция фильтра Баттерворта нижних частот будут рассматриваться здесь как его наиболее часто используемая функция.

Низкочастотный фильтр Баттерворта

Частотная характеристика аппроксимационной функции фильтра Баттерворта также часто называется «максимально плоской» (без пульсаций) характеристикой, поскольку полоса пропускания спроектирована так, чтобы иметь частотную характеристику, которая является настолько плоской, насколько это математически возможно, от 0 Гц (DC) до частоты среза -3 дБ без пульсаций. Более высокие частоты за пределами точки отсечки снижаются до нуля в полосе останова на уровне 20 дБ / декада или 6 дБ / октава. Это потому, что он имеет «фактор качества», «Q» всего 0,707.

Однако одним из основных недостатков фильтра Баттерворта является то, что он достигает этой плоскостности полосы пропускания за счет широкой полосы перехода, когда фильтр изменяется от полосы пропускания к полосе остановки. Он также имеет плохие фазовые характеристики. Идеальная частотная характеристика, называемая фильтром «кирпичной стены», и стандартные аппроксимации Баттерворта для различных порядков фильтра приведены ниже.

Идеальная частотная характеристика для фильтра Баттерворта

Обратите внимание, что чем выше порядок фильтра Баттерворта, тем больше количество каскадных ступеней в конструкции фильтра и тем ближе фильтр подходит к идеальному отклику «кирпичной стены».

Однако на практике идеальная частотная характеристика Баттерворта недостижима, поскольку она вызывает чрезмерную пульсацию в полосе пропускания.

Где обобщенное уравнение, представляющее фильтр Баттерворта «n-го» порядка, частотная характеристика дается как:

Где: n представляет порядок фильтра, ω равно 2πƒ, а ε — максимальное усиление полосы пропускания (A _max ).

Если A _max определено на частоте, равной угловой точке отсечки -3 дБ (ƒc), тогда ε будет равно единице и, следовательно, ε ² также будет равно единице. Однако, если вы теперь хотите определить A _max при другом значении усиления по напряжению, например, 1 дБ или 1.1220 (1 дБ = 20 * logA _max ), тогда новое значение ε находится по формуле :

Подставляя данные в уравнения, получаем:

Частотная характеристика фильтра может быть определена математически его передаточной функции с стандартом передачи напряжения Функция H (jω) и записывается в виде:

Примечание: (jω) также можно записать как (s) для обозначения S-области. и результирующая передаточная функция для фильтра нижних частот второго порядка задается как:

Нормализованные полиномы фильтра Баттерворта низких частот

Чтобы помочь в разработке своих фильтров нижних частот, Баттерворт создал стандартные таблицы нормализованных полиномов нижних частот второго порядка с учетом значений коэффициента, которые соответствуют частоте отсечки угла 1 радиан / с.

N	Нормализованные полиномы знаменателя в факторизованной форме
1	(1 + S)
2	(1 + 1,414 с + с ² )
3	(1 + с) (1 + с + с ² )
4	(1 + 0,765 с + с ² ) (1 + 1,848 с + с ² )
5	(1 + с) (1 + 0,618 с + с ² ) (1 + 1,618 с + с ² )
6	(1 + 0,518 с + с ² ) (1 + 1,414 с + с ² ) (1 + 1,932 с + с ² )
7	(1 + с) (1 + 0,445 с + с ² ) (1 + 1,247 с + с ² ) (1 + 1,802 с + с ² )
8	(1 + 0,390 с + с ² ) (1 + 1,111 с + с ² ) (1 + 1,663 с + с ² ) (1 + 1,962 с + с ² )
9	(1 + с) (1 + 0,347 с + с ² ) (1 + с + с ² ) (1 + 1,532 с + с ² ) (1 + 1,879 с + с ² )
10	(1 + 0,313 с + с ² ) (1 + 0,908 с + с ² ) (1 + 1,414 с + с ² ) (1 + 1,782 с + с ² ) (1 + 1,975 с + с ²)

Расчет и схема фильтра Баттерворта низких частот

Найти порядок активного фильтра Баттерворта нижних частот, чьи характеристики приведены в качестве: A _макс = 0,5 дБ на частоте полосы пропускания ( ωp ) 200 радиан / сек (31.8 гЦ), и A_min = -20 дБ на частоте полосы остановки ( ωs ) 800 радиан / сек. Также разработайте подходящую схему фильтра Баттерворта, соответствующую этим требованиям.

Во-первых, максимальное усиление полосы пропускания A _max = 0,5 дБ, которое равно усилению 1,0593 , помните, что: 0,5 дБ = 20 * log (A) на частоте ( ωp ) 200 рад / с, поэтому значение эпсилона ε находится по:

Во-вторых, минимальное усиление полосы остановки A _min = -20 дБ, которое равно усилению 10 (-20 дБ = 20 * log (A)) на частоте полосы остановки ( ωs ) 800 рад / с или 127,3 Гц.

Подстановка значений в общее уравнение для частотной характеристики фильтров Баттерворта дает нам следующее:

Так как n всегда должно быть целым числом, то следующим самым высоким значением 2,42 будет n = 3 , поэтому «требуется фильтр третьего порядка», и для создания фильтра Баттерворта третьего порядка, ступени фильтра второго порядка требуется каскадное соединение со ступенью фильтра первого порядка.

Из приведенной выше таблицы нормализованных полиномов Баттерворта низких частот коэффициент для фильтра третьего порядка дается как (1 + s) (1 + s + s ² ), и это дает нам усиление 3-A = 1 или A = 2 . В А = 1 + (Rf / R1) , выбирая значение как для резистора обратной связи Rf и резистора R1 дает нам значения 1 кОм и 1 кОм , соответственно, как: ( 1 кОм / 1 кОм) + 1 = 2 .

Мы знаем, что угловая частота отсечки, точка -3 дБ ( ω _o ) может быть найдена с помощью формулы 1 / CR , но нам нужно найти ω _o по частоте полосы пропускания ω _p ,

Таким образом, частота отсечки угла задается как 284 рад / с или 45,2 Гц (284 / 2π), и, используя знакомую формулу 1 / RC, мы можем найти значения резисторов и конденсаторов для нашей схемы третьего порядка.

Обратите внимание, что ближайшее предпочтительное значение до 0,352 мкФ будет 0,36 мкФ или 360 нФ .

И, наконец, наша схема низкочастотного фильтра Баттерворта третьего порядка с угловой частотой среза 284 рад / с или 45,2 Гц, максимальным усилением полосы пропускания 0,5 дБ и минимальным усилением полосы остановки 20 дБ строится следующим образом.

картинка-схема низкочастотного фильтра Баттерворта третьего порядка

Таким образом, для нашего фильтра низких частот Баттерворта 3-го порядка с угловой частотой 45,2 Гц, C = 360 нФ и R = 10 кОм

Универсальный перестраиваемый активный фильтр с регулировкой частоты и добротности.

Полосовой фильтр, режекторный фильтр, фильтр нижних (ФНЧ) и верхних частот
(ФВЧ) в одном флаконе.

Хорошо, когда всё хорошо, и от фильтра требуется стабильная работа на фиксированной частоте при заданном параметре добротности. Такие схемотехнические решения мы подробно рассмотрели на предыдущей странице.
Иногда, однако, возникает необходимость построения такой схемы, в которой резонансную частоту, добротность и коэффициент передачи было бы можно настраивать независимо друг от друга. А если в качестве бонуса возникает возможность придавать полученному изделию АЧХ различных типов фильтров, то тут уже, как говорится, не устройство, а — сам себе и швец, и жнец, и в дуду игрец.

На Рис.1 приведена схема фильтра, удовлетворяющая этим требованиям. Важной особенностью схемы является то, что она в зависимости от того, какой выход используется, работает одновременно как селективный (полосовой), заграждающий (режекторный), фильтр нижних частот и фильтр верхних частот.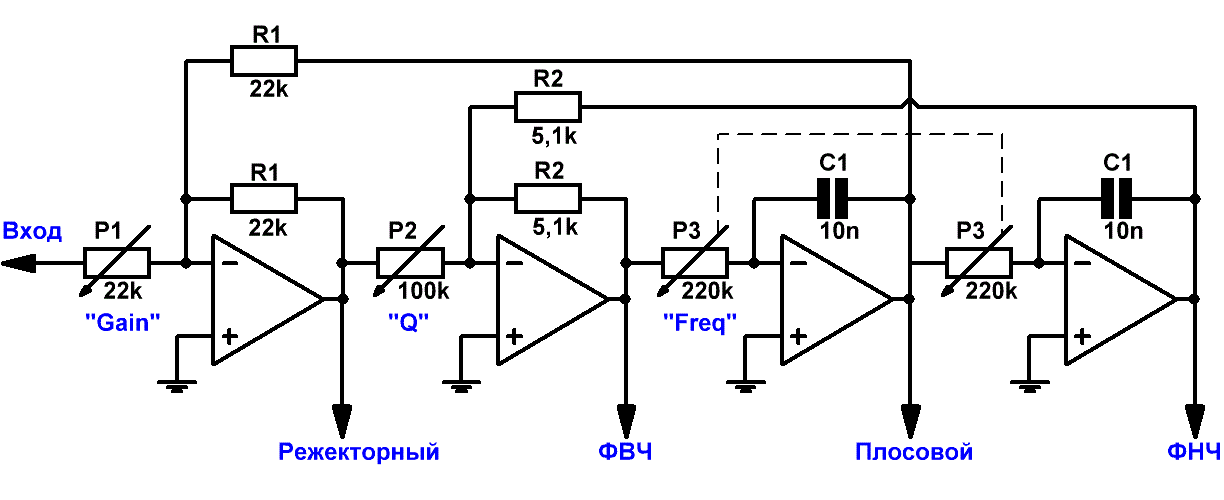

Рис.1

Расчёт элементов схемы следует производить исходя из простейших формул:
К_{передачи} = R₁/P₁ ; Q_{(добротность)} = P₂/R₂ ; F_{(частота)} = 1/(2*π*P₃*C₁) .

Частота среза/резонанса/режекции рассчитывается точно так же, как у простейших RC фильтров первого порядка. Для удобства перенесу сюда таблицу для расчёта этой частоты при фиксированных значениях сопротивления сдвоенного потенциометра Р3 и ёмкости конденсатора С1.

Теоретически, параметр добротности, при котором сохраняется устойчивость схемы без срыва в генерацию, может достигать 100. Однако повышение значения этого параметра выше единицы скорее важны для полосового и режекторного фильтров. У ФНЧ и ФВЧ при Q>1 изменяется форма АЧХ и они начинают приобретать свойства полосовых фильтров.
Продемонстрирую это утверждение диаграммами.

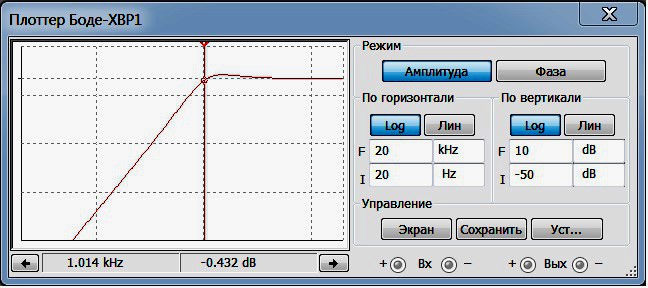
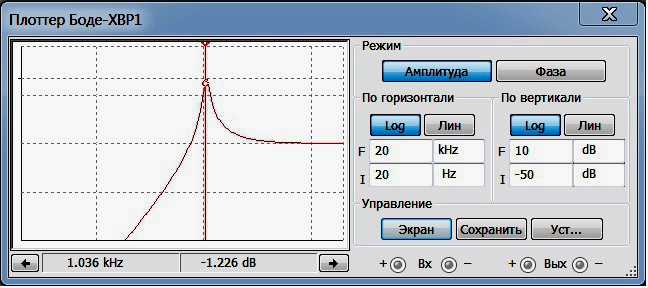
Рис.2

На Рис.2 сверху приведена АЧХ фильтра верхних частот с частотой среза 1кГц и добротностью, равной единице. Крутизна спада АЧХ этого фильтра в полосе подавления составляет — около 12 дБ/октаву, что эквивалентно фильтру Баттерворта 2-го порядка.
На Рис.2 снизу приведена АЧХ того же фильтра с добротностью, равной 10. Как можно увидеть, наряду с увеличением крутизны спада АЧХ, сама АЧХ напоминает нечто среднее между ФВЧ и ПФ.

И для сравнения на Рис.3 приведу АЧХ полосового фильтра при тех же самых значениях добротности

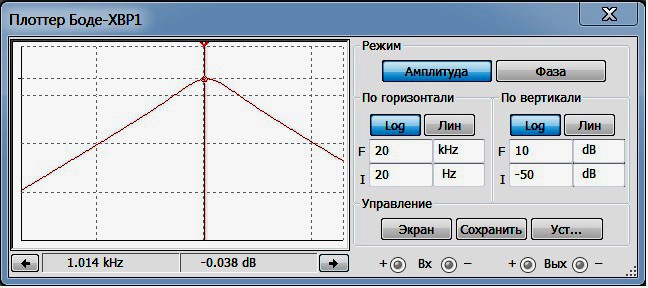
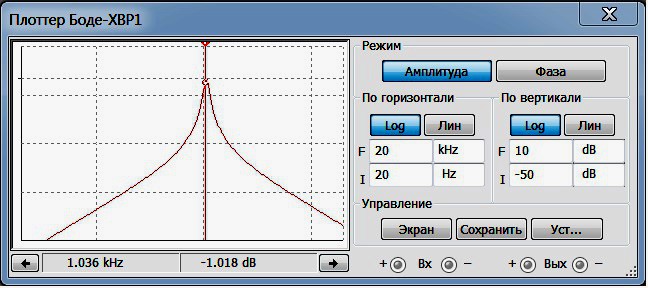
Рис.3

Ну вот, совсем другой коленкор! То, что доктор прописал, причём, для режекторного фильтра — картина будет несколько иной. На Рис.4 рассмотрим АЧХ РФ при тех же значениях добротности.

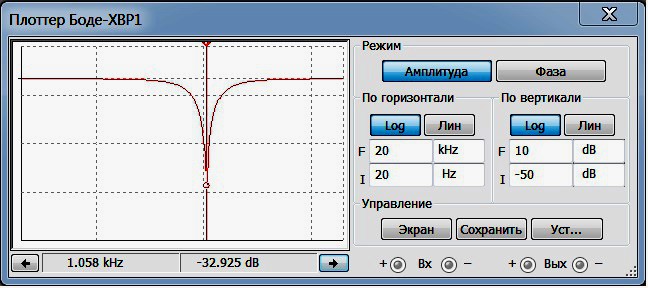
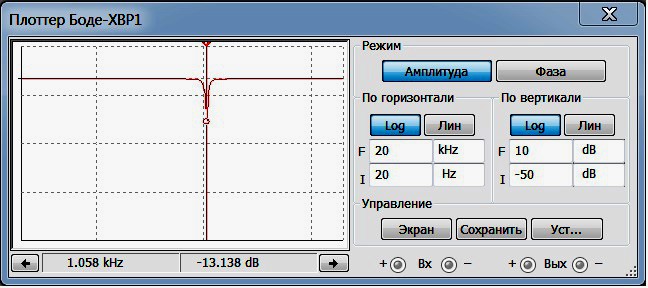
Рис.4

Здесь при увеличении параметра добротности, наряду с сужением полосы подавления, наблюдается и отчётливое снижение глубины режекции.

Вот такой он, северный олень — этот универсальный активный фильтр с регулировкой частоты и добротности.

На самом деле, данное схемотехническое решение является основой различных промышленных ИМС — программируемых универсальных фильтров. Они представляют собой устройства различных видов АЧХ и порядков (вплоть до 8-го), реализуемых за счёт последовательного включения каскадов, подобных описанному фильтру 2-го порядка.
Естественным образом, регулировка параметров ИМС ведётся не посредством вульгарного кручения переменных резисторов, а методом, основанном на периодической коммутации частотозадающих конденсаторов КМОП ключами и называемом в миру — методом коммутируемых (переключаемых) конденсаторов.
Но это уже другая песня и её мы исполним в другом гала-концерте, а на следующей странице перейдём к расчёту LC — фильтров.

мир электроники — Расчет частоты среза многозвенных RC фильтров

Расчет частоты среза многозвенных RC фильтров

категория

Расчеты по радиотехнике

материалы в категории

А. БРАЖНИКОВ, г. Пенза
Радио, 2002 год, № 12

Автор статьи рассказывает о некоторых аспектах построения многозвенных частотных RC-фильтров и выбора элементов для них.

Как известно, фильтр нижних частот (ФНЧ), схема которого изображена на рис. 1 ,а, пропускает в нагрузку сигналы от постоянного тока до частоты среза (полоса пропускания) и ослабляет сигналы более высокой частоты (полоса затухания). За частоту среза f₀ (рис. 1 ,б) принимают такую, на которой кривая амплитудно-частотной характеристики (АЧХ) фильтра снижается на 3 дБ (точнее в √2раз). Этот уровень выбирают потому, что при таком изменении напряжения мощность сигнала P=U²/r уменьшается в 2 раза.

Частота среза однозвенного (1-го порядка) RC-фильтра равна f₀=1/2πτ, где τ = RC. Его АЧХ очень полога, в полосе затухания спад характеристики — всего 6 дБ на октаву (при изменении частоты в два раза) или 20 дБ на декаду (в десять раз).

Для увеличения крутизны спада можно применять несколько RC-звеньев, включенных последовательно. Для того чтобы звенья не влияли одно на другое, их разделяют буферными повторителями напряжения, как показано на рис. 2, а.

У двузвенного фильтра спад АЧХ будет равен приблизительно 12 дБ/окт, у трехзвенного — 18 дБ/окт, у четырехзвенного — 24 дБ/окт и так далее (рис. 2,б; по вертикальной оси отложены значения нормированного коэффициента передачи). В общем случае АЧХ многозвенного фильтра будет произведением АЧХ его звеньев, а частота среза уменьшится в α = 1/√ⁿ√2-1 раз, где n — число звеньев.

На рис. 2, б показано уменьшение частоты среза f₀ с увеличением числа звеньев фильтра. В таблице указаны значения а для фильтров с числом звеньев от 2 до 10.

Такой фильтр может быть легко выполнен на любых усилителях с любым коэффициентом усиления (больше и меньше единицы), даже с разным знаком усиления (т. е. с инвертированием или без него). Просто общий коэффициент передачи по напряжению Кu в полосе пропускания будет равен произведению коэффициентов всех звеньев.

Еще одно достоинство такого фильтра — очень «мягкая», без колебаний и выбросов, реакция на скачки уровня входного сигнала.

Если на RC-звеньях строят фильтр не нижних, а верхних частот (рис. 3,а), то частота среза при добавлении каждого звена будет не уменьшаться, а увеличиваться (рис. 3, б), но численное значение коэффициента а остается прежним.

Такое изменение частоты среза необходимо учитывать при проектировании устройства с несколькими ступенями и соответствующим числом разделительных конденсаторов. Если, например, число разделительных конденсаторов равно 10, а нижняя частота среза должна быть равна 20 Гц, то каждый ФНЧ, образованный конденсатором вместе с входным сопротивлением следующей за ним ступени, должен иметь частоту среза примерно 5,4 Гц.

То же относится и к выбору корректирующих конденсаторов ОС, формирующих характеристику ФНЧ. Если таких конденсаторов несколько или имеются RC-цепи между узлами устройства, ограничивающие частотную полосу сверху, частоту среза каждой из них необходимо выбирать выше верхней рабочей частоты всего устройства в целом.

RC-фильтры

Фильтры — это схемы, которые пропускают без затухания (ослабления) определенную полосу частот и подавляют все остальные частоты. Частота, на которой начинается подавление, называется частотой среза f_с (рис.28.1).

Рис. 28.1. Частотная характеристика фильтра нижних (а) и верхних (б) частот.

Влияние фильтра на прямоугольный сигнал

Как уже говорилось в гл. 3, прямоугольный сигнал представляет собой сложное колебание, состоящее из основной гармоники и бесконечного количества нечетных гармоник. Низкочастотные составляющие формируют основание и плоскую вершину импульса, а высокочастотные — его фронт и срез.

Когда прямоугольный сигнал проходит через фильтр, его форма искажается. Фильтр нижних частот (ФНЧ) будет искажать главным образом Фронты и срезы, делая их менее крутыми и скругляя углы, как показано на рис. 28.7(б). ФНЧ оказывает на прямоугольный сигнал такое же Действие, как усилители с недостаточной шириной полосы пропускания. Фильтр верхних частот (ФВЧ), наоборот, искажает плоскую вершину и снование прямоугольного сигнала (рис. 28.5(б)).

RC— фильтры

Простейшим среди фильтров является RC-фильтр. Принцип его работы основан на том, что при изменении частоты реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а сопротивление резистора остается неизменным. На схеме рис. 28.2 конденсатор соединен последовательно с резистором. При подаче на вход такого фильтра низкочастотного сигнала реактивное сопротивление конденсатора С будет гораздо больше, чем сопротивление резистора R. В результате падение напряжения V_c на конденсаторе будет большим, а на резисторе V_r — малым. При подаче на вход этого фильтра высокочастотного сигнала картина будет обратная: V_c будет малым, а V_r — большим. Если теперь представить эту схему, как на рис. 28.3(б), где падение напряжения на конденсаторе является выходным, то в выходном сигнале будут преобладать НЧ-составляющие, а высокочастотные будут сильно ослабляться. Другими словами, мы получили фильтр нижних частот. И наоборот, если выходное напряжение снимать с резистора (рис. 28.3(а)), то получим фильтр верхних частот. Значения R и С определяют частоту среза фильтра.

Дифференциатор

Дифференциатор — это фильтр верхних частот. Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или «пички». На рис. 28.4 изображен RC-дифференциатор. Конденсатор С беспрепятственно пропускает ВЧ-составляющие входного сигнала, образующие фронт импульса АВ, а затем начинает заряжаться до 10 В.

Если постоянная времени (произведение RC) мала в сравнении с периодом входных импульсов, конденсатор успеет полностью зарядиться до 10 В, прежде чем придет следующая ВЧ-составляющая импульса — срез CD (рис. 28.5(а)). Когда конденсатор полностью зарядится, ток прекращается и падение напряжения на резисторе, т. е. на выходе, равно нулю. Срез CD представляет собой перепад напряжения 10 В и состоит из ВЧ-компонент. Поэтому он свободно пройдет через конденсатор и напряжение на выходе скачком упадет до –10 В. После этого конденсатор начнет перезаряжаться до –10 В, и, если постоянная времени мала, он успеет полностью зарядиться до этого напряжения. При этом выходное напряжение спадет до нуля и будет оставаться таким до прихода следующего фронта и т. д. Если постоянная времени больше, чем период входных импульсов, то выходной сигнал будет иметь форму, как на рис. 28.5(б).

Рис. 28.4. RC-дифференциатор.

Рис. 28.5. Сигнал на выходе дифференциатора,

изображенного на рис. 28.4, при малой (а) и большой (б) постоянной времени.

Интегрирующая RC-цепъ

Интегрирующая RC-цепь (интегратор) является фильтром нижних частот (ФНЧ) и при подаче на его вход прямоугольного сигнала выдает на выходе сигнал треугольной (пилообразной) формы. На рис. 28.6 изображен RC-интегратор. При подаче на его вход фронта прямоугольного импульса (рис. 28.7) конденсатор начинает заряжаться до напряжения +10 В. Еслизадать постоянную времени RC, большую в сравнении с периодом входного сигнала, то срез CD импульса поступит прежде, чем конденсатор успеет полностью зарядиться (рис. 28.7(а)). После этого конденсатор начинает заряжаться в обратном направлении. И опять в связи с большой постоянной времени фронт FE следующего импульса придет прежде, чем конденсатор успеет полностью зарядиться в отрицательном направлении и т.д. В результате на выходе получается сигнал треугольной формы, амплитуда которого меньше, чем амплитуда входного сигнала.

Если постоянная времени мала в сравнении с периодом входного сигнала, то выходной сигнал будет иметь вид, как на рис. 28.7(б). Обратите внимание, что и в интеграторе, и в дифференциаторе постоянная времени всегда сравнивается с периодом входного сигнала. Например, постоянная времени 100 мкс является большой по сравнению с периодом, скажем, 5 мкс (частота входного сигнала 200 кГц), но малой в сравнении с периодом 5 мс (частота входного сигнала 200 Гц).

Влияние RC-цети на синусоидальный сигнал

Синусоидальный сигнал является простым гармоническим колебанием и не содержит высших гармоник, поэтому при подаче такого сигнала на фильтр любого типа его форма не изменяется. Амплитуда выходного синусоидального сигнала может уменьшиться в зависимости от того, находится его частота в пределах полосы пропускания или нет. В первом случае синусоидальный сигнал претерпевает очень малое затухание, во втором случае затухание может быть очень большим.

Воздействие RC-цепи на пилообразный сигнал

Интегратор скругляет острые кромки пилообразного сигнала (рис. 28.8). Степень скругления определяется постоянной времени схемы. При очень большой постоянной времени выходной сигнал будет иметь вид, как на рис.28.8(б).

Рис. 28.8. Влияние интегрирующей цепочки

на форму пилообразного напряжения.

Рис. 28.9. Влияние дифференцирующей цепочки