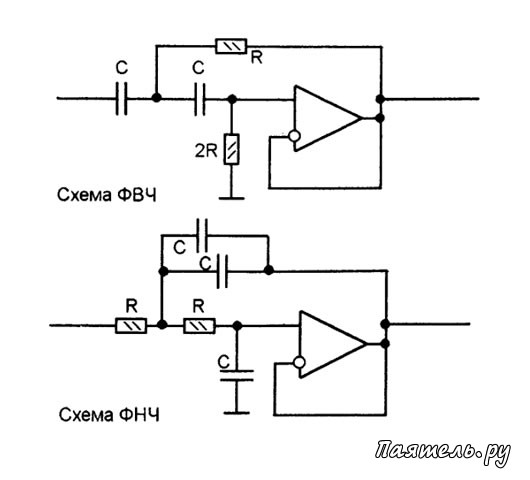
Расчет активного фильтра
Пассивная часть схемы представляет собой многополюсник, состоящий из резистивных и емкостных элементов рис. Предположим, что RC -многополюсник имеет структуру, показанную на рис. Это означает, что потенциал зажима 3 равен нулю. Составим уравнение узлов 4 и Разрешая второе уравнение этой системы относительно выходного напряжения U 2 , то есть , и подставляя результат в первое уравнение, после не сложных преобразований получим выражение для коэффициента передачи по напряжению:.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Расчёт звена активного фильтра низких частот на операционном усилителе
- Расчет активного фильтра
Схемы активных фильтров - Проектирование и анализ активного электрического фильтра
- Расчет фильтров нижних и верхних частот
- Активные фильтры
- Схемы активных фильтров
- Вы точно человек?
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Как сделать эффективный фильтр НЧ своими руками/Кроссовер под сабвуфер
youtube.com/embed/2c-8SizF1qY» frameborder=»0″ allowfullscreen=»»/>Расчёт звена активного фильтра низких частот на операционном усилителе
Понятно, что для необходимого затухания достаточно фильтра 4 порядка. Общий график для передаточной функции фильтра Баттерворта:. Чтобы желаемая схема имела желаемую амплитудно-частотную характеристику, входящие в неё элементы могут быть подобраны с не очень высокой точностью, что является плюсом данной схемы. В данной схеме коэффициент усиления операционного усилителя должен иметь строго определённое значение, а коэффициент передачи данной схемы будет не больше 3.
Поэтому данную схему можно отбросить. Данный фильтр построен на четырех операционниках, что увеличивает помехи и сложность расчёта данной схемы, поэтому её мы также отбрасываем. Определение передаточной функции. Они отрицательные, так как данные каскады являются инвертирующими, однако их произведение даёт положительный коэффициент передачи.
Для расчёта схемы лучше задаться емкостями конденсаторов, при этом для того, чтобы значение R 2 было действительным, должно выполняться условие.
При выборе ОУ необходимо учитывать диапазон частот фильтра: частота единичного усиления ОУ на которой коэффициент усиления равен единице должна быть больше произведения частоты среза и коэффициента усиления фильтра K у.
Другим важным параметром ОУ является его входное сопротивление. Оно должно быть больше десятикратного максимального сопротивления резистора схемы. Максимальное сопротивление в схеме равно Так же необходимо учитывать нагрузочную способность ОУ. Для современных ОУ минимальное сопротивление нагрузки составляет 2 кОм.
Учитывая, что сопротивление R1 и R4 равны соответственно Последнее добавление статей: Ремонт крышек люков полувагонов. Технология ремонта кузова полувагона. Организация обслуживания и ремонта вагонов в депо. Передатчик базовой станции стандарта GSM — Исследование морфологической структуры целлюлозы.
Расчет и проектирование лесосушильной камеры. Передатчик телевизионных вещательных радиостанций. Конструкции из дерева и пластмасс. Автоматизация котла Е Атоматизации средств контроля системы отображения.
Проектирование однозального кинотеатра. Проект станции технического обслуживания легковых автомобилей. Визуальной оценки цветового различия.
Автоматизации котельной. Производство дихлорэтана оксихлорированием этилена. Технология судоремонта. Разработка бескорпусной интегральной микросборки. ИС учета и поверки контрольно-измерительного оборудования.
Адсорбционная установка. Разработка схемы автоматизации процесса шлихтования. Расчеты по статике корабля. Система водоснабжения жилого поселка и промышленного предприятия.
Система автоматического регулирования температуры швейной иглы. Разработка ассортимента женской верхней одежды для швейного предприятия. Установка и расчет направляющих в шахте пассажирского лифта. Измерение ph фактора при шлихтовании. Разработка энергетической установка сухогрузного судна. Электрическая часть АЭС. Оценка точности стандартного метода определения линейных размеров.
Установка и расчет направляющих в шахте пассажирского лифта. Измерение ph фактора при шлихтовании. Разработка энергетической установка сухогрузного судна. Электрическая часть АЭС. Оценка точности стандартного метода определения линейных размеров.
Трикотажное производство. Разработка технологической последовательности по изготовлению женского пальто. Проектирование рельсовой колеи и одиночного обыкновенного стрелочного перевода. Сети без линий. Проектирование конструктивного мидель шпангоута. Расчет состава позиций поточной линии изготовления секций корпуса судна.
Цилиндр высокого давления паровой турбины. Картографические проекции в программном продукте ArcGIS. Статистический анализ временных рядов. Проектирование производственных участков предприятия.
Кинотеатральный громкоговоритель. Проектирование швейного потока. Разработка технологического процесса механической обработки детали. Разработка конструкции редуктора. Устройство для контроля запыленности специальных производственных помещений.
Расчеты по залу бумагоделательных машин. Электронная записная книжка. Проектирование элементов машиностроительного изделия. Пролетный клистрон. Устройство управления работой индикатора. Составление проекта на разведку месторождения полезного ископаемого. Проектирование системы управления микроволновой печью. Расчет воздухообмена системой кондиционирования. Информационная система учета и поверки. Технология производства кинофотоматериалов.
Маркетинговые исследования рынка мороженого. Расчёт фильтра с характеристикой Баттерворта Страница 1 из 2. Текст к Тексту, Powered by Joomla! Коэффициент передачи Общий график для передаточной функции фильтра Баттерворта: Определяем схемную реализацию фильтра: активный фильтр нижних частот четвёртого порядка со сложной отрицательной обратной связью: Чтобы желаемая схема имела желаемую амплитудно-частотную характеристику, входящие в неё элементы могут быть подобраны с не очень высокой точностью, что является плюсом данной схемы.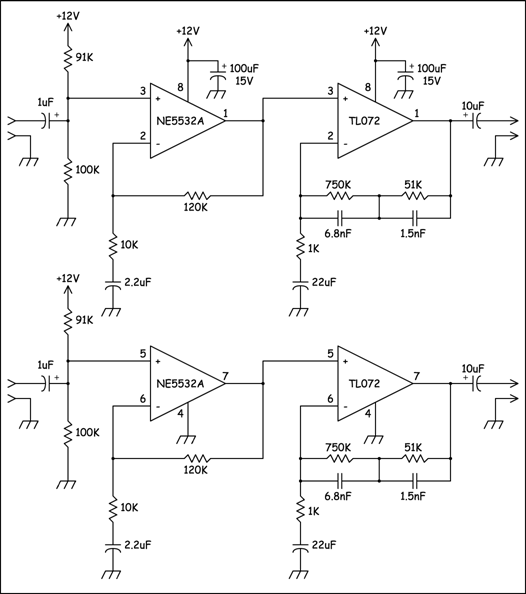
Титце, К. Далее используются формулы из У. Рассчитываем значения сопротивлений для первого каскада: Значения сопротивлений второго каскада: Выбор ОУ При выборе ОУ необходимо учитывать диапазон частот фильтра: частота единичного усиления ОУ на которой коэффициент усиления равен единице должна быть больше произведения частоты среза и коэффициента усиления фильтра K у.
Расчет активного фильтра
Спроектировать активный RC — фильтр нижних частот с ограниченной полосой пропускания, удовлетворяющий следующим требованиям:. Тенденция к микроминиатюризации радиоэлектронной аппаратуры в очень острой форме ставит вопрос о путях дальнейшего развития техники селективных устройств. Уменьшение габаритов LC — фильтров ограничено тем, что добротность катушек индуктивности падает с уменьшением их размеров. Выбирая величину нагрузочного сопротивления LC — фильтра, можно уменьшить индуктивность но при этом необходимо во столько же раз увеличить емкость, т.
Онлайн калькулятор для расчета мощности активного фильтра в электроустановке низкого напряжения.
Схемы активных фильтров
В данной работе проводится расчёт активного фильтра нижних частот Чебышева. Определяется порядок фильтра и значения компонентов. Исследуется влияние разброса параметров резисторов и конденсаторов относительно номинальных. Анализ и проектирование выполнены с помощью компьютерной программы Microcap. Передача и обработка цифровых сигналов электросвязи, сигналов радио и телевидения и т. Этими устройствами являются электрические фильтры. Они бывают реактивными и активными. В данной работе будет рассмотрено проектирование активного электрического фильтра.
Проектирование и анализ активного электрического фильтра
Применение положительной обратной связи позволяет увеличивать добротность полюса фильтра. При этом полюс фильтра можно реализовать на RC элементах, которые значительно дешевле и в данном диапазоне частот меньше по габаритам индуктивностей. Кроме того, величина емкости конденсатора, входящего в состав активного фильтра может быть уменьшена, так как в ряде случаев усилительный элемент позволяет увеличивать ее значение. Применение конденсаторов с малой емкостью позволяет выбирать их типы, обладающие малыми потерями и высокой стабильностью параметров.
Применение конденсаторов с малой емкостью позволяет выбирать их типы, обладающие малыми потерями и высокой стабильностью параметров.
Понятно, что для необходимого затухания достаточно фильтра 4 порядка. Общий график для передаточной функции фильтра Баттерворта:.
Расчет фильтров нижних и верхних частот
Вы используете устаревший браузер Internet Explorer. Некоторые функции сайта им не поддерживаются. Рекомендуем установить один из следующих браузеров: Firefox , Opera или Chrome. Аннотация А. Плехов, Д. Титов, Е.
Активные фильтры
Точный расчет необходимого количества активных фильтров является сложной задачей, которую решает квалифицированный инженер на основании замеров параметров качества электрической энергии или математической модели, учитывающей разные варианты переключений в электроустановке и различные режимы работы технологического оборудования. Для предварительного расчета бюджета по установке активных фильтров можно применить наш калькулятор. Предварительный расчет необходимого количества активных фильтров Точный расчет необходимого количества активных фильтров является сложной задачей, которую решает квалифицированный инженер на основании замеров параметров качества электрической энергии или математической модели, учитывающей разные варианты переключений в электроустановке и различные режимы работы технологического оборудования.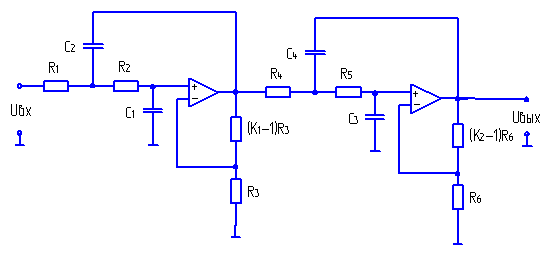 Введите необходимые данные для расчета: Pvfd — cуммарная мощность преобразователей частоты, кВт. Pdol — cуммарная мощность двигателей прямого пуска, кВт. Примечание: Если Вы не ввели значение, то оно считается равным нулю. Результат расчета Требуемый ток компенсации активного фильтра Icomp, А.
Введите необходимые данные для расчета: Pvfd — cуммарная мощность преобразователей частоты, кВт. Pdol — cуммарная мощность двигателей прямого пуска, кВт. Примечание: Если Вы не ввели значение, то оно считается равным нулю. Результат расчета Требуемый ток компенсации активного фильтра Icomp, А.
Структурная схема активного фильтра гармоник (АФГ) показана на рис. 1. АФГ предназначен для компенсации высших гармонических.
Схемы активных фильтров
В ходе лабораторной работы мы изучили принцип действия и схем интеграторов, и дифференциаторов. Схемы дифференцирующего и интегрирующего операционного усилителя и их сравнительные характеристики приведены в основной части работы. Для стабилизации схемы в передаточную функцию вводится полюс за счет добавления резистора R i.
Вы точно человек?
ВИДЕО ПО ТЕМЕ: Лекция 64. Фильр высокой частоты
Моделирование пассивных фильтров низкой частоты: однозвенных и двухзвенных.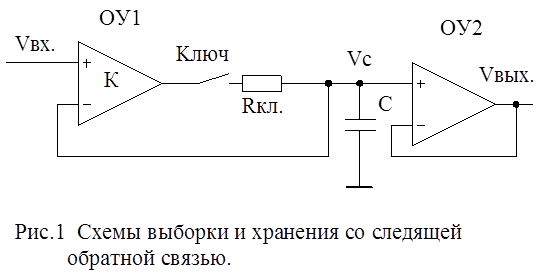
Джонсон, Дж. Джонсон, Г.
Практический расчет фильтров верхних и нижних частот RC и LC фильтров. Доброго дня уважаемые радиолюбители! А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры в статье много формул, но это не страшно, на самом деле все очень просто. Одним из ярких примеров их применения — цветомузыкальные устройства. Естественно, что такую конструкцию очень трудно назвать цветомузыкой.
Нужны еще сервисы? Архив Каталог тем Добавить статью. Как покупать?
Проектирование активных фильтров в Analog Filter Wizard 2.0
Активные фильтры являются одним из наиболее часто используемых элементов радиотехнических устройств. Особенно это касается аудиотехники, систем обработки сигналов, измерительных приборов, электронных музыкальных инструментов и т. п. В настоящее время имеется большой выбор программных продуктов, позволяющих выполнить расчеты и моделирование фильтров. Однако большинство этих продуктов или ограничивают возможности проектировщика, или доступны в пиратских копиях, часто некорректно работающих. Не все программы обеспечивают расчет фильтров для инфранизких частот. Так, например, программа FilterPro v3.1 (от Texas Instruments) не рассчитывала фильтры с частотой среза ниже 10 Гц, что и подтвердил официально Бьерн Гойбэль (Bjoern Goebel), инженер службы технической поддержи компании, в переписке с автором этой статьи.
п. В настоящее время имеется большой выбор программных продуктов, позволяющих выполнить расчеты и моделирование фильтров. Однако большинство этих продуктов или ограничивают возможности проектировщика, или доступны в пиратских копиях, часто некорректно работающих. Не все программы обеспечивают расчет фильтров для инфранизких частот. Так, например, программа FilterPro v3.1 (от Texas Instruments) не рассчитывала фильтры с частотой среза ниже 10 Гц, что и подтвердил официально Бьерн Гойбэль (Bjoern Goebel), инженер службы технической поддержи компании, в переписке с автором этой статьи.
В начале этого года компания Analog Devices открыла на своем сайте свободный доступ к своему новейшему программному продукту — бета-версии on-line (интерактивного) калькулятора по расчету аналоговых фильтров Analog Filter Wizard 2.0. Это новая версия хорошо зарекомендовавшего себя on-line калькулятора Analog Filter Wizard v1.0 (последняя версия — 1.0.28.22). (Analog Filter Wizard v1.0 сейчас опять доступен через ссылку [1]. ) И хотя новый Analog Filter Wizard 2.0 пока позволяет выполнить расчеты только полосовых фильтров, фильтров высоких и низких частот и ограничен в выборе топологии фильтров, он стоит того, чтобы уделить ему внимание и освоить его использование.
) И хотя новый Analog Filter Wizard 2.0 пока позволяет выполнить расчеты только полосовых фильтров, фильтров высоких и низких частот и ограничен в выборе топологии фильтров, он стоит того, чтобы уделить ему внимание и освоить его использование.
Доступ к Analog Filter Wizard 2.0 открывается с основного сайта компании www.analog.com. Вход — через вкладку All Design Tools. В ней выбираем Op Amp и активируем Filter. Все это можно выполнить без предварительной регистрации на сайте компании. Если же вы войдете на сайт через поисковик, то сайт откроется в русскоязычной версии. В ней доступ к этому программному продукту «пропустили», поэтому переключите язык на английский (English — в верхнем правом углу окна). Системные требования не очень высокие, при наличии Java все работает даже под Windows 2000, но медленно, а под Windows XP уже достаточно быстро. Вход в программу осуществляется через вкладку Design Support (рис. 1).
Войти в программу можно и по прямой ссылке [2]. В обоих случаях открывается окно Select your filter type (рис. 2).
2).
Впоследствии с этой страницы можно будет загружать ранее выполненный вами проект. Это осуществляется через опцию Load Design, но только при наличии у вас регистрации в системе myAnalog.
Программа содержит русификатор. Его активация осуществляется в окне Select a Language. Русификатор толковый, но, как обычно, во вкладках не все будет переведено, а там, где это сделано, имеют место неточности в терминах и пропуски. Однако, в отличие от других программ, на русском языке дается очень качественный, грамотный и полезный вариант помощи (вход через пиктограмму «?»). Необходимо учитывать, что для этой программы при включении русификатора на этапах проектирования происходит сброс всех настроек, и работу придется начинать заново. Лучше использовать программу на родном ей языке — английском.
Первый шаг — выбор типа фильтра. Здесь не возникает путаницы в понятиях фильтр нижних или верхних частот, так как виртуальные кнопки выбора типа фильтра представляют собой пиктограммы с изображением передаточных функций. Для иллюстрации работы программы произведем расчет фильтра низких частот (ФНЧ, в англоязычной терминологии — Low-pass filter) с частотой среза 60 Гц по уровню –3 дБ и подавлением частоты 100 Гц на 40 дБ. Нажимаем на пиктограмму Low-pass. Пиктограмма подсвечивается, и открывается окно установки технических условий (рис. 3). В окне подсвечивается указатель Specifications. Это указывает, на какой стадии разработки вы находитесь. Здесь же активируются (подсвечиваются зеленым) кнопки Go to Component Selection и Back. Последняя опция в любом из окон позволяет вернуться на шаг назад. В данном случае мы можем ввернуться к выбору типа фильтра через Back to Type.
Для иллюстрации работы программы произведем расчет фильтра низких частот (ФНЧ, в англоязычной терминологии — Low-pass filter) с частотой среза 60 Гц по уровню –3 дБ и подавлением частоты 100 Гц на 40 дБ. Нажимаем на пиктограмму Low-pass. Пиктограмма подсвечивается, и открывается окно установки технических условий (рис. 3). В окне подсвечивается указатель Specifications. Это указывает, на какой стадии разработки вы находитесь. Здесь же активируются (подсвечиваются зеленым) кнопки Go to Component Selection и Back. Последняя опция в любом из окон позволяет вернуться на шаг назад. В данном случае мы можем ввернуться к выбору типа фильтра через Back to Type.
Вводим в разделы Passband и Stopband необходимые для проектирования условия и данные.
Для Passband вводим:
- Усиление в полосе пропускания Gain (устанавливаем 0 дБ, в противном случае все будет рассчитываться от установленной величины усиления). Программа позволяет устанавливать усиление и в кратности, для этого нужно просто изменить размерность Gain с dB на V/V.

- Частота среза в Гц по нужному уровню (дБ). При вводе больших значений программа автоматически переведет их в кГц и МГц (добавив к числу k или M и убрав нули). В отличие от других программ уровень затухания на частоте среза можно устанавливать на свое усмотрение, что, несомненно, очень удобно. Устанавливаем для Passband частоту 60 Гц по стандартному уровню –3 дБ.
Для Stopband вводим частоту в Гц по нужному уровню (дБ) и обращаемся к движку Filter Response. Устанавливаем для Stopband частоту 100 Гц по уровню 40 дБ.
Движок Filter Response позволяет нам настроить фильтр по приемлемому полиному аппроксимирующей функции, амплитудночастотной и фазо-частотной характеристикам фильтра, определиться с его порядком и количеством операционных усилителей (ОУ), необходимых для его реализации. Сдвиг движка в сторону Fewest Stage уменьшает порядок фильтра и, следовательно, косхемотехника личество ОУ, но ухудшает реакцию фильтра на импульсные воздействия, увеличивает время задержки фильтра и приводит к неравномерности АЧХ в полосе пропускания.
Здесь будут доминировать полиномы аппроксимации Чебышева с различной неравномерностью. Сдвиг движка в сторону Fastest Setting меняет полином аппроксимирующей функции от полинома Баттерворта до полинома Бесселя. При этом количество требуемых ОУ и порядок фильтра увеличиваются. Чтобы лучше понять особенности этого вопроса, рекомендуем включить русификатор и активировать справку по Filter Response. К сожалению, при этом придется вернуться в начало проектирования.
Поскольку наш фильтр будет работать в области очень низких частот, в которой не ожидается быстрых скачкообразных изменений сигнала, то можно сократить порядок фильтра, используя полином Чебышева сприемлемой неравномерностью. Остановим свой выбор на фильтре шестого порядка (затраты — три ОУ) с неравномерностью в полосе пропускания 0,09 дБ. Выбор АЧХ сразу будет отражен в окне View: Magnitude (dB) (рис. 3). Переключиться на фазовую характеристику и групповое время задержки можно через View, активировав его подменю. Через опцию View целесообразно сразу оценить каскады фильтра, включив режим Stages (рис. 4).
4).
Это позволяет оценить распределение усиления, посмотреть частоты среза каждой ступени и их добротность. Все это поможет в будущем при проверке и наладке фильтра. Затем можно перейти к выбору компонентов фильтра, активировав окно Component Selection. Если проверка ожидаемых характеристик фильтра дает неудовлетворительные результаты, то в этом окне можно изменить вводные данные или установить движок Filter Response на новый полином передаточной функции. Оставляем введенные параметры без изменений и переходим к выбору элементов фильтра. После активации Component Selection открывается окно выбора компонентов фильтра (рис. 5).
По умолчанию установлен режим оптимизации Low Power, то есть оптимизация по минимальной потребляемой мощности. Однако можно, развернув меню, выполнить оптимизацию по минимальному уровню собственных шумов или перейти в режим свободного выбора компонентов — Specific Components. Особенностью программы является то, что в режимах оптимизации предлагается только одно решение. Возможно, оно является самым оптимальным, но отсутствие хоть какого-либо альтернативного выбора в этих режимах накладывает ограничения при проектировании.
Возможно, оно является самым оптимальным, но отсутствие хоть какого-либо альтернативного выбора в этих режимах накладывает ограничения при проектировании.
Автор статьи был неприятно удивлен, когда впервые перешел от привычного Analog Filter Wizard v1.0 к этой версии, включил режим Low Noise и получил не только не подходящий ему ОУ, но и элементы схемы в виде электролитических конденсаторов внушительных номиналов с допуском 5%. Переписка с разработчиком этого программного продукта помогла найти приемлемое решение: это переход к режиму свободного выбора компонентов фильтра.
Но сначала необходимо установить значения питающего напряжения. Это делается во вкладке Op Amp Voltage Supplies. Если требуется вариант однополярного питания, то устанавливают значение –Vs, равное нулю. Схема будет автоматически переведена в режим расщепления однополярного источника на два с делением напряжения пополам (используется дополнительный ОУ). Оставим значение питающих напряжений +Vs = 5 В и –Vs = –5 В (знак «–» обязателен!).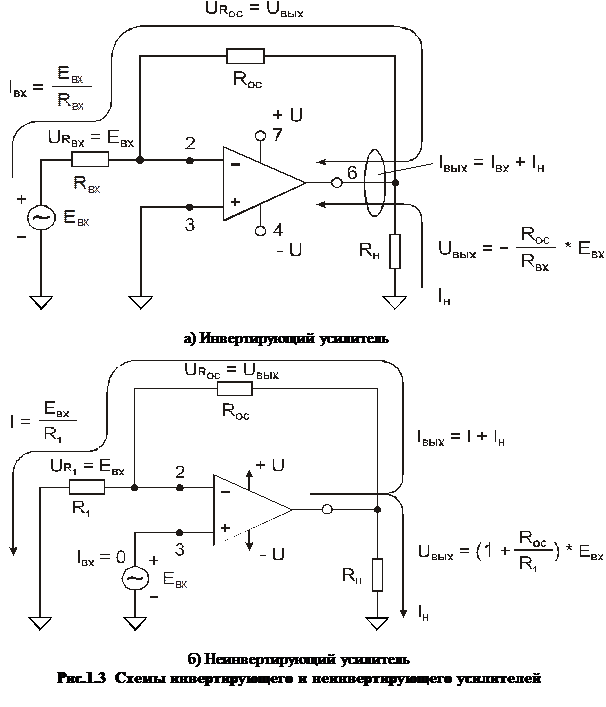 Активируем режим Specific Components. Левая сторона вкладки переключится в режим выбора элементов каждой секции фильтра (рис. 6).
Активируем режим Specific Components. Левая сторона вкладки переключится в режим выбора элементов каждой секции фильтра (рис. 6).
Дополнительно будет предложено учесть Compensate for GBW. Что имеется в виду? Обратимся к справке, активировав пиктограмму «?». Получаем ответ: «Если оставить этот элемент управления отключенным, то программа вычисляет номиналы резисторов и конденсаторов, предполагая, что ОУ является идеальным и обладает бесконечно широкой полосой, аналогично тому, как сделали бы вы, воспользовавшись справочником по проектированию фильтров. Реальные ОУ обладают конечной полосой пропускания, и это ограничение может повлиять на частотную характеристику фильтра. Если включить этот элемент управления, то программа корректирует номиналы резисторов и конденсаторов для компенсации влияния ограниченного произведения полосы на коэффициент усиления таким образом, чтобы окончательный результат был ближе к требуемому».
Поскольку наш фильтр будет работать в области очень низких частот, то компенсацию можно не включать. Однако впоследствии, если не учесть это в установках ОУ, возникнут проблемы, о которых будет сказано ниже.
Однако впоследствии, если не учесть это в установках ОУ, возникнут проблемы, о которых будет сказано ниже.
Перейдем к выбору компонентов фильтра. Сначала решим вопрос о приемлемых для нашего проекта допусках элементов будущего фильтра. Активируем опцию Component Tolerances: открывается вкладка, показанная на рис. 7.
Программа позволяет установить нулевые отклонения номиналов, то есть считать элементы идеальными, или задать допустимые отклонения. При этом в схеме будут устанавливаться элементы по соответствующим рядам номинальных значений. Для конденсаторов допустим выбор элементов с отклонением в 1, 5, 10 или 20%; для резисторов — 0,1, 0,5, 1 или 5%. Для ОУ можно выбрать разброс по GBW 20% (рекомендуем это значение не изменять и оставить по умолчанию). Здесь же можно посмотреть, к чему приведет выбранный нами вариант предельных отклонений от номинальных значений. Для этого в окне View можно переключиться в режим просмотра АЧХ, фазово-частотных характеристик, времени задержки или отклика на скачок напряжения.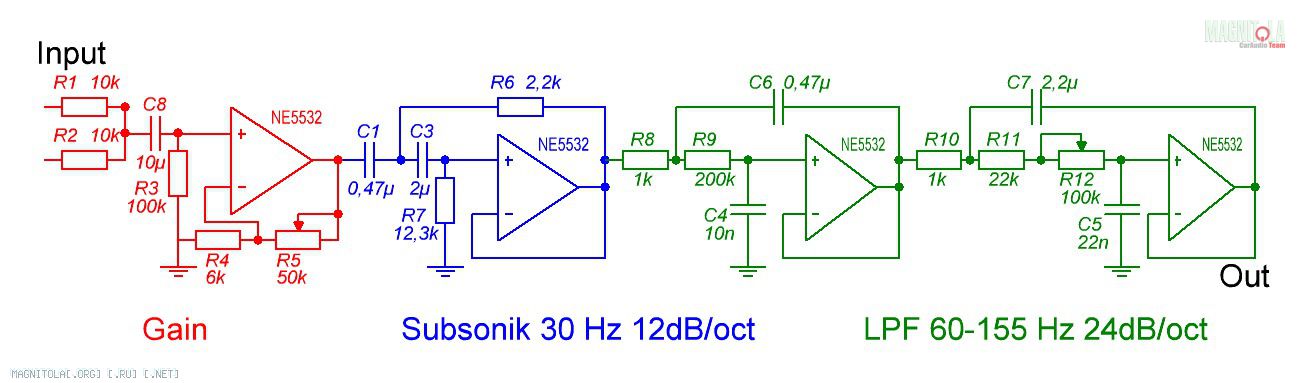 Остановим свой выбор на конденсаторах с отклонением 5% (более точные конденсаторы таких номиналов купить проблематично) и резисторах с допуском 1%. Посмотрим на АЧХ (рис. 8).
Остановим свой выбор на конденсаторах с отклонением 5% (более точные конденсаторы таких номиналов купить проблематично) и резисторах с допуском 1%. Посмотрим на АЧХ (рис. 8).
Подавление на частоте 100 Гц при самой худшей комбинации предельных отклонений будет в пределах –45…–37,5 дБ. Если проанализировать ситуацию, то можно увидеть, что основным виновником такого отклонения являются конденсаторы. Придется или мириться с этим, или повышать порядок фильтра. Если такие отклонения АЧХ для проекта недопустимы, придется вернуться в Specification (можно непосредственно из этого окна через опцию Back to Component Selection) и изменить начальные условия проектирования.
Допустим, нас устраивает полученный результат. Возвращаемся в раздел выбора элементов фильтра. (Напоминаем, ряды номинальных значений пассивных компонентов уже заданы.) Переключаем окно View на Circuit, активируем Back to Component Selection (внизу окна) и открываем первую секцию фильтра — Stage A (рис. 9).
К сожалению, пока программа не позволяет выбирать топологию фильтра.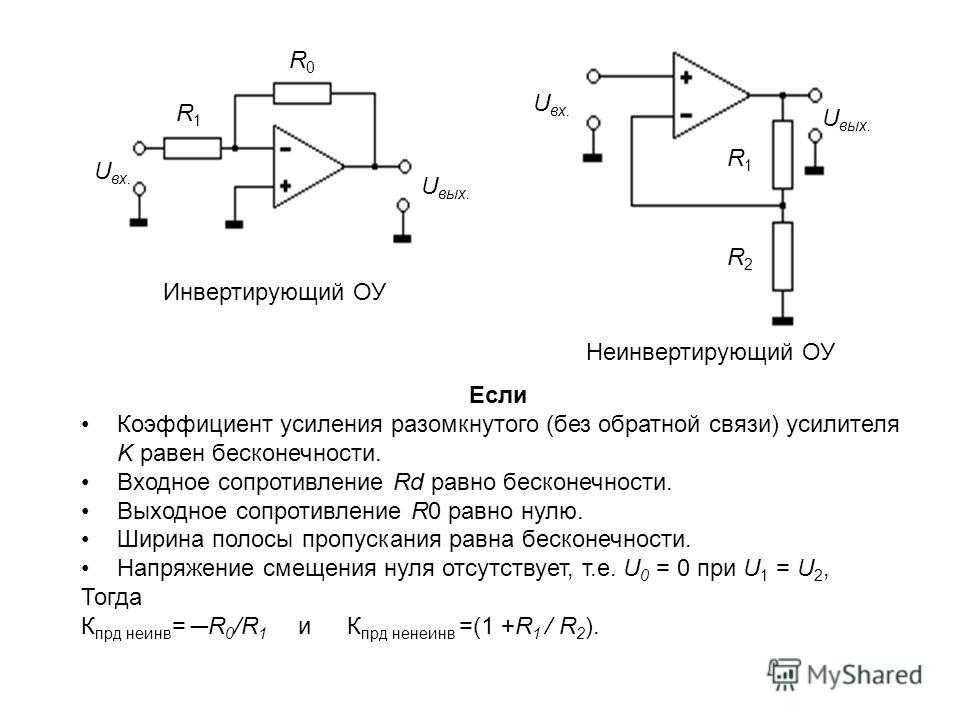 В Analog Filter Wizard 2.0 доступен только фильтр СалленаКи и активный фильтр первого порядка как добавка к фильтрам нечетных порядков (3, 5, 7 схемотехника и т.д.). Analog Filter Wizard v1.0 давал возможность выбрать одну из четырех топологий:
В Analog Filter Wizard 2.0 доступен только фильтр СалленаКи и активный фильтр первого порядка как добавка к фильтрам нечетных порядков (3, 5, 7 схемотехника и т.д.). Analog Filter Wizard v1.0 давал возможность выбрать одну из четырех топологий:
- фильтр Саллена-Ки;
- фильтр с топологией многопетлевой обратной связи;
- биквадратный фильтр;
- фильтр с изменяемыми параметрами.
Звено первого порядка в этой программе можно задать как активным, так и пассивным. Кроме того, в Analog Filter Wizard 2.0 для фильтров низкой частоты (ФНЧ) ни конденсаторы, ни резисторы не имеют по умолчанию одинаковых номиналов, и только при выборе варианта фильтра высокой частоты (ФВЧ) конденсаторы по умолчанию равны по номинальному значению. То есть нельзя установить или подобрать топологию равнокомпонентного фильтра. В равнокомпонентном фильтре Саллена-Ки номиналы резисторов и конденсаторов в частотозадающих цепях имеют одинаковые величины, что, без сомнения, удобно и технологично, особенно в случае применения прецизионных резисторов и конденсаторов в фильтрах высокого порядка.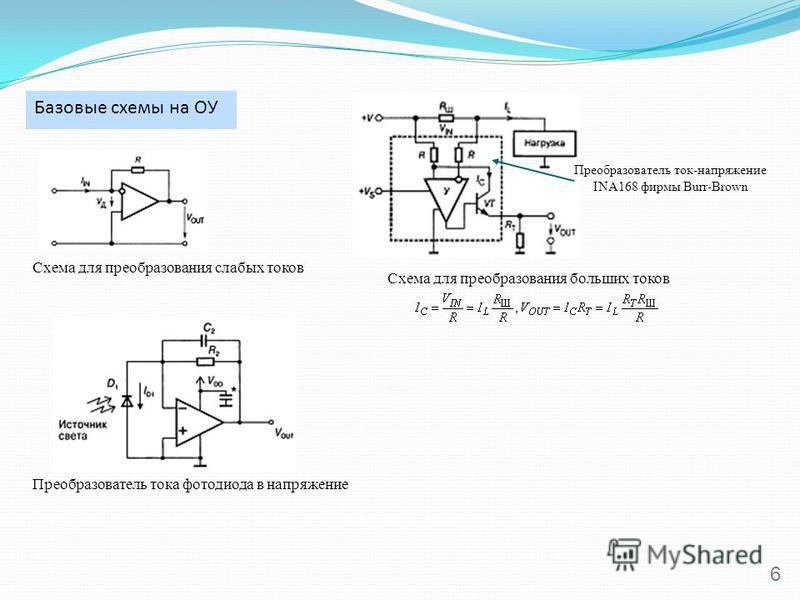 В этом отношении новая программа пока явно проигрывает.
В этом отношении новая программа пока явно проигрывает.
Для начала рекомендуется выбрать подходящий ОУ. Для этого активируем опцию Change рядом с рекомендуемым программой ОУ AD8657. Откроется таблица выбора ОУ: естественно, что все предлагаемые ОУ будут от компании Analog Devices. Подходящие для текущего проекта ОУ будут иметь отметку recommended. Для остальных будет дано объяснение, почему они не подходят.
В этом окне можно воспользоваться рядом фильтров, облегчающих выбор ОУ. Они расположены в верхней строке и позволяют выбрать ОУ по полосе пропускания, питающим напряжениям или сразу высветить только ОУ, рекомендованные для данного проекта. Если вы устанавливаете фильтр, не забывайте активировать его, нажав на Apply Filter. Выбираем подходящий на наш взгляд ОУ, например AD822, и активируем кнопку Select. Программа вернется в раздел Component Selection, и в схеме первой ступени ОУ AD8657 будет заменен на выбранный нами AD822. Опять активируем Stage A и, изменяя положение движка Component Sizing, настроим номинальные значения компоненты этого звена на приемлемые для нас величины. Естественно, что на первом месте будет выбор номиналов конденсаторов. Перемещение движка влево будет приводить к увеличению емкости конденсаторов и уменьшению номиналов резисторов и наоборот. Напоминаем, что номиналы элементов будут меняться не плавно, а в соответствии с заданными рядами номинальных значений во вкладке Component Tolerances. Повторяем описанную выше операцию для секций В и С фильтра.
Естественно, что на первом месте будет выбор номиналов конденсаторов. Перемещение движка влево будет приводить к увеличению емкости конденсаторов и уменьшению номиналов резисторов и наоборот. Напоминаем, что номиналы элементов будут меняться не плавно, а в соответствии с заданными рядами номинальных значений во вкладке Component Tolerances. Повторяем описанную выше операцию для секций В и С фильтра.
Обращаем ваше внимание на еще одну неточность программы. Иногда номинал конденсатора на этой вкладке (обычно это происходит для последней секции фильтра) не вписывается в выбранный ряд номинальных значений. Например, вы увидите конденсатор 4,71 нФ вместо ожидаемого 4,7 нФ. Перейдите на вкладку Component Tolerances: все будет показано точно.
Еще одно важное замечание: не забывайте устанавливать значение 20% для GBW во вкладке Component Tolerances. В противном случае вы не выведете конечные результаты.
Для завершения проекта можно оценить ряд дополнительных параметров фильтра, учитывающих выбранные номиналы элементов и тип ОУ.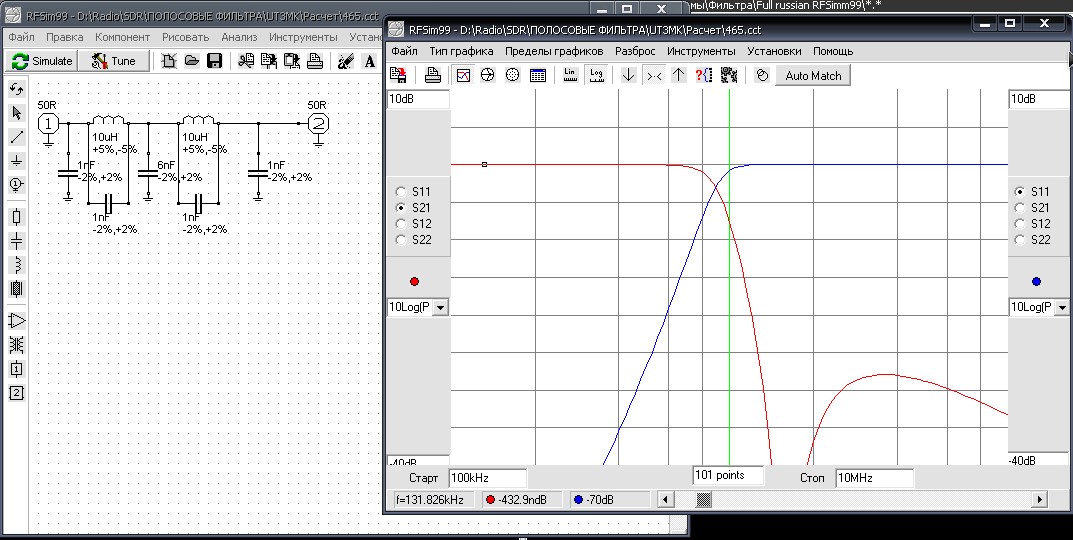 Через View предлагаются: спектральная мощность шумов Noise (но, к сожалению, без учета шумов 1/f ), потребляемая мощность Power (но без учета нагрузки, то есть это только то, что потребляют ИМС) и динамические характеристики Voltage range — максимально допустимый размах входного и выходного напряжения каждой секции фильтра.
Через View предлагаются: спектральная мощность шумов Noise (но, к сожалению, без учета шумов 1/f ), потребляемая мощность Power (но без учета нагрузки, то есть это только то, что потребляют ИМС) и динамические характеристики Voltage range — максимально допустимый размах входного и выходного напряжения каждой секции фильтра.
Завершение проекта находится во вкладке Final Results. После ее активации в открывшемся окне будет выведена полная схема фильтра с учетом даже блокировочных конденсаторов по цепям питания (рис. 10).
К недостаткам бета-версии программы можно отнести и то, что пока она не умеет группировать ОУ по корпусам ИМС. Так, на схеме, если ее развернуть прокруткой, и в присланной вам документации вы увидите свободные половинки ОУ AD822 (он сдвоенный). Тем не менее этот программный продукт даже в таком виде дает много того, чего нет в аналогичных продуктах других компаний.
Здесь на рис. 10 (через View) можно увидеть перечень элементов (Bill of Material) и, при необходимости, еще раз все характеристики фильтра.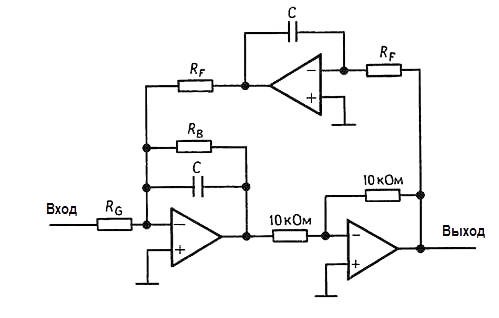
Если вы еще не прошли регистрацию в системе myAnalog, ваша работа на этом этапе будет закончена. Для продолжения — зарегистрируйтесь или активируйте вашу учетную запись. Тогда вы сможете сохранить проект в системе myAnalog (активировав Save to myAnalog), отправить результаты по почте (через Mail to Colleague), получить копию всей документации проекта, включая файлы для изготовления печатной платы как в варианте минимального занимаемого пространства, так и в варианте типовой отладочной платы. Если бы вы жили, например, в США, то могли бы заказать отладочную плату (через опцию заказа платы — Order Eval Board).
Вам на e-mail, который был указан при регистрации (но не сразу, придется подождать, и далеко не обещанные несколько минут), придет письмо с URL-ссылкой, по которой вы сможете загрузить файлы своего проекта. Перейдя по ссылке, вы загрузите полный комплект документации, включая таблицы и файлы CAD для изготовления печатной платы. Однако и здесь есть проблемы. Все таблицы, представленные в виде Excel-файлов, придут с расширением cvr. Низкими версиями Excel (например, Microsoft Office Excel 2003) они не форматируются и воспринимаются как текстовые файлы. Необходимо пользоваться последними версиями Excel или Openoffice (автор статьи этот путь не проверял). Если вы отправили результаты коллеге по почте, то он сможет увидеть их только после регистрации в системе myAnalog. Здесь есть еще одно неудобство. Если вы отправили проект себе на почтовый ящик, который не был зарегистрирован в системе myAnalog, вы не получите доступ к файлам. Придется перерегистрироваться с этого почтового ящика.
Низкими версиями Excel (например, Microsoft Office Excel 2003) они не форматируются и воспринимаются как текстовые файлы. Необходимо пользоваться последними версиями Excel или Openoffice (автор статьи этот путь не проверял). Если вы отправили результаты коллеге по почте, то он сможет увидеть их только после регистрации в системе myAnalog. Здесь есть еще одно неудобство. Если вы отправили проект себе на почтовый ящик, который не был зарегистрирован в системе myAnalog, вы не получите доступ к файлам. Придется перерегистрироваться с этого почтового ящика.
Несмотря на ограниченность бета-версии Analog Filter Wizard 2.0 и ряд выявленных автором при ее тестировании неудобств и погрешностей, этот программный продукт заслуживает внимания и, несомненно, будет развиваться в полноценный on-line калькулятор. Во всяком случае результаты расчетов совпали с результатами, полученными при моделировании на PSpice-симуляторе Multisim 12 и при практической проверке спроектированных фильтров.
Если у вас возникли трудности, то с любой вкладки можно отправить запрос через опцию Feedback.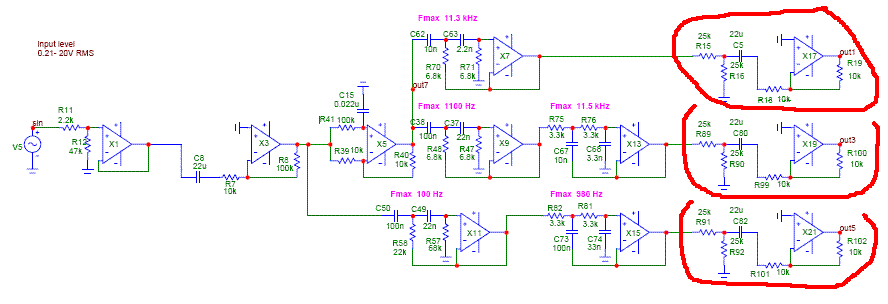 Она каждый раз высвечивается в нижнем правом углу вкладок. По опыту автора, компания Analog Devices всегда оперативно и грамотно оказывает полноценную помощь по всем вопросам, касающимся ее продуктов, но бесплатный (и даже платный) заказ образцов и отладочных плат, например, на Украину недоступен. Хотя в практике сотрудничества с Analog Devices образцы новых ИМС автору статьи были предоставлены. Тут, как говорится, просите — и дано вам будет. Учебный обзорный фильм по описанной программе подготовлен ее автором Меттом Даффом (Mett Daff), инженером по разработке прикладного программного обеспечения компании Analog Devices, и в настоящее время доступен в YouTube [3].
Она каждый раз высвечивается в нижнем правом углу вкладок. По опыту автора, компания Analog Devices всегда оперативно и грамотно оказывает полноценную помощь по всем вопросам, касающимся ее продуктов, но бесплатный (и даже платный) заказ образцов и отладочных плат, например, на Украину недоступен. Хотя в практике сотрудничества с Analog Devices образцы новых ИМС автору статьи были предоставлены. Тут, как говорится, просите — и дано вам будет. Учебный обзорный фильм по описанной программе подготовлен ее автором Меттом Даффом (Mett Daff), инженером по разработке прикладного программного обеспечения компании Analog Devices, и в настоящее время доступен в YouTube [3].
Примечание. Компания Analog Devices проводит корректировку и усовершенствование программы Analog Filter Wizard 2.0, так что некоторые моменты ко времени выхода статьи могут измениться.
Литература
- http://www.analog.com/Wizard/filter/filterUserEntry.asp
- http://www.analog.com/designtools/en/filterwizard/#/type
- http://www.
 youtube.com/watch?v=yCb3UvilJKU
youtube.com/watch?v=yCb3UvilJKU
Проектирование и расчёт полосного фильтра (стр. 1 из 2)
Проектирование и расчёт полосного фильтра
Реферат
Курсовая работа: 18с., 8 рис., 2 табл., 3 источника.
Объект исследования – активный полосовой фильтр на операционном усилителе.
Цель работы – расчёт и синтез схемы полосового фильтра на интегральном операционном усилителе, анализ амплитудно-частотной характеристики полученного устройства.
Метод исследования – формирование виртуальной модели фильтра, определение электрических параметров (по средствам ЭВМ).
Спроектирован фильтр на операционном усилителе с многопетлевой обратной связью. Устройство характеризуется следующими параметрами: частота среза
, полоса пропускания Δf=250 Гц, коэффициентом передачи в полосе пропускания
, наклон АЧХ 40(дБ/дек). Установлено, что выбранная схема фильтра является одной из наиболее дешёвых в реализации, при соблюдении предъявляемых к ней требований.
Ключевые слова:
ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ, ПОЛОСОВОЙ ФИЛЬТР, АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА, ЧАСТОТА СРЕЗА, ПОЛОСА ПРОПУСКАНИЯ, ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ.
Содержание
Введение
1 Анализ технического задания
2 Синтез схемы и расчет элементов фильтра
3 Расчет АЧХ фильтра на ЭВМ
4 Подбор элементов для схемы
Выводы
Список использованных источников
Введение
Цепи фильтрации сигналов – важная и неотъемлемая часть многих систем связи и электрических контрольно-измерительных устройств. Они служат для формирования частотных каналов в системах коммутации, разделения и преобразования электрических сигналов.
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определённых частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие частоты), полосно-пропускающие фильтры (которые пропускают полосу частот и задерживают те частоты, которые расположены выше или ниже этой полосы) и полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают те частоты, которые расположены выше или ниже этой полосы).
На практике невозможно реализовать идеальную амплитудно-частотную характеристику фильтра, поскольку требуется сформировать очень узкую переходную область. Следовательно, основная проблема при конструировании фильтра заключается в приближении реализованной реальной характеристики с заданной степенью точности к идеальной.
1. Анализ технического задания
Фильтры — это частотно-избирательные устройства, которые пропускают или задерживают сигналы, лежащие в определенных полосах частот. До 60-х годов для реализации фильтров применялись, в основном, пассивные элементы, т.е. индуктивности, конденсаторы и резисторы. Основной проблемой при реализации таких фильтров оказывается размер катушек индуктивности (на низких частотах они становятся слишком громоздкими). С разработкой в 60-х годах интегральных операционных усилителей появилось новое направление проектирования активных фильтров на базе ОУ. В активных фильтрах применяются резисторы, конденсаторы и усилители (активные компоненты), но в них нет катушек индуктивности.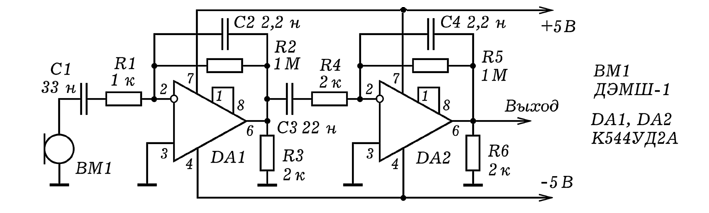 В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приемниках, традиционные пассивные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.
В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приемниках, традиционные пассивные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.
Сейчас во многих случаях аналоговые фильтры заменяются цифровыми. Работа цифровых фильтров обеспечивается, в основном, программными средствами, поэтому они оказываются значительно более гибкими в применении по сравнению с аналоговыми. С помощью цифровых фильтров можно реализовать такие передаточные функции, которые очень трудно получить обычными методами. Тем не менее, цифровые фильтры пока не могут заменить аналоговые во всех ситуациях, поэтому сохраняется потребность в наиболее популярных аналоговых фильтрах — активных RС-фильтрах.
Фильтры можно классифицировать по их частотным характеристикам, что в условном виде показано на рис. 1.1. На этом рисунке изображены характеристики фильтра нижних частот (ФНЧ), фильтра верхних частот (ФВЧ), полосового фильтра (ПФ), полосно-подавляющего фильтра (ППФ) и фильтра — «пробки» (режекторного фильтра — РФ). Характеристика фазового фильтра (ФФ) на рисунке не показана, т.к. его коэффициент передачи не изменяется с частотой. Основная функция любого фильтра заключается в том, чтобы ослабить сигналы, лежащие в определенных полосах частот, внести в них различные фазовые сдвиги или ввести временную задержку между входным и выходным сигналами.
1.1. На этом рисунке изображены характеристики фильтра нижних частот (ФНЧ), фильтра верхних частот (ФВЧ), полосового фильтра (ПФ), полосно-подавляющего фильтра (ППФ) и фильтра — «пробки» (режекторного фильтра — РФ). Характеристика фазового фильтра (ФФ) на рисунке не показана, т.к. его коэффициент передачи не изменяется с частотой. Основная функция любого фильтра заключается в том, чтобы ослабить сигналы, лежащие в определенных полосах частот, внести в них различные фазовые сдвиги или ввести временную задержку между входным и выходным сигналами.
С помощью активных RС-фильтров нельзя получить идеальные формы частотных характеристик в виде показанных на рис. 1.1 прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью ее реализации.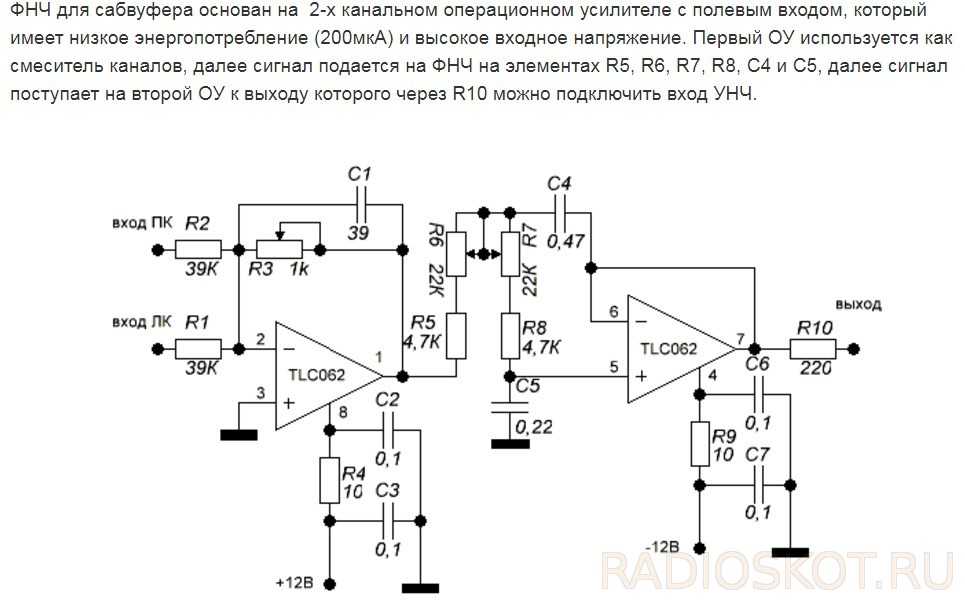 Это называется «проблемой аппроксимации». Во многих случаях требования к качеству фильтрации позволяют обойтись простейшимифильтрами первого или второго порядков. Проектирование фильтра в этом случае сводится к выбору схемы с наиболее подходящей конфигурацией и последующему расчету значений номиналов элементов для конкретных частот.
Это называется «проблемой аппроксимации». Во многих случаях требования к качеству фильтрации позволяют обойтись простейшимифильтрами первого или второго порядков. Проектирование фильтра в этом случае сводится к выбору схемы с наиболее подходящей конфигурацией и последующему расчету значений номиналов элементов для конкретных частот.
Однако бывают ситуации, когда требования к фильтрации сигнала могут оказаться гораздо более жесткими, и могут потребоваться схемы фильтров с характеристиками более высоких порядков, чем первый или второй.
Рисунок 1.1- Основные типы фильтров.
Реальные характеристики фильтров, а именно нижних частот, верхних частот и полосового фильтра, — показаны на рисунке 1.2.
Рисунок 1.2 – АЧХ фильтров.
На этих рисунках сплошными линиями изображены идеальные характеристики фильтров. Пунктирные линии показывают отклонение реальных характеристик от идеальных.Основными параметрами фильтров нижних и верхних частот являются частота среза f0, коэффициент передачи в полосе пропускания Ко, наклон АЧХ в полосе ограничения п и неравномерность АЧХ в полосе пропускания. Дляполосовых фильтров по аналогии с избирательными усилителями вводят понятие добротности Q и усиления Ко на частоте f0.
Дляполосовых фильтров по аналогии с избирательными усилителями вводят понятие добротности Q и усиления Ко на частоте f0.
2. Синтез схемы и расчет элементов фильтра
2.1 Исходные данные и требования для проектирования фильтра
| Типфильтра – ПФ | ||
| Частота среза, f0 | 5000 | Гц |
| Коэффициент передачи в полосе пропускания, К0 | 6 | |
| Наклон АЧХ в полосе ограничения, n | 40 | дБ/дек |
| Неравномерность АЧХ в полосе пропускания, ΔК | 20 | дБ |
| Полоса пропускания, Δf | 250 | Гц |
2.2 Разработка функциональной схемы
На рис. 2.1 приведена структурная схема фильтра с многопетлевой обратной связью. Каждый пассивный двухполюсный элемент в этой схеме может быть либо резистором, либо конденсатором.
Рисунок 2.1 – структурная схема фильтра
Передаточная функция для данной схемы имеет вид
(2.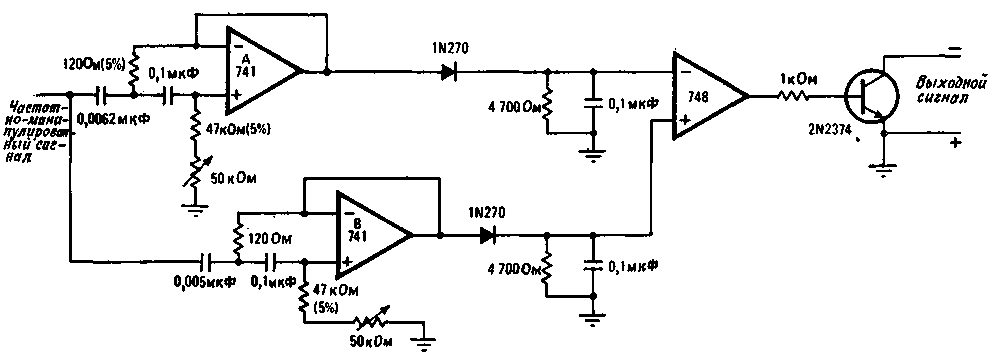 1)
1)
Для того чтобы схема на рис. 2.1 выделяла полосу частот, передаточную функцию (2.1) необходимо привести к передаточной функции, соответствующей полосовому звену второго порядка:
(2.2)
где ωо = 2лf0, H =α·К0.
Сравнивая выражения (2.1) и (2.2), нетрудно заметить, что, для того чтобы числитель не был функцией р, в качестве У1 и У4 должны использоваться резистивные проводимости; для того чтобы получить член с р2 в знаменателе, в качестве У3 и У5 должны использоваться емкостные проводимости; для того чтобы получить в знаменателе член, независимый от р, в качестве У2 должна использоваться резистивная проводимость.
Итак, однозначно определяются пассивные элементы схемы на рис. 2.1:
Y1=1/R1, Y2= pC1, Y3=1/R2, Y4= pC2, Y5=1/R3.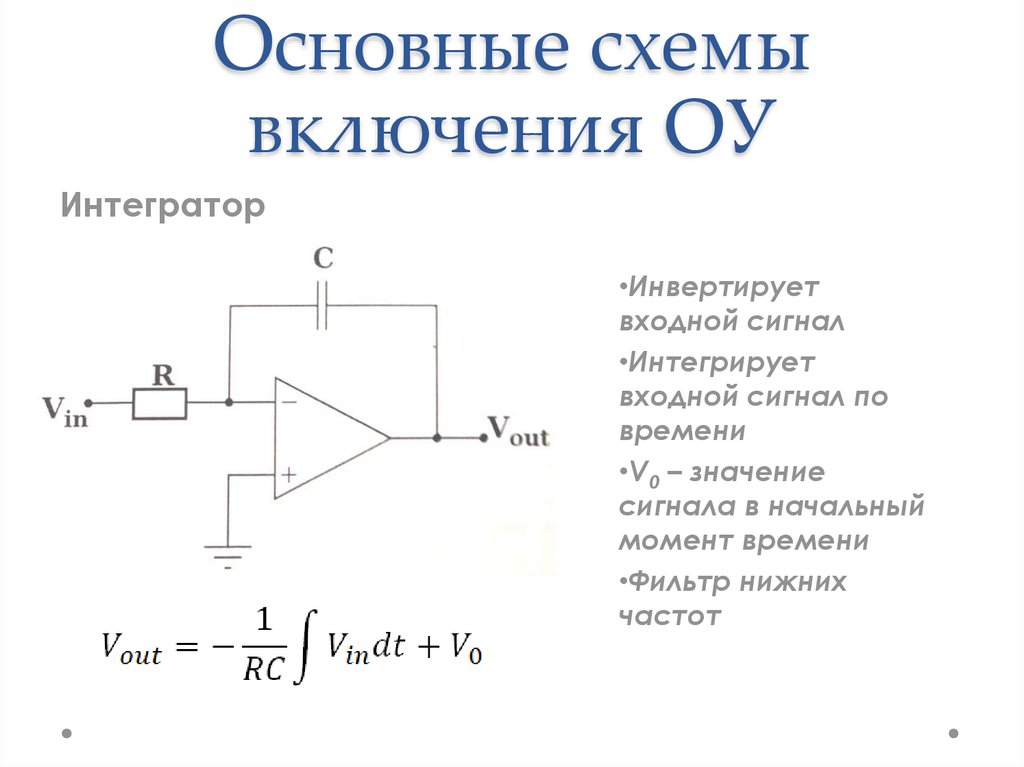
Схема полученного полосового фильтра приведена на рис. 2.2.
Рисунок 2.2 – Схема полосового фильтра
Передаточная функция имеет вид
(2.3)
Сравнивая последнее выражение с (2.2), получаем соотношения, необходимые для расчета фильтра:
(2.4)
В том случае, если
и
, имеем:
Глава 15, Схемы активных фильтров Решения для видео, электрические схемы
Вопросы по главе
Проблема 1
Найдите передаточную функцию $V_{o} / V_{i}$ для схемы, показанной на рис. P15.1, если $Z_{f}$ — эквивалентное сопротивление цепи обратной связи, $Z_{i}$ — эквивалентное сопротивление входной цепи, а операционный усилитель идеален.
Заходите скорее!
Проблема 2
а) Используя результаты задачи 15.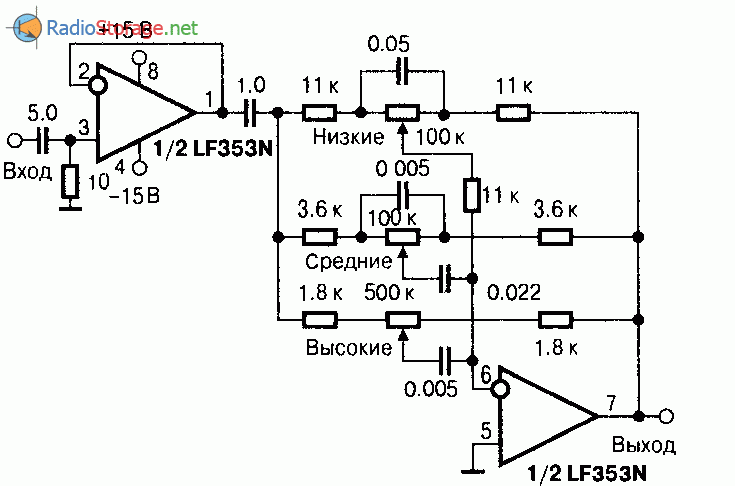 1, найдите передаточную функцию схемы, показанной на рис. P15.2.
1, найдите передаточную функцию схемы, показанной на рис. P15.2.
b) Каков коэффициент усиления схемы при $\omega \rightarrow 0 ?$
c) Каков коэффициент усиления схемы при $\omega \rightarrow \infty ?$
d) Ответьте на вопросы (b) и
(c) имеет смысл с точки зрения известного поведения схемы?
Заходите скорее!
Проблема 3
Повторите задачу $15.2,$, используя схему, показанную на рис. PIS.3.
Заходите скорее!
Проблема 4
а) Используя схему, показанную на рис. 15.1, спроектируйте фильтр нижних частот с коэффициентом усиления в полосе пропускания $15 \mathrm{дБ}$ и частотой среза $10 \mathrm{кГц}$. Предположим, имеется конденсатор $5 \mathrm{nF}$.
b) Начертите принципиальную схему и обозначьте все компоненты.
Заходите скорее!
Проблема 5
Разработайте фильтр нижних частот на основе операционного усилителя с частотой среза $500 \mathrm{Hz}$ и коэффициентом усиления в полосе пропускания, равным 1, с использованием конденсатора $50 \mathrm{nF}$.
а) Нарисуйте схему, обозначив номиналы компонентов и выходное напряжение.
б) Если номинал резистора обратной связи в заполнителе изменился, а номинал резистора в прямом тракте не изменился, то какая характеристика фильтра изменится?
Заходите скорее!
Проблема 6
Входной сигнал фильтра нижних частот, разработанного в задаче 15.5, равен 200 cos$w$ $t$ m $V$
а) Предположим, что источники питания равны $\pm V_{c c}$. При каком наименьшем значении $V_{\mathrm{cc}}$ операционный усилитель все еще будет работать в своей линейной области?
б) Найти выходное напряжение при $\omega=\omega_{c}$
в) Найти выходное напряжение при $\omega=0.100$
г) Найти выходное напряжение при $\omega=1000$
Заходите скорее!
Задача 7
а) Используйте схему из $\mathrm{Fig}$. 15.4 разработать фильтр верхних частот с частотой среза $40 \mathrm{кГц}$ и коэффициентом усиления в полосе пропускания 12 дБ. Используйте конденсатор емкостью 680 пФ в конструкции
Используйте конденсатор емкостью 680 пФ в конструкции
. б) Начертите принципиальную схему фильтра и обозначьте все компоненты.
Заходите скорее!
Задача 8
Разработайте фильтр верхних частот на основе операционного усилителя с отсечкой. частота отключения $300 \mathrm{Гц}$ и коэффициент усиления полосы пропускания 5 с использованием конденсатора 100 нФ.
а) Нарисуйте схему, обозначив номиналы компонентов и выходное напряжение.
б) Если номинал резистора обратной связи в фильтре изменился, а номинал резистора в прямом тракте не изменился, какая характеристика фильтра изменилась?
Заходите скорее!
Задача 9
Входной сигнал фильтра верхних частот, разработанного в задаче 15.8, составляет $150 \cos \omega t \mathrm{m} \mathrm{V}$
a) Предположим, что источники питания $\pm V_{c c}$. При каком наименьшем значении $V_{c c}$ операционный усилитель все еще будет работать в своей линейной области?
б) Найти выходное напряжение при $\omega=\omega_{c}$
в) Найти выходное напряжение при $\omega=0,1 \omega_{0}$
г) Найти выходное напряжение при $\omega =10 \omega_{0}$
Заходите скорее! 9{2}+\left(\frac{1}{Q}\right)\left(\frac{s}{k_{f}}\right)+1}$$
Вернитесь позже!
Задача 13
a) Укажите значения компонентов для прототипа пассивного полосового фильтра, описанного в задаче 15.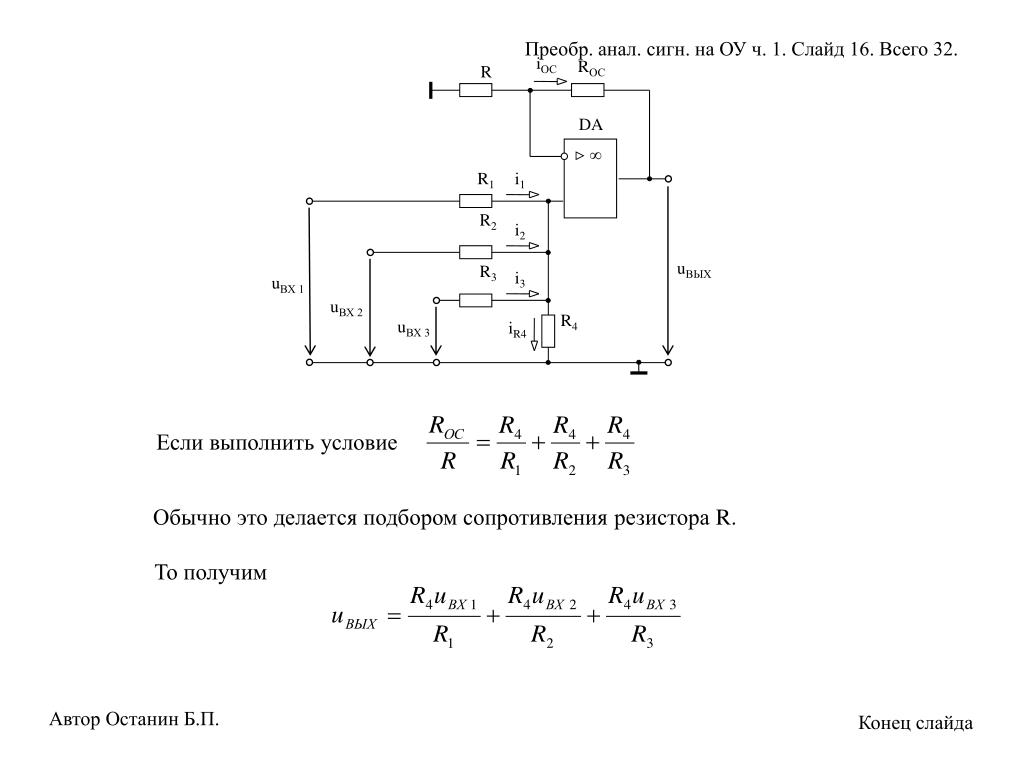 12, если добротность фильтра равна 25
12, если добротность фильтра равна 25
b) Укажите значения компонентов для полосового фильтра, описанного в задаче 15.12, если добротность равна $25 ;$ центральная, или резонансная, частота составляет $100 \mathrm{krad} / \mathrm{s} ;$, а импеданс в резонансе $3,6 \mathrm{k} \Omega$
c) Нарисуйте принципиальную схему масштабированного фильтра и обозначьте все компоненты.
Заходите скорее!
Задача 14
Альтернативой прототипу полосового фильтра, показанному на рис. $\mathrm{P} 15.12$, является создание $\omega_{o}=1 \mathrm{rad} / \mathrm{s}$ $R=1 \Omega, $ и $L=Q$ Генри.
а) Каково значение $C$ в схеме фильтра-прототипа?
b) Какова передаточная функция фильтра-прототипа?
c) Используйте только что описанную альтернативную схему прототипа для разработки пассивного полосового фильтра с добротностью $20$, центральной частотой $50 \mathrm{krad} / \mathrm{s}$ и импедансом $5 \mathrm{ k} \Omega$ в резонансе.
d) Нарисуйте схему масштабированного фильтра и обозначьте все компоненты.
д) Используя результаты, полученные в задаче 15.12, напишите передаточную функцию масштабированной схемы.
Заходите скорее!
Задача 15
Пассивный полосовой фильтр, показанный на рис. 14.22, имеет две прототипные схемы. В первом прототипе схемы $\omega_{o}=1 \mathrm{rad} / \mathrm{s}, \quad C=1 \mathrm{F}, \quad L=1 \mathrm{H}, \quad $ и
$R=Q$ Ом. Схема второго прототипа. $\omega_{o}=1 \mathrm{rad} / \mathrm{s}, \quad R=1 \Omega, \quad C=Q \quad$ фарад и $L=(1 / Q)$ генри.
a) Используйте один из этих прототипов схем (на ваш выбор) для разработки пассивного полосового фильтра с добротностью 16 и центральной частотой $80 \mathrm{krad} / \mathrm{s}$. Резистор $R$ равен $80 \mathrm{k} \Omega$ 9{2}+\left(\frac{R}{L}\right) s+\left(\frac{1}{L C}\right)}$$
Покажите, что если схема масштабируется как по величине, так и по частоте, передаточная функция масштабированной схемы равна передаточной функции немасштабированной схемы с заменой s на $\left(s / k_{f}\right),$, где $k_{f}$ — масштабный коэффициент частоты.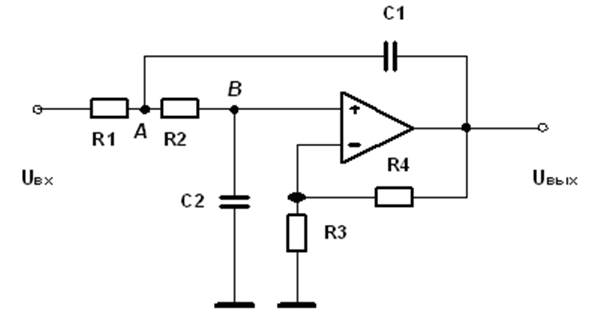
Заходите скорее!
Задача 17
Покажите, что наблюдение, сделанное в задаче 16 в отношении передаточной функции для схемы на рис. $14.28(\mathrm{a})$, также применимо к схеме режекторного фильтра (нижняя) на рис. 14.31 9{2}+\left(\frac{1}{Q}\right) s+1}$$
b) Напишите передаточную функцию для полосового фильтра. ter с центральной частотой $50 \mathrm{krad} / \mathrm{s}$ и добротностью 5
Вернитесь позже!
Задача 19
Два прототипа пассивной ленты. режекторный фильтр, показанный на рис. 14.31 (нижняя схема), показан на рис. P15.19(a) и (b).
Покажите, что передаточная функция для любой версии равна 9{\prime}$ значения резистора, катушки индуктивности и двух частых частот масштабированного фильтра.
Заходите скорее!
Задача 21
Масштабируйте режекторный фильтр в задаче 14,33, чтобы получить центральную частоту $500 \mathrm{krad} / \mathrm{s},$, используя катушку индуктивности $50 \mu \mathrm{H}$. Определите значения резистора, конденсатор и полоса пропускания масштабированного фильтра.
Определите значения резистора, конденсатор и полоса пропускания масштабированного фильтра.
Заходите скорее!
Задача 22
Схема на рис. $P 13.26$ масштабирована таким образом, что резистор $4 \mathrm{k} \Omega$ заменен резистором $20 \mathrm{k} \Omega$, а конденсатор $5 \mathrm{nF}$ заменен конденсатором $100 \mathrm{pF}$.
a) Каково масштабированное значение $L ?$
b) Каково выражение для $i_{o}$ в масштабированной схеме?
Заходите скорее!
Задача 23
Масштабируйте схему в задаче 13.29 так, чтобы резистор $10 \Omega$ увеличился до $1 \mathrm{k} \Omega$, а частота отклика по напряжению увеличилась в $1000 раз .$ Найти $v_{o}( t)$
Заходите скорее!
Задача 24
а) Покажите, что если схема фильтра нижних частот, показанная на рис. 15.1, масштабируется как по величине, так и по частоте, передаточная функция масштабированной схемы будет такой же, как в уравнении. 15.1 с заменой $s$ на $s/k_{f}$, где $k_{f}$ — масштабный коэффициент частоты.
15.1, масштабируется как по величине, так и по частоте, передаточная функция масштабированной схемы будет такой же, как в уравнении. 15.1 с заменой $s$ на $s/k_{f}$, где $k_{f}$ — масштабный коэффициент частоты.
б) В прототипе схемы ФНЧ на рис. $15.1, \omega_{c}=1 \mathrm{rad} / \mathrm{s}, C=1 \mathrm{F}$ $R_{ 2}=1 \Omega,$ и $R_{1}=1 / K$ Ом. Какова передаточная функция схемы-прототипа?
c) Используя результат, полученный в (а), выведите передаточную функцию масштабированного фильтра.
Заходите скорее!
Задача 25
а) Покажите, что если фильтр верхних частот, показанный на рис. 15.4, масштабирован как по величине, так и по частоте, передаточная функция будет такой же, как в уравнении. 15.4 с заменой $s$ на $s/k_{f},$, где $k_{f}$ — масштабный коэффициент частоты.
б) В прототипе схемы ФВЧ на рис. =1 \mathrm{F},$ и $R_{2}=K$ Ом. Какова передаточная функция схемы-прототипа?
c) Используя результат (а), выведите передаточную функцию масштабированного фильтра.
Заходите скорее!
Задача 26
a) Используя конденсаторы емкостью 20 нФ, спроектируйте активный широкополосный полосовой фильтр первого порядка с нижней частотой среза $2000 \mathrm{Гц}$, верхней частотой среза $8000 \mathrm{Гц}$ и коэффициентом усиления в полосе пропускания 10 дБ. Используйте прототипы фильтров нижних и верхних частот в процессе проектирования (см. задачи 15.24 и 15.25).
b) Напишите передаточную функцию для масштабированного фильтра.
c) Используйте передаточную функцию, полученную в части (b), чтобы найти $H\left(j \omega_{o}\right),$, где $\omega_{\theta}$ — центральная частота фильтра.
d) Каково усиление в полосе пропускания (в децибелах) фильтра при $\omega_{o} ?$
e) Используя компьютерную программу по вашему выбору, постройте график величины Боде для фильтра.
Заходите скорее!
Задача 27
а) Используя конденсаторы $5 \mathrm{нФ}$, спроектируйте активный широкополосный режекторный фильтр первого порядка с нижней частотой среза $1000 \mathrm{Гц}$, верхней частотой среза $5000 \mathrm{Гц}$ и усиление в полосе пропускания $10 \mathrm{dB}$.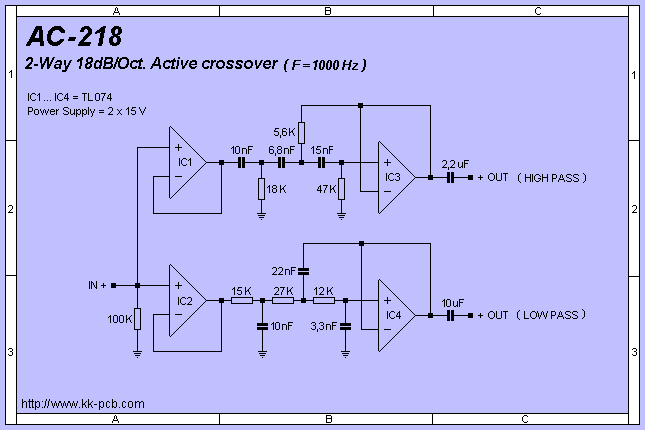 Используйте прототипы схем фильтров, представленные в задачах 15.24 и 15.25, в процессе проектирования.
Используйте прототипы схем фильтров, представленные в задачах 15.24 и 15.25, в процессе проектирования.
б) Начертите принципиальную схему фильтра и обозначьте все компоненты.
c) Какова передаточная функция масштабированного фильтра?
d) Оцените передаточную функцию, полученную в (c), на центральной частоте фильтра.
e) Каково усиление (в децибелах) на центральной частоте?
f) Используя компьютерную программу по вашему выбору, постройте график величины Боде для передаточной функции фильтра.
Заходите скорее!
Задача 28
Покажите, что схема на рис. $P 15.28$ ведет себя как полосовой фильтр. (Подсказка: найдите передаточную функцию для этой схемы и покажите, что она имеет тот же вид, что и передаточная функция для полосового фильтра. Используйте результат задачи $15.1.$ 9{2}$ для трех цепей на рис., P15.29, когда
$$H(s)=\frac{V_{0}}{V_{i}}$$
Вернитесь позже!
Задача 30
Разработайте полосовой фильтр с единичным усилением, используя каскадное соединение, чтобы получить центральную частоту $50 \mathrm{krad} / \mathrm{s}$ и полосу пропускания $300 \mathrm{krad} / \mathrm{s}$ .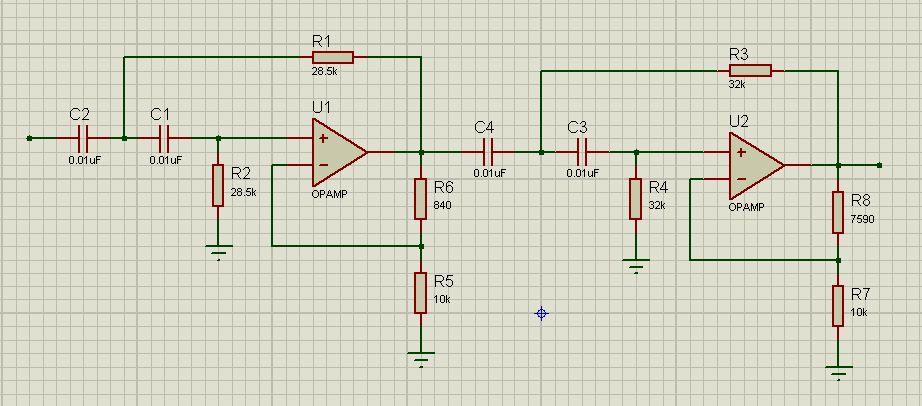 Используйте конденсаторы $150 \mathrm{nF}$. Укажите $f_{d} \cdot f_{c}, R_{L}$ и $R_{H}$
Используйте конденсаторы $150 \mathrm{nF}$. Укажите $f_{d} \cdot f_{c}, R_{L}$ и $R_{H}$
Повторите попытку позже!
Задача 31
Разработайте параллельный режекторный фильтр с центральной частотой. частота $\$ \mathrm{kHz}$, полоса пропускания $30 \mathrm{kHz}$ и пропуск. полосовое усиление $4 .$ Используйте конденсаторы 250 af и укажите все номиналы резисторов.
Заходите скорее!
Задача 32
Цель этой задачи состоит в том, чтобы проиллюстрировать преимущество низкочастотного фильтра Баттерворта $n$-го порядка над каскадом из $n$ идентичных низкочастотных участков, облегчающих вычисления, пусть $y$ представляет магнит. значение графика (в децибелах), и пусть $x=\log _{11}$ Затем вычислите $d y / d x$ в $\omega_{c}$ для каждого графика. 9{1 / n}} \mathrm{dB} / \mathrm{dec}$$
c) Вычислить $d y / d x$ для каждого типа фильтра при $n=1,2,3,4,$ и $\infty $
d) Обсудить значимость результатов, полученных в части (c)
Загляните позже!
Задача 33
a) Определить порядок фильтра нижних частот Butterwort с частотой среза $1000 \mathrm{Hz}$ и коэффициентом усиления не менее $-40 \mathrm{dB}$ при $4000 \mathrm{Hz}$
b) Каково фактическое усиление в децибелах при частоте $4000 \mathrm{Hz}$ ? 9{2} C_{1} C_{2}}}$$
Заходите позже!
Задача 35
a) Напишите передаточную функцию для полученного прототипа низкочастотного фильтра Баттерворта.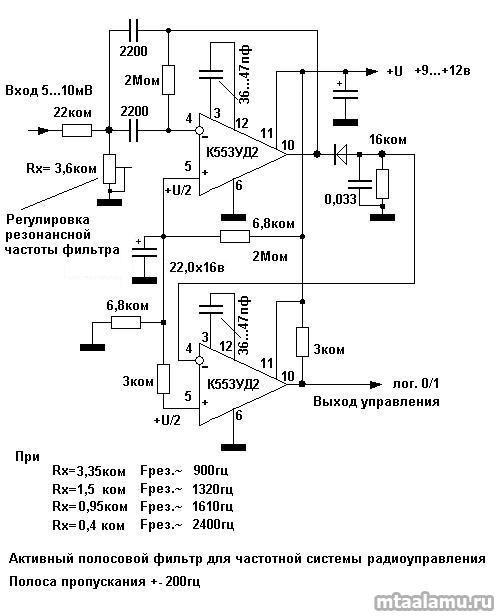 Задача $15.33(\mathrm{a})$
Задача $15.33(\mathrm{a})$
b) Запишите передаточную функцию для масштабированного наполнителя в (a) (см. задачу 15.34).
c) Проверьте выражение, полученное в части (b), используя его для расчета усиления (в децибелах) $4000 \mathrm{Hz}$. Сравните свой результат с найденным Задача $15.33(\mathrm{b})$
Заходите скорее!
Задача 36
а) Используя резисторы $2 \mathrm{kS}$ и идеальные операционные усилители, спроектируйте схему, реализующую фильтр нижних частот Баттерворта, указанный в задаче 15.33. Коэффициент усиления в полосе пропускания равен единице.
b) Постройте принципиальную схему и обозначьте номиналы всех компонентов.
Заходите скорее!
Задача 37
а) Используя конденсаторы емкостью 25 нФ и идеальные операционные усилители, спроектируйте высокочастотный фильтр Баттерворта с единичным коэффициентом усиления с частотой среза $5 \mathrm{кГц}$ и коэффициентом усиления не менее $-25 \mathrm{дБ}$ на $1 \mathrm{kHz}$
b) Начертите принципиальную схему фильтра и обозначьте номиналы всех компонентов.
Заходите скорее!
Задача 38
Проверьте записи в таблице 15.1 для $n=5$ и $n=6$.
Заходите скорее!
9{2}}}$$Таким образом, передаточная функция масштабированной схемы получается из передаточной функции немасштабированной схемы простой заменой $s$ в немасштабированной передаточной функции на $s / k_{f},$, где $k_ {f}$ — коэффициент масштабирования частоты.
Заходите скорее!
Задача 40
а) Используя резисторы $3 \mathrm{k} \Omega$ и идеальные операционные усилители, спроектируйте низкочастотный фильтр Баттерворта с единичным коэффициентом усиления, который имеет частоту среза $20 \mathrm{кГц}$ и понижение не менее $25 \mathrm {дБ}$ при 100$ \mathrm{кГц}$
б) Нарисуйте принципиальную схему фильтра и обозначьте все компоненты.
Заходите скорее!
Задача 41
Фильтр верхних частот, разработанный в задаче 15.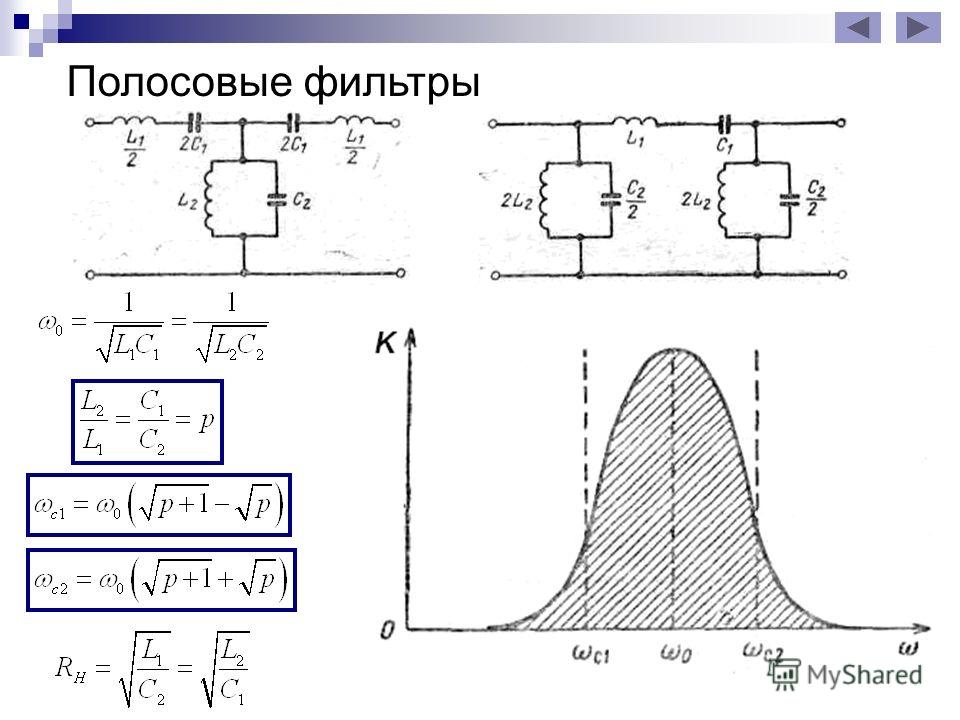 37, каскадируется с фильтром нижних частот, разработанным в задаче 15.40
37, каскадируется с фильтром нижних частот, разработанным в задаче 15.40
а) Опишите тип фильтра, образованного этой взаимосвязью.
b) Укажите частоты среза, среднюю частоту и добротность фильтра.
c) Используйте результаты задач 15.33 и 15.38, чтобы получить масштабированную передаточную функцию фильтра.
d) Проверьте вывод (c), используя его для вычисления $H\left(j \omega_{n}\right),$, где $\omega_{0}$ — средняя частота фильтра.
Заходите скорее!
Задача 42
а) Используйте конденсаторы емкостью 300 пФ в схеме на рис. 15.26, чтобы спроектировать полосовой фильтр с добротностью $20$, центральной частотой $8\mathrm{кГц}$ и коэффициентом усиления полосы пропускания $40\mathrm{дБ} $
б) Начертите принципиальную схему фильтра и обозначьте все компоненты. 9{2}-K} \\
R_{3}=2 Q
\end{array}
\end{aligned}$$
Заходите скорее!
Задача 44
а) Разработайте широкополосный полосовой фильтр Баттерворта с нижней частотой среза $1000 \mathrm{Гц}$ и верхней частотой среза $8000 \mathrm{Гц}$. Коэффициент усиления в полосе пропускания фильтра составляет $10 \mathrm{dB}$. Усиление должно снизиться как минимум на $20 \mathrm{dB}$ при $400 \mathrm{Hz}$ и $20 \mathrm{kHz}$. Используйте конденсаторы 50 нФ в цепи верхних частот и резисторы $5 \mathrm{k} \Omega$ в цепи нижних частот.
Коэффициент усиления в полосе пропускания фильтра составляет $10 \mathrm{dB}$. Усиление должно снизиться как минимум на $20 \mathrm{dB}$ при $400 \mathrm{Hz}$ и $20 \mathrm{kHz}$. Используйте конденсаторы 50 нФ в цепи верхних частот и резисторы $5 \mathrm{k} \Omega$ в цепи нижних частот.
б) Нарисуйте принципиальную схему фильтра и обозначьте все компоненты.
Заходите скорее!
Задача 45
a) Получите выражение для масштабированной передаточной функции для фильтра, разработанного в задаче 15.44
b) Используя выражение, полученное в (a), найдите коэффициент усиления (в децибелах) при $500 \mathrm{Hz}$ и $5000 \mathrm{ Гц}$
c) Удовлетворяют ли значения, полученные в части (b), требованиям фильтрации, указанным в задаче $15.44 ?$
Заходите скорее!
Задача 46
Получите передаточную функцию прототипа фильтра верхних частот Баттерворта соответствующего порядка, сначала написав передаточную функцию для прототипа фильтра нижних частот Баттерворта пятого порядка, а затем заменив $s$ на $1/s$ в выражении нижних частот.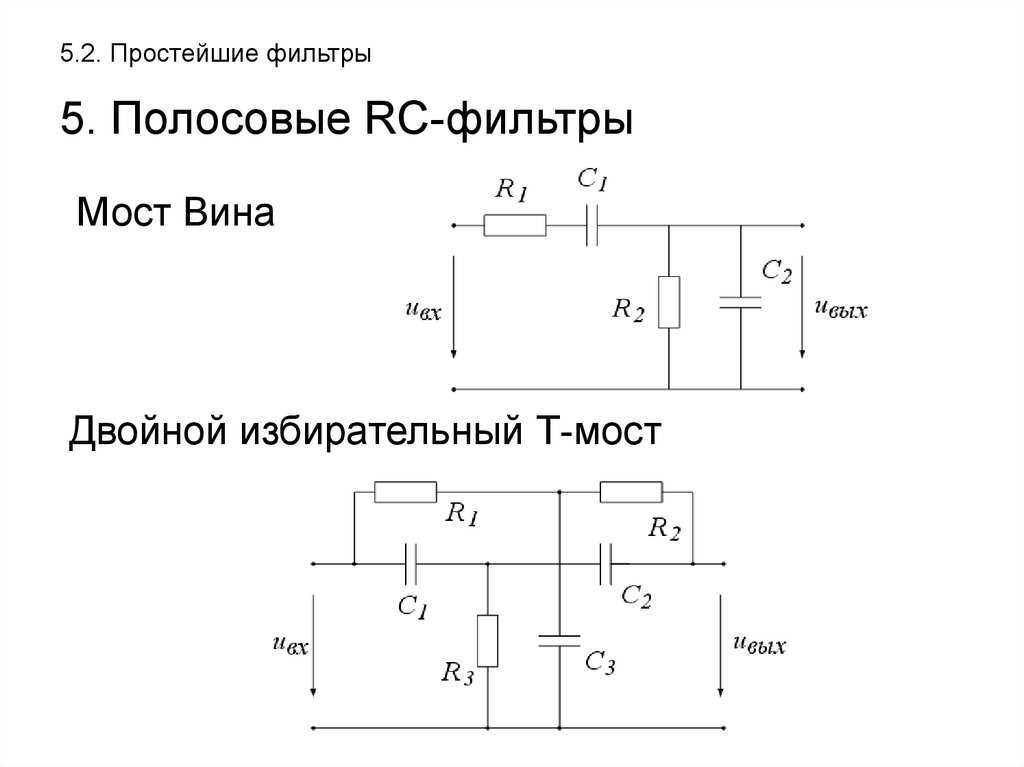
Заходите скорее!
Задача 47
Фильтр Баттерворта пятого порядка в задаче 15.46 используется в системе, где частота среза равна
$10 \mathrm{krad} / \mathrm{s}$
а) Какова масштабированная передаточная функция фильтра?
b) Проверьте свое выражение, найдя усиление (в децибелах) на частоте среза.
Заходите скорее!
Задача 48
Цель этой задачи — провести вас через анализ, необходимый для создания процедуры проектирования для определения компонентов схемы в схеме фильтра. Анализируемая схема показана на рис. $P 15.48$
a) Качественно проанализируйте схему и убедитесь, что схема представляет собой фильтр нижних частот с коэффициентом усиления в полосе пропускания $R_{2} / R_{1}$
b) Подкрепите свой качественный анализ выводом передаточной функции $V_{ о} / V_{i}$. (Подсказка: при выводе передаточной функции представьте резисторы с их эквивалентными проводимостями, то есть $G_{1}=1 / R_{1}$ и т. {2}+b_{1} s+b_{o}}$$ 9{*}}$ На первый взгляд кажется, что у нас есть два бесплатных варианта из пяти компонентов. Однако, когда мы исследуем отношения между компонентами схемы и ограничениями передаточной функции, мы видим, что при выборе $C_{2}$ существует верхний предел для $C_{1}$, чтобы $R_{2} \left(G_{2}\right)$ реализуемо. Имея это в виду, покажите, что если $C_{2}=1 \mathrm{F}$, три проводимости задаются выражениями
{2}+b_{1} s+b_{o}}$$ 9{*}}$ На первый взгляд кажется, что у нас есть два бесплатных варианта из пяти компонентов. Однако, когда мы исследуем отношения между компонентами схемы и ограничениями передаточной функции, мы видим, что при выборе $C_{2}$ существует верхний предел для $C_{1}$, чтобы $R_{2} \left(G_{2}\right)$ реализуемо. Имея это в виду, покажите, что если $C_{2}=1 \mathrm{F}$, три проводимости задаются выражениями
$$\begin{aligned}
&G_{1}=K G_{2}\ \
&G_{3}=\left(\frac{b_{o}}{G_{2}}\right) C_{1}\\ 9{2}}{4 b_{0}(1+K)}$$
d) На основе результатов, полученных в (c), наметьте процедуру проектирования для выбора компонентов схемы один раз $K, b_{0},$ и $b,$ известны.
Заходите скорее!
Задача 49
Предположим, что схема, анализируемая в задаче 15.48, является частью фильтра Баттерворта нижних частот третьего порядка с коэффициентом усиления в полосе пропускания, равным 8
а) Если $C_{2}=1 \mathrm{F}$ в секции второго порядка прототипа , каков верхний предел для $C_{1}$ ?
b) Если выбрано предельное значение $C_{1}$, каковы прототипные значения $R_{1}, R_{2},$ и $R_{3}?$
c) Если угловая частота фильтра 50 кГц и $C_{2}$ выбрано равным 250 пФ, рассчитайте масштабированные значения $C_{1}, R_{1}, R_{2},$ и $R_{3}$
d) Укажите масштабированные значения резисторов и конденсатора в секции первого порядка фильтра
. e) Постройте принципиальную схему фильтра и обозначьте номиналы всех компонентов на диаграмме.
e) Постройте принципиальную схему фильтра и обозначьте номиналы всех компонентов на диаграмме.
Заходите скорее!
Задача 50
Поменять местами $R \mathrm{s}$ и $C \mathrm{s}$ в схеме на рис. $P 15.48 ;$, то есть заменить $R_{1}$ на $C_{1}, R_{ 2}$ с $C_{3}$ $R_{3}$ с $C_{3}, C_{1}$ с $R_{1},$ и $C_{2}$ с $R_{2}$
а) Опишите тип фильтра, реализованного в результате обмена.
б) Подтвердите тип фильтра, описанный в (а), определив передаточную функцию $V_{o} / V_{i}$. Запишите передаточную функцию в форме, которая делает ее совместимой с таблицей 15.1.9.0014 c) Положим $C_{2}=C_{3}=1 \mathrm{F}$ и получим выражения для $C_{1}, R_{1},$ и $R_{2}$ через $ K, b_{1},$ и $b_{r}, 1,5 c$ Задача 15.48 для определения $b_{1}$ и $b_{n}$ )
d) Предположим, что фильтр, описанный в (a ) используется в том же типе фильтра Баттерворта третьего порядка, имеет усиление в полосе пропускания 8 . С $C_{2}=C_{3}$ вычислите прототипные значения $C_{1}, R_{1}$ в секции второго порядка фильтра.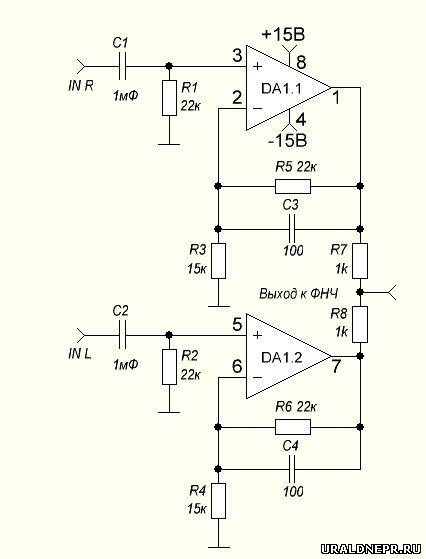
Заходите скорее!
Задача 51
a) Используйте схемы, проанализированные в задачах 15.48 и 15.50, для реализации широкополосного режекторного фильтра с коэффициентом усиления в полосе пропускания $20 \mathrm{dB}$, нижней угловой частотой $800 \mathrm{Гц}$, верхней угловой частотой $7200. \mathrm{Гц}$, и затухание не менее $20 \mathrm{дБ}$ как при $1500 \mathrm{Гц}$, так и при $13,5 \mathrm{кГц}$. По возможности используйте конденсаторы $50 \mathrm{nF}$
b) Начертите принципиальную схему фильтра и обозначьте все компоненты.
Заходите скорее!
Задача 52
a) Получите передаточную функцию для режекторного фильтра, описанного в задаче 15.51.
b) Используйте передаточную функцию, полученную в части (a), чтобы найти затухание (в децибелах) на центральной частоте фильтра.
Заходите скорее!
Задача 53
Целью этой задачи является разработка расчетных уравнений для схемы на рис.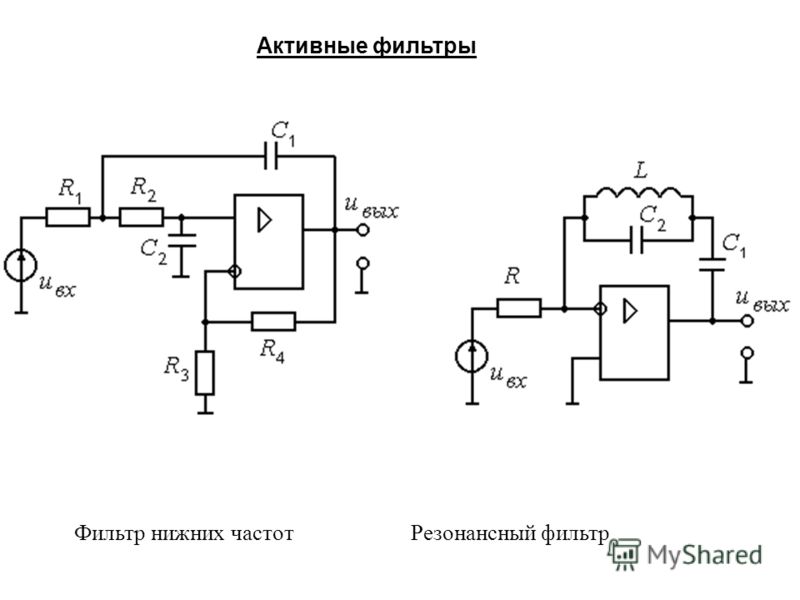 P15.53. (См. задачу 15.48 для предложений по разработке уравнений плана.
P15.53. (См. задачу 15.48 для предложений по разработке уравнений плана.
а) На основе качественного анализа опишите тип фильтра, реализованного в схеме.
b) Проверьте вывод, сделанный в (а), вычислив передаточную функцию $V_{o} / V_{i} .$ Запишите передаточную функцию в форме, которая делает ее совместимой с данными в таблице 15.1
c) Сколько Есть ли свободный выбор при выборе компонентов схемы?
d) Получите выражения для проводимостей $G_{1}=1 / R_{1}$ и $G_{2}=1 / R_{2}$ через $C_{1}, C_{2}$ и коэффициенты $b_{o}$ и $b_{1}$. (См. задачу $\left.15.48 \text { для определения } b_{o} \text { и } b_{1} .\right)$
e) Существуют ли какие-либо ограничения для $C_{1}$ или $C_{2}$ ?
f) Предположим, что схема на рис. $P 15.53$ используется для разработки фильтра Баттерворта нижних частот четвертого порядка с единичным коэффициентом усиления. Укажите прототипные значения $R_{1}$ и $R_{2}$ в каждой секции второго порядка, если в схеме прототипа используются конденсаторы $1 \mathrm{F}$.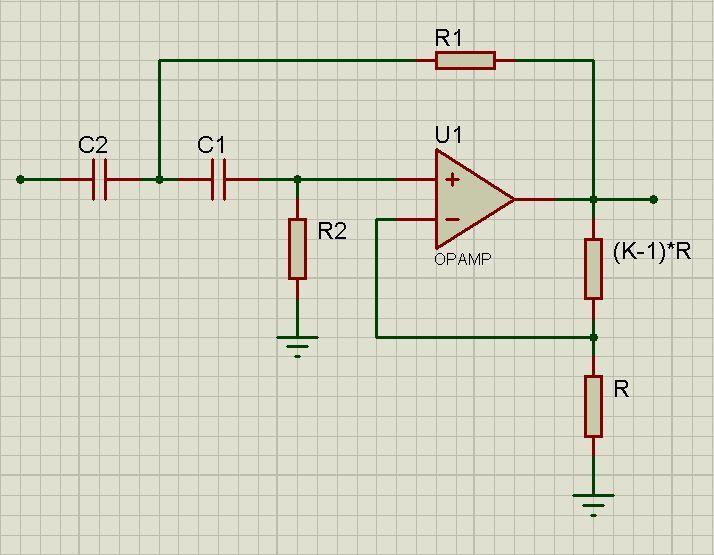
Заходите скорее!
Задача 54
Низкочастотный фильтр Баттерворта четвертого порядка с единичным коэффициентом усиления в задаче 15.53 используется в системе с частотой среза $25 \mathrm{кГц}$. Фильтр имеет конденсаторы $750 \mathrm{pf}$
а) Укажите числовые значения $R_{1}$ и $R_{2}$ в каждой секции фильтра
б) Начертите принципиальную схему фильтра и обозначьте все компоненты.
Заходите скорее!
Задача 55
Поменять местами $R$ s и $C$ s в схеме на рис. $P 15.53,$, то есть заменить $R_{1}$ на $C_{1}, R_{2}$ на $C_{2 }$ и наоборот.
а) Качественно проанализируйте схему и предскажите тип фильтра, реализованного в схеме.
b) Проверьте вывод, сделанный в (а), выведя передаточную функцию $V_{o} / V_{i} .$ Запишите передаточную функцию в форме, которая делает ее совместимой с данными в таблице 15.1
c) Сколько Есть ли свободный выбор при выборе компонентов схемы?
d) Найдите $R_{1}$ и $R_{2}$ как функции $b_{n}, b_{1}, C_{1},$ и $C_{2}$
e) Существуют ли ограничения на $C_{1}$ и $C_{2} ?$
f) Предположим, что схема используется в фильтре Баттерворта третьего порядка типа, найденного в (a). Укажите значения прототипа $R_{1}$ и $R_{2}$ в разделе второго порядка фильтра, если $C_{1}=C_{2}=1 \mathrm{F}$
Укажите значения прототипа $R_{1}$ и $R_{2}$ в разделе второго порядка фильтра, если $C_{1}=C_{2}=1 \mathrm{F}$
Заходите скорее!
Задача 56
а) Схема из задачи 15.55 используется в третьем. закажите фильтр Баттерворта верхних частот с частотой среза $40\mathrm{кГц}$. Укажите значения $R_{1}$ и $R_{2}$, если для построения фильтра доступны конденсаторы емкостью 360 пФ.
б) Укажите значения сопротивления и емкости в секции первого порядка фильтра.
c) Начертите принципиальную схему и обозначьте все компоненты. 9{2}+(1 / Q) s+1}$$
б) Используйте результат, полученный в (а), чтобы найти передаточную функцию фильтра, разработанного в примере 15.13.
Заходите скорее!
Задача 58
а) Используя схему, показанную на рис. $15.29,$, спроектируйте узкополосный режекторный фильтр с центральной частотой $4 \mathrm{кГц}$ и добротностью 15. Базируйте проект на $C=150 \mathrm{nF }$
Базируйте проект на $C=150 \mathrm{nF }$
б) Нарисуйте принципиальную схему фильтра и обозначьте номиналы всех компонентов на диаграмме.
c) Какова масштабированная передаточная функция фильтра?
Заходите скорее!
Задача 59
Используя схему на рис. $15.32(\mathrm{a})$, спроектируйте схему регулировки громкости, обеспечивающую максимальное усиление $20 \mathrm{dB}$ и усиление $17 \mathrm{dB}$ на частоте $40. \mathrm{Гц}$. Используйте резистор $11,1 \mathrm{k} \Omega$ и потенциометр $100 \mathrm{k} \Omega$. Протестируйте свою конструкцию, рассчитав максимальное усиление при $\omega=0$ и усиление при $\omega=1 / R_{2} C_{1}$, используя выбранные значения $R_{1}, R_{2}, $ и $C_{1}$
Заходите скорее!
Задача 60
Используйте схему на рис. $15.32(\mathrm{a})$ для разработки схемы управления громкостью баса с максимальным коэффициентом усиления $13,98 \mathrm{dB}$, который падает до $3 \mathrm{dB}$ при $50 \mathrm. {Гц}$.
{Гц}$.
Заходите скорее!
Задача 61
Постройте график зависимости максимального усиления в децибелах от $\alpha$ при $\omega=0$ для схемы, разработанной в задаче 15.59.. Пусть $\alpha$ изменяется от 0 до 1 с шагом 0,1
Вернитесь позже!
Задача 62
а) Покажите, что схемы на рис. $P 15.62(a)$ и $(b)$ эквивалентны.
b) Покажите, что точки, обозначенные $x$ и $y$ на рис. $P 15,62(b)$, всегда имеют одинаковый потенциал.
c) Используя информацию, представленную в (a) и (b), покажите, что схема на рис. 15,33 может быть изображена так, как показано на рис. 15.62(c)$ имеет вид схемы из $\mathrm{Fig}, 15.2,$, где 9{3}}\\
&Z_{f}=\frac{R_{1}+\alpha R_{2}+R_{1} R_{2} C_{1} s}{1+R_{2} C_{ 1} s}
\end{align}$$
Возвращайтесь скорее!
Задача 63
Руководитель технического проекта получил предложение от подчиненного, который утверждает, что схема, показанная на рис.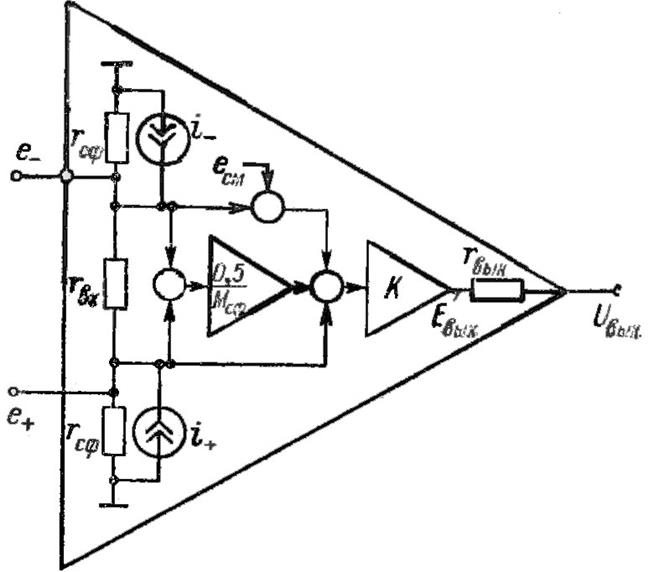 $P 15.63$, может использоваться в качестве схемы регулировки громкости высоких частот, если $R_{4} \gg R_{1}+R_{3}+ 2 р_{2}$. Подчиненный далее утверждает, что передаточная функция напряжения для цепи составляет
$P 15.63$, может использоваться в качестве схемы регулировки громкости высоких частот, если $R_{4} \gg R_{1}+R_{3}+ 2 р_{2}$. Подчиненный далее утверждает, что передаточная функция напряжения для цепи составляет
$$H(s)=\frac{V_{o}}{V_{s}}$$
$$=\frac{-\left\{\left(2 R_{3}+R_{4}\ вправо)+\влево[(1-\beta) R_{4}+R_{0}\вправо]\влево(\beta R_{4}+R_{3}\вправо) C_{2} s\вправо)} {\ влево \ {\ влево (2 R_ {3} + R_ {4} \ вправо) + \ влево [(1- \ бета) R_ {4} + R_ {3} \ вправо] \ влево (\ бета R_ { 4}+R_{0}\right) C_{1} s\right.}$$
Где $R_{o}=R_{1}+R_{3}+2 R_{2}$. К счастью, у инженера-проектировщика есть аспирант по электротехнике в качестве стажера, и поэтому он поручает студенту проверить претензию подчиненного.
Учащегося просят проверить поведение функции Ирансфера при $\omega \rightarrow 0 ;$ при $\omega \rightarrow \infty:$ и поведение, когда $60=\infty$ и $\beta$ варьируются между 0 и После тестирования передаточной функции вы думаете, что эту схему можно использовать в качестве регулятора громкости высоких частот? Объясните
Заходите скорее!
Задача 64
В схеме рис. $P 15.63$ значения компонентов $\operatorname{arc} R_{1}=R_{2}=20 \mathrm{k} \Omega, R_{3}=5,9 \mathrm{k} \Omega, R_{4}=500 \mathrm{k} \Omega$ и $C_{2}=2,7 \mathrm{nF}$
$P 15.63$ значения компонентов $\operatorname{arc} R_{1}=R_{2}=20 \mathrm{k} \Omega, R_{3}=5,9 \mathrm{k} \Omega, R_{4}=500 \mathrm{k} \Omega$ и $C_{2}=2,7 \mathrm{nF}$
а) Рассчитайте максимальное усиление в децибелах.
b) Рассчитайте максимальное сокращение в децибелах.
c) Значительно ли $R_{4}$ больше, чем $R_{0} ?$
d) Когда $\beta=1$, каково усиление в децибелах, когда $\omega=1 / R_{3} C_{ 2} ?$
e) Когда $\beta=0,$, каково сокращение в децибелах, когда $\omega=1 / R_{3} C_{2} ?$
f) На основании результатов, полученных в (d) и (e) . каково значение частоты $1 / R_{3} C_{2}$, когда $R_{4} \gg R_{0} ?$
Вернитесь позже!
Задача 65
Используя значения компонентов, данные в задаче 15.64, постройте график зависимости максимального усиления в децибелах от $\beta$ при $\omega=0$. Пусть $\beta$ изменяется от 0 до 1 с шагом 0,1
Заходите скорее!
Рисунок 1
Рисунок 2
Рисунок 3
Рис.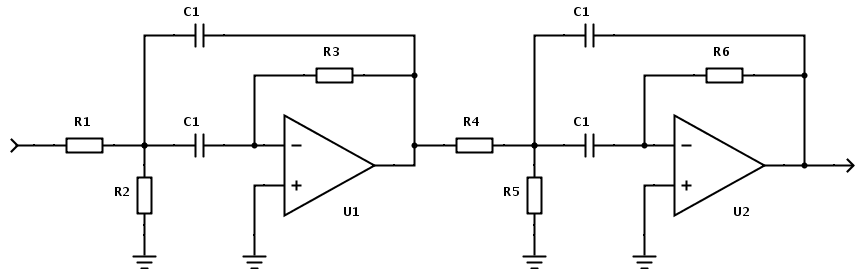 4. Частотная характеристика 4. Частотная характеристика
Рис. 5. 2-, 4-, 6- и 8-полюсный низкочастотный фильтр Баттерворта
Рис. 6. 8-полюсный низкочастотный фильтр, характеристика групповой задержкиБаттерворта, Бесселя, с постоянной задержкой, эллиптическая
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10
Рисунок 11
Рисунок 12
Рисунок 13
Рисунок 14
Рисунок 15
Рисунок 16
Рисунок 17
|
Лаборатория 2: Активные и пассивные фильтры
Компания NI
- Внутренние инструменты
Эта лабораторная работа знакомит учащихся с базовой терминологией и характеристиками фильтров, такими как наклон фильтра, полоса пропускания, полоса задерживания и частота среза. Студенты узнают о передаточных функциях фильтра для пассивных и активных фильтров, а также пассивных фильтров более высокого порядка и применят свои знания, моделируя и строя эти схемы. Продвинутые учащиеся могут бросить себе вызов, исследуя реализации активных фильтров более высокого порядка (например, Чебышева и Баттерворта) и то, как эти реализации максимизируют различные характеристики фильтров.
Студенты узнают о передаточных функциях фильтра для пассивных и активных фильтров, а также пассивных фильтров более высокого порядка и применят свои знания, моделируя и строя эти схемы. Продвинутые учащиеся могут бросить себе вызов, исследуя реализации активных фильтров более высокого порядка (например, Чебышева и Баттерворта) и то, как эти реализации максимизируют различные характеристики фильтров.
Введение
В первой лаборатории вы познакомились с базовым фильтром RC , однако мы не обсуждали характеристики фильтра. Схемы фильтров играют важную роль во многих электронных устройствах. Они в основном используются для передачи полезных сигналов при блокировании нежелательных сигналов. Фильтры можно разделить на две основные категории: аналоговые и цифровые фильтры, и каждая категория может быть дополнительно разделена на множество подгрупп, таких как пассивные фильтры, активные фильтры, КИХ-фильтры или БИХ-фильтры. Каждая подгруппа фильтров имеет свои преимущества и недостатки.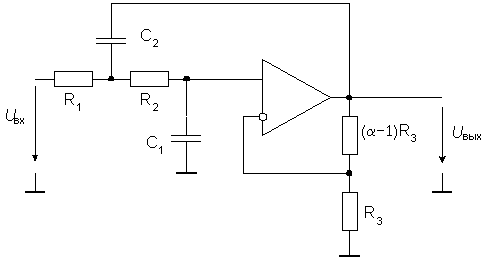 Изучение различий между каждым фильтром позволит инженеру-проектировщику фильтров выбрать лучший тип фильтра для данного приложения.
Изучение различий между каждым фильтром позволит инженеру-проектировщику фильтров выбрать лучший тип фильтра для данного приложения.
Проверка всех типов фильтров заняла бы слишком много времени для одной лаборатории. Чтобы сузить фокус, в этой лабораторной работе мы будем использовать аналоговые фильтры, чтобы представить основные характеристики фильтров и их конструкцию. Мы также поговорим о разнице между пассивными и активными фильтрами и о том, как они могут повлиять на выбор дизайна.
Цели обучения
В этом разделе студенты будут:
Имитация пассивного фильтра RC
Создать активный фильтр с помощью операционного усилителя
Список деталей
Для эксперимента необходимо следующее оборудование:
Оборудование
Analog Discovery Studio
Холст макетной платы
Электролитический конденсатор 1 мкФ
Керамический конденсатор 0,1 мкФ
Резистор 10 кОм
2 резистора 1 кОм
OP27 или совместимый операционный усилитель
Теория цепей и моделирование
Пассивный фильтр
Пассивные фильтры — это фильтры, состоящие только из пассивных компонентов, таких как резисторы, конденсаторы и катушки индуктивности ( RLC ).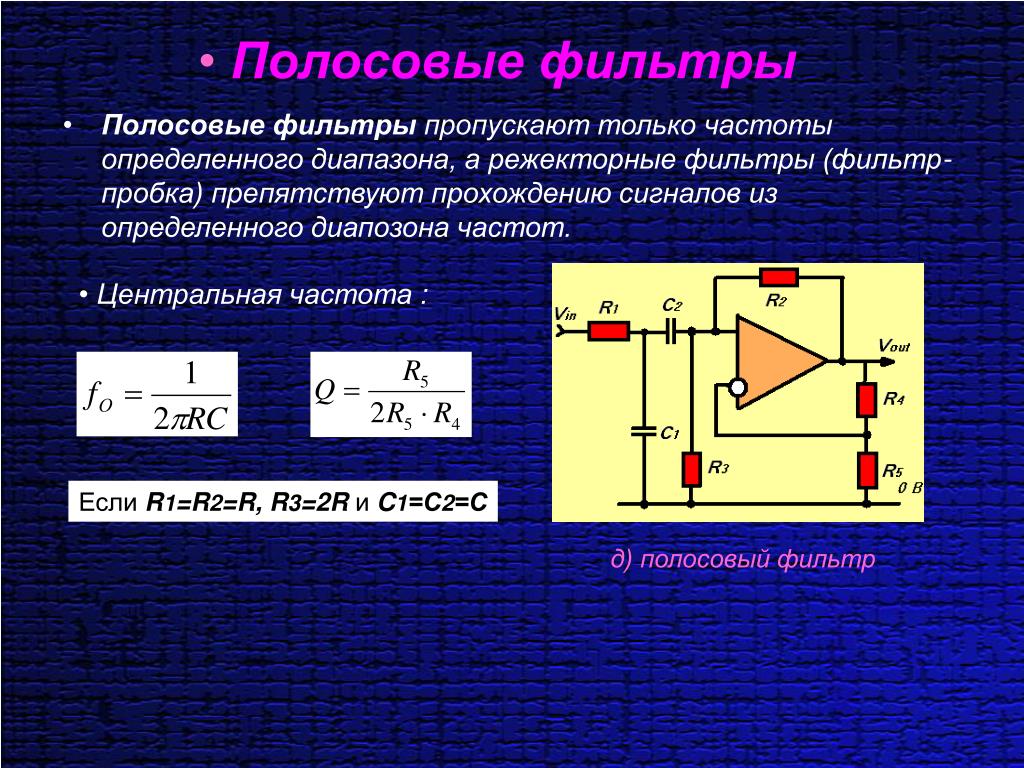 Для низкочастотных приложений используются фильтры RC , поскольку физический размер катушки индуктивности может быть очень большим для низкочастотных приложений. По мере увеличения рабочей частоты размер индуктора может быть меньше, что делает его хорошим выбором для RF приложений, которые работают в диапазоне МГц . В этом разделе вы будете работать с фильтром RC , но концепции, которые вы изучите, также применимы к фильтрам RL и RLC .
Для низкочастотных приложений используются фильтры RC , поскольку физический размер катушки индуктивности может быть очень большим для низкочастотных приложений. По мере увеличения рабочей частоты размер индуктора может быть меньше, что делает его хорошим выбором для RF приложений, которые работают в диапазоне МГц . В этом разделе вы будете работать с фильтром RC , но концепции, которые вы изучите, также применимы к фильтрам RL и RLC .
Характеристики фильтра нижних частот RC :
Полоса пропускания – диапазон частот, в котором входная частота не затухает по сравнению с выходной.
Полоса заграждения – диапазон частот, в котором начинается затухание входного сигнала.

Частота среза – граница перехода между полосой пропускания и полосой заграждения, это когда Vout равно 1√2 от Vin или 0,0707. По шкале децибел значение составляет -3 дБ.
Наклон – наклон определяет скорость затухания сигнала после частоты среза. Наклон является основным соображением, которое разработчик принимает во внимание при создании фильтра.
Фазовый сдвиг – разность фаз между входным и выходным сигналом.
ось Y – амплитуда сигнала, выраженная в децибелах (дБ).
ось абсцисс – частота, выраженная в логарифмическом масштабе.
Теперь, когда характеристики фильтра определены, давайте рассмотрим, как получить эти значения математически.
В s-области импеданс конденсатора определяется как: $X_C=\frac{1}{sC}$,
где $s=j\omega$ или $s=j2{\pi}f$, а j представляет собой комплексное число. Резистор в s-области — это просто его значение сопротивления.
Передаточная функция часто используется для определения характеристики фильтра, это просто выходной сигнал, деленный на входной: $H(s)=\frac{V_{out}(s)}{V_{in}(s)}$
Резистор в s-области — это просто его значение сопротивления.
Передаточная функция часто используется для определения характеристики фильтра, это просто выходной сигнал, деленный на входной: $H(s)=\frac{V_{out}(s)}{V_{in}(s)}$
Для фильтра RC можно использовать правило делителя напряжения, чтобы найти выходной сигнал: $V_{out}=\frac{X_C}{R+X_C}V_{in}$
Если мы заменим Xc и R их представлением в s-области, а затем перестроим, передаточная функция RC будет следующей: $H(s)=\frac{\frac{1}{Cs}}{R+\frac{1}{ Cs}}=\frac{1}{sRC+1}$
Подставив jω вместо s, передаточные функции примут вид: $H({\omega})=\frac{1}{j{\omega}RC+1}$
Анализ AC Sweep в Multisim показывает отклик фильтра в зависимости от амплитуды и частоты, поэтому будет полезно выразить передаточную функцию как амплитуду. Величина передаточной функции может быть рассчитана как: $|H({\omega})|=\frac{1}{\sqrt{({\omega}RC)^2+1}}$
Второй график анализа развертки переменного тока представляет собой разность фаз между входом и выходом. Мы можем вычислить угол, используя формулу: ${\theta}=-arctan({\omega}RC)$
Мы можем вычислить угол, используя формулу: ${\theta}=-arctan({\omega}RC)$
Часто отклик фильтра выражается как усиление в децибелах и задается следующим уравнением: $A(s)=-20log(\frac{V_{out}}{V_{in}})[dB]$
Частота среза фильтра находится в точке -3 дБ. Для фильтра RC это происходит, когда $X_C$ равно R: $R=X_C=\frac{1}{2{\pi}f_{c}C}$ → $f_c=\frac{1}{ 2{\pi}RC}$, где $f_c$ — частота среза. 9Фильтр порядка {st}$, и вы можете видеть, что наклон постепенный. Чтобы спроектировать фильтр ближе к идеальному фильтру, который имеет резкое падение частоты среза, вы должны увеличить порядок фильтра. Одним из простых способов увеличить порядок фильтрации фильтров RC является каскадирование нескольких фильтров нижних частот RC в многоступенчатую сеть.
Каждая дополнительная пара резистор-конденсатор, которую вы добавляете, увеличивает порядок фильтра на 1.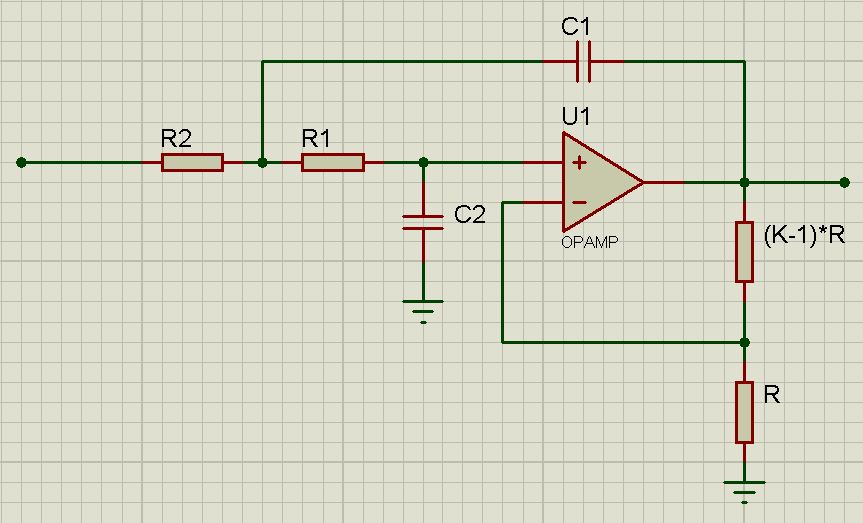
Чтобы получить передаточную функцию приведенной выше схемы, вы можете использовать закон тока Кирхгофа: 92R_1R_2C_1C_2+s(R_1C_1+R_1C_2+R_2C_2)+1}$
Активный фильтр
Как мы видели, пассивные фильтры легко настроить и спроектировать. Это делает пассивный фильтр жизнеспособным во многих приложениях, но у него есть некоторые недостатки. Например, если сопротивление нагрузки изменится, это вызовет изменение частотной характеристики, что затруднит управление для систем с переменным сопротивлением нагрузки. Вот тут-то и появляется активный фильтр. Активный фильтр имеет активный компонент, обычно операционный усилитель. Поскольку активный фильтр имеет операционный усилитель, мы также можем разработать фильтр с высоким входным импедансом и низким выходным импедансом. При такой конфигурации нагрузка будет мало влиять на частотную характеристику. 92+1}}$
Фазовый угол определяется выражением: ${\phi}H(s)=180-arctan(R_2C_1{\omega})$
Усиление берется, когда частота равна нулю, и это отношение между: $A=-\frac{R_2}{R_1}$
Вы можете установить частоту спада фильтра следующим образом: $f_c=\frac{1}{2{\pi}R_2C_1}$
Построение и измерение схемы
В первой лабораторной работе был построен фильтр RC , и вы использовали осциллограф для просмотра выходного сигнала при увеличении частоты функционального генератора.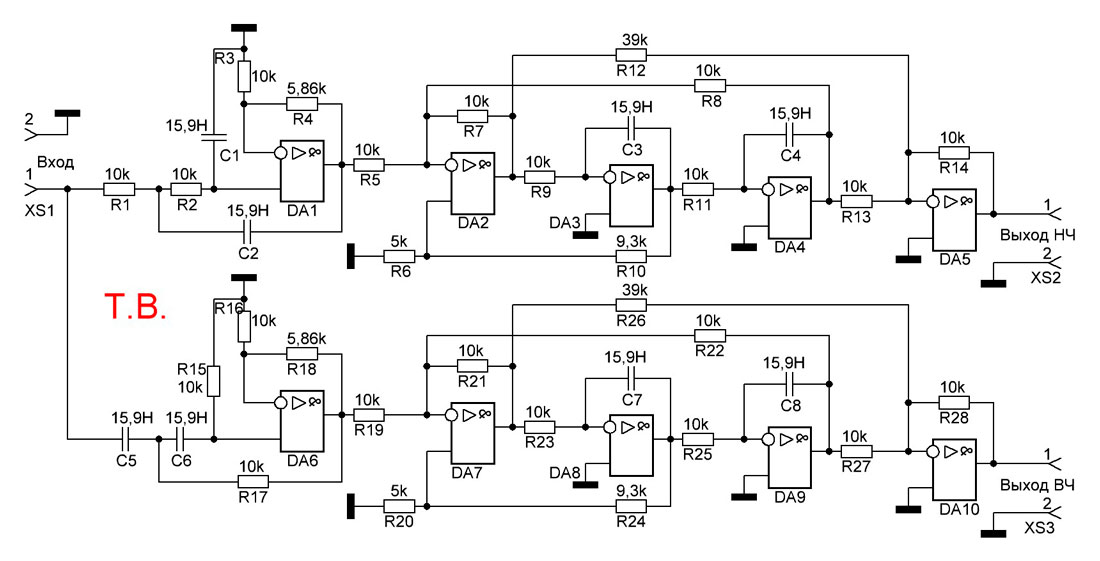 Вы также использовали Network Analyzer для просмотра отклика в частотной области. Для этой лабораторной работы входной сигнал представляет собой синусоидальную волну с шумом, и вы будете использовать 9Фильтр 1749 RC для удаления шума из сигнала.
Вы также использовали Network Analyzer для просмотра отклика в частотной области. Для этой лабораторной работы входной сигнал представляет собой синусоидальную волну с шумом, и вы будете использовать 9Фильтр 1749 RC для удаления шума из сигнала.
Пассивный фильтр
Подключите один вывод резистора к выводу W1 генератора сигналов, другой к положительному выводу конденсатора. Подключите отрицательный контакт конденсатора к заземленному контакту генератора сигналов. Подключите второй канал осциллографа 2+ (синий провод) к соединению между резистором и конденсатором, затем канал осциллографа 2- (бело-голубой провод) к отрицательному выводу конденсатора. Подключите первый канал осциллографа 1+ (оранжевый провод) к контакту W1 генератора сигналов (желтый провод), а канал осциллографа 1- (оранжево-белый провод) к отрицательному контакту конденсатора (этот контакт заземлен).
Не забудьте повернуть переключатели Scope Channel 1 и 2 в сторону заголовков MTE.
Схему подключения можно скачать здесь: wire_diagram_fr.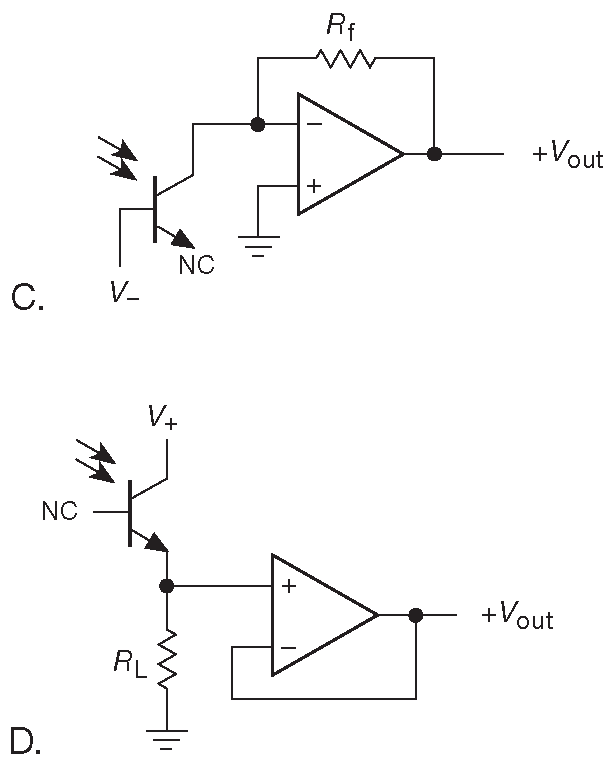 zip
zip
Запустите WaveForms и откройте инструмент Wavegen , затем выберите Custom и нажмите New . Во вкладке Math введите следующее соотношение: $sin(2*PI*X)+0,1*sin(30*PI*X)$, которое сгенерирует следующий сигнал: $V(t)=sin(2{ \pi}ft)+0,1sin(30{\pi}ft)$, где $sin(2{\pi}ft)$ — входной сигнал, а $0,1sin(30{\pi}ft)$ — шум при частота в 15 раз выше входного сигнала.
Нажмите на Создать .
Установите частоту на 10 Гц и запустите прибор. Используйте осциллограф Scope для просмотра отклика схемы во временной области.
Активный фильтр
Создайте схему, представленную в активном фильтре, на холсте макета. Вам нужно будет запитать операционный усилитель ± 5 В от переменного источника питания (красный и белый провода). Подсоедините канал W1 генератора функций (желтый провод) и канал осциллографа 1+ (оранжевый провод) к входу схемы, а канал 2+ осциллографа (синий провод) к выходу схемы.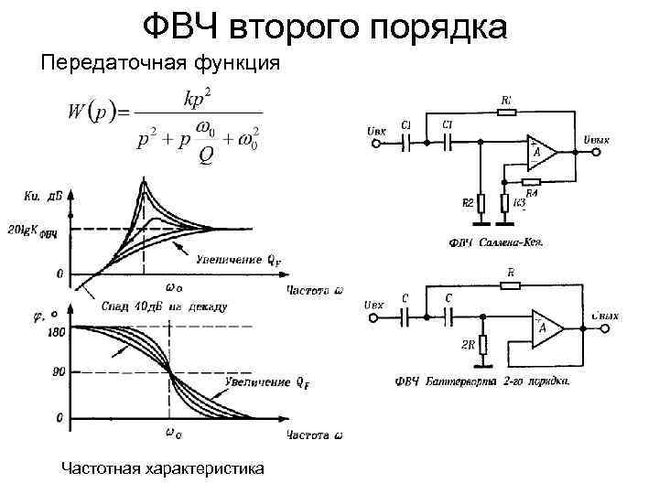 Соедините с землей 1-й и 2-й каналы осциллографа (оранжево-белый и сине-белый провода), землю функционального генератора и плюсовой вход ОУ.
Соедините с землей 1-й и 2-й каналы осциллографа (оранжево-белый и сине-белый провода), землю функционального генератора и плюсовой вход ОУ.
Не забудьте повернуть переключатели Scope Channel 1 и Scope Channel 2 в сторону разъемов MTE, а переключатель V+ в сторону надписи POWER .
Схему подключения можно скачать здесь: wire_diagram_active.zip
В WaveForms запустите прибор Supplies , установите напряжения на +5 В и -5 В и включите мастер, чтобы включить питание микросхемы. В приборе Wavegen установите ранее представленный зашумленный синусоидальный сигнал и установите частоту 500 Гц. Используйте Scope для просмотра отклика канала во временной области.
Используйте сетевой анализатор для просмотра отклика активного фильтра.
Дальнейшее исследование
В разделе ниже представлен способ продолжить исследование после завершения лабораторной работы.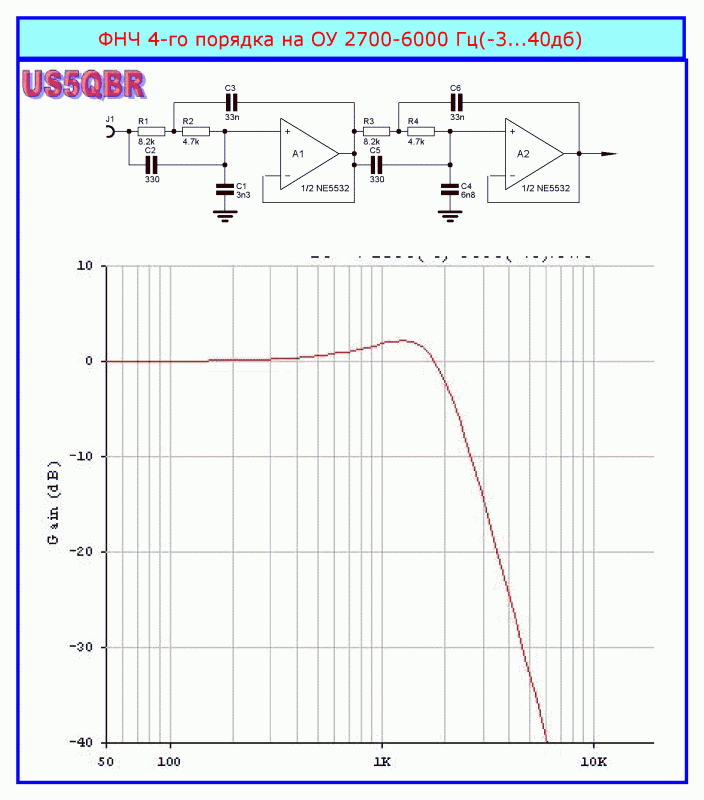 Он охватывает несколько ордеров в активных фильтрах и различные типы ответов фильтров.
Он охватывает несколько ордеров в активных фильтрах и различные типы ответов фильтров.
Активные фильтры высшего порядка
В этой лаборатории мы говорили о том, как сделать пассивные фильтры более высокого порядка, чтобы увеличить спад наклона. При обсуждении активных фильтров более высокого порядка на самом деле существует несколько общих решений для передаточной функции фильтра, которые были разработаны на протяжении многих лет, причем каждое решение максимизирует различные аспекты фильтра. Двумя распространенными примерами таких решений являются решения Баттерворта и Чебышева.
Откройте схемы в Multisim и сравните реализации фильтров Баттерворта и Чебышева. Поскольку они используют одну и ту же схемную архитектуру, чем отличаются эти две конструкции? Выполните анализ переменного тока на двух цепях фильтра. Чем АЧХ фильтра Баттерворта отличается от АЧХ фильтра Чебышева?
Оба фильтра рассчитаны на частоту среза 1 кГц. Идеальным откликом фильтра была бы «кирпичная стена», плоская в полосе пропускания и имеющая немедленный спад по вертикали на частоте среза.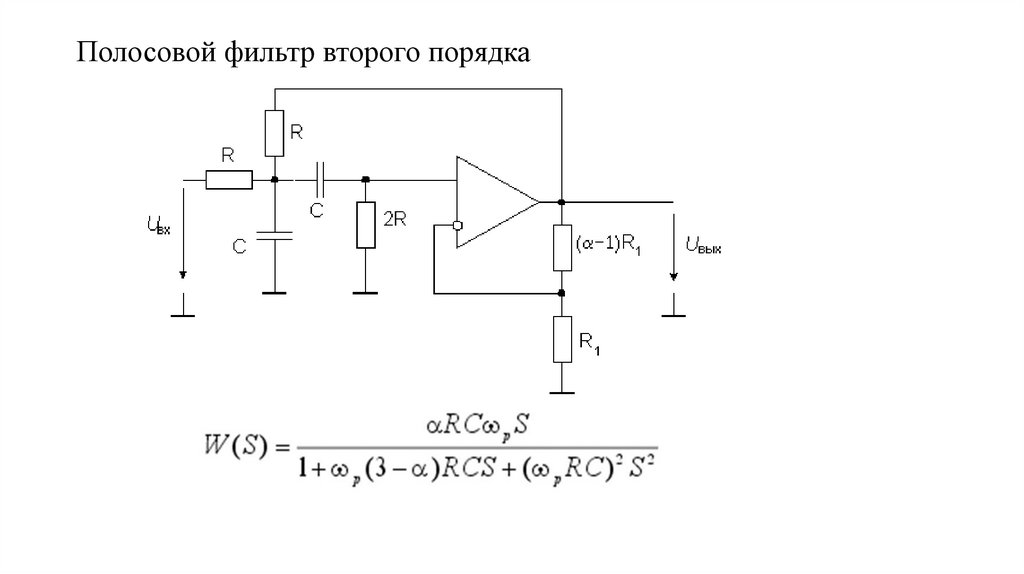


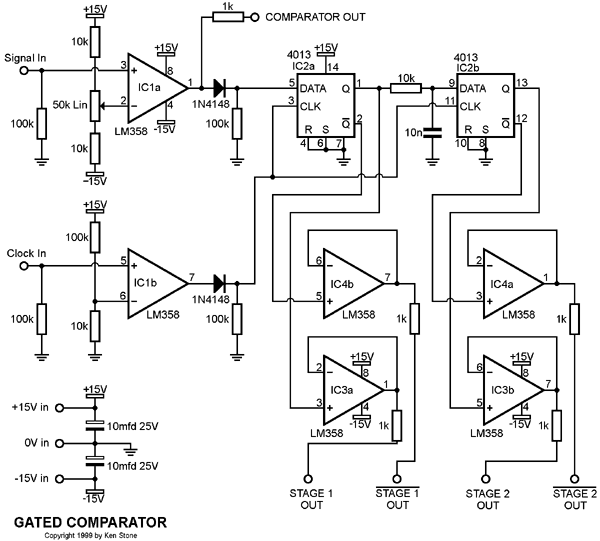
 youtube.com/watch?v=yCb3UvilJKU
youtube.com/watch?v=yCb3UvilJKU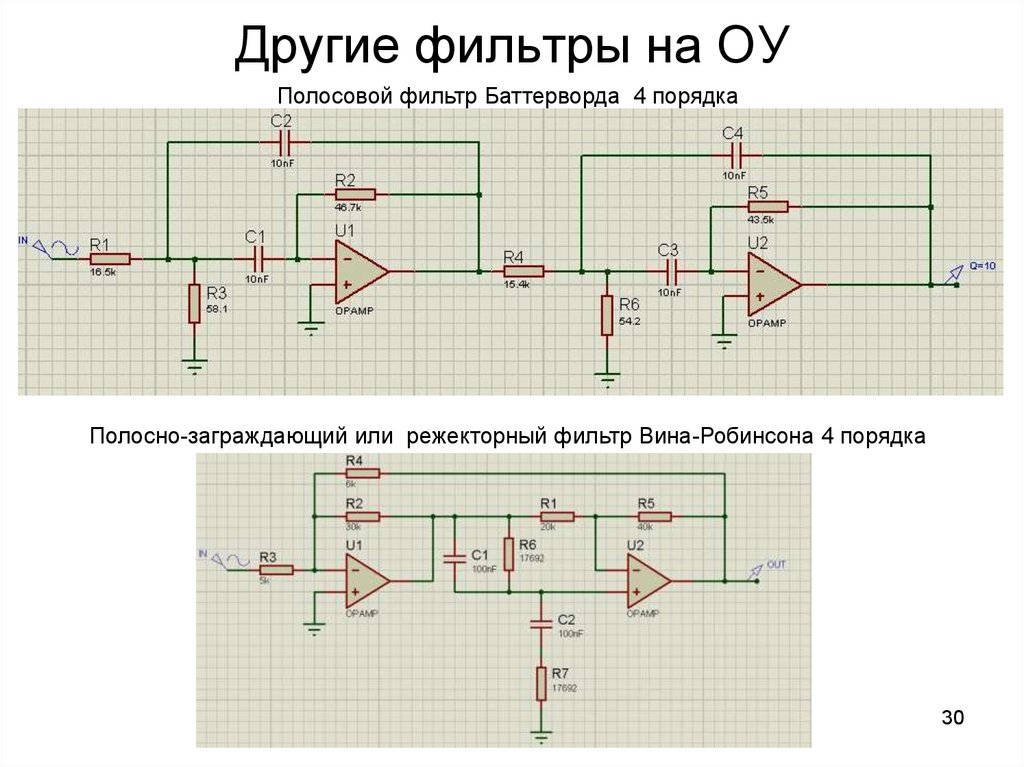 Эффективная работа с этими сигналами часто требует фильтрации, дискретизации и оцифровки аналоговых данных с помощью аналого-цифровых преобразователей. Преобразованные цифровые данные затем могут быть обработаны математически. Многие системы сбора данных также должны создавать представление исходного сигнала из потока цифровых данных.
Эффективная работа с этими сигналами часто требует фильтрации, дискретизации и оцифровки аналоговых данных с помощью аналого-цифровых преобразователей. Преобразованные цифровые данные затем могут быть обработаны математически. Многие системы сбора данных также должны создавать представление исходного сигнала из потока цифровых данных. Чтобы исправить изображение в примере с фильмом, частота кадров должна была бы вдвое превышать скорость вращения колеса (или его спиц) или лопастей вертолета. Никакая практическая система сбора данных не может производить выборку достаточно быстро, чтобы уловить все компоненты реального сигнала. Частоты выше Найквиста появляются как ложные низкочастотные псевдонимы. Например, На рис. 1 показан результат дискретизации сигнала частотой 900 Гц на частоте 1 кГц.
Чтобы исправить изображение в примере с фильмом, частота кадров должна была бы вдвое превышать скорость вращения колеса (или его спиц) или лопастей вертолета. Никакая практическая система сбора данных не может производить выборку достаточно быстро, чтобы уловить все компоненты реального сигнала. Частоты выше Найквиста появляются как ложные низкочастотные псевдонимы. Например, На рис. 1 показан результат дискретизации сигнала частотой 900 Гц на частоте 1 кГц.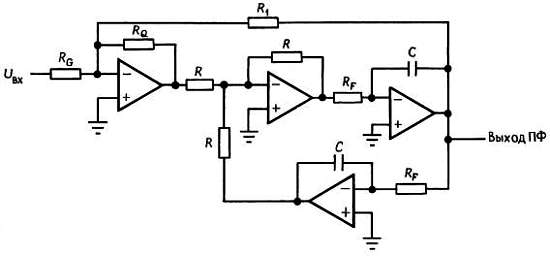


 Полосовые фильтры пропускают только компоненты сигнала в пределах полосы вокруг центральной частоты f o . Идеальный полосовой фильтр должен иметь переходы типа «кирпичная стена» на частотах f L и f H , подавляя все частоты сигнала. вне этого диапазона. Полосовые фильтры применяются в ситуациях, требующих выделения определенного тона, например тестового тона, из соседних тонов или широкополосного шума.
Полосовые фильтры пропускают только компоненты сигнала в пределах полосы вокруг центральной частоты f o . Идеальный полосовой фильтр должен иметь переходы типа «кирпичная стена» на частотах f L и f H , подавляя все частоты сигнала. вне этого диапазона. Полосовые фильтры применяются в ситуациях, требующих выделения определенного тона, например тестового тона, из соседних тонов или широкополосного шума.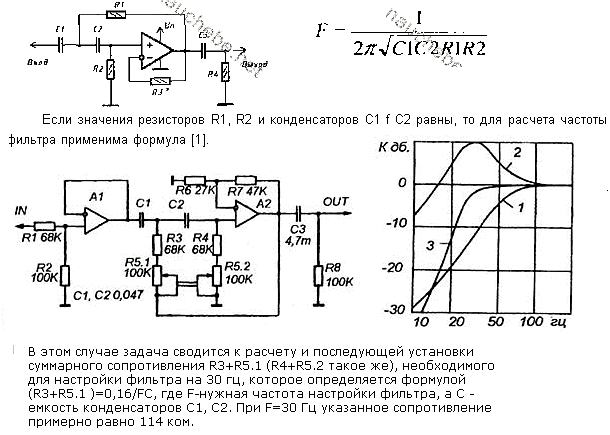 Следовательно, какой-то метод фильтрации должен отделить их друг от друга, прежде чем можно будет начать обработку и анализ. Реальные фильтры далеки от идеала. Они подвергают входные сигналы математическим передаточным функциям с такими именами, как Баттерворт, Бессель, постоянная задержка и эллиптическая функция, которые только приближаются к идеальному поведению. Вместо четко определенного перехода, представленного идеальными фильтрами, реальные фильтры содержат переходную область между полосой пропускания и полосой задерживания, как показано на рис.0600 Рисунок 3 .
Следовательно, какой-то метод фильтрации должен отделить их друг от друга, прежде чем можно будет начать обработку и анализ. Реальные фильтры далеки от идеала. Они подвергают входные сигналы математическим передаточным функциям с такими именами, как Баттерворт, Бессель, постоянная задержка и эллиптическая функция, которые только приближаются к идеальному поведению. Вместо четко определенного перехода, представленного идеальными фильтрами, реальные фильтры содержат переходную область между полосой пропускания и полосой задерживания, как показано на рис.0600 Рисунок 3 .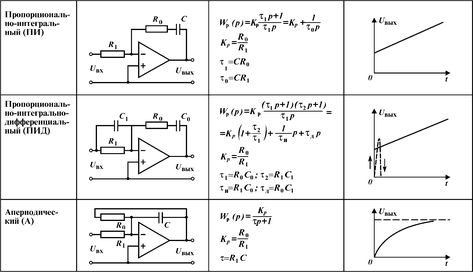 При выборе фильтра эти нормализованные данные позволяют разработчику сравнить теоретические характеристики амплитуды, фазы и задержки каждого типа фильтра.
При выборе фильтра эти нормализованные данные позволяют разработчику сравнить теоретические характеристики амплитуды, фазы и задержки каждого типа фильтра. Для большинства форм фильтров величина фазового сдвига изменяется в зависимости от частоты входного сигнала. Обычный способ представить это изменение в фазе через понятие Групповая задержка , производная фазового сдвига через фильтр по частоте.
Для большинства форм фильтров величина фазового сдвига изменяется в зависимости от частоты входного сигнала. Обычный способ представить это изменение в фазе через понятие Групповая задержка , производная фазового сдвига через фильтр по частоте.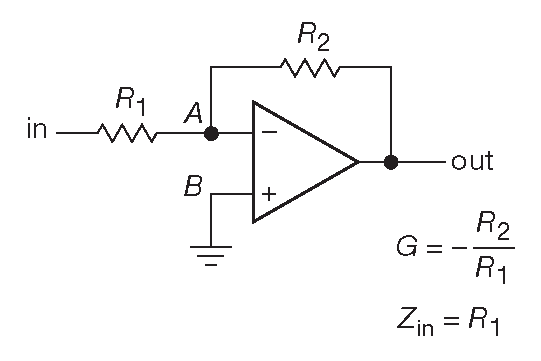
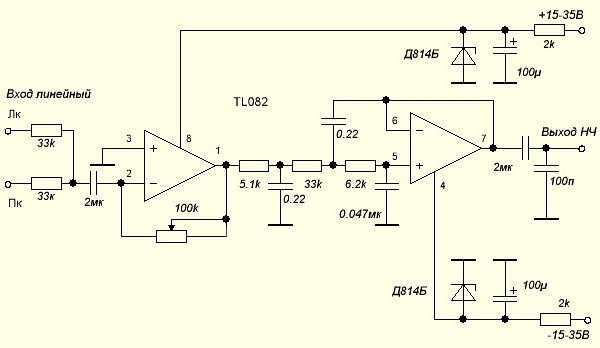 Спецификации фильтра могут также включать shape factor (sf) требование, описывающее скорость затухания сигналов во время перехода. sf представляет собой отношение между частотой среза/пульсаций и тем, где фильтр достигает желаемого уровня затухания, скажем (-80 дБ).
Спецификации фильтра могут также включать shape factor (sf) требование, описывающее скорость затухания сигналов во время перехода. sf представляет собой отношение между частотой среза/пульсаций и тем, где фильтр достигает желаемого уровня затухания, скажем (-80 дБ).
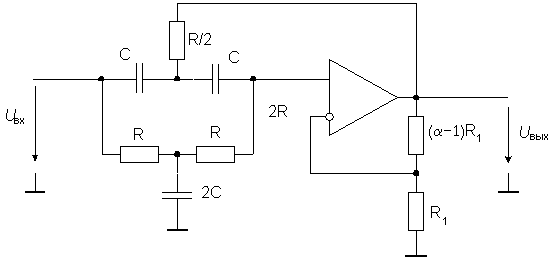 105
105 Для полосовых фильтров коэффициент формы показывает отношение ширины полосы пропускания при некотором уровне ослабления (например, — 80 дБ) до заданной ширины полосы пропускания (полоса пропускания на -3 дБ). Его коэффициент формы при -80 дБ составляет 10:1.
Для полосовых фильтров коэффициент формы показывает отношение ширины полосы пропускания при некотором уровне ослабления (например, — 80 дБ) до заданной ширины полосы пропускания (полоса пропускания на -3 дБ). Его коэффициент формы при -80 дБ составляет 10:1. 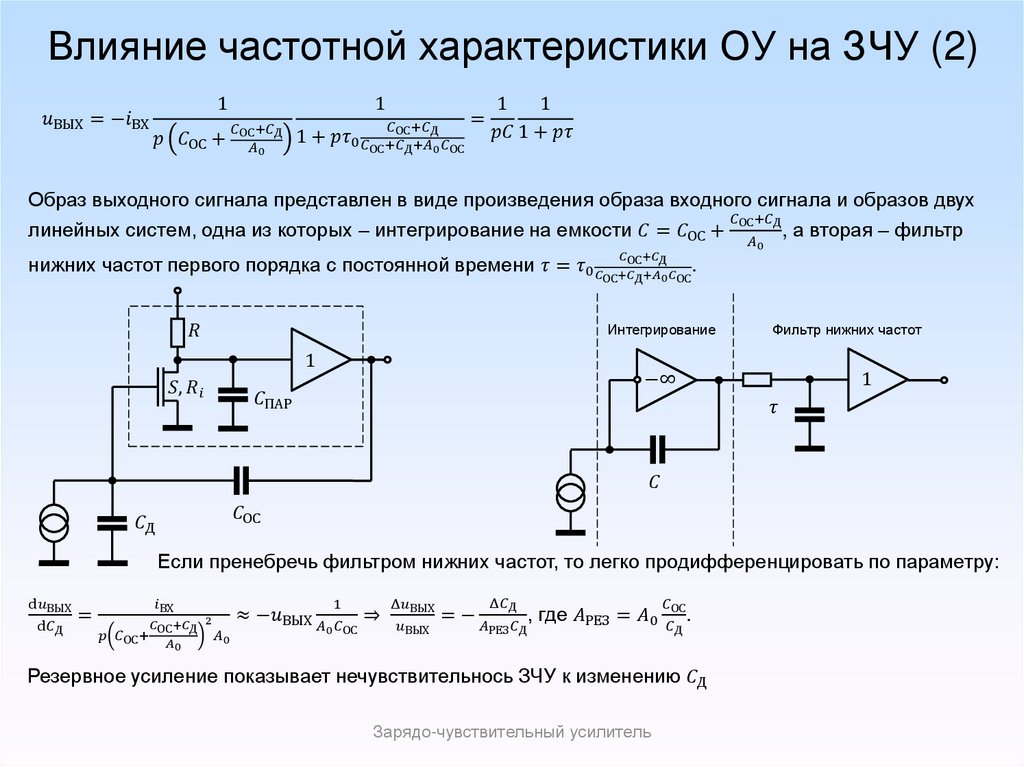 Два полюса, два нуля, фильтр нижних частот можно выразить как:
Два полюса, два нуля, фильтр нижних частот можно выразить как: Рассмотрим функцию второго порядка, которая создает кривую зависимости амплитуды от частоты в (рис. 9 ).
Рассмотрим функцию второго порядка, которая создает кривую зависимости амплитуды от частоты в (рис. 9 ). Каскадирование секций фильтров первого и второго порядка позволяет легко получить трех-, четырех-, пяти-, шести-, семи- и восьмиполюсные характеристики спада. Производительность так же хороша, как и у операционных усилителей, которые они содержат. При соответствующем выборе компонентов эти фильтры вносят небольшой широкополосный шум и могут достигать уровней искажений ниже -100 дБ. Полупроводниковые переключатели позволяют программировать угловую частоту без значительного шума, искажений или других нежелательных эффектов. Эти фильтры обычно меньше пассивных типов для частот менее 100 кГц. Угловые частоты секции фильтра и, следовательно, точность и форма фазовых и амплитудных кривых зависят от характеристик усилителя, точности и стабильности пассивных компонентов.
Каскадирование секций фильтров первого и второго порядка позволяет легко получить трех-, четырех-, пяти-, шести-, семи- и восьмиполюсные характеристики спада. Производительность так же хороша, как и у операционных усилителей, которые они содержат. При соответствующем выборе компонентов эти фильтры вносят небольшой широкополосный шум и могут достигать уровней искажений ниже -100 дБ. Полупроводниковые переключатели позволяют программировать угловую частоту без значительного шума, искажений или других нежелательных эффектов. Эти фильтры обычно меньше пассивных типов для частот менее 100 кГц. Угловые частоты секции фильтра и, следовательно, точность и форма фазовых и амплитудных кривых зависят от характеристик усилителя, точности и стабильности пассивных компонентов.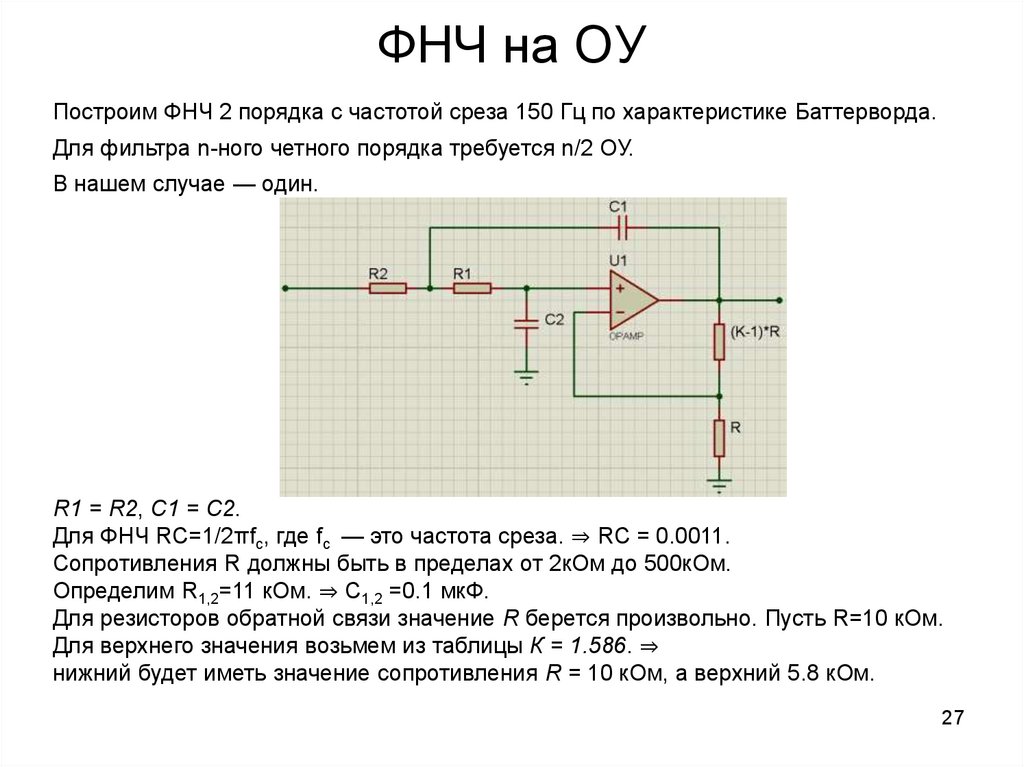 Это обеспечивает очень точное единичное усиление в полосе пропускания фильтра. Искажения могут быть проблемой для конструкции Саллена-Ки, так как большинство операционных усилителей не допускают больших колебаний синфазного сигнала без добавления искажений к сигналу. Для построения двухполюсной секции фильтра требуется только один операционный усилитель.
Это обеспечивает очень точное единичное усиление в полосе пропускания фильтра. Искажения могут быть проблемой для конструкции Саллена-Ки, так как большинство операционных усилителей не допускают больших колебаний синфазного сигнала без добавления искажений к сигналу. Для построения двухполюсной секции фильтра требуется только один операционный усилитель.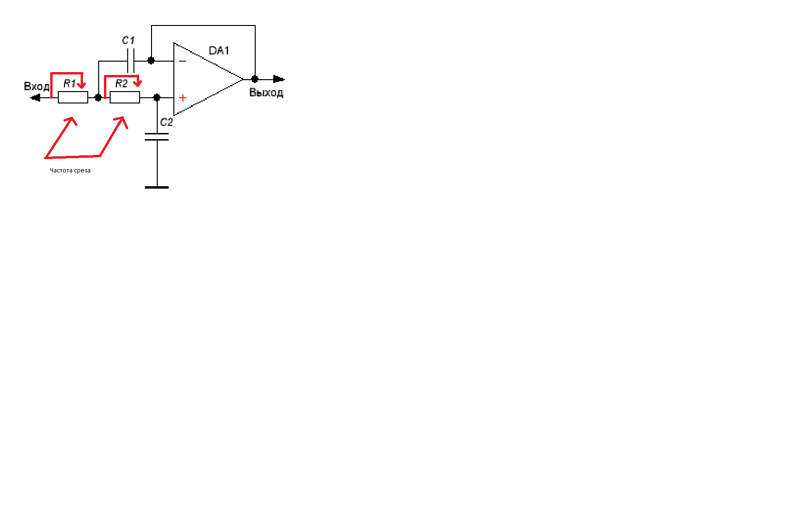 Невозможно построить несколько фильтров обратной связи с нулями. Топологии с множественной обратной связью не так универсальны, как другие топологии.
Невозможно построить несколько фильтров обратной связи с нулями. Топологии с множественной обратной связью не так универсальны, как другие топологии. Эта ошибка обычно стабильна во времени и мало меняется при изменении температуры. Усилители также добавляют гармонические искажения к выходному сигналу фильтра. Однако, поскольку активные фильтры могут достигать уровней искажений менее -100 дБ на частотах до 100 кГц и -110 дБ на частотах до 20 кГц, они могут легко предварительно фильтровать 16-битные (-96 дБ) и 18-битные (- 108 дБ) аналого-цифровые преобразователи.
Эта ошибка обычно стабильна во времени и мало меняется при изменении температуры. Усилители также добавляют гармонические искажения к выходному сигналу фильтра. Однако, поскольку активные фильтры могут достигать уровней искажений менее -100 дБ на частотах до 100 кГц и -110 дБ на частотах до 20 кГц, они могут легко предварительно фильтровать 16-битные (-96 дБ) и 18-битные (- 108 дБ) аналого-цифровые преобразователи. Вероятно, наиболее распространенной передаточной функцией амплитудного фильтра является функция Баттерворта , которая состоит из массива полюсов, равномерно распределенных по единичной окружности в левой полуплоскости, как в на рис. 10А . Такая схема обеспечивает максимально плоскую АЧХ в полосе пропускания (первые 2n — 1 производных АЧХ равны нулю, где n — число полюсов). Следовательно, амплитудная характеристика монотонно спадает (равномерный наклон) по мере увеличения частоты в полосе задерживания.
Вероятно, наиболее распространенной передаточной функцией амплитудного фильтра является функция Баттерворта , которая состоит из массива полюсов, равномерно распределенных по единичной окружности в левой полуплоскости, как в на рис. 10А . Такая схема обеспечивает максимально плоскую АЧХ в полосе пропускания (первые 2n — 1 производных АЧХ равны нулю, где n — число полюсов). Следовательно, амплитудная характеристика монотонно спадает (равномерный наклон) по мере увеличения частоты в полосе задерживания.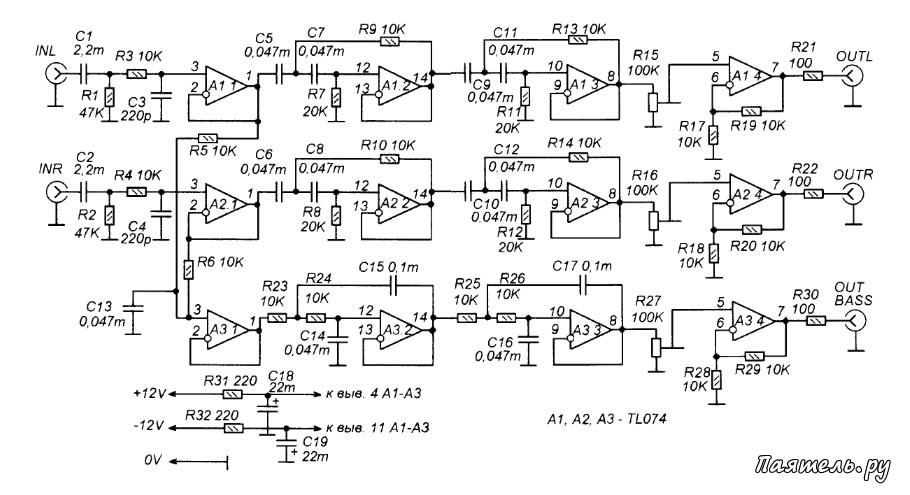
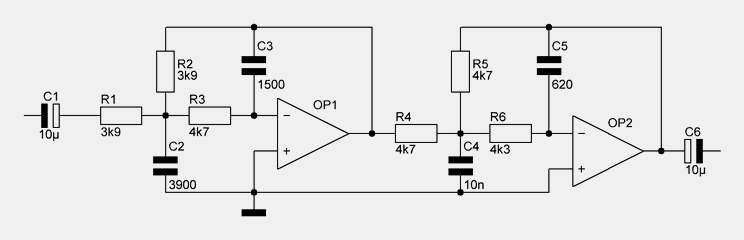 Неравномерность означает, что амплитуда в полосе пропускания изменяется от 1 до (1 + 2 ), где всегда меньше 1. Частоты полюсов более разбросаны, а добротность секций выше, чем добротность сравнимой секции. Баттерворта. Определение местоположения полюсов включает применение гиперболических тригонометрических функций к каждому полюсу фильтра Баттерворта того же порядка. Как и в случае Баттерворта, чебычевский спад в полосе задерживания является монотонным. Важно отметить, что многие проектировщики избегают передаточных функций Чебышева в пользу эллиптических альтернатив Кауэра, потому что сечение Q выше для Чебычева, чем с эллиптическими функциями, которые обеспечивают более быстрый спад в переходной полосе.
Неравномерность означает, что амплитуда в полосе пропускания изменяется от 1 до (1 + 2 ), где всегда меньше 1. Частоты полюсов более разбросаны, а добротность секций выше, чем добротность сравнимой секции. Баттерворта. Определение местоположения полюсов включает применение гиперболических тригонометрических функций к каждому полюсу фильтра Баттерворта того же порядка. Как и в случае Баттерворта, чебычевский спад в полосе задерживания является монотонным. Важно отметить, что многие проектировщики избегают передаточных функций Чебышева в пользу эллиптических альтернатив Кауэра, потому что сечение Q выше для Чебычева, чем с эллиптическими функциями, которые обеспечивают более быстрый спад в переходной полосе.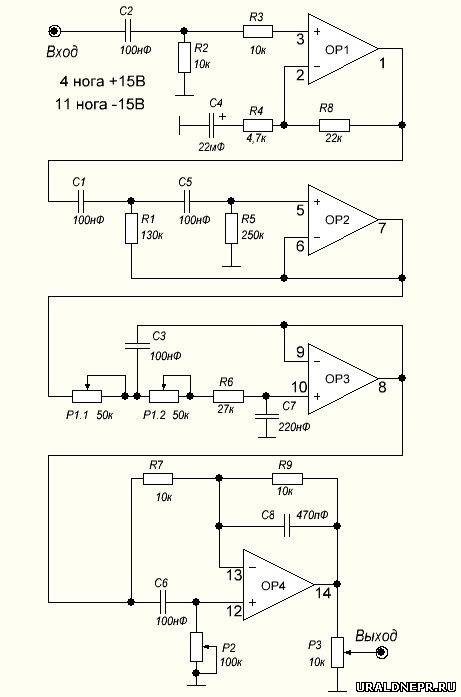 Хотя эллиптический фильтр обеспечивает более быстрый спад, чем фильтры Баттерворта или Чебычева , он вносит пульсации как в полосу пропускания, так и в полосу задерживания. Кроме того, спад эллиптического фильтра не является монотонным и в конечном итоге достигает предела затухания, называемого нижней границей полосы задерживания.
Хотя эллиптический фильтр обеспечивает более быстрый спад, чем фильтры Баттерворта или Чебычева , он вносит пульсации как в полосу пропускания, так и в полосу задерживания. Кроме того, спад эллиптического фильтра не является монотонным и в конечном итоге достигает предела затухания, называемого нижней границей полосы задерживания.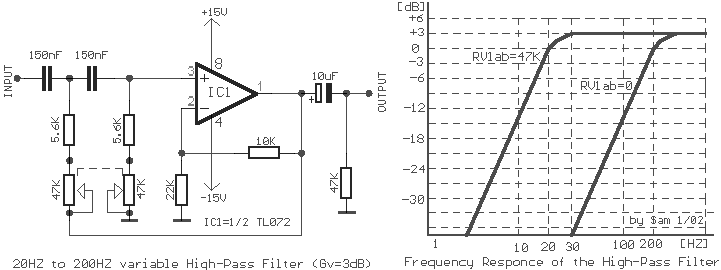 Другим критическим элементом в форме эллиптического фильтра является частота f s , которая обозначает первую частоту, на которой затухание достигает нижней границы полосы задерживания.
Другим критическим элементом в форме эллиптического фильтра является частота f s , которая обозначает первую частоту, на которой затухание достигает нижней границы полосы задерживания. рис. 6, ).
рис. 6, ).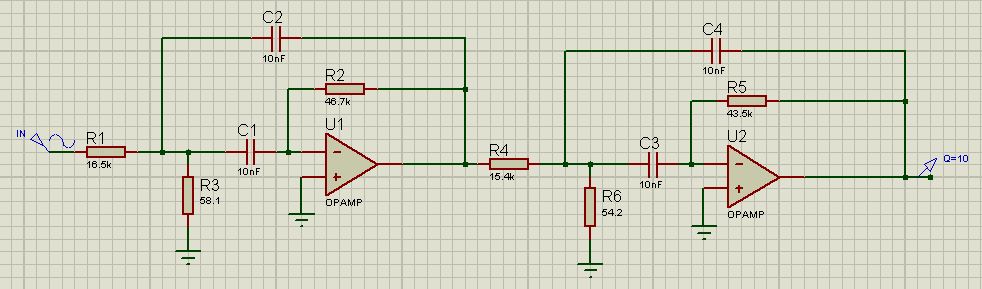 Самый распространенный линейно-фазовый фильтр основан на функциях Бесселя (иногда называемых Томпсоном). Фильтры Бесселя обеспечивают очень линейную фазовую характеристику и небольшие искажения задержки (постоянная групповая задержка) в полосе пропускания. Они не показывают перерегулирования в ответ на ступенчатый вход и монотонно спадают в полосе задерживания. Они также демонстрируют гораздо более медленное затухание в переходной полосе, чем амплитудные фильтры. На рис. 13 представлены кривые амплитуды и задержки для 8-полюсного датчика Бесселя. Другие типы фазовых фильтров включают в себя фильтры с постоянной задержкой (модифицированный Бессель), равноволновую фазу, равноволновую задержку и передаточные функции Гаусса. Они либо имеют больший спад амплитуды в полосе пропускания лишь для небольшого улучшения фазовой линейности, либо лишь немного меньший спад в полосе пропускания за счет ухудшения фазовой линейности.
Самый распространенный линейно-фазовый фильтр основан на функциях Бесселя (иногда называемых Томпсоном). Фильтры Бесселя обеспечивают очень линейную фазовую характеристику и небольшие искажения задержки (постоянная групповая задержка) в полосе пропускания. Они не показывают перерегулирования в ответ на ступенчатый вход и монотонно спадают в полосе задерживания. Они также демонстрируют гораздо более медленное затухание в переходной полосе, чем амплитудные фильтры. На рис. 13 представлены кривые амплитуды и задержки для 8-полюсного датчика Бесселя. Другие типы фазовых фильтров включают в себя фильтры с постоянной задержкой (модифицированный Бессель), равноволновую фазу, равноволновую задержку и передаточные функции Гаусса. Они либо имеют больший спад амплитуды в полосе пропускания лишь для небольшого улучшения фазовой линейности, либо лишь немного меньший спад в полосе пропускания за счет ухудшения фазовой линейности.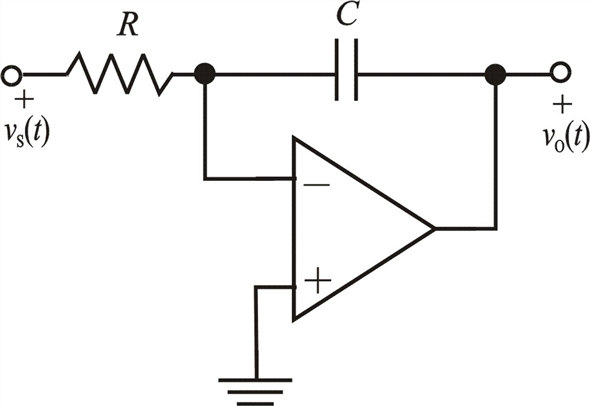 Для достижения этих целей доступны два метода: выравнивание амплитуды и выравнивание задержки. Оба усложняют конструкцию фильтра и имеют теоретические и практические ограничения.
Для достижения этих целей доступны два метода: выравнивание амплитуды и выравнивание задержки. Оба усложняют конструкцию фильтра и имеют теоретические и практические ограничения. Нули оси j создают «мягкий» или закругленный спад около частоты среза. Эти нули вносят основной вклад в форму кривой затухания, препятствуя дальнейшему улучшению формы угловой частоты.
Нули оси j создают «мягкий» или закругленный спад около частоты среза. Эти нули вносят основной вклад в форму кривой затухания, препятствуя дальнейшему улучшению формы угловой частоты. Положения полюса и нуля определяют фазовый сдвиг, хотя добавленный фазовый сдвиг не меняет амплитудную характеристику фильтра. Добавление фазового сдвига в соответствующих местах полосы пропускания позволяет «выпрямить» фазовую кривую амплитудного фильтра. Каждая пара полюс-ноль всепропускающего фильтра увеличивает фазовый сдвиг приблизительно с 90º при f c до целых 180º при 10-кратном увеличении f c . Следовательно, добавление секций эквалайзера увеличивает общий фазовый сдвиг для сети фильтра/эквалайзера.
Положения полюса и нуля определяют фазовый сдвиг, хотя добавленный фазовый сдвиг не меняет амплитудную характеристику фильтра. Добавление фазового сдвига в соответствующих местах полосы пропускания позволяет «выпрямить» фазовую кривую амплитудного фильтра. Каждая пара полюс-ноль всепропускающего фильтра увеличивает фазовый сдвиг приблизительно с 90º при f c до целых 180º при 10-кратном увеличении f c . Следовательно, добавление секций эквалайзера увеличивает общий фазовый сдвиг для сети фильтра/эквалайзера.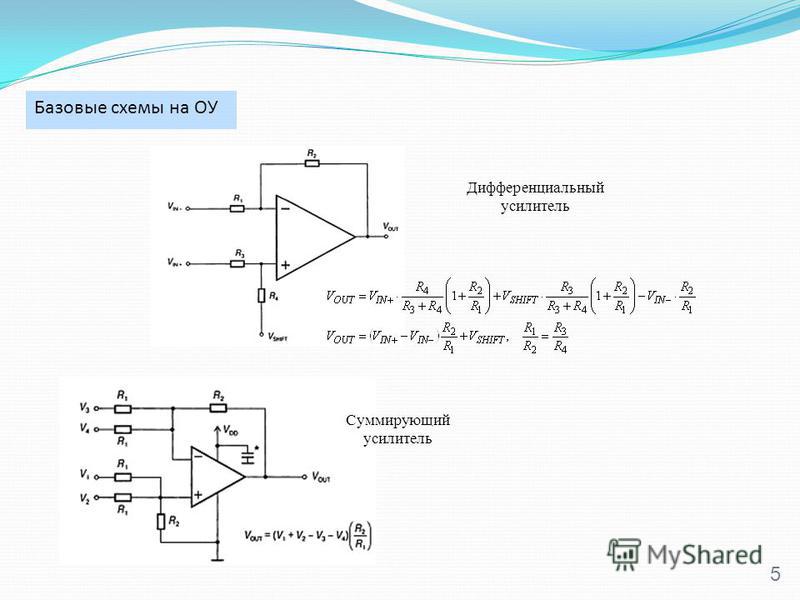
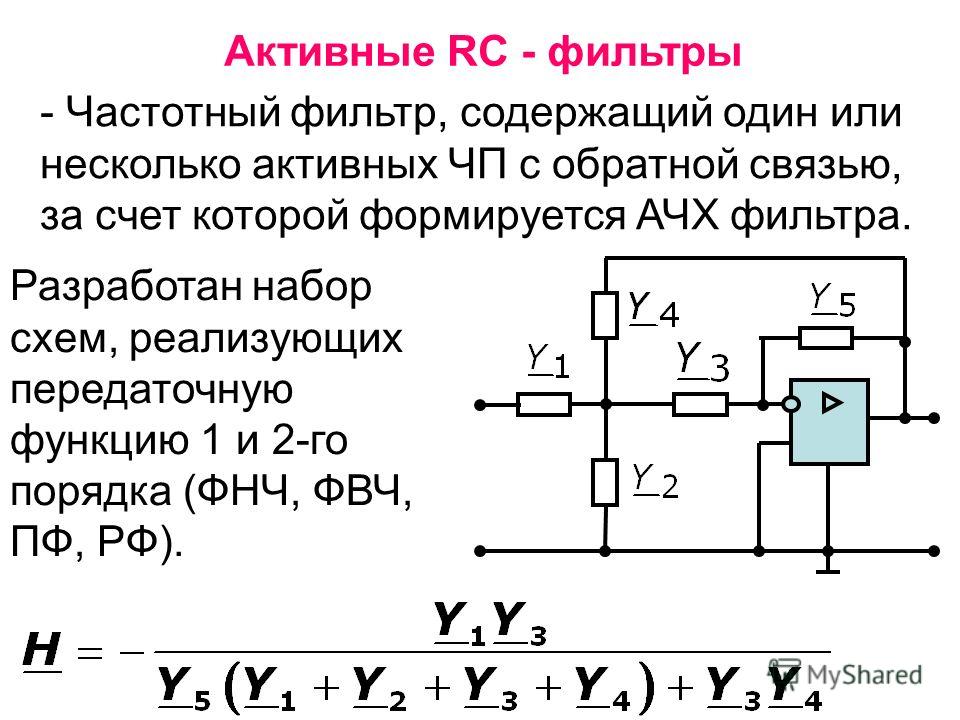 Общее правило для времени установления заключается в том, что чем больше фильтр приближается к приближению «кирпичной стены», тем больше времени требуется для установления. Таким образом, восьмиполюсный фильтр будет устанавливаться дольше, чем четырехполюсный фильтр.
Общее правило для времени установления заключается в том, что чем больше фильтр приближается к приближению «кирпичной стены», тем больше времени требуется для установления. Таким образом, восьмиполюсный фильтр будет устанавливаться дольше, чем четырехполюсный фильтр.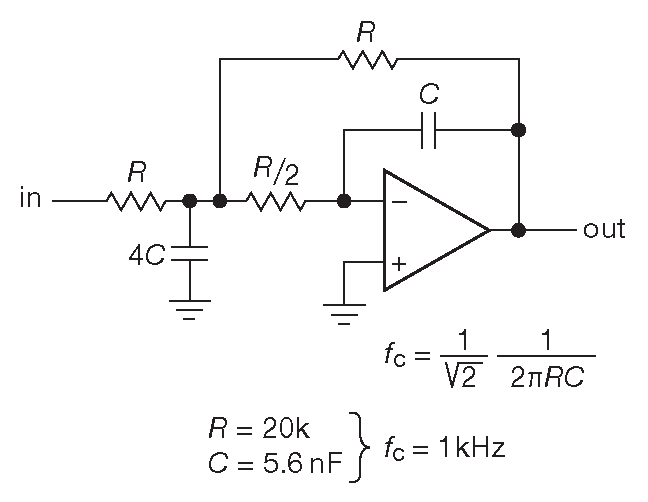 Для программируемых фильтров смещение постоянного тока может варьироваться в зависимости от настроек частоты среза.
Для программируемых фильтров смещение постоянного тока может варьироваться в зависимости от настроек частоты среза.
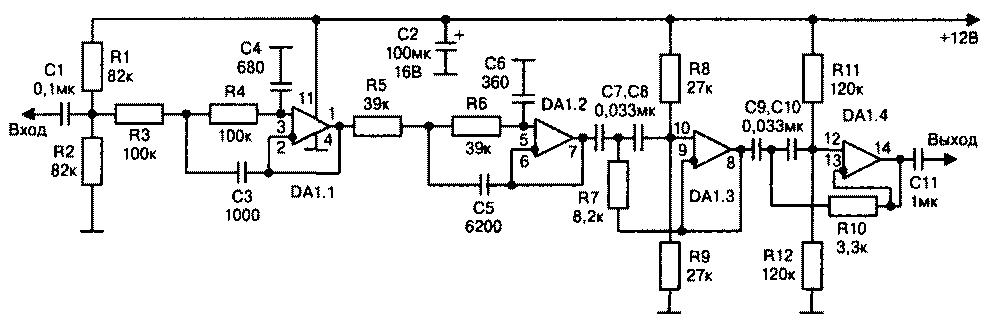 Это среднеквадратическая сумма отдельных гармонических искажений (например, 2 и , 3 и , — и т. д.), которые создаются нелинейностями активных и пассивных компонентов в цепи, когда она управляется чистый синусоидальный вход с заданной амплитудой и частотой.
Это среднеквадратическая сумма отдельных гармонических искажений (например, 2 и , 3 и , — и т. д.), которые создаются нелинейностями активных и пассивных компонентов в цепи, когда она управляется чистый синусоидальный вход с заданной амплитудой и частотой.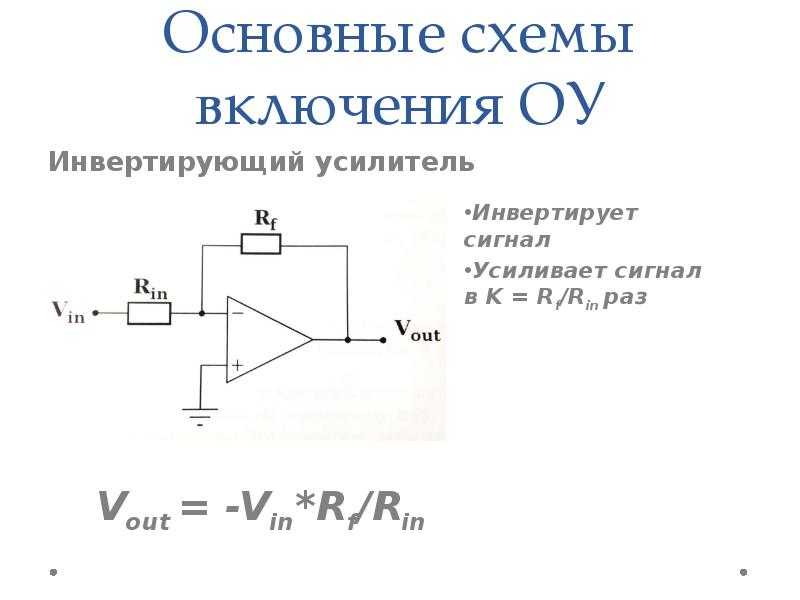 Однако это измерение также будет включать любой шум, который находится в пределах полосы пропускания измерителя и обычно упоминается как THD + NOISE или THD + N.
Однако это измерение также будет включать любой шум, который находится в пределах полосы пропускания измерителя и обычно упоминается как THD + NOISE или THD + N.
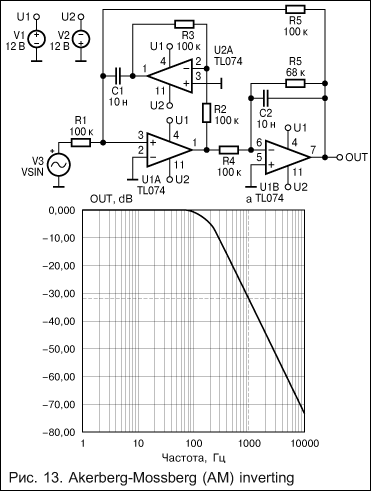 Спектральный анализ, например, включает только амплитуду каждой частотной составляющей входного сигнала. Большая часть передачи голоса и данных также требует целостности только амплитуд, как и многие формы модального анализа, который определяет резонансные частоты структур и объектов.
Спектральный анализ, например, включает только амплитуду каждой частотной составляющей входного сигнала. Большая часть передачи голоса и данных также требует целостности только амплитуд, как и многие формы модального анализа, который определяет резонансные частоты структур и объектов.