Работа силы равна формула. Механическая работа
Энергия — универсальная мера различных форм движения и взаимодействия. Изменение механического движения тела вызывается силами , действующими на него со стороны других тел. Работы силы — процесс обмена энергией между взаимодействующими телами.
Если на тело движуещаеся прямолинейно действует постоянная сила F, которая составляет некоторый угол с направлением перемещения, то работа этой силы равна произведению проекции силы F s на направление перемещения, умноженной на перемещение точки приложения силы: (1)
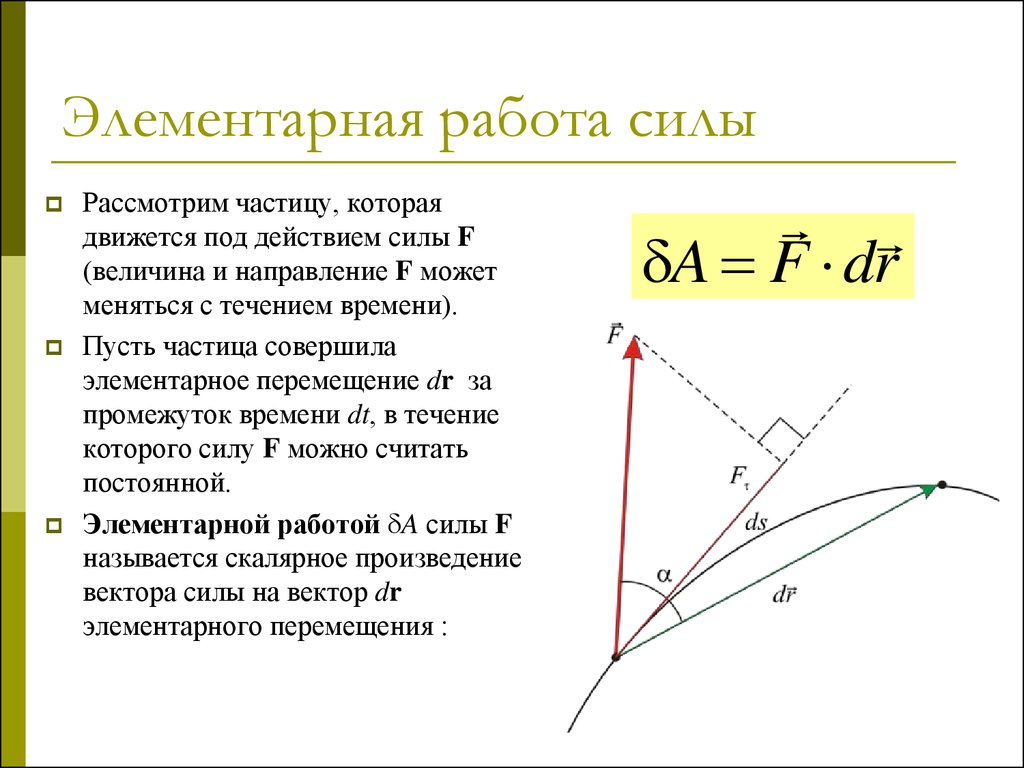
В бщем случае сила может изменяться как по модулю, так и по направлению, поэтому скалярная величина элементарной работоы силы F на перемещении dr:
где — угол между векторами F и dr; ds = |dr| — элементарный путь; F s — проекция вектора F на вектор dr рис. 1
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути: (2)
где s — пройденный телом. При /2
работа силы отрицательна. При =/2
(сила перпендикулярна перемещению)
работа силы равна нулю.
При /2
работа силы отрицательна. При =/2
(сила перпендикулярна перемещению)
работа силы равна нулю.
Единица работы — джоуль (Дж): работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н м).
Мощность – величина скорости совершения работы: (3)
За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент ремени:(4)
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.
Единица мощности — ватт
Кинетическая и потенциальная энергии
Кинетическая энергия механической системы — энергия механического движения этой системы.
Сила
F, действуя на покоящееся тело и вызывая
его движение, совершает работу, а изм-е
энергии движущегося тела(dT ) возрастает на величину затраченной
работы dA . Т. е. dA
= dТ
Т. е. dA
= dТ
Используя второй закон Ньютона(F=mdV/dt) и ряд др-х преобразований получаем
(5) — кинетическая энергия тела массой m, движущееся со скоростью v .
Кинетическая энергия зависит только от массы и скорости тела.
В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Т. о., кинетическая энергия зависит от выбора системы отсчета.
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
В сл-е взаимодействия тел осуществл-х посредством силовых полей(поля упругих, гравитационных сил), работа, совершаемая действующими силами при перемещении тела, не зависит от траектории этого перемещения, а зависит только от начального и конечного положений тела. Такие поля называются
 Если же работа, совершаемая силой,
зависит от траектории перемещения тела
из одной точки в другую, то такая сила
называется диссипативной (сила
трения). Тело, находясь в потенциальном
поле сил, обладает потенциальной энергией
П. Работа консервативных сил при
элементарном(бесконечно малом) изменении
конфигурации системы равна приращению
потенциальной энергии, взятому со знаком
минус: dA=
— dП
(6)
Если же работа, совершаемая силой,
зависит от траектории перемещения тела
из одной точки в другую, то такая сила
называется диссипативной (сила
трения). Тело, находясь в потенциальном
поле сил, обладает потенциальной энергией
П. Работа консервативных сил при
элементарном(бесконечно малом) изменении
конфигурации системы равна приращению
потенциальной энергии, взятому со знаком
минус: dA=
— dП
(6)Работа dA — скалярное произведение силы F на перемещение dr и выражение (6) можно записать: Fdr= -dП (7)
При расчётах потенциальную энергию тела в каком-то определенном положении считают равной нулю(выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня.
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна (8)
где
высота h отсчитывается от нулевого уровня, для
которого П 0 =0.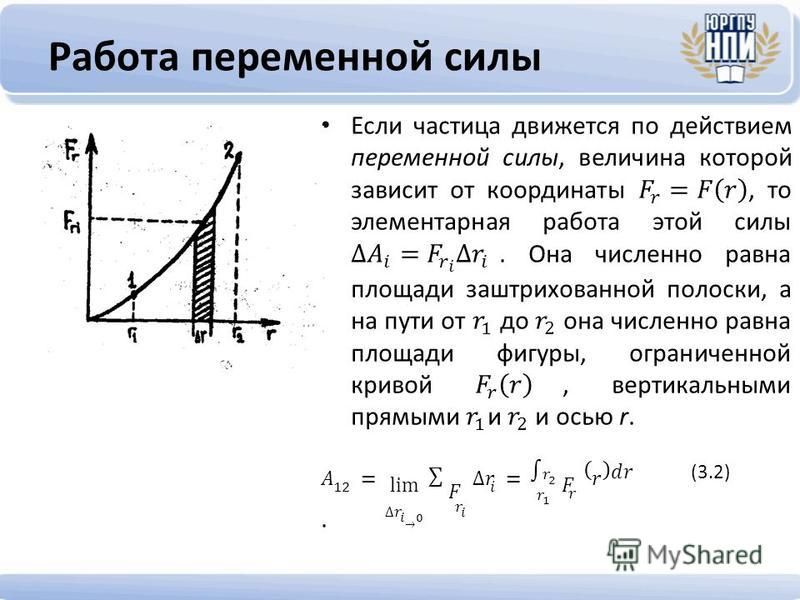
Т. к. начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение(кинетическая энергия всегда положительна!).
Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы равна сумме кинетической и потенциальной энергий: E=T+П.
Одно из важнейших понятий механики – работа силы .
Работа силы
Все физические тела в окружающем нас мире приводятся в движение с помощью силы. Если на движущееся тело в попутном или противоположном направлении действует сила или несколько сил со стороны одного или нескольких тел, то говорят, что

То есть, механическая работу совершает действующая на тело сила. Так, сила тяги электровоза приводит в движение весь поезд, тем самым совершая механическую работу. Велосипед приводится в движение мускульной силой ног велосипедиста. Следовательно, эта сила также совершает механическую работу.
В физике работой силы называют физическую величину, равную произведению модуля силы, модуля перемещения точки приложения силы и косинуса угла между векторами силы и перемещения.
A = F · s · cos (F, s) ,
где F модульсилы,
s – модуль перемещения.
Работа совершается всегда, если угол между ветрами силы и перемещения не равен нулю. Если сила действует в направлении, противоположном направлению движения, величина работы имеет отрицательное значение.
Работа не совершается, если на тело не действуют силы, или если угол между приложенной силой и направлением движения равен 90 о (cos
90 o
= 0).
Если лошадь тянет телегу, то мускульная сила лошади, или сила тяги, направленная по ходу движения телеги, совершает работу. А сила тяжести, с которой извозчик давит на телегу, работы не совершает, так как она направлена вниз, перпендикулярно направлению перемещения.
Работа силы – величина скалярная.
Единица работы в системе измерений СИ — джоуль. 1 джоуль – это работа, которую совершает сила величиной в 1 ньютон на расстоянии 1 м, если направления силы и перемещения совпадают.
Если на тело или материальную точку действуют несколько сил, то говорят о работе, совершаемой их равнодействующей силой.
В случае, если приложенная сила непостоянна, то её работа вычисляется как интеграл:
Мощность
Сила, приводящая в движение тело, совершает механическую работу. Но как совершается эта работа, быстро или медленно, иногда очень важно знать на практике. Ведь одна и та же работа может быть совершена за разное время. Работу, которую выполняет большой электромотор, может выполнить и маленький моторчик.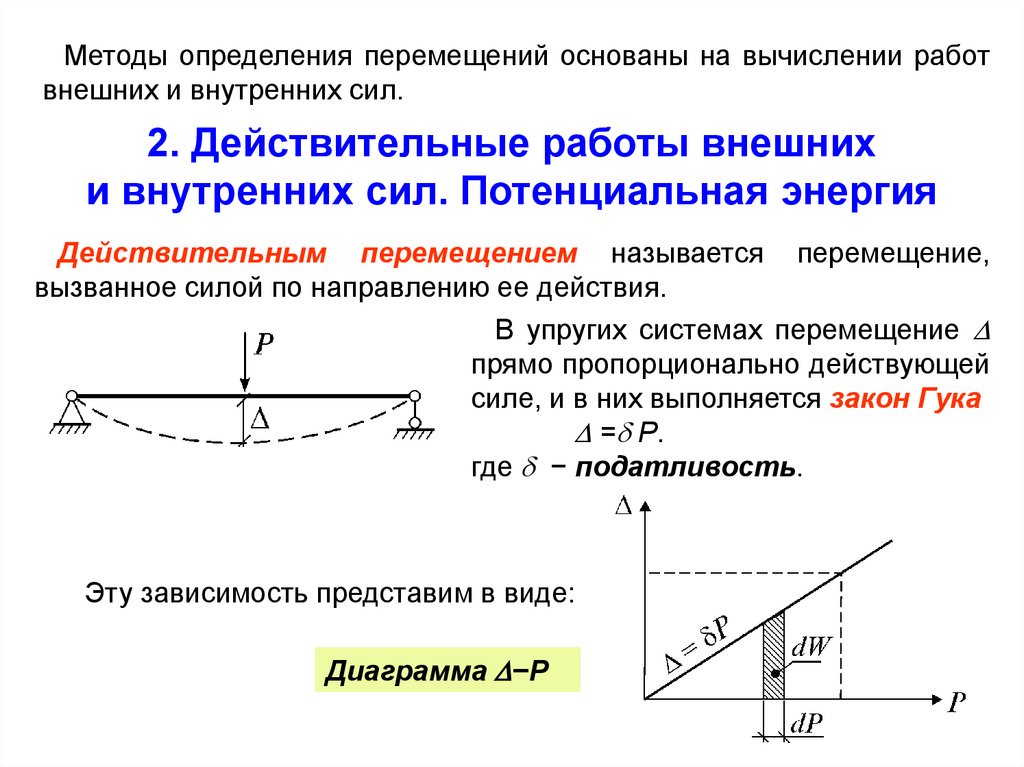 Но ему для этого понадобится гораздо больше времени.
Но ему для этого понадобится гораздо больше времени.
В механике существует величина, характеризующая быстроту выполнения работы. Эта величина называется мощностью .
Мощность – это отношение работы, выполненной за определённый промежуток времени, к величине этого промежутка.
По определению А = F · s · cos α , а s/∆ t = v , следовательно
N = F · v · cos α = F · v ,
где F – сила, v скорость, α – угол между направлением силы и направление скорости.
То есть мощность – это скалярное произведение вектора силы на вектор скорости движения тела .
В международной системе СИ мощность измеряется в ваттах (Вт).
Мощность в 1 ватт – это работа в 1 джоуль (Дж), совершаемая за 1 секунду (с).
Мощность можно увеличить, если увеличить силу, совершающую работу, или скорость, с которой эта работа совершается.
Основные теоретические сведения
Механическая работа
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы . Работой, совершаемой постоянной силой F , называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S :
Работа является скалярной величиной. Она может быть как положительна (0° ≤
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (F упр = kx ).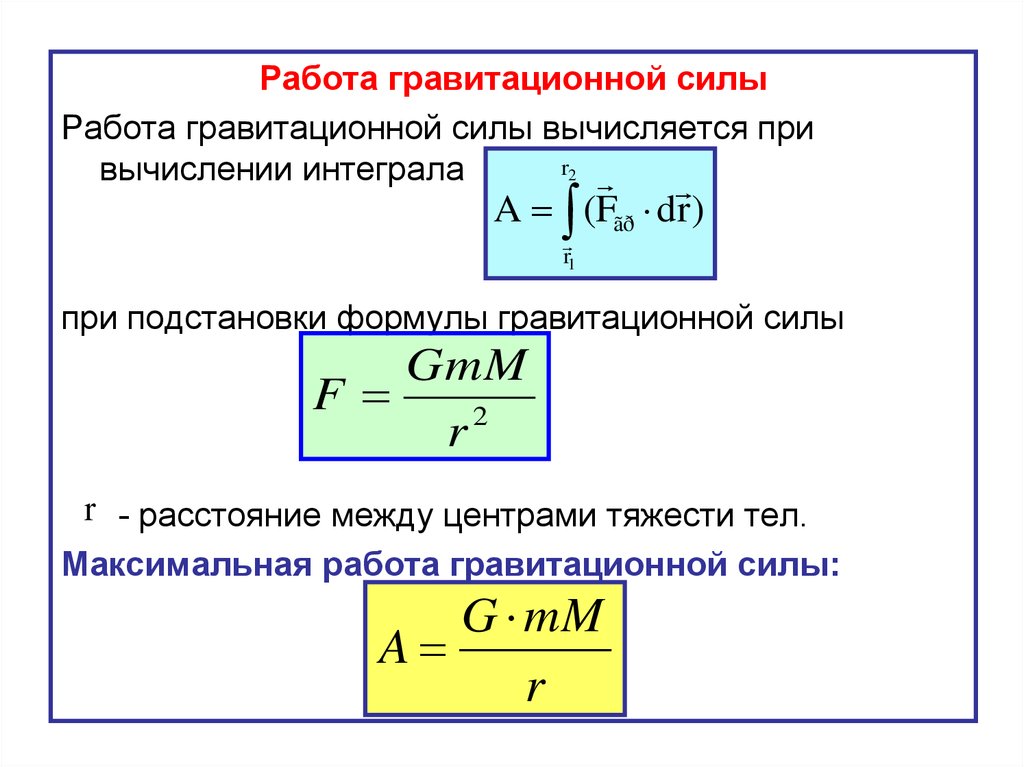
Мощность
Работа силы, совершаемая в единицу времени, называется мощностью . Мощность P (иногда обозначают буквой N ) – физическая величина, равная отношению работы A к промежутку времени t , в течение которого совершена эта работа:
По этой формуле рассчитывается средняя мощность , т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
КПД – коэффициент полезного действия , равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:
Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.
Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).
В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Кинетическая энергия
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения) :
То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Е к = 100 кДж и способен совершить работу в 100 кДж.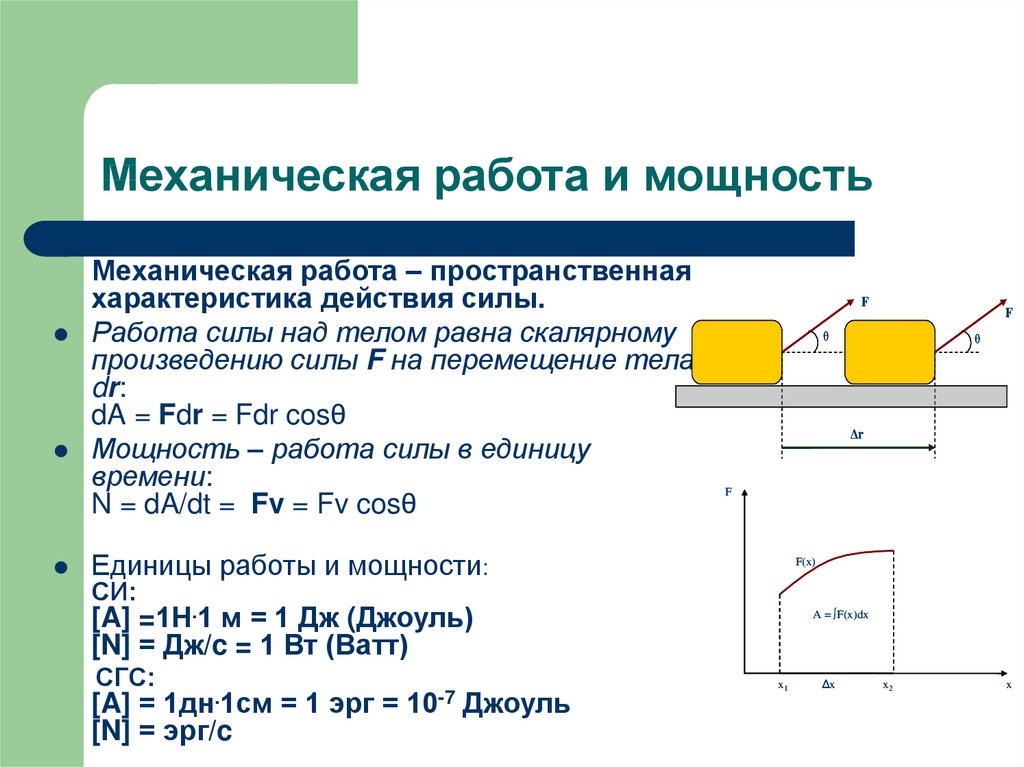 Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v , то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.
Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.
Потенциальная энергия
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел .
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы ). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x 1 , тогда при переходе в новое состояние с удлинением x 2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы ). Понятие потенциальной энергии для силы трения вводить нельзя.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.
В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.
Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.
Закон сохранения механической энергии
Полной механической энергией называется сумма кинетической энергии (т. е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:
Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах . Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Алгоритм решения задач на закон сохранения энергии:
- Найти точки начального и конечного положения тела.
- Записать какой или какими энергиями обладает тело в данных точках.
- Приравнять начальную и конечную энергию тела.
- Добавить другие необходимые уравнения из предыдущих тем по физике.
- Решить полученное уравнение или систему уравнений математическими методами.
Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.
Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии .
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Разные задачи на работу
Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:
- Работу можно найти по формуле: A = FS ∙cosα .
 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения. - Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
- Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh , где h – высота, на которую поднимается центр тяжести тела .
- Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt .
- Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.
Закон сохранения энергии и динамика вращательного движения
Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
Решение будет сводиться к следующей последовательности действий:
- Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
- Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
- Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
- В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
- Провести остальные необходимые математические операции для получения окончательного результата.
При решении задач надо помнить, что:
- Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.

- При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
- Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.
Неупругие соударения
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары .
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).
Абсолютно упругий удар
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
Законы сохранения. Сложные задачи
Несколько тел
В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.
Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:
- выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
- записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
- учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
- при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда
В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.
Столкновения с тяжёлой плитой
Пусть навстречу тяжёлой плите, которая движется со скоростью v , движется лёгкий шарик массой m со скоростью u н. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты . В таком случае, для конечной скорости шарика получим:
Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
По физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ.
 После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами. - Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называетсязамкнутой .
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьегозаконов Ньютона.
Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через и По третьему закону Ньютона Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: Применим к этим телам второй закон Ньютона:
где
и
–
импульсы тел в начальный момент времени,
и
–
импульсы тел в конце взаимодействия. Из этих соотношений следует:
Из этих соотношений следует:
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, то есть векторную сумму импульсов всех тел, входящих в эту систему.
Механическая работа и мощность
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения (рис. 1.1.9):
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
Если проекция силы на направление перемещения не остается постоянной, работу следует вычислять для малых перемещений и суммировать результаты:
Примером силы, модуль
которой зависит от координаты, может
служить упругая сила пружины, подчиняющаяся закону Гука . Для того, чтобы растянуть
пружину, к ней нужно приложить внешнюю
силу
модуль
которой пропорционален удлинению
пружины (рис. 1.1.11).
Для того, чтобы растянуть
пружину, к ней нужно приложить внешнюю
силу
модуль
которой пропорционален удлинению
пружины (рис. 1.1.11).
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.1.12).
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы равна по модулю работе внешней силы и противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами, и равна работе равнодействующей приложенных сил.
Работа силы, совершаемая в единицу времени, называется мощностью . Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа.
Формула работы в физике
Содержание:
- Определение и формула работы
- Элементарная работа
- Работа силы на конечном участке траектории
- Единицы измерения работы
- Примеры решения задач
Определение и формула работы
Определение
В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила
совершает работу. {2}}{2}(1)$$
{2}}{2}(1)$$
Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи величины перемещения, которое совершает рассматриваемое тело под действием силы ($\bar{F}$).
Элементарная работа
Элментарная реабота $(\delta A)$ некоторой силы $\bar{F}$ определяется как скалярное произведение:
$$\delta A=\bar{F} \cdot d \bar{r}=F \cdot d s \cdot \cos \alpha(2)$$
$\bar{r}$ радиус – вектор точки, к которой приложена сила, $\bar{r}$ — элементарное перемещение точки по траектории, $\alpha$ – угол между векторами $d s=|d \bar{r}|$ и $d \bar{r}$. Если $\alpha$ является тупым углом работа меньше нуля, если угол $\alpha$ острый, то работа положительная, при $\alpha=\frac{\pi}{2} \delta A=0$
В декартовых координатах формула (2) имеет вид:
$$\delta A=F_{x} d x+F_{y} d y+F_{z} d z(3)$$
где Fx,Fy,Fz – проекции вектора
$\bar{F}$ на декартовы оси. {n} \bar{F}_{i} \bar{v}_{i} d t(5)$$
{n} \bar{F}_{i} \bar{v}_{i} d t(5)$$
где проводится суммирование элементарных работ всех сил, dt – малый промежуток времени, за который совершается элементарная работа $\delta$ над системой.
Результирующая работа внутренних сил, даже если твердое тело движется, равна нулю.
Пусть твердое тело вращается около неподвижной точки — начала координат (или неподвижной оси, которая проходит через эту точку). В таком случае, элементарная работа всех внешних сил (допустим, что их число равно n), которые действуют на тело, равна:
$$\delta A=\bar{M} \bar{\omega} d t=\bar{M} d \bar{\varphi}(6)$$
где $\bar{M}$ – результирующий момент сил относительно точки вращения, $d \bar{\varphi}$ – вектор элементарного поворота, $\bar{w}$ – мгновенная угловая скорость.
Работа силы на конечном участке траектории
Если сила выполняет работу по перемещению тела на конечном участке траектории его движения, то работа может быть найдена как:
$$A=\int_{0}^{s} \bar{F} \cdot d \bar{r}(7)$$
В том случае, если вектор силы – величина постоянная на всем отрезке перемещения, то:
$$A=F_{\tau} \cdot s$$
где $F_{\tau}=F \cos \alpha$ – проекция силы на касательную к траектории. {4}$$
{4}$$
Ответ. n=4
Читать дальше: Формула силы Ампера.
Работа силы. Теорема об изменении кинетической энергии материальной точки. Частные случаи вычисления работы силы
Механика \ Теоретическая механика
Страницы работы
6 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
Работа силы.
Для того, чтобы рассмотреть теорему об изменении кинетической энергии, необходимо ввести новое понятие для силы – работу силы. Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении.
Пусть на материальное тело действует сила . Элементарная работа силы определяется выражением:
, (1)
где — алгебраическая величина проекции силы на
касательную в данной точке траектории, G – траекторная
координата.
Но , где — орт касательной, так как из кинематики точки известно, что , а , где — радиус-вектор.
Сила в проекциях на оси декартовой системы координат 0xyz:
, то есть
Элементарная работа силы окончательно определяется равенством:
(2)
Так как , где — радиус-вектор точки, то (2) может быть записано в форме скалярного произведения:
(3)
Так как , то
(4)
Элементарная работа силы может иметь еще одно выражение. Известно, что путь S, пройденный материальной точкой, величина существенно положительная и возрастающая, то есть , где G – траекторная координата (знак «+» — движение материальной точки в сторону положительных траекторных координат, рис. А, знак «-» — в сторону отрицательных, рис. Б).
Из рисунков видно, что (знак «+» — движение материальной точки в сторону положительных траекторных координат, знак «-» — в сторону отрицательных). То есть
(5)
Для определения полной работы силы на
перемещении от до нужно
просуммировать элементарные работы на элементарных перемещениях. В пределе из
(1) получаем криволинейный интеграл.
В пределе из
(1) получаем криволинейный интеграл.
(6)
Из (6)-(10) следует, что работа силы – скалярная (положительная или отрицательная) физическая величина, характеризующая действие этой силы на некотором конечном перемещении материальной точки. Аналогично:
(7)
(8)
(9)
— в этом случае криволинейный сводится к обычному определенному .
(10)
Из (10) следует, что если сила, действующая на материальную точку, перпендикулярна скорости этой точки во все время движения, то работа этой силы равна 0. Например, при движении материальной точки по горизонтальной плоскости работа силы тяжести этой точки равна 0.
Если сила приложена к точке, скорость которой равна 0, то работа этой силы также равна 0. Примером может служить работа силы трения скольжения, действующей на колесо, катящееся без скольжения по рельсу (точка касания колеса с рельсом – м.ц.е. колеса).
Пусть на материальную точку действует система сил . Из определения элементарной и полной работы следует: работа равнодействующей
системы сил, действующих на материальную точку, на данном перемещении ее равна
сумме работ всех сил данной системы на том же перемещении.
Из определения элементарной и полной работы следует: работа равнодействующей
системы сил, действующих на материальную точку, на данном перемещении ее равна
сумме работ всех сил данной системы на том же перемещении.
, где — работа равнодействующей системы сил, — работа силы данной системы сил.
Теорема об изменении кинетической энергии материальной точки.
Пусть материальная точка М массы m движется под действием системы сил () относительно некоторой системы отсчета по заданной траектории. В начальный момент времени точка занимала положение и имела в этот момент времени скорость . Под действием заданной системы сил материальная точка переместилась в положение М, при этом скорость ее стала равной .
Найдем связь между работой сил, приложенных к материальной точке, и изменением скорости точки. Для этого воспользуемся основным уравнением динамики
, где — равнодействующая всех сил, приложенных к
материальной точке. Умножим обе части его скалярно на дифференциал
радиуса-вектора .
Умножим обе части его скалярно на дифференциал
радиуса-вектора .
(*)
Половина произведения массы точки на квадрат ее скорости называется кинетической энергией материальной точки:
Кинетическая энергия материальной точки – скалярная положительная физическая величина, характеризующая динамическое состояние этой материальной точки в данный момент времени.
(*) – теорема об изменение кинетической энергии материальной точки в дифференциальной форме: полный дифференциал кинетической энергии материальной точки равен элементарной работе всех действующих на эту точку сил.
Проинтегрируем обе части (*) по кривой , получим теорему об изменении кинетической энергии в конечной форме:
(**)
Изменение кинетической энергии материальной точки при переходе ее из
начального в конечное положение равно сумме работ на этом перемещении всех сил,
приложенных к точке.
С помощью этой теоремы можно решать две задачи:
— Определять скорость материальной точки в конце или начале движения. (**) применяют, если работу можно вычислить, не зная закона движения.
— Вычисление работы силы по заданной скорости. (**) применяют, когда неизвестна аналитическая зависимость силы или трудно определить закон движения.
Частные случаи вычисления работы силы.
1. Работа центральной силы. Центральная сила – силы, линия действия которой во все время движения проходит через неподвижный центр (центр силы), а величина зависит от расстояния материальной точки до этого центра. Центральные силы могут быть силами притяжения (рис. А) или силами отталкивания (рис. Б).
, где
(«+» — сила отталкивания, «-» — притяжения), r – длина радиуса-вектора, — его орт.
Работа силы при перемещении материальной точки из в M:
Найдем алгебраические величины проекций силы на оси .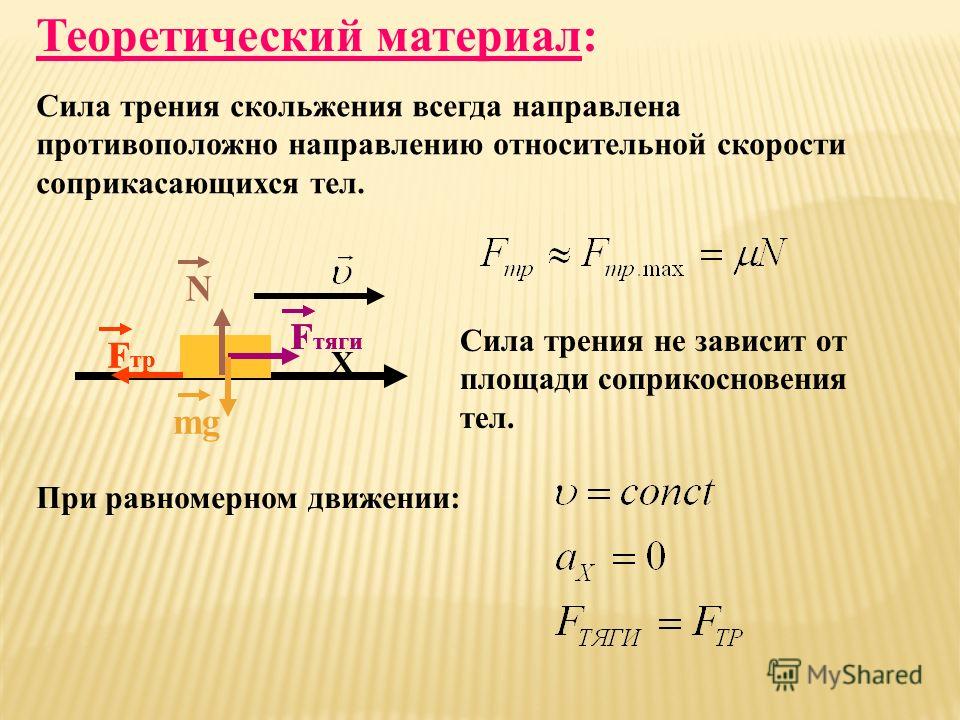
Орт:
Центральная сила:
То есть:
,
так как , то
Окончательно:
— работа центральной силы, переменной по величине и направлению, не зависит от формы траектории, по которой движется точка (а, значит, от длины пути, пройденного ею). А зависит только от начального и конечного положения.
Пример центральной силы – сила упругости пружины, величина которой прямопропорциональна ее удлинению, а линия действия проходит через неподвижную (.) О.
— длина пружины в недеформированном состоянии. Сила упругости , где c – коэффициент жесткости.
,
— удлинение пружины.
2. Работа постоянной по величине силы сопротивления. Сила сопротивления, действующая на материальную точку, направлена в сторону, противоположную скорости этой точки, то есть , где F=Const.
Работу этой силы при перемещении материальной точки из положения в положение M определим по формуле (10). Отсчет начала пути будет
совпадать с , а
Отсчет начала пути будет
совпадать с , а
, то есть работа постоянной по величине силы сопротивления будет зависеть от длины пути, пройденного материальной точкой при перемещении ее из в M.
3. Работа постоянной силы. Пусть на материальную точку действует постоянная сила . Вычислим работу этой силы на некотором перемещении точки из состояния в , .
— работа постоянной силы не зависит от формы траектории или от длины пути, пройденного точкой, а зависит лишь от начального и конечного положения точки на траектории.
Примером постоянной силы может служить сила тяжести. Вблизи поверхности Земли она равна по величине mg и направлена по вертикали вниз.
В системе координат с осью Z, направленной вертикально вверх, и плоскостью x0y горизонтальной, составляющие силы тяжести и работа силы при перемещении точки из положения в положение —
Работа будет положительной, если материальная точка движется вниз, и
отрицательной при ее движении вверх.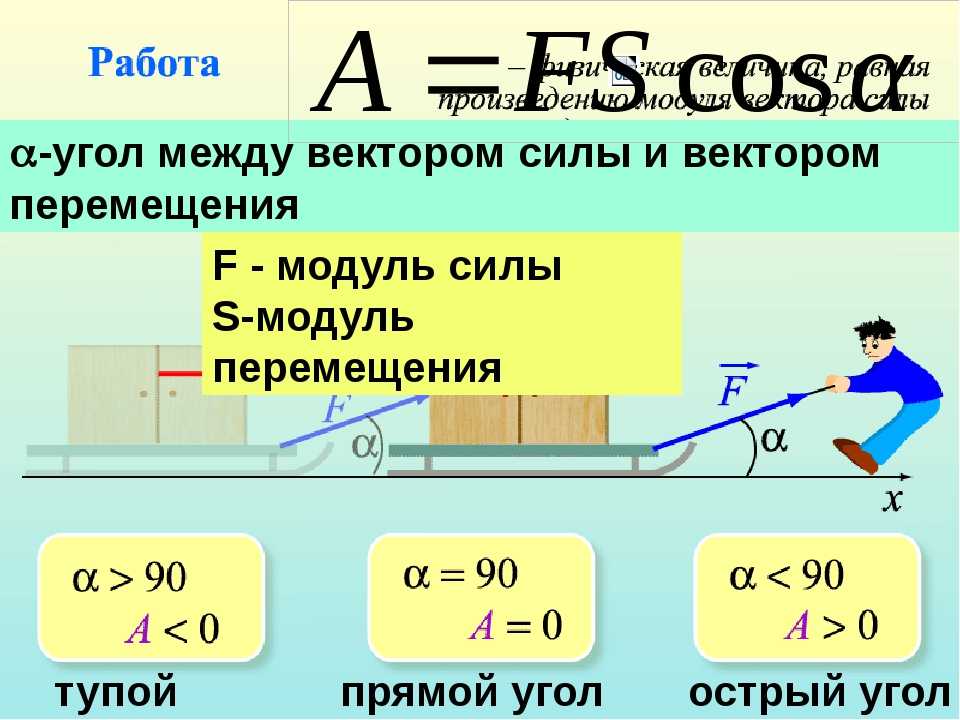
По виду производимой ими работы силы можно разделить на два класса. Консервативными называются силы, работа которых не зависит ни от формы траектории, ни от пути, проходимого точкой приложения силы, а зависит от начального и конечного положения этой точки. Силы, неудовлетворяющие этому условию, называются неконсервативными.
Похожие материалы
Информация о работе
Скачать файл
Q7 Напишите выражение для работы силы…
Перейти к
- Объективные вопросы
- Вопросы с короткими/длинными ответами
- Числа
- Иметь значение
- Физические величины и измерения
- Сила и давление
- Энергия
- Световая энергия
- Теплопередача
- Звук
- Электричество
Главная > Селина Солюшнс Класс 8 Физика > Глава 4 — Энергия > Упражнение: Вопросы с короткими/длинными ответами > Вопрос 7
Вопрос 7 Вопросы с короткими/длинными ответами
Q7) Запишите выражение для работы силы.
Ответ:
Решение:
Работа, совершенная приложением силы F, равна произведению силы, приложенной к телу, на расстояние, пройденное телом в направлении действия силы силы.
W = F \times D
Стенограмма видео
Добро пожаловать в Lido Learning’s
Вопрос:
и отвечайте на видео, теперь у нас есть
интересный вопрос перед нами
мы должны написать выражение для работы.
сделано
сила сейчас, чтобы понять это, давайте
взгляните на диаграмму ниже
мы так у нас есть тело
эта красная коробка-это наше тело да
и находится в положении а
мы прикладываем силу f, так что f
это сила здесь позвольте мне написать, что
вниз
так вынужден
это f и
это исходное положение
тело
то что происходит, когда мы применяем
заставить тело
перемещается в новое положение b или тело
идет в этом направлении
правильно и это конечная позиция или
Это
смещается, чтобы быть таким телом
смещается
из исходного положения вправо на b
от своего исходного положения
от а до б и сколько смещение
это d, мы также можем написать это как
столица д
или как вам нравится, так что это
расстояние или перемещение тела
правильно так работа сделана так что когда
к телу приложена сила
смещение
говорят, что в теле совершается работа
Итак, если к телу приложена сила f и
расстояние
или смещение тела
скажем д тогда работай
w задается как f
в d как видно здесь работа
Выполнено
равно силе в смещении
или расстояние, пройденное в этом направлении
силы
Таким образом, работа, совершаемая приложением силы f, равна
произведение силы, приложенной к телу
и расстояние, пройденное телом за
направление силы
поэтому ответ на наш вопрос
проделанная работа выражается как принуждение к
смещение
единица си для проделанной работы — это единица си
выполненной работы в джоулях также обозначается
с большой буквы, поэтому я надеюсь, что эта часть была
ясность и концепция работы, а также
понял
если у вас есть дополнительные вопросы, пожалуйста
размещайте свои комментарии ниже
Спасибо.
Связанные вопросы
Q1) Дайте определение работе.
2) Когда сила совершает работу?
Q3) Укажите два условия, при которых сила не совершает работу.
В4) В каком из следующих случаев совершается работа: а) мальчик толкает камень; б) мальчик карабкается…
Q5) Кули едет по дороге с багажом на голове. Совершает ли он работу против силы…
Q6) Луна вращается вокруг Земли по круговой траектории. Какую работу совершает Луна?
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Objective Questions
Short/Long Answer Questions
Numericals
Chapters
Matter
Physical Quantities and Measurement
Force and Pressure
Energy
Light Energy
Heat Transfer
Sound
Электричество
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Работа
Работа Чтобы совершить работу над объектом, к объекту должна быть приложена сила, и он должен двигаться в направлении действия силы. В частном случае постоянной силы работа может быть рассчитана путем умножения расстояния на компонент силы, действующей в направлении движения. | Индекс Принципы работы | ||
| Назад |
Чтобы совершить работу над объектом, к объекту должна быть приложена сила, и он должен двигаться в направлении действия силы. 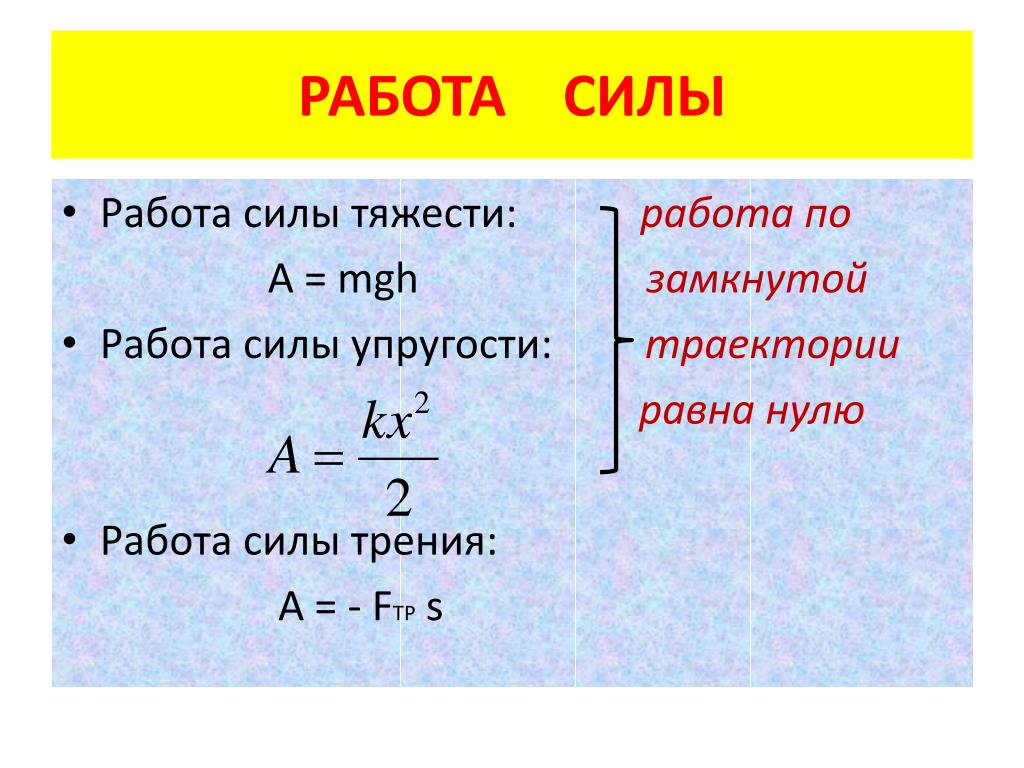 Данные в трех полях не будут принудительно согласованы, пока вы не нажмете на количество, которое нужно рассчитать. Работа =
N х
м =
Джоули Данные в трех полях не будут принудительно согласованы, пока вы не нажмете на количество, которое нужно рассчитать. Работа =
N х
м =
Джоули Работа = фунт х футов = фут фунт В частном случае постоянной силы работа может быть рассчитана путем умножения расстояния на компонент силы, действующей в направлении движения. | Индекс Принципы работы | ||
| Назад |
Для постоянной силы F, которая перемещает объект по прямой линии от x 1 до x 2 , работу силы можно изобразить как площадь, заключенную под силовой линией ниже Для более общего случая переменной силы F(x), которая является функцией x, работа по-прежнему является площадью под кривой силы, и выражение работы становится интегралом. | Индекс Принципы работы | ||
| Назад |
Сила без движения или сила, перпендикулярная движению, не работает Эти два примера сил, не совершающих работы, парадоксальны. Вы, конечно, можете чувствовать себя утомленным, когда делаете что-то из этого, так как же вы можете сказать, что работа не сделана? В случае слева, независимо от того, как сильно и как долго вы толкали ящик, если ящик не двигается, значит, вы не выполнили над ящиком никакой работы. Он сидит на том же месте! Почему же тогда вы чувствуете усталость (а также разочарование и т. д.). Решение этой дилеммы приходит к выводу, что, когда ваши мышцы используются для приложения силы к чему-либо, отдельные мышечные волокна находятся в постоянном процессе сокращения и расслабления, чтобы поддерживать общий коллективный результат постоянной силы, воздействующей на внешний объект. Пример справа — еще один стандартный парадокс в определении работы. Если ящик несут с постоянной скоростью, то нет необходимости в результирующей силе, чтобы удерживать его в движении. Сила, приложенная человеком, представляет собой направленную вверх силу, равную весу ящика, и эта сила перпендикулярна движению. Если нет движения в направлении силы, то эта сила не совершает никакой работы. Тем не менее, вы, безусловно, чувствуете, что выполняете работу, если несете тяжелую коробку. Разрешение парадокса аналогично первому примеру — ваши мышцы должны поддерживать дополнительное напряжение, чтобы оставаться в вертикальном положении под нагрузкой. Это требует большего внутреннего сокращения и высвобождения наших мышечных волокон и, следовательно, внутренней работы нашего тела. Есть много важных примеров сил, которые не совершают работы, потому что они действуют перпендикулярно движению. При круговом движении центростремительная сила всегда действует под прямым углом к движению. Он меняет направление движения, но не действует на объект. Это может быть применено к любой круговой орбите. | Индекс Принципы работы | ||
| Вернуться |
Работа
РаботаРабота
| Определение работы | Тепло и работа | Сохранение энергии | Внутренняя энергия |
| Взаимное превращение тепла и работы | Функции состояния | Калориметр | |
Определение работы
Работа может быть определена как произведение силы, используемой для перемещения
объект, умноженный на расстояние, на которое перемещается объект.
Ш = Ж x Г
Представьте себе систему, состоящую из образца аммиака, запертого в поршне и цилиндре, как показано на рисунке ниже. Предположим, что давление газа, давит на поршень просто уравновешивает вес поршня, так что объем газа остается постоянным. В настоящее время считать, что газ разлагается с образованием азота и водорода, увеличивая количество газа частицы в контейнере. Если температура и давление газа остаются постоянными, это означает, что объем газа должен увеличиться.
2 NH 3 ( г ) N 2 ( г ) + 3 H 2 ( г )
Объем газа можно увеличить, частично вытолкнув поршень из цилиндра.
Совершаемая работа равна произведению силы, действующей на поршень, на
расстояние, на которое перемещается поршень.
Ш = Ж x Г
Давление ( P ), которое газ оказывает на поршень, равно силе (F) с которой он давит на поршень, деленную на площадь поверхности ( A ) поршень.
Таким образом, сила, действующая на газ, равна произведению его давления на площадь поверхности поршня.
F = P x A
Подстановка этого выражения в уравнение, определяющее работу, дает следующее результат.
w = ( P x A ) x d
Произведение площади поршня на расстояние, на которое перемещается поршень, равно изменение объема системы при расширении газа. Условно, изменение объема представлено символом В .
В = А х д
Таким образом, величина работы, совершаемой при расширении газа, равна произведению
давление газа, умноженное на изменение объема газа.
| с | = П В
Джоуль — измерение теплоты и работы
По определению, один джоуль — это работа, совершаемая, когда сила в один ньютон используется для перемещения объект один метр.
1 Дж = 1 Н·м
Поскольку работа может быть преобразована в теплоту и наоборот, система СИ использует джоуль для измерять энергию в виде теплоты и работы.
Первый закон термодинамики: сохранение Энергия
Первый закон термодинамики гласит, что энергия не может быть создана или
уничтожен. Система может получать или терять энергию. Но любое изменение энергии системы
должно сопровождаться эквивалентным изменением энергии его окружения, потому что
полная энергия Вселенной постоянна. Первый закон термодинамики можно описать
следующим уравнением.
E универсальный = E сис + E доп. = 0
(Индексы univ , sys и surr обозначают вселенную, системы и ее окружения.)
Внутренняя энергия
Энергию системы часто называют внутренней энергией , потому что она представляет собой сумму кинетической и потенциальной энергий частиц, образующих систему. Потому что отсутствие взаимодействия между частицами, единственный вклад во внутреннюю энергию идеального газа есть кинетическая энергия частиц. Внутренняя энергия идеального газа равна следовательно, прямо пропорциональна температуре газа.
(В этом уравнении R — постоянная идеального газа, а T — температура газа в единицах Кельвина.)
Хотя трудно, если вообще возможно, написать уравнение для более сложных
системы, внутренняя энергия системы по-прежнему прямо пропорциональна ее
температура. Поэтому мы можем использовать изменения температуры системы для мониторинга.
изменение его внутренней энергии.
Поэтому мы можем использовать изменения температуры системы для мониторинга.
изменение его внутренней энергии.
Величина изменения внутренней энергии системы определяется как разница между начальным и конечным значениями этой величины.
Е сис = E окончательный — E начальный
Поскольку внутренняя энергия системы пропорциональна ее температуре, E положительна при повышении температуры системы.
Первый закон термодинамики: взаимопревращение тепла и работы
Энергия может передаваться между системой и ее окружением до тех пор, пока энергия энергия, полученная одним из этих компонентов Вселенной, равна энергии, потерянной Другой.
Е сис = — E закр
Энергия может передаваться между системой и ее окружением в виде либо
тепло ( q ) или рабочий ( w ).
Е сис = ч + ш
Когда тепло поступает в систему, это может привести к повышению температуры системы или Работа.
q = E сис — ш
Правила знаков для связи между внутренней энергией системы и тепла , которое пересекает границу между системой и ее окружением, задано на рисунке ниже.
- Когда тепло, поступающее в систему, увеличивает температуру системы, внутренний энергия системы возрастает, и E положительный.
- Когда температура системы снижается из-за выхода тепла из системы, E отрицательно.
Соглашение о знаках для отношения между работой и внутренней энергией система показана в левой части рисунка ниже.
- Когда система воздействует на окружающую среду, энергия теряется, и E отрицательно.

- Когда окружающая среда работает над системой, внутренняя энергия системы становится больше, поэтому E положительный.
Соотношение между величиной работы, совершаемой системой при ее расширении, и изменение объема системы ранее описывалось следующим уравнением.
| с | = П В
На приведенном выше рисунке показано, что можно включить соглашение о знаках для работы расширения. записав это уравнение следующим образом.
w = — P В
Функции состояния
Когда уравнения связывают два или более свойств, описывающих гос. системы, они называются уравнениями состояния . Например, закон идеального газа уравнение состояния.
PV = нРТ
Функция состояния s зависит только от состояния системы, а не от
путь, используемый для достижения этого состояния.
Температура является функцией состояния. Сколько бы раз мы ни нагревали, ни охлаждали, ни расширяли, сжать или иным образом изменить систему, чистое изменение температуры зависит только от на начальное и конечное состояния системы.
Т = T окончательный — T начальный
То же самое можно сказать об объеме, давлении и числе молей газа в образец. Все эти величины являются функциями состояния.
Теплота и работа являются , а не функциями состояния. Работа не может быть функцией государства, потому что она
пропорциональна расстоянию, на которое перемещается объект, которое зависит от пути, по которому он двигался
от начального до конечного состояния. Если работа не является функцией состояния, то теплота не может быть
государственная функция либо. Согласно первому закону термодинамики изменение
внутренняя энергия системы равна сумме переданной теплоты и работы
между системой и ее окружением.
Е сис = ч + ш
Если Е зависит не от пути перехода от начального состояния к конечному, а от количества работы зависит от используемого пути, количество отдаваемой или поглощаемой теплоты должно зависеть на пути.
Термодинамические свойства системы, являющиеся функциями состояния обычно обозначаются заглавными буквами ( T , V , P , E и так далее на). Термодинамические свойства, не являющиеся функциями состояния, часто описываются формулой строчные буквы ( q и w ).
| Практическая задача 3: Что из следующего свойства газа являются функциями состояния? (а) Температура, T (б) Объем, В (с) Давление, P (d) Количество молей газа, n (e) Внутренняя энергия, E Нажмите здесь, чтобы проверить свой ответ на практическое задание 3 |
Измерение тепла с помощью калориметра
Количество теплоты, выделяемой или поглощаемой в ходе химической реакции, можно измерить с помощью
калориметр, как показано на рисунке ниже.
Поскольку реакция происходит в закрытом сосуде при постоянном объеме, никакая работа расширение происходит во время реакции. Теплота, выделяемая или поглощаемая в результате реакции, равна равно изменению внутренней энергии системы за время реакция:
Е сис = q V .
Количество теплоты, отдаваемое или поглощаемое водой в калориметре, может быть рассчитывается исходя из теплоемкости воды.
| Практическая задача 4: Природный газ в метан реагирует с кислородом с образованием углекислого газа и воды. CH 4 ( г ) + 2 O 2 ( г ) CO 2 ( г ) + 2 H 2 O( ) Рассчитайте теплоту, выделяющуюся при взаимодействии 0,160 г метана с избытком кислорода в
бомбовый калориметр, если температура 1000 кг воды в ванне, окружающей
бомба увеличивается на 1,918 или С. |


 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.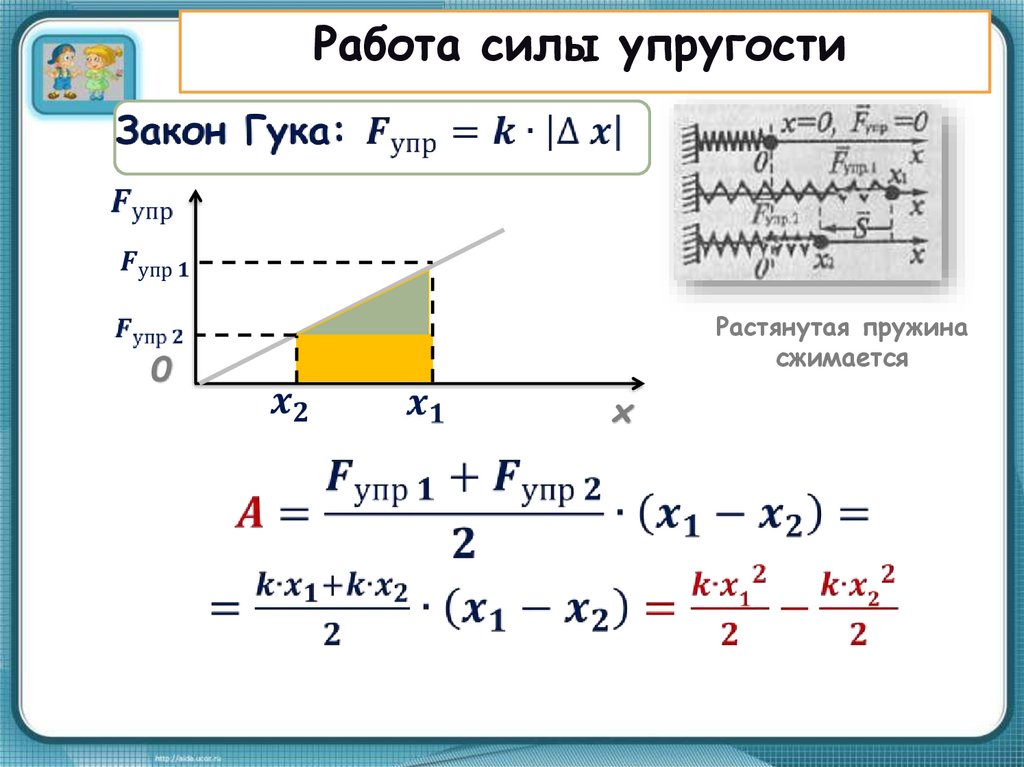

 После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами. Для выполнения работы требуется энергия, и основной единицей энергии в СИ является джоуль, количество энергии, необходимое для приложения силы в 1 ньютон на расстояние 1 метр (1 джоуль = 1 ньютон-метр).
Для выполнения работы требуется энергия, и основной единицей энергии в СИ является джоуль, количество энергии, необходимое для приложения силы в 1 ньютон на расстояние 1 метр (1 джоуль = 1 ньютон-метр).
 Это сокращение и расслабление включает в себя силу и движение и представляет собой внутреннюю работу в вашем теле. Энергия проявляется как разогрев мышечной ткани, но если ящик не движется, в ящике по-прежнему нет чистой работы.
Это сокращение и расслабление включает в себя силу и движение и представляет собой внутреннюю работу в вашем теле. Энергия проявляется как разогрев мышечной ткани, но если ящик не движется, в ящике по-прежнему нет чистой работы.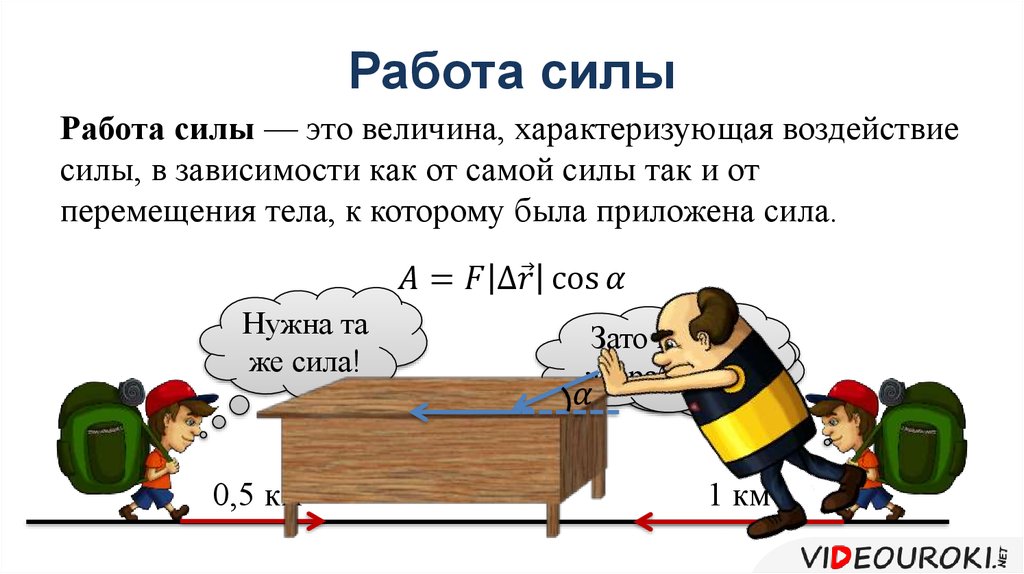 Но работа, совершаемая над ящиком, равна нулю, так как при движении по прямой с постоянной скоростью его энергия остается неизменной.
Но работа, совершаемая над ящиком, равна нулю, так как при движении по прямой с постоянной скоростью его энергия остается неизменной.
