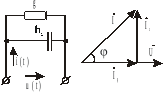
6. Электрическая цепьс соединением r-,l-,c- элементов.
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
по дисциплине «Электротехника и электроника»
для направления подготовки 151000.62 (ИНиГ, III курс, группа 1)
1. Основные законы и методы расчёта цепей постоянного тока
2. Расчёт электрической цепи постоянного тока методом контурных токов
3. Цепь переменного тока с активным и индуктивным сопротивлениями
4. Цепь переменного тока с активным и ёмкостным сопротивлениями
5. Цепь переменного тока с индуктивным и ёмкостным сопротивлениями
6. Электрическая цепь с соединением R-, L-, C – элементов
7. Метод расчета цепи с помощью комплексных чисел
8. Векторные диаграммы для цепей с соединением R-, L-, C – элементов
9. Векторные диаграммы для цепей с соединением R-, L– элементов.
10. Векторные диаграммы для цепей с соединением R-, C – элементов
11. Векторные диаграммы для цепей с соединением L-, C – элементов
12. Резонансные явления в электрических цепях переменного тока
13. Элементы трёхфазной электрической цепи; фазные, линейные токи, напряжения
14. Симметричный и несимметричный приемники в трёхфазных цепях, векторные
диаграмммы
15. Ток в нейтральном проводе в трёхфазных цепях
16. Режимы работы трёхфазного приёмника
17. Аварийные режимы в трёхфазных цепях
18. Активная, реактивная, полная мощности трёхфазной системы; измерение активной
мощности
19. Сравнение работы приемника при соединениях «треугольником» и «звездой»
20. Понятие магнитных цепей; закон полного тока для магнитной цепи
21. Сходство и различие электрических и магнитных цепей
22. Свойства ферромагнитных материалов, получение петли гистерезиса
23. Расчёт неразветвленной магнитной цепи
24. Схема замещения, векторная диаграмма катушки с магнитопроводом
25. Устройство и принцип действия трансформатора
26. Режим холостого хода трансформатора
27. Режим короткого замыкания трансформатора
28. Режим работы трансформатора под нагрузкой
29. Трёхфазные трансформаторы; группы соединений обмоток трансформаторов
30. Включение трансформаторов на параллельную работу
31. Устройство и принцип действия, режимы раоты асинхронного двигателя
32. Вращающееся магнитное поле статора асинхронного двигателя
33. Вращающееся магнитное поле ротора асинхронного двигателя
34. Рабочее вращающееся магнитное поле асинхронного двигателя
35. Механическая характеристика асинхронного двигателя
36. Устройство и принцип действия, области применения электрических машин
постоянного тока (МПТ)
37. Режимы работы электрических (МПТ)
38. Способы соединения цепей якоря и обмотки возбуждения электрических МПТ
39. Вольт-амперная характеристика полупроводникового диода
40. Устройство, принцип действия, схемы включения биполярного транзистора
41. Достижения полупроводниковой электроники
42. Преимущества и недостатки биполярного транзистора
43. Уравнение движения электропривода
44. Основные режимы работы электропривода
45. Выбор мощности двигателя в электроприводе
46. Выбор вида и типа двигателя в электроприводе
Основные законы и методы расчета цепей постоянного тока.
i

t
0

i – сила тока
i=f(t)
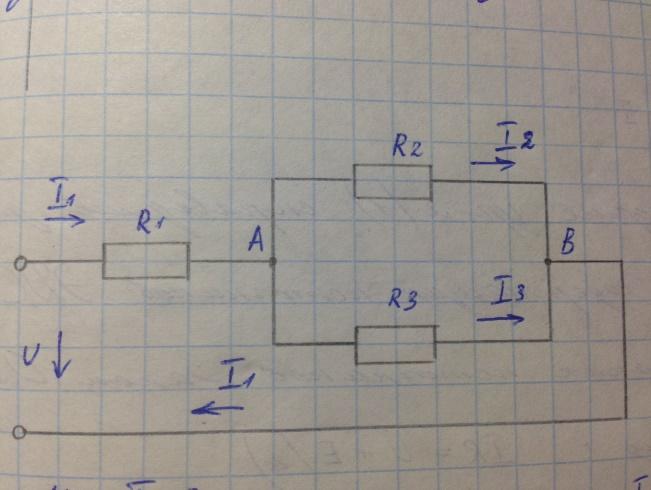
R1 =18 Ом
R2 =30 Ом
R3 =20 Ом
I2 =1,6 A
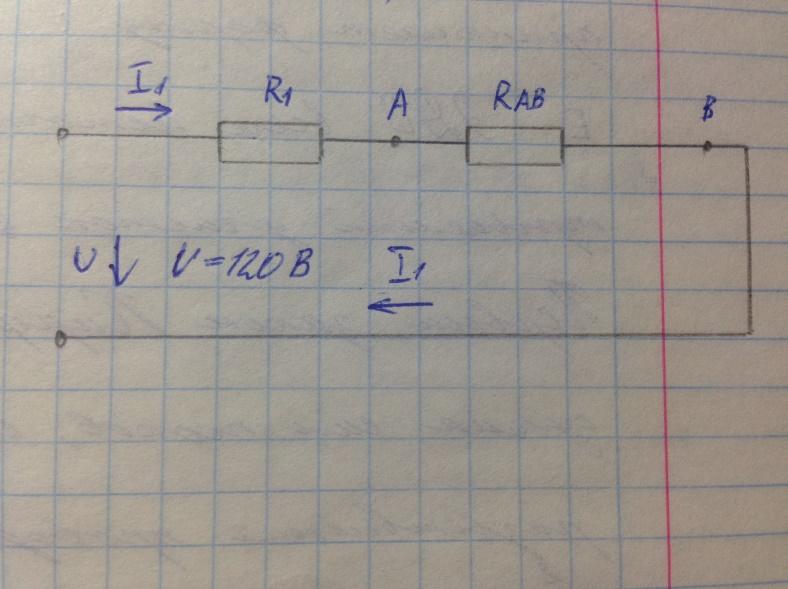
UAB = I2R2
UAB =1,6*30 =48 B
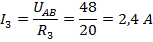
I1
U=I1*R
R=R1 +RAB
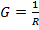 , См
(Сименс) проводимость
, См
(Сименс) проводимость
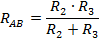
1)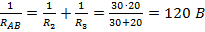
2) U=U1 +UAB= R1 I1 +UAB = 18*4+48=120 B.
Закон Ома
I
В.А.Х
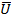
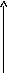


I
Закон Ома в форме ур-я (1) справедлив для участка цеп, не сод источников ЭДС. При наличии таких источников закон Ома принимает форму: IR=U+E (2)
E – ЭДС всех источников, вкл-ных в рассматр участок цепи.
Первый закон Кирхгофа: Алгебраическая сумма сил токов, сход-ся в любой точке разветвления проводников (или в узле) равна нулю.
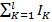 =0
=0
l- число токов, сх-ся в данном узле.
Причем токи, протекающие к узлу счит-ся +, токи вытекающие из узла –

I2
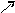
I1

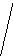

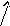
I3
l=3
I1 – I2 + I3 = 0
Второй
закон Кирхгофа:
В любом замкнутом контуре произвольно
выделяют в сложной сети проводников
алгебр сумма падений напря-ий на отдеьны
участках контура равна сумме ЭДС в этом
контуре: 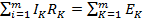
Где m – число участков в замкнутом контуре.
Расчёт электрической цепи постоянного тока методом контурных токов.
Основан на применении 2 закона Кирхгофа. Метод позволяет уменш число совместно решаемых уравнений до числа независимых контуров.
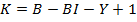
B – число ветвей в схеме цепи
BI – число ветвей, содержащие источники тока
Y – число узлов в схеме
Метод заключается в:
Выбираются независимые контуры и положительные направления контурных токов в них, каждый из которых протекает по всем элементам соответствующего контура.
Для схем, допускающих изображение на плоскости без пересечения ветвей дост условием выделением числа K незав контуров будет являться наличие в каждом из них хотя бы ветви, принадл-щей только этому контуру.
Для незав контуров сост-ся ур-я по по 2,3 Кирхгофа совместное решение которых опр-ет все контурные токи.
Ток каждой ветви опред-ся по 1,3 Кирхгофа, как алгебр сумма контурных токов соотв ветви.
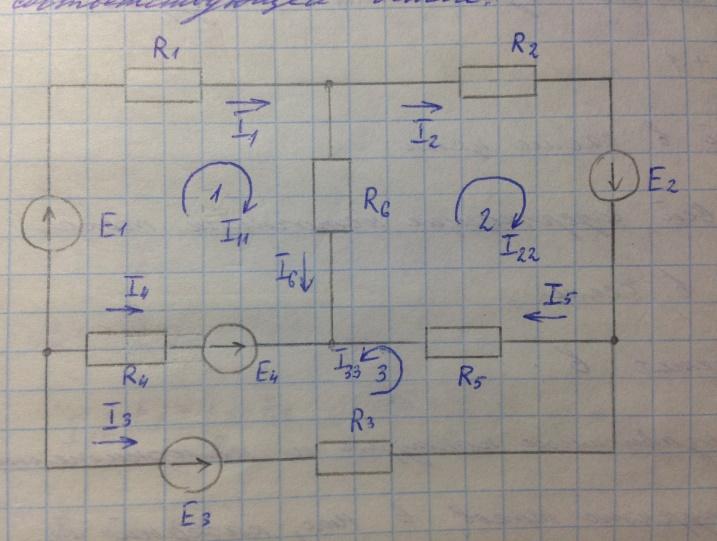
К=6-0-4+1=3
В левой части уравнений коэффициент при контурном токе рассматриваемого контура положителен и равен сумме сопротивлений его ветвей. Коэффициенты при контурных токах в контурах, имеющих общие ветви с рассматриваемым контуром, равны сумме сопротивлений общих ветвей со знаком плюс (минус), если направления контурных токов в общих ветвях совпадают (противоположны).
Правая часть уравнений содержит алгебраическую сумму ЭДС ветвей рассматриваемого контура, причем слагаемое записывается со знаком плюс (минус), если направления ЭДС и положительное направление контурного тока совпадают (противоположны).
1: 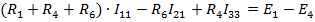
2: 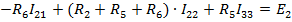
3: 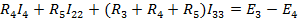
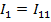
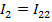
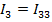
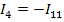
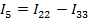
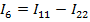 .
.
Цепь переменного тока с активным и индуктивным сопротивлениями.
Реальные цепи, содержащие индуктивность, всегда имеют и активное сопротивление: сопротивление провода обмотки и подводящих проводов. Рассмотрим электрическую цепь, в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток I = Im∙sinωt
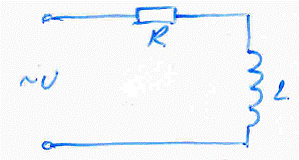
Через катушку и резистор протекает один и тот же ток, поэтому в качестве основного выберем вектор тока, и будем строить вектор напряжения, приложенного к этой цепи. Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе.
U = UL + UR (4.17)
Напряжение на резисторе будет совпадать по фазе с током:
UR = UmR∙sinωt (4.18), а напряжение на индуктивности будет равно ЭДС самоиндукции со знаком минус (по второму закону Кирхгофа).
UL = L∙ = Im∙ω∙L∙cosωt = UmL∙sin(ωt + π/2) (4.19)
Мы видим, что напряжение на индуктивности опережает ток на угол π/2. Построив векторы I, UR и UL и, воспользовавшись формулой (4.17), найдём вектор U. Векторная диаграмма показана на следующем рисунке.
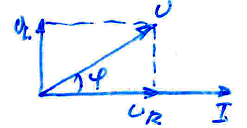
В рассматриваемой цепи ток I отстаёт по фазе от приложенного напряжения U, но не на
π / 2, как в случае с чистой индуктивностью, а на некоторый угол φ. Этот угол может принимать любые значения от 0 до π / 2 и при заданной индуктивности зависит от активного сопротивления. С увеличением R угол φ уменьшается. Как видно из диаграммы, модуль вектора U равен:
U == I∙= I∙ZL (4.20), где
ZL = (4.21) называется полным сопротивлением цепи с индуктивностью и активным сопротивлением. Сдвиг по фазе между током и напряжением в данной цепи также определяется из векторной диаграммы:
tg φ = UR / UL = ωL / R (4.22)
Цепь переменного тока с активным и емкостным сопротивлениями.
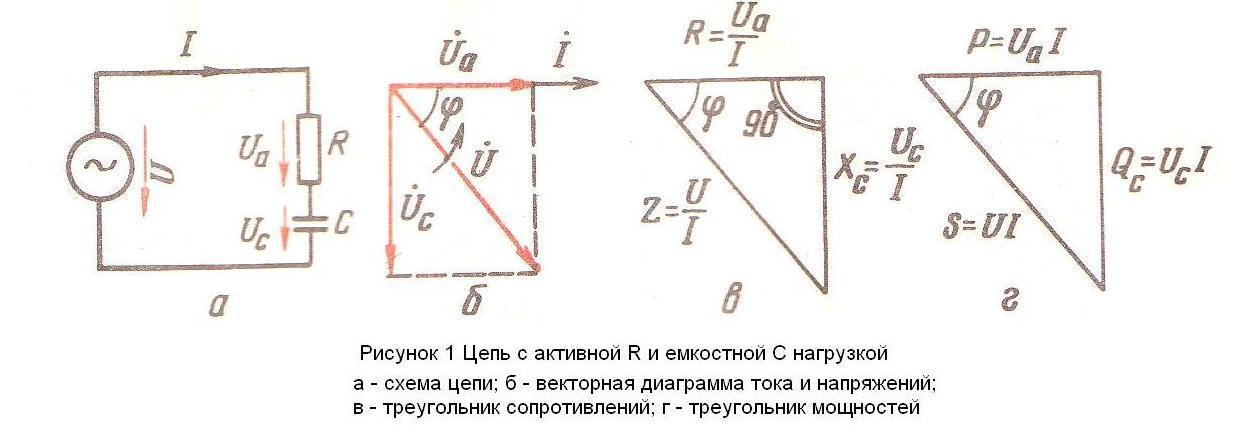
В реальных цепях переменного тока с ёмкостью всегда имеется активное сопротивление. Рассмотрим такую цепь.
Через конденсатор и резистор протекает один и тот же ток I = Im∙sinωt. Поэтому в качестве основного выберем вектор тока и будем строить вектор напряжения, приложенного к этой цепи.
U = Uc + UR (4.28).
Напряжение на резисторе будет совпадать по фазе с током:
UR = UmR∙sinωt (4.29).
Напряжение на конденсаторе будет отставать по фазе от тока на угол π / 2:
Uc = Umc∙sin(ωt — π/2 ) (4.30)
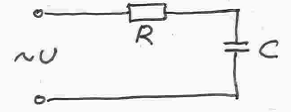
Построим векторы I, UR и Uc и, воспользовавшись формулой (4.28), найдём вектор U. Построим векторную диаграмму.
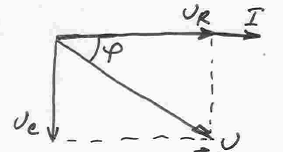
Из векторной диаграммы следует, что ток I опережает по фазе приложенное напряжение U , но не на угол π/2, как в случае чистой ёмкости, а на угол φ. Этот угол может изменяться от 0 до π/2 и при заданной ёмкости С зависит от значения активного сопротивления: с увеличением R угол φ уменьшается.
Модуль вектора U равен:
U
=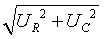 =
I
=
I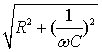 =
I∙Z1
(4.31), где
=
I∙Z1
(4.31), где
Z1 = 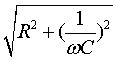 (4.32)
называется полным сопротивлением цепи.
(4.32)
называется полным сопротивлением цепи.
Сдвиг по фазе между током и напряжением:
tgφ = Uc/UR = (1/ωC)/R = 1/(ω∙R∙C) (4.33).
Электрическая цепь постоянного тока
С


Термин «сопротивление» для цепей переменного тока недостаточно полный, т.к. сопротивление переменному току оказывают не только те элементы, в которых энергия выделяется в виде тепла (их называют активным сопротивлением), но и те элементы цепи, в которых энергия запасается в энергетических или магнитных полях. Такие элементы называют реактивными, а их сопротивление переменному току – реактивным сопротивлением. Реактивным сопротивлением обладают индуктивность и емкость.
Установившийся синусоидальный ток в цепи с последовательным сопротивлением


Дифференциальное уравнение цепи:
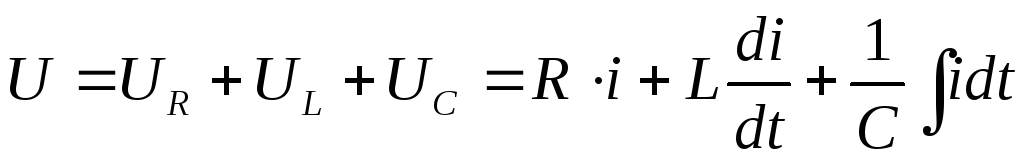 (*)
(*)
Приложенное
напряжение 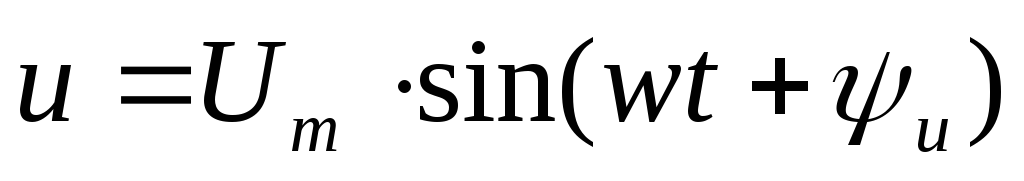 ,
при этом ток тоже синусоидальный:
,
при этом ток тоже синусоидальный: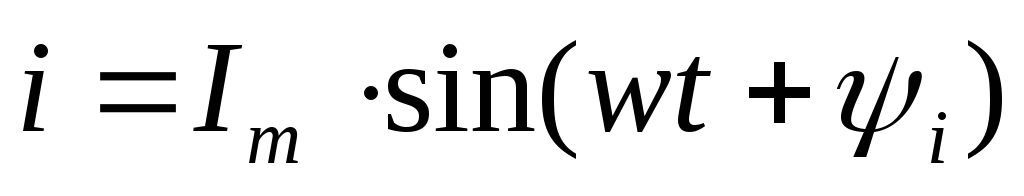
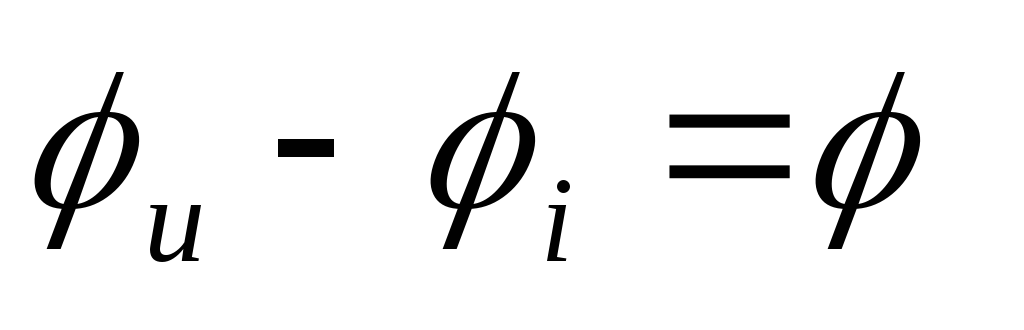
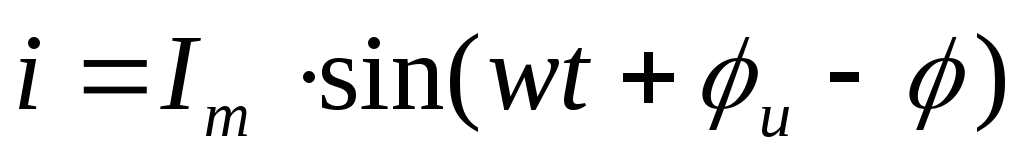
Целесообразно принять φu= φ, чтобы φu = 0 (так как ток в цепи общий), тогда
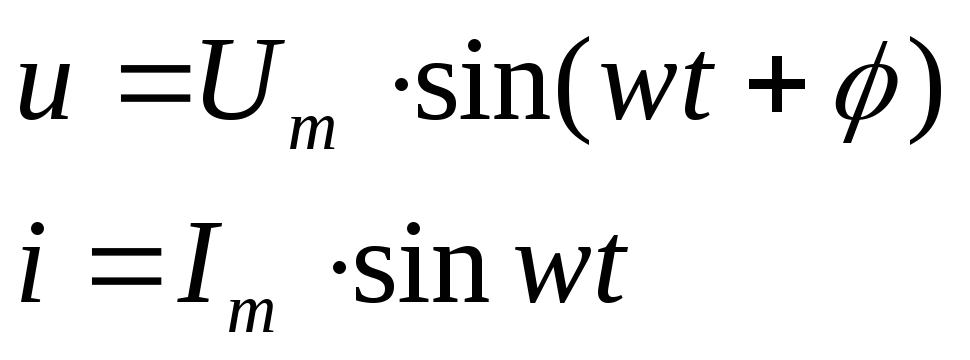
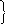 Подставим
в исходное уравнение (*) :
Подставим
в исходное уравнение (*) :
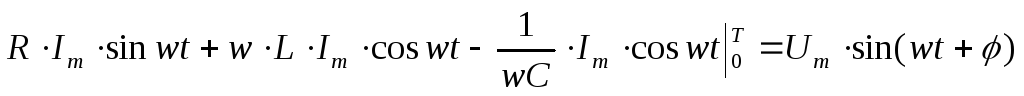
П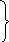 ри
ри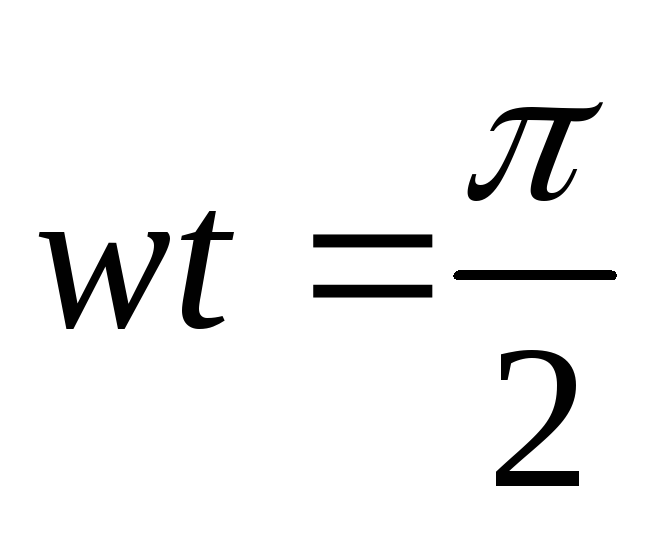 :
: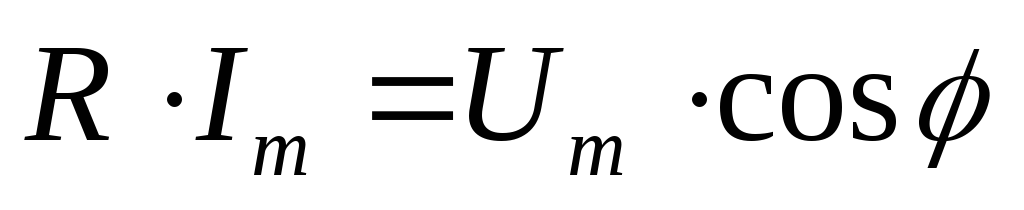 возведем
в квадрат и сложим:
возведем
в квадрат и сложим:
При 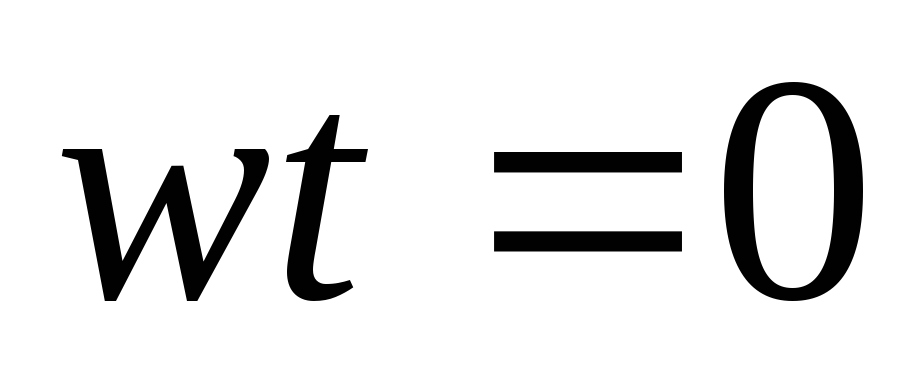 :
: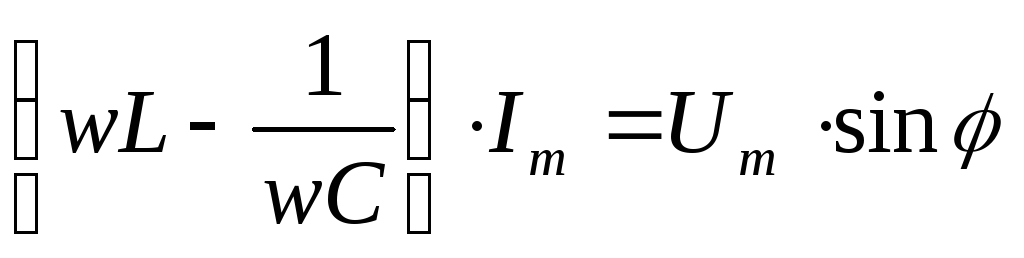
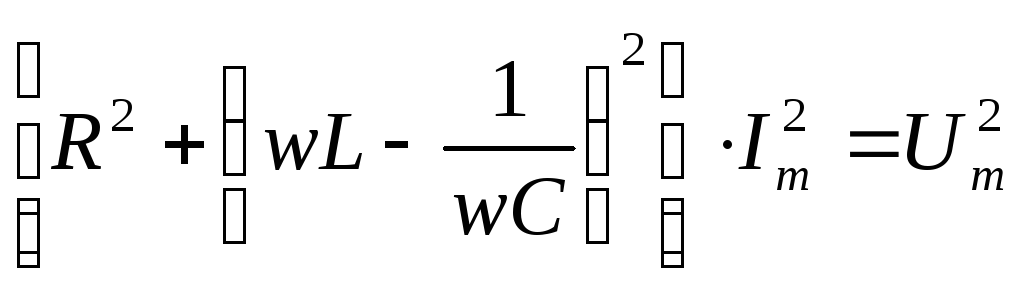 ,
откуда
,
откуда
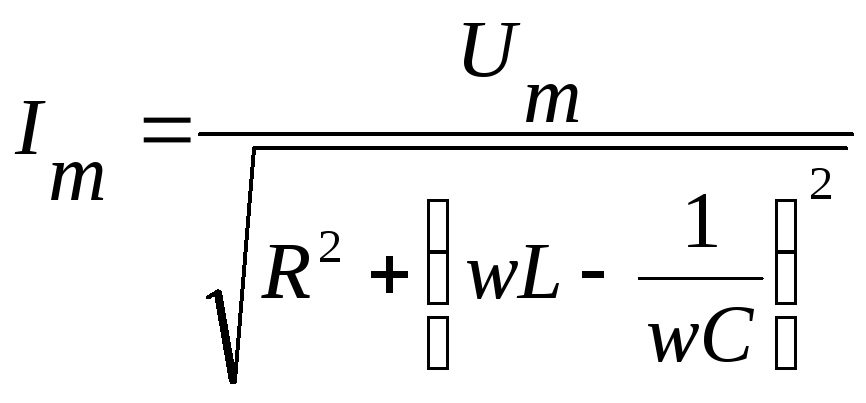
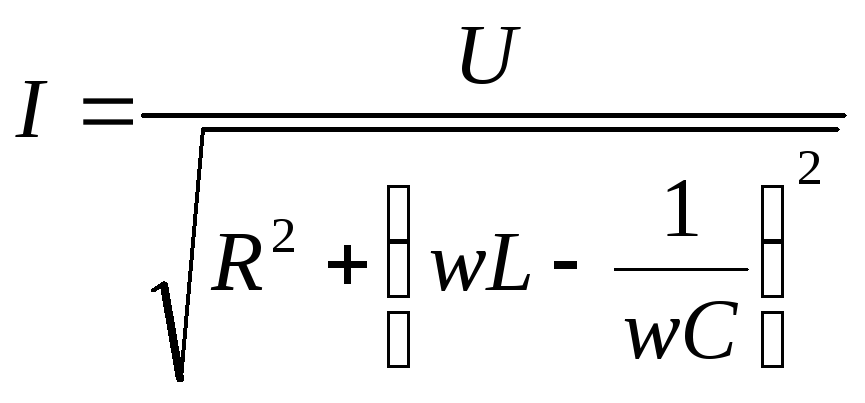
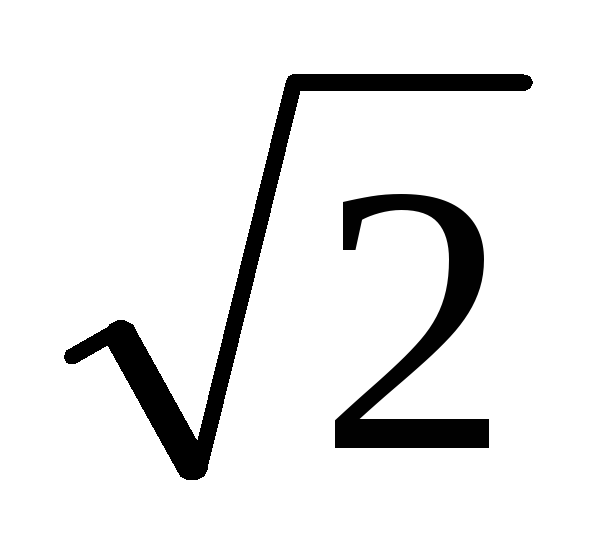 :
: 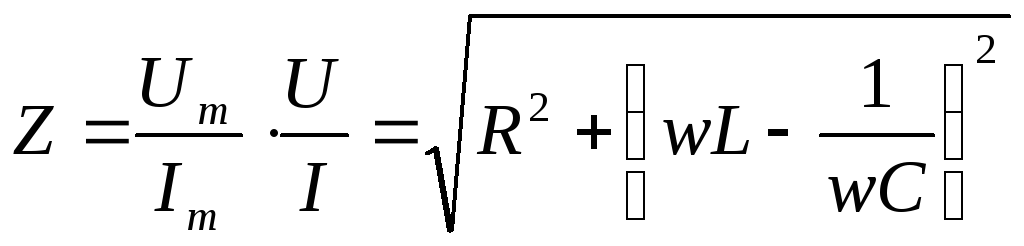
— полное сопротивление цепи
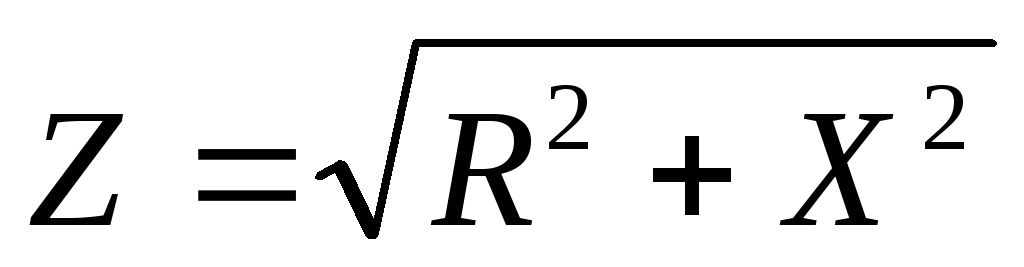
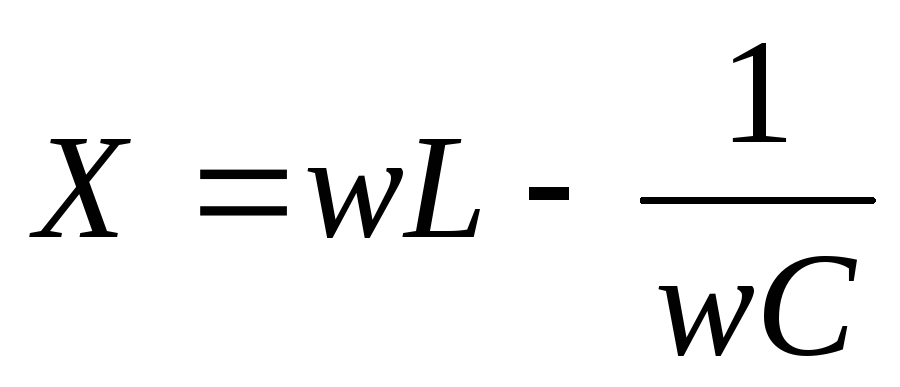
— реактивное сопротивление
Рассмотрим случай XL>XC

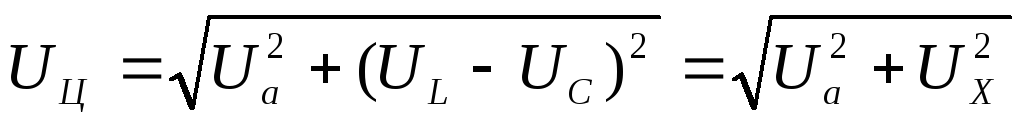
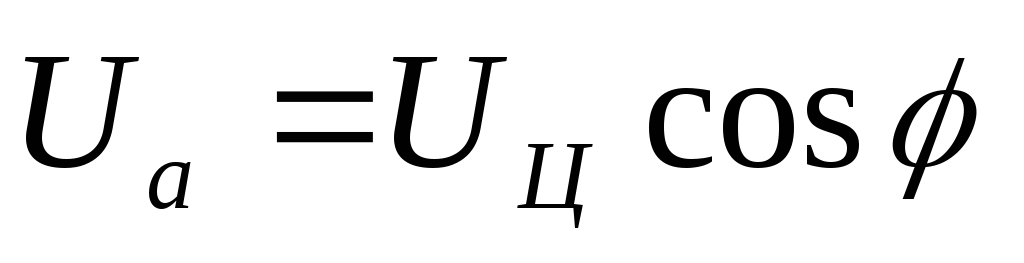 ;
; 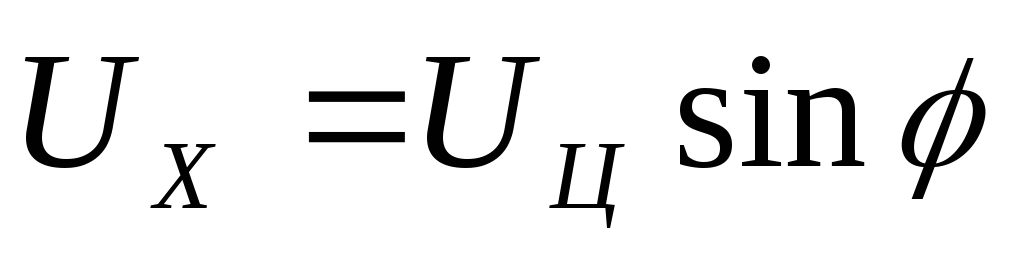 .
.

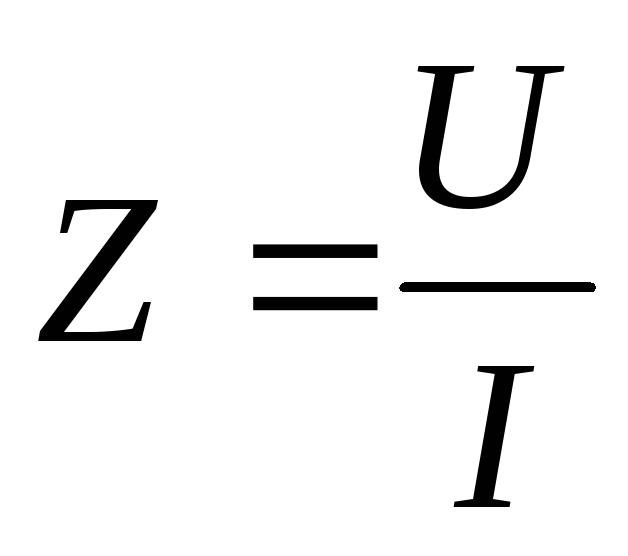
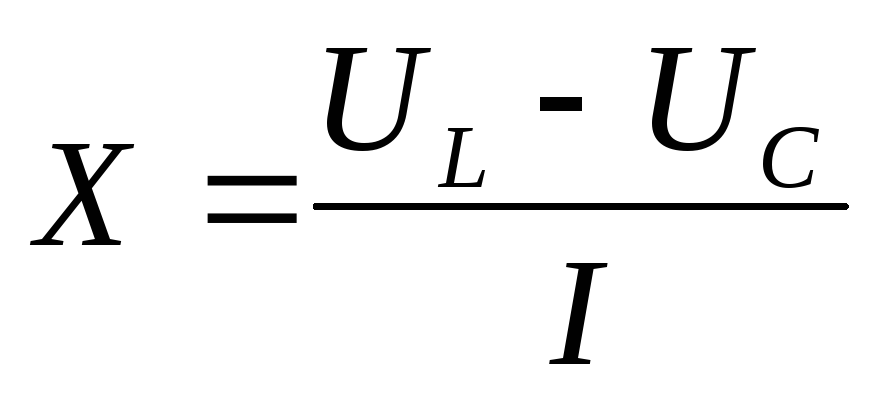
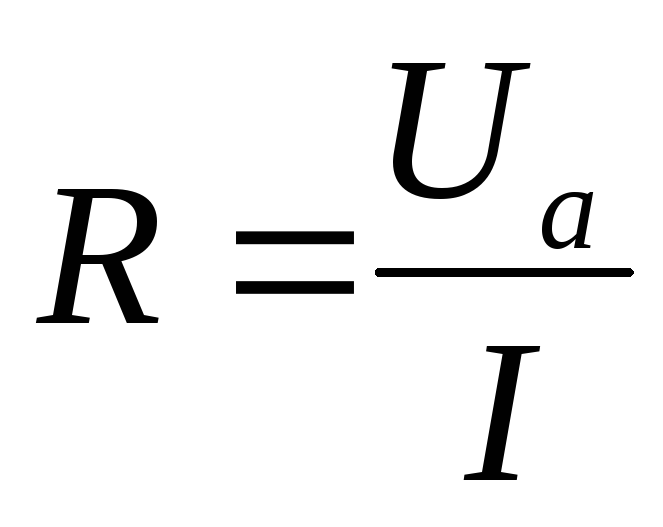
Треугольник сопротивлений
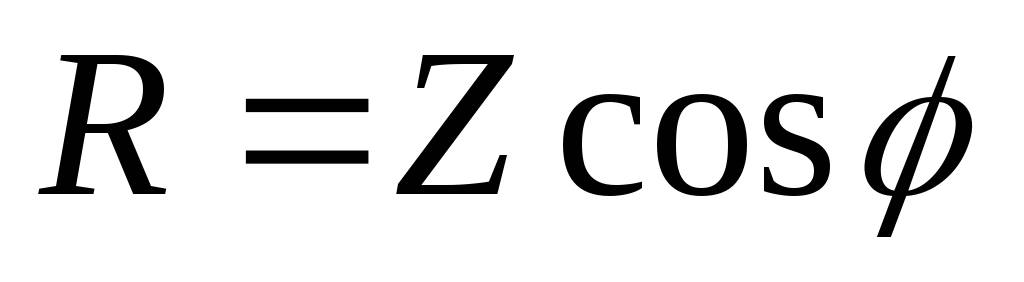
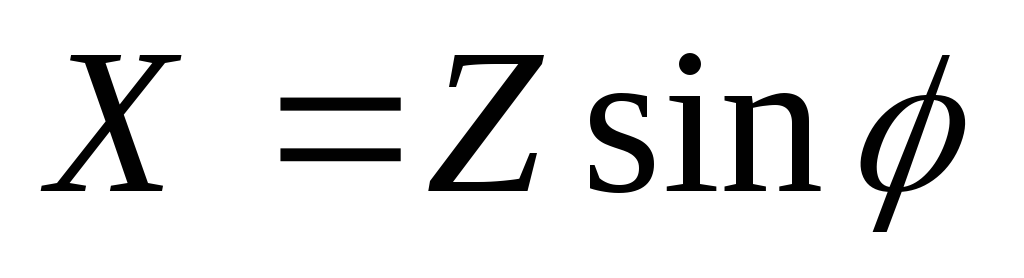
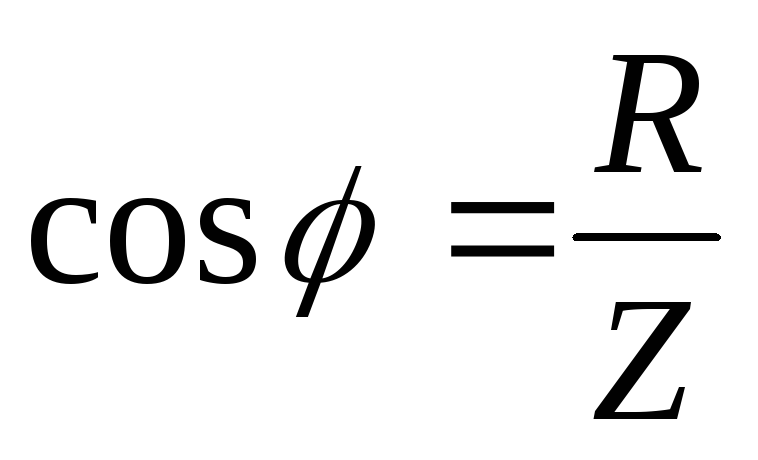
Синусоидальный ток в цепи с параллельным соединением R,L,C.

По первому закону Кирхгофа: i = iR+iL+iC
Согласно закону Ома:
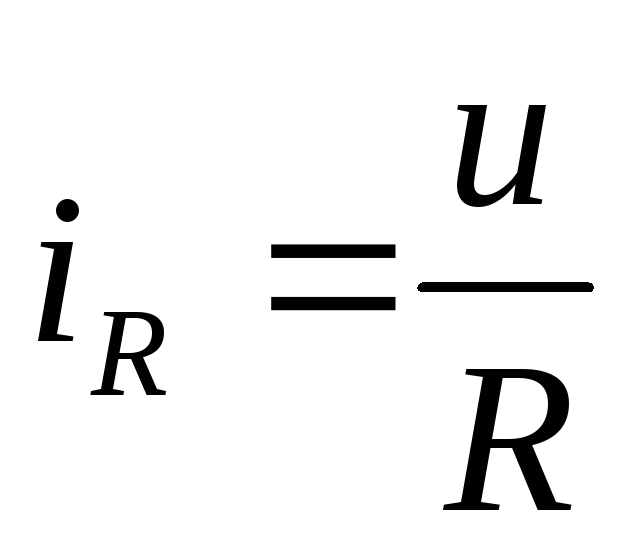
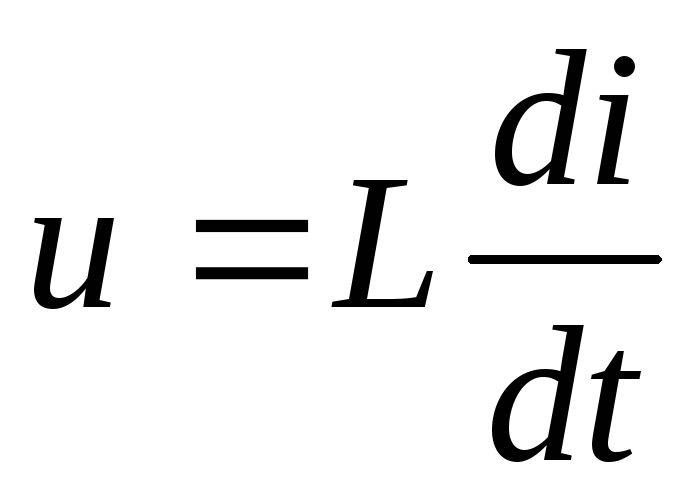
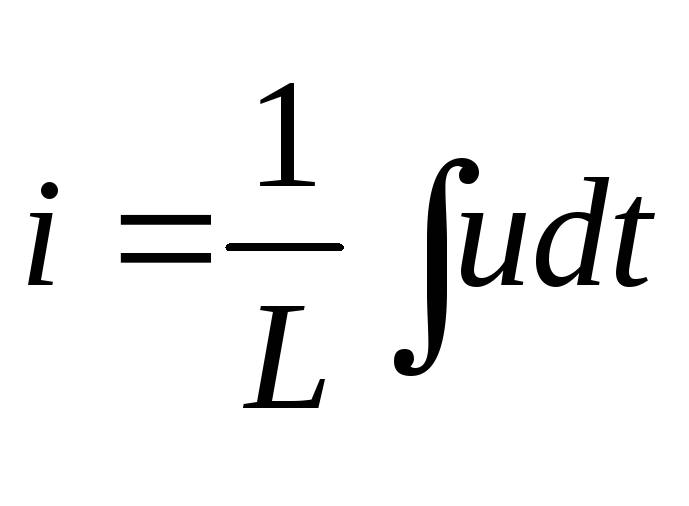
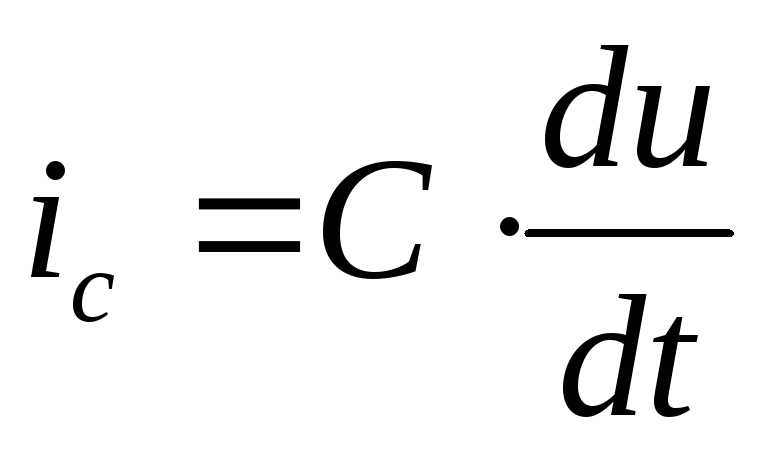
Таким образом, дифференциальное уравнение цепи с параллельным соединением имеет вид:
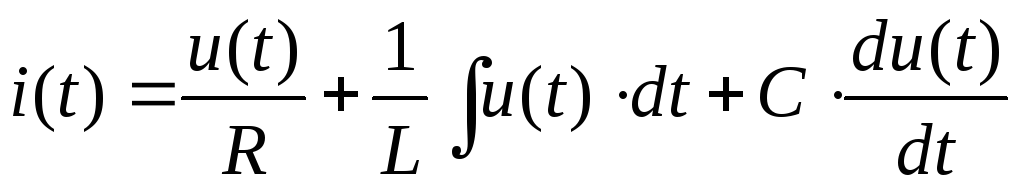
Примем 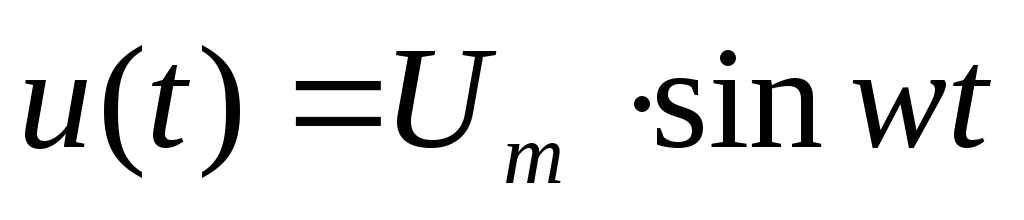
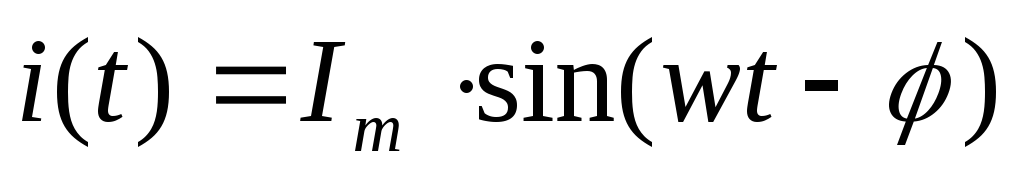 ,
так как
,
так как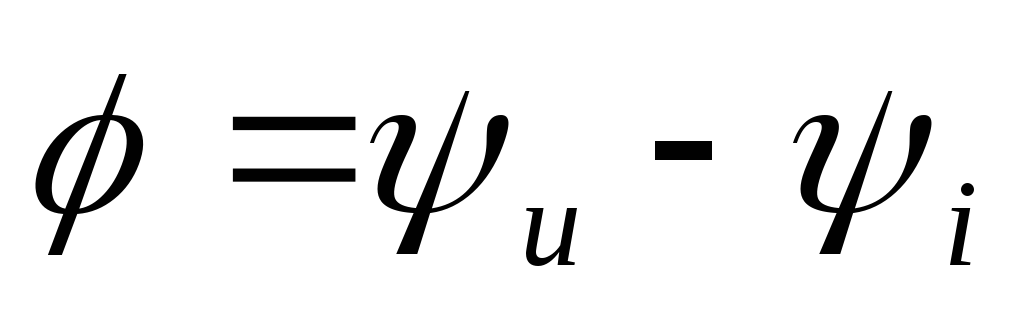
Подставляя в дифференциальное уравнение, получим
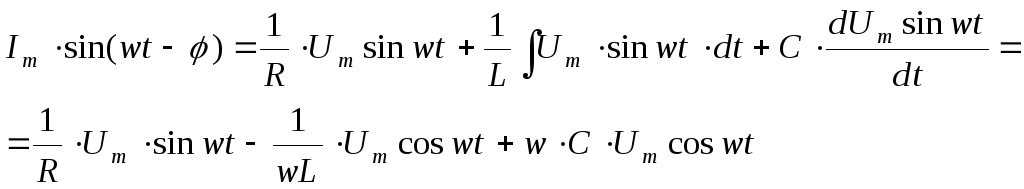
Рассмотрим 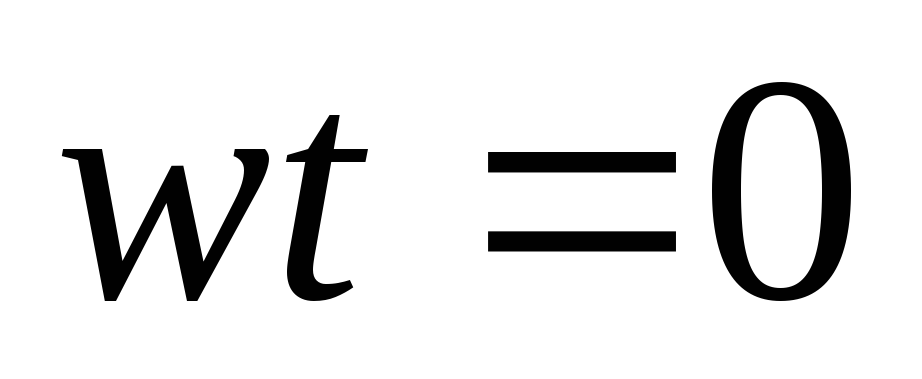 :
: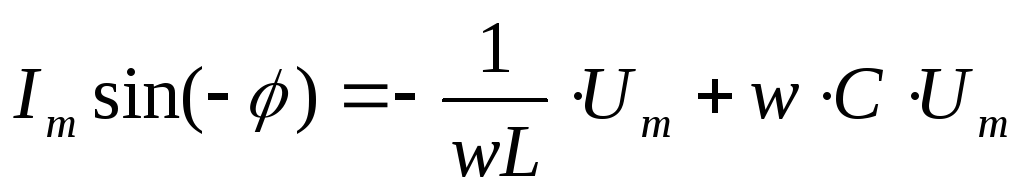 ,
,
Возведем
в квадрат: 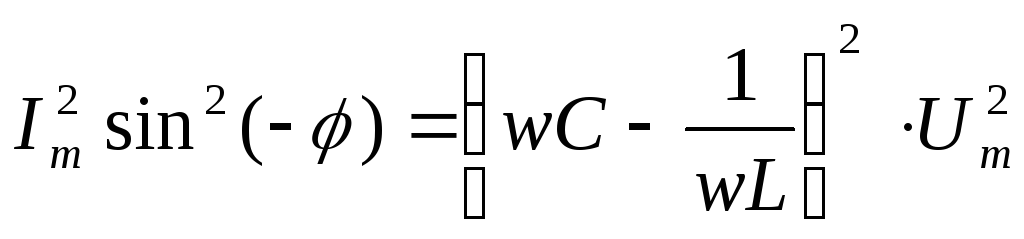 (*)
(*)
При 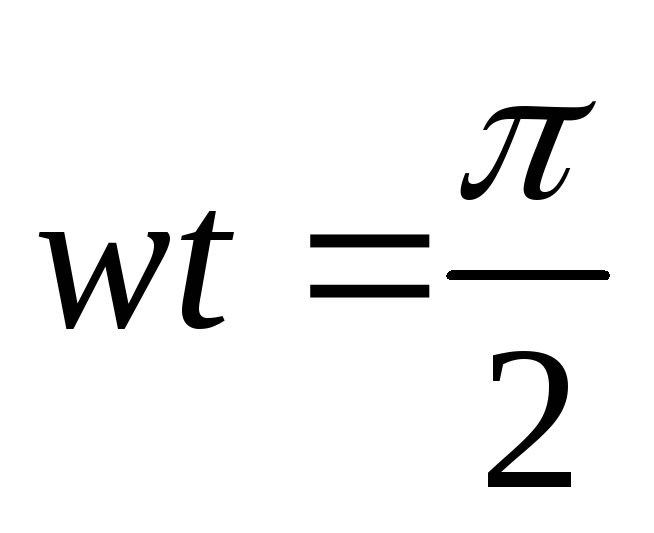 :
: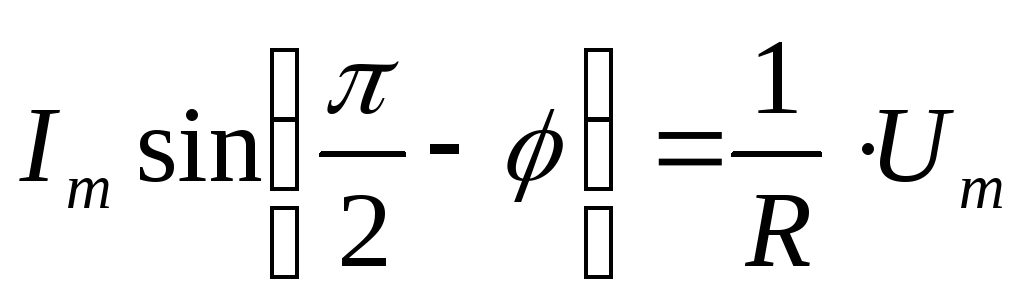 ,
или
,
или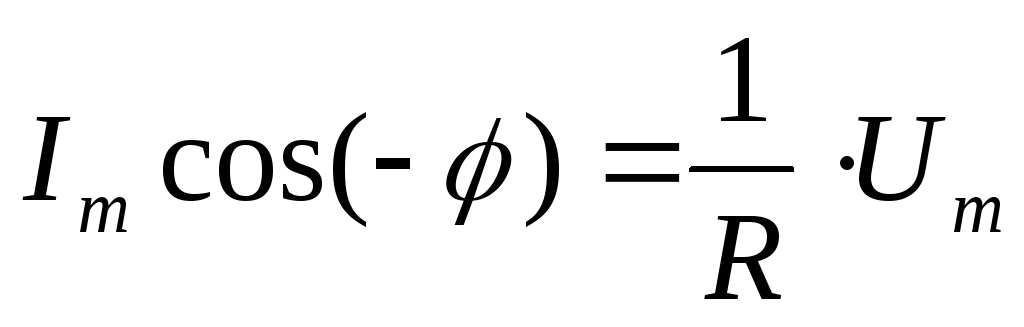 ,
,
Возведем
в квадрат: 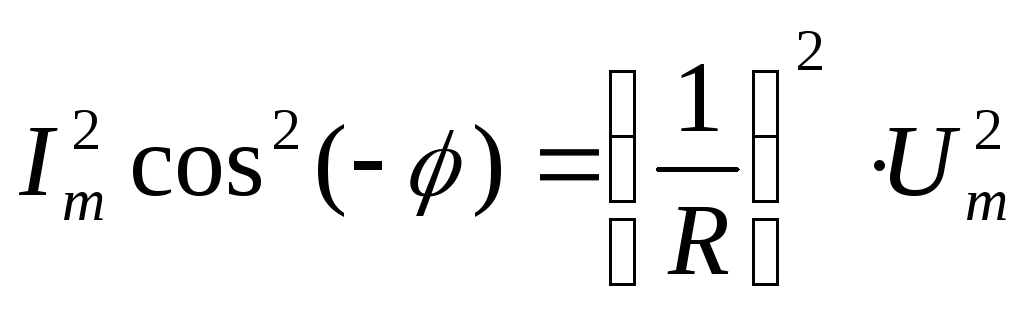 (**)
(**)
Сложив уравнения (*) и (**), получим:
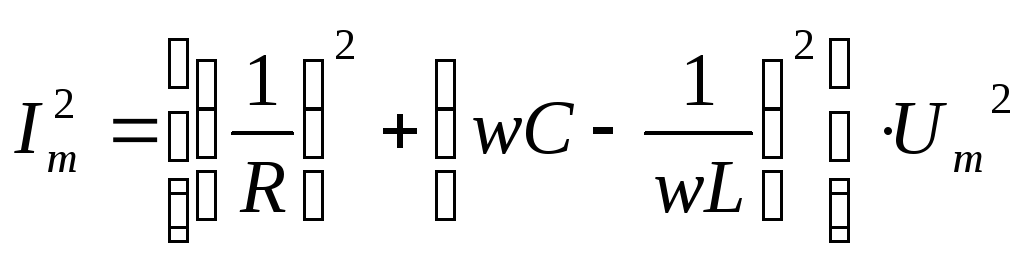 ,
или
,
или
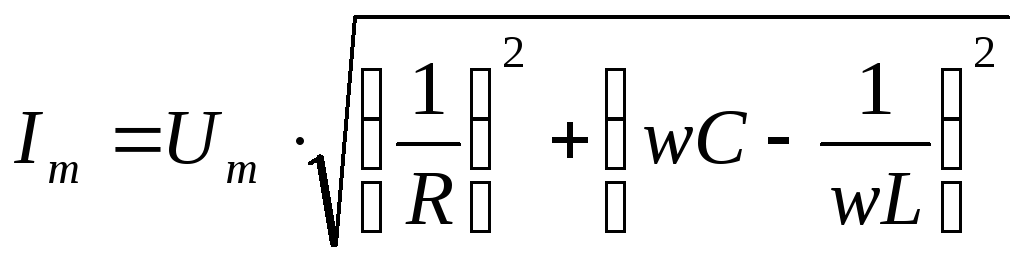
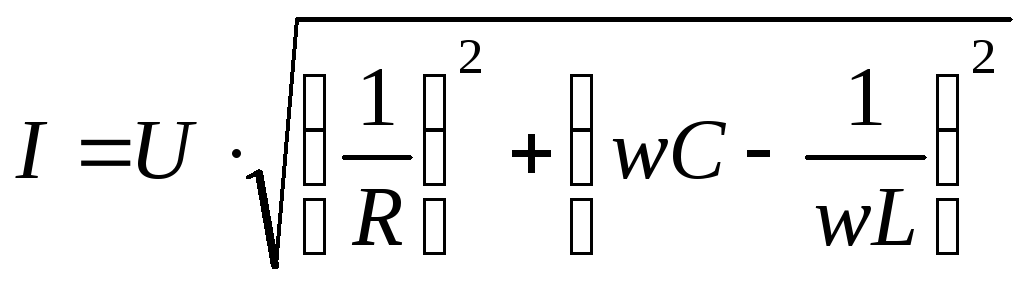
/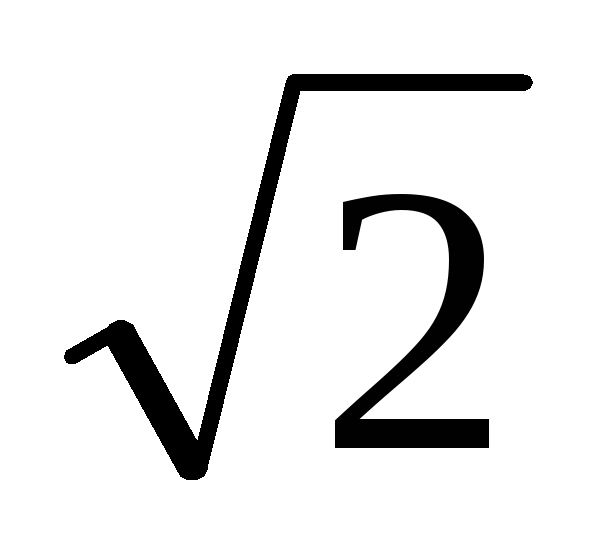 :
:
Введем
обозначение 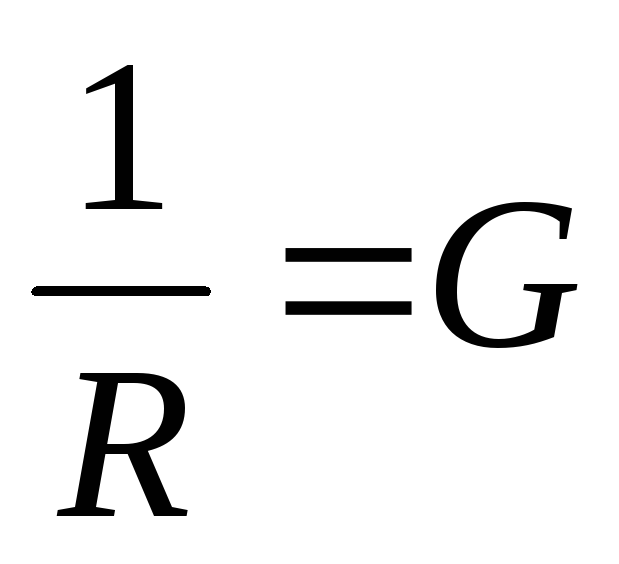 —
активная проводимость
—
активная проводимость
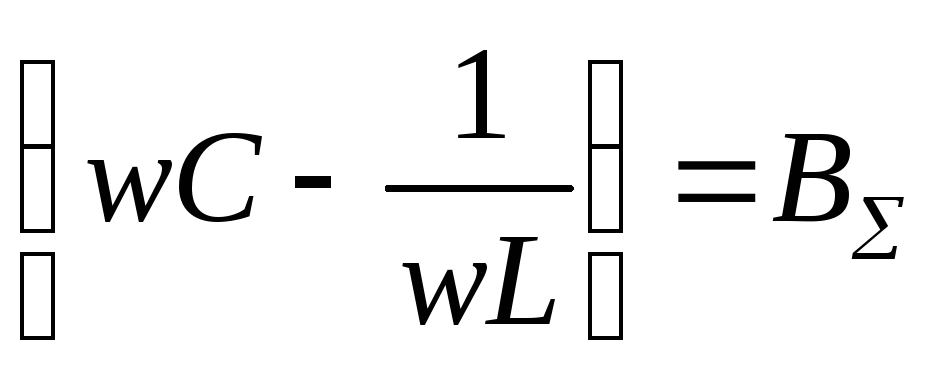 —
суммарная реактивная проводимость, при
чем
—
суммарная реактивная проводимость, при
чем 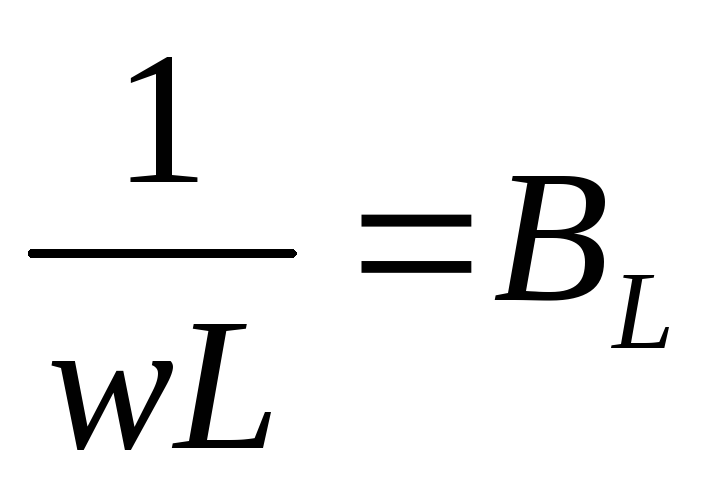 и
и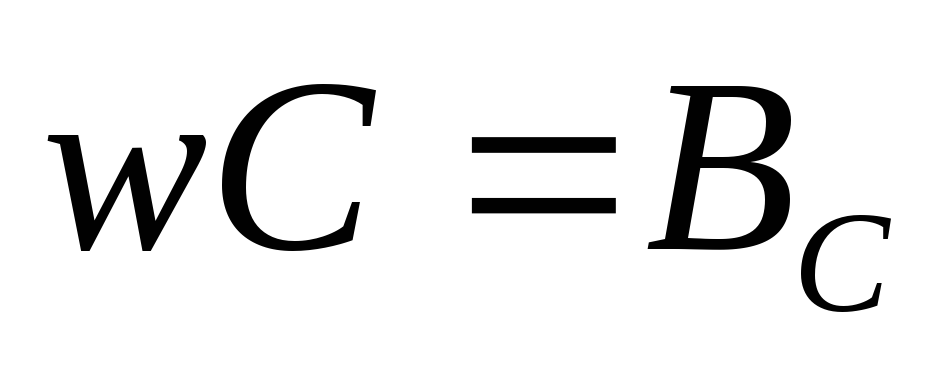
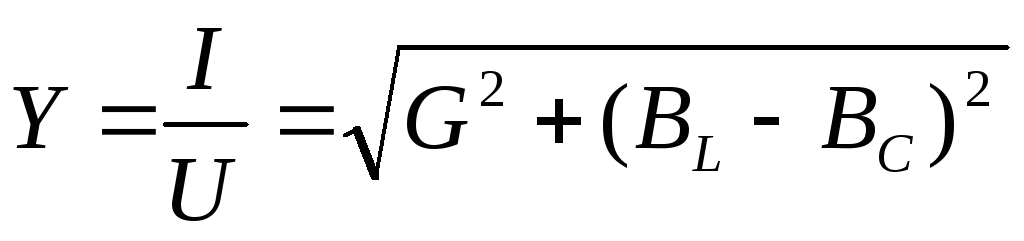 —
полная проводимость
—
полная проводимость
Сс
Закон Ома в комплексной форме
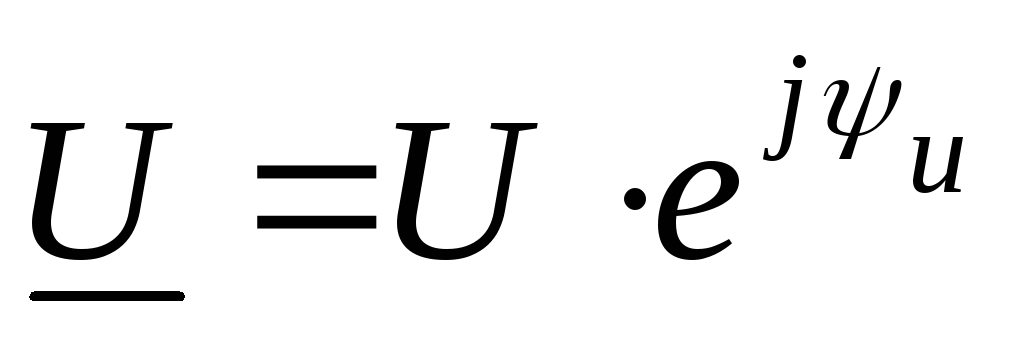 ;
; 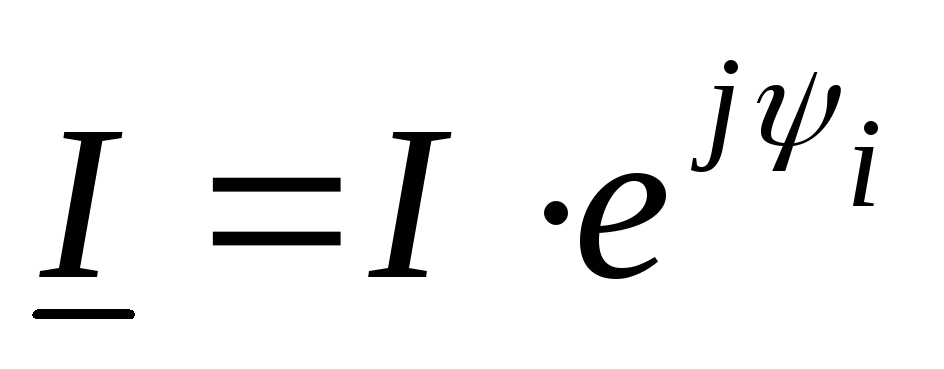
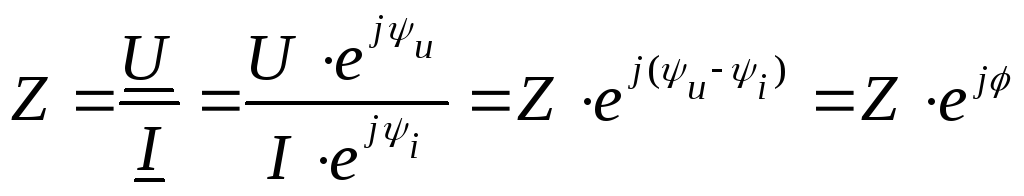
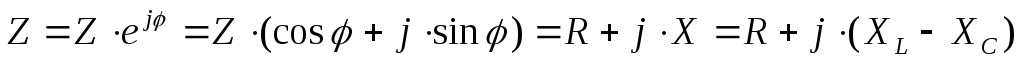
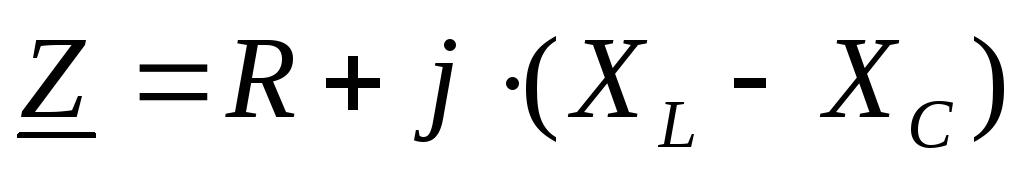
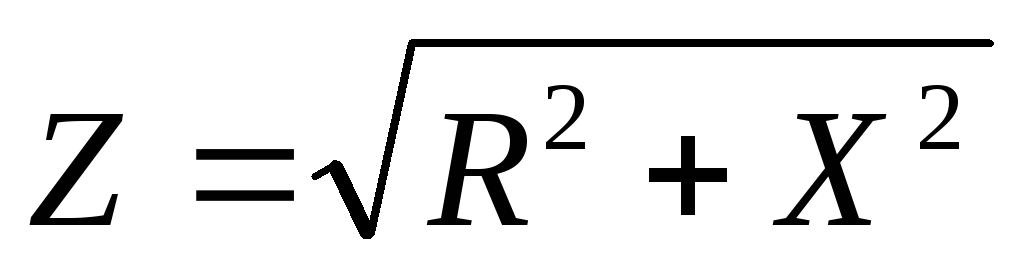
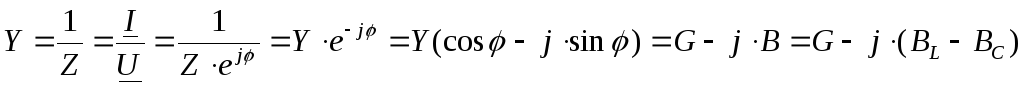
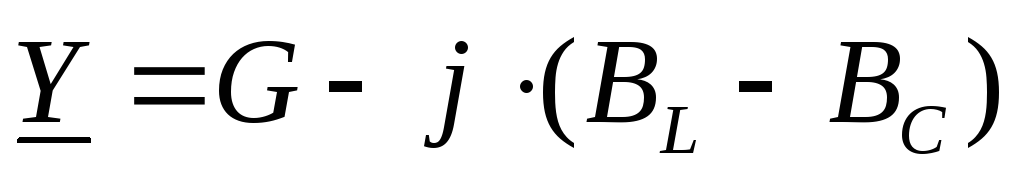
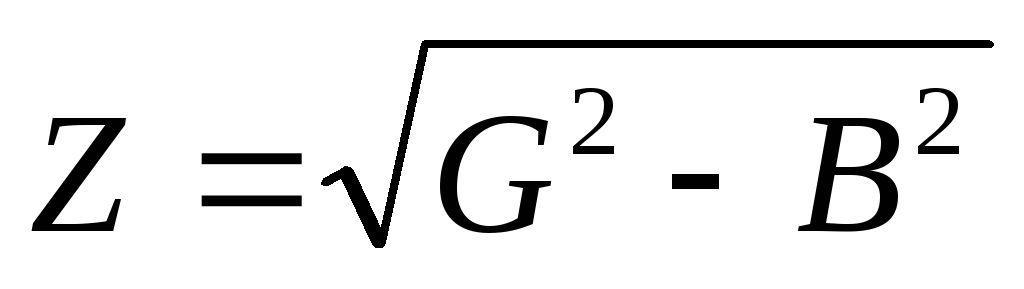
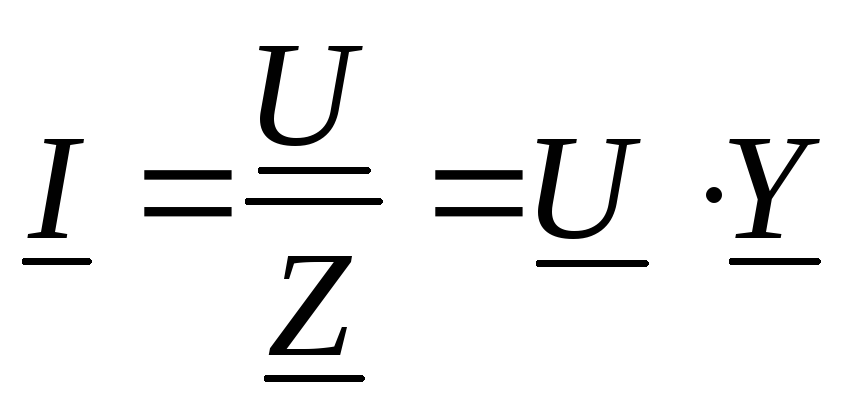
— закон Ома в комплексной форме
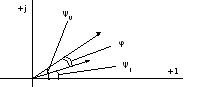
Мощность в комплексной форме
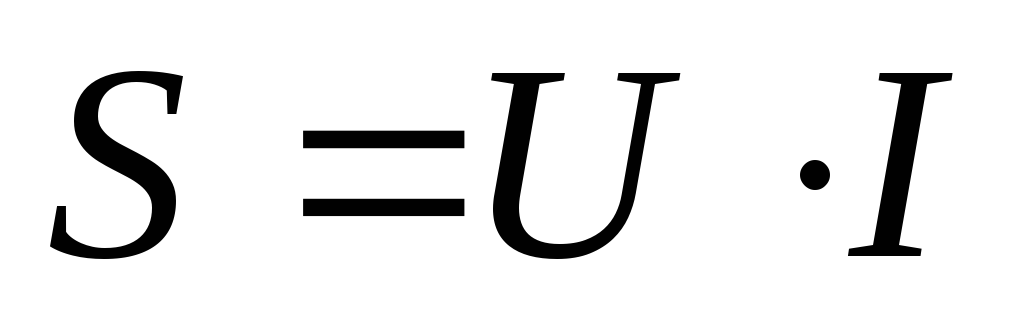
В
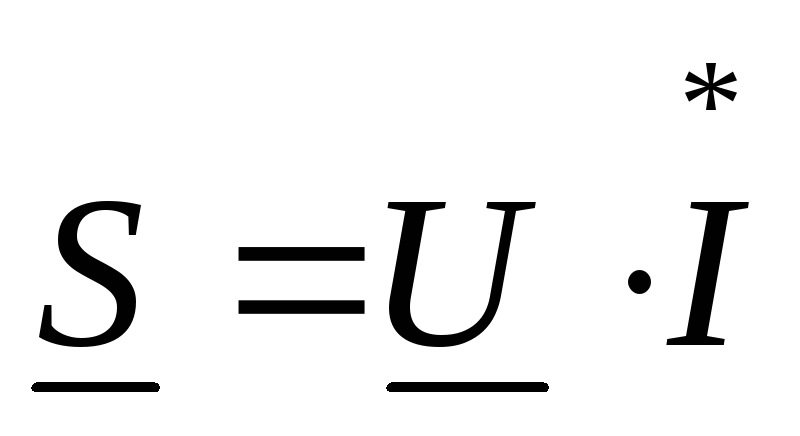
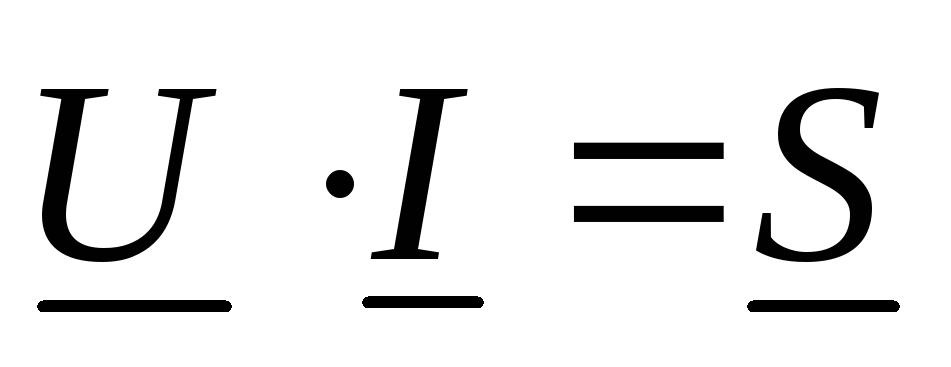 ,
тогда
,
тогда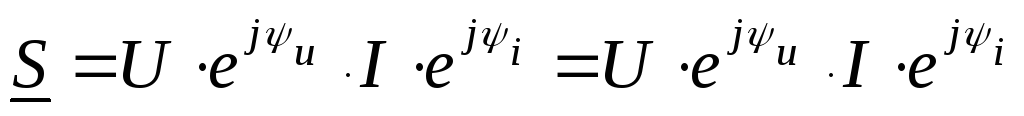 ,
так как Ψu – Ψi = φ, то:
,
так как Ψu – Ψi = φ, то: 


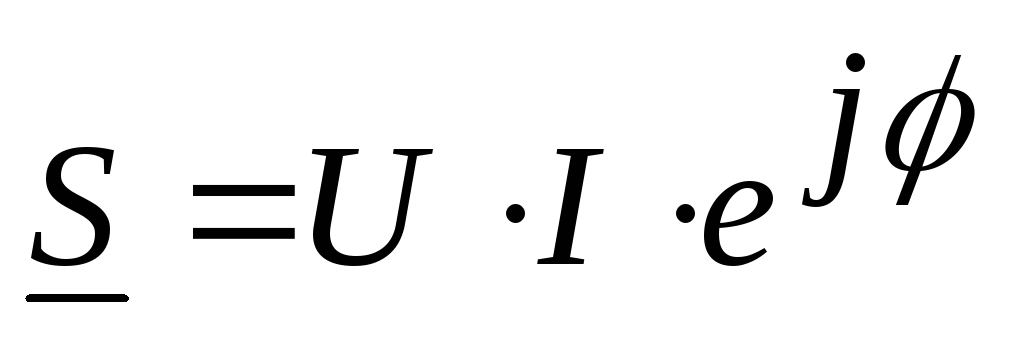
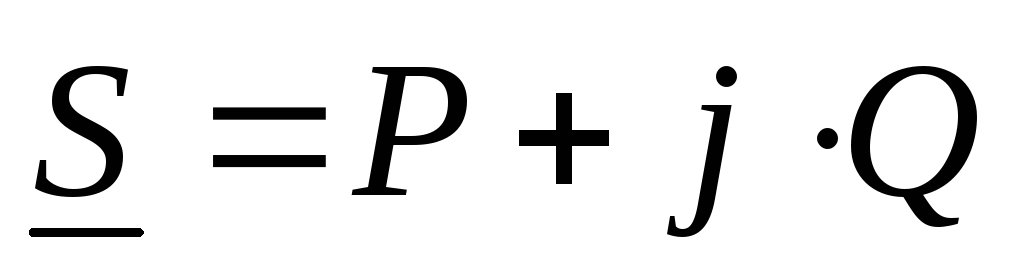

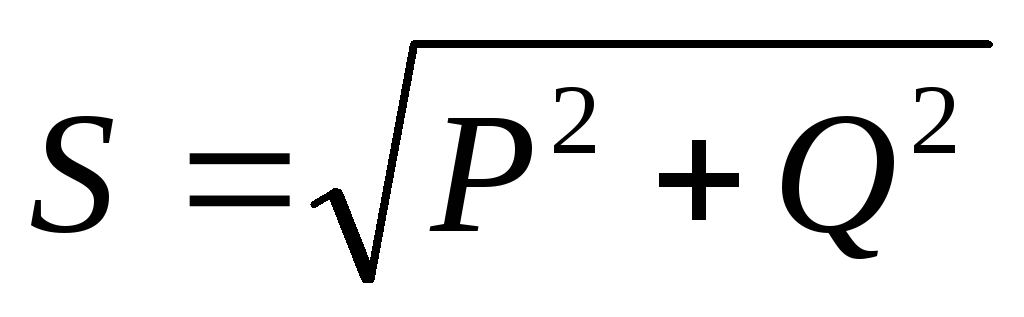
8. Векторные диаграммы для цепей с соединением R-,L-,C- элементов
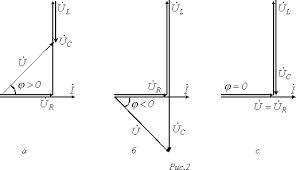
Для первого случая
XL˃XCUL=IXL
UL˃UCUc=IXc
Для второго случая
XL˂XCUL=IXL
UL˂UCUc=IXc
Для третьего случая
XL=XCUL=IXL
UL=UCUc=IXc
9. Векторные диаграммы для цепей с соединением R-,L- элементов
10. Векторные диаграммы с соединением R-,C-элементов
12. Резонансные явления в электрических цепях переменного тока.
Резонансом
напряжений в
электрических цепях называется режим
участка электрической цепи, содержащей
индуктивный и емкостной элементы, при
котором разность фаз между напряжением
и током равна нулю 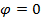 .
Режим резонанса может быть получен при
изменении частоты
.
Режим резонанса может быть получен при
изменении частоты 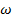 питающего
напряжения или изменением параметров
элементов L и С.
При последовательном
соединении возникает резонанс напряжения.
питающего
напряжения или изменением параметров
элементов L и С.
При последовательном
соединении возникает резонанс напряжения. 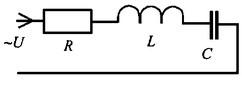 .
.
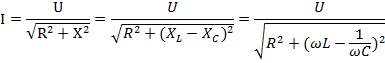
Резонанс токов. При параллельном соединении конденсатора и соленоида (смотри рисунок), так же как и при последовательном, сила тока в цепи зависит от значений емкости и индуктивности. При изменении емкости и индуктивности при определенном их соотношении сила тока в неразветвленном участке цепи оказывается минимальной (практически близкой к нулю). При определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения.Такое явление называется резонансом токов.
6 Переменный ток в цепи с последовательным соединением элементов r, l, c » СтудИзба
Переменный ток в цепи с последовательным соединением элементов r, l, c
|
Предположим, что имеется цепь, содержащая резистор R, катушку с индуктивностью L и конденсатор с емкостью С. Подведем к зажимам цепи переменное напряжение u. По цепи потечет переменный ток i. На отдельных участках цепи возникнут падения напряжений, для которых в соответствии со вторым законом Кирхгофа можно записать:
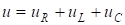 .
.
Определим, какую форму изменения будут иметь падения напряжений на участках цепи, если ток изменяется по закону:
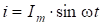 .
.
Падения напряжений на участках цепи определяются из соотношений известных из курса физики:
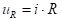 ,
, 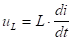 ,
, 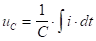 ( i=C
( i=C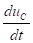 ).
).
После подстановки в исходные уравнения значения тока i получим:
 (т.к. (sin kx)’ = k cos kx, = k sin(kx+π/2 ))
(т.к. (sin kx)’ = k cos kx, = k sin(kx+π/2 ))
( т.к. ∫ sin kx dx = — 1/k cos kx).
Проанализируем полученные уравнения. Величины 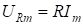 ,
, 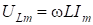 и
и 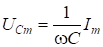 имеют размерность [B] и представляют собой соответственно амплитудные значения напряжений резисторе, катушке индуктивности и конденсаторе.
имеют размерность [B] и представляют собой соответственно амплитудные значения напряжений резисторе, катушке индуктивности и конденсаторе.
Величины R, 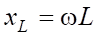 и
и 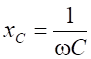 имеют размерность [Ом] и называются соответственно: R — активное сопротивление, xL — реактивное индуктивное сопротивление, xC — реактивное емкостное сопротивление.
имеют размерность [Ом] и называются соответственно: R — активное сопротивление, xL — реактивное индуктивное сопротивление, xC — реактивное емкостное сопротивление.
Активное сопротивление R не зависит от частоты тока, а реактивные сопротивления xL и xC являются функцией частоты тока  .
.
Сравнение фаз тока и напряжений позволяет сделать следующие выводы:
− в цепи с активным сопротивлением ток и напряжение совпадают по фазе j=0;
− в цепи с индуктивностью ток отстает от напряжения на угол 90°;
− в цепи с емкостью ток опережает напряжение на 90°.
Для соответствующих участков электрической цепи векторные диаграммы токов и напряжений будут выглядеть следующим образом.
|
Треугольники напряжений, сопротивлений и мощностей
На векторных диаграммах можно выделить прямоугольный треугольник напряжений.
В зависимости от соотношения xL и xCвозможны три режима работы цепи:
а) напряжение цепи опережает ток по фазе на угол j и цепь в целом имеет активно-индуктивный характер;
б) напряжение цепи отстает по фазе от тока на угол j и цепь в целом имеет активно-емкостный характер;
в) напряжение и ток совпадают по фазе, характер цепи в целом чисто активный. Такой режим цепи называется резонансом напряжений, при котором UL=UC, xL =xC. Настроить цепь в резонанс напряжений можно путем изменения xL или xC, т.е. изменяя C, L или f (частота, при которой наступает резонанс f = 1/(2π√LC) ). При резонансе напряжений сопротивление цепи минимально, а ток максимальный.
Цепи электроснабжения в строительной отрасли чаще всего имеют активно-индуктивный характер, поэтому далее рассмотрим соответствующие треугольники с положительным углом j.
|
По теореме Пифагора можно установить связь между полным напряжением цепи и напряжениями на ее отдельных участках:
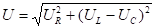 .
.
Если разделить стороны треугольника напряжений на ток (в цепи с последовательным соединением элементов ток одинаков во всех участках), то (в соответствии с законом Ома) получим треугольник сопротивлений.
|
Здесь х=xL — xC — реактивное сопротивление цепи, а Z — полное сопротивление цепи:
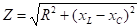 .
.
Полученное уравнение устанавливает связь межу различными сопротивлениями цепи.
Если умножить стороны треугольника напряжений на ток, то получим треугольник мощностей:
|
Здесь Р=URI — активная мощность, которая выделяется на активных сопротивлениях цепи. Она связана с необратимыми преобразованиями электрической энергии, то есть с совершением работы (полезной) в электроустановке. Активная мощность измеряется в ваттах [Вт].
Q=UxI — реактивная мощность. Связана в электроустановках с совершением обратимых преобразований энергии, полезной работы она не совершает. В электроустановках затрачивается на создание электрических (С) и магнитных (L) полей. Реактивная мощность измеряется вольт амперах реактивных [вар].
Реактивная мощность оказывает существенное влияние на режим работы электрической цепи. Циркулируя по проводам трансформаторов, генераторов, двигателей, линий электропередач, она нагревает их. Поэтому расчет проводов и других элементов устройств переменного тока производят из полной мощности, которая учитывает активную и реактивную мощности.
S=UI — полная мощность, измеряется в вольт амперах [В*А]. Из треугольника мощностей определим:
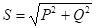 .
.
Коэффициент мощности
Из треугольника мощностей можно записать:
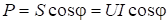 ,
,
откуда
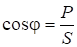 .
.
Множитель cosj — называется коэффициентом мощности. Коэффициент мощности это отношение активной мощности к полной. Он показывает, какая часть от полной мощности потребленной электроустановкой из сети затрачивается на совершение полезной работы. Очевидно, чем выше коэффициент мощности, тем эффективнее преобразование энергии в электроустановке. Наилучшее значение cosj=1, в этом случае вся потребленная из сети энергия затрачивается на совершение полезной работы.
И приведенных соотношений можно выразить ток, потребляемый электроустановкой из сети:
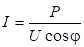 .
.
Из выражения следует, что чем ниже cosj, тем больший ток потребляет она из сети на совершение той же самой работы. На практике пропускная способность линий электропередач (ЛЭП) ограничена, поэтому снижение cosj электроприемников ведет к повышенной загрузке их током, и еще больше ограничивает их пропускную способность.
При снижении cosj повышаются потери энергии DР в ЛЭП, что следует из выражения:
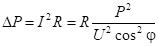 ,
,
здесь R — активное сопротивление ЛЭП. Увеличение потерь энергии ведет к возрастанию стоимости ее транспортировки.
Таким образом, задача повышения cosj является важной народно-хозяйственной проблемой.
Повысить cosj можно, уменьшив (желательно до нуля) потребляемую из сети реактивную мощность. Так как низкий cosj имеют электродвигатели, трансформаторы и т.п. электроустановки, работающие на холостом ходу или с недогрузкой, то для повышения cosj необходимо обеспечить полную загрузку этих электроустановок и своевременное их отключение. Указанные мероприятия называют организационными.
Для повышения cosj применяют синхронные компенсаторы и конденсаторные батареи. Эти устройства способны вырабатывать реактивную энергию необходимую потребителям.
Электрические цепи однофазного переменного тока с параллельным соединением элементов R, L, C
Цепь с параллельным соединением элементов состоит из ряда параллельных ветвей, включенных между двумя узлами. Рассмотрим простейшую цепь.
|
По первому закону Кирхгофа для токов можно записать:
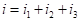 .
.
Действующие значения токов в отдельных ветвях будут определяться:
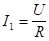 ,
, 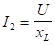 ,
, 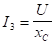 .
.
Построение векторных диаграмм для параллельного соединения элементов цепи начинают с вектора U (т.к. оно одинаково для всех участков цепи).
Цепь в зависимости от соотношения сопротивлений xL и xC также может иметь индуктивный, емкостный или чисто активный характер.
Режим, когда I1=I, т. е. I2 + I3 =0называют режимом резонанса токов. Для рассмотренной схемы условие возникновения резонанса также может быть записано:
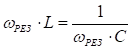 .
.
Уменьшение тока в цепи при резонансной частоте свидетельствует о значительном возрастании сопротивления цепи при этой частоте. Поэтому режим резонанса токов часто используется в электрических фильтрах, когда требуется подавить какую-либо гармонику в электрическом сигнале.
|
На построенных диаграммах можно выделить треугольник токов.
IA — активная составляющая тока;
IP — реактивная составляющая тока.
Связь между полным током и его составляющими выражается:
|
 .
.
Параллельное соединение реальных элементов электрической цепи
|
Реальные элементы электрической цепи отличаются от идеализированных, рассмотренных выше. Рассмотрим электрическую цепь.
К цепи подведено напряжение U. В соответствии с первым законом Кирхгофа для мгновенных значений токов получим:
i=i1+i2.
Действующие значения токов в ветвях равны:
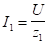 ,
, 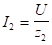 ,
,
где 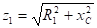 ,
, 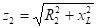 .
.
Построение векторной диаграммы начинают с вектора напряжения U. Затем откладывают токи I1 и I2 в ветвях. Токи сдвинуты по отношению к напряжению на фазы, соответственно j1 и j2, которые определяются из выражений:
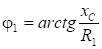 ,
, 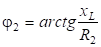 .
.
|
В ветви 1 (R1, C) ток опережает напряжение на угол j1. В ветви 2 (R2, L) ток отстает от напряжения на угол j2. Находим полный ток I как векторную сумму токов I1 и I2. Между общим напряжением и полным током обозначаем угол сдвига фаз j.
Далее откладывают падения напряжений на участках R1, R2, xC, xL.
Для ветви 1. Падение напряжения на R1 совпадает по фазе с током I1. Падение напряжения на xC перпендикулярно току I1 и отстает от него.
Для ветви 2. Падение напряжения на R2 совпадает по фазе с током I2. Падение напряжения на xL перпендикулярно току I2 и опережает его.
Однако сумма падений напряжений на ветвях равна напряжению на зажимах АB цепи.
22) Последовательная r-l-c цепь. Основные соотношения, полное комплексное сопротивление

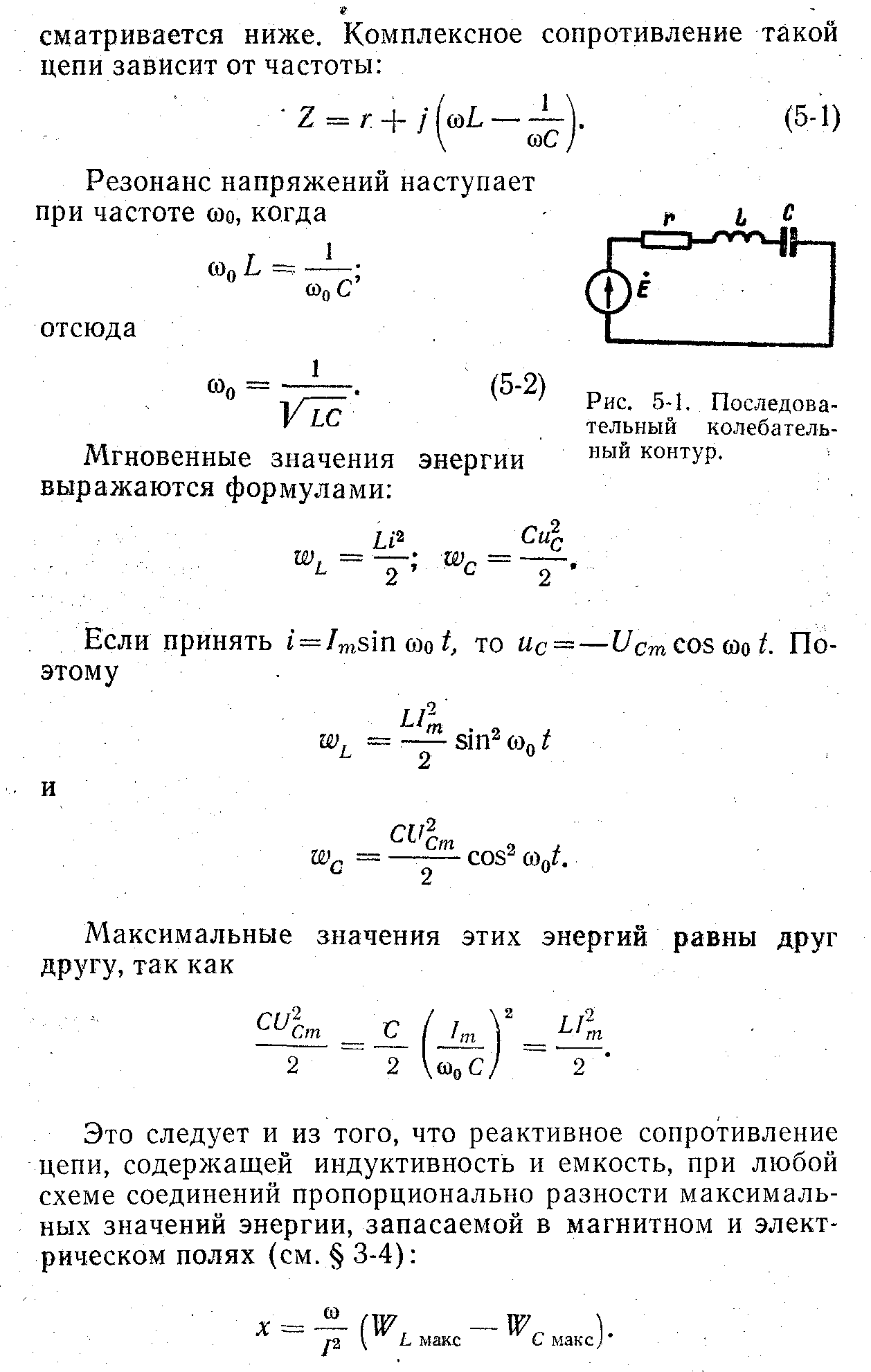



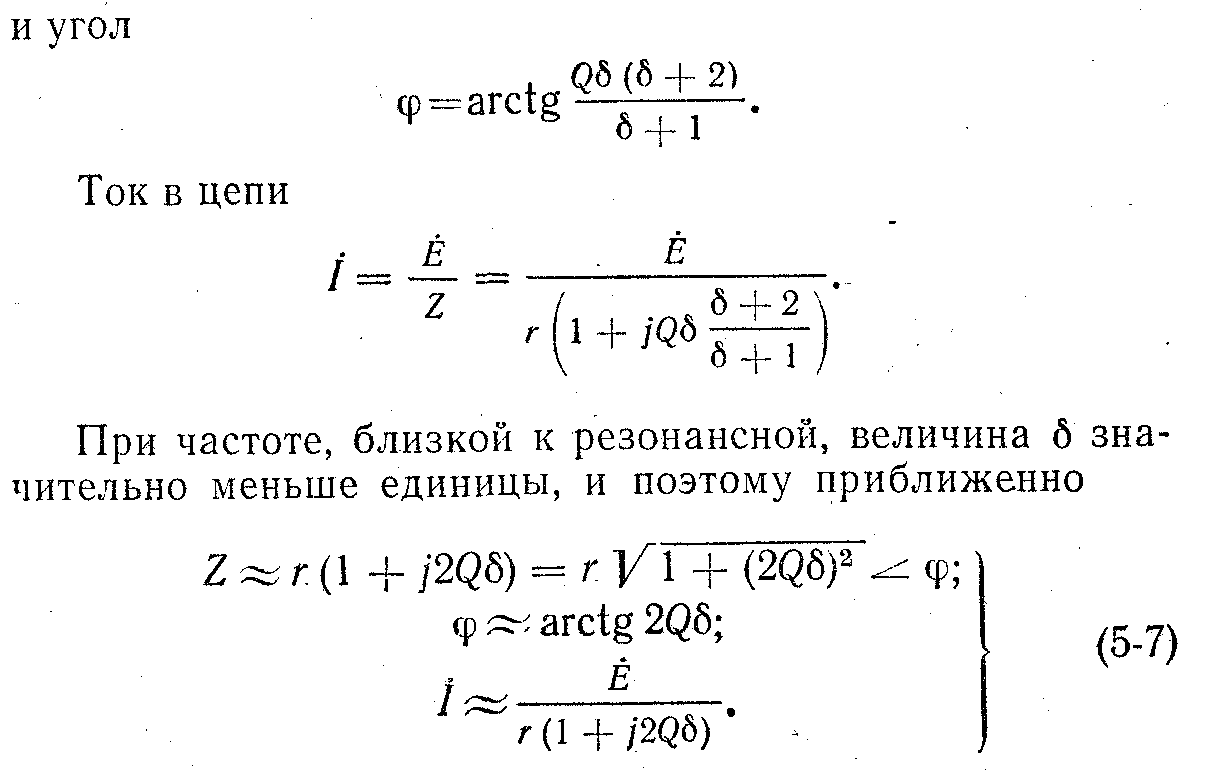


23) Мощность цепи синусоидального тока
Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:
| (1) |
Выражение для мгновенного значения мощности в электрических цепях имеет вид:
| (2) |
Приняв
начальную фазу напряжения за нуль, а
сдвиг фаз между напряжением и током за 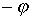 ,
получим:
,
получим:
| (3) |
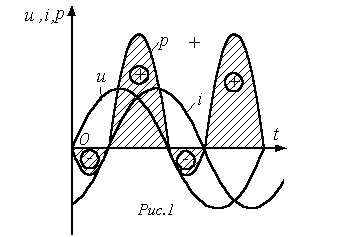
Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.
Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.
Такой
возврат энергии источнику происходит
за счет того, что энергия периодически
запасается в магнитных и электрических
полях соответственно индуктивных и
емкостных элементов, входящих в состав
двухполюсника. Энергия, отдаваемая
источником двухполюснику в течение
времени t равна 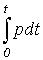 .
.
Среднее
за период значение мгновенной мощности
называется активной мощностью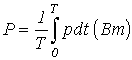 .
.
Принимая
во внимание, что 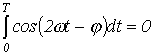 ,
из (3) получим:
,
из (3) получим:
| (4) |
Активная
мощность, потребляемая пассивным
двухполюсником, не может быть отрицательной
(иначе двухполюсник будет генерировать
энергию), поэтому 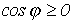 ,
т.е. на входе пассивного двухполюсника
,
т.е. на входе пассивного двухполюсника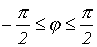 .
Случай Р=0,
.
Случай Р=0,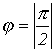 теоретически
возможен для двухполюсника, не имеющего
активных сопротивлений, а содержащего
только идеальные индуктивные и емкостные
элементы.
теоретически
возможен для двухполюсника, не имеющего
активных сопротивлений, а содержащего
только идеальные индуктивные и емкостные
элементы.
1. Резистор (идеальное активное сопротивление).

Здесь
напряжение и ток (см. рис. 2) совпадают
по фазе 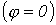 ,
поэтому мощность
,
поэтому мощность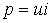 всегда
положительна, т.е. резистор потребляет
активную мощность
всегда
положительна, т.е. резистор потребляет
активную мощность
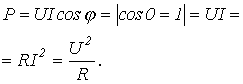
2. Катушка индуктивности (идеальная индуктивность)
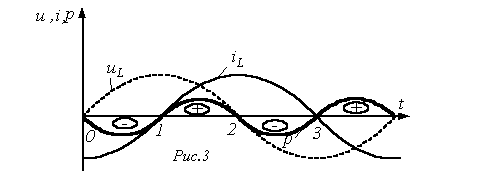
При
идеальной индуктивности ток отстает
от напряжения по фазе на 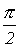 .
Поэтому в соответствии с (3) можно записать
.
Поэтому в соответствии с (3) можно записать .
.
Участок
1-2: энергия 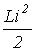 ,
запасаемая в магнитном поле катушки,
нарастает.
,
запасаемая в магнитном поле катушки,
нарастает.
Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.
3. Конденсатор (идеальная емкость)
Аналогичный
характер имеют процессы и для идеальной
емкости. Здесь 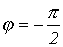 .
Поэтому из (3) вытекает, что
.
Поэтому из (3) вытекает, что .
Таким образом, в катушке индуктивности
и конденсаторе активная мощность не
потребляется (Р=0), так как в них не
происходит необратимого преобразования
энергии в другие виды энергии. Здесь
происходит только циркуляция энергии:
электрическая энергия запасается в
магнитном поле катушки или электрическом
поле конденсатора на протяжении четверти
периода, а на протяжении следующей
четверти периода энергия вновь
возвращается в сеть. В силу этого катушку
индуктивности и конденсатор называют
реактивными элементами, а их сопротивления
ХLи ХС, в отличие от
активного сопротивления R резистора, –
реактивными.
.
Таким образом, в катушке индуктивности
и конденсаторе активная мощность не
потребляется (Р=0), так как в них не
происходит необратимого преобразования
энергии в другие виды энергии. Здесь
происходит только циркуляция энергии:
электрическая энергия запасается в
магнитном поле катушки или электрическом
поле конденсатора на протяжении четверти
периода, а на протяжении следующей
четверти периода энергия вновь
возвращается в сеть. В силу этого катушку
индуктивности и конденсатор называют
реактивными элементами, а их сопротивления
ХLи ХС, в отличие от
активного сопротивления R резистора, –
реактивными.
Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.
В общем случае выражение для реактивной мощности имеет вид:
| (5) |
Она
положительна при отстающем токе
(индуктивная нагрузка- 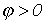 )
и отрицательна при опережающем токе
(емкостная нагрузка-
)
и отрицательна при опережающем токе
(емкостная нагрузка-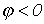 ).
Единицу мощности в применении к измерению
реактивной мощности называютвольт-ампер
реактивный(ВАр).
).
Единицу мощности в применении к измерению
реактивной мощности называютвольт-ампер
реактивный(ВАр).
В частности для катушки индуктивности имеем:
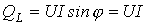 ,
так как
,
так как 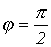 .
.
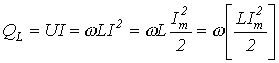 .
.
 Из
последнего видно, что реактивная мощность
для идеальной катушки индуктивности
пропорциональна частоте и максимальному
запасу энергии в катушке. Аналогично
можно получить для идеального конденсатора:
Из
последнего видно, что реактивная мощность
для идеальной катушки индуктивности
пропорциональна частоте и максимальному
запасу энергии в катушке. Аналогично
можно получить для идеального конденсатора:
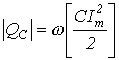 .
.
Полная мощность
Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:
| (6) |
Активная, реактивная и полная мощности связаны следующим соотношением:
| (7) |
Отношение
активной мощности к полной называют коэффициентом мощности. Из приведенных
выше соотношений видно, что коэффициент
мощности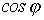 равен
косинусу угла сдвига между током и
напряжением. Итак,
равен
косинусу угла сдвига между током и
напряжением. Итак,
| (8) |
Комплексная мощность
Активную,
реактивную и полную мощности можно
определить, пользуясь комплексными
изображениями напряжения и тока. Пусть 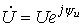 ,
а
,
а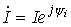 .
Тогда комплекс полной мощности:
.
Тогда комплекс полной мощности:
| (9) |
где 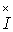 —
комплекс, сопряженный с комплексом
—
комплекс, сопряженный с комплексом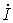 .
.
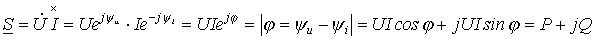 .
.
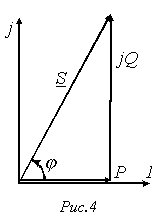
Комплексной
мощности можно поставить в соответствие
треугольник мощностей (см. рис. 4). Рис.
4 соответствует  (активно-индуктивная
нагрузка), для которого имеем:
(активно-индуктивная
нагрузка), для которого имеем:
.
Применение
статических конденсаторов для повышения
cos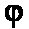
Как
уже указывалось, реактивная мощность 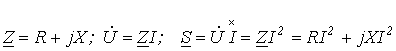 циркулирует
между источником и потребителем.
Реактивный ток, не совершая полезной
работы, приводит к дополнительным
потерям в силовом оборудовании и,
следовательно, к завышению его
установленной мощности. В этой связи
понятно стремление к увеличению
циркулирует
между источником и потребителем.
Реактивный ток, не совершая полезной
работы, приводит к дополнительным
потерям в силовом оборудовании и,
следовательно, к завышению его
установленной мощности. В этой связи
понятно стремление к увеличению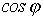 в
силовых электрических цепях.
в
силовых электрических цепях.
Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.

Если
параллельно такой нагрузке 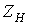 (см.
рис. 5), включить конденсатор С, то общий
ток
(см.
рис. 5), включить конденсатор С, то общий
ток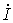 ,
как видно из векторной диаграммы (рис.
6), приближается по фазе к напряжению,
т.е.
,
как видно из векторной диаграммы (рис.
6), приближается по фазе к напряжению,
т.е.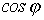 увеличивается,
а общая величина тока (а следовательно,
потери) уменьшается при постоянстве
активной мощности
увеличивается,
а общая величина тока (а следовательно,
потери) уменьшается при постоянстве
активной мощности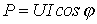 .
На этом основано применение конденсаторов
для повышения
.
На этом основано применение конденсаторов
для повышения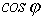 .
.
Какую
емкость С нужно взять, чтобы повысить
коэффициент мощности от значения 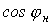 до
значения
до
значения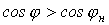 ?
?
Разложим 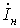 на
активную
на
активную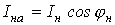 и
реактивную
и
реактивную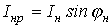 составляющие.
Ток через конденсаторкомпенсирует
часть реактивной составляющей тока
нагрузки
составляющие.
Ток через конденсаторкомпенсирует
часть реактивной составляющей тока
нагрузки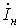 :
:
| (10) |
| (11) |
| (12) |
Из (11) и (12) с учетом (10) имеем
 ,
,
но 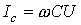 ,
откуда необходимая для повышения
,
откуда необходимая для повышения емкость:
емкость:
| (13) |
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
а) Постоянный ток
Для любой цепи постоянного тока выполняется соотношение:
| (14) |
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
б) Переменный ток.
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
| (15) |
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:
| (16) |
где
знак “+” относится к индуктивным
элементам  ,
“-” – к емкостным
,
“-” – к емкостным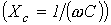 .
.
Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):
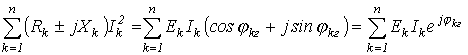
или
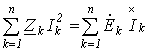 .
.
8. Последовательное соединение r, l, c при переменном токе
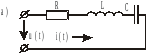
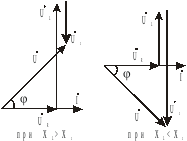
Рис. 7.
По закону Ома для мгновенного значения напряжения
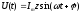
где  — полное сопротивление цепи раcсчитывается
по формуле
— полное сопротивление цепи раcсчитывается
по формуле
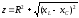
Угол сдвига фаз между приложенным напряжением и током
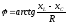
При последовательном соединении элементов векторную диаграмму удобно начинать строить с вектора общего тока, а затем учитывая II закон Кирхгофа строим вектора напряжений рис.7.
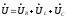
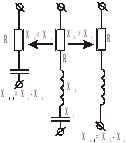
Рис. 8.
При последовательном
соединении 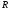 ,
,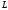 ,
,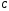 реактивные
сопротивления
реактивные
сопротивления 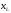 и
и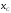 можно заменить одним эквивалентным,
а характер цепи будет определяться по
величине большего реактивного
сопротивления рис. 8.
можно заменить одним эквивалентным,
а характер цепи будет определяться по
величине большего реактивного
сопротивления рис. 8.
Реактивная мощность
цепи 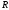 ,
,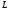 ,
, определяется:
определяется:
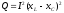
Полная мощность 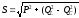
9. Параллельне соединения r и l в цепи переменного тока
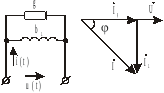
Рис. 9.
Мгновенные значения напряжения и тока в неразветвленной цепи

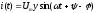
 ,где
,где —
полная проводимость цепи
—
полная проводимость цепи
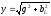
,где —
активная проводимость
—
активная проводимость
 —
реактивная проводимость индуктивности
—
реактивная проводимость индуктивности
Угол сдвига между приложенными напряжением и током
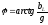
Параллельное соединение r с в цепи переменного тока

Рис. 10.
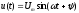
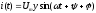 ,
,
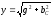 ,
, 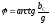
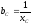 —
реактивная проводимость ёмкости.
—
реактивная проводимость ёмкости.
10. Параллельное соединение r , l , с в цепи переменного тока
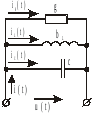
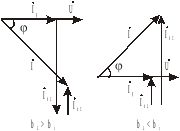
Рис. 11.
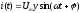
,где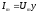
Полная проводимость определяется
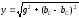
Угол сдвига между напряжением и током
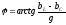
Для данной схемы соединения векторную диаграмму удобно начинать строить с вектора напряжения, а затем по 1 закону Кирхгофа (рис. 11)
При параллельном
соединении R , L,
С реактивные проводимости  и
и можно заменить одной эквивалентной, а
характер цепи будет определяться по
величине большей реактивной проводимости(рис.12)
можно заменить одной эквивалентной, а
характер цепи будет определяться по
величине большей реактивной проводимости(рис.12)
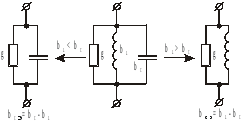
Замена последовательного соединения активных и реактивных сопротивлений в параллельно соединенные активные и реактивные проводимости и обратно: (Рис .13)
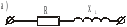
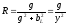 ,
, 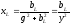
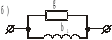
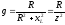 ,
, 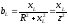

 ,
, 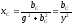
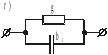
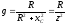 ,
, 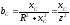
11. Анализ электрической цепи переменного тока методом проводимостей
Для расчетов токов I1,I2,I3 методом проводимостей в цепи (рис.14) необходимо перейти от разветвленной сложной схемы к простейшей последовательной цепи и определить ток в неразветвленном участке цепи I1, а затем в обратном порядке определим токи в параллельных ветвях I2 и I3.

Рис. 14.
Преобразуем
параллельный участок bc в последовательный.
Для этого определим активные проводимости 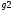 ,
,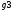 и реактивные
и реактивные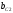 и
и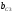 (Рис.15)
(Рис.15)
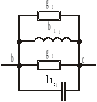
Рис. 15.
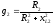
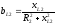
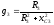
При параллельном соединении участка эквивалентная активная проводимость равна
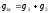
При двух реактивных
проводимостях разного характера,
характер эквивалентный проводимости
будет той, реактивная проводимость
которая больше и будет равна разности
проводимостей. Например,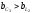 ,
тогда
,
тогда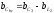
Схема (рис 15) примет такой вид (рис.16)
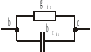
Рис. 16.
Далее перейдем от
проводимостей и к последовательно
соединенным сопротивлениям 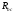 и
и (рис17)
(рис17)
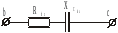
Рис.17.
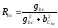
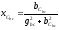
Данная разветвленная схема примет вид последовательно соединенных элементов (рис.18)

Рис. 18
При последовательном соединении активных сопротивлений эквивалентное активное сопротивление будет равно
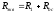
а при двух или нескольких соединенных последовательно реактивных сопротивлений, характер эквивалентного сопротивления будет таким, реактивное сопротивление которое больше и будет равна разности сопротивлений.
Например, 
тогда 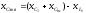
Схема рис. 18 примет такой вид (рис. 19) и будет носить активно-емкостной характер
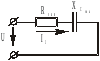
Рис. 19.
Полное сопротивление
цепи 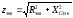
Ток в неразветвленном участке цепи
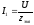 и фаза тока
и фаза тока 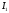

Затем определим
напряжение на участке 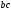
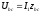 ,где
,где 
фаза напряжения 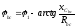
Знак »минус» показывает, что фаза напряжения при активно-
емкостном характере
отстаёт от фазы тока 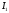 (Рис.18). После этого можно определить
токи в параллельных ветвях (Рис.14).
(Рис.18). После этого можно определить
токи в параллельных ветвях (Рис.14).
 ,где
,где 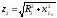
фаза тока 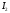
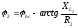
7. Электрическая цепь с последовательным соединением элементов r, l и c
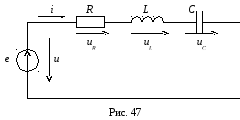
Пусть в заданной схеме с последовательным соединением элементов R, L и C (рис. 47) протекает переменный ток
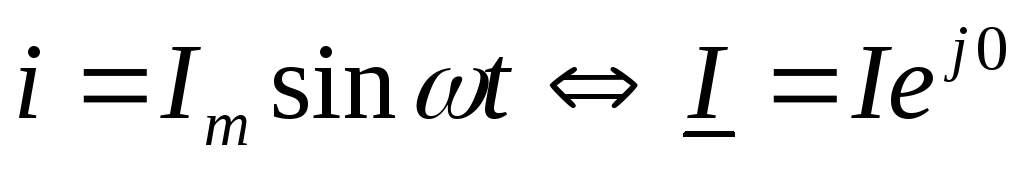 .
.
По 2-му закону Кирхгофа для мгновенных значений функций получим уравнение в дифференциальной форме:
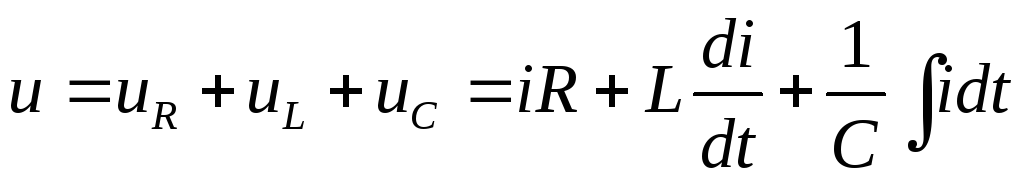 .
.
То же уравнение в комплексной форме получит вид:
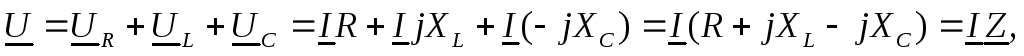
где 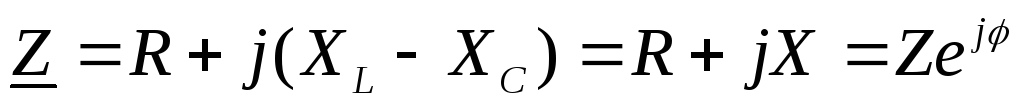
комплексное сопротивление,
комплексное сопротивление, 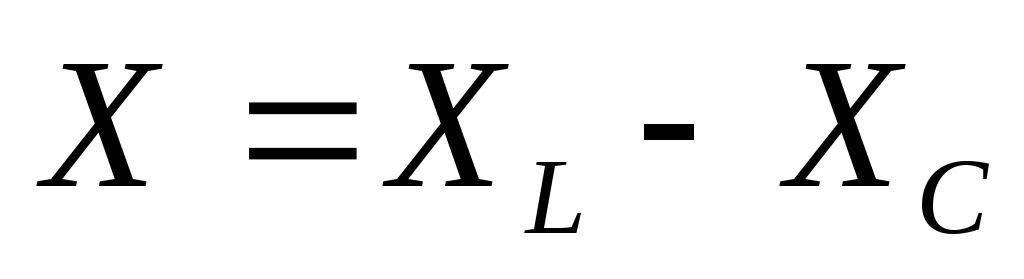
реактивное (эквивалентное) сопротивление,
реактивное (эквивалентное) сопротивление, 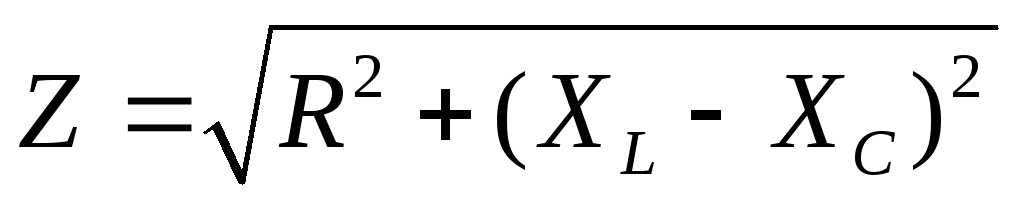
модуль комплексного или полное
сопротивление,
модуль комплексного или полное
сопротивление, 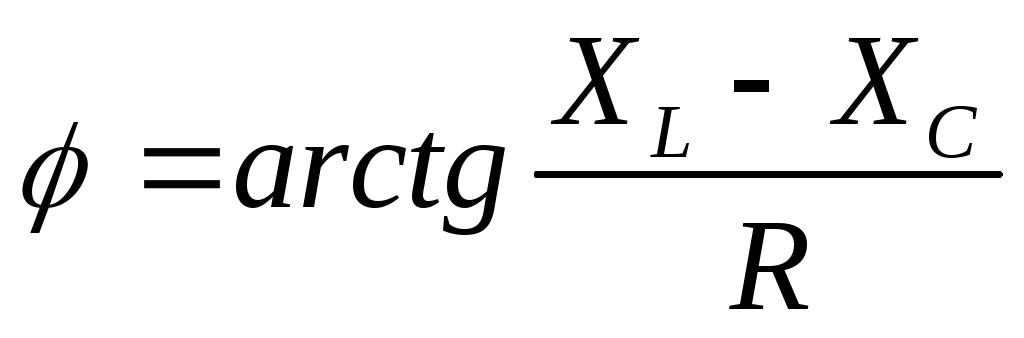
аргумент комплексного сопротивления
или угол сдвига фаз между напряжением
и током на входе схемы. При
аргумент комплексного сопротивления
или угол сдвига фаз между напряжением
и током на входе схемы. При 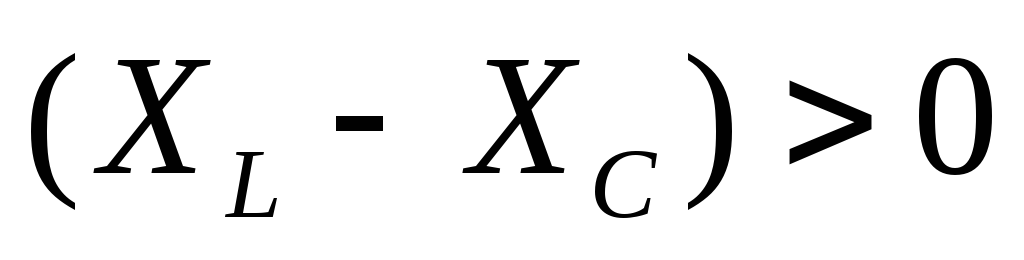 фазный уголφ>0,
при этом цепь в целом носит
активно-индуктивный характер, а при
фазный уголφ>0,
при этом цепь в целом носит
активно-индуктивный характер, а при  иφ<0
– цепь в целом носит активно-емкостный
характер.
иφ<0
– цепь в целом носит активно-емкостный
характер.
Уравнение закона Ома для последовательной схемы будет иметь вид:
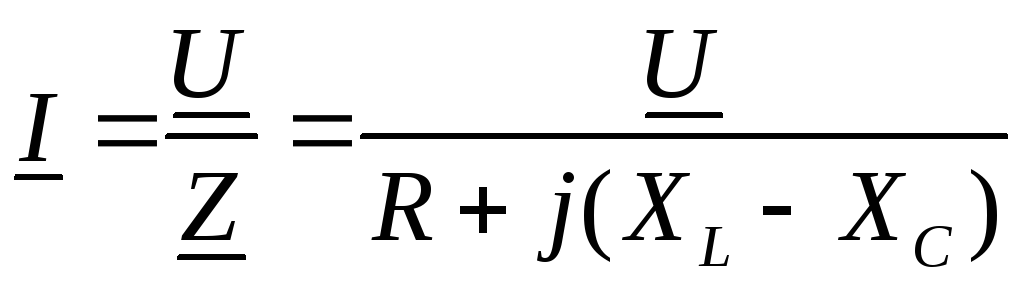 в
комплексной форме,
в
комплексной форме,
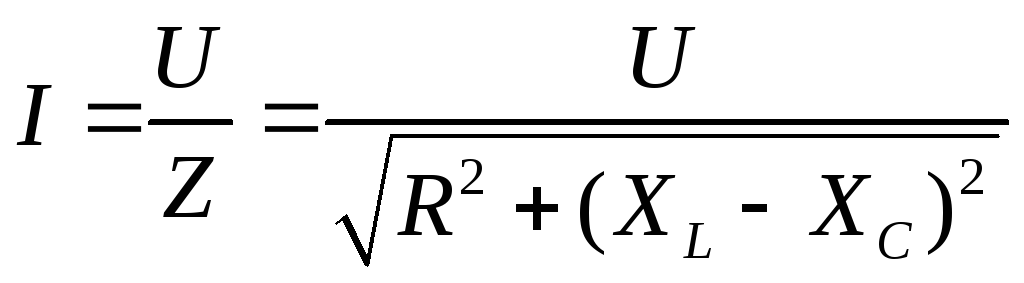 в
обычной форме для модулей.
в
обычной форме для модулей.
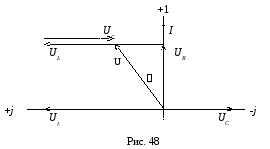
Векторная диаграмма тока и напряжений при φ>0 показана на рис. 48.
В рассматриваемой цепи на переменном токе будут происходить одновременно два физических процесса: преобразование энергии в другие виды в резисторе R (активный процесс) и взаимный обмен энергией между магнитным полем катушки, электрическим полем конденсатора и источником энергии (реактивный процесс).
8. Электрическая цепь с параллельным соединением элементов r, l и с
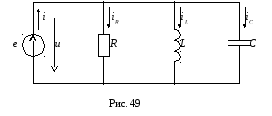
Пусть на входе схемы рис. 49 действует переменное напряжение:
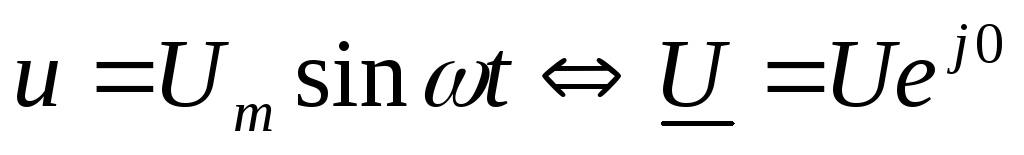
По 1-му закону Кирхгофа для мгновенных значений функций получаем уравнение в дифференциальной форме:
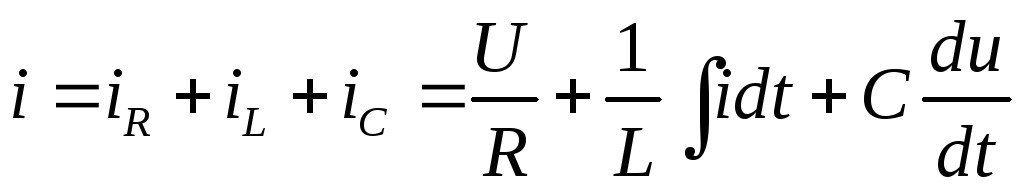
То же уравнение в комплексной форме получит вид:
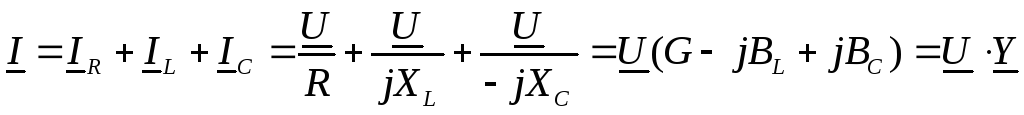 ,
,
где 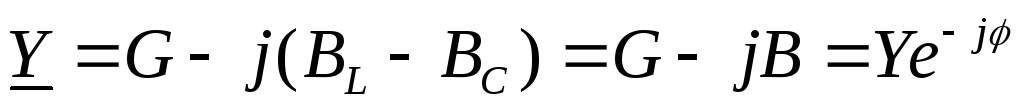
комплексная проводимость,
комплексная проводимость, 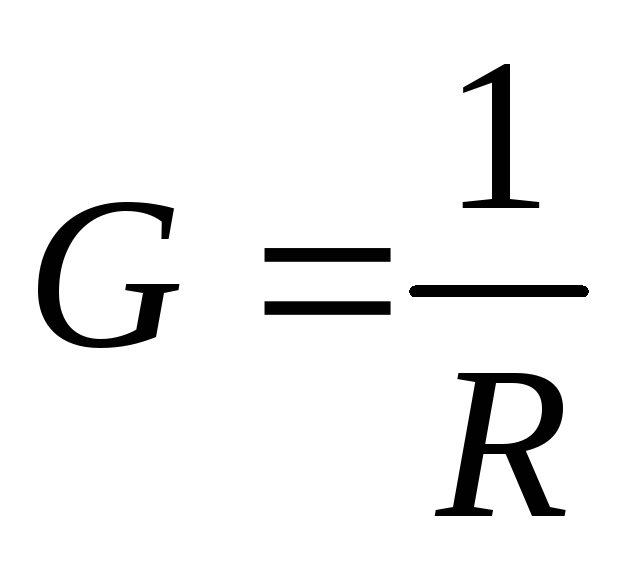
активная проводимость,
активная проводимость, 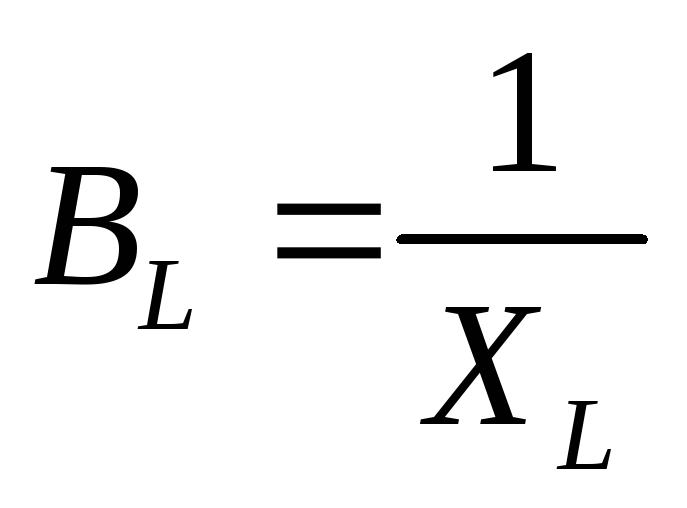
реактивная индуктивная проводимость,
реактивная индуктивная проводимость, 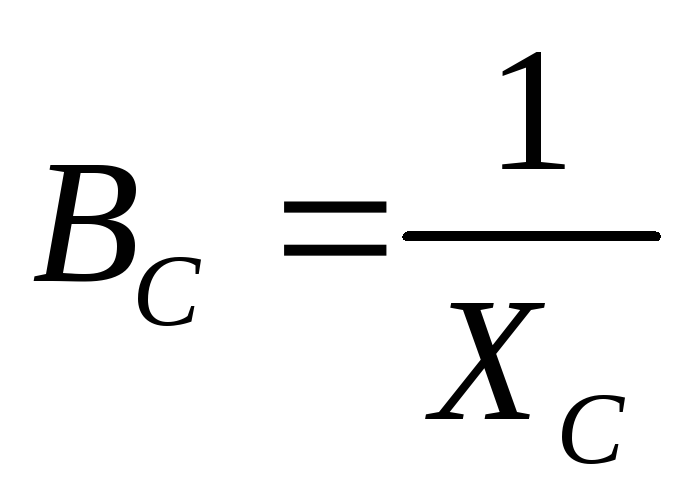
реактивная емкостная проводимость,
реактивная емкостная проводимость, 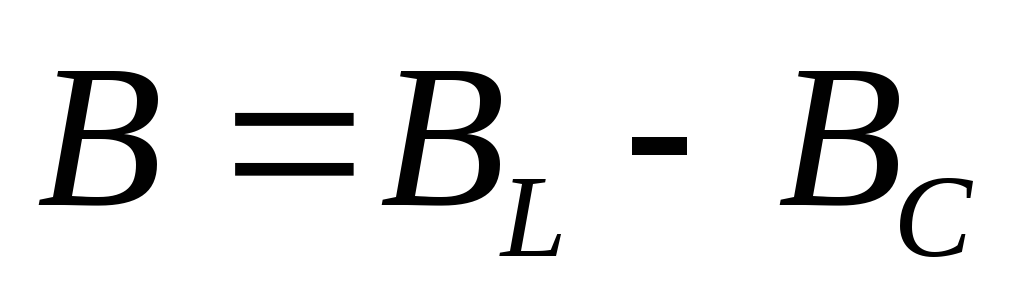
реактивная (эквивалентная) проводимость,
реактивная (эквивалентная) проводимость, 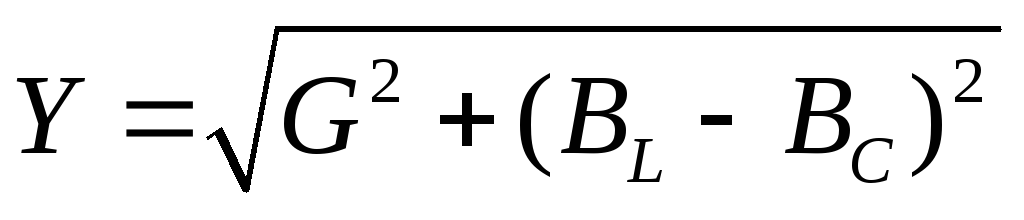
модуль комплексной проводимости или
полная проводимость,
модуль комплексной проводимости или
полная проводимость, 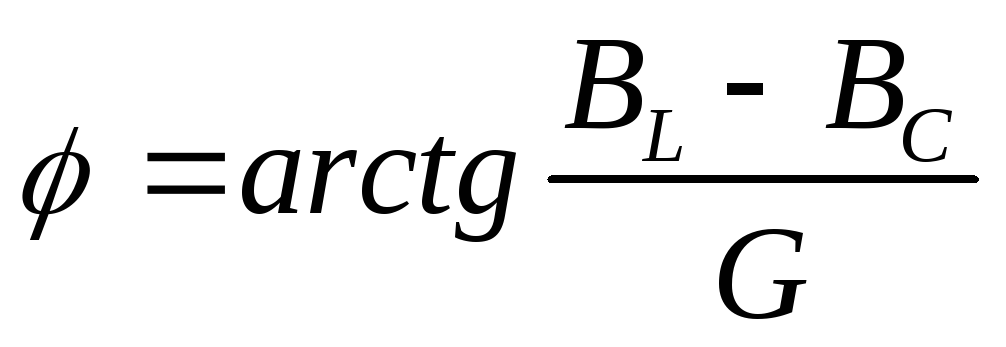
аргумент комплексной проводимости
или угол сдвига фаз между напряжением
и током на входе схемы. При
аргумент комплексной проводимости
или угол сдвига фаз между напряжением
и током на входе схемы. При 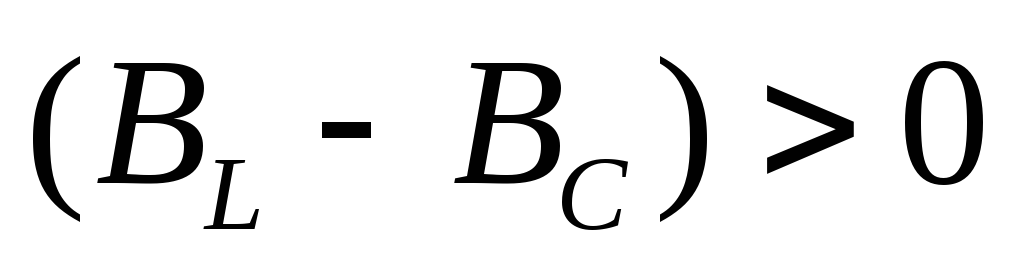 иφ>0
– цепь в целом носит активно-индуктивный
характер, а при
иφ>0
– цепь в целом носит активно-индуктивный
характер, а при 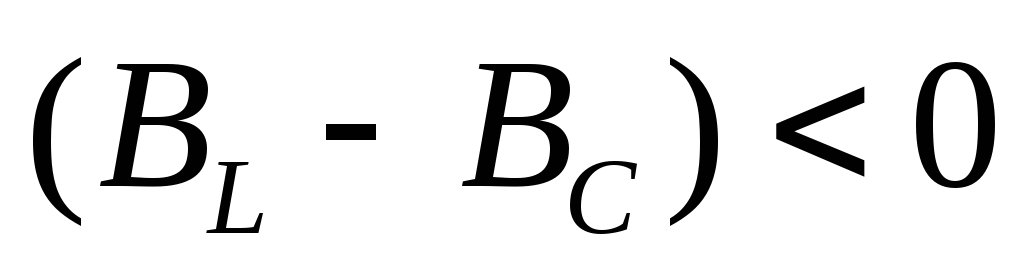 иφ<0
– цепь в целом носит активно-емкостный
характер.
иφ<0
– цепь в целом носит активно-емкостный
характер.
Уравнение закона Ома для параллельной схемы будет иметь вид:
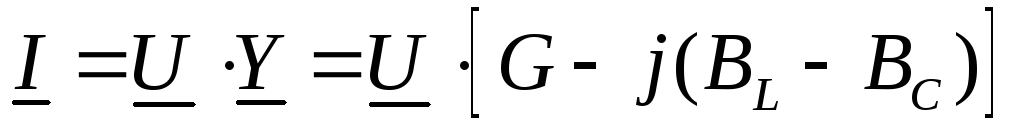 в
комплексной форме;
в
комплексной форме;
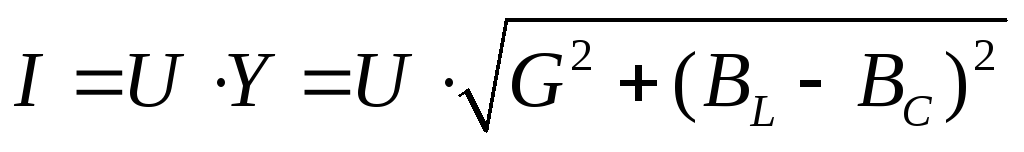 в
обычной форме для модулей.
в
обычной форме для модулей.
Векторная диаграмма токов и напряжения при φ>0 показана на рис. 50.
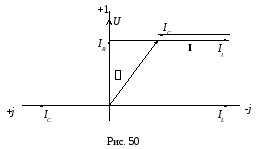
На переменном токе в рассматриваемой цепи будут происходить одновременно два физических процесса: преобразование электрической энергии в другие виды (активный процесс) и взаимный обмен энергией между магнитным полем катушки, электрическим полем конденсатора и источником энергии (реактивный процесс).
9. Активные и реактивные составляющие токов и напряжений
При расчете электрических цепей переменного тока реальные элементы цепи (приемники, источники) заменяются эквивалентными схемами замещения, состоящими из комбинации идеальных схемных элементов R, L и С.
Пусть некоторый приемник энергии носит в целом активно-индуктивный характер (например, электродвигатель). Такой приемник может быть представлен двумя простейшими схемами замещения, состоящими из 2-х схемных элементов R и L: а) последовательной (рис. 51а) и б) параллельной (рис. 51б):
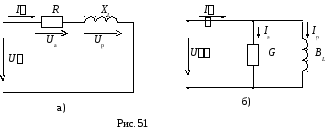
Обе
схемы будут эквивалентны друг другу
при условии равенства параметров
режима на входе: 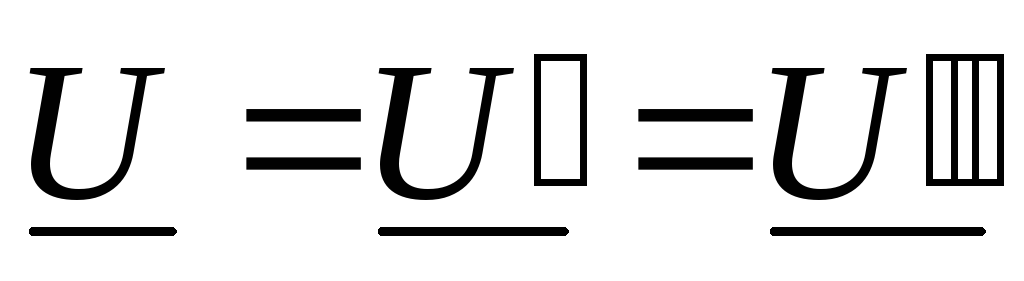 ,
,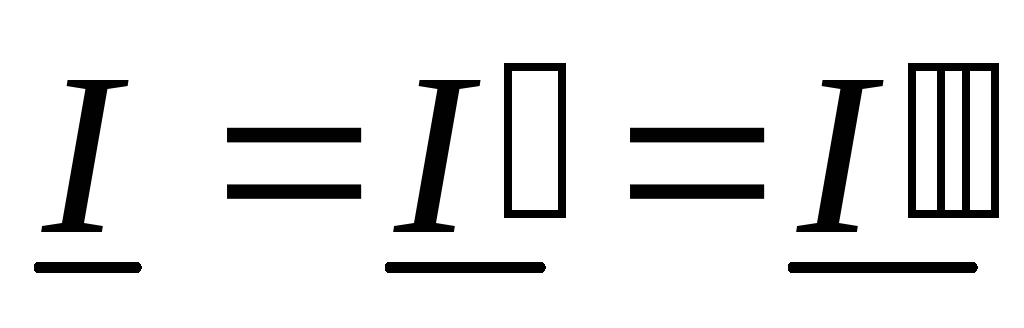 .
.
Для последовательной схемы (рис. 51а) справедливы соотношения:
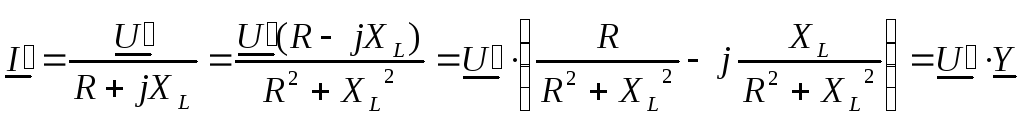 ,
,
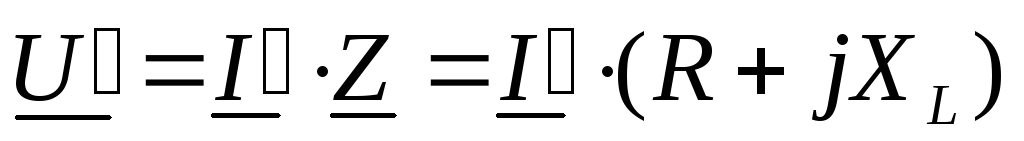 .
.
Для параллельной схемы (рис. 51б) справедливы соотношения:
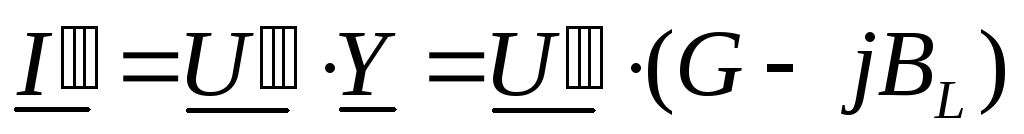 ,
,
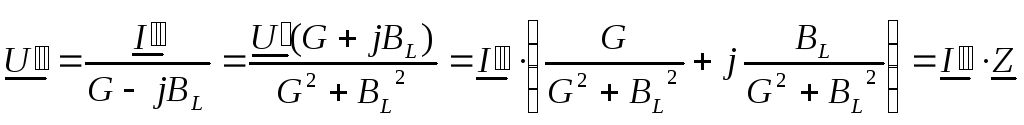 .
.
Сравнивая правые части уравнений для U и I, получим соотношения между параметрами эквивалентных схем:
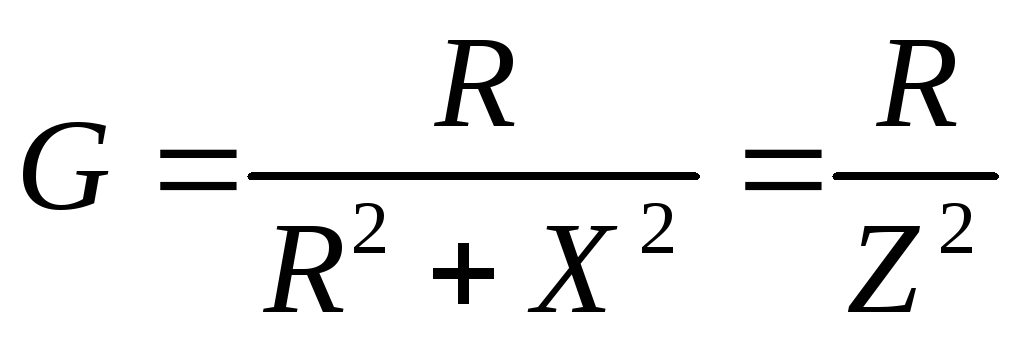 ,
, 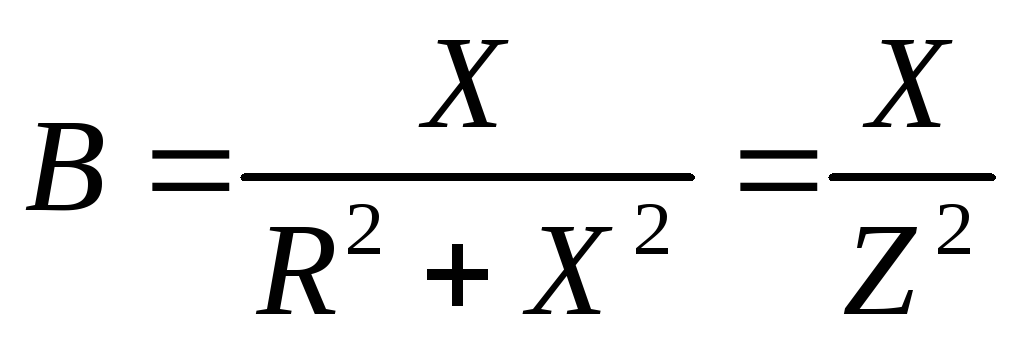 ,
,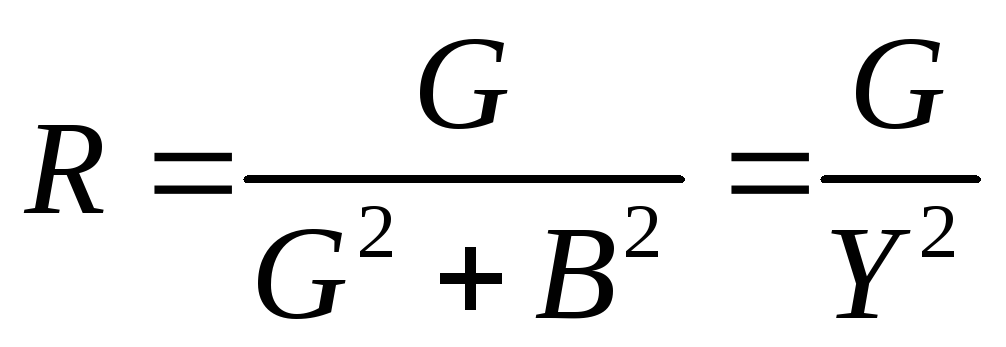 ,
,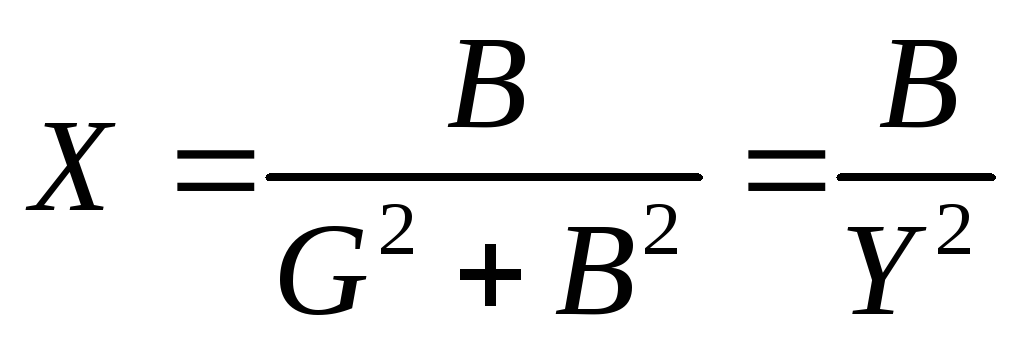 .
.
Из
анализа полученных уравнений следует
сделать вывод, что в общем случае 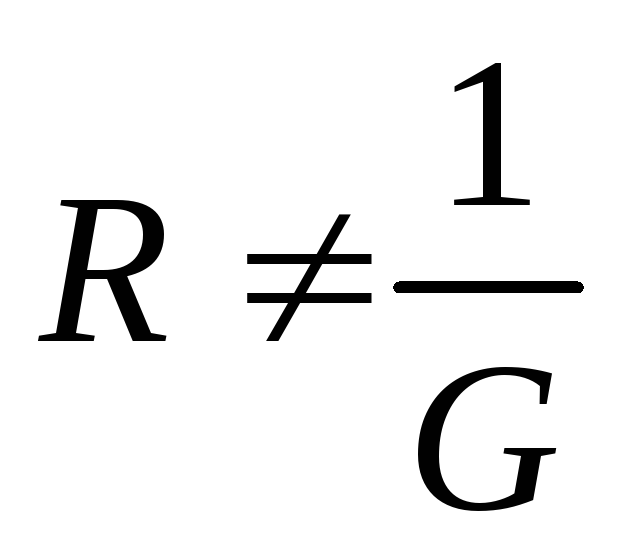 и
и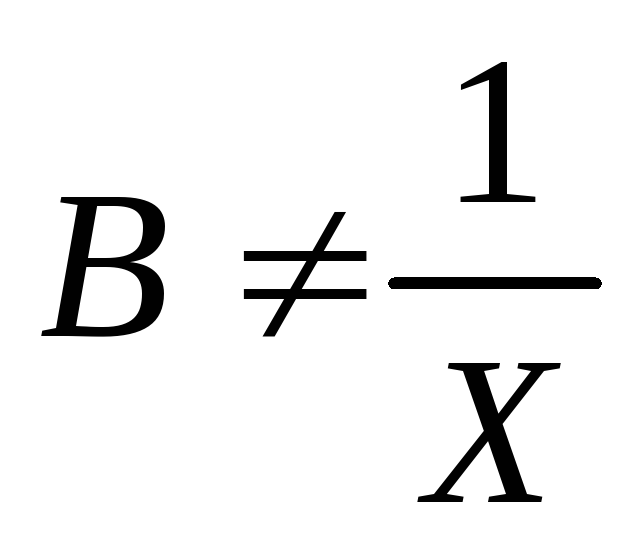 и соответственно
и соответственно и
и ,
как это имеет место для цепей постоянного
тока.
,
как это имеет место для цепей постоянного
тока.
Математически любой вектор можно представить состоящим из суммы нескольких векторов или составляющих.
Последовательной схеме замещения соответствует представление вектора напряжения в виде суммы двух составляющих: активной составляющей Uа, совпадающей с вектором тока I, и реактивной составляющей Uр, перпендикулярной к вектору тока (рис. 52а):

Из
геометрии рис. 52а следуют соотношения: 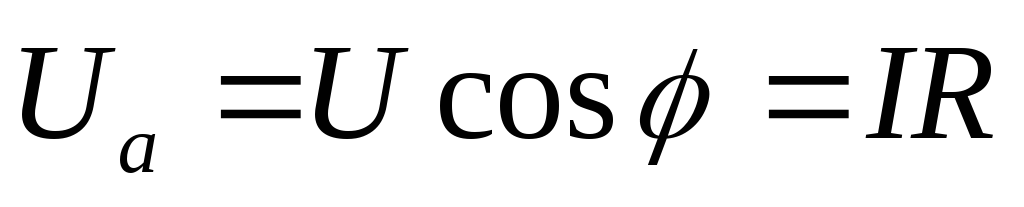 ,
,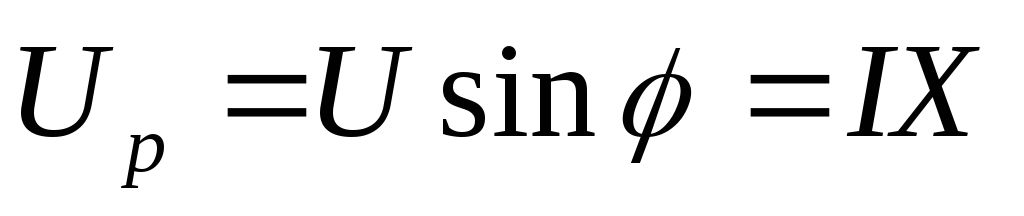 ,
, .
.
Треугольник,
составленный из векторов  ,
,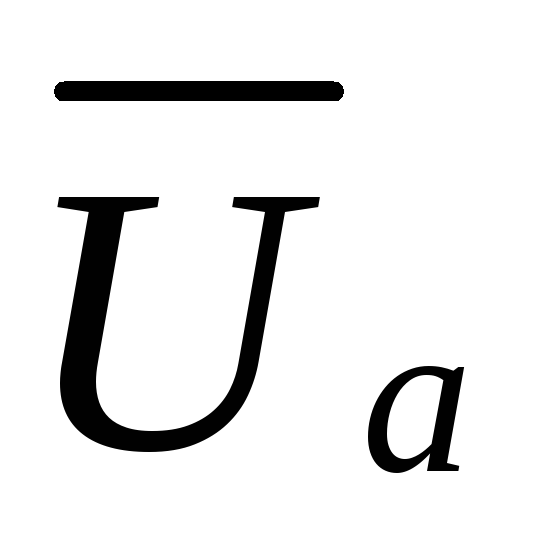 ,
, получил название треугольника
напряжений (рис. 52а).
получил название треугольника
напряжений (рис. 52а).
Если
стороны треугольника напряжений
разделить на ток I,
то получится новый треугольник,
подобный исходному, но сторонами которого
являются полное сопротивление Z,
активное сопротивление R и реактивное сопротивление X.
Треугольник со сторонами Z,
R, X называется
треугольником сопротивлений (рис.
52б). Из треугольника сопротивлений
следуют соотношения: R=Zcosφ,
X=Zsinφ, 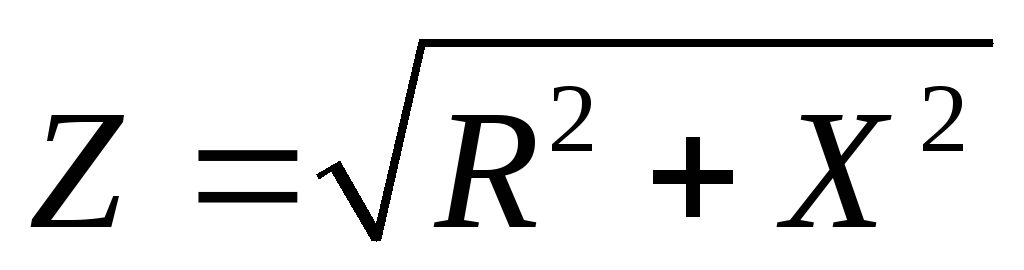 ,
,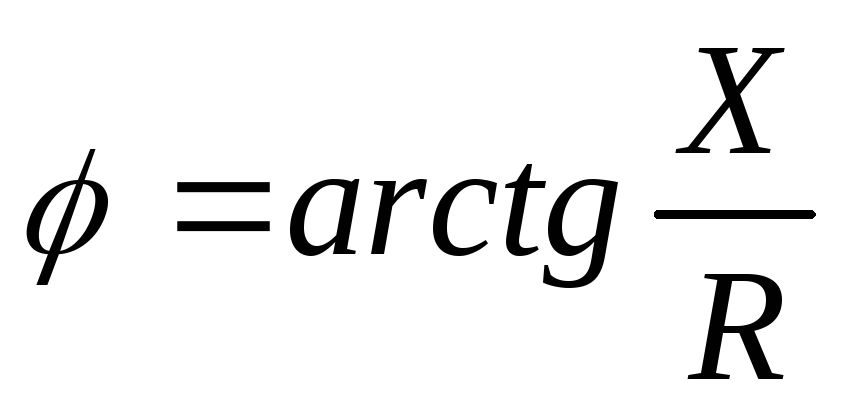 .
.
Параллельной схеме замещения соответствует представление вектора тока в виде суммы двух составляющих: активной составляющей Iа, совпадающей с вектором напряжения U, и реактивной составляющей Iр, перпендикулярной к вектору U (рис. 53а):
+1

Из геометрии рисунка следуют соотношения:
 ,
, 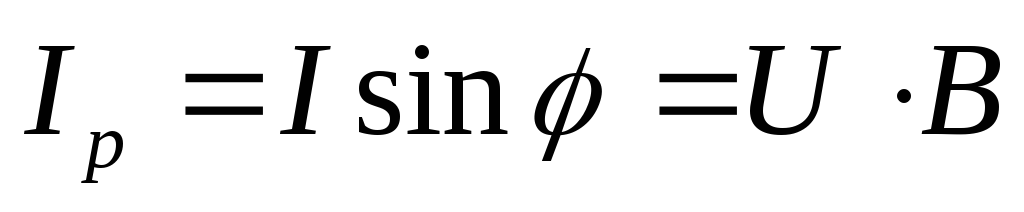 ,
,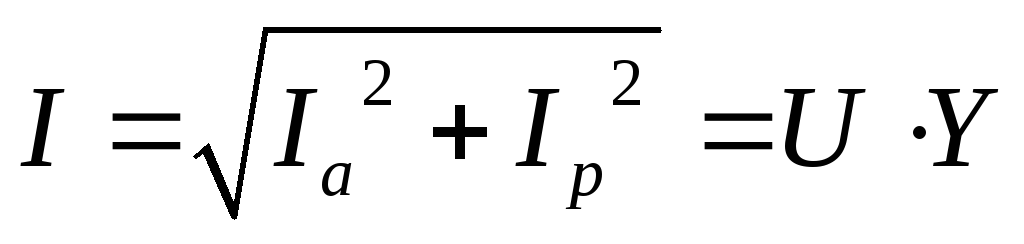 .
.
Треугольник,
составленный из векторов 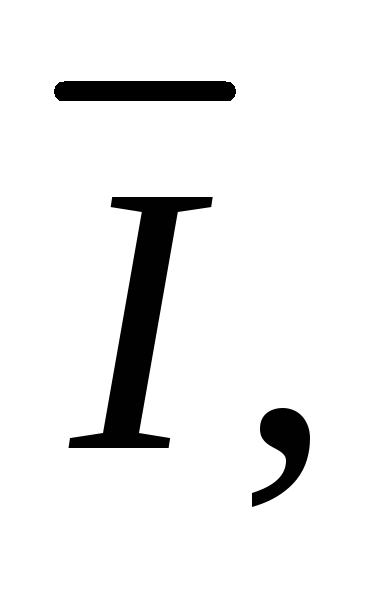
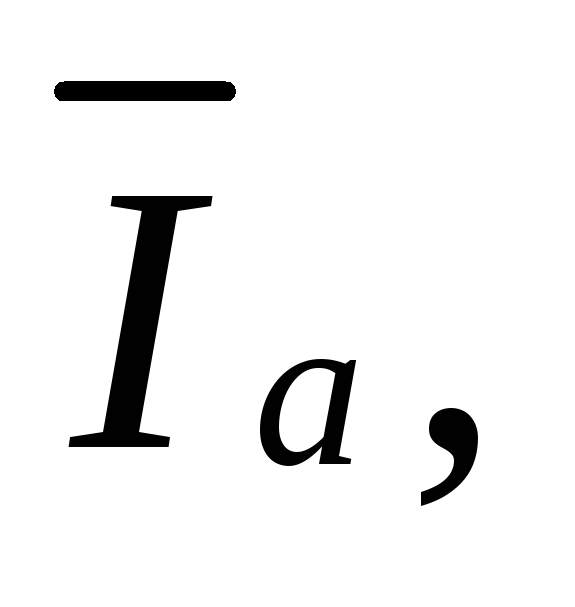
 получил название треугольника токов
(рис. 53а).
получил название треугольника токов
(рис. 53а).
Если стороны треугольника токов разделить на напряжение U, то получится новый треугольник, подобный исходному, но сторонами которого являются проводимости: полная – Y, активная G, реактивная – B (рис. 53б). Треугольник со сторонами Y, G, B называется треугольником проводимостей. Из треугольника проводимостей следуют соотношения:
 ,
, 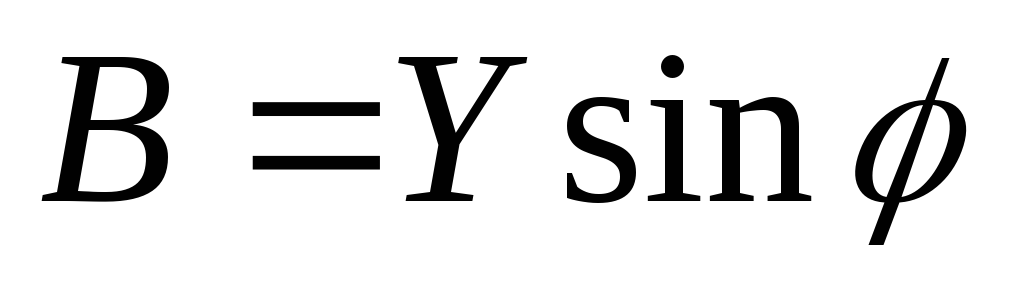 ,
,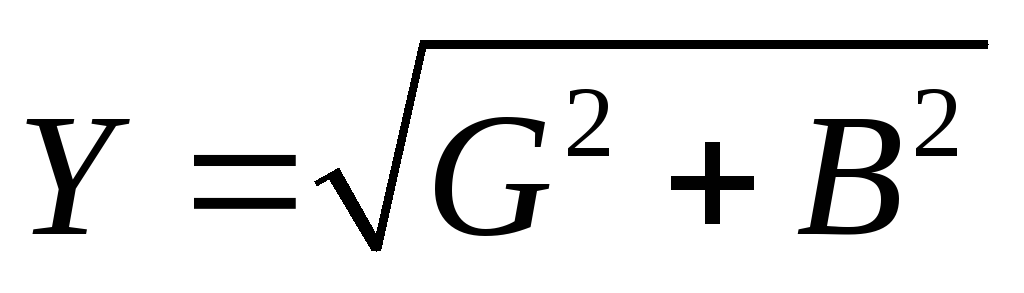 ,
,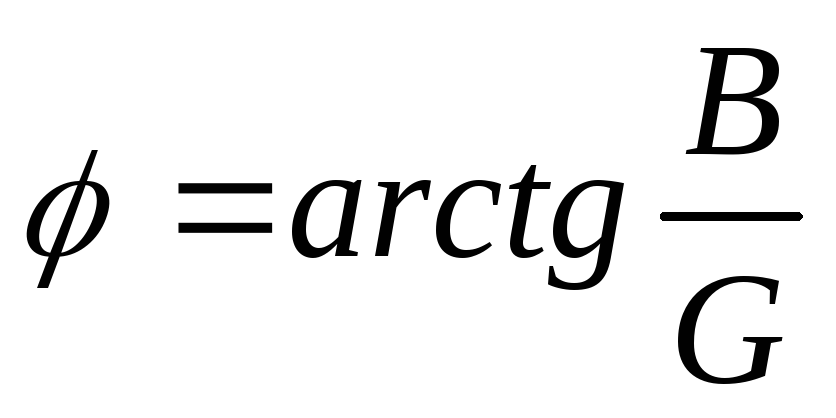 .
.
Разложение напряжений и токов на активные и реактивные составляющие является математическим приемом и применяется на практике для расчета сравнительно несложных цепей переменного тока.
Элементы r,l,c в цепи синусоидального тока
Пусть через каждый
элемент протекает синусоидальный ток  .
.
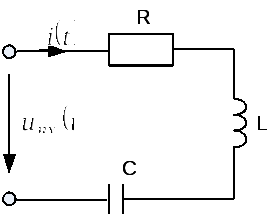
Тогда, согласно компонентным уравнениям и с учетом синусоидальности тока получаем:
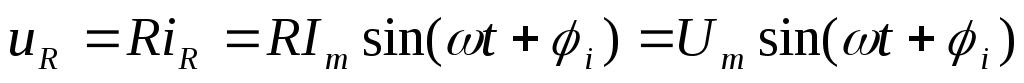 ;
;
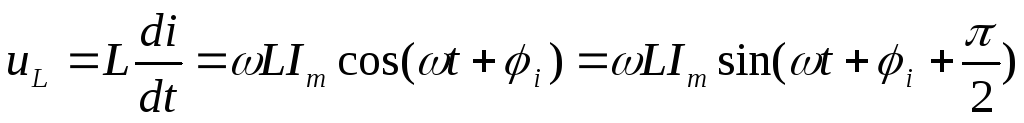 ;
;

Напряжения на
элементах в цепи синусоидального тока
так же синусоидальны и имеют ту же
частоту, но другие амплитуды и начальные
фазы. Учитывая стандартную запись
напряжения  ,
получаем
,
получаем
Напряжение на сопротивлении совпадает с током по фазе, напряжение на емкости отстает от тока на 900, напряжение на индуктивности опережает ток на 900.
Определим мгновенную и активную мощности на каждом элементе:

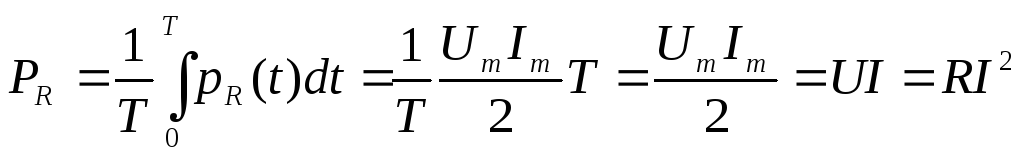 ;
;
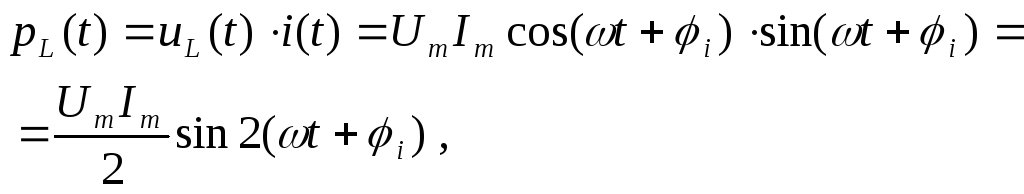
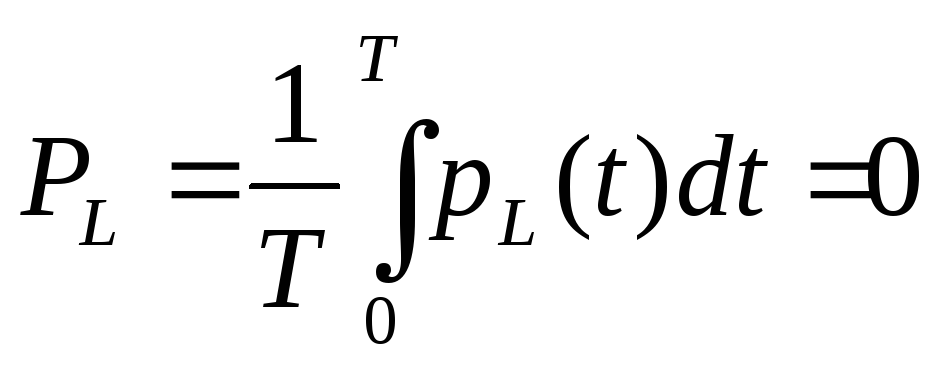 ;
;
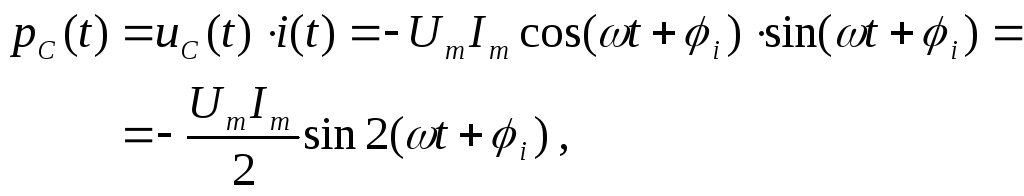
 .
.
Вопрос 7. Законы цепей в символической форме
1. Первый закон Кирхгофа
Алгебраическая
сумма мгновенных значений токов ветвей,
сходящихся в одном узле, равна нулю.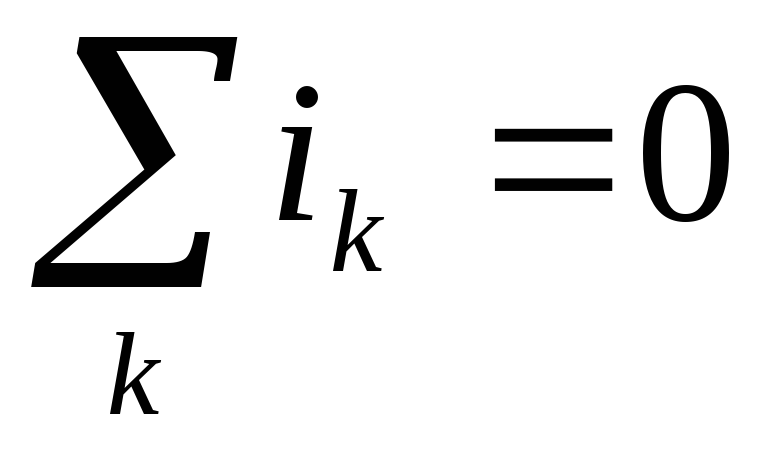 .
.
Подставим вместо
каждого мгновенного значения тока его
представление в виде комплекса
амплитудного значения, тогда 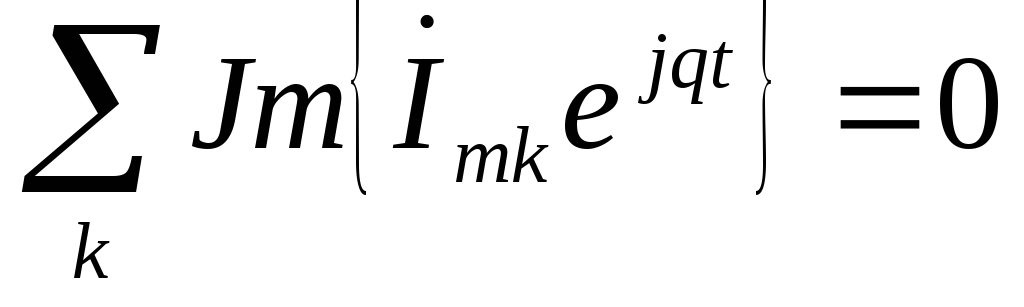 .
.
Так как в любой
момент времени нулю равна сумма проекций
вращающихся векторов, следовательно,
нулю должна равняться сумма самих
вращающихся векторов, т.е. получим 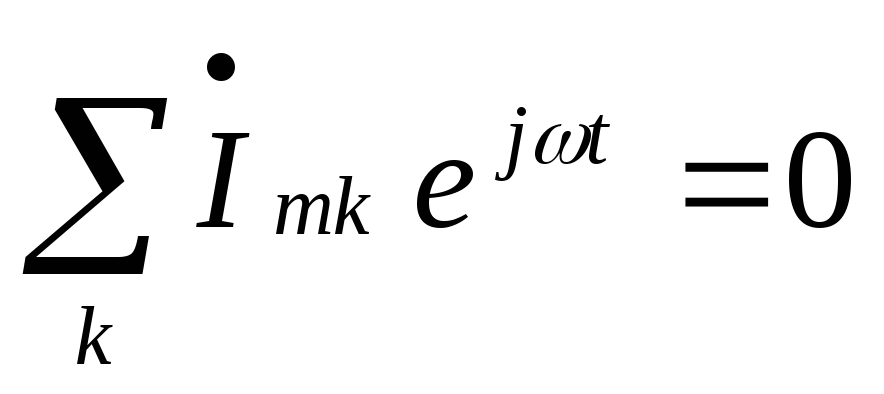 .
Так как
.
Так как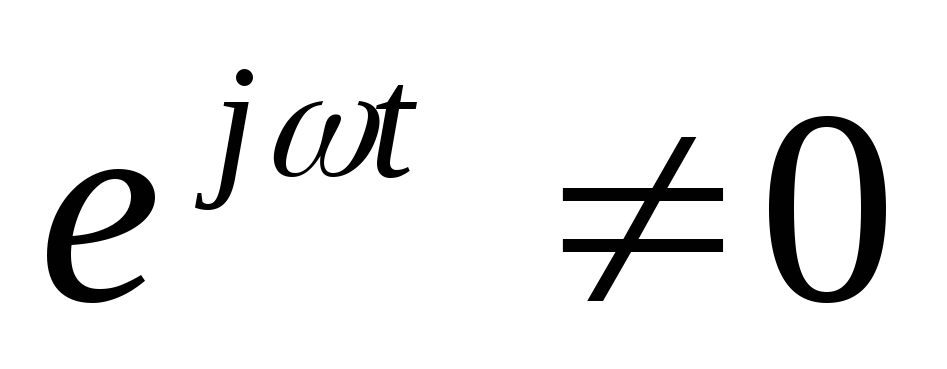 ,
то сократим на нее и получим
,
то сократим на нее и получим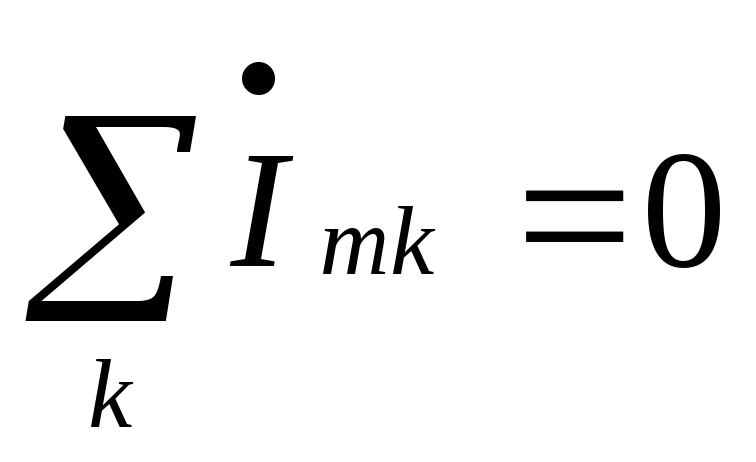 .
.
Алгебраическая сумма комплексов амплитудных значений токов ветвей, сходящихся в одном узле, равна нулю.
Поделив на 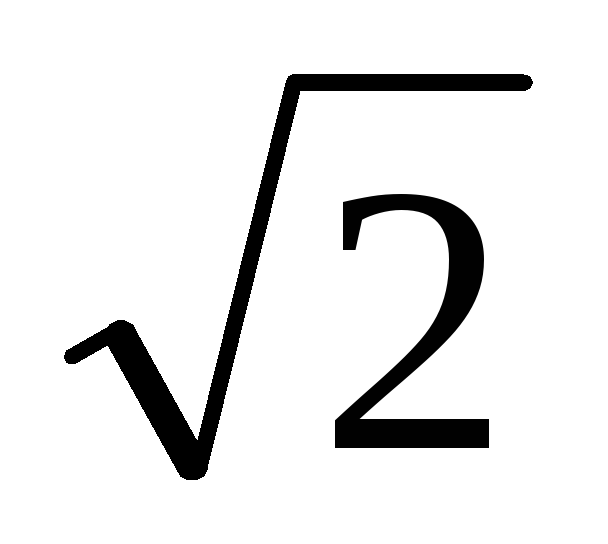 ,
получим первый закон Кирхгофа для
комплексов действующих значений.
,
получим первый закон Кирхгофа для
комплексов действующих значений.
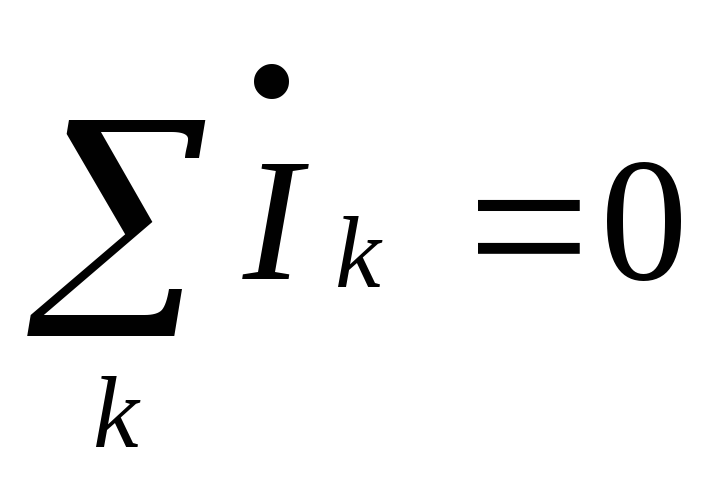
2. Второй закон Кирхгофа
После аналогичных преобразований получим:
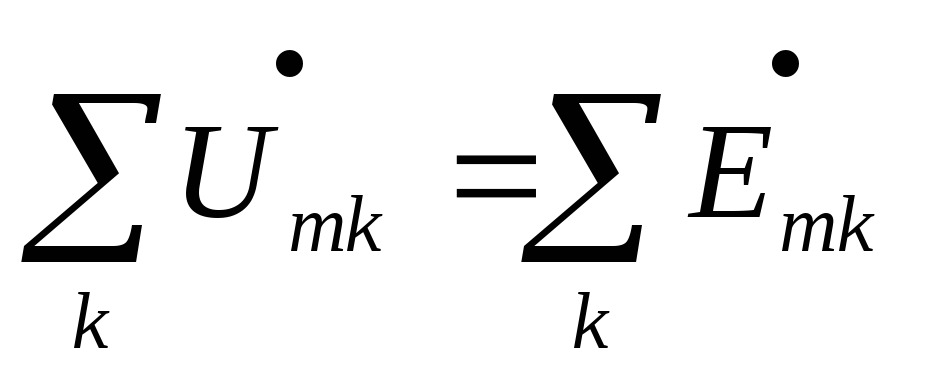 или
или 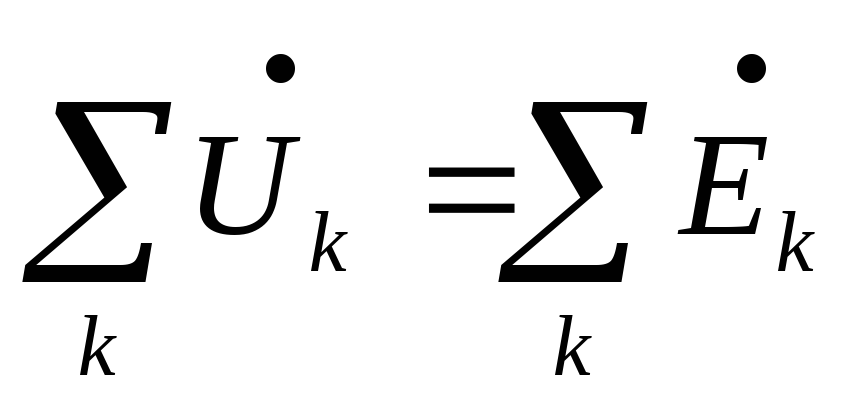 .
.
Алгебраическая сумма комплексов амплитудных (действующих) значений напряжений на всех элементах контура, кроме ЭДС равна алгебраической сумме комплексов амплитудных (действующих) значений ЭДС этого же контура.
Однако для самих амплитудных и действующих значений законы Кирхгофа не выполняются.
Вопрос 8. Фазовые соотношения между напряжением и током на элементах r,l,c Комплексы амплитуд напряжения и тока на элементах r,l,c связаны между собой.
Для R:
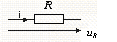
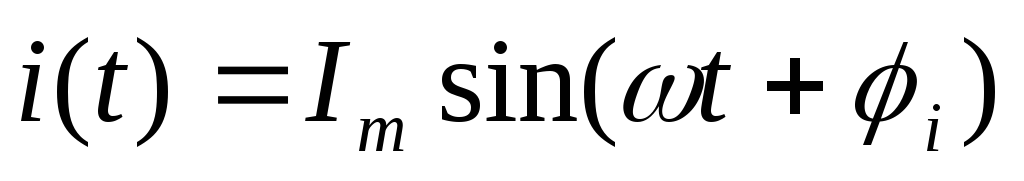 ,
, 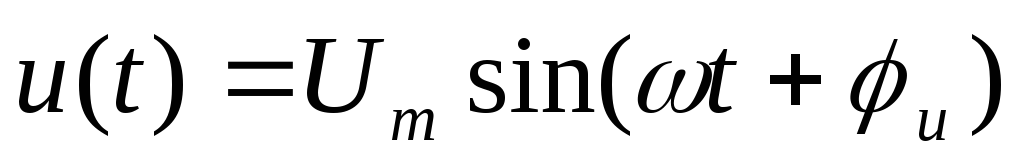 ,
гдеUm=RIm,, u=i
,
гдеUm=RIm,, u=i
Перейдем к проекциям вращающихся векторов:
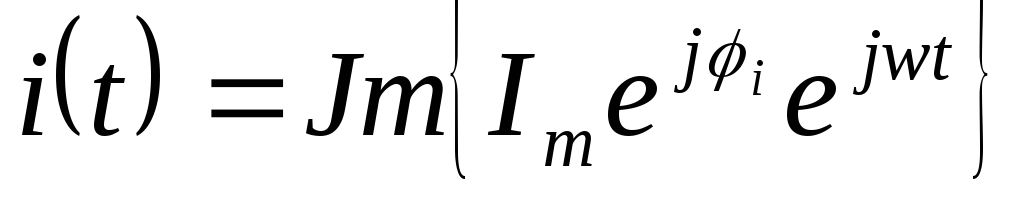 ,
, 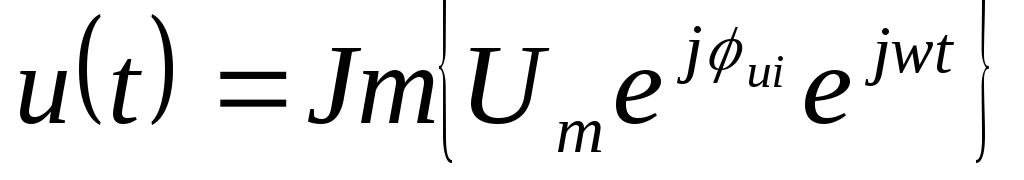 => Так как
=> Так как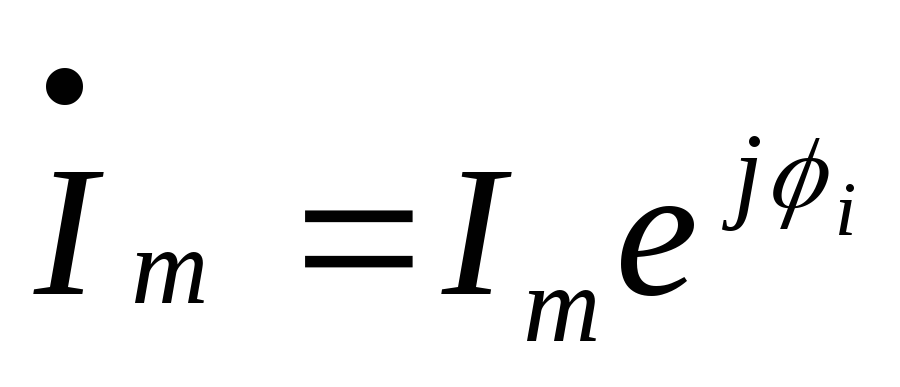 ,
,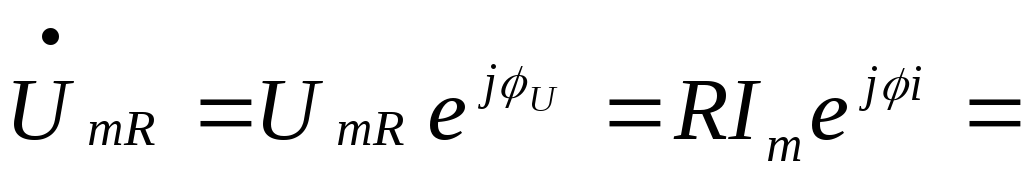
 .
Тогда
.
Тогда
 :
: 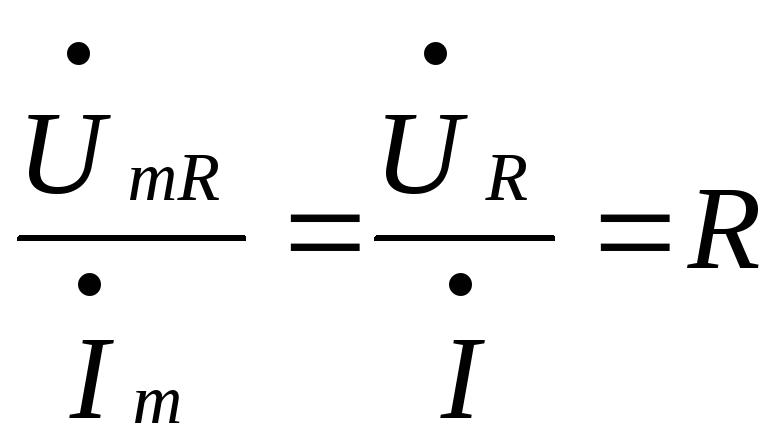
Для L:
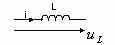
 ,
,
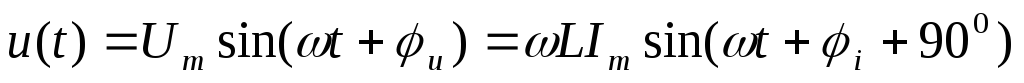 .
.
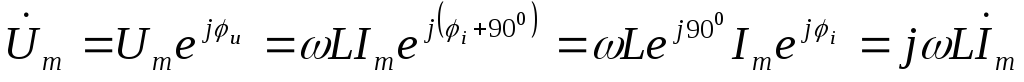 ,
,
u=i + 900.
 :
: 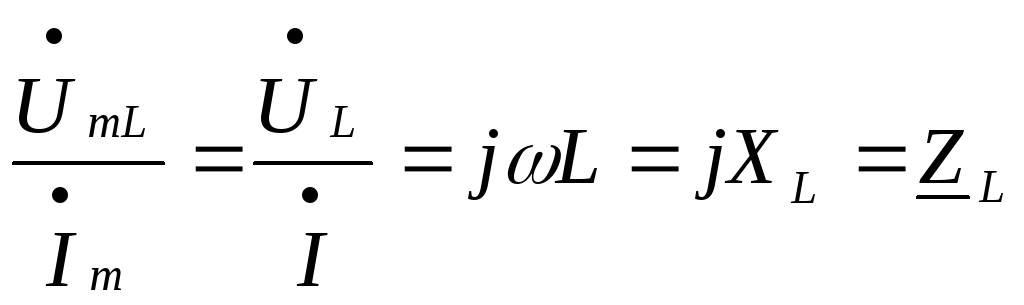 — комплексное сопротивление индуктивности.
— комплексное сопротивление индуктивности.
Для C:
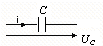
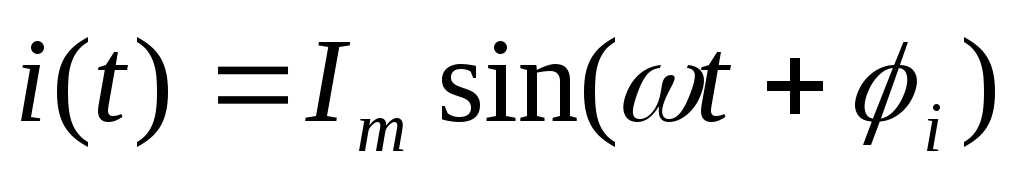 ,
,
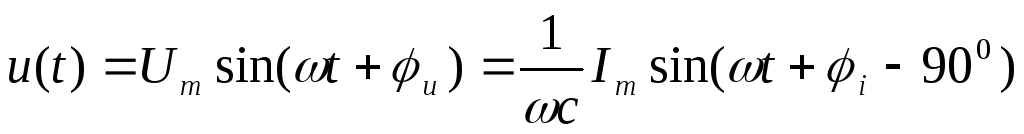
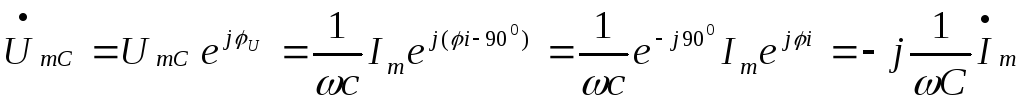 u=i — 900.
u=i — 900.
 :
: 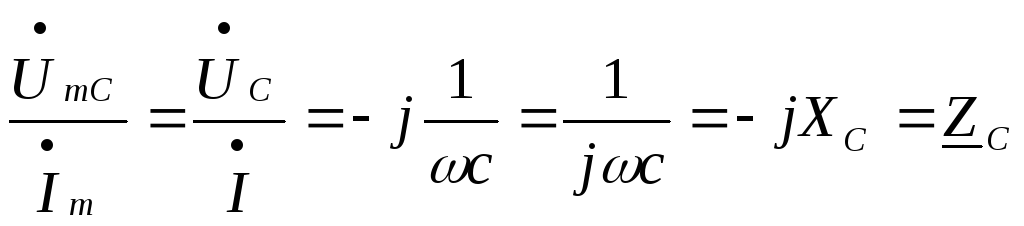 — комплексное сопротивление емкости.
— комплексное сопротивление емкости.
Таким образом, для
любого элемента в цепи синусоидального
тока 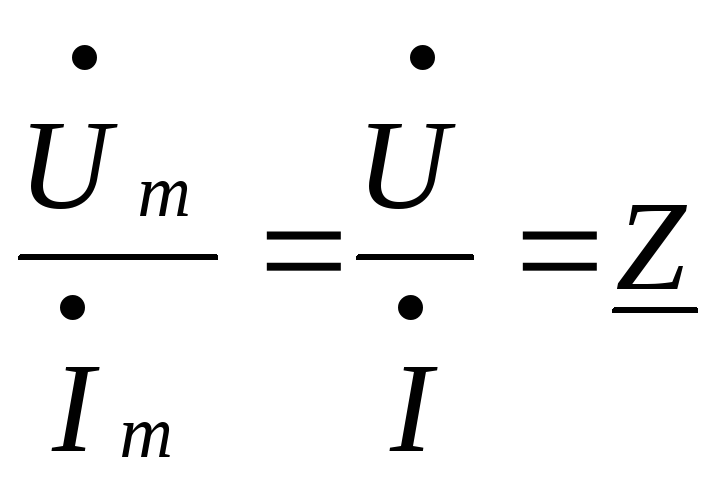 — некоторое комплексное число по
размерности оно соответствует
сопротивлению, и поэтому его называют
комплексом полного сопротивления и
обозначают
— некоторое комплексное число по
размерности оно соответствует
сопротивлению, и поэтому его называют
комплексом полного сопротивления и
обозначают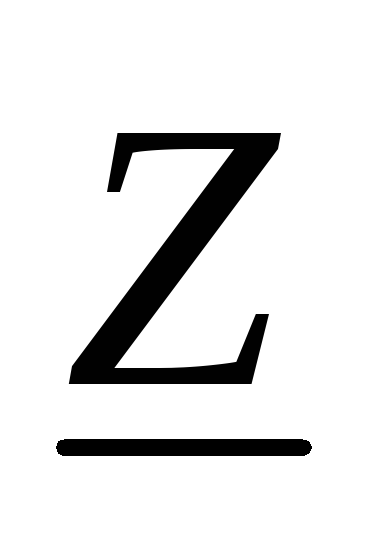 .
Тогда:
.
Тогда:
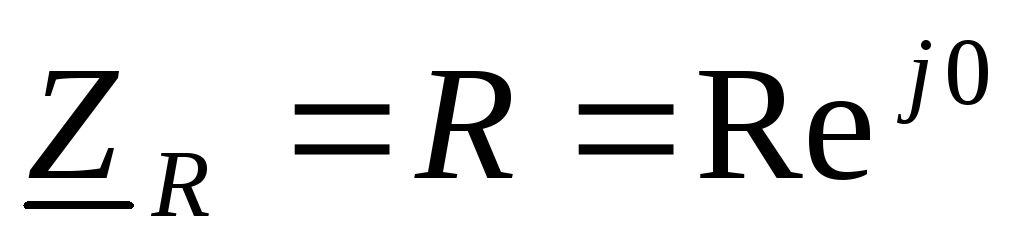 ,
,
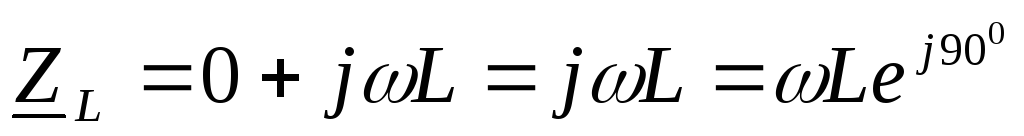 ,
,
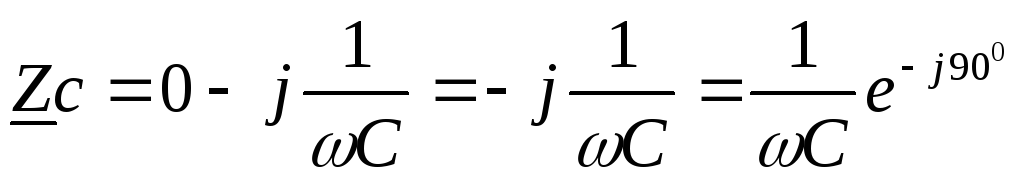 .
.
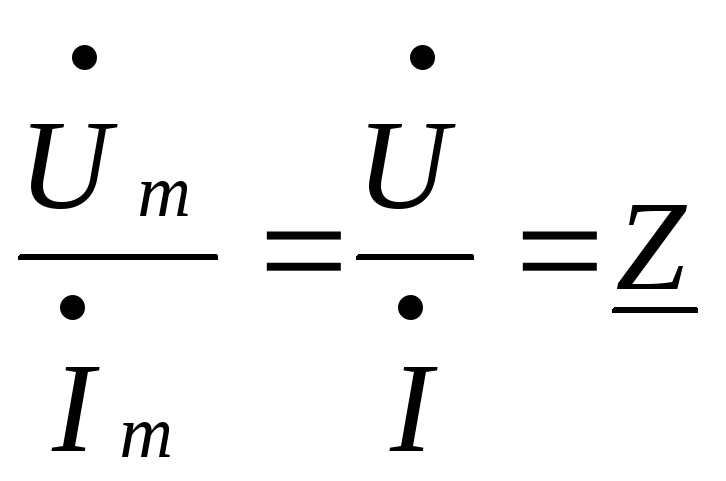 представляет закон
Ома в символической форме.
представляет закон
Ома в символической форме.
Комплекс полного сопротивления участка пассивной цепи синусоидального тока рассчитывают так же, как в цепи постоянного тока, если вместо элементов участка использовать комплексные сопротивления этих элементов.
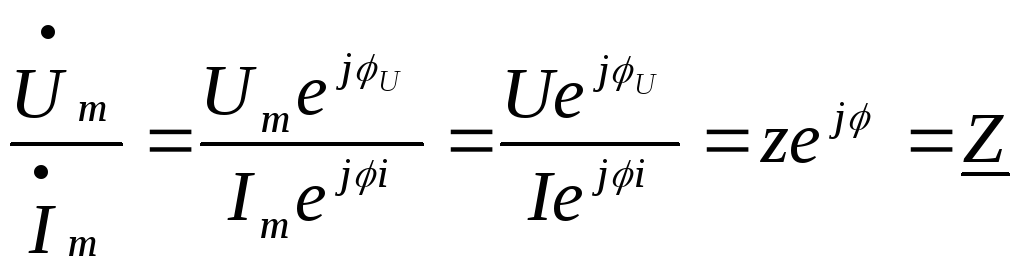 ,
,
где:
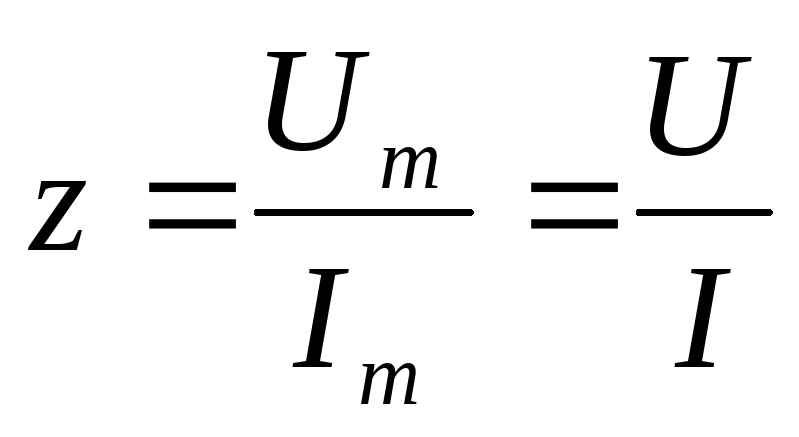 — коэффициент
пропорциональности между амплитудными
или действующими значениями напряжения
и тока на данном элементе;
— коэффициент
пропорциональности между амплитудными
или действующими значениями напряжения
и тока на данном элементе;
 показывает на
сколько фаза напряжения больше фазы
тока на данном элементе.
показывает на
сколько фаза напряжения больше фазы
тока на данном элементе.
Иногда строят треугольник сопротивлений. Фактически это и есть изображение комплекса полного сопротивления на комплексной плоскости.
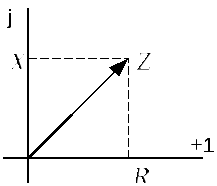
Величина  ,
как любое комплексное число, может быть
представлена в показательной,
тригонометрической или алгебраической
форме:
,
как любое комплексное число, может быть
представлена в показательной,
тригонометрической или алгебраической
форме:
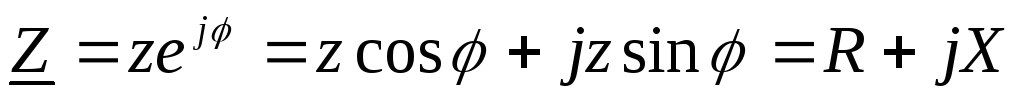 ,
,
где 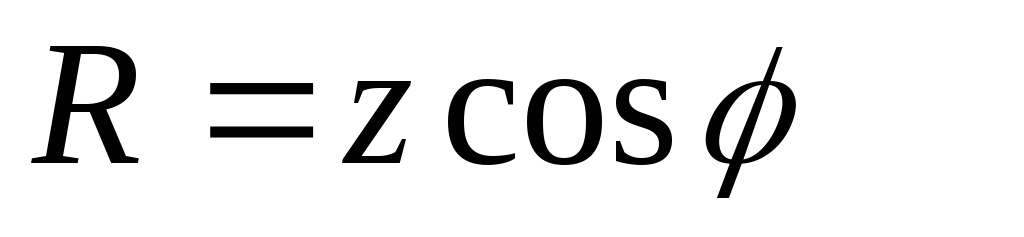 —
вещественная часть комплекса полного
сопротивления, ее называют активной
составляющей комплекса полного
сопротивления;
—
вещественная часть комплекса полного
сопротивления, ее называют активной
составляющей комплекса полного
сопротивления;
 —
мнимая часть комплекса полного
сопротивления, ее называют реактивной
составляющей комплекса полного
сопротивления;
—
мнимая часть комплекса полного
сопротивления, ее называют реактивной
составляющей комплекса полного
сопротивления;
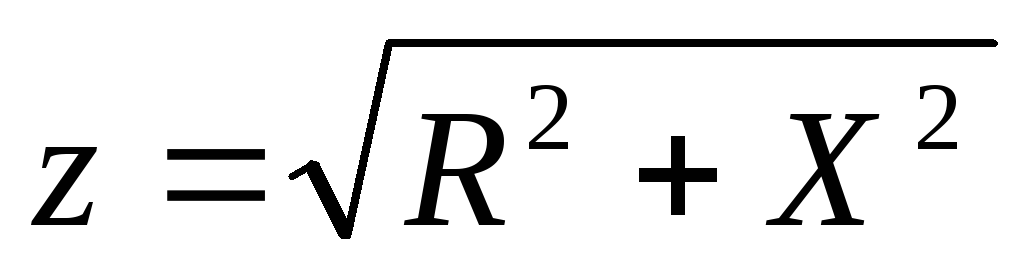 —
модуль комплекса полного сопротивления;
—
модуль комплекса полного сопротивления;
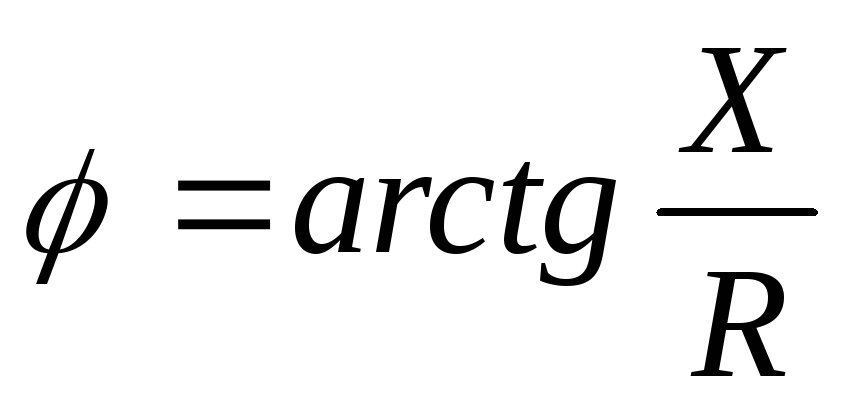 — фаза комплекса
полного сопротивления, изменяется в
пределах
— фаза комплекса
полного сопротивления, изменяется в
пределах 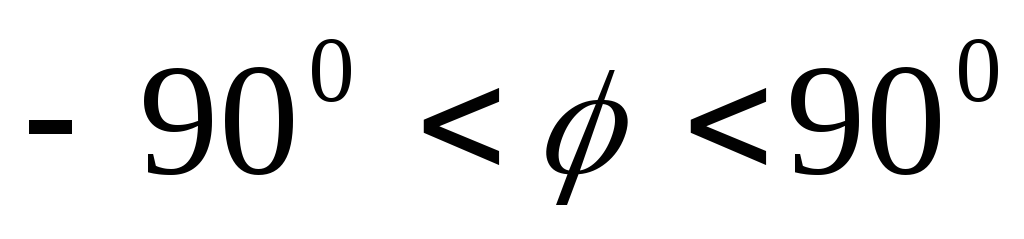 .
.
Величину обратную комплексу полного сопротивления называют комплексом полной проводимости (КПП):
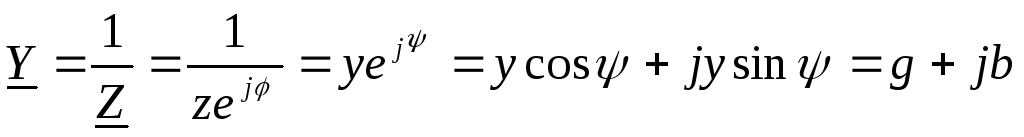 ,
где
,
где
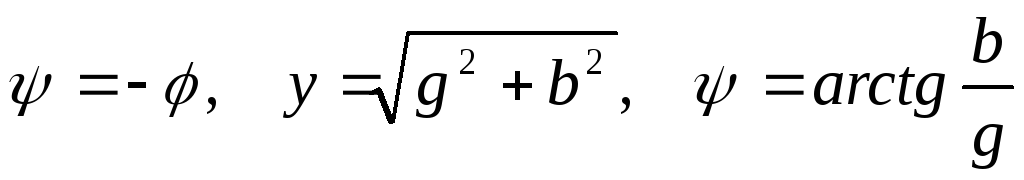 .
.
Для получения в «буквах» активной и реактивной составляющих комплекса полной проводимости по заданным в «буквах» активной и реактивной составляющим комплекса полного сопротивления:
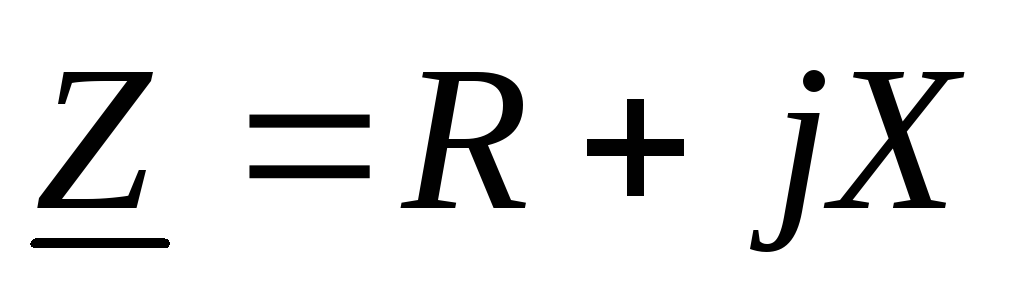
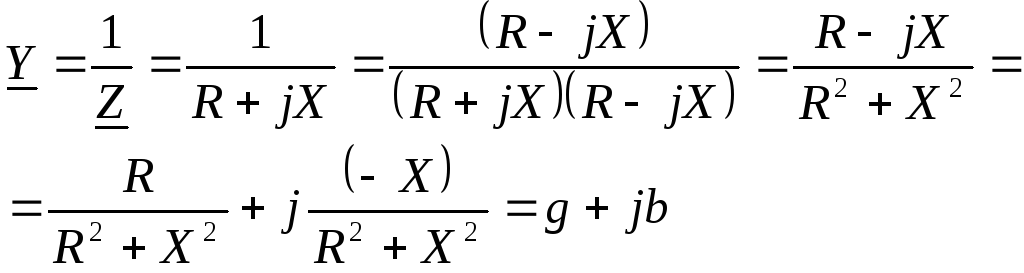
Параллельное соединение элементов r, l, c
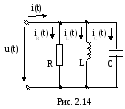
На вход электрической цепи (рис. 2.14), состоящей из соединенных параллельно элементов R,L,C, подано синусоидальное напряжение
u(t)=Umsin(ωt+ψu).
Запишем уравнение по первому закону Кирхгофа для мгновенных значений токов цепи:
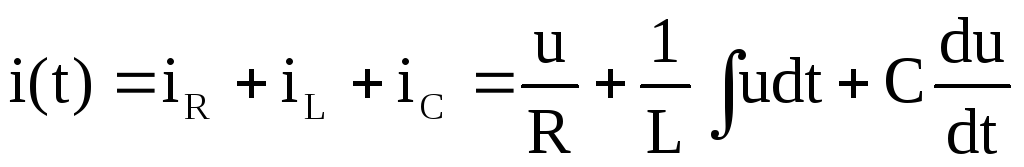 .
.
Сумме синусоидальных токов соответствует сумма изображающих их комплексных величин. И для действующих комплексных значений можно записать

Величину 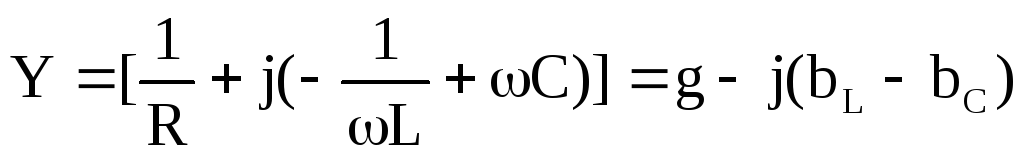 —
называют комплексной проводимостью
цепи с параллельным соединением элементовR,L,C,
которая определяется как сумма
проводимостей параллельных ветвей;
—
называют комплексной проводимостью
цепи с параллельным соединением элементовR,L,C,
которая определяется как сумма
проводимостей параллельных ветвей;
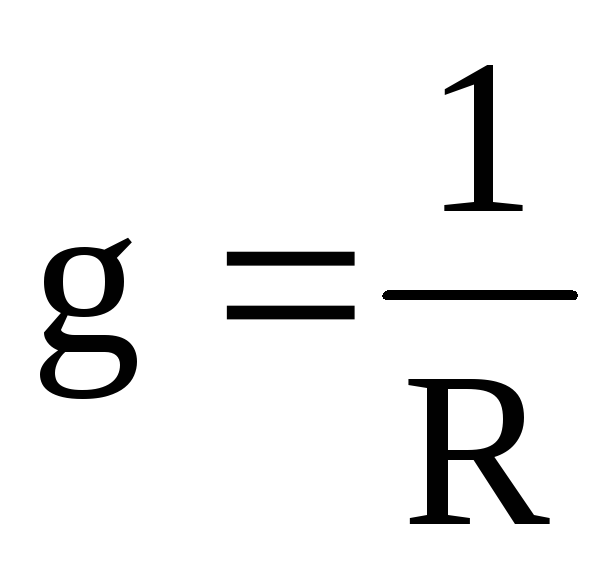 активная составляющая
проводимости;
активная составляющая
проводимости;
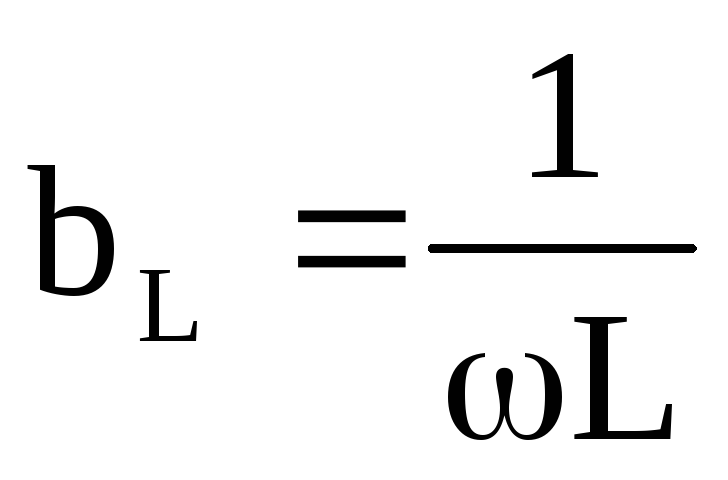 — реактивная
индуктивная составляющая проводимости;
— реактивная
индуктивная составляющая проводимости;
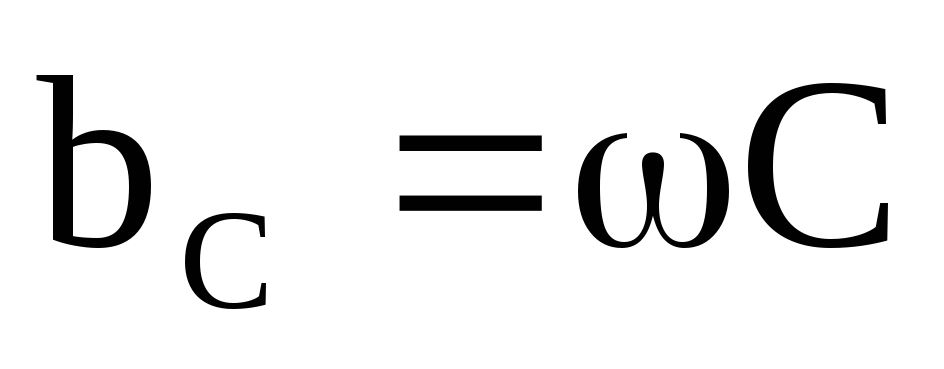 — реактивная
емкостная составляющая проводимости.
— реактивная
емкостная составляющая проводимости.
Запишем комплексную проводимость в показательной форме:
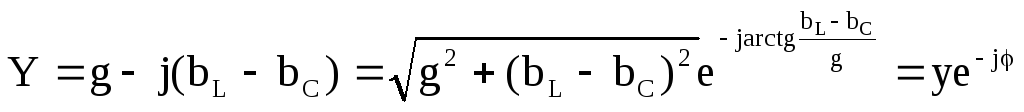 .
.
Тогда комплексный ток
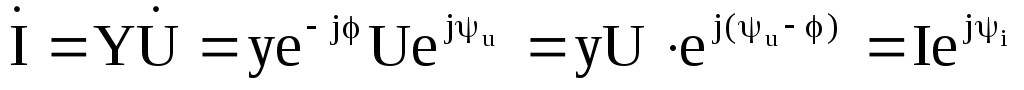 ,
,
где 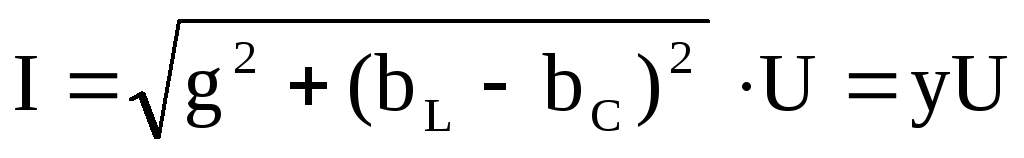 — действующее значение входного тока;
— действующее значение входного тока;
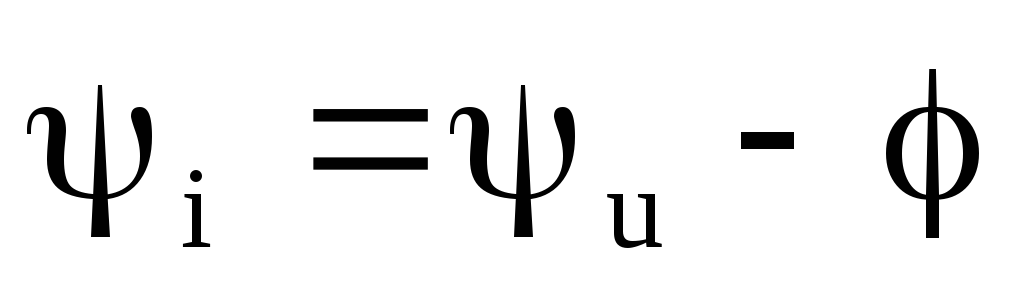 — начальная фаза тока;
— начальная фаза тока;
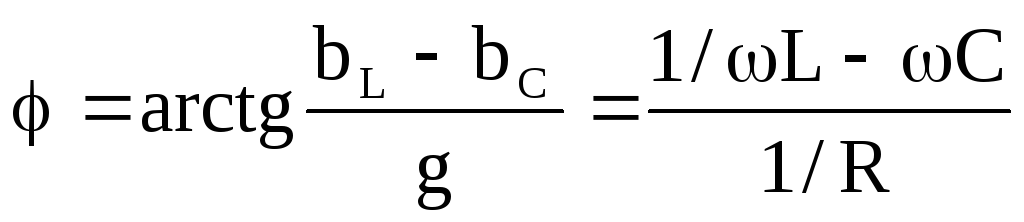 — угол сдвига фаз между напряжением на
зажимах цепи и входным током, который
определяется соотношением активной и
реактивной проводимостей.
— угол сдвига фаз между напряжением на
зажимах цепи и входным током, который
определяется соотношением активной и
реактивной проводимостей.
Построим векторную диаграмму токов и напряжений (рис. 2.15) на зажимах цепи, приняв начальную фазу напряжения за ноль.
Ток активного элемента совпадает по фазе с напряжением, поэтому на векторной диаграмме вектор этого тока изображается параллельно вектору напряжения. Ток индуктивного элемента отстает от напряжения на 90 градусов, поэтому на векторной диаграмме индуктивный ток повернут относительно вектора напряжения на 90 градусов по направлению движения часовой стрелки. Ток емкостного элемента опережает напряжение на 90 градусов, поэтому емкостный ток повернут относительно вектора напряжения против направления часовой стрелки на 90 градусов.
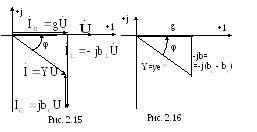 Необходимо
отметить, что ток индуктивного и
емкостного элементов находятся в
противофазе, вследствие чего в цепи
переменного тока при параллельном
соединении этих элементов могут
создаваться условия, невозможные для
цепей постоянного тока, когда токи
отдельных элементов будут значительно
превышать входной ток.
Необходимо
отметить, что ток индуктивного и
емкостного элементов находятся в
противофазе, вследствие чего в цепи
переменного тока при параллельном
соединении этих элементов могут
создаваться условия, невозможные для
цепей постоянного тока, когда токи
отдельных элементов будут значительно
превышать входной ток.
Треугольник, образованный векторами токов, принято называть треугольником токов.
Если каждую сторону треугольника токов поделить на вектор напряжения, то получим треугольник (рис. 2.16), подобный исходному и называемый треугольником проводимостей.
Как видно из полученных векторных диаграмм (рис. 2.15 и 2.16), угол сдвига фаз зависит от соотношения параметров цепи:
при IL>IC ( )
угол φ>0, ток отстает по фазе от
напряжения;
)
угол φ>0, ток отстает по фазе от
напряжения;
при IL<IC (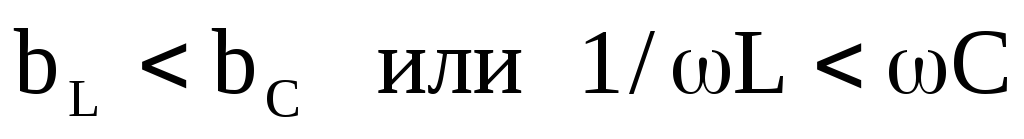 )
угол φ<0, ток опережает по фазе напряжение;
)
угол φ<0, ток опережает по фазе напряжение;
при IL=IC ( )
угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление; такой режим работы цепи
называется режимомрезонанса токов.
)
угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление; такой режим работы цепи
называется режимомрезонанса токов.
Расчет токов и напряжений при смешанном
соединении приемников
Расчет цепи переменного тока существенно облегчается, если синусоидально изменяющиеся токи, напряжения, ЭДС и т.д. изображать векторами и комплексными числами. Тогда для расчета цепей синусоидального тока можно применять все те методы, которые использовались для расчета цепей постоянного тока, только все токи, напряжения и сопротивления необходимо записывать в комплексной форме записи.
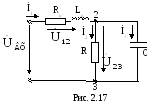
Рассмотрим решение прямой и обратной задачи для цепи с одним источником энергии рис. 2.17.
Прямая задача: при известных параметрах цепи R, Rк, Lк, C и токе третьей ветви I2 определить все остальные токи и напряжения. Частота питающей сети f. Расчет синусоидальных токов и напряжений удобно выполнять в комплексной форме записи.
Примем начальную фазу тока второй ветви равной нулю
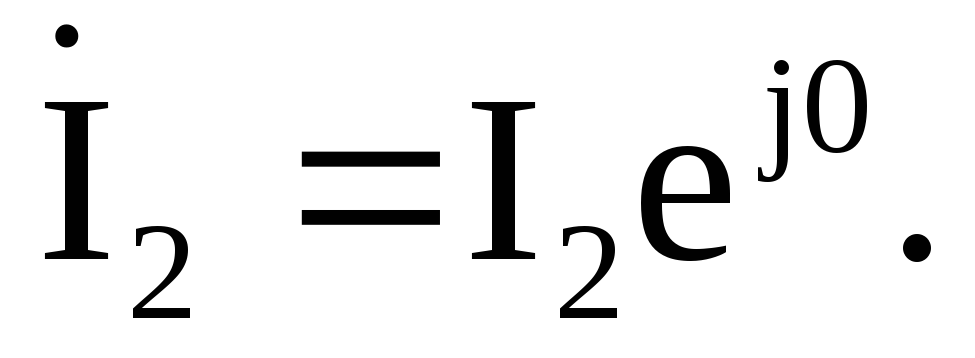
Комплексные сопротивления ветвей:
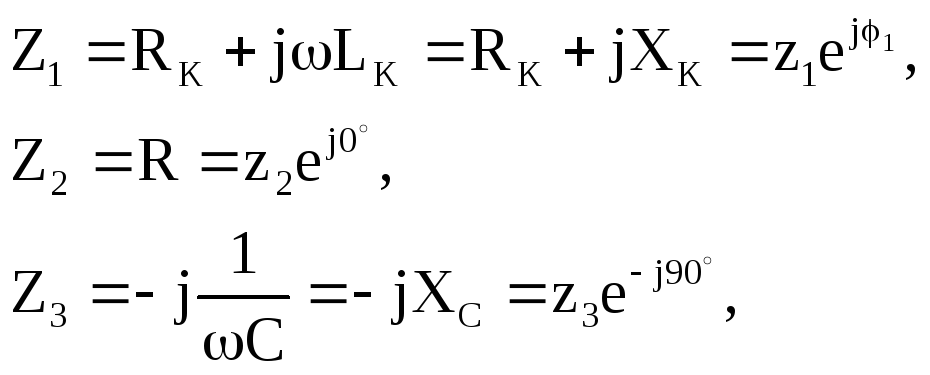
где 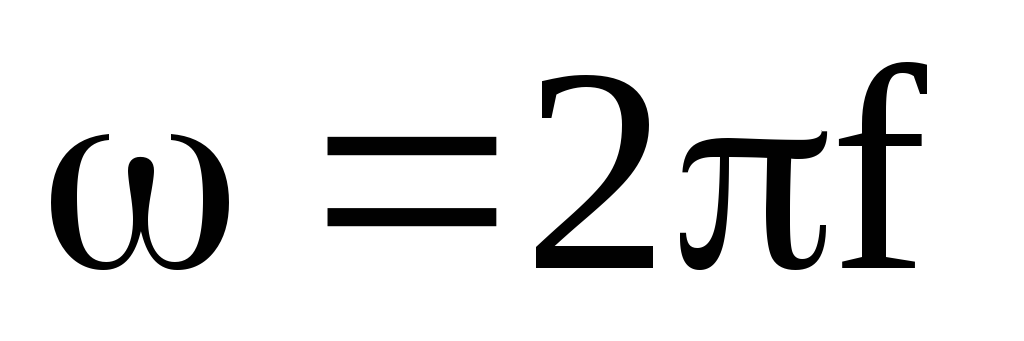 —
угловая частота.
—
угловая частота.
Зная ток I2 в одной из параллельных ветвей,
найдем напряжение на зажимах этих ветвей
по закону Ома: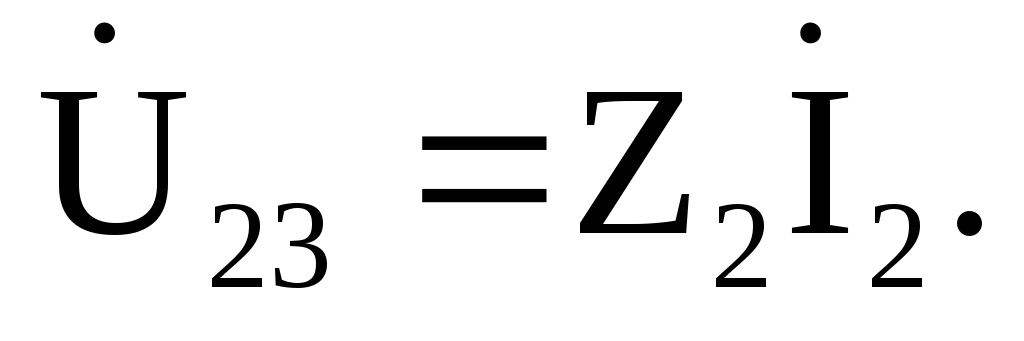
Ток третьей ветви
найдем: 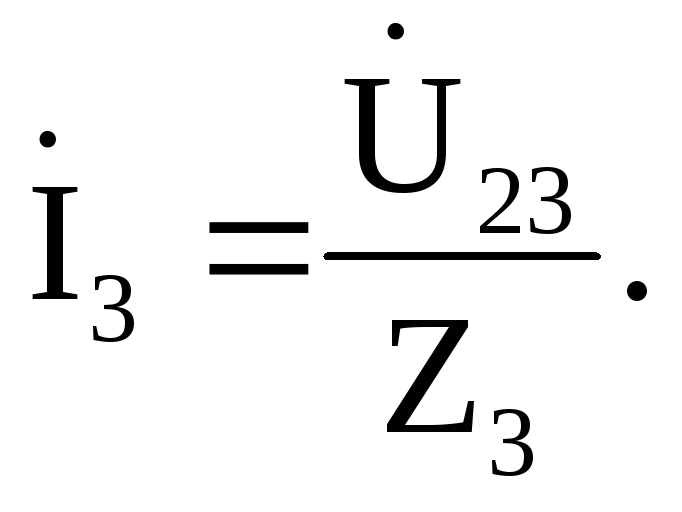
Ток I1 в неразветвленной части цепи найдем, составив уравнение по первому закону Кирхгофа для узла «2»:
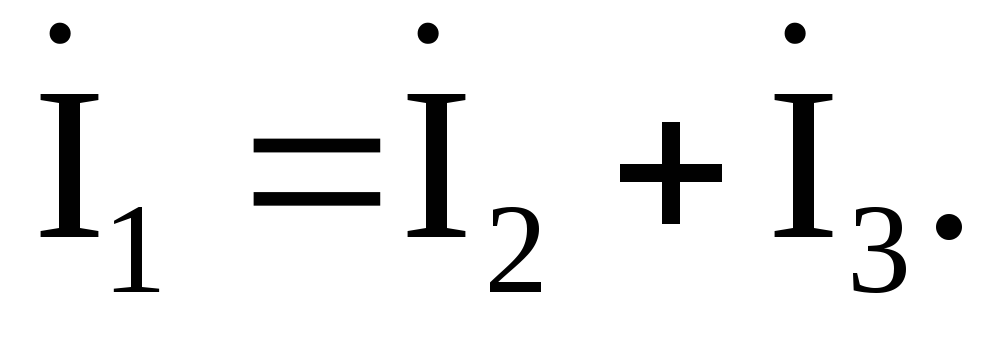
Напряжение на
зажимах первой ветви 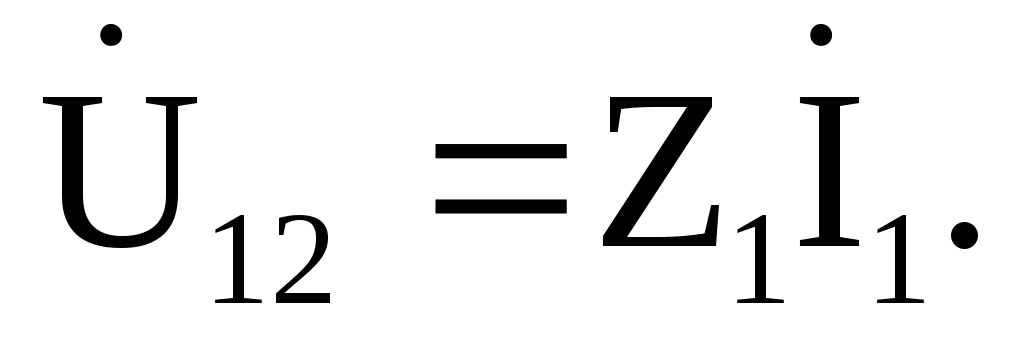
Напряжение на
зажимах цепи найдем, составив уравнение
по второму закону Кирхгофа: 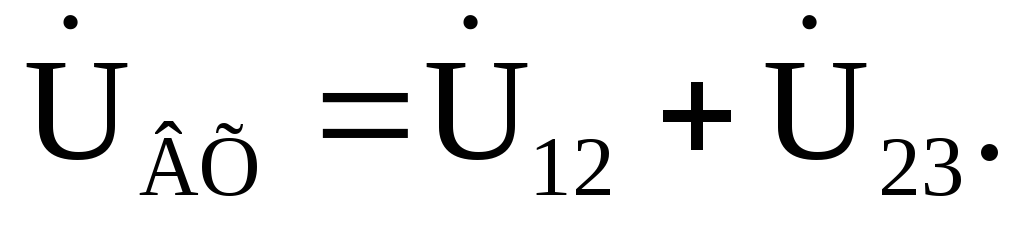
Построение векторной диаграммы удобно начинать с вектора тока второй ветви. Длины векторов токов и напряжений на векторной диаграмме откладываются в соответствующих масштабах по току miи напряжениюmu.
Начальная фаза
тока равна нулю 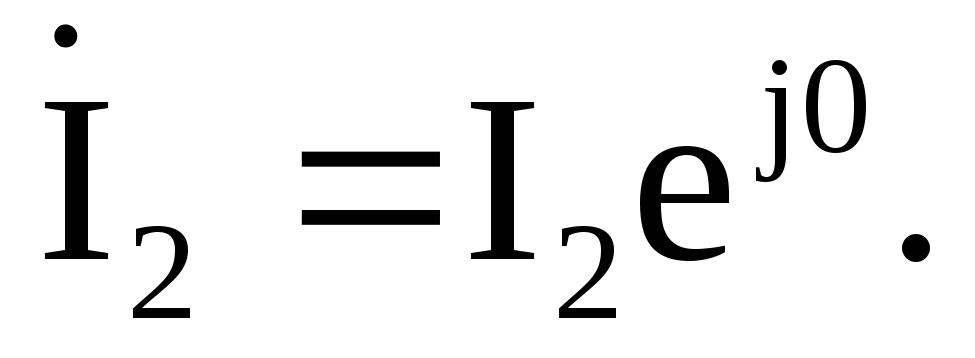 В соответствующем масштабе токов
изобразим вектор на комплексной
плоскости, совпадающим с осью действительных
чисел (рис. 2.18).
В соответствующем масштабе токов
изобразим вектор на комплексной
плоскости, совпадающим с осью действительных
чисел (рис. 2.18).
Н апряжение
апряжение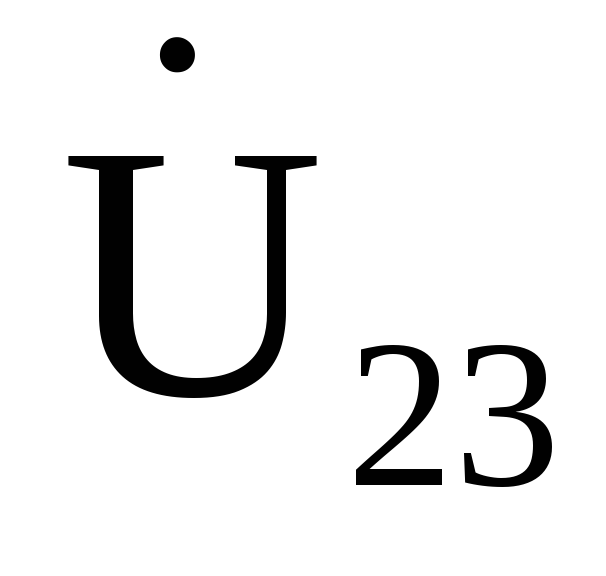 изображаем на векторной диаграмме
совпадающим по фазе с током второй
ветви, так как сопротивление этой ветви
чисто активное. Ток третьей ветви İ3, в которую включенидеальныйконденсатор, опережает напряжение
параллельных ветвей на угол 90°.
изображаем на векторной диаграмме
совпадающим по фазе с током второй
ветви, так как сопротивление этой ветви
чисто активное. Ток третьей ветви İ3, в которую включенидеальныйконденсатор, опережает напряжение
параллельных ветвей на угол 90°.
Согласно первому
закону Кирхгофа  .
По правилу параллелограмма складываем
вектора токов İ2, İ3 и получаем
вектор тока İ1.
.
По правилу параллелограмма складываем
вектора токов İ2, İ3 и получаем
вектор тока İ1.
Напряжение 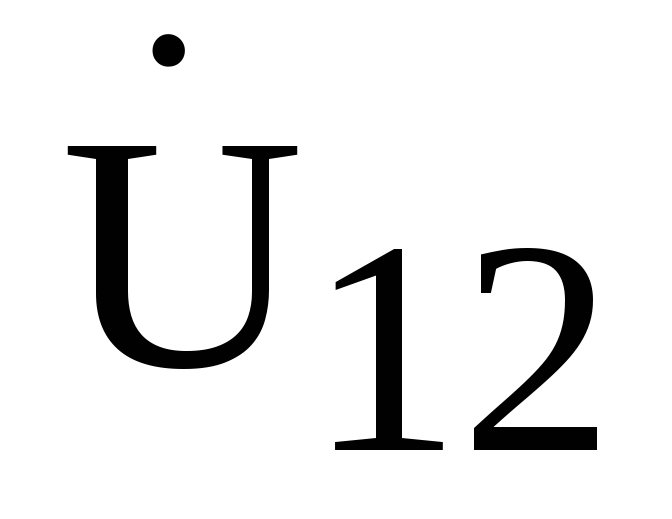 опережает
ток этого участка на угол φ1. Вектор
входного напряжения получаем путем
суммирования векторов согласно второму
закону Кирхгофa
опережает
ток этого участка на угол φ1. Вектор
входного напряжения получаем путем
суммирования векторов согласно второму
закону Кирхгофa
Начальные фазы, построенных токов и напряжений, должны совпадать с расчетными. Длины векторов в масштабе тока или напряжения должны соответствовать действующим значениям рассчитанных величин.
Обратная задача. Рассчитать токи и напряжения на всех участках электрической цепи, схема которой показана на рис. 2.7, питающейся от источника синусоидального напряжения с частотойf.
Известны параметры
цепи R,Rк,Lк,Cи величина напряжения на источнике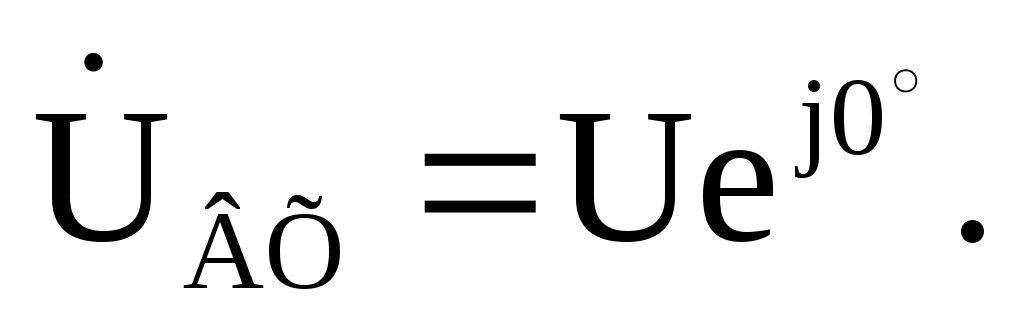
Комплексные сопротивления ветвей определяем аналогично предыдущей задаче:
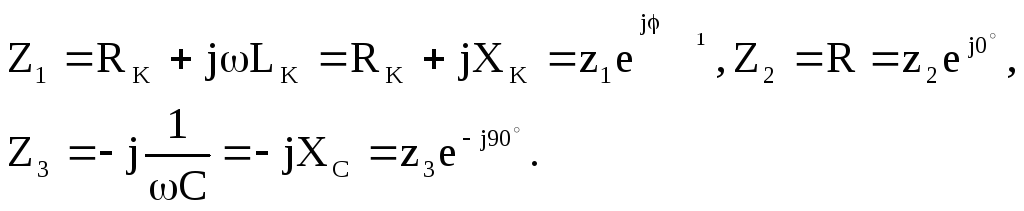
Для того, чтобы по закону Ома определить ток на входе цепи, необходимо рассчитать комплексное сопротивление цепи относительно входных зажимов.
Сопротивления второй и третьей ветвей соединены параллельно, поэтому эквивалентное сопротивление относительно зажимов «23» можно рассчитать:
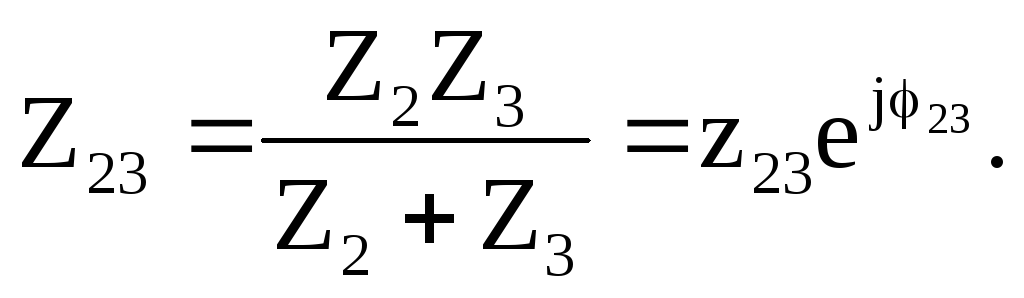
Относительно
входных зажимов сопротивление катушки
и сопротивление участка «23» соединены
последовательно, поэтому входное
сопротивление всей цепи можно определить
как сумму комплексных сопротивлений 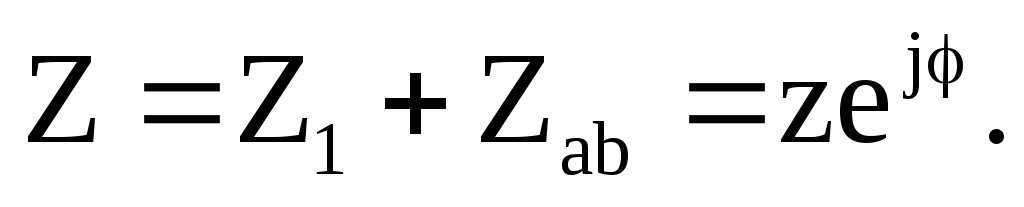
Определим входной
ток по закону Ома 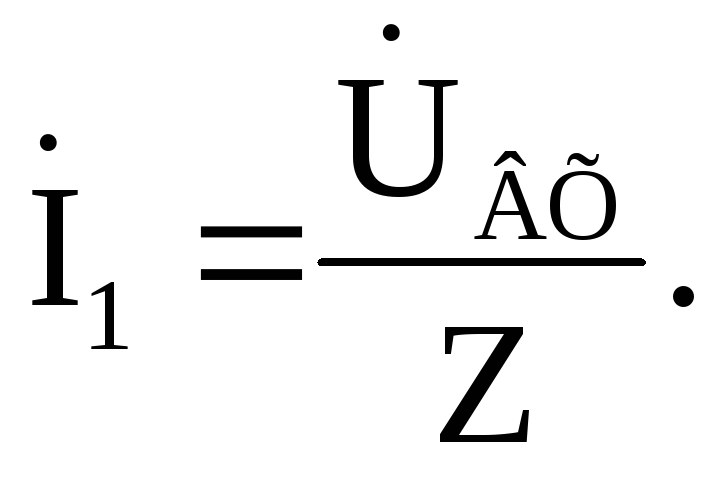
Напряжения на
участках цепи: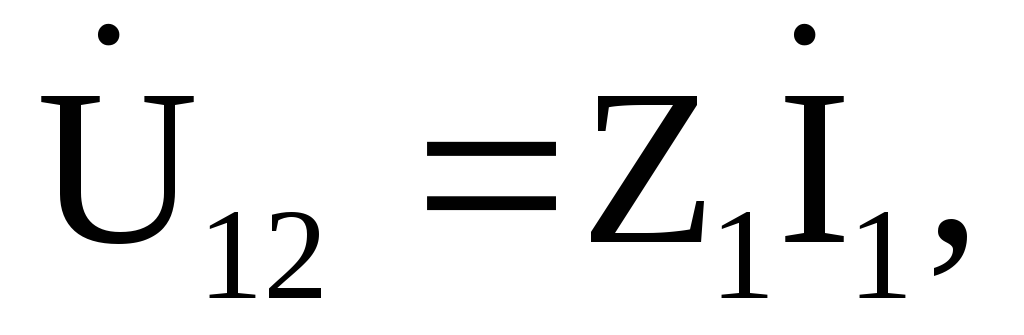
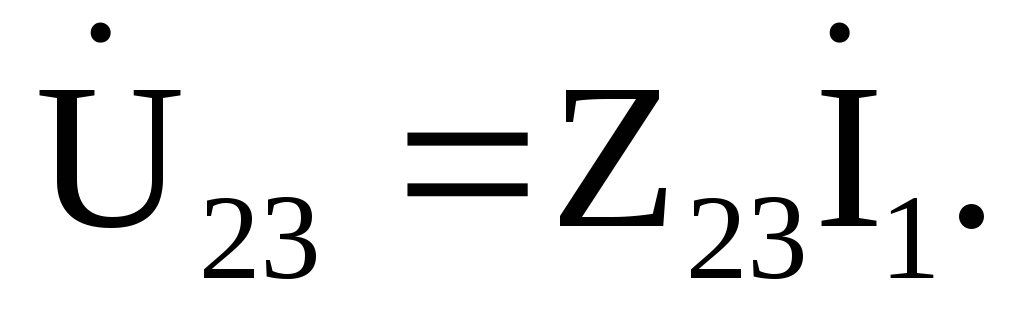
Т оки
параллельных ветвей определим по закону
Ома:
оки
параллельных ветвей определим по закону
Ома:

Построим векторную диаграмму токов и напряжений участков цепи (рис. 2.18). Для этого на комплексной плоскости в соответствующих масштабах тока miи напряженияmuпостроим вектора рассчитанных напряжений и токов со своими начальными фазами. На векторной диаграмме покажем выполнение законов Кирхгофа:
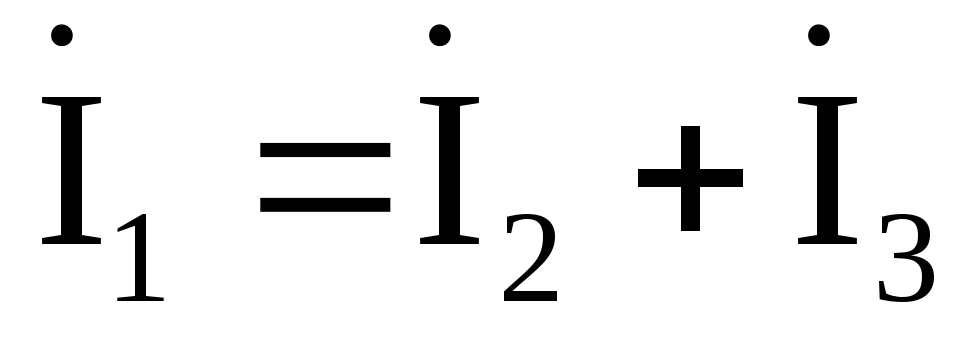 ,
, 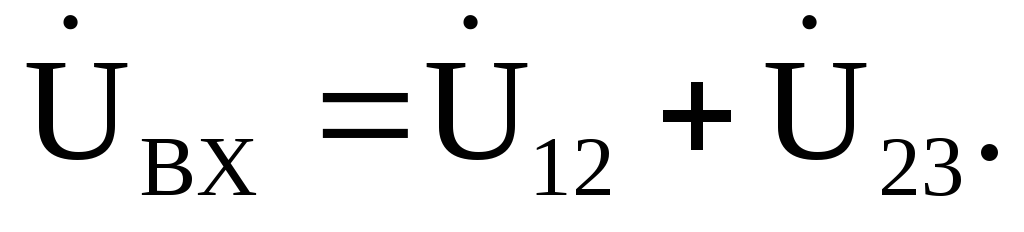
25


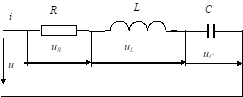
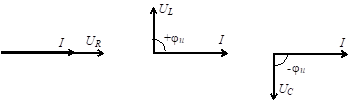
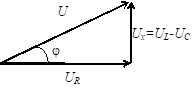
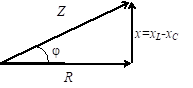
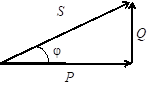

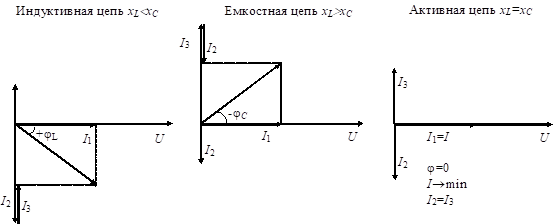
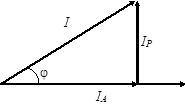
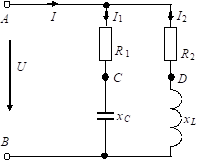
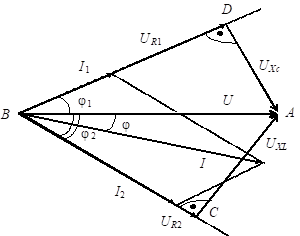
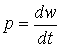 .
. 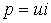 .
.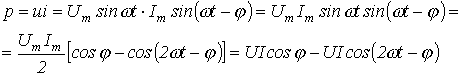 .
.  .
. 
 .
. 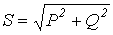 .
.  .
. 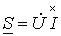 ,
,  ;
; 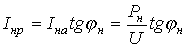 ;
; 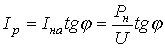 .
.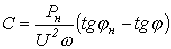 .
. 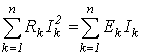
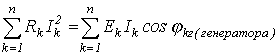
 ,
,