Элементы векторного исчисления

Лаптев Г. Ф. Элементы векторного исчисления. М., 1975 г. — 336 с. Книга представляет собой учебное руководство для студентов втузов. В пен содержится предусмотренный учебными программами материал но векторной алгебре, дифференциальной геометрии и теории поля. Изложение построено с учетом потребностей технических дисциплин, в которых используется векторное исчисление. Книга написана просто и ясно; это делает ее доступной пониманию студентов первого курса, впервые приступающих к изучению высшей математики. Книга окажется полезной и в условиях заочного обучения. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4. Скользящие и приложенные векторные величины. 5. Модуль вектора. 6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 2. Основные теоремы о скалярных проекциях § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме. 4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения. 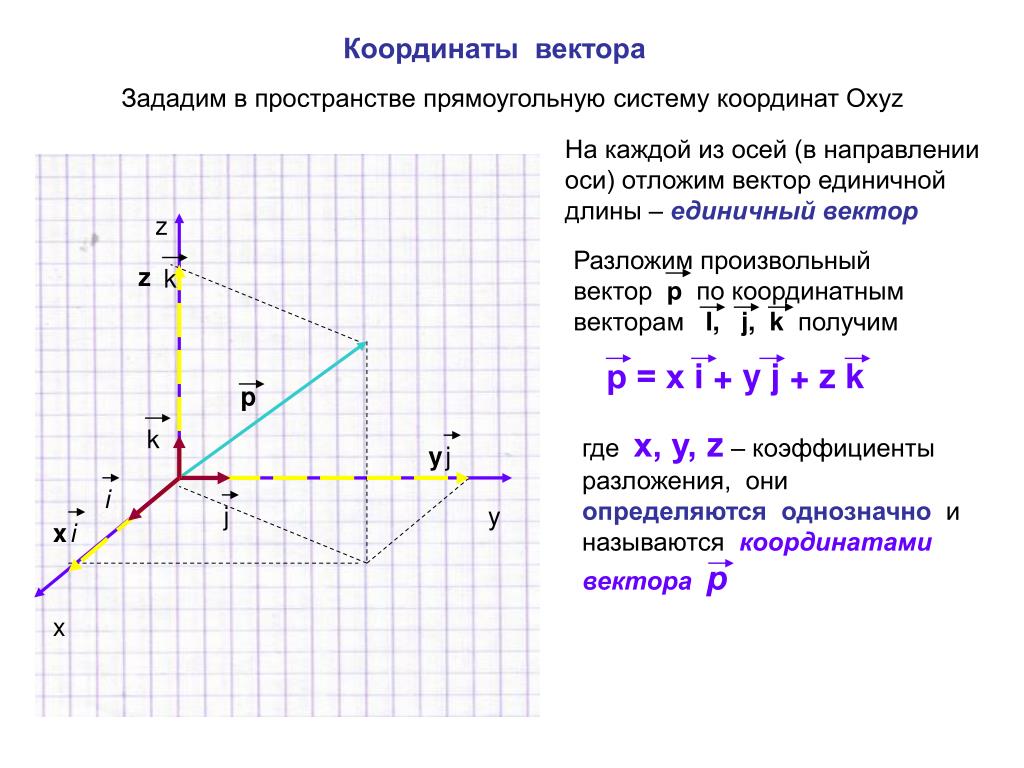§ 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов. 4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ § 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3. Круг кривизны § 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности. 5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2. 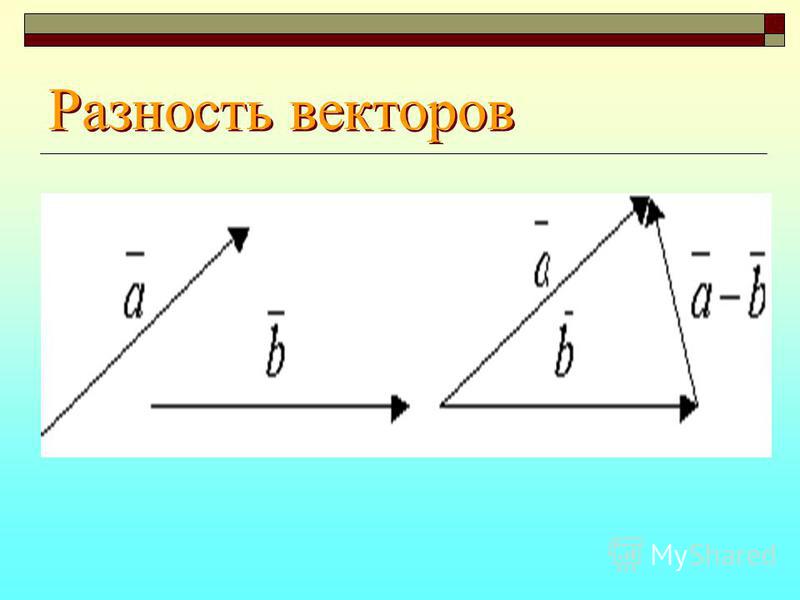Криволинейный интеграл от линейной формы по произвольной кривой. 3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV. ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ § 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII. 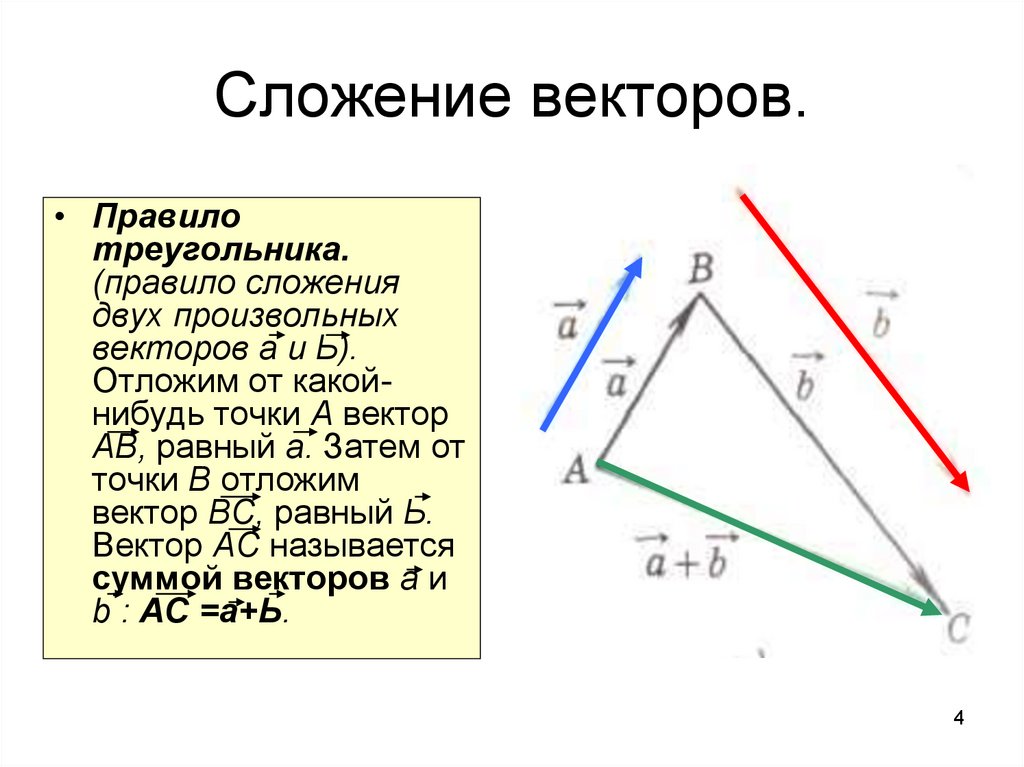ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ § 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах. § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты

3) Пусть – базис и пусть произвольный вектор. Проведем следующие построения.

Отложим все три базисных вектора  и вектор  от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы , плоскость  и плоскость ; далее через конец вектора  проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:

                             рис.4.

По правилу сложения векторов получаем равенство:

                        .                                     (1)

По построению . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число , такое что . Аналогично,  и , где . Теперь, подставляя эти равенства в (1), получаем:

                                             (2)

 и возможность разложения по базису доказана.

   Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису :

 и . Тогда

       .       (3)

   Заметим, что по условию векторы   некомпланарные, следовательно, они попарно неколлинеарные.

Возможны два случая:  или .

а) Пусть , тогда из равенства (3) следует:

           .                        (4)

Из равенства (4) следует, что вектор  раскладывается по базису , т.е. вектор  лежит в плоскости векторов  и, следовательно, векторы  компланарные, что противоречит условию.

б) Остается случай , т.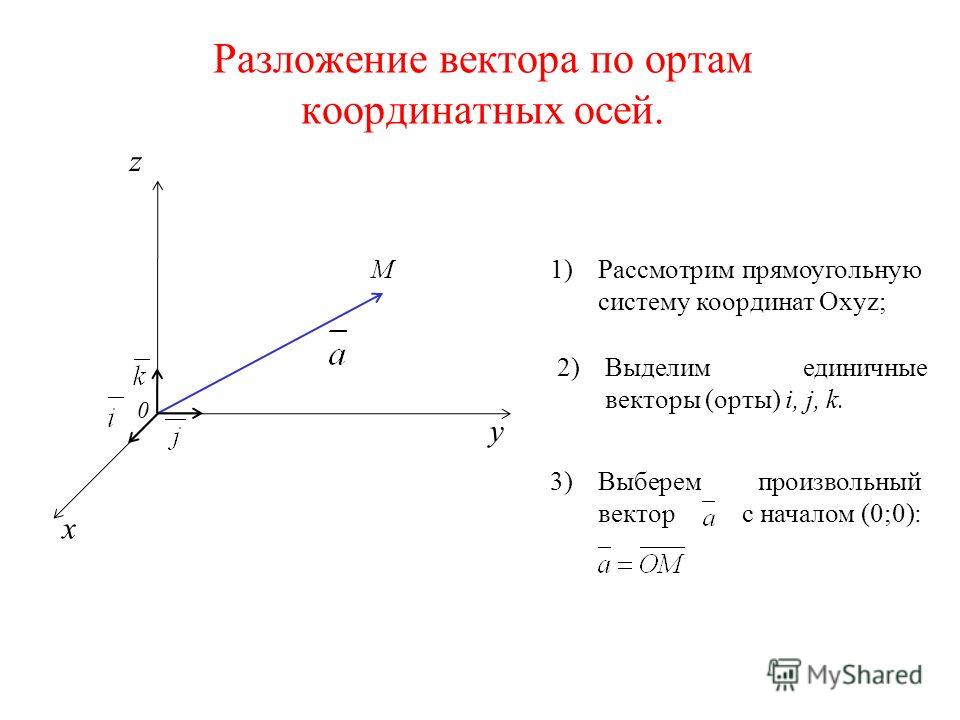 е. .  Тогда из равенства (3) получаем  или

             .                           (5)

Так как – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что  и , ч.т.д.

Теорема доказана.

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Если система векторов e₁, …, e_nn-мерного линейного пространства L_n образует базис в L_n, то любой вектор x из L_n может быть представлен в виде

x = С₁·e₁+ С₂·e₂+ …+ С_n· e_n.

Выражение x = С₁·e₁+ С₂·e₂+ . ..+ С_n· e_n называется разложением вектора по базису e₁, …, e_n, а числа С₁, С₂, …, С_n называются координатами вектора x  в базисе e₁, …, e_n.

Координаты вектора принято обозначать тем же символом, что и сам вектор:

x = x₁·e₁+ x₂·e₂+ …+ x_n· e_n.

Взаимно однозначное соответствие x = x₁·e₁+ x₂·e₂+ …+ x_n· e_n ⇐⇒ x = (x₁, x₂, …, x_n)

— изоморфизм L_n и R_n.

____________________________________________________________________________

№22

 —  -мерное векторное пространство над полем   с некоторыми базисами   и  .

Векторы одного базиса можно выразить через векторы другого:

.

Определение 4. Матрица, определенная коэффициентами вышеприведенного разложения

,

называется матрицей перехода⁷⁾ от базиса   к базису  .

Теорема.   Матрица перехода   от базиса   к   невырождена.

 Для любого базиса   и любой невырожденной квадратной матрицы   порядка  существует и при том единственный базис   с матрицей перехода   , т.е.   .

Теорема. Если   — матрица перехода от базиса   к   , то для любого вектора  справедливо равенство   , где   и   — столбцы координат вектора   в базисах  и   соответственно, т.е.   .

Теорема 1. Преобразование координат вектора при переходе от «старого» базиса e к «новому» базису f определяется формулой:

Доказательство. Обозначим координатные столбцы произвольного вектора x  X_n в «старом» базисе e

и в «новом» базисе f

Произвольный вектор x в базисе e имеет вид:

В базисе f тот же вектор имеет вид:

x = fX_f

и в силу формулы (1)

Сравнивая формулы (3) и (4), получаем

X_\e = C · X_f.

Умножая это равенство слева на C ⁻¹ , получаем формулу (2), которую требовалось доказать.

Рассмотрим прямоугольную систему координат в трехмерном пространстве OXYZ. Вектору  в данном пространстве соответствует тройка чисел (x,y,z), являющихся проекциями вектора на оси Ox, Oy, Oz. Эти числа называются координатами вектора  .

Числа получаются как разность соответствующих координат точек A(x₀,y₀,z₀) и B(x₁,y₁,z₁):

x= x₁-x₀ , y= y₁-y₀ , z= z₁-z₀ а модуль вектора  , равный его длине, вычисляется по теореме Пифагора:

 .

2.7. Преобразование координат вектора при переходе к новому базису

Пусть   и  — два базиса в n-мерном линейном пространстве L.

Матрицей перехода от базиса   к базису   называется матрица C, столбцами которой являются координаты векторов  в базисе  :

Вектор   линейно выражается через векторы обоих базисов. Тогда, если 

то координаты   вектора в базисе   , и его координаты   в базисе  связаны соотношениями

,

или 

где  ,   — матрица перехода от базиса   к базису   и обратная к ней;   — векторы-столбцы координат вектора   в соответствующих базисах.

Таким образом доказана следующая

Теорема. Пусть (e)={ } и (f)={ }— два базиса в n-мерном линейном пространстве L.

Координаты вектора  в базисе (e) и координаты  вектора  в базисе (f)связаны соотношением

где  ,   — матрица перехода от базиса (e) к базису (f) и обратная к ней.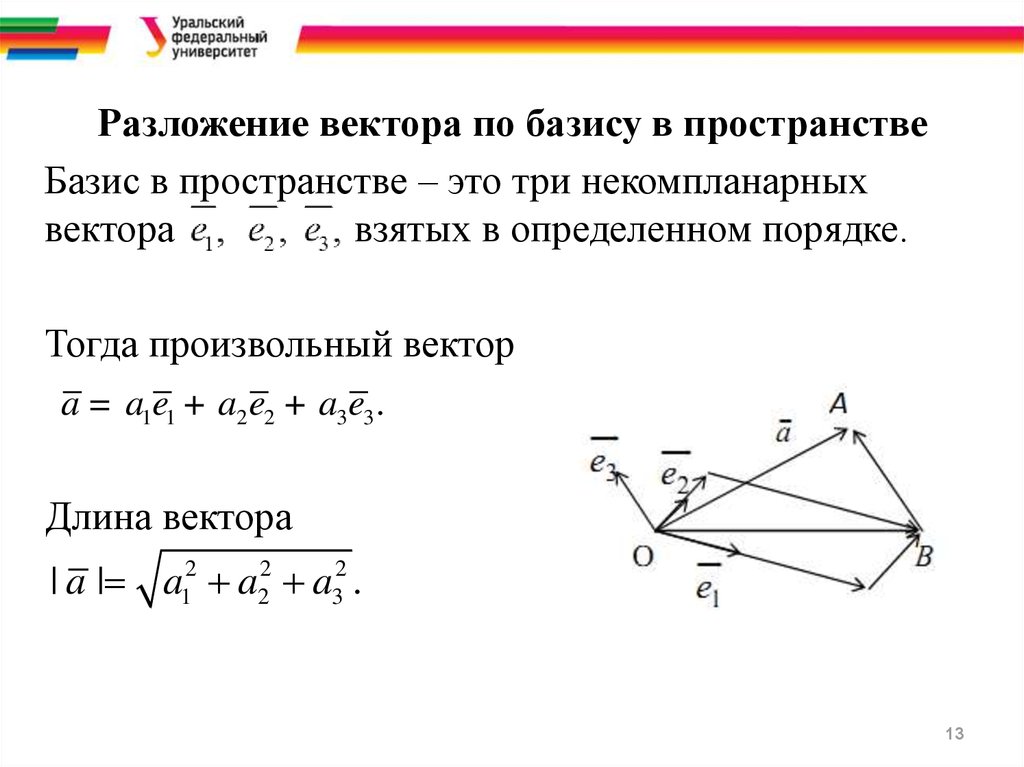

____________________________________________________________________________

№23

linear алгебра — Произвольные (т.е. не обязательно конечномерные) векторные пространства; справочный запрос.

Некоторые комментарии, кажется, подразумевают, что понятие базиса трудно определить для бесконечномерных пространств. Это не так. Определение

Если $V$ — векторное пространство над скалярным полем $K$, то семейство векторов $B=(b_i)_{i\in d}$ является базисом пространства $V$ в точности, если для каждого вектора $x$ существует единственное семейство $(x_i)_{i\in d}$ скаляров с $x_i \neq 0$ только для конечного числа $i$, такое что $x = \sum_{i \in d} c_ix_i$. Семейство $(x_i)_{i\in d} =: \mathfrak{C}_B(x)$ называется согласование $x$ в базе $B$.

работает для векторных пространств произвольной размерности. Обратите внимание, что решающим моментом является то, что каждый вектор должен быть представлен конечными линейными комбинациями базисных векторов. Большая часть свойств переносится из конечномерного случая — в частности, у вас все еще есть

.

Если $T \,:\, V \to V$ — линейное отображение, а $(b_i)_{i\in d}$ — базис $V$, то $T$ полностью определяется образами $b_i$ при $T$, т.е. на $(Tb_i)_{i\in d}$.

Из этого следует, что вы также можете обобщить матрицы, допустив сколь угодно большие наборы индексов, и (так же, как в конечномерном случае) потребовать, чтобы «столбцы» были изображениями базисных векторов.

Если $T \,:\, V \to V$ — линейное отображение, а $B$ — базис $V$, то семейство скалярных $(a_{ij})_{i,j\in d } =: \mathfrak{C}_B(T)$ были $$ (a_{ij})_{i \in d} = \mathfrak{C}_B(Tb_j) \text{ для всех $j \in d$,} $$ где $(a_{i,j})_{i\in d}$ при фиксированном $j$ — координатизация образа $b_j$ при $T$, называется координата $T$ в $B$ или матрица $T$ в $B$. Семейство $(a_{ij})_{i \in d}$ для фиксированного $j$ можно назвать $j$-м столбцом (из $(a_{ij})_{i,j\in d }$), и семейство $(a_{ij})_{j \in d}$ при фиксированном $i$ $i$-й строке. Каждая координация обладает тем свойством, что каждый столбец содержит только конечно ненулевые элементы.

Как и в конечномерном случае, вы можете определить $A\cdot x$ для пары координат $A=(a_{ij})_{i,j\in d}$ и $x=( x_j)_{j\in d}$, установив

$A\cdot x := (y_i)_{i\in d}$, где $y_i = \sum_{j \in d} a_{ij} x_j$.

Так как $x_i \neq 0$ только конечное число раз, ясно, что сумма всегда существует. Таким образом, остается вопрос, была ли эта координатизация всегда корректной, т. е. $y_i \neq 0$ тоже только конечное число раз? Можно ограничиться теми $n$ столбцами таблицы $A$, которые соответствуют ненулевым $x_j$. Поскольку каждый столбец координатизации $\mathfrak{C}_B(T)$ содержит только конечное число ненулевых элементов, скажем, $m_1,\ldots,m_n$ для интересующих $n$ столбцов, отсюда следует, что $y_i$ содержит не более $m_1+\ldots+m_n$ ненулевых записей.

Вы также получаете произведение матриц $A\cdot B$, собирая произведения $A\cdot x$, поскольку $x$ колеблется по столбцам $B$, т. n$, т. е. мы можем рассматривать матрицу как $$A=\begin{pmatrix}\vec r_1\\\vec r_2\\\vdots\\\vec r_m\end{pmatrix}.$$ (Проделать то же самое со столбцами тоже имеет смысл. В этом посте я буду описывать вещи со строками, их можно легко изменить для столбцов.)

Иногда бывает полезно проделать то же самое с векторами из произвольного векторного пространства $V$ над полем $F$. т. е. мы можем использовать обозначение $$\mathbf{B}=\begin{pmatrix}\vec v_1\\\vec v_2\\\vdots\\\vec v_m\end{pmatrix}.$$ Я буду использовать жирный шрифт для «матриц, состоящих из векторов».

Это просто другое обозначение упорядоченного $n$-набора векторов. Но по крайней мере в чем-то они похожи на матрицы. Например, мы можем умножить такую ​​матрицу на $A\in M_{k,m}(F)$ слева 9m a_{ij}\vec v_j$. (Если мы решим работать со столбцами, мы будем умножать справа.)

Мы также можем сложить эти матрицы и умножить их на скаляр. С этими определениями все еще сохраняются некоторые свойства обычного умножения матриц — для разрешенных произведений.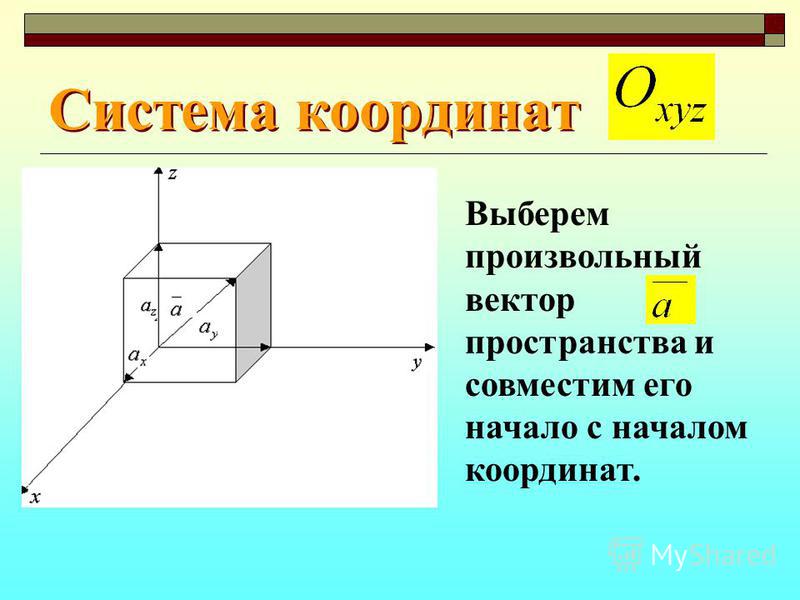 Например, ассоциативность $A(B\mathbf{C})=A(B\mathbf{C})$ или дистрибутивность — как $(A+B)\mathbf{C}$, так и $A(\mathbf{C} +\mathbf{D})$.

Также некоторые свойства, действительные для ранга, по-прежнему действительны для размерности векторного пространства, генерируемого строками. (Например, если $A$ обратима, то «ранг» $\mathbf B$ и $A\mathbf B$ одинаков. «Ранг» $A\mathbf B$ ограничен сверху рангом $A$, а также «рангом» $\mathbf B$.)

Мы не можем умножать справа, но мы все еще можем «отменять» справа в том смысле, что если строки $\mathbf B$ линейно независимы, то из $A\mathbf{B}=\mathbf{0}$ следует $A=0$ и $A_1\mathbf{B}=A_2\mathbf{B}$ подразумевает $A_1=A_2$.

Это обозначение можно использовать, например, для компактного обозначения матрицы перехода между двумя основаниями, записав $\mathbf B_2=M\mathbf{B_1}$. (И некоторые доказательства матриц перехода можно было бы записать довольно компактно, используя эту запись. Другое возможное преимущество этой записи состоит в том, что если мы будем осторожны, выполняя только «разрешенные» умножения, то мы сможем использовать многие свойства обычного умножения матриц.