Онлайн калькулятор умножения вектора на число
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Укажите размерность пространства 23
Укажите форму представления вектора Координаты точек начала и конца вектораКоординаты вектора
Задайте координаты вектора
Задайте значение числа q на которое нужно умножить вектор
q =
Как умножить вектор на число
Пример 1. Умножим вектор плоскости на число q. Координаты вектора заданны точками.
Умножим вектор плоскости на число q. Координаты вектора заданны точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Числа q на которое нужно умножить вектор AB = 12
Для того, чтобы вектор умножить на число, необходимо каждую координату вектора умножить на данное число.
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — A
AB ⋅ q = {ABx ⋅ q ; ABy ⋅ q} = {-7 ⋅ 12 ; 2 ⋅ 12} = {-84 ; 24}
Пример 2. Умножим вектор пространства на число q.
Координаты вектора a: (5 ; 9 ; -2)
Числа q на которое нужно умножить вектор a = 2.6
Для того, чтобы вектор умножить на число, необходимо каждую координату вектора умножить на данное число.
a ⋅ q = {ax ⋅ q ; ay ⋅ q ; az ⋅ q} = {5 ⋅ 2.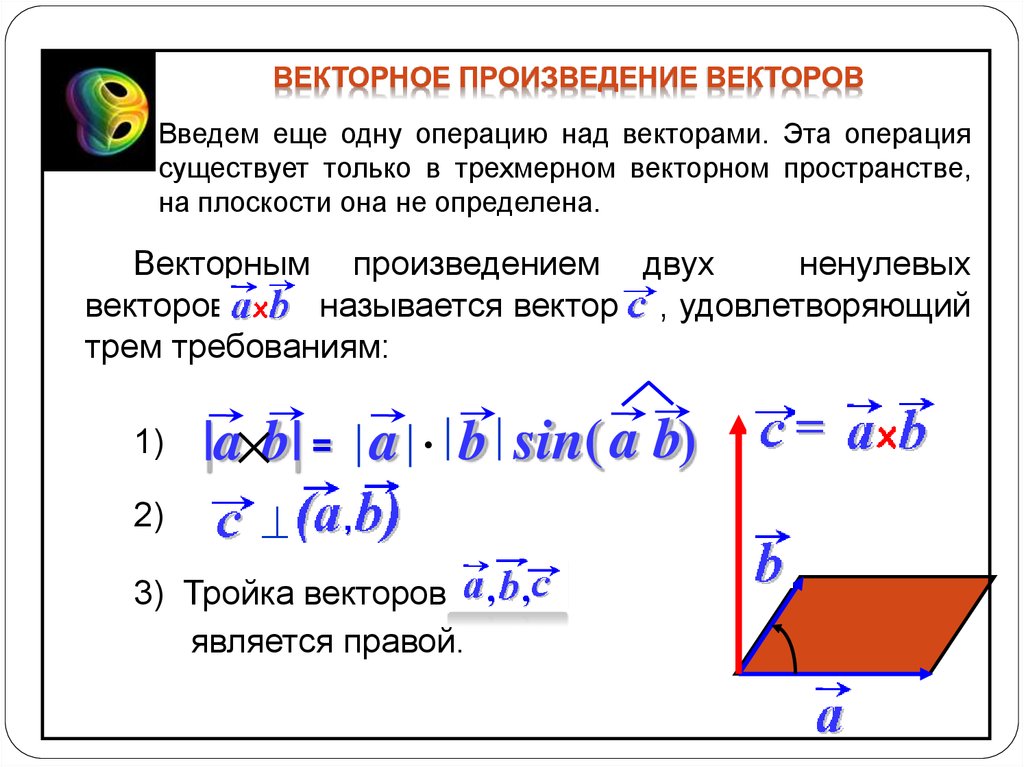
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Урок геометрии в 9-м классе «Действия над векторами». Тема: «Умножение вектора на число»
- Гордеева Марина Эвальдовна
Разделы: Математика, Урок с использованием электронного учебника
Класс: 9
Ключевые слова: Действия над векторами
УМК: «Геометрия: 9 класс» Атанасян Л. Г. и др.
Г. и др.
Основные дидактические цели урока:
- Формирование новых знаний и умений по теме: «Умножение вектора на число».
Задачи:
Для реализации поставленной цели учитель должен решить следующие задачи:
- Актуализировать знания и умения учащихся выполнять сложение и вычитание векторов; актуализировать умения строить данные векторы из одной точки; использовать правило треугольника, многоугольника;
- Подвести учащихся к выводу алгоритма нахождения результата умножения вектора на число;
- Сформировать умение нахождения результата произведения вектора на число;
- Создать условия для применения правила в различных ситуациях;
- Произвести первичный контроль усвоения знаний.
Формируемые результаты.
Предметные результаты:
- Знать: алгоритм умножения вектора на число.

- Уметь: находить произведение вектора на число; уметь строить исходный и полученный векторы.
Метапредметные результаты:
- уметь обобщать и делать выводы,
- уметь применять правило в различных ситуациях,
- уметь разрабатывать алгоритм действий,
- уметь использовать математические знания на уроках физики и др. наук.
Личностные результаты:
- уметь ставить перед собой цели, планировать свою деятельность,
- оценивать результаты своей работы и работы одноклассников, достигать поставленных целей.
Структура урока
- мотивация
- актуализация знаний и умений учащихся
- создание проблемной ситуации
- постановка темы и целей урока
- формирование новых знаний (введение понятия «произведение вектора на число» и свойств данного произведения)
- разработка алгоритма нахождения результата произведения вектора на число, вывод алгоритма определения одинакового и противоположного направления данного вектора и вектора, полученного при умножении его на положительное и отрицательное число; алгоритма определения длины результирующего вектора.

- первичное закрепление: отработка навыка нахождения результата умножения вектора на число с использованием свойств; самоконтроль усвоения новых знаний
- контроль усвоения, самооценка результатов своей деятельности
- рефлексия
- домашнее задание
Этап урока | Деятельность учителя | Деятельность учащихся |
Организационный | Приветствует учащихся. Предлагает записать дату в тетрадь | Записывают дату |
Мотивационный | Предлагает ответить на вопрос: «Как вы понимаете слова: «Каждый человек может ошибаться, каждый имеет право на ошибку, но при этом очень важно найти её, признать её и исправить». | Поясняют услышанное высказывание. |
| Актуализация знаний и умений: — выполнять сложение и вычитание векторов | Предлагает ответить на вопросы: — что такое вектор? | — направленный отрезок…. |
| — какие векторные величины вы знаете? | — сила, скорость…. | |
| — что такое сила тяжести и от чего она зависит? | — сила тяжести — это сила, с которой…., она зависит от массы тела. | |
| — что такое сила трения? | — сила трения — это сила……. | |
| — что такое сила упругости? | — сила упругости — это сила…… | |
Предлагает выполнить задания, записанные на доске: | Выполняют задания: №2. №3. Рассмотрите рисунок и ответьте на вопрос: будет ли тело двигаться вниз по наклонной плоскости? №4. Масса первого тела 2 кг. Сила тяжести, действующая на 1 тело 20H. Изобразите ее отрезком 4 см. Изобразите вектор силы тяжести, действующей на 2 и 3 тела, если их массы соответственно 4 кг и 0,5кг. Учащиеся легко выполняют задания 1-3, но при выполнении задания №4 испытывают затруднения. | |
| Постановка темы и целей урока | Учитель, используя методику проблемного диалога, учитель подводит учащихся к постановке темы урока. | |
| Какова формула силы тяжести? | F=mg | |
| Если для 1 тела массой 2 кг сила тяжести изображается вектором, длиной 4см, то какова длина вектора силы тяжести для тела массой 4кг, если она прямо пропорционально зависит от массы тела? | Если масса тела увеличена в 2 р, то и длина вектора увеличится в 2р и будет 8 см. | |
| А для тела, массой 0,5кг? | Соответственно в 2 р меньше и будет 2 см. | |
| Какое действие с векторами мы сейчас производили? | Умножение и деление вектора на число. | |
| Можно ли деление на число, заменить умножением? | Деление на число, можно заменить умножением на число, обратное делителю. | |
| Какова же тема урока? (учитель на доску прикрепляет лист А-4 с темой урока) | Умножение вектора на число. | |
Какие цели урока «Умножение вектора на число»? (учитель прикрепляет на доску лист А-4 с целями урока) и уточняет цели урока (при необходимости) | Узнать, как умножать вектор на число. | |
Формирование новых знаний | Предлагает просмотреть видео с сайта Инфоурок, с целью введения понятия «произведение вектора на число». Что такое произведение вектора на число? | Смотрят фильм. |
Работа с учебником | Чтобы узнать свойства произведения, откройте учебник на стр.202-203 прочтите и запишите свойства. | Читают и записывают свойства. Читают свойства произведения чисел и свойства произведения векторов и находят аналогии, которые помогают осознать, понять свойства произведения векторов. |
Первичное закрепление | Предлагает открыть конверты, лежащие на столе, достать оттуда векторы. И показать их. Теперь предлагает изобразить вектор -0,5 данного вектора, -0,25 данного вектора, -2 данного вектора, -1/3 и 5/6 данного вектора. | Достают, показывают. Выполняют задания, уточняя направление данных векторов. |
Контроль усвоения | Предлагает выполнить самостоятельную работу. | Учащиеся, обучающиеся на 4-5 в парах садятся за ноутбуки, заходят на сайт ЯКЛАСС, выполняют тренировочную работу «Умножение вектора на число». По окончании работы учащихся оценивает программа сайта, и в итоге учитель видит на экране оценку. |
Самооценка результатов своей деятельности | Предлагает оценить свою деятельность на уроке. | Отвечают на вопросы. |
Домашнее задание | п.86 стр. 202-203 №775, 776 | Записывают задания. |
Операции над векторами: теория и примеры решений
- Линейные операции над геометрическими векторами
- Проекция вектора на ось
- Операции над векторами, заданными в координатной форме
- n— мерные векторы и операции над ними
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
На этом уроке освоим самые простые операции над векторами, достаточные для вхождения
в изучение векторной алгебры. Предварительно желательно ознакомиться с материалом о том, что такое
вообще векторы.
Прежде чем Вы узнаете всё об операциях над векторами, настройтесь на решение несложной задачи. Есть вектор Вашей предприимчивости и вектор Ваших инновационных способностей. Вектор предприимчивости ведёт Вас к Цели 1, а вектор инновационных способностей — к Цели 2. Правила игры таковы, что Вы не можете двигаться сразу по направлениям двух этих векторов и достигнуть сразу двух целей. Векторы взаимодействуют, или, если говорить математическим языком, над векторами производится некоторая операция. Результатом этой операции становится вектор «Результат», который приводит Вас к Цели 3.
А теперь скажите: результатом какой операции над векторами «Предприимчивость» и «Инновационные способности» является вектор «Результат»? Если не можете сказать сразу, не унывайте. По мере изучения этого урока Вы сможете ответить на этот вопрос.
Умножение вектора на число
Произведением вектора на число называется вектор, получающийся из вектора растяжением
(при ) или сжатием (при )
в раз, причём направление вектора
сохраняется, если ,
и меняется на противоположное, если .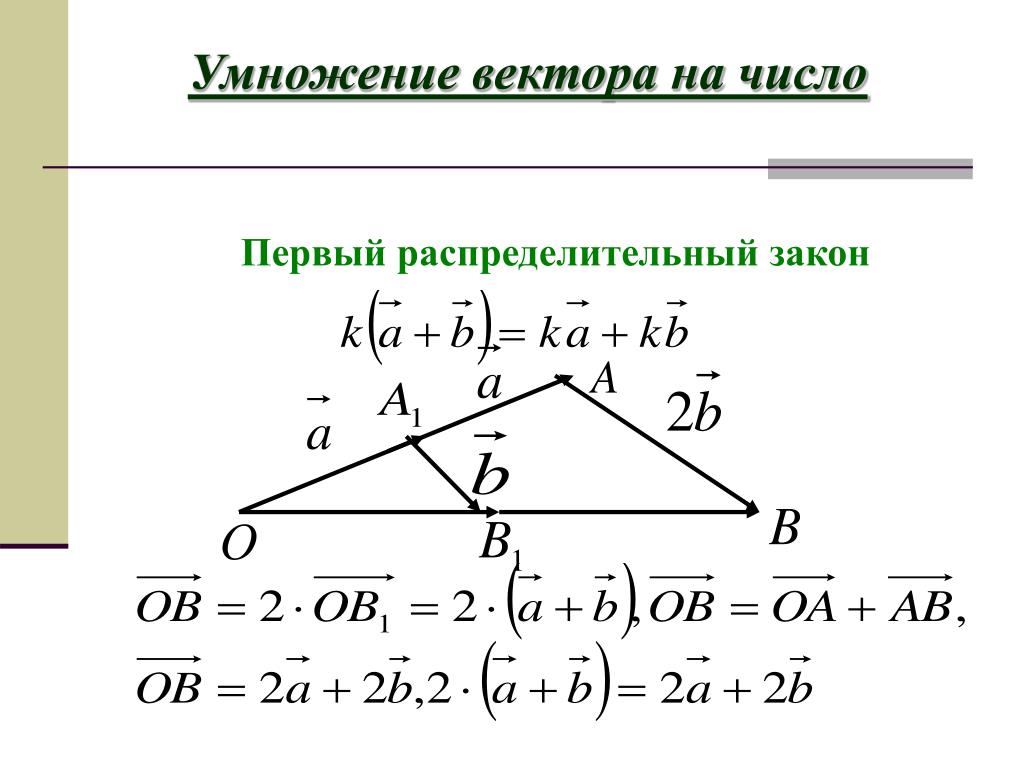 (Рис. 2)
(Рис. 2)
Из определения следует, что векторы и = всегда расположены на одной или на параллельных прямых. Такие векторы называются коллинеарными. (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить «коллинеарны».) Справедливо и обратное утверждение: если векторы и коллинеарны, то они связаны отношением
. (1)
Следовательно, равенство (1) выражает условие коллинеарности двух векторов.
Сложение и вычитание векторов
При сложении векторов нужно знать, что суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец — с концом вектора , при условии, что начало вектора приложено к концу вектора . (Рис. 3)
Это определение может быть распределено на любое конечное число векторов. Пусть в пространстве даны n свободных векторов . При сложении
нескольких векторов за их сумму принимают замыкающий вектор, начало которого
совпадает с началом первого вектора, а конец — с концом последнего вектора. То есть, если к концу вектора
приложить начало вектора , а к концу вектора
— начало вектора и т.д. и, наконец, к концу вектора
— начало вектора , то
суммой этих векторов служит замыкающий вектор , начало которого совпадает с началом первого вектора
, а конец — с концом последнего вектора . (Рис. 4)
То есть, если к концу вектора
приложить начало вектора , а к концу вектора
— начало вектора и т.д. и, наконец, к концу вектора
— начало вектора , то
суммой этих векторов служит замыкающий вектор , начало которого совпадает с началом первого вектора
, а конец — с концом последнего вектора . (Рис. 4)
Слагаемые называются составляющими вектора , а сформулированное правило — правилом многоугольника. Этот многоугольник может и не быть плоским.
При умножении вектора на число -1 получается противоположный вектор . Векторы и имеют одинаковые длины и противоположные направления. Их сумма даёт нулевой вектор, длина которого равна нулю. Направление нулевого вектора не определено.
В векторной алгебре нет необходимости рассматривать отдельно операцию вычитания: вычесть из вектора вектор означает прибавить к вектору противоположный вектор , т.е.
Пример 1. Упростить выражение:
.
Решение:
,
то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности, также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед вычислением произведений векторов.
Пример 2. Векторы и служат диагоналями параллелограмма ABCD (рис. 4а). Выразить через и векторы , , и , являющиеся сторонами этого параллелограмма.
Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам. Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Результат — требуемые в условии задачи векторы:
Есть все основания полагать, что теперь Вы правильно ответили на вопрос о векторах «Предприимчивость»
и «Инновационные способности» в начале этого урока. Правильный ответ: над этими векторами производится
операция сложения.
Правильный ответ: над этими векторами производится
операция сложения.
Решить задачи на векторы самостоятельно, а затем посмотреть решения
Пример 3. Даны векторы
и
. Построить на
чертеже векторы
1) ,
2) ,
3) ,
4) .
Правильное решение.
Пример 4. Даны векторы
и
. Построить на
чертеже векторы
1) ,
2) ,
3) ,
4) .
Правильное решение.
Как найти длину суммы векторов?
Эта задача занимает особое место в операциях с векторами, так как предполагает использование тригонометрических свойств. Допустим, Вам попалась задача вроде следующей:
Даны длины векторов и длина суммы этих векторов . Найти длину разности этих векторов .
Решения этой и других подобных задач и объяснения, как их решать — в
уроке «Сложение векторов: длина суммы векторов и теорема косинусов«.
А проверить решение таких задач можно на Калькуляторе онлайн «Неизвестная сторона треугольника (сложение векторов и теорема косинусов)».
А где произведения векторов?
Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки «Скалярное произведение векторов» и «Векторное и смешанное произведения векторов».
Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
Как известно, проекцией точки A на прямую (плоскость) служит основание перпендикуляра , опущенного из этой точки на прямую (плоскость).
Пусть —
произвольный вектор (Рис. 5), а и —
проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим
через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
Пересечение прямой и плоскости определит требуемую проекцию.
Составляющей вектора на оси l называется такой вектор , лежащий на этой оси, начало которого совпадает с проекцией начала, а конец — с проекцией конца вектора .
Проекцией вектора на ось l называется число
,
равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l, и со знаком минус, если эти направления противоположны.
Основные свойства проекций вектора на ось:
1. Проекции равных векторов на одну и ту же ось равны между собой.
2. При умножении вектора на число его проекция умножается на это же число.
3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.
4. Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 5. Рассчитать проекцию суммы векторов на ось l,
если , а углы —
Рассчитать проекцию суммы векторов на ось l,
если , а углы —
.
Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:
Находим окончательную проекцию суммы векторов:
.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
Перед решением задач этого параграфа желательно ознакомиться с материалом о координатах вектора.
Пусть даны два вектора и , заданные своими проекциями:
или
или
Укажем действия над этими векторами.
1.Сложение:
или, что то же
(при сложении двух векторов одноимённые координаты складываются).
2.Вычитание:
или, что то же
,
(при вычитании двух векторов одноимённые координаты вычитаются).
3.Умножение вектора на число:
или, что то же
,
(при умножении вектора на число все координаты умножаются на это число).
Пример 6. Даны два вектора, заданные координатами:
.
Найти заданный координатами вектор, являющийся суммой этих векторов: .
Решение:
.
Пример 7. Даны четыре вектора:
, , , .
Найти координаты векторов и .
Решение.
.
.
Решить задачи на векторы самостоятельно, а затем посмотреть решение
Пример 8. На плоскости даны векторы
и
. Найти
координаты векторов ,
и
.
На плоскости даны векторы
и
. Найти
координаты векторов ,
и
.
Правильное решение и ответ.
Пример 9. Точка конца вектора — точка . Найти точку начала этого вектора.
Правильное решение и ответ
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
При изучении многих вопросов, в частности, экономических, оказалось удобным
обобщить рассмотренные приёмы установления соответствия между числами и точками двумерного и трёхмерного пространства
и рассматривать последовательности n действительных чисел как «точки» некоторого абстрактного
«n-мерного пространства», а сами числа — как «координаты» этих точек. За составляющие n-мерного вектора можно принимать такие данные, как урожайность различных культур, объёмы продаж товаров, технические коэффициенты, номенклатура товаров на складах и т. д.
д.
n-мерным вектором называется упорядоченный набор из n действительных чисел, записываемых в виде
,
где — i – й элемент (или i – я координата) вектора x.
Возможна и другая запись вектора – в виде столбца координат:
Размерность вектора определяется числом его координат и является его отличительной характеристикой. Например, (2; 5) – двухмерный вектор, (2; -3; 0) – трёхмерный, (1; 3; -2; -4; 7) – пятимерный,
—
n – мерный вектор.
Нулевым вектором называется вектор, все координаты которого равны нулю:
0 = (0; 0; …; 0).
Введём операции над n-мерными векторами.
Произведением вектора
на действительное число называется вектор
(при умножении вектора на число каждая его координата умножается на это число).
Зная вектор
можно получить противоположный вектор
Суммой векторов
и
называется вектор
,
(при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются).
Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж
,
где
—
продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m .
Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех m предприятий сети:
Сумма противоположных векторов даёт нулевой вектор:
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:
Операции над n-мерными векторами удовлетворяют следующим свойствам.
Свойство 1.
Свойство 2.
Свойство 3.
Свойство 4.
Свойство 5.
Свойство 6.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
Поделиться с друзьями
Весь блок «Аналитическая геометрия»
- Векторы
- Понятие вектора, операции над векторами
- Сложение векторов: длина суммы векторов и теорема косинусов
- Скалярное произведение векторов, угол между двумя векторами
- Линейная зависимость векторов
- Базис системы векторов. Аффинные координаты
- Векторное произведение векторов, смешанное произведение векторов
- Плоскость
- Уравнения плоскости, взаимное расположение плоскостей
- Прямая на плоскости
- Уравнение прямой с угловым коэффициентом
- Общее уравнение прямой на плоскости
- Уравнение прямой в отрезках
- Каноническое уравнение прямой на плоскости
- Параметрические уравнения прямой на плоскости
- Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
Как производится умножение вектора на скаляр
Содержание
- Векторные компоненты
- Единичный вектор
- Сложение векторов
- Умножение вектора на скаляр
- Скалярное произведение двух векторов
- Векторное произведение двух векторов
- Смешанное произведение трех векторов
- Задача обучения
- Основные пункты
- Термины
- Обзор
- Пример
Основы векторного исчисления
Вектором называется количественная характеристика, имеющая не только числовую величину, но и направление. Иногда говорят, что вектор это направленный отрезок.
Иногда говорят, что вектор это направленный отрезок.
Векторная система обозначений имеет два существенных преимущества.
1. Формулировки физических законов в векторной форме не зависят от выбора осей координат. Векторная система обозначений представляет собой такой язык, в котором формулировки имеют физическое содержание даже без введения системы координат.
2. Векторная система обозначений является компактной. Многие физические законы выражаются через векторные величины.
Определим основные операции, которые можно производить с векторами.
Равенство двух векторов
Два вектора и равны, если они имеют одинаковую абсолютную величину и одинаковое направление, можно сравнивать два вектора, определенные в разных точках пространства и в разные моменты времени. Параллельный перенос не меняет значения вектора.
Сложение векторов
Суммой двух векторов называют вектор , проведенный из начальной точки вектора к конечной точке вектора , если вектор перенести параллельно самому себе так, чтобы его начало совпадало с концом вектора . Причем = + = + , если совместить начало векторов и , то вектор = + = + является диагональю параллелограмма, построенного на векторах и как на его сторонах и выходящий из общего начала. Сумма векторов не зависит от порядка, в котором складываются векторы.
Причем = + = + , если совместить начало векторов и , то вектор = + = + является диагональю параллелограмма, построенного на векторах и как на его сторонах и выходящий из общего начала. Сумма векторов не зависит от порядка, в котором складываются векторы.
Умножение вектора на скаляр
Произведением вектора на число называется вектор , длина которого равна длине первого вектора, умноженной на модуль числа, а направление либо совпадает с начальным вектором, либо противоположно.
и , если и , если .
Произведение числа 0 на любой вектор дает нулевой вектор, который по сути таковым не является ибо он не имеет длины она равна “нулю” и не имеет направления в пространстве. Сумма двух векторов равна нулю тогда и только тогда, когда они равны по модулю и противоположны по направлению. Если k – число, то т. е. умножение вектора на скаляр дистрибутивно.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9375 — | 7304 — или читать все.
9375 — | 7304 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В статье узнаете что такое вектор, векторные компоненты, единичный вектор, как складывать вектора, умножать вектора на скаляр, скалярное, векторное и смешанное произведение двух векторов.
Сохранение физической величины с вектором обычно означает совершенно иную ситуацию, чем просто сохранение ее скалярной длины. Постоянное значение импульса p (скаляр) может означать совершенно иную ситуацию, чем постоянный вектор p.
Вектор должен иметь три необходимые характеристики: значение (длина), направление, начало и конец.
Любое изменение любого из этих признаков — длины, направления или начало с концом — означает, что создан другой вектор. Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.
Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.
Векторные компоненты
Компонентами вектора являются его проекции на оси системы координат.
Также в трехмерном пространстве векторы A называются векторами, которые являются проекциями этого вектора A на оси системы координат.
Имея вектор A, мы погружаем его в систему координат x, y, z. Векторы, являющиеся проекциями вектора A на оси системы, называются векторными компонентами вектора A. Вектор A является векторной суммой составляющих векторов Ax, Ay и Az .
Единичный вектор
Единичный вектор, имеющий то же направление, что и вектор, на который он ссылается, важен, но его длина всегда равна 1.
Единичные векторы осей координат. Мы также присваиваем единичные векторы оси системы отсчета. а) относится к правовращающей системе и б) к левосторонней системе.
Сложение векторов
Сумма вектора обычно не совпадает с суммой скалярных величин:
Добавление двух или более векторов друг к другу сводится к добавлению их компонентов, то есть проекций на опорные оси. Результирующий вектор называется случайным вектором. Для двух векторов результирующий вектор является диагональю параллелограмма, построенного на этих векторах. Метод параллелограмма.
В случае большего числа векторов результирующий вектор получается путем рисования одного из этих векторов, затем в конце первого вектора мы начинаем второй, в конце второго мы даем начало третьего и так далее. Полученный вектор является вектором, начало которого находится в начале первого из добавленных векторов. и его конец в конце последнего. При изменении порядка сложения результирующий вектор (красный) не меняет длину, направление:
Это правило добавления векторов также действует в трехмерном пространстве:
Умножение вектора на скаляр
Самым простым умножением, выполняемым на векторах, является умножение вектора на скаляр (число). Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:
Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:
Скалярное произведение и векторное произведение двух векторов являются очень важными направления в физике и геометрии. Существует также смешанное произведение трех векторов.
Скалярное произведение двух векторов
Формально скалярное произведение векторов представляет собой точку, и ее значение определяется зависимостью
Скалярное произведение описывает способ, которым оба вектора видят друг друга, то есть как долго тень (проекция) отбрасывает каждый из векторов в своего партнера, когда угол между ними равен φ
B cos φ — длина тени, которую вектор B выбрасывает в вектор A. Аналогично, A cos φ — длина тени, которую вектор A выбрасывает в вектор B.
Когда длина проекции (тени) одного из векторов равна нулю, тогда длина проекции второго вектора равна нулю, то есть A • B = 0. Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.
Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.
Так как единичные векторы оси системы отсчета х, у и z, которые обозначают векторы ех, еYи еz, перпендикулярны друг к другу, то в виду того, что А • В = АВcosφ и что cos 0 = 1 и cos 90 o = 0, мы получаем произведение значений этих единичных векторов:
Выполнение аналогичного умножения на векторы A и B
мы получили новое выражение для скалярного произведения двух векторов A и B
Значение скалярного произведения двух векторов A и B можно записать в виде двух эквивалентных выражений:
Сравнивая оба выражения, мы находим выражение для угла между векторами A и B:
Векторное произведение двух векторов
Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.
В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.
В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:
Произведение векторов A и B , приводящее к третьему вектору C, отмечено диагональным крестом
Направление
Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.
Длина
вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.
Начало и конец
Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.
Изменение порядка применения векторов означает изменение знака векторного произведения.
Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A
В отличие от скалярного произведения, векторное произведение некоммутативно.
Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.
В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.
При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).
Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:
Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:
Удобнее всего рассчитать этот определитель, расширив относительно первой строки.
Смешанное произведение трех векторов
Смешанное произведение трех векторов является скалярным значением, равным значению детерминанта
Геометрическая интерпретация: смешанное произведение численно равно объему V параллелепипеда, растянутому по векторам A, B и C:
Циклическая корректировка векторов в смешанном произведении не меняет значение этого произведения, то есть:
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Физика > Умножение векторов на скаляр
Умножение векторов на число: описание терминов и определения вектора и скаляра, как провести умножение векторов, свойства вектора и скаляра, пример с графиком.
При умножении вектора на скаляр меняется величина вектора, но не направление.
Задача обучения
- Обобщить взаимодействие между векторами и скалярами.
Основные пункты
- Вектор характеризуется величиной и направлением.
- Скаляр отображается лишь величиной.
- Умножение вектора на скаляр эквивалентно умножению вектора величины на скаляр.
Термины
- Вектор – количество, обладающее величиной и направлением (между двумя точками).
- Скаляр – количество с величиной (лишено направления).
- Величина – число вектора, указывающее на длину.
Обзор
Вектор и скаляры отображают разные типы физических величин, но иногда вынуждены контактировать. Конечно, они обладают разными размерами в пространстве, поэтому добавление невозможно. Однако вектор можно умножить на скаляр, а вот умножить скаляр на вектор не получится.
Чтобы проделать подобную операцию, следует умножать компоненты, а именно величины. Это создаст новый вектор с тем же направлением, но будет уже результатом двух величин.
Пример
Допустим, вы располагаете вектором А с определенными величиной и направлением. Если умножить его на скаляр с величиной 0.5, то новый вектор будет вдвое меньше изначального. Если же величина 3, то втрое больше. Чтобы разобраться детальнее, возьмем силу гравитации. Сила отображает вектор с величиной, зависящей от скаляра (масса), а направление идет вниз. Если массу удвоить, то сила тяжести также удвоится.
(I) – Умножение вектора А на скаляр (а = 0.5) создает вектор В, который вдвое длиннее.
(Ii) – Умножение вектора А на 3 утраивает его длину.
(Iii) – Удвоение массы (скаляр) удваивает и силу тяжести (вектор).
В физике умножение вектора на число приносит много пользы. Большая часть единиц в векторных величинах выступает внутренними скалярами, умноженными на вектор. К примеру, м/с для отображения скорости состоит их двух величин: скаляр длины в метрах и скаляр времени в секундах. Теперь вы знаете, как проводить умножение векторов.
Теперь вы знаете, как проводить умножение векторов.
12.3: Скалярный продукт — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2588
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Вычислить скалярное произведение двух заданных векторов.
- Определить, перпендикулярны ли два заданных вектора.
- Найдите направляющие косинусы заданного вектора.
- Объясните, что подразумевается под векторной проекцией одного вектора на другой вектор, и опишите, как ее вычислить.
- Вычислите работу, совершаемую данной силой.

Если мы прикладываем силу к объекту, чтобы объект двигался, мы говорим, что работа совершается силой. Раньше мы рассматривали постоянную силу и предполагали, что сила приложена в направлении движения объекта. В этих условиях работу можно выразить как произведение силы, действующей на объект, и расстояния, которое этот объект перемещает. Однако в этой главе мы увидели, что и сила, и движение объекта могут быть представлены векторами.
В этом разделе мы разработаем операцию, называемую скалярным произведением, которая позволяет вычислить работу в случае, когда вектор силы и вектор движения имеют разные направления. Скалярное произведение, по сути, говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, пересекаются ли два вектора под прямым углом.
Скалярный продукт и его свойства
Мы уже научились складывать и вычитать векторы. В этой главе мы исследуем два типа умножения векторов. Первый тип векторного умножения называется скалярным произведением, основанным на обозначениях, которые мы используем для него, и определяется следующим образом:
В этой главе мы исследуем два типа умножения векторов. Первый тип векторного умножения называется скалярным произведением, основанным на обозначениях, которые мы используем для него, и определяется следующим образом:
Определение: скалярное произведение
скалярное произведение векторов \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3⟩\) задается суммой произведений компонент
\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3. \nonumber \]
Обратите внимание, что если \(u\) и \(v\) являются двумерными векторами, скалярное произведение вычисляется аналогичным образом. Таким образом, если \(\vecs{ u}=⟨u_1,u_2⟩\) и \(\vecs{ v}=⟨v_1,v_2⟩,\), то
\[\vecs{ u}⋅\vecs{ v }=u_1v_1+u_2v_2. \nonumber \]
Когда два вектора объединяются при сложении или вычитании, результатом является вектор. Когда два вектора объединяются с помощью скалярного произведения, результатом является скаляр. По этой причине скалярное произведение часто называют числом 9. 0056 скалярное произведение. Его также можно назвать внутренним продуктом .
0056 скалярное произведение. Его также можно назвать внутренним продуктом .
Пример \(\PageIndex{1}\): вычисление скалярных произведений
- Найдите скалярное произведение \(\vecs{ u}=⟨3,5,2⟩\) и \(\vecs{ v} =⟨−1,3,0⟩\).
- Найдите скалярное произведение \(\vecs{ p}=10\hat{\textbf i}−4 \hat{\textbf j}+7 \hat{\textbf k}\) и \(\vecs{ q} = −2 \ шляпа {\ textbf i} + \ шляпа {\ textbf j} +6 \ шляпа {\ textbf k}. \)
Раствор :
а. Подставляем компоненты вектора в формулу скалярного произведения:
\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 \\[4pt] &=12. \end{align*}\]
б. Расчет такой же, если векторы записываются с использованием стандартных единичных векторов. У нас все еще есть три компонента для каждого вектора, которые нужно подставить в формулу скалярного произведения:
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=p_1q_1+p_2q_2+p_3q_3 \\[4pt ] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42 \\[4pt] &=18. \end{align* }\]
\end{align* }\]
Упражнение \(\PageIndex{1}\)
Найти \(\vecs{ u}⋅\vecs{ v}\), где \(\vecs{ u}=⟨2,9,−1⟩\) и \(\vecs{v}=⟨−3,1,−4⟩.\)
- Подсказка
Умножьте соответствующие компоненты, а затем сложите их произведения.
- Ответить
\(7\)
Подобно сложению и вычитанию векторов, скалярное произведение имеет несколько алгебраических свойств. Мы докажем три из этих свойств, а остальные оставим в качестве упражнений.
Свойства скалярного произведения
Пусть \(\vecs{ u}\), \(\vecs{ v}\) и \(\vecs{ w}\) — векторы, и пусть \(c\) быть скаляром.
- Коммутативное свойство \[\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u} \nonumber \]
- Распределительное свойство \[\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w} \номер\]
- Ассоциативное свойство ) \номер\] 92 \номер \]
Доказательство
Пусть \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3⟩. \) Тогда
\) Тогда
\[ \begin{ выровнять*} \vecs{ u}⋅\vecs{ v} &=⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &= v_1u_1+v_2u_2+v_3u_3 \\[4pt] &= ⟨v_1,v_2,v_3⟩⋅⟨u_1,u_2,u_3⟩ \\[4pt] &=\vecs{ v}⋅\vecs{ u}.\end{align *}\]
Ассоциативное свойство похоже на ассоциативное свойство для умножения действительных чисел, но обратите особое внимание на разницу между скалярными и векторными объектами:
\[ \begin{align*} c(\vecs{ u}⋅\vecs{ v}) &=c(u_1v_1+u_2v_2+u_3v_3) \\[4pt] &=c(u_1v_1)+c(u_2v_2) +c(u_3v_3) \\[4pt] &=(cu_1)v_1+(cu_2)v_2+(cu_3)v_3 \\[4pt] &=⟨cu_1,cu_2,cu_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt ] &=c⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=(c\vecs{ u})⋅\vecs{ v}.\end{align*}\]
Доказательство \(c(\vecs{ u}⋅\vecs{ v})=\vecs{ u}⋅(c\vecs{ v})\) аналогично.
Четвертое свойство показывает связь между величиной вектора и его скалярным произведением на самого себя: 92.\end{align*}\]
□
Обратите внимание, что определение скалярного произведения дает \(\vecs{ 0}⋅\vecs{ v}=0. \) По свойству iv. если \(\vecs{ v}⋅\vecs{ v}=0,\), то \(\vecs{ v}=\vecs{ 0}.\)
\) По свойству iv. если \(\vecs{ v}⋅\vecs{ v}=0,\), то \(\vecs{ v}=\vecs{ 0}.\)
Пример \(\PageIndex{2}\): Использование Свойства скалярного произведения
Пусть \(\vecs{ a}=⟨1,2,−3⟩\), \(\vecs{ b}=⟨0,2,4⟩\) и \(\vecs { c} =⟨5,−1,3⟩\).
Найдите каждый из следующих продуктов.
- \(( \vecs{a} ⋅ \vecs{b}) \vecs{c} \)
- \(\vecs{a}⋅(2\vecs{c})\) 92\)
Раствор
а. Обратите внимание, что это выражение запрашивает скалярное число, кратное \(\vecs{ c}\) на \(\vecs{ a}⋅\vecs{ b}\):
\[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=( 1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=−8⟨5,−1,3⟩ \\[4pt] &= ⟨−40,8,−24⟩.\end{align*}\]
б. Это выражение представляет собой скалярное произведение вектора \(\vecs{ a}\) и скаляра, кратного 2\(\vecs{ c}\):
\[ \begin{align*} \vecs{ a}⋅(2\ vecs{ c}) &=2(\vecs{a}⋅\vecs{c}) \\[4pt] &=2(⟨1,2,−3⟩⋅⟨5,−1,3⟩) \\ [4pt] &=2(1(5)+2(-1)+(-3)(3)) \\[4pt] &=2(-6)=-12. \end{align*}\] 92=53\)
\end{align*}\] 92=53\)
Использование скалярного произведения для нахождения угла между двумя векторами
Когда два ненулевых вектора помещаются в стандартное положение, будь то в двух измерениях или в трех измерениях, они образуют между собой угол (рис. \(\PageIndex{1}\) ). Скалярное произведение позволяет найти меру этого угла. Это свойство является результатом того факта, что мы можем выразить скалярное произведение через косинус угла, образованного двумя векторами.
Рисунок \(\PageIndex{1}\): Пусть \(θ\) — угол между двумя ненулевыми векторами \(\vecs{ u}\) и \(\vecs{ v}\), такой, что \(0≤θ≤π\).Оценка скалярного произведения
Скалярное произведение двух векторов — это произведение величины каждого вектора на косинус угла между ними:
\[\vecs{ u}⋅\vecs{ v}=‖\ vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot} \]
Доказательство
Поместите векторы \(\vecs{ u}\) и \(\vecs{ v}\) в стандартное положение и рассмотрим вектор \(\vecs{ v}−\vecs { u}\) (Рисунок \(\PageIndex{2}\)).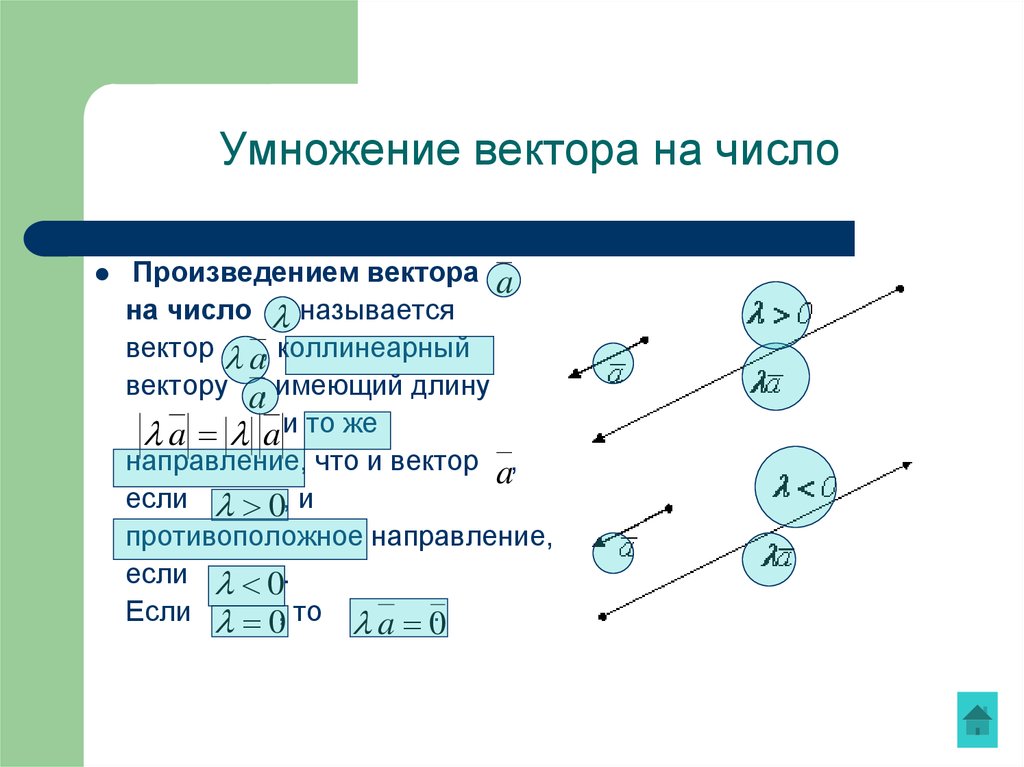 Эти три вектора образуют треугольник с длинами сторон \(‖\vecs{ u}‖,‖\vecs{ v}‖\) и \(‖\vecs{ v}−\vecs{ u}‖\). 92−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖ \vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]
Эти три вектора образуют треугольник с длинами сторон \(‖\vecs{ u}‖,‖\vecs{ v}‖\) и \(‖\vecs{ v}−\vecs{ u}‖\). 92−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖ \vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]
□
Мы можем использовать форму скалярного произведения в уравнении \ref{evaldot}, чтобы найти меру угла между двумя ненулевыми векторами, перестроив уравнение \ref{evaldot} для решения для косинуса угла:
\[\cos θ=\dfrac{\vecs{u}⋅\vecs{v}}{‖\vecs{u}‖‖\vecs{v}‖}. \метка{точка2} \]
Используя это уравнение, мы можем найти косинус угла между двумя ненулевыми векторами. Поскольку мы рассматриваем наименьший угол между векторами, мы предполагаем \(0°≤θ≤180°\) (или \(0≤θ≤π\), если мы работаем в радианах). Арккосинус уникален в этом диапазоне, поэтому мы можем определить меру угла \(θ\).
Пример \(\PageIndex{3}\): нахождение угла между двумя векторами
Найдите меру угла между каждой парой векторов.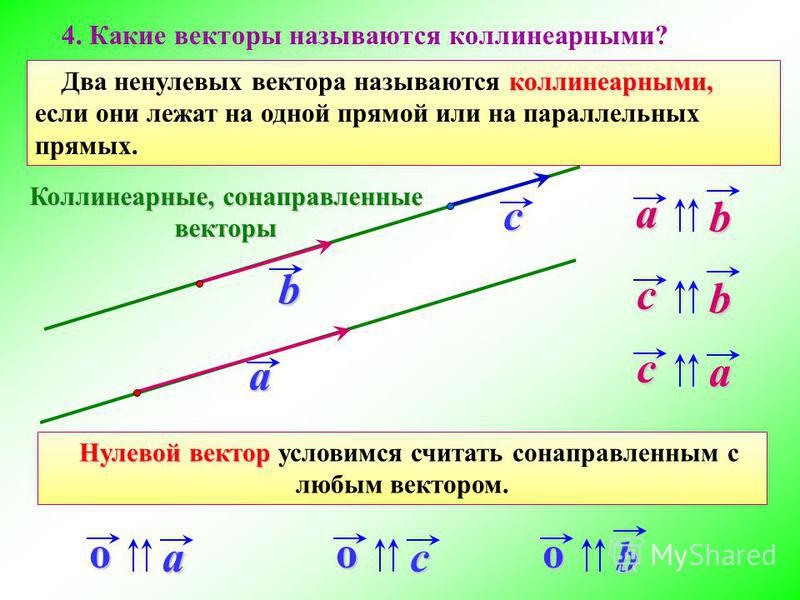 2}} \\[4pt] &=\dfrac{-2}{\sqrt{3}\sqrt{14}} =\ dfrac{−2}{\sqrt{42}}. \end{выравнивание*}\] 92}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]
2}} \\[4pt] &=\dfrac{-2}{\sqrt{3}\sqrt{14}} =\ dfrac{−2}{\sqrt{42}}. \end{выравнивание*}\] 92}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]
Теперь \(\cos θ=0\ ) и \(0≤θ≤π\), поэтому \(θ=π/2\).
Упражнение \(\PageIndex{3}\)
Найдите меру угла в радианах, образованного векторами \(\vecs{ a}=⟨1,2,0⟩\) и \(\vecs{ б}=⟨2,4,1⟩\). Округлить до сотых.
- Подсказка
Используйте уравнение \ref{dot2}.
- Ответить
\(θ≈0,22\) рад
Угол между двумя векторами может быть острым \((0<\cos θ<1),\), тупым \((−1<\cos θ<0)\) или прямым \((\cos θ=− 1)\). Если \(\cos θ=1\), то оба вектора имеют одинаковое направление. Если \(\cos θ=0\), то векторы в стандартном положении образуют прямой угол (рисунок \(\PageIndex{3}\)). Мы можем формализовать этот результат в виде теоремы об ортогональных (перпендикулярных) векторах.
Рисунок \(\PageIndex{3}\): (a) Острый угол имеет \(0<\cos θ<1\). (b) Тупой угол имеет \(−1<\cos θ<0.\) (c) Прямая линия имеет \(\cos θ=−1\). (d) Если векторы имеют одинаковое направление, \(\cos θ=1\). (e) Если векторы ортогональны (перпендикулярны), \(\cos θ=0.\)
(b) Тупой угол имеет \(−1<\cos θ<0.\) (c) Прямая линия имеет \(\cos θ=−1\). (d) Если векторы имеют одинаковое направление, \(\cos θ=1\). (e) Если векторы ортогональны (перпендикулярны), \(\cos θ=0.\)Ортогональные векторы
Ненулевые векторы \(\vecs{u}\) и \(\vecs{v}\) являются ортогональными векторами тогда и только тогда, когда \(\vecs{u}⋅\vecs{v}= 0.\)
Доказательство
Пусть \(\vecs{u}\) и \(\vecs{v}\) ненулевые векторы, и пусть \(θ\) обозначает угол между ними. Сначала предположим, что \(\vecs{u}⋅\vecs{v}=0.\)Затем
\[‖\vecs{u}‖‖\vecs{v}‖\cos θ=0. \nonumber \]
Однако \(‖\vecs{u}‖≠0\) и \(‖\vecs{v}‖≠0,\), поэтому мы должны иметь \(\cos θ=0\). Следовательно, \(θ=90°\) и векторы ортогональны.
Теперь предположим, что \(\vecs{u}\) и \(\vecs{v}\) ортогональны. Тогда \(θ=90°\) и мы имеем
\[ \begin{align*} \vecs{u}⋅\vecs{v} &=‖\vecs{ u}‖‖\vecs{ v}‖\ cos θ \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖\cos 90° \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖(0 ) \\[4pt] &=0. \end{align*}\]
\end{align*}\]
□
Термины ортогональный, перпендикулярный, и нормальный каждый указывает на то, что математические объекты пересекаются под прямым углом. Использование каждого термина определяется главным образом его контекстом. Мы говорим, что векторы ортогональны, а прямые перпендикулярны. Срок нормальный используется чаще всего при измерении угла, выполненного с плоскостью или другой поверхностью.
Пример \(\PageIndex{4}\): определение ортогональных векторов ,−2⟩\) — ортогональные векторы.
Решение
Используя определение, нам нужно только проверить скалярное произведение векторов:
\[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+ (5)(-2)=10+0-10=0. \nonumber \]
Поскольку \(\vecs{p}⋅\vecs{q}=0,\) векторы ортогональны (рис. \(\PageIndex{4}\)).
Рисунок \(\PageIndex{4}\): Векторы \(\vecs{ p}\) и \(\vecs{ q}\) образуют прямой угол, когда их начальные точки совпадают.Упражнение \(\PageIndex{4}\)
Для какого значения \(x\) \(\vecs{ p}=⟨2,8,−1⟩\) ортогонально \(\vecs{ q} =⟨x,−1,2⟩\)?
- Подсказка
Векторы \(\vecs{ p}\) и \(\vecs{ q}\) ортогональны тогда и только тогда, когда \(\vecs{ p}⋅\vecs{ q}=0\).

- Ответить
\(х=5\)
Пример \(\PageIndex{5}\): измерение угла, образованного двумя векторами
Пусть \(\vecs{ v}=⟨2,3,3⟩.\) Найдите меры углов, образованных двумя векторами следующие векторы.
- \(\vecs{v}\) и \(\mathbf{\шляпа i}\)
- \(\vecs{v}\) и \(\mathbf{\hat j}\)
- \(\vecs{v}\) и \(\mathbf{\шляпа k}\)
Решение
а. Пусть α будет углом, образованным \(\vecs{ v}\) и \(\mathbf{\hat i}\): 92}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt]γ &=\arccos\dfrac{3}{\sqrt{22}}≈0,877\,\text{ рад.} \end{align*}\]
Упражнение \(\PageIndex{5}\)
Пусть \(\vecs{ v}=⟨3,−5,1⟩.\) Найдите меру углы, образованные каждой парой векторов.
- \(\vecs{v}\) и \(\mathbf{\шляпа i}\)
- \(\vecs{v}\) и \(\mathbf{\hat j}\)
- \(\vecs{v}\) и \(\mathbf{\шляпа k}\)
- Подсказка
\(\mathbf{\hat i}=⟨1,0,0⟩, \mathbf{\hat j}=⟨0,1,0⟩,\) и \(\mathbf{\hat k}=⟨0 ,0,1⟩\)
- Ответить
\(а.
 α≈1,04\) рад; б. \(β≈2,58\) рад; в. \(γ≈1,40\) рад
α≈1,04\) рад; б. \(β≈2,58\) рад; в. \(γ≈1,40\) рад
Угол, образуемый вектором с каждой из осей координат, называемый углом направления, очень важен в практических вычислениях, особенно в таких областях, как инженерия. Например, в космонавтике угол запуска ракеты должен определяться очень точно. Очень маленькая ошибка в угле может привести к тому, что ракета отклонится от курса на сотни миль. Углы направления часто рассчитываются с помощью скалярного произведения и косинусов углов, называемых направляющими косинусами. Поэтому мы определяем как эти углы, так и их косинусы.
Определение: углы направления
Углы, образованные ненулевым вектором и осями координат, называются углами направления для вектора (рисунок \(\PageIndex{5}\)). Косинусы этих углов называются косинусами направления .
Рисунок \(\PageIndex{5}\): Угол \(α\) образован вектором \(\vecs{ v}\) и единичным вектором \(\mathbf{\hat i}\). Угол β образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat j}\). Угол γ образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat k}\).
Угол γ образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat k}\).В примере \(\PageIndex{5}\) направляющие косинусы \(\vecs{ v}=⟨2,3,3⟩\) равны \(\cos α=\dfrac{2}{\sqrt{ 22}}, \cos β=\dfrac{3}{\sqrt{22}},\) и \(\cos γ=\dfrac{3}{\sqrt{22}}\). Углы направления \(\vecs{v}\) равны \(α=1,130\) рад, \(β=0,877\) рад и \(γ=0,877\) рад.
До сих пор мы в основном фокусировались на векторах, связанных с силой, движением и положением в трехмерном физическом пространстве. Однако векторы часто используются более абстрактно. Например, предположим, что продавец фруктов продает яблоки, бананы и апельсины. В данный день он продает 30 яблок, 12 бананов и 18 апельсинов. Он может использовать количественный вектор \(\vecs{ q}=⟨30,12,18⟩,\) для представления количества фруктов, которое он продал в тот день. Точно так же он может захотеть использовать ценовой вектор \(\vecs{ p}=⟨0,50,0,25,1⟩,\), чтобы указать, что он продает свои яблоки по 50 центов за штуку, бананы по 25 центов за штуку и апельсины по 1 доллар за штуку. В этом примере, хотя мы все еще можем изобразить эти векторы, мы не интерпретируем их как буквальное представление положения в физическом мире. Мы просто используем векторы для отслеживания отдельных фрагментов информации о яблоках, бананах и апельсинах.
В этом примере, хотя мы все еще можем изобразить эти векторы, мы не интерпретируем их как буквальное представление положения в физическом мире. Мы просто используем векторы для отслеживания отдельных фрагментов информации о яблоках, бананах и апельсинах.
Эта идея может показаться немного странной, но если мы будем рассматривать векторы просто как способ упорядочивания и хранения данных, мы обнаружим, что они могут быть весьма мощным инструментом. Возвращаясь к продавцу фруктов, давайте подумаем о скалярном произведении \(\vecs{ q}⋅\vecs{ p}\). Мы вычисляем его, умножая количество проданных яблок (30) на цену одного яблока (50 центов), количество проданных бананов на цену одного банана и количество проданных апельсинов на цену одного апельсина. Затем мы складываем все эти значения вместе. Итак, в этом примере скалярный продукт говорит нам, сколько денег было у продавца фруктов в продажах в этот конкретный день.
Когда мы используем векторы более общим образом, нет причин ограничивать количество компонентов тремя. Что, если продавец фруктов решит начать продавать грейпфруты? В этом случае он хотел бы использовать четырехмерные векторы количества и цены для представления количества проданных яблок, бананов, апельсинов и грейпфрутов и их цены за единицу. Как и следовало ожидать, чтобы вычислить скалярное произведение четырехмерных векторов, мы просто складываем произведения компонентов, как и раньше, но сумма состоит из четырех членов вместо трех.
Что, если продавец фруктов решит начать продавать грейпфруты? В этом случае он хотел бы использовать четырехмерные векторы количества и цены для представления количества проданных яблок, бананов, апельсинов и грейпфрутов и их цены за единицу. Как и следовало ожидать, чтобы вычислить скалярное произведение четырехмерных векторов, мы просто складываем произведения компонентов, как и раньше, но сумма состоит из четырех членов вместо трех.
Пример \(\PageIndex{6}\): Использование векторов в экономическом контексте
Магазин товаров для вечеринок AAA продает приглашения, подарки для вечеринок, украшения и предметы общественного питания, такие как бумажные тарелки и салфетки. Когда AAA покупает свой инвентарь, она платит 25 центов за упаковку за приглашения и сувениры для вечеринок. Украшения стоят 50 центов AAA за штуку, а предметы общественного питания — 20 центов за упаковку. AAA продает приглашения по 2,50 доллара за упаковку и сувениры для вечеринок по 1,50 доллара за упаковку. Украшения продаются по 4,50 доллара за штуку, а предметы общественного питания по 1,25 доллара за упаковку.
Украшения продаются по 4,50 доллара за штуку, а предметы общественного питания по 1,25 доллара за упаковку.
В течение мая в магазине товаров для вечеринок AAA было продано 1258 приглашений, 342 сувенира для вечеринок, 2426 украшений и 1354 предмета общественного питания. Используйте векторы и скалярные произведения, чтобы рассчитать, сколько денег AAA заработала на продажах в мае месяце. Какую прибыль получил магазин?
Решение
Векторы стоимости, цены и количества: p} &=⟨2.50,1.50,4.50,1.25⟩ \\[4pt] \vecs{q} &=⟨1258,342,2426,1354⟩. \end{выравнивание*}\]
Продажи AAA в мае можно рассчитать с помощью скалярного произведения \(\vecs{ p}⋅\vecs{ q}\). У нас есть
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=⟨2.50,1.50,4.50,1.25⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] & =3145+513+10917+1692,5 \\[4pt] &= 16267,5. \end{align*}\]
Итак, в мае ААА заработала 16 267,50 долларов. Чтобы рассчитать прибыль, мы должны сначала подсчитать, сколько ААА заплатила за проданные товары. Мы используем скалярное произведение \(\vecs{c}⋅\vecs{q}\), чтобы получить
Мы используем скалярное произведение \(\vecs{c}⋅\vecs{q}\), чтобы получить
\[ \begin{align*} \vecs{ c}⋅\vecs{ q} &=⟨0,25,0,25,0,50,0,20⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=314,5+ 85,5+1213+270,8 \\[4pt] &=1883,8. \end{align*}\]
Итак, AAA заплатила 1 883,80 долларов за проданные товары. Таким образом, их прибыль равна
\[\vecs{ p}⋅\vecs{ q}−\vecs{ c}⋅\vecs{ q}=16267,5−1883,8 =14383,7. \nonumber \]
Таким образом, в мае магазин товаров для вечеринок AAA заработал 14 383,70 долларов США.
Упражнение \(\PageIndex{6}\)
1 июня магазин товаров для вечеринок AAA решил повысить цену на сувениры для вечеринок до 2 долларов за упаковку. Они также сменили поставщиков своих приглашений и теперь могут покупать приглашения всего за 10 центов за упаковку. Все остальные их расходы и цены остаются прежними. Если ААА продаст 1408 приглашений, 147 подарков для вечеринок, 2112 украшений и 1894 пункта общественного питания в июне месяце, используйте векторы и точечные произведения, чтобы рассчитать их общий объем продаж и прибыль за июнь.
- Подсказка
Используйте четырехмерные векторы для стоимости, цены и проданного количества.
- Ответить
Продажи = 15 685,50 долларов США; прибыль = 14 073,15
долларов США
Проекции
Как мы видели, сложение объединяет два вектора для создания результирующего вектора. Но что, если нам дан вектор и нужно найти его составные части? Мы используем векторные проекции для выполнения противоположного процесса; они могут разбить вектор на его компоненты. Величина векторной проекции является скалярной проекцией. Например, если ребенок тянет ручку тележки под углом 55°, мы можем использовать проекции, чтобы определить, какая сила на ручке фактически двигает тележку вперед (\(\PageIndex{6}\)) . Мы вернемся к этому примеру и научимся его решать после того, как увидим, как вычислять проекции.
Рисунок \(\PageIndex{6}\): Когда ребенок тянет тележку, только горизонтальная составляющая силы толкает тележку вперед.
Определение: вектор и проекция
Проекция вектора \(\vecs{ v}\) на \(\vecs{ u}\) — это вектор с меткой \(\text{proj}_\vecs{ u} \vecs{ v}\) на рисунке \(\PageIndex{7}\). Он имеет ту же начальную точку, что и \(\vecs{ u}\) и \(\vecs{ v}\), и то же направление, что и \(\vecs{ u}\), и представляет компонент \(\vecs { v}\), который действует в направлении \(\vecs{ u}\). Если \(θ\) представляет собой угол между \(\vecs{ u}\) и \(\vecs{ v}\), то по свойствам треугольников мы знаем длину \(\text{proj}_ \vecs{ u}\vecs{ v}\) равно \(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ.\) Когда выражая \(\cos θ\) через скалярное произведение, это становится 92}\vecs{у}. \nonumber \]
Длина этого вектора также известна как скалярная проекция из \(\vecs{ v}\) на \(\vecs{ u}\) и обозначается как
\[\| \text{proj}_\vecs{u}\vecs{v}\|=\text{comp}_\vecs{u}\vecs{v}=\dfrac{\vecs{u}⋅\vecs{v} }{‖\vecs{ u}‖.} \nonumber \]
Рисунок \(\PageIndex{7}\): Проекция \(\vecs{ v}\) на \(\vecs{ u}\) показывает компонента вектора \(\vecs{ v}\) в направлении \(\vecs{ u}\). 2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4, 3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{выравнивание*}\] 92}(\mathbf{\шляпа i}+6\mathbf{\шляпа j}) \\[4pt] &= -\dfrac{9}{37}(\mathbf{\шляпа i}+6\mathbf{\ шляпа j}) \\[4pt] &= -\dfrac{9}{37}\mathbf{\hat i}-\dfrac{54}{37}\mathbf{\hat j}.\end{align*} \]
2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4, 3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{выравнивание*}\] 92}(\mathbf{\шляпа i}+6\mathbf{\шляпа j}) \\[4pt] &= -\dfrac{9}{37}(\mathbf{\шляпа i}+6\mathbf{\ шляпа j}) \\[4pt] &= -\dfrac{9}{37}\mathbf{\hat i}-\dfrac{54}{37}\mathbf{\hat j}.\end{align*} \]Иногда бывает полезно разложить векторы, то есть разбить вектор на части в виде суммы. Этот процесс называется -разложением вектора на компоненты. Проекции позволяют нам идентифицировать два ортогональных вектора, имеющих желаемую сумму. Например, пусть \(\vecs{ v}=⟨6,−4⟩\) и пусть \(\vecs{ u}=⟨3,1⟩.\) Мы хотим разложить вектор \(\vecs{ v }\) на ортогональные компоненты, так что один из векторов компонентов имеет то же направление, что и \(\vecs{ u}\). 92}\vecs{ u} \\[4pt] = \dfrac{18−4}{9+1}\vecs{ u} \\[4pt] = \dfrac{7}{5}\vecs{ u}= \dfrac{7}{5}⟨3,1⟩=⟨\dfrac{21}{5},\dfrac{7}{5}⟩. \end{align*}\]
Теперь рассмотрим вектор \(\vecs{ q}=\vecs{ v}−\vecs{ p}. \) У нас есть
\) У нас есть
\[\begin{align*} \vecs { q} =\vecs{ v}−\vecs{ p} \\[4pt] = ⟨6,−4⟩−⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[ 4pt] = ⟨\dfrac{9}{5},−\dfrac{27}{5}⟩. \end{align*}\]
Очевидно, по тому, как мы определили \(\vecs{ q}\), имеем \(\vecs{ v}=\vecs{ q}+\vecs{ p},\ ) и
\[\begin{align*}\vecs{ q}⋅\vecs{ p} =⟨\dfrac{9}{5},−\dfrac{27}{5}⟩⋅⟨\dfrac{21}{5 },\dfrac{7}{5}⟩ \\[4pt] = \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt] = \dfrac{ 189}{25}−\dfrac{189}{25}=0. \end{align*}\]
Следовательно, \(\vecs{ q}\) и \(\vecs{ p}\) ортогональны.
Пример \(\PageIndex{8}\): преобразование векторов в компоненты
Выразите \(\vecs{ v}=⟨8,−3,−3⟩\) в виде суммы ортогональных вектора имеют то же направление, что и \(\vecs{ u}=⟨2,3,2⟩.\) 92}⟨2,3,2⟩ \\[4pt] &=\dfrac{1}{17}⟨2,3,2⟩ \\[4pt] &=⟨\dfrac{2}{17},\dfrac {3}{17},\dfrac{2}{17}⟩. \end{align*} \nonumber \]
Затем
\[ \begin{align*} \vecs{q} &=\vecs{v}-\vecs{p}=⟨8,-3,- 3⟩−⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩\\[4pt] &=⟨\dfrac{134}{17},−\ dfrac{54}{17},−\dfrac{53}{17}⟩. \end{align*} \nonumber \]
\end{align*} \nonumber \]
Чтобы проверить нашу работу, мы можем использовать скалярное произведение, чтобы убедиться, что векторы \(\vecs{ p}\) и \(\vecs{ q}\) являются ортогональными векторами:
\[ \begin{align*}\vecs{ p}⋅\vecs{ q}&=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩ ⋅⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩\\[4pt] &=\dfrac{268}{289}-\dfrac{162}{289}-\dfrac{106}{289}=0. \end{align*} \nonumber \]
Затем
\[\vecs{ v}=\vecs{ p}+\vecs{ q}=⟨\dfrac{2}{17},\dfrac{3 }{17},\dfrac{2}{17}⟩+⟨\dfrac{134}{17},-\dfrac{54}{17},-\dfrac{53}{17}⟩. \nonumber \]
Упражнение \(\PageIndex{7}\)
Выразите \(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\) как сумму ортогональных такие, что один из векторов имеет то же направление, что и \(\vecs{u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).
- Подсказка
Начните с нахождения проекции \(\vecs{ v}\) на \(\vecs{ u}\).
- Ответить
\(\vecs{v}=\vecs{p}+\vecs{q},\) где \(\vecs{p}=\dfrac{18}{5}\mathbf{\hat i}+\dfrac {9}{5}\mathbf{\hat j}\) и \(\vecs{q}=\dfrac{7}{5}\mathbf{\hat i}−\dfrac{14}{5}\mathbf {\ шляпа j} \)
Пример \(\PageIndex{9}\): Скалярная проекция скорости
Контейнеровоз выходит из порта и движется \(15°\) к северу от востока. Его двигатель развивает на этом пути скорость 20 узлов (см. следующий рисунок). Кроме того, океанское течение перемещает корабль на северо-восток со скоростью 2 узла. Учитывая и двигатель, и течение, с какой скоростью корабль движется в направлении \(15°\) к северу от востока? Округлите ответ до двух знаков после запятой.
Его двигатель развивает на этом пути скорость 20 узлов (см. следующий рисунок). Кроме того, океанское течение перемещает корабль на северо-восток со скоростью 2 узла. Учитывая и двигатель, и течение, с какой скоростью корабль движется в направлении \(15°\) к северу от востока? Округлите ответ до двух знаков после запятой.
Решение
Пусть \(\vecs{ v}\) будет вектором скорости, создаваемой двигателем, и пусть \(\vecs{w}\) будет вектором скорости течения. Мы уже знаем \(‖\vecs{ v}‖=20\) вдоль нужного маршрута. Нам просто нужно добавить скалярную проекцию \(\vecs{w}\) на \(\vecs{v}\). Получаем
\[ \begin{align*} \text{comp}_\vecs{ v}\vecs{w}=\dfrac{\vecs{ v}⋅\vecs{w}}{‖\vecs{ v }‖} \\[4pt] =\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} =‖\vecs{ w}‖ \cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1,73\,\text{узлы.}\end{align*}\]
Судно движется со скоростью 21,73 узла в направлении \(15°\) к северо-востоку.
Упражнение \(\PageIndex{8}\)
Повторите предыдущий пример, но предположите, что океанское течение движется на юго-восток, а не на северо-восток, как показано на следующем рисунке.
- Подсказка
Вычислить скалярную проекцию \(\vecs{w}\) на \(\vecs{v}\).
- Ответить
21 узел
Работа
Теперь, когда мы понимаем точечные произведения, мы можем увидеть, как их применять в реальных ситуациях. Чаще всего скалярное произведение двух векторов применяется для расчета работы.
Из физики мы знаем, что работа совершается, когда объект перемещается под действием силы. Когда сила постоянна и приложена в том же направлении, в котором движется объект, тогда мы определяем проделанную работу как произведение силы на расстояние, которое проходит объект: \(W=Fd\). Мы видели несколько примеров этого типа в предыдущих главах. Теперь представьте, что направление силы отличается от направления движения, как в примере с ребенком, тянущим тележку. Чтобы найти совершенную работу, нужно умножить составляющую силы, действующей в направлении движения, на величину перемещения. Скалярный продукт позволяет нам сделать именно это. Если представить приложенную силу вектором \(\vecs{ F}\), а перемещение объекта вектором \(\vecs{ s}\), то работа, выполненная силой , является скалярным произведением \(\vecs{F}\) и \(\vecs{s}\).
Скалярный продукт позволяет нам сделать именно это. Если представить приложенную силу вектором \(\vecs{ F}\), а перемещение объекта вектором \(\vecs{ s}\), то работа, выполненная силой , является скалярным произведением \(\vecs{F}\) и \(\vecs{s}\).
Определение: постоянная сила
Когда к объекту приложена постоянная сила, так что объект движется по прямой из точки \(P\) в точку \(Q\), работа \(W\), выполненная сила \(\vecs{ F}\), действующая под углом θ от линии движения, равна
\[W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F }∥∥\vecd{PQ}∥\cos θ. \nonumber \]
Давайте вернемся к проблеме детской тележки, представленной ранее. Предположим, ребенок тянет тележку с силой 8 фунтов на ручке под углом 55° . Если ребенок протащит тележку на 50 футов, найдите работу силы (рисунок \(\PageIndex{8}\)).
Рисунок \(\PageIndex{8}\): Горизонтальная составляющая силы представляет собой проекцию \(\vecs{ F}\) на положительную ось \(x\).Имеем
\[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb. } \nonumber \]
} \nonumber \]
В стандартных единицах США мы измеряем величину силы \(∥\vecs{ F}∥\) в фунтах. Величина вектора смещения \(∥\vecd{PQ}∥\) говорит нам, как далеко переместился объект, и измеряется в футах. Таким образом, общепринятой единицей измерения труда является футо-фунт. Один футо-фунт — это количество работы, необходимой для перемещения объекта весом 1 фунт на расстояние 1 фут по прямой. В метрической системе единицей измерения силы является ньютон (Н), а единицей измерения величины работы — ньютон-метр (Н·м) или джоуль (Дж).
Пример \(\PageIndex{10}\): Расчет работы
Конвейерная лента создает силу \(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\ mathbf{\hat k}\), который перемещает чемодан из точки \((1,1,1)\) в точку \((9,4,7)\) по прямой. Найдите работу, совершенную конвейерной лентой. Расстояние измеряется в метрах, а сила измеряется в ньютонах.
Решение
Вектор смещения \(\vecd{PQ}\) имеет начальную точку \((1,1,1)\) и конечную точку \((9,4,7)\):
\[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\шляпа i}+3 \mathbf{\шляпа j}+6\mathbf{\шляпа k}. \nonumber \]
\nonumber \]
Работа есть точечный продукт силы и перемещения:
\[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt] &= (5\ mathbf {\ шляпа i} −3 \ mathbf {\ шляпа j} + \ mathbf {\ шляпа k}) ⋅ (8 \ mathbf {\ шляпа i} +3 \ mathbf {\ шляпа j} +6 \ mathbf {\ шляпа k}) \\[4pt] = 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} \\[4pt] &= 37\,\text{J} \end{align*}\]
Упражнение \(\PageIndex{9}\)
Постоянная сила в 30 фунтов, приложенная под углом 60°, тянет ручную тележку на расстояние 10 футов по земле. Какую работу совершает эта сила?
- Подсказка
Используйте определение работы как скалярного произведения силы и расстояния.
- Ответить
150 фут-фунт
Ключевые понятия
- Скалярное произведение двух векторов \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3 ⟩\) равно \(\vecs{u}⋅\vecs{v}=u_1v_1+u_2v_2+u_3v_3\).
 92\)
92\)
 \)
\)Ключевые уравнения
- Скалярное произведение \(\vecs{ u}\) и \(\vecs{ v}\)
\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ\)
- Косинус образуемого угла по \(\vecs{u}\) и \(\vecs{v}\)
\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{v}}{‖\vecs{ u}‖‖\vecs{v}‖}\)
- Векторная проекция \ (\vecs{v}\) на 92}\vecs{ u}\)
- Скалярная проекция \(\vecs{ v}\) на \(\vecs{ u}\)
\(\text{comp}_\vecs{ u}\vecs{v}=\dfrac{\vecs{ u}⋅\vecs{v}}{‖\vecs{u}‖}\)
- Работа силы \(\vecs{ F}\) для перемещения объекта через вектор смещения \(\vecd{PQ}\)
\(W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ\)
Глоссарий
- Углы направления
- углы, образованные ненулевым вектором и осями координат
- направление косинусов
- косинусы углов, образованных ненулевым вектором и осями координат
- Скалярное произведение или скалярное произведение
- \(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\), где \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨ v_1,v_2,v_3⟩\)
- скалярная проекция
- величина векторной проекции вектора
- ортогональные векторы
- векторов, образующих прямой угол при размещении в стандартном положении
- векторная проекция
- составляющая вектора, следующего заданному направлению
- работа силы Под работой
- обычно понимается количество энергии, необходимое для перемещения объекта; если мы представим приложенную силу вектором \(\vecs{F}\), а перемещение объекта вектором \(\vecs{s}\), то работа, выполненная силой, будет скалярным произведением \ (\vecs{F}\) и \(\vecs{s}\).

Авторы и авторство
Эта страница под названием 12.3: Дот-продукт распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- углы направления
- направление косинусов
- скалярное произведение
- внутренний продукт
- ортогональных вектора
- скалярное произведение
- скалярная проекция
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 - Точечный продукт
- векторная проекция
- работа, совершенная силой
2.3 Точка, упс, ВНУТРЕННИЙ Продукт
2.3 Точка, упс, ВНУТРЕННЕЕ ПроизведениеКвантовая механика для инженеров © Леон ван Доммелен Далее: 2.  4 Операторы
4 Операторы
2.3 Точка, упс, ВНУТРЕННИЙ продуктСкалярное произведение векторов является важным инструментом. Это делает возможным чтобы найти длину вектора, умножив вектор сам на себя и извлечение квадратного корня. Он также используется для проверки того, что два вектора ортогональны: если их скалярный продукт равен нулю, они ортогональны. В этом подраздел, скалярное произведение определено для комплексных векторов и функции.
Обычное скалярное произведение двух векторов и может быть находится путем умножения компонентов с одинаковым индексом вместе и подводя итог, что:
(Выразительное равенство обычно используется для обозначения «является по определению равно» иливсегда равно.
) Рисунок 2.6 показаны умноженные компоненты одинаковыми цветами.Рисунок 2.  6: Формирование скалярного произведения двух векторов.
6: Формирование скалярного произведения двух векторов.Обратите внимание на использование числовых индексов, , и а не , и ; это означает тоже самое. Числовые индексы позволяют приведенной выше сумме трех членов записать более компактно как:
Это называется символом суммирования.
Длина вектора , обозначенного или просто , обычно вычисляется как
Однако это не работает правильно для сложных векторов. трудность заключается в том, что термины формы уже не обязательно положительные числа. Например, 1.Поэтому необходимо использовать обобщенное «скалярное произведение» для комплексных векторов, которое ставит комплексное сопряжение по первому вектору:
(2.7)
Если вектор действителен, комплексное сопряжение ничего не делает, и внутренний продукт такой же, как точка продукт . В противном случае во внутреннем произведении
и больше не взаимозаменяемы; в
сопряженные только по первому фактору, .
Замена и изменение внутреннего
стоимость продукта в его комплексно-сопряженную форму.
В противном случае во внутреннем произведении
и больше не взаимозаменяемы; в
сопряженные только по первому фактору, .
Замена и изменение внутреннего
стоимость продукта в его комплексно-сопряженную форму.Длина ненулевого вектора теперь всегда является положительным числом:
(2.8) Физики принимают скалярное произведение
за скобкой
устно. кроме как
и относятся к векторам как бюстгальтеры и кеты.Внутренний продукт функций определяется точно так же, как и для вектора, путем умножения значений в одной и той же позиции вместе и подведение итогов. Но так как значений бесконечно много, то сумма становится интегралом:
(2.9)
На рис. 2.7 показаны умноженные значения функции с использованием
одинаковые цвета:
2.7 показаны умноженные значения функции с использованием
одинаковые цвета:Рисунок 2.7: Формирование внутреннего произведения двух функций. Эквивалент длины вектора в случае функции назвал его «нормой»:
(2.10)
Двойные черты используются, чтобы избежать путаницы с абсолютным значением функция.Вектор или функция называются «нормализованными», если их длина или норма равна единице:
(2.11)
(«iff» действительно следует читать кактогда и только тогда, когда
)Два вектора или две функции и по определению ортогональны, если их внутренний продукт равен нулю:
(2.  12)
12)Наборы векторов или функций, которые все
- взаимно ортогональные, и
- нормализовано
часто используется ортогональный
. Этот документ будет правильно называть их ортонормированными.Итак, набор функций или векторов ортонормирован, если
а также
Ключевые точки
- Для сложных векторов и функций нормальное скалярное произведение становится внутренним продуктом.
- Чтобы получить скалярное произведение векторов,
- взять комплексные сопряжения компонентов первого вектора;
- перемножить соответствующие компоненты двух векторов вместе;
- сумма этих продуктов.

- Чтобы взять скалярное произведение функций,
- возьмем комплексно-сопряженную первую функцию;
- умножить две функции;
- интегрировать функцию продукта.
- Чтобы найти длину вектора, возьмем внутреннее произведение вектора с самим собой, а затем квадратный корень.
- Чтобы найти норму функции, возьмите внутренний продукт функции с самим собой, а затем квадратный корень.
- Пара векторов или пара функций ортогональны, если их внутренний продукт равен нулю.
- Набор векторов образует ортонормированный набор, если каждый ортогонален всем остальным, и каждый имеет единичную длину.
- Набор функций образует ортонормированный набор, если каждая из них ортогонален всем остальным, и каждый имеет единичную норму.
2.
 3 Контрольные вопросы
3 Контрольные вопросы - 1.
Найдите следующее внутреннее произведение двух векторов:
Раствор точка-а
- 2.
Найдите длину вектора
Раствор точка-б
- 3.
Найдите скалярное произведение функций и на интервале 0 1.
Раствор точка-с
- 4.
Покажите, что функции и ортогональны на интервале 0 .
Раствор точка-d
- 5.
Убедитесь, что это не нормализованная функция на интервале 0 , и нормализуйте ее, разделив на ее норму.
Раствор dot-e
- 6.
Убедитесь, что наиболее общее кратное этому, нормализованному на интервале 0, равно , где любое произвольное действительное число.
 Итак, используя формулу Эйлера, нормализуются следующие кратные: , (для 0), , (для ) и , (для 2).
Итак, используя формулу Эйлера, нормализуются следующие кратные: , (для 0), , (для ) и , (для 2).Раствор точка-f
- 7.
Покажите, что функции и являются ортонормированным множеством на интервале 0 1.
Раствор dot-g
Далее: 2.4 Операторы Инженерный колледж FAMU-FSU Обработано с помощью l2h Векторный продукт: определение, формула и соотношение
Что такое умножение \(4\) на \(5\), это \(20\), легко.
 Умножать числа довольно легко, и каждый может это сделать, но что, если вас попросили умножить два вектора, \(\vec{a}=2\hat{i} + 3\hat{j}\) и \(\vec {b}=\шляпа{i} — 3\шляпа{k}\), ну не все так просто. Векторы — это очень отдельная сущность, классические правила числового умножения здесь малопригодны. Чтобы получить произведение двух или более векторов, нам нужно понять концепцию векторного произведения 9.0059 .
Умножать числа довольно легко, и каждый может это сделать, но что, если вас попросили умножить два вектора, \(\vec{a}=2\hat{i} + 3\hat{j}\) и \(\vec {b}=\шляпа{i} — 3\шляпа{k}\), ну не все так просто. Векторы — это очень отдельная сущность, классические правила числового умножения здесь малопригодны. Чтобы получить произведение двух или более векторов, нам нужно понять концепцию векторного произведения 9.0059 .Определение векторного произведения
На этом этапе обычное умножение двух чисел хорошо определено. Но умножить два вектора не так просто. Произведение двух векторов можно выполнить двумя разными способами; либо по скалярному произведению, либо по векторному произведению. Скалярное произведение двух векторов дает скалярную величину, как следует из названия. В то время как векторное произведение двух векторов дает вектор, поэтому оно и называется векторным произведением.
Векторное произведение двух векторов дает вектор, который находится в направлении, перпендикулярном плоскости, образованной двумя векторами.
 Величина результирующего вектора является произведением величин двух исходных векторов и синуса угла между их направлениями.
Величина результирующего вектора является произведением величин двух исходных векторов и синуса угла между их направлениями.Предположим, есть два вектора, которые образуют панель xy между собой. Векторное произведение этих векторов будет перпендикулярно плоскости xy, то есть оси z.
Векторный производный продукт
Пусть есть два вектора, \(\vec{A}\) и \(\vec{B}\), и \(\theta\) — угол между ними.
Векторное произведение между ними обозначается \(\vec{A}\times\vec{B}\) (‘\(\times\)’ не следует путать со знаком умножения, здесь оно обозначает векторное произведение ) из-за символа креста векторное произведение также известно как перекрестное произведение . Теперь, когда векторы и угол между ними установлены, давайте еще раз посмотрим на определение, но в математической манере:
Векторное произведение двух ненулевых векторов \(\vec{A}\) и \(\vec{B}\) равно \(\vec{A}\times\vec{B}=AB\ space sin\theta\space\hat{n}\), где \(A\) и \(B\) — величины векторов, а \(\theta\) — острый угол между двумя векторами.
 И \(\шляпа{n}\) представляет собой единичный вектор в направлении, перпендикулярном плоскости, образованной двумя векторами.
И \(\шляпа{n}\) представляет собой единичный вектор в направлении, перпендикулярном плоскости, образованной двумя векторами.Важно указать, что ни один из векторов не является нулевым вектором, т. е. нулевым вектором. В этом случае векторное произведение не имеет геометрического значения. В результате векторного произведения получается вектор, имеющий величину \(AB\space sin\theta\) и указывающий в направлении, которое перпендикулярно плоскости, образованной двумя векторами, то есть перпендикулярно обоим векторам одновременно.
Чтобы продемонстрировать, как это выглядит, рассмотрите диаграмму ниже:
Два вектора A и B образуют другой вектор как их векторное произведение, StudySmarter Originals
Предположим, что векторы ориентированы таким образом, что они лежат в плоскости xy, т.е. z-компонента векторов равна 0. Если мы возьмем векторное произведение, его можно представить как поворот винта в направлении \(\vec{A}\) к \(\vec{B}\), что равно направление против часовой стрелки.
 Направление, в котором будет двигаться винт, — вертикально вверх, т. Е. Положительная ось z. Вертикальная стрелка — это в точности вектор, образованный их векторным произведением. На приведенной выше диаграмме \(\vec{A}\) и \(\vec{B}\) имеют одну и ту же начальную точку, но это не обязательно. На самом деле это могут быть любые два вектора, здесь они показаны только для наглядного представления концепции.
Направление, в котором будет двигаться винт, — вертикально вверх, т. Е. Положительная ось z. Вертикальная стрелка — это в точности вектор, образованный их векторным произведением. На приведенной выше диаграмме \(\vec{A}\) и \(\vec{B}\) имеют одну и ту же начальную точку, но это не обязательно. На самом деле это могут быть любые два вектора, здесь они показаны только для наглядного представления концепции.Обозначим полученный вектор как \(\vec{C}\), тогда по определению:
$$\vec{C}=AB\space sin\theta\space\hat{n}$$
, а величина определяется простым взятием абсолютного значения с обеих сторон,
$$|\vec{C}|=AB\space sin\theta$$
Величина единичного вектора становится \(1\ ), и все, что у нас осталось, это \(AB\space sin\theta\). Помните, что \(|\vec{C}|=C\), это просто вопрос удобства, какое обозначение предпочитается (то же самое касается \(\vec{A}\) и \(\vec{B} \) или любой другой вектор).
Чтобы визуализировать направление, в котором будет указывать результирующий вектор, очень полезно правило правого винта.
 Просто поверните пальцы в направлении вектора вращения и наблюдайте за направлением большого пальца. Поверните пальцы от \(\vec{A}\) к \(\vec{B}\), и направление большого пальца задает направление результирующего вектора.
Просто поверните пальцы в направлении вектора вращения и наблюдайте за направлением большого пальца. Поверните пальцы от \(\vec{A}\) к \(\vec{B}\), и направление большого пальца задает направление результирующего вектора.Компонентная форма векторного произведения
До сих пор вы знали, что геометрически означает векторное произведение. Теперь мы рассмотрим его алгебраическую форму более подробно. Чтобы обобщить векторное произведение:
Пусть A вектор такой, что \(\vec{A}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\), где \ (a_{1},a_{2} \space и \space a_{3}\) являются вещественными константами, такими, что они не являются одновременно \(0\) (иначе это был бы нулевой вектор) и \(\ vec{B}=b_{1}\шляпа{i}+b_{2}\шляпа{j}+b_{3}\шляпа{k}\) , где \(b_{1},b_{2} \ space и \space b_{3}\) являются вещественными константами и снова не являются одновременно \(0\). Здесь \(\hat{i}, \hat{j} \space и \space \hat{k}\) представляют единичные векторы по оси x, оси y и оси z соответственно.
 {o}=\vec{0}$$ 9{o}=0\), а величина всех единичных векторов равна \(1\). Точно так же \(\hat{j}\times\hat{j}=\vec{0}\) и \(\hat{k}\times\hat{k}=\vec{0}\), где \( \vec{0}\) представляет нулевой вектор. Вычисление других соотношений, например,
{o}=\vec{0}$$ 9{o}=0\), а величина всех единичных векторов равна \(1\). Точно так же \(\hat{j}\times\hat{j}=\vec{0}\) и \(\hat{k}\times\hat{k}=\vec{0}\), где \( \vec{0}\) представляет нулевой вектор. Вычисление других соотношений, например,$$\шляпа{i}\times\шляпа{j}=sin\left(\frac{\pi}{2}\right)\шляпа{k}=\шляпа{ k}$$
Поскольку угол между единичным вектором вдоль оси x и единичным вектором вдоль оси y равен \(\frac{\pi}{2}\) радианам, что дает синусоидальное значение \ (1\). Точно так же мы можем вычислить другие сущности, а именно:
$$\шляпа{j}\times\шляпа{i}=-\шляпа{k}, \пробел \шляпа{i}\times\шляпа{k}=-\шляпа{j}, \пробел \шляпа {k}\times\hat{i}=\hat{j}, \space \hat{j}\times\hat{k}=\hat{i} \space and \space \hat{k}\times\ hat{j}=-\hat{i}$$
Теперь, используя приведенные выше объекты для единичных векторов, мы можем вычислить \(\vec{A} \times \vec{B}\) следующим образом:
$ $\vec{A}\times\vec{B}=(a_{1}\шляпа{i}+a_{2}\шляпа{j}+a_{3}\шляпа{k})\times(b_{ 1}\шляпа{i}+b_{2}\шляпа{j}+b_{3}\шляпа{k})$$
$$\vec{A}\times\vec{B}=(a_{ 2}b_{3}-b_{2}a_{3})\шляпа{i}-(a_{1}b_{3}-a_{3}b_{1})\шляпа{j}+(a_{ 1}b_{2}-a_{2}b_{1})\шляпа{k}$$
Перекрестные произведения, которые привели к нулевому вектору, исключаются, и все, что у нас остается, это приведенное выше уравнение.
 Приведенное выше уравнение иногда может быть немного утомительным для запоминания и не очень удобным для записи. В результате приведенное выше уравнение часто представляется определителем \(3\) на \(3\), который равен:
Приведенное выше уравнение иногда может быть немного утомительным для запоминания и не очень удобным для записи. В результате приведенное выше уравнение часто представляется определителем \(3\) на \(3\), который равен:$$\vec{A}\times\vec{B}=\begin{vmatrix} \шляпа{i} & \шляпа{j} & \шляпа{k} \\ a_{1} & a_{2} & a_{3} \\b_{1} & b_{2} & b_{3} \ end{vmatrix}$$
, что в конечном итоге соответствует уравнению, полученному ранее. Но определитель относительно легко запомнить. Для словесного выражения элементов определителя первая строка состоит из единичных векторов, вторая и третья строки — из скалярных компонент векторов. Давайте рассмотрим пример, чтобы получить представление о вычислении таких определителей, в конечном счете, векторного произведения.
Тройное произведение векторов
Произведение векторов не ограничивается двумя векторами, но также может быть расширено до трех различных векторов. Пусть есть три ненулевых вектора \(\vec{A}, \space \vec{B} \space и \space \vec{C}\) и мы хотим вычислить векторное тройное произведение между ними: \(\ vec{A} \times (\vec{B} \times \vec{C})\), где порядок векторного произведения очень важен, так как \(\vec{A} \times (\vec{B} \times \vec{C}) \neq (\vec{A} \times \vec{B}) \times \vec{C}\) т.
 е. векторное тройное произведение не является ассоциативным. По сути, существует два способа вычисления векторного тройного произведения: во-первых, вычисление векторного произведения \(\vec{A}\) и \(\vec{B}\), а затем выполнение его векторного произведения с \( \vec{С}\). Это включает в себя выполнение двух векторных продуктов, одного за другим.
е. векторное тройное произведение не является ассоциативным. По сути, существует два способа вычисления векторного тройного произведения: во-первых, вычисление векторного произведения \(\vec{A}\) и \(\vec{B}\), а затем выполнение его векторного произведения с \( \vec{С}\). Это включает в себя выполнение двух векторных продуктов, одного за другим.Другой способ расчета векторного произведения — скалярное произведение:
$$ (\vec{A} \times \vec{B}) \times \vec{C}=(\vec{A} \cdot \ vec{C}) \vec{B}-(\vec{B} \cdot \vec{C}) \vec{A} $$
Как видно, эта формула включает скалярное произведение \(\ vec{A}\) с \(\vec{C}\), а затем \(\vec{B}\) с \(\vec{C}\). На практике оба вышеуказанных способа одинаково удобны.
Для векторов: \(\vec{a}=\hat{i}+\hat{j}+\hat{k}\), \(\vec{b}=2 \hat{i}-\ hat{k}\) и \(\vec{c}=\hat{j}-\hat{k}\), найдите векторное тройное произведение: \((\vec{a} \times \vec{b} ) \times \vec{c}\)
Решение:
Мы будем использовать следующую формулу
$$ (\vec{a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec {c}) \vec{b}-(\vec{b} \cdot \vec{c}) \vec{a} $$
Шаг 1: Оценка \(\vec{a} \cdot \vec {c}\) :
$$ \begin{aligned} \vec{a} \cdot \vec{c} &=(\hat{i}+\hat{j}+\hat{k}) \cdot (\шляпа{j}-\шляпа{к}) \\ &=0+1-1 \\ \поэтому \vec{a} \cdot \vec{c} &=0 \end{aligned} $$
Шаг 2: Оценка \(\vec{b} \cdot \vec{c}\) :
$$ \begin{выровнено} \vec{b} \cdot \vec{c} &=(2 \шляпа{i}-\шляпа{k}) \cdot(\шляпа{j}-\шляпа{k}) \\ &=0+0+1 \\ &=1 \end{выровнено} $$
Шаг 3: Замена \(\vec{a} \cdot \vec{c}\) и \(\vec{b} \cdot \vec{c}\) в \((\vec {a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{b} \cdot \vec{ c}) \vec{a}\):
$$ \begin{aligned} (\vec{a} \times \vec{b}) \times \vec{c} &=0-(1) \vec {a} \\ &=-\шляпа{i}-\шляпа{j}-\шляпа{k} \end{aligned} $$
Следовательно, \((\vec{a} \times \vec{b}) \times \vec{c}=-\hat{i}-\hat{j}-\hat{k}\)
Связь между векторным произведением и скалярным произведением
Хотя векторное произведение и скалярное произведение сильно различаются по геометрическому применению и их значению, мы все же можем связать их определенным образом.
 {2}\theta$$ 9{2}\) для векторов \(\vec{p}=2 \hat{i}-\hat{k}\) и \(\vec{q}=\hat{j}+\hat{k} \).
{2}\theta$$ 9{2}\) для векторов \(\vec{p}=2 \hat{i}-\hat{k}\) и \(\vec{q}=\hat{j}+\hat{k} \).Решение:
Шаг 1:
Сначала оценим \(\vec{p} \cdot \vec{q}\):
$$ \begin{aligned} \vec{p} \cdot \vec{q} &=(2 \шляпа{i}-\шляпа{k}) \cdot(\шляпа{j}+\шляпа{k}) \\ &=0+0-1 \\ \ поэтому \vec{p} \cdot \vec{q} &=1 \end{aligned} $$
Шаг 2:
Вычислить \(\vec{p} \times \vec{q}\) :
$$ \begin{aligned} \vec{p} \times \vec{q} &=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k } \\ 2 & 0 & -1 \\ 0 & 1 & 1 \end{массив}\right| \\ \поэтому \vec{p} \times \vec{q} &=\hat{i}(0+1)-\hat{j}(2+0)+\hat{k}(2-0) \\ \поэтому \vec{p} \times \vec{q} &=\hat{i}-2 \hat{j}+2 \hat{k} \end{aligned} $$ 9{2}\), мы уже вычислили его в шаге 3 :
$$ \text { RHS }=10 $$
Легко видеть, что
$$ \text{LHS}= \text {RHS} $$
Таким образом, личность подтверждена.
Векторное скалярное произведение
Векторное скалярное произведение, , также известное как Скалярное произведение, — это еще один способ умножения двух векторов помимо векторного произведения.
 Альтернативное, но одинаково используемое название для . Точечный продукт — 9.0058 Скалярное произведение.
Альтернативное, но одинаково используемое название для . Точечный продукт — 9.0058 Скалярное произведение. Скалярное произведение двух векторов дает скалярную величину, а не другой вектор. Основная причина существования скалярного произведения заключается в том, чтобы измерить величину вектора вдоль направления другого вектора.
Пусть \(\vec{a}\) и \(\vec{b}\) — два ненулевых вектора, образующих между собой острый угол \(\theta\). Формула для скалярного произведения дается следующим образом:
$$\vec{a} \cdot \vec{b}=ab \space cos\theta$$
9{2}}) \space cos(\pi/6)$$$$\vec{p} \cdot \vec{q}=(5)(10) \space \left( \frac{1}{ 2} \right)$$
$$\vec{p} \cdot \vec{q}=25$$
Следовательно, скалярное произведение двух векторов \(\vec{p}=4\hat{ i}+3\hat{j}\) и \(\vec{p}=6\hat{i}-8\hat{j}\) равно \(25\) единицам.
Примеры произведения векторов
Вычисление векторного произведения векторов \(\vec{C}=2\hat{i}+3\hat{j}-\hat{k}\) и \(\vec{D }=-\шляпа{i}+2\шляпа{k}\).

Решение:
Поместив единичные векторы и компоненты в детерминантную форму, как упоминалось ранее, мы получим
$$\vec{C}\times\vec{D}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & -1 \\- 1 & 0 & 2 \end{vmatrix}$$
Раскладывая определитель, получаем
$$\vec{C} \times \vec{D}=6\hat{i}-3\hat{j }+3\hat{k}$$
, который является результирующим вектором, полученным векторным произведением \(\vec{C}\) и \(\vec{D}\).
Для двух векторов \(\vec{p}=\hat{i}-2\hat{j}\) и \(\vec{q}=-2\hat{i}+\lambda\hat{j }\) такие, что их векторное произведение равно \(\vec{p} \times \vec{q}=2\hat{k}\). Вычислите значение \(\лямбда\).
Решение:
Используя полученную ранее формулу для вычисления векторного произведения двух векторов, мы имеем
$$\vec{p} \times \vec{q}=\lambda\hat{k}- 4\hat{k}=(\lambda-4)\hat{k}$$
Но также известно, что векторное произведение равно \(\vec{p} \times \vec{q}=2\hat {k}\), поэтому, сравнивая коэффициент единичного вектора, мы получаем
$$\lambda-4=2$$
, что дает \(\lambda=6\).

Продукт Vector — ключевые блюда на вынос
- Векторное произведение двух векторов — это вектор, указывающий в направлении, перпендикулярном плоскости, образованной двумя векторами.
- Для любых двух ненулевых векторов \(\vec{x}\) и \(\vec{y}\), образующих между собой острый угол \(\theta\), их векторное произведение равно \( |\vec{x} \times \vec{y}|=xy \space sin\theta \space \hat{n}\).
- Направление результирующего вектора можно определить с помощью правила правого винта, где пальцы указывают направление векторов, а большой палец указывает на результирующий вектор. 9{2}\).
Определение, формула, свойства, приложения и многое другое
Операции, которые можно выполнять с векторами, включают сложение и умножение. Умножение векторов может быть выполнено двумя способами: точечным произведением и перекрестным произведением. Скалярное произведение двух векторов составляется путем выбора компонентов вектора в направлении другого и умножения его на величину другого вектора.

Любая физическая величина, которая имеет как величину, так и направление, считается векторной величиной. В этой статье мы постараемся узнать об определении скалярного произведения с примерами, формулами, скалярным произведением двух векторов и многим другим. Давайте узнаем об основах вектора, прежде чем перейти к скалярному произведению векторов и его примерам.
Кроме того, здесь можно узнать о векторной алгебре.
Что такое скалярный продукт?Скалярное произведение — это один из способов умножения двух или более заданных векторов. Конечным результатом скалярного произведения векторов является скалярная величина. Следовательно, скалярное произведение также идентифицируется как скалярное произведение. Алгебраически это сумма произведений одинаковых записей двух строк чисел.
Геометрически векторное скалярное произведение определяется как произведение евклидовой величины двух векторов и косинуса угла, соединяющего их. Скалярное произведение векторов находит различные применения в геометрии, технике, механике и астрономии.
Формула скалярного произведения Оба определения аналогичны при работе с декартовыми координатами.
Оба определения аналогичны при работе с декартовыми координатами.Результирующая скалярного произведения двух векторов лежит в соответствующей плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом. Рассмотрим два вектора ‘x’ и ‘y’, тогда скалярное произведение двух векторов можно представить следующим образом:
\(\vec{x\ }.\vec{y}=\left|\vec{x}\right |\times\left|\vec{y}\right|\cos\theta\)
Что такое скалярное произведение двух векторов?
Здесь;
\(\left|\vec{x}\right| \text{ обозначают величину вектора } \vec{x}\text{ и }\left|\vec{y}\right| \text{ обозначают величина вектора} \vec{y}\ \text{ соответственно }\).
Также
\(\theta\text{ угол между векторами}\vec{x}\text{ и }\vec{y}\).Мы применяем векторы, которые нам нужны для представления координат в трехмерном пространстве или, чаще, для адресации списка чего-либо.
 Скалярное произведение двух векторов эквивалентно произведению величин двух векторов вместе с косинусом угла между двумя векторами.
Скалярное произведение двух векторов эквивалентно произведению величин двух векторов вместе с косинусом угла между двумя векторами.Узнайте больше о высоте и расстоянии в этой статье.
Термины, относящиеся к скалярному произведениюДавайте теперь разберемся с такими терминами, как величина двух векторов, угол между двумя векторами и проекция одного вектора на другой вектор, чтобы более точно понять формулу скалярного произведения двух векторов.
Величина вектораВектор описывает направление и величину. Величина данного вектора представляет собой квадратный корень из суммы квадратов конкретных элементов данного вектора. Величина вектора является положительной величиной. 9{2}}\).
Узнайте больше о наборах здесь.
Проекция вектораСкалярное произведение полезно для определения компонента одного вектора в направлении другого вектора. Проекция вектора одного вектора на другой вектор — это ширина тени представленного вектора на другой вектор.

Это достигается путем умножения величины представленных векторов на косеканс угла между двумя векторами. Конечным результатом формулы векторной проекции является скалярное значение.
Рассмотрим \(OA=\vec{p},OB=\vec{q}\), — два вектора, а θ — угол между \(\vec{p}\text{ и }\vec{ д}\). Нарисуйте линию AL, перпендикулярную OB.
Из прямоугольного треугольника OAL можно сказать, что:
\(\cosθ=\frac{OL}{OA}\).
\(OL=OA\cosθ=\left|\vec{p}\right|\cosθ\).
OL указывает на векторную проекцию a на b.
\(\vec{p}.\vec{q}=\left|\vec{p}\right|\left|\vec{q}\right|\cos\theta=\left|\vec{q }\право|ПР\).
\(=\left|\vec{q}\right|\left(\text{Проекция }\vec{p}\text{ на }\vec{q}\right)\).
Следовательно, проекция \(\text{проекция }\vec{p}\text{ на }\vec{q}=\frac{\vec{p}.\vec{q}}{\left|\ vec{q}\right|}\).
Аналогично, векторная проекция \(\vec{q}\text{ на }\vec{p}=\frac{\vec{p}.\vec{q}}{\left|\vec{p} \право|}\).
Прочтите эту статью о детерминантах.
Угол между двумя векторами с использованием скалярного произведения
Угол между двумя векторами вычисляется как косинус угла, соединяющего два вектора. Косинус угла между двумя векторами идентичен сумме произведения конкретных компонентов двух векторов, деленному на произведение величины двух векторов. Формула для угла между двумя векторами выглядит следующим образом. 9T}=\begin{bmatrix}A_1&A_2&A_3\end{bmatrix}\).
\(\begin{bmatrix}A_1&A_2&A_3\end{bmatrix}\begin{bmatrix}B_1\\
B_2\\
B_3\end{bmatrix}=A_1B_1+A_2B_2+A_3B_3=\vec{A}.\vec{ B}\)Матрица-строка и матрица-столбец перемножаются для получения суммы произведения соответствующих элементов двух векторов.
Прочтите эту статью об отношениях и функциях.
Как найти точечный продукт?Определение скалярного произведения можно представить двумя способами: алгебраическим и геометрическим. Хотя скалярное произведение двух векторов является произведением величины данных двух векторов и cos угла между ними.

Напомним, что векторы умножаются двумя способами:
- скалярное произведение векторов, также известное как скалярное произведение.
- векторное произведение векторов, также известное как векторное произведение.
Контраст между обоими методами заключается в том, что при использовании первого метода, то есть скалярного произведения, мы получаем скалярное значение в качестве результата, а при применении второго метода (перекрестного произведения) полученное значение снова является вектором по своей природе.
Давайте узнаем больше о формуле скалярного произведения векторов на примерах:
Если два вектора представлены в виде единичных векторов i, j, k вдоль осей x, y, z, то скалярное произведение берется следующим образом:
\(\text{ If } \vec{ x}=x_1\шляпа{i}+x_2\шляпа{j}+x_3\шляпа{k} \text{ и }\vec{y}=y_1\шляпа{i}+y_2\шляпа{j}+y_3\ шляпа {k}\ затем\)
\(\vec{x}.\vec{y}=\left(x_1\hat{i}+x_2\hat{j}+x_3\hat{k}\right) .\left(y_1\шляпа{i}+y_2\шляпа{j}+y_3\шляпа{k}\ \right)\)
\(\vec{x}.
 \ \vec{y}=x_1y_1+\ x_2y_2 +x_3y_3\)
\ \vec{y}=x_1y_1+\ x_2y_2 +x_3y_3\)Также читайте о статистике в этой статье.
Свойства скалярного произведенияНекоторые из важных свойств скалярного произведения векторов: коммутативность, ассоциативность, дистрибутивность и некоторые другие свойства скалярного произведения.
- Скалярное произведение коммутативно .
- Если \(\vec{x}\) и \(\vec{y}\) два ненулевых вектора, то:
- \(\vec{x} .\vec{y}=\vec{y }.\vec{x}\)
- Скалярное произведение ассоциативно относительно скалярного умножения:
- Если \(\vec{x}\) и \(\vec{y}\) любые два ненулевых вектора и λ является скаляром, то
- \(\vec{x}.\lambda\vec {y}=\lambda\left(\vec{x}.\vec{y}\right)\)
- Скалярное произведение является дистрибутивом относительно сложения векторов.
- Если \(\vec{x}\), \(\vec{y}\) и \(\vec{z}\) — любые три ненулевых вектора, то
- \(\vec{x }.
 \left(\vec{y}+\vec{z}\right)=\left(\vec{x} .\vec{y}\right)+\left(\vec{x}\ .\vec {z}\right)\)
\left(\vec{y}+\vec{z}\right)=\left(\vec{x} .\vec{y}\right)+\left(\vec{x}\ .\vec {z}\right)\) - \(\left(\vec{x}+\vec{y}\right).\vec{z}=\left(\vec{x}.\vec{z} \right)+\left(\vec{y}\ .\vec{z}\right)\)
- Скалярное произведение единичных векторов: скалярное произведение единичного вектора указано ниже.
- \(\шляпа{i}.\шляпа{i}=\шляпа{j}.\шляпа{j}=\шляпа{k}.\шляпа{k}=1\ \text{ и }\ \шляпа {i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
- Угол между одинаковыми векторами равен нулю градусов , и, следовательно, их скалярное произведение равно единице. При этом угол между двумя перпендикулярными векторами равен 90 градусов, а их скалярное произведение равно нулю.
- \(\text{Если } \theta=90 \text{ тогда }\ x_1y_1+\ x_2y_2+x_3y_3=0\text{ то есть} \vec{x}\text{ равно }\perp \text{ to } \ век{у}\) 92\)
- Умножение двух векторов.
- \(\text{ Если }\ \vec{x}=x_1\hat{i}+x_2\hat{j}+x_3\hat{k}\ \\text{ и }\ \vec{y}= y_1\шляпа{i}+y_2\шляпа{j}+y_3\шляпа{k}\ \\text{затем }\)
- \(\vec{x}.
 \vec{y}=x_1y_1+\ x_2y_2+x_3y_3 \)
\vec{y}=x_1y_1+\ x_2y_2+x_3y_3 \)
Другие темы по математике смотрите здесь.
Применение скалярного произведенияСкалярное произведение — это фундаментальный подход, с помощью которого мы можем соединить два вектора. Интуитивно это говорит нам что-то о том, насколько два заданных вектора указывают в соответствующем направлении.
- Использование скалярного произведения является оценкой проделанной работы. Произведение приложенной силы на перемещение называется работой. Если сила приложена под углом θ к смещению, проделанная работа рассчитывается как скалярное произведение силы и смещения по следующей формуле:
\(W=fd\cosθ\).
Скалярное произведение также используется для проверки того, являются ли два вектора ортогональными или нет. - \(\vec{p}.\vec{q}=\left|\vec{p}\right|\left|\vec{q}\right|\cos\theta=\left|\vec{p }\право|\лево|\vec{q}\право|\cos9{\circ}=\vec{p}.\vec{q}=0\)
- Скалярное произведение\скалярное произведение является шлюзом для умножения двух векторов.
 Геометрически скалярное произведение определяется как произведение длины векторов на угол косинуса между ними и определяется формулой:
Геометрически скалярное произведение определяется как произведение длины векторов на угол косинуса между ними и определяется формулой: - \(\vec{x\ }.\vec{y}=\left|\ vec{x}\right|\times\left|\vec{y}\right|\cos\theta\)
- Это скалярная величина, не имеющая направления. Его легко вычислить из суммы произведения элементов двух векторов.
- Скалярное произведение дополнительно помогает в измерении угла, создаваемого комбинацией векторов, а также помогает в определении положения вектора относительно оси координат.
- В трехмерном пространстве векторные операции используются для создания уравнений для представления линий, плоскостей и сфер.
Ознакомьтесь с примерами скалярного произведения двух векторов, чтобы узнать больше о том, как решать такие вопросы:
Пример 1: Если \(\vec{a}\) и \(\vec{b}\) являются двумя ненулевыми векторами и их скалярное произведение равно 0, то они:
- Под определенным углом
- Ни один из этих
Решение:
Скалярное произведение двух векторов \(=\vec{a}\cdot\vec{b}=\left|\vec{a}\ right|\cdot\left|\vec{b}\right|\cosα\)
Если \(\vec{a}\) и \(\vec{b}\) ненулевые векторы, если скалярное произведение быть 0 тогда. 9{\circ}\)
9{\circ}\)
Отсюда следует \(\vec{a}\perp \vec{b}\).
Пример 2: Две смежные стороны параллелограмма равны \(2\hat{i}-4\hat{j}+5\hat{k}\text{ и }\hat{i}-2\hat {j}-3\шляпа{к}\). Какова величина скалярного произведения векторов, представляющих его диагонали?
Расчет:
Здесь вектора a и b — смежные стороны параллелограмма
\(a=2\hat{i}-4\hat{j}+5\hat{k}\text{ и }b=\шляпа{i}-2\шляпа{j}-3\шляпа{k}\).
Пусть векторы c и d являются диагоналями параллелограмма.
Используя закон параллелограмма,
\(\vec{c}=\vec{a}+\vec{b}\).
\(=\влево(2\шляпа{i}-4\шляпа{j}+5\шляпа{k}\право)\ +\влево(\шляпа{i}-2\шляпа{j}-3 \шляпа{к}\право)\)
\(=3\шляпа{i}-6\шляпа{j}+2\шляпа{к}\)
Теперь с использованием закона треугольника,
\(\vec {a}=\vec{b}+\vec{d}\).
\(\vec{d}=\vec{a}-\vec{b}\)
\(=\left(2\hat{i}-4\hat{j}+5\hat{k }\справа)\-\слева(\шляпа{i}-2\шляпа{j}-3\шляпа{k}\справа)\).
\(=\шляпа{i}-\шляпа{2j}+8\шляпа{k}\)
\(\vec{c}.\vec{d}=\left(3\шляпа{i} -6\шляпа{j}+2\шляпа{k}\право).\влево(\шляпа{i}-2\шляпа{j}+8\шляпа{k}\право)\)
\(\ vec{c}.\vec{d}=3+12+16=31\)
Пример 3: Два вектора \(\vec{A}\text{ и }\vec{B}\) перпендикулярны относительно друг друга, и каждый имеет величину a. Тогда их скалярное произведение?
Решение:
КОНЦЕПЦИЯ:
Скалярное произведение или скаляр двух векторов задается как:
\(D=\vec{A}.\vec{B}=\left|\vec{A} \right|\times\left|\vec{B}\right|\cos\theta\) 9{\circ}=0\)
Следовательно, для двух векторов \(\vec{A}\text{ и }\vec{B}\), которые перпендикулярны друг другу и каждый из которых имеет величину a, скалярное произведение равно нулю .
Пример 4: Два вектора \(\vec{A}\text{ и }\vec{B}\) перпендикулярны друг другу. Тогда их перекрестный продукт?
Решение:
ПОНЯТИЕ:
Перекрестное произведение или вектор; произведение двух векторов задается как:
\(C=\vec{A}\times\vec{B}=\left|\ vec{A}\right|. \left|\vec{B}\right|\sin\theta\) 9{\circ}=\left|\vec{A}\right|.\left|\vec{B}\right|\)
\left|\vec{B}\right|\sin\theta\) 9{\circ}=\left|\vec{A}\right|.\left|\vec{B}\right|\)
Следовательно, для двух векторов \(\vec{A}\text{ и }\ vec{B}\), которые перпендикулярны друг другу, векторное произведение или векторное произведение двух векторов задается как: \(\left|\vec{A}\right|.\left|\vec{B}\right |\).
Мы надеемся, что приведенная выше статья о скалярном произведении поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о точечном продуктеВ.1 Что такое точечный продукт?
Ответ 1 Скалярное произведение — это один из способов умножения двух или более заданных векторов. Конечным результатом скалярного произведения векторов является скалярная величина. Следовательно, скалярное произведение также идентифицируется как скалярное произведение. Алгебраически это сумма произведений одинаковых записей двух строк чисел.
Следовательно, скалярное произведение также идентифицируется как скалярное произведение. Алгебраически это сумма произведений одинаковых записей двух строк чисел.
Q.2 Каковы типы векторов?
Ответ 2 Различные типы векторов: нулевой вектор, единичный вектор, вектор положения, ко-начальный вектор, похожие и разные векторы, копланарный вектор, коллинеарный вектор, равный вектор, вектор смещения и отрицательные векторы.
Q.3 В чем разница между вектором и единичным вектором?
Ответ 3 Любая физическая величина, которая имеет как величину, так и направление, называется векторной величиной. Принимая во внимание, что вектор, который имеет величину один, называется единичным вектором.
Q.4 Как найти скалярное произведение двух векторов?
Ответ 4 Определение скалярного произведения может быть представлено двумя способами, т. е. алгебраическим и геометрическим. Хотя скалярное произведение двух векторов является произведением величины данных двух векторов и cos угла между ними.
Хотя скалярное произведение двух векторов является произведением величины данных двух векторов и cos угла между ними.
В.5 Что представляет собой скалярное произведение?
Ответ 5 Скалярное произведение показывает, какая часть вектора силы приложена в направлении предполагаемого вектора. Скалярное произведение также может помочь нам оценить угол, образуемый парой векторов, и статус вектора, соответствующего осям координат.
Q.6 Является ли скалярное произведение проекцией?
Ответ 6 Скалярное произведение — это просто проекция одного вектора на другой, умноженная на величину другого вектора. Скалярное произведение говорит нам, на сколько один вектор перемещается в направлении другого.
В.7 Почему используется скалярное произведение?
Ответ 7 Скалярное произведение векторов позволяет оценить работу, когда вектор силы и вектор движения имеют разные направления. Скалярное произведение дополнительно помогает в измерении угла, создаваемого комбинацией векторов, а также помогает в нахождении положения вектора относительно оси координат.
Скалярное произведение дополнительно помогает в измерении угла, создаваемого комбинацией векторов, а также помогает в нахождении положения вектора относительно оси координат.
В.8 Что означает, что скалярное произведение равно 1?
Ответ 8 Если скалярное произведение двух векторов приближается к единице, это означает, что векторы находятся в одном направлении.
В.9 Что означает, что скалярное произведение равно 0?
Ответ 9 Скалярное произведение или внутреннее произведение векторов представляет собой сумму произведений соответствующих компонентов. Если скалярное произведение между двумя векторами равно нулю, то данные векторы ортогональны.
Q.10 Каковы свойства скалярных произведений?
Ответ 10 Ниже перечислены некоторые важные свойства скалярных произведений: Скалярное произведение коммутативно. Скалярное произведение ассоциативно относительно скалярного умножения. Скалярное произведение является дистрибутивным относительно сложения векторов.
Скалярное произведение является дистрибутивным относительно сложения векторов.
| Рефлексивное отношение: значение, формула, примеры и основные выводы |
| Типы матриц: определение, различные типы матриц с примерами и сводной таблицей |
| Алкены: формула, структура, типы, получение, свойства, использование алкенов с примерами |
| Теорема Байеса: Изучите определение, связанные термины, формулу, доказательство и применение здесь! |
Наглядное введение в скалярный продукт | Робин Линдерборг
Говорят, что лучший способ учиться — это учить, так что здесь я попытаюсь объяснить некоторые основы, касающиеся векторов и скалярного произведения.
Под вектором , мы подразумеваем просто список чисел. Например, v = [1, 3]. Этот конкретный вектор и состоит из двух чисел, но вектор может содержать любое количество ну… чисел.
Мы говорим, что v есть вектор в двумерном пространстве. У этого пространства есть замечательное свойство, заключающееся в том, что мы можем легко изобразить его на плоской поверхности. Вот что v выглядит так.
Вектор [1, 3] расположен на 1 единицу вправо и на 3 единицы вверх.Давайте добавим еще один вектор u = [2, 2] .
Так же, как и с обычными числами, мы можем выполнять обычные алгебраические операции над нашими двумя векторами. Сложение и вычитание векторов просто означает сложение и вычитание их отдельных компонентов, в результате чего получается новый вектор той же формы, что и исходные.
Итак, дано v=[3,1] и u=[2,2] , вычитаем следующим образом: v-u=[3–2,1–2]=[1,-1] . Эквивалентно добавление векторов дает новый вектор [5,3] .
Вычитание вектора u из вектора v (слева) и их сложение (справа). Обратите внимание, что вычитание одного вектора из другого дает вектор, соединяющий два исходных вектора, если результирующий вектор рисуется из конечной точки одного из них.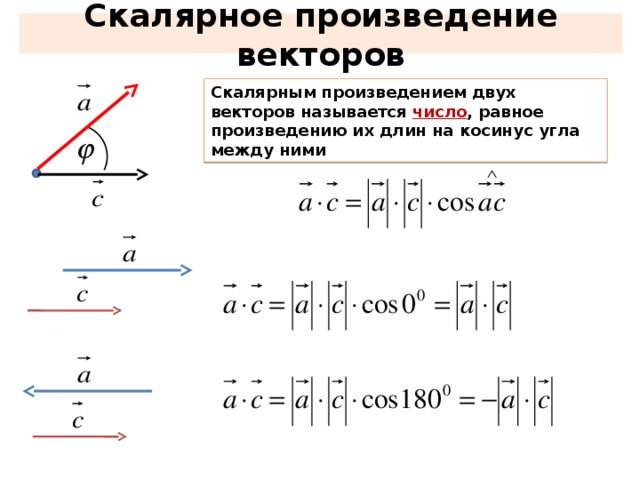 Возможно, это проще проиллюстрировать на другом графике.
Возможно, это проще проиллюстрировать на другом графике.
Это все хорошо, но как насчет того, чтобы их перемножить? Что ж, как оказалось, на самом деле существует несколько способов умножения векторов. Вы можете умножать компоненты так же, как мы добавляли и вычитали их выше. Но мы рассмотрим здесь гораздо более интересную операцию. Тот, который вообще не производит вектор, а именно скалярное произведение .
Вычисление скалярного произведения двух векторов фактически включает две операции: умножение и сложение. Начнем с поэлементного умножения компонент векторов, т.е. [1,3]*[2,2]=[2,6] . Затем мы складываем компоненты результирующего вектора вместе, чтобы получить одно число, то есть 2+6=8 . Вуаля!
Таким образом, скалярное произведение на и на равно 8. Отлично! Но зачем нам это? Скалярное произведение, при всей его простоте, на самом деле раскрывает довольно много полезной информации о взаимосвязи между двумя перемножаемыми векторами.
Скалярное произведение можно использовать для определения длины (также называемой размером или величиной) вектора. Длина вектора v обозначается |v| . И мы можем использовать скалярное произведение, чтобы получить наш ответ.
Помните теорему Пифагора, которая помогает нам найти длину гипотенузы в прямоугольном треугольнике, если мы знаем длины других сторон.
Теорема Пифагора.Теперь мы можем использовать эту теорему для определения длины нашего исходного вектора v=[1,3]. Поскольку v состоит из 1 шага в направлении x и 3 шагов в направлении y, мы можем составить прямоугольный треугольник из его компонентов и просто подставить значения в формулу. Вы только представьте v занимает место c на графике выше, b равно 1 и a равно 3. Таким образом,
означает, что длина v равна √10.
Вот интересная вещь: то, что мы только что сделали, было эквивалентно взятию скалярного произведения на самого себя. Мы умножили компоненты на сами на себя и сложили их, что и означает 3² + 1². Таким образом, длина вектора v — это просто квадратный корень из скалярного произведения между против и против .
Мы умножили компоненты на сами на себя и сложили их, что и означает 3² + 1². Таким образом, длина вектора v — это просто квадратный корень из скалярного произведения между против и против .
Возможно, вы еще не совсем убедились в полезности скалярного произведения. Вот еще одна интересная связь для вас. Если два вектора перпендикулярны (что в двумерном пространстве означает, что они образуют угол 90 градусов, но обобщаются на любое n -мерное пространство), их скалярное произведение всегда будет равно 0. Давайте копнем немного глубже и посмотрим, почему это так.
Теорема Пифагора на самом деле является частным случаем более общего правила, называемого закон косинусов. Последнее применимо к любому треугольнику, тогда как первое работает только с прямоугольными треугольниками. Он включает в себя третий член, который принимает во внимание угол между a и b .
Здесь cos θ относится к косинусу угла между a и b . Помните, что косинус угла равен 1, когда угол равен 90 градусов. Поскольку угол θ всегда равен 90° в прямоугольных треугольниках (это само определение прямоугольного треугольника), весь третий член в нашем уравнении равен 0, и мы остаемся с теоремой Пифагора.
Помните, что косинус угла равен 1, когда угол равен 90 градусов. Поскольку угол θ всегда равен 90° в прямоугольных треугольниках (это само определение прямоугольного треугольника), весь третий член в нашем уравнении равен 0, и мы остаемся с теоремой Пифагора.
Переведем закон косинусов в векторное представление. Мы начинаем с того, что рисуем то, с чем работаем.
Таким образом, в векторной записи закон косинусов переводится в следующее (это может выглядеть немного сложнее, но просто помните, что запись |x| относится к длине векторов, подобных сторонам треугольника) .
Из этой версии закона косинусов мы можем вывести более простое уравнение.
Шаг 1
Умножьте левую часть уравнения. И имейте в виду, что вектор, усеянный самой собой, — это длина вектора в степени 2.
Шаг 2
Отмените члены в левой и правой частях уравнения.
Итак, получается, что скалярное произведение двух векторов равно произведению их соответствующих длин на косинус угла, образованного между ними. А если угол равен 90 градусов, косинус равен 0, поэтому все выражение оценивается как 0.
А если угол равен 90 градусов, косинус равен 0, поэтому все выражение оценивается как 0.
Отлично!
Как написать скалярное произведение в LaTeX 2022
Как написать скалярное произведение в LaTeX
Джоанна В.
Последнее обновление:
Этот пост может содержать партнерские ссылки, которые позволяют нам получать комиссию бесплатно для вас. Узнать больше
Цель этой статьи показать вам простой способ создания символа точки в LaTeX .
В физике и математике большую часть времени при работе с векторами вам потребуется вычислить скалярное произведение двух векторов. Вот почему сегодня вы узнаете, как написать скалярное произведение в LaTeX 9.0046
Содержание
Скалярное произведение Начнем с двух векторов A и B . Скалярное произведение определяется как произведение двух заданных векторов, в результате которого получается положительное действительное число, также известное как скаляр. Это означает, что вы получаете число, а не вектор.
Это означает, что вы получаете число, а не вектор.
Скалярное произведение A и B представлено точечным символом между обоими векторами, например,
Символ точки умножения, одна точка Символ оператора точки в LaTeXЧтобы написать символ оператора точки, вам понадобится математический режим и одна простая команда, команда \cdot, и, как вы видите, она не требует аргументов. Поскольку команда уже находится в LaTeX, для нее не нужен дополнительный пакет.
Допустим, у нас есть векторы U и V, скалярное произведение будет
\documentclass{article}
\начать{документ}
$$\vec{U} \cdot \vec{V}$$
\конец{документ}
Вывод команды \cdotОдин вариант, который вам может понадобиться, это векторы с жирным шрифтом и стрелкой, опять же без пакетов.
\documentclass{статья}
\начать{документ}
$$\vec{\mathbf{U}} \cdot \vec{\mathbf{V}}$$
\конец{документ}
Жирные символы с символом скалярного произведения Скалярное произведение Угол/Вектор/Матричная форма Теперь скалярное произведение между двумя векторами может иметь 3 основных представления, каждое из которых может использоваться в зависимости от контекста, и их можно вставлять в Латекс. Ниже у вас будут примеры для каждого из них.
Ниже у вас будут примеры для каждого из них.
Первая форма ( Форма угла ) включает в себя угол тета между векторами, поэтому вам понадобится команда \theta и символ нормы вектора, все они должны быть в математическом режиме. Например, при заданных R и B скалярное произведение в угловой форме будет равно 9.0046
\begin{document}
$$\vec{R} \cdot \vec{B} = \Vert\vec{R}\Vert \Vert\vec{B}\Vert \cos(\theta)$$
\конец{документ}
Дает результат
Вторая форма ( Векторная форма ) чаще используется, когда вы знаете каждый компонент двух векторов одинакового размера. В физике довольно часто умножают два вектора, используя эту форму. Требуется математический режим.
\documentclass{статья}
\начать{документ}
$$\vec{a}=(x_{1}\шляпа{i}+y_{1}\шляпа{i}+z_{1}\шляпа{i})$$
$$\vec{b}=(x_{2}\шляпа{i}+y_{2}\шляпа{i}+z_{2}\шляпа{i})$$
\vspace{2pt}
$$\vec{a}\cdot\vec{b}=x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}$$
\конец{документ}
Выдает результат
Третья и последняя форма ( Матричная форма ) более распространена в линейной алгебре, когда вы работаете с векторами. Вам нужно будет использовать среду pmatrix (требуется математический режим), а также \\ и & для строк и столбцов, давайте посмотрим на пример
Вам нужно будет использовать среду pmatrix (требуется математический режим), а также \\ и & для строк и столбцов, давайте посмотрим на пример
\documentclass{article}
\usepackage{аммат}
\начать{документ}
Учитывая $\vec{R}$ и $\vec{B}$, скалярный продукт определяется как
$$\vec{R}\cdot\vec{B}=\begin{pmatrix} x_{1} & y_{1} & z_{1}
\end{pматрица}
\begin{pmatrix} x_{2}\\ y_{2}\\ z_{2} \end{pmatrix}$$
\конец{документ}
Мы используем & для определения позиции каждого нового столбца и \ \ для позиции каждой строки или строки. Единственное, на что следует обратить внимание, это необходимость пакета amsmath для среды pmatrix, но обычно у этого пакета нет проблем с совместимостью с другими пакетами. Приведенный выше код дает результат
. Результат будет представлен после умножения обеих матриц и сложения их значений. Тройное векторное произведение Имея три вектора A, B и C, вы можете выполнить так называемое тройное векторное произведение.





 Вектор FA обозначили вектором a, вектор ED обозначили вектором b. Выразите через векторы а и b векторы: ЕF, CD, AB, DA,OC.
Вектор FA обозначили вектором a, вектор ED обозначили вектором b. Выразите через векторы а и b векторы: ЕF, CD, AB, DA,OC.
 Предлагает рассмотреть свойства и найти сходство.
Предлагает рассмотреть свойства и найти сходство.



 α≈1,04\) рад; б. \(β≈2,58\) рад; в. \(γ≈1,40\) рад
α≈1,04\) рад; б. \(β≈2,58\) рад; в. \(γ≈1,40\) рад 92\)
92\)
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 4 Операторы
4 Операторы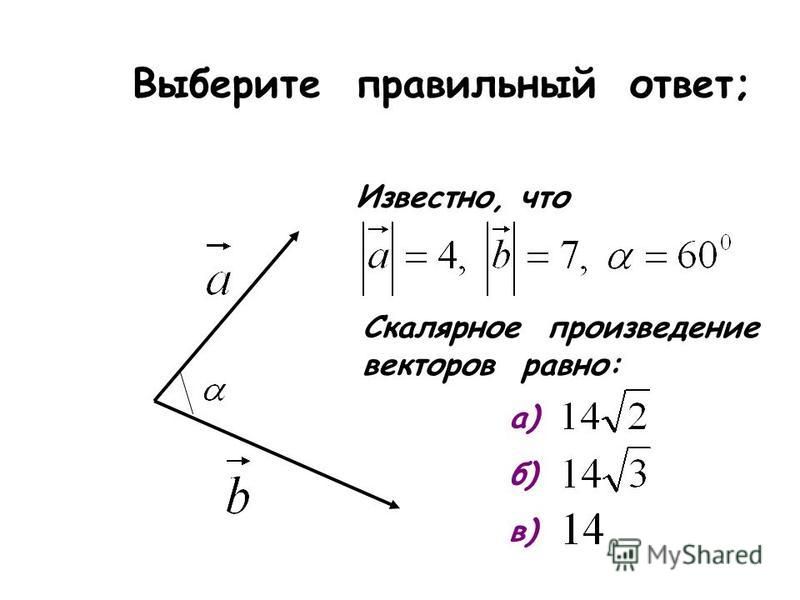 6: Формирование скалярного произведения двух векторов.
6: Формирование скалярного произведения двух векторов. В противном случае во внутреннем произведении
и больше не взаимозаменяемы; в
сопряженные только по первому фактору, .
Замена и изменение внутреннего
стоимость продукта в его комплексно-сопряженную форму.
В противном случае во внутреннем произведении
и больше не взаимозаменяемы; в
сопряженные только по первому фактору, .
Замена и изменение внутреннего
стоимость продукта в его комплексно-сопряженную форму. 2.7 показаны умноженные значения функции с использованием
одинаковые цвета:
2.7 показаны умноженные значения функции с использованием
одинаковые цвета: 12)
12)
 3 Контрольные вопросы
3 Контрольные вопросы  Итак, используя формулу Эйлера, нормализуются следующие кратные: , (для 0), , (для ) и , (для 2).
Итак, используя формулу Эйлера, нормализуются следующие кратные: , (для 0), , (для ) и , (для 2). Умножать числа довольно легко, и каждый может это сделать, но что, если вас попросили умножить два вектора, \(\vec{a}=2\hat{i} + 3\hat{j}\) и \(\vec {b}=\шляпа{i} — 3\шляпа{k}\), ну не все так просто. Векторы — это очень отдельная сущность, классические правила числового умножения здесь малопригодны. Чтобы получить произведение двух или более векторов, нам нужно понять концепцию векторного произведения 9.0059 .
Умножать числа довольно легко, и каждый может это сделать, но что, если вас попросили умножить два вектора, \(\vec{a}=2\hat{i} + 3\hat{j}\) и \(\vec {b}=\шляпа{i} — 3\шляпа{k}\), ну не все так просто. Векторы — это очень отдельная сущность, классические правила числового умножения здесь малопригодны. Чтобы получить произведение двух или более векторов, нам нужно понять концепцию векторного произведения 9.0059 . Величина результирующего вектора является произведением величин двух исходных векторов и синуса угла между их направлениями.
Величина результирующего вектора является произведением величин двух исходных векторов и синуса угла между их направлениями. И \(\шляпа{n}\) представляет собой единичный вектор в направлении, перпендикулярном плоскости, образованной двумя векторами.
И \(\шляпа{n}\) представляет собой единичный вектор в направлении, перпендикулярном плоскости, образованной двумя векторами. Направление, в котором будет двигаться винт, — вертикально вверх, т. Е. Положительная ось z. Вертикальная стрелка — это в точности вектор, образованный их векторным произведением. На приведенной выше диаграмме \(\vec{A}\) и \(\vec{B}\) имеют одну и ту же начальную точку, но это не обязательно. На самом деле это могут быть любые два вектора, здесь они показаны только для наглядного представления концепции.
Направление, в котором будет двигаться винт, — вертикально вверх, т. Е. Положительная ось z. Вертикальная стрелка — это в точности вектор, образованный их векторным произведением. На приведенной выше диаграмме \(\vec{A}\) и \(\vec{B}\) имеют одну и ту же начальную точку, но это не обязательно. На самом деле это могут быть любые два вектора, здесь они показаны только для наглядного представления концепции. Просто поверните пальцы в направлении вектора вращения и наблюдайте за направлением большого пальца. Поверните пальцы от \(\vec{A}\) к \(\vec{B}\), и направление большого пальца задает направление результирующего вектора.
Просто поверните пальцы в направлении вектора вращения и наблюдайте за направлением большого пальца. Поверните пальцы от \(\vec{A}\) к \(\vec{B}\), и направление большого пальца задает направление результирующего вектора. {o}=\vec{0}$$ 9{o}=0\), а величина всех единичных векторов равна \(1\). Точно так же \(\hat{j}\times\hat{j}=\vec{0}\) и \(\hat{k}\times\hat{k}=\vec{0}\), где \( \vec{0}\) представляет нулевой вектор. Вычисление других соотношений, например,
{o}=\vec{0}$$ 9{o}=0\), а величина всех единичных векторов равна \(1\). Точно так же \(\hat{j}\times\hat{j}=\vec{0}\) и \(\hat{k}\times\hat{k}=\vec{0}\), где \( \vec{0}\) представляет нулевой вектор. Вычисление других соотношений, например,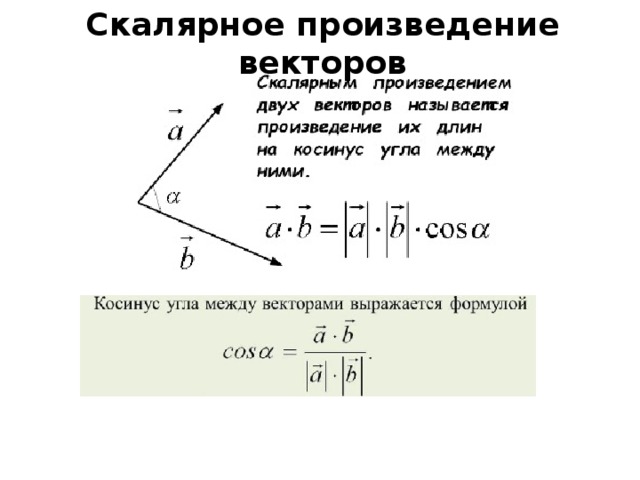 Приведенное выше уравнение иногда может быть немного утомительным для запоминания и не очень удобным для записи. В результате приведенное выше уравнение часто представляется определителем \(3\) на \(3\), который равен:
Приведенное выше уравнение иногда может быть немного утомительным для запоминания и не очень удобным для записи. В результате приведенное выше уравнение часто представляется определителем \(3\) на \(3\), который равен: е. векторное тройное произведение не является ассоциативным. По сути, существует два способа вычисления векторного тройного произведения: во-первых, вычисление векторного произведения \(\vec{A}\) и \(\vec{B}\), а затем выполнение его векторного произведения с \( \vec{С}\). Это включает в себя выполнение двух векторных продуктов, одного за другим.
е. векторное тройное произведение не является ассоциативным. По сути, существует два способа вычисления векторного тройного произведения: во-первых, вычисление векторного произведения \(\vec{A}\) и \(\vec{B}\), а затем выполнение его векторного произведения с \( \vec{С}\). Это включает в себя выполнение двух векторных продуктов, одного за другим. {2}\theta$$ 9{2}\) для векторов \(\vec{p}=2 \hat{i}-\hat{k}\) и \(\vec{q}=\hat{j}+\hat{k} \).
{2}\theta$$ 9{2}\) для векторов \(\vec{p}=2 \hat{i}-\hat{k}\) и \(\vec{q}=\hat{j}+\hat{k} \). Альтернативное, но одинаково используемое название для . Точечный продукт — 9.0058 Скалярное произведение.
Альтернативное, но одинаково используемое название для . Точечный продукт — 9.0058 Скалярное произведение. 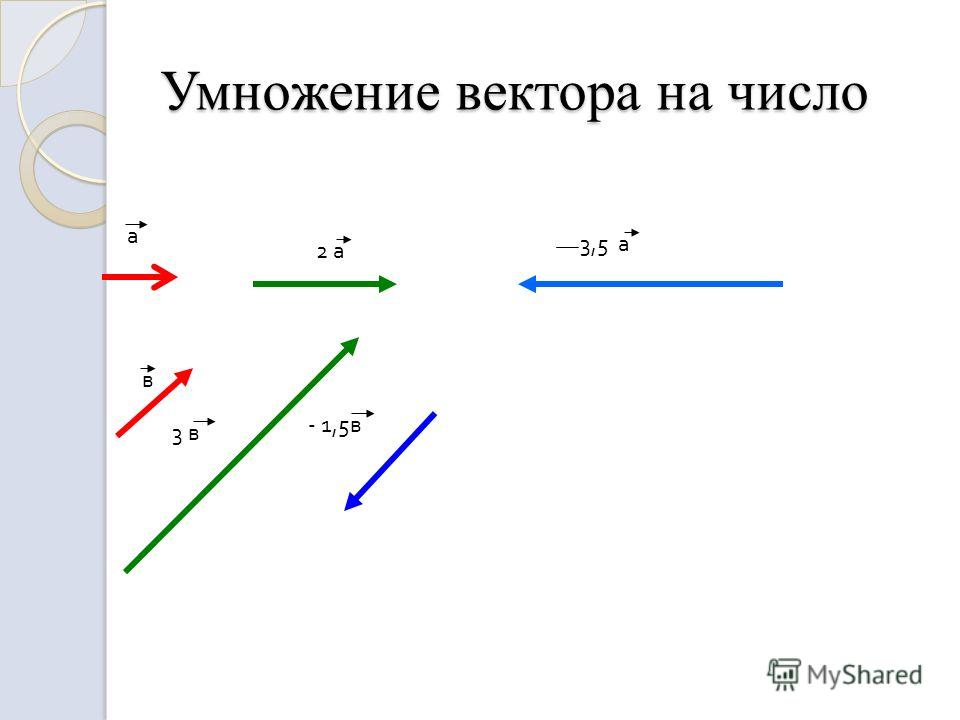


 Оба определения аналогичны при работе с декартовыми координатами.
Оба определения аналогичны при работе с декартовыми координатами. Скалярное произведение двух векторов эквивалентно произведению величин двух векторов вместе с косинусом угла между двумя векторами.
Скалярное произведение двух векторов эквивалентно произведению величин двух векторов вместе с косинусом угла между двумя векторами.


 \ \vec{y}=x_1y_1+\ x_2y_2 +x_3y_3\)
\ \vec{y}=x_1y_1+\ x_2y_2 +x_3y_3\)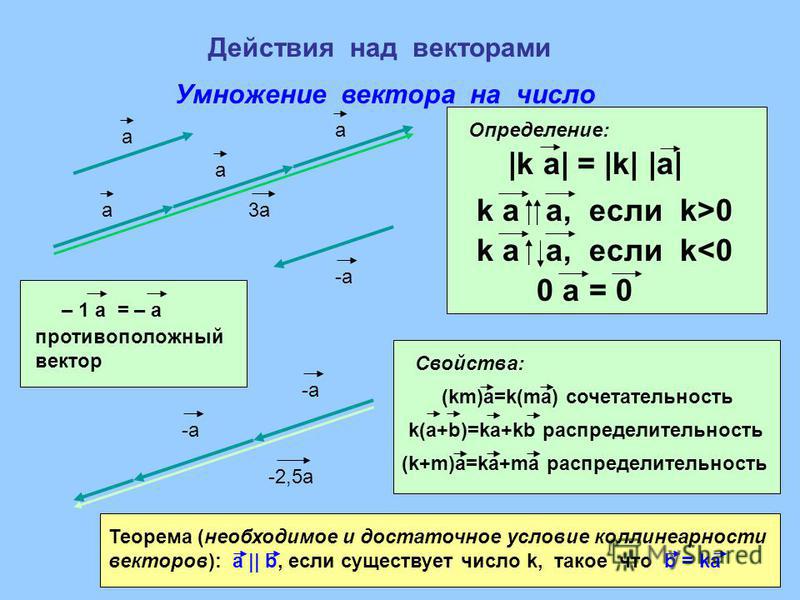 \left(\vec{y}+\vec{z}\right)=\left(\vec{x} .\vec{y}\right)+\left(\vec{x}\ .\vec {z}\right)\)
\left(\vec{y}+\vec{z}\right)=\left(\vec{x} .\vec{y}\right)+\left(\vec{x}\ .\vec {z}\right)\) \vec{y}=x_1y_1+\ x_2y_2+x_3y_3 \)
\vec{y}=x_1y_1+\ x_2y_2+x_3y_3 \) Геометрически скалярное произведение определяется как произведение длины векторов на угол косинуса между ними и определяется формулой:
Геометрически скалярное произведение определяется как произведение длины векторов на угол косинуса между ними и определяется формулой: