Векторное произведение векторов в координатах
С векторами, заданными в координатах, всё тоже просто и прозрачно. Сразу обращаю внимание на то, что разговор пойдёт о координатах ортонормированного базиса. В общем случае аффинного базиса нижеприведённая формула будет нерабочей. Кстати, кто ещё не успел ознакомиться с базисами, рекомендую статью Линейная (не) зависимость векторов. Базис векторов.
Векторное
произведение векторов 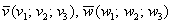 ,
заданных в ортонормированном базисе
,
заданных в ортонормированном базисе 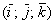 , выражается
формулой:
, выражается
формулой:
в
верхнюю строку определителя записываем
координатные векторы, во вторую и третью
строки «укладываем» координаты векторов 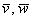
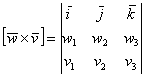
Согласно свойствам определителя, если в определителе две строки переставить местами, то он сменит знак. Этот факт полностью соответствует свойству антикоммутативности векторного произведения.
Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше. Если есть трудности с определителями и формула не очень понятна, пожалуйста, посетите урок
Что получается в результате раскрытия определителя?
В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор.
Пример 6
Найти
векторное произведение векторов  и его длину.
и его длину.
Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину.
1) Найдём векторное произведение:

В результате получен вектор
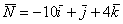 ,
,
или, ещё можно записать
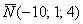 .
.
Существует
очень хороший способ проверки: как
следует из определения, вектор 
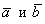 .
Ортогональность векторов, как мы
разбирались, проверяется с помощью скалярного
произведения:
.
Ортогональность векторов, как мы
разбирались, проверяется с помощью скалярного
произведения:Если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя. коллинеарный вектор координата множитель
2) Вычислим длину векторного произведения. Используем формулу для вычисления длины вектора

Ответ:
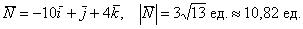
Аналогичный пример для самостоятельного решения:
Пример 7
Даны векторы
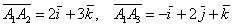 .
.
Найти 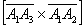 и вычислить
и вычислить 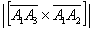 .
.
Решение с ответом в конце урока. Будьте внимательны!
Огонь камина в самом разгаре, и самое время добавить живительный геометрический смысл в наши задачи:
Пример 8
Даны вершины треугольника
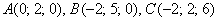 .
.
Найти его площадь.
Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:
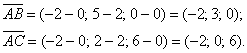
Затем векторное произведение:
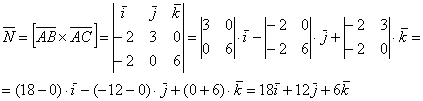
Вычислим его длину:
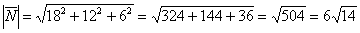
Формулы площадей параллелограмма и треугольника, само собой, остаются те же самые:

Ответ:

Рассмотренную
задачу можно решить ещё двумя способами
– было не обязательно выбирать стороны 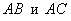
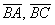 либо
либо  .
Желающие могут проверить, что во всех
трёх случаях получится один и тот же
ответ. Настоятельно рекомендую выполнить
схематический рисунок, чтобы лучше
понять вышесказанное.
.
Желающие могут проверить, что во всех
трёх случаях получится один и тот же
ответ. Настоятельно рекомендую выполнить
схематический рисунок, чтобы лучше
понять вышесказанное. Еще
одна важная особенность состоит в том,
что в
задачах на нахождение площади фигуры порядок векторов
не имеет значения. Действительно, если
находить 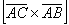
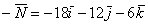 ,
но формула вычисления длины вектора
всё равно «съест» эти минусы. Заметьте,
что такую перестановку нельзя делать
в Примерах №№6,7, поскольку там требовалось
найти вполне конкретный вектор.
,
но формула вычисления длины вектора
всё равно «съест» эти минусы. Заметьте,
что такую перестановку нельзя делать
в Примерах №№6,7, поскольку там требовалось
найти вполне конкретный вектор.Скалярное произведение в координатах. Свойство скалярного произведения
На этом уроке мы выведем формулу, которая позволяет находить скалярное произведение векторов через их координаты, и рассмотрим свойства скалярного произведения.
Вначале сформулируем и докажем формулу для выражения скалярного произведения через координаты для неколлинеарных векторов. Далее рассмотрим скалярное произведение в координатах для коллинеарных векторов – сонаправленных и противоположно направленных. Рассмотрим следствия из полученной формулы в координатах о перпендикулярных векторах и о косинусе угла между ненулевыми векторами. Сформулируем и докажем свойства скалярного произведения: переместительный, распределительный и сочетательный законы и неотрицательность скалярного квадрата.
Тема: Соотношения между сторонами и углами треугольника. Раздел 3. Скалярное произведение векторов
Урок: Скалярное произведение векторов в координатах
Тема урока: «Скалярное произведение векторов в координатах. Свойства скалярного произведения». На этом уроке мы выведем формулу вычисления скалярного произведения через координаты векторов, рассмотрим свойства скалярного произведения и решим задачу на использование свойств скалярного произведения векторов.
Сформулируем и докажем центральную теорему урока.
Теорема. Скалярное произведение векторов 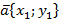 и
и 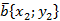 выражается формулой
выражается формулой
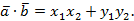

Доказательство.
1. При 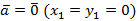 или
или 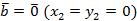 теорема очевидна.
теорема очевидна.
2. Пусть 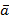 и
и 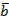
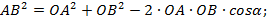
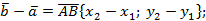
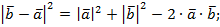
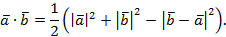
Перейдем в этой формуле к координатам.
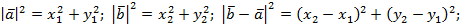
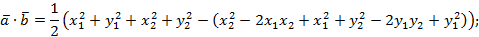

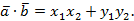
Уточним, что теорема доказана для случая неколлинеарных векторов, в доказательстве был использован треугольник, теорема косинусов, поэтому случай коллинеарных векторов тоже рассмотрим, при этом учтем, что угол между коллинеарными векторами может быть равен 180° или 0°.
3. Пусть 
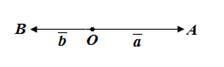
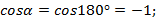
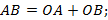

Подгоним это равенство под формулу, полученную при доказательстве теоремы.

Формула та же самая, если записать ее в координатах, то получим
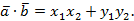
4. Аналогично рассмотрим случай 

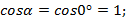

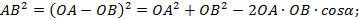
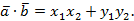
Вывод: 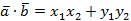 для всех векторов
для всех векторов 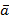 и
и 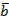 .
.
Сформулируем следствия из доказанной теоремы.
Следствие 1. Ненулевые векторы 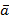 и
и 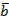 перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда 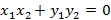 .
.
Действительно,  .
.
Следствие 2. Косинус угла между ненулевыми векторами 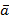 и
и 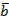 выражается формулой:
выражается формулой:
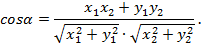
Действительно, 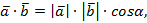

Рассмотрим свойства скалярного произведения векторов.
Для любых векторов  и любого числа k справедливы соотношения:
и любого числа k справедливы соотношения:
1. 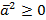 , причем
, причем 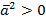 при
при 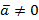 .
.
Доказательство.
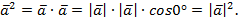
Но  при
при  .
.
2. 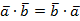 (переместительный закон).
(переместительный закон).
Доказательство (из определения).

3. 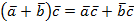 (распределительный закон).
(распределительный закон).
Доказательство.
Для доказательства используем метод координат.
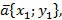
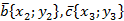 , тогда
, тогда
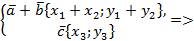
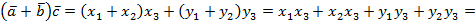
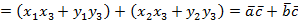 .
.
4. 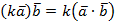 (сочетательный закон).
(сочетательный закон).
Доказательство.
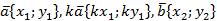 , значит,
, значит,
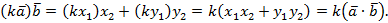
Замечание. Распределительный закон справедлив и в случае нескольких слагаемых, например,
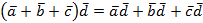 .
.
Задача. Вычислить скалярное произведение векторов 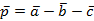 и
и  , если
, если 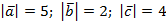 и
и 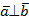 .
.
Решение.
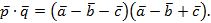
По свойствам скалярного произведения
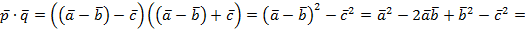
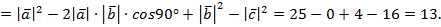
Ответ: 13.
Итак, мы вывели формулу вычисления скалярного произведения векторов через координаты векторов, доказали свойства скалярного произведения и решили задачу на вычисление скалярного произведения с использованием свойств скалярного произведения.
На следующем уроке мы рассмотрим решение задач на вычисление скалярного произведения.
Список литературы
- Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
- Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А. В. Геометрия. Уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- E-science.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Атанасян Л. С. и др. Геометрия 7–9 классы. №№1044, 1048.
Векторное произведение векторов, формула и примеры
Определение и формула векторного произведения векторов
ОПРЕДЕЛЕНИЕ Векторным произведением двух векторов и называется вектор , перпендикулярный к плоскости этих векторов и направленный так, что наименьший поворот от вектора к вектору происходит против хода часовой стрелки, если смотреть с конца вектора (рис. 1), причем
Если векторы и заданы своими координатами: , то их векторное произведение вычисляется по формуле:
где – орты координатных осей соответственно.
Если раскрыть этот определитель по первой строке:
то получаем, что
ПРИМЕР
| Задание | Найти векторное произведение векторов и |
| Решение |
Для нахождения векторного произведения составим определитель, в первой строке которого записаны орты координатных осей, а во второй и третьей строках координаты векторов и соответственно:
Вычислим этот определитель, разложив его по элементам первой строки:
|
| Ответ |
Свойства векторного произведения векторов
1. Геометрический смысл векторного произведения. Модуль векторного произведения двух векторов и равен площади параллелограмма построенного на этих векторах:
ЗАМЕЧАНИЕ Площадь треугольника построенного на векторах и равна половине модуля векторного произведения указанных векторов:
2. Векторное произведение двух ненулевых векторов и равно нулю тогда и только тогда, когда эти векторы коллинеарны.
3. .
4. .
5. .
ПРИМЕР| Задание | Найти площадь треугольника, образованного векторами и , если известно, что , а угол между этими векторами . |
| Решение |
Известно, что площадь треугольника, построенного на двух векторах, равна половине длины вектора, который есть их векторным произведением. Модуль векторного произведения векторов и равен произведению модулей этих векторов на синус угла между ними. То есть имеем:
(кв. ед.). |
| Ответ | (кв. ед.) |
§14. Векторное произведение векторов в координатной форме
Пусть в прямоугольной системе координат заданы векторы =
(x1,y1,z1),=(x2,у2,z2). Из определения векторного произведения легко установить следующие соотношения для векторов ,,(Рис. 27):
x=x==x=0 (1.35)
x=;x=;x=.
Из свойства векторного произведения векторов, получаем:
Рис.28
=(x1+y1+z1)х(x2+y2+z2)=x1y2(х)+
34
Последнее равенство можно записать символически как определитель третьего порядка в его разложении по элементам первой строю, т.е.
(1.36)
Итак,
(1.37)
Тогда
(1.38)
ПРИМЕР 1.1. Векторы =(-3,-2,6) и=(-2,4,4) служат сторонами треугольника АВС. Найти высоту AD треугольника АВС. РЕШЕНИЕ. Найдем площадь треугольника АВС.
С другой стороны, . Следовательно,
35
§15. Смешанное произведение векторов в координатной форме
Пусть в прямоугольной системе координат заданы векторы =
(х1,у1,z1), =(x2,y2,z2) и(x3,y3,z3)тогда
Теперь, используя равенство (1.34). можно записать, что
(1.39)
Из (1.39) следует, что векторы ,икомпланарны тогда и только тогда, когда выполняется равенство:
=0. (1.40)
§16. Полярные координаты
Возьмем на плоскости произвольную точку 0, которую назовем
полюсом, и ось ОР, задаваемую единичным вектором , которую назовем полярной осью. Тогда положение произвольной точки М плоскости можно определить двумя числами:r-длина отрезка ОМ и (φ — угол, который образует отрезок ОМ с осью ОР в положительном направлении, т.е. при движении против часовой стрелки (Рис. 28). Величиныrи (φ называются полярными координатами течки
Рис.28
М, r-полярный радиус, φ-полярный угол. При этом считаем, что полярные координаты точек плоскости изменяются в следующих пределах:. Таким образом получаем систему
36
координат, которая называется полярной системой координат.
Рассмотрим одновременно такую прямоугольную систему координат, для которой полюс полярной системы совпадает с началом декартовой, а полярная ось направлена в положительном направлении с осью ОХ. Пусть в прямоугольной системе координат точка имеет координаты х и у. Тогда, очевидно,
х=rcosφ, у=гsinφ (1.41)
формулы, выражающие прямоугольные координаты через полярные. Так как х2+у2=r2, то
(1.42)
формулы, выражающие полярные координаты через прямоугольные.
ПРИМЕР 1.2. Найти полярные координаты точки. М(, -1).
РЕШЕНИЕ. и так какx>0, y>0
То
Итак, r=2, φ=11π/6
§17. Цилиндрические координаты
Пусть в плоскости α определена полярная система координат с полюсом 0 и полярной осью ОХ. Проведем ось OZ, перпендикулярную плоскости α и направленную так, чтобы положительное вращение в плоскости α (т.е. против часовой стрелки) наблюдалось с конца полуоси OZ, против часовой стрелки (Рис. 29). Тогда положение произвольной точки М в пространстве можно задать упорядоченной тройкой чисел r, φ, z, гдеrи φ — полярные координаты точки М1, являющейся ортогональной проекцией точки М на плоскость α, z — ортогональная проекция точки М на ось OZ. Эта упорядоченная тройка чисел называетсяцилиндрическими координатами
37
точкиМ.
Цилиндрические координаты изменяются в следующих пределах:
Установим связь между цилиндрическими и прямоугольными координатами. Для этого расположим оси прямоугольной система OXYZ так, как указано на рис. 29. Тогда декартовы координаты х, у, z точки М будут связаны с ее цилиндрическими координатами r, φ, z соотношениями:
Х=rcosφ. у=rsinφ
z = z. (1.43)
Отметим, что наименование «цилиндрические координаты» связано
Рис.29
с тем, что все точки пространства,которые имеют одно и то же значение координаты г, расположена на цилиндре.
Свойства векторного произведения Геометрические свойства
Векторное произведение
 равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
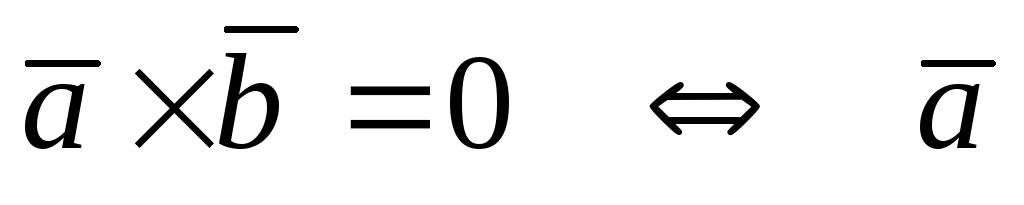 ||
||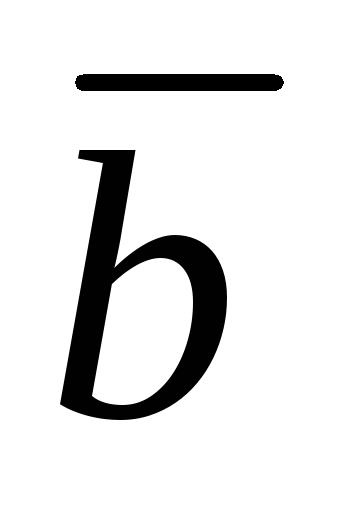 .
.
Доказательство. Пусть угол между векторами  и
и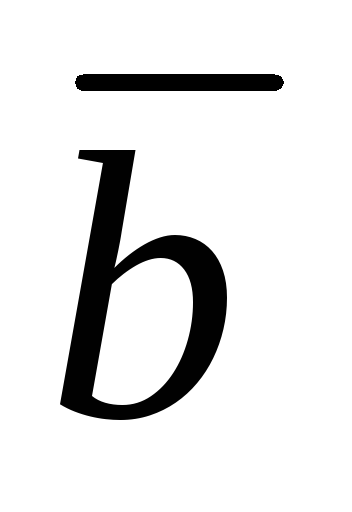 равен
равен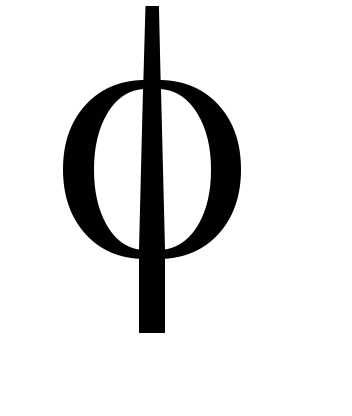 .
.
a)
Докажем, что  .
.
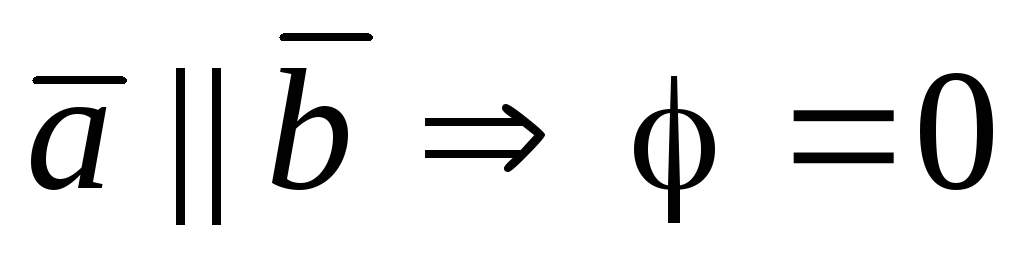 или
или  1800
1800 .
.
б)
Докажем, что 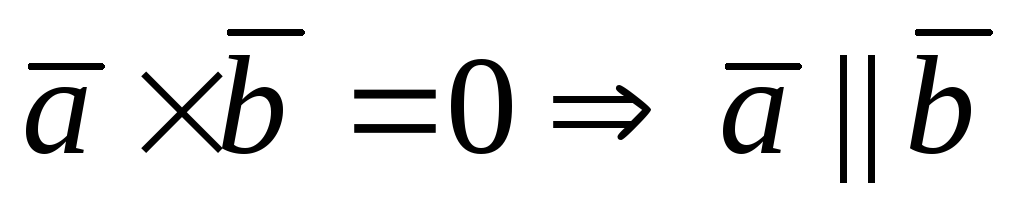 .
.

если 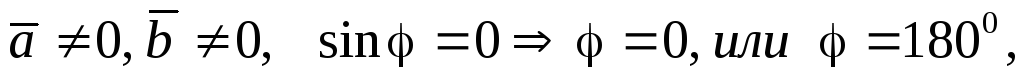
 .
.
Если  ,
или
,
или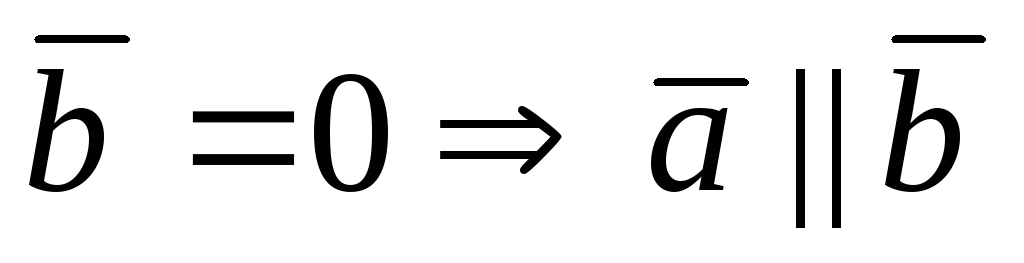 .
.
Модуль векторного произведения
 равен площади параллелограмма,
построенного на этих векторах.
равен площади параллелограмма,
построенного на этих векторах.
Доказательство.
Из курса геометрии 
Из
свойства 2 следует, что  ,
где
,
где – единичный вектор, перпендикулярный
векторам
– единичный вектор, перпендикулярный
векторам и
и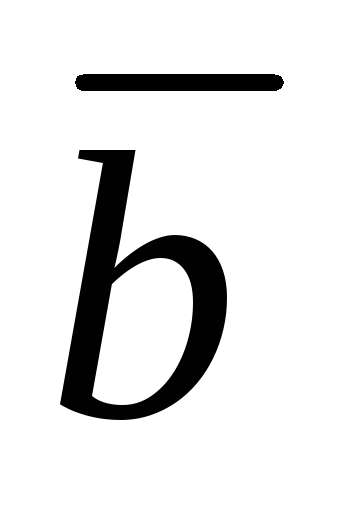 и
образующий с ними правую тройку:
и
образующий с ними правую тройку:
а) 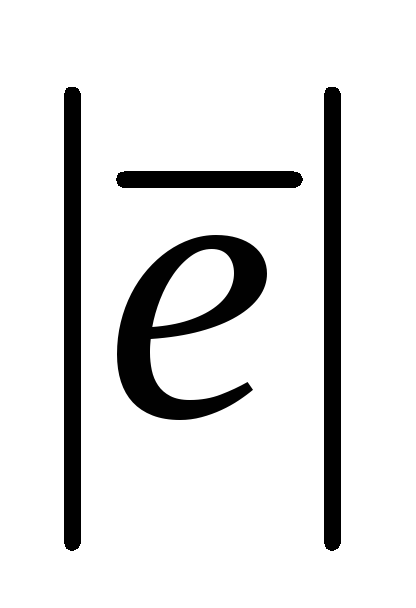 =1,
=1,
б) 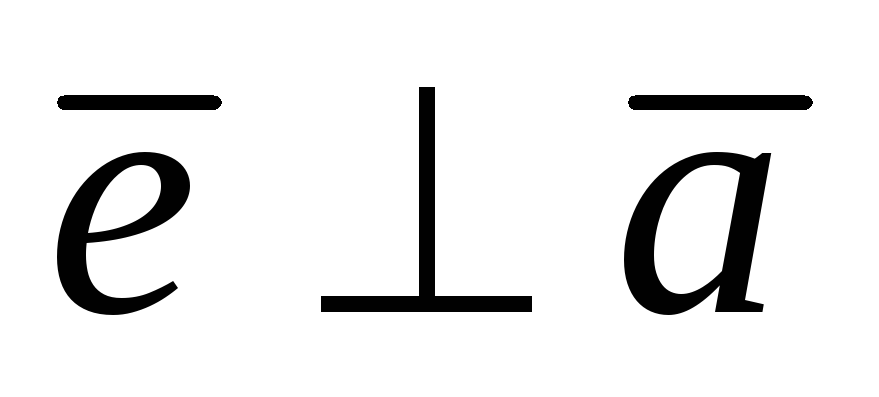 ,
,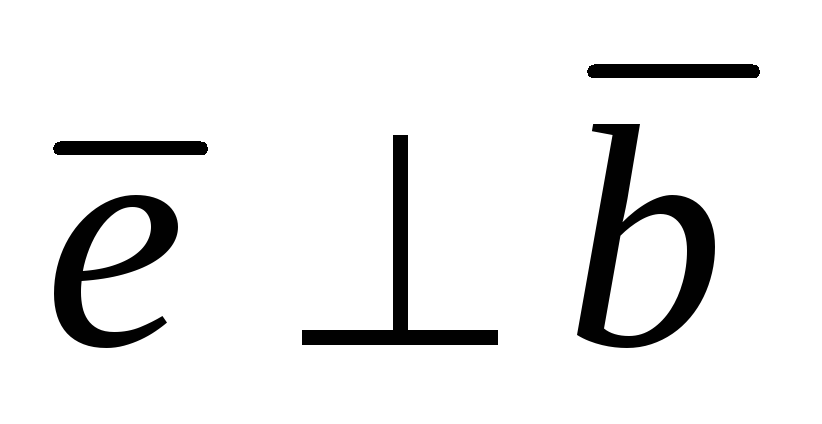 ,
,
в)  ,,
,, – правая тройка.
– правая тройка.
Алгебраические свойства
Антикоммутативность:
 =
= 
Доказательство.
Модули векторов 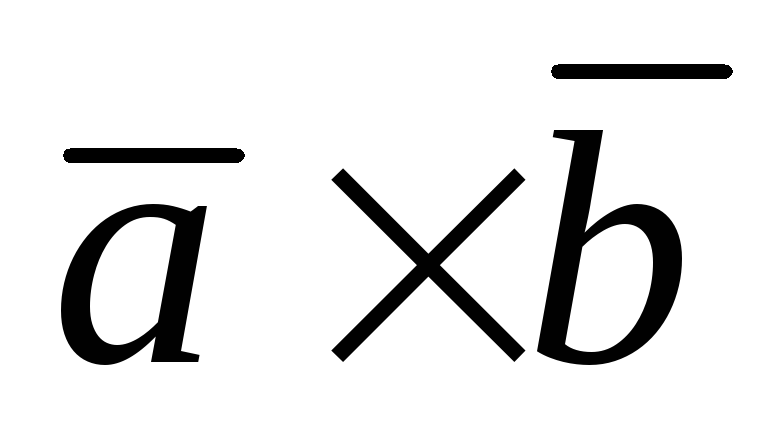 и
и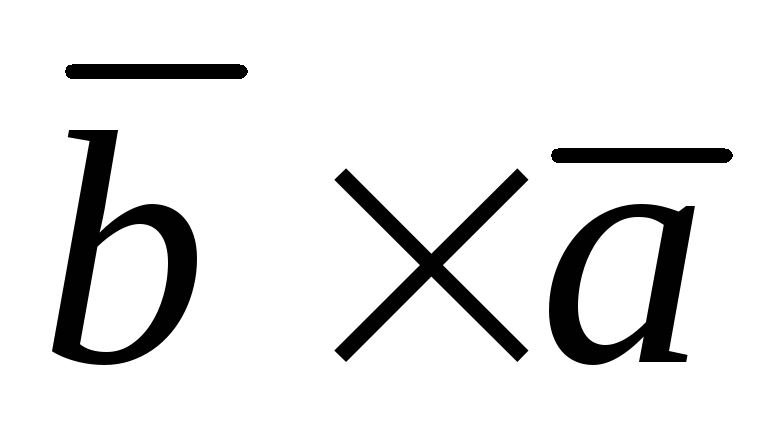 равны по определению векторного
произведения. Проверим их направление:
равны по определению векторного
произведения. Проверим их направление:
а)  ||
||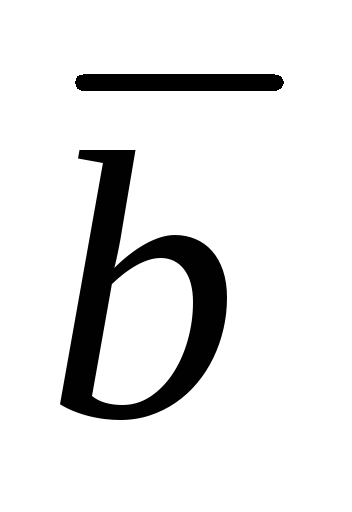
 равенство выполняется;
равенство выполняется;
б)  и
и не
параллельны. Но
не
параллельны. Но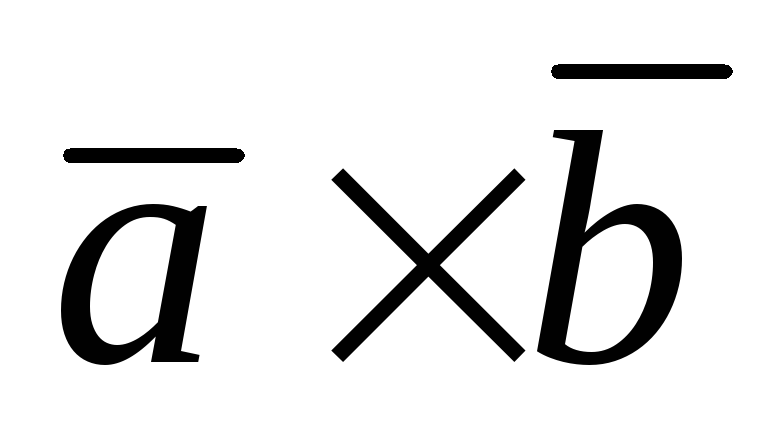 ||
||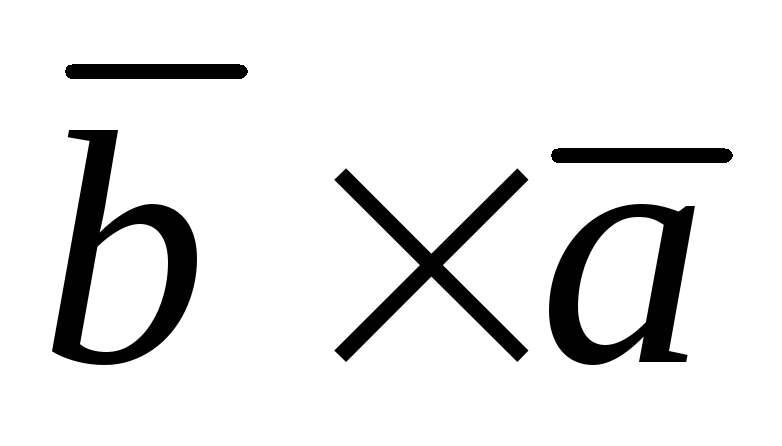 по определению векторного произведения,
тогда либо
по определению векторного произведения,
тогда либо ,
либо
,
либо .
Пусть
.
Пусть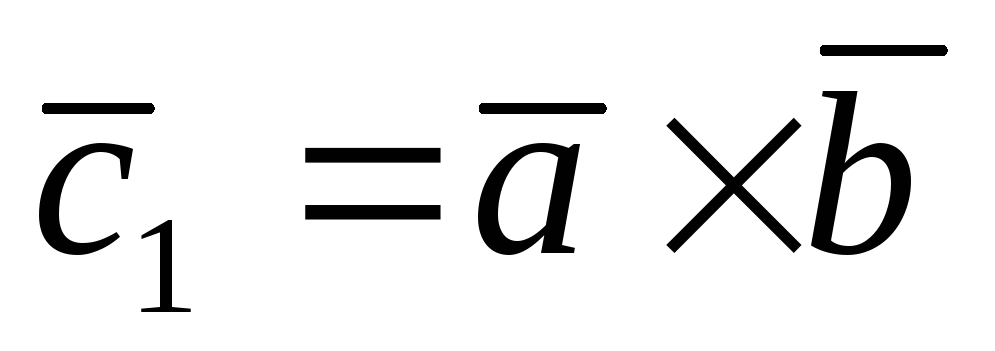 ,
а
,
а .
Тройка векторов
.
Тройка векторов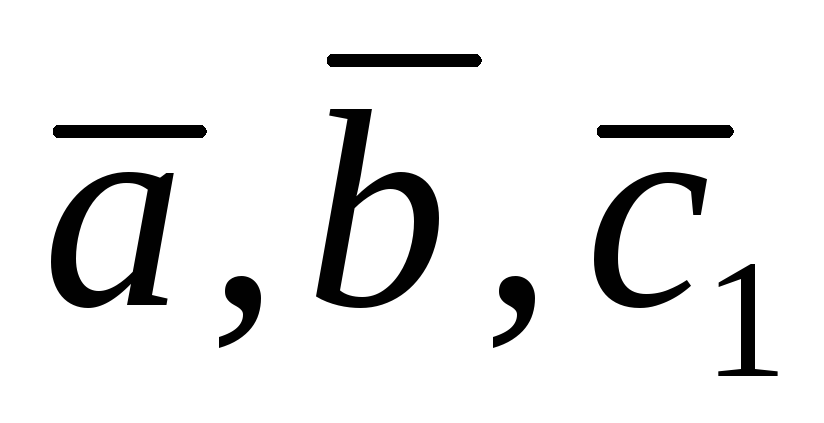 правая, а тройка
правая, а тройка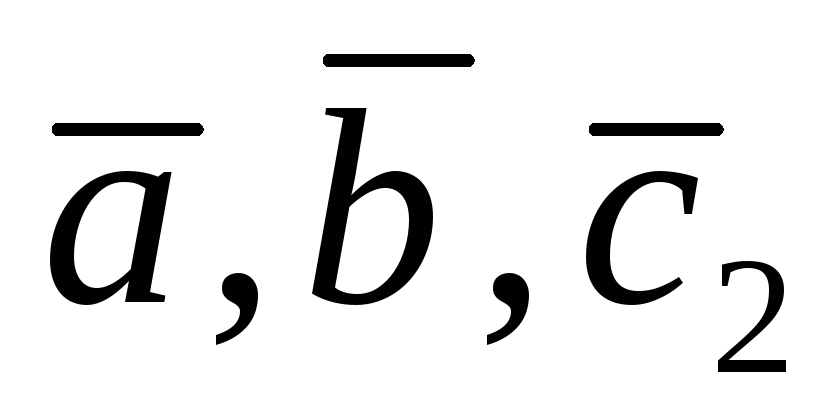 – левая. Следовательно,
– левая. Следовательно,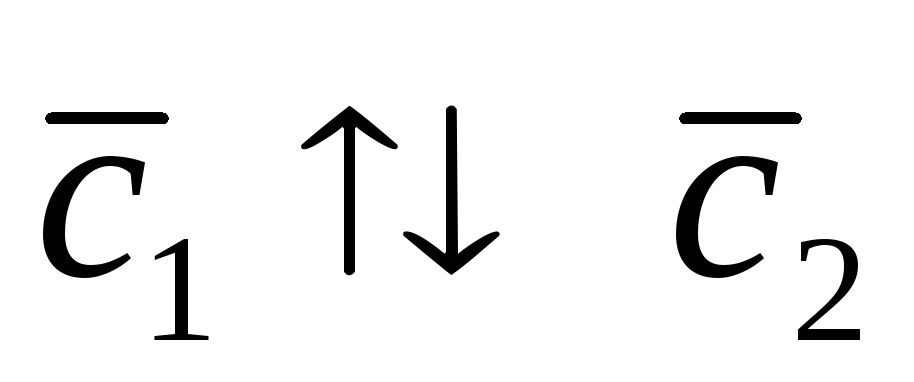 и
и 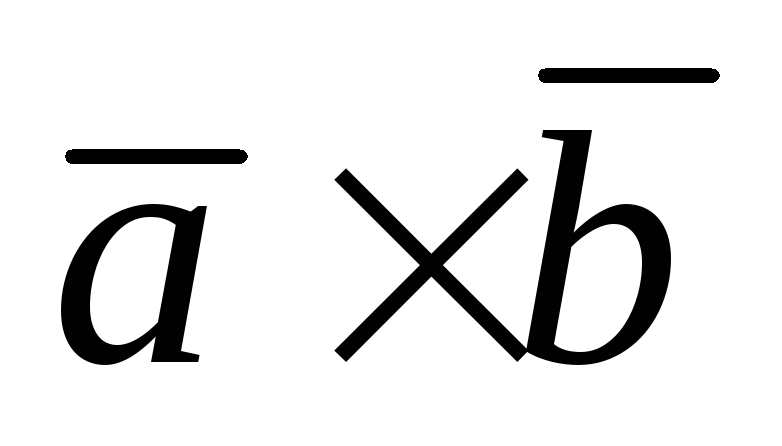 =
= 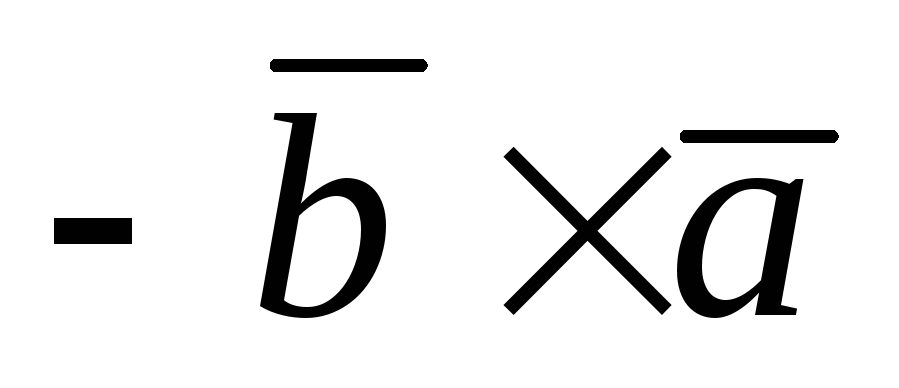 .
.
Ассоциативность относительно умножения на число.
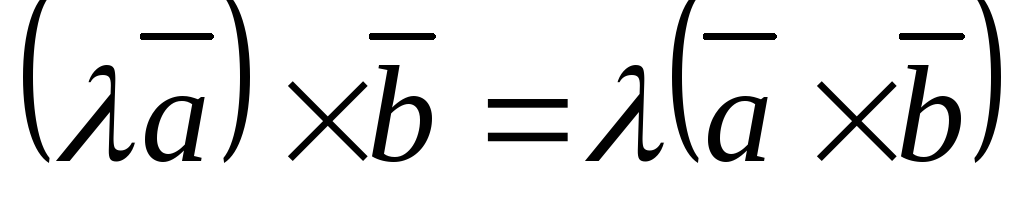

проверяем модуль:
а)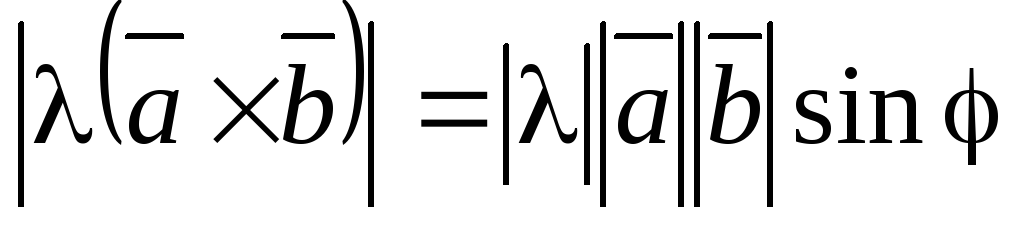 ,
,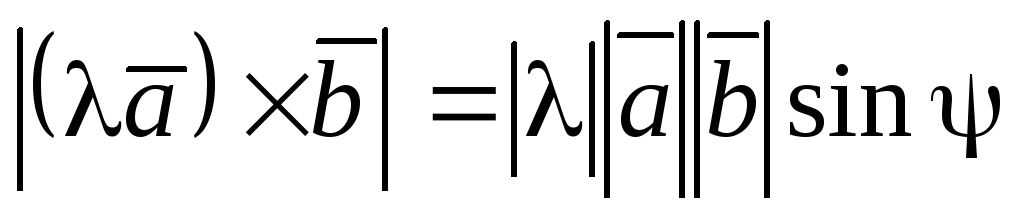 ,
,
где  – угол между векторами
– угол между векторами и
и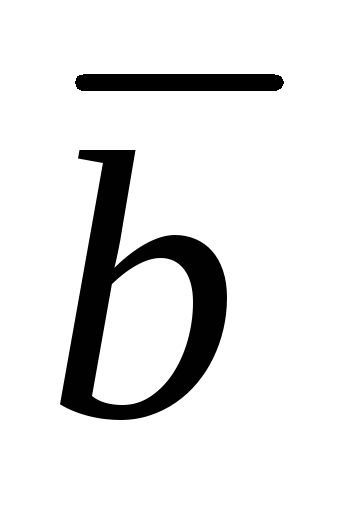 ,
а
,
а – угол между векторами
– угол между векторами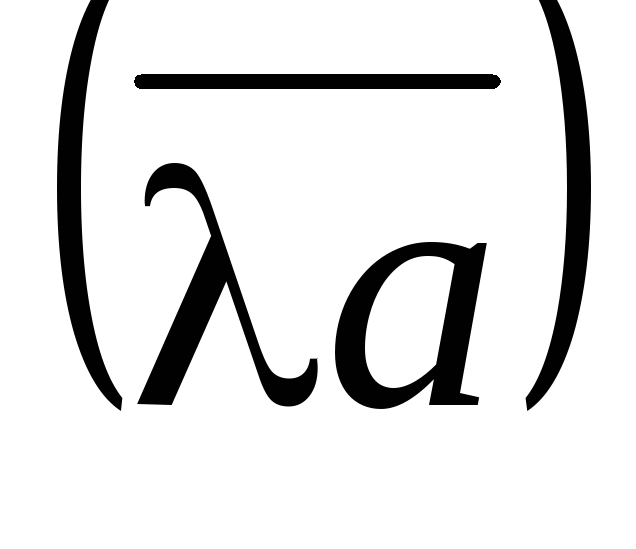 и
и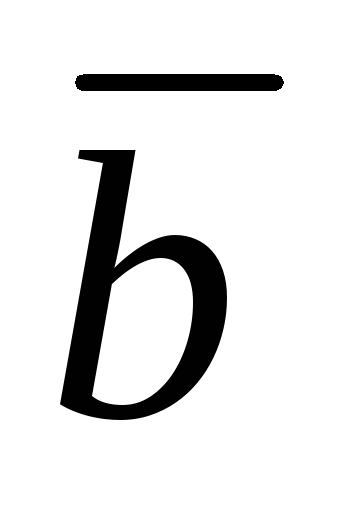 .
.
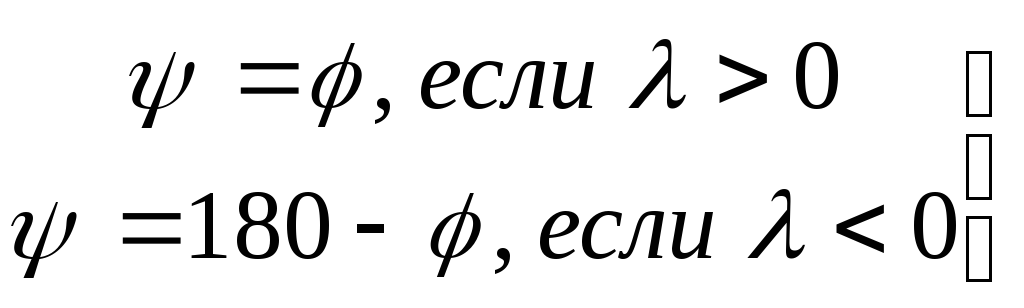 =>
=> 
поверяем направление:
б)
если 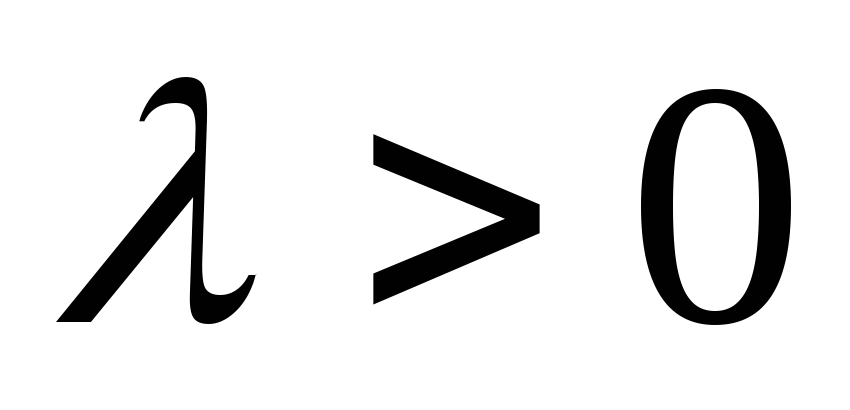
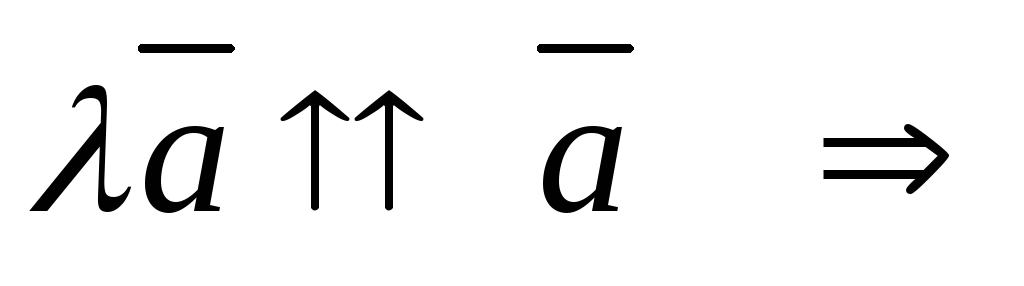
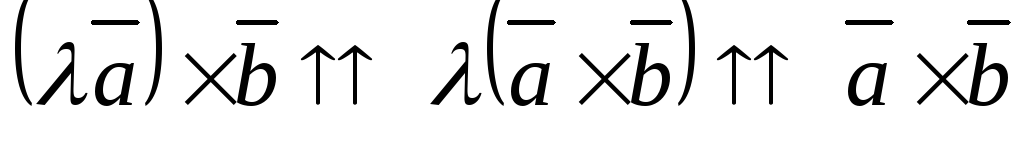
если 
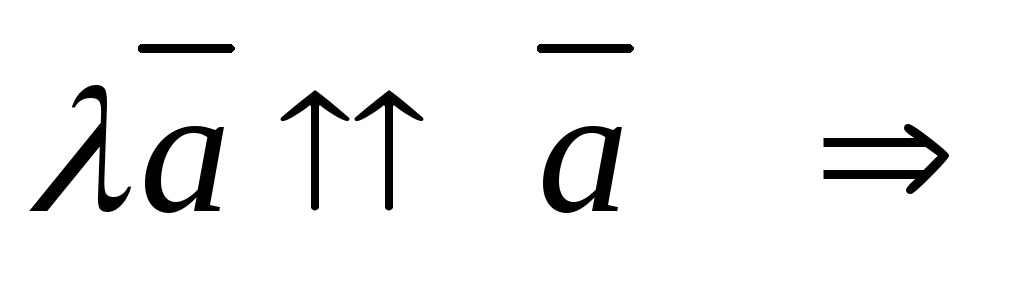
 и
и 

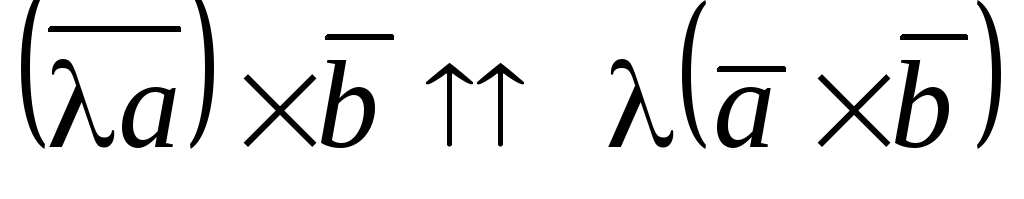 .
.
5. Дистрибутивность относительно сложения векторов

Выражение векторного произведения через координаты сомножителей
Теорема
1. Пусть
векторы  и
и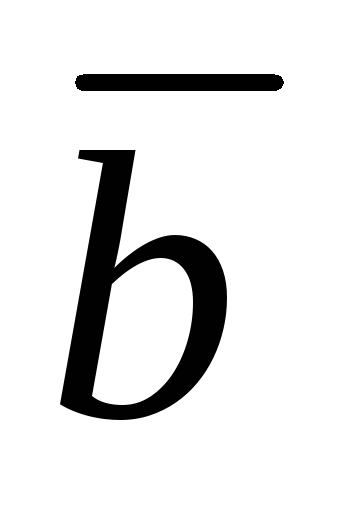 имеют координаты
имеют координаты
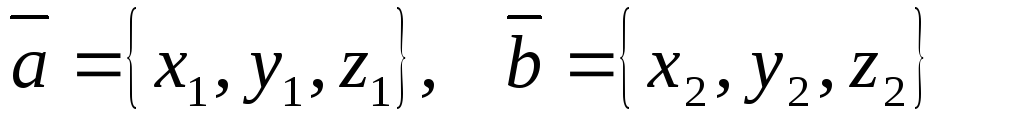 .
.
Векторное произведение этих векторов имеет координаты
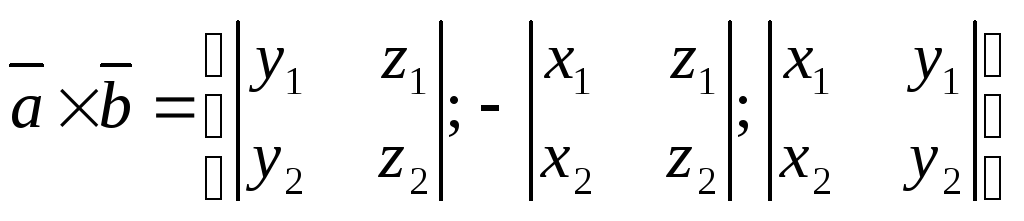 . (16)
. (16)
Можно расписать определители:
 (16’)
(16’)
или представить в виде
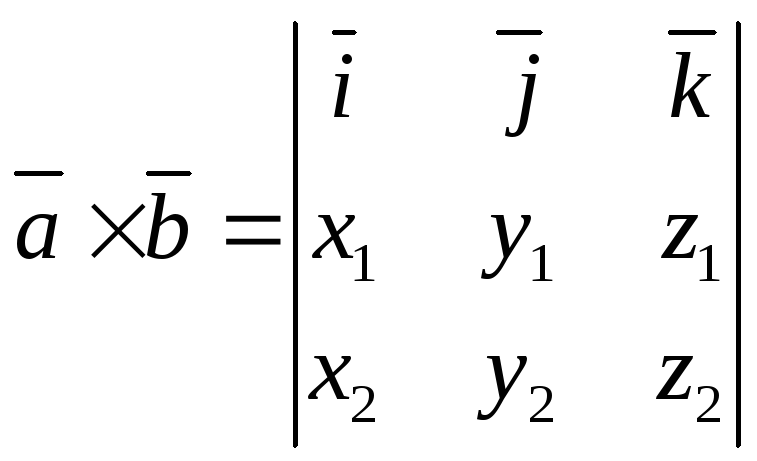 . (16’’)
. (16’’)
Доказательство. Рассмотрим векторные произведения базисных векторов:
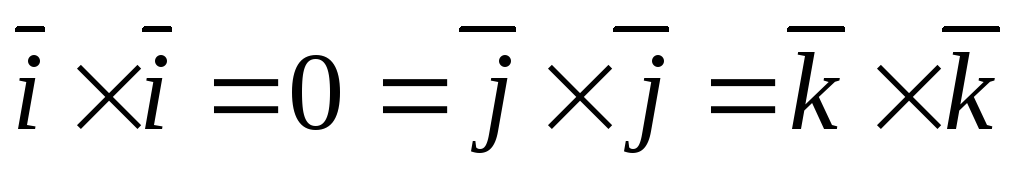
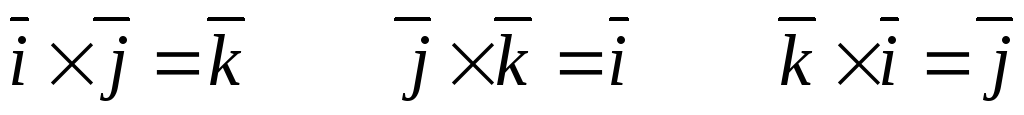 (17)
(17)
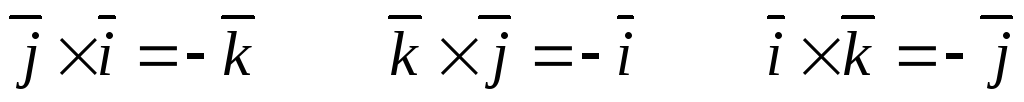 .
.
Разложим
векторы  и
и по базису
по базису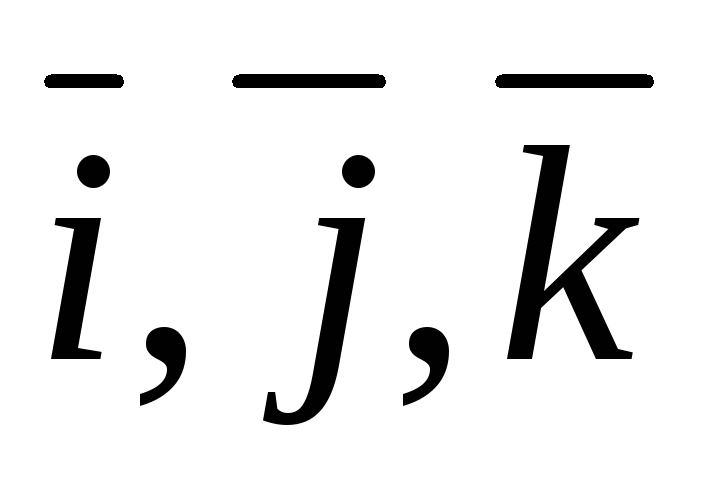 :
:

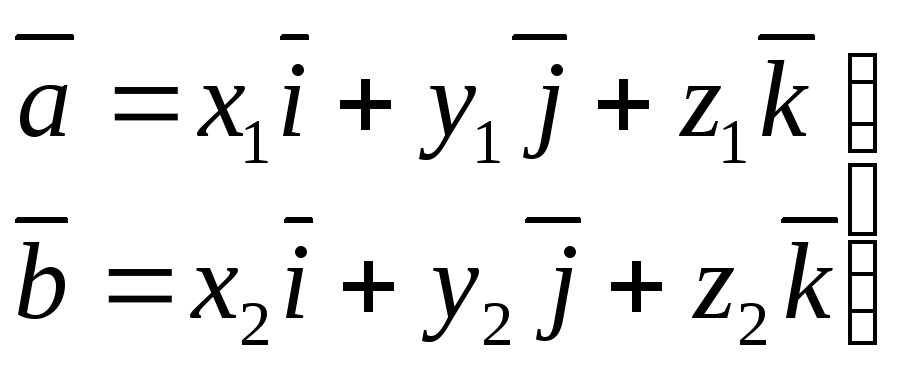 .
.
На основании свойств векторного произведения мы можем перемножать правые части почленно:
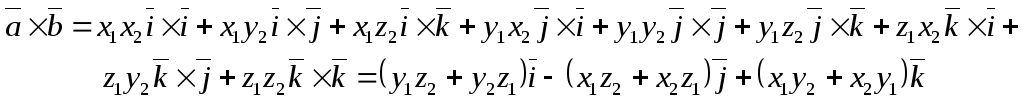
с учетом формул (17).
Пример 1. Найти координаты векторного произведения векторов
 .
.
Решение.
Пусть 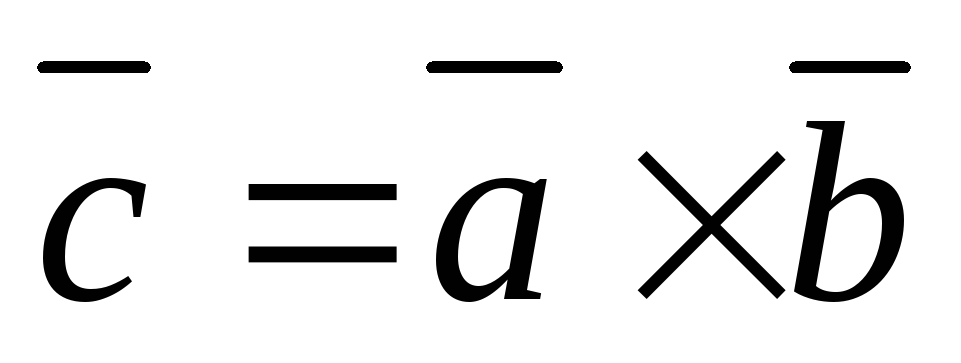 .
.
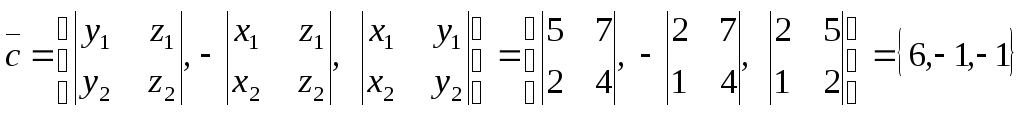 .
.
Пример
2: Даны три
точки:  .
.
Найти
площадь треугольника АВС (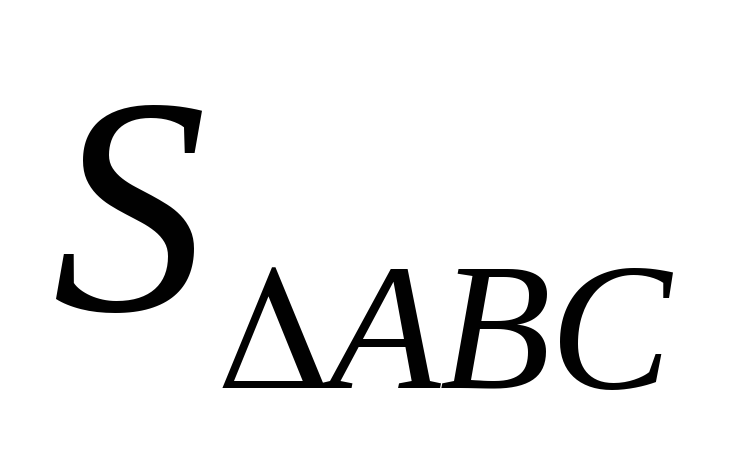 ).
).
Решение.
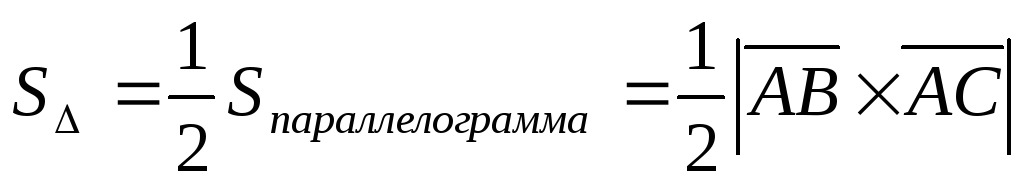 .
.
Найдем
координаты векторов 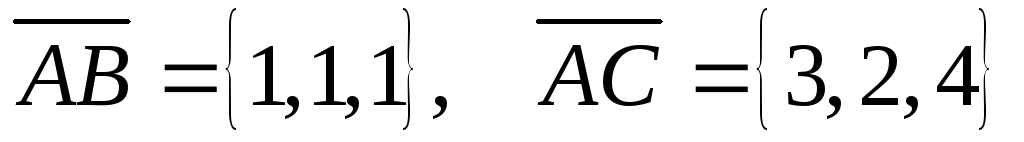 .
.
 .
.
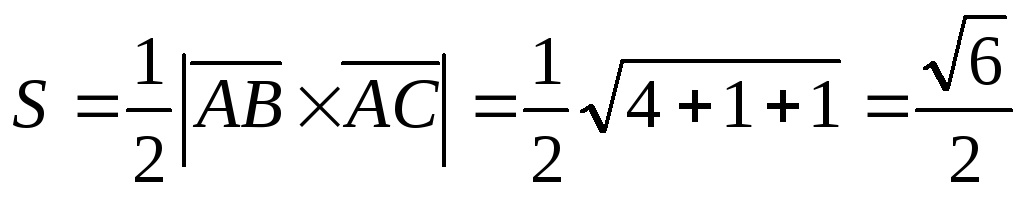 .
.
Смешанное произведение трёх векторов
Даны
при произвольных вектора 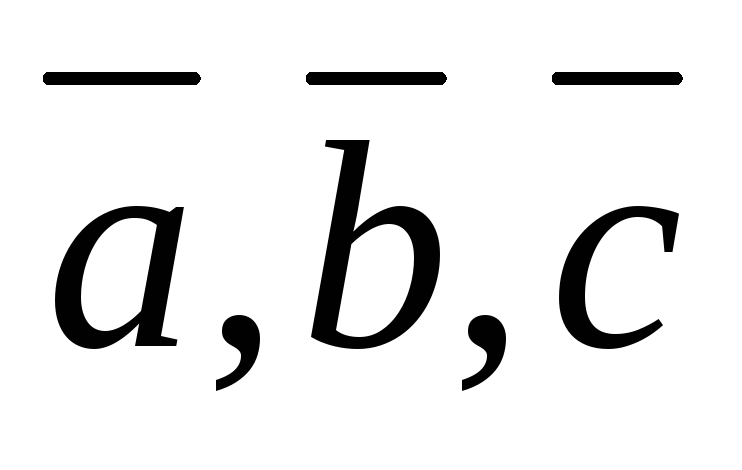 .
.
Определение.
Если результат векторного произведения  скалярно умножить на вектор
скалярно умножить на вектор  ,
то
,
то 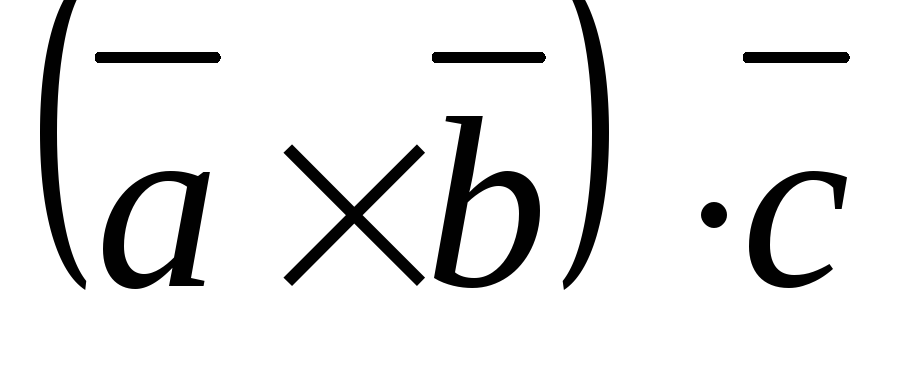 – это смешанное произведение векторов
– это смешанное произведение векторов 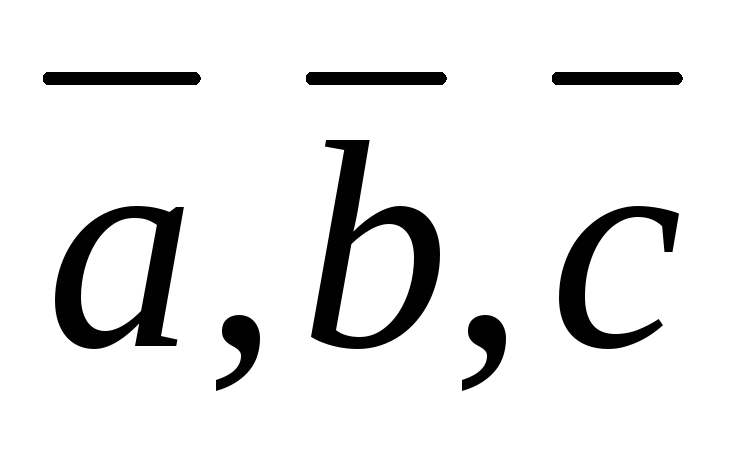 .
.
Геометрический смысл смешанного произведения
Теорема
2. Смешанное
произведение 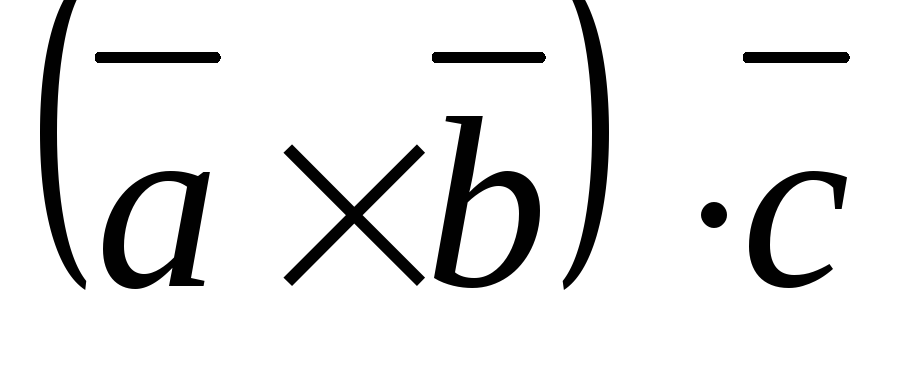 равно объему параллелепипеда, построенному
на приведённых к общему началу векторах,
взятому со знаком <+>, если
равно объему параллелепипеда, построенному
на приведённых к общему началу векторах,
взятому со знаком <+>, если  –
правая тройка векторов, и со знаком <->,
если тройка
–
правая тройка векторов, и со знаком <->,
если тройка –
левая.
–
левая.
Если
векторы 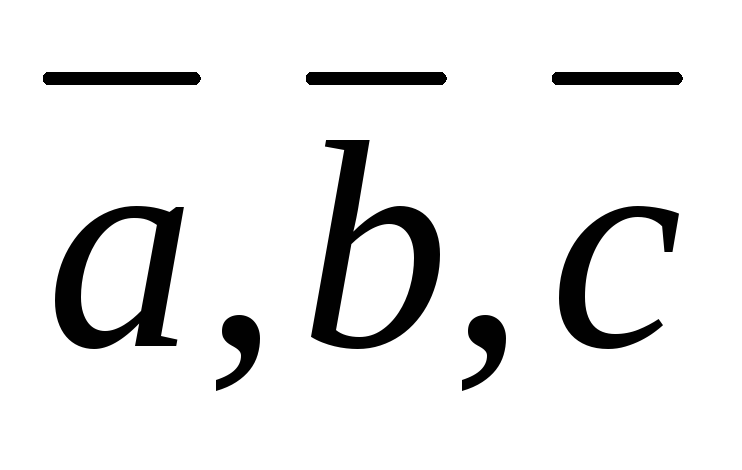 –
компланарны, то объем равен нулю, и
–
компланарны, то объем равен нулю, и  .
.
Доказательство.
Пусть S – площадь параллелограмма, построенного
на векторах  ,
,  – единичный вектор, перпендикулярный
к векторам
– единичный вектор, перпендикулярный
к векторам  и образующий с ними правую тройку.
(Вектор
и образующий с ними правую тройку.
(Вектор – орт векторного произведения
– орт векторного произведения  .)
.)
Из геометрического свойства 2 векторного произведения
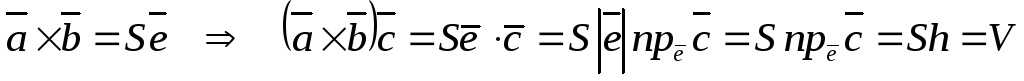 (18)
(18)
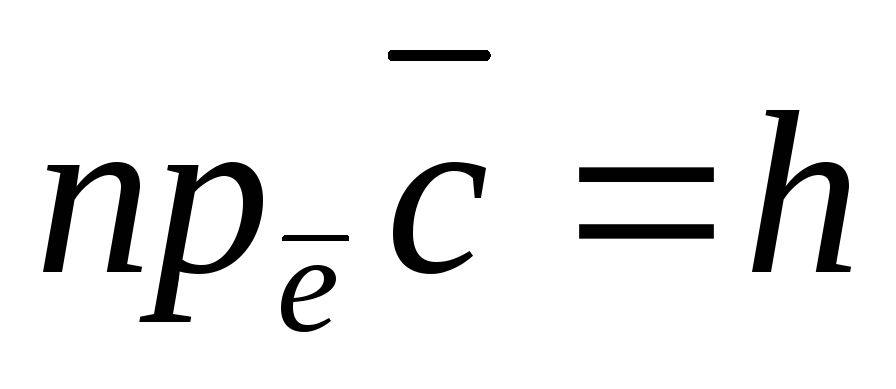 –высота
параллелепипеда, построенного на
векторах
–высота
параллелепипеда, построенного на
векторах 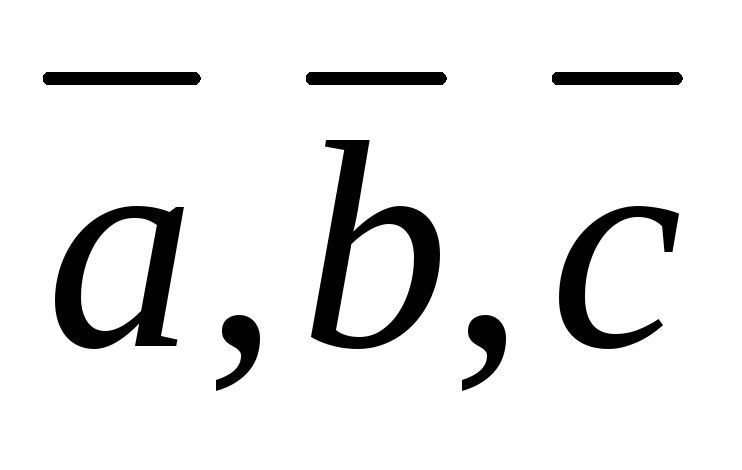 ,
с основанием S.
,
с основанием S.
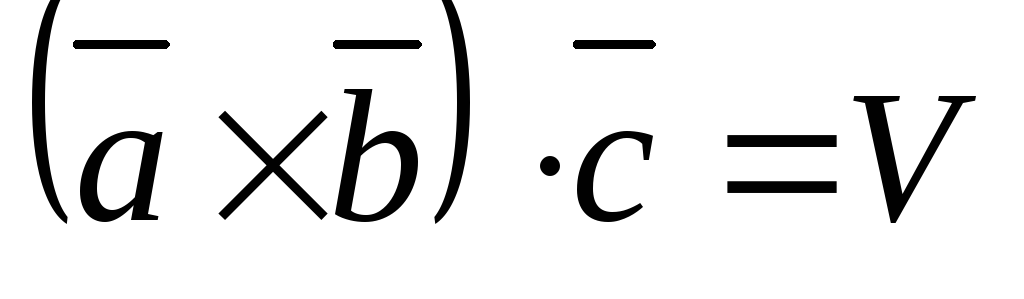 ,
а
,
а 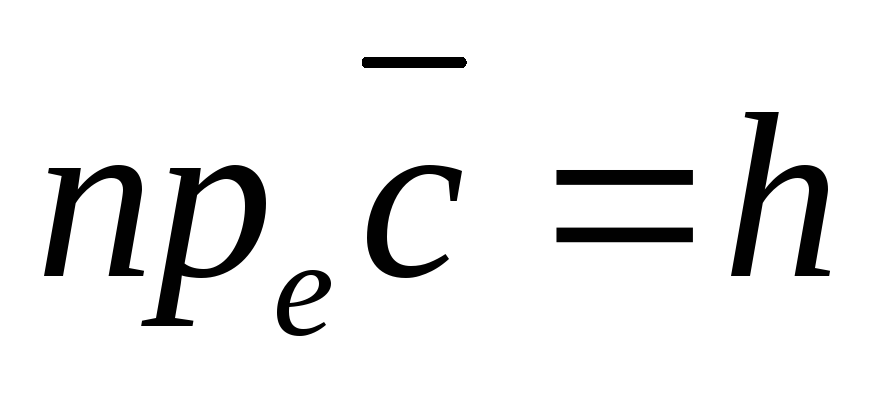 ,
если
,
если 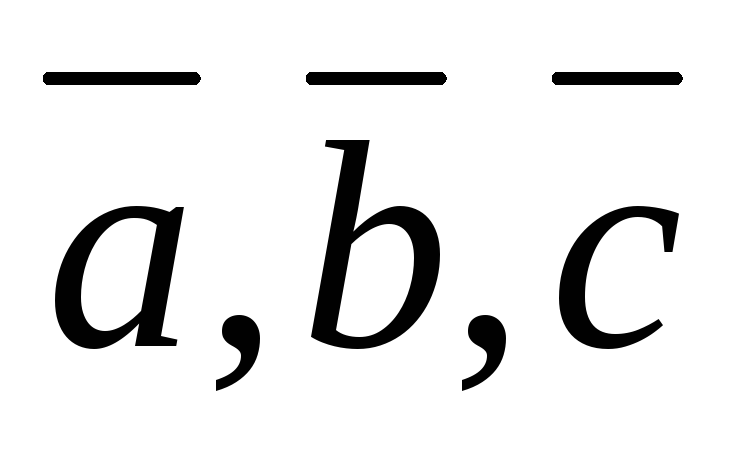 правая тройка, то есть той же ориентации,
что и
правая тройка, то есть той же ориентации,
что и 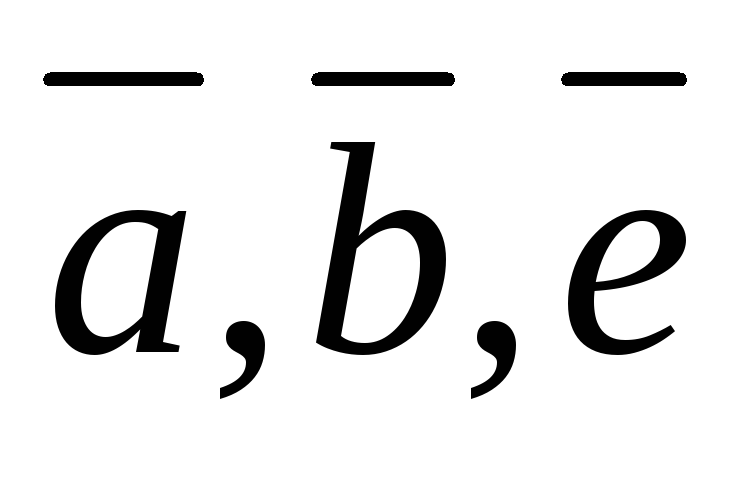 .
.
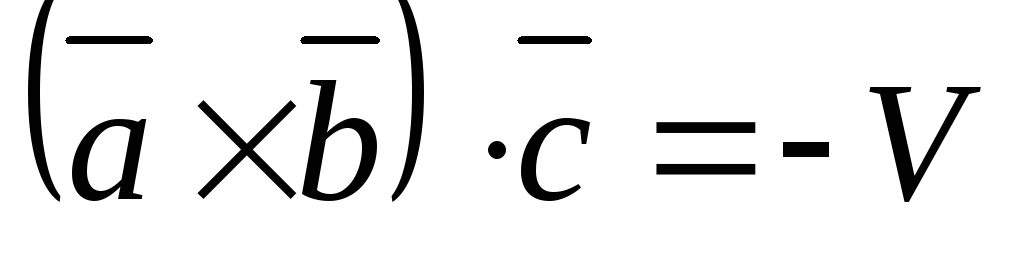 ,
а
,
а  ,
если тройка
,
если тройка  левая.
левая.
Если
векторы  –
компланарны, то
–
компланарны, то  .
.
Следствие
1. 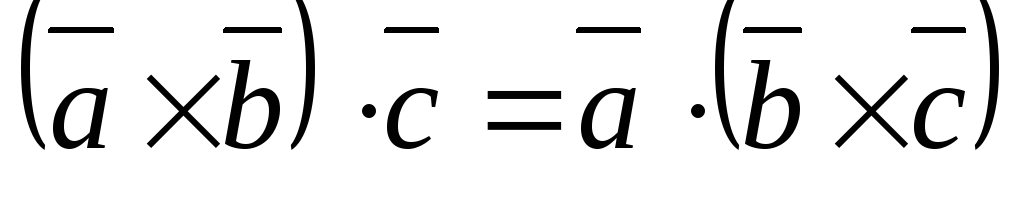 .
.
Доказательство. Скалярное произведение векторов коммутативно, следовательно
 .
.
По
теореме 2: 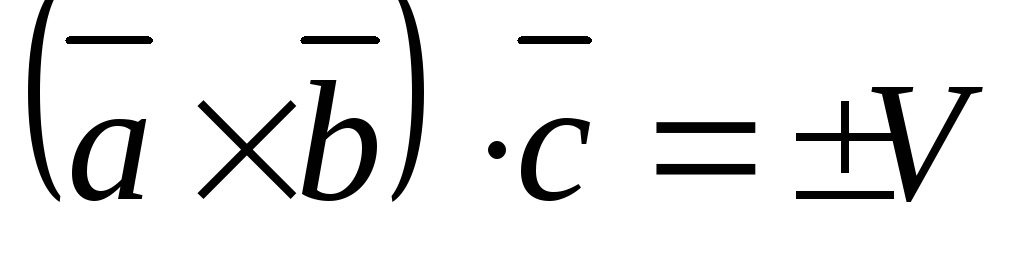 ,
,  .
.
Далее
будем обозначать смешанное произведение  ,
так как
.
,
так как
.
Следствие 2. Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны.
Выражение смешанного произведения через координаты векторов
Теорема
3. Пусть векторы 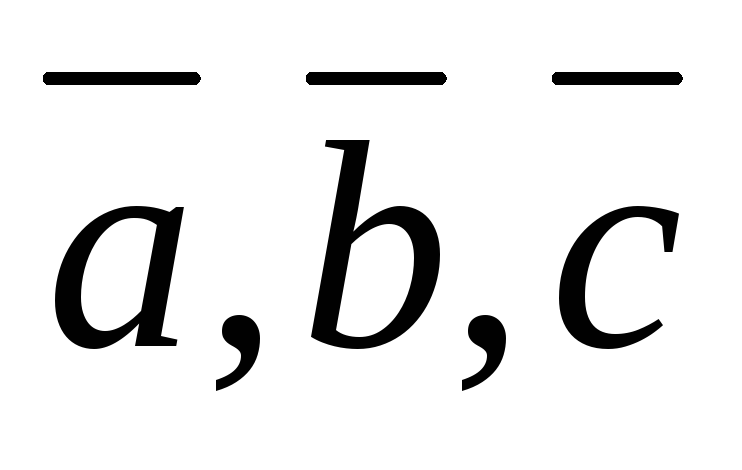 имеют в ортонормированном базисе
координаты
имеют в ортонормированном базисе
координаты  .
Тогда смешанное произведение этих
векторов можно представить в виде
.
Тогда смешанное произведение этих
векторов можно представить в виде
 .
.
Доказательство. 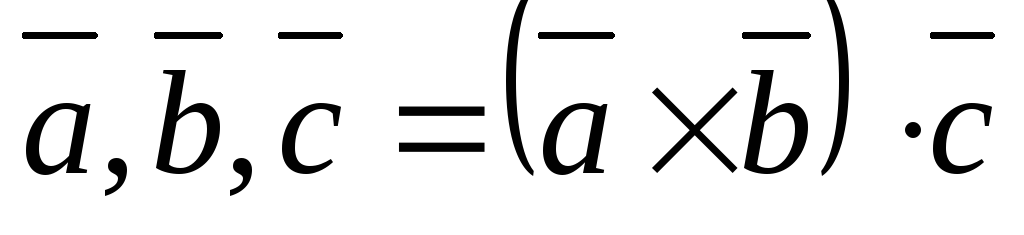 .
.
По теореме о векторном произведении:
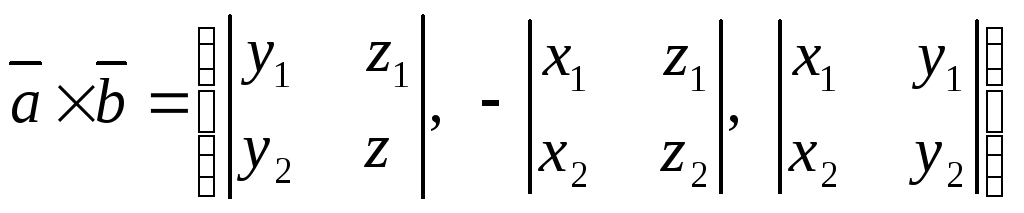 .
.
Умножим
векторное произведение скалярно на
вектор  :
:
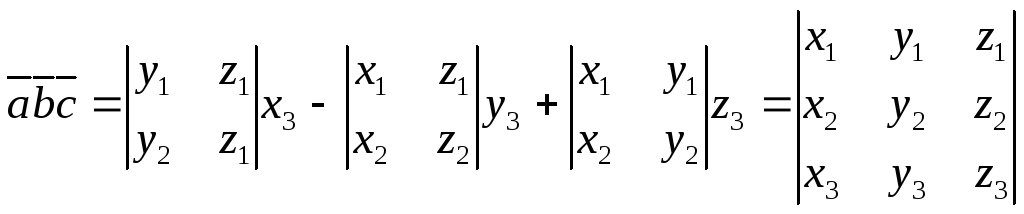 .
.
По следствию 2 необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, составленного из координат векторов:
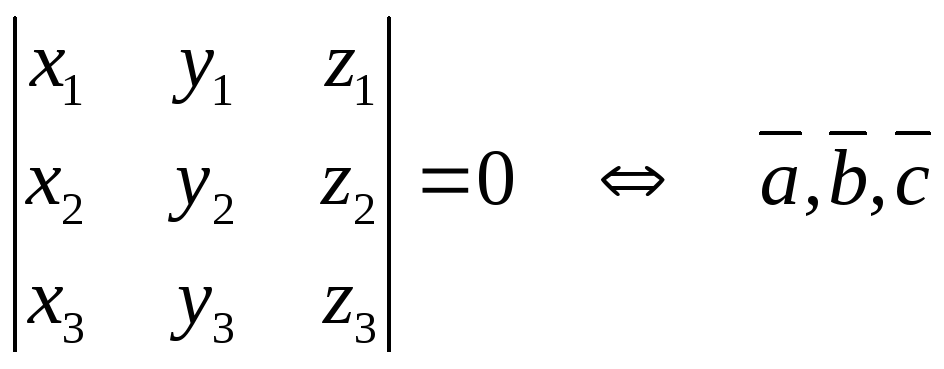 компланарны.
компланарны.
Пример
3. Даны четыре точки: 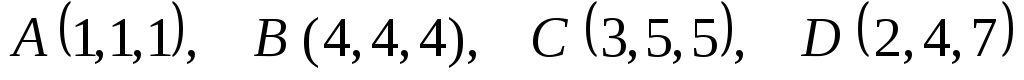 .
Найти объем тетраэдраАВСD.
.
Найти объем тетраэдраАВСD.
Решение. Объем тетраэдра равен одной шестой объема параллелепипеда с теми же основанием и высотой:
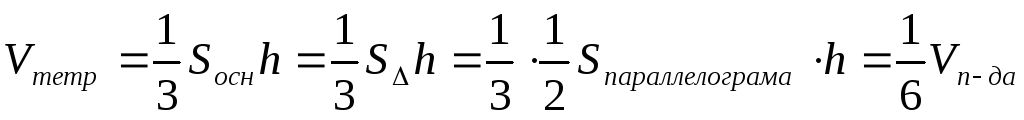 .
.
Координаты векторов .
По теореме 3
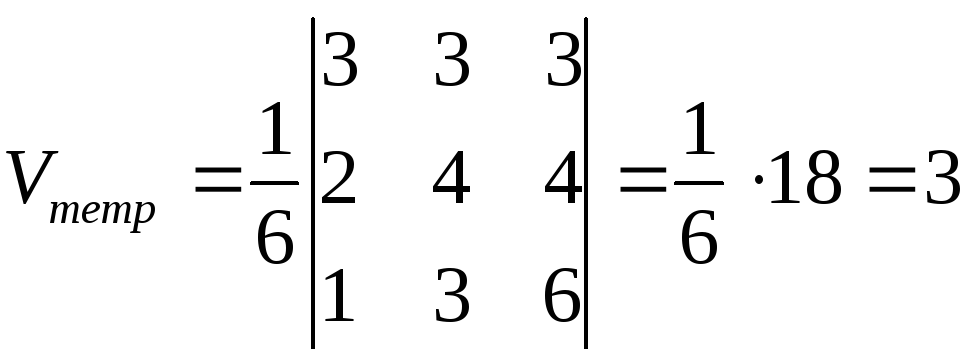 .
.
Скалярное произведение векторов
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; … ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Примеры задач на вычисление скалярного произведения векторов
Примеры вычисления скалярного произведения векторов для плоских задач
Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b == 5 |a|2 + 12 a · b — 9 |b|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ — 9 · 22 = 45 +36 -36 = 45.
Пример 4. Найти скалярное произведение векторов (a + 2i)·(b — 2j),если a = {1; 2} и b = {4; -8}.Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:
a = i + 2jb = 4i — 8j
Тогда используя свойства ортов (i2 = 1, j2 = 1, i·j = 0)
(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i2 — 30i·j + 12j·i — 20j2 = 12 — 0 + 0 — 20 = -8
Пример вычисления скалярного произведения векторов для пространственных задач
Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.
Скалярное произведение в координатах / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
- Скалярное произведение в координатах
Теорема
Доказательство
Дано: 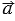
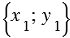 ,
, 
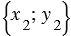
Доказать: 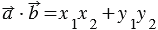
Доказательство:
Каждая координата вектора равна разности соответствующих координат его конца и начала, поэтому если хотя бы один из векторов нулевой, то справедливость равенства очевидна, так как координаты нулевого вектора равны нулю.
Рассмотрим ненулевые векторы 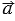 и
и  . Отложим от произвольной точки О векторы
. Отложим от произвольной точки О векторы 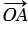 =
= 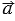 и
и 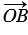 =
=  :
:
1 случай: векторы 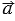 и
и  не коллинеарны:
не коллинеарны:

Тогда по теореме косинусов получаем
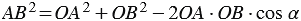 . (2)
. (2)
2 случай: векторы 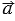 и
и  сонаправленные:
сонаправленные:

Тогда 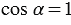 и получаем, что
и получаем, что

3 случай: векторы 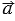 и
и  противоположно направленные:
противоположно направленные:
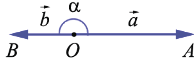
Тогда 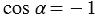 и получаем, что
и получаем, что

Итак, мы получили, что равенство (2) верно для любых двух ненулевых векторов 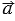 и
и  .
.
Так как 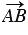 =
=  —
— 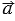 ,
, 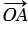 =
= 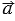 ,
, 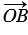 =
=  , то равенство (2) можно записать следующим образом:
, то равенство (2) можно записать следующим образом:

Следовательно,
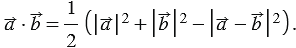
Вектора имеют следующие координаты 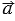
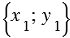 ,
, 
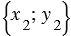 и (
и ( —
— 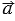 )
)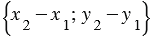 , при этом длина вектора равна квадратному корню из суммы квадратов координат данного вектора, поэтому
, при этом длина вектора равна квадратному корню из суммы квадратов координат данного вектора, поэтому
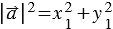 ,
, 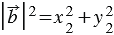
Учитывая это, получаем

Итак, 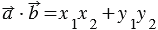 , что и требовалось доказать. Теорема доказана.
, что и требовалось доказать. Теорема доказана.
Следствие 1
Следствие 2
Косинус угла
|
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Теорема синусов
Теорема косинусов
Решение треугольников
Измерительные работы
Угол между векторами
Скалярное произведение векторов
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1044, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1073, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright


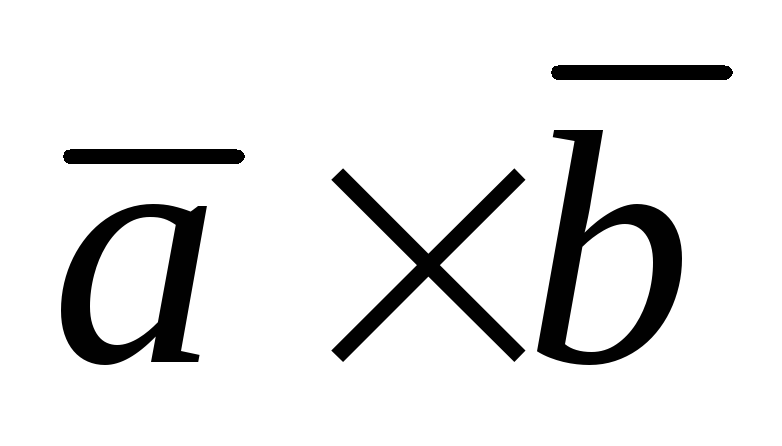 равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
равно нулю тогда и только тогда, когда
эти векторы коллинеарны: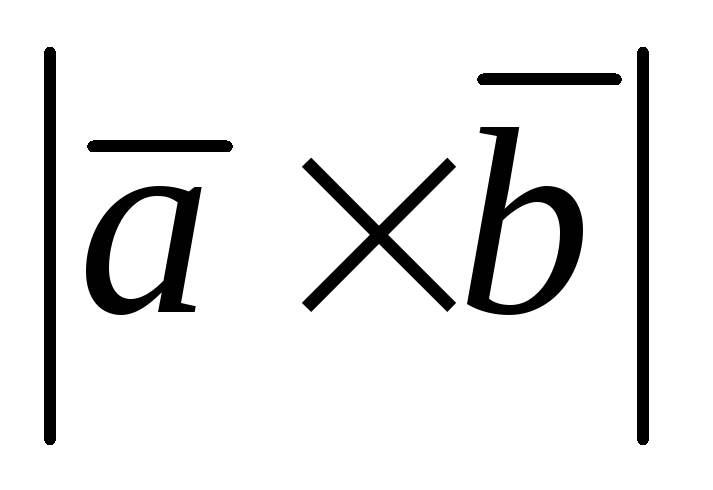 равен площади параллелограмма,
построенного на этих векторах.
равен площади параллелограмма,
построенного на этих векторах.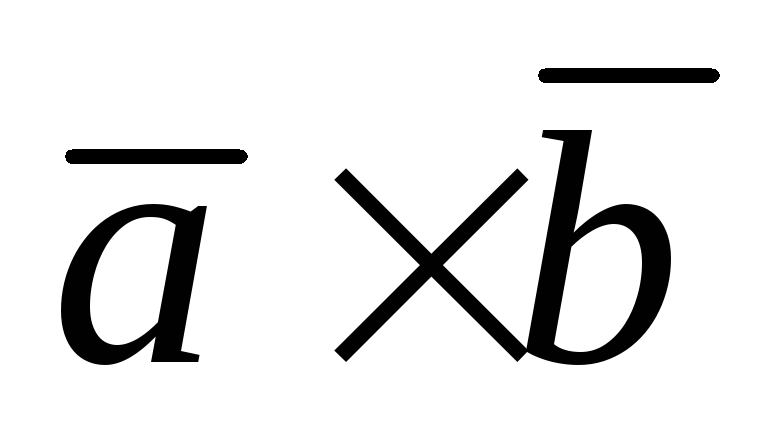 =
= 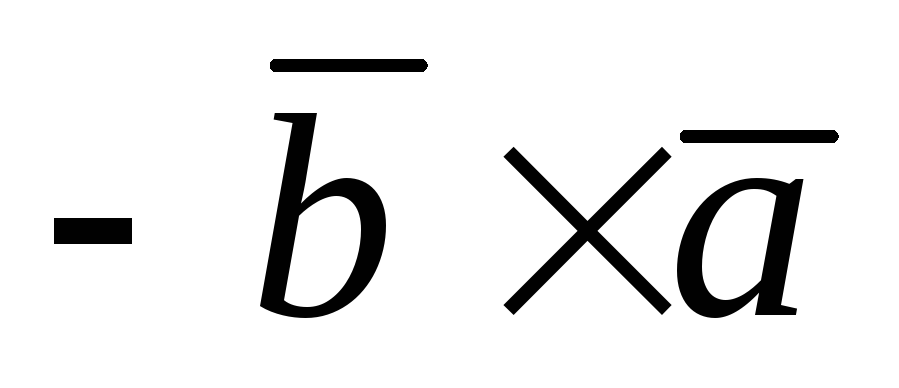
 между ненулевыми векторами
между ненулевыми векторами  и
и  выражается формулой
выражается формулой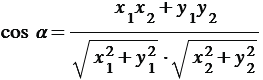 .
.