{2}$ и называется скалярный квадрат.

3  Если $\overline{a} \neq \overline{0}$, то

4  Если $\overline{a} \neq \overline{0}$ и $\overline{b} \neq \overline{0}$ и $(\overline{a}, \overline{b})=0$, то $\overline{a} \perp \overline{b}$. Верно и обратное утверждение.

5  $(\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c})$

6  $(\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b})$

7  $(\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d})$

Если векторы $\overline{a}$ и $\overline{b}$ заданы своими координатами: $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$ , то их скалярное произведение вычисляется по формуле:

1

$(\overline{a}, \overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}$

Определение

Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат. {\circ}$$

Читать дальше: векторное произведение векторов.

Скалярное произведение векторов — урок. Геометрия, 9 класс.

Скалярным произведением двух векторов a→ и b→ будет скалярная величина (число), равная произведению модулей этих векторов, умноженная на косинус угла между ними:

a→⋅b→=a→⋅b→⋅cosα.

 

Очень важно правильно определить угол между векторами. Если векторы не имеют общей начальной точки, необходимо представить, какой угол бы образовался, если их переместить к общей начальной точке.

 

Угол между векторами обозначают a→b→ˆ=α.

 

1. Если векторы сонаправлены, то a→b→ˆ=0°.

 

Обрати внимание!

Так как косинус угла в \(0\) градусов равен \(1\), то скалярное произведение сонаправленных векторов является произведением их длин.

Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.

2. Если векторы противоположно направлены, то a→b→ˆ=180°.

 

Обрати внимание!

Так как косинус угла в \(180\) градусов равен \(-1\), то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.

3. Векторы называют перпендикулярными, если a→b→ˆ=90°.

 

Обрати внимание!

Так как косинус прямого угла равен \(0\), то скалярное произведение перпендикулярных векторов равно \(0\).

4. Необходимо внимательно рассмотреть ситуации, когда векторы образуют тупой угол.

 

 

Обрати внимание!

Так как косинус тупого угла отрицательный, то скалярное произведение таких векторов, которые образуют тупой угол, является отрицательным.

Скалярное произведение векторов, заданных координатами

Если a→xa;ya и b→xb;yb, то a→⋅b→=xa⋅xb+ya⋅yb.

 

Так как в координатах a→=xa2+ya2 и b→=xb2+yb2, то можно определить косинус угла между векторами и, следовательно, величину угла.

 

cosα=a→⋅b→a→⋅b→;cosα=xa⋅xb+ya⋅ybxa2+ya2⋅xb2+yb2.

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нулю. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору.

 

a→⋅a→>0;0→⋅0→=0.

2. Скалярное произведение вектора самого на себя равно квадрату его модуля:

a→⋅a→=a→2.

 

3. Для скалярного произведения в силе переместительный закон:

a→⋅b→=b→⋅a→.

 

4. Для скалярного произведения в силе распределительный закон:

 

a→+b→⋅c→=a→⋅c→+b→⋅c→.

 

5.  Для скалярного произведения в силе сочетательный закон:

 

k⋅a→⋅b→=k⋅a→⋅b→.

 

6. Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны.

Скалярное произведение в координатах

На прошлых занятиях к уже известным действиям над векторами, а именно сложению, вычитанию и умножению вектора на число, мы добавили скалярное умножение векторов.

Мы говорили, что результатом первых трёх действий является некоторый вектор, а вот результатом скалярного умножения векторов — число.

Причём скалярное произведение равно 0, если хотя бы один из векторов нулевой. В случае, когда оба вектора ненулевые, скалярное произведение может принимать положительное значение, если угол между векторами острый, отрицательное значение, если угол между векторами тупой. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Вы знаете, что каждый вектор имеет свои координаты. В связи с этим ранее нами были получены правила, позволяющие выражать координаты вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

Так каждая координата вектора суммы равна сумме соответствующих координат данных векторов.

,

Каждая координата вектора разности двух векторов равна разности соответствующих координат данных векторов.

,

И каждая координата произведения вектора на число равна произведению соответствующих координат данного вектора на это число.

Понятно, что и скалярное произведение векторов можно выразить некоторым образом через координаты данных векторов.

Теорема. В прямоугольной системе координат скалярное произведение векторов  и  выражается формулой:

Доказательство.

,

,

,

, , то

 

 

,

 

Что и требовалось доказать.

Скалярное произведение векторов равно сумме произведений их соответствующих координат.

Выполним задание, где применим эту формулу.

Задача. Найти скалярное произведение векторов , , , если , , .

Решение.

Получается, что, зная координаты векторов, мы можем выяснить, перпендикулярны они или нет.

И в связи с изученной сегодня формулой, можно записать следствие из теоремы.

Следствие 1. Ненулевые векторы  и  перпендикулярны тогда и только тогда, когда .

Какие из данных векторов являются перпендикулярными для вектора ?

                                                   

Для этого сумма произведений соответствующих координат векторов должна быть равна нулю.

Составим такие выражения для вектора с каждым из векторов ,   и .

Проверим пары векторов.

 

 

 

 

Мы получили, что только два вектора,  и , являются перпендикулярными вектору .

А теперь рассмотрим ещё одно следствие из теоремы.

Следствие 2. Косинус угла  между ненулевыми векторами  и  выражается формулой: .

 

Действительно, из формулы скалярного произведения

.

Найти косинусы углов между векторами , , .  Если , , , , , .

Запишем формулу косинуса угла между векторами

Так мы рассмотрели примеры вычисления косинуса угла между векторами по их координатам.

А теперь выполним такое задание.

Задача. Определить, при каких значениях переменной  .

,

,

,

,

Решение.

По следствию, записанному сегодня, можно записать, что для того, чтобы векторы  были перпендикулярны, сумма произведений их координат должна равняться нулю.

 

  

 

 

 

 

 

 

 

 

 

В каждом из этих пунктов мы определили значение переменной x, при котором векторы будут перпендикулярны.

Задача. Доказать, что треугольник с вершинами ,  и  тупоугольный и найти косинус тупого угла.

Решение.

Нужно доказать, что треугольник с вершинами А, B и C тупоугольный и найти косинус тупого угла.

В нашем треугольнике ABC три угла. Чтобы доказать, что он тупоугольный достаточно найти косинус каждого угла и проанализировать его величину.

Если косинус одного из углов окажется меньшим нуля, то тем самым мы докажем, что данный угол тупой, а треугольник — тупоугольный.

Мы умеем находить косинус угла между векторами по их координатам.

Чтобы воспользоваться изученной формулой косинуса угла между векторами, нужно знать их координаты.

Найдём их как разности соответствующих координат конца и начала вектора.

 

 острый

 острый

 тупой

Тем самым мы доказали, что треугольник ABC — тупоугольный, и нашли косинус тупого угла.

Что и требовалось доказать.

Ответ: .

Подведём итоги урока.

Сегодня мы с вами получили формулу скалярного произведения векторов в координатах.

А также сформулировали следствия из данной теоремы.

Первое из них гласит, что ненулевые векторы перпендикулярны тогда и только тогда, когда сумма произведений их соответствующих координат равна нулю.

Второе следствие позволяет находить косинус угла между векторами через их координаты.

Скалярное произведение векторов.

Навигация по странице:

Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В случае плоской задачи скалярное произведение векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Формула скалярного произведения n -мерных векторов

В случае n-мерного пространства скалярное произведение векторов a = {a

1 ; a₂ ; . .. ; a_n} и b = {b₁ ; b₂ ; … ; b_n} можно найти воспользовавшись следующей формулой:

a · b = a₁ · b₁ + a₂ · b₂ + … + a_n · b_n

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:

   a · a ≥ 0

2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:

   a · a = 0   <=>   a = 0

3. Скалярное произведение вектора самого на себя равно квадрату его модуля:

   a · a = |a|²

4. Операция скалярного умножения коммуникативна:

   a · b = b · a

5. Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

   a ≠ 0, b ≠ 0, a · b = 0   <=>   a ┴ b

6. (αa) · b = α(a · b)

7. Операция скалярного умножения дистрибутивна:

   (a + b) · c = a · c + b · c

Примеры задач на вычисление скалярного произведения векторов

Примеры вычисления скалярного произведения векторов для плоских задач

Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.

Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.

Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.

Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.

Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.

Решение:

p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =

= 5 |a|² + 12 a · b — 9 |b|² = 5 · 3² + 12 · 3 · 2 · cos 60˚ — 9 · 2² = 45 +36 -36 = 45.

Пример вычисления скалярного произведения векторов для пространственных задач

Пример 4. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.

Пример вычисления скалярного произведения для n -мерных векторов

Пример 5. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Скалярное умножение

Скалярное умножение

В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников

Суперобложка / Обложка / Содержание

 

 

Пусть нам даны два вектора и , которые заданы своими координатами в произвольной косоугольной системе координат , и :

; .

Как вычислить скалярное произведение этих векторов? Чему равно

Если бы речь шла о декартовой системе координат, то все было бы просто: . Однако для произвольной системы координат это равенство не выполняется. Тем не менее мы можем им воспользоваться. Для этого нам всего лишь необходимо перейти от произвольной системы координат к декартовой.

и

.

Теперь мы можем записать:

.

Введем обозначение:

 

.

Матрицу будем называть таблицей или матрицей координат метрического тензора.

Очевидно, что , или

.

Перепишем теперь формулу для скалярного умножения с учетом введенных обозначений:

, и в индексной форме:

.

Данная формула для скалярного произведения является общей. Она справедлива для произвольной косоугольной системы координат. В декартовой же системе матрица координат метрического тензора совпадает с единичной матрицей.

В самом деле, для декартовой системы

, и , следовательно, и

.

 

Метрический тензор представляет собой набор коэффициентов , привязанный к определенной системе координат. Если мы переходим к другой системе, то в общем случае будем иметь и другие коэффициенты метрического тензора, которые принято называть координатами. Координаты метрического тензора зависят от выбранной координатной системы и непосредственно выражаются через ее базисные векторы. Тем не менее метрический тензор, также как и вектор, отражает вполне определенную геометрическую реальность, поскольку его координаты в различных координатных системах связаны известным законом преобразования.

Найдем закон преобразования координат метрического тензора.

, следовательно,

и есть искомый закон преобразования координат метрического тензора в индексной и в матричной формах. Мы обвели этот закон рамочкой, поскольку в тензорной алгебре он играет принципиальную роль, а нам он встретился впервые. В дальнейшем мы сможем убедиться, что этот закон проявляется при изучении самых разнообразных объектов. Для начала следует обратить внимание на принципиальное сходство его с законом преобразования координат вектора:

Закон преобразования координат вектора	Закон преобразования координат метрического тензора

Свойства метрического тензора.

1. Матрица координат метрического тензора симметрична.

Это свойство непосредственно следует из определения. В самом деле:

, но и, следовательно, .

2. Матрица метрического тензора определяет линейные размеры базисных векторов и углы между ними.

и .

.

В этих формулах не используется правило суммирования по повторяющимся индексам.

Метрический тензор аккумулирует в себе информацию о метрических свойствах пространства. Он необходим для вычисления длин векторов, углов между ними, расстояний между точками, площадей фигур и объемов тел. Иногда даже говорят, что метрический тензор определяет метрику пространства, хотя, если мы имеем дело с классической евклидовой геометрией, метрика всегда предполагается заданной. Необходимо только определиться с масштабами длин и углов. Но если мы имеем дело с некоторым абстрактным векторным пространством, понимая под векторами нечто отличное от направленных отрезков, мы можем столкнуться со случаями, когда расстояние между точками пространства определяется по другим правилам. Возможны также случаи, когда расстояние вообще нельзя никак определить. Векторные пространства, в которых правила для определения расстояниями между его точками не определены или не имеют смысла, называются аффинными, а свойства таких пространств изучает аффинная геометрия. Так вот, аффинную геометрию можно наделить метрическими свойствами и можно это сделать различными способами. Выбор способа и конкретного правила зависит от того, какую реальность мы хотим таким образом смоделировать. Одним из таких способов и является задание координат метрического тензора. В этом случае метрический тензор будет определять метрику пространства.

3. Матрица метрического тензора в ортонормированном базисе совпадает с единичной.

4. Закон преобразования координат метрического тензора

.

5. Определитель матрицы метрического тензора на плоскости равен квадрату площади базисного параллелограмма.

Докажем это.

Рис. 42

Обозначим площадь базисного параллелограмма , тогда .

Но . А . Следовательно,

.

Учитывая, что , получаем: .

6. Определитель матрицы метрического тензора в трехмерном пространстве равен квадрату объема базисного параллелепипеда.

Рис. 43

Построим параллелепипед на векторах , и (рис. 43). Из конца вектора опустим перпендикуляр h на основание: параллелограмм, построенный на векторах и . Объем параллелепипеда равен , где – площадь основания.

.

Для того чтобы вычислить объем, нам осталось найти высоту параллелепипеда h. Из точки пересечения высоты h и плоскости основания опустим перпендикуляры x и y на боковые ребра параллелепипеда. Перпендикуляры отсекут на ребрах при этом отрезки a и b. Длины отрезков мы можем найти как

, .

Из уравнения мы смогли бы найти h, если бы знали x.

Для того чтобы найти x, обратимся к рис. 44, на котором изображен вид сверху на плоскость основания параллелепипеда.

Рис. 44

Точка O является основанием высоты h, которая на рисунке не показана. x и y – перпендикуляры, опущенные на стороны параллелограмма, следовательно, треугольники и прямоугольные. Вертикальные углы и равны углу .

Катет BC прямоугольного треугольника с одной стороны равен

, с другой стороны, тот же катет равен .

Приравнивая эти выражения и умножая на , получаем первое уравнение:

.

Рассматривая второй прямоугольный треугольник , мы приходим ко второму уравнению: .

Заменяя a и b соответствующими выражениями, мы приходим к системе уравнений:

,

решая которую, находим x; y нам не нужен.

.

Подставляя x в уравнение , получаем:

.

Решая уравнение относительно , получаем:

.

Подставим полученное выражение в формулу для объема и произведем необходимые преобразования

.

Вот и все, осталось только узнать в полученном результате выражение для определителя. Развернем определитель метрического тензора, учитывая симметрию его элементов.

.

Теперь мы можем констатировать, что определитель матрицы метрического тензора равен квадрату объема параллелепипеда, построенного на векторах базиса:

.

Определитель метрического тензора часто возникает в уравнениях, поэтому для него используется специальное обозначение: .

Приведенное нами доказательство является чисто геометрическим. Оно не зависит от случайностей произвольного выбора координатных систем, оно использует только испытанные и вызывающие доверие приемы элементарной геометрии и в этом его достоинство. Однако, как и многие другие прямые геометрические доказательства, оно трудоемко и требует терпения и аккуратности. Развивая алгебраические идеи теории векторов, мы готовы дать другое, менее мучительное доказательство шестого свойства метрического тензора.

Воспользуемся законом преобразования координат метрического тензора. Пусть нам известны координаты метрического тензора в некоторой системе координат:

.

Перейдем к некоторой ортонормированной системе и найдем координаты метрического тензора в ней, воспользовавшись для этого законом преобразования координат.

, где звездочкой обозначен, как всегда, индекс, соответствующий названиям базисных векторов декартовой системы координат, а – матрица метрического тензора в декартовой системе. Но в декартовой системе координат матрица метрического тензора совпадет с единичной матрицей, следовательно: . Умножив полученное уравнение справа и слева на матрицы и , получим:

.

Теперь вспомнив, что ,

выразим .

Чтобы яснее было видно, что получилось, выпишем матрицы подробно:

.

Матрица составлена из координат векторов базиса в ортонормированной системе координат. Следовательно, ее определитель равен ориентированному объему параллелепипеда, построенного на векторах , и . А так как определитель произведения матриц равен произведению определителей, и определитель матрицы не изменяется от ее транспонирования, то:

, где s означает, как всегда, знак ориентированного объема.

Продемонстрируем еще одну идею доказательства.

Воспользуемся на этот раз определением

.

Воспользуемся некоторой ортонормированной системой координат. Выражая скалярные произведения через координаты векторов , и в ортонормированной системе, получим:

.

Ну а дальше, все как в предыдущем доказательстве.

7. Матрица метрического тензора симметричная и положительно определенная.

О том, что матрица симметричная мы уже говорили в первом нашем свойстве. Но между первым свойством и седьмым мы говорили об очень многих разных вещах, так что не грех будет и повториться. Что касается положительной определенности (напомним, что положительно определенной матрицей называется матрица, определитель которой больше нуля), то из шестого свойства сразу следует .

На этом, пожалуй, можно и закончить разговор о метрическом тензоре.

 

 

Скалярное и векторное произведения. Проекция вектора на вектор

В данной статье будут изложены основные инструкции, относительно векторов. С их помощью Вы будете знать что с ними можно делать, а что нет. Поэтому переходим к изучению операций над векторами.

І. Суммой двух -мерных векторов

и называют-мерный вектор , координаты которого равны сумме соответствующих координат векторов — слагаемых:

Например, если ,

то

Из этого правила следует, что разностью двух векторов будет вектор, координаты которого является разницей соответствующих координат векторов

ІІ. Произведением числа (скаляра) на -мерный вектор называется -мерный вектор , координаты которого равны произведению числа на соответствующие координаты вектора

Например

Операции сложения векторов и умножения числа на вектор ( — некоторые числа) обладают свойствами:

1)

2)

3)

4)

5)

6)

7) Для произвольного вектора существует противоположный вектор такой, что

ІІІ. Скалярным произведением двух -мерных векторов и называют число, равное сумме произведений соответствующих координат векторов:

Например,

если, то

Согласно другому определению, скалярное произведение двух векторов это число, равное произведению длин векторов (их модулей) на косинус угла между ними

Из приведенного выше определения можно получить формулу для вычисления угла между векторами

или в координатной форме

Также есть формулировка согласно которой скалярное произведение двух векторов равен модулю одного из них умноженному на проекцию второй вектор на направление первого

Из последнего определения вытекают формулы для нахождения проекции вектора на вектор

или в координатной форме

Примеры нахождения скалярного произведения, угла между векторами и проекции одного вектора на другой будут рассмотрены ниже.

Алгебраические свойства скалярного произведения векторов:

1)

2)

3)

4)Равенство имеет место при условии

Геометрические свойства скалярного произведения

1)векторы перпендикулярны между собой, если

2) угол между векторами острый в случаях, когда

3) угол между векторами тупой в случаях, когда

ІV. Векторным произведением или двух векторов называется вектор , который отвечает следующим условиям:

1) модуль вектора равен произведению модулей векторов и на синус угла между ними

2) вектор нормальный к плоскости, построенной на векторах и ;

3) вектор направлен так, что с его конца кратчайший поворот от вектора к происходит против часовой стрелки. Иными словами, векторы образуют правую тройку.

Векторное произведение имеет следующие геометрические свойства:

Его модуль равен площади параллелограмма построенного на векторах и

Поэтому площадь треугольника построенного на векторах и равна модулю половины векторного произведения этих векторов

Алгебраические свойства векторного произведения

1) векторное произведение равно нулю в случае коллинеарности векторов или когда один из них нулевой;

2) от перестановки векторов векторное произведение меняет знак на противоположный

3)

4)

На практике важно иметь под рукой формулу для вычисления векторного произведения в координатной форме, поэтому запишем и ее

Рассмотрим конкретные примеры для усвоения пройденного материала.

———————————————

Задача 1.

Заданы векторы и

Найти следующие величины

1) сумму векторов

2) скалярное произведение векторов

3) ) векторное произведение площадь треугольника построенного на векторах

4) угол между векторами

5) проекцию каждого из векторов на другой

Решение

1) Проведем вычисления

2) Скалярное произведение будет равно

3) Векторное произведение вычисляем по формуле

Площадь треугольника будет равна

4) Найдем угол между векторами по формуле

В ней скалярное произведение уже найдено поэтому находим длины векторов

Подставляем нужные значения в формулу

Находим значение угла

5) Найдем проекции векторов

Проекции векторов можно искать через косинус угла между векторами, результат от этого не изменится

На этом урок окончен. Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.

——————————————————

Посмотреть материалы:

Урок геометрии в 9 классе по теме «Скалярное произведение векторов в координатах»

Тема урока: Скалярное произведение векторов в координатах

Задачи урока:

• закрепить умение находить угол между векторами;

• повторить понятие скалярного произведения и закрепить умение применять его при решении задач;

• сформулировать и доказать теорему о скалярном произведении двух векторов в координатах и ее следствия;

• познакомить учащихся со свойствами скалярного произведения векторов;

• показать применение скалярного произведения векторов в координатах при решении задач.

I. Проверка домашней работы

Вспомним: очень важно правильно определить угол между векторами. Если векторы не имеют общей начальной точки, необходимо представить, какой угол бы образовался, если их переместить к общей начальной точке.

№ 1039. Решение:

Вспомним свойства квадрата:

1. Все углы квадрата прямые.

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Переместим векторы АС и BD в общую начальную точку О.

Тогда .

ж)

Переместим вектор DB в общую точку А, получится вектор АМ. Тогда

з)

Векторы АО и ОС — сонаправленные. Значит .

Выполните решение следующей задачи в тетради. К каждому случаю сделайте чертеж.

Дан квадрат ABCD, точка O пересечения диагоналей AC и BD. Найдите угол между векторами: 1) CD и CA, 2) AO и OА, 3) AD и ВD, 4) АO и СO, 5)  AC и DВ.  

II. Повторение (организуется в виде фронтального опроса)

a⃗  и b⃗  называется произведение их длин (модулей этих векторов) на косинус угла между ними: a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cosα.

1. Если векторы сонаправлены, то a⃗ˆb⃗ =0°:

0 равен 1, то скалярное произведение сонаправленных векторов является произведением их длин: a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 0=|a⃗|⋅|b⃗|⋅1=|a⃗|⋅|b⃗|.

Если два вектора равны, то такое скалярное произведение называют скалярным квадратом: a⃗⋅a⃗ =|a⃗|⋅| a⃗|⋅cos 0=|a⃗|⋅| a⃗|⋅1=|a⃗|²= a⃗².

2. Если векторы противоположно направлены, то a⃗ˆb⃗ =180°:

Так как косинус угла в 180 равен (-1), то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин:

a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 180=|a⃗|⋅|b⃗|⋅(-1) = — |a⃗|⋅|b⃗|.

3. Векторы называют перпендикулярными, если a⃗ˆb⃗ =90°:

, то скалярное произведение перпендикулярных векторов равно 0: a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 90=0.

4. Внимательно рассматриваются ситуации, когда векторы образуют тупой угол:

 

Таблица значений синуса, косинуса, тангенса и котангенса некоторых углов

Пример 1. Учащийся у доски

Решение:

Пример 2. Выполнить самостоятельно по вариантам в тетрадях

1 вариант (Ответ в первой задаче ).

2 вариант (Ответ в первой задаче ).

III. Новый материал

1) Сформулируем и докажем центральную теорему урока

Теорема. Скалярное произведение векторов  и  выражается формулой

Доказательство.

1. При  или  теорема очевидна.

2. Пусть  и  – ненулевые векторы. Тогда по теореме косинусов

Перейдем в этой формуле к координатам.

Уточним, что теорема доказана для случая неколлинеарных векторов, в доказательстве был использован треугольник, теорема косинусов, поэтому случай коллинеарных векторов тоже рассмотрим, при этом учтем, что угол между коллинеарными векторами может быть равен 180° или 0°.

3. Пусть

Подгоним это равенство под формулу, полученную при доказательстве теоремы.

Формула та же самая, если записать ее в координатах, то получим

4. Аналогично рассмотрим случай 

Вывод:  для всех векторов   и .

2) Следствия из теоремы

Сформулируем следствия из доказанной теоремы.

Следствие 1. Ненулевые векторы  и  перпендикулярны тогда и только тогда, когда  .

Действительно,  .

Следствие 2. Косинус угла между ненулевыми векторами  и  выражается формулой:

Действительно,

3) Свойства скалярного произведения векторов

Рассмотрим свойства скалярного произведения векторов.

Для любых векторов  и любого числа k справедливы соотношения:

1. , причем  при  .

Доказательство.

Но  при  .

2.  (переместительный закон).

Доказательство (из определения).

3.  (распределительный закон).

Доказательство.

Для доказательства используем метод координат.

 , тогда

.

 

4.   (сочетательный закон).

Доказательство.

, значит,

Замечание. Распределительный закон справедлив и в случае нескольких слагаемых, например,

.

IV Закрепление. Пример 1. Записать в тетрадь

Решение:

Пример 2. Выполнить самостоятельно по вариантам в тетрадях

1 вариант

2 вариант

Пример 3. Записать в тетрадь

Решение:

Пример 4. Выполнить самостоятельно по вариантам в тетрадях

1 вариант

2 вариант

Выводы:

1. Повторили понятие угла между векторами, понятие скалярного произведения.

2. Повторили, как определять угол между векторами, повторили, как вычислять скалярное произведение, если известны длины векторов и угол между ними.

3. Научились вычислять скалярное произведение в координатах, научились находить угол между векторами по их координатам.

4. Сформулировали и доказали теорему о скалярном произведении двух векторов в координатах и ее следствия.

5. Познакомились со свойствами скалярного произведения векторов.

6. Научились вычислять скалярное произведение векторов в координатах, научились вычислять угол между векторами.

Домашнее задание: № 1044(а, б, в), № 1048.

Использованные источники:

1. Атанасян Л. С. и др. Геометрия 7–9 классы.

2. http://www.yaklass.ru/p/geometria/9-klass/sootnoshenie-mezhdu-storonami-i-uglami-treugolnika-skaliarnoe-proizvedenie_-9222/skaliarnoe-proizvedenie-vektorov

3. https://interneturok.ru/geometry/9-klass/skalyarnoe-proizvedenie-vektorov/skalyarnoe-proizvedenie-v-koordinatah-svoystvo-skalyarnogo-proizvedeniya

Как умножить векторы — Скалярное (точечное) произведение

Как умножить векторы

Ключевые термины

Единичный вектор

Скалярное (точечное) произведение

Цели

Определите концепцию единичных векторов

Использовать единичные векторы для алгебраического представления векторов

Определить умножение скаляра и вектора

Используйте скалярное произведение, чтобы вычислить длину вектора

В этой статье мы рассмотрим другое представление векторов, а также основы умножения векторов.

Единичные векторы

Хотя координатная форма для представления векторов ясна, мы также можем представить их в виде алгебраических выражений с использованием единичных векторов. В наших стандартных прямоугольных (или евклидовых) координатах ( x, y, и z ) единичный вектор — это вектор длины 1, параллельный одной из осей. В двумерной координатной плоскости единичные векторы часто называются i и j, , как показано на графике ниже.Для трех измерений мы добавляем единичный вектор k , соответствующий направлению оси z . Эти векторы определяются алгебраически следующим образом.

i = (1, 0) или (1, 0, 0)

j = (0, 1) или (0, 1, 0)

к = (0, 0, 1)

Прежде чем мы представим алгебраическое представление векторов с помощью единичных векторов, мы должны сначала ввести умножение векторов — в данном случае на скаляры.

Умножение вектора на скаляр

Умножение векторов сложнее, чем умножение только скаляров, поэтому мы должны относиться к предмету осторожно. Начнем с простейшего случая: умножения вектора на скаляр. Ниже приведено определение умножения скаляра c на вектор a, , где a = ( x, y ). (Опять же, мы можем легко расширить эти принципы до трех измерений.)

Скалярное умножение коммутативно, поэтому . Но что означает это умножение? Как оказалось, умножение на скаляр c увеличивает длину вектора в c. Это наиболее ясно видно с единичными векторами, но это применимо к любому вектору. (Однако умножение на отрицательный скаляр меняет направление вектора на противоположное.На приведенном ниже графике показаны некоторые примеры с использованием c = 2. (Напомним, что расположение вектора не влияет на его значение.)

Практическая задача: Для вектора a = (3, 1) найдите вектор в том же направлении, что и a , но вдвое больше его длины.

Решение: Когда мы умножаем вектор на скаляр, направление вектора произведения совпадает с направлением множителя.Единственная разница в том, что длина умножается на скаляр. Итак, чтобы получить вектор, который в два раза длиннее a , но в том же направлении, что и a, просто умножьте на 2.

2 a = 2 • (3, 1) = (2 • 3, 2 • 1) = (6, 2)

Алгебраическое представление векторов

Мы можем использовать скалярное умножение с векторами для алгебраического представления векторов.Обратите внимание, что любой двумерный вектор v может быть представлен как сумма длины, умноженной на единичный вектор i , и другой длины, умноженной на единичный вектор j. Например, рассмотрим вектор (2, 4). Примените правила векторов, которые мы узнали до сих пор:

(2, 4) = (2, 0) + (0, 4) (правило сложения для векторов)

(2, 4) = 2 • (1, 0) + 4 • (0, 1) (правило умножения для скаляров и векторов)

(2, 4) = 2 i + 4 j

Графически мы складываем два вектора в единичных направлениях, чтобы получить произвольный вектор.

Обратите внимание, что единичные векторы действуют почти идентично переменным. Таким образом, мы можем сложить два вектора a и b следующим образом.

a = 3 i — 2 j b = i + 3 j

a + b = (3 i — 2 j ) + ( i + 3 j ) = 3 i + i — 2 j + 3 j = 4 i + j

Это представление обеспечивает большую гибкость, чем представление координат, но оно эквивалентно.

Практическая задача: Вычислить сумму и разность ( t — u ) векторов t = -2 i + 3 j и u = 6 i — 4 j .

Решение: Мы можем довольно легко решить эту задачу алгебраически.

t + u = (-2 i + 3 j ) + (6 i — 4 j ) = 4 i — j = (4, -1)

t — u = (-2 i + 3 j ) — (6 i — 4 j ) = -2 i + 3 j — 6 i + 4 j = -8 i + 7 j = (-8, 7)

Векторное умножение: скалярное (точечное) произведение

Умножение двух векторов немного сложнее, чем скалярное умножение. Определены два типа умножения с участием двух векторов: так называемое скалярное произведение (или «скалярное произведение») и так называемое векторное произведение (или «перекрестное произведение»). Для простоты мы обратимся только к скалярному произведению, но на этом этапе у вас должна быть достаточная математическая основа, чтобы понять и векторное произведение. Скалярное произведение (или скалярное произведение ) двух векторов определяется следующим образом в двух измерениях. Как всегда, это определение можно легко расширить до трех измерений — просто следуйте шаблону.Обратите внимание, что операция всегда должна обозначаться точкой (•), чтобы отличать от векторного произведения, в котором используется символ времени () — отсюда и названия скалярное произведение и перекрестное произведение .

Однако значение этого продукта может быть вам не совсем понятно на данном этапе. Мы можем проиллюстрировать это, посмотрев на простой случай: скалярное произведение произвольного вектора v и единичных векторов i и j.

Таким образом, v • i является «частью» вектора v в направлении I.

Однако это объяснение работает только для векторов длины 1.Когда два произвольных вектора умножаются, скалярное произведение имеет аналогичное значение, но величина числа немного отличается. Мы не будем углубляться в это, но мы можем рассмотреть особый случай, когда скалярное произведение дает ценную информацию.

Длина вектора

Рассмотрим случай скалярного произведения вектора v на себя.

Давайте посмотрим на эту ситуацию графически.

В результате получается прямоугольный треугольник с горизонтальным участком длиной x и вертикальным участком длиной y. Эти длины соответствуют длинам составляющих векторов x i и y j, соответственно. Но мы знаем из теоремы Пифагора, что — это квадрат длины вектора v . Не случайно, это то же самое, что скалярное произведение v на себя. Таким образом, длина любого вектора v, , записанного как (или иногда ), является квадратным корнем из скалярного произведения.

В простом случае единичных векторов

Эти простые случаи помогают проверить эту интерпретацию скалярного произведения.

Практическая задача: Рассчитайте длины следующих векторов.

а. г. 3 i + 2 j — k c. (2, –1) d. 5 к

Решение: В каждом случае просто возьмите квадратный корень из скалярного произведения вектора на себя. Результат — длина вектора в каждом случае. Что касается части b, просто расширите определение скалярного произведения до трех измерений.

а.

г.

г.

г.

Векторы Вектор — это величина, имеющая величину и направление. Для математического описания вектора используется система координат обычно выбирают с ортогональными осями. В этом тексте используется декартовой, круговой цилиндрической и сферической координат системы. В этих трехмерных системах любой вектор полностью описывается тремя скалярными величинами. Например, в декартовом координаты, вектор описывается со ссылкой на взаимно ортогональные оси координат. Тогда величина и ориентация вектор описывается указанием трех проекций вектор на три оси координат. При математическом представлении вектора A его направление по трем ортогональным координатным осям.В направление каждой оси представлено единичным вектором i , что есть, вектор единичной величины, направленный вдоль оси. В картезианском координаты, три единичных вектора обозначены i x , i y , i z . В цилиндрических координатах это i r , i , i z , а в сферических координатах i r , i , я . А , значит, имеет три компоненты вектора, каждый компонент соответствует проекции по трем осям. В декартовых координатах a вектор определяется в терминах его компонентов как Эти компоненты показаны на рис. А.1.1. 1 Обычно указываются векторы либо с полужирным шрифтом, например, A , либо путем рисования линия (или стрелка) над символом, чтобы указать на его векторную природу, как в \ bar A или \ vec A . Рисунок A.1.1 Вектор A , представленный его компонентами в декартовых координатах и ​​единичных векторах i . Сложение вектора Сумма двух векторов A = A x i x + A y i y + A z i z и B = B x i x + B y i y + B z i z осуществляется путем сложения коэффициентов каждого из компонентов, как показаны в двух измерениях на рис. A.1.2a. Таким образом, из (2) должно быть ясно, что сложение векторов одновременно коммутативный, A + B = B + A , и ассоциативный, ( A + B ) + C = A + ( B + C ) . Рисунок A.1.2 (a) Графическое представление сложения векторов в терминах определенных координат. (b) Представление сложения векторов независимо от конкретных координат.Графически суммирование векторов может выполняться без учета систему координат, как показано на рис. A.1.2b, заметив, что сумма A + B является вектором, направленным вдоль диагональ параллелограмма, образованная A и B . Следует отметить, что представление вектора в терминах его компоненты зависят от системы координат, в которой он выполненный. То есть для изменения системы координат потребуется соответствующее векторное преобразование.Кроме того, используемые переменные также должны преобразиться. Преобразование переменных и векторов из одного система координат в другую проиллюстрирована рассмотрением одной преобразование декартовых координат в сферические. Пример 1.2.1. Преобразование переменных и векторов Нам даны переменные в терминах x, y и z , а также векторы, такие как A = A x i x + A y i y + A z i z .Мы хотите получить переменные в терминах r, и и векторы, выраженные как A = A r i r + A i + А i . На рис. A.1.3a мы видим, что точка P имеет два представления, в одном из которых входят переменные x, y и z , а прочие, r, и . В частности, из Инжир.A.1.3b, x связано со сферическими координатами соотношением Рисунок A. 1.3 Задание точки P в декартовых и сферических координатах. (b) Преобразование из декартовых координат x в сферические координаты. (c) Преобразование единичного вектора в направлении x в сферические координаты Аналогичным образом переменные y и z оцениваются в сферическом координаты могут быть показаны как Вектор A преобразуется путем разрешения каждой единицы векторов i x , i y , i z в терминах единичных векторов в сферические координаты.Например, i x может быть сначала разрешено на компоненты в ортогональных координатах (x ‘, y ‘, z) показано на рис. A.1.3c. По определению, y ‘ находится на пересечении константы = и самолеты x-y . Также в плоскости x — y x ‘ , что составляет перпендикулярно плоскости y ‘ — z . Таким образом, sin, cos и 0 являются компонентами i x вдоль x ‘, y ‘ и z осей соответственно.Эти компоненты в свою очередь разделены на компоненты по сферическим координатным направлениям с помощью распознавая, что компонент согрешает на вдоль оси x ‘ находится в направлении — i , а составляющая cos по оси y ‘ разлагается на составляющие cos cos в направлении i и cos sin в направлении i r .Таким образом, По аналогии, Следует подчеркнуть, что понятие вектора не зависит от системы координат. (В том же смысле в главах 2 и 4 векторные операции определяются независимо от системы координат в котором они выражены.) A вектор может быть визуализирован как имеющий направление и величину элемент линии со стрелкой. Эта картина дает возможность разобраться с векторами на геометрическом языке, который не зависит от выбор конкретной системы координат, которая теперь будет использоваться для определить наиболее важные векторные операции. Для аналитических или численных целей операции обычно выполняется в координатной записи. Затем, как показано на рисунке, либо в следующем тексте, либо в задачах каждая операция будет оцениваться в декартовой системе координат. Определение скалярного произведения Для векторов A и B , как показано на рис. A.1.4, скаляр или скалярное произведение между двумя векторами определяется как где — угол между двумя векторами. Рисунок A.1.4 Иллюстрация для определения скалярного произведения. Непосредственно из его определения следует, что скалярное произведение равно коммутативный. Скалярное произведение также является распределительным. Чтобы увидеть это, обратите внимание, что A C — это проекция A на C раз величину C , | C | и B C — проекция B на C раз | C | . Поскольку проекции аддитивны, следует (11). Эти два свойства можно использовать для определения скалярного произведения в члены векторных компонент в декартовых координатах. В соответствии к определению единичных векторов, С A и B , выраженными в терминах этих компонентов, из дистрибутивных и коммутативных свойств следует, что Таким образом, в соответствии с (9) квадрат величины вектора является Определение векторного произведения Перекрестное произведение векторов A и B является вектором C имеющий величину и имеющий направление, перпендикулярное как A, , так и B .Геометрически величина C — это площадь параллелограмм, образованный векторами A и B . Вектор C имеет направление продвижения правого винта, как будто забитый путем поворота A в B . Другими словами, правая координата Система состоит из A — B — C , как показано на рис.А.1.5. Общепринятое обозначение для перекрестного произведения: Рисунок A.1.5 Иллюстрация для определения векторного произведения Полезно отметить, что если вектор A разлагается на два взаимно перпендикулярные векторы, A = A \ perp + A \ parallel , где A \ perp лежит в плоскости A и B и является перпендикулярно B и A \ параллельно параллельно B , тогда Это равенство следует из того факта, что оба перекрестных произведения имеют равные величина (поскольку | A \ perp x B | = | A \ perp || B | и | A | \ perp | = | A | sin ) и направление (перпендикулярно обоим A и B ). Распределительное свойство для кросс-продукта, может быть показан с использованием (17) и геометрической конструкции на рис. A.1.6 как следует. Во-первых, обратите внимание, что ( A + B ) \ perp = ( A \ perp + B \ perp ) , где \ perp обозначает компонент в самолеты A и D или B и D , соответственно и перпендикулярно к D .Таким образом, Рисунок A.1.6 Графическое представление, показывающее, что векторное произведение является дистрибутивным. Теперь нам нужно только показать, что Это уравнение графически представлено на рис. А.1.6 векторами A \ perp , B \ perp и их сумма. С точностью до фактора | D | , три вектора A \ perp x D , B \ perp x D и их sum, являются, соответственно, векторами A \ perp , B \ perp и их сумма, повернутая на 90 градусов. Таким образом, свойство сложения векторов уже показано для A \ perp + B \ perp также относится к A \ перп x D + B \ перп x D . Поскольку для изменения порядка двух векторов требуется переназначение направления вектора продукта (направление C на рис. A.1.5) коммутативность не выполняется.Скорее, Используя закон распределения, векторное произведение двух векторов может быть построенные в их декартовых координатах, используя следующие свойства векторных произведений единичных векторов. Таким образом, Полезная мнемоника для поиска перекрестного произведения в декартовой системе координат. координат реализуется с учетом того, что правая часть (23) — определитель матрицы: Скалярное тройное произведение Определение скалярного тройного произведения векторов A , B и C следует из рис. A.1.7, и определение скалярных и векторных произведений. Рисунок A.1.7 Графическое представление скалярного тройного произведения. Скалярное тройное произведение равно объему параллелепипеда. имея три вектора для своих трех оснований. То есть в (25) второй член в квадратных скобках — это площадь базового параллелограмма на рис. A.1.7, а первая — высота параллелепипеда. Скалярное тройное произведение положительно, если три вектора образуют в правой системе координат в том порядке, в котором они написано; в противном случае — отрицательно.Следовательно, циклическая перестановка в порядок векторов оставляет ценность продукта неизменной. Отсюда следует, что размещение креста и точки в скаляре тройное произведение произвольно. Крестик и точка можно поменять местами не влияя на продукт. Используя правила для оценки скалярного произведения и перекрестное произведение в декартовых координатах, мы имеем Двойное перекрестное произведение Рассмотрим векторное произведение A x ( B x C ) . Является есть другой, иногда более полезный способ выражения этого двойного кросс-продукт? Поскольку продукт B x C является перпендикулярно к самолет, определяемый B и C , затем конечный продукт A x ( B x C ) должен лежать в самолет B и C . Следовательно, векторное произведение должен быть выражен как линейный комбинация векторов B и C .Один из способов найти коэффициентов этой линейной комбинации, чтобы оценить продукт в Декартовы координаты. Здесь мы предпочитаем использовать геометрический вывод. Поскольку вектор B x C перпендикулярен плоскости определяется векторами B и C , из рис. A.1.7 следует, что где A ‘ — проекция A на плоскость определяется B и C .Затем мы разделяем вектор C на компонент, параллельный B , C \ parallel , и компонент перпендикулярно к B , C \ perp , как показано на рис. A.1.8, поэтому что Рисунок A.1.8 Графическое представление двойного перекрестного произведения. Тогда, согласно свойствам перекрестного произведения, величина векторного произведения задается формулой а направление векторного произведения ортогонально A ‘ и лежит в плоскости, определяемой векторами B и C , как показано на рис.А.1.8 Правило построения вектора, перпендикулярного заданному вектор, A ‘ , в x — y Самолет выглядит следующим образом. Во-первых, два компонента A ‘ относительно любых двух ортогональных осей определяются (x, y) . Вот направления C \ perp и B с компоненты A ‘ C \ perp и A ‘ \ cdot B соответственно.Потом новый вектор создается путем замены компонентов x и y и меняя знак одного из них. Согласно этому правилу, Рис. A.1.8 показывает, что вектор A x ( B x C ) задается Теперь, поскольку C \ parallel имеет то же направление, что и B , и добавление (31) дает Теперь обратите внимание, что A ‘ C = A \ cdot C и A ‘ B = A \ cdot B (которые следуют из определение A ‘ как проекция A в B — C плоскость), и двойное перекрестное произведение становится Этот результат особенно удобен, потому что не содержат каких-либо специальных обозначений или проекций. Векторные тождества, найденные в этом Приложении, кратко изложены в Таблица III в конце текста.

ВЕКТОРНЫЕ МЕТОДЫ

ВЕКТОРНЫЕ МЕТОДЫ

Приоритетные направления:

1. Векторы и сложение векторов
2. Единичные векторы
3. Базовые векторы и компоненты вектора
4. Прямоугольные координаты в 2-D
5. Прямоугольные координаты в 3-D
6. А вектор, соединяющий две точки
7. Точечный продукт
8. Перекрестное произведение
9. Тройной продукт
10. Тройное векторное произведение

Векторы и сложение вектора:

Скаляр — это величина, подобная массе или температуре, имеющая только величина. » на жирном символе (т.е., ). Следовательно,

Любой вектор можно превратить в единичный вектор, разделив его на длину.

Любой вектор можно полностью представить, указав его величину и единицу. вектор по его направлению.

База векторы и компоненты вектора:

Базовые векторы — это набор векторов, выбранных в качестве базовых для представления всех другие векторы.Идея состоит в том, чтобы построить каждый вектор из добавления векторы по базовым направлениям. Например, вектор на рисунке может можно записать как сумму трех векторов u ₁ , u ₂ , и u ₃ , каждый по направлению одного из оснований векторы e ₁ , e ₂ и e ₃ , так что

Каждый из векторов u ₁ , u ₂ и u ₃ параллельно одному из базовых векторов и может быть записывается как скалярное кратное этой базе. Пусть u ₁ , u ₂ , и u ₃ обозначают эти скалярные множители, так что получается

Оригинальный вектор u банка теперь будет записано как

Скалярные множители u ₁ , u ₂ и u ₃ известны как компоненты u в базе описывается базовыми векторами e ₁ , e ₂ , и e ₃ .Если базовые векторы являются единичными векторами, то компоненты представляют собой соответственно длины трех векторов u ₁ , u ₂ и u ₃ . Если базовые векторы единичные векторов и взаимно ортогональны, то основание известно как ортонормированное, евклидово или декартово основание.

Вектор может быть разрешен по любым двум направлениям в плоскости, содержащей Это. На рисунке показано, как правило параллелограмма используется для построения векторов. a и b , что в сумме дает c .

В трех измерениях вектор может быть разрешен по любым трем направлениям. некопланарные линии. На рисунке показано, как можно разрешить вектор вдоль в трех направлениях, сначала найдя вектор в плоскости двух из направлениях, а затем разрешив этот новый вектор по двум направлениям в самолет.

Когда векторы представлены в виде базовых векторов и компонентов, сложение двух векторов приводит к сложению компонентов векторы.Следовательно, если представлены два вектора A и B по

тогда,

Прямоугольные компоненты в 2-D:

Даны базовые векторы прямоугольной системы координат x-y . единичными векторами а также вдоль направлениях x и y соответственно.

Используя базовые векторы, можно представить любой вектор F как

Из-за ортогональности базисов имеют место следующие соотношения.

Прямоугольные координаты в 3-D:

Базовые векторы прямоугольной системы координат задаются набором три взаимно ортогональных единичных вектора, обозначаемых , , а также что находятся вдоль координатных направлений x , y и z , соответственно, как показано на рисунке.

Показанная система является системой для правшей, поскольку большой палец правой руки рука указывает в направлении z , если пальцы таковы, что они представляют поворот вокруг оси z от x до y . Эту систему можно превратить в левую, перевернув направление любой из координатных линий и связанный с ней базовый вектор.

В прямоугольной системе координат компонентами вектора являются проекции вектора вдоль x , y и z направления. Например, на рисунке проекции вектора A вдоль x, y, и z направления задаются A _x , A _y , и A _z соответственно.

В результате теоремы Пифагора и ортогональности базы векторов, величина вектора в прямоугольной системе координат может быть рассчитано по

Направляющий косинус:

Направляющие косинусы определены как

где углы , , а также находятся углы, показанные на рисунке.Как показано на рисунке, направление косинусы представляют собой косинусы углов между вектором и три координатных направления.

Направляющие косинусы могут быть вычислены из компоненты вектора и его величина через отношения

Три направляющих косинуса не являются независимыми и должно удовлетворять соотношению

Эти результаты формируют тот факт, что

Единичный вектор может быть построен вдоль вектора используя направляющие косинусы в качестве компонентов вдоль x , y , и z направлений. Например, единичный вектор вдоль вектор A получается из

Следовательно,

Вектор соединение двух точек:

Вектор, соединяющий точку A с точкой B выдается

Единичный вектор вдоль линии A-B может быть получен из

Вектор F по линии A-B и величиной F может таким образом получается из соотношения

точка товар:

Скалярное произведение обозначается «» между двумя векторами.Скалярное произведение векторов A и B приводит к скаляру, задаваемому соотношением

где является угол между двумя векторами. Порядок не важен в скалярном произведении как видно из определения скалярных произведений. В результате получается

Скалярное произведение имеет следующие свойства.

Поскольку косинус 90 ^o равен нулю, скалярное произведение двух ортогональные векторы приведут к нулю.

Поскольку угол между вектором и самим собой равен нулю, а косинус ноль равен единице, величина вектора может быть записана через точку продукт по правилу

Прямоугольные координаты:

При работе с векторами, представленными в прямоугольная система координат по составляющим

, то скалярное произведение можно оценить из отношение

Это можно проверить прямым умножением векторов и отмечая, что из-за ортогональности базовых векторов прямоугольная система

Проекция вектора на линию:

Ортогональная проекция вектора на линия получается перемещением одного конца вектора на линию и опусканием перпендикуляр на линию от другого конца вектора. В Результирующий отрезок на прямой является ортогональной проекцией вектора или просто его проекция.

Скалярная проекция вектора A вдоль единичный вектор является длина ортогонального выступа A по линии, параллельной , и может быть оценен с помощью скалярного произведения. Соотношение для проекции это

Проекция вектора А вдоль агрегата. вектор просто умножает скалярную проекцию на единичный вектор к получить вектор .Это дает соотношение

перекрестное произведение:

Перекрестное произведение векторов a и b является вектором перпендикулярно как a , так и b и имеет величину, равную Площадь параллелограмма, полученная из a и b . В направление перекрестного произведения задается правилом правой руки.Крест продукт обозначается знаком «» между векторами

Порядок важен в перекрестном произведении. Если порядок операций изменения в перекрестном произведении направление результирующего вектора наоборот. То есть

Перекрестное произведение имеет следующие свойства.

Прямоугольные координаты:

При работе в прямоугольных системах координат, перекрестное произведение векторов a и b , заданных

можно оценить с помощью правила

Можно также использовать прямое умножение базовые векторы с использованием соотношений

тройное произведение:

Дано тройное произведение векторов a , b и c . по

Стоимость тройного произведения равна объему параллелепипед, построенный из векторов.Это видно из цифра с

Тройной продукт имеет следующие свойства

Прямоугольные координаты:

Рассмотрим векторы, описанные в прямоугольной форме. система координат как

Тройное произведение можно оценить с помощью отношение

Трехместный векторное произведение:

Произведение тройного вектора имеет свойства

Умножение векторов

Векторы — что это такое? дает введение в предмет.

Есть два полезных определения умножения векторов в в одном произведение — скаляр, а в другом — произведение вектор. Нет операции деления векторов. В некоторых школьные программы вы встретите скалярные произведения, но не векторные продуктов, но мы обсуждаем оба типа умножения векторов в в этой статье, чтобы дать более полное представление об основах субъект

Скалярное умножение

Скалярное произведение векторы $ {\ bf u} = (u_1, u_2, u_3) $ и $ {\ bf v} = (v_1, v_2, v_3) $ — скаляр, определяемый как $$ {\ bf u.2 \ quad (2), $$ и если $ {\ bf i, j, k} $ — единичные векторы вдоль оси тогда $$ {\ bf i. i} = {\ bf j.j} = {\ bf k.k} = 1, \ quad {\ rm и} \ quad {\ bf i.j} = {\ bf j.k} = {\ bf k.i} = 0 \ quad (3). $$ Это оставлено читателю, чтобы проверить из определения, что $$ {\ bf u.v} = {\ bf v.u}, \ {\ rm и} \ ({\ bf u + v}). {\ bf w} = {\ bf u.w} + {\ bf v.w}. $$ Это показывает, что мы можем расширять или умножать $$ {\ bf u.v} = (u_1 {\ bf i} + u_2 {\ bf j} + u_3 {\ bf k}). (v_1 {\ bf i} + v_2 {\ bf j} + u_3 {\ bf k}) $$ дает девять терминов. Используя уравнение (3), шесть из этих членов равны ноль, а остальные три дают выражение $ u_1v_1 + u_2v_2 + u_3v_3 $ в соответствии с определением в уравнении (1).{-1} \ left ({{\ bf u.v} \ over | {\ bf u} ||| {\ bf v} |} \ right) \ quad (7). $$ В трех измерениях мы можем использовать более интуитивное определение угла с точки зрения поворота, но в более высокие размеры необходимо иметь определение угла например, формула (7). Если мы воспользуемся этой формулой для определения угла, тогда Правило косинуса следует прямо, поскольку они эквивалентны.

Обратите внимание, что произведение вектора-строки и вектора-столбца равно определяется в терминах скалярного произведения, и это согласуется с матричное умножение.$$ (u_1 \ u_2 \ u_3) \ left (\ begin {array} {cc} v_1 \\ v_2 \\ v_3 \ end {array} \ right) = u_1v_1 + u_2v_2 + u_3v_3. $$

Векторное умножение

Векторное произведение двух векторы $ {\ bf b} $ и $ {\ bf c} $, записываемые как $ {\ bf b} \ times {\ bf c} $ (и иногда называют крестом product), это вектор $$ {\ bf b} \ times {\ bf c} = \ left ( \ begin {array} {cc} b_2c_3-b_3c_2 \\ b_3c_1 -b_1c_3 \\ b_1c_2 -b_2c_1 \ end {array} \ right) \ quad (8). $$ Существует альтернативное определение векторного произведения, а именно, что $ {\ bf b} \ times {\ bf c} $ является вектор величины $ | {\ bf b} || {\ bf c} | \ sin \ theta $ перпендикулярно $ {\ bf b} $ и $ {\ bf c} $ и подчиняясь «правилу правой руки», и докажем, что этот результат следует из данного определения и что эти два определения эквивалентны. Приведено доказательство позже для полноты, но сначала рассмотрим $ {\ bf b} \ times {\ bf c} $ выражается через компоненты в направлениях $ {\ bf i, j, k} $.

Из этого определения видно, что $ {\ bf b} \ times {\ bf c} = — {\ bf c} \ times {\ bf b} $, поэтому эта операция не коммутативна. Если $ {\ bf i, j, k} $ — единичные векторы вдоль осей, тогда из этого определения: $$ {\ bf i} \ times {\ bf i} = {\ bf j} \ times {\ bf j} = {\ bf k} \ times {\ bf k}, $$ и $$ \ eqalign {{\ bf i} \ times {\ bf j} & = {\ bf k}, \ quad {\ bf j} \ times {\ bf i} = — {\ bf k} \ cr {\ bf j} \ times {\ bf k} & = {\ bf i}, \ quad {\ bf k} \ times {\ bf j} = — {\ bf i} \ cr {\ bf k} \ times {\ bf i} & = {\ bf j}, \ quad {\ bf i} \ times {\ bf k} = — {\ bf j}.} $$ Из определения следует, что $$ k ({\ bf b} \ times {\ bf c}) = (k {\ bf b}) \ times {\ bf c} = {\ bf b} \ times (k {\ bf c}), \ quad \ quad ({\ bf a + b}) \ times {\ bf c} = ({\ bf a} \ times {\ bf c}) + ({\ bf b} \ times {\ bf c}). $$ Расширение выражения $$ {\ bf b} \ times {\ bf c} = (b_1 {\ bf i} + b_2 {\ bf j} + b_3 {\ bf k}) \ times (c_1 {\ bf i} + c_2 {\ bf j} + c_3 {\ bf k}) $$ дает $$ (b_2c_3-b_3c_2) {\ bf i} + (b_3c_1-b_1c_3) {\ bf j} + (b_1c_2-b_2c_1) {\ bf k} \ quad (9) $$ который — формула для векторного произведения, заданная в уравнении (8).

Теперь мы докажем, что два определения умножения векторов эквивалент. На схеме показаны направления векторов $ {\ bf b} $, $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $, которые образуют правую вручил набор ».

Вы можете закончить чтение здесь, и это действительно больше важно понимать, что есть два определения вектора продукт, который может быть доказан как эквивалентный, чем он механически проработать детали доказательства.

Теорема Вектор произведение двух векторов $ {\ bf b} $ и $ {\ bf c} $ является вектором $ {\ bf b} \ times {\ bf c} $ со следующими свойствами:

(i) $ {\ bf b} \ times {\ bf c} $ имеет величина $ | {\ bf b} || {\ bf c} | \ sin \ theta $, где $ \ theta $ — угол между направлениями $ {\ bf b} $ и $ {\ bf c} $;

(ii) $ {\ bf b} \ times {\ bf c} $ — это перпендикулярно $ {\ bf b} $ и $ {\ bf c} $ с направлением, таким, что векторы $ {\ bf b} $, $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $ образуют правый набор, как на схеме, так что $ {\ bf b} \ times {\ bf c} $ и $ {\ bf c} \ times {\ bf b} $ направлены в противоположные стороны.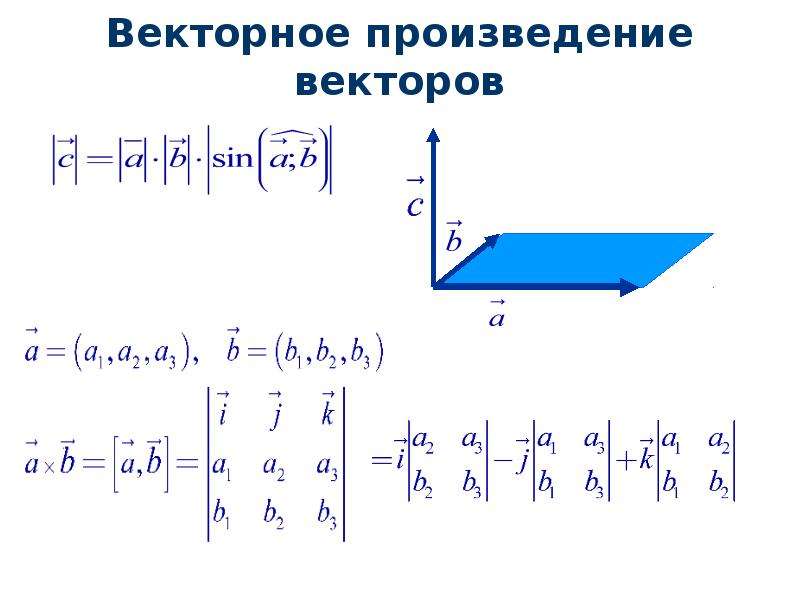 2 $.2} \ cr & = | {\ bf b} \ times {\ bf c} |. } $$

Доказательство части (ii) Кому показать, что $ {\ bf b} $ и $ {\ bf b} \ times {\ bf c} $ перпендикулярны покажем, что скалярное произведение равно нулю: $$ {\ bf b}. {\ bf b} \ times {\ bf c} = b_1 (b_2c_3-b_3c_2) + b_2 (b_3c_1-b_1c_3) + b_3 (b_1c_2-b_2c_1) = 0, $$ и аналогично скалярное произведение $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $ равен нулю, поэтому эти векторы перпендикулярны.

Перекрестное произведение

Вектор имеет величину , (длина) и направление :

Два вектора можно умножить на с помощью «перекрестного произведения » (см. Также скалярное произведение)

Перекрестное произведение a × b двух векторов — это другой вектор , который находится под прямым углом к ​​обоим:

И все это происходит в трех измерениях!

Величина (длина) векторного произведения равна площади параллелограмма с векторами a и b для сторон:

Посмотрите, как он меняется под разными углами:

Перекрестное произведение ( синий ):

• нулевой длины, когда векторы a и b указывают в том же или противоположном направлении
• достигает максимальной длины, когда векторы a и b расположены под прямым углом

И это может указывать в ту или иную сторону!

Так как же это вычислить?

Расчет

Мы можем вычислить перекрестное произведение следующим образом:

a × b = | a | | b | sin (θ) n

• | a | величина (длина) вектора a
• | b | величина (длина) вектора b
• θ — угол между a и b
• n — единичный вектор под прямым углом к ​​ a и b

Таким образом, длина равна: длина a умноженная на длину b умноженная на синус угла между a и b ,

Затем мы умножаем на вектор n , чтобы он направлялся в правильном направлении (под прямым углом к ​​ a и b ).

ИЛИ мы можем вычислить это так:

Когда a и b начинаются в исходной точке (0,0,0), перекрестное произведение заканчивается на:

• c _x = a _y b _z — a _z b _y
• c _y = a _z b _x — a _x b _z
• c _z = a _x b _y — a _y b _x

Пример: перекрестное произведение

a = (2,3,4) и b = (5,6,7)

• c _x = a _y b _z — a _z b _y = 3 × 7 — 4 × 6 = −3
• c _y = a _z b _x — a _x b _z = 4 × 5 — 2 × 7 = 6
• c _z = a _x b _y — a _y b _x = 2 × 6 — 3 × 5 = −3

Ответ: a × b = (−3,6, −3)

В каком направлении?

Перекрестное произведение может указывать в совершенно противоположном направлении и по-прежнему находиться под прямым углом к ​​двум другим векторам, поэтому мы имеем:

«Правило правой руки»

Правой рукой укажите указательным пальцем вдоль вектора a , а средним пальцем — вдоль вектора b : перекрестное произведение идет в направлении большого пальца.

Точечный продукт

Перекрестное произведение дает векторный ответ и иногда называется векторным произведением .

Но есть также точечное произведение, которое дает скаляр , (обычное число), и его иногда называют скалярным произведением .

Вопрос: Что получится, если скрестить слона с бананом?

Ответ: | слон | | банан | sin (θ) n

Векторная алгебра:

ВЕКТОРНЫЕ МЕТОДЫ

Приоритетные направления:

1. Векторы и векторное сложение
2. Единичные векторы
3. Базовые векторы и компоненты вектора
4. прямоугольный координаты в 2-D
5. прямоугольный координаты в 3-D
6. Вектор соединение двух точек
7. Точечный продукт
8. Перекрестное произведение
9. Трехместный товар
10. Трехместный векторный продукт

Векторы и векторное сложение:

Скаляр — это величина, такая как масса или температура, которая имеет только величину. » на жирном символе (т.е.,). Следовательно,

Любой вектор можно превратить в единичный вектор, разделив его на длину.

Любой вектор можно полностью представить, указав его величину и единицу. вектор по его направлению.

Базовые векторы и компоненты вектора:

Базовые векторы — это набор векторов, выбранных в качестве базовых для представления всех остальных векторы.Идея состоит в том, чтобы построить каждый вектор из сложения векторов по базовым направлениям. Например, вектор на рисунке можно записать как сумма трех векторов u ₁ , u ₂ и u ₃ , каждый по направлению одного из базовых векторов e ₁ , e ₂ и e ₃ , так что

Каждый из векторов u ₁ , u ₂ и u ₃ параллельна одному из базовых векторов и может быть записана как скалярное кратное эта база. Пусть u ₁ , u ₂ и u ₃ обозначим эти скалярные множители так, чтобы получилось

Оригинальный вектор u банка теперь будет записано как

Скалярные множители u ₁ , u ₂ и u ₃ известны как компоненты и в базе, описываемой базой векторы e ₁ , e ₂ и e ₃ .Если базовые векторы являются единичными векторами, то компоненты представляют собой длины трех векторов соответственно u ₁ , u ₂ , и u ₃ . Если базовые векторы являются единичными векторами и взаимно ортогонально, то основание называется ортонормированным, евклидовым или декартовым база.

Вектор может быть разрешен по любым двум направлениям в плоскости, содержащей его. На рисунке показано, как правило параллелограмма используется для построения векторов и . и b , что в сумме дает c .

В трех измерениях вектор может быть разрешен вдоль любых трех некомпланарных линий. На рисунке показано, как можно разрешить вектор по трем направлениям. сначала найдя вектор в плоскости двух направлений, а затем разрешение этого нового вектора по двум направлениям на плоскости.

Когда векторы представлены в виде базовых векторов и компонентов, сложение двух векторов приводит к сложению компонентов векторы.Следовательно, если два вектора A и B представлены как

тогда,

прямоугольный компоненты в 2-D:

Базовые векторы прямоугольной системы координат x-y задаются формулой единичные векторы и вдоль x и y направления соответственно.

Используя базовые векторы, можно представить любой вектор F как

Из-за ортогональности базисов имеют место следующие соотношения.

прямоугольный координаты в 3-D:

Базовые векторы прямоугольной системы координат задаются набором три взаимно ортогональных единичных вектора, обозначенных,, и что находятся вдоль координатных направлений x , y и z , соответственно, как показано на рисунке.

Показанная система является системой для правой руки, поскольку большой палец правой руки указывает в направлении z , если пальцы таковы, что представляют вращение вокруг оси z от x до y . Эта система может можно превратить в левостороннюю систему, изменив направление любого из координатные линии и связанный с ними базовый вектор.

В прямоугольной системе координат компонентами вектора являются проекции вектора вдоль x , y и z направления. Например, на рисунке проекции вектора A по x, y, и z направлениям задаются A _x , A _y , и A _z соответственно.

В результате теоремы Пифагора и ортогональности базы векторов, величина вектора в прямоугольной системе координат может быть рассчитано по

Направляющий косинус:

Направляющие косинусы определены как

где углы, и — углы показаны на рисунке.Как показано на рисунке, направляющие косинусы представляют собой косинусы углов между вектором и тремя координаты направления.

Направляющие косинусы могут быть вычислены из компоненты вектора и его величина через отношения

Три направляющих косинуса не являются независимыми и должно удовлетворять соотношению

Эти результаты формируют тот факт, что

Единичный вектор может быть построен вдоль вектора используя направляющие косинусы в качестве компонентов вдоль x , y и z направлений.Например, единичный вектор вдоль вектора A получается из

Следовательно,

Вектор соединение двух точек:

Вектор, соединяющий точку A с точкой B дается

Единичный вектор вдоль линии A-B может быть получен из

Вектор F по линии A-B и величиной F может таким образом получается из соотношения

Точечный продукт:

Скалярное произведение обозначается «» между двумя векторами.В скалярное произведение векторов A и B приводит к скаляру, заданному отношение

где — угол между двумя векторами. Порядок не важен в скалярное произведение, как видно из определения скалярных произведений. В результате один получает

Скалярное произведение имеет следующие свойства.

Поскольку косинус 90 ^o равен нулю, скалярное произведение двух ортогональные векторы приведут к нулю.

Поскольку угол между вектором и самим собой равен нулю, а косинус нуля единица, величина вектора может быть записана в терминах скалярного произведения используя правило

Прямоугольные координаты:

При работе с векторами, представленными в прямоугольная система координат по составляющим

, то скалярное произведение можно оценить из отношение

Это можно проверить прямым умножением векторы и отмечая, что из-за ортогональности базовых векторов прямоугольная система

Проекция вектора на линию:

Ортогональная проекция вектора вдоль прямой получается перемещением одного конца вектора на линию и опусканием перпендикулярно линии от другого конца вектора.Результирующий отрезок на прямой — это ортогональная проекция вектора или просто его проекция.

Скалярная проекция вектора A вдоль направления единичный вектор — длина ортогональной проекции A вдоль линии, параллельной, и может быть оценен с помощью скалярного произведения. В отношение для проекции

Проекция вектора А вдоль агрегата. вектор просто умножает скалярную проекцию на единичный вектор, чтобы получить вектор вместе.Это дает соотношение

Крест товар:

Перекрестное произведение векторов a и b представляет собой вектор, перпендикулярный как a и b и имеет величину, равную площади параллелограмм, полученный из a и b . Направление креста продукт определяется правилом правой руки.Перекрестное произведение обозначается «» между векторами

Порядок важен в перекрестном произведении. Если порядок операций изменится в перекрестном произведении направление результирующего вектора меняется на противоположное. То есть

Перекрестное произведение имеет следующие свойства.

Прямоугольные координаты:

При работе в прямоугольных системах координат, перекрестное произведение векторов a и b , заданных

можно оценить с помощью правила

Можно также использовать прямое умножение основания векторов с использованием соотношений

Тройной товар:

Тройное произведение векторов a , b и c равно

Стоимость тройного произведения равна объему параллелепипеда. построенный из векторов.Это видно из рисунка с

г.

Тройной продукт имеет следующие свойства

Прямоугольные координаты:

Рассмотрим векторы, описанные в прямоугольной форме. система координат как

Тройное произведение можно оценить с помощью отношение

Тройной вектор товар:

Произведение тройного вектора имеет свойства

Точечный продукт | Блестящая вики по математике и науке

В декартовых координатах скалярное произведение принимает удобную форму.Предположим, что a⃗ \ vec {a} a и b⃗ \ vec {b} b образуют углы α \ alpha α и β \ beta β соответственно с осью x x x. Напомним, что представление в декартовых координатах становится

.

a⃗ = (xa, ya) \ vec {a} = (x_a, y_a) a = (xa, ya)

и

b⃗ = (xb, yb), \ vec {b} = (x_b, y_b), b = (xb, yb),

, где xa = ∣a⃗∣cos⁡α x_a = | \ vec {a} | \ cos {\ alpha} xa = ∣a∣cosα, ya = ∣a⃗∣sin⁡α y_a = | \ vec {a} | \ sin {\ alpha} ya = ∣a∣sinα, xb = ∣b⃗∣cos⁡β x_b = | \ vec {b} | \ cos {\ beta} xb = ∣b∣cosβ и yb = ∣b⃗∣sin⁡β y_b = | \ vec {b} | \ sin {\ beta} yb = ∣b∣sinβ.

Следовательно,

a⃗⋅b⃗ = ∥a⃗∥∥b⃗∥cos⁡ (β − α) = ∥a⃗∥∥b⃗∥ (cos⁡αcos⁡β + sin⁡αsin⁡β) = (∥a⃗∥cos⁡α) (∥b⃗ ∥cos⁡β) + (∥a⃗∥sin⁡α) (∥b⃗∥sin⁡β) = xaxb + yayb. \ begin {выровнено} \ vec {a} \ cdot \ vec {b} & = \ left \ | \ vec {a} \ right \ | \ left \ | \ vec {b} \ right \ | \ соз (\ бета — \ альфа) \\ & = \ left \ | \ vec {a} \ right \ | \ left \ | \ vec {b} \ right \ | (\ cos {\ alpha} \ cos {\ beta} + \ sin {\ alpha} \ sin {\ beta}) \\ & = \ left (\ left \ | \ vec {a} \ right \ | \ cos {\ alpha} \ right) \ left (\ left \ | \ vec {b} \ right \ | \ cos {\ beta} \ right) + \ left (\ left \ | \ vec {a} \ right \ | \ sin {\ alpha} \ right) \ left (\ left \ | \ vec {b} \ right \ | \ sin {\ beta} \верно) \\ & = x_a x_b + y_a y_b.\ end {выровнен} a⋅b = ∥a∥∥∥∥ b∥∥∥ cos (β − α) = ∥a∥∥∥∥ b∥∥∥ (cosαcosβ + sinαsinβ) = (∥a∥cosα) (∥ ∥∥ b∥∥∥ cosβ) + (∥a∥sinα) (∥∥∥ b∥∥∥ sinβ) = xa xb + ya yb.

Другими словами, произведение двух векторов в декартовых координатах — это просто сумма произведения каждого из соответствующих компонентов двух векторов. То же самое относится к векторам более чем в двух измерениях.

Точечное произведение в декартовых координатах:

Предположим, что a⃗ = (a1, a2,…, an) \ vec {a} = (a_1, a_2, \ ldots, a_n) a = (a1, a2,…, an) и b⃗ = (b1, b2 ,…, An) \ vec {b} = (b_1, b_2, \ ldots, a_n) b = (b1, b2,…, an).Тогда

a⃗⋅b⃗ = a1b1 + a2b2 + ⋯ + anbn. □ \ vec {a} \ cdot \ vec {b} = a_1 b_1 + a_2 b_2 + \ cdots + a_n b_n. \ _ \ squarea⋅b = a1 b1 + a2 b2 + ⋯ + an bn. □

Векторы u⃗ \ vec {u} u, v⃗ \ vec {v} v и u⃗ − v⃗ \ vec {u} — \ vec {v} u − v образуют треугольник, где θ \ thetaθ — угол между u⃗ \ vec { u} u и v⃗ \ vec {v} v. Следовательно, мы можем применить теорему косинусов к этому треугольнику:

∥u⃗ − v⃗∥2 = ∥u⃗∥2 + ∥v⃗∥2−2∥u⃗∥∥v⃗∥cos⁡θ∑i = 1n (ui − vi) 2 = ∑i = 1nui2 + ∑i = 1nvi2−2∥ u⃗∥∥v⃗∥cos⁡θ − 2∑i = 1nuivi = −2∥u⃗∥∥v⃗∥cos⁡θuTv = ∥u⃗∥∥v⃗∥cos⁡θ \ begin {выровнено} \ left \ | \ vec {u} — \ vec {v} \ right \ | ^ {2} & = \ left \ | \ vec {u} \ right \ | ^ {2} + \ left \ | \ vec {v} \ right \ | ^ {2 } — 2 \ left \ | \ vec {u} \ right \ | \ left \ | \ vec {v} \ right \ | \ cos {\ theta} \\ \ sum_ {i = 1} ^ {n} (u_ {i} — v_ {i}) ^ {2} & = \ sum_ {i = 1} ^ {n} u_ {i} ^ {2} + \ sum_ {i = 1} ^ {n} v_ {i} ^ {2} — 2 \ left \ | \ vec {u} \ right \ | \ left \ | \ vec {v} \ right \ | \ cos {\ theta} \\ -2 \ sum_ {i = 1} ^ {n} u_ {i} v_ {i} & = -2 \ left \ | \ vec {u} \ right \ | \ left \ | \ vec {v} \ right \ | \ cos {\ theta} \\ u ^ {T} v & = \ left \ | \ vec {u} \ right \ | \ left \ | \ vec {v} \ right \ | \ cos {\ theta} \ end {выровнено} ∥u − v∥2i = 1∑n (ui −vi) 2−2i = 1∑n ui vi uTv = ∥u∥2 + ∥v∥2−2∥u∥∥v∥cosθ = i = 1∑ n ui2 + i = 1∑n vi2 −2∥u∥∥v∥cosθ = −2∥u∥∥v∥cosθ = ∥u∥∥v∥cosθ

Найдите косинус угла между каждой из следующих пар векторов:

a) a⃗ = (3,0), b⃗ = (3,4) \ vec {a} = (3,0), \ vec {b} = (3,4) a = (3,0) , b = (3,4)
b) a⃗ = 3i + 2j, b⃗ = 5i − j \ vec {a} = 3i + 2j, \ vec {b} = 5i-ja = 3i + 2j, b = 5i − j. {\ circ}.{\ circ} 45∘. □ _ \ квадрат □

Больше 90 градусов Менее 90 градусов Он равен 90 градусам Недостаточная информация

Три точки A, B, A, B, A, B и CCC в трехмерном евклидовом пространстве имеют соответствующие координаты (−6,2, −4), (- 1,1, −2), (-6 , 2, -4), (-1, 1, -2), (- 6,2, −4), (- 1,1, −2) и (−2,2,1).(-2, 2, 1). (- 2,2,1). Какова мера ∠ABC? \ Угла ABC? ∠ABC?

Отправьте свой ответ

для

A = (1,4,7), B = (2,6,4), C = (1,9,8), A = (1, 4, 7), B = (2, 6, 4) , C = (1, 9, 8), A = (1,4,7), B = (2,6,4), C = (1,9,8),

каково скалярное произведение AAA и (B-C)? (B-C)? (B-C)?

Отправьте свой ответ

Для векторов

u = (2,7,5), v = (3, −8, −1), u = (2, 7, 5), \ quad v = (3, -8, -1), u = ( 2,7,5), v = (3, −8, −1),

каково значение скалярного произведения u⋅v? U \ cdot v? U⋅v?

Отправьте свой ответ

Даны два вектора u⃗ \ vec {u} u и v⃗ \ vec {v} v такие, что ∥u⃗∥ = 5 \ | \ vec {u} \ | = 5∥u∥ = 5 и ∥v⃗∥ = 8 \ | \ vec {v} \ | = 8∥v∥ = 8, какова положительная разница между наибольшим и наименьшим возможным значением u⃗⋅v⃗? \ Vec {u} \ cdot \ vec {v}? U⋅v?

2∥A⃗∥ = ∥B⃗∥2 \ left \ | \ vec A \ right \ | = \ left \ | \ vec B \ right \ | 2∥∥∥ A∥∥∥ = ∥∥∥ B∥∥∥ ∥A⃗∥ = ∥B⃗∥ \ left \ | \ vec A \ right \ | = \ left \ | \ vec B \ right \ | ∥∥∥ A∥∥∥ = ∥∥∥ B∥∥∥ ∥A⃗∥ = 2∥B⃗∥ \ left \ | \ vec A \ right \ | = \ sqrt 2 \ left \ | \ vec B \ right \ | ∥∥∥ A∥∥∥ = 2 ∥∥∥ B∥∥∥ ∥A⃗∥ = 2∥B⃗∥ \ left \ | \ vec A \ right \ | = 2 \ влево \ | \ vec B \ right \ | ∥∥∥ A∥∥∥ = 2∥∥∥ B∥∥∥

Если A⃗ \ vec AA и B⃗ \ vec BB — два вектора, такие что A⃗ + B⃗ \ vec A + \ vec BA + B перпендикулярно B⃗ \ vec BB, а A⃗ + 2B⃗ \ vec A + 2 \ vec BA + 2B — перпендикулярно A⃗ \ vec AA, что из следующего верно?

Пояснение: Векторы A⃗ \ vec AA и B⃗ \ vec BB не равны нулю.