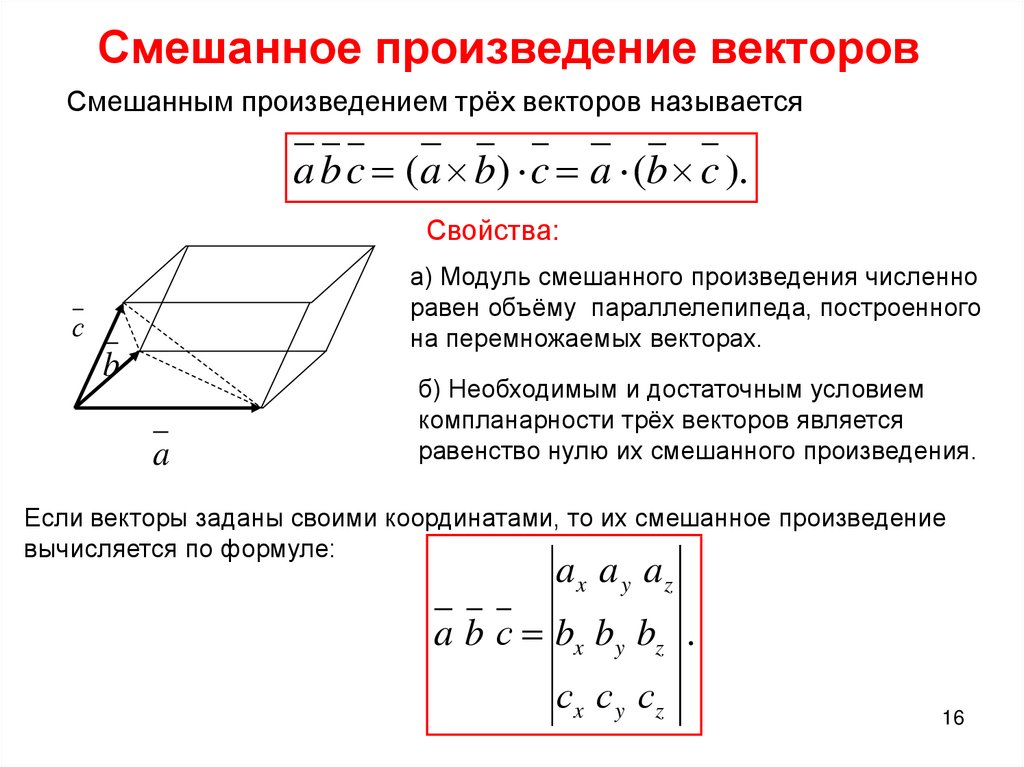
Смешанное произведение трех векторов и его свойства
Смешанным произведением трех векторов а, b, с называется число, равное скалярному произведению вектора [а; b] на вектор с.
Смешанное произведение векторов a, b и с обозначается (а; b; с). Следовательно,
(а; b;с) = | [а; b] | • |с| • cos ψ, (1)
где ψ — угол между векторами [а; b] и с.
Теорема 1. Модуль смешанного произведения трех некомпланарных векторов а, b и с равен объему параллелепипеда, построенного на векторах-множителях.
Как известно, площадь S параллелограмма, построенного на векторах а и b, равна | [а; b] |. Поэтому из формулы (1) следует, что
(а; b;с) = S • |с | • cos ψ.
С другой стороны, объем V параллелепипеда, построенного на векторах а, b, с (рис.
58), равен произведению площади его основания S на высоту h, причем h = |AA2|, где А2 — проекция вершины А1 на ось, определяемую вектором [а; b].
Так как |AA2| = |с | • cos ψ, то
V = S • h = S • | c | • | cos ψ | = | (а; b; с) |.
Из формулы (1) видно, что если смешанное произведение трех векторов не равно кулю, то его знак совпадает со знаком cos ψ. Поэтому смешанное произведение положительно, если вектор с направлен в ту же сторону от плоскости векторов а и b, что и вектор [а; b], т. е. если тройка векторов а, b, с правая.
Смешанное произведение отрицательно, когда вектор с и вектор [а; b] направлены в противоположные стороны от плоскости векторов а и b, т. е. когда тройка векторов а, b, с левая.
Итак, если векторы а, b, с образуют правую тройку, то (а; b;с) > 0, если левую, то (а; b;с) < 0.
Теорема 2. Смешанное произведение трех векторов равно нулю тогда и только тогда, когда векторы компланарны.
Необходимость. Пусть (а; b, с) = 0. Предположим, что векторы а, b и с некомпланарны. Построим на этих векторах параллелепипед.
Его объем V > 0, но по теореме 1 | (а; b;с) | = V, что противоречит предположению.
Достаточность. Пусть векторы а, b и с компланарны. Тогда вектор [а; b] перпендикулярен вектору с, но скалярное произведение перпендикулярных векторов равно нулю, т. е. [а; b] • c = (а; b;с) = 0.
Рассмотрим некоторые свойства смешанного произведения.
1. Для любых векторов а, b и с справедливы равенства
(а; b;с) = (b; с, а) = (с; а; b),
т. е. при циклической перестановке множителей смешанное произведение не изменяется.
Достаточно доказать первое равенство, так как второе следует из первого.
Если векторы а, b и с компланарны, то равенство (а; b;с) = (b; с, а) очевидно; обе части равенства равны нулю.
Пусть векторы а, b и с некомпланарны. Тогда в силу теоремы 1
| (a;b;c) | = V и | (b;c;a) | = V,
где V — объем параллелепипеда, построенного на данных трех векторах. Но тройки векторов а, b, с и b, с, а являются одновременно либо правыми, либо левыми, поэтому знаки чисел (a;b;c) и (b;c;a) совпадают.
2. Для любых векторов а, b и с справедливы равенства
(a;b;c) = — (b; а;с) = — (а; с; b),
т. е. при перестановке двух соседних множителей знак смешанного произведения изменяется на противоположный.
b) =150°,| а | = | b | = 4, | c | = 3
По определению
(a;b;c) = [а; b] • с = | а | • | b | • sin 150° • | c | • cos 0° = 4 • 4 • 3 • 1/2 = 24.
Задача 2. Вычислить ( i + j; j — 2i; k ), где i, j, k — взаимно перпендикулярные единичные векторы, образующие правую тройку.
( i + j; j — 2i; k ) = [i + j; j — 2i] • k = ([i; j] — 2[i; i] + [j; j] — 2[j; i]) • k =
= 3[i; j] • k = 3 (i; j; k) = 3.
Смешанное произведение трех векторов14
Смешанным
произведением трех векторов называется скалярное произведение
векторного произведения первых двух
векторов на третий.
Если векторы заданы в декартовом ортонормированном базисе , то есть если
,
то их смешанное произведение равно определителю третьего порядка, в первой строке которого находятся координаты первого вектора, во второй — координаты второго, в третьей – координаты третьего,
. ( 23 )
Пример. Смешанное произведение векторов
на основании формулы (23) равно
.
Из формулы (23) и свойств определителей вытекают два следующих соотношения, касающиеся возможности переставлять местами сомножители смешанного произведения:
На основании формулы (17) для скалярного произведения мы можем записать следующую формулу для смешанного произведения:
.
Из нее, в частности, вытекает
Геометрический
смысл смешанного произведения.
Абсолютная
величина смешанного произведения
векторов равна объему параллелепипеда, построенного на этих
векторах как на сторонах,
=. ( 24 )
Действительно, площадь основания и высота такого параллелепипеда соответственно равны
, ,
откуда следует формула (24).
Условие компланарности трех векторов. Три ненулевых вектора компланарны тогда и только тогда, если их смешанное произведение равно нулю.
Пример. Векторы пре-дыдущего примера компланарны, так как их смешанное произве-дение равно нулю.
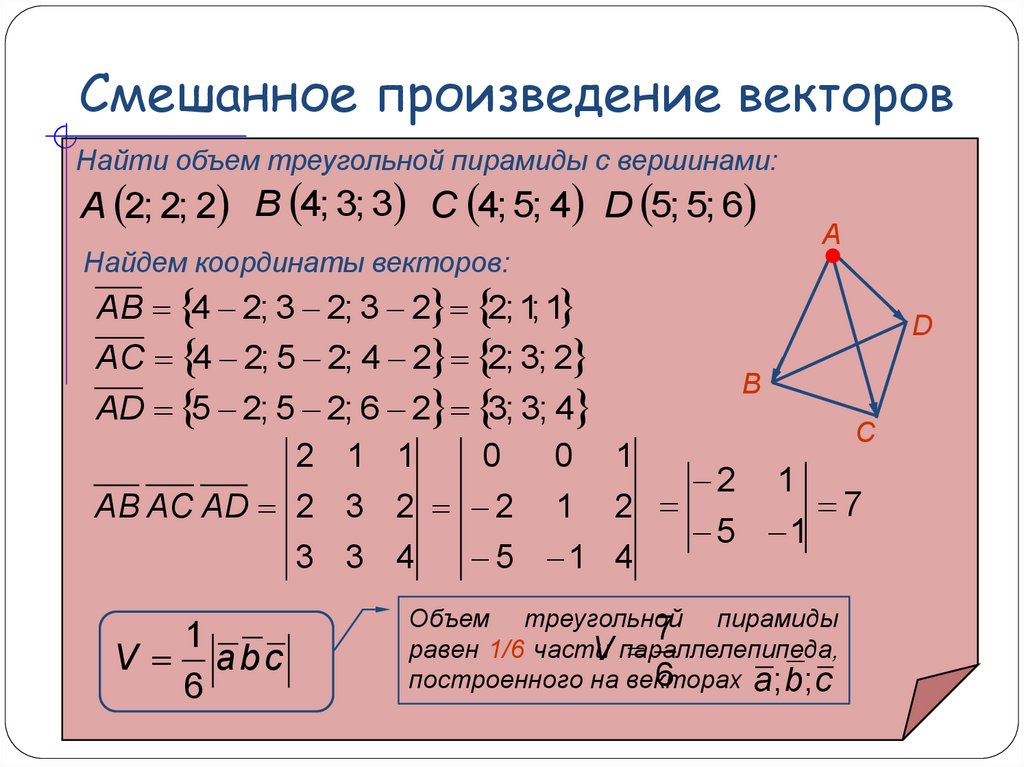
Пример. Найти объем треугольной пирамиды с вершинами
, Рис. 10 и длину ее высоты , опущенной из вершины (рис. 10).
Введем в рассмотрение векторы
.
Данная пирамида
построена на них как на сторонах.
куб.единиц
Длину высоты находим, исходя из известной школьной формулы. Именно:
Так как
получаем
лин.единиц.
Что такое вектор и его орт?
Дать определение равных векторов; противоположных векторов.
Какие векторы называются коллинеарными? компланарными?
Как можно определить сумму векторов? разность векторов? произведение вектора на число?
Что такое составляющая вектора вдоль оси? проекция вектора на ось?
По какой формуле можно найти проекцию вектора на ось?
Что такое базис на плоскости? в пространстве?
Что такое декартов ортонормированный базис?
Сформулировать теорему о разложении вектора по базису.
Что такое координаты вектора в данном базисе? что представляют собой координаты вектора в декартовом ортонормированном базисе?
Какая существует связь между линейными операциями над векторами и операциями над их координатами?
Сформулировать необходимое и достаточное условие коллинеарности двух векторов; (не)компланарности трех векторов.
Как найти координаты вектора, зная координаты его начала и конца?
Как найти длину, направляющие косинусы и орт вектора, заданного в декартовом ортонормированном базисе?
Перечислите основные способы задания векторов.
Дать определение скалярного произведения двух векторов.
Какая существует связь между скалярным произведением и проекцией вектора на ось?
Перечислите свойства скалярного произведения.
Как найти скалярное произведение векторов, заданных в декартовом ортонормированном базисе?
Как найти угол между двумя векторами с помощью скалярного произведения?
Как найти проекцию вектора на ось с помощью скалярного произведения?
Дать определение правой тройки векторов.
Дать определение векторного произведения двух векторов.
В чем состоит геометрический смысл модуля (длины) векторного произведения?
Перечислите свойства векторного произведения.
Как найти векторное произведение векторов, заданных в правом декартовом ортонормированном базисе?
Дать определение смешанного произведения трех векторов.
Как найти смешанное произведение векторов, заданных в декартовом ортонормированном базисе?
В чем состоит геометрический смысл смешанного произведения?
Beliebtester Live Sex Chat with Free-Cams bei BongaCams
Sexyste Новичок
#аршфиккен #schwanzlutschen
играй со мной bb // приватное шоу открыто // каждые 50 tkns злоупотребляют ее горлом
#блазен #сперма в Мунде #танзен #facial
8Alexandra8s Чат
[нет] перед стриптизом, Tits52/ Pussy114/ Blowjob136/ Dildoshow376/ Squirt577
#танзен #кеин фикен #муширайбен #Русский
Чат CherryMilfas
#минет #чаттен #сперма в киске #Mobile Live
PLATINUM-Ss Чат
NEW GRL ALERT♥ COME N PLAY W ME♥ C2C ON/725TKNS♥ PVT ON♥ LOVE FUCKING MY PUSSY SO HARD♥[none]: TOPLESS
#сквирт #Русский
Diana0999s Чат
зефирка-2022с Чат
#дилдофикен #харт фикен #handjob
Чат h5ngry-Bunnys
Красотка здесь #teen #худышка #smalltits #petite #ass
#раухен #ловенсе #Шпиле #Русский
муррррдс чат
#бдсм #бласен #абспритцен #küssen
LisaAndJhons Чат
Interaktiv (Lovense, Fickmaschine и т.
д.)
#танзен #лючен #ловенсе #König des Raums
KROSHKA_Ns Чат
#кунилингус #натурмуши лекен #Spiele
Не показывать сиськи! Группа голая, ТОЛЬКО полный приват — ваши Спецкоманды 50 111 157 500 токенов. Частный менее
#минет #абспритцен #бутерброд #раухен
406:Соси член и кончи на лицо с сиськами!ЛЮБОВЬ.
ВИБРО 11 и 33! СЛУЧАЙНЫЙ-77-ВОЛНА-88-ИМПУЛЬС-111-ВЗРЫВ-160-ЗЕМЛЯ-E 185!
#вичсен #лекен #киска #Мобильный Live
Мне в подарок 8088 ❤️ Lovense работает от 2-х жетонов. Небольшая вибрация 2-3с/12-10с. Средний 51-30с /91-55с. Большой 301-90с
#аршфиккен #genießend #фистинг #киска фикен
lera-oks Чат
#по фикен #фаллоимитатор #lecken
НОВАЯ ИГРУШКА!! Только жесткое вибро 2,11,50,111,333,555,100 для посещения туалета 200
#фингерал #лицо #ficken
Привет, ребята, приходите ко мне, чтобы открыть для себя мои самые сокровенные желания и удовольствия.
Я целую тебя и жду, когда ты сыграешь в тоге
#анмачен #Ауфнембар
Здравствуйте, я Юлия, у меня ловенс работает от 2 токенов Максимум вибро 21
#аршфиккен #минет #руббельн #Мобильный Live
ТРАХНИ МЕНЯ ❤️ ПОДПИСАТЬСЯ❤️ 2665 собрано, 247335 ОСТАЛОСЬ ЛЮБИМЫЕ ВИБРАЦИИ ❤️201 ❤️101 ❤️50 ЖЕЛЕЗ ФЕЙЕРВЕРК 80 ЗЕМЛЯQ
#глубокая глотка #фикен #Englisch
ОгонЕчеКККс Чат
#fingeranal
95317 tk — на новогодний подарок.
Любимая вибрация — 333 тк. Рандом — 44 ТК. Хожу в группу, приват и полный приват.
#фикен #дрочка #раздеть #муширайбен
Эй, ребята, тут много народу Сиськи 199, задница 401 здесь Перед приватом дополнительные 500 за приват с игрой в жопу
Heißeste Sex Shows Live
#минет #Mobile Live
2500 — обратный отсчет: 1158 собрано, 1342 жестко дрочат
#танзен #мастурбация #натурмуши лекен
Переписка в личку 50 ток
#дилдофикен #Русский
Всем привет! Я Натали!❤️ ❤️Lovens работает от 2x Режимы: Случайный 25__Волна 55__Импульс 222__Фейерверк 333__Землетрясение
#по фикен #дрочка #lutschen
дариас Чат
Нет тегов
Инст: Ali_ce2298 [нет]
#айерлекен #sperma-Swapping
Привет ребята)❤MENU LOVENSE!!!❤самая сильная вибрация 50 тк❤ у кого есть токены и у кого есть статус сидит и не поддерживает меня
#бутерброд #фикен #киска #сквирт
Тебе нравятся волосатые киски? Тогда вот вам! Ежедневные горячие шоу: БДСМ, Ролевые игры, Анал, Двойное проникновение, Фистинг,
#бдсм #мастурбация #Spiele
Привет пацаны!)) Любимые вибрации 55/101/201.
Назойливые нищие сидят молча. Всем хорошего дня, ярких оргазмов,
#харт фикен #сквирт #Spiele
[нет]! [none] поднято, [none] осталось до начала шоу***show Чулки в киске 10000
#танзен #глубокая глотка #дрочка #Englisch
Привет,я Лена!Собираю на оплату кредита 283143 собрал 16857
#минет #глубокая глотка #genießend #Mobile Live
5 ток — 1 раз шлепнуть по заднице Вибратор — от 2 токов 33333 — обратный отсчет, 5588 — готово, 27745 — аудиосистема
#фаллоимитатор #куссен #лекен #Russisch
СПЕЦИАЛЬНЫЕ КОМАНДЫ 23,51,99,102.
222.333 LOVENSE IN ass
Использование скалярного тройного произведения для доказательства копланарности векторов — Криста Кинг Математика
Формула скалярного тройного произведения
Скалярное тройное произведение ???|a\cdot(b\times c)|??? из трех векторов ???a\langle{a_1},a_2,a_3\rangle???, ???b\langle{b_1},b_2,b_3\rangle??? и ???c\langle{c_1},c_2,c_3\rangle??? будет равно ???0??? когда векторы компланарны, что означает, что все векторы лежат в одной плоскости.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.
???a???, ???b??? и ???c??? компланарны, если ???|a\cdot(b\times c)|=0???
???б\раз с??? является перекрестным произведением ???b??? и ???c???, и мы найдем его, используя ???3\times 3??? матрица
???\begin{vmatrix}\bold i&\bold j&\bold k\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}=\bold i\begin{vmatrix}b_2&b_3\\c_2&c_3\end{vmatrix}- \bold j\begin{vmatrix}b_1&b_3\\c_1&c_3\end{vmatrix}+\bold k\begin{vmatrix}b_1&b_2\\c_1&c_2\end{vmatrix}???
???=\жирный i(b_2c_3-b_3c_2)-\жирный j(b_1c_3-b_3c_1)+\жирный k(b_1c_2-b_2c_1)???
Мы преобразуем результат перекрестного произведения в стандартную векторную форму, а затем возьмем скалярное произведение ???a\langle{a_1},a_2,a_3\rangle??? и векторный результат ???b\times c???.
???|a\cdot(b\times c)|???
Окончательный ответ — скалярное тройное произведение. Если он равен ???0???, то мы доказали, что векторы компланарны.
Как использовать скалярное тройное произведение для проверки того, что три вектора компланарны (что они лежат в одной плоскости)
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Доказательство компланарности векторов
Пример
Докажите компланарность векторов.
???a\langle3,3,-3\rangle???
???b\langle1,0,-2\rangle???
???c\langle2,3,-1\rangle???
Мы будем использовать скалярное тройное произведение и начнем с вычисления перекрестного произведения ???b??? и ???с???, ???б\раз с???.
???b\times c=\begin{vmatrix}\bold i&\bold j&\bold k\\1&0&-2\\2&3&-1\end{vmatrix}???
???b\times c=\bold i\begin{vmatrix}0&-2\\3&-1\end{vmatrix}-\bold j\begin{vmatrix}1&-2\\2&-1\end {vmatrix}+\bold k\begin{vmatrix}1&0\\2&3\end{vmatrix}???
???b\times c=\жирный i[(0)(-1)-(-2)(3)]-\жирный j[(1)(-1)-(-2)(2) ]+\жирный k[(1)(3)-(0)(2)]???
???b\times c=\жирный i(0+6)-\жирный j(-1+4)+\жирный k(3-0)???
???b\times c=6\жирный i-3\жирный j+3\жирный k???
???b\times c=\langle6,-3,3\rangle???
Конечным ответом является скалярное тройное произведение.
