Плечо силы. Определение и примеры расчета плеча силы

Плечо силы — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения).

Определяется длинной нормали (перпендикуляра) к линии усилия проведенной из рассматриваемой точки.

Обозначается: L, l или h. Измеряется в метрах [м].

Плечо силы – один из двух множителей определяющих момент силы.

Наш короткий видеоурок про момент и плечо силы с примерами:
Момент и плечо силы (видео)

О плече силы можно говорить только тогда, когда есть прямая связь между силой и точкой относительно которой возникает момент.

Порядок нахождения плеча силы

Рассмотрим порядок нахождения плеча силы F относительно точки A.

Для этого покажем прямую a, по направлению действия силы F

Из точки A опустим перпендикуляр к прямой a.

Длина этого перпендикуляра является плечом силы.

Примеры определения плеча силы

1. Сила расположена перпендикулярно оси стержня и известно расстояние между точками A и B.
   
   Плечо силы относительно точки A равно длине отрезка AB.
2. Сила расположена под определенным углом к оси стержня
   
   Плечо силы относительно точки B составляет AB×cos30°
3. Известно расстояние от точки до линии действия силы
   
   Плечо силы относительно точки B равно 3м.

Момент силы >>

Момент действующей силы. Формула Сила, плечо силы

Момент силы — физическая величина, равная произведению силы на плечо силы.

Плечо силы — кратчайшее расстояние (перпендикуляр) между линией действия силы и точкой вращения тела.

Таким образом, формульно определим момент силы как:

(1)

Практическое применение момента силы необходимо в задачах, в которых тело НЕ участвует во вращательном движении.

Рис. 1. Момент сил

Проиллюстрируем способ поиска моментов сил, действующих на тело. Пусть на тело действуют три независимые силы (рис. 1). Тело представляет собой длинную балку, помещённую на неподвижную ось (в точке О), одним из размеров которых пренебречь нельзя.

Рис. 2. Момент сил. Линии действия сил

По определению (1), найдём моменты действующих сил, проиллюстрировав поиск плеча каждой силы рисунком. Проведём линии действия каждой из сил (зелёный цвет) (рис. 2).

Рис. 3. Момент сил. Плечо силы

Далее проведём плечо каждой силы. По определению, для поиска плеча силы достаточно провести перпендикуляр из точки вращения (О) на линию действия силы (рис. 3).

Тогда:

(2)

(3)

(4)

Таким образом, для нахождения момента силы необходимо решить геометрическую задачу (чаще всего с использованием теоремы Пифагора).

Вывод: поиск момента силы всегда происходит через определение (1). Иногда поиск плеча силы — геометрическая задача на теорему Пифагора.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

Формула плеча силы в физике

Определение и формула плеча силы

Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${\overline{F}}_1$ и ${\overline{F}}_2$, действующие на рычаг направлены в одну сторону.

Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.

Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $\left|OA\right|=d_1$- плечо силы $F_1$; $\left|OA\right|=d_2$- плечо силы $F_2$.

Рычаг находится в состоянии равновесия, если выполняется равенство:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1\right).\]

Предположим, что материальная точка движется по окружности (рис.2) под действием силы $\overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($\varepsilon $) точки определяется тангенциальной составляющей ($F_{\tau }$) силы $\overline{F}$:

\[mR\varepsilon =F_{\tau }\left(2\right),\]

где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{\tau }$ — проекция силы на направление скорости движения точки.

Если угол $\alpha $ — это угол между вектором силы $\overline{F}$ и радиус — вектором $\overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:

\[F_{\tau }=F{\sin \alpha \ \left(3\right).\ }\]

Расстояние $d$ между центром O и линией действия силы $\overline{F}$ называют плечом силы. Из рис.2 следует, что:

\[d=R{\sin \alpha \ \left(4\right).\ }\]

Если на точку будет действовать сила ($\overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $\alpha $ станет равен $\frac{\pi }{2}$.

Момент силы и плечо

Понятие плечо силы иногда используют, для записи величины момента силы ($\overline{M}$), который равен:

\[\overline{M}=\left[\overline{r}\overline{F}\right]\left(5\right),\]

где $\overline{r}$ — радиус — вектор проведенный к точке продолжения силы$\ \overline{F}$. Модуль вектора момента силы равен:

\[M=F{r\sin \alpha =\ }Fd\ \left(6\right).\]

Построение плеча силы

И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.

Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).

Примеры задач с решением

Рычаг — Википедия

Использование рычага для получения бо́льшего усилия на коротком плече, за счёт приложения меньшей силы на длинном.

Рыча́г — твёрдое тело, которое может вращаться вокруг неподвижной опоры.

Рычаг относится к простейшим механизмам. Представляет собой любой предмет, имеющий возможность вращаться вокруг неподвижной точки опоры (подвеса). Части предмета от точки опоры до точки приложения сил называют плечами рычага. Относительно точки опоры места приложения сил могут быть по разные стороны (рычаг I рода) или с одной стороны (рычаг II рода)

[1].

Рычаг используется для создания большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие.

Частными случаями рычага являются также два других простейших механизма: дифференциальный ворот и блок.

Человек стал использовать рычаг ещё в доисторические времена, интуитивно понимая его принцип. Такие инструменты, как мотыга или весло, применялись, чтобы уменьшить силу, которую необходимо было прикладывать человеку. В пятом тысячелетии до нашей эры в Месопотамии применялись весы, использовавшие принцип рычага для достижения равновесия.^[2][3] Позже, в Греции, был изобретён безмен, позволивший изменять плечо приложения силы, что сделало использование весов более удобным. Около 1500 года до н. э. в Египте и Индии появляется шадуф (колодец с «журавлём»), прародитель современных кранов, устройство для поднимания сосудов с водой.^[4]

Гравюра из «Журнала механики», изданного в Лондоне в 1842 году, изображающая Архимеда, переворачивающего Землю с помощью рычага.

Неизвестно, пытались ли мыслители тех времён объяснить принцип работы рычага. Первое письменное объяснение дал в III веке до н. э. Архимед, связав понятия силы, груза и плеча. Закон равновесия, сформулированный им, используется до сих пор и звучит как: «Усилие, умноженное на плечо приложения силы, равно нагрузке, умноженной на плечо приложения нагрузки, где плечо приложения силы — это расстояние от точки приложения силы до опоры, а плечо приложения нагрузки — это расстояние от точки приложения нагрузки до опоры». По легенде, осознав значение своего открытия, Архимед воскликнул: «Дайте мне точку опоры, и я переверну Землю!» ^[4].

В современном мире принцип действия рычага используется повсеместно. Практически любой механизм, преобразующий механическое движение, в том или ином виде использует рычаги. Подъёмные краны, двигатели, плоскогубцы, ножницы, а также тысячи других механизмов и инструментов используют рычаги в своей конструкции.

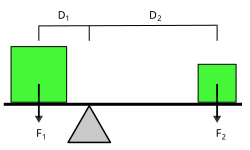Схема рычага. В равновесии F1D1=F2D2{\displaystyle F_{1}D_{1}=F_{2}D_{2}}

Принцип работы рычага является прямым следствием закона сохранения энергии. Чтобы переместить рычаг на расстояние Δh2{\displaystyle \Delta h_{1}} сила, действующая со стороны груза, должна совершить работу равную:

 A1=F1Δh2{\displaystyle \ A_{1}=F_{1}\Delta h_{1}}.

Если посмотреть с другой стороны, сила, приложенная с другой стороны, должна совершать работу

 A2=F2Δh3{\displaystyle \ A_{2}=F_{2}\Delta h_{2}},

где Δh3{\displaystyle \Delta h_{2}} — это перемещение конца рычага, к которому приложена сила F2{\displaystyle F_{2}}. Чтобы выполнялся закон сохранения энергии для замкнутой системы, работа действующей и противодействующей сил должны быть равны, то есть:

 A1=A2{\displaystyle \ A_{1}=A_{2}},

 F1Δh2=F2Δh3{\displaystyle \ F_{1}\Delta h_{1}=F_{2}\Delta h_{2}}.

По определению подобия треугольников, отношение перемещений двух концов рычага будет равно отношению его плеч:

Δh2Δh3=D1D2{\displaystyle {\frac {\Delta h_{1}}{\Delta h_{2}}}={\frac {D_{1}}{D_{2}}}}, следовательно

 F1D1=F2D2{\displaystyle \ F_{1}D_{1}=F_{2}D_{2}}.

Учитывая, что произведение силы и расстояния от точки опоры до линии действия силы является модулем момента силы, можно сформулировать принцип равновесия для рычага. Рычаг находится в равновесии, если сумма моментов сил (с учётом знака), приложенных к нему, равна нулю. (Точнее, если векторная сумма моментов сил, приложенных к нему, равна нулю.)

Для рычагов, как и для других механизмов, вводят характеристику, показывающую механический эффект, который можно получить за счёт рычага. Такой характеристикой является передаточное отношение, оно показывает, как соотносятся нагрузка и приложенная сила:

i=F1F2=D2D1{\displaystyle i={\frac {F_{1}}{F_{2}}}={\frac {D_{2}}{D_{1}}}}.

Нужно отметить, что как и у любого механизма, у рычага полезная работа меньше полной. Например, у большинства рычагов коэффициент полезного действия (КПД) равен ~ 80 %. Остальные 20 процентов работы расходуются на преодоление силы трения и т. п.

В специальной теории относительности теория рычага существенно отличается от принятой в классической механике (парадокс рычага).

Составной рычаг представляет собой систему из двух и более простых рычагов, соединённых таким образом, что выходное усилие одного рычага является входным для следующего. Например, для системы из двух последовательно связанных рычагов, если на входное плечо первого рычага приложена сила F1{\displaystyle F_{1}}, на другом конце этого рычага выходное усилие окажется F2{\displaystyle F_{2}}, и связаны они будут с помощью передаточного отношения:

i1=F1F2{\displaystyle i_{1}={\frac {F_{1}}{F_{2}}}}.

При этом на входное плечо второго рычага будет воздействовать такое же усилие F2{\displaystyle F_{2}}, а выходным усилием второго рычага и всей системы будет F3{\displaystyle F_{3}}, передаточное отношение второй ступени будет равно:

i2=F2F3{\displaystyle i_{2}={\frac {F_{2}}{F_{3}}}}.

При этом механический эффект всей системы, то есть всего составного рычага, будет вычисляться как отношение входного и выходного усилия для всей системы, то есть:

i=F1F3=F1F3F2F2=F1F2F2F3=i1i2{\displaystyle i={\frac {F_{1}}{F_{3}}}={\frac {F_{1}}{F_{3}}}{\frac {F_{2}}{F_{2}}}={\frac {F_{1}}{F_{2}}}{\frac {F_{2}}{F_{3}}}=i_{1}i_{2}}.

Таким образом, передаточное отношение составного рычага, состоящего из двух простых будет равно произведению передаточных отношений входящих в него простых рычагов.

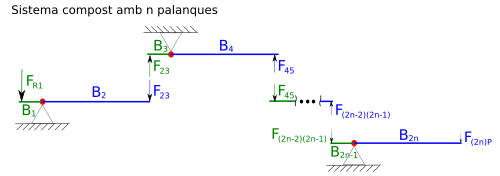Составной рычаг в общем случае, состоящий из n простых рычагов

Такой же подход решения можно применять и для более сложной системы, состоящей, в общем случае из n рычагов. В этом случае в системе будет присутствовать 2n плеч. Передаточное отношение для такой системы будет вычисляться по формуле:

iC=FR1F(2n−1)−P=FR1F23⋅F23F45⋅…⋅F(2n−2)−(2n−1)F(2n−1)−P=B2B1⋅B4B3⋅…⋅B(2n)B(2n−1){\displaystyle i_{C}={\frac {F_{R1}}{F_{(2n-1)-P}}}={\frac {F_{R1}}{F_{23}}}\cdot {\frac {F_{23}}{F_{45}}}\cdot …\cdot {\frac {F_{(2n-2)-(2n-1)}}{F_{(2n-1)-P}}}={\frac {B_{2}}{B_{1}}}\cdot {\frac {B_{4}}{B_{3}}}\cdot …\cdot {\frac {B_{(2n)}}{B_{(2n-1)}}}},

где:

•  Bi{\displaystyle \ B_{i}} — это i-ое плечо системы;
•  F(i−1)i{\displaystyle \ F_{(i-1)i}} — сила, передаваемая с плеча (i-1) на плечо i;
•  iC{\displaystyle \ i_{C}} — передаточное отношение всей системы.

Как видно из формулы для этого случая также верно, что передаточное отношение составного рычага равно произведению передаточных отношений входящих в него элементов.

Различают рычаги 1 рода, в которых точка опоры располагается между точками приложения сил, и рычаги 2 рода, в которых точки приложения сил располагаются по одну сторону от опоры. Среди рычагов 2 рода выделяют рычаги 3 рода^[5], с точкой приложения внешней силы ближе к точке опоры, чем нагрузки, что даёт выигрыш в скорости и пути.

Примеры: рычаги первого рода — детские качели (перекладина), ножницы; рычаги второго рода — тачка (точка опоры — колесо), приподнимание предмета ломом движением вверх; рычаги третьего рода — метла дворника, грабли; задняя дверь багажника или капот легковых автомобилей на гидравлических телескопических упорах, подъём кузова самосвала (с гидроцилиндром в центре), движение мышцами рук и ног человека и животных.

Конспект «Рычаг. Равновесие рычага. Момент силы»

«Рычаг. Равновесие рычага.
Момент силы. Правило моментов»

Рычагом называют твердое тело, которое может вращаться вокруг неподвижной точки. Неподвижную точку называют точкой опоры. Расстояние от точки опоры до линии действия силы называют плечом этой силы.

Условие равновесия рычага: рычаг находится в равновесии, если приложенные к рычагу силы F₁ и F₂ стремятся вращать его в противоположных направлениях, причем модули сил обратно пропорциональны плечам этих сил: F₁/F₂ = l₂/l₁ Это правило было установлено Архимедом. По легенде он воскликнул: Дайте мне точку опоры и я подниму Землю.

Для рычага выполняется «золотое правило» механики (если можно пренебречь трением и массой рычага).

Прикладывая к длинному рычагу некоторую силу, можно другим концом рычага поднимать груз, вес которого намного превышает эту силу. Это означает, что, используя рычаг, можно получить выигрыш в силе. При использовании рычага выигрыш в силе обязательно сопровождается таким же проигрышем в пути.

Момент силы. Правило моментов

Произведение модуля силы на ее плечо называют моментом силы. M = Fl, где М — момент силы, F — сила, l — плечо силы.

Правило моментов: рычаг находится в равновесии, если сумма моментов сил, стремящихся вращать рычаг в одном направлении, равна сумме моментов сил, стремящихся вращать его в противоположном направлении. Это правило справедливо для любого твердого тела, способного вращаться вокруг закрепленной оси.

Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от ее плеча. Именно поэтому, например, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. С помощью небольшой силы при этом создают значительный момент, и дверь открывается. Открыть ее, оказывая давление около петель, значительно труднее. По той же причине гайку легче отворачивать более длинным гаечным ключом, шуруп легче вывернуть с помощью отвертки с более широкой ручкой и т. д.

Единицей момента силы в СИ является ньютон-метр (1 Н*м). Это момент силы 1 Н, имеющей плечо 1 м.

 

---

Конспект урока «Рычаги. Равновесие рычага. Момент силы».

Следующая тема: «Механическая энергия. Закон сохранения энергии».

 

Плечо силы, определение и построение перпендикуляра. Направление вектора момента силы. Центр тяжести, массы. Формулы, примеры

Тестирование онлайн

Плечо силы

Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!

На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F₁ и F₂

Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке

Плечо силы реакции опоры определяется аналогично

Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F₂

Плечо силы F₁

Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.

При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.

Плечи сил F₁, F₂ и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d₁. Плечо силы трения — это длина d₂.

Момент силы

Это векторная величина, определяется по формуле

Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.

Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки

Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки

Если точка О выбрана на теле

Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки

Статика. Условие неподвижности тела. Момент силы. Правило моментов | LAMPA

Отлично! С плечом силы и моментом силы мы разобрались. Стоп! А зачем вообще они нам нужны-то? Не разобрались ли мы случайно в совершенно не нужных нам вещах? Нет. Момент силы — нужная нам вещь.

Напомним, что мы говорили об условии неподвижности тела. Мы получили одно условие: векторная сумма всех сил должна быть равна нулю F⃗1+F⃗2+…+F⃗N=0.\vec{F}_1+\vec{F}_2+…+\vec{F}_N=0{.}F⃗1​+F⃗2​+…+F⃗N​=0. Условие логичное — равнодействующая всех сил равна нулю.

Но мы видели пример (толкание ручки двумя пальцами), когда равнодействующая равна нулю, но тем не менее тело двигается. Так происходит, когда моменты сил, вращающих тело против часовой стрелки , не компенсируют моменты сил, вращающих тело по часовой стрелке.

Правило моментов. Для того чтобы тело было неподвижно, нужно, чтобы моменты сил, вращающих тело против часовой стрелки, в точности компенсировали моменты сил, вращающих тело по часовой стрелке: (M1+M2+…+MN)ПРОТИВ ЧАС. СТР.=(M_1+M_2+…+M_N)_{\text{ПРОТИВ ЧАС. СТР.}}=(M1​+M2​+…+MN​)ПРОТИВ ЧАС. СТР.​==(M1′+M2′+…+MN′)ПО ЧАС. СТР.=(M_1’+M_2’+…+M_N’)_{\text{ПО ЧАС. СТР.}}=(M1′​+M2′​+…+MN′​)ПО ЧАС. СТР.​

Вспомните пример с ручкой, которую мы толкали указательными пальцами обеих рук. Ручка вращалась из-за того, что моменты двух сил от наших пальцев вращали ее в одну и ту же сторону — против часовой стрелки. А «противостоять» этим моментам никакие другие силы не могли. Вот ручка и вращалась.

Проиллюстрировать это правило лучше всего на конкретном примере.

Условие

К левому концу невесомого стержня прикреплен груз массой 333 кг (см. рисунок). Стержень расположили на опоре, отстоящей от его левого конца на 0,20,20,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

(Источник: сайт reshuege.ru)

Решение

Итак, мы знаем, что стержень не будет вращаться в том случае, если моменты сил, вращающих его по часовой стрелке и против часовой стрелки, компенсируют друг друга. Значит, для начала нам нужно:

• нарисовать силы, действующие на рычаг
• найти и обозначить на рисунке плечи этих сил
• определиться с тем, в какую сторону эти силы вращают стержень (по часовой или же против часовой стрелки).

Итого у нас три силы:

• сила тяжести первого груза m1g⃗m_1\vec{g}m1​g⃗​; плечо этой силы d1=xd_1=xd1​=x (здесь xxx — длина маленького отрезка между темно-синими отметками на стержне)
• сила тяжести второго груза m2g⃗m_2\vec{g}m2​g⃗​; плечо этой силы d2=4xd_2=4xd2​=4x
• сила реакции треугольной опоры N⃗\vec{N}N⃗; плечо этой силы d=0d=0d=0, поскольку ось вращения (точка вращения) совпадает с точкой приложения силы, то есть лежит как раз на прямой, содержащей вектор силы N⃗\vec{N}N⃗; момент этой силы равен нулю.

Больше никаких сил к стержню не приложено. Сила тяжести самого стержня здесь отсутствует, поскольку в условии указано, что стержень «невесомый» — масса его равна нулю.

Из рисунка видно, что сила тяжести первого груза m1g⃗m_1\vec{g}m1​g⃗​ «пытается» повернуть стержень против часовой стрелки, а сила тяжести второго груза m2g⃗m_2\vec{g}m2​g⃗​ «пытается» повернуть стержень по часовой стрелке. Момент силы реакции опоры никуда ничего не поворачивает, поскольку плечо силы реакции опоры равно нулю. Поэтому для равновесия стержня момент силы тяжести m1g⃗m_1\vec{g}m1​g⃗​ должен быть равен моменту силы тяжести m2g⃗m_2\vec{g}m2​g⃗​:

m1g⋅d1=m2g⋅d2m_1g\cdot d_1=m_2g\cdot d_2m1​g⋅d1​=m2​g⋅d2​,

m1g⋅x=m2g⋅4xm_1g\cdot x=m_2g\cdot 4xm1​g⋅x=m2​g⋅4x,

m1g=4m2gm_1g=4m_2gm1​g=4m2​g,

m1=4m2m_1=4m_2m1​=4m2​,

m2=m14=3 кг4=0,75 кгm_2=\frac{m_1}{4}=\frac{3\text{ кг}}{4}=0,75\text{ кг}m2​=4m1​​=43 кг​=0,75 кг.

Ответ. 0,750,750,75 кг.

Замечание. Мы использовали при решении задачи только правило равенства моментов. А что нам дает первое условие — равенство нулю векторной суммы всех сил? Оно бывает полезно. Но используется не всегда. В нашем случае оно выглядит так:

m1g⃗+N⃗+m2g⃗=0m_1\vec{g}+\vec{N}+m_2\vec{g}=0m1​g⃗​+N⃗+m2​g⃗​=0.

Или в проекциях на вертикальную ось, направленную вверх:

−m1g+N−m2g=0-m_1g+N-m_2g=0−m1​g+N−m2​g=0,

N=m1g+m2gN=m_1g+m_2gN=m1​g+m2​g.

Вполне логичный результат: сила реакции опоры компенсирует две силы тяжести, приложенные к концам стержня. Это условие используется в случае «неудачно» выбранного положения оси вращения. Это не наш случай. В 90%90\%90% задач условие равенства нулю равнодействующей силы не понадобится.

Разберем еще одну задачу.

Условие

Под действием силы тяжести mgmgmg груза и силы FFF рычаг, представленный на рисунке, находится в равновесии.

Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную ось указаны на рисунке. Модуль силы FFF равен 600600600 Н. Найдите модуль силы тяжести, действующей на груз.

(Источник: сайт reshuege.ru)

Решение

Прежде всего, комментарий, который хочется высказать и нам, и вам: «Кошмарная задача». Согласимся с вами: задача внушает ужас. Все это обозначения длин, отрезков. Ужас.

Но возьмем себя в руки и попытаемся разобраться. Рычаг невесомый, поэтому на него действуют только три силы:

• сила тяжести груза mg⃗m\vec{g}mg⃗​
• сила F⃗\vec{F}F⃗
• сила реакции опоры «круглой штуки», на которую опирается рычаг, N⃗\vec{N}N⃗.

Рычаг вращается относительно точки касания «круглой штуки». Поэтому плечо силы реакции опоры N⃗\vec{N}N⃗ равно нулю. Момент этой силы равен нулю.

Из рисунка также видно, что сила тяжести груза mg⃗m\vec{g}mg⃗​ пытается вращать рычаг по часовой стрелке, а сила F⃗\vec{F}F⃗ — против часовой стрелки. Значит, для равновесия моменты этих сил должны компенсировать друг друга:

MF=MmgM_F=M_{mg}MF​=Mmg​.

Осталось найти плечи этих сил.