Глава 10. Статика

Статика — это раздел динамики, в котором рассматривается равновесие тел, и формулируются условия, при выполнении которых тела находятся в равновесии. Для успешного решения задач «на статику» необходимо уметь вычислять моменты сил, знать и уметь использовать условия равновесия тел. При этом следует помнить, что при вычислении моментов распределенных сил (тяжести, трения, реакции) возникает понятие центра тяжести тела, как точки, к которой надо приложить суммарную распределенную силу для вычисления ее момента.

Момент силы определяется по отношению к некоторой точке, которую будем называть началом отсчета моментов, и которая выбирается произвольно. Моментом силы называется произведение модуля силы на ее «плечо» , которое определяется как длина перпендикуляра, опущенного из начала отсчета момента на прямую, вдоль которой действует сила

(10. 1)

Например, плечом силы относительно точки (см. рисунок) является отрезок . Знак момента определяется следующим образом. Надо представить, что через точку проходит ось вращения тела, на которое действует сила . Если сила стремится закрутить тело по часовой стрелке относительно этой оси, то момент силы отрицателен, если против часовой стрелки — положителен. (Следует иметь в виду, что знак момента можно было выбирать и наоборот. Дело в том, что момент силы — это вектор. В школьном курсе, однако, определение вектора момент не вводится, и рассматриваются только такие ситуации, когда векторы момента направлены вдоль одной оси. Данное выше определение момента — это определение проекции вектора момента на эту ось. А поскольку направление оси никак не определяется, то важен только относительный знак проекций момента.) Из определения момента (10.1) следует, что момент силы равняется нулю, если прямая, вдоль которой она действует, проходит через начало отсчета момента.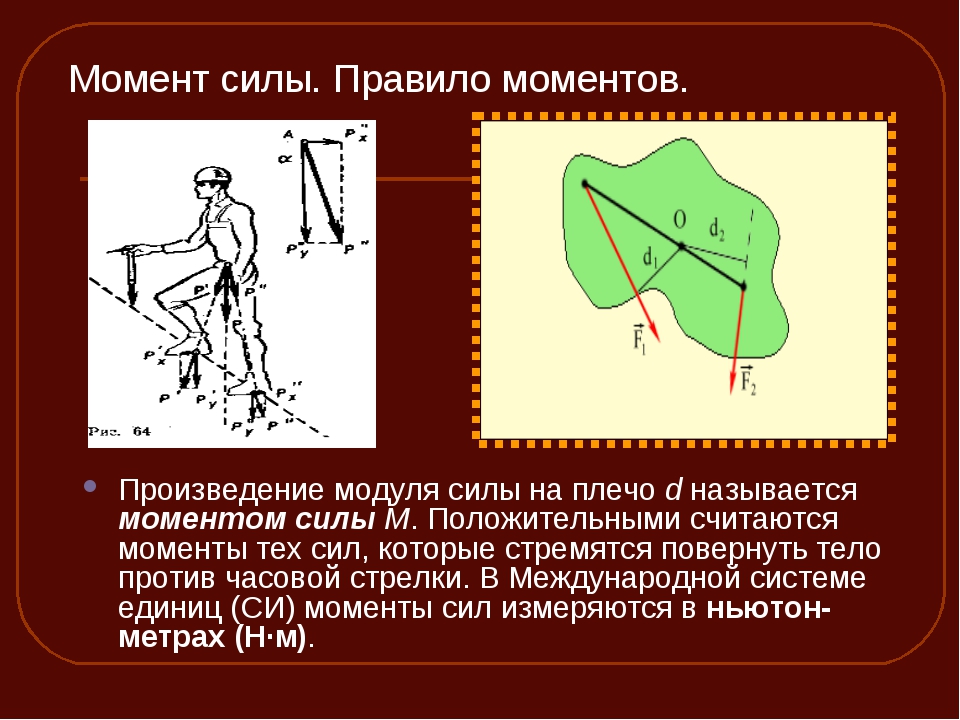

Если на неточечное тело действуют силы, у которых нет определенной точки приложения, например, сила тяжести, сила трения, сила реакции (такие силы принято называть распределенными), то для вычисления их моментов можно поступить следующим образом. Необходимо разбить это тело на бесконечно малые элементы, вычислить момент силы, действующей на каждый элемент, просуммировать полученные моменты. Оказывается, что если распределенные силы пропорциональны массам элементов и одинаково направлены, для вычисления момента распределенной силы нужно суммарную распределенную силу приложить к некоторой точке, которая называется центром тяжести тела. Центр тяжести тела, обладающего центральной симметрией (а только такие тела и могут встретиться школьникам), находится в геометрическом центре тела.

Тело находится в равновесии по отношению к инерциальной системе отсчета, если сумма всех сил, действующих на тело, равна нулю

(10. 2)

и сумма моментов этих сил, вычисленных относительно произвольного начала отсчета, равна нулю

(10.3)

Условия (10.2), (10.3) можно использовать для определения сил, действующих на тело, которое находится в равновесии.

В задаче 10.1.1 начало отсчета моментов (точка ) лежит на линии действия силы . Поэтому момент этой силы относительно точки равен нулю (ответ

3).

На рисунке числами 1, 2, 3 и 4 отмечены отрезки (толстые сплошные линии), которые представляют собой плечи сил , , или (задача 10.1.2) относительно точки (линии действия сил показаны тонким пунктиром). Из этого рисунка видим, что из этих сил наибольшее плечо имеет сила (правильный ответ в этой задаче – 2).

Для момента первой силы из задачи 10.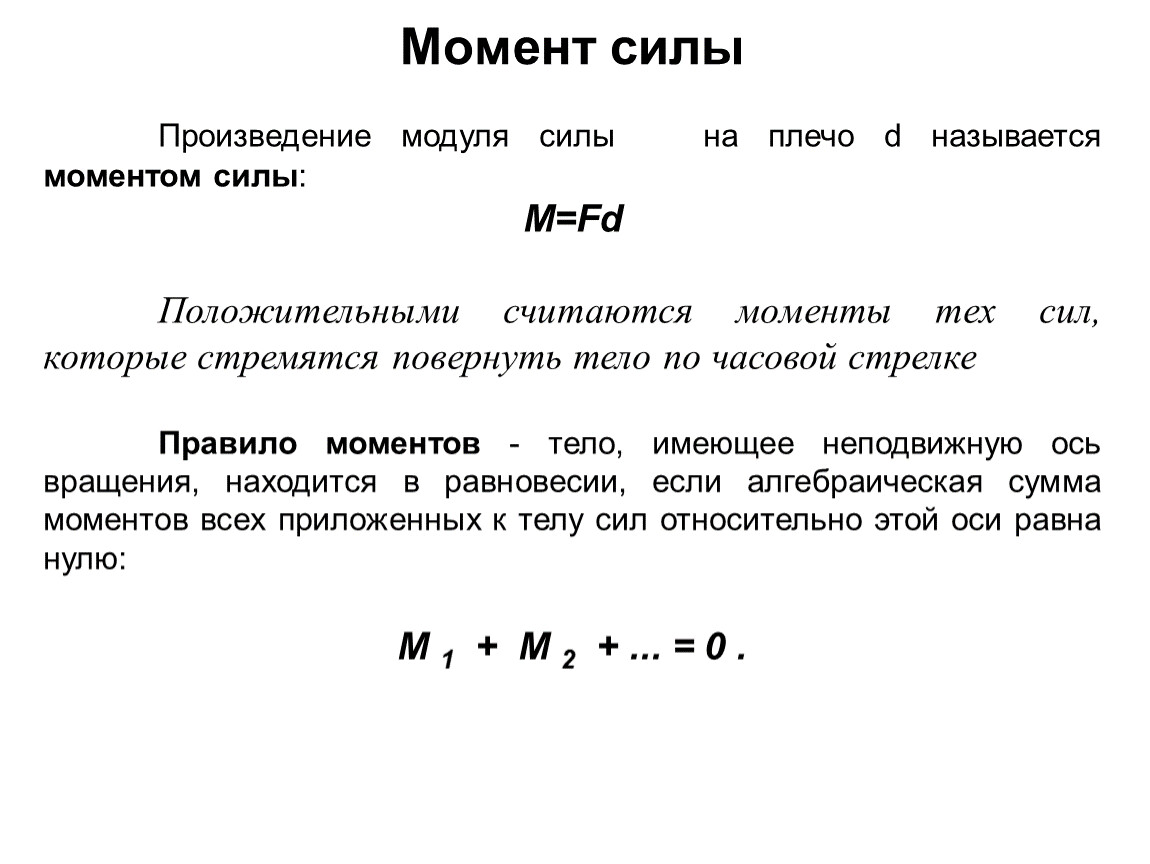 1.3 имеем

Тогда для момента второй силы получаем

т.е. момент второй силы в раз больше момента первой силы (ответ

1).

По определению плечо силы — это перпендикуляр опущенный из начала отсчета момента (точки в задаче 10.1.4) на линию действия силы. Поэтому плечо силы реакции — отрезок (или , который равен отрезку ). Следовательно, плечо силы реакции вертикальной стенки, действующей на лестницу, равно длине отрезка . Правильный ответ в задаче – 1.

Плечо силы в задаче 10.1.5 равно отрезку (см. рисунок). Из прямоугольного треугольника получаем для плеча силы — . Поэтому момент силы равен

(ответ 1).

На тело массой , находящееся на наклонной плоскости с углом наклона (

задача 10.1.6), со стороны плоскости действует сила реакции, направленная перпендикулярно плоскости и равная . Поэтому момент этой силы относительно основания плоскости длиной (см. рисунок в условии задачи) равен (ответ 2).

Чтобы рычаг был в равновесии сумма моментов всех сил, действующих на рычаг, должна равняться нулю, причем относительно любой точки — начала отсчета моментов. На рычаг в задаче 10.1.7 действуют: сила 3 Н на плечо длиной 0,1 м, искомая сила — на плечо длиной 0,3 м и сила со стороны оси вращения. Помещая начало отсчета моментов на оси вращения и находя моменты сил, действующих на плечи рычага, получаем из условия равновесия (10.3)

(момент силы, действующей на рычаг со стороны оси вращения равен нулю относительно выбранного начала). Отсюда находим, что (ответ 1).

Ось вращения стержня в задаче 10.1.8 надо расположить в такой точке, чтобы сумма моментов сил и относительно этой оси равнялась бы нулю. При этом очевидно, что ось должна располагаться справа от точки приложения силы .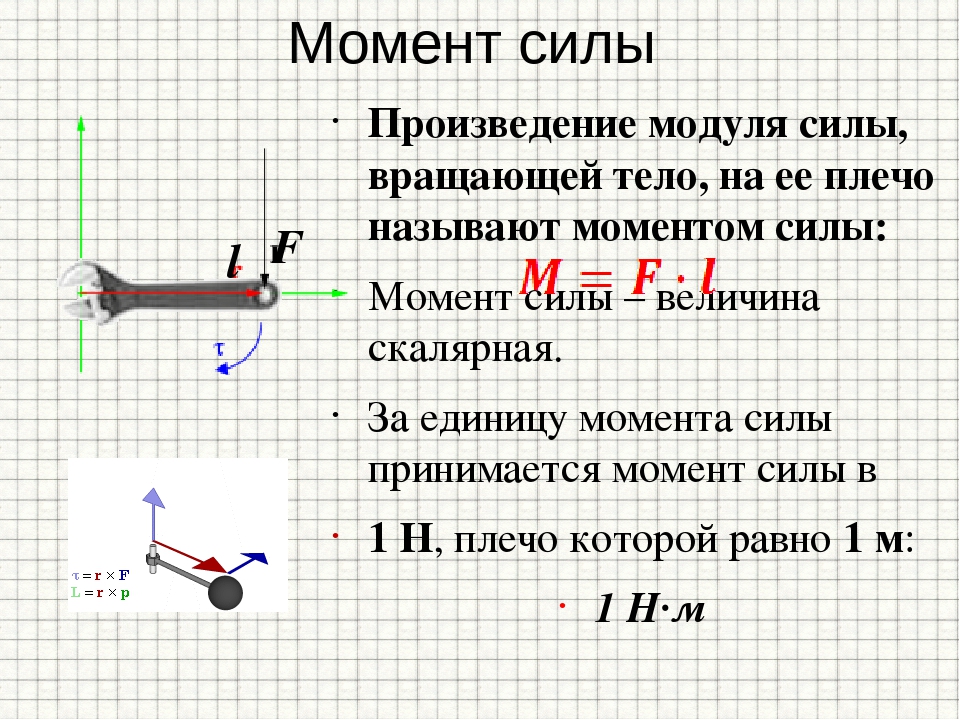 Поскольку величина силы втрое больше величины силы , то плечо силы должно быть втрое меньше плеча силы . Поэтому правильный ответ в задаче —

4.

Приравнивая величины моментов сил тяжести, действующих на тела, относительно опоры (задача 10.1.9), получим

где — расстояние от опоры до левого груза. Отсюда находим (ответ 2). Аналогично в задаче 10.1.10 получим (ответ 4).

В задаче 10.2.1 на невесомый стержень действуют две силы натяжения нитей и , и сила со стороны груза, равная его силе тяжести (см. рисунок). Используем условие равновесия стержня (10.3). Моменты удобно вычислять относительно начала отсчета , помещенного около правого конца стержня. Относительно этого начала имеем , , (здесь использовано, что точка крепления груза делит стержень в отношении 1:3). Поэтому из условия (10.3) получаем . Отсюда 4 кг (ответ

4).

Из условия равенства моментов, вращающих рычаг в задаче 10. 2.2 по и против часовой стрелки, получаем (ответ 4).

Как отмечалось во введении к настоящей главе, для нахождения момента распределенной силы (в данном случае момента силы тяжести) нужно силу тяжести, действующую на весь стержень, «приложить» к геометрическому центру стержня (к его середине) и вычислять момент этой силы так, как будто бы она является сосредоточенной (см. рисунок). Поэтому плечо силы тяжести относительно точки в

задаче 10.2.3 равно — длина стержня), и момент силы тяжести относительно точки равен — ответ 3. Здесь — масса стержня.

Используя это значение момента силы тяжести, можно найти силу натяжения нити в задаче 10.2.4. Условие равновесия (10.3) относительно точки дает

где — момент силы натяжения относительно точки . Отсюда находим (ответ 3).

С одной стороны, если к стержню приложена минимальная необходимая для переворота сила (задача 10.

2.5), сила реакции, действующая на стержень со стороны стола, будет приложена к точке, находящейся над самым краем. С другой стороны, если к концу стержня приложена именно такая сила, стержень практически находится в равновесии. Поэтому в том случае, когда на тело действует минимальная необходимая для переворота сила, сумма моментов силы тяжести и искомой силы относительно края стола равна нулю

Отсюда находим (ответ 2).

На стержень из задачи 10.2.6 действуют сила тяжести , реакции стенки и пола , а также сила трения со стороны пола, направленная так, как показано на рисунке, причем сила тяжести приложена к середине стержня. Используем условие равенства нулю суммы моментов внешних сил (10.3) относительно нижней точки стержня. Поскольку моменты силы трения и силы реакции относительно нижней точки стержня равны нулю, условие (10.3) дает

где — угол между стержнем и горизонтальной поверхностью (отмечен на рисунке дугой).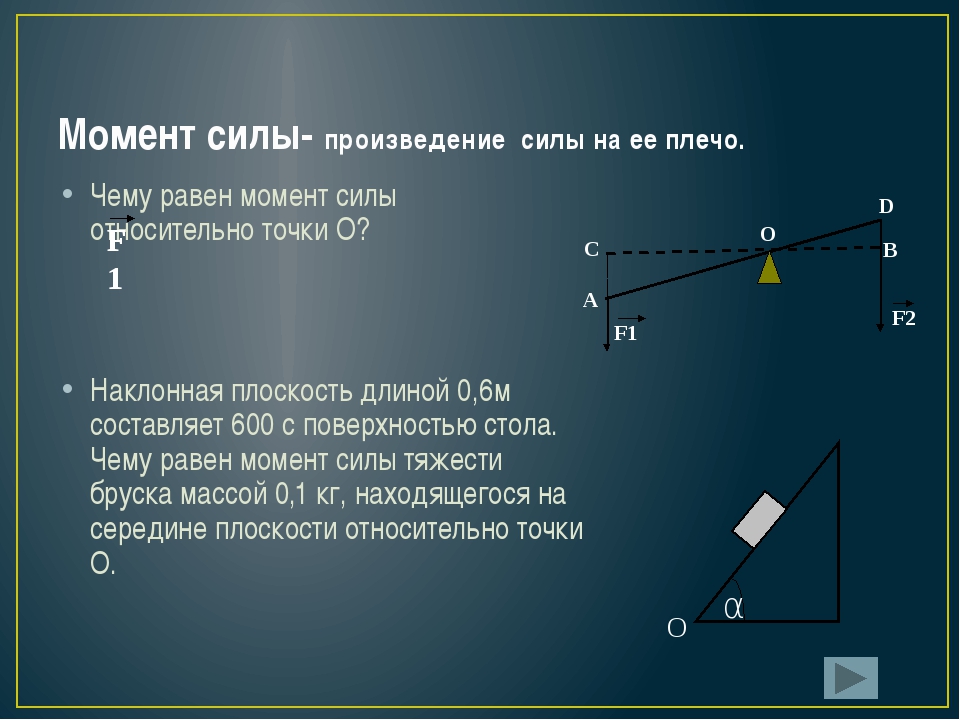 Отсюда находим

Поскольку для рассматриваемого случая , , то (ответ 1).

При приложении к концу стержня минимально необходимой для отрыва этого конца от поверхности (задача 10.2.7) силы одновременно выполнены два следующих условия. Поскольку стержень практически находится в равновесии, то еще выполнены уравнения статики — сумма моментов сил, действующих на стержень, равна нулю. С другой стороны, в этот момент стержень уже начинает отрываться от поверхности, и сила реакции опоры будет приложена к другому концу стержня (см. рисунок). Поэтому сумма моментов силы и силы тяжести относительно левого конца стержня должна равняться нулю . Отсюда (ответ 4).

При приложении к бруску минимально необходимой для его переворота силы (задача 10.2.8) сумма моментов сил тяжести и относительно упора (см. рисунок в условии) равна нулю. Этот вывод обосновывается так же, как и в предыдущей задаче. Поэтому (ответ 3).

В задаче 10.2.9 проще всего сравнить силы реакции упоров, из условия равенства нулю суммы всех сил, действующих на стержень (формула (10.2)). На стержень действуют три силы: тяжести , и две силы реакции и (см. рисунок), сумма которых равна нулю, или . Поэтому сила реакции нижнего упора больше, чем верхнего (ответ 2).

Треугольник в задаче 10.2.10 находится в равновесии, если его центр тяжести лежит на вертикальной прямой, проходящей через шарнир. Это связано с тем, что на треугольник действуют две силы — тяжести и реакции шарнира — и, чтобы выполнялось условие моментов относительно шарнира, момент силы тяжести относительно шарнира должен равняться нулю. Докажем, что центр тяжести треугольника лежит в точке пересечения его медиан. Действительно, если разбить треугольник на тонкие полоски, параллельные одной из сторон, то центр тяжести каждой из них лежит в ее середине. Поэтому и центры тяжести всех полосок (а, значит, и всего треугольника) лежат на его медиане (см. рисунок; медиана показана пунктиром). А поскольку треугольник можно разделить на слои, параллельные второй и третьей его стороне, то центр тяжести лежит и на этих медианах, т.е. в точке их пересечения (правильный ответ 1).

Момент силы.

Теоретическая механика



Момент силы

Говорят, что когда-то великий Архимед изрек фразу: «Дайте мне точку опоры, и я переверну Землю». Современная физика утверждает, что с практической точки зрения, мудрый грек, конечно же, погорячился – даже сдвинуть на доли миллиметра такой массив, как планета с помощью мускульной силы человека – занятие не одного года, а уж перевернуть Землю…
Тем не менее, с теоретической точки зрения Архимед прав – если найти соответствующую точку опоры, то с помощью рычага Землю сдвинуть с места может даже комар. Дело в том, что здесь играет роль не сила, как таковая, а ее момент.

Что же такое – момент силы? Следует сразу оговориться, что момент силы — понятие относительное, поскольку без указания того, относительно какой точки он рассматривается, понятие момента силы теряет смысл (не путать с моментом пары сил, о котором речь пойдет в следующих статьях).

Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие.
Если взять более длинный ключ, то гайку можно завернуть значительно сильнее, прикладывая одинаковое усилие. Из этого следует, что одной и той же силой можно выполнить различное по эффективности вращающее действие на какое-либо тело. В этом и кроется понятие момента силы – это вращающее действие силы относительно какой-либо точки в пространстве.

Понятие момента силы относительно точки ввел гениальный итальянец Леонардо да Винчи (1452-1519), который известен потомкам не только, как великий художник, но и видный ученый своего времени.

Итак, по определению, момент силы относительно точки – это произведение модуля силы на ее плечо.
Плечом в данном случае называется кратчайшее расстояние от рассматриваемой точки до линии действия силы, т. е. перпендикуляр, опущенный из точки на линию действия силы (см. рисунок b).
Математически это определение можно представить в виде формулы:

М₀(F) = Fh,     где h – плечо силы относительно точки 0.

Точка, относительно которой рассматривается момент силы, называется центром момента.

Из приведенной выше формулы очевидно, что единицей измерения момента силы является ньютон × метр (Нм).



Теперь можно оценить справедливость высказывания Архимеда относительно возможности перевернуть Землю — при определенном плече силы, которую способны развить человеческие мускулы, это сделать теоретически возможно, но рука Архимеда должна была описать путь длиной в сотни тысяч километров для того, чтобы сдвинуть земной шар на доли миллиметра, поскольку потребовался бы огромной длины рычаг. Как вы понимаете, практически осуществить подобный подвиг нереально даже для такого уважаемого гения, как Архимед.

Впрочем, бытующее утверждение о трудностях, связанных с перемещением Земли человеческой рукой не совсем безгрешны. Ведь мы, как обыватели, привыкли рассматривать Землю, как весомый предмет, забывая что она, будучи в космическом пространстве, обладает совсем другими весовыми категориями. Поэтому справедливее будет рассматривать не расстояние, на которое мог бы сдвинуть земной шар Архимед, а ускорение, с которым он попытался бы сдвинуть планету со своего места, т. е. фактически — побороть силу инерции Земли, как тела.
И тогда ему не потребовался бы рычаг непомерной длины — прикладывая незначительную силу, сдвинуть Землю можно было бы и двухметровой палкой, но здесь уже возник бы вопрос о времени, в течении которого необходимо было давить на рычаг, чтобы побороть инертность земного шара (как вы понимаете, мускульная сила человека не способна придать планете существенного ускорения).
Опять же, возникает еще одна проблема — Архимеду потребовался бы надежный упор для ног, способный противостоять возмущению Земли на нахальную попытку Архимеда сдвинуть ее с места, а где его найти в открытом космосе?…

Осталось разобраться со знаками для момента силы, ведь он, как и сила, является векторной величиной, т. е. характеризуется не только модулем, но и направлением своего вращающего действия.
При расчетах в технической механике условно считают, что если момент силы стремиться вращать свое плечо вокруг центра момента против часовой стрелки, то он является положительным, если по часовой стрелке — отрицательным (см. рисунок a).

Одна и та же сила относительно разных точек может вызывать и положительный, и отрицательный момент (см. рисунок a).

Отдельный случай, когда рассматриваемая точка (центр момента) лежит на линии действия силы. Очевидно, что в этом случае момент силы относительно этой точки будет равен нулю, поскольку плечо отсутствует (расстояние от линии действия силы до точки равно нулю).

И еще одна важная деталь, которая следует из определения момента силы относительно точки: если переносить силу вдоль линии ее действия, то момент силы относительно любой точки не изменится, поскольку не изменится и расстояние от этой точки до линии действия силы, т. е. плечо (см. рисунок с).

***

Плоская система пар сил



Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

Статика твёрдого тела — материалы для подготовки к ЕГЭ по Физике

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: момент силы, условия равновесия твёрдого тела.

Статика изучает равновесие тел под действием приложенных к ним сил. Равновесие — это состояние тела, при котором каждая его точка остаётся всё время неподвижной в некоторой инерциальной системе отсчёта.

Условием равновесия материальной точки является равенство нулю равнодействующей (т. е. векторной суммы) всех сил, приложенных к точке. В этом случае наша точка будет двигаться равномерно и прямолинейно в произвольной инерциальной системе отсчёта. Значит, система отсчёта, связанная с точкой, также будет инерциальной, и в ней точка будет покоиться.

В случае твёрдого тела ситуация сложнее. Прежде всего, важно учитывать точку приложения каждой силы.

-Сила тяжести приложена в центре тяжести тела. Для тела простой формы центр тяжести совпадает с центром симметрии.

-Силы упругости и трения приложены в точке или в плоскости контакта тела с соприкасающимся телом.

Прямая линия, проходящая через точку приложения вдоль вектора силы, называется линией действия силы. Оказывается, точку приложения силы можно переносить вдоль линии её действия — от этого механическое состояние тела не изменится (в частности, равновесие не нарушится).

Для равновесия твёрдого тела недостаточно потребовать равенства нулю векторной суммы всех приложенных к телу сил.

В качестве примера рассмотрим пару сил — так называются две равные по модулю противоположно направленные силы, линии действия которых не совпадают. Пусть пара сил и приложена к твёрдому стержню (рис. 1).

Рис. 1. Пара сил

 

Векторная сумма этих сил равна нулю. Но стержень покоиться не будет: он начнёт вращаться. В данном случае не выполнено второе условие равновесия твёрдого тела. Чтобы его сформулировать, нужно ввести понятие момента силы.

Как должна быть направлена линия действия силы, чтобы тело стало вращаться вокруг неподвижной оси? Для начала заметим следующее.

— Если линия действия силы параллельна данной оси, то вращения не будет.
— Если линия действия силы пересекает данную ось, то вращения не будет.

В каждом из этих случаев действие силы вызывает лишь деформацию твёрдого тела.

Чтобы началось вращение, линия действия силы и ось вращения должны быть скрещивающимися прямыми.

Без ограничения общности можно считать эти прямые перпендикулярными друг другу. Мы всегда можем этого добиться, разложив силу на две составляющие — параллельную и перпендикулярную оси вращения — и отбросив параллельную составляющую как не вызывающую вращения. Поэтому везде далее мы считаем, что все силы, действующие на тело, перпендикулярны оси вращения.

Момент силы.

 

Плечо силы — это расстояние от оси вращения до линия действия силы (т. е. длина общего перпендикуляра к двум этим прямым).

В качестве примера на рис. 2 изображён диск, к которому приложена сила . Ось вращения перпендикулярна плоскости чертежа и проходит через точку . Плечом силы является величина , где — основание перпендикуляра, опущенного из точки на линию действия
силы.

Рис. 2. Плечо силы

 

Момент силы относительно оси вращения — это произведение силы на плечо:

.

Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.

Условия равновесия.

 

Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов . Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения.

В общем случае, когда твёрдое тело может совершать как поступательное, так и вращательное движение, мы имеем два условия равновесия.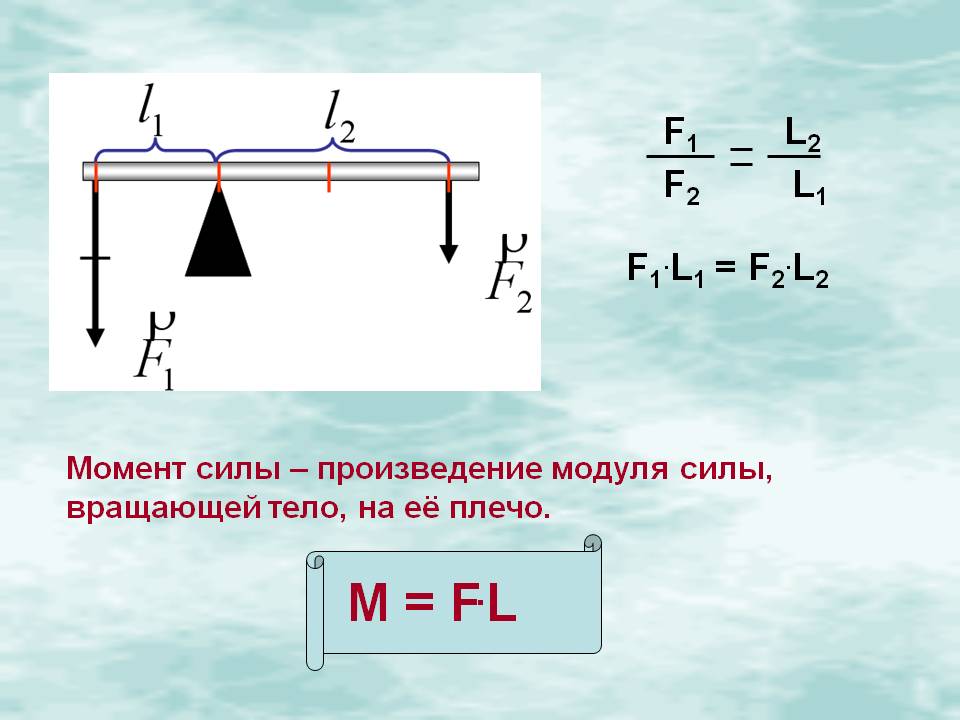

1. Равна нулю векторная сумма всех сил, приложенных к телу.
2. Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.

Так, в примере на рис. 1 алгебраическая сумма моментов пары сил не обращается нуль (оба момента положительны). Поэтому стержень не находится в равновесии.

При решении задач удобно использовать сформулированные выше условия равновесия в следующем виде.

1′. Силы уравновешены вдоль любой оси.
2′. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.

Сейчас мы разберём одну достаточно содержательную задачу по статике и посмотрим, как работают наши условия равновесия.

Задача. Однородная лестница опирается на гладкую вертикальную стену, образуя с ней угол . При каком максимальном значении лестница будет покоиться? Коэффициент трения между лестницей и полом равен .

Решение. Пусть лестница опирается о пол и стену в точках и соответственно (рис. 3). Расставим силы, действующие на лестницу.

Рис. 3. К задаче

 

Поскольку лестница однородная, сила тяжести приложена в середине лестницы. Сила упругости пола и сила трения приложены в точке . На рис. 3 точка приложения этих сил немного смещена от точки внутрь лестницы; тем самым мы однозначно указываем, что силы приложены именно к лестнице (а не к полу).

Точно так же сила упругости стены приложена в точке . Поскольку стена гладкая, сила трения между стеной и лестницей отсутствует.
Воспользуемся условием 1′. Вдоль горизонтальной оси силы уравновешены:

. (1)

Вдоль вертикальной оси силы также уравновешены:

. (2)

Теперь переходим к правилу моментов — условию 2′. Какую ось вращения выбрать? Удобнее всего взять ось, проходящую через точку (перпендикулярно плоскости рисунка). В таком случае моменты сразу двух сил и обратятся в нуль — ведь плечи этих сил относительно точки равны нулю (поскольку линии действия сил проходят через эту точку). Ненулевые моменты относительно точки имеют силы и , которые стремятся вращать лестницу в разные стороны; стало быть, моменты данных сил должны быть равны друг другу.

Плечо силы — это длина перпендикуляра , опущенного из точки на линию действия силы . Плечо силы — это длина перпендикуляра , опущенного из точки на линию действия силы . Согласно правилу моментов имеем:

Пусть длина лестницы равна . Тогда . Подставляем эти соотношения в равенство моментов:

откуда

(3)

С учётом равенства (1) имеем вместо (3):

(4)

Вспомним теперь, что в условии спрашивается максимальное значение . При максимальном угле лестница пока ещё стоит, но уже находится на грани проскальзывания. Это означает, что сила трения достигла своего максимального значения, равного силе трения скольжения:

.

Теперь из (4) получаем:

,

а с учётом равенства (2):

.

Отсюда получаем искомую максимальную величину :

.

 

Урок по теме «Момент силы»

План – конспект урока № 49/4.

Тема: Момент силы.

Цель: познакомиться с новой физической величиной, которая характеризует состояние тел с точкой вращения Раскрыть сущность изучаемых явлений.

Задачи:

а) образовательная проконтролировать знания учащихся, полученные на предыдущем уроке, сформировать представления о структуре и содержании изучаемой физической теории, организовать усвоение основных определений по данной теме, познакомить с основными физическими величинами, сформулировать основные законы по данной теме.

б) развивающая формировать мотивацию постановкой познавательных задач, раскрытием связи теории и опыта, формировать умение анализировать факты при наблюдении или объяснении явлений, при работе с текстом учебника, развивать внимание, память, логическое и творческое мышления.

в) воспитательная формирование интереса к физике при анализе физических явлений, при демонстрации опытов, при решении задач, стимуляция работы учащихся, формирование научного мировоззрения учащихся.

Методы: объяснительно – иллюстративный, проблемный, репродуктивный, эвристический.

Оборудование: учебник, демонстрационное оборудование.

План урока:

1. Организационный момент (1 – 2 минуты).

2. Домашнее задание (2 – 3 минуты).

3. Проверка домашнего задания (10-15 минут).

4. Изложение нового материала (15 – 22 минуты).

5. Закрепление нового материала (5 – 10 минут).

6. Итог урока (1-2 минуты)

Ход урока:

1. Организационный момент

2. Домашнее задание §57, упр. 30 (2). Подг к л/р. №9.

3. Проверка домашнего задания

При проверке домашнего задания двое-трое учащихся отвечают на вопросы в конце §20. Еще два ученика у доски графически определяют плечи сил, действующих на рычаги. Примерами задания могут быть следующие:

4. Изложение нового материала

Переходя к изложению основного материала, следует отталкиваться от основного соотношения:

Этому соотношению французский ученый П.Вариньон придал наиболее общую форму, введя такое понятие как момент силы.

Под моментом силы понимают произведение силы на плечо:

где F — сила, l — плечо силы.

Можно легко доказать, что рычаг находится в равновесии, если момент силы, вращающий рычаг по часовой стрелке равен моменту силы, вращающей рычаг против часовой стрелки.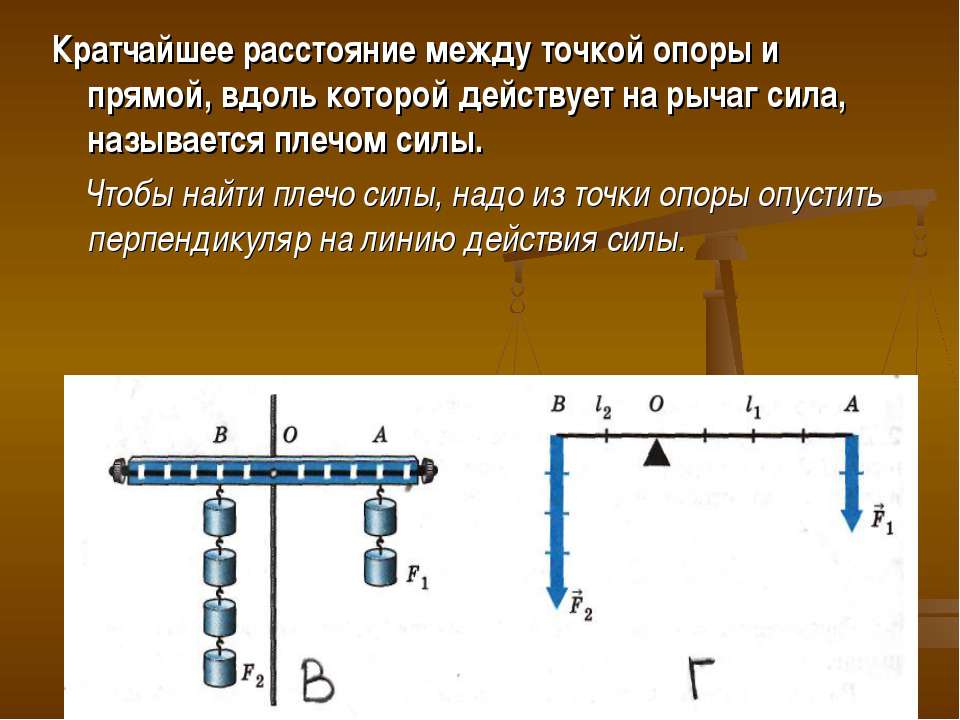

Согласно (1), используя свойство пропорции можно получить:

В выражении (3) М₁ = F₁l_1, а М₂ = F₂l₂.

М₂ стремится повернуть рычаг по часовой стрелке, a M₁ — против часовой стрелки. Таким образом:

Правило моментов справедливо для любого твердого тела, которое имеет закрепленную ось вращения. При этом важно выполнение условия (4), а не число «положительных» и «отрицательных» моментов.

При определении плеча силы следует всегда проводить линию действия силы, на которую из точки вращения опускают перпендикуляр, длина которого и есть плечо данной силы.

Согласно (2) даже небольшая сила может создавать большой вращающий момент.

Для этого нужно брать значение плеча. Это широко используют в технике и быту. Отвертки с широкой рукояткой, гаечные ключи, ножницы по металлу — все эти устройства имеют большие плечи.

5. Закрепление

№ 743, 747, 748

743°. На рычаге грузы по 1 Н каждый уравновешиваются растянутой пружиной динамометра (рис. 212). Определите цену деления динамометра. (На динамометр действует сила F = 6 Н. Он показывает шесть делений => цена деления динамометра 1 Н.)

747. Длина меньшего плеча рычага 5 см, большего 30 см. На меньшее плечо действует сила 12 Н. Какую силу надо приложить к большему плечу, чтобы уравновесить рычаг? (Сделайте рисунок. Весом рычага пренебречь.)

748. При помощи кусачек перекусывают гвоздь. Расстояние от оси вращения кусачек до гвоздя 2 см, а до точки приложения силы руки 16 см. Рука сжимает кусачки с силой 200 Н. Определите силу, действующую на гвоздь.

Домашние опыты: изучение равновесия рычага

1. Возьмите карандаш, линейку и три-четыре одинаковые старательные резинки.

2. Положите линейку на карандаш так, чтобы она опиралась точно посередине и лежала горизонтально.

3. Положите на расстоянии 10 см от карандаша резинку. Убедитесь, что для равновесия линейки, вторую резинку нужно положить также на расстоянии 10си по другую сторону от карандаша.

4. На одну из резинок положите еще одну. Убедитесь, что для равновесия линейки, теперь необходимо вдвое уменьшить расстояние этих двух резинок до карандаша.

6. Подведение итогов урока. Выставление оценок.

Издательство «Поли Медиа Пресс»

Александр Давидович Шварц, известный ученый и врач, высококлассный профессионал, чья диссертация о бюгельном протезировании в свое время в ЦНИИСе считалась как «Библия ортопедической стоматологии» (со слов А. Ш.). Он считается патриархом, ведущим специалистом и общепризнанным авторитетом в областях протезирования с применением съемных опирающихся протезов и биомеханики зубочелюстной системы. Подробно с его концепциями и идеями можно познакомиться из многочисленных публикаций в различных изданиях. Мы же начинаем публиковать статьи Александра Давидовича на страницах газеты «Стоматология Сегодня» и первым материалом печатаем краткий вариант концепции ортопедического лечения дефектов зубных рядов, переданный нам автором вместе с добрыми пожеланиями успехов в работе, в качестве уважения к нашему труду.

При ортопедическом лечении дефектов зубных рядов учитывается общее состояние здоровья больного, т.е. осуществляется системный подход. Однако, наряду с оценкой состояния внутренних органов, недостаточное внимание уделяется функции жевательных мышц, которые при открывании и закрывании полости рта, при дроблении пищи, при боковых сдвигах нижней челюсти осуществляют физиологическую, механическую работу.  
    При этом на скатах окклюзионной поверхности возникают силы нормальной реакции (упругости) — N и трения (F), равнодействующей которых являются силы опорных реакций (Rn). Однако, для представления об устойчивости (равновесии) зуба необходимо учитывать все силы опорных реакций, для чего надо определить полное давление (реакцию) — R. 
    Только учитывая угол между реакцией (R) и осью зуба, врач может правильно определить углы наклонов скатов жевательной поверхности и передать эти данные в лабораторию. К сожалению, зубной техник в настоящее время не имеет этих данных и самостоятельно решает вопросы степени наклонов скатов бугорков, в то время как от этого зависит устойчивость зубов. 
    Полное давление всей окклюзионной поверхности — R должно действовать вдоль оси зуба или под незначительным углом (18-20°) относительно оси зуба. Наиболее важным для сохранения зубов при протезировании является учет моментов сил (М), расшатывающих зубы. Момент силы возникает всегда при глотании пищи, т.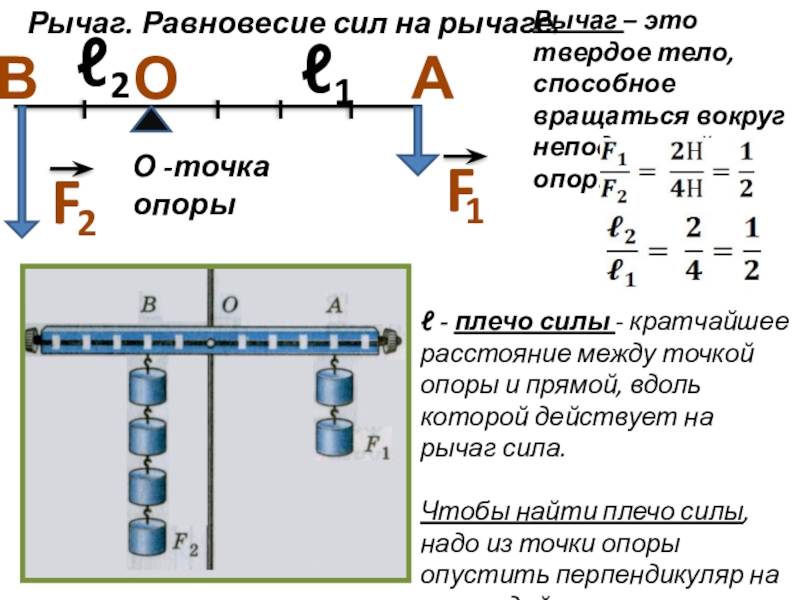 е. несколько тысяч раз в день. Но, если силы толерантности организма и пародонта зубов превышают величину момента силы, то зубы будут устойчивы. Однако, нередко может быть противоположная картина, при которой зубы подлежат удалению. Момент силы — это произведение силы реакции на расстояние между ней и центром зуба M=R*L. Момент силы является основным параметром, характеризующим устойчивость, расшатывание зуба. 
    Опасный момент можно исключить при соотношении бугорков зуба 5:3. В таком случае при глотании пищи реакция реакция равна 0, следовательно, отсутствует плечо силы. 
    Поэтому, при протезировании следует ознакомиться с общим состоянием организма больного и в последующем — направлением действия силовых параметров (N, F, L, Rn, R ), возникающих со стороны жевательных мышщ. 
    Во всех случаях врач должен провести статический анализ (на листе бумаги), на котором зарисовать контуры опорных боковых зубов, углы наклона их продольных осей, а затем все необходимые параметры. Такой статический анализ учитывает наиболее важные показатели зубов при протезировании, каковыми являются направления силовых параметров, т.к. без них можно рассчитывать только на силы организма, а не на планирование. 
    К сожалению, нередко врачи недооценивают, что началом пищеварительной системы является полость рта, зубы, осуществляющие жевательную функцию. 
    Поэтому, статический анализ направления действия силовых параметров должен стать обязательным для каждого ортопеда. 
    Все это соответствует уровню квалификационного стоматолога-ортопеда XXI-го века. Без этого врач может уподобиться зубному врачу прошлого столетия. 
    
    Аксиомы физики и клиника ортопедической стоматологии 
    1. Действие 2-х сил на скатах жевательной поверхности = Упругости (нормальной реакции) N и трения — F, их равнодействующая — сила опорной реакции Rn — давление каждого ската. 
    2. Расстояние от центра корня зуба на его оси до силы Rn — плечо силы — L.  
    3. Определение полного давления R и его направления относительно оси зуба — иначе моделирование искусственной коронки будет неточным. Давление должно действовать примерно вдоль оси. 
    4. M — момент силы, характеризующий устойчивость, расшатывание зуба : 
    — при давлении пищи на один скат 
    — при пище на всей жевательной поверхности 
    — при глотании пищевого комка 
    — относительное «равенство моментов» 
    — при действии силы на вершину бугорка 
    — в зависимости от протяженности окклюзионных накладок. 
    5. «Биомеханический гомеостаз» — амортизация, демпфирование давления 
    6. R и M — два параметра, характеризующие положение зуба при центральной окклюзии (IKR) и центральном соотношении (RKP) 
    Момент силы, расшатывающий зуб, особенно при глотании, должент быть равен 0 или крайне незначительным по величине. 
    7. Проведение мероприятий при дефекте 1-го зуба, замедляющие наклон смежных зубов.  
    8. Действие 2-х сил — при наличии бугорков зуба и 1-силы при стирающейся окклюзии. Само торможение, конус трения, синдром ВНЧС. 
    9. Соотношение бугорков: 2:1; 2,5: 1,5; 5:3. 
    10. Моделирование бугорков окклюзионной поверхности зубов с соотношением 5:3 
    11. Постановка зубов (5:3) для съемного протезирования со скатами 15 и 25°. 
    12. Модификация постановки зубов, выпускающихся в настоящее время. 
    13. Коррекция режущей поверхности (резцовой площадки) фронтальных зубов. 
    14. Схематическое изображение сил N, F, Rn при наклонах скатов 15, 30, 45, 60, 75, 81,5°. 
    15. Нижняя челюсть, как рычаг III — го рода — выигрыш в силе при глотании пищи. 
    16. Вертикальное и наклонное (под углом) действие давления на скат, горизонтальное действие давления на коронку зуба. 
    17. Лингвализированная окклюзия (1:1). Зависимость наклонов скатов от осей зубов. 
    18. То же, при наличии имплантатов (1:1) 
    19. То же при соотношении бугорков (5:3) 
    20. Моделирование скатов окклюзионной поверхности, при которых в RKP давление действует вдоль оси зуба (М=0) 
    21. Параметры силы: 
    — величина (полное давление, распределенное на все 28 зубов) 
    — направление действия (под углом не более 18-20°) 
    — точка приложения давления (посредине жевательной поверхности возможны только при соотношении бугорков 5:3, что соответствует закону, разработанному одним из известных ортопедов Германии A. Motsch (1978), в котором одним из признаков гармонической окклюзии является минимум мышечных затрат при максимуме эффективности акта жевания.

Глава 4

Вам уже известно правило равновесия рычага:

.

Пользуясь свойством пропорции (произведение её крайних членов равно произведению средних членов), запишем его в таком виде:

F₁l₁ = F₂l₂.

В левой части равенства стоит произведение силы F₁ на её плечо l₁, а в правой — произведение силы F₂ на её плечо l₂.

Произведение модуля силы, вращающей тело, на её плечо называется моментом силы; он обозначается буквой M. Следовательно,

M = Fl.

Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.

Это правило, называемое правилом моментов, можно записать в виде формулы:

M₁ = M₂.

Действительно, в рассмотренном нами опыте (§ 58) действующие на рычаг силы были равны 2 Н и 4 Н, их плечи соответственно составляли 4 и 2 деления рычага, т. е. моменты этих сил одинаковы при равновесии рычага.

Момент силы, как и всякая физическая величина, может быть измерен. За единицу момента силы принимается момент силы в 1 Н, плечо которой равно 1 м.

Эту единицу называют ньютон-метр (Н•м).

Момент силы характеризует действие силы и показывает, что оно зависит одновременно и от модуля силы, и от её плеча. Действительно, мы уже знаем, например, что действие силы на дверь зависит и от модуля силы, и от того, где приложена сила. Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на неё сила. Гайку легче отвернуть длинным гаечным ключом, чем коротким. Ведро тем легче поднять из колодца, чем длиннее ручка во́рота, и т. д.

1. Что называется моментом силы? Как выражается момент силы через модуль силы и её плечо? 2. В чём состоит правило моментов? 3. Что принимают за единицу момента силы? Как называется эта единица?

Плечо силы относительно точки — Энциклопедия по машиностроению XXL

Плечо силы относительно точки С Знак момента относительно точки С тс  [c.53]

Расстояние от точки С до линии действия силы называется плечом силы относительно точки С например, р есть плечо силы Р относительно точки С. Произведение силы на плечо представляет собой числовое значение величины, называемой моментом силы относительно данной точки.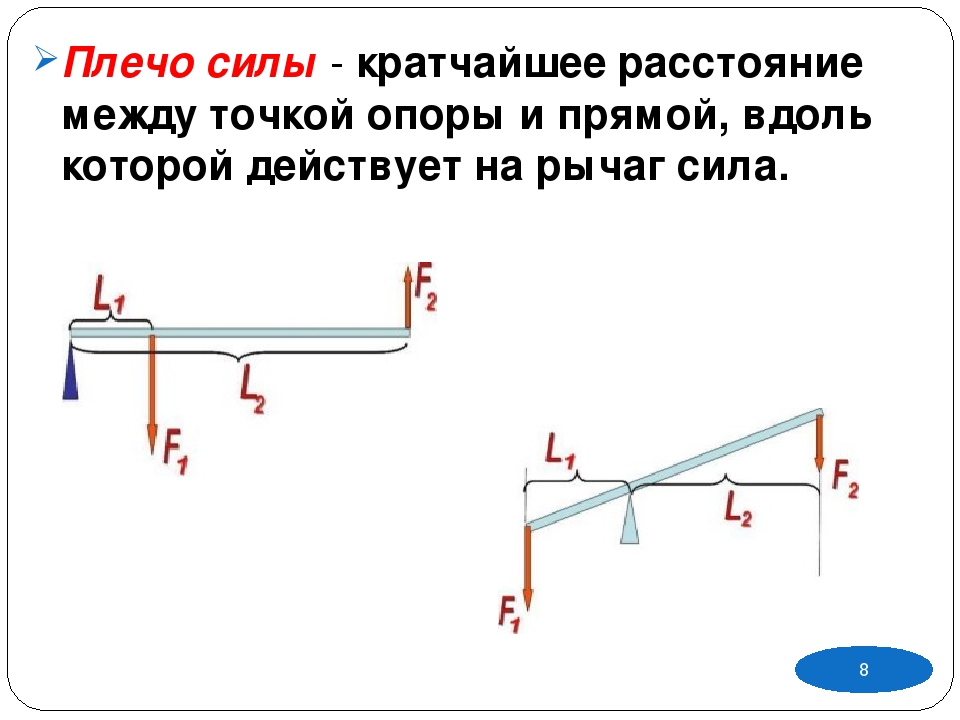 Таким образом, формула (3) показывает, что моменты параллельных сил относительно любой точки, находящейся на линии действия их равнодействующей, равны между собой по числовому значению.  [c.206]

Но, как видно из чертежа, АС sin а = /г. Называя плечом силы относительно точки длину перпендикуляра, опущенного из точки на линию действия силы, находим, что и в этом случае момент силы равен произведению модуля силы на плечо  [c.228]

Плечо силы относительно точки О равно Ь, а поворот ее с конца оси X виден происходящим по ходу часовой стрелки, следовательно  [c.163]

В самом деле, момент силы реакции Ко относительно оси х равен нулю, так как эта реакция проходит через ось х. Момент силы Рх относительно оси х равен Р г, где г — плечо силы относительно точки О.  [c.615]

А. Неправильно. Плечо силы относительно точки —длина перпендикуляра, опущенного из точки на линию действия силы.  [c.273]

Перпендикуляр а, опущенный из точки на линию действия силы, называется плечом силы относительно точки о.  [c.59]

Здесь /г —плечо силы относительно точки О (рис. 3.6) если наблюдатель видит со стороны положительного направления оси г, что сила Рху стремится повернуть тело вокруг оси г против хода часовой стрелки, то берется знак плюс , и в противном случае —знак минус .  [c.48]

Вычисляя момент наклонной силы, учитывайте обе ее составляющие. Пе забывайте, что плечо силы относительно точки равно расстоянию от точки до линии действия силы, а не до точки приложения силы.  [c.37]

Находим момент силы Р,. Плечом силы относительно точки А является отрезок АС, так как сила направлена к АС перпендикулярно. Величина момента отрицательная  [c.69]

Т. е. радиус инерции сечения относительно оси оп, параллельной нулевой линии, будет средней пропорциональной между плечом силы относительно той же оси и расстоянием нулевой линии от оси ОУ (все три отрезка лежат на одной прямой ои, перпендикулярной к оси ov). Имея величины и г ,, указанным ранее построением найдем четвертую пропорциональную и . Поскольку все  [c.434]

Легко доказать, что момент системы сил относительно точки О будет равен произведению Рй. где й— плечо силы относительно точки О.  [c.159]

Плечо силы относительно точки с Знак момента относительно точки с  [c.53]

Произведение величины силы Fi на плечо /ij представляет собой величину момента А/р (Fi) этой силы относительно точки р полюса плана скоростей. Так как все скорости на плане повернуты в одну сторону, то знак момента для всех сил совпадает со знаком элементарной работы силы, следовательно,  [c.328]

Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.  [c.25]

Плечом h силы относительно точки О называют кратчайшее расстояние от этой точки до линии действия силы.  [c.25]

Момент силы относительно точки (А. И. Аркуша, 1.10) при решении задач по статике, а затем и по динамике имеет не менее важное значение, чем проекции сил. Поэтому нужно уметь определять эту величину безошибочно. Обычно его числовое значение находят неправильно из-за ошибок, допускаемых при определении плеча.  [c.75]

Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо.  [c.75]

Точка О, относительно которой берется момент силы, называется центром момента ОВ=1 — кратчайшее расстояние от центра момента до линии действия силы— называется плечом силы относительно данной точки знак плюс ставится в случае, если сила Р стремится повернуть плечо I против хода часовой стрелки, а знак минус — в противоположном случае (правило знаков то же, что и у моментов пар сил). Рис. 1.38  [c.33]

Как известно, сила — скользящий вектор, поэтому при переносе силы р по линиям действия из точки А в любую другую точку Ль Ла и т. д. (рис. 1.38) длина плеча не изменится, а значит не изменится и значение момента силы относительно точки.  [c.33]

Момент силы относительно точки. Равновесие твердого тела с одной неподвижной точкой. Момент силы Р относительно точки О, который записывается в виде т (Р), для плоской системы сил равен по абсолютной величине произведению модуля силы Р на расстояние А от точки О до линии действия силы Р, называемое плечом.  [c.36]

Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю. Например  [c.37]

При составлении суммы моментов сил относительно точки С сила Р, приложенная в центре катка О, разложена на две составляющие — горизонтальную (Р os а) и вертикальную (Р sin а), и использована теорема Вариньона. При этом, как принято всегда делать, при вычислении момента горизонтальной составляющей силы Р мы пренебрегли изменением ее плеча, считая, что оно равно радиусу катка г.  [c.111]

Для определения момента силы F относительно оси у спроектируем эту силу на плоскость xz, перпендикулярную к оси у, т. е. определим F . Нетрудно видеть, что = E os 30°. Остается взять момент силы относительно точки пересечения оси у с перпендикулярной плоскостью хг, т. е. точки О. Плечом является ребро  [c.159]

Отсюда следует, во-первых, что числовое значение главного момента плоской системы сил можно вычислять как алгебраическую сумму моментов этих сил относительно центра О, т. е. если А — плечи сил F , то  [c.242]

Моментом силы относительно точки (центра) О называется вектор, численно равный произведению модуля силы на плечо (расстояние от центра до линии действия силы) н направленный перпендикулярно плоскости, проходящей через точку О и линию действия силы в ту сторону, откуда сила видна направленной относительно точки О против хода часовой стрелки. Если точка приложения силы F определяется радиусом-вектором г относительно точки О, то Мо Р) = гХ , т. е. момент силы равен векторному произведению вектора г на вектор Х. Проекция в тора момента силы Мо (Р) на ось называется моментом силы Г относительно оси. Момент равнодействующей силы относительно оси равен алгебраической сумме моментов сил данной системы сил относительно этой оси.  [c.50]

Будем называть расстояние от точки опоры до линии действия силы плечом силы, а произведение модуля силы на плечо—моментом силы относительно точки опоры С. Момент мы считаем положительным, если сила стремится повернуть рычаг против вращения стрелок часов, и отрицательным, если сила стремится повернуть плечо в ту же сторону, в какую поворачиваются стрелки часов. Момент  [c.54]

Плечо h силы относительно точки О определим из треугольника ОМ N  [c.137]

Момент пары, подобно моменту силы относительно точки,— векторная величина. Вектор момента пары перпендикулярен плоскости пары. Но у всякой плоскости имеется две стороны. Условились вектор момента восставлять с той стороны, с которой пара представляется поворачивающей свое плечо против хода часовой стрелки (рис. 83, а). Таким образом, вектор момента пары сил характеризует не только величину воздействия пары на тело, но и плоскость пары, а также и направление, в котором силы пары стремятся повернуть тело.  [c.149]

Применим эту теорему к решению данной задачи. Определим главный момент внешних сил относительно точки О. Внешними силами являются вес гироскопа и реакция в точке О (рис. 118, в). Главный момент внешних сил относительно точки О направлен перпендикулярно вертикальной плоскости, проходящей через ОС, и равен произведению веса mg на плечо O Sin По теореме Резаля  [c.160]

Длину перпендикуляра СА и СВ), опущенного из точки С на линию действия силы, называют плечом этой силы относительно точки С, а произведение модуля силы на плечо называют моментом силы относительно точки С  [c. 228]

Если сила стремится повернуть плечо вокруг точки С против вращения стрелок часов, то момент силы относительно точки С считают положительным, а если по вращению стрелок часов, то отрицательным. Так, момент силы относительно точки С на рис. 68, а положительный (Mi > 0), а момент силы F2 относительно той же точки отрицательный М с [c.228]

Момент силы относительно оси равен нулю, если линия действия еилы пересекает эту ось. В этом случае линия действия проекции сил1т на плоскость, перпендикулярную оси, проходит через точку пересечения оси о плоскостью и, следовательно, равно нулю плечо силы относительно точки О.  [c.24]

Возьмем систему уравнений равновесия в виде (2.14). Выгодно за центры моментов принять опорные точки А и В, так как момент одной из искомых реакций относительно ее точки приложения будет равен нулю, и тем самым в каждое уравнение равновесия войдет только одна неизвестная величина. В данной задаче выгодно, чтобы не проводить и не вычислять значения плеч сил относительно точек А и В, разлоятть силы Р а Р на горизонтальную и вертикальную составляющие (по правилу параллелограмма) и затем применить теорему Бариньона (1. 31) + д, причем sin р,  [c.47]

Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относителыю этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).  [c.25]

Сила, действующая на элементарную площадь ids (рис. V.14), равна, очевидно, ztds, а крутящий момент этой элементарной силы относительно произвольной точки О, лежащей в плоскости сечения, равен Ttdsp, где р — плечо действия силы относительно точки О.  [c.124]

---

Amazon.com: Shoulder Cold Kompressor — Cold Compression Brace: Health & Personal Care

---

В настоящее время недоступен.
Мы не знаем, когда и появится ли этот товар в наличии.

Размер	Универсальный
Марка	Подтяжки G-Force
Материал	Гель
Показания	Хроническая боль в плече, послеоперационный отек или после тренировки
Цвет	Чернить

---

• Восстановление после операции, физической активности или хронической боли
• Съемный гелевый пакет
• Легкое нанесение и удаление
• Уменьшение боли и отека
• Регулируемое сжатие

Портер-Йошида и Ко.Сумка через плечо Force

ПОЛНЫЙ РАЗНООБРАЗИЕ.
Повседневная серия с военным оттенком и мотивом случайных цветовых различий, которые редко встречаются на военной технике. Самая большая особенность — это небольшая разница в цвете между передним карманом и телом, что позволяет создавать образы разных партий.

Особенности:

• W280 / h300 / D85
• 365 грамм
• Промышленный материал
• Оранжевая подкладка

Характеристики	Водоотталкивающий
Ширина	28 год см
Высота	20 см
Глубина	85 см
Масса	365 грамм
Крепление	Почтовый индекс
Отделения	Внутреннее отделение Внутреннее отделение Внешние отсеки
Детали	Применение логотипа
Сделано в	Япония
Арт.№:	XEQPT005000
MPN	05457-855

Strike Force II 150 Shoulder Pad

-NEW рифленые арки и погоны для легкости и прочности. С помощью этой технологии мы можем добавить больше отверстий в пластик для лучшей воздухопроницаемости и снижения веса.Уменьшая вес, игрок получает более широкий диапазон движений и становится менее утомленным.

-7% легче наших старых колодок Strikeforce и на 16% легче традиционных колодок.

-Наша система обивки из HDOC и 2x EVA и стальных пружинных арок прилегает к корпусу игроков, обеспечивая наилучшую посадку, комфорт и диапазон движений. Кроме того, благодаря нашему регулируемому открытию шеи игрок получает лучшую индивидуальную посадку.

-Velcro® прикрепляет заднюю пластину, шейный валик и съемную дельтовидную подушку.

-Легкая поворотная передняя и задняя система закрытия. Благодаря этой системе тренерам не нужно беспокоиться о неправильном размещении или срывании шнуровки во время тренировки или в игре. Вертлюги перемещаются вместе с телом игрока для большего диапазона движений и отводят энергию от тела.

-1 дюйм система крепления ремня и пряжки.

— Металлические изделия из нержавеющей стали.

-Низкопрофильный.
ПРЕДУПРЕЖДЕНИЕ:

Футбол — опасный вид спорта, который может привести к серьезным травмам или даже смерти.Несмотря на то, что наше оборудование предназначено для снижения риска таких травм, нет гарантии, что использование этого оборудования позволит предотвратить травмы. Любые модификации или изменения без разрешения производителя могут снизить защиту этого оборудования.

Аксессуары

TAG разработаны для обеспечения максимальной защиты и производительности оборудования TAG. Использование аксессуаров сторонних производителей ставит под угрозу качество и защиту оборудования TAG. Использование аксессуаров сторонних производителей на оборудовании TAG приведет к аннулированию гарантии TAG.

Все цвета на основе цветов PMS

РАЗМЕР	ПЛЕЧО	СУНДУК
МАЛЫЙ	16 «-17»	36 «-38»
СРЕДНЯЯ	17–18 дюймов	38 «-40»
БОЛЬШОЙ	18 «-19»	40 «-42»
XL	19 «-20»	42 «-44»
2XL	20 «-21»	44 «-46»
3XL	21 «-22»	46 «-48»
4XL	22 «-23»	48 «-50»

12 Распространенных проблем с плечом и как их лечить

Плечи — это суставы, в которых встречаются кости плеча (плечевая кость), лопатки (лопатка) и ключица (ключица).Плечевая кость входит в округлую впадину лопатки с каждой стороны тела. Каждое плечо удерживается на месте группой из четырех мышц и сухожилий, называемой вращающей манжетой, которая покрывает и защищает плечевую кость, а также позволяет поднимать и перемещать руку.

Боль в плече может иметь множество причин. Вы можете повредить его при падении или несчастном случае, или вы могли перестараться с рутинной работой, например с покраской. Иногда боль в плече возникает из-за такого состояния, как артрит. Это может даже быть вызвано проблемами в других частях вашего тела, которые называются отраженной болью.

Симптомы травмы плеча

Задайте себе несколько вопросов, которые помогут вам решить, есть ли у вас травма плеча:

• Можете ли вы нормально двигать рукой, или ваше плечо слишком жесткое или болезненное?

• Вы чувствуете, что плечо может выскочить из гнезда?

• Достаточно ли крепко ваше плечо для обычных занятий?

Некоторые травмы плеча можно лечить дома в течение нескольких дней с отдыхом и льдом.При необходимости вы можете перевязать его, чтобы удерживать на месте, и поднять над сердцем. Но при некоторых травмах требуется профессиональная помощь. Вот признаки того, что вам нужно немедленно обратиться к врачу:

• Ваш плечевой сустав выглядит деформированным.

• Вы вообще не можете использовать плечо.

• Боль сильная.

• Плечо внезапно опухает.

• Ваша рука слабая или онемевшая.

Причины боли в плече и факторы риска

Распространенные травмы плеча

• Вывих. Если ваше плечо слишком сильно отведено назад или повернуто слишком далеко, верхняя часть руки может выскочить из гнезда. Вы почувствуете боль и слабость в плече. У вас также могут быть отек, онемение и синяки.

• Разделение. Эта травма поражает сустав, в котором соединяются ключица и лопатка. Он называется акромиально-ключичным (АК) суставом. Падение или сильный удар разрывают скрепляющие его связки. Если вытолкнуть ключицу с места, на плече появится шишка.

• Перелом. Кость может сломаться или треснуть, если вы упадете или получите сильный удар. Чаще всего возникают переломы ключицы (ключицы) и плечевой кости (кости руки, ближайшей к плечу). У вас будет сильная боль, и может появиться синяк. Если у вас сломана ключица, ваше плечо может провиснуть, и вы не сможете поднять руку.

• Разрыв хряща. Вы можете повредить хрящ (эластичную подушечку), окружающий край плечевого сустава.Это может происходить после повторения одного и того же движения снова и снова. Вы также можете повредить его при падении или в любой момент, когда ваше плечо поглощает большую силу. При этом типе травмы вы можете почувствовать боль, когда протянете руку через голову, и ваше плечо может показаться слабым. Также может показаться, что он цепляется, блокируется или скрежещет.

• Разрыв вращательной манжеты. Поворотная манжета — это группа мышц и сухожилий плеча, которые удерживают руку на месте и позволяют поднять ее над головой.Вы можете повредить его из-за чрезмерного использования или при падении. С возрастом он также начинает изнашиваться. Плечо может болеть ночью или при попытке поднять что-нибудь. При перемещении вы можете услышать треск.

• Застывшее плечо. Это условие ограничивает подвижность сустава. В суставе накапливаются аномальные тканевые полосы (спайки), которые мешают вашему плечу свободно двигаться. Ваше плечо может «замерзнуть», потому что боль или операция заставили вас меньше его использовать, что приведет к нарастанию спаек.

• Удар. Это происходит, когда сухожилия вращательной манжеты защемляются в костях плеча. Это может вызвать отек и боль. Если вы часто поднимаете руки над головой, это может сработать.

• Бурсит. Бурса (наполненный жидкостью мешок, который смягчает сустав) может опухнуть и раздражаться, если вы будете повторять одни и те же движения снова и снова. Но это также может быть вызвано падением или другой травмой. Если у вас бурсит, вы можете больше всего ощущать боль при движении плеча.

Другие причины боли в плече

• Остеоартроз. Это наиболее распространенная форма артрита, также называемая дегенеративным заболеванием суставов. Это может повлиять на любой сустав, включая ваши плечи. Хрящ между костями разрушается, и они трутся друг о друга. Это может вызвать боль и скованность.

• Ревматоидный артрит. Это заболевание, при котором иммунная система вашего тела атакует защитную оболочку суставов.Это также может вызвать боль и скованность в плечах.

• Реферированная боль. Иногда у вас болят плечи, когда с ними все в порядке. Это может быть признаком проблем с желчным пузырем, печенью или другим органом.

• Сердечный приступ. Если у вас болит плечо, и у вас проблемы с дыханием, или чувствуете себя стесненным в груди, вам может немедленно потребоваться неотложная медицинская помощь.

• Тендинит. Это происходит при воспалении сухожилий, составляющих вращательную манжету.Это может происходить медленно с течением времени или в результате падения или прямого удара в плечо.

• Костные шпоры. Также известные как «остеофиты», эти маленькие гладкие кусочки кости трутся о вращающую манжету и надеваются на нее, не позволяя плечу двигаться должным образом. Они могут привести к тендиниту или разрыву вращательной манжеты плеча.

Диагностика боли в плече

Ваш врач начнет с медицинского осмотра, чтобы проверить наличие каких-либо структурных проблем и исключить все, что может касаться вашего позвоночника или шеи.

Затем они проверит ваш диапазон движений, чтобы определить, насколько сильное и гибкое ваше плечо. Это будет включать в себя движение рук различными способами, например, над головой, поперек тела или позади себя, а также поворот на 90 или 180 градусов.

Ваш врач также может порекомендовать один или несколько тестов визуализации, чтобы лучше рассмотреть:

• Рентгеновские снимки. Они могут помочь вашему врачу найти костные шпоры, артрит и другие связанные с костями причины боли в плече. Ваш врач также может порекомендовать артрограмму, которая включает в себя укол красителя, чтобы детали были более четкими.

• Магнитно-резонансная томография (МРТ). Он использует радиоволны и мощный магнит для детального изображения вашего плеча.

• Компьютерная томография (КТ). Это серия рентгеновских снимков, сделанных под разными углами. Когда они собраны вместе, они могут дать врачу возможность лучше понять, что происходит с вашим плечом.

• Электромиография (ЭМГ). Измеряет электрическую активность мышц, чтобы определить, есть ли проблемы с нервами.

• Артроскопия. Это хирургическая процедура, позволяющая с помощью крошечной оптоволоконной камеры показать врачу изображения вашего плеча в высоком разрешении. В некоторых случаях ваш врач может решить проблему во время процедуры.

Лечение боли в плече и домашние средства

При вывихах, расслоениях и переломах вам понадобится помощь врача, чтобы вернуть плечо в правильное положение, а затем перевязку, чтобы удерживать его на месте, пока оно заживет.

При многих других проблемах ваш врач может посоветовать покой, тепло или лед и такие лекарства, как ибупрофен или аспирин, чтобы уменьшить боль и отек.

Если после этих первых шагов состояние вашего плеча не улучшится, врач может попробовать ввести кортикостероид (противовоспалительное лекарство) прямо в сустав, чтобы уменьшить отек и боль.

Иногда разрывы хряща, разрывы вращающей манжеты и замерзание плеча не проходят без отдыха и лекарств. Ваш врач может порекомендовать операцию.

При любой проблеме с плечом в план лечения, вероятно, будут включены упражнения, которые помогут вам растянуть и укрепить сустав, а также улучшить диапазон движений.

Профилактика боли в плече

Учитывая, как часто вы используете плечо каждый день — на работе и на отдыхе, — разумно принять меры по его защите:

• Если вы работаете за столом, убедитесь, что на вашем стуле есть правильная поддержка спины и способствует хорошей осанке.

• Сделайте перерыв и двигайтесь не реже одного раза в час.

• Если ваша работа требует подъема тяжестей, используйте правильную технику: встаньте лицом к лицу с тем, что вы поднимаете, держите спину прямо и согните колени, чтобы использовать ноги в качестве силы.

• Дотянувшись до чего-то тяжелого над головой, воспользуйтесь табуреткой или лестницей, чтобы занять более удобное положение.

• Спросите своего врача о программе кондиционирования, чтобы укрепить мышцы вокруг плеч и сохранить их гибкость.

Влияние пояснично-тазового контроля на кинетику плеча и локтя у элитных бейсбольных питчеров

Задний план: Исследования показали, что ослабление пояснично-тазового контроля отрицательно сказывается на характеристиках качки и может привести к увеличению числа дней в списке инвалидов.Несмотря на выявленную корреляцию между пояснично-тазовым контролем и травмой, нет исследований, которые показали бы, увеличивает ли недостаточный пояснично-тазовый контроль усилие, прикладываемое к руке, выполняющей метание.

Методы: В соревнованиях приняли участие 43 бессимптомных питчера Национальной студенческой спортивной ассоциации I дивизиона и профессиональных бейсбольных питчеров низшей лиги. Мы измерили двусторонний переднезадний пояснично-тазовый наклон во время теста устойчивости туловища в стойке на одной ноге.Мы измерили кинетику плеча и локтя бросающей руки во время качки с помощью трехмерной высокоскоростной системы видеозахвата. Мы использовали двусторонние коэффициенты корреляции продукта-момента Пирсона (r), чтобы определить силу взаимосвязей между переменными (P <0,05).

Полученные результаты: Не было значимой связи между шагом шага и какой-либо из кинетических переменных качки (r <0.23, P> 0,14). Точно так же не было значимой взаимосвязи между ведущей ногой и максимальной силой отвлечения плеча, крутящим моментом внешнего вращения плеча или силой отвлечения локтя (r <-0,24, P> 0,13). Однако ведущая опора имела значительную взаимосвязь как с максимальным горизонтальным крутящим моментом на плече (r = 0,44, P = 0,003), так и с крутящим моментом вальгусной локтевой части (r = 0,46, P = 0,002).

Выводы: Наши результаты показывают, что существует взаимосвязь между пояснично-тазовым контролем ведущей ноги и как горизонтальным моментом плеча, так и вальгусным моментом локтевого сустава во время метательного движения.Из-за этих взаимоотношений клиницисты должны рассмотреть возможность включения упражнений на контроль пояснично-тазового отдела, чтобы свести к минимуму кинетическую силу, воздействующую на плечо и локоть при броске во время качки.

Ключевые слова: Основной; остаток средств; совместная сила; стабильность; метание спортсмена; метательная механика.

Сумка через плечо Fydelity Jambox G-Force с динамиками … | 92410

Описание

FYDELITY Стереопакеты! Включите, подключитесь и оторвитесь! Сумки, рюкзаки и холодильники с усиленными динамиками, которые подключаются к вашему смартфону или MP3-плееру.Вечеринка в сумке! Представляем FYDELITY Stereobags, единственную коллекцию модных сумок и рюкзаков, в которых музыка является саундтреком к вашей жизни. FYDELITY Стереопакеты подключаются к любому MP3-плееру или смартфону и имеют встроенный усилитель и динамики, которые позволяют слушать музыку без наушников. В стильных аксессуарах FYDELITY сочетаются экипировка, гаджеты и музыкальные инструменты. FYDELITY Stereobags, уходящий корнями в культуру бумбоксов 80-х, время, когда музыка пришла с улиц, отключает «общий доступ к файлам», «гиперссылки» и «социальные сети», чтобы объединять людей и возвращать их к музыке.Вечеринка в сумке!

Производитель: Fydelity (США)

http://eu.highfydelity.com/

Код продукта: 92410

Цвет: Черный (с динамиками)

Внутренний размер: 35х20х10см

Материал: пластик, кожзаменитель

Масса, кг: 0,4

Объем, л: 7

Яркая модель с твердым днищем в виде кассетной ленты ретро.Плотно сплетенная и удобная застежка «молния» с логотипом компании обеспечит герметичность изделия. Подкладка обрамлена актуальными фирменными принтами. Внутри одной комнаты потайной карман и один подвесной двигатель, который спрятан в блоке и проводах к водонепроницаемым стереодинамикам Hi-Fi с усилителем на 3 Вт. Отношение сигнал / шум: 60 дБ. Легко подключайте свой телефон, mp3, проигрыватель компакт-дисков, iPod / iPad через стереоразъем 3,5 мм. Карманы для iPod / iPhone для быстрого и легкого доступа к плееру. Питание: 4 батарейки AA (фонарик), для непрерывного 10-часового звука.АЧХ: 150 Гц ~ 20 кГц.Отличная удобная сумка, подходящая как для тренировок, так и для ежедневных прогулок и активного отдыха!

http://americankids.eu/

Упаковано в полиэтиленовый пакет.

Описание

FYDELITY Стереопакеты! Включите, подключитесь и оторвитесь! Сумки, рюкзаки и холодильники с усиленными динамиками, которые подключаются к вашему смартфону или MP3-плееру.Вечеринка в сумке! Представляем FYDELITY Stereobags, единственную коллекцию модных сумок и рюкзаков, в которых музыка является саундтреком к вашей жизни. FYDELITY Стереопакеты подключаются к любому MP3-плееру или смартфону и имеют встроенный усилитель и динамики, которые позволяют слушать музыку без наушников. В стильных аксессуарах FYDELITY сочетаются экипировка, гаджеты и музыкальные инструменты. FYDELITY Stereobags, уходящий корнями в культуру бумбоксов 80-х, время, когда музыка пришла с улиц, отключает «общий доступ к файлам», «гиперссылки» и «социальные сети», чтобы объединять людей и возвращать их к музыке.Вечеринка в сумке!

Производитель: Fydelity (США)

http: //eu.hi

Porter Сумка на ремне PORTER FORCE SHOULDER POUCH

Описание

Размер

Ш150 / В280 (см)

Ш59,1 / В70,9 (дюйм)

Вес

120 г

Это новый тип повседневной военной серии «PORTER FORCE», анонсированной на 2012 A / W.Серия, которая в основном состояла из предметов большого размера, была дополнительно расширена за счет добавления небольших вариаций и новых предметов.

Мотив — это случайная разница в цвете ткани, которая иногда встречается в военных товарах, и, кажется, используется большая разница в ткани за счет тонкой разницы в цвете между тканью переднего кармана и тканью корпуса сумки. Это самая большая особенность.

При окрашивании ткани индивидуальные различия (некоторая размытость цвета) возникают в каждой производственной партии, поэтому обычно из одной и той же партии ткани изготавливают одно изделие, чтобы не было разницы в цвете между деталями.Однако в военной одежде и сумках бывают редкие случаи, когда некоторые детали имеют различия в цвете ткани (изделия частично используют много разных тканей), и эта серия случайно производится нерегулярно. Мне интересно цветовое решение и я намеренно его создаю.

Внешняя ткань изготовлена ​​из промышленного материала, сотканного из прочной нейлоновой пряжи 210 денье 6. Эта ткань изначально использовалась в качестве основного материала для резиновых лодок и т. Д. И не производилась для того, чтобы ее окрашивали, как ткань для одежды или сумок.Цель состоит в том, чтобы создать ощущение милитари с целью создания отличительного впечатления, создаваемого уникальным глянцем и вертикальными полосами, возникающими при окрашивании этой ткани.

Представьте себе подкладку военной куртки, внутреннюю часть оранжевого цвета аварийного цвета и простеганную ткань из нейлона рипстоп. Снаружи сумка представляет собой нейлон, но это первое использование материала, позволяющего впервые почувствовать легкость и мягкость стеганого шитья, когда вы держите его в руках.

Используемая нейлоновая лента зависит от предмета, но для каждой части используется до 4 типов (4 цвета), и создается реалистичное ощущение милитари.

За исключением наплечного мешочка, внутри есть съемный карман, который можно использовать как единый мешочек. ПОРТФЕЛЬ 3WAY отличается от других предметов формой съемного мешочка.

※ Прилагается оригинальная бирка для подвешивания.

※ Рост мужской модели: 173 см
※ Рост женской модели: 161 см

.