Умножение вектора на число

Умножение вектора на число

Навигация по странице:

• Геометрическая интерпретация умножения вектора на число.
• Алгебраическая интерпретация умножения вектора на число.
• Формулы умножения вектора на число
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Свойства вектора умноженного на число
• Примеры задач на умножение вектора и числа
  • плоская задача
  • пространственных задача

Онлайн калькулятор. Умножение вектора на число.

Геометрическая интерпретация.

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; . .. ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a₁; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2.

Найти произведение вектора a = {1; 2; -5} на -2.

Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Сложение двух векторов.

Произведение вектора на число.Разложение вектора по базису.

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ -Рассмотрим правила сложения векторов. Если слагаемые векторы путем их параллельного переноса последовательно пристраивать один за другим так, что начало последующего вектора, совпадает с концом предыдущего, то вектор, замыкающий получившуюся ломаную, является суммой данных слагаемых, причём его начало совпадает с началом первого из слагаемых векторов, а конец – с концом последнего. Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала. Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти векторы переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего — с концом второго и т. д., сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную). Сложение векторов с использованием координат. Каждая координата (см. Базис и разложение по базису) суммы векторов есть сумма соответствующей координаты всех (двух или более) суммируемых векторов. Например, для двумерного случая:   -Геометрически произведение ненулевого вектора на число k – это вектор, длина которого равна ka, где a = – длина данного вектора, а направление, приa ≠ 0, совпадает с направлением вектора , если k > 0 и противоположно, если k< 0. Если хотя бы один из сомножителей – вектор или число – равен нулю, то и произведение равно нулю. При умножении вектора на число каждая из его координат умножается на это число. Операция умножения вектора на число подчиняется законам, аналогичным законам обычного умножения —Разложение вектора по базису. Определение. Пусть – произвольный вектор, – произвольная система векторов. Если выполняется равенство , (1) то говорят, что вектор представлен в виде линейной комбинации данной системы векторов. Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора относительно базиса . Теорема. (О разложении вектора по базису.) Любой вектор векторного пространства можно разложить по его базису и притом единственным способом. Доказательство. 1) Пусть L произвольная прямая (или ось) и –базис . Возьмем произвольный вектор . Так как оба вектора и коллинеарные одной и той же прямой L, то . Воспользуемся теоремой о коллинеарности двух векторов. Так как , то найдется (существует) такое число , что и тем самым мы получили разложение вектора по базису векторного пространства . Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства : и , где . Тогда и используя закон дистрибутивности, получаем: . Так как , то из последнего равенства следует, что , ч.т.д. ⇐ Предыдущая1234Следующая ⇒ Читайте также:  Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США 

Последнее изменение этой страницы: 2017-01-19; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)

математика — Нахождение 2 векторов, зная их векторное произведение и одно ограничение

спросил 6 лет, 4 месяца назад

Изменено 6 лет, 4 месяца назад

Просмотрено 2к раз

Мне нужно найти два вектора в трехмерном пространстве, a и b таких a x b = c , где известно c . Я также знаю одно ограничение, скажем, что a_y = 0
Итак, я должен искать эти 2 вектора на плоскости (c_x)x+(c_y)y+(c_z)z=0 , для вектора a я могу упростите его до (c_x)x+(c_z)z=0
для вектора b , так как он перпендикулярен a , а также должен находиться на пересечении плоскости (a_x)x+(a_z)z=0 и (c_x)x+(c_y)y+(c_z)z=0 плоскости.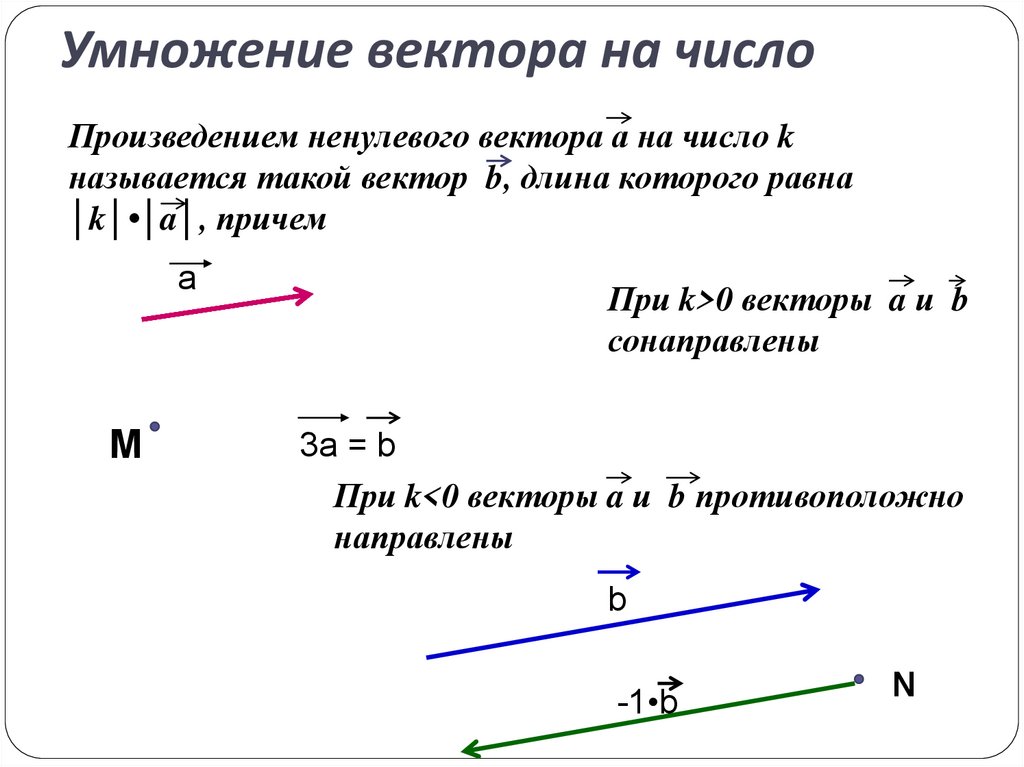
После добавления к этому уравнению перекрестного произведения у меня есть 4 уравнений и 5 неизвестных (a_x,a_z,b_x,b_y,b_z) . Как я могу это решить?
Заранее спасибо.

РЕДАКТИРОВАТЬ: Может быть, объяснение, для чего мне это нужно, как-то поможет.
У меня есть вектор направления камеры, и мне нужен вектор, указывающий вправо от экрана, и второй, указывающий вверх.

• математика
• вектор
• 3d
• линейная алгебра

2

1. определение проблемы

    А,Б=?
   С=!
   Ай=!
   А х В = С
    

   предполагаемые свойства скалярного и перекрестного произведения из-за перпендикулярности:

    (переменный ток) = 0
   (BC) = 0
   |А|.|Б| = |С|
    

2. установить длину для одного из векторов на любую известную константу, например 1

    |А|=1
   |В|=|С|
    

   Это также упоминается John Moeller в его комментарии

3. 92

   Если вы расширите векторное произведение, вы получите 5 уравнений и 3 неизвестных. Итак, решите систему (выберите любые 3 из нетривиальных уравнений).

PS Похоже, это для создания аналогии вашей матрицы NEH

Итак, если это так, то все 3 вектора перпендикулярны друг другу, а один указывает на определенное направление ( вверх или север …) и размеры обычно 1 для всех векторов.

Итак, предположим, что вектор D является известным вектором выравнивания:

 A'= C x D
В = С х А'
А = С х В
 

Вы можете изменить порядок операндов, чтобы получить нужные вам указания. Если D неизвестен, вы можете использовать (1,0,0) или (0,1,0) или (0,0,1) , вместо этого выберите тот, который не параллелен . C … или самый большой (C.D) . Также взгляните на:

• Как узнать координаты точки обзора? 92)
  

  Зарегистрируйтесь или войдите в систему

  Зарегистрируйтесь с помощью Google

  Зарегистрироваться через Facebook

  Зарегистрируйтесь, используя электронную почту и пароль

  Опубликовать как гость

  Электронная почта

  Обязательно, но не отображается

  Опубликовать как гость

  Электронная почта

  Требуется, но не отображается

  Как найти перпендикулярный вектор

  Обновлено 25 апреля 2017 г.

  Ариэль Балтер, доктор философии.

  Чтобы построить вектор, перпендикулярный другому заданному вектору, можно использовать методы, основанные на скалярном и перекрестном произведениях векторов. Скалярное произведение векторов A = (a1, a2, a3) и B = (b1, b2, b3) равно сумме произведений соответствующих компонент: A∙B = a1_b2 + a2_b2 + a3_b3. Если два вектора перпендикулярны, то их скалярное произведение равно нулю. Перекрестное произведение двух векторов определяется как A×B = (a2_b3 — a3_b2, a3_b1 — a1_b3, a1_b2 — a2*b1). Произведение двух непараллельных векторов — это вектор, перпендикулярный им обоим.

  Два измерения — скалярное произведение

  Запишите гипотетический неизвестный вектор V = (v1, v2).

  Вычислите скалярное произведение этого вектора и заданного вектора. Если вам дано U = (-3,10), то скалярное произведение равно V∙U = -3 v1 + 10 v2.

  Установите скалярное произведение равным 0 и найдите один неизвестный компонент через другой: v2 = (3/10) v1.

  Выберите любое значение для v1. Например, пусть v1 = 1.

  Решите для v2: v2 = 0,3. Вектор V = (1,0,3) перпендикулярен U = (-3,10). Если вы выбрали v1 = -1, вы получите вектор V’ = (-1, -0,3), который указывает в направлении, противоположном первому решению. Это единственные два направления в двумерной плоскости, перпендикулярные данному вектору. Вы можете масштабировать новый вектор до любой желаемой величины. Например, чтобы сделать его единичным вектором с величиной 1, вы должны построить W = V/(величина v) = V/(sqrt(10) = (1/sqrt(10), 0,3/sqrt(10)).0005

  Три измерения — скалярное произведение

  Запишите гипотетический неизвестный вектор V = (v1, v2, v3).

  Вычислите скалярное произведение этого вектора и заданного вектора. Если вам дано U = (10, 4, -1), то V∙U = 10 v1 + 4 v2 — v3.

  Установить скалярное произведение равным нулю. Это уравнение плоскости в трех измерениях. Любой вектор в этой плоскости перпендикулярен U.