Скалярное произведение двух векторов
Скалярным произведением аb двух векторов а и b называют число (скаляр), равное произведению их длин на косинус угла между ними — cos :
аb = а b cos
Свойства скалярного произведения:
1) аb = 0, если хотя бы один векторов — нуль-вектор, или вектора перпендикулярны;
2) аа = а2
3) аb = bа;
4) аb = а пра b = b прb a;
5) (a + b) c = ac + bc;
6) m(аb) = (ma)b = a(mb).
Пусть вектора а иbразложены по ортам:
a
b = bx i + by j + bz k.
Используя свойства скалярного произведения мы можем найти его выражение через координаты. Так как орты взаимно перпендику-лярны, то произведения ij = ji = ik = ki = jk = kj = 0,тогда как
ii = jj = kk = 1
Поэтому
ab = (a
= axbx (ii) + aybx(ji) + azbx(ki) +
+ axby(ij) + ayby(jj
+ axbz(ik) + aybz(jk) + azbz(kk) =
= axbx + ayby + azbz .
Таким образом скалярное произведение двух векторов равно сумме произведений соответствующих координат:
a
Используя скалярное произведение и зная координаты векторов можно найти и угол между ними по формуле
,
Условием перпендикулярностидвух векторов служит равенство нулю их скалярного произведения.
ab= axbx + ayby + azbz = 0
В частности нуль-вектор перпендикулярен любому другому.
Векторное произведение двух векторов
Векторным произведением a
1. Модуль вектора с равен площади параллелограмма,
построенного на векторах a,
b:
Модуль вектора с равен площади параллелограмма,
построенного на векторах a,
b:
c=a b sin
где —угол между векторамиa, b.
2. Вектор с перпендикулярен вектору a и вектору b.
3. Вектора a, b, с должны образовывать правую тройку, то есть кратчайший поворот от первого вектора —
Свойства векторного произведения
1) аb = 0, если хотя бы один векторов — нуль-вектор, или вектора параллельны;
2) аа = 0
3) аb = — bа;
4) (m+n)(аb) = m(аb) + n(аb)
5) (a + b) c
6) m(аb)
= (ma)b = a(mb).
Рассмотрим теперь как выражается векторное произведение через координаты сомножителей:
ab = (ax i + ay j + az k)
= axbx (ii) + aybx(ji) + azbx(ki) +
+ axby(ij)
+ ayb
+ axbz(ik) + aybz(jk) + azbz(kk)
Принимая во внимание, что ii = jj = kk = 0,а
(ij) = -(
(ik) = -(ki) = j,
(jk) = -(kj) = i,
получим:
ab = aybx(-k) + azbx(-j) +axbyk + azby(-i) + axbz
= (aybz — azby)i — (azbx— axbz)j + (axby— aybx)k ,
Последнее выражение есть ни что иное, как определитель 3-го порядка
.
Смешанное (векторно-скалярное) произведение 3-х векторов.
Смешанным или векторно-скалярным произведением трех векторов a, b, c называют произведение вида (
Абсолютная величина смещанного произведения равна объема пареллелипипеда, построенного на данных трех векторах:
Смешанное произведение положительно, если вектора a, b, c образуют правую тройку, и отрицательно — если левую.
Свойства смешанного произведения:
1) Смещанное произведение не изменяется
а) если перемножаемые вектора переставлять в круговом порядке
(ab)c = (с
б) если поменять местами векторное и скалярное произведение
(ab)c = a(bс)
Этот факт позволяет записывать смешанное произведение без указания порядка векторного и скалярного умножения:
(ab)c
= abс.
2) Перестановка в abслюбых двух векторов изменяет знак произведения
abс = -baс abс = — cba, …
3) Смешанное произведение равно 0, если
а) хотя бы один из трех векторов есть нуль-вектор;
б) два из перемножаемых векторов колинеарны;
в) три вектора компланарны.
Разлагая все вектора по ортам нетрудно получить выражение смешанного произведения через координаты:
Очевидно, что условием компланарноститрех векторов будет служить равенство нулю их смешанного произведения:
= 0.
Геометрия Метод координат в пространстве. Скалярное произведение векторов
Для изучения новой темы понадобится повторить теорему о трех перпендикулярах.
Если прямая а, проведенная на плоскости α через основание О наклонной с, перпендикулярна её проекции в, то она перпендикулярна и самой наклонной.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Скалярное произведение двух векторов это число.
Скалярное произведение двух векторов это число.
Скалярное произведение векторов и обозначается так: (произведение вектора а на вектор бэ).
Таким образом:
(произведение вектора а на вектор бэ равно произведению модуль вектора а на модуль вектора бэ и на косинус угла между векторами а и бэ)
Справедливы утверждения:
1°. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Действительно, скалярное произведение вектора A на вектор B равно произведению их длин на косинус угла между ними. Но cos 90° = 0 следовательно b= 0.
2°. Скалярный квадрат вектора (то есть скалярное произведение вектора на себя) равен квадрату его длины.
Скалярное произведение двух векторов можно вычислить через произведение соответственных координат этих векторов:
скалярное произведение векторов {х1; у1; z1} и {х2; у2; z2} выражается формулой:
х1х2 + у1у2 + z1z2 (скалярное произведение двух векторов равно сумме произведений соответственных координат этих векторов).
Докажем утверждение:
Косинус угла α между ненулевыми векторами {х1; у1; z1} и {х2; у2; z2}
вычисляется по формуле:
cos α =Косинус угла альфа равен частному от деления суммы произведений соответственных координат векторов, которые составляют угол альфа, на произведение длин, выраженных координатами этих векторов
косинус угла альфа равен частному от деления скалярного произведения векторов на произведение их длин.
Таким образом, подставив вместо скалярного произведения вектора формулу суммы произведений соответственных координат векторов х1х2 + у1у2 + z1z2 , а также заменив произведение длин векторов на произведение длин векторов, выраженных через координаты
Получим: косинус угла альфа равен частному от деления скалярного произведения векторов на произведение их длин, отсюда следует, что косинус угла альфа равен частному от деления суммы произведений соответственных координат векторов, которые составляют угол альфа, на произведение длин, выраженных координатами этих векторов
Что и требовалось доказать.
Сформулируем основные свойства скалярного произведения векторов.
Для любых векторов и любого числа k справедливо следующее:
1°.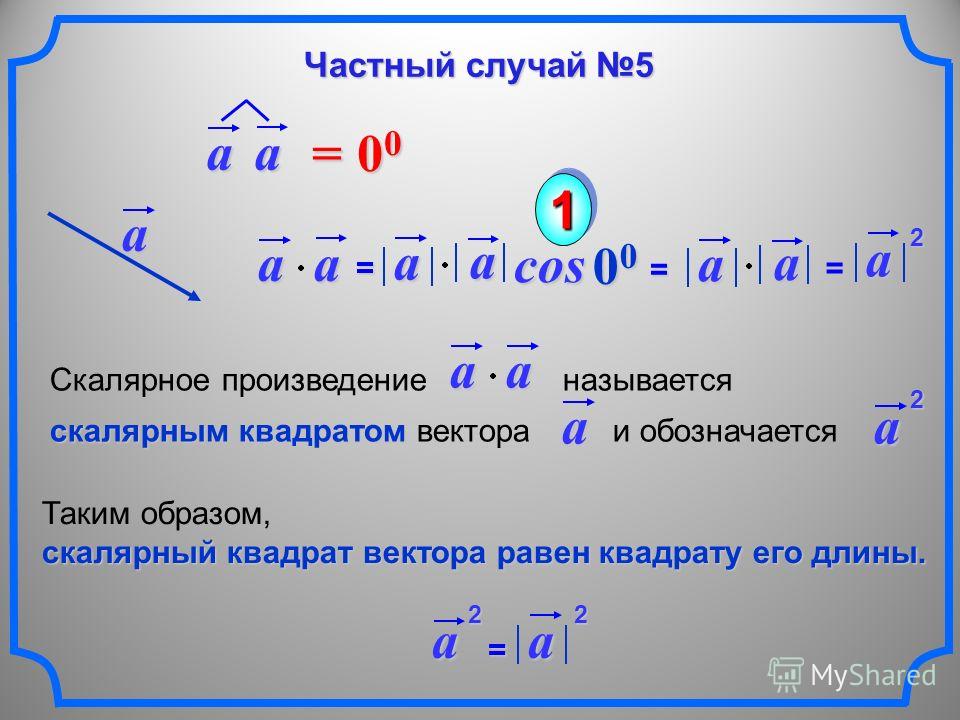 Скалярный квадрат вектора всегда больше либо равен нулю
Скалярный квадрат вектора всегда больше либо равен нулю
2.переместительный закон – от перестановки мест векторов в скалярном произведении скалярное произведение не меняется.
3 (распределительный закон – скалярное произведение суммы двух
ВведениеСкалярное произведение — это значение, выражающее угловое соотношение между двумя векторы. В этой статье мы узнаем, как рассчитывается это значение, его математическое значение и несколько способов использования этой функции в 3D-приложения. Расчет скалярного произведения Скалярное произведение — это скалярное значение, являющееся результатом операции двух
вектора с одинаковым количеством компонент. A B = A 1 B 1 + … + A n B n Таким образом, скалярный продукт представляет собой сумму произведений каждая компонента двух векторов. Например, если A и B были трехмерными векторами: A B = A.x * B.x + A.y * B.y + A.z * B.z Универсальная функция C++ для реализации скалярного произведения на двух векторах с плавающей запятой любых размеров может выглядеть примерно так: Этот образец кода предоставлен исключительно для демонстрации универсального
функция, поясняющая, как рассчитывается скалярный продукт; DirectX предоставляет
несколько реализаций этой функции для вас, как вы увидите
далее, хотя, если вам нужно написать свой собственный
функции (например, при использовании C++ без библиотек D3DX) вы, вероятно,
просто напишите отдельные функции для обработки обычно используемых типов векторов
(2D,3D,4D) как встроенный код. Что это значит?Ранее мы говорили, что скалярное произведение представляет угловое отношение между двумя векторами, и остановились на этом. Сейчас мы познакомимся поближе что представляет собой это значение. Допустим, у нас есть два вектора, A и B, как показано слева. значения |А| и |Б| представляют длины векторов A и B соответственно, и Θ — угол между двумя векторами. Скалярное произведение векторов A и B будет иметь следующее отношение к этим значения: А В = |А| * |Б| * cos( Θ ) Другими словами, скалярное произведение двух векторов будет быть равным косинусу угла между векторами, умноженному на длины каждый из векторов.
Учитывая характеристики функции косинуса, мы можем вывести три возможных условия:
Приведенные выше характеристики верны для любых векторов ненулевой длины. Кроме того, существует особый случай, когда оба вектора являются единичными векторами, т. е. есть векторы длиной один (1,0). В этом случае длины векторы не вносят вклад в уравнение, упрощая до: А В = |А| * |Б| * cos( Θ ) В этом случае скалярное произведение равно
косинус угла между векторами. Θ = acos(A B)
Углы между неединичными векторами (векторами с длины, не равные 1,0) можно рассчитать либо путем предварительной нормализации векторов или путем деления скалярного произведения неединичных векторов на длину каждый вектор.
Скалярное произведение вектора против самого себя (т.е. A A) приводит к значению, равному квадрату длины вектора. Это известная часть уравнения расстояния, d=sqrt(x*x+y*y+z*z).
Если бы кто-то взял
скалярное произведение единичного вектора A и второго вектора B любой ненулевой длины,
результатом является длина вектора B, спроецированная в направлении вектора A (см. Реализации DirectXDirectX Graphics предоставляет несколько реализаций функции скалярного произведения:
|
numpy.dot — Руководство NumPy v1.23
- numpy.dot( a , b , out=None )
Скалярное произведение двух массивов. В частности,
Если оба a и b являются одномерными массивами, это внутреннее произведение векторов (без комплексного сопряжения).
Если оба a и b являются двумерными массивами, это умножение матриц, но предпочтительнее использовать
matmulилиa @ b.Если либо a , либо b 0-D (скаляр), это эквивалентно
, умноженному на. и использованиеnumpy.multiply(a, b)илиa * bпредпочтительнее.Если a представляет собой массив N-D, а b представляет собой массив 1-D, это произведение суммы по последняя ось а и б .

Если a является массивом N-D, а b является массивом MD (где
M>=2), это произведение суммы по последней оси a и предпоследней оси b :точка (a, b) [i, j, k, m] = сумма (a [i, j,:] * b [k,:, m])
- Параметры
- a array_like
Первый аргумент.
- б array_like
Второй аргумент.
- out ndarray, необязательный
Выходной аргумент. Это должно иметь точный вид, который будет возвращен если он не использовался. В частности, он должен иметь правильный тип, должен быть C-непрерывный, и его dtype должен быть возвращенным dtype для точка(а,б) . Это особенность производительности. Следовательно, если эти условия не выполняются, вместо попытки быть гибким.
- Возвращает
- output ndarray
Возвращает скалярное произведение a и b .
 Если a и b оба
скаляры или оба одномерных массива, то возвращается скаляр; в противном случае
возвращается массив.
Если дано из , то оно возвращается.
Если a и b оба
скаляры или оба одномерных массива, то возвращается скаляр; в противном случае
возвращается массив.
Если дано из , то оно возвращается.
- Поднимает
- ValueError
Если последнее измерение и не такого размера, как предпоследнее измерение b .
См. также
-
vdot Комплексно-сопряженное скалярное произведение.
-
тензордот Суммирование произведений по произвольным осям.
-
einsum Соглашение Эйнштейна о суммировании.
-
matmul Оператор @ как метод без параметра.
-
linalg.multi_dot Скалярное произведение.
Примеры
>>> np.dot(3, 4) 12
Ни один из аргументов не является комплексно сопряженным:
>>> np.



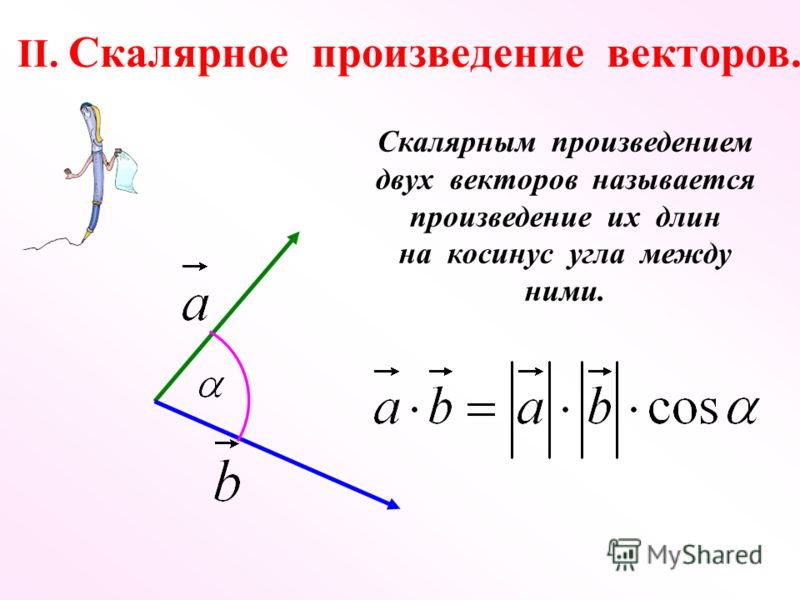
 Даны два вектора A и B каждый
с n компонентов скалярное произведение рассчитывается как:
Даны два вектора A и B каждый
с n компонентов скалярное произведение рассчитывается как:
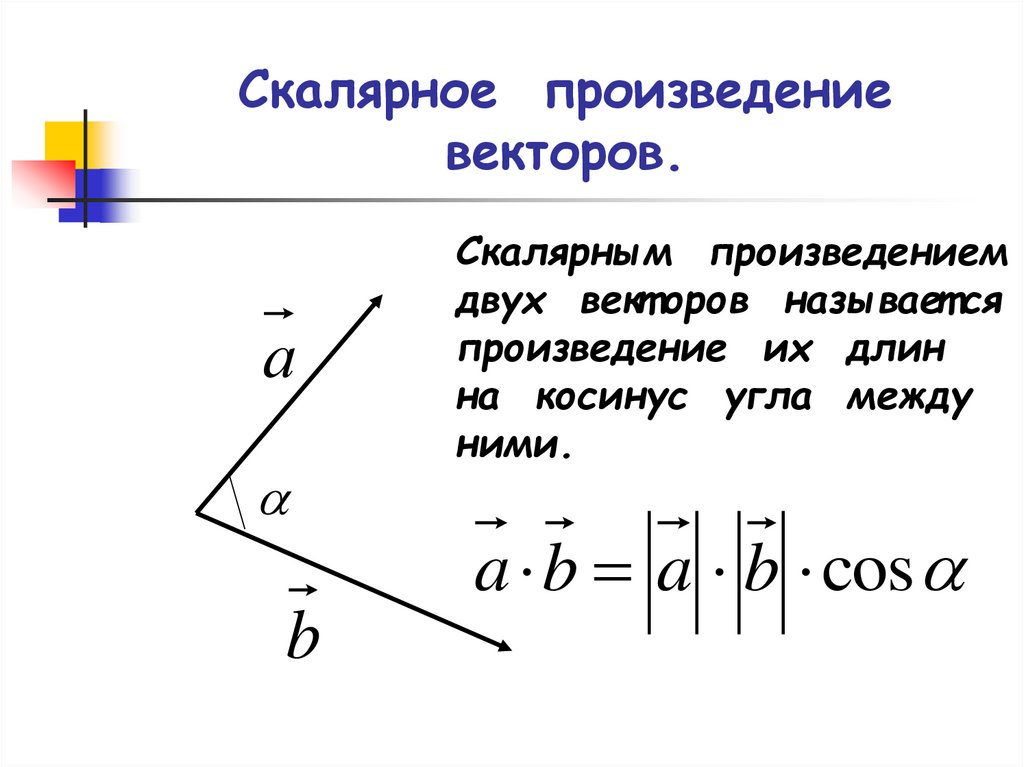 Таким образом, угол между единицей
векторов можно рассчитать как:
Таким образом, угол между единицей
векторов можно рассчитать как: иллюстрацию слева). Это используется несколькими способами, такими как столкновение
реакции и преобразования векторов из одной системы координат в другую (это
лежит в основе матричных преобразований).
иллюстрацию слева). Это используется несколькими способами, такими как столкновение
реакции и преобразования векторов из одной системы координат в другую (это
лежит в основе матричных преобразований). 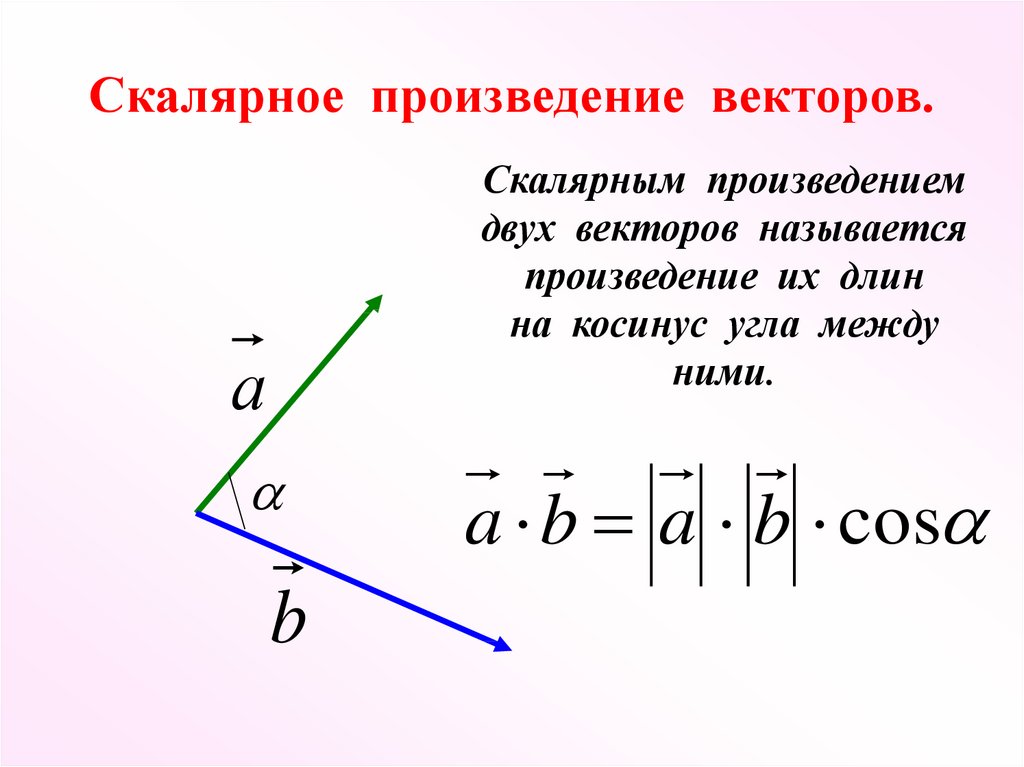 {x|y|z|w}
{x|y|z|w} 
 Если a и b оба
скаляры или оба одномерных массива, то возвращается скаляр; в противном случае
возвращается массив.
Если дано из , то оно возвращается.
Если a и b оба
скаляры или оба одномерных массива, то возвращается скаляр; в противном случае
возвращается массив.
Если дано из , то оно возвращается.