Урок 4. Векторные и скалярные величины
ВИДЕО УРОК
Перемещение – это особая величина. Особая потому, что она задаётся не только определённым числом, но и направлением. Таких величин в физике известно много. Скорость, ускорение, сила и ряд других физических величин характеризуются не только численным значением, но и направлением. Эти величины называют векторными величинами или просто векторами.
Величины, характеризуемые как численным значением, так и направлением, называются векторными величинами, или векторами.
Вектор графически изображается стрелкой, длина которой (в некоторых произвольных единицах длины) равна численному значению рассматриваемой величины, а направление показывает направление вектора.
а его численное значение – этой же буквой без стрелки (s).
Модуль (или длина) вектора перемещения – число, показывающее, скольким единицам длины (метрам, километрам и т. д.) равно перемещение. Модуль вектора обозначается той же буквой со стрелкой, что и сам вектор, но перед буквой и за ней ставятся вертикальные линии.
ПРИМЕР:
Вектор определяется его модулем и направлением.
Два вектора считаются равными, если равны их модули и они одинаково направлены.
Величины, которые определяются только численными значениями, называются скалярными величинами, или скалярами
ПРИМЕР:
Температура, время, масса, объём и др.
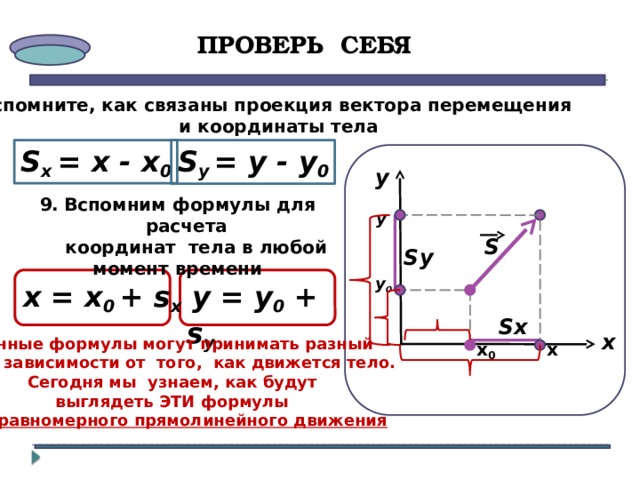
Зная вектор перемещения и координаты начального положения тела, можно найти значения координат его конечного положения.
ПРИМЕР:
Выберем систему координат XOY.
Начальное положение тела М0 определяется координатами х0 и у0. Приставим к точке М0 вектор
перемещения тела.
Как найти координаты х и у конечного положения тела (точки М) ?
Опустим из начала
Перпендикуляры М0N0 и MN на ось Х и перпендикуляры М0L0 и ML на ось Y. Точки N0 и N – это проекции точек М0 и М на ось X, а точки L0 и L – на ось Y. Проведём вектор от точки N0
Точки N0 и N – это проекции точек М0 и М на ось X, а точки L0 и L – на ось Y. Проведём вектор от точки N0
к точке N
Вектор
Аналогично построим вектор
Из рисунка видно, что направление вектора
совпадает с направлением оси координат. В этом случае, чтобы найти координату х точки М, нужно к начальной координате х0 прибавить длину отрезка N0N.
Направление вектора
может быть и противоположно направлению оси координат
 Таким образом,
Таким образом,х = х0 + N0N, если вектор
направлен также, как ось Х, и
х = х0 – N0N,
если направление вектора
Этот вывод можно записать короче, если ввести понятие проекции вектора
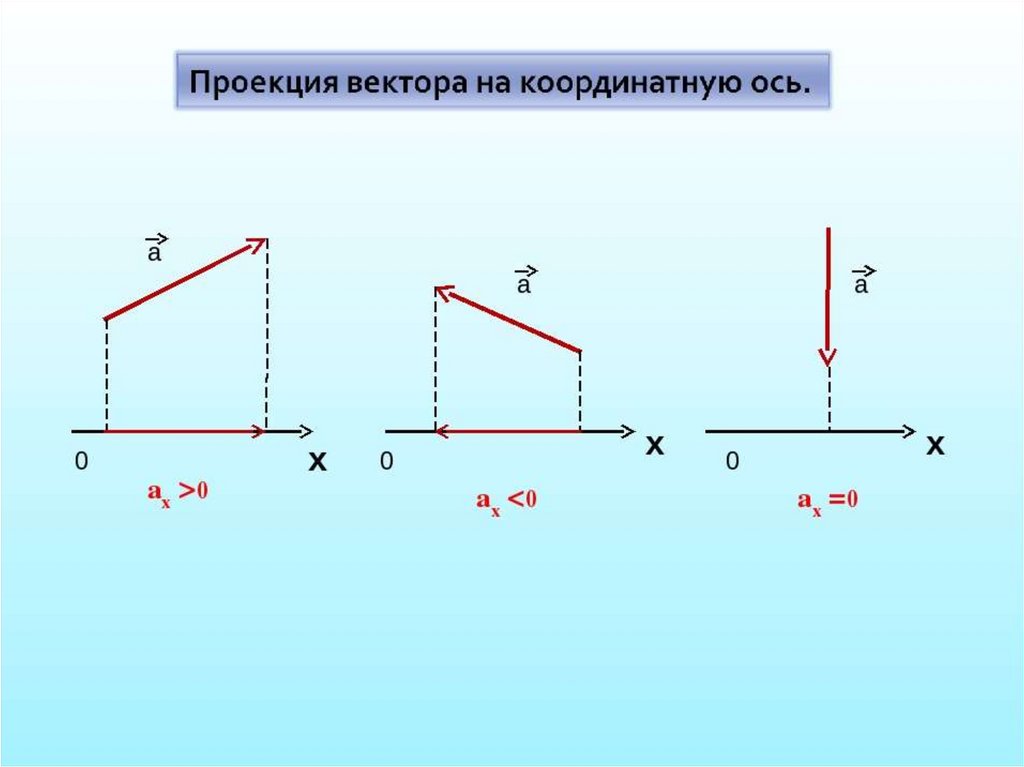
Проекцией вектора на ось Х называют скалярную величину, численно равную длине составляющей вектора по этой оси.
Проекция будет положительной, если составляющая вектора
по данной оси координат направлена также, как и ось координат, и отрицательной в противоположном случае.
Проекцию вектора на оси координат обозначают той же буквой, что и вектор, но без стрелки над ней и с индексом, показывающим, к какой оси относится проекция:
Если имеется только одна ось, то индекс у проекции вектора не пишется.
Во всех случаях, как бы ни был направлен вектор
координата х равна: х = х0 + sx,
координата у равна: у = у0 + sу
поэтому, зная перемещение, а значит и его проекции на оси координат, можно найти координаты тела.
Если вектор
направлен так же, как ось Х, то проекция sx положительна
(sx = N0N).
Если направление вектора
(sx = – N0N).
ПРИМЕР:
Пусть тело движется так, что вектор перемещения всё время остаётся параллельным одной из координатных осей, например оси Х.
Тогда его проекция на ось Y будет равна нулю. Это означает, что координата у при движении не изменяется. Проекция же вектора перемещения
на ось Х по абсолютной величине равна длине самого вектора
Для случая, показанного на рисунке
она положительна, а для случая, показанного на рисунке
отрицательна.
Но в том и другом случае координата х определяется формулой:
х = х0 + sx
ЗАДАЧА
Турист шёл из точки, расположенной в
РЕШЕНИЕ:
Поместим начало координат у перекрёстка дорог и направим оси Х и Y соответственно на восток и на север.
Начальное положение туриста (точка А) задано координатами
 Из этой точки проведём под углом 135° к оси Х вектор перемещения
Из этой точки проведём под углом 135° к оси Х вектор перемещенияНадо найти координаты х и у точки В.
Спроецируем вектор
на оси Х и Y.
Проекции sx и sу вектора перемещения, как видно из рисунка, равны по абсолютной величине длинам катетов прямоугольного равнобедренного треугольника АВС. Обозначим катет треугольника через а, тогда согласно теореме Пифагора
а2 + а2 = s2,
2а2 = s2.
Отсюда
sx = –а = –3,5 км,
sу = а = 3,5 км.
Конечные координаты туриста мы найдём по формулам:
х = х0 + sx и у = у0 + sу
Подставив в эти формулы соответствующие значения, получим:
х = 2 км – 3,5 км = –1,5 км,
у = 1 км + 3,5 км = 4,5 км.
Перемещение при прямолинейном равномерном движении.
Для того чтобы найти положение тела в какой-то момент времени, нужно знать вектор перемещения, потому что именно он связан с изменением координат движущегося тела. Проекции вектора перемещения точки на координатные оси просто равны изменениям её координат. При движении тела вдоль прямой в одном направлении перемещение тела непрерывно возрастает. Чтобы найти перемещение за время t, надо знать, как быстро оно возрастает. Быстроту этого возрастания определяют отношением перемещения к значению промежутка времени t, в течении которого оно произошло. Это отношение называют скоростью движения и обозначают буквой v. Так как перемещение – величина векторная, а время – скалярная, то скорость тоже векторная величина:
При движении тела вдоль прямой в одном направлении перемещение тела непрерывно возрастает. Чтобы найти перемещение за время t, надо знать, как быстро оно возрастает. Быстроту этого возрастания определяют отношением перемещения к значению промежутка времени t, в течении которого оно произошло. Это отношение называют скоростью движения и обозначают буквой v. Так как перемещение – величина векторная, а время – скалярная, то скорость тоже векторная величина:
Скоростью равномерного прямолинейного движения тела называют вектор, направленный так же, как перемещение тела, и равный по модулю отношению численных значений перемещения и промежутка времени, в течении которого это перемещение произошло.
Скорость, таким образом, показывает, какое перемещение тело совершает в единицу времени. Следовательно, для того чтобы найти перемещение тела за данное время t, надо знать его скорость
Тогда перемещение тела можно вычислить по формуле:
По формулам, написанным в векторной форме, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия.
Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия.
При прямолинейном движении траекторией является прямая линия. Естественно поэтому направить координатную ось вдоль этой прямой. В этом случае при движении тела будет изменяться только одна координата, например координата х, если выбранную ось обозначить через Х. Вдоль этой оси будут направлены и вектор скорости, и вектор перемещения тела.
Так как векторы
равны, то равны и их проекции на ось Х, т. е.
Мы выбрали координатную ось Х так, чтобы она была направлена вдоль той прямой, по которой движется тело. В таком случае, как мы условились, индекс при проекциях векторов перемещения и скорости можно не ставить, так что вместо sx и vx можно писать s и v.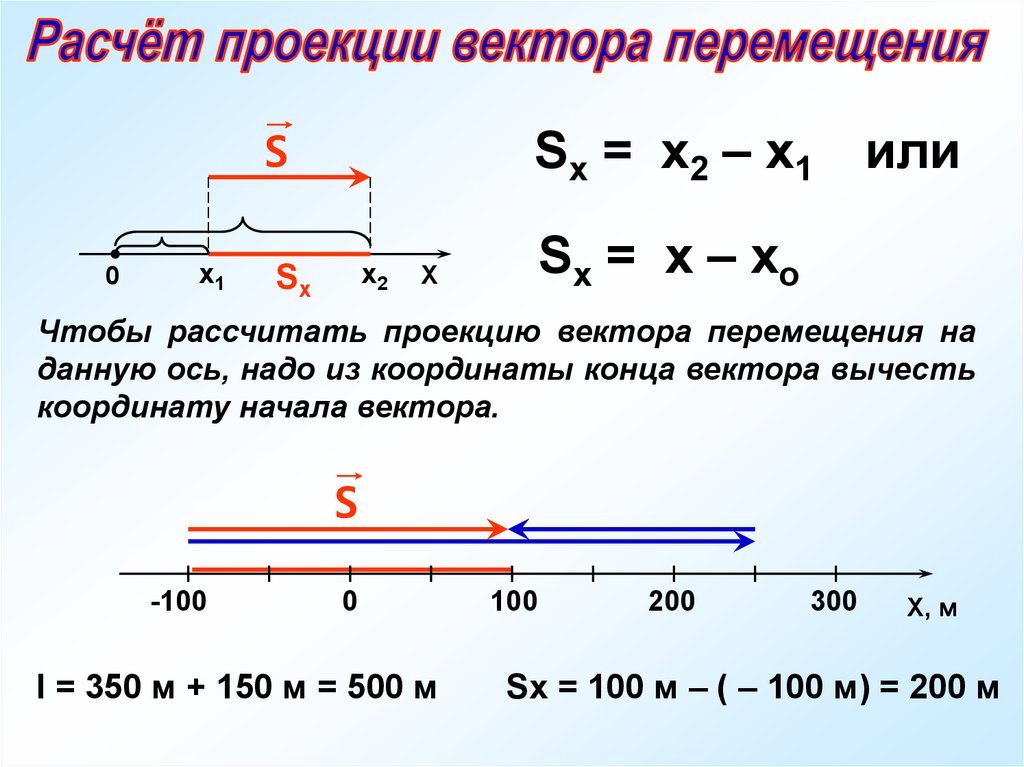 Тогда
Тогда
s = vt.
Теперь можно получить формулу для вычисления координаты тела x в любой момент времени. Известно, что
x = x0 + sx,
следовательно,
x = x0 + vt.
Необходимо помнить, что в этой формуле v – это проекция вектора скорости. А она, как всякая проекция вектора, может быть положительной и отрицательной. Если вектор скорости направлен так же, как ось Х
то проекция его на ось Х положительна. Если же направление вектора скорости противоположно направлению оси Х
то его проекция на эту ось отрицательна. Координата начального положения тела тоже может быть положительной и отрицательной: в начальный момент времени тело может находиться и по одну и по другую сторону от начала отсчёта.
Так же эта формула позволяет найти положение тела (материальной точки) в любой момент времени при прямолинейном равномерном движении. Для этого нужно знать начальную координату тела (точки) x0 и проекцию вектора скорости на ось, вдоль которой движется тело (нужно, следовательно, знать вектор скорости!). эта формула показывает, какой смысл имеет величина <<скорость>>.
Если движение происходит вдоль оси Х, то проекция вектора скорости на эту ось равна
Но х – х0 – это изменение координаты х, а t – время, за которое такое изменение произошло. Следовательно:
При прямолинейном равномерном движении проекция скорости тела на ось координат равна изменению координаты тела за единицу времени.
Можно сказать, что скорость показывает быстроту изменения координаты.
Когда тело движется вдоль оси, то по значению проекции его скорости на эту ось можно найти и сам вектор скорости. Ведь их абсолютные значения совпадают, а знак проекции определяет направление скорости. Поэтому в дальнейшем в таких случаях для краткости будем называть скоростью значение её проекции на ось. По тем же причинам проекцию перемещения будем называть перемещением.
Для решения задачи механики необходимо знать вектор скорости, а не его модуль. Спидометры, устанавливаемые в автомобилях, показывают именно модуль скорости. Им <<всё равно>>, куда движутся автомобили. По их показаниям поэтому нельзя определить ни направления движения автомобиля, ни его положения в любой момент времени.
ЗАДАЧА:
По дороге навстречу друг другу движутся два автомобиля: один со скоростью 60 км/час, другой – 90 км/час. У заправочной станции автомобили встретились и после этого продолжали свой путь.
У заправочной станции автомобили встретились и после этого продолжали свой путь.
Определить положение каждого автомобиля через 30 мин после встречи и расстояние между ними в этот момент.
РЕШЕНИЕ:
За начало координат примем заправочную станцию, а момент встречи автомобилей – за начало отсчёта времени. Координатную ось (обозначим её буквой Х) направим слева направо. Тогда координаты автомобилей через 0,5 час после встречи можно вычислить по формулам:
x1 = х01 + v1t и x2 = х02 + v2t
Начальные координаты х01 и х02 у обоих автомобилей равны нулю.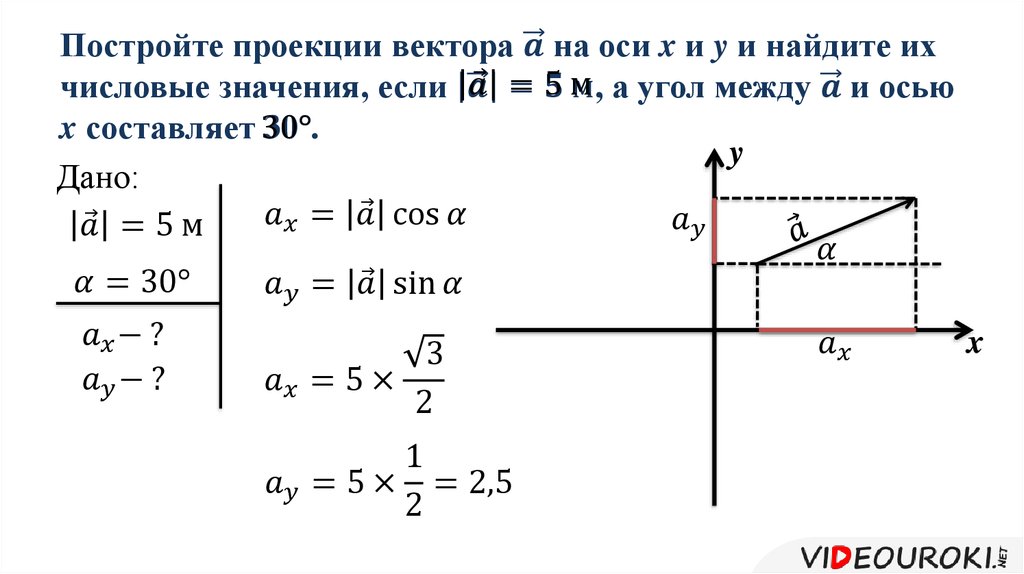 Поэтому
Поэтому
x1 = v1t и x2 = v2t
Проекция v1 скорости первого автомобиля положительна, потому что вектор его скорости направлен так же, как ось Х. Она равна v1 = +60 км/час. Проекция v2 скорости второго автомобиля отрицательна, так как вектор его скорости направлен против положительного направления оси Х, так что v2 = –90 км/час.
Следовательно,
x1 = 60 км/час × 0,5 час = 30 км,
x2 = –90 км/час × 0,5 час = –45 км.
Расстояние l между автомобилями равно разности их координат:
l = x1 – x2 = 30 км – (–45 км) = 75 км.
Задания к уроку 4
Физика 9 кл. Вектор. Проекция вектора на координатную ось
- Подробности
- Просмотров: 444
О векторных величинах
1. Какая величина называется векторной (или просто вектором)?
Физическая величина, которая характеризуется не только числовым значением (модулем), но и направлением, называется векторной величиной (или просто вектором).
Для векторной величины одинаково важны числовое значение (модуль) и направление.
Примеры векторных величин:
— скорость,
— перемещение,
— сила.
2. Какая величина называются скалярной (или просто скаляром)?
Величины, которые не имеют направления и задаются только числом, называются скалярными величинами или скалярами.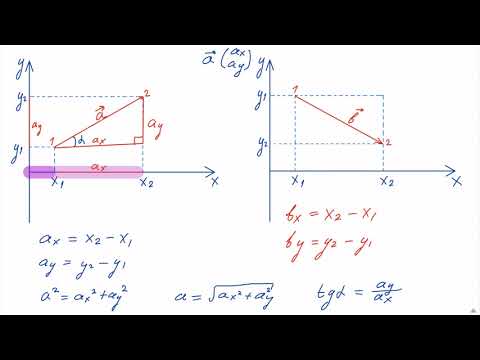
Примеры скалярных величин:
— число книг на полке,
— длина карандаша,
—
высота комнаты.
Модуль вектора — тоже скаляр.
3. Как изображают векторную величину?
Векторную величину изображают в виде стрелки, которая начинается в некоторой точке и заканчивается острием, указывающим направление..
Такой отрезок-стрелка называется вектором.
Длина стрелки в выбранном масштабе выражает модуль векторной величины.
Векторы обозначают буквами со стрелкой над ними.
Такой же буквой, но без стрелки обозначают модуль вектора.
4. Если два вектора равны друг другу по модулю, но направления векторов различны, то можно ли сказать, что эти векторы равны друг другу?
Нет, нельзя.
Равными считаются векторы, у которых одинаковы и модули, и направления.
5. Чем отличается векториая величина от скалярной?
Векторная величина характеризуется модулем (величиной) и направлением, а скалярная величина — только модулем.
Вектор имеет направление, а скаляр не имеет направления.
Проекция вектора на координатную ось
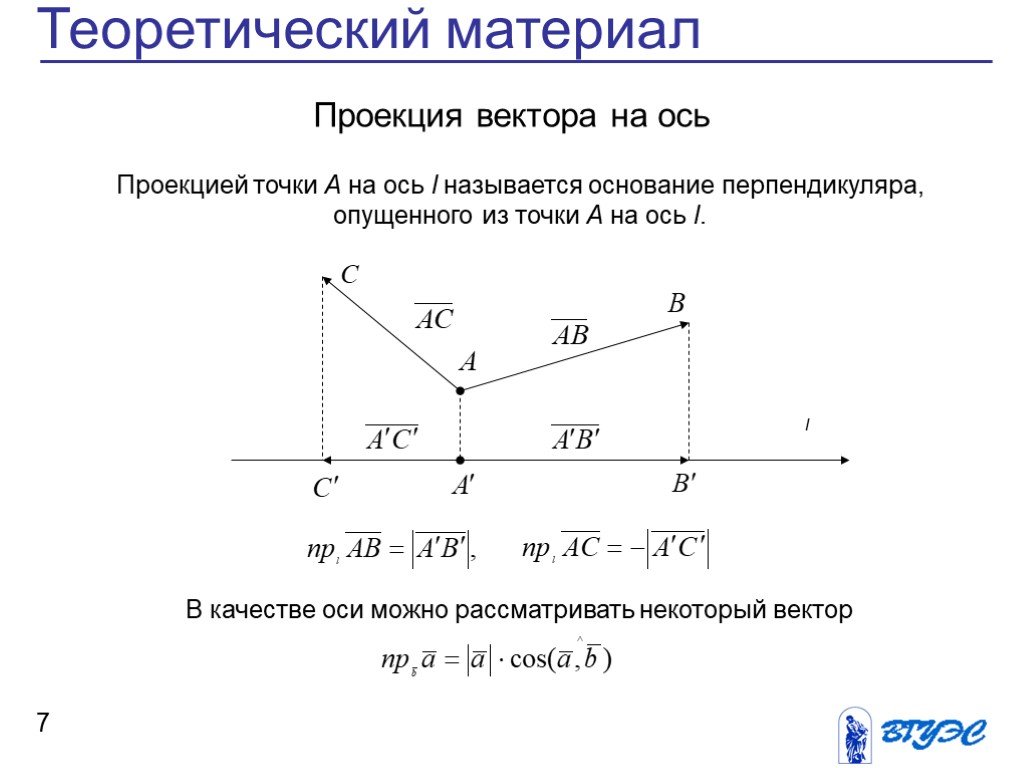
1. Как построить проекцию вектора на координатную ось?
Есть вектор а.
Опустим из точки А (начало вектора) и точки В (конец вектора) перпендикуляры на ось ОX.
Получим на оси точки ха и хв — это проекции точек А и В на ось ОX.
Длину отрезка ха-хв между проекциями начала и конца вектора называют проекцией вектора а на ось ОX и обозначают, как ах.
Проекцию вектора на ось обозначают той же буквой, что и вектор, но без стрелки и с индексом оси.
Проекция вектора — величина скалярная.
2. Если вектор перемещения параллелен координатной оси, то чему равен модуль проекции вектора на эту ось?
Если вектор параллелен оси координат, то модуль его проекции ( |ax| ) равен модулю ( a ) самого вектора.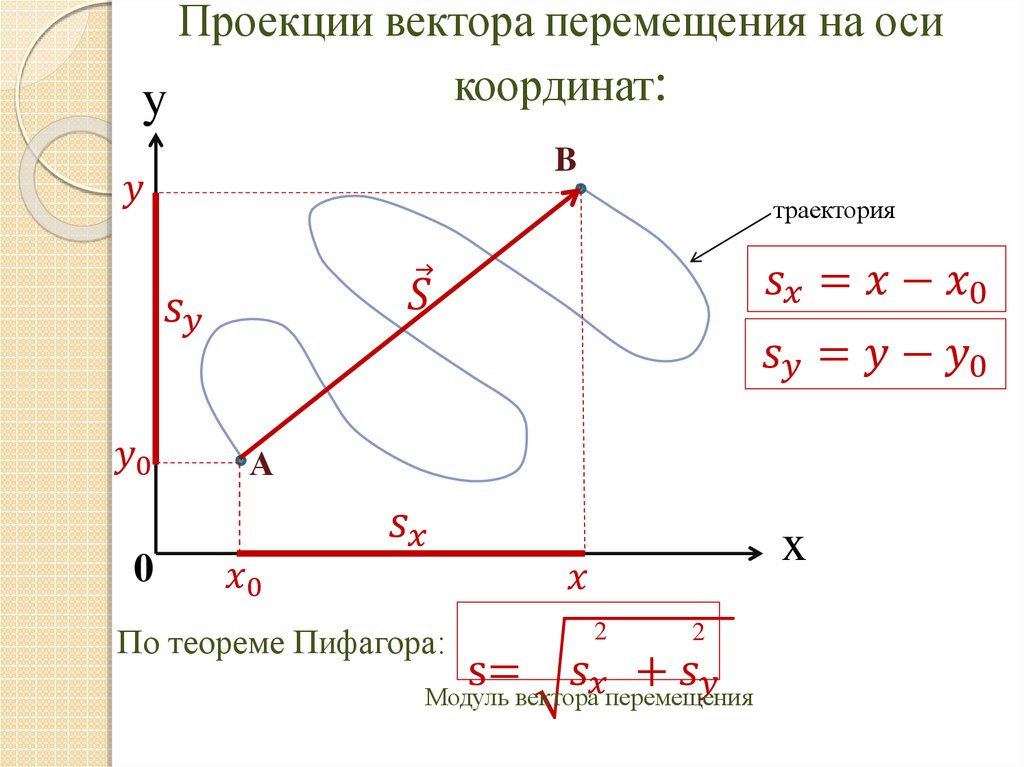
3. Что называют проекцией вектора на координатную ось?
Длину отрезка на координатной оси между проекциями начала и конца вектора, взятую со знаком « + » или « —», называют проекцией вектора а на координатную ось.
3. Когда проекция вектора на ось будет положительной, а когда — отрицательной?
Проекция вектора на координатную ось может быть, как положительной, так и отрицательной.
Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью.
Проекция вектора на ось считается отрицательной, если вектор направлен противоположно оси.
Если вектор перпендикулярен координатной оси, то при любом направлении вектора его проекция на ось равна нулю.
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
Формула скалярной и векторной проекции
Улучшить статью
Сохранить статью
Перед векторной проекцией мы должны взглянуть на скалярную проекцию, или, как правило, мы говорим проекция , что означает, что вектор производит проекцию на вектор . Проекции в основном бывают двух типов: скалярные проекции и векторные проекции. Скалярная проекция говорит нам о величине проекции, а векторная проекция говорит нам о себе и единичном векторе проекции.
Проекции в основном бывают двух типов: скалярные проекции и векторные проекции. Скалярная проекция говорит нам о величине проекции, а векторная проекция говорит нам о себе и единичном векторе проекции.
Проекция
Рассмотрим два вектора, и эти два вектора близки друг к другу с одной стороны и образуют угол θ между ними. Вектор проецируется на вектор . Для лучшего понимания вы можете предположить, что есть две палочки, как положение вектора. мы ставим факел на условие над вектором . Затем вы видите тень на векторе первой палочки, которая является проекцией второй палочки (вектора) на первую палочку ().
Скалярная проекция
Проекция
Аналогично,
Проекция
Векторная проекция
Векторная проекция определяется как произведение единичного вектора на скаляр. Векторная проекция
Аналогично,
Векторная проекция
Примеры задач
Задача 1: Если [Tex] [/Tex] и [Tex] [/Tex] 9002. затем найдите проекцию вектора a на b.
затем найдите проекцию вектора a на b.
Решение:
здесь и проекция =
Проекция =
=
Проблема 2: Найдите проекцию вектора A + B на C -Vect, здесь , и
.Решение:
здесь, и
Проекция вектора на
Задача 3: Найдите проекцию A на B -вектор, здесь, .0028 и Решение: LET и Проекция = = = 0 Задача 4: Найдите скалярную проекцию A на B, здесь, \ overlightRow {a} = 2 \ hat hat. {i} – \шляпа{j} + \шляпа{k}, \overrightarrow{b} = \шляпа{i} -2\шляпа{j} +\шляпа{k} Решение: Пусть и Проекция = = 5/6 Проблема 5: Найдите значение λ, когда скалярная проекция A на B равен 4, здесь, , Решение: Здесь, проекция и . 4 = 4 = 28 = 2λ + 18 λ = 5 Задача 6: Проекция вектора A на B, здесь = и Solution: = and Projection of the vector = Problem 7: Find the vector projection of m on n vector, here and Solution: Here , и Векторная проекция = = Вектор проекции дает проекцию одного вектора на другой вектор. Проекция вектора является скалярной величиной. Векторная проекция одного вектора на другой получается путем умножения данного вектора на косеканс угла между двумя векторами. Векторная проекция имеет множество применений в физике и технике для представления вектора силы относительно другого вектора. Давайте узнаем больше о формуле векторной проекции, выводе, а также проверим примеры.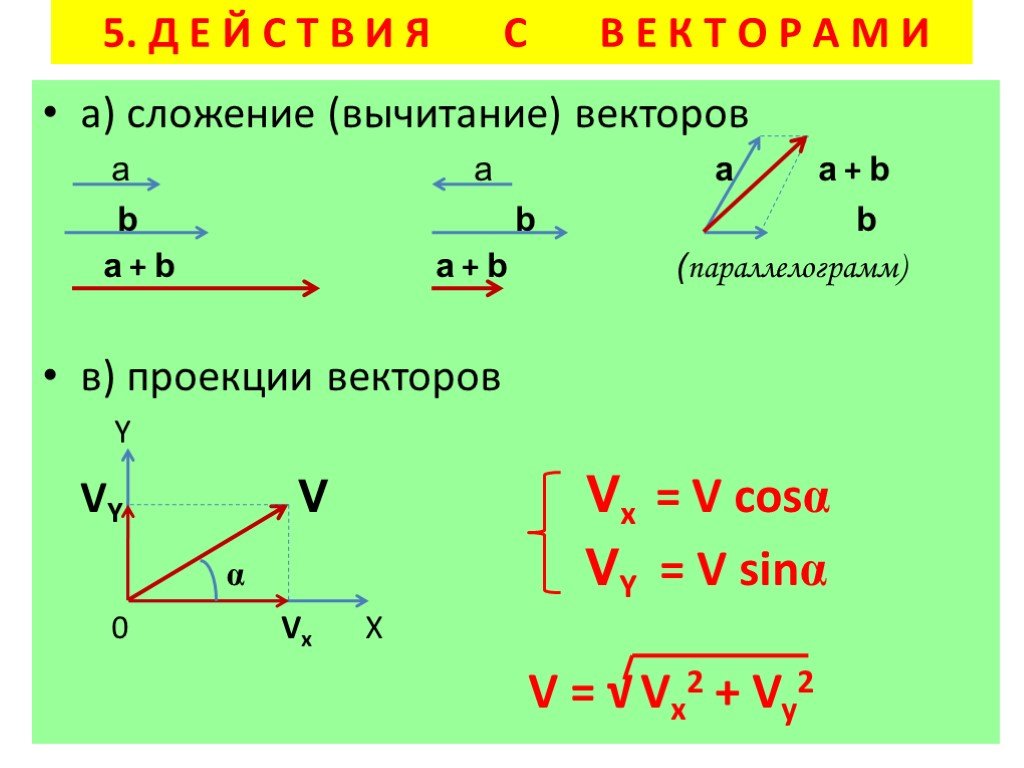 Проекция на на на на на на на стационарной наступлении на на на на на на стационарной наступлении на на на на на на стационарных =
Проекция на на на на на на на стационарной наступлении на на на на на на стационарной наступлении на на на на на на стационарных = Вектор проекции – формула, определение, вывод, пример
1. Что такое вектор проекции? 2. Формула вектора проекции 3. Вывод формулы вектора проекции 4. Понятия, относящиеся к вектору проекции 5. Примеры проекционного вектора 6. Практические вопросы 7. Часто задаваемые вопросы о Projection Vector Что такое вектор проекции?
Векторная проекция одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.
Результатом формулы векторной проекции является скалярное значение.
Проекция вектора \(\vec a\) на вектор \(\vec b \) получается произведением вектора a на косеканс угла между векторами a и b. Это еще больше упрощается, чтобы получить окончательное значение вектора проекции. Вектор проекции имеет величину, которая является частью величины вектора a, и имеет то же направление, что и вектор b.
Формула вектора проекции
Формула вектора проекции в векторной алгебре для проекции вектора a на вектор b равна скалярному произведению вектора a и вектора b, деленному на величину вектора b. Результат скалярного произведения является скалярным значением, и величина вектора b также является скалярным значением. Следовательно, величина и аргумент ответа вектора проекции являются скалярным значением и находятся в направлении вектора b..
\(\text{Проекция вектора} {a} \ \text{на вектор} {b} = \dfrac{a. b}{| b|}\)
Вывод формулы вектора проекции
Следующий вывод помогает четко понять и вывести формулу вектора проекции для проекции одного вектора на другой вектор.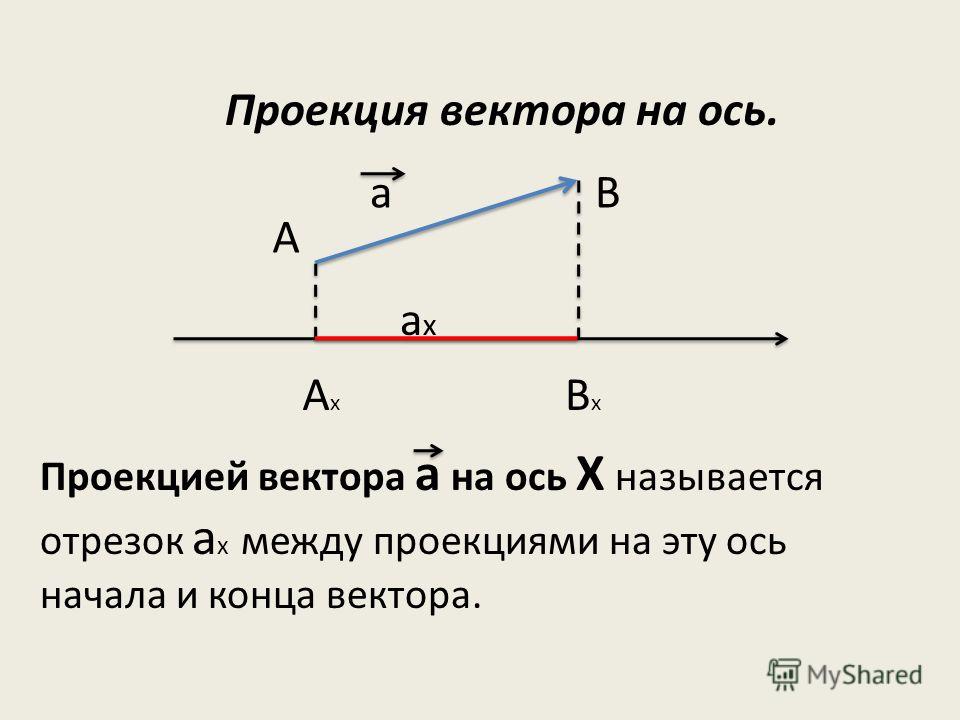 Пусть OA = \(\overrightarrow a\), OB = \(\overrightarrow b\) — два вектора, а θ — угол между \(\overrightarrow a\) и \(\overrightarrow b\). Это составляющая вектора a относительно вектора b. Проведите AL перпендикулярно OB.
Пусть OA = \(\overrightarrow a\), OB = \(\overrightarrow b\) — два вектора, а θ — угол между \(\overrightarrow a\) и \(\overrightarrow b\). Это составляющая вектора a относительно вектора b. Проведите AL перпендикулярно OB.
Из прямоугольного треугольника OAL , cos θ = OL/OA
OL = OA cos θ
OL = \(|\overrightarrow a|\) cos θ
OL — вектор проекции вектора a на вектор b.
\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ
\(\overrightarrow a. \overrightarrow b\)= \(|\overrightarrow b |(|\overrightarrow a|\) cos θ)
\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow b|\) OL
OL = \(\dfrac{\overrightarrow a. \ overrightarrow b}{|\overrightarrow b|}\)
Таким образом, формула проецирования вектора \(\overrightarrow a\) на вектор \(\overrightarrow b = \dfrac{\overrightarrow a. \overrightarrow b}{|\overrightarrow b|}\). Точно так же проекция вектора \(\overrightarrow b\) на вектор \(\overrightarrow a = \dfrac{\overrightarrow a. 2}}\)
2}}\)
Скалярное произведение двух векторов
Скалярное произведение двух векторов также называется скалярным произведением. Если два вектора выразить через единичные векторы i, j, k вдоль осей x, y, z, то скалярное произведение получается следующим образом:
Если \(\overrightarrow a = a_1\hat i + a_2 \hat j + a_3 \hat k\) и \(\overrightarrow b = b_1 \hat i + b_2 \hat j + b_3\hat k\), тогда
\(\overrightarrow a. \overrightarrow b\) = \((a_1 \ шляпа i + a_2 \ шляпа j + a_3 \ шляпа k)(b_1 \ шляпа i + b_2 \ шляпа j + b_3 \ шляпа k)\)
\(\overrightarrow a. \overrightarrow b\) = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\)
Связанные темы
Следующие темы помогают лучше понять проекцию вектор.
- Векторные формулы
- Скалярный продукт
- Единичный вектор
- Вектор положения
- Типы векторов
- Векторы
Часто задаваемые вопросы о Projection Vector
Что такое вектор проекции?
Вектор проекции является тенью одного вектора поверх другого вектора.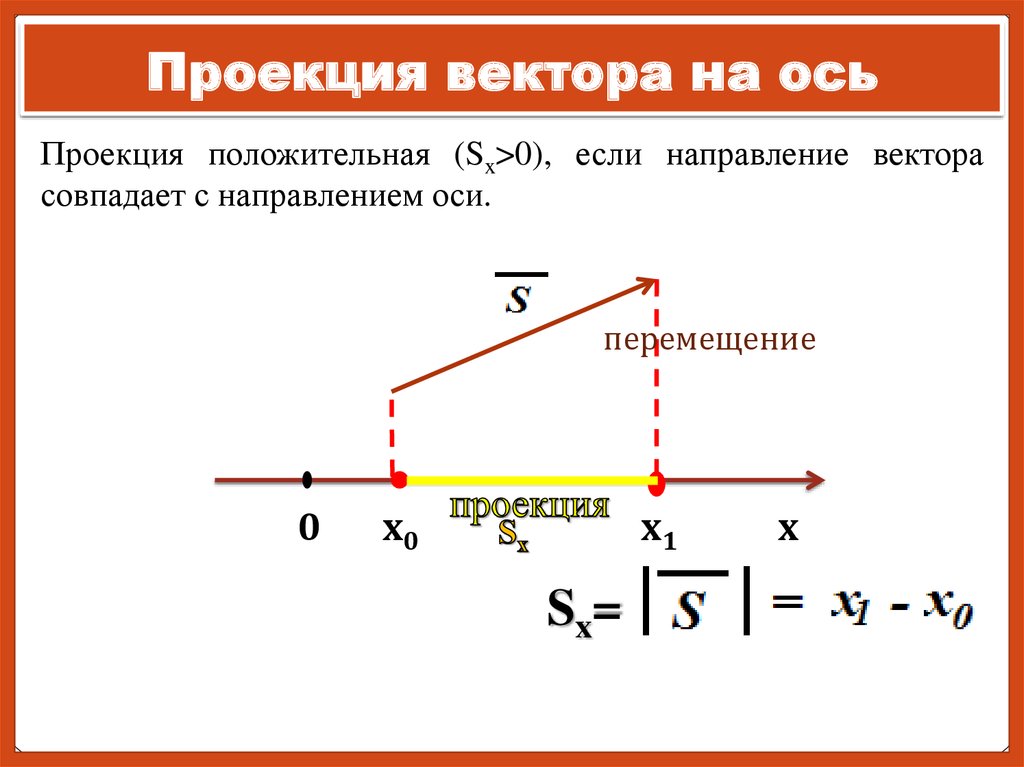 Векторная проекция одного вектора на другой получается путем умножения данного вектора на косеканс угла между двумя векторами.
Векторная проекция одного вектора на другой получается путем умножения данного вектора на косеканс угла между двумя векторами.
Что такое формула вектора проекции?
Формула векторной проекции дает проекцию вектора a на вектор b. Формула вектора проекции: \(\text{Проекция вектора} \vec {a} \\text{на вектор} \vec{b} = \dfrac{\vec{a}. \vec{b}}{| \ vec{b}|}\). Формула вектора проекции, представляющая проекцию вектора a на вектор b, равна скалярному произведению двух векторов, деленному на величину вектора b.
Как найти вектор проекции?
Проекция вектора \(\vec a\) на вектор \(\vec b \) получается побочным произведением вектора a на косеканс угла между векторами a и векторами b. Это можно упростить, чтобы получить следующую формулу вектора проекции.
\(\text{Проекция вектора } \vec {a} \ \text{на вектор } \vec{b} = \dfrac{\vec{a}. \vec{b}}{| \vec{b }|}\).
Что требуется для нахождения вектора проекции?
Чтобы найти вектор проекции, нам нужны два вектора и угол между ними.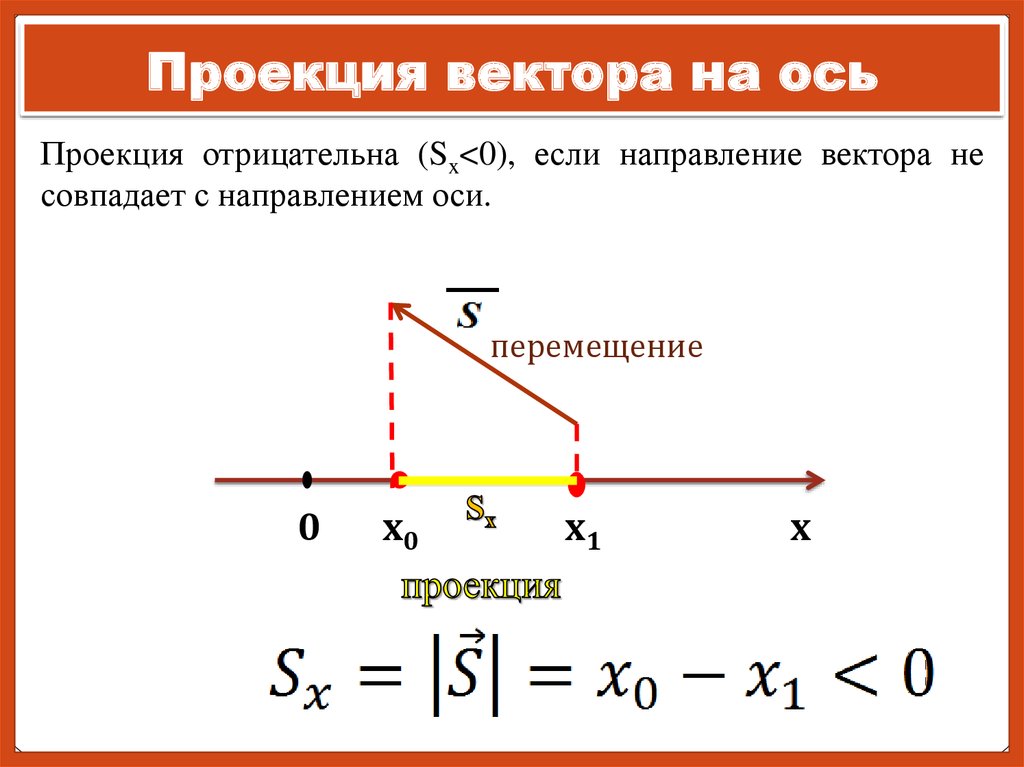 Кроме того, нам нужно знать вектор, для которого должен быть рассчитан вектор проекции, по отношению к другому вектору.
Кроме того, нам нужно знать вектор, для которого должен быть рассчитан вектор проекции, по отношению к другому вектору.
Как найти угол между двумя векторами из вектора проекции?
Угол между двумя векторами можно вычислить, разделив проекцию вектора на заданный вектор. Этими двумя векторами являются \(\vec a\) и \(\vec b \), а проекция вектора \(\vec a\) есть |aCosθ|. Таким образом, деление этой проекции на величину вектора дает косеканс угла между двумя векторами.
Как использовать скалярное произведение для нахождения вектора проекции?
Формула для проекции \(\vec a\) на вектор \(\vec b \) равна \(\text{Проекция вектора} \vec {a} \ \text{на вектор} \vec{ b} = \dfrac{\vec{a}.\vec{b}}{| \vec{b}|}\). Здесь в формуле мы наблюдаем скалярное произведение \(\vec a\) и \(\vec b \) в формуле проекции.
Каковы применения Projection Vector?
Векторная проекция имеет множество применений в физике и технике для представления вектора силы относительно другого вектора.