Принцип ферма вывод законов отражения и преломления: Занятие 2. Принцип Ферма. – Геометрическая оптика — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Занятие 2. Принцип Ферма.

Принцип минимального времени

В 1660 г. П. Ферма, сформулировал принцип, который явился обобщенным законом и геометрической оптики. В простейшей формулировке этот принцип звучит так.

В вакууме скорость света максимальна. В оптической среде с показателем преломления п время прохождения светом того же расстояния увеличивается в п раз. Величина s, равная пpoизведению абсолютного показателя преломления n на пройденном расстояние l (s = nl), называется оптической длиной пути. Принцип Ферма относится именно к оптической длине пути

Прямолинейность распространения света.

Используя принцип Ферма, можно получить закон прямолинейного распространении света. Свет из одной точки в другую распространяется по кратчайшему расстоянию. В однородной среде кратчайшим оптически и путем является прямая линия.

Однако в неоднородной среде кратчайшим оптическим путем может оказаться некоторая кривая (или ломаная) линия, вдоль которой показатель преломления меньше, чем вдоль геометрической прямой. Этим объясняется явление преломления света и искривление световых лучей в неоднородной среде — явление рефракции.

Закон отражения.

Пусть на зеркальную поверхность падает свет из точки А. В точке А’ собираются лучи, отраженные от зеркала. Предположим, что свет из точки А в точку А’ может распространяться двумя путями — отражаясь от точек О и О’. Время, которое потребуется свету, чтобы пройти из источника А в точку А’ через точку О, можно определить из выражения

Здесь u — скорость распространения света. Покажем, что время прохождения света по траектории АОА’ меньше, чем по любой другой траектории АО’А’.

Продифференцируем выражение и приравняем производную нулю в соответствии с принципом Ферма.

Учтем, что sin a = x/AO, sin a’ = (L — х) /ОА’. Получим:

Отсюда получаем sin a = sin a ‘; а так как оба угла острые, то отсюда следует равенство углов:

a = a ‘

Мы получили соотношение, выражающее закон отражения угол отражения a’ равен углу падения a . Из принципа Ферма следует и вторая часть этого закона: отраженный луч

лежит в плоскости, проходящей через падающий луч и нормаль сражающей поверхности. Ведь если бы эти лучи лежали в разных плоскостях, то не был бы минимальным путь АОА’.

Закон преломления света

Закон преломления света. Аналогичным образом, используя принцип Ферма, рассмотрим явление, происходящее на границе раздела двух сред. Пусть в среде I скорость света u₁, в среде II — u₂. Для прохождения света из точки А₁ в точку A₂ будет затрачено время

Выберем из всех возможных траекторий распространения света ту, которой соответствует минимальное время распространения света. Продифференцировав и положив производную равной пулю, получим:

Учитывая, что sin a1 = x/A1O, sin a2 = (L — х) /ОА2 получим : Откуда следует :

Это и есть закон преломления света. Запишем его в более удобной форме.

Из построений и принципа Ферма следует также, что преломленный луч лежит в плоскости, проходящей через падающий луч и перпендикуляр к поверхности раздела двух сред.

Рассматривая падение светового пучка на границу раздела двух сред, мы говорили раздельно об отражении и преломлении света. Это было вызвано необходимостью вывода законов отражения и преломления света. Однако практически всегда на границе раздела двух сред световой пучок разделяется на два — отраженный и преломленный.

Геометрическая оптика

Основные законы геометрической оптики известны ещё с древних времен. Так, Платон (430 г. до н.э.) установил закон прямолинейного распространения света. В трактатах Евклида формулируется закон прямолинейного распространения света и закон равенства углов падения и отражения. Аристотель и Птолемей изучали преломление света. Но точных формулировок этих законов геометрической оптики греческим философам найти не удалось.

Геометрическая оптика является предельным случаем волновой оптики, когда

длина световой волны стремится к нулю.

Простейшие оптические явления, например возникновение теней и получение изображений в оптических приборах, могут быть поняты в рамках геометрической оптики.

В основу формального построения геометрической оптики положено четыре закона, установленных опытным путем:

· закон прямолинейного распространения света;

· закон независимости световых лучей;

· закон отражения;

· закон преломления света.

Для анализа этих законов Х. Гюйгенс предложил простой и наглядный метод, названный впоследствии принципом Гюйгенса.

Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.

Гюйгенс Христиан (1629–1695), нидерландский ученый. В 1665–1681 гг. работал в Париже. Изобрел (1657) маятниковые часы со спусковым механизмом, дал их теорию, установил законы колебаний физического маятника. Опубликовал в 1690 г. созданную им в 1678 г. волновую теорию света, объяснил двойное лучепреломление. Усовершенствовал телескоп; сконструировал окуляр, названный его именем. Открыл кольцо у Сатурна и его спутник Титан. Автор одного из первых трудов по теории вероятностей (1657 г.).

Основываясь на своем методе, Гюйгенс объяснил прямолинейность распространения света и вывел законы отражения и преломления.

Закон прямолинейного распространения света

· свет в оптически однородной среде распространяется прямолинейно.

Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их источниками малых размеров.

Тщательные эксперименты показали, однако, что этот закон нарушается, если свет проходит через очень малые отверстия, причем отклонение от прямолинейности распространения тем больше, чем меньше отверстия.

Тень, отбрасываемая предметом, обусловлена прямолинейностью распространения световых лучей в оптически однородных средах.

Рис 7.1

Астрономической иллюстрацией прямолинейного распространения света и, в частности, образования тени и полутени может служить затенение одних планет другими, например затмение Луны, когда Луна попадает в тень Земли (рис. 7.1). Вследствие взаимного движения Луны и Земли тень Земли перемещается по поверхности Луны, и лунное затмение проходит через несколько частных фаз (рис. 7.2).

Рис. 7.2

Закон независимости световых пучков:

· эффект, производимый отдельным пучком, не зависит от того

, действуют ли одновременно остальные пучки или они устранены.

Разбивая световой поток на отдельные световые пучки (например, с помощью диафрагм), можно показать, что действие выделенных световых пучков независимо.

Закон отражения (рис. 7.3):

       ·        отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;

       ·       угол падения α равен углу отражения γ: α = γ



Рис. 7.3                                                     Рис. 7.4

      Для вывода закона отражения воспользуемся принципом Гюйгенса. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред (рис. 7.4). Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.

       ·       Для прохождения волной расстояния ВС требуется время             Δt = BC/υ.
За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.

      Закон преломления (закон Снелиуса) (рис. 7.5):

       ·     луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;

       ·     отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.



Рис. 7.5                                           Рис. 7.6

      Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна u (рис. 7.6).

      Пусть время, затрачиваемое волной для прохождения пути ВС, равно Dt. Тогда ВС = сDt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = uDt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. 7.6 видно, что

       ,       т.е.       .

      Отсюда следует закон Снелиуса:

.

      Несколько иная формулировка закона распространения света была дана французским математиком и физиком П. Ферма.

Ферма Пьер (1601–1665) – французский математик и физик. Родился в Бомон-де-Ломань. Получил юридическое образование. С 1631 г. был советником парламента в Тулузе.
      Физические исследования относятся большей частью к оптике, где он установил в 1662 г. основной принцип геометрической оптики (принцип Ферма). Аналогия между принципом Ферма и вариационными принципами механики сыграла значительную роль в развитии современной динамики и теории оптических инструментов.

      Согласно принципу Ферма, свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.

      Покажем применение этого принципа к решению той же задачи о преломлении света.

      Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела (рис. 7.7).

Рис. 7.7

      В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:

.

      Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:

,

      отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса: .

      Принцип Ферма сохранил свое значение до наших дней и послужил основой для общей формулировки законов механики (в том числе теории относительности и квантовой механики).

      Из принципа Ферма вытекает несколько следствий.

      Обратимость световых лучей: если обратить луч III (рис. 7.7), заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.

      Другой пример – мираж, который часто наблюдают путешественники на раскаленных солнцем дорогах. Они видят впереди оазис, но когда приходят туда, кругом оказывается песок. Сущность в том, что мы видим в этом случае свет, прошедший над песком. Воздух сильно раскален над самой дорогой, а в верхних слоях холоднее. Горячий воздух, расширяясь, становится более разреженным и скорость света в нем больше, чем в холодном. Поэтому свет проходит не по прямой, а по траектории с наименьшим временем, заворачивая в теплые слои воздуха.

      Если свет распространяется из среды с большим показателем преломления (оптически более плотной) в среду с меньшим показателем преломления (оптически менее плотной) ( > ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α (рис. 7.8 а).

Рис.7.8

      С увеличением угла падения увеличивается угол преломления (рис. 7.8 б, в), до тех пор, пока при некотором угле падения ( ) угол преломления не окажется равным π/2.

      Угол называется предельным углом. При углах падения α > весь падающий свет полностью отражается (рис. 7.8 г).

       ·       По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.

       ·     Если , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 7.8 г).

       ·     Таким образом, при углах падения в пределах от до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

      Предельный угол определим из формулы:

;

.

      Явление полного отражения используется в призмах полного отражения (Рис. 7.9).

Рис. 7.9

      Показатель преломления стекла равен n » 1,5, поэтому предельный угол для границы стекло – воздух   = arcsin (1/1,5) = 42°.

      При падении света на границу стекло – воздух при α > 42° всегда будет иметь место полное отражение.

      На рис. 7.9 показаны призмы полного отражения, позволяющие:

      а) повернуть луч на 90°;

      б) повернуть изображение;

      в) обернуть лучи.

      Призмы полного отражения применяются в оптических приборах (например, в биноклях, перископах), а также в рефрактометрах, позволяющих определять показатели преломления тел (по закону преломления, измеряя , определяем относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления второй среды известен).

Явление полного отражения используется также в световодах, представляющих собой тонкие, произвольным образом изогнутые нити (волокна) из оптически прозрачного материала.
Рис. 7.10

      В волоконных деталях применяют стеклянное волокно, световедущая жила (сердцевина) которого окружается стеклом – оболочкой из другого стекла с меньшим показателем преломления. Свет, падающий на торец световода под углам больше предельного, претерпевает на поверхности раздела сердцевины и оболочки полное отражение и распространяется только по световедущей жиле.

      Световоды используются при создании телеграфно-телефонных кабелей большой емкости. Кабель состоит из сотен и тысяч оптических волокон тонких, как человеческий волос. По такому кабелю, толщиной в обычный карандаш, можно одновременно передавать до восьмидесяти тысяч телефонных разговоров.

      Кроме того, световоды используются в оптоволоконных электронно-лучевых трубках, в электронно-счетных машинах, для кодирования информации, в медицине (например, диагностика желудка), для целей интегральной оптики.

Оптика и волны
Корпускулярная теория очень просто объясняла явления геометрической оптики, описываемые в терминах распространения световых лучей. С точки зрения волновой теории, лучи — это нормали к фронту волны. Принцип Гюйгенса также позволяет объяснить законы геометрической оптики на основе волновых представлений о природе света.

Закон отражения
Когда световые волны достигают границы раздела двух сред, направление их распространения изменяется. Если они остаются в той же среде, то происходит отражение света.

Отражение света — это изменение направления световой волны при падении на границу раздела двух сред, в результате чего волна продолжает распространяться в первой среде.

Закон отражения света хорошо известен:

Падающий луч, перпендикуляр к границе раздела двух сред в точке падения и отраженный луч лежат в одной плоскости, причем угол падения равен углу отражения.

Направления распространения падающей и отраженной волн показаны на рис. 3.2.
Рис. 3.2. Отражение света от плоской поверхности
Видео 3.1 Трехсантиметровые волны: закон отражения (металл).
Видео 3.2 Трехсантиметровые волны: закон отражения (диэлектрик).
Видео 3.3 Решетка — зеркало для трехсантиметровых волн. (диэлектрик).
Закон отражения может быть выведен из принципа Гюйгенса. Действительно, допустим, что плоская волна, распространяющаяся в изотропной среде, падает на границу раздела двух сред АС (рис. 3.3).
Рис. 3.3. Применение принципа Гюйгенса к выводу закона отражения
Достаточно рассмотреть два параллельных луча I и в падающем пучке. Углом падения называют угол между нормалью п к поверхности раздела и падающим лучом I. Плоский фронт AD падающей волны сначала достигнет границы раздела двух сред в точке А, которая станет источником вторичных волн. Согласно принципу Гюйгенса, из нее, как из центра, будет распространяться сферическая волна. Через время
,
то есть с запаздыванием во времени на , луч из падающего пучка придет в точку С, которая в этот момент времени также станет источником вторичной волны. Но, к этому моменту вторичная сферическая волна, распространяющаяся из точки А, уже будет иметь радиус (как и должно быть: ). Мы знаем теперь положение двух точек фронта отраженной волны — С и В. Чтобы не загромождать рисунок, мы не показываем вторичных волн, испущенных точками между А и С, но линия CD будет касательной (огибающей) ко всем из них. Стало быть, CВ действительно является фронтом отраженной волны. Направление ее распространения (лучи II и ) ортогонально фронту CD. Из равенства треугольников ABC и ADC вытекает равенство углов
что, в свою очередь, приводит к закону отражения
На рис. 3.4 представлена интерактивная модель отражения света.
Рис. 3.4. Изучение закона отражения света

Закон преломления
Если световые волны достигают границы раздела двух сред и проникают в другую среду, то направление их распространения также изменяется — происходит преломление света.

Преломление света — это изменение направления распространения световой волны при переходе из одной прозрачной среды в другую.

Направление распространения падающей и преломленной волны показано на рис. 3.5.

Рис. 3.5. Преломление света на плоской границе раздела двух прозрачных сред
Закон преломления гласит:

Падающий луч, перпендикуляр к границе раздела сред в точке падения и преломленный луч лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления постоянно для данной пары сред и равно показателю преломления второй среды относительно первой

Здесь показатель преломления среды, в которой распространяется преломленная волна, показатель преломления среды, в которой распространяется падающая волна.
Закон отражения также вытекает из принципа Гюйгенса. Рассмотрим (рис. 3.6) плоскую волну (фронт АВ), которая распространяется в среде с показателем преломления , вдоль направления I со скоростью
Эта волна падает на границу раздела со средой, в которой показатель преломления равен , а скорость распространения
Рис. 3.6. К выводу закона преломления света с помощью принципа Гюйгенса
Время, затрачиваемое падающей волной для прохождения пути ВС, равно
За это же время фронт вторичной волны, возбуждаемой в точке А во второй среде, достигнет точек полусферы с радиусом
В соответствии с принципом Гюйгенса положение фронта преломленной волны в этот момент времени задается плоскостью DC, а направление ее распространения — лучом III, перпендикулярным к DC. Из треугольников и следует
откуда

(3.1)

Таким образом, закон преломления света записывается так:

(3.2)

Видео 3.4 Полное внутреннее отражение (видимый свет)
Видео 3.5 Модель световода
Видео 3.6 Куб и призма на пути трехсантиметровой волны.
На рис. 3.7 представлена интерактивная модель преломления света на границе раздела двух сред.
Рис. 3.7. Изучение закона преломления
Для еще одной иллюстрации применения принципа Гюйгенса рассмотрим пример.
Пример. На плоскую границу раздела двух сред падает нормально луч света. Показатель преломления среды непрерывно увеличивается от ее левого края к правому (рис. 3.8). Определим, как будет идти луч света в этой неоднородной среде.
Рис. 3.8. Искривление луча света в неоднородной среде
Пусть фронт волны АА подошел к границе раздела сред. Точки раздела сред можно рассматривать как центры вторичных волн. Через время   испущенные вторичные сферические волны достигают точек на расстоянии от фронта АА. Поскольку показатель преломления среды растет слева направо, эти расстояния убывают слева направо. Огибающая к вторичным волнам — новый фронт ВВ — повернется. Если теперь взять точки фронта ВВ за источники вторичных волн, то за время они породят волны, образующие фронт СС. Он еще более повернут. Его точки порождают фронт DD и т. д. Проводя нормаль к волновым фронтам в разные моменты времени, получаем путь светового луча в среде с переменным показателем преломления (зеленая линия). Видно, что луч искривляется в сторону увеличения показателя преломления. Аналогия: если притормозить левые колеса автомобиля, его повернет налево. Для света степень «торможения» растет с ростом показателя преломления среды: .
Эта задача имеет отношение к явлению, наблюдающемуся на море. Когда ветер дует с берега, иногда возникает так называемая «зона молчания»: звук колокола с судна не достигает берега. Обычно говорят, что звук относится ветром. Но даже при сильном урагане скорость ветра примерно в 10 раз меньше скорости звука, так что «отнести» звук ветер никак не может. Объяснение заключается в том, что скорость встречного ветра у поверхности моря вследствие трения меньше, чем на высоте. Поэтому скорость звука у поверхности больше, и линия распространения звука загибается кверху, не попадая на берег.

Дополнительная информация
http://allphysics.ru/perelman/otrazhenie-i-prelomlenie-sveta – Я.И.Перельман, «Занимательная физика». Отражение и преломление света.
http://www.nvtc.ee/e-oppe/Sidorova/objects/index.html – Законы преломления, отражения света. Зеркала. Теория и примеры задач. В «Итоговых заданиях» — кроссворд.
http://files.school-collection.edu.ru/dlrstore/1461c067-705e-4f5f-9d18-152a8eec1564/7_16.swf – Слайд-шоу «Рассеянное отражение света».
http://www.youtube.com/watch?v=KQvtIEITg5s&feature=endscreen&NR=1 – Видео о преломлении света около магнитов и в линзах.
http://allphysics.ru/feynman/kak-voznikaet-pokazatel-prelomleniya – Фейнмановские лекции по физике. Как возникает показатель преломления.
http://publ.lib.ru/ARCHIVES/B/… – Тарасов Л.В., Тарасова А.Н., «Беседы о преломлении света».

Принцип Ферма.
Итак, волновая оптика способна объяснить явления отражения и преломления света столь же успешно, как и геометрическая оптика. В основу последней, трактующей явления на основе законов распространения лучей, положен принцип Ферма:

Свет распространяется по такому пути, для прохождения которого требуется минимальное время.

Для прохождения участка пути свету требуется время
где v=с/п — скорость света в среде. Таким образом, время t, затрачиваемое светом на путь от точки 1 до точки 2, равно

(3.3)

Введем величину с размерностью длины, которая называется оптической длиной пути:

(3.4)

Пропорциональность t и L позволяет сформулировать принцип Ферма следующим образом:

Свет распространяется по такому пути, оптическая длина которого минимальна.

Рассмотрим путь света из точки S в точку С после отражения от плоскости АВ (рис. 3.9).
Рис. 3.9. Применение принципа Ферма к отражению света
Непосредственное попадание света из S в С невозможно из-за экрана. Нам надо найти точку О, отразившись в которой луч попадет в точку С. Среда, в которой проходит луч, однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины. Рассмотрим зеркальное изображение S’ точки S. Геометрические длины путей SOC и S’OC равны. Поэтому минимальность длины SOC эквивалентна минимальности длины S’OC. А минимальная геометрическая длина пути из S’ в С будет соответствовать прямой, соединяющей точки S’ и С. Пересечение этой прямой с плоскостью раздела сред дает положение точки О. Отсюда следует равенство углов:
то есть закон отражения света.
Рассмотрим теперь явление преломления света (рис. 3.10).
Рис. 3.10. Применение принципа Ферма к преломлению света
Видео 3.7 Искривление луча в неоднородной среде.
Видео 3.8 Трехсантиметровые волны: диэлектрическая линза.
Видео 3.9 Трехсантиметровые волны: диэлектрическая призма.
Определим положение точки О, в которой должен преломиться луч, распространяясь от S к С, чтобы оптическая длина пути L была минимальна. Выражение для L имеет вид

(3.5)

Найдем величину х, соответствующую экстремуму оптической длины пути:

(3.6)

Отсюда следует

(3.7)

или
Мы получили закон преломления света.
Принцип Ферма является частным случаем так называемого принципа наименьшего действия, имеющего приложения практически ко всем областям физики. Всякий раз из всех возможных движений системы осуществляется то, для которого некая величина (ее называют действием) минимальна (точнее, имеет экстремум). В этом проявляется некая «экономность» природы, выбирающей оптимальные пути для перехода системы из одного состояния в другое.

Дополнительная информация
Геометрическая оптика
http://allphysics.ru/feynman/geometricheskaya-optika – Фейнмановские лекции по физике. Геометрическая оптика.
http://www.ph5s.ru/book_ph_opt_geom.html – Ссылки на книги по геометрической оптики. Сайт бывшего преподавателя МИФИ А.Н. Варгина.
http://school-collection.edu.ru/catalog/rubr/ef4b174a-8fec-c03a-df26-ae730713bc30/79292/?interface=themcol – Интерактивные модели по физике. Геометрическая оптика.
http://diplomivanov.narod.ru/ – Сайт о геометрической оптике: теория и задачи.
http://eqworld.ipmnet.ru/ru/library/books/Begunov1966ru.djvu – Бегунов Б.Н., учебник по геометрической оптике.
http://www.physel.ru/a-mainmenu-55.html – Материалы по геометрической оптике.
http://www.youtube.com/watch?v=mRwRy24hbg8&feature=related – Ход лучей в линзе.
http://physbook.ru/index.php/Kvant… – Задачи на оптические построения.
http://physbook.ru/index.php/Kvant… – Геометрия тонкой линзы.
http://physbook.ru/index.php/Kvant… – Тонкие линзы. Нулевые линзы.
http://physbook.ru/index.php/Kvant… – Фокус шара.
http://www.youtube.com/watch?v=MNea-aK6VuQ – Оптическая разность хода. Видео.
http://sfiz.ru/list.php?c=geomoptika – Геометрическая оптика. Учебные материалы.

Учебники и лекции по оптике
http://www.plib.ru/library/book/16969.html – Бутиков Е.И. Учебник по оптике.
http://www.plib.ru/library/book/16986.html – Годжаев Н.М. Учебник по оптике.
http://www.plib.ru/library/book/15479.html – Клаудер Дж, Сударшан Э. «Основы квантовой оптики».
http://www.alleng.ru/d/phys/phys106.htm – Сивухин, учебник по оптике.
http://www.abitura.com/handbook/index.html – Справочник по физике (в т. ч. по оптике).
http://sfiz.ru/page.php?id=103 – Словарь по оптике.
http://uti.tpu.ru/edu/chairs/eno/opt.pdf – Е.В. Полицинский «Оптика. Конспекты лекций.» Учебное пособие.
http://physoptika.ru/ – Лекции по оптике. Примеры решения задач.
http://www.phys.spbu.ru/content/File/Library/Books/GenPhys/crowellOptics.pdf – B. Crowell. «Optics»
http://www.physbook.ru/ – Электронный учебник по физике.
http://eqworld.ipmnet.ru/ru/library/books/BornVolf1973ru.djvu – М. Борн, Э. Вольф, «Основы оптики».
http://eqworld.ipmnet.ru/ru/library/books/GorbunovaZajcevaKrasnikov1977ru.djvu – Горбунова О.И., Зайцева А.М., Красников С.Н., «Задачник-практикум по общей физике. Оптика. Атомная физика».
http://eqworld.ipmnet.ru/ru/library/books/DetlafYavorskij_t3_1979ru.djvu – Детлаф А.А., Яворский Б.М. Курс физики. Том 3. Волновые процессы. Оптика. Атомная и ядерная физика.
http://www.physics.spbstu.ru/forstudents/practice/vasyliev_phys_optica_manual.pdf – А.Э. Васильев. «Физика. Оптика.» Учебное пособие.
http://www.phys.spbu.ru/library/studentlectures/krylov/krylov/ – И.Р. Крылов. «Методическое пособие по курсу оптики».
http://jamshyt.ru/wnopa/f2/ – Оптика. Материалы.
http://fn.bmstu.ru/phys/bib/physbook/tom4/content.htm – О.С. Литвинов, К.Б. Павлов, В.С. Горелик «Электромагнитные волны и оптика» Онлайн-учебник.
http://www.laser-portal.ru/content_3 – История и законы оптики, оптические эффекты, материалы, компоненты оптических схем, природа света.
http://www.harmony-guild.ru/index.php?option=com_content&view=article&id=190:2011-05-31-07-27-31&catid=34:demo-category&Itemid=78 – Излучение Вавилова-Черенкова. Механизм, интересные следствия.
http://files.school-collection.edu.ru/dlrstore/5ee6b93b-cb19-46e1-9e74-30aa92a167fa/7_18.swf – Слайд-шоу «Зеркальный телескоп».
http://media.dm-centre.ru/index.php?option=com_content&view=article&id=25&Itemid=29 – Опыты по оптике. Видео.
http://eqworld.ipmnet.ru/ru/library/books/Savelev_t3_1971ru.djvu – Савельев И.В. Курс общей физики, том З. Оптика. Атомная физика.
http://allphysics.ru/feynman/optika-printsip-naimenshego-vremeni – Фейнмановские лекции по физике. Оптика. принцип наименьшего времени.
http://allphysics.ru/feynman/tsvetovoe-zrenie – Фейнмановские лекции по физике. Цветовое зрение.
http://allphysics.ru/feynman/mehanizm-zreniya – Фейнмановские лекции по физике. Механизм зрения.

Тесты и задачи
http://physbook.ru/index.php/Kvant… – Задачи на распространение света.
http://www.reppofiz.info/ege.html – Задачи из ЕГЭ по оптике (и не только) с решениями.
http://eqworld.ipmnet.ru/ru/library/books/RussoMate1976ru.djvu – Руссо М., Матье Ж.П. Задачи по оптике.
http://www.testent.ru/load/testy/fizika/optika/39-1-0-1824 – Тесты по оптике.
http://window.edu.ru/window_catalog/files/r72644/stup538.pdf – Сборник задач ЕГЭ по оптике.

Другие ресурсы по оптике
http://www3.crimea.edu/tnu/structure/physic_fac/departments/general/common_phys/all/opt.htm – Кратко об основных аспектах оптики.
http://repetitor.mathematic.of.by/spravka_fizika3.htm#M1 – Основные формулы по оптике.
http://shkola.lv/index.php?mode=cht&chtid=91 – Основные положения, законы, формулы.
http://school-collection.edu.ru/catalog/search/?text=%EE%EF%F2%E8%EA%E0&tg=&interface=catalog – Коллекция ресурсов по оптике: статьи, эксперименты, лабораторные.
http://power-p.ru/load/fizika/optika/14-1-0-331 – Презентации по оптике: устройство глаза, фотоаппарата, микроскопа, телескопа и другое.
http://pymath.ru/viewtopic.php?f=77&t=809&sid=63be0a3e99f9a32260b53dcfaad3c271 – Видеоурок «Разрешающая способность».

Интересные факты
http://physbook.ru/index.php/Kvant… – Физическая оптика: на каком расстоянии можно отличить двугорбого верблюда от одногорбого?
http://physbook.ru/index.php/Kvant… – Древняя оптика: почему ошибался Птоломей?
http://physbook.ru/index.php/Kvant… – Лучи и волны.
http://physbook.ru/index.php/Kvant… – Волны на пляже.
http://physbook.ru/index.php/Kvant… – Предельные возможность оптического микроскопа.
http://physbook.ru/index.php/Kvant… – Электрический микроскоп. Можно ли в микроскопе разглядеть молекулу?
http://physbook.ru/index.php/Kvant… – Как устроен глаз? Эффект «Полета» луны.
http://elkin52.narod.ru/optika.htm – Занимательная оптика в вопросах и ответах.
http://www.osa-univer.org.ua/DiscoveryKit_Rus.pdf – Занимательная оптика, набор наглядных пособий.
http://www.youtube.com/watch?v=NwH7qx5468o – Распространение луча лазера в воде: опыт Джона Тилдана.
http://www.youtube.com/watch?v=C_R9GnBAC1E – Бесконечное зеркало.
http://www.vokrugsveta.ru/quiz/615/ – Почему небо голубое? Объяснение «на пальцах».
http://www.laser-portal.ru/content_5 – Лазеры. Область их применения.
http://our-lectures.ru/interesting/physics/27-pochemy-nebo-golyboe.html Почему небо голубое? Объяснение с математическими выкладками.
http://www.sveticvet.ru/iskrivlenie-svetovyx-luchej-v-atmosfere/mirazh-v-miniatyure/index.php – Статья о миражах.
http://optika8.narod.ru/History.htm – Краткая история развития оптики.
http://laser-portal.ru/content_7 – История развития оптики.
http://allphysics.ru/perelman/luchi-sveta – Я.И.Перельман, «Занимательная физика». Лучи света.
http://allphysics.ru/perelman/zrenie-odnim-i-dvumya-glazami – Я.И.Перельман, «Занимательная физика». Зрение одним и двумя глазами.
http://www.youtube.com/watch?v=uGTV5OxcKDs – Видео о свете и зеркалах (плоских, выпуклых и вогнутых), цветных фильтрах, люминофорах, черных телах, призмах.
Принцип ферма — fiziku5.ru
Задача 1. Параллельный пучок света c длиной волны 500 нм падает на экран с круглым отверстием диаметра d. Прошедший сквозь отверстие свет, попадает на экран для наблюдения, расположенный на расстоянии L от экрана с отверстием. Каков будет диаметр светлого пятна? Используя полученный результат, получите критерий применимости геометрической оптики.
3. Закон отражения
3.1 Принцип Ферма
Законы геометрической оптики: закон прямолинейного распространения света в оптически однородной среде, закон отражения и закон преломления света могут быть получены из принципа Ферма, который формулируется так:
В пространстве между двумя точками свет распространяется по такому пути, вдоль которого время его прохождения минимально.
Задача 2. Используя принцип Ферма, выведите закон отражения света.
Решение. Пусть свет от точечного источника S, отразившись от зеркала, попадает в точку P. Будем исходить из установленного ранее факта, что свет в однородной среде распространяется прямолинейно. Изменение направления происходит при отражении света от зеркала.
Рассмотрим произвольный ход луча SOP. Пусть угол между перпендикуляром к зеркалу OH и направлением падающего луча равен a, а угол между перпендикуляром к зеркалу и направлением отраженного луча равен b. Время между выходом из источника и достижением светом точки P равно длине ломаной SOP, деленной на скорость распространения c. Так как скорость распространения света везде одна и та же, минимальность времени прохождения траектории эквивалентна минимальности длины ломаной SOP. Таким образом, формулировка задачи об отыскании траектории минимального времени достижения точки P превращается в новую формулировку об отыскании кратчайшей траектории SOP.
Проведем геометрическое решение. Решение сводится к нахождению такого расположения точки O на зеркале, которое обеспечит минимальность длины ломаной SOP. Построим дополнительную точку S`, которая расположена симметрично точке S относительно поверхности зеркала. Из построения точки S` ясно, что длина ломаной SOP равна длине ломаной S`OP. Получаем еще одну формулировку задачи — надо найти такое положение точки O, которое обеспечит минимальность длины ломаной S`OP. Очевидно, что кратчайшее расстояние между точками S` и P — расстояние вдоль прямой, соединяющей эти точки. Искомое положение точки O находится на прямой, соединяющей точки S` и P. Из этого сразу становится ясным простое доказательство того, что падающий, отраженный лучи и перпендикуляр к отражающей поверхности лежат в одной и той же плоскости, и угол отражения равен углу падения.
3.2 Построение изображения в плоском зеркале
Дополнительная точка S`, которая использовалась при доказательстве закона отражения является ничем иным, как изображением источника S. Изображение источника расположено в его зеркальном отражении относительно плоскости отражения. Наблюдатель может увидеть изображение не из любой точки. Чтобы изображение было видимым, необходимо, чтобы прямая, соединяющая изображение и точку наблюдения, пересекала плоскость отражения. Отсюда также ясно, что между источником и его видимым изображением необязательно должна находиться отражающая поверхность.
Оптическое отражение является физическим воплощением одноименной математической операции симметрии.
Задача 3. Горящая миниатюрная лампочка находится вблизи прямого угла, образованного двумя плоскими зеркалами. Сколько изображений имеет лампочка? Постройте все изображения.
Задача 4. Луч света падает под углом a на одно из двух зеркал, образующих друг с другом прямой угол. Каково направление отраженного от системы зеркал луча?
3.3 Построение изображения в сферическом зеркале
3.3.1 Основные точки и линии сферического зеркала
Изображение предмета создается светом, отраженным от предмета, прошедшим оптическую систему и попавшим в глаза наблюдателю. Для построения изображения предмета можно пользоваться любыми из лучей, однако, изо всех лучей есть наиболее удобные для этих целей. У сферического зеркала есть несколько опорных линий и точек, используемых при построении изображения. Они показаны на рисунке 81. Во-первых, ось симметрии зеркала PP` — главная оптическая ось. Далее: центр кривизны зеркала O, точка P — полюс зеркала, точка F — фокус, он расположен на главной оптической оси зеркала на расстоянии R/2 от центра. Фокус вогнутого зеркала находится перед, а выпуклого — за зеркалом. Фокус вогнутого зеркала замечателен тем, что все лучи, идущие параллельно главной оптической оси, пересекаются в фокусе. Это свойство используется при построении изображения.
3.3.2 Построение изображения в вогнутом зеркале
Пусть AB — предмет, изображение которого следует построить (рисунок 81). Из всех лучей, которые идут из точки B и отражаются от зеркала, выберем луч BC, параллельный главной оптической оси и луч BD, проходящий через фокус. Эти лучи, а, значит, и все остальные отраженные, пересекутся в точке B`. Наблюдатель будет видеть свет, исходящий из точки B`, т. е. точка B` является изображением точки B. Точно так же можно построить изображение каждой точки тела AB (на рисунке изображение обозначено более бледно, чем сам предмет).
При построении изображения точки, лежащей на главной оптической оси, используется одна из побочных оптических осей (прямая, проходящая через полюс). Все лучи, идущие параллельно побочной оптической оси пересекаются в точке, лежащей на фокальной плоскости.
3.3.3 Формула сферического зеркала
Задача 5. Выведите уравнение, связывающее фокусное расстояние F с расстояниями от предмета и изображения до полюса зеркала a и b:
. (1)
Отдельно рассмотрите случаи: a>F; a<F. Что означает результат b<0? (Величина называется оптической силой зеркала, измеряется в
м-1 или диоптриях.)
Формула сферического зеркала (1) применима и для выпуклого зеркала. Для выпуклого зеркала F<0. При этом надо иметь в виду, что расстояние дор изображения может быть также отрицательным. Это означает, что изображение находится по ту же сторону от линзы, что и сам предмет.
Задача 6. Свеча длины h=20 см стоит в фокусе выпуклого зеркала. Определите увеличение зеркала , если F=30 см.
4. Закон преломления
4.1 Повторение содержания закона преломления
Вопрос 1. На рисунке 82 показан ход луча через границу раздела двух прозрачных сред с разными показателями преломления.
а) В какой среде показатель преломления больше?
б) Укажите какие из обозначенных на рисунке углов являются: углом падения, углом отражения, углом преломления?
в) Сформулируйте закон преломления и запишите его математическое выражение.
4.2 Полное внутреннее отражение
При падении луча на границу двух сред из более в менее плотную оптическую среду (из среды с большим в среду с меньшим показателем преломления) угол преломления оказывается больше угла падения. По мере увеличения угла падения угол преломления приближается к прямому углу. Угол падения g0, при котором угол преломления становится прямым, называется углом полного внутреннего отражения.
Задание 1. Выразите угол полного внутреннего отражения через показатели преломления сред. Как изменится формула для границы раздела среды и вакуума?
4.3 Решение задач
Задача 7. Луч света падает на границу раздела двух сред под углом 30о. Показатель преломления первой среды равен 2,4. Определите показатель преломления второй среды, если отраженный и преломленный лучи перпендикулярны друг другу.
Задача 8. В блоке оптического стекла с показателем преломления имеется наполненная воздухом полость в виде плоскопараллельной пластинки толщиной 0,2 см. Луч света падает на границу раздела стекло-воздух под углом 30о. Определите смещение луча после прохождения через воздушную полость.
Задача 9. Сечение стеклянной призмы имеет форму равностороннего треугольника. Луч света падает из воздуха на одну из граней перпендикулярно ей. Найдите угол между лучом, выходящим из призмы, и продолжением падающего луча. Показатель преломления стекла равен 1,5.
5. Домашнее задание
5.2 Решение задач
Задача 1. Человек видит свое изображение в плоском зеркале. На какое расстояние нужно передвинуть зеркало, чтобы изображение сместилось на 1 м от человека,
Задача 2. Отражающая поверхность зеркала составляет с плоскостью стола угол 1350. По направлению к зеркалу катится шар со скоростью
2 м/с. В каком направлении и с какой скоростью движется изображение шара?
Основные понятия геометрической оптики. Принцип Ферма Оптика

Основные понятия геометрической оптики. Принцип Ферма

Оптика— раздел физики, который занимается изучением природы света, законов распространения и взаимодействия с веществом.
Свет— это электромагнитное излучение в диапазоне длин волн от до (ф 0,4-0,79 мкм кр).
Видимый свет– это излучение в интервале длин волн: . Геометрическая оптика – раздел физики занимающийся изучением законов распространения света и получением изображений в оптических приборах. В основу геометрической оптики положено понятие светового луча (это линия указывающая направление распространения света) и световой пучок (это область пространства, в пределах которой распространяется свет). Световые пучки являются независимыми: каждый световой пучок при взаимном пересечении ведет себя самостоятельно, независимо от других пучков и не оказывает никакого влияния на другие пучки света. В основу г. о. положен принцип Ферма.
Принцип Ферма (первая формулировка): свет распространяется по такому пути, для прохождения которого ему требуется минимальное время. Пусть свет распространяется из точки 1 в точку 2 .Для прохождения элементарного участка dS свету потребуется время. Абсолютный показатель преломления среды , где с – скорость света, – скорость света в среде, то . Вторая формулировка:величина называется оптической длиной пути.Если среда однородна (n=сonst), то L=nS, т. е. оптическая длина пути равнапроизведению показателя преломления среды на геометрическое расстояние между точками. Если заменить , т. е. пр. Ферма: свет распространяется по такому пути, длина которого минимальна, где s- геометрическая длина пути.
Оптические свойства вещества характеризуются величиной, называемой абсолютным показателем преломления n.
Абсолютный показатель преломления показывает во сколько раз скорость света в вакууме с больше скорости света в веществе v
n = c/v.

Относительный показатель преломления равен отношению абсолютных показателей преломления в двух средах:
n₂₁ = n₂/n₁;    n₂₁ = v₁/v₂.

где v₁и v₂ — скорость света в первой и во второй среде соответственно.
2. Основные законы геометрической оптики.
1) З-н прямолинейного распространения света: в однородной прозрачной среде свет распространяется прямолинейно.
2) З-н обратимости хода светового луча.( закон независимости световых лучей;)
3) З-н отражения света:
а)луч падающий, луч отраженный и перпендикуляр восстановленный в точку падения луча на границе раздела 2 сред, лежат в одной пл-ти.
б)угол падения= углу отражения.
4) закон независимости световых пучков. ·     (эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены.
      Разбивая световой поток на отдельные световые пучки (например, с помощью диафрагм), можно показать, что действие выделенных световых пучков независимо. )
5) З-н преломления света:
а)луч падающий, луч преломляющий и перпендикуляр восстановленный в точку падения луча на границе раздела 2 сред, лежат в одной плоскости.
б)отношение sin угла падения к sin угла преломления есть величина постоянная, равная относительному показателю двух сред, где – относительный показатель преломления, – абсолютный показатель света.
      Закон отражения (рис. 7.3):
       ·        отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
       ·       угол падения α равен углу отражения γ: α = γ
          Для вывода закона отражения воспользуемся принципом Гюйгенса. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред (рис. 7.4). Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.
       ·       Для прохождения волной расстояния ВС требуется время             Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.
      Закон преломления (закон Снелиуса) (рис. 7.5):
       ·     луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
       ·     отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.
      Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна u (рис. 7.6).
      Пусть время, затрачиваемое волной для прохождения пути ВС, равно Dt. Тогда ВС = сDt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = uDt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. 7.6 видно, что
       ,       т.е.       .
      Отсюда следует закон Снелиуса:
.
3. Применение принципа Ферма к доказательству законов отражения и преломления.
Принцип Ферма – основной принцип геометрической оптики. Простейшая форма принципа Ферма – утверждение, что луч света всегда распространяется в пространстве между двумя точками по тому пути, по которому время его прохождения меньше, чем по любому из всех других путей, соединяющих эти точки. Время прохождения светом расстояния l, заполненного средой с показателем преломления n, пропорционально оптической длине пути S; S = l•n для однородной среды, а при переменном n
S = ∫ndl,
Поэтому можно сказать, что принцип Ферма есть принцип наименьшей оптической длины пути. В первоначальной формулировке самого П. Ферма (около 1660) принцип имел смысл наиболее общего закона распространения света, из которого следовали все (к тому времени уже известные) законы геометрической оптики: для однородной среды он приводит к закону прямолинейности светового луча (в соответствии с геометрическим положением о том, что прямая есть кратчайшее расстояние между двумя точками), а для случая падения луча на границу различных сред из принципа Ферма можно получить законы отражения света и преломления света. В более строгой формулировке принцип Ферма представляет собой вариационный принцип, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, по которой время его прохождения экстремально или одинаково по сравнению с временами прохождения по всем другим линиям, соединяющим эти точки. Это означает, что оптическая длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям, соединяющим указанные точки. Примерами минимального пути служат упомянутые распространение света в однородной среде и прохождение светом границы двух сред с разными показателями преломления n. Все три случая (минимальности, максимальности и стационарности пути) можно проиллюстрировать, анализируя отражение луча света от вогнутого зеркала (рис.1).
Действительный путь света соответствует экстремальному времени распространения
Рис.1

Если зеркало имеет форму эллипсоида вращения, а свет распространяется от одного его фокуса Р к другому Q (причём путь без отражения невозможен), то оптическая длина пути луча PO’ + O’Q по свойствам эллипсоида равна всем остальным возможным, например PO» + О» Q; если на пути между теми же точками свет отражается от зеркала меньшей, чем у эллипсоида, кривизны (MM), реализуется минимальный путь, если же большей (зеркало NN) – максимальный. Условие экстремальности оптической длины пути сводится к требованию, чтобы была равна нулю вариация от интеграла
,
где А и В – точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку принципа Ферма.
В волновой теории света принцип Ферма представляет собой предельный случай принципа Гюйгенса – Френеля и применим, когда можно пренебречь дифракцией света (когда длина световой волны достаточно мала по сравнению с характерными для задачи размерами): рассматривая лучи как нормали к волновым поверхностям, легко показать, что при всяком распространении света оптической длины их путей будут иметь экстремальные значения. Во всех случаях, когда необходимо учитывать дифракцию, принцип Ферма перестаёт быть применимым.
4.Преломоение света на плоской границе раздела 2-х сред. Полное внутреннее отражение
Если световой пучок падает на поверхность, разделяющую две прозрачные среды разной оптической плотности, например воздух и воду, то часть света отражается от этой поверхности, а другая часть — проникает во вторую среду. При переходе из одной среды в другую луч света изменяет направление на границе этих сред. Это явление называется преломлением света.
Законы преломления света.
Из всего сказанного заключаем:

1 . На границе раздела двух сред различной оптической плотности луч света при переходе из одной среды в другую меняет своё направление.
2. При переходе луча света в среду с большей оптической плотностью угол преломления меньше угла падения; при переходе луча света из оптически более плотной среды в среду менее плотную угол преломления больше угла падения.
Преломление света сопровождается отражением, причём с увеличением угла падения яркость отражённого пучка возрастает, а преломлённого ослабевает. Это можно увидеть проводя опыт, изображённом на рисунке. Следовательно, отражённый пучок уносит с собой тем больше   световой   энергии,   чем   больше   угол   падения.
Пусть MN -граница раздела двух про зрачных сред, например, воздуха и воды, АО-падающий луч, ОВ — преломленный луч, -угол падения, -угол преломления, -скорость распространения света в первой среде, — скорость распространения света во второй среде .
Первый закон преломления звучит так: отношение синуса угла падения к синусу угла преломления является постоянной величиной для данных двух сред:
, где — относительный показатель преломления (показатель преломления второй среды относительно первой).
Второй закон преломления света очень напоминает второй закон отражения света:
падающий луч, луч преломленный и перпендикуляр, проведенный в точку падения луча, лежит в одной плоскости.
Полное внутреннее отражение
Наблюдается для электромагнитных или звуковых волн на границе раздела двух сред, когда волна падает из среды с меньшей скоростью распространения (в случае световых лучей это соответствует бо́льшему показателю преломления).
С увеличением угла падения , угол преломления также возрастает, при этом интенсивность отражённого луча растет, а преломленного — падает (их сумма равна интенсивности падающего луча). При некотором критическом значении интенсивность преломленного луча становится равной нулю и происходит полное отражение света. Значение критического угла падения можно найти, положив в законе преломления угол преломления равным 90°:
5. Призмы
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена. Виды призм: Дисперсионные призмы. Отражательные призмы. Поляризационные призмы.
Дисперсионные призмы Дисперсионные призмы используют в спектральных приборах для пространственного разделения излучений различных длин волн.
Отражательные призмы Отражательные призмы используют для изменения хода лучей, изменения направления оптической оси, изменения направления линии визирования, для уменьшения габаритных размеров приборов. Классифицируются отражательные призмы по нескольким признакам:

количеству отражений в призме

наличию или отсутствию «крыши»

характеру конструкции призмы

углу излома оптической оси

Также, особую нишу среди отражательных призм занимают составные призмы, — состоящие из нескольких частей, разделённых воздушными промежутками. Некоторые широко распространённые призмы получили собственные имена.

Призма Аббе

Призма Аббе-Порро
6. Тонкие линзы. Формула тонкой линзы
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой. Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше Линзы входят в состав практически всех оптических устройств. Линзы (Рис.3) делятся на собирающие и рассеивающие
Схема тонкой линзы
Рис.3,Собирающие (a) и рассеивающие (b) линзы и их условные обозначения.
Главной оптической осью линзы считается ось, прожодящая через центры кривизны её поверхностей. В тонкой линзе точки пересечения главной оптической оси с обеими поверхностями линзы сливаются в одну точку О.(Т.к. очень большие радиусы кривизны приближаются к плоскостям, то сферические поверхности теоретически сливаються в одну плоскость ). Эта точка называется оптическим центром линзы. Тонкая линза имеет одну главную плоскость, которая общая для двух сферических поверхностей и проходит через центр призмы и перпендикулярна к главной оптической оси. Все прямые, проходящие через оптический центр линзы, называются побочными оптическими осями линзы. Важным является то, что все лучи, идущие через оптический центр линзы, не преломляются.
Поток монохроматических параллельных лучей или пучков лучей с осями их узких конусов , нормалльных к сферической границе раздела (к главной плоскости, называют парксиальными (приосевыми) пучками. При этом, пройдя через неё сходятся в главном фокусе линзы F₂. Главные фокусы линзы лежат на главной оптической оси линзы. Точки, расположенные на главной оптической оси линзы с двух сторон оптического центра на равных расстояниях f₂., называются главными фокусами линзы . Плоскости, проходящие через главные фокусы f₂ линзы и перпендикулярные к её главной оптической оси, называются фокальными плоскостями линзы .
Формула тонкой линзы.
Формула тонкой линзы связывает между; собой три величины: расстояние от предмета до линзы d, расстояние от линзы до изображения f и фокус ное расстояние линзы F:
В формуле тонкой линзы фокусное расстояние ОF обозначается буквой F. Если линза собирающая, то > 0, если линза рассеивающая, то перед ставится знак «минус». Если изображение действительное, то > 0; если изображение воображаемое, то перед ставиться знак «минус». Все величины в формулу линзы подставляются в метрах.
7. Построение изображений в линзах
Опыт показывает, что параксиальные лучи света, выходящие из одной светящейся точки, после прохождения через линзу сходятся также в одной точке, которая является изображением светящейся точки. Поэтому для построения изображения точки достаточно взять два любых луча, но лучше те, ход которых после преломления заранее известен: 1 — луч, идущий через оптический центр; 2 — луч, параллельный главной оптической оси; 3 — луч, проходящий через передний фокус собирающей линзы (или продолжение луча 3 проходит через задний фокус рассеивающей линзы) (рис. 16.41).
Рис. 16.41
Положение изображения действительного предмета и егоразмеры зависят от положения предмета относительно линзы. Пусть d — расстояние от предмета до линзы, f — расстояние от линзы до изображения. Построим изображение плоского предмета АВ, расположенного на различных расстояниях d от линзы. Если линза собирающая, то при d>2F (рис. 16.42) изображение действительное, перевернутое, уменьшенное,F
При F (рис. 16.43) изображение действительное, перевернутое, увеличенное, f>2F.

Рис. 16.43
При d (рис. 16.44) изображение мнимое, прямое, увеличенное, находится с той же стороны от линзы, что и сам предмет, но дальше предмета (f>d).

Рис. 16.44
В рассеивающей линзе (рис. 16.45) изображение действительного предмета всегда мнимое, прямое, уменьшенное, находится между линзой и ее фокусом со стороны изображаемого предмета.
8.Глаз как оптический прибор. Лупа, Микроскоп, фотоаппарат.
Глаз. Основным источником зрения является глазное яблоко, за зрачком находится хрусталик, а сзади сетчатка. Оптическую роль в глазе выполняет элемент, имеющий форму двояковыпуклой линзы и наз-ся хрусталиком. К краям хрусталика прикреплены мышцы, которые сжимают или растягивают хрусталик, в результате меняются радиусы кривизны сферич. пов-ти хрусталика и соответственно фокусные расстояния. При изменении расстояния d до наблюдаемого объекта, расстояние f от хрусталика до сетчатки остается неизменным, а меняется фокусное расстояние. Недостатки зрения – близорукость и дальнозоркость.
Лупой называют собирающую тонкую линзу с малым фокусным расстоянием (5-10 см).увеличение лупы: , расстояние наилучшего зрения.
34.Вывод законов отражения и преломления из принципов Гюйгенса и принципа Ферма.
К нахождению закона преломления волн. ОВ — поверхность падающей волны, ab — поверхность раздела двух сред, NC — поверхность преломленной волны угол i с перпендикуляром к поверхности раздела. Согласно закону преломления пучок преломленных лучей будет распространяться по направлению, задаваемому углом r. Согласно волновым представлениям описанная задача сводится к следующему. На поверхность раздела падает плоская волна, поверхность которой составляет угол i с поверхностью раздела. Скорость распространения волны в первой среде есть v1, во второй — v2. Принцип Гюйгенса можно сформулировать следующим образом: Каждая точка, до которой доходит световое возбуждение, является в свою очередь центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны. В физике исключительное значение имеет метод принципов, позволяющий на основе небольшого числа общих предположений — принципов — обосновать известные законы некоторого круга явлений и предсказать еще неоткрытые закономерности.В геометрической оптике таким принципом является принцип кратчайшего оптического пути (или минимального времени распространения), именуемым также принципом Ферма. По определениюоптической длиной пути называется величина.
35. Методы наблюдения интерференции света. Когерентность.
  Образование интерференционной картины можно наблюдать в опыте Юнга, использующем метод деления волнового фронта  Прошедший через узкую длинную щель S свет, вследствие дифракции образует расходящийся пучок, который падает на второй экран B с двумя, параллельными между собой узкими щелями S₁ и S₂, расположенными близко друг к другу на равных расстояниях от S. Эти щели действуют как вторичные синфазные источники, и исходящие от них волны, перекрываясь, создают интерференционную картину, наблюдаемую на удаленном экране C. Расстояние между соседними полосами равно:
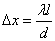. Зеркала Френеля.Другой интерференционный опыт, аналогичный опыту Юнга, но в меньшей степени осложненный явлениями дифракции и более светосильный, был осуществлен О. Френелем в 1816 г. Две когерентные световые волны получаются в результате отражения от двух зеркал М и N, плоскости которых наклонены под небольшим углом φ друг к другу.Бипризма Френеля:  В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180°. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы. Можно считать, что здесь образуются два близких мнимых изображения S₁ и S₂ источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол 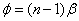.Билинза Бийе:  Аналогичное бипризме Френеля устройство, в котором роль когерентных источников играют действительные изображения ярко освещенной щели, получается, если собирающую линзу разрезать по диаметру и половинки немного раздвинуть . Прорезь закрывается непрозрачным экраном А, а падающие на линзу лучи проходят через действительные изображения щел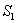и  и 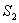 и дальше перекрываются, образуя интерференционное поле. В физике когерентностью называется скоррелированность нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.
Основные законы геометрической оптики, принцип Ферма, доказательство закона преломления на основании принципа Ферма.
Основу геометрической оптики образуют четыре закона: 1) закон прямолинейного распространения света; 2) закон независимости световых лучей; 3) закон отражения света; 4) закон преломления света.

Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны.

Луч света распространяется прямолинейно, если на пути его распространения среда однородна, абсолютный показатель преломления среды везде одинаков. Однако, если показатель преломления среды плавно изменяется на трассе луча, траектория луча света искривляется (рис.1.2), причём луч смещается в сторону увеличения показателя преломления.

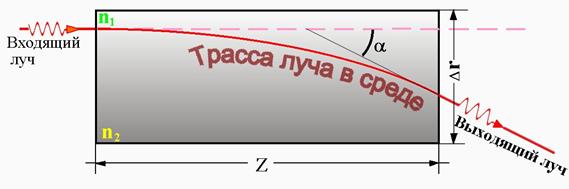Рис.1.2
Это явление получило название рефракция излучения, хотя в буквальном переводе слово рефракция означает преломление. Рассмотрим преломление солнечных лучей на закате или восходе, когда Солнце практически находится за горизонтом. Известно, что плотность атмосферы Земли меняется с высотой, чем выше слои атмосферы, тем меньше их плотность. Абсолютный показатель преломления связан с плотностью среды, поэтому с высотой он также будет уменьшаться. Разобьем атмосферу Земли на параллельные слои. Каждый слой будет характеризоваться своим показателем. Чем выше слой атмосферы от Земли, тем его показатель становится меньше.

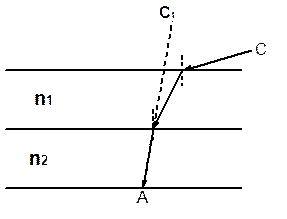Рис.1.3
Рассмотрим ход лучей ( рисунок 1.3), идущих от точки С (С- это точка, лежащая на Солнце, которое почти спряталось за горизонт). Луч искривляется, так как каждый последующий слой атмосферы имеет больший показатель преломления и в каждом последующем слое луч света приближается к перпендикуляру восстановленному в точку падения . Наблюдатель, находящийся в точке А, видит изображение Солнца в точке С₁. Зашедшее Солнце за счет преломления остается видимым еще несколько минут, поэтому продолжительность дня оказывается на 7-8 минут больше, чем она была бы в отсутствии преломления. Сплюснутая форма Солнца при восходе и заходе объясняется, тем, что лучи, идущие от разных частей Солнца отклоняются от прямой линии на разные углы.
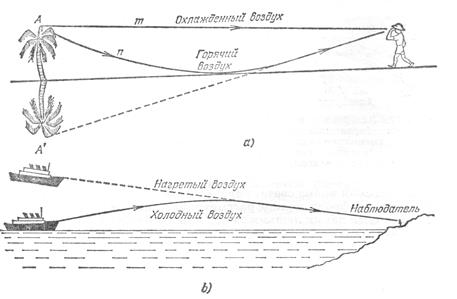Рис.1.4
Миражисвязаны с тем, что абсолютный показатель преломления в разных атмосферных слоях оказывается разным. Обычно наблюдается верхний или нижний мираж. Нижний мираж наблюдается в пустынях и в степях в теплое время года, когда прилегающий к земной поверхности слой воздуха сильно нагрет, а его плотность и показатель преломления быстро возрастают с высотой. На рисунке 1.4,а показано каким образом горячий песок позволяет видеть макушку дерева А. Луч света n преломляется при прохождении вниз от холодного к нагретому воздуху, следовательно, угол преломления будет возрастать, а линия, по которой свет распространяется, искривляется (рис.1.5. В точке Влуч света испытает полное внутреннее отражение, преломленный луч исчезнет. Вся световая энергия сосредотачивается в отраженном луче, поэтому луч как бы изменил свое направление.

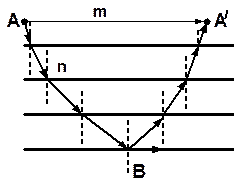Рис.1.5
Поэтому, когда он попадает в глаз наблюдателя, то кажется, что он исходит из точки А^¢, а не точки А.

Верхний мираж может наблюдаться близ воды. Так как около поверхности воды может находиться слой холодного воздуха, над которым расположен слой теплого воздуха.

В результате отдаленный корабль на море может казаться плавающим в небе, как показано на рисунке 1.4б., так как лучи света описывают большую дугу и возвращаются вниз за десятки километров от источника. С Лазурного берега иногда можно увидеть Корсику, расположенную за 200 километров оттуда. Жители бельгийского города Вервье в 1815 году увидели в небе целую армию. За сто километров от этого города в это утро произошла битва при Ватерлоо.

Закон независимости световых пучков утверждает, что лучи при пересечении не возмущают друг друга. Пересечения лучей не мешает каждому из них распространяться независимо друг от друга.

Если две изотропные среды с разными показателями преломления соприкасаются друг с другом, то между ними образуется граница раздела этих сред. Луч света, попадая на эту границу, частично отражается, частично преломляется (см. рис.1.6)

Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

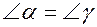(1.7)

Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред и равна отношению абсолютного показателя преломления второй среды относительно показателя преломления первой среды:

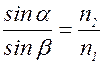(1.8)

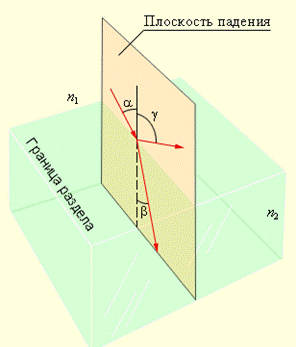Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом (1621 г.)

Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ₁ к скорости их распространения во второй среде υ₂:

Рис 1.6 иллюстрирует законы отражения и преломления света.

Принцип Ферма

В основу геометрической оптики может быть положен принцип, установленный французским математиком Ферма в середине 17 столетия. Из этого принципа вытекают законы прямолинейного распространения света, отражения и преломления света. В формулировке самого Ферма принцип гласит, что свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.

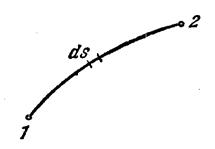Рис.1.7
Пусть луч распространяется из точки 1 в точку пространства 2 (рис.1.7). Разобьем траекторию распространения света на прямолинейные участки, на которых показатель преломления будет константой, тогда чтобы свету пройти путь 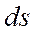требуется время

,

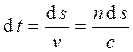Следовательно, время, затрачиваемое светом на прохождение пути 1-2 равно

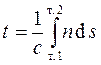
Величина 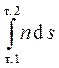имеет размерность длины и эту величину называют оптическим ходом луча или оптической длиной пути света

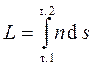(1,9)

В однородной изотропной среде оптическая длина пути света равна

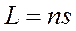(1.10)

Пропорциональность времени t прохождения оптической длине пути луча L дает возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути, оптическая длина которого экстремальна. Из принципа Ферма вытекает обратимость хода световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется минимальным и в случае распространения света из точки 2 в точку 1.

С помощью принципа Ферма можно доказать законы геометрической оптики, например, закон преломления света.

Дата добавления: 2017-10-04; просмотров: 1681;
Похожие статьи: