Сила тяжести в физике — формулы и определения с примерами
Содержание:
Сила тяжести:
Почему все подброшенные вверх тела падают на Землю ? Почему на санках легко съезжать с горки, а вверх их нужно тянуть?
Подбросьте вверх мяч. Поднявшись на некоторую высоту, он начнёт двигаться вниз и упадёт на Землю. Парашютист, выпрыгнувший из самолёта, падает вниз и после раскрытия парашюта. С появлением дождевой тучи на Землю падает густой дождь. Как бы высоко мы не прыгали вверх, всегда опускаемся на Землю.
Все тела, находящиеся на Земле или вблизи неё, взаимодействуют с ней: Земля притягивает тела, а они притягивают Землю.
Поскольку масса у Земли очень большая, то в результате взаимодействия с нею заметно изменяют свои скорости и положения именно тела, а Земля практически остаётся на месте.
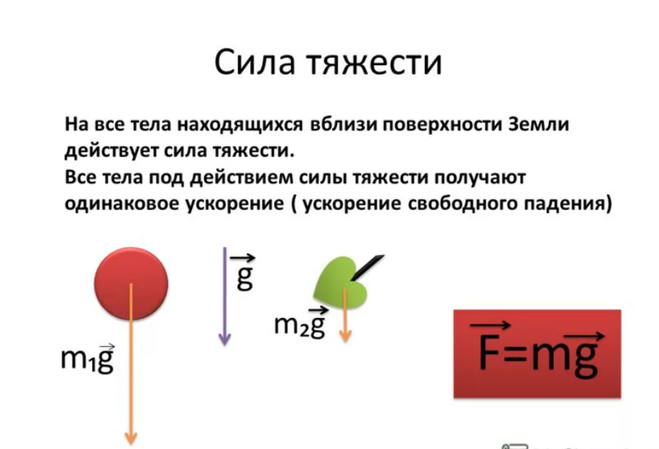
Силу, с которой Земля притягивает к себе любое тело, называют силой тяжести.
От чего зависит сила тяжести
Из опыта с яблоками, выполненного ранее, можем сделать вывод, что на два яблока, подвешенных на пружине, действует сила тяжести больше, чем на одно, так как масса двух яблок больше массы одного. Силу тяжести обозначают
Силу тяжести обозначают
Единицей силы тяжести, как и любой другой, в СИ является один ньютон (1Н). Эта единица названа в честь английского учёного Исаака Ньютона, впервые сформулировавшего основные законы движения тел и законы тяготения. 1 ньютон (1 Н) равен силе тяжести, которая действует на тело массой приблизительно 102 г.
Тогда на тело массой 1кг действует сила тяжести 9,81 Н, т. е.
Как, пользуясь единицей силы 1 Н, определить силу тяжести, которая действует на тело любой массы?
Поскольку на тело массой 1 кг действует сила тяжести 9,81 Н, то на тело массой т будет действовать сила тяжести, в т раз большая.
Чтобы определить силу тяжести , действующую на тело, нужно постоянную для данной местности величину = 9,81 умножить на массу тела , выраженную в килограммах:
Но притяжение существует не только между Землёй и телами на ней или вблизи неё. Все тела притягиваются друг к другу. Например, притягиваются между собой Земля и Луна, Солнце и Земля или другие планеты, корабли в море, предметы в комнате. Вследствие притяжения Земли к Луне на Земле возникают приливы и отливы (рис. 69).
Вследствие притяжения Земли к Луне на Земле возникают приливы и отливы (рис. 69).
Вода в океанах поднимается дважды в сутки на несколько метров.
Благодаря силе тяжести атмосфера удерживается возле Земли, реки текут сверху вниз, Луна удерживается возле Земли, планеты двигаются по орбитам вокруг Солнца.
Явление притяжения всех тел Вселенной друг к другу называют всемирным тяготением.
Исаак Ньютон доказал, что сила притяжения между телами тем больше, чем больше массы этих тел и чем меньше расстояние между телами. Если бы сила тяжести на Земле вдруг исчезла, то все незакреплённые на ее поверхности тела от любого небольшого толчка разлетелись бы во все стороны в космическом пространстве.
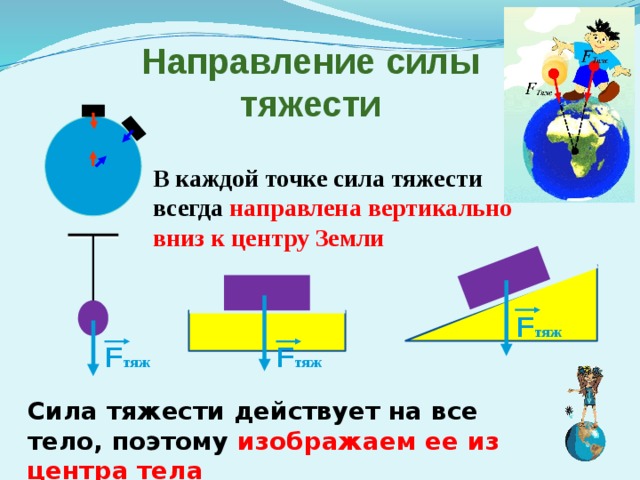
Каково направление силы тяжести
Опыт. Если взять отвес или привязанный к нити какой-либо предмет (рис. 70), то увидим, что нить с грузиком вследствие действия на него силы тяжести всегда направлена к Земли вдоль прямой, которую называют вертикалью.
Выполнив этот опыт во всех точках Земли, учёные убедились, что сила тяжести всегда направлена к центру Земли.
Силу тяжести изображают в виде вертикальной стрелки, направленной вниз и приложенной к определённой точке тела (рис. 71 а, б).
Кстати:
Кроме планет с их спутниками вокруг Солнца двигаются малые планеты, которые еще называют астероидами. Наибольшая из них — Церера — имеет статус карликовой планеты и радиусом почти в 20 раз, а по массе в 7500 раз меньше Земли. Сила тяжести на ней настолько мала, что человек, оттолкнувшись от поверхности планеты, мог бы улететь с нее.
Вот как описывает основатель теории космонавтики К,Э. Циолковский в рассказе «Путь к звездам» условия пребывания человека на этом астероиде: «На Земле я могу свободно нести еще одного человека такого же веса, как я. На Весте так же легко могу нести в 30 раз больше. На Земле я могу подпрыгнуть на 50см. На Весте такое же усилие дает прыжок в 30м. Это высота десятиэтажного дома или огромной сосны.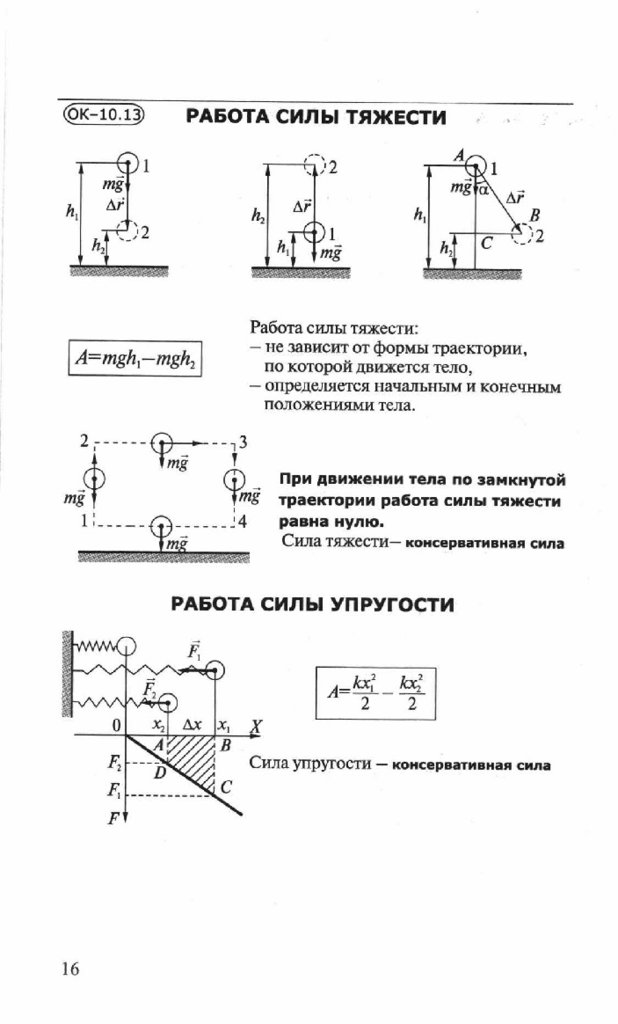 Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона».
Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона».
Все тела возле Земли падают на ее поверхность, если их ничто не удерживает. В чем причина этого явления?
Как тела падают на ЗемлюРассмотрим фотографию падения шарика, на которой положение шарика фиксировалось на пленке через равные интервалы времени (рис. 45). Если линейкой отмерить расстояние между изображениями шарика в различные моменты времени, то можно заметить, что эти расстояния постепенно увеличиваются. Это свидетельствует о том, что скорость шарика при падении постепенно увеличивается.
Как увеличивается скорость падающего телаЕсли вспомнить определение силы, по которому сила изменяет скорость тела, то можно сделать вывод, что на шарик действует сила, направленная к Земле.
Силу, действующую на каждое тело со стороны Земли, называют силой тяготения.
Измерения показывают, что скорость тела, падающего на поверхность Земли при отсутствии сопротивления воздуха, каждую секунду увеличивается на 9,8 .
Как рассчитать силу тяготенияЕсли знать массу тела, то можно рассчитать силу тяготения. Способ таких расчетов подсказывают результаты опытов.
Возьмем динамометр и подвесим к нему гирьку массой 102 г, стрелка динамометра остановится на отметке 1 Н. Если подвесить два таких груза, то динамометр покажет силу 2 Н и т. д. С этого опыта можно сделать вывод, что сила тяжести пропорциональна массе тела.
Сила тяготения пропорциональна массе тела:
Коэффициент пропорциональности равен приблизительно
Для расчетов при решении задач иногда принимают, что
Если знать такую зависимость силы тяготения от массы, то можно заранее рассчитать ее значение.
Например, необходимо определить, что покажет динамометр, если на его крючок повесить гирю массой 500 г.
Дано:
Решение
Ответ. Стрелка динамометра покажет 4,9 Н.
Стрелка динамометра покажет 4,9 Н.
Сила тяготения является проявлением общего закона природы, действующего во всей Вселенной закона всемирного тяготения. Открытый и сформулированный в XVII в. английским физиком Ньютоном, он утверждает, что сила гравитационного притяжения во Вселенной пропорциональна массам взаимодействующих тел и зависит от расстояния между ними.
где R — расстояние между телами, m1 и m2 — массы взаимодействующих тел, — гравитационная постоянная.
Сила тяготения, как проявление гравитационного взаимодействия Земли, является следствием взаимодействия всех тел с Землей. Поэтому в расчетах силы тяготения пользуются только массой данного тела. Характеристики Земли отображены в обобщенной форме в коэффициенте
Работа силы тяжестиКаждая сила, действующая на движущееся тело, совершает работу. Проанализируем более подробно работу, совершаемую силой тяжести. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Пусть тело массой m падает с высоты h1 до высоты h2 (рис. 132). Модуль перемещения равен при этом h1 —h2 . Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:
Проанализируем более подробно работу, совершаемую силой тяжести. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Пусть тело массой m падает с высоты h1 до высоты h2 (рис. 132). Модуль перемещения равен при этом h1 —h2 . Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:
(1)
Рис. 132
Высоты h1 и h2 можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола класса или поверхности стола и т. д. Высоту выбранного уровня принимают равной пулю. Поэтому этот уровень называют нулевым.
Если тело падает с высоты
(2)
Теперь выясним, какую работу совершает сила тяжести, если тело движется не по вертикали. Для этого рассмотрим движение тела по наклонной плоскости.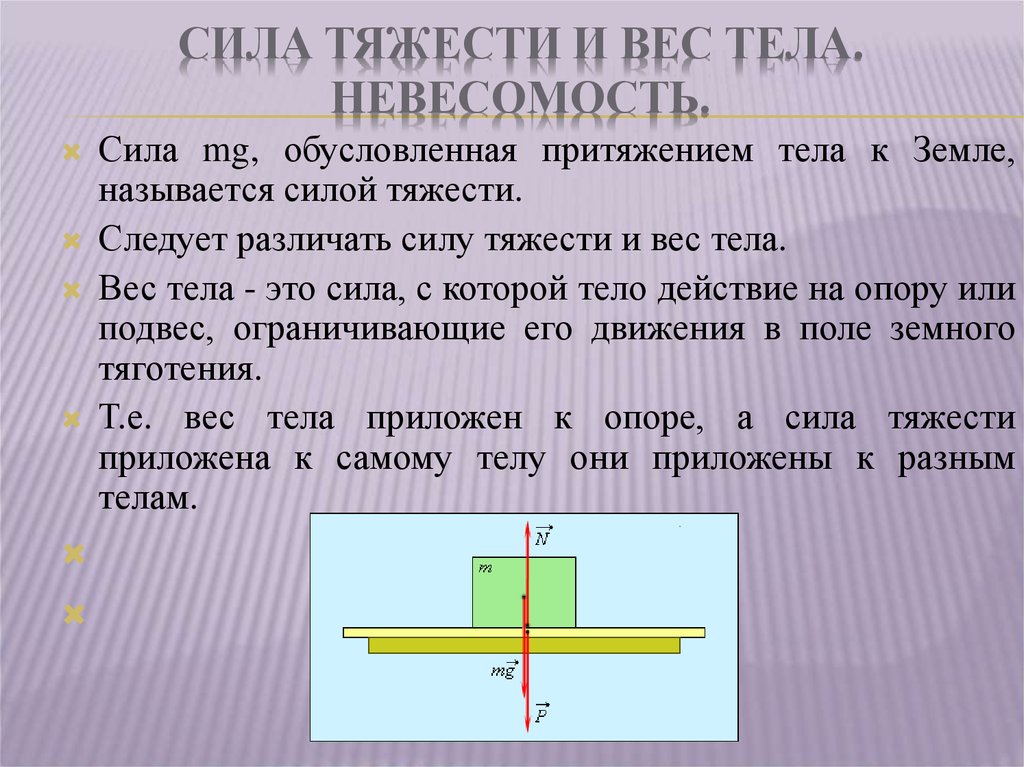 Пусть тело массой m совершило перемещение , равное по модулю длине наклонной плоскости (рис. 133). Работа силы тяжести в этом случае равна: , где — угол между вектором перемещения и вектором силы тяжести. Из рисунка видно, что . Поэтому
Пусть тело массой m совершило перемещение , равное по модулю длине наклонной плоскости (рис. 133). Работа силы тяжести в этом случае равна: , где — угол между вектором перемещения и вектором силы тяжести. Из рисунка видно, что . Поэтому
Рис. 133
Мы получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали (см. формулу (2)). Отсюда следует, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. Работа силы тяжести определяется только изменением высоты относительно некоторого уровня.
Теперь докажем, что работа силы тяжести определяется формулой (2) при движении по любой траектории. Например, некоторое тело бросили горизонтально с высоты h (рис. 134). Как известно, траекторией такого движения является парабола. Мысленно разобьем траекторию на маленькие участки , такие, что их можно считать прямыми линиями. Каждый из них можно считать маленькой наклонной плоскостью, а движение по траектории AB рассматривать как движение по множеству наклонных плоскостей.
Рис. 134
Таким образом, работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела, т. е. вычисляется но формуле (1). Отсюда следует, что если тело движется по замкнутой траектории, где начальное и конечное положения тела совпадают, то работа силы тяжести равна нулю. Такие силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела в пространстве, называются
Для потенциальных сил можно ввести понятие потенциальной энергии. Действительно, формула (I) может быть переписана следующим образом:
Действительно, формула (I) может быть переписана следующим образом:
A = mg(hl — h2)= -(mgh
Правая часть этого равенства представляет собой изменение величины mgh, взятое с противоположным знаком.
Понятие кинетической энергии, изменение которой равно работе сил, действующих на тело. Теперь мы встретились еще с одной величиной, изменение которой (но с противоположным знаком) тоже равно работе силы — в данном случае работе силы тяжести. Величину, равную mgh, называют потенциальной энергией П тела в гравитационном поле. Тогда формулу (3) можно записать в виде:
(4)
Говорят, что работа силы тяжести равна убыли потенциальной энергии тела в гравитационном поле Земли.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна его начальной потенциальной энергии:
Следовательно, потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты. Например, этим пользуются при забивании свай на строительных площадках (рис. 135). Чтобы поднять тело с нулевого уровня на эту же высоту, должна быть совершена работа другой силой, направленной против силы тяжести.
Например, этим пользуются при забивании свай на строительных площадках (рис. 135). Чтобы поднять тело с нулевого уровня на эту же высоту, должна быть совершена работа другой силой, направленной против силы тяжести.
Рис. 135
Потенциальная энергия зависит от положения тела относительно нулевого уровня и, следовательно, от координат тела. Так как пулевой уровень может быть выбран произвольно, то и потенциальная энергия определяется неоднозначно. Однако физический смысл имеет разность потенциальных энергий тела
Сила тяжести является силой, с которой Земля притягивает тело. Тело обладает потенциальной энергией, потому что оно взаимодействует с Землей. Не было бы Земли, не было бы и силы притяжения, а следовательно, и потенциальной энергии тела. Поэтому потенциальная энергия — это энергия взаимодействия, в данном случае тела и Земли.
Главные выводы:
- Работа силы тяжести не зависит от формы траектории, а определяется начальным и конечным положениями тела.

- Работа силы тяжести равна нулю, если тело возвращается в исходное положение.
- Сила тяжести является потенциальной силой.
- Потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты.
- Потенциальная энергия — это энергия взаимодействия тел.
Как вы знаете, по современным научным представлениям взаимное притяжение между телами осуществляется посредством особого вида материи — гравитационного поля. Каждое тело вокруг себя создает гравитационное поле. Как и другие физические поля, гравитационное поле имеет свою силовую характеристику — напряженность гравитационного поля.
Напряженность гравитационного поля — это векторная физическая величина, равная отношению силы притяжения, действующей на материальную точку (тело) в гравитационном поле, к его массе:
Где — напряженность гравитационного поля, — масса материальной точки (тела), — сила притяжения, действующая на материальную точку в гравитационном поле.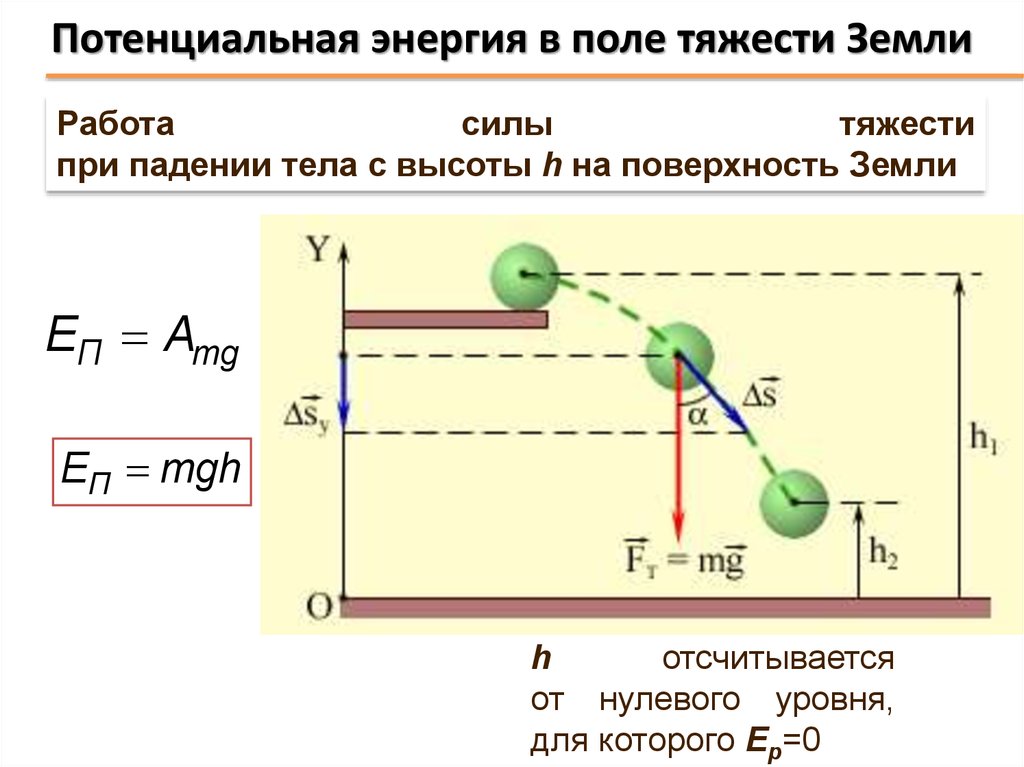
Чтобы ответить на этот вопрос, определим модуль напряженности гравитационного поля для произвольной точки на поверхности Земли и на высоте от поверхности Земли:
Здесь и — силы притяжения на поверхности Земли и на высоте h соответственно, — масса Земли, — радиус Земли.
- Заказать решение задач по физике
Модуль напряженности гравитационного поля в некоторой точке прямо пропорционален массе источника данного поля и обратно пропорционален
квадрату расстояния до этой точки. Модуль напряженности гравитационного поля не зависит от массы тела, помещенного в это поле. Вектор напряженности гравитационного поля в произвольной точке поля направлен вдоль радиуса к центру источника поля (b). В данной точке гравитационного поля модуль и направление напряженности гравитационного поля совпадают с модулем и направлением ускорения свободного падения.
На помещенное в гравитационное поле произвольное тело действует сила притяжения со стороны источника поля. В результате тело получает ускорение (ускорение свободного падения), направленное к центру источника поля (например, центру Земли). Это ускорение сообщается телу действующей на него силой тяжести гравитационного поля.
Сила тяжести — это сила, с которой Земля (планета) притягивает тела. Сила тяжести равна произведению массы тела, помещенного в гравитационное поле Земли (планеты), на ускорение свободного падения:
Сила тяжести всегда приложена к центру массы тела и направлена вертикально вниз (перпендикулярно к горизонтальной поверхности) к центру Земли (планеты) (с).
Из вышесказанного ясно, что понятия «напряженность гравитационного поля» и «ускорение свободного падения» имеют разный физический смысл. Так, напряженность гравитационного поля появляется в случае возникновения поля, а ускорение свободного падения возникает в результате действия силы тяжести при помещении в это поле произвольного тела (пробное тело).
Так, напряженность гравитационного поля появляется в случае возникновения поля, а ускорение свободного падения возникает в результате действия силы тяжести при помещении в это поле произвольного тела (пробное тело).
Если выпустить из рук карандаш, он обязательно упадет. Если поставить рюкзак на скамейку, она (хоть и незаметно для глаз) прогнется. Если подвесить к резиновому шнуру какое-нибудь тело, шнур растянется. Все это — следствия притяжения Земли. При этом репортажи с космических станций демонстрируют нам вроде бы «исчезновение» земного притяжения — космонавты и все вещи на борту находятся в состоянии невесомости.
Гравитационное взаимодействие:
Почему любой предмет, например выпущенный из руки карандаш, капля дождя, лист дерева и т. д., падает вниз? Почему стрела, выпущенная из лука, не летит все время прямо, а в конце концов падает на землю? Почему Луна движется вокруг Земли? Причина всех этих явлений в том, что Земля притягивает к себе все тела (рис.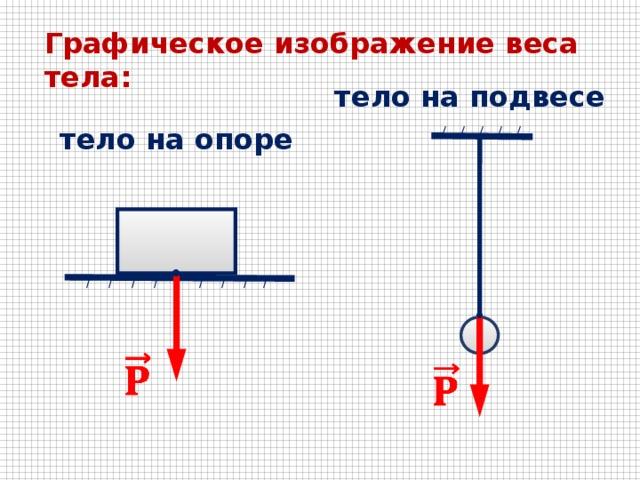 20.1).
20.1).
При этом все тела притягивают к себе Землю. Например, притяжение к Луне вызывает на Земле приливы и отливы (рис. 20.2). В результате притяжения к Солнцу наша планета и все другие планеты Солнечной системы движутся вокруг Солнца по определенным орбитам. В 1687 г. Исаак Ньютон сформулировал закон, согласно которому между всеми телами Вселенной существует взаимное притяжение. Такое взаимное притяжение объектов называют гравитационным взаимодействием или всемирным тяготением. Опираясь на опыты и математические расчеты, Ньютон доказал, что интенсивность гравитационного взаимодействия увеличивается с увеличением масс взаимодействующих тел. Именно поэтому легко убедиться в том, что всех нас притягивает Земля, и при этом мы совсем не ощущаем притяжение соседа по парте.
В физике силу гравитационного притяжения Земли, действующую на тела вблизи ее поверхности*, называют силой тяжести.
Сила тяжести — это сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее.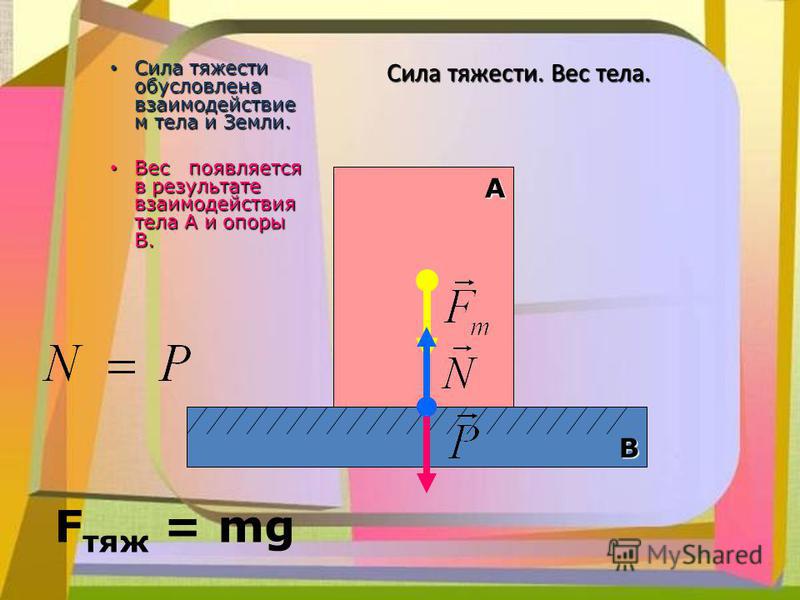
Сила тяжести приложена к телу, которое притягивается Землей, и направлена вертикально вниз, к центру Земли (рис. 20.3).
Многочисленными опытами доказано, что сила тяжести, действующая на тело, прямо пропорциональна массе этого тела: где — значение силы тяжести; m — масса тела; g — коэффициент пропорциональности, который называют ускорением свободного падения.
Будем считать, что, когда говорят «вблизи поверхности Земли», имеют в виду расстояние, не превышающее нескольких десятков километров.
Вблизи поверхности Земли ускорение свободного падения равно приблизительно 9,8 ньютона на килограмм: Значение ускорения свободного падения несущественно изменяется на экваторе и полюсах Земли (рис. 20.4), при подъеме над поверхностью Земли и при спуске в шахту. Используя рис. 20.4, определите, на сколько сила тяжести, действующая на вас, на экваторе меньше, чем на полюсе.
Что физики называют весом телаИз-за притяжения к Земле все тела сжимают или прогибают опору либо растягивают подвес. Сила, которая характеризует такое действие тел, называется весом тела (рис. 20.5).
Сила, которая характеризует такое действие тел, называется весом тела (рис. 20.5).
Вес тела — это сила, с которой вследствие притяжения к Земле тело давит на горизонтальную опору или растягивает вертикальный подвес. Единица веса в СИ, как и любой другой силы,— ньютон Если тело находится в состоянии покоя или прямолинейного равномерного движения, то его вес совпадает по направлению с силой тяжести и равен ей по значению: P=mg. Однако в отличие от силы тяжести, которая приложена к телу, вес приложен к опоре или подвесу (рис. 20.6).
Для упрощения расчетов в случаях, когда большая точность не существенна, можно считать, что g= 10 Н/кг.
Состояние невесомостиВы наверняка хорошо знаете термин «невесомость», но его значение многие понимают неправильно. Например, считают, что невесомость — это состояние, которое наблюдается только в космосе, где нет воздуха, или там, где отсутствует гравитация. Но это не так! Отсутствие воздуха само по себе не вызывает невесомости, а от гравитации вообще не спрячешься — во Вселенной нет ни одного уголка, где бы не действовали силы всемирного тяготения*. На самом деле невесомость — это отсутствие веса. Уберите у тела опору или подвес — и оно окажется в состоянии невесомости. (Обратите внимание: сопротивление воздуха тоже является своего рода опорой!)
Но это не так! Отсутствие воздуха само по себе не вызывает невесомости, а от гравитации вообще не спрячешься — во Вселенной нет ни одного уголка, где бы не действовали силы всемирного тяготения*. На самом деле невесомость — это отсутствие веса. Уберите у тела опору или подвес — и оно окажется в состоянии невесомости. (Обратите внимание: сопротивление воздуха тоже является своего рода опорой!)
Невесомость — это такое состояние тела, при котором тело не действует на опору или подвес. Тело вблизи поверхности Земли находится в состоянии невесомости, если на него действует только одна сила — сила тяжести. На короткое время невесомость легко создать и дома. Можно, например, подпрыгнуть — и вы на мгновение окажетесь в состоянии невесомости: в данном случае, пока выдвигаетесь вниз, сопротивление воздуха пренебрежимо мало и можно считать, что на вас действует только сила тяжести. Постоянно в состоянии невесомости находятся космические орбитальные станции и все, что на них находится (рис. 20.7). Это связано с тем, что космические корабли «постоянно падают» на Землю из-за ее притяжения и в то же время остаются на орбите благодаря своей огромной скорости. У нетренированного человека длительное пребывание в состоянии невесомости, как правило, сопровождается тошнотой, нарушением работы мышц, вестибулярного аппарата**, нервными расстройствами, именно поэтому космонавты проходят серьезную физическую подготовку (рис. 20.8).
20.7). Это связано с тем, что космические корабли «постоянно падают» на Землю из-за ее притяжения и в то же время остаются на орбите благодаря своей огромной скорости. У нетренированного человека длительное пребывание в состоянии невесомости, как правило, сопровождается тошнотой, нарушением работы мышц, вестибулярного аппарата**, нервными расстройствами, именно поэтому космонавты проходят серьезную физическую подготовку (рис. 20.8).
Плотность материи в нашей Вселенной очень мала (2-3 атома Гидрогена на 1 м3), потому во Вселенной в среднем очень мала и гравитация. Ее называют микрогравитацией. Вестибулярный аппарат — орган чувств у людей и позвоночных животных, воспринимающий изменение положения тела в пространстве и направление движения. Этот орган отвечает, например, за способность человека различать в темноте, где верх, а где низ.
Итоги:
Во Вселенной все тела притягиваются друг к другу. Такое взаимное притяжение тел называют всемирным тяготением. Сила тяжести — сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее. Сила тяжести вычисляется по формуле и направлена вертикально вниз, к центру Земли. Вес тела — это сила, с которой вследствие притяжения к Земле тело действует на горизонтальную опору или вертикальный подвес. Следует различать силу тяжести и вес тела: сила тяжести приложена к самому телу, а вес — к опоре или подвесу; вес тела равен по значению силе тяжести (P=mg) только в состоянии покоя тела или его равномерного прямолинейного движения. Когда тело движется под действием только силы тяжести, то оно находится в состоянии невесомости (его вес равен нулю).
Сила тяжести — сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее. Сила тяжести вычисляется по формуле и направлена вертикально вниз, к центру Земли. Вес тела — это сила, с которой вследствие притяжения к Земле тело действует на горизонтальную опору или вертикальный подвес. Следует различать силу тяжести и вес тела: сила тяжести приложена к самому телу, а вес — к опоре или подвесу; вес тела равен по значению силе тяжести (P=mg) только в состоянии покоя тела или его равномерного прямолинейного движения. Когда тело движется под действием только силы тяжести, то оно находится в состоянии невесомости (его вес равен нулю).
11 примеров силы поля в повседневной жизни
Наша повседневная жизнь наполнена полевыми силами. В этом посте мы рассмотрим 10 реальных примеров полевых сил.
Примеры Полевой силы в повседневной жизни: Сила гравитации:Планеты, движущиеся вокруг Солнца:Мы можем заметить эффект этого глубокого силового поля в нашей Солнечной системе.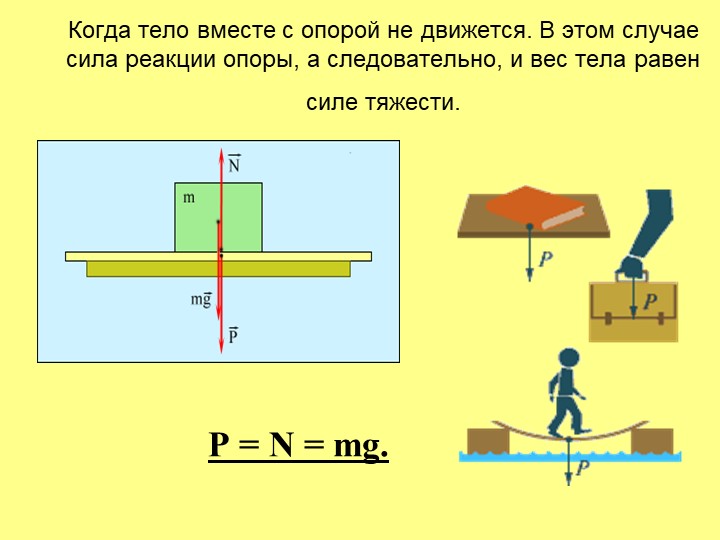 Солнце больше планет нашей солнечной системы. А как мы знаем, сила гравитации пропорциональна массе тела. Следовательно, большая масса объектов приведет к сильной силе гравитационного притяжения между объектами. Таким образом, он может оказывать сильное гравитационное силовое поле, которое удерживает планеты, существующие в нашей солнечной системе, на орбите.
Солнце больше планет нашей солнечной системы. А как мы знаем, сила гравитации пропорциональна массе тела. Следовательно, большая масса объектов приведет к сильной силе гравитационного притяжения между объектами. Таким образом, он может оказывать сильное гравитационное силовое поле, которое удерживает планеты, существующие в нашей солнечной системе, на орбите.
Другое название силы тяжести — вес. Вес любого объекта — это просто величина силы, на которую действует сила тяжести. Сколько весит любой объект на Земле, аналогично тому, как Земля тянет его вниз.
Когда парашютист выпрыгивает из самолета, он не имеет контакта, но все же приближается к земле из-за силы тяжести.
Даже эта сила тяжести удерживает воду в нашем стакане.
Сила притяжения Луны другая, то есть 1/6th в сравнении с землей. Так ваш вес уменьшится на 1/6th раз на Луне, чем на Земле. В то время как гравитация Юпитера в 2.5 раза больше, чем у Земли, и, таким образом, ваш вес увеличится в 2.5 раза, когда вы находитесь на Юпитере.
В то время как гравитация Юпитера в 2.5 раза больше, чем у Земли, и, таким образом, ваш вес увеличится в 2.5 раза, когда вы находитесь на Юпитере.
Мы знаем, что сила тяжести обратно пропорциональна квадрату расстояния между двумя объектами. Это означает, что по мере того, как объект удаляется от другого объекта, сила тяжести уменьшается.
По мере того, как человек удаляется от центра Земли, действие гравитационного поля постепенно уменьшается, и в космосе отсутствует сила тяжести. Из-за этого мы обнаружили, что астронавты часто плавают в космосе.
Отталкивание ракеты:Как известно, гравитация притягивает к себе все. Вот почему мы должны приложить большое количество силы, чтобы преодолеть гравитационную силу Земли при движении ракеты.
Изображение кредита: http://NASA/OpenStax University Physics, CNX UPhysics 09 07 Шаттл, CC BY 4.0Примеры полевых сил в повседневной жизни:
Электрическая сила:Втирание баллона в волосы:Когда мы трём две поверхности из-за силы трения, электроны передаются от одного объекта к другому.
Когда вы расчесываете сухие волосы, электроны передаются на расческу из-за силы трения, и она становится отрицательно заряженной. Поле теперь формируется вокруг гребенки, которая оказывает притяжение или отталкивание в зависимости от заряда другого приближающегося объекта. Когда вы кладете его рядом с кусочками бумаги, они сразу же прилипают к расческе, потому что статическое электричество генерируется в диапазоне полей, развиваемых гребенкой.
Кредит изображения: «Файл: Аттракцион-и-отталкивающая-электрическая-демонстрация-с-зарядами.jpg» by МайкРан под лицензией CC BY-SA 4.0Электрическое поле в проводе:Провода, которые обеспечивают нас электричеством, содержат большое количество беспорядочно движущихся электронов. Поток этих электронов создается за счет приложения электрической силы.
Изображение кредита: https://www.maxpixel.net/static/photo/1x/Lap-Wire-Electric-Power-Power-Line-2945750.jpgОблачная молния:При повышении температуры воздух становится теплым, и он поднимается. Когда этот теплый воздух поднимается вверх, водяной пар становится холодным, образуя облака. Из-за такой разницы температур облако будет заряжаться. Более легкий и положительный заряд будет формировать верхнюю часть облака, в то время как более тяжелые и отрицательно заряженные частицы будут формировать нижнюю часть облака.
Когда этот теплый воздух поднимается вверх, водяной пар становится холодным, образуя облака. Из-за такой разницы температур облако будет заряжаться. Более легкий и положительный заряд будет формировать верхнюю часть облака, в то время как более тяжелые и отрицательно заряженные частицы будут формировать нижнюю часть облака.
Когда эти заряды становятся достаточно большими, то внутри облака между двумя зарядами возникает гигантская искра или молния. Вот как молния также возникает из-за электрического силовое поле, развитое внутри облака.
Изображение кредита: https://p2.piqsels.com/preview/2/219/726/lightning-storm-arizona-monsoon.jpgПримеры полевых сил в повседневной жизни:
Магнитная силаМагнитная сила, притяжение или отталкивание, возникающие между электрически заряженными частицами из-за их движения. Магнитная сила на движущийся заряд действует под прямым углом к плоскости, образованной направлением его скорости и направлением окружающего магнитного поля.
Первым интересом Альберта Эйнштейна к науке была таинственная бесконтактная сила, которую он наблюдал с помощью магнитов. Позже эту силу назвали магнитной силой.
Сила магнитного поля между полюсами магнита:Каждый магнит имеет два полюса: северный (N) полюс и южный (S) полюс.
У каждого есть собственное поле вокруг него, которое можно показать воображаемыми линиями, называемыми линиями поля. Направление силовых линий — от северного полюса к южному полюсу.
Когда мы приближаем такие два магнита друг к другу, они либо притягивают, либо отталкивают друг друга, в зависимости от полюса другого магнита, потому что силовые линии обоих магнитов интерферируют.
Когда одинаковые полюса магнита расположены ближе друг к другу, то они будут отталкиваться. В то время как в случае противоположных полюсов они притягиваются друг к другу, так как будет конструктивное вмешательство между линиями поля.
Кредит изображения: Компьютерщик3, Цилиндрические магниты VFPt отталкивающие, CC BY-SA 3. 0Схемотехнические помехи:
0Схемотехнические помехи:Аппаратное обеспечение телевизора состоит из множества электронных компонентов, которые связаны друг с другом. Когда ток проходит через электрическую схему телевизора, компоненты, состоящие из проводников, формируют вокруг себя поля из-за разности потенциалов и протекания через них электрического тока. Силовые линии каждого компонента будут мешать друг другу и создавать шумовой сигнал. Таким образом, интерференция также является полевой силой.
Изображение кредита: https://p0.pxfuel.com/preview/129/47/820/cpu-technology-computer-semiconductor.jpgЮжное и северное сияние:Такое явление, как южное или северное сияние, возникает из-за магнитного поля Земли.Когда заряженные частицы, вылетающие из Солнца, достигают поверхности Земли, некоторые из них оказываются в ловушке магнитного поля Земли вокруг земной атмосферы, называемых поясами. Когда заряженные частицы стремятся покинуть это магнитное поле, они будут двигаться по спирали вдоль силовых линий магнитного поля к магнитным полюсам. И через него они попадают в атмосферу Земли и взаимодействуют с частицами атмосферного газа, что и является причиной красивых световых шоу.
И через него они попадают в атмосферу Земли и взаимодействуют с частицами атмосферного газа, что и является причиной красивых световых шоу.
Игровой автомат Работа сделанная сила вычисляется скалярным произведением силы и смещения объекта из-за приложенной силы.
Теперь сила, чья сеть совершается круговым движением, возвращающимся в то место, откуда вы начали, равна нулю. Тогда эти силы известны как консервативные силы.
Работа, выполняемая этой силой, не будет зависеть от пути, пройденного объектом, скорее, от начальной и конечной позиции этого объекта.
Гравитационная сила и электрическая сила — консервативные силовые поля.
Пример консервативного силового поля:- Когда вы берете мяч и перемещаете его по некоторому сложному пути, тогда работа, совершаемая силой тяжести на мяч, зависит только от конечных точек, или мы можем сказать, что разница в высоте.
 Таким образом, не имеет значения, решите ли вы идти прямо вниз или решите спускаться и подниматься по некоторому большому пути и в конечном итоге оказаться в одном и том же месте. Работа, совершаемая силой тяжести, останется прежней. Более того, он также будет равен нулю, если вы будете наблюдать за общей работой, проделанной по замкнутому пути.
Таким образом, не имеет значения, решите ли вы идти прямо вниз или решите спускаться и подниматься по некоторому большому пути и в конечном итоге оказаться в одном и том же месте. Работа, совершаемая силой тяжести, останется прежней. Более того, он также будет равен нулю, если вы будете наблюдать за общей работой, проделанной по замкнутому пути. - Рассмотрим электрическое поле, которое создается из-за заряда Q. Теперь, если мы поместим тестовый заряд ‘q’, тогда работа, проделанная для переноса этого тестового заряда ‘q’ от A к B на расстояние d, не будет зависеть от пути за ним. Электрическое поле зависит только от начального и конечного положения, следовательно, только от положения A и B, а не от пути, по которому следует пробный заряд «q». Более того, работа, проделанная для перемещения заряда по замкнутому пути, то есть от A к B и затем от B к A, будет равна нулю согласно этой теории.
Таким образом, мы можем сказать, что электрическая сила — это консервативная сила поля.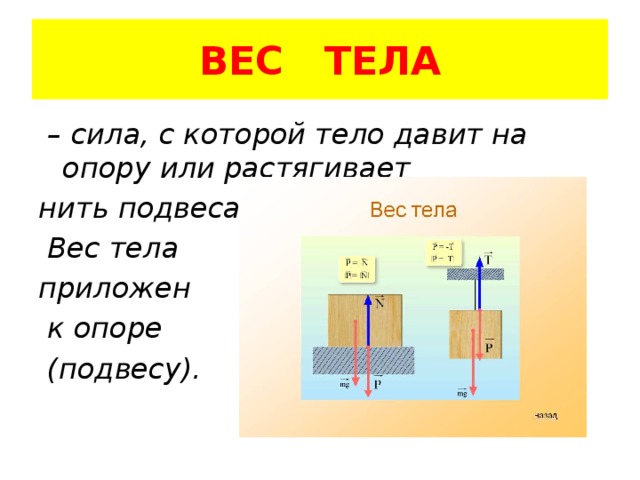
Как он используется в медицинских / лабораторных целях?Центростремительная сила — это результирующая сила, которая удерживает объект в движении по круговой траектории. Таким образом, мы можем сказать, что она является причиной равномерного кругового движения.
В области медицины в лабораторных центрифугах центростремительная сила используется для ускорения осаждения частиц, взвешенных в образцах крови.
По мере того, как мы ускоряем образец крови (обычно центрифуга может обеспечить ускорение от 600 до 2000 раз, нормальное к силе тяжести), это предотвращает осаждение клеток крови с образцом цельной крови.
Частицы, которые являются более тяжелыми по массе, здесь тяжелые эритроциты будут притягиваться к дну пробирки, а компоненты, присутствующие в растворе, будут оседать слоями в соответствии с их плотностью.
Таким образом, теперь можно легко разделить клетки крови и другие компоненты.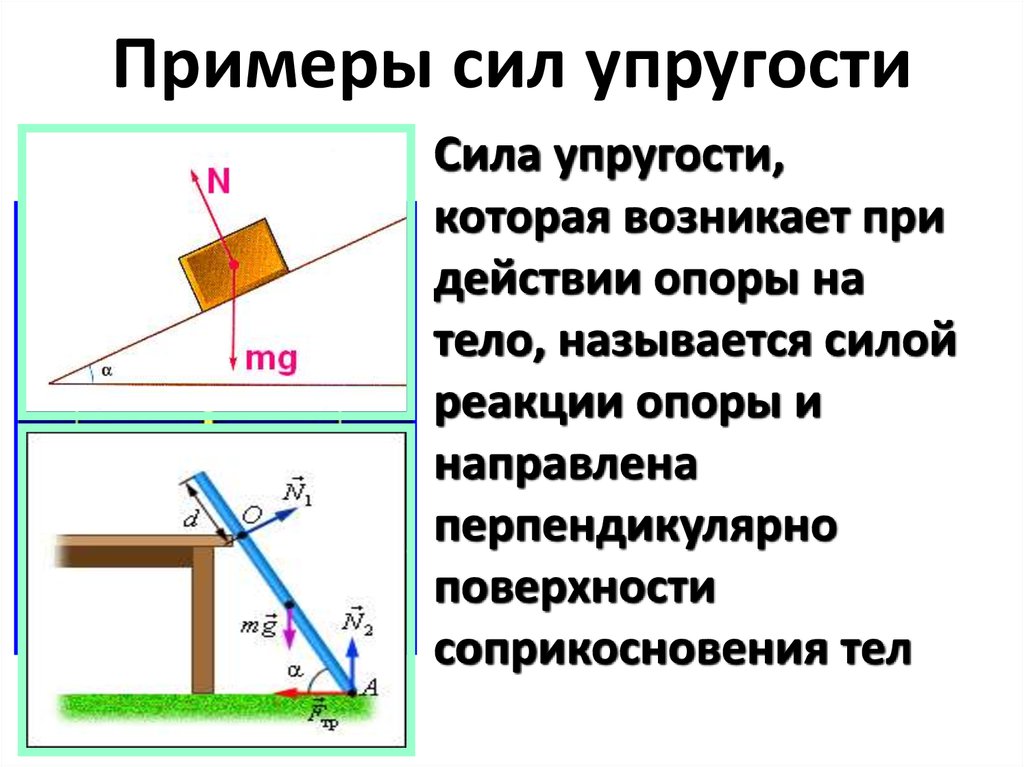
Автоматизация полевой службы — это процесс сбора информации о полевой службе. Затем эта задокументированная информация немедленно передается через беспроводное соединение, такое как Wi-Fi, спутники, и синхронизируется с основной системой, обеспечивая доступ к данным в реальном времени через мобильный интерфейс.
Использование одного из них может повысить продуктивность полевых работ, а также сократить временную задержку. Информация будет у вас под рукой.
В сфере общественных работ или социальных услуг государственные учреждения сложны и разнообразны в зависимости от сообщества, которое они обслуживают. Но у всех них есть одна общая черта: куда бы они ни пошли, доступ к информации и обмен ею.
По мере роста спроса на услуги видеокамеры, дроны и датчики играют важную роль в предоставлении ценных источников данных полевым работникам агентства.
Автоматизируя повседневные операции на местах с помощью интеграции и интеллектуальных устройств, он упрощает нашу жизнь. Например, предположим, что нам дают электроэнергию от любой организации XYZ. Кроме того, если возникнут какие-либо проблемы, мы, несомненно, сможем связаться с ними, используя их приложение, и пожаловаться им. Кроме того, таким образом вы сможете быстрее решить вашу жалобу и ускорить техническое обслуживание с помощью автоматизации полевых работ.
Например, предположим, что нам дают электроэнергию от любой организации XYZ. Кроме того, если возникнут какие-либо проблемы, мы, несомненно, сможем связаться с ними, используя их приложение, и пожаловаться им. Кроме того, таким образом вы сможете быстрее решить вашу жалобу и ускорить техническое обслуживание с помощью автоматизации полевых работ.
В наши дни мы покупаем вещи в Интернете. Мы можем без особой растяжки точно знать, когда мы получим то, что мы купили, отслеживая это.
Часто задаваемые вопросы | Часто задаваемые вопросы о Field Force ПримерыВ. Что такое сила?Отв. Сила — это внешний агент, из-за которого тело меняет состояние покоя или движения. Следовательно, это означает, что сила является причиной изменения или, говоря техническим языком, движения в теле.
В. Какие бывают типы силы?Ответ Есть два типа сил:
- Контактная сила.
- Бесконтактная сила или полевая сила.

Отв. Как следует из названия, это сила, которая действует только тогда, когда объекты находятся в прямом контакте друг с другом, тогда этот тип силы называется контактной силой.
В. Приведите примеры контактной силы в повседневной жизни..Ответ Примеры контактной силы приведены ниже:
Мышечная сила:Можете ли вы сдвинуть стол, не касаясь его?
Можете ли вы приложить силу к столу, не касаясь его?
И ваш ответ будет нет. Чтобы сдвинуть или передвинуть стол, необходим контакт с мышцами вашего тела.
Удар по мячу:Ударяя по футбольному мячу, вы касаетесь футбольного мяча ногой и прикладываете силу. Таким образом, это еще и контактная сила.
Кредит изображения: Pixabay бесплатные изображенияСила трения:Когда вы перетаскиваете какой-либо объект по полу, он прикладывает силу трения к нижней части объекта, чтобы противодействовать движению объекта.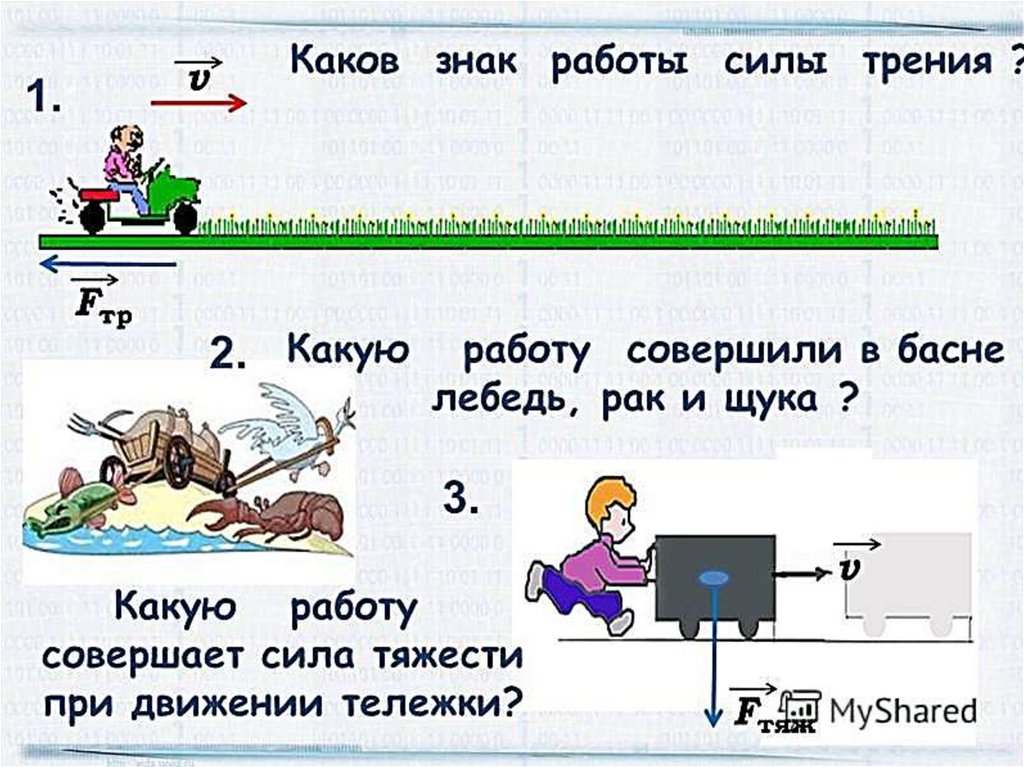 Таким образом, сила трения также является контактной силой, потому что, если объект не соприкасается с полом, силы трения не будет, чтобы противодействовать его движению.
Таким образом, сила трения также является контактной силой, потому что, если объект не соприкасается с полом, силы трения не будет, чтобы противодействовать его движению.
Когда объект покоится на любой поверхности, он оказывает на поверхность силу. Эта сила реакции находится под прямым углом к поверхности и известна как нормальная сила.
Мешок на столе оказывает на стол силу, перпендикулярную поверхности стола, и представляет собой нормальную силу. Следовательно, если нормальная сила и сила тяжести уравновешены, мешок будет лежать на столе.
В. Что такое силовое поле? Приведите примеры Field Force.Отв. Сила, которая не требует прямого контакта с другим объектом, тогда этот тип силы называется бесконтактной силой. Невидимое поле всегда связано с этими силами, называемыми силами поля.
Фундаментальные силы природы, гравитационная сила, электрическая сила, магнитная сила, — это силы поля.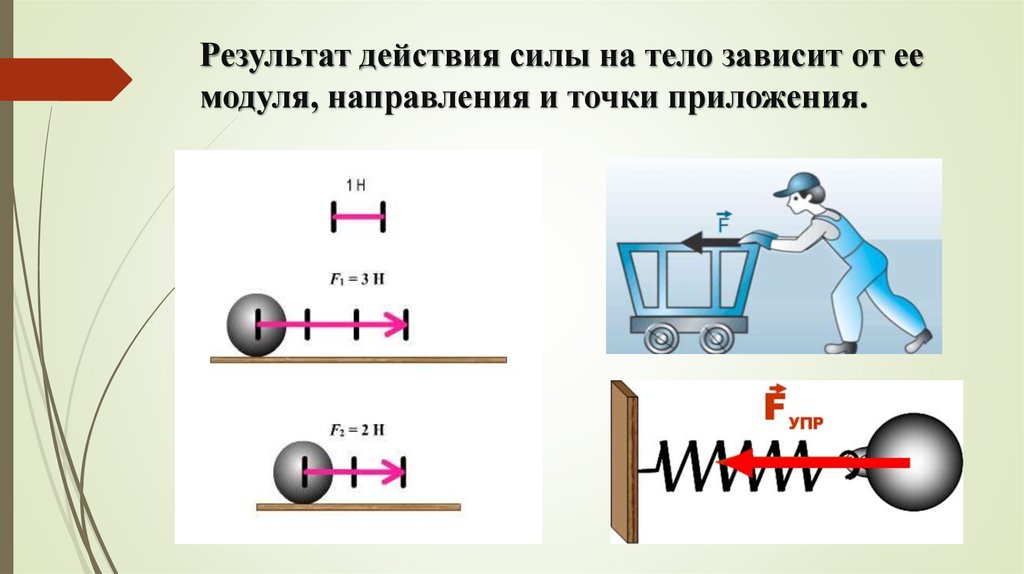 .
.
Ответ Сила поля может создать ограниченную область, где другое тело может почувствовать влияние силы.
Поле — это область объекта, где другой объект ощущает влияние силы, ответственной за силу поля.
В. Приведите примеры силового поля в нашей повседневной жизни.Ответ Примеры различных полевых сил или бесконтактных сил приведены в следующих источниках:
- Мы остаемся на земле из-за гравитационного силового поля.
- Сила гравитационного поля удерживает воду внутри стакана.
- Любой объект или тело, которое упадет с любой высоты, упадет на землю из-за силы гравитационного поля (наблюдение Ньютона яблока, падающего с дерева)
- Капли дождя падают на землю из-за силы гравитационного поля.
- Когда два магнита приближаются друг к другу, они либо притягиваются, либо отталкиваются друг от друга, что является примером силы магнитного поля.

- Без какого-либо физического контакта железные булавки притягиваются к магниту как сила поля.
- Ток в проводе, поток электронов также происходит за счет силы электрического поля.
- Заряженный гребень притягивается к листу бумаги из-за электростатической силы.
- Электромагнетизм также является примером Силы поля.
Q.
Сравните и сопоставьте контактные силы с полевыми войсками.Ответ Сравнение между контактной силой и полевой силой приведено ниже:
| Контактная сила | Полевая сила |
| Этот тип силы возникает только тогда, когда два объекта находятся в физическом контакте друг с другом. | Для силового поля не потребуется никакого физического контакта друг с другом соответственно. |
| Никакое поле не связано с контактной силой. | Всегда есть поле, связанное с бесконтактным или силовым полем.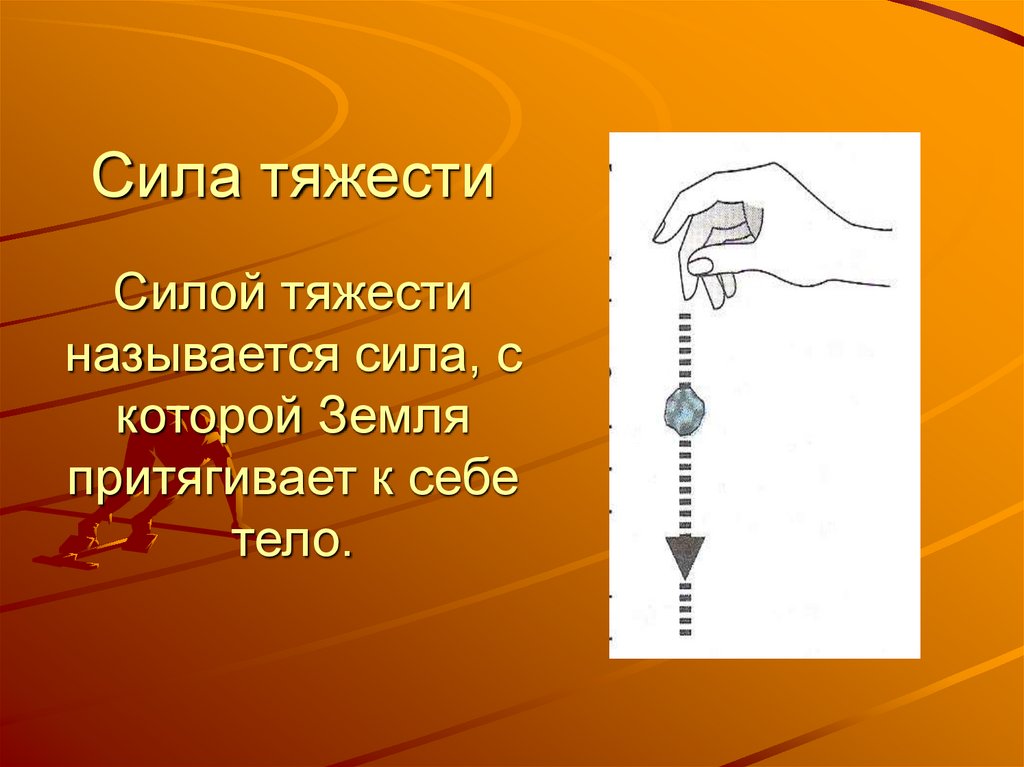 |
| Сила трения, мышечная сила, нормальная сила, натяжение и т. Д. Являются примерами контактной силы. | Фундаментальные силы, такие как гравитационная сила, электростатическая сила, магнитная сила являются примерами силы поля. |
Ответ Примеры контактной силы и силы поля приведены ниже:
- Контактные силы: Мышечная сила, сила трения, сила натяжения, норма сила и сила пружины являются контактом силы.
- Полевая сила: Гравитационная сила, электрическая сила, магнитная сила и электромагнитные силы являются примерами силы поля.
Ответ Скалярные поля — это те, каждая точка поля которых имеет скалярное значение.
Поле температуры, поле влажности и поле давления являются образцами скалярного поля.
В. Каковы некоторые примеры неуравновешенных сил?Ответ Когда результирующая сила, приложенная к телу, не равна нулю, силы, действующие на тело, неуравновешены.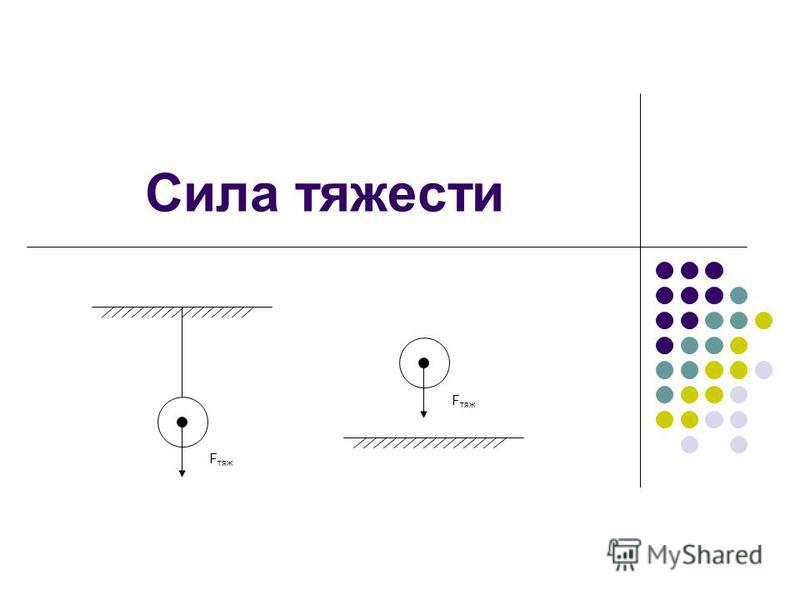 Таким образом, когда что-либо движется, это происходит потому, что действующие на него силы неуравновешены. Примеры приведены ниже:
Таким образом, когда что-либо движется, это происходит потому, что действующие на него силы неуравновешены. Примеры приведены ниже:
- Когда вы пинаете мяч, он перемещается с одного места на другое
- Движение ракеты
- Вождение автомобиля
- Потянув за дверь, вы можете открыть ее
- Когда вы толкаете стену, она не двигается из-за несбалансированной силы
| Действия учителя | Действия учеников | УУД |
| 1. Актуализация знаний и умений | ||
Приветствует учащихся. – Ребята, сегодня мы продолжаем изучение раздела «Взаимодействие тел». Чтобы продвинуться дальше в этом разделе вспомним и повторим некоторые понятия изученные нами ранее. Что мы подразумеваем под взаимодействием тел? – Приведите примеры взаимодействия тел. Задаёт вопросы, направленные на проверку имеющихся знаний.
Давайте резюмируем информацию и сделаем выводы о причинах изменения скорости тела. | Приветствуют учителя, демонстрируют готовность к уроку. Учащиеся отвечают на вопрос учителя. – Действие одного тела на другое не может быть односторонним, оба тела действуют друг на друга, т.е. взаимодействуют) – Бильярдные шары, тележки при столкновении и т.п. Отвечают на вопросы учителя. – Не может. – Пока действует на него другое тело – Большую скорость приобретает тело с меньшей массой. Формулируют выводы. – Скорость тела изменяется под действием на него другого тела. | умение слушать и вступать в диалог (К), |
| 2. Постановка учебной задачи | ||
– Что же по вашему мнению является причиной изменения скорости движения тел? – Ваши догадки недалеки от истины. Причиной изменения скорости движения тел является сила. Давайте сформулируем цель нашего урока. – Итак, откройте ваши тетради и запишите тему урока: «Сила. Единицы силы. Сила тяжести». Цели нашего урока:
| Высказывают свои предположения, обосновывают ответы Формулируют тему, цель урока, высказывают свои предположения по ходу урока. Записывают дату и тему урока. | самостоятельная постановка новых учебных целей и задач (Р) |
| 3. Мотивация учебной деятельности | ||
– Сила – очень важная физическая величина. О ней сложено немало пословиц, поговорок и песен. Давайте вспомним некоторые из них. – Что же, вы только что убедились, какое важное место занимает понятие «сила» в русском фольклоре. А теперь давайте определим, какую роль играет сила в мире физики. | Приводят примеры пословиц, поговорок и песен, в которых встречается слово «сила». | формирование выраженной устойчиво-познавательной мотивации и интереса к учению (Л) |
4. Выявление места и причины затруднения Выявление места и причины затруднения | ||
– Часто не указывают, какое тело и как действовало на другое тело. Просто говорят, что на тело действует сила. Почему мяч и брусок с гирей пришли в движение, а пружина сжалась? Демонстрация. Катит по столу мяч и тянет брусок с гирей за нитку. Сжимает пружину. – Вы правы, это произошло вследствие воздействия силы. Демонстрация. Пружина на штативе, пластилин. К пружине подвешивается груз и она растягивается. Пластилин сжимается пальцами руки и изменяется его форма. – Сила, действующая на тело, может не только изменить скорость всего тела, но и отдельных его частей. Какие проявления силы вы могли наблюдать в проделанном опыте? – Приведите примеры деформаций. | -На них подействовала сила. Записывают в тетрадь, как обозначается сила
Растяжение пружины, деформация пластилина
Приводят 2-3 примера. | проведение наблюдения и эксперимента под руководством учителя (П), объяснение явлений, процессов выявляемых в ходе эксперимента (П)
|
| 5. Построение проекта выхода из затруднения | ||
– Запишите в тетрадях: деформация-изменение формы или размера тела. – Теперь выясним, от чего зависит результат действия силы. Для этого вам необходимо работать в парах. На столах у обучающихся собрана установка: на лабораторных штативах подвешены грузики на нитях (маятники). Фронтальный эксперимент: – Толкаем грузик легонько рукой, затем толкаем чуть сильнее. – Толкаем грузик в одну сторону, а затем в другую. – Исходя из результатов проведённого вами эксперимента, сделайте выводы о том, от чего зависит действие силы (действие силы зависит от ее модуля, действие силы зависит от направления) Просит троих учеников поочерёдно подойти к двери и толкнуть её в местах обозначенных цифрами 1, 2, 3. Просит сформулировать третью составляющую, от которой зависит действие силы (точка приложения). Выводит на экран слайд №8. Просит записать информацию, данную на слайде, в тетрадь. (Приложение 2) | Записывают в тетрадях определение понятия «деформация». Разбиваются на пары. Выполняют указания учителя по проведению фронтального эксперимента. Делают выводы о том, от чего зависит действие силы. Подходят к двери, поочерёдно толкают её. Определяют, кто из них приложил большую силу, а кто меньшую. Делают предположения относительно третьей составляющей, от которой зависит действие силы. Смотрят на слайд, записывают в тетрадь от чего зависит действие силы. | осуществление взаимного контроля и оказание в сотрудничестве необходимую взаимопомощь (К), осуществление сравнения при самостоятельном выборе оснований и критериев для указанной логической операции (П), установление причинно-следственных связей (П) |
6. Физкультминутка Физкультминутка | ||
Давайте немного отдохнём.Включает видео на ноутбуке, выводит на проектор. www.youtube.com/watch?v=4zVbT-bxlaw | Выполняют упражнения |
|
| 7. Реализация построенного проекта | ||
– Сила измеряется в Н (Ньютонах) Запишем в тетрадях: [F]=Н (Ньютон). На рисунках и чертежах силу обозначают в виде направленного отрезка. Начало его – точка приложения силы, длина его – модуль силы в заданном масштабе. (Рисунок 60 учебника). | Записывают необходимую информацию в тетрадь, смотрят на рисунок 60 в учебнике. |
|
| 8. Самостоятельная работа с самопроверкой по эталону | ||
– Выполним по вариантам задания. По одному человеку с каждого варианта выполняют у доски (В-1 №359, В-2 № 360) [2] – А теперь давайте проверим правильность выполнения заданий. Выводит на проектор правильные решения задач. | По одному человеку с каждого варианта выполняют задание у доски. Остальные – на местах. Сверяют свои решения с образцом-эталоном. Учащиеся на местах оценивают работу товарищей, выполнявших задания у доски. | самостоятельный анализ условий достижения цели, на основе учёта выделенных учителем ориентиров действия в новом учебном материале (Р), осуществление контроля, коррекции, оценки действий партнёра (К) |
| 9. Первичное закрепление с проговариванием во внешней речи | ||
– Ну, а сейчас посмотрим небольшой фильм. Вы при его просмотре должны что-то заметить. (Демонстрация фильма 1 минута). Приложение 1. – Что вы заметили? – Звезды, планеты, спутники притягиваются к Солнцу и друг к другу. Притяжение всех тел во Вселенной – Всемирное тяготение. Ньютон сформулировал закон Всемирного тяготения (качественная формулировка закона). Сила, с которой Земля притягивает к себе все тела – сила тяжести. Запишем в тетрадь ее обозначение. Fтяж – сила тяжести. Направлена она всегда вертикально вниз в любой точке земного шара (к центру Земли). Картинки «Сила тяжести» показ <Рисунок 1> и <Рисунок 2>. |
Высказывают свои предположения.
Записывают данные в тетрадь. | обобщение понятий – осуществление логической операции перехода от видовых признаков к родовому (П) |
| 10. Включение в систему знаний и повторения | ||
Решение задачи 293 из [2] | Решают задачи в тетради | умение самостоятельно контролировать своё время и управлять им (Р), адекватная самостоятельная оценка правильности выполнения действия (Р) и внесение необходимых коррективов в исполнение как в конце действия, так и по ходу его реализации (Р) |
11. Информация о домашнем задании Информация о домашнем задании | ||
-Запишите домашнее задание на следующий урок. § 24,25 №№ 291,292, 365 [2] | Записывают домашнее задание |
|
| 12. Рефлексия учебной деятельности на уроке | ||
У каждого ученика на столе набор карточек: красная, желтая и зеленая. Нужно поднять карточку нужного цвета, ответив на высказывание учителя:
Выставляет оценки, завершает урок. | Показывают учителю одну из трёх карточек, оценивают свою работу на уроке | формирование навыков рефлексии (Л) |
Явление инерции.
 Сила. Явление тяготения и сила тяжести. Вес.
Сила. Явление тяготения и сила тяжести. Вес.Раздел долгосрочного планирования: Давление | Школа: ШГ № 31 | ||
Дата : | ФИО учителя: Парыгина Юлия Юрьевна | ||
класс: 7 | Присутствовали: | Отсутствовали: | |
Тема урока | Явление инерции. Сила. Явление тяготения и сила тяжести. Вес. | ||
Цели обучения, достигаемые на этом уроке (Ссылка на учебный план) | 7.2.2.1 — объяснять явление инерции и приводить примеры 7.2.2.2 -приводить примеры действия сил из повседневной жизни 7.2.2.10 -различать вес и силу тяжести | ||
Цель урока | — формулируют отличительные признаки инерции; — объяснить сущность явления тяготения; — различают силу тяжести и вес. | ||
Критерии оценивания | — выделяют физические признаки силы тяжести и веса; — записывают единицы измерения ; — умеют графически определятьнаправление силы тяжести и веса. | ||
Языковые задачи | — описывают в устной и письменной форме понятия инерции, силы тяжести и веса; — проговаривают термины по теме: инерция, сила, вес, Ньютон, ускорение свободного падения, опора, подвес. | ||
Воспитание ценностей | — умеют организовать свою работу; — планируют работу в группе; — воспринимают чужую точку зрения и выражают свою. | ||
Межпредметная связь | естествознание, математика | ||
Предыдущие знания | Механическое движение. | ||
Ход урока
Этапы | Деятельность учителя | Деятельность ученика | Оценивание | Дифференциация | Ресурсы к уроку |
Вовлечение учащихся в учебную деятельность | Приветствие учащихся. Коллективная работа класса. Определение темы и цели урока отвечая на вопросы: — Что называют механическим движением? — Может ли тело, находящееся в относительном покое, само собой изменить скорость? (Нет). Демонстрация с мячом, который на столе. — Как можно изменить скорость тел? (Подтолкнуть, т.е. подействовать рукой)? Мяч начинает двигаться. Перестаю действовать, что наблюдаете? (Мяч останавливается). — Как же можно изменить скорость движения тела? Учитель демонстрирует тему урока по слайдам . | Отвечают устно на вопросы Записывают и формулируют тему урока и цель урока. Скорость тела изменяется, если на него действуют другие тела!!! Направление скорости тела изменяется, если на него действуют другие тела!!! | Оборудование к уроку по теме. | ||
Исследование/практика | Работа в парах. (см. Приложение 1) Выяснить, как будет двигаться тело при отсутствии внешнего воздействия. Опыт: Наблюдают за движением шара по наклонному желобу: сначала с тканью, а после без неё, т.е. без воздействия. Вывод: чем меньше действие другого тела, тем дольше сохраняется скорость движения и тем ближе оно к равномерному. Вывод: явление сохранения скорости тела, при отсутствии действия на него других тел называется инерцией. Эксперимент. — Посмотрите, на нити висит шарик. Что произойдет если мы оборвем нить? -Подбросьте шарик вверх. Наблюдайте за движением шарика. Как он движется Куда? -Пронаблюдайте за движением шарика по желобу.Обратите внимание, что шарик меняет свою траектория движения, после скатывания с желоба его траектория – кривая линия. Эксперимент с динамометром: Динамометр – прибор для измерения веса тела. Динамометр показывает силу, с которой на него действует тело, то есть вес груза. Просим учеников медленно перемещать динамометр влево-вправо по горизонтали. Показания динамометров не изменяются. Медленно перемещаем динамометр вверх-вниз. Показания динамометров изменяются. | Отвечают на поставленные вопросы. Результаты исследований оформляют в тетради: в первом случае скорость шарика уменьшилась очень быстро, движение было неравномерным, но во втором случае уменьшили трение, т.е. убрали ткань, шарик катится дальше, т.к. скорость шарика изменяется медленнее, т.е. дольше сохраняется, а движение шарика становится ближе к равномерному прямолинейному, но шарик снова останавливается. Формулируют вывод. Отвечают на вопросы и формулирую вывод. В чем же причина наблюдаемых явлений? Дело в том, что на все тела действует сила притяжения к Земле. Поэтому тела падаю на Землю. Существует притяжение не только между Землей и телами, находящимися на ней. Притяжение всех тел Вселенной друг к другу называется всемирным тяготением. Сила, с которой Земля притягивает к себе тело, называется силой тяжести. F = mg g – ускорение свободного падения, равное 9,8 м/ или 9,8 Н/кг) [ F ] = [ Ньютон ] = [ H ] Сила, с которой тело вследствие притяжения к Земле действует на опору или подвес, называется весом тела. P = F = mg [ P ] = [ Ньютон ] = [ H ] | Подбор заданий | Оборудование на каждой парте у учащихся, карточки с правилами работы с оборудованием и вопросами. | |
Информация/модерация | После проведения исследовательской работы проводится взаимопроверка (рядом сидящие пары обмениваются результатами, проговаривают результаты своих исследований) и сравнение с ответами предложенными учителем на слайде, исправляют неточности. | Учащиеся объясняют, анализируют, формулируют новые понятия инерция, сила тяготения и вес. | Формативное оценивание в процессе микрообучения- заполнение таблицы. | Результат от конкретного ученика, оказание индивидуальной поддержки учащемуся. | Презентация |
Практика/тренажер | Решение задач: 1. Масса груза 5 кг. Какая сила тяжести действует на него? 2. Сила тяжести, действующая на тело 196 Н. Какова масса тела? (см. Приложение 3) | Решают задачи. | |||
Обратная связь/Рефлексия | Итоги урока: мини-тест (см. Приложение 2) Ответ УСПЕХ Проводит рефлексию. Кратко написать самое важное, что уяснил с урока с пожеланиями соседу по парте и отправить. — Чему научил вас урок? | Проговаривают определения инерция, сила тяжести и вес. Выполняют мини-тест . | Формативное оценивание во время работы с мини-теста. |
Приложение 1.
Тема: Явление инерции. Сила. Явление тяготения и сила тяжести. Вес.
Цель: Научить находить в окружающем мире примеры проявления инерции, силы тяжести и веса и объяснять их.
Критерии:
1.Может проводить эксперименты по плану.
2. Оформляет результаты исследования в тетради.
Результаты исследований оформите в тетради.
1. Эксперимент: Наблюдайте за движением шара по наклонному желобу: сначала с тканью, а после без неё, т.е. без воздействия. Выясните, как будет двигаться тело при отсутствии внешнего воздействия.
Вывод: чем меньше действие другого тела, тем дольше сохраняется скорость движения и тем ближе оно к равномерному.
Вывод: явление сохранения скорости тела, при отсутствии действия на него других тел называется инерцией.
2. Эксперимент: На нити висит шарик. Что произойдет если мы оборвем нить?
Подбросьте шарик вверх. Наблюдайте за движением шарика. Как он движется Куда?
Пронаблюдайте за движением шарика по желобу.Обратить внимание, что шарик меняет свою траектория движения, после скатывания с желоба его траектория – кривая линия.
Вывод: Притяжение всех тел Вселенной друг к другу называется всемирным тяготением.
Сила, с которой Земля притягивает к себе тело, называется силой тяжести. F = mg
g – ускорение свободного падения, g= 9,8 м/ или 9,8 Н/кг) [ F ] = [ Ньютон ] = [ H ]
Сила, с которой тело вследствие притяжения к Земле действует на опору или подвес, называется весом тела. P = F = mg
[ P ] = [ Ньютон ] = [ H ]
3.Эксперимент с динамометром: Динамометр – прибор для измерения веса тела.
Динамометр показывает силу, с которой на него действует тело, то есть вес груза.
а) Медленно перемещайте динамометр влево-вправо по горизонтали.
б) Медленно перемещаем динамометр вверх-вниз. Как меняются показания динамометра?
Приложение 2. Мини-тест
Критериии:
1. Выделяет признаки инерции, силы тяжести и веса.
2. Указывает в таблице правильные ответы.
Впишите в таблицу ответов буквы, соответствующие верному ответу на каждый вопрос.
1. Что такое инерция?
Г. Свойство тел сохранять скорость.
У. Явление сохранения скорости тела при отсутствии действия на него других тел.
В. Изменение скорости тела под действием других тел.
2. Что произойдет с бруском, если резко его дёрнуть вперёд за нить?
С. Упадёт назад.
Д. Упадёт вперед.
Е. Останется неподвижным.
3. В каком случае наблюдается проявление инерции?
А.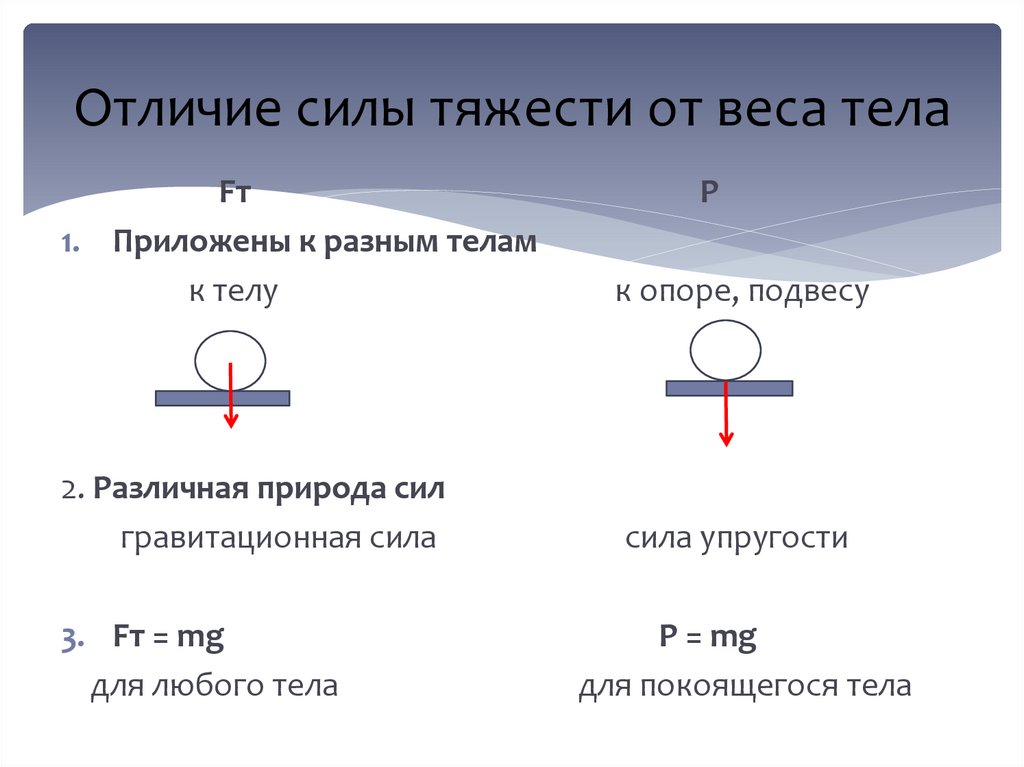 Камень падает на дно ущелья.
Камень падает на дно ущелья.
П. Пыль выбивают из ковра.
Н. Мяч отскочил от стенки после удара.
4. Какое изменение произошло в движении автобуса, если пассажиры отклонились влево?
И. Автобус остановился.
Е. Автобус повернул направо.
Ч. Автобус повернул налево.
5. Для чего делают разбег при прыжках в длину?
К. Чтобы выше подпрыгнуть.
Л. Чтобы увеличить длину траектории движения тела.
Х. Чтобы набрать скорость для толчка.
Приложение 3. Решение задач.
1. Масса груза 5 кг. Какая сила тяжести действует на него?
2. Сила тяжести, действующая на тело 196 Н. Какова масса тела?
Приложение 4.
Рефлексия: Кратко написать самое важное, что уяснил с урока с пожеланиями соседу по парте и отправить.
-Чему научил вас урок ?
— Какое впечатление осталось у вас от урока?
По какой формуле находят силу тяжести.
 Сила тяжести: формула, определение
Сила тяжести: формула, определениеОпределение
Под воздействием силы притяжения к Земле все тела падают с одинаковыми по отношению к ее поверхности ускорениями. Такое ускорение называют ускорением свободного падения и обозначают: g. Его величина в системе СИ считается равной g=9,80665 м/с 2 – это так называемое, стандартное значение.
Вышесказанное обозначает то, что в системе отсчета, которая связывается с Землей, на любое тела обладающее массой m действует сила равная:
которая называется силой тяжести.
Если тело находится в состоянии покоя на поверхности Земли, тогда сила тяжести уравновешивается реакцией подвеса или опоры, которая удерживает тело от падения (вес тела).
Различие между силой тяжести и силой притяжения к Земле
Если быть точным, то следует заметить, что в результате неинерциальности системы отсчета, которая связывается с Землей,
сила тяжести отличается от силы притяжения к Земле. Ускорение, которое соответствует движению по орбите существенно меньше,
чем ускорение, которое связывается с суточным вращением Земли. Система отсчета, связанная с Землей, осуществляет вращение по
отношению к инерциальным системам с угловой скоростью =const. Поэтому в случае
рассмотрения перемещения тел по отношению к Земле следует учитывать центробежную силу инерции (F in), равную:
Система отсчета, связанная с Землей, осуществляет вращение по
отношению к инерциальным системам с угловой скоростью =const. Поэтому в случае
рассмотрения перемещения тел по отношению к Земле следует учитывать центробежную силу инерции (F in), равную:
где m – масса тела, r – расстояние от оси Земли. Если тело расположено не высоко от поверхности Земли (в сравнении с радиусом Земли), то можно считать, что
где R Z – радиус земли, – широта местности.
В таком случае ускорение свободного падения (g) по отношению к Земле будет определено действием сил: силы притяжения к Земле () и силы инерции (). При этом сила тяжести — есть результирующая этих сил:
Так как сила тяжести сообщает телу, обладающему массой m ускорение равное , то соотношение (1) является справедливым.
Разница между силой тяжести и силой притяжения к Земле небольшая. Так как .
Как и всякая сила, сила тяжести – векторная величина. Направление силы
, например, совпадает с направлением нити, натянутой грузом,
которое называют направлением отвеса. Сила
направлена к центру Земли. Значит, нить отвеса направлена
также только на полюсах и экваторе. На других широтах угол отклонения ()
от направления к центру Земли составляет величину, равную:
Сила
направлена к центру Земли. Значит, нить отвеса направлена
также только на полюсах и экваторе. На других широтах угол отклонения ()
от направления к центру Земли составляет величину, равную:
Разница между F g -P максимальна на экваторе, она составляет 0,3% от величины силы F g . Так как земной шар является сплюснутым около полюсов, то F g имеет некоторые вариации по широте. Так она у экватора на 0,2% меньше, чем у полюсов. В результате ускорение g изменяется с широтой от 9,780 м/с 2 (экватор) до 9,832 м/с 2 (полюса).
По отношению к инерциальной системе отсчета (например, гелиоцентрической СО) тело в свободном падении будет перемещаться с ускорением (a) отличающимся от g, равным по модулю:
и совпадающим по направлению с направлением силы .
Единицы измерения силы тяжести
Основной единицей измерения силы тяжести в системе СИ является: [P]=H
В СГС: [P]=дин
Примеры решения задач
Пример
Задание. Определите во сколько раз величина силы тяжести на Земле
(P 1) больше, чем сила тяжести на Луне (P 2). 2 .
2 .
Таким образом, для ответа на поставленный вопрос следует найти отношение:
Проведем вычисления:
Ответ.
Пример
Задание. Получите выражение, которое связывает широту и угол, который образуют вектор силы тяжести и вектор силы притяжения к Земле.
Решение. Угол, который образуется между направлениями силы притяжения к Земле и направлением силы тяжести можно оценить, если рассмотреть рис.1 и применить теорему синусов. На рис.1 изображены: – центробежная сила инерции, которая возникает за счет вращения Земли вокруг оси, – сила тяжести, – сила притяжения тела к Земле. Угол — широта местности на Земле.
Я не понял урок на физике и не знаю как определить силу тяжести!
Ответ
Сила тяжести — это свойство тел с массой притягиваться друг к другу. Тела, которые имеют массу, всегда притягиваются друг к другу. Притяжения тел с очень большими массами в астрономических масштабах создает значительные силы, благодаря которым мир является таким, каким мы его знаем.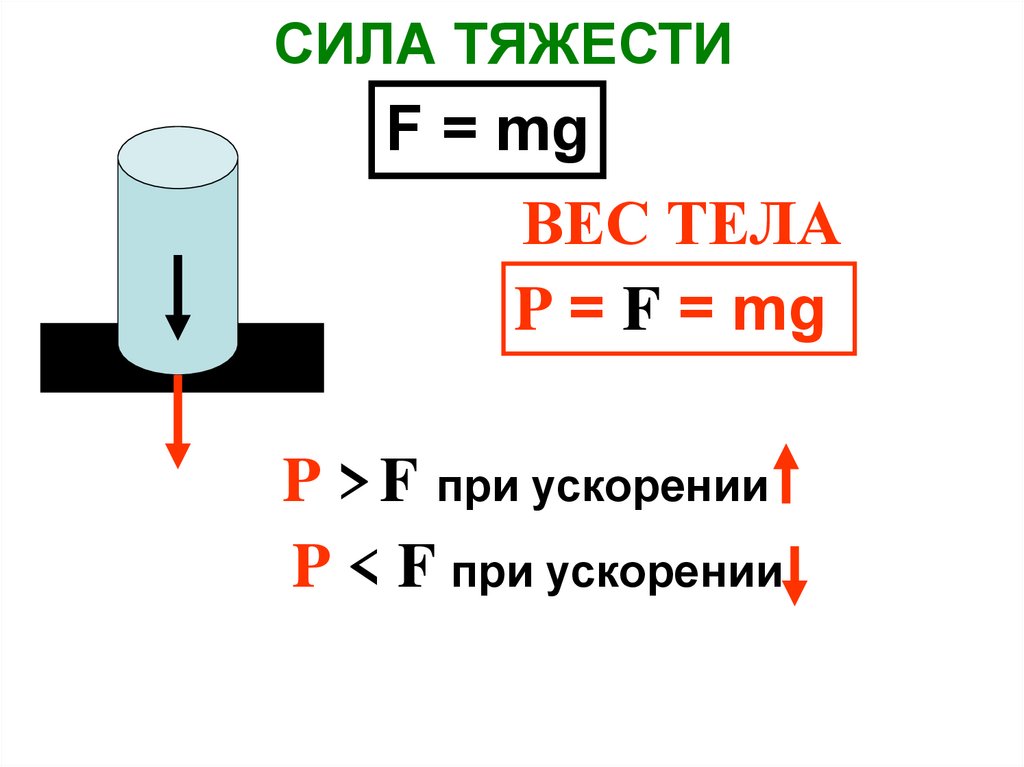
Сила притяжения является причиной земного притяжения, в результате которого предметы падают на нее. Благодаря силе притяжения Луна вращается вокруг Земли, Земля и другие планеты — вокруг Солнца, Солнечная система — вокруг центра Галактики.
В физике сила тяжести — это сила, с которой тело действует на опору или вертикальный подвес. Эта сила направлена всегда вертикально вниз.
F — сила с которой действует тело. Измеряется в ньютонах (Н).
m — масса (вес) тела. Измеряется в килограммах (кг)
g — ускорение свободного падения. Измеряется в ньютонах разделенных на килограмм (Н/кг). Ее величина постоянная и в среднем по земной поверхности равна 9,8 Н/кг.
Как определить силу притяжения?
Пример:
Пусть масса чемодана равна 15 кг, тогда чтобы найти силу притяжения чемодана к Земле воспользуемся формулой:
F= m*g = 15*9,8 = 147 Н.
То есть сила притяжения чемодана составляет 147 ньютонов.
Значение g для планеты Земля неодинаково — на экваторе оно составляет 9,83 Н/кг, а на полюсах 9,78 Н/кг. Поэтому и берут среднее значение, которое мы использовали для расчета. Точные значения для различных регионов планеты используют в авиакосмической отрасли, а также на них обращают внимания в спорте, при тренировках спортсменов для участия в соревнованиях в других странах.
Поэтому и берут среднее значение, которое мы использовали для расчета. Точные значения для различных регионов планеты используют в авиакосмической отрасли, а также на них обращают внимания в спорте, при тренировках спортсменов для участия в соревнованиях в других странах.
Историческая справка: впервые посчитал g и вывел формулу силы тяжести, а если точнее формулу силы с которой тело действует на другие тела, в 1687 году известный английский физик Исаак Ньютон. Именно в его честь и названа единица измерения силы. Существует легенда, что Ньютон начал исследовать вопрос силы тяжести после того, как ему упало на голову яблоко.
Сила тяжести – величина, на которую тело притягивается к земле под действием ее притяжения. Данный показатель напрямую зависит от веса человека или массы предмета. Чем больше вес, тем он выше. В этой статье мы расскажем, как найти силу тяжести.
Из школьного курса физики: сила притяжения прямо пропорциональна весу тела. Рассчитать величину можно по формуле F=m*g, где g – коэффициент, равный 9,8 м/с 2 . Соответственно для человека, который весит 100 кг, сила притяжения равна 980. Стоит отметить, что на практике все немного иначе, и на силу тяжести влияет множество факторов.
Рассчитать величину можно по формуле F=m*g, где g – коэффициент, равный 9,8 м/с 2 . Соответственно для человека, который весит 100 кг, сила притяжения равна 980. Стоит отметить, что на практике все немного иначе, и на силу тяжести влияет множество факторов.
Факторы, влияющие на силу тяжести:
- расстояние от земли;
- географическое расположение тела;
- время суток.
Запомните, что на северном полюсе постоянная g равна не 9,8, а 9,83. Это возможно из-за наличия в земле залежей полезных ископаемых, которые обладают магнитными свойствами. Незначительно увеличивается коэффициент в местах залежей железной руды. На экваторе коэффициент равен 9,78.
Если тело находится не на земле или в движении, то для определения силы притяжения необходимо знать ускорение предмета. Для этого можно воспользоваться специальными приборами – секундомером, спидометром или акселерометром. Для расчета ускорения определите конечную и начальную скорости движения объекта.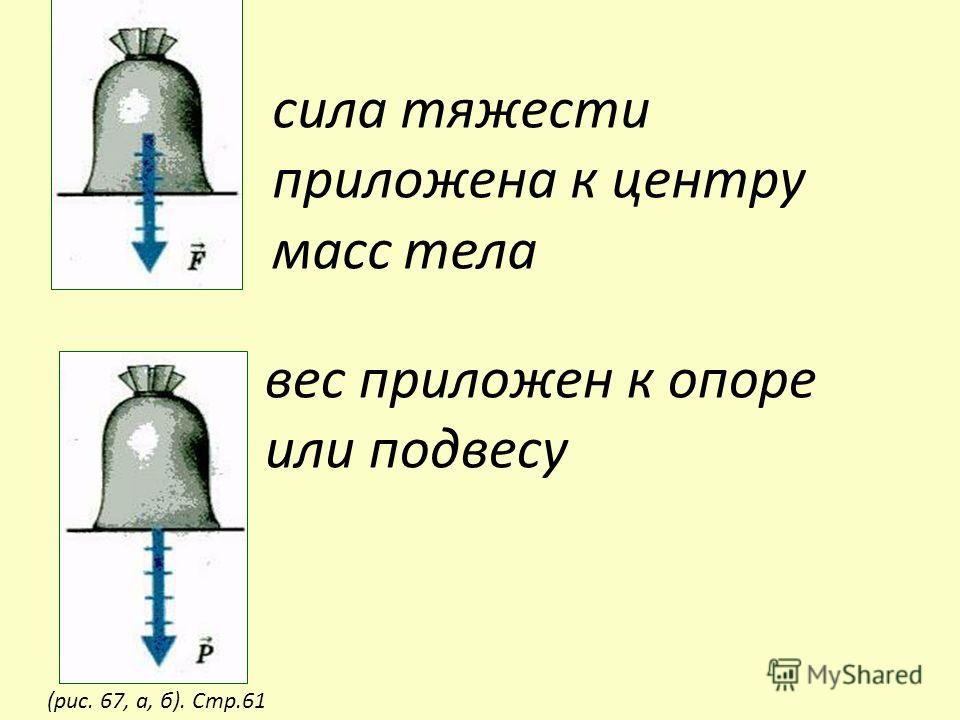 Отнимите от конечной величины начальную скорость, а полученную разницу разделите на время, за которое предмет прошел расстояние.
Можно подсчитать ускорение, подвигав предмет. Для этого необходимо передвинуть тело из состояния покоя. Теперь расстояние умножьте на два. Полученную величину разделите на время, возведенное в квадрат. Этот способ расчета ускорения подходит, если тело вначале находится в состоянии покоя.
Если имеется спидометр, то для определения ускорения необходимо возвести в квадрат начальную и конечную скорости тела. Найдите разницу квадратов конечной и начальной скоростей. Полученный результат разделите на время, умноженное на 2. Если тело движется по окружности, то оно имеет свое ускорение, даже при постоянной скорости. Для нахождения ускорения возведите скорость тела в квадрат и разделите на радиус окружности, по которой оно движется. Радиус необходимо указывать в метрах.
Отнимите от конечной величины начальную скорость, а полученную разницу разделите на время, за которое предмет прошел расстояние.
Можно подсчитать ускорение, подвигав предмет. Для этого необходимо передвинуть тело из состояния покоя. Теперь расстояние умножьте на два. Полученную величину разделите на время, возведенное в квадрат. Этот способ расчета ускорения подходит, если тело вначале находится в состоянии покоя.
Если имеется спидометр, то для определения ускорения необходимо возвести в квадрат начальную и конечную скорости тела. Найдите разницу квадратов конечной и начальной скоростей. Полученный результат разделите на время, умноженное на 2. Если тело движется по окружности, то оно имеет свое ускорение, даже при постоянной скорости. Для нахождения ускорения возведите скорость тела в квадрат и разделите на радиус окружности, по которой оно движется. Радиус необходимо указывать в метрах.
Для определения мгновенного ускорения используйте акселерометр. Если вы получили отрицательное значение ускорения, это значит, что предмет тормозит, то есть его скорость уменьшается. Соответственно при положительном значении предмет разгоняется, а его скорость увеличивается. Помните, коэффициент 9,8 можно использовать лишь в том случае, если сила тяжести определяется для предмета, который находится на земле. Если тело установлено на опору, следует учесть сопротивление опоры. Эта величина зависит от материала, из которого изготовлена опора.
Если вы получили отрицательное значение ускорения, это значит, что предмет тормозит, то есть его скорость уменьшается. Соответственно при положительном значении предмет разгоняется, а его скорость увеличивается. Помните, коэффициент 9,8 можно использовать лишь в том случае, если сила тяжести определяется для предмета, который находится на земле. Если тело установлено на опору, следует учесть сопротивление опоры. Эта величина зависит от материала, из которого изготовлена опора.
Если тело волочат не в горизонтальном направлении, то стоит взять во внимание угол, на который отклоняется предмет от горизонта. В итоге формула будет иметь следующий вид: F=m*g – Fтяги*sin. Измеряется сила тяжести в ньютонах. Для проведения расчетов используйте скорость, измеренную в м/с. Для этого поделите скорость в км/час на 3,6.
В данном параграфе мы напомним Вам о силе тяжести, центростримительном ускорение и весе тела
На каждое тело, находящееся на планете, действует гравитация Земли .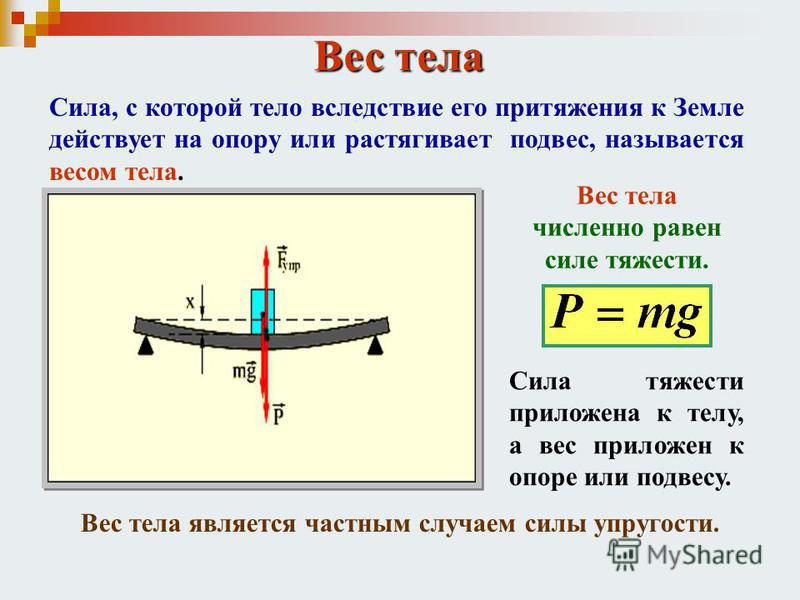 Сила, с которой Земля притягивает каждое тело, определяется по формуле
Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз .
Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести
F т =GMm/R 2
где М — масса Земли; R — радиус Земли.
Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле
F
т =GMm/R
2 модуль ускорения свободного падения g находят по формуле
g=F т /m=GM/R 2 .
Из формулы (2.29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде
F т =mg
В § 5 было отмечено, что поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы
F
т =GMm/R
2 видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.
Из формулы
F
т =GMm/R
2 видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.
Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела, например опоры, нити подвеса и т. п. Тела, ограничивающие движение других тел, называют связями. Под действием силы тяжести связи деформируются и сила реакции деформированной связи по третьему закону Ньютона уравновешивает силу тяжести.
На ускорение свободного падения влияет вращение Земли. Это влияние объясняется так. Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета — Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.
Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно 9,8 м/с 2 .
Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле
g=GM/(R+h) 2.
Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 1 м/с2.
Следовательно, вблизи Земли (до высот нескольких километров) сила тяжести практически не изменяется, а потому свободное падение тел вблизи Земли является движением равноускоренным.
 Невесомость и перегрузки
Невесомость и перегрузки Силу, в которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес — это упругая сила, приложенная к опоре или подвесу (т. е. к связи).
Наблюдения показывают, что вес тела Р, определяемый на пружинных весах, равен действующей на тело силе тяжести F т только в том случае, если весы с телом относительно Земли покоятся или движутся равномерно и прямолинейно; В этом случае
Р=F т =mg.
Если же тело движется ускоренно, то его вес зависит от значения этого ускорения и от его направления относительно направления ускорения свободного падения.
Когда тело подвешено на пружинных весах, на него действуют две силы: сила тяжести F т =mg и сила упругости F yп пружины. Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил F т и F уп дает равнодействующую, вызывающую ускорение тела, т. е.
е.
F т + F уп =mа.
Согласно приведенному выше определению понятия «вес», можно написать, что Р=-F yп. Из формулы: F т + F уп =mа. с учетом того, что F т =mg, следует, что mg-mа=-F yп . Следовательно, Р=m(g-а).
Силы F т и F уп направлены по одной вертикальной прямой. Поэтому если ускорение тела а направлено вниз (т.е. совпадает по направлению с ускорением свободного падения g), то по модулю
P=m(g-a)
Если же ускорение тела направлено вверх (т. е. противоположно направлению ускорения свободного падения), то
Р = m = m(g+а).
Следовательно, вес тела, ускорение которого совпадает по направлению с ускорением свободного падения, меньше веса покоящегося тела, а вес тела, ускорение которого противоположно направлению ускорения свободного падения, больше веса покоящегося тела. Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.
При свободном падении a=g. Из формулы: P=m(g-a)
следует, что в таком случае Р=0, т. е. вес отсутствует. Следовательно, если тела движутся только под действием силы тяжести (т. е. свободно падают), они находятся в состоянии невесомости . Характерным признаком этого состояния является отсутствие у свободно падающих тел деформаций и внутренних напряжений, которые вызываются у покоящихся тел силой тяжести. Причина невесомости тел заключается в том, что сила тяжести сообщает свободно падающему телу и его опоре (или подвесу) одинаковые ускорения.
е. вес отсутствует. Следовательно, если тела движутся только под действием силы тяжести (т. е. свободно падают), они находятся в состоянии невесомости . Характерным признаком этого состояния является отсутствие у свободно падающих тел деформаций и внутренних напряжений, которые вызываются у покоящихся тел силой тяжести. Причина невесомости тел заключается в том, что сила тяжести сообщает свободно падающему телу и его опоре (или подвесу) одинаковые ускорения.
Определение 1
Сила тяжести считается приложением к центру тяжести тела, определяемому путем подвешивания тела на нити за его различные точки. При этом точка пересечения всех направлений, которые отмечены нитью, и будет считаться центром тяжести тела.
Понятие силы тяжести
Силой тяжести в физике считают силу, действующую на любое физическое тело, пребывающее вблизи земной поверхности либо иного астрономического тела. Сила тяжести на поверхности планеты, по определению, будет складываться из гравитационного притяжения планеты, а также центробежной силы инерции, спровоцированной суточным вращением планеты.
Иные силы (например, притяжение Солнца и Луны) по причине их малости не учитываются или изучаются отдельно в формате временных изменений гравитационного поля Земли. Сила тяжести сообщает всем телам, в независимости от их массы, равное ускорение, представляя при этом консервативную силу. Она вычисляется на основании формулы:
$\vec {P} = m\vec{g}$,
где $\vec{g}$-ускорение, которое сообщается телу силой тяжести, обозначенное как ускорение свободного падения.
На тела, передвигающиеся относительно поверхности Земли, помимо силы тяжести, также оказывает непосредственное воздействие сила Кориолиса, представляющая силу, используемую при изучении движения материальной точки по отношению к вращающейся системе отсчета. Присоединение силы Кориолиса к воздействующим на материальную точку физическим силам позволит учитывать воздействие вращения системы отсчета на подобное движение.
Важные формулы для расчета
Соответственно закону всемирного тяготения, сила гравитационного притяжения, воздействующая на материальную точку с ее массой $m$ на поверхности астрономического сферически симметричного тела с массой $M$, будет определяться соотношением:
$F={G}\frac{Mm}{R^2}$, где:
- $G$-гравитационная постоянная,
- $R$- радиус тела.
 2\vec{R_0}}$, где:
2\vec{R_0}}$, где:$\vec {R_0}$- вектор, перпендикулярный оси вращения, который проведен от нее к указанной материальной точке, пребывающей вблизи поверхности Земли.
При этом сила тяжести $\vec {P}$ будет равнозначна сумме $\vec {F}$ и $\vec {Q}$:
$\vec{P} = \vec{F} = \vec{Q}$
Закон притяжения
Без присутствия силы тяжести стало бы невозможным происхождение многих, сейчас кажущихся нам естественными, вещей: так, не было бы схождение с гор лавин, течения рек, дождей. Атмосфера Земли может сохраняться исключительно благодаря воздействию силы тяжести. Планеты с меньшей массой, например, Луна или Меркурий, растеряли всю свою атмосферу довольно стремительными темпами и стали беззащитными перед потоками агрессивного космического излучения.
Атмосфера Земли сыграла решающее значение при процессе формирования жизни на Земле, ее. Помимо силы тяжести, на Земле воздействует также сила притяжения Луны. За счет ее близкого соседства (в космических масштабах), на Земле возможно существование отливов и приливов, а многие биологические ритмы являются совпадающими с лунным календарем.
 Силу тяжести, таким образом, нужно рассматривать в формате полезного и важного закона природы.
Силу тяжести, таким образом, нужно рассматривать в формате полезного и важного закона природы.Замечание 2
Закон притяжения считается универсальным и возможен к применению в отношении любых двух тел, обладающих определенной массой.
В ситуации, если масса одного взаимодействующего тела оказывается намного больше массы второго, говорится о частном случае гравитационной силы, для которого существует специальный термин, такой как «сила тяжести». Он применим к задачам, ориентированным на определение силы притяжения на Земле или иных небесных телах. При подставлении значения силы тяжести в формулу второго закона Ньютона, получаем:
Здесь $а$ – ускорение силы тяжести, принуждающее тела стремиться друг к другу. В задачах, связанных с задействованием ускорения свободного падения, такое ускорение обозначают буквой $g$. С помощью собственного интегрального исчисления, Ньютону математически удалось доказать постоянную сосредоточенность силы тяжести в центре большего тела.
Пространственные спектры и фрактальность рельефа, силы тяжести и снимков / Хабр
Взаимосвязь рельефа и силы тяжести напоминает известную проблему «курицы и яйца».
 С одной стороны, рельеф несомненно влияет на измеряемую на его поверхности силу тяжести — уровень рельефа определяет расстояние до центра масс планеты, а возвышения рельефа содержат дополнительные притягивающие массы. С другой стороны, сила тяжести так же несомненно влияет на рельеф, что особенно заметно в океанах, форма поверхности которых повторяет аномалии силы тяжести. Мало этого, на поверхность рельефа воздействуют ветровая и водная эрозия и множество других факторов, так что характер взаимосвязи рельефа и силы тяжести становится сложно предсказать. Космические снимки также воспроизводят формы рельефа — вместе с формами и цветами растительности и всего прочего на этом рельефе, так что характер взаимосвязи снимков и рельефа оказывается еще менее очевидным.
С одной стороны, рельеф несомненно влияет на измеряемую на его поверхности силу тяжести — уровень рельефа определяет расстояние до центра масс планеты, а возвышения рельефа содержат дополнительные притягивающие массы. С другой стороны, сила тяжести так же несомненно влияет на рельеф, что особенно заметно в океанах, форма поверхности которых повторяет аномалии силы тяжести. Мало этого, на поверхность рельефа воздействуют ветровая и водная эрозия и множество других факторов, так что характер взаимосвязи рельефа и силы тяжести становится сложно предсказать. Космические снимки также воспроизводят формы рельефа — вместе с формами и цветами растительности и всего прочего на этом рельефе, так что характер взаимосвязи снимков и рельефа оказывается еще менее очевидным.К счастью, поле силы тяжести и рельеф поверхности нашей планеты обладают свойством фрактальности, то есть самоподобия на разных масштабах, что и является ключом для определения характера связи между ними.
Измерение фрактальной размерности
Существует множество способов определения фрактальной размерности, и общего у них только наличие характерного пространственного масштаба.
 Можно производить вычисления фрактальности в пространственной области, а можно и в частотной (компоненты пространственного спектра), дифференцировать и интегрировать… Секрет в том, что всё многообразие способов дает схожие результаты и выбор конкретного способа довольно произволен, важно лишь понимать, как результаты выбранного метода вычислений сопоставить с результатами других методов (Gneiting et al., 2012).
Можно производить вычисления фрактальности в пространственной области, а можно и в частотной (компоненты пространственного спектра), дифференцировать и интегрировать… Секрет в том, что всё многообразие способов дает схожие результаты и выбор конкретного способа довольно произволен, важно лишь понимать, как результаты выбранного метода вычислений сопоставить с результатами других методов (Gneiting et al., 2012).Возможно, фундаментальная математика это совсем не то, что вы ожидаете найти в этой публикации, но нам и не потребуются серьезные знания в области интегродифференциального и кумулянтного исчислений — мы ограничимся обзорной экскурсией в некоторые из их свойств.
Производная (или дифференциал) означает наклон или приращение кривой, а интеграл (или отрицательная производная) означает заполнение или площадь под кривой. Таким образом, для произвольной кривой (одномерного сигнала) дифференциальный способ оперирует ломаной, характеризующей границу кривой, а интегральный способ — площадью под кривой.
 Удивительно здесь то, что и дифференцирование и интегрирование задают пространственный масштаб, или окно вычислений. С интегралом сразу понятно, ведь площадь, очевидно, зависит от ширины фигуры под кривой, а вот с дифференциалом все не так просто. Подумаем, сколько значений минимально необходимо для вычисления первого дифференциала. Очевидно, два — ведь нам нужно посчитать разницу между ними. А для второго дифференциала нам нужно вычислить разницу между двумя первыми дифференциалами, каждый из которых требует два значения и, если взять одно общее значение для вычисления первых дифференциалов, то потребуется три значения. Как видим, для вычисления N-го дифференциала необходимо N+1 значений. Значит, степень производной (дифференциала) также определяет пространственный масштаб. Таким образом, можно определить фрактальную размерность через интегрирование по отрезку изменяемого размера (окну), или через производные разных порядков (включая дробные и отрицательные, при этом последние соответствуют одной из первообразных, то есть интегралам).
Удивительно здесь то, что и дифференцирование и интегрирование задают пространственный масштаб, или окно вычислений. С интегралом сразу понятно, ведь площадь, очевидно, зависит от ширины фигуры под кривой, а вот с дифференциалом все не так просто. Подумаем, сколько значений минимально необходимо для вычисления первого дифференциала. Очевидно, два — ведь нам нужно посчитать разницу между ними. А для второго дифференциала нам нужно вычислить разницу между двумя первыми дифференциалами, каждый из которых требует два значения и, если взять одно общее значение для вычисления первых дифференциалов, то потребуется три значения. Как видим, для вычисления N-го дифференциала необходимо N+1 значений. Значит, степень производной (дифференциала) также определяет пространственный масштаб. Таким образом, можно определить фрактальную размерность через интегрирование по отрезку изменяемого размера (окну), или через производные разных порядков (включая дробные и отрицательные, при этом последние соответствуют одной из первообразных, то есть интегралам). За подробностями рекомендую обратиться к публикациям ныне покойного профессора Нижегоро́дского госуда́рственного университе́та и́мени Н. И. Лобаче́вского (Университет Лобачевского, ННГУ) — Александра Ивановича Саичева, в которых я и нашел связь фрактальности с дробными производными (Саичев, В. А. Филимонов, 2008).
За подробностями рекомендую обратиться к публикациям ныне покойного профессора Нижегоро́дского госуда́рственного университе́та и́мени Н. И. Лобаче́вского (Университет Лобачевского, ННГУ) — Александра Ивановича Саичева, в которых я и нашел связь фрактальности с дробными производными (Саичев, В. А. Филимонов, 2008).Корреляционная размерность и (поли)спектры определяются наборами значений с заданными расстояниями между ними, то есть содержат пространственный масштаб. Через них, соответственно, тоже можно определять фрактальную размерность. Основой для описания и понимания (поли)спектрального и корреляционного видов анализа является анализ кумулянтный (Дубков, Малахов, 1973). Для детального ознакомления рекомендую к прочтению теоретические и практические работы по кумулянтному и биспектральному (полиспектральному) анализу от преподавателей ННГУ Александра Александровича Дубкова и Германа Николаевича Бочкова, у которых мне посчастливилось учиться. Пользуюсь случаем поблагодарить их обоих, а Германа Николаевича еще и поздравить с юбилеем 80 лет!
Далее мы будем пользоваться вычислением фрактальной размерности через дисперсию компонентов оконного дискретного спектра мощности.
 В пространственной области аналогичный анализ выполняется круговым преобразованием Радона с дисперсией как базовой функцией. Иными словами, если в ранее нами использованном круговом преобразовании Радона, см. Методы компьютерного зрения для решения обратной задачи геофизики, заменить вычисление среднего значения на дисперсию (стандартное отклонение), тоже получится способ вычисления фрактальной размерности, притом довольно популярный (хотя и под разными названиями) в геологической литературе (см. ссылки в конце статьи). В радиофизике для описания подобных преобразований есть так называемые методы синтеза апертуры, то есть получения большого количества отсчетов вместо одного. Классический пример — локатор бокового обзора (эхолот, в том числе) излучает и принимает отраженные сигналы непрерывно и для вычисления расстояния до каждой точки береговой линии или рельефа дна используется множество измерений, что позволяет сильно улучшить точность. Для нашей задачи рассмотрим простой пример — можем ли мы определить фрактальность в одной точке рельефа разрешением 10 м? Очевидно, нет.
В пространственной области аналогичный анализ выполняется круговым преобразованием Радона с дисперсией как базовой функцией. Иными словами, если в ранее нами использованном круговом преобразовании Радона, см. Методы компьютерного зрения для решения обратной задачи геофизики, заменить вычисление среднего значения на дисперсию (стандартное отклонение), тоже получится способ вычисления фрактальной размерности, притом довольно популярный (хотя и под разными названиями) в геологической литературе (см. ссылки в конце статьи). В радиофизике для описания подобных преобразований есть так называемые методы синтеза апертуры, то есть получения большого количества отсчетов вместо одного. Классический пример — локатор бокового обзора (эхолот, в том числе) излучает и принимает отраженные сигналы непрерывно и для вычисления расстояния до каждой точки береговой линии или рельефа дна используется множество измерений, что позволяет сильно улучшить точность. Для нашей задачи рассмотрим простой пример — можем ли мы определить фрактальность в одной точке рельефа разрешением 10 м? Очевидно, нет. Если же мы проанализируем все точки в кольцах радиуса от 1 до 1000 пикселов (в диапазоне 10 м… 10 км для заданного разрешения), включающих от 4х до ~6000 пикселов (2πR, где R это радиус кольца), то сможем с высокой точностью вычислить фрактальную размерность. При этом точность вычисления пропорциональна квадратному корню из числа пикселов или радиуса колец. А теперь в игру вступают силы природы — если мы наблюдаем фрактальность на масштабе от 1 пиксела и более, эта же фрактальность гарантированно присутствует и на меньших масштабах, хотя мы не можем определить точно граничный масштаб. Небольшое отступление: в лабораторных экспериментах с моделированием динамики фотополимеров мы находили этот граничный масштаб в области сотен нанометров (где молекулы образуют сетчатые структуры и не гауссовые и не фрактальные), так что для геологических исследований граничного масштаба просто нет. Таким образом, благодаря самой сути явления фрактальности, становится возможным обнаружить области залегания фрактальных рудных тел размером значительно менее метра при анализе спутниковых оптических или радарных снимков 5-10 м разрешения (например, Sentinel-1 и Sentinel-2).
Если же мы проанализируем все точки в кольцах радиуса от 1 до 1000 пикселов (в диапазоне 10 м… 10 км для заданного разрешения), включающих от 4х до ~6000 пикселов (2πR, где R это радиус кольца), то сможем с высокой точностью вычислить фрактальную размерность. При этом точность вычисления пропорциональна квадратному корню из числа пикселов или радиуса колец. А теперь в игру вступают силы природы — если мы наблюдаем фрактальность на масштабе от 1 пиксела и более, эта же фрактальность гарантированно присутствует и на меньших масштабах, хотя мы не можем определить точно граничный масштаб. Небольшое отступление: в лабораторных экспериментах с моделированием динамики фотополимеров мы находили этот граничный масштаб в области сотен нанометров (где молекулы образуют сетчатые структуры и не гауссовые и не фрактальные), так что для геологических исследований граничного масштаба просто нет. Таким образом, благодаря самой сути явления фрактальности, становится возможным обнаружить области залегания фрактальных рудных тел размером значительно менее метра при анализе спутниковых оптических или радарных снимков 5-10 м разрешения (например, Sentinel-1 и Sentinel-2). Смотрите практические примеры в публикации Ударим биспектром по бездорожью, или как найти золото в Сибири. Обратите внимание, что сегодня мы рассматриваем спектральный метод, а не биспектральный, который обладает дополнительным важным свойством исключения гауссовых сигналов и, таким образом, значительно более чувствителен за счет полного «игнорирования» всех гауссовых помех, представляющих неразрешимую проблему для спектрального анализа на субпиксельных масштабах.
Смотрите практические примеры в публикации Ударим биспектром по бездорожью, или как найти золото в Сибири. Обратите внимание, что сегодня мы рассматриваем спектральный метод, а не биспектральный, который обладает дополнительным важным свойством исключения гауссовых сигналов и, таким образом, значительно более чувствителен за счет полного «игнорирования» всех гауссовых помех, представляющих неразрешимую проблему для спектрального анализа на субпиксельных масштабах.Отдельно отметим, что нет принципиальной разницы между двумерным и одномерным анализом фрактальности. Например, для вышеуказанного метода кольцевого преобразования Радона с базовой функцией дисперсией анализ является одномерным (в кольцах) для двумерных исходных данных. Этому методу можно сопоставить двумерный с вычислением дисперсии в кругах или даже квадратах (упрощаются вычисления ценой ухудшения точности из-за потери радиальной симметрии — вариация расстояний от центра до границы квадрата искажает масштаб) соответствующего масштаба.
 Практическая разница возникает при наличии гауссовых помех, которые мы хотим исключить — очевидно, что радиально симметричный анализ более применим для такого случая. В литературе можно встретить вариацию указанных подходов с вычислением количества пикселов, превышающих среднее значение (в кольцах, кругах или квадратах) вместо более устойчивого вычисления дисперсии.
Практическая разница возникает при наличии гауссовых помех, которые мы хотим исключить — очевидно, что радиально симметричный анализ более применим для такого случая. В литературе можно встретить вариацию указанных подходов с вычислением количества пикселов, превышающих среднее значение (в кольцах, кругах или квадратах) вместо более устойчивого вычисления дисперсии.Изостазия и граница фрактальности рельефа и силы тяжести
В статье Легенды и мифы геофизики мы узнали, что среди геофизиков существует миф об отсутствии связи между рельефом и силой тяжести, и показали, что на самом эта связь существует для определенного диапазона масштабов. А теперь разберемся с ней подробнее.
Как мы обсудили выше, нижнего предела масштаба фрактальности рельефа для практических целей не существует, а вот верхний предел есть и геологам он хорошо известен как глубина изостазии:
ИЗОСТАЗИ́Я (от изо… и греч. στάσις – состояние), состояние механич. равновесия поверхностной оболочки Земли, при котором на некоторой глубине (обычно принимаемой равной 100–150 км) в верхней мантии давление вышележащих пород становится одинаковым.
 В этом случае избыток или недостаток масс на поверхности Земли компенсируется соответствующим перераспределением масс в её недрах. [Большая Российская Энциклопедия — Изостазия]
В этом случае избыток или недостаток масс на поверхности Земли компенсируется соответствующим перераспределением масс в её недрах. [Большая Российская Энциклопедия — Изостазия]Заметим, что это определение означает, что ниже глубины изостазии недра нашей планеты ведут себя подобно жидкости, а твердые породы располагаются выше этой границы (см. предыдущую ссылку):
… кора плавает в вязкой мантии в соответствии с законом Архимеда, т. е. находится в состоянии гидростатич. равновесия. [Большая Российская Энциклопедия — Изостазия]
С учетом известного нам соотношения между длиной волны и глубиной ее гравитационного источника, см. Методы компьютерного зрения для решения обратной задачи геофизики, для пространственных компонент рельефа и поля силы тяжести верхняя граница фрактальности составляет примерно 150-300 км, варьируясь для разных регионов планеты. Вполне очевидно, что (сжатая вязкая) жидкость не обладает свойством фрактальности, в отличие от твердых тел, что и является причиной исчезновения эффекта.

Что интересно, известно об эффекте изостазии уже почти три столетия, и первооткрывателем был тот самый Буге (Бугер), результаты работ которого и сегодня вызывают столько недопонимания, см. Легенды и мифы геофизики:
Данные о том, что вес горного сооружения компенсируется более лёгкими массами на глубине, впервые получил П. Бугер в 1749. Проанализировав результаты экспедиции 1736, он обнаружил, что в предгорьях Анд угол уклонения отвеса от вертикали значительно меньше того, который должны создавать массы горного рельефа. [Большая Российская Энциклопедия — Изостазия]
Определение границы Мохоровича (Мохо) по значениям фрактальности и корреляции пространственных спектров рельефа и силы тяжести
Обратимся снова к вышеупомянутой статье энциклопедии:
Амер. геолог Дж. Баррелл в 1914–15 и нидерл. геофизик Ф. Вейнинг-Мейнец в 1931 развили эту схему изостатич.
 компенсации. Они предположили, что верхняя часть литосферы является упругой, и использовали решение задачи об изгибе внешними силами упругой плиты, плавающей на жидком основании. [Большая Российская Энциклопедия — Изостазия]
компенсации. Они предположили, что верхняя часть литосферы является упругой, и использовали решение задачи об изгибе внешними силами упругой плиты, плавающей на жидком основании. [Большая Российская Энциклопедия — Изостазия]Из вышесказанного становится понятно, что фрактальность проявляется максимально для твердого слоя (земной коры), далее резко снижается для слоя упругого и совсем исчезает при переходе к вязкой магме. Граница, или подошва, твердой земной коры определяется так называемой границей Мохоровича (Мохо), и до этой границы наблюдаются высокая фрактальность и корреляция пространственных спектров силы поля тяжести и рельефа близка к единице (100%).
Посмотрим на графики из публикации Легенды и мифы геофизики:
Здесь правый график является диагональным сечением левого. Смещение в начале оси абсцисс на графиках соответствует глубине океана на рассматриваемой территории (2.5 — 5 км). Очень высокая корреляция (90% и выше) наблюдается до маштаба ~15 км, высокая корреляция (75% и выше) до ~35 км, и дальше наблюдается плавный спад значимости корреляции.
 Как мы рассмотрели ранее, масштаб, на котором исчезает значимая корреляция, и будет соответствовать достижению изостазии. Для океанского дна на рассматриваемой нами территории граница Мохо расположена на глубине 11 км согласно модели CRUST 1.0: A New Global Crustal Model at 1×1 Degrees, что соответствует длине волны 15 км, как мы и видим на графиках. Граница слоя упругости составит около 25 км (длина волны 35 км). Таким образом, по корреляции компонентов пространственных спектров поля силы тяжести и рельефа можно определить границы Мохоровича (Мохо), упругого слоя и изостазии.
Как мы рассмотрели ранее, масштаб, на котором исчезает значимая корреляция, и будет соответствовать достижению изостазии. Для океанского дна на рассматриваемой нами территории граница Мохо расположена на глубине 11 км согласно модели CRUST 1.0: A New Global Crustal Model at 1×1 Degrees, что соответствует длине волны 15 км, как мы и видим на графиках. Граница слоя упругости составит около 25 км (длина волны 35 км). Таким образом, по корреляции компонентов пространственных спектров поля силы тяжести и рельефа можно определить границы Мохоровича (Мохо), упругого слоя и изостазии.Посмотрим также графики значений геологической плотности, вычисленной по фрактальной размерности батиметрии и поля силы тяжести на поверхности из того же ноутбука:
Горизонтальное смещение кривых плотности вызвано приведением поля силы тяжести к поверхности, а батиметрии, очевидно, ко дну океана. Здесь мы также легко выделяем области пространственных масштабов около 15 км и 35 км, как и на предыдущих графиках.
 Как будет показано далее, значение фрактальной плотности по данным рельефа является оценкой сверху для геологической плотности и при увеличении площади наблюдения при ее неоднородности приводит к систематическому завышению оценки плотности фрактальным методом.
Как будет показано далее, значение фрактальной плотности по данным рельефа является оценкой сверху для геологической плотности и при увеличении площади наблюдения при ее неоднородности приводит к систематическому завышению оценки плотности фрактальным методом.Сила Кориолиса и фрактальность рельефа и силы тяжести
Теперь вспомним, что закон Архимеда, на который ссылается статья энциклопедии выше, является гравитационным выталкиванием (кстати, космонавты на орбите живут без силы Архимеда) и становится ясно, что вся геология определяется гравитационными и инерционными силами в твердых и жидких частях планеты. Инерционные силы, включая силу Кориолиса, чрезвычайно важны для рассмотрения как поверхностных потоков, так и мантийных плюмов и их выходов на поверхность (вулканизм). Хотя всем знакомо явление закручивания жидкости в стоках раковины или ванны, но не все знают, что это направление зависит от полушария, равно как и расположение обрывистого и пологого берегов рек. Ранее я уже показывал детальные геологические модели, и на них легко заметить асимметрию, вызванную силой Кориолиса — поэтому, в зависимости от полушария, бурить следует в разных частях рудо- или нефтегазоконтролирующих структур.
 Кстати, это и еще один способ проверить корректность построенных моделей. Направление тектонических разломов также меняется из-за воздействия силы Кориолиса на тектонические плиты, особенно интересно это проявляется при пересечении экватора. Таким образом, на поверхности планеты появляются асимметричные фрактальные структуры рельефа и поля силы тяжести масштабов до сотен километров, при этом, направление асимметрии сохраняется и до намного больших масштабов.
Кстати, это и еще один способ проверить корректность построенных моделей. Направление тектонических разломов также меняется из-за воздействия силы Кориолиса на тектонические плиты, особенно интересно это проявляется при пересечении экватора. Таким образом, на поверхности планеты появляются асимметричные фрактальные структуры рельефа и поля силы тяжести масштабов до сотен километров, при этом, направление асимметрии сохраняется и до намного больших масштабов.Если мы рассмотрим острова Индонезии в Южном полушарии, то потоки гидротермальных растворы с минералами под действием силы Кориолиса должны отклоняться влево от направления движения. Посмотрим на региональную модель из статьи Ищем рудное золото на острове Сумбава, Индонезия:
Зная про влияние силы Кориолиса, мы делаем вывод, что гидротермальные растворы двигались из глубины в центре модели — и теперь мы можем указать возможное расположение золоторудных выходов для всей западной части острова Сумбава. Из-за радиального распространения рудоконтролирующих структур без учета силы Кориолиса расположение золоторудных выходов кажется хаотическим, хотя, на самом деле, подчиняется строгой закономерности.

В Западной Сибири, расположенной в Северном полушарии, гидротермальные потоки отклоняются вправо. Вернемся к модели из статье Ударим биспектром по бездорожью, или как найти золото в Сибири:
Здесь золотое и молибденовое месторождения расположены с разных сторон выхода глубинной структуры — следовательно, контролирующие их гидротермальные потоки двигались в разных направлениях и мы можем на большей модели отследить их источники и найти другие их выходы. Также имеет смысл проанализировать более детальную модель, чтобы выделить две независимые структуры, сливающиеся в единую на рассматриваемом масштабе.
Замечу, что в геологической литературе описания указанной закономерности я никогда не встречал, хотя все это очевидно из школьного курса физики — если знать, на что смотреть.
И снова о редукции Бугера (Буге)
В уже упомянутой выше публикации Легенды и мифы геофизики мы показали, что на самом деле, редукция Буге не удаляет (полностью) корреляцию спектральных компонентов измеренной силы тяжести и рельефа.
 Стоит отметить, что основная проблема проявляется для диапазона масштабов до 20 км, что вовсе не было проблемой для самого Буге, поскольку детальность его данных была ниже и для них придуманная им редукция работала практически идеально. Поскольку это просто классический «секрет Полишинеля», то придуманы и способы исправить ситуацию — например, исходя из равной фрактальности рельефа и силы тяжести, можно подобрать параметры преобразования Буге, чтобы несколько уменьшить фрактальность (Miranda et al., 2015). В работе (Zhang, Featherstone, 2019) для территории Австралии методами фрактального и спектрального анализа показано, что топография, редукция Буге и аномалии в свободном воздухе имеют почти идентичные фрактальные размерности и спектры, при этом использование редукции Буге приводит к наибольшим ошибкам.
Стоит отметить, что основная проблема проявляется для диапазона масштабов до 20 км, что вовсе не было проблемой для самого Буге, поскольку детальность его данных была ниже и для них придуманная им редукция работала практически идеально. Поскольку это просто классический «секрет Полишинеля», то придуманы и способы исправить ситуацию — например, исходя из равной фрактальности рельефа и силы тяжести, можно подобрать параметры преобразования Буге, чтобы несколько уменьшить фрактальность (Miranda et al., 2015). В работе (Zhang, Featherstone, 2019) для территории Австралии методами фрактального и спектрального анализа показано, что топография, редукция Буге и аномалии в свободном воздухе имеют почти идентичные фрактальные размерности и спектры, при этом использование редукции Буге приводит к наибольшим ошибкам.Но зачем же так нужен этот святой Грааль геофизики, «идеальная» редукция Буге (идеализация, которой не существует)? Ответ прост — плоскую карту измеренных значений силы тяжести сложно вручную сопоставлять с плоской же картой рельефа.
 А результатом редукции Буге должна быть плоская карта с показанными на ней аномалиями силы тяжести, полностью соответствующими аномалиям плотности, не требующая сопоставления с рельефом. Поскольку при этом игнорируется глубинное расположение аномалий, то из-за неоднозначности по глубине, очевидно, часть аномалий плотности будут потеряны — что, опять же, не представляло проблемы для самого Буге в силу масштаба его измерений (малые аномалии, которые можно было бы потерять при таком преобразовании, он просто не мог измерить).
А результатом редукции Буге должна быть плоская карта с показанными на ней аномалиями силы тяжести, полностью соответствующими аномалиям плотности, не требующая сопоставления с рельефом. Поскольку при этом игнорируется глубинное расположение аномалий, то из-за неоднозначности по глубине, очевидно, часть аномалий плотности будут потеряны — что, опять же, не представляло проблемы для самого Буге в силу масштаба его измерений (малые аномалии, которые можно было бы потерять при таком преобразовании, он просто не мог измерить).Фрактальность рельефа, силы тяжести и снимков
При моделировании поля силы тяжести от набора гауссовых глубинных источников 3D Density Inversion by Circular Hough Transform (Focal Average) and Fractality Index оказывается, что это поле на поверхности обладает выраженной фрактальной размерностью, причем эта размерность пропорциональна распределению плотности с глубиной. Таким образом, становится ясно, что первопричиной является фрактальность гравитационного поля, которая с высочайшей корреляцией проявляется и в рельефе, следовательно, эрозионные процессы не нарушают эту взаимосвязь.
 Для космических или ортофотоснимков значение фрактальности оказывается выше за счет вариаций цвета, не связанных с изменениями рельефа. Выбирая подходящий спектральный диапазон, в котором поверхность имеет наименьшую спектральную размерность, мы можем оценить плотность пород поверхности. Обратимся к доступному на GitHub ноутбуку Geological Fractality on ALOS DEM AW3D30 and Sentinel-2 SUrface Reflectance Image for Ravar, Kerman Province, Iran:
Для космических или ортофотоснимков значение фрактальности оказывается выше за счет вариаций цвета, не связанных с изменениями рельефа. Выбирая подходящий спектральный диапазон, в котором поверхность имеет наименьшую спектральную размерность, мы можем оценить плотность пород поверхности. Обратимся к доступному на GitHub ноутбуку Geological Fractality on ALOS DEM AW3D30 and Sentinel-2 SUrface Reflectance Image for Ravar, Kerman Province, Iran:Плотность, вычисленная по фрактальной размерности рельефа, равна ρ=3200 kg/m³ при R²=0.99, что вполне согласуется с плотностью магматических пород, образующих эту территорию. По космическому снимку значение плотности выше и составляет ρ=3500 kg/m³ при R²=1.00, что соответствует плотности поверхностных метаморфических пород, вероятно покрывающих часть территории. При этом следует учитывать, что индекс фрактальной размерности рассчитывается по вариации значений и систематически завышает оценку в том случае, если территория неоднородна по составу.
 Таким образом, полученные нами значения являются оценкой сверху. Для получения более точных значений необходимо сегментировать территорию на гомогенные участки и выполнить вычисления для них по отдельности. Кроме того, перегибы кривой фрактальной размерности пропорциональны глубинам, на которых геологическая плотность изменяется.
Таким образом, полученные нами значения являются оценкой сверху. Для получения более точных значений необходимо сегментировать территорию на гомогенные участки и выполнить вычисления для них по отдельности. Кроме того, перегибы кривой фрактальной размерности пропорциональны глубинам, на которых геологическая плотность изменяется.Заключение
Если вы все же дочитали статью до конца (надеюсь), то я искренне рад за вас! Действительно, это было не так просто — ведь мы связали воедино множество подходов из разных наук, начиная от фундаментальной физики и математики, продолжая численным моделированием и заканчивая геологией и геофизикой. Теперь вы знаете множество определений и методов вычисления фрактальности, а главное — видите то единственное, что есть у них общего. А еще понимаете, как и почему проявляется фрактальность в природе и, возможно, даже сможете найти золото на далеких теплых островах или в холодной Сибири по открытым данным космической съемки для геологического анализа любой детальности, воспользовавшись современной математикой и физикой для анализа негауссовых процессов и фрактальности.

Также смотрите
- Мои статьи на Хабре
- Теоретические и практические статьи и посты на LinkedIn
- Геологические модели и код на GitHub
- YouTube канал с геологическими моделями
- Геологические модели в виртуальной/дополненной реальности (VR/AR)
Ссылки
Кумулянтный анализ функционального нелинейного преобразования негауссовых случайных процессов и полей, А. А. Дубков, А. Н. Малахов, 1973. http://m.mathnet.ru/links/cd623304046883b7c36697e2e9f9b1d0/dan39067.pdf
Кумулянтный анализ случайных негауссовых процессов и их преобразований, Малахов А.Н.,1978. https://ikfia.ysn.ru/wp-content/uploads/2018/01/Malahov1978ru.pdf
Численное моделирование реализаций и спектры квазимультифрактального диффузионного процесса, А. И. Саичев, В. А. Филимонов, 2008. http://www.mathnet.ru/links/2a351947644994381a8272c4fc3ba0dd/jetpl108.pdf
Numerical simulation of the realizations and spectra of a quasi-multifractal diffusion process, A.
 I. Saichev & V. A. Filimonov, https://link.springer.com/article/10.1134/S0021364008090129
I. Saichev & V. A. Filimonov, https://link.springer.com/article/10.1134/S0021364008090129Gneiting, T., Ševčíková, H. & Percival, D. B. Estimators of Fractal Dimension: Assessing the Roughness of Time Series and Spatial Data. Statist. Sci. 27, 247–277 (2012).
Zhang, K. & Featherstone, W. Exploring the Detailed Structure of the Local Earth’s Gravity Field Using Fractal and Fourier Power Spectrum Techniques. (2019).
Miranda, S. A. et al. Fractalness of land gravity data and residual isostatic anomalies map of Argentina, Chile and western Uruguay. Geofísica internacional 54, 315–322 (2015).
6 примеров гравитационной силы в нашей повседневной жизни
Распространите любовь
Хотите знать, какие 6 эксклюзивных примеров гравитационной силы встречаются в повседневной жизни? Если да, то не смотрите дальше…!!! Потому что в этой эксклюзивной статье я собираюсь раскрыть некоторые известные примеры из повседневной жизни, которые вы видели, но никогда не думали о них как о примере гравитации в действии.

Так что же такое гравитационная сила? Откровенно говоря, никто не знает, что такое гравитация! Но что мы знаем наверняка о гравитации, так это то, как она работает. Гравитационная сила — это сила притяжения, которая притягивает два объекта друг к другу.
Точнее, когда два тела притягиваются друг к другу в силу того, что их массы находятся на расстоянии друг от друга. Наблюдается сила тяжести. Независимо от того, является ли рассматриваемый объект самым маленьким или самым большим, каждый из них оказывает гравитационное воздействие на любой другой объект.
Другими словами, все, что имеет массу, воздействует на другой объект силой тяжести. В гравитации так много загадок, которых мы до сих пор не знаем! Например, почему гравитация является только силой притяжения? Почему бы не отталкивающую, как и все остальные основные силы природы.
Примеры гравитационной силы в нашей повседневной жизни
Если вы думаете, что не можете привести примеры гравитационной силы в повседневной жизни.
 Ну, вот ваш шанс подумать еще раз.
Ну, вот ваш шанс подумать еще раз.- Приливы в Ocean
- Water in Glass
- Яблоко, падающее с дерева
- Вы не можете летать
- Революция Луны вокруг Земли
- Дожди
Самым первым в моем списке 6 лучших примеров гравитационных сил в повседневной жизни являются приливы и отливы в океане. Приливы и отливы в океане обычно происходят из-за гравитационного притяжения, вызванного солнцем, а также нашим естественным спутником, то есть Луной.
Приливные силы (вызванные Луной) воздействуют на Землю, поэтому ее вода внутри океана выпячивается в сторону, ближайшую к Луне. В результате мы видим приливы в океане. Точно так же, когда Луна находится дальше всего от той стороны Земли, с которой она обращена, гравитационное притяжение отсутствует из-за гравитации Луны. В результате мы видим отливы в океане.
Эту же формулу можно применить к гравитационному притяжению Солнца и тому, как оно вызывает приливы и отливы в океане.
Вода в стакане Источник изображения: BBC Science Focus Magazine Только потому, что существует гравитационное притяжение из-за гравитации Солнца и Луны, мы можем извлекать приливную энергию, которую позже используем для производства электричества.
Только потому, что существует гравитационное притяжение из-за гравитации Солнца и Луны, мы можем извлекать приливную энергию, которую позже используем для производства электричества.Вы когда-нибудь задумывались, когда вы наливаете воду в стакан, почему он всегда остается на дне? Позвольте мне перефразировать это для вас…!!! Вы когда-нибудь задумывались, когда вы наливаете воду в стакан, почему она никогда не парит и не поднимается до верха стакана?
Вода остается на дне стакана под действием силы тяжести. Гравитационное притяжение, вызванное землей к воде, никогда не позволяло ей подняться до краев. Поэтому в результате вода, которую вы наливаете, всегда остается на дне стакана.
Яблоко, падающее с дерева Источник изображения: Mega InterestВсе мы слышали истории о том, как Ньютон увидел, как яблоко падает с дерева, и таким образом открыл идею гравитации.
 Он просто задал несколько основных фундаментальных вопросов о гравитации и пришел к выводу, что яблоко должно было упасть на землю из-за гравитационной силы, действующей на яблоко со стороны земли.
Он просто задал несколько основных фундаментальных вопросов о гравитации и пришел к выводу, что яблоко должно было упасть на землю из-за гравитационной силы, действующей на яблоко со стороны земли.Не говоря уже о том, что когда я учился в школе, мой учитель физики часто говорил, что мы, возможно, никогда не открыли бы законы гравитации, если бы в тот день яблоко не упало на голову Ньютона. Ну, у меня другое мнение по этому вопросу.
Согласно имеющимся индийским научным писаниям, родившийся в 12 веке индийский математик и астроном Бхаскарачарья или Бхаскара II уже сформулировал законы гравитации. В четвертой части своего трактата «Сидданта Широмани», то есть в Грахаганите (математике планет), он писал:
Источник изображения: StoryWeaver«Предметы падают на землю из-за силы притяжения земли. Следовательно, Земля, планеты, созвездия, Луна и Солнце удерживаются на орбите благодаря этому притяжению». ‘t Fly
Следующим в моем списке 6 лучших примеров силы гравитации в повседневной жизни является то, что вы не можете летать.
 Все, что вы можете делать, это ходить, бегать или даже прыгать, но, к сожалению, в конце концов вам придется вернуться на поверхность земли. Должен ли я говорить вам, почему? Ну, это происходит из-за гравитационной силы, которую оказывает на вас земля.
Все, что вы можете делать, это ходить, бегать или даже прыгать, но, к сожалению, в конце концов вам придется вернуться на поверхность земли. Должен ли я говорить вам, почему? Ну, это происходит из-за гравитационной силы, которую оказывает на вас земля.Неудивительно, что вы можете летать только и только если у вас есть крылья, как у птиц. Но все же подобно птицам, наконец, вам придется снова вернуться на поверхность земли и оставаться в непосредственном контакте с землей.
Выбор редакции: Аристотелевская Вселенная: Земля-центрированная Вселенная
Вращение Луны вокруг Земли Источник изображения: NSTAДа, вы меня правильно поняли. Вращение Луны вокруг Земли является прямым следствием гравитационной силы, которую Земля оказывает на Луну. Правильное выравнивание, как и плавное обращение Луны вокруг Земли, будет невозможно, если между ними не будет гравитационного притяжения.
Не только вращение Луны вокруг Земли, но и все планеты в нашей Солнечной системе (включая Землю) также вращаются вокруг Солнца из-за гравитационного притяжения между Солнцем и другими небесными телами.

Если вы не знаете, даже если есть правильное выравнивание между Землей и Луной из-за сил гравитации, Луна удаляется от Земли. Но не о чем беспокоиться. Потому что Луна удаляется от Земли со скоростью примерно 3,78 см. Это означает, что для полного распада на самом деле потребуются миллиарды лет.
Выбор редактора: Закон движения планет Кеплера — гелиоцентрическая модель
Осадки Источник изображения: VCCircle известен как Дождь. Благодаря силам гравитации дождь в конечном итоге падает на землю, а не поднимается вверх.Осадки являются частью непрерывного движения воды изнутри, снаружи и на поверхности земли. Солнце нагревает воду в морях и океанах. В результате вода из океана и морей испаряется, образуя водяной пар в воздухе.
Когда воздух охлаждается до точки росы и становится насыщенным. Водяной пар в воздухе конденсируется, образуя облака. Позже эти облака выпадают обратно на землю в виде дождя, снега или ледяных крупинок, очевидно, из-за гравитации.

Выбор редакции: Тихоническая модель: геогелиоцентрическая модель Вселенной
Некоторые другие примеры гравитационных сил в повседневной жизни
Помимо упомянутых выше, я также упоминаю некоторые из них.
- Кусок бумаги, падающий на землю
- Газы в звездах
- Ребенок, катающийся в парке
- Подброшенный вверх мяч всегда падает
- Устойчивость предметов
- Все, что вы роняете, падает вниз по склону
- Глобальная система позиционирования (GPS) и т. д.
Это все для этого поста. Если вам понравилась эта статья, поделитесь ею, если хотите, лайкните, если поделитесь. Вы также можете найти нас на Mix, Twitter, Pinterest и Facebook. Эй, чувак, если ты зашел так далеко, дай нам отзыв в разделе комментариев. Это сделало бы мой день. Вы также можете сделать пожертвование . Ваши пожертвования помогут нам запустить наш веб-сайт и обслуживать вас ЛУЧШЕ. Ваше здоровье!!!
Пожертвовать сейчас
Вам также может понравиться:
- 6 лучших примеров силы трения за ШЕСТЬ минут
- 6 лучших примеров равномерного движения в повседневной жизни (все новые)
- 6 примеров неравномерного движения за ШЕСТЬ минут
- 0 Top 6 примеров периодического движения в реальной жизни
- 6 основных примеров непериодического движения в повседневной жизни
Распространение любви
Простое определение и примеры + изображения
от Admin
По названию вы можете догадаться о значении этой силы.
Гравитационная сила — это сила, создаваемая гравитацией .
В физике определение гравитационной силы можно сформулировать следующим образом:
«Каждый объект во Вселенной, большой или маленький, оказывает силу на любой другой объект. Эта сила известна как Гравитационная сила “
Не правильно поняли?
Не волнуйтесь. Давайте возьмем несколько примеров из реальной жизни, чтобы понять приведенное выше утверждение.
(Так вы получите точное представление)
Сила гравитации Примеры из нашей повседневной жизни
Вот список примеров силы гравитации из повседневной жизни:
- Яблоко, падающее с дерева кран
- Мяч упал с некоторой высоты
- Вода, падающая с водопада
- Слипы монет из рук
- Прыжок в бассейне
- Теннис, выпадающий в воздух
- Теннис, выпавшие в воздухе
- .
 небо
небо
- И еще…
Давайте по порядку разберем каждый из этих примеров с картинками.
#1 Яблоко падает с дерева
Здесь яблоко падает с дерева.
Когда яблоко падает с дерева, гравитация притягивает яблоко вниз.
Этот тип силы, действующей на объект, который не требует физического контакта, известен как Гравитационная сила .
(Сила гравитации всегда направлена вниз)
#2 Вода, падающая из крана
Здесь вода льется из крана.
Когда вода падает из-под крана, сила тяжести притягивает воду вниз.
Этот тип силы, действующей на объект, который не требует физического контакта, известен как Гравитационная Сила .
(Сила гравитации всегда направлена вниз)
#3 Мяч падает с некоторой высоты
Здесь мальчик роняет мяч с некоторой высоты.
Когда мяч падает с некоторой высоты, гравитация притягивает мяч вниз.
Этот тип силы, действующей на объект, который не требует какого-либо физического контакта, известен как Гравитационная сила .

(Сила гравитации всегда направлена вниз)
#4 Вода падает из водопада
Здесь вода падает из водопада.
Когда вода падает из водопада, гравитация притягивает воду вниз.
Этот тип силы, действующей на объект, который не требует физического контакта, известен как Гравитационная сила .
(Сила гравитации всегда действует вниз)
#5 Монета выпадает из руки
Что происходит, когда монета выскальзывает из руки?
Когда монета выскальзывает из вашей руки, гравитация притягивает монету вниз.
Этот тип силы, действующей на объект, который не требует физического контакта, известен как Гравитационная сила .
(Сила гравитации всегда направлена вниз)
#6 Пловец прыгает в бассейн
Здесь пловец прыгает в бассейн.
Когда пловец прыгает в бассейн, гравитация притягивает пловца вниз.
Этот тип силы, действующей на объект, который не требует физического контакта, известен как Гравитационная сила .

(Сила гравитации всегда направлена вниз)
#7 Теннисный мяч, подброшенный в воздух
Здесь теннисный мяч подброшен в воздух.
Когда теннисный мяч подбрасывается в воздух, гравитация притягивает теннисный мяч вниз.
Этот тип силы, действующей на объект, который не требует физического контакта, известен как Гравитационная Сила .
(Сила гравитации всегда направлена вниз)
#8 Воздушный змей падает с неба
Здесь воздушный змей падает с неба.
Когда воздушный змей падает с неба, гравитация притягивает его вниз.
Этот тип силы, действующей на объект, который не требует какого-либо физического контакта, известен как Гравитационная сила .
(Сила гравитации всегда действует вниз)
.
.
.Есть так много других примеров силы гравитации, с которыми мы сталкиваемся в нашей повседневной жизни.
Резюме
Из вышеприведенных примеров понятно одно.

Если сила создается гравитацией , то говорят, что сила является гравитационной силой.
Вот как легко запомнить определение гравитационной силы:
«Каждый объект во вселенной, будь то маленький или большой, воздействует на любой другой объект. Эта сила известна как Гравитационная Сила «
».
.
.Как вы думаете, легко ли вам понять эту концепцию гравитационной силы?
(Дайте мне знать в комментариях ниже)
Связанный:
- Что такое Сила?
- Различные виды сил
- Contact Force
- Не контактная сила
- Сбалансированная сила
- Бесбалансированная сила
GRAITATION FIRCE: определение, формула и примеры
Что такая гравитационная сила?
Все объекты, имеющие массу, притягиваются друг к другу с силой, известной как гравитационная сила.
 Это весьма заметно в астрономических объектах, таких как Солнце, Земля и Луна, которые имеют огромные массы. Причина в том, что сила пропорциональна произведениям масс объектов. Он отвечает за поддержание движения планет вокруг Солнца и Луны вокруг Земли. Даже люди оказывают друг на друга силу, но она совершенно незначительна из-за относительно малых масс.
Это весьма заметно в астрономических объектах, таких как Солнце, Земля и Луна, которые имеют огромные массы. Причина в том, что сила пропорциональна произведениям масс объектов. Он отвечает за поддержание движения планет вокруг Солнца и Луны вокруг Земли. Даже люди оказывают друг на друга силу, но она совершенно незначительна из-за относительно малых масс.Гравитационная сила бесконтактна, так как нет контакта между объектами. Он центростремительный, так как направлен к центру орбиты, вокруг которой движется объект. Он отвечает за удержание тела на орбите. Вращающееся тело ощущает рывок, направленный от центра. Этот рывок называется центробежной силой. Гравитационное взаимодействие является самым слабым из всех фундаментальных взаимодействий.
Gravitational ForceМногие известные ученые внесли значительный вклад в изучение гравитации. Итальянский астроном Галилео Галилей в начале 1799 г.0396-го -го века, установили, что все объекты одинаково ускоряются по направлению к центру Земли.
 Английский математик Исаак Ньютон первым открыл законы гравитации в своей основополагающей работе 1687 года.
Английский математик Исаак Ньютон первым открыл законы гравитации в своей основополагающей работе 1687 года.Универсальные законы всемирного тяготения
Закон, также известный как закон всемирного тяготения Ньютона, гласит, что все объекты во вселенной, обладающие массой, притягиваются друг к другу с силой, которая
- прямо пропорциональна произведению масс
- обратно пропорциональна квадрату расстояния между их центрами
Это два фактора, которые влияют на гравитационную силу. Значение высокое для массивных объектов и когда тела находятся ближе друг к другу.
Универсальные законы гравитацииОбщая формула гравитационной силы
Предположим, что M 1 и M 2 — массы двух тел, а R — расстояния между их центрами. Следующее уравнение дает гравитационную силу между двумя объектами. 92} \hspace{2 cm} (1) \]
Единица гравитационной силы: Н или Ньютон
Здесь G называется универсальной гравитационной постоянной.
Универсальные законы гравитации Это эмпирическая физическая константа, которая имеет значение 6,67 X 10 -11 Н·м 2 /кг 2 . Его размерная формула: M -1 L -3 T -2 . Зная массы M 1 и M 2 и расстояние между ними d , можно вычислить звездную величину F .
Это эмпирическая физическая константа, которая имеет значение 6,67 X 10 -11 Н·м 2 /кг 2 . Его размерная формула: M -1 L -3 T -2 . Зная массы M 1 и M 2 и расстояние между ними d , можно вычислить звездную величину F .Свойства гравитационной силы
Вот некоторые факты и характеристики гравитационной силы.
- Привлекательная
- Бесконтактная
- Дальняя
- Не требует среды
- Прямо пропорциональна произведению масс объектов
- Обратно пропорциональна квадрату расстояния между объектами
- Постоянная величина на поверхности Земли
- Самая слабая из всех фундаментальных сил
- Действует вдоль линии, соединяющей любые два тела
Примеры силы гравитации
предмет подброшен в воздух, он возвращается на поверхность за счет земного притяжения.
Сила гравитации Пример Ниже приведены еще несколько примеров.
Ниже приведены еще несколько примеров.1. Сила гравитации Земли
Земля оказывает гравитационную силу на каждый объект, явление, известное как гравитация. Гравитация удерживает нас на поверхности и не дает свободно парить в воздухе. Мы воздействуем на Землю с той же силой, что и Земля на нас. Однако Земля настолько массивна, что невозмутима. Подвешенный в воздухе объект, если его отпустить, свободно упадет к центру Земли. 92} \hspace{2 cm} (5) \]
Приведенный выше термин называется ускорением под действием силы тяжести. Его значение составляет 9,81 м/с 2 на поверхности Земли. Умножение г на массу человека дает вес человека Вт .
\[ W = mg \hspace{2 см} (6) \]
Ускорение свободного падения в космосе равно нулю, поэтому космонавты чувствуют себя невесомыми и свободно парят.
Следующее выражение дает работу силы тяжести Земли, когда объект массой м падает с высоты ч над поверхностью Земли.

\[ \text{Проделанная работа} = mgh \hspace{2 см} (7) \]
Эта работа представляет собой изменение потенциальной энергии объекта при падении объекта в воздухе.
Спутники обращаются вокруг Земли по фиксированным орбитам благодаря гравитационному притяжению. Если бы не было гравитации, спутники были бы выброшены в космос.
Гравитация в полярной области выше, чем на экваторе. Причина в том, что полюса ближе к центру Земли, чем экватор.
Сила гравитации между Землей и Луной
Луна вращается вокруг Земли, потому что гравитационные силы удерживают их вместе. Мы помещаем их массы и расстояние между их двумя центрами в уравнение (1), чтобы вычислить эту силу.
Масса Земли: M E = 6,0 x 10 24 кг
Масса Луны: M M = 7,35 x 10 22 кг
Среднее расстояние между Землей и Луной ЕМ = 3,844 х 10 9{20} \hspace{0,1 см} Н \]
Таким образом, сила притяжения между Землей и Луной равна 2 x 10 20 Н.

2. Сила гравитации Солнца
Сила гравитации Солнца из-за его массы, которая настолько велика, что его влияние распространяется очень широко. Все планеты вращаются вокруг Солнца по эллиптическим орбитам из-за этой силы притяжения. Гравитационная сила между Солнцем и Землей может быть рассчитана с помощью уравнения (1).
Масса Солнца: M с 9{22} \hspace{0,1 см} Н \]
Таким образом, сила притяжения между Солнцем и Землей равна 3,5 x 10 22 Н.
Точно так же сила притяжения между Солнцем и другими планетами будет зависеть от их массы и расстояния.
Гравитационная сила между Землей и Солнцем3. Гравитационная сила планет
Все планеты Солнечной системы имеют свою гравитационную силу. Значения ускорения свободного падения приведены ниже.
- Mercury: 3.7 m/s 2
- Venus and Uranus: 8.87 m/s 2
- Mars: 3.
 71 m/s 2
71 m/s 2 - Jupiter: 24.79 m/s 2
- Сатурн: 10,44 м/с 2
- Нептун: 11,15 м/с 2
. Помимо гравита луны 1,62 м/с
2
. По сравнению с Землей это примерно 1/6 th .
Преимущества и недостатки силы гравитации
Сила гравитации имеет большое значение, которое влияет на нашу повседневную жизнь. Вот некоторые из его преимуществ.
- Постоянно на поверхности Земли
- Поддерживает работу мышц и костей
- Позволяет Земле сохранять свою атмосферу
- Позволяет водяным плотинам накапливать энергию
Вот некоторые из его недостатков.
- Затрудняет полеты в открытый космос, так как ракетам приходится преодолевать силу тяжести
- Заставляет нас падать и получать травмы
- Ограничивает высоту высотных зданий во время строительства
- Тяжело воздействует на кости и суставы с возрастом
Часто задаваемые вопросы
Q. 1. Консервативна ли гравитационная сила?
1. Консервативна ли гравитационная сила?
Ответ. Да. Сила гравитации консервативна, поскольку работа, совершаемая ею на близком пути, равна нулю.
Q.2. Существует ли сила гравитации в вакууме?
Ответ . Да. В вакууме может существовать сила гравитации.
Q.3. Каков диапазон гравитационной силы?
Ответ. Диапазон гравитационной силы бесконечен, хотя он становится слабее по мере увеличения расстояния между объектами.
Q.4. Какое измерение изменяется в зависимости от силы гравитации?
Ответ. Вес. Вес человека на Земле не одинаков на Луне из-за разницы в гравитационных силах.
Q.5. Какая сила сильнее? Гравитационная или электрическая?
Ответ. Электрическая сила сильнее силы гравитации.
Электрическая сила сильнее силы гравитации.
Задачи и решения гравитационных сил
Задача 1. Какова сила притяжения между двумя твердыми телами массами 110 и 130 кг и расстоянием между ними 80 см? Дано, G = 6,67 x 10 -11 Нм 2 /кг 2 .
Solution:
Given
M 1 = 110 kg
M 2 = 130 kg
d = 80 cm or 0.8 m
F = G M 1 M 2 / d 2
= 6.67 x 10 -11 N.m 2 /kg 2 x 110 kg x 130 kg / (0.8) 2
= 1.5 X 10 -6 N
Ссылки
Последний раз статья рецензировалась в воскресенье, 4 сентября 2022 г.
10+ примеров гравитационной потенциальной энергии – Лямбда-гики .
Нас интересует гравитационная потенциальная энергия груза, которая удерживается в объекте в результате его вертикального положения или гравитационного притяжения объекта к Земле. Масса объекта и его высота над нулевой точкой отсчета являются определяющими факторами гравитационной потенциальной энергии. В этой статье перечислены некоторые распространенные примеры гравитационных потенциальная энергия в нашей повседневной жизни.
Масса объекта и его высота над нулевой точкой отсчета являются определяющими факторами гравитационной потенциальной энергии. В этой статье перечислены некоторые распространенные примеры гравитационных потенциальная энергия в нашей повседневной жизни.
Само введение дает предпосылку для этого примера.
Рассмотрим груз m, который поднимается вертикально на высоту h против силы тяжести через систему шкивов. Здесь сила, возникающая при подъеме ящика, и сила тяжести F g равны. Следовательно, чистая проделанная работа равна потенциальной энергии гравитации и рассчитывается путем умножения величины гравитационной силы, F г , по вертикальному расстоянию h, пройденному грузом.
Устранение этих сил приведет к тому, что объект упадет обратно на землю, тем самым преобразуя гравитационную потенциальную энергию в кинетическую энергию. Предполагается, что гравитационная потенциальная энергия на заданной высоте h остается постоянной. Любопытно, что нуль гравитационной потенциальной энергии — произвольное значение. Отрицательную гравитационную потенциальную энергию можно наблюдать ниже нулевой точки, которую также называют исходной точкой.
Предполагается, что гравитационная потенциальная энергия на заданной высоте h остается постоянной. Любопытно, что нуль гравитационной потенциальной энергии — произвольное значение. Отрицательную гравитационную потенциальную энергию можно наблюдать ниже нулевой точки, которую также называют исходной точкой.
Косвенные способы использования гравитационной потенциальной энергии можно увидеть в гидроэнергетике.
Накопление гравитационной потенциальной энергии обусловлено разницей высоты воды за плотиной ГЭС и воды на противоположной стороне. Падение воды с высоты преобразует ее потенциальную энергию в кинетическую энергию, которая вращает турбину для выработки электроэнергии.
Автомобиль, припаркованный на вершине холмаТранспортное средство преобразует кинетическую энергию в потенциальную при подъеме на холм.
Подъем транспортного средства на определенную высоту над уровнем земли позволил ему достичь гравитационной потенциальной энергии mgh, где m — масса транспортного средства, g — гравитационная постоянная, а h — достигнутая высота над землей.
Как только транспортное средство начинает спускаться с холма, оно развивает скорость, которая преобразует потенциальную энергию в кинетическую энергию. Потенциальная энергия, запасенная в месте расположения автомобиля на гребне склона, преобразуется в кинетическую энергию .
Йо-йо ждет освобожденияЙо-йо становится свидетелем накопления определенной потенциальной энергии перед ее высвобождением.
Йо-йо обладает гравитационной потенциальной энергией, пока оно удерживается над землей, так как гравитация уже тянет его вниз. Эта потенциальная энергия в йо-йо преобразуется в кинетическую энергию при падении, которая увеличивается по мере уменьшения расстояния между йо-йо и землей. Когда йо-йо снова поднимают, оно снова преобразует кинетическую энергию и сохраняет ее в виде потенциальной энергии.
Гравитационная потенциальная энергия существует в воде на вершине действительно высокого водопада.
Высокая скорость воды, падающей с вершины водопада, преобразует гравитационную потенциальную энергию в кинетическую энергию. Когда текущая сверху вода сталкивается с массой воды у основания водопада, вода бурно и хаотично разбрызгивается во всех областях.
Часть кинетической энергии, получаемой водой , теперь преобразуется в кинетическую энергию динамического равновесия. Это поднимает внутреннюю энергию воды и нагревает ее на дне водопада.
Книга на столе прямо перед падением Книга на краю стола, всего в нескольких шагах от места падения, также проявляет гравитационную потенциальную энергию.
Гравитационному притяжению противодействуют некоторые внешние силы, когда книга поднимается над землей, чтобы удержать ее на столе . Гравитационное притяжение придает книге притягательную энергию, если она падает обратно на пол. Действие книги, падающей со стола, испытывает ускорение под действием силы тяжести, что вызывает преобразование потенциальной энергии в кинетическую энергию.
Высота, масса и сила объекта влияют на всю его энергию гравитации больше, чем точка отсчета. Таким образом, книга на столе обладает меньшей энергией гравитации, чем книга на крыше большого офиса, и меньшей энергией гравитации, чем более тяжелая книга на отдельном столе.
Ребенок наверху горкиГравитационная потенциальная энергия — это любая накопленная энергия, которая может падать или двигаться.
Любое существо, находящееся на грани падения, испытывает гравитационную потенциальную энергию. В начале у юноши есть гравитационная потенциальная энергия на горке. Поскольку часть энергии была преобразована в тепло из-за трения о скольжение, когда ребенок достигает дна, он или она обладает как кинетической, так и тепловой энергией.
Поскольку часть энергии была преобразована в тепло из-за трения о скольжение, когда ребенок достигает дна, он или она обладает как кинетической, так и тепловой энергией.
Гравитационная потенциальная энергия шара для разрушения определяется большой массой шара и высотой, на которую он поднят.
Между гравитационной потенциальной энергией и массой объекта, а также его высотой над исходной точкой существует прямая зависимость. Высота вызывает увеличение гравитационной потенциальной энергии объекта.
Примеры гравитационной потенциальной энергии: Разрушающий шар; Источник изображения: Стефан Кюн, Абриссбирн, CC BY-SA 3.0 Ребенок на качеляхРебенок, катающийся на качелях при движении вперед и назад, благодаря своей высоте над землей развивает гравитационную потенциальную энергию.
Гравитационная потенциальная энергия ребенка может быть рассчитана путем измерения массы и высоты ребенка над землей. Гравитационная потенциальная энергия объекта увеличивается во столько раз, сколько раз увеличивается высота над землей.
Гравитационная потенциальная энергия объекта увеличивается во столько раз, сколько раз увеличивается высота над землей.
Кинетическая и гравитационная потенциальная энергия любого объекта, который поднимается или падает, изменяется.
Сила гравитации — это притяжение между двумя или более точками или огромными массами, подобное притяжению между массами и землей. Это определяющий фактор в идентификации веса и, следовательно, в этом состоянии плод обладает гравитационной энергией.
Примеры гравитационной потенциальной энергии: Фрукты, свисающие с дерева; Источник изображения: publicdomainvectors.org Птица, сидящая на ветке дереваПтица, сидящая на ветке дерева, обладает гравитационной потенциальной энергией.
Это связано с тем, что пока он на дереве, он находится дальше от земли, чем на земле.
Цветочный горшок, свисающий с референса, является еще одним примером.
Висячий цветочный горшок обладает гравитационной потенциальной энергией благодаря своей массе на определенной высоте от земли или исходной точки.
Самолет летит над головойКогда самолет взлетает, двигатели выделяют химическую энергию в виде топлива, которое во время полета преобразуется в механическую энергию, приводящую в действие механические операции, такие как вращение лопастей вентилятора, пропеллеров и т. д.
Механическая энергия создает тягу, которая увеличивает скорость самолета. Механическая энергия превращается в кинетическую, когда скорость самолета увеличивается. Когда самолет начинает набирать высоту, эта механическая энергия начинает преобразовываться в гравитационную потенциальную энергию.
Примеры гравитационной потенциальной энергии: Взлет самолета; Источник изображения: pixabayГравитация и движение спутников — Science Learning Hub
Добавить в коллекцию
Гравитация — это сила, которая притягивает все объекты друг к другу. Люди притягиваются к Земле и Земля к людям, Луна и Земля притягиваются друг к другу, а Солнце и Земля притягиваются друг к другу. Все эти притяжения вызваны гравитацией. Гравитационное притяжение больше для более массивных объектов. Гравитация уменьшается по мере увеличения расстояния между объектами.
Люди притягиваются к Земле и Земля к людям, Луна и Земля притягиваются друг к другу, а Солнце и Земля притягиваются друг к другу. Все эти притяжения вызваны гравитацией. Гравитационное притяжение больше для более массивных объектов. Гравитация уменьшается по мере увеличения расстояния между объектами.
Гравитация притягивает все друг к другу
Каждый объект во Вселенной притягивается ко всем другим объектам силой гравитации. Это означает, что во Вселенной нет места, где не действует гравитация. Примеры гравитации в действии:
- Гравитация удерживает атмосферу вокруг Земли.
- Гравитация удерживает людей на поверхности Земли.
- Гравитация удерживает Международную космическую станцию на орбите вокруг Земли.
- Гравитация удерживает Луну на орбите вокруг Земли.
- Гравитация удерживает Землю на орбите вокруг Солнца.
Исаак Ньютон первым пришел к выводу, что все объекты притягиваются друг к другу под действием силы тяжести. Даже людей притягивает друг к другу гравитация, но эта сила настолько мала, что не заметна. Гравитация становится заметной только в том случае, если один (или оба) объекта имеют большую массу, например Земля.
Даже людей притягивает друг к другу гравитация, но эта сила настолько мала, что не заметна. Гравитация становится заметной только в том случае, если один (или оба) объекта имеют большую массу, например Земля.
В космосе есть гравитация
Гравитация не исчезает только потому, что вы находитесь над атмосферой. Даже если объект находится высоко над атмосферой Земли, все равно будет действовать сильная сила гравитации, притягивающая его к центру Земли. На высоте 30 км вы бы находились над 99% земной атмосферы. На расстоянии 100 км вы бы официально оказались в космосе, но сила тяжести осталась бы почти такой же. Вы и Земля все еще были бы притянуты друг к другу.
Ньютон выяснил, что если расстояние от центра Земли удвоится, гравитация станет вчетверо меньше, чем на поверхности. Спутник массой 1000 кг имеет силу тяжести 9800 Н у поверхности Земли. Радиус Земли составляет около 6 366 км, поэтому на высоте 6 366 км над поверхностью Земли расстояние от центра Земли удвоится. Сила веса, притягивающая его к центру Земли, теперь будет только в четверть меньше, но все равно будет равна 2450 Н.
Сила веса, притягивающая его к центру Земли, теперь будет только в четверть меньше, но все равно будет равна 2450 Н.
Так почему же спутник массой 1000 кг просто не упадет обратно на Землю?
Боковая скорость удерживает спутники на орбите
На высоте 100 км вы бы были так высоко, что увидели бы черное небо и звезды, если бы посмотрели вверх. Если вы поднимете спутник на такую высоту и отпустите его, он все равно упадет на Землю, потому что сила тяжести почти такая же, как у поверхности Земли.
Однако, если спутнику придать скорость в любом направлении, горизонтальном относительно поверхности Земли, он будет двигаться дальше, прежде чем упадет на Землю. Если ему придать достаточную скорость, он продвинется так далеко, что, поворачиваясь к Земле, вообще не попадет в Землю. При правильной скорости он будет двигаться вокруг Земли по кругу. Этот тип движения и путь, по которому движется спутник, называется орбитой.
Рядом с Землей на высоте 100 км спутник должен двигаться со скоростью 8 километров в секунду (28 000 км/ч), чтобы оставаться на орбите. На больших высотах спутникам не нужно двигаться так быстро. Спутники телевизионной связи находятся на большей высоте 36 000 км, и им нужно двигаться со скоростью всего 3 км / с (11 000 км / ч).
На больших высотах спутникам не нужно двигаться так быстро. Спутники телевизионной связи находятся на большей высоте 36 000 км, и им нужно двигаться со скоростью всего 3 км / с (11 000 км / ч).
Луна находится на расстоянии 360 000 км от Земли, и ей нужно двигаться со скоростью всего 1 км/с, чтобы оставаться на орбите вокруг Земли.
Если в космосе есть гравитация, почему астронавты кажутся невесомыми?
Астронавты кажутся невесомыми по той же причине, по которой человек на батуте чувствует себя невесомым в воздухе. Сила тяжести остается прежней, но пол не давит на космонавта вверх, поэтому сила веса не ощущается.
Если бы человек находился в лифте, а тросы порвались и отказали тормоза (нас уверяют, что такого не может быть), то человек и лифт упали бы на Землю с одинаковой скоростью. Пол не будет удерживать человека вверх, поэтому человек сможет насладиться ощущением невесомости (ненадолго).
То же самое для астронавтов высоко над атмосферой на Международной космической станции (МКС) на высоте около 400 км. Гравитация все еще сильна, но астронавт и МКС падают на землю с одинаковой скоростью. Они также оба движутся горизонтально со скоростью 28 000 км/ч. Когда они падают на землю, они движутся так быстро по горизонтали, что вообще не касаются Земли и совершают оборот вокруг Земли каждые 90 минут.
Гравитация все еще сильна, но астронавт и МКС падают на землю с одинаковой скоростью. Они также оба движутся горизонтально со скоростью 28 000 км/ч. Когда они падают на землю, они движутся так быстро по горизонтали, что вообще не касаются Земли и совершают оборот вокруг Земли каждые 90 минут.
Природа науки
Научные идеи со временем меняются. Мировоззрение Ньютона, основанное на гравитации, с тех пор было заменено идеями Эйнштейна о том, что все массы искажают пространство и время. Это подчеркивает тот факт, что наука не является фиксированной совокупностью знаний. Хотя теория Эйнштейна широко признана, закон всемирного тяготения Ньютона до сих пор используется для практических ситуаций, таких как движение спутников.
Полезные ссылки
Посетите веб-сайт обсерватории и планетария Stardome, чтобы узнать о ресурсах и мероприятиях, связанных с орбитами — часть раздела Солнечной системы.
Используйте эту симуляцию Университета Колорадо, чтобы поэкспериментировать с движением снаряда.
Опубликовано 27 марта 2013 г., обновлено 20 мая 2015 г.0002 Загрузить 0 шт.
Загрузить все
Гравитация – определение, объяснение, примеры и ответы на часто задаваемые вопросы
Какая сила удерживает нас на Земле и не дает взлететь в космос? Если вы знаете ответ на этот вопрос, то знаете, что такое гравитация. Гравитация — одна из фундаментальных сил вселенной, которые доминируют в каждый момент нашего сознательного существования. Она помогает нам ходить по земле, притягивает баскетбольные и бейсбольные мячи к земле, а гравитация — это то, с чем наши мышцы не могут бороться. История гравитации идет рука об руку с историей физики, и многие известные физики нашли способы выяснить, что вызывает гравитацию.
Ученые определили четыре типа сил во вселенной, которые либо притягивают, либо отталкивают один объект от другого. Это:
(изображения будут загружены в ближайшее время)
Из этих 4 типов сил сильные и слабые взаимодействия действуют в центре атомов объекта. ЭМ-сила распространяется на объекты с избыточным зарядом (электроны, протоны), например носки, которые шаркают по пушистому ковру.
ЭМ-сила распространяется на объекты с избыточным зарядом (электроны, протоны), например носки, которые шаркают по пушистому ковру.
Гравитация — это сила, действующая на объекты, имеющие массу. Это всепроникающая сила, которая удерживает нашу ногу на земле, но для многих она до сих пор остается загадкой и ответом на вопрос, что вы подразумеваете под гравитацией.
Что вы подразумеваете под гравитационной силой
Гравитацию можно определить как силу, с которой планета (или тело) воздействует на другие объекты и притягивает их к своему центру. Именно эта сила гравитации удерживает все планеты на своих орбитах вокруг Солнца.
(изображение скоро будет загружено)
Ньютон объяснил, что подразумевается под силой тяготения в его законе всемирного тяготения как сила притяжения, которая существует между любыми двумя объектами, имеющими массу. Эта сила прямо пропорциональна массам тел и обратно пропорциональна расстоянию между ними. Это математически выражается как:
Это математически выражается как:
F = G * (м1 м2) / R2
Где F — сила тяжести.
G — Гравитационная постоянная и ее значение составляет 6,67 x 10-11 Н * м2/кг2.
R — Расстояние между объектами.
Из чего состоит гравитация
Гравитация Земли создается всей ее массой. Вся масса Земли оказывает комбинированное гравитационное притяжение на массу вашего тела. Именно это гравитационное притяжение земли дает вам ваш вес. Так что если вы находитесь на планете, масса которой меньше земной, то и весить вы там будете меньше. Вы и Земля оказываете гравитационное воздействие друг на друга, но, поскольку масса Земли намного больше вашего веса, ваша сила не влияет на планету.
(изображение будет загружено в ближайшее время)
Группа ученых, базирующихся на Южном полюсе, обнаружила небесный отпечаток пальца с помощью телескопа BICEP2. Этот отпечаток объясняет начало времени и раскрывает микроскопические детали гравитации. Квантовые частицы в зачаточной Вселенной породили «инфляцию», которая является причиной того, что Вселенная взорвалась наружу.
Квантовые частицы в зачаточной Вселенной породили «инфляцию», которая является причиной того, что Вселенная взорвалась наружу.
Также выяснилось, что гравитация состоит из квантовых частиц, называемых гравитонами. Отдельный гравитон слишком мал и не имеет массы, но квантовые флуктуации этих гравитонов в зарождающейся Вселенной искривляют карманы этого крошечного пространства-времени.
Что такое гравитационная сила Земли
Гравитация Земли обозначается буквой g и определяется как чистое ускорение, вызываемое объектами под действием гравитации (распределения массы внутри Земли) и центробежной силы, обусловленной действием силы тяжести Земли. вращение.
Ускорение Земли под действием силы тяжести составляет 9,8 м/с 2 вблизи ее поверхности (также называемое 1g). Гравитация уменьшается по мере удаления от Земли.
Гравитация на Земле везде разная
Притяжение Солнца удерживает Землю в таком положении, что мы можем наслаждаться солнечным светом, не обжигаясь. Гравитация удерживает всю нашу атмосферу и воздух, которым мы дышим, поэтому жизнь без гравитации для нас невозможна.
Гравитация удерживает всю нашу атмосферу и воздух, которым мы дышим, поэтому жизнь без гравитации для нас невозможна.
Но сила тяжести не одинакова во всех частях нашей планеты Земля. В местах, где подземная масса больше, гравитация больше, чем в местах с меньшей подземной массой. Сила гравитации также зависит от того, где вы стоите, возле экватора или дальше от него. Это связано с тем, что Земля вращается вокруг своей оси; следовательно, сила тяжести на экваторе меньше (90,789 м/с 2 ), чем сила тяжести на полюсах (9,832 м/с 2 ). Это означает, что на полюсах вы будете весить немного больше, чем на экваторе из-за центростремительной силы.
НАСА запустило 2 космических корабля для измерения этих изменений гравитации Земли. Эти космические аппараты являются частью GRACE (эксперимент по восстановлению гравитации и климату).
GRACE может обнаруживать небольшие изменения гравитации с течением времени и раскрыла важные подробности о Земле. Например, GRACE отслеживает уровень моря, и его изменения могут определять изменения в земной коре, вызванные землетрясениями.
Например, GRACE отслеживает уровень моря, и его изменения могут определять изменения в земной коре, вызванные землетрясениями.
Примеры гравитации
Некоторые интересные примеры гравитации:
Гравитация является самой слабой силой среди всех известных фундаментальных сил. Стержневой магнит может тянуть скрепку вверх из-за электромагнитной силы, которая сильнее, чем гравитационное притяжение всей Земли на эту скрепку.
Под действием силы тяжести автомобиль катится вниз по склону, даже если вы не нажимаете на педаль газа.
Гравитация удерживает Землю и все планеты вокруг Солнца в правильном положении и на их орбитах.
Сила гравитации удерживает газы внутри Солнца.
Приливы в океанах определяются силой притяжения Луны.
Звезды и планеты были созданы гравитацией, которая объединила материалы, из которых они состоят.



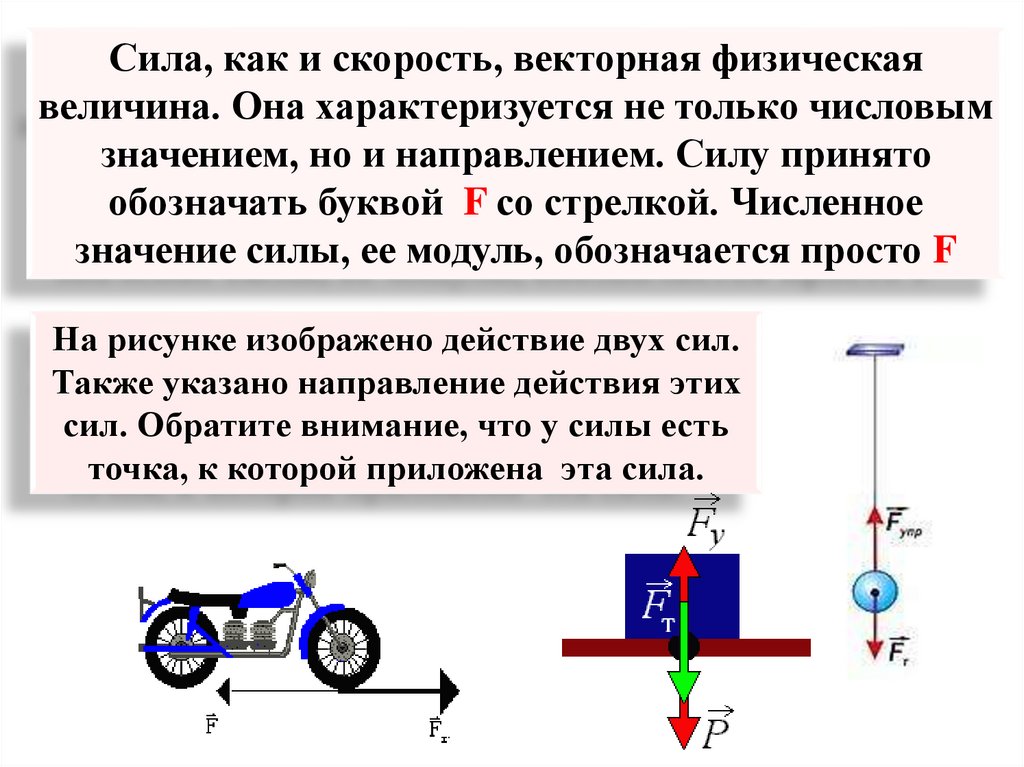
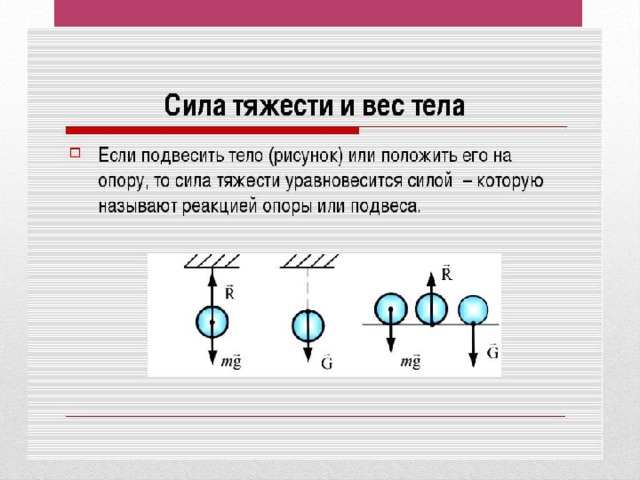 Таким образом, не имеет значения, решите ли вы идти прямо вниз или решите спускаться и подниматься по некоторому большому пути и в конечном итоге оказаться в одном и том же месте. Работа, совершаемая силой тяжести, останется прежней. Более того, он также будет равен нулю, если вы будете наблюдать за общей работой, проделанной по замкнутому пути.
Таким образом, не имеет значения, решите ли вы идти прямо вниз или решите спускаться и подниматься по некоторому большому пути и в конечном итоге оказаться в одном и том же месте. Работа, совершаемая силой тяжести, останется прежней. Более того, он также будет равен нулю, если вы будете наблюдать за общей работой, проделанной по замкнутому пути.
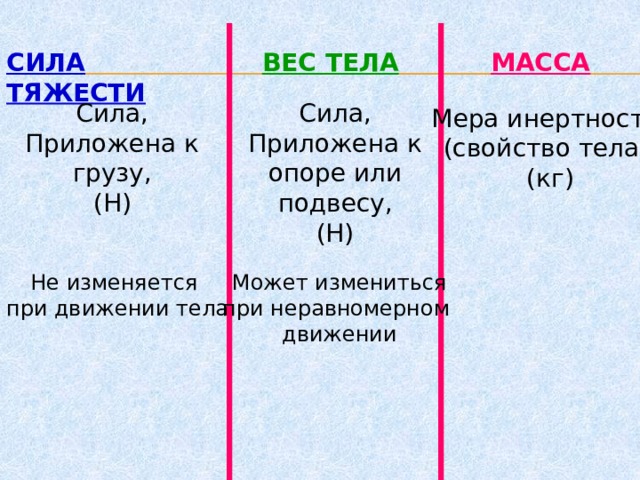

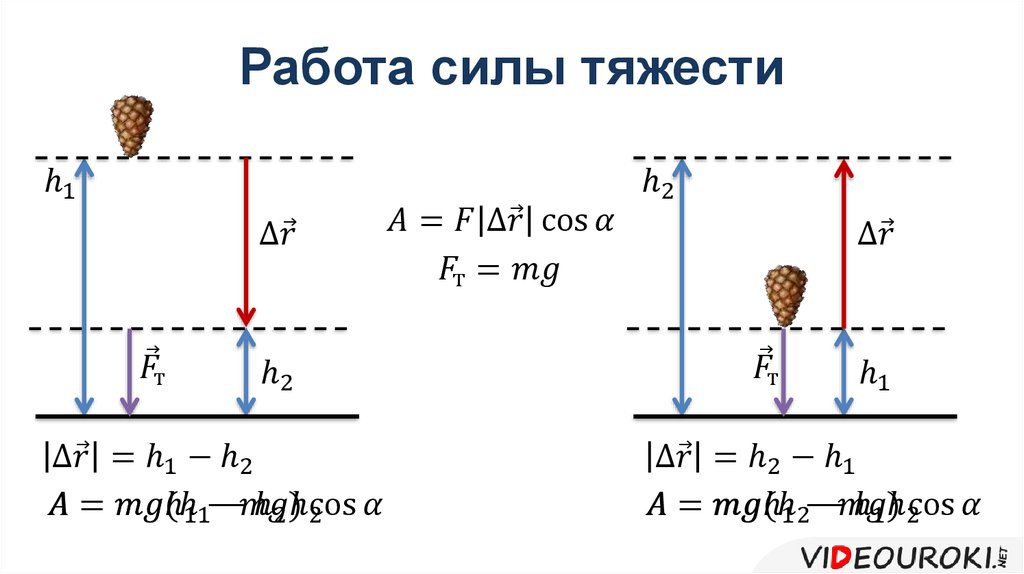


 Просит определить, кто из них приложил большую силу для открытия двери, а кто меньшую.
Просит определить, кто из них приложил большую силу для открытия двери, а кто меньшую.

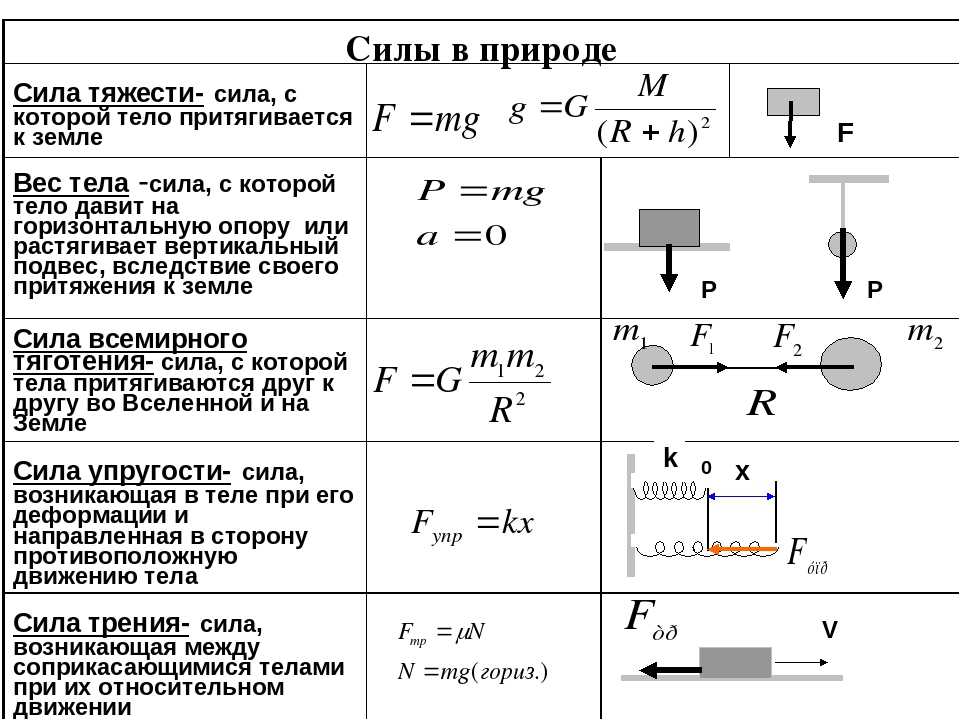
 Виды механического движения.
Виды механического движения.
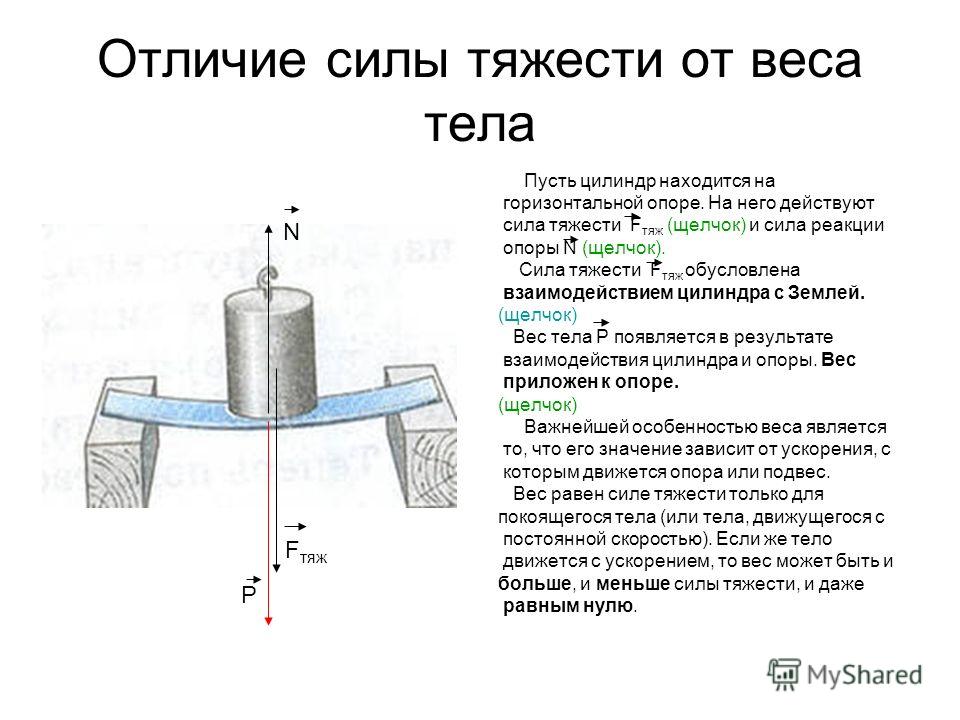

 Все тела притягиваются друг к другу. В свою очередь, и Земля притягивается к этим телам.
Все тела притягиваются друг к другу. В свою очередь, и Земля притягивается к этим телам.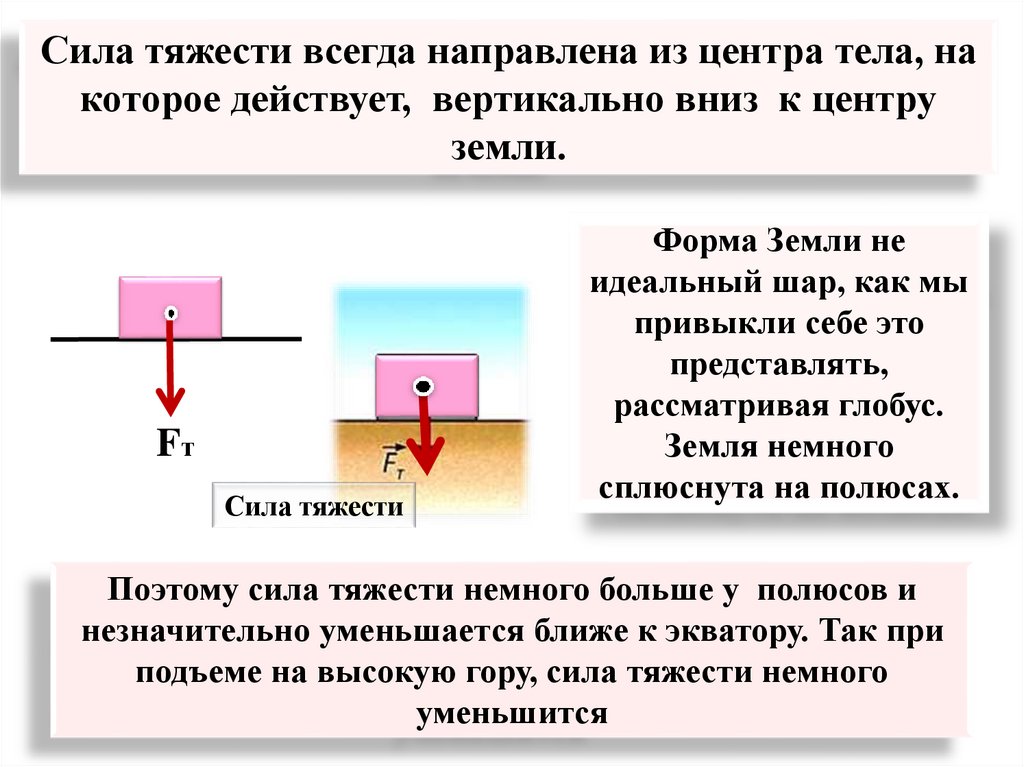
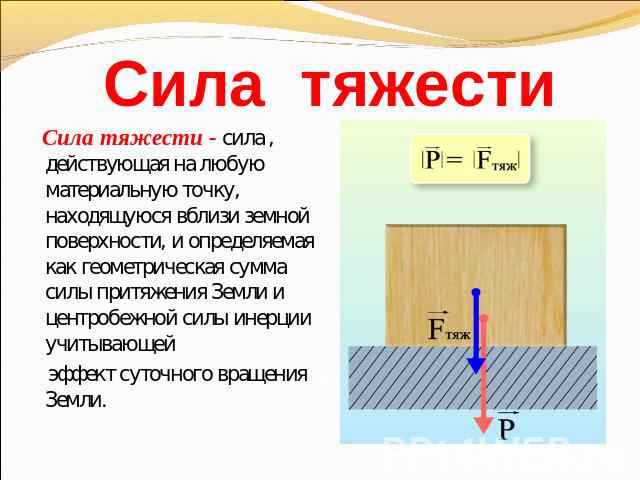
 2\vec{R_0}}$, где:
2\vec{R_0}}$, где: Силу тяжести, таким образом, нужно рассматривать в формате полезного и важного закона природы.
Силу тяжести, таким образом, нужно рассматривать в формате полезного и важного закона природы. С одной стороны, рельеф несомненно влияет на измеряемую на его поверхности силу тяжести — уровень рельефа определяет расстояние до центра масс планеты, а возвышения рельефа содержат дополнительные притягивающие массы. С другой стороны, сила тяжести так же несомненно влияет на рельеф, что особенно заметно в океанах, форма поверхности которых повторяет аномалии силы тяжести. Мало этого, на поверхность рельефа воздействуют ветровая и водная эрозия и множество других факторов, так что характер взаимосвязи рельефа и силы тяжести становится сложно предсказать. Космические снимки также воспроизводят формы рельефа — вместе с формами и цветами растительности и всего прочего на этом рельефе, так что характер взаимосвязи снимков и рельефа оказывается еще менее очевидным.
С одной стороны, рельеф несомненно влияет на измеряемую на его поверхности силу тяжести — уровень рельефа определяет расстояние до центра масс планеты, а возвышения рельефа содержат дополнительные притягивающие массы. С другой стороны, сила тяжести так же несомненно влияет на рельеф, что особенно заметно в океанах, форма поверхности которых повторяет аномалии силы тяжести. Мало этого, на поверхность рельефа воздействуют ветровая и водная эрозия и множество других факторов, так что характер взаимосвязи рельефа и силы тяжести становится сложно предсказать. Космические снимки также воспроизводят формы рельефа — вместе с формами и цветами растительности и всего прочего на этом рельефе, так что характер взаимосвязи снимков и рельефа оказывается еще менее очевидным. Можно производить вычисления фрактальности в пространственной области, а можно и в частотной (компоненты пространственного спектра), дифференцировать и интегрировать… Секрет в том, что всё многообразие способов дает схожие результаты и выбор конкретного способа довольно произволен, важно лишь понимать, как результаты выбранного метода вычислений сопоставить с результатами других методов (Gneiting et al., 2012).
Можно производить вычисления фрактальности в пространственной области, а можно и в частотной (компоненты пространственного спектра), дифференцировать и интегрировать… Секрет в том, что всё многообразие способов дает схожие результаты и выбор конкретного способа довольно произволен, важно лишь понимать, как результаты выбранного метода вычислений сопоставить с результатами других методов (Gneiting et al., 2012). Удивительно здесь то, что и дифференцирование и интегрирование задают пространственный масштаб, или окно вычислений. С интегралом сразу понятно, ведь площадь, очевидно, зависит от ширины фигуры под кривой, а вот с дифференциалом все не так просто. Подумаем, сколько значений минимально необходимо для вычисления первого дифференциала. Очевидно, два — ведь нам нужно посчитать разницу между ними. А для второго дифференциала нам нужно вычислить разницу между двумя первыми дифференциалами, каждый из которых требует два значения и, если взять одно общее значение для вычисления первых дифференциалов, то потребуется три значения. Как видим, для вычисления N-го дифференциала необходимо N+1 значений. Значит, степень производной (дифференциала) также определяет пространственный масштаб. Таким образом, можно определить фрактальную размерность через интегрирование по отрезку изменяемого размера (окну), или через производные разных порядков (включая дробные и отрицательные, при этом последние соответствуют одной из первообразных, то есть интегралам).
Удивительно здесь то, что и дифференцирование и интегрирование задают пространственный масштаб, или окно вычислений. С интегралом сразу понятно, ведь площадь, очевидно, зависит от ширины фигуры под кривой, а вот с дифференциалом все не так просто. Подумаем, сколько значений минимально необходимо для вычисления первого дифференциала. Очевидно, два — ведь нам нужно посчитать разницу между ними. А для второго дифференциала нам нужно вычислить разницу между двумя первыми дифференциалами, каждый из которых требует два значения и, если взять одно общее значение для вычисления первых дифференциалов, то потребуется три значения. Как видим, для вычисления N-го дифференциала необходимо N+1 значений. Значит, степень производной (дифференциала) также определяет пространственный масштаб. Таким образом, можно определить фрактальную размерность через интегрирование по отрезку изменяемого размера (окну), или через производные разных порядков (включая дробные и отрицательные, при этом последние соответствуют одной из первообразных, то есть интегралам). За подробностями рекомендую обратиться к публикациям ныне покойного профессора Нижегоро́дского госуда́рственного университе́та и́мени Н. И. Лобаче́вского (Университет Лобачевского, ННГУ) — Александра Ивановича Саичева, в которых я и нашел связь фрактальности с дробными производными (Саичев, В. А. Филимонов, 2008).
За подробностями рекомендую обратиться к публикациям ныне покойного профессора Нижегоро́дского госуда́рственного университе́та и́мени Н. И. Лобаче́вского (Университет Лобачевского, ННГУ) — Александра Ивановича Саичева, в которых я и нашел связь фрактальности с дробными производными (Саичев, В. А. Филимонов, 2008). В пространственной области аналогичный анализ выполняется круговым преобразованием Радона с дисперсией как базовой функцией. Иными словами, если в ранее нами использованном круговом преобразовании Радона, см. Методы компьютерного зрения для решения обратной задачи геофизики, заменить вычисление среднего значения на дисперсию (стандартное отклонение), тоже получится способ вычисления фрактальной размерности, притом довольно популярный (хотя и под разными названиями) в геологической литературе (см. ссылки в конце статьи). В радиофизике для описания подобных преобразований есть так называемые методы синтеза апертуры, то есть получения большого количества отсчетов вместо одного. Классический пример — локатор бокового обзора (эхолот, в том числе) излучает и принимает отраженные сигналы непрерывно и для вычисления расстояния до каждой точки береговой линии или рельефа дна используется множество измерений, что позволяет сильно улучшить точность. Для нашей задачи рассмотрим простой пример — можем ли мы определить фрактальность в одной точке рельефа разрешением 10 м? Очевидно, нет.
В пространственной области аналогичный анализ выполняется круговым преобразованием Радона с дисперсией как базовой функцией. Иными словами, если в ранее нами использованном круговом преобразовании Радона, см. Методы компьютерного зрения для решения обратной задачи геофизики, заменить вычисление среднего значения на дисперсию (стандартное отклонение), тоже получится способ вычисления фрактальной размерности, притом довольно популярный (хотя и под разными названиями) в геологической литературе (см. ссылки в конце статьи). В радиофизике для описания подобных преобразований есть так называемые методы синтеза апертуры, то есть получения большого количества отсчетов вместо одного. Классический пример — локатор бокового обзора (эхолот, в том числе) излучает и принимает отраженные сигналы непрерывно и для вычисления расстояния до каждой точки береговой линии или рельефа дна используется множество измерений, что позволяет сильно улучшить точность. Для нашей задачи рассмотрим простой пример — можем ли мы определить фрактальность в одной точке рельефа разрешением 10 м? Очевидно, нет. Если же мы проанализируем все точки в кольцах радиуса от 1 до 1000 пикселов (в диапазоне 10 м… 10 км для заданного разрешения), включающих от 4х до ~6000 пикселов (2πR, где R это радиус кольца), то сможем с высокой точностью вычислить фрактальную размерность. При этом точность вычисления пропорциональна квадратному корню из числа пикселов или радиуса колец. А теперь в игру вступают силы природы — если мы наблюдаем фрактальность на масштабе от 1 пиксела и более, эта же фрактальность гарантированно присутствует и на меньших масштабах, хотя мы не можем определить точно граничный масштаб. Небольшое отступление: в лабораторных экспериментах с моделированием динамики фотополимеров мы находили этот граничный масштаб в области сотен нанометров (где молекулы образуют сетчатые структуры и не гауссовые и не фрактальные), так что для геологических исследований граничного масштаба просто нет. Таким образом, благодаря самой сути явления фрактальности, становится возможным обнаружить области залегания фрактальных рудных тел размером значительно менее метра при анализе спутниковых оптических или радарных снимков 5-10 м разрешения (например, Sentinel-1 и Sentinel-2).
Если же мы проанализируем все точки в кольцах радиуса от 1 до 1000 пикселов (в диапазоне 10 м… 10 км для заданного разрешения), включающих от 4х до ~6000 пикселов (2πR, где R это радиус кольца), то сможем с высокой точностью вычислить фрактальную размерность. При этом точность вычисления пропорциональна квадратному корню из числа пикселов или радиуса колец. А теперь в игру вступают силы природы — если мы наблюдаем фрактальность на масштабе от 1 пиксела и более, эта же фрактальность гарантированно присутствует и на меньших масштабах, хотя мы не можем определить точно граничный масштаб. Небольшое отступление: в лабораторных экспериментах с моделированием динамики фотополимеров мы находили этот граничный масштаб в области сотен нанометров (где молекулы образуют сетчатые структуры и не гауссовые и не фрактальные), так что для геологических исследований граничного масштаба просто нет. Таким образом, благодаря самой сути явления фрактальности, становится возможным обнаружить области залегания фрактальных рудных тел размером значительно менее метра при анализе спутниковых оптических или радарных снимков 5-10 м разрешения (например, Sentinel-1 и Sentinel-2). Смотрите практические примеры в публикации Ударим биспектром по бездорожью, или как найти золото в Сибири. Обратите внимание, что сегодня мы рассматриваем спектральный метод, а не биспектральный, который обладает дополнительным важным свойством исключения гауссовых сигналов и, таким образом, значительно более чувствителен за счет полного «игнорирования» всех гауссовых помех, представляющих неразрешимую проблему для спектрального анализа на субпиксельных масштабах.
Смотрите практические примеры в публикации Ударим биспектром по бездорожью, или как найти золото в Сибири. Обратите внимание, что сегодня мы рассматриваем спектральный метод, а не биспектральный, который обладает дополнительным важным свойством исключения гауссовых сигналов и, таким образом, значительно более чувствителен за счет полного «игнорирования» всех гауссовых помех, представляющих неразрешимую проблему для спектрального анализа на субпиксельных масштабах.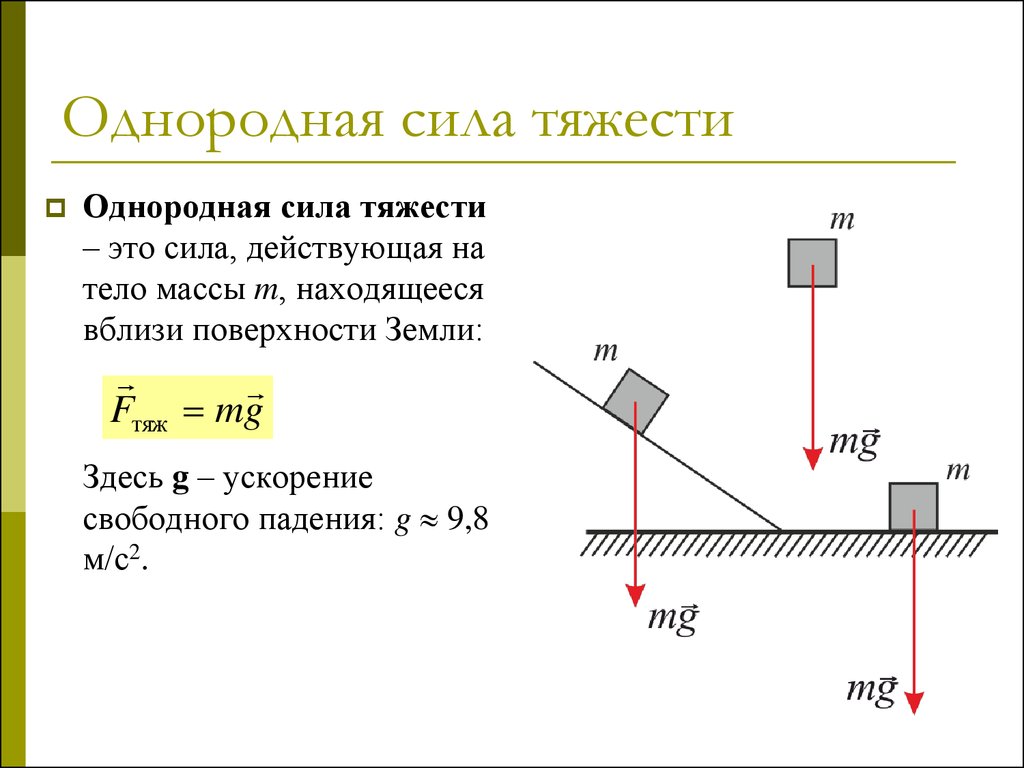 Практическая разница возникает при наличии гауссовых помех, которые мы хотим исключить — очевидно, что радиально симметричный анализ более применим для такого случая. В литературе можно встретить вариацию указанных подходов с вычислением количества пикселов, превышающих среднее значение (в кольцах, кругах или квадратах) вместо более устойчивого вычисления дисперсии.
Практическая разница возникает при наличии гауссовых помех, которые мы хотим исключить — очевидно, что радиально симметричный анализ более применим для такого случая. В литературе можно встретить вариацию указанных подходов с вычислением количества пикселов, превышающих среднее значение (в кольцах, кругах или квадратах) вместо более устойчивого вычисления дисперсии.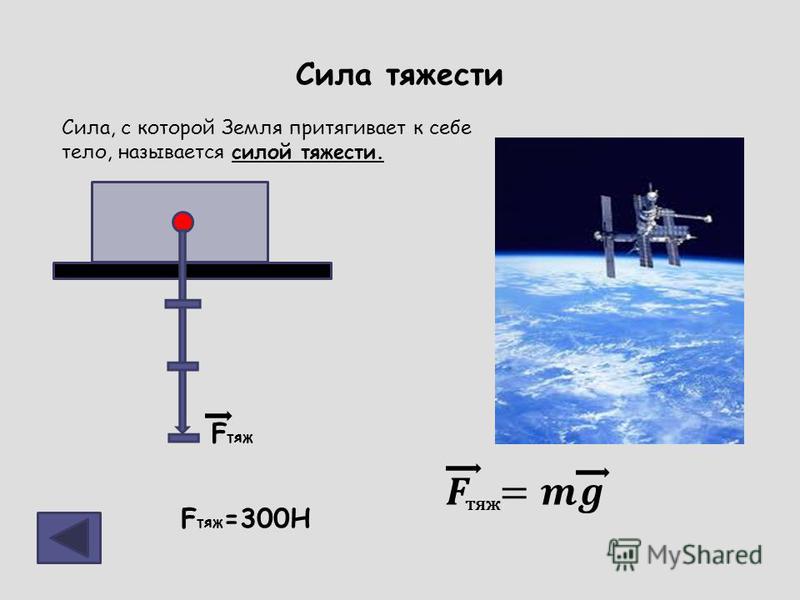 В этом случае избыток или недостаток масс на поверхности Земли компенсируется соответствующим перераспределением масс в её недрах. [Большая Российская Энциклопедия — Изостазия]
В этом случае избыток или недостаток масс на поверхности Земли компенсируется соответствующим перераспределением масс в её недрах. [Большая Российская Энциклопедия — Изостазия]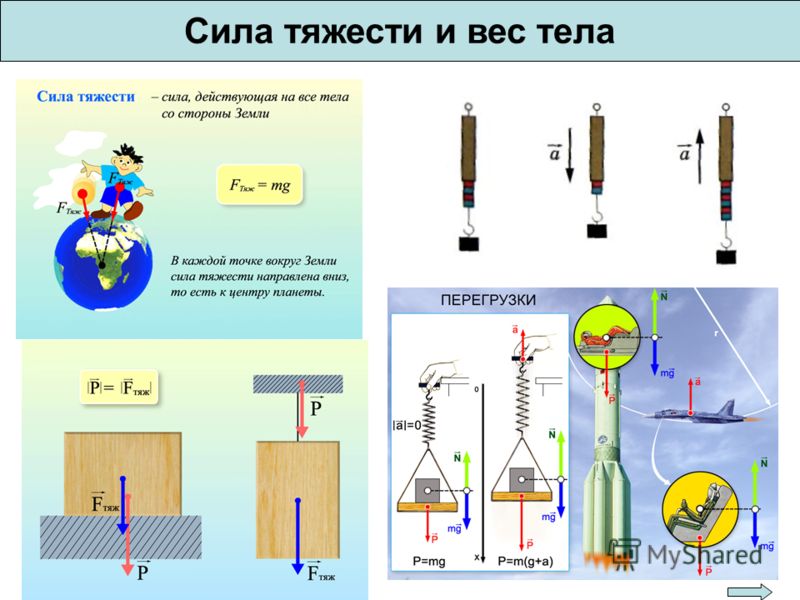
 компенсации. Они предположили, что верхняя часть литосферы является упругой, и использовали решение задачи об изгибе внешними силами упругой плиты, плавающей на жидком основании. [Большая Российская Энциклопедия — Изостазия]
компенсации. Они предположили, что верхняя часть литосферы является упругой, и использовали решение задачи об изгибе внешними силами упругой плиты, плавающей на жидком основании. [Большая Российская Энциклопедия — Изостазия] Как мы рассмотрели ранее, масштаб, на котором исчезает значимая корреляция, и будет соответствовать достижению изостазии. Для океанского дна на рассматриваемой нами территории граница Мохо расположена на глубине 11 км согласно модели CRUST 1.0: A New Global Crustal Model at 1×1 Degrees, что соответствует длине волны 15 км, как мы и видим на графиках. Граница слоя упругости составит около 25 км (длина волны 35 км). Таким образом, по корреляции компонентов пространственных спектров поля силы тяжести и рельефа можно определить границы Мохоровича (Мохо), упругого слоя и изостазии.
Как мы рассмотрели ранее, масштаб, на котором исчезает значимая корреляция, и будет соответствовать достижению изостазии. Для океанского дна на рассматриваемой нами территории граница Мохо расположена на глубине 11 км согласно модели CRUST 1.0: A New Global Crustal Model at 1×1 Degrees, что соответствует длине волны 15 км, как мы и видим на графиках. Граница слоя упругости составит около 25 км (длина волны 35 км). Таким образом, по корреляции компонентов пространственных спектров поля силы тяжести и рельефа можно определить границы Мохоровича (Мохо), упругого слоя и изостазии.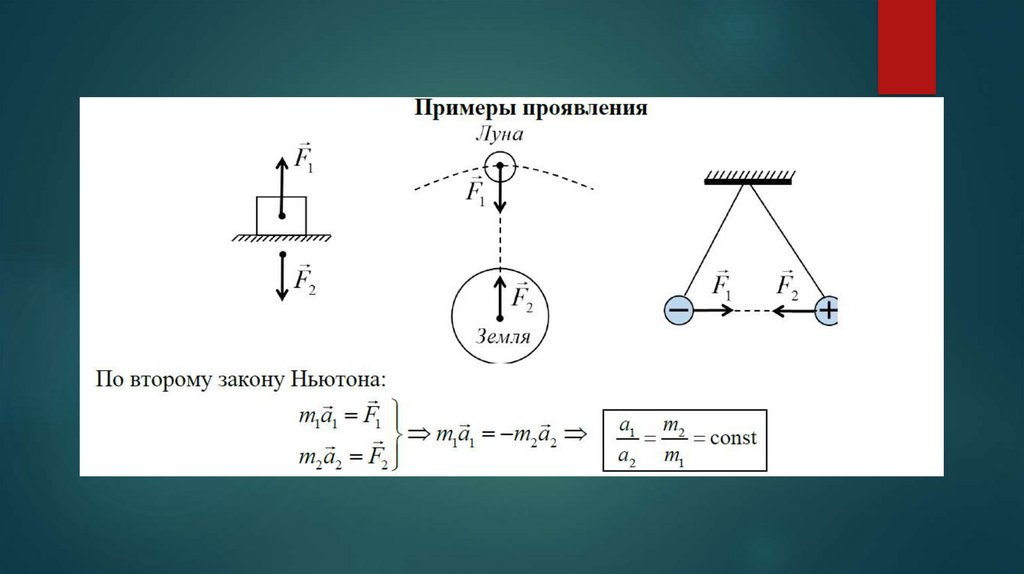 Как будет показано далее, значение фрактальной плотности по данным рельефа является оценкой сверху для геологической плотности и при увеличении площади наблюдения при ее неоднородности приводит к систематическому завышению оценки плотности фрактальным методом.
Как будет показано далее, значение фрактальной плотности по данным рельефа является оценкой сверху для геологической плотности и при увеличении площади наблюдения при ее неоднородности приводит к систематическому завышению оценки плотности фрактальным методом. Кстати, это и еще один способ проверить корректность построенных моделей. Направление тектонических разломов также меняется из-за воздействия силы Кориолиса на тектонические плиты, особенно интересно это проявляется при пересечении экватора. Таким образом, на поверхности планеты появляются асимметричные фрактальные структуры рельефа и поля силы тяжести масштабов до сотен километров, при этом, направление асимметрии сохраняется и до намного больших масштабов.
Кстати, это и еще один способ проверить корректность построенных моделей. Направление тектонических разломов также меняется из-за воздействия силы Кориолиса на тектонические плиты, особенно интересно это проявляется при пересечении экватора. Таким образом, на поверхности планеты появляются асимметричные фрактальные структуры рельефа и поля силы тяжести масштабов до сотен километров, при этом, направление асимметрии сохраняется и до намного больших масштабов.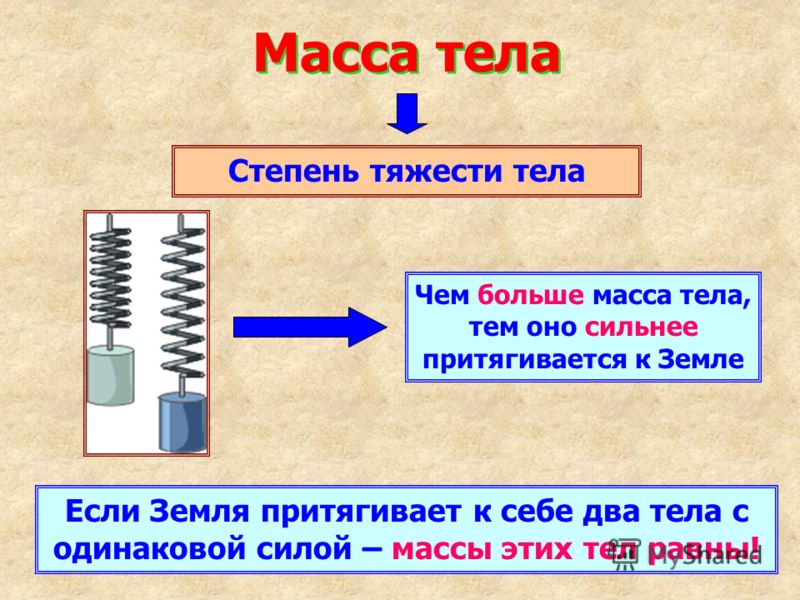
 Стоит отметить, что основная проблема проявляется для диапазона масштабов до 20 км, что вовсе не было проблемой для самого Буге, поскольку детальность его данных была ниже и для них придуманная им редукция работала практически идеально. Поскольку это просто классический «секрет Полишинеля», то придуманы и способы исправить ситуацию — например, исходя из равной фрактальности рельефа и силы тяжести, можно подобрать параметры преобразования Буге, чтобы несколько уменьшить фрактальность (Miranda et al., 2015). В работе (Zhang, Featherstone, 2019) для территории Австралии методами фрактального и спектрального анализа показано, что топография, редукция Буге и аномалии в свободном воздухе имеют почти идентичные фрактальные размерности и спектры, при этом использование редукции Буге приводит к наибольшим ошибкам.
Стоит отметить, что основная проблема проявляется для диапазона масштабов до 20 км, что вовсе не было проблемой для самого Буге, поскольку детальность его данных была ниже и для них придуманная им редукция работала практически идеально. Поскольку это просто классический «секрет Полишинеля», то придуманы и способы исправить ситуацию — например, исходя из равной фрактальности рельефа и силы тяжести, можно подобрать параметры преобразования Буге, чтобы несколько уменьшить фрактальность (Miranda et al., 2015). В работе (Zhang, Featherstone, 2019) для территории Австралии методами фрактального и спектрального анализа показано, что топография, редукция Буге и аномалии в свободном воздухе имеют почти идентичные фрактальные размерности и спектры, при этом использование редукции Буге приводит к наибольшим ошибкам. А результатом редукции Буге должна быть плоская карта с показанными на ней аномалиями силы тяжести, полностью соответствующими аномалиям плотности, не требующая сопоставления с рельефом. Поскольку при этом игнорируется глубинное расположение аномалий, то из-за неоднозначности по глубине, очевидно, часть аномалий плотности будут потеряны — что, опять же, не представляло проблемы для самого Буге в силу масштаба его измерений (малые аномалии, которые можно было бы потерять при таком преобразовании, он просто не мог измерить).
А результатом редукции Буге должна быть плоская карта с показанными на ней аномалиями силы тяжести, полностью соответствующими аномалиям плотности, не требующая сопоставления с рельефом. Поскольку при этом игнорируется глубинное расположение аномалий, то из-за неоднозначности по глубине, очевидно, часть аномалий плотности будут потеряны — что, опять же, не представляло проблемы для самого Буге в силу масштаба его измерений (малые аномалии, которые можно было бы потерять при таком преобразовании, он просто не мог измерить). Для космических или ортофотоснимков значение фрактальности оказывается выше за счет вариаций цвета, не связанных с изменениями рельефа. Выбирая подходящий спектральный диапазон, в котором поверхность имеет наименьшую спектральную размерность, мы можем оценить плотность пород поверхности. Обратимся к доступному на GitHub ноутбуку Geological Fractality on ALOS DEM AW3D30 and Sentinel-2 SUrface Reflectance Image for Ravar, Kerman Province, Iran:
Для космических или ортофотоснимков значение фрактальности оказывается выше за счет вариаций цвета, не связанных с изменениями рельефа. Выбирая подходящий спектральный диапазон, в котором поверхность имеет наименьшую спектральную размерность, мы можем оценить плотность пород поверхности. Обратимся к доступному на GitHub ноутбуку Geological Fractality on ALOS DEM AW3D30 and Sentinel-2 SUrface Reflectance Image for Ravar, Kerman Province, Iran: Таким образом, полученные нами значения являются оценкой сверху. Для получения более точных значений необходимо сегментировать территорию на гомогенные участки и выполнить вычисления для них по отдельности. Кроме того, перегибы кривой фрактальной размерности пропорциональны глубинам, на которых геологическая плотность изменяется.
Таким образом, полученные нами значения являются оценкой сверху. Для получения более точных значений необходимо сегментировать территорию на гомогенные участки и выполнить вычисления для них по отдельности. Кроме того, перегибы кривой фрактальной размерности пропорциональны глубинам, на которых геологическая плотность изменяется.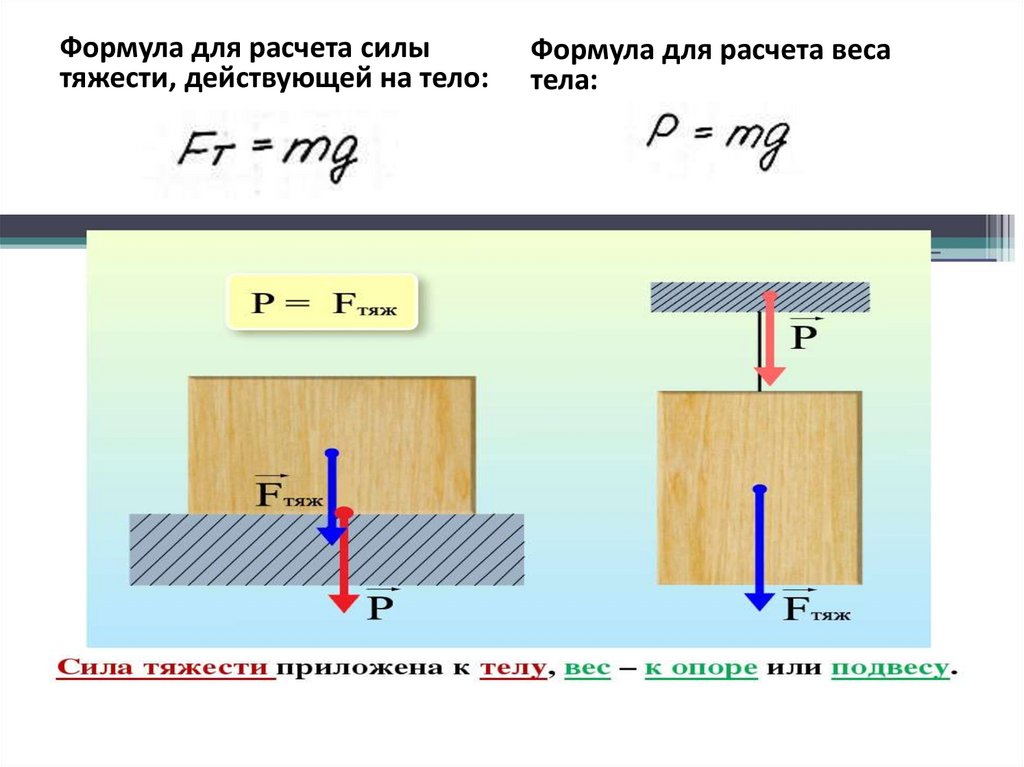
 I. Saichev & V. A. Filimonov, https://link.springer.com/article/10.1134/S0021364008090129
I. Saichev & V. A. Filimonov, https://link.springer.com/article/10.1134/S0021364008090129
 Ну, вот ваш шанс подумать еще раз.
Ну, вот ваш шанс подумать еще раз. Только потому, что существует гравитационное притяжение из-за гравитации Солнца и Луны, мы можем извлекать приливную энергию, которую позже используем для производства электричества.
Только потому, что существует гравитационное притяжение из-за гравитации Солнца и Луны, мы можем извлекать приливную энергию, которую позже используем для производства электричества.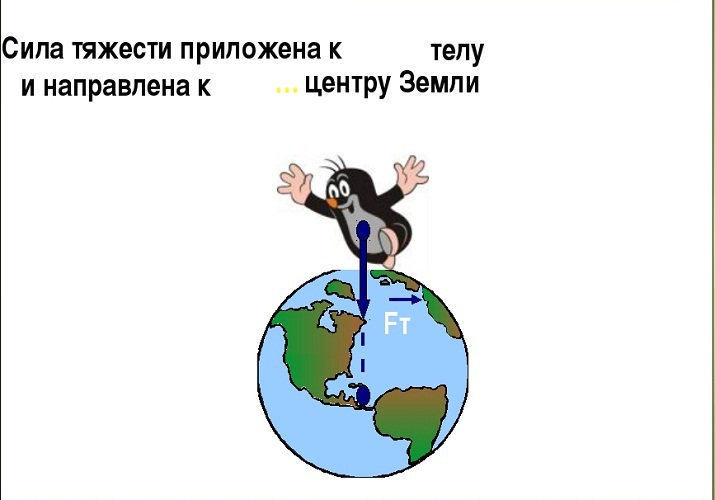 Он просто задал несколько основных фундаментальных вопросов о гравитации и пришел к выводу, что яблоко должно было упасть на землю из-за гравитационной силы, действующей на яблоко со стороны земли.
Он просто задал несколько основных фундаментальных вопросов о гравитации и пришел к выводу, что яблоко должно было упасть на землю из-за гравитационной силы, действующей на яблоко со стороны земли. Все, что вы можете делать, это ходить, бегать или даже прыгать, но, к сожалению, в конце концов вам придется вернуться на поверхность земли. Должен ли я говорить вам, почему? Ну, это происходит из-за гравитационной силы, которую оказывает на вас земля.
Все, что вы можете делать, это ходить, бегать или даже прыгать, но, к сожалению, в конце концов вам придется вернуться на поверхность земли. Должен ли я говорить вам, почему? Ну, это происходит из-за гравитационной силы, которую оказывает на вас земля.

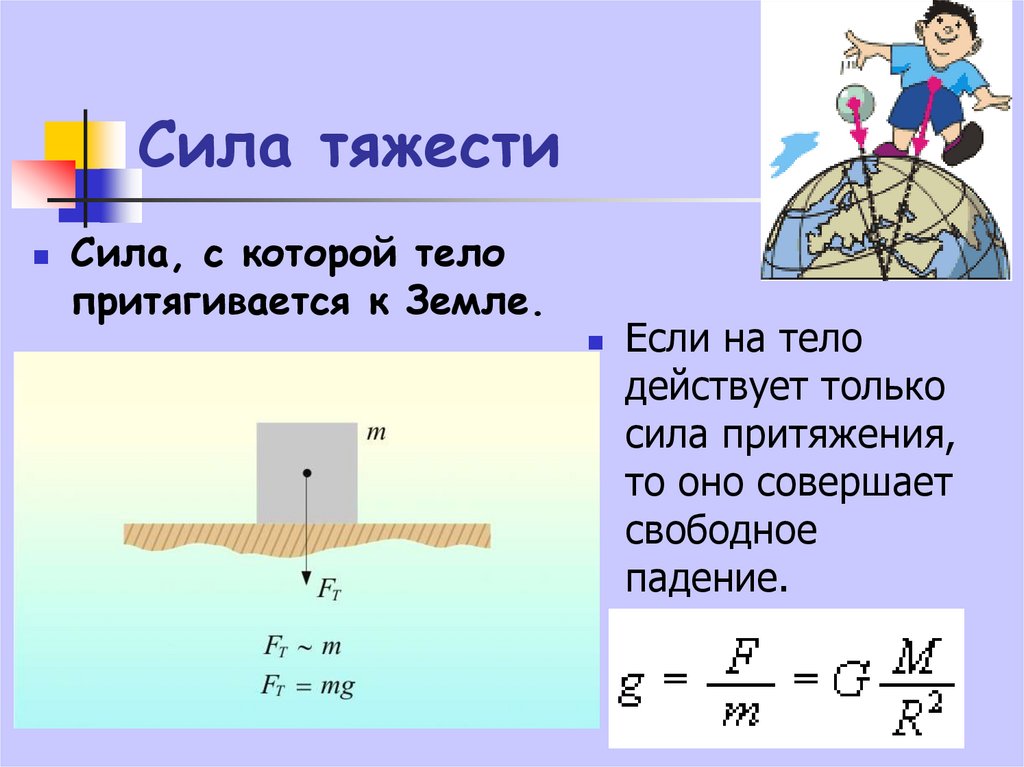 небо
небо