Прикладная теория цифровых автоматов
Прикладная теория цифровых автоматов
ОглавлениеПРЕДИСЛОВИЕГлава 1. ИНФОРМАЦИОННЫЕ ОСНОВЫ ЦИФРОВЫХ АВТОМАТОВ  1. ПОНЯТИЕ ИНФОРМАЦИИ 1. ПОНЯТИЕ ИНФОРМАЦИИ1.2. КОЛИЧЕСТВО ИНФОРМАЦИИ И ЭНТРОПИЯ 1.3. ДИСКРЕТИЗАЦИЯ ИНФОРМАЦИИ 1.4. АЛФАВИТНОЕ ПРЕДСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ ИНФОРМАЦИИ Глава 2. СИСТЕМЫ СЧИСЛЕНИЯ И ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ В ЭВМ 2.1. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.2. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.3. КОДИРОВАННЫЕ ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.4. СИСТЕМЫ СЧИСЛЕНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ 2.5. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ С НЕПОСТОЯННЫМИ ВЕСАМИ РАЗРЯДОВ 2.6. СИМВОЛИЧЕСКИЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.7. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ 2.8. ВЫБОР СИСТЕМЫ СЧИСЛЕНИЯ ДЛЯ ПРИМЕНЕНИЯ ЭВМ 2.9. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ 2.10. ПРЕДСТАВЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ В ЭВМ Глава 3. ВЫПОЛНЕНИЕ ОПЕРАЦИЯ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ И СДВИГА В ЭВМ 3.2. ОПЕРАЦИЯ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ В ЭВМ 3.3. ОПЕРАЦИЯ СДВИГА 3.4. СЛОЖЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 3.5. ОКРУГЛЕНИЕ ЧИСЕЛ В ЭВМ Особенности округления чисел, заданных инверсными кодами Погрешности выполнения арифметических операций 3.  6. ТОЧНОСТЬ ВЫПОЛНЕНИЯ ОПЕРАЦИИ В МАШИНЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 6. ТОЧНОСТЬ ВЫПОЛНЕНИЯ ОПЕРАЦИИ В МАШИНЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ3.7. ВЫЧИСЛЕНИЯ С ДВОЙНОЙ ТОЧНОСТЬЮ Глава 4. ВЫПОЛНЕНИЕ ОПЕРАЦИИ УМНОЖЕНИЯ И ДЕЛЕНИЯ В ЭВМ 4.2. УМНОЖЕНИЕ, ВЫПОЛНЯЕМОЕ МЕТОДОМ НАКОПЛЕНИЯ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ 4.4. МЕТОДЫ УСКОРЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ Матричный метод умножения Быстрое умножение чисел большой разрядности 4.5. УМНОЖЕНИЕ ЧИСЕЛ, ЗАДАННЫХ В ДОПОЛНИТЕЛЬНОМ КОДЕ 4.6. УМНОЖЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 4.7. ОСОБЕННОСТИ ВЫПОЛНЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ В СОВРЕМЕННЫХ ЭВМ 4.8. ДЕЛЕНИЕ ЧИСЕЛ С ВОССТАНОВЛЕНИЕМ ОСТАТКОВ 4.9. ДЕЛЕНИЕ БЕЗ ВОССТАНОВЛЕНИЯ ОСТАТКОВ 4.10. МАШИННЫЕ СХЕМЫ ДЕЛЕНИЯ 4.11. ДЕЛЕНИЕ ЧИСЕЛ В ДОПОЛНИТЕЛЬНОМ КОДЕ 4.12. СПОСОБЫ УСКОРЕННОГО ДЕЛЕНИЯ 4.13. ДЕЛЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 4.14. ДЕЛЕНИЕ ЧИСЕЛ В ЭВМ СОВРЕМЕННЫХ МОДЕЛЕЙ Глава 5. НЕОСНОВНЫЕ АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ 5.  2. ВЫЧИСЛЕНИЕ СУММ ПАРНЫХ ПРОИЗВЕДЕНИИ 2. ВЫЧИСЛЕНИЕ СУММ ПАРНЫХ ПРОИЗВЕДЕНИИ5.3. АРИФМЕТИКА КОМПЛЕКСНЫХ ЧИСЕЛ 5.4. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ Глава 6. ДВОИЧНО-ДЕСЯТИЧНАЯ АРИФМЕТИКА 6.2. СЛОЖЕНИЕ ЧИСЕЛ В ИНВЕРСНЫХ Д-КОДАХ 6.3. СДВИГ Д-КОДОВ 6.4. УМНОЖЕНИЕ ЧИСЕЛ В Д-КОДАХ 6.5. ДЕЛЕНИЕ ЧИСЕЛ В Д-КОДАХ 6.6. ПЕРЕВОД ЧИСЕЛ В Д-КОДАХ Глава 7. ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ В СИСТЕМАХ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ 7.2. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В МИНУС-ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ 7.3. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ 8.2. ВЫБОР МОДУЛЯ ДЛЯ КОНТРОЛЯ 8.8. КОНТРОЛЬ ЛОГИЧЕСКИХ ОПЕРАЦИЙ 8.4. КОНТРОЛЬ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ Глава 9. БУЛЕВЫ ФУНКЦИИ 9.2. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БУЛЕВЫХ ФУНКЦИИ 9.3. ФУНКЦИОНАЛЬНО ПОЛНЫЕ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ 9.4. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ 9.5. МИНИМИЗАЦИЯ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ 9.6. АБСОЛЮТНО МИНИМАЛЬНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ 9.7. МНОГОЗНАЧНЫЕ ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ Глава 10.  АБСТРАКТНЫЕ ЦИФРОВЫЕ АВТОМАТЫ АБСТРАКТНЫЕ ЦИФРОВЫЕ АВТОМАТЫ10.2. ДЕКОМПОЗИЦИЯ АБСТРАКТНЫХ АВТОМАТОВ Глава 11. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ 11.2. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ В БУЛЕВОМ И МОНОФУНКЦИОНАЛЬНОМ БАЗИСАХ 11.4. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ДЕШИФРАТОРАХ И МУЛЬТИПЛЕКСОРАХ 11.5. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ПЗУ 11.6. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ПЛМ 11.7. АСИМПТОТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ Глава 12. ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ АВТОМАТОВ С ПАМЯТЬЮ 12.1. КАНОНИЧЕСКИЙ МЕТОД СТРУКТУРНОГО СИНТЕЗА АВТОМАТОВ С ПАМЯТЬЮ 12.2. ОБЕСПЕЧЕНИЕ УСТОЙЧИВОСТИ ФУНКЦИОНИРОВАНИЯ ЦИФРОВЫХ АВТОМАТОВ 12.8. СТРУКТУРНЫЙ СИНТЕЗ ЭКОНОМИЧНЫХ СХЕМ АВТОМАТОВ С ПАМЯТЬЮ 12.4. МИКРОПРОГРАММНЫЕ АВТОМАТЫ Глава 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ 13.3. ЦИКЛИЧЕСКИЕ КОДЫ Глава 14. КОНТРОЛЬ ЦИФРОВЫХ АВТОМАТОВ 14.  2. ОБЩИЕ МЕТОДЫ ФУНКЦИОНАЛЬНОГО КОНТРОЛЯ ЦИФРОВЫХ АВТОМАТОВ 2. ОБЩИЕ МЕТОДЫ ФУНКЦИОНАЛЬНОГО КОНТРОЛЯ ЦИФРОВЫХ АВТОМАТОВ14.3. ФУНКЦИОНАЛЬНЫЙ КОНТРОЛЬ ЦИФРОВЫХ АВТОМАТОВ ПРИ ИСПОЛЬЗОВАНИИ ЛИНЕЙНЫХ ГРУППОВЫХ КОДОВ 14.4. ЭЛЕМЕНТЫ ТЕОРИИ САМОПРОВЕРЯЕМЫХ ЦИФРОВЫХ АВТОМАТОВ 14.5. ТЕСТОВЫЙ КОНТРОЛЬ 14.6. САМОДИАГНОСТИРУЕМЫЕ ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ |
Двоичная система счисления | Презентация к уроку:
Слайд 1
Двоичная система счисления Система счисления. Часть2
Слайд 2
Историческая справка 1703г. – великий немецкий математик Лейбниц ввел в математику двоичную систему счисления. 1936-1938гг. – американский инженер и математик Клод Шеннон предложил использовать двоичную систему счисления для конструирования электрических схем. В двоичной системе счисления для записи чисел используются всего две цифры: 0 и 1, q = 2 .
Слайд 3
Перевод чисел из двоичной системы счисления в десятичную ( N 2 N 10 ) ( через развернутую форму записи числа ) Пример: 1011,01 2 =1*2 3 +0*2 2 +1*2 1 +1*2 0 +0*2 -1 +1*2 -2 =8+2+1+ ¼ =11 ¼ . Таблица степеней числа 2 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7 2 8 2 9 2 10 ___________________________________________________________________________________________________________________ 2 4 8 16 32 64 128 256 512 1024 Задание 8: переведите в десятичную систему счисления 10110,011 2 110101,1 2 10101,101 2
Таблица степеней числа 2 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7 2 8 2 9 2 10 ___________________________________________________________________________________________________________________ 2 4 8 16 32 64 128 256 512 1024 Задание 8: переведите в десятичную систему счисления 10110,011 2 110101,1 2 10101,101 2
Слайд 4
Перевод целых чисел из десятичной системы счисления в двоичную ( N 10 N 2 ) Способ – деление на основание системы счисления 22 10 =10110 2 Задание 9: переведите десятичные числа 27; 35; 54; 66 в двоичную систему счисления
Слайд 5
Арифметические операции с двоичными числами. Рассмотрим правила выполнения арифметических операций над одноразрядными числами. Представим их в виде таблиц. Правило сложения Правило вычитания Правило умножения 0+0=0 0-0=0 0*0=0 0+1=1 1-0=1 0*1=0 1+0=1 1-1=0 1*0=0 1+1=10 0-1=-1 1*1=1 1+1+1=11
Слайд 6
Арифметические операции с двоичными числами. Примеры. 1. 1010+10101=11111 1010 10101 11111 2. 10101-1010=1011 10101 1010 1011 3. 10111*11=1000101 10111 11 10111 10111 1000101
10111*11=1000101 10111 11 10111 10111 1000101
Слайд 7
Упражнения Произведите сложение двоичных чисел: 111+101; 11011+1110 Выполните вычитание двоичных чисел: 111-101; 11011-01110 Умножьте двоичные числа: 111*101; 11011*1110
Слайд 8
Перевод десятичных дробей в двоичную систему счисления ( N 10 N 2 ) (умножением на 2) Пример: 0,5625 10 = N 2 = 0,1001 2 0, 5625 2 1 1250 2 0 2500 2 0 5000 2 1 0000 Задание 10: переведите десятичные дроби в двоичную систему счисления с точностью до 6 знаков после запятой: 0,7 10 0,4622 10 0,5198 10 0,5803 10
Слайд 9
Перевод смешанных чисел из десятичной системы счисления в двоичную Алгоритм перевода: 1) перевести целую часть; 2) перевести дробную часть; 3) сложить полученные результаты. Пример : перевести 17,25 10 в двоичную систему счисления. Решение: 17 10 = 10001 2 0,25 10 = 0,01 2 17,25 10 = 10001,01 2 Задание 11: переведите в двоичную систему счисления числа: 40,5 10 31,75 10 124,25 10
Слайд 10
Упражнения: Переведите в двоичную запись десятичные числа: 17; 48; 193; 513 используя правило деления на 2. 2. Переведите в десятичную запись двоичные числа: 1001; 10111; 1011000; 10111011
2. Переведите в десятичную запись двоичные числа: 1001; 10111; 1011000; 10111011
Слайд 11
Основной недостаток двоичной системы – ее громоздкость. Более компактной является восьмеричная система счисления с основанием 8. В ней используется восемь символов 0,1,2,3,4,5,6,7, заимствованных из десятичной. Для представления двоичных чисел восьмеричными цифрами разряды двоичного числа объединяют в группы по три (триады), начиная с младшего разряда, а дробную часть, со старшего и каждую триаду преобразуют в восьмеричный эквивалент: 11111101 2 = 011 111 101 =375 =3*8 2 +7*8 1 +5*8 0 =253 Восьмеричная и шестнадцатиричная система счисления.
Слайд 12
Если для образования триад не хватает разрядов, то добавляют незначащие нули. Еще более компактную форму записи двоичных чисел дает шестнадцатиричная система счисления, в которой используется 16 символов: 0,1,2,3,4,5,6,7,8,9,А,В,С, D ,Е, F . Десять символов заимствованы из десятичной системы, а в качестве недостающих использованы буквы латинского алфавита: А-10, В-11, С-12, D -13, Е-14, F -15. Процедура преобразования двоичного числа в шестнадцатиричное довольно проста. Двоичное число разбивается на четверки (тетрады),начиная с младшего разряда, а дробная часть со старшего и каждая тетрада заменяется шестнадцатиничным символом: 10101011111101 =0010 1010 1111 1101 =2А FD 1111000101111011 2 = Восьмеричная и шестнадцатиричная система счисления.
Процедура преобразования двоичного числа в шестнадцатиричное довольно проста. Двоичное число разбивается на четверки (тетрады),начиная с младшего разряда, а дробная часть со старшего и каждая тетрада заменяется шестнадцатиничным символом: 10101011111101 =0010 1010 1111 1101 =2А FD 1111000101111011 2 = Восьмеричная и шестнадцатиричная система счисления.
Слайд 13
Таблица двоичных кодов десятичных и шестнадцатеричных 1 2 3 4 5 6 7 8 9 A B C D E F 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
Слайд 14
1111000101111011 2 = F17B 16 Ответ
Слайд 15
1. выполните сложение и проведите проверку 11010101 2 +1110 2 2. выполните вычитание и результат переведите в десятичную СС: 110101110 2 -10111111 2 3. выполните умножение и результат переведите в десятичную СС: 111100 2 *100100 2 4. переведите из 10-ой СС в 2-ичную, 8 –ричную,16- ричную СС числа: 126, 533 5. запишите в развернутом виде (по формуле) числа: 657; 15А12 Самостоятельная работа
Двоичная система счисления, преобразование, шаги с решением Пример
Двоичные числа представляются просто двумя символами или цифрами в компьютерных приложениях, а именно 0 (ноль) и 1 (единица). Двоичная система счисления была самой влиятельной системой счисления в истории технического развития.
Двоичная система счисления была самой влиятельной системой счисления в истории технического развития.
В этой статье мы изучим, что такое двоичная система счисления, кто ее изобрел, сколько цифр в ней используется, таблица преобразования, преобразование двоичного в десятичное, шестнадцатеричное и восьмеричное, решенные примеры, использование и преимущества двоичной системы счисления и часто задаваемые вопросы.
Что такое двоичная система счисления?
Двоичная система счисления или система с основанием 2 состоит только из двух цифр, равных 0 и 1. Компьютеры обрабатывают и хранят все свои данные, включая числа, слова, фильмы, изображения и музыку, используя двоичную систему счисления. Поскольку числа «2» в этой системе не существует, 1 + 1 = 10.
Определение двоичной системы счисления
В математике двоичная система счисления представляет собой позиционную систему счисления, в которой в качестве основания используется 2, и, следовательно, требуется только два отдельных символа для его цифр, 0 и 1, вместо обычных десяти символов, необходимых в десятичной системе.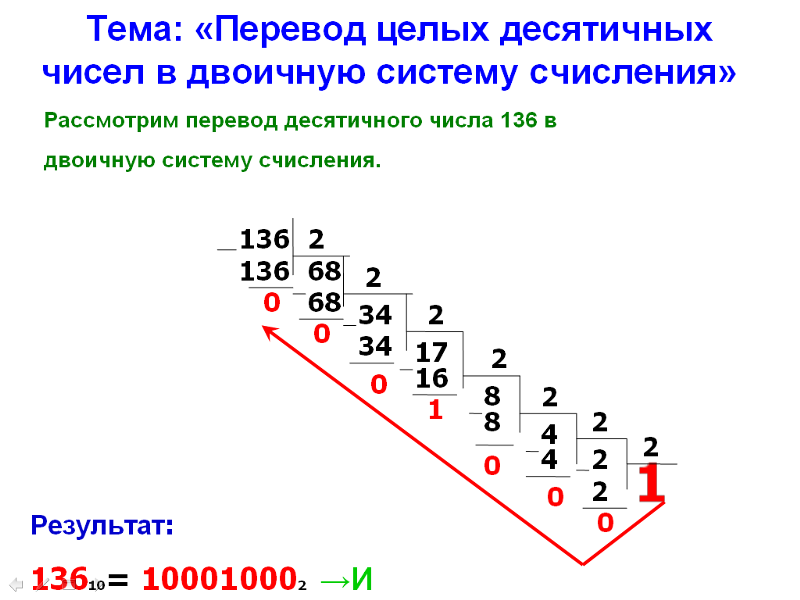 Полезность двоичной системы в теории информации и компьютерных технологиях связана, прежде всего, с компактным и надежным представлением нулей и единиц в электромеханических устройствах с двумя состояниями, такими как «включено-выключено», «открыто-закрыто» или «идет-не идет». ”
Полезность двоичной системы в теории информации и компьютерных технологиях связана, прежде всего, с компактным и надежным представлением нулей и единиц в электромеханических устройствах с двумя состояниями, такими как «включено-выключено», «открыто-закрыто» или «идет-не идет». ”
Прочитайте обо всех системах счисления здесь.
Кто изобрел двоичную систему счисления?
Готфриду Вильгельму Лейбницу приписывают разработку двоичной системы в 17 веке. Лейбниц предложил двоичную систему счисления в своей статье «Объяснение двоичной арифметики».
Однако новые данные свидетельствуют о том, что более ранние цивилизации в Египте и Китае, с другой стороны, использовали двоичную систему для основного счета и арифметики. Некоторые ученые искали в словаре Мангареву, небольшой остров с населением менее 2000 человек и площадью всего 7 квадратных миль (18 квадратных километров) на полпути между островом Пасхи и Таити.
Согласно ученым, у мангареванцев были термины для чисел от 1 до 10. Они использовали двоичную систему для чисел от 20 до 80 с отдельными именами из одного слова для 20, 40 и 80. Они использовали степени от десяти по крайней мере до 10 миллионов для действительно больших чисел.
Они использовали двоичную систему для чисел от 20 до 80 с отдельными именами из одного слова для 20, 40 и 80. Они использовали степени от десяти по крайней мере до 10 миллионов для действительно больших чисел.
Джордж Буль, британский математик, написал в 1854 г. основополагающую работу, описывающую алгебраическую систему логики, основанную на бинарной системе, которая стала известна как булева алгебра. Его логическое исчисление сыграет ключевую роль в развитии цифровых электрических схем.
Сколько цифр используется в двоичной системе счисления?
Двоичная система счисления — это позиционная система счисления, в которой используются только два символа — 0 и 1, а не десять, как требуется в десятичной системе. Основание двоичной системы счисления равно 2, что означает, что любое представление числа может иметь только два числовых значения. В двоичном формате числа от 0 до 10 равны 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001 и 1010.
Также узнайте больше о других геометрических фигурах здесь.
Таблица двоичных систем счисления
Вот таблица преобразования систем счисления, которая пригодится при решении задач, основанных на двоичных системах счисления.
| Binary Base-2 | Decimal Base-10 | Octal Base-8 | Hexadecimal Base-16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 8 | 10 | 8 |
| 1001 | 9 | 11 | 9 |
| 1010 | 10 | 12 | A |
| 1011 | 11 | 13 | B |
| 1100 | 12 | 14 | C |
| 1101 | 13 | 15 | D |
| 1110 | 14 | 16 | E |
| 1111 | 15 | 17 | F |
| 10000 | 16 | 20 | 10 |
| 10001 | 17 | 21 | 11 |
| 10010 | 18 | 22 | 12 |
| 10011 | 1 | 23 | 13 666666666666666666666666666666666666666666666666666 | 23 | 13666666666666666666666669 | 23 | 23 | 004720 | 24 | 14 |
| 10101 | 21 | 25 | 15 |
| 10110 | 22 | 26 | 16 |
| 10111 | 23 | 27 | 17 |
| 11000 | 24 | 30 | 18 |
| 11001 | 25 | 31 | 19 |
| 11010 | 26 | 32 | 1A |
| 11011 | 27 | 33 | 1B |
| 11100 | 28 | 34 | 1C |
| 11101 | 29 | 35 | 1D |
| 11110 | 30 | 36 | 1E |
| 11111 | 31 | 37 | 1F |
| 100000 | 32 | 40 | 20 |
Преобразование двоичной системы счисления
Существует четыре основных типа систем счисления:
- : Имеет основание 8.

- Шестнадцатеричная система счисления: Имеет основание 16.
На экзаменах часто требуется преобразовать одну форму системы в другую форму. Давайте посмотрим, как мы можем преобразовать двоичную систему счисления в десятичную, шестнадцатеричную и восьмеричную.
Преобразование двоичного числа в десятичное
Для преобразования двоичного числа в десятичное существует два основных метода: позиционная запись и удвоение. Эти методы описаны в разделах ниже.
Использование позиционной записи
Существует два основных метода преобразования двоичного числа в десятичное: позиционная запись и удвоение. Эти методы описаны в разделах ниже.
| Старший бит (MSB) 90\) = 128+64+0+0+8+0+2+0 = (202) Преобразование двоичного числа в шестнадцатеричное Шестнадцатеричная система счисления упрощает преобразование больших двоичных значений в меньшие, более компактные группы. \(= (6A)_{16}\), что является ответом. Узнайте больше о линиях регрессии здесь. По группировке Поскольку шестнадцатеричная система счисления имеет только 16 цифр (от 0 до 7 и от A до F), мы можем выразить каждую шестнадцатеричную цифру, используя только четыре бита, как показано ниже.
Процессы преобразования двоичного числа в шестнадцатеричное следующие. Решенный пример Преобразование двоичного числа 1010101101001 в шестнадцатеричное число. Таким образом, преобразование из двоичного в шестнадцатеричное равно: \(= (1010101101001)_2\) \(= (1 0101 0110 1001)_2\) 100001 1)\(= (1 5 6 9)_{16}\) \(= (1569)_{16}\) Также проверьте концепции линейной алгебры здесь, когда вы закончите с концепциями системы счисления! Преобразование двоичного кода в восьмеричный Восьмеричная система счисления упрощает преобразование огромных двоичных значений в более мелкие и компактные группы. Двоичное число можно преобразовать в восьмеричное различными способами.
Процессы преобразования двоичного числа в восьмеричное следующие. Пример решена Преобразование двоичного числа 1010111100 в восьмеричное. Следовательно, двоично-восьмеричное. = (1010111100) = (001 010 111 100) = (1 2 7 4) = (1274) Подробнее о круговой диаграмме см. здесь. Использование и преимущества двоичной системы счисленияДвоичная система счисления является одним из типов техники представления чисел. Вот его использование и преимущества. Использование Наиболее распространенный и широко используемый в цифровых системах. Двоичная система используется для описания двоичных величин, которые могут быть представлены любым устройством только с двумя возможными рабочими состояниями. Выключатель, например, имеет только два состояния: открыто и закрыто. Наиболее распространенное применение этой системы счисления можно найти в компьютерных технологиях. В конце концов, каждый компьютерный язык и программирование основаны на двузначной системе счисления, используемой в цифровом кодировании. Процесс цифрового кодирования включает в себя получение данных и их отображение с ограниченными фрагментами информации. Нули и единицы двоичной системы составляют ограниченную информацию. 916\) может представлять почти 65 тысяч цветов. Кроме того, применение двоичной системы счисления можно найти в области математики, называемой булевой алгеброй. Этот предмет математики связан с логикой и значениями истинности. Утверждениям в этой программе присваиваются 0 или 1 в зависимости от того, истинны они или ложны. Преимущества Двоичная система счисления может использоваться для различных целей. Компьютер, например, щелкает переключателями, чтобы добавить числа. Вы можете стимулировать компьютерное добавление, добавляя двоичные числа в систему. Надеюсь, что эта статья о двоичных системах счисления была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас! Часто задаваемые вопросы о двоичной системе счисленияQ.1 Что такое двоичная система счисления на примере? Ответ 1 В математике двоичная система счисления представляет собой позиционную систему счисления, которая использует 2 в качестве основания и, следовательно, требует только два отдельных символа для своих цифр, 0 и 1, а не обычные десять необходимых символов в десятичной системе. Полезность двоичной системы в теории информации и компьютерных технологиях связана, прежде всего, с компактным и надежным представлением нулей и единиц в электромеханических устройствах с двумя состояниями, такими как «включено-выключено», «открыто-закрыто» или «идет-не идет». В.2 Что такое шестнадцатеричное число? Ответ 2 Шестнадцатеричная система представлена с основанием 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Шестнадцатеричная (иногда известная как основание 16 или просто шестнадцатеричная) система счисления представляет собой позиционную систему счисления, используемую в математике и вычислительной технике. Шестнадцатеричное используется в кодировке передачи Base16, которая делит каждый байт открытого текста на два 4-битных значения и две шестнадцатеричные цифры. Шестнадцатеричные числа обычно используются разработчиками программного обеспечения и проектировщиками систем, поскольку они обеспечивают удобное для человека представление данных в двоичном коде. В.3 Кто изобрел двоичную систему счисления? Ответ 3 Готфриду Вильгельму Лейбницу приписывают разработку двоичной системы в 17 веке. Лейбниц предложил двоичную систему счисления в своей статье «Объяснение двоичной арифметики». Однако новые данные свидетельствуют о том, что более ранние цивилизации в Египте и Китае, с другой стороны, использовали двоичную систему для основного счета и арифметики. Некоторые ученые искали в словаре Мангареву, небольшой остров с населением менее 2000 человек и площадью всего 7 квадратных миль (18 квадратных километров) на полпути между островом Пасхи и Таити. По мнению ученых, у мангареванцев были термины для чисел от 1 до 10. Они использовали двоичную систему для чисел от 20 до 80 с отдельными именами из одного слова для 20, 40 и 80. Они использовали степени от десяти по крайней мере до 10 миллионов для действительно больших чисел. В.4 Что такое двоичные числа? Ответ 4 Двоичная система счисления или система с основанием 2 состоит только из двух цифр, равных 0 и 1. Компьютеры обрабатывают и хранят все свои данные, включая числа, слова, фильмы, изображения и музыку, используя двоичную систему счисления. Поскольку числа «2» в этой системе не существует, 1 + 1 = 10. Джордж Буль, британский математик, в 1854 году написал основополагающую работу, описывающую алгебраическую систему логики, основанную на бинарной системе, которая стала известна как булева алгебра. Его логическое исчисление сыграет ключевую роль в развитии цифровых электрических схем. В.5 Что такое восьмеричные числа? Ответ 5 Восьмеричная система счисления представлена с основанием 8, то есть она и использует цифры от 0 до 7, т.е. 0, 1, 2, 3, 4, 5, 6 и 7 для представления чисел. Термин восьмеричный используется для описания чисел с восьмизначным основанием. Двоичная система счисления — Арифметические вычисления в двоичной системе счисленияДля определения числа в двоичной системе используется двоичная система счисления. Двоичная система представляет собой представление чисел с помощью нулей и единиц. Двоичная система счисления обычно используется в компьютерных языках, таких как Java, C++. Это связано с тем, что компьютер понимает только двоичный язык, равный 0 или 1. Все вводимые компьютеру данные декодируются в последовательность нулей или единиц. Система счисления обычно используется для представления чисел в компьютерной архитектуре.
И в математике, и в цифровой электронике двоичная система счисления представляет собой способ представления чисел, основание которых равно 2, а то же самое представляет собой комбинацию нулей и единиц. Здесь мы предоставили пример двоичной системы счисления. Взглянем! 110100 История двоичной системы счисления Томас Харриот, Готфрид Лейбниц и Хуан Карамуэль-и-Лобковиц изучали двоичную систему счисления в 16 и 17 веках. Это называется современной бинарной системой. Томас Харриот, Готфрид Лейбниц и Хуан Карамуэль-и-Лобковиц изучали двоичную систему в 16 и 17 веках. Это называется современной бинарной системой. Тем не менее, другие методы представления двоичных чисел были найдены в более раннее время в различных странах, таких как Индия, Китай, Египет и т. д. In the following table, you will get to see the values of decimal to binary numbers from 1 to 30. Decimal to Binary Numbers From 1 to 30
Почти все виды основных арифметических операций, таких как сложение, вычитание, умножение и деление, возможны с двоичными цифрами. Изучим их по отдельности. Суммирование двоичных чисел — простейшая операция, использующая форму переноса. 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0, здесь переносим 1, так как 1 + 1 равно 2, что равно 0 + (1 x 21) Дополнение из двух цифр (здесь «1») дает ноль, а перенос необходимо добавить ко второму числу. 5 + 5 = 0 и перенос 1 Здесь вы можете проверить пример, показывающий сложение двух двоичных выражений. Add 10101 and 11011 Binary Number System Addition
Подобно сложению, вычитание следует той же процедуре: 90 936 0 – 1 = 1, одолжить 1 1 – 0 = 1 1 – 1 = 0 Когда вы вычитаете 1 из 0, получается 1, и то же самое нужно уменьшить из следующего числа. Здесь вы можете проверить пример, показывающий вычитание двух двоичных выражений. Subtract 1010110 – 101010 Binary Number System Subtraction
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 Двоичное число можно преобразовать в шестнадцатеричное различными способами. Для преобразования можно использовать как прямой, так и косвенный подходы. Для начала вы должны преобразовать двоичную систему в другую базовую систему (например, в десятичную или в восьмеричную). После этого вы должны преобразовать его в шестнадцатеричное число. 90\)
Двоичное число можно преобразовать в шестнадцатеричное различными способами. Для преобразования можно использовать как прямой, так и косвенный подходы. Для начала вы должны преобразовать двоичную систему в другую базовую систему (например, в десятичную или в восьмеричную). После этого вы должны преобразовать его в шестнадцатеричное число. 90\) Рассмотрим двоичное число. Для целочисленной части разбейте двоичные цифры на четыре группы (начиная справа), а для дробной части начните слева. Каждый набор из четырех двоичных цифр должен быть преобразован в одну шестнадцатеричную цифру. Это базовый алгоритм, в котором вы комбинируете двоичные числа и заменяете их шестнадцатеричными эквивалентами.
Рассмотрим двоичное число. Для целочисленной части разбейте двоичные цифры на четыре группы (начиная справа), а для дробной части начните слева. Каждый набор из четырех двоичных цифр должен быть преобразован в одну шестнадцатеричную цифру. Это базовый алгоритм, в котором вы комбинируете двоичные числа и заменяете их шестнадцатеричными эквивалентами.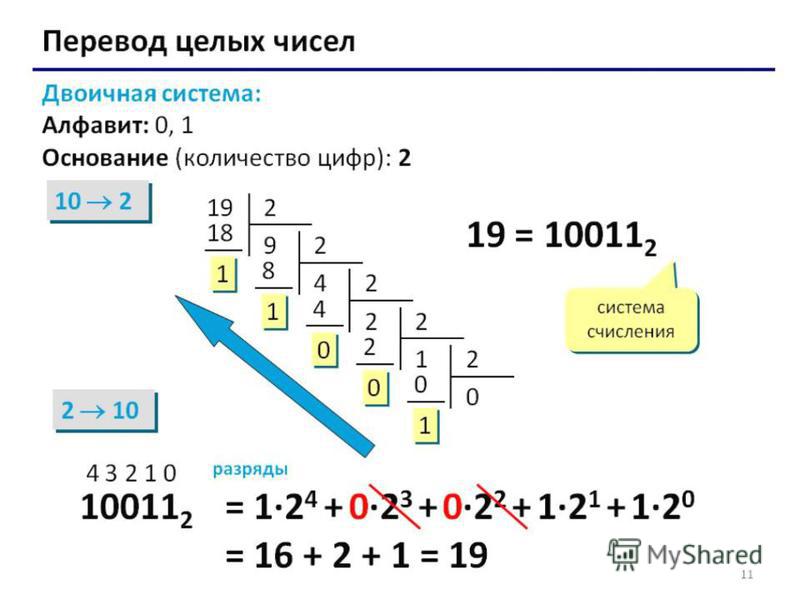 Для преобразования можно использовать как прямой, так и косвенный подходы. Для начала вы должны преобразовать двоичный код в другую базовую систему (например, в десятичную или шестнадцатеричную). После этого вы должны преобразовать его в восьмеричное число.
Для преобразования можно использовать как прямой, так и косвенный подходы. Для начала вы должны преобразовать двоичный код в другую базовую систему (например, в десятичную или шестнадцатеричную). После этого вы должны преобразовать его в восьмеричное число. Рассмотрим двоичное число. Для целочисленной части разбейте двоичные цифры на три группы (начиная справа), а для дробной части начните слева. Каждый набор из трех двоичных цифр должен быть преобразован в одну восьмеричную цифру.
Рассмотрим двоичное число. Для целочисленной части разбейте двоичные цифры на три группы (начиная справа), а для дробной части начните слева. Каждый набор из трех двоичных цифр должен быть преобразован в одну восьмеричную цифру.
 Есть две основные причины, по которым компьютеры должны использовать эту схему нумерации. Во-первых, он может обеспечить надежный диапазон безопасности. Во-вторых, что наиболее важно, это помогает уменьшить количество необходимых схем. Это уменьшает количество необходимого пространства, количество используемой энергии и количество потраченных денег.
Есть две основные причины, по которым компьютеры должны использовать эту схему нумерации. Во-первых, он может обеспечить надежный диапазон безопасности. Во-вторых, что наиболее важно, это помогает уменьшить количество необходимых схем. Это уменьшает количество необходимого пространства, количество используемой энергии и количество потраченных денег.


 Восьмеричные числа имеют широкий спектр применения и значения, включая использование в компьютерах и цифровых системах счисления. При запросе наземным радаром транспондеры самолетов передают код «кваканья», который выражается в виде четырех восьмеричных цифр. На экране радара этот код используется для идентификации разных самолетов. 9{-2}+ …\)
Восьмеричные числа имеют широкий спектр применения и значения, включая использование в компьютерах и цифровых системах счисления. При запросе наземным радаром транспондеры самолетов передают код «кваканья», который выражается в виде четырех восьмеричных цифр. На экране радара этот код используется для идентификации разных самолетов. 9{-2}+ …\) Система счисления подразделяется на четыре типа:
Система счисления подразделяется на четыре типа: Тем не менее, другие методы представления двоичных чисел были найдены в более раннее время в различных странах, таких как Индия, Китай, Египет и т. д.
Тем не менее, другие методы представления двоичных чисел были найдены в более раннее время в различных странах, таких как Индия, Китай, Египет и т. д. 0003
0003 Это точно так же, как мы делаем в десятичной системе при сложении двух однозначных чисел. Например:
Это точно так же, как мы делаем в десятичной системе при сложении двух однозначных чисел. Например: Это называется заимствование.
Это называется заимствование.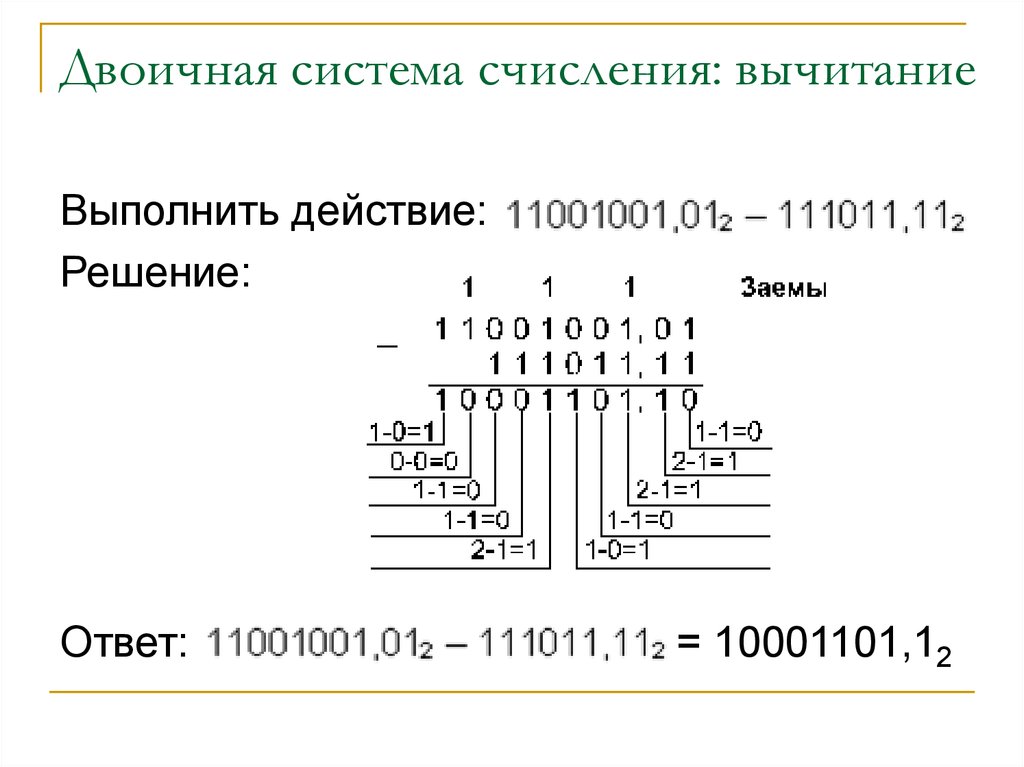 36 1
36 1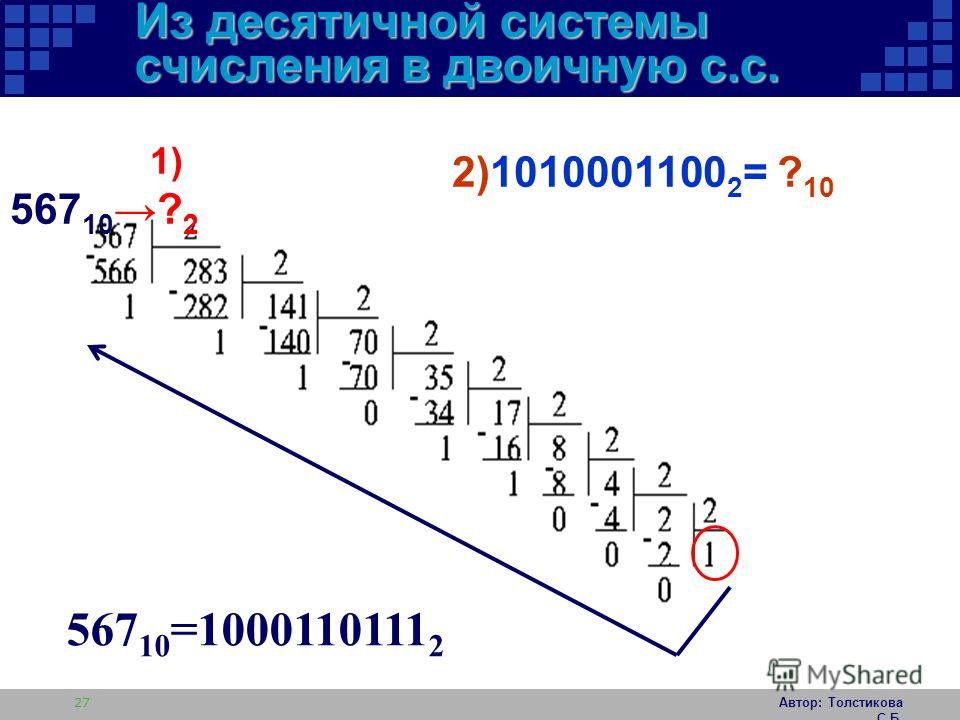 Проверьте пример ниже:
Проверьте пример ниже: Преобразуйте следующее двоичное число в десятичное число.
Преобразуйте следующее двоичное число в десятичное число. Аналогичным образом мы можем выполнять операции сложения, вычитания, умножения и деления над двоичными числами.
Аналогичным образом мы можем выполнять операции сложения, вычитания, умножения и деления над двоичными числами.
