Применение закон био савара лапласа: Закон Био — Савара — Лапласа и его применение к расчету магнитного поля — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

1.3. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля. @

Вопрос второй.

Магнитостатика. Магнитное поле в вакууме.

2.1.Магнитное поле и его источники. Вектор магнитной индукции,свойства магнитного поля.

Многочисленные опыты начала XIX века показали, что каждый проводник с током и постоянный магнит способны оказывать силовое воздействие через пространство на другие проводники с током или магниты. Это происходит из-за того, что вокруг проводников с током и магнитов возникает поле, которое было названо магнитным.

Рассмотрим ряд опытов, которые позволили установить основные свойства магнитного поля:

Если заряженный шарик из диэлектрика подвесить на нити вблизи магнитной стрелки, стрелка и шарик остаются неподвижными. Следовательно, постоянные магниты не действуют на неподвижные заряды и неподвижные заряды не создают магнитного поля.
Если магнитную стрелку поместить под прямолинейным проводником с током, то она будет поворачиваться, стремясь расположиться перпендикулярно проводнику (опыт Эрстеда). Смена направления тока на противоположное вызовет переориентацию стрелки на 180˚С.
Рис.1.2 Силовые линии
магнитного поля прямолинейного тока и правило правой руки.
Пучок движущихся электронов оказывает действие на магнитную стрелку аналогичное проводнику с током (опыт Иоффе).
Конвекционные токи, образуемые движущимися заряженными телами, по своему действию на магнитную стрелку подобны токам проводимости (опыт Эйхенвальда).

На основании данных опытов был сделан вывод о том, что магнитное поле создается только движущимися зарядами или движущимися заряженными телами, а также постоянными магнитами.

Основной характеристикой магнитного поля является вектор магнитной индукции .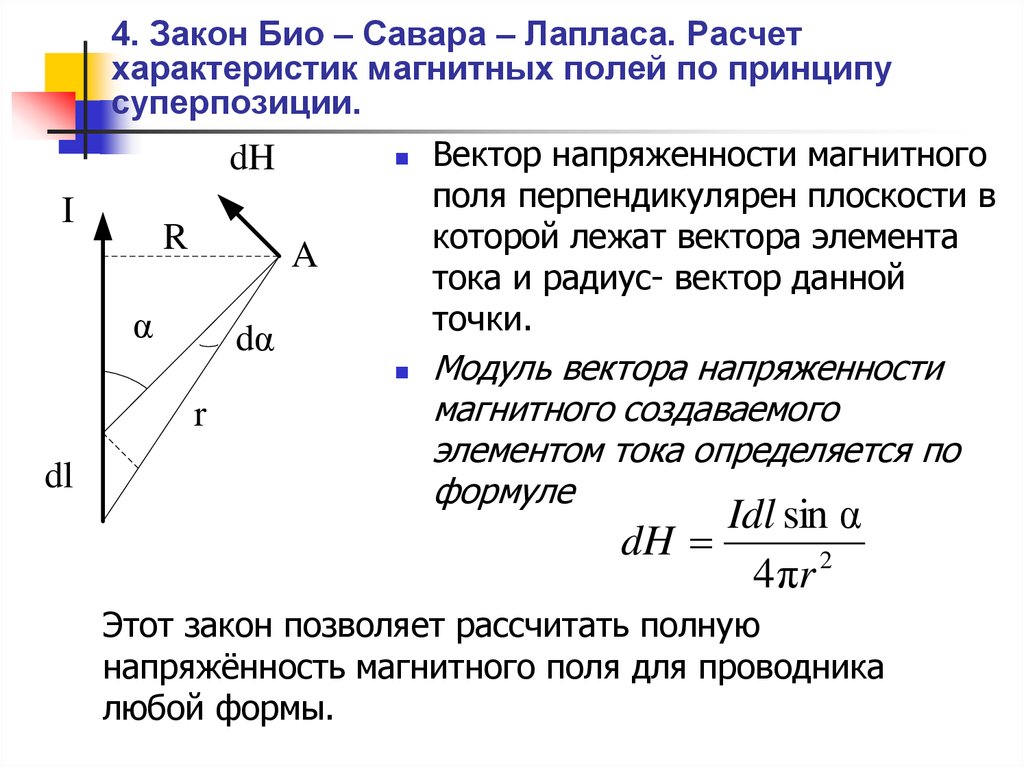 За направление магнитной индукции в данной точке поля принимают направление, по которому в данной точке располагается ось магнитной стрелки отS кN (рис.1.1). Графически магнитные поля изображаются силовыми линиями магнитной индукции, то есть кривыми, касательные к которым в каждой точке совпадают с направлением вектора В.

Как определить направление вектора около проводника с током? Это можно сделать с помощьюправила правой руки,которое иллюстрируется рис. 1.2. Большой палец правой руки ориентируют в направлении тока, тогда остальные пальцы в согнутом положении указывают направление силовых линий магнитного поля.

Магнитная индукция в системе СИ измеряется в Н/(А∙м), этой величине присвоено специальное наименование – тесла [Tл].

2.2 Сила Ампера, сила Лоренца.

В 1820 г. А.Ампер установил, что сила, с которой магнитное поле действует на элементарный проводник с током Iи длиной:

Вектор совпадает по направлению с током. Данная формула выражаетзакон Ампера:сила, действующая на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника и магнитной индукции поля.

Если поместить проводник с током между полюсов постоянного магнита, то сила Ампера будет действовать на него в направлении, показанном на рис. 1.4.

Направление может быть найдено по правилу левой руки: если ладонь левой руки расположить так, чтобы вектор был направлен в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отставленный под прямым углом большой палец укажет направление силы, действующей на элемент проводника с током (рис.4.5).

Модуль силы Ампера вычисляется по формуле:

, где α –угол между векторамии. Чтобы найти силу, действующую на проводник конечной длиныв магнитном поле, необходимо определить геометрическую сумму сил, действующих на все малые элементы данного проводника, т.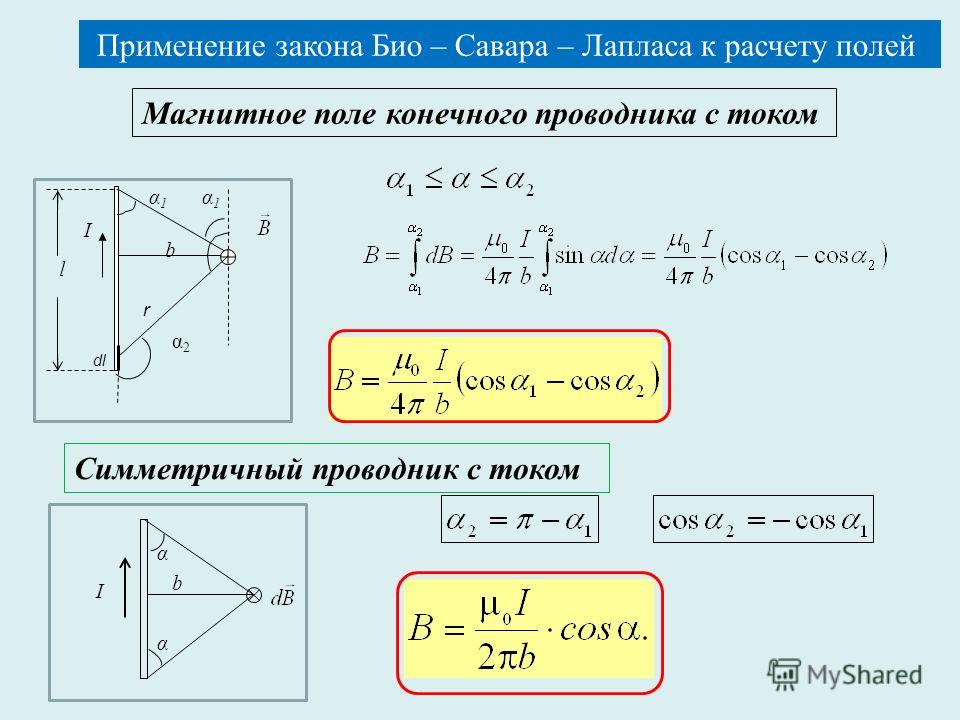

е.

Пусть элемент проводника с током перпендикулярен направлению магнитного поля. Тогда sinα=1 и dF=IВ. Отсюда получаем

Последнее выражение помогает определить физический смысл величины В: магнитная индукция численно равна силе, действующей со стороны магнитного поля на 1 м проводника, по которому течет ток в 1 А и который расположен перпендикулярно направлению магнитного поля.Таким образом, магнитная индукция является силовой характеристикой магнитного поля.

Из закона Ампера следует, что магнитные силы нецентральные, так как они направлены перпендикулярно силовым линиям магнитного поля. Напомним, что электростатические силы – центральные.

Сила Лоренца

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.

Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.

Сила Лоренца определяется соотношением:

F_л = q·V·B·sin

где q –величина движущегося заряда; V — модуль его скорости; B — модуль вектора индукции магнитного поля;  — угол между вектором скорости заряда и вектором магнитной индукции.

Обратите внимание, что сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно

Сила Лоренца перпендикулярна векторам В и v , и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.

Сила Лоренца зависит от модулей скорости частицы и индукции магнитного поля. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Частица равномерно движется по окружности радиуса r.

2.3 Закон Био-Савара-Лапласса и его применение к расчету магнитного поля.

Французские физики Ф. Савар и Ж.Б. Био изучали магнитное поле, создаваемое проводниками с постоянным током различной формы. На основании многочисленных опытов они пришли к выводу, что магнитная индукция поля проводника с током пропорциональна силе тока I, зависит от формы и размеров проводника, а также от расположения рассматриваемой точки по отношению к проводнику. Био и Савар пытались получить самый общий закон – для проводника любой формы и любой точки поля. Однако сделать это им не удалось. По их просьбе этой проблемой занялся французский математик П.С.Лаплас. Он высказал важную гипотезу о том, что при наложении магнитных полей справедлив принцип суперпозиции, т.

е. принцип независимости действия полей. Если имеется несколько проводников с током, каждый из которых создает в исследуемой точке магнитное поле с индукциями …, то результирующая магнитная индукция будет равна векторной сумме всех:. Если перейти к малым отрезкам провода с током, то суммирование надо заменить интегрированием и тогда индукция, создаваемая всем проводником с токомI, будет равна:где– индукция, создаваемая элементом длины проводникаdℓ, интегрирование проводится по всей длине проводника. Лаплас обобщил экспериментальные результаты Био и Савара в виде дифференциального закона, называемого законом Био – Савара – Лапласа, по которому магнитная индукция , создаваемая в некоторой точке А элементом проводникаdℓ с током I

, определяется формулой

Выберем произвольную точку А вблизи проводника. Вектор направлен в точке А перпендикулярно плоскости, построенной на векторахипо правилу правого винта (буравчика), и совпадает с направлением касательной к линии индукции в точке А (пунктирный круг) (рис. 1.7). Коэффициент пропорциональностиkзависит от выбора системы единиц. В СИ это размерная величина, равная μ₀/4π, где μ₀— магнитная постоянная, равная 4π∙10^-7Гн/м. Все выше изложенное относится к вакууму.

Таким образом, магнитную индукцию поля, создаваемую в вакууме током I, текущим по проводу конечной длины ℓ и любой формы, можно найти по формуле

1.Магнитное поле в центре кругового проводника с током.Рассмотрим круговой проводник с током, изображенный на рис.1.8. Все элементы данного проводникаdℓ создают в его центре (точке А) магнитные поляодинакового направления – вдоль нормали к площади витка. Поэтому, как и в предыдущем случае, сложение векторов можно заменить сложением их модулей. Элементыdℓ перпендикулярныRиsinα=1. Используя закон Био-Савара-Лапласа, получим:

2.Магнитное поле прямолинейного проводника с током. Представим себе ток, текущий по тонкому прямому проводу бесконечной длины (рис. 1.9). Возьмем произвольную точку А на расстоянииRот проводника. Согласно правилу правого винта (буравчика), векторыот каждого элемента токаdℓ_iимеют одинаковое направление, перпендикулярное плоскости чертежа (на нас). Поэтому сложение векторовможно заменить сложением их модулей. При суммировании всехбудет меняться уголαмеждуrиdℓ, поэтому выберемαв качестве переменной интегрирования. Выразим черезαвсе остальные величины, полагая, что отрезок АD≈rиз-за малостиdℓ.

Итак, из треугольника АСЕ выразим rчерез известное нам расстояниеRи переменнуюα:

По закону Био-Савара-Лапласа получим:

В данном выражении α₁и α₂— значения угла α для крайних точек проводника. Если прямолинейный проводник бесконечно длинный, то α₁= 0, α₂= π. Магнитная индукция в любой точке поля такого проводника с током:

Напомним, что линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.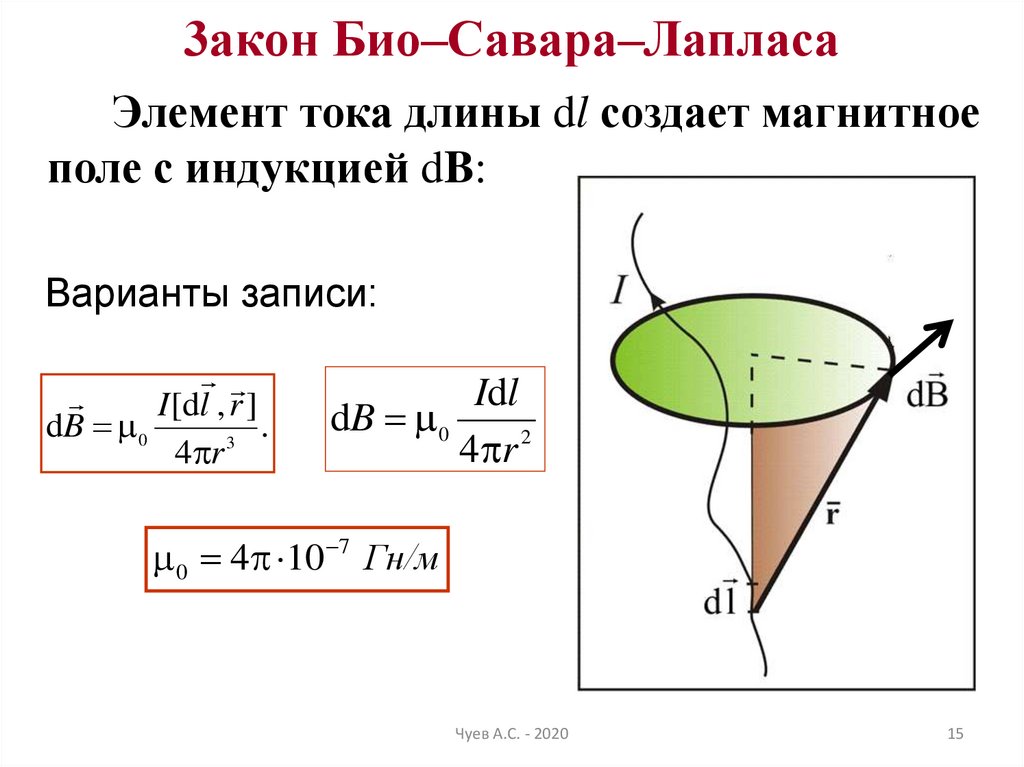

3.Магнитное поле соленоида. Если витки соленоида расположены вплотную друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью. Обозначим черезLдлину соленоида, а черезn- число витков, приходящихся на единицу длины соленоида. Магнитная индукция поля соленоида В равна геометрической сумме магнитных индукций В_iполей всех его витков. ЕслиL>>R(радиуса витков), тогда В в точке А, лежащей на оси вдали от концов такого соленоида, вычисляется по формуле (без вывода): В = μ₀nI.

2.4 Расчет магнитных полей для простейших систем. ХРЕН ЗНАЕТ ТО ИЛИ НЕ ТО,ДРУГОГО НЕТ! Или это то,что выше….то,что под цифрами 1,2,3

Законы Био – Савара – Лапласа и Ампера применяются для определения силы взаимодействия двух параллельных проводников с током. Рассмотрим два бесконечных прямолинейных проводника с токами I1 и I2 , расстояние между которыми равно а. На рис. 1.10 проводники расположены перпендикулярно чертежу. Токи в них направлены одинаково (из-за чертежа на нас) и обозначены точками. Каждый из проводников создает магнитное поле, которое действует на другой проводник. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление определяется правилом правого винта, а его модуль по закону Био – Савара – Лапласа . Согласно проведенным выше расчетам модуль равен сТогда, согласно закону Ампера, dF1=I2B1dl илии аналогично. Направление силы, с которой поледействует на участокdℓ второго проводника с токомI₂(рис.1.10), определяется по правилу левой руки (см. разд. 1.2). Как видно из рис.1.10 и расчетов, силыодинаковы по модулю и противоположны по направлению. В нашем случае они направлены навстречу друг другу и проводники притягиваются. Если токи текут в противоположных направлениях, то возникающие между ними силы отталкивают проводники друг от друга. Итак, параллельные токи (одного направления) притягиваются, а антипараллельные ( противоположных направлений ) — отталкиваются.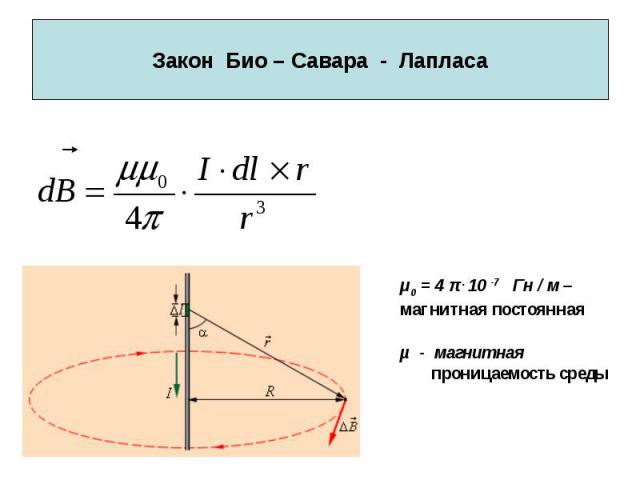 Для определения силы F, действующей на проводник конечной длины ℓ, необходимо проинтегрировать полученное равенство по ℓ от 0 до ℓ : При магнитном взаимодействии выполняется закон действия и противодействия, т.е. третий закон Ньютона:

2.5 Работа по перемещению проводника с током в магнитном поле. ВРОДЕ ТО,ХЗ

Закон Био — Савара — Лапласа и его применение к расчету магнитного поля

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде

(110.1)

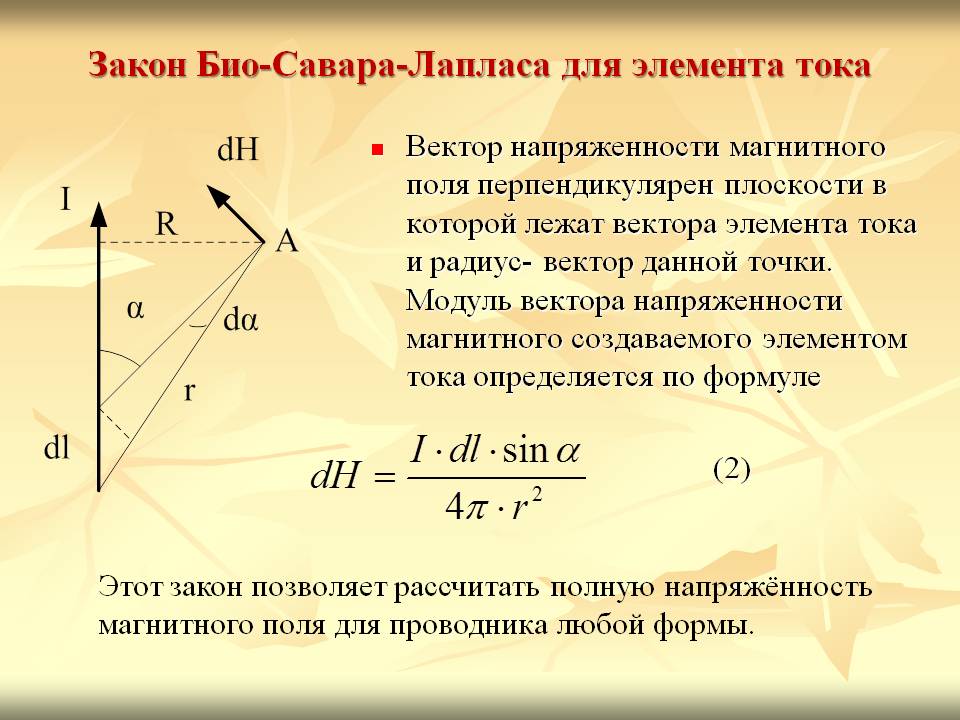
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется выражением

(110. 2)

где a — угол между векторами dl и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

(110.3)

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

(110.4)

Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

(110.5)

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током

Электромагнетизм — из архива библиотеки Wolfram

Электромагнетизм

Пол Эббот

Организация:

Университет Западной Австралии

Отдел:

9004 9003 9003 9003 9005. 9004.

.. 9005 9005 9003 9003 9003 9003 9003 9003 9003 9003 9005. 9004. 9004.3 9005 9003 9003 9005. 9004. 9004. 9004.....3 9005 9003 9003 9003. uwa.edu.au/people/paul.c.abbott
Колледж

Курс физики второго курса бакалавриата состоит из 13 лекций. Сочетание векторного исчисления и волновой физики часто может быть трудным при первом знакомстве. Хороший способ обрести уверенность — применять их в задачах.

Mathematica используется как средство для заметок и заданий по курсу, а также как средство расчета и визуализации.

Рекомендуемое чтение:

Введение в электродинамику Гриффитс
Электромагнетизм: принципы и приложения Лоррен и Корсон
Том 2 из Фейнмановские лекции по физике

Темы:
Эти конспекты лекций основаны на заметках доктора Тома Р. Марша с факультета физики и астрономии Саутгемптонского университета. Введение:

Aims
Structure
References
Assessment
Notes
Conventions

Introduction
The gradient
Summary

Introduction
Преобразование Кулона в закон Гаусса Применение закона Гаусса
Вычисление дивергенции
Уравнение Пуассона, уравнение Лапласа и теорема Гаусса
Резюме

Магнитные поля
Введение
Закон Био-Савара
Закон об амперах
Summary

Introduction
The displacement current
Summary of Maxwell’s Equations
General properties of waves
Wave equation from Maxwell’s Equations
Relations between fields and the wave vector
Summary
Vector тождества полей

Определения
Примеры

Примеры
Определение
Последовательность
Три измерения

Наука > Физика > Электромагнетизм

Укажите закон Био-Савара (закон Лапласа) для магнитной индукции, создаваемой элементом тока. Выразите его в векторной форме. — Sarthaks eConnect

← Предыдущий вопрос Следующий вопрос →

1 ответ

+1 голос

3 марта 2022 г.

Лучший ответ

Рассмотрим очень короткий отрезок длины dl провода, по которому течет ток I. Произведение I \(\vec{dl}\) называется элементом тока; направление вектора \(\vec{dl}\) – вдоль провода в направлении тока.

Закон Био-Савара (закон Лапласа): Величина приращения магнитной индукции \(\vec{dB}\) вырабатываемой элементом тока I \(\vec{dl}\) на расстоянии r от него прямо пропорциональна величине Idl текущего элемента, синусу угла между текущим элементом I \(\vec{dl}\) и единичным вектором \(\hat r\), направленным от текущего элемента к точке в вопросе и обратно пропорциональна квадрату расстояния точки от текущего элемента; магнитная индукция направлена перпендикулярно к I \(\vec{dl}\) и \(\hat r\) в соответствии с правилом векторного произведения.

Где \(\hat r\) = \(\cfrac{\vec r}r\) и константа \(\mu_0\) – проницаемость свободного пространства. Уравнения (1) и (2) называются законом Био-Савара.

Инкрементальная магнитная индукция \(\vec{дБ}\) определяется правилом винтов правой руки векторного перекрестного произведения I \(\vec{dl}\) x \(\hat r\). На рисунке ниже текущий элемент I \(\vec{dl}\) и \(\hat r\) находится в плоскости страницы, так что \(\vec{dB}\) указывает за пределы страницы в точке точка P обозначена ⊙; в точке Q \(\vec{dB}\) указывает на страницу, отмеченную знаком ⊗. 92}\)

[Примечания : (1) Приведенный выше закон основан на экспериментах Жана Батиста Био (1774-1862) и Феликса Савара (1791-1841), французских физиков. Из их наблюдений Лаплас вывел закон математически. (2) Закон Био-Савара играет в магнитостатике ту же роль, что и закон Кулона в электростатике.]

← Предыдущий вопрос Следующий вопрос →

1.3. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля. @

Закон Био — Савара — Лапласа и его применение к расчету магнитного поля

Электромагнетизм — из архива библиотеки Wolfram

Укажите закон Био-Савара (закон Лапласа) для магнитной индукции, создаваемой элементом тока. Выразите его в векторной форме. — Sarthaks eConnect

1 ответ

Похожие вопросы

Категории

alexxlab

Добавить комментарий Отменить ответ

Рубрики