Векторы в жизни — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Векторы в жизни
ПРЕЗЕНТАЦИЮ ПОДГОТОВИЛИСТУДЕНТЫ ГРУППЫ 11КС-11
ЕГОРКИН АРТЁМ
МОГИЛЬНЫЙ ВЛАДИСЛАВ
ШПАКОВСКИЙ АНТОН
2. Цели исследования
Рассмотреть вопросы применения понятия вектора в другихнауках:
в физике, химии, биологии, географии, экономике, психологии.
Выяснить, встречаются ли векторы в повседневной жизни и
нужны ли они в различных профессиях.

3. Векторы в литературе
Басня И. А.Крылова«Лебедь, рак и щука»
Воз и ныне там, т.к.
равнодействующая всех сил,
приложенных к возу,
равна нулю
4. Векторы в физике
Магнитное полепостоянных
магнитов
Кинематический
винт
Скалярное произедение в физике
5. Строение атома азота
Стрелками изображаетсяэлектрон,
а направление
соответствует
направлению спина
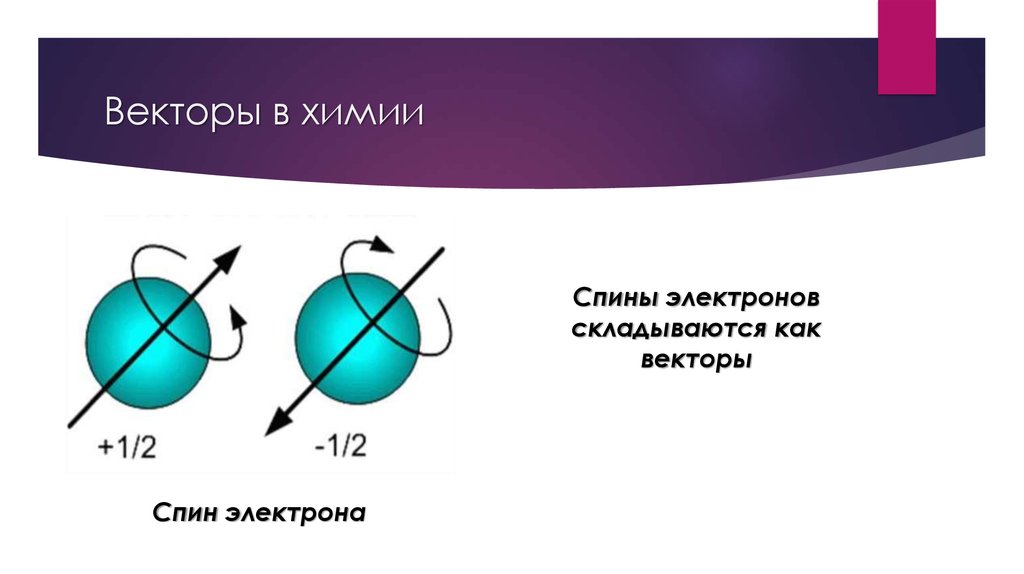
6. Векторы в химии
Спины электроновскладываются как
векторы
Спин электрона
7. Векторы в химии
Химические реакции записываются с помощьюуравнений, в записи которых используются векторы.
Пример, реакция обмена, взаимодействие хлорида
кальция и нитрата серебра с образованием осадка
хлорида серебра:
CaCl2(ж) + 2AgNO3(ж) Ca(NO3)2(ж) + 2AgCl(тв)
8. Векторы в биологии
Молекула ДНК –векторное изображение
Молекула ДНК
Нуклеиновые кислоты – природные высокомолекулярные
органические соединения, обеспечивающие хранение и
передачу наследственной (генетической) информации в
живых организмах
9.
 Синтез лекарственных препаратов
Синтез лекарственных препаратов10. Векторы в географии
С помощью векторовпоказывают направление
движения воздушных масс
в циклонах и антициклонах
11. Векторы в экономике
12. Векторы в психологии
13. Векторы в повседневности
В жизни мы можем наблюдать векторыв деревьях, в частности ели –
направление её ствола это вектор,
направления ее “лапок” от ствола. Еще
мы можем видеть векторы в фонарных
столбах, лавочках и т.д.
14. Векторы в дорожных знаках
Пешеходы и автолюбители могут наблюдатьвекторы в дорожных знаках, также столбы,
на которых крепятся знаки, являются
векторами
15. Благодарю за внимание!
(Данная картинка сделана в векторной графике)English Русский Правила
Творческая работа «Применение векторов»
Содержание:
1 | Введение…………………………………………………… | 3 |
2 | Возникновение понятия «вектор»…………………………. | 4 |
3 | Использование векторов | 5 |
3.1. | В физике……………………………………………………… | 5 |
3.2. | В химии………………………………………………………. | 7 |
3.3. | В биологии…………………………………………………… | 8 |
3.4. | В географии………………………………………………….. | 8 |
4 | Векторы в профессиях | 10 |
5 | Выводы | 11 |
Литература | 12 |
Введение
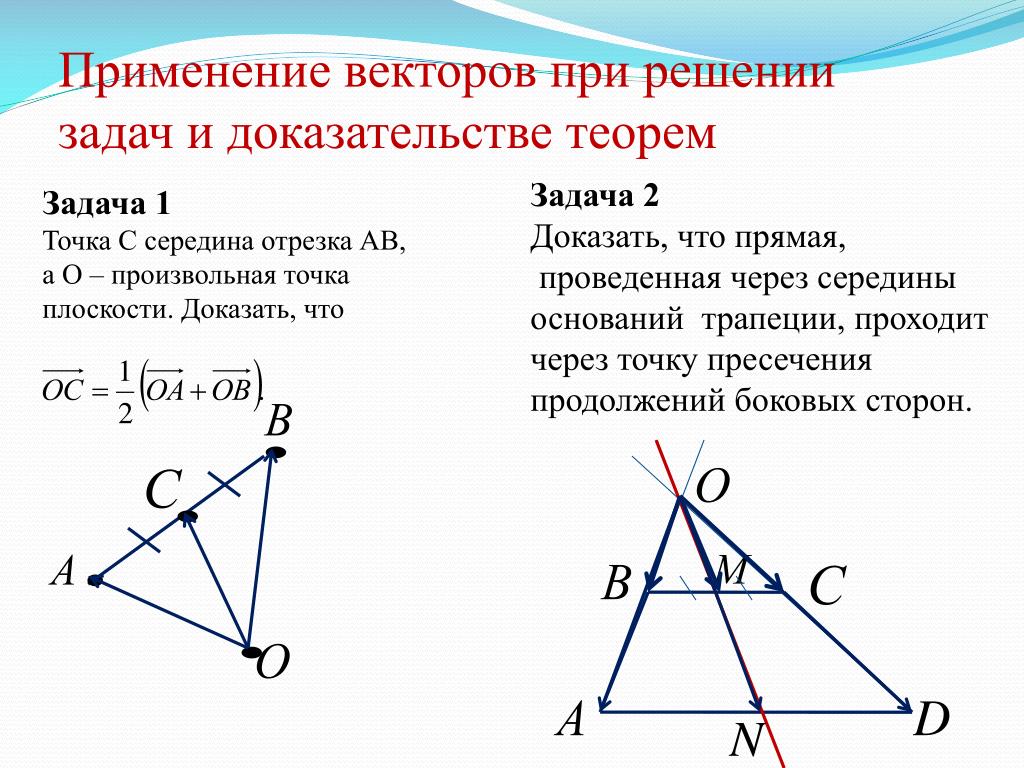
С понятием вектор я познакомилась на уроках геометрии. Особого интереса она у меня не вызвала. Однако, практически сразу понятие «вектор» встретилось и на уроках физики. Тогда стало ясно, что вектор не сугубо математическое понятие, оно применяется и в других областях науки. Вектор — это направленный отрезок. А зачем они нужны? Встречаются ли они в жизни? Может, стоит присмотреться? Если вы начинаете утро с прогноза погоды, то слышали, к примеру: «Ветер северо-западный, скорость 18 метров в секунду». Нельзя не согласится,, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости. Идем в школу: видим дорожные знаки, вроде этих:
Особого интереса она у меня не вызвала. Однако, практически сразу понятие «вектор» встретилось и на уроках физики. Тогда стало ясно, что вектор не сугубо математическое понятие, оно применяется и в других областях науки. Вектор — это направленный отрезок. А зачем они нужны? Встречаются ли они в жизни? Может, стоит присмотреться? Если вы начинаете утро с прогноза погоды, то слышали, к примеру: «Ветер северо-западный, скорость 18 метров в секунду». Нельзя не согласится,, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости. Идем в школу: видим дорожные знаки, вроде этих:
Придя в школу или на работу, видим направляющие знаки:
«Выход», например
Примеры направляющих знаков вы можете увидеть в Приложении 1. Видим, что векторы присутствуют в нашей жизни.
Актуальность изучения данной темы связано с многообразием сфер применения векторов: от искусства до сложных задач моделирования реальных процессов.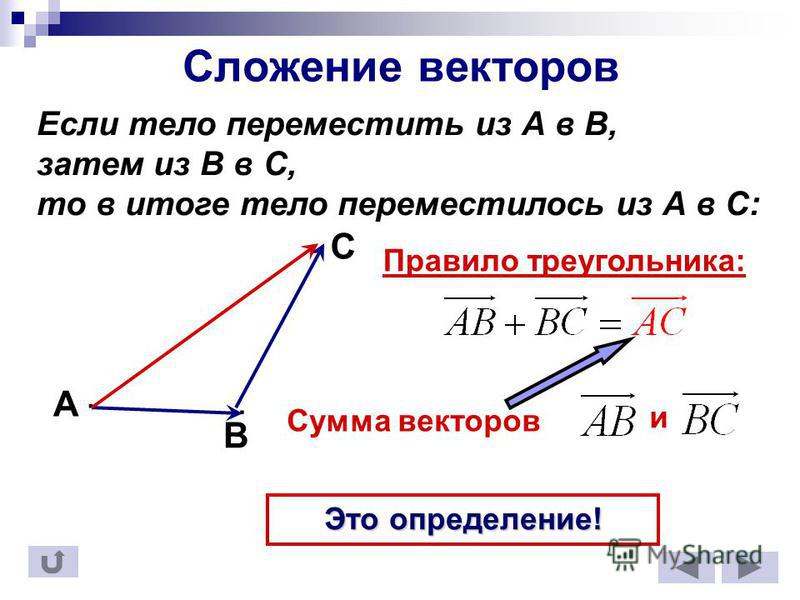 Понятие вектора используется во многих приложениях математики, таких, как современная алгебра и геометрия, теория функций и теория вероятностей. Учебники по таким, на первый взгляд, далеким от математики предметам, как электротехника, радиотехника, теория антенн и др., очень широко используют векторы.
Понятие вектора используется во многих приложениях математики, таких, как современная алгебра и геометрия, теория функций и теория вероятностей. Учебники по таким, на первый взгляд, далеким от математики предметам, как электротехника, радиотехника, теория антенн и др., очень широко используют векторы.
Я решила выяснить, в каких именно областях науки применяются векторы, насколько это понятие актуально в жизни.
Целью моей работы:
Рассмотреть векторы как математические модели реальных процессов.
Перед собой я поставила такие задачи:
Изучить литературу по данной теме;
Изучить понятие «вектор» в предметах естественно-научного цикла;
Узнать, как осуществляется моделирование с помощью векторов.
Установить, используется ли данное понятие в жизни;
Возникновение понятия «вектор»
Одним из основных понятий математики являются «вектор». Развитие этого понятия происходило благодаря широкому использованию его в различных областях математики, информатики, механики, а так же в технике.
Развитие этого понятия происходило благодаря широкому использованию его в различных областях математики, информатики, механики, а так же в технике.
Вектор – молодое математическое понятие. Этот термин впервые употребил ирландский математик Уильям Гамильтон в 1845 году в своих работах по построению числовых систем, обобщающих комплексные числа. Также он ввел термины «скаляр», «скалярное произведение», «векторное произведение». Исследования в этой области проводил ещё немецкий физик-математик Г.Грассман. Его идеи об абстрактных векторных пространствах привели к важному открытию – возможности рассматривать цветовые ощущения как трехмерные векторы. Это легло в основу современного учения о свете. Им были установлены законы сложения цветов.
Понятие «вектор» стало широко использоваться в математике в XIX веке, когда стал активно развиваться раздел математики «Комплексные числа». Векторы использовались для наглядного представления таких чисел. В школах эта тема изучается с 1963 года. Сейчас понятие вектора стало одним из ведущих понятий школьного курса математики.
Сейчас понятие вектора стало одним из ведущих понятий школьного курса математики.
Есть такое высказывание: «Карьера начинается в школе», поэтому я решила глубже изучить понятие «вектор», рассмотреть его значение в математическом моделировании и выяснить в каких профессиях применяется данное понятие.
Использование векторов в различных науках:
В физике
Векторы — мощный инструмент не только математики, но и физики. Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Многие физические величины, такие, как сила, скорость, ускорение, характеризуются не только числовым значением, но и направлением. Эти величины очень удобно изображать в виде направленных отрезков. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. Векторная алгебра является фундаментом, на котором построена классическая физика. С помощью векторов можно моделировать различные физические процессы. Например, некоторые физические поля (магнитное и электромагнитное, сила тяжести) рассматриваются как векторные поля. Такая модель позволяет применять к изучаемым понятиям удобные методы математических расчётов.
Векторная алгебра является фундаментом, на котором построена классическая физика. С помощью векторов можно моделировать различные физические процессы. Например, некоторые физические поля (магнитное и электромагнитное, сила тяжести) рассматриваются как векторные поля. Такая модель позволяет применять к изучаемым понятиям удобные методы математических расчётов.
Векторные величины в физике: скорость, перемещение, ускорение, сила, импульс, напряженность электрического поля, магнитная индукция, момент силы. Для этих величин важно «сколько» и «куда».
Скорость изучается на уроках математики и на уроках физики, и при решении многих задач на скорость необходимо сделать рисунок, на котором направление движения показывается стрелками. Векторами удобно моделировать движение в одном направлении, в разных направлениях, движение по кругу, движение по воде. Составленная таким образом схема-модель поможет решить задачу.
Пример схем некоторых задач на движение:
Тело с большей скоростью догоняет тело с меньшей скоростью:
Движение в противоположные стороны:
Равномерным движением по окружности называется такое движение, при котором скорость не меняется по модулю, а меняется лишь её направление. При этом вектор ускорения перпендикулярен вектору скорости. Вектор скорости направлен по касательной к окружности.
При этом вектор ускорения перпендикулярен вектору скорости. Вектор скорости направлен по касательной к окружности.
Еще одна физическая векторная величина, которую я хотела бы рассмотреть – это сила. Сила определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Результат действия силы зависит от направления. На рисунке вы можете видеть модель направления силы тяжести и всемирного тяготения.
В физике можно найти ещё много примеров, где векторы применяются как средство моделирования физических процессов.
В химии
Также векторы помогают создавать математические модели некоторых химических процессов. Например, для того, чтобы показать строение атома используются всё те же векторы.
На схеме вы можете видеть строение атома азота:
На таких схемах стрелками изображается электрон, а направление соответствует направлению спина (собственного магнитного момента электрона). Операции над спинами производятся так же, как и операции над векторами, что позволяет трактовать химические процессы языком математики. Примером векторных частиц, имеющих спин служат: фотон, глюон, W- и Z-бозоны, векторные мезоны, ортопозитроний.
Операции над спинами производятся так же, как и операции над векторами, что позволяет трактовать химические процессы языком математики. Примером векторных частиц, имеющих спин служат: фотон, глюон, W- и Z-бозоны, векторные мезоны, ортопозитроний.
Химические реакции записываются с помощью уравнений, в записи которых используются векторы.
Пример, реакция обмена, взаимодействие хлорида кальция и нитрата серебра с образованием осадка хлорида серебра:
CaCl2(ж) + 2AgNO3(ж) Ca(NO3)2(ж) + 2AgCl(тв)
3.3.В биологии
Биология относится к наукам естественно-математического цикла. Часто для того, чтобы смоделировать тот или иной процесс, приходится использовать язык математики или переносить суть математических понятий на понятия биологические. Суть понятия «вектор» — это направленность. В биологии этим словом называют организм, который переносит паразита от одного организма к другому.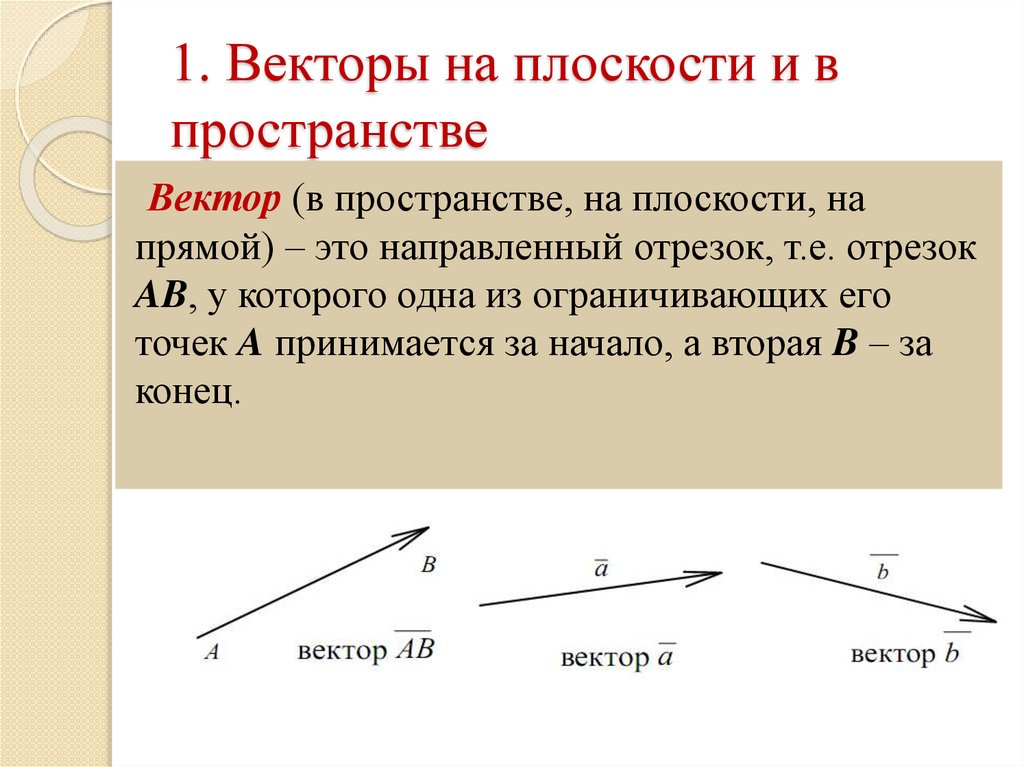 Например, клещи являются переносчиками вируса, вызывающего энцефалит. В генетике вектором считается молекула нуклеиновой кислоты, которая используется для передачи генетического материала другой клетке. С помощью организмов векторов синтезируются различные лекарственные средства, в том числе и антибиотики, ферменты, необходимые человеку (инсулин).
Например, клещи являются переносчиками вируса, вызывающего энцефалит. В генетике вектором считается молекула нуклеиновой кислоты, которая используется для передачи генетического материала другой клетке. С помощью организмов векторов синтезируются различные лекарственные средства, в том числе и антибиотики, ферменты, необходимые человеку (инсулин).
В настоящее время создана векторная модель для доставки в клетки костного мозга гена, кодирующего гранулоцитарный колониестимулирующий фактор человека. Данный белок относится увеличивает продолжительность жизни клеток костного мозга, усиливает функциональную активность зрелых нейтрофилов. Созданный вектор представляет собой многослойную конструкцию. Эффективность описанной векторной модели была доказана опытным путем. При конструировании противовирусных вакцин немаловажное значение имеет создание специального вектора-носителя, обеспечивающего адресную доставку генов и их защиту от действия нуклеаз крови.
В географии
Оказывается, векторы, как отрезки, показывающие направление нашли своё отражение и в географии. Так, ветер – характеризуемый величиной и направлением, рассматривается как вектор. Распределение ветра исследуется в векторной форме. Таким образом, ветер (горизонтальное движение воздушных частиц относительно подстилающей поверхности) – векторная величина и описывается двумя параметрами – скоростью ( м/с) и направлением. Вектор – модель ветра. Аналогично, с помощью векторов показывают направление движения воздушных масс в циклонах и антициклонах.
Так, ветер – характеризуемый величиной и направлением, рассматривается как вектор. Распределение ветра исследуется в векторной форме. Таким образом, ветер (горизонтальное движение воздушных частиц относительно подстилающей поверхности) – векторная величина и описывается двумя параметрами – скоростью ( м/с) и направлением. Вектор – модель ветра. Аналогично, с помощью векторов показывают направление движения воздушных масс в циклонах и антициклонах.
Вектор также служит моделью всевозможных течений. Горизонтальные перемещения водных масс в морях и океанах называются морскими течениями. К элементам, характеризующим течение, относятся направление и скорость. Значит, течение – векторная величина. С помощью векторов и действий над ними осуществляется учет приливно-отливных течений.
Течение реки, подводные течения океанов показывают с помощью векторов.
С помощью векторов составляют карты миграции птиц и животных.
Используя действия над векторами можно рассчитать пролетные пути перелетных птиц.
Векторы в профессиях.
Я выяснила, что векторы используются во многих науках для моделирования самых различных процессов и явлений. Значит, это понятие потребуется во всех технических профессиях, профессиях, связанных с компьютерном деле, в медицине, химии и т.д. Векторы нужны для освоения профессии строителя и архитектора, так как особое место вектору отводится в сопромате, ведь нагрузка на разные элементы конструкций является разложением вектора по базису векторов силы тяжести и других приложенных к конструкции сил. В самолетостроении, судостроении, автомобилестроении при конструировании транспорта также применяются векторы и их свойства.
В науке судовождение используются векторы и их свойства для определения кажущегося ветра во время движения судна. В штилевую погоду на судне, имеющего ход, всегда ощущается встречный ветер, равный скорости судна. Он имеет название курсовой ветер и имеет направление, противоположное движению судна. Таким образом, на движущемся судне наблюдается кажущийся ветер, вектор которого равен геометрической сумме истинного и курсового ветров. Для определения направления ветра используется способ построения векторного треугольника.
Он имеет название курсовой ветер и имеет направление, противоположное движению судна. Таким образом, на движущемся судне наблюдается кажущийся ветер, вектор которого равен геометрической сумме истинного и курсового ветров. Для определения направления ветра используется способ построения векторного треугольника.
Векторы понадобятся и портному для правильного составления выкроек одежды.
Выводы
Выполнив работу, я увидела, что векторы находят широкое применение в геометрии и в прикладных науках, где используются для представления величин, имеющих направление (силы, скорости и т. п.).
Вектор может служить моделью для любого явления, характеризующегося величиной и направлением. Так, в физике – это сила, ускорение, скорость; в химии – это изображения строения атома, изображения химических реакций; в биологии – это модель переноса вирусов, процессов клонирования и создания вакцин; в географии – это модель ветра, течения. Таким образом, векторное исчисление является универсальным инструментом, позволяющим создавать математические модели физических, химических и биологических процессов. Векторы широко используются в экономике и компьютерной графике, при построении вычислительных нейронных структур и всем известных популярных социальных сетей. Умение оперировать с объектами посредством векторного исчисления помогает находить удобные и наглядные пути решения сложных задач, поэтому хорошее знание этого раздела школьной математики необходимо каждому, чья будущая профессия связана с техникой, компьютерами, естественными науками, пространственным мышлением.
Таким образом, векторное исчисление является универсальным инструментом, позволяющим создавать математические модели физических, химических и биологических процессов. Векторы широко используются в экономике и компьютерной графике, при построении вычислительных нейронных структур и всем известных популярных социальных сетей. Умение оперировать с объектами посредством векторного исчисления помогает находить удобные и наглядные пути решения сложных задач, поэтому хорошее знание этого раздела школьной математики необходимо каждому, чья будущая профессия связана с техникой, компьютерами, естественными науками, пространственным мышлением.
Литература:
Башмаков М.А. Что такое вектор?-2-е изд., стер.- М.: Квант, 1976.-221с.
Выгодский М.Я. Справочник по элементарной математике.-3-е изд., стер. — М.: Наука, 1978.-186с.
Гусятников П.Б. Векторная алгебра в примерах и задачах.-2-е изд., стер.- М.: Высшая школа, 1985. -302с.
-302с.
Зайцев
В.В. Элементарная математика. Повторительный курс.-3-е изд., стер.- М.: Наука,1976.-156с.
Коксетер Г.С. Новые встречи с геометрией.-2-е изд., стер. — М.: Наука,1978.-324с.
Погорелов А.В. Аналитическая геометрия.- 3-е изд., стер. — М.: Квант,1968.-235с.
Интернет –источники:
https://dic.academic.ru/dic.nsf/ruwiki/401756
http://www.microarticles.ru/article/primenenie-vektorov-v-prikladnih-naykah.html
http://online.mephi.ru/courses/physics/atomic_physics/data/course/5/5.5.html
http://www.sworld.com.ua/konfer47/32.pdf
https://flot.com/publications/books/shelf/rulkov/24.htm
Приложение 1.
8
12: Векторы в космосе — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2585
- Гилберт Стрэнг и Эдвин «Джед» Герман
- OpenStax
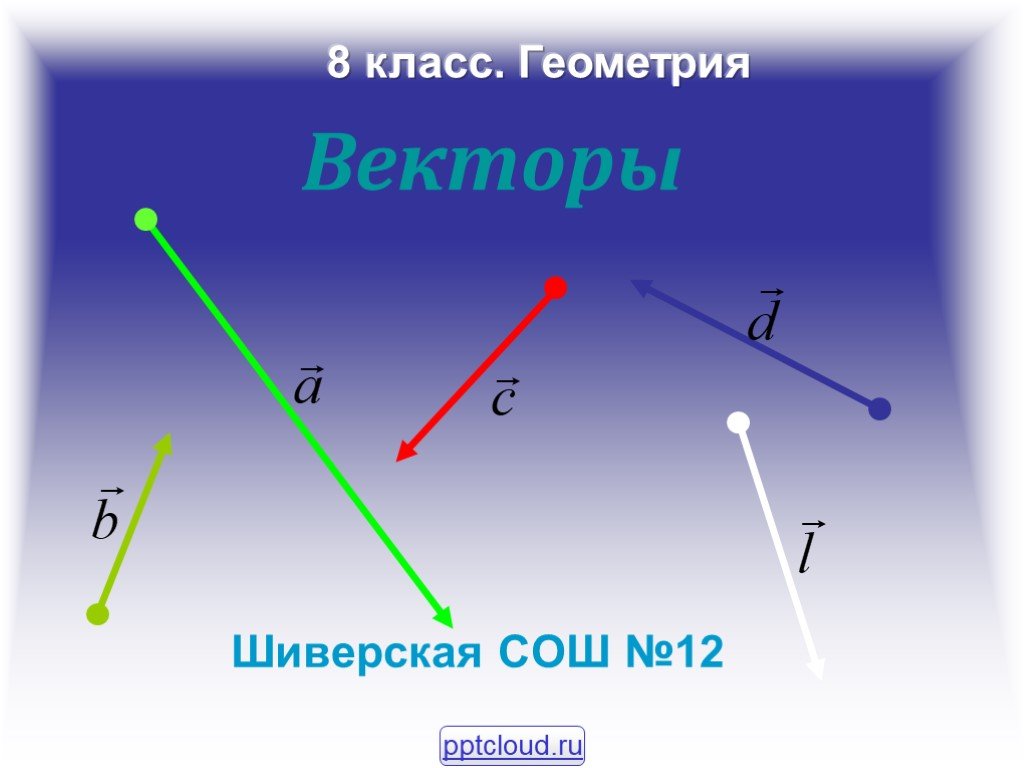
Величина, имеющая величину и направление, называется вектором .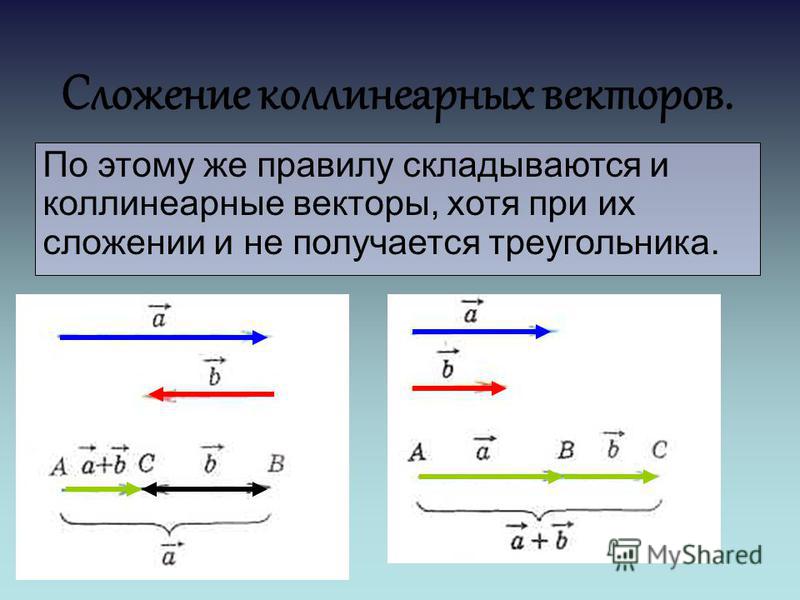 Векторы имеют множество применений в реальной жизни, включая ситуации, связанные с силой или скоростью. Например, рассмотрим силы, действующие на лодку, пересекающую реку. Мотор лодки создает силу в одном направлении, а течение реки создает силу в другом направлении. Обе силы являются векторами. Мы должны учитывать как величину, так и направление каждой силы, если хотим знать, куда направится лодка.
Векторы имеют множество применений в реальной жизни, включая ситуации, связанные с силой или скоростью. Например, рассмотрим силы, действующие на лодку, пересекающую реку. Мотор лодки создает силу в одном направлении, а течение реки создает силу в другом направлении. Обе силы являются векторами. Мы должны учитывать как величину, так и направление каждой силы, если хотим знать, куда направится лодка.
- 12.0: Прелюдия к векторам в космосе
- 12.1: Векторы в самолете
- При измерении силы, такой как тяга двигателей самолета, важно описать не только мощность этой силы, но и направления, в котором она приложена. Некоторые величины, такие как сила, определяются с точки зрения как размера (также называемого величиной), так и направления. Величина, имеющая величину и направление, называется вектором.
- 12.1E: Упражнения к разделу 12.1
- 12.

- пространство. В этом разделе представлено естественное расширение двумерной декартовой координатной плоскости на три измерения.
- 12.2E: Упражнения к разделу 12.2
- 12.
- 12.3: Скалярное произведение
- В этом разделе мы разработаем операцию, называемую скалярным произведением, которая позволяет нам вычислять работу в случае, когда вектор силы и вектор движения имеют разные направления. Скалярное произведение, по сути, говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат.
- 12.3E: упражнения к разделу 12.3
- 12.4: перекрестное произведение
- векторы. Вычисление крутящего момента является важным применением векторных произведений, и мы более подробно рассмотрим крутящий момент позже в этом разделе.

- 12.4E: Упражнения к разделу 12.4
- 12.5: Уравнения прямых и плоскостей в пространстве
- Чтобы написать уравнение прямой, мы должны знать две точки на прямой или мы должны знать направление прямой и хотя бы одну точку, через которую проходит прямая . В двух измерениях мы используем понятие наклона для описания ориентации или направления линии. В трех измерениях мы описываем направление линии, используя вектор, параллельный линии. В этом разделе мы рассмотрим, как использовать уравнения для описания линий и плоскостей в пространстве.
- 12.5E: упражнения к разделу 12.5
- 12.6: квадратичные поверхности
- и сферы. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями, для изучения множества других поверхностей, которые можно изобразить в трехмерной системе координат.

- 12.6E: Упражнения к разделу 12.6
- 12.7: Цилиндрические и сферические координаты
- о расширениях полярных координат. Как следует из названия, цилиндрические координаты полезны для решения задач, связанных с цилиндрами, таких как вычисление объема круглого резервуара для воды или количества масла, протекающего по трубе. Точно так же сферические координаты полезны для решения задач, связанных со сферами, таких как определение объема куполообразных структур.
- 12.7 4.0, автором, ремиксом и/или куратором которого выступили Гилберт Странг и Эдвин «Джед» Херман (OpenStax) с использованием исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Глава
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
Типы, решаемые примеры с формулой
Применение векторов включает приложения в реальной жизни, применение векторного пространства, применение векторной алгебры, применение вектора в технике, применение скалярного произведения векторов и многое другое. В этой статье мы изучим все приложения векторов.
Введение в вектор
Величина, которая может быть полностью описана с использованием как величины, так и направления, называется векторной величиной. Пример: перемещение, сила, напряженность электрического поля и т. д.
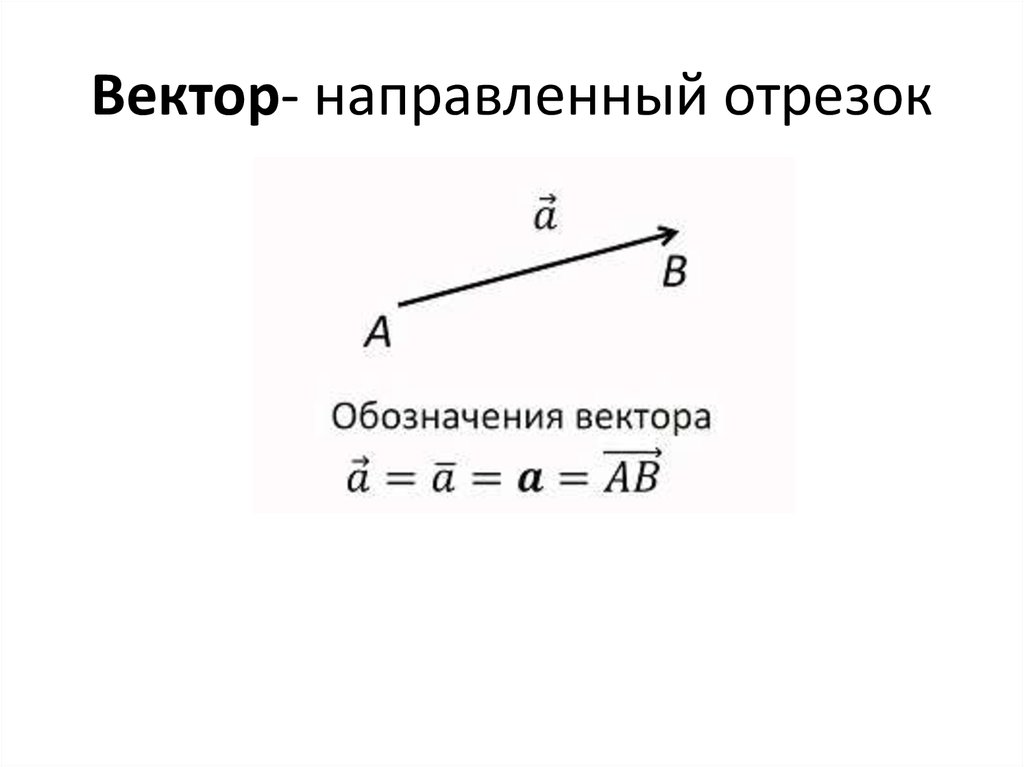
Векторная алгебра — это огромный мир математики, использующий чистую логику. Геометрически вектор представляет собой направленный отрезок прямой. Если AB является отрезком и если он указан направлением с помощью стрелки, как показано на рисунке, то направленный отрезок AB имеет не только направление, но и величину.
Отрезок AB с направлением из A в B представлен вектором \(\bar{AB}\), а отрезок AB с направлением из B в A обозначает вектор \(\bar{BA}\).
 3\)
3\)Векторное исчисление играет важную роль в дифференциальной геометрии и при изучении уравнений в частных производных. Векторное исчисление также имеет дело с двумя интегралами, известными как линейные интегралы и поверхностные интегралы.
Дивергенция и скручивание — две важные операции над векторным полем. Они важны для исчисления по нескольким причинам, включая использование ротора и дивергенции для разработки некоторых многомерных версий Фундаментальной теоремы исчисления. Кроме того, завихрение и дивергенция появляются в математических описаниях механики жидкости, электромагнетизма и теории упругости, которые являются важными понятиями в физике и технике.
Применение векторного исчисления
Он широко используется в физике и технике, особенно при описании электромагнитных полей, гравитационных полей и потоков жидкости.
Векторное исчисление используется в
- Геодезические на поверхности
- Электрическое поле от распределенного заряда
- Построение среза векторного поля
- Чтобы найти скорость изменения массы потока жидкости.

- В динамике твердого тела при прямолинейном и плоскокриволинейном движении по траекториям и при прямоугольном движении. 92\hat{k}\), который является касательным вектором к кривой в любой точке t.
- Они используются в преобразовании Фурье
- Векторные пространства предоставляют абстрактный, бескоординатный способ работы с геометрическими и физическими объектами, такими как тензоры.
- Применение векторного пространства в информатике: минимаксная теорема теории игр, утверждающая существование уникального выигрыша, когда все игроки играют оптимально, может быть сформулирована и доказана с использованием методов векторных пространств.

- Применение векторного пространства в линейной алгебре: Квантовая механика полностью основана на нем. Также важен для теории управления во временной области (пространстве состояний) и напряжений в материалах с использованием тензоров.
- В дифференциальной геометрии касательная плоскость к поверхности в точке, естественно, является векторным пространством, начало которого отождествляется с точкой касания.
- Во многих физических ситуациях нам часто нужно знать направление вектора. Например, мы можем захотеть узнать направление вектора магнитного поля в какой-то точке или направление движения объекта.

- Векторная алгебра полезна для нахождения составляющей силы в определенном направлении.
- В кинематике для нахождения результирующих векторов перемещений и результирующих векторов скорости.
- В механике для нахождения равнодействующих векторов сил и равнодействующих многих производных векторных величин.
- В области электричества и магнетизма для нахождения результирующих электрических или магнитных векторных полей.
- Применение векторов в физике: Векторы можно использовать для представления физических величин. Чаще всего в физике векторы используются для представления смещения, скорости и ускорения. Векторы представляют собой комбинацию величины и направления и изображаются в виде стрелок.
- Рахул поворачивает рукоятку, чтобы опустить ковш воды в колодец.Определить полную работу, совершаемую ковшом, если вес ковша равен 15 Н, а сила натяжения каната 13 Н. Ковш поднимается на расстояние 4,5 м, пока он вращается вертикально вниз. направление
- Веревка совершает отрицательную работу над ведром, потому что движение и сила действуют в противоположных направлениях. Если сила измеряется в ньютонах, а перемещение в метрах, то работа измеряется в джоулях.
- Определить магнитную силу между двумя параллельными проводниками длиной 1 м, отстоящими друг от друга на 50 см в воздухе и по которым текут токи 30 А в том же направлении и в противоположном направлении.

- Навигация по воздуху и на лодке обычно осуществляется с использованием векторов.
- Самолетам задается вектор движения, и они используют свою скорость, чтобы определить, какое расстояние им нужно пройти, прежде чем развернуться или приземлиться. Планы полета составляются с использованием серии векторов.
- Спортивные инструкции основаны на использовании векторов. Например, широкие принимающие, играющие в американский футбол, могут пробежать маршрут, по которому они пробегают семь метров по полю, прежде чем повернуть налево на 45 градусов и бежать в этом направлении.
 Спортивный комментарий также зависит от векторов. Только в некоторых видах спорта есть поля с сетками, поэтому обсуждения вращаются вокруг направления и скорости игрока.
Спортивный комментарий также зависит от векторов. Только в некоторых видах спорта есть поля с сетками, поэтому обсуждения вращаются вокруг направления и скорости игрока.
Пусть \(\vec{x}\) & \(\vec{y}\) — касательные векторы к кривой в моменты времени t = 1 и t = -1 соответственно, тогда
\(\vec{x }=2\шляпа{i}+2\шляпа{j}-3\шляпа{k} и \vec{y}=-2\шляпа{i}+2\шляпа{j}-3\шляпа{k} \)
Пусть 𝜃 будет углом между касательными \(\vec{x}\) и \(\vec{y}\), тогда
\(cos\theta={\vec{x}.\vec{ y}\over{|\vec{x}|.|\vec{y}|}}={(2\шляпа{i}+2\шляпа{j}-3\шляпа{k}).(-2 \шляпа{i}+2\шляпа{j}-3\шляпа{k})\over{|2\шляпа{i}+2\шляпа{j}-3\шляпа{k}|.|-2\ шляпа{i}+2\шляпа{j}-3\шляпа{k}|}}={-4+4+9\over{\sqrt{17}\sqrt{17}}}={9\over{17}}\)
Векторное пространство
В математике, физике и технике векторное пространство представляет собой набор объектов, называемых векторами , которые можно складывать и умножать на числа, называемые скалярами.
 Скаляры часто являются действительными числами, но в некоторых векторных пространствах есть скалярное умножение на комплексные числа или, как правило, на скаляр из любой математической области. Самый простой пример векторного пространства — тривиальный: {0}, который содержит только нулевой вектор
Скаляры часто являются действительными числами, но в некоторых векторных пространствах есть скалярное умножение на комплексные числа или, как правило, на скаляр из любой математической области. Самый простой пример векторного пространства — тривиальный: {0}, который содержит только нулевой векторПрименение векторного пространства
Применение векторного пространства требуется в инженерии и информатике. Векторные пространства имеют множество применений, поскольку они часто встречаются в обычных обстоятельствах, а именно везде, где задействованы функции со значениями в каком-либо поле.
Векторная алгебра
Векторная алгебра — это, в частности, основные алгебраические операции сложения векторов и скалярного умножения. Векторная алгебра включает в себя сложение и вычитание векторов, деление и умножение векторов, а также скалярное произведение и векторное произведение.
Применение векторной алгебры
В приведенном ниже списке перечислены некоторые из наиболее распространенных применений векторной алгебры.
Узнайте больше о логарифмических функциях здесь.
Применение разрешения векторов в повседневной жизни
Применение разрешения векторов в повседневной жизни, как указано ниже:
Обвалы дорог
Дорога на поворотах приподнята на дальнем конце кривизны.
 Угол крена Ф. Нормальная реакция земли – N. Машины наклонены к вертикали на угол Ф. N cos Ф уравновешивает массу mg транспортного средства по вертикали. N sin Ф обеспечивает центростремительную силу по радиусу кривизны. Это определяет максимальную скорость автомобиля, чтобы избежать скольжения.
Угол крена Ф. Нормальная реакция земли – N. Машины наклонены к вертикали на угол Ф. N cos Ф уравновешивает массу mg транспортного средства по вертикали. N sin Ф обеспечивает центростремительную силу по радиусу кривизны. Это определяет максимальную скорость автомобиля, чтобы избежать скольжения.Движение снаряда
Снаряд (камень), брошенный с начальной скоростью u под углом Ф к горизонту, имеет вертикальную составляющую (u sin Ф – g t) и горизонтальную составляющую u cos Ф под компонентами вектора.
Заточка деревянного карандаша с лезвием
Карандаш срезаем под углом. Составляющая силы в направлении, перпендикулярном карандашу, режет карандаш. Составляющая силы в направлении, параллельном карандашу, удаляет тонкую деревянную деталь.
Магнитное поле Земли
Магнитное поле Земли имеет две составляющие B и H: перпендикулярную поверхности Земли и параллельную поверхности.
Маятник
Натяжение струны состоит из двух компонентов, которые уравновешивают вес и создают центростремительную силу.

Реальное применение закона параллелограмма векторов
Пусть P и Q — два вектора, действующие одновременно в точке и представленные как по величине, так и по направлению двумя соседними сторонами OA и OD параллелограмма OABD, как показано на рисунке. 92+2\times6\times10cos60}\)
\(R = \sqrt{196}\)
R = 14
Общие примеры применения векторных величин
В приведенном ниже списке приведены некоторые из наиболее распространенных применений векторов. .
Работа
В физике термин работа используется для описания энергии, которая добавляется или удаляется от объекта или системы, когда к ним прилагается сила. В результате эксперимента было установлено, что работа максимальна, когда приложенная сила параллельна движению объекта, и что работа не совершается, когда сила прикладывается перпендикулярно движению. Следовательно, работа, совершаемая силой, может быть описана скалярным произведением вектора силы и вектора перемещения.
Используя векторное исчисление, мы можем найти формулу для работы.
 Формула работы: W = \(\vec{F}·\vec{d}\). Это означает, что работа является скалярной величиной. Это скалярное произведение двух векторов.
Формула работы: W = \(\vec{F}·\vec{d}\). Это означает, что работа является скалярной величиной. Это скалярное произведение двух векторов.Следовательно, W = \(Fdcos\theta\), где \(\theta — угол между силой и перемещением.
Решенный пример: применение скалярного произведения векторов
= −58,5 Дж
Сила веса совершает положительную работу над ковшом, потому что движение и сила действуют в одном направлении.
\(W_{вес}=\vec{F_{вес}}\vec{d}cosθ\)
= (15N) (4,5 м) cos 0∘
= 67,5 Дж
Общая проделанная работа =\ (W_{веревка} + W_{вес}\) = −58,5 Дж + 67,5 Дж = 9.
 0J
0JМагнитная сила
Сила, с которой магнитное поле действует на заряженную частицу, наиболее велика, когда частица движется перпендикулярно полю, а магнитная сила, действующая на частицу, равна нулю, когда она движется параллельно полю. Следовательно, магнитная сила может быть описана с помощью векторного произведения вектора напряженности поля и вектора скорости частицы: \(\vec{F}=q\vec{v}\times\vec{B}\), где \(\ vec{F}\) — сила, действующая на частицу, q — заряд частицы, \(\vec{v}\) — скорость частицы, а \(\vec{B}\) — вектор представляет магнитное поле. Если скорость измеряется в м/с, а магнитное поле измеряется в теслах, сила будет измеряться в ньютонах, метрической базовой единице силы. Это означает, что магнитная сила является векторной величиной. Это перекрестное произведение двух векторов.
Отсюда \(F = qvBsin\theta.\)
Решенный пример: Применение векторного произведения векторов
A: Дано как,
\(i_1 = i_2\) = 30 A,
d = 0,5 м,
L = 1 м
Магнитная сила между двумя проводниками равна,
9{-3}}N\)Применение векторного магнитного потенциала
Векторный потенциал определен в соответствии с законом Ампера и может быть выражен либо через ток i, либо через плотность тока j (источники магнитного поля). В различных текстах это определение принимает формы
\(A={\mu_{0}i\over{4\pi}}\oint{\vec{dl}\over{r}}\)
Крутящий момент
Когда вы поднимаете бейсбольный мяч со стола, вы прилагаете силу, которая перемещает объект как единое целое. Когда вы прикладываете силу к дверной ручке, вы заставляете дверь вращаться на петлях. Ученые используют термин крутящий момент для описания силового свойства, влияющего на вращение объекта. Крутящий момент можно описать с помощью векторного произведения вектора силы и плеча рычага, вектора, направленного радиально наружу от оси вращения к точке приложения силы к объекту: \(\vec{tau}=\ vec{r}\times\vec{F}\), где \(\vec{tau}\) — крутящий момент, \(\vec{r}\) — перпендикулярное расстояние, а \(\vec{F} \) — приложенная сила.
 Это означает, что крутящий момент является векторной величиной. Это перекрестное произведение двух векторов. 9{−2}Нм\)
Это означает, что крутящий момент является векторной величиной. Это перекрестное произведение двух векторов. 9{−2}Нм\)В соответствии с правилом правой руки направление крутящего момента находится за пределами страницы. Тип вращения, вызванный крутящим моментом, — против часовой стрелки.
Применение векторов в повседневной жизни
Ниже приведены примеры применения векторов в повседневной жизни
Надеюсь, что эта статья о применении векторов была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о применении векторов
В.1. Каково применение векторов в реальной жизни?
Ответ 1 Навигация по воздуху и на лодке обычно осуществляется с использованием векторов. Самолетам дается вектор движения, и они используют свою скорость, чтобы определить, какое расстояние им нужно пройти, прежде чем развернуться или приземлиться. Планы полета составляются с использованием серии векторов. Спортивные инструкции основаны на использовании векторов. Например, широкие принимающие, играющие в американский футбол, могут пробежать маршрут, по которому они пробегают семь метров по полю, прежде чем повернуть налево на 45 градусов и бежать в этом направлении.

Q.2 Каково основное применение векторов в технике?
Ответ 2 Векторы используются в инженерной механике для представления величин, которые имеют как величину, так и направление. Многие инженерные величины, такие как силы, перемещения, скорости и ускорения, необходимо будет представить в виде векторов для анализа.
Q.3 Что является распространенным примером вектора?
Ответ 3 Векторы могут использоваться для описания любых физических явлений, которые имеют как величину, так и направление. Они полезны для описания смещения или скорости движущегося объекта, когда одно число не может дать адекватного описания. Величина, которая может быть полностью описана с использованием как величины, так и направления, называется векторной величиной.

- 12.7 4.0, автором, ремиксом и/или куратором которого выступили Гилберт Странг и Эдвин «Джед» Херман (OpenStax) с использованием исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.




 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 3\)
3\)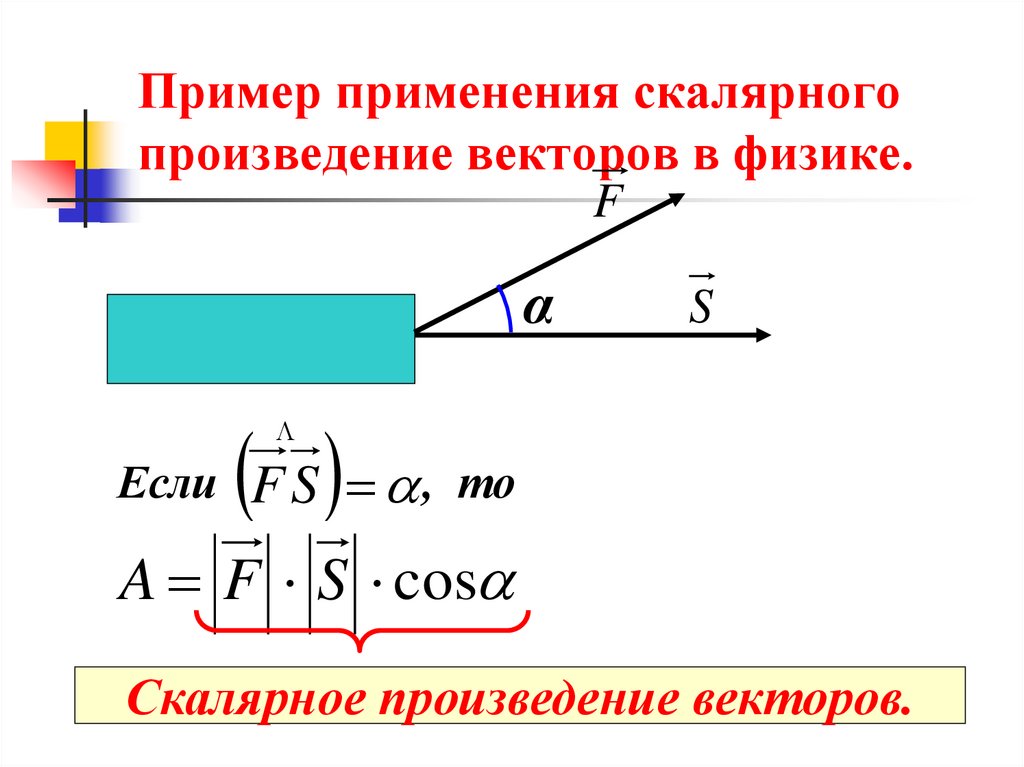
 Скаляры часто являются действительными числами, но в некоторых векторных пространствах есть скалярное умножение на комплексные числа или, как правило, на скаляр из любой математической области. Самый простой пример векторного пространства — тривиальный: {0}, который содержит только нулевой вектор
Скаляры часто являются действительными числами, но в некоторых векторных пространствах есть скалярное умножение на комплексные числа или, как правило, на скаляр из любой математической области. Самый простой пример векторного пространства — тривиальный: {0}, который содержит только нулевой вектор

 Угол крена Ф. Нормальная реакция земли – N. Машины наклонены к вертикали на угол Ф. N cos Ф уравновешивает массу mg транспортного средства по вертикали. N sin Ф обеспечивает центростремительную силу по радиусу кривизны. Это определяет максимальную скорость автомобиля, чтобы избежать скольжения.
Угол крена Ф. Нормальная реакция земли – N. Машины наклонены к вертикали на угол Ф. N cos Ф уравновешивает массу mg транспортного средства по вертикали. N sin Ф обеспечивает центростремительную силу по радиусу кривизны. Это определяет максимальную скорость автомобиля, чтобы избежать скольжения.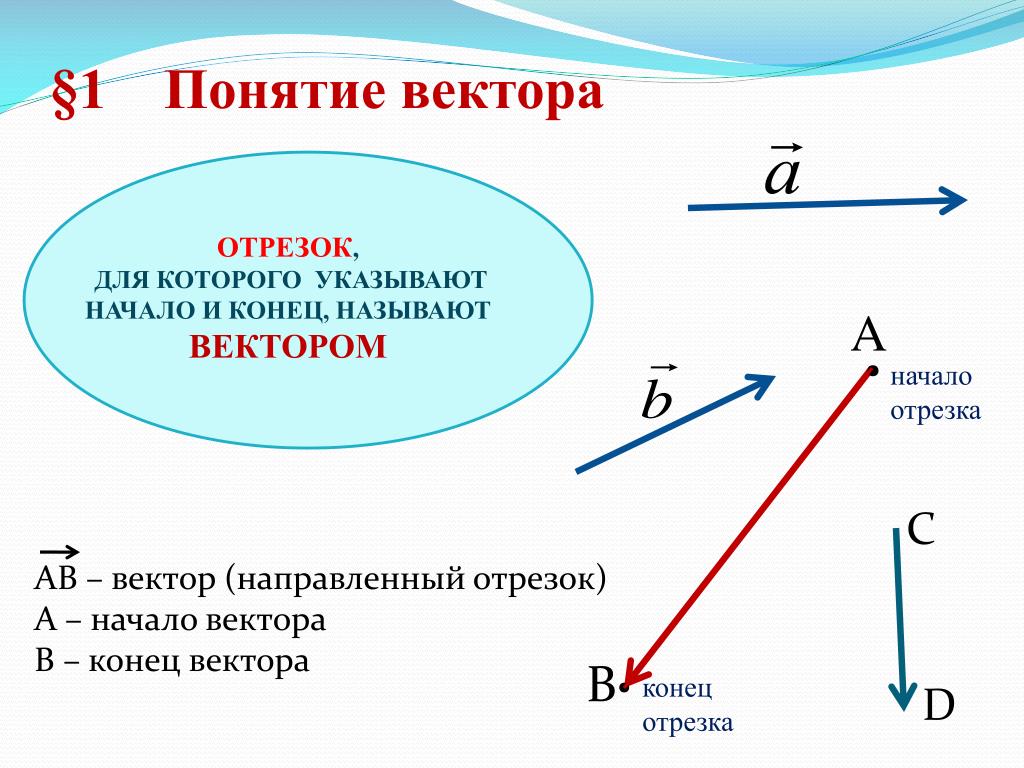
 Формула работы: W = \(\vec{F}·\vec{d}\). Это означает, что работа является скалярной величиной. Это скалярное произведение двух векторов.
Формула работы: W = \(\vec{F}·\vec{d}\). Это означает, что работа является скалярной величиной. Это скалярное произведение двух векторов. 0J
0J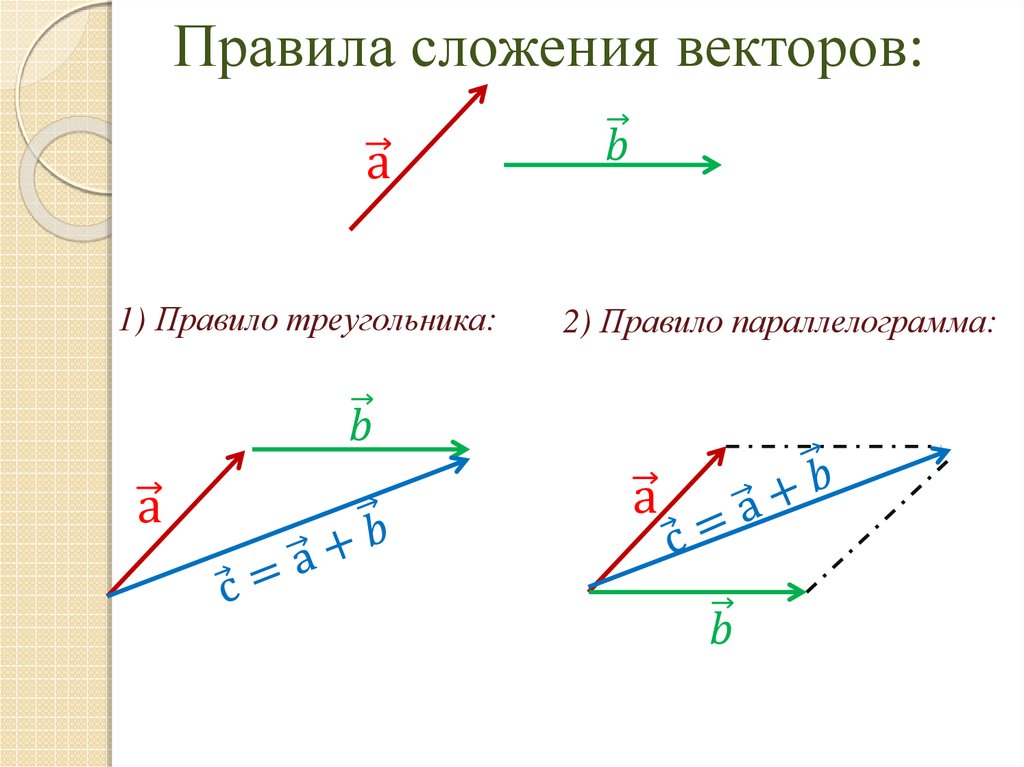
 Это означает, что крутящий момент является векторной величиной. Это перекрестное произведение двух векторов. 9{−2}Нм\)
Это означает, что крутящий момент является векторной величиной. Это перекрестное произведение двух векторов. 9{−2}Нм\) Спортивный комментарий также зависит от векторов. Только в некоторых видах спорта есть поля с сетками, поэтому обсуждения вращаются вокруг направления и скорости игрока.
Спортивный комментарий также зависит от векторов. Только в некоторых видах спорта есть поля с сетками, поэтому обсуждения вращаются вокруг направления и скорости игрока.