Элементарный учебник физики Т2

Элементарный учебник физики Т2

Ландсберг Г.С. Элементарный учебник физики. Т.2. Электричество и магнетизм. — М.: Наука, 1985. — 479 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ Глава I. Электрические заряды § 1. Электрическое взаимодействие. § 2. Проводники и диэлектрики. § 3. Разделение тел на проводники и диэлектрики § 4. Положительные и отрицательные заряды § 5. Что происходит при электризации? § 6. Электронная теория. § 7. Электризация трением. § 8. Электризация через влияние. § 9. Электризация под действием света. § 10. Закон Кулона. § 11. Единица заряда. Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 12. Действие электрического заряда на окружающие тела. § 13. Понятие об электрическом поле. § 14. Напряженность электрического поля. § 15. Сложение полей. § 16. Электрическое поле в диэлектриках и в проводниках. § 17. Графическое изображение полей. § 18. Основные особенности электрических карт. § 19. Применение метода линий поля к задачам электростатики. § 20. Работа при перемещении заряда в электрическом поле. § 21. Разность потенциалов (электрическое напряжение). § 22. Эквипотенциальные поверхности. § 23. В чем смысл введения разности потенциалов? § 24. Условия равновесия зарядов в проводниках. § 25. Электрометр. § 26. В чем различие между электрометром и электроскопом? § 27. Соединение с Землей. § 28. Измерение разности потенциалов в воздухе. Электрический зонд. § 29. Электрическое поле Земли. § 30. Простейшие электрические поля. § 31. Распределение зарядов в проводнике. Клетка Фарадея. § 32. Поверхностная плотность заряда. § 33. Конденсаторы. § 34. Различные типы конденсаторов. § 35. Параллельное и последовательное соединение конденсаторов. § 36. Диэлектрическая проницаемость. § 37. Почему электрическое поле ослабляется внутри диэлектрика? § 38. Энергия заряженных тел. Энергия электрического поля. Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 39. Электрический ток и электродвижущая сила. § 40. Признаки электрического тока. § 41. Направление тока. § 42. Сила тока. § 43. «Скорость электрического тока» и скорость движения носителей заряда. § 44. Гальванометр. § 45. Распределение напряжения в проводнике с током. § 46. Закон Ома. § 47. Сопротивление проводов. § 48. Зависимость сопротивления от температуры. § 49. Сверхпроводимость. § 50. Последовательное и параллельное соединение проводников. § 51. Реостаты. § 52. Распределение напряжения в цепи. § 53. Вольтметр. § 54. Каким должно быть сопротивление вольтметра и амперметра? § 55. Шунтирование измерительных приборов. Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА § 56. Нагревание током. Закон Джоуля-Ленца. § 57. Работа, совершаемая электрическим током. § 58. Мощность электрического тока. § 59. Контактная сварка. § 60. Электрические нагревательные приборы. Электрические печи. § 61. Понятие о расчете нагревательных приборов. § 62. Лампы накаливания. § 63. Короткое замыкание. § 64. Электрическая проводка. Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ § 65. Первый закон Фарадея. § 66. Второй закон Фарадея. § 67. Ионная проводимость электролитов. § 68. Движение ионов в электролитах. § 69. Элементарный электрический заряд. § 70. Первичные и вторичные процессы при электролизе. § 71. Электролитическая диссоциация. § 72. Градуировка амперметров при помощи электролиза. § 73. Технические применения электролиза. Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА § 74. Введение. Открытие Вольты. § 75. Правило Вольты. Гальванический элемент. § 76. Как возникают э. д. с. и ток в гальваническом элементе? § 77. Поляризация электродов. § 78. Деполяризация в гальванических элементах. § 79. Аккумуляторы. § 80. Закон Ома для замкнутой цепи. § 81. Напряжение на зажимах источника тока и э. д. с. § 82. Соединение источников тока. § 83. Термоэлементы. § 84. Термоэлементы в качестве генераторов. § 85. Измерение температуры с помощью термоэлементов. Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ § 86. Электронная проводимость металлов. § 87. Строение металлов. § 88. Причина электрического сопротивления. § 89. Работа выхода. § 90. Испускание электронов накаленными телами. Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ § 91. Самостоятельная и несамостоятельная проводимость газов. § 92. Несамостоятельная проводимость газа. § 93. Искровой разряд. § 94. Молния. § 95. Коронный разряд. § 96. Применения коронного разряда. § 97. Громоотвод. § 98. Электрическая дуга. § 99. Применения дугового разряда. § 100. Тлеющий разряд. § 101. Что происходит при тлеющем разряде? § 102. Катодные лучи. § 103. Природа катодных лучей. § 104. Каналовые лучи. § 105. Электронная проводимость в высоком вакууме. § 106. Электронные лампы. § 107. Электроннолучевая трубка. Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ § 108. Природа электрического тока в полупроводниках. § 109. Движение электронов в полупроводниках. § 110. Полупроводниковые выпрямители. § 111. Полупроводниковые фотоэлементы. Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ § 112. Естественные и искусственные магниты. § 113. Полюсы магнита и его нейтральная зона. § 114. Магнитное действие электрического тока. § 115. Магнитные действия токов и постоянных магнитов. § 116. Происхождение магнитного поля постоянных магнитов. § 117. Гипотеза Ампера об элементарных электрических токах. Глава XI. МАГНИТНОЕ ПОЛЕ § 118. Магнитное поле и его проявления. Магнитная индукция. § 119. Магнитный момент. Единица магнитной индукции. § 120. Измерение магнитной индукции поля с помощью магнитной стрелки. § 121. Сложение магнитных полей. § 122. Линии магнитного поля. § 123. Приборы для измерения магнитной индукции. Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ § 124. Магнитное поле прямолинейного проводника и кругового витка с током. § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита. § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля. § 127. Магнитное поле движущихся зарядов. Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ § 128. Магнитное поле Земли. § 129. Элементы земного магнетизма. § 130. Магнитные аномалии и магнитная разведка полезных ископаемых. § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури. Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ § 132. Введение. § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки. § 134. Действие магнитного поля на виток или соленоид с током. § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока. § 136. Сила Лоренца. § 137. Сила Лоренца и полярные сияния. Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 138. Условия возникновения индукционного тока. § 139. Направление индукционного тока. Правило Ленца. § 140. Основной закон электромагнитной индукции. § 141. Электродвижущая сила индукции. § 142. Электромагнитная индукция и сила Лоренца. § 143. Индукционные токи в массивных проводниках. Токи Фуко. Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ § 144. Магнитная проницаемость железа. § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные. § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея. § 147. Молекулярная теория магнетизма. § 148. Магнитная защита. § 149. Особенности ферромагнитных тел. § 150. Основы теории ферромагнетизма. Глава XVII. ПЕРЕМЕННЫЙ ТОК § 151. Постоянная и переменная электродвижущая сила. § 152. Опытное исследование формы переменного тока. Осциллограф. § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения. § 154. Сила переменного тока. § 155. Амперметры и вольтметры переменного тока. § 156. Самоиндукция. § 157. Индуктивность катушки. § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью. § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления. § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока. § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока. § 162. Сдвиг фаз между током и напряжением. § 163. Мощность переменного тока. § 164. Трансформаторы. § 165. Централизованное производство и распределение электрической энергии. § 166. Выпрямление переменного тока. Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ § 167. Генераторы переменного тока. § 168. Генераторы постоянного тока. § 169. Генераторы с независимым возбуждением и с самовозбуждением. § 170. Трехфазный ток. § 171. Трехфазный электродвигатель. § 172. Электродвигатели постоянного тока. § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением. § 174. Коэффициент полезного действия генератора и двигателя. § 175. Обратимость электрических генераторов постоянного тока. § 176. Электромагниты. § 177. Применение электромагнитов. § 178. Реле и их применения в технике и автоматике. Ответы и решения к упражнениям Приложения Предметный указатель Таблицы

А.1. Урок-презентация на тему: «Закон Ома для полной цепи»

Слайд 1

ФИЗИКА Электростатика и постоянный ток

Слайд 2

Электростатика 2 Это раздел электродинамики, в котором изучается взаимодействие неподвижных электрических зарядов.

Слайд 3

3 Электрический заряд – это физическая величина, определяющая интенсивность электромагнитного взаимодействия заряженных тел. Заряд любого тела дискретен и кратен элементарному заряду: [ q ] = A  c = Кл Заряд протона q p = e , заряд электрона q e = – e . Электрон ( др.греч. ἤλεκτρον ) – янтарь . Процесс сообщения телу электрического заряда – электризация – состоит в перераспределении подвижных электрических зарядов между взаимодействующими телами. Если N p = N e , то тело электрически нейтрально, q = 0 . Если N p > N e , то заряд тела q > 0 . Если N p

Слайд 4

4 В изолированной (замкнутой) системе нет обмена зарядами с внешними телами. Заряды лишь перераспределяются между телами системы или смещаются в пределах одного тела. Закон сохранения электрического заряда : алгебраическая сумма электрических зарядов замкнутой системы есть величина постоянная Электрический заряд обладает свойством инвариантности: величина заряда не изменяется при переходе от одной инерциальной системы отсчета к другой.

Слайд 5

5 Закон Кулона: сила взаимодействия двух неподвижных точечных электрических зарядов прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними: Электрические заряды взаимодействуют друг с другом: одноименные заряды отталкиваются, разноименные притягиваются . Формула справедлива также для тел сферической формы; в таком случае r – расстояние между центрами этих сфер.

Слайд 6

6 .  – диэлектрическая проницаемость среды между зарядами. Величина  показывает, во сколько раз сила F взаимодействия зарядов в данной среде меньше силы Fo их взаимодействия в вакууме: – электрическая постоянная ; Взаимодействие электрически заряженных тел осуществляется посредством электрического поля. .

Слайд 7

7 Электрическое поле – одна из форм материи, осуществляющая взаимодействие между заряженными телами. Поле неподвижного заряда называется электростатическим . Источники электрического поля: электрические заряды; переменное магнитное поле. Наличие электрического поля проявляется в его силовом воздействии на электрический заряд. Напряженностью электрического поля называется векторная величина, равная отношению силы, действующей на положительный пробный заряд, помещенный в данную точку поля, к величине этого заряда [E] = Н/Кл = В/м

Слайд 8

8 Направление вектора напряженности совпадает с направлением силы, действующей на пробный заряд. Пробный заряд является инструментом для измерения поля. Графически электростатическое поле изображается с помощью линий напряженности (силовых линий). Это линии, касательная к которым в каждой точке совпадает с направлением вектора напряженности, а густота (плотность) линий пропорциональна величине напряженности в данном месте пространства. Линии напряженности могут начинаться или заканчиваться на зарядах, либо уходить в бесконечность.

Слайд 9

9 Используя закон Кулона, можно получить выражение для напряженности электростатического поля точечного заряда q на расстоянии r от него: Если электрическое поле создано несколькими точечными зарядами, то, согласно принципу суперпозиции , напряженность результирующего поля равна геометрической сумме напряженностей, созданных каждым зарядом в отдельности:

Слайд 10

10 Потоком вектора напряженности через элементарную площадку dS называется скалярная величина d Ф , равная скалярному произведению вектора напряженности электрического поля на единичный вектор нормали к этой площадке, умноженному на площадь dS Величина d Ф пропорциональна числу силовых линий, пронизывающих площадку dS . Поток через поверхность S конечных размеров

Слайд 11

11 Теорема Гаусса для электростатического поля в вакууме Определим поток вектора напряженности поля одного точечного заряда q через сферическую поверхность радиуса R : Для любой точки на поверхности сферы Если заряд q находится в центре сферы, то для любой элементарной площадки dS этой поверхности угол  = 0 , то есть cos  = 1 . Для вакуума  = 1 , поэтому Полученный результат справедлив также для случая, когда заряд находится внутри любой замкнутой поверхности.

Слайд 12

12 Рассмотрим наиболее общий случай: замкнутая поверхность произвольной формы окружает несколько зарядов. Согласно принципу суперпозиции напряженность результирующего поля Это теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на электрическую постоянную  о . Если заряд находится вне замкнутой поверхности, то поток вектора Е через нее равен нулю.

Слайд 13

13 Доказанная теорема упрощает расчет электрических полей системы электрических зарядов. Для примера рассчитаем напряженность электрического поля бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда . В качестве замкнутой поверхности выберем цилиндр с основанием S . Поток напряженности через оба основания цилиндра Ф = 2 SE . Поток напряженности через боковую поверхность Ф = 0 . Заряд внутри этой поверхности q = S . По теореме Гаусса

Слайд 14

14 Работа электростатического поля Пусть поле создано неподвижным точечным зарядом q . Работа поля на элементарном участке dl траектории равна Работа поля вдоль всей траектории движения Работа не зависит от формы траектории и определяется только положением начальной и конечной точки, поэтому электростатическое поле точечного заряда потенциально , а электростатические силы консервативны .

Слайд 15

15 Известно, что работа консервативной силы равна убыли потенциальной энергии: Потенциальная энергия взаимодействия точечных зарядов Отношение W p / q o является энергетической характеристикой электростатического поля, которая называется потенциалом Потенциал – это скалярная величина, равная потенциальной энергии единичного положительного заряда, помещенного в данную точку электростатического поля. [ [  ] = Дж/Кл = В

Слайд 16

16 Выражение для работы можно обобщить на случай любого электростатического поля: Величина называется циркуляцией вектора вдоль траектории L . Циркуляция вектора напряженности равна работе сил поля по перемещению единичного положительного заряда вдоль данной траектории. Если траектория замкнута, то и тогда Циркуляция напряженности электростатического поля вдоль произвольного замкнутого контура L равна нулю. Это положение справедливо только для электростатического поля. Это выражение является математическим критерием потенциальности поля.

Слайд 17

17 Потенциал поля точечного заряда q на расстоянии r от него Работа, совершаемая силами электростатического поля при перемещении точечного заряда q из точки с потенциалом  1 в точку с потенциалом  2

Слайд 18

18 . Связь между напряженностью и потенциалом Работа сил электростатического поля при бесконечно малом перемещении dx Ту же работу можно выразить через потенциал: Повторив аналогичные действия для осей OY и OZ , получим Напряженность электростатического поля равна градиенту потенциала, взятому со знаком минус . Вектор градиента направлен в сторону наибольшего возрастания потенциала, а вектор напряженности – в противоположную сторону.

Слайд 19

19 Графически электростатическое поле изображается не только с помощью линий напряженности, но с использованием эквипотенциальных поверхностей – совокупности точек с одинаковым потенциалом . Вектор напряженности в каждой точке направлен по нормали к эквипотенциальной поверхности в сторону уменьшения потенциала. Густота эквипотенциальных поверхностей пропорциональна величине и направлении напряженности в разных точках. На рисунке пунктирными линиями показаны сечения эквипотенциальных поверхностей плоскостью чертежа.

Слайд 20

20 Электроемкость Потенциал уединенного проводника пропорционален его заряду и зависит только от формы и размеров проводника: где С – называется электроемкостью или емкостью проводника. Величина С зависит от размеров и формы проводника, но не зависит от заряда. Емкость Земного шара С  700 мкФ. Конденсатором называется система двух проводников, разноименно заряженных равными по модулю зарядами.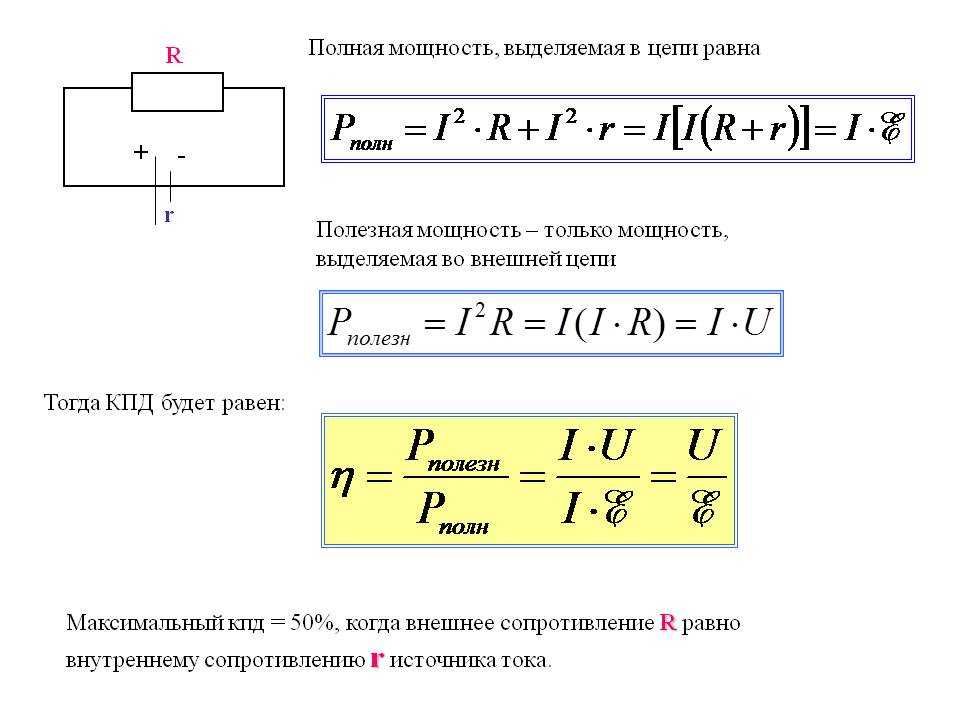 Заряд конденсатора прямо пропорционален разности потенциалов его обкладок:

Слайд 21

21 Ёмкость плоского конденсатора где S – площадь обкладки; d – расстояние между обкладками . При параллельном соединении n конденсаторов При последовательном соединении n конденсаторов

Слайд 22

22 Энергия электростатического поля Энергия заряженного проводника – это потенциальная энергия взаимодействия зарядов проводника. Сообщение проводнику заряда связано с совершением работы по преодолению электростатических сил отталкивания между одноименными зарядами. Процесс заряжания конденсатора можно представить, как перенос заряда с одной обкладки на другую. При переносе заряда dq с обкладки 2 на обкладку 1 внешние силы совершают работу Работа внешних сил при увеличении заряда от нуля до q Энергия электрического поля заряженного конденсатора

Слайд 23

23 Энергию конденсатора можно рассматривать как энергию электростатического поля всех зарядов конденсатора. Выразим данную энергию через величину, характеризующую само электрическое поле – через напряженность. Плотность энергии электрического поля Носителем энергии является поле . Это выражение справедливо и для переменного электрического поля, в котором поле существует независимо от зарядов.

Слайд 24

При внесении вещества в электромагнитное поле наблюдается воздействие на заряды и магнитные моменты молекул вещества. Смысл воздействия поля на вещество – это ориентирующее действие на дипольные и магнитные моменты. . Диэлектрики в электрическом поле

Слайд 25

25 Электрическим диполем называется система двух разноименных одинаковых по модулю электрических зарядов, расположенным на расстоянии l друг от друга. Дипольным моментом называется вектор где вектор проведен от отрицательного заряда к положительному заряду.

Слайд 26

26 Все вещества по их электрическим свойствам можно разделить на проводники, полупроводники и диэлектрики. Диэлектрики – это вещества, которые не проводят электрический ток. В диэлектриках практически отсутствуют свободные заряды. Диэлектрики бывают неполярные, полярные и сегнетоэлектрики.

Слайд 27

27 Неполярные диэлектрики состоят из симметричных молекул, в которых «центры тяжести» положительных и отрицательных зарядов совпадают ( l = 0) ( H 2 , N 2 , O 2 , CO 2 ) . Собственный дипольный момент молекул неполярных диэлектриков равен нулю. Во внешнем электрическом поле происходит смещение зарядов (деформация молекулы), и молекула приобретает дипольный момент, ориентированный по полю. Величина смещения зарядов зависит от упругих свойств заряда в молекуле.

Слайд 28

28 Полярные диэлектрики состоят из молекул, которые имеют отличный от нуля собственный дипольный момент ( H 2 O, NH 3 , HCl и др. ). До внесения в поле эти моменты ориентированы хаотично, что поддерживается тепловым движением. При внесении полярного диэлектрика в электрическое поле возникает преимущественная ориентация диполей по направлению поля, но тепловое движение мешает этому процессу. С увеличением температуры поляризация уменьшается.

Слайд 29

29 Количественной мерой поляризации любого диэлектрика является вектор поляризованности где суммируются все дипольные моменты молекул в объеме  V . Поляризованность – это электрический (дипольный) момент единицы объема. При внесении диэлектрика во внешнее электростатическое поле напряженностью Е о вследствие поляризации внутри диэлектрика образуется поле связанных зарядов напряженностью Е  , которое направлено навстречу внешнему полю Е о . Согласно принципу суперпозиции напряженность поля в диэлектрике

Слайд 30

. Электрическое смещение (электрическая индукция): При переходе из одной среды в другую величина D не изменяется, в то время как значение напряженности электрического поля Е испытывает скачок на границе раздела сред с различными свойствами.

Слайд 31

Поляризованность пропорциональна напряженности внешнего поля Безразмерная величина  называется электрической восприимчивостью , она показывает, насколько вещество воспринимает поле. где величина называется диэлектрической проницаемостью . Величины ,  и Р являются характеристиками вещества . Вектор — это характеристика источника электрического поля, которым являются свободные заряды.

Слайд 32

32 Условия на границе двух диэлектриков

Слайд 33

Для вакуума где суммируются все свободные заряды в объеме, ограниченном замкнутой поверхностью S . Других зарядов в вакууме просто нет. Вектор D от свойств среды не зависит, следовательно, он описывает электростатическое поле, созданное свободными зарядами, но при таком их расположении, которое устанавливается при наличии диэлектрика. Поток вектора смещения электростатического поля в диэлектрике через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов внутри этой поверхности . Основное уравнение электростатики в веществе

Слайд 34

34 СЕГНЕТОЭЛЕКТРИКИ это кристаллические диэлектрики, обладающие спонтанной (самопроизвольной) поляризованностью в определенном интервале температуры. ( Сегнетова соль, титанат бария и др . ) Сегнетоэлектрики имеют следующие отличительные свойства. Большие значения диэлектрической  проницаемости. Например, для титаната бария  ~ 10 4 . Нелинейный характер зависимости диэлектрической проницаемости от напряженности электрического поля.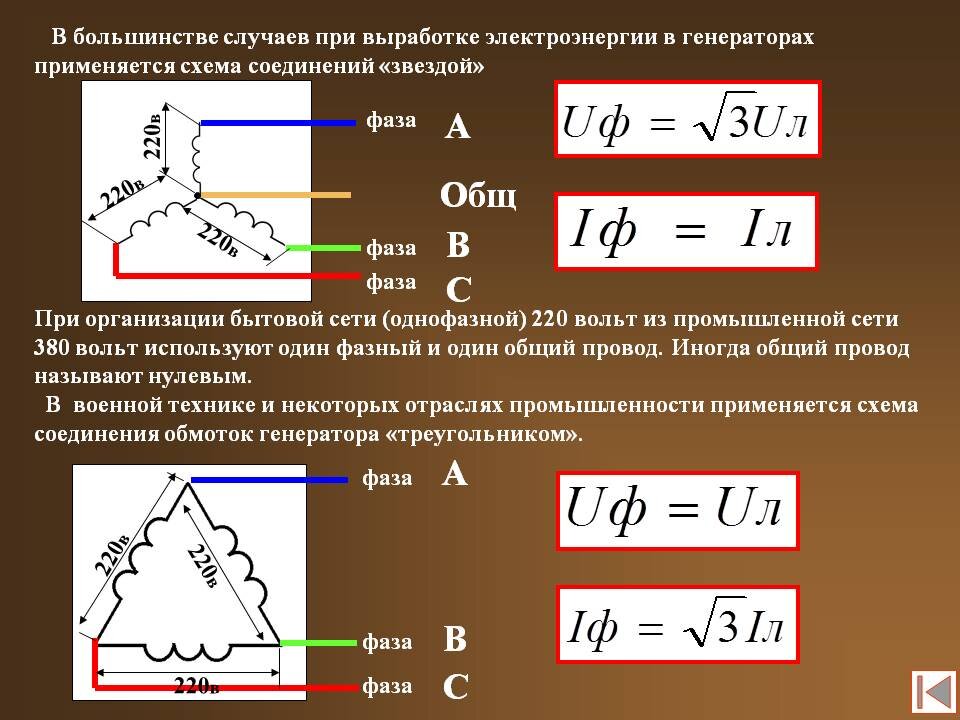 Наличие гистерезиса, т.е. зависимости поляризованности от предыстории образца.

Слайд 35

35 Доменная структура : существуют макроскопические области, в пределах которых наблюдается одинаковая спонтанная ориентация дипольных молекул вещества. Поляризация сегнетоэлектриков во внешнем поле заключается: в смещении границ доменов и росте размеров тех доменов, моменты которых близки по направлению к направлению внешнего поля; в повороте моментов доменов по полю. Наличие так называемой точки Кюри – критической температуры, выше которой сегнетоэлектрические свойства исчезают, и вещество переходит в полярный диэлектрик. Например, для сегнетовой соли сегнетоэлектрические свойства проявляются в температурном интервале Т = (255…297) К . Сегнетоэлектрики используются, в частности, для изготовления конденсаторов малых размеров, но большой электроемкости. А также для модуляции частоты электромагнитных колебаний.

Слайд 36

Постоянный электрический ток 36

Слайд 37

37 Электрическим током называется упорядоченное движение заряженных частиц . За направление электрического тока принято направление движения положительного заряда. Различают ток проводимости и конвекционный ток. Конвекционным током называется движение заряженного макроскопического тела.

Слайд 38

38 [ Током проводимости называется упорядоченное движение свободных зарядов. Свободные заряды способны перемещаться на любые расстояния в пределах проводника. Необходимыми и достаточными условиями существования тока проводимости являются: наличие свободных зарядов; наличие силы, действующей на свободные заряды в определенном направлении. (Чаще всего, источником такой силы является электрическое поле.)

Слайд 39

39 Количественной характеристикой электрического тока является сила тока , которая равна заряду, переносимому через рассматриваемую поверхность за единицу времени: Если сила тока и его направление не изменяются с течением времени, то электрический ток называется постоянным . [ I ] = А = Кл/с

Слайд 40

40 Плотности тока – это отношение силы тока dI через элементарную площадку dS , перпендикулярную направлению тока, к ее площади Направление вектора совпадает с направлением движения зарядов в данной точке.

Слайд 41

41 . Сила тока через поверхность S конечных размеров  — угол между направлением тока через элементарную площадку dS и нормалью к ней; j n — проекция вектора плотности тока на нормаль к площадке dS . Сила тока проводимости через поверхность S равна потоку плотности тока через эту поверхность.

Слайд 42

42 Пусть через площадку dS за время dt переносится заряд q – заряд носителя тока; n – концентрация носителей тока; dV – элементарный объем. Так как векторы и совпадают по направлению, то плотность тока проводимости — скорость дрейфа.

Слайд 43

43 Классическая электронная теория электропроводности металлов В классической теории ( Друде-Лоренца ) электроны проводимости рассматриваются как электронный газ, обладающий свойствами идеального одноатомного газа. В отсутствии электрического поля электроны проводимости хаотически движутся и сталкиваются с ионами металла, которые совершают беспорядочные тепловые колебания в узлах кристаллической решетки. Считается, что средняя длина свободного пробега электронов имеет порядок расстояния между узлами кристаллической решетки.

Слайд 44

44 В присутствии электрического поля электроны наряду с тепловым движением приобретают некоторую скорость упорядоченного движения в направлении, противоположном вектору напряженности. Считается, что при столкновении с ионами электроны полностью теряют свою скорость упорядоченного движения. Это означает, что электрон движется ускоренно лишь на длине свободного пробега, стартуя всякий раз после столкновения с ионом от нулевой скорости. Так как средняя длина свободного пробега электрона мала, то средняя скорость упорядоченного движения электронов много меньше их средней скорости теплового движения:

Слайд 45

45 Закон Видемана-Франца Для металлов отношение коэффициента теплопроводности  к удельной электрической проводимости  пропорционально температуре Т : где L = 2,47  10 –8 Вт  Ом /К 2 – постоянная Лоренца. Взаимная связь электрической проводимости и теплопроводности объясняется тем, что оба эти свойства металлов, в основном, обусловлены движением свободных электронов. Коэффициент теплопроводности увеличивается пропорционально средней скорости частиц, так как ускоряется перенос энергии. Электропроводность, наоборот, падает, потому что соударения при большой скорости частиц значительно затрудняют перенос энергии. Закон Видемана-Франца стал триумфом теории свободных электронов.

Слайд 46

46 Закон Ома в дифференциальной форме Уравнение движения электронов на длине свободного пробега На этом участке электроны движутся равноускоренно, поэтому Интегрируя по времени в пределах от 0 до средней продолжительности свободного пробега  , получим Подставив это в выражение (*) для плотности тока, получим

Слайд 47

47 Величину  называют удельной электропроводностью а величину  = 1/  — удельным сопротивлением . Закон Ома в дифференциальной форме: плотность тока проводимости равна произведению удельной электропроводности проводника на напряженность электрического поля в проводнике.

Слайд 48

48 Для поддержания тока проводимости необходимо действие на носители тока не только электростатических (кулоновских ) сил, но и некоторых сторонних сил. Электродвижущая сила (ЭДС)

Слайд 49

49 Под действием сторонних сил носители тока внутри источника тока движутся против сил электростатического поля, так что на концах внешней цепи поддерживается постоянная разность потенциалов, и в цепи длительное время течет электрический ток. Такие силы действуют в гальванических элементах, аккумуляторах, генераторах и т.п.

Слайд 50

50 Электродвижущая сила (ЭДС) равна работе сторонних сил по перемещению единичного положительного заряда [ E ] = Дж/Кл = В Перемещая заряды, сторонние силы совершают работу за счет энергии источника тока. В генераторах – это механическая энергия, в гальванических элементах – это энергия химических реакций на электродах.

Слайд 51

51 Разность потенциалов концов участка цепи 1-2 равна работе электростатических сил по перемещению единичного положительного заряда вдоль этого участка

Слайд 52

52 . Напряжением на участке цепи 1-2 называется величина, равная суммарной работе электростатических и сторонних сил по перемещению единичного положительного заряда из точки 1 в точку 2: [ U ] = Дж/Кл = В

Слайд 53

53 Закон Ома для участка цепи в интегральной форме Сила тока в участке цепи пропорциональна напряжению на его концах и обратно пропорциональна его электрическому сопротивлению R 12 – сопротивление участка 1-2 цепи; U 12 – напряжение на концах участка.

Слайд 54

54 Закон Ома для замкнутой цепи Сила тока в цепи пропорциональна суммарной ЭДС и обратно пропорциональна полному сопротивлению цепи R 12 = R + r – полное сопротивление участка 1-2 цепи; R – внешнее сопротивление цепи; r – внутреннее сопротивление источника тока.

Слайд 55

55 Сопротивление – способность проводника препятствовать протеканию электрического тока. Сопротивление однородного проводника постоянного сечения l – длина проводника; S – площадь его поперечного сечения; – удельное электрическое сопротивление, зависящее от материала и температуры:  о – удельное сопротивление при t = 0 С;  — температурный коэффициент сопротивления материала.

Слайд 56

56 Работа электрического тока Умножив напряжение U 12 на величину заряда dq , прошедшего за время dt по цепи , получим элементарную работу по перемещению этого заряда вдоль участка 1-2: За конечное время t работа тока Если постоянный электрический ток течет в цепи, состоящей из неподвижных проводников, то эта работа тока целиком расходуется на нагревание проводника: Q = A 12 . Мощность тока

Слайд 57

57 Литература Хавруняк В. Г. Курс физики. — М.: НИЦ ИНФРА-М, 2014. — 400 с. — ЭБС » Знаниум «. Рогачев Н. М. Курс физики. — М.: Лань, 2010. — 448 с. . — ЭБС «Лань». Трофимова Т.И. Курс физики.- М. : Академия, 2010. — 560 с. «Физика. Лабораторный практикум» . — ЭБС «ВГЛТУ» «Магнетизм» 5.3 (27) «Колебания и волны» 6.2 (30) и 6.5 (32) «Волновая оптика» 7.1 (35)

Слайд 58

58 Номер варианта выбирается по последней цифре номера зачетной книжки . Контрольная работа №1 Контрольная работа №2 Вари-ант Номера задач Вари-ант Номера задач 1 2 3 4 5 6 7 8 9 0 1.11 1.42 2.13 2.44 3.05 3.46 1.12 1.43 2.14 2.45 3.06 3.47 1.13 1.44 2.15 2.46 3.07 3.48 1.14 1.45 2.16 2.47 3.08 3.49 1.15 1.46 2.17 2.48 3.09 3.50 1.21 1.31 2.26 2.56 3.12 3.53 1.22 1.32 2.27 2.57 3.13 3.54 1.23 1.33 2.28 2.58 3.14 3.55 1.24 1.34 2.29 2.59 3.15 3.56 1.25 1.35 2.30 2.55 3.16 3.57 1 2 3 4 5 6 7 8 9 0 4.01 4.42 5.13 5.44 6.10 6.51 4.02 4.43 5.14 5.45 6.11 6.52 4.03 4.44 5.15 5.46 6. 07 6.53 4.04 4.45 5.16 5.47 6.09 6.54 4.05 4.46 5.17 5.48 6.15 6.55 4.11 4.31 5.06 5.35 6.22 6.56 4.12 4.32 5.07 5.36 6.27 6.57 4.13 4.33 5.08 5.37 6.29 6.58 4.14 4.34 5.09 5.38 6.31 6.59 4.15 4.35 5.10 5.39 6.32 6.60 5. Физика. Методическое пособие и задания к контрольным работам для студентов факультета заочного обучения специальностей: «Автомобили и автомобильное хозяйство», «Автомобили и автомобильное хозяйство» (сокращенная программа), «Технология деревообработки»/ Б.М. Кумицкий , А.М. Бомбин , И.П. Бирюкова ; ГОУ ВПО «ВГЛТА».– Воронеж, 2009.– 94 с

Слайд 59

Лекция окончена

электричества — Когда температура внешнего резистора увеличивается, почему расчетное значение внутреннего сопротивления выше?

спросил 3 года 9 месяцев назад

Изменено 12 месяцев назад

Просмотрено 511 раз

$\begingroup$

Допустим, у нас есть схема с ячейкой (с внутренним сопротивлением) и внешним резистором 10 $ \Omega$, как показано:

Затем резистор $10\Omega$ нагревается, что приводит к увеличению сопротивления этого резистора. Я думал, что поскольку резистор $10\Omega$ теперь имеет значение выше, чем $10\Omega$, на этом резисторе падает больше напряжения. Поскольку ваша ЭДС постоянна, на внутреннем резисторе должно падать меньшее напряжение. Меньшее падение напряжения означает меньшее сопротивление. Где ошибка в моей логике?

• электричество
• электрические цепи
• температура
• электрическое сопротивление
• батареи

$\endgroup$

2

$\begingroup$

Недостаток в утверждении «Меньшее падение напряжения означает меньшее сопротивление». Уменьшение разности потенциалов между двумя точками может быть вызвано либо уменьшением сопротивления, либо уменьшением тока, в зависимости от обстоятельств.

Общее падение напряжения на внутреннем и внешнем сопротивлениях распределяется между двумя элементами пропорционально их сопротивлению. Если внешнее сопротивление увеличится, то на него будет приходиться большая доля общего падения напряжения. В крайнем случае:

— при бесконечном внешнем сопротивлении не будет падения напряжения на внутреннем сопротивлении;

— при стремлении внешнего сопротивления к нулю все падение напряжения приходится на внутреннее сопротивление.

$\endgroup$

$\begingroup$

Ваша логика не ошибочна (при условии, что внутреннее сопротивление постоянно). Однако, если внутреннее сопротивление намного меньше сопротивления нагрузки, увеличение напряжения на сопротивлении нагрузки может быть трудно измерить. Это связано с тем, что небольшое изменение сопротивления нагрузки мало повлияет на напряжение на клеммах элемента. Другими словами, батарея станет источником постоянного (идеального) напряжения (напряжение на клеммах = ЭДС).

Надеюсь, это поможет.

$\endgroup$

$\begingroup$

Поскольку ваша ЭДС постоянна, меньшее напряжение должно падать на внутренней резистор

Под постоянной ЭДС я понимаю, что вольтиметр показывает одно и то же значение между полюсами ячейки, независимо от того, если внешнее сопротивление равно $10\Omega$ или больше. Итак, по определению падение напряжения не меняется, но ток уменьшается от своего начального значения при повышении температуры резистора.

$\endgroup$

1

$\begingroup$

Закон Ома гласит, что если внешнее сопротивление увеличивается, ток уменьшается. Напряжение является постоянным, если вы игнорируете внутреннее сопротивление источника напряжения. Если учесть малое внутреннее сопротивление, напряжение источника немного возрастает.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

10.3 Батареи и внутреннее сопротивление | Электрические цепи

Предыдущий 10.2 Последовательные и параллельные резисторные сети (пересмотр)

Следующий 10.4 Оценка внутреннего сопротивления в цепях

10.3 Батареи и внутреннее сопротивление (ESCPV)

До сих пор мы имели дело с идеальными батареями в том смысле, что на них не влияет цепью или током каким-либо образом и обеспечивать точное напряжение до тех пор, пока они не станут плоскими.

Если вы измеряете разность потенциалов на клеммах батарея сама по себе вы получить значение, отличное от того, что вы измеряете, когда оно находится в полной цепи. Значение будет меньше, когда батарея включена в полную цепь. Иногда разница называется потерянных вольт . Ничто не на самом деле было потеряно, но энергия была передана.

Настоящие батареи сделаны из материалов, обладающих сопротивлением. Это значит, что настоящие батареи являются не только источниками разности потенциалов (напряжения), но и также обладают внутренним сопротивлением. Если источник полной разности потенциалов называется ЭДС, \(\mathcal{E}\), то настоящая батарея может быть представлена ​​в виде ЭДС, соединенной последовательно с резистором \(r\). внутренний сопротивление батареи обозначается символом \(r\).

Нагрузка

Внешнее сопротивление в цепи называется нагрузкой.

Предположим, что батарея с ЭДС \(\mathcal{E}\) и внутренним сопротивлением \(r\) пропускает ток \(I\) через внешний нагрузочный резистор \(R\). Тогда разность потенциалов на нагрузочном резисторе равна разности потенциалов батарея:

\[V_{\text{нагрузка}}=I\cdot R\]

Аналогично, по закону Ома разность потенциалов на внутреннем сопротивлении равна:

\[{V}_{\text{внутреннее сопротивление}}=I\cdot r\]

Разность потенциалов \(V\) батареи связана с ее ЭДС \(\mathcal{E}\) и внутренним сопротивлением \(r\) автор:

\начать{выравнивать*} \mathcal{E}& = V+Ir\\ &\текст{или}\\ V& = \mathcal{E}-Ir \конец{выравнивание*}

Аккумуляторная батарея является источником энергии и энергии, обеспечиваемой на единицу проходящего заряда (ЭДС).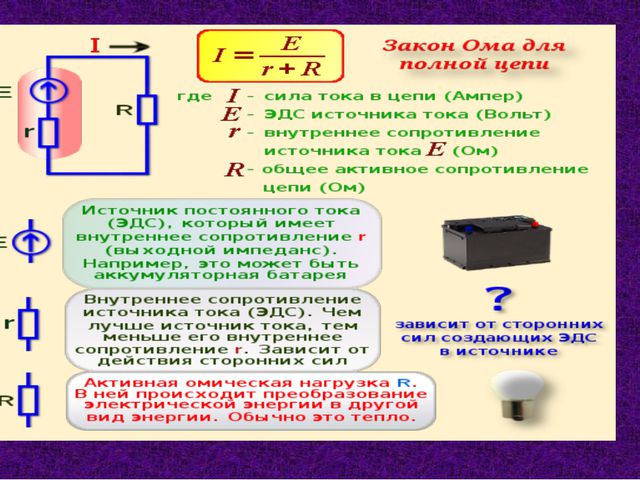 через батарею равна полной работе (разнице потенциалов) через компоненты в цепи. Это можно проиллюстрировать, показав энергию на единицу заряда в зависимости от положения в цепи. Заряд получает энергию при движении через батареи и теряет энергию при движении через резисторы.

1. Положительная работа совершается при единичном заряде аккумулятором, передающим энергию, равную ЭДС.
2. Заряд работает для преодоления внутреннего сопротивления батареи. Выполнение работы требует, чтобы заряд теряет часть энергии. Работа, совершенная для преодоления внутреннего сопротивления, равна \(V _ {\ text {внутреннее сопротивление}} = Ir \).
3. Когда единичный заряд покидает аккумулятор, он имеет меньше энергии, чем первоначальная ЭДС. Теперь это общая энергия, которую он может использовать для выполнения работы, перемещающейся по цепи, \ (V _ {\ text {load}} = \ mathcal {E} -Ir \).
4. Когда заряд движется по цепи, он совершает работу, проходя через каждый компонент, равный в \(ИК\).

ЭДС батареи практически постоянна, поскольку зависит только от химическая реакция (которая преобразует химическую энергию в электрическую энергию), происходящая внутри батареи. Таким образом, мы видим, что разность потенциалов на клеммы аккумулятора зависит от тока, потребляемого нагрузкой. чем выше ток, тем меньше разность потенциалов на клеммах, потому что ЭДС постоянна. По той же причине разность потенциалов равна ЭДС только тогда, когда ток очень мал.

Ток, который может потребляться от батареи, ограничен критическим максимальным значением \({I}_{c}\). Чем больше сопротивление в цепи, тем меньше будет ток. Представьте, что у вас есть провод без сопротивления, который вы использовать для соединения клемм аккумулятора. Цепь завершена, ток будет течь и добавление любого сопротивления в цепь уменьшит ток. Ток без внешнего сопротивления будет \({I}_{c}\). В ток \({I}_{c}\), \(V=\text{0}\text{V}\), поскольку в цепи нет нагрузки. Тогда уравнение становится:

\начать{выравнивать*} \text{0}& = \mathcal{E}-{I}_{c}r\\ {I}_{c}r& = \mathcal{E}\\ {I}_{c}& = \frac{\mathcal{E}}{r} \конец{выравнивание*}

Максимальный ток, который можно получить от батареи, меньше \(\frac{\mathcal{E}}{r}\).

Рабочий пример 6: Внутреннее сопротивление

Определить внутреннее сопротивление батареи с ЭДС \(\text{12,00}\) \(\text{V}\) и имеет разность потенциалов на его выводах \(\text{10,00}\) \(\text{V}\) когда ток \(\text{4,00}\) \(\text{A}\) течет через аккумулятор при включении в цепь.

Определите, как подойти к проблеме

Это проблема внутреннего сопротивления. Итак, мы используем уравнение:

\начать{выравнивать*} \mathcal{E}& = V+Ir \конец{выравнивание*}

Решить проблему

\начать{выравнивать*} \mathcal{E}& = V+Ir\\ \text{12}& = \text{10}+\text{4}\left(r\right)\\ г & = \текст{0,5}\текст{Ом} \конец{выравнивание*}

Напишите окончательный ответ

Внутреннее сопротивление батареи равно \(\text{0,50}\) \(\text{Ом}\).

temp text

Определение внутреннего сопротивления батареи

Цель

Для определения внутреннего сопротивления батареи.

Аппарат

Для этого эксперимента вам понадобятся следующие предметы:

Метод

Мы создадим цепь, содержащую батарею, которую мы хотим изучить, последовательно. с резистором. Затем измерим разность потенциалов на нагрузке а также ток для ряда различных резисторов/реостатов в схема. Не имеет значения, если это каждый раз другой резистор или больше резисторы последовательно или параллельно. Важно то, что общее сопротивление схема меняется так, что ток каждый раз разный. Причина что это может сказать нам о внутреннем сопротивлении батареи потому что разность потенциалов на внутреннем сопротивлении \(V_{\text{внутреннее сопротивление}}=I\cdot r\), и мы можем изменять I, изменяя сопротивление схема. Если разность потенциалов на внутреннем сопротивлении меняется и мы складываем все потенциальные разности, \(\ mathcal{E} = V_{\text{нагрузка}}+V_{\text{внутреннее сопротивление}}\) мы можем определить внутреннее сопротивление.

Для этого мы построим график зависимости \(V_{\text{load}}\) от \(I\), а затем воспользуемся функциями график для определения \(\mathcal{E}\) и \(r\). Чтобы понять, почему построение графика поможет нам, начнем с уравнение для величины \(\mathcal{E}\) и заменить закон Ома и перестроить следующим образом: \начать{выравнивать*} \mathcal{E} & = V_{\text{нагрузка}} + V_{\text{внутреннее сопротивление}} \\ \mathcal{E} & = V_{\text{load}} + I\cdot r \\ V _ {\ text {load}} & = \ mathcal {E} -I \ cdot r \\ V _ {\ text {load}} & = -r \ cdot I + \ mathcal {E} \\ \ underbrace {V _ {\ text {load}}} _ {y} & = \ underbrace {-r} _ {m} \ cdot \ underbrace {I} _x + \ underbrace{\ mathcal {E}} _ {c} \конец{выравнивание*} Если мы построим график \(V_{\text{load}}\) по сравнению с \(I\), мы будем отображать данные, которые регулируются этим соотношением.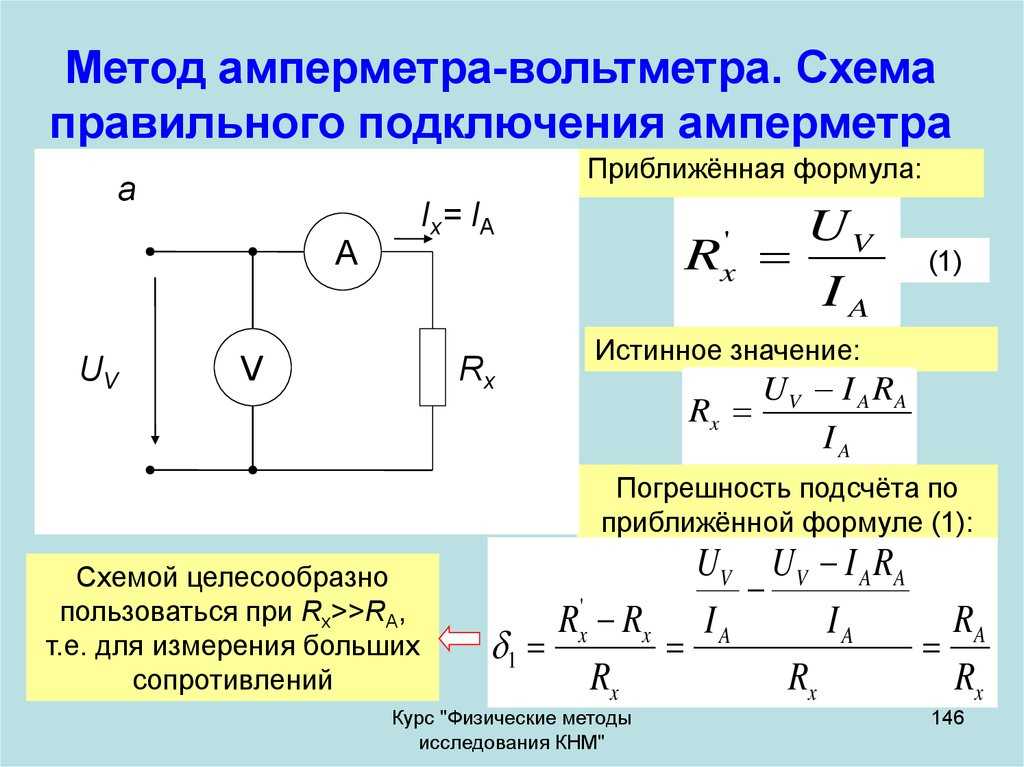 Это позволяет нам сделать вывод, что наклон графика \(m\) будет равен \(-r\), а вертикальная ось пересечения, \(c\), будет ЭДС \(\mathcal{E}\).

Результаты

Запишите свои результаты в таблицу, подобную приведенной ниже. Вы можете взять больше показаний, если хотите.

Настройка	\(V_{\text{нагрузка}}\) (\(\text{V}\))	\(Я\) (\(\текст{А}\))
Сопротивление 1
Сопротивление 2
Сопротивление 3
Сопротивление 4
Сопротивление 5

Обсуждение и заключение

Нанесите данные на набор осей, как в этом примере.