Умножение вектора на число — Студопедия

Поделись  

10.11.2021г. Геометрия 11 класс

Цели урока: рассмотреть правило умножения вектора на число и основные свойства этого действия, а так же их применение при решении задач; повторить и систематизировать знания по теме «Векторы»;совершенствовать навыки выполнения действий над векторами.

 Личностные результаты: умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности;

Метапредметные результаты:умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в учёбе;

Предметные результаты: представление об основных понятиях, идеях и методах геометрии;

 Тип урока: урок открытия новых знаний

Ход урока

1. Организационный момент.

2. Постановка цели и задач урока

3. Актуализация опорных знаний (задания для выполнения с последующей проверкой)

№ 1. Найти:

(Ответы: .)

4. Первичное усвоение новых знаний. Сформулировать правило умножения вектора на число: если то при при k < 0. Если Подробно рассмотрим на примерах свойства умножения вектора на число.

Умножение вектора на число

Сочетательный закон

Первый распределительный закон

Второй распределительный закон

 

Обратите внимание, что так же, как и в планиметрии, можно доказать следующее утверждение: если векторы коллинеарные и то существует число k, такое, что

 5. Первичное закрепление.

1) Решение задач из учебника

Задача № 345

Точки Е и F — середины сторон АВ и ВС параллелограмма ABCD, а О — произвольная точка пространства. Выразите вектор через вектор (рис. 4).

 

 

Решение: Так как EF — средняя линия треугольника ABC, то EF || АС и EF = 1/2AС. Поэтому

Задача № 347

а) Упростите выражение

Решение:

Задача № 348

Дан параллелепипед ABCDA1В1C1D1.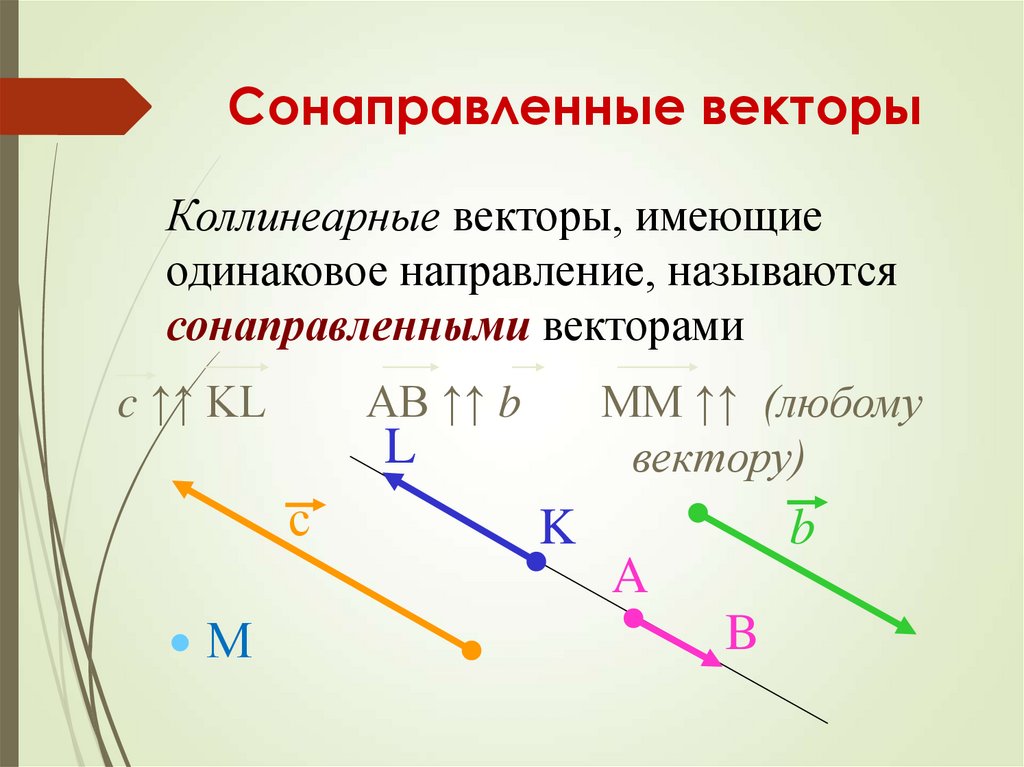 (рис. 5).

Докажите, что Решение: Из рисунка видно, что

6. Первичная проверка понимания

— Что называется произведением ненулевого вектора на число?

— Что называется произведением нулевого вектора на число?

— Свойства умножения вектора на число.

 — Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарные; б) любые два коллинеарных вектора сонаправлены; в) любые два равных вектора коллинеарные; г) любые два сонаправленные вектора равны.

Домашнее задание Прочитать п. 42, выполнить №344,  № 347(б), № 341*

Ребята,

1.прочитайте п. 42,

2. выучите определения и свойства умножения вектора на число,

3. прочитайте конспект урока и разберите задачи,

4. выполните №344, № 347(б), № 341*



Векторы для чайников. Часть 1. Сложение, разность, умножение на число. — Блог

Векторы для чайников.

Часть 1. Сложение, разность, умножение на число.

18 июня 2021 0 Marina Pashnina

Есть на баше одна уже старая шутка про черного кота, которая звучит как-то так:

— Если чёрный кот перешел дорогу туда и обратно, это значит, что он удвоил наказание или отменил своё решение? 
— Кот скалярный или векторный? Если скалярный — то удвоил, если векторный — то отменил.

В общем, с этой ноты и начинается статья про то, что было бы, если бы уже знакомый нам кот по имени Котаненс был векторным или скалярным, или статья о векторах.
 

 

Вектор — это направленный отрезок и главное, что нужно знать о векторе — у него есть величина и направление. Тут пока все сходится с котом, переходящим дорогу: кот идет в определенном направлении и проходит при этом определенное расстояние. 

 

 

 

В школьном курсе геометрии рассматриваются некоторые действия над векторами: сложение векторов, умножение вектора на число, разность векторов. В основном, эти действия интуитивно понятные, достаточно только представить или нарисовать вектор или пару векторов. Давайте коротко рассмотрим эти действия.

Отдельно оговорюсь о существовании нулевых векторов — таких векторов, у которых начало и конец находятся в одной точке. Для упрощения материала этот нулевой вектор будет местами игнорироваться ввиду малой практической значимости.

Что ж, начнем.

 

Сложение векторов

Есть несколько методов сложения векторов, которые руководствуются похожими принципами. 
 

Для сложения двух векторов нам понадобятся вектора ā  и b̅ (кто бы мог подумать?) .

 

Отложим вектор b̅ от вектора ā и проведем от конца вектора ā до начала вектора b̅ результирующий вектор.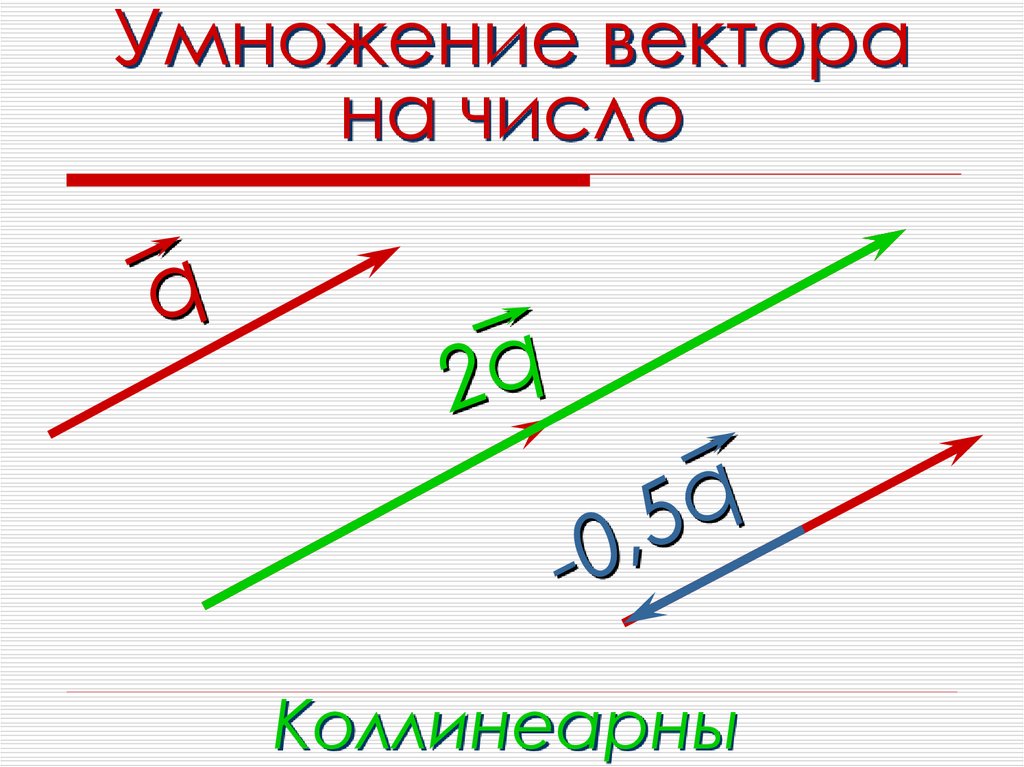 Этот прием называется правило треугольника.

 

 

Результатом сложения будет вектор ā + b̅. Всё также, как с котом: сначала кот прошел по вектору ā (определенное расстояние в определенном направлении),  затем по вектору b̅. То, что он прошел в итоге — это и есть результирующий вектор ā + b̅.

 

Это же работает и для сложения нескольких векторов: кот может пробежать по зиг-загу, или же статно пройти по результирующему вектору.

 

Если же вектор b̅ отложить не от конца, а от начала вектора ā, то получится правило параллелограмма.

 

 

Тут можно вспомнить векторного кота из шутки — если векторный кот пройдет туда-обратно, результирующий вектор, по которому он пройдет — будет равняться 0, а значит — кот отменит свое проклятье.

 

Скалярный же кот при проходе туда-обратно сложит длины векторов и получит число в 2 раза больше изначального, а значит и проклятье удвоится.
 

Разность векторов

 

Разность векторов ā и b̅ также можно рассчитать несколькими способами.

 

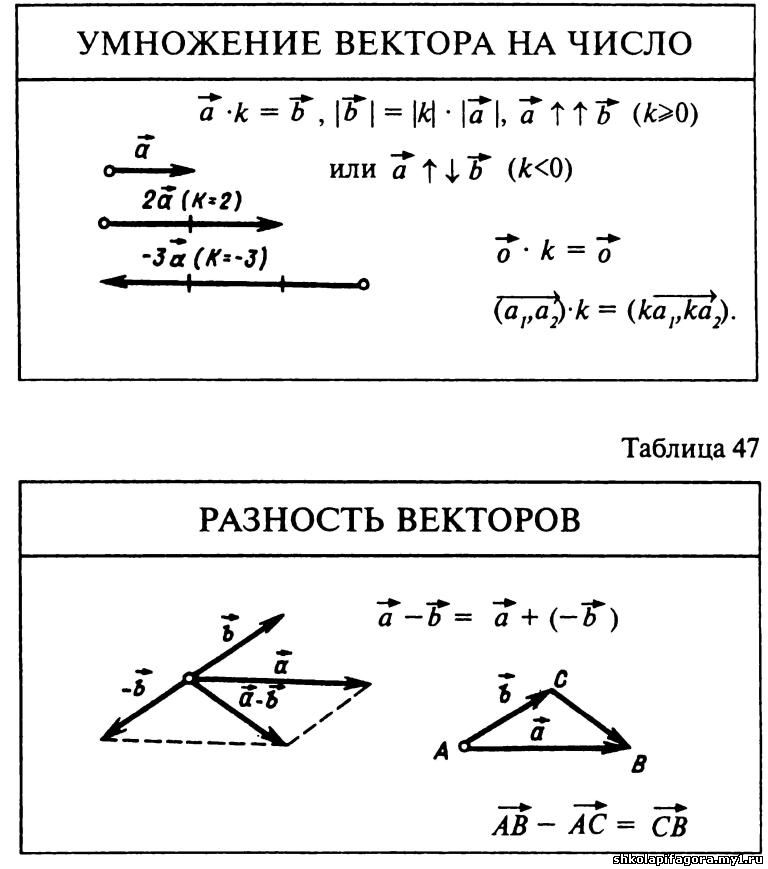
ā — b̅, как частный случай сложения — это сложение вектора ā с вектором, обратному b̅, т.е.  ā + (-b̅).

 

Вектор  -b̅, обратный к вектору  b̅  сделать просто: кот просто должен пойти в обратную сторону.

 

А дальше просто складываем этот вектор с вектором  ā.

 

Второй способ получить разность векторов чуть сложнее для осознания: разностью векторов ā и b̅ называется такой вектор, сумма которого с вектором b̅ дает вектор  ā. Для понимания достаточно просто нарисовать на листочке и все станет ясно. 

 

 

 

Умножение вектора на число

 

Умножение вектора a на число n создает такой вектор, длина которого равна |ā| * | n |, где  |ā| — это длина вектора a, а направление сохраняется при n >= 0 и меняется при n < 0.

 

 

Эта статья оказалась достаточно объемной, поэтому я рещила разделить ее на 2 части: во второй части статьи будет рассказано про векторное и скалярное произведение векторов и об этом можно почитать в статье «Векторы для чайников. Часть 2.».

Умножение векторов – типы, процесс и примеры

Умножение векторов помогает нам понять, как ведут себя два вектора при объединении. Эта векторная операция имеет широкое применение в физике, инженерии и астрономии, поэтому нам необходимо изучить эти методы, особенно если мы изучаем высшую математику. Умножение векторов охватывает два важных метода векторных операций: скалярное произведение и векторное произведение. Изучение умножения векторов также может помочь нам освежить наши знания о векторах и темах их применения. В этой статье мы обсудим два типа векторного умножения и узнаем разницу между ними. Обязательно держите свои заметки по следующим понятиям под рукой, так как нам, возможно, придется освежить их, изучая векторное умножение.

• Понимание различных компонентов, составляющих вектор.
• Посмотрите, как мы складываем и вычитаем векторы.
• Понять, как скалярный фактор влияет на заданный вектор.

А пока давайте продолжим и изучим два важных метода векторного умножения.

Когда мы умножаем два или более векторов, важно определить, хотим ли мы получить произведение, имеющее скалярную величину или векторную величину. Техника, которую нам нужно будет применить, зависит от нашего ответа на этот вопрос. На самом деле существует три возможных продукта векторного умножения: вектор, умноженный на скалярный множитель, точечный (или скалярный) продукт и перекрестный (или векторный) продукт.

• К этому моменту мы должны были узнать о распределении скалярных коэффициентов по вектору, и это первая процедура. Обязательно проверьте ссылки, которые мы включили в первый раздел.
• Скалярное произведение, известное как скалярное произведение, как вы уже догадались, возвращает скалярную величину.
• Аналогично, векторное произведение возвращает векторную величину.

Наше обсуждение сосредоточится на двух последних методах: точечных произведениях и перекрестных произведениях. Эти имена помогут вам определить операцию, которую необходимо выполнить, поскольку их операторы представляют собой точку ($\cdot$) и крестик ($\times$) соответственно.

Каковы правила умножения векторов?

Два продукта будут иметь разные результаты и процессы. Вот почему нам нужно понять, что представляют собой точечные и перекрестные произведения. Скалярный продукт и его правила Скалярное произведение представляет собой проекцию одного вектора на другой вектор. Допустим, у нас есть $\overrightarrow{A}$ и $\overrightarrow{B}$, скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ — это просто проекция $\overrightarrow{A} $ на вектор $\overrightarrow{B}$. Вот визуализация того, что происходит, когда мы находим скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$. Что происходит, так это то, что мы используем векторную составляющую $\overrightarrow{A}$ вдоль направления $\overrightarrow{B}$ и умножаем эту составляющую на величину $\overrightarrow{B}$.

\begin{align}\overrightarrow{A} \cdot \overrightarrow{B} &= (A \cos\theta)(B)\\&= AB\cos\theta\end{align} Это означает, что

скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ ($\overrightarrow{A} \cdot \overrightarrow{B})$ – это просто произведение двух векторов’ величин и косинус угла между ними . Полученное произведение является скалярным, поэтому -точечное произведение также известно как скалярное произведение. Вот некоторые важные свойства скалярного произведения, о которых следует помнить:

• Скалярное произведение коммутативно: $\overrightarrow{A} \cdot \overrightarrow{B} = \overrightarrow{B} \cdot \overrightarrow{A}$. 9{\circ}$ равно $0$).

Есть еще один способ вычислить скалярное произведение двух векторов: мы умножаем их соответствующие декартовы компоненты на . Допустим, $\mathbf{i}$, $\mathbf{j}$ и $\mathbf{k}$ — единичные векторы вдоль осей $x$, $y$ и $z$ соответственно, мы можем найдите произведение $\overrightarrow{A}$ и $\overrightarrow{B}$, как показано ниже. \begin{align}\overrightarrow{A} &= A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}\\\overrightarrow{B} &= B_1\mathbf{i} + B_2\ mathbf{j} + B_3\mathbf{k}\\\\\overrightarrow{A} \cdot \overrightarrow{B}&=A_1B_1 + A_2B_2 +A_3B_3 \end{выровнено} Мы можем вычислить эти два способа скалярного произведения (или скалярного произведения) двух векторов. Теперь давайте перейдем ко второму важному результату векторного умножения: перекрестному или векторному произведению. Перекрестное произведение и его правила Возможно, вы уже видели здесь шаблон — для векторных произведений мы используем оператор $\times$, и результирующее произведение является вектором. Из-за этого перекрестное или векторное произведение предполагает, что мы будем учитывать направление. Отличный способ визуализировать векторное произведение двух векторов — определить площадь параллелограмма по векторам. Отсюда мы видим, что перекрестное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ равно произведению $A\sin\theta$ и $\overrightarrow{B}$. \begin{align}\overrightarrow{A} \times \overrightarrow{B} &= (A \sin \theta)(B)\\&= AB \sin \theta \mathbf{n} \end{align} Имейте в виду, что $\mathbf{n}$ — это просто единичный вектор, перпендикулярный и $\overrightarrow{A}$, и $\overrightarrow{B}$. Это означает, что мы можем найти перекрестное произведение на умножение величин двух векторов при наличии двух векторов и угла между ними . Затем мы можем умножить результат на синус угла между двумя векторами . Вот некоторые важные свойства векторных или кросс-произведений, которые могут пригодиться:

• Векторные или перекрестные произведения антикоммутативны: $\overrightarrow{A} \times \overrightarrow{B} = -\overrightarrow{B} \times \overrightarrow{A}$.
• Векторное произведение является дистрибутивным относительно сложения: $\overrightarrow{A} \times (\overrightarrow{B}\times \overrightarrow{C}) = \overrightarrow{A} \times \overrightarrow{B} + \overrightarrow{A} \ раз \overrightarrow{C}$.
• Перемножение двух параллельных векторов всегда будет равно $0$.

Как и в случае со скалярными произведениями, мы также можем найти векторное произведение двух векторов, учитывая их декартовы формы. Используя те же единичные векторы, мы имеем $\overrightarrow{A} = A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}$ и $\overrightarrow{B} = B_1\mathbf{i} + B_2\mathbf{j}+ B_3\mathbf{k}$. Важным свойством для наблюдения являются векторные произведения векторов с тремя единицами. Мы собрали для вас продукты: Мы можем разработать формулу векторного произведения, распределив два вектора на сложение и используя векторные произведения единичных векторов. Однако, чтобы упростить обсуждение, вот как мы можем вычислить векторное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$. \begin{выровнено}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k }\конец{выровнено} Если вы уже изучали детерминанты в прошлом, есть еще один способ понять векторное произведение, и вы также можете помочь себе запомнить операцию.

• Мы можем записать единичные векторы в первый массив.
• Компоненты двух векторов в следующих двух массивах.
• Чтобы найти коэффициент перед $\mathbf{i}$, мы находим определитель оставшейся матрицы $2\times2$ после того, как покроем строку и столбец, содержащие $\mathbf{i}$.
• Примените аналогичный процесс, чтобы найти компоненты для $\mathbf{j}$ и $\mathbf{k}$ .

\begin{align}\overrightarrow{A} \times \overrightarrow{B}&=\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ A_1 & A_2 & A_3\\ B_1 & B_2 & B_3\end{vmatrix}\\&=\begin{vmatrix}  A_2 & A_3\\B_2 & B_3\end{vmatrix}\mathbf{i}- \begin{vmatrix}  A_1 & A_3\\B_1 & B_3\end{vmatrix}\mathbf{j}+\begin{vmatrix}  A_1 & A_2\\B_1 & B_2\end{vmatrix}\mathbf{k}\\&=(A_2B_3 – A_3B_2)\mathbf{i} — (A_1B_3 – A_3B_1)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k}\end{выровнено} Независимо от подхода, он все равно должен возвращать одни и те же результаты. Это все, что нам нужно узнать о векторном умножении, так почему бы нам не попробовать решить приведенные ниже задачи, чтобы лучше понять векторные произведения и скалярные произведения? 9{\ circ} $

Раствор

Эта задача требует, чтобы мы умножили величины $\overrightarrow{F}$ и $\overrightarrow{s}$ и косинус образовавшегося угла $\theta$. Короче говоря, нам нужно скалярное произведение $|\overrightarrow{F}| $ и $|\overrightarrow{s}| . \begin{align}\overrightarrow{F} \cdot \overrightarrow{s} &= |\overrightarrow{F}||\overrightarrow{s}|\cos \theta \end{align} Мы будем использовать одну и ту же формулу для всех трех значений, поэтому продолжим и суммируем расчеты в одной таблице. 9{\circ}\\&= 600 \cdot \dfrac{1}{2}\\&=300 \end{выровнено} \begin{выровнено}\overrightarrow{F} \cdot \overrightarrow{s} &=300 \text{N}\cdot\text{m}\end{выровнено}

Это отличный способ применить нашу формулу скалярного произведения, а также получить представление об одном из многих приложений векторного умножения. Пример 2 Найдите выражения для $\overrightarrow{A} \cdot \overrightarrow{B}$ и $\overrightarrow{A} \times \overrightarrow{B}$ для следующих векторов: \begin{align} \overrightarrow{A} &= 2\mathbf{i} – 3\mathbf{j}\\\overrightarrow{B} &=3\mathbf{i}+ 2\mathbf{j}\end{ выровнено}

Решение

Зная декартовы формы векторов, мы все еще можем найти их точечные и перекрестные произведения.

• Мы можем перемножить коэффициенты соответствующих компонентов, а затем сложить произведения, чтобы найти скалярный продукт.
• Для перекрестного произведения вида $a\mathbf{i} + b\mathbf{j}$ мы распределяем члены алгебраически и сокращаем перекрестные произведения одних и тех же единичных векторов.

Почему мы не работаем с $\overrightarrow{A} = 2\mathbf{i} – 3\mathbf{j}$ и $\overrightarrow{B} =3\mathbf{i} + 2\mathbf{j}$ сначала лучше понять процесс? Скалярное произведение будет простым — мы умножаем коэффициенты перед $\mathbf{i}$ и $\mathbf{j}$. \begin{align}\overrightarrow{A} \cdot\overrightarrow{B}&= ({\color{blue}2}\mathbf{i} – {\color{red}3}\mathbf{j}) \cdot ({\ color{blue}3}\mathbf{i} + {\color{red}2}\mathbf{j})\\&= ({\color{blue}2})({\color{blue} 3}) + ({\color{red}-3})({\color{red}2})\\&= 6 – 6\\&= 0\end{выровнено} Это означает, что скалярное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$ равно $0$. Поскольку векторное произведение является дистрибутивным относительно сложения, мы можем распределить члены алгебраически и сократить $\mathbf{i}\times\mathbf{i}$ или $\mathbf{j}\times\mathbf{j}$ . \begin{align}\overrightarrow{A} \times\overrightarrow{B}&= (2\mathbf{i} – 3\mathbf{j}) \times (3\mathbf{i} + 2\mathbf{j} )\\&= (2\mathbf{i})\times (3\mathbf{i} + 2\mathbf{j}) – 3\mathbf{j}\times (3\mathbf{i} + 2\mathbf {j})\\&= [(2)(3) \mathbf{i}\times\mathbf{i} +(2)(2) \mathbf{i}\times\mathbf{j}]+[( -3)(3) \mathbf{j}\times\mathbf{i} + (-3)(2)\mathbf{j}\times\mathbf{j}]\end{выровнено} Напомним, что перекрестное произведение идентичных векторов будет равно нулю, поэтому давайте воспользуемся этим, чтобы сократить члены. Кроме того, просмотрите руководство, которое мы предоставили для векторных произведений других единичных векторов. \begin{выровнено}\overrightarrow{A} \times\overrightarrow{B}&= (0 + 4\mathbf{k})+(-9(\mathbf{-k} )+ 0)  \\&= (4 + 9)\mathbf{k}\\&= 13\mathbf{k}\end{align} Таким образом, мы показали, как можно найти перекрестное и скалярное произведения двух векторов вида $a\mathbf{i} + b\mathbf{j}$. Пример 3 Оцените следующие выражения, учитывая декартовы формы трех векторов, показанных ниже. \begin{align} \overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4 \mathbf{j}- 3\mathbf{k}\\\overrightarrow{C} &=3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k}\end{align} а. $\overrightarrow{A} \times\overrightarrow{B}$ б.$\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{B})$ в. $(\overrightarrow{A} \times \overrightarrow{B})\times \overrightarrow{C}$

Решение

У нас есть два способа найти векторное произведение $\overrightarrow{A}$ и $\overrightarrow{B}$: используя формулу, полученную из распределения двух векторов, или используя наши знания об определителях.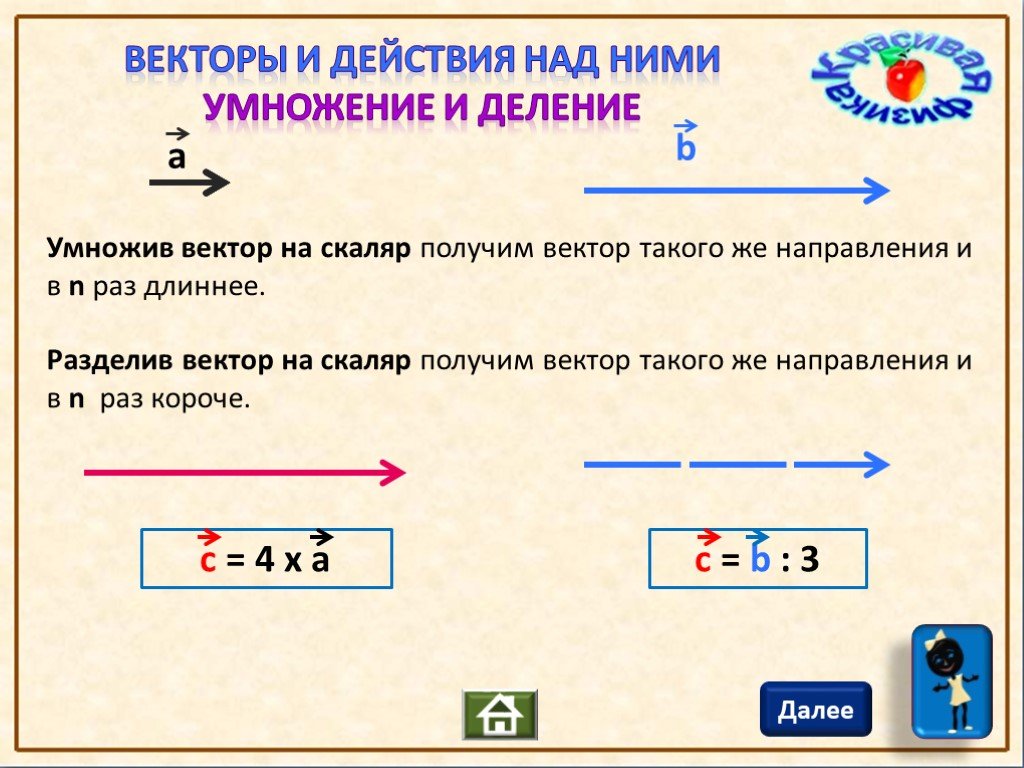 Мы пока будем использовать первый вариант: \begin{выровнено}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k }\конец{выровнено} Следовательно, мы имеем векторное произведение двух векторов: \begin{align}\overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4 \mathbf{j}- 3\mathbf{k}\\\overrightarrow{A} \times \overrightarrow{B}&=(-5\cdot -3 – 6\cdot 4)\mathbf{i} +(-3 \cdot 4 – 4\cdot -3)\mathbf{j}+(4\cdot 4 – -5\cdot -2)\mathbf{k}\\&=-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}\\&=-9\mathbf{i} +6\mathbf{k}\end{выровнено} Мы будем использовать этот результат для следующих двух задач, поэтому давайте назначим $\overrightarrow{M}$ для представления $-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}$ или $ -9\mathbf{i} +6\mathbf{k}$. Чтобы найти $\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B})$, мы просто умножаем коэффициенты соответствующих единичных векторов как $\overrightarrow{A}$, так и полученного вектор, $\overrightarrow{M}$. \begin{align}\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B}) &=\overrightarrow{B}\cdot\overrightarrow{M}\\&=(-2\mathbf{ i}+ 4\mathbf{j}- 3\mathbf{k})\cdot(-9\mathbf{i}+0\mathbf{j}+6\mathbf{k})\\&= (-2)(-9)+ (4)(0) +(-3)(6)\\& =18-18\\&=0\конец{выровнено} Для третьей задачи найдем перекрестное произведение $(\overrightarrow{A} \times \overrightarrow{B}) = \overrightarrow{M}$ и $\overrightarrow{C}$, взяв определители коэффициентов. \begin{align}(\overrightarrow{A}\times\overrightarrow{B}) \times\overrightarrow{C} &=\overrightarrow{M}\times\overrightarrow{C}\\&=(-9\mathbf{ i}+0\mathbf{j}+6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})\end{выровнено} Давайте перепишем их в матричной форме и начнем вычислять определители полученных матриц $2\times2$, как показано ниже. \begin{выровнено}(-9\mathbf{i}+ 0\mathbf{j} +6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})&=\begin{vmatrix }\mathbf{i} & \mathbf{j} & \mathbf{k}\\ -9 & 0 & 6\\3 & 2 & -6\end{vmatrix}\\&=\begin{vmatrix}  0 & 6\\2 & -6\end{vmatrix}\mathbf{i}-\begin{vmatrix}  -9 & 6\\3 & -6\end{vmatrix}\mathbf{j}+\begin{vmatrix}  — 9 & 0\\3 & 2\end{vmatrix}\mathbf{k}\\&=(0 — 12)\mathbf{i} -(54 — 18)\mathbf{j}+(-18- 0) \mathbf{k}\\&=-12\mathbf{i} -36\mathbf{j}-18\mathbf{k}\end{выровнено} 9{\circ}$?

$37,5$ N$\cdot$m

$37,5\sqrt{2}$ N$\cdot$m

$75$ N$\cdot$m

$75\sqrt{3}$ N$\cdot$m

4. Что из следующего показывает выражение для $\overrightarrow{A} \cdot \overrightarrow{B}$ для следующих векторов?
\begin{выровнено}\overrightarrow{A} &= 4\mathbf{i} + 2\mathbf{j}\\\overrightarrow{B} &=-6\mathbf{i}- 5\mathbf{j}\ конец {выровнен}

$-17$

$-34$

$17$

$34$

5. Что из следующего показывает выражение для $\overrightarrow{A} \times \overrightarrow{B}$ для следующих векторов?
\begin{выровнено}\overrightarrow{A} &= 4\mathbf{i} + 2\mathbf{j}\\\overrightarrow{B} &=-6\mathbf{i}- 5\mathbf{j}\ end{align}

$-4 \mathbf{j}$

$-4 \mathbf{k}$

$-8 \mathbf{j}$

$-8 \mathbf{k}$

6. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:

\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{align}

Какие из следующего эквивалентно $\overrightarrow{A} \cdot \overrightarrow{C}$?

18$

27$

36$

54$

7. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:

\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{align}

Какие из следующего эквивалентно $\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{C})$?

18$

27$

36$

54$

8. Предположим, что у нас есть следующие выражения для $\overrightarrow{A}$, $\overrightarrow{B}$ и $\overrightarrow{C}$:

\begin{align} \overrightarrow{A} &= 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}\\\overrightarrow{B} &=6\mathbf{i}- 3\mathbf{j}+ 3\mathbf{k}\\\overrightarrow{C} &=4\mathbf{i}- 5\mathbf{j}+ 8\mathbf{j}\end{align}

Какие из следующего эквивалентно $(\overrightarrow{A} \times \overrightarrow{C})\times \overrightarrow{B}$?

$ ​​-99\mathbf{i} -60\mathbf{j} +12\mathbf{k}$

$ ​​-33\mathbf{i} -20\mathbf{j} +6\mathbf{k}$

$ ​​33\mathbf{i} +20\mathbf{j} -6\mathbf{k}$

$99\mathbf{i} +60\mathbf{j} +12\mathbf{k}$

 

Изображения/математические чертежи создаются с помощью GeoGebra.

Предыдущий урок | Главная страница | Следующий урок

Умножение векторов: векторное произведение

Мы видели в предыдущем разделе о точке продукты, которые точка продукт принимает два вектора и производит скаляр, что делает его примером скалярного произведения. В этом разделе мы введем вектор произведение, правило умножения, которое берет два вектора и производит новый вектор. Мы обнаружим, что эта новая операция, перекрестное произведение, действительны только для наших 3-мерных векторов и не могут быть определены в 2-мерных векторах. габаритный случай. Причины этого станут ясны, когда мы обсудим виды свойств, которые мы хотим, чтобы перекрестный продукт имел.

Вращательная инвариантность

Одна важная особенность скалярного произведения, о которой мы не упоминали в предыдущем сечением является его -инвариантность относительно вращений. Другими словами, если мы возьмем пару векторов на плоскости и повернуть их на один и тот же угол (представьте, например, что векторы сидят на записи и вращают запись), их скалярный продукт останется прежним. Рассмотрим длину одного вектора (которое дается скалярным произведением): если вектор вращается вокруг начала координат под некоторым углом его длина не изменится, даже если его направление может измениться весьма драматично! Точно так же из геометрической формулы скалярного произведения мы видим, что результат зависит только от длин двух векторов и угол между ними. Ни одна из этих величин не меняется, когда мы поворачиваем два векторы вместе, так что их скалярное произведение тоже не может. Вот что мы имеем в виду, когда мы говорим, что скалярное произведение равно инвариант при вращении.

Вращательная инвариантность оказывается очень важным свойством в физике. Представьте себе, что вы записываете векторные уравнения для описания некоторой физической ситуации, принимая поставить на стол. Теперь поверните стол (или оставьте стол неподвижным и поверните себя под некоторым углом вокруг стола). Вы действительно ничего не изменили о физике на столе, просто повернув все на какой-то фиксированный угол. Из-за этого вы должны ожидать, что ваши уравнения сохранят свою форму. Этот означает, что если эти уравнения включают произведения векторов, эти произведения лучше быть вращательно инвариантным. Скалярный продукт уже прошел этот тест, так как мы отмечено выше. Теперь мы хотим потребовать того же от перекрестного произведения.

Ужесточение требования вращательной инвариантности для кросса произведение, нам нужно перекрестное произведение двух векторов, чтобы получить другое вектор. Рассмотрим, например, два трехмерных вектора u и v в плоскость (два непараллельных вектора всегда определяют плоскость точно так же, как две строки делают. Если мы повернем эту плоскость, векторы изменят направление, но нам не нужно перекрестное произведение w = u × v менять вообще. Однако, если w имеет любые ненулевые компоненты в плоскости u и v , эти компоненты будут обязательно меняются при вращении (вращаются, как и все остальное). Единственные векторы, которые совсем не изменятся при вращении плоскости u — v это те векторы, которые перпендикулярны плоскости. Следовательно, векторное произведение двух векторов u и v должно дать новый вектор, который перпендикулярно обоим и и против .

Это простое наблюдение на самом деле в значительной степени ограничивает наши возможности. варианты того, как мы можем определить перекрестный продукт. Например, мы можем видеть сразу, что нельзя определить перекрестное произведение для двух- размерные векторы, , так как нет направления, перпендикулярного плоскости двумерных векторов! (Для этого нам понадобится третье измерение).

Теперь, когда мы знаем направление в котором векторное произведение двух векторов точек, звездная величина результирующего вектора еще не определена. Если я возьму векторное произведение двух векторов в плоскости x — y , я теперь знаю, что результирующий вектор должен указывать строго в направлении z . Но если это направлена ​​вверх (т. е. лежит вдоль положительной оси z ) или должна указывать вниз? Как долго должно быть?

Начнем с определения векторного произведения единичных векторов i , j и k . Так как все векторы могут быть разложены по единичным векторам (см. Единичные векторы), как только мы определили векторные произведения для этого особого случая, и будет легко расширить определение, включив в него все векторы. Как мы отмечено выше, перекрестное произведение между i и j (поскольку они оба лежат в плоскости x — y ) должно указывать чисто в направлении z . Следовательно:

i × j = c k

для некоторой константы c . Потому что позже нам понадобится величина чтобы результирующий вектор имел геометрическую значимость, нам нужно, чтобы c k имели единичную длину. Другими словами, c может быть либо +1, либо -1. Теперь мы делаем совершенно произвольный выбор в соответствии с соглашением: мы выбираем c = + 1. Факт что мы выбрали c , чтобы быть положительным, известно как Правило правой руки (мы могли бы так же легко выбрать c = — 1, и все математические расчеты будут одинаковыми, если мы будем последовательны — но мы должны выбрать одно или другое, и нет смысла идти против того, что делают все остальные.) Оказывается, чтобы быть последовательным с правой рукой Правило, все перекрестные произведения между единичными векторами определены однозначно:

i × j	=	k = — j × i
j × k	=	i = — k × j
к × i	=	j = — i × k

В частности, обратите внимание, что порядок векторов в векторных произведениях имеет значение. В общем u × v = — v × u . Отсюда мы видим, что перекрестное произведение вектора с самим собой всегда равно нулю, так как по приведенному выше правилу u × u = — u × u , а это означает, что обе стороны должны исчезнуть, чтобы сохранялось равенство. Теперь мы можем завершить наш список перекрестных продуктов между единичные векторы, заметив, что:

i × i = j × j = к × к = 0

Чтобы взять векторное произведение двух общих векторов, мы сначала разложим векторы используя единичные векторы i , j и k , а затем продолжить распределить перекрестное произведение по суммам, используя приведенные выше правила для выполнения перекрестного произведения произведения между единичными векторами. Мы можем сделать это для произвольных векторов u = ( u ₁ , u ₂ , u ₃ ) и v = ( v ₁ , v ₂ , v 90 ) для получения общей формулы 9 508 , v 90 .

u	=	u 1 i + u 2 j + u 3 k
v	=	v 1 i + v 2 j + v 3 k
u × v	=	( u 1 i + u 2 j + u 3 k )×( v 1 i + v 2 j + v 3 к )
	=	u 1 v 1 ( i × i ) + u 1 v 2 ( i × j ) + u 1 v 3 ( i × k ) + . ..(всего 9 членов!)
	=	( u 1 v 2 — u 2 v 1 ) k + ( u 3 v 1 — u 1 v 3 ) j + ( u 2 v 3 — u 3 v 2 ) i

К сожалению, это настолько просто, насколько это возможно, когда дело доходит до написания креста. произведение явно через компоненты вектора. Наверное, это хорошо, чтобы сохранить эта формула удобна до тех пор, пока вы не привыкнете к вычислению векторных перекрестных произведений.

Геометрическая формула векторного произведения

К счастью, как и в случае со скалярным произведением, существует простая геометрическая формула для вычисления перекрестного произведения двух векторов, если их соответствующие длины и угол между ними известен. Рассмотрим перекрестное произведение двух (не обязательно единичной длины) векторы, лежащие строго вдоль осей x и y (как i и j сделать). Таким образом, мы можем записать векторы как u = и и и v = b j , для некоторых констант a и b . Таким образом, векторное произведение u × v равно равно

u × v = ab ( i × j ) = ab 7 k

Обратите внимание, что величина результирующего вектора равна площади прямоугольник со стороной и и против ! Как и было обещано выше, величина креста произведение между двумя векторами, | u × v |, имеет геометрическую интерпретацию. В в общем случае она равна площади параллелограмма, состоящего из двух данных векторы как его стороны (см. ).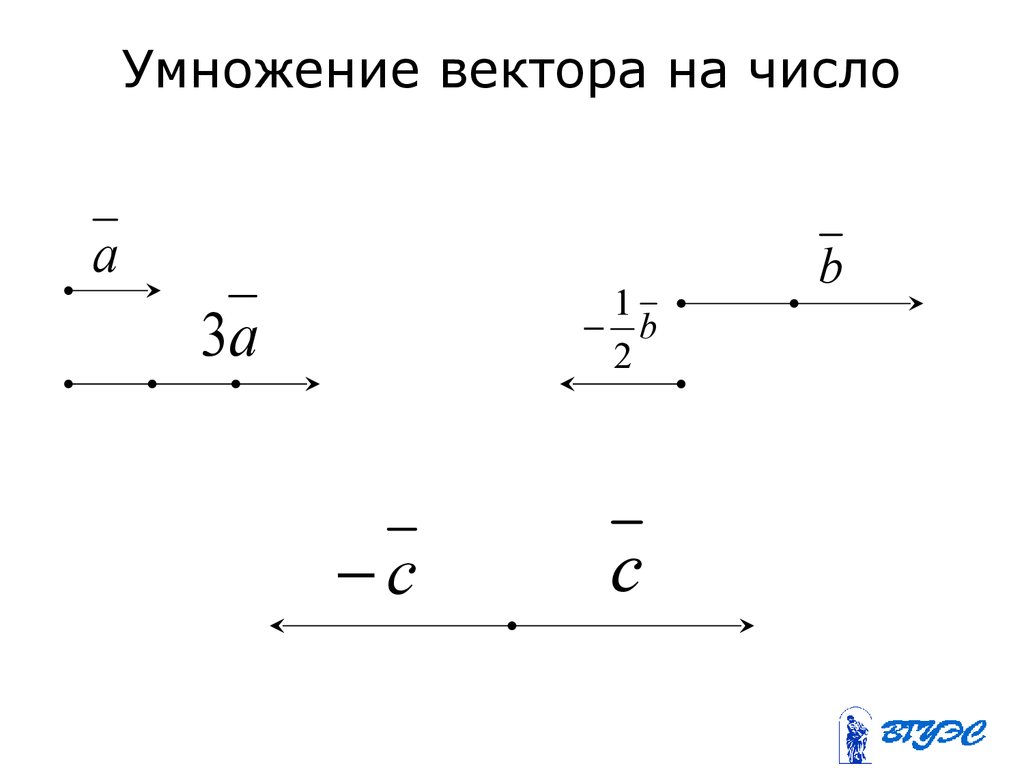

Из базовой геометрии мы знаем, что эта площадь определяется выражением площадь = | и || против | sin θ , где | и | и | против | это длины сторон параллелограмм и θ — угол между двумя векторами. Уведомление что когда два вектора перпендикулярны друг другу, θ = 90 градусов, поэтому sin θ = 1 и мы восстанавливаем знакомую формулу площади квадрата. С другой стороны, когда два вектора параллельны, θ = 0 градусов, и sin θ = 0, что означает, что площадь равна нулю (как мы и ожидали). В общем, тогда мы найти, что величина векторного произведения между двумя векторами u и v которые разделены углом θ (идя по часовой стрелке от u до v , как определяется правилом правой руки) определяется как:

| и × против | = | и || против | грех θ

В частности, это означает, что для двух параллельных векторов векторное произведение равно 0.