Определение и применение на практике закона Джоуля-Ленца — формула и правила расчета

Физики из Англии Джеймс Джоуль и Эмилий Ленц, по отдельности, но примерно в одно время 1841-1842 годах выяснили взаимосвязь количества тепла и поток тока внутри проводника. Эта зависимость была названа «Закон Джоуля-Ленца».

Английский физик заметил эту зависимость, раньше, чем русский физик на 1 год, однако назвали закон, соединив обе фамилии, т.к. как вклад каждого из них был велик. Закон Джоуля-Ленца описывает не теорию, а практику.

Давайте рассмотрим закон Джоуля-Ленца, его определение и применение в жизни.

Когда в проводнике протекает ток, то происходит работа поперек силам трения. При движении электроном через провод происходит столкновение электронов с иными электронами, атомами и другими частицами, в следствие чего вырабатывается тепло.

Рассматриваемый нами закон объясняет то количество тепла, которое вырабатывается при движении тока по проводнику.

При увеличении силы тока, сопротивления и времени протекания, количество тепла тоже увеличится, и наоборот при уменьшении этих показателей произойдет уменьшение количества тепла.

Формула закона Джоуля-Ленца представлена на рисунке.рис.1

Рисунок 1. Формула закона Джоуля-Ленца, при последовательном соединении

Сила тока – I считается в амперах, сопротивление- R в омах, время t- в секундах. Теплота Q измеряется в джоулях. Для перевода в калории умножаем на 0,24. 1 калория рассчитывается, как то тепло, которое необходимо дать воде, чтобы повысить ее на 1 градус.

Эта формула применяется, если проводники соединяются последовательно, при проходе равной величины тока, а на концах падает разное напряжение. Мощность определяется как сила тока в квадрате, умноженная на сопротивление.

Увеличение мощности сопровождает увеличение квадрата напряжения и уменьшает сопротивление, и наоборот. Если электрические цепи соединяются параллельно, то закон Джоуля-Ленца выглядит: рис. 2

Рисунок 2. Формула закона Джоуля-Ленца, при параллельном соединении

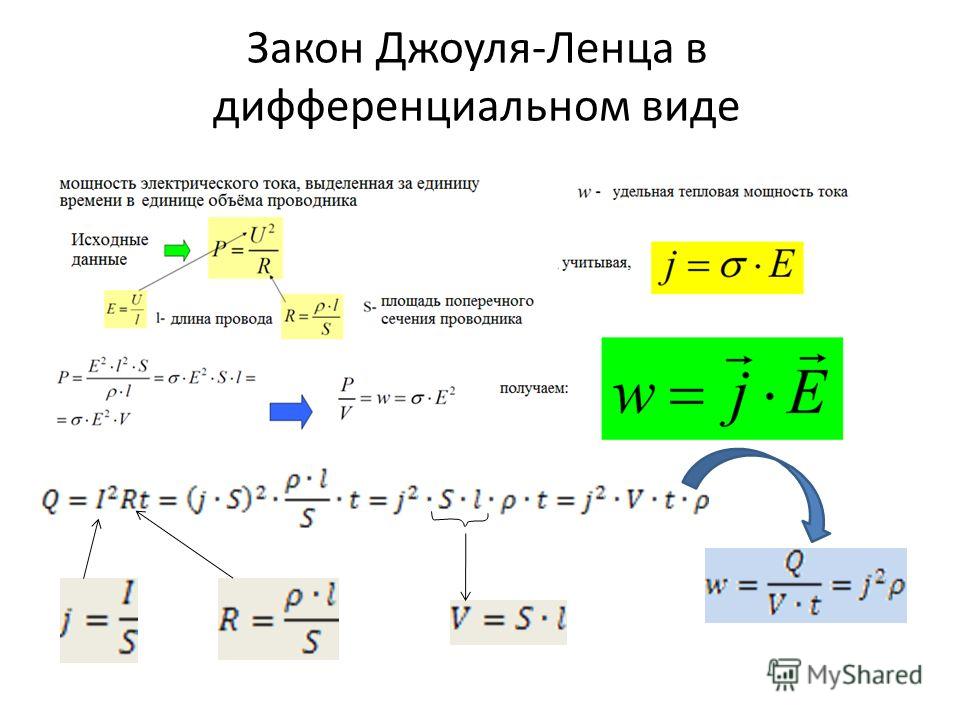
При использовании дифференциальной формы, формула такая: рис.3

Рисунок 3. Дифференциальная форма формулы закона Джоуля-Ленца

j является плотностью тока в А/см2, E — напряженностью электрического поля, сигма — удельным сопротивлением проводника.

Если участок цепи однородный, то сопротивление будет одинаково. При наличии в цепях проводников с различным сопротивлением, то самое большое тепло выделится там, где находится максимальное сопротивление. К такому выводу мы приходим, анализируя формулу Джоуля-Ленца.

Нередкие проблемы

Итак, проблема нахождения времени, т.е. тот период, когда ток проходит по проводнику (замкнутая цепь)

Вторая проблема, нахождение сопротивления проводника. Используется формула рельс:рис.4

Рисунок 2. Формула нахождение сопротивления проводника

«Р» удельное сопротивление, измеряемое в Ом*м/см2, l и S является длина и площадь поперечного сечения.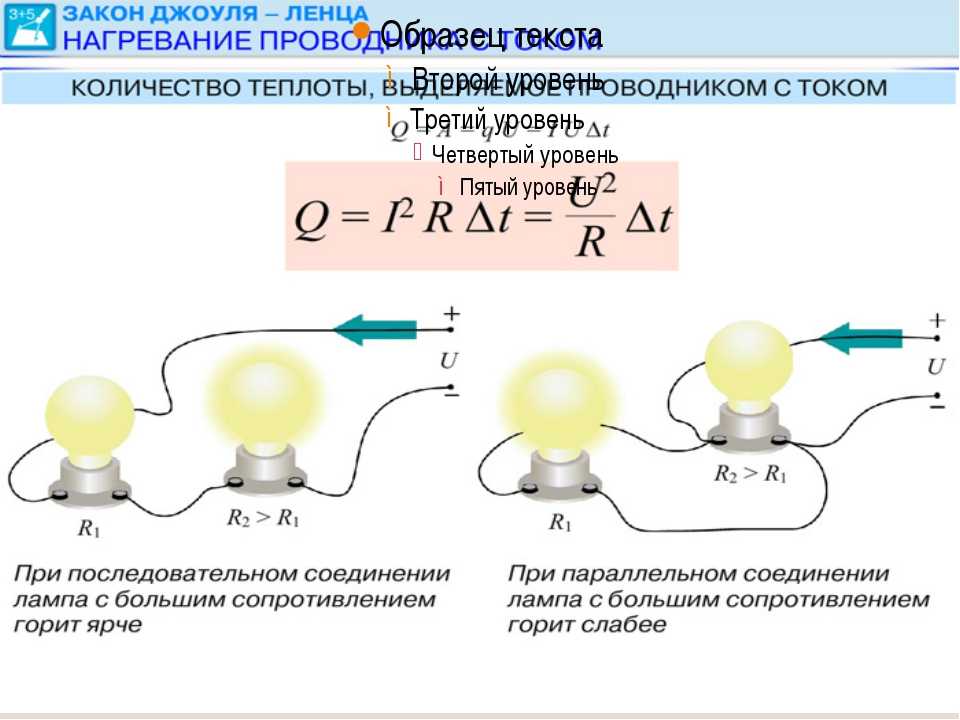 При математических операциях метры и сантиметры2 сокращаются и получаются Омы.

Удельным сопротивлением является величина, указанная в таблице, индивидуальная для каждого металла. Рассмотрим с какой целью это используется.

При электротехнических подсчетах широко используется закон Джоуля-Ленца. Можно использовать его, когда рассчитываются приборы нагревания. Нагревающий элемент – проводник с высоким сопротивлением, например нихром.

Для расчета мощности тепла прибора нужно определить, что и в каком объеме нужно нагреть, количество теплоты и времени на передачу тепла телу.

После расчета определится сопротивление и сила тока в данной цепи. Учитывая полученные данные, выбирается материал сечение и длина проводника.

Использование закона Джоуля-Ленца для передачи электроэнергии на расстояние

Закон Джоуля-Ленца

Когда происходит передача электричества на расстояние, появляется проблема потери на линиях передач. Закон показывает количество тепла, которое выделяется проводником при проходе тока.

ЛЭП используются предприятиями и городами, следственно необходимо больше мощности и больше тока.

Количество теплоты связано с сопротивлением тока и проводника, для того чтобы избежать нагрева, необходимо уменьшить количество тепла.

Не всегда можно использовать сечение провода, это дорого стоит из-за цены меди и веса кабелей, следовательно, увеличивается  стоимость несущей конструкции.

На рисунке показаны высоковольтные линии электропередач. Это огромные конструкции из металла, создающиеся для поднятия кабеля на высоту, безопасную для людей на земле, чтобы избежать удара током.

Для этого необходимо снизить ток, следовательно, повышается напряжение.

Линии электропередач между городами используют напряжение 220 и 110 кВ, а у того, кто потребляет, понижают до необходимой величины, используя трансформатные подстанции. Или множеством КТП медленно понижая до безопасной величины, например, 6кВ.

То есть ток уменьшится в тысячи раз, но при той же потребляемой мощности. По закону Джоуля-Ленца, теплота в данном случае определится мощностью, которая теряется на кабеле.

Плавкие предохранители

Закон Джоуля-Ленца используется для расчета плавких предохранителей. Это элементы, защищающие электрическое устройство от высоких для него токов, которые могут появится из-за скачка напряжения, короткого замыкания для охраны от поломки электрической системы и пожара. Они представляют собой корпус, изолятор и тонкую проволоку.

Проволока используется с сечением, подходящим для прохода номинального тока через нее, но при увеличении выделения тепла, она пережигается.

Следовательно, можно сделать вывод, что рассматриваемый нами закон Джоуля-Ленца очень широко применяется и сильно значим для электротехники.

Используя информацию про количество теплоты, исчисляемое по рассмотренным формулам, можно разузнать о режимах работы устройств, определить подходящий материал и сечение для обеспечения безопасности, увеличения срока использования прибора или цепи.

На этом я закончу данную статью. Надеюсь, эта информация стала полезной и интересной для вас.

Вопрос 2.4. Вывод Закона Джоуля- Ленца.

При столкновении с узлами кристаллической решетки, энергия которую приобретает электрон за счет Эл. поля передается кристаллической решетки, поэтому при протекании электрического тока, проводники нагреваются и в проводнике выделяется теплота, которая называется Джоулевой теплотой. Кинетическая энергия электрона перед столкновением.

, т.к. ; , Число столкновений одного электрона за единицу времени с узлами решетки: , поэтому единицы объема проводника за единицу времени электронами кристаллической решетки передается энергия. . Т.к. , тогда — удельная мощность электрического тока.(Закон Джоуля – Ленца в дифференциальной форме)

Т.к. jE=j, то , с учетом: ; Отсюда , W=IU – мощность электрического тока, где V=Sl – объем проводника. Теплота, выделяемая в проводнике за время t: Q=Wt=IUt.

Q=IUt – алгебраический закон Джоуля – Ленца. С учетом: I=U/R,

2.7. Последовательное и параллельное Соединение проводников.

При последовательном соединении через каждый проводник, резистор проходит один и тот же ток: I=I₁=I₂=…=I_n (1), Как видно из схемы разность потенциалов между концами цепи равняется сумме разности потенциалов на отдельных резисторах U=U₁+U₂+…+U_n (2). Используя закон Ома U_i=I_iR_i(3) (напряженность однородного участка цепи) и соотношения (1) и (2) R=R₁+R₂+…+R

n (4).

Параллельное соединение проводниковПри параллельном соединении общий ток разветвляется по отдельным проводникам, поэтому исходя из закона сохранения электрического заряда I=I₁+I₂+…+I_n (5). Все проводники подсоединены к одним и тем же точка 0 и 1. поэтому разность потенциалов на всех проводниках одна и та же U=U₁=U₂=U₃=…=U_n (6). Используя закон Ома и соотношение (5), (6) Получим формулу

Вопрос 2.8. Правило Кирхгофа. Разветвленные цепи.

В электрических схемах радиотехнических устройств встречаются различные комбинированные соединения множества элементов. Не всегда удается выяснить, каким образом соединены отдельные элементы, для расчета таких цепей применяют правило Кирхгофа, которое является следствием из закона Ома. Для применения правила Кирхгофа используется ряд понятий:

1) узел – это точка соединения более чем двух проводников, токи идущие к узлу считаются положительными, а выходящие из узла отрицательными.

2) участок цепи – это часть цепи между двумя узлами, каждый участок может содержать несколько источников тока и несколько электронных элементов.

В пределах участка направление и величина тока не меняется.

I правило Кирхгофа.Алгебраическая сумма сил токов, сходящихся в узле равняется нулю

II правило Кирхгофа.

Для замкнутого контура разветвленной цепи, алгебраическая сумма произведений сил токов на сопротивление соответствующих участков равняется алгебраической сумме ЭДС источников, входящих в данной контур . Для записи по правилам Кирхгофа необходимо придерживаться определенной последовательности:

1) для каждого участка произвольно выбирается направление тока и указывается на схеме. Если после решения системы Ур-ий некоторые токи окажутся отрицательными, это значит, что на данном участке направление тока противоположно. Численно значение тока при этом верное.

2) произвольно выбирается направление обхода контуров одинаковое для всех и указывается стрелкой около схемы.

3) Записывается столько уравнений сколько неизвестных при этом уравнение должны быть линейно независимы.

Для этого каждое последующее уравнение должно содержать хотя бы одно неизвестное, не входившее в предыдущее уравнение. В систему Ур-ий должно входить все источники и элементы (сопротивления).

4) знак при произведении I_iR_i берется положительным, если для данного участка направление тока совпадает с направление обхода контура.

5) Знак ЭДС берется положительным, если при обходе первым встречаются отрицательный полюс источника, в противном случае берется знак «-».

Закон Ленца и сохранение энергии

При входе в торговый центр/кинозал/аэропорт/вокзал вы можете столкнуться с охранником с металлоискателем в руке для проверки безопасности. Возможно, вы также использовали кредитную/дебетовую карту для оплаты счетов, вставив ее в устройство, называемое устройством для чтения карт. Возможно, вы также видели генератор переменного тока. Все это работает по принципу закона Ленца. В этой статье мы поговорим о законе Ленца.

Электромагнитная индукция: Явление производства ЭДС индукции из-за изменения магнитного потока (количества силовых линий магнитного поля), соединенных с замкнутой цепью, называется электромагнитной индукцией.

Что такое закон Ленца?

Ленц утверждает, что направление индукционного тока в цепи таково, что оно препятствует изменению магнитного потока. Закон Ленца назван в честь немецкого физика Эмиля Ленца, сформулировавшего его в 1834 году. 

Это научный закон, который определяет направление индуцированного тока, но ничего не говорит о его величине. Магнитный поток, подключенный к замкнутому контуру, усиливает поток индуцированного тока таким образом, что он создает магнитный поток в направлении, противоположном первоначальному магнитному потоку. Магнитный поток, подключенный к замкнутой цепи, уменьшает индуцированный ток в таком направлении, что магнитный поток создается в направлении первоначального тока.

Формула закона Ленца имеет следующий вид:

E= -N(d∅/dt)

Здесь отрицательный знак указывает на то, что направление ЭДС индукции таково, что оно препятствует изменению магнитного потока).

  Иллюстрация 1:

Как показано на рисунке выше, когда северный полюс стержневого магнита перемещается к катушке, индуцированный ток в катушке течет в направлении против часовой стрелки, если мы видим его из стороне магнита. Лицевая сторона катушки развивает северную полярность. Как мы знаем, тот самый полюс отталкивает, поэтому северный полюс-северный полюс отталкивает. Значит, он противостоит движению северного полюса магнита.

Заключение: Движение магнита увеличивает поток через катушку, и поток будет генерироваться в противоположном направлении за счет индуцированного тока.

Иллюстрация 2:

Как показано на рисунке, когда северный полюс стержневого магнита удален от катушки, индуцированный ток в катушке течет по часовой стрелке. Лицевая сторона катушки развивает южную полярность. Мы знаем, что противоположные полюса притягиваются. Итак, северный полюс и южный полюс притягиваются друг к другу.

Вывод: Движение магнита уменьшает поток через катушку. Поток генерируется в том же направлении за счет индуцированного тока, следовательно, противодействует потоку и увеличивает его.

Important uses of Lenz’s law are:

• The braking system in trains
• AC generators
• Balancing Eddy current
• Metal detector
• Microphones
• Eddy’s current dynamic meter
• Card reader

Lenz’s law and the Закон сохранения энергии

Закон Ленца является следствием закона сохранения энергии. Закон сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена, но может переходить из одной формы в другую. Закон Ленца гласит, что направление тока таково, что оно препятствует изменению магнитного потока. Таким образом, требуется дополнительное усилие, чтобы совершить работу против противоположных сил. Эта дополнительная работа приводит к периодическим изменениям магнитного потока, поэтому индуцируется больший ток. Таким образом, дополнительное усилие преобразуется только в электрическую энергию, что является не чем иным, как законом сохранения энергии.

Магнитный поток увеличивается, когда северный полюс магнита приближается к нему, и падает, когда он отталкивается в приведенной выше активности. В первом сценарии противодействие причине включает в себя перемещение магнита, и лицо, обращенное к катушке, приобретает северную полярность. Северный полюс магнита и северный полюс катушки отталкиваются друг от друга. Чтобы противодействовать силе отталкивания, необходимо совершить механическое действие, чтобы приблизить магнит к катушке. Эта механическая энергия преобразуется в электрическую энергию. Благодаря эффекту Джоуля эта электрическая энергия превращается в тепловую энергию.

Когда магнит отодвигают от катушки, ближняя сторона катушки приобретает южную полярность. В этом случае создаваемая ЭДС будет противодействовать движению магнита наружу. Чтобы противостоять силе притяжения между северным полюсом магнита и южным полюсом катушки, необходимо еще раз выполнить механическую работу. Этот труд превращается в электрическую энергию.

Механическая работа не совершается, если магнит не перемещается, следовательно, в катушке не индуцируется ЭДС.

В результате закон Ленца согласуется с законом сохранения энергии.

Закон электромагнитной индукции Фарадея:

Первый закон: Он гласит, что всякий раз, когда магнитный поток связан с изменением замкнутого контура, в нем индуцируется ЭДС, которая длится только до тех пор, пока изменяется поток происходит. Если цепь замкнута, то внутри цепи также индуцируется ток, который называется «Индуцированный ток».

Магнитные поля можно изменить:

• Перемещение стержневого магнита к катушке или от нее.
• Перемещение катушки в магнитное поле или вне магнитного поля.
• Вращение катушки относительно магнита.
• Изменение площади катушки, помещенной в магнитное поле.

Второй закон: Он гласит, что величина ЭДС индукции равна скорости изменения магнитного потока, связанного с замкнутой цепью.

|∈| = dⲫ/dt

E = -N dⲫ/dt

E = -N (ⲫ2-ⲫ1)/t ⇢ («t» – время)

Примеры вопросов

Вопрос 1. Что следует из закона Ленца?

Ответ:

Закон Ленца является следствием закона сохранения энергии.

Вопрос 2: Что произойдет, если закон Ленца изменить на противоположный?

Ответ:

Индуцированный ток будет создавать поток в том же направлении при первоначальном изменении.

Вопрос 3: Как закон Ленца используется в реальной жизни?

Ответ:

Закон Ленца используется в электромагнитных тормозах в поездах. Он также применяется в электрогенераторах, генераторах переменного тока.

Вопрос 4: Замкнутый контур обычно движется в статическом электрическом поле между пластинами большого конденсатора. Какова сила тока, когда этот конденсатор полностью находится в области между пластинами?

Ответ:

Ток не может быть вызван изменением электрического потока. Таким образом, ток не возникает, когда он полностью находится внутри области между пластинами конденсатора.  

Вопрос 5: Отличие закона Фарадея от закона Ленца?

Ответ:

Закон Ленца определяет направление индукционного тока.

Закон Фарадея гласит, что величина ЭДС, индуцированной в цепи, пропорциональна скорости изменения магнитного потока.

Вопрос 6: Какой закон используется для определения направления тока в генераторе переменного тока?

Ответ:

Закон Ленца используется для нахождения направления тока в генераторе переменного тока.

Вопрос 7: Какой закон используется для определения направления вихревого тока?

Ответ:

Поскольку мы знаем, что вихревые токи также препятствуют изменению магнитного потока, поэтому направление определяется законом Ленца.

Physics for Science & Engineering II

9.1 Магнитный поток, закон Фрадея и закон Ленца из Office of Academic Technologies на Vimeo.

9.1 Магнитный поток Закон Фрадея и закон Ленца

Ранее мы видели, что если мы поместим петлю с током во внешнее магнитное поле, то магнитное поле создаст чистый крутящий момент в этой петле с током и под влиянием этот крутящий момент, петля вращается. Так во время процесса электрическая потенциальная энергия преобразуется в энергию движения или кинетическую энергию. Мы называем этот тип системы, которая устроена таким образом, что петля вращается только в одном направлении, называемой «электрическим двигателем», устройством, которое преобразует электрическую потенциальную энергию в кинетическую энергию.

Глядя на эту систему, всегда можно задать симметричный вопрос: если взять ту же систему, но в этом случае, вместо того, чтобы пропускать ток через проводящую петлю, если мы просто провернем петлю при определенном угла скорости, мы получим ток, протекающий через эту петлю? Ответ на этот вопрос – да. По сути, это полностью симметричная система по отношению к предыдущему случаю. Как вы помните в предыдущем случае, чтобы иметь возможность вращения контура только в одном направлении, нужно было менять направление тока в каждом полупериоде.

Теперь, во втором случае, если мы провернем петлю, другими словами, если мы начнем с кинетической энергии и проверим ее только в одном направлении, мы действительно индуцируем ток вдоль этой петли, и этот ток изменит направление поток через каждые пол-оборота, так как петля вращается только в одном направлении. Следовательно, в этой системе мы действительно окажемся с током. Она будет менять направление в каждом полупериоде и в процессе, поэтому, начиная с кинетической энергии, энергия вращающегося контура будет преобразовываться в энергию движущихся зарядов, которая представляет собой электрическую потенциальную энергию.

Эти системы, эти устройства, производящие это преобразование, мы называем «генераторами».

Сейчас мы поймем, почему это происходит, но прежде чем мы углубимся в это подробно, давайте рассмотрим пару интересных наблюдений, которые можно сделать. Предположим, что у нас есть катушка, которая подключена к прибору, называемому гальванометром. Гальванометр — это не что иное, как очень чувствительный амперметр, определяющий низкий уровень электрического тока.

Теперь, очевидно, в схеме, примерно такой, нет источника питания. Между любыми двумя точками этой петли нет разности потенциалов. Мы не сможем обнаружить никакого тока. Другими словами, в этом положении шкала гальванометра не прогибается. Ну, если мы держим стержневой магнит напротив этой петли, мы, конечно, знаем, что стержневой магнит будет генерировать свои собственные уникальные силовые линии магнитного поля, и они будут выходить из северного полюса и входить в южный полюс. Таким образом, на некотором расстоянии от петли некоторые из этих линий будут проходить через область, окруженную этой петлей.

Опять же, мы не увидим никакого отклонения в циферблате гальванометра, и если мы переместим магнит рядом с катушкой, в этом случае все силовые линии, создаваемые этим магнитом, будут проходить через область, окруженную этой катушки, но опять же, пока мы держим магнит в этом положении, мы не увидим никакого отклонения шкалы гальванометра. Таким образом, когда магнит находится вдали, небольшое количество силовых линий проходит через область, окруженную катушкой, а когда магнит находится рядом с катушкой, то максимальное количество силовых линий будет проходить через область, окруженную катушкой. эта катушка. В обоих случаях, когда магнит покоится, мы не будем наблюдать никакого отклонения стрелки гальванометра.

Когда мы делаем это наблюдение, если мы внимательно посмотрим, мы увидим, что когда магнит движется к катушке, мы наблюдаем отклонение шкалы гальванометра. Мы также увидим, что всякий раз, когда он движется быстро или быстрее к катушке, это отклонение будет увеличиваться. Кроме того, всякий раз, когда мы отодвигаем катушку от катушки, мы снова будем наблюдать отклонение шкалы гальванометра, но на этот раз оно будет в противоположном направлении.

Опять же, для медленной скорости или низкой скорости, когда катушка удаляется или приближается, отклонение шкалы гальванометра будет небольшим, но всякий раз, когда она движется быстрее, мы увидим, что она будет двигаться для большего отклонения. Направление этих отклонений будет противоположным в зависимости от того, движется ли магнит к катушке или от катушки.

Конечно, отклонение шкалы гальванометра подскажет нам, что в этих случаях через эту катушку протекает определенный ток. Кроме того, поскольку отклонения происходят в противоположных направлениях по отношению к движению магнита к катушке или от нее, это будет указывать на то, что направление протекания тока будет в противоположных направлениях относительно того, движется ли магнит к катушке или движется подальше от катушки.

Действительно, мы получаем некоторый наведенный ток при движении магнита относительно катушки. Этот ток не имеет ничего общего с количеством силовых линий, проходящих через область, окруженную этой катушкой, но он имеет прямое отношение к тому, как эти силовые линии, проходящие через область, окруженную этой катушкой, меняются, как быстро они меняются. увеличиваются или насколько быстро они уменьшаются. Это подводит нас к понятию магнитного потока.

Ранее мы определили понятие потока в различных случаях. Сначала мы рассмотрели поток двигателя, а затем ввели поток электрического поля, изучая закон Гаусса. Здесь, используя аналогичный подход, мы определим магнитный поток. Магнитный поток определяется как, как вы помните, чтобы иметь возможность определить поток, нам нужна площадь, поверхность, и векторное поле, усеянное этой поверхностью, даст нам поток этих векторов через эту поверхность.

Магнитный поток определяется как интеграл от B точка d A . Как вы помните, мы определили поток электрического поля как интеграл от E dot d A , интегрированный по замкнутой поверхности s . Здесь магнитный поток определяется как интеграл от B dot d A по открытой поверхности. Это различие напрямую связано со свойствами силовых линий магнитного поля.

В случае с силовыми линиями электрического поля мы всегда могли получить открытые силовые линии электрического поля, потому что мы всегда могли изолировать положительный или отрицательный заряд. Как вы помните, силовые линии электрического поля исходят из положительного заряда и идут радиально наружу в бесконечность, а для отрицательного заряда все было как раз наоборот. Чтобы определить общий поток, связанный с этими линиями поля, мы должны выбрать замкнутую поверхность, которая охватит все эти линии поля.

В то время как в случае силовых линий магнитного поля, поскольку не может быть магнитного монополя, магнитные полюса всегда имеют форму диполей, то силовые линии магнитного поля всегда замыкаются сами на себя. Если мы выберем закрытую поверхность для блокировки, то количество силовых линий, входящих в эту закрытую поверхность, всегда будет равно количеству силовых линий, выходящих из этой поверхности. Поэтому чистый поток всегда будет давать нам 0 для замкнутой поверхности.

В результате этого, чтобы иметь возможность определить поток магнитного поля, мы всегда выбираем открытую поверхность, другими словами, поверхность, которая не заключает в себе объем. Так вот, в этом примере основная величина, связанная с индуцированным током вдоль этого контура, это не величина магнитного поля или не площадь, окруженная этой катушкой, а то, насколько быстро или насколько медленно движется магнитный поток через область, окруженную этой катушкой. катушка меняется.

Это явление было открыто Майклом Фарадеем в 1831 году и сформулировано как индуцированная электродвижущая сила, которая вызывает появление индуцированного тока вдоль этого замкнутого проводящего контура, когда магнитный поток изменяется через площадь, окруженную контуром, равен минус скорость изменения магнитного потока. Итак, здесь ε представляет собой индуцированную электродвижущую силу, а Φ B — это, опять же, магнитный поток, и отрицательный знак в этом соотношении проявляется из-за другого закона, известного как «закон Ленца». Вся эта взаимосвязь снова известна как «закон индукции Фарадея».

Хорошо. Ну это в том случае, если у нас есть только один виток для нашей катушки. Если у нас есть n число витков, в этом случае закон Фарадея принимает форму – N умножить на dΦ B на dt , потому что в этом случае поток через каждый контур будет связан со следующим петли, и, следовательно, индуцированная электродвижущая сила будет равна Н, умноженной на скорости изменения потока. Другими словами, поток через область, окруженную каждым из этих витков.

Прежде чем перейти к закону Ленца, давайте также введем единицу измерения магнитного потока. Поскольку Φ B является произведением магнитного поля и площади в системе единиц СИ, поэтому оно будет иметь единицы тесла, умноженные на метр в квадрате. У нас есть специальное название для этого продукта. Называется «Вебер». Мы собираемся апробировать этот блок с «Wb». Следовательно, мы можем выразить закон Фарадея как индуцированную электродвижущую силу в цепи, равную отрицательной скорости изменения магнитного потока.

Если мы посмотрим на единицы измерения правой части закона Фарадея, мы увидим, что это действительно приведет к размерам разности потенциалов. Поскольку ε равно числу витков, умноженному на скорость изменения потока, это будет равно веберам в секунду, а в явном виде это будет тесла-метры в квадрате в секунду, что будет равно единице тесла и явной формы тесла, мы можем выразить это, взглянув на магнитную силу.

Магнитная сила была равна q v пересекают B и в системе единиц СИ поэтому слева у нас ньютоны, кулоны метры в секунду и единица магнитного поля, если все эти величины в системе единиц СИ, то единицей магнитного поля был тесла. Таким образом, мы можем выразить Тесла в явной форме как ньютоны, умноженные на секунды, деленные на кулоны на метр, и тогда мы получим умножение на метры в квадрате на секунду. Здесь этот метр и тот метр в квадрате отменятся, секунды отменятся, и двигаясь дальше, ε будет равно ньютонам на кулон.

Ньютоны — это сила, которая представляет собой массу, умноженную на ускорение, и она будет равна тогда килограммам метрам в секунду в квадрате и разделенным на кулоны, оставленные в знаменателе, у нас есть еще метры здесь.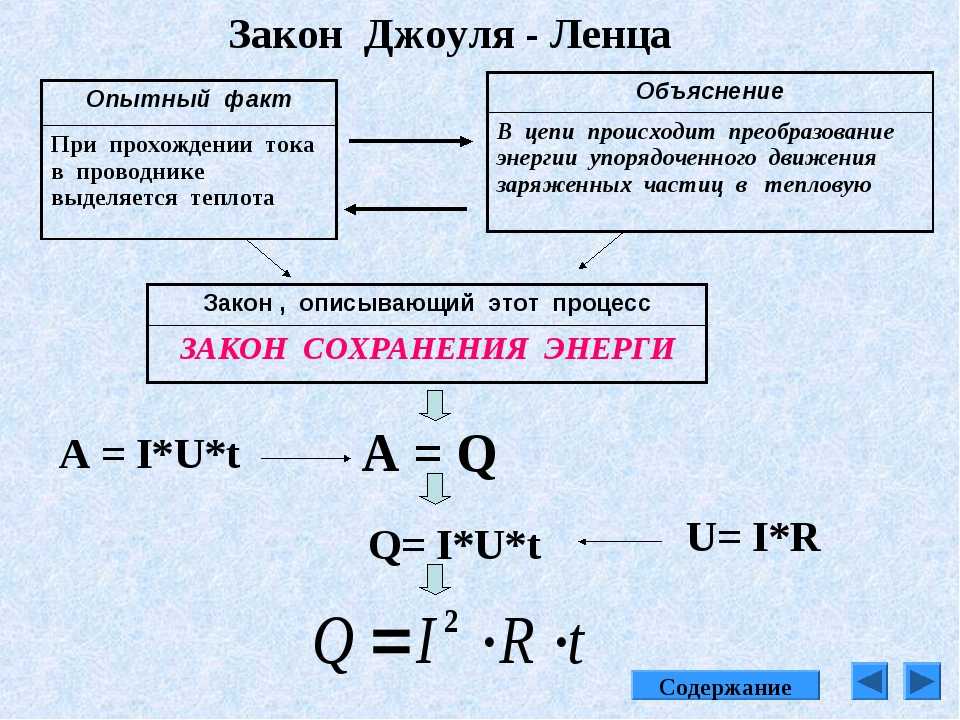 Итак, килограмм-метры в квадрате на секунду в квадрате или ньютон-метр — это не что иное, как единица энергии, работы, поэтому она будет равна джоулю. У нас будет джоуль на кулон. Джоуль на кулон — это, по определению, электрическая потенциальная энергия на единицу заряда, по определению — не что иное, как электрический потенциал. Следовательно, это будет в единицах вольт в системе единиц СИ. Действительно, это отношение будет иметь размеры электрического потенциала.

Хорошо. Ранее мы говорили, что в законе Фарадея справа стоит отрицательный знак, и этот отрицательный знак появляется из-за другого закона, известного как закон Ленца. Закон Ленца просто гласит, что индуцированная электродвижущая сила или ток в замкнутом проводящем контуре будет появляться в таком направлении потока, что будет противодействовать его причине. Другими словами, он будет противодействовать изменению, которое его производит.

Хорошо. Рассмотрим этот закон на примере. Предположим, что у нас есть внешнее магнитное поле, направленное в плоскость, и мы поместим петлю проводимости, окружность или провод, скажем, внутри этой области. Для первого случая предположим, что это внешнее магнитное поле однородно. Другими словами, он не меняется. Следовательно, магнитное поле, проходящее через область, окруженную этой петлей, которая является этой областью, не будет изменяться. Это также означает, что магнитный поток через эту область постоянен. Если поток через эту область постоянный, то, поскольку ЭДС индукции равна – dΦ B над dt для такой одновитковой катушки, а производная постоянной равна 0, поэтому вдоль этого проводящего контура не будет наведенной ЭДС, а это означает, что i наведенная тоже идет быть равным 0.

Теперь возьмем эту же систему. Магнитное поле направлено в плоскость, но в данном случае B не однородно, а нарастает в плоскость. Магнитное поле увеличивается. В этом случае, когда мы поместим нашу проводящую петлю внутрь этой области, поскольку магнитное поле увеличивается в плоскости, поток через область, окруженную этой проводящей петлей, будет увеличиваться. Это означает, что Φ B увеличивается. Это означает, что он будет меняться со временем. В результате этого мы получим некоторую индуцированную электродвижущую силу вдоль этой петли, поэтому ε будет отличаться от 0, и, естественно, эта индуцированная электродвижущая сила вызовет индуцированный ток. Это тоже будет отличаться от 0.

Давайте посмотрим на направление потока этого индуцированного тока. Что ж, изменение потока, согласно закону Фарадея, создаст индуцированную электродвижущую силу. Индуцированная электродвижущая сила будет генерировать индуцированный ток. Закон Ленца гласит, что этот ток проявится вдоль этой проводящей петли так, что попытается противостоять своей причине. Причиной этого индуцированного тока является увеличение магнитного потока. Магнитный поток увеличивается из-за увеличения магнитных полей.

Следовательно, индуцированный ток будет протекать через эту петлю таким образом, что он попытается противодействовать увеличению этого внешнего магнитного поля. Единственный способ сделать это, генерируя магнитное поле, будет направлен в противоположную сторону от направления внешнего магнитного поля. Следовательно, магнитное поле индуцированного тока должно быть направлено не в плоскости.

Итак, используя правило правой руки, если магнитное поле через область, окруженную этой проводящей петлей, выходит из плоскости, и мы знаем, что силовые линии магнитного поля всегда имеют форму концентрических окружностей, огибающих провод, поэтому, если линия магнитного поля выходит отсюда для этого индуцированного тока, она будет уходить в плоскость вне контура. Чтобы иметь возможность иметь линии поля в этом направлении, мы просто держим пальцы правой руки в направлении линий магнитного поля, которые вращаются по часовой стрелке, а большой палец укажет нам направление соответствующего электрического тока.

Следовательно, в этом случае ток должен течь против часовой стрелки. Потому что, если ток движется против часовой стрелки, используя большой палец в направлении потока тока и вращая пальцы правой руки вокруг большого пальца, мы увидим, что соответствующие силовые линии будут выходить из плоскости через область, окруженная этим током и уходящая в плоскость вне контура. В результате этого магнитное поле на интересующей поверхности будет противодействовать внешнему магнитному полю, поэтому оно попытается уменьшить его силу или избежать ее увеличения, но оно никогда не достигнет достаточно высокого значения для этого, поэтому мы получаем индуцированная электродвижущая сила и связанный с ней ток, который будет протекать через эту проводящую петлю против часовой стрелки.

Для последнего случая, если рассматривать магнитное поле, опять же, в плоскости, но в этом случае B уменьшается, так как магнитное поле меняется, это вызовет поток через область, окруженную этой проводящей петлей, к изменяться и изменяться таким образом, что из-за уменьшающегося магнитного поля поток будет уменьшаться через область, окруженную этим контуром. Это означает, что мы снова получим индуцированную электродвижущую силу и, следовательно, индуцированный ток.

Если мы попытаемся определить направление течения тока, опять же по закону Ленца, ток должен течь в таком направлении, чтобы он противодействовал своей причине.