Сложение и вычитание векторов – правила
4.6
Средняя оценка: 4.6
Всего получено оценок: 697.
Обновлено 11 Января, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 697.
Обновлено 11 Января, 2021
Сложение и вычитание векторов – это одно из немногих действий на стыке математики и геометрии. Дело в том, что выражения из векторов можно складывать и вычитать арифметически, ориентируясь только на буквенные обозначения векторов, но для того, чтобы получить числовой результат или его геометрическое отображение придется выполнить ряд построений. Разберемся подробнее в правилах сложения и вычитания векторов.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Что такое вектор?
Вектор – это отрезок с направлением.
Вектор и луч часто путают и допускают грубую ошибку. Вектор – это направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой.
Вектор иногда помещают в декартову систему координат. Тогда, проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси Ох и Оу. Каждая из этих проекций будет отрезком. При этом, если из проекций составить прямоугольник, то его гипотенуза и будет начальным вектором. Это иногда используется при сложении векторов.
Рис. 1. Вектор в системе координат.Сложение и вычитание векторов
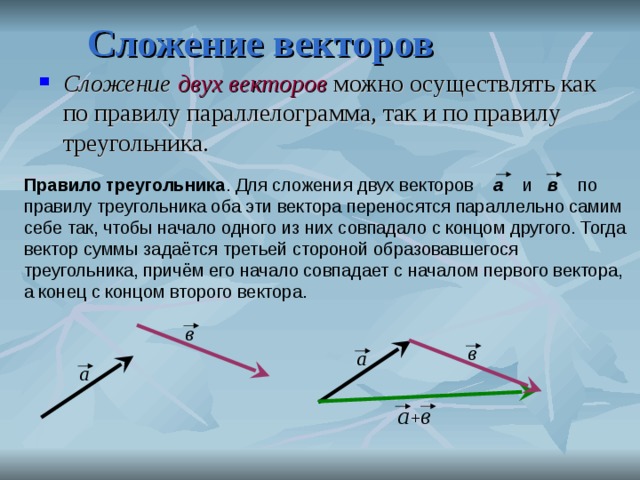
Способов и методов сложения векторов всего два. Существует и третий, но его не считают отдельным методом, так как он вытекает из первых двух. Но мы его рассмотрим отдельно, чтобы не возникало вопросов при дальнейшем изучении темы.
Правило многоугольника
Для того, чтобы сложить векторы правилом многоугольника, необходимо параллельным переносом совместить конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не кончатся векторы, которые необходимо сложить.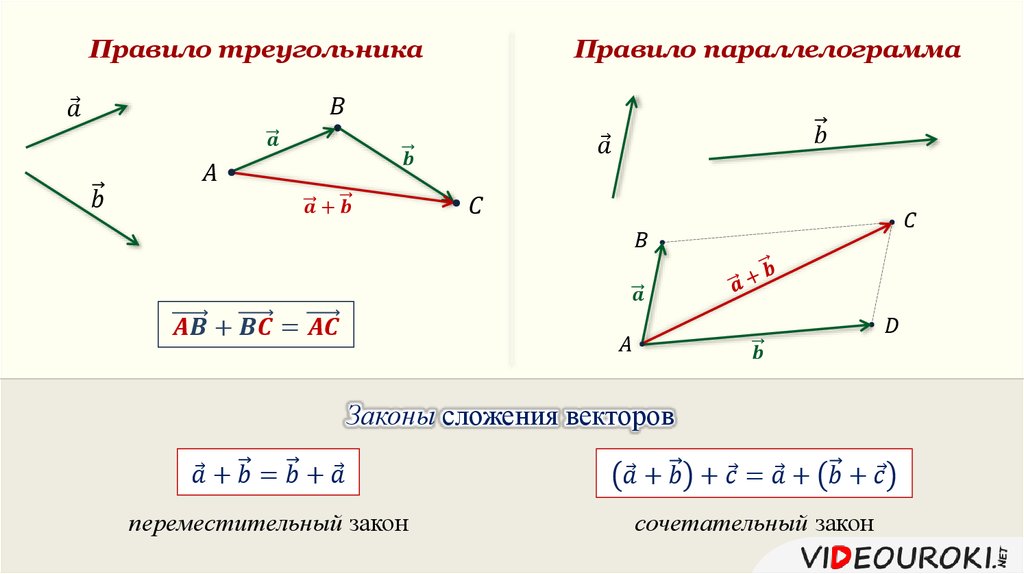
После этого нужно начало первого вектора соединить с концом последнего последнего вектора и указать направление. Получившийся вектор будет направлен в сторону последнего из участвовавших в сложении.
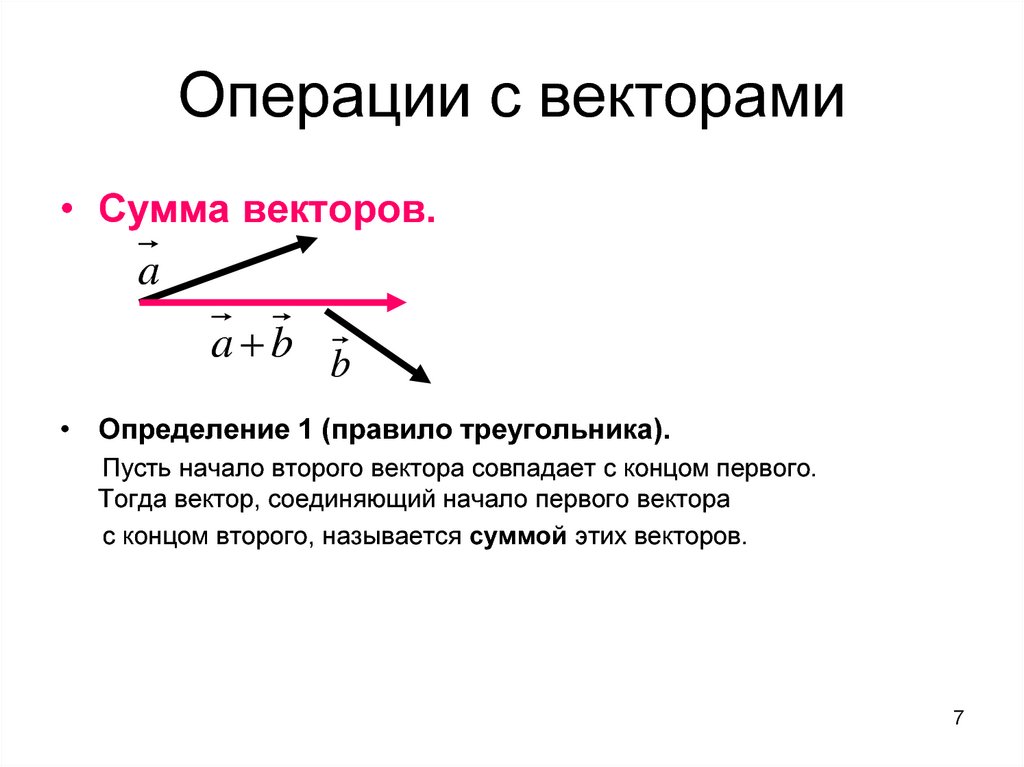
Складывать таким способом можно любое количество векторов. Если так складывается только два вектора, то способ называют правилом треугольника
Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер. Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.
Рис. 2. Правило многоугольника.Правило параллелограмма
Правило параллелограмма сложнее, его можно применять только для 2 векторов. Если вам нужно этим способом сложить большее количество векторов, например, три, то действие выполняют в следующем порядке:
- Складывают два любых вектора правилом параллелограмма. Результатом будет некий вектор и у нас остается еще один, который в сложении не участвовал.
- Получившийся и оставшийся векторы складывают по тому же правилу.
- Этот процесс можно повторять столько раз, сколько требуется по условию задачи.
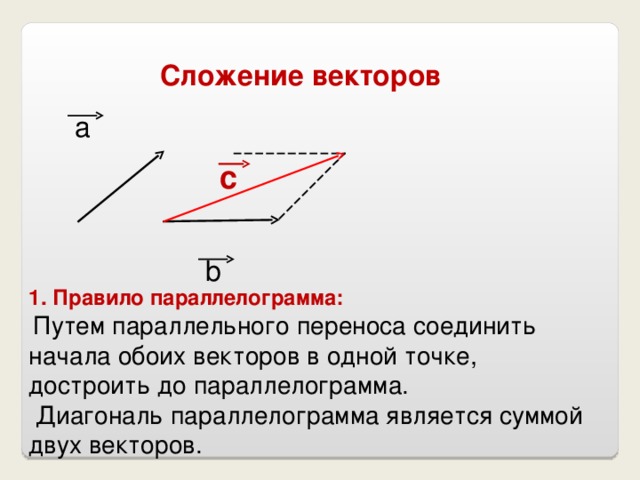
Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого получившуюся фигуру достраивают до параллелограмма. Диагональ, которая выходит из начала двух векторов и есть результат сложения. Вектор должен быть направлен в противоположную сторону от совмещенного начала двух векторов.
Для того чтобы вычесть векторы любым способом, направление вектора, который является вычитаемым, меняют на противоположное. Получившиеся векторы складывают любым из методов.
Рис. 3. Правило многоугольника.Сложение в декартовой системе
В декартовой системе все векторы раскладывают на проекции, после чего отрезки проекций складывают: проекции на ось Ох отдельно, на ось Оу отдельно. После из получившихся двух проекций снова собирают вектор.
Что мы узнали?
Мы узнали, что такое вектор.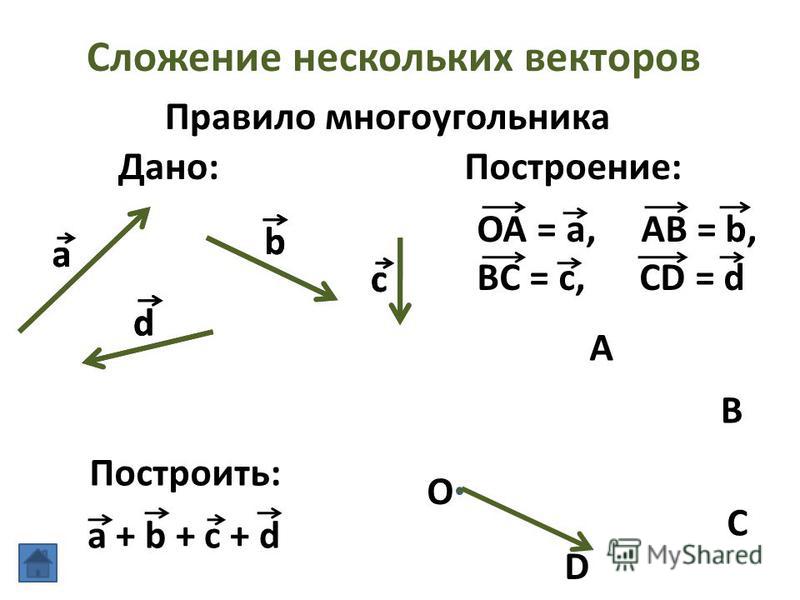
Поговорили о правилах сложения и вычитания векторов. Обсудили, чем отличается вектор от луча и обсудили метод действий с векторами в декартовой системе координат.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Нина Трофимова
8/10
Vlad Turlov
10/10
Никита Негин
10/10
Evgeniy Salakov
10/10
Артем Карнаух
8/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 697.
А какая ваша оценка?
Сумма нескольких векторов
Урок 6. Геометрия 9 класс ФГОС
В этом уроке излагается правило сложения нескольких векторов — правило многоугольника. Так же на конкретных примерах рассматриваются его частные случаи.
Конспект урока «Сумма нескольких векторов»
Вам
уже известны правила сложения двух векторов.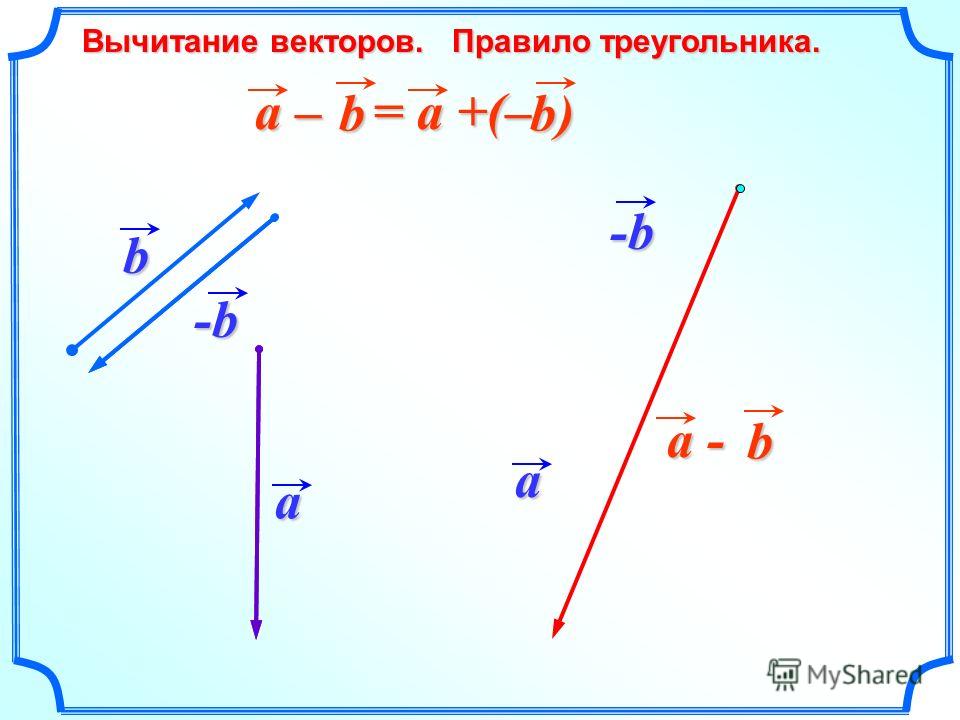
Cегодня мы будем учиться складывать несколько векторов.
Построим
вектор суммы векторов , , .
От некоторой точки А отложим вектор
. Далее от точки B
отложим вектор .
А от точки C отложим вектор
.
Будем последовательно складывать наши векторы, пользуясь правилом треугольника.
Сумма векторов , равна вектору .
Теперь к вектору добавим вектор . В результате мы получаем вектор .
Тогда можем сказать, что сумма .
Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.
Такое правило построения суммы векторов называют правилом многоугольника.
Сформулируем его в общем виде.
Если А1, А2, …, An — произвольные точки плоскости, то сумма векторов
.
Это
равенство справедливо для любых точек А1, А2, …, An.
И, в частности, для случая, когда некоторые из них совпадают.
Например, если начало первого вектора совпадает с концом последнего, то сумма данных векторов равна нулевому вектору.
Задача. Построить вектор суммы попарно неколлинеарных векторов , , , и .
Построение
.
Задача. В соответствии с правилом многоугольника составить равенство,выражающее сумму нескольких векторов.
Посмотрим на первый рисунок. Мы видим, что последовательно складывают векторы . Но, так как начало вектора совпадает с концом вектора , то сумма данных векторов равна нулевому вектору .
Перейдём к следующему случаю.
Видим, что сумма состоит из векторов . А вот вектор , как раз таки, и равен ей.
На рисунке в
последовательно, друг за другом, отложены векторы Ну, а вектор
равен их
сумме.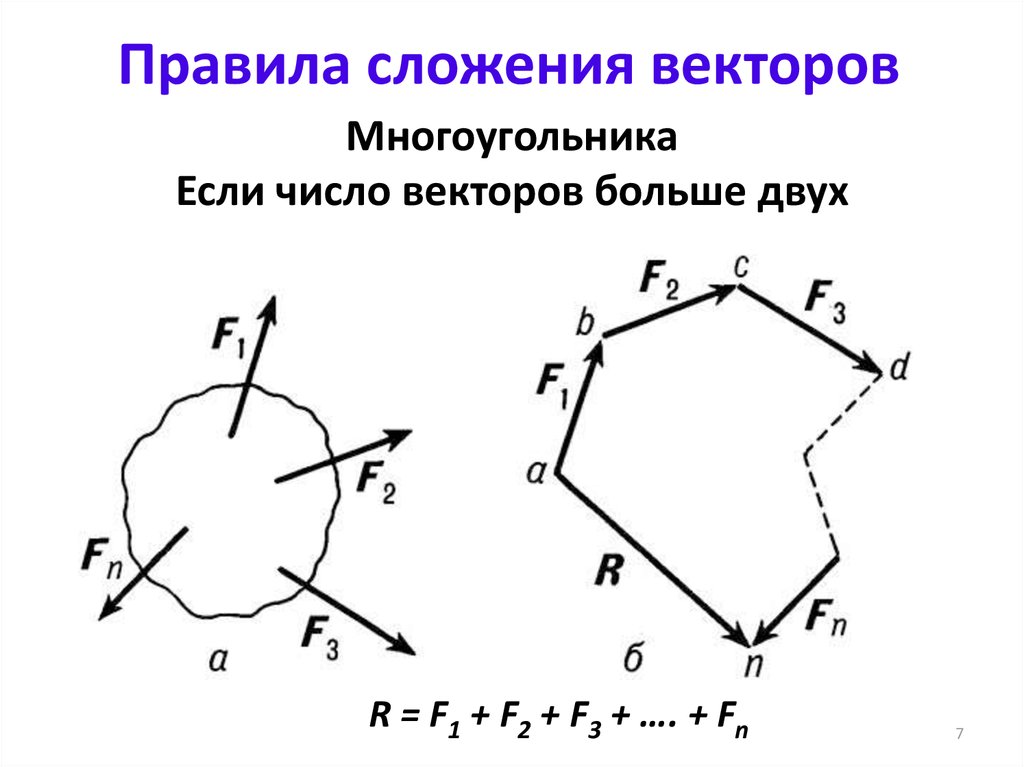
На последнем рисунке последовательно, друг за другом, отложены векторы . При этом Начало вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна нулевому вектору .
Задача. равнобокая трапеция. и — её основания, боковая сторона равна . Построить вектор и найти его длину.
Построение
Решение.
Ответ:
А теперь подведём итоги нашего урока.
Сегодня мы познакомились с правилом многоугольника, которое позволяет строить вектор суммы нескольких векторов.
Его суть заключается в том, что векторы-слагаемые последовательно откладывают друг от друга, суммой является вектор, начало которого совпадает с началом первого вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого.
Если эти точки совпадают, то сумма данных векторов равна нулевому вектору.
Предыдущий урок 5
Законы сложения векторов.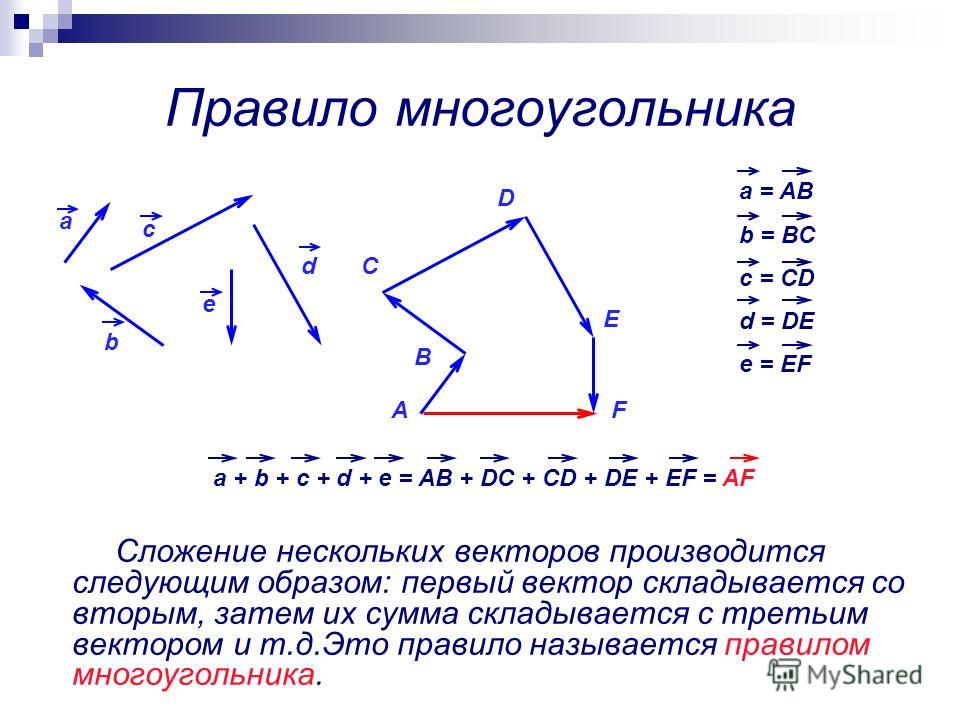
Следующий урок 7 Вычитание векторов
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Векторное произведение векторов
Векторное произведение векторовВекторное произведение и скалярное произведение — два способа умножения векторов, наиболее часто применяемые в физике и астрономии. Величину векторного произведения двух векторов можно получить, взяв произведение величин векторов на синус угла ( и направление определяется по правилу правой руки. Если векторы выразить через единичные векторы i, j и k в направлениях x, y и z, то векторное произведение может быть выражено в довольно громоздкой форме: , что может быть сформулировано несколько более компактно в виде определителя. | Индекс Векторные понятия Приложения | |||
| Назад |
Векторное произведение компактно записывается в виде определителя, который для случая 3×3 имеет удобную процедуру вычисления: После того, как вы познакомитесь со схемой вычисления определителя, это удобный способ восстановить расширенную форму: | Индекс Векторные концепции | ||
| Назад |
Вы можете ввести значения в любое из полей ниже. Затем щелкните символ векторного произведения или угла. | Индекс Векторные концепции | ||
| Назад |
Геометрически векторное произведение полезно как метод построения вектора, перпендикулярного плоскости, если у вас есть два вектора на плоскости. Физически появляется при расчете крутящего момента и при расчете магнитной силы на подвижном заряде. | Индекс Векторные концепции | ||
| Назад |
Направление векторного произведения можно визуализировать с помощью правила правой руки. Если согнуть пальцы правой руки так, чтобы они вращались от вектора А к вектору В, то большой палец будет указывать в направлении векторного произведения. Векторное произведение A и B всегда перпендикулярно обоим A и B. Другой способ утверждения, который заключается в том, что векторное произведение перпендикулярно плоскости, образованной векторами A и B. Это правостороннее правило математически определяется выражением векторного произведения. | Индекс Векторные концепции | ||
| вернуться назад |
Как соответствовать требованиям векторного пространства
BY: Мэри Джейн Стерлинг и
Обновлено: 03-26-2016
Из книги: 6666666666666666666666666 гг. Для чайников
Исследовать книгу Купить на Amazon
В линейной алгебре набор элементов называется векторным пространством , когда выполняются определенные требования.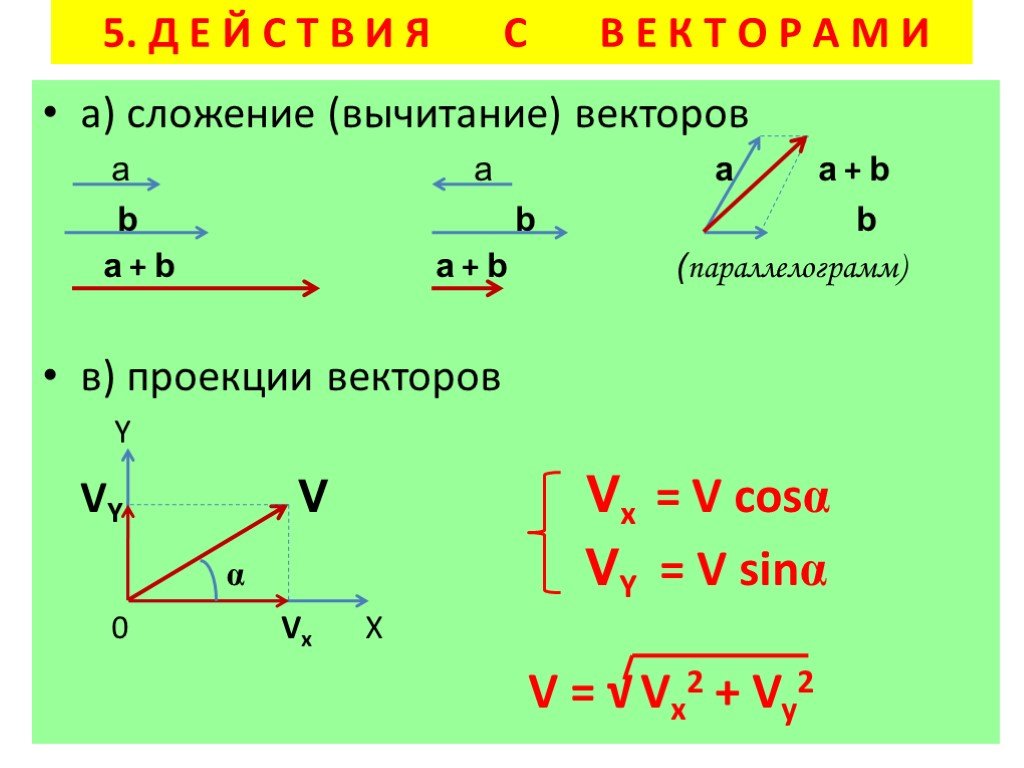
Например, пусть набор состоит из векторов u , v и w . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям:
Закрытие. u ⊕ v есть в наборе.
Коммутативность. и ⊕ v = v ⊕ и.
Ассоциативность. ты ⊕ ( v ⊕ w ) = ( u ⊕ v ) ⊕ w.
Элемент идентичности 0. u ⊕ 0 = 0 ⊕ u = u для любого элемента u.
Обратный элемент −u. и ⊕ — и = — и ⊕ и = 0
Под действием ⊗ множество является векторным пространством, если оно удовлетворяет следующим требованиям:
Закрытие.
