Сложение и вычитание векторов – правила

4.6

Средняя оценка: 4.6

Всего получено оценок: 747.

4.6

Средняя оценка: 4.6

Всего получено оценок: 747.

Сложение и вычитание векторов – это одно из немногих действий на стыке математики и геометрии. Дело в том, что выражения из векторов можно складывать и вычитать арифметически, ориентируясь только на буквенные обозначения векторов, но для того, чтобы получить числовой результат или его геометрическое отображение придется выполнить ряд построений. Разберемся подробнее в правилах сложения и вычитания векторов.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Что такое вектор?

Вектор – это отрезок с направлением.

Вектор и луч часто путают и допускают грубую ошибку. Вектор – это направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой. Луч имеет начало и направление, но он бесконечен, то есть измерить его невозможно. Так же, как нельзя и складывать лучи между собой или луч с вектором.

Вектор иногда помещают в декартову систему координат. Тогда, проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси Ох и Оу. Каждая из этих проекций будет отрезком. При этом, если из проекций составить прямоугольник, то его гипотенуза и будет начальным вектором. Это иногда используется при сложении векторов.

Рис. 1. Вектор в системе координат.

Сложение и вычитание векторов

Способов и методов сложения векторов всего два. Существует и третий, но его не считают отдельным методом, так как он вытекает из первых двух. Но мы его рассмотрим отдельно, чтобы не возникало вопросов при дальнейшем изучении темы.

Правило многоугольника

Для того, чтобы сложить векторы правилом многоугольника, необходимо параллельным переносом совместить конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не кончатся векторы, которые необходимо сложить.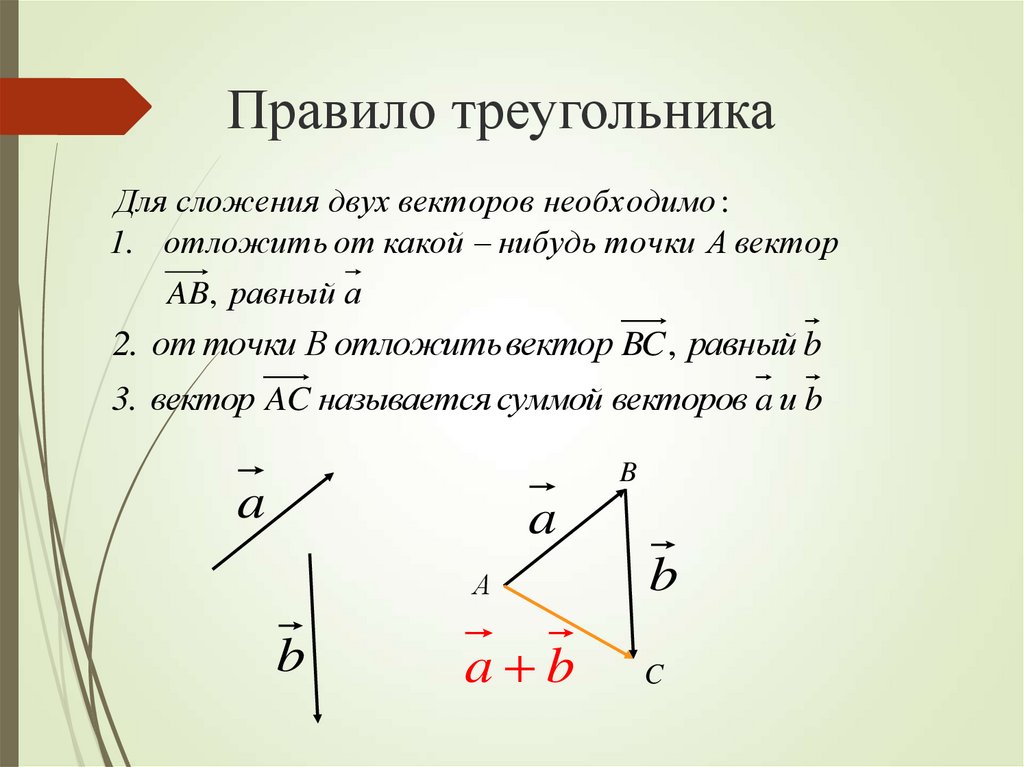

После этого нужно начало первого вектора соединить с концом последнего последнего вектора и указать направление. Получившийся вектор будет направлен в сторону последнего из участвовавших в сложении.

Складывать таким способом можно любое количество векторов. Если так складывается только два вектора, то способ называют правилом треугольника

Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер. Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.

Рис. 2. Правило многоугольника.

Правило параллелограмма

Правило параллелограмма сложнее, его можно применять только для 2 векторов. Если вам нужно этим способом сложить большее количество векторов, например, три, то действие выполняют в следующем порядке:

• Складывают два любых вектора правилом параллелограмма. Результатом будет некий вектор и у нас остается еще один, который в сложении не участвовал.
• Получившийся и оставшийся векторы складывают по тому же правилу.
• Этот процесс можно повторять столько раз, сколько требуется по условию задачи.

Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого получившуюся фигуру достраивают до параллелограмма. Диагональ, которая выходит из начала двух векторов и есть результат сложения. Вектор должен быть направлен в противоположную сторону от совмещенного начала двух векторов.

Для того чтобы вычесть векторы любым способом, направление вектора, который является вычитаемым, меняют на противоположное. Получившиеся векторы складывают любым из методов.

Рис. 3. Правило многоугольника.

Сложение в декартовой системе

В декартовой системе все векторы раскладывают на проекции, после чего отрезки проекций складывают: проекции на ось Ох отдельно, на ось Оу отдельно. После из получившихся двух проекций снова собирают вектор.

Что мы узнали?

Мы узнали, что такое вектор. Поговорили о правилах сложения и вычитания векторов. Обсудили, чем отличается вектор от луча и обсудили метод действий с векторами в декартовой системе координат.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Нина Трофимова

  8/10

• Vlad Turlov

  10/10

• Никита Негин

  10/10

• Evgeniy Salakov

  10/10

• Артем Карнаух

  8/10

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 747.

---

А какая ваша оценка?

Вычитание векторов. Правило вычитания векторов. Геометрия вычитание векторов.

• Альфашкола
• org/ListItem»>Статьи
• Правила вычитания векторов

В этой статье мы узнаем как вычесть вектора. Вектор — это величина, имеющая величину размер и направление. Вычитание вектора равносильно добавлению вектора с отрицательным знаком. Разность векторов \(\overline{a}\) и \(\overline{-b}\)  равна сумме \(\overline{a}\) и \(\overline{-b}\):

Перемещение векторов

Наша задача — найти способ четко и последовательно представлять векторы. Графически это просто: поскольку мы можем перемещать вектор в любом месте, давайте всегда будем располагать «хвост» вектора в начале координатной плоскости. Теперь, когда хвост вектора помещен в конец другого вектора (помните, мы можем перемещать вектор в любом месте, пока мы сохраняем его направление и длину). Проводим от начала вектора \(\overline{b}\) (вычитаемого вектора) вектор \(\overline{c}\)  к началу вектора \(\overline{a}\) (уменьшаемого вектора) получаем разость вектор \(\overline{c}\) :

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Елена Сергеевна Чаплина

Репетитор по математике

Стаж (лет)

Образование:

Омский государственный педагогический институт им. А.М.Горького

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Альфинур Самерхановна Мурзабаева

Репетитор по математике

Стаж (лет)

Образование:

Стерлитамакская государственная педагогическая академия

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Анна Иосифовна Баталова

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по химии для подготовки к ЕГЭ
• Репетитор по химии для подготовки к ОГЭ
• Репетитор для подготовки к ОГЭ по физике
• Репетитор по русскому языку для подготовки к ЕГЭ
• Репетитор по русскому языку для подготовки к ОГЭ
• Подготовка к олимпиадам по английскому языку
• Репетитор для подготовки к ЕГЭ по истории
• Репетитор по биологии для подготовки к ОГЭ
• Репетитор по географии для подготовки к ЕГЭ
• Подготовка к ОГЭ по литературе

Похожие статьи

• Объем и площадь параллелепипеда
• Центральный угол окружности
• Биография Ломоносова Михаила Васильевича(Часть 1)
• Задачи на вклады в банк
• Решаем ОГЭ. Задание 21
• Задачи на вычисление степенных выражений
• Неуверенный ребенок: что мешает его самооценке и как помочь повысить
• Первая школьная любовь и как помочь подростку пережить ее?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Векторная алгебра — определение, операции, пример

Векторная алгебра — одна из важнейших тем алгебры. Изучает алгебру векторных величин. Как мы знаем, есть два типа физических величин, скаляры и векторы . Скалярная величина имеет только величину, тогда как векторная величина имеет и величину, и направление.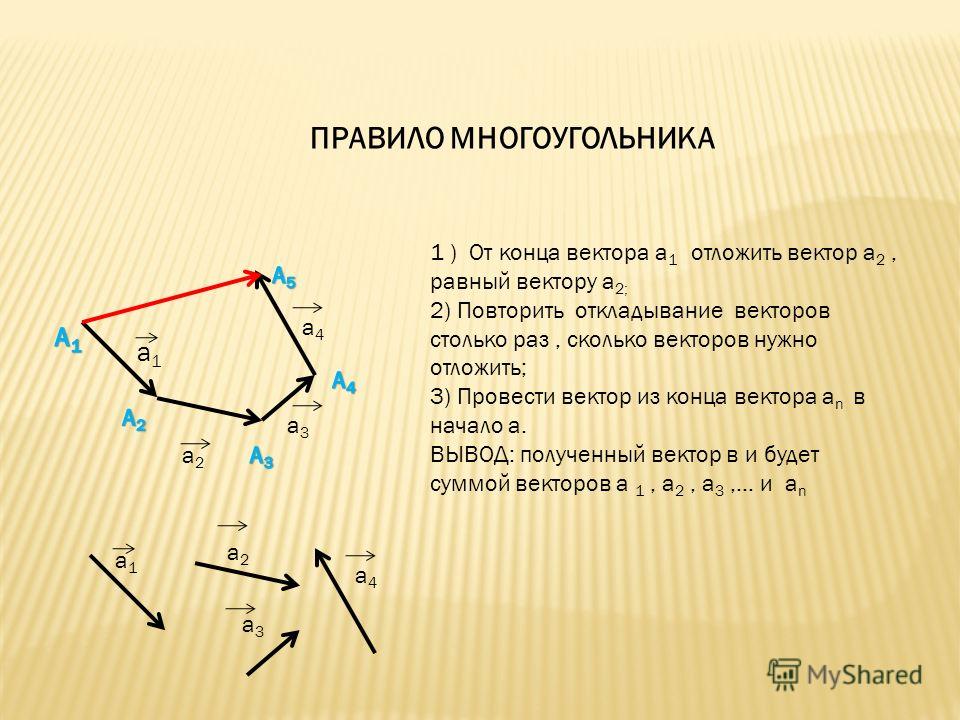 Узнайте о величине вектора здесь.

Алгебра является важным предметом в математике, где мы используем универсальные символы или буквы для обозначения величин, чисел и переменных. Эти символы позже используются во многих выражениях, уравнениях и формулах для выполнения алгебраических операций. У него много ответвлений.

По сути, векторная алгебра — это алгебра, в которой основные элементы обычно обозначают векторы. Мы выполняем алгебраические операции над векторами и векторными пространствами. В этой ветви есть правила и гипотезы, основанные на свойствах и поведении векторов. Здесь вы изучите различные концепции, основанные на основах векторной алгебры и некоторых решенных примерах.

Также читайте:

Определение

Вектор — это объект, который имеет как величину, так и направление. Обычно это изображается стрелкой, указывающей направление (→), а ее длина показывает величину. Стрелка, указывающая на вектор, имеет острие, а ее противоположный конец — хвост.

\(\begin{array}{l}\text{Обозначается как }\vec{V}.\end{array} \)

 Величина вектора представлена ​​как |V|. Два вектора называются равными, если они имеют одинаковые величины и одинаковое направление.

Операции векторной алгебры

Как и в обычной алгебре, мы также выполняем арифметические операции, такие как сложение, вычитание, умножение над векторами. Однако в случае умножения векторы имеют две терминологии, такие как скалярное произведение и перекрестное произведение.

Добавление векторов

Предположим, что есть два вектора P и Q, тогда суммирование этих двух векторов можно произвести, когда хвост вектора Q встречается с головой вектора A. И при этом сложении величина и направление векторов не должны изменять. Сложение векторов следует двум важным законам:

• Коммутативное право:  P + Q = Q + P
• Ассоциативный закон: P + (Q + R) = (P + Q) + R

Вычитание векторов

Здесь направление других векторов меняется на обратное, а затем выполняется сложение обоих заданных векторов.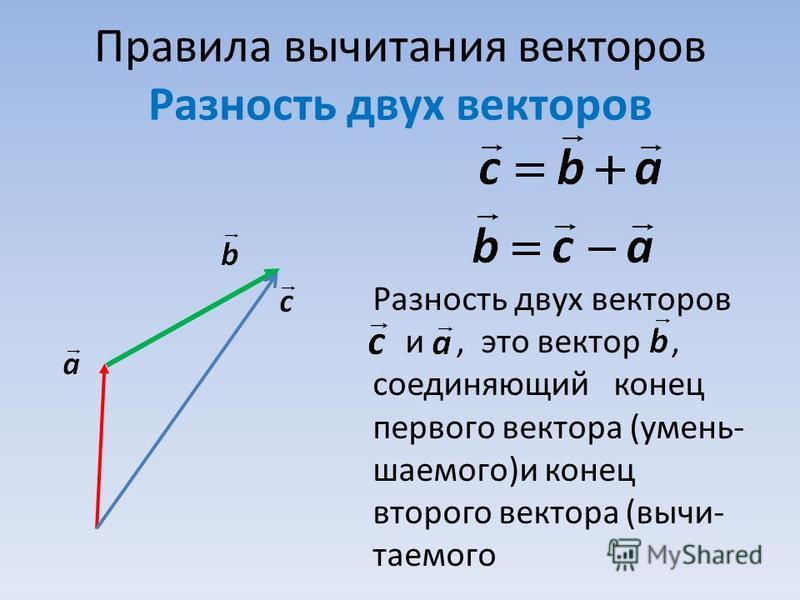 Если P и Q являются векторами, для которых необходимо выполнить метод вычитания, то мы инвертируем направление другого вектора, скажем, для Q, делаем его -Q. Теперь нам нужно добавить вектор P и -Q. Таким образом, направления векторов противоположны друг другу, но величина остается прежней.

• Р – Q = Р + (-Q)

Умножение векторов

Если k является скалярной величиной и умножается на вектор A, то скалярное умножение дается kA. Если k положительное, то направление вектора kA совпадает с направлением вектора A, но если значение k отрицательное, то направление вектора kA будет противоположно направлению вектора A. И модуль вектора kA задается как |kA|.

Скалярный продукт

Скалярное произведение часто называют скалярным произведением. Он представлен точкой (.) между двумя векторами. Здесь два координатных вектора одинаковой длины перемножаются таким образом, что в результате получается одно число. Таким образом, когда мы берем скалярное произведение двух векторов, результатом является либо число скалярной величины.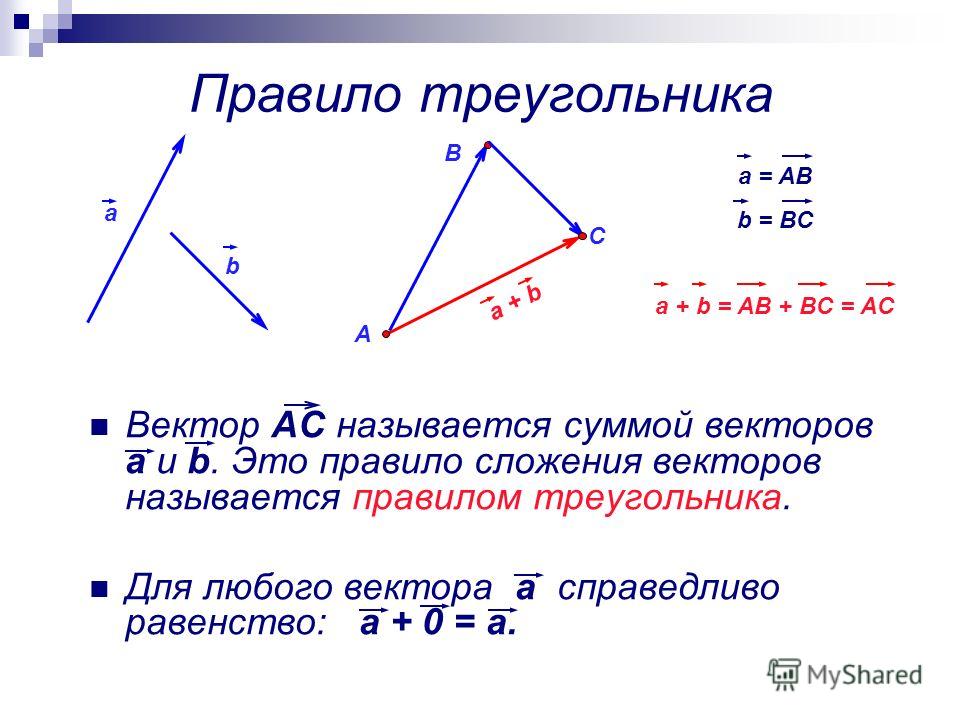 Предположим, что P и Q — два вектора, тогда скалярное произведение для обоих векторов определяется выражением;

• P.Q = |P| |В| cos θ

Если P и Q направлены в одном направлении, т. е. θ = 0°, то;

• P.Q = |P| |В|

Если P и Q ортогональны, т. е. θ = 90°, то;

• P.Q = 0 [поскольку cos 90° = 0]

В векторной алгебре, если два вектора заданы как;

P = [P ₁ ,P ₂ ,P ₃ ,P ₄ ,….,P _n ] и Q = [Q ₁ ,Q ₂ ,Q ₃ ,Q ₄ ,….,Q _n ]

Тогда их скалярное произведение равно;

• с.

Перекрестное произведение

Перекрестное произведение обозначается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, определенная в трехмерной системе. Если P и Q — два независимых вектора, то результат перекрестного произведения этих двух векторов (P x Q) перпендикулярен обоим векторам и нормален к плоскости, содержащей оба вектора. Он представлен; 92}\end{массив} \)

.

Предположим, что для любого вектора r — величина, (l, m, n) — направляющие косинусы и (a, b, c) — отношения направлений, тогда:
l = a/r, m = b/r, п = с/р

\(\begin{array}{l}\text{Пусть } |\vec{a}| \text{ любой вектор, тогда единичный вектор в направлении }|\vec{a}| \text{ определяется как } \hat{a}=\frac{\vec{a}}{|\vec{a}|}\end{array} \)

\(\begin{array}{l}\text{Вектор положения точки P, разделяющей отрезок, соединяющий точки A и B, чьи} \\ \text{ векторы положения равны }|\vec{a}| \text{ и }|\vec{b}| \text{соответственно, в соотношении m : n внутренне задается } \frac{n\vec{a}+m\vec{b}}{m+n} \конец{массив} \)

\(\begin{array}{l}\text{В случае внешнего деления формула принимает вид: } \frac{m\vec{b}-n\vec{a}}{m-n}\end{ массив} \)

\(\begin{array}{l}\text{Матричное представление перекрестного произведения двух векторов задается следующим образом: } \vec{a}\times\vec{b}=\begin{vmatrix} \hat{ i} &\шляпа{j} &\шляпа{k} \\ a_1 &b_1 &c_1 \\ a_2 &b_2 & c_2 \end{vmatrix}\end{массив} \)

Пример векторной алгебры

Вопрос: Найдите скалярное произведение векторов P(1, 3, -4) и Q(3,−5, 2).

Ответ: Согласно определению векторной алгебры скалярного произведения, мы знаем;

P.Q = P ₁ Q ₁ +P ₂ Q ₂ +P ₃ Q ₃ +……….P _{0 904} Q

3

Следовательно,

P.Q = 1,3 + 3,(-5) + (-4).2

= 3 – 15 – 8

= -20

Часто задаваемые вопросы

Что такое векторная алгебра?

Векторная алгебра определяется как тип алгебры, в которой элементы представлены в векторной форме, а их алгебраические операции подчиняются векторным законам.

Каковы законы сложения векторов?

Два основных закона сложения векторов:

Коммутативный закон: A + B = B + A
Ассоциативный закон: A + (B + C) = (A + B) + C

Какие существуют типы векторов Умножение?

Существует два типа умножения векторов:

Скалярное произведение: P • Q = |P| |В| cos θ

Перекрестное произведение: P × Q = |P| |В| грех θ

Определение, формула, правила и примеры

Возможно, мы этого не осознаем, но каждый день мы что-то добавляем. Мы делаем это, когда идем в продуктовый магазин, чтобы купить что-то, мы делаем это, когда добавляем ингредиенты в еду во время приготовления пищи и даже когда играем с друзьями. Это часть нашей повседневной жизни, и ее также можно применять к более сложным вещам, таким как векторы.

В этой статье мы узнаем о векторах и различных способах добавления векторов.

Определение сложения векторов

Сложение векторов можно определить как процедуру сложения двух или более векторов.

Вектор, образованный сложением векторов, называется результирующим вектором и обычно обозначается как r⇀ . Способ добавления этих векторов может различаться в зависимости от того, заданы ли они в виде точек или в геометрическом представлении. Хотя сложение можно выполнить с помощью математики для точек, практично использовать закон параллелограмма, когда они представлены геометрически.

Формула сложения векторов

Предположим, что A и B являются точками на плоскости с их координатами, заданными как A=(a1,a2) и B=(b1,b2) соответственно. Тогда формула сложения векторов для A⇀+B⇀ может быть записана как:

A⇀+B⇀=(a1+b1,a2+b2)

Свойства сложения векторов :

Изменение порядка векторов не меняет сумму. A+B=B+A

Ассоциативность: Изменение группировки дополнений не меняет сумму. А+(В+С)=(А+В)+С

Нулевой элемент: Добавление точки к нулю равно точке. Если нулевой элемент равен O=(0,0), то A+O=A

Обратный аддитив: Если точка A есть A=(a1,a2), то ее обратный равен -A=(- а1,-а2). Когда эти векторы складываются, в результате получается ноль.

A+(-A)=(a1,a2)+(-a1,-a2)=(a1-a1,a2-a2)=(0,0)

Графическое сложение векторов

Как сложение векторов будет выполняться графически? Ниже приведены различные методы.

Треугольный закон сложения векторов

Треугольный закон сложения векторов. Он также известен как метод «голова к хвосту» , потому что головы и хвосты задействованных векторов помещаются друг на друга при попытке найти их сумму. На рисунке ниже показано, как выглядят голова и хвост вектора.

Рис.1 Показ головы и хвоста вектора

Давайте посмотрим, как используется этот закон. Рассмотрим векторы A и B ниже.

Рис. 2 Два вектора A и B

Чтобы сложить два вектора прямым методом, выполните следующие действия.

1. Поместите конец второго вектора на начало первого вектора.
2. Чтобы найти сумму, нарисуйте результирующий вектор, чтобы соединить хвост первого вектора с головой второго вектора.

Рис.3 Сложение двух векторов

На приведенном выше рисунке A⇀+B⇀=C⇀.

Если есть третий вектор, вы продолжаете размещать хвост третьего вектора на голове второго вектора. Результирующий вектор будет нарисован так, чтобы соединить хвост первого вектора с головой второго вектора.

Вектор можно перемещать по своей плоскости до тех пор, пока длина/направление не меняются.

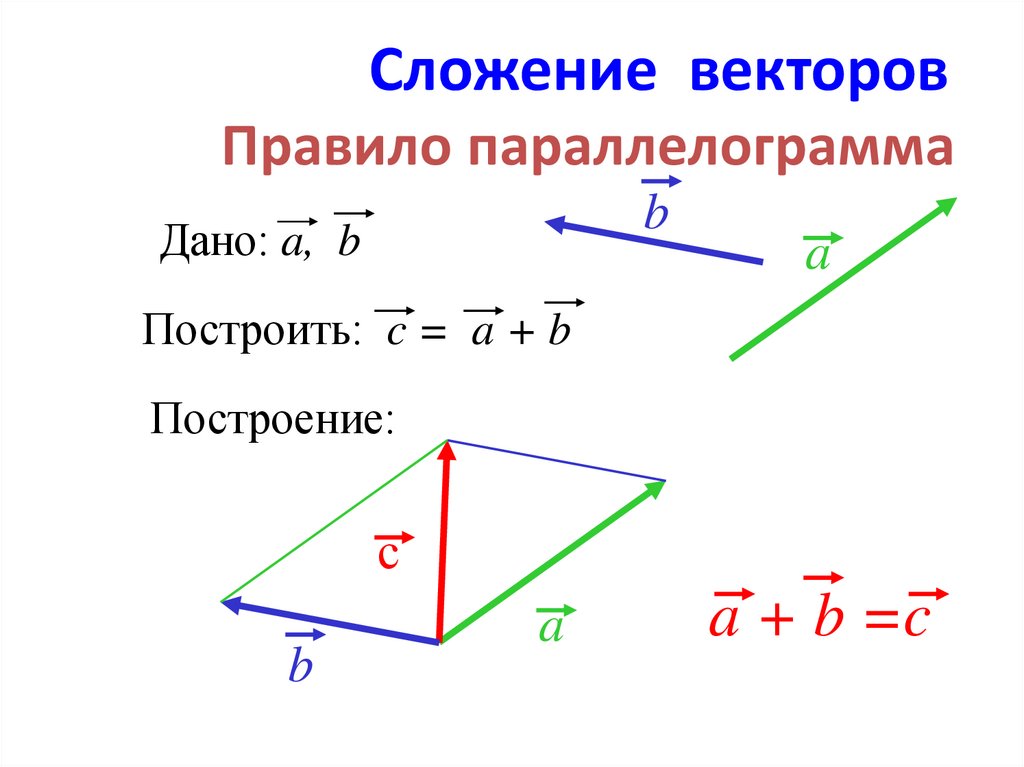
Закон сложения векторов в виде параллелограмма

Согласно закону параллелограмма, если два вектора можно представить как две смежные стороны, исходящие из общей вершины, а затем дополнить их так, как если бы они образовывали параллелограмм, то результирующий вектор можно найти из диагонали этого параллелограмма.

Чтобы найти u→+w→:

1. Соедините хвосты векторов

2. Завершите параллелограмм, начертив две параллельные стороны.

3. После завершения параллелограмма нарисуйте диагональ, начинающуюся в вершине исходного вектора, как показано на рисунке ниже.

Рис.4. Сложение двух векторов

Закон параллелограмма также можно использовать, когда заданы векторы, определенные как координаты.

Для точек A=(2,3) и B=(1,3) сумму можно найти по закону параллелограмма, показанному на рис. 2.

Вычитание вектора

Чтобы понять вычитание, нужно сначала понять, что такое отрицательное значение вектора. Допустим, есть вектор A. Отрицательное значение этого вектора определяется как -A. Отрицательный вектор вектора А имеет ту же величину, что и вектор А, однако они направлены в противоположные стороны.

Рис. 6 Разница между вектором A и отрицательным значением вектора A

Закон параллелограмма для векторного вычитания

Чтобы найти u→-w→, его следует представить как u→+(-w→). Имея это в виду, мы получаем цифру ниже:

Рис.7 Закон параллелограмма для вычитания векторов

Примеры сложения векторов

Давайте рассмотрим несколько примеров.

Если A=(2,4) и B=(-2,5) — две векторные точки, какова сумма векторов?

Ответ.

Формула сложения векторов:

A+B=(a1+b1,a2+b2)

Приведены точки A=(2,4) и B=(-2,5)

From набрано очков:

a1=2a2=4b1=-2b2=5

Если подставить в формулу сложения векторов, то получится:

A+B=(2+(-2),4+5)=(0,9)

Если A=(1,7) и B=(5,-7) — две точки вектора, найдите сумма векторов.

Ответ.

Полученные баллы:

A=(1,7)B=(5,-7)

Формула сложения векторов:

A+B=(a1+b1,a2+b2)

Из точек имеем:

a1=1a2=7b1=5b2=-7

Применяя формулу сложения векторов:

A+B=(1+5,7+(-7))=(6,0)

Возьмем другой пример.

Игрушечная машинка переместилась на 10 см на восток и на 24 см на север. Используя закон треугольника, найдите результирующий вектор двух векторов.

Ответ.

У нас есть два вектора величиной 10 см и 24 см. Назовем их A и B.

A→=10смB→=24см

Направление A→ — это восток, а направление B→ — север. Таким образом, мы имеем:

Рис. 8

Обратите внимание, что хвост второго вектора расположен на голове первого вектора, как и говорит закон. Чтобы найти результирующий вектор, мы завершим треугольник, нарисовав линию, соединяющую хвост первого вектора с головой второго вектора, а затем добавим обе величины.

Обозначим результирующий вектор C.

Рис. 9

Результирующий вектор:

C→=10см+24см=34см

Возьмем другой пример.

Рассмотрим векторы A→=5см в восточном направлении, B→=4см в северном направлении и C→=7см в восточном направлении. Используя правило треугольника, найдите результирующий вектор.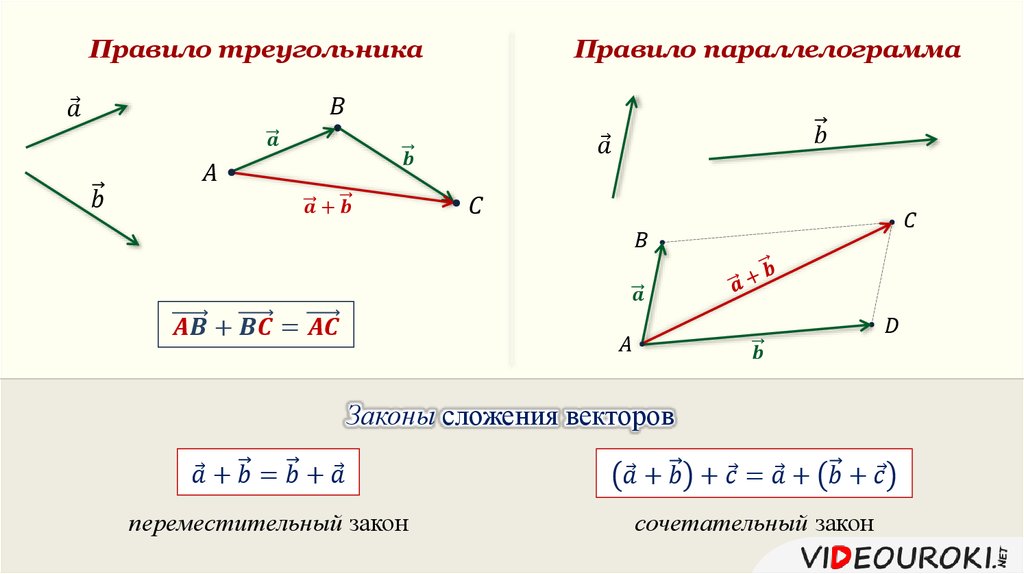

Ответы.

Во-первых, нам нужно нарисовать векторы в соответствии с их направлениями. При этом имейте в виду, что хвост одного вектора должен располагаться над головой другого вектора.

Рис. 10

Как видно из рисунка выше, хвост второго вектора помещается на голову первого вектора, а хвост третьего вектора — на голову второго вектора.

Результирующий вектор будет суммой величин всех векторов.

Рис. 11

Чтобы найти результирующий вектор, была проведена линия, соединяющая хвост первого вектора с головой третьего вектора. результирующий вектор:

C→=5см+4см+7см=16см

Рис. 12

Используя рисунок выше, найдите векторы A→+B→,B→+C→, A→-B→ и B→-C→ по закону параллелограмма.

Решение

• Чтобы найти A→+B→, можно применить закон параллелограмма, как показано на рисунке. Диагональ параллелограмма представляет собой сумму векторов, как на рисунке ниже.