Электричество и магнетизм

Приведем пример расчета токов в разветвленной цепи (рис. 4.25).

Рис. 4.25. Пример разветвленной цепи 

Направления действия ЭДС показаны синими стрелками. В этой цепи у нас имеется два узла — точки b и d (m = 2), и три ветви — участок b–а–d с током I₁, участок b–d с током I₂ и участок b–c–d с током I₃ (n = 3). Значит, мы можем написать одно (m – 1 = 2 – 1 = 1) уравнение на основе первого правила Кирхгофа и два (n – m + 1 = 3 – 2 + 1 = 2) уравнения на основе второго правила Кирхгофа. Как же это делается на практике? 

Шаг первый. Выберем направления токов, текущих в каждой из ветвей цепи. Как эти направления выбрать — совершенно неважно. Если мы угадали, в окончательном результате значение этого тока получится положительным, если нет и направление должно быть обратным — значение этого тока получится отрицательным.

В нашем примере мы выбрали направления токов как показано на рисунке. Важно подчеркнуть, что направления действия ЭДС не произвольны, они определяются способом подключения полюсов источников тока (см. рис. 4.25). 

Шаг второй. Записываем первое правило Кирхгофа для всех узлов кроме одного (в последнем узле, выбор которого произволен, это правило будет выполняться автоматически). В нашем случае мы можем записать уравнение для узла

b, куда входит ток I₂ и выходят токи I₁ и I₃

(4.45)

Шаг третий. Нам осталось написать уравнения (в нашем случае — два) для второго правила Кирхгофа. Для этого надо выбрать два независимых замкнутых контура. В рассматриваемом примере имеются три такие возможности: путь по левому контуру b–a–d–b, путь по правому контуру b–c–d–b и путь вокруг всей цепи

b–a–d–c–b. Достаточно взять любые два из них, тогда для третьего контура второе правило Кирхгофа будет выполнено автоматически. Направление обхода контура роли не играет, но при обходе ток будет браться со знаком плюс, если он течет в направлении обхода, и со знаком минус, если ток течет в противоположном направлении. Это же относится к знакам ЭДС.

Возьмем для начала контур b–a–d–b. Мы выходим из точки b и движемся против часовой стрелки. На нашем пути встретятся два тока,

I₁ и I₂, направления которых совпадают с выбранным направлением обхода. ЭДС также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как

(4.46)

В качестве второго замкнутого пути для разнообразия выберем путь b–a–d–c–b вокруг всей цепи. На этом пути мы встречаем два тока

I₁ и I₃, из которых первый войдет со знаком плюс, а второй — со знаком минус. Мы встретимся также с двумя ЭДС, из которых  войдет в уравнения со знаком плюс, а  — со знаком минус. Уравнение для этого замкнутого пути имеет вид

(4.47)

 

Шаг четвертый. Мы нашли три уравнения для трех неизвестных токов в цепи. Решение произвольной системы линейных уравнений описывается в курсе математики. Для наших целей (цепь достаточна проста) можно просто выразить I₃ через

I₁ из уравнения (4.47)

(4.48)

I₂ через I₁ с помощью уравнения (4. 46)

(4.49)

и подставить (4.48), (4.49) в уравнение первого правила Кирхгофа (4.45). Это уравнение содержит лишь неизвестное

I₁, которое находится без труда

(4.50)

Подставляя это выражение в (4.48), (4.49), находим соответственно токи I₂, I₃

(4.51)

Правила Кирхгофа — это… Что такое Правила Кирхгофа?

Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.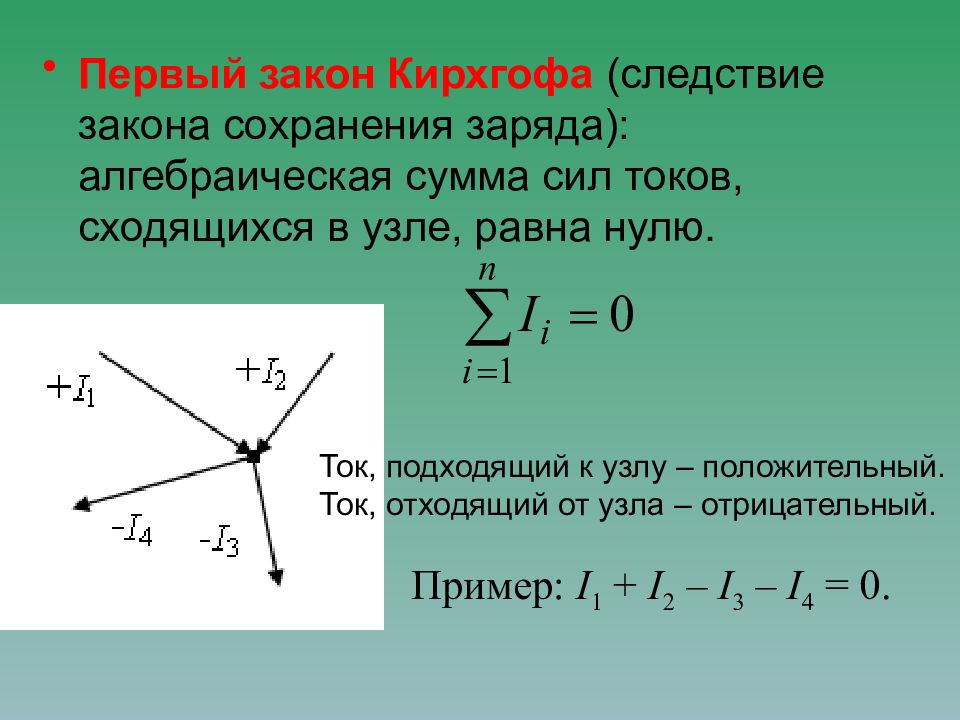

Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.^[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Формулировка правил

Определения

Для формулировки правил Кирхгофа, вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U

1, I₁ есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутые циклы из ветвей. Термин замкнутый цикл означает, что начав с некоторого узла цепи и пройдя по нескольким ветвям и узлам однократно можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что каждая ветвь и узел может одновременно принадлежать нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает. i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений

для переменных напряжений

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Пример

На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым правилом выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

Снова, полученная система уравнений, полностью описывает анализируемую цепь и её решение определяет все токи и все напряжения ветвей, такой подход к анализу цепи принято называть методом узловых потенциалов.

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит узлов, то она описывается уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений.

• Правила Кирхгофа, записанные для узлов или контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр. : по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение, в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники.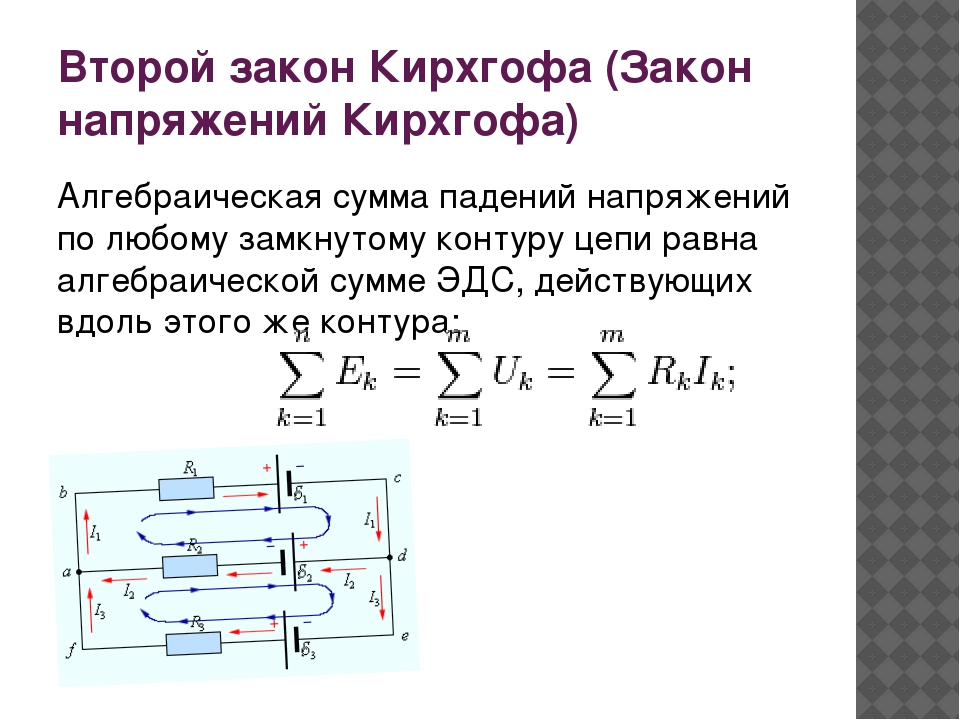 Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Закон излучения Кирхгофа

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа в химии

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

Примечания

Литература

• Матвеев А. Н. Электричество и магнетизм. — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество. — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи.  — 11-е издание. — М.: Гардарики, 2007.

1.2 Правила Кирхгофа — Законы постоянного тока

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.

В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рисунок 1.1) Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.

Рисунок 1.1
Узел электрической цепи. I1, I2 > 0; I3,I4 < 0

В узлах цепи постоянного тока не может происходить накопление зарядов.

Первое правило Кирхгофа:

Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I1 + I2 + I3 + … + In = 0.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называютсямконтурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).

Рисунок 1.2
Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef)

В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.

Второе правило Кирхгофа является следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис.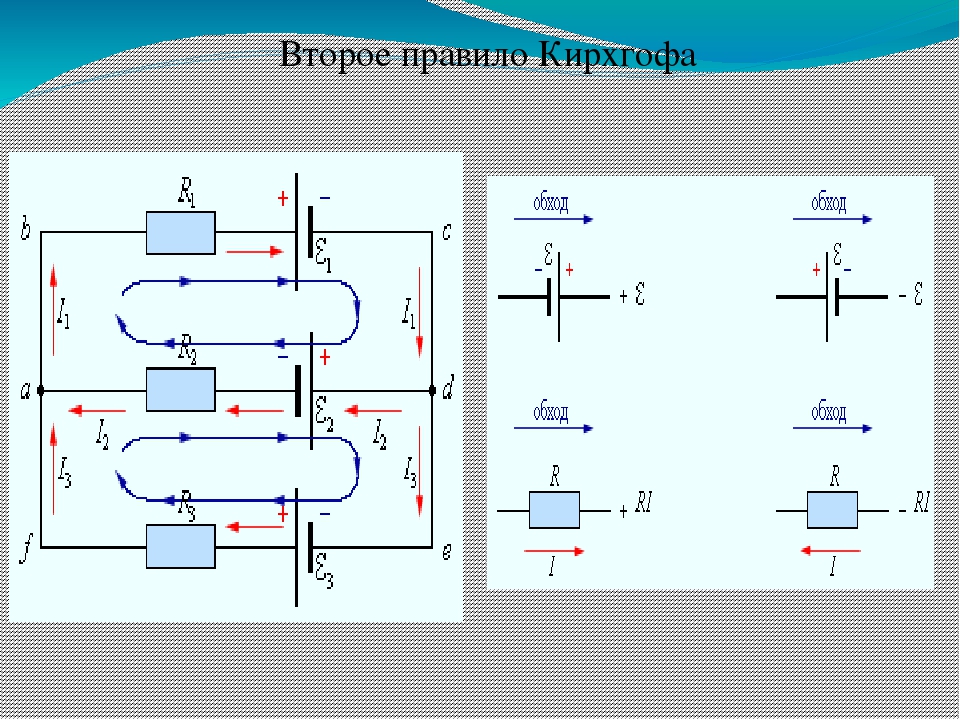 1.3.

Рисунок 1.3.
«Правила знаков»

Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc: I1R1 = Δφbc – 1.

Для участка da: I2R2 = Δφda – 2.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:

I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = –1 – 2.

Аналогично, для контура adef можно записать:

– I2R2 + I3R3 = 2 + 3.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:

I1R1 + I2R2 = – 1 – 2,

– I2R2 + I3R3 = 2 + 3,

– I1 + I2 + I3 = 0.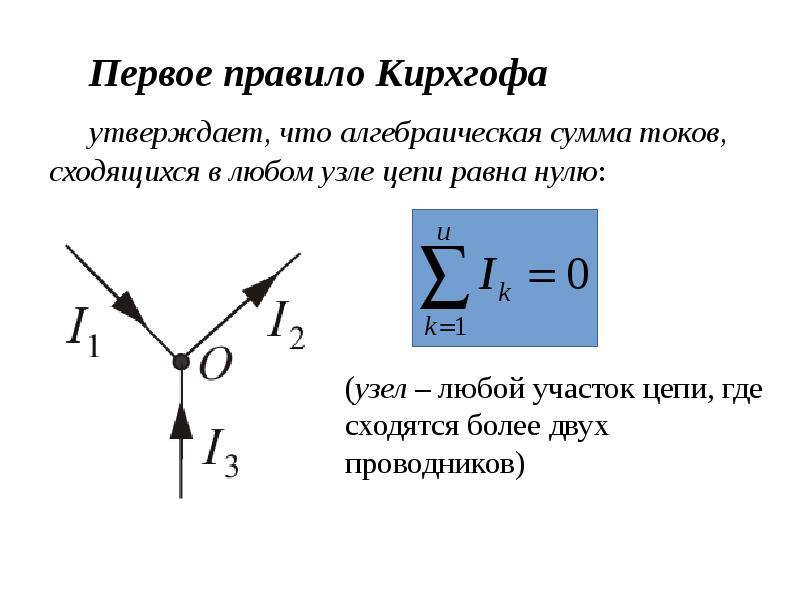

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

Модель. Цепи постоянного тока

Модель. Конденсаторы в цепях постоянного тока

Уравнения Кирхгофа для электрических цепей

Расчет сложных (разветвленных) сетей постоянного тока заключается в отыскании по заданным сопротивлениям участков цепи и приложенных к ним ЭДС сил токов в каждом участке. Для решения этой группы задач применяют правила (иногда в литературе их называют законами, что не корректно) Кирхгофа.

Сформулируем правила (уравнения) Кирхгофа. Но прежде, определим, что узлом в разветвленной цепи называют точку (на рисунке это точка А), в которой имеется более двух возможных направлений тока (рис. 1). В узле сходится более двух проводников.

рис. 1

Первое правило (уравнение) Кирхгофа

Первое правило Кирхгофа (правило узлов): алгебраическая сумма токов сходящихся в узле, равна нулю:

   

где n- количество проводников, сходящихся в узле. Надо отметить, что положительными считают токи, подходящие к узлу, отрицательными – токи, отходящие от него. Если рассмотреть рис. 1, то , а остальные токи отрицательные.

Второе правило (уравнение) Кирхгофа

Второе правило Кирхгофа (правило контуров): в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме приложенных в нем ЭДС :

   

При использовании второго правила Кирхгофа выбирают определенное направление обхода контура. Токи , совпадающие по направлению с направлением обхода, считают положительными. ЭДС источников тока считают положительными, если они создают токи, направленные в сторону обхода контура.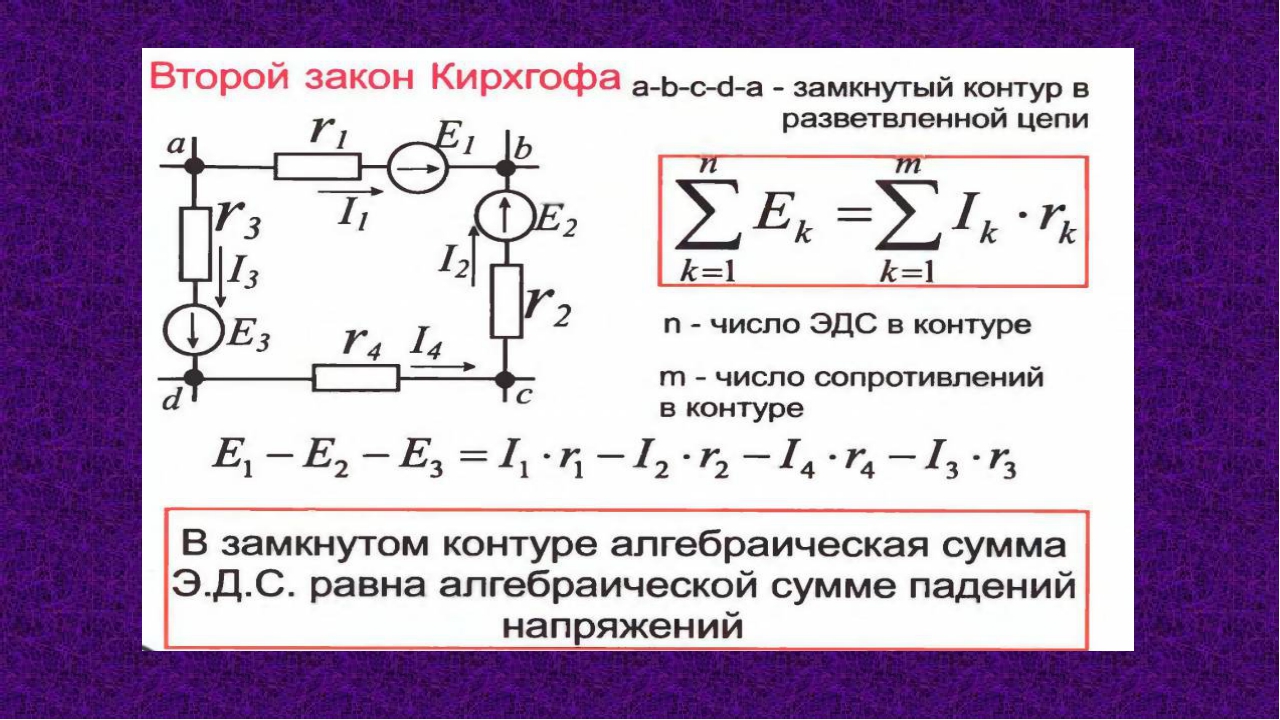

Таким образом, порядок расчёта цепи постоянного тока с использованием правил Кирхгофа следующий:

1. произвольным образом выбираем направления токов во всех участках цепи;
2. для m узлов цепи записываем m-1 независимых уравнений правила узлов;
3. выделяем произвольные замкнутые контуры так, чтобы каждый новый контур содержал хотя бы один участок цепи, не входящий в уже рассмотренные контуры. В разветвленной цепи, состоящей из p ветвей (участков цепи между соседними узлами) и m узлов, число независимых уравнений правила контуров равно p-m+1.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

4.

4. Разветвленные цепи. Правила Кирхгофа

Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными немецким физиком Г. Р. Кирхгофом. Этих правил два.

Первое из них относится к узлам цепи. Узлом называется точка, в которой сходится более чем два проводника (рис. 4.4). Ток, текущий к узлу, считается положительным, текущий от узла имеет противоположный знак. Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:

.

Это правило вытекает из уравнения непрерывности, т. е., в конечном счете, из закона сохранения заряда. Число уравнений, составленных по первому правилу Кирхгофа, должно быть на одно меньше, чем число узлов в исследуемой цепи. Этим обеспечивается линейная независимость получаемых уравнений.

Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (например, 1-3-2) (см. рис. 4.5). Зададим направление обхода, изобразив его стрелкой. Применим к каждому из неразветвленных участков контура закон Ома:

; .

При сложении этих выражений получается одно из уравнений

; ,

которое выражает второе правило Кирхгофа: для любого замкнутого контура алгебраическая сумма всех падений напряжения равна сумме всех ЭДС в этом контуре.

Подобные уравнения могут быть составлены для всех замкнутых контуров, существующих в данной разветвленной цепи, однако их число должно быть ограничено уравнениями для независимых контуров, в которых встречается хотя бы один ток, не входящий в остальные.

При составлении уравнений согласно второму правилу Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода.

Например, ток нужно считать положительным, он течет по направлению обхода. ЭДС также нужно приписать знак «плюс», так как она действует в направлении обхода. Току и ЭДС приписывается знак «минус».

На практике, при решении задач, при составлении уравнений направления токов выбирают произвольно и в соответствии с этим применяют правило знаков.

Действительное направление токов определится решением задачи: если какой-либо ток окажется положительным, то его направление выбрано правильно, если отрицательным, то в действительности он течет противоположно выбранному направлению.

Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, равно числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления, то могут быть вычислены все токи.

---

Вопросы

1) На чем основаны правила Кирхгофа
2) Сколько независимых уравнений необходимо составить при использовании первого правила Кирхгофа
3) Сколько независимых уравнений, составленных по второму правилу Кирхгофа, необходимо, для вычисления токов в цепи

§ 32. ПРАВИЛА КИРХГОФА ДЛЯ ЛИНЕЙНЫХ РАЗВЕТВЛЕННЫХ ЦЕПЕЙ

Элемент электрической цепи называется линейным, если его параметры не зависят от напряжения и силы тока, т. е. вольт-амперная характеристика прямая.

Электрическая цепь называется линейной если она состоит из линейных элементов.

Применение закона Ома для расчета сложных разветвленных цепей, содержащих несколько источников довольно сложно. Для расчетов таких цепей используют два правила немецкого физика Г. Кирхгофа, первое из которых вытекает из закона сохранения заряда, а второе является обобщением закона Ома на произвольное число источников сторонних ЭДС в изолированном замкнутом контуре.

Для того чтобы использовать правила Кирхгофа необходимо ввести несколько понятий.

Электрическая схема – графическое изображение электрической цепи.

Ветвь электрической цепи – один или несколько последовательно соединенных элементов цепи, по которым течет один и тот же ток.

Узел – соединение трех или большего количества ветвей. Ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Например, для узла на рис.64 I1-I2+I3-I4-I5=0

РИС.64 РИС.65

Контур – любой замкнутый путь, проходящий по нескольким ветвям. Положительное направление обхода контура выбирается произвольно, но одно и то же для всех контуров электрической цепи. Токи совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода – отрицательными. ЭДС считаются положительными, если они создают ток, направленный в сторону обхода контура.

Рассмотрим цепь, содержащую три источника (рис.65). Пусть R1, R2, R3 общие сопротивления ветвей АВ, ВС, СА соответственно. Положительное направление обхода примем по часовой стрелке. Применим к каждой ветви закон Ома для неоднородного участка цепи.

Сложив почленно эти уравнения, получим

Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1.выбрать произвольное направление токов на всех участках цепи; действительное направление токов выяснится при решении: если искомый ток получится положительным, то его направление было выбрано правильно, а если отрицательным, то его истинное направление противоположно выбранному;

2.выбрать направление обхода контуров и строго его придерживаться; записывая со соответствующими знаками токи и ЭДС;

3.составить количество уравнений равное количеству искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи).

Теория по физике для ЕГЭ, пособия по подготовке и справочные материалы в Москве

Первое правило Кирхгофа

Алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю.

Также можно легко запомнить первый закон Кирхгофа следующим образом: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Здесь ток \(I_1\) — ток, втекающий в узел, а токи \(I_2\) и \(I_3\) — токи, вытекающие из узла. Тогда можно записать:

\(I_1 = I_2 + I_3,\ (1)\)

Перенесем токи \(I_2\) и \(I_3\) в левую часть выражения (1), тем самым получим:

\(I_1 — I_2 — I_3 = 0,\ (2)\)

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «—».

Второе правило Кирхгофа

Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.

Термин «алгебраическая сумма» означает, что как величина ЭДС, так и величина падения напряжения на элементах может быть как со знаком «+», так и со знаком «—». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта: либо по часовой стрелке, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура, записываются со знаком «+», в противном случае ЭДС записываются со знаком «—».

— напряжения, падающие на элементах цепи, записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «—».

Например, рассмотрим цепь на рисунке и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке и выбрав направление токов через резисторы, как показано на рисунке.

Получим:

\(E_1- E_2 = -UR_1 — UR_2\) или \(E_1 = E_2 — UR_1 — UR_2\)

правил Кирхгофа | Физика

Найдите токи, протекающие в цепи, показанной на Рисунке 5.

Рис. 5. Эта схема аналогична схеме на рис. 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви обозначены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа.Токи обозначены на рисунке I ₁ , I ₂ и I ₃ , и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Начнем с применения правила Кирхгофа первого или перекрестка в точке а.Это дает

I ₁ = I ₂ + I ₃ ,

, так как I ₁ течет в стык, а I ₂ и I ₃ вытекает. Применение правила соединения в e дает точно такое же уравнение, так что новая информация не получается. Это одно уравнение с тремя неизвестными — необходимы три независимых уравнения, поэтому необходимо применять правило цикла.Теперь рассмотрим цикл abcdea. Двигаясь от a к b, мы проходим R ₂ в том же (предполагаемом) направлении тока I ₂ , поэтому изменение потенциала составляет — I ₂ R ₂ . Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала составляет + ЭДС ₁ . Прохождение внутреннего сопротивления r ₁ от c до d дает — I ₂ r ₁ .Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала — I ₁ R ₁ . Правило цикла гласит, что изменения в потенциале равны нулю. Таким образом,

— I ₂ R ₂ + ЭДС ₁ — I ₂ r ₁ — I ₁ R ₁ = — I ₂ ( R ₂ + r ₁ ) + ЭДС ₁ — I ₁ R ₁ = 0.

Подставляя значения из принципиальной схемы для сопротивлений и ЭДС и отменяя единицу измерения ампер, получаем

−3 I ₂ + 18 — 6 I ₁ = 0.

Теперь, применяя правило цикла к aefgha (мы могли бы также выбрать abcdefgha), аналогично дает

+ I ₁ R ₁ + I ₃ R ₃ + I ₃ r ₂ — ЭДС ₂ = + I ₁ R ₁ + I ₃ ( R ₃ + r ₂ ) — ЭДС ₂ = 0.

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении. С введенными значениями это становится

+6 I ₁ + 2 I ₃ — 45 = 0.

Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение относительно I ₂ :

I ₂ = 6 — 2 I ₁ .

Теперь решите третье уравнение относительно I ₃ :

I ₃ = 22,5 — 3 I ₁ .

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для I ₁ :

I ₁ = I ₂ + I ₃ = (6−2 I ₁ ) + (22,5− 3 I ₁ ) = 28,5 — 5 Я ₁ .

Объединение терминов дает

6 I ₁ = 28,5 и

I ₁ = 4,75 А.

Подставляя это значение вместо I ₁ обратно в четвертое уравнение, получаем

I ₂ = 6 — 2 I ₁ = 6 — 9,50

I ₂ = −3,50 A.

Знак минус означает, что I ₂ течет в направлении, противоположном предполагаемому на рисунке 5.Наконец, подстановка значения I ₁ в пятое уравнение дает

I ₃ = 22,5 — 3 I ₁ = 22,5 — 14. 25

I ₃ = 8,25 А.

Обсуждение

В качестве проверки отметим, что действительно I ₁ = I ₂ + I ₃ . Результаты также можно было проверить, введя все значения в уравнение для цикла abcdefgha.

6.3 Правила Кирхгофа — Введение в электричество, магнетизм и электрические цепи

ЦЕЛИ ОБУЧЕНИЯ

---

По окончании раздела вы сможете:

• Государственное правило Кирхгофа
• Государственное правило петли Кирхгофа
• Анализировать сложные схемы по правилам Кирхгофа

Мы только что видели, что некоторые схемы можно проанализировать, сведя схему к одному источнику напряжения и эквивалентному сопротивлению. Многие сложные схемы не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в предыдущих разделах.В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рисунке 6.3.1 известна как многоконтурная схема , которая состоит из переходов. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить. Попробуйте. Резисторы

и

включены последовательно и могут быть уменьшены до эквивалентного сопротивления.То же самое и с резисторами и. Но что же тогда делать?

Несмотря на то, что эта схема не может быть проанализирована с помощью уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной. Правила известны как правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

(рисунок 6.3.1)

Рисунок 6.3.1 Эта схема не может быть сведена к комбинации последовательного и параллельного соединения.Однако мы можем использовать правила Кирхгофа для его анализа.

ПРАВИЛА КИРХГОФА

---

• Первое правило Кирхгофа — правило соединения . Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
  

  (6.3.1)

• Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любого пути (контура) замкнутой цепи должна быть равна нулю:
  

  (6.3.2)

Теперь мы даем объяснения этих двух правил, сопровождаемые советами по решению проблем по их применению и работающим примером, в котором они используются.

Первое правило Кирхгофа

Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рисунок 6.3.2). Как указывалось ранее, соединение или узел — это соединение трех или более проводов. Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.

(рисунок 6.3.2)

Рисунок 6.3.2 Заряд должен сохраняться, поэтому сумма токов в переходе должна быть равна сумме токов на выходе.

Хотя это и является чрезмерным упрощением, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разводке. Если провода на рис. 6.3.2 были заменены водопроводными трубами, а вода считалась несжимаемой, объем воды, поступающей в разветвление, должен был равняться объему воды, вытекающей из разветвления.

Второе правило Кирхгофа

Второе правило Кирхгофа (правило петли ) применяется к разности потенциалов. Правило цикла сформулировано в терминах потенциала

, а не потенциальной энергии, но они связаны между собой.В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна быть передана в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простую петлю без стыков, как на рис. 6.3.3.

(рисунок 6.3.3)

Рисунок 6.3.3 Простая петля без стыков. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.

Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Ярлыки

,

,, и служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Цепь обозначается как Цикл, и метки помогают отслеживать разницу напряжений при перемещении по цепи.Начните с точки и двигайтесь к ней. Напряжение источника напряжения добавляется к уравнению, а падение потенциала на резисторе вычитается. От точки до потенциальный перепад вычитается. От до вычитается потенциальный перепад. От пунктов до ничего не делается, потому что нет компонентов.

На рис. 6.3.4 показан график напряжения при перемещении по контуру. Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор.Падение потенциала , или изменение электрического потенциала, равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

(рисунок 6.3.4)

Рисунок 6.3.4 График напряжения при движении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Тогда правило петли Кирхгофа утверждает

Уравнение контура можно использовать для определения тока в контуре:

Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.

Применение правил Кирхгофа

Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах. Это могут быть токи, напряжения или сопротивления.Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.

Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.

---

Стратегия решения проблем: правила Кирхгофа

1. Обозначьте точки на принципиальной схеме строчными буквами. Эти метки просто помогают сориентироваться.
2. Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов.Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что хотя бы один ток направлен на соединение и хотя бы один ток выходит из соединения.
3. Выберите петли в схеме. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
4. Примените правило соединения. Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
5. Примените правило цикла.Используйте карту на рисунке 6.3.5.

(рисунок 6.3.5)

Рисунок 6.3.5 Каждый из этих резисторов и источников напряжения проходит от до. (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала. (c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала.(d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.

Давайте рассмотрим некоторые этапы этой процедуры более подробно. При размещении переходов в цепи не обращайте внимания на направление токов. Если направление потока тока неочевидно, выбора любого направления достаточно, если хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения. Если стрелка находится в направлении, противоположном обычному потоку тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.

Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.

Рассмотрим рисунок 6.3.6. В этой цепи два перехода: переход

,

и переход. Точки,, и не являются соединениями, потому что соединение должно иметь три или более соединений. Уравнение для соединения есть, а уравнение для соединения есть.Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.

(рисунок 6.3.6)

Рисунок 6.3.6 На первый взгляд, эта схема содержит два соединения, соединение и соединение, но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.

При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рис. 6.3.7 показаны четыре варианта петель для решения типовой схемы; варианты (a), (b) и (c) имеют достаточное количество циклов для полного решения схемы.Вариант (d) отражает больше петель, чем необходимо для решения схемы.

(рисунок 6.3.7)

Рисунок 6.3.7 Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы. На панели (d) показаны три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.

Рассмотрим схему на Рисунке 6.3.8 (a). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).

(рисунок 6.3.8)

Рисунок 6.3.8 (a) Многоконтурная схема. (b) Пометьте схему, чтобы облегчить ориентацию.

Далее определяем перекрестки. В этой схеме точки

и

имеют по три соединенных провода, что делает их соединениями. Начните применять правило соединения Кирхгофа, нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 6.3.9 (б). Junction показывает это, а Junction это показывает. Поскольку Junction предоставляет ту же информацию, что и Junction, ее можно не принимать во внимание. Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.

(рисунок 6.3.9)

Рисунок 6.3.9 (a) Эта схема имеет два соединения, обозначенных b и e, но в анализе используется только узел b. (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.

Далее нам нужно выбрать петли.На рисунке 6.3.10 контур

включает в себя источник напряжения, резисторы и. Цикл начинается с точки, затем проходит через точки, и, а затем возвращается к точке. Вторая петля, петля, начинается в точке и включает резисторы и источник напряжения.

(рисунок 6.3.10)

Рисунок 6.3.10 Выберите петли в схеме.

Теперь мы можем применить правило цикла Кирхгофа, используя карту на рис. 6.3.5. Начиная с точки

и двигаясь к точке, резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается.При перемещении от точки к точке резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается. При перемещении от точки к точке источник напряжения пересекается от отрицательной клеммы к положительной, поэтому добавляется. Между точками и нет компонентов. Сумма разностей напряжений должна равняться нулю:

Наконец, мы проверяем цикл

. Мы начинаем с точки и переходим к точке, пересекаясь в направлении, противоположном текущему потоку.Потенциальное падение добавлено. Затем мы пересекаем и в том же направлении, что и ток, и вычитаем падение потенциала и. Обратите внимание, что через резисторы и ток одинаковый, потому что они соединены последовательно. Наконец, источник напряжения пересекается с положительной клеммы на отрицательную, а источник напряжения вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура

Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.

Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока

. Сначала добавьте уравнение. (1) раз к формуле. (2). Результат обозначен как уравнение. (4):

Затем вычтите уравнение. (3) из уравнения. (2). Результат обозначен как уравнение. (5):

Мы можем решить уравнения. (4) и (5) для текущего

. Сложив семь раз уравнение. (4) и троекратное уравнение.(5) приводит к, или. Используя уравнение. (4) приводит к. Наконец, уравнение. (1) дает. Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:

Обратите внимание, что решение для текущего

отрицательное. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока.Питание от второго источника напряжения есть и нет.

ПРИМЕР 6.3.1

---

Расчет тока по правилам Кирхгофа

Найдите токи, протекающие в цепи, показанной на рисунке 6.3.11.

(рисунок 6.3.11)

Рисунок 6.3.11 Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения. Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи обозначены на рисунке

, и, и были сделаны предположения об их направлениях. Места на схеме отмечены сквозными буквами. В решении мы применяем правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.

Упростите уравнения, поместив неизвестные в одну сторону уравнений.

Упростите уравнения. Уравнение первого цикла можно упростить, разделив обе части на

. Уравнение второго цикла можно упростить, разделив обе части на.

Результатов:

Значение

Метод проверки расчетов заключается в вычислении мощности, рассеиваемой резисторами, и мощности, подаваемой источниками напряжения:

Подаваемая мощность равна мощности, рассеиваемой резисторами.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.6

---

При рассмотрении следующей схемы и мощности, подаваемой и потребляемой схемой, всегда ли источник напряжения обеспечивает питание схемы или может ли источник напряжения потреблять энергию?

ПРИМЕР 6.3.2

---

Расчет тока по правилам Кирхгофа

Найдите ток, протекающий в цепи, показанной на рисунке 6.3.12.

(рисунок 6.3.12)

Рисунок 6.3.12 Эта схема состоит из трех последовательно соединенных резисторов и двух батарей. Обратите внимание, что батареи подключены с противоположной полярностью.

Стратегия

Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только один цикл и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки

до точки. Рассмотрим цикл и воспользуйтесь рисунком 6.3.5, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 6.3.5, батарея будет добавлена, а батарея будет вычтена.

Решение

Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение:

Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.

Значение

Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее

протекает через батарею от положительной клеммы к отрицательной клемме и потребляет мощность.

Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей

.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.7

---

При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в Примере 6.3.2 направление тока было выбрано по часовой стрелке от точки a до точки b .Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки

к точке?

Несколько источников напряжения

Для многих устройств требуется более одной батареи. Несколько источников напряжения, таких как батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.

Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи. Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно.Две последовательно соединенные батареи показаны на рисунке 6.3.13. Использование правила петли Кирхгофа для схемы в части (b) дает результат

(рисунок 6.3.13)

Рисунок 6.3.13 (a) Две батареи, подключенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннее сопротивление.

Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать, а их ЭДС можно складывать вместе, чтобы получить общие значения.Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке 6.3.13 напряжение на клеммах равно

.

Обратите внимание, что одинаковый ток

присутствует в каждой батарее, потому что они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.

Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь.Например, светодиодный фонарик может иметь две батареи типа AAA, каждая с напряжением на клеммах

, для обеспечения фонарика.

Любое количество батарей можно подключить последовательно. Для аккумуляторов

последовательно напряжение на зажимах равно

(6.3.3)

, где эквивалентное сопротивление равно

.

Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке 6.3.14, мы можем найти ток:

Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.

(рисунок 6.3.14)

Рисунок 6.3.14 Две батареи подключаются последовательно к светодиодной лампе, как в фонарике.

Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке 6.3.15 показаны две батареи с одинаковыми ЭДС, включенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, а отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам.Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.

(рисунок 6.3.15)

Рисунок 6.3.15 (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый помечен значком), соединенные параллельно, которые создают одинаковую ЭДС.

Рассмотрим анализ Кирхгофа схемы на рис. 6.3.15 (b). Есть две петли и узел в точке

,

и.

Расчет тока через нагрузочный резистор дает

, где. Напряжение на клеммах равно падению потенциала на нагрузочном резисторе. Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.

Параллельно можно подключить любое количество батарей. Для

параллельно включенных аккумуляторов

напряжение на зажимах равно

(6.3.4)

, где эквивалентное сопротивление равно

.

Например, в некоторых дизельных грузовиках параллельно используются две батареи

; они производят полную ЭДС, но могут обеспечить больший ток, необходимый для запуска дизельного двигателя.

Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления.Аккумуляторы подключаются последовательно для увеличения напряжения на клеммах нагрузки. Аккумуляторы подключаются параллельно для увеличения тока нагрузки.

Массив солнечных батарей

Другой пример, имеющий дело с несколькими источниками напряжения, — комбинация солнечных элементов , соединенных как последовательно, так и параллельно, чтобы обеспечить желаемое напряжение и ток. Фотогальваническая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте.Фотоэлектрический эффект выходит за рамки этого учебника, но, как правило, фотоны, ударяясь о поверхность солнечного элемента, создают в нем электрический ток.

Большинство солнечных элементов изготовлено из чистого кремния. Большинство отдельных элементов имеют выходное напряжение около

, в то время как выходной ток зависит от количества солнечного света, падающего на элемент (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические элементы производят ток на единицу площади примерно равной площади поверхности ячейки.

Отдельные солнечные элементы электрически соединены в модулях для удовлетворения потребностей в электроэнергии. Их можно соединить последовательно или параллельно — как батареи, о которых говорилось ранее. Матрица или модуль солнечных элементов обычно состоит из

и

элементов с выходной мощностью до.

Солнечные элементы, как и батареи, вырабатывают напряжение постоянного тока. Ток от источника постоянного напряжения однонаправлен. Большинству бытовых приборов требуется переменное напряжение.

Кандела Цитаты

Лицензионный контент CC, особая атрибуция

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

10.4: Правила Кирхгофа — Physics LibreTexts

Мы только что видели, что некоторые схемы можно анализировать, сводя схему к одному источнику напряжения и эквивалентному сопротивлению.Многие сложные схемы не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рисунке \ (\ PageIndex {1} \) известна как многоконтурная схема , которая состоит из переходов. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить.Попробуйте. Резисторы \ (R_1 \) и \ (R_2 \) включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами \ (R_4 \) и \ (R_5 \). Но что же тогда делать?

Несмотря на то, что эта схема не может быть проанализирована с использованием уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

Теперь мы даем объяснения этих двух правил, за которыми следуют советы по их применению и рабочий пример, в котором они используются.

Первое правило Кирхгофа

Первое правило Кирхгофа (правило соединения ) применяется к заряду, входящему в соединение и выходящему из него (рисунок \ (\ PageIndex {2} \)). Как указывалось ранее, соединение или узел — это соединение трех или более проводов. Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.

Рисунок \ (\ PageIndex {2} \): Заряд должен сохраняться, поэтому сумма токов в переходе должна быть равна сумме токов на выходе.

Хотя это и является чрезмерным упрощением, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разводке. Если провода на рисунке \ (\ PageIndex {2} \) были заменены водопроводными трубами и вода считалась несжимаемой, объем воды, текущей в соединение, должен быть равен объему воды, вытекающей из соединения.

Второе правило Кирхгофа

Второе правило Кирхгофа (правило петли ) применяется к разности потенциалов. Правило цикла сформулировано в терминах потенциала В , а не потенциальной энергии, но они связаны между собой, поскольку \ (U = qV \).В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна быть передана в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простой цикл без соединений, как на рисунке \ (\ PageIndex {3} \).

Рисунок \ (\ PageIndex {3} \): простой цикл без соединений. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.

Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Ярлыки a , b , c и d служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Цепь обозначается как Loop abcda , и метки помогают отслеживать разницу напряжений при перемещении по цепи.Начните с точки a и двигайтесь к точке b . Напряжение источника напряжения добавляется к уравнению и вычитается падение потенциала резистора \ (R_1 \). От точки b до c падение потенциала на \ (R_2 \) вычитается. Из c до d вычитается падение потенциала на \ (R_3 \). От точек d до a ничего не делается, потому что нет компонентов.

На рисунке \ (\ PageIndex {4} \) показан график напряжения при перемещении по контуру.Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор. Падение потенциала , или изменение электрического потенциала, равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Рисунок \ (\ PageIndex {4} \): график напряжения при движении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор.Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Тогда правило петли Кирхгофа утверждает

\ [V — IR_1 — IR_2 — IR_3 = 0. \]

Уравнение контура можно использовать для определения тока в контуре:

\ [I = \ frac {V} {R_1 + R_2 + R_3} = \ frac {12.00 \, V} {1.00 \, \ Omega + 2.00 \, \ Omega + 3.00 \, \ Omega} = 2.00 \, A . \]

Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.

Применение правил Кирхгофа

Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах. Это могут быть токи, напряжения или сопротивления. Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.

Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.

Стратегия решения проблем: правила Кирхгофа

1. Обозначьте точки на принципиальной схеме строчными буквами a , b , c ,….Эти метки просто помогают сориентироваться.
2. Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов. Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что хотя бы один ток направлен на соединение и хотя бы один ток выходит из соединения.
3. Выберите петли в схеме. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
4. Примените правило соединения. Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
5. Примените правило цикла. Используйте карту на рисунке \ (\ PageIndex {5} \).

Рисунок \ (\ PageIndex {5} \): Каждый из этих резисторов и источников напряжения проходит от до до до . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала.(c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.

Давайте рассмотрим некоторые этапы этой процедуры более подробно. При размещении переходов в цепи не обращайте внимания на направление токов. Если направление потока тока неочевидно, выбора любого направления достаточно, если хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения.Если стрелка находится в направлении, противоположном обычному потоку тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.

Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.

Рассмотрим рисунок \ (\ PageIndex {6} \). В этой цепи два перехода: переход b и переход e .Точки a , c , d и f не являются перекрестками, потому что стык должен иметь три или более соединений. Уравнение для соединения b — \ (I_1 = I_2 + I_3 \), а уравнение для соединения e — \ (I_2 + I_3 = I_1 \). Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.

Рисунок \ (\ PageIndex {6} \): На первый взгляд, эта схема содержит два соединения, соединение b и соединение e , но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.

При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рисунке \ (\ PageIndex {7} \) показаны четыре варианта циклов для решения примерной схемы; варианты (a), (b) и (c) имеют достаточное количество циклов для полного решения схемы. Вариант (d) отражает больше петель, чем необходимо для решения схемы.

Рисунок \ (\ PageIndex {7} \): Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы.На панели (d) показаны три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.

Рассмотрим схему на рисунке \ (\ PageIndex {8a} \). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).

Рисунок \ (\ PageIndex {8} \): (a) Многоконтурная схема. (b) Пометьте схему, чтобы облегчить ориентацию.

Далее определяем перекрестки.В этой схеме точки b и e имеют по три соединенных провода, что делает их соединениями. Начните применять правило соединения Кирхгофа \ (\ left (\ sum I_ {in} = \ sum I_ {out} \ right) \), рисуя стрелки, представляющие токи, и маркируя каждую стрелку, как показано на рисунке \ (\ PageIndex {9 } \). Соединение b показывает, что \ (I_1 = I_2 + I_3 \), а соединение e показывает, что \ (I_2 + I_3 = I_1 \). Поскольку соединение e дает ту же информацию, что и соединение b , ее можно не принимать во внимание.Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.

Рисунок \ (\ PageIndex {9} \): (a) Эта схема имеет два соединения, помеченных b и e, но в анализе используется только узел b. (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.

Далее нам нужно выбрать петли. На рисунке \ (\ PageIndex {10} \) контур abefa включает источник напряжения \ (V_1 \) и резисторы \ (R_1 \) и \ (R_2 \). Цикл начинается в точке a , затем проходит через точки b , e и f , а затем возвращается к точке a .Второй контур, Loop ebcde , начинается в точке e и включает резисторы \ (R_2 \) и \ (R_3 \), а также источник напряжения \ (V_2 \).

Рисунок \ (\ PageIndex {10} \): Выберите петли в схеме.

Теперь мы можем применить правило цикла Кирхгофа, используя карту на рисунке \ (\ PageIndex {5} \). Начиная с точки a и двигаясь к точке b , резистор \ (R_1 \) пересекается в том же направлении, что и ток \ (I_1 \), поэтому падение потенциала \ (I_1R_1 \) вычитается.Двигаясь от точки b к точке e , резистор \ (R_2 \) пересекается в том же направлении, что и ток \ (I_2 \), поэтому падение потенциала \ (I_2R_2 \) вычитается. При перемещении от точки e к точке f источник напряжения \ (V_1 \) пересекается от отрицательной клеммы к положительной клемме, поэтому добавляется \ (V_1 \). Между точками f и a нет компонентов. Сумма разностей напряжений должна равняться нулю:

\ [Петля \, abefa: \, -I_1R_1 — I_2R_2 + V_1 = 0 \ или \, V_1 = I_1R_1 + I_2R_2.\]

Наконец, проверяем цикл ebcde . Мы начинаем с точки e и переходим к точке b , пересекая \ (R_2 \) в направлении, противоположном текущему потоку \ (I_2 \). Потенциальное падение \ (I_2R_2 \) добавлено. Затем мы пересекаем \ (R_3 \) и \ (R_4 \) в том же направлении, что и текущий поток \ (I_3 \), и вычитаем потенциальные падения \ (I_3R_3 \) и \ (I_3R_4 \). Обратите внимание, что ток через резисторы \ (R_3 \) и \ (R_4 \) одинаков, потому что они соединены последовательно. Наконец, источник напряжения пересекается с положительной клеммы на отрицательную, а источник напряжения \ (V_2 \) вычитается.Сумма этих разностей напряжений равна нулю и дает уравнение контура

\ [Петля \, ebcde: \, I_2R_2 — I_3 (R_3 + R_4) — V_2 = 0. \]

Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.

\ [\ text {Перекресток b:} \, I_1 — I_2 — I_3 = 0. \ label {eq1} \]

\ [\ text {Петля abefa:} \, I_1R_1 + I_2R_2 = V_1. \ label {eq2} \]

\ [\ text {Loop ebcde:} \, I_2R_2 — I_3 (R_3 + R_4) = V_2. \ label {eq3} \]

Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока \ (I_2 \).Сначала добавьте уравнение \ ref {eq1} times \ (R_2 \) к уравнению \ ref {eq2}. Результатом будет уравнение \ ref {eq4}:

.

\ [(R_1 + R_2) I_1 — R_2I_3 = V_1. \]

\ [6 \, \ Omega I_1 — 3 \ Omega I_3 = 24 \, V. \ label {eq4} \]

Затем вычтите уравнение \ ref {eq3} из уравнения \ ref {eq2}. Результатом будет уравнение \ ref {eq5}:

.

\ [I_1R_1 + I_3 (R_3 + R_4) = V_1 — V_2. \]

\ [3 \ Omega I_1 + 7 \ Omega I_3 = -5 \, V. \ label {eq5} \]

Мы можем решить уравнения \ ref {eq4} и \ ref {eq5} для тока \ (I_1 \).Если сложить семикратное уравнение \ ref {eq4} и трехкратное уравнение \ ref {eq5}, получится \ (51 \, \ Omega I_1 = 153 \, V \) или \ (I_1 = 3.00 \, A \). Использование уравнения \ ref {eq4} приводит к \ (I_3 = -2,00 \, A \). Наконец, уравнение \ ref {eq1} дает \ (I_2 = I_1 — I_3 = 5,00 \, A \). Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:

\ [P_ {in} = I_1V_1 + I_3V_2 = 130 \, W, \ nonumber \]

\ [P_ {out} = I_1 ^ 2R_1 + I_2 ^ 2R_2 + I_3 ^ 2R_3 + I_3 ^ 2R_4 = 130 \, W.\ nonumber \]

Обратите внимание, что решение для текущего \ (I_3 \) отрицательно. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока. Мощность, отдаваемая вторым источником напряжения, составляет 58 Вт, а не −58 Вт.

Пример \ (\ PageIndex {1} \): расчет тока с использованием правил Кирхгофа

Найдите токи, протекающие в цепи, показанной на рисунке \ (\ PageIndex {11} \).

Рисунок \ (\ PageIndex {11} \): Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения.Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены \ (I_1, \, I_2 \) и \ (I_3 \), и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от до до h .В решении мы применяем правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.

\ [Перекресток \, c: \, I_1 + I_2 = I_3. \]

\ [Петля \, abcdefa: \, I_1 (R_1 + R_4) — I_2 (R_2 + R_5 + R_6) = V_1 — V_3. \]

\ [Петля \, cdefc: \, I_2 (R_2 + R_5 + R_6) + I_3R_3 = V_2 + V_3.\]

Упростите уравнения, поместив неизвестные в одну сторону уравнений.

\ [Перекресток \, c: \, I_1 + I_2 — I_3 = 0. \]

\ [Петля \, abcdefa: \, I_1 (3 \ Omega) — I_2 (8 \ Omega) = 0,5 \, V — 2,30 \, V. \]

\ [Цикл \, cdefc: \, I_2 (8 \ Omega) + I_3 (1 \ Omega) = 0,6 \, V + 2. 2R_1 = 0.2R_1 = 0,18 \, W. \]

\ [P_ {disipated} = 1.09 \, W. \]

\ [P_ {источник} = I_1V_1 + I_2V_3 + I_3V_2 = 0,10 \, + 0,69 \, W + 0,30 \, W = 1,09 \, W. \]

Подаваемая мощность равна мощности, рассеиваемой резисторами.

Упражнение \ (\ PageIndex {1} \)

При рассмотрении следующей схемы и мощности, подаваемой и потребляемой схемой, всегда ли источник напряжения обеспечивает питание схемы или может ли источник напряжения потреблять энергию?

Ответ

Схема может быть проанализирована с использованием правила петли Кирхгофа.2R_2 = 7,2 \, мВт. \)

Пример \ (\ PageIndex {2} \): расчет тока с использованием правил Кирхгофа

Найдите ток, протекающий в цепи, показанной на рисунке \ (\ PageIndex {12} \).

Рисунок \ (\ PageIndex {12} \): Эта схема состоит из трех резисторов и двух последовательно соединенных батарей. Обратите внимание, что батареи подключены с противоположной полярностью.

Стратегия

Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только один цикл и нет узлов.Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки a до точки b . Рассмотрим цикл abcda и воспользуйтесь рисунком \ (\ PageIndex {5} \), чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку \ (\ PageIndex {5} \), батарея \ (V_1 \) будет добавлена, а батарея \ (V_2 \) вычтена.

Решение

Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение:

\ [Цикл \, abcda: \, -IR_1 -V_1 -IR_2 + V_2 -IR_3 = 0.\]

Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.

\ [I (R_1 + R_2 + R_3) = V_2 — V_1. \]

\ [I = \ frac {V_2 — V_1} {R_1 + R_2 + R_3} = \ frac {24 \, V — 12 \, V} {10.0 \, \ Omega + 30.0 \, \ Omega + 10.0 \, \ Омега} = 0,20 \, А. \]

Значение

Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее \ (V_1 \) течет через батарею от положительной клеммы к отрицательной клемме и потребляет энергию.2R_3 = 0,80 \, Вт \]

\ [P_ {V_1} = IV_1 = 2,40 \, W \]

\ [P_ {рассеивается} = 4.80 \, Вт \]

\ [P_ {источник} = IV_2 = 4.80 \, W \]

Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей \ (V_1 \).

Упражнение \ (\ PageIndex {2} \)

При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в примере \ (\ PageIndex {2} \) было выбрано направление тока по часовой стрелке от точки a до точки b .Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки b до точки a ?

Ответ

Расчетный ток будет равен \ (I = -0.20 \, A \) вместо \ (I = 0.20 \, A \). Сумма рассеиваемой мощности и потребляемой мощности все равно будет равна подаваемой мощности.

Несколько источников напряжения

Для многих устройств требуется более одной батареи.Несколько источников напряжения, таких как батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.

Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи. Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно. Две последовательно соединенные батареи показаны на рисунке \ (\ PageIndex {13} \). Использование правила петли Кирхгофа для схемы в части (b) дает результат

\ [\ epsilon_1 — Ir_1 + \ epsilon_2 — Ir_2 — IR = 0, \]

\ [[(\ epsilon_1 + \ epsilon_2) — I (r_1 + r_2)] — IR = 0.\]

Рисунок \ (\ PageIndex {13} \): (a) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннее сопротивление.

Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать, а их ЭДС можно складывать вместе, чтобы получить общие значения. Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах.Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке \ (\ PageIndex {13} \) напряжение на клеммах равно

.

\ [V_ {терминал} = (\ epsilon_1 — Ir_1) + (\ epsilon_2 — Ir_2) = [(\ epsilon_1 + \ epsilon_2) — I (r_1 + r_2) — I (r_1 + r_2)] = (\ epsilon_1 + \ epsilon_2) + Ir_ {eq}. \]

Обратите внимание, что одинаковый ток I присутствует в каждой батарее, потому что они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.

Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батарейки типа AAA, каждая с напряжением на клеммах 1,5 В, чтобы обеспечить 3,0 В для фонарика.

Любое количество батарей можно подключить последовательно. Для последовательно включенных батарей N напряжение на зажимах равно

Примечание

\ [V_ {терминал} = (\ epsilon_1 + \ epsilon_2 +… + \ Epsilon_ {N-1} + \ epsilon_N) — I (r_1 + r_2 +.№ р_и \]

Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке \ (\ PageIndex {14} \), мы можем найти ток:

\ [(\ epsilon_1 — Ir_1) + (\ epsilon_2 — Ir_2) = IR, \]

\ [Ir_1 + Ir_2 + IR = \ epsilon_1 + \ epsilon_2, \]

\ [I = \ frac {\ epsilon_1 + \ epsilon_2} {r_1 + r_2 + R}. \]

Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.

Рисунок \ (\ PageIndex {14} \): две батареи подключаются последовательно к светодиодной лампе, как в фонарике.

Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке \ (\ PageIndex {15} \) показаны две батареи с одинаковыми ЭДС, соединенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, а отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам. Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.

Рисунок \ (\ PageIndex {15} \): (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый помечен как \ (\ epsilon \)), соединенные параллельно, которые производят одинаковую ЭДС.

Рассмотрим анализ Кирхгофа схемы на рисунке \ (\ PageIndex {15b} \). {- 1} \]

Например, в некоторых грузовиках с дизельным двигателем параллельно используются две батареи на 12 В; они производят полную ЭДС 12 В, но могут обеспечивать больший ток, необходимый для запуска дизельного двигателя.

Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления. Аккумуляторы подключаются последовательно для увеличения напряжения на клеммах нагрузки.Аккумуляторы подключаются параллельно для увеличения тока нагрузки.

21.3 Правила Кирхгофа — College Physics

Расчет силы тока: с использованием правил Кирхгофа

Найдите токи, протекающие в цепи, показанной на рисунке 21.25.

Рисунок 21.25 Эта схема аналогична схеме на рисунке 21.21, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви обозначены и предполагается, что они движутся в показанных направлениях.В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи обозначены как I1I1 размер 12 {I rSub {размер 8 {1}}} {}, I2I2 размер 12 {I rSub {размер 8 {2}}} {} и I3I3 размер 12 {I rSub {размер 8 {3 }}} {} на рисунке, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h.В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Начнем с применения правила Кирхгофа первого или перекрестка в точке а. Это дает

I1 = I2 + I3, I1 = I2 + I3, размер 12 {I rSub {размер 8 {1}} = I rSub {размер 8 {2}} + I rSub {размер 8 {3}}} {}

21,54

, поскольку I1I1 размером 12 {I rSub {размер 8 {1}}} {} течет в соединение, в то время как I2I2 размером 12 {I rSub {размер 8 {2}}} {} и I3I3 размером 12 {I rSub {размер 8 {3}}} {} вытекать.Применение правила соединения в e дает точно такое же уравнение, так что новая информация не получается. Это одно уравнение с тремя неизвестными — необходимы три независимых уравнения, поэтому необходимо применять правило цикла.

Теперь рассмотрим цикл abcdea. Двигаясь от a к b, мы пересекаем R2R2 размера 12 {R rSub {size 8 {2}}} {} в том же (предполагаемом) направлении, что и текущий размер I2I2 12 {I rSub {size 8 {2}}} {} , поэтому изменение потенциала равно −I2R2-I2R2 размер 12 {- I rSub {размер 8 {2}} R rSub {размер 8 {2}}} {}.Затем, переходя от b к c, мы переходим от –– к +, так что изменение потенциала составляет + emf1 + emf1 размер 12 {+ «emf» rSub {size 8 {1}}} {}. Пересечение внутреннего сопротивления r1r1 размером 12 {r rSub {размер 8 {1}}} {} от c до d дает −I2r1-I2r1 размер 12 {- I rSub {размер 8 {2}} r rSub {размер 8 {1} }} {}. Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала −I1R1 − I1R1 размер 12 {- I rSub {размер 8 {1}} R rSub {размер 8 { 1}}} {}.

Правило цикла гласит, что сумма изменений потенциала равна нулю.Таким образом,

−I2R2 + emf1 − I2r1 − I1R1 = −I2 (R2 + r1) + emf1 − I1R1 = 0. − I2R2 + emf1 − I2r1 − I1R1 = −I2 (R2 + r1) + emf1 − I1R1 = 0. размер 12 {- I rSub {размер 8 {2}} R rSub {размер 8 {2}} + «emf» rSub {размер 8 {1}} — I rSub {размер 8 {2}} r rSub {размер 8 { 1}} — I rSub {размер 8 {1}} R rSub {размер 8 {1}} = — I rSub {размер 8 {2}} \ (R rSub {размер 8 {2}} + r rSub {размер 8 {1}} \) + «emf» rSub {size 8 {1}} — I rSub {size 8 {1}} R rSub {size 8 {1}} = 0} {}

21,55

Подстановка значений из Принципиальная схема для сопротивлений и ЭДС, а при отмене единицы ампер дает

−3I2 + 18−6I1 = 0.−3I2 + 18−6I1 = 0. размер 12 {- 3I rSub {размер 8 {2}} + «18» — 6I rSub {размер 8 {1}} = 0} {}

21,56

Теперь применим правило цикла к aefgha (мы могли бы выбрать abcdefgha как ну) аналогично дает

+ I1R1 + I3R3 + I3r2 − emf2 = + I1R1 + I3R3 + r2 − emf2 = 0. + I1R1 + I3R3 + I3r2 − emf2 = + I1R1 + I3R3 + r2 − emf2 = 0. размер 12 {+ I rSub {размер 8 {1}} R rSub {размер 8 {1}} + I rSub {размер 8 {3}} R rSub {размер 8 {3}} + I rSub {размер 8 {3} } r rSub {размер 8 {2}} — «emf» rSub {размер 8 {2}} «= +» I rSub {размер 8 {1}} R rSub {размер 8 {1}} + I rSub {размер 8 {3}} слева (R rSub {размер 8 {3}} + r rSub {размер 8 {2}} справа) — «emf» rSub {size 8 {2}} = 0} {}

21.57

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении. С введенными значениями это становится

+ 6I1 + 2I3−45 = 0. + 6I1 + 2I3−45 = 0. размер 12 {+ 6I rSub {размер 8 {1}} + 2I rSub {размер 8 {3}} — «45» = 0} {}

21,58

Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение для I2I2 размером 12 {I rSub {size 8 {2}}} {}:

I2 = 6−2I1.I2 = 6−2I1. размер 12 {I rSub {размер 8 {2}} = 6 — 2I rSub {размер 8 {1}}} {}

21.59

Теперь решите третье уравнение для I3I3 размера 12 {I rSub {size 8 {3}}} {}:

I3 = 22,5−3I1.I3 = 22,5−3I1. размер 12 {I rSub {размер 8 {3}} = «22» «.» 5 — 3I rSub {size 8 {1}}} {}

21.60

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для I1I1 размера 12 {I rSub {size 8 {1}}} {} :

I1 = I2 + I3 = (6−2I1) + (22,5−3I1) = 28,5−5I1.I1 = I2 + I3 = (6−2I1) + (22,5−3I1) = 28,5−5I1. размер 12 {I rSub {размер 8 {1}} = I rSub {размер 8 {2}} + I rSub {размер 8 {3}} = \ (6 — 2I rSub {размер 8 {1}} \) + \ («22» ».»5 — 3I rSub {size 8 {1}} \) =» 28 «». «5 — 5I rSub {size 8 {1}}} {}

21,61

Объединение терминов дает

6I1 = 28,5 и 6I1 = 28,5, а размер 12 {6I rSub {size 8 {1}} = «28» «.» 5} {}

21,62

I1 = 4,75 A.I1 = 4,75 A. размер 12 {I rSub {size 8 {1}} = 4 «.» «75» «A»} {}

21,63

Подставляя это значение для I1I1 размера 12 {I rSub {size 8 {1}}} {} обратно в четвертое уравнение, получаем

I2 = 6−2I1 = 6−9,50 I2 = 6−2I1 = 6−9,50 размер 12 {I rSub {size 8 {2}} = 6 — 2I rSub {size 8 {1}} = 6–9 дюймов.»» 50 «} {}

21,64

I2 = −3,50 A.I2 = −3,50 A. размер 12 {I rSub {size 8 {2}} = — 3″. «» 50 «» A «} {}

21.65

Знак минус означает, что I2I2 размером 12 {I rSub {size 8 {2}}} {} течет в направлении, противоположном предполагаемому на рисунке 21.25.

Наконец, подстановка значения для I1I1 размера 12 {I rSub {size 8 {1}}} {} в пятое уравнение дает

I3 = 22,5−3I1 = 22,5−14,25 I3 = 22,5−3I1 = 22,5−14,25 размер 12 {I rSub {size 8 {3}} = «22» «.» 5 — 3I rSub {size 8 {1}} = «22» «.»5 -» 14 «». «» 25 «} {}

21,66

I3 = 8,25 A.I3 = 8,25 A. размер 12 {I rSub {size 8 {3}} = 8″. «» 25 «» A «} {}

21,67

Обсуждение

Для проверки отметим, что действительно I1 = I2 + I3I1 = I2 + I3 размер 12 {I rSub {размер 8 {1}} = I rSub {размер 8 {2}} + I rSub {размер 8 {3} }} {}. Результаты также можно было проверить, введя все значения в уравнение для цикла abcdefgha.

21.3 Правила Кирхгофа — Колледж Физики, главы 1-17

Применяя правила Кирхгофа, мы генерируем уравнения, которые позволяют нам находить неизвестные в схемах.Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете в результате применения правил.

Рисунок 4 и следующие пункты помогут правильно определить знаки плюса и минуса при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b.Во многих схемах потребуется построить более одного контура. Проходя каждый цикл, нужно быть последовательным в отношении знака изменения потенциала. (См. Пример 1.)

Пример 1: Расчет силы тока: с использованием правил Кирхгофа

Найдите токи, протекающие в цепи, показанной на Рисунке 5.

Рисунок 5. Эта схема похожа на схему на Рисунке 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви обозначены и предполагается, что они движутся в показанных направлениях.В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены [латекс] \ boldsymbol {I_1} [/ latex], [latex] \ boldsymbol {I_2} [/ latex] и [latex] \ boldsymbol {I_3} [/ latex], и были сделаны предположения сделал о своих направлениях. Места на схеме обозначены буквами от a до h.В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Начнем с применения правила Кирхгофа первого или перекрестка в точке а. Это дает

[латекс] \ boldsymbol {I_1 = I_2 + I_3}, [/ латекс]

, так как [latex] \ boldsymbol {I_1} [/ latex] течет в соединение, а [latex] \ boldsymbol {I_2} [/ latex] и [latex] \ boldsymbol {I_3} [/ latex] вытекает. Применение правила соединения в e дает точно такое же уравнение, так что новая информация не получается.Это одно уравнение с тремя неизвестными — необходимы три независимых уравнения, поэтому необходимо применять правило цикла.

Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем [латекс] \ boldsymbol {R_2} [/ latex] в том же (предполагаемом) направлении, что и текущий [латекс] \ boldsymbol {I_2} [/ latex], и поэтому изменение потенциала [латекс] \ boldsymbol {-I_2R_2} [/ латекс]. Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала составляет [latex] \ boldsymbol {+ \ textbf {emf} _1} [/ latex].Если пересечь внутреннее сопротивление [латекс] \ boldsymbol {r_1} [/ latex] от c до d, получим [латекс] \ boldsymbol {-I_2r_1} [/ latex]. Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала [latex] \ boldsymbol {-I_1R_1} [/ latex].

Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,

[латекс] \ boldsymbol {-I_2R_2 + \ textbf {emf} _1 — I_2r_1 — I_1R_1 = -I_2 (R_2 + r_1) + \ textbf {emf} _1 — I_1R_1 = 0}.[/ латекс]

Подставляя значения из принципиальной схемы для сопротивлений и ЭДС и отменяя единицу измерения ампер, получаем

[латекс] \ boldsymbol {-3I_2 + 18 -6I_1 = 0}. [/ Латекс]

Теперь, применяя правило цикла к aefgha (мы могли бы также выбрать abcdefgha), аналогично дает

[латекс] \ boldsymbol {+ I_1R_1 + I_3R_3 + I_3r_2 — \ textbf {emf} _2 = + I_1R_1 + I_3 (R_3 + r_2) — \ textbf {emf} _2 = 0}. [/ Латекс]

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении.С введенными значениями это становится

[латекс] \ boldsymbol {+ 6I_1 + 2I_3 — 45 = 0}. [/ Latex]

Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение для [латекса] \ boldsymbol {I_2} [/ latex]:

[латекс] \ boldsymbol {I_2 = 6 — 2I_1}. [/ Латекс]

Теперь решите третье уравнение для [латекса] \ boldsymbol {I_3} [/ latex]:

[латекс] \ boldsymbol {I_3 = 22,5 — 3I_1}. [/ Latex]

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для [latex] \ boldsymbol {I_1} [/ latex]:

[латекс] \ boldsymbol {I_1 = I_2 + I_3 = (6 — 2I_1) + (22.5 — 3I_1) = 28,5 — 5I_1}. [/ Latex]

Объединение терминов дает

[латекс] \ boldsymbol {6I_1 = 28,5} [/ латекс] и

[латекс] \ boldsymbol {I_1 = 4.75 \; \ textbf {A}}. [/ Latex]

Подставляя это значение вместо [latex] \ boldsymbol {I_1} [/ latex] обратно в четвертое уравнение, получаем

[латекс] \ boldsymbol {I_2 = 6 — 2I_1 = 6 — 9,50} [/ латекс]

[латекс] \ boldsymbol {I_2 = -3,50 \; \ textbf {A}}. [/ Latex]

Знак минус означает, что [латекс] \ boldsymbol {I_2} [/ latex] течет в направлении, противоположном предполагаемому на рисунке 5.

Наконец, подстановка значения [latex] \ boldsymbol {I_1} [/ latex] в пятое уравнение дает

[латекс] \ boldsymbol {I_3 = 22,5 — 3I_1 = 22,5 — 14,25} [/ латекс]

[латекс] \ boldsymbol {I_3 = 8.25 \; \ textbf {A}}. [/ Latex]

Обсуждение

Для проверки отметим, что действительно [латекс] \ boldsymbol {I_1 = I_2 + I_3} [/ latex]. Результаты также можно было проверить, введя все значения в уравнение для цикла abcdefgha.

Материал в этом разделе теоретически верен. Мы должны иметь возможность проверить это, измерив ток и напряжение. Фактически, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и будут рассмотрены в следующих модулях. Как мы увидим, результат очень основного, даже глубокого факта — выполнение измерения изменяет измеряемую величину.

Правила Кирхгофа

Правила Кирхгофа
Далее: Конденсаторы в цепях постоянного тока Up: Электрический ток Предыдущий: Последовательные резисторы и Теперь мы знаем почти все, что нам нужно знать об ЭДС и резисторах.Тем не мение, было бы удобно, если бы мы могли обобщить наши знания в ряд удобных правил, которые затем можно использовать для анализа любой цепи постоянного тока. По сути, это то, что сделал немецкий физик Густав Кирхгоф в 1845 году. когда он предложил два простых правила для работы с цепями постоянного тока.

Первое правило Кирхгофа применяется к точкам соединения в цепях постоянного тока (, т. Е. , точки соединения трех или более проводов). Правило соединения:

Сумма всех токов, входящих в любую точку соединения, равна сумма всех токов, выходящих из этой точки соединения.

Это правило легко понять. Как мы уже отмечали, если это правило не были удовлетворены, то в точках стыковки накапливались бы заряды, нарушая наши фундаментальное установившееся предположение.

Второе правило Кирхгофа применяется к контурам в цепях постоянного тока. Правило цикла:

Алгебраическая сумма изменений электрического потенциала, встречающихся в полный обход любого замкнутого контура равен нулю.

Это правило тоже легко понять. Мы уже видели (в разделе 5) что нулевая чистая работа сделана в медленном перемещении заряда по некоторому замкнутому контуру в электростатическом поле. Поскольку проделанная работа равна произведению заряда и разницы по электрическому потенциалу между начальной и конечной точками из цикла следует, что эта разница должна быть равна нулю. Таким образом, если мы применим это результат к частному случаю петли в цепи постоянного тока, мы сразу приходим ко второму правилу Кирхгофа.При использовании этого правила мы сначала выбираем замкнутый контур в цепи постоянного тока, который мы анализируем. Далее мы решаем, собираемся ли мы пройти через это петля по часовой стрелке или против часовой стрелки (выбор произвольный). Если пересечь источник ЭДС в направлении увеличения потенциала тогда изменение потенциала. Однако, если ЭДС проходит в противоположном направлении, то изменение потенциала будет. Если резистор, несущий ток, проходит в направлении тока, то изменение потенциал есть.Наконец, если резистор проходит в в противоположном направлении, то изменение потенциала равно.

Токи, протекающие по общей цепи постоянного тока, всегда можно найти, применив Первое правило Кирхгофа для всех узловых точек, Второе правило Кирхгофа для всех петель, а затем решение Полученные таким образом совместные алгебраические уравнения. Эта процедура работает независимо от того, насколько сложна рассматриваемая схема (, например, , Кирхгоф правила используются в полупроводниковой промышленности для анализа невероятно сложные схемы, вытравленные на поверхности кремниевых пластин, которые используются для построить центральные процессоры компьютеров).

---

Далее: Конденсаторы в цепях постоянного тока Up: Электрический ток Предыдущий: Последовательные резисторы и

Ричард Фицпатрик 2007-07-14

Когда использовать законы Кирхгофа

Когда использовать законы Кирхгофа

Когда использовать законы Кирхгофа

Вот три типичных принципиальные схемы, которые, возможно, потребуется решить (например, с учетом сопротивлений всех резисторов и напряжений всех батарей, найдите все токов).

Рисунок слева можно легко решить с помощью правила добавления сопротивлений параллельно и последовательно. Резисторы R ₃ , р ₄ и R ₅ можно рассматривать, как если бы они были одним резистором сопротивления Р ₃₄₅ .Это эффективное сопротивление можно добавить параллельно с р ₂ дать еще одно эффективное сопротивление Р ₂₃₄₅ . Наконец, это эффективное сопротивление может быть добавлено последовательно с р ₁ для расчета чистого сопротивления R = ₁ + R ₂₃₄₅ видел аккумулятор.Это значение R можно использовать для вычисления тока, производимого аккумулятор. Ток от батареи весь течет через R ₁ , поэтому падение напряжения на р ₁ можно вычислить по закону Ома. Поскольку напряжение аккумулятора известно, вы можете затем вычислите падение напряжения на Р ₂ . Сейчас применяя закон Ома к р ₂ сообщает вам ток через него; и т.п.Таким образом вы в конечном итоге выясните токи и падения напряжения. везде в цепи.

Середина и правые фигуры не могут быть решены такой простой (?) стратегией. Вместо, вы должны записать законы Кирхгофа и решить уравнения.

Для В качестве примера рассмотрим правую фигуру. Дайте имена неизвестные токи i 1 , i 2 и i 3 через 3 резистора (выбирая направления ad lib).Эти неизвестные токи можно найти, решив 3 уравнения:

1. Первый уравнение описывает текущее сохранение в узле.