Длинный соленоид — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Длинные соленоиды и относительно сильные магниты также представляют собой простые электронно-оптические и ионно-оп-тические элементы, поскольку магнитные поля внутри соленоида и вдали от краев магнитных полюсов практически однородны. Разумеется, однородное магнитное поле является такой же идеализацией, как и однородное электрическое поле. На практике всегда приходится учитывать краевые эффекты. Посредством введения эффективной длины реальное поле всегда можно заменить однородным полем, оказывающим приблизительно такое же воздействие, как и исходное поле.  [1]

Длинный соленоид с плотной намоткой размещен на цилиндрическом железном сердечнике с магнитной проницаемостью р, и проводимостью А. Радиус сердечника го, утечки в конденсаторе несущественны, обмотку и соединительные провода можно считать идеально проводящими.  [2]

Длинный соленоид с разомкнутыми концами расположен вдоль постоянного магнитного поля с индукцией В 2 Тл.

 [3]

Длинный соленоид, по которому течет ток, содержит N 500 витков. Определить длину соленоида, если напряженность магнитного поля на его оси Н 1000 А / м, а сила тока в нем / 0 4 А.  [4]

Длинный соленоид с разомкнутыми концами расположен вдоль постоянного магнитного поля с индукцией В 1 Тл.  [5]

Поверх длинного соленоида, имеющего A t витков, длину / и площадь сечения S, вплотную намотан по всей длине второй соленоид, имеющий Nt витков и такое же сечение S.  [6]

Поверх длинного соленоида вплотную намотана катушка. Ток в соленоиде нарастает прямо пропорционально времени.  [7]

Поверх длинного соленоида, имеющего длину /, сечение S и число витков NI, вплотную по всей длине намотан второй соленоид, имеющий число витков ЛГ2 и такое же сечение, S, как и первый.  [8]

Поверх длинного соленоида вплотную намотана катушка. Ток в соленоиде нарастает прямо пропорционально времени.  [9]

Имеется длинный соленоид с током I.  [10]

Дан узкий длинный соленоид ( / — 15 см, 1500 витков, 51 см2, / 0, 1 А), В середине соленоида возникает магнитный поток Фп [ 6я — 10 — 5 В — С.  [11]

Имеется очень длинный соленоид с плотностью намотки п витков на 1 м длины.  [12]

Намоткой длинного соленоида с радиу ом сечения а служит тонкая лента-проводник шириной h, намотанная в один, слой практически вплотную.  [13]

У длинного соленоида с плотной обмоткой магнитное поле внутри практически однородно.  [14]

Замена длинного соленоида, создающего однородное поле, рядом коротких катушек позволяет существенно уменьшить размеры и вес фокусирующей системы и расход электроэнергии на ее питание. Магнитная система становится особенно экономичной при использовании для создания периодически изменяющегося по длине пучка магнитного поля постоянных магнитов.

 [15]

Страницы:      1    2    3    4

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3. 1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5. 2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Плотно намотанный длинный соленоид имеет n витков на единицу длины, радиус r и течет ток i. Частица с зарядом q и массой m брошена из точки на оси в направлении, перпендикулярном оси.

Максимальная скорость, при которой частица не ударяется о соленоид, будет равна –\[\begin{align} & \text{A)}\dfrac{{{\mu }_{0}}qrni}{2m} \\ & \text{B}}\dfrac{{{\mu}_{0}}qrni}{m} \\ & \text{C}}\dfrac{2{{\mu}_{0}}qrni} {3m} \\ & \text{D) Ничего из перечисленного} \\ \end{align}\]

Ответ

Проверено

236.7k+ просмотров

Подсказка: Нам дано, что заряженная частица вылетает из оси внутри соленоида. Мы можем использовать уравнение для магнитной силы Лоренца и центростремительной силы, чтобы определить максимальный радиус, при котором частица может совершить круговое движение.

Полный пошаговый ответ:
Нам дано, что соленоид плотно намотан на ось, проходящую через точку О, как показано ниже. Кроме того, мы знаем, что заряженные частицы вылетают из этой оси перпендикулярно ей, так что частица может совершать круговое движение внутри соленоида.
 

Мы знаем, что заряженная частица, брошенная перпендикулярно магнитному полю, будет совершать круговое движение. Итак, данная частица, сброшенная внутрь соленоида, также совершает круговое движение.
Дано, что радиус соленоида равен «r». Чтобы заряженная частица не попала в соленоид, максимальный радиус, в котором она может совершить круговое движение, будет равен половине радиуса соленоида, как показано на рисунке.
Мы можем найти этот радиус, приравняв силу Лоренца и центростремительную силу, действующую на заряженную частицу. Что дается как — 9{2}}}{\dfrac{r}{2}} \\
 & \Rightarrow v=\dfrac{qrB}{2m} \\
\end{align}\]
Но мы также знаем магнитное поле из-за к соленоиду мы ‘n’ оборотов на единицу длины как –
\[B={{\mu }_{0}}ni\]
Подставляя это в уравнение для скорости, получаем –
\[\поэтому v=\dfrac {q{{\mu }_{0}}nir}{2m}\]
Скорость, с которой движется частица, должна быть меньше или равна \[\dfrac{{{\mu }_{0}}qnir {2м}\].

Правильный ответ — вариант А.

Примечание:
Заряженная частица в магнитном поле будет совершать круговое движение, если она имеет перпендикулярную составляющую вдоль направления магнитного поля. Сила Лоренца, действующая на частицу, будет равна нулю, если частица двигалась вдоль оси и, следовательно, не совершала кругового движения.

Недавно обновленные страницы

Большинство эубактериальных антибиотиков получают из биологии Rhizobium класса 12 NEET_UG

Саламиновые биоинсектициды были извлечены из биологии класса A 12 NEET_UG

Какое из следующих утверждений относительно бакуловирусов класса 12 биологии NEET_UG

Канализационные или городские канализационные трубы не должны быть непосредственно классом биологии 12 NEET_UG

Очистка сточных вод осуществляется микробами A Микробы B Удобрения класса 12 биологии NEET_UG

Ферментная иммобилизация активный фермент класса 12 биологии NEET_UG

Большинство эубактериальных антибиотиков получают из биологии класса 12 ризобий NEET_UG

Саламиновые биоинсектициды были извлечены из биологии класса А 12 NEET_UG

Какое из следующих утверждений относительно бакуловирусов класса 12 биологии NEET_UG

Канализационные или городские канализационные трубы не должны быть непосредственно классом биологии 12 NEET_UG

Очистка сточных вод осуществляется микробами A Микробы B Удобрения класса 12 биологии NEET_UG

Ферментная иммобилизация активный фермент биологии класса 12 NEET_UG

Тенденции сомнений

Магнитное поле соленоида

Магнитное поле соленоида
Следующий: Происхождение постоянного магнетизма Вверх: Магнетизм Предыдущий: Закон Ампера о круговых движениях Соленоид представляет собой плотно намотанную спиральную катушку проволоки, диаметр которой мал по сравнению с к его длине. Магнитное поле, создаваемое в центре или сердечнике , соленоида с током по существу равномерна и направлена ​​вдоль оси соленоида. Вне соленоида магнитное поле намного слабее. На рис. 27 показано (довольно схематично) магнитное поле, создаваемое типичным соленоидом. Соленоид намотан из одного спирального провода, по которому течет ток. Обмотка достаточно тугая, чтобы каждый виток соленоида хорошо приблизительно как круглая проволочная петля, лежащая в плоскости, перпендикулярной оси соленоид, по которому течет ток. Предположим, что там таких витков на единицу осевой длины соленоида. Что это величина магнитного поля в сердечнике соленоида?

Рисунок 27: Соленоид.

Чтобы ответить на этот вопрос, применим схему Ампера. закон к прямоугольной петле. Сначала нужно найти линейный интеграл магнитного поля вокруг. Вдоль и магнитное поле практически перпендикулярна петле, поэтому вклада в линейный интеграл от этих участков контура.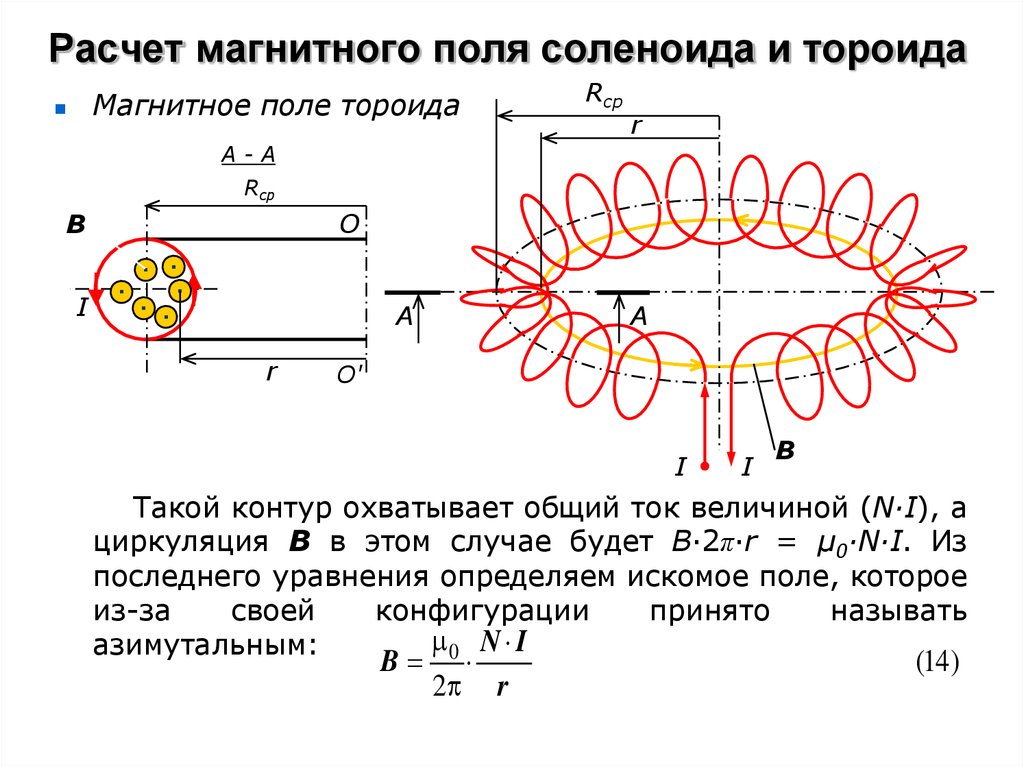

Вдоль магнитного поля примерно однородно, величины , скажем, и направлена ​​параллельно петле. Таким образом вклад в линейный интеграл от этого участка контура , где длина . Вдоль магнитного поля напряженность практически незначительна, поэтому этот участок цикла не влияет на линию интеграл. Отсюда следует, что линейный интеграл магнитное поле вокруг просто

(178)

По круговому закону Ампера этот линейный интеграл равен умножить на алгебраическую сумму токи, протекающие по контуру. Так как длина петля по оси соленоида , петля пересекает витков соленоида, через каждый из которых протекает ток. Таким образом, общая ток, протекающий по контуру, равен . Этот ток считается положительный ток, так как если мы посмотрим против направления токи текут в каждом витке ( т. е. , на страницу на рисунке), цикл циркулирует эти токи против часовой стрелки.