Поток вектора напряженности
Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:
Рис. 2.5
Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности ФЕ через эту поверхность.
В векторной форме можно записать – скалярное произведение двух векторов, где вектор .
Таким образом, поток вектора есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.
Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.
| Рис. 2.6 | Рис. 2.7 | ||
Для рисунка 2.6 – поверхность А1 окружает положительный заряд и поток здесь направлен наружу, т.е. Поверхность А2 – окружает отрицательный заряд, здесь и направлен внутрь. Общий поток через поверхность
Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность А отрицательный (подсчитайте число силовых линий).
Таким образом, поток вектора напряженности зависит от заряда. В этом смысл теоремы Остроградского-Гаусса.
Электричество и магнетизм
Теорема установлена М.В. Остроградским (рис. 1.33) в виде общей математической теоремы для любого векторного поля и К. Гауссом — применительно к электростатическому полю.
Рис. 1.33. М. Острогра́дский (1801–1861) — российский математик и механик
Закон Кулона и принцип суперпозиции позволяют вычислить потенциал поля любого распределения заряда
.
Используя связь или непосредственно с помощью закона Кулона и принципа суперпозиции, можно вычислить и напряженность поля
Однако, практическое вычисление написанных выше сумм и интегралов далеко не всегда так просто, как просто выглядят сами суммы и интегралы. Они вычисляются достаточно непринужденно, когда зарядов два, три, может быть, десяток. Если же речь идет о макроскопических заряженных телах, когда число точечных зарядов (протонов, электронов и т. п.) макроскопически велико, прямое вычисление подобных выражений становится очень сложной задачей. В первую очередь это касается написанных выше сумм, а не интегралов.
Мы хотим подчеркнуть, что при решении макроскопических задач, в подавляющем большинстве случаев, можно считать, что заряд распределён непрерывно, соответственно, вычислять надо не суммы, а интегралы. Поэтому встает задача: на базе закона Кулона и принципа суперпозиции, написать интегральные и/или дифференциальные уравнения, которым удовлетворяет напряженность поля произвольного распределения зарядов. Эту задачу в ряде случаев успешно решает обсуждаемая в этом параграфе теорема Гаусса для вектора .
Рассмотрим некоторую поверхность и на ней бесконечно малый участок (бесконечно малую площадку) площадью (рис. 1.34).
Рис. 1.34. Бесконечно малый участок поверхности
Показанный на рисунке «вектор площадки» имеет следующий смысл: 1) он направлен по нормали к поверхности в той её точке, в окрестности которой находится площадка; 2) его модуль равен площади площадки . Вектор , а вместе с ним и вектор всегда направлены по перпендикуляру к поверхности в данном её месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен. Здесь и ниже, если иное специально не оговорено, будут использоваться указанные выше общепринятые правила: внешняя нормаль и правый винт.
Электрический поток
Физика > Электрический поток
Рассмотрите скорость электрического поля – электрический поток. Читайте про равномерное и неравномерное электрическое поле, теорему Гаусса, формула, вольтметр.
Электрический поток – скорость движения электрического поля по указанной площади.
Задача обучения
Основные пункты
- Если электрическое поле выступает равномерным, то электрический поток на поверхности (S) вычисляется как ΦE = E ⋅ S = ES cosθ.
- Единица измерения – вольтметры.
Термин
- Электрическое поле – участок вокруг заряженной частицы или между двумя зарядами.
Электрический поток – скорость перемещения электрического поля сквозь указанную площадь. Выступает пропорциональным количеству линий, пронизывающих виртуальную поверхность.

Если в электрическом поле присутствует равномерное распределение, то используем формулу ΦE = E ⋅ S = ES cosθ (E – величина электрического поля, S – поверхностная площадь, а θ – угол между линиями электрического поля и перпендикуляром к S.
Для неравномерного электрического поля: dΦE = E ⋅ dS (электрическое поле E, умноженное на компонент области, перпендикулярной полю).
Электрический поток над поверхностью характеризуется также законом Гаусса (теорема Гаусса) в виде поверхностного интеграла: ΦE = ∬SE ⋅ dS (Е – электрическое поле, dS – дифференциальная площадь на замкнутой поверхности S с наружной поверхностью, определяющей его направление).
Если на электрический поток не воздействуют заряды внутри замкнутой поверхности, то поле в формуле Гаусса может зависеть от зарядов вне закрытой поверхности. Закон полезен исключительно для ручных расчетов, когда в электрическом поле присутствует высокая степень симметрии (сферическая и цилиндрическая).
Единицы измерения – вольтметры. Если расписать, то базовой будет кг · м3 · с-3 · А-1.
Поток векторного поля — Википедия
Материал из Википедии — свободной энциклопедии
В математике поток векторного поля используется для двух различных понятий:
- Фазовый поток — поток векторного поля A→{\displaystyle {\vec {A}}} — однопараметрическое семейство диффеоморфизмов Γt{\displaystyle \Gamma _{t}}, определяемых дифференциальным уравнением A→(Γt(x))=dΓt(x)dt{\displaystyle {\vec {A}}(\Gamma _{t}(x))={\frac {d\Gamma _{t}(x)}{dt}}}.
Поток векторного поля через поверхность[править | править код]
Поток векторного поля через поверхность — поверхностный интеграл второго рода по поверхности S{\displaystyle S}. По определению ΦF=∬SF⋅ndS{\displaystyle {{\Phi }_{F}}=\iint \limits _{S}{\mathbf {F} \cdot \mathbf {n} \,dS}}
где F=F(X){\displaystyle \mathbf {F} =\mathbf {F(X)} } — векторное поле (вектор-функция векторного аргумента — точки пространства), n{\displaystyle \mathbf {n} } — единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — то есть для дифференцируемой поверхности — так, чтобы n{\displaystyle \mathbf {n} } было непрерывно; для неориентируемой поверхности это не важно, так как поток через неё всегда ноль), dS{\displaystyle dS} — элемент поверхности.
- В трёхмерном случае X=(x,y,z),F=F(X)=(Fx(X),Fy(X),Fz(X)){\displaystyle \mathbf {X} =(x,y,z),\mathbf {F} =\mathbf {F(X)} =\left(F_{x}(\mathbf {X} ),F_{y}(\mathbf {X} ),F_{z}(\mathbf {X} )\right)}, а поверхностью является обычная двумерная поверхность.
Иногда, особенно в физике, применяется обозначение
dS=ndS{\displaystyle d\mathbf {S} =\mathbf {n} \,dS}
тогда поток записывается в виде
ΦF=∬SF⋅dS{\displaystyle {{\Phi }_{F}}=\iint \limits _{S}{\mathbf {F} \cdot d\mathbf {S} }}.
Физическая интерпретация[править | править код]
Пусть движение несжимаемой жидкости единичной плотности в пространстве задано векторным полем скорости течения v=v(x,y,z){\displaystyle \mathbf {v} =\mathbf {v} (x,y,z)}. Тогда объём жидкости, который протечёт за единицу времени через поверхность S{\displaystyle S}, будет равен потоку векторного поля v{\displaystyle \mathbf {v} }.
Поток вектора напряженности электрического поля
Число линий вектора  ,
пронизывающих некоторую поверхность,
называетсяпотоком N вектора напряженностичерез эту
поверхность. Если поверхностьSплоская и перпендикулярна силовым
линиям, а поле (Е) однородно (рис.3.2,а), то
очевидно, что
,
пронизывающих некоторую поверхность,
называетсяпотоком N вектора напряженностичерез эту
поверхность. Если поверхностьSплоская и перпендикулярна силовым
линиям, а поле (Е) однородно (рис.3.2,а), то
очевидно, что
N=ES.
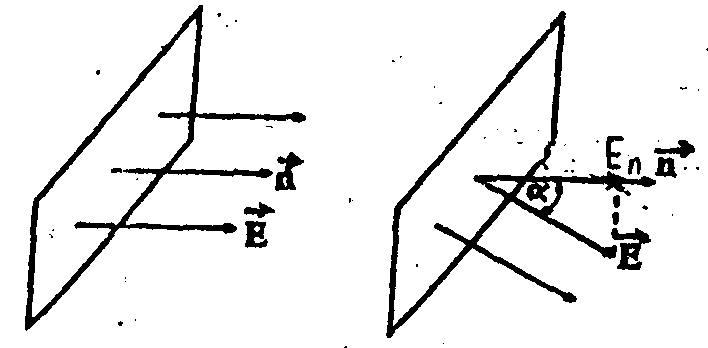
а) б)
Рис.3.2
Если нормаль к плоской поверхности составляет угол α с силовыми линиями (рис.3.2, б), то:
N=EScosα=En·S (3.5)
Наконец, в случае неоднородного поля и произвольной формы поверхности, разобьем ее на элементарные площадки dS. ПотокdNчерез такую площадкуdSравен:
dN=EndS, (3.6)
где En=E·cosα–
проекция векторана нормаль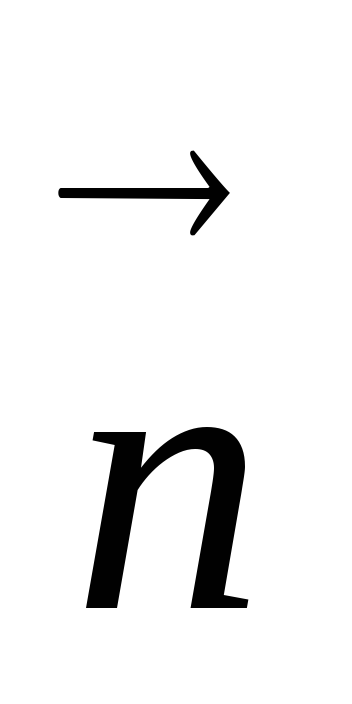 ,
а поток через всю поверхность
,
а поток через всю поверхность
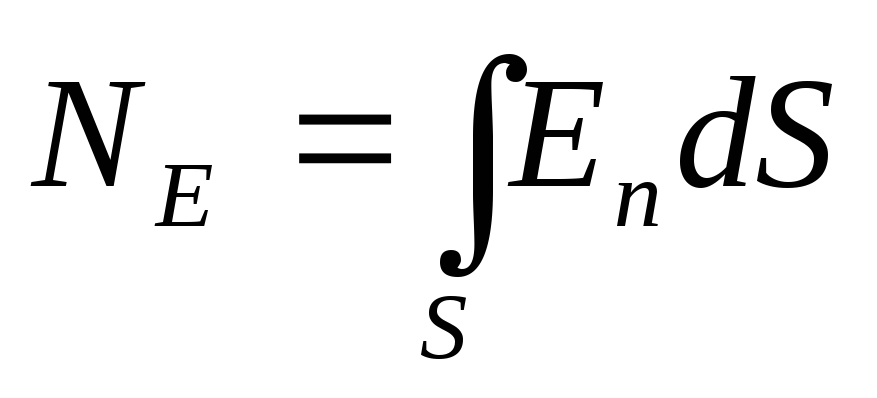 (3.7)
(3.7)
Теорема Остроградского – Гаусса и ее применение к расчету полей
Определим поток Nвектора напряженности поля зарядовQ1,Q2, …Qnчерез произвольнуюзамкнутуюповерхность, окружающую эти заряды.
Рассмотрим сначала случай сферической поверхности Sсфрадиусомr, в центре которой в вакууме (ε =1) находится точечный зарядQ(рис.3.3)
Рис.3.3
Напряженность Е во всех точках поверхности сферы одинакова, а линии вектора Е перпендикулярны поверхности сферы. Тогда согласно (3.4) и (3.7) поток NEв вакууме
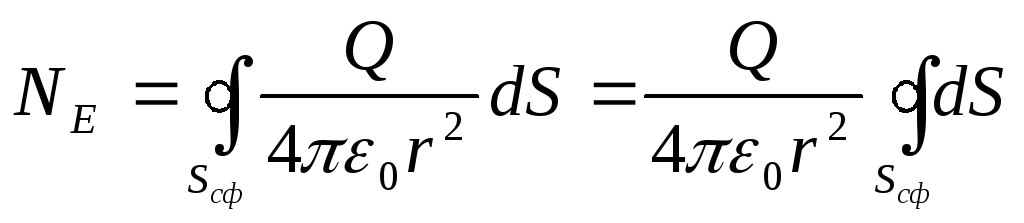
Так как площадь поверхности сферы S = 4πr2, то
 ,
,
и поток вектора напряженности заряда Q
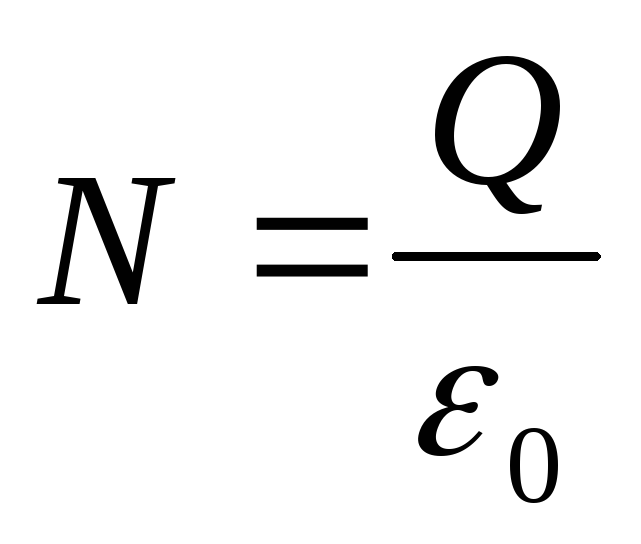 (3.8)
(3.8)
Окружим теперь заряд замкнутой поверхностью Sпроизвольной формы. Как видно из рис. 3.3, каждая силовая линия, пронизывающая сферу, пронижет и поверхностьS. Следовательно, формула (3.8) справедлива и для любой замкнутой поверхности.
Если поток Nсоздаетсяnзарядами, то он равен сумме потоков, создаваемых каждым из зарядов:
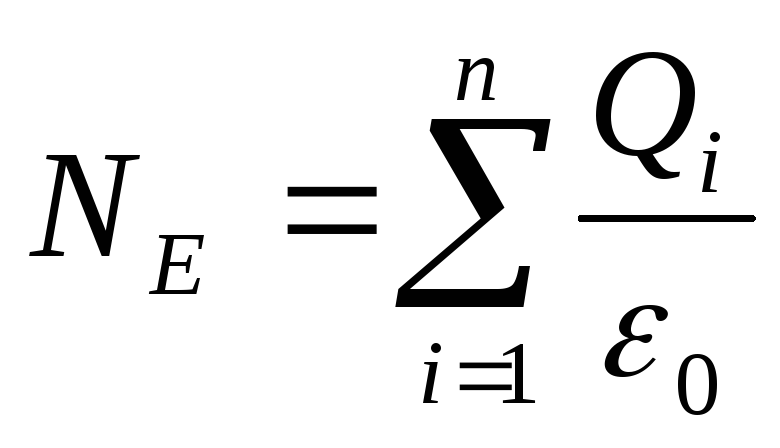
или окончательно:
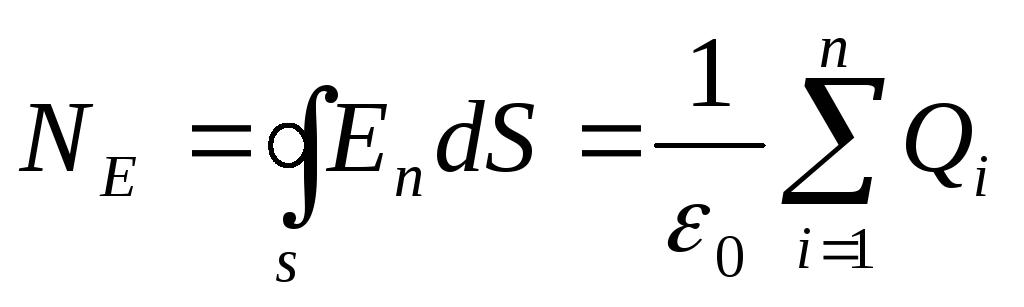 (3.9)
(3.9)
Формула (3.9) выражает теорему Остроградского-Гаусса:поток вектора напряженности N через любую замкнутую поверхность, пропорционален алгебраической сумме зарядов, находящихся внутри этой поверхности.
В случае равномерного распределения
заряда по объему Vтела с
объемной плотностьюρформула (3.9)
может быть записана .
.
Поле равномерного заряженной бесконечной прямолинейной нити
Пусть бесконечная нить или тонкий цилиндр (рис3.4) заряжен равномерно с линейной плотностью заряда τ(τ=dQ/dℓ— заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии вектора Е радиально расходятся от нити перпендикулярно ей: Е=Еn

Рис.3.4
Окружим участок нити длиной ℓ коаксиальной с ней цилиндрической замкнутой поверхностью радиусом r. ПотокNчерез ее торцы равен нулю и, следовательно, полный поток равен потоку через боковую поверхность:
NЕ=ES=E2πrℓ
По теореме Остроградского-Гаусса (3.9)
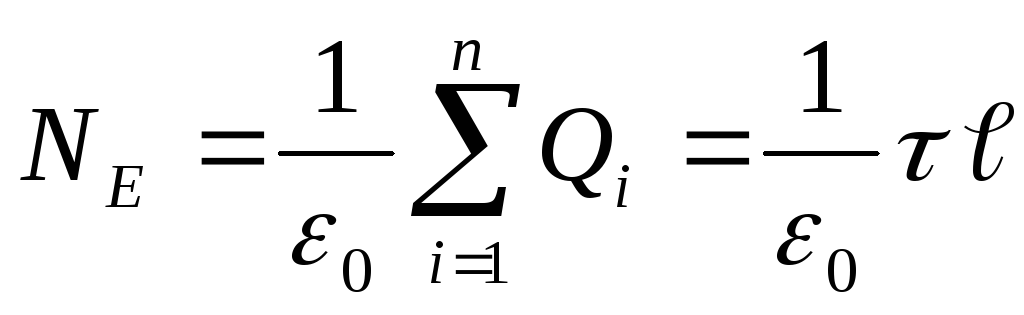
Приравняв правые части, получим
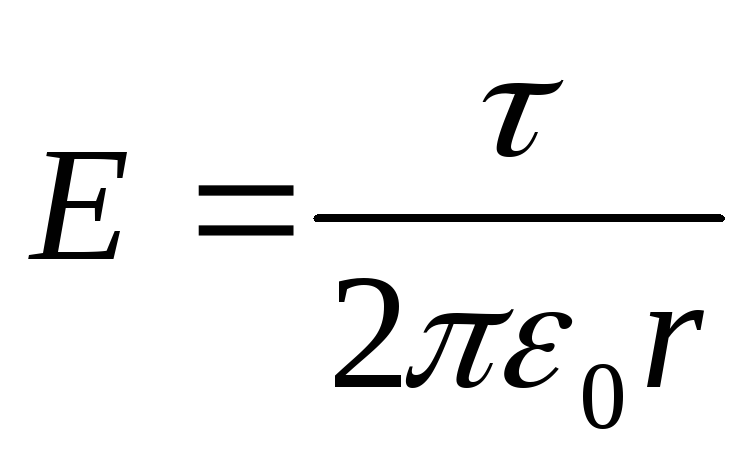 .
(3.10)
.
(3.10)
Если у нас цилиндр радиуса Rи зарядQсосредоточен на поверхности, то для точекr<R(т.е. внутри цилиндра) Е=О.
Электричество и магнетизм
Основные понятия электростатики. Закон Кулона. Понятие электрического поля. Напряженность электрического поля. Линии напряженности. Принцип суперпозиции.

Закон Кулона.
Закон Кулона: сила электростатического взаимодействия двух точечных зарядов q1 и q2 в вакууме прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния r между ними.
В
системе единиц СИ закон Кулона записывается
для модуля силы Кулона 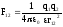 и
для вектора силы
и
для вектора силы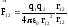 ,
где0=8.8510-12 Кл2/(Нм2)
и называется электрической
постоянной.
,
где0=8.8510-12 Кл2/(Нм2)
и называется электрической
постоянной.


Поток вектора Е. Теорема Гаусса для электростатического поля в вакууме. Работа электростатического поля. Циркуляция вектора Е. Потенциал электростатического поля.
Поток вектора напряженности электростатического поля
Чтобы
с помощью силовых линий можно было
характеризовать не только направление,
но и величину напряженности
электростатического поля, их условились
проводить с определенной густотой.
Число
линий напряженности, пронизывающих
единицу площади перпендикулярной
им поверхности, должно быть равно модулю
вектора 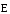 .
Число
силовых линий, пронизывающих
элементарную площадку dS, называется
потоком вектора напряженности dФЕ через площадку dS.
Эта величина считается по формуле
dФЕ=ЕdScos(),
где — угол
между вектором нормали
.
Число
силовых линий, пронизывающих
элементарную площадку dS, называется
потоком вектора напряженности dФЕ через площадку dS.
Эта величина считается по формуле
dФЕ=ЕdScos(),
где — угол
между вектором нормали  к площадкеdS
и вектором
к площадкеdS
и вектором 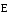 . Представим
величину элемента поверхности в виде
вектора
. Представим
величину элемента поверхности в виде
вектора 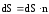 .
Таким образом
.
Таким образом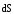 — это вектор, численно равный площади
элемента поверхности и совпадающий
по направлению с наружной нормалью
к нему. Тогда Еn=Еcos
— есть проекция вектора
— это вектор, численно равный площади
элемента поверхности и совпадающий
по направлению с наружной нормалью
к нему. Тогда Еn=Еcos
— есть проекция вектора 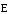 на нормаль
на нормаль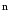 к площадкеdS
(рис.1.6) и
к площадкеdS
(рис.1.6) и 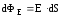 .
.
Если
плоская поверхность S
перпендикулярна силовым линиям
однородного электрического поля, то
поток напряженности через нее равен
ФЕ=ЕS.
Если площадка dS
параллельна линиям напряженности, то
поток dФЕ через нее равен нулю, так как в этом
случае 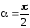 и Еn= 0.
Если поверхность S
произвольной формы, а поле неоднородное,
то поверхность разбивают на малые
элементарные площадки dS,
на каждой из которых напряженность
поля
и Еn= 0.
Если поверхность S
произвольной формы, а поле неоднородное,
то поверхность разбивают на малые
элементарные площадки dS,
на каждой из которых напряженность
поля 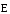 постоянная. Поток напряженности через
каждую элементарную площадку равенdФЕ=ЕndS,
а поток напряженности поля через всю
поверхность представится суммой
элементарных потоков и в итоге будет
равен
постоянная. Поток напряженности через
каждую элементарную площадку равенdФЕ=ЕndS,
а поток напряженности поля через всю
поверхность представится суммой
элементарных потоков и в итоге будет
равен 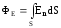 .
.
Теорема Гаусса для электростатического поля в вакууме.
Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную 0. Эта формулировка представляет собой теорему К.Гаусса.
В
общем случае электрические заряды могут
быть распределены с некоторой объемной
плотностью 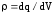 ,
различной в разных местах пространства.
Тогда суммарный заряд объемаV,
охватываемого замкнутой поверхностью
S
равен
,
различной в разных местах пространства.
Тогда суммарный заряд объемаV,
охватываемого замкнутой поверхностью
S
равен 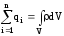 и теорему Гаусса следует записать в
виде
и теорему Гаусса следует записать в
виде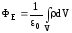 .
.

Циркуляция вектора напряженности электрического поля.
Работа, совершаемая силами электрического поля при перемещении единичногоположительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:
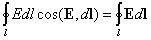
Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.
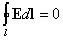 .
.
Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле — потенциальным
Электрический диполь. Полярные, неполярные и ионные диэлектрики. Поляризация диэлектриков. Поляризованность. Диэлектрическая проницаемость. Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике.
2. Теорема Гаусса.
Использование теоремы Гаусса для расчета полей
(Примеры решения задач)
Поток электрического поля
Пример 2.1.
Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найдите поток вектора напряженности через круг радиуса R, плоскость которого перпендикулярна отрезку прямой, соединяющей заряды, и проходит через его середину.
Решение.
Рассмотрим
элементарный поток результирующего
электрического поля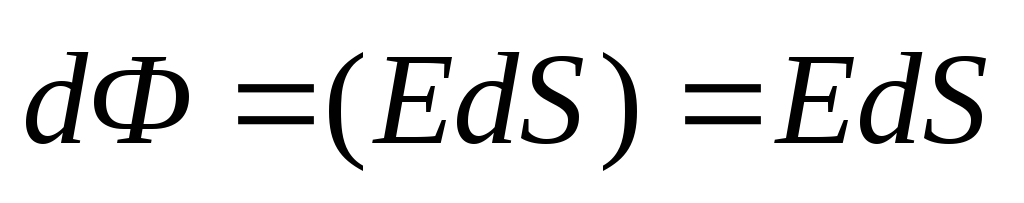 через бесконечно малую кольцевую зону
круга радиуса
через бесконечно малую кольцевую зону
круга радиуса и ширины
и ширины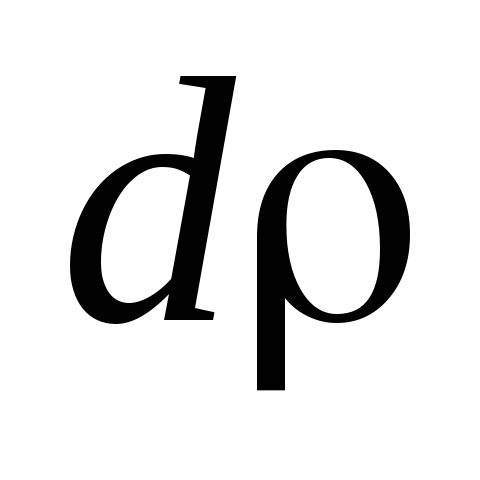 (см.рис)
(см.рис)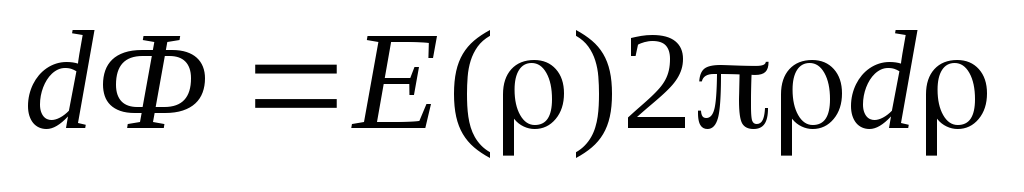 .
В записи потока учтено, что вектор
.
В записи потока учтено, что вектор перпендикулярен поверхности круга.
Выразим напряженность электрического
поля через
перпендикулярен поверхности круга.
Выразим напряженность электрического
поля через ,
используя подобие треугольников
показанных на рисунке:
,
используя подобие треугольников
показанных на рисунке: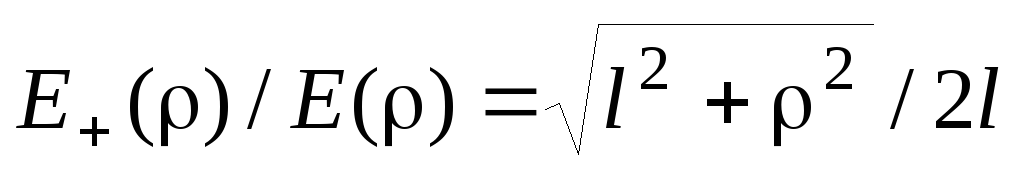 ,
,
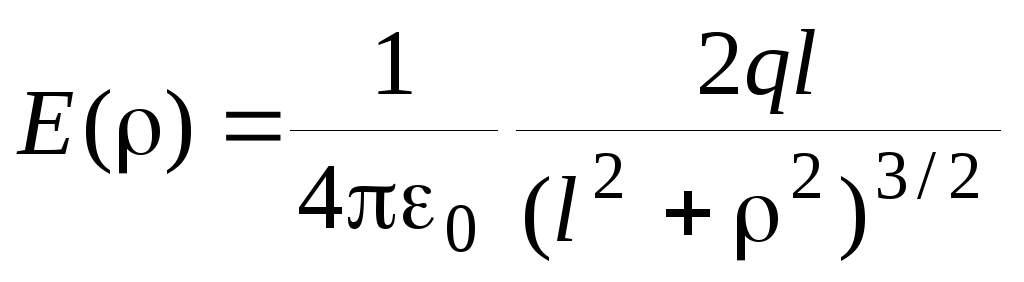 .
.
Вычисление потока сводится к взятию интеграла:
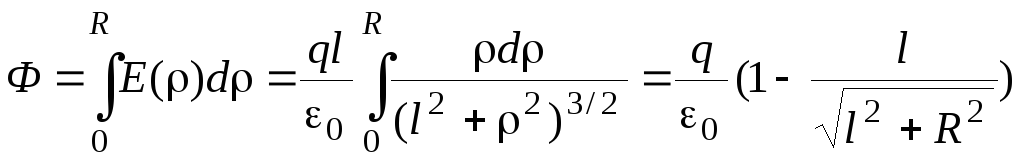
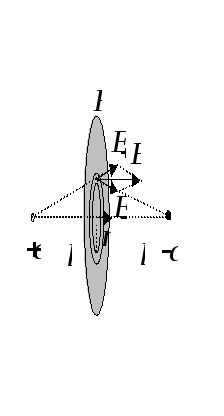 .
.
Электрическое поле заряженной сферы
Пример 2.2.
По поверхности сферы радиуса 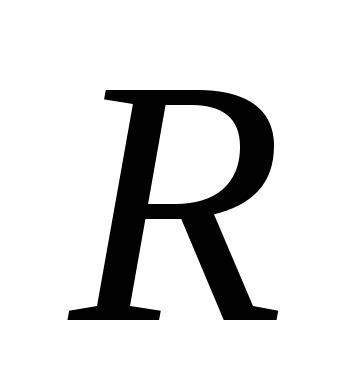 однородно распределен заряд
однородно распределен заряд .
Определите напряженность электрического
поля в произвольной точке пространства
вне сферы и внутри нее. Полученный
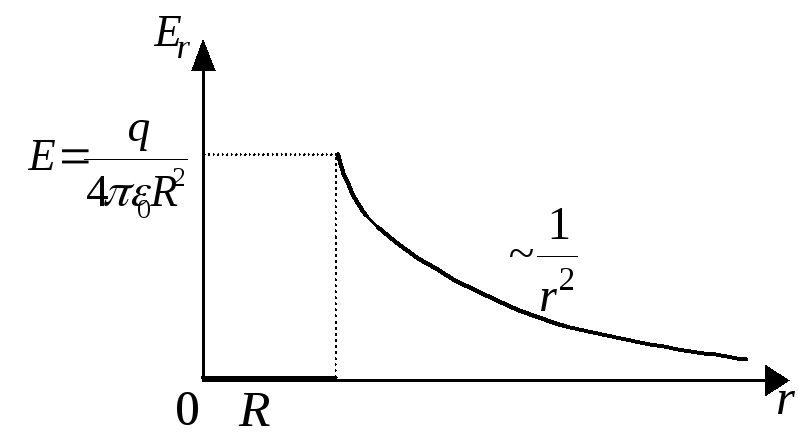
результат представьте на графике
.
Определите напряженность электрического
поля в произвольной точке пространства
вне сферы и внутри нее. Полученный
результат представьте на графике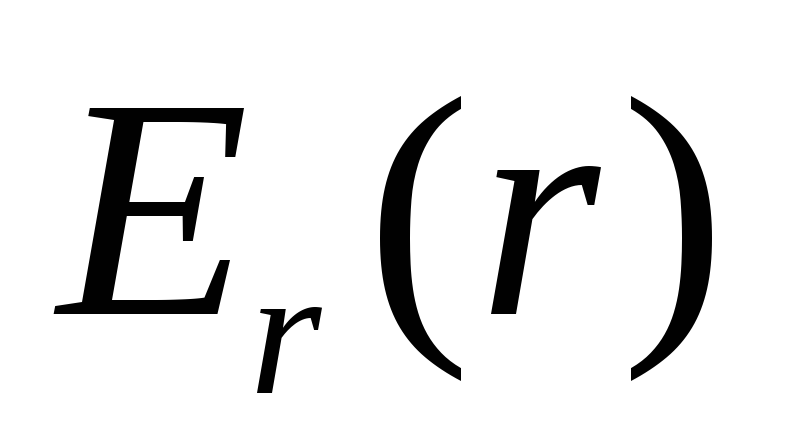 ,
где
,
где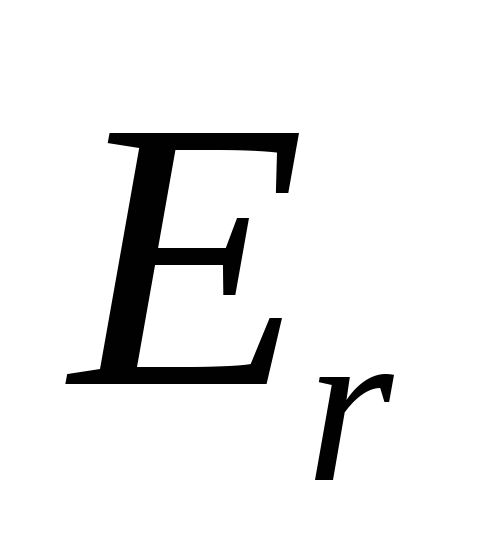 проекция вектора напряженности на осьr, проведенную из
центра сферы.
проекция вектора напряженности на осьr, проведенную из
центра сферы.
Решение.
Электрическое поле, порождаемое
сферически-симметричным распределением
заряда сферы, в любой точке пространства
направлено вдоль луча от центра сферы
и в равноудаленных точках имеет одинаковую
величину, т.е. 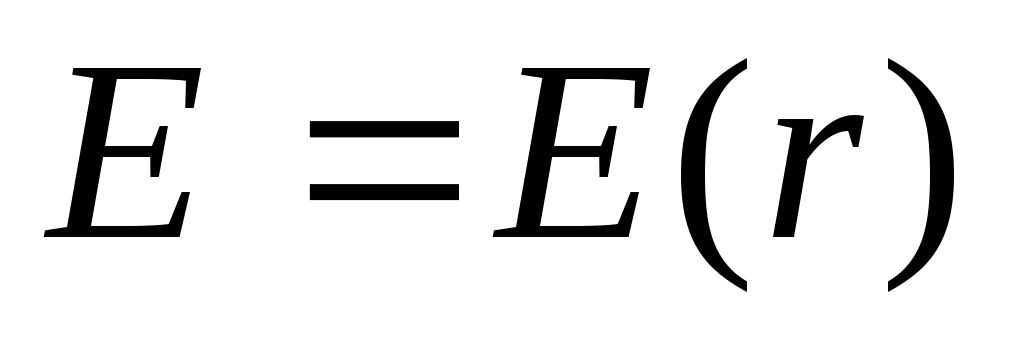 .
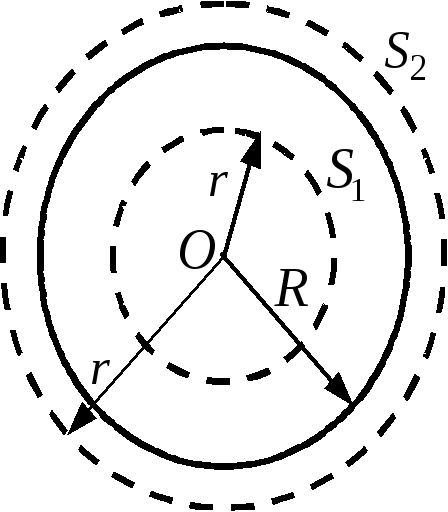
При таком свойстве симметрии поля в
качестве замкнутой гауссовой поверхности
возьмем концентрическую сферу радиуса
.
При таком свойстве симметрии поля в
качестве замкнутой гауссовой поверхности
возьмем концентрическую сферу радиуса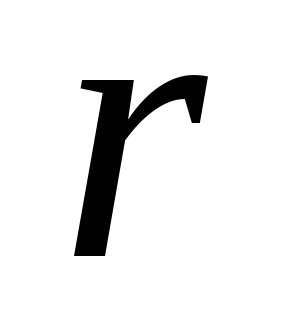 .
Поток сквозь выбранную поверхность
равен
.
Поток сквозь выбранную поверхность
равен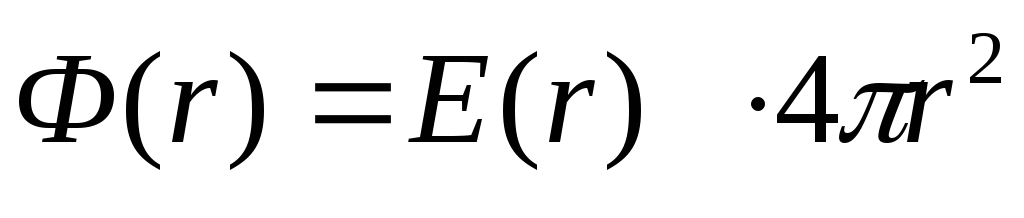 .
Согласно теореме Гаусса, он определяется
зарядом внутри гауссовой поверхности.
При
.
Согласно теореме Гаусса, он определяется
зарядом внутри гауссовой поверхности.
При заряд внутри поверхности равен заряду
сферы
заряд внутри поверхности равен заряду
сферы ,
а при
,
а при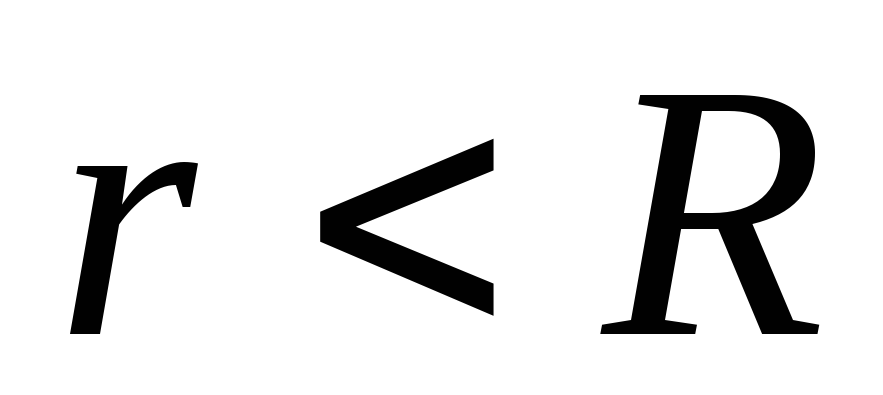 равен нулю. Поэтому:
равен нулю. Поэтому:
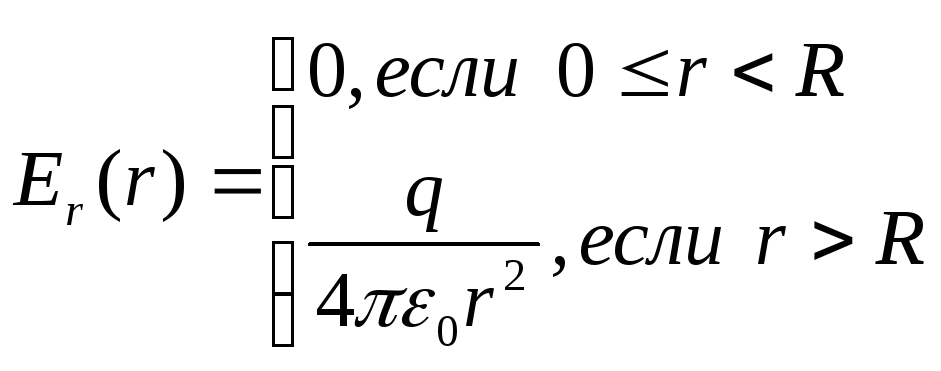
Знак заряда  определяет знак проекции
определяет знак проекции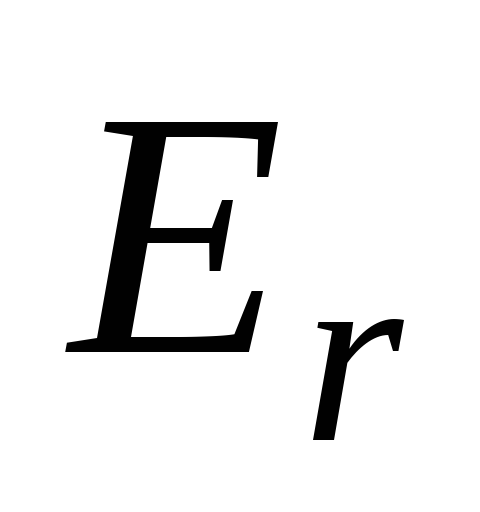 ,
а следовательно и направление самого
вектора
,
а следовательно и направление самого
вектора .
Он направлен от центра заряженной сферы
(
.
Он направлен от центра заряженной сферы
(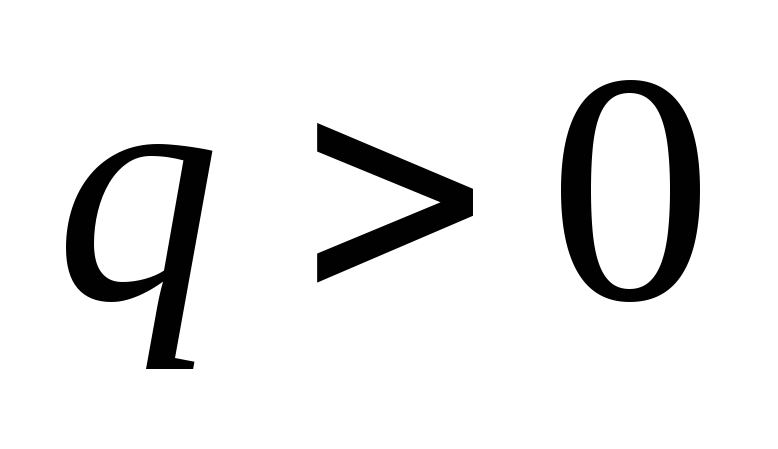 )
или к центру (
)
или к центру (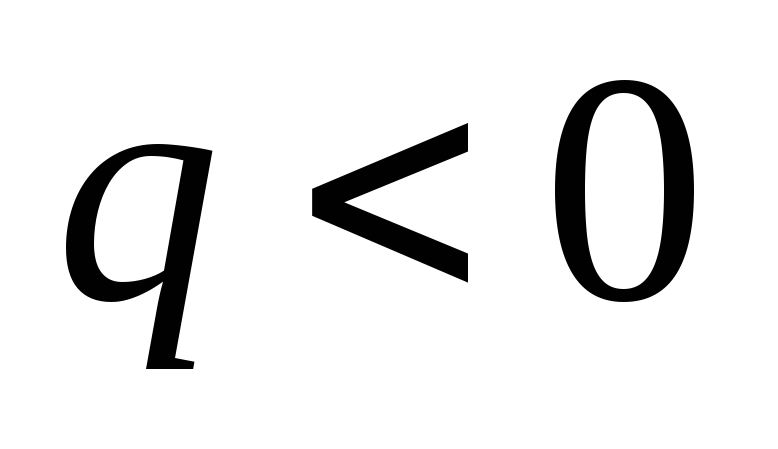 ).
Внутри однородно заряженной сферической
поверхности электрическое поле
отсутствует. График зависимости проекции
вектора напряженности
).
Внутри однородно заряженной сферической
поверхности электрическое поле
отсутствует. График зависимости проекции
вектора напряженности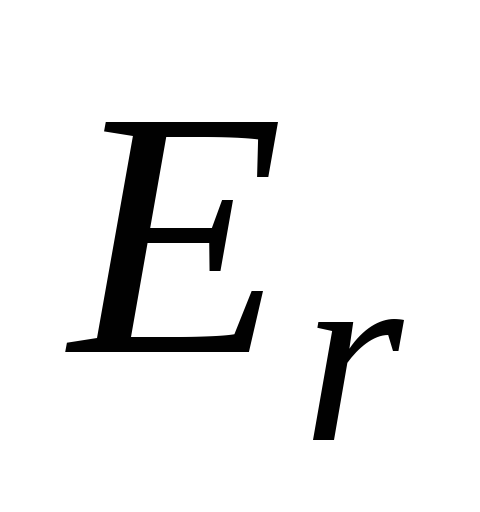 на ось
на ось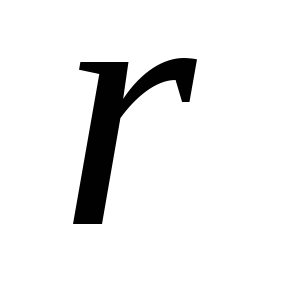 ,
проведенную из центра сферы, показан
на Рис. 1 в предположении
,
проведенную из центра сферы, показан
на Рис. 1 в предположении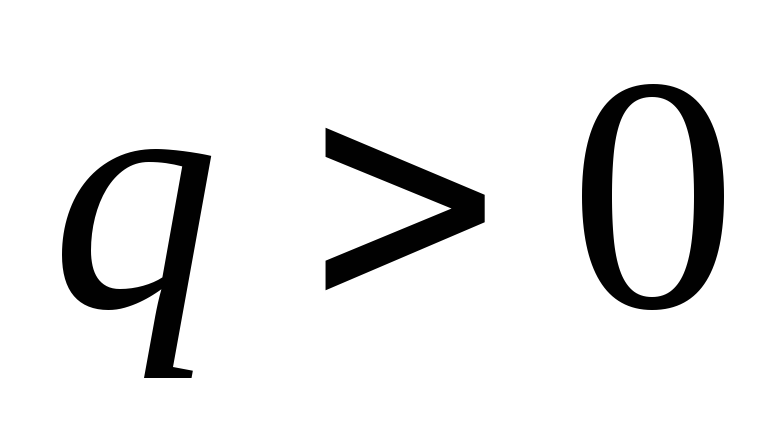 .
.
|
Рис 1 |
Электрическое поле заряженного шара
Пример 2.3.
По объему шара 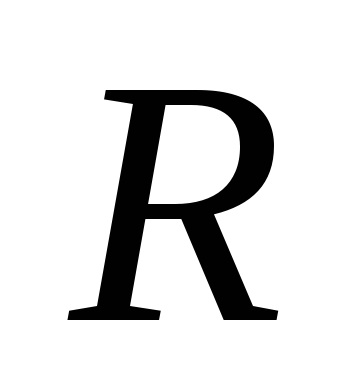 однородно
распределен заряд
однородно
распределен заряд .
Пренебрегая влиянием вещества шара,
определите напряженность электрического
поля в произвольной точке пространства
вне шара и внутри него. Полученный
результат представьте на графике
.
Пренебрегая влиянием вещества шара,
определите напряженность электрического
поля в произвольной точке пространства
вне шара и внутри него. Полученный
результат представьте на графике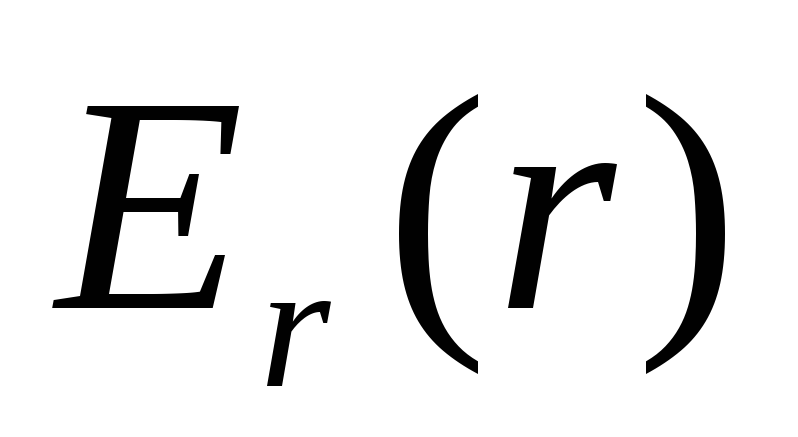 ,
где
,
где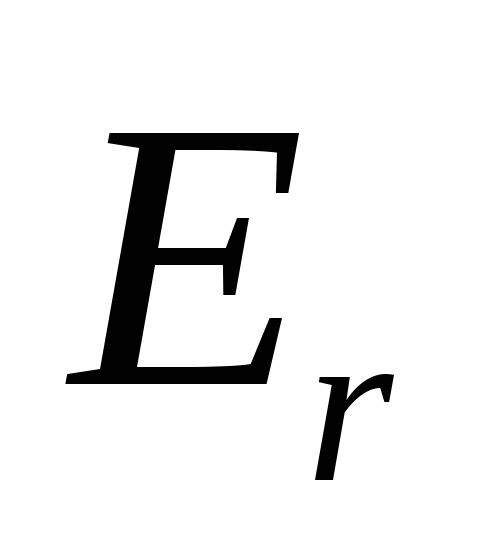 проекция вектора напряженности на осьr, проведенную из
центра шара.
проекция вектора напряженности на осьr, проведенную из
центра шара.
Решение.
Поле такой системы зарядов
центрально-симметричное, поэтому в
качестве гауссовой замкнутой поверхности
следует взять концентрическую сферу
радиуса 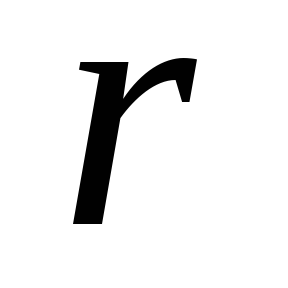 .
.
1) Найдем напряженность электрического
поля внутри шара 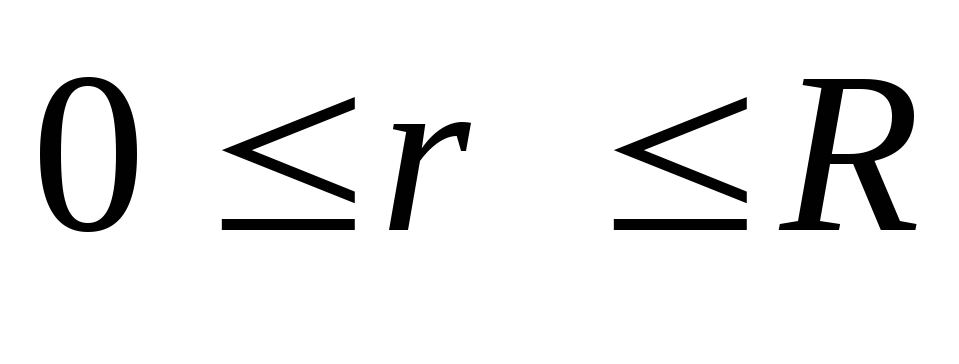 .
Векторы напряженности
.
Векторы напряженности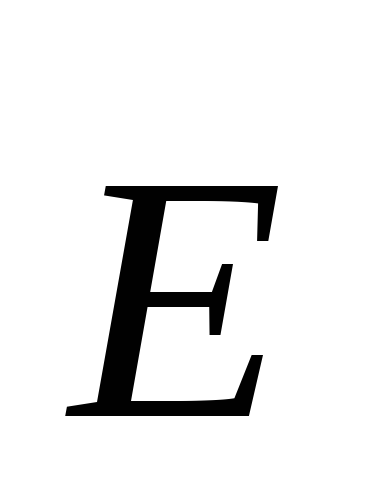 направлены по радиусам выбранной сферы,
а модули векторов
направлены по радиусам выбранной сферы,
а модули векторов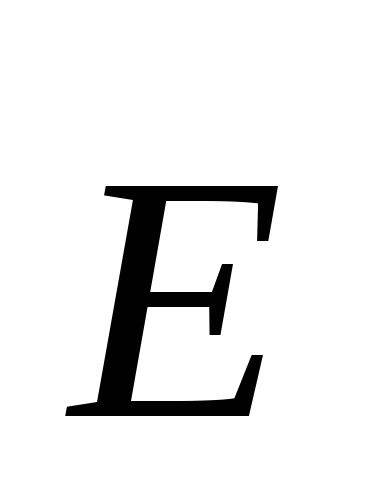 зависят только от расстояния
зависят только от расстояния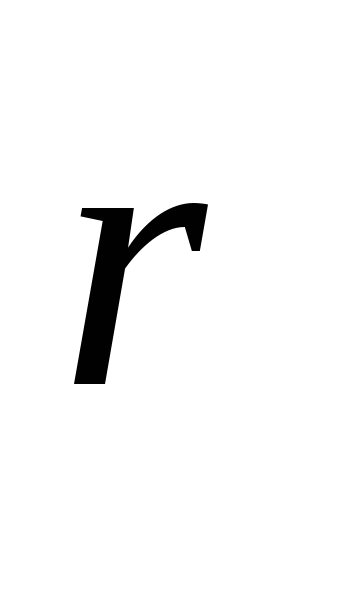 до центра сферы, то есть, одинаковы по
поверхности сферы. Поэтому поток поля
вектора
до центра сферы, то есть, одинаковы по
поверхности сферы. Поэтому поток поля
вектора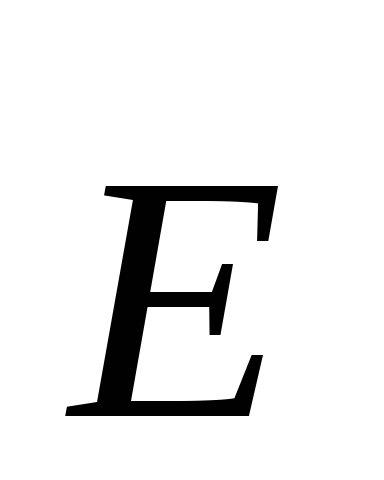 через выбранную сферу
через выбранную сферу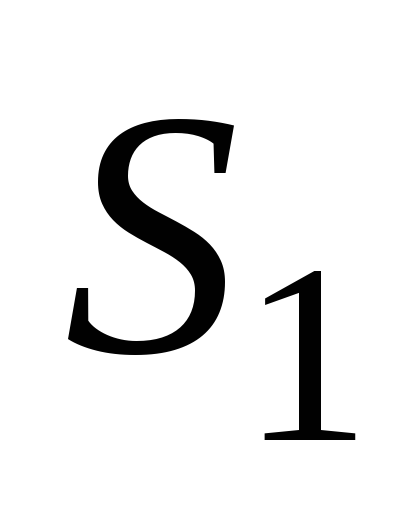 можно записать
можно записать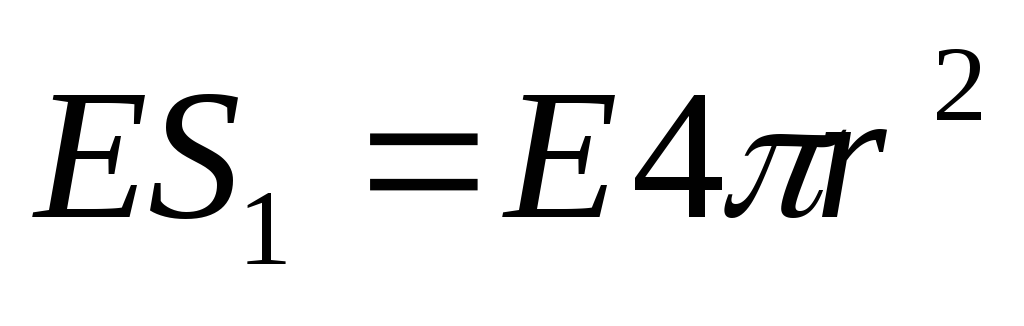 (Рис.2а).
(Рис.2а).
Заряд, охватываемый сферой 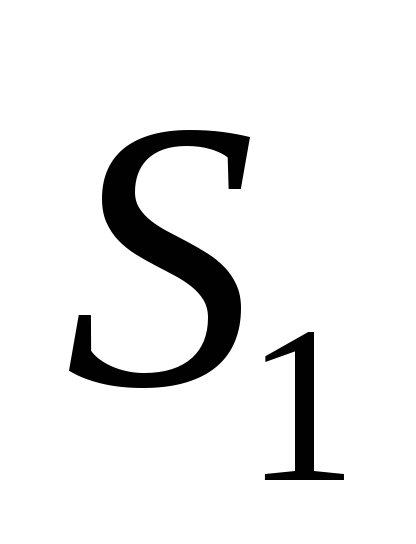 ,
равен
,
равен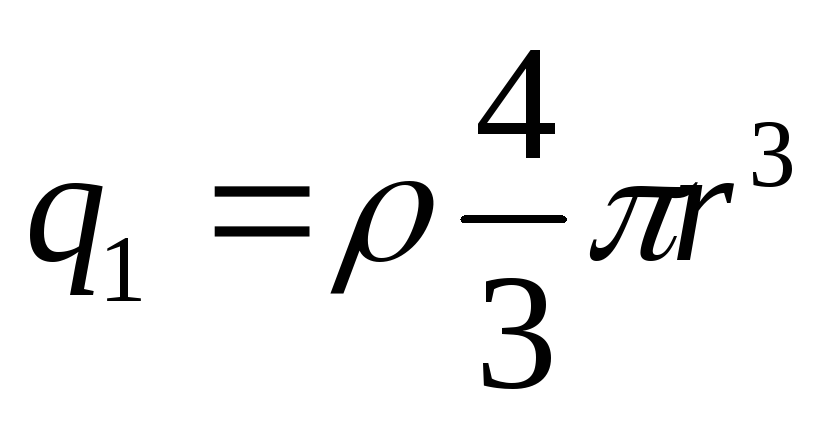 ,
где
,
где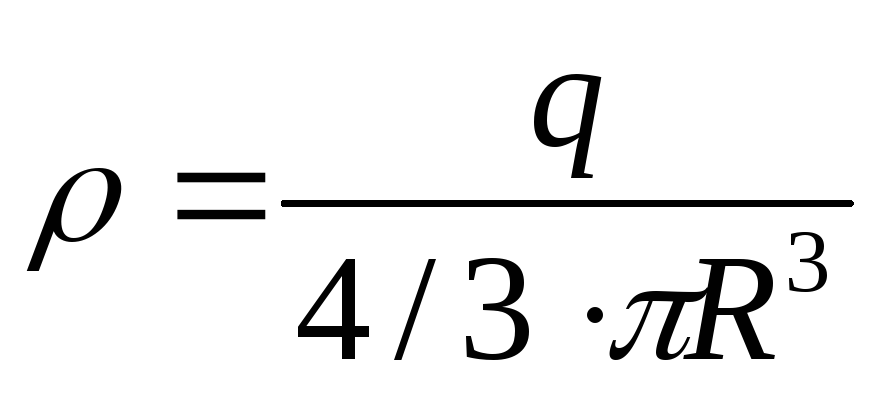 —
объемная плотность заряда. Согласно
теореме Гаусса
—
объемная плотность заряда. Согласно
теореме Гаусса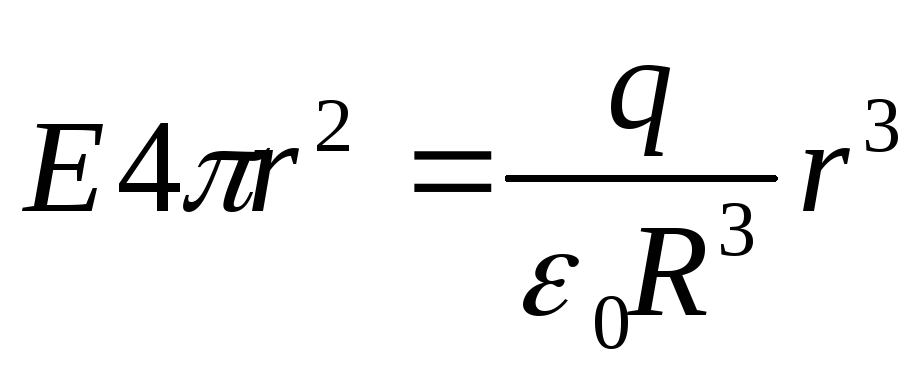 .
В результате напряженность поля внутри
однородно заряженного шара равна:
.
В результате напряженность поля внутри
однородно заряженного шара равна:
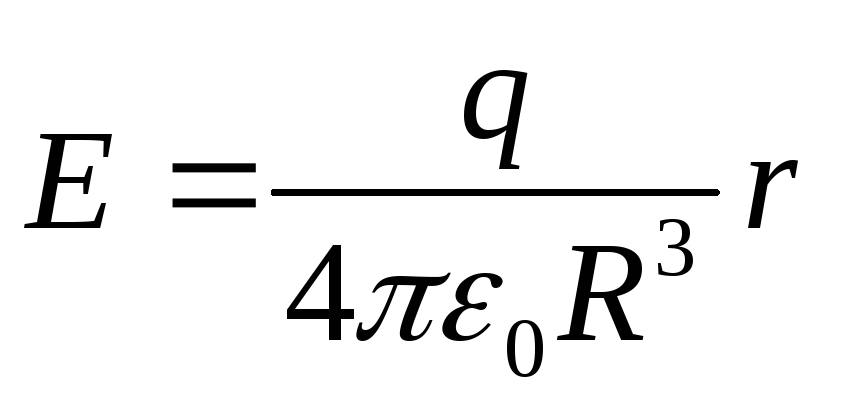 ,
,
т.е. поле  внутри
шара возрастает по линейному закону от
нуля в центре до значения
внутри
шара возрастает по линейному закону от
нуля в центре до значения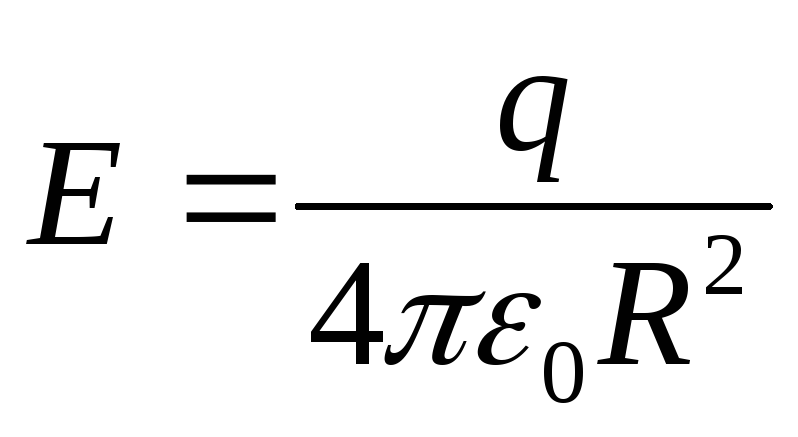 на
его поверхности.
на
его поверхности.
2) Найдем напряженность электрического
поля вне шара 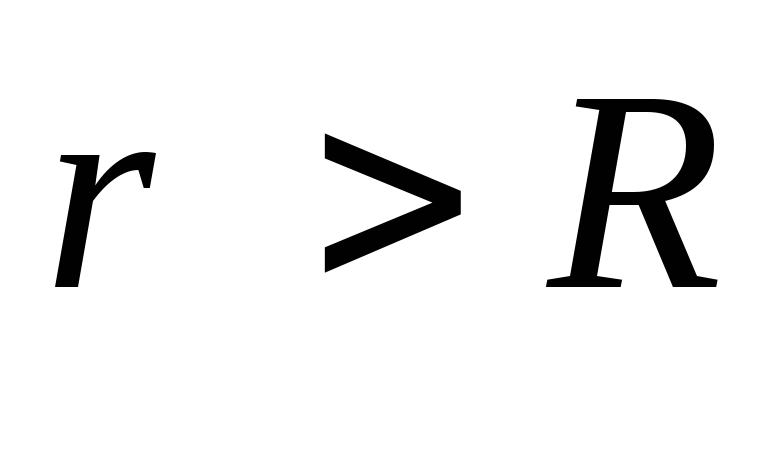 .
Свойство симметрии поля остается
неизменным. Поэтому гауссову поверхность
представим концентрической сферой
.
Свойство симметрии поля остается
неизменным. Поэтому гауссову поверхность
представим концентрической сферой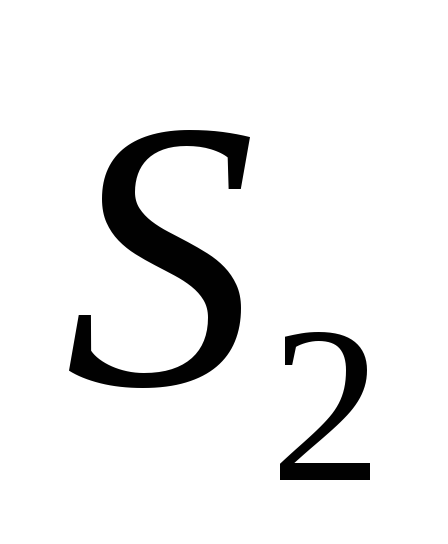 радиуса
радиуса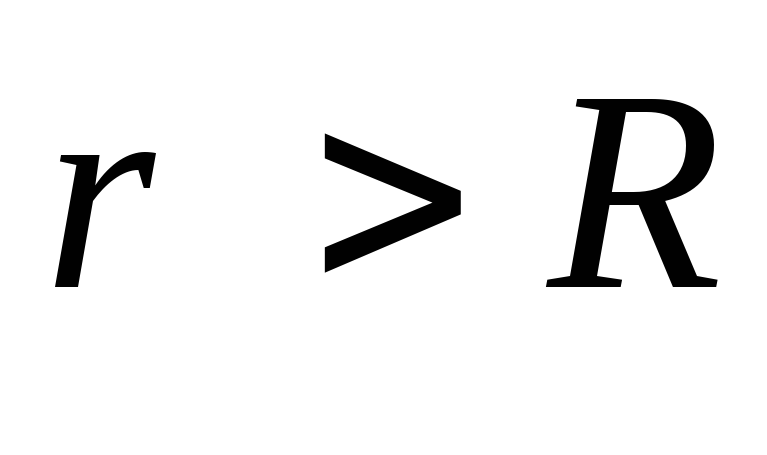 (Рис.2а). Согласно теореме Гаусса имеем:
(Рис.2а). Согласно теореме Гаусса имеем: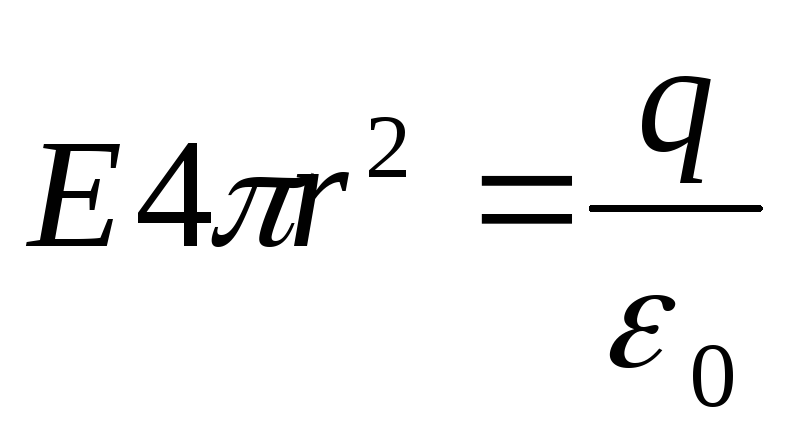 ,
где
,
где заряд шара. Для величины напряженности
поля получим:
заряд шара. Для величины напряженности
поля получим:
 .
.
Поле  вне однородно заряженного шара убывает
обратно пропорционально
вне однородно заряженного шара убывает
обратно пропорционально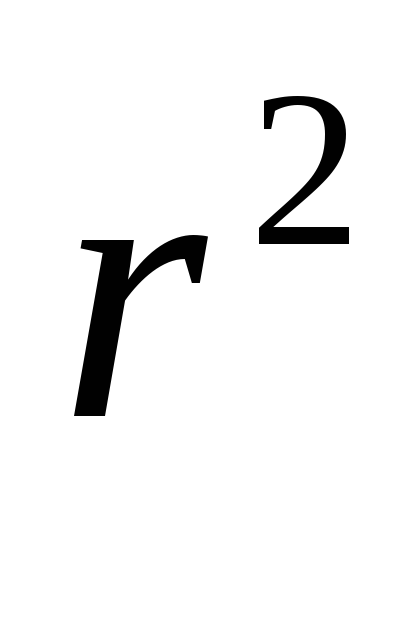 .
.
Объединяя полученные зависимости, запишем:
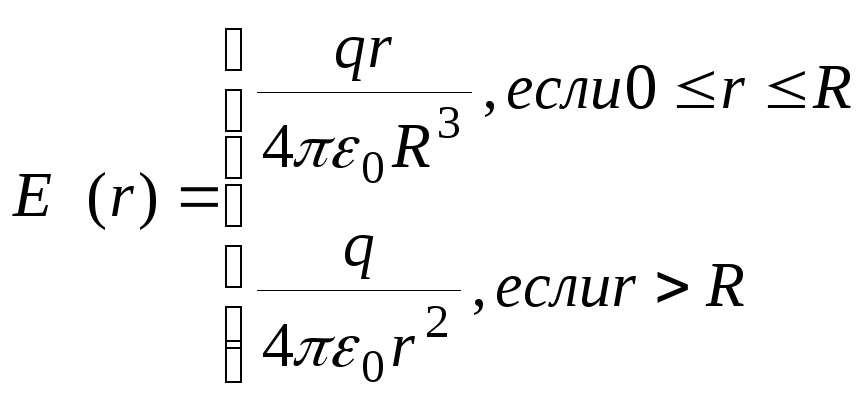 .
.
График зависимости проекции вектора
напряженности 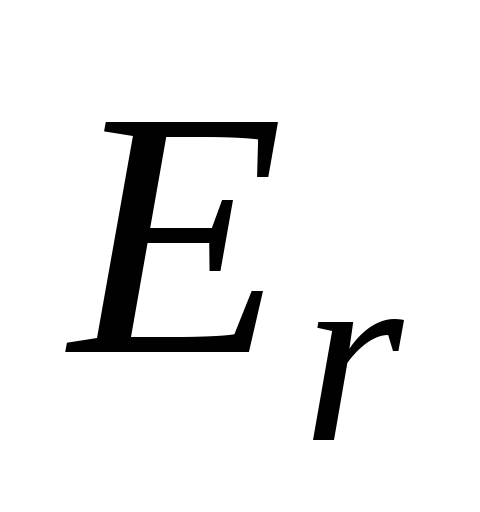 на ось
на ось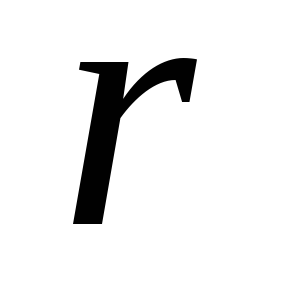 ,
проведенную из центра шара, представлен
на Рис. 2б.
,
проведенную из центра шара, представлен
на Рис. 2б.


Рис.2а
Рис.2б
Пример 2.4.
Шар заряжен однородно с объемной
плотностью  .
В шаре сделана сферическая полость,
положение центра которой характеризуется
радиусом-вектором
.
В шаре сделана сферическая полость,
положение центра которой характеризуется
радиусом-вектором (этот вектор проведен из центра шара в
центр полости). Найти поле
(этот вектор проведен из центра шара в
центр полости). Найти поле в полости.
в полости.
Решение.
Представим, что имеем два шара с центрами
в точках 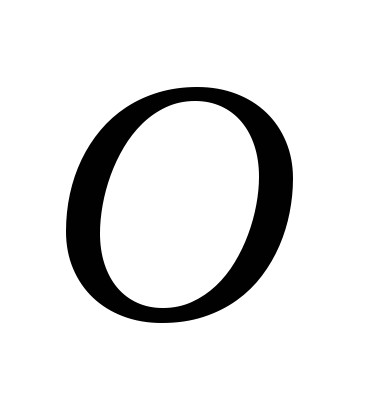 и
и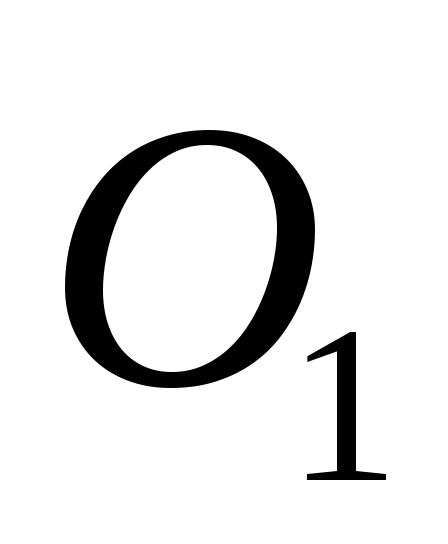 ,
заряженные однородно с объемной
плотностью
,
заряженные однородно с объемной
плотностью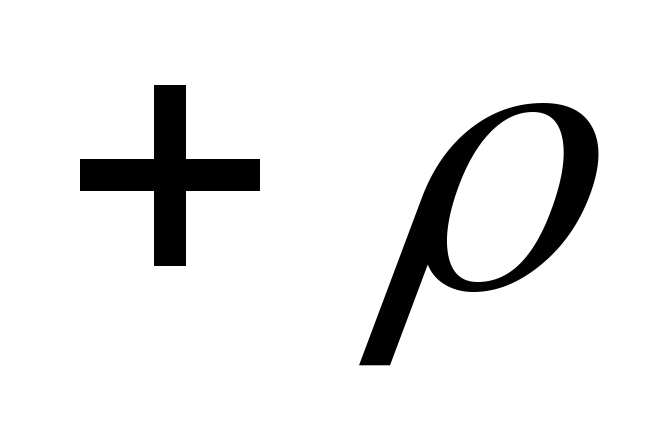 первый и
первый и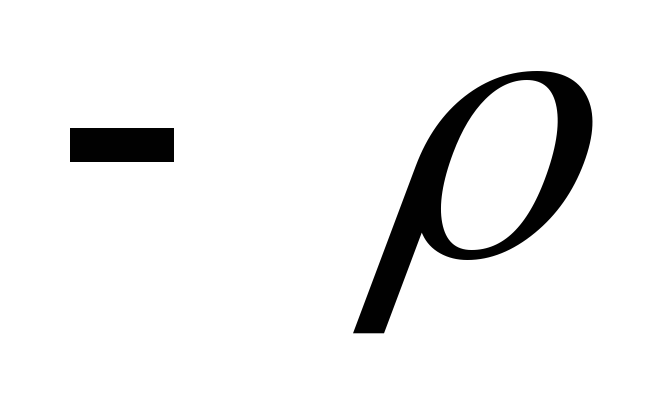 второй. Выберем произвольную точку
второй. Выберем произвольную точку ,
которая принадлежит обоим шарам.
Воспользовавшись решениемпримера
2.3., для первого шара в точке
,
которая принадлежит обоим шарам.
Воспользовавшись решениемпримера
2.3., для первого шара в точке поле равно:
поле равно:
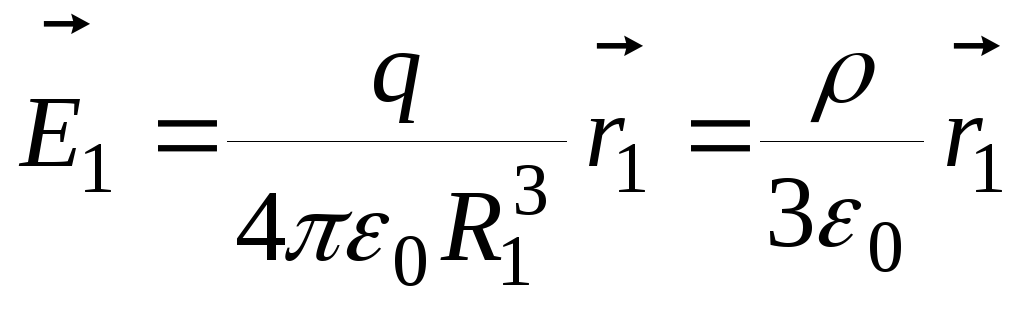 (
(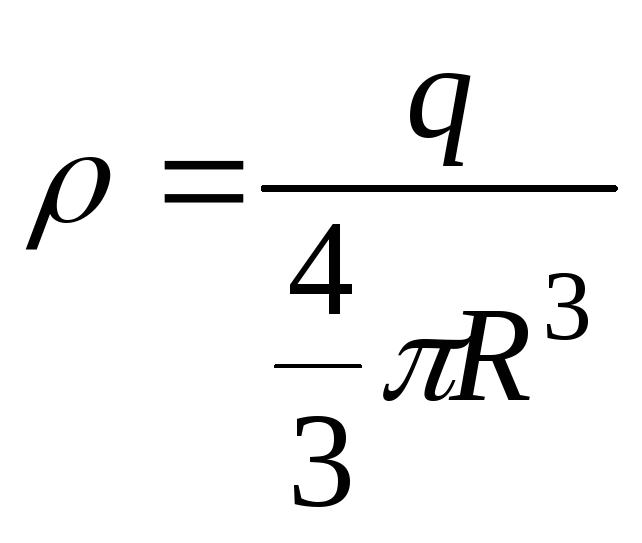 ).
).
Для второго шара в точке  поле равно:
поле равно:
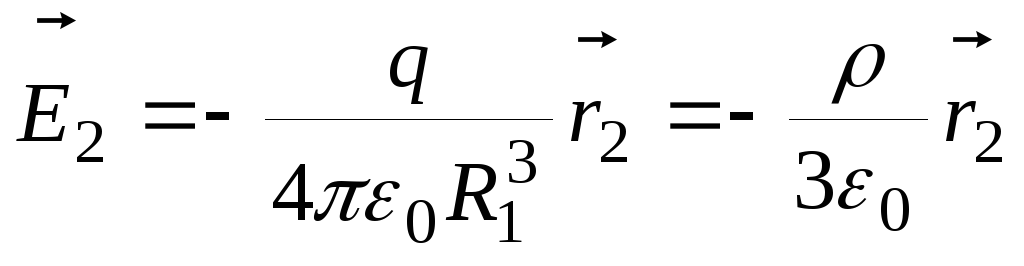 .
.
|
Рис.3 |
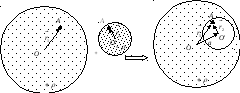
Чтобы определить напряженность поля в
полости наложим распределение зарядов
двух шаров, как показано на Рис.3. Тогда
по принципу суперпозиции найдем поле
в полости: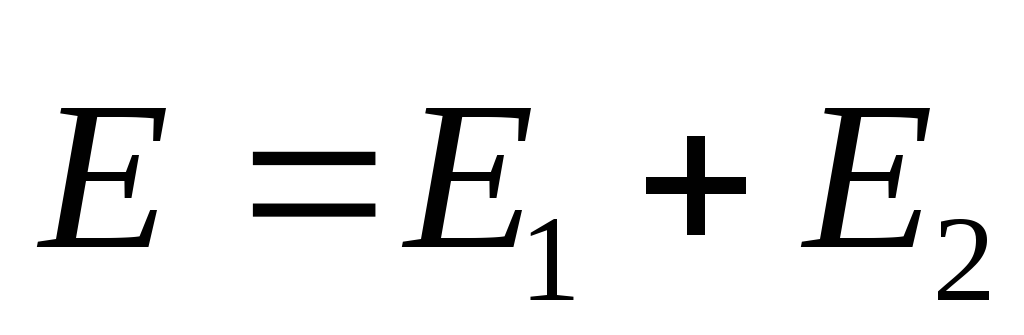
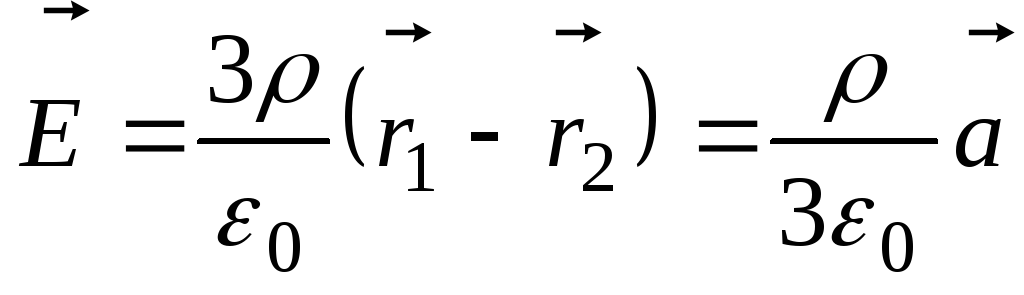 .
.
Заметим, что поле внутри полости однородно
заряженного шара оказывается однородным,
а его величина и направление определяется
вектором смещения  .
.
Пример 2.5.
Шар радиуса 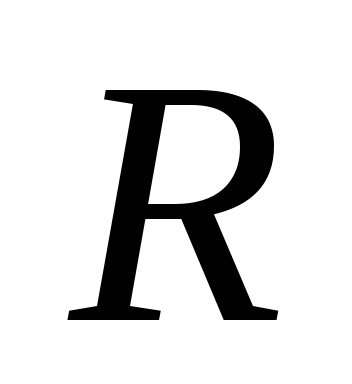 имеет положительный заряд, объемная
плотность которого зависит от расстоянияrдо его центра как
имеет положительный заряд, объемная
плотность которого зависит от расстоянияrдо его центра как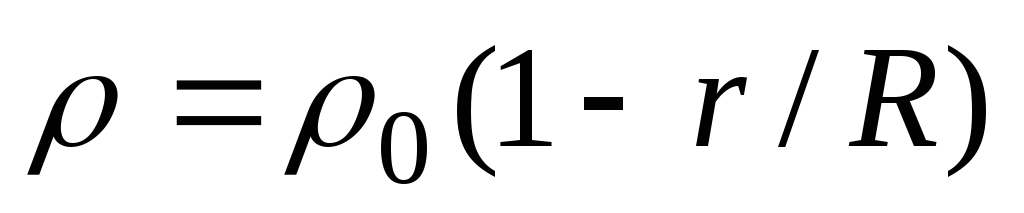 ,
где
,
где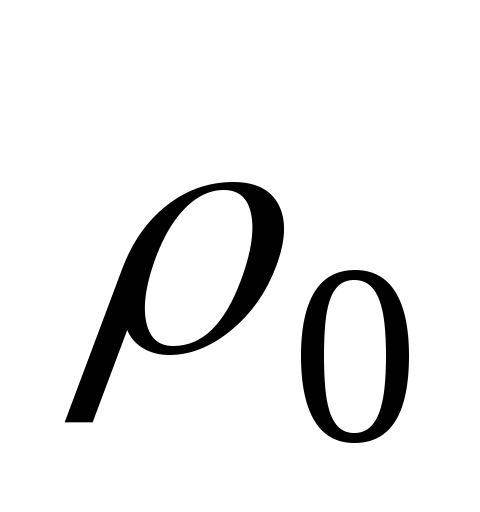 — положительная постоянная. Пренебрегая
влиянием вещества шара, найдите модуль
вектора напряженности электрического
поля внутри и вне шара как функциюr.
— положительная постоянная. Пренебрегая
влиянием вещества шара, найдите модуль
вектора напряженности электрического
поля внутри и вне шара как функциюr.
Решение.
Поле этой системы зарядов центрально-симметричное, поэтому в качестве замкнутой гауссовой поверхности выберем сферу, концентрическую с шаром.
1) Для нахождения поля вне шара радиус
сферы 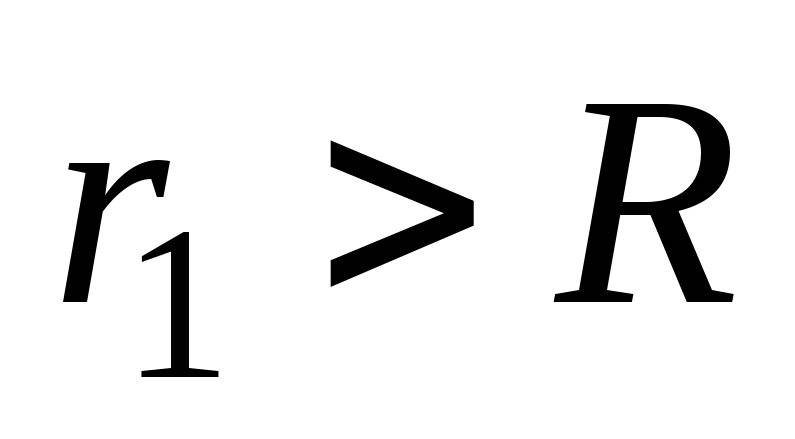 ,
согласно теореме Гаусса:
,
согласно теореме Гаусса:
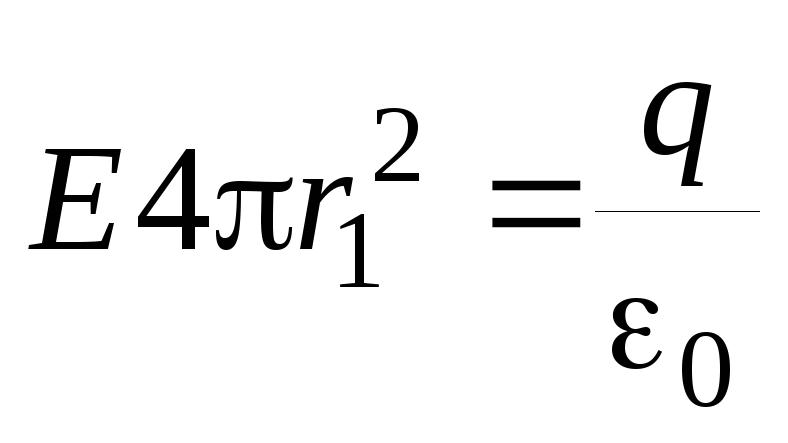 ,
,
где  полный заряд шара. Чтобы найти
полный заряд шара. Чтобы найти ,
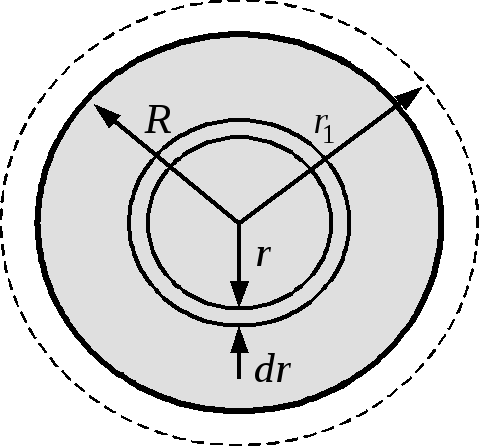
мысленно представим шар в виде набора
бесконечно тонких шаровых слоев радиуса
,
мысленно представим шар в виде набора
бесконечно тонких шаровых слоев радиуса ширины
ширины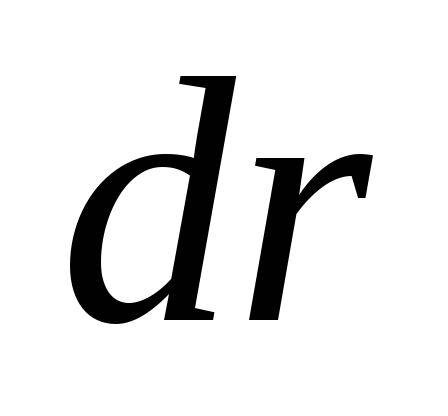 (Рис.4а). Объем шарового слоя
(Рис.4а). Объем шарового слоя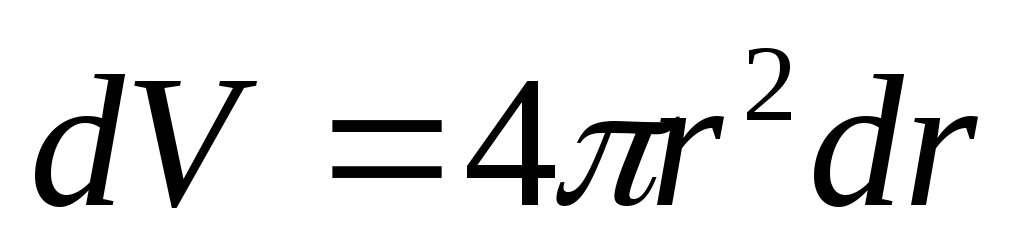 ,
тогда
,
тогда ,
а
,
а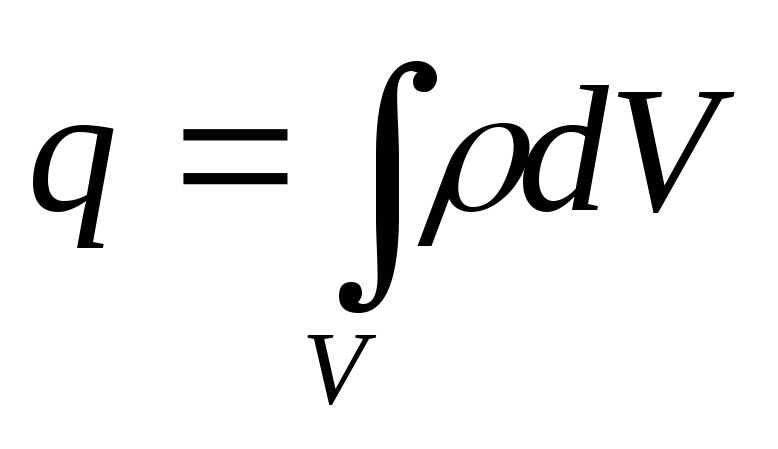 .Интегрируя,
получим:
.Интегрируя,
получим:
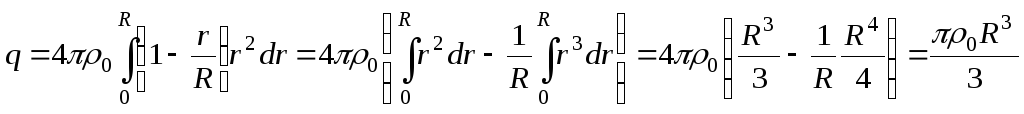
Подставив полученное выражение для  в правую часть соотношения для потока,
получим напряженность поля вне шара:
в правую часть соотношения для потока,
получим напряженность поля вне шара:
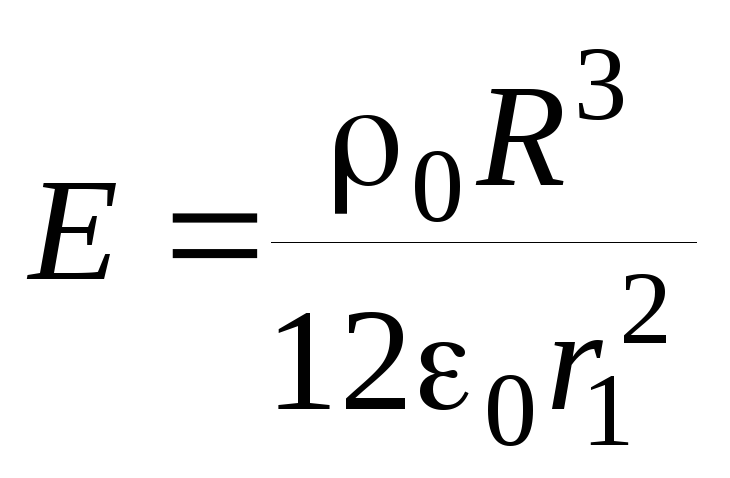 .
.
2) Найдем напряженность электрического
поля внутри шара. В качестве замкнутой
гауссовой поверхности снова выберем
сферу, концентрическую с шаром, радиус
которой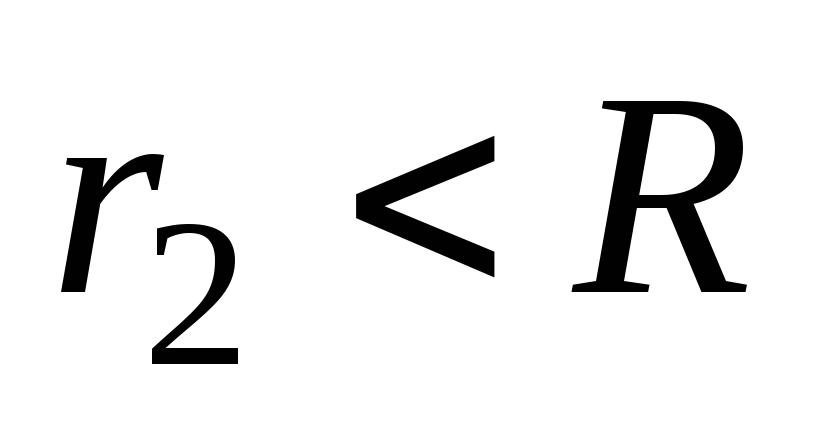 (рис.4б).
(рис.4б).
Согласно теореме Гаусса
 ,
,
где 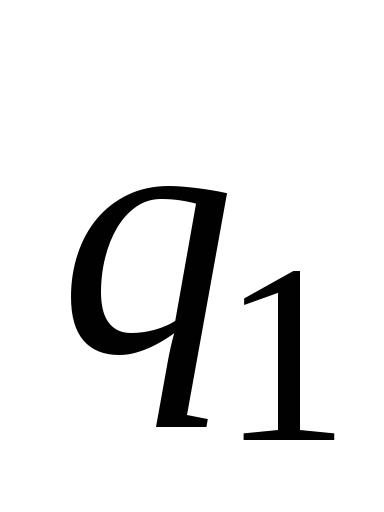 заряд внутри выбранной сферы. Величину
заряд внутри выбранной сферы. Величину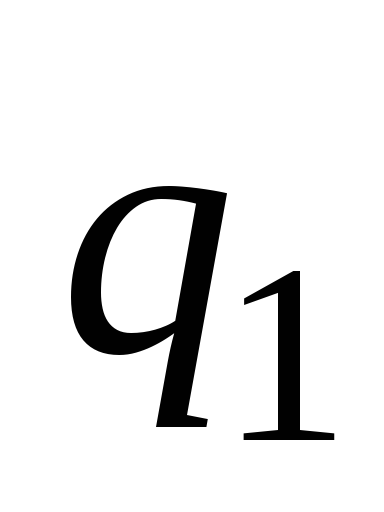 найдем также как и в пункте 1), подставив
соответствующие пределы интегрирования:
найдем также как и в пункте 1), подставив
соответствующие пределы интегрирования:
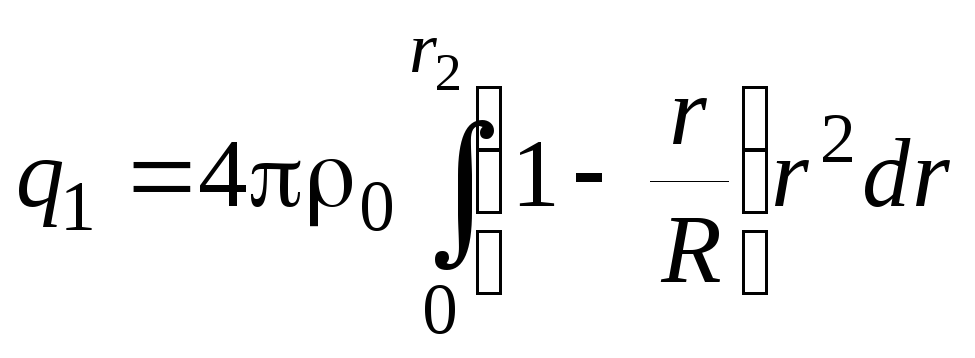
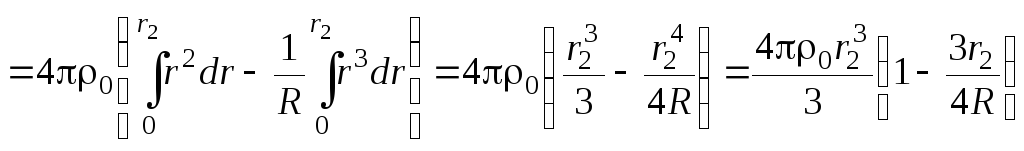 .
.
Подставив величину заряда 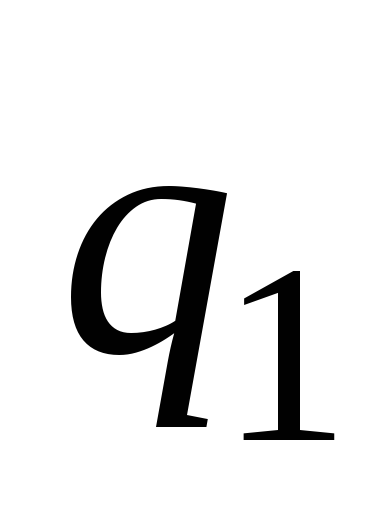 в соотношение для потока, найдем:
в соотношение для потока, найдем:
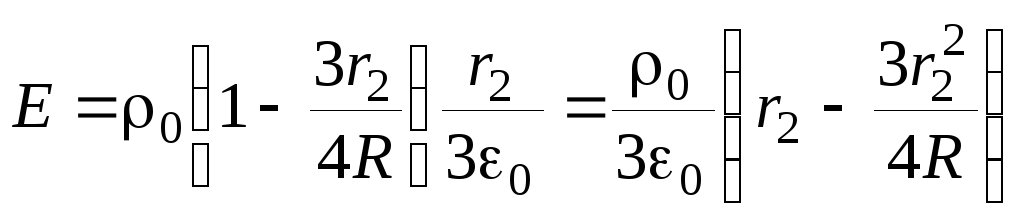 .
.
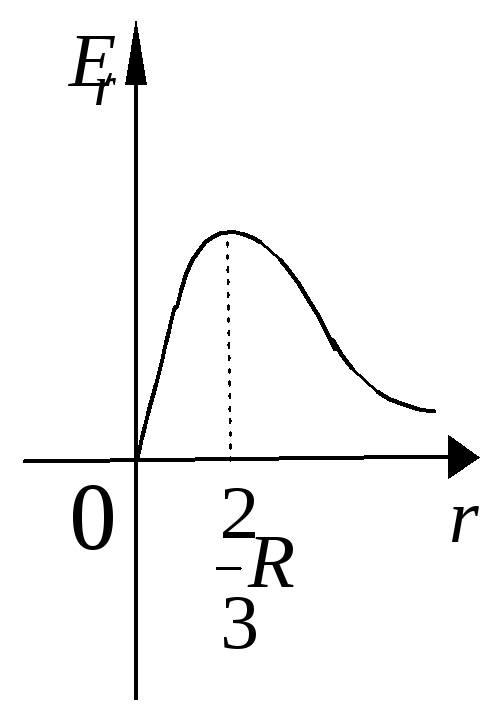
График зависимости проекции вектора 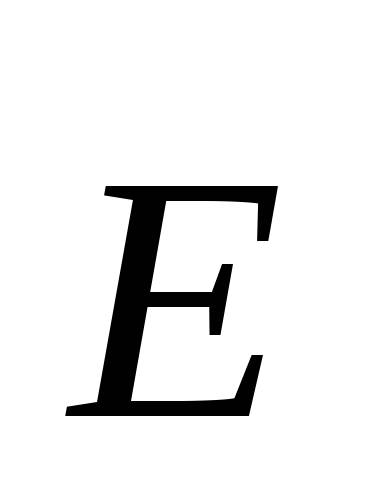 на ось
на ось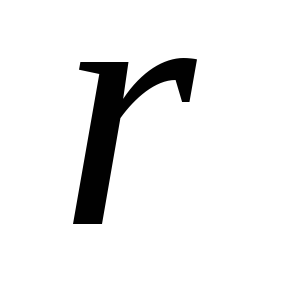 ,
проведенную из центра шара, показан на
Рис.4в, из которого видно, что напряженность
достигает максимума на расстоянии
,
проведенную из центра шара, показан на
Рис.4в, из которого видно, что напряженность
достигает максимума на расстоянии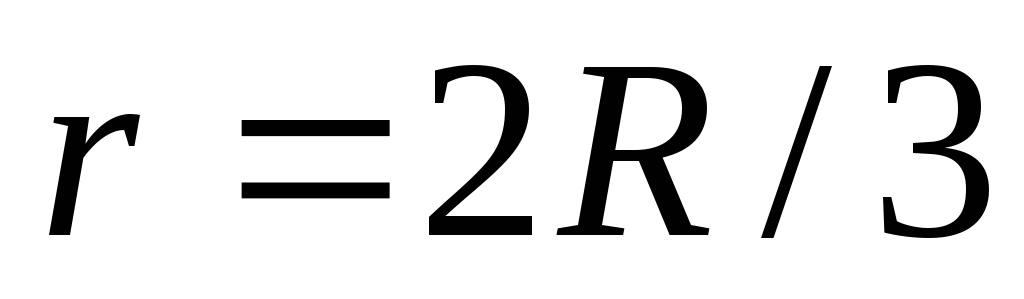 от центра шара.
от центра шара.
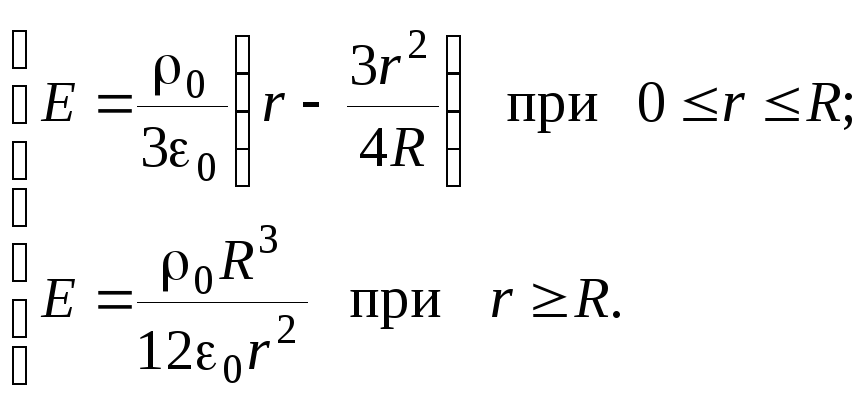
|
|
|
Рис.4а | Рис.4б | Рис.4в |