Электричество и магнетизм

Теорема установлена М.В. Остроградским (рис. 1.33) в виде общей математической теоремы для любого векторного поля и К. Гауссом — применительно к электростатическому полю.

 Рис. 1.33. М. Острогра́дский (1801–1861) — российский математик и механик 

Закон Кулона и принцип суперпозиции позволяют вычислить потенциал поля любого распределения заряда                    

 .

Используя связь  или непосредственно с помощью закона Кулона и принципа суперпозиции, можно вычислить и напряженность поля             

 

Однако, практическое вычисление написанных выше сумм и интегралов далеко не всегда так просто, как просто выглядят сами суммы и интегралы. Они вычисляются достаточно непринужденно, когда зарядов два, три, может быть, десяток. Если же речь идет о макроскопических заряженных телах, когда число точечных зарядов (протонов, электронов и т. п.) макроскопически велико, прямое вычисление подобных выражений становится очень сложной задачей.

В первую очередь это касается написанных выше сумм, а не интегралов.

Мы хотим подчеркнуть, что при решении макроскопических задач, в подавляющем большинстве случаев, можно считать, что заряд распределён непрерывно, соответственно, вычислять надо не суммы, а интегралы. Поэтому встает задача: на базе закона Кулона и принципа суперпозиции, написать интегральные и/или дифференциальные уравнения, которым удовлетворяет напряженность поля произвольного распределения зарядов. Эту задачу в ряде случаев успешно решает обсуждаемая в этом параграфе теорема Гаусса для вектора . 

Рассмотрим некоторую поверхность  и на ней бесконечно малый участок (бесконечно малую площадку) площадью  (рис. 1.34).  

Рис. 1.34. Бесконечно малый участок поверхности

 Показанный на рисунке «вектор площадки»  имеет следующий смысл: 1) он направлен по нормали  к поверхности  в той её точке, в окрестности которой находится площадка; 2) его модуль равен площади площадки . Вектор , а вместе с ним и вектор  всегда направлены по перпендикуляру к поверхности в данном её месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается  на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен.

Здесь и ниже, если иное специально не оговорено, будут использоваться указанные выше общепринятые правила: внешняя нормаль и правый винт.

Введём в рассмотрение поток  произвольного вектора  через выбранную площадку. По определению:

Поток  вектора  через бесконечно малую площадку  есть скалярное произведение вектора  на вектор площадки :

Формально рассматривается бесконечно малая площадка, фактически (например, при численном суммировании) она должна быть настолько мала, чтобы в её пределах вектор  можно было считать неизменным (однородным), а саму площадку плоской, тогда не возникает проблемы, в какой точке внутри площадки проводить нормаль к ней.

Для общности определения (в физике рассматриваются потоки и других векторов) выше был рассмотрен произвольный вектор , применительно к вектору напряженности электрического поля , с учетом замечания о размерах площадки, определение потока иллюстрирует рис.

1.35.

 Рис. 1.35. Поток вектора напряженности электрического поля  через бесконечно малую площадку

 Согласно определению, поток вектора напряженности  через площадку  равен (здесь и в дальнейшем, для краткости, когда это будет удобным, будем писать: «площадка» и указывать при этом вектор  этой площадки, которым полностью определены и её площадь и ориентация):

(1.43)

где α — угол между векторами  и ,   — нормальная к поверхности составляющая вектора . Подчеркнем, что изменение направления нормали   как и изменение направления  вектора  напряженности на обратное меняет знак потока на противоположный, таким образом, поток вектора — величина алгебраическая. 

Поток вектора  через произвольную поверхность S равен сумме потоков через все площадки, на которые разбита поверхность S, то есть интегралу по этой поверхности вида: 

(1. 32)

Если векторное поле  однородно, то есть  , а поверхность плоская, то  

 

Здесь S — площадь этой поверхности. Для обозначения интеграла по замкнутой поверхности используется специальный значок интеграла, а именно: с кружком в середине (S — замкнутая поверхность) (рис. 1.36):

   

Рис. 1.36. Поток вектора напряженности электрического поля через замкнутую поверхность

 Для уяснения смысла такой величины как поток вектора весьма полезно, в силу наглядности, рассмотрение потока жидкости, например, в реке или в трубе.

 Пусть, для простоты несжимаемая жидкость, с плотностью  течет со скоростью . Указание зависимости вектора скорости от координат точки и времени означает задание векторного поля, в данном случае: поля вектора скорости . Как и всякое векторное поле, поле  скоростей удобно изобразить с помощью линий поля, которые в данном случае принято называть «линиями тока». По определению, в любой точке вектор скорости жидкости направлен по касательной к линии тока. Выделим внутри жидкости площадку  (см. рис. 1.37) настолько малую, что скорость  во всех точках этой площадки можно считать одной и той же. Возьмем временной интервал  настолько малый, что скорость  за это время сколько-нибудь заметно измениться не успевает и поставим такой вопрос: «Какая масса  жидкости протекает сквозь площадку

 за время ?». Очевидно, что за указанное время сквозь площадку пройдут те частицы жидкости, которые были от неё не дальше (вдоль потока), чем на расстоянии . Более дальние, имея скорость , просто не успеют «добраться» до площадки за интересующее нас время .

Рис. 1.37. К выводу соотношения для потока вектора

На рисунке выше жидкость, которая успеет за время  пересечь площадку , занимает заштрихованный объём ^{, величина которого, как видно из рисунка равна  . Соответственно, масса жидкости проходящей сквозь площадку}

 за время  равна 

 , где

В написанной выше формуле вектор  есть характеристика именно потока жидкости, определяемая её плотностью и скоростью течения. Величины  и  являются параметрами «постановки эксперимента». При том же потоке жидкости можно рассмотреть другую площадку и выбрать другое время регистрации массы. Вектор  называется вектором плотности потока массы. Единица его измерения  наглядно демонстрирует его физический смысл: величина вектора показывает, сколько килограмм жидкости протекает за секунду через квадратный метр площадки перпендикулярной потоку. Такой же смысл имеют его проекции на оси, с тем отличием, что  численно равно массе жидкости протекающей за секунду сквозь квадратный метр площадки перпендикулярной оси

ОХ,  – … оси ОУ  и так далее.

Если разделить  на плотность  получится  — вектор плотности потока объёма, измеряемый в  . Модуль этого вектора численно равен числу кубометров жидкости проходящих за секунду сквозь квадратный метр площадки перпендикулярной потоку жидкости. Знание этого вектора требуется, например, при расчете пропускной способности газо- или нефтепровода, как впрочем, и водопровода.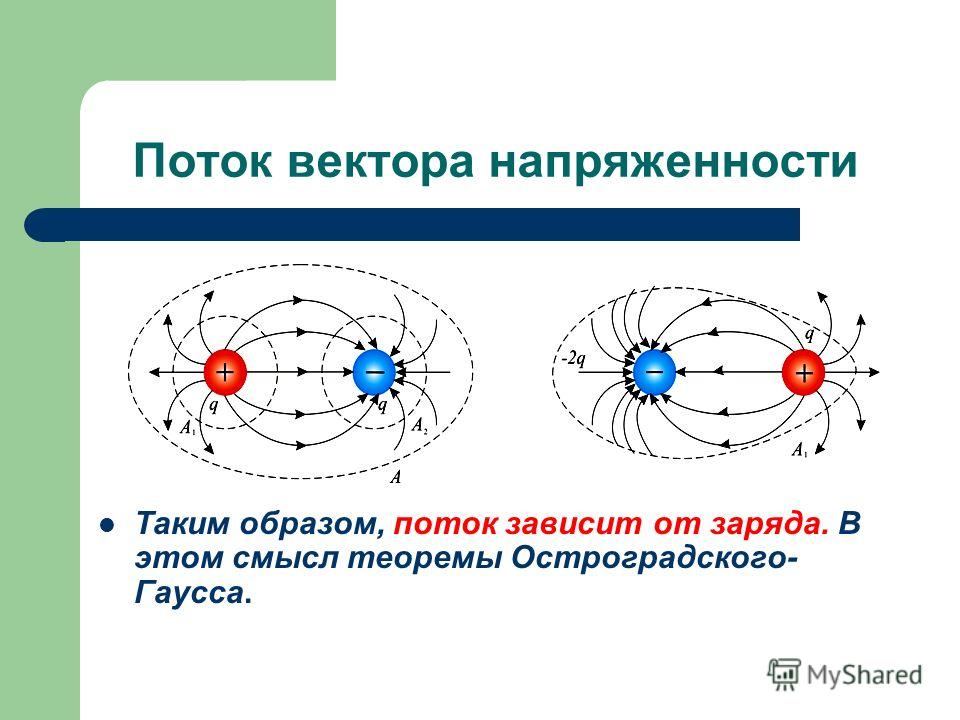

Доказанная ниже теорема Гаусса для вектора  (см. соотношение ) показывает, что источниками электростатического поля являются электрические заряды. 

Рассмотрим для начала частный, но очень простой, пример прямого вычисления потока вектора через поверхность. 

Пример 6. Полусфера радиусом R с плоским основанием помещена в постоянное однородное электрическое поле E, перпендикулярное основанию полусферы (рис. 1.38). Найти поток вектора напряженности через основание полусферы, саму полусферу  и через всю замкнутую поверхность этого тела. 

 Рис. 1.38. Пример расчета потока вектора напряженности электрического поля 

Решение. Проще всего рассчитать поток  через основание полусферы. Направим ось z вдоль поля. Направление вектора внешней нормали к основанию обратно направлению вектора E. При этом вектор E одинаков во всех точках основания. Поток через основание получается равным взятому с обратным знаком произведению E  на площадь основания

 Найдем теперь поток напряженности через поверхность полусферы. Используя сферические координаты — углы  и  — для определения положения точки на полусфере, мы видим, что

и

 

Поэтому поток через элементарную площадку на полусфере равен  

Учитывая, что

а

записываем поток в виде

откуда находим полный поток через поверхность полусферы

 

Мы получили, что поток через поверхность полусферы равен по абсолютной величине потоку через ее основание, так что с учетом знаков полный поток через замкнутую поверхность равен нулю

. 

Теорема Гаусса для вектора  позволяет связать поток вектора напряженности через некоторую замкнутую поверхность с величиной зарядов, находящихся внутри этой поверхности.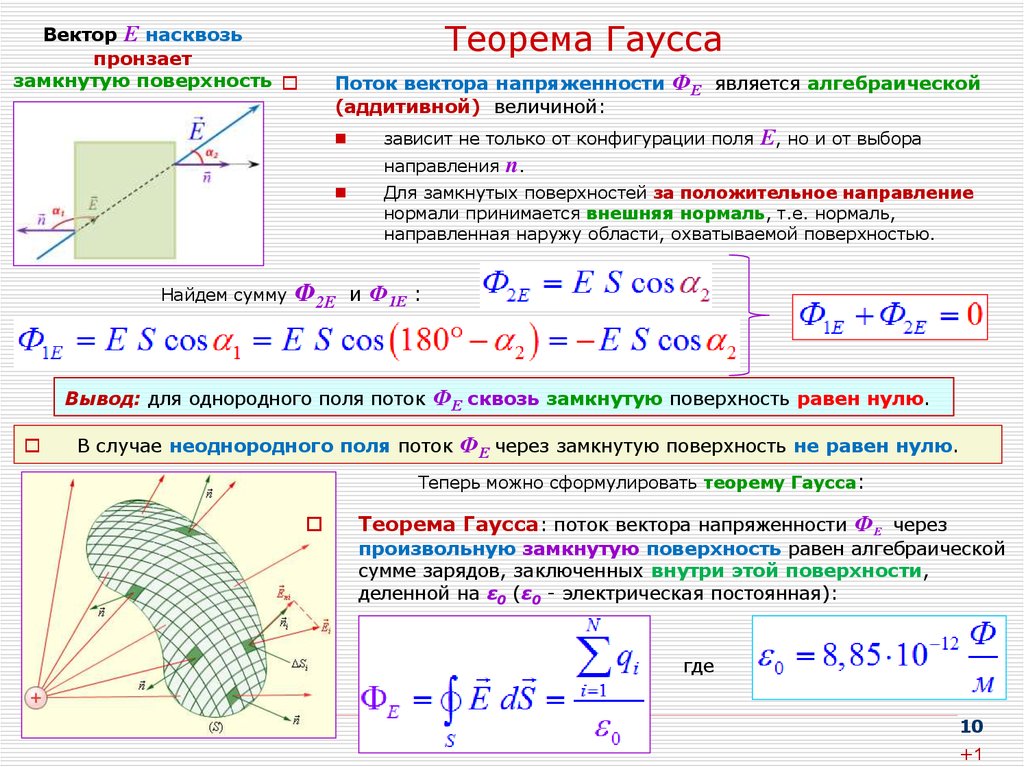 Рассмотрим для начала частный случай, а именно: определим поток вектора напряженности через произвольную воображаемую сферическую поверхность, в центре которой расположен точечный заряд. 

Линии напряжённости векторного поля  точечного заряда представляют собой радиальные прямые, направленные от заряда, если он положителен, и к заряду, если он отрицателен (см. рис. 1.12). Поток вектора напряженности поля точечного заряда через сферическую поверхность радиусом r, центр которой совпадает с положением заряда и началом координат, равен  

(1.33)

Здесь , где   — элемент телесного угла, мы воспользовались значением полного телесного угла

  

Можно показать, что поток вектора напряженности через любую замкнутую поверхность, охватывающую заряд q, не зависит от формы поверхности и равен  так же, как и для сферы. Физический смысл этого утверждения опять-таки заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности (показана на рис. 1.39-1 пунктиром) не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы  (см. рис. 1.39-1). 

 

Рис. 1.39. Поток вектора Е через замкнутую поверхность:
1 —  заряд находится внутри поверхности; 2 —  заряд находится вне поверхности  

Если же заряд находится вне ограниченного замкнутой поверхностью пространства, то линии напряжённости пронизывают поверхность чётное число раз (снаружи внутрь и изнутри наружу), в результате полный поток через поверхность, не охватывающую заряд, равен нулю (рис. 1.39-2). 

Вывод теоремы Гаусса для точечного заряда, расположенного в произвольной точке, приведен в Дополнении 5.

Пусть теперь внутри и вне данной замкнутой поверхности имеется произвольное число точечных зарядов любого знака. В силу принципа суперпозиции суммарная напряженность поля будет представлять собой векторную сумму напряженностей полей каждого из зарядов

 

Полный поток напряженности поля через эту поверхность есть

 

Используя , получаем соотношение, известное как теорема Гаусса для вектора : 

Поток вектора напряженности электрического поля через замкнутую поверхность равен полному заряду внутри этой поверхности делённому на                               (1.34)

Подчеркнем еще раз тривиальное, но важное обстоятельство: если внутри поверхности нет зарядов, то поток вектора  через эту поверхность равен нулю (рис. 1.40). Источниками электростатического поля являются электрические заряды и суммарная мощность источников электростатического поля внутри поверхности  равна . Присутствие в последней формуле электрической постоянной  есть результат выбора  системы единиц (СИ) и физического смысла не имеет.

Рис. 1.40. Если внутри поверхности нет зарядов, то поток вектора  через эту поверхность равен нулю 

При непрерывном распределении заряда по объёму теорему Гаусса естественно записать в следующем виде 

(1.35)

В правой части этого соотношения интеграл берется по объёму  ограниченному поверхностью , поток  через которую вычисляется в левой его части. При непрерывном распределении заряда по некоторой поверхности справа будет стоять интеграл вида  только по той части  несущей заряд поверхности, которая оказалась внутри поверхности , стоящей слева. При непрерывном распределении заряда вдоль некоторой линии  справа будет стоять интеграл вида  также только по той части  несущей заряд линии, которая оказалась внутри поверхности . Короче, необходимо любым приемлемым способом вычислить заряд внутри той замкнутой поверхности, по которой вычисляется поток вектора напряженности электрического поля.

Примеры расчёта полей, в которых главным инструментом является теорема Гаусса, даны в следующем разделе 1.5.

5/7

2.2. Поток вектора напряженности

Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью пронизывают некоторую площадкуS, топоток вектора напряженности(число силовых линий через площадку) будет определяться формулой

где E_n– произведение векторана нормальк данной площадке (рисунок 2.5).

Рисунок 2.5

Полное число силовых линий, проходящих через поверхность S, называется потоком вектора напряженности Ф_Е через эту поверхность.

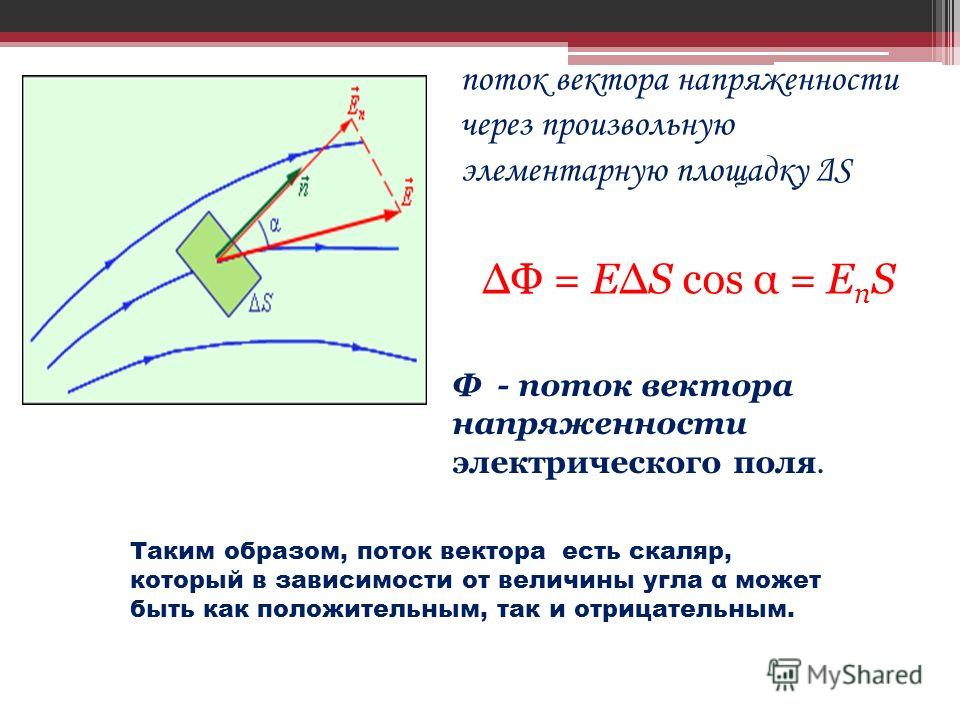
Элементарный поток вектора напряженности через площадку dS(рис. 5) определится соотношением:

,

где – проекцияна направление нормали.

В векторной форме можно записать – скалярное произведение двух векторов, где вектор.

Таким образом, поток вектора есть скаляр, который в зависимости от величины углаα может быть как положительным, так и отрицательным.

Полный поток вектора напряженности через любую площадку Sможно определить тогда, а поток через замкнутую поверхность, окружающую заряд или заряженное тело равен.

Так как напряженность поля, созданного в любой точке пространства зависит от величины заряда, создающего это поле, то поток вектора напряженности электростатического поля через любую площадку, находящуюся в этом поле также зависит от величины заряда.

Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.

Рисунок 2.6 Рисунок 2. 7

Для рисунка 2.6 – поверхность А₁ окружает положительный заряд и поток здесь направлен наружу, т.е.ПоверхностьА₂– окружает отрицательный заряд, здесьи направлен внутрь. Общий поток через поверхностьАравен нулю.

Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность Аотрицательный.

Таким образом, поток вектора напряженности зависит от заряда.

К.Ф. Гаусс (1777–1855) выдающийся немецкий математик, астроном и физик в 1839г. предложил теорему, которая устанавливает связь потока вектора напряженности электрического поля череззамкнутую поверхность со значением зарядаq, находящегося внутри этой поверхности.Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.

Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :

.

Докажем эту теорему. Пусть поле создается точечным зарядом q. Окружим заряд замкнутой поверхностьюSпроизвольной формы. Разобьем замкнутую поверхность на элементарные площадкиdS, к каждой из которых проведем вектор нормали.

Элементарный поток вектора напряженности через площадкуdS(рис. 2.8) определится соотношением:

,

где –проекцияна направление нормали. Тогда, где- элементарный телесный угол, под которым элементвиден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхностьSот точечного зарядаq, находящегося внутри этой поверхности.

,

так как , то

.

Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS₁иdS₂, находящиеся внутри телесного углаdΩ(рис. 2.9) равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Тогда , следовательно, поток напряженности электрического поля через любую поверхностьS, не охватывающую заряды равен нулю, т.е.Ф_Е=0.

Пусть внутри замкнутой поверхности имеется зарядов, тогда алгебраическим суммированием (согласно принципу суперпозиции) находим, что общий поток вектора напряженности через замкнутую поверхность равен .

Теорема доказана.

Таким образом теорему Гаусса можно сформулировать следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :

(1),

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то теорема Гаусса имеет вид:

(2)

где интеграл справа берется по объему V, охватываемому поверхностьюS.

Необходимо обратить внимание на следующее обстоятельство: в то время как само поле зависит от конфигурации всех зарядов, потоксквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхностиS. Это значит, чтоесли передвинуть заряды внутри замкнутой поверхности, тоизменится всюду, и на поверхностиS, апоток вектора через эту поверхность останется прежним.

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на , то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.

Рассмотрим примеры применения теоремы Гаусса.

Электрический поток | Определение и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Britannica Beyond
  Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Связанный контент

17.

1: Поток электрического поля

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

19487

• Howard Martin пересмотрено Аланом Нг
• University of Wisconsin-Madison

Закон Гаусса использует понятие «поток». Поток всегда определяется на основе:

• Поверхность А.
• Векторное поле (например, электрическое поле).

и может рассматриваться как мера количества силовых линий от векторного поля, которые пересекают данную поверхность. По этой причине обычно говорят о «потоке электрического поля через поверхность». Это показано на рисунке \(\PageIndex{1}\) для однородного горизонтального электрического поля и плоской поверхности, вектор нормали которой \(\vec A\) показан. Если поверхность перпендикулярна полю (левая панель) и, таким образом, вектор поля параллелен вектору \(\vec A\), то поток через эту поверхность максимален. Если поверхность параллельна полю (правая панель), то никакие силовые линии не пересекают эту поверхность, и поток через эту поверхность равен нулю. Если поверхность вращается относительно электрического поля, как на средней панели, то поток через поверхность находится между нулем и максимальным значением.

Рисунок \(\PageIndex{1}\): Поток электрического поля через поверхность, образующую разные углы по отношению к электрическому полю. На крайнем левом рисунке поверхность ориентирована так, чтобы поток через нее был максимальным. На самой правой панели нет силовых линий, пересекающих поверхность, поэтому поток через поверхность равен нулю.

Определим вектор \(\vec A\), связанный с поверхностью, так что величина \(\vec A\) равна площади поверхности, а направление \(\vec A\) таков, что он перпендикулярен поверхности, как показано на рисунке \(\PageIndex{1}\). Мы определяем поток \(\Phi_E\) электрического поля \(\vec E\) через поверхность, представленную вектором, \(\vec A\), как: \[\begin{aligned} \ Phi_E=\vec E\cdot \vec A=EA\cos\theta\end{aligned}\], так как это будет иметь те же свойства, которые мы описали выше (например, отсутствие потока, когда \(\vec E\) и \(\ vec A\) перпендикулярны, поток пропорционален числу силовых линий, пересекающих поверхность). Обратите внимание, что поток определяется только до общего знака, поскольку есть два возможных выбора направления вектора \(\vec A\), поскольку требуется, чтобы он был перпендикулярен поверхности. По соглашению мы обычно выбираем \(\vec A\) так, чтобы поток был положительным.

Упражнение \(\PageIndex{1}\)

Каковы единицы измерения электрического потока в системе СИ?

1. \(\text{N}\cdot\text{m/C}\)
2. \(\текст{V}\cdot\текст{м}\)
3. \(\text{В/м}\)
4. Единицы потока зависят от размеров заряженного объекта.

Ответить

Единицы потока зависят от размеров заряженного объекта.

Пример \(\PageIndex{1}\)

Однородное электрическое поле задается формулой: \(\vec E=E\cos\theta\hat x+E\sin\theta\hat y\) во всем пространстве. Прямоугольная поверхность определяется четырьмя точками \((0,0,0)\), \((0,0,H)\), \((L,0,0)\), \((L, 0,Н)\). Чему равен поток электрического поля через поверхность?

Решение :

Заданная поверхность соответствует прямоугольнику на плоскости \(xz\) с площадью \(A=LH\). Поскольку прямоугольник лежит в плоскости \(xz\), вектор, перпендикулярный поверхности, будет направлен в направлении \(y\). Мы выбираем положительное направление \(y\), так как это даст положительное число для потока (поскольку электрическое поле имеет положительную составляющую в направлении \(y\)). Вектор \(\vec A\) определяется как: \[\begin{aligned} \vec A =A\hat y=LH\hat y\end{aligned}\] Таким образом, поток через поверхность определяется как: \[\begin{align} \Phi_E&=\vec E\cdot \vec A=(E\cos\theta\hat x+E\sin\theta\hat y)\cdot(LH\hat y)\\ &= ELH\sin\theta\end{aligned}\], где следует отметить, что угол \(\theta\) в данном случае не является углом между \(\vec E\) и \(\vec A\) , а скорее дополнение этого угла.

Обсуждение:

В этом примере мы рассчитали поток однородного электрического поля через прямоугольник площадью \(A=LH\). Поскольку мы знали компоненты вектора электрического поля \(\vec E\) и поверхностного вектора \(\vec A\), мы использовали их скалярное произведение для определения потока через поверхность. В некоторых случаях проще работать с величиной векторов и углом между ними для определения скалярного произведения (хотя обратите внимание, что в этом примере угол между \(\vec E\) и \(\vec A\ ) равно \(9{\circ}-\тета\)).

Неоднородные поля

До сих пор мы рассматривали поток однородного электрического поля \(\vec E\) через поверхность \(S\), описываемую вектором \(\vec A\ ). В этом случае поток \(\Phi_E\) определяется как: \[\begin{aligned} \Phi_E=\vec E\cdot \vec A\end{aligned}\] Однако, если электрическое поле не постоянны по величине и/или по направлению на всей поверхности, то мы разделяем поверхность \(S\) на множество бесконечно малых поверхностей \(dS\) и суммируем (интегрируем) потоки от этих бесконечно малых поверхностей:

\[\Phi_{E}=\int\vec E\cdot d\vec A\]

где \(d\vec A\) — вектор нормали к бесконечно малой поверхности, \(dS\) . Это показано на рисунке \(\PageIndex{2}\), на левой панели которого показана поверхность, для которой электрическое поле изменяет величину вдоль поверхности (поскольку силовые линии ближе в нижней левой части поверхности). ), а на правой панели — сценарий, в котором направление и величина электрического поля меняются вдоль поверхности.

Рисунок \(\PageIndex{2}\): Примеры поверхностей, которые необходимо разделить, чтобы определить суммарный поток через них. Поверхность слева должна быть разделена, потому что электрическое поле меняет величину над поверхностью, тогда как поверхность справа должна быть разделена, потому что угол между \(\vec E\) и \(d\vec A\) не равен постоянна (и величина \(\vec E\) также меняется вдоль поверхности).

Чтобы вычислить поток через всю поверхность, мы сначала вычисляем поток через бесконечно малую поверхность \(dS\), над которой мы предполагаем, что \(\vec E\) постоянна по величине и направлению, а затем, мы суммируем (интегрируем) потоки со всех бесконечно малых поверхностей вместе. Помните, что поток через поверхность связан с количеством силовых линий, пересекающих эту поверхность; таким образом, имеет смысл подсчитать линии, пересекающие бесконечно малую поверхность, \(dS\), а затем сложить их вместе по всем бесконечно малым поверхностям, чтобы определить поток через всю поверхность, \(S\).

Пример \(\PageIndex{2}\)

Электрическое поле указывает в направлении \(z\) повсюду в пространстве. Величина электрического поля линейно зависит от положения \(x\) в пространстве, так что вектор электрического поля определяется выражением: \(\vec E=(a-bx)\hat z\), где \( a\) и \(b\) являются константами. Чему равен поток электрического поля через квадрат со стороной \(L\), расположенный в положительной плоскости \(ху\) с одним из углов в начале координат? Нам нужно вычислить поток электрического поля через квадрат со стороной \(L\) в плоскости \(xy\). Электрическое поле всегда направлено \(z\), поэтому угол между \(\vec E\) и \(d\vec A\) (вектор нормали для любого бесконечно малого элемента площади) будет оставаться постоянным.

Решение :

Мы можем вычислить поток через квадрат, разделив квадрат на тонкие полоски длиной \(L\) в направлении \(y\) и бесконечно малой шириной \(dx\) в \ (x\), как показано на рисунке \(\PageIndex{3}\). В этом случае, поскольку электрическое поле не изменяется с \(y\), размерность бесконечно малого элемента площади в направлении \(y\) конечна (\(L\)). Если бы электрическое поле менялось как в зависимости от \(х\), так и от \(у\), мы начали бы с элементов площади, имеющих бесконечно малые размеры как в направлениях \(х\), так и в направлениях \(у).

Рисунок \(\PageIndex{3}\): Разделение квадрата в плоскости \(xy\) на тонкие полосы длины \(L\) и ширины \(dx\).

Как показано на рисунке \(\PageIndex{3}\), сначала мы вычисляем поток через тонкую полоску площади \(dA=Ldx\), расположенную в позиции \(x\) вдоль \(x\) ось. При выборе \(d\vec A\) в направлении, обеспечивающем положительный поток, поток через показанную полосу определяется как: \[\begin{aligned} d\Phi_E=\vec E\cdot d\ vec A=EdA=(ax-b)Ldx\end{aligned}\] где \(\vec E\cdot d\vec A=EdA\), так как угол между \(\vec E\) и \(\ vec A\) равно нулю. 2\end{выровнено}\]

Обсуждение:

В этом примере мы показали, как рассчитать поток электрического поля, величина которого меняется в зависимости от положения. Мы смоделировали квадрат со стороной \(L\) состоящим из множества тонких полосок длины \(L\) и ширины \(dx\). Затем мы рассчитали поток через каждую полосу и сложили их вместе, чтобы получить общий поток через квадрат.

Закрытые поверхности

Различают «закрытую» и «открытую» поверхности. Поверхность называется замкнутой, если она полностью определяет объем, который можно было бы, например, заполнить жидкостью. Замкнутая поверхность имеет четкое «внутри» и «снаружи». Например, поверхность сферы, куба или цилиндра — все это примеры замкнутых поверхностей. С другой стороны, плоскость, треугольник и диск являются примерами «открытых поверхностей».

Для замкнутой поверхности можно однозначно определить направление вектора \(\vec A\) (или \(d\vec A\)) как направление, в котором он перпендикулярен поверхности и указывает наружу . Таким образом, знак потока за пределы замкнутой поверхности имеет смысл. Поток будет положительным, если есть чистое количество силовых линий, выходящих из объема, определяемого поверхностью (поскольку \(\vec E\) и \(\vec A\) будут в среднем параллельны), а поток будет отрицательным если в объем входит чистое количество линий поля (поскольку \(\vec E\) и \(\vec A\) в среднем будут антипараллельными). Таким образом, поток через замкнутую поверхность равен нулю, если количество силовых линий, входящих в поверхность, равно количеству силовых линий, выходящих из поверхности.

При расчете потока над замкнутой поверхностью мы используем другой символ интегрирования, чтобы показать, что поверхность замкнута: \[\begin{aligned} \Phi_E=\oint \vec E\cdot d\vec A\end{aligned }\], который является тем же символом интегрирования, который мы использовали для обозначения интеграла по путям, когда начальная и конечная точки совпадают (см., например, раздел 8.1).

Упражнение \(\PageIndex{2}\)

Рисунок \(\PageIndex{4}\): Неоднородное электрическое поле, протекающее через замкнутую поверхность неправильной формы.

Неоднородное электрическое поле \(\vec E\) протекает через замкнутую поверхность неправильной формы, как показано на рисунке \(\PageIndex{4}\). Поток через поверхность

1. положительный.
2. ноль.
3. отрицательный.

Ответить

Пример \(\PageIndex{3}\)

Отрицательный электрический заряд \(-Q\) расположен в начале системы координат. Вычислите поток электрического поля через сферическую поверхность радиуса \(R\) с центром в начале координат. 92}\end{aligned}\] согласно закону Кулона для точечного заряда. Хотя вектор \(\vec E\) меняет направление повсюду вдоль поверхности, он всегда образует один и тот же угол (-180) с соответствующим вектором \(d\vec A\) в любом конкретном месте. Действительно, для точечного заряда электрическое поле указывает в радиальном направлении (внутрь для отрицательного заряда) и, таким образом, перпендикулярно сферической поверхности во всех точках. 2\). Поток через сферическую поверхность отрицательный, потому что заряд отрицательный, а силовые линии направлены в сторону \(-Q\). 92)=-\frac{Q}{\epsilon_0}\end{aligned}\], что, как ни странно, не зависит от радиуса сферической поверхности. Обратите внимание, что мы использовали \(\epsilon_0\) вместо константы Кулона, \(k\), так как результат более чистый без дополнительного множителя \(4\pi\).

Обсуждение:

В этом примере мы вычислили поток электрического поля от отрицательного точечного заряда через сферическую поверхность, концентрическую с зарядом. Мы обнаружили, что поток отрицателен, что имеет смысл, поскольку силовые линии направляются к отрицательному заряду, и, таким образом, на сферическую поверхность попадает определенное количество силовых линий. Возможно, неожиданно мы обнаружили, что полный поток через поверхность не зависит от радиуса поверхности! На самом деле это утверждение в точности соответствует закону Гаусса: суммарный поток от замкнутой поверхности зависит только от количества заряда, содержащегося на этой поверхности (и константы \(\epsilon_0\)).