Урок 27. напряжённость и потенциал электростатического поля. разность потенциалов — Физика — 10 класс

Физика, 10 класс

Урок 27. Напряжённость и потенциал электростатического поля. Разность потенциалов

Перечень вопросов, рассматриваемых на уроке:

1) Теория дальнодействия;

2) Теория близкодействия;

3) Электрическое поле;

4) Скорость электрического поля;

5) Напряжённость электрического поля;

6) Однородное и неоднородное электрическое поле;

7) Принцип суперпозиции полей;

8) Диэлектрическая проницаемость;

9) Электростатическая защита

10) Работа электрического поля;

11) Потенциал и разность потенциалов.

Глоссарий по теме:

Напряжённость — отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.

Потенциал точки электростатического поля -отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.

Напряжение – разность потенциалов.

Потенциальное поле – поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю.

Напряжённость направлена в сторону убывания потенциала.

Эквипотенциальные поверхности – поверхности равного потенциала.

Свободные заряды — заряженные частицы, способные свободно перемещаться в проводнике под влиянием электрического поля.

Электростатическая индукция – явление разделения зарядов и их распределение по поверхности проводника во внешнем электрическом поле.

Основная и дополнительная литература

Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 290 – 320.

Рымкевич А.П. Сборник задач по физике. 9 – 11 класс. М. Дрофа, 1999 – С. 93 — 102

Теоретический материал для самостоятельного изучения

Согласно идее Фарадея электрические заряды не действуют друг на друга непосредственно. Каждый из них создаёт в окружающем пространстве электрическое поле.

Электрическое поле — это особый вид материи, посредством которой происходит взаимодействие зарядов. Скорость распространения электрического поля в вакууме равна 300000 км/с.

Напряжённость Е — силовая характеристика электрического поля.

Электрическое поле, напряженность которого одинакова во всех точках, называется однородным. Поле между параллельными пластинами однородно

Главное свойство электрического поля – это действие его на электрические заряды с некоторой силой.

Напряжённость-это отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.

Если в данной точке пространства различные заряженные частицы создают поля, напряжённости которых Е₁, Е₂, то результирующая напряжённость поля в этой точке равна геометрической сумме напряжённостей этих полей. В этом состоит принцип суперпозиции полей.

Заряд, помещенный в электрическое поле обладает потенциальной энергией.

Потенциалом φ точки электростатического поля называют отношение потенциальной энергии Wn заряда, помещённого в данную точку, к этому заряду q.

Напряжение – это работа, совершаемая полем при перемещении заряда 1Кл.

Примеры и разбор решения заданий

1. К каждой позиции первого столбца подберите соответствующую позицию второго

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Напряженность
Потенциал
Потенциальная энергия заряда в однородном электростатическом поле
Разность потенциалов	qΕd

Решение: вспомнив формулы величин, можем установить:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Напряженность
Потенциал
Потенциальная энергия заряда в однородном электростатическом поле	qΕd
Разность потенциалов

2.

В однородном электрическом поле напряжённостью 1 В/м переместили заряд -25 нКл в направлении силовой линии на 2 см. Найти работу поля, изменение потенциальной энергии заряда и напряжение между начальной и конечной точками перемещения.

Решение.

Работа электрического поля при перемещении заряда вдоль силовой линии:

ΔA = — qΕΔd,

при этом изменение потенциальной энергии равно:

Напряжение между начальной и конечной точками перемещения равно:

Вычисления:

ΔA = -25 · 10^-9 Kл · 10³ B/м · 0,02 м = -0,5 мкДж;

Ответ:

Потенциальность электростатического поля

Определение 1

Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.

Что такое потенциальное поле

Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).

Определение 2

Поле называется потенциальным, если при перемещении по любому замкнутому контуру работа сил поля равняется 0.

Известно, что сила гравитации FG~1r2, которая убывает обратно пропорционально квадрату расстояния, является потенциальной, при этом ее потенциальность обусловлена именно обратно пропорциональной зависимостью от расстояния. Сила Кулона тоже обратно пропорциональна квадрату расстояния. Напомним закон Кулона FE~1r2. Все математическое описание потенциала создавалось при изучении сил гравитации. Понятие о потенциале появилось в работах Ж. Л. Лагранжа в 1777 году. Определение «потенциал» было введено в науку намного позже Дж. Грином и К. Ф. Гауссом.

Определение 3

На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.

Доказательство 1

Легко докажем это математически.

Циркуляция вектора напряженности поля точечного заряда Ei→ по любому замкнутому контуру равняется 0:

∮LEi→ds→=0.

Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:

E→=∑iEi→.

Находим интеграл:

∮LE→ds→=∮L∑iEi→ds→=∑i∮LEi→ds→=∑i0=0.

Приведенный выше критерий потенциальности поля не дифференциален, поэтому его трудно применять. Нужно проверять равенство 0 работы по замкнутому контуру. А это означает, что необходимо анализировать бесконечное число циклов, что, в конечном итоге, невозможно. Критерий потенциальности применим лишь в случае, когда известна аналитическая формула работы, что не всегда возможно. Поэтому нужно отыскать другой критерий потенциальности поля, который был бы прост в применении. Данным критерием является дифференциальная формулировка. Она определяется при помощи понятия ротор вектора rot A→.

Что такое ротор. Практические задачи

Определение 4

Ротор − это вектор, проекция которого на направление единичного вектора n→ определяется таким образом:

rotnA→=lim∆S→0∮A→·ds→∆S,

где ∆S − это площадь, которая лежит в плоскости перпендикулярной к n→, ограниченная малым контуром L, на контуре L − это направление положительного обхода связано с n→ правилом правого винта.

Замечание 1

Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:

rot A→=∇×A→=i→j→k→∂∂x∂∂y∂∂zAxAyAk.

Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:

∫AL1BE→·ds→=∫AL2BE→·ds→.

где L1 и L2− это различные пути между точками А и В. При замене местами пределов интегрирования получаем:

∫AL2BE→·ds→=-∫BL2AE→·ds→.

Выражение ∫AL1BE→·ds→=∫AL2BE→·ds→ представим в виде:

∫AL1BE→·ds→=∫BL2AE→·ds→=∮LE→·ds→=0.

где L=L1+L2. Применяем формулу Стокса:

∫Srot A→·dS→=∮LA→·ds→,

к уравнению выше, получаем:

∮LE→·ds→=∫Srot E→·dS→=0,

где S− это поверхность, ограниченная контуром L. Поскольку поверхность произвольная, то интеграл в выражении ∮LE→·ds→=∫Srot E→·dS→=0 может равняться 0, только если равняется 0 подынтегральное выражение, а поскольку dS→≠0 то есть:

Определение 5

rot E→=0.

Это дифференциальная формулировка потенциальности электростатического поля

.

Пример 1

Необходимо найти rotn υ→ для точек оси вращения, если υ→ − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n→

Решение

Рисунок 1

В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1). Известно, что:

υ=ωR,∆S=πR2.

Обозначим υds. ds как скалярное значение элемента окружности. Для этого используем формулу определения ротора, получаем:

rotn υ→=limR→0∮ωR→·ds→πR2=limR→0ωR2πRπR2=2ω,

где ∮ds=2πR − это длина окружности.

Ответ: Ротор линейной скорости точек вращающегося тела равняется rotn υ→=2ω.

Пример 2

Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.

Решение

Поскольку электростатическое поле потенциально, тогда выполняется равенство:

A=∮LE→ds→=0.

Рисунок 2

Определение 6

Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.

Пример 3

Допустим обратное. Пускай вдоль поверхности S (рисунок 2) непрерывности нет. Это означает, что если 1, 2 и 3, 4 разделенные поверхностью S, но бесконечно близкие друг к другу точки, тогда работа электростатических сил на пути 1→2 отличается на конечную величину от работы тех же сил на пути 3→ 4. Так как мы считаем, что отрезки 1→2 и 3→ 4 бесконечно малы, силы конечны, значит, и работа, которую выполняют электрические силы на заданных отрезках, бесконечно малая величина. Выходит, что работа на пути 1→2→3→4→1 не должна равняться 0. То есть работа сил по перемещению пробного заряда по замкнутому контуру не равняется 0. Это невозможно, поскольку электростатическое поле потенциально. Мы показали, что тангенциальные составляющие напряженности электростатического поля не непрерывны.

Потенциальное электрическое поле — Технический словарь Том V

Потенциальное электрическое поле — поле, в котором работа, совершаемая электрической силой при перемещении электрического заряда, зависит только от положения начальной и конечной точек пути, по которому происходит перемещение электрического заряда, но не зависит от пути, по которому происходит перемещение.
Потенциальное электрическое поле — поле, в котором работа, совершаемая электрической силой при перемещении электрического заряда, зависит только от положения начальной и конечной точек пути перемещения электрического заряда, но не зависит от формы этого пути.
Потенциальное электрическое поле источника здесь отсутствует, однако в зоне разреза создаются наведенные электрические заряды с плотностью а. Эти заряды вызывают искривление пути вихревого тока i.
Создание потенциального электрического поля, в котором распределение потенциалов описывалось бы бигармоническим уравнением, невозможно.
В потенциальном электрическом поле напряжение между двумя точками совпадает по величине с разностью потенциалов между ними.
Мы ограничимся случаем чисто потенциального электрического поля ( Е — — Уф) при равном нулю магнитном поле и предположим, что возмущению подвергается только электронное распределение при неизменном распределении ионов.
Мы ограничимся случаем чисто потенциального электрического поля ( Е — 7 ( р) при равном нулю магнитном поле и предположим, что возмущению подвергается только электронное распределение при неизменном распределении ионов.
Отсюда ясно, в частности, что любое потенциальное электрическое поле не дает возбуждения, а приводит лишь к разделению электрических зарядов.
Рассмотрим вопрос о распределении электронов плазмы в медленно включаемом потенциальном электрическом поле.
Рассмотрим вопрос о распределении электронов плазмы в медленно включаемом потенциальном электрическом поле.
Кажущаяся эквивалентность, однако, рушится при появлении в среде потенциального электрического поля. В частности, оно обязательно возникает при образовании в сплошной среде полостей.
Ускоритель заряженных частиц, в котором ускоряемые частицы под действием ведущего магнитного поля движутся по близким к замкнутым или спиральным траекториям Ускоритель заряженных частиц, в котором ускорение частиц осуществляется потенциальным электрическим полем.
Если же в рассматриваемой области пространства имеются заряды и токи, то наряду с вихревыми полями со сцепленными линиями мы обнаружим вихревое магнитное поле, линии которого замкнуты около токов, и потенциальное электрическое поле, линии которого начинаются в положительных и кончаются в отрицательных зарядах.
В потенциальном электрическом поле ( электростатическом поле) работа по перемещению электрического заряда не зависит от пути, по которому перемещается заряд.
Движущийся электрический заряд наряду с электрическим создает магнитное поле. В отличие от потенциального электрического поля, постоянное магнитное поле, создаваемое стационарными токами, является соленоидальным, или вихревым: его силовые линии всегда замкнуты. Другими словами, магнитное поле не имеет источников — магнитных зарядов.

Для наглядного изображения магнитных полей используют силовые линии. В отличие от потенциального электрического поля, где силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных, магнитное поле является соленоидалъным или вихревым: его силовые линии всегда замкнуты. Другими словами, магнитное поле не имеет источников — магнитных зарядов.
Электрические силы являются консервативными; их работа не зависит от формы траектории и определяется только значениями потенциала начальной и конечной точек пути. Отсюда следует, что потенциальное электрическое поле не способно заставить электрические заряды перемещаться по замкнутой траектории.
Электрические силы являются консервативными; их работа не зависит от формы траектории и определяется только значениями потенциала начальной и конечной точек пути. Отсюда следует, что потенциальное электрическое поле неспособно заставить электрические заряды перемещаться по замкнутой траектории.
Электрические силы являются консервативными; их работа не зависит от формы траектории и определяется только значениями потенциала начальной и конечной точек пути. Отсюда следует, что потенциальное электрическое поле неспособно заставить электрические заряды перемещаться по замкнутой траектории.
У поля электрических зарядов силовые линии всегда начинаются и кончаются на зарядах, а силовые линии электрического поля, обусловленного электромагнитной индукцией, не связаны с зарядами и являются замкнутыми. Поэтому поле электрических зарядов — это всегда потенциальное электрическое поле, а электрическое поле, возбуждаемое электромагнитной индукцией, не потенциальное, а вихревое. Работа, совершаемая таким полем при продвижении электрических зарядов, может зависеть не только от положения начальной и конечной точек перемещения, но и от пути движения зарядов. Поэтому при продвижении зарядов по замкнутому пути эта работа может быть отлична от нуля.
Распределение электронов по периметру образца. В процессе эксперимента было установлено, что изменение потенциала смещения не вызывает сколь-нибудь заметного изменения тока. Это легко объяснить тем, что градиент потенциального электрического поля вблизи поверхности анода достаточно велик, чтобы полностью исключить переброс вторичных электронов малой энергии между соседними пластинками.
Потенциальная составляющая электрического поля существует как в диэлектрике, окружающем проводящее тело, так и в самом теле вследствие протекания в нем тока и появления напряжения между точками тела из-за конечной удельной электрической проводимости вещества. Так как потенциалы точек поверхности тела различны, то, следовательно, существует потенциальное электрическое поле и его потенциальная составляющая в окружающем тело диэлектрике.
Одно из основных различий между электростатическим полем и полем постоянных токов обусловлено наличием в цепях с токами источников энергии, без которых невозможны ни возникновение тока, ни его стационарный характер. В источниках энергии движение заряженных частиц ( электронов и ионов) связано с воздействием на них не только сил потенциального электрического поля, но и сил другого происхождения.
Электрический потенциал, характеризующий данное поле, может быть определен лишь с точностью до произвольной постоянной, зависящей от произвольного выбора точки Р, в которой потенциал тфитншаеггся равным — пулю. Электрическое поле, которое может быть в каждой точке охарактеризовано с точностью до произвольной постоянной скалярной величины, именуемой электрическим потенциалом, носит название потенциального электрического поля. Таковыми, в частности, являются электростатическое поле, а также электрическое поле постоянных токов, протекающих по неподвижным проводникам, при условии, что поле рассматривается вне области действия источников электродвижущих сил. Действительно, распределение зарядов на проводниках при этом остается, как и в электростатике, неизменным во времени. Оговорка о необходимости ограничения областью вне источников ЭДС для того, чтобы поле было потенциальным, будет рассмотрена в конце этого параграфа.
Легко представить себе механизм такого возбуждения. Следовательно, более легкие электроны обладают большим ускорением Vpjmen. Радиальное различие ускорений е и р уравновешено потенциальным электрическим полем.
В чисто безвихревом поле не может быть постоянного тока. Такой расход энергии не может быть обеспечен безвихревым полем. Постоянные токи возможны только в том случае, если есть источники поля, которые создают потенциальное электрическое поле. Обычно говорят, что такие источники создают стороннюю электродвижущую силу.

Поле электрического потенциала — Studreferaty

Потенциал электрического поля – Основы электроники

В зависимости от количества зарядов и их величины изменяется энергия электрического поля, создаваемого этими зарядами. Очевидно, что величина энергии электрического поля, образованного одним ‘зарядом, будет отличаться от величины энергии поля, образованного двумя или тремя такими же зарядами.

В практике очень часто приходится сравнивать различные по величине поля.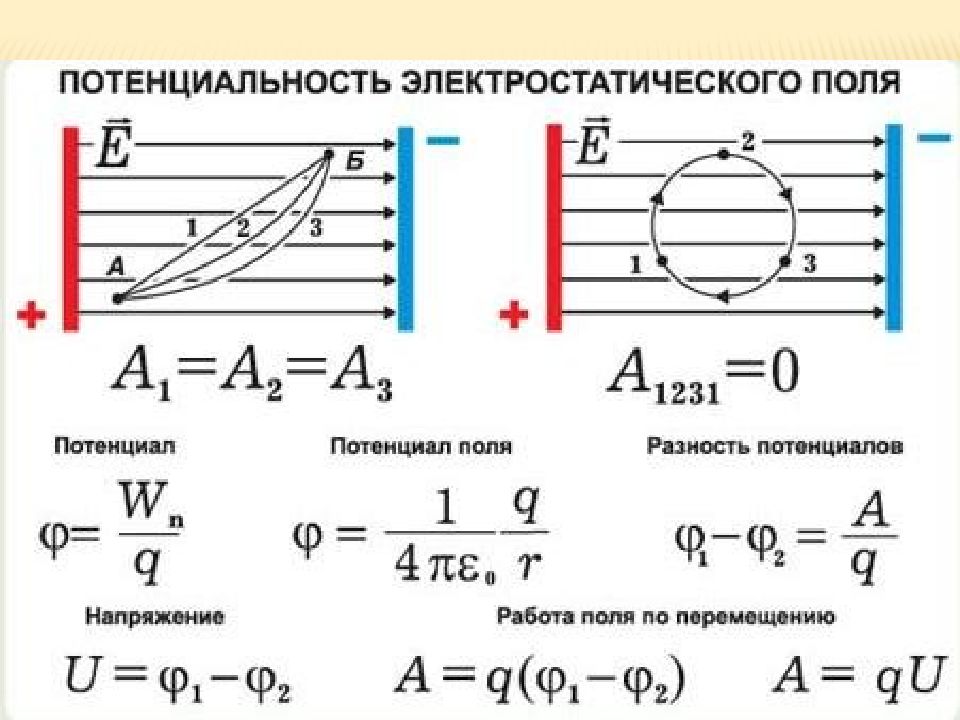 Это сравнение производится по действиям полей на единичный положительный заряд (так называемый пробный заряд). Поясним это.

Определение:  Единичным называется заряд, величина которого равна одной единице заряда.

Пусть, например, поле образовано некоторым положительным зарядом. Чтобы внести в какую-то точку этого поля единичный положительный заряд, необходимо затратить определенную работу на преодоление силы отталкивания между основным и единичным зарядами. Величина потенциальной энергии поля при этом возрастает.

Попробуем теперь внести единичный заряд в другое поле, образованное в два раза большим электрическим зарядом. Очевидно, что при этом придется затратить большую работу, чем в первом случае. Следовательно, и потенциальная энергия поля возрастет больше, чем в первом случае.

В электротехнике для характеристики поля вводится специальное понятие — электрический потенциал.

Определение; Электрический потенциал некоторой точки поля численно равен работе, затрачиваемой при внесении единичного положительного заряда из-за пределов поля в данную точку.

Измеряется потенциал электрического поля в вольтах. Такое название единицы для измерения потенциала дано по имени итальянского физика Алессандро Вольта (1745—1827), открывшего закон взаимодействия электрических токов и предложившего первую гипотезу для объяснения магнитных свойств вещества.

Характеристика поля с помощью электрического потенциала очень удобна. Она позволяет сравнивать не только различные электрические поля, но и отдельные точки одного и того же поля. Вместо того, например, чтобы говорить «шар А наэлектризован более сильно, чем шар Б», можно сказать: «потенциал шара А выше потенциала шара Б». Потенциал точки поля обычно обозначается буквой φ.

Электрическое поле может создаваться не только положительным или отрицательным зарядом, но и их совокупностью. В таком поле отдельные точки могут иметь как отрицательные, так и положительные потенциалы. Чтобы в этом случае сравнивать потенциалы различных точек, ввели условное понятие о точке с нулевым потенциалом, т. е.

стали считать, что одна из точек (или несколько точек) имеет потенциал, равный нулю. Потенциалы остальных точек поля определяются относительно точки нулевого потенциала. Этот метод аналогичен методу измерения температур.

Там также определенная температура (температура тающего льда) принимается за нулевую точку и по отношению к ней определяется температура других тел.

В электротехнике условно считают, что нулевой потенциал имеет поверхность земли.

Если потенциал в данной точке выше потенциала земли, то мы говорим, что точка обладает положительным потенциалом. Если же, наоборот, потенциал точки ниже потенциала земли, то точка обладает отрицательным потенциалом.

Измеряя потенциалы различных точек электрического поля относительно земли, можно убедиться в том, что они неодинаковы. Значит, между отдельными точками может быть некоторая разность потенциалов.

Определение:  Разность потенциалов между двумя точками электрического поля называется напряжением. Напряжение, так же как и потенциал, измеряется в вольтах.

Сказанное поясним примером.

На рис. 1 мы условно показали четыре точки: А—с потенциалом + 20 в, Б — с потенциалом +40 в, В — с нулевым потенциалом (земля) и Г — с потенциалом—15 в.

Рисунок 1. Разность потенциалов между различными точками электрического поля

Разность потенциалов между точками Б и А =40—20=20 в;

Разность потенциалов между точками А и В =20— 0=20 в;

Разность потенциалов между точками Б и В =40— 0=40 в;

Разность потенциалов между точками А и Г=20—(—15) =35 в.

Потенциал точки Б выше потенциалов точек А, В и Г. Потенциал точки А выше потенциалов точек В и Г, но ниже потенциала точки Б.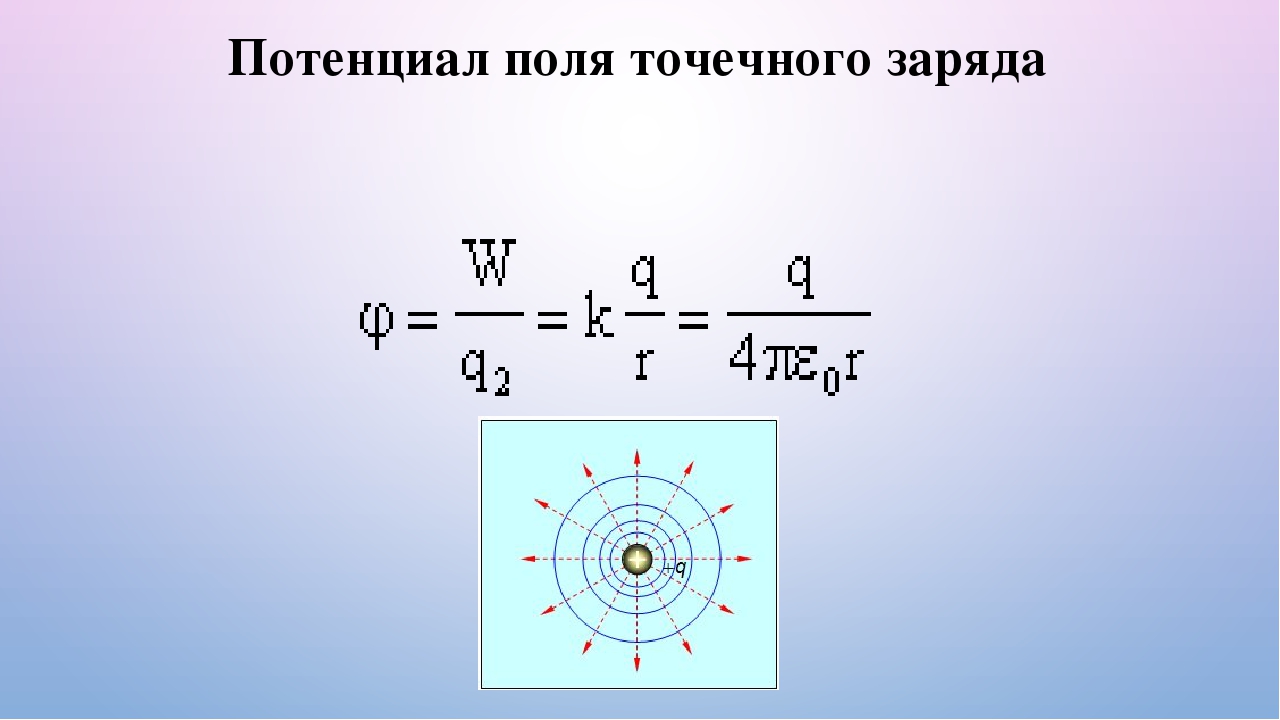 Потенциал точки В ниже потенциалов точек А и Б, но выше потенциала точки Г.

Следует обратить внимание на то, что точки отрицательного потенциала имеют более низкий потенциал, чем тонки нулевого потенциала.

Можно и иначе определить напряжение между двумя точками. Для этого рассмотрим две точки А и Б электрического поля.

Допустим, что потенциал точки А равен φА потенциал точки Б равен φБ. Потенциал точки А (или Б) определяется той работой, которую необходимо затратить на перенос единичного положительного заряда из-за пределов поля в точку А (или Б).

Если для переноса единичного положительного заряда из-за предела поля в точку А и в точку Б требуется затратить различную по величине работу, то φА не равно φБ и между точками А и Б существует некоторая разность потенциалов, или напряжение. Это напряжение определяется разностью φА – φБ т. е.

работой, совершаемой силами поля при переносе единичного положительного заряда из точки А в точку Б.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник: http://www.sxemotehnika.ru/potentcial-elektricheskogo-polia.html

Потенциал электрического поля: потенциальная энергия, потенциал поля, эквипотенциальные поверхности

В статье расскажем про потенциальную энергию и потенциал поля Е, узнаете что такое линии напряженности электрического поля и эквипотенциальные поверхности, а так же про потенциальный градиент.

Потенциальная энергия U нагрузки в поле E и потенциал поля V E

Энергетический подход очень эффективен при описании электрических явлений, поскольку можно определить потенциальную энергию U заряда в электрическом поле. Рассмотрим электрическое поле между двумя параллельными пластинами, на которых есть нагрузки одинаковой величины, но с противоположными знаками.

 Размер плит велик по сравнению с расстоянием между ними, и, таким образом, в большинстве областей поле между ними можно рассматривать как однородное.

 Небольшой положительный точечный заряд +q имеет наибольшую потенциальную энергию U, когда он находится в точке на поверхности положительного электрода, как на чертеже.

Это означает, что в этот момент заряд +q обладает наибольшей способностью выполнять работу при его возврате к отрицательному электроду.

 Нам нужно дать эту энергию заряда U, выполняя работу по переносу этого заряда с отрицательного на положительный электрод.

 Работа выполняется против силы электростатического отталкивания F = Q*E . В разделе dl мы сделаем работу dW равной:

или

Работа по переносу заряда +q между двумя электродами, то есть потенциальной энергии U этого заряда на положительном электроде, равна:

Поскольку электрическое поле является потенциальным полем, работа по переносу заряда из точки а в точку b не зависит от формы пути нагрузки между этими точками.

Ранее мы определяли напряженность электрического поля, как силу, действующую на единицу нагрузку.

 Аналогичным образом мы определяем электрический потенциал V или просто потенциал как отношение потенциальной энергии, которую заряд q имеет в электрическом поле, к величине заряда.

 Следовательно, если любой заряд q имеет потенциальную энергию U в некоторой точке поля, то потенциал поля V в этой точке равен:

В общем случае, когда поле E не является однородным, мы должны написать общее соотношение, которое также верно и для однородного поля:

Теперь мы можем выразить напряженность поля E, уменьшив потенциал dV на участке dl:

Когда направление сдвига dl не параллельно направлению поля E, тогда общее соотношение между обсуждаемыми значениями будет получено путем записи его в векторной форме.  Тогда падение dV-потенциала будет скалярным произведением, и в общем случае неоднородного поля приращения dU и dV равны:

Разность потенциалов Vab между точками А и В на рисунке выше, даже если поле было неоднородным, получим интегрированием:

Линии напряженности электрического поля и эквипотенциальные поверхности

Назовем линии E-поля дорожками тест-положительных зарядов, движущимися под действием этого поля. Поверхности, где электрический потенциал имеет одинаковое значение, называются эквипотенциальными поверхностями. Линии поля E (зеленые) всегда перпендикулярны эквипотенциальным поверхностям (красные). На рисунке ниже показано окружение точки нагрузки.

Распределение линий E (зеленые), перпендикулярных эквипотенциальным поверхностям (красные), окруженным диполем, можно представить следующим образом:

Поверхность металла всегда является эквипотенциальной поверхностью.  Таким образом, когда нагрузки в состоянии покоя распределяются по поверхности металла, электрическое поле непосредственно над поверхностью металла должно быть перпендикулярно его поверхности в каждой точке.

Потенциальный градиент и поле E

Поскольку, как мы показали выше, интенсивность поля E связана с уменьшением потенциала dV и расстояния dl, на котором это уменьшение происходит с помощью формулы:

Этот вектор напряженности поля E может быть определен непосредственно как градиент потенциала:

Полученная связь между вектором поля E и градиентом потенциала:

Как мы помним из свойств векторных функций, градиент скалярной функции (в данном случае потенциал V) равен размеру вектора E. Компоненты этого вектора выражаются частными производными (уменьшаются по x, y и z)

Если поле E является постоянным и однородным, то градиент потенциала также является постоянным, и теперь очень простым и удобным правилом для определения разности потенциалов V (напряжения) в этом поле является отношение, которое напрямую вытекает из соотношения между E и градиентом потенциала:

где расстояние l отсчитывается вдоль поля.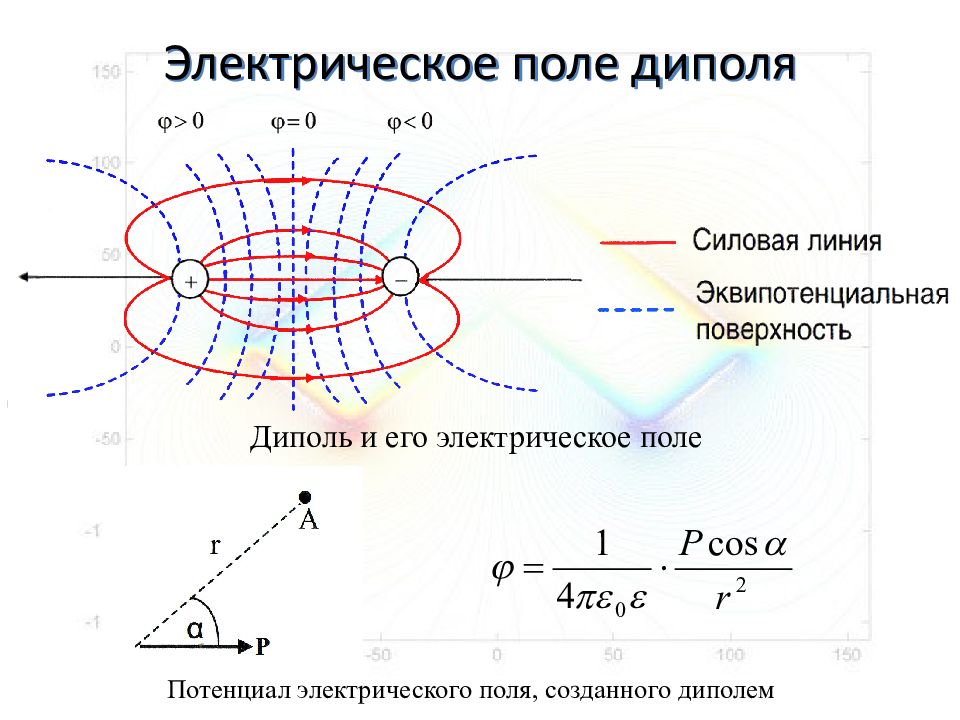  Это правило зависит от изменения напряжения, показанного вольтметром, если мы плавно изменим положение его клемм, касаясь провода сопротивления, по которому течет ток.

Напряжение, определяемое по этому правилу, называется шаговым напряжением. Название «шаговое напряжение» возникает из-за риска поражения электрическим током, когда мы предпринимаем длинные шаги (например, бегаем), а удар молнии рядом с нами ударит о землю.

 Ступенчатое напряжение опасно для скота, остающегося на поляне во время шторма.

Только разность потенциалов может быть измерена в эксперименте. Единица измерения электрического потенциала и разности потенциалов составляет 1 вольт (1 В = 1 Дж / 1 С).

Источник: https://meanders.ru/potencial-jelektricheskogo-polja.shtml

Потенциал электрического поля. Разность потенциалов. урок. Физика 10 Класс

Электрическое поле действует на помещенный в него заряд с силой, которая определяется величиной заряда и напряженностью поля в данной точке.

Если эта сила перемещает заряд – то она совершает работу. Даже если заряда в поле нет, то потенциально эта работа все равно может быть совершена, как только он там окажется. Из опыта других разделов физики мы знаем, что работа связана с энергией.

Для решения некоторых задач удобно использовать энергетическую модель описания электрического поля. Проведем аналогию с гравитационным полем.

Если мы поднимем тело массы , лежащее на земле на высоту  (см. рис. 1), мы изменим его потенциальную энергию на величину . Именно такую работу  и необходимо совершить для этого подъема.

Рис. 1. Изменение потенциальной энергии

Для любой массы  разница энергий на высоте 0 и  будет равна  (см. рис. 2).

Рис. 2. Разница потенциальных энергий

Если разделить значение потенциальной энергии  на массу, мы получим величину, характеризующую гравитационное поле в данной точке. Выражение  уже не зависит от массы, оно показывает работу, которую необходимо совершить для переноса тела, с некоторой массой, на высоту , деленную на эту массу.

Теперь посмотрим, как ввести аналог потенциальной энергии приведенной на единицу массы в электрическом поле.

На заряд , находящийся в поле другого заряда , закрепленного в некоторой точке пространства, действует сила Кулона . Эта сила может переместить заряд , совершив при этом работу. Значит, система двух зарядов, находящихся на определенном расстоянии, обладает потенциальной энергией, зависящей от величины зарядов и расстояния между ними.

Если по аналогии с гравитационным полем рассмотреть величину, равную этой энергии, деленной на заряд , то она уже не будет зависеть от заряда  и охарактеризует только поле заряда  в данной точке. То есть будет являться функцией заряда  и расстояния между зарядами. Эта величина и называется потенциалом электрического поля.

Разность потенциалов двух точек, умноженная на величину заряда , равна работе, необходимой для перемещения этого заряда между этими точками. То есть разность потенциалов двух точек поля – это работа по перемещению между ними единичного заряда.

Как и в поле сил тяжести, эта работа не зависит от траектории  и определяется только положением точек, между которыми перемещается единичный заряд. Такие поля называют консервативными. В разделе «Механика» мы уже говорили, что энергия – величина, требующая для измерения задания «начала отсчета».

Например, в гравитационном поле мы можем считать нулевой потенциальную энергию тела, находящегося на уровне земли. В случае электростатического поля, создаваемого зарядом, естественно считать нулевой потенциальной энергией некоторого заряда, находящегося в поле, его энергию на бесконечном удалении от заряда, в поле которого он находится.

Это и есть «точка отсчета» для потенциальной энергии поля заряда.

Потенциал поля в некоторой точке равен работе по перемещению единичного заряда из этой точки на бесконечность.

Пусть положительный заряд  находится на расстоянии  от положительного заряда  (см. рис. 3).

Рис. 3. Изначальное положение заряда

Какую работу совершит электрическое поле при перемещении заряда  вдоль радиуса в точку, отдаленную на  от ? (См. рис. 4.)

Рис. 4. Конечное положение заряда

По определению работа силы равна этой силе, умноженной на перемещение:

В данном случае действует сила электрического взаимодействия (см. рис. 5), по закону Кулона .

Рис. 5. Действие силы электрического взаимодействия

Сила и перемещение в нашем случае сонаправлены,  и . Так мы можем находить работу для случая, когда сила постоянна на всей траектории. Здесь же сила изменяется по мере отдаления зарядов друг от друга.

Обозначим перемещение заряда (см. рис. 6).

Рис. 6. Перемещение заряда

По мере перемещения заряда  сила изменяется, но на малом (в сравнении с расстоянием до заряда ) отрезке можем считать ее постоянной и находить работу по определению, которое мы привели выше.

Работа, совершаемая силой Кулона на таком малом отрезке  равна , где силу  можно считать постоянной на всем отрезке . Тогда работа при перемещении на расстояние  будет равна сумме работ на  участках (), на каждом из которых сила Кулона постоянна и равна .

Эта сумма будет равна 

Подробный вывод этой формулы вы можете проследить в ответвлении.

Работа при перемещении электрического заряда

Работа по перемещению заряда на малом участке  равна:

Работа на участке  равна сумме работ на каждом участке :

Воспользуемся приближенным равенством:

Прежде чем его применить, покажем, что равенство справедливо. Приведем правую часть к общему знаменателю:

Раскроем скобки:

Заметим, что  – пренебрежимо малая по сравнению с  величина,  не может считаться пренебрежимо малой, т. к. количество  участков  велико. Поэтому в знаменателе можем пренебречь членами  и .

Вернемся к нахождению работы. Распишем выражение по полученной формуле:

Распишем сумму:

Мы знаем, что работа связана с энергией. Система обладает энергией, если силы, возникающие в системе, могут выполнить работу (в нашем случае это сила электростатического взаимодействия зарядов). Работа равна уменьшению потенциальной энергии:

Сравнив с выражением , делаем вывод, что  – это потенциальная энергия взаимодействия двух зарядов. Ранее мы приняли, что потенциальная энергия заряда, отдаленного от источника электрического поля на бесконечность, равна нулю. Посмотрим, как с этим согласуется полученная формула:

Действительно,  будет равна нулю на бесконечном отдалении от заряда , т. к.  при .

Теперь проверим, как полученный результат соотносится с моделью, в которой разноименные заряды обозначены знаками плюс и минус. Если заряды одноименные, то потенциальная энергия взаимодействия положительна .

Система стремится к состоянию с наименьшей потенциальной энергией (как и, например, камень на некоторой высоте  над поверхностью земли, предоставленный сам себе, будет падать вниз, т. е.

уменьшать высоту и с ней потенциальную энергию )

Действительно, заряды будут отталкиваться и сила электрического взаимодействия будет вызывать перемещение заряда на большее расстояние, потенциальная энергия  будет уменьшаться.

Если заряды разноименные, то потенциальная энергия взаимодействия  имеет знак минус. Заряды притягиваются, и сила их взаимодействия вызывает перемещение заряда на меньшее расстояние , потенциальная энергия  уменьшается.

Энергия заряда  в поле заряда , равная , зависит от величин обоих зарядов. Характеристика поля, созданного зарядом , естественно, не должна зависеть от величины помещенного в него заряда. Разделим  на  и получим .

Эта величина называется потенциалом электрического поля и обозначается буквой . Эта характеристика поля показывает, какой энергией обладает положительный заряд, помещенный в данную точку поля.

Как и энергия, потенциал – скалярная величина, измеряется в вольтах.

В нашем случае  – потенциал поля точечного заряда. Точка отсчета потенциалов в нашем случае естественным образом является бесконечно отдаленной точкой (см. рис. 7).

Рис. 7. Точка отсчета потенциалов

В зависимости от задачи точкой отсчета выбирают потенциал поверхности Земли, потенциал отрицательно заряженной пластины конденсатора или потенциал любой другой точки, удобной для решения задачи.

Таким образом, пользуясь определением потенциала, можно вычислить потенциальную энергию заряда, находящегося в электростатическом поле:

и работу поля по перемещению заряда из точки с потенциалом  в точку с потенциалом :

Электрическое поле является консервативным, его работа не зависит от траектории движения заряда, а зависит только от перемещения.

Заряд всегда распределен на каком-то теле, имеющем геометрические размеры. На расстояниях, много больших размеров тела, поле слабо зависит от объема и формы этого тела, и потому модели точечного заряда достаточно. Например, потенциал поля заряженного металлического шара при  эквивалентен потенциалу поля точечного заряда (см. рис. 8):

Рис. 8. Потенциал поля при

.

Внутри шара потенциал во всех точках одинаков и равен потенциалу на поверхности шара (см. рис. 9):

Рис. 9. Потенциал внутри шара

.

Если бы это было не так, то потенциальная энергия в разных точках внутри шара отличалась бы, а, так как внутри металла есть свободные носители заряда, поле выполняло бы работу по перемещению зарядов. В итоге электроны переместились бы в область большего потенциала, тем самым уменьшив его. Таким образом, потенциал во всех точках приравнивается.

Потенциал подчиняется принципу суперпозиции. При наличии нескольких источников поля складываются как векторы напряженности поля, так и потенциалы:

При перемещении заряда между точками с разностью потенциалов 1 кВ электрическое поле совершило работу 40 мкДж. Чему равен заряд?

Это простая задача на понимание смысла величины разности потенциалов.

Разность потенциалов равна работе по переносу заряда, деленной на величину этого заряда.

Выразим значение заряда:

И вычислим ответ:

Ответ: 

Какую работу надо совершить, чтобы перенести заряд 5 мкКл из бесконечности в точку поля, удаленную от центра заряженного шара на 18 см? Заряд шара – 20 мкКл.

Порассуждаем.

– Потенциал поля заряженного шара на бесконечности равен нулю. Следовательно, приближая заряд от бесконечности к шару, внешней силе нужно совершать работу для преодоления силы электростатического взаимодействия. Численно эта работа будет равна работе электрического поля заряженного шара по перемещения заряда с расстояния 18 см на бесконечность.

– Работа по переносу заряда в электрическом поле связана с разностью потенциалов между начальной и конечной точками траектории и величиной заряда.

– Величина переносимого заряда у нас есть.

– Потенциал поля заряженного шара на бесконечности, как мы уже отметили, равен нулю. А в конечной точке траектории мы сможем его вычислить, пользуясь формулой для потенциала поля точечного заряда, которая справедлива и для поля вне заряженного шара.

Приступим к решению.

Найдем потенциал электрического поля заряженного шара в конечной точке траектории.

Потенциал электрического поля заряженного шара на бесконечности равен нулю.

Разность потенциалов электрического поля по переносу заряда из точки с потенциалом  в точку с потенциалом  будет равна:

В то же время она будет равна работе электрического поля по переносу заряда, деленной на заряд:

Величина работы внешних сил, которую надо совершить, чтобы перенести заряд из точки с меньшим потенциалом в точку с большим потенциалом, равна работе электрического поля по переносу такого же заряда в обратном направлении.

Таким образом, мы получили систему из пяти уравнений, решив которую найдем искомую величину. Пронаблюдать математическую часть решения задачи вы можете в свертке.

Ответ: .

Математическая часть решения задачи 2

Подставим выражения для потенциалов из первого и второго уравнений в третье:

Подставим полученную разность потенциалов в четвертое уравнение.

И выразим работу электрического поля:

Согласно пятому уравнению это и есть искомая работа .

Подставим данные из условия и рассчитаем ответ:

Задача решена.

На этом наш урок закончен. Спасибо за внимание.

Список литературы

1. Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

2. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.  

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт phyzika.ru (Источник)        

2. Интернет-сайт physics.ru (Источник)  

3. Интернет-сайт knowlegeport.narod.ru (Источник)

Домашнее задание

1. Какой вид имеет формула для работы электрического поля?

2. Что такое потенциал электрического поля?

3. Решите задачу: точечный заряд , находясь в некоторой точке поля, обладает потенциальной энергией 1 мкДж. Найдите потенциал этой точки поля.

Источник: https://interneturok.ru/lesson/physics/10-klass/osnovy-elektrodinamiki-2/potentsial-elektricheskogo-polya-raznost-potentsialov

Электрическое поле: определение, классификация, характеристики

Нас окружает материальный мир. Материю мы воспринимаем с помощью зрения и других органов чувств. Отдельным видом материи является электрическое поле, которое можно выявить только через его влияние на заряженные тела или с помощью приборов. Оно порождает магнитные поля и взаимодействует с ними. Эти взаимодействия нашли широкое практическое применение.

Определение

Электрическое поле неразрывно связано с магнитным полем, и возникает в результате его изменения. Эти два вида материи являются компонентами электромагнитных полей, заполняющих пространство вокруг заряженных частиц или заряженных тел.

Таким образом, данный термин означает особый вид материи, обладающий собственной энергией, являющийся составным компонентом векторного электромагнитного поля. У электрического поля нет границ, однако его силовое воздействие стремится к нулю, при удалении от источника – заряженного тела или точечных зарядов [1].

Важным свойством полевой формы материи является способность электрического поля поддерживать упорядоченное перемещение носителей зарядов.

Рис. 1. Определение понятия «электрическое поле»

Энергия электрического поля подчиняется действию закона сохранения. Её можно преобразовать в другие виды или направить на выполнение работы.

Силовой характеристикой полей выступает их напряжённость – векторная величина, численное значение которой определяется как отношение силы, действующей на пробный положительный заряд, к величине этого заряда.

Характерные физические свойства:

• реагирует на присутствие заряженных частиц;
• взаимодействует с магнитными полями;
• является движущей силой по перемещению зарядов – как положительных ионов, таки отрицательных зарядов в металлических проводниках;
• поддаётся определению только по результатам наблюдения за проявлением действия.

Оно всегда окружает неподвижные статичные (не меняющиеся со временем) заряды, поэтому получило название – электростатическое. Опыты подтверждают, что в  электростатическом поле действуют такие же силы, как и в электрическом.

Электростатическое взаимодействие поля на заряженные тела можно наблюдать при поднесении наэлектризованной эбонитовой палочки к мелким предметам. В зависимости от полярности наэлектризованных частиц, они будут либо притягиваться, либо отталкиваться от палочки.

Сильные электростатические поля образуются вблизи мощных электрических разрядов. На поверхности проводника, оказавшегося в зоне действия разряда, происходит перераспределение зарядов.

Вследствие распределения зарядов проводник становится заряженным, что является признаком влияния электрического поля.

Классификация

Электрические поля бывают двух видов: однородные и неоднородные.

Однородноеэлектрическое поле

Состояние поля определяется пространственным расположением линий напряжённости. Если векторы напряжённости идентичны по модулю и они при этом сонаправлены во всех точках пространства, то электрическое поле – однородно. В нём линии напряжённости расположены параллельно.

В качестве примера является электрическое поле, образованное разноимёнными зарядами на участке плоских металлических пластин (см. рис. 2).

Рис. 2. Пример однородности

Неоднородное электрическое поле

Чаще встречаются поля, напряжённости которых в разных точках отличаются. Линии напряжённости у них имеют сложную конфигурацию.

Простейшим примером неоднородности является электрический диполь, то есть система из двух разноимённых зарядов, влияющих друг на друга (см. рис. 3).

Несмотря на то, что векторы напряжённости электрического диполя образуют красивые линии, но поскольку они не равны, то такое поле неоднородно. Более сложную конфигурацию имеют вихревые поля (рис 4).  Их неоднородность очевидна.

Рис. 3. Электрический диполь Рис. 4. Вихревые поля

Характеристики

Основными характеристиками являются:

• потенциал;
• напряжённость;
• напряжение.

Потенциал

Термин означает отношение потенциальной энергии W, которой обладает пробный заряд q′ в данной точке к его величине. Выражение φ=W/q′. называется потенциалом электрического поля в этой точке.

Другими словами: количество накопленной энергии, которая потенциально может быть потрачена на выполнение работы, направленной на перемещение единичного заряда в бесконечность, или в другую точку с условно нулевой энергией,  называется потенциалом рассматриваемого электрического поля в данной точке.

Энергия поля учитывается по отношению к данной точке. Её ещё называют потенциалом в данной точке. Общий потенциал системы равен сумме потенциалов отдельных зарядов. Это одна из важнейших характеристик поля. Потенциал можно сравнить с энергией сжатой пружины, которая при высвобождении способна выполнить определённую работу.

Единица измерения потенциала – 1 вольт. При бесконечном удалении точки от наэлектризованного тела, потенциал в этой точке уменьшается до 0: φ∞=0.

Напряжённость поля

Достоверно известно, что электрическое поле отдельно взятого заряда q действует с определённой силой F на точечный пробный заряд, независимо от того, на каком расстоянии он находится. Сила, действующая на изолированный положительный пробный заряд, называется напряжённостью и обозначается символом E.

Напряжённость – векторная величина. Значение модуля вектора напряжённости: E=F/q′.

Линиями напряжённости электрического поля (известные как силовые линии), называются касательные, которые в точках касания совпадают с ориентацией векторов напряжённости. Плотность силовых линий определяет величину напряжённости.

Рис. 5. Электрическое поле положительного и отрицательного вектора напряжённости

Напряженность вокруг точечного заряда Q на расстоянии r от него, определяется по закону Кулона: E = 14πε0⋅Qr2. Такие поля называют кулоновскими.

Векторы напряженности положительного точечного заряда направлены от него, а отрицательного – до центра (к заряду). Направления векторов кулоновского поля видно на рис. 6.

Рис. 6. Направление линий напряжённости положительных и отрицательных зарядов

Для кулоновских полей справедлив принцип суперпозиции. Суть принципа в следующем:вектор напряжённости нескольких зарядов может быть представлен в виде геометрической суммы напряжённостей, создаваемых каждым отдельно взятым зарядом, входящих в эту систему.

Для общего случая распределения зарядов имеем:

Линии напряжённости схематически изображены на рисунке 7. На картинке видно линии, характерные для полей:

• электростатического;
• дипольного;
• системы и одноимённых зарядов;
• однородного поля.

Рис. 7. Линии напряжённости различных полей

Напряжение

Поскольку силы электрического поля способны выполнять работу по перемещению носителей элементарных зарядов, то наличие поля является условием для существования электрического тока. Электроны и другие элементарные заряды всегда двигаются от точки, обладающей более высоким потенциалом, к точке с низшим потенциалом. При этом часть энергии расходуется на выполнение работы по перемещению.

Для поддержания постоянного тока (упорядоченного движения носителей элементарных зарядов) необходимо на концах проводника поддерживать разницу потенциалов, которую ещё называют напряжением. Чем больше эта разница, тем активнее выполняется работа, тем мощнее ток на этом участке. Функции по поддержанию разницы потенциалов возложены на источники тока.

Методы обнаружения

Органы чувств человека не воспринимают электрических полей. Поэтому мы не можем их увидеть, попробовать на вкус или определить по запаху. Единственное, что может ощутить человек – это выпрямление волос вдоль линий напряжённости. Наличие слабых воздействий мы просто не замечаем.

Обнаружить их можно через воздействие на мелкие кусочки бумаги, бузиновые шарики и т.п. Электрическое поле воздействует на электроскоп – его лепестки реагируют на такие воздействия.

Очень простой и эффективный метод обнаружения с помощью стрелки компаса. Она всегда располагается вдоль линий напряжённости.

Существуют очень чувствительные электронные приборы, с лёгкостью определяющие наличие электростатических полей.

Методы расчета электрического поля

Для расчётов параметров используются различные аналитические или численные методы:

• метод сеток или конечных разностей;
• метод эквивалентных зарядов;
• вариационные методы;
• расчёты с использованием интегральных уравнений и другие.

Выбор конкретного метода зависит от сложности задачи, но в основном используются численные методы, приведённые в списке.

Использование

Изучение свойств электрического поля открыло перед человечеством огромные возможности. Способность поля перемещать электроны в проводнике позволила создавать источники тока.

На свойствах электрических полей создано различное оборудование, применяемое в медицине, химической промышленности, в электротехнике. Разрабатываются приборы, применяемые в сфере беспроводной передачи энергии к потребителю. Примером могут послужить устройства беспроводной зарядки гаджетов. Это пока только первые шаги на пути к передачи электричества на большие расстояния.

Сегодня, благодаря знаниям о свойствах полевой формы материи, разработаны уникальные фильтры для очистки воды. Этот способ оказался дешевле, чем использование традиционных сменных картриджей.

К сожалению, иногда приходится нейтрализовать силы полей. Обладая способностью электризации предметов, оказавшихся в зоне действия, электрические поля создают серьёзные препятствия для нормальной работы радиоэлектронной аппаратуры. Накопленное статическое электричество часто является причиной выхода из строя интегральных микросхем и полевых транзисторов.

Источник: https://www.asutpp.ru/elektricheskoe-pole.html

Работа в электрическом поле. Потенциал

Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆l→ формулу работы можно записать так: ∆A=F·∆l·cos α=Eq∆lcos α=Elq∆l.

Рисунок 1.4.1. Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.

Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.

Определение 1

При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.

У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.

Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:

Определение 2

Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0. Поле, обладающее таким свойством, называется консервативным, или потенциальным.

Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q, а также две траектории перемещения пробного заряда q в другую точку. Символом ∆l→  на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:

∆A=F∆lcos α=Eq∆r=14πε0Qqr2∆r.

Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δr. Проинтегрируем данное выражение на интервале от r=r1 до r=r2 и получим следующее:

A=∫r1r2E·q·dr=Qq4πε01r1-1r2.

Рисунок 1.4.2. Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.

Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны.

Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е.

заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.

Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов.

Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле.

Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.

Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за 0.

Определение 3

Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.

Обозначив энергию как W, а работу, совершаемую зарядом, как A10, запишем следующую формулу:

Wp1=A10.

Обратите внимание, что энергия обозначается именно буквой W, а не E, поскольку в электростатике E – это напряженность поля.

Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки).

На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет.

Важна лишь разность ее значений в начальной и конечной точке пространства.

Определение 4

Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки 1 в точку 2, нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.

A12=A10+ A02= A10 – A20 =Wp1 – Wp2.

Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.

Понятие потенциала электрического поля

Определение 5

Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.

Он обозначается буквой φ. Это важная энергетическая характеристика электростатического поля.

φ=Wpq.

Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.

A12=Wp1–Wp2=qφ1–qφ2=q(φ1 – φ2).

Потенциал электрического поля измеряется в вольтах (В).

1 В=1 Дж1 Кл.

Разность потенциалов в формулах обычно обозначается Δφ.

Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:

Определение 6

Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.

φ∞=A∞q.

Чтобы вычислить потенциал точечного заряда на расстоянии r, на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:

φ=φ∞=1q∫r∞Edr=Q4πε0∫r∞drr2=14πε0Qr

С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при r≥R, что следует из теоремы Гаусса.

Изображение электрических полей с помощью эквипотенциальных поверхностей

Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.

Определение 7

Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.

Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.

Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.

Рисунок 1.4.3. Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.

Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.

В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:

ΔA12=qEΔl=q(φ1–φ2)=–qΔφ,

где Δφ=φ1-φ2 – изменение потенциала. Отсюда выводится, что: 

E=-∆φ∆l, (∆l→0) или E=-dφdl.

Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.

Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:

φ=φ1+φ2+φ3+…

Источник: https://Zaochnik.com/spravochnik/fizika/elektricheskoe-pole/rabota-v-elektricheskom-pole-potentsial/

Электрический потенциал

Электрический потенциал – это скалярная физическая величина, характеризующая напряжённость поля. Через параметр также выражается электрическое напряжение.

Физический смысл электрического поля

Учёные давно ломают голову над субстанциями электрического и магнитного полей, но пока сие для них загадка, как и гравитация. существование не оспаривается, но суть неясна. Не секрет электричество люди знали задолго до нашей эры, а к изучению не стремились.

Главные достижения по изучению электричества случились бы минимум на 20 лет раньше, нежели в действительности.

До Эрстеда влияние провода с током на магнитную стрелку отмечал Джованни Доменико Романьози в 1802 году.

Это подтверждённые официальными изданиями данные, а собственно событие, возможно, произошло раньше. Заслуга Эрстеда лишь в заострении внимания общественности на замеченном факте.

Подобных примеров тьма. Порой учёные вне зависимости друг от друга делали открытия, изобретения. Встречались случаи, когда муж науки думал, что его измышления не новы.

Потом удивлялся, когда оказывалось, что авторство теперь принадлежит постороннему человеку, хотя собственное открытие случилось раньше по времени. Замалчивание гарантировало переход доли известности к описавшему событие.

Так происходило в XIX веке – учёные постоянно сотрудничали, что-то обсуждали, порой тяжело найти концы.

К примеру, Фарадея упрекали за плагиат конструкции первого человеческого двигателя, а Википедия приписала ему авторство катушки индуктивности, придуманной Лапласом, на которое Майкл не претендовал. Впрочем, когда речь заходит о материи полей, учёные хранят дружное молчание. Единственным исключением стал Никола Тесла, утверждавший, что все во Вселенной состоит из гармонических колебаний.

Итак, учёные не знают о поле ничего, а электрический потенциал это характеристика поля. Субстанцию никто не видел, долго не могли зарегистрировать и с трудом представляют поныне! Не верите – попробуйте нарисовать в воображении электромагнитную волну:

1. Известно, что колебание представляет суперпозицию электрического и магнитного полей, изменяющихся во времени.
2. Вектор напряжённости магнитный перпендикулярен вектору электрическому, связаны через константу среды (некая физическая величина).
3. На вид это две перпендикулярные волны… стоп! Что такое волна?

Так выглядит современная физика. Никто точно не знает, как выглядят поле, колебание, волна, как это нарисовать. Понятно лишь: картинки из учебника слабо описывают происходящее.

Дело усугубляется неспособностью человека видеть и чувствовать электромагнитное излучение. Колебание не выглядит синусоидальным, рассматривается для одной точки, линии, фронта и пр.

Это, скорее, уплотнение и растяжение эфира, нечто напоминающее трёхмерную неописуемую фигуру.

Длинное предисловие свидетельствует, насколько неизведанным остаётся то, что используется в повседневной жизни. И порой таит реальную опасность для человека.

К примеру, доказано, что излучение СВЧ печи постепенно «портит» пищу. Человек, регулярно питающийся из микроволновки, рискует получить в собственное распоряжение обширный список недугов.

В первую очередь – болезни крови. Небезопасна для людей и сетевая частота 50 Гц.

Характеристики электрического поля

Человек быстро понял, что электрическое поле есть, уже в XVIII веке – либо раньше – нарисована опилками его картина. Люди увидели линии, выходившие из полюсов. По аналогии стали пытаться изобразить электрическое поле.

К примеру, Шарль Кулон на исходе восемнадцатого столетия открыл закон притяжения и отталкивания зарядов.

Записав формулу, понял, что эквипотенциальные линии силы взаимодействия концентрически расходятся вокруг точечного скопления электричества, а траектории движения – прямолинейны.

Так оказалась изображена первая картина электрического поля. Напоминает картину, как исследователи представляли магнитное, но с гигантской разницей: в природе нашлись заряды обоих знаков. Линии напряжённости уходят в бесконечность (в теории, безусловно, закончатся). А магнитные заряды поодиночке не найдены, линии их всегда замыкаются в видимой области пространства.

Первая картина электрического поля

В остальном нашлось много общего, к примеру, заряды одинакового знака отталкиваются, а разных – притягиваются. Это справедливо для магнитов и электричества.

Гильберт заметил, что магнетизм – сильная субстанция, которую сложно экранировать или уничтожить, а электричество легко разрушается влагой и прочими веществами.

Дёгтя в бочку добавил Кулон, который, следуя Бенджамину Франклину, присвоил электронам отрицательный заряд. Хотя речь шла о количестве флюида. И избыток электронов следовало назвать положительным.

Как результат, линии напряжённости поля располагаются в направлении обратном правильному. Потенциал растёт не туда… Главными характеристиками электрического поля считаются:

1. Напряжённость – показывает, какая сила действует на положительный единичный заряд в данной точке со стороны поля.
2. Потенциал – показывает, какую работу способно затратить поле, чтобы переместить единичный пробный положительный заряд в бесконечно удалённую точку.
3. Напряжение – разность потенциалов между двумя точками. Напряжение определяется исключительно относительно некоторого уровня.

Наиболее вероятно происхождение терминов из латинского языка. Напряжённость ввёл в обиход, предположительно, Алессандро Вольта, а потенциал называется по наименованию типа поля, которое указанной величиной характеризуется: работа по перемещению заряда не зависит от траектории, равна разнице потенциалов начальной и конечной точки. Следовательно, на замкнутой траектории равна нулю.

Нулевой потенциал и потенциальное поле

Электрическое поле считается потенциальным, значит, работа по перемещению в нем заряда не зависит от траектории и определяется единственно потенциалом. Потенциал – универсальное физическое понятие, часто применяемое. К примеру, для гравитационного поля Земли, происхождение которого поныне необъяснимо. Известно, что массы притягиваются по закону, напоминающему выведенный Шарлем Кулоном.

Зарисовка напряжённости поля

В электрическом поле Земной шар становится началом отсчёта. Нет разницы, относительно чего исчислять потенциал, но люди быстро поняли, что смоляное электричество бьётся, стеклянное кусается током, а грунт не причиняет вреда. Следовательно, в полном соответствии с логикой принят за нуль.

В этом плюс: Земля громадная по объёму, на планету стекают без труда гигантские токи, статические и переменные. Доказано, что на теле заряд пытается распределиться взаимно на максимальной дистанции. Что соответствует поверхности планеты.

При таком раскладе плотность заряда получается несущественной, много меньше, чем на любом наэлектризованном теле.

На Земле потенциал за редким исключением измеряется относительно грунта, значение называют электрическим напряжением. Из контекста становится понятно, что напряжение бывает положительным и отрицательным.

Впрочем, не всегда. На ЛЭП порой считается выгодным использовать схемы с изолированной нейтралью. Тогда потенциал любой точки не считается относительно Земли, отсутствует нейтраль.

Это становится возможным в трёхфазных цепях.

На местной подстанции ставят разделительный трансформатор, нейтраль вторичной обмотки которого заземляют, чтобы поставлять потребителям фазное напряжение 220 В, а не линейное.

Порой люди наивно думают, что планета единая, следовательно, не нужна нейтраль, ток всё равно потечёт. Но потечёт через грунт, вызывая немалый экономический ущерб и представляя опасность для людей созданием шагового напряжения.

Медный нулевой проводник – называли в первой половине XIX века возвратным – имеет малое сопротивление и гарантированно не причинит вреда.

В цепях с изолированной нейтралью потенциал не отсчитывается относительно уровня грунта, а напряжение измеряется между двумя точками.

Уместно упомянуть, что по закону Ома ток, протекая через проводник, создаёт разность потенциалов. Поэтому нельзя браться при аварии за контур заземления.

Малое сопротивление способно оказаться причиной образования здесь немалой разницы потенциалов. А человек обязан помнить об опасности напряжения прикосновения.

Однако цепи с изолированной нейтралью используются и в целях безопасности.

Если напряжение создаётся между двумя точками вторичной обмотки разделительного трансформатора, ток на землю через неосторожно взявшегося за оголённый провод человека не пойдёт – разница потенциалов относительно грунта меньше. Следовательно, разделительный трансформатор становится мерой защиты и часто используется на практике.

Падение потенциала во внешней электрической цепи

Внешней электрической цепью называется участок, находящийся за пределами источника. На практике ЭДС вырабатывается на вторичных обмотках трёхфазного трансформатора подстанции, считаясь источником. Начиная с вывода, идёт внешняя цепь.

На ней потенциал падает от фазного напряжения до нейтрали. Речь идёт о рядовых потребителях. Когда в дом приходит электричество, это неизменно система трёхфазного тока. Нейтраль глухо заземлена, чтобы обеспечить нужный уровень безопасности.

Жилой дом не гарантирует равномерную загрузку всех фаз, через нейтраль потечёт ток. Если цепь использовать для защиты, не возникает полной гарантии безопасности: путь тока способен пролечь через человека, неожиданно взявшегося за заземлитель.

Следовательно, нужно обеспечить два нулевых проводника: рабочий и защитный. Через первый производится зануление металлических частей объекта, через второй – заземление.

Причём за рубежом принято делить две ветви на две разные линии, а в РФ они объединяются в районе контура заземления. Первое сделано для надёжной защиты, второе – для возможности работы в здании трёхфазного оборудования (вдруг пригодится!).

Если в промышленной установке оставить лишь заземление корпуса, это плохо окончится для неудачника, попавшего под электрический потенциал.

Следовательно, западная система хороша для однофазного оборудования. Но за счёт унифицированности система РФ сложнее. Импортное оборудование плохо сочетается с российскими условиями: фильтры питания рассчитаны так, чтобы защитный и рабочий нулевые проводники не пересекались. Причина в электрическом потенциале:

1. На защитном проводнике всегда потенциал грунта – нуль.
2. На рабочем допустимо иное значение за счёт падения напряжения на проводах линии электроснабжения.

Система TN-C-S

Чтобы выровнять разницу, линии на входе в здание объединяют и заводят на контур громоотвода. Что для импортной техники не становится идеальным решением, предприятия-поставщики электроэнергии несут потери. Это известная система TN-C-S, применяющаяся в РФ. Дома, возведенные ещё в СССР, понемногу переоборудуются.

Источник: https://VashTehnik.ru/enciklopediya/elektricheskij-potencial.html

Потенциал электрического поля

Важным свойством электрического поля, как поля не имеющего вихрей и созданного одними неподвижными источниками, является его потенциальность.

Электрическое поле называется потенциальным, если работа, которую совершает носитель заряда в таком поле, при перемещении его по любому замкнутому контуру равняется нулю.

Гравитационное поле силы тяжести также является потенциальным.

Если поднять груз определенной массы на некоторую высоту, а затем опустить его обратно на поверхность Земли, в прежнюю точку, то полная механическая работа будет также равна нулю.

Причем, совершенно не важно по какой траектории осуществлялся подъем и спуск груза. Источником такого гравитационного поля является в этом примере Земля (тело с массой во много раз большей чем масса поднимаемого груза).

Электростатическое поле, то есть такое поле, которое образовано неподвижными электрическими зарядами, также обладает аналогичной потенциальностью.

Работа носителя заряда при его перемещении по замкнутому контуру в электростатическом поле будет равняться нулю.

Траектория такого перемещения замкнута и называется контуром и эта траектория может быть любого вида, принципиальное значение имеет ее замкнутость, а не форма.

На рисунке изображены разные траектории движения заряда в электростатическом поле плоского конденсатора. Не имеет значения по какому маршруту двигался заряд (картинка слева), совершенная им работа будет одинаковой, то есть A1=A2=A3.

На правом изображении показано движение заряда по замкнутому контуру. Начальная и конечная точки поля совпадают. Заряд двигался из точки 1, затем 2, 3, и снова прибыл в точку 1, тем самым образовав замкнутую траекторию, то есть контур.

В этом случае говорят, что совершенная им механическая работа равна нулю.

Потенциальная энергия

Известное в механике понятие потенциальной энергии также относится к потенциальному полю. При отсутствии потенциального поля не может быть никакой речи о потенциальной энергии.

Потенциальной энергией тела мы как раз и называем ту работу, которую необходимо затратить, чтобы переместить это тело из бесконечности в данную точку. Иначе говоря, требуется затратить энергию, чтобы перенести тело из области с нулевым потенциалом в область с высоким потенциалом.

Опять же, если затрачиваемая работа зависит от формы пути, то нет потенциального поля, а значит невозможно говорить о потенциальной энергии.

Как было уже сказано выше, потенциал — это энергетическая характеристика поля и потому достаточно легко определить потенциальную энергию через потенциал.

Потенциальная энергия Up равна произведению заряда q на потенциал φ.

Дата: 01.05.2015

© Valentin Grigoryev (Валентин Григорьев)

Источник: http://electricity-automation.com/page/potentsial-elektricheskogo-polya

Курс по математическому анализу

Вашему вниманию предлагается курс по математическому анализу.

 

 

Наверх

1. Предел числовой последовательности.

Последовательность  — это функция, заданная на множестве натуральных чисел . Число  называется пределом последовательности , если для любого положительного числа , как бы мало оно ни было, существует такой номер, что для всех  c номерами  справедливо неравенство . Неравенство , эквивалентное неравенству , означает, что для любого существует такой номер , что все  c номерами расположены между и . Последовательность, предел которой — конечное число , называется сходящейся, и ее предел обозначают. Если изобразить элементы последовательности на плоскости точками с координатами  , то неравенства означают, что все точки  с номерами расположены между параллельными оси абсцисс прямыми и .

 

Бесконечно малая последовательность. Последовательность  , предел которой равен нулю , называется бесконечно малой.   

Бесконечно большая последовательность. Последовательность называется бесконечно большой, если для любого положительного числа  , как бы велико оно ни было, существует такой номер  , что для всех с номерамисправедливо неравенство  , записываем .

 

 

Наверх

2. Методы вычисления пределов последовательностей.

Пусть заданы две последовательности  и . Если существуют  и , то существуют и пределы суммы и произведения последовательностей, а при и предел частного, причем   ,        ,  . Для правильного применения этих теорем очень важно существование пределов каждой последовательности.

Неопределенности и их раскрытие.

Если    и  , то может существовать  . В этом случае говорят, что имеем неопределенность типа  . Также может существовать   , в этом случае имеем неопределенность типа  . Если   и  , то может существовать . В этом случае говорят, что имеем неопределенность типа   . Поскольку в перечисленных случаях не применимы теоремы о пределе суммы, произведения и частного, используют другие способы вычисления, которые называют методами раскрытия неопределенностей. Это, как правило, алгебраические преобразования, приводящие выражения к виду, при котором можно пользоваться упомянутыми теоремами.

 

 

Наверх

3. Предел функции в точке.

 

Рассмотрим функцию , определенную в некоторой окрестности точки  , , , за исключением, быть может, самой точки  . Число  называется пределом функции  при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех   , удовлетворяющих неравенству  , справедливо неравенство . Говорят “предел функции  в точке  ” и обозначают  . Неравенство  для всех , эквивалентное неравенствам , , означают, что для любого существует такое , что для  график функции   расположен на плоскости в прямоугольнике . При вычислениях на компьютере мы имеем дело с дискретными значениями переменных. Поэтому удобнее пользоваться другим, эквивалентным приведенному, определением предела. А именно:  , если для любой, сходящейся к  последовательности значений аргумента , соответствующая последовательность значений функции  сходится к числу . Отсюда следует, в частности, что для любого существует такое , что для любой последовательности , сходящейся к , точки с координатами  находятся на плоскости внутри прямоугольника   . 

Бесконечно большие функции.

Если для любой последовательности  значений аргумента соответствующая последовательность значений функции бесконечно большая, то функция называется бесконечно большой в точке . Если  бесконечно большая в точке , то для любого положительного числа , как бы велико оно ни было, существует такое число , что для всех , удовлетворяющих неравенству , справедливо неравенство ; обозначают  .

 

 

Наверх

4. Бесконечно малые функции. Сравнение бесконечно малых функций.

Рассмотрим функцию, определенную в некоторой окрестности точки , ,  за исключением, быть может, самой точки . Функция  называется бесконечно малой при , стремящемся к , если . Если — бесконечно малая в точке , то для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех , удовлетворяющих неравенству , справедливо неравенство . Неравенства  для всех , эквивалентные неравенствам , , означают, что для любого существует такое , что для график функции расположен на плоскости в прямоугольнике . Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию.  При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.   

Сравнение бесконечно малых функций.

Пусть и  — две функции, бесконечно малые в точке . Если , то говорят, что  более высокого порядка малости, чем и обозначают . Если же , то  более высокого порядка малости, чем ; обозначают . Бесконечно малые функции  и называются бесконечно малыми одного порядка малости, если  , обозначают  .  И, наконец, если   не существует, то бесконечно малые функции и  несравнимы.   

Эквивалентные бесконечно малые функции.

Если , то бесконечно малые функции и  называются эквивалентными, обозначают ~ .

 

 

Наверх

5. Методы вычисления пределов функций.

Пусть заданы две функции и . Если существуют  и  , то существуют и пределы суммы и произведения этих функций, а при и предел частного, причем        

,

,      

 .

Для правильного применения этих теорем очень важно существование пределов каждой функции. Не трудно доказать, что предел постоянной функции равен этой постоянной, то есть   . Из приведенных формул следует полезное утверждение: 

 , то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной , то вычисление предела при  всегда можно свести к вычислению предела при . Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке  в выражение для функции. 

 

Неопределенности и их раскрытие.

Существуют случаи, когда не применимы теоремы о пределах суммы, произведения, частного, но предел существует и может быть вычислен. Если  и   , то может существовать . В этом случае говорят, что имеем неопределенность типа . Также может существовать   , в этом случае имеем неопределенность типа   . Если   и   , то может существовать  .   В этом случае говорят, что имеем неопределенность типа . Если     и   , то может существовать  — неопределенность типа  . Рассматривают также неопределенности типа , и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой в выражение для функции. Полезно запомнить замечательные пределы: 

      (е = 2.71828… — основание натуральных логарифмов) — неопределенность типа .

       — неопределенность типа .

Использование эквивалентных бесконечно малых.

Если мы имеем неопределенность типа    , то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке  равен нулю. Пусть, , ,  — бесконечно малые функции при  , причем эквивалентна  , т.е. ~ , ~ (напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда, т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную. 

Правило Лопиталя.

Неопределенности типа  или удобно раскрывать с помощью правила Лопиталя. Пусть  и  две бесконечно малые или бесконечно большие функции при  и существует предел отношения их производных при . Тогда  . Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз. 

 

Формула Тейлора.

Пусть функция имеет в точке  производные всех порядков до -го включительно. Тогда для    справедлива формула Тейлора:

где  называется остаточным членом формулы Тейлора.

 

 

Наверх

6. Непрерывность функции в точке, на отрезке.

Рассмотрим функцию , определенную на некотором промежутке . Функция  непрерывна в точке , если предел функции в точке  равен значению функции в этой точке,. 

Свойства функций, непрерывных на отрезке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Для функции, непрерывной на отрезке , справедливы следующие утверждения. 

Функция, непрерывная на отрезке  , достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке  существуют точки  такие, что

. 

Если функция  непрерывна на отрезке  и принимает на концах значения разных знаков, то на интервале  существует точка   , в которой функция обращается в нуль, т.е.   . Это утверждение применяют для отделения корней уравнений  с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.

Если функция   непрерывна на отрезке    , дифференцируема хотя бы на интервале  , то на интервале  существует точка , такая, что  . Это свойство называют формулой Лагранжа или формулой конечных приращений.

 

 

Наверх

7. Классификация точек разрыва

Рассмотрим функцию  , определенную на некотором промежутке . Функция непрерывна в точке , если предел функции в точке  равен значению функции в этой точке, . 

Односторонние пределы функции в точке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Если функция определена на промежутке , , то при исследовании поведения функции в окрестности точки  имеет смысл говорить о пределе функции  в точке  справа, а при исследовании в окрестности точки — о пределе функции в точке  слева. Число называется пределом справа функции при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех  , удовлетворяющих неравенству , справедливо неравенство  . Говорят “предел справа функции в точке ” и обозначают . Аналогично говорят “предел слева функции в точке ” и обозначают , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство  . Для существования предела функции в точке, необходимо и достаточно, чтобы существовали и совпадали односторонние пределы функции в этой точке. По той же схеме вводится понятие непрерывности слева и непрерывности справа. Функция, определенная на отрезке , , непрерывна справа в точке , если и непрерывна слева в точке  , если. Для того чтобы функция была непрерывна в точке  необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:. Если хотя бы одно из равенств нарушается, говорят о разрыве в точке . 

Классификация разрывов.

Если хотя бы одно из равенств  нарушается, говорят о разрыве в точке . Если  и односторонние пределы конечны, то разрыв в точке называется устранимым. Если и оба односторонние пределы конечны, то говорят о скачке функции в точке . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

 

 

Наверх

8. Производная, ее вычисление, геометрический смысл.

Производная функции в точке — Пусть функция  определена на промежутке . Точка — произвольная точка из области определения функции,   — приращение функции в точке , вызванное приращением независимой переменной .  Производной функции по независимой переменной  в точке ,  называется предел отношения приращения функции к приращению  при стремлении  к нулю, т.е.   

,  

— производная функции в точке . 

Односторонние производные — Если определена при , то можно определить правую производную функции в точке :

Аналогично, если  определена при , определяется левая производная функции в точке :

 Функция  имеет в точке  производную тогда и только тогда, когда в точкесовпадают ее левая и правая производные:  . 

Секущая графика функции — Пусть — функция, определенная на промежутке . Прямая, проходящая через точки , , ,  называется секущей графика функции  . Угловой коэффициент  секущей равен   и ее уравнение имеет вид  . 

Касательная и нормаль к графику функции — Касательной к графику функции  в точке  называется предельное положение секущей, проходящей через точки  , , когда . Угловой коэффициент касательной равен значению производной в точке и ее уравнение имеет вид . Нормалью к графику функции  в точке называется прямая , проходящая через эту точку перпендикулярно касательной. Угловой коэффициент нормали равен    и ее уравнение имеет вид  .

 

 

Наверх

9. Производные сложных, обратных функций.

Пусть    — функция, дифференцируемая в точке  ,   — функция, дифференцируемая в точке   , причем  . Тогда   — сложная функция независимого переменного , дифференцируема в точке    и ее производная в этой точке вычисляется по формуле   .

Обычно    называют внешней функцией, а — внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции. 

Производная обратной функции.

Пусть функция дифференцируема и строго монотонна на . Пусть также в точке производная . Тогда в точке   определена дифференцируемая функция , которую называют обратной к  , а ее производная вычисляется по формуле .

 

 

Наверх

10. Дифференцируемость, дифференциал.

Дифференцируемость функции в точке.

Пусть функция  определена в некоторой окрестности точки  . Рассмотрим приращение функции в этой точке:  . Функция называется дифференцируемой в точке , если ее приращение можно записать в виде , где — приращение независимой переменной, А – постоянная, не зависящая от , — бесконечно малая функция при . 

Дифференциал функции.

Дифференциалом функции  в точке называется линейная по  часть приращения . Дифференциал обозначается   , то есть  . Рассматривая функцию , нетрудно убедиться, что  , если  — независимая переменная. 

Связь дифференциала и производной.

Воспользуемся определением производной для дифференцируемой функции в точке : . Таким образом, дифференциал функции выражается формулой  , то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на  . Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная. 

 

 

Наверх

11. Производные и дифференциалы высших порядков.

Производные высших порядков.

Рассмотрим функцию  , определенную на некотором промежутке   . Вычислим производную , которая также является функцией на . Производной второго порядка от функции  называется производная от ее производной:   . Аналогично определяют производную любого порядка:  . 

Дифференциалы высших порядков.

Рассмотрим дифференциал функции  в произвольной точке промежутка : . Здесь  — приращение независимой переменной, которое является числом и не зависит от . Сам же дифференциал есть функция от , и можно вычислить дифференциал от этой функции:   При  этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле Аналогично вычисляется дифференциал любого порядка .

Понятие инвариантности формы дифференциала.

Рассмотрим дифференциал функции  в произвольной точке промежутка : . Здесь — приращение независимой переменной, которое является числом и не зависит от . Пусть теперь   — функция независимого переменного , определенная на промежутке  . Тогда  — сложная функция переменного . Вычислим ее дифференциал, используя формулу для производной сложной функции: . Заметим, что и выражение для дифференциала принимает ту же форму , хотя здесь  уже функция переменного  . Это свойство дифференциала первого порядка называется инвариантностью (т.е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что  — функция переменного  . Поэтому и форма второго (а также и всех следующих) дифференциала неинвариантна.

 

 

Наверх

12. Исследование функций и построение графиков.

Рассмотрим функцию , определенную на промежутке (возможно,  ) . Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения. 

Если , то график функции пересекает ось абсцисс в точке  . 

Если , то график функции пересекает ось ординат в точке  .

Если в точке  функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту  (Если расстояние от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты стремится к нулю при справа, слева или с обеих сторон). 

Если , или , существуют и конечны пределы и , то прямая — асимптота графика функции. 

Если , то график функции имеет на левой границе области сходимости вертикальную асимптоту  ; аналогично, если , то график функции имеет на правой границе области сходимости вертикальную асимптоту . 

Если и существует такое число , что для любого , то исследуемая функция периодична с периодом ; в этом случае достаточно построить график функции на промежутке  и доопределить его по периодичности на всю числовую ось.

Если , то исследуемая функция четная; этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке и отобразить его симметрично относительно оси ординат на . 

Если  , то исследуемая функция нечетная; этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке  и отобразить его симметрично относительно начала координат на . 

Исследование функций с помощью производной.

Если функция дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум (точки максимума и точки минимума функции имеют общее название — точки экстремума), используя следующие утверждения. 

Для того, чтобы дифференцируемая на функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы () на . 

Пусть в точке  производная  или не существует. Если существует окрестность точки , такая, что для  из этой окрестности при  и при , то функция имеет в точке максимум. Если же при  и  при  , то функция имеет в точке  минимум (в этом случае говорят, что “производная меняет знак при переходе через точку ”).

Если непрерывная в точке функция дифференцируема на , при этом на  и на , то функция имеет в точке максимум; если же при  и  при , то функция имеет в точке  минимум.   

Исследование функций с помощью второй производной.

Если функция дважды дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости и вогнутости.

График функции называется выпуклым (выпуклым вниз) на промежутке , если он расположен выше касательной, проведенной в любой точке , . Если же график функции лежит ниже касательной, — то он называется вогнутым (выпуклым вверх). 

Если дважды дифференцируемая на промежутке  функция имеет на нем положительную вторую производную, то функция выпуклая на . Если же вторая производная отрицательна на промежутке , то функция на нем вогнута. 

Если вторая производная равна нулю в точке , а слева и справа от нее имеет значения разных знаков, точка  — точка перегиба.

 

 

Наверх

13. Кривые на плоскости.

Кривые на плоскости в декартовых координатах.

Кривая на плоскости в прямоугольных (декартовых) координатах — это множество точек, координаты которых связаны соотношениями , , , или ; первые два соотношения задают кривую явно, последнее — неявно. Кривая, заданная уравнением  , , называется гладкой, если функция дифференцируема на промежутке . В каждой точкегладкой кривой можно провести касательную , уравнение которой . Уравнение нормали в той же точке имеет вид  или  . Кривая, заданная неявно уравнением , называется гладкой, если на ней нет особых точек (точка линии называется особой, если в ней одновременно обращаются в нуль обе частные производные функции : ). Уравнения касательной и нормали к такой кривой, проходящих через точку , , имеют соответственно вид   и

Кривые, заданные параметрически.

Уравнения , , устанавливающие зависимость декартовых координат точки плоскости от значения параметра , определяют на плоскости кривую, заданную в параметрической форме (говорят еще — заданную параметрически). Поскольку производная функции , заданной параметрически уравнениями , в точке, которая не является особой точкой кривой, вычисляется по формуле , то уравнения касательной и нормали к кривой, проходящих через точку , имеют соответственно вид: .   

Кривые в полярных координатах.

Декартовы координаты точки  на плоскости связаны с полярными координатамисоотношениями . Многие кривые на плоскости удобно описывать как функции радиуса-вектора и полярного угла — в полярных координатах. Так, уравнение единичной окружности в полярных координатах имеет вид  . Уравнение кривой в полярных координатахобычно имеет вид . Угловой коэффициент касательной к графику функции, заданной уравнением , в точке   равен   , а декартовы координаты точки равны соответственно  и   .

 

 

Наверх

14. Формула Тейлора.

Остаточный член формулы Тейлора — Пусть функция имеет в точке  производные всех порядков до -го включительно. Тогда для справедлива формула Тейлора:

 ,

где ,  называется остаточным членом формулы Тейлора в форме Пеано; — бесконечно малая более высокого порядка малости, чем . Если отбросить остаточный член, то получится приближенная формула Тейлора

 

,

правая часть которой называется многочленом Тейлора функции ; его обозначают . Приближенная формула позволяет заменять в различных математических расчетах (аналитических и численных) произвольную функцию ее многочленом Тейлора. 

Из формулы Тейлора видно, что чем точка  ближе к точке , тем выше точность такой аппроксимации и эта точность растет с ростом степени многочлена. Это означает, в свою очередь, что чем больше производных имеет функция в некоторой окрестности точки , тем выше точность, с которой многочлен Тейлора аппроксимирует функцию в этой окрестности. 

Разложение основных элементарных функций — Положив  и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций: 

Разложение функций с использованием стандартных разложений — Для разложения по формуле Тейлора функции в окрестности произвольной точки необходимо сделать замену переменной , то есть  , и воспользоваться одним из приведенных выше разложений основных функций в окрестности точки  .

 

 

Наверх

15. Неопределенный интеграл, простейшие методы интегрирования.

Первообразная и неопределенный интеграл — Рассмотрим функцию , определенную на промежутке (здесь возможно ). Дифференцируемая на промежутке     функция , производная которой в каждой точке равна , называется первообразной функции  : . Поскольку  , то можно говорить о семействе первообразных — множестве функций вида  , . Семейство первообразных   функции называется неопределенным интегралом функции  и обозначается символом : для всех . Здесь    — знак интеграла, — подынтегральное выражение,  — подынтегральная функция,  — переменная интегрирования, — значение неопределенного интеграла, семейство первообразных функции , . То есть производнаянеопределенного интеграла равна подынтегральной функции. Наоборот,    , следовательно, дифференцирование и вычисление неопределенного интеграла, – взаимно обратные операции. Не представляет труда с помощью таблицы производных составить таблицу неопределенных интегралов. Важным свойством неопределенного интеграла является линейность: , здесь    — постоянные. Вычисление неопределенного интеграла обычно сводится к преобразованию подынтегрального выражения так, чтобы можно было воспользоваться таблицей интегралов. 

Интегрирование заменой переменной — Если — непрерывно дифференцируемая функция, то, полагая   , получим формулу интегрирования заменой переменной    . Если замена переменной выбрана правильно, то интеграл в правой части должен легко вычисляться. Для некоторых классов функций существуют стандартные замены, сводящие интеграл к табличному. 

Интегрирование по частям — Пусть   — непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям . Название “по частям” связано с тем, что для записи интеграла в правой части нужно проинтегрировать “часть”     подынтегрального выражения в левой части. Метод интегрирования по частям используется для интегралов вида   ,  ,  ,  и некоторых других.

 

 

Наверх

16. Интегрирование некоторых классов функций.

Интегрирование рациональных функций — Функция называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов: . Если , рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого: 

Если , выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена   , а именно: 

Каждому действительному корню кратности 1 в разложении соответствует член   . 

Каждому действительному корню  кратности  в разложении соответствует набор из  членов     . 

Каждой паре комплексно сопряженных корней   кратности 1 в разложении соответствует член    ( — корни уравнения ).

Каждой паре комплексно сопряженных корней кратности  в разложении соответствует набор из членов       . 

В приведенных выражениях — неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю , приравнивая полученные коэффициенты при степенях   к соответствующим коэффициентам  и решая систему относительно  . 

Наконец, полученное разложение интегрируем почленно. 

Интегрирование тригонометрических функций — Интегралы вида , где  — рациональная функция своих аргументов, вычисляются с помощью универсальной замены переменной  . При этом . Однако универсальная замена обычно связана с большими вычислениями, поэтому в некоторых случаях можно ее избежать. 

Интегралы вида   вычисляются с помощью замены  . Интегралы вида  вычисляются с помощью замены  . Интегралы вида  , если , то есть четная рациональная функция своих аргументов вычисляются с помощью замены    . 

Интегралы вида  вычисляются с помощью формул понижения степени  . 

Интегрирование иррациональных функций — Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен. 

Интегралы вида , где  — рациональная функция своих аргументов, вычисляются заменой . 

Интегралы вида   вычисляются заменой или . 

Интегралы вида   вычисляются заменой   или . Интегралы вида вычисляются заменой или .

 

 

Наверх

17. Определенный интеграл. Формула Ньютона-Лейбница.

Определенный интеграл, его геометрический смысл.

Рассмотрим функцию , определенную на промежутке . Разобьем промежуток на  произвольных частей точками   и обозначим , , . На каждом промежутке    возьмем произвольную точку  и вычислим в ней значение функции. Выражение   называется интегральной суммой функции на  .Если при  существует и конечен предел последовательности частичных сумм  , не зависящий ни от способа разбиения промежутка  точками  , ни от выбора , то этот предел называют определенным интегралом от функции по промежутку , а саму функцию — интегрируемой на . Обозначают    . 

Из приведенного определения естественно следует геометрический смысл определенного интеграла: если , то   равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми . 

Формула Ньютона-Лейбница.

Значение определенного интеграла может быть вычислено по формуле Ньютона-Лейбница =, здесь символ  означает, что из значения  при верхнем пределе b нужно вычесть значение при нижнем пределе a , — первообразная функция для . Таким образом, вычисление определенного интеграла сводится к нахождению первообразной, то есть неопределенного интеграла. 

Методы вычисления определенного интеграла.

Если — непрерывно дифференцируемая на отрезке  функция, , и , когда  изменяется на  , то, положив  , получим формулу замены переменной в определенном интеграле  .

Пусть  — непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям   . Эта формула применяется для тех же классов функций, что и при вычислении неопределенного интеграла.

 

 

Наверх

18. Применение определенного интеграла для площадей и длин дуг.

Вычисление площадей и длин дуг кривых в декартовых координатах.

Пусть на плоскости задана область, ограниченная снизу кривой  , заданной в декартовых координатах, сверху – кривой  , слева – прямой   (ее может и не быть, если  ), справа – прямой  . Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле   . Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, , то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия. 

Пусть на отрезке  уравнением  задана плоская кривая. Ее длина вычисляется по формуле  

Вычисление площадей и длин дуг при параметрическом задании кривых.

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть   , при этом  , а сверху – кривой   . Тогда площадь такой плоской фигуры вычисляем по формуле . Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что  . 

Пусть кривая на плоскости задана параметрически   . Тогда длина этой кривой вычисляется по формуле  .

Вычисление площадей и длин дуг кривых в полярных координатах.

Когда кривая, ограничивающая область, задана в полярных координатах , то площадь этой области вычисляем по формуле  . Основная трудность в использовании этой формулы заключается в определении пределов интегрирования  . Здесь нужно понимать, что кривая  определена только, если . Поскольку в формуле присутствует , то она учтет и не существующую площадь, когда  . Решив уравнение , найдем пределы интегрирования. 

Если кривая, ограничивающая область, задана в полярных координатах  , то ее длина вычисляется по формуле . Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.

 

 

Наверх

19. Несобственные интегралы.

Интеграл как функция верхнего предела.

Для функции , интегрируемой для всех  , значение интеграла  зависит от значения верхнего предела ; можно рассмотреть функцию переменной : каждому значению ставится в соответствие число, равное значению интеграла  . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: ; функция определена в области интегрируемости подынтегральной функции . Если — первообразная для , то значение можно вычислить по формуле Ньютона—Лейбница: . Функцию можно исследовать, не вычисляя первообразной. Для интегрируемой при функции справедливы следующие утверждения:   непрерывна на промежутке , причем ; если при , то     монотонно возрастает на промежутке ; если непрерывна при , то дифференцируема на промежутке , причем . 

Несобственные интегралы по неограниченному промежутку.

Пусть функция  интегрируема для всех  и   . Если существует предел , то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его  . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл для интегрируемой при  функции  и интеграл для функции , интегрируемой на . Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится. 

Несобственные интегралы от неограниченных функций.

Пусть функция  интегрируема на любом отрезке, целиком содержащемся в промежутке, и бесконечно большая в точке . Если существует предел , то этот предел называют несобственным интегралом от неограниченной функции по и обозначают его . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл от интегрируемой на любом конечном отрезке, содержащемся в , бесконечно большой в точке  функции . Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится. 

Исследование несобственных интегралов на сходимость.

Вычисление несобственных интегралов сводится к вычислению первообразной, использованию формулы Ньютона-Лейбница и вычислению предела. Каждый из этапов сам по себе достаточно сложен, и разумно приступать к ним, если есть уверенность, что интеграл сходится, то есть предел конечен. Поэтому, в конечном счете, самым важным в теории несобственных интегралов является исследование их на сходимость: если интеграл расходится, то его и вычислять не надо. Одним из главных инструментов исследования несобственных интегралов на сходимость являются теоремы сравнения.

Рассмотрим две неотрицательные функции  и , определенные при . Пусть  для всех  , начиная с некоторого числа . Тогда, если сходится интеграл от большей функции , то сходится и интеграл от меньшей, то есть. Если расходится интеграл от меньшей функции  ,то расходится и интеграл от большей — . 

Если   , то несобственные интегралы от этих функций или оба сходятся или оба расходятся. 

Аналогичные утверждения, которые называют признаками сравнения, имеют место и для интегралов по конечному промежутку от неограниченных функций.

 

 

Наверх

20. Числовые ряды.

Числовой ряд. Рассмотрим произвольную числовую последовательность и формально составим сумму ее членов    Это выражение называют числовым рядом, или просто рядом. Члены последовательности называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда . Эта сумма называется n-ой частичной суммой. 

 

Сходимость числового ряда. Ряд    называют сходящимся, если существует и конечен предел последовательности     частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают   , . Если предел частичных сумм не существует или бесконечен, то ряд расходится. Разность  называется остатком ряда. Очевидно, что для сходящегося ряда    . Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то  (необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться. 

 

 

Суммирование числовых рядов. Если возможно найти общий член последовательности    , то по определению можно найти и сумму ряда, вычисляя предел этой последовательности.

 

 

Наверх

21. Сходимость знакоположительных рядов.

Теоремы сравнения.

1. Рассмотрим два числовых ряда с неотрицательными членами   и  , . Если при всех n, начиная с некоторого номера,  , то из сходимости ряда  следует сходимость ряда. Наоборот, из расходимости ряда следует расходимость ряда. 

2. Если для таких же двух рядов   , то оба ряда или сходятся или расходятся одновременно. При использовании теорем сравнения нужно иметь ряд-эталон, с которым сравнивать и про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд   , который сходится при и расходится при , или геометрический ряд , который сходится при  и расходится при  . 

Признаки сходимости. Признаки сходимости Даламбера. Для ряда с положительными членами , вычислим   . Если , то ряд сходится, — расходится. При признак Даламбера ответа не дает: ряд может как сходиться, так и расходиться. 

Признак сходимости Коши. Для ряда с неотрицательными членами   , вычислим . Если   , то ряд сходится, — расходится. При    признак Коши ответа не дает: ряд может как сходиться, так и расходиться.

 

 

Наверх

22. Сходимость знакопеременных рядов.

Абсолютная и условная сходимость. Если в последовательности  бесконечно много положительных и отрицательных членов, то ряд называется знакопеременным. Ряд   называется знакочередующимся. Знакопеременный ряд   называется абсолютно сходящимся, если сходится ряд   . Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда   начинают с исследования на сходимость ряда из модулей  методами для рядов с неотрицательными членами. Если такой ряд сходится, то получен ответ: ряд сходится абсолютно. 

 

Исследование знакочередующихся рядов. Если ряд из модулей расходится, то для знакочередующегося ряда можно применить признак Лейбница: если последовательность   стремится к нулю, монотонно убывая,   , то ряд    сходится, по крайней мере, условно. Для знакочередующегося ряда очень просто оценивается остаток ряда: .

 

 

Наверх

23. Функциональные ряды, равномерная сходимость.

Функциональный ряд, его сходимость. Рассмотрим ряд,   , членами которого являются функции, определенные на промежутке   . При каждом фиксированном   имеем числовой ряд, сходимость которого может быть исследована рассмотренными ранее методами. Сумма функционального ряда   также является функцией от х:   . По определению предела последовательности: если для   можно указать номер  ( что интересно, для каждого фиксированного   — свой номер, т.е.  ), такой, что для    выполняется неравенство  , то это и означает, что функциональный ряд сходится к функции. Множество , для которого это выполняется, называется областью сходимости функционального ряда. 

 

Равномерная сходимость функционального ряда. Пусть   , т.е. функциональный ряд сходится. Если для   можно указать номер  независимо от  , такой, что для выполняется неравенство  , то говорят, что функциональный ряд сходится равномерно на множестве .   

  

Исследование на равномерную сходимость. Признак Вейерштрасса равномерной сходимости функционального ряда: если существует сходящийся числовой ряд   с положительными членами, такой, что для всех  , начиная с некоторого номера и всех  выполняется неравенство , то функциональный ряд   сходится на равномерно. Числовой ряд   в этом случае называют мажорантой для функционального ряда.

 

 

Наверх

24. Ряд Тейлора.

Степенные ряды. Функциональный ряд     , где — числовая последовательность, называется степенным рядом. Степенной ряд сходится на интервале   с центром в точке   . Число  — радиус сходимости степенного ряда может быть вычислено по формулам , или     . Степенной ряд сходится равномерно на любом отрезке, целиком лежащем внутри интервала сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда. 

 

Разложение функций в ряд Тейлора. При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция   определена в некоторой окрестности точки   и имеет в этой точке производные всех порядков. Ряд 

называется рядом Тейлора для функции    в точке . При такой ряд называют также рядом Маклорена:    . Функция  может быть разложена в степенной ряд на интервале , если существует степенной ряд, сходящийся к  на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки , то это ряд Тейлора. Пусть функция   бесконечно дифференцируема на интервале и все ее производные ограничены в совокупности на этом интервале, то есть существует число   , такое, что для всех    и для всех   справедливо неравенство . Тогда ряд Тейлора сходится к   для всех   . Приведем разложения в ряд Тейлора для основных элементарных функций. 

 

 

Наверх

25. Ряд Фурье.

Ряд Фурье, его сходимость. Пусть функция  абсолютно интегрируема на отрезке  , то есть существует   . Тогда ей можно поставить в соответствие ее тригонометрический ряд Фурье: . Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера-Фурье: . Если функция  кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если   — сумма ряда Фурье, то для любого        . То есть, если   непрерывна в точке  , то   . Если в точке   у   разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке . 

  

Разложение в ряд Фурье на произвольном отрезке. Для кусочно-гладкой на отрезке  функции задача о разложении в ряд Фурье на этом отрезке линейной заменой сводится к задаче о разложении функции на отрезке  :   , .

 

 

Наверх

26. Сходимость ряда Фурье.

Сходимость ряда Фурье, явление Гиббса. Если функция  кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если — сумма ряда Фурье, то для любого  . То есть, если  непрерывна в точке  , то  . Если в точке  у     разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке  . В окрестности точек непрерывности функции   разность между значением функции в точке и значением частичной суммы ряда в этой точке стремится к нулю при  , что полностью соответствует теории, поскольку в этом случае   . В окрестности точек разрыва   частичные суммы ряда Фурье ведут себя иначе. Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Оно состоит в том, что для некоторых функций в точке ее скачка      существуют такие значения    , что

Это не противоречит теории, поскольку у Гиббса рассмотрен предел  , а в теории v     . 

Приближение функций, минимальное свойство коэффициентов Фурье. Функция , где    — произвольные числа, называется тригонометрическим многочленом. Тригонометрическим многочленом наилучшего приближения n-ой степени для функции     на отрезке   называется такой многочлен , среднеквадратичное отклонение  которого от функции  минимально:    . Для любой ограниченной интегрируемой на    функции частичная сумма   ее ряда Фурье является тригонометрическим многочленом наилучшего приближения n-ой степени. 

 

Зависимость скорости сходимости от гладкости функций. Скорость сходимости ряда Фурье функции зависит от ее гладкости (количества непрерывных производных). Если   непрерывно дифференцируема r раз на отрезке   , то справедливо неравенство , где  . Для среднеквадратичного отклонения справедлива оценка   , где  .

 

 

Наверх

27. Функции многих переменных.

Функция двух переменных. Переменная  (с областью изменения  ) называется функцией независимых переменных  в множестве  , если каждой паре их значений из   по некоторому правилу или закону ставится в соответствие одно определенное значение   из множества . Множество v область определения функции, множество   v область ее значений. Функциональная зависимость   от обозначается так:  и т.п. Выберем в пространстве систему координат  , изобразим на плоскости   множество  ; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение . Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных. 

Линии и поверхности уровня. Линией уровня функции двух переменных   называется геометрическое место точек на плоскости   , в которых функция    принимает одно и то же значение. Линии уровня функции определяются уравнением  , где . Изучая линии уровня функции, можно исследовать характер ее изменения, не прибегая к пространственному графику. Поверхностью уровня функции трех переменных    называется геометрическое место точек в пространстве, в которых функция  принимает одно и то же значение. Уравнение поверхностей уровня имеет вид:  . Поскольку график функции трех переменных нам недоступен, поверхности уровня являются единственным средством изучения таких функций. 

  

Локальные экстремумы. Точка называется точкой локального минимума (максимума) функции , определенной в области , если существует окрестность этой точки, такая, что  для всех точек этой окрестности, отличных от . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.

 

 

Наверх

28. Частные производные, градиент.

Частные производные. Пусть  — функция двух переменных, определенная в некоторой окрестности точки . Если существует конечный предел   , то говорят, что функция   имеет в точке частную производную по переменной   . Аналогично определяется частная производная по    . Обозначают:

 . 

Пусть — функция n переменных, определенная в области   n-мерного пространства. Частной производной функции по переменной  называется предел 

. 

Из определения частной производной следует правило: при вычислении производной по одной из переменных все остальные переменные считаем постоянными, учитывая, что производная постоянной равна нулю и постоянную можно выносить за знак производной.  

Производная по направлению. Если в n-мерном пространстве задан единичный вектор , то изменение дифференцируемой функции в направлении этого вектора характеризуется производной по направлению: . В частности, для функции трех переменных   ,  — направляющие косинусы вектора  . 

Градиент. Производная по направлению представляет собой скалярное произведение вектора   и вектора с координатами   , который называется градиентом функции    и обозначается    . Поскольку   , где   — угол между   и   , то вектор указывает направление скорейшего возрастания функции   , а его модуль равен производной по этому направлению. 

Полный дифференцал. Для приращения дифференцируемой функции   справедливо равенство    . Линейная по приращениям аргументов часть приращения функции называется полным дифференциалом функции и обозначается    . 

Производные и дифференциалы высших порядков. Дифференцируя частную производную как функцию нескольких переменных по одной из переменных, получим производные второго порядка. Например, для функции двух переменных: . Если смешанные производные     и     непрерывны, то они равны, то есть не зависят от порядка дифференцирования. Аналогично определяются, например,     . Если при вычислении полного дифференциала от дифференциала первого порядка учесть, что приращения аргументов есть числа и оставить их неизменными, то получим дифференциал второго порядка. Например, для функции двух переменных:    . Здесь учтено равенство смешанных производных второго порядка и принято    . При этих допущениях формулу дифференциала любого порядка можно получить из символического выражения:   .

 

 

Наверх

29. Неявные функции.

Неявная функция одной переменной. Пусть в некоторой области   плоскости задана функция , и пусть линия уровня этой функции , определяемая уравнением   , является графиком некоторой функции   , определяемой уравнением    . В этом случае говорят, что функция    задана неявно уравнением   . Для существования неявной функции требуется выполнение следующих условий: функция   и ее частная производная по    непрерывны в     , . Тогда в некоторой окрестности точки   существует единственная непрерывная функция     , задаваемая уравнением   , так, что в этой окрестности   . 

  

Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение     задает неявно функцию   . Это же уравнение может задавать неявно функцию или      . 

 

Производная неявной функции. При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение  : . Отсюда получим формулу для производной функции    , заданной неявно:   . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением   : , .

 

 

Наверх

30. Формула Тейлора для многих переменных.

Формулы Тейлора и Маклорена. Если функция   имеет в некоторой окрестности точки непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки из этой окрестности справедлива формула Тейлора n-го порядка:  , где ,

 ,

 

и т.д. Формула Тейлора, записанная в окрестности точки (0,0) называется формулой Маклорена. Например, для функции двух переменных при n=2: . 

 

Аппроксимация функции многочленом. Выражение

называется многочленом Тейлора n-го порядка. Поскольку , то в окрестности точки функцию можно приближенно заменить, или, как говорят, аппроксимировать, ее многочленом Тейлора, т.е.  . Чем ближе точка  к точке , тем выше точность такой аппроксимации; кроме того, точность возрастает с ростом n. Это означает, что, чем больше непрерывных производных имеет функция  , тем точнее представляет ее многочлен Тейлора.

 

 

Наверх

31. Исследование на экстремум.

Локальные экстремумы. Точка   называется точкой локального минимума (максимума) функции , определенной в области , если существует окрестность этой точки, такая, что   для всех точек этой окрестности, отличных от . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства. 

 

Исследование на экстремум функции двух переменных. Обозначим через приращение функции   в точке  . Если — точка локального минимума функции  , то существует окрестность   , в которой   (обратное неравенство в случае максимума). Из формулы Тейлора первого порядка   следует, что приращение   дважды непрерывно дифференцируемой функции   может сохранять знак, если главная линейная часть приращения функции в точке экстремума (максимума или минимума) равна нулю, т.е. выполнено необходимое условие экстремума: если точка   — точка экстремума, то   . Такая точка называется стационарной точкой функции. Приращение функции в стационарной точке имеет вид . Обозначим . Справедливо следующее достаточное условие экстремума. Пусть функция    дважды непрерывно дифференцируема в окрестности точки   и  . Если   , то в точке  функция достигает экстремума. Если при этом , то этот экстремум v минимум, при — максимум. Если же    , то в точке   экстремума нет. Геометрически достаточное условие означает, что в окрестности экстремума график функции   близок к поверхности . Если    , то для определения знака приращения   необходимо изучить члены формулы Тейлора более высокого порядка.

 

 

Наверх

32. Условный экстремум.

Условные экстремумы. Пусть функция  определена в некоторой области  и в этой области задана кривая уравнением . Условным экстремумом функции двух переменных  называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить , то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной . 

 

Метод множителей Лагранжа. Если уравнение  не разрешимо ни относительно  , ни относительно , то рассматривают функцию Лагранжа. Необходимым условием существования условного экстремума функции  при условии  является равенство нулю всех частных производных функции Лагранжа:   . 

  

Наибольшее и наименьшее значение функции в области. Поскольку функция  , непрерывная в ограниченной замкнутой области достигает в ней своего наибольшего и наименьшего значений, задача об их нахождении разделяется на две части: найти экстремумы функции двух переменных внутри области, найти ее условные экстремумы на границе области, при условии, что граница задана уравнением .

 

 

Наверх

33. Двойной и тройной интегралы.

Двойной интеграл в декартовых координатах. Пусть   ограниченная замкнутая область плоскости с кусочно-гладкой границей и пусть функция определена и ограничена на  . Посредством сетки кусочно-гладких кривых разобьем на конечное число элементарных областей с площадями  (разбиение ). Пусть — наибольший из диаметров областей , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число    называется интегральной суммой и ставится в соответствие каждому разбиению и каждому выбору точек . Если существует    и он не зависит от выбора разбиения  и точек , то функция называется интегрируемой по Риману в области , а сам предел называется двойным интегралом от функции  по области и обозначается    или   . Двойной интеграл существует, если  непрерывна на . Допустимы точки разрыва первого рода, лежащие на конечном числе гладких кривых в . 

 

Свойства двойного интеграла. Свойства двойного интеграла аналогичны свойствам определенного интеграла: 

Линейность:  

. Аддитивность: 

, если S1 и S2 две области без общих внутренних точек. 

Если для каждой точки  выполнено неравенство  , то . 

Если  интегрируема на , то функция   также интегрируема, причем . 

Если  и  наименьшее и наибольшее значения функции в области, а ее  площадь, то . 

Теорема о среднем значении: если  непрерывна в связной области , то существует, по крайней мере, одна точка такая, что   . 

Вычисление двойного интеграла. 

Если  , где —    непрерывные на функции, то двойной интеграл может быть вычислен двумя последовательными интегрированиями: . Аналогично, если , то     . 

Тройной интеграл и его свойства. Пусть — ограниченная замкнутая пространственная область, границей которой является кусочно-гладкая поверхность, и пусть функция  определена и ограничена в  . Посредством сетки кусочно-гладких поверхностей разобьем на конечное число элементарных областей   с объемами  (разбиение). Пусть . наибольший из диаметров областей  , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число ставится в соответствие каждому разбиению  и каждому выбору точек и называется интегральной суммой. Если существует   и он не зависит от выбора разбиения и точек,  то функция называется интегрируемой по Риману в области  , а сам предел называется тройным интегралом от функции   по области  и обозначается  . Свойства тройных интегралов такие же, как и у двойных интегралов. 

Вычисление тройного интеграла в декартовых координатах. Пусть  является цилиндрическим телом, проекция которого на плоскость  есть область  и которое ограничено снизу поверхностью , а сверху v поверхностью , где   — непрерывные функции в . Тогда , то есть интегрированием по z тройной интеграл сводится к двойному интегралу по области . Для областей более сложной формы вычисление двойных и тройных интегралов производится разбиением областей на конечное число простых областей с уже рассмотренными свойствами.

 

 

Наверх

34. Замена переменных в кратных интегралах.

Замена переменных в двойном интеграле. Пусть функции взаимно однозначно отображают открытое множество, содержащее область плоскости на открытое множество, содержащее область , и пусть является образом . Если и их частные производные непрерывны, а определитель   , то . Выражение  называется элементом площади в криволинейных координатах, функциональный определитель — якобианом. 

 

Вычисление площади.

Замена переменных в тройном интеграле. Пусть посредством функций производится взаимно однозначное отображение открытого множества, содержащего область пространства на открытое множество, содержащее область пространства и  есть образ . Если эти три функции непрерывны вместе со своими первыми частными производными в области и якобиан, то . Выражение  называется элементом объема в криволинейных координатах . 

 

Вычисление объема.

Двойной интеграл в полярных координатах. Введем на плоскости полярные координаты. Пусть — область, полученная взаимно однозначным отображением области плоскости , определяемым функциями . Тогда , а двойной интеграл в полярных координатах вычисляется по формуле: .Элемент площади в полярных координатах есть .

 

 

Наверх

35. Сферические и цилиндрические координаты.

Тройной интеграл в цилиндрических координатах. Введем в пространстве цилиндрические координаты. Для этого на плоскости используем полярные координаты, а третья координата произвольной точки остается . Учитывая связь полярных координат с декартовыми, получим выражение декартовых координат через цилиндрические:  . Тогда  и тройной интеграл в цилиндрических координатах вычисляется по формуле: . Элемент объема в цилиндрической системе координат есть  . 

  

Тройной интеграл в сферических координатах. Введем в пространстве сферическую систему координат. Для этого рассмотрим произвольную точку  в декартовой системе координат. Спроектируем ее на плоскость , получив точку  . Положение точки в пространстве будем характеризовать ее расстоянием от начала координат , углом между отрезком и положительной полуосью , углом между отрезком и положительной полуосью . Декартовы координаты точки выражаются через сферические по формулам: . В этом случае    . Тогда тройной интеграл в сферических координатах вычисляется по формуле: 

.

Элемент объема в сферической системе координат есть  .

 

 

Наверх

36. Поверхностный интеграл по площади поверхности.

Площадь гладкой поверхности. Рассмотрим кусок поверхности  , заданной уравнением . Пусть выполняется условие , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Разобьем поверхность сеткой гладких кривых на элементарные области ( разбиение ). Пусть   — наибольший из диаметров элементарных областей. Если независимо от разбиения  существует , то он и называется площадью данной поверхности. Пусть    однозначно проектируется на плоскость и  — эта проекция. Элементу площади области на плоскости  соответствует элемент площади поверхности , равный , где — угол между нормалью к поверхности и осью . Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла  по проекции поверхности на плоскость. Если поверхность задана уравнением , то     и площадь поверхности вычисляется по формуле   , здесь — проекция поверхности на плоскость . Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности. 

 

Поверхностный интеграл 1-го рода. Пусть некоторая функция определена и ограничена на гладкой поверхности . Выберем разбиение поверхности и точки на каждой элементарной области   и составим интегральную сумму . Если независимо от выбора разбиения и точек существует , то он называется поверхностным интегралом по площади поверхности (1-го рода) от функции и обозначается    . 

 

Свойства и вычисление поверхностного интеграла по площади поверхности. Если поверхность задана уравнением  и однозначно проектируется на плоскость , то поверхностный интеграл 1-го рода вычисляется по формуле . Нетрудно получить аналогичные формулы, если поверхность однозначно проектируется на другие координатные плоскости. Поскольку вычисление поверхностного интеграла сводится к двойному интегралу, то, естественно, все свойства поверхностного интеграла 1-го рода такие же, как и у двойного.

 

 

Наверх

37. Криволинейный интеграл по длине дуги.

Криволинейный интеграл 1-го рода. Пусть — отрезок кусочно-гладкой кривой с началом в точке и концом в точке и — ограниченная функция, определенная в некоторой области, содержащей кривую . Выберем на кривой произвольные точки , разбивая ее на элементарные отрезки (разбиение ), длина каждого  . Обозначим . Пусть  — произвольная точка на элементарном отрезке . Составим интегральную сумму . Если независимо от разбиения и выбора точек существует    , то он называется криволинейным интегралом по длине кривой (1-го рода) и обозначается  . Аналогично определяется криволинейный интеграл 1-го рода      от функции трех переменных   по отрезку пространственной кривой. 

 

Свойства и вычисление криволинейного интеграла по длине дуги. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой , то есть. Это единственное свойство, которое не совпадает с обычными свойствами интегралов, определеямых через предел интегральной суммы. Если — отрезок кусочно-гладкой кривой, заданной параметрически:

 , то криволинейный интеграл вычисляется по формуле:

. Если плоская кривая задана в явном виде, то криволинейный интеграл вычисляется по формуле: .

 

 

Наверх

38. Скалярное поле.

Скалярное поле. Если каждой точке пространства ставится в соответствие скалярная величина , то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также

 или      . Поле может быть плоским, если   , центральным (сферическим), если   , цилиндрическим, если .

 

Поверхности и линии уровня. Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых   принимает постоянное значение. Их уравнение:  . В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение:   . В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые. 

 

Производная по направлению и градиент скалярного поля. Пусть   — единичный вектор с координатами  ,  — скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле  . Производная по направлению представляет собой скалярное произведение вектора   и вектора с координатами  , который называется градиентом функции  и обозначается  . Поскольку  , где  — угол между   и  , то вектор  указывает   направление скорейшего возрастания поля , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента: 

 

 

Наверх

39. Векторное поле.

Векторное поле. Если каждой точке пространства ставится в соответствие вектор , то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде: . Скалярные функции однозначно определяют векторное поле. Векторное поле может быть плоским, если , сферическим, когда , , цилиндрическим, когда , . 

 Векторные линии (линии тока). Для наглядного представления векторных полей используют векторные линии (линии тока). Это кривые, в каждой точке которых вектор является касательным вектором. Через каждую точку проходит одна линия тока. За исключением точек, где поле не определено или , линии тока никогда не пересекаются. В декартовых координатах дифференциальные уравнения линий тока имеют вид:

 

 

Наверх

40. Поток векторного поля.

Поток векторного поля. Рассмотрим кусок поверхности , заданной уравнением . Пусть выполняется условие  , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Выберем одну из сторон поверхности следующим образом: построим на поверхности достаточно малый замкнутый контур, на котором задано направление обхода. Построим вектор нормали в точке поверхности, лежащей внутри контура. Если из конца вектора нормали обход контура кажется происходящим против часовой стрелки, то будем называть сторону поверхности, обращенную к вектору нормали положительной стороной. Таким образом, будем рассматривать ориентированную двухстороннюю поверхность, а односторонние поверхности лист Мебиуса, бутылку Клейна оставим в покое. Потоком векторного поля   через ориентированную поверхность называется поверхностный интеграл по площади поверхности (1-го рода)  , где —     единичный вектор нормали, направленный в положительную сторону. Выбор положительной стороны обычно диктуется физическими условиями задачи. 

 

Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции , где  — компоненты векторного поля,  — направляющие косинусы вектора нормали.

 

 

Наверх

41. Формула Остроградского.

Поток векторного поля через замкнутую поверхность. Рассмотрим кусочно-гладкую двухстороннюю замкнутую ориентированную поверхность  . Поток векторного поля   через замкнутую поверхность является важной характеристикой поля и позволяет судить о наличии источников и стоков поля. При непосредственном вычислении потока через замкнутую поверхность приходится разбивать ее на части, однозначно проектируемые на координатные плоскости. 

Формула Остроградского. Пусть замкнутая поверхность ограничивает некоторый объем  . Тогда в декартовых координатах справедлива формула Остроградского: , где  — компоненты векторного поля. 

 

 

Дивергенция векторного поля. Дивергенцией   векторного поля  называется . Точка  находится внутри замкнутой поверхности , ограничивающей объем   , который при вычислении предела стягивается в эту точку.  является скалярной величиной и служит мерой источников поля. Если в некоторой области поля  , то источников поля в этой области нет. Такое поле называют соленоидальным. Используя формулу Остроградского, нетрудно получить выражение для вычисления дивергенции в декартовых координатах: . Из свойств частных производных следуют свойства дивергенции векторного поля: 

 

 

Наверх

42. Криволинейный интеграл в векторном поле.

Криволинейный интеграл в векторном поле. Пусть заданы некоторое векторное поле  и кривая АВ (А — начальная точка, В — конечная). Криволинейный интеграл в векторном поле     есть скаляр, полученный следующим образом: 

Разобьем кривую точками А=А0, А1, А2-Аn=В на n частей, приближенно изображаемых векторами  (разбиение ). 

Обозначим  . 

На границе или внутри каждой элементарной дуги Аi-1Ai выберем точку, которой соответствует радиус-вектор   и составим интегральную сумму   . 

Если существует     и он не зависит от разбиения  и выбора точек, то этот предел называется криволинейным интегралом в векторном поле. В декартовой системе координат:, где — компоненты векторного поля.

Если кривая задана в параметрической форме:

, то вычисление криволинейного интеграла сводится к определенному интегралу: 

. Используя определение и формулу для вычисления нетрудно получить свойства криволинейного интеграла: 

Подчеркнем, что, в отличие от криволинейного интеграла по длине дуги, криволинейный интеграл в векторном поле меняет знак при изменении направления интегрирования. 

Если   векторное поле, описывающее физическое силовое поле, то криволинейный интеграл выражает работу, которую совершает   сила при переносе материальной точки из пункта А в пункт В вдоль кривой АВ. 

 

Циркуляция векторного поля. Важной характеристикой векторного поля является циркуляция векторного поля, которая равна криволинейному интегралу по замкнутой кривой в области поля, или, как говорят, по замкнутому контуру:   . Циркуляция векторного поля является скалярной величиной и характеризует вихревые свойства поля. Если в некоторой области поля циркуляция равна нулю, то поле называют безвихревым.

 

 

Наверх

43. Формула Стокса.

Формула Стокса. Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности , край которой образуется кусочно-гладкой кривой . Выберем положительную сторону поверхности (из конца единичного вектора нормали      обход границы представляется против часовой стрелки). Для циркуляции векторного поля     вдоль контура границы имеет место формула Стокса: , где   — компоненты векторного поля,   — направляющие косинусы вектора нормали. 

  

Ротор векторного поля. Рассмотрим в пространстве замкнутый контур  с выбранным направлением обхода, лежащий в ориентированной плоскости на ее положительной стороне (из конца единичного вектора нормали   обход контура представляется против часовой стрелки). Ротором    (или вихрем) векторного поля в точке  называется вектор, проекция которого на направление вектора нормали есть    . Точка лежит  на плоскости внутри контура  , который стягивается в эту точку при вычислении предела. Поскольку ротор поля определяется через циркуляцию, то он тоже является мерой завихренности поля. Найдем компоненты ротора в декартовой системе координат, воспользовавшись формулой Стокса. Для этого выберем сначала координатную плоскость y0z с нормальным вектором   , затем x0z,     , затем x0y,   . Применяя каждый раз теорему о среднем для интеграла, получим:    

Теперь теорема Стокса может быть сформулирована следующим образом: циркуляция векторного поля вдоль контура равна потоку ротора поля через поверхность, натянутую на этот контур. Выражение для ротора поля проще запомнить, если записать его в виде определителя:. Используя свойства частных производных и определителей, получим следующие свойства ротора векторного поля:

 

 

 

Наверх

44. Потенциальное поле.

Потенциальное поле. Если векторное поле  , то оно называется потенциальным, а скалярное поле , соответственно, его потенциалом. Самым известным примером такого соответствия является электрическое поле, напряженность которого  , где — потенциал электрического поля. Минус в формуле связан с историческим выбором направления вектора напряженности от плюса к минусу, когда уже умели тереть шерсть об янтарь, но не знали, как это описывать математически. 

  

Условие потенциальности поля. Пусть задано скалярное поле  , причем данная функция дважды непрерывно дифференцируема. Напомним, что в этом случае смешанные частные производные второго порядка не зависят от порядка дифференцирования. Вычислим  . 

Нетрудно видеть, что при этих условиях получается тождественный ноль. То есть, если поле потенциальное, то его  . 

 

 

Вычисление потенциала векторного поля. Если мы убедились, что поле  является потенциальным, то есть его ротор равен нулю, то представляет интерес вычислить потенциал этого поля. Для этого рассмотрим криволинейный интеграл в данном векторном поле:  , где точки А и В — начальная и конечная точки кривой. Поскольку  , то скалярное произведение векторов     и      является полным дифференциалом функции  : . Поэтому из свойств криволинейного интеграла следует, что . Смысл полученной формулы состоит в том, что работа поля по перемещению материальной точки из А в В не зависит от пути интегрирования, а только от конечной и начальной точек, точнее, от разности потенциалов в этих точках. Понятие разности потенциалов хорошо известно из физики. Для вычисления потенциала поля в произвольной точке В выберем начальную точку А, от которой начнем отсчет (в физике часто это — бесконечно удаленная точка). Тогда . Поскольку интеграл не зависит от пути интегрирования, то выберем его так, как нам удобно: сначала параллельно оси 0х, потом параллельно 0у, наконец, параллельно 0z. Обозначая , получим: 

.

Здесь    — компоненты векторного поля    . Поскольку выбор начальной точки произволен, потенциал поля определяется с точностью до произвольной постоянной, которая определяется физическими соображениями.

3 ПОТЕНЦИАЛЬНЫЙ ХАРАКТЕР ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Основные теоретические сведения

Тема: Основы электростатики Д/З -4 Сав 3. 4. Д-Я План:. Основные понятия и определения. основные характеристики электростатического поля 3. графическое изображение электростатического поля 4. закон Кулона

Подробнее

2 ЭЛЕКТРОСТАТИЧЕСКАЯ ТЕОРЕМА ГАУССА

2 ЭЛЕКТРОСТАТИЧЕСКАЯ ТЕОРЕМА ГАУССА Поток вектора напряжённости электростатического поля сквозь поверхность. Используя закон Кулона, можно доказать электростатическую теорему Гаусса. Для этого необходимо

Подробнее

Таким образом, мы пришли к закону (5).

Конспект лекций по курсу общей физики Часть II Электричество и магнетизм Лекция. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ (продолжение).4. Теорема Остроградского Гаусса. Применение теоремы Докажем теорему для частного

Подробнее

Теория электромагнитного поля. Лекция 1.

Теория электромагнитного поля. Лекция 1. Кафедра ТОЭ, СПбГПУ, доц. А.Г. Калимов 15.10.2014 1 Разработка курса Автор курса Калимов Александр Гелиевич, доцент кафедры Теоретических Основ Электротехники Санкт-Петербургского

Подробнее

Теоретическая справка к лекции 5

Теоретическая справка к лекции 5 Электрический заряд. 19 Элементарный электрический заряд e 1, 6 1 Кл. Заряд электрона отрицательный ( e e), заряд протона положительный ( p N e электронов и N P протонов

Подробнее

КЛ 3 Вариант 1 КЛ 3 Вариант 2 КЛ 3 Вариант 3

КЛ 3 Вариант 1 1. Записать формулу для вектора напряженности электрического поля, если известен электростатический потенциал. Пояснить действие оператора градиента на скалярную функцию. 2. Вывести уравнение

Подробнее

1.10. Общая задача электростатики

1 110 Общая задача электростатики Вектор напряженности электрического поля неподвижного точечного заряда вычисляется по формуле 1 Q E =, (1) 3 4π Используя принцип суперпозиции, нетрудно вычислить напряженность

Подробнее

ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

3. Лабораторная работа 21 ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ Цели работы: 1) экспериментально исследовать квазистационарное электрическое поле, построить картину эквипотенциальных поверхностей и линий

Подробнее

) (Плотность линий поля E ) ~ E, здесь ds

Экзамен. Линии электрического поля E. Линия векторного поля это линия, касательная в каждой точке к которой совпадает с направлением векторного поля. В физике к линиям поля есть дополнительное требование.

Подробнее

9 ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

9 ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ Рассмотрим точечную частицу с электрическим зарядом q, которая находится во внешнем электростатическом поле, потенциал которого в точке нахождения частицы равен. При этом

Подробнее

Функции нескольких переменных

И В Яковлев Материалы по физике MathUsru Функции нескольких переменных «Всё зависит только от тебя» так говорят люди не знакомые с понятием функции многих переменных Неизвестный автор Данный листок возник

Подробнее

И. В. СЕМЧЕНКО ОСНОВЫ ЭЛЕКТРОМАГНЕТИЗМА

И. В. СЕМЧЕНКО ОСНОВЫ ЭЛЕКТРОМАГНЕТИЗМА Допущено Министерством образования Республики Беларусь в качестве учебного пособия для студентов учреждений высшего образования по физическим специальностям МИНСК

Подробнее

Семестр 3. Лекция 2. E,dS. E S

Семестр Лекция Лекция Теорема Гаусса для электростатического поля Поток вектора напряжённости электрического поля Теорема Гаусса в интегральной и дифференциальной формах в вакууме и её применение для расчёта

Подробнее

2. ЭЛЕКТРОМАГНЕТИЗМ 2.1. ЭЛЕКТРОСТАТИКА

ЭЛЕКТРОМАГНЕТИЗМ ЭЛЕКТРОСТАТИКА Согласно закону Кулона сила с которой точечный заряд ‘ находящийся в точке с радиусвектором действует в вакууме на точечный заряд находящийся в точке с радиус-вектором (рис

Подробнее

1.3. Теорема Гаусса.

1 1.3. Теорема Гаусса. 1.3.1. Поток вектора через поверхность. Поток вектора через поверхность одно из важнейших понятий любого векторного поля, в частности электрического d d. Рассмотрим маленькую площадку

Подробнее

ϕ =, если положить потенциал на

. ПОТЕНЦИАЛ. РАБОТА СИЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ Потенциал, создаваемый точечным зарядом в точке A, находящейся на, если положить потенциал на бесконечности равным нулю: φ( ). Потенциал, создаваемый в

Подробнее

Закон сохранения заряда: Закон Кулона:

«ЭЛЕКТРОСТАТИКА» Электрический заряд ( ) фундаментальное неотъемлемое свойство некоторых элементарных частиц (электронов, протонов), проявляющееся в способности к взаимодействию посредством особо организованной

Подробнее

A 2b 1. Поэтому сумма A1a2

Лекция Работа сил электростатического поля по переносу точечного заряда Найдем элементарную работу сил электростатического поля этого заряда по перемещению заряда из точки в точку : Как известно из курса

Подробнее

Напряжённость электрического поля

И. В. Яковлев Материалы по физике MathUs.ru Напряжённость электрического поля Темы кодификатора ЕГЭ: действие электрического поля на электрические заряды, напряжённость электрического поля, принцип суперпозиции

Подробнее

поле называют потенциальным.

Л7 Потенциальные поля Если силы, действующие на тело при его движении, в любой точке пространства удовлетворяют условию F F F x y z ( x, y, z) x ( x, y, z) y ( x, y, z) z где Φ(x,y,z) — некоторая скалярная

Подробнее

4. Электромагнитная индукция

1 4 Электромагнитная индукция 41 Закон электромагнитной индукции Правило Ленца В 1831 г Фарадей открыл одно из наиболее фундаментальных явлений в электродинамике явление электромагнитной индукции: в замкнутом

Подробнее

Потенциал электрического поля

И. В. Яковлев Материалы по физике MathUs.ru Потенциал электрического поля Темы кодификатора ЕГЭ: потенциальность электростатического поля, потенциал электрического поля, разность потенциалов. Мы начнём

Подробнее

Лекц ия 29 Электромагнитное поле

Лекц ия 29 Электромагнитное поле Вопросы. Ток смещения. Опыты Роуланда и Эйхенвальда. Уравнения Максвелла в интегральной и дифференциальной формах. 29.1. Ток смещения Согласно закону электромагнитной индукции

Подробнее

Глава 14. ЭЛЕКТРОСТАТИКА. ПОТЕНЦИАЛ

Глава 4. ЭЛЕКТРОСТАТИКА. ПОТЕНЦИАЛ 4.. Потенциальность электростатического поля Сразу же подчеркнём, что речь идёт не о любом электрическом поле, а о поле, созданном зарядами. Вспомним рисунок векторного

Подробнее

10. Векторный и скалярный потенциалы

Векторный и скалярный потенциалы Уравнения Максвелла это, в общем случае, сложные интегральнодифференциальные уравнения, поэтому непосредственно их решать относительно трудно Были введены две вспомогательные

Подробнее

ГЛАВА 2.2}$), тоже потенциальна. Все математическое описание потенциала было создано при исследовании сил гравитации. Понятие о потенциале возникло в работах Ж.Л. Лагранжа в 1777 г. Термин «потенциал» ввели в науку гораздо позднее Дж. Грин и К.Ф. Гаусс.

На основании принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля. Математически доказать это очень просто. Циркуляция вектора напряженности поля точечного заряда ($\overrightarrow{E_i}$) по любому замкнутому контуру равна нулю:

\[\oint\limits_L{\overrightarrow{E_i}d\overrightarrow{s}=0\ \left(1\right).}\]

Если поле создается N точечными зарядами, то по принципу суперпозиции мы можем результирующее поле найти как:

\[\overrightarrow{E}=\sum\nolimits_i{\overrightarrow{E_i}}\ \left(2\right).\]

Найдем интеграл:

\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=\oint\limits_L{\sum\nolimits_i{\overrightarrow{E_i}}}d\overrightarrow{s}=\sum\nolimits_i{\oint\limits_L{\overrightarrow{E_i}d\overrightarrow{s}}}=\sum\nolimits_i{0}=0\ \left(3\right).}\]

Выше описанный критерий потенциальности поля не является дифференциальным, вследствие чего, его бывает трудно применять. Приходится проверять равенство нулю работы по замкнутому контуру. Это значит необходимо исследовать бесконечное количество циклов, что, в конечном счете, невозможно. Критерий потенциальности можно применить только тогда, когда известна аналитическая формула работы, что бывает совсем не всегда. Следовательно, необходимо найти другой критерий потенциальности поля, который был бы легок в применении. Таким критерием стала дифференциальная формулировка. Она дается с помощью понятия ротор вектора ($rot\overrightarrow{A}$).

Что такое ротор

(Обратите внимание, что здесь большой буквой $S$ обозначается площадь, маленько буквой $s$ — линейное перемещение.)

Ротор характеризует интенсивность «завихрения» вектора. При практическом вычислении ротора используют формулы:

\[rot\ \overrightarrow{A}=\overrightarrow{\nabla }\times \overrightarrow{A}=\left| \begin{array}{ccc} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ A_x & A_y & A_k \end{array} \ \right|\left(5\right).A_{ \begin{array}{c} B \\ L_2 \end{array} }{\overrightarrow{E}\cdot d\overrightarrow{s}=\oint\limits_L{\overrightarrow{E}\cdot d\overrightarrow{s}}=0\ (8),}}\]

где $L=L_1+L_2$. Применим формулу Стокса:

\[\int\limits_S{rot}\overrightarrow{A}\cdot d\overrightarrow{S}=\oint\limits_L{\overrightarrow{A}\cdot d\overrightarrow{s}(9)}\]

к уравнению (8), получим:

\[\oint\limits_L{\overrightarrow{E}\cdot d\overrightarrow{s}}=\int\limits_S{rot\overrightarrow{E}\cdot d\overrightarrow{S}}=0\ \left(9\right),\]

где $S$ — поверхность, которая ограничена контуром $L$. Так как поверхность произвольна, то интеграл в выражении (9) может быть равен нулю, только если равно нулю подынтегральное выражение, а так как $d\overrightarrow{S}\ne 0$ то есть:

\[rot\overrightarrow{E}=0\left(10\right).\]

Формула (10) является дифференциальной формулировкой потенциальности электростатического поля.

Пример 1

Задание: Найти $rot_n\overrightarrow{v}\ $для точек оси вращения, если $\overrightarrow{v}$ — вектор скорости точек твердого тела, которое вращается с угловой скоростью $\omega$ вокруг оси коллинеарной $\overrightarrow{n}$.2}\ }=2\omega \ \left(1.3\right),\]

где $\oint{ds}=2\pi R$- длина окружности.

Ответ: Ротор линейной скорости точек вращающегося тела равен ${rot}_n\overrightarrow{v}=2\omega .$

Пример 2

Задание: Доказать, что из условия потенциальности поля следует, что тангенциальные составляющие напряженности электростатического поля не прерываются.

Решение:

Так как электростатическое поле потенциально, то выполняется равенство:

\[A=\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=0\ \left(2.1\right).}\]

Рис. 2

Тангенциальные составляющие — это касательные к произвольной поверхности в любой ее точке. Непрерывность означает, что касательные составляющие напряженности имеют одинаковые значения по обе стороны поверхности. Допустим обратное. Пусть вдоль поверхности S (рис.2) непрерывность не выполняется. Это значит, что если 1,2 и 3,4 разделенные поверхностью S, но при этом бесконечно близкие друг к другу точки, то работа электростатических сил на пути $1\to 2$ отличается на конечную величину от работы тех же сил на пути $3\to 4$. Так как мы считаем, что отрезки $1\to 2$ и $3\to 4$ бесконечно малые, силы конечны, следовательно, и работа, выполняемая электрическими силами на заданных отрезках — бесконечно малая величина. Получается, что работа на пути $1\to 2\to 3\to 4\to 1$ должна быть не равна нулю. То есть работа сил по перемещению пробного заряда по замкнутому контуру не равна нулю. Такое невозможно, так как электростатическое поле потенциальное. Мы показали, что тангенциальные составляющие напряженности электростатического поля ненепрерывны.

Обзор | Безграничная физика

Связь между электрическим потенциалом и полем

Электрический потенциал и поле связаны между собой в том смысле, что потенциал — это свойство поля, которое описывает действие поля.

Цели обучения

Объясните взаимосвязь между электрическим потенциалом и электрическим полем

Основные выводы

Ключевые моменты

• Электрическое поле — мера силы на единицу заряда; электрический потенциал — это мера энергии на единицу заряда.
• Для однородного поля соотношение между электрическим полем (E), разностью потенциалов между точками A и B (Δ) и расстоянием между точками A и B (d) составляет: [latex] \ text {E} = — \ frac {\ Delta \ phi} {\ text {d}} [/ latex] Если поле неоднородно, для решения требуется исчисление.
• Потенциал — это свойство поля, которое описывает действие поля на объект.

Ключевые термины

• электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
• электрический потенциал : потенциальная энергия на единицу заряда в точке в статическом электрическом поле; Напряжение.

Связь между электрическим потенциалом и полем аналогична взаимосвязи между гравитационным потенциалом и полем в том смысле, что потенциал — это свойство поля, описывающее действие поля на объект (см.).

Электрическое поле и потенциал в одном измерении : Наличие электрического поля вокруг статического точечного заряда (большая красная точка) создает разность потенциалов, в результате чего тестовый заряд (маленькая красная точка) испытывает силу и перемещается.

Электрическое поле похоже на любое другое векторное поле — оно создает силу, основанную на стимуле, и имеет единицы силы, умноженные на обратный стимул. В случае электрического поля стимулом является заряд, и, следовательно, единицы измерения NC ^-1 . Другими словами, электрическое поле — это мера силы на единицу заряда.

Электрический потенциал в точке — это отношение потенциальной энергии любой заряженной частицы в этой точке к заряду этой частицы. Его единицы — JC ^-1 .Таким образом, электрический потенциал — это мера энергии на единицу заряда.

В единицах измерения электрический потенциал и заряд тесно связаны. У них общий коэффициент обратных кулонов (C ^-1 ), в то время как сила и энергия различаются только на коэффициент расстояния (энергия — это произведение силы на расстояние).

Таким образом, для однородного поля соотношение между электрическим полем (E), разностью потенциалов между точками A и B (Δ) и расстоянием между точками A и B (d) составляет:

[латекс] \ text {E} = — \ frac {\ Delta \ phi} {\ text {d}} [/ latex].

Коэффициент -1 возникает из-за отталкивания положительных зарядов: положительный заряд будет отталкиваться от положительно заряженной пластины к месту с более высоким напряжением.

Приведенное выше уравнение представляет собой алгебраическое соотношение для однородного поля. В более чистом смысле, без предположения об однородности поля, электрическое поле — это градиент электрического потенциала в направлении x:

[латекс] \ text {E} _ \ text {x} = — \ frac {\ text {dV}} {\ text {dx}} [/ latex].

Это можно вывести из основных принципов.Учитывая, что ∆P = W (изменение энергии заряда равно работе, выполненной над этим зарядом), применяя закон сохранения энергии, мы можем заменить ∆P и W другими членами. ∆P может быть заменен на его определение как произведение заряда (q) и дифференциала потенциала (dV). Затем мы можем заменить W на его определение как произведение q, электрического поля (E) и разницы расстояний в направлении x (dx):

[латекс] \ text {qdV} = — \ text {qE} _ \ text {xdx} [/ latex].

Разделив обе части уравнения на q, получим предыдущее уравнение.

Электрическая потенциальная энергия и разность потенциалов

Электрическая потенциальная энергия возникает в результате сил между зарядами; разность потенциалов — это энергия, необходимая для перемещения заряда из точки A в точку B.

Цели обучения

Вычислить потенциальную энергию между зарядами

Основные выводы

Ключевые моменты

• Электрическая потенциальная энергия — это тип потенциальной энергии, возникающей в результате действия кулоновских сил. Потенциальная энергия (UE) между зарядами q и Q может быть вычислена как функция расстояния между зарядами (r): [latex] \ text {U} _ \ text {E} (\ text {r}) = \ frac {\ text {qQ}} {4 \ pi \ epsilon_0 \ text {r}} [/ latex].
• Формула для потенциальной энергии может быть изменена для потенциала между многими зарядами, если учитываются взаимодействия каждого заряда с каждым другим зарядом в системе. Например, потенциал между тремя зарядами можно определить с помощью следующей формулы: [latex] \ text {U} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0 \ text {r}} (\ frac {\ text {Q} _1 \ text {Q} _2} {\ text {r} {12}} + \ frac {\ text {Q} _2 \ text {Q} _3} {\ text {r} {23} } + \ frac {\ text {Q} _1 \ text {Q} _3} {\ text {r} {13}}) [/ latex].
• Разность потенциалов или напряжение — это разница в электрической потенциальной энергии между двумя точками.Он обозначается ∆V и измеряется в вольтах или джоулях на кулон.

Ключевые термины

• кулон : В Международной системе единиц производная единица электрического заряда; количество электрического заряда, переносимого током в 1 ампер, протекающим в течение 1 секунды. Символ: C
.
• потенциальная энергия : энергия, которой обладает объект из-за его положения (в гравитационном или электрическом поле) или его состояния (в виде растянутой или сжатой пружины, в качестве химического реагента или благодаря наличию массы покоя)

Электрическая потенциальная энергия — это тип потенциальной энергии, возникающей в результате действия кулоновских сил.Он измеряется в джоулях и зависит от расположения заряженных частиц относительно друг друга, а также от величины их соответствующих зарядов.

Потенциальная энергия (U _E ) между зарядами q и Q может быть рассчитана как функция расстояния между зарядами (r):

[латекс] \ text {U} _ \ text {E} (\ text {r}) = \ frac {\ text {qQ}} {4 \ pi \ epsilon_0 \ text {r}} [/ latex]

Если имеется три или более зарядов, приведенная выше формула может быть изменена так, чтобы потенциальные энергии между всеми зарядами суммировались.Рассмотрим, например, случай с обвинениями Q ₁ , Q ₂ и Q ₃ :

[латекс] \ text {U} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0 \ text {r}} (\ frac {\ text {Q} _1 \ text {Q} _2} {\ text {r} {12}} + \ frac {\ text {Q} _2 \ text {Q} _3} {\ text {r} {23}} + \ frac {\ text {Q} _1 \ text { Q} _3} {\ text {r} {13}}) [/ latex]

В этом примере r ₁₂ представляет расстояние между Q ₁ и Q ₂ , r ₂₃ представляет расстояние между Q ₂ и Q ₃ , а r ₁₃ представляет расстояние между Q ₁ и Q ₃ .Вышеуказанная формула может быть изменена для любого количества зарядов.

Потенциальная разница

Разность потенциалов или напряжение — это разница в электрической потенциальной энергии между двумя точками. Он обозначается ∆V и измеряется в вольтах или джоулях на кулон.

Разность электрических потенциалов : Краткий обзор разности электрических потенциалов и электрической потенциальной энергии для начинающих студентов-физиков.

Напряжение — это работа на единицу заряда, которую необходимо совершить против статического электрического поля, чтобы переместить заряд из одной точки в другую.Он может представлять собой источник энергии или потерянную, сохраненную или использованную энергию. Напряжение также определяется таким образом, что отрицательные заряды тянутся к более высоким напряжениям, а положительные заряды перемещаются к более низким напряжениям. Таким образом, ток в проводах течет от более высокого напряжения к более низкому.

Разница потенциалов не зависит от пути, пройденного от одной точки до другой, и может быть измерена любым из множества инструментов. К ним относятся вольтметр, потенциометр и осциллограф. Чаще всего его измеряют в схемах, и в таких ситуациях его можно вычислить с помощью закона Ома, который будет рассмотрен в более позднем атоме.

Разность потенциалов в статическом поле : Когда заряд q перемещается из точки A в точку B, разность потенциалов не зависит от пройденного пути.

Электрическое поле и изменение электрического потенциала

Электрическое поле — это градиент потенциала, который обратно пропорционален расстоянию от точки интереса до заряда.

Цели обучения

Вычислить электрический потенциал, создаваемый распределением заряда постоянного значения

Основные выводы

Ключевые моменты

• Для любого заряда постоянной величины (Q) потенциал (VE) на определенном расстоянии от него (r) можно рассчитать по формуле: [latex] \ text {V} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0} \ frac {\ text {Q}} {\ text {r}} [/ latex] Где ε0 — электрическая постоянная, также известная как диэлектрическая проницаемость свободного пространства.
• Для одного точечного заряда потенциал будет постоянным для всех точек на определенном радиальном расстоянии. Несколько точек с одинаковым потенциалом известны как эквипотенциальные.
• Когда несколько зарядов создают поле, эквипотенциальные линии приобретают неправильную форму. Это связано с тем, что поля, создаваемые каждым зарядом, перекрываются, таким образом, потенциал увеличивается в любой точке по сравнению с тем, который возник бы от одного или другого заряда.

Ключевые термины

• эквипотенциальный : область, каждая точка которой имеет одинаковый потенциал.
• радиальный : Движение по радиусу.

Любой заряд создает вокруг себя векторное поле (известное как электрическое поле). Электрическое поле — это градиент потенциала, который обратно пропорционален расстоянию от точки интереса до заряда. Размещение второго заряда в системе («пробный заряд») приводит к тому, что два заряда испытывают силу (единицы поля — ньютоны, мера силы на кулон), заставляя заряды перемещаться относительно друг друга.Проще всего смоделировать взаимодействия между двумя зарядами так, чтобы один считался неподвижным, пока пробный заряд движется.

По мере движения пробного заряда потенциал между ним и другим зарядом изменяется, как и электрическое поле. Связь между потенциалом и полем (E) является дифференциальной: электрическое поле — это градиент потенциала (V) в направлении x. Это может быть представлено как:

[латекс] \ text {E} _ \ text {x} = — \ frac {\ text {dV}} {\ text {dx}} [/ latex].

Эквипотенциальные линии : Изолированный точечный заряд Q с его линиями электрического поля (синий) и эквипотенциальными линиями (зеленый)

Таким образом, когда тестовый заряд перемещается в направлении x, скорость его изменения потенциала является величиной электрического поля.

В момент перед движением пробного заряда его потенциальная энергия максимальна, а его кинетическая энергия равна 0. Для любого заряда постоянной величины (Q) потенциал на определенном расстоянии от него (r) может быть рассчитан из следующее уравнение:

[латекс] \ text {V} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0} \ frac {\ text {Q}} {\ text {r}} [/ latex],

, где ε ₀ — электрическая постоянная, также известная как диэлектрическая проницаемость свободного пространства. Движение к заряду и от него приводит к изменению потенциала; соотношение между расстоянием и потенциалом обратное.

Для одного точечного заряда потенциал будет постоянным для всех точек на определенном радиальном расстоянии. Несколько точек с одинаковым потенциалом известны как эквипотенциальные. В случае полей, созданных одиночным точечным зарядом, все точки на любом круге с центром вокруг точечного заряда будут эквипотенциальными, как показано на.

показывает, что когда несколько зарядов создают поле, эквипотенциальные линии приобретают неправильную форму. Это связано с тем, что поля, создаваемые каждым зарядом, перекрываются, таким образом, потенциал увеличивается в любой точке по сравнению с тем, который возник бы от одного или другого заряда.

Потенциалы и заряженные проводники

Электрический потенциал внутри заряженного проводника равен нулю, но может быть вычислен как ненулевое значение вне заряженного проводника.

Цели обучения

Определить электрический потенциал внутри и снаружи заряженного проводника

Основные выводы

Ключевые моменты

• Электрический потенциал (∆V) и поле (E) связаны согласно интегралу: [latex] \ Delta \ text {V} = — \ int _ {\ text {i}} ^ {\ text {f}} \ ! \ vec {\ text {E}} \ cdot \ mathrm {\ text {d}} \ vec {\ text {l}} [/ latex], где l — расстояние между двумя точками, между которыми определяется разность потенциалов.
• Учитывая, что электрическое поле постоянно равно 0 для любого места внутри заряженного проводника, разность потенциалов в том же объеме не может иметь никакого значения, кроме 0.
• Для точек вне проводника потенциал отличен от нуля и может быть рассчитан в соответствии с полем и расстоянием от проводника.

Ключевые термины

• электрический потенциал : потенциальная энергия на единицу заряда в точке в статическом электрическом поле; Напряжение.
• электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
• работа : Мера энергии, затрачиваемой на перемещение объекта; чаще всего, сила, умноженная на смещение. Если объект не двигается, работа не выполняется.

Когда проводник становится заряженным, этот заряд распространяется по его поверхности, пока не будет достигнуто электростатическое равновесие. Его поверхность эквипотенциальная.

Все точки внутри заряженного проводника испытывают электрическое поле равным 0. Это связано с тем, что силовые линии от зарядов на поверхности проводника одинаково противостоят друг другу. Однако, имея электрическое поле, равное нулю во всех точках внутри проводника, электрический потенциал внутри проводника не обязательно равен нулю для всех точек внутри того же проводника. Это можно доказать, связав электрическое поле и потенциал.

Электрический заряд на острой части проводника : Силы отталкивания в направлении более резко изогнутой поверхности справа направлены больше наружу, чем вдоль поверхности проводника.\ text {f} \! \ vec {\ text {E}} \ cdot \ mathrm {\ text {d}} \ vec {\ text {l}} [/ latex]

Наконец, мы выводим уравнение:

[латекс] \ text {dV} = — \ vec {\ text {E}} \ cdot \ mathrm {\ text {d}} \ vec {\ text {l}} = 0 [/ латекс]

Таким образом, мы можем заключить, что, учитывая, что электрическое поле постоянно равно 0 для любого места внутри заряженного проводника, разность потенциалов в том же объеме должна быть постоянной и равной 0.

С другой стороны, для точек вне проводника потенциал отличен от нуля и может быть определен тем же самым уравнением в зависимости от поля и расстояния от проводника.

Равномерное электрическое поле

Электрическое поле, которое является однородным, — это такое поле, которое достигает недостижимой стабильности, будучи постоянным повсюду.

Цели обучения

Описание свойств и приближения однородного электрического поля

Основные выводы

Ключевые моменты

• Однородное электрическое поле — это приближение, позволяющее выполнять простые вычисления, не требующие дифференциального исчисления. Каждое поле будет иметь по крайней мере некоторую неровность, хотя некоторые могут быть почти однородными.
• Уравнение для величины однородного электрического поля: [latex] \ text {E} = \ frac {- \ Delta \ phi} {\ text {d}} [/ latex] где E — поле, Δ — разность потенциалов между пластинами, а d — расстояние между пластинами.
• Для случая, когда положительный заряд q перемещается из точки A с определенным потенциалом (V ₁ ) в точку B с другим потенциалом (V ₂ ), это уравнение выглядит следующим образом: [латекс] \ text { W} = — \ text {q} (\ text {V} _2- \ text {V} _1) [/ latex] Разница (V ₂ -V ₁ ) также может быть представлена ​​как ∆V или V _АБ .
• В однородных полях также просто вычислить разность потенциалов: [latex] \ text {V} _ {\ text {AB}} = \ text {Ed} [/ latex] В этом случае напряженность поля E, а расстояние между точками A и B находится d.

Ключевые термины

• разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
• электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.

Однородное поле — это то, в котором электрическое поле постоянно на всем протяжении. Как и так называемая «поверхность без трения» в механике, однородное поле является идеальной, но нереальной ситуацией, которая упрощает вычисления. Уравнения с неоднородными электрическими полями требуют использования дифференциального исчисления.

Однородность электрического поля можно приблизительно определить, поместив две проводящие пластины параллельно друг другу и создав между ними разность потенциалов.В таком случае поле возле его краев будет немного изменяться, но оно будет примерно постоянным во всех остальных областях.

Уравнение величины однородного электрического поля:

[латекс] \ text {E} = \ frac {- \ Delta \ phi} {\ text {d}} [/ latex]

где E — поле, Δ — разность потенциалов между пластинами, а d — расстояние между пластинами. Коэффициент -1 возникает из-за того, что положительные заряды отталкиваются, и, таким образом, положительный заряд будет отталкиваться от положительной пластины в направлении, противоположном направлению увеличения напряжения.

Однородность электрического поля позволяет легко рассчитать работу, выполняемую при перемещении испытательного заряда. Для случая, когда положительный заряд q перемещается из точки A с определенным потенциалом (V ₁ ) в точку B с другим потенциалом (V ₂ ), это уравнение имеет вид:

[латекс] \ text {W} = — \ text {q} (\ text {V} _2- \ text {V} _1) [/ латекс]

Разница (V ₂ -V ₁ ) также может быть представлена ​​как ∆V или V _AB .В однородных полях также просто связать ∆V с напряженностью поля и расстоянием (d) между точками A и B:

[латекс] \ text {V} _ {\ text {AB}} = \ text {Ed} [/ latex]

Взаимосвязи в однородном электрическом поле : На этом изображении работа (W), напряженность поля (E) и разность потенциалов (∆V) определены для точек A и B в рамках построения однородного потенциального поля между положительными и отрицательные пластины.

Энергосбережение

Энергия сохраняется при движении заряженной частицы через электрическое поле, как и в любой другой физической ситуации.

Цели обучения

Сформулировать принцип сохранения энергии заряженной частицы в электрическом поле

Основные выводы

Ключевые моменты

• При наличии стационарного испытательного заряда в определенном месте приложенное электрическое поле заставит заряд переместиться в один или другой конец, в зависимости от заряда.
• Положительные тестовые заряды будут двигаться в направлении поля; отрицательные заряды будут двигаться в противоположном направлении.
• В момент приложения поля неподвижный пробный заряд имеет нулевую кинетическую энергию, а его электрическая потенциальная энергия максимальна.Затем заряд ускоряется, и его кинетическая энергия (от движения) увеличивается по мере уменьшения его потенциальной энергии. Сумма энергий всегда постоянна.
• Формулу, иллюстрирующую сохранение энергии, можно записать разными способами, но все выражения основаны на простой предпосылке приравнивания начальной и конечной сумм кинетической и потенциальной энергии.

Ключевые термины

• кинетическая энергия : энергия, которой обладает объект из-за его движения, равная половине массы тела, умноженной на квадрат его скорости.
• разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
• потенциальная энергия : энергия, которой обладает объект из-за его положения (в гравитационном или электрическом поле) или его состояния (в виде растянутой или сжатой пружины, в качестве химического реагента или благодаря наличию массы покоя)

Энергия сохраняется при движении заряженной частицы через электрическое поле, как и в любой другой физической ситуации.Это явление можно выразить как равенство суммарной кинетической ( E _кинет ) и электрической потенциальной ( E _el ) энергий:

[латекс] (\ text {E} _ {\ text {kin}} + \ text {E} _ {\ text {el}}) _ {\ text {initial}} = (\ text {E} _ { \ text {kin}} + \ text {E} _ {\ text {el}}) _ {\ text {final}} [/ latex]

При наличии стационарного испытательного заряда в определенном месте приложенное электрическое поле заставит заряд переместиться в один или другой конец, в зависимости от заряда (положительные испытательные заряды будут двигаться в направлении поля; отрицательные заряды будут двигаться внутрь). 2 + \ text {U}) _ {\ text {final}} [/ latex]

, где m и v — масса и скорость электрона, соответственно, а U — электрическая потенциальная энергия. U можно рассчитать следующим образом:

[латекс] \ text {U} = \ text {q} _0 \ text {V} = \ text {k} \ frac {\ text {q} _0 \ text {q}} {\ text {r}} [ / латекс]

, где В, — разность потенциалов, к, — постоянная, q , _0, — пробный заряд, q — другой заряд, и r — расстояние между зарядами.

Члены формулы сохранения энергии можно переписать разными способами, но все выражения основаны на простой предпосылке уравнивания начальной и конечной сумм кинетической и потенциальной энергии.

Сходства между действием гравитационного и электрического полей на объекте : Заряд + q перемещается вниз по электрическому полю так же, как объект m перемещается вниз по склону. В обоих случаях движущаяся частица переходит из состояния с более высокой потенциальной энергией в состояние с более низкой потенциальной энергией.

Электрон-вольт

Электрон-вольт — единица энергии, используемая в физике элементарных зарядов и электричества.

Цели обучения

Преобразование электронвольт в единицы энергии СИ

Основные выводы

Ключевые моменты

• Электрон-вольт определяется как количество энергии, полученной или потерянной зарядом электрона, перемещающегося через разность электрических потенциалов в один вольт.Его значение примерно равно 1,602 × 10 ^-19 Дж.
.
• Электрон-вольт стал полезным благодаря экспериментам. Ученые, работающие с электростатическими ускорителями частиц, обычно использовали в своей работе соотношение между энергией (E), зарядом (q) и разностью потенциалов (V). Это соотношение: E = qV.
• В качестве энергии электрон-вольт может использоваться во многих вычислениях, включая импульс, массу, длину волны и температуру.

Ключевые термины

• разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
• ускоритель частиц : Устройство, которое ускоряет электрически заряженные частицы до чрезвычайно высоких скоростей с целью инициирования высокоэнергетических реакций или получения высокоэнергетического излучения.
• электрон-вольт : Устройство для измерения энергии субатомных частиц; энергия равна энергии, полученной электроном, движущимся через разность потенциалов в один вольт. Эквивалентно 1,6022 x 10-19 джоулей.

Обзор

Электрон-вольт, обозначаемый как эВ, а иногда и как электронвольт, — это единица энергии, используемая в физике элементарных зарядов и электричества.

Электрон-вольт определяется как количество энергии, полученной или потерянной зарядом электрона, перемещающегося через разность электрических потенциалов в один вольт. Таким образом, он равен произведению одного вольта (1 Дж / Кл) и одного элементарного заряда, что дает ему значение в джоулях, приблизительно равное 1,602 × 10 ^-19 Дж.

.

Электрон-вольт сам по себе не является единицей СИ, он стал полезен в результате экспериментов. Ученые, работающие с электростатическими ускорителями частиц, обычно использовали соотношение между энергией (E), зарядом (q) и разностью потенциалов (V) в своей работе:

[латекс] \ text {E} = \ text {qV} [/ латекс]

Все вычисления энергии по приведенному выше уравнению были квантованы как кратные элементарному заряду q для данного напряжения, и, таким образом, возникло обычное использование электрон-вольта в качестве единицы измерения.

Импульс

И электрон-вольт, и импульс являются мерой энергии, и они связаны между собой в физике высоких энергий. Приложение разности потенциалов к электрону дает ему энергию, которая проявляется в движении электрона через него. Учитывая, что у электрона есть масса и скорость, у него есть импульс. Деление электрон-вольт на константу с единицами измерения скорости дает импульс.

Масса

Учитывая, что масса эквивалентна энергии, электрон-вольт может измерять массу.2} [/ латекс]

Длина волны

Энергия E , частота v и длина волны λ фотона связаны соотношением

[латекс] \ text {E} (\ text {eV}) = \ text {hv} = \ frac {\ text {hc}} {\ lambda} [/ latex]

где h — постоянная Планка, c — скорость света. Таким образом, фотон с длиной волны 532 нм (зеленый свет) будет иметь энергию примерно 2,33 эВ. Точно так же 1 эВ соответствует инфракрасному фотону с длиной волны 1240 нм и так далее.

Энергия фотонов в видимом спектре : Связь между длиной волны и энергией, выраженная в электрон-вольтах.

Температура

В физике плазмы электрон-вольт может использоваться как единица измерения температуры. Чтобы преобразовать в Кельвины, просто разделите значение 1 эВ (в Джоулях) на постоянную Больцмана (1,3806505 (24) × 10 ^-23 Дж / К).

Дипольные моменты

Электрический дипольный момент — это мера полярности в системе.

Цели обучения

Свяжите электрический дипольный момент с полярностью в системе

Основные выводы

Ключевые моменты

• Электрические дипольные моменты используются для измерения разделения положительных и отрицательных зарядов (полярности) в системе. Они измеряются в кулонах-метрах (Км).
• Для точечных зарядов со значениями + q и -q электрический дипольный момент (p) может быть определен как: [latex] \ text {p} = \ text {qd} [/ latex], где q представляет собой заряды, а d представляет собой вектор смещения.Вектор смещения имеет величину расстояния между зарядами и направление от отрицательного заряда к положительному.
• Все диполи испытывают крутящий момент, который вращает диполь, выравнивая его с электрическим полем. Этот крутящий момент можно рассчитать как произведение электрического дипольного момента и электрического поля.

Ключевые термины

• дипольный момент : векторное произведение заряда на любом полюсе диполя на расстояние, разделяющее их.
• вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
• крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)

Электрический дипольный момент — это мера полярности, которая представляет собой разделение положительных и отрицательных зарядов в системе. Он измеряется в кулонах-метрах (См · м). Существует много различных типов дипольных моментов, включая электрические дипольные моменты, магнитные дипольные моменты и топологические дипольные моменты.

К подмножеству электрических дипольных моментов относятся дипольные моменты переходов, дипольные моменты молекул, дипольные моменты связей и электрические дипольные моменты электронов. Для целей этого атома мы сосредоточимся на широком обзоре электрического дипольного момента в статических ситуациях.

Молекулярный дипольный момент в воде : Эта молекула воды (H ₂ O) имеет высокую плотность электронов (обозначена красной штриховкой) около красного атома O. Ближе к белым атомам H наблюдается малая плотность электронов.Следовательно, молекула является диполем, с отрицательностью около O и положительностью ближе к атомам H.

Определение

По сути, для случая точечных зарядов со значениями + q и -q электрический дипольный момент (p) может быть определен как векторное произведение зарядов и вектора смещения d:

[латекс] \ text {p} = \ text {qd} [/ latex]

Вектор смещения — это вектор с величиной, равной расстоянию между зарядами, и направлением, указывающим от отрицательного заряда к положительному.По сути, он взаимозаменяем с переменной «радиус» во многих других уравнениях (например, в тех, которые определяют гравитационные и электростатические силы), за исключением того, что он включает фактор направления.

Момент

Все диполи испытывают крутящую силу или крутящий момент, когда они помещаются во внешние электрические поля. Этот крутящий момент вращает диполь, чтобы выровнять его с полем. Это вызвано необходимостью минимизировать потенциальную энергию. Крутящий момент (τ) можно рассчитать как произведение электрического дипольного момента и электрического поля (E), предполагая, что E пространственно однородно:

[латекс] \ tau = \ text {p} \ times \ text {E} [/ latex]

Электрический потенциал и электрическое поле

Электрический потенциал и электрическое поле
следующий: Электрический потенциал a Up: Электрический потенциал Предыдущее: Электрический потенциал

Электрический потенциал и электрическое поле Мы видели, что разница в электрическом потенциале двух произвольные точки в пространстве — это функция электрического поля, пронизывающего пространство, но не зависит от испытательного заряда, используемого для измерения этой разницы.Давайте исследуем связь между электрическим потенциалом и электрическим поле.

Рассмотрим заряд, который медленно перемещается на бесконечно малое расстояние по оси. Предположим, что разность электрических потенциалов между конечным и начальным положениями заряда есть. По определению изменение в электрической потенциальной энергии заряда дан кем-то

(84)

Из уравнения.(76) работа, которую мы совершаем при перемещении заряда, равна

(85)

где — местная напряженность электрического поля, а — угол наклона между направлением поля и осью. По определению, , где — -компонента локального электрического поля. Энергосбережение требует, чтобы (, то есть , увеличение энергии заряда соответствует работа сделана на зарядке), или

(86)

что сводится к

(87)

Мы называем это количество градиентом электрический потенциал в -направлении.Он в основном измеряет, насколько быстро потенциал меняется при изменении координаты (но координаты и остаются постоянными). Таким образом, приведенная выше формула говорит что -компонента электрического поля в данной точке пространства равна до минус локальный градиент электрического потенциала в -направление.

Согласно формуле. (87) напряженность электрического поля имеет размеры разности потенциалов по длине. Отсюда следует, что единицами измерения электрического поля являются вольты. на метр ( .Конечно, эти новые агрегаты полностью эквивалентны ньютонов на кулон: , т.е. ,

(88)

Рассмотрим частный случай однородно направленного электрического поля. генерируется двумя равномерно заряженными параллельными плоскостями, перпендикулярными оси -оси. это ясно, из уравнения. (87), что если между пластинами должно быть постоянным тогда должно изменяться линейно с в этом регионе. На самом деле это легко показать, что

(89)

где — произвольная постоянная.Согласно формуле. (89) электрический потенциал уменьшается непрерывно, пока мы двигаемся по направлению электрического поля. Поскольку положительный заряд ускоренных в этом направлении, мы заключаем, что положительные заряды ускорял до градиентов электрического потенциала почти таким же образом когда массы падают вниз по градиентам гравитационного потенциала (что, конечно, пропорционально высоте). Таким же образом ускоряются отрицательные заряды с до . градиенты электрического потенциала.

Согласно формуле. (87) -компонента электрического поля равна к минусу градиента электрического потенциала в -направлении. Поскольку в -направлении нет ничего особенного, аналогичные правила должны существовать для — и -компонентов поля. Эти три правила можно объединить, чтобы получить

(90)

Здесь производная берется постоянной и, и т. Д. Вышеприведенное выражение показывает, как электрическое поле , которое является векторным полем, связано с электрическим потенциал, который является скалярным полем.

Мы видели, что электрические поля суперпозиционны. То есть электрический поле, создаваемое набором зарядов, распределенных в пространстве, равно просто векторная сумма электрических полей, создаваемых каждым зарядом взяты отдельно. Что ж, если электрические поля наложены друг на друга, отсюда следует из уравнения. (90) что электрические потенциалы также должны быть суперпозиционными. Таким образом, электрический потенциал, создаваемый набором зарядов, распределенных в пространстве это просто скалярная сумма потенциалов, генерируемых каждым отдельно взятым зарядом.Ясно, что гораздо проще определить потенциал, генерируемый множеством зарядов, чем для определения электрического поля, так как мы можем суммировать потенциалы генерируется отдельными зарядами алгебраически, и вам не нужно беспокоиться о их направления (так как у них нет направлений).

Уравнение (90) выглядит довольно устрашающе. К счастью, однако, это возможно. переписать это уравнение в более привлекательной форме. Рассмотрим два соседних точки и. Предположим, что — векторное смещение точки относительно точки.Пусть будет разность электрического потенциала между этими двумя точками. Предположим, что мы путешествуем из в, сначала пройдя расстояние по оси, затем двигаясь по оси, и, наконец, двигаясь по оси. Чистый прирост в электрическом потенциале, когда мы переходим от к представляет собой просто сумму увеличения по мере движения по оси -оси, при движении по оси -ax и по оси-оси:

(91)

Но, согласно формуле.(90), , и др. Итак, получаем

(92)

что эквивалентно

(93)

где — угол между вектором и местное электрическое поле. Обратите внимание, что достигает его наиболее отрицательное значение, когда. Другими словами, направление электрическое поле в точке соответствует направлению, в котором электрическое поле потенциал снижается наиболее быстро.Положительный заряд помещен в точку ускоряется в этом направлении. Точно так же отрицательный заряд, помещенный на ускоряется в том направлении, в котором потенциал увеличивается наиболее быстро ( т.е. , ). Предположим, что мы переходим от точки к соседней точке в направлении, перпендикулярном направлению местного электрического поле ( т.е. , ). В этом случае из уравнения (93) что точки и лежат при одном и том же электрическом потенциале (, т.е. ,). Геометрическое место всех точек в окрестности точки, лежащих в тот же потенциал, что и плоскость, перпендикулярная направлению местный электрический поле.В более общем смысле, поверхности постоянного электрического потенциала, так называемые эквипотенциальных поверхностей , существуют как набор не взаимоблокирующихся поверхностей, которые везде перпендикулярно направлению электрического поля. На рисунке 14 показан эквипотенциальные поверхности (пунктирные линии) и силовые линии электрического поля (сплошные линии) генерируется положительным точечным зарядом. В этом случае эквипотенциальные поверхности имеют вид сферы с центром в заряде.

Рисунок 14: Эквипотенциальные поверхности (пунктирные линии) и электрические силовые линии (сплошные линии) точечного положительного заряда.

в разд. 4.3, мы обнаружили, что электрическое поле непосредственно над поверхностью проводник направлен перпендикулярно этой поверхности. Таким образом, ясно, что поверхность проводника должна соответствовать эквипотенциальной поверхности. Фактически, поскольку там нет электрического поля внутри проводника (и, следовательно, нет градиента в электрическом поле). потенциал), следует, что весь проводник (, т. е. , как поверхность, так и интерьер) находится при том же электрическом потенциале.

---

следующий: Электрический потенциал a Up: Электрический потенциал Предыдущее: Электрический потенциал

Ричард Фицпатрик 2007-07-14

Electric Potential — The Physics Hypertextbook

Обсуждение

введение

Вспомните историю развития электростатики.

1. Начисления существуют.
2. Заряды действуют друг на друга.
3. Эта сила проявляется на расстояниях любого размера.

У нас с вами нет проблем с этой последней идеей, но в свое время она называлась «действие на расстоянии» — довольно вежливое оскорбление. Чтобы избежать концептуальных проблем, связанных с бестелесной силой, Майкл Фарадей изобрел электрическое поле, и мир остался доволен.

Ну, какое-то время доволен. Затем кто-то указал, что электрическое поле является векторной величиной, и они вспомнили, что векторы громоздки и с ними трудно работать. Концептуальный комфорт был получен, но практическая реализация осталась неизменной.Будь прокляты эти ученые. Всегда ищу лучшее из всех возможных миров. Они хотели чего-то и концептуально удовлетворительного, и математически простого. Какая безрассудность!

Хотите верьте, хотите нет, но проблема уже была решена физиками и математиками, работающими над темами, не имеющими ничего общего с электричеством. Вода, ветер, тепло и растворенные вещества текут. Некоторые концептуальные и математические приемы, используемые для понимания этих предметов, также могут быть использованы для понимания электричества, а затем магнетизма и гравитации.

Что такое силовые линии, если не какая-то схема течения? Линии электрического поля «перетекают» от положительных зарядов к отрицательным. Положительный заряд — это как открытый кран, а отрицательный — как открытый сток. Любой, у кого есть исправная раковина, может сделать грубую модель электрического диполя на кухне или в ванной одним движением руки. Аналогичные аналогии существуют для ветра, тепла и растворенных веществ. (Технически тепло и растворенные вещества диффундируют, а не текут, поэтому здесь аналогии немного слабее.)

Подумайте на мгновение о других вещах, которые текут, и подумайте о том, что заставляет их течь. Это будет ответ на нашу следующую концептуальную проблему. Создадим таблицу, в которой сравниваются похожие явления. Во всех случаях будет что-то, что течет, и что-то, что вызывает поток.

поток…	вызвано разницей в…
река (жидкая вода)	высота
ветер (атмосферные газы)	атмосферное давление
тепло (внутренняя энергия)	температура
растворенные вещества (растворенные вещества)	концентрация

В каждом случае то, что течет, может быть описано векторным полем (величина, имеющая величину и направление в любом месте), а то, что вызывает поток, может быть описано разницей в скалярном поле (величина который имеет величину только в любом месте).

поток…	вызвано разницей в…
векторное поле	скалярное поле

Если мы сможем идентифицировать электрическое скалярное поле, которое вызывает электрическое векторное поле, мы упростили все электричество математически, поскольку скаляры математически проще векторов. «Определить», вероятно, не подходящее слово. «Define» больше нравится. Мы собираемся определить величину, которая играет ту же роль, что высота для рек, давление — для ветра, температура — для тепла, а концентрация — для растворенных веществ.

«Поток» электрического поля «вызван» разностью электрического потенциала .

поток…	вызвано разницей в…
электрическое поле (пробные заряды)	электрический потенциал

Теперь вы должны спросить себя, что такое «электрический потенциал».

Во-первых, вторая половина термина «потенциал» не подразумевает, что у него есть возможность произойти или что-то, что может привести к будущей полезности.Электрический потенциал места в космосе буквально не «может стать электрическим». Это неверное представление основано на другом значении слова «потенциал».

Настоящее значение слова «потенциал» в этом контексте сейчас неясно и, таким образом, является источником потенциальной путаницы. В контексте этого обсуждения потенциал означает нечто более близкое к тому, что дает силу, мощь, мощь или способность. Для физика существительное «потенциал» более тесно связано с прилагательными «мощный» или «потенция».В наши дни слово «потенциал» кажется скорее бессильным, чем мощным. «У меня есть power » — фраза, которая вдохновляет. «У меня есть потенциал » — это фраза в поисках вдохновения.

Во-вторых, когда я писал термин «электрический потенциал», я не отрезал две трети пути от записи электрической потенциальной энергии. Это две отдельные (но взаимосвязанные) концепции. Посмотрите, сможете ли вы проследить эту цепочку рассуждений. Обратите внимание, как я сказал «рассуждение», а не «логику». Это не доказательство.Математика покажет, как все взаимосвязано.

Разница в электрическом потенциале порождает электрическое поле. (Это концепция, которую я представляю вам в этой главе, которую вы сейчас читаете.) Электрическое поле — это сила, приходящаяся на заряд, действующая на воображаемый пробный заряд в любом месте в космосе. (Эта концепция была представлена ​​в главе перед этой.) Работа, проделанная путем помещения действительного заряда в электрическое поле, дает заряду электрическую потенциальную энергию. (Эта концепция называется теоремой работы-энергии и была представлена ​​очень давно, в одной далекой-далекой главе.) По переходному свойству (я полагаю) электрический потенциал порождает электрическую потенциальную энергию; и, согласно рефлексивному свойству (другое предположение), электрический потенциал — это энергия на заряд, которую воображаемый пробный заряд имеет в любом месте в космосе.

Это слова. Нам нужна математика. Мы можем сделать это трудным путем (без исчисления) или простым способом (с исчислением). Твой выбор.

В любом случае, вот правила для символов, специфичных для этой темы…

• Электрическое поле выделено жирным шрифтом в верхнем регистре. E .Полужирно, потому что это векторная величина. Это прописные буквы из-за произвольного выбора. Это буква E, потому что это имеет смысл. Если вы видите символ, написанный курсивом с полосой в верхней части, например, E , это означает, что вы используете только среднее значение величины. Иногда этого достаточно.
• Обозначение электрической потенциальной энергии курсивом, прописными буквами U . Оно выделено курсивом, потому что это скалярная величина. Это прописные буквы, потому что… никто не знает.Это U, потому что вам нужно использовать какую-то букву. Думаю, теперь очередь за вами. Поскольку мы имеем дело с электрической потенциальной энергией, мы должны добавить нижний индекс в верхнем регистре E. Это дает нам U _E . Если я забыл добавить подпись E, это потому, что вы должны знать из контекста, что это электрическая потенциальная энергия, а не что-то еще.
• Обозначение электрического потенциала выделено курсивом в верхнем регистре. V . Оно выделено курсивом, потому что это скалярная величина. Это заглавные буквы, чтобы соответствовать электрической потенциальной энергии (возможно).Это V, потому что V следует за U в алфавите… я думаю. Возможно, это также связано с названием единицы измерения электрического потенциала — вольт. Вы можете подумать, что я должен добавить к этому символу нижний индекс E в верхнем регистре, например, V _E , но я не буду. Никто не делает. Так редко обсуждают неэлектрические формы скалярного потенциала, что добавление нижнего индекса делается только для исключений — например, для гравитационного потенциала, V _g .

без исчисления

Начнем с теоремы об энергии работы.Когда работа закончена ( W ), энергия изменяется (∆ E ).

W = ∆ E

Более конкретно, когда работа выполняется против электрической силы ( F _E ), электрическая потенциальная энергия изменяется (∆ U _E ). Напомним, что работа — это сила, умноженная на смещение ( d ). Над символом силы есть полоса, указывающая, что мы будем использовать среднее значение. Это одно из ограничений выводов без исчисления.

F _E d = ∆ U _E

Разделите обе стороны по заряду ( q ).

Немного переставить.

Отношение силы к заряду слева называется электрическим полем ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Единственное, что изменилось, это то, что сейчас мы имеем дело со средними значениями. Отношение энергии к заряду справа называется , электрический потенциал ( В, ).Это новая идея, которая сейчас обсуждается в этой книге.

Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в космосе. Поскольку оно происходит от силы, это векторное поле. Электрический потенциал — это электрическая потенциальная энергия пробного заряда, деленная на его заряд для каждого места в космосе. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.

Электрическое поле и электрический потенциал связаны смещением.Временное смещение поля потенциальное…

Ed = ∆ V

или поле является потенциально избыточным смещением, если хотите.

На языке причудливых математических вычислений поле — это градиент потенциала, потому что реальный мир причудлив, я имею в виду трехмерный. Градиент — это трехмерный эквивалент наклона. Обычный уклон одномерный, потому что линия одномерная (даже если она не прямая). При движении по кривой нужно принимать только одно решение.Мне идти вперед или вернуться? В обычном евклидовом пространстве у нас есть три варианта. Вверх или вниз? Влево или вправо? Вперед или назад?

исчисление

Начнем с теоремы об энергии работы. Когда работа закончена ( W ), энергия изменяется (∆ E ).

W = ∆ E

Более конкретно, когда работа выполняется против электрической силы ( F _E ), электрическая потенциальная энергия изменяется (∆ U _E ).Напомним, что работа — это интеграл сила-перемещение.

–

⌠ ⌡

F E · d r = ∆ U E

Разделите обе стороны по заряду ( q ).

–	1	⌠ ⌡	F E · d r =	1	∆ U E
	кв			q

Немного переставить.

–	⌠ ⌡	Ф E	· d r =	∆ U E
		кв		q

Отношение силы к заряду слева называется электрическим полем ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Отношение энергии к заряду справа называется , электрический потенциал ( В, ).Это новая идея, которая сейчас обсуждается в этой книге.

Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в космосе. Поскольку оно происходит от силы, это векторное поле. Электрический потенциал — это электрическая потенциальная энергия пробного заряда, деленная на его заряд для каждого места в космосе. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.

Электрическое поле и электрический потенциал связаны интегралом по путям, который работает для всех видов ситуаций.Мой совет при работе с интегралом по путям — всегда выбирать самый простой путь для работы. Электричество — это консервативная сила, поэтому выполняемая им работа не зависит от выбранного пути. Это уравнение говорит о более поразительном. Интеграл слева настолько независим от пути, что его значение зависит только от электрического потенциала в начале и в конце пути. Если вам удастся найти эти два числа и вычесть их, вы сделали интеграл целиком. Если бы таким образом работало больше интегралов, студенты не зацикливались бы на исчислении.

–

⌠ ⌡

E · d r = ∆ V

Электрическое поле и электрический потенциал также связаны производной, которая работает только для одномерных ситуаций — ситуаций со сферической, цилиндрической или плоской симметрией.

E = —	д	V r̂
	др

В терминах более причудливого исчисления поле — это градиент потенциала, потому что реальный мир более интересен, чем одномерная задача.Градиент является эквивалентом производной в более высоких измерениях (в этой книге — двух и трех измерениях). Это соотношение работает для всех видов симметрии и несимметрии.

E = −∇ V

Греческая буква , дельта выглядит как треугольник, направленный вверх (∆). Перевернутая дельта называется дель (∇). Символы дельта и дель являются примерами математических устройств, называемых операторами , — символами, указывающими, что над переменной необходимо выполнить операцию.Дельта-оператор неоднократно обсуждался в этой книге. Оператор del немного реже.

Оператор дельты используется всякий раз, когда требуется изменение или разность количества. Вернемся немного назад к уравнению, которое связывает электрическое поле с электрическим потенциалом через интеграл по путям.

–

⌠ ⌡

E · d r = ∆ V

Здесь ∆ V означает разность электрического потенциала между двумя точками — обычно начальным или начальным положением (обозначено в этой книге с нижним индексом ноль) и конечным или конечным положением (указанным в этой книге без подстрочного индекса). .

	р
–	⌠ ⌡	E · d r = V — V 0
	r 0

В декартовых координатах оператор del представляет собой сумму частных производных в трех направлениях единичного вектора. (В некартовых координатах del немного сложнее).

∇ = î	∂	+ ĵ	∂	+ кО	∂
	∂ x		∂ y		∂ z

Когда оператор del применяется к скалярному полю, результирующая операция известна как градиент . Вернитесь немного назад. Уравнение, которое говорит, что электрическое поле — это градиент электрического потенциала…

E = −∇ V

выглядит так при раскрытии оператора del…

E = — î	∂	В — ĵ	∂	V — k	∂	В
	∂ x		∂ y		∂ z

и тому подобное, когда члены переставлены так, что скаляры предшествуют векторам…

E = —	∂	В до —	∂	В ĵ —	∂	V k
	∂ x		∂ y		∂ z

Возможно, теперь вы понимаете, почему был изобретен символ дель.В компактном уравнении 5 символов (не считая пробелов). В расширенном уравнении 23 (с учетом «шляп», но без учета пробелов).

Подождите. В чем дело со всеми этими знаками минус? Позвольте мне объяснить… позже.

шт.

электрический потенциал

Что нового в этой главе этой книги? Все понятие электрического потенциала. Я представил электрический потенциал как способ решить проблемы векторной природы электрического поля, но электрический потенциал — это концепция, которая имеет право на существование сама по себе.Электрический потенциал — это электрическая потенциальная энергия тестового заряда, деленная на заряд этого тестового заряда.

Старые вещи. SI — это сокращение от le Système international d’unités на французском языке или International System of Units на английском языке. Единица измерения энергии в системе СИ — джоуль, названная в честь Джеймса Джоуля, английского пивовара, ставшего физиком, который определил, что тепло и электричество являются формами энергии, эквивалентными другим формам механической энергии, таким как гравитационная потенциальная энергия и кинетическая энергия.Единицей заряда в системе СИ является кулон, названный в честь Шарля-Огюстена Кулона, французского дворянина и солдата, ставшего физиком, открывшего правило обратных квадратов электростатической силы. Единица смещения (или расстояния) в системе СИ — это метр — слово, названное в честь никого и в конечном счете образованное от греческого слова для обозначения меры (μετρον, metron ).

Новинки. Единица измерения электрического потенциала в системе СИ — вольт, названная в честь итальянского дворянина, ставшего физиком Алессандро Вольта, полное имя которого — удивительно длинный граф Алессандро Джузеппе Антонио Анастасио Вольта.Сегодняшняя шутка состоит в том, что полное имя Вольты было настолько длинным, что, когда они сократили его до названия подразделения, они зашли слишком далеко и отрезали последнюю букву «а». Единицей электрического потенциала по праву следует называть вольта, а не вольт (шутка, которую ценят только педантичные из нас). Граф Вольта известен прежде всего как изобретатель электрохимической ячейки — того, что мы теперь ошибочно называем батареей (еще одно отличие, которое ценится только педантиками — батарея — это совокупность электрохимических ячеек).Для тех, кто заботится о важных вещах, вольт — это джоуль на кулон.

[V = J / C]

Разность электрических потенциалов между двумя точками равна одному вольт, если для перемещения одного кулона заряда из одного места в другое требуется один джоуль работы.

электрическое поле

Электрический потенциал — это способ объяснить «сложное» векторное поле в терминах «легкого» скалярного поля. По определению, электрическое поле — это сила, приходящаяся на заряд воображаемого пробного заряда.

Посредством длинного объяснения, электрическое поле — это также градиент электрического потенциала (скорость изменения электрического потенциала со смещением).

Установите две величины равными…

, а затем установите их единицы равными.

[N / C = В / м]

Ньютон на кулон и вольт на метр являются эквивалентными единицами измерения электрического поля. Вольт на метр чаще используют те, кто действительно измеряет вещи, потому что вольт (который можно измерить с помощью вольтметра) и измеритель (который можно измерить линейкой любого размера, включая метрическую палочку с соответствующим названием) намного больше. легче измерить, чем силу (которую, я полагаю, можно измерить с помощью пружинной шкалы или тензодатчика, прикрепленного к заряженному объекту) и заряд (который можно измерить с помощью какого-либо известного мне устройства).

электрическая потенциальная энергия

Если вольт — это джоуль на кулон, то джоуль — это кулон-вольт. Когда один кулон заряда перемещается через разность электрических потенциалов в один вольт, его энергия изменяется на один джоуль.

[J = CV]

Для некоторых приложений джоуль слишком велик, в основном потому, что кулон слишком велик. Обычная малая единица заряда — элементарный заряд [е]. Это самый маленький заряд, который когда-либо наблюдался. Некоторые частицы, такие как протон, имеют этот заряд со знаком плюс ( q _протон = +1 e), а некоторые, как электрон, имеют его со знаком минус ( q _{электрон} = −1 e ).Когда один элементарный заряд перемещается через разность электрических потенциалов в один вольт, его энергия изменяется на один электронвольт, [эВ] — плюс или минус один электронвольт в зависимости от знака заряда и знака разности потенциалов. Электронвольт используется для некоторых приложений в электромагнетизме; твердое тело, атомная физика, ядерная физика и физика элементарных частиц; и смежные науки, такие как биофизика, химия и астрономия. Это хороший маленький блок для небольших физических систем, таких как атомы и молекулы.На самом деле это слишком мало для ядерной физики и физики элементарных частиц, но следующей по величине единицей СИ является джоуль, который на 19 порядков больше.

qV =	qV
1 электронвольт =	(1 элементарный заряд) (1 вольт)
1 электронвольт =	(1,6 × 10 −19 кулонов) (1 вольт)
1 электронвольт =	1,6 × 10 −19 джоулей
1 эВ =	1.6 × 10 −19 Дж

Электронвольт на самом деле не является единицей СИ, поскольку элементарный заряд не определяется как единица измерения. Заряд электрона, протона или чего-либо еще с элементарным зарядом должен быть получен экспериментально и, следовательно, не определен. Электронвольт был «принят для использования» с SI CIPM ( le Comité international des poids et mesures или Международный комитет мер и весов).

эксперимент милликена

Роберт Милликен (1865–1953) США

аппарат

выводов

Учебное пособие по физике: Электрический потенциал

В предыдущем разделе Урока 1 было рассмотрено, что движение положительного тестового заряда в электрическом поле сопровождается изменениями потенциальной энергии.Гравитационная аналогия использовалась для объяснения причин взаимосвязи между местоположением и потенциальной энергией. Перемещение положительного пробного заряда против направления электрического поля похоже на перемещение массы вверх в пределах гравитационного поля Земли. Оба движения были бы подобны , идущему против природы , и потребовали бы работы внешней силы. Эта работа, в свою очередь, увеличит потенциальную энергию объекта. С другой стороны, движение положительного пробного заряда в направлении электрического поля будет похоже на падение массы в гравитационном поле Земли.Оба движения были бы похожи на , идущие по природе , и происходили бы без необходимости работы внешней силы. Это движение приведет к потере потенциальной энергии. Потенциальная энергия — это запасенная энергия положения объекта, и она связана с расположением объекта в поле. В этом разделе Урока 1 мы представим понятие электрического потенциала и свяжем это понятие с потенциальной энергией положительного тестового заряда в различных местах в пределах электрического поля.

Возвращение к гравитационной аналогии

Вокруг Земли существует гравитационное поле, которое оказывает гравитационное влияние на все массы, находящиеся в окружающем ее пространстве. Перемещение объекта вверх против гравитационного поля увеличивает его гравитационную потенциальную энергию. Объект, движущийся вниз в пределах гравитационного поля, потерял бы потенциальную гравитационную энергию. Когда гравитационная потенциальная энергия была введена в Блоке 5 Физического Класса, она была определена как энергия, запасенная в объекте из-за его вертикального положения над Землей.Количество гравитационной потенциальной энергии, хранящейся в объекте, зависело от количества массы, которым обладал объект, и величины высоты, на которую он был поднят. Гравитационная потенциальная энергия зависела от массы объекта и его высоты. У объекта с удвоенной массой будет вдвое больше потенциальной энергии, а у объекта с удвоенной высотой будет вдвое больше потенциальной энергии. Обычно высокие позиции называют локациями с высоким потенциалом энергии. Взгляд на диаграмму справа показывает ошибочность такого утверждения.Обратите внимание, что груз весом 1 кг, удерживаемый на высоте 2 метра, имеет такую ​​же потенциальную энергию, как и масса весом 2 кг, удерживаемая на высоте 1 метр. Потенциальная энергия зависит не только от местоположения; это также зависит от массы. В этом смысле потенциальная гравитационная энергия зависит как минимум от двух типов величин:

1) Масса — свойство объекта, испытывающего гравитационное поле, и

2) Высота — положение в гравитационном поле

Таким образом, неправильно называть высокие позиции в гравитационном поле Земли позициями с высокой потенциальной энергией.Но есть ли какое-то количество, которое можно было бы использовать для оценки таких высот как имеющих большой потенциал обеспечения больших количеств потенциальной энергии массам, которые там находятся? Да! Хотя это не обсуждается во время блока по гравитационной потенциальной энергии, можно было бы ввести величину, известную как гравитационный потенциал — потенциальная энергия на килограмм. Гравитационный потенциал — это величина, которую можно использовать для оценки различных местоположений на поверхности Земли с точки зрения того, сколько потенциальной энергии будет обладать каждый килограмм массы, когда он будет помещен туда.Величина гравитационного потенциала определяется как ПЭ / масса. Поскольку числитель и знаменатель PE / масса пропорциональны массе объекта, выражение становится независимым от массы. Гравитационный потенциал — это величина, зависящая от местоположения, которая не зависит от массы объекта, испытывающего поле. Гравитационный потенциал описывает эффекты гравитационного поля на объекты, которые находятся в различных местах внутри него.

Если гравитационный потенциал — это средство оценки различных мест внутри гравитационного поля с точки зрения количества потенциальной энергии на единицу массы, тогда концепция электрического потенциала должна иметь аналогичное значение.Рассмотрим электрическое поле, создаваемое положительно заряженным генератором Ван де Граафа. Направление электрического поля находится в том направлении, в котором будет проталкиваться положительный испытательный заряд; в этом случае направление направлено наружу от сферы Ван де Граафа. Потребуется работа, чтобы переместить положительный испытательный заряд к сфере против электрического поля. Количество силы, задействованной при выполнении работы, зависит от количества перемещаемого заряда (согласно закону электрической силы Кулона).Чем больше заряд на испытательном заряде, тем больше сила отталкивания и тем больше работы, которая должна быть проделана с ним, чтобы переместить его на такое же расстояние. Если два объекта с разным зарядом — один из которых в два раза больше заряда другого — перемещаются на одинаковое расстояние в электрическое поле, то объект с двойным зарядом потребует вдвое большей силы и, следовательно, в два раза больше работы. Эта работа изменит потенциальную энергию на величину, равную количеству проделанной работы. Таким образом, электрическая потенциальная энергия зависит от количества заряда на объекте, испытывающем поле, и от местоположения внутри поля.Так же, как и потенциальная гравитационная энергия, электрическая потенциальная энергия зависит как минимум от двух типов величин:

1) Электрический заряд — свойство объекта, испытывающего электрическое поле, и

2) Расстояние от источника — местоположение в пределах электрического поля

В то время как электрическая потенциальная энергия зависит от заряда объекта, испытывающего электрическое поле, электрический потенциал зависит исключительно от местоположения.Электрический потенциал — это потенциальная энергия на заряд.

Понятие электрического потенциала используется для выражения эффекта электрического поля источника с точки зрения местоположения внутри электрического поля. Пробный заряд с удвоенным количеством заряда будет обладать удвоенной потенциальной энергией в данном месте; однако его электрический потенциал в этом месте будет таким же, как и у любого другого испытательного заряда. Положительный тестовый заряд будет иметь высокий электрический потенциал, когда он удерживается рядом с положительным зарядом источника, и с более низким электрическим потенциалом, когда он находится дальше.В этом смысле электрический потенциал становится просто свойством местоположения внутри электрического поля. Предположим, что электрический потенциал в данном месте составляет 12 джоулей на кулон, тогда это электрический потенциал заряженного объекта в 1 или 2 кулона. Утверждение, что электрический потенциал в данном месте составляет 12 джоулей на кулон, будет означать, что 2-кулоновский объект будет обладать 24 джоулями потенциальной энергии в этом месте, а объект 0,5 кулонов будет испытывать 6 джоулей потенциальной энергии в этом месте.

Электрический потенциал в цепях

Когда мы начнем обсуждать электрические схемы, мы заметим, что электрическая цепь с батарейным питанием имеет места с высоким и низким потенциалом. Заряд, движущийся по проводам цепи, будет сталкиваться с изменениями электрического потенциала при прохождении по цепи. В электрохимических элементах батареи между двумя выводами создается электрическое поле, направленное от положительного вывода к отрицательному.Таким образом, перемещение положительного тестового заряда через ячейки от отрицательного вывода к положительному потребует работы, таким образом увеличивая потенциальную энергию каждого кулоновского заряда, который движется по этому пути. Это соответствует движению положительного заряда против электрического поля. По этой причине положительный вывод описывается как вывод с высоким потенциалом. Подобные рассуждения привели бы к заключению, что движение положительного заряда по проводам от положительного вывода к отрицательному будет происходить естественным образом.Такое движение положительного испытательного заряда должно происходить в направлении электрического поля и не требует работы. Заряд будет терять потенциальную энергию при движении через внешнюю цепь от положительного вывода к отрицательному. Отрицательная клемма описывается как клемма с низким потенциалом. Это назначение высокого и низкого потенциала клеммам электрохимической ячейки предполагает традиционное соглашение о том, что электрические поля основаны на направлении движения положительных тестовых зарядов.

В определенном смысле электрическая цепь — это не что иное, как система преобразования энергии. В электрохимических элементах электрической цепи с батарейным питанием химическая энергия используется для работы с положительным испытательным зарядом, чтобы переместить его с клеммы с низким потенциалом на клемму с высоким потенциалом. Химическая энергия преобразуется в электрическую потенциальную энергию во внутренней цепи (то есть в батарее). Попав на клемму с высоким потенциалом, положительный тестовый заряд будет перемещаться по внешней цепи и воздействовать на лампочку, двигатель или катушки нагревателя, преобразовывая свою электрическую потенциальную энергию в полезные формы, для которых схема была разработана.Положительный тестовый заряд возвращается к отрицательной клемме с низкой энергией и низким потенциалом, готовый к повторению цикла (или, лучше сказать, цепи , ) снова и снова.

Проверьте свое понимание

1. Величина электрического потенциала определяется как величина _____.

а. электрическая потенциальная энергия

г. сила, действующая на заряд

г.потенциальная энергия на заряд

г. сила на заряд

2. Заполните следующую запись:

Когда над положительным испытательным зарядом выполняется работа с помощью внешней силы по перемещению его из одного места в другое, потенциальная энергия _________ (увеличивается, уменьшается) и электрический потенциал _________ (увеличивается, уменьшается).

3.На следующих диаграммах показано электрическое поле (представленное стрелками) и две точки, обозначенные A и B, расположенные внутри электрического поля. Положительный тестовый заряд показан в точке A. Для каждой диаграммы укажите, должна ли работа выполняться с зарядом, чтобы переместить его из точки A в точку B. Наконец, укажите точку (A или B) с наибольшей электрической потенциальной энергией и наибольший электрический потенциал.

электричества | Определение, факты и типы

Электростатика — это изучение электромагнитных явлений, возникающих при отсутствии движущихся зарядов, т.е.е., после установления статического равновесия. Заряды быстро достигают положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов. И наоборот, имея набор проводников с известными потенциалами, можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников.Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы, можно также считать, что энергия находится в электрическом поле, создаваемом этой сборкой зарядов. Наконец, энергия может храниться в конденсаторе; энергия, необходимая для зарядки такого устройства, хранится в нем как электростатическая энергия электрического поля.

Изучите, что происходит с электронами двух нейтральных объектов, соприкасающихся друг с другом в сухой среде.

Объяснение статического электричества и его проявлений в повседневной жизни.

Encyclopædia Britannica, Inc. Посмотреть все видео к этой статье

Статическое электричество — это знакомое электрическое явление, при котором заряженные частицы передаются от одного тела к другому. Например, если два предмета трутся друг о друга, особенно если они являются изоляторами, а окружающий воздух сухой, предметы приобретают одинаковые и противоположные заряды, и между ними возникает сила притяжения. Объект, теряющий электроны, становится заряженным положительно, а другой — отрицательно.Сила — это просто притяжение между зарядами противоположного знака. Свойства этой силы описаны выше; они включены в математическое соотношение, известное как закон Кулона. Электрическая сила, действующая на заряд Q ₁ в этих условиях, вызванная зарядом Q ₂ на расстоянии r , задается законом Кулона,

Жирным шрифтом в уравнении обозначается вектор характер силы, а единичный вектор r̂ — это вектор, размер которого равен единице, и который направлен от заряда Q ₂ к заряду Q ₁ .Константа пропорциональности k равна 10 ⁻⁷ c ² , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 ⁹ ньютон-квадратный метр на квадратный кулон (Нм ² / C ² ). На рисунке 1 показано усилие на Q ₁ из-за Q ₂ . Числовой пример поможет проиллюстрировать эту силу. И Q ₁ , и Q ₂ выбраны произвольно в качестве положительных зарядов, каждый с величиной 10 ⁻⁶ кулонов.Заряд Q ₁ расположен в координатах x , y , z со значениями 0,03, 0, 0 соответственно, а Q ₂ имеет координаты 0, 0,04, 0. Все координаты даны в метрах. Таким образом, расстояние между Q ₁ и Q ₂ составляет 0,05 метра.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Величина силы F на заряде Q ₁ , рассчитанная с использованием уравнения (1), равна 3.6 ньютонов; его направление показано на рисунке 1. Сила, действующая на Q ₂ из-за Q ₁ , составляет — F , что также имеет величину 3,6 ньютона; его направление, однако, противоположно направлению F . Сила F может быть выражена через ее компоненты по осям x и y , поскольку вектор силы лежит в плоскости x y . Это делается с помощью элементарной тригонометрии из геометрии рисунка 1, а результаты показаны на рисунке 2.Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрической силы между зарядами в состоянии покоя. Если заряды имеют противоположные знаки, сила будет притягивающей; притяжение было бы указано в уравнении (1) отрицательным коэффициентом единичного вектора r̂. Таким образом, электрическая сила на Q ₁ будет иметь направление, противоположное единичному вектору r̂ , и будет указывать от Q ₁ к Q ₂ .В декартовых координатах это привело бы к изменению знаков компонентов силы x и y в уравнении (2).

компоненты кулоновской силы

Рисунок 2: Компоненты x и y силы F на рисунке 4 (см. Текст).

Предоставлено Департаментом физики и астрономии Университета штата Мичиган

Как можно понять эту электрическую силу, действующую на Q ₁ ? По сути, сила возникает из-за наличия электрического поля в позиции Q ₁ .Поле создается вторым зарядом Q ₂ и имеет величину, пропорциональную размеру Q ₂ . При взаимодействии с этим полем первый заряд на некотором расстоянии либо притягивается, либо отталкивается от второго заряда, в зависимости от знака первого заряда.

2.2: Электростатический потенциал — Physics LibreTexts

Испытательные заряды

Альтернативный способ взглянуть на электрические поля из того, что мы сделали в разделе 1.2 — с точки зрения испытательного заряда . Идея состоит в том, чтобы использовать заряженную точечную частицу как средство измерения векторов электрической силы в различных точках пространства. Когда все векторы силы нанесены на карту, мы затем делим их на заряд точечной частицы, и новые векторы становятся векторами электрического поля. Распространенный (но несколько странный) способ записать это математически:

\ [\ overrightarrow E \ left (\ overrightarrow r \ right) = \ lim \ limits_ {q_ {test} \ rightarrow 0} \ dfrac {\ overrightarrow F_ {on \; q_ {test}}} {q_ {test} }, \; \; \; \; \; \; \ text {где} \ overrightarrow r \ text {- позиция} q_ {test} \]

Область вокруг скопления заряда аналогичным образом может быть протестирована с заряженной точечной частицей.В каждой точке пространства можно измерить потенциальную энергию, которая существует, когда испытательный заряд переносится из бесконечности в заданное положение, а затем количество испытательного заряда может быть разделено, так что все, что остается, является функцией источника. обвинения. Запишем это так:

\ [V \ left (\ overrightarrow r \ right) = \ lim \ limits_ {q_ {test} \ rightarrow 0} \ dfrac {\ Delta U \ left (q_ {test}: \ infty \ rightarrow \ overrightarrow r \ right )} {q_ {test}}, \; \; \; \; \; \; \ text {где} \ overrightarrow r \ text {- вектор положения} q_ {test} \]

Этот процесс отображает скалярное поле , поскольку с каждой точкой в ​​пространстве связано число (а не вектор, как в случае электрического поля), и все эти числа относятся к произвольно выбранному значению нуля в точке бесконечность.Так же, как векторы электрического поля не совпадают с векторами сил, значения в этом скалярном поле не являются потенциальными энергиями — более того, это можно увидеть даже в единицах этих чисел, которые представляют собой джоули, разделенные на кулоны. Отношение джоулей на кулон получило собственное название: вольт, . Созданное нами скалярное поле называется электростатическим потенциалом . Подобно вектору электрического поля, это величина, которая определяется в каждой точке пространства вблизи некоторого электрического заряда.В отличие от векторов электрического поля, эти величины являются скалярами — у них нет направления.

Предупреждение

Возможно, самая большая проблема для студентов, плохо знакомых с электростатикой, — это использование слова «потенциал» в слове «электростатический потенциал». Это название происходит от того факта, что оно связано с электрической потенциальной энергией, но эти величины очень разные, и читателю рекомендуется помнить об этом. {th} \) заряда до положения в пространстве, обозначенного вектором положения \ (\ overrightarrow r \).Следует подчеркнуть, что \ (U \ left (q_ {test} \ right) \) , а не , представляет собой полную потенциальную энергию полной сборки заряда (нет терминов, включающих такие факторы, как \ (q_1q_2 \), например) — он представляет только часть потенциальной энергии, полученной системой из-за введения испытательного заряда, переносимого из бесконечности. Таким образом, электростатический потенциал рассматривает все заряды, которые не являются пробным зарядом, как коллективный источник скалярного поля.Обратите внимание, что, приняв соглашение \ (U \ left (\ infty \ right) = 0 \), мы также сделали это для электростатического потенциала. И, как и в случае с потенциальной энергией, положение, которое мы выбираем для обозначения нулевого электрического потенциала, произвольно.

Все вещи, которые мы разработали для электрических полей, также применимы к потенциалам, с той лишь разницей, что потенциалы накладываются друг на друга как скаляры, а не векторы (что на самом деле упрощает работу с ними во многих случаях). Суть в том, что когда у нас есть набор исходных зарядов, включая непрерывное распределение, мы можем определить потенциал в каждой точке пространства, и если мы поместим туда точечный заряд, мы можем определить его потенциальную энергию, умножив заряд на электрический потенциал:

\ [U = qV \ left (\ overrightarrow r \ right), \; \; \; \; \; \; \ text {where} \ overrightarrow r = \ text {вектор положения заряда} q \]

Сходство с уравнением 1.2.2 очевиден — мы просто заменили силу и поле энергией и потенциалом.

Предупреждение

Мы часто будем использовать такой язык, как «потенциальная энергия точечного заряда», но, как и в случае со всей потенциальной энергией, на самом деле мы имеем в виду «потенциальную энергию, добавленную к системе благодаря наличию точечного заряда». Чтобы ввести потенциальную энергию, требуется взаимодействие через консервативную силу, а для взаимодействия требуются две сущности. Например, у объекта не может быть собственной гравитационной потенциальной энергии (хотя мы часто относимся к нему именно так) — он должен взаимодействовать с Землей. {- 1} \).]

Обратите внимание, что знаки поменялись местами с обеих сторон уравнения. Величина слева обычно обозначается как падение потенциала от A до B . Конечно, потенциал не имеет , поэтому, возможно, потенциальное изменение — лучший язык. Причина этой формулировки, вероятно, уходит корнями в конкретный случай выполнения интеграла по пути, который следует направлению электрического поля. Обратите внимание, что в этом случае \ (\ overrightarrow E \) всегда в том же направлении, что и \ (\ overrightarrow {dl} \), что дает положительный линейный интеграл.Если линейный интеграл положительный, то \ (U_A> U_B \), что означает, что потенциал падает с \ (A \) до \ (B \). Это дает нам полезное практическое правило:

Электрические поля указывают в направлении уменьшения электрического потенциала.

Всякий раз, когда у нас есть интегральное отношение, подобное этому, тогда, как мы видели для закона Гаусса, также доступно дифференциальное (локальное) отношение. Мы действительно видели это в нашем исследовании механики, и это также проявляется здесь:

\ [\ overrightarrow F = — \ overrightarrow \ nabla U \; \; \; \Правая стрелка \;\;\; \ overrightarrow E = — \ overrightarrow \ nabla V \]

Хотя это интересно, читателя можно простить, если он спросит, для чего это нужно.Последнее соотношение особенно действенно по следующей причине. Предположим, мы хотим вычислить электрическое поле распределения заряда. Предполагая, что у нас нет умного способа использовать для этого закон Гаусса, мы должны выполнить вычисление, как мы делали в разделе 1.3. Часть того, что делает эти вычисления сложными, — это отслеживание трех различных компонентов вектора электрического поля (то есть трех отдельных интегралов). Если вместо этого вычислить потенциальное поле (один интеграл без векторов), мы можем взять производных (градиент), чтобы получить электрическое поле.В следующем разделе мы увидим, как вычислить потенциальное поле по распределению заряда.

Предупреждение

Связь между полем и потенциалом часто понимается неправильно, в еще одном воплощении путаницы величины с изменением этой величины (например, ошибочное принятие ускорения со скоростью. Так же, как нулевая мгновенная скорость не означает, что ускорение равно нулю, нулевой потенциал при точка в пространстве не означает, что поле там равно нулю. В самом деле, мы можем определить потенциал равным нулю где угодно, независимо от того, что это за поле! Это скорость изменения потенциала, которая определяет поле, а не значение потенциала.

Формулы градиента

Еще в разделе 1.6 мы впервые столкнулись с использованием векторного исчисления, когда узнали, что нам придется учитывать расходимости электрических полей, чтобы применить закон Гаусса в определенных приложениях. Теперь мы сталкиваемся с одним из родственников операции дивергенции — градиентом. Как и в случае с расхождением, полезно рассмотреть некоторые формулы градиентов в определенных особых обстоятельствах. Как и в случае с дивергенцией, формула градиента в декартовых координатах работает во всех случаях, тогда как градиент в цилиндрических и сферических координатах упрощается только тогда, когда скалярная функция зависит только от \ (r \) (как и раньше, в цилиндрических координатах это — расстояние до оси, а в сферических координатах — расстояние до точки):

Декартовы координаты

\ [\ overrightarrow \ nabla V \ left (x, \; y, \; z \ right) = \ dfrac {\ partial V} {\ partial x} \ widehat i + \ dfrac {\ partial V} {\ partial y } \ widehat j + \ dfrac {\ partial V} {\ partial z} \ widehat k \]

Цилиндрические координаты

\ [\ overrightarrow \ nabla V \ left (r, \ cancel {\ phi}, \ cancel {z} \ right) = \ dfrac {\ partial V} {\ partial r} \ widehat r \]

Сферические координаты

\ [\ overrightarrow \ nabla V \ left (r, \ cancel {\ theta}, \ cancel {\ phi} \ right) = \ dfrac {\ partial V} {\ partial r} \ widehat r \]

Пример \ (\ PageIndex {1} \)

В определенной области пространства вокруг начала координат электростатическое потенциальное поле удовлетворяет:

\ [V \ left (x, y, z \ right) = \ alpha \; х + \ бета \; у ^ 2 + \ гамма \; z ^ 3 \ nonumber \]

Найдите плотность заряда в начале координат в терминах \ (\ alpha \), \ (\ beta \) и \ (\ gamma \).2 \; \ widehat k \ nonumber \]

Теперь дивергенция поля дает нам плотность заряда (закон Гаусса в локальной форме):

\ [\ dfrac {\ rho \ left (x, y, z \ right)} {\ epsilon_o} = \ nabla \ cdot \ overrightarrow E = \ dfrac {\ partial E_x} {\ partial x} + \ dfrac { \ partial E_y} {\ partial y} + \ dfrac {\ partial E_z} {\ partial z} = 0-2 \ beta-6 \ gamma \; z \; \; \; \Правая стрелка \;\;\; \ в коробке {\ rho \ left (0,0,0 \ right) = — 2 \ beta \ epsilon_o} \ nonumber \]

Обратите внимание, что в начале координат потенциал равен нулю, но электрическое поле нет, равно как и плотность заряда.

Идентичность из векторного исчисления

Мы вывели зависимость отрицательного градиента между потенциалом и электрическим полем из той же связи между консервативной силой и связанной с ней потенциальной энергией (уравнение 2.2.7). Чтобы сила имела связанную потенциальную энергию, необходимо, чтобы она была консервативной. Мы все время предполагали, что электрическая сила консервативна. Как мы увидим позже, на самом деле это не всегда так.Оказывается, что электромагнитное поле является консервативным, но магнитное поле может передавать энергию в / из электрического поля, что само по себе делает электрическое поле неконсервативным. Для этого необходимо, чтобы заряды источника двигались, и, поскольку мы все еще обсуждаем только электро статику , мы можем безопасно продолжать использовать электростатический потенциал и соотношение отрицательного градиента.

Существование функции потенциальной энергии достаточно, чтобы доказать, что сила консервативна, хотя доказать это может быть проблематично без инструментов, предоставляемых векторным исчислением.Простой тест на консервативность силы — исчезновение ее изгиба:

\ [\ overrightarrow \ nabla \ times \ overrightarrow F = 0 \; \; \; \ leftrightarrow \; \; \; F \; является \; консервативным \; \; \; \ leftrightarrow \; \; \; \ overrightarrow F = — \ overrightarrow \ nabla U \]

Причина, по которой это работает как тест, заключается в том, что геометрия завитка и градиента такова, что завиток векторного поля, возникающий из градиента скалярного поля, всегда одинаково равен нулю:

\ [\ overrightarrow \ nabla \ times \ left [\ overrightarrow \ nabla \ left (что угодно \ вправо) \ вправо] \ эквив 0 \]

Итак, если силу можно записать как отрицательный градиент функции потенциальной энергии, то ее изгиб должен исчезнуть, и это соответствует консервативной силе.Распространяя это на электростатику, мы видим, что если электрическое поле можно выразить как отрицательный градиент потенциала, то его ротор исчезает. Итак, имеем:

\ [\ overrightarrow \ nabla \ times \ overrightarrow E = 0 \; \; \; \ leftrightarrow \; \; \; электростатика \; \; \; \ leftrightarrow \; \; \; \ overrightarrow E = — \ overrightarrow \ nabla V \]

Эквипотенциальные поверхности

Следствием градиентного отношения является то, что их взаимосвязь имеет геометрическую природу. Первое проявление этого состоит в том, что градиент скалярного поля указывает в том направлении, где скалярные значения растут быстрее всего.Таким образом, имея отрицательный знак, мы заключаем, что электрическое поле направлено в направлении самого быстрого спуска электрического потенциала. Это подтверждает установленное выше эмпирическое правило.

Мы можем продемонстрировать эту геометрическую взаимосвязь с помощью диаграммы. Давайте представим, что мы начинаем с определенной точки пространства и измеряем там потенциал (после обозначения нулевой точки). Затем мы отбираем близлежащие точки и находим направление, в котором мы можем переместить наш детектор, чтобы потенциал не изменился.Если мы продолжим эту процедуру и нанесем на карту все пространство, где потенциал не меняется, мы обнаружим, что это поверхность. Поскольку эта воображаемая поверхность существует с одним равным потенциалом, она называется эквипотенциальной поверхностью . Вот двухмерное изображение набора таких поверхностей:

Рисунок 2.2.1 — Эквипотенциальные поверхности

При положительном заряде источника силовые линии направлены наружу, что действительно указывает от более высокого потенциала к более низкому, но есть кое-что более конкретное, из чего мы можем сделать вывод о геометрической взаимосвязи поля и потенциала.Б \ overrightarrow E \ cdot \ overrightarrow {dl} \]

Конечно, электрическое поле не равно нулю везде, где мы идем, и расстояние, которое мы проходим, не равно нулю, так как же этот интеграл может оказаться равным нулю? Может быть, часть этого отменяет другие части? Нет, потому что это происходит на каждом пути, который мы выбираем, между любыми двумя точками, пока этот путь остается на эквипотенциальном уровне. Ответ заключается в том, что этот интеграл может быть равен нулю только тогда, когда в каждой точке эквипотенциала электрическое поле перпендикулярно \ (\ overrightarrow {dl} \).Другими словами:

Электрическое поле везде перпендикулярно эквипотенциальным поверхностям.

То, что электрические поля перпендикулярны эквипотенциальным поверхностям, звучит очень знакомо. То же самое мы сказали о проводящих поверхностях для электростатики. Действительно, сразу делаем вывод, что для электростатики:

Проводники эквипотенциальные.

Обратите внимание, что это утверждение выходит за рамки только поверхности проводника. Мы знаем, что внутри металла проводника нет электрического поля, поэтому, когда мы идем от поверхности проводника к металлу, электрический потенциал не может изменяться (электрические поля возникают из-за изменений электрического потенциала), поэтому электрический потенциал одинаков во всем проводнике.

Когда нам предоставляют несколько эквипотенциальных поверхностей, как мы здесь, мы можем сделать вывод об электрическом поле больше, чем просто о его направлении. Операция градиента измеряет направленную скорость изменения . Это означает, что если каждая показанная эквипотенциальная поверхность разделена одинаковым числом вольт (как на диаграмме выше), то области, где эти поверхности находятся ближе всего друг к другу, изменяются быстрее всего, что означает, что величина электрического поля там больше всего.

Пример \ (\ PageIndex {2} \)

Заряженная частица движется в электрическом поле, эквипотенциальные поверхности которого показаны на схеме. Единственная сила, испытываемая зарядом, возникает из-за этого поля. Заряд движется медленнее в точке \ (A \), чем в точке \ (B \).

1. Заряд частицы: положительный / отрицательный / не могу определить
2. Величина ускорения заряда больше в: точка A / точка B / не могу сказать.
3. Каково направление ускорения заряда в каждой точке?

Решение

а. Кинетическая энергия частицы увеличилась от точки A к точке B, что означает, что ее потенциальная энергия снизилась. Но его электростатический потенциал вырос, поэтому, поскольку \ (\ Delta U = q \ Delta V \), то \ (\ Delta U <0 \) и \ (\ Delta V> 0 \) означает, что \ (q <0 \ ).

г. Все эквипотенциалы отличаются одинаковым напряжением, поэтому те, которые расположены ближе друг к другу, указывают на область, где электрическое поле сильнее.Следовательно, поле сильнее в точке A, а это означает, что на него действует большая результирующая сила, чем в точке B.

г. Сила, создаваемая электрическим полем, должна быть параллельна электрическому полю, которое должно быть перпендикулярно эквипотенциальной поверхности. Итак, силы в точках A и B должны быть либо слева, либо справа, но можем ли мы сказать, в какую сторону? Поле указывает от более высокого потенциала к более низкому потенциалу, поэтому в точке A оно указывает влево, а в точке B — вправо.{\ mathbf {r} _ {2}} \ mathbf {E} \ cdot d \ mathbf {l} \ label {m0064_eV12} \]

Этот метод вычисления разности потенциалов часто бывает немного неудобным. Чтобы понять, почему, рассмотрим пример из теории схем, показанный на рисунке \ (\ PageIndex {1} \). В этом примере, состоящем из одного резистора и узла заземления, мы выделили четыре величины:

• Сопротивление \ (R \)
• Ток \ (I \) через резистор
• Узловое напряжение \ (V_1 \), которое представляет собой разность потенциалов, измеренную от земли до левой стороны резистора
.
• Узловое напряжение \ (V_2 \), которое представляет собой разность потенциалов, измеренную от земли до правой стороны резистора
.

Допустим, мы хотим вычислить разность потенциалов \ (V_ {21} \) на резисторе.Это можно сделать двумя способами:

• \ (V_ {21} = — IR \)
• \ (V_ {21} = V_2-V_1 \)

Преимущество второго метода в том, что нет необходимости знать \ (I \), \ (R \) или что-либо еще о том, что происходит между узлами; нужно только знать напряжения в узлах. Дело в том, что часто бывает удобно иметь общую точку отсчета — в этом примере — землю — относительно которой могут быть определены разности потенциалов во всех других интересующих точках.Когда у нас есть это, вычисление разностей потенциалов сводится к простому вычитанию заранее определенных узловых потенциалов.

Рисунок \ (\ PageIndex {1} \): резистор в более крупной схеме, используемый в качестве примера для демонстрации концепции узловых напряжений. (CC BY SA 4.0; К. Киккери).

Итак, можем ли мы установить точку отсчета для общих электростатических проблем, которая работает таким же образом? Ответ положительный. Датум произвольно выбран как сфера, охватывающая вселенную; т.е. сфера радиуса \ (\ to \ infty \).{\ bf r} {\ bf E} \ cdot d {\ bf l}} \ label {m0064_eVP} \]

Электрический потенциал в точке, заданный уравнением \ ref {m0064_eVP}, определяется как измеренная разность потенциалов, начиная с сферы бесконечного радиуса и заканчивая точкой \ ({\ bf r} \). 2} \ right] \ cdot d {\ bf l} \]

Принцип независимости пути (Раздел 5.{r}
\ end {align}

т.

\ [\ boxed {V ({\ bf r}) = + \ frac {q} {4 \ pi \ epsilon r}} \ label {m0064_eV} \]

(Предложение: подтвердите, что уравнение \ ref {m0064_eV} размерно правильное.) В контексте приведенного выше примера теории схем это «узловое напряжение» в \ ({\ bf r} \), когда датум определен как — поверхность бесконечно удаленной сферы. Впоследствии мы можем вычислить разность потенциалов от любой точки \ ({\ bf r} _1 \) до любой другой точки \ ({\ bf r} _2 \) как \ [V_ {21} = V ({\ bf r} _2) -V ({\ bf r} _1) \], и это обычно будет легче, чем при использовании уравнения \ ref {m0064_eV12} лот .

Нечасто имеют дело с системами, состоящими из одной заряженной частицы. Итак, чтобы описанная выше методика была действительно полезной, нам нужен простой способ определения потенциального поля \ (V ({\ bf r}) \) для произвольных распределений заряда. Первым шагом в разработке более общего выражения является определение результата для частицы, находящейся в точке \ ({\ bf r} ‘\) где-то в другом месте, кроме начала координат. Поскольку уравнение \ ref {m0064_eV} зависит только от заряда и расстояния между точкой поля \ ({\ bf r} \) и \ ({\ bf r} ‘\), мы имеем

\ [V ({\ bf r}; {\ bf r} ‘) \ треугольникq + \ frac {q’} {4 \ pi \ epsilon \ left | {\ bf r} — {\ bf r} ‘\ right |} \ label {m0064_eVd} \]

, где для единообразия обозначений мы используем символ \ (q ‘\) для обозначения заряда.N {\ frac {q_n} {\ left | {\ bf r} — {\ bf r} _n \ right |}}} \ label {m0064_eVN} \]

Уравнение \ ref {m0064_eVN} дает электрический потенциал в указанном месте из-за конечного числа заряженных частиц.

Потенциальное поле из-за непрерывного распределения заряда рассматривается в разделе 5.13.

Авторы и авторство

.