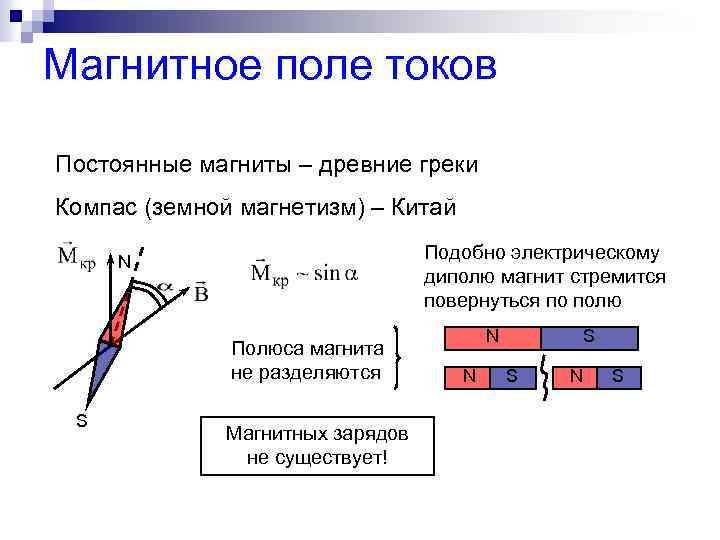
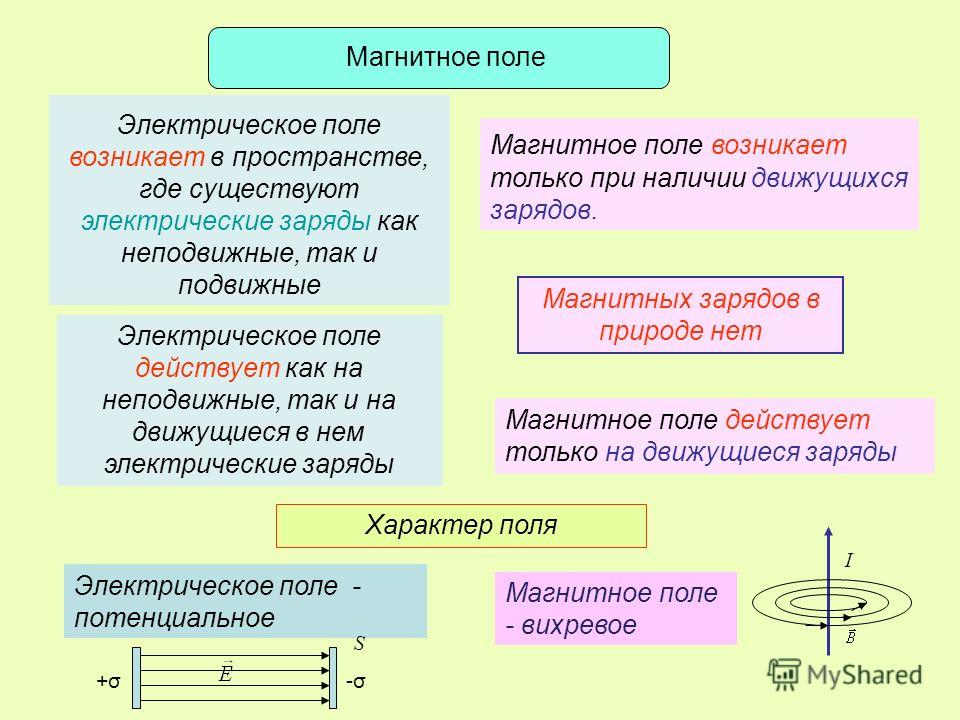
Потенциальное и вихревое поле
Различают два основных типа векторных полей: потенциальные (безвихревые) и вихревые (соленоидальные) поля. Физические свойства их различны.
Потенциальное поле тесно связано со своим источником, линии поля имеют начало (исток) и конец (сток). Линии вихревого поля всегда непрерывны и не имеют источников (рисунок Рисунок 12 ).
−Потенциальное и вихревое поля
Для потенциального поля имеем
,
то есть циркуляция вектора по любому замкнутому контуруравна нулю.
Если поле является вихревым, то поток вектора через любую замкнутую поверхность равен нулю:
.
В дальнейшем будет показано, что электростатическое поле является только потенциальным, магнитное – вихревым.
Градиент, оператор Гамильтона
Далее мы рассмотрим некоторые
дифференциальные операции с векторыми
и скалярными полями, а именно градиент,
дивергенцию (расхождение) и ротор
(вихрь).
Каждое поле порождает собой еще три поля, которые мы и будем рассматривать: векторные поля градиента и ротора и скалярное поле дивергенции.
Градиентом скалярного поля называется вектор, имеющий направление быстрейшего увеличенияи по величине равный производной по этому направлению.
В векторном анализе часто удобно использовать условный вектор, т.н. оператор Гамильтона. В декартовых координатах он имеет вид
.
Тогда можно записать
.
Градиент совпадает по направлению с нормалью к поверхности уровня и направлен в ту сторону, кудавозрастает (рисунок Рисунок 13 ).
−Градиент
Градиент будет применяться при анализе потенциальных векторных полей. Другое применение вектора градиента – численная оптимизация функций.
Дивергенция, физический смысл дивергенции
Для анализа явлений, происходящих в
электромагнитном поле, важно знать, где
находятся источники того или иного
вектора. За меру источника можно выбрать
поток вектора через замкнутую поверхность,
но внутри данной замкнутой поверхности
могут быть источники разных знаков,
взаимно уничтожающие свое действие.
Чтобы выявить распределение источников
в пространстве, можно устремить эту
замкнутую поверхность к нулю, но тогда
поток вектора через эту бесконечно
малую поверхность будет бесконечно
малым. Это затруднение ликвидируется
тем, что поток вектора через замкнутую
поверхность делят на объем, окруженный
этой поверхностью. Устремляя объем к
нулю, получим предел этого отношения,
который и называется дивергенцией.
За меру источника можно выбрать
поток вектора через замкнутую поверхность,
но внутри данной замкнутой поверхности
могут быть источники разных знаков,
взаимно уничтожающие свое действие.
Чтобы выявить распределение источников
в пространстве, можно устремить эту
замкнутую поверхность к нулю, но тогда
поток вектора через эту бесконечно
малую поверхность будет бесконечно
малым. Это затруднение ликвидируется
тем, что поток вектора через замкнутую
поверхность делят на объем, окруженный
этой поверхностью. Устремляя объем к
нулю, получим предел этого отношения,
который и называется дивергенцией.
Дивергенция дает возможность точно указать, в каких точках пространства расположились источники вектора.
Возьмем какую-либо точку поля
,
окружим ее малым объемоми вычислим поток векторачерез поверхность,
ограничивающую объем.
Разделим этот поток на,
чтобы отнести его к единице объема и
перейдем к пределу, устремляя к нулю
все размеры,
что мы будем обозначать символом.
При этом объембудет стягиваться к точке.
В векторном анализе доказывается, что
или, с применением оператора Гамильтона,
,
т.е., скалярное произведение оператора набла на вектор .
Рассмотрим значения дивергенции для разных случаев поля (рисунок Рисунок 14 ).
−Дивергенция
При положительной в точке дивергенции внутри областипоток векторачерез ограничивающую поверхность больше нуля, то есть линии вектора расходятся из этой области. Таким образом, внутринаходятся источники вектора. При отрицательной дивергенции, наоборот, линии вектора сходятся в областьи тогда внутри нее находятся стоки векторного поля.
Если же во всех точках некоторой области
поля дивергенция оказывается равной
нулю, что силовые линии поля либо
пронизывают ее, либо являются замкнутыми.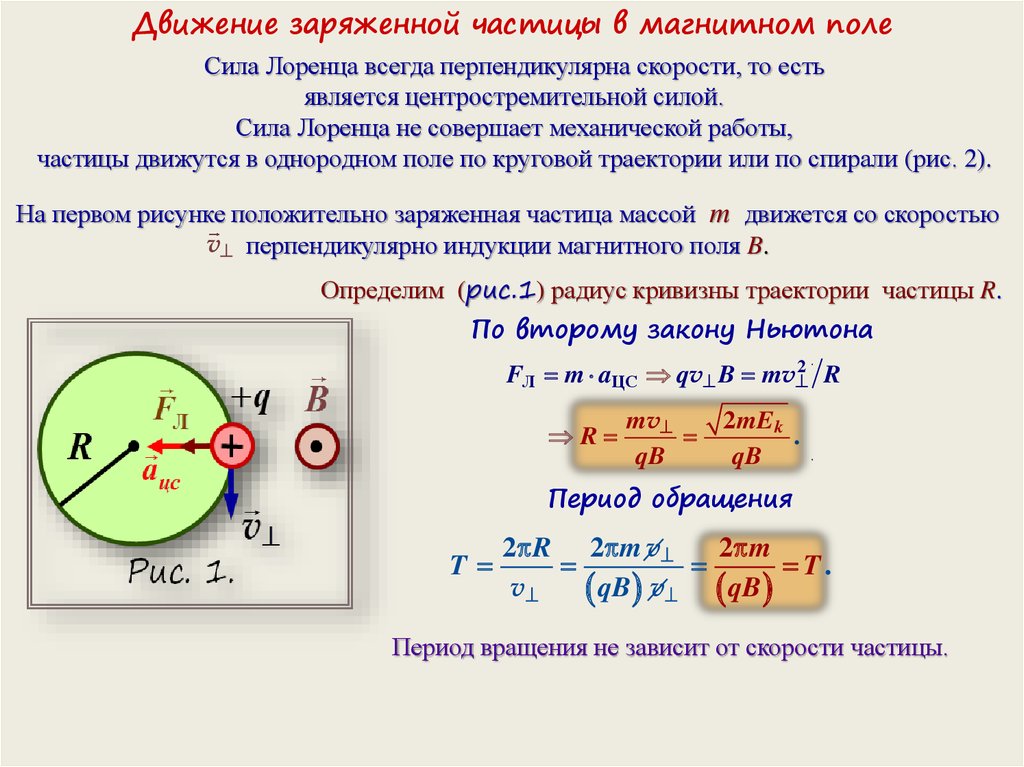
Вихревой характер магнитного поля
Определение 1Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.
Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.
Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:
Определение вихревого поля также выполнимо другим способом.
Вихревое магнитное поле
Определение 2Векторные поля, вектор которых не равен нулю – это вихревые магнитные поля.
Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:
rot B→=μ0j→ (2), где j→ считается объемной плотностью тока, и второй формы определения вихревого поля можно заключить, что магнитное поле будет вихревым там, где проходят токи, а безвихревым там, где их нет.
При отсутствии токов вектор магнитной индукции B→ представляется в виде градиента скалярного магнитного потенциала φm:
B→=-gradφm (3).
Если имеются токи, то данное представление невозможно.
Различие между потенциальными и вихревыми полями
Основными уравнениями магнитного поля постоянных токов считаются выражения вида:
rot B→=μ0j→div B→=0 (4).
Произведем сравнение с основными уравнениями электростатики:
rot E→=0div E→=1ε0ρ (5).
Рассматривая систему (5), видно, что электрическое поле всегда потенциально, а его источниками являются электростатические (неподвижные) заряды.
Магнитное поле считается вихревым при наличии токов. Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.
Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.
Электрические токи являются источниками поля. Магнитное поле считается вихревым, так как его дивергенция везде равна нулю. Его также называют соленоидальным. Определение потенциального электростатического поля возможно при заданной дивергенции напряженности div E→ (x, y, z) в качестве функции координат. Полное определение вихревого магнитного поля реально, когда имеется мощность его вихрей, то есть rot B→ (x, y, z) как функция координат.
Показать, почему для вихревого магнитного поля нельзя представить вектор индукции B→ в виде градиента магнитного потенциала φm.
Решение
Возьмем формулу:
B→=-gradφm (1.1).
Для выражения (1.1) можно применить операцию rot:
rot B→=-rot gradφm (1.2).
Известно значение rot:
rot (gradφm)=0 (1.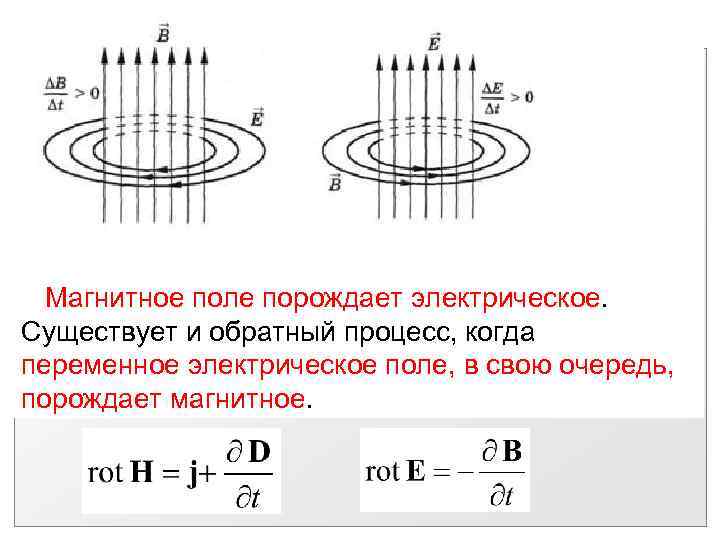 3).
3).
При подстановке (1.3) в (1.2) имеем:
rot B→=0.
Ответ: Вспомнив теорему о циркуляции, получаем отсутствие токов. В данном случае, представление вектора индукции магнитного поля невозможно в виде магнитного потенциала в области, где проходят токи.
Пример 2Применение понятия скалярного магнитного потенциала φm возможно только в области пространства, где j→=0. Данная часть пространства φm характеризуется неоднозначностью функции. Показать это.
Решение
Необходимо рассмотреть магнитное поле возле контура с током, как изображено на рисунке 1. По теореме о циркуляции для любого контура выполнимо равенство:
∮LB→dl→=0.
Рисунок 1
Если токов нет, магнитное поле становится потенциальным, интеграл, который необходимо взять между A и B, не зависит от пути интегрирования, то запись примет вид:
∫AaBB→dl→=∫AbBB→dl→ (2.2).
Отсюда следует:
∫AbBB→dl→=∫ABB→dl→=φmA-φmB (2.3).
Выражение (2. 3) может быть рассмотрено в качестве разности скалярных магнитных потенциалов в точках A и B. Можно пойти иным путем и принять значение потенциала равным нулю в точке В, как выполнялось для нахождения потенциала в электростатике:
3) может быть рассмотрено в качестве разности скалярных магнитных потенциалов в точках A и B. Можно пойти иным путем и принять значение потенциала равным нулю в точке В, как выполнялось для нахождения потенциала в электростатике:
∫ABB→dl→=φmA (2.4).
При выборе контура, охватывающего какой-либо ток (контур AcbB), как показано на рисунке 1, линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет не равен нулю:
∮AcbBB→dl→≠0 (2.5).
Или
∮AcbBB→dl→≠∫AcBB→dl→-∫AbBB→dl→=I≠0 (2.6)
Тогда:
∫AcBB→dl→=∫AbBB→dl→+I=φmA-φmB+I (2.7).
При выборе какого-либо пути AnB, охватывающего ток в количестве n раз, имеем:
∫AnBB→dl→=φmA-φmB+nI (2.8).
Следует задать нулевой потенциал в точке В:
∫AnBB→dl→=φmA+nI (2.9).
Ответ: Получив уравнение (2.9), очевидно, что скалярный магнитный потенциал является неоднозначной величиной.
Автор: Роман Адамчук
Преподаватель физики
Магнитный векторный потенциал | Brilliant Math & Science Wiki
июль Томас внес
Содержание
- Расчет магнитного векторного потенциала
- Магнитное поле
- Электрическое поле
Магнитный векторный потенциал, обусловленный длиной \(d\vec{s}\) с текущим через него током \(I\), равен 92} + L {R} \bigg) \шляпа{z} \end{выравнивание} \]
Магнитное поле представляет собой ротор векторного потенциала.
\[\vec{B} = \nabla \times \vec{A}\]
Найти магнитное поле в области с магнитным векторным потенциалом \(\vec{A} = \sin(\theta)\hat{r} — r\hat{\theta}.\)
Поскольку \(\vec{A}\) находится в сферических координатах, используйте сферическое определение завитка.
\[\begin{выравнивание} \vec{B} = \frac{1}{r\sin\theta} \left( \ гидроразрыва {\ парциальное} {\ парциальное \ тета} \ влево (А_ \ varphi \ грех \ тета \ вправо) — \ гидроразрыва {\ парциальное А_ \ тета} {\ парциальное \ varphi} \справа) &\шляпа{\mathbf r} \\ {}+ \frac{1}{r} \left( \frac{1}{\sin\theta} \frac{\partial A_r}{\partial \varphi} — \frac{\partial}{\partial r} \left( r A_\varphi \right) \справа) &\шляпа{\boldsymbol \theta} \\ {}+ \frac{1}{r} \left( \frac{\partial}{\partial r} \left( r A _{\theta} \right) — \ гидроразрыва {\ парциальное A_r} {\ парциальное \ тета} \справа) &\шляпа{\boldsymbol \varphi} \конец{выравнивание}\]
Единственная часть, которая выживет для данного \(\vec{A}\), это
\[ \начать{выравнивать} \vec{B} &= \frac{1}{r} \big( \frac{\partial}{\partial r} (r A_\theta) — \frac{\partial A_r}{\partial \theta} \big) \hat{ \varphi} \\ &= \frac{1}{r} \big( 2r — \cos(\theta) \big) \\ &= 2 — \ гидроразрыва {\ соз (\ тета)} {r} \end{выравнивание} \]
Частная производная магнитного векторного потенциала частично вносит вклад в индуцированное электрическое поле в соответствии с законом Фарадея.
\[\vec{E} = — \frac{\partial \vec{A} }{\partial t} \]
Вспомним закон Фарадея:
\[\nabla \times \vec{E} = — \frac{\partial \vec{B} }{\partial t}\]
\[\nabla \times \vec{E} = — \frac{\partial \big( \nabla \times \vec{A} \big) }{\partial t}\]
\[\nabla \times \vec{E} = — \nabla \times \frac{ \partial \vec{A} }{\partial t}\]
\[\rightarrow \vec{E} = — \frac{ \partial \vec{A} }{\partial t}\]
Цитировать как: Магнитный векторный потенциал. Brilliant.org . Извлекаются из https://brilliant.org/wiki/магнитный-векторный-потенциал/
Магнитный потенциал | Энциклопедия MDPI
Термин «магнитный потенциал» может использоваться для обозначения любой из двух величин в классическом электромагнетизме: векторного магнитного потенциала или просто векторного потенциала, A; и магнитный скалярный потенциал ψ. Обе величины могут использоваться при определенных обстоятельствах для расчета магнитного поля B.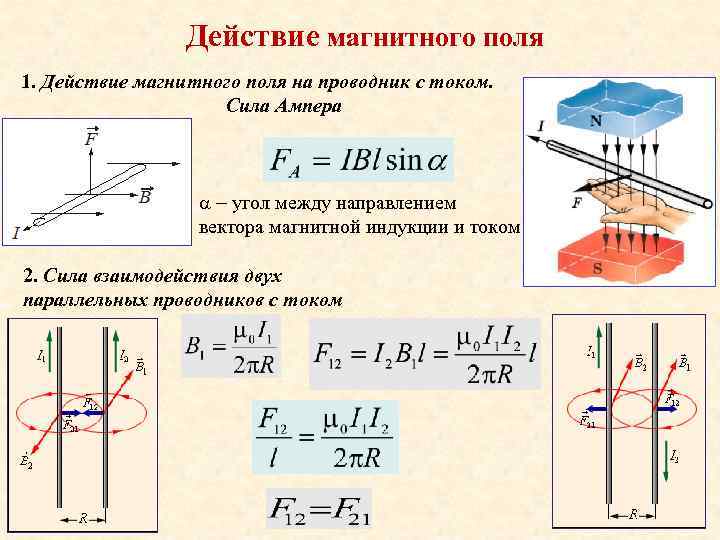 Более часто используемый магнитный векторный потенциал определяется так, что его ротор равен магнитному полю: [math]\displaystyle{ \nabla \times \mathbf{A} =\mathbf{B}\, }[/math]. Вместе с электрическим потенциалом φ магнитный векторный потенциал также может использоваться для определения электрического поля E. Следовательно, многие уравнения электромагнетизма могут быть записаны либо в терминах полей E и B, либо, что эквивалентно, в терминах потенциалов φ и A. В более продвинутых теориях, таких как квантовая механика, в большинстве уравнений используются потенциалы, а не поля. Магнитный скалярный потенциал ψ иногда используется для определения магнитного H-поля в случаях, когда нет свободных токов, аналогично использованию электрического потенциала для определения электрического поля в электростатике. Одним из важных применений ψ является определение магнитного поля, создаваемого постоянными магнитами, когда известна их намагниченность. С некоторой осторожностью скалярный потенциал можно распространить и на свободные токи.
Более часто используемый магнитный векторный потенциал определяется так, что его ротор равен магнитному полю: [math]\displaystyle{ \nabla \times \mathbf{A} =\mathbf{B}\, }[/math]. Вместе с электрическим потенциалом φ магнитный векторный потенциал также может использоваться для определения электрического поля E. Следовательно, многие уравнения электромагнетизма могут быть записаны либо в терминах полей E и B, либо, что эквивалентно, в терминах потенциалов φ и A. В более продвинутых теориях, таких как квантовая механика, в большинстве уравнений используются потенциалы, а не поля. Магнитный скалярный потенциал ψ иногда используется для определения магнитного H-поля в случаях, когда нет свободных токов, аналогично использованию электрического потенциала для определения электрического поля в электростатике. Одним из важных применений ψ является определение магнитного поля, создаваемого постоянными магнитами, когда известна их намагниченность. С некоторой осторожностью скалярный потенциал можно распространить и на свободные токи. Исторически лорд Кельвин впервые ввел векторный потенциал в 1851 году вместе с формулой, связывающей его с магнитным полем.
Исторически лорд Кельвин впервые ввел векторный потенциал в 1851 году вместе с формулой, связывающей его с магнитным полем.
1. Магнитный векторный потенциал
Магнитный векторный потенциал A представляет собой векторное поле, определяемое вместе с электрическим потенциалом ϕ (скалярное поле) уравнениями: [1]
- [математика] \displaystyle{ \mathbf{B} = \nabla \times \mathbf{A}\,\quad \mathbf{E} = -\nabla\phi — \frac{ \partial \mathbf{A} }{ \partial t }\,}[/математика]
, где B — магнитное поле, а E — электрическое поле. В магнитостатике, где нет изменяющегося во времени распределения заряда, необходимо только первое уравнение. (В контексте электродинамики члены векторный потенциал и скалярный потенциал используются для магнитного векторного потенциала и электрического потенциала соответственно. В математике векторный потенциал и скалярный потенциал могут быть обобщены на более высокие измерения.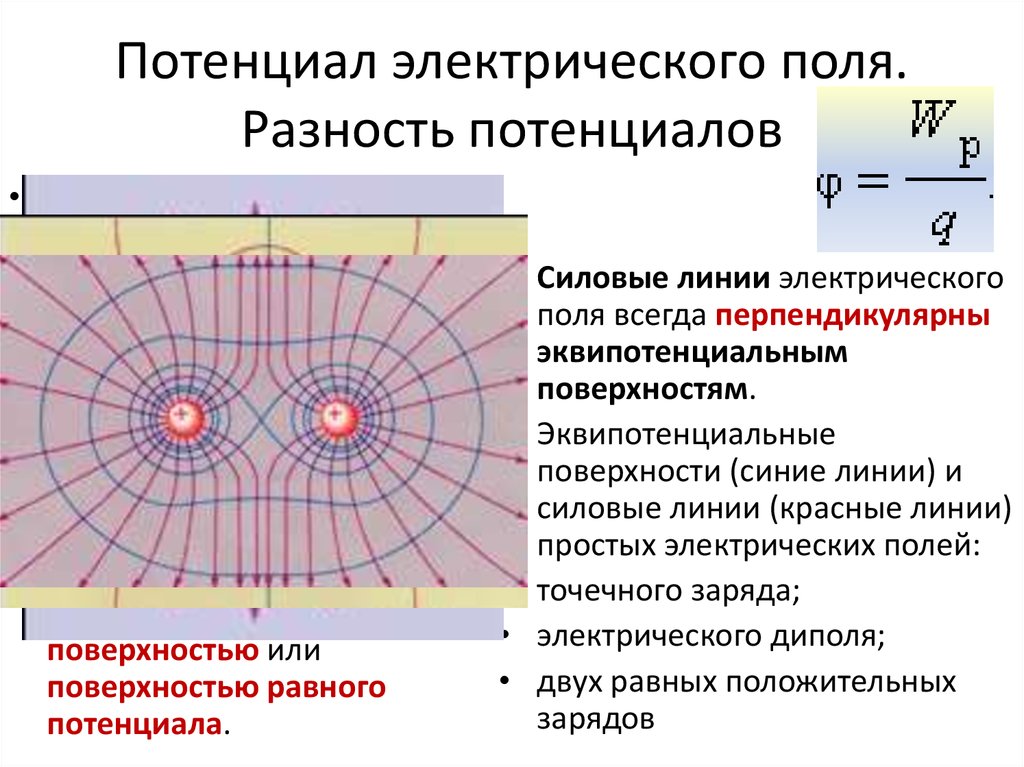 )
)
Если электрические и магнитные поля определяются, как указано выше, из потенциалов, они автоматически удовлетворяют двум уравнениям Максвелла: закону Гаусса для магнетизма и закону Фарадея. Например, если A является непрерывным и везде четко определенным, то это гарантированно не приведет к магнитным монополям. (В математической теории магнитных монополей В некоторых местах число может быть либо неопределенным, либо многозначным; подробности см. в разделе магнитный монополь).
Начиная с приведенных выше определений:
- [math]\displaystyle{ \begin{align} \nabla \cdot \mathbf{B} &= \nabla \cdot \left(\nabla \times \mathbf{A}\ справа) = 0 \\ \nabla \times \mathbf{E} &= \nabla \times \left( -\nabla\phi — \frac{ \partial\mathbf{A} }{ \partial t } \right) = -\frac{ \partial }{ \partial t } \left(\nabla \times \mathbf{A}\right) = -\frac{ \partial \mathbf{B} }{ \partial t }. \end{выравнивание} }[/math]
Альтернативно, существование A и ϕ гарантируется этими двумя законами с помощью теоремы Гельмгольца.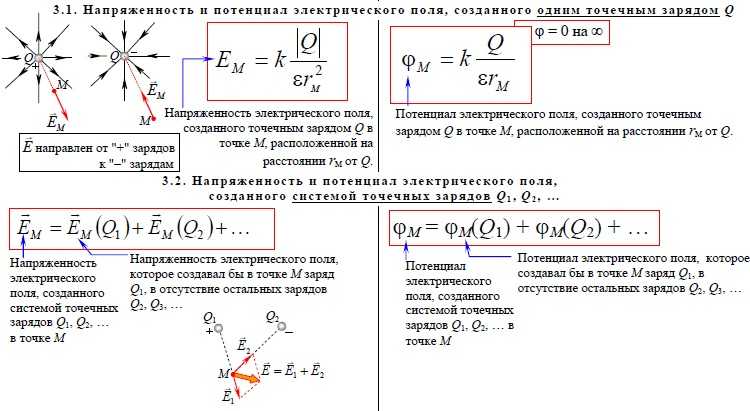 Например, поскольку магнитное поле не имеет дивергенции (закон Гаусса для магнетизма, т. Е. ∇ ⋅ B = 0), всегда существует A , удовлетворяющее приведенному выше определению.
Например, поскольку магнитное поле не имеет дивергенции (закон Гаусса для магнетизма, т. Е. ∇ ⋅ B = 0), всегда существует A , удовлетворяющее приведенному выше определению.
Векторный потенциал A используется при изучении лагранжиана в классической механике и в квантовой механике (см. уравнение Шредингера для заряженных частиц, уравнение Дирака, эффект Ааронова–Бома).
В системе СИ единицами измерения A являются В·с·м −1 , и они совпадают с импульсом на единицу заряда или силой на единицу тока.
Линейный интеграл A по замкнутому контуру равен магнитному потоку через замкнутую поверхность:
- [math]\displaystyle{ \oint_\Gamma \mathbf{A}\, \cdot\, d{ \mathbf{\Gamma}} = \iint_S \nabla\times\mathbf{A}\, \cdot\, d\mathbf{S}=\Phi_B. }[/математика]
Таким образом, единицы из A также эквивалентны Weber на метр. Приведенное выше уравнение полезно при квантовании потока сверхпроводящих петель.
Приведенное выше уравнение полезно при квантовании потока сверхпроводящих петель.
Хотя магнитное поле B представляет собой псевдовектор (также называемый аксиальным вектором), векторный потенциал A является полярным вектором. [2] Это означает, что если бы правило правой руки для перекрестных произведений было заменено правилом левой руки, но без изменения каких-либо других уравнений или определений, то B поменял бы знаки, но A не изменится. Это пример общей теоремы: ротор полярного вектора является псевдовектором, и наоборот. [2]
1.1. Выбор манометра
- Основная страница: Физика: Крепление манометра
Приведенное выше определение не дает однозначного определения магнитного векторного потенциала, потому что по определению мы можем произвольно добавлять компоненты без завитков к магнитному потенциалу без изменения наблюдаемого магнитного поля.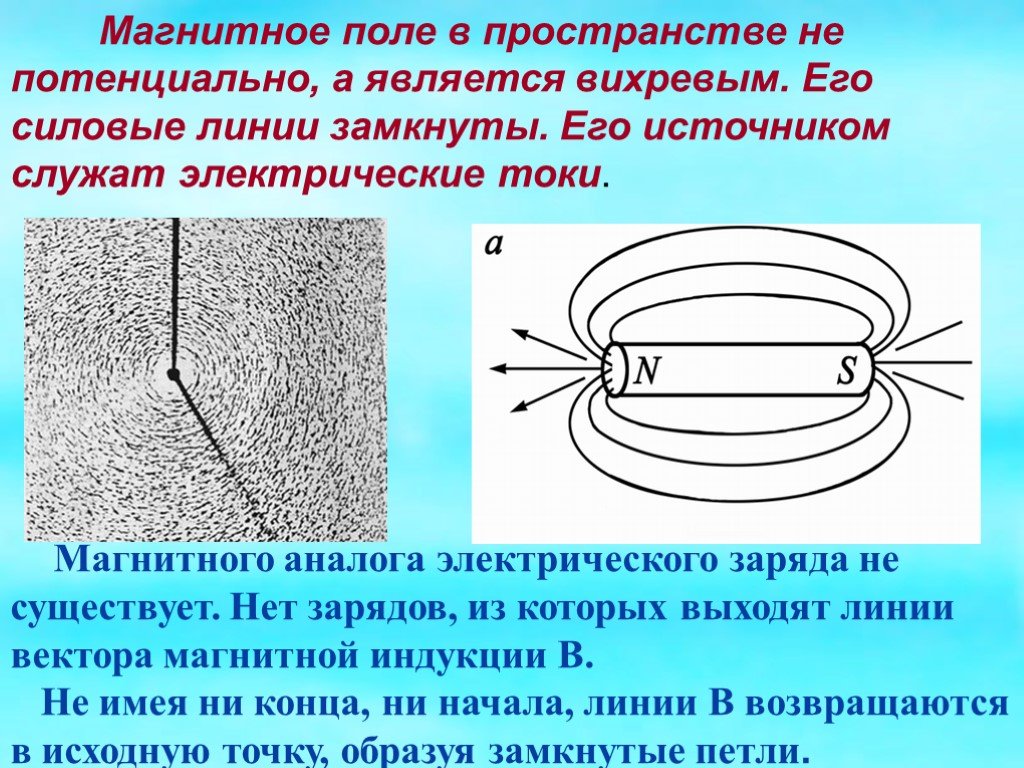 Таким образом, имеется некоторая степень свободы при выборе 92} &= -\mu_0 \mathbf{J} \end{align} }[/math]
Таким образом, имеется некоторая степень свободы при выборе 92} &= -\mu_0 \mathbf{J} \end{align} }[/math]
В других датчиках уравнения другие. Другая запись для записи тех же уравнений (с использованием четырех векторов) показана ниже.
1.3. Расчет потенциалов по исходным распределениям
- Главная страница: Физика:Запаздывающий потенциал
Решения уравнений Максвелла в калибровке Лоренца (см. Фейнман [1] и Джексон [3] ) с граничным условием, что оба потенциала достаточно быстро стремятся к нулю по мере их приближения к бесконечности, называются запаздывающими потенциалами, которые магнитный векторный потенциал A ( R , T ) и электрический скалярный потенциал ϕ ( R , T ) из -за распределения тока токовой плотности J ( R ′, T r r r r r r r r r r r r r r r r . , где поля в векторе положения r и времени t вычисляются из источников в удаленном положении r ′ в более раннее время t ′. Местоположение r ′ является исходной точкой в распределении заряда или тока (также переменной интегрирования в пределах объема Ω). Более раннее время t ′ называется запаздывающим временем и рассчитывается как В других калибрах формула для A и ϕ отличается; например, см. Представляя векторный потенциал магнитного поля кулоновской калибровки A , плотность магнитного потока B и плотность тока Дж полей вокруг тороидального индуктора круглого поперечного сечения. Более толстые линии указывают линии поля с более высокой средней интенсивностью. Кружки в поперечном сечении сердечника обозначают поле B , выходящее за пределы изображения, знаки плюс обозначают поле B , входящее в изображение. 9B) — собственная работа, общественное достояние, https://commons.wikimedia.org/w/index.php?curid=19608361 См. Feynman [5] для изображения поля A вокруг длинного тонкого соленоид. Начиная с в предположении квазистатических условий, т. линии и контуры A относятся к B так же, как линии и контуры B относятся к j . Таким образом, изображение поля A вокруг контура потока B (которое будет создаваться в тороидальном индукторе) качественно такое же, как поле B вокруг контура тока. Рисунок справа представляет собой художественное изображение поля A . Более толстые линии указывают пути с более высокой средней интенсивностью (более короткие пути имеют более высокую интенсивность, так что интеграл пути тот же). Линии нарисованы, чтобы (эстетически) придать общий вид А — поле. На чертеже подразумевается, что ∇ ⋅ A = 0, верно при одном из следующих предположений: В контексте специальной теории относительности естественно объединить магнитный векторный потенциал вместе с (скалярным) электрическим потенциалом в электромагнитный потенциал, также называемый четырехпотенциальным . Одной из причин для этого является то, что 4-потенциал является математическим 4-вектором. Таким образом, используя стандартные правила четырехвекторного преобразования, если электрические и магнитные потенциалы известны в одной инерциальной системе отсчета, их можно просто вычислить в любой другой инерциальной системе отсчета. 9\mu A_\mu &= 0 \\ \Box A_\mu &= \frac{4\pi}{c} J_\mu \end{align} }[/math] , где □ — д’Аламбериан, а J — четырехпоток. Первое уравнение представляет собой калибровочное условие Лоренца, а второе содержит уравнения Максвелла. Четырехпотенциал также играет очень важную роль в квантовой электродинамике. Магнитный скалярный потенциал плоских цилиндрических магнитов, закодированный как цвет от положительного (фуксия) через ноль (желтый) до отрицательного (голубой). Автор Geek3 — собственная работа, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=82804692 Скалярный потенциал — еще одна полезная величина для описания магнитного поля, особенно для постоянных магнитов. В односвязной области, где нет свободного тока, , следовательно, мы можем определить магнитный скалярный потенциал , ψ , как [6] \psi = -\nabla\cdot\mathbf{H} = \nabla\cdot\mathbf{M}. }[/математика] Здесь ∇ ⋅ M действует как источник магнитного поля, так же как ∇ ⋅ P действует как источник электрического поля. 3\mathbf{r}’ \end{align} }[ /математика]
3\mathbf{r}’ \end{align} }[ /математика]
93\mathbf{r}’ \end{align} }[/math]
 Кулоновскую калибровку для другой возможности.
Кулоновскую калибровку для другой возможности. 1.4. Изображение поля А
 е. B} \, }[/math]
е. B} \, }[/math] 1.
 5. Электромагнитный четырехпотенциальный
5. Электромагнитный четырехпотенциальный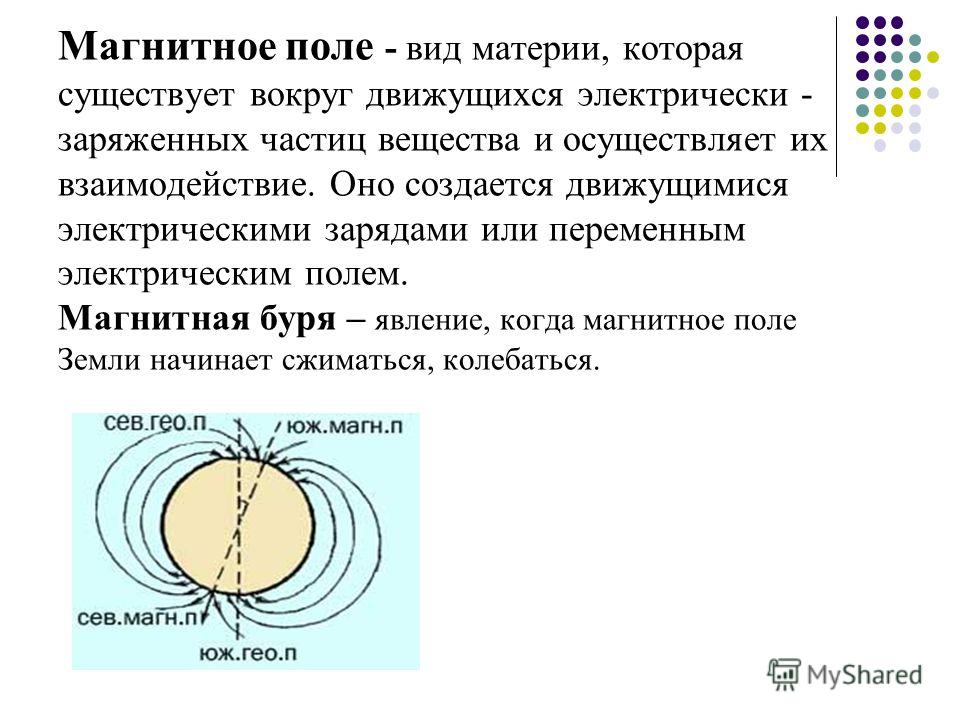
2. Магнитный скалярный потенциал