Потенциал электростатического поля и разность потенциалов

Подробности

Просмотров: 686

«Физика — 10 класс»

Обладает ли электрическое поле энергией? В чём это выражается?
Как рассчитать энергию поля?

В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это силовая характеристика. Теперь введём энергетическую характеристику — потенциал.

Потенциал поля.

Работа любого электростатического поля при перемещении в нём заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля.

На замкнутой траектории работа электростатического поля всегда равна нулю.

Поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю, называют потенциальным

.

Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.

Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = — (W_п2 — W_п1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой (14.14).

Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля (см. формулу (14.14)), так и для неоднородного. Следовательно, отношение потенциальной энергии к заряду не зависит от помещённого в поле заряда.

Это позволяет ввести новую количественную характеристику поля —

потенциал, не зависящую от заряда, помещённого в поле.

Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень её отсчёта. При определении потенциала поля, созданного системой зарядов, как правило, предполагается, что потенциал в бесконечно удалённой точке поля равен нулю.

Потенциалом точки электростатического поля называют отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.

Согласно данному определению потенциал равен:

Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:

Напряжённость поля — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.

Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:

Разность потенциалов.

Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.

Изменение потенциала не зависит от выбора нулевого уровня отсчёта потенциала.

Так как потенциальная энергия Wn = дчр, то работа сил поля равна:

А = — (W_п2 — W_п1) = -q(φ₂ — φ₁) = q(φ₁ — φ₂) = qU.         (14.17)

Здесь

U = φ₁ — φ₂ —         (14.18)

разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.

Разность потенциалов называют также напряжением.

Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:

Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.

Единица разности потенциалов.

Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах.

Разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В): 1 В = 1 Дж/1 Кл.

Выразим единицу разности потенциалов через основные единицы СИ. Так как

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Следующая страница «Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности»

Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Электростатика — Физика, учебник для 10 класса — Класс!ная физика

Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона.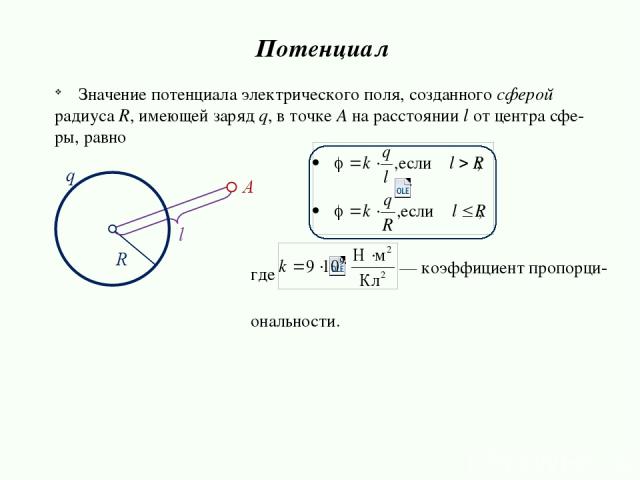 Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара. Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора.

Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

§10. Напряженность и потенциал электростатического поля Основные формулы

Напряженность электрического поля определяется выражением

,

где – сила, действующая на точечный заряд q, помещенный в данную точку поля.

Потенциал электростатического поля равен

,

где П – потенциальная энергия точечного заряда q, находящегося в данной точке поля .

Сила, действующая на точечный заряд, находящийся в электри­ческом поле, и потенциальная энергия этого заряда определяются из соотношений

, .

Принцип суперпозиции электрических полей: напряженность или потенциал поля, созданного системой то­чечных зарядов, равны сумме напряженностей или потенциалов полей каждого из зарядов, то есть

, ,

где – напряженность и потенциал в данной точке поля, созда­нного

i – м зарядом.

Напряженность и потенциал поля, созданного точечным зарядом, определяются из соотношений:

, ,

где r – расстояние от заряда Q до точки, в которой определяются напряженность и потенциал электростатического поля.

Теорема Остроградского – Гаусса для электростатического поля имеет вид

,

где – поток вектора напряженности электростатического поля сквозь произвольную замкнутую поверхность S; – сумма зарядов, охваченных данной поверхностью.

Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиуса R , заряд которой q , на расстоянии r от центра сферы, определяются формулами:

а) если то ,

б) если , то ,

в) если то , .

Напряженность поля, создаваемого прямой бесконечной равномерно заряженной линией или бесконечно длинным цилиндром, равна

,

где r – расстояние от нити или оси цилиндра до точки, в которой вычисляется напряженность поля.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, определяется выражением

,

где – поверхностная плотность заряда на плоскости.

Вектор электрического смещения связан с вектором напряженности электрического поля соотношением

,

где – электрическая постоянная, – диэлектрическая проницаемость вещества.

Связь потенциала с напряженностью выражается уравнениями:

а) в общем случае или ;

б) в случае однородного поля ,

где и – потенциалы точек двух эквипотенциальных поверхностей; d – расстояние между этими поверхностями;

в) в случае поля, обладающего центральной или осевой симметрией,

.

Электрический момент диполя определяется формулой

,

где Q – заряд диполя; – плечо диполя, то есть вектор, направленный от отрицательного заряда к положительному и численно равный расстоянию между зарядами.

Работа сил электростатического поля по перемещению заряда q из точки поля с потенциалом в точку с потенциалом равна

, или .

Задачи

10.1. Определить напряжен­ность Е электрического поля, создаваемого точечным зарядом q = 10 нКл на расстоянии r =10 см от него. Диэлектрик – масло.

10.2. Расстояние d между двумя точечными зарядами q₁ = 8 нКл и q₂= -5,3 нКл равно 40 см. Вычислить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напря­женность, если второй заряд будет положительным?

10.3. Электрическое поле создано двумя точечными зарядами q₁ = 10 нКл и q₂ = -20 нКл, находящимися на расстоянии d = 20 см друг от друга. Определить напряженность Е поля в точке, удален­ной от первого заряда на r₁ = 30 см и от второго на r₂ = 50 см.

10.4. Расстояние d между двумя точечными положительными за­рядами q₁ = 9q и q₂ = q равно 8 см. На каком расстоянии r от перво­го заряда находится точка, в которой напряженность Е поля заря­дов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?

10.5. Два точечных заряда q₁= 2q и q₂ = —q находятся на рас­стоянии d друг от друга. Найти положение точки на прямой, про­ходящей через эти заряды, напряженность поля Е в которой равна нулю.

10.6. Электрическое поле создано двумя точечными зарядами q₁ = 40 нКл и q₂= -10 нКл, находящимися на расстоянии d = 10 см друг от друга. Определить напряженность поля Е в точке, удален­ной от первого заряда на r₁ = 12 см и от второго на r₂ = 6 см.

10.7. Тонкое кольцо радиусом R = 8 см несет заряд, равномерно распределенный с линейной плотностью τ = 10 нКл/м. Какова на­пряженность электрического поля Е в точке, равноудаленной от всех точек кольца на расстояние r = 10 см?

10.8. Тонкое полукольцо радиуса R = 20 см заряжено равно­ мерно зарядом q = 0,70 нКл. Найти модуль напряженности электрического поля в центре кривизны этого полукольца.

10. 9. Полусфера несет заряд, равномерно распределенный с по­верхностной плотностью σ = 1 нКл/м². Найти напряженность электрического поля Е в геометрическом центре полусферы.

10.10. На металлической сфере радиусом R = 10 см находится заряд q = l нКл. Определить напряженность электрического поля Е в следующих точках: 1) на расстоянии r₁ = 8 см от центра сферы; 2) на её поверхности; 3) на расстоянии r₂ = 15 см от центра сферы. Построить график зависимости Е от r.

10.11. Две концентрические металлические заряженные сферы радиусами R₁ = 6 см и R₂ = 10 см несут соответственно заряды q₁ = 1 нКл и q₂ = -0,5 нКл. Найти напряженность электростатического поля Е в точках, отстоящих от центра сфер на расстояниях r₁ = 5 см, r₂ = 9 см, r₃ = 15 см. Построить график зависимости Е (r).

10.12. Очень длинная тонкая прямая проволока несет заряд, равномерно распределенный по всей ее длине. Вычислить линейную плотность заряда , если напряженность Е поля на расстоянии а = 0,5 м от проволоки против ее середины равна 200 В/м.

10.13. Расстояние d между двумя длинными тонкими проволо­ками, расположенными параллельно друг другу, равно 16 см. Про­волоки равномерно заряжены разноименными зарядами с линейной плотностью τ = 150 мкКл/м. Какова напряженность Е поля в точ­ке, удаленной на r = 10 см как от первой, так и от второй проволоки?

10.14. Прямой металлический стержень диаметром d = 5 см и длиной l = 4 м несет равномерно распределенный по его поверхности заряд q = 500 нКл. Определить напряженность Е поля в точке, находящейся против середины стержня на расстоянии а = 1 см от его поверхности.

10.15. Бесконечно длинная тонкостенная металлическая трубка радиусом R = 2 см несет равномерно распределенный по поверхно­сти заряд (σ = 1 нКл/м²). Определить напряженность Е поля в точ­ках, отстоящих от оси трубки на расстояниях r₁ = l см, r₂ = 3 см. Построить график зависимости Е(r).

10.16. На отрезке тонкого прямого проводника длиной l = 10 см равномерно распределен заряд с линейной плотностью = 3 мкКл/м. Вычислить напряженность Е поля, создаваемого этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего кон­ца отрезка на расстояние, равное длине этого отрезка.

10.17. Тонкий стержень длиной l = 12 см заряжен с линейной плотностью τ = 200 нКл/м. Найти напряженность Е электрического поля в точке, находящейся на расстоянии r = 5 см от стержня против его середины.

10.18. Тонкий стержень длиной l = 10 см заряжен с линейной плотностью = 400 нКл/м. Найти напряженность Е электрического поля в точке, расположенной на перпендикуляре к стержню, про­веденном через один из его концов, на расстоянии r = 8 см от этого конца.

10.19. Электрическое поле создано двумя бесконечными парал­лельными пластинами, несущими одинаковый равномерно распре­деленный по площади заряд (σ= 1 нКл/м²). Определить напряжен­ность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.

10.20. Электрическое поле создано двумя бесконечными парал­лельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями = 2 нКл/м² и = -5 нКл/м². Определить напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напря­женности вдоль линии, перпендикулярной пластинам.

10.21. Две бесконечные параллельные пластины равномерно за­ряжены с поверхностной плотностью = 10 нКл/м² и = 30 нКл/м². Определить силу взаимодействия между пластинами, приходящуюся на площадь S, равную 1 м².

10.22. Эбонитовый сплошной шар радиусом R = 5 см несет заряд, равномерно распределенный с объемной плотностью ρ = 10 нКл/м³. Определить напряженность Е и смещение D электрического поля в точках: 1) на расстоянии r₁ = 3 см от центра сферы; 2) на поверхно­сти сферы; 3) на расстоянии r₂ = 10 см от центра сферы. Построить графики зависимостей Е(r) и D(r).

10.23. Длинный парафиновый цилиндр радиусом R = 2 см несет заряд, равномер­но распределенный по объему с объемной плотностью ρ = 10 нКл/м³. Определить на­пряженность Е и смещение D электричес­кого поля в точках, находящихся от оси цилиндра на расстоянии: 1) r₁ = 1 см; 2) r₂ = 3 см. Обе точки равноудалены от концов цилиндра. Построить графики зависимостей Е(r) и D (r).

10.24. Тонкая нить несет равномерно распределенный по длине заряд с линейной плотностью τ = 2 мкКл/м. Вблизи средней части нити на расстоянии r = 1 см, малом по сравнению с ее длиной, нахо­дится точечный заряд q = 0,l мкКл. Определить силу F, действую­щую на заряд.

10.25. Большая металлическая пластина несет равномерно рас­пределенный по поверхности заряд (σ= 10 нКл/м²). На малом рас­стоянии от пластины находится точечный заряд q = 100 нКл. Найти силу F, действующую на заряд.

10.26. Между пластинами плоского конденсатора находится то­чечный заряд q = 30 нКл. Поле конденсатора действует на заряд с силой F₁ = 10 мН. Определить силу F₂ взаимного притяжения плас­тин, если площадь S каждой пластины равна 100 см².

10.27. Две одинаковые круглые пластины площадью по S = 100 см² каждая расположены параллельно друг другу. Заряд одной пла­стины равен q₁ = 100 нКл, другой q₂ = -100 нКл. Определить силу F взаимного притяжения пластин в двух случаях, когда расстояние между ними: 1) r₁ = 2 см; 2) r₂ = 10 м.

10.28. Две параллельные, бесконечно длинные прямые нити несут заряд, равномерно распределенный по длине с линейными плотностями = 0,1 мкКл/м и = 0,2 мкКл/м. Определить силу F взаимодействия, приходящуюся на отрезок нити длиной 1 м. Рас­стояние r между нитями равно 10 см.

10.29. Металлический шар имеет заряд q₁ = 0,1 мкКл. На рас­стоянии от его поверхности, равном радиусу шара, находится конец нити, вытянутой вдоль силовой линии. Нить несет равномерно рас­пределенный по длине заряд q₂ = 10 нКл.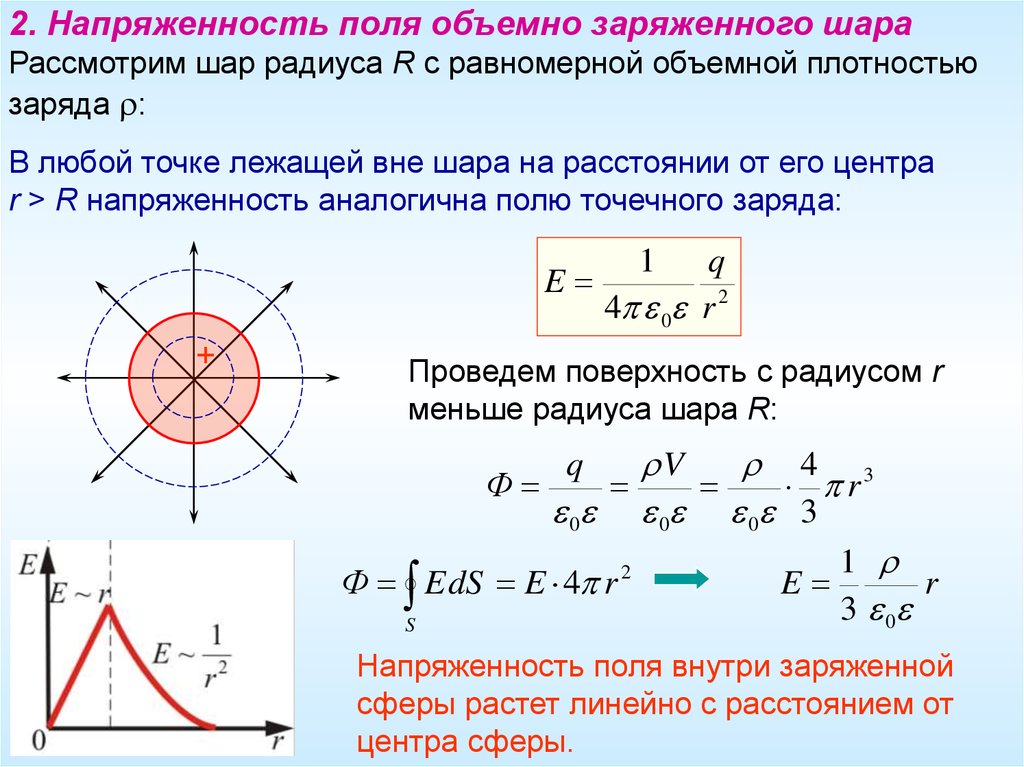 Длина нити равна радиусу шара. Определить силу F, действующую на нить, если радиус R шара равен 10 см.

10.30. Точечный заряд q = 10 нКл, находясь в некоторой точке поля, обладает потенциальной энергией П = 10 мкДж. Найти потенциал этой точки поля.

10.31. При перемещении заряда q = 20 нКл между двумя точками поля внешними силами была совершена работа А = 4 мкДж. Определить работу А₁ сил поля и разность потенциалов этих точек поля.

10.32. Поле создано точечным зарядом q = l нКл. Определить потенциал φ поля в точке, удаленной от заряда на расстояние r = 20 см.

10.33. Определить потенциал φ электрического поля в точке, удаленной от зарядов q₁ = -0,2 мкКл и q₂ = 0,5 мкКл соответственно на r₁ = 15 см и r₂ = 25 см.

10.34. Заряды q₁ = l мкКл и q₂ = -1 мкКл находятся на расстоянии d = 10 см. Определить напряженность Е и потенциал поля в точке, удаленной на расстояние r = 10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно направлению от q₁ к q₂.

10.35. Вычислить потенциальную энергию П системы двух точечных зарядов q₁ = 100 нКл и q₂ = 10 нКл, находящихся на расстоянии d = 10 см друг от друга.

10.36. Какова потенциальная энергия П системы четырех одинаковых точечных зарядов q = 10 нКл, расположенных в верши­нах квадрата со стороной длиной а = 10 см?

10.37. По тонкому кольцу радиусом R = 10 см равномерно рас­пределен заряд с линейной плотностью τ = 10 нКл/м. Определить потенциал φ в точке, лежащей на оси кольца, на расстоянии а = 5 см от центра.

10.38. На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Вычислить потенциал φ поля, создаваемого этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.

10.39. Тонкий стержень длиной l = 10 см несет равномерно распределенный заряд q = l нКл. Определить потенциал электрического поля в точке, лежащей на оси стержня на расстоянии а = 20 см от ближайшего его конца.

10.40. Тонкие стержни образуют квадрат со стороной а. Стержни заряжены с линейной плотностью заряда τ = 1,33 нКл/м. Найти потенциал φ электрического поля в центре квадрата.

10.41. Бесконечно длинная тонкая прямая нить несет равномерно распределенный по длине нити заряд с линейной плотностью τ = 0,01 мкКл/м. Определить разность потенциалов двух точек поля, удаленных от нити на r₁ = 2 см и r₂ = 4 см.

10.42. Имеются две концентрические металлические сферы ра­диусами R₁ = 3 см и R₂ = 6 см. Пространство между сферами запол­нено парафином. Заряд q₁ внутренней сферы равен -1 нКл, заряд внеш­ней сферы q₂ = 2 нКл. Найти потенциал φ электрического поля на рас­стоянии от центра сфер: 1) r₁ = l см; 2) r₂ = 5 см; 3) r₃ = 9 см.

10.43. Металлический шар радиусом R = 5 см несет заряд q = 1 нКл. Шар окружен слоем эбонита толщиной d = 2 см. Вычислить потенциал электрического поля на расстоянии от центра шара: 1) r₁ = 3 см; 2) r₂ = 6 см; 3) r₃ = 9 см. Построить график зависи­мости (r).

10.44. Заряд распределен равномерно по бесконечной плоскости с поверхностной плотностью σ = 10 нКл/м². Определить разность потенциалов двух точек поля, одна из которых находится на плоскости, а другая удалена от плоскости на расстояние d = 10 см.

10.45. Определить потенциал φ, до которого можно зарядить уединенный металлический шар радиусом R = 10 см, если напряженность Е поля, при которой происходит пробой воздуха, равна 3 МВ/м. Найти также максимальную поверхностную плотность σ электрических зарядов перед пробоем.

10.46. Две бесконечные параллельные плоскости находятся на расстоянии d = 0,5 см друг от друга. На плоскостях равномерно распределены заряды с поверхностными плотностями = 0,2 мкКл/м² и = -0,3 мкКл/м². Определить разность потенциалов U между плоскостями.

10. 47. Металлический шарик диаметром d = 2 см заряжен отрицательно до потенциала φ = 150 В. Сколько электронов находится на поверхности шарика?

10.48. Сто одинаковых капель ртути, заряженных до потенциала φ = 20 В, сливаются в одну большую каплю. Каков потенциал φ₁ образовавшейся капли?

10.49. Сплошной парафиновый шар радиусом R = 10 см равномерно заряжен с объемной плотностью ρ = 1 мкКл/м³. Определить потенциал электрического поля в центре шара и на его поверхности. Построить график зависимости (r).

10.50. Эбонитовый толстостенный полый шар несет равномерно распределенный по объему заряд с плотностью ρ = 2 мкКл/м³. Внут­ренний радиус R₁шара равен 3 см, наружный R₂= 6 см. Определить потенциал поля в следующих точках: 1) на наружной поверхности шара; 2) на внутренней поверхности шара; 3) в центре шара.

10.51. Напряженность Е однородного электрического поля в не­которой точке равна 600 В/м. Вычислить разность потенциалов U между этой точкой и другой, лежащей на прямой, составляющей угол α = 60° с направлением вектора напряженности. Расстояние между точками равно 2 мм.

10.52. Электрическое поле создано положительным точечным зарядом. Потенциал φ поля в точке, удаленной от заряда на r = 12 см, равен 24 В. Определить значение и направление градиента потенциала в этой точке.

10.53. Точечные заряды q₁ = l мкКл и q₂ = 0,1 мкКл находятся на расстоянии r₁ = 10 см друг от друга. Какую работу А совершат силы поля, если второй заряд, отталкиваясь от первого, удалится от него на расстояние: 1) r₂ = 10 м; 2) r₃ = ?

10.54. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью τ = 133 нКл/м. Какую работу А надо совер­шить, чтобы перенести заряд q = 6,7 нКл из центра полукольца в бесконечность?

10.55. Тонкий стержень согнут в кольцо радиусом R = 10 см. Он заряжен с линейной плотностью τ = 300 нКл/м. Какую работу А надо совершить, чтобы перенести заряд q = 5 нКл из центра кольца в точку, расположенную на оси кольца на рас­стоянии l = 20 см от его центра?

10.56. Электрон находится в однородном электрическом поле напряженностью E = 200 кВ/м. Какой путь пройдет электрон за время t = 1 нс, если его начальная скорость была равна нулю? Какой скоростью будет обладать электрон в конце этого интервала времени?

10.57. Какая ускоряющая разность потенциалов U требуется для того, чтобы сообщить скорость v = 30 Мм/с: 1) электрону; 2) про­тону?

10.58. Разность потенциалов U между катодом и анодом элект­ронной лампы равна 90 В, расстояние r = 1 мм.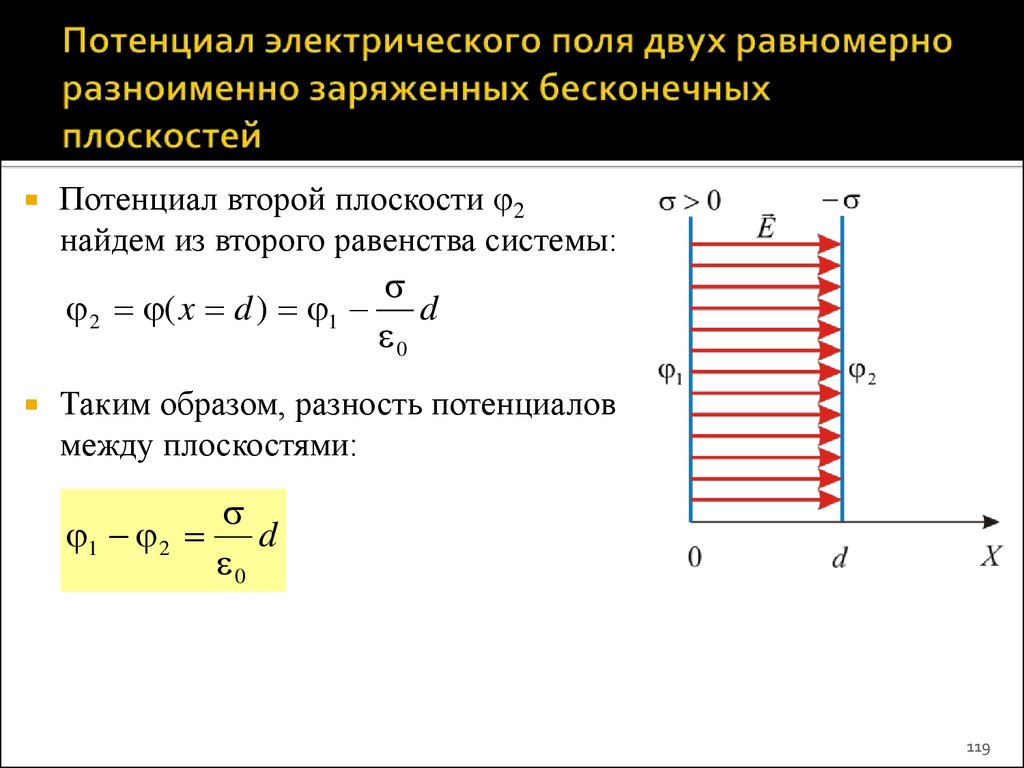 С каким ускорением а движется электрон от катода к аноду? Какова скорость v электро­на в момент удара об анод? За какое время t электрон пролетает расстояние от катода до анода? Поле считать однородным.

10.59. Пылинка массой m = 1 мг, несущая на себе пять электро­нов, прошла в вакууме ускоряющую разность потенциалов U = 3 MB. Какова кинетическая энергия Т пылинки? Какую скорость v приобрела пылинка?

10.60. Заряженная частица, пройдя ускоряющую разность потенциалов U = 600 кВ, приобрела скорость v = 5,4 Мм/с. Определить удельный заряд частицы (отношение заряда в массе).

10.61. Электрон, летевший горизонтально со скоростью v₀ = 1,6 Мм/с, влетел в однородное электрическое поле с напряжен­ностью E = 90 В/см, направленное вертикально вверх. Какова будет по модулю и направлению скорость v электрона через 1 нc?

10.62. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом = 100 В электрон имел скорость V₁ = 6 Мм/с. Определить потенциал точки поля, в которой скорость V₂ электрона будет равна 0,5V₁.

10.63. Электрон с начальной скоростью v₀ = 3 Мм/с влетел в однородное электрическое поле напряженностью E = 150 В/м. Вектор начальной скорости перпендикулярен линиям напряженно­сти электрического поля. Найти: 1) силу F, действующую на элек­трон; 2) ускорение а, приобретаемое электроном; 2) скорость v электрона через t = 0,1 мкс.

10.64. Электрон влетел в пространство между пластинами плоского конденсатора со скоростью v₀ = 10 Мм/с, направленной параллельно пластинам. На сколько приблизится электрон к положительно заряженной пластине за время движения внутри конден­сатора (поле считать однородным), если расстояние d между пласти­нами равно 16 мм, разность потенциалов U = 30 В и длина l пластин равна 6 см?

10. 65. Положительно заряженная частица, заряд которой равен элементарному заряду e, прошла ускоряющую разность потенциа­лов U = 60 кВ и летит на ядро атома лития, заряд которого равен трем элементарным зарядам. На какое наименьшее расстояние r_min частица может приблизиться к ядру? Начальное расстояние ча­стицы от ядра можно считать бесконечно большим, а массу частицы – пренебрежимо малой по сравнению с массой ядра.

10.66. Два электрона, находящиеся на большом расстоянии друг от друга, сближаются с относительной начальной скоростью v = 10 Мм/с. Определить минимальное расстояние r_min, на которое они могут подойти друг к другу.

10.67. Три одинаковых шарика, расположенные в вершинах равностороннего треугольника со стороной а, соединены друг с другом нитями. Заряд и масса каждого шарика равны q и m. Одну из нитей пережгли. Найти максимальную скорость среднего шарика.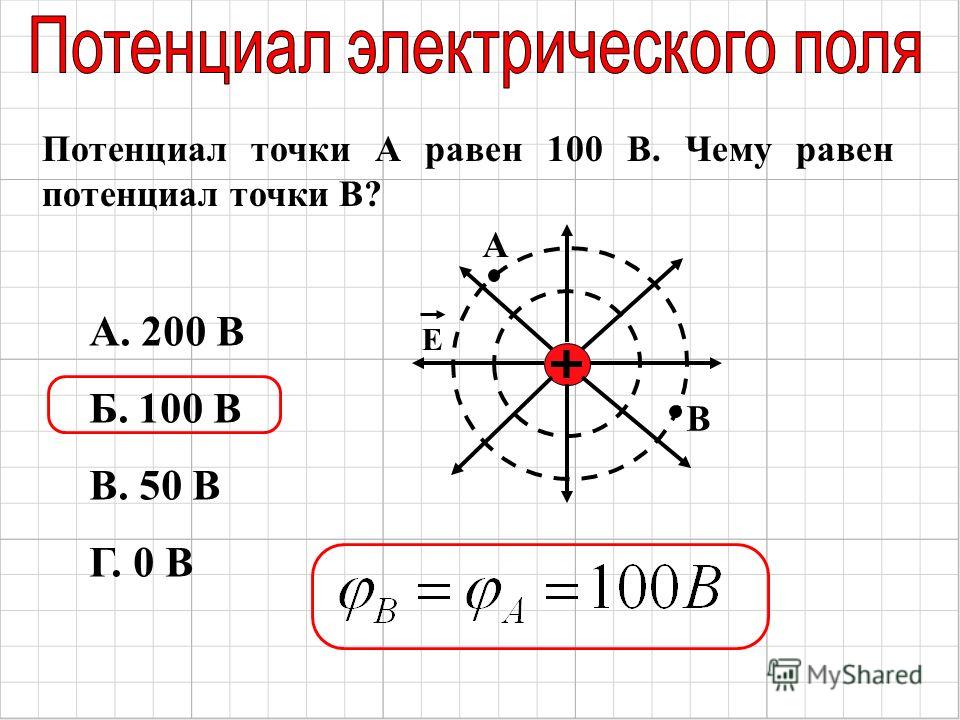 Сил тяжести нет.

10.68. Небольшой шарик висит над горизонтальной проводящей плоскостью на изолирующей упругой нити жесткости k. После того, как шарик зарядили, он опустился на х см, и его расстояние от проводящей плоскости стало равным l. Найти заряд шарика.

10.69. Точечный заряд q = 100 мкКл находится на расстоянии l = 1,5 см от проводящей плоскости. Какую работу надо совершить против электрических сил, чтобы медленно удалить этот заряд на очень большое расстояние от плоскости?

10.70. Два точечных заряда, q и —q, расположены на расстоянии l друг от друга и на одинаковом расстоянии l/2 от проводящей плоскости с одной стороны от нее. Найти модуль электрической силы, действующей на каждый заряд.

10.71. Точечный заряд q = 2 мкКл находится между двумя проводящими взаимно перпендикулярными полуплоскостями. Расстояние от заряда до каждой полуплоскости l = 5 см.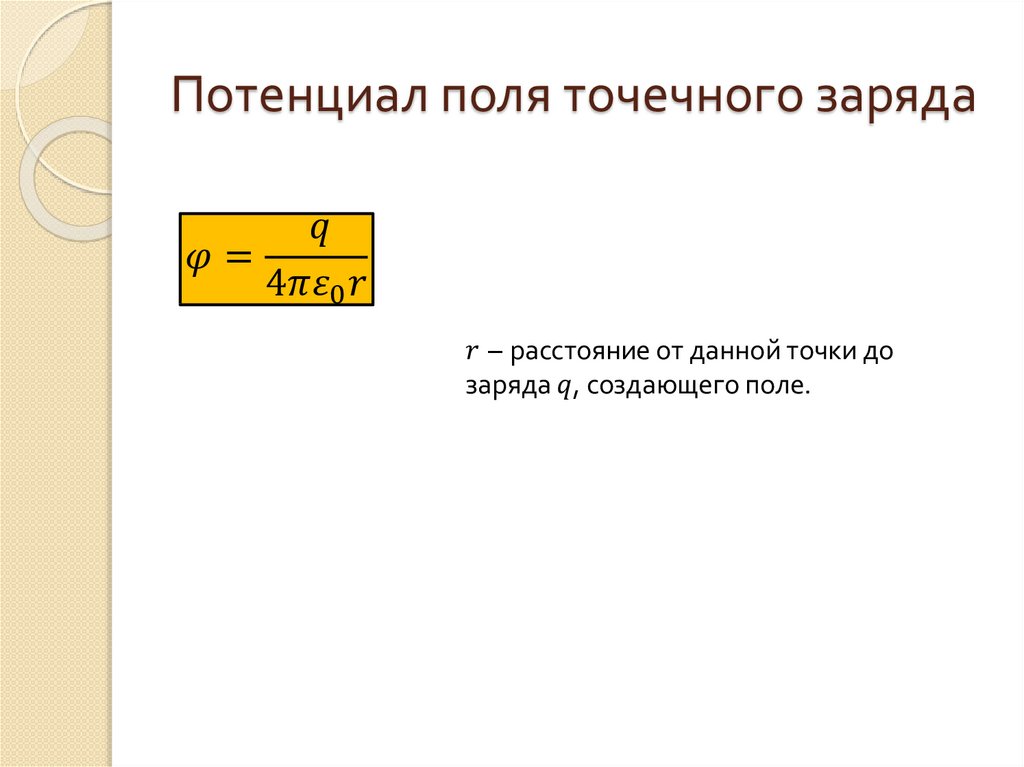 Найти модуль силы, действующей на заряд.

10.71. Найти потенциал незаряженной проводящей сферы, вне которой на расстоянии l = 30 см от ее центра находится точечный заряд q = 0,5 мкКл.

10.72. Три электрона, находившихся на расстоянии а = 10 мм друг от друга, начали симметрично разлетаться под действием взаимного отталкивания. Найти их максимальные скорости.

10.73. Определить суммарную энергию взаимодействия точечных зарядов, расположенных в вершинах квадрата со стороной а в системах, которые показаны на рис. 10.1.

10.74. Точечный заряд q находится на расстоянии l от проводящей плоскости. Найти энергию взаимодействия этого заряда с зарядами, индуцированными на плоскости.

5.12: Поле электрического потенциала, обусловленное точечными зарядами

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

6313

• Стивен В. Эллингсон
• Политехнический институт Вирджинии и Государственный университет через Инициативу открытого образования Технологических библиотек Вирджинии 9{ \mathbf { r } _ { 2 } } \ mathbf { E } \ cdot d \ mathbf { l } \ label {m0064_eV12} \]

  Этот метод расчета разности потенциалов часто немного неудобен. Чтобы понять почему, рассмотрим пример из теории схем, показанный на рисунке \(\PageIndex{1}\). В этом примере, состоящем из одного резистора и заземляющего узла, мы определили четыре величины:

  .
  • Сопротивление \(R\)
  • Ток \(I\) через резистор
  • Напряжение узла \(V_1\), представляющее собой разность потенциалов, измеренную от земли до левой стороны резистора
  • Напряжение узла \(V_2\), представляющее собой разность потенциалов, измеренную от земли до правой стороны резистора

  Допустим, мы хотим рассчитать разность потенциалов \(V_{21}\) на резисторе. Это можно сделать двумя способами:

  • \(V_{21}=-ИК\)
  • \(В_{21}=В_2-В_1\)

  Преимущество второго метода в том, что нет необходимости знать \(I\), \(R\) или вообще что-либо о том, что происходит между узлами; необходимо знать только узловые напряжения. Дело в том, что часто бывает удобно иметь общие датум — в данном примере земля — относительно которого можно определить разность потенциалов во всех других интересующих местах. Когда у нас есть это, вычисление разностей потенциалов сводится к простому вычитанию предварительно определенных потенциалов узлов.

  Рисунок \(\PageIndex{1}\): Резистор в более крупной цепи используется в качестве примера для демонстрации концепции узловых напряжений. (CC BY SA 4.0; К. Киккери).

  Итак, можем ли мы установить данное в общих электростатических задачах, которое работает таким же образом? Ответ положительный. Данное значение произвольно выбрано как сфера, охватывающая вселенную; т. е. сфера с радиусом \(\to\infty\). Используя этот выбор данных, мы можем использовать уравнение \ref{m0064_eV12} для определения \(V({\bf r})\), потенциала в точке \({\bf r}\) следующим образом:{\bf r} {\bf E} \cdot d{\bf l} } \label{m0064_eVP} \]

  Электрический потенциал в точке, определяемый уравнением \ref{m0064_eVP}, определяется как разность потенциалов, измеренная начиная со сферы бесконечного радиуса и заканчивая точкой \({\bf r}\). 2} \right] \cdot d{\bf l} \nonumber \] 9{г}
  \конец{выровнено}

  так

  \[\boxed{V({\bf r}) = + \frac{q}{4\pi\epsilon r} } \label{m0064_eV} \]

  (Предложение: Подтвердите, что уравнение \ref{m0064_eV} является правильным по размерам.) В контексте вышеприведенного примера теории цепей это «узловое напряжение» в \({\bf r}\), когда данное значение определено как быть поверхностью сферы на бесконечности. Впоследствии мы можем вычислить разность потенциалов от любой точки \({\bf r}_1\) до любой другой точки \({\bf r}_2\) как \[V_{21} = V({\bf r} _2)-V({\bf r}_1) \nonumber \] и обычно это лот проще, чем использовать уравнение \ref{m0064_eV12}.

  Нечасто приходится иметь дело с системами, состоящими из одной заряженной частицы. Таким образом, чтобы описанная выше техника была действительно полезной, нам нужен простой способ определения потенциального поля \(V({\bf r})\) для произвольных распределений заряда. Первым шагом в построении более общего выражения является определение результата для частицы, находящейся в точке \({\bf r}’\) где-то еще, кроме начала координат. Поскольку уравнение \ref{m0064_eV} зависит только от заряда и расстояния между точками поля \({\bf r}\) и \({\bf r}’\), мы имеем 9N { \frac{q_n}{\left|{\bf r}-{\bf r}_n\right|} } } \label{m0064_eVN} \]

  Уравнение \ref{m0064_eVN} дает электрический потенциал в определенном месте из-за конечного числа заряженных частиц.

  Потенциальное поле из-за непрерывного распределения заряда рассматривается в разделе 5.13.

  ---

  Эта страница под названием 5.12: Поле электрического потенциала из-за точечных зарядов распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Стивеном В. Эллингсоном (Инициатива открытого образования технических библиотек Вирджинии) через источник контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

  1. Наверх
  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или Страница

     Автор

     Стивен В. Эллингсон

     Лицензия

     CC BY-SA

     Версия лицензии

     4,0

     Программа OER или Publisher

     Инициатива открытого образования технических библиотек Вирджинии

     Показать оглавление

     нет

  2. Теги

     1. источник@https://doi.org/10.21061/electromagnetics-vol-1

  домашнее задание и упражнения — Электрическое поле и электрический потенциал точечного заряда в 2D и 1D

  спросил 10 лет, 1 месяц назад

  Изменено 4 года, 6 месяцев назад

  Просмотрено 20 тысяч раз

  $\begingroup$

  в 3D электрическое поле заряда пиона обратно пропорционально квадрату расстояния, а потенциал обратно пропорционально расстоянию. Мы можем вывести его из закона Кулона. однако я не знаю, как вывести формулу в 2D и 1D. Я читал в книге, что электрический потенциал точечного заряда в 2D пропорционален логарифму расстояния. Как это доказать?

  • домашние задания и упражнения
  • электростатика
  • закон Гаусса
  • пространственно-временные измерения
  • закон кулона

  $\endgroup$

  $\begingroup$

  Кулоновский потенциал имеет следующие формы для положительного заряда в каждой размерности: \начать{выравнивать} \Phi_{\operatorname{1-d}}(r) &= -\frac{\sigma}{2\epsilon_0} r, \\ \Phi_{\operatorname{2-d}}(r) &= -\frac{\lambda}{2\pi \epsilon_0} \ln(r),\\mathrm{and} \\ \Phi_{\operatorname{3-d}}(r) &= \frac{q}{4\pi\epsilon_0} \left(\frac{1}{r}\right). \end{выравнивание} Причина этого в том, что электрическое поле, определяемое как $-\nabla\Phi$ в общем случае и $-\dfrac{\partial\Phi}{\partial r} \hat{r}$ в данном случае, умножается на меру границы «шара» должна быть постоянной. 2}\ правильно). \end{выравнивание}

  Название закона, который подразумевает это, известно как закон Гаусса.

  $\endgroup$

  6

  $\begingroup$

  Хитрость заключается в использовании закона Гаусса.

  Предположим, что пространство представляет собой двумерную плоскость (Флатландия!), и в начале координат находится заряд $q$. Закон Гаусса гласит, что если мы заключим заряд в 1-сферу $S$ (также известную как круг), то мы должны иметь $\int_S \langle \vec{E} , \vec{n}\rangle = 2 \pi q$ (в удобных единицах), где $\vec{n}$ — вектор нормали к окружности. Если предположить, что $\vec{E}$ осесимметрично, т. е. $\vec{E} = E(r) \hat{r}$, это превращается в $E(r) 2\pi r = 2\pi q$, откуда следует, что $E(r) = q/r$. Интегрирование поля, похожего на $1/r$, дает вам логарифмический потенциал.

  Вы также можете использовать закон Гаусса в 1d, заключая заряд в $0$-сферу (две точки, равноудаленные от начала координат). Я оставлю это вам, чтобы попробовать это.

  $\endgroup$

  6

  $\begingroup$

  Вычислить электрическое поле для двумерного мира можно несколькими способами. Это будет зависеть от того, какое поведение электростатического взаимодействия вы хотите сохранить в этом мире. 92$, то такой мир не подчинялся бы закону Гаусса. И если вы заставите этот мир следовать закону Гаусса, то Кулон, живущий в этом двумерном мире, вместо этого нашел бы закон $1/r$.

  Итак, какое из двух свойств является более фундаментальным? На мой взгляд, закон Гаусса действует, но у меня нет возможности доказать это, поскольку нет двумерного мира, с которым можно было бы экспериментировать.

  Мой ответ на ваш вопрос Книга, которую вы читали, основывала свое утверждение об электрическом потенциале точечного заряда в 2D, неявно предполагая, что закон Гаусса выполняется для любого мира независимо от измерений.