1.Потенциал данной точки электрического поля:
Потенциал φ данной точки электрического поля равен отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда. φ = Wp/q, где
φ – потенциал поля в данной точке, Wp – энергия заряда в данной точке, q – величина заряда в данной точке.
φ = Wp/q’ – если q’= 1Кл, то из формулы следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. φ = [W]/[q](Джоуль/Кулон). В СИ единица измерения потенциала называется (Вольт) – названа в честь итальянца Александро Вольта.
2.Связь потенциала с напряженностью электростатического поля.
Работа по перемещению
точки положительного электрического
заряда из одной точки поля в другую
вдоль оси X
на малую величину есть dA=q*Ex*dx,
так же равна dA=-q*dφ. Получим связь между напряжением поля
и его потенциалом. E
Получим связь между напряжением поля
и его потенциалом. E
Е=-gradφ, (знак «-» говорит о направлении вектора Е)
3.Работа сил электpостатического поля по перемещению заряда.
Работа сил электрического поля при перемещении заряда из одной точки поля в другую равна: φ
-работа при перемещении заряда между двумя точками в электростатическом поле
— не зависит от формы траектории, а зависит от
положения этих точек.
— равна убыли потенциальной энергии заряда в этом поле;
— работа по замкнутой траектории равна нулю.
W=qEr — потенциальная энергия заряда в данной точке электростатического поля. Зависит от выбора начальной точки отсчета потенциальной энергии.
Тогда можно записать, что работа равна А=W1—W2
3.Работа электpостатического поля по перемещению заряженной частицы с данной точки на бесконечность.
Работа сил электростатического поля равна A12=-q*(φ2— φ1)
Потенциал поля на бесконечности, где φ2=0 => А1∞=q*φ1
А1∞ — работа электростатического поля, q- заряд, φ1- потенциал.
А потенциал равен отношению φ1 =А1∞/
4.
 Циpкуляция напpяженности электростатического поля.
Циpкуляция напpяженности электростатического поля.Элементарная работа сил поля при перемещении заряда из точки 1 в близко расположенную точку 2 равна:
Полная работа будет равна A=∫21 E*dl – интеграл называется циркуляцией вектора Е.
5.Теоpема о циpкуляции вектора напряженности электростатического поля.
Из независимости Кри от пути между двумя точками следует, что работа по произв. Замкнутого пути равна 0.
=∫21 E*dl=0 – теорема о циркуляции.
Лекция 5 ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ЭЛЕКТРОЕМКОСТЬ.
1.изическая величина, равная отношению модуля напряженности внешнего электрического поля в вакууме к модулю напряженности полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.
При
отсутствии внешнего электрического
поля оси молекулярных диполей из-за
теплового движения ориентированы
хаотично, так что на поверхности
диэлектрика и в любом элементе объема
электрический заряд в среднем равен
нулю.
При внесении диэлектрика во внешнее поле возникает частичная ориентация молекулярных диполей. В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле направленное навстречу внешнему полю (рис. 1.5.3).
Рисунок 1.5.3.
Ориентационный механизм поляризации полярного диэлектрика
Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, то напряженность поля создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:
2. Поверхностная плотность заряда — предел, к которому стремится отношение электрического заряда к площади, на которой этот заряд расположен, при условии, что площадь стремится к нулю.
3. Будем рассматривать
уединенный проводник, т. е. проводник,
значительно удаленный от других
проводников, тел и зарядов. Его потенциал,
как известно, прямо пропорционален
заряду проводника. Из опыта известно,
что разные проводники, будучи при этом
одинаково заряженными, имеют различные
потенциалы.
Величину
называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
4. Конденсатором называют систему двух разноименно заряженных проводников, разделенных диэлектриком (например, воздухом).
Свойство конденсаторов накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется величиной, называемой электроемкостью конденсатора. Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U:C = Q/U.
В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.
5. Если его пластины образуют параллельные плоскости, то его называют плоским.
— емкость плоского конденсатора.
Зависит
от площади его пластин S; от расстояния
между его пластинами d; от материала,
заполняющего пространство между
пластинами ε. При изготовлении конденсатора
большой емкости стремятся сделать
большое S при малом d, а также заполнить
его пространство веществами с большим
ε.
При изготовлении конденсатора
большой емкости стремятся сделать
большое S при малом d, а также заполнить
его пространство веществами с большим
ε.
6. Параллельное соединение конденсаторов:На рис. 1 изображено параллельное соединение нескольких конденсаторов. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U, Q2 = C2U, Q3 = C3U, а заряд, полученный отисточника Q = Q1 + Q2 + Q3.
Общая емкость равнозначного (эквивалентного) конденсатора:
C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3,
7. Последовательное соединение конденсаторов
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q
Действительно,
от источника питания заряды поступают
лишь на внешние обкладки цепи конденсаторов,
а на соединенных между собой внутренних
обкладках смежных конденсаторов
происходит лишь перенос такого же по
величине заряда с одной обкладки на
другую (наблюдается электростатическая
индукция), поэтому и на них по- являются
равные и разноименые электрические
заряды.
Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.
Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.
Лекция 7 ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК.
Потенциал электрического поля. Потенциал поля точечного заряда, системы зарядов.
Потенциал
электрического поля. Потенциал поля
точечного заряда, системы зарядов.Внося
в данную точку поля различные пробные
заряды мы
будем, соответственно, изменять
потенциальную энергию, т.е. получим
различные .
Но отношение потенциальной энергии к
заряду остается величиной постоянной.
Следовательно для характеристики поля
можем использовать это отношение. Обычно
оно обозначается буквой и
называется потенциалом поля в данной
точке
Потенциал
является энергетической характеристикой
поля.
Связь между напряжённостью и потенциалом.

электрическое поле характеризуется двумя физическими величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика). Выясним как они связаны между собой. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал , на близко расположенную эквипотенциальную поверхность, имеющую потенциал Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения С другой стороны Из этих уравнений получаем знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.
Энергия системы зарядов, заряженного проводника, конденсатора. Энергия электрического поля, объёмная плотность энергии.
Внося
в данную точку поля различные пробные
заряды мы будем, соответственно, изменять
потенциальную энергию, т. е. получим
различные Но отношение потенциальной энергии к
заряду остается величиной постоянной.
Следовательно для характеристики поля
можем использовать это отношение. Обычно
оно обозначается буквой и называется потенциалом поля в данной
точке
е. получим
различные Но отношение потенциальной энергии к
заряду остается величиной постоянной.
Следовательно для характеристики поля
можем использовать это отношение. Обычно
оно обозначается буквой и называется потенциалом поля в данной
точке
Потенциал
является энергетической характеристикой
поля. Он численно равен работе, которую
надо затратить против сил электрического
поля при перенесении единичного
положительного точечного заряда из
бесконечности в данную точку поля.
Единица измерения потенциала — вольт. Когда поле образовано несколькими
произвольно расположенными зарядами
, потенциал его
в данной точке равен алгебраической
сумме потенциалов создаваемых каждым зарядом в отдельности,
т.е. Если из точки “а” в точку “b”
электрического поля перемещается заряд
q’, то при этом совершается работа против
электрических сил, равная где — потенциалы поля в точках “а” и ” b”.
В СИ за единицу разности потенциалов
принимают Вольт (В), Разность потенциалов
между двумя точками поля равна одному
Вольту, если для перемещения между ними
заряда в один Кулон нужно совершить
работу в один Джоуль В атомной физике и электронике часто
употребляют для измерения работы и
энергии, величину называемую электронвольтом
(эВ). Один электронвольт равен работе,
совершаемой при перемещении заряда,
равного заряду электрона, между двумя
точками поля с разностью потенциалов
один вольт.
Один электронвольт равен работе,
совершаемой при перемещении заряда,
равного заряду электрона, между двумя
точками поля с разностью потенциалов
один вольт.
Найдем сначала выражение для потенциальной энергии системы двух точечных зарядов находящихся на расстоянии Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние . При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая к . .Работа переноса заряда из бесконечности в точку, удаленную от на
где
потенциал, создаваемый зарядом
в той точке, в которую перемещается
заряд
Аналогично работа переноса заряда
из бесконечности в точку, удаленную от
на
равна где
— потенциал, создаваемый зарядом
в той точке, в которую перемещается
заряд
. Значение работ в обоих случаях одинаковы,
и каждое из них выражает энергию системы Для того чтобы в выражение энергии
системы оба заряда входили симметрично,
запишем его следующим образом: Эта формула дает энергию системы двух
зарядов. Перенесем из бесконечности
еще один заряд и поместим его в точку, находящуюся на
расстоянии от
и от
. При этом совершим работу где — потенциал,
создаваемый зарядами и в той точке, в которую мы поместили заряд .
В сумме с или работа будет равна энергии трех зарядов: Последнее выражение можно привести к
виду Добавляя к системе Зарядов последовательно и т.д., можно убедиться в том, что в случае
n зарядов потенциальная энергия системы
равна где потенциал, создаваемый в той точке, где
находится , всеми зарядами, кроме i-го.
Перенесем из бесконечности
еще один заряд и поместим его в точку, находящуюся на
расстоянии от
и от
. При этом совершим работу где — потенциал,
создаваемый зарядами и в той точке, в которую мы поместили заряд .
В сумме с или работа будет равна энергии трех зарядов: Последнее выражение можно привести к
виду Добавляя к системе Зарядов последовательно и т.д., можно убедиться в том, что в случае
n зарядов потенциальная энергия системы
равна где потенциал, создаваемый в той точке, где
находится , всеми зарядами, кроме i-го.
Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен , а емкость — С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная . Но потенциал электростатического поля данного проводника в бесконечности равен нулю .
При переносе заряда dq с проводника в
бесконечность такую же работу совершают
силы электростатического поля. Следовательно, при увеличении заряда
проводника на величину dq возрастает
потенциальная энергия поля, т.е.
Следовательно, при увеличении заряда
проводника на величину dq возрастает
потенциальная энергия поля, т.е.
Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:
Применяя соотношение , можно получить следующие выражения для потенциальной энергии W:
(16.2) |
Для заряженного конденсатора разность потенциалов (напряжение) равна поэтому соотношение для полной энергии его электростатического поля имеют вид
Объемная плотность!!!Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна . Для плоского конденсатора, объем которого Sd, где S — площадь пластин, d — расстояние между пластинами, имеем С учетом, что и или |
19.
 3 Электрический потенциал, обусловленный точечным зарядом – College Physics
3 Электрический потенциал, обусловленный точечным зарядом – College PhysicsРезюме
- Объясните точечные заряды и составьте уравнение для электрического потенциала точечного заряда.
- Различать электрический потенциал и электрическое поле.
- Определить электрический потенциал точечного заряда при заданном заряде и расстоянии.
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферические распределения заряда (как на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование вычислений для определения работы, необходимой для перемещения пробного заряда [латекс]\boldsymbol{q}[/латекс] с большого расстояния на расстояние [латекс]\boldsymbol{r}[/латекс] от точечного заряда [ латекс]\boldsymbol{Q}[/latex], и учитывая связь между работой и потенциалом [латекс]\boldsymbol{(W = -q \Delta V)}[/latex], можно показать, что 92 . }[/латекс]
}[/латекс]
Электрический потенциал
В точечного зарядаЭлектрический потенциал [латекс]\boldsymbol{V}[/latex] точечного заряда определяется выражением
[латекс]\boldsymbol{V =}[/latex] [ латекс]\boldsymbol{\frac{kQ}{r}}[/latex] [латекс]\boldsymbol{( \textbf{Point Charge}),}[/latex]
Потенциал на бесконечности выбран равным нулю. Таким образом, [латекс]\boldsymbol{V}[/latex] для точечного заряда уменьшается с расстоянием, тогда как [латекс]\boldsymbol{E}[/латекс] для точечного заряда уменьшается с квадратом расстояния: 92}}.[/латекс]
Напомним, что электрический потенциал [latex]\boldsymbol{V}[/latex] является скаляром и не имеет направления, тогда как электрическое поле [latex]\textbf{E}[/latex] является вектором. Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов , принимая во внимание величину и направление. Это согласуется с тем фактом, что [latex]\boldsymbol{V}[/latex] тесно связан с энергией, скаляром, тогда как [latex]\textbf{E}[/latex] тесно связан с силой, то есть вектором.
Это согласуется с тем фактом, что [latex]\boldsymbol{V}[/latex] тесно связан с энергией, скаляром, тогда как [latex]\textbf{E}[/latex] тесно связан с силой, то есть вектором.
Пример 1. Какое напряжение создает небольшой заряд на металлическом шаре?
Заряды статического электричества обычно находятся в диапазоне от нанокулонов (нКл) до микрокулонов [латекс]\boldsymbol{( \mu \textbf{C})}[/latex]. Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд -3,00 нКл?
Стратегия
Как мы обсуждали в главе 18 Электрический заряд и электрическое поле, заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре. Таким образом, мы можем найти напряжение, используя уравнение [латекс]\boldsymbol{V = kQ/r}[/латекс] . 9{2} \;\textbf{m}})} \\[1em] & \boldsymbol{-539 \;\textbf{V}}. \end{array}[/latex]
Обсуждение
Отрицательное значение напряжения означает, что положительный заряд будет притягиваться с большего расстояния, поскольку потенциал ниже (более отрицательный), чем на больших расстояниях.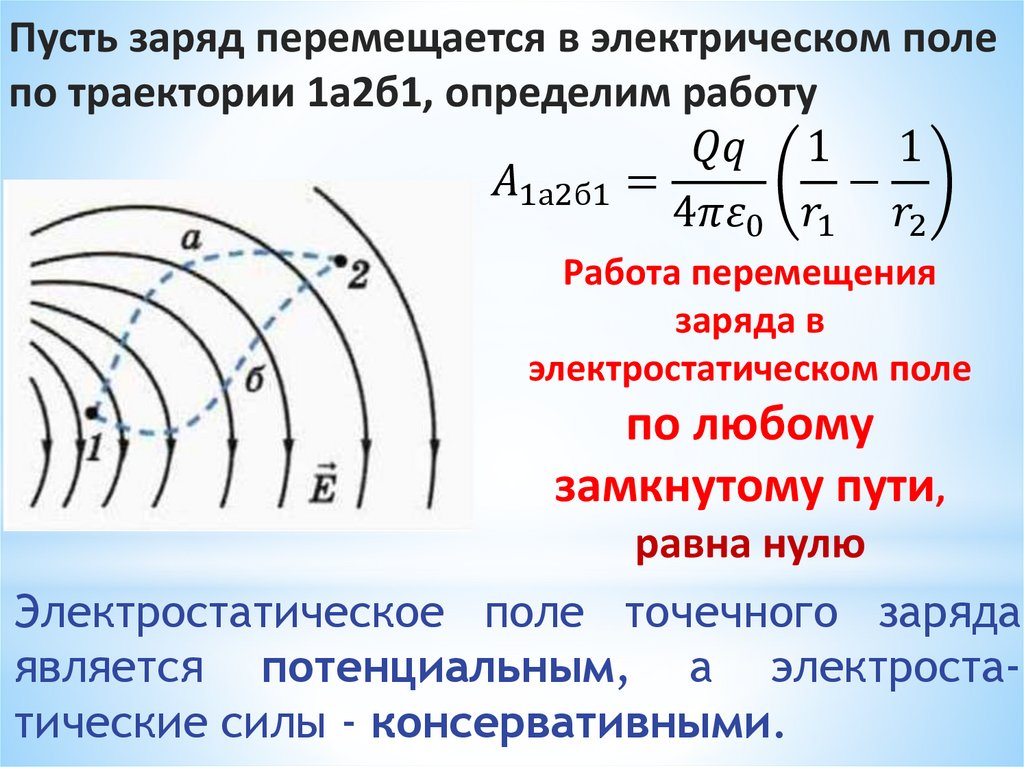 И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
Пример 2. Что такое избыточный заряд генератора Ван де Граафа
Демонстрационный генератор Ван де Граафа имеет металлическую сферу диаметром 25,0 см, которая создает напряжение 100 кВ вблизи своей поверхности. (См. рис. 1.) Какой избыточный заряд находится на сфере? (Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.)
Рисунок 1. Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.Стратегия
Потенциал на поверхности будет таким же, как у точечного заряда в центре сферы на расстоянии 12,5 см. (Радиус сферы равен 12,5 см.) Таким образом, мы можем определить избыточный заряд, используя уравнение 9{-6} \;\textbf{C} = 1,39 \;\mu \textbf{C}}. \end{array}[/latex]
\end{array}[/latex]
Обсуждение
Это относительно небольшой заряд, но он производит довольно большое напряжение. У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
Напряжения в обоих этих примерах можно измерить с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли. Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов. Это аналогично тому, как уровень моря принимается за [латекс]\boldsymbol{h = 0}[/latex] при рассмотрении гравитационной потенциальной энергии, [латекс]\boldsymbol{\textbf{PE}_g = мгх}[/латекс].
- Электрический потенциал точечного заряда [латекс]\boldsymbol{V = kQ/r}[/латекс].
 2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?
2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?8: Исследовательский генератор Ван де Граафа имеет металлический шар диаметром 2,00 м с зарядом 5,00 мКл. а) Каков потенциал вблизи его поверхности? б) На каком расстоянии от его центра находится потенциал 1,00 МВ? (в) Атом кислорода с тремя недостающими электронами высвобождается вблизи генератора Ван де Граафа. Какова его энергия в МэВ на этом расстоянии?
9: Электростатический распылитель краски представляет собой металлическую сферу диаметром 0,200 м с потенциалом 25,0 кВ, которая отбрасывает капли краски на заземленный объект. а) Какой заряд находится на шаре? б) Какой заряд должен иметь капля краски массой 0,100 мг, чтобы достичь предмета со скоростью 10,0 м/с?
10: В одном из классических экспериментов по ядерной физике в начале 20-го века альфа-частица была ускорена к ядру золота, и ее траектория была существенно отклонена кулоновским взаимодействием.
 Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится?
Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится?11: (а) Каков потенциал между двумя точками, расположенными на расстоянии 10 см и 20 см от точечного заряда [латекс]\boldsymbol{3,0 мк\текстбф{С}}[/латекс]? б) В какое место следует переместить точку на расстоянии 20 см, чтобы разность потенциалов увеличилась в два раза?
12: необоснованные результаты
(a) Какова конечная скорость электрона, ускоренного из состояния покоя при напряжении 25,0 МВ отрицательно заряженным выводом Ван де Граафа?
(b) Что неразумного в этом результате?
(c) Какие предположения являются ответственными?
Электрическая потенциальная энергия – формула, определение, решаемые примеры
Электрическая потенциальная энергия обладает объектом благодаря двум элементам: заряду, которым обладает сам объект, и относительному положению объекта по отношению к другим электрически заряженные объекты.
 величина электрического потенциала зависит от количества работы, совершаемой при перемещении объекта из одной точки в другую против электрического поля.
величина электрического потенциала зависит от количества работы, совершаемой при перемещении объекта из одной точки в другую против электрического поля.Когда объект перемещается против электрического поля, он получает некоторое количество энергии, которое определяется как электрическая потенциальная энергия . Для любого заряда электрический потенциал получается делением потенциальной энергии на количество заряда.
JEE Main 2021 LIVE Physics Paper Solutions 24 февраля Shift-1 На основе памяти
Содержание
- Определение
- Формула
- Происхождение
- Электрический потенциал точечного заряда
- Несколько зарядов
- Важные моменты
- Решенные примеры
Что такое электрическая потенциальная энергия?
Электрическая потенциальная энергия любого данного заряда или системы изменений называется полной работой, выполненной внешним агентом для перевода заряда или системы зарядов из бесконечности в текущую конфигурацию без какого-либо ускорения.

Определение: Электрическая потенциальная энергия определяется как полная потенциальная энергия, которой будет обладать единичный заряд, если он находится в любой точке космического пространства.
Обзор
Электрическая потенциальная энергия является скалярной величиной и имеет только величину и не имеет направления. Он измеряется в джоулях и обозначается буквой V. Он имеет размерную формулу ML 2 T -3 A -1 .
Электрический потенциал Обозначается как В, ∆В, У, ∆У Размер: МЛ 2 Т -3 А -1 Общая формула Напряжение = Энергия/Заряд Единица СИ Вольт Есть два ключевых элемента, от которых зависит электрическая потенциальная энергия объекта.

- Собственный электрический заряд.
- Это относительное положение с другими электрически заряженными объектами.
- Электростатика
- Эквипотенциальная поверхность
Формула электрического потенциала:
Заряд, помещенный в электрическое поле, обладает потенциальной энергией и измеряется работой, совершаемой при перемещении заряда из бесконечности в эту точку против электрического поля. Если два заряда q 1 и q 2 разделены расстоянием d, e электрическая потенциальная энергия системы равна;
U = [1/(4πε o )] × [q 1 q 2 /d]
Если два одинаковых заряда (два протона или два электрона) сблизить, потенциальная энергия системы увеличивается. Если два разноименных заряда, то есть протон и электрон, приблизить друг к другу, электрическая потенциальная энергия системы уменьшится.

Формула электрического потенциала
Метод 1:
Электрический потенциал в любой точке вокруг точечного заряда q определяется по формуле: В = k × [q/r]
Где,
- В = электрическая потенциальная энергия
- q = начисление очков
- r = расстояние от любой точки вокруг заряда до точечного заряда
- k = постоянная Кулона; k = 9,0 × 10 9 Н
Метод 2: Использование закона Кулона
Электростатический потенциал между любыми двумя произвольными зарядами q 1 , q 2 , разделенными расстоянием r, определяется законом Кулона и математически записывается как: U = k × [q 1 q 2 /r 2 ]
Где,
- U – электростатическая потенциальная энергия,
- q 1 и q 2 — это два заряда.

Примечание: Электрический потенциал на бесконечности равен нулю (так как r = ∞ в приведенной выше формуле).
Расчет электрического потенциала
Рассмотрим заряд q 1 . Допустим, они расположены на расстоянии «r» друг от друга. Полный электрический потенциал заряда определяется как полная работа, совершаемая внешней силой по перемещению заряда из бесконечности в данную точку.
Мы можем записать это как -∫ (r a → r b ) F.dr = – (U a – U б )
Здесь мы видим, что точка r b находится в бесконечности, а точка r a есть r.
Подставив значения, которые мы можем написать, -∫ (r →∞) F.dr = – (U r – U ∞ )
Как известно, U бесконечность равна нулю.
Следовательно, -∫ (r → ∞) F.dr = -U R
Используя закон Кулона, между двумя зарядами можно написать:
⇒ -∫ (r →∞) [-kqq o ]/r 2 др = -У Р
Или, -k × qq o × [1/r] = U R
Следовательно, U R = -kqq o /r
Электрический потенциал точечного заряда
Рассмотрим точечный заряд «q» в присутствии другого заряда «Q» с бесконечным расстоянием между ними.

U E (r) = k e × [qQ/r]
где k e = 1/4πε o = постоянная Колумба
Рассмотрим точечный заряд q при наличии нескольких точечных зарядов Q i с бесконечным расстоянием между ними.
U E (r) = k e q × ∑ n i = 1 [Q i /r i ]
4- 54
Электрический потенциал для нескольких зарядов
В случае 3 зарядов:
Если три заряда q 1 , q 2 и q 3 расположены в вершинах треугольника, то потенциальная энергия системы равна
U = U 12 + U 23 + U 31 = (1 /4πε O ) × [Q 1 Q 2 /D 1 Q Q Q Q Q Q Q + Q + Q + Q Q Q Q Q . 3 /d 2 + q 3 q 1 /d 3 ]
В случае 4 сборов:
Если четыре заряда q 1 , q 2 , q 3 и q 4 расположены в углах квадрата, электрическая потенциальная энергия системы равна,
U = (1/4πε o ) × [(q 1 q 2 /d) + (q 2 q 3 /d) + (q 3 /d 8 q 4 ) + (q 4 q 1 /d) + (q 4 q 2 /√2d) + (q 3 q 1 /√2d)]
Особый случай:
В поле заряда Q, если заряд q перемещается против электрического поля с расстояния «a» на расстояние «b» от Q, работа определяется выражением,
Вт = (V б – V a ) × q = [1/4πε o × (Qq/b)] – [1/4πε o × (Qq/a)] = Qq/4πε o [1/b – 1/a] = (Qq/4πε o )[(a-b)/ab]
Важные моменты
- В точке посередине между двумя равными и противоположными зарядами электрический потенциал равен нулю, но электрическое поле не равно нулю.

- Говорят, что электрический потенциал в точке равен одному вольту , если работа в один джоуль совершается при перемещении одного коломба заряда против электрического поля.
- Если отрицательный заряд перемещается из точки А в точку В, электрический потенциал системы увеличивается.
- Базовый уровень, используемый для определения электрического потенциала в точке, равен бесконечности. Это означает, что сила на пробном заряде равна нулю на эталонном уровне.
- Предполагается, что поверхность земли имеет нулевой потенциал, поскольку земля настолько велика, что добавление или снятие с нее заряда не изменит ее электрическое состояние.
⇒ Проверить: Закон Гаусса и его приложения
Что такое разность электрических потенциалов?
В электрической цепи потенциал между двумя точками (E) определяется как количество работы, выполненной (Вт) внешним агентом при перемещении единичного заряда (Q) из одной точки в другую.

Математически мы можем сказать, что
Э = В/К
Где,
- E = разность электрических потенциалов между двумя точками
- Вт = Работа, совершенная при перемещении заряда из одной точки в другую
- Q = количество заряда в кулонах
Электрическая потенциальная энергия – видеоурок
Решенные примеры для электрического потенциала
Задача 1: Частица массой 40 мг, несущая заряд 5×10 -9 Кл, движется прямо к неподвижному точечному положительному заряду величиной 10 -8 Кл. Находясь на расстоянии 10 см от неподвижного точечного заряда он имеет скорость 50 см/с. На каком расстоянии от неподвижного точечного заряда частица на мгновение остановится? Постоянно ли ускорение во время движения?
Решение:
Если частица на мгновение останавливается на расстоянии r от фиксированного заряда, из закона сохранения энергии мы имеем
Общая энергия системы = константа
(КЭ + ПЭ) = константа
(1/2)mu 2 + 1/4πε o × [Qq/a] = (1/4πε o ) × [Qq/r]
Подставляя данные, получаем;
⇒ 1/2 × 40 × 10 -6 × 1/2 × 1/2 = 9 × 10 9 × 10 -8 × 5 × 10 -9 × [ 1/r – 1/(10 × 10 -2 )]
или [1/r – 10] = (5×10 -5 )/(9×5×10 -8 ) = 100/9
или 1/r = (100/9) + 10 = 190/9 м
т.
 е. r = 4,7 × 10 -2 м
е. r = 4,7 × 10 -2 мПоскольку F = [1/4πε o ] × [Qq/r 2 ]
Следовательно, ускорение = F/m ∝ 1/r 2 , т. е. ускорение не постоянно во время движения.
Задача 2: Мяч массой 5 г и зарядом 10 -7 C перемещается из точки A, потенциал которой равен 500 В, в точку B, потенциал которой равен нулю. Какова скорость мяча в точке А, если в точке В она равна 25 см в секунду?
Решение:
Пусть u — скорость мяча в точке A.
Работа выполнена на заряд полем;
Вт = q × (V A – V B ) = 10 -7 × (500 – 0) = 5 × 10 -5 J
Появляется из-за повышенной кинетической энергии.
∴ Вт = (1/2) мв 2 – (1/2) мю 2
5 × 10 -5 = (1/2) × 5/1000 [(1/4) 2 – u 2 ]
2 × 10 -2 = 1/16 – U 2
u 2 = (1/16) – 0,02
= (1-0,32)/16
= 0,0425
Следовательно, u = 0,206 м/с = 20,6 см/с.

Следовательно, u = 20,6 см/сек.
Пример 3: Допустим, у нас есть два заряда величиной 1C и 2C, расположенные на расстоянии 2 метров друг от друга. Вычислите электрический потенциал между этими двумя зарядами. (Возьмите: k = 1)
Решение:
При этом величины зарядов равны q 1 = 1 Кл и q 2 = 2 Кл.
Расстояние между этими двумя зарядами равно r = 2 м.
Электрический потенциал между этими двумя зарядами определяется выражением U r = -[kqq o ]/r
Подставляя данные значения в приведенное выше уравнение, мы получаем,
U r = -1 Дж.
Пример 4: Какую работу необходимо совершить, чтобы перенести два заряда величиной 3C и 5C с расстояния бесконечного расстояния на расстояние 0,5 м?
Решение:
∆E = E 0 – E г
= 0 – [-(9 × 10 9 × 5 × 3)/0,5] = 27 × 10 10 .




 2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?
2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?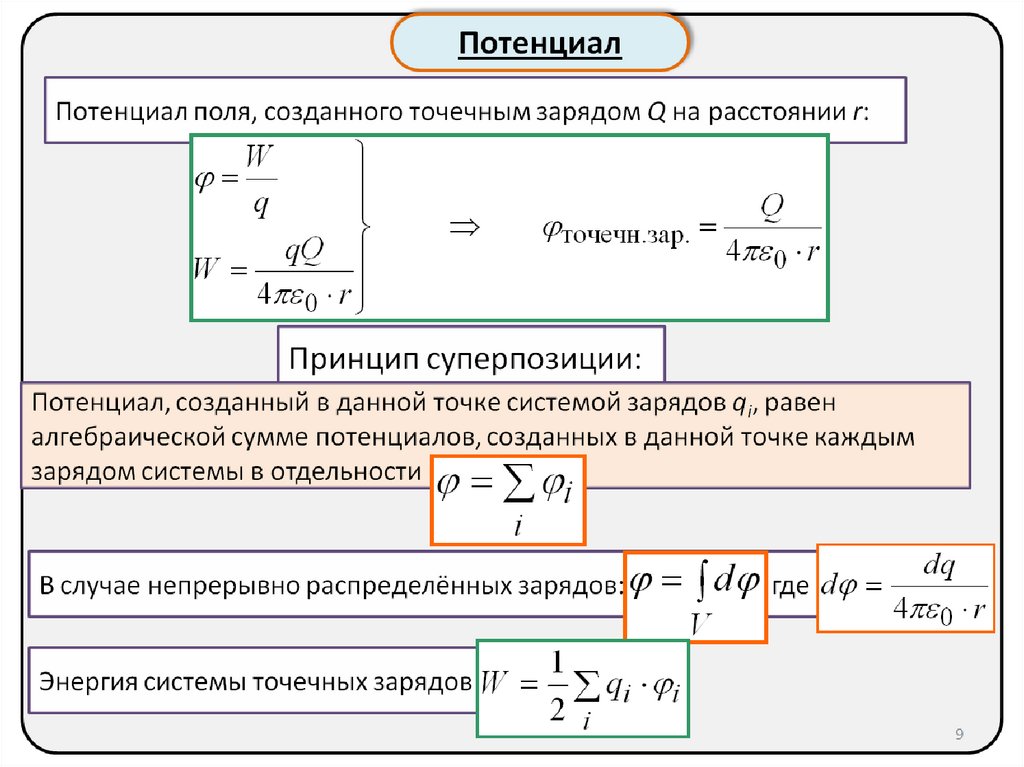 Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится?
Если энергия двухзарядного альфа-ядра была 5,00 МэВ, насколько близко к ядру золота (79протоны) может ли он прийти до того, как отклонится? величина электрического потенциала зависит от количества работы, совершаемой при перемещении объекта из одной точки в другую против электрического поля.
величина электрического потенциала зависит от количества работы, совершаемой при перемещении объекта из одной точки в другую против электрического поля.






 е. r = 4,7 × 10 -2 м
е. r = 4,7 × 10 -2 м
