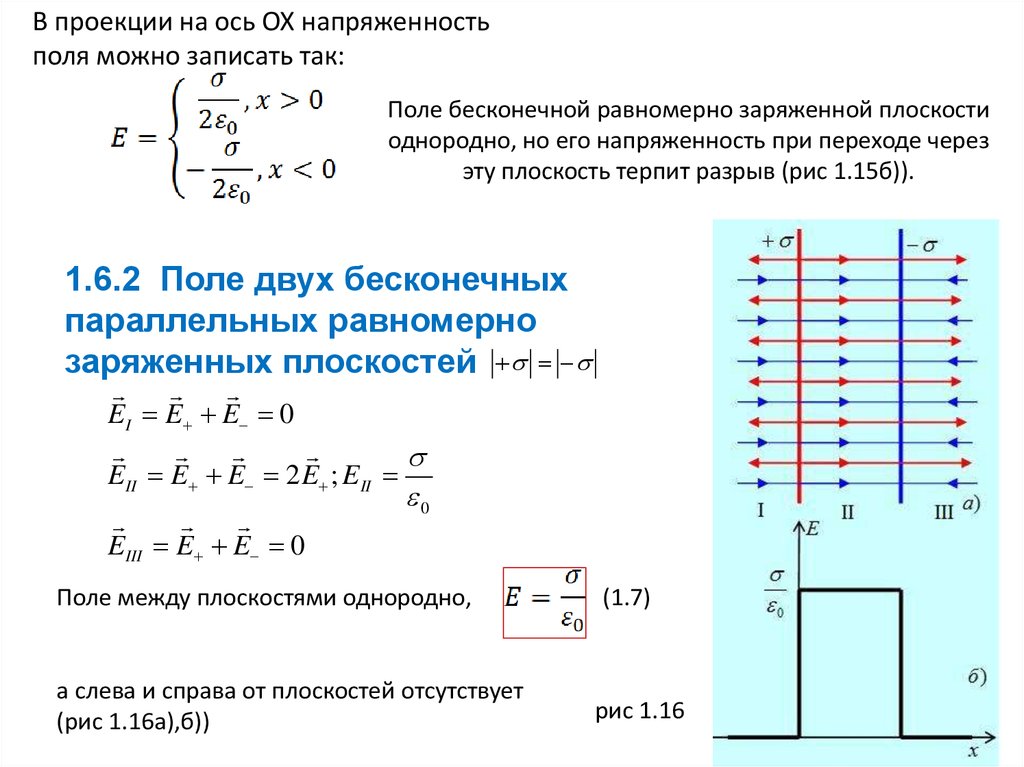
Потенциал электростатического поля
В отличие от вектора напряженности электрического поля потенциал является скалярной величиной. Зная значения потенциала в окрестности некоторой точки, можно по формулам (3) вычислить напряженность поля в этой точке.
Пример. Найти напряженность электрического поля, потенциал которого зависит от координат x и y по закону , гдеa – постоянная.
Решение. ,,,.
Обычно потенциал удается измерить или рассчитать в конечном числе точек, расположенных в некоторой области. Пусть, например, известны значения потенциала в близко расположенных узлах прямоугольной сетки (рис.1). Тогда вектор напряженности электрического поля в точке 0 имеет проекции на осиXиY:
, .
Рис.1.
Для приемлемой точности необходимо, чтобы в рассматриваемой окрестности точки 0 электрическое поле менялось слабо и, очевидно, что точность этих формул увеличивается с уменьшением
 Заметим, что замена производной
отношением малых приращений функции и
аргумента широко используется в численных
методах и в экспериментальной технике.
Заметим, что замена производной
отношением малых приращений функции и
аргумента широко используется в численных
методах и в экспериментальной технике.Рис.2. Рис.3.
Электростатические поля удобно изображать при помощи эквипотенциальных поверхностей — поверхностей равного потенциала. Возьмем на эквипотенциальной поверхности произвольную точку 0 и введем локальную систему координат с началом в этой точке (рис.2). ОсьZнаправим по нормалик эквипотенциальной поверхности в сторону возрастания потенциала. Это направление примем за положительное направление нормали. Координатная плоскостьочевидно совместится с касательной плоскостью к эквипотенциальной поверхности. Тогда в точке 0. Кроме того, орт оси,. Формула (6) переходит в
. (4)
Функция
возрастает наиболее быстро в направлении
нормали.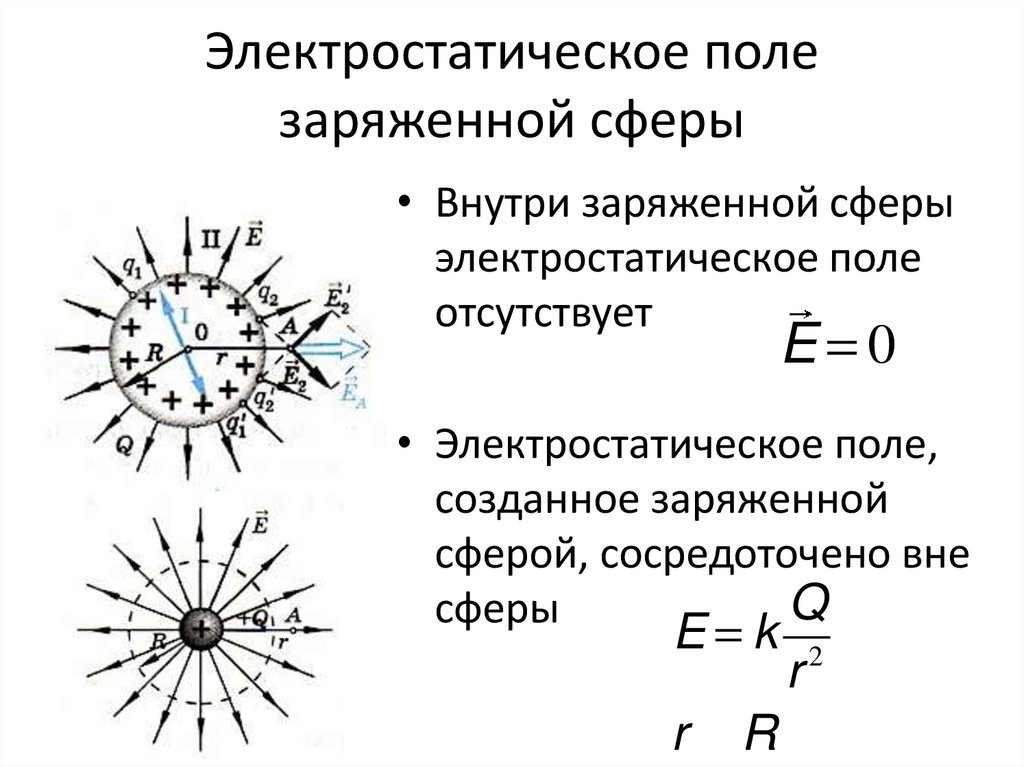 Поэтому, согласно (8),вектор напряженности
электрического поля в каждой точке
пространства перпендикулярен
эквипотенциальной поверхности и
направлен в сторону максимального
убывания потенциала. Модуль вектора
напряженности равен модулю производной
функции
в том же направлении.
Поэтому, согласно (8),вектор напряженности
электрического поля в каждой точке
пространства перпендикулярен
эквипотенциальной поверхности и
направлен в сторону максимального
убывания потенциала. Модуль вектора
напряженности равен модулю производной
функции
в том же направлении.
Поясним сказанное на примере. На рис.3 изображены две эквипотенциальные поверхности, соответствующие двум близким значениям потенциала и.- вектор нормали, направленный в сторону увеличения потенциала. Видно, что производная по направлениюбольше, чем производная, вычисленная по любому другому направлению. Вектор напряженности направлен в сторону, противоположную, и его модуль.
Очевидно, что эквипотенциальная поверхность не может самопересекаться, поскольку в точках пересечения можно было бы провести две касательные плоскости и определить два различных направления вектора напряженности (рис.4.). Исключение составляют особые точки, где .
Рис.4.
Рис. 5.
5.
Существуют различные методы решения дифференциальных уравнений. В некоторых частных случаях решение удается получить аналитически (выразить через элементарные функции), но чаще всего приходится использовать численные методы и компьютерные расчеты.
Будем исходить из того, что уже разработана компьютерная программа, которая с высокой точностью находит решение уравнения Лапласа , удовлетворяющее заданным граничным условиям на поверхности тел, входящих в систему. Такое решение будет совпадать с экспериментом, если все проводники являются однородными, неподвижными и в поле отсутствуют диэлектрики. Поэтому к результатам таких компьютерных расчетов можно относиться как к «компьютерному эксперименту», моделирующему эксперимент реальный. Наша задача состоит в выполнении «компьютерного эксперимента» и в анализе получаемых результатов.
Работа
с компьютерными программами обычно
включает два этапа. Во-первых, необходимо
убедиться в правильности работы
программы. Для этого программу «испытывают»
на частных задачах и в специальных
случаях, когда решение точно (или
приближенно) известно. Компьютерный
эксперимент должен подтверждать
известные закономерности, а также
показывать отклонение от теоретических
результатов, полученных в рамках
некоторых предположений, нарушающихся
в компьютерном эксперименте.
Компьютерный
эксперимент должен подтверждать
известные закономерности, а также
показывать отклонение от теоретических
результатов, полученных в рамках
некоторых предположений, нарушающихся
в компьютерном эксперименте.
Например, потенциал и модуль вектора напряженности электрического поля, созданного точечнымдиполем в точке, положение которой задано радиус-вектором(рис.5), определяются формулами
, (5)
. (6)
где электрический момент диполя (дипольный момент),– вектор, проведенный ототрицательногозаряда к положительному,- угол между векторамии. Формулы (5), (6) получены для точечного диполя, когда длина

После «испытания» компьютерной программы можно приступить к поиску новых закономерностей. Вам будет предложено исследовать распределение заряда по поверхности заряженного проводящего эллипсоида, а также по поверхности проводящей сферы, расположенной в поле точечного заряда. Эти задачи являются для Вас новыми в том смысле, что их не удается решить, напрямую воспользовавшись формулой (1) и принципом суперпозиции.
Для «экспериментального» определения плотности поверхностного заряда следует воспользоваться результатом, строго вытекающим из теоремы Гаусса: во внешнем пространстве вблизи поверхности проводника поле перпендикулярно к поверхности проводника и определяется формулой
, (7)
где — нормаль, проведенная наружу от поверхности проводника,- поверхностная плотность заряда в данной точке поверхности.
Электродинамика в задачах
Задача №580 | ||
| ||
Показать решение | ||
Задача №552 | ||
| ||
Задача №540 | ||
| ||
Показать решение | ||
Задача №520 | ||
| ||
Показать решение | ||
Задача №507 | ||
| ||
Показать решение | ||
Задача №477 | ||
| ||
Показать решение | ||
Задача №438 | ||
| ||
Показать решение | ||
Задача №294 | ||
| ||
Показать решение | ||
Задача №282 | ||
| ||
Показать решение | ||
Задача №270 | ||
| ||
Показать решение | ||
Задача №254 | ||
| ||
Показать решение | ||
Задача №246 | ||
| ||
Показать решение | ||
Задача №181 | ||
| ||
Показать решение | ||
Задача №111 | ||
| ||
| {i\omega t}$ помещен тонкий проводящий круглый диск, расположение и размеры которого указаны на рисунке ($d\ll h$). Считая, что частота $\omega$ и проводимость материала диска $\sigma$ удовлетворяют сильному неравенству $\frac{c}{\sqrt{2\pi \sigma \omega}} \gg h \rm{tg}\theta_0$ (то есть скин-эффект слабый), определить интенсивность тепловыделения в диске. | ||
Показать решение
Задача №42
В волноводе с металлическими стенками квадратного сечения $a\times a$
область $z\leqslant 0$ заполнена диэлектриком с $\varepsilon
_{1}$ $=$ 3$\varepsilon_{0}$, а область $z>0$ —
диэлектриком с $\varepsilon_{2}$ $=$ $\varepsilon_{0}$. По диэлектрику
$\varepsilon_{1}$ к плоской границе идет волна H$_{10}$. В каком
диапазоне частот $\omega_{1}\div\omega_{2}$ должна находиться
частота волны, чтобы произошло полное отражение волны. По диэлектрику
$\varepsilon_{1}$ к плоской границе идет волна H$_{10}$. В каком
диапазоне частот $\omega_{1}\div\omega_{2}$ должна находиться
частота волны, чтобы произошло полное отражение волны. |
Показать решение
Задача №9
Длинный цилиндрический конденсатор (радиусы обкладок $a$ и $c$, длина $L$) имеет заполнение в виде двух концентрических слоев с различными
проводимостями ($\sigma_1$ и $\sigma_2$) и диэлектрическими проницаемостями ($\varepsilon_1$ и $\varepsilon_2$),
причем $\sigma_1/\varepsilon_1=\sigma_2/\varepsilon_2$. Радиус границы раздела слоев – $b$.
Внутренняя обкладка конденсатора заземлена, к внешней приложено постоянное напряжение $U$. В некоторый момент времени $t = t_0$ внешнюю обкладку мгновенно отключают от источника напряжения и соединяют с землей
через сопротивление $R$. Найти ток через сопротивление $I_R(t)$
В некоторый момент времени $t = t_0$ внешнюю обкладку мгновенно отключают от источника напряжения и соединяют с землей
через сопротивление $R$. Найти ток через сопротивление $I_R(t)$ |
Показать решение
Пересмотр концепции поля – Колледж физики, главы 1-17
18 Электрический заряд и электрическое поле
Резюме
- Описать силовое поле и рассчитать напряженность электрического поля, создаваемого точечным зарядом.
- Рассчитайте силу, действующую на пробный заряд со стороны электрического поля.
- Объясните взаимосвязь между электрической силой (F) на испытательном заряде и напряженностью электрического поля (E).

Контактные силы, такие как между бейсбольным мячом и битой, объясняются в малом масштабе взаимодействием зарядов в атомах и молекулах в непосредственной близости. Они взаимодействуют через силы, включающие Кулоновская сила . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.
Например, заряженная резиновая расческа притягивает нейтральные кусочки бумаги на расстоянии под действием кулоновской силы. Очень полезно представить объект, окруженный в пространстве силовым полем . Силовое поле переносит силу на другой объект (называемый тестовым объектом) на некотором расстоянии.
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю (и все другие массы), представляет собой гравитационную силу, которая могла бы возникнуть, если бы в данной точке поля была помещена другая масса.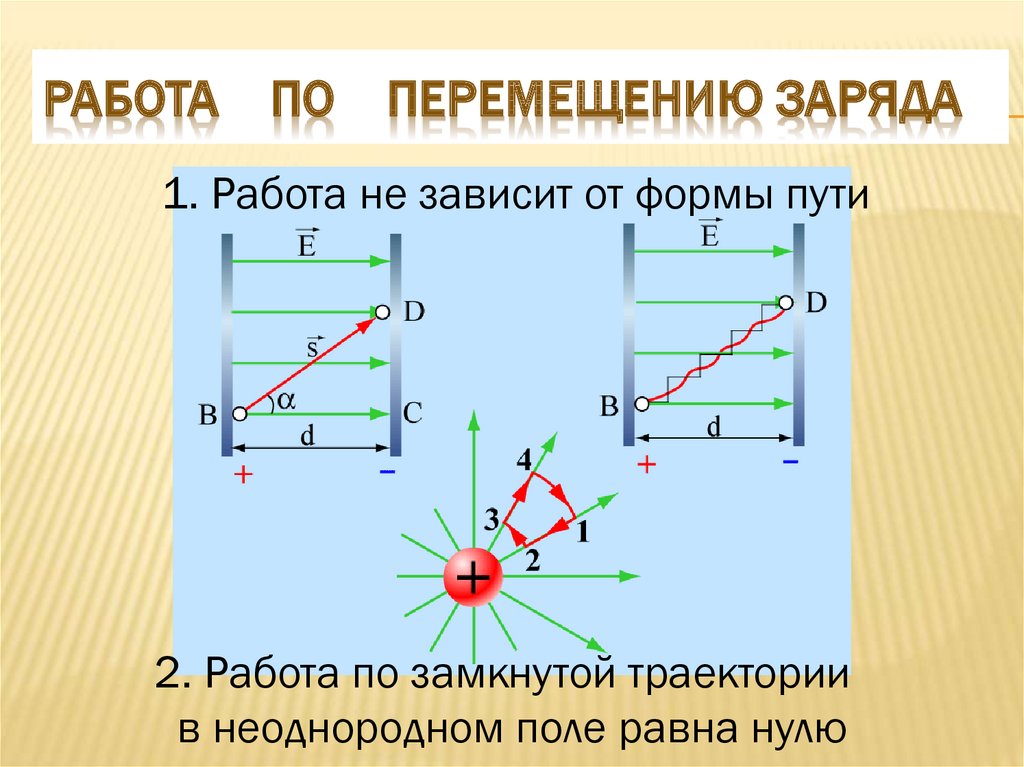 2}[/latex], для точечный заряд (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующий на пробный заряд [латекс]\boldsymbol{q}[/латекс] на расстоянии [латекс]\boldsymbol {r}[/latex] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс].
2}[/latex], для точечный заряд (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующий на пробный заряд [латекс]\boldsymbol{q}[/латекс] на расстоянии [латекс]\boldsymbol {r}[/latex] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс].
 Ф 1 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0017 q 1 и q 2 а также плата Q .
Ф 1 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0017 q 1 и q 2 а также плата Q .Для упрощения мы бы предпочли иметь поле, зависящее только от [латекс]\boldsymbol{Q}[/латекс], а не от тестового заряда [латекс]\жирныйсимвол{q}[/латекс]. Электрическое поле определяется таким образом, что оно представляет собой только создающий его заряд и уникально в каждой точке пространства. В частности, электрическое поле [латекс]\boldsymbol{E}[/латекс] определяется как отношение кулоновской силы к пробному заряду:
[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{\frac{F}{q}}[/латекс],
где [латекс]\boldsymbol{F}[/латекс] — электростатическая сила (или кулоновская сила), действующая на положительный пробный заряд
[латекс]\boldsymbol{q}[/латекс]. 2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс]
2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс]
Таким образом видно, что электрическое поле зависит только от заряда [латекс]\boldsymbol{Q}[/латекс] и расстояния [латекс]\boldsymbol{r}[/латекс]; он полностью не зависит от тестового заряда [латекс]\boldsymbol{q}[/латекс].
Расчет электрического поля точечного заряда
Расчет напряженности и направления электрического поля [латекс]\boldsymbol{E}[/латекс], создаваемого точечным зарядом 2,00 нКл (нанокулонов) на расстоянии 5,00 мм от заряда. 95 \;\textbf{N} / \textbf{C}.} \end{array}[/latex]
Обсуждение
Эта напряженность электрического поля одинакова в любой точке на расстоянии 5,00 мм от заряда [latex]\boldsymbol{Q}[/latex], который создает поле. Он положительный, что означает, что он имеет направление, указывающее в сторону от заряда [латекс]\boldsymbol{Q}[/латекс].
Расчет силы, действующей на точечный заряд электрическим полем
Какую силу электрическое поле, найденное в предыдущем примере, действует на точечный заряд [латекс]\boldsymbol{-0,250 \;\mu \textbf{C}} [/латекс]?
Стратегия
Поскольку мы знаем напряженность электрического поля и заряд в поле, силу, действующую на этот заряд, можно рассчитать, используя определение электрического поля [латекс]\boldsymbol{\textbf{E} = \textbf{ F}/q}[/latex] заменены на [latex]\boldsymbol{ \textbf{F} = q \textbf{E}}[/latex]. 5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]
5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]
Потому что [латекс] \boldsymbol{q}[/latex] отрицательна, сила направлена против направления поля.
Обсуждение
Сила притяжения, как и ожидалось для разных зарядов. (Поле было создано положительным зарядом и здесь действует на отрицательный заряд.) Заряды в этом примере типичны для обычного статического электричества, а полученная умеренная сила притяжения аналогична силам, возникающим при статическом прилипании и подобных ситуациях.
PhET Explorations: Electric Field of Dreams
Играй в мяч! Добавьте заряды в Поле Снов и посмотрите, как они реагируют на электрическое поле. Включите фоновое электрическое поле и отрегулируйте направление и величину.
Рисунок 2. Электрическое поле мечты- Поле электростатической силы, окружающее заряженный объект, распространяется в пространстве во всех направлениях.

- Электростатическая сила, действующая точечным зарядом на пробный заряд на расстоянии [латекс]\boldsymbol{r}[/латекс], зависит от заряда обоих зарядов, а также от расстояния между ними.
- Электрическое поле [latex]\textbf{E}[/latex] определяется как
[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{\frac{\textbf{F}}{q,}}[/латекс]
, где [латекс]\textbf{F}[/латекс] — кулоновская или электростатическая сила, действующая на небольшой положительный пробный заряд [латекс]\boldsymbol{q}[/латекс]. [latex]\textbf{E}[/latex] имеет единицы N/C.
- Величина электрического поля [латекс]\textbf{E}[/латекс], создаваемого точечным зарядом [латекс]\boldsymbol{Q}[/латекс] , равна
92}}.[/латекс]
, где [латекс]\boldsymbol{r}[/латекс] — расстояние от [латекс]\жирныйсимвол{Q}[/латекс]. Электрическое поле [латекс]\boldsymbol{E}[/латекс] является вектором, а поля из-за множественных зарядов складываются подобными векторами.
- поле
- карта величины и направления силы, действующей на другие объекты, простирающейся в космос
- Точечная оплата
- Заряженная частица, обозначенная как [латекс]\boldsymbol{Q}[/латекс], создающая электрическое поле
- испытательный заряд
- Частица (обозначается как [латекс]\жирный символ{q}[/латекс]) с положительным или отрицательным зарядом, помещенная в электрическое поле, создаваемое точечным зарядом
электростатика — Электрическое поле в сферических координатах
$\begingroup$
Предположим, я хочу найти линейный интеграл электрического поля вдоль некоторого пути $ab$, как показано здесь.



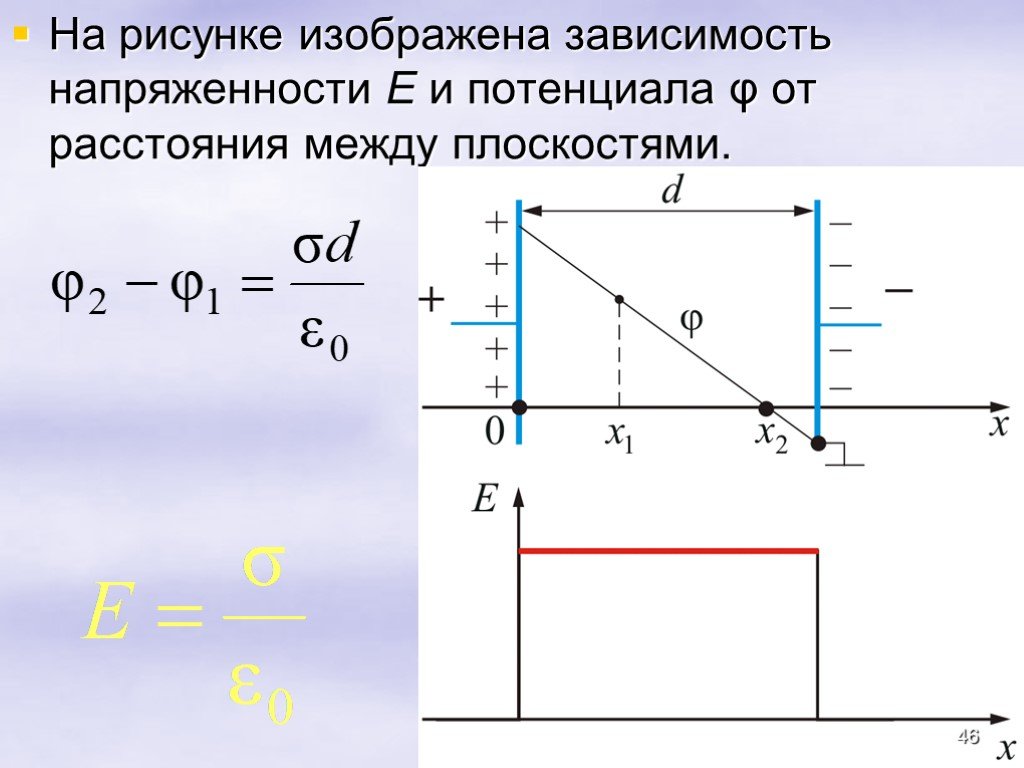 Найти емкость конденсатора.
Найти емкость конденсатора. Если в плоскости $xy$ поместить экран 1) с отверстием в виде трех одинаковых сердечек (см. рисунок),
то интенсивность в точке $P$ станет равна $I_1$. Если же вместо экрана 1) поместить дополнительный к нему экран 2),
то интенсивность станет равна $I_2$. Чему будет равна интенсивность $I_3$ в точке $P$,
если вместо экрана 2) поставить его треть (экран 3)?
Если в плоскости $xy$ поместить экран 1) с отверстием в виде трех одинаковых сердечек (см. рисунок),
то интенсивность в точке $P$ станет равна $I_1$. Если же вместо экрана 1) поместить дополнительный к нему экран 2),
то интенсивность станет равна $I_2$. Чему будет равна интенсивность $I_3$ в точке $P$,
если вместо экрана 2) поставить его треть (экран 3)? n f(x-nd)$, где $f(x)$ – одиночный импульс (см. рисунок).
Фурье-образ функции $f(x)$ считать известным и равным $\tilde{f}(k)$.
n f(x-nd)$, где $f(x)$ – одиночный импульс (см. рисунок).
Фурье-образ функции $f(x)$ считать известным и равным $\tilde{f}(k)$. Считать, что $\Delta\omega \ll \omega_0$.
Считать, что $\Delta\omega \ll \omega_0$.
 {-5}$ см).
{-5}$ см). Плоскость полуокружности перпендикулярна полупрямым (см. рис.). Найти магнитное поле в точке $O$.
Плоскость полуокружности перпендикулярна полупрямым (см. рис.). Найти магнитное поле в точке $O$.