19Потенциальная энергия. Потенциальное пол
Потенциальная энергия 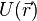 — скалярная физическая
величина, представляющая собой часть
полной механической
энергии системы, находящейся
вполе консервативных
сил. Зависит от положения материальных
точек, составляющих систему, и
характеризует работу,
совершаемую полем при их перемещении[1].
Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане системы,
и описывающая взаимодействие элементов
системы[2].
Термин «потенциальная энергия» был
введен в XIX веке шотландским инженером
и физикомУильямом
Ренкином.
— скалярная физическая
величина, представляющая собой часть
полной механической
энергии системы, находящейся
вполе консервативных
сил. Зависит от положения материальных
точек, составляющих систему, и
характеризует работу,
совершаемую полем при их перемещении[1].
Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане системы,
и описывающая взаимодействие элементов
системы[2].
Термин «потенциальная энергия» был
введен в XIX веке шотландским инженером
и физикомУильямом
Ренкином.
Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.
Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными (потенциальными).
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
Потенциальная энергия в поле тяготения Земли
Потенциальная
энергия тела 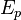 в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
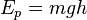
где 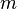 — масса тела,
— масса тела, 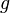 — ускорение
свободного падения,
— ускорение
свободного падения, 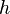 —
высота положения центра
масс тела над произвольно выбранным
нулевым уровнем.
—
высота положения центра
масс тела над произвольно выбранным
нулевым уровнем.
О физическом смысле понятия потенциальной энергии
В то время, как кинетическая энергия всегда характеризует тело относительно выбранной системы отсчёта, потенциальная энергия всегда характеризует тело относительно источника силы.
Кинетическая энергия характеризуется скоростью относительно системы отсчёта; потенциальная — расположением тел в поле.
Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.
Потенциальное поле
Потенциальное поле — это поле, в котором работа силы не зависит от формы пути, а зависит лишь от положений начальной и конечной точек траектории, а силы, действующие в нем, — консервативными.
Консервативные (потенциальные) силы — это силы, зависящие только от координат точек системы и работа которых не зависит от пути перехода из начального в конечное положение, а определяется только начальным и конечным положением.
В потенциальном поле работа сил по любому замкнутому контуру равна нулю.
Связь между силовой и энергетической характеристиками в потенциальном силовом поле.
В потенциальном силовом поле и E и F являются функциями координат. Пусть сила F направлена вдоль перемещения, тогда приращение Ep:
-dE = Fdr = Frdr
Fr = -dEp/dr
«-» указывает на то, что сила направлена в сторону убывания потенциальной энергии.
В случае, когда вектор F имеет произвольное направление в пространстве, необходимо поставить в соответствие сколярному полю Ep вектор F.
Эту задачу решает градиент:
F = — grad Ep.
консервативное поле, векторное поле, циркуляция которого вдоль любой замкнутой траектории равнанулю. Если П. п.силовое поле, то это означает равенство нулю работы сил поля вдоль замкнутойтраектории.
4.3.Потенциальное поле сил. Консервативные силы
Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что эта частица находится в поле сил. Например, вблизи поверхности Земли частица находится в поле силы тяжести.
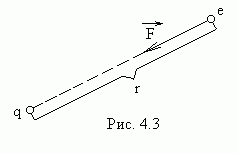 В электрическом
поле неподвижного точечного заряда
В электрическом
поле неподвижного точечного заряда  на заряженную частицу действует поле,
характерное тем, что направление силы,
действующей на частицу в любой точке
пространства, проходит через неподвижный
центр (заряд
на заряженную частицу действует поле,
характерное тем, что направление силы,
действующей на частицу в любой точке
пространства, проходит через неподвижный
центр (заряд ),
а величина силы зависит только от
расстояния до этого центра:
),
а величина силы зависит только от
расстояния до этого центра: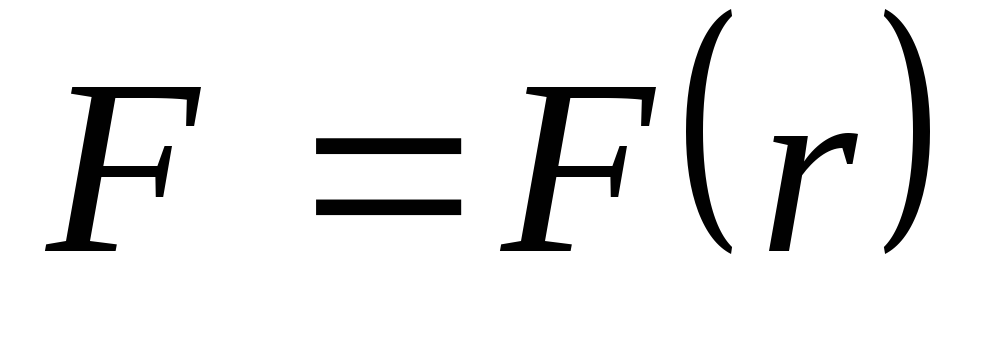 .
Такое поле называется центральным
(рис.4.3).
.
Такое поле называется центральным
(рис.4.3).
Если в каждой точке поля сила, действующая на частицу, одинакова по величине и направлению, поле называется однородным.
Силовое поле,
которое можно описать с помощью функции 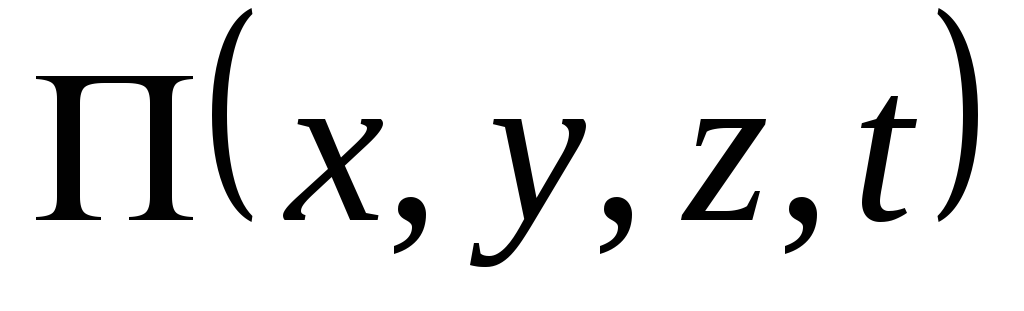 такой, что
такой, что
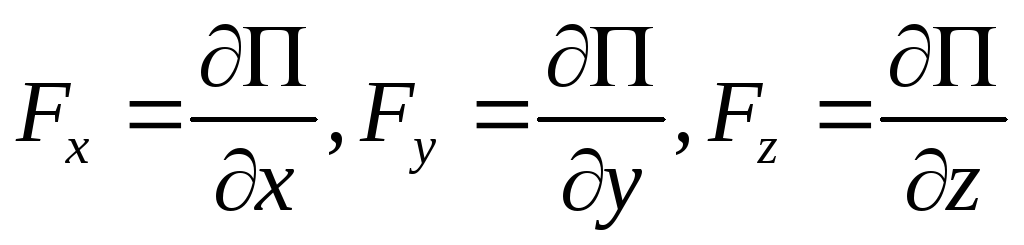 (4.6)
(4.6)
называется
потенциальным. Функция 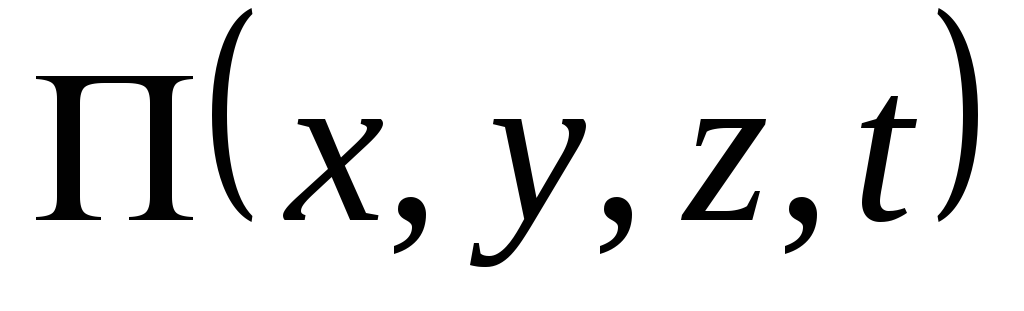 называется потенциальной функцией или
потенциалом. Если поле не изменяется
со временем, оно называется стационарным,
в этом случае
называется потенциальной функцией или
потенциалом. Если поле не изменяется
со временем, оно называется стационарным,
в этом случае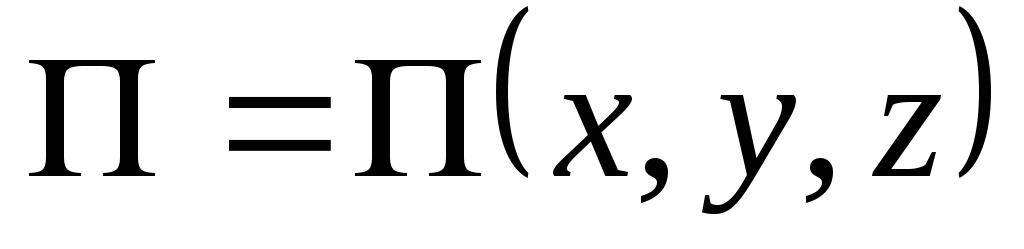
Добавление к
функции  произвольной постоянной величины не
изменяет значений
,
вычисляемых по формулам (4.6) . Поэтому
потенциальная функция определяется с
точностью до произвольной аддитивной
постоянной. Однако при фиксированном
значении этой постоянной
произвольной постоянной величины не
изменяет значений
,
вычисляемых по формулам (4.6) . Поэтому
потенциальная функция определяется с
точностью до произвольной аддитивной
постоянной. Однако при фиксированном
значении этой постоянной 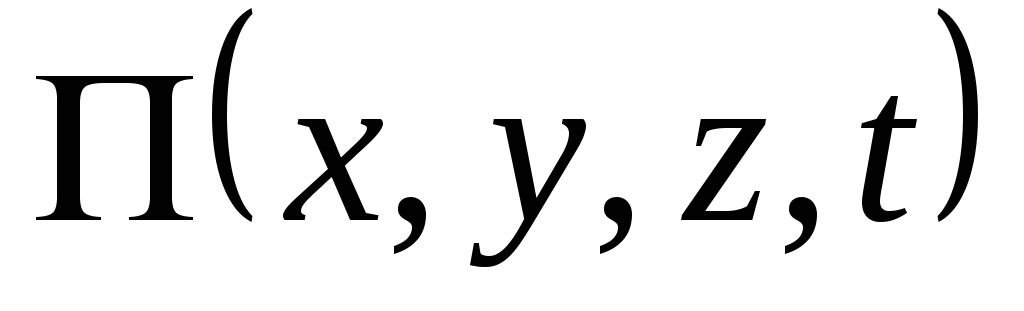 становится однозначной функцией
координат и времени.
становится однозначной функцией
координат и времени.
Вектор с
компонентами 
 —
скалярная функция координат, называется
градиентом функции
—
скалярная функция координат, называется
градиентом функции и обозначается
и обозначается либо
либо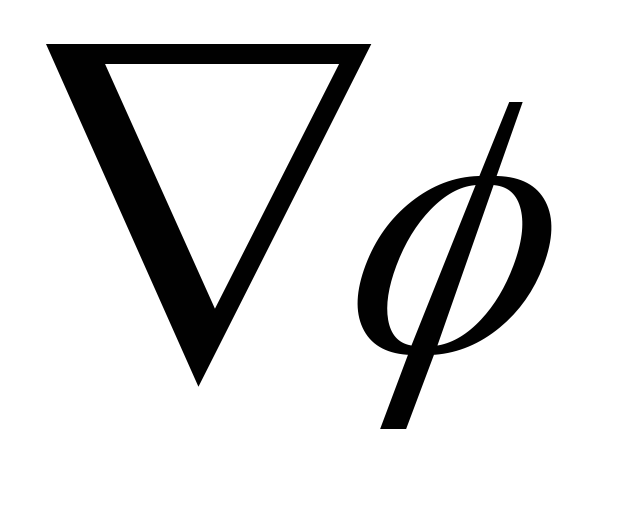 (
( называется оператором набла,
называется оператором набла,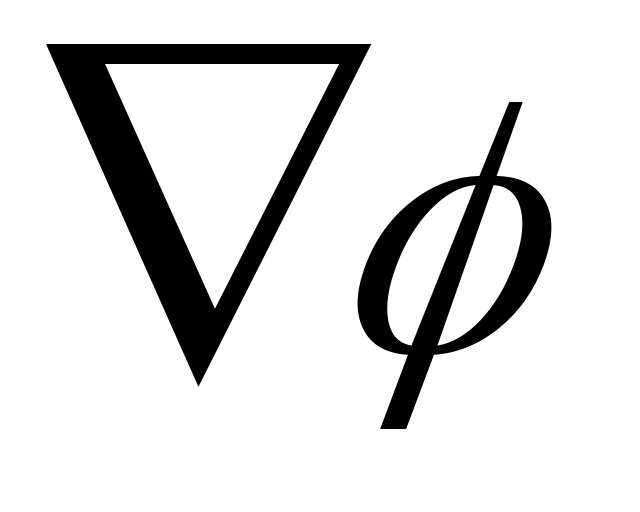 читается:
«набла фи» или «градиент фи»). Из
определения градиента следует, что
читается:
«набла фи» или «градиент фи»). Из
определения градиента следует, что 
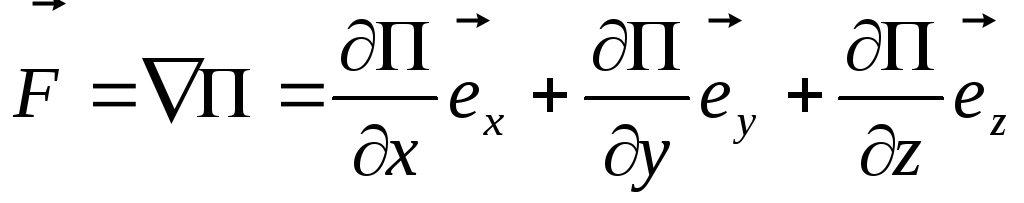 .
(4.7)
.
(4.7)
Работа силы, удовлетворяющей условию (4.7), равна
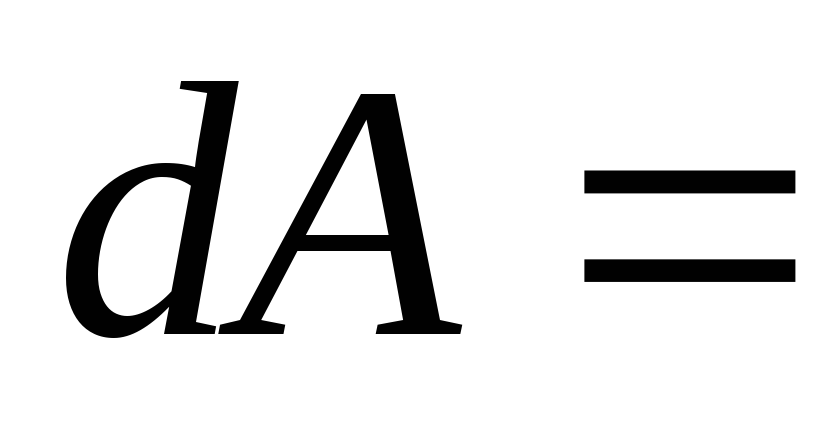
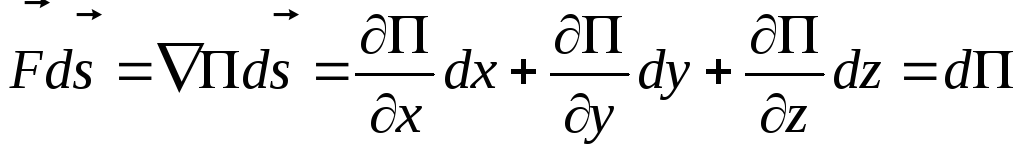 ,
(4.8)
,
(4.8)
т.е. представляет
собой полный дифференциал функции 
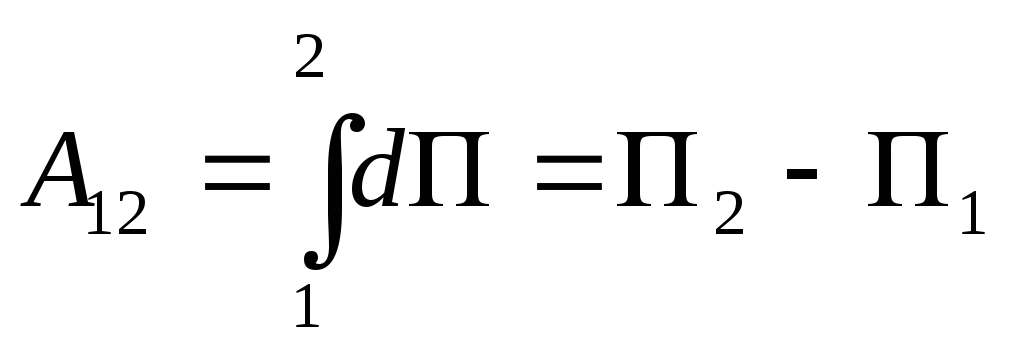 .
(4.9)
.
(4.9)
Форма траектории, по которой осуществлялось интегрирование, была совершенно произвольной. Таким образом, работа, совершаемая над частицей силами стационарного потенциального поля, не зависит от пути, по которому двигалась частица, а определяется только начальным и конечным положениями частицы в пространстве.
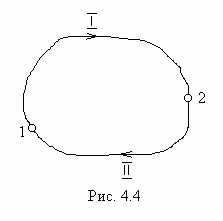
Из независимости
работы консервативных сил от пути
вытекает, что работа таких сил на
замкнутом пути равна нулю. Чтобы доказать
это, разобьем произвольный замкнутый
путь (рис.4.4) на две части: путь 1, по
которому частица переходит из точки 1
в точку 2, и путь  ,
по которому частица переходит из точки
2 в точку 1. При этом точки 1 и 2 выбраны
произвольно.
,
по которому частица переходит из точки
2 в точку 1. При этом точки 1 и 2 выбраны
произвольно.
Работа на всем замкнутом пути равна сумме работ, совершаемых на каждом из участков:
 .
(4.10)
.
(4.10)
Очевидно, работы 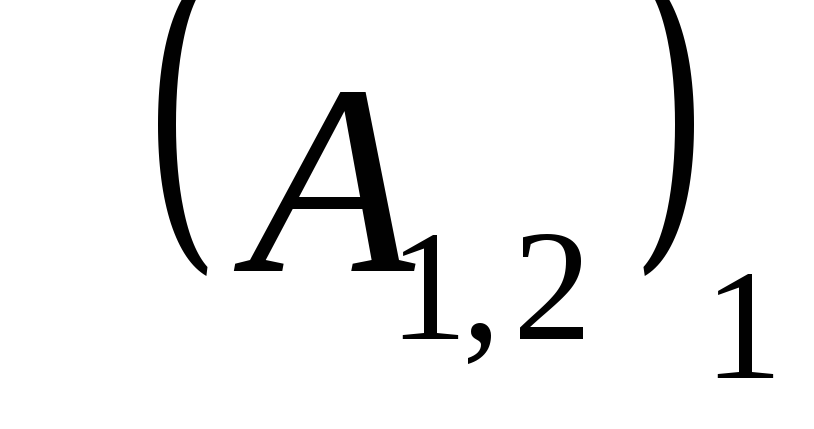 и
и  отличаются
только знаком. Действительно, изменение
направления движения на обратное
приводит к замене
отличаются
только знаком. Действительно, изменение
направления движения на обратное
приводит к замене  на
—
на
— ,
поэтому значение интеграла
,
поэтому значение интеграла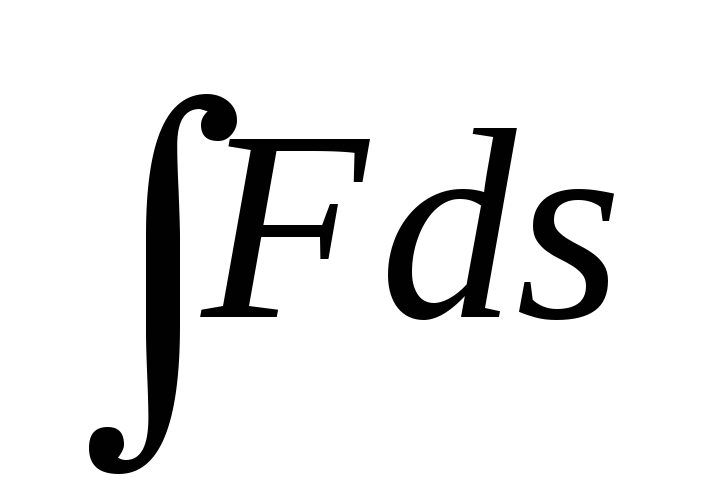 изменяет знак на обратный.
изменяет знак на обратный.
Поэтому равенство
(4.10) можно записать в виде:  .Так
как работа не зависит от пути, то
.Так
как работа не зависит от пути, то 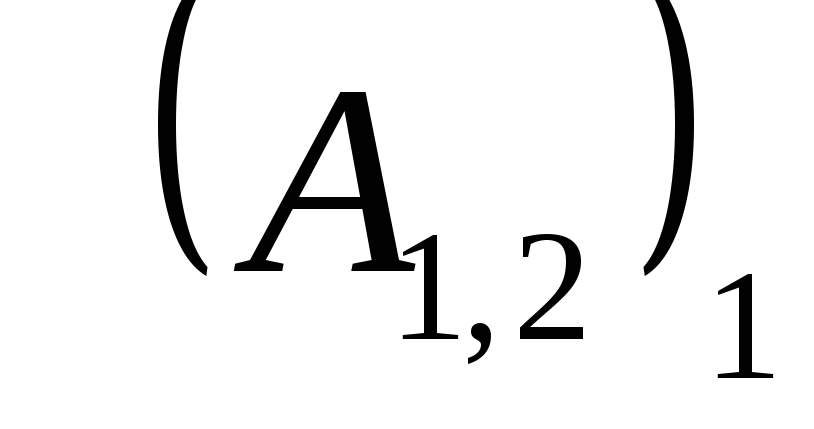 =
—
=
—  ,
и
,
и 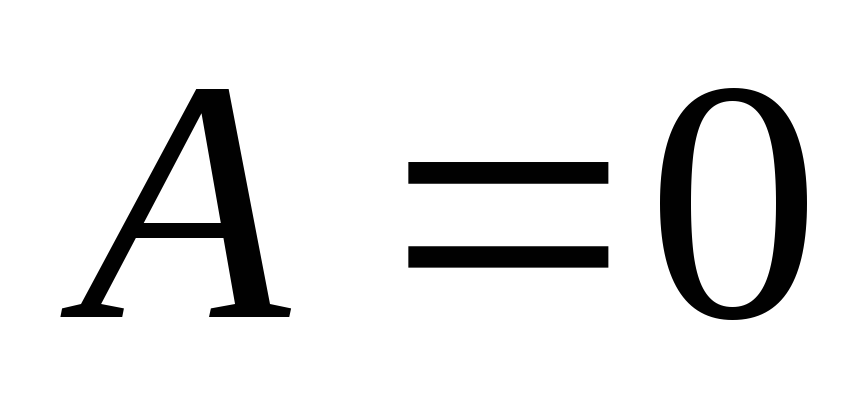 .
.
Кроме консервативных сил существуют неконсервативные силы. К ним относятся диссипативные силы, переводящие механическую энергию во внутреннюю ( это силы трения, сопротивления среды), а также гироскопические силы, перпендикулярные скорости ( сила Кореолиса, сила Лоренца), работа которых всегда равна нулю. Для неконсервативных сил соотношение (4.7) не выполняется.
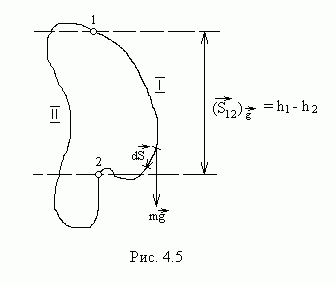 Докажем, что сила
тяжести является консервативной. Эта
сила в любой точке имеет одинаковые
величину и направление – вниз по
вертикали (рис.4.5). Поэтому, независимо
от того, по какому из путей 1 или II
движется частица, работа определяется
выражением:
Докажем, что сила
тяжести является консервативной. Эта
сила в любой точке имеет одинаковые
величину и направление – вниз по
вертикали (рис.4.5). Поэтому, независимо
от того, по какому из путей 1 или II
движется частица, работа определяется
выражением: 
Из рис.4.5 видно,
что проекция вектора 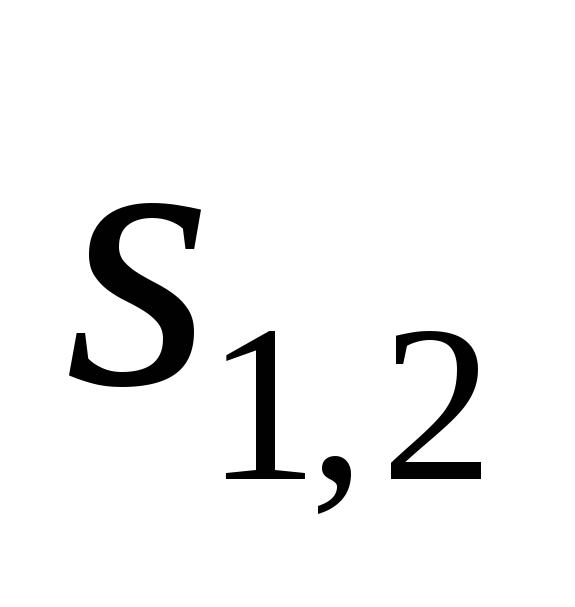 на направление
на направление  равна разности высот
равна разности высот  .
Тогда работа
.
Тогда работа 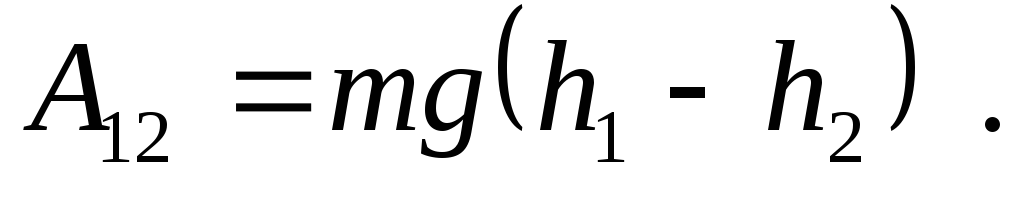
Это выражение не зависит от пути, следовательно, сила тяжести консервативна.
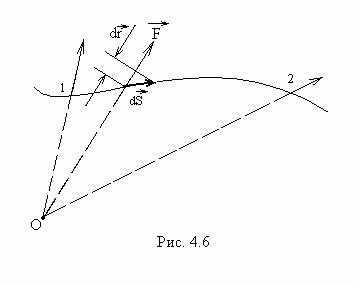 Силы, действующие
на частицу в центральном поле, также
консервативны (рис.4.6). Элементарная
работа центральной силы на пути
Силы, действующие
на частицу в центральном поле, также
консервативны (рис.4.6). Элементарная
работа центральной силы на пути  равна
равна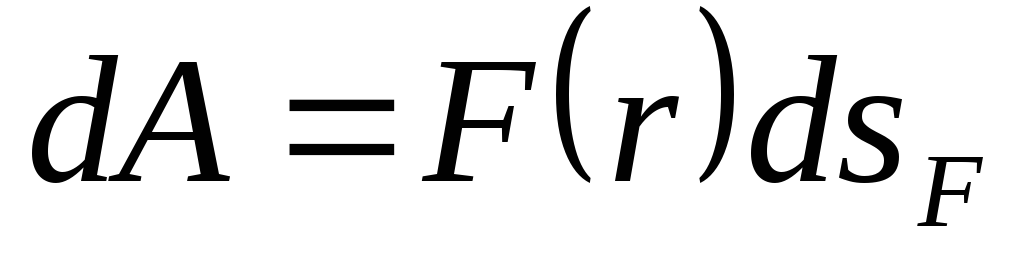 .
Проекция
.
Проекция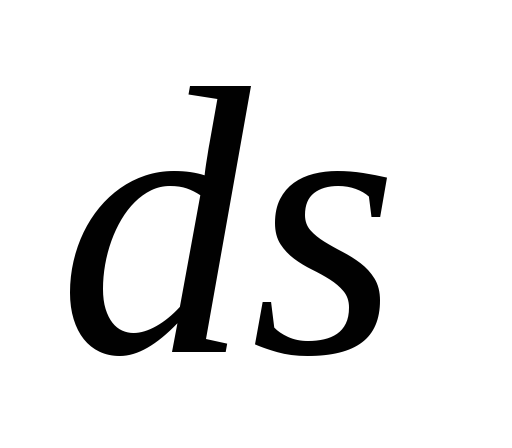 на направление силы в данном месте –
это проекция на направление радиуса-вектора
на направление силы в данном месте –
это проекция на направление радиуса-вектора , она равна приращению расстояния частицы
до центра силового поля О:
, она равна приращению расстояния частицы
до центра силового поля О:
 .
Работа на всем пути
.
Работа на всем пути 
Это выражение
зависит только от вида функции 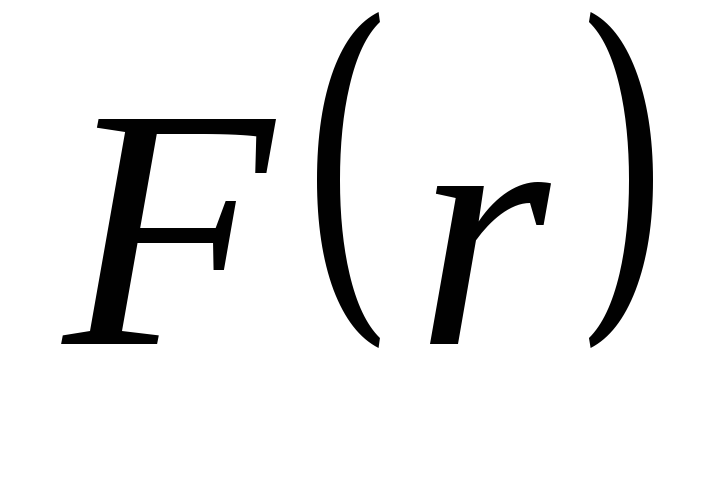 и от значений
и от значений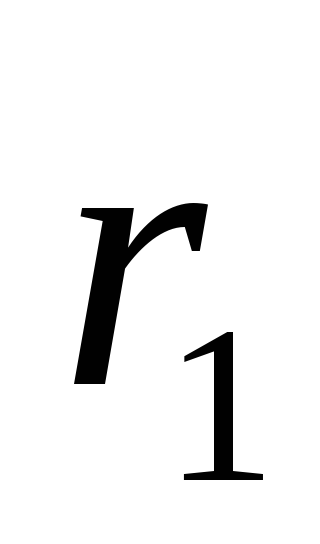 и
и .
От вида траектории оно не зависит,
следовательно, центральная сила
консервативна.
.
От вида траектории оно не зависит,
следовательно, центральная сила
консервативна.
4.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ВО ВНЕШНЕМ ПОЛЕ СИЛ
Из выражения (4.9) следует, что работа равна приращению потенциальной функции, и эта работа идет на приращение кинетической энергии частицы, как показывает (4.5). Таким образом,
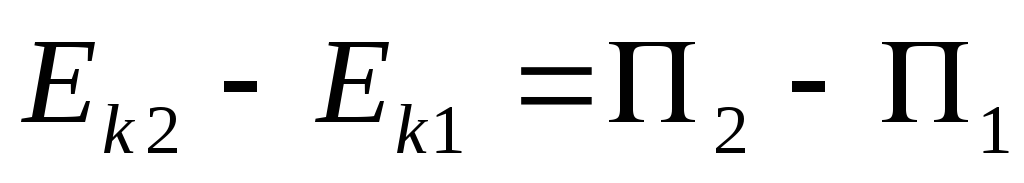 .
(4.11)
.
(4.11)
Перейдем от
функции  к
функции
к
функции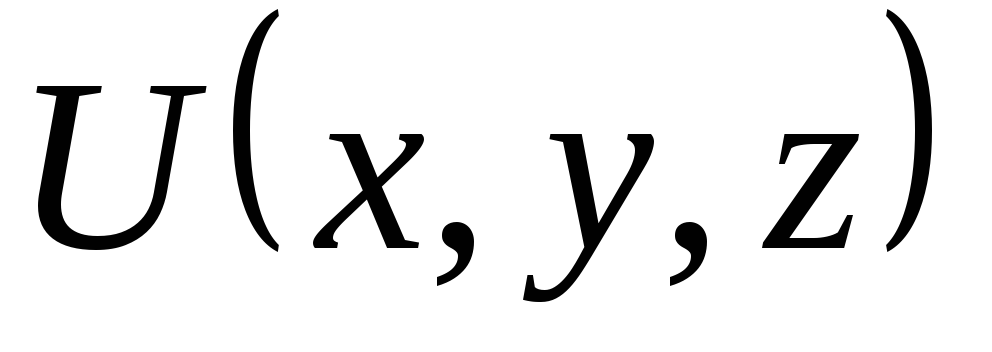 ,
связанной с
,
связанной с соотношением
соотношением
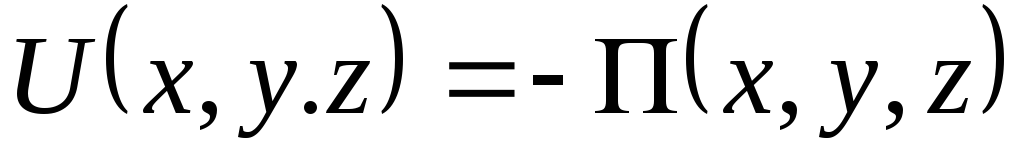 .
(4.12)
.
(4.12)
Тогда из (4.11)
получаем: 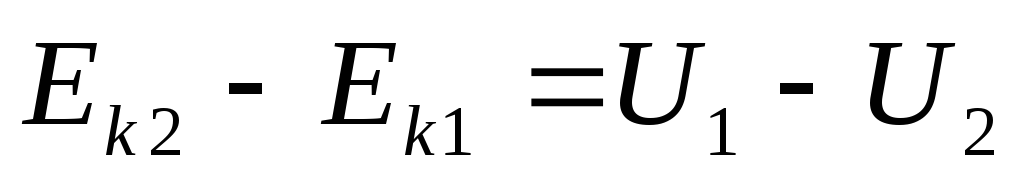 ,
или
,
или .
.
Полученный результат
означает, что величина 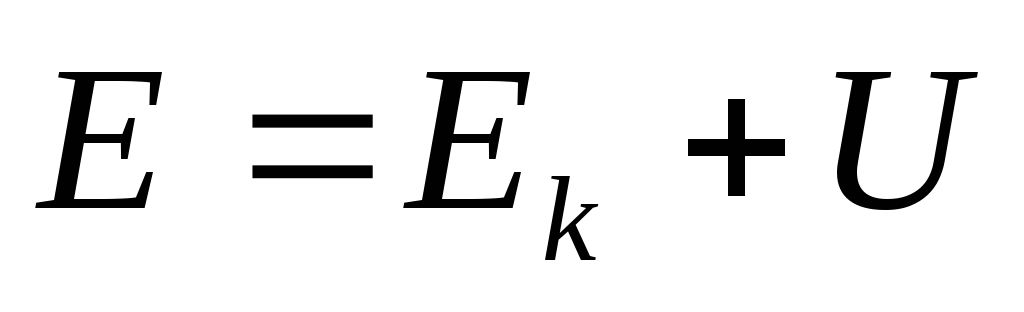 для частицы, находящейся в поле
консервативных сил, остается постоянной,
т.е. является интегралом движения.
Функция
для частицы, находящейся в поле
консервативных сил, остается постоянной,
т.е. является интегралом движения.
Функция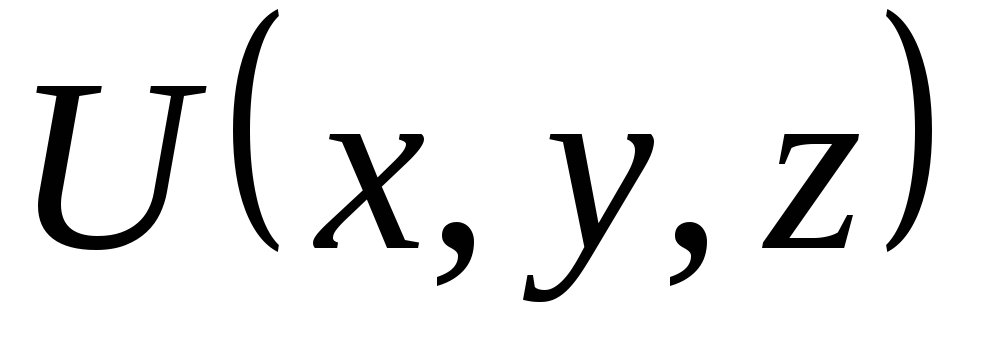 называется потенциальной энергией
частицы во внешнем поле сил. Таким
образом, потенциальная энергия
характеризует взаимодействие частицы
с полем сил и зависит от положения
частицы в этом поле, т.е. от координат.
Величину
называется потенциальной энергией
частицы во внешнем поле сил. Таким
образом, потенциальная энергия
характеризует взаимодействие частицы
с полем сил и зависит от положения
частицы в этом поле, т.е. от координат.
Величину ,
равную сумме кинетической и потенциальной
энергии, называют полной механической
энергией частицы.
,
равную сумме кинетической и потенциальной
энергии, называют полной механической
энергией частицы.
Из выражения (4.9) с учетом (4.12) получаем
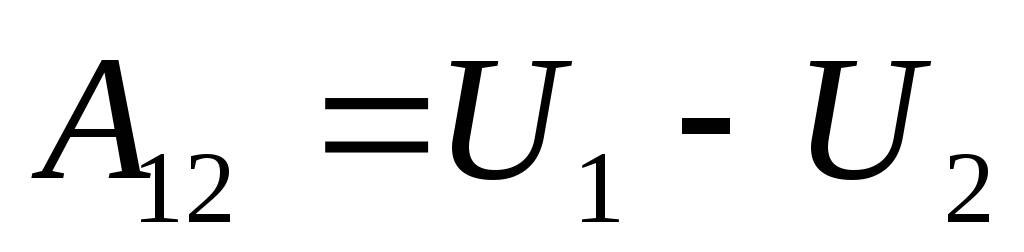
-работа, совершаемая над частицей силами консервативного поля, равна убыли потенциальной энергии частицы, т.е. работа совершается за счет запаса потенциальной энергии.
Выражение (4.7) с учетом (4.12) принимает вид
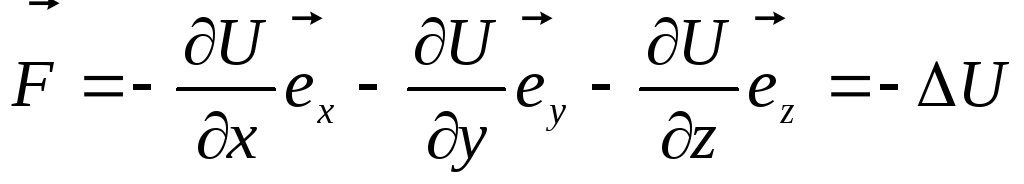
–сила, действующая на частицу в стационарном поле сил, равна градиенту потенциальной энергии частицы в этом поле, взятому с обратным знаком.
Пусть на частицу,
кроме сил стационарного потенциального
поля, действует также неконсервативная
сила  .
Тогда при переходе частицы из точки 1 в
точку 2 над ней будет совершаться работа
.
Тогда при переходе частицы из точки 1 в
точку 2 над ней будет совершаться работа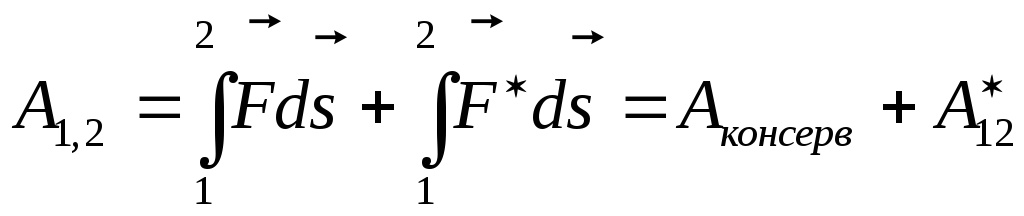 ,гд
,гд е
е — работа неконсервативной силы. Работа
консервативных сил равна убыли
потенциальной энергии. Тогда
— работа неконсервативной силы. Работа
консервативных сил равна убыли
потенциальной энергии. Тогда
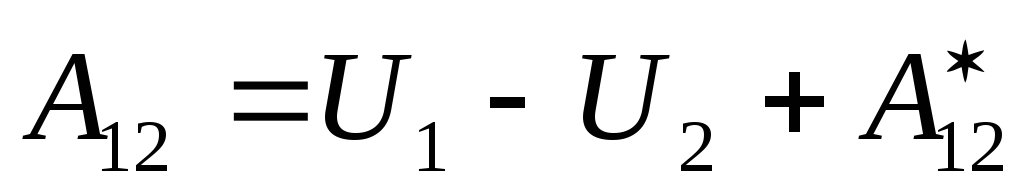 .
.
Суммарная работа
всех приложенных к частице сил идет на
приращение ее кинетической энергии: 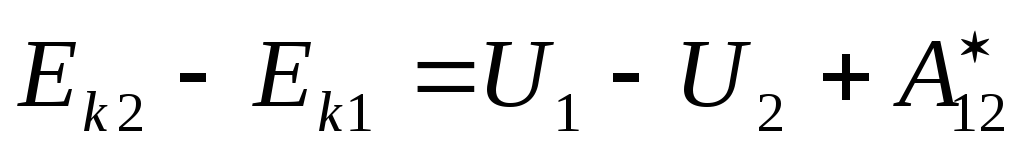 ,
или
,
или
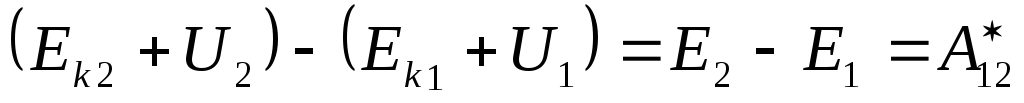
-работа неконсервативных сил затрачивается на приращение полной механической энергии частицы.
Потенциальная
энергия, как и потенциальная функция,
определяется с точностью до произвольной
аддитивной постоянной. Однако, это не
имеет значения, так как во все функции
входит либо разность значений потенциальной
энергии, либо ее производные. В каждой
конкретной задаче выбирается начало
отсчета потенциальной энергии, от
которого ведут расчет энергии в других
положениях. Поэтому 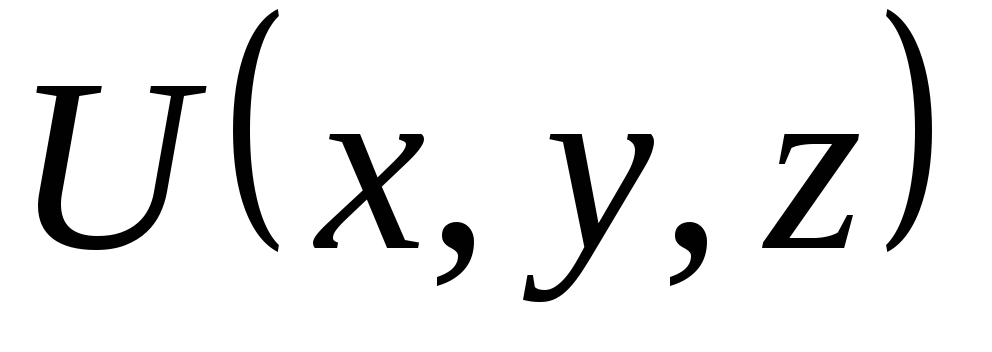 может
иметь как положительные, так и отрицательные
значения.
может
иметь как положительные, так и отрицательные
значения.
Конкретный вид
функции  зависит
от характера силового поля. В поле
тяжести
зависит
от характера силового поля. В поле
тяжести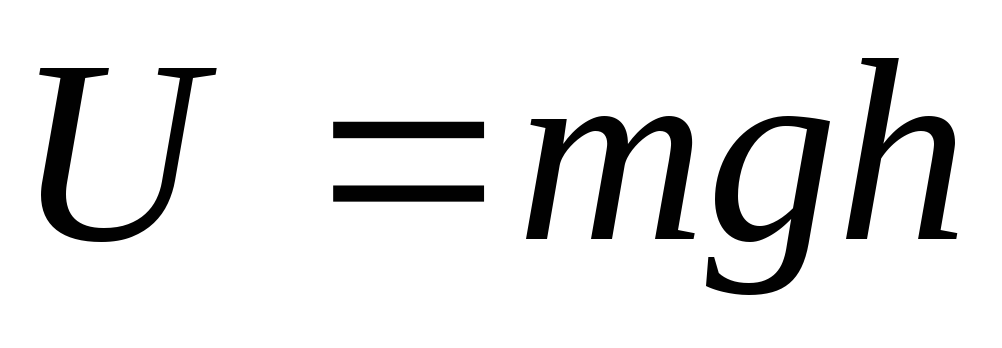 ,
где
,
где отсчитывается
от произвольного уровня.
отсчитывается
от произвольного уровня.
Рассмотрим
систему, состоящую из невзаимодействующих между собой частиц,
находящихся в поле консервативных сил.
Каждая из частиц обладает кинетической
невзаимодействующих между собой частиц,
находящихся в поле консервативных сил.
Каждая из частиц обладает кинетической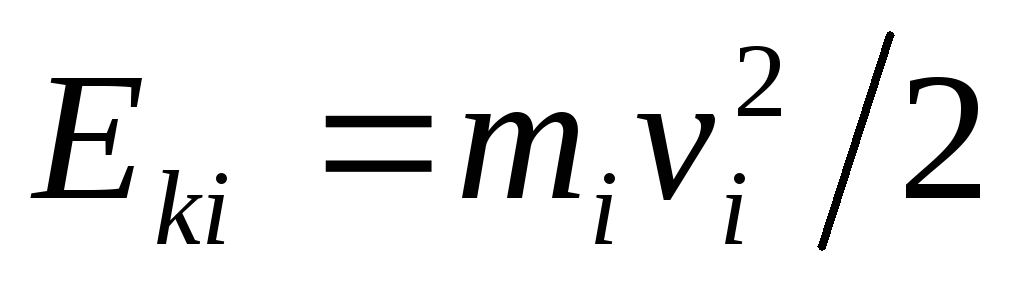 и потенциальной энергией
и потенциальной энергией номер
частицы, тогда для каждой частицы можно
записать
номер
частицы, тогда для каждой частицы можно
записать
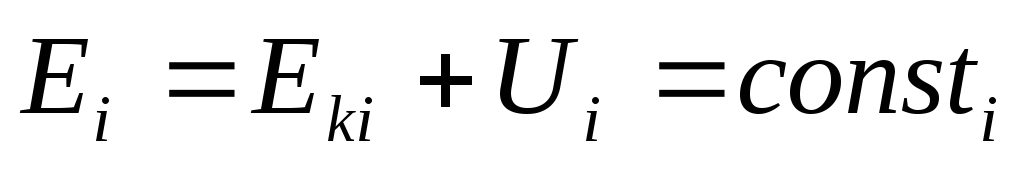
Просуммировав эти выражения для всех частиц, получаем
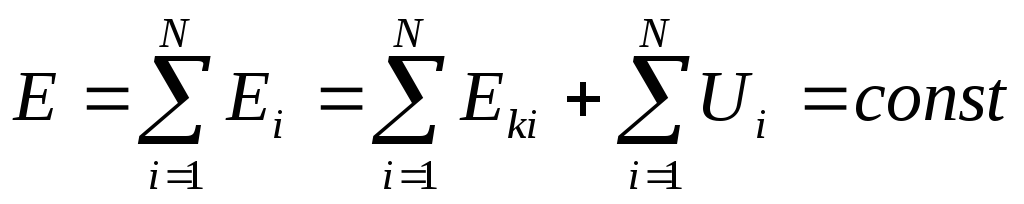
— полная механическая энергия системы невзаимодействующих частиц, на которые действуют только консервативные силы, остается постоянной.
4.5.ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ
 Рассмотрим
замкнутую систему, состоящую из двух
взаимодействующих частиц (рис.4.7). Введем
вектор
Рассмотрим
замкнутую систему, состоящую из двух
взаимодействующих частиц (рис.4.7). Введем
вектор 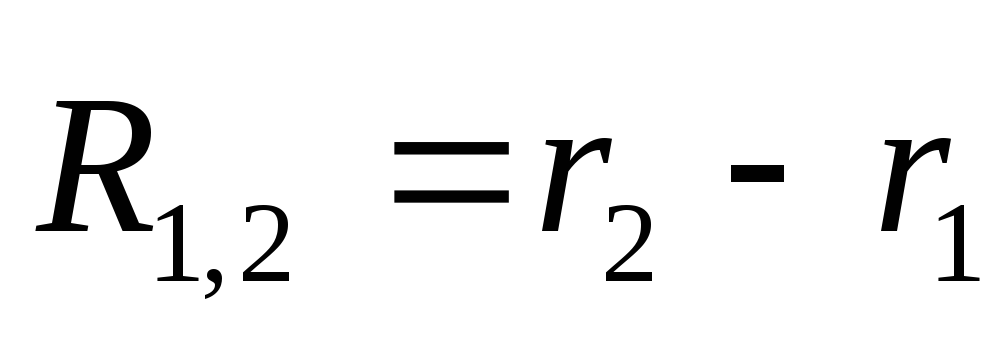 ,
где
,
где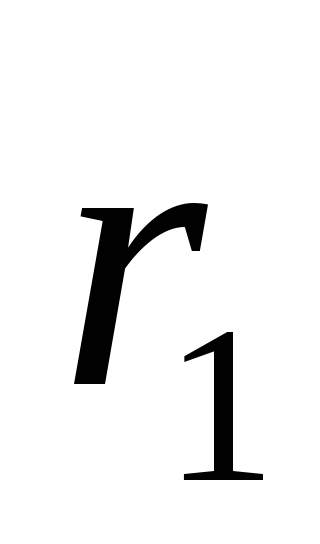 и
и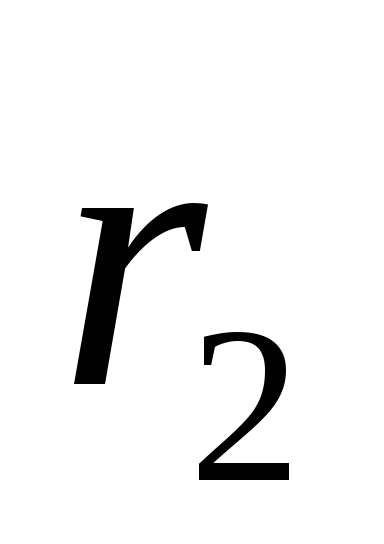 —
радиус-векторы частиц. Расстояние между
частицами равно модулю этого вектора.
Будем считать, что силы взаимодействия
частиц
—
радиус-векторы частиц. Расстояние между
частицами равно модулю этого вектора.
Будем считать, что силы взаимодействия
частиц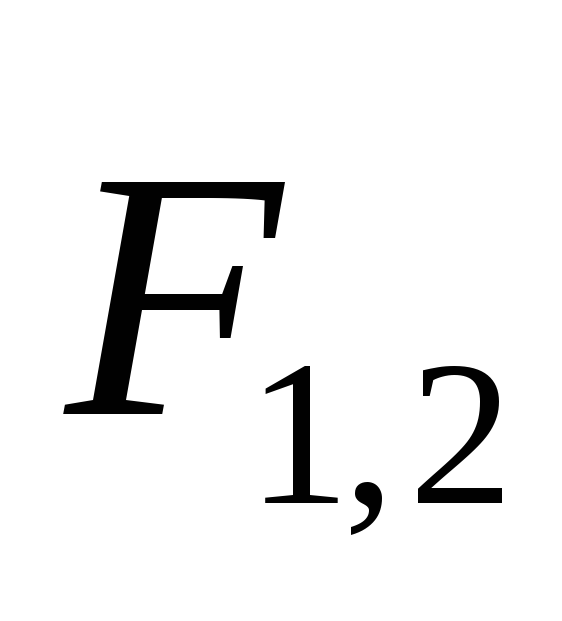 и
и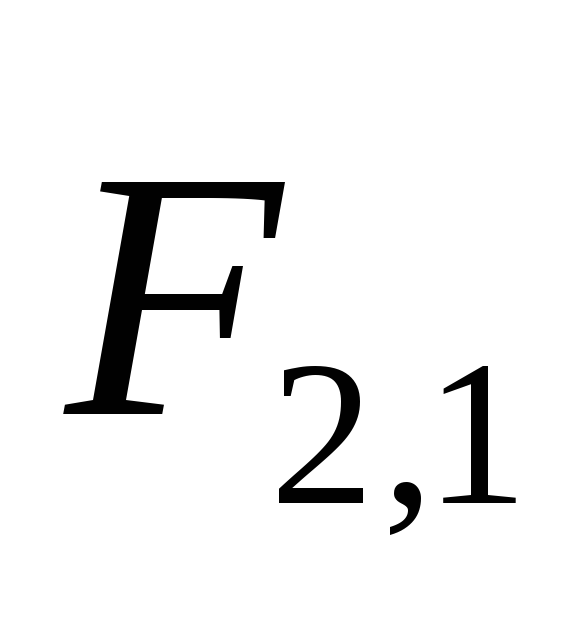 зависят только от расстояния
зависят только от расстояния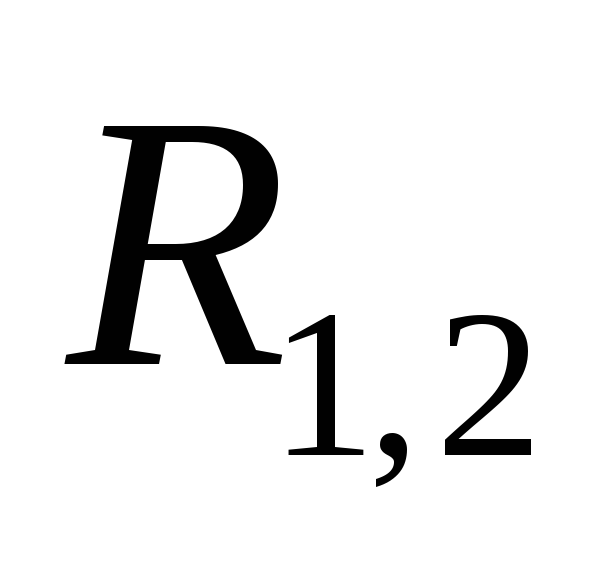 между ними, и направлены вдоль прямой,
соединяющей частицы:
между ними, и направлены вдоль прямой,
соединяющей частицы:
 ,
(4.13)
,
(4.13)
г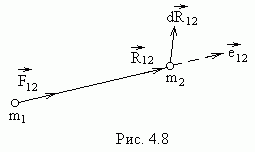 де
де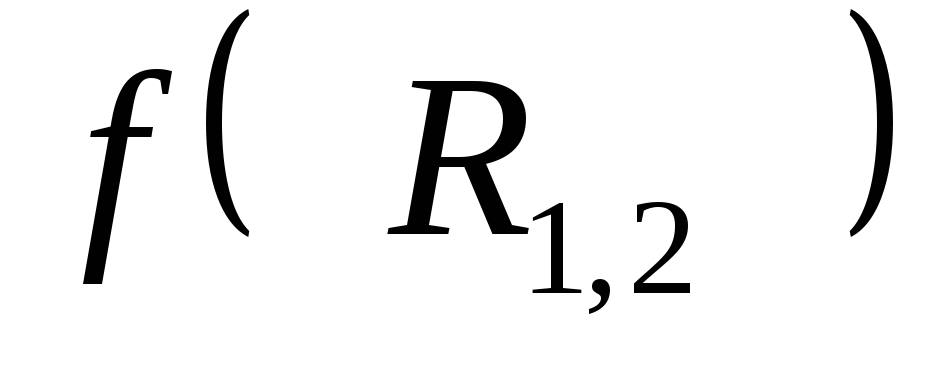 — некоторая функция
— некоторая функция ,
,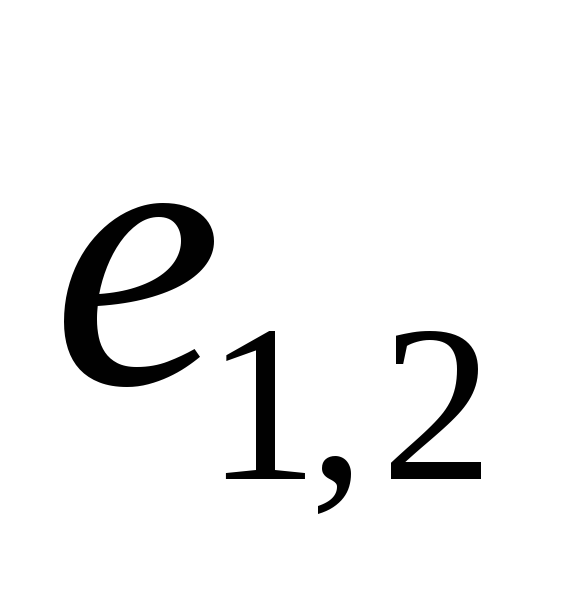 —
орт вектора
—
орт вектора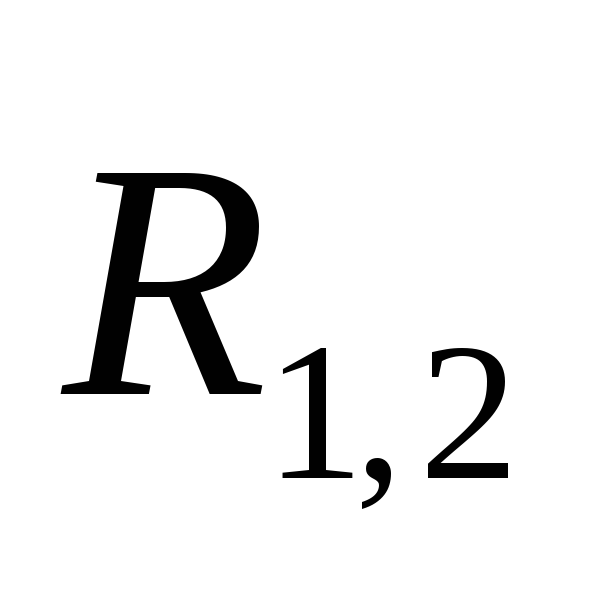 (рис.4.8).
По третьему закону Ньютона
(рис.4.8).
По третьему закону Ньютона =
=  .
Уравнения движения частиц
.
Уравнения движения частиц
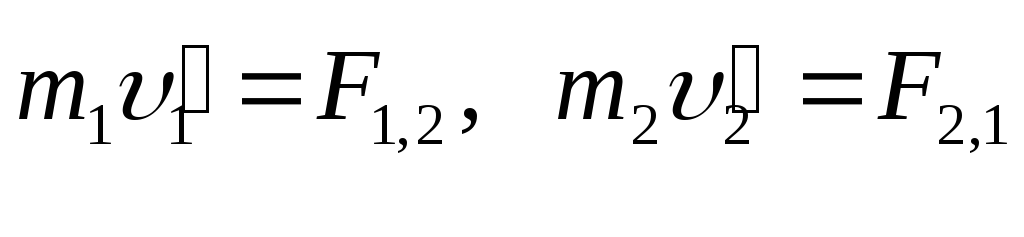 .
.
Умножим первое
уравнение на  ,
второе – на
,
второе – на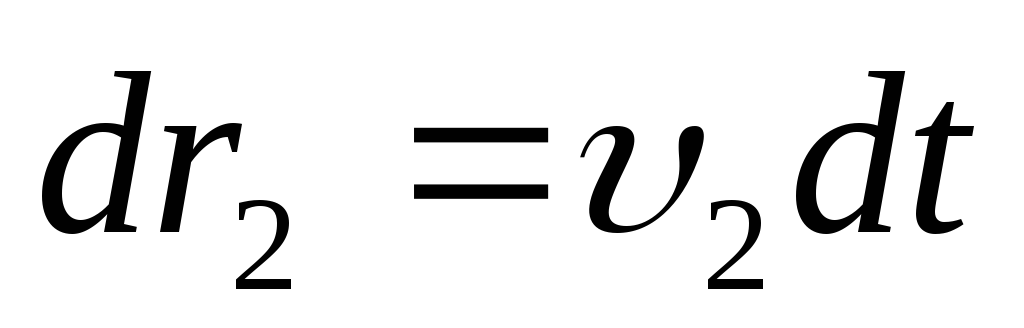 и сложим:
и сложим:
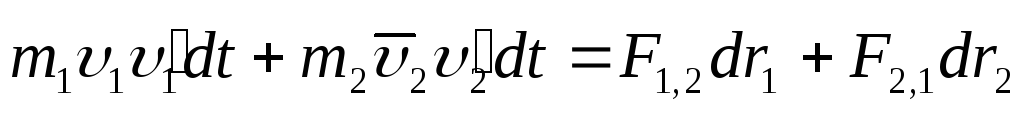 .
(4.14)
.
(4.14)
Левая часть этого
выражения представляет собой приращение
кинетической энергии системы за время 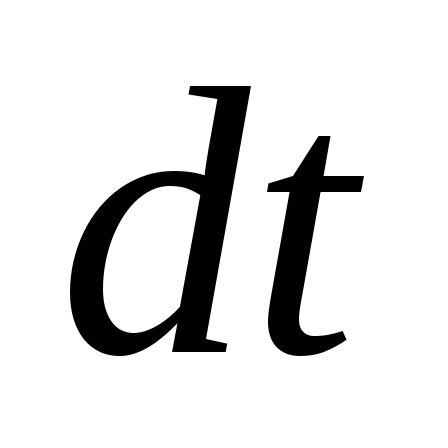 , а правая часть – работу внутренних
сил за то же время:
, а правая часть – работу внутренних
сил за то же время:
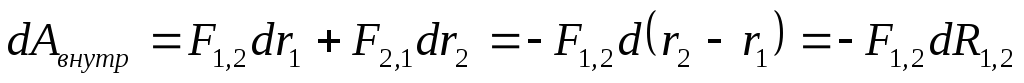 .
.
Подставив в это выражение формулу (4.13), получаем
 .
.
Из рис.4.7 видно,
что скалярное произведение  равно приращению расстояния между
частицами. Тогда
равно приращению расстояния между
частицами. Тогда
 .
.
Выражение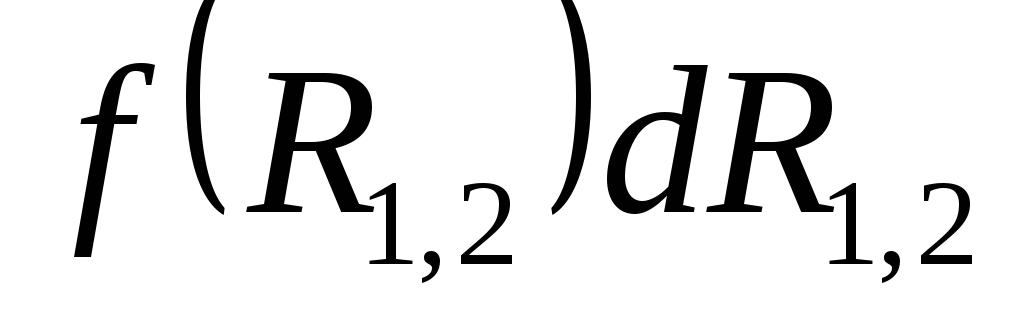 есть
приращение некоторой функции от
есть
приращение некоторой функции от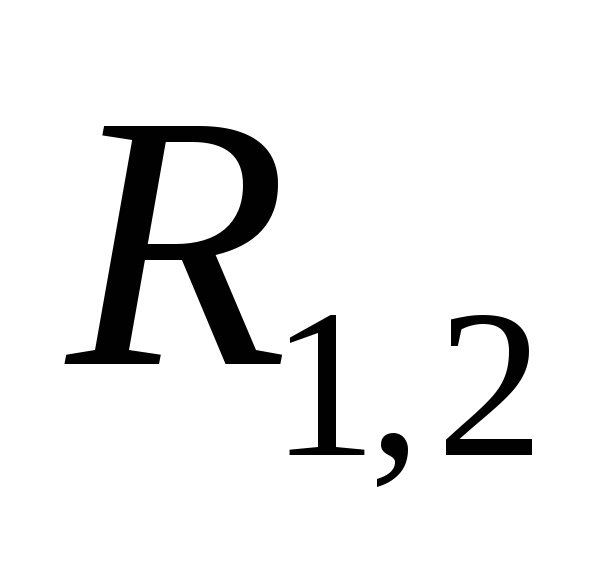 :
:
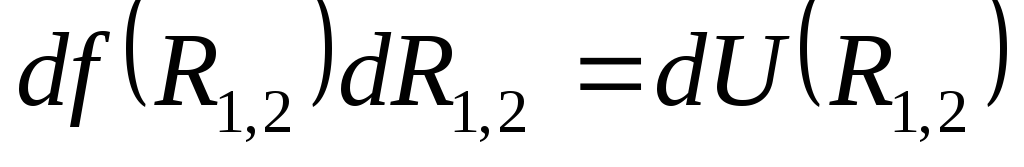 .
.
Следовательно,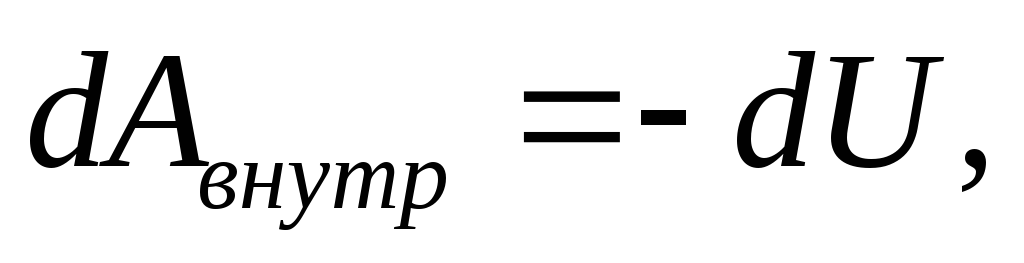 и
выражение (4.14) можно представить в виде:
и
выражение (4.14) можно представить в виде:
 .
.
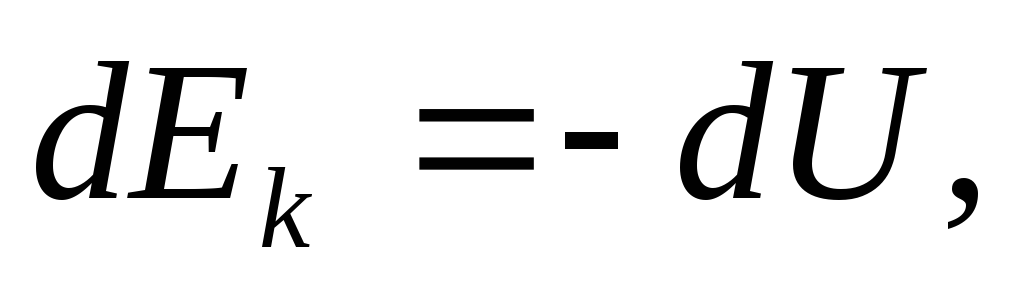 или
или 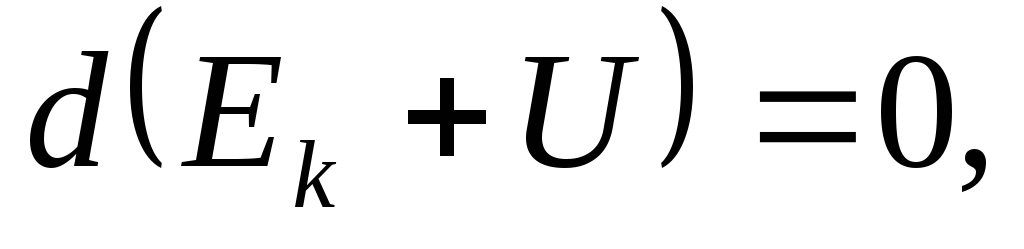 таким
образом, величина
таким
образом, величина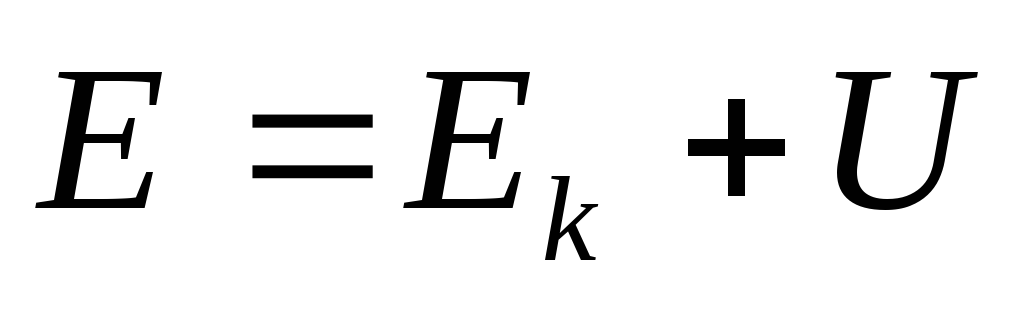 для
замкнутой системы сохраняется. Функция
для
замкнутой системы сохраняется. Функция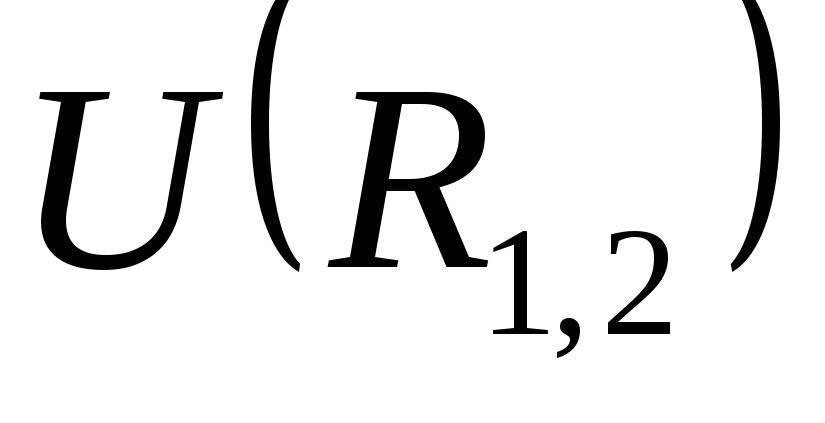 представляет собой потенциальную
энергию взаимодействия. Она зависит от
расстояния между частицами. Работа
внутренних сил
представляет собой потенциальную
энергию взаимодействия. Она зависит от
расстояния между частицами. Работа
внутренних сил
Т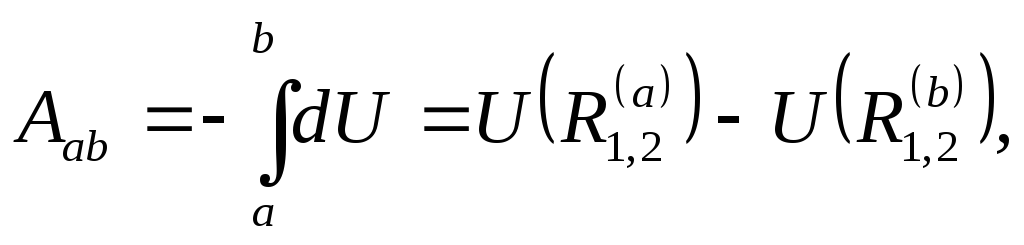 .е.
не зависит от путей, по которым перемещались
частицы, а определяется только начальными
и конечными расстояниями между частицами.
Таким образом, силы взаимодействия вида
(4.13) являются консервативными.
.е.
не зависит от путей, по которым перемещались
частицы, а определяется только начальными
и конечными расстояниями между частицами.
Таким образом, силы взаимодействия вида
(4.13) являются консервативными.
Центральные силы и их поля — Википедия
Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка K{\displaystyle K} на рис.1)[1].
Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды.
Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой[2]. Распределенные системы, в которых действуют центральные силы, в общем случае[3] не могут быть представлены конечным количеством материальных точек. В случае распределённых систем общим подходом является разбиение их на очень большое (в пределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый (которые и рассматриваются как материальные точки), между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией) таких элементарных сил.
Классическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы. [4]
Рис.1 К определению центральной силы: α{\displaystyle \alpha } частица в поле атомного ядра.(опыт Резерфорда)- Для любой центральной силы F→{\displaystyle {\vec {F}}} выполняется соотношение
- M→=r→×F→=0,{\displaystyle {\vec {M}}={\vec {r}}\times {\vec {F}}=0,}
(где M — момент сил, r→{\displaystyle {\vec {r}}} — радиус-вектор с началом в центре силы), свидетельствующее о равенстве нулю момента силы относительно центра силы:
Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения). Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.
Величина, характеризующая интенсивность центрального силового поля, представляет собой вектор, направленный по линии, соединяющей точечный источник и заданную точку поля.
Потенциальные центральные поля[править | править код]
Работа центральной силы[править | править код]
Элементарная работа dA{\displaystyle dA} силы, в том числе и центральной силы, есть скалярная величина, исчисляемая изменением энергии при перемещении точки приложения силы F→{\displaystyle {\vec {F}}} (в общем случае изменяющей свою величину и направление), при перемещении на столь малый отрезок своей траектории, что на нём вектор силы может считаться неизменным, то есть на расстояние d→r{\displaystyle {\vec {d}}r} :
dA=F→d→r=Fcosαdr{\displaystyle dA={\vec {F}}{\vec {d}}r=F\cos \alpha dr} (5)
где α{\displaystyle \alpha } есть угол между этими векторами. Поскольку cosα=cos(−α){\displaystyle \cos \alpha =\cos(-\alpha )}, то направление отсчёта угла значения не имеет.
При перемещении на расстояние от r1{\displaystyle r_{1}} до r2{\displaystyle r_{2}}, весь пройденный путь можно разбить на i{\displaystyle i} элементарных участков. И тогда полная работа A{\displaystyle A} будет суммой этих элементарных работ с тем большей точностью, чем на большее количество участков n{\displaystyle n} будет разбита траектории, что выражается знаком интеграла, как предела этой суммы :
A=lim∑i=1nFicosiαi dri=∫r1r2F→rdr→(6){\displaystyle A=\lim \sum _{i=1}^{n}{F_{i}}\cos _{i}\alpha _{i}\ dr_{i}=\int \limits _{r_{1}}^{r_{2}}{\vec {F}}_{r}d{\vec {r}}(6)}
Рассматривая движение в декартовой системе координат, центральную силу можно представить в виде геометрической суммы её проекций на координатные оси:
F→=F→x+F→y+F→z=Fxi→+Fyj→+Fzk→(7){\displaystyle {\vec {F}}={\vec {F}}_{x}+{\vec {F}}_{y}+{\vec {F}}_{z}=F_{x}{\vec {i}}+F_{y}{\vec {j}}+F_{z}{\vec {k}}(7)}
где i→{\displaystyle {\vec {i}}} ,j→{\displaystyle {\vec {j}}} ,k→{\displaystyle {\vec {k}}} суть единичные векторы (орты) для своих осей.
Потенциал поля[править | править код]
Не для всякого поля силы совершаемая ею работа зависит лишь от положения начальной и конечной точек движения. Иными словами, не зависит от формы пути.
Упомянутый интеграл не будет зависеть от формы пути лишь в том случае, если будет существовать некая первообразная функция U{\displaystyle U}, в выражении полного дифференциала которой:
- dU=∂U∂xdx+∂U∂ydy+∂U∂zdz(8){\displaystyle dU={\frac {\partial U}{\partial x}}dx+{\frac {\partial U}{\partial y}}dy+{\frac {\partial U}{\partial z}}dz(8)}
её частные производные будут соответствовать проекциями силы (по существующему обычному соглашению — с точностью до знака):
- dU=−Fxdx−Fydy−Fzdz(9){\displaystyle dU=-F_{x}dx-F_{y}dy-F_{z}dz(9)}
В этом случае функция U{\displaystyle U} будет называться потенциальной функцией, а поле силы — потенциальным полем.[5]
Но это станет возможным лишь при одновременном выполнении равенств:
∂Fy∂z=∂Fz∂y;∂Fz∂x=∂Fx∂z;∂Fx∂y=∂Fy∂x(10){\displaystyle {\frac {\partial F_{y}}{\partial z}}={\frac {\partial F_{z}}{\partial y}};{\frac {\partial F_{z}}{\partial x}}={\frac {\partial F_{x}}{\partial z}};{\frac {\partial F_{x}}{\partial y}}={\frac {\partial F_{y}}{\partial x}}(10)}
Для центральных сил это условие выполняется. Поле, в котором выполнены эти условия, называется безвихревым полем. Поэтому потенциальные поля суть поля безвихревые.[5]
Знак минус в формуле, связывающей потенциальную функцию и силу, определяется желанием отождествить потенциальную функцию с потенциальной энергией[6] (в противном случае можно было бы обойтись без знака минус, что иногда и делается при введении потенциальной функции чисто формально, особенно для векторного поля, не имеющего характера силы).
Связь с потенциальной энергией естественно осуществляется через работу.
Представляется естественным считать, что вектор напряжённости поля направлен ОТ источника поля, (что привычно принимается при описании электростатического поля при взаимодействии одноимённых зарядов[7]) Тогда, зафиксировав точку, находящуюся на расстоянии r1{\displaystyle r_{1}} от центрального заряда и предоставив ему свободу, получим, что он под действием силы будет удаляться в бесконечность. При этом совершённая полем работа будет равна:
Ar1=∫r11F→rdr→(11){\displaystyle A_{r_{1}}=\int \limits _{r_{1}}^{\mathcal {1}}{\vec {F}}_{r}d{\vec {r}}(11)}.
То же можно сказать и в случае, если поле продвинуло тело дальше r2>r1{\displaystyle r_{2}>r_{1}} и, следовательно, проделало больше работы и потому разница работ на пути между точками больше нуля.
И эти работы может быть названа с точностью до постоянной потенциалом точки: Ul1{\displaystyle U_{l1}} и Ul2{\displaystyle U_{l2}}, подразумевая под потенциалом возможность совершить работу, которая для более близкой точки выше, чем у более далёкой.
Тогда совершённая полем работа будет равна разности потенциалов, взятой со знаком «минус»
A=∫r1r2F→rdr→=Ul1−Ul2=−ΔU(12){\displaystyle A=\int \limits _{r_{1}}^{r_{2}}{\vec {F}}_{r}d{\vec {r}}=U_{l1}-U_{l2}=-\Delta U(12)}
Таким образом работа силы на пути из начальной точки в конечную равна изменению потенциальной функции, являющейся скалярной функцией расстояния. В таком случае для каждой точки пути можно с точностью до постоянной величины приписать свой потенциал:U{\displaystyle U}
Поле как градиент потенциала[править | править код]
В поле центральной силы её составляющая по данной оси представляет собой скорость изменения потенциальной функции по этой же оси или же градиент функции по заданному направлению.
Для описания изменения потенциальной функции по произвольному направлению в теории поля введён векторный дифференциальный оператор, имеющий вид:
- ∇≡∂∂xi→+∂∂yj→+∂∂zk→(13){\displaystyle \nabla \equiv {\frac {\partial }{\partial x}}{\vec {i}}+{\frac {\partial }{\partial y}}{\vec {j}}+{\frac {\partial }{\partial z}}{\vec {k}}(13)}
Применяя этот оператор к потенциальной функции получаем, что в данной точке поля сила является (с точностью до знака) градиентом потенциала:
- F→=Fxi→+Fyj→+Fzk→=F→x+F→y+F→z=−∇U≡−gradU(14).{\displaystyle {\vec {F}}=F_{x}{\vec {i}}+F_{y}{\vec {j}}+F_{z}{\vec {k}}={\vec {F}}_{x}+{\vec {F}}_{y}+{\vec {F}}_{z}=-\nabla U\equiv -\mathbf {grad} U(14).}
Знак минус, по обычному соглашению присутствующий в этой формуле, связан с тем, чтобы функция U могла быть отождествлена с потенциальной энергией (хотя чисто формально потенциальная функция могла бы быть выбрана и с другим знаком, если такого отождествления не предполагается).
Кулоновское поле[править | править код]
Напряженность кулоновского поля определяется вектором E→{\displaystyle {\vec {E}}}, равным:
E→=CQQr→r3(15){\displaystyle {\vec {E}}=C_{Q}{\frac {Q{\vec {r}}}{r^{3}}}(15)}
или, переходя, к скалярной форме записи:
E=CQQr2(16){\displaystyle E=C_{Q}{\frac {Q}{r^{2}}}(16)}
Здесь E=‖E→‖{\displaystyle E=\lVert {\vec {E}}\rVert }; Q{\displaystyle Q} — заряд тела -источника силы; r=‖r→‖{\displaystyle r=\lVert {\vec {r}}\rVert },есть расстояние до точки, где определяется интенсивность, а константа CQ{\displaystyle C_{Q}} зависит от диэлектрической постоянной среды ε{\displaystyle \varepsilon }, (для пустого пространства равная 1), в которой существует поле:
CQ=14πεε0{\displaystyle C_{Q}={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}}, где:
ε0{\displaystyle \varepsilon _{0}} есть диэлектрическая постоянная вакуума. В таком случае для вакуума
CQ=14πε0{\displaystyle C_{Q}={\frac {1}{4\pi \varepsilon _{0}}}} = 1010{\displaystyle 10^{10}} Vm/As в Международной системе единиц[8],
Кулоновские силы[править | править код]
Объектом действия кулоновского поля является материальное тело, несущее заряд q{\displaystyle q}
В таком случае на него действует механическая (ньютонова) сила электрического происхождения, равная произведению величины заряда на напряжённость поля:
или, с учётом ():
F→q=CQqQr→r3(17){\displaystyle {\vec {F}}_{q}=C_{Q}{\frac {qQ{\vec {r}}}{r^{3}}}(17)} или, в скалярном представлении:
Fq=CQqQr2(18){\displaystyle F_{q}=C_{Q}{\frac {qQ}{r^{2}}}(18)}
Специфической особенностью кулоновского поля является то, что вектор его напряжённости направлен либо ОТ источника поля в случае совпадение знака заряда источника и объекта взаимодействия, либо направлен К источнику в случае разноимённости зарядов. Это значит, что заряженные материальные тела в первом случае будут испытывать отталкивающую силу, а в противоположном — силу сближающую их.
Ещё одним свойством кулоновского поля является техническая возможность выделить область пространства, в котором оно будет в требуемой степени отсутствовать (клетка Фарадея)
Поле гравитации[править | править код]
В русскоязычной литературе интенсивность поля тяготения называют «ускорением свободного падения» g→{\displaystyle {\vec {g}}}, за рубежом иногда её называют напряжённостью гравитационного поля.
g→=GMr→r3(19){\displaystyle {\vec {g}}=G{\frac {M{\vec {r}}}{r^{3}}}(19)}
Или, переходя к скалярной форме записи: g=GMr2(20){\displaystyle g=G{\frac {M}{r^{2}}}(20)}
Здесь g=‖g→‖{\displaystyle g=\lVert {\vec {g}}\rVert }; M{\displaystyle M} — масса тела -источника гравитации; r=‖r→‖{\displaystyle r=\lVert {\vec {r}}\rVert } есть расстояние до точки, где определяется интенсивность, а константа G{\displaystyle G} есть гравитационная постоянная, равная по современным данным G=6,6742∗10−11m3kg∗s2{\displaystyle G=6,6742*10^{-11}{\frac {m^{3}}{kg*s^{2}}}}, [9]
Силы гравитации[править | править код]
Объектом действия поля гравитации является материальное тело, имеющее массу m{\displaystyle m}
В таком случае на него действует механическая сила, равная произведению массы m{\displaystyle m} тела на напряжённость поля. Существенно, что между массой, входящей во второй закон Ньютона и массой того же тела, подверженного действию гравитации, нет никакой разницы в величине. Тогда, с учётом ():
F→g=mg→(21){\displaystyle {\vec {F}}_{g}=m{\vec {g}}(21)}
или, в скалярном представлении:
Fg=mg (22){\displaystyle F_{g}=mg\ (22)}
Специфической особенностью сил гравитации является то, что они всегда являются силами притяжения. Кроме того, силы гравитации всепроникающи, и от них невозможно защититься никаким экраном. Это свойство объединяет силы гравитации с фиктивными силами инерции, существующими в любой неинерциальной системе отсчёта. Подобная аналогия имеет своей основой фундаментальные свойства пространства, изучения которых выходит за рамки классической физики.[10]
Потенциал поля гравитации[править | править код]
Подставляя в (6) значение силы Всемирного тяготения из (20), получаем с учётом того, что работа была совершена против поля:
A=−GmM∫r1r2r→r3dr→=−GmM(1r2−1r1)=U2−U1{\displaystyle A=-GmM\int \limits _{r_{1}}^{r_{2}}{\frac {\vec {r}}{r^{3}}}d{\vec {r}}=-GmM\left({\frac {1}{r_{2}}}-{\frac {1}{r_{1}}}\right)=U_{2}-U_{1}} (23)
Таким образом каждой точке гравитационного поля можно с точностью до постоянной присвоить свой потенциал, как:
Ur=−GmM(1r){\displaystyle U_{r}=-GmM\left({\frac {1}{r}}\right)}[11](24)
Движение под действием центральной силы[править | править код]
В общем случае любую траекторию тела, рассматриваемого как материальная точка, можно представить в виде пространственной кривой, состоящей из сопряжённых поворотов в различных плоскостях вокруг мгновенных центров поворота с различными значениями радиуса поворота rc{\displaystyle r_{c}} на том же Рис 1.Применение представления о траектории реального трёхмерного тела смысла не имеет.
Но кривизна траектории отнюдь не значит, что на тело действует некая сила, для каждого момента являющейся силой центростремительной.
Замечание
Последняя оговорка весьма существенна. Так, например, для земного наблюдателя бомба, сброшенная с летящего равномерно и прямолинейно летательного аппарата движется по параболе. Но для пилота она падает вертикально под действием единственной в данном случае силы тяжести (если не принимать во внимание снос из-за сопротивления воздуха). Никаких сил, вызывающих искривление траектории, здесь нет. Центростремительные силы возникают не потому, что траектория крива, но потому, что они являются выражением реально имеющего место силового взаимодействия движущегося объекта со своим окружением.
Считается, что в центре силы находится источник силы, которым может быть тяготеющая масса, либо электрический заряд в случае, если рассматриваемая сила есть характеристика соответствующего силового поля. Центр силы в общем случае не совпадает с мгновенным центром поворота — точка C{\displaystyle C} на Рис. Это совпадение имеет место лишь при повороте тела по дуге окружности. [4]
Как видно на Рис.1 единственная действующая между телами α{\displaystyle \alpha } и K{\displaystyle K} сила F→{\displaystyle {\vec {F}}} может быть разложена на две составляющие: F→=F→t+F→n{\displaystyle {\vec {F}}={\vec {F}}_{t}+{\vec {F}}_{n}} (2)
При этом F→t{\displaystyle {\vec {F}}_{t}} есть тангенциальная сила, в зависимости от направления движения тела по своей траектории на рисунке либо тормозящая его движение, либо ускоряющая его.
F→n{\displaystyle {\vec {F}}_{n}} есть сила, направленная по нормали к касательной к траектории в сторону мгновенного центра и потому являющаяся центростремительной силой.[12]
Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса) следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела L→{\displaystyle {\vec {L}}} прямо пропорциональна величине приложенного к телу момента силы M→{\displaystyle {\vec {M}}}:
dL→dt=M→(3){\displaystyle {\frac {d{\vec {L}}}{dt}}={\vec {M}}(3)}
Однако в поле центральной силы её момент всегда равен нулю (Формула (1)). Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:
L→=const(4){\displaystyle {\vec {L}}=const(4)}. Но, поскольку постоянство вектора есть одновременно и сохранение его направления в пространстве, то заметаемая при движении тела площадка всегда лежит в одной и той же плоскости. Из этого следует, что любая траектория движения тела под действием центральной силы есть плоская кривая.
Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где преобладают гравитационные воздействия, и потому изучаемая система взаимодействующих сил может рассматриваться как консервативная система, то есть такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.[4]
E=Wk+Wp{\displaystyle E=W_{k}+W_{p}} (25), где:
Wk=m2(vn2+vt2)(26){\displaystyle W_{k}={\frac {m}{2}}(v_{n}^{2}+v_{t}^{2})(26)} причём vn{\displaystyle v_{n}} и vt{\displaystyle v_{t}} соответствуют скоростям, создаваемым нормальной и тангенциальной составляющей действующей на тело силы на Рис.1
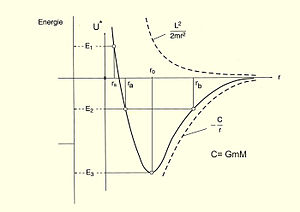 Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты
Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планетыВоспользовавшись определением кинетического момента:L=mrvt{\displaystyle L=mrv_{t}} получаем для кинетической энергии тангенциального движения соотношение:
Wk(t)=L22mr2(27){\displaystyle W_{k}(t)={\frac {L^{2}}{2mr^{2}}}(27)} .
А для движения по нормали к траектории: Wk(n)=mvn22(28){\displaystyle W_{k}(n)={\frac {mv_{n}^{2}}{2}}(28)}
Wp=GmMr(29){\displaystyle W_{p}={\frac {GmM}{r}}(29)}
Тогда выражение для полной энергии тела будет иметь вид:
E=mvn22+L22mr2−GmMr(30){\displaystyle E={\frac {mv_{n}^{2}}{2}}+{\frac {L^{2}}{2mr^{2}}}-{\frac {GmM}{r}}(30)}
Введя в рассмотрение эффективный потенциал U∗{\displaystyle U^{*}} :
U∗=L22mr2−GmMr(31){\displaystyle U^{*}={\frac {L^{2}}{2mr^{2}}}-{\frac {GmM}{r}}(31)}
Получаем возможность связать диапазон изменения длины радиус-вектора траектории тела с запасённой им энергией, что представлено на рис.2[13]
Так при минимальной энергии движущегося тела E3{\displaystyle E_{3}} тело движется по круговой орбите с радиусом
Потенциальное поле и его свойства
Векторное
поле 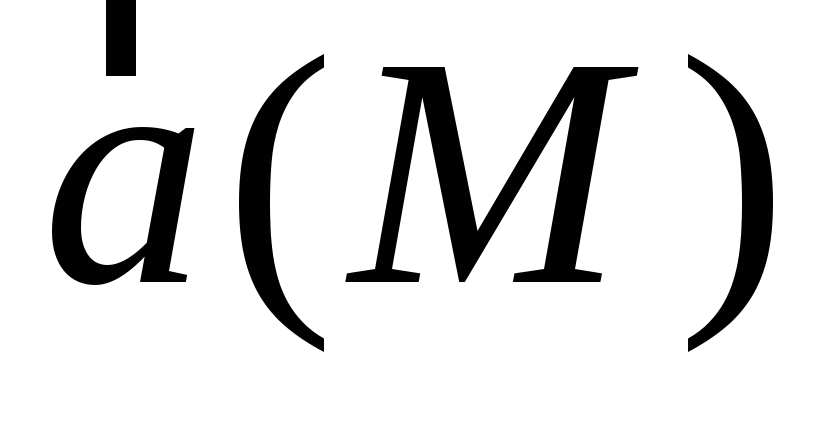 называетсяпотенциальным,
если существует такое скалярное поле
называетсяпотенциальным,
если существует такое скалярное поле  (потенциал векторного поля
(потенциал векторного поля 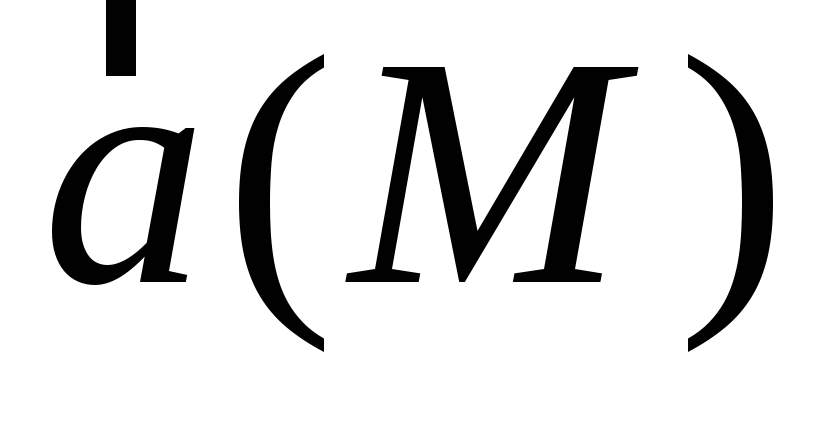 ),
что
),
что =
=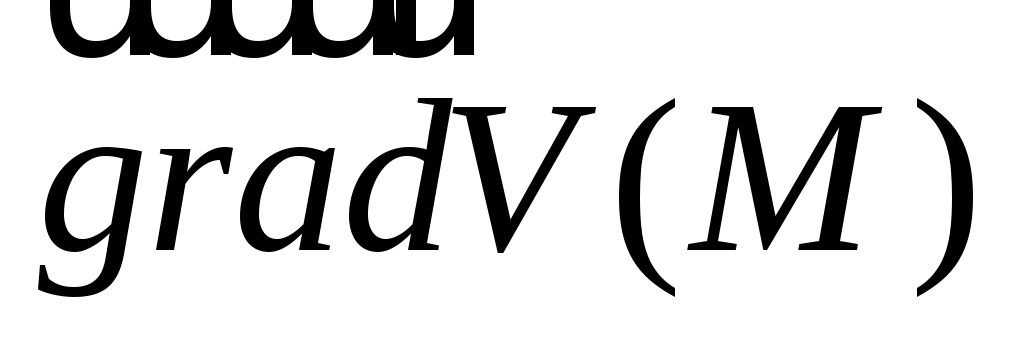 .
.
Замечание.
Если поле 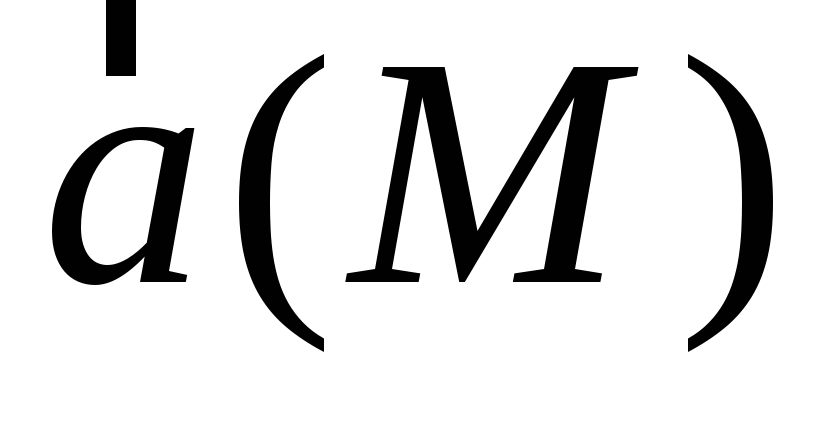 — потенциально, то
— потенциально, то
 =
=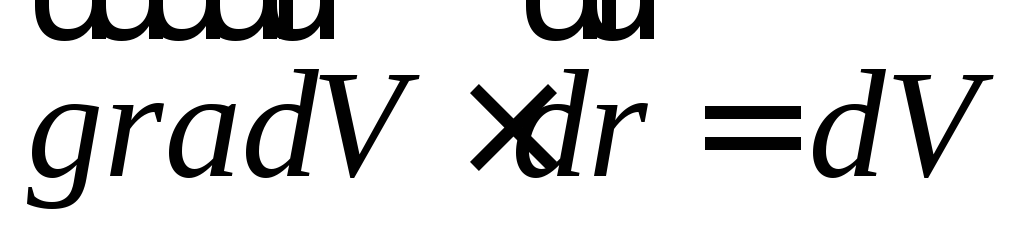 —
полный дифференциал. Тогда
—
полный дифференциал. Тогда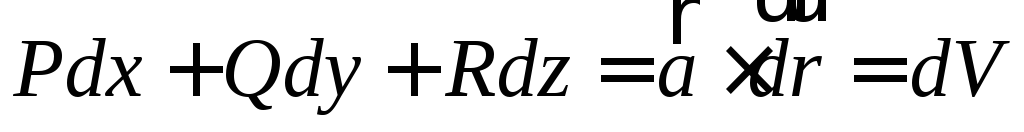 —
полный дифференциал. Поэтому свойства
потенциального поля можно сформулировать
и доказать как следствия теоремы о
полном дифференциале.
—
полный дифференциал. Поэтому свойства
потенциального поля можно сформулировать
и доказать как следствия теоремы о
полном дифференциале.
Свойства потенциального поля.
Линейный интеграл потенциального поля
 не зависит от формы дугиL
=
не зависит от формы дугиL
=  ,
а зависит только от начальной и конечной
точек дуги.
,
а зависит только от начальной и конечной
точек дуги.
В
самом деле, 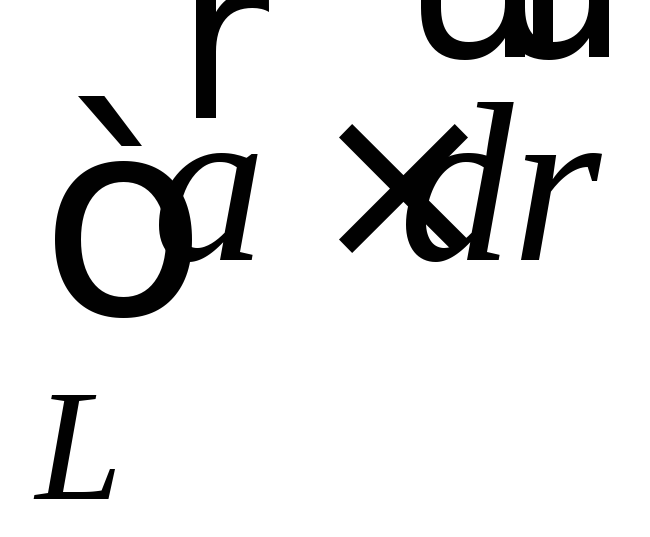 =
=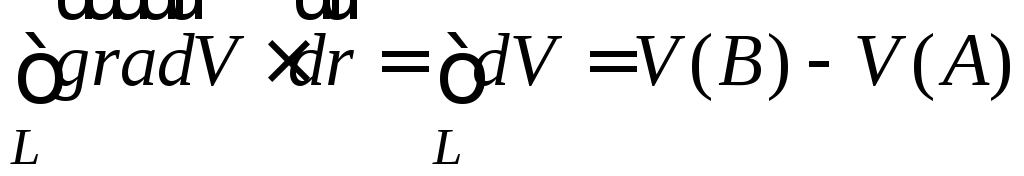 .
.
Циркуляция потенциального поля равна нулю
Полагая
дугу АВ замкнутой (A
= B),
получаем 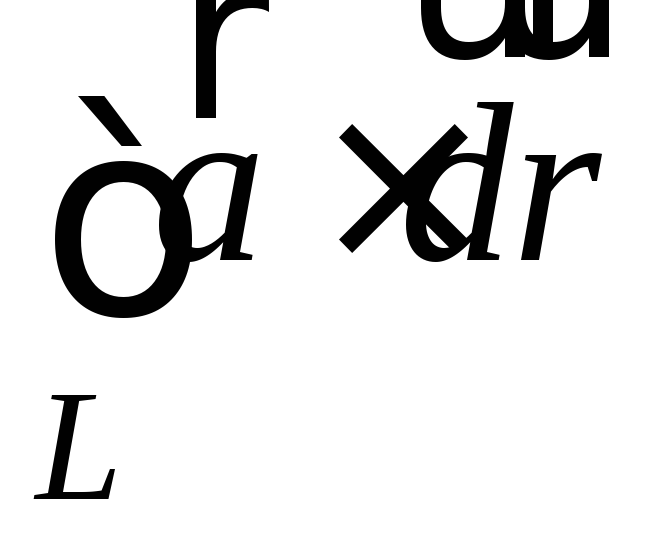 =
=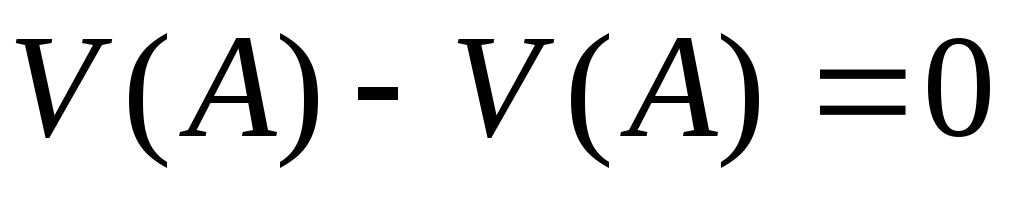
Потенциальное поле является безвихревым, т.е.

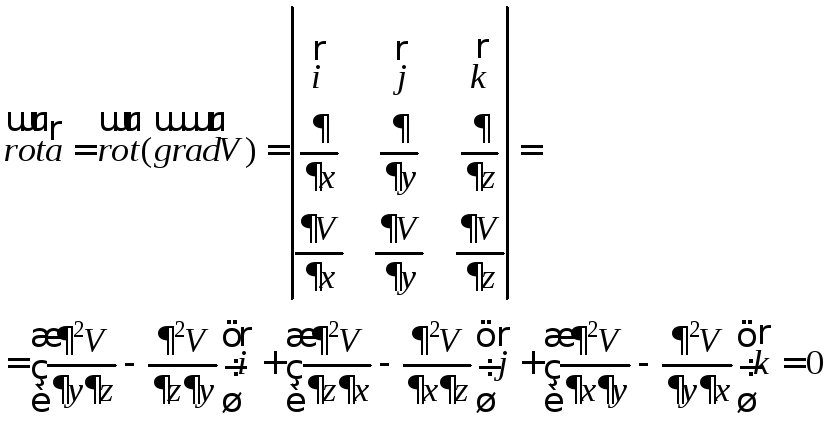
Оператор Гамильтона
Оператор
Гамильтона 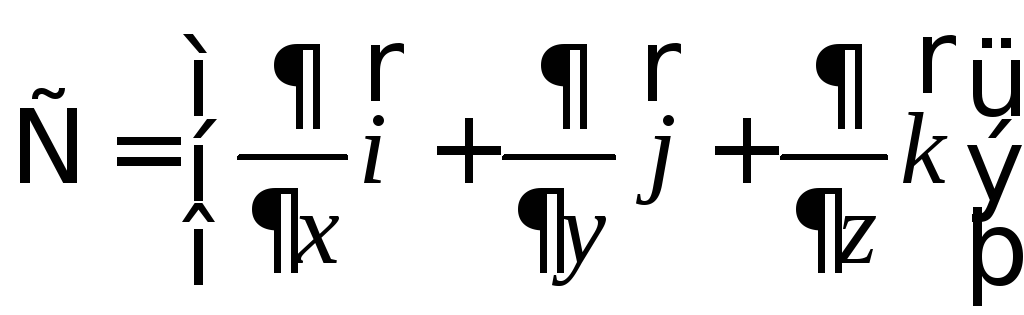 .
.
Применим
оператор Гамильтона к скалярному полю 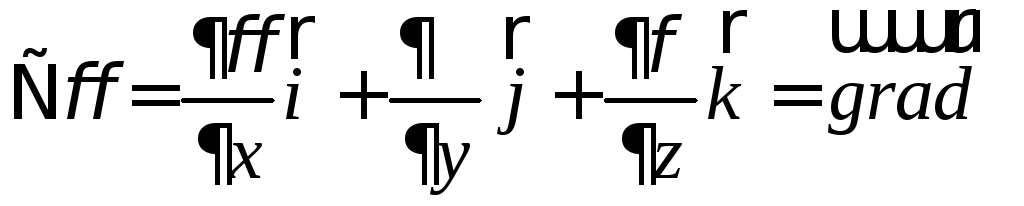 .
.
Оператор
Гамильтона представляет собой
вектор-оператор. Его можно скалярно или
векторно умножить на векторное поле 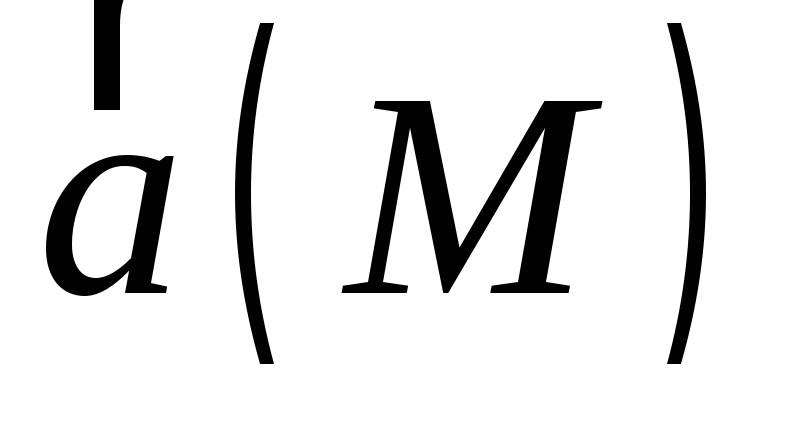 .
.
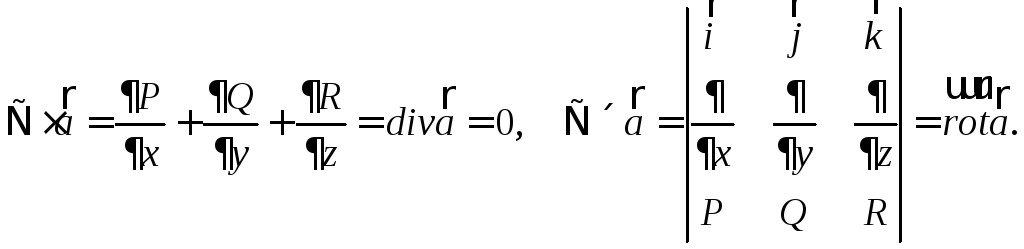
Это дифференциальные операции первого порядка над скалярным и векторным полями. От скалярного поля можно взять градиент, от векторного поля можно взять дивергенцию и ротор.
Дифференциальные операции второго порядка
В
результате дифференциальных операций
первого порядка мы получаем скалярные
и векторные поля  .
.
К ним вновь можно применить дифференциальные операции первого порядка.
От
скалярного поля 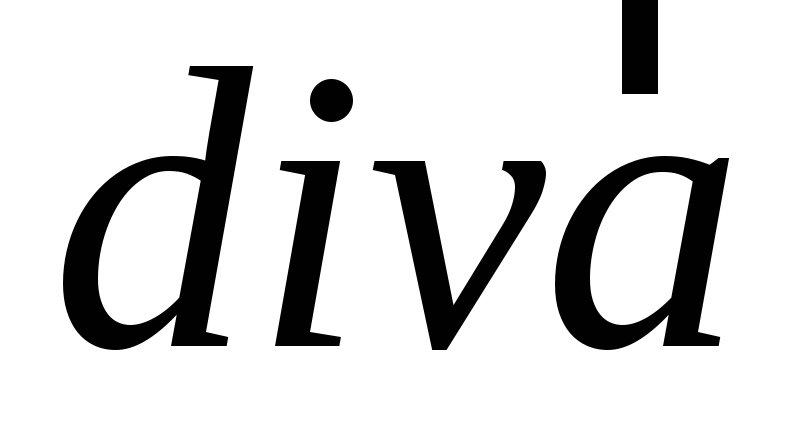 можно
взять градиент, получив векторное поле
можно
взять градиент, получив векторное поле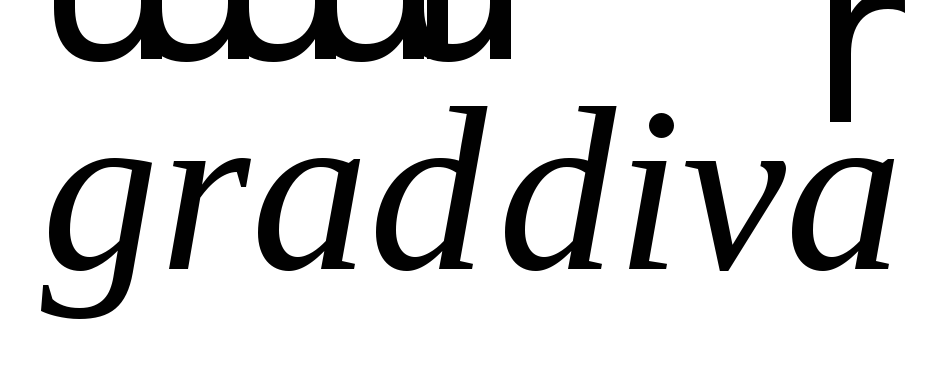 .
.
От
векторных полей  можно
взять ротор и дивергенцию, получив
скалярные поля
можно
взять ротор и дивергенцию, получив
скалярные поля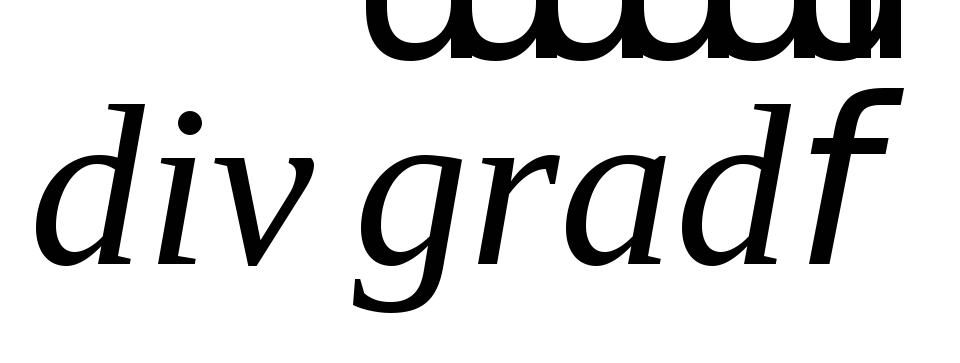 ,
, и
векторные поля
и
векторные поля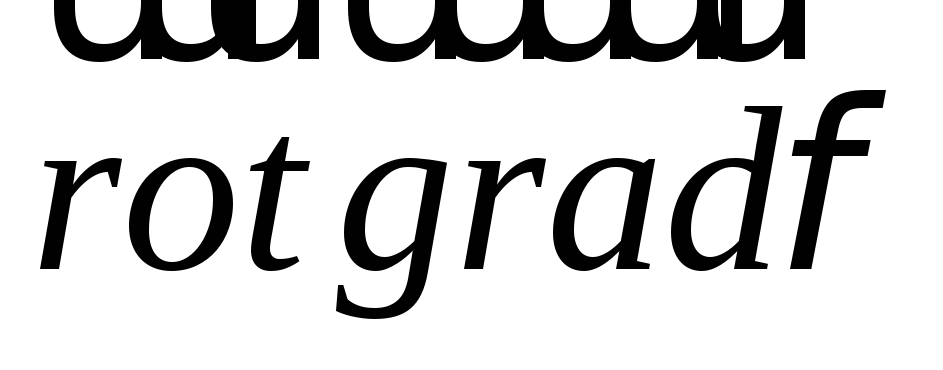 ,
,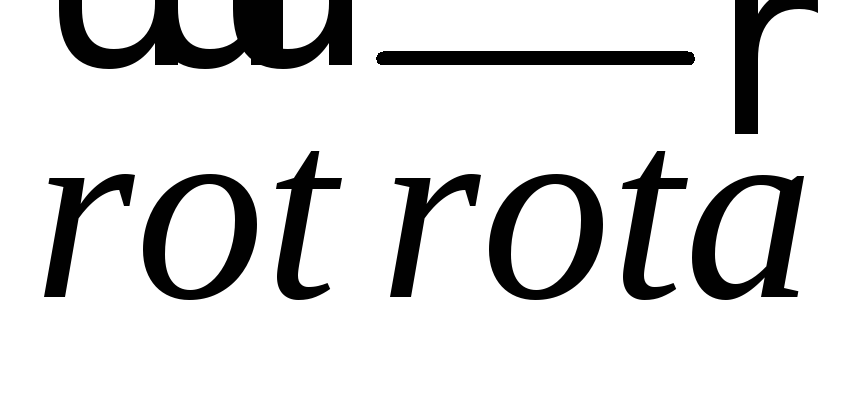 .
.
Итак,
дифференциальные операции второго
порядка позволяют получить скалярные
поля  ,
, и векторные поля
и векторные поля ,
,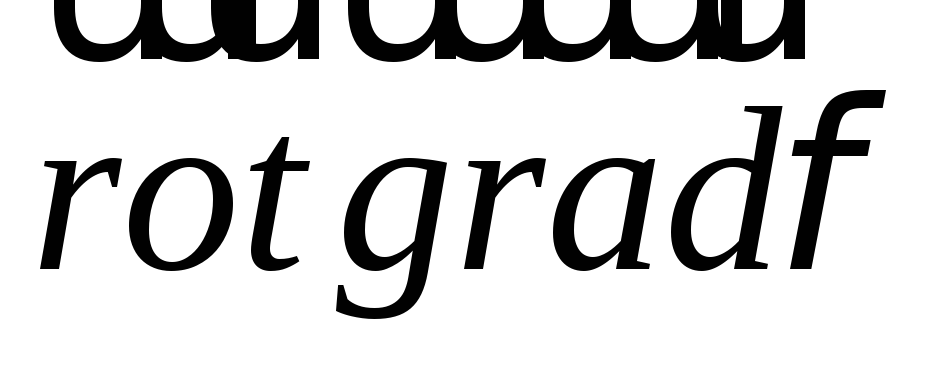 ,
, .
.
Ранее
было показано, что потенциальное
поле – безвихревое,
т.е.  =0.
=0.
Покажем,
что поле
ротора – соленоидальное поле,
т.е.  =0.
=0.
Доказательство.
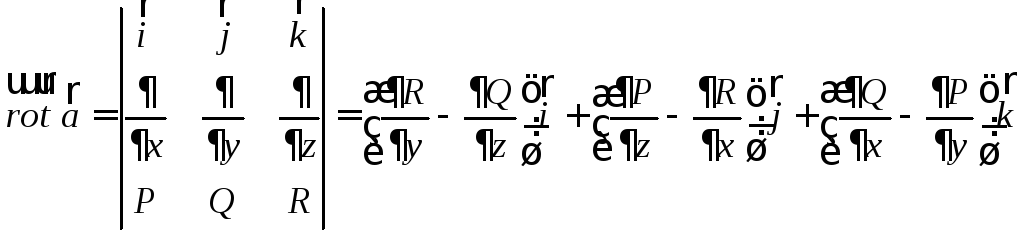
 =
= 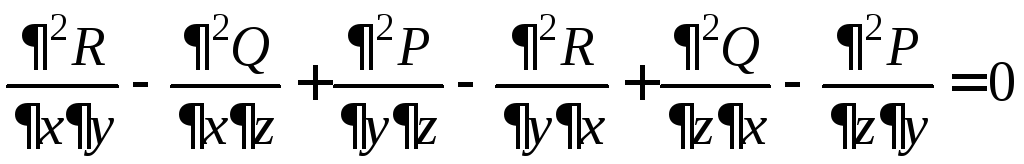 .
.
Три остальных векторных поля связаны друг с другом. Это становится ясным, если рассматривать векторные операции с оператором Гамильтона «набла» аналогично обычным векторным операциям. Однако, эти аналогии не совсем верны, см. подробнее о свойствах оператора «набла» выпуск 7 учебника.
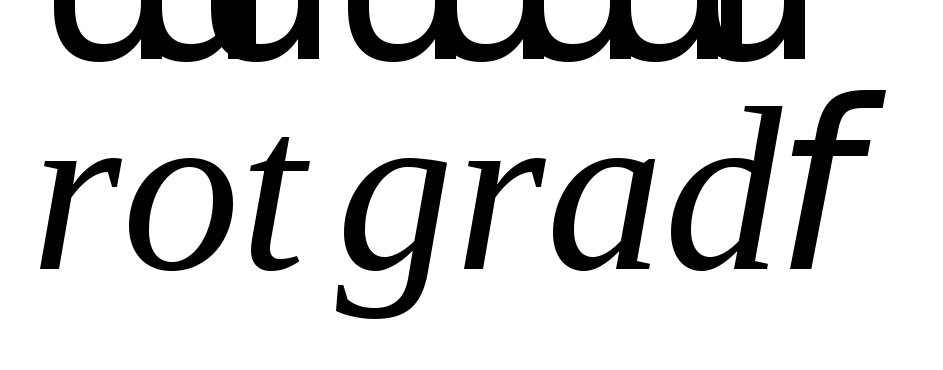 =
= ,
,
 =
=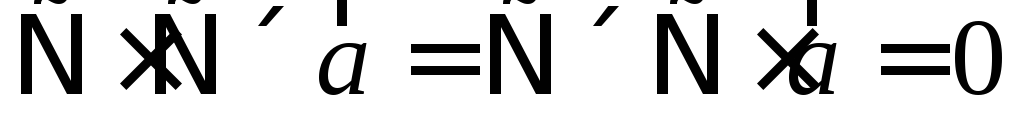
Известно
соотношение 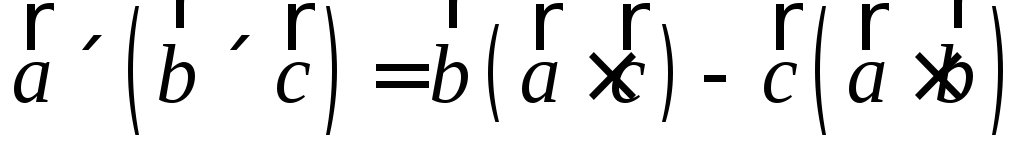 .
Перенося это правила на действия с
оператором «набла», получим
.
Перенося это правила на действия с
оператором «набла», получим
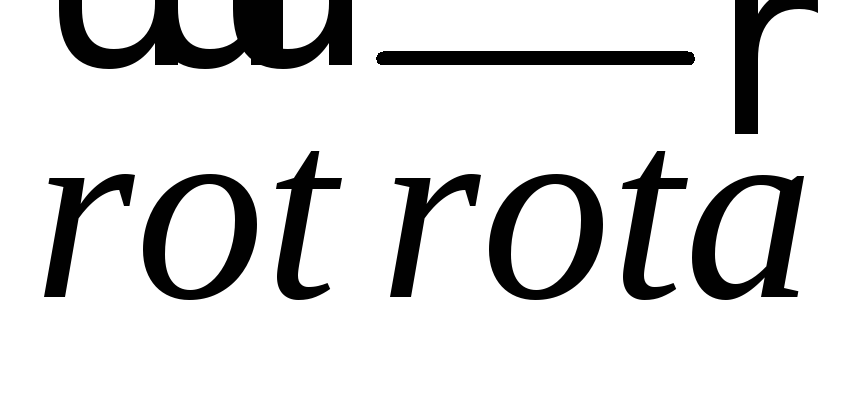
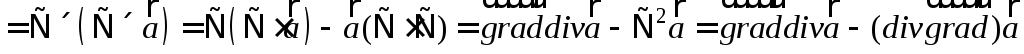 .
.
Здесь  — оператор Лапласа (скаляр – оператор).
— оператор Лапласа (скаляр – оператор).
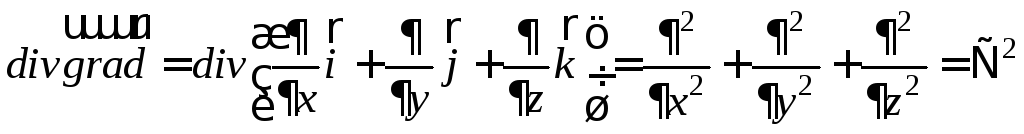 .
.
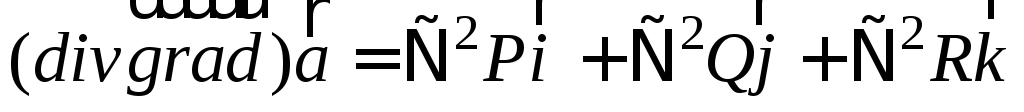 —
произведение скаляр-оператора Лапласа
на вектор
—
произведение скаляр-оператора Лапласа
на вектор  .
.
Гармоническое поле
Скалярное
поле 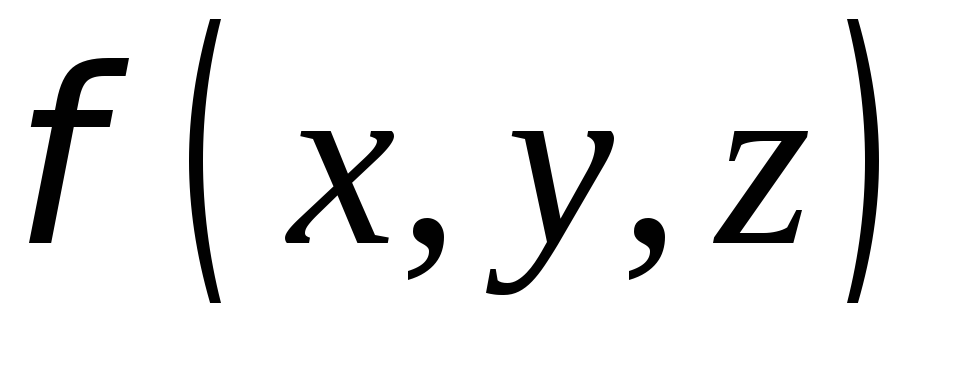 называется гармоническим, если
называется гармоническим, если
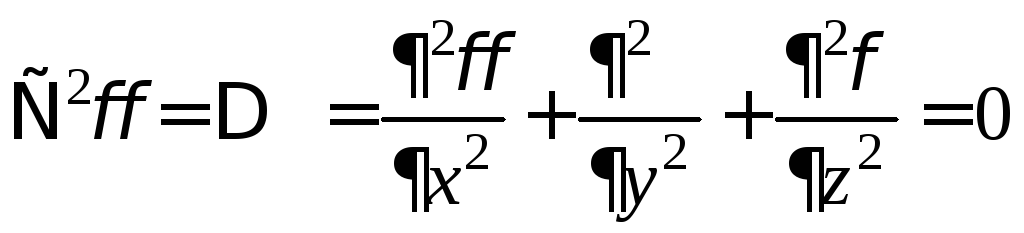 — уравнение
Лапласа.
— уравнение
Лапласа.
Векторное
поле называется гармоническим, если
оно потенциальное ( ),
а потенциал
),
а потенциал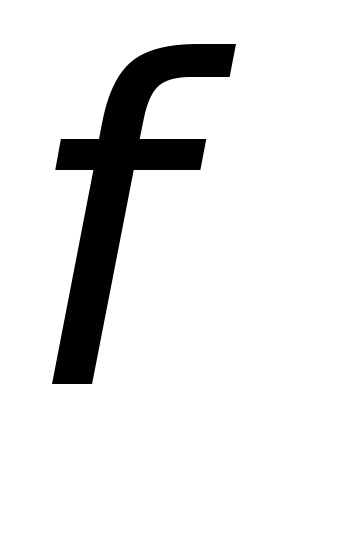 — гармоническое скалярное поле, т.е.
— гармоническое скалярное поле, т.е.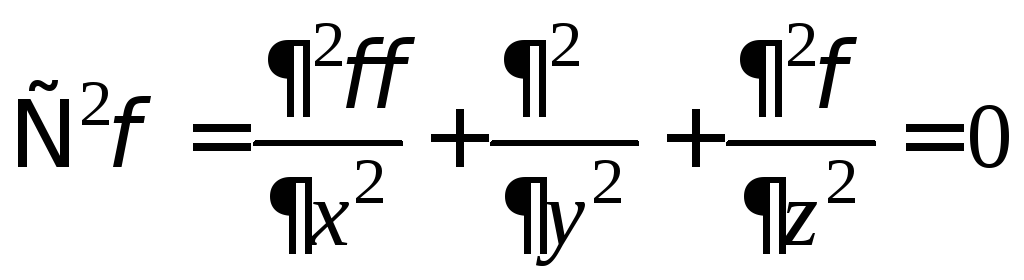 .
.
Теорема. Для того,
чтобы векторное поле  было гармоническим, необходимо и
достаточно чтобы оно было соленоидальным
и потенциальным.
было гармоническим, необходимо и
достаточно чтобы оно было соленоидальным
и потенциальным.
Необходимость.
Если векторное поле 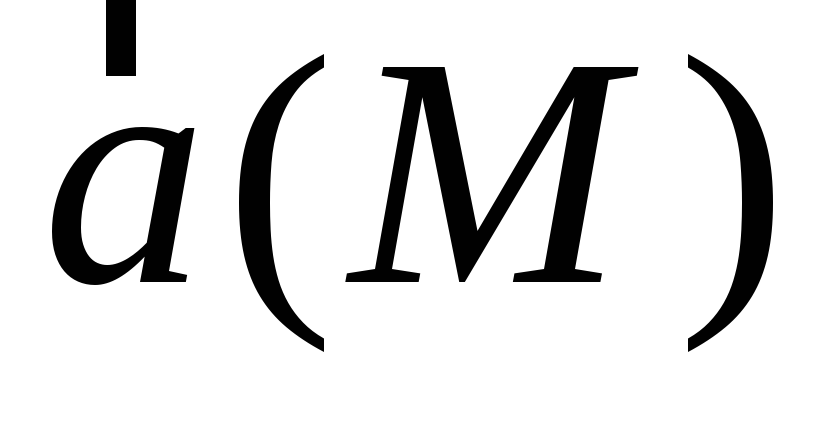 — гармоническое, то оно потенциальное,
т.е.
— гармоническое, то оно потенциальное,
т.е.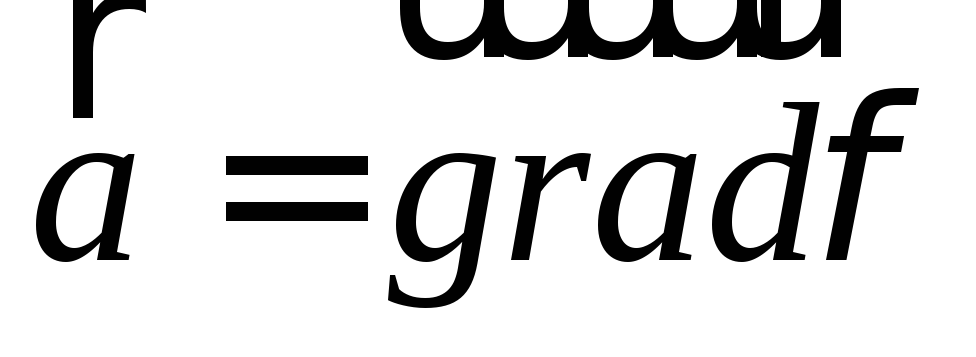 ,
тогда оно соленоидально, так как
,
тогда оно соленоидально, так как .
.
Достаточность.
Если векторное поле  потенциальное, то
потенциальное, то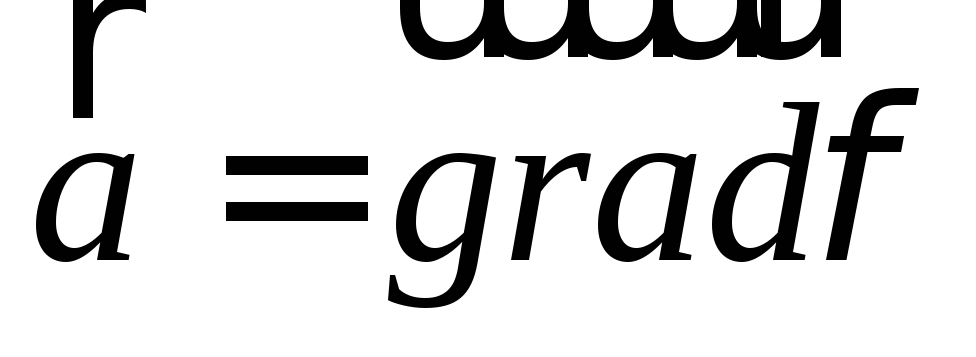 .
Так как оно еще и соленоидально, то 0 =
.
Так как оно еще и соленоидально, то 0 =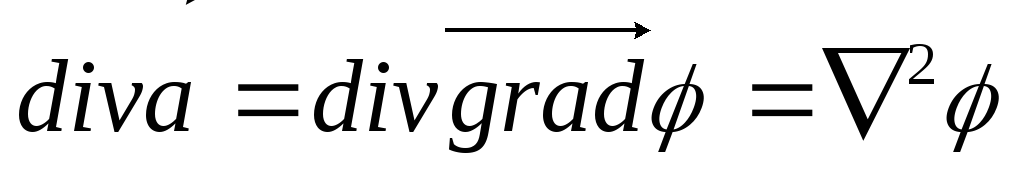 .
Следовательно, поле потенциально и его
потенциал удовлетворяет уравнению
Лапласа, поэтому векторное поле –
гармоническое.
.
Следовательно, поле потенциально и его
потенциал удовлетворяет уравнению
Лапласа, поэтому векторное поле –
гармоническое.
Так как гармоническое поле потенциально и соленоидально, то его свойства – свойства соленоидального поля и свойства потенциального поля.
Часть 2. Числовые и функциональные ряды Лекция 10. Числовые ряды и их свойства
Числовой
ряд  –
это сумма бесконечного количества
чисел, выбранных по определенному
алгоритму. Обычно задают формулу общего
члена ряда
–
это сумма бесконечного количества
чисел, выбранных по определенному
алгоритму. Обычно задают формулу общего
члена ряда  .
.
Примеры
1+
 —
бесконечно убывающая геометрическая
прогрессия со знаменателем
—
бесконечно убывающая геометрическая
прогрессия со знаменателем .
Ее сумма равна
.
Ее сумма равна ,
,1+1+1+…..Сумма этого ряда бесконечна.
1-1+1-1… Сумма этого ряда не существует (ни конечная, ни бесконечная).
При
изучении рядов возникает основной
вопрос: «Сходится ли ряд». Отвечая на
этот вопрос для геометрической прогрессии,
мы вычисляем последовательно  1+
1+ ,
, =1+
=1+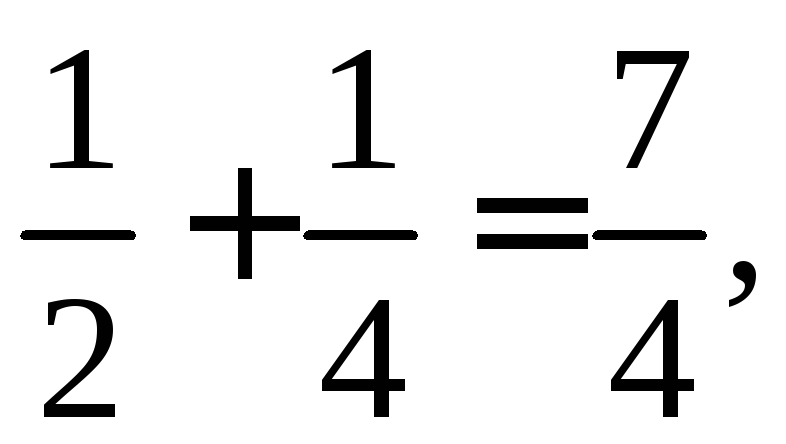 1+
1+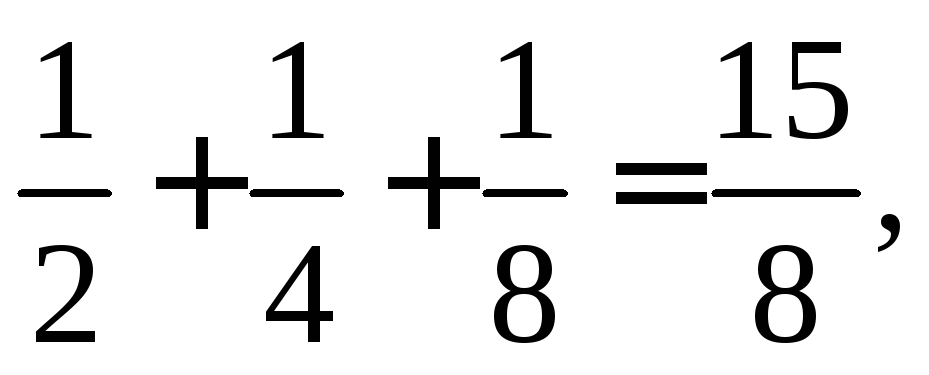 — суммыn членов ряда – частичные
суммы ряда
— суммыn членов ряда – частичные
суммы ряда 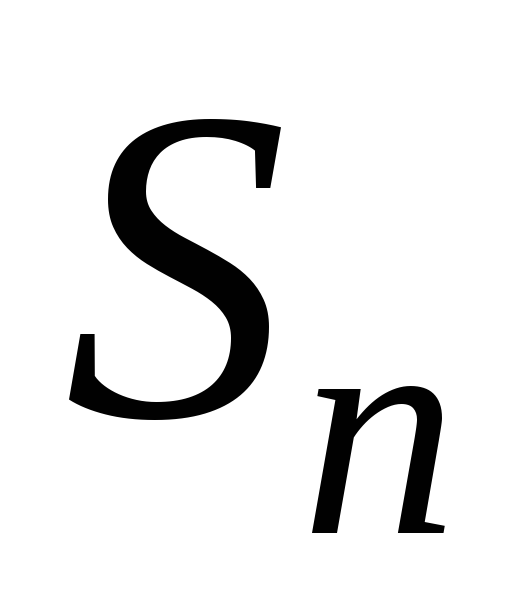 .
.
Ряд 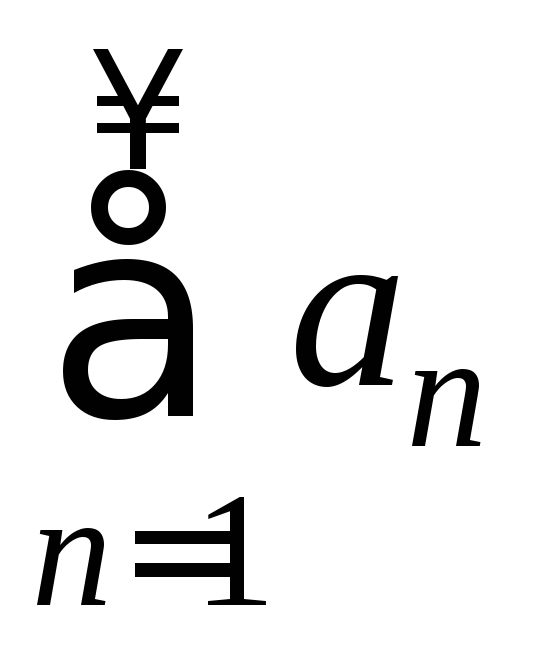 называетсясходящимся, если существует
конечный предел последовательности
частичных сумм ряда – он называется
суммой ряда
называетсясходящимся, если существует
конечный предел последовательности
частичных сумм ряда – он называется
суммой ряда 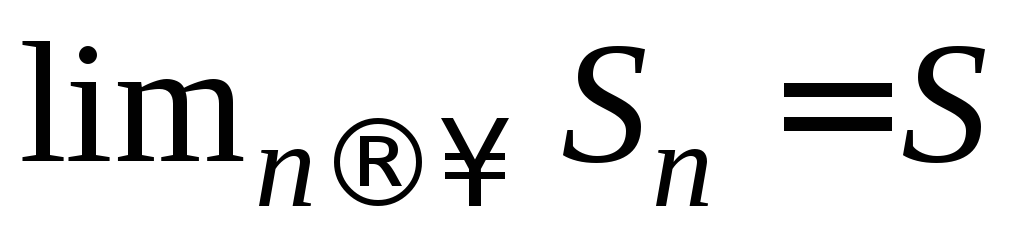 .
.
Ряд называется расходящимся, если предел частичных сумм ряда бесконечен или вообще не существует.
Потенциальное векторное поле — это… Что такое Потенциальное векторное поле?
Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. Однако это условие не является достаточным (например, в многосвязной области у безвихревого поля может не существовать скалярный потенциал).
В физике, имеющей дело с силовыми полями, математическое условие потенциальности силового поля можно представить как требование равенства нулю работы при мгновенном перемещении частицы, на которую действует поле, по замкнутому контуру. Этот контур не обязан быть траекторией частицы, движущейся под действием только данных сил. В качестве потенциала поля в этом случае можно выбрать работу по мгновенному перемещению пробной частицы из некоторой произвольно выбранной исходной точки в заданную точку (по определению эта работа не зависит от пути перемещения). Например, потенциальными являются статическое электрическое поле, а также гравитационное поле в ньютоновой теории гравитации.
В некоторых источниках потенциальным полем сил считается только поле с потенциалом, не зависящим от времени. Это связано с тем, что потенциал для сил, зависящий от времени, вообще говоря, не является потенциальной энергией тела, движущегося под действием этих сил. Поскольку силы совершают работу не одномоментно, работа сил над телом будет зависеть от его траектории и от скорости прохождения по ней. В этих условиях сама потенциальная энергия не определена, так как по определению должна зависеть только от положения тела, но не от пути. Тем не менее, и для этого случая потенциал для сил может существовать, и может входить в уравнения движения так же, как и потенциальная энергия для тех случаев, когда она существует.
Пусть — потенциальное векторное поле; оно выражается через потенциал как
- (или в другой записи ).
Для поля сил и потенциала сил эта же формула записывается как
- ,
то есть для сил потенциалом является . Когда U не зависит от времени, оно является потенциальной энергией, и тогда знак «-» возникает просто по определению. В противном случае знак сохраняется ради единообразия.
Для поля выполняется свойство независимости интеграла от пути :
- ,
Это равносильно
- .
Интеграл по замкнутому контуру обращается в 0, поскольку начальная и конечная точка совпадают. И наоборот, предыдущую формулу можно вывести из этой, если разбить замкнутый контур на два незамкнутых.
Необходимое условие записывается как (или в другой записи ).
На языке дифференциальных форм потенциальное поле — это точная 1-форма — то есть форма, которая является (внешним) дифференциалом 0-формы (функции). Градиенту соответствует взятие внешнего дифференциала от 0-формы (потенциала), ротору соответствует взятие внешнего дифференциала от 1-формы (поля). Необходимое условие следует из того, что второй внешний дифференциал всегда равен нулю: . Интегральные формулы следуют из (обобщённой) теоремы Стокса.
 |
См. также
14. Потенциальные и непотенциальные поля. Консервативные и диссипативные силы. Потенциальная энергия.

Силу  ,
действующую на материальную точку,
называют консервативной или потенциальной,
если работа
,
действующую на материальную точку,
называют консервативной или потенциальной,
если работа  ,
совершаемая этой силой при перемещении
этой точки из произвольного положения
1 в другое 2, не зависит от того, по какой
траектории это перемещение произошло:
,
совершаемая этой силой при перемещении
этой точки из произвольного положения
1 в другое 2, не зависит от того, по какой
траектории это перемещение произошло:

Изменение
направления движения точки вдоль
траектории на противоположное вызывает
изменение знака консервативной силы,
так как величина 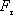 меняет
знак. Поэтому при перемещении материальной
точки вдоль замкнутой траектории
меняет
знак. Поэтому при перемещении материальной
точки вдоль замкнутой траектории 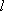 ,
например
,
например 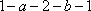 ,
работа консервативной силы равна нулю.
,
работа консервативной силы равна нулю.

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.
Потенциальные силы создают стационарное поле, в котором работа силы зависит только от начального и конечного положений перемещаемой точки
Работа потенциальной силы при перемещении точки по замкнутой траектории L равна нулю
Если внешние тела, создающие рассматриваемое поле, могут двигаться относительно инерциальной системы, то это поле не будет стационарным. Но нестационарное поле потенциально, если работа, совершаемая силой F при мгновенном переносе точки ее приложения вдоль любой траектории L, равна нулю
К непотенциальным относятся диссипативные и гироскопические силы. Диссипативными силами называются силы, суммарная работа которых при любых перемещениях замкнутой системы всегда отрицательна (например, силы трения). Гироскопическими силами называются силы, зависящие от скорости материальной точки, на которую они действуют, и направленные перпендикулярно к этой скорости (например, сила Лоренца, действующая со стороны магнитного поля на движущуюся в нем заряженную частицу). Работа гироскопических сил всегда равна нулю.
Потенциальная
энергия — это энергия, обусловленная
взаимным расположением тел и характером
их взаимодействия. При соответствующих
условиях возможно изменение потенциальной
энергии, за счет чего совершается
работа. Для поднятия тела массой m на
высоту  необходимо
совершить работу против сил тяготения
Р:
необходимо
совершить работу против сил тяготения
Р:
 ,
,
знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h.
Проинтегрируем это выражение:
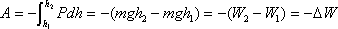
Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна
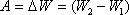
Считая
поверхности Земли  ,
получим
,
получим

Эта
энергия 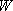 системы
тело — Земля и является потенциальной
энергией тела, поднятого на высоту h:
системы
тело — Земля и является потенциальной
энергией тела, поднятого на высоту h:
|
15. Закон всемирного тяготения. Поле тяготения, его напряженность и потенциальная энергия гравитационного взаимодействия.
Между всякими 2 материальными точками действуют силы взаимного притяжения, которые прямо пропорциональны массам точек и обратно пропорциональны квадрату расстояния между ними (закон всемирного тяготения)
Где F-
сила взаимного притяжения мат точек,
m1
и m2
– их массы, r
– расстояние м/у точками, G
– гравитационная постоян. = 6,67*
Гравитационное поле (поле тяготения) – один из видов физического поля, посредством которого осущ гравитац взаимодейств (притяжение) тел.
Пример. Солнце и планеты солнечной системы, планеты и их спутники.
Силовой хар-ой полей служит напряженность – векторная величина, где F – сила тяготения, действ на матер точку массой m, помещен в некоторую точку поля. Напряженность гравит поля, создав планетой массу M которой можно считать распределен сферич-симметрич, где r – расстояние от центра планеты до интерес нас точки поля, наход вне планеты.
Потенциалом гравитац поля назыв скалярная величина, где П – потенциальн энергия матер точки массой m, помещен в данную точку поля.
Потенц энергию бесконечно удаленных друг от друга матер точек принято считать = 0.
Определение векторного поля. Поле градиента. Потенциальные поля, условия потенциальности.
Векторное поле. Если каждой точке М некоторой области V пространства
соответствует значение некоторой
векторной величины 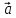 (M),
то говорят, что в области V задано
векторное поле
(M),
то говорят, что в области V задано
векторное поле 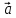 (M).
Примеры векторных полей – поле тяготения,
поля электрической и магнитной
напряжённостей, поле скоростей частиц
движущейся жидкости.
(M).
Примеры векторных полей – поле тяготения,
поля электрической и магнитной
напряжённостей, поле скоростей частиц
движущейся жидкости.
Если в некоторой
декартовой системе координат вектор  (M)
имеет координаты Р(M), Q(M), R(M),
то
(M)
имеет координаты Р(M), Q(M), R(M),
то 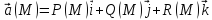 .
Таким образом,
задание векторного поля
.
Таким образом,
задание векторного поля 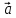 (M)
эквивалентно заданию трёх скалярных
полей Р(M), Q(M), R(M).
Будем называть векторное поле гладким,
если его координатные функции — гладкие
скалярные поля.
(M)
эквивалентно заданию трёх скалярных
полей Р(M), Q(M), R(M).
Будем называть векторное поле гладким,
если его координатные функции — гладкие
скалярные поля.
Градиентом дифференцируемого скалярного поля
u(M)=u(x,y,z) называется вектор 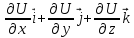 .
Т.е. сумма частных производных умноженных
на соответствующие единичные вектора.
.
Т.е. сумма частных производных умноженных
на соответствующие единичные вектора.
В общем случае градиент вводится как векторная характеристика скалярного поля — то есть области, каждой точке которой соответствует значение определенного скаляра. Градиент характеризует, насколько быстро меняется скалярная величина в том или ином месте этого поля.
Потенциальные
векторные поля. Векторное
поле A = {Ax, Ay, Az} называется потенциальным,
если вектор А является градиентом
некоторой скалярной функции u = u(x, y,
z): A
= grad
u
= 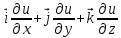 (16.7).
(16.7).
При этом функция u называется потенциалом данного векторного поля.
Выясним, при каких
условиях векторное поле является
потенциальным.
Так как из (16.7) следует, что  ,
То
,
То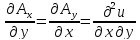 ,
, =
= ,
, =
= .
так как смешанная производная второго
порядка не зависит от порядка
дифференцирования. Из этих равенств
легко получаем, что rot A = 0 —условие
потенциальности векторного поля.
.
так как смешанная производная второго
порядка не зависит от порядка
дифференцирования. Из этих равенств
легко получаем, что rot A = 0 —условие
потенциальности векторного поля.
Ротором векторного
поля 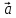 (M)
в точке
(M)
в точке 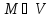 называется векторная величина (векторное
поле):
называется векторная величина (векторное
поле):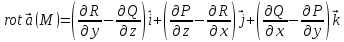 .
Если выразить
.
Если выразить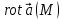 через оператор Гамильтона набла:
через оператор Гамильтона набла: равен векторному произведению
равен векторному произведению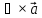 .
Действительно,
.
Действительно,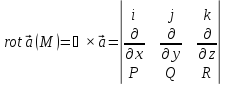 .
.
Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.
Поток
векторного поля через поверхность. Пусть в области D
задано непрерывное векторное поле 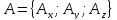 ,
, .
Возьмем в этом векторном поле некоторую
поверхностьS
и выберем ее определенную сторону. Пусть
.
Возьмем в этом векторном поле некоторую
поверхностьS
и выберем ее определенную сторону. Пусть 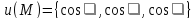 – поле единичных нормалей к поверхности,
соответствующее выбранной стороне.
Тогда поверхностный интеграл 2-ого рода
– поле единичных нормалей к поверхности,
соответствующее выбранной стороне.
Тогда поверхностный интеграл 2-ого рода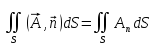 (т.к.
(т.к.  )называется потоком вектора A через поверхность S в указанную сторону.
)называется потоком вектора A через поверхность S в указанную сторону.
Пусть 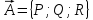 .
Формула Гаусса-Остроградского:
.
Формула Гаусса-Остроградского: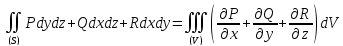

Левую часть можно
записать так: 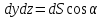 ,
,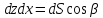 ,
,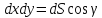 .
Следовательно:
.
Следовательно: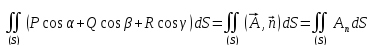 ,
так как
,
так как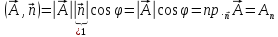 .
Это поток вектора через замкнутую
поверхность. Правую часть можно записать
какдивергенцию (расходимость):
.
Это поток вектора через замкнутую
поверхность. Правую часть можно записать
какдивергенцию (расходимость):  .
.
Дивергенцией векторного поля A в точке MÎV
называется производная функции  по объему в этой точке:
по объему в этой точке: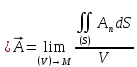 .
Дивергенцию можно записать и с помощью оператора
Набла:
.
Дивергенцию можно записать и с помощью оператора
Набла: 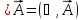 .Дивергенция
в декартовых координатах:
.Дивергенция
в декартовых координатах:  .
.
Свойства дивергенции:
 .
. .
.
Другие свойства (на лекции не разбирали, на усмотрение сдающего):
Если u – скалярное поле, а F – векторное:
 .
.Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором:
 .
.Дивергенция от ротора равна нулю:
 .
.
Соленоидальные векторные поля, условия соленоидальности.
Пусть в некоторой
области D
задано непрерывное векторное поле 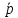 (M)=
(M)=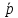 (x,y,z). Потоком
векторного поля
(x,y,z). Потоком
векторного поля 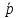 через ориентированную кусочно-гладкую
поверхность S,
расположенную в области D,
называется интеграл
через ориентированную кусочно-гладкую
поверхность S,
расположенную в области D,
называется интеграл 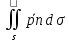 ,
где
,
где 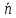 –единичный
вектор нормали к поверхности S,
указывающий на ее ориентацию, а
–единичный
вектор нормали к поверхности S,
указывающий на ее ориентацию, а 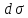 –элемент
площади поверхности S.
–элемент
площади поверхности S.
Векторное поле 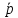 называетсясоленоидальным в области D, если поток
этого поля через любую кусочно-гладкую
несамопересекающуюся поверхность,
расположенную в D
и представляющую собой границу некоторой
ограниченной подобласти области D, равен нулю.
называетсясоленоидальным в области D, если поток
этого поля через любую кусочно-гладкую
несамопересекающуюся поверхность,
расположенную в D
и представляющую собой границу некоторой
ограниченной подобласти области D, равен нулю.
Если дивергенция
равна нулю, то есть 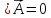 ,
то поле вектора
,
то поле вектора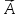 называетсясоленоидальным.
называетсясоленоидальным.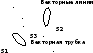
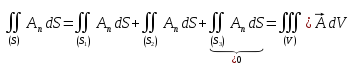
 ,
поэтому поток везде, на каждом сечении
трубки, одинаков.
,
поэтому поток везде, на каждом сечении
трубки, одинаков.
Для того чтобы
непрерывно дифференцируемое векторное
поле  былосоленоидальным в объемно-односвязной области D, необходимо и
достаточно,
чтобы во всех точках D
выполнялось равенство
былосоленоидальным в объемно-односвязной области D, необходимо и
достаточно,
чтобы во всех точках D
выполнялось равенство 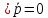 .
Где дивергенцией (“расходимость”)
векторного поля
.
Где дивергенцией (“расходимость”)
векторного поля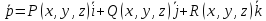 называется скалярная функция
называется скалярная функция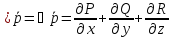


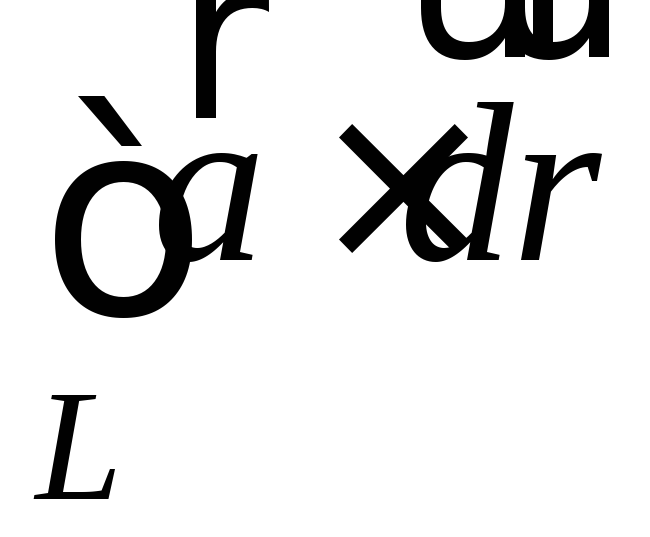 не зависит от формы дугиL
=
не зависит от формы дугиL
=  ,
а зависит только от начальной и конечной
точек дуги.
,
а зависит только от начальной и конечной
точек дуги.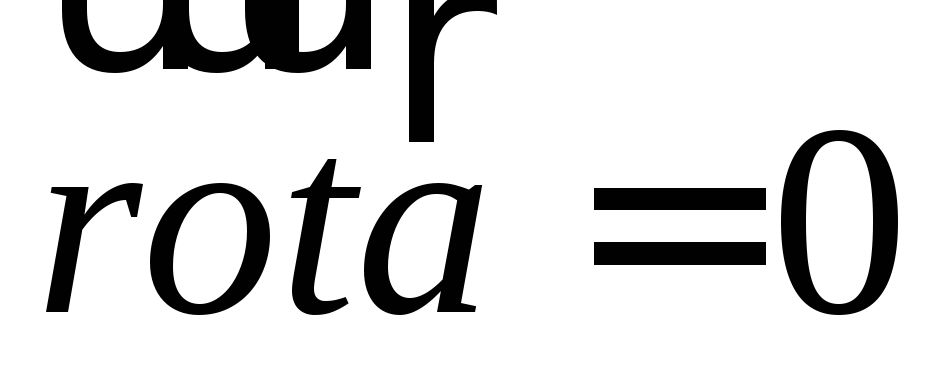
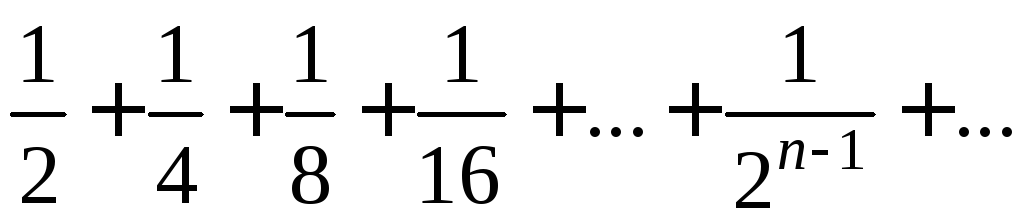 —
бесконечно убывающая геометрическая
прогрессия со знаменателем
—
бесконечно убывающая геометрическая
прогрессия со знаменателем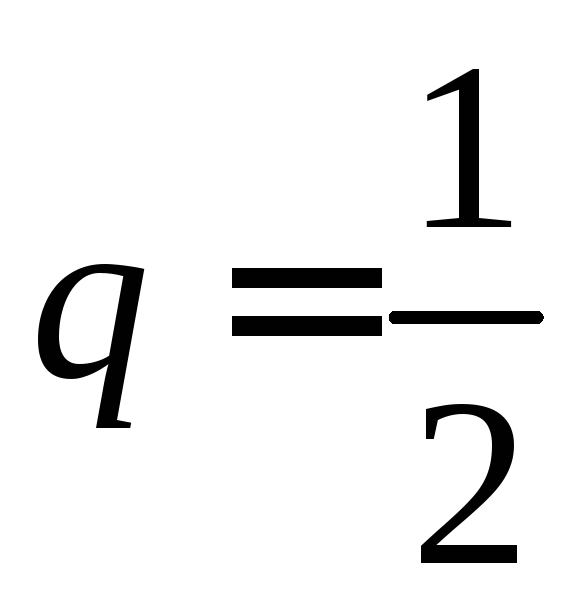 .
Ее сумма равна
.
Ее сумма равна ,
,
 .
. .
.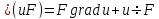 .
. .
.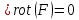 .
.