Потенциал электрического поля. Разность потенциалов. Видеоурок. Физика 10 Класс
Электрическое поле действует на помещенный в него заряд с силой, которая определяется величиной заряда и напряженностью поля в данной точке.
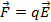
Если эта сила перемещает заряд – то она совершает работу. Даже если заряда в поле нет, то потенциально эта работа все равно может быть совершена, как только он там окажется. Из опыта других разделов физики мы знаем, что работа связана с энергией.
Для решения некоторых задач удобно использовать энергетическую модель описания электрического поля. Проведем аналогию с гравитационным полем.
Если мы поднимем тело массы 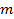 , лежащее на земле на высоту
, лежащее на земле на высоту 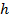
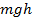 . Именно такую работу
. Именно такую работу 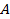 и необходимо совершить для этого подъема.
и необходимо совершить для этого подъема.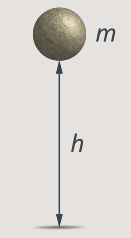
Рис. 1. Изменение потенциальной энергии

Для любой массы 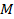 разница энергий на высоте 0 и
разница энергий на высоте 0 и 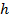 будет равна
будет равна 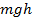 (см. рис. 2).
(см. рис. 2).
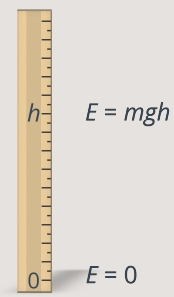
Рис. 2. Разница потенциальных энергий
Если разделить значение потенциальной энергии 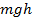
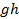 уже не зависит от массы, оно показывает работу, которую необходимо совершить для переноса тела, с некоторой массой, на высоту
уже не зависит от массы, оно показывает работу, которую необходимо совершить для переноса тела, с некоторой массой, на высоту 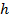 , деленную на эту массу.
, деленную на эту массу.Теперь посмотрим, как ввести аналог потенциальной энергии приведенной на единицу массы в электрическом поле.
На заряд 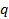 , находящийся в поле другого заряда
, находящийся в поле другого заряда  , закрепленного в некоторой точке пространства, действует сила Кулона
, закрепленного в некоторой точке пространства, действует сила Кулона 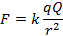 . Эта сила может переместить заряд
. Эта сила может переместить заряд 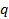
Если по аналогии с гравитационным полем рассмотреть величину, равную этой энергии, деленной на заряд 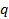 , то она уже не будет зависеть от заряда
, то она уже не будет зависеть от заряда 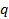 и охарактеризует только поле заряда
и охарактеризует только поле заряда 
 и расстояния между зарядами. Эта величина и называется потенциалом электрического поля.
и расстояния между зарядами. Эта величина и называется потенциалом электрического поля.Разность потенциалов двух точек, умноженная на величину заряда 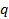 , равна работе, необходимой для перемещения этого заряда между этими точками. То есть разность потенциалов двух точек поля – это работа по перемещению между ними единичного заряда.
, равна работе, необходимой для перемещения этого заряда между этими точками. То есть разность потенциалов двух точек поля – это работа по перемещению между ними единичного заряда.
Как и в поле сил тяжести, эта работа не зависит от траектории и определяется только положением точек, между которыми перемещается единичный заряд. Такие поля называют консервативными. В разделе «Механика» мы уже говорили, что энергия – величина, требующая для измерения задания «начала отсчета». Например, в гравитационном поле мы можем считать нулевой потенциальную энергию тела, находящегося на уровне земли. В случае электростатического поля, создаваемого зарядом, естественно считать нулевой потенциальной энергией некоторого заряда, находящегося в поле, его энергию на бесконечном удалении от заряда, в поле которого он находится. Это и есть «точка отсчета» для потенциальной энергии поля заряда.
Потенциал поля в некоторой точке равен работе по перемещению единичного заряда из этой точки на бесконечность.
Пусть положительный заряд 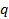 находится на расстоянии
находится на расстоянии 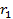 от положительного заряда
от положительного заряда  (см. рис. 3).
(см. рис. 3).

Рис. 3. Изначальное положение заряда 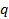
Какую работу совершит электрическое поле при перемещении заряда 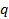 вдоль радиуса в точку, отдаленную на
вдоль радиуса в точку, отдаленную на 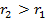 от
от 
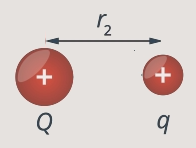
Рис. 4. Конечное положение заряда 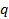
По определению работа силы равна этой силе, умноженной на перемещение:
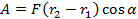
В данном случае действует сила электрического взаимодействия (см. рис. 5), по закону Кулона 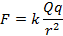
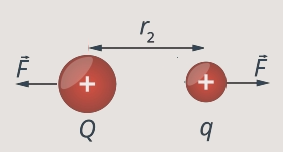
Рис. 5. Действие силы электрического взаимодействия
Сила и перемещение в нашем случае сонаправлены, 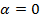 и
и 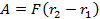 . Так мы можем находить работу для случая, когда сила постоянна на всей траектории. Здесь же сила изменяется по мере отдаления зарядов друг от друга.
. Так мы можем находить работу для случая, когда сила постоянна на всей траектории. Здесь же сила изменяется по мере отдаления зарядов друг от друга.
Обозначим перемещение заряда 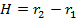 (см. рис. 6).
(см. рис. 6).
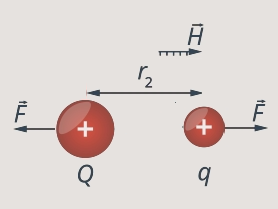
Рис. 6. Перемещение заряда
По мере перемещения заряда 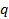 сила изменяется, но на малом (в сравнении с расстоянием до заряда
сила изменяется, но на малом (в сравнении с расстоянием до заряда 
Работа, совершаемая силой Кулона на таком малом отрезке 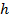 равна
равна 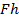 , где силу
, где силу 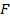 можно считать постоянной на всем отрезке
можно считать постоянной на всем отрезке 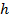 . Тогда работа при перемещении на расстояние
. Тогда работа при перемещении на расстояние 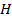 будет равна сумме работ на
будет равна сумме работ на 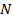 участках (
участках (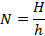 ), на каждом из которых сила Кулона постоянна и равна
), на каждом из которых сила Кулона постоянна и равна 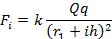 .
.
Эта сумма будет равна 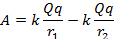
Подробный вывод этой формулы вы можете проследить в ответвлении.
Работа при перемещении электрического заряда
Работа по перемещению заряда на малом участке 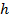 равна:
равна:
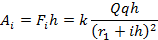
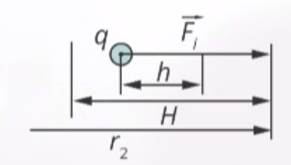
Работа на участке 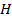 равна сумме работ на каждом участке
равна сумме работ на каждом участке 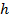 :
:
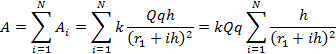
Воспользуемся приближенным равенством:
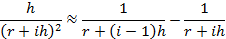
Прежде чем его применить, покажем, что равенство справедливо. Приведем правую часть к общему знаменателю:
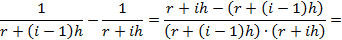
Раскроем скобки:
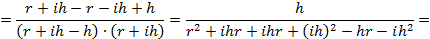
Заметим, что 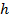 – пренебрежимо малая по сравнению с
– пренебрежимо малая по сравнению с 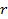 величина,
величина, 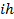 не может считаться пренебрежимо малой, т. к. количество
не может считаться пренебрежимо малой, т. к. количество 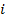 участков
участков 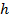 велико. Поэтому в знаменателе можем пренебречь членами
велико. Поэтому в знаменателе можем пренебречь членами 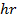 и
и 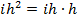 .
.

Вернемся к нахождению работы. Распишем выражение по полученной формуле:
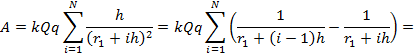
Распишем сумму:
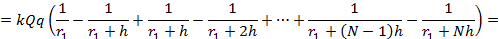

Мы знаем, что работа связана с энергией. Система обладает энергией, если силы, возникающие в системе, могут выполнить работу (в нашем случае это сила электростатического взаимодействия зарядов). Работа равна уменьшению потенциальной энергии:
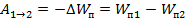
Сравнив с выражением 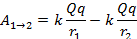 , делаем вывод, что
, делаем вывод, что 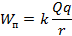 – это потенциальная энергия
– это потенциальная энергия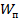 взаимодействия двух зарядов. Ранее мы приняли, что потенциальная энергия заряда, отдаленного от источника электрического поля на бесконечность, равна нулю. Посмотрим, как с этим согласуется полученная формула:
взаимодействия двух зарядов. Ранее мы приняли, что потенциальная энергия заряда, отдаленного от источника электрического поля на бесконечность, равна нулю. Посмотрим, как с этим согласуется полученная формула:
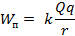
Действительно, 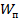 будет равна нулю на бесконечном отдалении от заряда
будет равна нулю на бесконечном отдалении от заряда  , т. к.
, т. к. 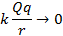 при
при 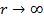 .
.
Теперь проверим, как полученный результат соотносится с моделью, в которой разноименные заряды обозначены знаками плюс и минус. Если заряды одноименные, то потенциальная энергия взаимодействия положительна 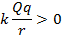 . Система стремится к состоянию с наименьшей потенциальной энергией (как и, например, камень на некоторой высоте
. Система стремится к состоянию с наименьшей потенциальной энергией (как и, например, камень на некоторой высоте 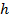 над поверхностью земли, предоставленный сам себе, будет падать вниз, т. е. уменьшать высоту и с ней потенциальную энергию
над поверхностью земли, предоставленный сам себе, будет падать вниз, т. е. уменьшать высоту и с ней потенциальную энергию 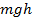 )
)
Действительно, заряды будут отталкиваться и сила электрического взаимодействия будет вызывать перемещение заряда на большее расстояние, потенциальная энергия 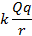 будет уменьшаться.
будет уменьшаться.
Если заряды разноименные, то потенциальная энергия взаимодействия 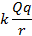 имеет знак минус. Заряды притягиваются, и сила их взаимодействия вызывает перемещение заряда на меньшее расстояние
имеет знак минус. Заряды притягиваются, и сила их взаимодействия вызывает перемещение заряда на меньшее расстояние 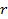 , потенциальная энергия
, потенциальная энергия 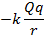 уменьшается.
уменьшается.
Энергия заряда 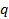 в поле заряда
в поле заряда  , равная
, равная 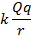 , зависит от величин обоих зарядов. Характеристика поля, созданного зарядом
, зависит от величин обоих зарядов. Характеристика поля, созданного зарядом  , естественно, не должна зависеть от величины помещенного в него заряда. Разделим
, естественно, не должна зависеть от величины помещенного в него заряда. Разделим 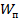 на
на 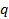 и получим
и получим 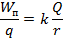 . Эта величина называется потенциалом электрического поля и обозначается буквой
. Эта величина называется потенциалом электрического поля и обозначается буквой 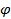 . Эта характеристика поля показывает, какой энергией обладает положительный заряд, помещенный в данную точку поля. Как и энергия, потенциал – скалярная величина, измеряется в вольтах.
. Эта характеристика поля показывает, какой энергией обладает положительный заряд, помещенный в данную точку поля. Как и энергия, потенциал – скалярная величина, измеряется в вольтах.
В нашем случае  – потенциал поля точечного заряда. Точка отсчета потенциалов в нашем случае естественным образом является бесконечно отдаленной точкой (см. рис. 7).
– потенциал поля точечного заряда. Точка отсчета потенциалов в нашем случае естественным образом является бесконечно отдаленной точкой (см. рис. 7).
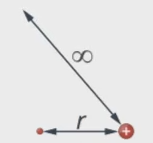
Рис. 7. Точка отсчета потенциалов
В зависимости от задачи точкой отсчета выбирают потенциал поверхности Земли, потенциал отрицательно заряженной пластины конденсатора или потенциал любой другой точки, удобной для решения задачи.
Таким образом, пользуясь определением потенциала, можно вычислить потенциальную энергию заряда, находящегося в электростатическом поле:
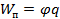
и работу поля по перемещению заряда из точки с потенциалом 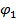 в точку с потенциалом
в точку с потенциалом 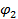 :
:
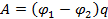
Электрическое поле является консервативным, его работа не зависит от траектории движения заряда, а зависит только от перемещения.
Заряд всегда распределен на каком-то теле, имеющем геометрические размеры. На расстояниях, много больших размеров тела, поле слабо зависит от объема и формы этого тела, и потому модели точечного заряда достаточно. Например, потенциал поля заряженного металлического шара при 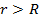 эквивалентен потенциалу поля точечного заряда (см. рис. 8):
эквивалентен потенциалу поля точечного заряда (см. рис. 8):

Рис. 8. Потенциал поля при 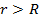
 .
.
Внутри шара потенциал во всех точках одинаков и равен потенциалу на поверхности шара (см. рис. 9):
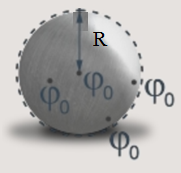
Рис. 9. Потенциал внутри шара
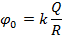 .
.
Если бы это было не так, то потенциальная энергия в разных точках внутри шара отличалась бы, а, так как внутри металла есть свободные носители заряда, поле выполняло бы работу по перемещению зарядов. В итоге электроны переместились бы в область большего потенциала, тем самым уменьшив его. Таким образом, потенциал во всех точках приравнивается.
Потенциал подчиняется принципу суперпозиции. При наличии нескольких источников поля складываются как векторы напряженности поля, так и потенциалы:
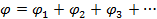
При перемещении заряда между точками с разностью потенциалов 1 кВ электрическое поле совершило работу 40 мкДж. Чему равен заряд?
Это про
Потенциальное векторное поле — Википедия
Материал из Википедии — свободной энциклопедии
Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат. Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. Однако это условие не является достаточным — если рассматриваемая область пространства не является односвязной, то скалярный потенциал может быть многозначной функцией.
В физике, имеющей дело с силовыми полями, математическое условие потенциальности силового поля можно представить как требование равенства нулю работы при мгновенном перемещении частицы, на которую действует поле, по замкнутому контуру. Этот контур не обязан быть траекторией частицы, движущейся под действием только данных сил. В качестве потенциала поля в этом случае можно выбрать работу по мгновенному перемещению пробной частицы из некоторой произвольно выбранной исходной точки в заданную точку (по определению эта работа не зависит от пути перемещения). Например, потенциальными являются статическое электрическое поле, а также гравитационное поле в ньютоновой теории гравитации.
В некоторых источниках потенциальным полем сил считается только поле с потенциалом, не зависящим от времени. Это связано с тем, что потенциал для сил, зависящий от времени, вообще говоря, не является потенциальной энергией тела, движущегося под действием этих сил. Поскольку силы совершают работу не одномоментно, работа сил над телом будет зависеть от его траектории и от скорости прохождения по ней. В этих условиях сама потенциальная энергия не определена, так как по определению должна зависеть только от положения тела, но не от пути. Тем не менее, и для этого случая потенциал для сил может существовать, и может входить в уравнения движения так же, как и потенциальная энергия для тех случаев, когда она существует.
Пусть v→{\displaystyle {\vec {v}}} — потенциальное векторное поле; оно выражается через потенциал ϕ{\displaystyle \phi } как
- v→=∇ϕ{\displaystyle {\vec {v}}=\nabla \phi } (или в другой записи v→=gradϕ{\displaystyle {\vec {v}}=\operatorname {grad} \phi }).
Для поля сил и потенциала сил эта же формула записывается как
- F→(r→,t)=−∇U(r→,t){\displaystyle {\vec {F}}({\vec {r}},t)=-\nabla U({\vec {r}},t)},
то есть для сил потенциалом ϕ{\displaystyle \phi } является −U{\displaystyle -U}. Когда U не зависит от времени, оно является потенциальной энергией, и тогда знак «-» возникает просто по определению. В противном случае знак сохраняется ради единообразия.
Для поля ϕ{\displaystyle \phi } выполняется свойство независимости интеграла от пути P{\displaystyle P}:
- ∫Pv→⋅dr→=ϕ(B)−ϕ(A){\displaystyle \int _{P}{\vec {v}}\cdot d{\vec {r}}=\phi (B)-\phi (A)},
Это равносильно
- ∮v→⋅dr→=0{\displaystyle \oint {\vec {v}}\cdot d{\vec {r}}=0}.
Интеграл по замкнутому контуру обращается в 0, поскольку начальная и конечная точка совпадают. И наоборот, предыдущую формулу можно вывести из этой, если разбить замкнутый контур на два незамкнутых.
Необходимое условие записывается как ∇×v→=0{\displaystyle \nabla \times {\vec {v}}=0} (или в другой записи rotv→=0{\displaystyle \operatorname {rot} {\vec {v}}=0}).
На языке дифференциальных форм потенциальное поле — это точная 1-форма — то есть форма, которая является (внешним) дифференциалом 0-формы (функции). Градиенту соответствует взятие внешнего дифференциала от 0-формы (потенциала), ротору соответствует взятие внешнего дифференциала от 1-формы (поля). Необходимое условие следует из того, что второй внешний дифференциал всегда равен нулю: d2=0{\displaystyle d^{2}=0}. Интегральные формулы следуют из (обобщённой) теоремы Стокса.
Электростатический потенциал — Википедия
У этого термина существуют и другие значения, см. Потенциал.Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).
Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.
Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
- φ=Wpqp.{\displaystyle \varphi ={\frac {W_{p}}{q_{p}}}.}
Напряжённость электростатического поля E{\displaystyle \mathbf {E} } и потенциал φ{\displaystyle \varphi } связаны соотношением[1]
- ∫ABE⋅dl=φ(A)−φ(B),{\displaystyle \int \limits _{A}^{B}\mathbf {E} \cdot \mathbf {dl} =\varphi (A)-\varphi (B),}
или обратно[2]:
- E=−∇φ.{\displaystyle \mathbf {E} =-\nabla \varphi .}
Здесь ∇{\displaystyle \nabla } — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля ∇⋅E=ρε0{\displaystyle \mathbf {\nabla } \cdot \mathbf {E} ={\rho \over \varepsilon _{0}}}, легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:
- ∇2φ=−ρε0,{\displaystyle {\nabla }^{2}\varphi =-{\rho \over \varepsilon _{0}},}
где φ{\displaystyle \varphi } — электростатический потенциал (в вольтах), ρ{\displaystyle \rho } — объёмная плотность заряда (в кулонах на кубический метр), а ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная (в фарадах на метр).
Неоднозначность определения потенциала[править | править код]
Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:
- φ1−φ2=Afq∗1→2q∗,{\displaystyle \varphi _{1}-\varphi _{2}={\frac {A_{f}^{q^{*}1\to 2}}{q^{*}}},}
где:
- φ1{\displaystyle \varphi _{1}} — потенциал в точке 1,
- φ2{\displaystyle \varphi _{2}} — потенциал в точке 2,
- Afq∗1→2{\displaystyle A_{f}^{q^{*}1\to 2}} — работа, совершаемая полем при переносе пробного заряда q∗{\displaystyle q^{*}} из точки 1 в точку 2.
При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).
Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произволом выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).
В СИ за единицу разности потенциалов принимают вольт (В).
Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT−3I−1).
В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг.
Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ.
Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов.
Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.
Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния 1r{\displaystyle {\frac {1}{r}}} (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.
Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:
- φ=kqr,{\displaystyle \varphi =k{\frac {q}{r}},}
где k{\displaystyle k} обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ:
- k=14πε0{\displaystyle k={\frac {1}{4\pi \varepsilon _{0}}}} = 9·109 В·м/Кл,
q{\displaystyle q} — величина заряда, r{\displaystyle r} — расстояние от заряда-источника до точки, для которой рассчитывается потенциал.
- Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть, например, над поверхностью шара, а не внутри его.
- Кулоновский потенциал в приведенном выше виде используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):
- W=∑i<jkqiqjrij=12∑i≠jkqiqjrij.{\displaystyle W=\sum _{i<j}k{\frac {q_{i}q_{j}}{r_{ij}}}={\frac {1}{2}}\sum _{i\neq j}k{\frac {q_{i}q_{j}}{r_{ij}}}.}
Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция ∫CE⋅dℓ{\displaystyle \textstyle \int _{C}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}} зависит от пути, потому что ∇×E≠0{\displaystyle \mathbf {\nabla } \times \mathbf {E} \neq \mathbf {0} } (см. Закон индукции Фарадея).
Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности, А определен так чтобы
- B=∇×A,{\displaystyle \mathbf {B} =\mathbf {\nabla } \times \mathbf {A} ,\,}
где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. Учитывая это, величина
- F=E+∂A∂t{\displaystyle \mathbf {F} =\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}}
является консервативным полем по закону Фарадея, и поэтому можно написать
- E=−∇V−∂A∂t,{\displaystyle \mathbf {E} =-\mathbf {\nabla } V-{\frac {\partial \mathbf {A} }{\partial t}},\,}
где V — скалярный потенциал, определённый консервативным полем F.
Электростатический потенциал — это частный случай этого определения, где A не зависит от времени. С другой стороны, для изменяющихся во времени полей,
- −∫abE⋅dℓ≠V(b)−V(a),{\displaystyle -\int _{a}^{b}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)},\,}
в отличие от электростатики.
Потенциальное электрическое поле — Большая Энциклопедия Нефти и Газа, статья, страница 1
Потенциальное электрическое поле
Cтраница 1
Потенциальное электрическое поле — поле, в котором работа, совершаемая электрической силой при перемещении электрического заряда, зависит только от положения начальной и конечной точек пути, по которому происходит перемещение электрического заряда, но не зависит от пути, по которому происходит перемещение. [1]
Потенциальное электрическое поле — поле, в котором работа, совершаемая электрической силой при перемещении электрического заряда, зависит только от положения начальной и конечной точек пути перемещения электрического заряда, но не зависит от формы этого пути. [2]
Потенциальное электрическое поле источника здесь отсутствует, однако в зоне разреза создаются наведенные электрические заряды с плотностью а. Эти заряды вызывают искривление пути вихревого тока i. [3]
Создание потенциального электрического поля, в котором распределение потенциалов описывалось бы бигармоническим уравнением, невозможно. [4]
В потенциальном электрическом поле напряжение между двумя точками совпадает по величине с разностью потенциалов между ними. [5]
Мы ограничимся случаем чисто потенциального электрического поля ( Е — — Уф) при равном нулю магнитном поле и предположим, что возмущению подвергается только электронное распределение при неизменном распределении ионов. [6]
Мы ограничимся случаем чисто потенциального электрического поля ( Е — 7 ( р) при равном нулю магнитном поле и предположим, что возмущению подвергается только электронное распределение при неизменном распределении ионов. [7]
Отсюда ясно, в частности, что любое потенциальное электрическое поле не дает возбуждения, а приводит лишь к разделению электрических зарядов. [8]
Рассмотрим вопрос о распределении электронов плазмы в медленно включаемом потенциальном электрическом поле. [9]
Рассмотрим вопрос о распределении электронов плазмы в медленно включаемом потенциальном электрическом поле. [10]
Кажущаяся эквивалентность, однако, рушится при появлении в среде потенциального электрического поля. В частности, оно обязательно возникает при образовании в сплошной среде полостей. [11]
Ускоритель заряженных частиц, в котором ускоряемые частицы под действием ведущего магнитного поля движутся по близким к замкнутым или спиральным траекториям Ускоритель заряженных частиц, в котором ускорение частиц осуществляется потенциальным электрическим полем. [12]
Если же в рассматриваемой области пространства имеются заряды и токи, то наряду с вихревыми полями со сцепленными линиями мы обнаружим вихревое магнитное поле, линии которого замкнуты около токов, и потенциальное электрическое поле, линии которого начинаются в положительных и кончаются в отрицательных зарядах. [13]
В потенциальном электрическом поле ( электростатическом поле) работа по перемещению электрического заряда не зависит от пути, по которому перемещается заряд. [14]
Движущийся электрический заряд наряду с электрическим создает магнитное поле. В отличие от потенциального электрического поля, постоянное магнитное поле, создаваемое стационарными токами, является соленоидальным, или вихревым: его силовые линии всегда замкнуты. Другими словами, магнитное поле не имеет источников — магнитных зарядов. [15]
Страницы: 1 2
Потенциал электрического поля
Потенциальность поля
Важным свойством электрического поля, как поля не имеющего вихрей и созданного одними неподвижными источниками, является его потенциальность.
Электрическое поле называется потенциальным, если работа, которую совершает носитель заряда в таком поле, при перемещении его по любому замкнутому контуру равняется нулю.
Гравитационное поле силы тяжести также является потенциальным. Если поднять груз определенной массы на некоторую высоту, а затем опустить его обратно на поверхность Земли, в прежнюю точку, то полная механическая работа будет также равна нулю. Причем, совершенно не важно по какой траектории осуществлялся подъем и спуск груза. Источником такого гравитационного поля является в этом примере Земля (тело с массой во много раз большей чем масса поднимаемого груза).
Электростатическое поле, то есть такое поле, которое образовано неподвижными электрическими зарядами, также обладает аналогичной потенциальностью. Работа носителя заряда при его перемещении по замкнутому контуру в электростатическом поле будет равняться нулю. Траектория такого перемещения замкнута и называется контуром и эта траектория может быть любого вида, принципиальное значение имеет ее замкнутость, а не форма.
На рисунке изображены разные траектории движения заряда в электростатическом поле плоского конденсатора. Не имеет значения по какому маршруту двигался заряд (картинка слева), совершенная им работа будет одинаковой, то есть A1=A2=A3. На правом изображении показано движение заряда по замкнутому контуру. Начальная и конечная точки поля совпадают. Заряд двигался из точки 1, затем 2, 3, и снова прибыл в точку 1, тем самым образовав замкнутую траекторию, то есть контур. В этом случае говорят, что совершенная им механическая работа равна нулю.
Потенциал
Так как электростатическое поле является потенциальным, то в нем каждая точка пространства имеет потенциал характеризующий это поле. Для гравитационного поля это будет гравитационный потенциал, а для электрического — электрический потенциал. Что же такое потенциал и как он определяется?
Потенциалом φ точки электрического поля называется работа, которую нужно затратить, чтобы переместить заряд +q в количестве одного Кулона из бесконечности в данную точку поля, или же работа по перемещению этого же заряда +q из данной точки в бесконечность.
Из определения потенциала получается, что потенциал — это показатель характеризующий работу заряда, то есть это по-сути энергетическая характеристика поля. Что же следует понимать под бесконечностью? Это всё-таки некоторое расстояние, а не математическое понятие ∞. Под бесконечностью в определении потенциала следует понимать такое расстояние в пространстве, на котором поле можно считать равным нулю, то есть напряженность поля в ней настолько мала, что ее можно принять за ноль. Силовые линии электрического поля одиночного заряда уходят в бесконечность и даже в этой бесконечности с противоположной стороны вполне может встретится заряд противоположного знака, и тогда эти две бесконечности встретятся. Вот такое место встречи и есть то место, где влияние поля одиночного заряда равно нулю. Это место нулевого потенциала, где потенциал φ=0, после перехода этой зоны нулевого потенциала его значения поменяют свой знак. В реальной природе, во вселенной, каждый заряд имеет свою противоположную пару и потому точка бесконечности — это точка равновесия, баланса.
Из практических соображений бывает удобно принять некоторую линию или поверхность (эквипотенциальную) равной нулю. Это значит, что относительно некоторого источника электрического поля она всё же имеет некоторое значение, но принимается за ноль из практической необходимости. Получается обоснованная относительная система отсчета потенциалов поля. На этот счёт есть аналогия с гравитационным полем Земли (отсчет от уровня моря), когда влияние гравитации Солнца несущественно, но для высоких орбит космических спутников следует учитывать и гравитацию Солнца. При значительном приближении космического аппарата к Луне, влияние гравитационного потенциала Луны станет первостепенным и потребуется лунная система отсчета. Подобным образом обстоят дела и с электрическим полем Земли. Если в физике при рассмотрении теоретических вопросов выбирают бесконечность, то в электротехнике поступают иначе, и принимают за нулевой потенциал поверхность Земли. Соответственно на определенной высоте от поверхности Земли, в атмосфере, потенциал будет иметь некоторое отличное от нуля значение.
В каком случае понятие потенциала теряет смысл? Если при движении заряда по разным траекториям будет совершатся разная работа, то есть она будет зависеть от формы пути, то здесь потенциал поля не имеет смысла. Итак, понятие потенциала относится только к потенциальному полю.
Потенциальная энергия
Известное в механике понятие потенциальной энергии также относится к потенциальному полю. При отсутствии потенциального поля не может быть никакой речи о потенциальной энергии. Потенциальной энергией тела мы как раз и называем ту работу, которую необходимо затратить, чтобы переместить это тело из бесконечности в данную точку. Иначе говоря, требуется затратить энергию, чтобы перенести тело из области с нулевым потенциалом в область с высоким потенциалом. Опять же, если затрачиваемая работа зависит от формы пути, то нет потенциального поля, а значит невозможно говорить о потенциальной энергии.
Как было уже сказано выше, потенциал — это энергетическая характеристика поля и потому достаточно легко определить потенциальную энергию через потенциал.
Потенциальная энергия Up равна произведению заряда q на потенциал φ.
Дата: 01.05.2015
© Valentin Grigoryev (Валентин Григорьев)
Потенциал электрического поля
Электростатическое поле точечного заряда – центральное, поэтому оно потенциально. В силу принципа суперпозиции потенциально любое электростатическое поле.
Потенциальная энергия заряда в электростатическом поле (Wp) – физическая величина, равная работе электростатического поля при перемещении заряда из его положения на нулевой уровень. Как правило, в электростатике принимается, что нулевой уровень находится на бесконечности.
Работа перемещения заряда в электростатическом поле равна изменению потенциальной энергии заряда, взятому с противоположным знаком: A = – (Wp2 – Wp1).
Потенциал электростатического поля (j) – физическая величина, равная отношению потенциальной энергии заряда в поле к его значению.
Потенциал – величина скалярная. За его единицу в системе СИ принимается вольт (1 В = 1 Дж/Кл).
Принцип суперпозиции для потенциала. Потенциал электростатического поля, одновременно создаваемого в некоторой точке пространства несколькими зарядами, равна сумме потенциалов электростатических полей, которые создавались бы в этой же точке каждым из зарядов по отдельности j = j1 + j2 + … .
Эквипотенциальная поверхность – поверхность, во всех точках которой потенциал имеет одинаковые значения. Для поля точечного заряда эквипотенциальными поверхностями являются сферы с центром в точке расположения заряда.
Работа
электрического поля на криволинейном
участке траектории
.
Циркуляция электростатического поля
на замкнутой траектории 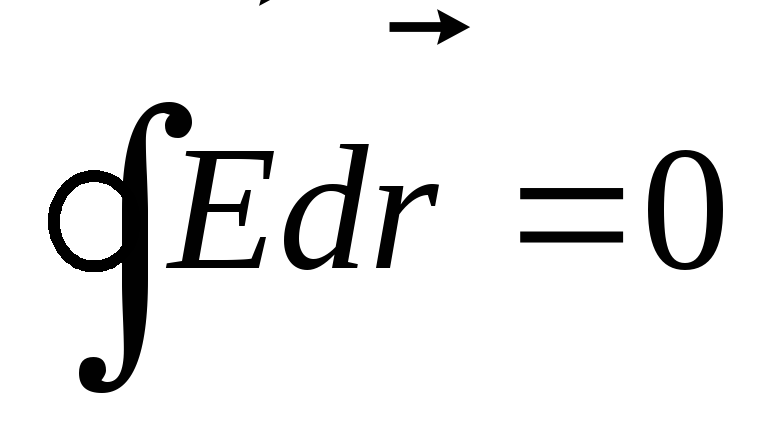 .
Потенциал электростатического поля
точечного заряда
.
Потенциал электростатического поля
точечного заряда 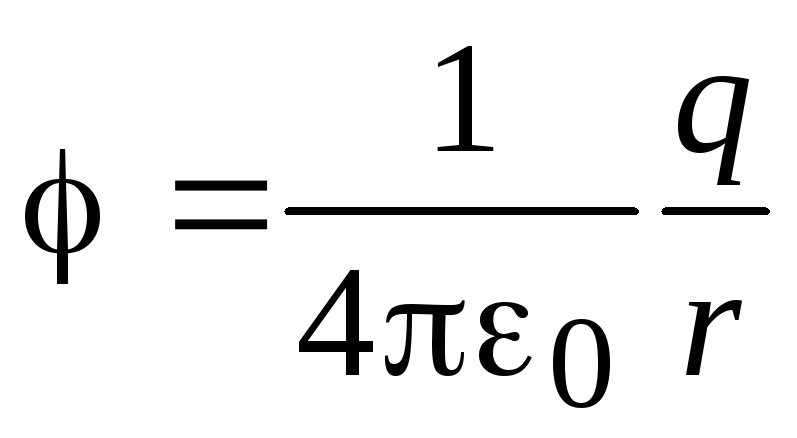 .
Потенциальная энергия взаимодействия
двух зарядов
.
Потенциальная энергия взаимодействия
двух зарядов 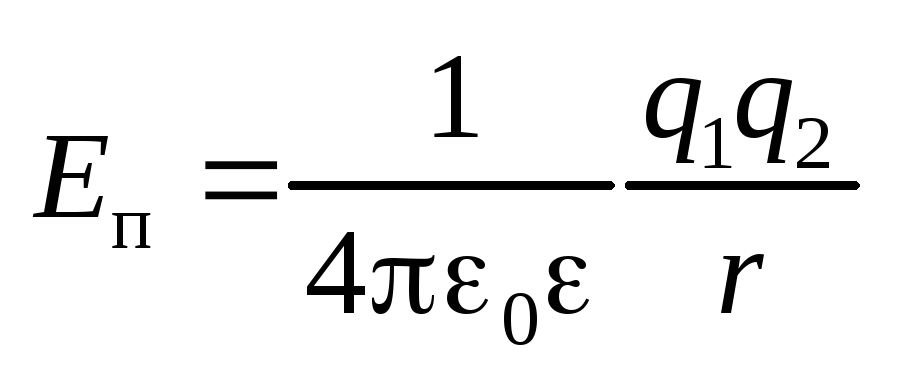 .
Потенциал электростатического поля
(определение)
.
Потенциал электростатического поля
(определение) 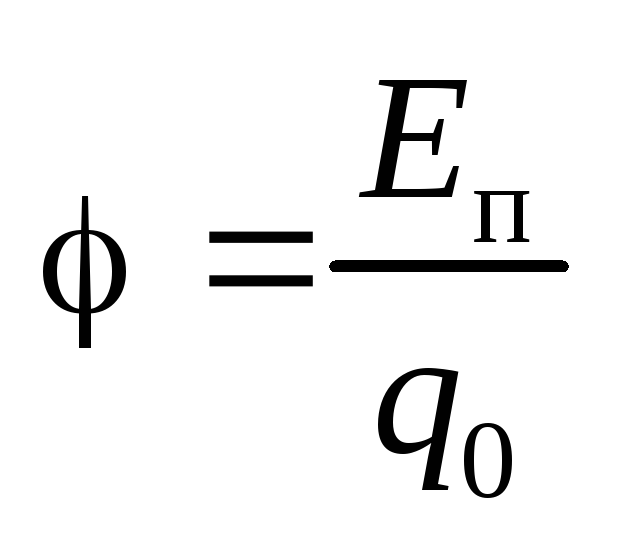 .
Связь работы электростатического поля
с разностью потенциалов
.
Связь работы электростатического поля
с разностью потенциалов 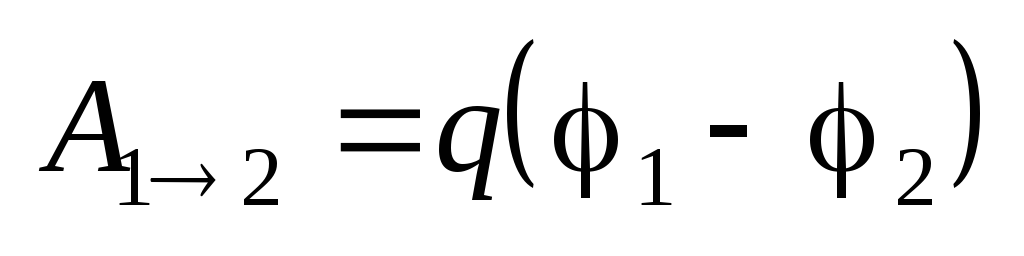 .
Выражение потенциала поля через работу
пробного заряда
.
Выражение потенциала поля через работу
пробного заряда 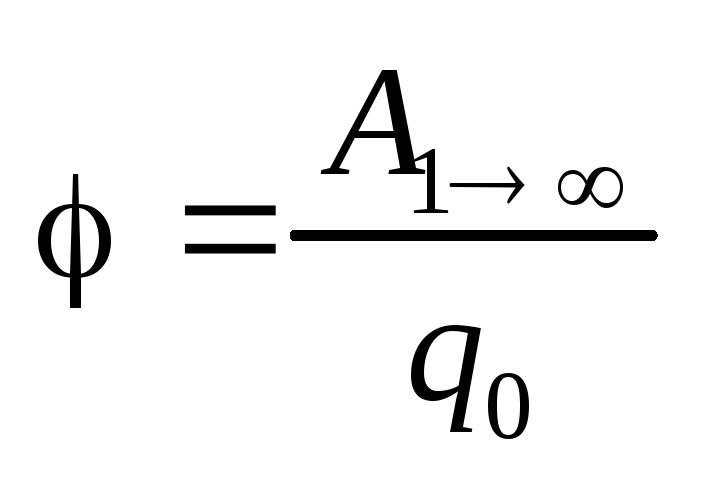 .
Расчет потенциала по распределению
напряженности поля
.
Расчет потенциала по распределению
напряженности поля 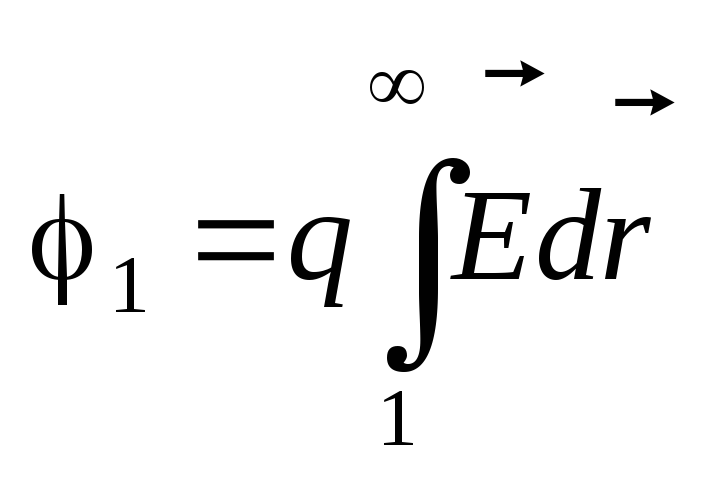 .
Расчет напряженности поля по распределению
потенциала
.
Расчет напряженности поля по распределению
потенциала 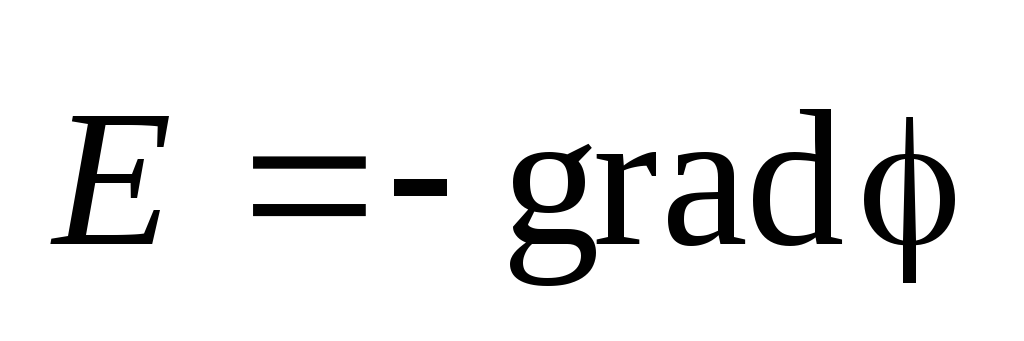 .
Связь между напряжением и напряженностью
для однородного поля
.
Связь между напряжением и напряженностью
для однородного поля 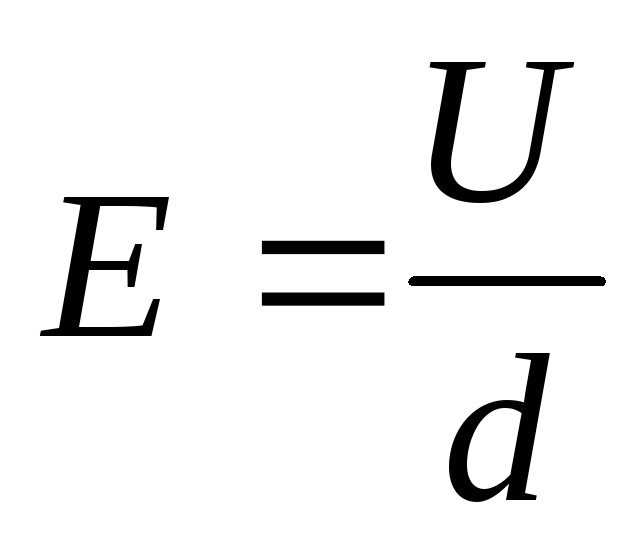 .
Дипольный момент электрического диполя
.
Дипольный момент электрического диполя 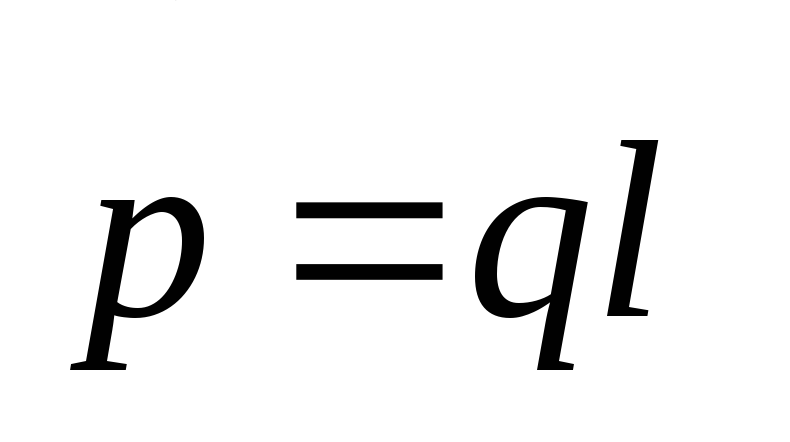 .
Момент сил, действующих на электрический
диполь в электрическом поле
.
Момент сил, действующих на электрический
диполь в электрическом поле 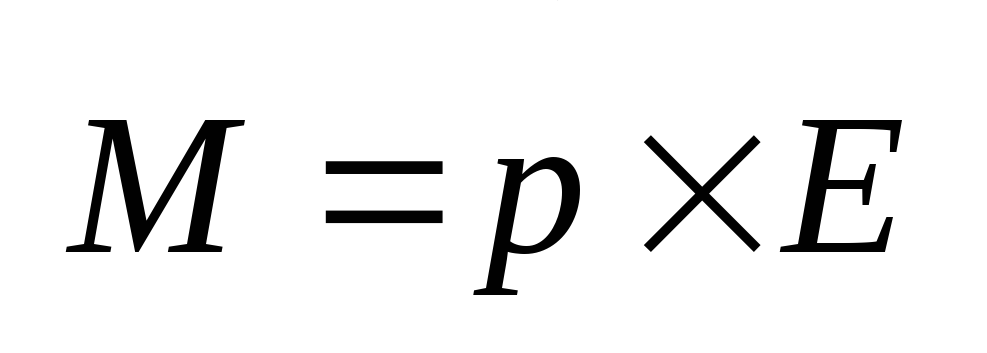 ;
; 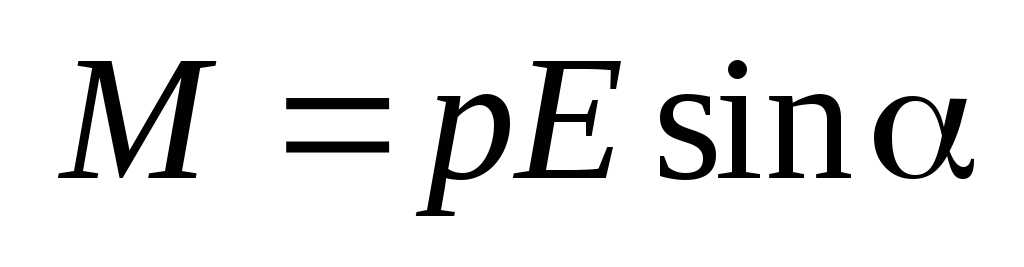 .
Потенциальная энергия электрического
диполя во внешнем электрическом поле
.
Потенциальная энергия электрического
диполя во внешнем электрическом поле 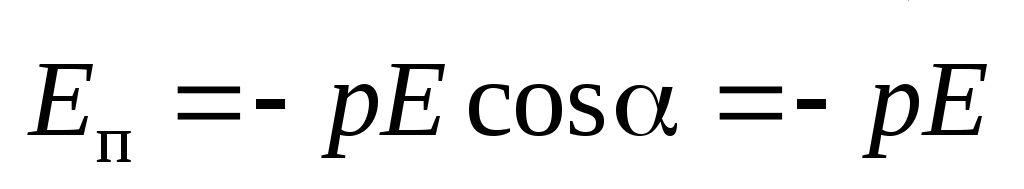 .
.
Проводник в электростатическом поле
Проводники – вещества, в которых имеются свободные заряды, способные перемещаться под действием электрического поля.
Электростатическая индукция – явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле.
Свободные заряды в проводнике, находящемся во внешнем электростатическом поле, перераспределяются так, что создаваемое ими собственное поле компенсирует внешнее, в результате чего напряженность результирующего поля в проводнике становится равной нулю. На этом явлении основана электростатическая защита – защита чувствительных к электрическому полю приборов с помощью замкнутой металлической оболочки, т. к. внутри нее электрическое поле отсутствует.
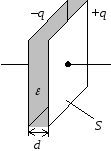
Конденсатор – устройство для накопления значительных по величине разноименных электрических зарядов. Конденсатор состоит из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Электроемкость конденсатора – физическая величина, равная отношению заряда одной из пластин конденсатора (по модулю) к напряжению между его обкладками.
Свойства
электростатического поля внутри
проводника 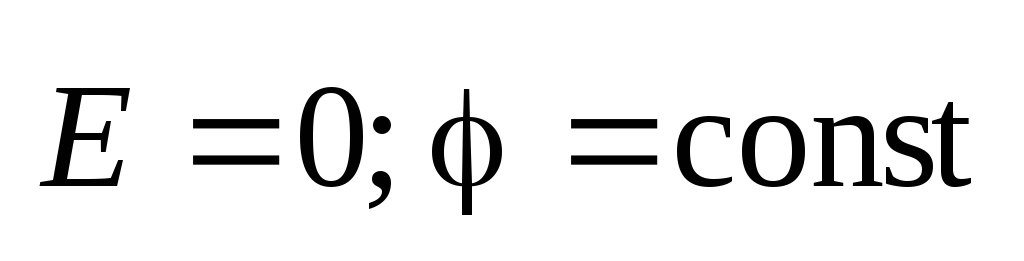 .
Свойства электростатического поля вне
проводника около его поверхности
.
Свойства электростатического поля вне
проводника около его поверхности 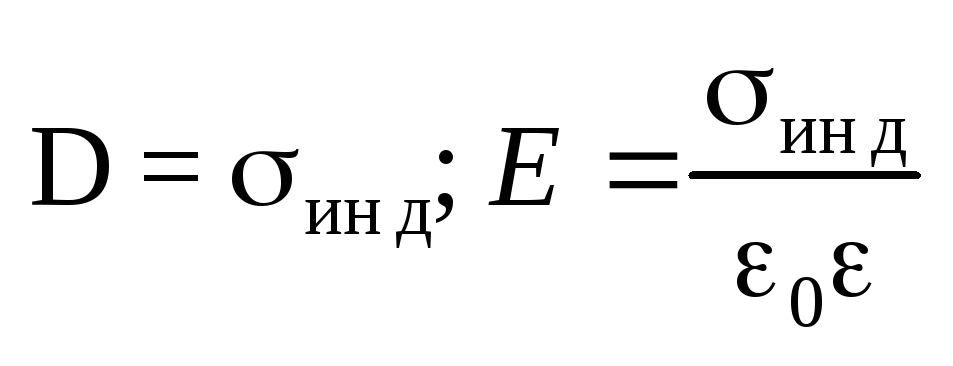 .
Электроемкость уединенного проводника
(определение)
.
Электроемкость уединенного проводника
(определение) 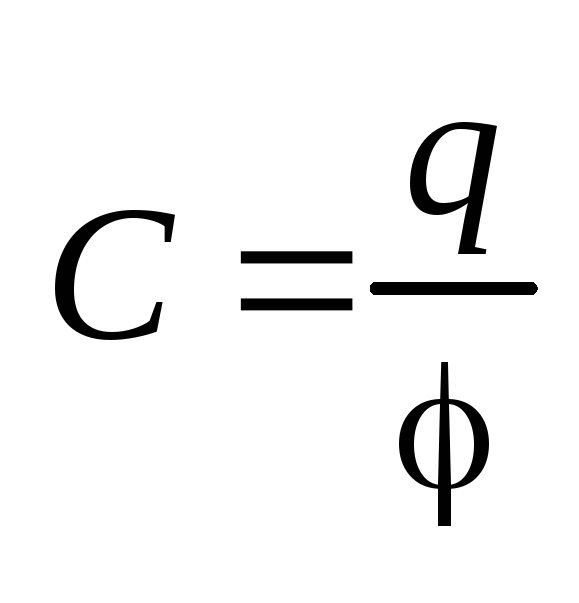 .
Электроемкость шара
.
Электроемкость шара 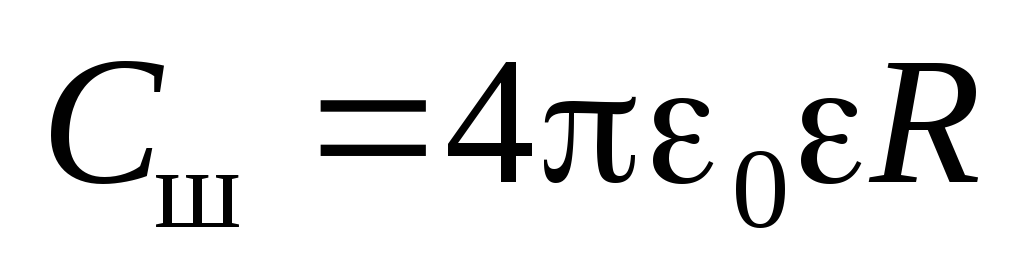 .
Электроемкость конденсатора (определение)
.
Электроемкость конденсатора (определение)  .
Электроемкость плоского конденсатора
.
Электроемкость плоского конденсатора 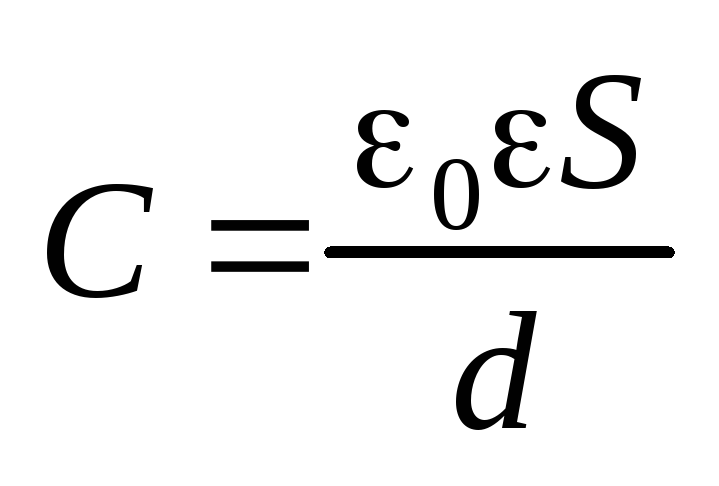 .
Электроемкость цилиндрического
конденсатора
.
Электроемкость цилиндрического
конденсатора 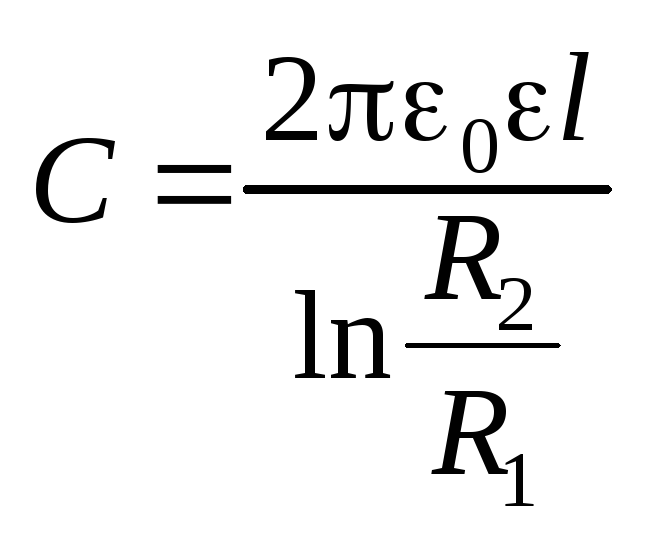 .
Электроемкость сферического конденсатора
.
Электроемкость сферического конденсатора 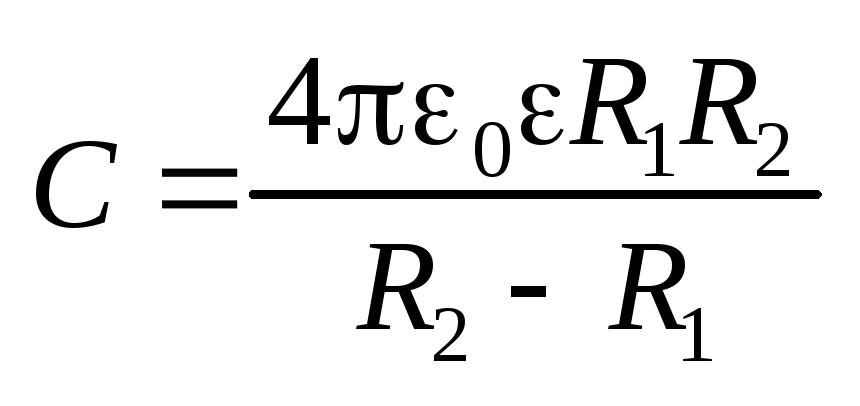 .
Электроемкость параллельно соединенных
конденсаторов
.
Электроемкость параллельно соединенных
конденсаторов 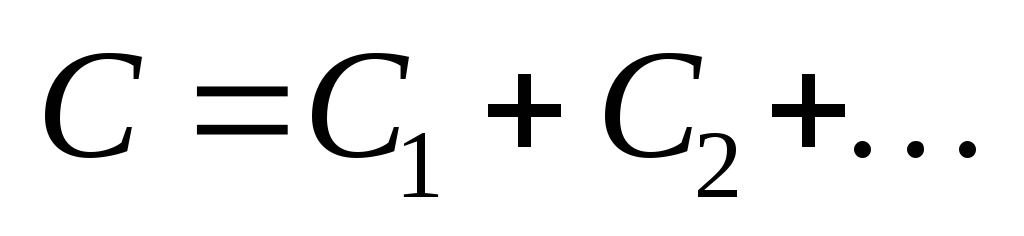 .
Электроемкость последовательно
соединенных конденсаторов
.
Электроемкость последовательно
соединенных конденсаторов  .
Потенциальная энергия системы
электрических зарядов
.
Потенциальная энергия системы
электрических зарядов 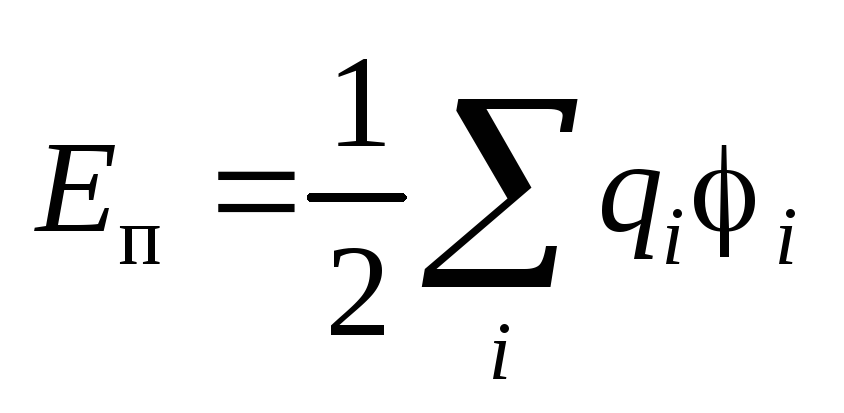 .
Потенциальная энергия уединенного
проводника
.
Потенциальная энергия уединенного
проводника 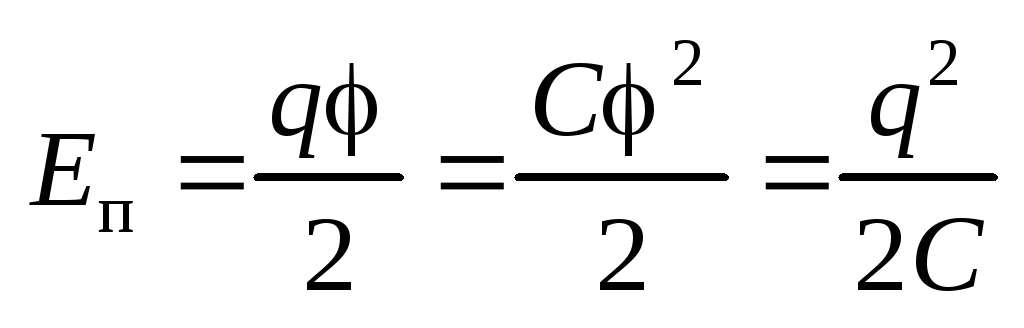 .
Потенциальная энергия конденсатора
.
Потенциальная энергия конденсатора  .
Объемная плотность энергии электрического
поля
.
Объемная плотность энергии электрического
поля 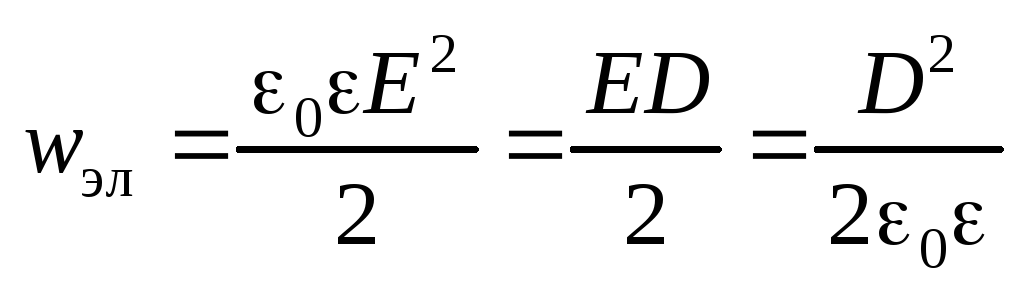 .
Условия на границе раздела двух
диэлектриков
.
Условия на границе раздела двух
диэлектриков 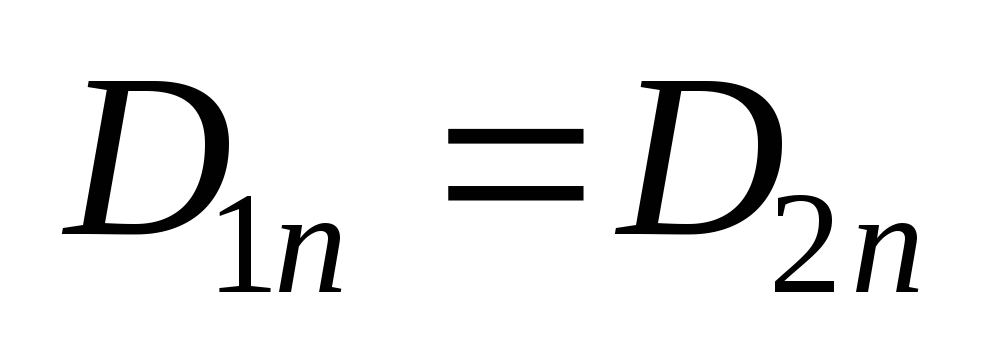 ;
; 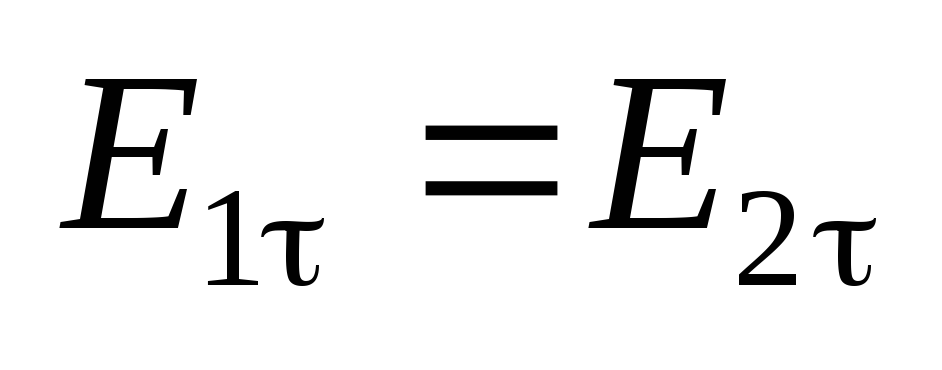 .
.
|
|
|
Плоский конденсатор | Параллельное соединение | Последовательное соединение |
Электрическое поле – FIZI4KA

Электродинамика – раздел физики, изучающий свойства и взаимодействия электрических зарядов, осуществляемые посредством электромагнитного поля.
Электростатикой называется раздел электродинамики, в котором рассматриваются свойства и взаимодействия неподвижных электрически заряженных тел или частиц.
Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.
Точечный заряд – заряженное тело, размер которого мал по сравнению с расстоянием, на котором оценивается его действие.
Электризация тел
Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.
Способы электризации:
- трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
- через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
- при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
- при ударе;
- под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.
Взаимодействие зарядов. Два вида зарядов
Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.
Обозначение – \( q \), единица измерения в СИ – кулон (Кл).
Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10-19 Кл), наименьший положительный заряд (1,6·10-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.
Величина заряда тела будет равна


где \( N \) — число избыточных или недостающих электронов;
\( e \) — элементарный заряд, равный 1,6·10-19 Кл.
Важно!
Частица может не иметь заряда, но заряд без частицы не существует.
Электрические заряды взаимодействуют:
- заряды одного знака отталкиваются:

- заряды противоположных знаков притягиваются:


Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.

Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.

Закон сохранения электрического заряда
Систему называют замкнутой (электрически изолированной), если в ней не происходит обмена зарядами с окружающей средой.
В любой замкнутой (электрически изолированной) системе сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.
Полный электрический заряд \( (q) \) системы равен алгебраической сумме ее положительных и отрицательных зарядов \( (q_1, q_2 … q_N) \):


Важно!
В природе не возникают и не исчезают заряды одного знака: положительный и отрицательный заряды могут взаимно нейтрализовать друг друга, если они равны по модулю.
Закон Кулона
Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.
Закон Кулона формулируется так:
сила взаимодействия \( F \) двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям \( q_1 \) и \( q_2 \) и обратно пропорциональна квадрату расстояния между ними \( r \):
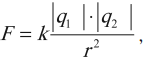
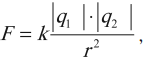
где \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (Н·м2)/Кл2 – коэффициент пропорциональности,
\( \varepsilon_0=8.85\cdot10^{-12} \) Кл2/(Н·м2) – электрическая постоянная.
Коэффициент \( k \) численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.
Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.
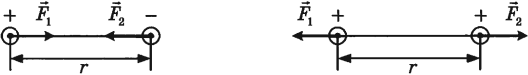
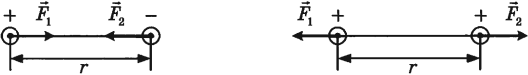
Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:
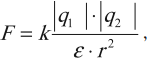
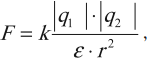
где \( \varepsilon \) – диэлектрическая проницаемость среды.
Закон Кулона применим к взаимодействию
- неподвижных точечных зарядов;
- равномерно заряженных тел сферической формы.
В этом случае \( r \) – расстояние между центрами сферических поверхностей.
Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции).
Действие электрического поля на электрические заряды
Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.
Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.
Свойства электрического поля заключаются в том, что оно:
- материально;
- создается зарядом;
- обнаруживается по действию на заряд;
- непрерывно распределено в пространстве;
- ослабевает с увеличением расстояния от заряда.
Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.
Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:
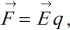
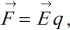
где \( \vec{E} \) – напряженность электрического поля, \( q \) – заряд.
Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.
Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:
- сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
- записать для заряда условие равновесия или основное уравнение динамики материальной точки;
- выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
- если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
- записать математически все вспомогательные условия;
- решить полученную систему уравнений относительно неизвестной величины;
- проверить решение
Напряженность электрического поля
Напряженность электрического поля \( \vec{E} \) – векторная физическая величина, равная отношению силы \( F \), действующей на пробный точечный заряд, к величине этого заряда \( q \):


Обозначение – \( \vec{E} \), единица измерения в СИ – Н/Кл или В/м.
Напряженность поля точечного заряда в вакууме вычисляется по формуле:
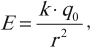
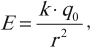
где \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (Н·м2)/Кл2,
\( q_0 \) – заряд, создающий поле,
\( r \) – расстояние от заряда, создающего поле, до данной точки.
Напряженность поля точечного заряда в среде вычисляется по формуле:
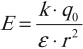
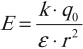
где \( \varepsilon \) – диэлектрическая проницаемость среды.
Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле.
Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.
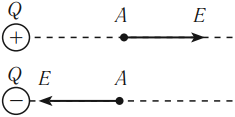

Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности \( \vec{E} \).
Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.
Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.
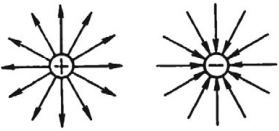

Определяя направление вектора \( \vec{E} \) в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.
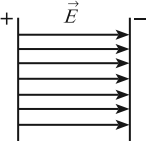

Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.
Принцип суперпозиции электрических полей
Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.
Принцип суперпозиции электрических полей: напряженность электрического поля системы \( N \) зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:
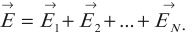
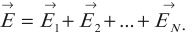
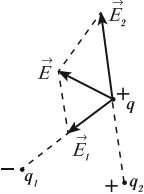

Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.
Потенциальность электростатического поля
Электрическое поле с напряженностью \( \vec{E} \) при перемещении заряда \( q \) совершает работу. Работа \( A \) электростатического поля вычисляется по формуле:
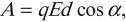
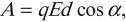
где \( d \) – расстояние, на которое перемещается заряд,
\( \alpha \) – угол между векторами напряженности электрического поля и перемещения заряда.
Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле.
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.
Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.
Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным.
Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой \( W \), так как буквой \( E \) обозначают напряженность поля:
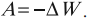
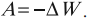
Потенциальная энергия заряда \( q \), помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.
Потенциал электрического поля. Разность потенциалов
Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.
Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).
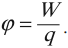
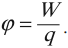
Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.
Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:
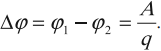
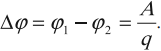
Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).
Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.
Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:
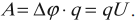
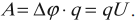
Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле.
В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:
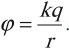
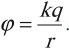
Для наглядного представления электрического поля используют эквипотенциальные поверхности.
Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю.
Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.
Свойства эквипотенциальных поверхностей
- Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
- Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.


Разность потенциалов и напряженность связаны формулой:


Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:
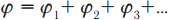
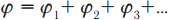
Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.
Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.
Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.
Алгоритм решения таких задач:
- установить характер и особенности электростатических взаимодействий объектов системы;
- ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
- записать законы сохранения и движения для объектов;
- выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
- составить систему уравнений и решить ее относительно искомой величины;
- проверить решение.
Проводники в электрическом поле
Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.
Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.
Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.
Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.
Важно!
Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита.
Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.
Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.
Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны).
Диэлектрики в электрическом поле
Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.
В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.
В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.
Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.
Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.
Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.
Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.
Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:
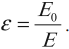
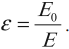
В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.
Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.
Электрическая емкость. Конденсатор
Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.
Обозначение – \( C \), единица измерения в СИ – фарад (Ф).
Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.
Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:
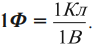
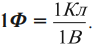
Формула для вычисления электроемкости:


где \( q \) – заряд проводника, \( \varphi \) – его потенциал.
Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.
Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.
Электроемкость конденсатора рассчитывается по формуле:
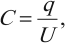
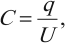
где \( q \) – модуль заряда одной из обкладок,
\( U \) – разность потенциалов между обкладками.
Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.
Плоский конденсатор представляет две параллельные пластины площадью \( S \), находящиеся на расстоянии \( d \) друг от друга.
Электроемкость плоского конденсатора:
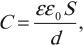
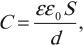
где \( \varepsilon \) – диэлектрическая проницаемость вещества между обкладками,
\( \varepsilon_0 \) – электрическая постоянная.
На электрической схеме конденсатор обозначается:


Виды конденсаторов:
- по типу диэлектрика – воздушный, бумажный и т. д.;
- по форме – плоский, цилиндрический, сферический;
- по электроемкости – постоянной и переменной емкости.
Конденсаторы можно соединять между собой.
Параллельное соединение конденсаторов
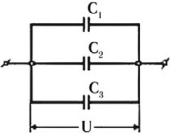

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:
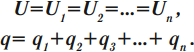
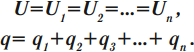
Общая емкость:
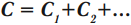
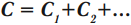
Последовательное соединение конденсаторов
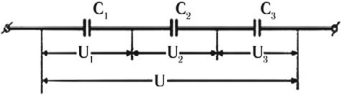

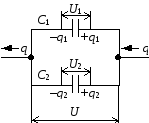
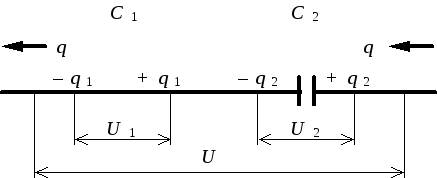
При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.
Заряды конденсаторов при таком соединении равны:
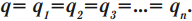
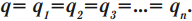
Общее напряжение:
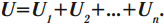
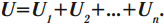
Величина, обратная общей емкости:
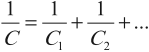
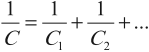
При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.
Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости.
Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.
Энергия электрического поля конденсатора
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:
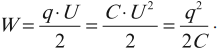
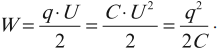
Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.
Плотность энергии электрического поля:
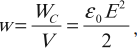
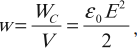
где \( V \) – объем пространства между обкладками конденсатора.
Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.
Основные формулы раздела «Электрическое поле»






Электрическое поле
5 (100%) 1 vote