Статья на тему Основы безвихревой электродинамики Потенциальное магнитное поле

                                        
УДК  537. 87. 872                                   
                         Основы безвихревой электродинамики.
                                                  Кузнецов Ю.Н.
                       Часть1. Потенциальное магнитное поле.
             На примере механического воздействия на тело даётся представление о
       симметрийно-физических переходах в природных явлениях.
             Распространение идеи переходов на магнитостатику предсказывает существование потенциального магнитного поля.
            Излагаются логические доказательства истинности предсказания.
            Даётся описание подтверждающих экспериментов.
Симметрийно-физический переход в механическом явлении.
Геометрии природных явлений и участвующих в них объектов обладают той, или иной степенью симметрии. В настоящей статье затрагиваются предельные цилиндрообразный и шарообразный варианты, характеризуемые преобразованием  явления (объекта) самого в себя при непрерывном повороте вокруг одной, или двух имеющихся осей симметрии.
Согласно фактам предельная симметрия больше, чем разновидность геометрической формы. Она реально проявляет себя как действенная сторона явления, находящаяся в неразрывной связи с физическими свойствами участников и причинно-следственными отношениями между ними.
Зависимость физики явления от степени его предельной геометрической симметрии зримо проявляется в процессе практического осуществления симметрийного перехода, который происходит всегда ступенчато.
В качестве примера приведём симметрийно-физический переход в области механических явлений. В таблице 1 иллюстрируется факт физического перехода в явлении силового воздействия на тело при повороте одной из двух однонаправленных сил () на 180°.
       При изменении симметрии действующих сил ускорение тела сменяется его деформацией, а вместо инерционного проявляется другое своё же свойство тела — его упругость.
       Ньютоновская причинно-следственная связь переходит в гуковскую.
       Симметрийно-физический переход в магнитостатике.
       Симметрийный аспект. По аналогии с механическим примером возможен переход физических свойств магнитного поля (таблица 2) при повороте одного из двух однонаправленных токов (i2) на 180°.
       Известные электромагнитные поля, с точки зрения их геометрической структуры, обладают либо замкнутыми, либо разомкнутыми силовыми линиями. Других вариантов в электромагнетизме нет.
       . Поэтому безальтернативно выдвигается предположение о замене в центрально-симметричной магнитостатике исходного циркуляционного свойства магнитного поля с цилиндрообразной симметрией на потенциальное, обладающее шарообразной симметри-
                                                                                                                                     Таблица 2.
ей, подобной симметрии поля электрического заряда. Новое отношение между центрально-симметричным токовым источником и его более симметричным потенциальным магнитным полем предполагается аналогичным гауссовой причинно-следственной связи для электростатики.
В природном явлении предельные симметрии причины и следствия не могут быть разными. Исскуственный перевод причины (токового источника)  к более симметричному виду предположительно сопровождается  аналогичным переходом в следствии (в магнитном поле).
 Идея о потенциальном  магнитном поле с шарообразной симметрией присутствует в гипотезе Дирака о магнитном микромонополе.
Физический аспект. Известные знания о протяжённых структурах полей получены из эмпирических  фактов о результатах их локальных воздействий на электрические заряды.
Следовательно, предполагаемый переход к другой структуре магнитного поля может быть подтверждён только доказательством перехода к другой направленности локальных магнитных сил в рамках их релятивистской природы.
       Для ясного понимания причины и непосредственного видения механизма такого перехода в последующем изложении приводятся в сопоставлении два одинаковых по своей сути примера, сочетающих логику и очевидность.
       Суть парселловской идеи в том, что в областях сгущений силовых линий воздействие каждого токового заряда  на пробный усиливается, а в областях разряжения — уменьшается. Общая релятивистская составляющая силового воздействия при однонаправленных токах наглядно представляется ориентированной поперечно к скорости движения пробного заряда и подчиняющейся правилу левой руки.
       Автором был предложен [2] аналогичный пример, основывающийся на той же парселловской идее. В нём, как и в таблице 2, всего лишь изменяется на 180° направление тока i2, сопровождаемое соответствующим поворотом диаграмм релятивистских «сплющиваний». В результате общая релятивистская составляющая силового воздействия  становится ориентированной вдоль скорости движения пробного заряда (Рис.2).
       Форма и количество релятивистского эффекта в поле каждого движущегося заряда,
как в однонаправленных, так и в центрально-симметричных токах, соответствуют специальной теории относительности. Разнятся лишь симметрии их наложения в области
пробного заряда, что и является истинной причиной существования поперечного и
продольного направлений магнитной силы.
                            i1                                                                   i2
 

             ∑V

Усиление притягивания

Ослабление отталкивания

Ослабление притягивания

Усиление отталкивания

Ослабление отталкивания

                                                                              Q
                         
                                                                  Рис.1
              
                         i1                                                                         i2

 

             ∑V

Усиление притягивания

Ослабление отталкивания

Ослабление отталкивания

Усиление притягивания

                                                                    Q

 

                                                       
                                                                   Рис.2                                                          
       Изменению магнитообрузующего свойства токового источника (более симметричному сочетанию диаграмм релятивистских эффектов) соответствует изменение взаимодействующего свойства общего поля движущихся зарядов (более симметричная направленность магнитной силы).
Примером монопольного источника потенциального магнитного поля является равномерное в обе стороны растяжение упругой электрически заряженной нити, приводя-
щее к образованию центрально-симметричных (противонаправленных) токов переноса зарядов.
        Материальный аспект. Приведенное обоснование подтвердим другим подходом, опирающимся на фундаментальные природные принципы.
       В удалённых от центрально-симметричного токового источника локальных областях пространства геометрическое суммирование равных и противоположно направленных векторов магнитной напряжённости Н и магнитного потенциала А везде даёт в итоге нуль-векторы. Математически корректные нуль-векторы с физической точки зрения иррациональны, поскольку не отвечают принципу наблюдаемости (измеряемости) природного объекта.
      Вместе с тем, после осуществления симметрийного перехода магнитная энергия во всём пространстве остаётся неизменной, поскольку составляющие однонаправленных и центрально-симметричных токов i1, i2, расположены на одной прямой линии (Рис.1,2).
      В обоих случаях нет причин для превращения даже части магнитной энергии в другие формы при условном сближении вдоль общей прямой линии левой и правой токовых составляющих из бесконечности, так как на  всей её протяжённости магнитное поле равно нулю. Поэтому однонаправленные и противонаправленные токовые составляющие одинаково не взаимодействуют между собой  ни силовым, ни индукционным способами.
       При использовании известных знаний для описания магнитного поля противотоков выявляется истинное противоречие между результатами применения принципов суперпозиции и сохранения энергии – физически иррациональное нуль-векторное поле обладает реальной магнитной энергией.
       Его разрешение начнём с первого естественного утверждения о необходимости создания другого теоретического описания, адекватного центрально-симметричной магнитостатике.
       Вторым пунктом теоретически обоснованно утверждается, что, вследствие сохранения магнитной энергии (следовательно – и взаимодействующих свойств поля), в новом теоретическом описании для характеристик локальных плотностей энергий сохраняются модули, векторы которых утратили свойство направленности. Эти модули образуют неоднородное скалярное поле.
      Третий пункт является центральным в разрешении противоречия. Полагается, что градиент радиально ориентированной неоднородности скалярного поля модулей взаимно скомпенсировавшихся векторов магнитного потенциала (оно линейно зависит от расстояния до токового источника) описывает новые радиально ориентированные векторы магнитной напряжённости
                                                    .                                                                (1)                                                                         
Последним пунктом итогово констатируется следующее понимание противоречия и его разрешения.
В условиях запрета принципом суперпозиции на образование центрально-симметричными противотоками циркуляционного свойства общего магнитного поля взамен, в меру сохраняющейся магнитной энергии, неизбежно образуется другое известное полевое свойство – потенциальное.
Нуль-векторная полевая ситуация свидетельствует не о взаимной компенсации накладывающихся магнитных полей токовых зарядов, что нарушало бы принцип сохранения энергии, а лишь исходных циркуляционных свойств.
Опытная регистрация эффекта стационарного потенциального магнитного поля. Стационарное потенциальное магнитное поле не взаимодействует силовым образом с замкнутыми токами, с постоянными магнитами.
Для его обнаружения использовался магнито-термический эффект, аналогичный известному охлаждению электропроводника циркуляционным магнитным полем.
       Уменьшение температуры электропроводника объясняется уменьшением энтропии системы заряженных частиц в нём в связи с некоторым упорядочением их движения магнитным полем. Потенциальное магнитное поле, в отличие от циркуляционного, спо
собно изменять не только траекторную, но и скоростную картину движения заряженных частиц.
       В качестве охлаждаемого тела в опытах использовался полупроводниковый. кристалл стабилитрона. Наличие у него сильной температурно-омической связи  (200 кОм/град. в обратном направлении в интервале 0,8…1,9 мОм) позволяло фиксировать магнито-термический эффект (МТЭ) по регистрируемому цифровым омметром увеличению омического сопротивления стабилитрона.
  В качестве дипольного источника потенциального магнитного поля применялись противонаправленные токи в паре рядом расположенных в одной плоскости прямоугольных многовитковых ( n = 300)  рамок с стационарным током (i =  0,55 А в каждой).

На рисунках  3,4   показаны схемы опытов.
                                                     R                      (МТЭ)
                                                                                             (НДТ)
          — i
                                                         I                II                   III         t
                                                                                                               
                                                                                       Рис.3
                                                        R
                                                                                                                 (НДТ)
               — i
                                                                    I                      II                 III                 t
                                                                                      Рис.4
   
  Стабилитрон размещался в латунной экранирующей втулке. С целью разделения во времени магнитного охлаждения кристалла стабилитрона и его нагрева джоулевым теплом (НДТ) термозащитный кожух выполнен из алебастра и имеет массу, равную 0,5 кг.
  Свободно пропуская магнитное поле, он в значительной мере аккумулирует в себе первоначальный слабый поток джоулева тепла, задерживая на некоторое время его влияние на стабилитрон.
В начале каждого опыта, в отсутствии исследуемого поля, оценивалась теплообменная ситуация между стабилитроном и окружающим пространством (зона I графиков).
       Горизонтальная ломанная  линия на первом участке графика указывает на неизменность во времени температуры стабилитрона.
       В зоне II подъём ломанной линии графика над горизонтальной средней указывает на увеличение омического сопротивления стабилитрона под воздействием магнитного охлаждения и этот факт является опытным доказательством образования центрально-
симметричными токами потенциального магнитного поля. Иного объяснения наблюдаемому факту автор не находит.
        В ряде опытов экранирующая втулка с стабилитроном  размещалась внутри толстостенной стальной втулки (d = 1, 4 см, D = 3, 2 см., ℓ = 6,5 см.). Однако проявление магнито-термического эффекта по-прежнему имело место, что подтверждает естественное
предположение об отсутствии взаимодействия потенциального магнитного поля с спиновыми магнитными моментами ферромагнитного материала. Второй опытный факт является весомым дополнением к искомому доказательству.
        В зоне III проявлялось преимущественное влияние джоулева тепла, образуемого токами в рамках. Ломанная линия графика уходит вниз вследствие нагревания экранирующей втулки и  стабилитрона тепловым потоком, преодолевшим тепловую защиту.
       В экспериментах с однонаправленными стационарными токами в паре рамок (Рис.4) магнитное охлаждение заметным образом не проявлялось.
Опытная регистрация эффекта переменного потенциального магнитного поля.
Из математической модели безвихревой электродинамики [ 2 ] имеем  следующую формулу для вычисления ЭДС, образуемой в проводнике посредством бесциркуляционного магнитного поля
                                                       ε ,                                                                                 (2)
которая упрощается в приближении однородности поля
                                             ε  = — d/dt ℓІ                                                                         (3)
По сравнению с вихревой электродинамикой в (3) вместо площади поверхности отображается квадрат протяжённости проводника.
Мощность потерь электромагнитной энергии поперечной ЭМВ в проводнике пропорциональна площади его поверхности, ортогональной вектору потока плотности  электромагнитной энергии 
                                                N1 = 0,5 ZВ ∫ НІdf,                                                      (4)                                                                    
где  ZВ  описывает волновое сопротивление проводника.
Для случая безвихревого электромагнитного поля площадь поверхности заменяется квадратом длины проводника, ориентированного вдоль вектора потока плотности электромагнитной энергии (вдоль возвратно-поступательных индукционных токов)
                                             N2 = 0,5 ZВ ℓ ∫ НІdℓ.                                                              (5)                                                                             
В приближении однородности поля по длине проводника имеем
                                              N2 =  0,5 ZВ  (Н ℓ )І                                                              (6)                                                                                  
В качестве источника переменного магнитного поля применялась та же пара рамок с переменными токами в них (по 0,55 А в каждой, f = 50 гц.).
Стабилитрон использовался другой. Коэффициент термоомической связи был вдвое меньше (100 кОм/град.).
Если в первой серии опытов охлаждался непосредственно кристалл стабилитрона=а, то во второй нагреваемым элементом была алюминиевая экранирующая втулка ( D = 1см, d = 0,8см, ℓ = 3 см, m = 2,4 г).
      Методика экспериментов заключалась в регистрации отрезка времени между моментами включения переменного тока и первым уменьшением показания цифрового омметра  на одну цифру, что указывало на нагрев стабилитрона (и алюминиевой втулки) на 0,01є.
Такому изменению температуры алюминиевой втулки эквивалентно увеличение энергии её теплосодержания на
                                         W =  4,187 с m Δ t                                                                    (7)                                                                      
                                         W = 2, 1 10 ˉ І ДЖ.                                                                                                       (8)                                                                                          
Малая начальная мощность нагрева втулки на 0,01є  позволяет использовать линейное приближение для определения времени достижения этой температуры
                                                 N =  W/Δt                                                                   (9)                                                
В опытах с стационарными противонаправленными токами в паре рамок, когда имел место только нагрев джоулевым теплом, были получены отрезки времени  в следующем интервале их разброса
                                      Δt = (10,4…12,2) мин.                                                                (10)                                              
Подставляя в (9) опытные результаты (10) получаем мощность нагрева втулки джо
улевым теплом
                                  N1 = (2,56…3,39) 10ˉ⁵     ВТ.                                                                                        (11)
В опытах с переменными противонаправленными токами к установленной величине мощности нагрева втулки джоулевым теплом ожидалось добавление мощности нагрева возвратно-поступательными индукционными токами.
Полученное существенное уменьшение регистрируемых отрезков времени
                                    Δt = (3,66…4,58) мин.                                                                  (12)
подтвердило ожидание, что и явилось по мнению автора,  опытным доказательством существования безвихревого вида электромагнитной индукции.                                                                                                                         
Подставляя в (9) результаты из (12) получаем суммарную мощность теплового нагрева втулки
                                 N2 = (7,84…9,54) 10ˉ⁵      Вт.                                                          (13)                                                                      
Для выявления составляющей мощности индукционного нагрева втулки использовалась формула
                                       N3 =  N2    —   N1                                                                                                                 (14)
                                       N3 = ( 4,77…6,09) 10 ˉ⁵    ВТ.                                                                                 (15)
Теоретическое вычисление мощности индукционного нагрева с использованием (6) даёт результат
                                      N3 = 6,5 10ˉ  Вт.
Его удовлетворительное совпадение с (15) придаёт дополнительную уверенность автору в истинности сформулированных им логических выводов об образовании центрально-симметричными токами потенциального магнитного поля, в существовании безвихревых электродинамических явлений.
В опытах с однонаправленными переменными токами эффект дополнительного нагрева втулки заметным образом не проявлялся.
Во второй части статьи  будет дана информация о сути продольных ЭМВ. Об опытном подтверждении автором  их существования. Об устройствах для излучения. О трактовке светового диапозона продольных ЭМВ. Об идеях получения и регистрации продольных фотонов.
       В третьей части будет изложена 4-мерная математическая модель безвихревой электродинамики и некоторые дополнительные суждения.
.
                                                                   
                                                        Литература.
1.Парселл Э. Электричество и магнетизм. М., Высшая школа.,!980г., стр. 191,192.
         2. Кузнецов Ю. Н. Научный журнал русского физического общества, 1-6, 1995 г
Сведения об авторе.
     Кузнецов Юрий Николаевич
     контактный телефон     677-26-65

Магнитный потенциал — Magnetic potential

Термин магнитный потенциал может быть использован для любого из двух величин в классической электромагнетизма : на магнитный векторный потенциал , или просто векторный потенциал , A ; и магнитный скалярный потенциал ψ . Обе величины могут быть использованы при определенных обстоятельствах для расчета магнитного поля B .

Более часто используется магнитный векторный потенциал определяется таким образом , что его ротор равен магнитному полю: завиток A = B . Вместе с электрическим потенциалом ф , магнитный векторный потенциал может быть использован для определения электрического поля Е , а также. Поэтому многие уравнения электромагнетизма можно записать либо в терминах полей Е и В , или что то же самое в терминах потенциалов А и ф . В более продвинутых теорий , таких как квантовая механика , большинство уравнений использовать потенциалы , а не полей.

Магнитный скалярный потенциал

ψ иногда используются для указания магнитного H -пол в тех случаях , когда нет свободных токов , таким образом , аналогично использования электрического потенциала для определения электрического поля в электростатиках . Одним из важного использования ф , чтобы определить магнитное поле из — за постоянные магниты , когда их намагниченность известна. С некоторой осторожностью скалярный потенциал может быть расширен для включения свободных токов , а также.

Исторически сложилось так , Лорд Кельвин впервые представлен векторный потенциал в 1851 году, наряду с формулой , касающейся его к магнитному полю.

Магнитный векторный потенциал

Магнитный векторный потенциал является векторное поле , определяемое вместе с электрическим потенциалом

ф (а скалярное поле ) с помощью уравнений:

Взнак равно∇×A,Езнак равно-∇φ-∂A∂T,{\ Displaystyle \ mathbf {B} = \ набла \ раз \ mathbf {A}, \ ,, \ четырехъядерных \ mathbf {E} = — \ набла \ фи — {\ гидроразрыва {\ парциальное \ mathbf {A}} {\ парциальное т}} \ ,,}

где В представляет собой магнитное поле и Е представляет собой электрическое поле . В магнитостатике , где нет времени , изменяющегося распределения заряда , требуются только первое уравнение. (В контексте электродинамики , термины векторного потенциала и скалярный потенциал используются для магнитного векторного потенциала

и электрического потенциала , соответственно. В математике, векторный потенциал и скалярный потенциал можно обобщить на более высокие измерения.)

Если электрические и магнитные поля определяются как выше от потенциалов, они автоматически удовлетворяют два уравнения Максвелла : закон Гаусса для магнетизма и закона Фарадея . Например, если непрерывна и хорошо определена всюду, то он гарантированно не приводит к магнитных монополей . (В математической теории магнитных монополей, позволено быть либо не определены или многозначны в некоторых местах, см магнитного монополя для деталей).

Начиная с приведенными выше определениями:

∇⋅Взнак равно∇⋅(∇×A)знак равно0∇×Езнак равно∇×(-∇φ-∂A∂T)знак равно-∂∂T(∇×A)знак равно-∂В∂T,{\ Displaystyle {\ {начинается выровнена} \ набли \ CDOT \ mathbf {B} = & \ наб \ CDOT \ влево (\ набла \ раза \ mathbf {A}, \ справа) = 0 \\\ наб \ раза \ mathbf { Е} & = \ набла \ раза \ влево (- \ Nabla \ Phi — {\ гидроразрыва {\ парциального \ mathbf {A}} {\ парциального т}} \ справа) = — {\ гидроразрыв {\ парциального} {\ парциального т}} \ влево (\ наб \ раза \ mathbf {A}, \ справа) = — {\ гидроразрыв {\ парциального \ mathbf {B}.} {\ парциального т}} \ {конец выровнен}}}

С другой стороны , существование A и φ гарантируются из этих двух законов , используя теорему Гельмгольца . Например, поскольку магнитное поле расходимость -бесплатно (Ряд Гаусса, т.е.

∇ ⋅ B = 0 ), всегда существует , который удовлетворяет приведенному выше определению.

Векторный потенциал используется при изучении Лагранжа в классической механике и в квантовой механике (см уравнение Шредингера для заряженных частиц , уравнение Дирака , Ааронова-Бома ).

В системе СИ , единицы A являются V · с · м ^-1 , и такие же , как и у импульса на единицу заряда .

Несмотря на то, магнитное поле B является псевдовектором (также называемый аксиальным вектором ), вектор — потенциал является полярным вектором . Это означает , что если правило правой руки для кросс — продуктов были заменены правило левой, но без изменения каких — либо других уравнений или определения, то

B переключит признаки, но не изменится. Это пример общей теоремы: Завиток полярного вектора псевдовектор, и наоборот.

выбор манометров

Приведенное выше определение не определяет магнитный векторный потенциал однозначно , потому что, по определению, мы можем произвольно добавить локон компоненты -свободной к магнитному потенциалу без изменения наблюдаемого магнитного поля. Таким образом, есть степень свободы доступной при выборе . Это условие известно как калибровочная инвариантность .

Уравнения Максвелла в терминах векторного потенциала

Используя приведенное выше определение потенциалов и применение его к двум другим уравнениям Максвелла (те, которые автоматически не удовлетворены) приводит к сложному дифференциальному уравнению , которое может быть упрощено с помощью манометра Lorenz , где выбираются так, чтобы удовлетворять:

∇⋅A+1с2∂φ∂Tзнак равно0.{\ Displaystyle \ набли \ CDOT \ mathbf {А} + {\ гидроразрыва {1} {с ^ {2}}} {\ гидроразрыва {\ парциального \ Phi} {\ парциального т}} = 0.}

С помощью индикатора Лоренца, уравнения Максвелла можно записать компактно в терминах магнитного векторного потенциала А и электрического скалярного потенциала ф :

∇2φ-1с2∂2φ∂T2знак равно-ρε0∇2A-1с2∂2A∂T2знак равно-μ0J{\ Displaystyle {\ начинаются {выровнен} \ набла ^ {2} \ фи — {\ гидроразрыва {1} {с ^ {2}}} {\ гидроразрыва {\ парциальное ^ {2} \ Phi} {\ парциальное т ^ {2}}} & = — {\ гидроразрыва {\ Rho} {\ эпсилон _ {0}}} \\\ набла ^ {2} \ mathbf {A} — {\ гидроразрыва {1} {с ^ {2} }} {\ гидроразрыва {\ парциальное ^ {2} \ mathbf {A}} {\ парциальное т ^ {2}}} & = — \ му _ {0} \ mathbf {j} \ {конец выровнен}}}

В других калибрах , уравнения различны. Различные обозначения , чтобы записать это же уравнение (используя четыре-векторов ) приведено ниже.

Расчет потенциалов от исходных распределений

Решения уравнений Максвелла в калибровке Лоренца (см Фейману и Джексон) с граничным условием , что оба потенциала к нулю достаточно быстро , поскольку они приближаются к бесконечности, называются запаздывающие потенциалы , которые являются магнитный векторный потенциал ( г , т ) и электрические скалярный потенциал φ ( г , т ) из — за текущее распределение плотности тока J ( г ‘, т ‘) , плотность заряда ρ ( г ‘, т ‘) , а объем Ω, в пределах которых ρ и J является не- нулю , по крайней мере иногда и некоторые места):

A(р,T)знак равноμ04π∫ΩJ(р’,T’)|р-р’|d3р’φ(р,T)знак равно14πε0∫Ωρ(р’,T’)|р-р’|d3р'{\ Displaystyle {\ начинаются {выровнен} \ mathbf {A} \ влево (\ mathbf {г}, т \ справа) & = {\ гидроразрыва {\ му _ {0}} {4 \ пи}} \ Int _ { \ Omega} {\ гидроразрыва {\ mathbf {J} \ влево (\ mathbf {г} ‘т’ \ справа)} {\ влево | \ mathbf {г} — \ mathbf {г} «\ право |}} \ , \ mathrm {d} ^ {3} \ mathbf {г} «\\\ Phi \ влево (\ mathbf {г}, т \ вправо) & = {\ гидроразрыва {1} {4 \ пи \ эпсилон _ {0 }}} \ int _ {\ Omega} {\ гидроразрыва {\ Rho \ влево (\ mathbf {г} ‘т’ \ справа)} {\ влево | \ mathbf {г} — \ mathbf {г} «\ вправо |}} \, \ mathrm {d} ^ {3} \ mathbf {г} «\ {конец выровнен}}}

где поля на позиции вектора г и времени т вычисляются из источников в отдаленном положении г ‘на более раннее время т ‘. Расположение г ‘представляет собой точечный источник в заряде или распределения тока (также переменного интегрирование, в пределах объема Ом ). Чем раньше времени т ‘называется запаздывающим время , и рассчитывается как

T’знак равноT-|р-р’|с{\ Displaystyle т ‘= т — {\ гидроразрыва {\ влево | \ mathbf {г} — \ mathbf {г}’ \ право |} {с}}},

Есть несколько заметных вещей о А и ф , вычисленные таким образом:

• (The датчик состояние Лоренц ): выполнено.∇⋅A+1с2∂φ∂Tзнак равно0{\ Displaystyle \ набли \ CDOT \ mathbf {А} + {\ гидроразрыва {1} {с ^ {2}}} {\ гидроразрыва {\ парциального \ Phi} {\ парциального т}} = 0}
• Положение г , точка , в которой значение для φ и A найдены только входит в уравнение как часть скалярного расстояния от р ‘к р . Направление от р ‘к р не входит в уравнение. Единственное , что имеет значение около точки источника, как далеко он находится.
• Подынтегральная использует замедленное время , т ‘. Это просто отражает тот факт , что изменения в источниках распространяются со скоростью света. Следовательно, плотность заряд и ток , влияющая на электрический и магнитный потенциал на г и т , из удаленного местоположения г ‘также должен быть в каком — то предшествующее время T ‘.
• Уравнение для А является векторным уравнением. В декартовых координатах уравнение разделяется на три скалярное уравнение:

  AИкс(р,T)знак равноμ04π∫ΩJИкс(р’,T’)|р-р’|d3р’AY(р,T)знак равноμ04π∫ΩJY(р’,T’)|р-р’|d3р’AZ(р,T)знак равноμ04π∫ΩJZ(р’,T’)|р-р’|d3р'{\ Displaystyle {\ начинаются {выровнены} А_ {х} \ слева (\ mathbf {R}, т \ справа) & = {\ гидроразрыва {\ му _ {0}} {4 \ пи}} \ Int _ {\ Omega} {\ гидроразрыва {J_ {х} \ влево (\ mathbf {г} ‘т’ \ справа)} {\ влево | \ mathbf {г} — \ mathbf {г} «\ право |}} \, \ mathrm {d} ^ {3} \ mathbf {г} «\\ А_ {у} \ ​​слева (\ mathbf {R}, т \ справа) & = {\ гидроразрыва {\ му _ {0} {4} \ пи }} \ int _ {\ Omega} {\ гидроразрыва {J_ {у} \ ​​влево (\ mathbf {г} ‘т’ \ справа)} {\ влево | \ mathbf {г} — \ mathbf {г} «\ право |}} \, \ mathrm {d} ^ {3} \ mathbf {г} «\\ А_ {г} \ слева (\ mathbf {R}, т \ справа) & = {\ гидроразрыва {\ му _ { 0}} {4 \ пи}} \ int _ {\ Omega} {\ гидроразрыва {J_ {г} \ влево (\ mathbf {г} ‘т’ \ справа)} {\ влево | \ mathbf {г} — \ mathbf {г} ‘\ право |}} \, \ mathrm {d} ^ {3} \ mathbf {г}’ \ {конец выровнен}}}

В этой форме легко видеть , что компонент А в заданном направлении , зависит только от компонентов J , которые находятся в том же направлении. Если ток переносятся в длинном прямом проводе, в A точках в том же направлении, что и провод.

В других датчиках, формула для А и ф отличается; например, см кулоновского датчик для другой возможности.

Живописание А-поле

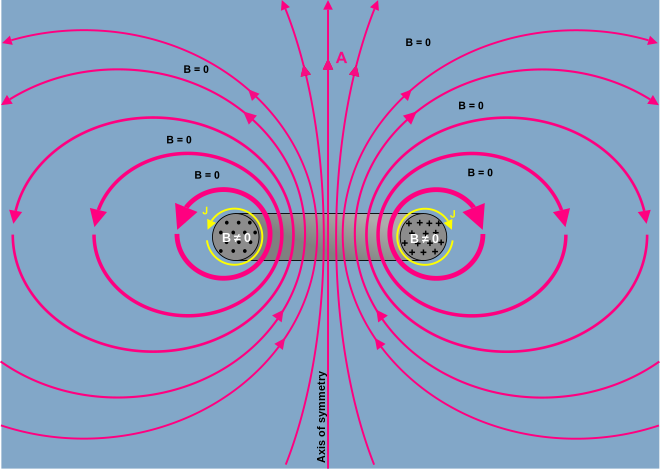Представляя кулоновское калибровочную магнитный векторный потенциал А , плотность магнитного потока В , а плотность тока J поля вокруг тороидальной катушки индуктивности круглого сечения . Более толстые линии обозначают линии поля высокой средней интенсивности. Круги в поперечном сечении сердечника представляют B -поле , выходящий из картины, а также знаки представляют собой B -field собирается в картину. ∇ ⋅ = 0 предполагалось.

См Фейнман для изображения А полей вокруг длинного тонкого соленоида .

поскольку

∇×Взнак равноμ0J{\ Displaystyle \ набла \ раз \ mathbf {B} = \ му _ {0} \ mathbf {j}}

при условии квазистатических условий, т.е.

∂Е∂T→0∇×Aзнак равноВ,{\ Displaystyle {\ гидроразрыва {\ парциального Е} {\ парциального т}} \ RightArrow 0 \, \ четырехъядерная \ наб \ раза \ mathbf {A} = \ mathbf {B}, \ ,,}

линии и контуры А относятся к B , как линии и контуры B относятся к J . Таким образом, изображение в A поля вокруг петли B потока (как будет производиться в тороидальной катушке индуктивности ) качественно такой же , как B поля вокруг петли тока.

На рисунке справа изображение художника из A поля. Более толстые линии указывают пути более высокой средней интенсивности (более короткие пути имеют более высокую интенсивность , так что интеграл пути то же самое). Линии тянутся к (эстетический) придают общий вид А — поле.

Чертеж молчаливо предполагает ∇ ⋅ = 0 , правда , при одном из следующих предположений:

• кулоновское датчик предполагается
• датчик Лоренца предполагается , и нет никакого распределения заряда, ρ = 0 ,
• датчик Лоренц предполагается , и предполагается , что нулевой частоте
• датчик Лоренца предполагаются и ненулевая частота , которая является достаточно низким пренебречь предполагаются1с∂φ∂T{\ Displaystyle {\ гидроразрыва {1} {C}} {\ гидроразрыва {\ парциального \ Phi} {\ парциального т}}}

Электромагнитный четыре потенциала

В контексте специальной теории относительности , то естественно , чтобы присоединиться магнитным векторный потенциал вместе с (скалярным) электрическим потенциалом в электромагнитный потенциал , называемом также четыре-потенциалом .

Одной из причин для этого является то , что четыре-потенциалом является математическим четыре-вектором . Таким образом, используя стандартные правила преобразования четырехмерный вектор, если электрические и магнитные потенциалы известны в одной инерциальной системе отсчета, то они могут быть просто вычислены в любой другой инерциальной системе отсчета.

Другой, связанных с мотивацией является то , что содержание классического электромагнетизма можно записать в краткой и удобной форме , используя электромагнитный потенциал, особенно , когда датчик Лоренц используется. В частности, в абстрактном индексе записи , множество уравнений Максвелла (в калибровке Лоренца) можно записать (в гауссовых единицах ) следующим образом :

∂μAμзнак равно0◻Aμзнак равно4πсJμ{\ Displaystyle {\ начинают {выровнены} \ парциальное ^ {\ му} A _ {\ му} & = 0 \\\ Вставка A _ {\ му} & = {\ гидроразрыва {4 \ пи} {C}} J _ {\ му} \ {конец выровнен}}}

где □ является даламбертианом и J представляет собой четыре тока . Первое уравнение представляет собой датчик состояние Лоренца , а вторые содержат уравнения Максвелла. Четыре потенциала также играет очень важную роль в квантовой электродинамике .

Магнитный скалярный потенциал

Скалярный потенциал это еще один полезный объем при описании магнитного поля, особенно для постоянных магнитов .

В односвязной области , где нет ни одного свободного тока,

∇×ЧАСзнак равно0,{\ Displaystyle \ наб \ раза \ mathbf {H} = 0,}

следовательно , мы можем определить магнитный скалярный потенциал , ψ , а

ЧАСзнак равно-∇ψ,{\ Displaystyle \ mathbf {H} = — \ набла \ фунтов на квадратный дюйм.}

Используя определение H :

∇⋅Взнак равноμ0∇⋅(ЧАС+M)знак равно0,{\ Displaystyle \ набла \ CDOT \ mathbf {B} = \ му _ {0} \ набла \ CDOT \ влево (\ mathbf {H} + \ mathbf {М} \ справа) = 0,}

это следует из того

∇2ψзнак равно-∇⋅ЧАСзнак равно∇⋅M,{\ Displaystyle \ набла ^ {2} \ фунты на квадратный дюйм = -. \ Наб \ CDOT \ mathbf {H} = \ наб \ CDOT \ mathbf {M}}

Здесь, ∇ ⋅ М действует в качестве источника магнитного поля, так же, как ∇ ⋅ P действует как источник для электрического поля. Поэтому аналогично связанный электрический заряд , величина

ρмзнак равно-∇⋅M{\ Displaystyle \ Rho _ {т} = — \ набла \ CDOT \ mathbf {M}}

называется связанный магнитный заряд .

Если есть свободный ток, можно вычесть вклад свободного тока в законе Био-Савара от общего магнитного поля и решить остаток с скалярного потенциала методом. На сегодняшний день не было никаких воспроизводимые доказательств существования магнитных монополей.

Смотрите также

Заметки

Рекомендации

• Даффина, WJ (1990). Электричество и магнетизм, четвертое издание . McGraw-Hill.

• Фейнман, Ричард P; Leighton, Роберт B; Пески, Мэтью (1964). Фейнмановские лекции по физике Том 2 . Addison-Wesley. ISBN  0-201-02117-X .

• Kraus, Джон Д. (1984), электромагнетизм (3 — е изд.), McGraw-Hill, ISBN  0-07-035423-5

• Ulaby, Фавваз (2007). Основы прикладной электродинамики, пятое издание . Pearson Prentice Hall. стр. 226-228. ISBN  0-13-241326-4 .

Помогите решить / разобраться (Ф)

Немного дополню прозвучавшие ответы.

Магнитное поле постоянного магнита вихревое или потенциальное?

Поле постоянного магнита вне магнита — и вихревое, и потенциальное. Надо хорошо понимать, что это не взаимоисключающие возможности. Такие поля (одновременно вихревые и потенциальные) называются Laplacian vector field.

Слова вихревое поле и соленоидальное поле — синонимы, но «вихревое поле» не совсем удачно: кажется, что это поле с ненулевым вихрем (ротором) 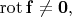в отличие от безвихревого 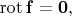но это не так. На самом деле, определение вихревого (соленоидального) поля — это нулевая дивергенция 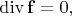а ротор может быть и нулевым, и ненулевым.

Поле постоянного магнита вне магнита удовлетворяет обоим условиям: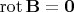
— поле потенциальное
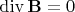— поле вихревое (соленоидальное)

—————-

Поле внутри постоянного магнита сложнее. В разных учебниках излагаются разные части общей картины. Но внутренность магнита вас не интересует, поэтому буду краток:
— есть истинное микроскопическое магнитное поле. Оно, вообще говоря, квантовое, и поэтому вообще не является просто векторным полем — это более сложный математический объект. В некотором смысле (который надо отдельно оговаривать математически), оно является вихревым, но не потенциальным. Кроме того, его трудно измерять непосредственно, и его свойства остаются теоретическими, и косвенно влияющими на результаты косвенных экспериментов.
— есть макроскопические магнитные поля, которые легко измерить в экспериментах. Они были введены ещё в 19 веке. По своей сути, они являются усреднениями истинного микроскопического поля, так чтобы «не замечать» неоднородностей поля на масштабах атомов и молекул. Но такое усреднение можно сделать по-разному, и поэтому приняты два разных макроскопических поля:

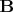— магнитная индукция, для которой источниками являются «токи Ампера» по боковой поверхности магнита;
— напряжённость магнитного поля, для которой источниками являются «магнитные заряды» на торце магнита.
Между ними действует соотношение 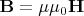(в магнитных веществах сложнее за счёт нелинейности и явления гистерезиса).

Так вот, внутри постоянного магнита, и во всём пространстве, включающем в себя внутренность постоянного магнита:
— поле 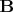вихревое, но не потенциальное;
— поле потенциальное, но не вихревое.

— 15.01.2014 18:08:41 —

Свободных магнитных зарядов в ближайшей к нам части Вселенной не наблюдается.

Ещё Кулон использовал в качестве пробного магнитного заряда конец длинного тонкого постоянного магнита.Если под работой вы имеете в виду интеграл 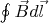, то да, «работа» отлична от нуля.
Это верно только для интегралов, контур которых проходит через вещество постоянного магнита (и то не для всех, а только для охватывающих ненулевую часть «токов Ампера»). Если контур расположен вне магнита, то такой интеграл (он называется циркуляцией поля по контуру, сообщаю для tasfinder) будет равен нулю.

Таким образом, мы должны уточнить и этот тезис:

пробный магнитный заряд совершив круг по полю и вернувшись в ту же точку совершит работу, значит поле вихревое.

Это будет выполняться только для пробных магнитных зарядов, проходящих сквозь вещество постоянного магнита. Экспериментально это сделать нельзя 🙂 (Никакие щели в постоянном магните не сработают — они приведут к работе противоположного знака внутри щели.)Вопрос вполне содержателен. А ответ на него ясен. Плотность энергии магнитного поля 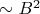Есть поле пробного магнита 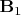и внешнее поле 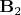. Поэтому плотность энергии магнитного поля 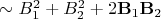. Если внешнее поле неоднородно, то при перемещении пробного магнита интеграл от последнего слагаемого меняется. Энергия магнитного поля переходит в энергию движения магнита.
Но разумеется, в подобной интерпретации нельзя совершить пробным магнитом (или пробным магнитным полюсом) полный круг, и при этом извлечь энергию. В этом смысле, магнитное поле потенциально.

Основы безвихревой электродинамики Потенциальное магнитное поле

8

УДК 537. 87. 872

Основы безвихревой электродинамики.

Кузнецов Ю.Н.

Часть1. Потенциальное магнитное поле.

На примере механического воздействия на тело даётся представление о

симметрийно-физических переходах в природных явлениях.

Распространение идеи переходов на магнитостатику предсказывает существование потенциального магнитного поля.

Излагаются логические доказательства истинности предсказания.

Даётся описание подтверждающих экспериментов.

Симметрийно-физический переход в механическом явлении.

Геометрии природных явлений и участвующих в них объектов обладают той, или иной степенью симметрии. В настоящей статье затрагиваются предельные цилиндрообразный и шарообразный варианты, характеризуемые преобразованием явления (объекта) самого в себя при непрерывном повороте вокруг одной, или двух имеющихся осей симметрии.

Согласно фактам предельная симметрия больше, чем разновидность геометрической формы. Она реально проявляет себя как действенная сторона явления, находящаяся в неразрывной связи с физическими свойствами участников и причинно-следственными отношениями между ними.

Зависимость физики явления от степени его предельной геометрической симметрии зримо проявляется в процессе практического осуществления симметрийного перехода, который происходит всегда ступенчато.

В качестве примера приведём симметрийно-физический переход в области механических явлений. В таблице 1 иллюстрируется факт физического перехода в явлении силового воздействия на тело при повороте одной из двух однонаправленных сил () на 180°.

Закон Ньютона

Однонаправленным силам

пропорционально ускорение тела

При изменении симметрии действующих сил ускорение тела сменяется его деформацией, а вместо инерционного проявляется другое своё же свойство тела — его упругость.

Ньютоновская причинно-следственная связь переходит в гуковскую.

Симметрийно-физический переход в магнитостатике.

Симметрийный аспект. По аналогии с механическим примером возможен переход физических свойств магнитного поля (таблица 2) при повороте одного из двух однонаправленных токов (i2) на 180°.

Известные электромагнитные поля, с точки зрения их геометрической структуры, обладают либо замкнутыми, либо разомкнутыми силовыми линиями. Других вариантов в электромагнетизме нет.

. Поэтому безальтернативно выдвигается предположение о замене в центрально-симметричной магнитостатике исходного циркуляционного свойства магнитного поля с цилиндрообразной симметрией на потенциальное, обладающее шарообразной симметри-

Таблица 2.

Теорема

о циркуляции магнитного вектора.

i1 i2

Однонаправленным токам

пропорциональна циркуляция вектора магнитной напряжённости поля вдоль замкнутой линии, охватывающей токи.

ей, подобной симметрии поля электрического заряда. Новое отношение между центрально-симметричным токовым источником и его более симметричным потенциальным магнитным полем предполагается аналогичным гауссовой причинно-следственной связи для электростатики.

В природном явлении предельные симметрии причины и следствия не могут быть разными. Исскуственный перевод причины (токового источника) к более симметричному виду предположительно сопровождается аналогичным переходом в следствии (в магнитном поле).

Идея о потенциальном магнитном поле с шарообразной симметрией присутствует в гипотезе Дирака о магнитном микромонополе.

Физический аспект. Известные знания о протяжённых структурах полей получены из эмпирических фактов о результатах их локальных воздействий на электрические заряды.

Следовательно, предполагаемый переход к другой структуре магнитного поля может быть подтверждён только доказательством перехода к другой направленности локальных магнитных сил в рамках их релятивистской природы.

Для ясного понимания причины и непосредственного видения механизма такого перехода в последующем изложении приводятся в сопоставлении два одинаковых по своей сути примера, сочетающих логику и очевидность.

Суть парселловской идеи в том, что в областях сгущений силовых линий воздействие каждого токового заряда на пробный усиливается, а в областях разряжения — уменьшается. Общая релятивистская составляющая силового воздействия при однонаправленных токах наглядно представляется ориентированной поперечно к скорости движения пробного заряда и подчиняющейся правилу левой руки.

Автором был предложен [2] аналогичный пример, основывающийся на той же парселловской идее. В нём, как и в таблице 2, всего лишь изменяется на 180° направление тока i2, сопровождаемое соответствующим поворотом диаграмм релятивистских «сплющиваний». В результате общая релятивистская составляющая силового воздействия становится ориентированной вдоль скорости движения пробного заряда (Рис.2).

Форма и количество релятивистского эффекта в поле каждого движущегося заряда,

как в однонаправленных, так и в центрально-симметричных токах, соответствуют специальной теории относительности. Разнятся лишь симметрии их наложения в области

пробного заряда, что и является истинной причиной существования поперечного и

продольного направлений магнитной силы.

i1 i2

∑V

Усиление

отталкивания

Усиление

притягивания

Ослабление

отталкивания

Ослабление

притягивания

Ослабление

отталкивания

Q

Рис.1

i1 i2

∑V

Ослабление

отталкивания

Усиление

притягивания

Ослабление

отталкивания

Усиление

притягивания

Q

Рис.2

Изменению магнитообрузующего свойства токового источника (более симметричному сочетанию диаграмм релятивистских эффектов) соответствует изменение взаимодействующего свойства общего поля движущихся зарядов (более симметричная направленность магнитной силы).

Примером монопольного источника потенциального магнитного поля является равномерное в обе стороны растяжение упругой электрически заряженной нити, приводя-

щее к образованию центрально-симметричных (противонаправленных) токов переноса зарядов.

Материальный аспект. Приведенное обоснование подтвердим другим подходом, опирающимся на фундаментальные природные принципы.

В удалённых от центрально-симметричного токового источника локальных областях пространства геометрическое суммирование равных и противоположно направленных векторов магнитной напряжённости Н и магнитного потенциала А везде даёт в итоге нуль-векторы. Математически корректные нуль-векторы с физической точки зрения иррациональны, поскольку не отвечают принципу наблюдаемости (измеряемости) природного объекта.

Вместе с тем, после осуществления симметрийного перехода магнитная энергия во всём пространстве остаётся неизменной, поскольку составляющие однонаправленных и центрально-симметричных токов i1, i2, расположены на одной прямой линии (Рис.1,2).

В обоих случаях нет причин для превращения даже части магнитной энергии в другие формы при условном сближении вдоль общей прямой линии левой и правой токовых составляющих из бесконечности, так как на всей её протяжённости магнитное поле равно нулю. Поэтому однонаправленные и противонаправленные токовые составляющие одинаково не взаимодействуют между собой ни силовым, ни индукционным способами.

При использовании известных знаний для описания магнитного поля противотоков выявляется истинное противоречие между результатами применения принципов суперпозиции и сохранения энергии – физически иррациональное нуль-векторное поле обладает реальной магнитной энергией.

Его разрешение начнём с первого естественного утверждения о необходимости создания другого теоретического описания, адекватного центрально-симметричной магнитостатике.

Вторым пунктом теоретически обоснованно утверждается, что, вследствие сохранения магнитной энергии (следовательно – и взаимодействующих свойств поля), в новом теоретическом описании для характеристик локальных плотностей энергий сохраняются модули, векторы которых утратили свойство направленности. Эти модули образуют неоднородное скалярное поле.

Третий пункт является центральным в разрешении противоречия. Полагается, что градиент радиально ориентированной неоднородности скалярного поля модулей взаимно скомпенсировавшихся векторов магнитного потенциала (оно линейно зависит от расстояния до токового источника) описывает новые радиально ориентированные векторы магнитной напряжённости

. (1)

Последним пунктом итогово констатируется следующее понимание противоречия и его разрешения.

В условиях запрета принципом суперпозиции на образование центрально-симметричными противотоками циркуляционного свойства общего магнитного поля взамен, в меру сохраняющейся магнитной энергии, неизбежно образуется другое известное полевое свойство – потенциальное.

Нуль-векторная полевая ситуация свидетельствует не о взаимной компенсации накладывающихся магнитных полей токовых зарядов, что нарушало бы принцип сохранения энергии, а лишь исходных циркуляционных свойств.

Опытная регистрация эффекта стационарного потенциального магнитного поля. Стационарное потенциальное магнитное поле не взаимодействует силовым образом с замкнутыми токами, с постоянными магнитами.

Для его обнаружения использовался магнито-термический эффект, аналогичный известному охлаждению электропроводника циркуляционным магнитным полем.

Уменьшение температуры электропроводника объясняется уменьшением энтропии системы заряженных частиц в нём в связи с некоторым упорядочением их движения магнитным полем. Потенциальное магнитное поле, в отличие от циркуляционного, спо

собно изменять не только траекторную, но и скоростную картину движения заряженных частиц.

В качестве охлаждаемого тела в опытах использовался полупроводниковый. кристалл стабилитрона. Наличие у него сильной температурно-омической связи (200 кОм/град. в обратном направлении в интервале 0,8…1,9 мОм) позволяло фиксировать магнито-термический эффект (МТЭ) по регистрируемому цифровым омметром увеличению омического сопротивления стабилитрона.

В качестве дипольного источника потенциального магнитного поля применялись противонаправленные токи в паре рядом расположенных в одной плоскости прямоугольных многовитковых ( n = 300) рамок с стационарным током (i = 0,55 А в каждой).

На рисунках 3,4 показаны схемы опытов.

R (МТЭ)

(НДТ)

— i

I II III 

Рис.3

R

(НДТ)

— i

I II III 

Рис.4

Стабилитрон размещался в латунной экранирующей втулке. С целью разделения во времени магнитного охлаждения кристалла стабилитрона и его нагрева джоулевым теплом (НДТ) термозащитный кожух выполнен из алебастра и имеет массу, равную 0,5 кг.

Свободно пропуская магнитное поле, он в значительной мере аккумулирует в себе первоначальный слабый поток джоулева тепла, задерживая на некоторое время его влияние на стабилитрон.

В начале каждого опыта, в отсутствии исследуемого поля, оценивалась теплообменная ситуация между стабилитроном и окружающим пространством (зона I графиков).

Горизонтальная ломанная линия на первом участке графика указывает на неизменность во времени температуры стабилитрона.

В зоне II подъём ломанной линии графика над горизонтальной средней указывает на увеличение омического сопротивления стабилитрона под воздействием магнитного охлаждения и этот факт является опытным доказательством образования центрально-

симметричными токами потенциального магнитного поля. Иного объяснения наблюдаемому факту автор не находит.

В ряде опытов экранирующая втулка с стабилитроном размещалась внутри толстостенной стальной втулки (d = 1, 4 см, D = 3, 2 см., ℓ = 6,5 см.). Однако проявление магнито-термического эффекта по-прежнему имело место, что подтверждает естественное

предположение об отсутствии взаимодействия потенциального магнитного поля с спиновыми магнитными моментами ферромагнитного материала. Второй опытный факт является весомым дополнением к искомому доказательству.

В зоне III проявлялось преимущественное влияние джоулева тепла, образуемого токами в рамках. Ломанная линия графика уходит вниз вследствие нагревания экранирующей втулки и стабилитрона тепловым потоком, преодолевшим тепловую защиту.

В экспериментах с однонаправленными стационарными токами в паре рамок (Рис.4) магнитное охлаждение заметным образом не проявлялось.

Опытная регистрация эффекта переменного потенциального магнитного поля.

Из математической модели безвихревой электродинамики [ 2 ] имеем следующую формулу для вычисления ЭДС, образуемой в проводнике посредством бесциркуляционного магнитного поля

ε , (2)

которая упрощается в приближении однородности поля

ε = — d/dt ℓІ (3)

По сравнению с вихревой электродинамикой в (3) вместо площади поверхности отображается квадрат протяжённости проводника.

Мощность потерь электромагнитной энергии поперечной ЭМВ в проводнике пропорциональна площади его поверхности, ортогональной вектору потока плотности электромагнитной энергии

N1 = 0,5 ZВ ∫ НІdf, (4)

где ZВ описывает волновое сопротивление проводника.

Для случая безвихревого электромагнитного поля площадь поверхности заменяется квадратом длины проводника, ориентированного вдоль вектора потока плотности электромагнитной энергии (вдоль возвратно-поступательных индукционных токов)

N2 = 0,5 ZВ ℓ ∫ НІdℓ. (5)

В приближении однородности поля по длине проводника имеем

N2 = 0,5 ZВ (Н ℓ )І (6)

В качестве источника переменного магнитного поля применялась та же пара рамок с переменными токами в них (по 0,55 А в каждой, f = 50 гц.).

Стабилитрон использовался другой. Коэффициент термоомической связи был вдвое меньше (100 кОм/град.).

Если в первой серии опытов охлаждался непосредственно кристалл стабилитрона=а, то во второй нагреваемым элементом была алюминиевая экранирующая втулка ( D = 1см, d = 0,8см, ℓ = 3 см, m = 2,4 г).

Методика экспериментов заключалась в регистрации отрезка времени между моментами включения переменного тока и первым уменьшением показания цифрового омметра на одну цифру, что указывало на нагрев стабилитрона (и алюминиевой втулки) на 0,01є.

Такому изменению температуры алюминиевой втулки эквивалентно увеличение энергии её теплосодержания на

W = 4,187 с m Δ t (7)

W = 2, 1 10 ˉ І ДЖ. (8)

Малая начальная мощность нагрева втулки на 0,01є позволяет использовать линейное приближение для определения времени достижения этой температуры

N = W/Δt (9)

В опытах с стационарными противонаправленными токами в паре рамок, когда имел место только нагрев джоулевым теплом, были получены отрезки времени в следующем интервале их разброса

Δ = (10,4…12,2) мин. (10)

Подставляя в (9) опытные результаты (10) получаем мощность нагрева втулки джо

улевым теплом

N1 = (2,56…3,39) 10ˉ⁵ВТ. (11)

В опытах с переменными противонаправленными токами к установленной величине мощности нагрева втулки джоулевым теплом ожидалось добавление мощности нагрева возвратно-поступательными индукционными токами.

Полученное существенное уменьшение регистрируемых отрезков времени

Δ = (3,66…4,58) мин. (12)

подтвердило ожидание, что и явилось по мнению автора, опытным доказательством существования безвихревого вида электромагнитной индукции.

Подставляя в (9) результаты из (12) получаем суммарную мощность теплового нагрева втулки

N2 = (7,84…9,54) 10ˉ⁵ Вт. (13)

Для выявления составляющей мощности индукционного нагрева втулки использовалась формула

N3 = N2 — N1 (14)

N3 = ( 4,77…6,09) 10 ˉ⁵ВТ. (15)

Теоретическое вычисление мощности индукционного нагрева с использованием (6) даёт результат

N3 = 6,5 10ˉ Вт.

Его удовлетворительное совпадение с (15) придаёт дополнительную уверенность автору в истинности сформулированных им логических выводов об образовании центрально-симметричными токами потенциального магнитного поля, в существовании безвихревых электродинамических явлений.

В опытах с однонаправленными переменными токами эффект дополнительного нагрева втулки заметным образом не проявлялся.

Во второй части статьи будет дана информация о сути продольных ЭМВ. Об опытном подтверждении автором их существования. Об устройствах для излучения. О трактовке светового диапозона продольных ЭМВ. Об идеях получения и регистрации продольных фотонов.

В третьей части будет изложена 4-мерная математическая модель безвихревой электродинамики и некоторые дополнительные суждения.

.

Литература.

1.Парселл Э. Электричество и магнетизм. М., Высшая школа.,!980г., стр. 191,192.

2. Кузнецов Ю. Н. Научный журнал русского физического общества, 1-6, 1995 г

Сведения об авторе.

Кузнецов Юрий Николаевич

контактный телефон 677-26-65

Гауссоподобная теорема о потоке магнитных векторов. i1 i2 Центрально-симметричным (противонаправленным) токам прапор- ционален поток векторов магнитной напряжённости поля по замкнутой поверхности, охватывающей токи.

Каковы различия потенциального и вихревого силовых полей — MOREREMONTA

Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.

Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.

Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:

Определение вихревого поля также выполнимо другим способом.

Вихревое магнитное поле

Векторные поля, вектор которых не равен нулю – это вихревые магнитные поля.

Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:

r o t B → = μ 0 j → ( 2 ) , где j → считается объемной плотностью тока, и второй формы определения вихревого поля можно заключить, что магнитное поле будет вихревым там, где проходят токи, а безвихревым там, где их нет.

При отсутствии токов вектор магнитной индукции B → представляется в виде градиента скалярного магнитного потенциала φ m :

B → = — g r a d φ m ( 3 ) .

Если имеются токи, то данное представление невозможно.

Различие между потенциальными и вихревыми полями

Основными уравнениями магнитного поля постоянных токов считаются выражения вида:

r o t B → = μ 0 j → d i v B → = 0 ( 4 ) .

Произведем сравнение с основными уравнениями электростатики:

r o t E → = 0 d i v E → = 1 ε 0 ρ ( 5 ) .

Рассматривая систему ( 5 ) , видно, что электрическое поле всегда потенциально, а его источниками являются электростатические (неподвижные) заряды.

Магнитное поле считается вихревым при наличии токов. Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.

Электрические токи являются источниками поля. Магнитное поле считается вихревым, так как его дивергенция везде равна нулю. Его также называют соленоидальным. Определение потенциального электростатического поля возможно при заданной дивергенции напряженности d i v E → ( x , y , z ) в качестве функции координат. Полное определение вихревого магнитного поля реально, когда имеется мощность его вихрей, то есть r o t B → ( x , y , z ) как функция координат.

Показать, почему для вихревого магнитного поля нельзя представить вектор индукции B → в виде градиента магнитного потенциала φ m .

B → = — g r a d φ m ( 1 . 1 ) .

Для выражения ( 1 . 1 ) можно применить операцию r o t :

r o t B → = — r o t g r a d φ m ( 1 . 2 ) .

Известно значение r o t :

r o t ( g r a d φ m ) = 0 ( 1 . 3 ) .

При подстановке ( 1 . 3 ) в ( 1 . 2 ) имеем:

Ответ: Вспомнив теорему о циркуляции, получаем отсутствие токов. В данном случае, представление вектора индукции магнитного поля невозможно в виде магнитного потенциала в области, где проходят токи.

Применение понятия скалярного магнитного потенциала φ m возможно только в области пространства, где j → = 0 . Данная часть пространства φ m характеризуется неоднозначностью функции. Показать это.

Необходимо рассмотреть магнитное поле возле контура с током, как изображено на рисунке 1 . По теореме о циркуляции для любого контура выполнимо равенство:

Если токов нет, магнитное поле становится потенциальным, интеграл, который необходимо взять между A и B , не зависит от пути интегрирования, то запись примет вид:

∫ A a B B → d l → = ∫ A b B B → d l → ( 2 . 2 ) .

∫ A b B B → d l → = ∫ A B B → d l → = φ m A — φ m B ( 2 . 3 ) .

Выражение ( 2 . 3 ) может быть рассмотрено в качестве разности скалярных магнитных потенциалов в точках A и B . Можно пойти иным путем и принять значение потенциала равным нулю в точке В , как выполнялось для нахождения потенциала в электростатике:

∫ A B B → d l → = φ m A ( 2 . 4 ) .

При выборе контура, охватывающего какой-либо ток (контур A c b B ), как показано на рисунке 1 , линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет не равен нулю:

∮ A c b B B → d l → ≠ 0 ( 2 . 5 ) .

∮ A c b B B → d l → ≠ ∫ A c B B → d l → — ∫ A b B B → d l → = I ≠ 0 ( 2 . 6 )

∫ A c B B → d l → = ∫ A b B B → d l → + I = φ m A — φ m B + I ( 2 . 7 ) .

При выборе какого-либо пути A n B , охватывающего ток в количестве n раз, имеем:

∫ A n B B → d l → = φ m A — φ m B + n I ( 2 . 8 ) .

Следует задать нулевой потенциал в точке В :

∫ A n B B → d l → = φ m A + n I ( 2 . 9 ) .

Ответ: Получив уравнение ( 2 . 9 ) , очевидно, что скалярный магнитный потенциал является неоднозначной величиной.

Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.

Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.

Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:

Определение вихревого поля также выполнимо другим способом.

Вихревое магнитное поле

Векторные поля, вектор которых не равен нулю – это вихревые магнитные поля.

Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:

r o t B → = μ 0 j → ( 2 ) , где j → считается объемной плотностью тока, и второй формы определения вихревого поля можно заключить, что магнитное поле будет вихревым там, где проходят токи, а безвихревым там, где их нет.

При отсутствии токов вектор магнитной индукции B → представляется в виде градиента скалярного магнитного потенциала φ m :

B → = — g r a d φ m ( 3 ) .

Если имеются токи, то данное представление невозможно.

Различие между потенциальными и вихревыми полями

Основными уравнениями магнитного поля постоянных токов считаются выражения вида:

r o t B → = μ 0 j → d i v B → = 0 ( 4 ) .

Произведем сравнение с основными уравнениями электростатики:

r o t E → = 0 d i v E → = 1 ε 0 ρ ( 5 ) .

Рассматривая систему ( 5 ) , видно, что электрическое поле всегда потенциально, а его источниками являются электростатические (неподвижные) заряды.

Магнитное поле считается вихревым при наличии токов. Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.

Электрические токи являются источниками поля. Магнитное поле считается вихревым, так как его дивергенция везде равна нулю. Его также называют соленоидальным. Определение потенциального электростатического поля возможно при заданной дивергенции напряженности d i v E → ( x , y , z ) в качестве функции координат. Полное определение вихревого магнитного поля реально, когда имеется мощность его вихрей, то есть r o t B → ( x , y , z ) как функция координат.

Показать, почему для вихревого магнитного поля нельзя представить вектор индукции B → в виде градиента магнитного потенциала φ m .

B → = — g r a d φ m ( 1 . 1 ) .

Для выражения ( 1 . 1 ) можно применить операцию r o t :

r o t B → = — r o t g r a d φ m ( 1 . 2 ) .

Известно значение r o t :

r o t ( g r a d φ m ) = 0 ( 1 . 3 ) .

При подстановке ( 1 . 3 ) в ( 1 . 2 ) имеем:

Ответ: Вспомнив теорему о циркуляции, получаем отсутствие токов. В данном случае, представление вектора индукции магнитного поля невозможно в виде магнитного потенциала в области, где проходят токи.

Применение понятия скалярного магнитного потенциала φ m возможно только в области пространства, где j → = 0 . Данная часть пространства φ m характеризуется неоднозначностью функции. Показать это.

Необходимо рассмотреть магнитное поле возле контура с током, как изображено на рисунке 1 . По теореме о циркуляции для любого контура выполнимо равенство:

Если токов нет, магнитное поле становится потенциальным, интеграл, который необходимо взять между A и B , не зависит от пути интегрирования, то запись примет вид:

∫ A a B B → d l → = ∫ A b B B → d l → ( 2 . 2 ) .

∫ A b B B → d l → = ∫ A B B → d l → = φ m A — φ m B ( 2 . 3 ) .

Выражение ( 2 . 3 ) может быть рассмотрено в качестве разности скалярных магнитных потенциалов в точках A и B . Можно пойти иным путем и принять значение потенциала равным нулю в точке В , как выполнялось для нахождения потенциала в электростатике:

∫ A B B → d l → = φ m A ( 2 . 4 ) .

При выборе контура, охватывающего какой-либо ток (контур A c b B ), как показано на рисунке 1 , линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет не равен нулю:

∮ A c b B B → d l → ≠ 0 ( 2 . 5 ) .

∮ A c b B B → d l → ≠ ∫ A c B B → d l → — ∫ A b B B → d l → = I ≠ 0 ( 2 . 6 )

∫ A c B B → d l → = ∫ A b B B → d l → + I = φ m A — φ m B + I ( 2 . 7 ) .

При выборе какого-либо пути A n B , охватывающего ток в количестве n раз, имеем:

∫ A n B B → d l → = φ m A — φ m B + n I ( 2 . 8 ) .

Следует задать нулевой потенциал в точке В :

∫ A n B B → d l → = φ m A + n I ( 2 . 9 ) .

Ответ: Получив уравнение ( 2 . 9 ) , очевидно, что скалярный магнитный потенциал является неоднозначной величиной.

Различают два основных типа векторных полей: потенциальные (безвихревые) и вихревые (соленоидальные) поля. Физические свойства их различны.

Потенциальное поле тесно связано со своим источником, линии поля имеют начало (исток) и конец (сток). Линии вихревого поля всегда непрерывны и не имеют источников (рисунок 12).

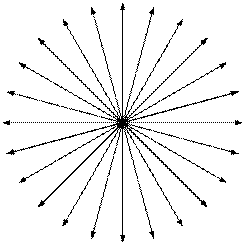
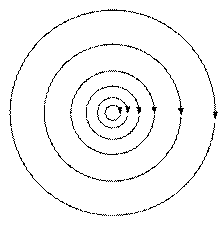
Рисунок 12 − Потенциальное и вихревое поля

Для потенциального поля 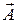имеем

,

то есть циркуляция вектора 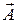по любому замкнутому контуру 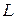равна нулю.

Если поле является вихревым, то поток вектора 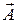через любую замкнутую поверхность равен нулю:

.

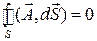В дальнейшем будет показано, что электростатическое поле является только потенциальным, магнитное – вихревым.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10458 — | 7917 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно