Site Loader
Posted on 10.09.2020

Химический потенциал — Википедия

У этого термина существуют и другие значения, см. Потенциал.

Хими́ческий потенциа́л μ{\displaystyle \mu } — термодинамическая функция, применяемая при описании состояния систем с переменным числом частиц. Определяет изменение термодинамических потенциалов (энергии Гиббса, внутренней энергии, энтальпии и т. д.) при изменении числа частиц в системе. Представляет собой энергию добавления одной частицы в систему без совершения работы. Применяется для описания материального взаимодействия. Определение химического потенциала можно записать в виде:

dE=TdS−PdV+μdN,{\displaystyle dE=TdS-PdV+\mu dN,}

где E{\displaystyle E} — энергия системы, S{\displaystyle S} — её энтропия, N{\displaystyle N} — количество частиц в системе.

Эта формула определяет, кроме химического потенциала μ{\displaystyle \mu }, также давление P{\displaystyle P} и температуру T{\displaystyle T}.

Для систем, состоящих из одного компонента, химический потенциал задаётся формулой

μ=E−TS+PVN=GN,{\displaystyle \mu ={E-TS+PV \over N}={G \over N},}

где G{\displaystyle G} — потенциал Гиббса.

Если энергия системы зависит не от объёма, а от других термодинамических параметров A1,A2…{\displaystyle A_{1},A_{2}…}, исходная формула принимает вид

dE=TdS−∑iaidAi+μdN.{\displaystyle dE=TdS-\sum _{i}a_{i}dA_{i}+\mu dN.}

Если в системе имеется несколько разных типов частиц, есть столько же разных химических потенциалов.

Химический потенциал служит естественной независимой переменной для большого термодинамического потенциала.

Важность химического потенциала для термодинамики обусловлена, помимо прочего, тем, что одним из условий термодинамического равновесия в системе является одинаковость химического потенциала любого компонента системы в различных фазах и в разных точках одной фазы

[1].

Для однородных многокомпонентных систем открытых систем

dE=TdS−PdV+∑jμjdmj,{\displaystyle dE=TdS-PdV+\sum _{j}\mu _{j}dm_{j},}

где mj{\displaystyle m_{j}} — масса j{\displaystyle j}-го компонента[K 1], μj{\displaystyle \mu _{j}} — химический потенциал этого компонента, по определению равный[K 2][2][3][4]

μk≡(∂E∂mk)S,V,{mj≠k}.{\displaystyle \mu _{k}\equiv \left({\frac {\partial E}{\partial m_{k}}}\right)_{S,V,\{m_{j\neq k}\}}.}(Дефиниция химического потенциала компонента)

Величину изменение энергии системы за счёт вариации масс составляющих систему веществ

z≡∑jμjdmj,{\displaystyle z\equiv \sum _{j}\mu _{j}dm_{j},}(Химическая работа бесконечно малого процесса в открытой однородной системе)

не имеющую общепринятого названия, чаще всего называют элементарной химической работой[K 3][5][6][7][8][9][10][11][12][13][14][15][16][17][18]

[19][20], а также массовой работой[21], работой переноса массы[5][16], работой перераспределения масс веществ[22], энергией, передаваемой при обмене веществом[23], энергией, передаваемой при переносе массы[24][25]. Химическая работа не является независимо измеряемой величиной — таковой является сумма энтропийной и химической составляющих изменения энергии в рассматриваемом процессе. Но если положить теплоту бесконечно малого процесса равной[26][27][28][29]

q≡TdS{\displaystyle q\equiv T\mathrm {d} S}(Теплота бесконечно малого процесса в открытой однородной системе)

и учесть, что элементарная работа расширения/сжатия равна

w=−PdV,{\displaystyle w=-P\mathrm {d} V,}(Элементарная работа расширения/сжатия в однородной системе)

то химическая работа может быть вычислена[29]:

z=∑jμjdmj=dE−q−w=dE−TdS+PdV.{\displaystyle z=\sum _{j}\mu _{j}\mathrm {d} m_{j}=\mathrm {d} E-q-w=\mathrm {d} E-T\mathrm {d} S+P\mathrm {d} V.}

Для системы в пространственно неоднородном внешнем поле следует учитывать зависимость химического потенциала компонента от напряжённости поля[1].

Если система находится в электрическом поле, то химический потенциал электрически заряженных частиц называют электрохимическим потенциалом

[30][31] (термин предложен в 1929 г. Э. А. Гуггенгеймом[32]). Специальный термин понадобился по причине принятого в литературе условного разбиения электрохимического потенциала на неэлектрическую и электрическую части. С теоретической точки зрения такое разделение носит чисто формальный характер, поскольку носителями заряда служат те же самые формульные единицы, с которыми соотносится обычный химический потенциал, и поэтому нет способа раздельного определения его химической и электрической составляющих. Практически же разделение электрохимического потенциала на две части оказывается хорошим приближением в случае заряженных частиц малой массы (электронов и позитронов), для которых вследствие малости их массы вклад неэлектрической части в электрохимический потенциал пренебрежимо мал по сравнению со вкладом электрической составляющей
[33][34].

Если система находится в гравитационном поле, то условием её равновесия служит постоянство суммы химического потенциала компонента в отсутствие поля и его гравитационного потенциала[35][36] (конкретизация этого условия для идеального газа даёт барометрическую формулу[1]), и по аналогии с электрохимическим потенциалом химический потенциал компонента в поле тяготения можно назвать гравихимическим потенциалом

; химический потенциал компонента в гравитационном поле при наличии электрического поля есть потенциал электрогравихимический. Деление химического потенциала в силовых полях на чисто химическую и полевые (электрическую, магнитную и гравитационную) части носит формальный характер, поскольку нет способа экспериментального определения химической составляющей отдельно от полевых.

Химический потенциал анизотропного тела есть тензор второго ранга, зависящий от тензора напряжений[37]. Как и тензор напряжений, который в изотропных средах становится шаровым[38][39], в изотропных средах для задания шарового тензора химического потенциала достаточно единственной скалярной величины

[40].

  1. ↑ Под компонентом в данной формуле можно понимать как независимый компонент, так и составляющее вещество: использование масс независимых компонентов, а не масс составляющих систему веществ означает отказ от прямого рассмотрения влияния химических реакций на массы веществ в системе, ибо химические превращения в ней уже учтены при подсчёте числа компонентов.
  2. ↑ Индексы у частной производной означают постоянство энтропии, объёма и масс всех компонентов, кроме k{\displaystyle k}-го.
  3. ↑ В понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии», связанное с переносом массы j{\displaystyle j}-го компонента через
    контрольную поверхность    , в качестве которой в гетерогенной системе обычно выступает поверхность раздела фаз. В гомогенной системе контрольная поверхность ограничивает очень малую по сравнению со всей системой, но всё ещё макроскопическую её часть, то есть мысленно выделяемую однородную макроскопическую область (элементарный объём) сплошной среды, размеры которой бесконечно малы по сравнению с неоднородностями среды и бесконечно велики по отношению к размерам частиц (атомов, ионов, молекул и т. п.) этой среды.
  1. ↑ 1 2
    3     Физическая энциклопедия, т. 5, 1998, с. 413.
  2. ↑ Chemical potential, μ // IUPAC Gold Book.
  3. ↑ Гамбург Ю. Д., Химическая термодинамика, 2016, уравнение (1.29), с. 28.
  4. ↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, уравнение (5.2), с. 54.
  5. ↑ 1 2 Борщевский А. Я., Физическая химия, т. 1, 2017, с. 242.
  6. ↑ Гамбург Ю. Д., Химическая термодинамика, 2016, с. 28.
  7. ↑ Кириллин В. А. и др., Техническая термодинамика, 2016, с. 467.
  8. ↑ Аминов Л. К., Термодинамика и статистическая физика, 2015, уравнение (3.6), с. 56.
  9. ↑ Морачевский А. Г., Фирсова Е. Г.
    , Физическая химия. Термодинамика химических реакций, 2015, с. 14.
  10. ↑ Кокотов Ю. А., Химический потенциал, 2010, с. 14, 16.
  11. ↑ Lebon G. e. a., Understanding Non-equilibrium Thermodynamics, 2008, expression (1.22), p. 14.
  12. ↑ Тер Хаар Д., Вергеланд Г., Основы термодинамики, 2006, с. 171.
  13. ↑ Борисов И. М., Введение в химическую термодинамику, 2005, уравнение (1.103), с. 80.
  14. ↑ Еремин В. В. и др., Основы физической химии, 2005, уравнение (2.2), с. 29.
  15. ↑ Жариков В. А., Основы физической геохимии, 2005, уравнение (2.4), с. 31.
  16. ↑ 1 2
    Воронин Г. Ф.    , Основы термодинамики, 1987, с. 62.
  17. ↑ Emanuel G., Advanced classical thermodynamics, 1987, expression (6.11), p. 119.
  18. ↑ Callen H. B., Thermodynamics and an Introduction to Thermostatistics, 1985, expression (2.9), p. 36.
  19. ↑ Путилов К. А., Термодинамика, 1971, с. 125.
  20. ↑ Зоммерфельд А., Термодинамика и статистическая физика, 1955, с. 147.
  21. ↑ Свиридов В. В., Свиридов А. В., Физическая химия, 2016, уравнения (4.47)—(4.50), с. 120—121.
  22. ↑ Тамм М. Е., Третьяков Ю. Д., Физико-химические основы неорганической химии, 2004, уравнения (1.3), с. 11.
  23. ↑ Пригожин И., Кондепуди Д., Современная термодинамика, 2002, подпись к рис. (2.4), с. 53.
  24. ↑ Зубарев Д. Н., Первое начало термодинамики, 1992, с. 555.
  25. ↑ Кубо Р., Термодинамика, 1970, с. 16.
  26. ↑ Базаров И. П., Термодинамика, 2010, с. 29.
  27. ↑ Кокотов Ю. А., Химический потенциал, 2010, с. 16.
  28. ↑ Callen H. B., Thermodynamics and an Introduction to Thermostatistics, 1985, expression (2.8), p. 36.
  29. ↑ 1 2 Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 54.
  30. ↑ Гуггенгейм, 1941, с. 122—123.
  31. ↑ Callen H. B., Thermodynamics and an Introduction to Thermostatistics, 1985, p. 35.
  32. ↑ Guggenheim, 1985, p. 300.
  33. ↑ Русанов, 2013, с. 19.
  34. ↑ Салем, 2004, с. 245.
  35. ↑ Зимон А. Д., Коллоидная химия, 2015, с. 147.
  36. ↑ Гуггенгейм, 1941, с. 141.
  37. ↑ Русанов, 2013, с. 21.
  38. ↑ Заславский, 1986, с. 189.
  39. ↑ Мейз, 1974, с. 87.
  40. ↑ Русанов, 2013, с. 25.
  • Аминов Л. К. Термодинамика и статистическая физика. Конспекты лекций и задачи. — Казань: Казан. ун-т, 2015. — 180 с.
  • Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3. (недоступная ссылка)
  • Химический потенциал // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
  • Большая физическая энциклопедия в 5-ти томах. Гл. ред. А. М. Прохоров. Москва «Советская энциклопедия» 1988 г.
  • Борисов И. М. Введение в химическую термодинамику. Классическая термодинамика. — Уфа: РИО БашГУ, 2005. — 208 с. — ISBN 5-7477-1212-8. (недоступная ссылка)
  • Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4. (недоступная ссылка)
  • Воронин Г. Ф. Основы термодинамики. — М.: Изд-во Моск. ун-та, 1987. — 192 с. (недоступная ссылка)
  • Гамбург Ю. Д. Химическая термодинамика. — М.: Лаборатория знаний, 2016. — 237 с. — (Учебник для высшей школы). — ISBN 978-5-906828-74-3. (недоступная ссылка)
  • Гуггенгейм. Современная термодинамика, изложенная по методу У. Гиббса / Пер. под ред. проф. С. А. Щукарева. — Л.—М.: Госхимиздат, 1941. — 188 с.
  • Еремин В. В., Каргов С. И., Успенская И. А. и др. Основы физической химии. Теория и задачи. — М.: Экзамен, 2005. — 481 с. — (Классический университетский учебник). — ISBN 5-472-00834-4.
  • Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
  • Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с. (недоступная ссылка)
  • Заславский Б. В. Краткий курс сопротивления материалов. — М.: Машиностроение, 1986. — 328 с.
  • Зимон А. Д. Коллоидная химия: Общий курс. — 6-е изд. — М.: Красанд, 2015. — 342 с. — ISBN 978-5-396-00641-6.
  • Зоммерфельд А. Термодинамика и статистическая физика / Пер. с нем. — М.: ИЛ, 1955. — 480 с. Архивная копия от 25 сентября 2017 на Wayback Machine
  • Зубарев Д. Н. Первое начало термодинамики (рус.) // Физическая энциклопедия. — Большая Российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 555.
  • Кириллин В. А., Сычев В. В., Шейндлин А. Е. Техническая термодинамика. — М.: Изд. дом МЭИ, 2016. — 496 с. — ISBN 978-5-383-01024-2. (недоступная ссылка)
  • Кокотов Ю. А. Химический потенциал. — СПб.: Нестор-История, 2010. — 412 с. — ISBN 978-5-98187-668-4. (недоступная ссылка)
  • Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с. (недоступная ссылка)
  • Мейз Дж. Теория и задачи механики сплошных сред. — М.: Мир, 1974. — 319 с.
  • Морачевский А. Г., Фирсова Е. Г. Физическая химия. Термодинамика химических реакций. — 2-е изд., испр. — СПб.: Лань, 2015. — 101 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1858-9. (недоступная ссылка)
  • Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур / Пер. с англ. — М.: Мир, 2002. — 461 с. — (Лучший зарубежный учебник). — ISBN 5-03-003538-9. Архивная копия от 23 сентября 2017 на Wayback Machine
  • Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с. (недоступная ссылка)
  • Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. М., Наука, 1977. 552 с.
  • Русанов А. И. Лекции по термодинамике поверхностей. — СПб.—М.—Краснодар: Лань, 2013. — 237 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1487-1.
  • Салем Р. Р. Физическая химия. Термодинамика. — М.: Физматлит, 2004. — 351 с. — ISBN 5-9221-0078-5.
  • Свиридов В. В., Свиридов А. В. Физическая химия. — СПб.: Лань, 2016. — 597 с. — ISBN 978-5-8114-2262-3. (недоступная ссылка)
  • Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
  • Тер Хаар Д., Вергеланд Г. Основы термодинамики / Пер. с англ.. — М.: Вузовская книга, 2006. — 200 с. — ISBN 5-9502-0197-3.
  • Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5: Стробоскопические приборы — Яркость. — 760 с. — ISBN 5-85270-101-7.
  • Каллен Г.[en]. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — xvi + 493 p. — ISBN 0471862568, 9780471862567. (недоступная ссылка)
  • Cook G., Dickerson R. H.Understanding the chemical potential // American Journal of Physics.— 1995.—63.— pp. 737—742
  • Guggenheim E. A. Thermodynamics: An Advanced Treatment for Chemists and Physicists. — Amsterdam: North-Holland, 1985. — xxiv + 390 с. — ISBN 0 444 86951 4.
  • Kaplan T. A.The Chemical Potential // Journal of Statistical Physics .—2006.—122.— pp. 1237—1260

Стандартный электродный потенциал — Википедия

В электрохимии стандартный электродный потенциал, обозначаемый Eo, E0, или Eθ, является мерой индивидуального потенциала обратимого электрода (в равновесии) в стандартном состоянии, которое осуществляется в растворах при эффективной концентрации в 1 моль/кг и в газах при давлении в 1 атмосферу или 100 кПа (килопаскалей). Объёмы чаще всего взяты при 25 °C. Основой для электрохимической ячейки, такой, как гальваническая ячейка, всегда является окислительно-восстановительная реакция, которая может быть разбита на две полуреакции: окисление на аноде (потеря электрона) и восстановление на катоде (приобретение электрона). Электричество вырабатывается вследствие различия электростатического потенциала двух электродов. Эта разность потенциалов создаётся в результате различий индивидуальных потенциалов двух металлов электродов по отношению к электролиту.

Вычисление стандартных электродных потенциалов[править | править код]

Электродный потенциал не может быть получен эмпирически. Потенциал гальванической ячейки вытекает из «пары» электродов. Таким образом, невозможно определить величину для каждого электрода в паре, используя эмпирически полученный потенциал гальванической ячейки. Для этого установлен водородный электрод, для которого этот потенциал принят равным 0,00 В, и любой электрод, для которого электродный потенциал ещё неизвестен, может быть соотнесён со стандартным водородным электродом с образованием гальванической ячейки — и в этом случае потенциал гальванической ячейки даёт потенциал неизвестного электрода.

Так как электродные потенциалы традиционно определяют как восстановительные потенциалы, знак окисляющегося металлического электрода должен быть изменён на противоположный при подсчёте общего потенциала ячейки. Также нужно иметь в виду, что потенциалы не зависят от количества передаваемых электронов в полуреакциях (даже если оно различно), так как они рассчитаны на 1 моль переданных электронов. Отсюда при расчёте какого-либо электродного потенциала на основании двух других следует проявлять внимательность.

Например:

Fe3+ + 3e− → Fe(тв) −0,036 В

Fe2+ + 2e− → Fe(тв) −0,44 В

Для получения третьего уравнения:

Fe3+ + e− → Fe2+ (+0,77 В)

следует умножить потенциал первого уравнения на 3, перевернуть второе уравнение(поменять знак) и умножить его потенциал на 2. Сложение этих двух потенциалов даст стандартный потенциал третьего уравнения.[источник не указан 414 дней]

Таблица стандартных электродных потенциалов[править | править код]

Чем больше стандартные восстановительные потенциалы, тем легче их можно восстановить, другими словами, тем более сильными окислителями они являются. И наоборот: низкий отрицательный потенциал означает, что данная форма является сильным восстановителем. Например, F2 имеет 2,87 В, а Li+ имеет −3,05 В, фтор — окислитель, литий — восстановитель. Таким образом, Zn2+, стандартный восстановительный потенциал которого равен −0,76 В, может быть окислен любым другим электродом, стандартный потенциал которого больше −0,76 В. (напр., H+(0 В), Cu2+(0,16 В), F2(2,87 В)) и может быть восстановлен любым электродом, стандартный потенциал которого меньше −0,76 В (напр., H−(−2,23 В), Na+(−2,71 В), Li+(−3,05 В)).

В гальванической ячейке, где самопроизвольная окислительно-восстановительная реакция заставляет ячейку производить электрический потенциал, Энергия Гиббса ΔGo должна быть отрицательной в соответствии со следующим уравнением:

ΔGoяч = -nFEoяч

где n это количество молей электронов на моль продуктов, а F является постоянной Фарадея, ~96485 Кл/моль. Таким образом применимы следующие правила:

если Eoяч> 0, тогда процесс самопроизвольный (гальваническая ячейка)
если Eoяч< 0, тогда процесс несамопроизвольный (электролитическая ячейка)

Стандартные электродные потенциалы даны при стандартных условиях. Однако реальные ячейки могут действовать и при нестандартных условиях. При данном стандартном потенциале потенциал при нестандартных эффективных концентрациях может быть вычислен с использованием уравнения Нернста:

E=E0+RTnFln⁡aOxaRed{\displaystyle E=E^{0}+{\frac {RT}{nF}}\ln {\frac {a_{\rm {Ox}}}{a_{\rm {Red}}}}}

Величины E0 зависят от температуры (кроме стандартного водородного электрода) и обычно относятся к стандартному водородному электроду при этой температуре. Для конденсированных фаз величины потенциалов также зависят от давления.

  • Zumdahl, Steven S., Zumdahl, Susan A (2000) Chemistry (5th ed.), Houghton Mifflin Company. ISBN 0-395-98583-8
  • Atkins, Peter, Jones, Loretta (2005) Chemical Principles (3rd ed.), W.H. Freeman and Company. ISBN 0-7167-5701-X
  • Zu, Y, Couture, MM, Kolling, DR, Crofts, AR, Eltis, LD, Fee, JA, Hirst, J (2003) Biochemistry, 42, 12400-12408
  • Shuttleworth, SJ (1820) Electrochemistry (50th ed.), Harper Collins.

XuMuK.ru — СТАНДАРТНЫЙ ПОТЕНЦИАЛ — Химическая энциклопедия

СТАНДАРТНЫЙ ПОТЕНЦИАЛ (нормальный потенциал), значение электродного потенциала, измеренное в стандартных условиях относительно выбранного электрода сравнения (стандартного электрода). Обычно стандартные потенциалы находят в условиях, когда термодинамич. активности а всех компонентов потенциалопределяющей р-ции, протекающей на исследуемом электроде, равны 1, а давление газа (для газовых электродов) равно 1,01 · 105 Па (1 атм). Для водных р-ров в качестве стандартного электрода используют водородный электрод (Pt; H2 [1,01·105Па], Н+ [a=1]), потенциал к-рого при всех т-рах принимается равным нулю (см. Электроды сравнения): стандартный потенциал равен эдс электрохимической цепи, составленной из исследуемого и стандартного электродов. Согласно рекомендациям ИЮПАК (1953), при схематич. изображении цепи (гальванич. ячейки) водородный электрод всегда записывается слева, исследуемый-справа. Потенциал исследуемого электрода считается положительным, если в режиме «источник тока» слева направо во внеш. цепи движутся электроны, а в р-ре — положительно заряженные частицы. Напр., стандартный потенциал хлорсеребряного электрода равен эдс гальванич. ячейки

-Pt, Н2[1,01·105Па]|НС1(аb=l)|AgCl, Ag|Pt +

Для любой электродной р-ции, включающей перенос n электронов, электродный потенциал определяется ур-нием:


где Е°-стандартный потенциал электрода, R-газовая постоянная, Т-абс. т-ра, F- постоянная Фарадея, аi-термодинамич. активность частиц (как заряженных, так и незаряженных), участвующих в электродной р-ции, vi-стехиометрич. коэффициенты (положит. числа для продуктов р-ций и отрицат. числа для исходных в-в, если при записи стехиометрич. ур-ния элек-трохим. процесса электроны входят в левую часть ур-ния, напр. AgCl + е : Ag + С1—). Значения стандартных потенциалов для ряда электродных процессов в водной среде приведены в таблице в порядке убывания окислит. способности соответствующих систем. Стандартные потенциалы металлов и водорода, расположенные в порядке их возрастания, составляют электрохимический ряд напряжений.

Стандартный потенциал определяется либо непосредственными измерениями эдс соответствующих электрохим. цепей с экстраполяцией на бесконечно разб. р-ры, либо расчетом — по данным о стандартных значениях изменения энергии Гиббса хим. р-ции DG0. В последнем случае р-цию представляют в виде суммы двух (или более) электродных р-ций, одна из к-рых -окис-лит.-восстановит. р-ция с искомым стандартным потенциалом , а другая-с известным стандартным потенциалом .. Если в условной схеме ячейки 1-й электрод записан слева, то


Из ур-ния следует, что стандартные потенциалы, в свою очередь, м.б. использованы для расчета DG0 и константы равновесия К р-ции (ln К = — DG°/RT). Значения E0, рассчитанные на основе значений DG0, представлены в таблице; они далеко не всегда м. б. реализованы в электрохим. цепях из-за того, что предполагаемое равновесие электродной р-ции в действительности может не устанавливаться (это характерно для щелочных, щел.-зем. металлов и большинства орг. в-в в водных р-рах).

В неводных р-рителях стандартные потенциалы также определяют по отношению к потенциалу водородного электрода для каждого отдельного р-рителя. Ведется поиск стандартного электрода, потенциал к-рого можно было бы считать практически не зависящим от природы р-рителя, что позволило бы создать единую шкалу электродных потенциалов. В качестве таких электродов предложены системы: рубидий/ион рубидия, ферроцен/ферроциний-катион и бис(дифенил)хром(I)/ /бис(дифенил)хром(0), потенциалы к-рых из-за большого размера ионов и соотв. малой их сольватации незначительно (по сравнению с потенциалом водородного электрода) зависят от природы р-рителя. Последние два электрода рекомендованы в 1984 ИЮПАК в качестве электродов сравнения в неводных орг. средах.

Выбор электрода сравнения и стандартного состояния исследуемого электрода в системах с расплавами и твердым электролитом в большой мере определяется природой как исследуемого электродного процесса, так и ионного проводника. В широко используемых в качестве электролитов расплавах хлоридов металлов стандартный потенциал берется в хлорной шкале, т. е. в качестве стандартного пользуются хлорным электродом в расплавленном хлориде (графит, Сl2 [1,01 · 105 Па], MC1z [расплав]), где М-металл (на практике обычно берут смесь хлоридов металла). Активность катионов Мz+ в индивидуальном расплаве принимается равной 1. В ряде высокотемпературных гальванич. элементов с твердым электролитом в качестве электрода сравнения применяют оксидные электроды, в частности вюститовый (Pt; Fe, FeO).

Лит.: Электрохимия металлов в неводных растворах, пер. с англ., М., 1974; Методы измерения в электрохимии, т. 1, пер. с англ., М., 1977; Шаталов А. Я., Введение в электрохимическую термодинамику, М., 1984; Дамаскин Б. Б., Петрий О. А., Электрохимия, М., 1987; Standard Potentials in aqueous solution, ed. by A.J. Bard, N.Y.-Basel, 1985. Б.И. Подловченко.

3.1.5 Потенциальность электростатического поля

Видеоурок: Работа электрического поля. Потенциал. Электрическое напряжение

Лекция: Потенциальность электростатического поля


Потенциальная энергия поля

Некоторую силу можно назвать консервативной только в том случае, когда она не зависит от траектории, по которой двигается тело. Работа всех консервативных сил равна разности потенциальных энергий рассматриваемого тела A = W1 — W2

Сила взаимодействия между зарядами также является консервативной, а так как это сила приводит к тому, что заряды начинают двигаться, то она так же выполняет работу. При этом существует важный факт — работа в данном случае абсолютно не зависит от траектории, по которой двигается данной тело, а определяется она только начальным и конечным положением тела. При этом, как и любая работа консервативных сил, если траектория перемещения — замкнутая линия, то работа равна нулю.

Потенциальная энергия поля равна:


Можно заметить, что практически вся теория электродинамики достаточно сильно напоминает механику. Постарайтесь вспомнить потенциальную энергию тела. Она зависела от массы, высоты и ускорения свободного падения. Можно провести аналогию. Более того, напряженность электрического поля из закона Кулона выводится точно так же, как и ускорение свободного падения из закона гравитационного взаимодействия.

Основным и главным отличием потенциальной энергии материальных точек от энергии зарядов являются граничные значения. Потенциальная энергия заряженных тел увеличивается с уменьшением расстояния между зарядами и стремится к нулю, когда заряды удаляют на бесконечность.


Потенциал

Исходя из формулы, можно сделать вывод, что потенциальная энергия поля пропорциональна величине рассматриваемого заряда. Величина, являющая коэффициентом пропорциональности, называется потенциалом поля. Как видно из формулы, он также зависит от величины заряда.


Потенциал обозначается буквой «фи» и измеряется в Вольтах (В).

Если напряженность — это силовая характеристика имеющегося поля, то потенциал является его энергетической характеристикой.


Разность потенциалов

Из полученной формулы можно вывести значение энергии через потенциал. И если учесть, что разность потенциальных энергий — это работа, получим:


Полученная величина называется разностью потенциалов. Если некоторый пробный заряд отдалять на какое-то расстояние от заряженного тела, то будет совершаться работа, позволяющая изменить энергетическую характеристику поля.

Разность потенциалов еще называют напряжением. Если некоторый заряд удаляют на бесконечное расстояние, то напряжение такого поля равно начальному потенциалу.


Для того, чтобы изменить потенциал поля необходимо совершить работу по перемещению заряда.



Эквипотенциальная поверхность

Для наглядного понимания того, что такое потенциалы и их изменения, используют эквипотенциальные поверхности. Это поверхности, которые расположены перпендикулярно к силовым линиям. На всей такой поверхности значение потенциала одинаково. Чем дальше эквипотенциальная поверхность находится от заряда, тем меньше там потенциал.

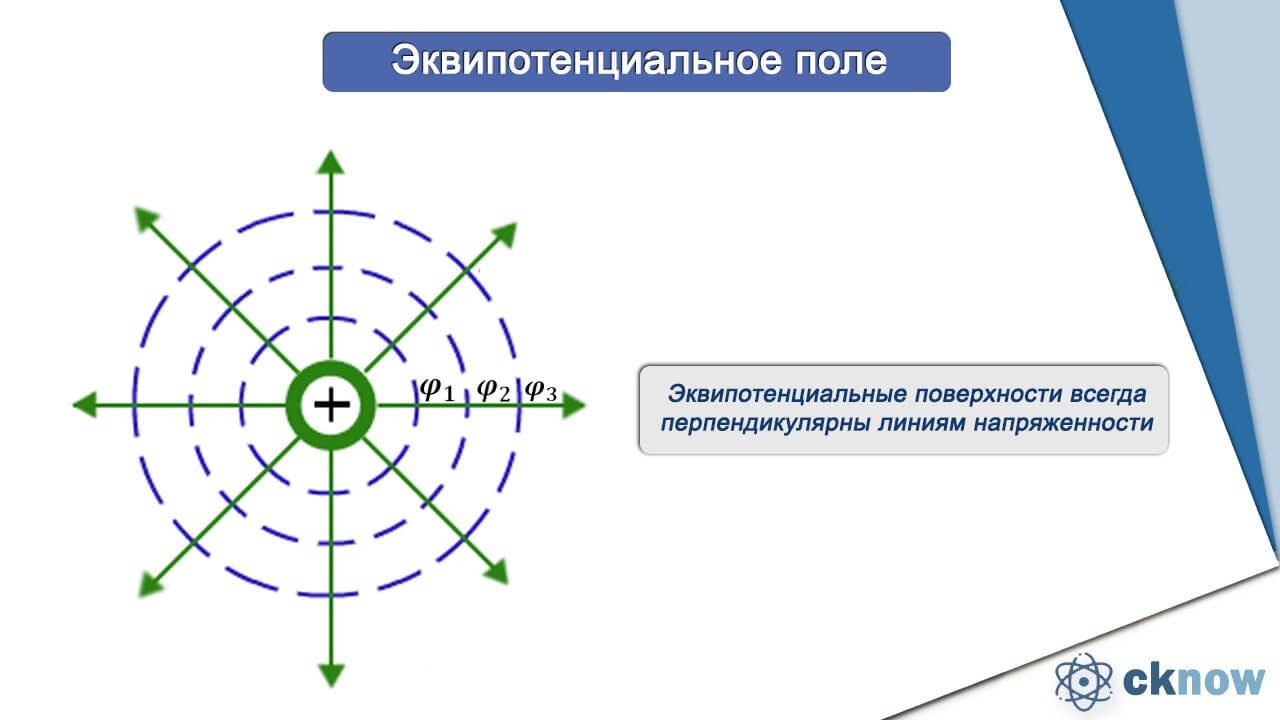
На рисунке мы можем наблюдать поперечное сечение поверхности. Они располагаются перпендикулярно к экрану, на который вы смотрите. Направление перемещения заряда всегда находится под углом 90 градусов к поверхностям.


Контактная разность потенциалов — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 марта 2017; проверки требуют 9 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 марта 2017; проверки требуют 9 правок.

Контактная разность потенциалов (в англоязычной литературе — потенциал Вольты) — это разность потенциалов, возникающая при соприкосновении двух различных твердых проводников, имеющих одинаковую температуру. Различают внутреннюю и внешнюю разности потенциалов в зависимости от того, рассматриваются ли потенциалы эквипотенциального объема контактирующих проводников или же потенциалы вблизи их поверхности[1].

Контактная разность потенциалов не может быть измерена вольтметром напрямую, однако может проявляться на вольт-амперных характеристиках контакта. Примером устройства, где внешняя контактная разность потенциалов двух металлов влияет на ВАХ, может служить ламповый диод. Внутренняя контактная разность потенциалов лежит в основе работы таких полупроводниковых приборов, как диод на p-n переходе, диод с контактом металл-полупроводник, транзистор, а также ряда других.

При соприкосновении двух проводников с разными работами выхода в приконтактной области появляются электрические заряды. А между их свободными концами возникает разность потенциалов. Значение внешней контактной разности потенциалов равно разности работ выхода, отнесенной к заряду электрона. Если проводники соединить в кольцо, то ЭДС в кольце будет равна 0. Для разных пар металлов значение контактной разности потенциалов колеблется от десятых долей вольта до единиц вольт[2].

Для объяснения внутренней контактной разности потенциалов в металлах прибегают к модели свободных электронов и к зонной теории. Рассмотрим энергетическую диаграмму, изображающую полную энергию одного электрона. Полная энергия электрона равна сумме потенциальной энергии в электрических полях и кинетической энергии. Нулевая полная энергия на энергетической диаграмме соответствует неподвижному электрону вдали от металла (это т.н. энергетический уровень вакуума). Для электрона внутри металла полная энергия будет отрицательна; электрон находится в потенциальной яме.

Рассмотрим вначале энергетическую структуру изолированного металла. Предположим, что температура металла равна 0 К. Энергетическая структура металла в простейшем случае определяется двумя величинами: работой выхода (т.е. расстоянием от уровня Ферми до уровня вакуума) и степенью заполнения верхней зоны электронами (энергия Ферми). Все энергетические уровни от начала энергетической зоны вплоть до уровня Ферми будут заполнены электронами. Максимальная кинетическая энергия электрона, в соответствии с зонной теорией металлов, равна энергии Ферми. Положение уровня Ферми на шкале полных энергий из-за принципа Паули будет являться значением химического потенциала данной системы электронов.

Приведение металлов в соприкосновение выводит систему из равновесия (поскольку химические потенциалы двух металлов не совпадают), происходит диффузия электронов в сторону уменьшения их энергии, приводящая к изменению заряда и электрического потенциала металлов. В приконтактной области начинается рост электрического поля. Появление электрического поля сдвигает все энергетические уровни электронов этих металлов, и вслед за ними будет двигаться уровень Ферми. Когда положение уровня Ферми (химического потенциала) обоих металлов на шкале энергии сравняются, заряд в приконтактной области перестанет меняться, наступит диффузионно-дрейфовое равновесие. Необходимо подчеркнуть, что диффузия электронов практически не меняет ни концентрацию электронов, ни величину энергии Ферми каждого металла. Разность положений нижних краев энергетической зоны в первом и втором металле, отнесенная к заряду электрона, и будет называться внутренней контактной разностью потенциалов.

Вольта доказал существование разности потенциалов следующим опытом. На стержень электроскопа насажены два диска из разных материалов (цинк и медь), покрытых тонким слоем диэлектрика и приведенных в соприкосновение. На короткое время диски замыкаются медной проволокой. При этом между ними возникает контактная разность потенциалов, причём цинк заряжается положительно, а медь — отрицательно. При этом наблюдается небольшое расхождение листочков электроскопа. Для увеличения показаний электроскопа снимается медная проволока и диски раздвигаются. Так как заряд образованного из двух дисков конденсатора не изменяется, а ёмкость уменьшается, то напряжение на конденсаторе возрастает. При этом листочки электроскопа расходятся на большее расстояние.

Измерение контактной разности потенциалов[править | править код]

Электродный потенциал — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 мая 2017; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 мая 2017; проверки требуют 3 правки. У этого термина существуют и другие значения, см. Потенциал.

Электро́дный потенциа́л — ЭДС элемента, составленного из данного электрода и стандартного водородного электрода, электродный потенциал которого принят равным нулю. При этом знак электродного потенциала считают положительным, если в таком гальваническом элементе испытуемый электрод является катодом, и отрицательным, если испытуемый электрод является анодом. Необходимо отметить, что иногда электродный потенциал определяют как «разность потенциалов на границе электрод  – раствор», т.е. считают его тождественным потенциалу ЭДС, что не вполне правильно (хотя эти величины взаимосвязаны)..

Возникновение электродного потенциала обусловлено переносом заряженных частиц через границу раздела фаз, специфической адсорбцией ионов, а при наличии полярных молекул (в том числе молекул растворителя) — ориентационной адсорбцией их. Величина электродного потенциала в неравновесном состоянии зависит как от природы и состава контактирующих фаз, так и от кинетических закономерностей электродных реакций на границе раздела фаз.

Равновесное значение скачка потенциалов на границе раздела электрод/раствор определяется исключительно особенностями электродной реакции и не зависит от природы электрода и адсорбции на нём поверхностно-активных веществ. Эту абсолютную разность потенциалов между точками, находящимися в двух разных фазах, нельзя измерить экспериментально или рассчитать теоретически.

Практическое значение имеют относительные электродные потенциалы, обычно называемые просто электродные потенциалы, представляющие собой разность электродных потенциалов рассматриваемого электрода и электрода сравнения — чаще всего нормального водородного электрода, электродный потенциал которого условно принимается равным нулю (для водных систем).

Способы устранения омической составляющей при измерении[править | править код]

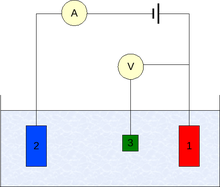Трёхэлектродная схема
  • Компенсационная схема
  • Трёхэлектродная схема

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *