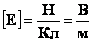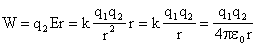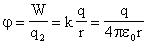Электричество и магнетизм
В Дополнении 3 разобран пример использования этих соотношений.
|
В СИ единицей измерения потенциала электрического поля является вольт (В):
|
Напряженность поля определяет силу, действующую в поле на точечный заряд, а потенциал — его потенциальную энергию в этом поле. Поэтому, следуя смыслу соотношений и, напряженность электрического поля называют силовой характеристикой поля, а потенциал — его энергетической характеристикой.
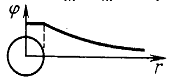
Как и потенциальная энергия, потенциал поля всегда определен с точностью до аддитивной постоянной. Это видно из : поскольку набла есть дифференциальный оператор, потенциалы и физически тождественны, так как им соответствует поле одной и той же напряженности
.
Это позволяет нормировать потенциал, произвольно выбирая некоторую точку и полагая потенциал в этой точке равным нулю
|
|
(1.16) |
Учитывая, что и напряженность поля, и потенциал поля убывают с ростом расстояния до системы зарядов, создающей поле, во всех тех случаях, когда конечный заряд распределен по конечной области пространства, нормировать потенциал естественно и удобно на «нуль на бесконечности», то есть полагать его равным нулю на бесконечном удалении от системы зарядов
|
|
(1.17) |
О тех идеализированных случаях, когда нормировка на нуль на бесконечности, именно в силу идеализированности задачи, лишена смысла, будет сказано далее.
Соотношение (1.13) позволяет вычислить напряженность поля по известному потенциалу;
|
|
(1.18) |
Получим «обратную» связь: выразим потенциал поля через его напряженность. Для этого сравним три выражения: выражение для из (1.18), выражение для вектора бесконечно малого перемещения и выражение для полного дифференциала функции :
Нетрудно видеть, что скалярное произведение двух первых векторов равно полному дифференциалу потенциала
|
|
(1.19) |
или, с учетом
|
|
|
На самом деле это соотношение не новое. Если умножить (1.20) на заряд и учесть связи (1.14) и (1.15), мы получим знакомое по главе 4 раздела «Механика» соотношение, связывающее работу консервативной силы и убыль потенциальной энергии
.
Там же, в разделе «Механика» было показано, что стационарное потенциальное поле консервативно. Из соотношения (1.18) вытекает, что электростатическое поле консервативно во всех тех случаях, когда потенциал поля не зависит от времени.
Интегрируя соотношение (1.20) от точки , потенциал в которой принят равным нулю, до некоторой точки , потенциал в которой нас интересует, вдоль произвольной, удобной для вычислений кривой (поле консервативно и от формы кривой результат не зависти), получаем
|
|
(1.21) |
Вычислим с помощью (1.21) потенциал поля точечного заряда , находящегося в начале координат, нормировав его на нуль на бесконечном удалении от этого заряда. Воспользуемся для этого законом Кулона в форме (1.9):
|
|
(1.22) |
При вычислении использовано тождество , справедливое для любого вектора : и являющееся результатом простого дифференцирования определения модуля любого вектора: .
Таким образом, потенциал поля точечного заряда находящегося в начале координат имеет вид
|
|
(1.23) |
и поле это, как уже отмечалось ранее, центральное: фактически потенциал поля зависит только от .
Глава 18. Напряженность и потенциал электрического поля.Силовые линии электрического поля
Для характеристики создаваемого зарядами электрического поля вводятся две величины — напряженность электрического поля и его потенциал. Напряженность характеризует силу, действующую со стороны поля на внесенный в него пробный заряд. Если в какой-то точке поля на заряд действует сила , то напряженность электрического поля в этой точке равна
(18.1) |
где — заряд, который мы взяли, чтобы «попробовать» поле в данной точке. Такой заряд называется «пробным». Пробный заряд не должен искажать распределение зарядов, создающих поле, и потому должен быть достаточно мал. В формулу (18.1) пробный заряд входит со своим знаком (не модуль), поэтому, как следует из (18.1), вектор напряженности поля в некоторой точке направлен так же, как и вектор силы, действующей в этой точке на положительный пробный заряд.
Найдем напряженность электрического поля, создаваемого точечным зарядом . Для этого возьмем произвольный пробный заряд и поместим его в точку, находящуюся на расстоянии от заряда . Сила, действующую на пробный заряд со стороны заряда , определяется законом Кулона (17.1), (17.2). Поэтому согласно (18.1) имеем
(18.2) |
где . Направлен вектор напряженности от заряда , если , и к нему, если .
Пусть поле создается несколькими зарядами … В этом случае его напряженность равна векторной сумме напряженностей тех полей, которые создаются каждым зарядом в отдельности. Действительно, из принципа суперпозиции следует, что на пробный заряд в этом случае действует сила …, где … — силы, действующие на пробный заряд со стороны каждого заряда … Поэтому из (18.1) получаем
(18.3) |
где … — напряженности тех полей, которые создавались бы каждым зарядом в отдельности в отсутствие других зарядов. Утверждение (18.3) называется принципом суперпозиции для полей. Формула (18.2) и принцип суперпозиции позволяют вычислить поле, создаваемое любым заряженным телом — с помощью мысленного разбиения его на точечные части и суммирования напряженностей, создаваемых всеми таким частями. Однако из-за математической сложности такой процедуры, она не входит в программу школьного курса физики. Школьник должен знать без вывода результат ее применения к заряженным сферам и плоскостям. Из формул (17.4), (17.5) получаем для напряженности поля сферы радиуса , равномерно заряженной зарядом , в точке на расстоянии от центра сферы:
(18.4) |
где , а из формулы (17.6) для напряженности поля равномерно заряженной плоскости
(18.5) |
где — заряд плоскости, — площадь, — поверхностная плотность зарядов плоскости.
Электрическое поле можно изобразить графически (на современном русском языке — визуализировать) с помощью силовых линий. Силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке. Вообще говоря, силовые линии проходят через каждую точку поля (кроме тех точек, где ), но поскольку так их нарисовать нельзя, условились проводить их с определенной густотой в зависимости от величины поля: чем гуще расположены силовые линии, тем больше величина напряженности поля.
Второй характеристикой электрического поля является его потенциал. Основная идея введения этой величины заключается в следующем. Если электрический заряд перемещается в электрическом поле (созданном другими зарядами), то со стороны поля на него действуют силы, и, следовательно, поле совершает работу. Потенциал поля — это такая функция точки поля , что работа , совершаемая полем над точечным пробным зарядом при его перемещении из точки с радиусом-вектором в точку с радиусом-вектором , равна
(18.6) |
(именно в такой последовательности). Из формулы (18.6) следует, что работа, которую совершает поле при перемещении заряда, не зависит от формы траектории, а определяется только начальной и конечной ее точками. В частности, при перемещении тела по замкнутой траектории поле совершает нулевую работу.
Поскольку в формулу (18.6), входит разность потенциалов двух точек поля, потенциал определен с точностью до постоянной. Эту постоянную всегда можно выбрать так, что потенциал любой заданной точки поля можно сделать равным нулю. Как правило, в качестве такой точки выбирают бесконечно удаленную от зарядов точку поля, считая ее потенциал равным нулю. Из формулы (18.6) следует, что потенциал любой точки поля равен отношению работы, которую совершает электрическое поле при перемещении пробного заряда из этой точки в ту точку, потенциал которой выбран равным нулю, к пробному заряду.
Можно доказать, что если поле создается точечным зарядом , то потенциал на расстоянии от заряда при условии, что потенциал бесконечно удаленной точки принят за нуль, равен
(18.7) |
Важно отметить, что в формулу (18.7) входит заряд со знаком (не модуль!), т.е. потенциал поля, создаваемого положительным зарядом, — положительный, отрицательным — отрицательный.
Для потенциалов справедлив принцип суперпозиции: если поле создается несколькими точечными зарядами, то потенциал любой его точке равен алгебраической сумме потенциалов (18.7), создаваемых в этой точке каждым точечным зарядом. Это правило позволяет найти потенциал поля, создаваемого протяженным заряженным телом: нужно мысленно разделить тело на малые («точечные») части, по формуле (18.7) найти потенциал поля, создаваемого каждой такой частью, а затем сложить полученные результаты.
Для решения задач ЕГЭ нужно знать (без вывода) формулу потенциала поля равномерно заряженной сферы. Пусть имеется сфера радиуса , равномерно заряженная зарядом . Тогда потенциал точки поля, расположенной на расстоянии центра сферы, равен
(18.8) |
(точка нулевого потенциала выбрана на бесконечности).
Часто в задачах ЕГЭ по физике используется связь напряженности однородного электрического поля и разности потенциалов двух точек поля, лежащих на одной силовой линии. Для нахождения этой связи возьмем положительный пробный заряд , перенесем его из первой точки во вторую вдоль силовой линии и найдем работу, которую совершает при этом электрическое поле. Поскольку поле действует на заряд с постоянной силой , угол между перемещением и этой силой равен нулю (заряд движется вдоль силовой линии), поэтому работа сил поля равна , где — расстояние между исследуемыми точками. С другой стороны, по определению потенциала работа поля равна . Приравнивая эти работы, находим
(18.9) |
Подчеркнем, что формула (18.9) справедлива только для однородного поля, а точки 1 и 2 должны лежать на одной силовой линии.
Рассмотрим теперь задачи.
Величина напряженности электрического поля, создаваемого точечным зарядом (задача 18.1.1), определяется формулой (18.2)
где (ответ 1).
Размерность напряженности электрического поля (задача 18.1.2) можно найти из связи напряженности поля и потенциала (см. формулу (18.9)). А поскольку размерность потенциала в международной системе единиц СИ – вольт, из формулы (18.9) имеем:
где квадратные скобки обозначают размерность (ответ 3).
Для определения напряженности поля используют пробный заряд (см. формулу (18.1)). Однако напряженность (18.1) ни от знака, ни от величины пробного заряда не зависят (задача 18.1.3). Это связано с тем, что сила в (18.1) линейно зависит от пробного заряда , и он сокращается в (18.1). Если взять пробный заряд отрицательным, то направление вектора числителе (18.1) изменится по сравнению со случаем положительного пробного заряда, но отношение будет направлено противоположно вектору , т.е. направление вектора не изменится (ответ 4).
Для нахождения поля, созданного двумя точечными зарядами (задача 18.1.4), используем принцип суперпозиции. Напряженности полей, создаваемых в точке каждым зарядом в отдельности, показаны тонкими векторами и отмечены как и . Поскольку модули этих векторов равны, вектор их суммы направлен вертикально вниз (ответ 4).
По определению силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке (задача 18.1.5 — ответ 4).
Поскольку силовые линии поля в задаче 18.1.6 направлены направо, то направо направлен и вектор напряженности в каждой точке. Поэтому направо будет направлен и вектор силы, действующий со стороны этого поля на положительные точечный заряд (ответ 2).
Поскольку все траектории движения заряда I, II и III в задаче 18.1.7 начинаются и заканчиваются в тех же точках, то работа поля над зарядом при его движении по всем трем траекториям одинакова (ответ 4).
Разность потенциалов двух точек однородного электрического поля (задача 18.1.8) найдем по формуле (18.9):
(ответ 1).
Поскольку вектор напряженности электрического поля в любой точке направлен от заряда, то силовые линии поля расходятся радиально, являясь везде прямыми (см.рисунок). Таким образом, правильный ответ в задаче 18.1.9 — 1.
По определению потенциала имеем для работы поля в задаче 18.1.10
(ответ 3).
Силовые линии электрического поля строятся так, что их густота пропорциональна величине поля: чем гуще силовые линии, тем больше величина напряженности. Поэтому в задаче 18.2.1 (ответ 2).
Рисунок в задаче 18.2.2 — тот же самый, что и в предыдущей задаче, однако логика получения ответа совсем другая. Чтобы сравнить потенциалы в точках 1 и 2 перенесем из первой точке во вторую положительный пробный заряд и найдем работу поля. Так как , и если работа положительна, то , если отрицательна — наоборот. Очевидно, работа поля при перемещении положительного заряда из точки 1 в точку 2 положительна. Действительно, стрелки на силовых линиях направлены вправо, следовательно, и сила, действующая на положительный заряд, направлена вправо, туда же направлен и вектор перемещения заряда, поэтому косинус угла между силой и перемещением положителен на всех элементарных участках траектории, поэтому положительна работа. Таким образом (ответ 1), причем этот результат является следствием направления стрелок на силовых линиях, а не переменной густоты силовых линий.
В задаче 18.2.3 используем формулу для потенциала поля точечного заряда. Поскольку потенциал поля обратно пропорционален расстоянию до заряда, создающего поле (см. формулу (18.7)),
(ответ 2). Другими словами, на втрое большем расстоянии от точечного заряда потенциал его поля втрое меньше.
Очевидно, искомая в задаче 18.2.4 точка, находится между зарядами. В этой точке величины напряженностей полей и , создаваемых каждым зарядом, должны быть равны (см. рисунок). Используя формулу (18.2), получаем
где . Отсюда находим (ответ 3).
Используя принцип суперпозиции для потенциалов и формулу для потенциала поля точечного заряда (18.7), получим для искомой точки (задача 18.2.5)
где . Отсюда находим (ответ 2).
Поскольку все заряды в задаче 18.2.6 одинаковы, то напряженность поля, созданного в центре квадрата каждой парой зарядов, лежащих на одной диагонали, равна нулю. Поэтому равна нулю и напряженность электрического поля, созданного всеми четырьмя зарядами (ответ 2).
В задачах 18.2.7 и 18.2.8 используем принцип суперпозиции. Векторы напряженности полей, создаваемых верхней и нижней пластинами и соответственно показаны на рисунках (левый рисунок относится к задаче 18.2.7, правый — к 18.2.8). Из этих рисунков следует, что в области II для задачи 18.2.7 и в областях I и III для задачи 18.2.8 векторы и направлены противоположно. А поскольку величина напряженности поля плоскости не зависит от расстояния до нее (формула (18.5)), а заряды плоскостей одинаковы по величине, напряженность суммарного поля в этих областях равна нулю.
Таким образом, правильный ответ в задаче 18.2.7 — 2, в задаче 18.2.8 — 3. Отметим, что полученный результат является приближенным и справедлив в пределе бесконечно больших пластин. Для конечных пластин поле в указанных областях будет малым, но отличным от нуля, причем величина поля будет наибольшей около краев пластин.
По принципу суперпозиции для потенциалов имеем (задача 18.2.9) . Если убрать либо первый, либо второй заряды, то потенциал в исследуемой точке станет равным соответственно или . Отсюда находим (ответ 2).
Согласно формуле (18.8) потенциал поля в любой точке внутри сферы равен потенциалу на ее поверхности
где . Поэтому правильный ответ в задаче 18.2.10 — 4.
Потенциал. Разность потенциалов. Напряжение. | |
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
— следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
Разность потенциалов | |
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
Связь между напряженностью и напряжением. | |
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
Из этого соотношения видно:
|
|
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
Потенциал поля точечного заряда |
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
|
Основные законы и формулы
58
ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК
Закон Кулона:
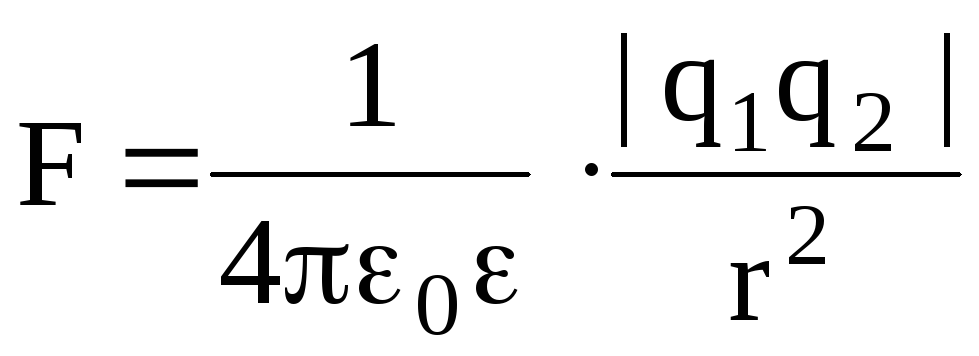 ,
,
где F – сила взаимодействия двух точечных зарядов q1 и q2; r – расстояние между зарядами; — диэлектрическая проницаемость среды; 0 — электрическая постоянная
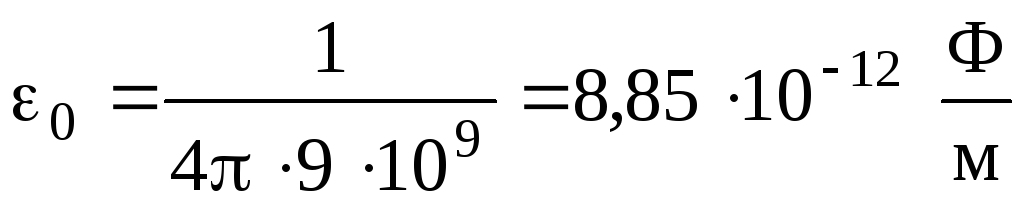 .
.
Закон сохранения заряда:
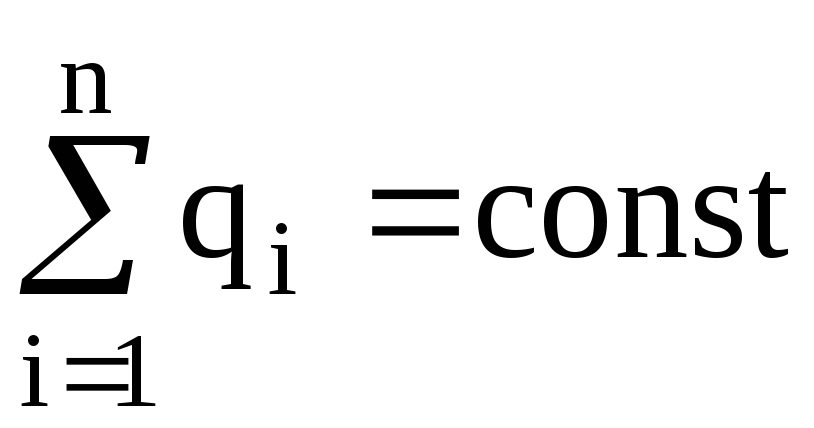 ,
,
где 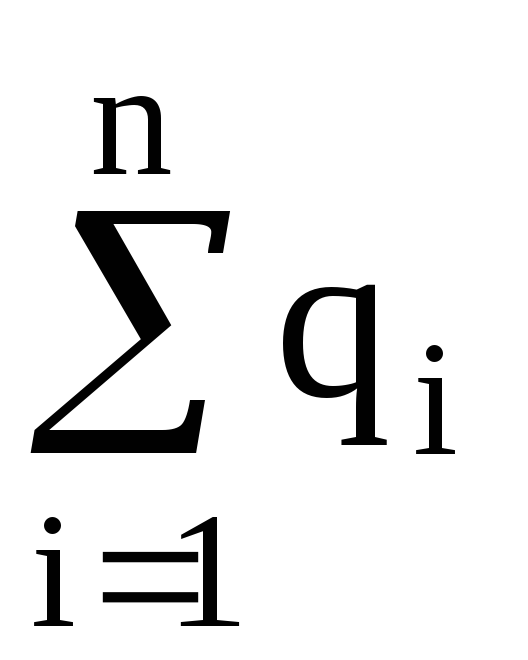 – алгебраическая сумма зарядов, входящих
в изолированную систему;n
– число зарядов.
– алгебраическая сумма зарядов, входящих
в изолированную систему;n
– число зарядов.
Напряженность и потенциал электростатического поля:
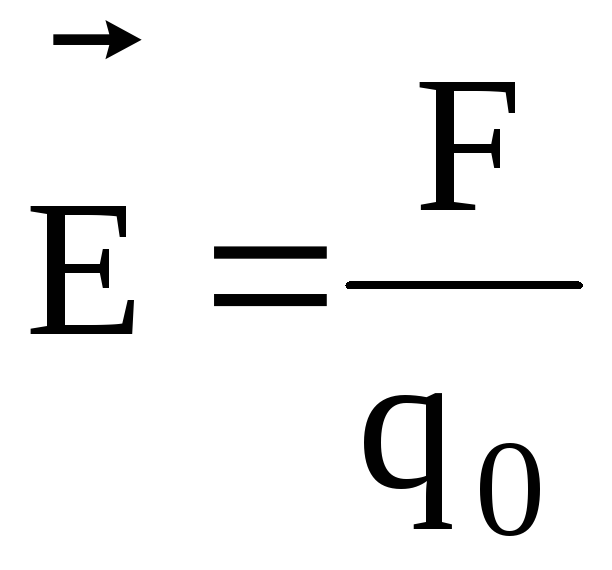 ;
; 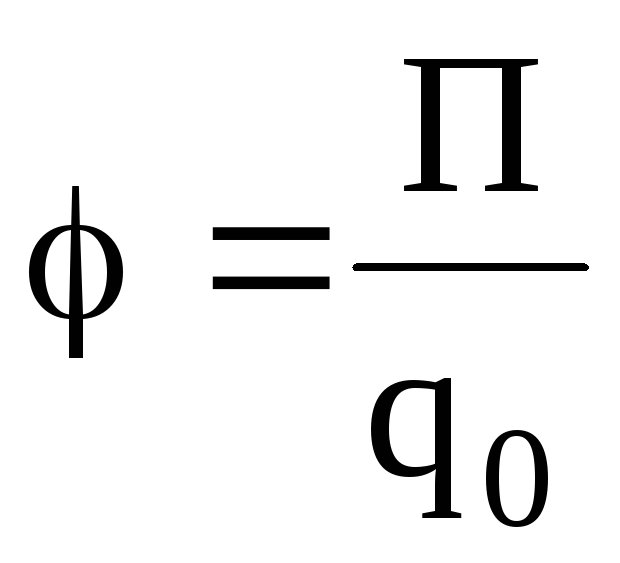 ,
или
,
или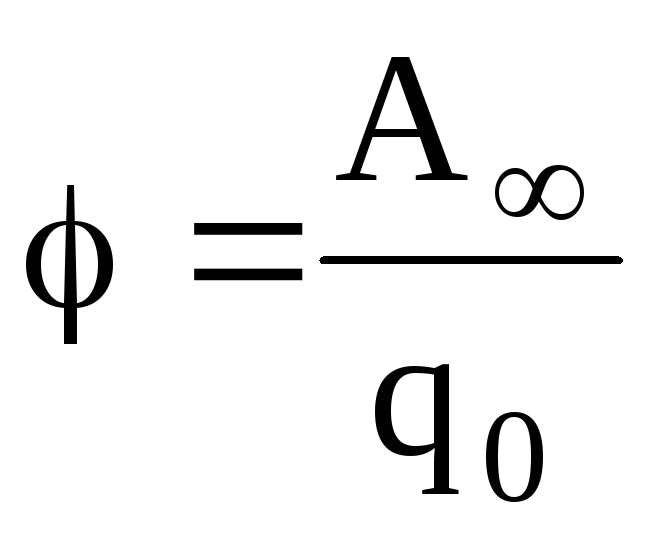 ,
,
где  – сила, действующая на точечный
положительный зарядq0,
помещенный в данную точку поля; П –
потенциальная энергия заряда; А∞ — работа,
затраченная на перемещение заряда q0 из данной точки поля в бесконечность.
– сила, действующая на точечный
положительный зарядq0,
помещенный в данную точку поля; П –
потенциальная энергия заряда; А∞ — работа,
затраченная на перемещение заряда q0 из данной точки поля в бесконечность.
Поток
вектора напряженности  электрического поля:
электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
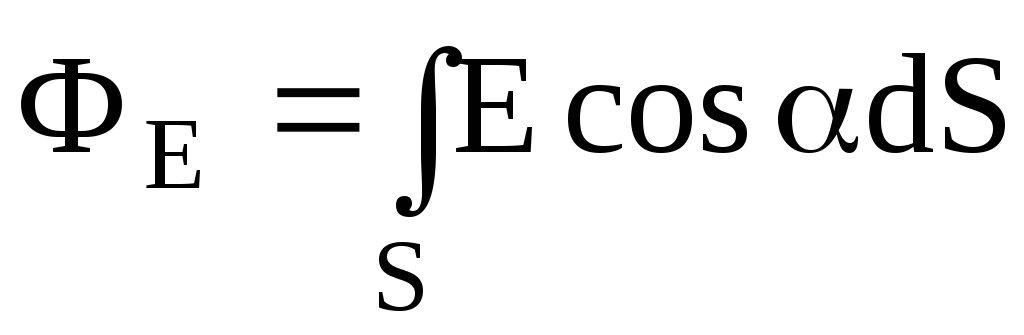 ,
или
,
или 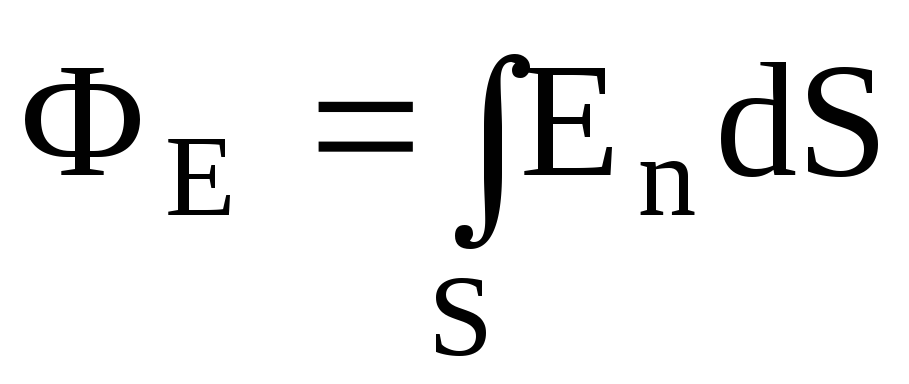 ,
,
где
– угол между вектором напряженности  и нормалью
и нормалью к элементу поверхности;dS
– площадь элемента поверхности; En – проекция вектора напряженности на
нормаль;
к элементу поверхности;dS
– площадь элемента поверхности; En – проекция вектора напряженности на
нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
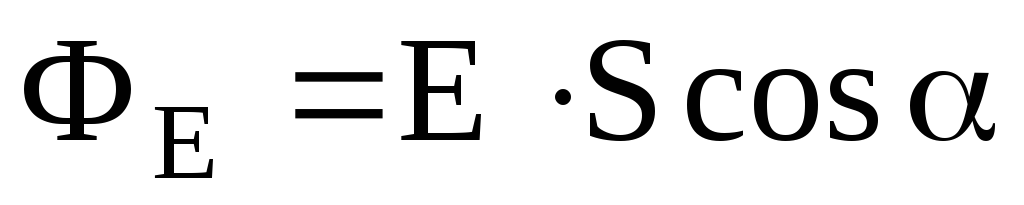 .
.
Поток
вектора напряженности  через замкнутую поверхность –
через замкнутую поверхность –
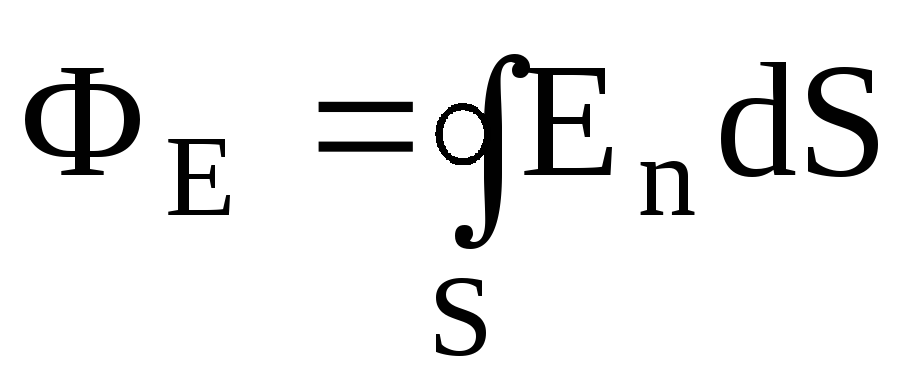
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
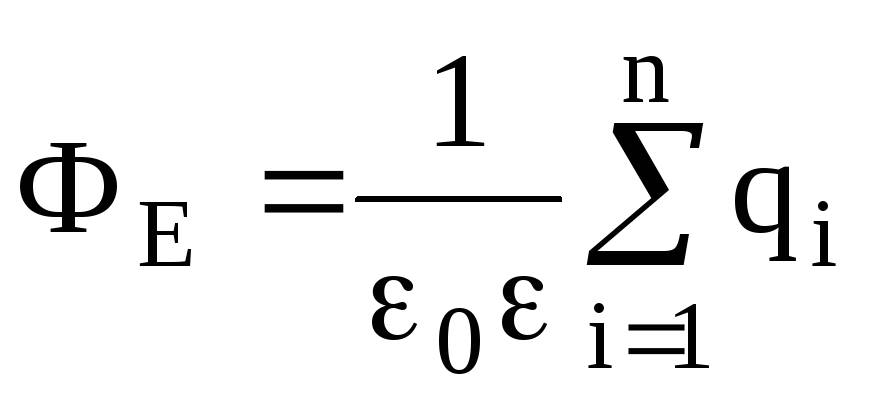 ,
,
где 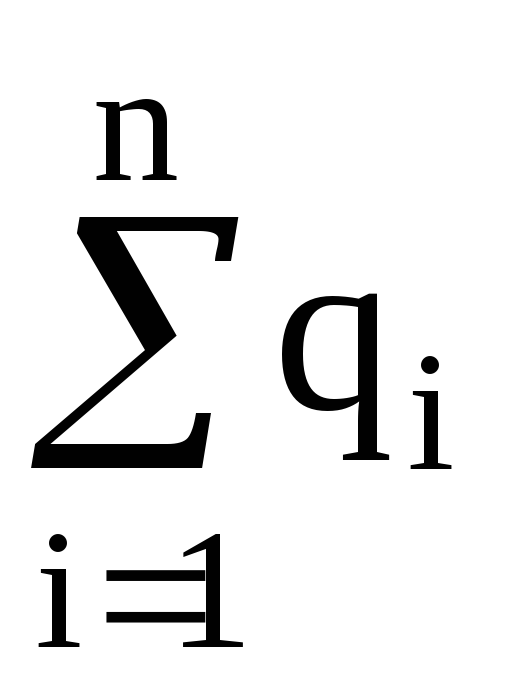 – алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; n
– число зарядов.
– алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; n
– число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
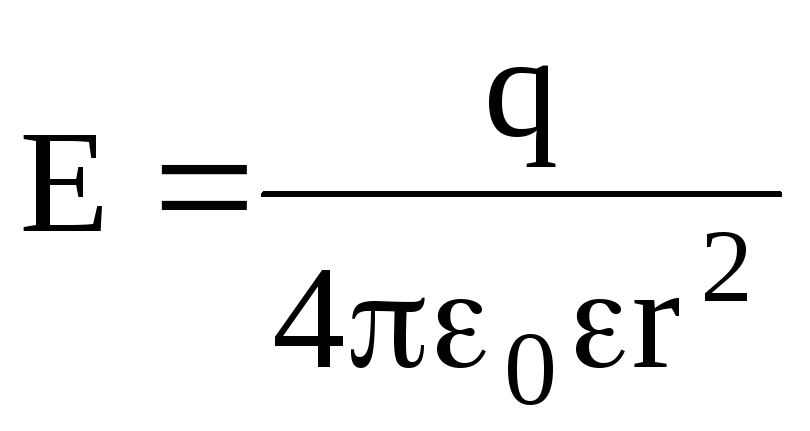 .
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на
поверхности сферы (r=R) 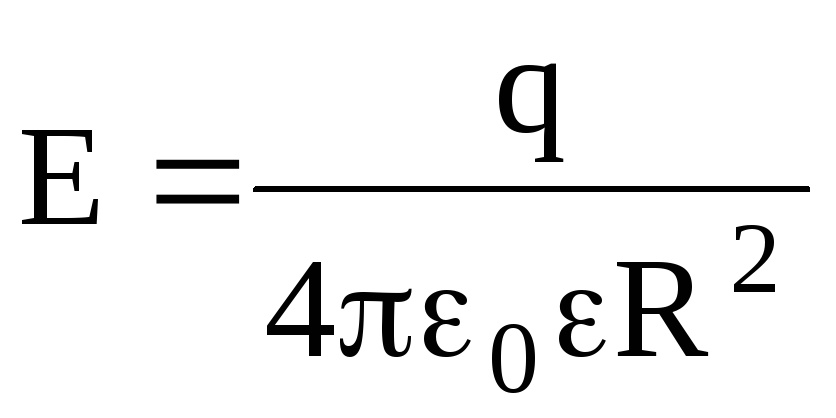 ;
;
вне
сферы (r
R) 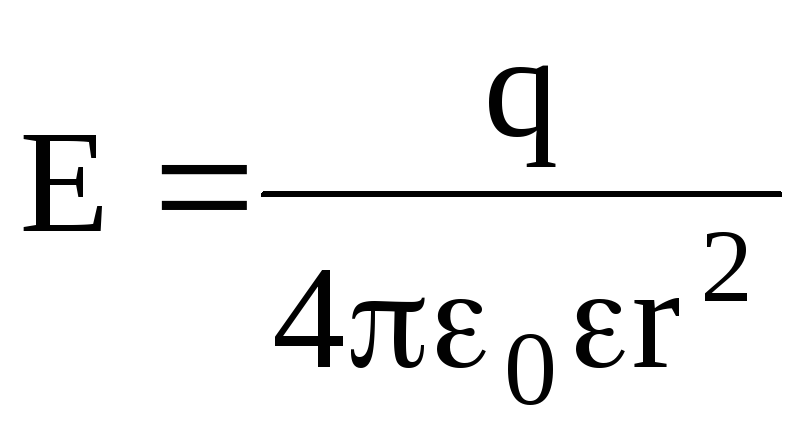 .
.
Принцип суперпозиции (наложения)
электростатических полей, согласно
которому напряженность  результирующего поля, созданного двумя
(и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей,
выражается формулой
результирующего поля, созданного двумя
(и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей,
выражается формулой
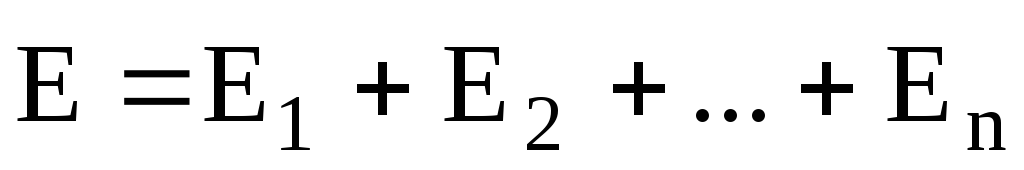 .
.
В
случае двух электрических полей с
напряженностями 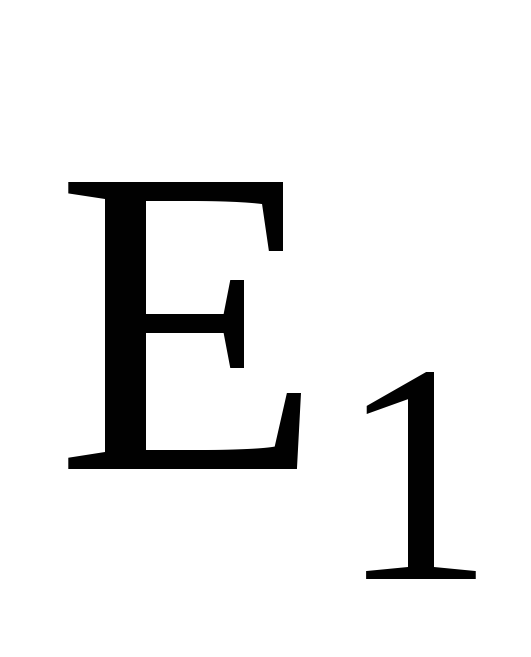 иабсолютное значение вектора напряженности
составляет
иабсолютное значение вектора напряженности
составляет
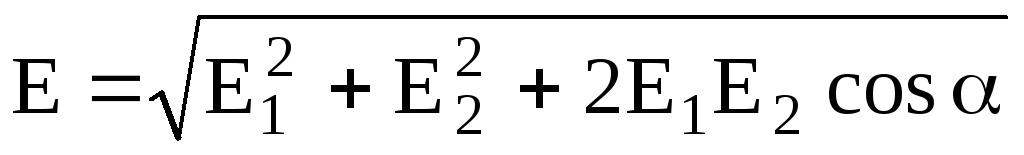 ,
,
где
— угол между векторами 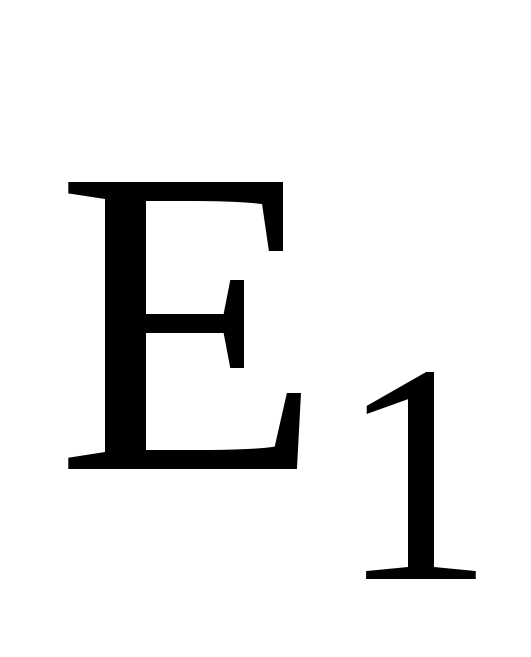 и
и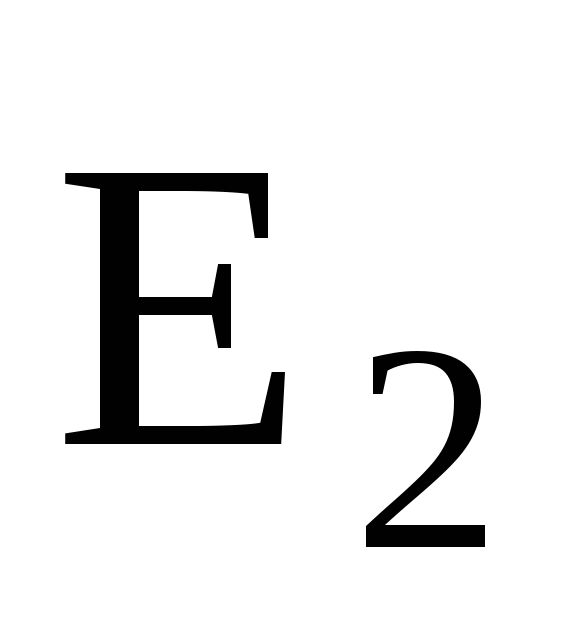 .
.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –
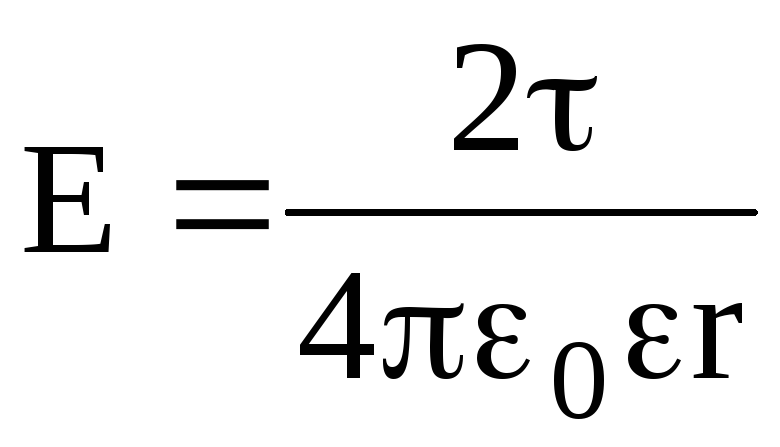 ,
,
где — линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
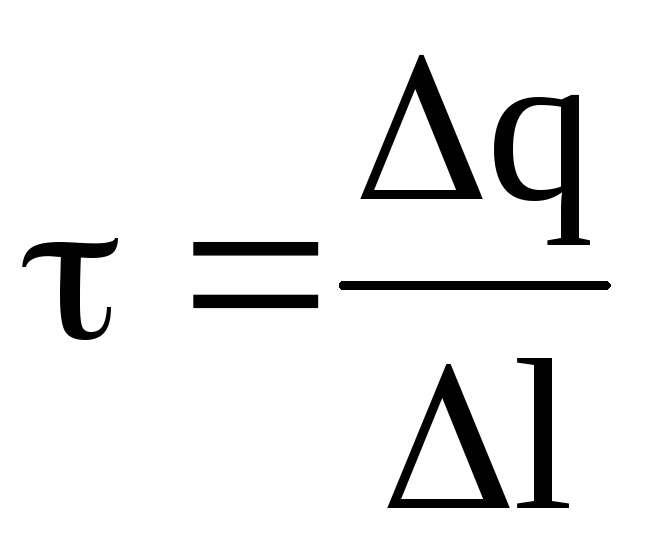 .
.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –
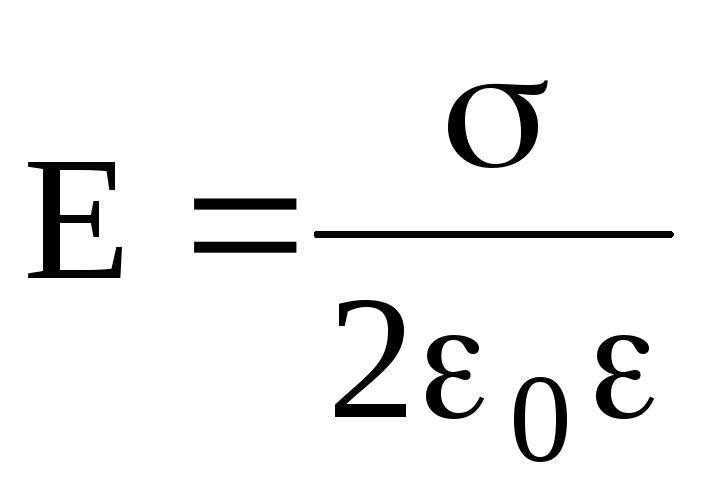 ,
,
где — поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:
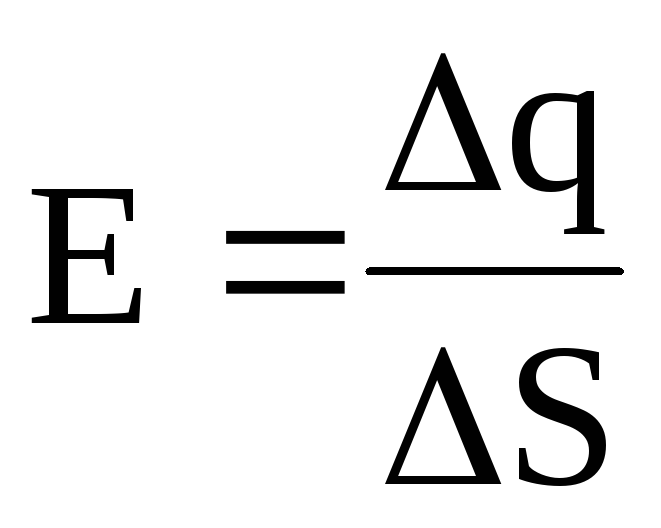 .
.
Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –
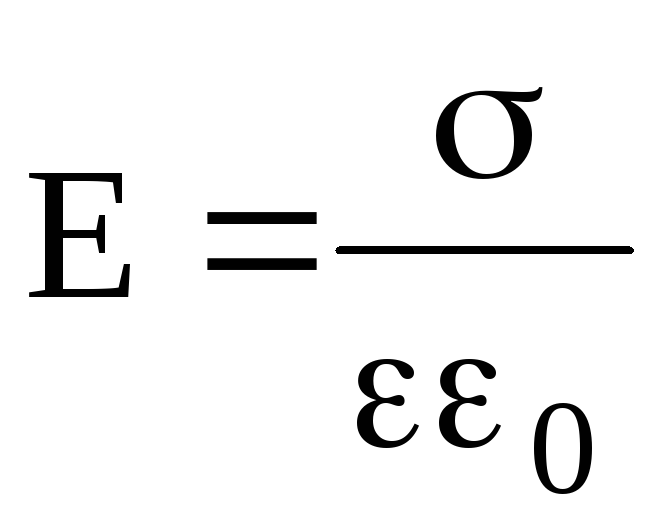 .
.
Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.
Электрическое
смещение  связано с напряженностью
связано с напряженностью электрического поля соотношением
электрического поля соотношением
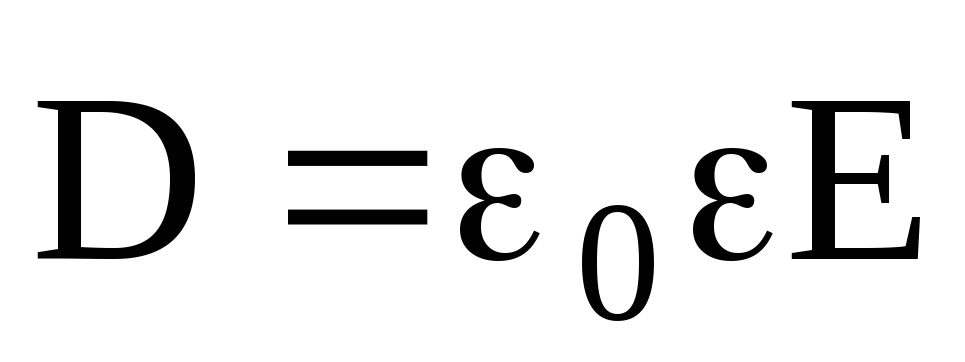 ,
,
которое справедливо только для изотропных диэлектриков.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:
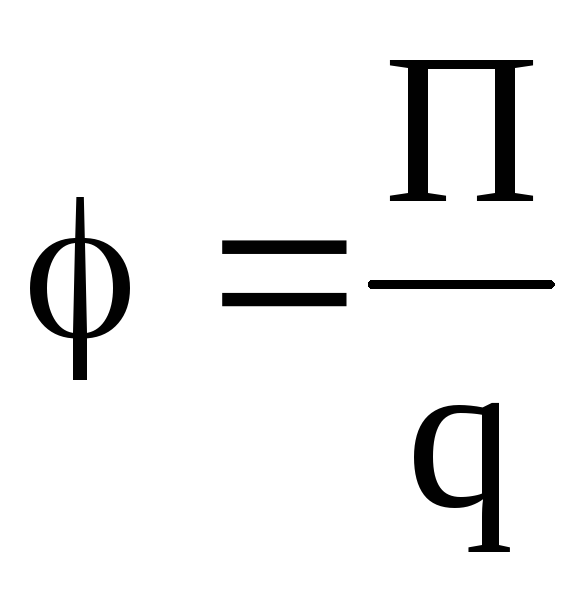 .
.
Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:
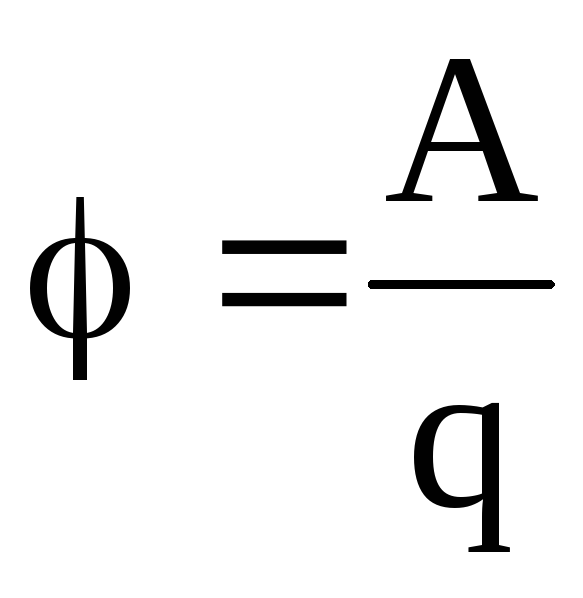 .
.
Потенциал электрического поля в бесконечности условно принят равным нулю.
Потенциал электрического поля, создаваемый точечным зарядом q на
расстоянии r от заряда, –
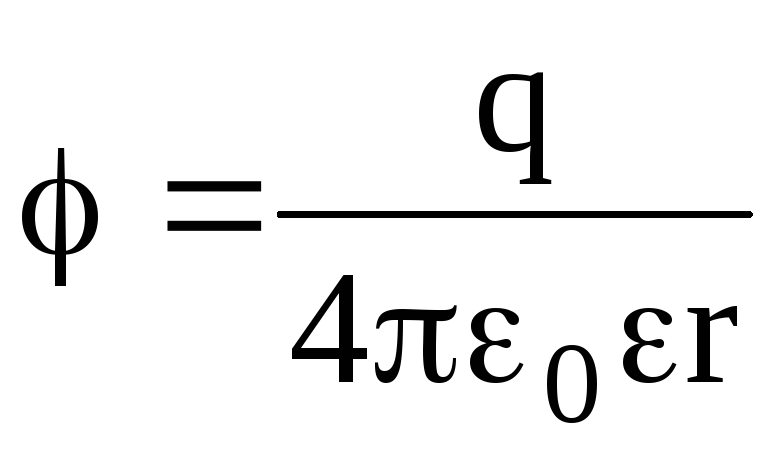 .
.
Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:
внутри
сферы (r
R) 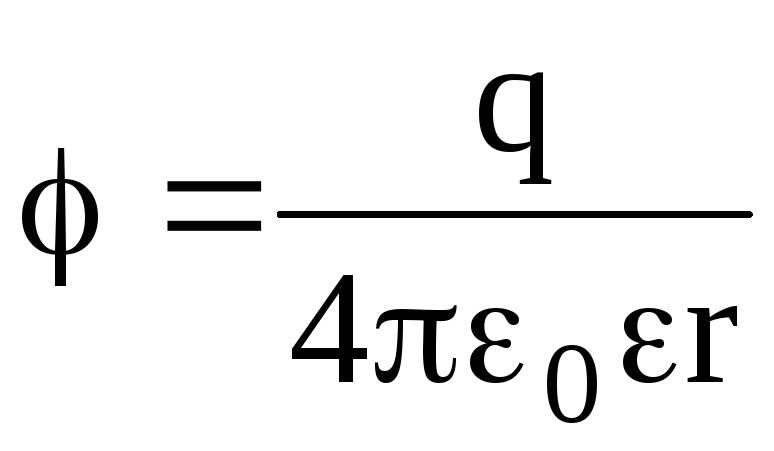 ;
;
на
поверхности сферы (r
= R) 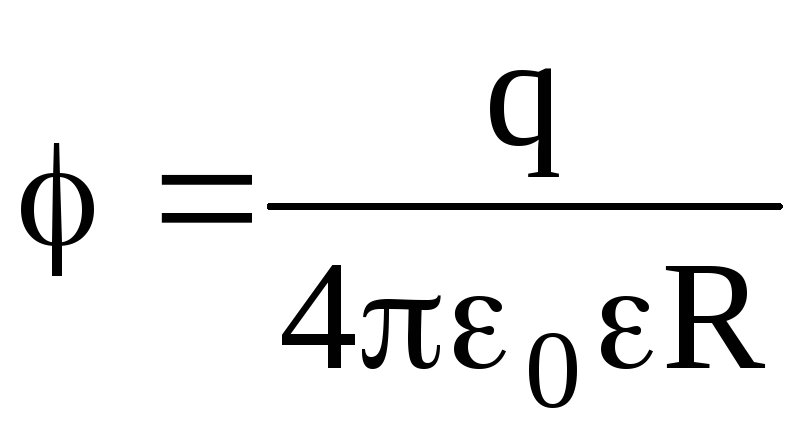 ;
;
вне
сферы (r
R) 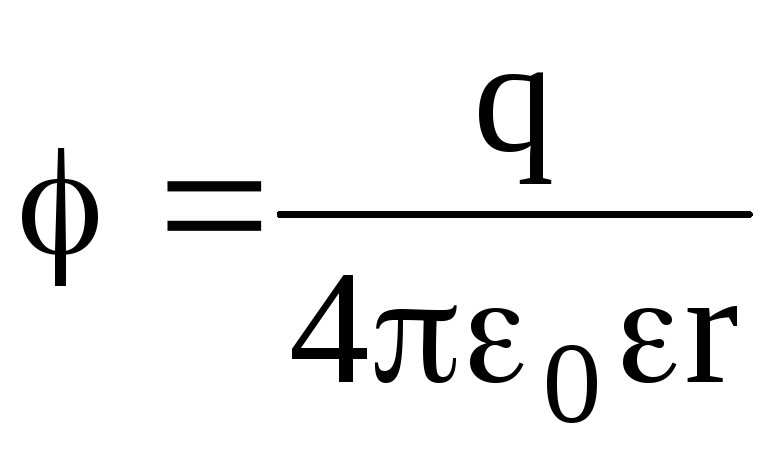 .
.
Во всех формулах, приведенных для потенциала заряженной сферы, есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал
электрического поля, образуемого
системой n
точечных зарядов в данной точке в
соответствии с принципом суперпозиции
электрических полей, равен алгебраической
сумме потенциалов 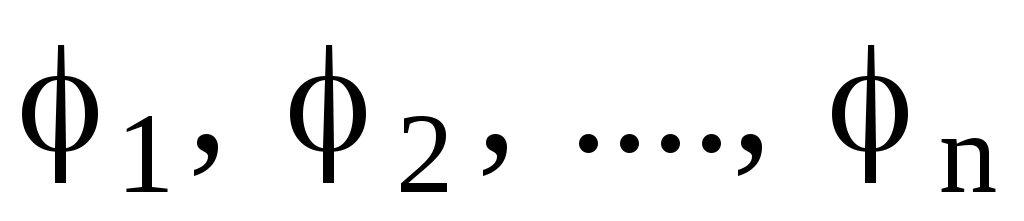 ,
создаваемых отдельными точечными
зарядами
,
создаваемых отдельными точечными
зарядами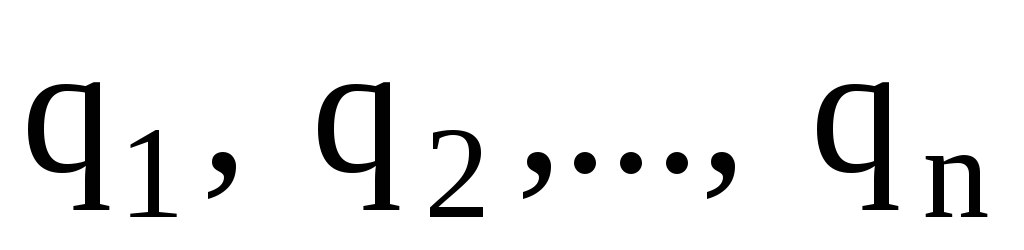 :
:
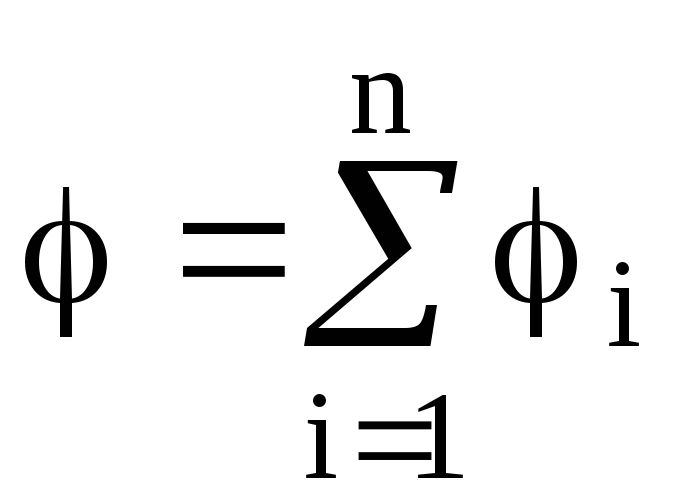 .
.
Энергия
W
взаимодействия системы точечных зарядов 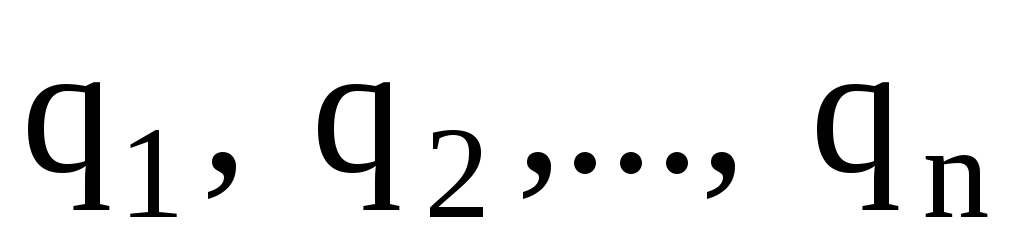 определяется работой, которую эта
система может совершить при удалении
их относительно друг друга в бесконечность,
и выражается формулой
определяется работой, которую эта
система может совершить при удалении
их относительно друг друга в бесконечность,
и выражается формулой
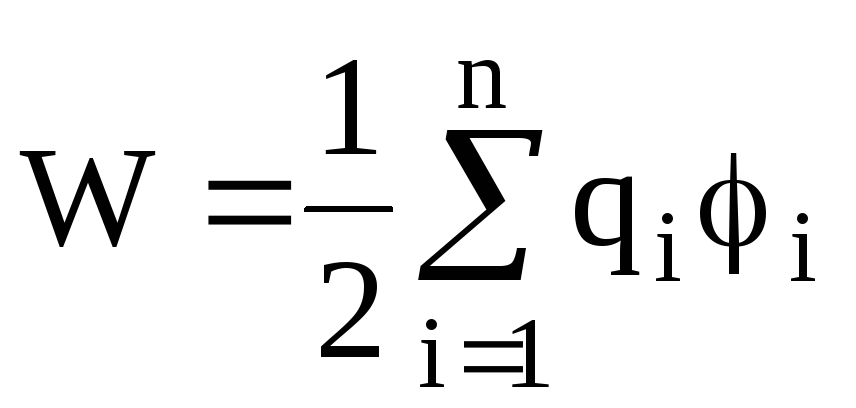 ,
,
где  — потенциал поля, создаваемый всеми
(n-1)
зарядами (за исключением i-го)
в точке, где находится заряд
— потенциал поля, создаваемый всеми
(n-1)
зарядами (за исключением i-го)
в точке, где находится заряд 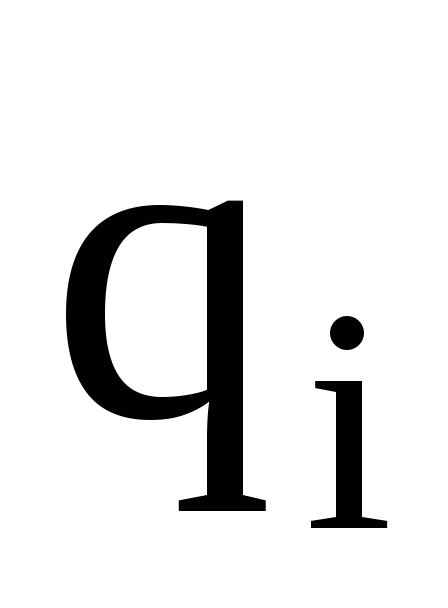 .
.
Потенциал связан с напряженностью электрического поля соотношением
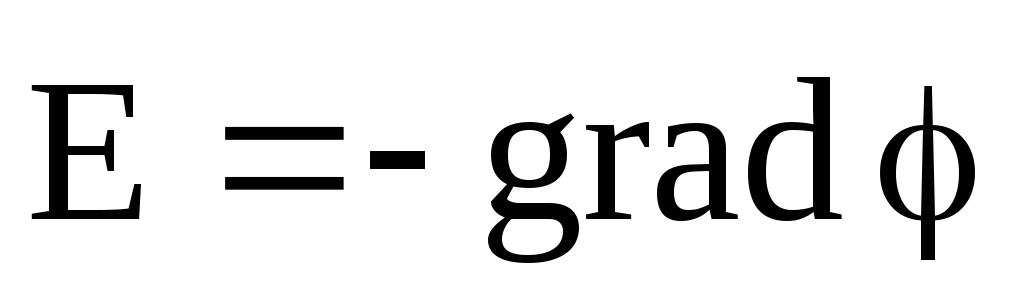 .
.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой
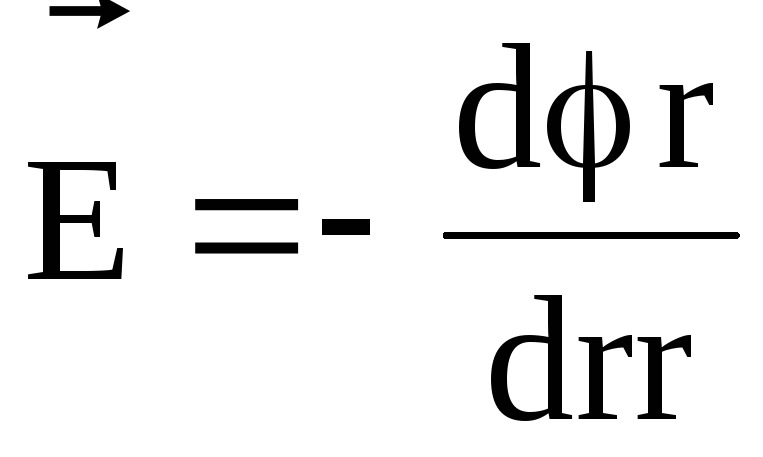 ,
,
или в скалярной форме
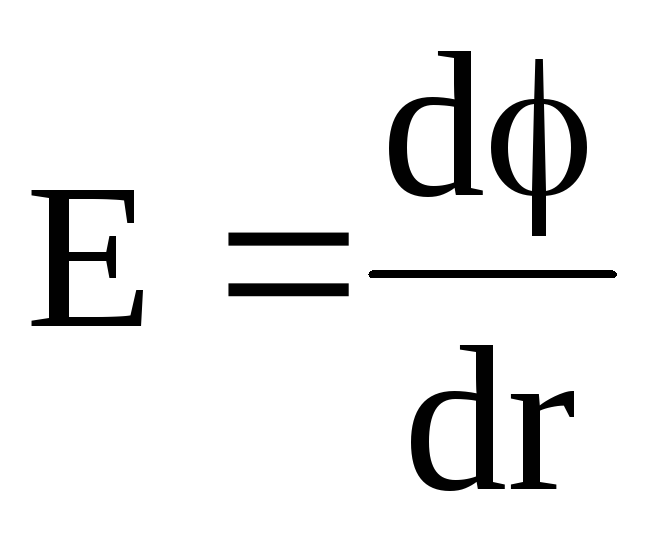 .
.
В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –
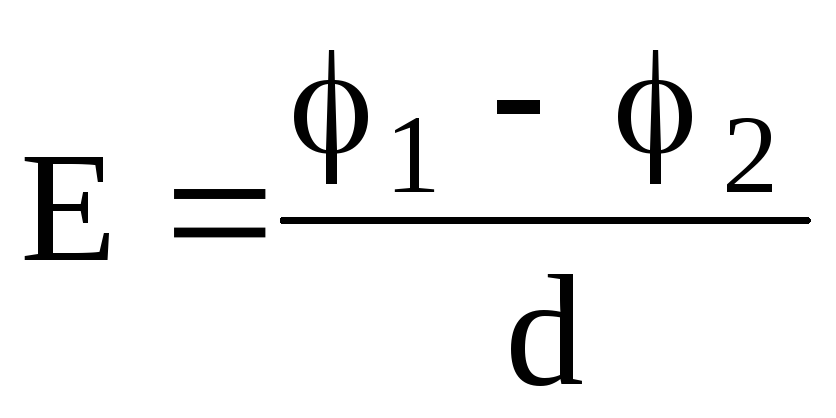 ,
,
где 1 и 2 – потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал 1, в другую, имеющую потенциал 2, равна
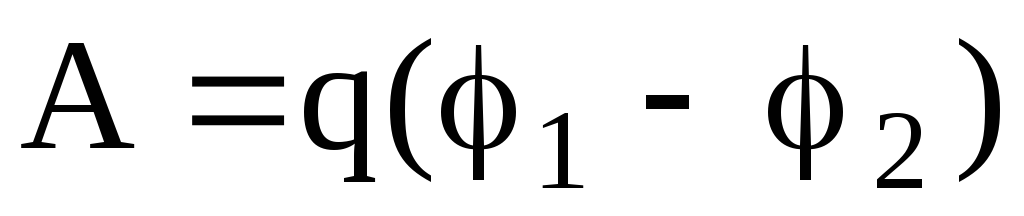 ,
или
,
или 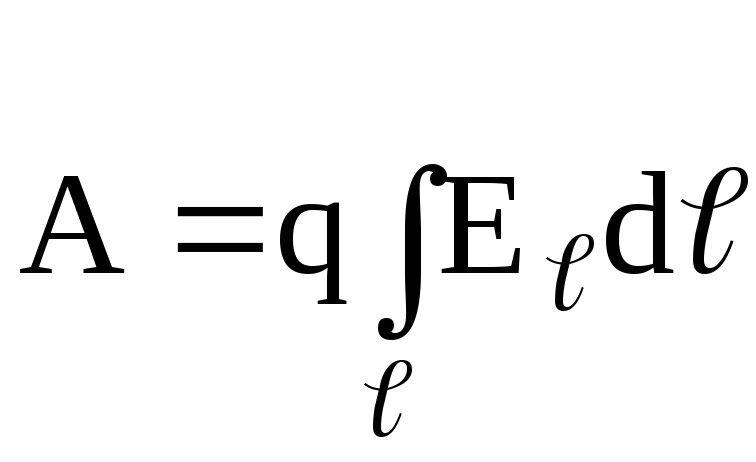 ,
,
где
E – проекция вектора
– проекция вектора  на направление перемещения;
на направление перемещения; — перемещение.
— перемещение.
В случае однородного поля последняя формула принимает вид
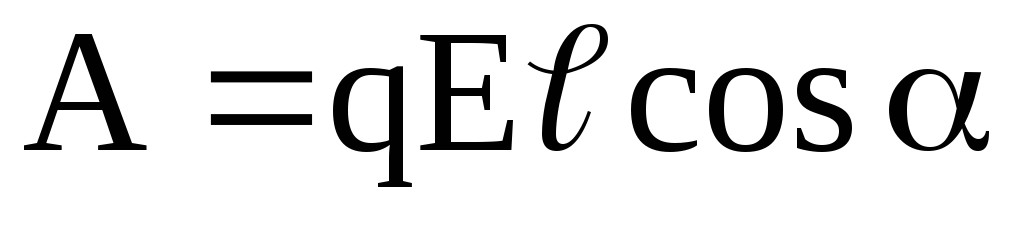 ,
,
где 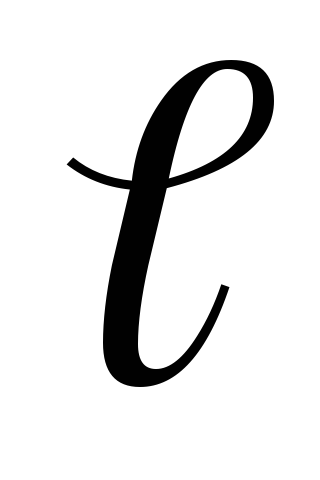 – перемещение;
— угол между направлениями вектора
– перемещение;
— угол между направлениями вектора  и перемеще-ния
и перемеще-ния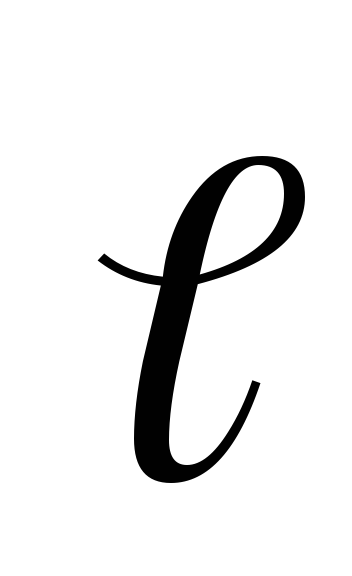 .
.
Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.
Электрический
момент  диполя есть вектор, направленный от
отрицательного заряда к положительному,
равный произведению заряда
диполя есть вектор, направленный от
отрицательного заряда к положительному,
равный произведению заряда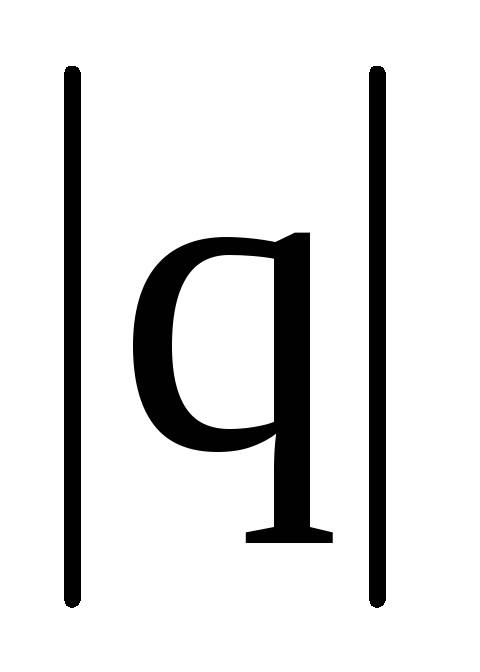 на вектор
на вектор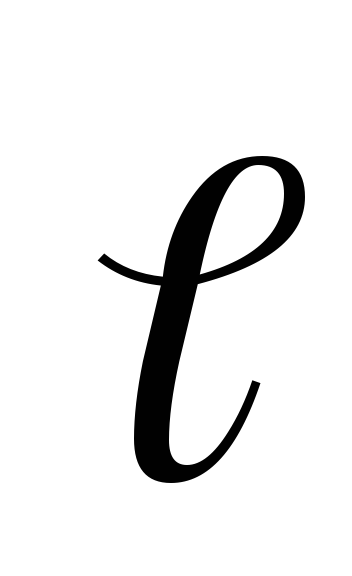 ,
проведенный от отрицательного заряда
к положительному, и называемый плечом
диполя, т.е.
,
проведенный от отрицательного заряда
к положительному, и называемый плечом
диполя, т.е.
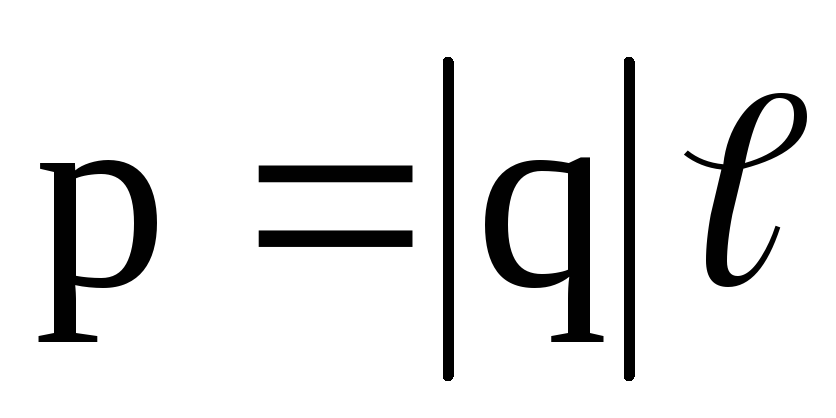 .
.
Диполь
называется точечным, если его плечо 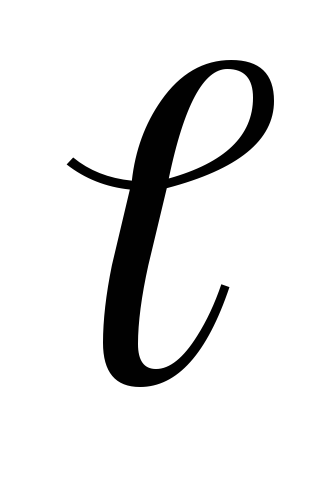 намного меньше расстоянияr
от центра диполя до точки, в которой нас
интересует действие диполя (
намного меньше расстоянияr
от центра диполя до точки, в которой нас
интересует действие диполя (
r),
см. рис. 1.
r),
см. рис. 1.
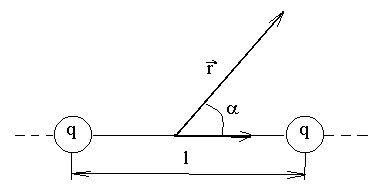
Рис. 1
Напряженность поля точечного диполя:
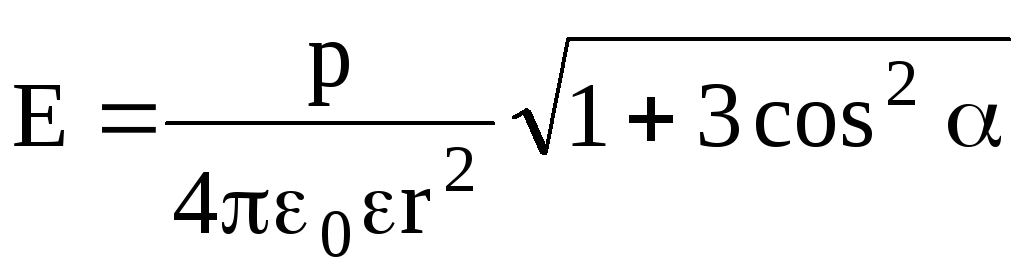 ,
,
где
р – электрический момент диполя; r
– абсолютное значение радиус-вектора,
проведенного от центра диполя к точке,
напряженность поля в которой нас
интересует;
— угол между радиус-вектором 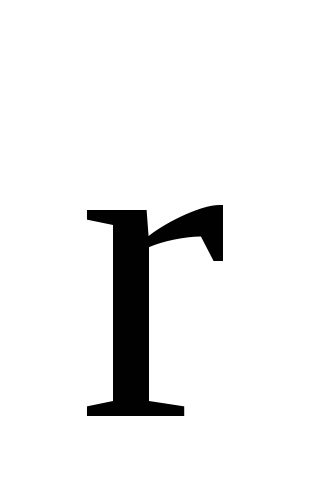 и плечом
и плечом диполя.
диполя.
Напряженность поля точечного диполя в точке, лежащей на оси диполя
(=0), находится по формуле
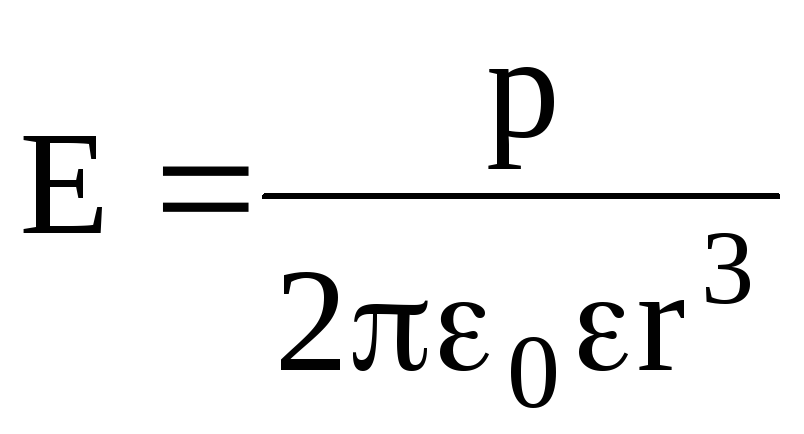 ;
;
в
точке, лежащей на перпендикуляре к плечу
диполя, восстановленном из его середины  ,
– по формуле
,
– по формуле
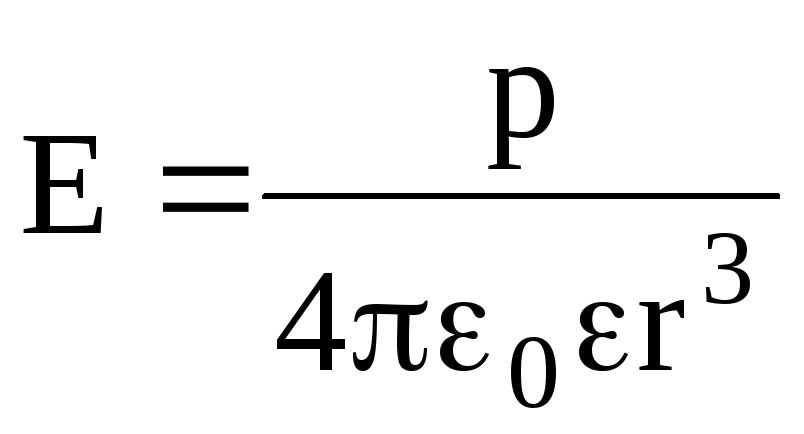 .
.
Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет
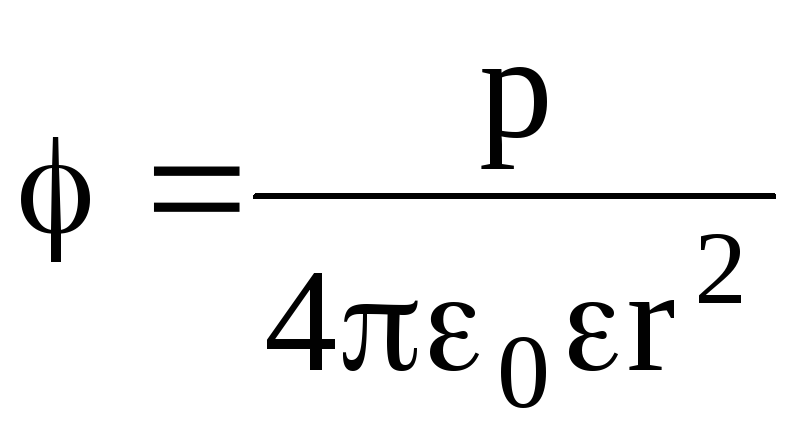 ,
,
а
в точке, лежащей на перпендикуляре к
плечу диполя, восстановленном из его
середины  ,
–
,
–
=0.
Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.
Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –
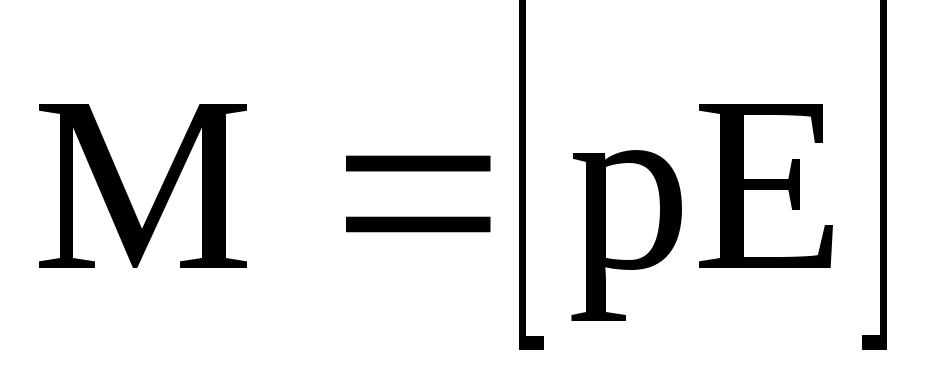 ,
или
,
или 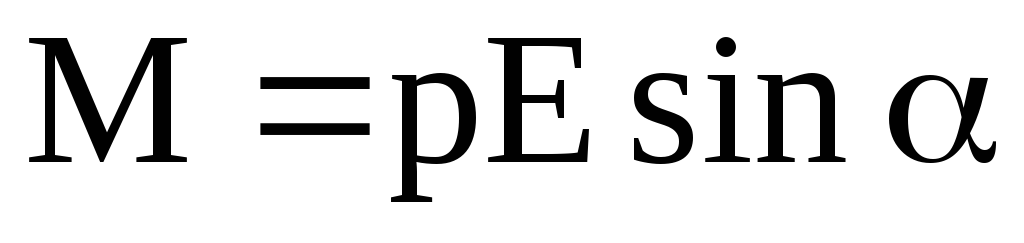 ,
,
где
— угол между направлениями векторов 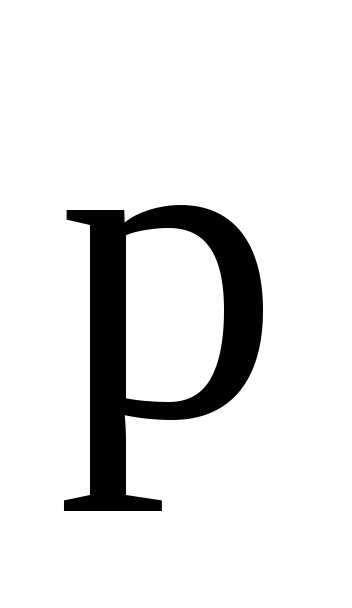 и
и .
.
Электроемкость уединенного проводника или конденсатора –
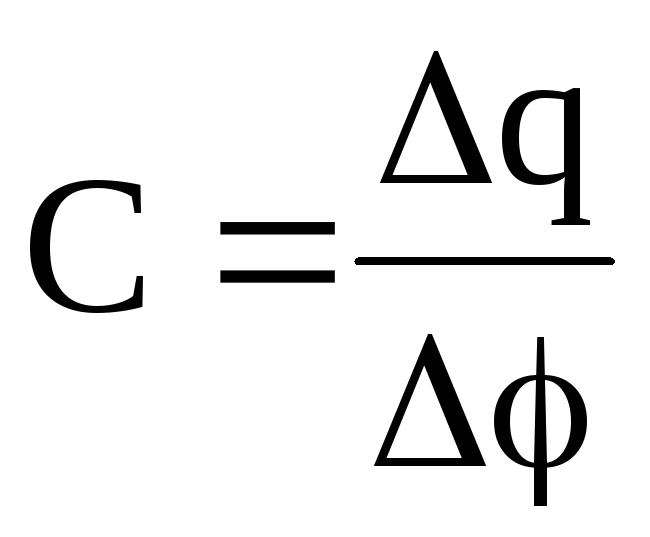 ,
,
где
q
– заряд, сообщенный проводнику;  —
изменение потенциала,
вызванное этим зарядом.
—
изменение потенциала,
вызванное этим зарядом.
Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –
 .
.
Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.
Электроемкость плоского конденсатора:
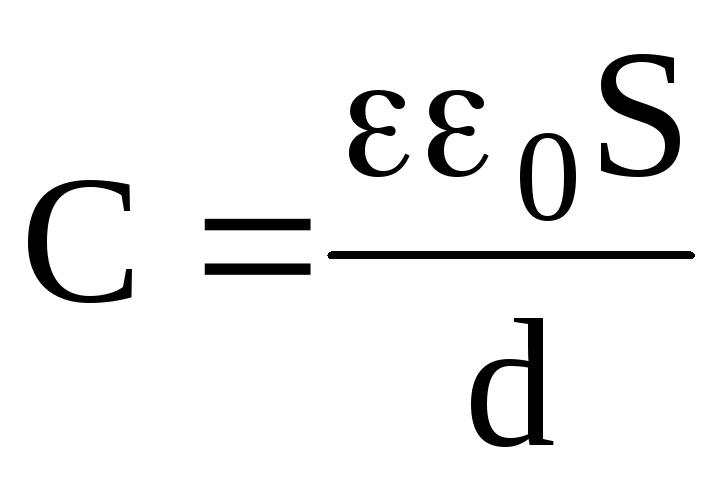 ,
,
где S – площадь каждой пластины конденсатора; d – расстояние между пластинами; — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.
Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной di и диэлектрической проницаемостью i каждый (слоистый конденсатор), составляет
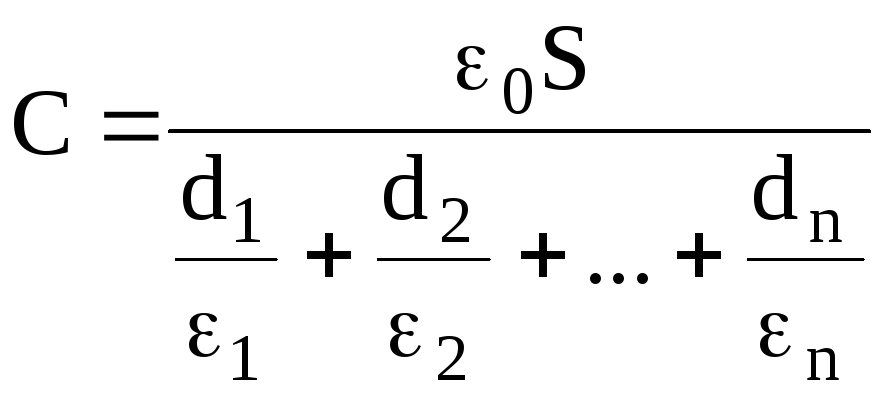 .
.
Электроемкость сферического конденсатора (две концентрические сферы радиусом R1 и R2 , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:
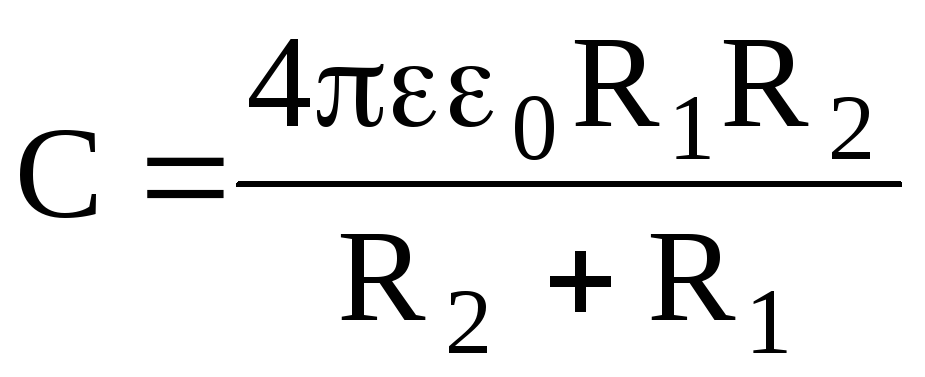 .
.
Электроемкость последовательно соединенных конденсаторов составляет:
в общем случае –
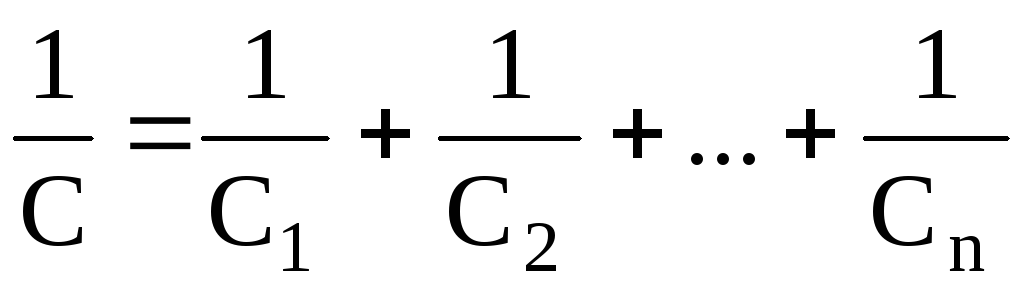 ,
,
где n – число конденсаторов;
в случае двух конденсаторов –
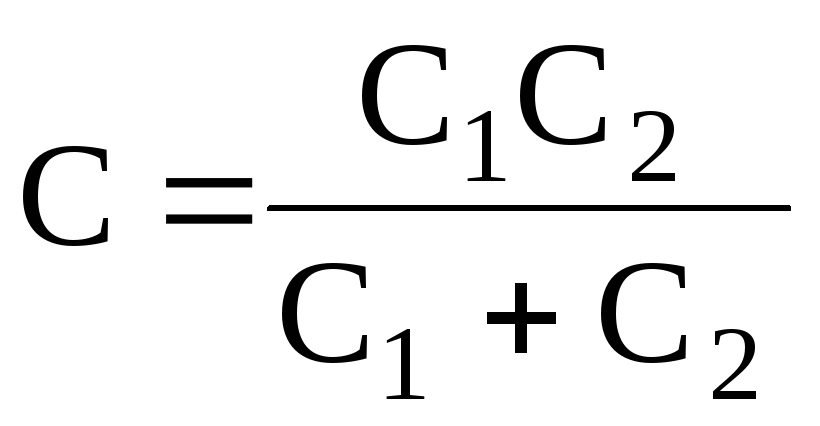 ;
;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
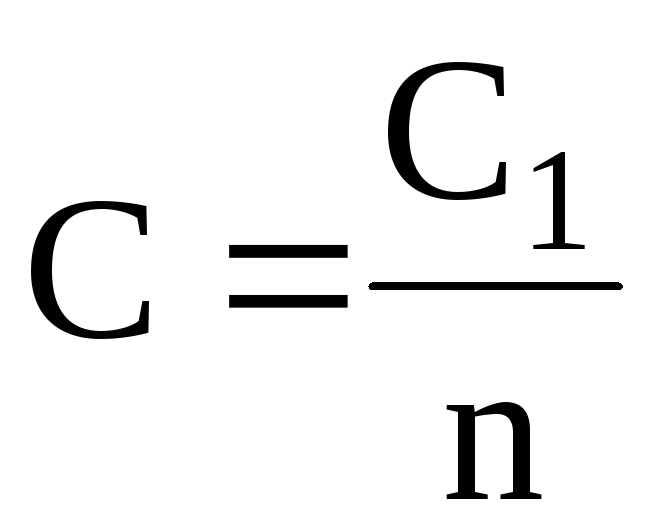 .
.
Электроемкость параллельно соединенных конденсаторов определяется следующим образом:
в общем случае –
С=С1+С2+…+Сn;
в случае двух конденсаторов –
С= С1+С2;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
С=nС1.
Энергия заряженного проводника выражается через заряд q, потенциал и электроемкость С проводника следующим образом:
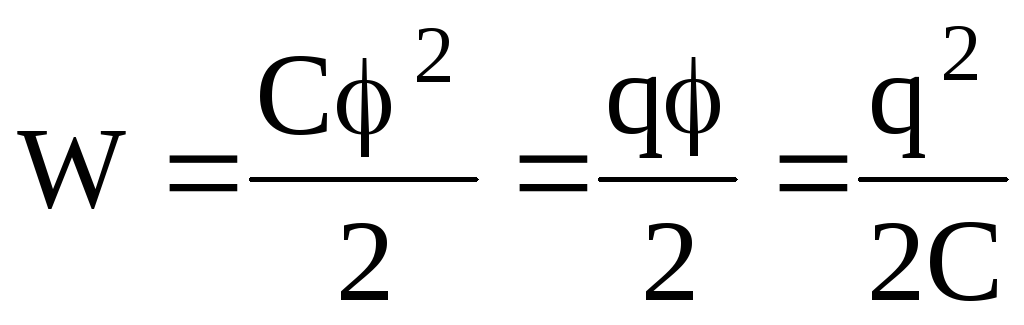 .
.
Энергия заряженного конденсатора –
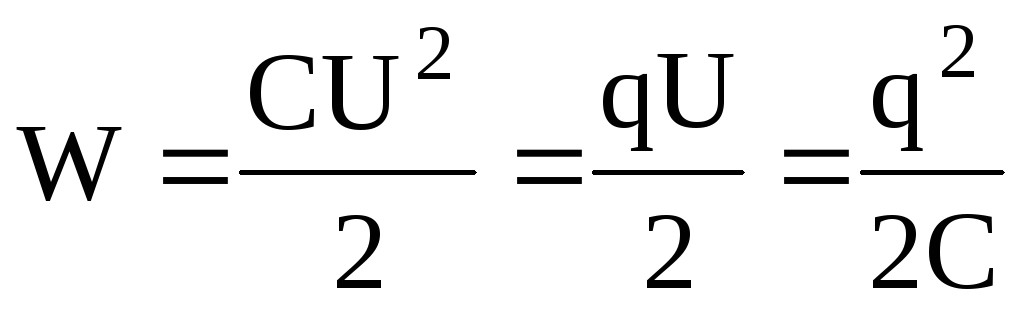 ,
,
где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.
2. Электрическое поле. Напряженность поля, электрический потенциал и напряжение.
В пространстве вокруг электрически заряженного тела существует электрическое
п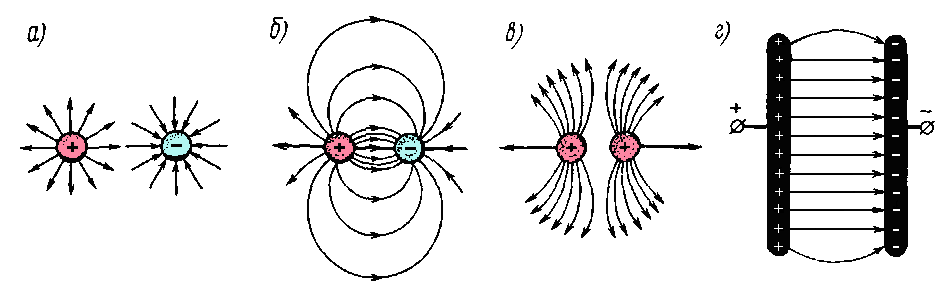 оле,
представляющее собой один из видов
материи. Электрическое поле обладает
энергией, которая проявляется в виде
сил, действующих на находящиеся в поле
заряженные тела.
оле,
представляющее собой один из видов
материи. Электрическое поле обладает
энергией, которая проявляется в виде
сил, действующих на находящиеся в поле
заряженные тела.
Э
 лектрическое
поле условно изображают в виде силовых
линий, которые направлены в ту сторону,
в которую двигалась бы в поле положительно
заряженная частица.
лектрическое
поле условно изображают в виде силовых
линий, которые направлены в ту сторону,
в которую двигалась бы в поле положительно
заряженная частица.
Н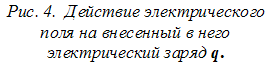 апряженность
поля.
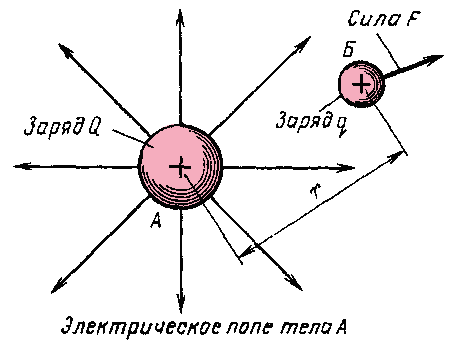
Электрическое поле действует на внесенный
в него заряд q (рис. 4) с некоторой силой F.
Следовательно, об интенсивности
электрического поля можно судить по
значению силы, с которой притягивается
или отталкивается некоторый электрический
заряд. В электротехнике интенсивность
поля характеризуют напряженностью
электрического поля Е, под которой понимают отношение силы F,
действующей на заряженное тело в данной
точке поля, к заряду q этого тела:
апряженность
поля.
Электрическое поле действует на внесенный
в него заряд q (рис. 4) с некоторой силой F.
Следовательно, об интенсивности
электрического поля можно судить по
значению силы, с которой притягивается
или отталкивается некоторый электрический
заряд. В электротехнике интенсивность
поля характеризуют напряженностью
электрического поля Е, под которой понимают отношение силы F,
действующей на заряженное тело в данной
точке поля, к заряду q этого тела:
E= F/q
По мере удаления от заряженного тела силовые линии электрического поля располагаются реже, т. е. напряженность поля E уменьшается (рис. 3,а,б и в). Только в однородном электрическом поле (рис. 3,г) напряженность одинакова во всех его точках.
Электрический потенциал. Электрическое поле обладает определенным запасом энергии, т. е. способностью совершать работу, которая может быть реализована, если внести в него какой-либо заряд. Этот заряд будет перемещаться по направлению силовых линий, совершая определенную работу. Для характеристики энергии, запасенной в каждой точке электрического поля, введено специальное понятие — электрический потенциал. Электрический потенциал φ поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля.
За нулевой потенциал условно принимают потенциал, который имеет поверхность земли.
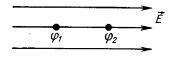
Э лектрическое
напряжение.Разные
точки электрического поля обладают
разными потенциалами. Обычно нас мало
интересует абсолютная величина
потенциалов отдельных точек электрического
поля, важнее знать разность потенциалов φ1-φ2 между двумя точками поля А и Б (рис. 5). Разность потенциалов φ1 и φ2 двух точек поля характеризует собой
работу, затрачиваемую силами поля на
перемещение заряда из одной точки поля
с большим потенциалом в другую — точку
с меньшим потенциалом и носит название электрического
лектрическое
напряжение.Разные
точки электрического поля обладают
разными потенциалами. Обычно нас мало
интересует абсолютная величина
потенциалов отдельных точек электрического
поля, важнее знать разность потенциалов φ1-φ2 между двумя точками поля А и Б (рис. 5). Разность потенциалов φ1 и φ2 двух точек поля характеризует собой
работу, затрачиваемую силами поля на
перемещение заряда из одной точки поля
с большим потенциалом в другую — точку
с меньшим потенциалом и носит название электрического
 напряжения. Электрическое напряжение обозначают
буквой U.
напряжения. Электрическое напряжение обозначают
буквой U.
Единицей электрического напряжения служит Вольт (В).
3. Электрический ток и электропроводность вещества.
В веществе, помещенном в электрическое поле, возникает процесс направленного движения элементарных носителей электричества. Заряженными частицами являются электроны или ионы. Движение этих электрически заряженных частиц называется электрическим током.
Единицей силы тока служит Ампер (А). Это такой ток, при котором через поперечное сечение проводника каждую секунду проходит количество электричества, равное 1 Кл. В формулах ток обозначают буквой I.
В электротехнике широко применяют как постоянный, так и переменный ток. Постоянным называют ток, значение и направление которого в любой момент времени остаются неизменными (рис. 6, а). Токи, значение и направление которых не остаются постоянными, называют изменяющимися, или переменными.
Свойство вещества проводить электрический ток под действием электрического поля называют электропроводностью. Электропроводность различных веществ зависит от концентрации свободных электрически заряженных частиц. Чем их больше, тем больше электропроводность данного вещества. Все вещества в зависимости от электропроводности делят на три группы: проводники, диэлектрики (изолирующие материалы) и полупроводники.
Высокая электропроводность металлов объясняется электронной теорией строения атома, согласно которой атомы металлов имеют такое строение, при котором электроны на последней электронной орбите сравнительно слабо связаны с ядрами атомов. Поэтому они свободно перемещаются между атомами, переходя от одного к другому и заполняя пространство между ними. Эти электроны называются свободными.
Если внести металлический проводник в электрическое поле, то свободные электроны под действием сил поля начнут перемещаться в сторону положительного полюса, создавая электрический ток. Таким образом, электрическим током в металлических проводниках называется упорядоченное (направленное) движение свободных электронов.
Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей.
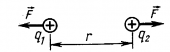
Взаимодействие электрических зарядов осуществляется через особый вид материи, порождаемой заряженными частицами — электрическое поле. Электрические заряды изменяют свойства окружающего их пространства. Проявляется это в том, что на помещенный вблизи заряженного тела другой заряд (назовем его пробным) действует сила (рис. 2). По величине этой силы можно судить об «интенсивности» поля, созданного зарядом q. Для того, чтобы сила, действующая на пробный заряд, характеризовала электрическое поле именно в данной точке пространства, пробный заряд, очевидно, должен быть точечным.
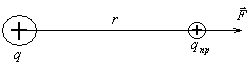
Рисунок 2
Поместив пробный заряд qпр на некотором расстоянии r от заряда q (рис. 2), мы обнаружим, что на него действует сила, величина которой зависит от величины взятого пробного заряда qпр.
Л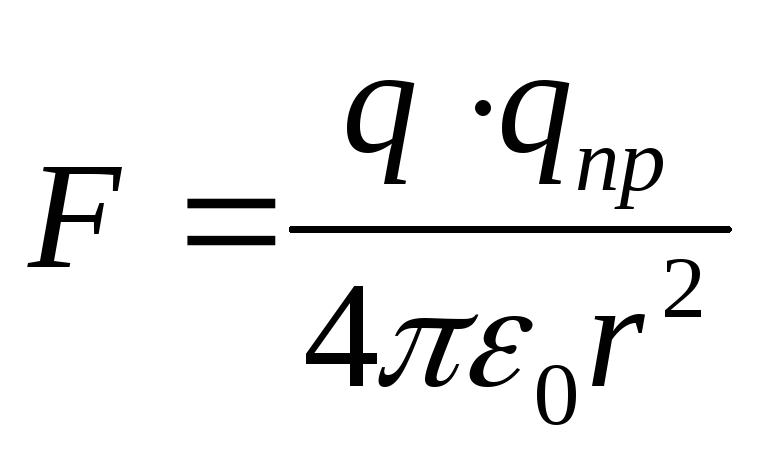 егко,
однако, видеть, что для всех пробных
зарядов отношениеF/ qпр будет
одно и тоже и зависит лишь от величин q и r , определяющих поле заряда q в данной точке r.
Естественно, поэтому, принять это
отношение за величину, характеризующую
«интенсивность» или, как говорят, напряженность электрического
поля (в данном случае поля точечного
заряда):
егко,
однако, видеть, что для всех пробных
зарядов отношениеF/ qпр будет
одно и тоже и зависит лишь от величин q и r , определяющих поле заряда q в данной точке r.
Естественно, поэтому, принять это
отношение за величину, характеризующую
«интенсивность» или, как говорят, напряженность электрического
поля (в данном случае поля точечного
заряда):

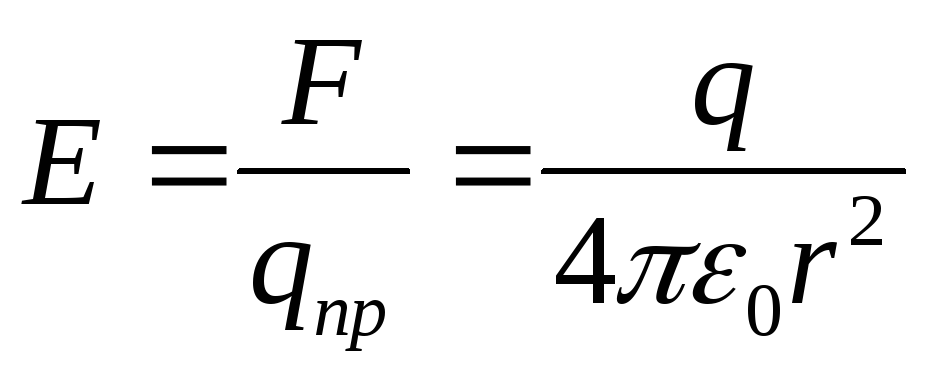 .
.
Таким образом, напряженность электрического поля является его силовой характеристикой. Численно она равна силе, действующий на пробный заряд qпр = +1, помещенный в данное поле.
Напряженность
поля – вектор.
Его направление совпадает с направлением вектора
силы,
действующей на точечный заряд, помещенный
в это поле. Следовательно, если в
электрическое поле напряженностью 
 поместить
точечный зарядq,
то на него будет действовать сила:
поместить
точечный зарядq,
то на него будет действовать сила: 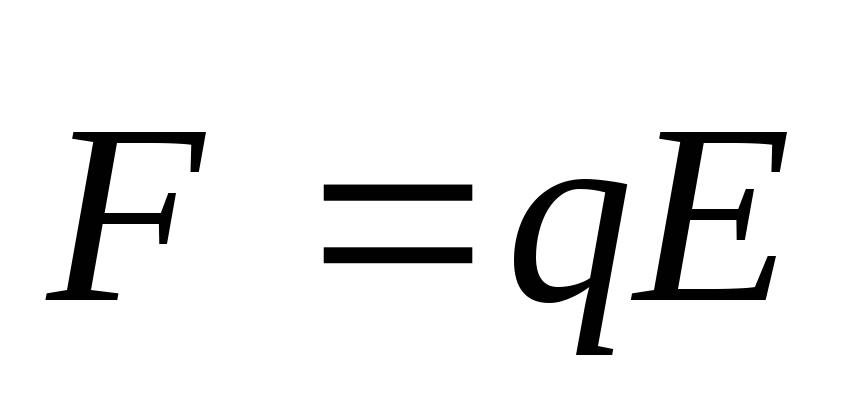
Размерность
напряженности электрического поля в
СИ: 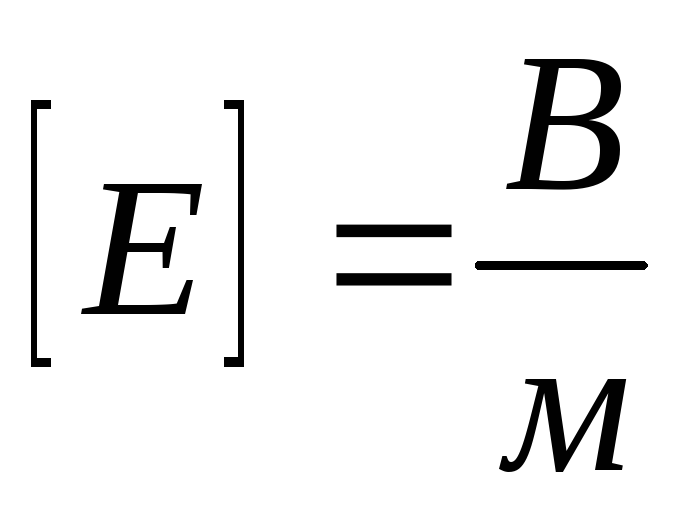 .
.
Электрическое поле удобно изображать с помощью силовых линий. Силовая линия – линия, вектор касательной к которой в каждой точке совпадает с направлением вектора напряженности электрического поля в этой точке. Принято считать, что силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность) и нигде не прерываются.
 Электрическое
поле подчиняется принципу
суперпозиции (сложения), который можно сформулировать
следующим образом: напряженность
электрического поля, созданного в
некоторой точке пространства системой
зарядов, равна векторной сумме
напряженностей электрических полей,
созданных в этой же точке пространства
каждым из зарядов в отдельности:
Электрическое
поле подчиняется принципу
суперпозиции (сложения), который можно сформулировать
следующим образом: напряженность
электрического поля, созданного в
некоторой точке пространства системой
зарядов, равна векторной сумме
напряженностей электрических полей,
созданных в этой же точке пространства
каждым из зарядов в отдельности:
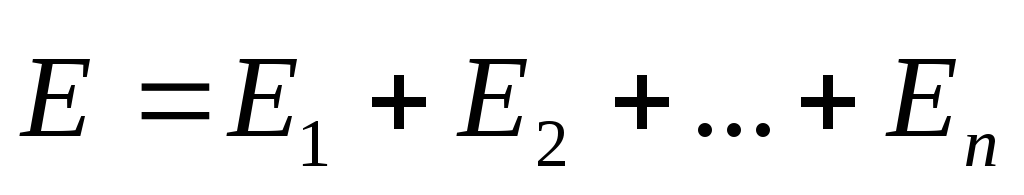 .
.
Работа сил электростатического поля, потенциал. Консервативность электростатических сил, связь между е и . Потенциал точечного и распределенного заряда.
Как следует из закона Кулона, сила, действующая на точечный заряд q в электрическом поле, созданном другими зарядами, является центральной. Напомним, что центральной называется сила, линия действия которой направлена по радиус-вектору, соединяющему некоторую неподвижную точку О (центр поля) с любой точкой траектории. Из «Механики» известно, что все центральные силы являются потенциальными. Работа этих сил не зависит от формы пути перемещения тела, на которое они действуют, и равна нулю по любому замкнутому контуру (пути перемещения). В применении к электростатическому полю:
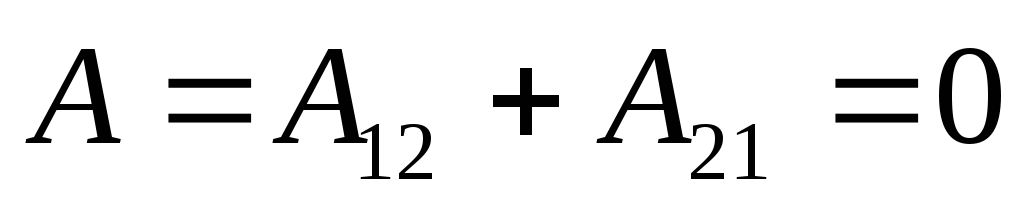
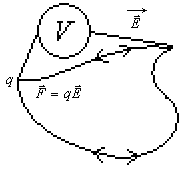 .
.
То есть, работа сил поля по перемещению заряда q из точки 1 в точку 2 равна по величине и противоположна по знаку работе по перемещению заряда из точки 2 в точку 1, независимо формы пути перемещения. Следовательно, работа сил поля по перемещению заряда может быть представлена разностью потенциальных энергий заряда в начальной и конечной точках пути перемещения:
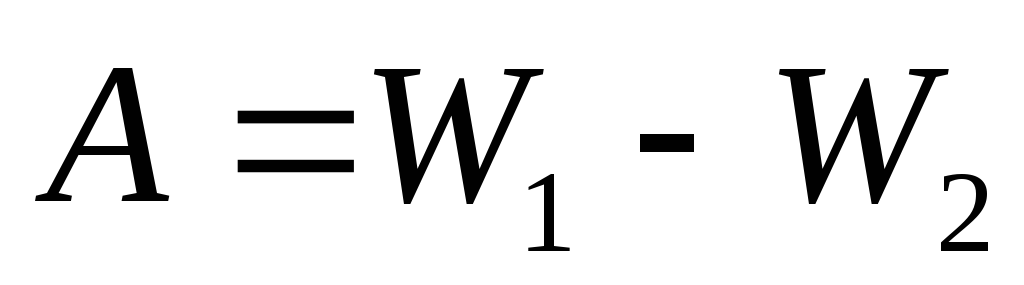 .
.
Введем потенциал электростатического поля φ, задав его как отношение:

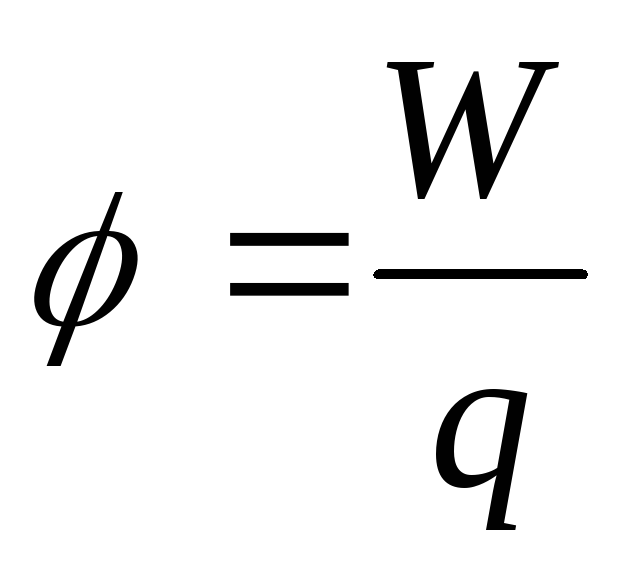 ,
(размерность
в СИ:
,
(размерность
в СИ: 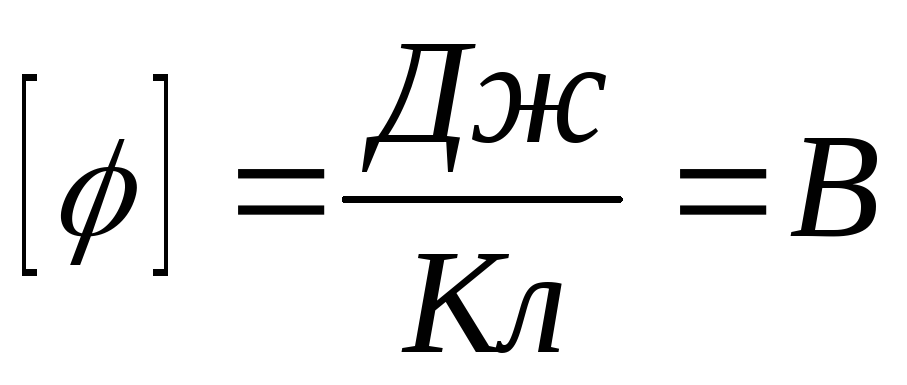 ).
).
Тогда работа сил поля по перемещению точечного заряда q из точки 1 в точку 2 будет:
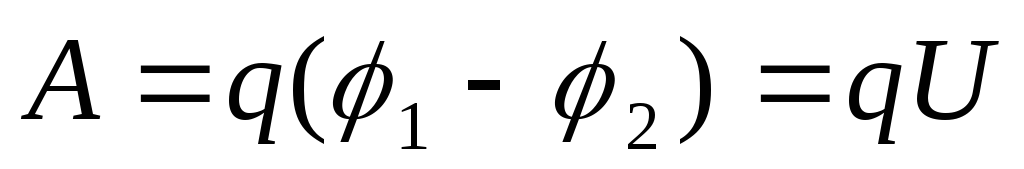
Разность
потенциалов 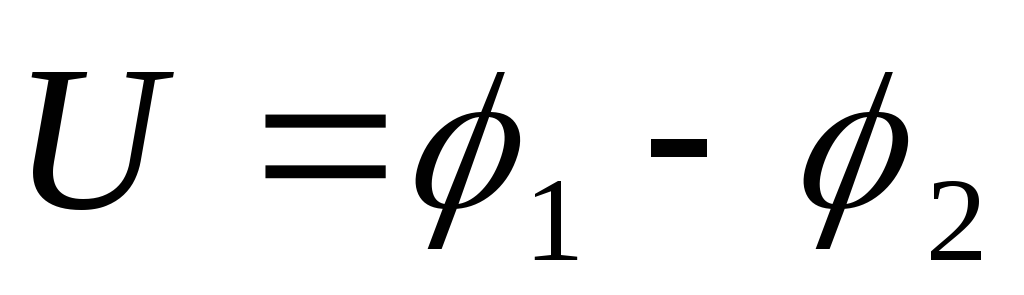 называется электрическим напряжением.
Размерность напряжения, как и потенциала,
[U]
= B.
называется электрическим напряжением.
Размерность напряжения, как и потенциала,
[U]
= B.
Считается,
что на бесконечности электрические
поля отсутствуют, и значит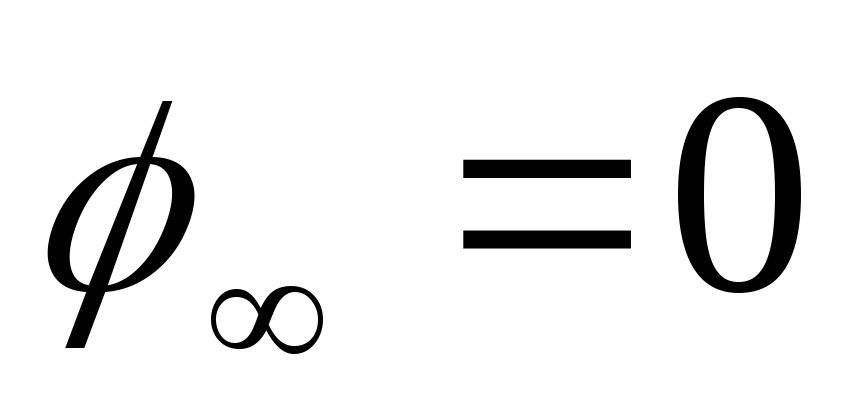 .
Это позволяет датьопределение
потенциала как работы,
которую нужно совершить, чтобы
переместить заряд q = +1 из бесконечности в данную точку
пространства. Таким образом, потенциал электрического
поля является его энергетической
характеристикой.
.
Это позволяет датьопределение
потенциала как работы,
которую нужно совершить, чтобы
переместить заряд q = +1 из бесконечности в данную точку
пространства. Таким образом, потенциал электрического
поля является его энергетической
характеристикой.
Циркуляция вектора напряженности. Связь напряженности и потенциала
Р ассмотрим
работу сил электрического поля при
перемещении зарядаQ0 из точки 1 по замкнутому контуру L
(рис. 75). Эта работа на элементарном
отрезке dl контура будет равна
ассмотрим
работу сил электрического поля при
перемещении зарядаQ0 из точки 1 по замкнутому контуру L
(рис. 75). Эта работа на элементарном
отрезке dl контура будет равна 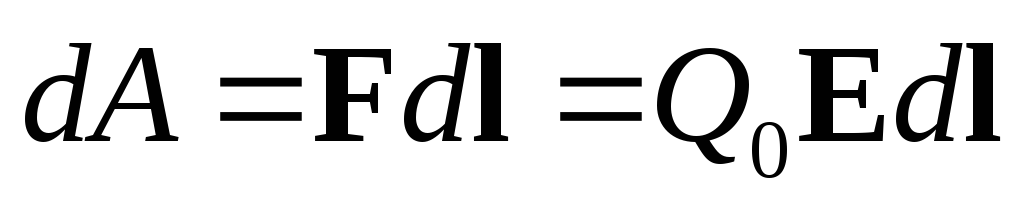 ,
а на всём контуре
,
а на всём контуре
Если в результате перемещения мы вернулись опять в точку 1, то работа по перемещению заряда Q0 , будет равна
A = Q0 (φ1 – φ1) = 0.
Следовательно, 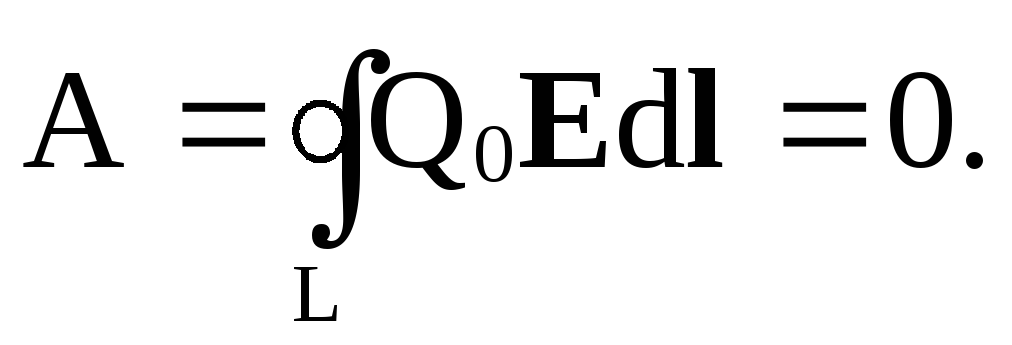 Так
как Q0
Так
как Q0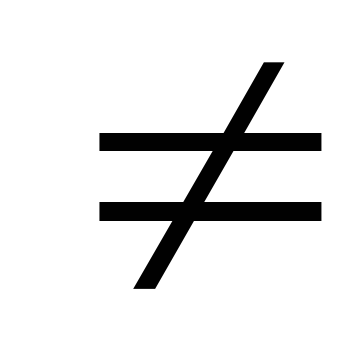 0,
то
0,
то 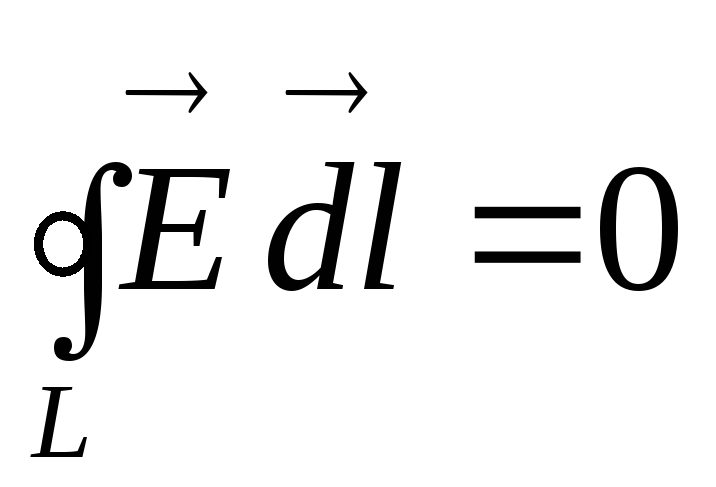 .
.
Такой интеграл называют циркуляцией вектора Е по замкнутому контуру L. Записанное равенство читается так: циркуляция вектора напряженности электрического поля по замкнутому контуру равна нулю. Это справедливо для электростатических полей, т.е. полей, создаваемых неподвижными зарядами. Или более обще – для потенциальных полей.
Электрические поля можно описать с помощью силовой характеристики – вектора Е, а также с помощью энергетической характеристики – скаляра φ – потенциала. Очевидно, что между этими величинами должна существовать связь.
Рассмотрим электрическое поле, создаваемое зарядом Q. В этом поле возьмем 2 точки с координатами х и х + Δх (рис.76). Пусть потенциал, создаваемый этим зарядом, описывается некоторой функцией φ (х). Расстояние между точками возьмем
столь малым, чтобы для приращения потенциала Δφ можно было записать
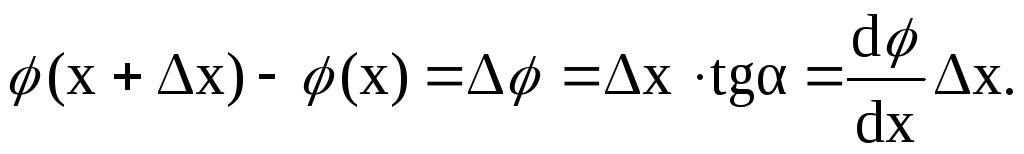
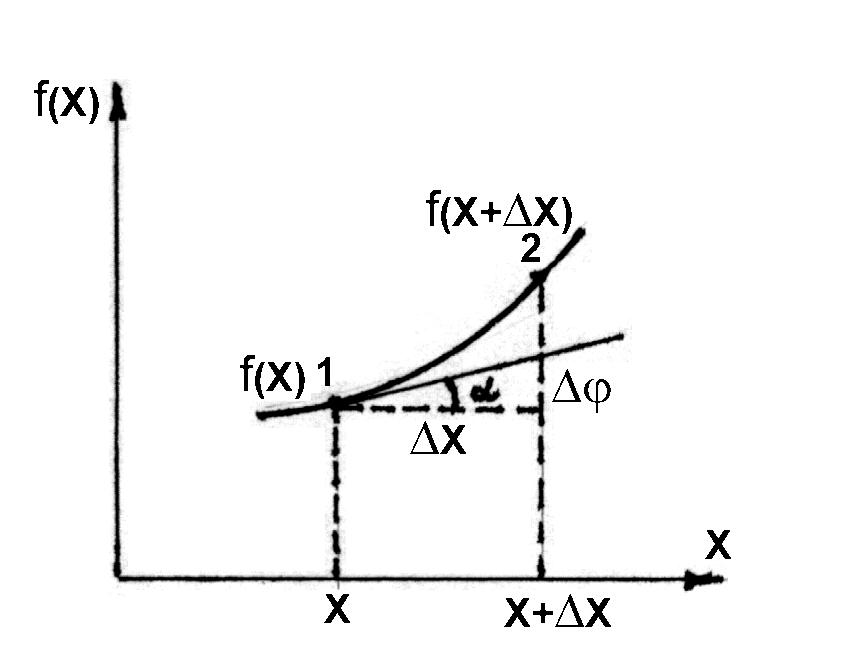
Рис.76
Тогда работа А по перемещению заряда Q/ из точки 1 в точку 2 будет равна
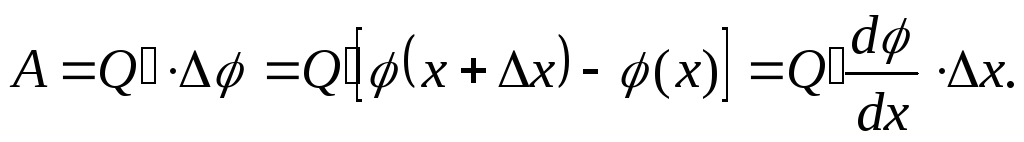
Для этой же работы можно написать ее выражение через силу
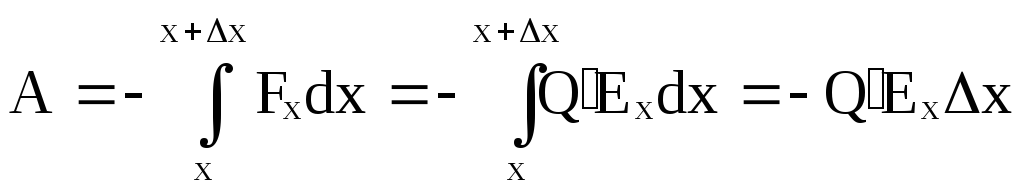
Расстояние Δх надо выбирать таким малым, чтобы на этом отрезке считать Fx и Exпостоянными. Знак ( — ) означает, что работа совершается против сил поля.
Приравнивая эти выражения для работы, получаем
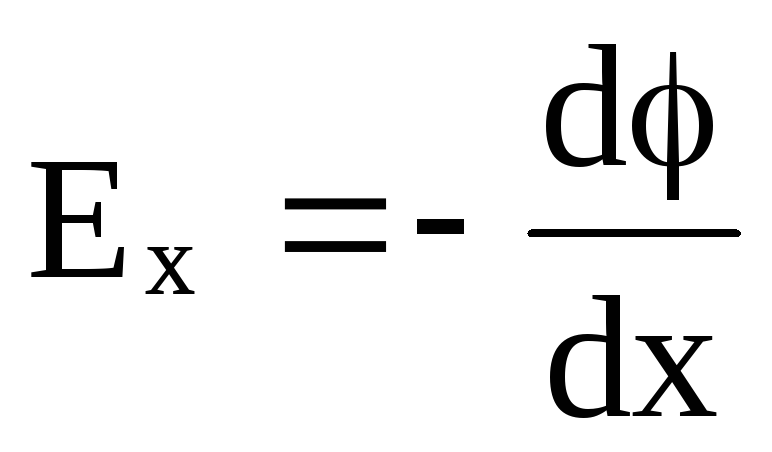 .
.
Здесь мы рассмотрели изменение потенциала и напряженности поля вдоль одной координаты х. Но в силу однородности пространства это равенство справедливо и для других координат:
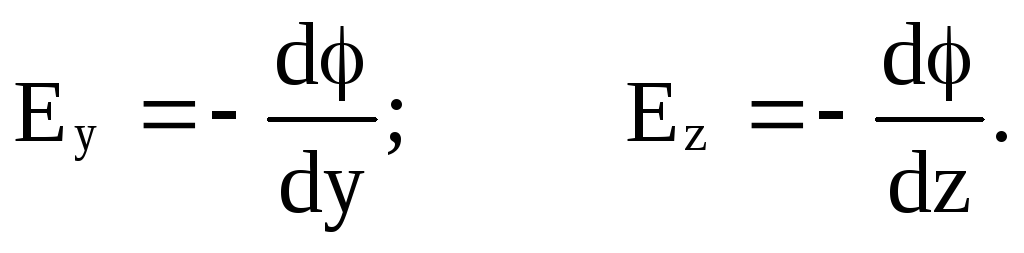
Или, если записать в векторном виде
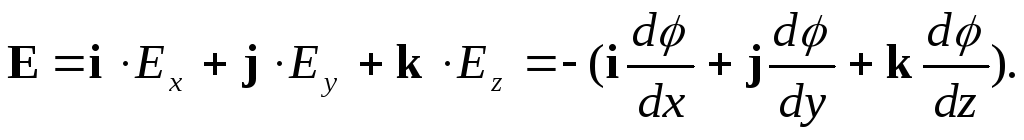
Выражение, стоящее в скобках, называется градиентом функции т.е. градиентом потенциала φ
Е = — grad φ,
т.е. напряженность характеризует быстроту изменения потенциала, или разность потенциалов, приходящуюся на единицу длины силовой линии. Если поле однородно, то напряженность поля равна (например, для плоского конденсатора с разностью потенциалов U и расстоянием между его обкладками d) E = U/d. Отсюда видно, что напряженность можно измерять в В/м.
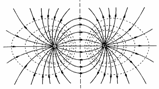
Напряженность и потенциал электрического поля диполя
Электрический диполь – это система из двух равных по величине разноименных зарядов Q1-Q2=Q расположенных на малом расстоянии l друг от друга.
Расстояние между зарядами l – вектор, направленный по полю от -Q к +Q, называют плечом диполя (рис. 77).
Величина р, равная p = Q∙l называется электрическим моментом диполя.
Л
Рис. 77
иния, проходящая через оба заряда, называетсяосью диполя. Определим напряженность поля, создаваемую диполем на его оси. В точке, расположенной на оси посредине между зарядами (рис.77а), напряженность поля обоих зарядов равна и будет суммироватьсяЕ = Е1 + Е2 = 2Е1 = 2Е2.
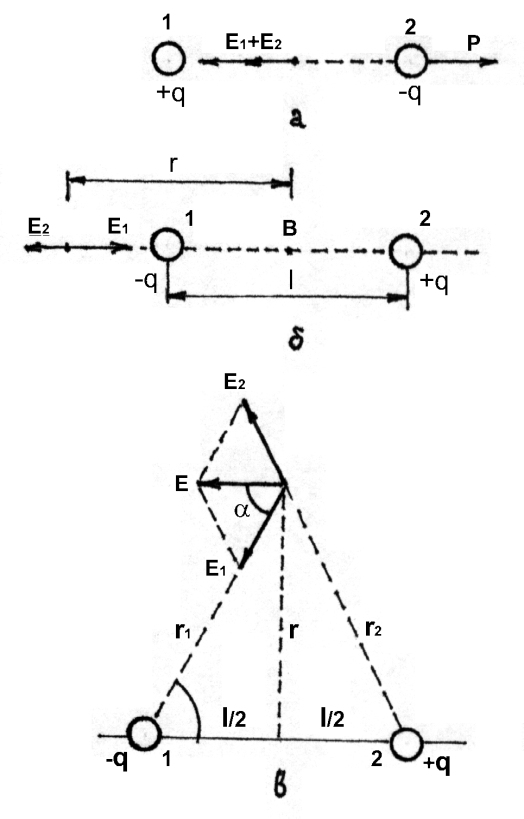 Напряженность
поля в точке А, лежащей на продолжении
оси диполя на расстоянии r
от средней точки диполя В, (рис. 77б) будет
равна геометрической сумме напряженностей Е1 и Е2 от обоих зарядов. По абсолютной величине
Е будет равно
Напряженность
поля в точке А, лежащей на продолжении
оси диполя на расстоянии r
от средней точки диполя В, (рис. 77б) будет
равна геометрической сумме напряженностей Е1 и Е2 от обоих зарядов. По абсолютной величине
Е будет равно
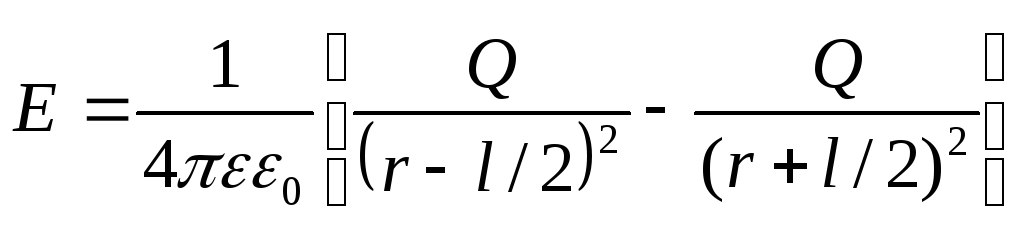
Рис. 77
Принимая во
внимание, что l r
можно пренебречь значениями l2 в знаменателе. Тогда получим
r
можно пренебречь значениями l2 в знаменателе. Тогда получим
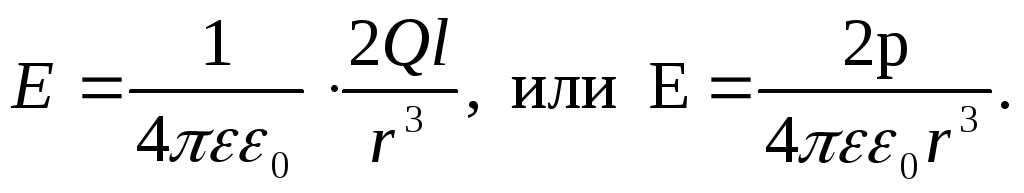
Вычислим напряженность поля в точке С, лежащей на расстоянии r на перпендикуляре, восстановленном из средней точки В (рис. 77в). Так как r1 = r2, то очевидно
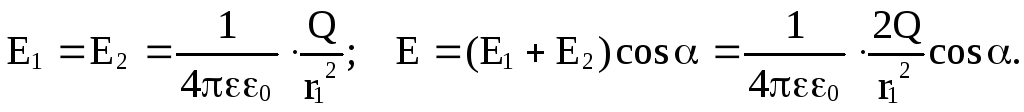
Из рисунка видно, что cos α = l/2r1 , тогда
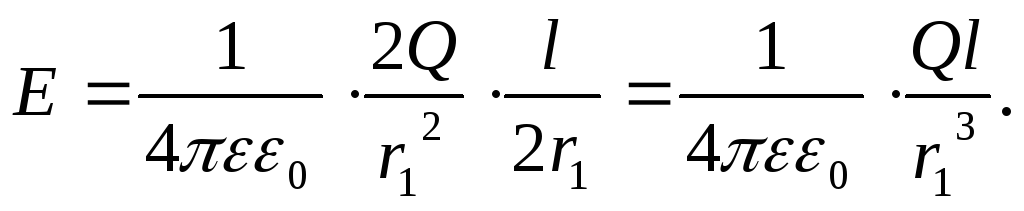
Так как r
»l , то можно считать, что r  r1,
и тогда
r1,
и тогда 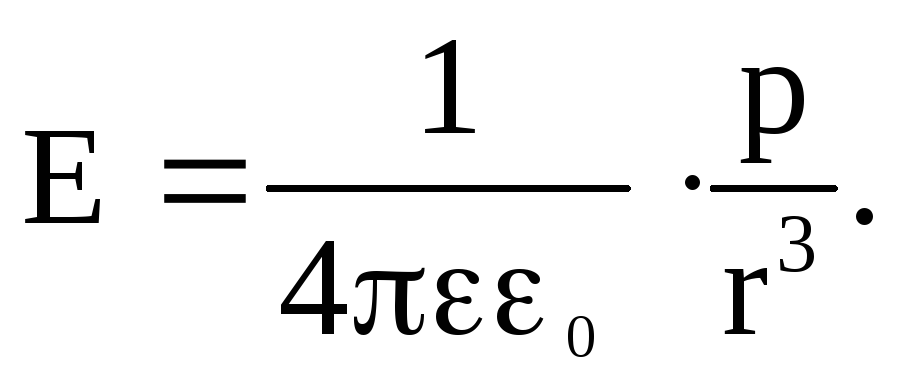
Напряженность поля в произвольной точке пространства определяется по формуле
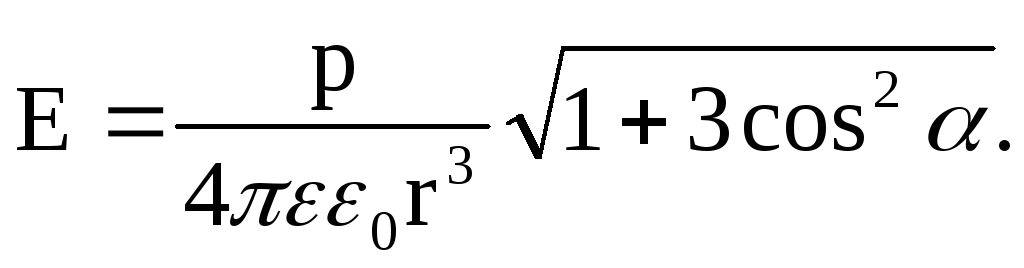
При α = π получаем напряженность на оси диполя.
При α = π/2 получаем напряженность на перпендикуляре к оси диполя.



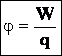


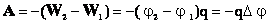
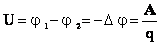

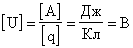
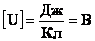
 →
→ 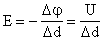
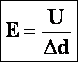
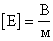 — Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
— Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.