Когда потенциал равен нулю — MOREREMONTA

Потенциал

Электростатическое поле является потенциальным. Что такое потенциальное поле? Пусть электростатическое поле перемещает заряд между двумя точками. Работа сил поля по перемещению заряда между этими точками не зависит от формы пути, а зависит только от положения самих точек. Такое поле и называется потенциальным.

Так как электростатическое поле потенциально, то для него возможно ввести понятие потенциала.

А почему нужно перемещать заряд в бесконечность? Считается, что в бесконечности поле равно нулю и потенциал равен нулю. Если ещё раз прочесть определение потенциала, то можно понять, что перемещая заряд в бесконечность, мы перемещаем его в точку, в которой потенциал равен нулю. В качестве точки с нулевым потенциалом можно было бы выбрать любую точку, но обычно выбирается бесконечность.

Ещё вопрос: почему важно для определения потенциала то, что электростатическое поле потенциально? В потенциальном поле работа не зависит от формы пути, значит потенциал может характеризовать поле в точке. Ведь если бы работа поля по перемещению заряда в бесконечность зависила от формы пути, то премещая заряд разными путями, мы получили бы различные значения потенциала для одной точки. Но работа в случае электростатического поля

не зависит от формы пути, значит значение потенциала в точке будет только одно, а это означает, что потенциал может характеризовать поле в данной точке.

Для различных точек электростатического поля мы можем однозначно указать значение потенциала. Правда здесь есть одна тонкость: перед тем как указывать значение потенциала для любой точки нужно значение потенциала в определённой точке принять равным нулю (или какой-то определённой величине). Таковой точкой мы выбрали бесконечность. Здесь важно понять, что когда мы говорим о потенциале поля в данной точке, то другая точка, куда (или откуда) будем перемещать заряд, заранее известна.

Потенциал является скалярной величиной.

Формула потенциала φ точки электростатического поля заряда q на расстоянии r от него:

Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:

,

Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.

Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространс­тва определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:

.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.

Вектор напряженности (как и сила ) перпендикулярен эквипотенциальным поверхнос­тям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.

Напряжение и напряженность однородного поля .

В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ₁, и φ₂ равна:

,

.

Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.

Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы , , разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.

Автор Влад Шестаков задал вопрос в разделе ВУЗы, Колледжи

Если напряженность электростатического поля в некоторой точке равна нулю.обязательно ли что потенциал в этой точке = 0? и получил лучший ответ

Ответ от Vladimir Shchookin[гуру]

Копирую первую часть ответа АНДРЕЯ (Так, как напряженность электрического поля равна градиенту потенциала, то если потенциал в этой точке будет равен постоянной величине (константе) , т. е. не зависеть от координат, то электростатическое поле в точке будет равно 0, т. к. в этом случае производные от потенциала по координатам будут равны 0.) и говорю, что вовсе нет. Пример: поле двух параллельных плоскостей, заряженных разноимённо с равными по абсолютному значению поверхностными плотностями зарядов.
JELAYU USPEXOV .
Vladimir Shchookin.

Векторный потенциал — Википедия

У этого термина существуют и другие значения, см. Потенциал.

В векторном анализе

векторный потенциал — это векторное поле, ротор которого равен заданному векторному полю. Он аналогичен скалярному потенциалу, который определяется как скалярное поле, градиент которого равен заданному векторному полю.

Формально, если v{\displaystyle \mathbf {v} } — векторное поле, векторным потенциалом называется векторное поле A{\displaystyle \mathbf {A} } такое, что

v=∇×A.{\displaystyle \mathbf {v} =\nabla \times \mathbf {A} .}

Если A{\displaystyle \mathbf {A} } является векторным потенциалом для поля v{\displaystyle \mathbf {v} }, то из тождества

∇⋅(∇×A)=0{\displaystyle \nabla \cdot (\nabla \times \mathbf {A} )=0}

(дивергенция ротора равна нулю) следует

∇⋅v=∇⋅(∇×A)=0,{\displaystyle \nabla \cdot \mathbf {v} =\nabla \cdot (\nabla \times \mathbf {A} )=0,}

то есть v{\displaystyle \mathbf {v} } должно быть соленоидальным векторным полем.

Для любого соленоидального векторного поля, удовлетворяющего определённым условиям, существует векторный потенциал. В частности, его существование зависит от области, на которой определено поле — в случае многосвязной области потенциал вихревого поля обычно не существует.

Пусть

v:R3→R3{\displaystyle \mathbf {v} :\mathbb {R} ^{3}\to \mathbb {R} ^{3}}

— дважды непрерывно дифференцируемое соленоидальное векторное поле. Предположим, что v(x){\displaystyle \mathbf {v} \left(\mathbf {x} \right)} убывает достаточно быстро при ‖x‖→∞{\displaystyle \|\mathbf {x} \|\rightarrow \infty }. Определим

A(x)=14π∇×∫R3v(y)‖x−y‖dy.{\displaystyle \mathbf {A} (\mathbf {x} )={\frac {1}{4\pi }}\nabla \times \int \limits _{\mathbb {R} ^{3}}{\frac {\mathbf {v} (\mathbf {y} )}{\left\|\mathbf {x} -\mathbf {y} \right\|}}\,d\mathbf {y} .}

Тогда A{\displaystyle \mathbf {A} } является векторным потенциалом для v{\displaystyle \mathbf {v} }, то есть

∇×A=v.{\displaystyle \nabla \times \mathbf {A} =\mathbf {v} .}

Обобщением этой теоремы является разложение Гельмгольца, согласно которому любое векторное поле может быть представлено как сумма соленоидального векторного поля и безвихревого векторного поля.

Векторный потенциал соленоидального векторного поля определяется неоднозначно. Если A{\displaystyle \mathbf {A} } является векторным потенциалом для v{\displaystyle \mathbf {v} }, также им является

A+∇m,{\displaystyle \mathbf {A} +\nabla m,}

где m{\displaystyle m} — любая непрерывно дифференцируемая скалярная функция. Это является следствием того факта, что ротор градиента равен нулю.

В электродинамике это даёт неоднозначность при определении потенциалов электромагнитного поля и решается наложением на потенциал дополнительного условия калибровки.

Уравнения Максвелла[править | править код]

Одним из способов записи уравнений Максвелла является формулировка в терминах векторного и скалярного потенциалов. Векторный потенциал A{\displaystyle \mathbf {A} } вводится таким образом, что

μ0H=B=rot⁡A{\displaystyle \mu _{0}\mathbf {H} =\mathbf {B} =\operatorname {rot} \mathbf {A} } (в системе СИ).

При этом уравнение div⁡B=0{\displaystyle \operatorname {div} \mathbf {B} =0} удовлетворяется автоматически.

Подстановка выражения для A{\displaystyle \mathbf {A} } в

rot⁡E=−∂B∂t{\displaystyle \operatorname {rot} \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}

приводит к уравнению

rot⁡(E+∂A∂t)=0,{\displaystyle \operatorname {rot} \left(\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}\right)=0,}

согласно которому, так же как и в электростатике вводится скалярный потенциал. Однако теперь в E{\displaystyle \mathbf {E} } вносят вклад и скалярный и векторный потенциал:

E=−gradφ−∂A∂t.{\displaystyle \mathbf {E} =-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}.}

Из уравнения rot⁡H=j+∂D∂t{\displaystyle \operatorname {rot} \mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}} следует

rotrot⁡A=μ0j+ε0μ0∂∂t(−gradφ−∂A∂t).{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\mu _{0}\mathbf {j} +\varepsilon _{0}\mu _{0}{\frac {\partial }{\partial t}}\left(-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}\right).}

Используя равенство rotrot⁡A=graddiv⁡A−∇2A{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\operatorname {grad} \;\operatorname {div} \mathbf {A} -\nabla ^{2}\mathbf {A} }, уравнения для векторного и скалярного потенциалов можно записать в виде

ΔA−grad⁡(div⁡A+1c2∂φ∂t)−1c2∂2A∂t2=−μ0j,{\displaystyle \Delta \mathbf {A} -\operatorname {grad} \left(\operatorname {div} \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}\right)-{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}=-\mu _{0}\mathbf {j} ,}

Δφ+∂∂tdiv⁡A=−ρε0.{\displaystyle \Delta \varphi +{\frac {\partial }{\partial t}}\operatorname {div} \mathbf {A} =-{\frac {\rho }{\varepsilon _{0}}}.}

Физический смысл векторного потенциала[править | править код]

В классической электродинамике векторный потенциал достаточно часто трактовался как величина, не имеющая непосредственного физического смысла, формально вводимая лишь для удобства выкладок, хотя уже в структуре действия для классической электродинамики векторный потенциал входит таким прямым образом, что это наводит на мысль о его фундаментальном характере.

В квантовой теории это имеет прозрачный физический смысл прямого влияния векторного потенциала на фазу волновой функции движущейся в магнитном поле частицы. Более того, удалось поставить квантовые эксперименты, показавшие, что векторный потенциал доступен достаточно непосредственному в некотором смысле измерению (по крайней мере, речь идёт о том, что векторный потенциал может влиять наблюдаемым измеримым образом на квантовую частицу даже тогда, когда напряженность магнитного поля в областях, доступных частице, всюду равна нулю, то есть магнитное поле не может оказывать воздействие на частицу через напряженность, а лишь прямо — через векторный потенциал; см. Эффект Ааронова — Бома).

Подобно тому, как скалярный потенциал связан с понятием энергии, векторный потенциал обнаруживает тесную связь с понятием импульса. Так, в случае быстрого отключения магнитного поля частица, находившаяся в нём, получает дополнительный импульс qA.

Электростатический потенциал — это… Что такое Электростатический потенциал?

У этого термина существуют и другие значения, см. Потенциал.

Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда (для любой системы единиц; подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля и потенциал связаны соотношением^[1]

или обратно^[2]:

Здесь  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона. В единицах системы СИ:

где  — электростатический потенциал (в вольтах),  — объёмная плотность заряда (в кулонах на кубический метр), а  — диэлектрическая проницаемость вакуума (в фарадах на метр).

Неоднозначность определения потенциала

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

где:  — потенциал в точке 1,  — потенциал в точке 2,  — работа, совершаемая полем при переносе пробного заряда из точки 1 в точку 2. При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положнения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произволом выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

Единицы измерения

В СИ за единицу разности потенциалов принимают вольт (В). Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1В = 1 Дж/Кл (L²MT⁻³I⁻¹). В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг. Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ

Использование термина

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала.

Кулоновский потенциал

Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала, как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Чаще всего под кулоновским потенциалом имеют в виду электростатический потенциал одного точечного заряда (или нескольких точечных зарядов, полученный сложением кулоновского потенциала каждого из них). Зачастую даже в случае, когда имеется в виду потенциал, созданный непрерывно распределенными зарядами, если его называют кулоновским, это может подразумевать, что он выражен (или может быть выражен) всё же в виде суммы (интеграла) пусть и бесконечного числа элементов, на которые разбит заряженный объем, но всё же потенциал каждого рассчитан как потенциал точечного заряда. Однако, поскольку электростатический потенциал в принципе может быть выражен таким образом практически всегда (подробнее см. чуть ниже), то разграничение терминов всё же достаточно размывается.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния 1/r (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда:

(где K обозначен коэффициент, зависящий от системы единиц измерения — например в СИ K = 1/(4πε₀), q — величина заряда, r — расстояние от заряда-источника до точки, для которой рассчитывается потенциал).

• Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть например над поверхностью шара, а не внутри его.
• Кулоновский потенциал в виде приведенной выше формулы используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

См. также

Примечания

Векторный потенциал электромагнитного поля — Википедия

Ве́кторный потенциа́л электромагни́тного по́ля (вектор-потенциал, магнитный потенциал) — в электродинамике, векторный потенциал, ротор которого равен магнитной индукции:

B=rot⁡A=∇×A.{\displaystyle \mathbf {B} =\operatorname {rot} \mathbf {A} =\nabla \times \mathbf {A} .}

Вектор-потенциал является пространственной компонентой 4-вектора электромагнитного потенциала.

Одним из способов записи уравнений Максвелла является формулировка в терминах векторного и скалярного потенциалов.

При этом уравнение div⁡B=0{\displaystyle \operatorname {div} \mathbf {B} =0} удовлетворяется автоматически.

Подстановка выражения для A{\displaystyle \mathbf {A} } в

rot⁡E=−∂B∂t{\displaystyle \operatorname {rot} \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}

приводит к уравнению

rot⁡(E+∂A∂t)=0,{\displaystyle \operatorname {rot} \left(\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}\right)=0,}

согласно которому, так же как и в электростатике вводится скалярный потенциал. Однако теперь в E{\displaystyle \mathbf {E} } вносят вклад и скалярный и векторный потенциал:

E=−gradφ−∂A∂t.{\displaystyle \mathbf {E} =-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}.}

Из уравнения rot⁡H=j+∂D∂t{\displaystyle \operatorname {rot} \mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}} следует

rotrot⁡A=μ0j+ε0μ0∂∂t(−gradφ−∂A∂t).{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\mu _{0}\mathbf {j} +\varepsilon _{0}\mu _{0}{\frac {\partial }{\partial t}}\left(-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}\right).}

Используя равенство rotrot⁡A=graddiv⁡A−∇2A{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\operatorname {grad} \;\operatorname {div} \mathbf {A} -\nabla ^{2}\mathbf {A} }, уравнения для векторного и скалярного потенциалов можно записать в виде

ΔA−grad⁡(div⁡A+1c2∂φ∂t)−1c2∂2A∂t2=−μ0j,{\displaystyle \Delta \mathbf {A} -\operatorname {grad} \left(\operatorname {div} \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}\right)-{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}=-\mu _{0}\mathbf {j} ,}

Δφ+∂∂tdiv⁡A=−ρε0.{\displaystyle \Delta \varphi +{\frac {\partial }{\partial t}}\operatorname {div} \mathbf {A} =-{\frac {\rho }{\varepsilon _{0}}}.}

Вектор-потенциал и магнитный поток[править | править код]

В соответствии с теоремой Стокса, магнитный поток Φ{\displaystyle \Phi } через контур L{\displaystyle L} легко выразить через циркуляцию векторного потенциала A{\displaystyle \mathbf {A} } по этому контуру:

Φ=∮L⁡A⋅dl.{\displaystyle \Phi =\oint \limits _{L}\mathbf {A} \cdot \mathbf {dl} .}

Легко убедиться, что преобразования

A→A+∇ψ,{\displaystyle \mathbf {A} \rightarrow \mathbf {A} +\nabla \psi ,}

φ→φ−∂ψ∂t,{\displaystyle \varphi \rightarrow \varphi -{\frac {\partial \psi }{\partial t}},}

где ψ{\displaystyle \psi } — произвольная скалярная функция координат и времени, не изменяют уравнений Максвелла (калибровочная инвариантность, по теореме Нётер ей соответствует закон сохранения электрического заряда). Для удобства решения этих уравнений накладывают дополнительное искусственное условие, называемое калибровкой потенциала. При решении различного класса задач удобнее бывает та или иная калибровка. Широкое распространение получили две — калибровка Кулона и калибровка Лоренца.

Калибровка Кулона[править | править код]

Калибровкой Кулона называют выражение:

div⁡A=0.{\displaystyle \operatorname {div} \mathbf {A} =0.}

Эта калибровка удобна для рассмотрения магнитостатических задач (с постоянными во времени токами).

Калибровка Лоренца[править | править код]

Калибровкой Лоренца называют условие равенства нулю 4-дивергенции потенциала (в СИ):

∇μAμ=div⁡A+1c2∂φ∂t=0.{\displaystyle \nabla _{\mu }A_{\mu }=\operatorname {div} \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}=0.}

В этом случае уравнения переписываются в виде даламбертианов:

◻A≡ΔA−1c2∂2A∂t2=−μ0j,{\displaystyle \square \mathbf {A} \equiv \Delta \mathbf {A} -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}=-\mu _{0}\mathbf {j} ,}

◻φ≡Δφ−1c2∂2φ∂t2=−ρε0.{\displaystyle \square \varphi \equiv \Delta \varphi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\varphi }{\partial t^{2}}}=-{\frac {\rho }{\varepsilon _{0}}}.}

Уравнения, записанные в таком виде, удобнее использовать для решения нестационарных задач.

Физический смысл векторного потенциала[править | править код]

Обычно считается, что векторный потенциал — величина, не имеющая непосредственного физического смысла, вводимая лишь для удобства выкладок. Однако удалось поставить эксперименты, показавшие, что векторный потенциал доступен непосредственному измерению. Подобно тому, как электростатический потенциал связан с понятием энергии, векторный потенциал обнаруживает тесную связь с понятием импульса.

Смещение квантовомеханической фазы[править | править код]

Влияние магнитного поля на движение квантовой частицы приводит к смещению фазы^[1][2]:

ΔφH=eℏc∫S(A,dl),{\displaystyle \Delta \varphi _{H}={\frac {e}{\hbar c}}\int _{S}^{}(\mathbf {A} ,\;d\mathbf {l} ),}

где e{\displaystyle e} — заряд электрона, c{\displaystyle c} — скорость света в вакууме, ℏ{\displaystyle \hbar } — приведенная постоянная Планка, A{\displaystyle \mathbf {A} } — векторный потенциал магнитного поля и dl{\displaystyle d\mathbf {l} } — элемент траектории движения частицы.

При этом смещение фазы возникает и тогда, когда частица проходит по областям, в которых B=0{\displaystyle \mathbf {B} =0}, не равен нулю только A{\displaystyle \mathbf {A} }. Например, это происходит при наблюдении эффекта Ааронова — Бома^[3].

Обобщённый импульс[править | править код]

При движении частицы в электромагнитном поле полный импульс P{\displaystyle \mathbf {P} } равен не просто p=mv1−v2/c2{\displaystyle \mathbf {p} ={\frac {m\mathbf {v} }{\sqrt {1-v^{2}/c^{2}}}}}, а p+qA{\displaystyle \mathbf {p} +q\mathbf {A} }. Следовательно, при движении частицы в чисто магнитном поле сохраняется именно эта величина. Налицо аналогия с полной энергией частицы E=T+U=mc21−v2/c2+qφ{\displaystyle E=T+U={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}+q\varphi }, которую можно считать суммой кинетической и потенциальной энергии.

Импульс частицы при быстром отключении магнитного поля[править | править код]

Если заряженная частица находится вблизи источника магнитного поля, которое в определённый момент времени быстро отключают, то она приобретает дополнительный импульс Δp=qA{\displaystyle \Delta \mathbf {p} =q\mathbf {A} } даже в том случае, если B{\displaystyle \mathbf {B} } в точке нахождения частицы было равно нулю (например, с внешней стороны соленоида). В частности, если частица до отключения поля покоилась, то она начинает движение с импульсом, равным qA{\displaystyle q\mathbf {A} }. Таким образом мы получаем возможность непосредственно измерить векторный потенциал в макроскопической системе.

В системе СИ единицей векторного потенциала является вебер на метр (Вб/м, размерность — В·с/м = кг·м·с⁻²·А⁻¹).

1. ↑ Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1966. — Т. 6. — 344 с.
2. ↑ Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. — М.: Мир, 1968. — 382 с.
3. ↑ Aharonov, Y. and D. Bohm. Significance of electromagnetic potentials in quantum theory // Phys. Rev.. — 1959. — Т. 115.

Потенциал действия — Википедия

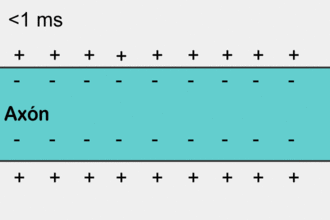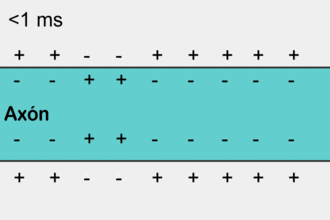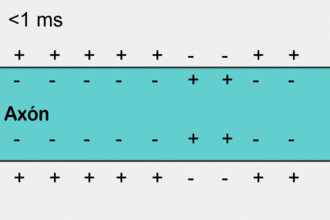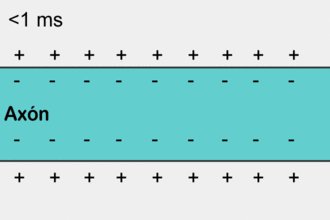Распространение потенциала действия по аксону

Потенциа́л де́йствия — волна возбуждения, перемещающаяся по мембране живой клетки в виде кратковременного изменения мембранного потенциала на небольшом участке возбудимой клетки (нейрона или кардиомиоцита), в результате которого наружная поверхность этого участка становится отрицательно заряженной по отношению к внутренней поверхности мембраны, в то время, как в покое она заряжена положительно. Потенциал действия является физиологической основой нервного импульса.

Благодаря работе «натрий-калиевого насоса» концентрация ионов натрия в цитоплазме клетки очень мала по сравнению с окружающей средой. При проведении потенциала действия открываются потенциал-зависимые натриевые каналы и положительно заряженные ионы натрия поступают в цитоплазму по градиенту концентрации, пока он не будет уравновешен положительным электрическим зарядом. Вслед за этим потенциал-зависимые каналы инактивируются и отрицательный потенциал покоя восстанавливается за счёт диффузии из клетки положительно заряженных ионов калия, концентрация которых в окружающей среде также значительно ниже внутриклеточной.

1. Предспайк — процесс медленной деполяризации мембраны до критического уровня деполяризации (местное возбуждение, локальный ответ).
2. Пиковый потенциал, или спайк, состоящий из восходящей части (деполяризация мембраны) и нисходящей части (реполяризация мембраны).
3. Отрицательный следовой потенциал — от критического уровня деполяризации до исходного уровня поляризации мембраны (следовая деполяризация).
4. Положительный следовой потенциал — увеличение мембранного потенциала и постепенное возвращение его к исходной величине (следовая гиперполяризация).

Рис. 2. A. Схематичное изображение идеализированного потенциала действия. B. Реальный потенциал действия пирамидного нейрона гиппокампа крысы. Форма реального потенциала действия обычно отличается от идеализированной.

Поляризация мембраны живой клетки обусловлена отличием ионного состава с её внутренней и наружной стороны. Когда клетка находится в спокойном (невозбуждённом) состоянии, ионы по разные стороны мембраны создают относительно стабильную разность потенциалов, называемую потенциалом покоя. Если ввести внутрь живой клетки электрод и измерить мембранный потенциал покоя, он будет иметь отрицательное значение (около −70 — −90 мВ). Это объясняется тем, что суммарный заряд на внутренней стороне мембраны существенно меньше, чем на внешней, хотя с обеих сторон содержатся и катионы, и анионы. Снаружи — на порядок больше ионов натрия, кальция и хлора, внутри — ионов калия и отрицательно заряженных белковых молекул, аминокислот, органических кислот, фосфатов, сульфатов. Надо понимать, что речь идёт именно о заряде поверхности мембраны — в целом среда и внутри, и снаружи клетки заряжена нейтрально.

Потенциал мембраны может изменяться под действием различных стимулов. Искусственным стимулом может служить электрический ток, подаваемый на внешнюю или внутреннюю сторону мембраны через электрод. В естественных условиях стимулом часто служит химический сигнал от соседних клеток, поступающий через синапс или путём диффузной передачи через межклеточную среду. Смещение мембранного потенциала может происходить в отрицательную (гиперполяризация) или положительную (деполяризация) сторону.

В нервной ткани потенциал действия, как правило, возникает при деполяризации — если деполяризация мембраны нейрона достигает некоторого порогового уровня или превышает его, клетка возбуждается, и от её тела к аксонам и дендритам распространяется волна электрического сигнала. (В реальных условиях на теле нейрона обычно возникают постсинаптические потенциалы, которые сильно отличаются от потенциала действия по своей природе — например, они не подчиняются принципу «всё или ничего». Эти потенциалы преобразуются в потенциал действия на особом немиелинезированном участке аксона — его начальном сегменте, и затем обратно распространяется на сому нейрона и дендриты.

Рис. 3. Простейшая схема, демонстрирующая мембрану с двумя натриевыми каналами в открытом и закрытом состоянии

Это обусловлено тем, что на мембране клетки находятся ионные каналы — белковые молекулы, образующие в мембране поры, через которые ионы могут проходить с внутренней стороны мембраны на наружную и наоборот. Большинство каналов ионо-специфичны — натриевый канал пропускает практически только ионы натрия и не пропускает другие (это явление называют селективностью). Мембрана клеток возбудимых тканей (нервной и мышечной) содержит большое количество потенциал-зависимых ионных каналов, способных быстро реагировать на смещение мембранного потенциала. Деполяризация мембраны в первую очередь вызывает открытие потенциал-зависимых натриевых каналов. Когда одновременно открывается достаточно много натриевых каналов, положительно заряженные ионы натрия устремляются через них на внутреннюю сторону мембраны. Движущая сила в данном случае обеспечивается градиентом концентрации (с внешней стороны мембраны находится намного больше положительно заряженных ионов натрия, чем внутри клетки) и отрицательным зарядом внутренней стороны мембраны (см. Рис. 2). Поток ионов натрия вызывает ещё бо́льшее и очень быстрое изменение мембранного потенциала, которое и называют потенциалом действия (в специальной литературе обозначается ПД).

Согласно закону «всё-или-ничего» мембрана клетки возбудимой ткани либо не отвечает на стимул совсем, либо отвечает с максимально возможной для неё на данный момент силой. То есть, если стимул слишком слаб и порог не достигнут, потенциал действия не возникает совсем; в то же время, пороговый стимул вызовет потенциал действия такой же амплитуды, как и стимул, превышающий пороговый. Это отнюдь не означает, что амплитуда потенциала действия всегда одинакова — один и тот же участок мембраны, находясь в разных состояниях, может генерировать потенциалы действия разной амплитуды.

После возбуждения нейрон на некоторое время оказывается в состоянии абсолютной рефрактерности, когда никакие сигналы не могут его возбудить снова, затем входит в фазу относительной рефрактерности, когда его могут возбудить исключительно сильные сигналы (при этом амплитуда ПД будет ниже, чем обычно). Рефрактерный период возникает из-за инактивации быстрого натриевого тока, то есть инактивации натриевых каналов (см. ниже).

Распространение потенциала действия[править | править код]

По немиелинизированным волокнам[править | править код]

По немиелинизированному волокну потенциал действия распространяется непрерывно. Проведение нервного импульса начинается с распространением электрического поля. Возникший потенциал действия за счет электрического поля способен деполяризовать мембрану соседнего участка до критического уровня, в результате чего на соседнем участке генерируются новые потенциалы. Сам потенциал действия не перемещается, он исчезает там же, где возник. Главную роль в возникновении нового потенциал действия играет предыдущий.

Если внутриклеточным электродом раздражать аксон посередине, то потенциал действия будет распространяться в обоих направлениях. Обычно же потенциал действия распространяется по аксону в одном направлении (от тела нейрона к нервным окончаниям), хотя деполяризация мембраны происходит по обе стороны от участка, где в данный момент возник потенциал. Одностороннее проведение потенциала действия обеспечивается свойствами натриевых каналов — после открытия они на некоторое время инактивируются и не могут открыться ни при каких значениях мембранного потенциала (свойство рефрактерности). Поэтому на ближнем к телу клетки участке, где до этого уже «прошел» потенциал действия, он не возникает.

При прочих равных условиях распространение потенциала действия по аксону происходит тем быстрее, чем больше диаметр волокна. По гигантским аксонам кальмара потенциал действия может распространяться почти с такой же скоростью, как и по миелинизированным волокнам позвоночных (около 100 м/c).

По миелинизированным волокнам[править | править код]

По миелинизированному волокну потенциал действия распространяется скачкообразно (сальтаторное проведение). Для миелинизированных волокон характерна концентрация потенциалзависимых ионных каналов только в областях перехватов Ранвье; здесь их плотность в 100 раз больше, чем в мембранах безмиелиновых волокон. В области миелиновых муфт потенциалзависимых каналов почти нет. Потенциал действия, возникший в одном перехвате Ранвье, за счет электрического поля деполяризует мембрану соседних перехватов до критического уровня, что приводит к возникновению в них новых потенциалов действия, то есть возбуждение переходит скачкообразно, от одного перехвата к другому. В случае повреждения одного перехвата Ранвье потенциал действия возбуждает 2-й, 3-й, 4-й и даже 5-й, поскольку электроизоляция, создаваемая миелиновыми муфтами, уменьшает рассеивание электрического поля.

«Скачкообразное распространение» увеличивает скорость распространения потенциала действия по миелинизированным волокнам по сравнению с немиелинизированными. Кроме того, миелинизированные волокна толще, а электрическое сопротивление более толстых волокон меньше, что тоже увеличивает скорость проведения импульса по миелинизированным волокнам. Другим преимуществом сальтаторного проведения является его экономичность в энергетическом плане, так как возбуждаются только перехваты Ранвье, площадь которых меньше 1 % мембраны, и, следовательно, необходимо значительно меньше энергии для восстановления трансмембранных градиентов Na

+ и K⁺, расходующихся в результате возникновения потенциал действия, что может иметь значение при высокой частоте разрядов, идущих по нервному волокну.

Чтобы представить, насколько эффективно может быть увеличена скорость проведения за счёт миелиновой оболочки, достаточно сравнить скорость распространения импульса по немиелинизированным и миелинизированным участкам нервной системы человека. При диаметре волокна около 2 µм и отсутствии миелиновой оболочки скорость проведения будет составлять ~1 м/с, а при наличии даже слабой миелинизации при том же диаметре волокна — 15—20 м/с. В волокнах большего диаметра, обладающих толстой миелинововой оболочкой, скорость проведения может достигать 120 м/с.

Скорость распространения потенциала действия по мембране отдельно взятого нервного волокна непостоянна — в зависимости от различных условий эта скорость может очень значительно уменьшаться и, соответственно, увеличиваться, возвращаясь к некоему исходному уровню.

Схема строения мембраны клетки.

Активные свойства мембраны, обеспечивающие возникновение потенциала действия, основываются главным образом на поведении потенциалзависимых натриевых (Na

+-) и калиевых (K⁺-) каналов. Начальная фаза ПД формируется входящим натриевым током, позже открываются калиевые каналы и выходящий K⁺-ток возвращает потенциал мембраны к исходному уровню. Исходную концентрацию ионов затем восстанавливает натрий-калиевый насос.

По ходу ПД каналы переходят из состояния в состояние: у Na⁺-каналов основных состояний три — закрытое, открытое и инактивированное (в реальности дело сложнее, но этих трёх достаточно для описания), у K⁺-каналов два — закрытое и открытое.

Поведение каналов, участвующих в формировании ПД, описывается через проводимость и вычисляется через коэффициенты переноса (трансфера).

Коэффициенты переноса были выведены Ходжкином и Хаксли.^[1][2]

Проводимость для калия G_K на единицу площади [S/cm²]

Проводимость для натрия G_Na на единицу площади [S/cm²]

рассчитывается сложнее, поскольку, как уже было сказано, у потенциал-зависимых Na⁺-каналов, помимо закрытого/открытого состояний, переход между которыми описывается параметром m{\displaystyle m}, есть ещё инактивированное/не-инактивированное состояния, переход между которыми описывается через параметр h{\displaystyle h}

Электрохимический потенциал — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 сентября 2017; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 сентября 2017; проверки требует 1 правка.

Электрохимический потенциал — химический потенциал электрически заряженных частиц и квазичастиц (ионы, электроны, дырки) в электрическом поле^[1][2][3][4] (термин предложен в 1929 г. Э. А. Гуггенгеймом^[5]). Специальный термин понадобился по причине принятого в литературе условного разбиения электрохимического потенциала на неэлектрическую и электрическую части. С теоретической точки зрения такое разделение носит чисто формальный характер, поскольку носителями заряда служат те же самые формульные единицы, с которыми соотносят обычный химический потенциал, и поэтому нет способа раздельного определения его химической и электрической составляющих. Практически же разделение электрохимического потенциала на две части иногда оказывается хорошим приближением, ибо в природе существуют частицы (электроны и позитроны), для которых вследствие малости их массы вклад неэлектрической части в электрохимический потенциал пренебрежимо мал по сравнению со вкладом электрической составляющей^[6][7].

Физический смысл электрохимического потенциала заключается в том, что его изменение равно работе для перехода системы из состояния 1{\displaystyle 1} в состояние 2{\displaystyle 2} с изменением химической, осмотической и электрической энергий: Δμ=μ2−μ1+RTln⁡C2C1+zF(φ2−φ1){\displaystyle \Delta \mu =\mu _{2}-\mu _{1}+RT\ln {\frac {C_{2}}{C_{1}}}+zF(\varphi _{2}-\varphi _{1})}. Здесь: μ2,μ1{\displaystyle \mu _{2},\mu _{1}} — химические потенциалы в состоянии 2{\displaystyle 2} и 1{\displaystyle 1},R{\displaystyle R} — универсальная газовая постоянная, T{\displaystyle T} — абсолютная температура, C1,C2{\displaystyle C_{1},C_{2}} — молярная концентрация, z{\displaystyle z} — заряд иона в единицах элементарного заряда, F=Nae=9,65∗107{\displaystyle F=N_{a}e=9,65*10^{7}} Кл/кмоль — постоянная Фарадея, φ2,φ1{\displaystyle \varphi _{2},\varphi _{1}} — разность потенциалов между растворами^[8].

1. ↑ Электрохимический потенциал // Физическая энциклопедия, т. 5, 1998, с. 595
2. ↑ Дамаскин Б. Б. Электрохимический потенциал // Химическая энциклопедия, т. 5, 1998, с. 464
3. ↑ Гуггенгейм, 1941, с. 122—123.
4. ↑ Callen, 1985, p. 35.
5. ↑ Guggenheim, 1985, p. 300.
6. ↑ Русанов, 2013, с. 19.
7. ↑ Салем, 2004, с. 245.
8. ↑ Владимиров, Ю. А., Рощупкин Д. И., Потапенко А. Я. Биофизика. — М. : Медицина, 1983. — c. 13

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — N. Y. e. a.: John Wiley, 1985. — xvi + 493 с. — ISBN 0471862568, 9780471862567.
• Guggenheim E. A. Thermodynamics: An Advanced Treatment for Chemists and Physicists. — Amsterdam: North-Holland, 1985. — xxiv + 390 с. — ISBN 0 444 86951 4.
• Гуггенгейм. Современная термодинамика, изложенная по методу У. Гиббса / Пер. под ред. проф. С. А. Щукарева. — Л.—М.: Госхимиздат, 1941. — 188 с.
• Русанов А. И. Лекции по термодинамике поверхностей. — СПб.—М.—Краснодар: Лань, 2013. — 237 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1487-1.
• Салем Р. Р. Физическая химия. Термодинамика. — М.: Физматлит, 2004. — 351 с. — ISBN 5-9221-0078-5.

Потенциал покоя — Википедия

Потенциа́л поко́я — мембранный потенциал возбудимой клетки (нейрона, кардиомиоцита) в невозбужденном состоянии. Он представляет собой разность электрических потенциалов, имеющихся на внутренней и наружной сторонах мембраны и составляет у теплокровных от −55 до −100 мВ^[1]. У нейронов и нервных волокон обычно составляет −70 мВ.

Возникает вследствие диффузии положительно заряженных ионов калия в окружающую среду из цитоплазмы клетки в процессе установления осмотического равновесия. Анионы органических кислот, нейтрализующие заряд ионов калия в цитоплазме, не могут выйти из клетки, однако ионы калия, концентрация которых в цитоплазме велика по сравнению с окружающей средой, диффундируют из цитоплазмы до тех пор, пока создаваемый ими электрический заряд не начнёт уравновешивать их градиент концентрации на клеточной мембране.

В 1902 году Юлиус Бернштейн выдвинул гипотезу, согласно которой клеточная мембрана пропускает внутрь клетки ионы К⁺, и они накапливаются в цитоплазме. Расчет величины потенциала покоя по уравнению Нернста для калиевого электрода удовлетворительно совпал с измеренным потенциалом между саркоплазмой мышцы и окружающей средой, который составлял около — 70 мВ.

Согласно теории Ю. Бернштейна, при возбуждении клетки её мембрана повреждается, и ионы К⁺ вытекают из клетки по концентрационному градиенту до тех пор, пока потенциал мембраны не становится равным нулю. Затем мембрана восстанавливает свою целостность, и потенциал возвращается к уровню потенциала покоя. Это утверждение, относящееся скорее к потенциалу действия, было опровергнуто Ходжкином и Хаксли в 1939 году.

Теорию Бернштейна касательно потенциала покоя подтвердил Кеннет Стюарт Коул (Kenneth Stewart Cole), иногда его инициалы ошибочно пишут как K.C. Cole, из-за его прозвища, Кейси («Kacy»). ПП и ПД изображены на известной иллюстрации Коула и Curtis, 1939. Этот рисунок стал эмблемой Membrane Biophysics Group of the Biophysical Society.

Для того, чтобы на мембране поддерживалась разность потенциалов, необходимо, чтобы была определенная разность концентрации различных ионов внутри и снаружи клетки.

Концентрации ионов в клетке скелетной мышцы и во внеклеточной среде

Ионы	Концентрация в саркоплазме (ммоль/л)	Концентрация вне клетки (ммоль/л)
K+	140	2,5
Na+	10	120
Cl—	3-4	120
Ca2+	<0,001	2
A— (полипептиды)	140	0

С помощью уравнения Нернста можно рассчитать равновесный трансмембранный потенциал для K⁺, который и определяет значение ПП. Но значение потенциала покоя полностью не совпадает с EK+, так как в создании его участвуют также ионы натрия и хлора, вернее, их равновесные потенциалы.

Впоследствии было доказано, что основной вклад в создание потенциала покоя вносит выходящий калиевый ток, который осуществляется через специфические белки-каналы — калиевые каналы постоянного тока. В покое калиевые каналы открыты, а натриевые каналы закрыты. Ионы калия выходят из клетки по градиенту концентрации, что создает на наружной стороне мембраны избыток положительных зарядов; при этом на внутренней стороне мембраны остаются отрицательные заряды. Некоторый (небольшой) вклад в создание потенциала покоя вносит также работа так называемого «натрий-калиевого насоса», который образован особым мембранным ферментом — натрий-калиевой АТФазой.

Потенциал покоя для большинства нейронов составляет величину порядка −60 мВ — −70 мВ. У клеток невозбудимых тканей на мембране также имеется разность потенциалов, разная для клеток разных тканей и организмов.

ПП формируется в два этапа.

Первый этап: создание незначительной (-10 мВ) отрицательности внутри клетки за счёт обмена Na⁺ на K⁺ в соотношении 3 : 2 (на каждые 3 иона натрия, выведенные наружу, приходится 2 иона калия, вобранные внутрь). Таким образом, клетка теряет больше положительного заряда, чем приобретает, и в результате заряжается отрицательно. Обмен ионов осуществляет натрий-калиевый насос с затратой энергии АТФ. До 70% всех энергозатрат нейрона может уходить на работу натрий-калиевых насосов.

Результаты деятельности мембранных ионных насосов-обменников на первом этапе формирования ПП таковы:

1. Дефицит ионов натрия (Na⁺) в клетке.

2. Избыток ионов калия (K⁺) в клетке.

3. Появление на мембране слабого электрического потенциала (-10 мВ).

Второй этап: создание значительной (-60 мВ) отрицательности внутри клетки за счёт утечки из неё через мембрану ионов K⁺. Ионы калия K⁺ покидают клетку и уносят с собой из неё положительные заряды, доводя отрицательность до −70 мВ.

Итак, мембранный потенциал покоя — это дефицит положительных зарядов внутри клетки, возникающий за счёт работы натрий-калиевого насоса и (в большей мере) последующей утечки из клетки положительных ионов калия.

• Дудель Й., Рюэгг Й., Шмидт Р. и др. Физиология человека: в 3-х томах. Пер. с англ / под ред Р. Шмидта и Г. Тевса. — 3. — М.: Мир, 2007. — Т. 1. — 323 с илл. с. — 1500 экз. — ISBN 5-03-000575-3.