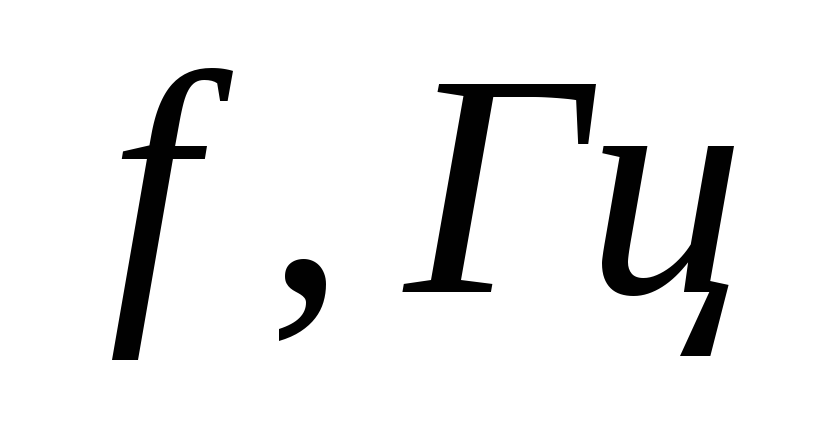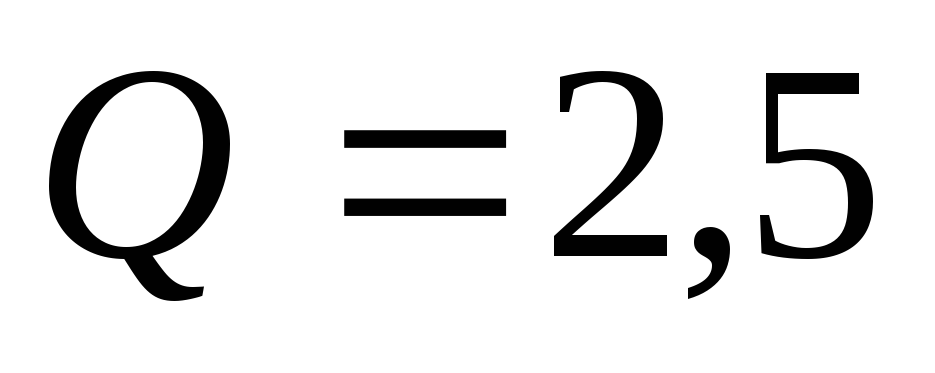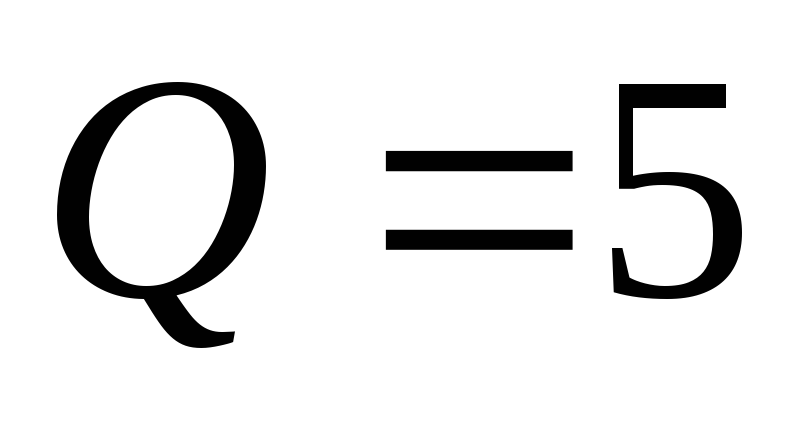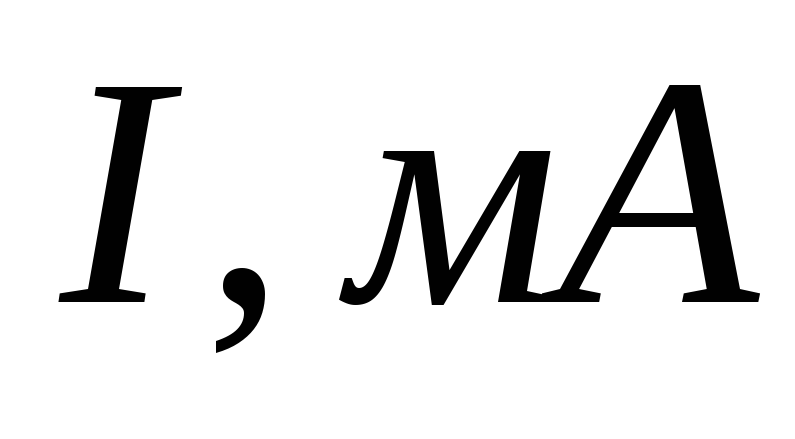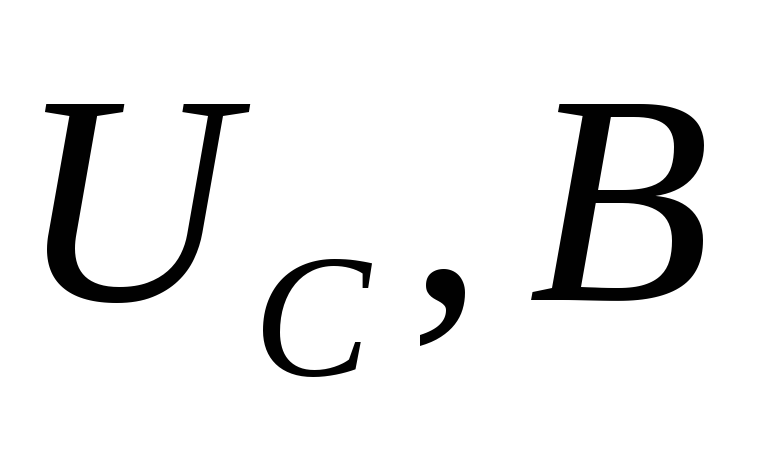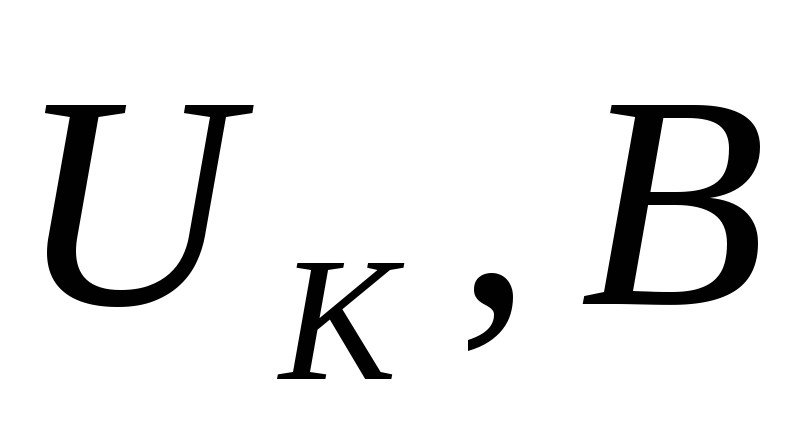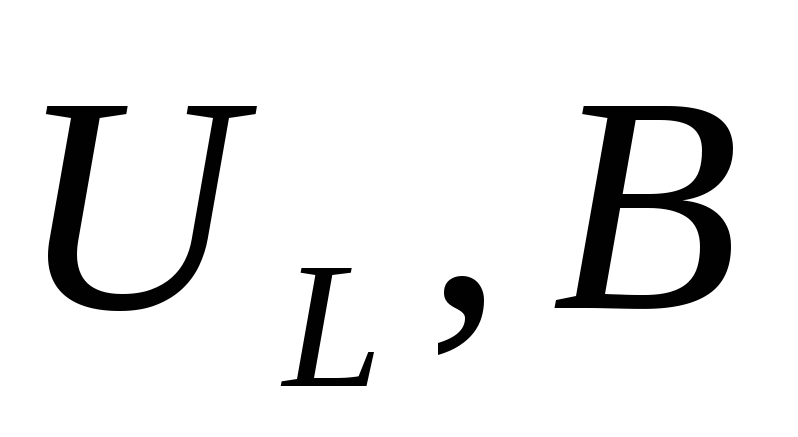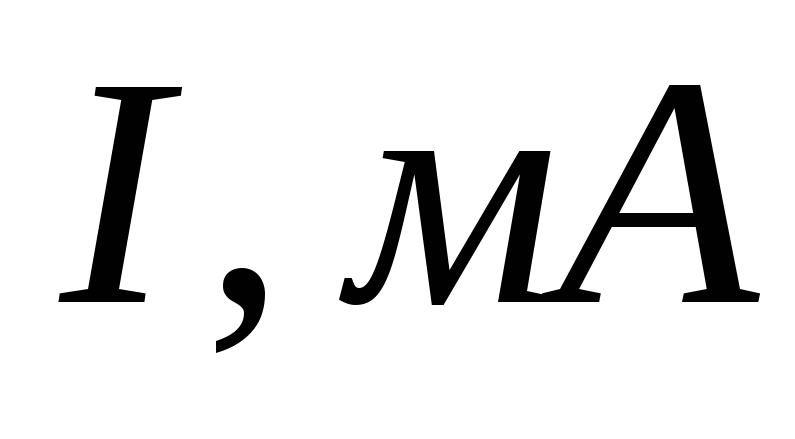Методическая разработка по физике (11 класс) по теме: «Исследование зависимости емкостного и индуктивного сопротивления от частоты переменного тока».
Тема урока:
«Исследование зависимости емкостного и индуктивного сопротивления от частоты переменного тока».
Цель урока:
Изучить зависимость емкостного и индуктивного сопротивления от частоты переменного тока при постоянных параметрах элементов.
Урок по данной теме проведён
в 11 классе
в МОУ «СОШ № 75» г. Чусового
учителем физики
Широковой
Людмилой Николаевной
(Районный семинар физиков)
Учебно-методический комплекс
(1час в кабинете информатики)
Тема учебного занятия:
«Исследование зависимости емкостного и индуктивного сопротивления от частоты переменного тока».
Форма учебного занятия: комбинированный урок с использованием информационных технологий.
Класс: 11 класс «Средняя общеобразовательная школа № 75»
Цель урока: Изучить зависимость емкостного и индуктивного сопротивления от частоты переменного тока при постоянных параметрах элементов.
Задачи урока:
`продолжить усвоение понятий «емкостного» и «индуктивного» сопротивлений в цепи переменного тока
`формирование практических навыков экспериментирования в виртуальной физической лаборатории
`продолжить формирование умений самостоятельно работать с полученной информацией
Тип урока: комбинированный (с использованием ИКТ).
Оборудование:
компьютер, мультимедийный проектор, экран, презентация к уроку, конструктор —
«Виртуальная лаборатория», лист отчета.
Ход урока.
I. Актуализация знаний.
Организационный момент. Тема. Цель урока.
Слайд № 5, 6, 7
Повторение
∙ Что понимают под емкостным сопротивлением? От чего оно зависит?
∙ Что понимают под индуктивным сопротивлением? От чего оно зависит?
Мы это постараемся проверить сегодня на уроке, но вспомним закон Ома.
II. Лабораторная работа
Слайд № 8, 9
Ход работы
собираем виртуальную схему на монтажном столе ПК;
записываем показания вольтметров на листе отчета обеих схем;
выполняем математические вычисления в тетради;
строим график в тетради;
делаем вывод;
отвечаем на контрольный вопрос;
сдаем тетрадь вместе с листом отчета.
Выполнение работы
а) катушка в цепи переменного тока
собираем виртуальную цепь, указанную на схеме отчетного листа,
задаем параметры элементов цепи:
— резистор R = 100 Ом
— мощность Р = 500 Вт
— индуктивность катушки L = 100мГн = 0,1гн
— напряжение на генераторе U = 100в
Изменяя частоту генератора, записать показания вольтметров (напряжения на резисторе UR и напряжение на катушке UL) в таблицу 1
б) конденсатор в цепи переменного тока
собираем виртуальную цепь, указанную на схеме отчетного листа,
задаем параметры элементов цепи:
— рабочее напряжение U = 400В
— емкость конденсатора С = 10 мкФ
— резистор сопротивлением R = 100.Ом
Изменяя частоту генератора, записать показания вольтметров (напряжения на резисторе UR и напряжение на катушке UС) в таблицу 2
Построить, и проанализировать графики зависимости индуктивного и емкостного сопротивлений от частоты переменного тока.
Сформулировать вывод.
Ответить на контрольный вопрос.
По окончании работы тетради сдаются учителю.
Подведение итогов, рефлексия.
Слайд № 10,11,12 Подведение итогов урока
Я научился собирать виртуальные электрические цепи, производить измерения и убедился, что индуктивное сопротивление прямо пропорционально частоте переменного тока, а емкостное сопротивление обратно пропорционально частоте переменного тока,
и это подтверждает правильность теории.
Слайд № 13 Домашнее задание
Перышкин А.В. § 32 -34 повторить
Рымкевич А.П. № 974,975,978,979.
Виртуальная лабораторная работа.
Тема урока: «Исследование зависимости емкостного и индуктивного сопротивления от частоты переменного тока
Цель урока: Изучить зависимость емкостного и индуктивного сопротивления от частоты переменного тока при постоянных параметрах элементов.
Порядок выполнения работы:
I). Катушка в цепи переменного тока.
1. собрать цепь, задать параметры →
катушка — индуктивности L = 0,1Гн; резистор – сопротивление R = 100.Ом
2. Изменяя частоту генератора, записать показания вольтметров (напряжения на резисторе UR и
напряжение на катушке UL) в таблицу 1
3. Рассчитать значение токов, текущих в цепи, в зависимости от частоты (для этого надо напряжение на резисторе разделить на его сопротивление I = UR /R). Запишите полученные данные в таблицу 1.
4. Определите индуктивные сопротивления для соответствующих частот (для этого надо напряжение
на катушке разделить на силу тока ХL = UL /I). Запишите данные в таблицу 1.
5. Построить график зависимости индуктивного сопротивления от частоты переменного тока.
6. Сформулируйте вывод.
ḬI). Конденсатор в цепи переменного тока
1. собрать цепь, задать параметры →
Конденсатор — емкость С = 1ОмкФ; резистор – сопротивление R = 100.Ом
2. Изменяя частоту генератора, записать показания вольтметров (напряжения на резисторе UR и
напряжение на конденсаторе UС) в таблицу 2.
3. Рассчитать значение токов, текущих в цепи, в зависимости от частоты (для этого надо напряжение
на резисторе разделить на его сопротивление I = UR /R). Запишите полученные данные в таблицу 2.
4. Определите емкостные сопротивления для соответствующих частот (для этого надо напряжение на
конденсаторе разделить на силу тока ХС = UС /I). Запишите данные в таблицу 2.
5. Построить график зависимости емкостного сопротивления от частоты переменного тока.
6. Сформулируйте вывод.
Контрольный вопрос: Почему с увеличением частоты индуктивное сопротивление увеличивается, а емкостное уменьшается?
V
V
R
L
V
V
R
С
Урок 45. Лабораторная работа № 11. Исследование зависимости силы тока от электроемкости конденсатора в цепи переменного тока
Лабораторная работа №11
Исследование зависимости силы тока от электроёмкости конденсатора в цепи переменного тока
Цель работы: изучить влияние электроёмкости на силу переменного тока.
Оборудование: набор неполярных конденсаторов известной ёмкости, регулируемый источник переменного тока ЛАТР, миллиамперметр с пределом измерения до 100 мА переменного тока, вольтметр с пределом измерения до 75 В переменного напряжения, соединительные провода.
Теория
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Если же включить конденсатор в цепь переменного тока, то заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течёт переменный ток. Сила тока тем больше, чем больше ёмкость конденсатора и чем чаще происходит его перезарядка, т.е. чем больше частота переменного тока.
Сопротивление, обусловленное наличием электрической ёмкости в цепи переменного тока, называют ёмкостным сопротивлением XC. Оно обратно пропорционально ёмкости С и круговой частоте ω:
или, с учётом, что ω=2πν, где ν- частота переменного тока, (1).
Из закона Ома для участка цепи переменного тока, содержащего ёмкостное сопротивление, действующее значение тока в цепи равно: (2).
Из формулы (2) следует, что в цепи с конденсатором переменный ток изменяется прямо пропорционально изменению ёмкости конденсатора при неизменной частоте тока.
Графически зависимость силы тока от электроёмкости конденсатора в цепи переменного тока изображается прямой линией (рис.1).
В этом и предстоит убедиться опытным путём в данной работе.
Ход работы.
1. Собрать электрическую схему согласно рисунка 2 и перечертить её в тетрадь:
2. Подготовить таблицу для результатов измерений и вычислений:
|
Частота тока ν, Гц |
Напряжение на конденсаторе U, В |
Ёмкость конденсатора С, мкФ |
Ток в цепи I, мА |
Ёмкостное сопротивление , Ом |
|
|
измеренное |
вычисленное |
||||
|
50 |
50 |
|
|
||
|
|
|||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
3. Для каждого конденсатора из набора измерить силу тока при напряжении 50 В.
4. В каждом опыте рассчитать ёмкостное сопротивление по закону Ома для участка цепи переменного тока: , здесь I — действующее значение тока в мА,
5. В каждом опыте вычислите ёмкостное сопротивление по заданным значениям частоты переменного тока ν=50Гц и ёмкости конденсатора С: , здесь С — ёмкость в мкФ.
6. Сравните результаты расчётов в п.4 и в п.5 и сделайте вывод о выполнимости закона Ома для участка цепи переменного тока содержащего электроёмкость с учётом погрешности измерений.
7. Постройте график зависимости силы тока от электроёмкости конденсатора в цепи переменного тока:
8. Запишите вывод по результатам опытов и ответьте на контрольные вопросы.
1. Почему постоянный ток не проходит через конденсатор?
2. Какое сопротивление называется ёмкостным? Почему оно является реактивным сопротивлением?
3. От чего и как зависит ёмкостное сопротивление?
4. Выполняется ли закон Ома для участка цепи переменного тока, содержащего ёмкостное сопротивление?
5. Напряжение на конденсаторе изменяется по закону . Запишите уравнение переменного тока в цепи с конденсатором.
ИССЛЕДОВАНИЕ RLC-КОНТУРА | sibac.info
Тихонов Владимир
класс 11 «Б», ОПШМТ № 11, г. Павлодар
Гордова Наталья Владимировна
научный руководитель, преподаватель физики, ОПШМТ № 11, г. Павлодар
E—mail: etih@yandex.ru
Введение
Интерес, проявляемый в настоящее время к колебательным процессам, весьма широк и далеко выходит за пределы изучения качаний маятника, как это было в начале XVII века, когда ученые только начали интересоваться колебаниями.
По современным представлениям науки звуковые, тепловые, световые, электромагнитные явления, т. е. важнейшие физические процессы окружающего нас мира, являются различными видами колебаний. Они играют исключительную роль в таких ведущих отраслях техники, как электричество и радио.
Выработка, передача и потребление электрической энергии, телефония, телеграфия, радиовещание, радиолокация — все эти важные и сложные отрасли техники основаны на использовании электрических и электромагнитных колебаний.
Среди различных колебательных систем особое место занимают электромагнитные системы, при которых электрические величины (токи, заряды) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей.
Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур. Колебательный контур — это электрическая цепь, состоящая из последовательно включенных резистора, катушки индуктивности и конденсатора. Именно такой колебательный контур нашел широкое применение в радиоаппаратуре.
Цель данной работы — исследовать механизм электромагнитных колебаний в RLC контуре на примере его компьютерной модели и подтвердить теоретические выводы, используя реальный RLC-контур, на практике.
Для этого необходимо решить следующие задачи:
· исследовать компьютерную модель RLC-контура в программе «Открытая физика», найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления, построить графики.
· исследовать реальный RLC-контур с использованием компьютерной программы «Audiotester», а в качестве генератора частоты — звуковую плату компьютера. Также найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления и построить графики.
· сделать выводы о совпадении теоретических и практических результатов.
Новизна данной работы заключается в том, что в практической части используется компьютер, звуковая плата которого заменяет генератор переменной частоты и вольтметр переменного напряжения. Для управления звуковой платой и обработки информации применяется специальная программа «Audiotester».
1. Основные положения
Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями
Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой W, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте W0.
Если частота W0 свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте W внешнего источника
Явление возрастания амплитуды колебаний тока при совпадении частоты W внешнего источника с собственной частотой W0 электрической цепи называется электрическим резонансом. При последовательном резонансе (W = W0) амплитуды UCи UL напряжений на конденсаторе и катушке резко возрастают.
Существует понятие добротности RLC-контура. Она равна отношению амплитуды напряжения на конденсаторе Uc к амплитуде напряжения генератора U: Q = Uc/U.
На рисунке изображен последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рисунок 1):
e(t) = 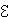 0 cos ωt,
0 cos ωt,
где: 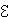 0 — амплитуда,
0 — амплитуда,
ω — круговая частота.
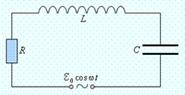
Рисунок 1. Вынужденные колебания в контуре.
2. Исследование компьютерной модели RLC-контура.
Изучим механизм возникновения вынужденных электрических колебаний и вхождения системы в резонанс; определим зависимость тока в контуре от частоты генератора. Для этого будем использовать программу «Открытая физика 1.1» [1, c. 135] .
Запустим на компьютере модель RLC-контура. Появившееся окно эксперимента разбито на несколько частей (рисунок 2). В левой верхней части окна изображена электрическая схема контура. В правой верхней части окна расположена резонансная кривая контура. В левой нижней части находятся движки изменения сопротивления, индуктивности, емкости контура и частоты колебаний генератора. В правой нижней части окна показана векторная диаграмма напряжений и тока в элементах контура. Кнопки вверху слева вызывают звуковое сопровождение, документ с теоретической частью и справочную информацию.
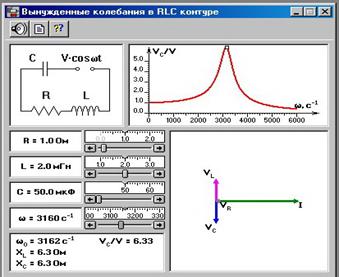
Рисунок 2.
В компьютерной модели можно изменять параметры RLC-контура, а также частоту W внешнего источника. При изменении параметров на дисплее высвечивается новая резонансная кривая, на которой точкой отмечается результат компьютерного эксперимента. Одновременно высвечивается векторная диаграмма, на которой с помощью векторов изображаются колебания тока и напряжений на элементах цепи.
Выбираем значения параметров RLC-контура: С=50 мкФ, R=1 Ом, L=2 мГн.
Рассчитаем собственную циклическую частоту Wo , собственную частоту fo контура и добротность Q.
Wo = 1/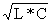 , fo = Wo/(2*П), Q = Uc/U.
, fo = Wo/(2*П), Q = Uc/U.
Получаем: Wo = 3162 с-¹, fo= 503,5 Гц , Q = 1,24
В состоянии резонанса будем увеличивать сопротивление R и отслежи-вать значение добротности контура Q на экране. Данные заносим в таблицу 1.
Таблица 1
R, Ом | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 5.0 | 6.0 |
Q | 12.66 | 6.33 | 4.22 | 3.16 | 2.53 | 2.11 | 1.81 | 1.58 | 1.27 | 1.05 |
Построим график зависимости добротности контура от активного сопро-тивления в состоянии резонанса (W=Wo):
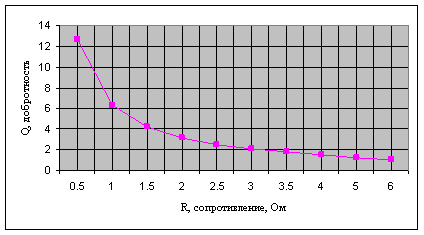
Рисунок 3. График зависимости добротности от активного сопротивления в состоянии резонанса
Из графика хорошо видно, что с увеличением сопротивления добротность контура падает.
Рассчитаем в состоянии резонанса реактивные сопротивления Хс и ХL для данной колебательной системы (С=50 мкФ, R=1 Ом, L=2 мГн) Хс = 1/(W*C) , XL = W*L. Получаем: Xc = 6.329 Ом, ХL = 6.32 Ом.
Смотрим на компьютерной модели значения Xc и ХL = 6,3 Ом (рисунок 2). Расчетные значения совпали со значениями модели почти точно.
Теперь изменяем параметры системы: емкость С = 50 мкФ, сопротивление R = 2 Ом, индуктивность L = 2 мГн.
Используя компьютерную модель, рассчитываем полное сопротивление цепи переменного тока, силу тока по формулам:
Z = 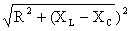 , I=U/Z и заполняем таблицу 2:
, I=U/Z и заполняем таблицу 2:
Таблица 2.
W, c | 1260 | 1880 | 2510 | 3140 | 3770 | 4400 | 5020 | 5650 |
Z, Ом | 13.55 | 7.09 | 3.6 | 2 | 2.97 | 4.74 | 6.32 | 8.05 |
I, A | 0.3 | 0.56 | 1.11 | 2 | 1.35 | 0.84 | 0.63 | 0.5 |
Xl | 2.5 | 3.8 | 5.0 | 6.3 | 7.5 | 8.8 | 10 | 11.3 |
Xc | 15.9 | 10.6 | 8.0 | 6.4 | 5.3 | 4.5 | 4 | 3.5 |
Q | 1.18 | 1.49 | 2.24 | 3.18 | 1.77 | 0.97 | 0.62 | 0.44 |
Строим график зависимости действующего значения тока в контуре от циклической частоты (рисунок 4):
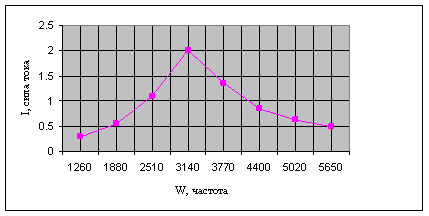
Рисунок 4. График зависимости силы тока от частоты
И график зависимости добротности от циклической частоты (рисунок 5):
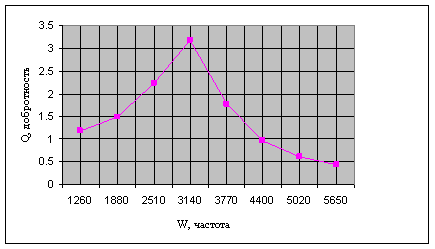
Рисунок 5. График зависимости добротности от частоты
Таким образом можно сделать следующие выводы:
· резонанс в цепи с колебательным контуром наступает при совпадении частоты генератора W c частотой колебательного контура Wo;
· с увеличением сопротивления добротность контура падает. Самая высокая добротность при небольших значениях сопротивления контура;
· самая высокая добротность контура ― на резонансной частоте;
· полное сопротивление контура минимально на резонансной частоте.
3. Экспериментальное исследование RLC-контура.
Теперь проведем экспериментальное исследование RLC контура с реальными катушкой индуктивности, конденсатором, сопротивлением и подтвердим совпадение теоретических и экспериментальных измерений. Для исследования RLC контура при различных значениях R будем использовать переменное сопротивление.
Для проведения эксперимента необходим генератор переменного напряжения, вольтметр или амперметр переменного тока и сам RLC контур. В качестве генератора переменного напряжения и вольтметра мы будем использовать компьютер, оснащенный аудиокартой. Существует ряд программ по управлению выходным сигналом аудиокарты и измерению входного сигнала, поступающего на аудиокарту, что и позволяет производить радиотехнические измерения с использованием реальных радиотехнических деталей.
Таким образом состав исследовательской установки включает в себя:
компьютер с аудиокартой, исследуемый RLC контур, комплекс программ AudioTester, вольтметр для калибровки аудиокарты компьютера, тестер для измерения сопротивления контура.
В комплекс компьютерной программы AudioTester входят три программы:
1.программа «Генератор», позволяющая получить на выходе аудиокарты переменные напряжения различной частоты, формы и амплитуды;
2.программа «Осциллограф», позволяющая на экране компьютера наблюдать сигналы, поступающие на вход аудиокарты;
3.и непосредственно сама программа AudioTester, позволяющая производить различные радиотехнические измерения.
Схема установки для исследования изображена на рисунке 6.
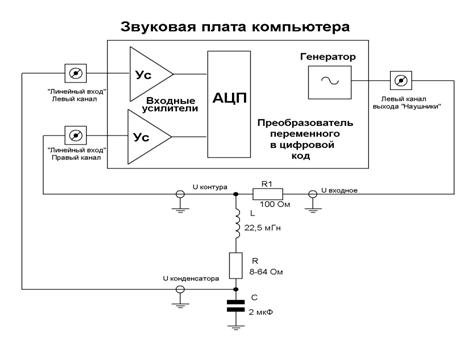
Рисунок 6. Схема измерительной установки
В теоретической части измерялся ток, здесь будем измерять напряжения на контуре и отдельно на конденсаторе. Так как сопротивление RLC контура, особенно на частоте резонанса, мало, в схему было добавлено сопротивление R1, ограничивающее ток через схему. Это позволило использовать относительно слабый выход звуковой платы (разъем «наушники») для получения переменного напряжения. Катушка и конденсатор выбраны таким образом, что частота резонанса контура не намного отличается от частоты контура, полученной в теоретической части.На фотографии показана собранная установка, представляющая собой RLC контур, подключенный к компьютеру.

Подготовка к измерениям и калибровка
Рассмотрим подробнее работу программы AudioTester. Эта программа была создана для проведения различных радиотехнических измерений. Программа позволяет получать на выходе аудиокарты сигналы различной частоты, формы и амплитуды, анализировать входной сигнал, поступающий на вход аудиокарты и сохранять все поступающие данные в файлы на диск компьютера. Между входом и выходом аудиокарты подключается исследуемое устройство. Таким образом, мы можем изменять параметры сигнала, подаваемого на вход исследуемого устройства и анализировать сигналы, поступающие с выхода исследуемого устройства. На рисунке 7 показано основное окно программы.
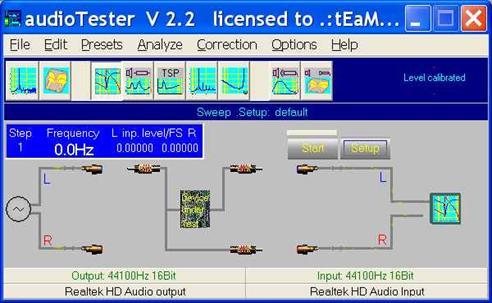
Рисунок 7.
В этом режиме программа позволяет генерировать сигнал с изменяемой частотой и измерять два напряжения, поступающие на левый и правый входы аудиокарты. Нажав на кнопку Setup, переходим в окно настроек (рисунок 8):
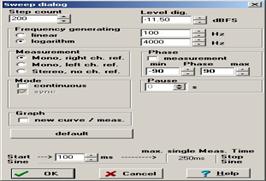
Рисунок 8.
Раздел настроек <Frequency generating> позволяет задавать начальную и конечную частоту генератора напряжения.Мы задали диапазон изменения частоты f от 100 до 4000 Гц.
В окне <Step count> задается количество точек, на которое будет разбит заданный частотный диапазон. В данном случае 200.
Для получения достоверных результатов необходимо произвести калибровку выхода аудиокарты (который является генератором) и линейного входа этой же аудиокарты (который используется как вольтметр переменного напряжения).
Калибровка генератора производилась по следующей методике. Задавался частотный диапазон 50—75 Герц, то есть частоты, далекие от частоты резонанса контура и измерялось напряжение на контуре с помощью лампового вольтметра переменного напряжения. Значение в окне <Level dig> подбиралось таким образом, чтобы вольтметр показывал напряжение 0,1 Вольт.
Следующий этап работы ― калибровка линейного входа аудиокарты. Для калибровки входного усилителя аудиокарты использовалось окно Calibration. Здесь выставлялось напряжение <mV rms> в секции <Soundcard input voltage calibration > таким образом, чтобы сигнал на графике зависимости напряжения на контуре от частоты генератора соответствовал 0,1 Вольт, генерируемого аудиокартой (рисунок 9):
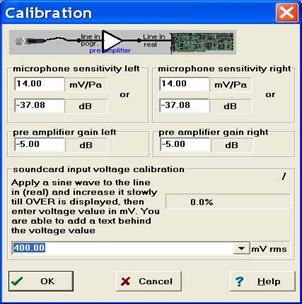
Рисунок 9.
Измерения
Запускаем программу Audiotester. Устанавливаем значение переменного сопротивления R2 = 8 Ом. Измерения напряжения проводились в частотном диапазоне от 100 Герц до 4000 Герц. Как видно из следующего графика, резонансная частота контура равна приблизительно 750 Герц (рисунок 10):
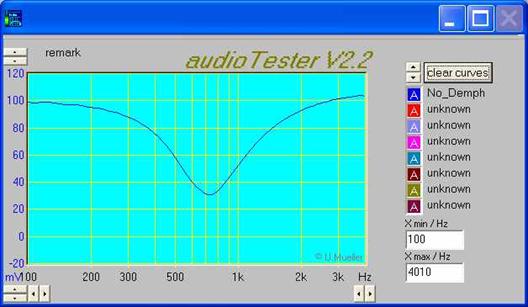
Рисунок 10.
Получим графики зависимости напряжения на контуре от частоты при различных значениях сопротивления контура R2. Нами измерялось суммарное сопротивление R2 и катушки контура. Это обусловлено тем, что у нас имеется не идеальная катушка, а вполне реальная, имеющая также свое активное сопротивление. Значения R2 устанавливаются равными от 8 до 64 Ом с шагом 8 Ом. Полученные графики представлены на рисунке 11.
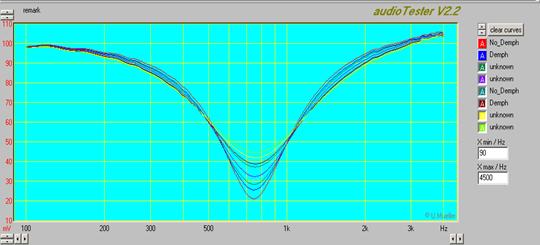
Рисунок 11.
Из графиков видно, что напряжение на контуре в точке резонанса существенно зависит от значения R контура. Нижняя кривая соответствует сопротивлению контура, равному 8 Ом, а верхняя ― 64 Ом. Таким образом, видно, что при увеличении значения R напряжение в точке резонанса также увеличивается. На рисунке 12 показаны графики зависимости напряжения на конденсаторе контура от частоты при различных значениях сопротивления R.
Верхняя кривая графика соответствует меньшему значению сопротивления, а нижняя ― большему.
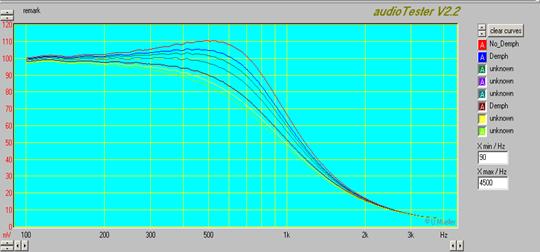
Рисунок 12.
Программа AudioTester позволяет сохранить полученные графики в виде табличных файлов. Далее эти данные были перемещены в Excel-таблицу, в которой и были произведены все необходимые вычисления.
Нам известно значение емкости конденсатора C, с помощью программы мы определили резонансную частоту контура fo = 750. Значение индуктивности можно вычислить по следующей формуле:
L = 1 / (2*П * fo) ² * C, L = 1/((2*П*750) ² * 2e-6) = 0,0225 Гн
Мы получили значение индуктивности 0,0225 Гн.
Затем, изменяя частоту генератора f, измеряем напряжение на контуре (Uк) и напряжение на конденсаторе контура (Uс). Получаем значение добротности для различных частот, которая вычисляется по формуле:
Q = Uс / Uк
Анализируя полученные результаты, можно сделать следующие выводы:
·добротность контура растет с увеличением частоты и достигает максимума на частоте резонанса. При дальнейшем увеличении частоты добротность уменьшается;
·значения добротности на краях заданного частотного диапазона практически не изменяются при изменении сопротивления контура;
·при исследовании изменения добротности на резонансной частоте видно, что значение добротности Q тем выше, чем меньше сопротивление контура R.
Выбрав из полученных результатов значение добротности на резонансной частоте контура для разных значений сопротивления, мы получаем следующую таблицу:
Таблица 3.
R, Ом | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 |
Q | 8,09 | 4,69 | 3,72 | 2,85 | 2,38 | 2,03 | 1,76 | 1,58 |
И график, соответствующий этой таблице:
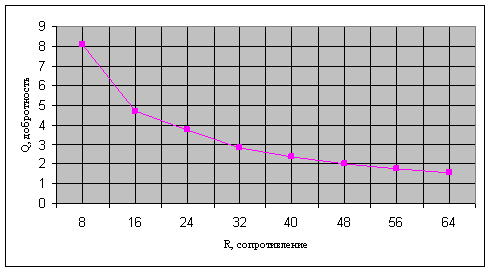
Рисунок 13. График зависимости добротности от сопротивления контура в состоянии резонанса.
Также была составлена таблица с результатами вычислений полного сопротивления контура, реактивных сопротивлений катушки индуктивности и конденсатора для различных значений частоты генератора. Активное сопротивление выбрано 8 Ом, С контура ― 2.0 мкФ,
ХL=2*П*f*L ,
Хс=1/(2*П*f*C),
Z= 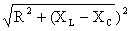
Приведем часть таблицы
Таблица 4.
f (Гц) | R = 8 Ом | ||
X (L) | Х(C) | Z контура | |
638.34 | 90.24 | 124.66 | 35.34 |
650.29 | 91.93 | 122.37 | 31.47 |
662.46 | 93.65 | 120.13 | 27.66 |
674.85 | 95.40 | 117.92 | 23.89 |
687.48 | 97.19 | 115.75 | 20.21 |
700.34 | 99.01 | 113.63 | 16.66 |
713.44 | 100.86 | 111.54 | 13.34 |
726.79 | 102.75 | 109.49 | 10.46 |
740.39 | 104.67 | 107.48 | 8.48 |
754.24 | 106.63 | 105.51 | 8.08 |
768.35 | 108.62 | 103.57 | 9.46 |
782.73 | 110.66 | 101.67 | 12.03 |
797.37 | 112.73 | 99.80 | 15.20 |
812.29 | 114.84 | 97.97 | 18.67 |
827.49 | 116.98 | 96.17 | 22.30 |
842.97 | 119.17 | 94.40 | 26.03 |
858.74 | 121.40 | 92.67 | 29.83 |
874.81 | 123.67 | 90.97 | 33.67 |
891.18 | 125.99 | 89.29 | 37.55 |
Выделенные значения соответствуют частоте резонанса контура. Видно, что на низких частотах емкостное сопротивление конденсатора Хс переменному току велико. При увеличении частоты емкостное сопротивление конденсатора Хс убывает. Индуктивное сопротивление ХL катушки мало на низких частотах, но увеличивается с ростом частоты.
На резонансной частоте индуктивное сопротивление ХL катушки равно емкостному сопротивлению конденсатора Хс. Полное сопротивление на частоте резонанса имеет минимальное значение (рисунок 14):
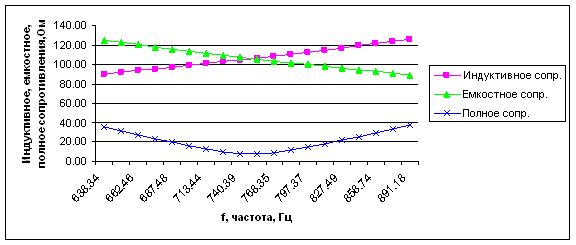
Рисунок 14. График зависимости индуктивного, ёмкостного и полного сопротивления от частоты генератора.
Полученные нами выводы в практической части работы полностью согласуются с выводами, сделанными нами в теоретической части при изучении компьютерной модели RLC-контура.
Заключение
Таким образом в данной работе проведены теоретические и практические исследования работы RLC-контура в цепи переменного тока.
Мы исследовали компьютерную модель RLC-контура в программе «Открытая физика», нашли резонансную частоту контура, на резонансной частоте исследовали зависимость добротности контура от сопротивления и построили графики.
В практической части работы исследовали реальный RLC-контур с использованием компьютерной программы «Audiotester». Нашли резонансную частоту контура, на резонансной частоте исследовали зависимость добротности контура от сопротивления и построили графики.
Выводы, сделанные нами в теоретической и практической части работы, совпали полностью.
Применение в практической части специальной программы «Audiotester» позволило провести исследования в широком диапазоне значений частоты без дополнительных измерительных приборов, получить и сохранить данные на компьютере, произвести их компьютерную обработку и построить графики на экране компьютера разных величинных зависимостей.
Список литературы:
1.Сорокин А.В., Торгашина Н.Г., Ходос Е.А., Чиганов А.С. Физика: наблюдение, эксперимент, моделирование. Элективный курс: Методическое пособие. М.: БИНОМ. Лаборатория знаний, 2006. ― 175 c.
Лабораторная работа №12. «Исследование зависимости ёмкостного сопротивления конденсатора от частоты переменного тока».
Лабораторная работа №12.
«Исследование зависимости ёмкостного сопротивления конденсатора от частоты переменного тока».
Цель работы: исследовать, как ёмкостное сопротивление конденсатора зависит от частоты переменного тока.
Оборудование: конденсатор 14,7 мкФ; лампа 6,3 В, 0,3 А; генератор звуковой частоты ГНЧ-1; ключ; соединительные провода — 4 шт.
Внимание!
При использовании в качестве источника переменного тока генератора звуковой частоты ГНЧ-1 по завершению опыта рекомендуем сначала уменьшить выходное напряжение генератора до нуля, разомкнуть ключ в собранной конструкции, только потом и выключить генератор.
При выключении генератора при замкнутой внешней цепи возможен вывод из строя элементов цепи (лампы, диода, и др.) чрезмерным током (скачком напряжения), возникающим за счёт явления самоиндукции.
Ход работы
Составьте таблицу для занесения результатов опыта.
- ν, Гц
Состояние лампы
100
Не горит
200
Загорается
500
Горит
1000
Горит ярко
2. Соберите цепь по рисунку, где соединённые последовательно конденсатор и лампа подключены к выходу звукового генератора.
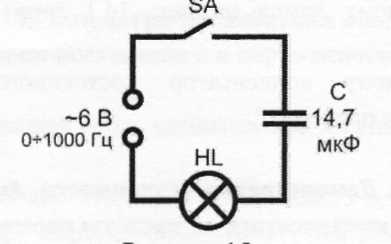
Установите частоту генератора на диапазон 100-1000 Гц и выходное напряжение 6 В. Включите генератор и замкните цепь. Изменяя частоту от 100 до 1000 Гц, следите за яркостью лампы, которая увеличивается при увеличении частоты. Это свидетельствует о том, что сопротивление конденсатора переменному току обратно пропорционально зависит от частоты тока.
Состояние лампы при различных частотах занесите в таблицу.
Примечание. У используемого генератора о частоте тока можно судит не только по шкале диапазона, но и воспринимать на слух, включив встроенный динамик.
Контрольные вопросы.
С какой частотой происходит перезарядка обкладок конденсатора, находящегося в цепи переменного тока?
Как сопротивление конденсатора переменному току зависит от частоты тока?
Колебательные контур — определение, виды, принцип действия, схемы и применение
В статье расскажем что такое колебательный контур. Последовательный и параллельный колебательный контур.Колебательный контур — устройство или электрическая цепь, содержащее необходимые радиоэлектронные элементы для создания электромагнитных колебаний. Разделяется на два типа в зависимости от соединения элементов: последовательный и параллельный.
Основная радиоэлементная база колебательного контура: Конденсатор, источник питания и катушка индуктивности.
Последовательный колебательный контур

Последовательный колебательный контур является простейшей резонансной (колебательной) цепью. Состоит последовательный колебательный контур, из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина которого вычисляется по закону Ома: I = U / ХΣ , где ХΣ — сумма реактивных сопротивлений последовательно включенных катушки и конденсатора (используется модуль суммы).
Для освежения памяти, вспомним как зависят реактивные сопротивления конденсатора и катушки индуктивности от частоты приложенного переменного напряжения. Для катушки индуктивности, эта зависимость будет иметь вид:

Из формулы видно, что при увеличении частоты, реактивное сопротивление катушки индуктивности увеличивается. Для конденсатора зависимость его реактивного сопротивления от частоты будет выглядеть следующим образом:

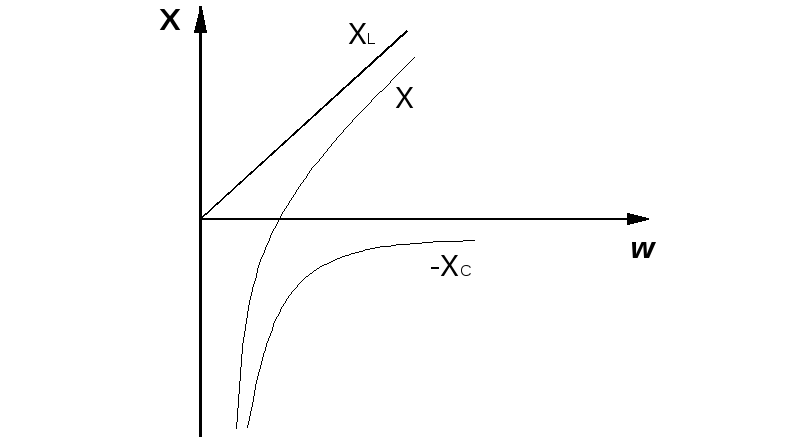
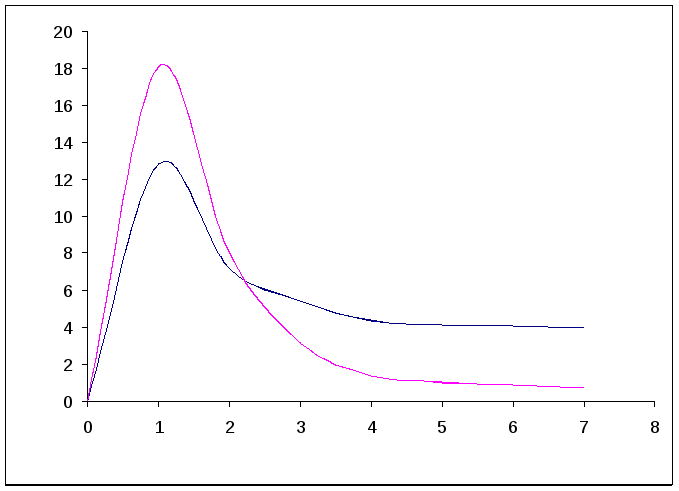
В отличии от индуктивности, у конденсатора всё происходит наоборот — при увеличении частоты, реактивное сопротивление уменьшается. На следующем рисунке графически представлены зависимости реактивных сопротивлений катушки XL и конденсатора ХC от циклической (круговой) частоты ω, а также график зависимости от частоты ω их алгебраической суммы ХΣ. График, по сути, показывает зависимость от частоты общего реактивного сопротивления последовательного колебательного контура.

Из графика видно, что на некоторой частоте ω=ωр , на которой реактивные сопротивления катушки и конденсатора равны по модулю (равны по значению, но противоположны по знаку), общее сопротивление цепи обращается в ноль. На этой частоте в цепи наблюдается максимум тока, который ограничен только омическими потерями в катушке индуктивности (т.е. активным сопротивлением провода обмотки катушки) и внутренним сопротивлением источника тока (генератора). Такую частоту, при которой наблюдается рассмотренное явление, называемое в физике резонансом, называют резонансной частотой или собственной частотой колебаний цепи. Также из графика видно, что на частотах, ниже частоты резонанса реактивное сопротивление последовательного колебательного контура носит емкостной характер, а на более высоких частотах — индуктивный. Что касается самой резонансной частоты, то она может быть вычислена при помощи формулы Томсона, которую мы можем вывести из формул реактивных сопротивлений катушки индуктивности и конденсатора, приравняв их реактивные сопротивления друг к другу:

На рисунке справа, изображена эквивалентная схема последовательного резонансного контура с учетом омических потерь R, подключенного к идеальному генератору гармонического напряжения с амплитудой U. Полное сопротивление (импеданс) такой цепи определяется: Z = √(R2+XΣ2), где XΣ = ω L-1/ωC. На резонансной частоте, когда величины реактивных сопротивлений катушки XL = ωL и конденсатора ХС= 1/ωС равны по модулю, величина XΣ обращается в нуль (следовательно, сопротивление цепи чисто активное), а ток в цепи определятся отношением амплитуды напряжения генератора к сопротивлению омических потерь: I= U/R. При этом на катушке и на конденсаторе, в которых запасена реактивная электрическая энергия, падает одинаковое напряжение UL = UС = IXL = IXС.

На любой другой частоте, отличной от резонансной, напряжения на катушке и конденсаторе неодинаковы — они определяются амплитудой тока в цепи и величинами модулей реактивных сопротивлений XL и XС.Поэтому резонанс в последовательном колебательном контуре принято называть резонансом напряжений. Резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер. Условие резонанса — это равенство величин реактивных сопротивлений катушки индуктивности и ёмкости.
Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое (или волновое) сопротивление ρ и добротность контура Q. Характеристическим (волновым) сопротивлением контура ρ называется величина реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = ХL = ХC при ω =ωр . Характеристическое сопротивление может быть вычислено следующим образом: ρ = √(L/C). Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура — катушкой (энергия магнитного поля) WL = (LI2)/2 и конденсатором (энергия электрического поля) WC=(CU2)/2. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает «качество».
Добротность колебательного контура — характеристика, определяющая амплитуду и ширину АЧХ резонанса и показывающая, во сколько раз запасы энергии в контуре больше, чем потери энергии за один период колебаний. Добротность учитывает наличие активного сопротивления нагрузки R.
Для последовательного колебательного контура в RLC цепях, в котором все три элемента включены последовательно, добротность вычисляется:

где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.
Величину, обратную добротности d = 1 / Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q = ρ / R, где R-сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р = I2R. Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.
Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ), при этом сами цепи рассматривают как четырёхполюсники. На рисунках ниже представлены два простейших четырехполюсника, содержащих последовательный колебательный контур и АЧХ этих цепей, которые приведены (показаны сплошными линями). По вертикальной оси графиков АЧХ отложена величина коэффициента передачи цепи по напряжению К, показывающая отношение выходного напряжения цепи к входному.

Для пассивных цепей (т.е. не содержащих усилительных элементов и источников энергии), величина К никогда не превышает единицу. Сопротивление переменному току изображённой на рисунке цепи, будет минимально при частоте воздействия, равной резонансной частоте контура. В этом случае коэффициент передачи цепи близок к единице (определяется омическими потерями в контуре). На частотах, сильно отличающихся от резонансной, сопротивление контура переменному току достаточно велико, а следовательно, и коэффициент передачи цепи будет падать практически до нуля.

При резонансе в этой цепи, источник входного сигнала оказывается фактически замкнутым накоротко малым сопротивлением контура, благодаря чему коэффициент передачи такой цепи на резонансной частоте падает практически до нуля (опять-таки в силу наличия конечного сопротивления потерь). Наоборот, при частотах входного воздействия, значительно отстоящих от резонансной, коэффициент передачи цепи оказывается близким к единице. Свойство колебательного контура в значительной степени изменять коэффициент передачи на частотах, близких к резонансной, широко используется на практике, когда требуется выделить сигнал с конкретной частотой из множества ненужных сигналов, расположенных на других частотах. Так, в любом радиоприемнике при помощи колебательных цепей обеспечивается настройка на частоту нужной радиостанции. Свойство колебательного контура выделять из множества частот одну принято называть селективностью или избирательностью. При этом интенсивность изменения коэффициента передачи цепи при отстройке частоты воздействия от резонанса принято оценивать при помощи параметра, называемого полосой пропускания. За полосу пропускания принимается диапазон частот, в пределах которого уменьшение (или увеличение — в зависимости от вида цепи) коэффициента передачи относительно его значения на резонансной частоте, не превышает величины 0,7 (3дБ).
Пунктирными линиями на графиках показаны АЧХ точно таких же цепей, колебательные контуры которых имеют такие же резонансные частоты, как и для случая рассмотренного выше, но обладающие меньшей добротностью (например, катушка индуктивности намотана проводом, обладающим большим сопротивлением постоянному току). Как видно из рисунков, при этом расширяется полоса пропускания цепи и ухудшаются ее селективные (избирательные) свойства. Исходя из этого, при расчете и конструировании колебательных контуров нужно стремиться к повышению их добротности. Однако, в ряде случаев, добротность контура, наоборот, приходится занижать (например, включая последовательно с катушкой индуктивности резистор небольшой величины сопротивления), что позволяет избежать искажений широкополосных сигналов. Хотя, если на практике требуется выделить достаточно широкополосный сигнал, селективные цепи, как правило, строятся не на одиночных колебательных контурах, а на более сложных связанных (многоконтурных) колебательных системах, в т.ч. многозвенных фильтрах.
Параллельный колебательный контур

В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рисунке приведена принципиальная схема параллельного колебательного контура. Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя — можно лишь складывать проводимости. На рисунке приведены графические зависимости реактивных проводимостей катушки индуктивности BL = 1/ωL, конденсатора ВC = -ωC, а также суммарной проводимости ВΣ, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току.

Если построить зависимость реактивного сопротивления контура от частоты XΣ = 1/BΣ, эта кривая, изображённая на следующем рисунке, в точке ω = ωр будет иметь разрыв второго рода. Сопротивление реального параллельного колебательного контура (т.е с потерями), разумеется, не равно бесконечности — оно тем меньше, чем больше омическое сопротивление потерь в контуре, т.е уменьшается прямо пропорционально уменьшению добротности контура. В целом, физический смысл понятий добротности, характеристического сопротивления и резонансной частоты колебательного контура, а также их расчетные формулы, справедливы как для последовательного, так и для параллельного колебательного контура.
Для параллельного колебательного контура, в котором индуктивность, емкость и сопротивление включены параллельно, добротность вычисляется:

где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.
Рассмотрим цепь, состоящую из генератора гармонических колебаний и параллельного колебательного контура. В случае, когда частота колебаний генератора совпадает с резонансной частотой контура его индуктивная и емкостная ветви оказывают равное сопротивление переменному току, в следствие чего токи в ветвях контура будут одинаковыми. В этом случае говорят, что в цепи имеет место резонанс токов. Как и в случае последовательного колебательного контура, реактивности катушки и конденсатора компенсируют друг друга, и сопротивление контура протекающему через него току становится чисто активным (резистивным). Величина этого сопротивления, часто называемого в технике эквивалентным, определяется произведением добротности контура на его характеристическое сопротивление Rэкв = Q·ρ. На частотах, отличных от резонансной, сопротивление контура уменьшается и приобретает реактивный характер на более низких частотах — индуктивный (поскольку реактивное сопротивление индуктивности падает при уменьшении частоты), а на более высоких — наоборот, емкостной (т к реактивное сопротивление емкости падает с ростом частоты).

В процессе работы контура, дважды за период колебаний, происходит энергетический обмен между катушкой и конденсатором (смотри рисунок). Энергия поочередно накапливается, то в виде энергии электрического поля заряженного конденсатора, то в виде энергии магнитного поля катушки индуктивности. При этом в контуре протекает собственный контурный ток Iк, превосходящий по величине ток во внешней цепи I в Q раз. В случае идеального контура (без потерь), добротность которого теоретически бесконечна, величина контурного тока также будет бесконечно большой. Но на практике, такого не бывает. В любом случае, качество элементов контура, их паразитные характеристики, электрические цепи, служащие для подвода энергии и отбора энергии из контура, не позволят контурному току расти.
Рассмотрим, как зависят коэффициенты передачи четырехполюсников от частоты, при включении в них не последовательных колебательных контуров, а параллельных.

Четырехполюсник, изображенный на рисунке, на резонансной частоте контура представляет собой огромное сопротивление току, поэтому при ω=ωр его коэффициент передачи будет близок к нулю (с учетом омических потерь). На частотах, отличных от резонансной, сопротивление контура будет уменьшатся, а коэффициент передачи четырехполюсника — возрастать.

Для четырехполюсника, приведенного на рисунке выше, ситуация будет противоположной — на резонансной частоте контур будет представлять собой очень большое сопротивление и практически все входное напряжение поступит на выходные клеммы (т.е коэффициент передачи будет максимален и близок к единице). При значительном отличии частоты входного воздействия от резонансной частоты контура, источник сигнала, подключаемый к входным клеммам четырехполюсника, окажется практически закороченном накоротко, а коэффициент передачи будет близок к нулю.
Видео по теме: Колебательный контур
Лабораторная работа «Элементы цепей переменного тока. Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров элементов»
Порядок выполнения работы
Соберите цепь показанную на рисунке 1.
Установите следующие значения параметров:
Генератор – напряжение (эффективное) 100 В, частота 100 Гц;
Конденсатор – рабочее напряжение 400 В, емкость 10 мкФ;
Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.
Изменяя емкость конденсатора от 5 до 50 мкФ (через 5 мкФ), запишите показания вольтметров (напряжение на конденсаторе и на резисторе).
С, емкость,мкФ | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
Uконд | ||||||||||
Uрез | ||||||||||
Iэф | ||||||||||
XC |
Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения емкости конденсатора (для этого надо напряжение на резисторе разделить на его сопротивление).
Определите значения емкостных сопротивлений конденсатора для соответствующих значений его емкости и сравните их с рассчитанными по формуле (3).
Установите емкость конденсатора 10 мкФ. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты емкостного сопротивления в зависимости от частоты переменного тока.
ω,частота,Гц | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Uконд | |||||||||
Uрез | |||||||||
XС |
С
оберите цепь показанную на рисунке 2.
Рис.1.Рис.2.
Установите следующие значения параметров:
Генератор – напряжение (эффективное) 100 В, частота 100 Гц;
Катушка — индуктивность 50 мГн;
Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.
Изменяя индуктивность катушки от 50 до 500 мГн (через 50 мГн), запишите показания вольтметров (напряжение на катушке и на резисторе).
L,индукт,мГн | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
Uкатушки | ||||||||||
Uрез | ||||||||||
Iэф | ||||||||||
XL |
Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения индуктивности катушки (для этого надо напряжение на резисторе разделить на его сопротивление).
Определите индуктивные сопротивления катушки для соответствующих значений ее индуктивности и сравните их с рассчитанными по формуле (1).
Установите индуктивность катушки 100 мГн. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты индуктивного сопротивления в зависимости от частоты переменного тока.
ω,частота,Гц | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Uконд | |||||||||
Uрез | |||||||||
XL |
Постройте графики зависимостей индуктивного и емкостного сопротивлений от частоты переменного тока.
3. Контрольные вопросы.
3.1. Почему емкостное сопротивление уменьшается с увеличением частоты переменного ток а, индуктивное сопротивление – увеличивается?
3.2. Каковы разницы фаз между током и напряжением для катушки и конденсатора?
3.3. В каких единицах измеряются емкостное и индуктивное сопротивления?
3.4. Как записывается аналог закона Ома для максимальных (эффективных) значений тока и напряжения для реактивных элементов – конденсатора и катушки индуктивности?
Лабы / 3 / Лаб№3
Цель работы:
Получение навыков экспериментального исследования резонансных явлений в электрических цепях.
Основные теоретические положения и ответы на вопросы подготовки:
1.Условие резонансного режима работы цепи:
Резонансом – называется процесс вынужденных колебаний при прочих равных условиях максимальна
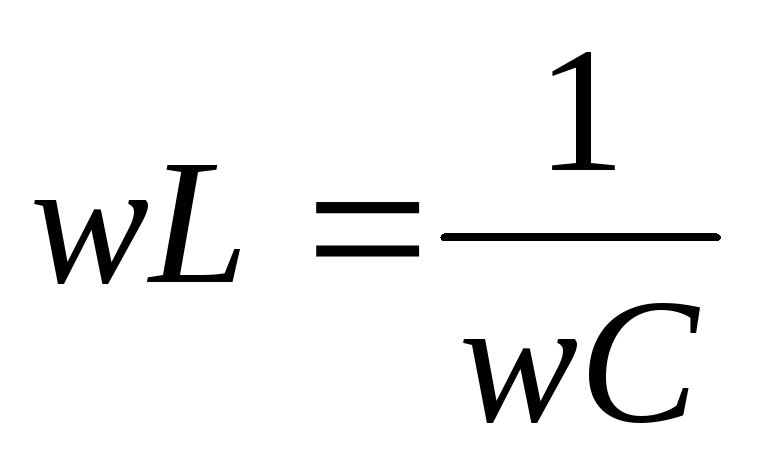 —
условие резонанса;
—
условие резонанса;
2,Схемы электрических цепей в которых возникает резонанс напряжений, резонанс токов:
При
последовательном соединении 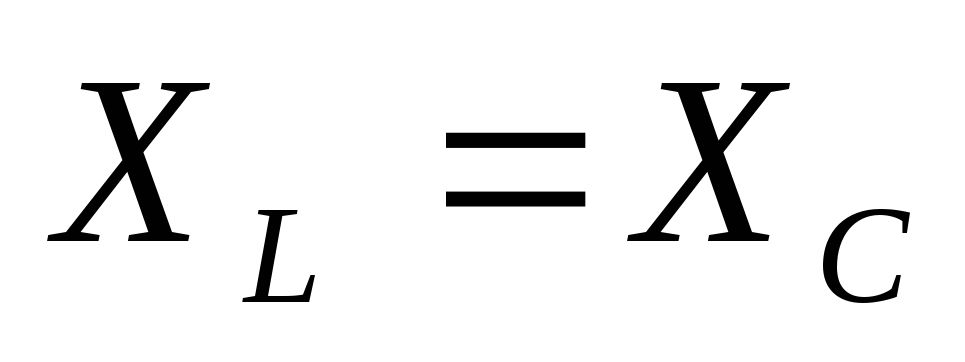 значения противоположных по фазе
напряжений на индуктивности и емкости
равны:
значения противоположных по фазе
напряжений на индуктивности и емкости
равны:
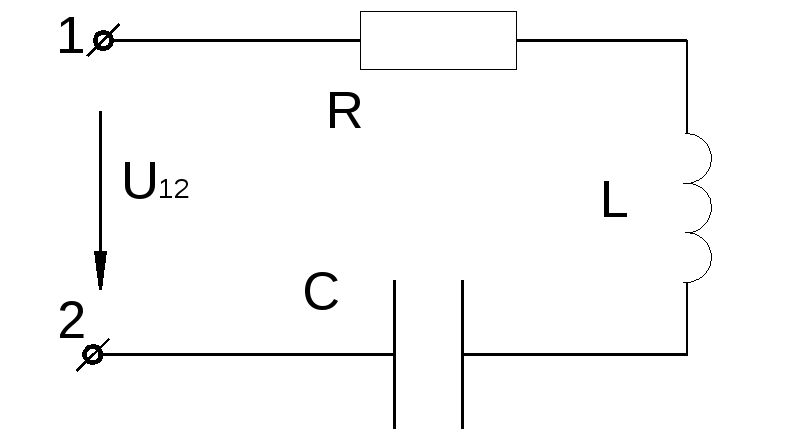
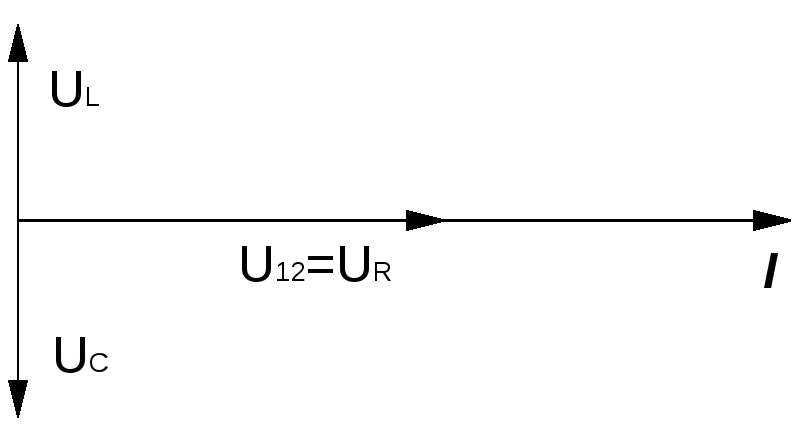
Поэтому резонанс в рассматриваемой цепи называется резонансом напряжения
Рассмотрим схему цепи с параллельным соединением
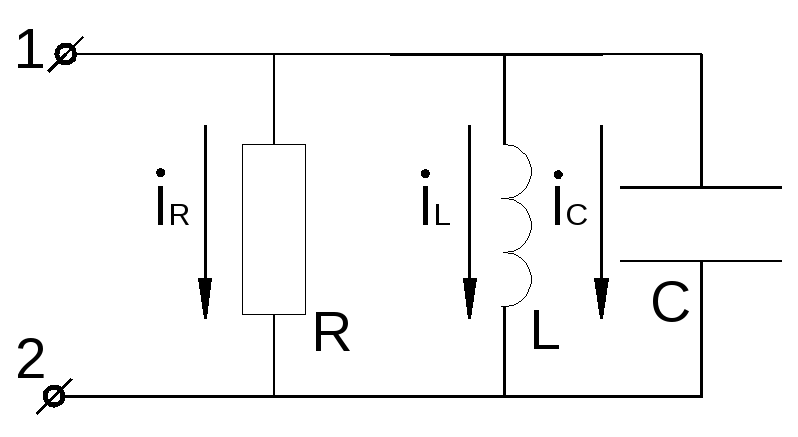
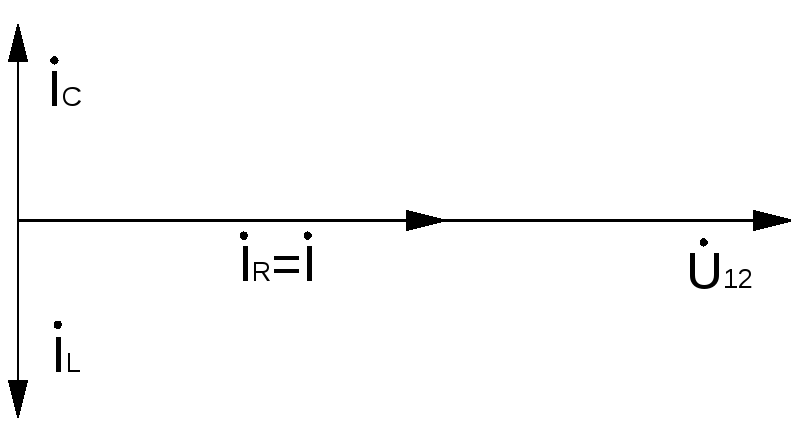
В данном случае резонанс токов
3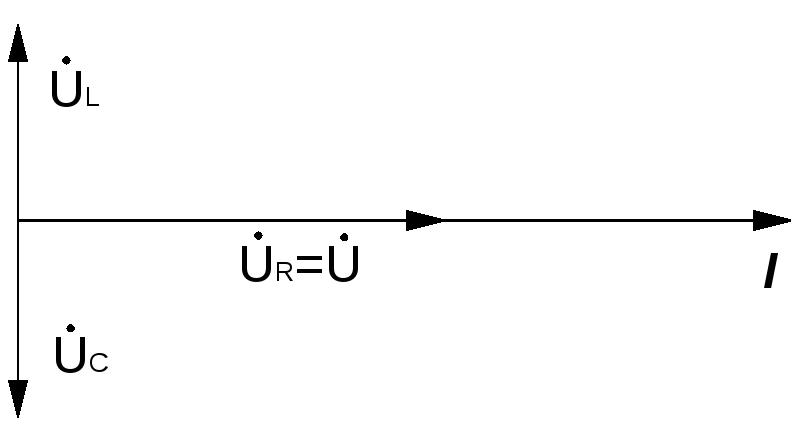 .
Условия возникновения в электрической
цепи резонанс напряжений:
.
Условия возникновения в электрической
цепи резонанс напряжений:
При последовательном соединении R,L,C:
Для
нее наступает резонанс при следующих
условиях 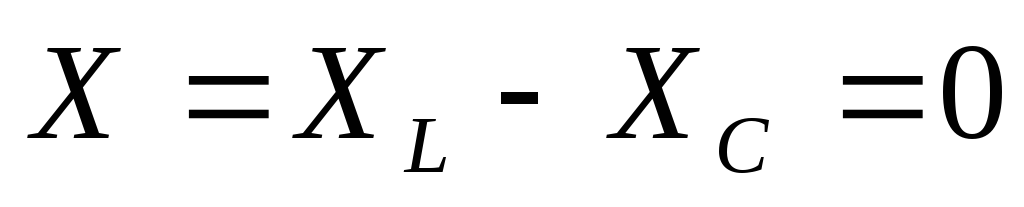 ,
т.е.
.
Значит
,
т.е.
.
Значит 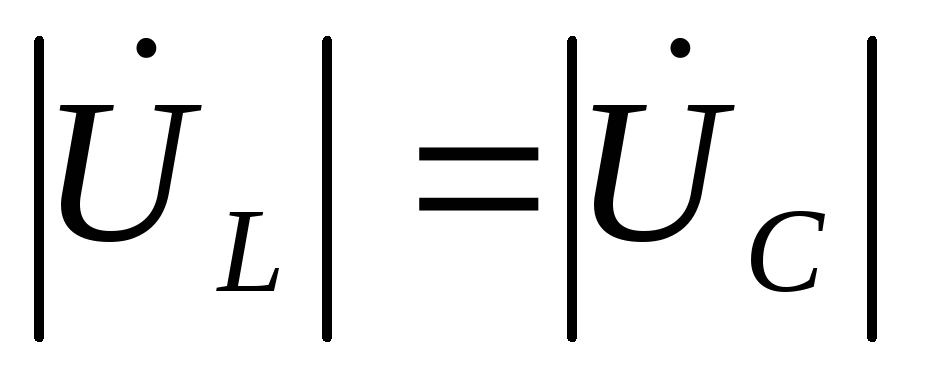 и
и 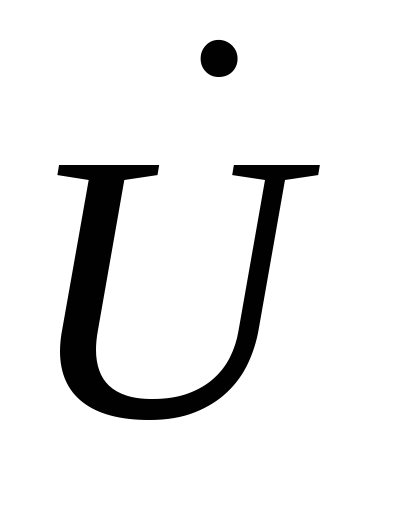 опережает
ток по фазе на
опережает
ток по фазе на  ,
а
,
а 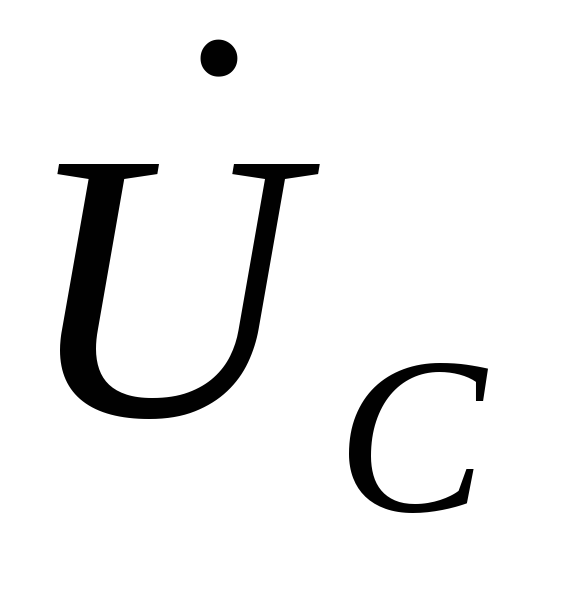 отстает
от тока на
отстает
от тока на 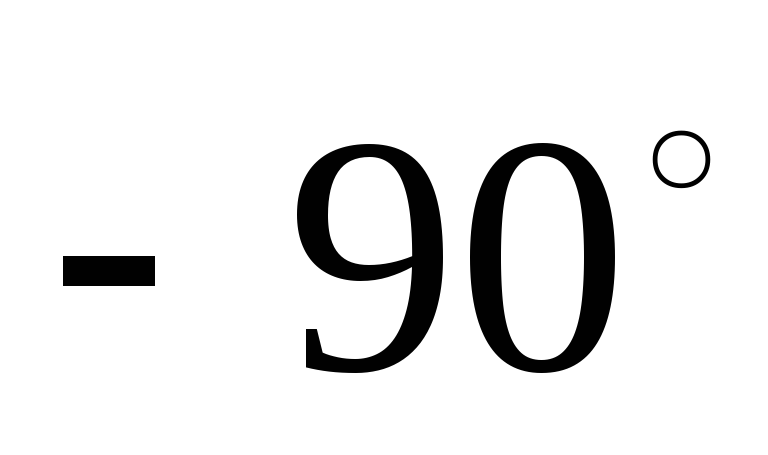 ,
, 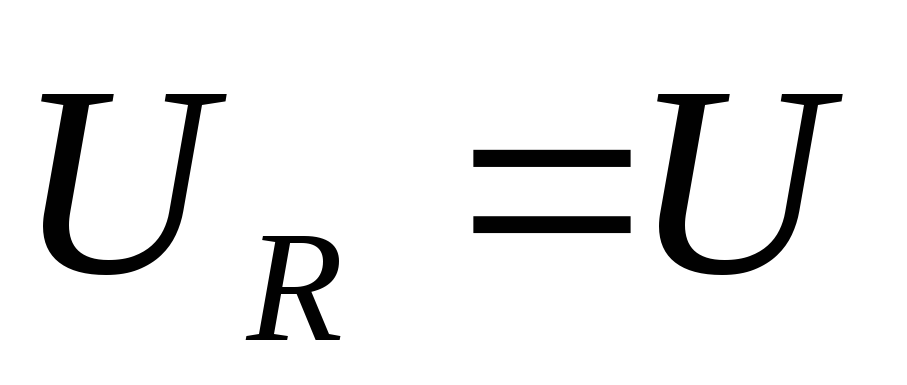 и совпадает по фазе с током
и совпадает по фазе с током 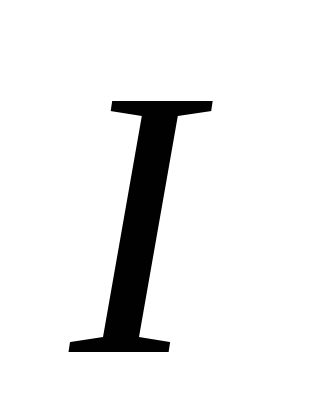
4.
Резонансная условная частота 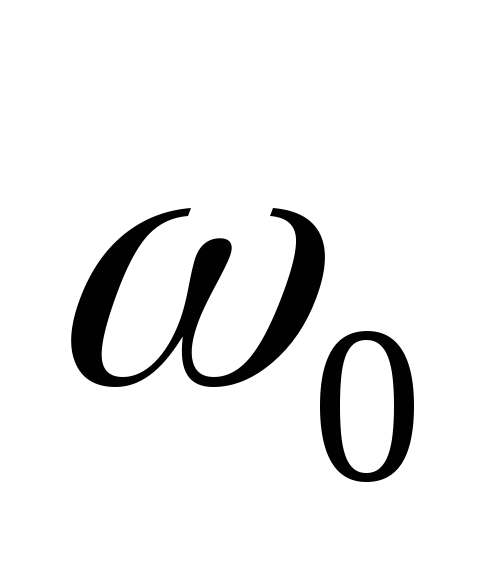 и резонансная угловая частота
и резонансная угловая частота 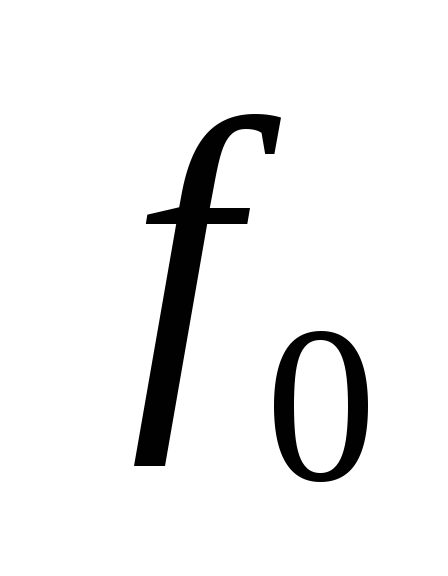 :
:
Резонасная
частота 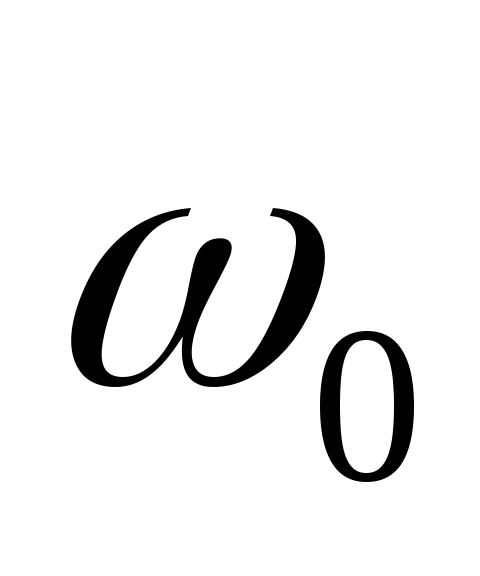 определяется из условия резонанса, т.
е.
определяется из условия резонанса, т.
е. 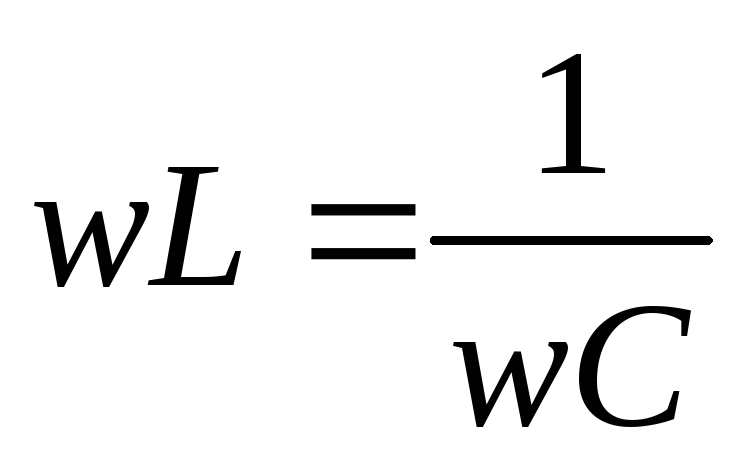 .
Значит резонанс достигается 3-мя
способами: изменением частоты напряжения
питания; изменением параметров цепи
(индуктивности или емкости).
.
Значит резонанс достигается 3-мя
способами: изменением частоты напряжения
питания; изменением параметров цепи
(индуктивности или емкости). 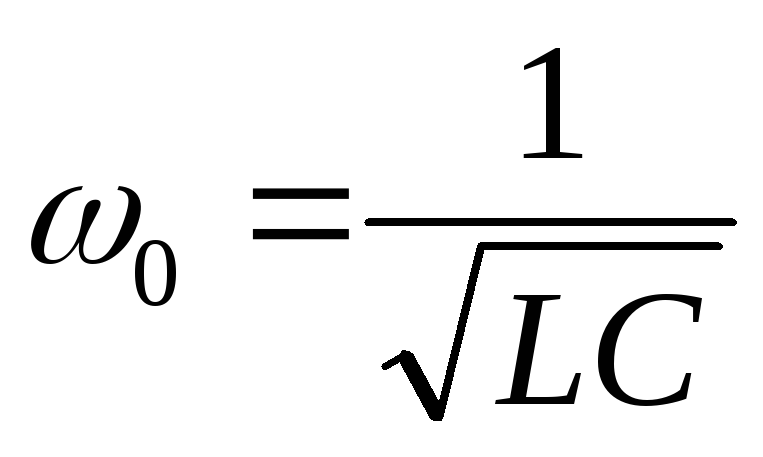
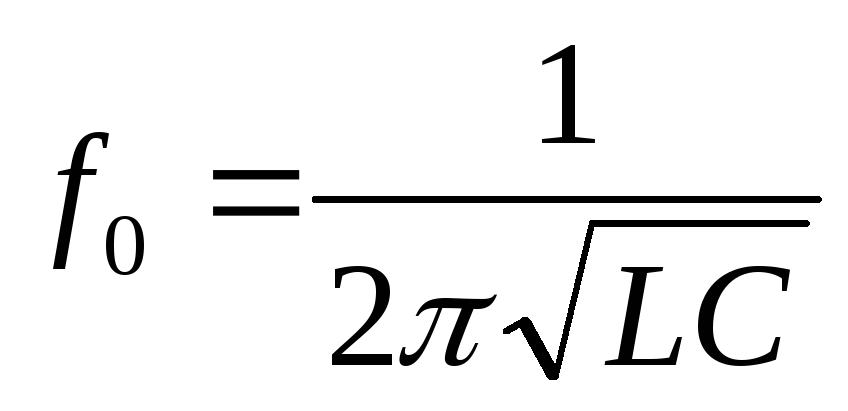
5. Характеристическое сопротивление контура:
Сопротивление 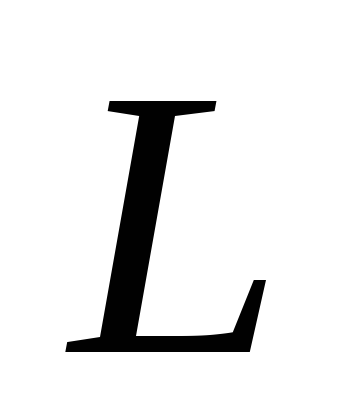 и
и  при резонансе называется характеристическим
сопротивлением
при резонансе называется характеристическим
сопротивлением  .
.
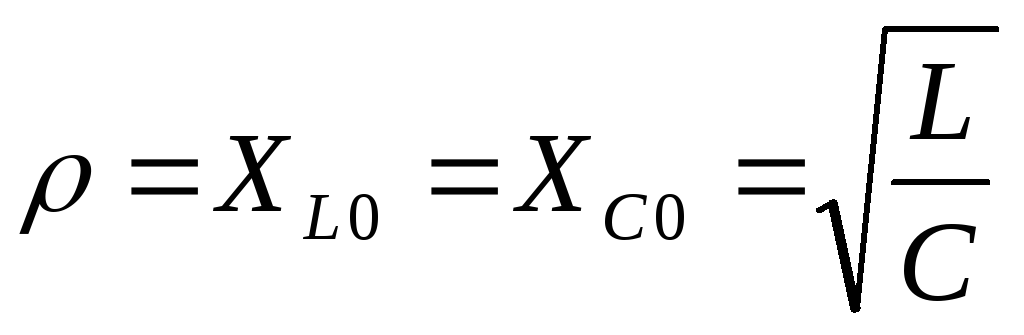
6. Формулы расчета полного сопротивления цепи и тока при резонансном напряжении :
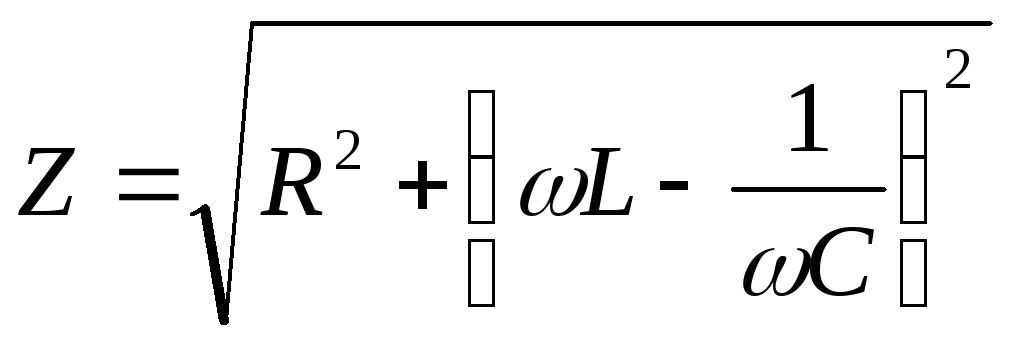 —
полное сопротивление цепи
—
полное сопротивление цепи 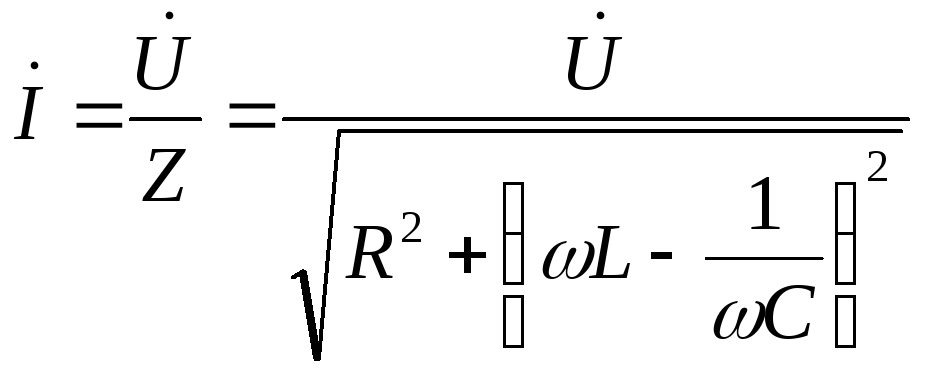 — ток
— ток
7. Расчет напряжений на индуктивности и емкости при резонансе напряжения:
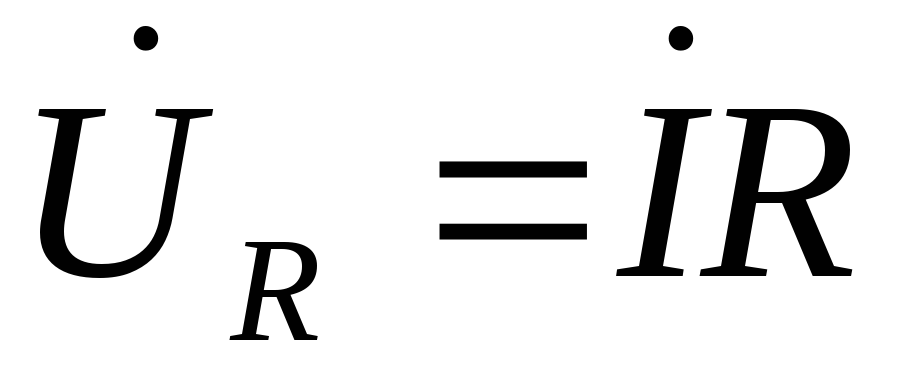
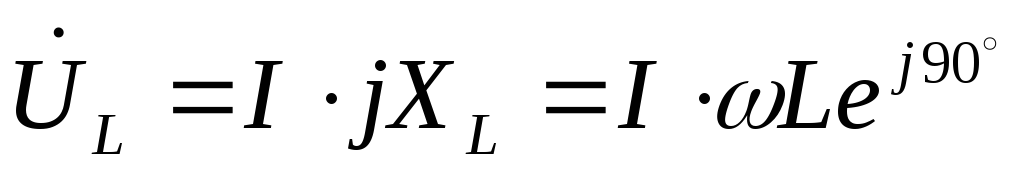
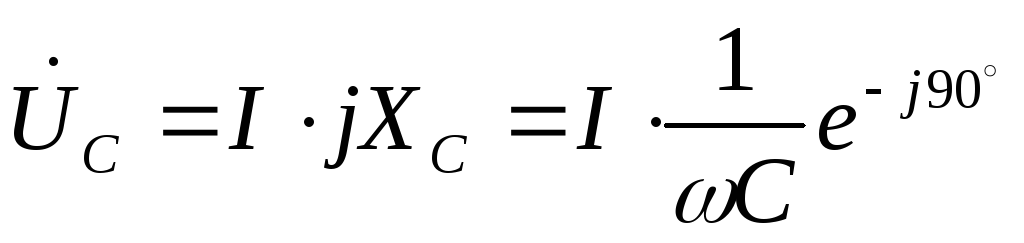
8. Добротность последовательного контура:
Добротность( )
– это величина , которая показывает во
сколько раз напряжение на
)
– это величина , которая показывает во
сколько раз напряжение на 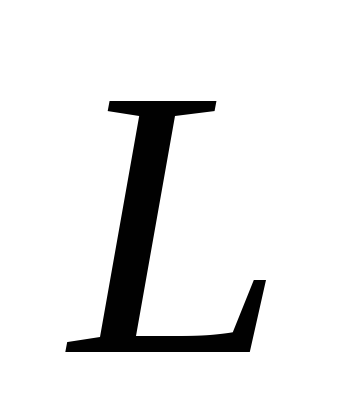 или на
или на  в режиме резонанса превосходит входное
напряжение:
в режиме резонанса превосходит входное
напряжение: 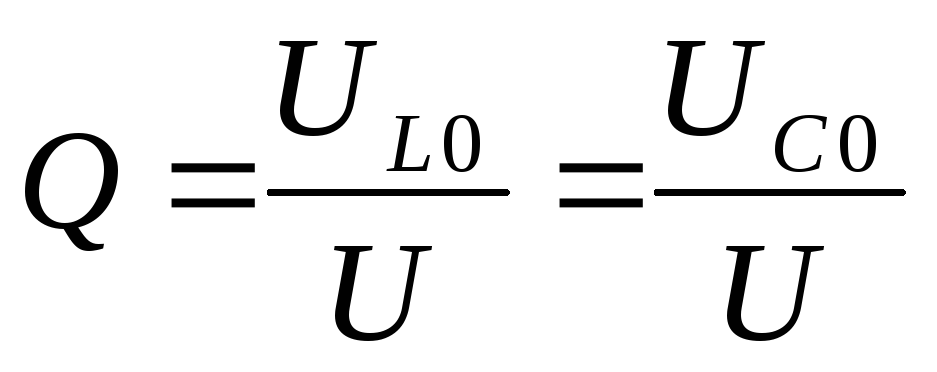
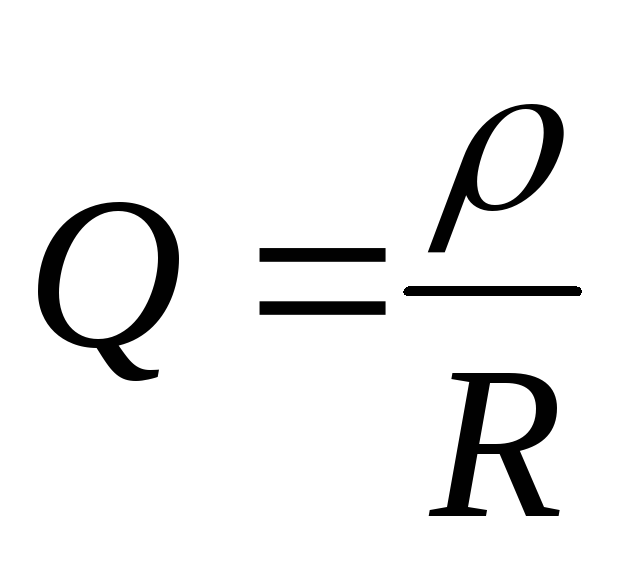
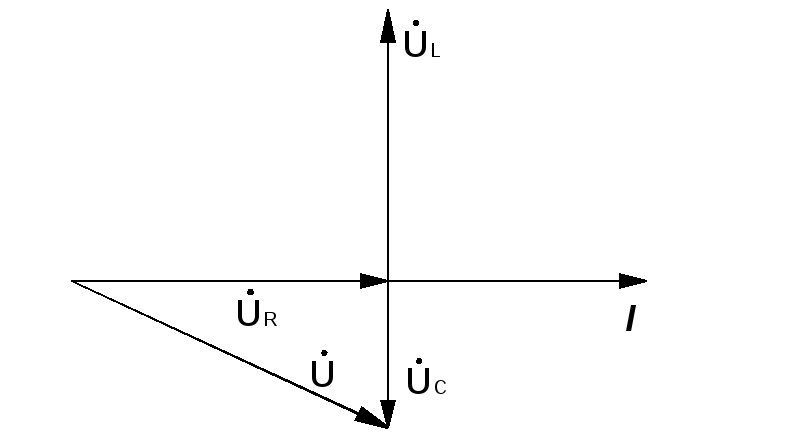
9. Векторная диаграмма для электрической цепи с последовательным соединением R,L,C:
а) до резонанса; б) при резонансе; в) после резонанса
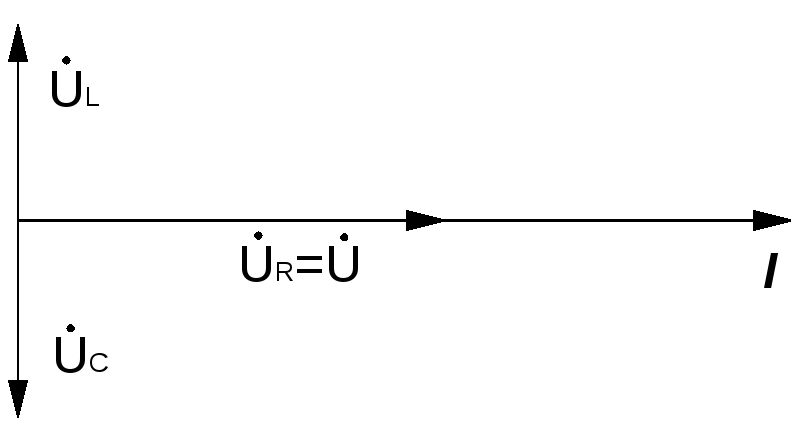
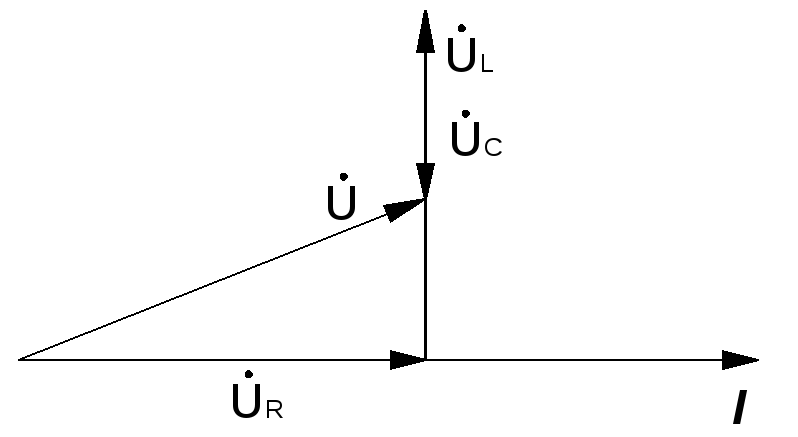
10.
Угол сдвига фаз 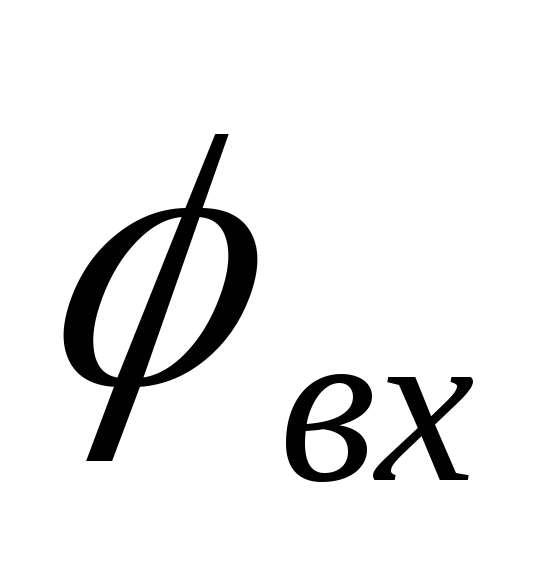 между током и напряжением на входе
последовательного колебательного
контура:
между током и напряжением на входе
последовательного колебательного
контура:
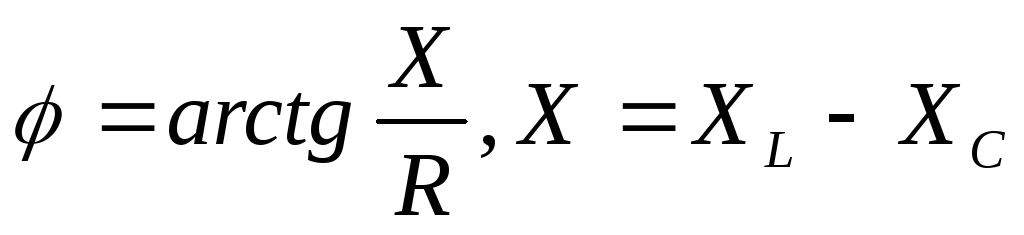
11.
График зависимости 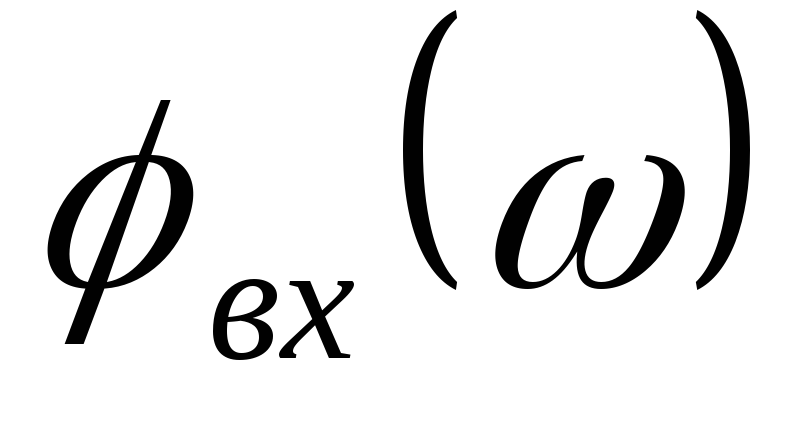 .
Значение угла сдвига фаз
.
Значение угла сдвига фаз 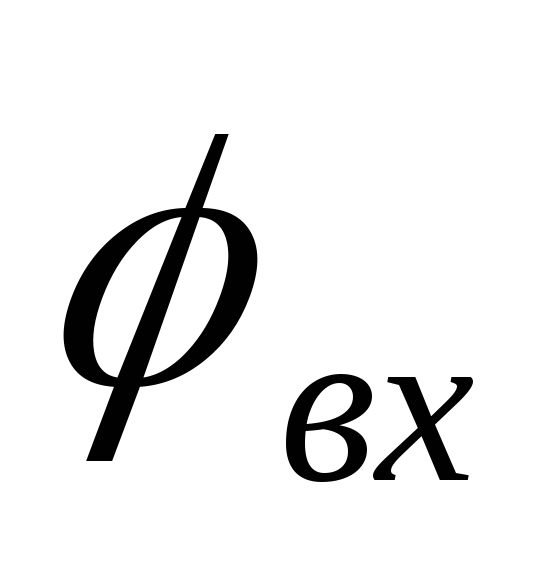 при резонансе:
при резонансе:
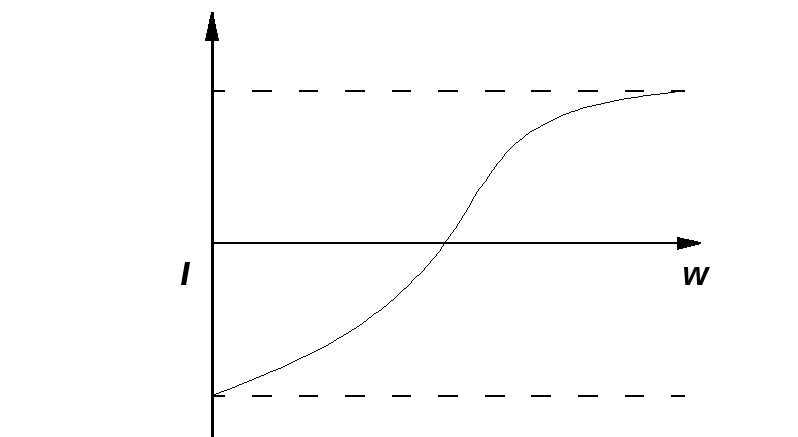
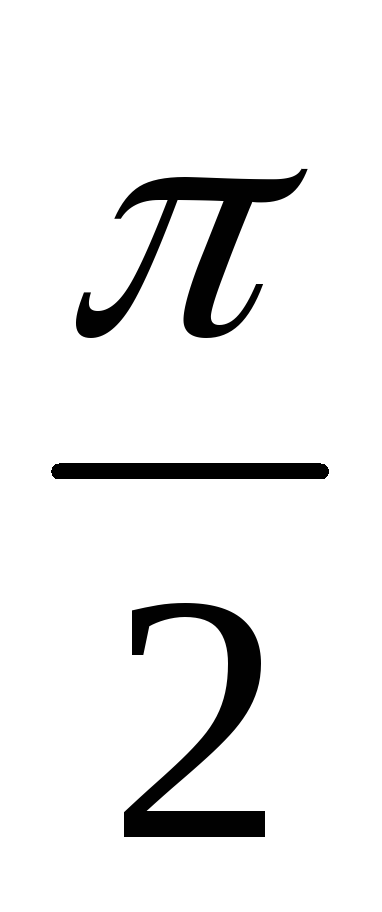

При
резонансе 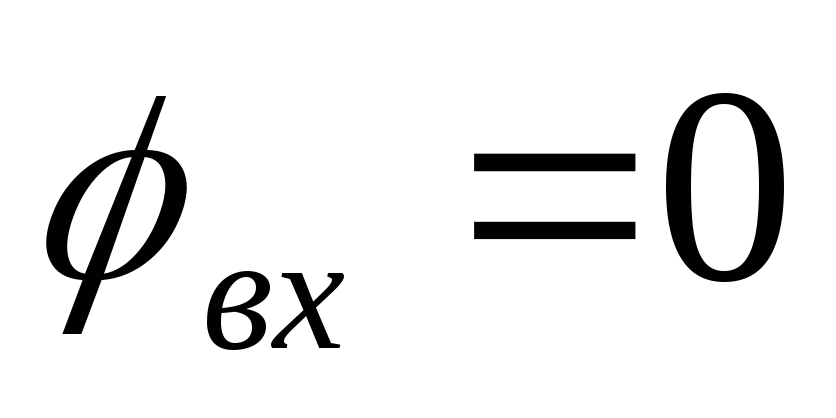
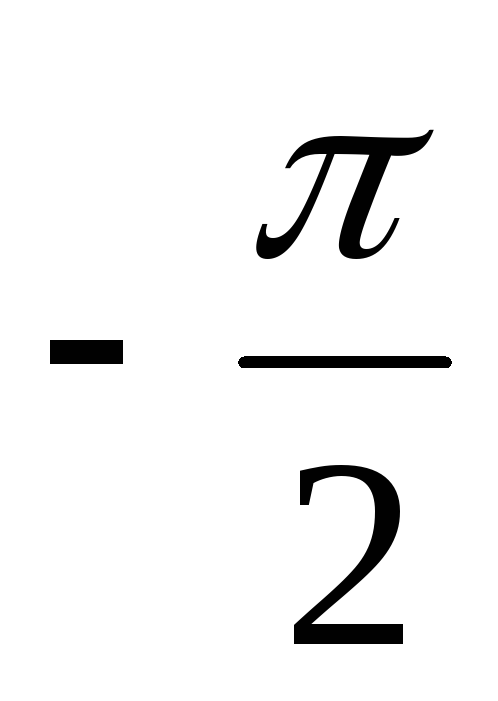
12. Частотные характеристики цепи 13. Построить резонансные кривые
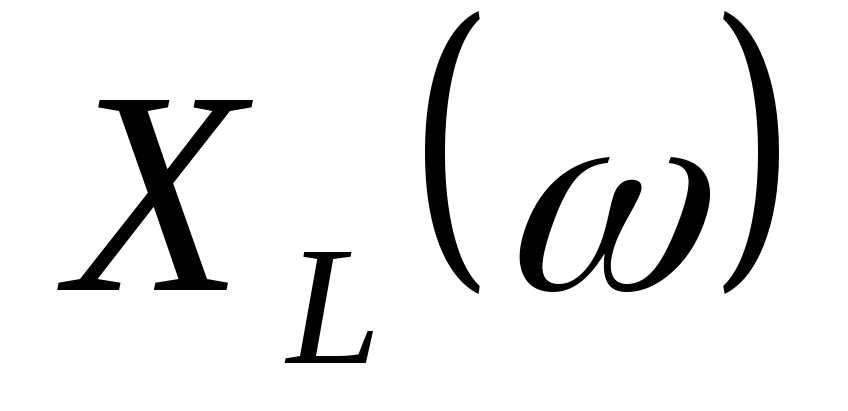 ,
, 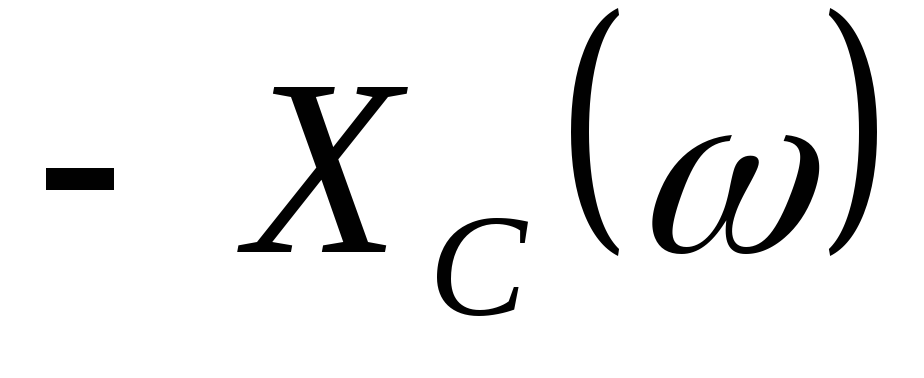 ,
, 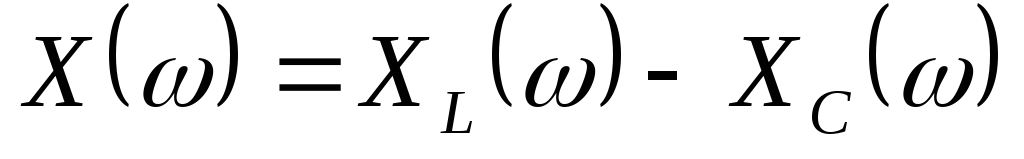 :
: 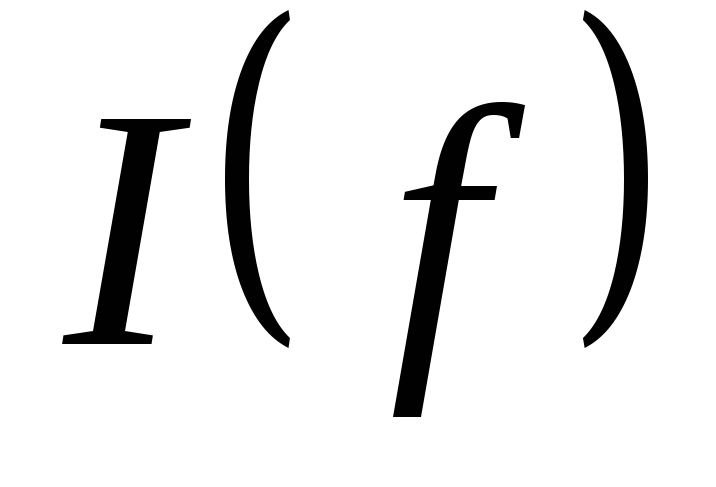 ,
, 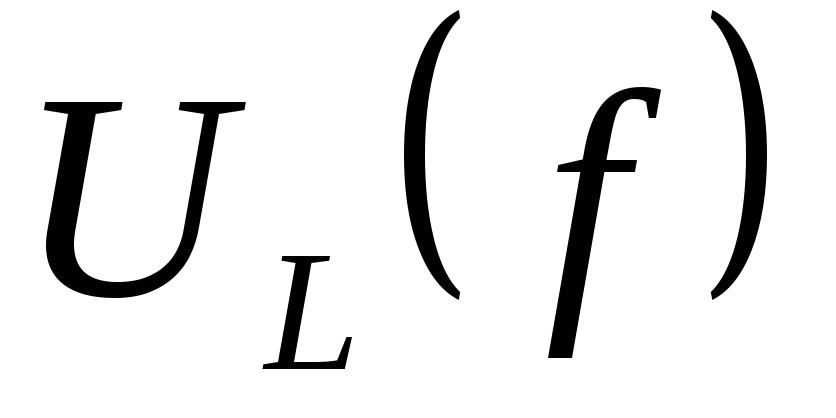 ,
, 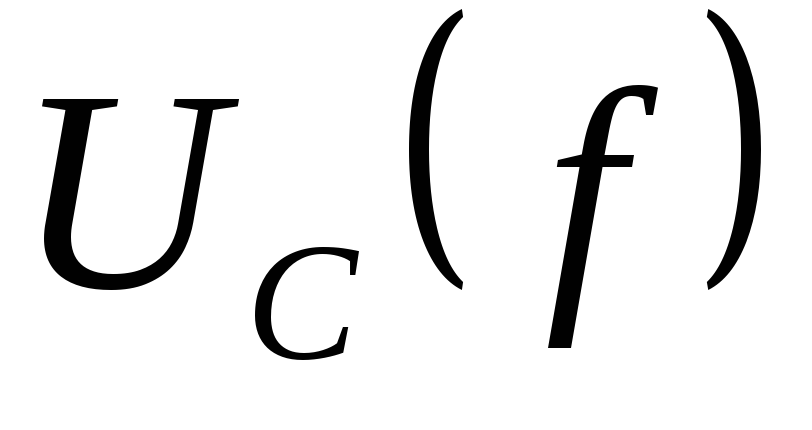
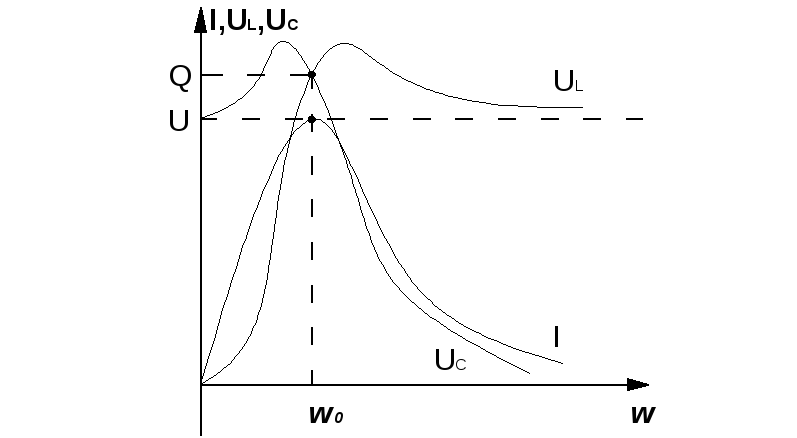
14.
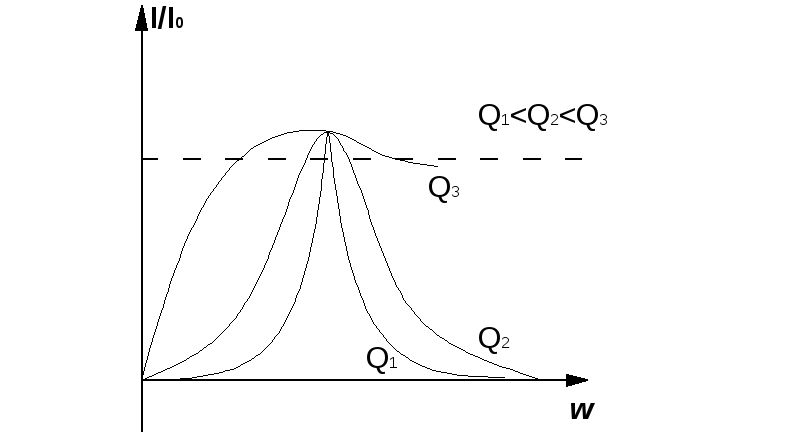
Резонансные кривые 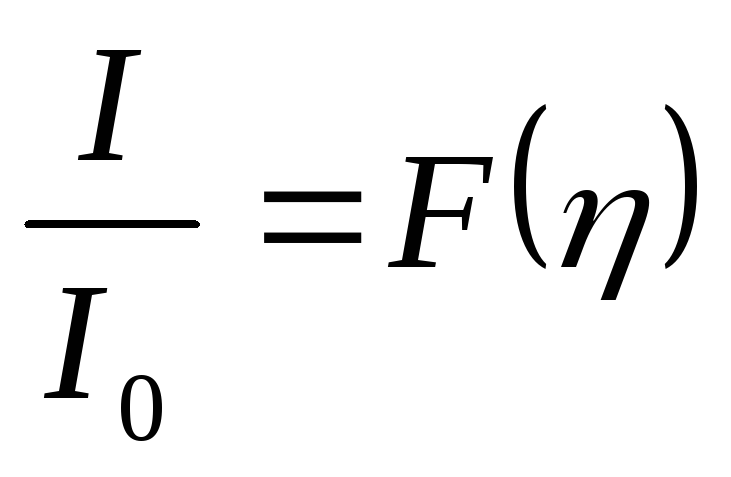 ,
, 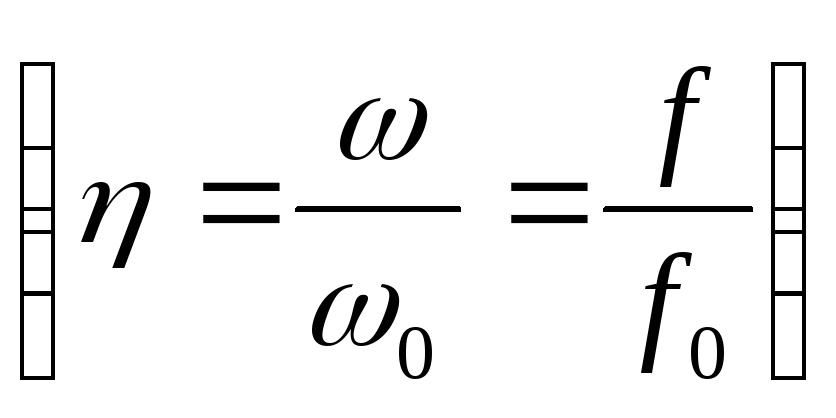 для последовательных колебательных
контуров с разной добротностью:
для последовательных колебательных
контуров с разной добротностью:
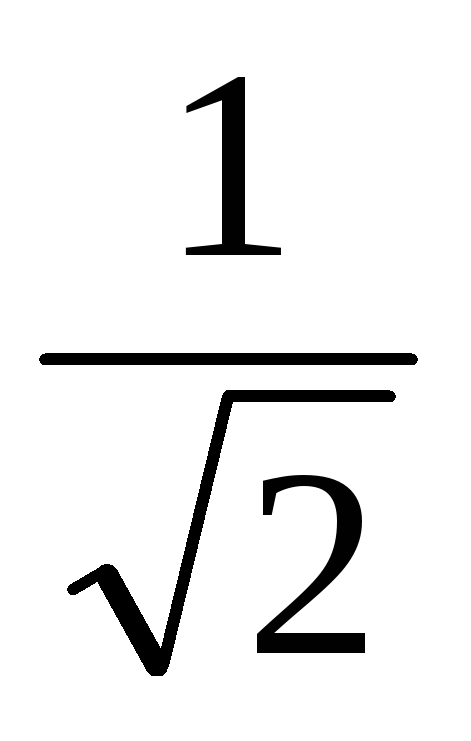
15. Определение полосы пропускания последовательного колебательного контура:
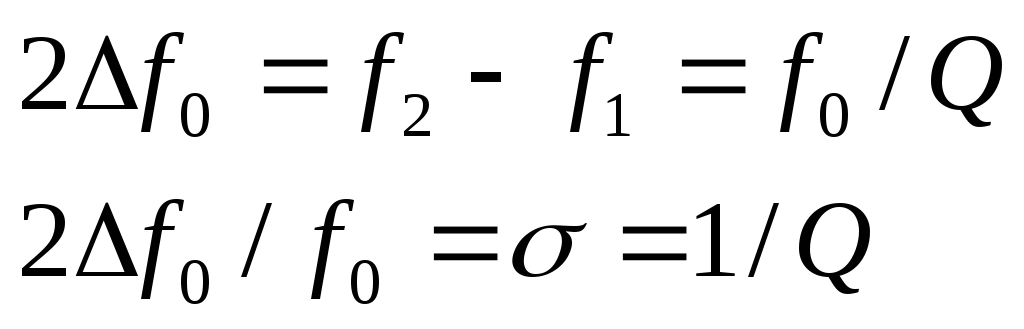
Порядок выполнения работы:
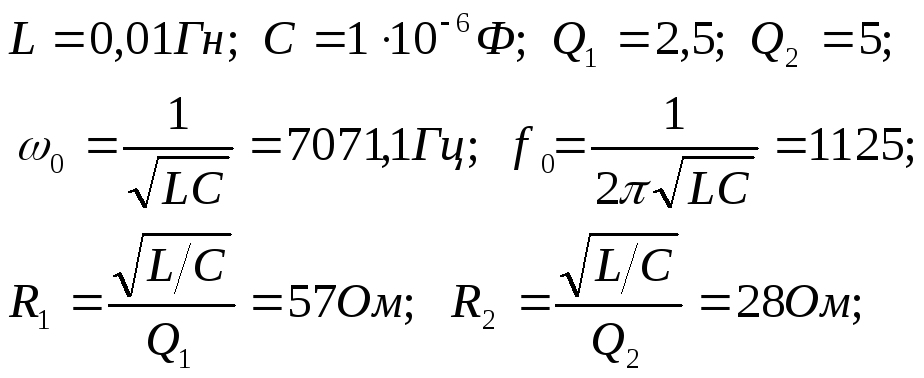
| Добротность | |||||
|
| |||||
|
|
|
|
|
| |
500 | 18,8 | 5,9 | 1,21 | 1,098 | -74° | 19,2 |
700 | 32,4 | 7,28 | 2,91 | 2,833 | -62° | 34,6 |
900 | 54,9 | 9,62 | 6,34 | 6,295 | -40° | 68,5 |
1100 | 74,6 | 10,69 | 10,63 | 10,581 | 0° | 127,7 |
1300 | 61 | 7,42 | 10,31 | 10,308 | 34° | 81,5 |
1500 | 44,5 | 4,72 | 8,73 | 8,709 | 52° | 51 |
1700 | 34,3 | 3,21 | 7,68 | 7,666 | 62° | 37 |
1) Рассчитаем значение 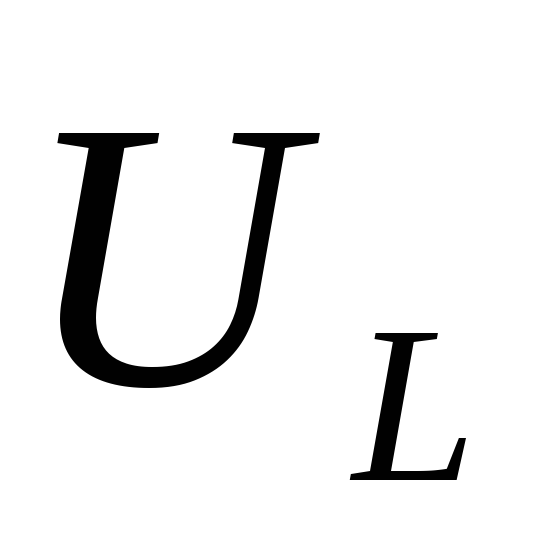 по экспериментальным данным:
по экспериментальным данным:
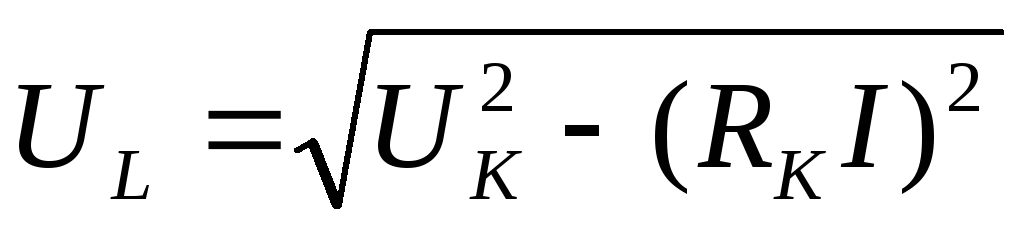 ,
где
,
где 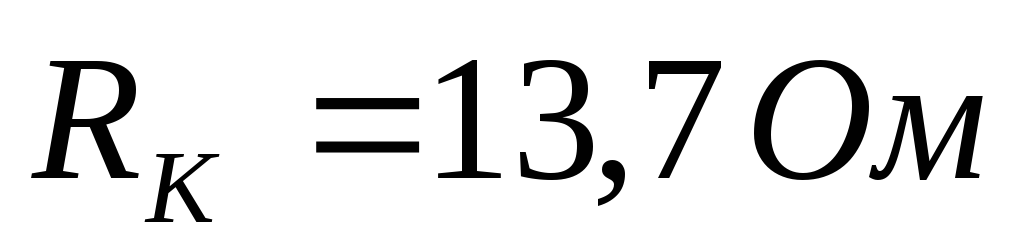
1: 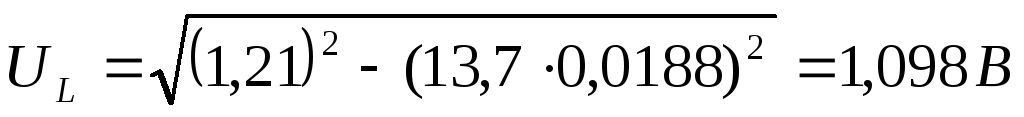 5:
5: 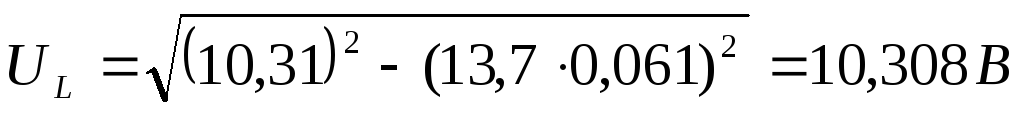
2: 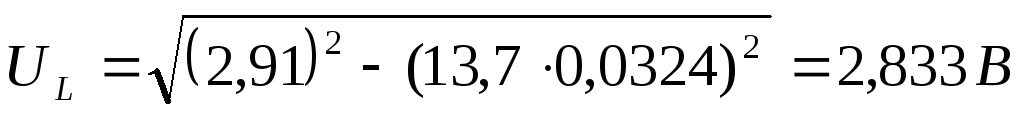 6:
6: 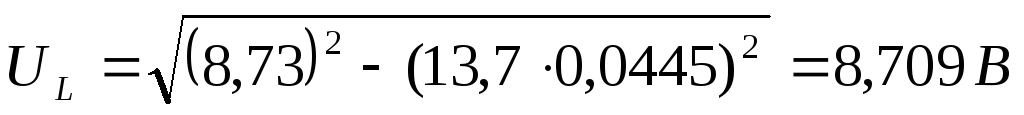
3: 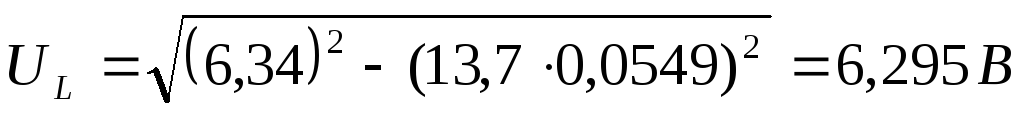 7:
7: 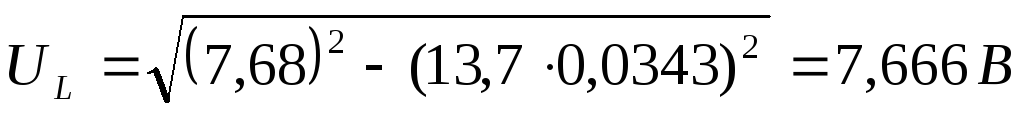
4: 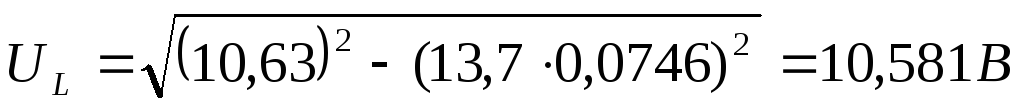
Р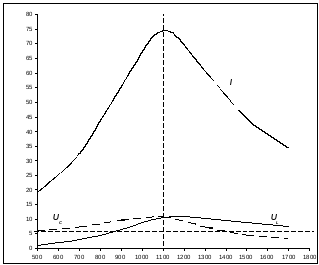 езонансные
кривые
езонансные
кривые  ,
, 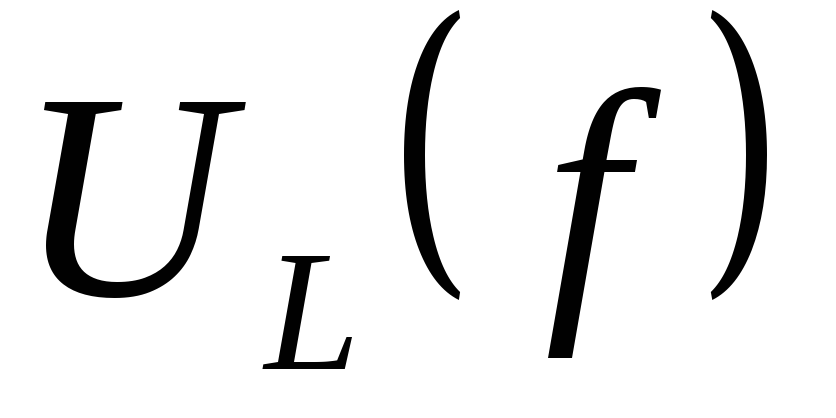 ,
, 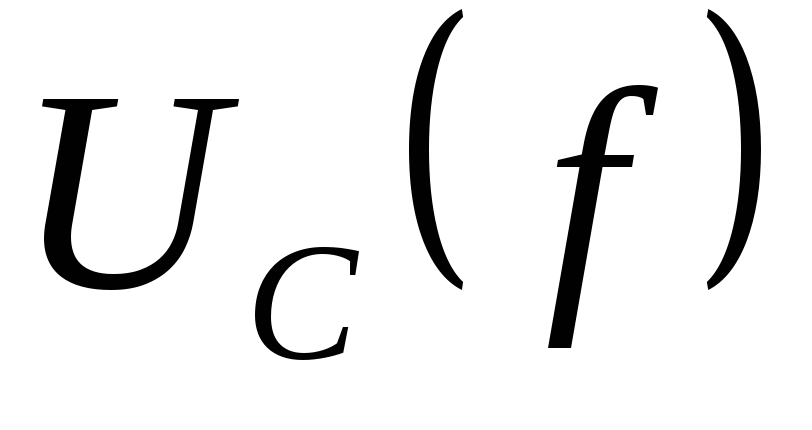 ,
по экспериментальным данным:
,
по экспериментальным данным:
2) Рассчитать зависимости 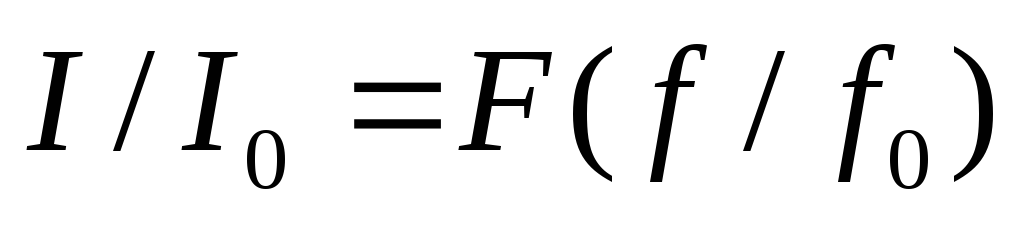 для добротностей
для добротностей 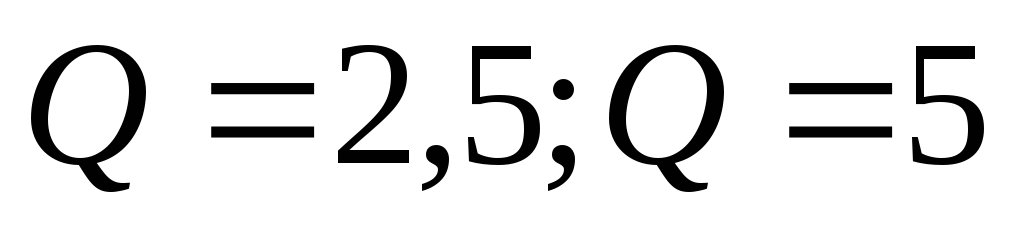 и
построить график зависимости
и
построить график зависимости 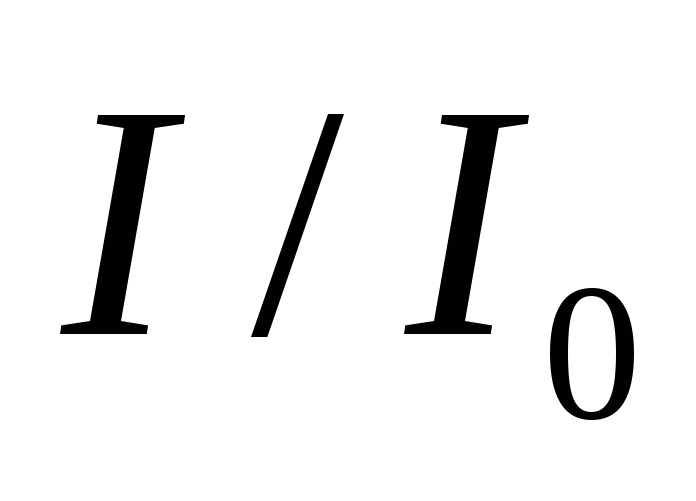 от
от 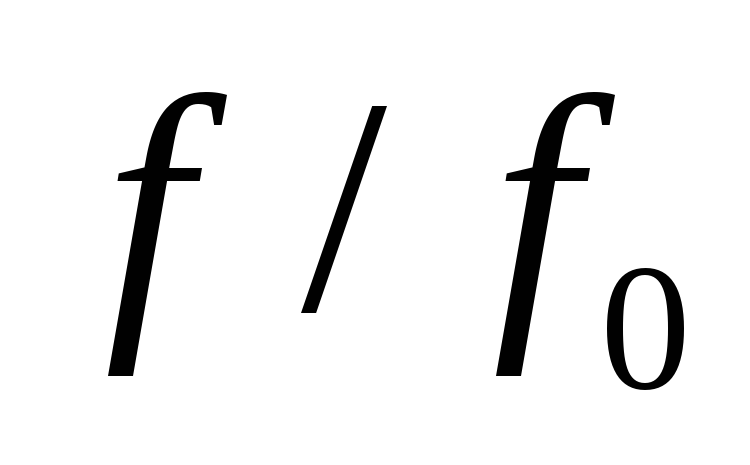 .
По резонансным кривым определить
граничные частоты
.
По резонансным кривым определить
граничные частоты 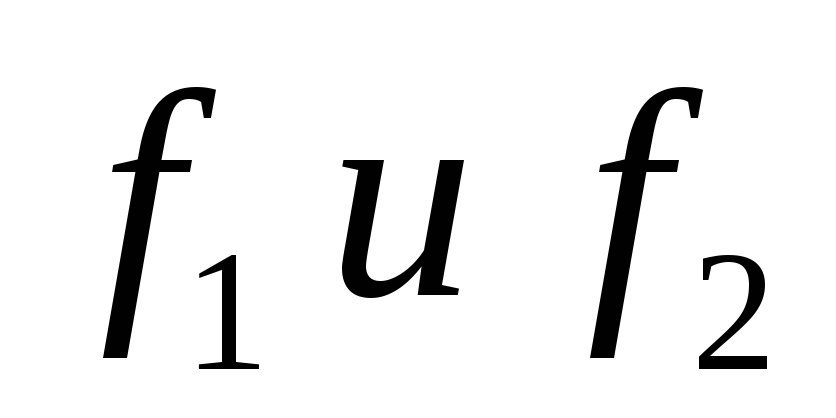 для двух значений добротности.
для двух значений добротности.
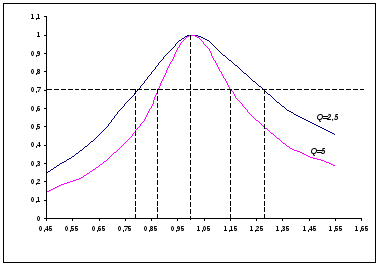

3) Из экспериментальных данных хорошо
видно по максимальному току в цепи при
неизменном входном напряжении, что
резонансная частота 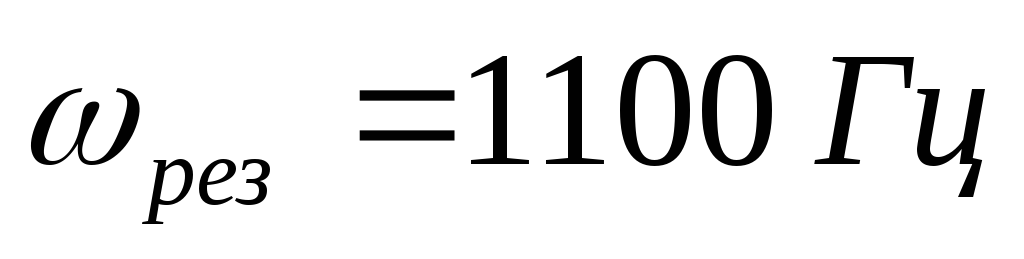
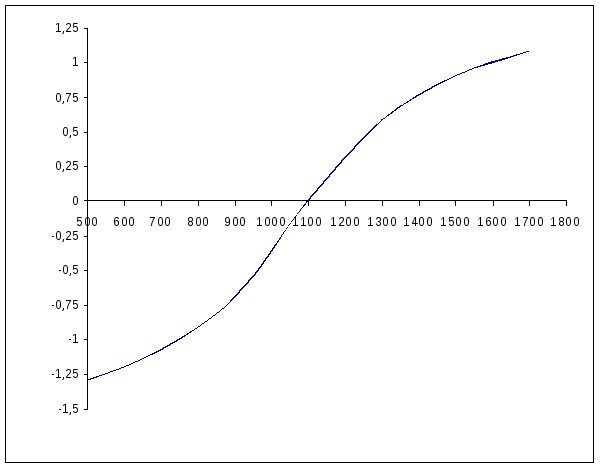
4) Рассчитаем и построим график зависимости
угла 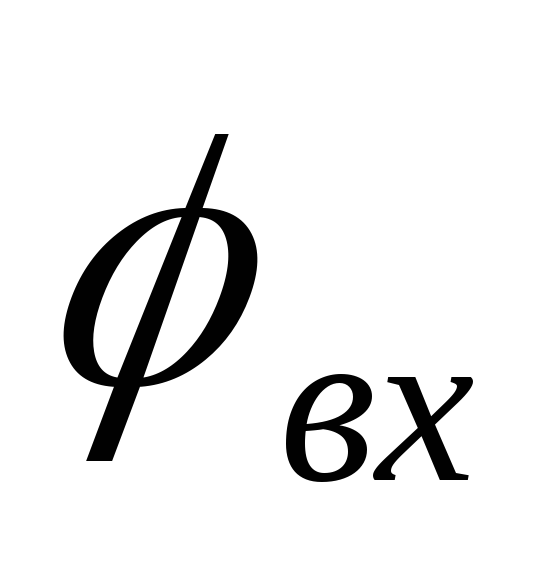 от частоты:
от частоты:
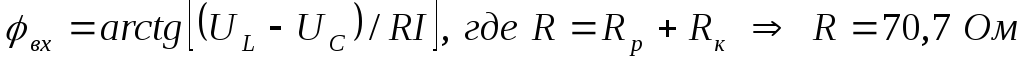
500; 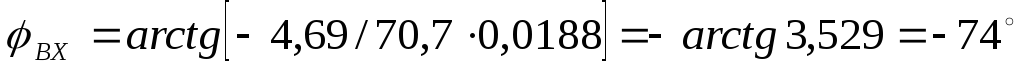
700; 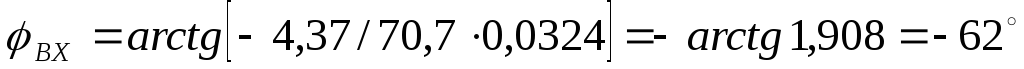
900; 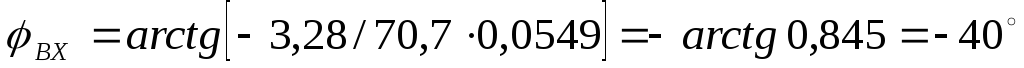
1
w
100;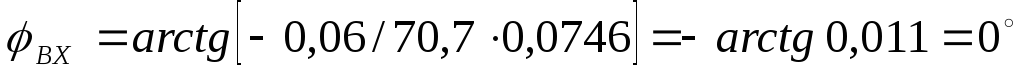
1300; 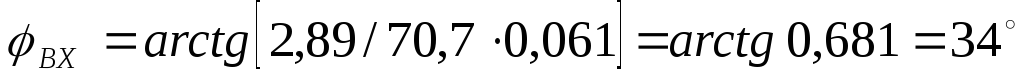
1500; 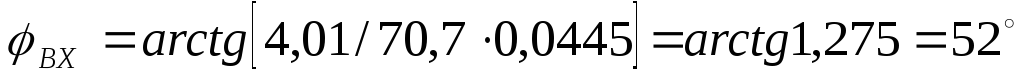
1700; 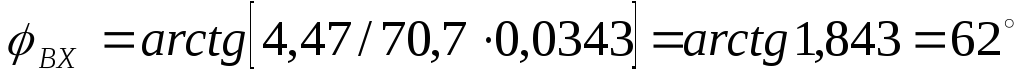
5) Полная и активная мощности при резонансе.
Активная мощность при резонансе.
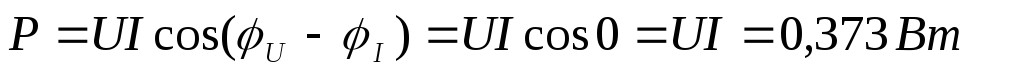
Полная мощность при резонансе.
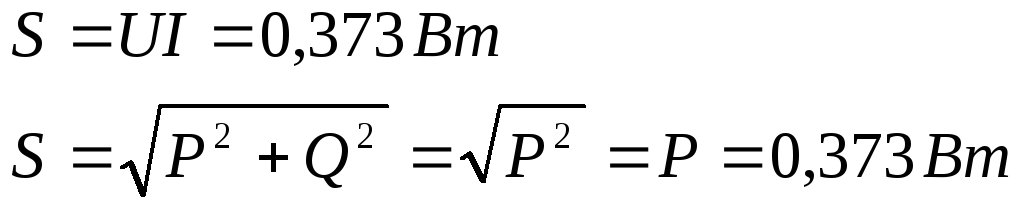
6) Определение добротности.
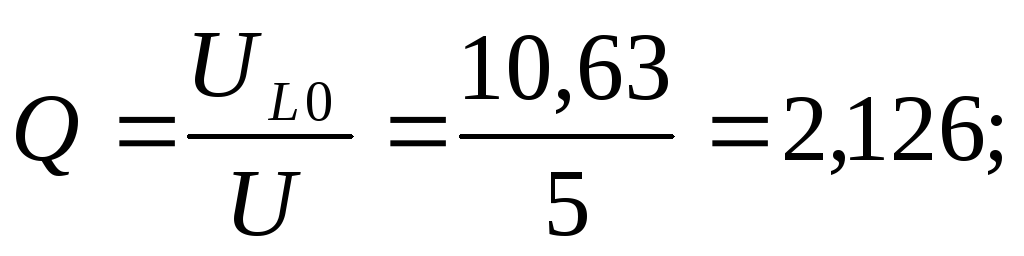
7) График зависимости 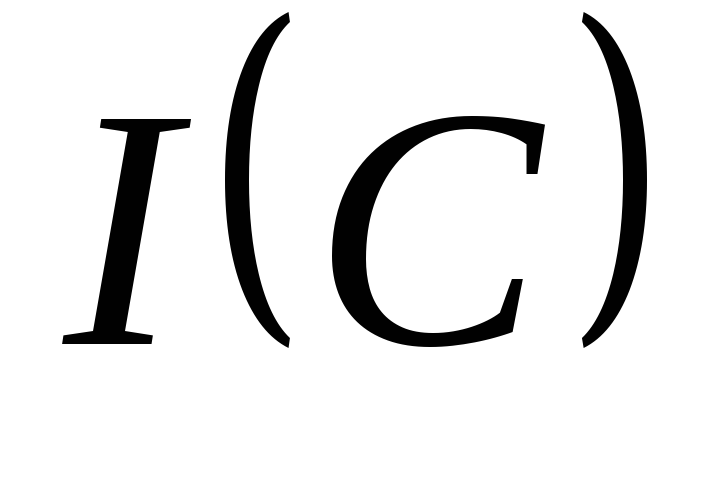 ,
, 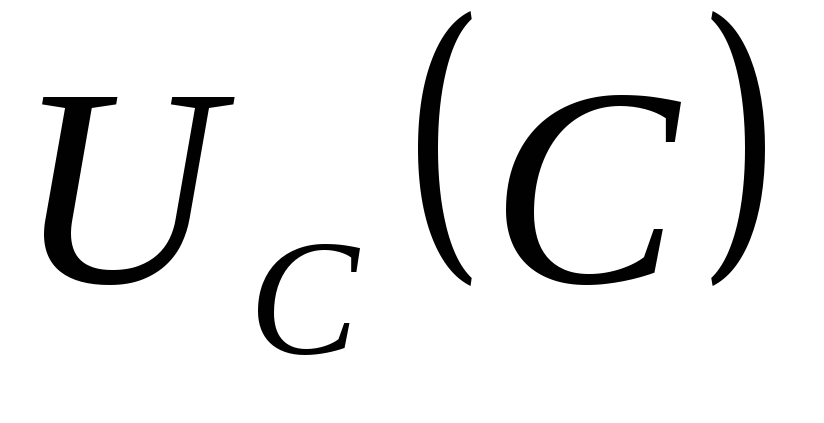 ,
по данным таблицы:
,
по данным таблицы:
C, мкФ
I, мА
UC, В
1
128
18,1
2
72,1
8
3
54,4
3,2
4
43,9
1,4
5
41,3
1
6
40,7
0,9
7
39,4
0,7
U
I
C
5