Что такое таблица истинности? Таблица, описывающая логическую функцию, называется таблицей истинности. В таблице истинности перечислены все возможные наборы входных переменных. В последнем столбце таблицы истинности выводится число, соответствующее значению функции, по которой строилась данная таблица истинности.
Рассмотрим пример: Допустим, у нас есть две булевых переменных x1 и x2. От этих переменных зависит логическая функция f(x1,x2) Для примера возьмем f(x1,x2)=x1∧x2∨x1. Так как x1, x2 булевы, то они принимают значния 0 или Все возможные варианты входных переменных x1 и x2 можно представить в таблице:
Подставим значения переменных f(0,0)= 0∧0∨0=0 f(0,1)= 0∧1∨0=0 f(1,0)= 1∧0∨1=1 f(1,1)= 1∧1∨1=1
Получившиеся значения запишем в последний столбец нашей таблицы:
Мы получили таблицу истинности функции f(x1,x2)=x1∧x2∨x1.
На нашем сайте вы можете построить таблицу истинности online. Для этого вам всего лишь нужно ввести функцию в поле и нажать вычислить.
Таблицы истинности основных булевых функций:
Унарные функции:
Бинарные функции
| |||||||||||||||||||||||||||||||
Урок по теме: Логические выражения и таблицы истинности | План-конспект урока по информатике и икт (9 класс) по теме:
Урок по информатике: Логические выражения и таблицы истинности
Цели: построение таблиц истинности логических выражений.
Задачи:
- Научить составлять логические выражения из высказываний;
- Ввести понятие “таблица истинности логического выражения”;
- Изучить последовательность действий построения таблиц истинности;
- Научить находить значение логических выражений посредством построения таблиц истинности;
- Ввести понятие равносильности логических выражений;
- Научить доказывать равносильность логических выражений, используя таблицы истинности;
- Закрепить навыки нахождения значений логических выражений посредством построения таблиц истинности.
Ожидаемые результаты обучения:
Учащиеся должны знать:
- таблицы истинности логических операций;
- этапы составления таблиц истинности логических выражений;
- понятие равносильные логические выражения.
Учащиеся должны уметь:
- строить и заполнять таблицу истинности логического выражения;
- находить значение логических выражений посредством построения таблиц истинности;
- доказывать равносильность логических выражений, используя таблицы истинности.

Ход урока
I. Оргмомент.
Здравствуйте, ребята. Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Составление логических выражений. Таблицы истинности». Изучив данную тему, вы научитесь, как из высказываний составляются логические формы, и определять их истинность посредством составления таблиц истинности.
II. Проверка домашнего задания.
III. Изложение нового материала.
1. Построение таблиц истинности.
Мы уже несколько уроков используем понятие “таблица истинности”, определим же его.
Опр.1 Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.
При построении таблиц истинности есть определенная последовательность действий:
- Необходимо определить количество строк в таблице истинности: количество строк равно 2n, где n — количество логических переменных.
- Необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

- Необходимо построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
- Заполнить столбцы входных переменных наборами значений;
- Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Пример. Построить таблицу истинности для составного высказывания:
1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2). Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно семи.
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Можно сначала выполнить логическое отрицание или найти значение сначала в первой скобке, затем инверсию и значение во второй скобке, затем значение между этими скобками.
A | B | |||||
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
2. Равносильные логические выражения.
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак “ = “.
Пример. Докажем, что логические выражения и равносильны.
Построим сначала таблицу истинности логического выражения:
1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2). Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум, а количество логических операции — трем, то есть количество столбцов таблицы истинности равно пяти.
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Сначала необходимо выполнить логическое отрицание А, а затем логическое отрицание В. Последним действием выполним логическое сложение.
A | B | |||
0 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 0 | 0 |
Теперь построим таблицу истинности логического выражения:
1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2). Определяем количество столбцов. В нашем случае количество переменных равно двум, а количество логических операции — двум, то есть количество столбцов таблицы истинности равно четырем.
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Сначала необходимо выполнить действие в скобках, а затем логическое отрицание.
A | B | ||
0 | 0 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 |
Построили таблицы. Теперь давайте, сравним значения в последних столбцах таблиц истинности, т.к. именно последние столбцы являются результирующими:
=
IV. Закрепление изученного материала.
1. Построить таблицу истинности для формулы: .
1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 3переменные: А, В и С.
Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 3переменные: А, В и С.
Количество строк в таблице истинности должно быть равно 23=8.
2). Определяем количество столбцов. В нашем случае количество переменных равно трем, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно восьми.
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Последовательность операций: инверсия, операции в скобках, операция за скобкой.
A | B | C | |||||
0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
2. Докажите с помощью таблиц истинности равносильность следующих логических выражений: и .
Докажите с помощью таблиц истинности равносильность следующих логических выражений: и .
Построим сначала таблицу истинности логического выражения: .
1). Определим количество строк в таблице: 22=4.
2). Определяем количество столбцов: 2+1=3.
3). Строим таблицу с указанным количеством строк и столбцов.
A | B | |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 0 |
1 | 1 | 1 |
Построим таблицу истинности логического выражения: .
1). Определим количество строк в таблице: 22=4.
2). Определяем количество столбцов: 2+2=4.
3). Строим таблицу с указанным количеством строк и столбцов.
A | B | ||
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
Вывод: данные логические выражения не равносильны.
V. Итог урока.
Обобщить пройденный материал, оценить работу активных учеников.
VI. Домашнее задание.
- Доказать, используя таблицы истинности, что логические выражения и равносильны.
Построить таблицу истинности для формулы:
Примечания к таблице истинности и логическим утверждениям
Таблица истинности логической функции содержит списки всех возможных значений, которые функция может получить для данного входа. Таблица истинности состоит из множества строк и столбцов, причем верхняя строка указывает логические переменные и их комбинации, а нижняя строка показывает конечную функцию с возрастающей сложностью. Таблица истинности логической системы представляет выходные данные системы для данного входа в виде строк и столбцов. Чтобы назвать столбцы таблицы истинности, используются входы и выходы со строками, представляющими все потенциальные входы и выходы схемы.
Что такое логические операторы? Логическое утверждение — это утверждение, которое возвращает либо истину, либо ложь, т. е. 0 или 1. Если оно возвращает истину, оно позволяет нам получить известный набор фактов или получить из них новый факт. Пример: Диагонали прямоугольника имеют одинаковую длину.
е. 0 или 1. Если оно возвращает истину, оно позволяет нам получить известный набор фактов или получить из них новый факт. Пример: Диагонали прямоугольника имеют одинаковую длину.
Здесь он вернет либо истину, либо ложь в зависимости от утверждения. Это декларативный тип оператора, который возвращает true или false.
Некоторые примеры логических утверждений:Примеры предложений, которые являются (или содержат) истинными утверждениями:
- «Том Круз — мужчина».
- «У треугольника три стороны».
- «Милан — столица Италии».
Примеры ложных предложений:
- «Все кулеры сделаны из чистого золота».
- «Два плюс два равно девять».
Примеры предложений, которые не являются (или не составляют) утверждениями: Эмоции, чувства, вопросы и т. д. не могут быть включены в логические утверждения.
- «Кто ты?»
- «Беги!»
- «Королева Англии мудра».
- «Пегас существует».

В логической функции есть три основные операции НЕ, ИЛИ и И:
- НЕ: Это также называется инверсией или отрицанием. Обозначается -. Это означает прямо противоположное или отрицательное значение.
- ИЛИ: Это также называется дизъюнкцией или сложением. Обозначается +. Это похоже на простое добавление значений. Функция возвращает истину, если хотя бы одно из ее значений истинно.
- И: Это также называется соединением или умножением. Он обозначается *. Это похоже на износ умножения для функции, возвращающей истину, оба значения должны быть истинными.
Унарные логические операторы содержат только один логический оператор. Это может быть либо Логическая Истина, либо Логическая Ложь.
Таблица истинности для логической истины: для каждого логического входа возвращает истинное значение.
Вход | Выход |
T | T |
F | T |
Таблица истинности для логической ошибки: для каждого логического входа возвращается ошибка значение
Вход | Выход |
T | 900 02 Ф |
Ф | F |
Таблица истинности для комплимента: возвращает значение, прямо противоположное логическому входу.
Вход | Выход(~) |
T | 9 0002 F |
F | T |
В двоичных операциях есть два логических входа. Над этими операторами выполняются операции И, ИЛИ и НЕ.
Таблица истинности для операции ИЛИ: Возвращает истину, если любой из входных данных верен, и ложь, если оба входа ложны.
А | В | А ИЛИ В |
| 9 0002 Т | Т | Т |
Т | F | Т |
Ф | T | T |
F | F | F 900 03 |
Таблица истинности для операции И: она возвращает истину только в том случае, если оба входа верны, в противном случае — ложь.
А | В | А И В |
| 90 002 Т | Т | Т |
T | F | F |
F | 9000 2 T | F |
F | F | F 90 074 |
Значения функций могут быть 0 или 1. Где логический 0 означает ложь, а логическая 1 означает истину. Таким образом, применяются следующие правила:
Если A = 0, то -A = 1
Если A = 1, то -A = 0
A+B = 0, если A = 0 и B = 0
A+B = 1, за исключением случаев, когда A = 0 и B = 0
A*B = 1 если A = 1 и B = 1
A*B = 0, за исключением случаев, когда A = 1 и B = 1
Как оценить значения логической функции: Пример: показать процесс оценки значений логическая функция -(A+B) * -(A*B).
Он определяется путем разбиения на более мелкие составные функции и вычисления их значений для достижения последнего шага. Это последовательный процесс. Необходимо выполнить следующие шаги:-
- Две логические переменные, A и B, перечислены вверху первых двух столбцов. Все возможные комбинации значений для A и B перечислены в этих столбцах путем подсчета двоичными числами: 00, 01, 10, 11.
- В третьем столбце значение (A+B) вычисляется с помощью операции ИЛИ. .
- В четвертом столбце минус (дополнение) третьего столбца берется, чтобы найти значения, связанные с функцией -(A+B)
- В пятом столбце мы вычисляем значения (A*B) с помощью AND операция.
- Мы находим отрицательное значение (A*B), чтобы вычислить значение -(A*B)
- В седьмом столбце мы находим И значений в четвертом столбце и шестом столбце, чтобы получить значение -(A+B )*-(A*B)
Таким же образом вычисляем таблицу истинности и значения для всех функций. Ниже приведена таблица выражения для -(A+B) * -(A*B).
Ниже приведена таблица выражения для -(A+B) * -(A*B).
А | Б | (А+В) | -(А+В) | (А*В) | -(А*В) | -(А+В) * -(А*В) |
0 | 0 | 1 | 0 | 1 | 1 900 03 | |
0 | 1 | 1 | 0 9007 4 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 1 | 900 710 |
Крайний правый (седьмой) столбец содержит последнюю функцию, которая должна быть оценена. Другие значения в других столбцах (3-й-6-й) определяются путем определения сложения и умножения, а затем отрицания значений.
Другие значения в других столбцах (3-й-6-й) определяются путем определения сложения и умножения, а затем отрицания значений.
Для все более сложных логических функций компьютеры используются для построения таблиц истинности. Некоторые функции имеют большое количество входных переменных и состоят из нескольких составляющих функций; может получиться таблица с сотнями строк и столбцов.
Мы можем использовать таблицы истинности, чтобы определить, правильна ли структура логического аргумента. Они широко используются в логике запросов к базе данных, а также в их оптимизации. Кроме того, для приложений, связанных с общей логикой, таких как экспертные системы. Любой анализ, вероятно, должен реализовать их в той или иной форме. Кроме того, они используются в структурах базовых решений (IF, Case/Switch, IIF и т. д.). Вы можете построить любое количество логических слоев, и было бы полезно их использовать. Они там на фоне системы.
Использование булевых теорем является альтернативой таблице истинности. Этот процесс используется для определения простейшей схемы, которая будет выполнять необходимую логическую функцию. Это уменьшает количество операций, необходимых для выполнения данной задачи, и, следовательно, повышает эффективность системы.
КоСТАРС
КоСТАРСБоковая панель CoSTARS №1:
Логические схемы
1.
Фон
На этой боковой панели мы узнаем о логических цепях, которые строительные блоки цифровых компьютеров. Мы будем использовать xLogicCircuits lab, фантастический инструмент обучения, разработанный Дэвид Эк в Колледжи Хобарта и Уильяма Смита в прекрасной Женеве, штат Нью-Йорк.
Обратите внимание, что д-р Эк дает прекрасное и подробное введение в свою лабораторию, и мы предоставит здесь всего несколько дополнительных комментариев. Итак, первый шаг в этом Боковая панель предназначена для использования лаборатории xLogicCircuits.
2. Лаборатория xLogicCircuits
Читайте о лаборатории xLogicCircuits здесь:
http://math.hws.edu/TMCM/java/labs/xLogicCircuitsLab1.htmlОбратите внимание, что лабораторную работу не следует запускать как апплет (не используйте кнопку «Запустить xLogicCircuits»), так как вы не сможете сохранить свою работу. Вместо этого используйте версию приложения, как описано в следующем шаге. Запустите приложение xLogicCircuits Lab (не апплет) отсюда:
http://math.hws.edu/TMCM/java/classes/xLogicCircuits.jar
Обратите внимание, что вам, возможно, придется сначала сохранить это на рабочем столе, а затем запустить оттуда.
Чтобы включить примеры из лаборатории, сохраните этот файл на рабочем столе и затем запустите лабораторное программное обеспечение и загрузите этот файл:FirstExamples.txt Если вас интересуют материалы, выходящие за рамки этих заметок, вы можете прочитать Вторая лаборатория цепей с веб-сайта TMCM, где обсуждаются схемы памяти.
В этом случае вам также понадобятся примеры из этой лаборатории, которые находятся в этот файл:
Цепи Памяти.txtЗадачи № 1–10. Выполните упражнения 1–10 из xLogicCircuitsLab.
3. Логический Функции, таблицы истинности и логические схемы
Вы уже знакомы с функциями из своей математики курсы. Итак, это функция:
f(х) = х + 5
И эта функция f(x) явно принимает число и прибавляет к нему 5. Только поскольку функции могут использовать числовые переменные, они также могут использовать логическое значение переменные. Вы должны помнить, что логические переменные могут иметь только один двух значений — true или false, которые мы также иногда пишем как 1 или 0, соответственно. Итак, у нас может быть эта функция:
г(х) = НЕ х
Это функция, как и f(x), но здесь переменная x должна быть числом . логическое значение (истина или ложь), а результат g(x) также является логическим значением (истина или ложно).На самом деле результатом g(x) является , противоположное 9.0570 х. Итак, если x истинно, НЕ x ложно, и наоборот . Определение. Булева логическая функция — это функция над логическими переменными, которая вычисляет логический результат.
Мы можем указать логическую функцию, используя таблицу истинности . Это таблица, в которой перечислены 90 569 все возможные значения 90 570 входных данных. переменные в функцию, и для каждой комбинации значений она также перечисляет вывод функции. Таким образом, поведение функции полностью описано.
Вот таблица истинности функции g(x) = NOT x:
x НЕ x
ложь истина
правда ложьВспомните, что мы часто пишем истину как 1 и ложь как 0, так что здесь это более сжатая форма этой таблицы:
х НЕ x
0 1
1 0Обратите внимание, что большинство булевых логических функций требуют более одного входная переменная.
Например, функция И принимает две переменные, и это правда только если обе его входных переменных верны и ложны в противном случае. Итак, (x AND y) истинно, если оба x и y истинны (посмотрите, почему это называется И?). Вот его таблица истинности:
х у х И у
0 0 0
0 1 0
1 0 0
1 1 1Обратите внимание, что таблица истинности требует четырех строк для список всех возможных допустимых значений для x и y. Также пока мы может перечислять строки этой таблицы в любом порядке, принято их перечислять таким образом: если две входные переменные рассматривались как одна 2-значное двоичное число, строки перечислены в порядке возрастания (00, 01, 10, 11). Видеть?
Другой важной логической функцией является ИЛИ, где (x ИЛИ y) true, если либо
x, либо y истинны, или если оба истинны. Здесь его таблица истинности: х у x ИЛИ у
0 0 0
0 1 1
1 0 1
1 1 1Итак, это якобы лаборатория логических схем , не логические функции.
Разница? Можно построить логические схемы как реальные физические устройства, которые вы можете держать, трогать и в некоторых случаях даже подключаются и используются для написания программ на Java (как, в конце концов, компьютеры построены из логических схем).
Мы можем построить логическую схему, эквивалентную ИЛИ функция. Для этого мы должны придать
физический смысл единицам. и 0 в таблице истинности. Поэтому мы говорим, что 1 означает, что есть присутствует напряжение или электричество, а 0 означает, что их нет. Затем, мы строим устройство с двумя входящими и одним выходящими проводами, как таковое:
Теперь в левой части картинки у нас есть два переключателя . Они похожи на выключатели на стене и могут включать провода A и B (1) или выключено (0). Также в правой части картинки у нас есть свет . Он будет светиться, если провод C включен (1), и не будет светиться, если он выключен (0).Волшебство вот в чем: инженеры-электрики выяснили, как создать устройство, называемое вентилем ИЛИ, поведение которого точно соответствует описывается булевой логической функцией ИЛИ.
То есть, если либо А, либо B включен, затем C будет включен, и свет загорится. Если оба A и B выключены, тогда C будет выключен, и линия не будет светиться. Если вы должны были построить таблицу, описывающую это поведение, она будет выглядеть так:
А B C
ВЫКЛ ВЫКЛ ВЫКЛ
ВЫКЛ ВКЛ ВКЛ
ВКЛ ВЫКЛ ВКЛ
ВКЛ ВКЛ ВКЛПереписывая ON как 1 и OFF как 0, мы имеем:
А Б С
0 0 0
0 1 1
1 0 1
1 1 1Если сравнить это с таблицей логического логического функции (x OR y), вы увидите, что таблиц тот же . Таким образом, в глубоком смысле физический логический элемент ИЛИ вычисляет логическое ИЛИ. схема. Это простой компьютер. Очень простой. Но тем не менее это компьютер!
Точно так же инженеры-электрики могут построить вентиль НЕ, который вычисляет функцию НЕ и логический элемент И, который вычисляет функцию И.
Теперь, пока мы можем свести логическую функцию к И, ИЛИ, и НЕ, то мы можем построить физическую схему (то есть набор физические ворота), который вычисляет эту функцию.
4. Логический Функции как двоичные арифметические функции
Когда мы думаем о компьютерах, мы думаем не только о логике , но и арифметика . Они кажутся разными на первый взгляд. Конечно, мы можем построить схему, которая вычисляет (x AND y), но как насчет x плюс у или х умножить на у?
Часть гениальности пионеров компьютеров заключается в том, что они связали эти две идеи вместе. Они придумали, как выполнять арифметические действия с помощью логических функций. Гений! Хитрость заключается в том, чтобы представить числа в двоичный код или основание 2. Вы уже знаете, как это сделать. Так, например, вы знаете, что 0101 в двоичном формате равно 4+1 или 5 в десятичном.
Но как это помогает?
Чтобы убедиться в этом, давайте решим простейшую арифметическую задачу: прибавим два одиночные биты. Мы обозначим входные биты A и B, и у нас есть это таблица:
А Б А + В
0 0 0
0 1 1
1 0 1
1 1 2Проблема с этой таблицей. Последняя цифра 2 (поскольку 1+1=2), и мы должны представить всю таблицу в двоичном виде. Так мы должны преобразовать это число в 10 (2 в двоичном формате), что даст нам:
А Б А + В
0 0 00
0 1 01
1 0 01
1 1 10Следующая часть гениальности заключалась в разбиении бинарного файла. число в отдельные двоичные биты. Видите, логические функции вроде И, ИЛИ, и НЕ имеют только один выходной бит , но ответы в этом таблица для A+B имеет два бита . Решение состоит в том, чтобы разделить эти биты в свои собственные столбцы, которые мы обозначим C и D, где мы думаем о число CD как вычисляемое число:
А Б А + B C D
0 0 00 0 0
0 1 01 0 1
1 0 01 0 1
1 1 10 1 0Видите, как CD эквивалентен (A+B)? Но теперь мы можно смотреть на C и D по отдельности, и у каждого своя логическая функция! Рассмотрим C:
А В С
0 0 0
0 1 0
1 0 0
1 1 1Мы уже видели эту функцию.
Это просто И функция! Итак, С = (А И В). Теперь на D:
А Б Д
0 0 0
0 1 1
1 0 1
1 1 0Это сложнее. D — новая для нас логическая функция. Это XOR, где (A XOR B) то же самое, что (A OR B), за исключением того, что ровно один и не оба должны быть истинными. Мы говорим XOR равно эксклюзив-или потому что оно исключает случай, когда и А, и В истинны. Теперь, если мы были ворота XOR, мы бы сделали. Если бы у нас не было вентиля XOR, однако мы могли бы использовать комбинацию вентилей И, ИЛИ и НЕ, чтобы получить задание сделано, потому что (A XOR B) эквивалентно (((NOT A) AND B) OR ((NOT B) AND Б))). Как мы это узнали? Мы скоро объясним. Но для Теперь мы можем видеть, что если мы соединим A и B с C с помощью вентиля И, и мы соедините A и B с D с помощью вентиля XOR (или его эквивалента), тогда мы будем иметь построил простое устройство, которое вычисляет 1-битное сложение.
Итак, мы сделали это! Мы преобразовали арифметическую задачу (дополнение) к логической задаче (путем разбиения ответа на отдельные биты и думать о каждом бите как о логической функции над входом). Затем мы преобразовали эти логические функции в настоящие физические схемы и таким образом мы построили арифметический компьютер!!!
Конечно, 1-битный сумматор не очень хорош для компьютера, но если мы можем сделать это для 1 бита, мы, конечно, можем сделать это для 2 или 32, если уж на то пошло. А если мы умеем складывать, то наверняка можем и вычитать, умножать и делить. Ты делать ставку! Итак, мы видим, как можно расширить эти идеи, чтобы сконструировать все арифметические схемы внутри современного компьютера!
Итак, 1-битный сумматор, который мы только что написали, называется Half-Adder . Изучите заметки xCircuitsLab, чтобы понять, как объединяются два полусумматора. чтобы сформировать один Full-Adder , а затем как четыре полных сумматора daisy соединили в 4-битный сумматор .
Вам важно понять, как последовательные полные сумматоры действительно соответствуют тому, как вы добавил бы два числа самостоятельно. Как только вы поймете, что такое 4-битный сумматор, затем используйте свои знания о представлении отрицательных чисел в дополнении до двух понять действие 4-бит минус .
Проблема 11. Используя только элементы И, ИЛИ и НЕ, создать свой собственный Half-Adder. Он должен принимать два бита A и B в качестве входных данных, и он должен иметь два бита C и D вывода, где A+B=CD. Договариваться ваши выходные биты, поэтому старший бит (бит 2) находится слева. Сохраните свой Half-Adder как схему с именем MyHalfAdder.
Проблема 12. Используя схему MyHalfAdder, создайте Full-Adder, называемый MyFullAdder.
Проблема 13. Использование схемы MyFullAdder, построить 2-битный сумматор, называемый MyTwoBitAdder. Это занимает два 2-битных числа (для 4 битов ввода) и производит их 3-битную сумму в качестве вывода.

5. Магазин ДеМоргана Законы
В классе мы обсуждали законы ДеМоргана:
(x И y) == (НЕ ((НЕ x) ИЛИ (НЕ y)))
и:
(x ИЛИ y) == (НЕ ((НЕ x) И (НЕ y)))Задача 14: Подтвердите, что каждый из этих законов true с использованием таблиц истинности. Для этого построим таблицу истинности для (x AND y), а затем еще один для (NOT ((NOT x) OR (NOT y))). Покажи то их последние столбцы одинаковы, поэтому два выражения эквивалентны. Сделайте то же самое для другого закона (x OR y).
Проблема 15. Подтвердите каждый из этих законов еще раз, используя схемы. Для этого постройте схему с двумя входами x и у, и два выхода. Первый вывод равен (x AND y). Второй вывод (НЕ ((НЕ x) ИЛИ (НЕ y))). Проверьте свою схему на всех четырех возможных комбинаций значений для x и y, и убедитесь, что два выхода одинаковы для каждого входа.
Сделайте то же самое для другого закона (x OR y).
Проблема 16. Мы можем переформулировать законы ДеМоргана следующим образом:
(НЕ (x И y)) == ((НЕ x) ИЛИ (НЕ y))
и
(НЕ (x ИЛИ y)) == ((НЕ x) И (НЕ y))
Объясните, почему это работает.Проблема 17. Мы видели, что (x XOR y) == ((NOT x) И y) ИЛИ ((x И (НЕ y)). Используйте повторяющиеся применения метода ДеМоргана. Закон (вместе с тем фактом, что НЕ НЕ х равно х), чтобы показать, что:
(x XOR y) == НЕ ((x ИЛИ (НЕ y)) И ((НЕ x) ИЛИ y)))
Показать свою работу! Кроме того, создайте таблицу истинности, которая проверяет этот результат.
Совет. Начните с ((НЕ x) И y) ИЛИ ((x И (НЕ y)). См. как это имеет форму (A OR B), где A — выражение ((NOT x) AND y) а В есть выражение (х И (НЕ у))? Итак, закон ДеМоргана. утверждает, что (A OR B) можно переписать как (NOT ((NOT A) AND (NOT B)), так что это, но замените A и B выражениями, которые они обозначают.Затем вам придется сделать это еще два раза, и, наконец, устранить все двойное отрицание (НЕ-НЕ).
Задача 18. В этой задаче возьмем первые шаги к созданию схемы, которая вычисляет 2-битное умножение . Эта схема должна иметь 4 входа, A, B, C и D, представляющие два двухбитные двоичные числа AB и CD и три выходных бита, E, F и G, представляющее 4-битное число EFGH (где E — цифра 8), полученное в результате умножение AB на CD. Обратите внимание, что самое большое 2-битное число равно 11, т.е. равно 3 в десятичном виде, поэтому наибольшее произведение равно 3×3 или 9., что требует 4 бита представлять. Вот почему у нас есть 4 бита вывода. Таким образом, для Например, если мы ввели 1011, то A=1, B=0, C=1, D=1, поэтому AB = 10 (в двоичный, что равно 2 в десятичном виде) и CD=11 (в двоичном формате, что равно 3 в десятичном формате). Теперь 2 умножить на 3 равно 6, поэтому 4-битный вывод должен равняться 6, что в двоичном виде равно 0110. Таким образом, наш вывод будет 0110.

Вот начало таблицы истинности, которую вы должны использовать для этой схемы:
А Б С D E F G H
0 0 0 0 0 0 0 0 (0 x 0 = 0)
0 0 0 1 0 0 0 0 (0 x 1 = 0)
0 0 1 0 0 0 0 0 (0 x 2 = 0)
0 0 1 1 0 0 0 0 (0 x 3 = 0)
0 1 0 0 0 0 0 0 (1 x 0 = 0)
0 1 0 1 0 0 0 1 (1 x 1 = 1)
0 1 1 0 0 0 1 0 (1 x 2 = 2)
0 1 1 1 0 0 1 1 (1 x 3 = 3)
1 0 0 0 0 0 0 0 (2 x 0 = 0)
1 0 0 1 0 0 1 0 (2 x 1 = 1)
1 0 1 0 0 1 0 0 (2 x 2 = 4)
1 0 1 1 0 1 1 0 (2 x 3 = 6)
…Убедитесь, что вы понимаете эту таблицу! Для этого проблема, вам просто нужно предоставить последние 4 строки таблицы.
Задача 19 (БОНУС): Завершите задачу №18, создав схема, определенная таблицей истинности, которую вы закончили. Эта схема имеет 4 входа, A, B, C и D, и 4 выхода, E, F, G и H.
Каждый из выходные строки можно рассматривать как собственную функцию над входными строками. Подумай об этом! Например, строка E (8-й бит) верно только когда вы умножаете 3×3, чтобы получить 9, так что это верно только тогда, когда все входные данные верны. То есть:
Е = (((А И В) И С) И D)
Отлично — осталось один (E) и еще три (F, G и H). Сделай это таким же образом, затем создайте свою схему в xCircuitsLab. Окончательно, проверьте, работает ли ваша схема, протестировав ее с различными выборочными входами (для например, как и в предыдущей задаче, когда вы вводите 1011, это представляет задача 2х3, а ответ 6, или 0110, поэтому ваша схема должна выводить 0110. Вы также захотите проверить другие входы и выходы.
6 . Дизъюнктивная нормальная форма
В классе мы также обсуждали дизъюнктивную нормальную форму или ДНФ. Существует простой способ создания DNF для любых логических .
функция:
Написать таблицу истинности функции;
Для каждой строки, которая равна 1 (истина), напишите конъюнкт (И) выбор входных переменных этой строки;
Итак, если у нас есть две входные переменные, x и y, и если x равно 0, а y равно 1, конъюнкт будет ((НЕ x) AND y). Обратите внимание, что это выражение верно только на этой одной строке . На любой другой строке либо (НЕ x) ложно или y ложно, поэтому ((НЕ x) AND y) ложно. Так что выражение выбирает одну строку из таблицы истинности.Соедините эти конъюнкты выбора строки с дизъюнктами (ОР), , так как выражение истинно для любой из этих строк.
Давайте еще раз рассмотрим это на примере. Давай работать с XOR. Итак, сначала составим таблицу истинности:
.х у x Исключающее ИЛИ у
0 0 0
0 1 1
1 0 1
1 1 0Теперь мы добавляем конъюнкты, которые выбирают строки, в которых есть единицы, как такие:
х г x XOR y соединение
0 0 0 —
0 1 1 (НЕ x) И y
1 0 1 x И (НЕ y)
1 1 0 —
Наконец, мы берем дизъюнкт этих конъюнктов, то есть мы ИЛИ их вместе, чтобы получить:x XOR y == ((NOT x) AND y) OR (x AND (NOT у))
Выражение справа представляет собой дизъюнктивную нормальную форму.
из (х исключающее ИЛИ у).
Обратите внимание, что мы можем применить эту же технику к любому логическая функция. Это большое дело, поэтому повторим:
Может быть (и часто есть) лучший способ выразить функцию, возможно, используя меньше вентилей, но вы всегда можете построить ДНФ. Более того, это механический процесс, как описано выше. Так что, если вы не видите хитрой схемы для какой-то функции, вы можете всегда используйте методом перебора и стройте для него ДНФ.
Задача 20. Постройте ДНФ для каждого из следующие функции. Затем создайте схему в xLogicCircuits и убедитесь, что схема работает так же, как исходное выражение.
((НЕ х) ИЛИ у)
(НЕ (х ИЛИ (НЕ у)))
7 . Логические основания ({И, Или, Не}, {И, Не}, {Или, Не}, {Ни}, {Ни}, другие?)
До сих пор мы видели, что можем сократить арифметические функции как сложение и умножение логических функций.
Затем мы увидели что мы можем свести любую булеву логическую функцию к дизъюнктивной нормальной Форма. Наконец, поскольку ДНФ использует только вентили И, ИЛИ и НЕ, мы сделать вывод, что мы можем построить компьютер, используя только вентили И, ИЛИ и НЕ. Стоит повторить:
Вау! Это восхитительно! Будем называть множество разных вентилей, которых вместе достаточно для построения любой логической функции (и Итак, любой компьютер) a логическая основа. Итак, мы только что определили удивительный факт, что множество {И, ИЛИ, НЕ} образует логическую основу. Можем мы сделать лучше? Можем ли мы использовать find меньший логический базис?
Да, можем. Для начала рассмотрим заявку Закон ДеМоргана: 90 544 (x И y) == (НЕ ((НЕ x) ИЛИ (НЕ y)))
и:
(x ИЛИ y) == (НЕ ((НЕ x) И (НЕ y)))Как только мы сведем выражение к его ДНФ, мы можем использовать первая форма закона ДеМоргана для замены каждого (x AND y) на (NOT ((НЕ х) ИЛИ (НЕ у))).
Но это устраняет все И, оставляя только ИЛИ и НЕ. Таким образом, {ИЛИ, НЕ} является логическим основанием. Точно так же мы мог бы использовать вторую форму закона Де Моргана, чтобы заменить OR на И и НЕ. Таким образом, {И, НЕ} также является логическим основанием! Ух ты.
Проблема 21. Используйте законы ДеМоргана, чтобы переписать ДНФ из задачи 20 выглядят следующим образом.
Перепишите ДНФ для ((НЕ x) ИЛИ y) так, чтобы она использует НЕ и ИЛИ (без И).
Перепишите ДНФ для (НЕ (x ИЛИ (НЕ y))) так, чтобы использует только НЕ и И (без ИЛИ).
Теперь осталось два вида ворот. Можем мы сделать лучше? Можем ли мы построить целый компьютер всего из один вид ворота? Давайте посмотрим. Рассмотрим вентиль ИЛИ-НЕ. Эти ворота, которые может быть построен в реальном мире из физических транзисторов, занимает два вводит x и y и выводит true, только если ни x , ни y не истинный.
Это отрицание ворот ИЛИ. Итак имеем:
(x ИЛИ y) == (НЕ (x ИЛИ y))
Со следующей таблицей истинности:
x y x ИЛИ y x ИЛИ y
0 0 0 1
0 1 1 0
1 0 1 0
1 1 1 0Теперь мы знаем, что {ИЛИ, НЕ} является логическим основанием, поэтому мы пытаемся построить каждое из этих двух ворот используют только ворота NOR. Во-первых, для НЕ мы видим далее:
х x ИЛИ x x ИЛИ x
0 0 1
1 1 0Убедитесь, что вы понимаете эту таблицу. Это показывает, что (х NOR x) эквивалентно (NOT x). Таким образом, мы можем переписать каждый вентиль НЕ с помощью ворота NOR. А ворота ИЛИ? Ну, так как NOR является отрицанием ИЛИ, НЕ-ИЛИ — это двойное отрицание, эквивалентное ИЛИ. Что это:
(НЕ (x ИЛИ y)) == (x ИЛИ y)
Но мы знаем, что (НЕ z) == (z НИ z), поэтому мы складываем их вместе, чтобы увидеть, что:
((x ИЛИ y) ИЛИ (x ИЛИ y)) == (x ИЛИ y)Мы сделали это! Мы показали, что {NOR} является логическая основа.
.Или, перефразируя, мы доказали этот удивительный факт:
Вау! Это невероятно. С достаточным количеством NOR-ворот, и достаточно терпения, вы можете собрать современный цифровой компьютер. На самом деле, вы бы использовали именно эти шаги:
Для каждой вычисляемой арифметической функции уменьшите к булевой логической функции.
Для каждой из этих булевых логических функций выразите функция в дизъюнктивной нормальной форме. Теперь у нас есть схемы с И, ИЛИ и НЕ.
Используйте закон ДеМоргана, чтобы заменить каждое И на ИЛИ и НЕ, потому что (x И y) == (НЕ ((НЕ x) ИЛИ (НЕ y))).
Затем замените каждое ИЛИ на НЕ с этим правилом: (x ИЛИ y) == ((x ИЛИ y) ИЛИ (x ИЛИ y))
Наконец, замените каждое NOT на NOR следующим правилом: (НЕ х) == (х НИ х)
Вот и все. Остались только ворота NOR ворота!
Проблема 22.
С помощью этого метода перепишите выражение в части (a) задачи 21, использующее только вентили ИЛИ-НЕ. Это скучный! Теперь, в качестве бонуса, создайте эту схему в xLogicCircuits. Обратите внимание, что вы можете построить вентиль НЕ-ИЛИ, очистив экран, построив простая схема, которая соединяет выход вентиля ИЛИ с вентилем НЕ и затем на выход, а затем назвав это «NOR» и нажав «iconify» кнопка. Теперь у вас есть вентиль ИЛИ-НЕ для построения схемы исключающего ИЛИ!
Проблема 23. Точно так же, как НЕ-ИЛИ (НЕ (x ИЛИ y)), НЕ-И (НЕ (х И у)). Кроме того, как NOR является логической основой, так и NAND. Докажите этот факт, показав, как преобразовать схемы, которые имеют только И и НЕ вентилируется в эквивалентные схемы, которые имеют только вентили НЕ-И. Аргумент следует за аналогичным аргументом для вентилей НЕ-ИЛИ, как только что описано.
8. Бонус: Схемы, которые помнят
Это только верхушка айсберга для цифровых схем, и гораздо больше ума требуется, чтобы построить настоящий современный компьютер.








 В этом случае вам также понадобятся примеры из этой лаборатории, которые находятся в
этот файл:
В этом случае вам также понадобятся примеры из этой лаборатории, которые находятся в
этот файл: 
 Например, функция И принимает две переменные, и
это правда только если обе его входных переменных верны и ложны
в противном случае. Итак, (x AND y) истинно, если оба x и y истинны (посмотрите, почему это
называется И?). Вот его таблица истинности:
Например, функция И принимает две переменные, и
это правда только если обе его входных переменных верны и ложны
в противном случае. Итак, (x AND y) истинно, если оба x и y истинны (посмотрите, почему это
называется И?). Вот его таблица истинности: Разница? Можно построить логические схемы как реальные физические устройства, которые вы можете держать, трогать и
в некоторых случаях даже подключаются и используются для написания программ на Java (как, в конце концов,
компьютеры построены из логических схем).
Разница? Можно построить логические схемы как реальные физические устройства, которые вы можете держать, трогать и
в некоторых случаях даже подключаются и используются для написания программ на Java (как, в конце концов,
компьютеры построены из логических схем). То есть, если либо А, либо
B включен, затем C будет включен, и свет загорится. Если оба
A и B выключены, тогда C будет выключен, и линия не будет светиться. Если
вы должны были построить таблицу, описывающую это поведение, она будет выглядеть так:
То есть, если либо А, либо
B включен, затем C будет включен, и свет загорится. Если оба
A и B выключены, тогда C будет выключен, и линия не будет светиться. Если
вы должны были построить таблицу, описывающую это поведение, она будет выглядеть так:
 Но как это помогает?
Но как это помогает? Это просто И
функция! Итак, С = (А И В). Теперь на D:
Это просто И
функция! Итак, С = (А И В). Теперь на D:
 Вам важно
понять, как последовательные полные сумматоры действительно соответствуют тому, как вы
добавил бы два числа самостоятельно. Как только вы поймете, что такое 4-битный сумматор,
затем используйте свои знания о представлении отрицательных чисел в дополнении до двух
понять действие 4-бит минус .
Вам важно
понять, как последовательные полные сумматоры действительно соответствуют тому, как вы
добавил бы два числа самостоятельно. Как только вы поймете, что такое 4-битный сумматор,
затем используйте свои знания о представлении отрицательных чисел в дополнении до двух
понять действие 4-бит минус .
 Сделайте то же самое для другого закона (x OR y).
Сделайте то же самое для другого закона (x OR y).  Затем
вам придется сделать это еще два раза, и, наконец, устранить все
двойное отрицание (НЕ-НЕ).
Затем
вам придется сделать это еще два раза, и, наконец, устранить все
двойное отрицание (НЕ-НЕ). 
 Каждый из
выходные строки можно рассматривать как собственную функцию над входными строками.
Подумай об этом! Например, строка E (8-й бит)
верно только когда вы умножаете 3×3, чтобы получить 9, так что это верно только тогда, когда все входные данные верны. То есть:
Каждый из
выходные строки можно рассматривать как собственную функцию над входными строками.
Подумай об этом! Например, строка E (8-й бит)
верно только когда вы умножаете 3×3, чтобы получить 9, так что это верно только тогда, когда все входные данные верны. То есть:  функция:
функция: из (х исключающее ИЛИ у).
из (х исключающее ИЛИ у).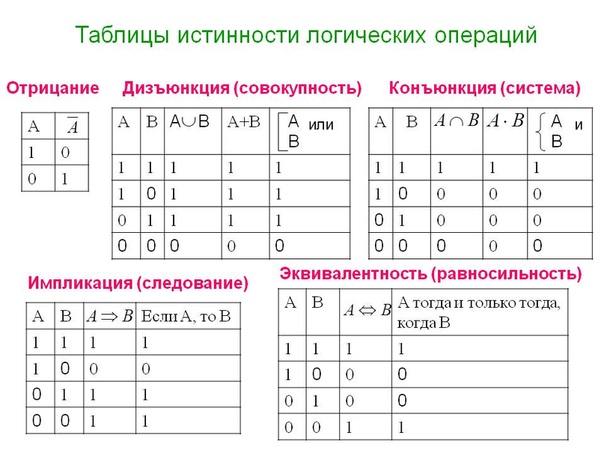 Затем мы увидели
что мы можем свести любую булеву логическую функцию к дизъюнктивной нормальной
Форма. Наконец, поскольку ДНФ использует только вентили И, ИЛИ и НЕ, мы
сделать вывод, что мы можем построить компьютер, используя только вентили И, ИЛИ и НЕ.
Стоит повторить:
Затем мы увидели
что мы можем свести любую булеву логическую функцию к дизъюнктивной нормальной
Форма. Наконец, поскольку ДНФ использует только вентили И, ИЛИ и НЕ, мы
сделать вывод, что мы можем построить компьютер, используя только вентили И, ИЛИ и НЕ.
Стоит повторить: Но это устраняет все И, оставляя только
ИЛИ и НЕ. Таким образом, {ИЛИ, НЕ} является логическим основанием. Точно так же мы
мог бы использовать вторую форму закона Де Моргана, чтобы заменить OR на
И и НЕ. Таким образом, {И, НЕ} также является логическим основанием! Ух ты.
Но это устраняет все И, оставляя только
ИЛИ и НЕ. Таким образом, {ИЛИ, НЕ} является логическим основанием. Точно так же мы
мог бы использовать вторую форму закона Де Моргана, чтобы заменить OR на
И и НЕ. Таким образом, {И, НЕ} также является логическим основанием! Ух ты. Это отрицание ворот ИЛИ. Итак имеем:
Это отрицание ворот ИЛИ. Итак имеем:  Или, перефразируя, мы доказали этот удивительный факт:
Или, перефразируя, мы доказали этот удивительный факт: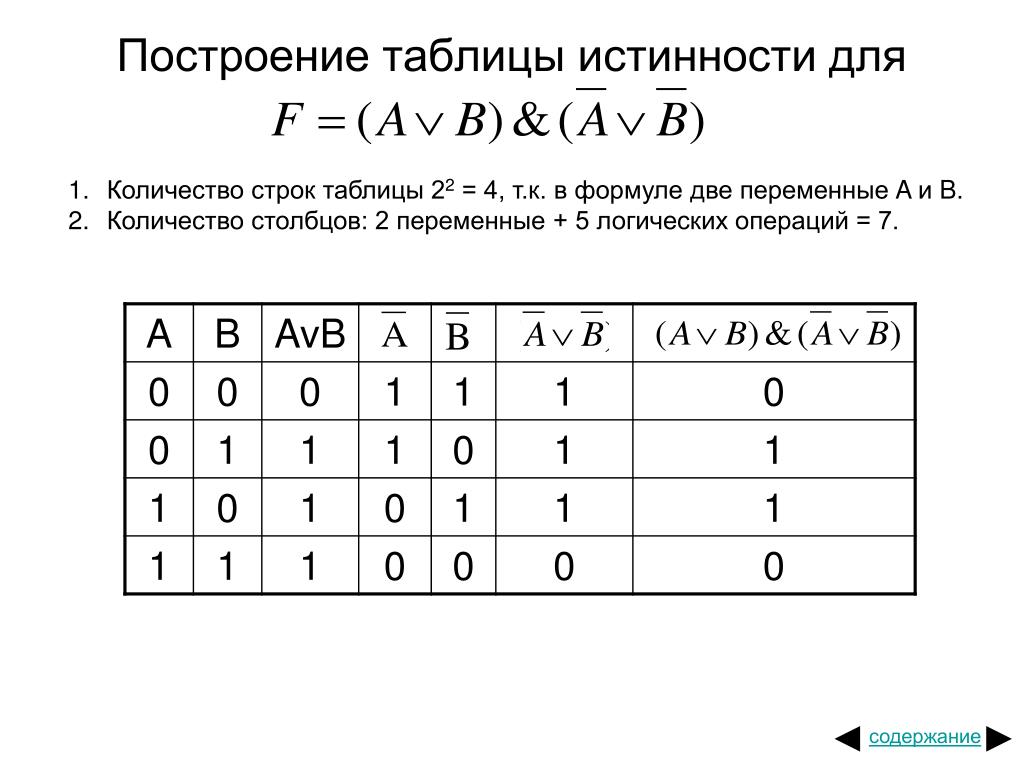 С помощью этого метода перепишите
выражение в части (a) задачи 21, использующее только вентили ИЛИ-НЕ. Это
скучный! Теперь, в качестве бонуса, создайте эту схему в xLogicCircuits.
Обратите внимание, что вы можете построить вентиль НЕ-ИЛИ, очистив экран, построив
простая схема, которая соединяет выход вентиля ИЛИ с вентилем НЕ и
затем на выход, а затем назвав это «NOR» и нажав «iconify»
кнопка. Теперь у вас есть вентиль ИЛИ-НЕ для построения схемы исключающего ИЛИ!
С помощью этого метода перепишите
выражение в части (a) задачи 21, использующее только вентили ИЛИ-НЕ. Это
скучный! Теперь, в качестве бонуса, создайте эту схему в xLogicCircuits.
Обратите внимание, что вы можете построить вентиль НЕ-ИЛИ, очистив экран, построив
простая схема, которая соединяет выход вентиля ИЛИ с вентилем НЕ и
затем на выход, а затем назвав это «NOR» и нажав «iconify»
кнопка. Теперь у вас есть вентиль ИЛИ-НЕ для построения схемы исключающего ИЛИ! 