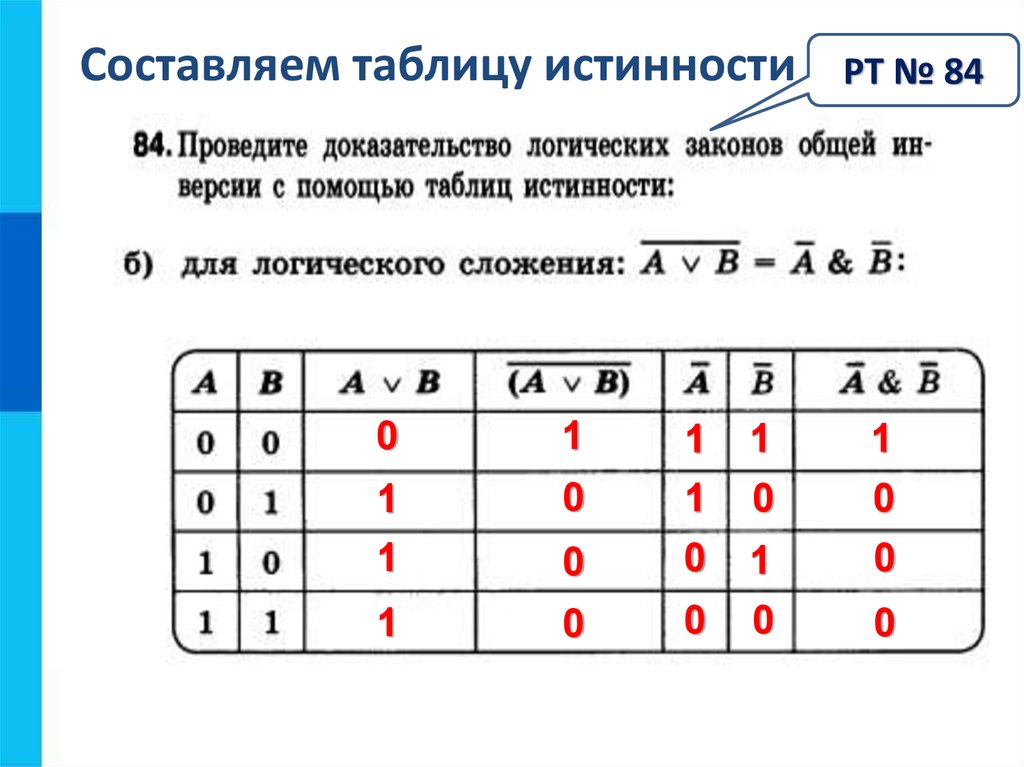
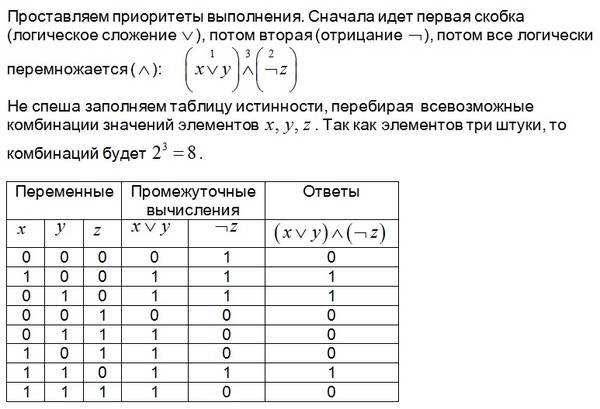
Разберите решение следующих примеров — Студопедия
Поделись
П р и м е р 1. Построить отрицание для следующих высказываний и определить их истинностное значение:
a) «11>0»;
б) «7 делится на 3»;
в) «3+4=7».
Решение. a) отрицанием истинного высказывания ”11>0» является ложное высказыванием «11 0».
б) отрицанием ложного высказывания «7 делится на 3» будет истинное высказывание «7 не делится на 3».
в) «3+4 7» ложное высказывание.
П р и м е р 2. Записать символически высказывание «15 делится на 3 и на 5».
Решение. Это высказывание есть конъюнкция двух высказываний «15 делится на 3» и «15 делится на 5». Поэтому получим:
П р и м е р 3. Прочитать по правилам русского языка символически записанное высказывание , если «2 – простое число», «2 – четное число».
Ответ: « 2 – простое и четное число».
П р и м е р 4. Пусть «Иван умен», «Петр умен»
Записать символически:
a) Иван умен и Петр глуп;
б) Иван и Петр оба глупы;
в) или Иван умен или Петр глуп;
г) если Иван умен, то Петр глуп.
Решение.
a)
б)
в)
г) .
П р и м е р 5. Пусть «У меня есть собака», «У меня есть кошка”. Перевести на разговорный язык:
a) ;
б) ;
в) ;
г) .
Решение. a)У меня есть собака или у меня нет кошки;
б) Если у меня есть собака, то у меня нет кошки;
в) Или у меня нет собаки и есть кошка, или у меня нет кошки;
г) Если у меня нет собаки, то у меня нет кошки.
П р и м е р 6. Какие из данных высказываний истинны?
a) 3 5;
б) 7 7;
в) 3 0.
Решение. a) имеем дизъюнкцию: Так как первый член дизъюнкции истинный, то и вся дизъюнкция истинна.
б) высказывание «7 7» истинно, так как «7=7» истинно.
в) «3 0» ложно, т.к. оба члена дизъюнкции ложны.
П р и м е р 7. Постройте импликацию высказывания «25 при делении на 7 дает остаток 2» и «11>0» и определите ее истинностное значение.
Решение. «Если 25 при делении на 7 дает остаток 2, то 11>0» – истинное высказывание, поскольку истинно его заключение.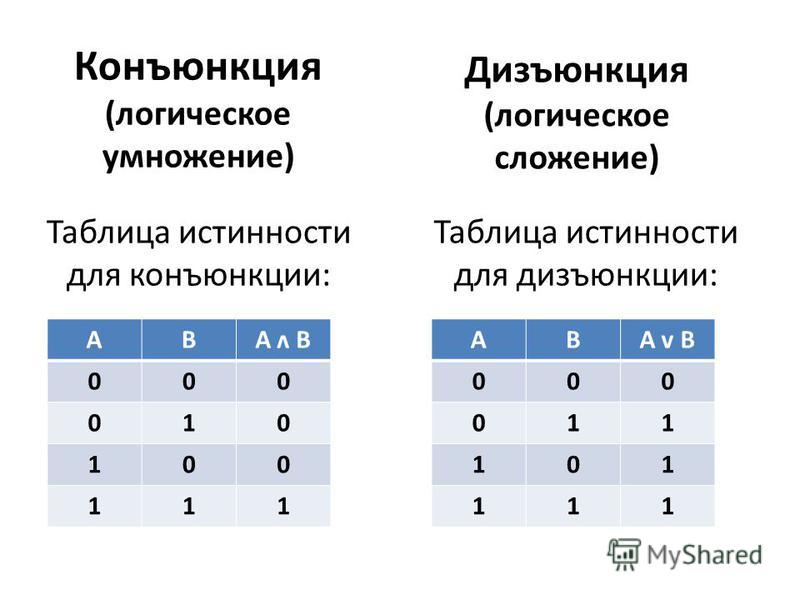
П р и м е р 8. Постройте эквиваленцию высказываний «25 при делении на 7 дает остаток 2» и «2 является конем уравнения », и определите ее истинное значение.
Решение. «25 при делении на 7 дает остаток 2 тогда и только тогда, когда 2 является конем уравнения ». Это высказывание истинно, как эквиваленция ложных высказываний.
П р и м е р 9.Какие из данных высказываний истинны:
a) ;
б) ;
в) ;
г) ;
д) ;
е) ;
ж) ;
з) .
Ответ: а), б), г), д), е) – истинны;
в), ж), з) – ложны.
П р и м е р 10. Построить таблицы истинности для следующих формул:
a) ;
б) ;
в) ;
г) .
Определить является ли каждая из формул тавтологией, противоречием или выполнимой.
Решение. Для сложной формулы F можно предложить следующий порядок заполнения таблицы истинности:
1.В строку выписываются сначала все атомы, а затем все подформулы F (не считая атомов), начиная с простых и кончая самой формулой F.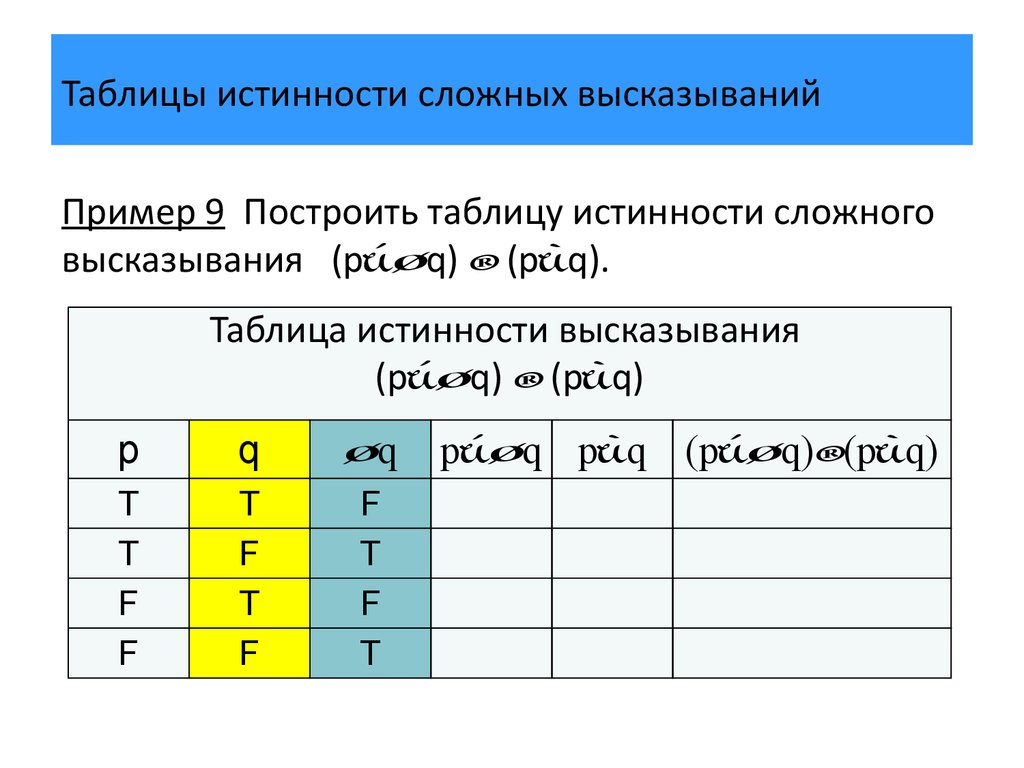
Для каждой записи подготавливается столбец.
2.Атомам формулы F даются всевозможные наборы значений из множества {1;0}, компоненты которых записываются в соответствующие столбцы. Можно показать, что различных наборов значений истинности атомов (значит и строк таблицы) будет всего , где n – число атомов формулы F. Для удобства значения располагают так: под первым атомом подряд пишут половину (т.е. ) значений 1, затем столько же значений 0; под вторым атомом пишут подряд четвертую часть (т.е. ) значений 1, затем столько же значений 0, повторяют это еще раз и т.д. Под последним атомом значений 1 и 0 чередуются.
3.Столбцы всех подформул формулы F и столбец самой формулы F заполняются согласно определениям соответствующих операций.
а) так как формула имеет две переменные, ее таблица истинности содержит четыре строки .
Так как последний столбец таблицы содержит только значения 1, то формула является тавтологией.
Заметим, что 3, 4, 5 столбцы являются вспомогательными и в таблице истинности могут отсутствовать.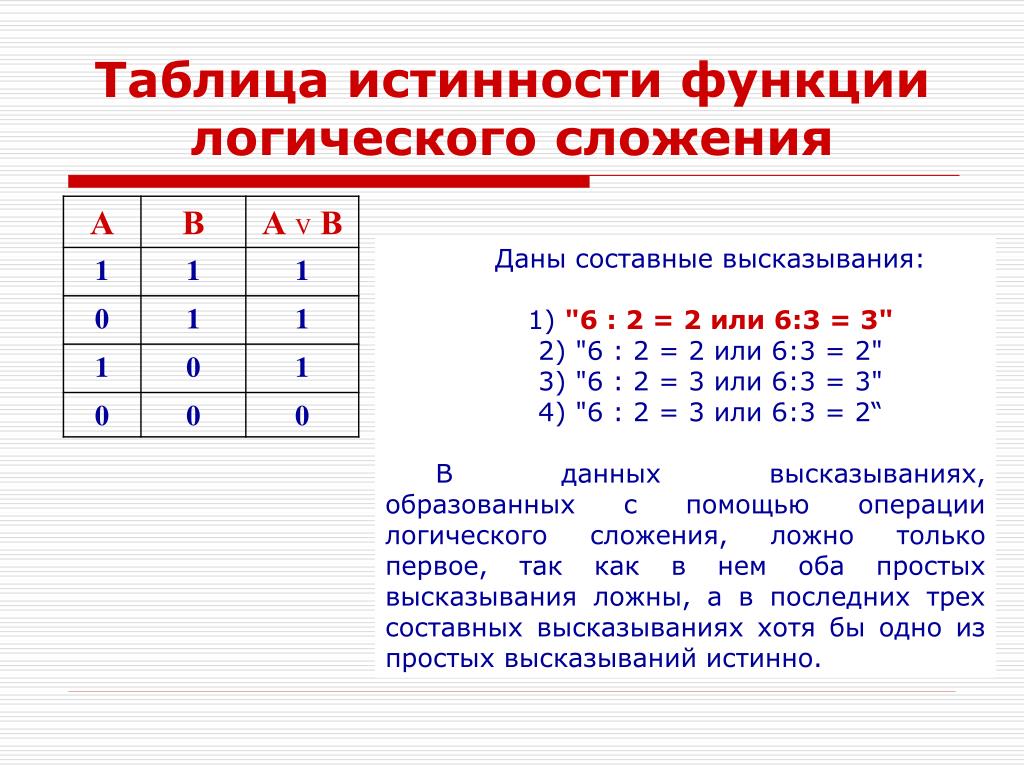
б) Поскольку формула содержит три высказывательные переменные, то ее таблица истинности содержит восемь строк .
Эта формула является одновременно выполнимой и опровержимой, так как на наборе значений переменных 0, 0, 0 формула принимает значение 1, а на остальных наборах формула принимает значение 0.
в)
В этой таблице не приведен вспомогательный столбец. Формула является противоречием.
г)
В построенной таблице не заполнены вспомогательные столбцы (сделайте это самостоятельно). Формула является одновременно выполнимой и опровержимой.
П р и м е р 11. Проверить являются ли следующие формулы равносильными:
a) и ;
б) и .
Решение.
а) составим таблицы истинности для данных формул (их удобно совместить). Получим:
Сравнивая два последних столбца, мы видим, что они одинаковые. Значит, формулы равносильны (или логически равны): .
б) составим таблицы истинности:
Сравнивая 6-й и 8-й столбцы таблицы, видим, истинностные значения формул различаются при значениях переменных , , .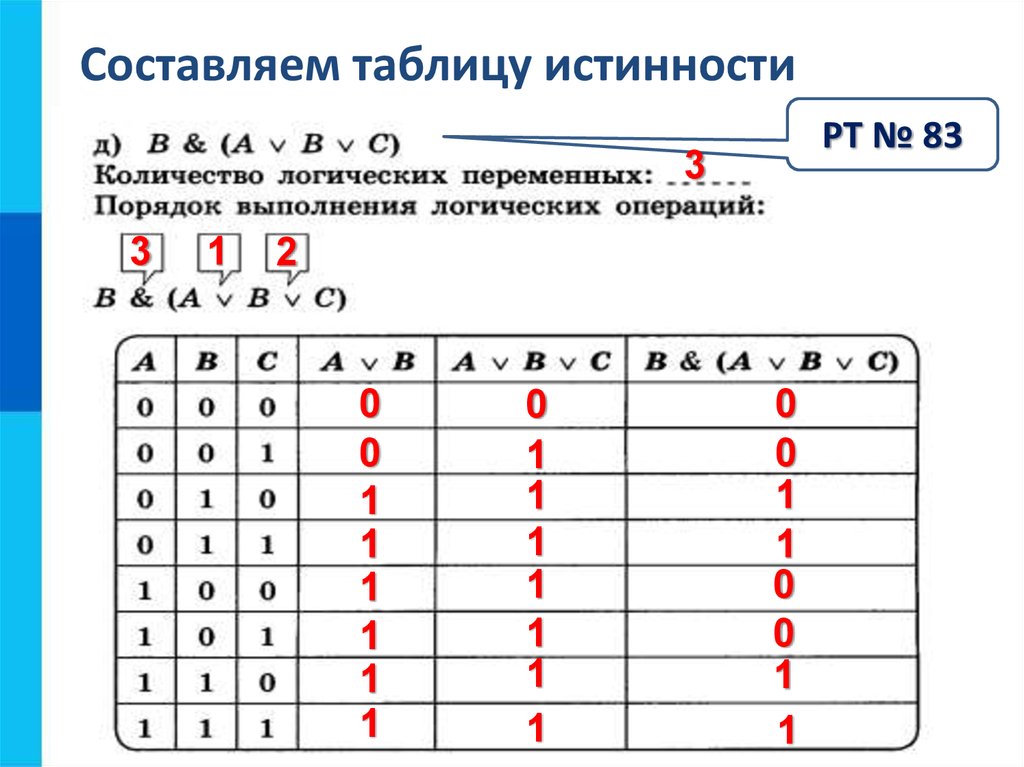
Следовательно, эти формулы не являются равносильными.
П р и м е р 12. Упросить формулы, применяя основные равносильности алгебры высказываний (стр. 32 учебного пособия Л.М.Мартынова).
а) ;
б) ;
в) ;
г) .
Решение.
а) (здесь применили дистрибутивный закон, закон противоречия 7
б) , т.к. если обозначить через Х, то получим по закону поглощения 4.
в) .
г)
.
П р и м е р 13. Записать формулу с помощью только конъюнкции и отрицания.
Решение.
.
П р и м е р 14. Доказать, что формула есть логическое следствие формул .
Решение. 1-й способ. Докажем, что по определению. Для этого составим всевозможные наборы истинностных значений для высказывательных переменных , вычислим для них соответствующие значения посылки и значения и сравним только те значения этих формул, при которых посылка истинна.
Легко понять, что первая формула принимает значение 1 лишь для набора истинностных значений 0,0.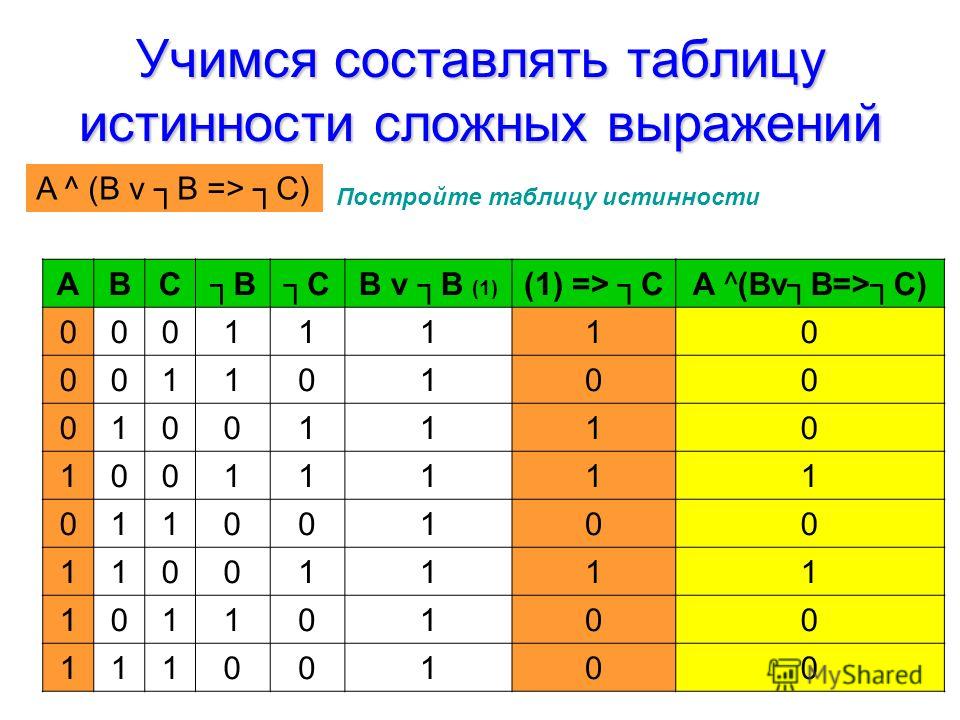
Требуемое логическое следование вытекает из фрагмента таблицы истинности
2-й способ. По признаку логического следования для высказывательных формул достаточно показать, что импликация , тождественно истинна (или тавтология).
Докажем это с помощью преобразований:
3-й способ. Методом от противного. Предположим, что формула не является логическим следствием формул и . Значит, при истинных посылках и формула принимает значение 0. Т.к. , то , . Но тогда мы получаем противоречие с предположением об истинности посылки . Полученное противоречие доказывает, что наше предположение неверно, и значит, формула является логическим следствием посылок и .
Приложения алгебры высказываний
Алгебра высказываний нашла применение в логико-математической практике. Во-первых, при анализе и синтезе контактных схем.
П р и м е р 15.Упростить релейно-контактную схему и определить условия ее работы.
Решение. Запишем функцию проводимости этой схемы и преобразуем ее с помощью основных равносильностей алгебры высказываний.
По новой функции проводимости строим упрощенную схему:
Из полученной формулы, очевидно, что . Это и есть условия работы данной схемы.
П р и м е р 16. Для комитета, состоящего из 4 человек сконструировать электрическую цепь так, чтобы лампочка зажигалась, если за данное предложение проголосовало меньшинство.
Решение. Для данных условий работы составим функцию проводимости:
Схема будет такой:
Во-вторых, в математике часто приходится формулировать утверждения, которые являются отрицаниями других утверждений, Обычно трудности вызывают формулировки отрицаний сложных предложений, в которых присутствует импликация. Процесс нахождения удобной формулировки отрицания некоторого предложения в алгебре высказываний получил название построения отрицания. Чаще всего для формулы , имеющей в записи импликации, построить отрицание означает следующее: для формулы найти равносильную и по возможности простую формулу , в которой нет импликаций, а знаки отрицания (если они есть) относятся только к атомам.
П р и м е р 17. Перевести предложение «Если я устал или голоден, то не могу заниматься» на логический язык, построить его отрицание и сформулировать это отрицание по-русски.
Введем атомы: «Я устал», «Я голоден»; наконец, «Я могу заниматься». Тогда заданное предложение запишется формулой . Далее
Значит, отрицание предложения формулируется так: «Я либо устал, либо голоден, но могу заниматься».
В-третьих, аппарат алгебры высказываний позволяет выяснять правильность выводов из некоторого списка положений.
П р и м е р 18. Проанализировать правильность вывода в рассуждении: «Если Коля дома, то у него горит свет и отрыто окно. Свет у Коли не горит. Значит, его нет дома».
Введем атомы: «Коля дома», «У Коли горит свет»; «У Коли открыто окно». Тогда заданное рассуждение запишется в виде . Чтобы убедиться в его правильности, достаточно показать, что формула является тождественно истинной.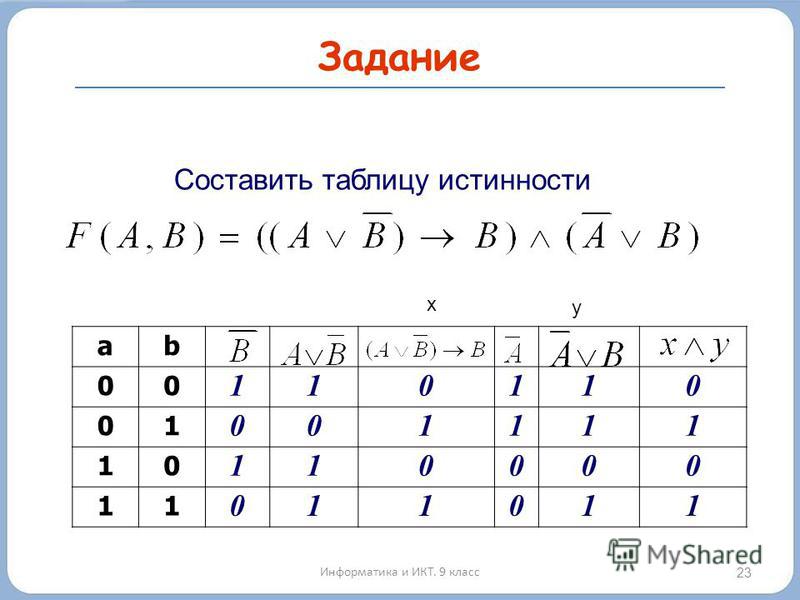
Имеем: .
И, наконец, с помощью алгебры высказываний можно решать различные логические задачи.
Обобщённый приём решения логических задач методом алгебры высказываний:
1.Выделяем и обозначаем все участвующие в задаче простые высказывания;
2. Строим из них содержащиеся в условии задачи сложные высказывания;
3.Рассматриваем конъюнкцию построенных посылок, она истинна по условию;
4,Преобразуем эту конъюнкцию с помощью логических равенств к более простому виду, удобному для получения требуемой в задаче информации;
5. Извлекаем эту информацию (ответы на вопросы задачи).
Воспользуемся данным приёмом при решении логической задачи.
П р и м е р 19. Согласно инструкции капитан должен находиться на судне всегда, за исключением случаев, когда с судна выгружают груз; если же груз не выгружают, то рулевой никогда не отсутствует, если не отсутствует капитан. В каких случаях рулевой обязан присутствовать на судне?
Решение.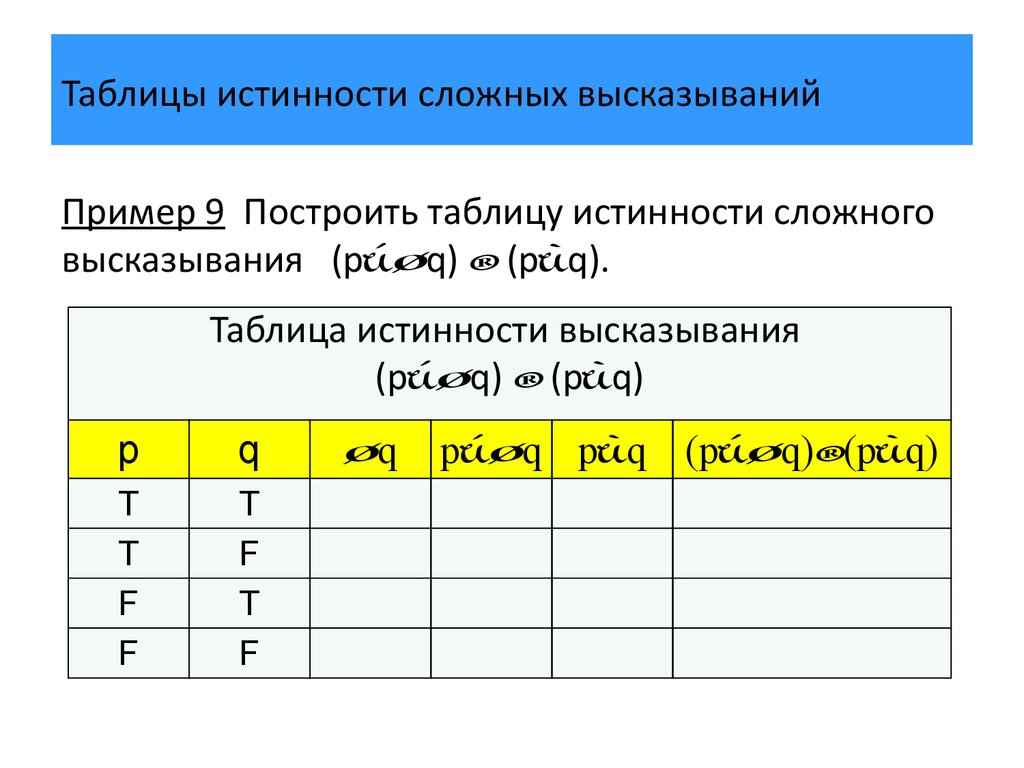
1. Введём обозначения, соответствующие простым высказываниям: «Капитан присутствует на судне»; «С судна выгружают груз»; «Рулевой присутствует на судне».
2. В инструкции могут быть выделены одно простое и два сложных высказывания: .
3. .
4. Упростим данную конъюнкцию: .
5. Ответ: Если с судна не выгружают груз, то рулевой обязан присутствовать вместе с капитаном.
П р и м е р 20. Три девушки: Аля, Валя и Катя ходили в театр. Одна из них была в красном платье, другая – в белом, третья – в синем. На вопрос, какое на каждой из девушек было платье, они дали ответ: Аля была в красном, Катя – не в синем, Валя – не в красном. В этом ответе из трех частей одна верна, две – не верны. В каком платье была каждая из девушек?
Решение. Введем обозначения:
– Аля в красном платье;
– Катя в синем платье;
– Валя в красном платье, и тогда ответ, который дали девушки, можно записать в виде конъюнкции . Так как по условию в этом ответе из трех частей одна верна, а две не верны, то истинна следующая дизъюнкция:
.
Упростив эту формулу, получаем
.
Поскольку первая и третья конъюнкции ложны, то истинна , то есть: Валя в красном платье, Катя в белом платье, Аля в синем платье.
Построение таблиц истинности презентация, доклад
«Построение таблиц истинности»
Информатика 10 класс
2 задание
Даны высказывания: А= «3*3=9»,В=»3*3=10» определить истинность высказываний
— А ∧ В — ложь
А ∧ В — истина
В ∨ А — ложь
А ∨ В — истина
1 задание
По мишеням произведено три выстрела. Рассмотрено высказывание: Рк= «мишень поражена к-ым выстрелом», где к=1,2,3. Что означают следующие высказывания.
1 задание
Р1 ∨ Р2 ∨ Р3
Одним из трех выстрелов попали в мишень
— Р1 ∧ Р2 ∧ Р3
Всеми тремя выстрелами попали в мишень
3 задание
заполнить таблицу
3 задание
Изучение нового материала
Таблица истинности – это таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний
Алгоритм построения таблицы истинности:
1.
подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице m = 2n;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов в таблице: число переменных плюс число операций;
6. выписать наборы входных переменных ;
7. провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной в п.4 последовательностью
Наборы входных переменных
а) определить количество наборов входных переменных;
б) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю —1;
в) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0;
г) продолжать деление колонок значений последующих переменных на 8, 16 и т.
д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа.
Приоритеты операций
отрицание
конъюнкция
дизъюнкция
импликация
эквивалентность
Построим таблицу истинности выражения
A∧ (B ∨ В∧С)
Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8.
Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.
установим последовательность выполнения логических операций с учетом скобок и приоритетов
заполним наборы входных переменных
заполним наборы входных переменных
заполним наборы входных переменных
проведем заполнение таблицы истинности по столбикам
проведем заполнение таблицы истинности по столбикам
проведем заполнение таблицы истинности по столбикам
проведем заполнение таблицы истинности по столбикам
Закрепление новых знаний
1.
Построить таблицы истинности для следующих выражений:
а) А∨ (В ∨ В)
б)А∧ (В ∧ В→С)
* в)А ∨(В ∨ В) ∧ А ∧(В→С)
Контроль и самопроверка знаний
Индивидуальная работа по карточкам, после выполнения заданий проверить правильность работы у соседа по парте с оцениванием.
Домашнее задание
Уровень знания: знать, что такое таблица истинности, уметь строить таблицу истинности
Уровень понимания: составить таблицы истинности и определить истинность формулы
1.( А→В) ∧ (А∧В) ∨ (А∧В)
2. А∨ А∨ B ∧ А∧В
Скачать презентацию
[Решено] 6.6.5 Вычисление значений истинности Вычисление значений истинности…
Получите больше от подписки*
- Доступ к более чем 100 миллионам учебных ресурсов по конкретным курсам
- Круглосуточная помощь опытных наставников по более чем 140 предметам
- Полный доступ к более чем 1 миллиону решений для учебников
*Вы можете изменить, приостановить или отменить в любое время
Вопрос от ConstableMaskPuppy246
6.
6.5 Вычисление значений истинности
Вычислите значения истинности следующих формул, где все A-L истинны, а M-Z ложны.
A. (A ∧ Q)
B. ((P ∧ B) <-> (L ∨ (Q ∧ ¬S)))
C. ((Q → (R → F)) → (( D → Q) → (C → R)))
D. (((R <-> S) ∨ (P ∧ ¬Q)) ∨ (¬R ∧ S))
E. (P ∧ (P ∧ (P ∧ (P ∧ P))))
F. (P ∧ (B ∧ (C ∧ (D ∧ P))))
G. [-[D <->-(X→ (Z • Q))] ∨ P]
H. -[[D <->-(X→ (Z • Q))] ∨ K]
I. -(P ∧ (P ∧ (P ∧ (P ∧ P))))
J. (P ∧ -(B ∧ (-C ∧ -(D ∧ P))))
K. (-((R <-> S) ∨ -(P ∧ ¬Q)) ∨ -(¬R ∧ S))
L. (-((D <-> S) ∨ -(E ∧ ¬Q)) ∨ -(¬B ∧ S))
M. ((Q → ((R → S)) → (P → Q) → (P → R)))
N. ((B → ((R → E)) → (A → Q) → (P → R)))
6.6.6 Таблицы истинности Классификация
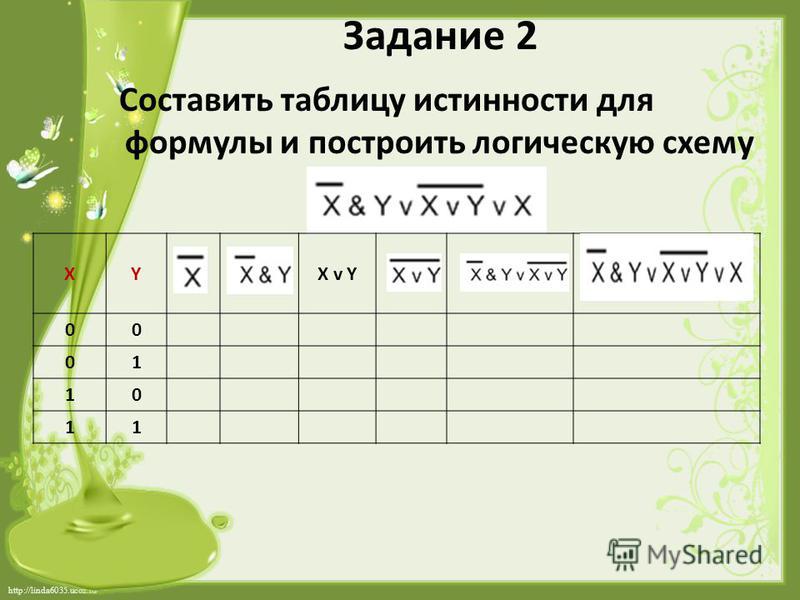
Постройте таблицу истинности для классификации следующих отдельных предложений:
A. -(P ∧ (P ∧ (P ∧ (P ∧ P))))
B. (((R <-> S) ∨ ( R ∧ ¬S)) ∨ (¬R ∧ S))
C. ((P ∧ R) <-> (P ∨ (R ∧ ¬P)))
D.
[-[D <-> — (E→ (F • D))] ∨ E]
E. (((P ∧ Q) ∨ R) <-> ((P ∨ R) ∧ (Q ∨ R)))
6.6.7 Истина Tables Compare
Постройте таблицу истинности для сравнения следующих наборов утверждений. Многие из них взяты с Carnap.io/book CC-BY 4.0 Intl License.
A. [~(B∧E)→I] / [(B∧E)→~I]
B. [-[Z <-> -(X→ (Z • Q))] ∨ Q] / Z / (X • Q)
C. (P → Q) / (~P ∨ Q) / (~Q → ~P)
D. ((P ∧ R) / (P ∨ (R ∧ ¬ P)))
E. -[D <-> -(E→ (E • D))] / [-D <-> (-E→ (E • D))]
F. (P → Q) / (Q <-> R) / (P → R)
6.6.8 Таблицы истинности Достоверность
Постройте таблицу истинности для проверки достоверности каждого из следующих выводов. Многие из них взяты с Carnap.io/book CC-BY 4.0 Intl License.
A. (P ∨ R) // (¬P → ¬¬R)
B. P // (P ∧ ¬(P → P))
C. (P → Q) // (Q → P)
D. A / (A → B) // (B → A)
E. D / (C → (C → (C→D)))
F. ¬P / (P <- > R) // (R <-> ¬(P → P))
G. ((P ∧ Q) <-> (P ∨ R)) // ((P ∧ Q) ∨ ¬(P ∨ R ))
Искусство и гуманитарные науки Философия
Ответ и объяснение
Решено проверенным экспертом
Рейтинг Полезно
Ответил jdespanola
ce dui lectus, congue vel laoreet ac, dictum vitae odio.
Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat
Разблокировать полный доступ к Course Hero
Изучите более 16 миллионов пошаговых ответов из нашей библиотеки
Подпишитесь, чтобы посмотреть ответ
ilisis. Pellentesq
ur laoree
ce dui lectus, congue vel laoreet ac, dictum vitae odio. Donec a
ur laoree
ipsum dolor sit amet, consectetur adipiscing eli
risus ant
inia pulvinar tortor nec facilisis. Pellentesque
risus ant
inia pulvinar tortor nec facilisis. Пеллентеск
ur laoree
dictum vitae odio. Донец Аликет. Lorem ipsum
risus ant
a molestie consequat, ultrices ac magna. Fusce du
ur laoree
fficitur laoreet.
Nam risus ante, dapibus a molestie c
risus ant
molestie consequat, ultrices ac magna. Fusce dui lectus, congue ve
molestie
ec aliquet. Lorem ipsum dolor sit amet, consectetur adipiscing elit
ur laoree
inia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur lao
ur laoree
nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ant
ur laoree
или nec facilisis. Pellentes
, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, co
acinia pulvinar tortor nec facilisis. Pellentesqu
lestie consequat,
congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem
s ante, dapibus a
a. Fusce dui lectus, congue vel laoreet ac, dict
lestie consequat,
, ultrices ac magna. Fusce dui lectus, congue
lestie consequat,
sus ante, dapibus a molestie consequat, ultrices ac magna. Fusce du
s ante, dapibus a
ac, dictum vitae odio.
Don
lestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolo
, ultrices ac magna. Fusce dui lectus, congue
inia pulvinar tort
lestie consequat, ultrices ac magna. Fusce dui lectus, congue vel
lestie consequ
cing elit. Nam lacinia pulvinar tortor nec facil
inia pulvinar tortor
fficitur laoreet. Nam risus ante, dapibus a mo
trices ac magna. F
s a molestie consequat, ultrices ac magna. Fusce dui lectus, congue ve
lestie consequ
congue vel laoreet ac, dictum vitae odio
lestie consequ
inia pulvinar tortor nec fa
congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar
нг элит. Nam lacinia pulvinar tortor nec fa
icitur laore
, dictum vitae odio. Донец Аликет
а. Fusce dui le
, consectetur adipiscing elit.
а. Fusce dui le
consectetur adipiscing elit. Nam la
e vel laoreet
m risus ante, dapibus a molestie conse
ultrices ac
risus ante, dapibus a molestie consequat, ultri
e vel laoreet
m risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui le
icitur laore
Пошаговое объяснение
ac, dictum vitae odio. Донец
облегчение. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie conequat,
sum dolor sitame
risus ant
at, ultrices ac magna. Fusce dui lectus, congue
рисус муравей
ipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesq
ur laoree
ce dui lectus, congue vel laoreet ac, dictum vitae odio. Donec a
risus ant
ipsum dolor sit amet, consectetur adipiscing eli
risus ant
inia pulvinar tortor nec facilisis. Pellentesque
risus ant
inia pulvinar tortor nec facilisis.
Pellentesque
ur laoree
dictum vitae odio. Донец Аликет. Лорем ипсум
risus ant
a molestie conequat, ultrices ac magna. Fusce du
ur laoree
fficitur laoreet. Nam risus ante, dapibus a molestie c
risus ant
molestie consequat, ultrices ac magna. Fusce dui lectus, congue ve
molestie
ec aliquet. Lorem ipsum dolor sit amet, consectetur adipiscing elit
ur laoree
inia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur lao
ur laoree
не включенные в другие группировки Pellentesque dapibus efficitur laoreet. Nam risus ant
ur laoree
или nec facilisis. Pellentes
, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, co
acinia pulvinar tortor nec facilisis. Pellentesqu
lestie consequat,
congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem
s ante, dapibus a
a. Fusce dui lectus, congue vel laoreet ac, dict
lestie consequat,
, ultrices ac magna.
Fusce dui lectus, congue
lestie consequat,
sus ante, dapibus a molestie consequat, ultrices ac magna. Fusce du
s ante, dapibus a
ac, dictum vitae odio. Don
lestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolo
, ultrices ac magna. Fusce dui lectus, congue
inia pulvinar tort
lestie consequat, ultrices ac magna. Fusce dui lectus, congue vel
dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentes
Cing elit. Nam lacinia pulvinar tortor nec facil
s ante, dapibus a molestie consequat, ultrices ac magna. Fu
fficitur laoreet. Nam risus ante, dapibus a mo
at, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dict
s a molestie consequat, ultrices ac magna. Fusce dui lectus, congue ve
sum dolor sit amet, consectetur adipiscing elit.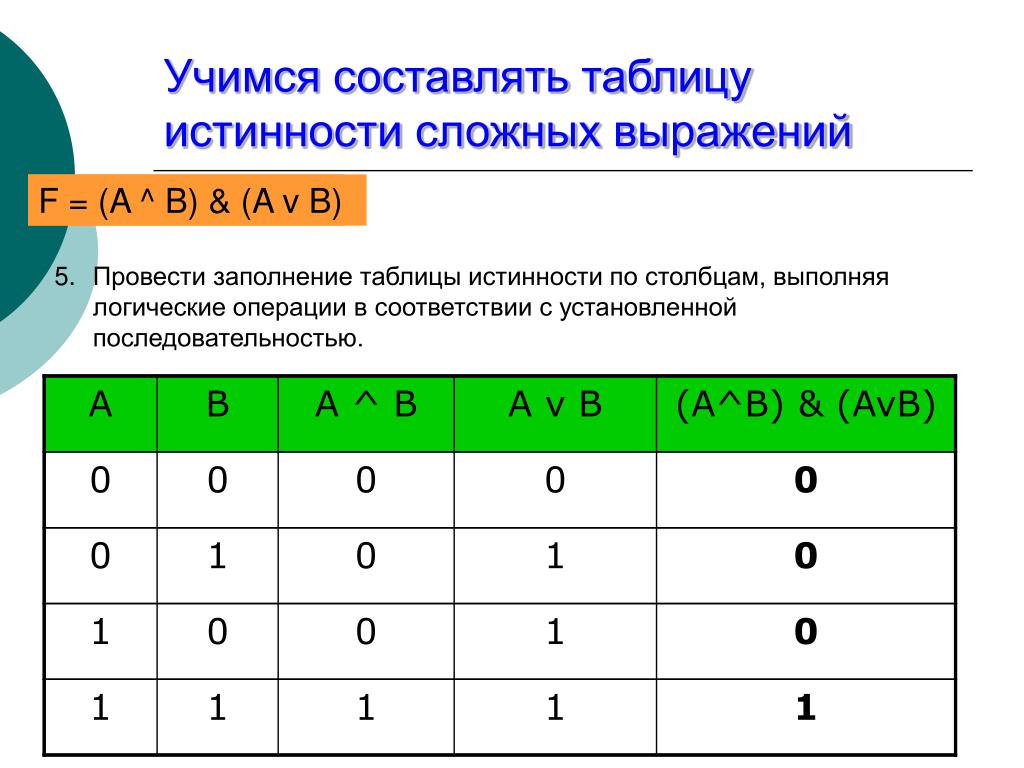
Nam lacin
congue vel laoreet ac, dictum vitae odio
fficitur laoreet. Nam risus ante, dapibus a molestie consequ
inia pulvinar tortor nec fa
a. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dol
ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur
20 вложений
png
png
png
png
png
png
png
png
png
png
png
png
png
png
png
png
png
png 100% (1 оценка)
Вычисление таблиц истинности с использованием вложенных типов
Этот пост содержит фрагменты кода на Haskell, которые после объединения должны привести к работающей программе на Haskell. Итак, вот преамбула с некоторыми функциями языка и библиотеками, которые мы будем здесь использовать:
{-# LANGUAGE LambdaCase #-}
{-# LANGUAGE FlexibleInstances #-}
модуль Главное где
импортировать Data.
Foldable(toList)
импорт Data.Map (Карта)
импортировать квалифицированные Data.Map как Map
Foldable(toList)
импорт Data.Map (Карта)
импортировать квалифицированные Data.Map как Map
Рассмотрим следующую задачу: по заданной булевой формуле с переменными построить ее таблицу истинности. Формулы определяются как следующий тип данных:
данные F = Вар Строка | Ф :&: Ф | Ф :|: Ф | Не Ф | Постоянная логическая получение (Показать)
Эту задачу довольно просто решить в два этапа: сначала пройтись по формуле, чтобы найти все свободные переменные, затем вычислить формулу для каждого возможного назначения этих переменных.
Однако, поскольку мы уже используем Haskell, почему бы не усложнить себе жизнь еще больше и не попробовать вычислить таблицу истинности за один проход формулы? Идея алгоритма достаточно проста: мы можем вычислить таблицы истинности подвыражений индуктивно:
Для константы верните таблицу из одной строки с этой константой в столбце значение .
Для переменной X вернуть
X значение 0 0 1 1 Для двоичных выражений вычислить таблицы истинности подвыражений, а затем соединить полученные таблицы по общим столбцам, применяя соответствующую функцию в значение столбец.
Вот вопрос, а как представить тип такой таблицы в Haskell? Простое решение будет выглядеть так:
type Assignment = [(String, Bool)] введите SimpleTable = [(Присвоение, Логическое значение)]
Но, как я уже говорил, этот пост не о простых решениях. Это представление, в частности, не навязывает многие свойства, которые мы хотим, чтобы они были истинными, такие как:
- Каждое
Назначениедолжно иметь каждую переменную только один раз - Каждый элемент
SimpleTableдолжен иметь одинаковый набор переменных - В результате должны присутствовать все возможные комбинации значений
Последние два из них мы можем реализовать, используя представление таблицы истинности вложенного типа :
data Truth a = Значение а | Вилка Строка (Правда (а, а)) получение (Показать)
Вложенные типы несколько загадочны, и поэтому вы можете немного прищуриться, чтобы убедиться, что каждое значение
Правдасодержит ровно n строк и 2 n значений типаa. Вы даже можете доказать это формально, используя индукцию по числу Forks в значении.Прежде всего, давайте узнаем, как преобразовать значение этого типа данных в обычную таблицу истинности. Это будет полезно для печати данных, поскольку автоматически сгенерированный экземпляр
Showна самом деле не удобочитаем.Следующий код для преобразования потребовал некоторых экспериментов с моей стороны, что заставило меня задуматься о том, существует ли хорошая методология для написания функций для вложенных типов: хотя я нахожу реализацию рекурсивной функции для обычных рекурсивных типов данных довольно простой, функции для вложенных типов я’ написанные до сих пор обычно требуют некоторого специального полиморфизма, и неясно, как искать, какие классы типов следует использовать.
В любом случае, хотя я не могу объяснить, как придумать следующий код, я могу, по крайней мере, показать другую функцию, которая оказалась полезной в качестве вдохновения: оказывается, легко реализовать экземпляр
Foldableдля.: Тип данных Truth экземпляр Foldable Truth где foldMap f = \case Значение v -> f v Fork _ v -> foldMap (uncurry mappend . fork f) vОбратите внимание, что эта функция по существу игнорирует все теги
String. Мы можем написать ещеfoldMap-подобная функция, которая не игнорирует их, а использует для построения простого представления таблицы истинности:trueFold::Monoid b => (a -> b) -> (Bool -> String -> б -> б) -> Истина а -> б trueFold f1 f2 = \case Значение v -> f1 v Fork s t -> trueFold (uncurry mappend . pointwise (f2 False s . f1, f2 True s . f1)) f2 t trueTable :: True Bool -> SimpleTable trueTable = trueFold (\b -> [([], b)]) (\k v ls -> map (onFirst ((v, k) :)) ls)
В приведенном выше фрагменте мы используем пару вспомогательных функций, которые, вероятно, доступны в
Control.Arrow, но мне было проще реализовать их самостоятельно, чем пытаться вспомнить, какая комбинация волнистых линий соответствует какой функция:поточечно (f1, f2) (x, y) = (f1 x, f2 y) вилка f (x, y) = (f x, f y) присоединиться (f1, f2) х = (f1 х, f2 х) onFirst f (x, y) = (f x, y)
Теперь перейдем к построению таблицы истинности.
Точно так же, как реализация Foldableоказался полезным для того, чтобы получить нужную нам функцию, оказалось, что реализацияFunctorиApplicativeоказалась крайне полезной при построении оценочной функции. Вот экземпляры:экземпляр Functor Truth где fmap f = \ case Значение x -> значение (f x) Вилка t v -> Вилка t $ fmap (форк f) v пример аппликативная истина, где чистый = значение tf <*> tv = случай (tf, tv) из (Значение f, Значение v) -> Значение (f v) (значение f, Fork t v) -> Fork t $ fmap (fork f) v (Fork t f, Value v) -> Fork t $fmap(fork($v)) f (Вилка t1 f, Вилка t2 v) -> случай сравнения t1 t2 из EQ -> Fork t1 (точечный <$> f <*> v) LT -> Форк t1 (объединить <$> f <*> tv) GT -> Fork t2 (fork <$> tf <*> v)Хотя экземпляр
Functorдовольно прост, у меня есть несколько замечаний по поводу экземпляраApplicative.<*> Операторна самом деле реализует соединение, и чтобы сделать его более эффективным и избежать перетасовки тегов, мы предполагаем, что теги (Stringчасть конструктораFork) отсортированы и сохраняйте это отсортированное свойство при объединении таблиц.Теперь, когда у нас есть операция соединения, пора реализовать сам вычислитель. Для этого нам понадобится класс типов для «логических» типов, например. типы, до которых мы можем поднять логические функции. Обратите внимание:
класс Boolean a где liftBool :: (Bool -> Bool) -> a -> a liftBool2 :: (Bool -> Bool -> Bool) -> a -> a -> a экземпляр Boolean Bool, где лифтБул = идентификатор liftBool2 = идентификатор instance Boolean a => Boolean (a, a), где liftBool f (x, y) = (liftBool f x, liftBool f y) liftBool2 f (x, y) (z, w) = (liftBool2 f x z, liftBool2 f y w) instance Boolean a => Boolean (Истина a), где liftBool f = \case Значение v -> Значение (liftBool f v) Внутренняя вилка -> Вилка (liftBool f внутренняя) liftBool2 f t1 t2 = liftBool2 f <$> t1 <*> t2Окончательная реализация представляет собой прямое использование этого класса типов:
eval :: F -> Truth Bool оценка = \ случай Константа b -> значение b Var v -> Fork v (значение (ложь, истина)) Not f -> liftBool not (eval f) f1 :&: f2 -> liftBool2 (&&) (eval f1) (eval f2) f1 :|: f2 -> liftBool2 (||) (оценка f1) (оценка f2)
Реализация, вероятно, не нуждается в этом дополнительном классе, и вместо этого может просто использовать некоторые обходы, но это код, который я получил на данный момент.
Вы даже можете доказать это формально, используя индукцию по числу 
Тип данных Truth 
Точно так же, как реализация 
