Методическая разработка занятия по математике по теме «Векторы в пространстве. Действия над векторами»

Занятие 111. «Векторы в пространстве. Действия над векторами»

План занятия:

1. Понятие вектора.

2. Координаты точки в пространстве.

3. Построение точки в пространстве.

1. Понятие вектора.

Вектором называется отрезок, для которого указано, какой из его концов считается началом, а какой — концом.

Любая точка пространства рассматривается как нулевой вектор.

2. Координаты точки и вектора в пространстве.

Любая точка М(x; y; z) в пространстве имеет 3 координаты: х-абсцисса, у-ордината, z-аппликата.

Любой вектор ={х; у; z} или { х₂ – х₁, у₂ – у₁, z₂ – z₁} в пространстве также имеет 3 координаты:

х — абсцисса, у- ордината, z- аппликата.

Радиус-вектором называют вектор, проведённый из начала координат в произвольную точку пространства. Радиус-вектор имеет координаты точки, в которую он проведён.

= ={х; у; z}

Координаты вектора выражаются через координаты его начала А (х₁; у₁; z₁) и конца В(х₂; у₂; z₂):

{ х₂ – х₁, у₂ – у₁, z₂ – z₁}.

Правило. Для определения координат вектора АВ нужно от координат конца вектора вычесть координаты начала.

Координаты равных векторов равны.

Длина вектора (модуль вектора) (х; у; z) вычисляется по формуле:

3. Действия с векторами в координатной форме:

Правило. Суммой (разностью) векторов (х₁; у₁; z₁) и (х₂; у₂; z₂) называется вектор = , координаты которого равны сумме (разности) соответствующих координат этих векторов:

(х₁ х₂; у₁ у₂; z₁ z₂).

Правило. Произведением вектора (х; у; z) на число k называется вектор

=k , координаты которого равны произведению числа k на координаты вектора :

=(kх; kу; kz).

П равило. Построение радиус-вектора в пространстве

Для построения радиус-вектора в пространстве необходимо:

1) Построить прямоугольную систему координат в пространстве Охуz.

2) Отложить первые две координаты конца вектора на соответствующих осях и провести их проекции;

3) Выполнить параллельный перенос третьей координаты в точку пересечения проекций;

4) Соединить полученную точку с началом координат и обозначить искомый вектор.

Правило. Построение вектора MN в пространстве

Для построения вектора MN в пространстве необходимо:

1) Построить прямоугольную систему координат в пространстве Охуz.

2) По правилу построить 2 точки — точку начала вектора M(-2;0;3) и точку конца N(2;1; -2).

3) Соединить полученные точки и обозначить искомый вектор.

Задание для самостоятельного выполнения

Задание 1. Сделать краткий конспект данной темы.

Задание 2. Выучить все формулировки определений и теорем.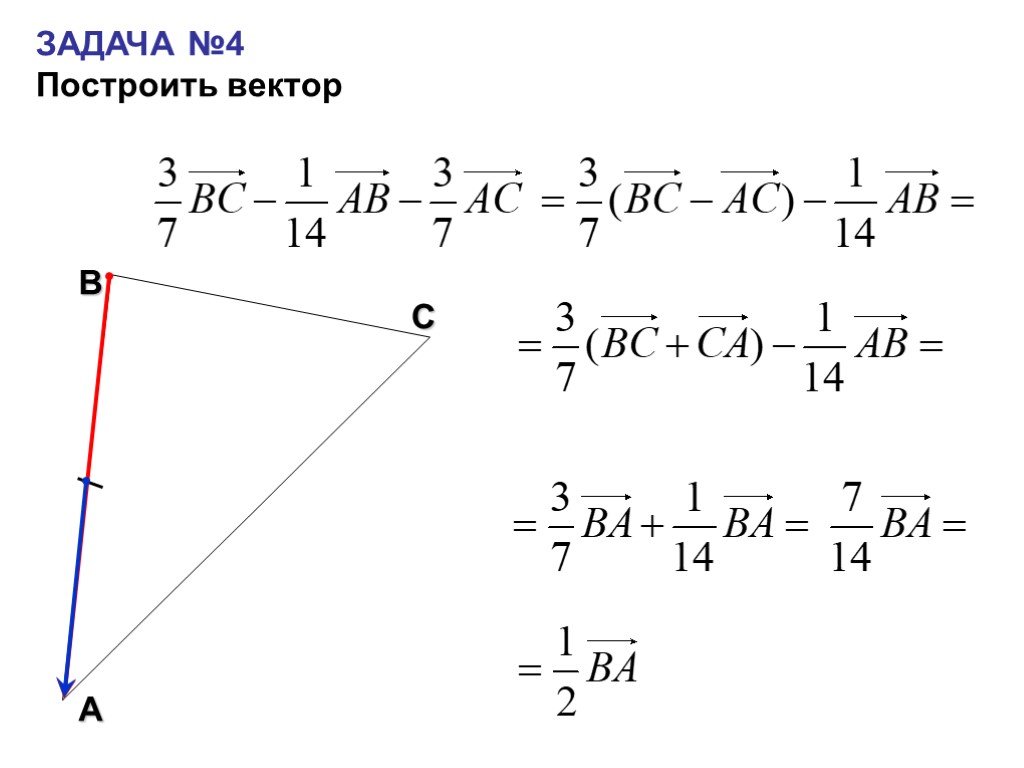

Задание 3.   Рассмотреть решение задач.

Задание 4. Решить задачи.

Задача 1. Найдите координаты вектора , если М(10; -4; 2) и К(16; 2 -5).

Задача 2. Найдите длину вектора ( — 5; 1; 2).

Задача 3. Найдите сумму векторов и , если А(2; 3; -1), С(3; -2; 0), В (3,6,0), Д (-2,5,-4)

Задача 4. Найдите разность векторов и , если В(3; 7; 10), С(1; 9; -6), А(-6,0,1)

Выполненные задания и вопросы по выполнению работ отправить на адрес электронной почты преподавателя: [email protected] Имя файла – фамилия студента и номер занятия. (например, Петров-111)

steps3D — Tutorials — Реализация bumpmapping’а

В этой статье мы рассмотрим два важных момента при эффективной реализации попиксельного освещения.

Нахождение базиса касательного пространства для набора треугольников

В рассматриваемых ранее примерах попиксельного освещения с учетом карты нормалей (bumpmap) возникала необходимость задания для каждой вершины всех выводимых граней базиса касательного пространства — векторов t, b и n.

Для случая простой геометрии объекта (например тора), эти вектора легко найти аналитически (что, собственно и делалось ранее). Однако при использовании более сложной геометрии возникает необходимость алгоритма вычисления этих векторов по данным в вершинах.

Проще всего дело обстоит с вектором внешней нормали n — в ряде случаев он просто явно задается для каждой вершины. Если же он не задан, то его легко можно найти по координатам вершин.

Если у нас задан треугольник v₀,v₁,v₂, то нормаль в точке v₀ легко можно найти через векторное произведение ребер:

Однако при использовании данной формулы нужно иметь в виду, что она может дать как внешнюю, так и внутреннюю нормаль. Проще всего бороться с этим путем задания для каждого треугольника вершин в таком порядке, чтобы эта формула всегда давала именно внешнюю нормаль.

Обратите также внимание, что эта формула вообще дает нормаль ко всему треугольнику, а не нормаль в какой-то вершине.

Для более точного определения вектора нормали в вершине можно воспользоваться тем, что вершина обычно принадлежит сразу нескольким граням, поэтому для каждой из таких граней вычисляется вектор нормали, а потом они складываются для получения нормали в вершине.

Полученное значение нормали должно быть нормировано для дальнейшего использования.

Для получения двух касательных векторов t и b одной геометрической информации (координат вершин) уже недостаточно и требуется информация о наложении текстурных координат (что вполне естественно, поскольку эти вектора используются именно для корректного наложения карты нормалей).

Рассмотрим сначала идеальный случай — пусть у нас есть гладкая поверхность с заданным на ней законом задания текстурных координат:

Пусть также задана точка v₀, соответствующая текстурным координатам (s₀,t₀).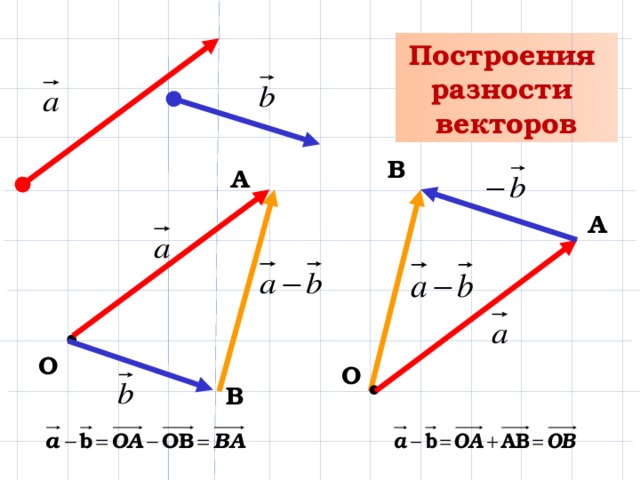

Тогда рассмотрим на этой поверхности линии линии, вдоль которых одна из текстурных координат будет постоянна. Нас интересует две таких линии — вдоль одной величина s принимает значение

s₀, а вдоль второй величина t принимает значение t₀.

Эти линии проходят через точку v₀ и пересекаются в ней. В случае, когда рассматриваемая поверхность и закон задания текстурных координат являются гладкими и невырожденными в точке v₀, то в этой точке можно построить касательный вектор к каждой из них.

В случае невырожденности закона задания текстурных координат эти вектора будут линейно независимы и если к ним добавить вектор нормали они будут являться базисом касательного пространства в этой точке.

Рассмотрим теперь, как можно найти эти касательные вектора без явного нахождения самих этих линий.

В силу невырожденности закона задания текстурных координат этот закон можно (хотя бы локально, т. е. в малой окрестности точки v₀) обратить, т.е. записать в виде:

Тогда интересующие нас касательные вектора будут равны (x’_s,y’_s,z’_s,) и (x’_t,y’_t,z’_t,).

Вернемся обратно к треугольнику v₀,v₁,v₂, считая, что в каждой его вершине явно заданы текстурные координаты

(s_i,t_i), используемые для обращения к карте нормалей.

Считая, что пространственные и текстурные координаты связаны некоторым законом (рассматриваемого ранее вида), можно приближенно записать следующие разностные отношения:

Используя заданные в вершинах треугольника значения пространственных и текстурных координат, можно записать три системы линейных уравнений следующего вида.

Для решения каждой из этих систем можно с успехом применить известное правило Крамера, т.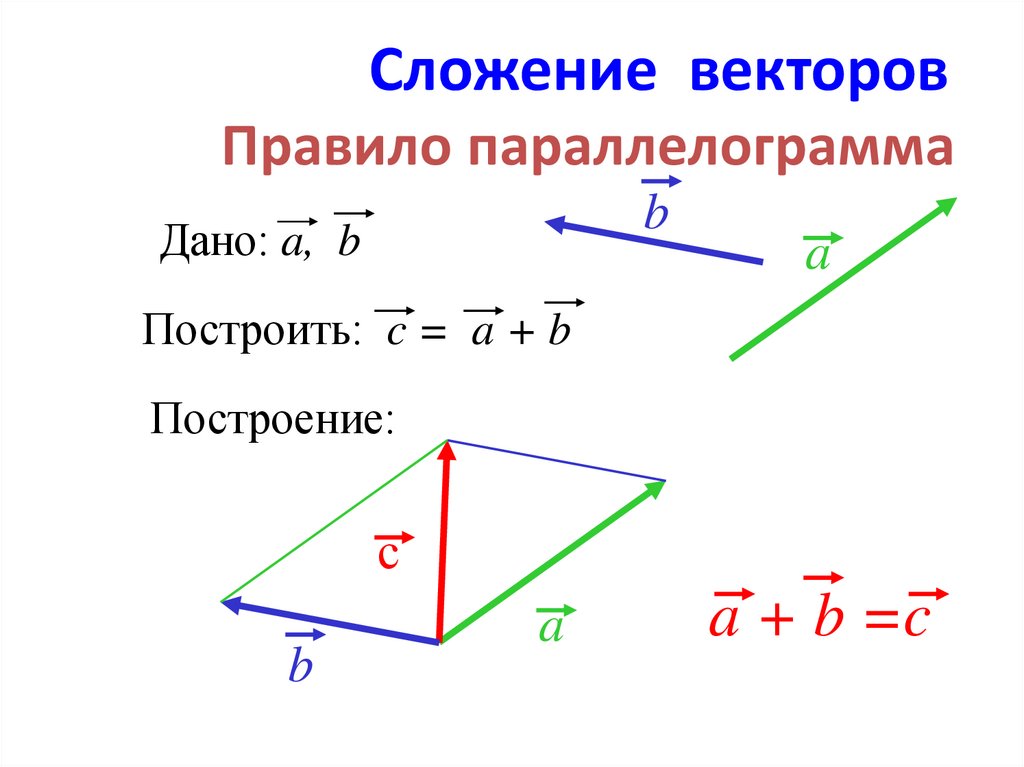

е. записать интересующие нас производные x’_s,x’_t в виде отношения двух определителей.

Можно упростить запись решения, путем введения следующих двух векторов:

Тогда каждый из необходимых определителей будет являться (с точностью до знака) одной из компонент векторного произведения векторов e0 и e1.

Ниже приводится процедура, реализующая описанный выше алгоритм для вычисления базиса касательного пространства в точке (при этом вектор нормали считается уже найденным).

Обратите внимание, что в конце процедуры проверяется ориентация полученного базиса (она может оказаться как левой так и правой и производится ее коррекция при необходимости).

Для повышения точности, можно вычислить вектора t и b используя несколько треугольников, проходящих через вершину v₀ и взять среднее из полученных значений.

Быстрая нормализация векторов

Способ нормирования векторов с использованием нормирующей кубической карты, хотя и прост, но требует использования текстурного блока и обращения к текстуре.

При использовании фрагментных программ нормирование вектора легко выполняется всего в три команды, однако без фрагментных программ и шейдерных языков высокого уровня, нормирование вектора осуществить довольно сложно.

Однако в ряде случаев можно воспользоваться приближенной формулой, которая для векторов, длины которых не сильно отличаются от единицы, дает достаточно хорошие результаты.

Возьмем за основу известную формулу (основанную на разложении по формуле Тейлора с точностью до первого члена).

Тогда, если обозначить t=(v,v)-1, то мы получим простую приближенную формулу

Естественно, что эта формула дает лишь приближенное значение и тем точнее, чем ближе длина вектора v к единице.

Vector Construction — Synbio Technologies

Перейти к содержимому

Конструкция Vector

Vector Constructionadmin2022-08-18T11:59:12-04:00

На основе наших платформ синтеза Syno ^®  2.0 и Syno ^®  3.0 Synbio Technologies предоставит любой синтетический вектор с высокой точностью и экономичной ценой, особенно для исследований в проектах shRNA, TALENT и CRISPR-Cas9.

Разработка и проверка кшРНК

РНК-интерференция (РНКи) — это быстрый, удобный и эффективный метод, который широко используется для подавления экспрессии генов. Используя кшРНК для молчания выбранного гена-мишени, РНКи чрезвычайно полезна в исследованиях вирусов, опухолей и генетических нарушений.

Разработка и проверка TALEN

TALEN (эффекторная нуклеаза, подобная активатору транскрипции) — это молекулярный инструмент, часто используемый для редактирования генома . Он точно вырезает целевые гены, что приводит к высокоточному редактированию генов. Система TALEN обеспечивает более легкий, простой и доступный метод подавления генов, чем технология нуклеазы цинковых пальцев (ZFN).

Создание и проверка CRISPR-Cas9

гРНК CRISPR-Cas9 (нуклеаза, управляемая РНК CRISPR-Cas9) — это самый последний прорыв в технологии редактирования генома после TALEN. Synbio Technologies предлагает создание и проверку системы CRISPR-Cas9 с помощью нашей запатентованной платформы Syno ^®  2.0 высокоэффективным и экономичным способом.

Спецификации услуг

Наименование услуг	Сведения об услуге	Результаты	Цена	Срок выполнения работ (рабочие дни)
Создание и проверка кшРНК	Услуги клеточной кшРНК Услуги кшРНК на основе лентивирусов Услуги кшРНК на основе аденовирусов Услуги shRNA на основе стволовых клеток Эффекты РНК-интерференции в стволовых клетках	Лиофилизированная плазмидная ДНК (2~5 мкг) Хроматограмма секвенирования Сертификат анализа (COA) Вирусная частица (необязательно) Линия клеток (необязательно)	Цитата	Цитата
TALEN Строительство и проверка	Плазмидная конструкция TALEN Проверка функции целевого локуса на основе TALEN Конструирование стабильных клеточных линий Конструкция стволовых клеток
Создание и проверка CRISPR-Cas9	Дизайн sgRNA на основе CRISPR-Cas9 Конструкция плазмиды на основе CRISPR-Cas9 Проверка целевого локуса на основе CRISPR-Cas9 Конструкция стабильной клеточной линии на основе CRISPR-Cas9 Конструкция стволовых клеток на основе CRISPR-Cas9

Родственные

Переключить скользящую панель Область

КОНТАКТЫ

• 4250 УС-1 Люкс 3 Соединение Монмут, Нью-Джерси 08852

• Тел. : +1 732-230-3003

• Факс: +1 609-228-5911

• Справки: [email protected]

Ссылка для загрузки страницы Перейти к началу

Служба создания и модификации пользовательских векторов

CBpromise   

Наше обещание вам:
Гарантированное качество продукции, квалифицированная поддержка клиентов.

24×7 СЛУЖБА КЛИЕНТА

СВЯЖИТЕСЬ С НАМИ, ЧТОБЫ ЗАКАЗАТЬ

Creative Biogene — ведущая биотехнологическая компания, обладающая обширными знаниями и опытом в предоставлении услуг по созданию и модификации пользовательских векторов для клиентов по всему миру. Современное оборудование, передовые технологии и высококвалифицированный персонал Creative Biogene готовы предоставить вам полный комплекс услуг по созданию и модификации пользовательских векторов, включая анализ последовательностей, синтез и клонирование генов, сборку фрагментов ДНК, секвенирование ДНК, сайт-направленный мутагенез и производство плазмид. и т. д. . Используя быстрые и эффективные методы построения и модификации, Creative Biogene может быстро создавать новые пользовательские векторные конструкции для больших или малых проектов.

В молекулярном клонировании вектор представляет собой молекулу ДНК, используемую в качестве носителя для искусственного переноса чужеродного генетического материала в другую клетку, где он может быть реплицирован и/или экспрессирован (например, плазмиды, космиды, фаги лямбда). Четыре основных типа векторов — это плазмиды, вирусные векторы, космиды и искусственные хромосомы. Среди них наиболее часто используемыми векторами являются плазмиды. В настоящее время коммерчески доступно большое разнообразие плазмидных векторов. Однако в некоторых случаях коммерческие векторы не могут наилучшим образом соответствовать конкретным потребностям исследователя, и исследователям приходится полагаться на собственную модификацию вектора.

Благодаря многолетнему развитию Creative Biogene может предоставлять услуги по конструированию и модификации пользовательских векторов для быстрого и надежного создания пользовательских специализированных плазмидных векторов с определенными характеристиками.