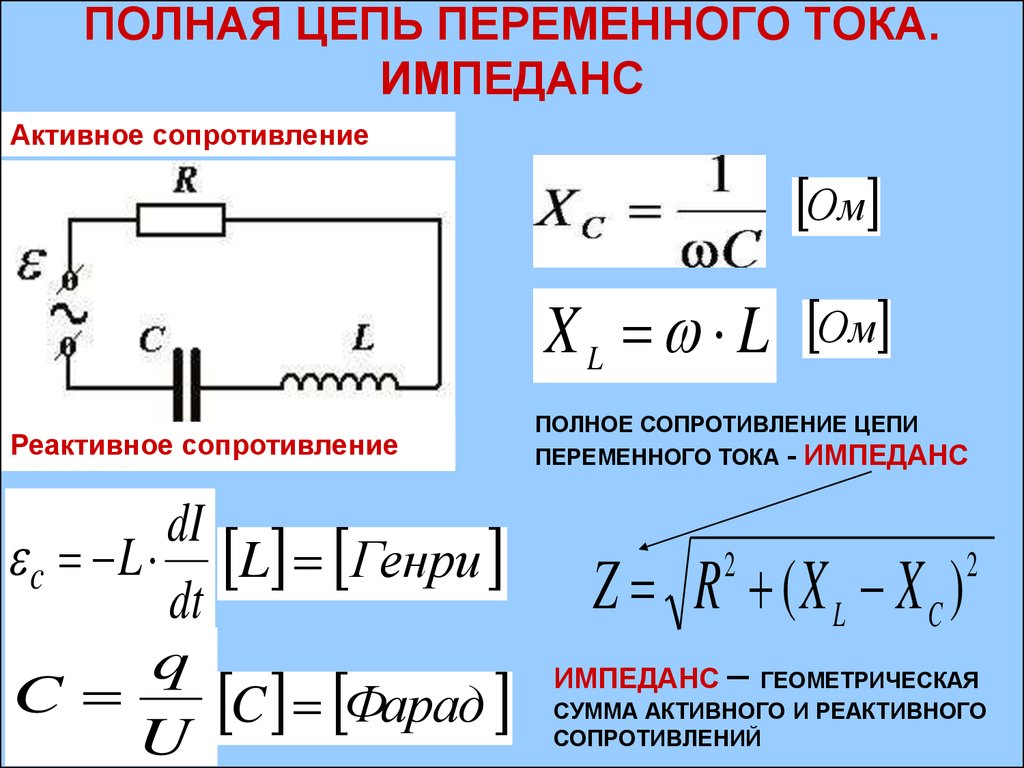
Постоянная времени цепи LR Калькулятор
✖Индуктивность – это свойство электрического проводника сопротивляться изменению протекающего по нему электрического тока.ⓘ Индуктивность [L] | AbhenryАттогенристолетиеДекагенриДецигенриEMU из ИндуктивностьESU индуктивностиExahenryFemtohenryГигагенриГектогенриГенрикилогенриМегагенриМикрогенриМиллигенриНаногенриPetahenryPicohenryStathenryТерагенриВебер / Ампер | +10% -10% | |
✖Сопротивление является мерой сопротивления току, протекающему в электрической цепи. Его единицей СИ является ом.ⓘ Сопротивление [R] | AbohmEMU сопротивленияESU сопротивленияExaohmГигаомкилооммегаоммикроомМиллиомНаномомПетаомПланка сопротивлениеКвантованная Hall СопротивлениеВзаимный СименсStatohmВольт на АмперYottaohmZettaohm | +10% -10% |
|
✖Постоянная времени цепи LR — это индуктивность цепи на единицу сопротивления. |
АттосекундаМиллиард летсантисекундаВекаЦикл переменного тока 60 ГцЦикл переменного токаДеньДесятилетиеДекасекундаДецисекундаExasecondФемтосекундаГигасекундагектосекундаЧаскилосекундаМегасекундамикросекундаМиллениумМиллион летМиллисекундаминутМесяцНаносекундаПетасекундаПикосекундаВторойСведбергТерасекундаТысяча летНеделюГодYoctosecondЙоттасекундаЗептосекундаЗеттасекунда |
⎘ копия |
👎
Формула
сбросить
👍
Постоянная времени цепи LR Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.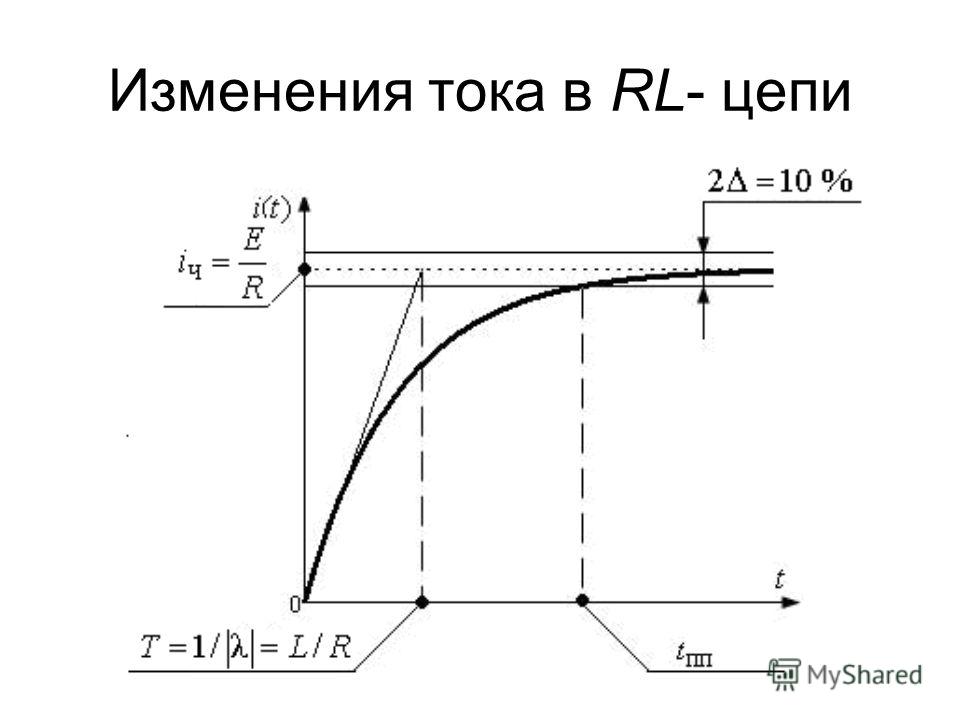 Преобразование входов в базовый блок
Преобразование входов в базовый блок
Индуктивность: 5.7 Генри —> 5.7 Генри Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.564356435643564 Второй —> Конверсия не требуется
< 10+ Электромагнитная индукция Калькуляторы
Постоянная времени цепи LR формула
Постоянная времени цепи LR = Индуктивность/Сопротивление
tau = L/R
Что такое схема LR?
Цепь резистор-индуктор, или RL-фильтр, или RL-сеть, представляет собой электрическую цепь, состоящую из резисторов и катушек индуктивности, приводимых в действие источником напряжения или тока.
Share
Copied!
26.
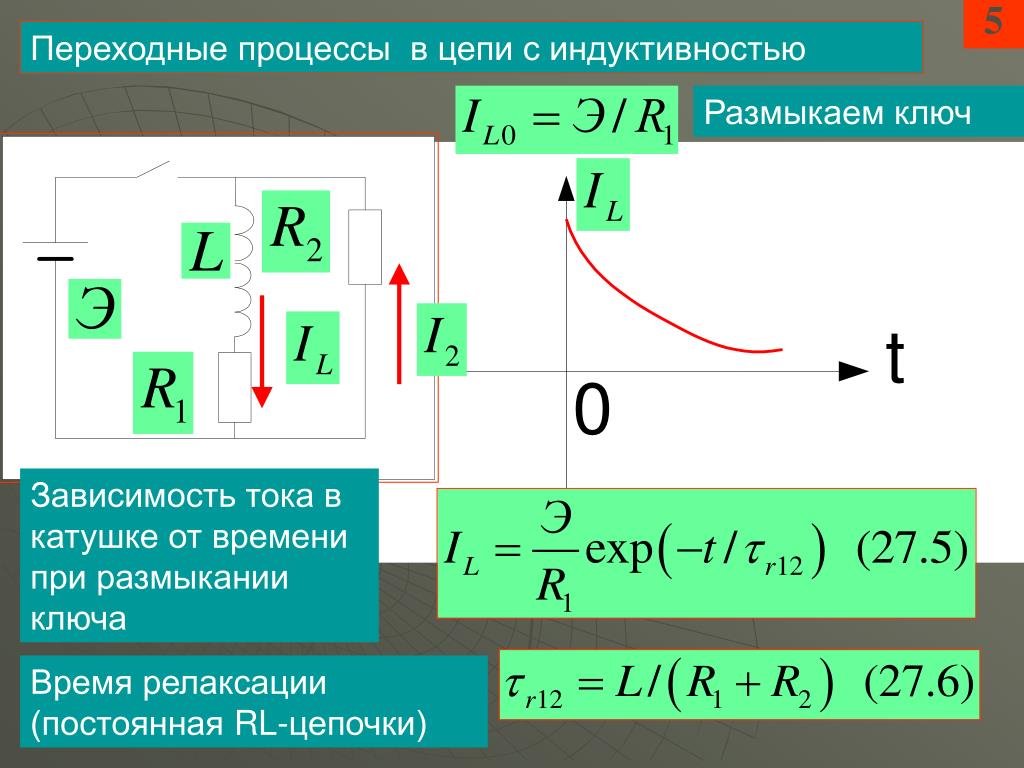
 Определение постоянной времени. Переходные процессы в…
Определение постоянной времени. Переходные процессы в…Привет, Вы узнаете про определение постоянной времени, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое определение постоянной времени, переходные процессы в r-l-c-цепи , настоятельно рекомендую прочитать все из категории Теоретические основы электротехники.
Переходные процессы в цепи с одним накопителем энергии и произвольным числом резисторов
Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение.
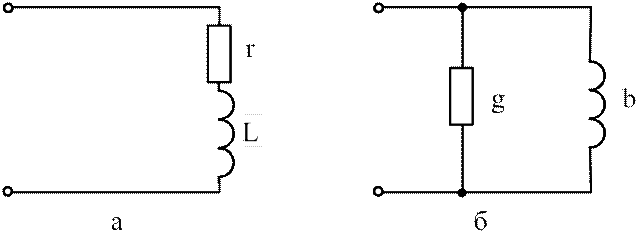
Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см.
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как:
,
и с емкостным, как:
,
где — входное сопротивление цепи по отношению к зажимам 1-2 подключения ветви, содержащей накопитель энергии.
Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать
,
где в соответствии с вышесказанным
.
Переходные процессы при подключении последовательной
R-L-C-цепи к источнику напряжения
Рассмотрим два случая:
а) ;
б) .
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
| . | (1) |
Тогда для первого случая принужденная составляющая этого напряжения
| . | (2) |
Характеристическое уравнение цепи
,
решая которое, получаем
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1. или , где — критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.
или , где — критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.
В этом случае
| . | (3) |
2. — предельный случай апериодического режима.
В этом случае и
| . | (4) |
3 . Об этом говорит сайт https://intellect.icu . — периодический (колебательный) характер переходного процесса.
В этом случае и
| , | (5) |
где — коэффициент затухания; — угловая частота собственных колебаний; — период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
.
Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации , запишем для t=0 два уравнения:
решая которые, получим
; .
Таким образом,
.
Тогда ток в цепи
и напряжение на катушке индуктивности
.
На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .
Для критического режима на основании (2) и (4) можно записать
.
При
Таким образом
и
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
.
Для нахождения постоянных интегрирования запишем
откуда и .
Тогда
.
На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
и
,
где ; ; .
Таким образом,
и .
Здесь также возможны три режима:
| 1. ; | 2. | 3. |
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 — ; 2 — ; 3 — , — которые представлены на рис. 6,а…6,в соответственно.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники.
 Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
Ответ: заряд.
Ответ: L=0,225 Гн.
Ответ: .
Ответ: .
- Как можно определить постоянную времени в цепи с одним накопителем энергии по осциллограмме тока или напряжения в какой-либо ветви?
- Определить, какой процесс: заряд или разряд конденсатора в цепи на рис. 2 – будет происходить быстрее?
- Влияет ли на постоянную времени цепи тип питающего устройства: источник напряжения или источник тока?
- В цепи на рис. 2 , С=10 мкФ. Чему должна быть равна индуктивность L катушки, устанавливаемой на место конденсатора, чтобы постоянная времени не изменилась?
- Как влияет на характер переходного процесса в R-L-C-контуре величина сопротивления R и почему?
- Определить ток через катушку индуктивности в цепи на рис.
 7, если ; ; ; ; .
7, если ; ; ; ; . - Определить ток в ветви с конденсатором в цепи на рис. 8, если ; ; ; .
В общем, мой друг ты одолел чтение этой статьи об определение постоянной времени. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках. Надеюсь, что теперь ты понял что такое определение постоянной времени, переходные процессы в r-l-c-цепи и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теоретические основы электротехники
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Что такое постоянная времени цепи RLC?
Ключевые выводы
- Цепи
RLC имеют демпфирование, поэтому они не будут мгновенно переходить между двумя разными состояниями и будут демонстрировать некоторое переходное поведение.

Постоянная времени RLC-цепи показывает, сколько времени потребуется для перехода между двумя разными состояниями возбуждения, аналогично случаю, когда конденсатор заряжается до полной емкости.
- Цепи
RLC могут иметь разные уровни демпфирования, что может усложнить определение постоянной времени.
Сложные RLC-цепи могут демонстрировать сложную реакцию во временной области.
Реактивные цепи являются основой реальных систем, от энергосистем до радиочастотных цепей. Они также важны для моделирования поведения сложных электрических цепей без четко определенной геометрии. Важной частью понимания реактивных цепей является их моделирование с использованием языка цепей RLC. Способ построения и объединения простых RLC-цепей может привести к сложному электрическому поведению, полезному для моделирования электрических откликов в более сложных системах.
Поскольку все цепи RLC являются линейными системами второго порядка, они имеют некоторый предельный цикл в своем переходном поведении, который определяет, как они достигают установившегося состояния при работе между двумя разными состояниями. Постоянная времени цепи RLC описывает, как система переходит между двумя состояниями управления во временной области, и это фундаментальная величина, используемая для описания более сложных систем с резонансами и переходным поведением. Если вы работаете со схемами RLC, вот как определить постоянную времени в переходной характеристике.
Постоянная времени цепи RLC
Системы первого и второго порядка (например, цепи RL, RC, LC или RLC) могут иметь некоторую постоянную времени, которая описывает, сколько времени требуется цепи для перехода между двумя состояниями. Такой переход может произойти, когда амплитуда источника возбуждения изменяется (например, источник ступенчатого напряжения/тока), когда источник возбуждения изменяет частоту или когда источник возбуждения включается или выключается. Из-за этого перехода между двумя разными состояниями управления естественно думать о цепи RLC с точки зрения ее постоянной времени.
Из-за этого перехода между двумя разными состояниями управления естественно думать о цепи RLC с точки зрения ее постоянной времени.
В действительности цепь RLC не имеет постоянной времени, как зарядный конденсатор. Вместо этого мы говорим, что система имеет константу демпфирования, которая определяет, как система переходит между двумя состояниями. Поскольку мы рассматриваем линейную систему второго порядка (или связанную с ней эквивалентную линейную систему первого порядка), система имеет две важные величины:
Постоянная демпфирования ( 𝛽 ): Определяет, как энергия, первоначально переданная системе, рассеивается (обычно в виде тепла).
Собственная частота ( 𝜔 0 ): определяет, как система будет колебаться, если в системе не будет демпфирования.
Постоянная времени в цепи RLC в основном равна 𝛽 , но реальная переходная характеристика в этих системах зависит от соотношения между 𝛽 и 𝜔 0 .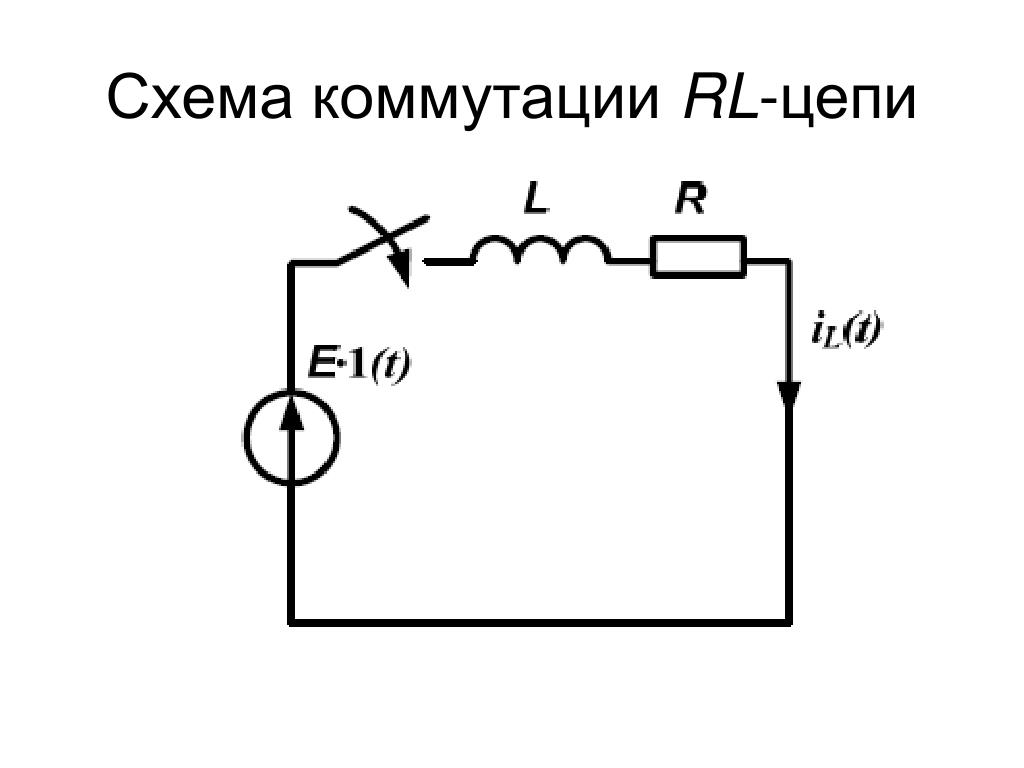 Системы второго порядка, такие как схемы RLC, представляют собой затухающие генераторы с четко определенными предельными циклами, поэтому они демонстрируют затухающие колебания в своей переходной характеристике. Условия для каждого типа переходной характеристики в демпфированном генераторе приведены в таблице ниже.
Системы второго порядка, такие как схемы RLC, представляют собой затухающие генераторы с четко определенными предельными циклами, поэтому они демонстрируют затухающие колебания в своей переходной характеристике. Условия для каждого типа переходной характеристики в демпфированном генераторе приведены в таблице ниже.
|
Для простых RLC-цепей с недостаточным демпфированием, таких как параллельные или последовательные RLC-цепи, константу демпфирования можно определить вручную. В противном случае, например, в сложных схемах со сложными передаточными функциями, постоянная времени должна быть извлечена из данных измерений или моделирования.
Извлечение постоянной времени цепи RLC из измерений
Если у вас есть некоторые измерения или данные моделирования из цепи RLC, вы можете легко извлечь постоянную времени из цепи с недостаточным демпфированием, используя регрессию. Давайте рассмотрим простой пример для генератора RLC с недостаточным демпфированием, а затем рассмотрим генераторы RLC с критическим и передним демпфированием.
Underdemped
На приведенном ниже графике показано, как это можно легко сделать для генератора с недостаточным демпфированием. Данные показывают зависимость полного тока в последовательной RLC-цепи от времени, обнаруживая сильно затухающие колебания. Последовательные максимумы отклика во временной области (слева) отмечены красными точками. Затем эти данные наносятся на график в натуральном логарифмическом масштабе как функция времени и подгоняются под линейную функцию. Наклон линейной функции равен 0,76, что равно постоянной затухания и постоянной времени. Для проверки те же данные на линейном графике (левая панель) были сопоставлены с экспоненциальной кривой; мы также находим, что постоянная времени на этой экспоненциальной кривой равна 0,76.
Данные показывают зависимость полного тока в последовательной RLC-цепи от времени, обнаруживая сильно затухающие колебания. Последовательные максимумы отклика во временной области (слева) отмечены красными точками. Затем эти данные наносятся на график в натуральном логарифмическом масштабе как функция времени и подгоняются под линейную функцию. Наклон линейной функции равен 0,76, что равно постоянной затухания и постоянной времени. Для проверки те же данные на линейном графике (левая панель) были сопоставлены с экспоненциальной кривой; мы также находим, что постоянная времени на этой экспоненциальной кривой равна 0,76.
Два способа получения постоянной времени демпфирования цепи RLC.
В приведенном выше примере постоянная времени для цепи RLC с недостаточным демпфированием равна постоянной демпфирования. Это не относится к цепи RLC с критическим демпфированием или избыточным демпфированием, и в этих двух других случаях следует выполнить регрессию.
Критическое демпфирование и сверхдемпфирование
В случае критического демпфирования постоянная времени зависит от начальных условий в системе, поскольку одно решение системы второго порядка является линейной функцией времени. В схеме с избыточным демпфированием постоянная времени больше не строго равна постоянной демпфирования. Вместо этого постоянная времени равна:
Постоянная времени цепи RLC с избыточным демпфированием.
Здесь у нас есть постоянная времени, полученная из суммы двух затухающих экспонент. Когда 𝜔 0 << 𝛽 , постоянная времени сходится к 𝛽 . Обсуждаемые здесь взаимосвязи действительны для простых цепей RLC с одним блоком RLC. Более сложные схемы требуют другого подхода для извлечения переходных характеристик и демпфирования.
Цепи RLC высшего порядка
Цепи RLC более высокого порядка имеют несколько блоков RLC, соединенных вместе уникальными способами, и они могут не иметь четко определенной постоянной времени, которая следует простому уравнению, показанному выше. В то время как, в принципе, вы можете рассчитать отклик в частотной области вручную, схемы с большим количеством RLC-элементов, соединенных последовательно и параллельно, решить очень сложно. Наблюдаемая вами постоянная времени зависит от нескольких факторов:
В то время как, в принципе, вы можете рассчитать отклик в частотной области вручную, схемы с большим количеством RLC-элементов, соединенных последовательно и параллельно, решить очень сложно. Наблюдаемая вами постоянная времени зависит от нескольких факторов:
Где расположены выходные порты схемы.
Как источники питания и компоненты расположены в более крупной топологии.
Какой источник напряжения используется для сравнения в передаточной функции цепи.
Пример цепи RLC более высокого порядка показан ниже. В этой схеме у нас есть несколько блоков RLC, каждый со своей постоянной демпфирования и собственной частотой.
Более сложная сеть RLC.
В основном это фильтр более высокого порядка, т. е. он объединяет несколько секций фильтра в большую сеть RLC. Этот тип цепи может иметь несколько резонансов/антирезонансов на разных частотах, и частоты могут не совпадать с собственной частотой каждой секции RLC. Это происходит из-за связи между различными участками цепи, создающей сложный набор резонансов/антирезонансов в частотной области.
Этот тип цепи может иметь несколько резонансов/антирезонансов на разных частотах, и частоты могут не совпадать с собственной частотой каждой секции RLC. Это происходит из-за связи между различными участками цепи, создающей сложный набор резонансов/антирезонансов в частотной области.
Существует два способа определения переходной характеристики и постоянной времени RLC-цепи на основе моделирования:
Использовать симуляцию переходного процесса, как обсуждалось выше; просто подгоните отклик схемы во временной области (натуральный логарифмический масштаб) и рассчитайте передаточную функцию по наклону.
Если вам нравится определять переходные характеристики вручную, вы можете использовать развертку по частоте для определения полюсов и нулей в передаточной функции.
Оба метода основаны на использовании мощного симулятора SPICE для расчета тока и напряжения на каждом компоненте цепи. Для сложных схем с несколькими блоками RLC анализ нулевого полюса является самым быстрым способом извлечения всей информации о переходном поведении, любых резонансных частотах и любых антирезонансных частотах.
Для сложных схем с несколькими блоками RLC анализ нулевого полюса является самым быстрым способом извлечения всей информации о переходном поведении, любых резонансных частотах и любых антирезонансных частотах.
Если вам нужно определить постоянную времени передемпфирования RLC-цепи, вы можете использовать программное обеспечение для проектирования переднего плана от Cadence, чтобы приступить к созданию схем и получить доступ к инструментам моделирования. Приложение PSpice Simulator позволяет легко определить константу демпфирования в цепи RLC при моделировании переходных процессов. Вы также можете выполнить более сложное моделирование полюса-ноля, чтобы определить все возможные переходные эффекты в сложной сети RLC.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетите вебсайт Больше контента от Cadence PCB Solutions
УЧИТЬ БОЛЬШЕRL естественный отклик — вывод
Мы исследуем естественный отклик цепи резистор-индуктор $(\text{RL})$. Это происхождение похоже на естественную реакцию RC.
Уравнение $i$-$v$ индуктора имеет вид $v = \text L \,di/dt$. Напряжение зависит от того, как ток меняется от момента к моменту. Формальный вывод требует понятий исчисления, особенно производных, для обработки этой зависимости от времени.
Естественная реакция $(\text{RL})$ аналогична естественной реакции RC. По сути, это точный сдвоенный . Если вы запишете математику для вывода RC и поменяете местами ток и напряжение, а L вместо C, математика будет точно такой же.
Автор Вилли Макаллистер.
Содержание
- Стратегия
- Моделирование компонентов
- Модель схемы
- Решите схему
- Постоянная времени 9{-\text Rt/\text L}$
- Это дифференциальное уравнение, потому что оно содержит производные.

- Это первого порядка , потому что старшая производная является первой производной $({di} / {dt})$.
- Это обычное , потому что существует только одна независимая переменная $(t)$ (в отличие от частных производных нескольких переменных).
- Придумаем функцию тока $i(t)$.
- Подставьте функцию в дифференциальное уравнение.
- Найдите константы, используя начальные условия. 9{-\text Rt/\text L}}$
Мне всегда нравится смотреть, как выглядят уравнения,
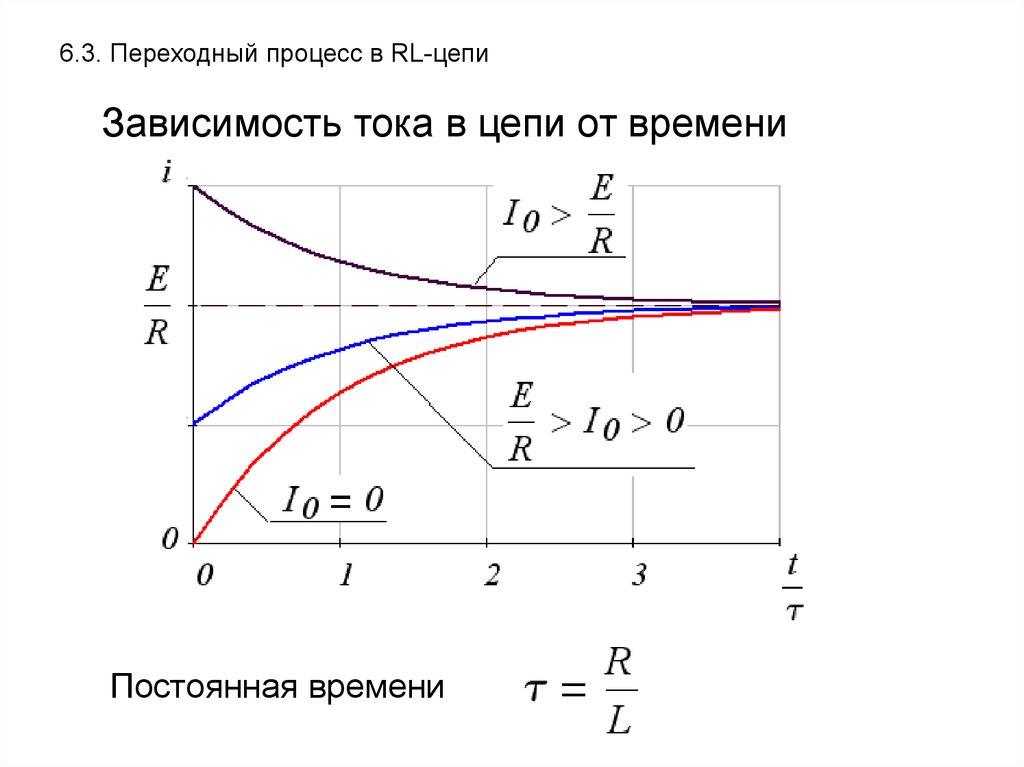
Перед замыканием переключателя ток равен $\text I_0$. Переключатель замыкается при $t=0$, и ток падает по экспоненциальной кривой до тех пор, пока не достигнет $0$.
Перед замыканием ключа напряжение на дросселе равно $0$. Он делает резкий скачок при $t=0$, как только ток начинает меняться. Пиковое напряжение зависит от начального тока $\text I_0$ и сопротивления $\text R$. Напряжение следует аналогичной экспоненциальной кривой, пока не упадет до $0$.
Сравните эти рассчитанные графики с теми, что мы нарисовали ранее. Эскизы имеют правильную форму.

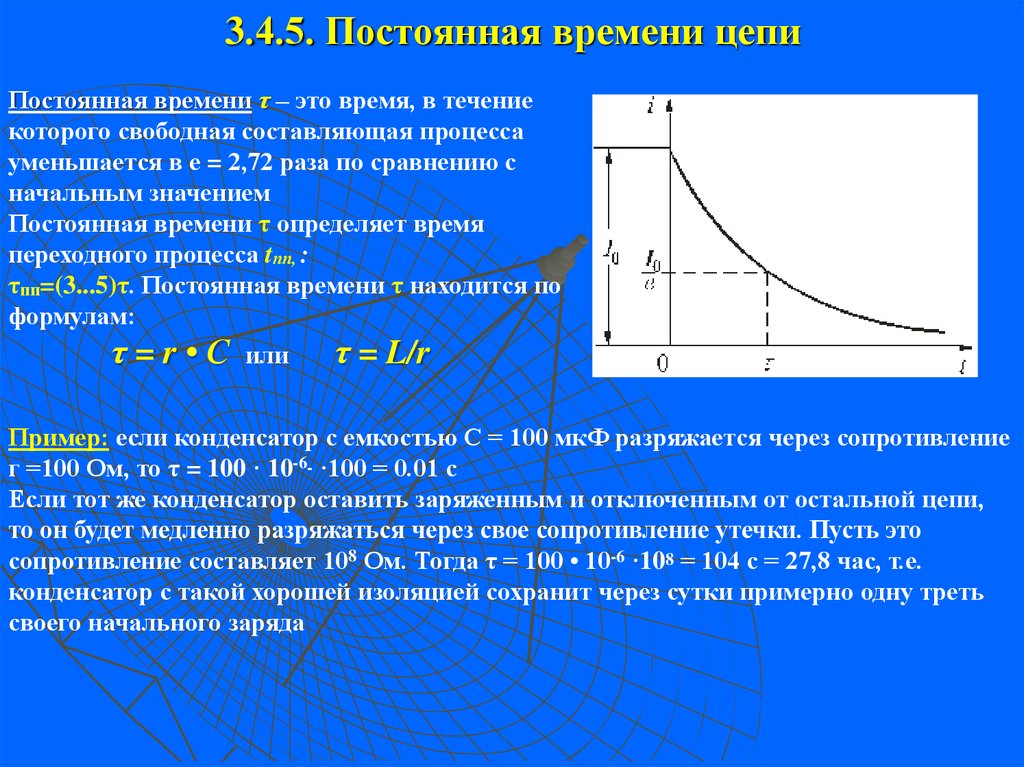
Постоянная времени
Показатель степени должен быть обычным числом. Не допускается наличие размеров. $\text{R}/\text L$ должен иметь единицы измерения $1/\text{time}$, чтобы можно было сократить $t$. Обратная величина, $\text L/\text R$, имеет единицы $\text{секунд}$, о чем вы, возможно, не догадались.
$\text L/\text R$ называется постоянной времени комбинации резистор-индуктор. Он обладает теми же свойствами, что и соответствующее произведение $\text R \cdot \text{C}$ в цепи резистор-конденсатор. Мы используем греческую букву $\tau$ (тау) как символ постоянной времени, 9{-t/\tau}$
Когда $t$ равно постоянной времени, показатель степени становится $-1$. Экспоненциальный член равен $1/e = 1/1,569$, или около $0,37$.
Постоянная времени определяет скорость снижения экспоненциальной кривой до нуля. По истечении $1$ постоянной времени ток падает до $37\%$ своего начального значения. Если вы подождете константы времени от $3$ до $5$, естественный отклик в значительной степени закончится.

Если увеличить катушку индуктивности, постоянная времени увеличится.
Если увеличить резистор, постоянная времени уменьшится.Это отличается от постоянной времени $\text{RC}$, $\tau_{\text{RC}}=\text{RC}$, которая становится длиннее с увеличением как $\text R$, так и $\text С$. Для $\text{RL}$, когда резистор имеет большую энергию, его рассеяние велико, и естественный отклик быстро затухает. Когда резистор мал, ток индуктора проходит через резистор более свободно, поэтому энергия рассеивается медленно, и ток циркулирует по кругу в течение длительного времени.
Постоянная времени RL равна , а не Р умножить на Л.Небольшое предостережение: несмотря на то, что мы называем это схемой $\text{RL}$, постоянная времени не является произведением $\text{RL}$. Это $\tau_{\text{LC}} = \dfrac{\text L}{\text R}$.
Для схемы $\text{RC}$ постоянная времени равна $\text{RC}$.
Сделайте все возможное, чтобы не попасть в ловушку.
Как вы помните порядок частного? $\text R$ сверху или $\text L$? Я помню $\text L/\text R$, потому что «el over r» начинается с hello! , а «arr over el» звучит как пират.

Рабочий пример
Давайте рассмотрим пример,
Задача 1
Что такое $\blueD i$, если переключатель замкнут?$i = $________ $\text{мА}$
показать ответКогда переключатель замкнут, весь ток от источника тока протекает через индуктор. $i = 8 \,\text{мА}$.
Задача 2
Что такое $\goldD v$, если переключатель замкнут?$i = $________ $\text{V}$
показать ответКогда переключатель замкнут, производная постоянного тока $di/dt = 0$.
Уравнение индуктора говорит нам, что $v = \text L\,\dfrac{di}{dt} = 0 \,\text{V}$.
Переключатель размыкается при $t=0$.
Задача 3
Чему равен $\blueD i$ в катушке индуктивности в момент после размыкания ключа?$i = $ ________ $\text{мА}$
показать ответВ тот момент, когда переключатель размыкается, ток в катушке индуктивности не меняется по сравнению с тем, что было до этого.
 $i = 8 \,\text{мА}$. Ток в катушке индуктивности не может измениться мгновенно. 9{-t/80\,\text{ns}}$
$i = 8 \,\text{мА}$. Ток в катушке индуктивности не может измениться мгновенно. 9{-t/80\,\text{ns}}$Естественный ответ выглядит так:
Имитационная модель
Попробуйте эту имитационную модель. Щелкните TRAN , чтобы выполнить анализ переходных процессов. Источник тока имеет собственный внутренний переключатель. Он начинается с $8\,\text{mA}$ и резко падает до $0$ при $t=0$. Убедитесь сами, что ток упал до $37\%$ от его значения $t(0)$ после одной постоянной времени.
Резюме
Естественный отклик схемы $\text{RL}$ является экспоненциальным, 9{-\text t/\tau}$
Приложение. Разделимое дифференциальное уравнение
Дифференциальное уравнение, которое мы вывели для схемы $\text{RL}$:
$\text L \dfrac{di}{dt} + i\,\text R = 0$
Это разделимое дифференциальное уравнение. Дифференциальное уравнение является разделимым, если можно отсортировать все $i$ и $di$ как произведение в одной части уравнения и получить все $dt$ в произведении в другой части.

, где $\text I_0$ — текущий ток в момент времени $t=0$. Это называется естественной реакцией .
Постоянная времени для схемы $\text{RL}$ равна $\tau = \dfrac{\text L}{\text R}$.
Естественный отклик схемы — это то, что схема делает «естественно», когда у нее есть некоторая внутренняя энергия, и мы позволяем ей рассеиваться. Это самое основное поведение схемы.
Почему мы изучаем естественную реакцию $\text{RL}$? Потому что он появляется каждый раз, когда провод включается в цепь.
 Если провод сформирован в катушку, мы называем это катушкой индуктивности. Даже если он не скручен, каждый провод и каждая дорожка на печатной плате имеют небольшую индуктивность, которая может иметь значение. Золотые провода в интегральной схеме имеют достаточную индуктивность, чтобы играть важную роль в очень быстрых схемах. Вокруг всегда есть индуктивность и всегда рядом сопротивление.
Если провод сформирован в катушку, мы называем это катушкой индуктивности. Даже если он не скручен, каждый провод и каждая дорожка на печатной плате имеют небольшую индуктивность, которая может иметь значение. Золотые провода в интегральной схеме имеют достаточную индуктивность, чтобы играть важную роль в очень быстрых схемах. Вокруг всегда есть индуктивность и всегда рядом сопротивление.Стратегия
Мы хотим получить естественную реакцию $\text{LC}$, $\blueD i$ и $\goldD v$ как функцию времени. Этот вывод следует тем же шагам, что и естественный ответ RC.
Предположим, что $\text I_0$ является начальным током, протекающим в катушке индуктивности.
Моделирование компонентов
$\text R$ и $\text L$ можно моделировать их характеристическими уравнениями $i$-$v$.
Резистор описывается законом Ома,
$v_\text R = i \,\text R$
Индуктор описывается уравнением $i$-$v$ для индуктора,
$v_\text L = \text L \,\dfrac{di}{dt}$
пассивный знакНапряжения резистора и катушки индуктивности ориентированы с использованием правил знаков для пассивных компонентов.
 Направление тока указано синей стрелкой, а два напряжения ориентированы таким образом, что ток течет в положительные клеммы напряжения $\text R$ и $\text L$.
Направление тока указано синей стрелкой, а два напряжения ориентированы таким образом, что ток течет в положительные клеммы напряжения $\text R$ и $\text L$.Мы осторожны с этим, потому что он определяет знаки в уравнениях, которые скоро появятся.
Моделирование схемы
Когда у нас есть модель для каждого компонента, мы создаем модель того, как они связаны с законом напряжения Кирхгофа. Начнем с верхнего левого угла схемы и пойдем против часовой стрелки,
$v_\text L + v_\text R = 0$
$\text L \,\dfrac{di}{dt} + i\, \text R = 0$
Это дифференциальное уравнение. Он моделирует цепь.
С этого момента мы будем называть $v_\text R$ просто $v$.
Решить схему
$\text L \,\dfrac{di}{dt} + i\,\text R = 0$
Это уравнение называется обыкновенным дифференциальным уравнением первого порядка (ОДУ). Что означает этот жаргон?
Теперь шаг за шагом рассмотрим решение ОДУ.
Наша цель — найти функцию $i(t$), которая при подключении делает ОДУ верным. Один из способов получить $i(t)$ — сделать обоснованное предположение и попробовать его. Мы будем угадывать решение, как мы это делали с естественной реакцией RC.
Есть ли другие способы?Это ОДУ оказывается разделимым дифференциальным уравнением. Способ решения этого разделимого уравнения находится в приложении в конце этой статьи. Когда вы используете этот метод, вам не нужно гадать.
Сэл углубляется в серию видеороликов о разделимых дифференциальных уравнениях.
У него также есть видео об угадывании решения дифференциальных уравнений второго порядка.
 Уравнения второго порядка возникают в электрических цепях, когда мы доходим до цепей $\text{LC}$ и $\text{RLC}$.
Уравнения второго порядка возникают в электрических цепях, когда мы доходим до цепей $\text{LC}$ и $\text{RLC}$.Чтобы решить дифференциальное уравнение,



 Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с. 7, если ; ; ; ; .
7, если ; ; ; ; .
 Переходная характеристика напоминает зарядку конденсатора.
Переходная характеристика напоминает зарядку конденсатора. Если провод сформирован в катушку, мы называем это катушкой индуктивности. Даже если он не скручен, каждый провод и каждая дорожка на печатной плате имеют небольшую индуктивность, которая может иметь значение. Золотые провода в интегральной схеме имеют достаточную индуктивность, чтобы играть важную роль в очень быстрых схемах. Вокруг всегда есть индуктивность и всегда рядом сопротивление.
Если провод сформирован в катушку, мы называем это катушкой индуктивности. Даже если он не скручен, каждый провод и каждая дорожка на печатной плате имеют небольшую индуктивность, которая может иметь значение. Золотые провода в интегральной схеме имеют достаточную индуктивность, чтобы играть важную роль в очень быстрых схемах. Вокруг всегда есть индуктивность и всегда рядом сопротивление. Направление тока указано синей стрелкой, а два напряжения ориентированы таким образом, что ток течет в положительные клеммы напряжения $\text R$ и $\text L$.
Направление тока указано синей стрелкой, а два напряжения ориентированы таким образом, что ток течет в положительные клеммы напряжения $\text R$ и $\text L$.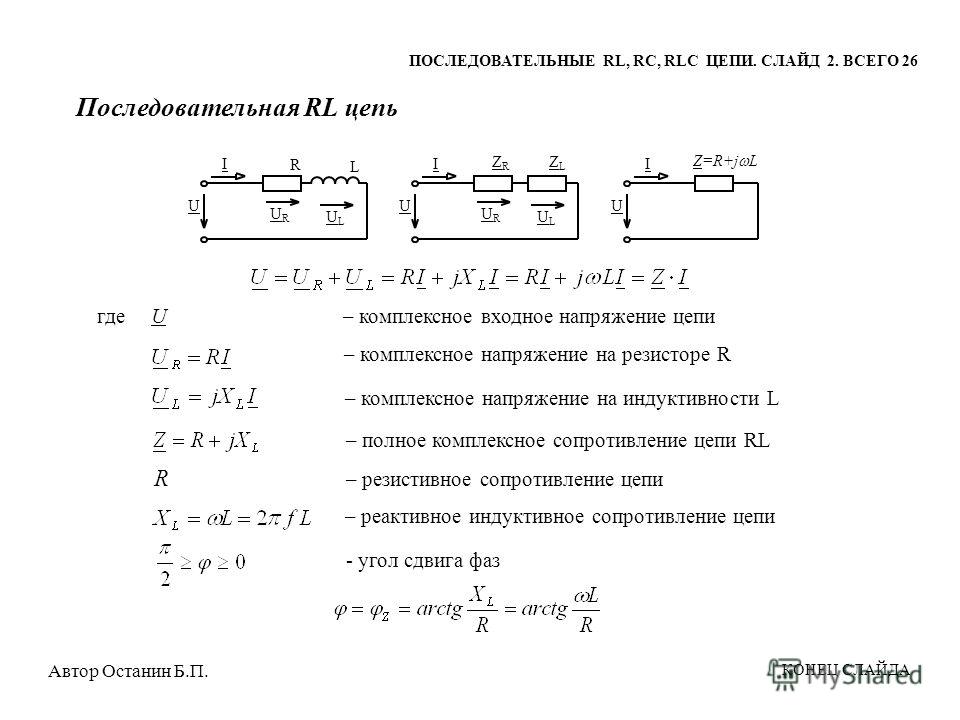
 Уравнения второго порядка возникают в электрических цепях, когда мы доходим до цепей $\text{LC}$ и $\text{RLC}$.
Уравнения второго порядка возникают в электрических цепях, когда мы доходим до цепей $\text{LC}$ и $\text{RLC}$.
 $i = 8 \,\text{мА}$. Ток в катушке индуктивности не может измениться мгновенно. 9{-t/80\,\text{ns}}$
$i = 8 \,\text{мА}$. Ток в катушке индуктивности не может измениться мгновенно. 9{-t/80\,\text{ns}}$