1.13. RC — цепи: изменения во времени напряжения и тока

ОСНОВЫ ЭЛЕКТРОНИКИ

Конденсаторы и цепи переменного тока

Для анализа цепей переменного тока (или в общем случае схем, работающих с изменяющимися напряжениями и токами) можно использовать характеристики двух типов. Во-первых, можно рассматривать изменения напряжения U и тока I во времени, а во-вторых — изменение амплитуды при изменении частоты сигнала. И те, и другие характеристики имеют свои преимущества, и в каждом практическом случае приходится выбирать наиболее подходящие. Мы начнем изучение цепей переменного тока с временных зависимостей, а в разд. 1.18 перейдем к частотным характеристикам.

Каковы же свойства схем, в состав которых входят конденсаторы? Для того чтобы ответить на этот вопрос, рассмотрим простейшую RC — цепь (рис. 1.29). Воспользуемся полученным ранее выражением для емкости:

C(dU/dt) = I = — U/R.

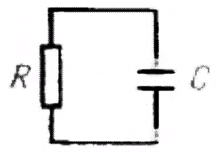
Рис. 1.29.

Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид:

U = Ae ^{— t/RC}.

Отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рис. 1.30.

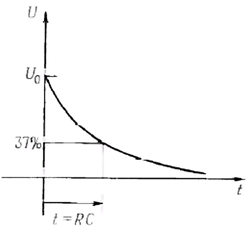
Рис. 1.30. Сигнал разряда RС — цепи.

Постоянная времени. Произведение RC называют постоянной времени цепи. Если R измерять в омах, а С — в фарадах, то произведение RC будет измеряться в секундах. Для конденсатора емкостью 1 мкФ, подключенного к резистору сопротивлением 1 кОм. постоянная времени составляет 1 мс, если конденсатор был предварительно заряжен и напряжение на нем составляет 1 В, то при подключении резистора в цепи появится ток, равный 1 мА.

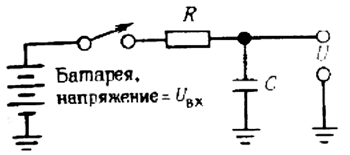
Рис. 1.31.

На рис. 1.31 показана несколько иная схема. В момент времени t = 0 схема подключается к батарее. Уравнение, описывающее работу такой схемы, выглядит следующим образом:

I = C(dU/dt) = (U_вх — U)/R.

и имеет решение

U = U_вх + Ae ^-t/RC.

Не пугайтесь, если не поняли, как выполнено математическое преобразование. Важно запомнить полученный результат. В дальнейшем мы будем многократно его использовать, не прибегая к математическим выкладкам. Постоянная величина А определяется из начальных условий (рис. 1.32): U = 0 при t = 0, откуда А = -U

вх и U = U_вх(1 — e ^-t/RC).

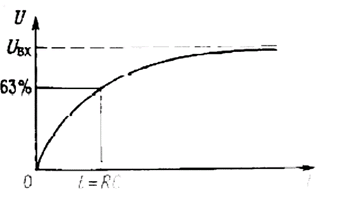
Рис. 1.32.

Установление равновесия. При условии t » RC напряжение достигает значения U_вх. (Советуем запомнить хорошее практическое правило, называемое правилом пяти RC. Оно гласит: за время, равное пяти постоянным времени, конденсатор заряжается или разряжается на 99%.) Если затем изменить входное напряжение U

вх (сделать его равным, например, нулю), то напряжение на конденсаторе U будет убывать, стремясь к новому значению по экспоненциальному закону e ^-t/RC. Например, если на вход подать прямоугольный сигнал U_вх, то сигнал на выходе U будет иметь форму, показанную на рис. 1.33.

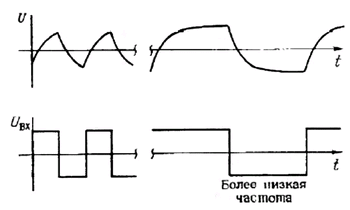
Рис. 1.33. Напряжение, снимаемое с конденсатора (верхние сигналы), при условии, что на него через резистор подается прямоугольный сигнал.

Упражнение 1.13. Докажите, что время нарастания сигнала (время, в течение которого сигнал изменяется от 10 до 90% своего максимального значения) составляет 2.2 RC.

У вас, наверное, возник вопрос: каков закон изменения для произвольного U^вх(t)? Для того чтобы ответить на него, нужно решить неоднородное дифференциальное уравнение (стандартные методы решения таких уравнений здесь не рассматриваются). В результате получим

U(t) = 1/RC ^t∫ _{— ∞}U_вхτe ^-t/RCdt.

Согласно полученному выражению, RC — цепь усредняет входное напряжение с коэффициентом пропорциональности e

-t/RC где Δt = τ — t. На практике, однако, такой вопрос возникает редко. Чаше всего рассматриваются частотные характеристики и определяют, какие изменения претерпевает каждая частотная составляющая входного сигнала. Скоро (разд. 1.18) мы также перейдем к этому немаловажную вопросу. А пока рассмотрим несколько интересных схем, хотя анализа которых достаточно временных зависимостей.

Упрощение с помощью эквивалентного преобразования Тевенина. Можно было бы приступить к анализу более сложных схем, пользуясь, как и раньше, методом решения дифференциальных уравнений. Однако чаше всего не стоит прибегать к решению дифференциальных уравнений. Большинство схем можно свести к RC — схеме. показанной на рис. 1.34. Пользуясь эквивалентным преобразованием для делителя напряжения, образованного резисторами R

1 и R₂, можно определить U(t) для скачка входного напряжения U_вх.

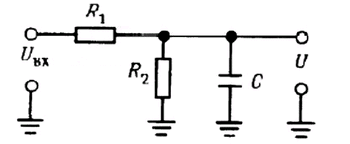
Рис. 1.34.

Упражнение 1.14. Для схемы, показанной на рис. 1.34. R₁ = R₂ = 10 кОм и С = 0,1 мкФ. Определите U(t) и изобразите полученную зависимость в виде графика.

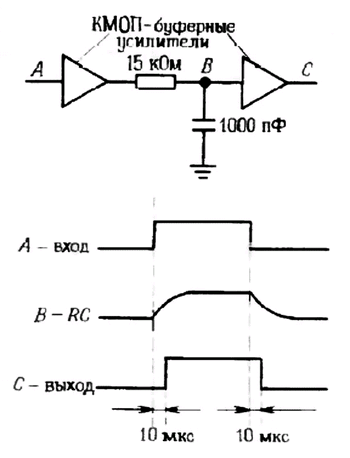
Пример: схема задержки. Мы уже упоминали логические уровни — напряжения, определяющие работу цифровых схем. На рис. 1.35 показано, как с помощью конденсаторов можно получить задержанный импульс. В виде треугольников изображены КМОП — буферные усилители. Они дают высокий уровень на выходе (более половины величины напряжения питания постоянного тока) и наоборот. Первый буферный усилитель воспроизводит входной сигнал и обеспечивает небольшое выходное сопротивление, предотвращая тем самым воздействие на источник сигнала RС — цепи (вопрос о нагрузке схемы мы рассмотрели в разд. 1.05). Согласно характеристике RС — цепи, выходной сигнал для нее задерживается относительно входного, поэтому выходной буферный усилитель переключается на 10 мкc позже скачка напряжения на входе (напряжение на выходе RС — цепи достигает 50% своего максимального значения через 0,7 RC). На практике приходится принимать во внимание отклонение входного порога буфера от величины, равной половине напряжения питания, так как это отклонение изменяет задержку и ширину выходного импульса. Иногда подобную схему используют для того, чтобы задержать импульс на время, в течение которого может произойти какое-либо событие. При проектировании схем лучше не прибегать к подобным трюкам, но иногда они бывают полезны.

Рис. 1.35. Использование RС — цепи для формирования задержанного цифрового сигнала.

Индуктивности и трансформаторы

RC-цепь. Дифференцирующие и интегрирующие RC-цепи.

Обсудив в предыдущих статьях устройство и принцип работы резисторов, конденсаторов и катушек индуктивности, мы имеем полное право перейти к рассмотрению цепей, состоящих из этих элементов! Этим мы сегодня и займемся. И первая RC-цепь, работу которой мы рассмотрим…

Дифференцирующая RC-цепь.

Из названия цепи, в принципе, уже понятно, что за элементы входят в ее состав – это конденсатор и резистор 🙂 И выглядит она следующим образом:

Работа данной схемы основана на том, что

ток, протекающий через конденсатор, прямо пропорционален скорости изменения напряжения, приложенного к нему:

i = C\medspace\frac{dU_c}{dt}

Напряжения в цепи связаны следующим образом (по закону Кирхгофа):

u_{out} = u_{in}\medspace-\medspace u_c

В то же время, по закону Ома мы можем записать:

u_{out} = i R = C R\medspace\frac{dU_c}{dt}

Выразим u_c из первого выражения и подставим во второе:

u_{out} = C R\medspace\frac{dU_c}{dt} = C R\medspace(\frac{dU_{in}}{dt}\medspace-\medspace \frac{dU_{out}}{dt}\medspace)

u_{out} = C R\medspace\frac{dU_{in}}{dt}\medspace-\medspace C R\medspace\frac{dU_{out}}{dt}

При условии, что C R\medspace\frac{dU_{out}}{dt} << u_{out} (то есть скорость изменения напряжения низкая) мы получаем приближенную зависимость для напряжения на выходе:

u_{out} \approx C R\medspace\frac{dU_{in}}{dt}

Таким образом, цепь полностью оправдывает свое название, ведь напряжение на выходе представляет из себя дифференциал входного сигнала. Но возможен еще и другой случай, когда C R\medspace\frac{dU_{out}}{dt} >> u_{out} (быстрое изменение напряжения). При выполнении этого равенства мы получаем такую ситуацию:

C R\medspace\frac{dU_{in}}{dt} = C R\medspace\frac{dU_{out}}{dt}

То есть: U_{out} \approx U_{in}.

Можно заметить, что условие C R\medspace\frac{dU_{out}}{dt} << u_{out} будет лучше выполняться при небольших значениях произведения C R, которое называют

постоянной времени цепи:

\tau = R C

Давайте разберемся, какой смысл несет в себе эта характеристика цепи 🙂 Заряд и разряд конденсатора происходит по экспоненциальному закону:

u = U_0\medspace e^{-t/\tau}

Здесь U_0 – напряжение на заряженном конденсаторе в начальный момент времени. Теперь посмотрим, каким будет значение напряжения по истечении времени \tau:

U_{\tau} = U_0\medspace e^{-\tau/\tau} = U_0\medspace e^{-1} \approx 0.37\medspace U_0

Напряжение на конденсаторе уменьшится до 37% от первоначального. Таким образом, \tau – это время, за которое конденсатор:

• при заряде – зарядится до 63%
• при разряде – разрядится на 63% (разрядится до 37%)

С постоянной времени цепи мы разобрались, давайте вернемся к дифференцирующей RC-цепи. Теоретические аспекты функционирования мы разобрали, так что давайте посмотрим, как она работает на практике. А для этого попробуем подавать на вход какой-нибудь сигнал и посмотрим, что получится на выходе. В качестве примера, подадим на вход последовательность прямоугольных импульсов:

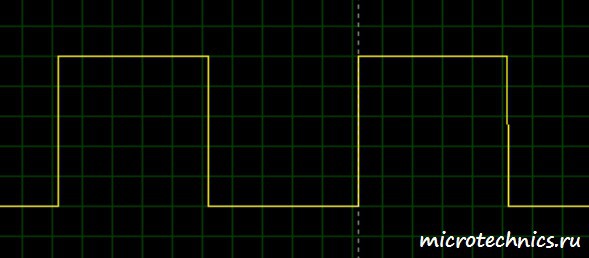
А вот как выглядит осциллограмма выходного сигнала (второй канал – синий цвет):

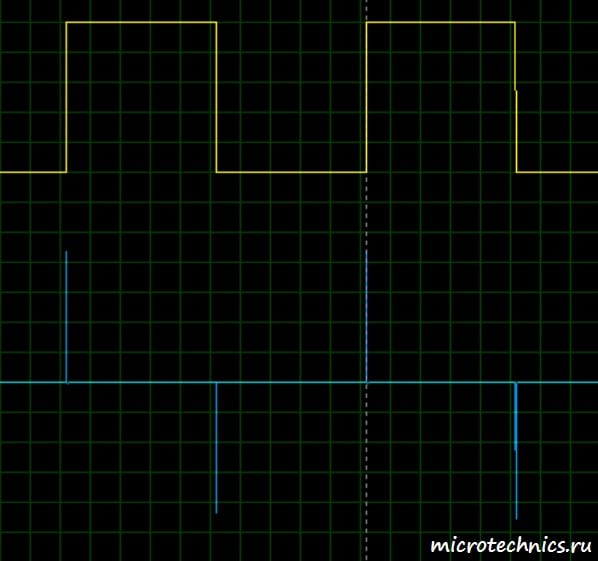
Что же мы тут видим?

Большую часть времени напряжение на входе неизменно, а значит его дифференциал равен 0 (производная константы = 0). Именно это мы и видим на графике, значит RC-цепь выполняет свою дифференцирующую функцию. А с чем же связаны всплески на выходной осциллограмме? Все просто – при “включении” входного сигнала происходит процесс зарядки конденсатора, то есть по цепи проходит ток зарядки и напряжение на выходе максимально. А затем по мере протекания процесса зарядки ток уменьшается по экспоненциальному закону до нулевого значения, а вместе с ним уменьшается напряжение на выходе, ведь оно равно U_{out} = i R. Давайте увеличим масштаб осциллограммы и тогда мы получим наглядную иллюстрацию процесса зарядки:

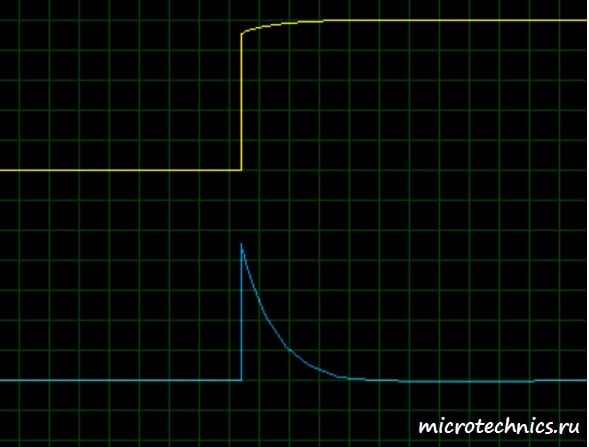
При “отключении” сигнала на входе дифференцирующей цепи происходит аналогичный переходный процесс, но только вызван он не зарядкой, а разрядкой конденсатора.

В данном случае постоянная времени цепи у нас имеет небольшую величину, поэтому цепь хорошо дифференцирует входной сигнал. По нашим теоретическим расчетам, чем больше мы будем увеличивать постоянную времени, тем больше выходной сигнал будет похож на входной. Давай проверим это на практике! Будем увеличивать сопротивление резистора, что и приведет к росту \tau:

Тут даже не надо ничего комментировать – результат налицо 🙂 Мы подтвердили теоретические выкладки, проведя практические эксперименты, так что давайте переходить к следующему вопросу – к интергрирующим RC-цепям.

Интегрирующая RC-цепь.

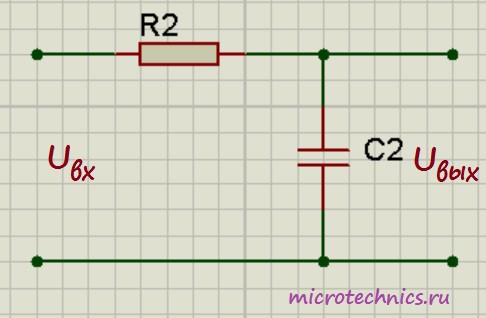
Запишем выражения для вычисления тока и напряжения данной цепи:

i = C\medspace\frac{du_{out}}{dt}

В то же время ток мы можем определить из Закона Ома:

i = \frac{u_R}{R} = \frac{u_{in}\medspace-\medspace u_{out}}{R}

Приравниваем эти выражения и получаем:

C\medspace\frac{du_{out}}{dt} = \frac{u_{in}\medspace-\medspace u_{out}}{R}

du_{out} = \frac{1}{C}\medspace\frac{u_{in}\medspace-\medspace u_{out}}{R}\enspace dt

Проинтегрируем правую и левую части равенства:

u_{out} = \frac{1}{R C}\medspace \int(u_{in}\medspace-\medspace u_{out})\medspace dt = \frac{1}{R C}\medspace \int u_{in}\medspace dt\medspace-\medspace \frac{1}{R C}\medspace \int u_{out}\medspace dt

Как и в случае с дифференцирующей RC-цепочкой здесь возможны два случая:

• Если u_{out} << \frac{1}{R C}\int u_{out}\medspace dt, то \frac{1}{R C}\int u_{in}\medspace dt\medspace-\medspace \frac{1}{R C}\int u_{out}\medspace dt \approx 0 и, соответственно, U_{out} \approx U_{in}. То есть сигнал на выходе приближенно повторяет входной сигнал. Для выполнения этого условия необходимо, чтобы постоянная времени цепи имела малую величину.
• Если u_{out} >> \frac{1}{R C}\int u_{out}\medspace dt, то u_{out} \approx \frac{1}{R C}\int u_{in} \medspace dt. В данном случае цепь хорошо выполняет свою интегрирующую функцию, и чем больше будет величина постоянной времени цепи, тем интегрирующие свойства будут лучше.

Для того, чтобы убедиться в работоспособности цепи, давайте подадим на ее вход точно такой же сигнал, какой мы использовали при анализе работы дифференцирующей цепи, то есть последовательность прямоугольных импульсов. При малых значениях \tau сигнал на выходе будет очень похож на входной сигнал, а при больших величинах постоянной времени цепи, на выходе мы увидим сигнал, приближенно равный интегралу входного. А какой это будет сигнал? Последовательность импульсов представляет собой участки равного напряжения, а интеграл от константы представляет из себя линейную функцию (\int Cdx = Cx). Таким образом, на выходе мы должны увидеть пилообразное напряжение. Проверим теоретические выкладки на практике:

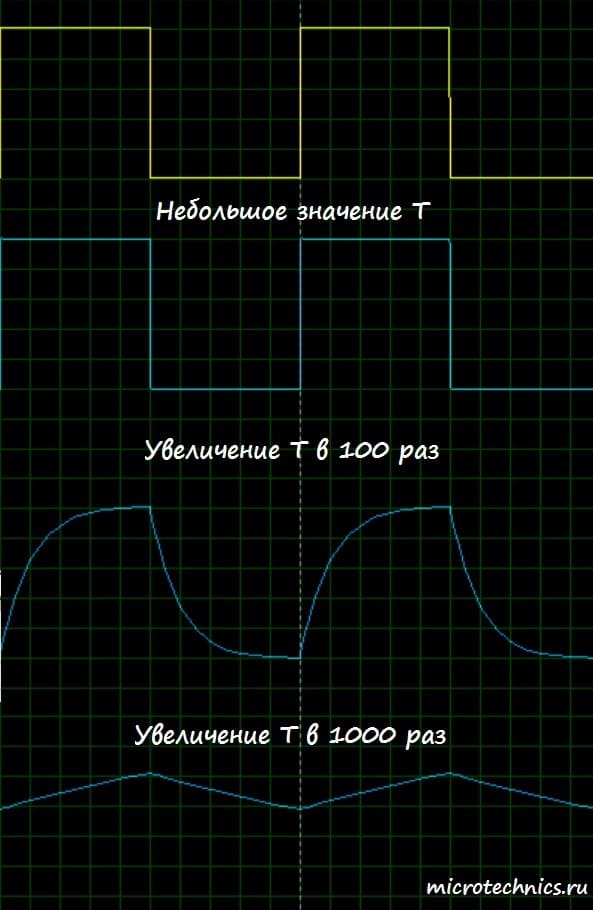
Желтым цветом здесь изображен сигнал на входе, а синим, соответственно, выходные сигналы при разных значениях постоянной времени цепи. Как видите, мы получили именно такой результат, который и ожидали увидеть 🙂

На этом мы и заканчиваем сегодняшнюю статью, но не заканчиваем изучать электронику, так что до встречи в новых статьях!

Постоянная времени цепи с развязывающим конденсатором

До сих пор мы рассматривали влияние развязывающего конденсатора в случае, когда постоянная времени была очень большой по сравнению с длительностью импульса. Если в схеме, показанной на рис. 10.12, уменьшить величину емкости конденсатора С с 10 мкФ до 10 нФ и подать на вход прямоугольный сигнал с частотой около 500 Гц, то наглядно проявится эффект несоответствия постоянной времени требованию неискаженной передачи. Примерный вид входного и выходного сигналов изображен на рис. 10.16: выходной сигнал имеет явный наклон на тех отрезках времени, на которые приходятся горизонтальные участки входного сигнала. Объяснение состоит в следующем: постоянная времени настолько мала, что конденсатор имеет возможность немного заряжаться и разряжаться в течение периода колебания; в действительности наклонные линии в выходном сигнале, вверху и внизу, представляют собой части экспоненциальных кривых заряда и разряда 7?С-цепи.

Наклон можно выразить также через нижнюю граничную частоту f_v определяемую по уровню —3 дБ. Как и в разд. 8.2, справедливо равенство: 2л/», = 1/RC, поэтому из уравнения (10.13) имеем:

Таким образом, для усиления длинных импульсов требуется, чтобы у усилителя была отличная характеристика в области нижних частот. Например, используя полученное выше соотношение, получаем, что в случае, £огда при длительности импульса 1 мс требуется, чтобы спад был менее 1 %, необходимо, чтобы нижняя граничная частота усилителя, определенная по уровню —3 дБ, была не выше 1,7 Гц. Когда нужно одновременно учесть это требование и решить проблему потери постоянной составляющей при прохождении сигнала через развязывающий конденсатор, легко понять, почему в импульсных усилителях связь по постоянному току предпочтительнее.

10.10. Дифференцирование и интегрирование

Рис. 10.16. Прохождение прямоугольного колебания через Л С-цепь с неправильно выбранной постоянной времени.

При малых отклонениях экспоненту v = Кехр (-t/RC) можно аппроксимировать прямой, учитывая только два первых члена разложения в ряд, то есть

Так, если длительность импульса равна t_w, то относительный спад сигнала, показанного на рис. 10.16, равен

Если в схеме с развязывающим конденсатором постоянную времени RC сделать очень малой по сравнению с длительностью импульса, то он искажается до неузнаваемости, выходной сигнал принимает вид продифференцированного входного сигнала. Если на вход RC-схемы с С = 1 нФ и R = 10 кОм

Рис. 10.17. Дифференцирующая цепь.

(рис. 10.17) подать импульсы (сформированные схемой, приведенной на рис. 10.2) с частотой 500 Гц, то выходной сигнал будет иметь вид, показанный на рис. 10.18, и его можно считать результатом крайнего несоответствия постоянной времени. Конденсатор сначала пропускает положительный фронт сигнала, но затем быстро заряжается до напряжения +9 В, давая на выходе только узкий импульс. Когда напряжение входного сигнала возвращается к нулю при отрицательном перепаде, выходное напряжение сначала падает до —9 В благодаря заряду на конденсаторе, но затем конденсатор быстро разряжается, а на выходе формируется только узкий импульс. Только в том случае, когда входной сигнал имеет время нарастания и спада много меньше постоянной времени RC, полный размах выходного импульсного сигнала равен ±9 В; затянутые фронты позволяют конденсатору зарядиться прежде, чем он полностью передаст амплитуду импульса.

Тот факт, что выходные импульсы появляются только тогда, когда входной сигнал изменяется, объясняет, почему эта схема называется дифференциатором. Отметим, что при положительной скорости изменения входного напряжения dv_BX /dt выходной импульс получается положительным, а при отрицательном значении dv_Bx/d/ получается отрицательный импульс. Легко найти теоретическую связь между входным и выходным сигналами для ЛС-дифференциатора. Согласно рис. 10.17, выходное напряжение есть просто разность потенциалов на резисторе R, то есть

Рис. 10.18. Типичная форма сигналов на входе и выходе дифференцирующей цепи.

Если q — мгновенное значение заряда на конденсаторе, то

Рис. 10.21. Интегрирование симметричного прямоугольного сигнала а дает треугольный сигнал на выходе б.

сигнала (равной, если отношение длительности импульса к интервалу

между импульсами равно единице) с наложенными на него пульсациями треугольной формы.

Лучшую временную диаграмму сигнала на выходе интегратора можно получить, преднамеренно удалив постоянную составляющую из входного сигнала и сделав его, таким образом, симметричным относительно нулевого уровня. Это легко сделать, расположив между источником прямоугольного сигнала и интегратором, приведенным на рис. 10.19, развязывающую ЛС-цепь, изображенную на рис. 10.12. В результате входной и выходной сигналы принимают вид, показанный на рис. 10.21. Положительные полуволны входного сигнала дают на выходе монотонно нарастающий сигнал, поскольку на этом отрезке времени происходит подсчет положительной площади, но затем за каждым положительным полупериодом следует отрицательный полупериод, в пределах которого также происходит интегрирование, давая на выходе сигнал с отрицательным наклоном и компенсируя аналогичный предыдущий сигнал с положительным наклоном. В результате получается треугольный сигнал, середина которого приходится на нулевой уровень. В действительности, этот сигнал состоит из отрезков экспоненциальных кривых заряда и разряда интегрирующего конденсатора. Если Rw С имеют значения, указанные на рис. 10.19, и частота сигнала равна 500 Гц или больше, то условиевыполняется; отрезки экспонент представляют

столь малые части всей функции, что их аппроксимируют прямой линией.

Электронные вычисления

Интересный эксперимент по проверке работы дифференциатора и интегратора состоит в интегрировании продифференцированного прямоугольного колебания. Математика говорит нам, что должна быть восстановлена исходная функция, то есть прямоугольный сигнал. Если показанная на рис. 10.19 интегрирующая цепь включена вслед за дифференцирующей цепью, приведенной на рис. 10.17, и на эту комбинацию подается прямоугольное колебание, то теорию можно проверить, наблюдая выходной сигнал с помощью осциллографа. Сносное изображение входного сигнала получится при частоте следования импульсов около 500 Гц. Попытайтесь объяснить неточность результата.

Литература: М.Х.Джонс, Электроника — практический курс Москва: Техносфера, 2006. – 512с. ISBN 5-94836-086-5

Постоянная времени RC — RC time constant

Времени RC — константа , которая также называется тау, то постоянное время (в секундах ) из цепи RC , равно произведению цепи сопротивления (в омах ) и монтажная емкость (в фарадах ), т.е.

τ знак равно р С {\ Displaystyle \ тау = RC}

Это время , необходимое для зарядки конденсатора через резистор , от начального напряжения заряда от нуля до приблизительно 63,2% от величины приложенного напряжения постоянного тока, или для разряда конденсатора через тот же резистор примерно 36,8% от его исходного напряжение заряда. Это значение является производным от математической константы е , в частности , или , относящиеся к напряжению на конденсаторе в зависимости от времени: 1 — е — 1 {\ Displaystyle 1-е ^ {- 1}} е — 1 {\ Displaystyle е ^ {- 1}}

Зарядка в направлении приложенного напряжения В 0 : В ( T ) знак равно В 0 ( 1 — е — T / τ ) {\ Displaystyle V_ {0}: \ четырехъядерных V (T) = V_ {0} (1-е ^ {- т / \ тау})}

Разрядка к нулю от начального напряжения В 0 : В ( T ) знак равно В 0 ( е — T / τ ) {\ Displaystyle V_ {0}: \ четырехъядерных V (T) = V_ {0} ({е ^ — т / \ тау})}

предельная частота

Постоянное время связанно с частотой среза ф _с , альтернативным параметром схемы RC, по τ {\ Displaystyle \ тау}

τ знак равно р С знак равно 1 2 π е с {\ Displaystyle \ тау = RC = {\ гидроразрыва {1} {2 \ пи F_ {C}}}}

или, что то же самое,

е с знак равно 1 2 π р С знак равно 1 2 π τ {\ Displaystyle F_ {C} = {\ гидроразрыва {1} {2 \ пи RC}} = {\ гидроразрыва {1} {2 \ пи \ тау}}}

где сопротивление в Оме и емкость в фарадах дают постоянное время в секундах или частоту в Гц.

Короткие условные уравнения с использованием значения для : 10 6 / ( 2 π ) {\ Displaystyle 10 ^ {6} / (2 \ р)}

е _с в Гц = 159155 / т в мкс

τ в мкс = 159155 / ф _с в Гц

Другие полезные уравнения:

время нарастания (от 20% до 80%) T р ≈ 1.4 τ ≈ 0,22 е с {\ Displaystyle T_ {г} \ около 1,4 \ тау \ около {\ гидроразрыва {0,22} {F_ {C}}}}

время нарастания (от 10% до 90%) T р ≈ 2,2 τ ≈ 0,35 е с {\ Displaystyle T_ {г} \ около 2,2 \ тау \ около {\ гидроразрыва {0,35} {F_ {C}}}}

В более сложных схемах , состоящие из более чем одного резистора и / или конденсатора, время холостого хода постоянная метод обеспечивает способ аппроксимации частоты среза путем вычисления суммы нескольких постоянного времени RC.

задержка

Задержка сигнала провода или другой цепи, измеренная , как групповая задержка или задержка фазы или эффективная задержка распространения в цифровом переходе, может быть доминируют резистивно-емкостными эффектами, в зависимости от расстояния и других параметров, или , альтернативно , может быть во власти индуктивные , волны и скорость света эффектов в других сферах.

Задержка Резистивного-емкостная или задержка RC, тормозит дальнейшее увеличение скорости в микроэлектронных интегральных схемах . Когда размер элемента становится все меньше и меньше , чтобы увеличить тактовую частоту , задержка RC играет все более важную роль. Эта задержка может быть уменьшена путем замены алюминия проводящую проволоку по меди , тем самым уменьшая сопротивление; он также может быть уменьшен путем изменения межслойного диэлектрика (обычно двуокись кремния) с низкой диэлектрической проницаемостью материалов, тем самым уменьшая емкость.

Типичная цифровая задержка распространения резистивной проволоки составляет около половины R раза C; поскольку оба R и С пропорциональны длине провода, задержка шкалы как квадрат длины провода. Заряд распространяется путем диффузии в такой проволоке, как пояснил лорд Кельвин в середине девятнадцатого века. До Хевисайд не обнаружил , что уравнения Максвелла подразумевают распространение волн при достаточной индуктивности в цепи, этот квадрат отношение диффузии думали обеспечить фундаментальный предел для совершенствования телеграфных кабелей дальней связи. Этот старый анализ был заменен в области телеграфной, но остается актуальной долго на чипе межсоединений.

Смотрите также

Рекомендации

внешняя ссылка

<img src=»https://en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Физические процессы при разрядке конденсатора на резистор и индуктивную катушку. Постоянная времени RC-цепи

Контрольные вопросы.

1.  Какие физические процессы происходят при разрядке конденсатора на резистор и индуктивную катушку?

При разрядке конденсатора на резистор напряжение на нем уменьшается по закону: 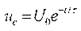 . При этом резистор может нагреваться(повышается температура резистора).

При разрядке конденсатора на индуктивную катушку напряжение на конденсаторе 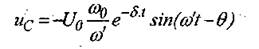. При этом катушка также нагревается.

2.  Как замедлить или ускорить процесс разряда конденсатора на резистор?

Увеличение сопротивления R при С=const замедляет разряд конденсатора. К замедлению разряда приводит также и увеличение емкости при R=const.

3.  Что такое постоянная времени RC-цепи? Как определить постоянную времени по осциллографу разряда конденсатора на резистор?

Постоянная времени RC-цепи – постоянная времени, определяющая промежуток времени, за которое напряжение u_c (и ток i) уменьшается в е раз.

Постоянную времени цепи можно найти графическим способом. Для этого нужно провести касательную к кривой напряжения в любой её точке. Постоянная времени выражается длиной подкасательной, выраженной в секундах (с).

4.  Каким должно быть сопротивление RLC-цепи, чтобы разряд конденсатора носил колебательный характер? Как влияет значение сопротивления   R на частоту (период) затухающих колебаний?

При условии 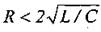 разряд носит колебательный характер. Увеличение сопротивления R цепи приводит к уменьшению угловой частоты  ω^’ и к увеличению периода затухающих колебаний   Т’=2π/ ω^’.

5.  Как с помощью декремента колебаний определить коэффициент затухания RLC-цепи?

Определить коэффициент затуханияRLC-цепи   с помощью дискремента затухания  можно по следующей формуле: δ = In Δ /Т^’.

6.  Как перевести колебательный разряд конденсатора в апериодический?

Колебательный разряд в апериодический можно перевести увеличением сопротивления резистора, включенного в RLC—цепь.  Но для этого нужно определенное условие: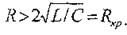  

постоянная времени rc- цепи — с английского на русский

См. также в других словарях:

• постоянная времени электрической цепи — Величина, характеризующая электрическую цепь, в которой преходящий электрический ток является экспоненциальной функцией времени, равная интервалу времени, в течение которого преходящий электрический ток в этой цепи убывает в е раз. Примечание… …   Справочник технического переводчика

• постоянная времени входной цепи — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN input time constant …   Справочник технического переводчика

• постоянная времени якорной цепи — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN armature circuit time constant …   Справочник технического переводчика

• Постоянная времени электрической цепи — 75. Постоянная времени электрической цепи По ГОСТ 19880 74* Источник: ГОСТ 20938 75: Трансформаторы малой мощности. Термины и определения …   Словарь-справочник терминов нормативно-технической документации

• Постоянная времени электрической цепи — 1. Величина, характеризующая электрическую цепь, в которой преходящий электрический ток является экспоненциальной функцией времени, равная интервалу времени, в течение которого преходящий электрический ток в этой цепи убывает в е раз… …   Телекоммуникационный словарь

• постоянная времени электрической цепи — Величина, характеризующая электрическую цепь, в которой свободный ток является экспоненциальной функцией времени, равная промежутку времени, в течение которого ток в этой цепи убывает в е = 2,718 раз …   Политехнический терминологический толковый словарь

• ПОСТОЯННАЯ ВРЕМЕНИ — величина, характеризующая инерционность динамической системы; имеет размерность времени. Напр., постоянная времени электрической цепи характеризует скорость изменения тока или напряжения в ней при переходном процессе …   Большой Энциклопедический словарь

• постоянная времени записи — Постоянная времени RC цепи, у которой частотная зависимость сопротивления или проводимости совпадает с амплитудно частотной характеристикой канала записи или с одной из слагаемых этой характеристики. [ГОСТ 13699 91] Тематики запись и… …   Справочник технического переводчика

• постоянная времени нагруженного трансформатора малой мощности — Постоянная времени электрической цепи нагруженного трансформатора, определяемая отношением индуктивности намагничивания к эквивалентному сопротивлению трансформатора [ГОСТ 20938 75] Тематики трансформатор Классификация >>> EN time… …   Справочник технического переводчика

• постоянная времени первичной обмотки трансформатора малой мощности — Постоянная времени электрической цепи первичной обмотки трансформатора, определяемая отношением индуктивности первичной обмотки к ее активному сопротивлению [ГОСТ 20938 75] Тематики трансформатор Классификация >>> EN time constant of a… …   Справочник технического переводчика

• постоянная времени — 3.2 постоянная времени: Величина, характеризующая инерционность динамической системы при изменении регистрируемого сигнала по экспоненциальному закону. Источник: ГОСТ Р 53375 2009: Скважины нефтяные и газовые. Геолого технологические исследования …   Словарь-справочник терминов нормативно-технической документации

постоянная времени rc- цепи — со всех языков на русский

См. также в других словарях:

• постоянная времени электрической цепи — Величина, характеризующая электрическую цепь, в которой преходящий электрический ток является экспоненциальной функцией времени, равная интервалу времени, в течение которого преходящий электрический ток в этой цепи убывает в е раз. Примечание… …   Справочник технического переводчика

• постоянная времени входной цепи — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN input time constant …   Справочник технического переводчика

• постоянная времени якорной цепи — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN armature circuit time constant …   Справочник технического переводчика

• Постоянная времени электрической цепи — 75. Постоянная времени электрической цепи По ГОСТ 19880 74* Источник: ГОСТ 20938 75: Трансформаторы малой мощности. Термины и определения …   Словарь-справочник терминов нормативно-технической документации

• Постоянная времени электрической цепи — 1. Величина, характеризующая электрическую цепь, в которой преходящий электрический ток является экспоненциальной функцией времени, равная интервалу времени, в течение которого преходящий электрический ток в этой цепи убывает в е раз… …   Телекоммуникационный словарь

• постоянная времени электрической цепи — Величина, характеризующая электрическую цепь, в которой свободный ток является экспоненциальной функцией времени, равная промежутку времени, в течение которого ток в этой цепи убывает в е = 2,718 раз …   Политехнический терминологический толковый словарь

• ПОСТОЯННАЯ ВРЕМЕНИ — величина, характеризующая инерционность динамической системы; имеет размерность времени. Напр., постоянная времени электрической цепи характеризует скорость изменения тока или напряжения в ней при переходном процессе …   Большой Энциклопедический словарь

• постоянная времени записи — Постоянная времени RC цепи, у которой частотная зависимость сопротивления или проводимости совпадает с амплитудно частотной характеристикой канала записи или с одной из слагаемых этой характеристики. [ГОСТ 13699 91] Тематики запись и… …   Справочник технического переводчика

• постоянная времени нагруженного трансформатора малой мощности — Постоянная времени электрической цепи нагруженного трансформатора, определяемая отношением индуктивности намагничивания к эквивалентному сопротивлению трансформатора [ГОСТ 20938 75] Тематики трансформатор Классификация >>> EN time… …   Справочник технического переводчика

• постоянная времени первичной обмотки трансформатора малой мощности — Постоянная времени электрической цепи первичной обмотки трансформатора, определяемая отношением индуктивности первичной обмотки к ее активному сопротивлению [ГОСТ 20938 75] Тематики трансформатор Классификация >>> EN time constant of a… …   Справочник технического переводчика

• постоянная времени — 3.2 постоянная времени: Величина, характеризующая инерционность динамической системы при изменении регистрируемого сигнала по экспоненциальному закону. Источник: ГОСТ Р 53375 2009: Скважины нефтяные и газовые. Геолого технологические исследования …   Словарь-справочник терминов нормативно-технической документации

Анализ постоянной времени цепи RC

Анализ, часть 2 — Шаги к решению дифференциального уравнения

Теперь у нас есть линейное дифференциальное уравнение первого порядка в форме y ‘+ P (x) y = Q (x).
Это уравнение довольно просто решить с помощью интегрирующего коэффициента.

Для этого типа уравнения мы можем использовать коэффициент интегрирования μ = e ^∫Pdx

Шаг 1:

В нашем случае, если мы сравним наше уравнение (5) со стандартной формой, мы обнаружим, что P равно 1 / RC, и мы также интегрируем по t, поэтому мы вычисляем интегрирующий коэффициент как:

μ = e ^∫Pdt = e ^{∫1 / RCdt} = e ^{t / RC}

Шаг 2:

Затем умножьте левую часть уравнения (5) на μ, получив:

e ^{t / RC} V _c ‘+ e ^{t / RC} (1 / RC) V _c

Но e ^{t / RC} (1 / RC) является производной e ^{t / RC} (функция правила функции, а также потому, что производная экспоненты e, возведенная в степень, есть сама по себе.То есть d / dx (e ^x ) = e ^x

Следовательно:

e ^{t / RC} V _c ‘+ e ^{t / RC} (1 / RC) V _c можно переписать как:

e ^{t / RC} V _c ‘+ Vc d / dt (e ^{t / RC} )

Однако, зная правило дифференциации продукта:

e ^{t / RC} V _c ‘+ Vc d / dt (e ^{t / RC} ) = d / dt (e ^{t / RC} Vc)

Итак, левая часть уравнения (5) была упрощена до:

d / dt (e ^{t / RC} Vc)

Приравнивая это к правой части уравнения (5) (которое нам также нужно умножить на коэффициент интегрирования e ^{t / RC} ), мы получим:

d / dt (e ^{t / RC} Vc) = e ^{t / RC} (V _s / RC)

Шаг 3:

Теперь проинтегрируйте обе части уравнения относительно t:

∫ d / dt (e ^{t / RC} Vc) dt = ∫ (e ^{t / RC} (V _s / RC)) dt = V _s ∫ (e ^{t / RC} (1 / RC)) дт

Левая часть представляет собой интеграл от производной e ^{t / RC} Vc, поэтому интеграл снова прибегает к e ^{t / RC} Vc.

В правой части уравнения, если вынести константу V _s за знак интеграла, мы получим e ^{t / RC} , умноженное на 1 / RC. Но 1 / RC — это производная от показателя t / RC. Таким образом, этот интеграл имеет вид ∫ f (u) u ‘dt = ∫f (u) du, а в нашем примере u = t / RC и f (u) = e ^{t / RC} Следовательно, мы можем использовать обратную цепочку Правило для интеграции.

Итак, пусть u = t / RC и f (u) = e ^u дает:

∫ f (u) u ‘dt = ∫ (e ^{t / RC} (1 / RC)) dt = ∫ f (u) du = ∫ e ^u du = e ^u = e ^{t / RC}

Таким образом, правая часть интеграла становится:

V _s ∫ (e ^{t / RC} (1 / RC)) dt = V _s e ^{t / RC}

Соединение левой и правой половин уравнения и включение постоянной интегрирования:

e ^{t / RC} Vc = V _s e ^{t / RC} + C

Разделите обе стороны на e ^{t / RC} , чтобы изолировать Vc:

Vc = V _s + Ce ^{-t / RC} …………….. Уравнение (6)

Шаг 4:

Оценка постоянной интеграции:

В момент времени t = 0 на конденсаторе нет напряжения. Итак, Vc = 0. Подставляем V _c = 0 и t = 0 в уравнение (6):

.

0 = V _с + Ce ^{-0 / RC} = V _с + Ce ⁰ = V _с + C 1 = Vs + C

Так C = — V _с

Заменить C обратно в уравнение (6):

Vc = V _s — V _s e ^{-t / RC} = V _s (1 — e ^{-t / RC} )

Итак, это дает нам окончательное уравнение для напряжения на конденсаторе как функции времени:

V _c (t) = V _s (1 — e ^{-t / RC} )………………… Уравнение (7)

Теперь, когда мы знаем это напряжение, легко вычислить и зарядный ток конденсатора. Как мы заметили ранее, ток конденсатора равен току резистора, потому что они соединены последовательно:

i (t) = (V _s — V _c (t)) / R

Замена V _c (t) из формулы (6):

i (t) = (Vs — V _s (1 — e ^{-t / RC} )) / R

= (V _{s e ^{-t / RC}} ) / R = V _s / R (e ^{-t / RC} )

Итак, наше окончательное уравнение для тока:

i (t) = V _s / R (e ^{-t / RC} )………………. Уравнение (8)

.

Постоянная времени RC

Измерение постоянной времени в RC-цепи

В этом лабораторном эксперименте мы будем измерять постоянную времени τ RC-цепи через три разных метода. На рисунке 1 мы нарисовали последовательную RC-цепь.

Рисунок 1 — Схема RC-цепи
Когда переключатель находится в положении 1, источник напряжения подает ток на резистор и конденсатор. На пластинах конденсатора оседает заряд. Вначале на пластинах очень мало заряда, однако со временем заряд идет на пластины накапливаются, и повышенное напряжение на конденсаторе уменьшит протекание тока через цепь.Мы можем увидеть это в следующем уравнении цикла:

V _o + V _r + V _c = 0
или
V _o — iR — q / C = 0

Поскольку q становится больше, я должен уменьшаться, чтобы компенсировать это. Со временем текущий со временем приблизится к нулю. Когда переключатель переводится в положение 2, аккумулятор извлекается из цепи, и заряд, накопившийся в конденсаторе, проходит через резистор. В этом случае уравнение выглядит так:

iR + q / C = 0
или
dq / dt R + q / C = 0

Это дифференциальное уравнение первого порядка имеет решение в виде экспоненты:
q (t) = q _o e ^{(- t / τ)}

Где τ = RC.Эта функция убывания изображена на рисунке 2:

.
Рисунок 2 — Экспоненциальное затухание

Учитывая значения R и C в большинстве схем, очень трудно «наблюдать» за распадом. В этой лабораторной работе мы немного схитрим, подключим нашу RC-цепь не к источнику напряжения. с переключателем, но с функциональным генератором, который выдает прямоугольный сигнал. Это будет действовать как «включено» и «выключено» напряжение питания сотни или тысячи раз в секунду. Затем мы можем наблюдать напряжение на схему на осциллографе и оттуда измерьте τ.

Процедура:
С помощью осциллографа измерьте прямоугольный выходной сигнал функционального генератора. Установить размах напряжения не менее десяти вольт и поместите форму сигнала на экран осциллографа таким образом, чтобы было легко измерить напряжения. При этом также убедитесь, что измеренный период на вашем осциллографе — это то, что вы ожидаете от частоты от функционального генератора. Распространенной ошибкой в ​​этой лабораторной работе является использование неоткалиброванной шкалы времени.

На макете последовательно подключите конденсатор и резистор.Выберите пару с RC 10 ^-4 секунд или меньше. Однако обратите внимание, что если вы выберете конденсатор с очень малой емкостью, то емкость остальной части схемы будет доминировать при измерении τ. Если ваши результаты для номера метода №1 категорически не согласен с методами №2 и №3, значит, вы проигнорировали предупреждение о выборе очень маленького емкость.

Метод № 1
Первый способ измерения τ — это считывание показаний R&C непосредственно с компонентов. самих себя.Поскольку конденсаторы обычно имеют погрешности ± 20%. Какая погрешность связана с этим измерением?

Метод № 2
Подключите осциллограф для измерения напряжения на конденсаторе. См. Рисунок 3. Обратите внимание, что конденсатор должен подключаться к земле, а не к резистору. Подумайте об этой детали, когда будете проводить измерения. если ты при неправильном измерении можно заземлить обе стороны конденсатора, фактически исключив его из цепи.

Рисунок 3 — Фотография RC-цепи

На вашем прицеле проверьте напряжение на конденсаторе.Это должно выглядеть примерно так, как показано на рисунке 4. Обратите внимание, что вам может потребоваться настроить запуск на вашем осциллографе .

Рисунок 4 — Вверху: диаграмма отклика напряжения Внизу: напряжение на конденсаторе на осциллографе

Увеличьте период работы генератора функций так, чтобы казалось, что конденсатор полностью заряжен. разрядка. «Увеличьте» этот участок графика, изменив временную шкалу, таким образом, вы можете осмотрите его более внимательно. Смотрите рисунок 5.
Рисунок 5 — «Раздутие» затухающей части сигнала

Нашим вторым методом измерения постоянной времени будет измерение «одной точки». Поскольку e ^-1 = 0,368, возьмите разницу между самым высоким и самым низким напряжениями, умножьте это на 0,368 и прибавьте к самому низкому напряжение. Который будет напряжение на конденсаторе после одного τ. Найдите этот уровень напряжения на экране и измерьте, сколько времени потребовалось для напряжение на конденсаторе снизится до этого значения.Поскольку напряжение соответствует одному затуханию τ, оно прямое измерение τ. Не забудьте указать в записной книжке оценку ошибки. Таким же образом оцените ошибку вы бы оценили погрешность измерения при использовании линейки.

Метод № 3
Последний способ измерения τ — это сбор данных во многих точках. Воспользуйтесь тем, что у нас есть цифровые осциллографы, сохраняя данные на карту памяти USB и импортируя данные в Excel. Если вы затем вычислите столбец, который представляет собой натуральный логарифм (ln) вашего напряжения, вы можете построить график этих значений. данные по времени и получить оценку τ (фактически -1 / τ).Используйте компьютеры в лаборатории, чтобы получить уклон и погрешность уклона. Помните, что некоторые из ваших данных более ценны, чем другие, и удалите точки, которые могут сбить вашу кривую (подумайте об относительной ошибке некоторых баллов по сравнению с другими).

В заключение обсудите RC-схему, сравните ваши значения τ с их погрешностями и включите свои мысли о лучший способ измерить τ. Обратите внимание, что ваш вывод должен быть прилично длиннее, чем те, которые вы написали, поэтому далеко для этого класса, и если ваше обсуждение не будет включать комментарии по поводу неопределенностей в вашем измерения не будут считаться завершенными.

,

Постоянная времени RC Деривация

Эталонные дизайнерские калькуляторы

Получение постоянной времени RC

На схеме показан резистор номиналом $ R $, соединенный с конденсатором номиналом $ C $.

Пусть импульсное напряжение V приложено в момент времени t = 0. Электрический ток начинает течь через резистор $ R $, и конденсатор начинает заряжаться. В результате на конденсаторе $ C $ возникает напряжение $ v (t) $. растет.Заряд $ q (t) $ на конденсаторе также начинает расти. Сумма заряда $ q (t) $ в любой момент времени $ t $ определяется выражением

$ q (t) = C.v (t) $

где $ C $ — емкость конденсатора.

Дифференцирование этого уравнения по времени дает

$ \ frac {dq (t)} {dt} = C. \ Frac {dv (t)} {dt} $

$ \ frac {dq (t)} {dt} $ — это скорость изменения заряда в цепи, которая представляет собой не что иное, как текущий ток.Итак, мы можем написать уравнение как

$ i (t) = C. \ Frac {dv (t)} {dt} $

Обратите внимание, что этот ток $ i (t) $ протекает через резистор.

Если $ v (t) $ — это напряжение на конденсаторе в момент времени t, то напряжение на резисторе в момент времени t определяется как $ V-v (t) $.

По закону Кирхгофа мы можем написать

$ V-v (t) = i (t). R $

Объединяя два уравнения, получаем

$ \ frac {V-v (t)} {R} = C.\ Гидроразрыва {DV (т)} {дт} $

Разделение переменных.

$ \ frac {dt} {RC} = \ frac {dv (t)} {V-v (t)} $

Решение этого уравнения приводит нас к

$ \ frac {t} {RC} = -ln (V-v (t)) + K $

где K — постоянная интегрирования.

Так как при t = 0 v (t) = 0, подстановкой получаем

$ K = ln (V) $

Следовательно, получаем

$ \ frac {t} {RC} = -ln (V-v (t)) + ln (V) $ или

$ ln \ frac {V-v (t)} {V} = — \ frac {t} {RC} $

Выражаясь в экспоненциальной форме, получаем

$ V -v (t) = e ^ {- \ frac {t} {RC}} $

, что упрощает

$ V -v (t) = V.{-1}) $ или около 63,2% от окончательного значения

& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp