Постоянная времени — Википедия

Материал из Википедии — свободной энциклопедии

Постоянная времени — характеристика экспоненциального процесса, определяющая время, через которое амплитуда процесса упадёт в «е» раз (е≈2,718).

В радиотехнике

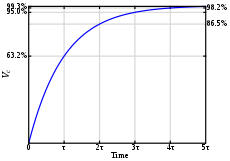
В радиотехнике постоянная времени τ{\displaystyle \tau } характеризует длительность протекания переходного процесса, обычно это тот промежуток времени, в течение которого реакция схемы на единичный скачок (функция Хевисайда) достигает 1−1/e≈63.2%{\displaystyle 1-1/e\approx 63.2\,\%} от своего конечного значения. Также постоянная времени характеризует время убывания реакции до уровня 1/e≈36.8%{\displaystyle 1/e\approx 36.8\,\%} от своего первоначального значения.

Фильтры

Постоянная времени связана с граничной частотой, либо с частотой пропускания фильтра нижних частот.

fgr=12πτ{\displaystyle f_{gr}={1 \over 2\pi \tau }}

Видео по теме

См. также

Ссылки

постоянная времени — это… Что такое постоянная времени?

3.2 постоянная времени: Величина, характеризующая инерционность динамической системы при изменении регистрируемого сигнала по экспоненциальному закону.

3.20 постоянная времени (time constant): Для системы первого порядка — время, необходимое для достижения выходным сигналом системы 63,2 % его конечной вариации после ступенчатого изменения ее входного сигнала.

Если система не является системой первого порядка, термин «постоянная времени» не применяют. Для системы более высокого порядка следует использовать термин «время реакции». [МЭК 62397]

Постоянная времени

Время перемещения клапана регулирующего органа на

2/₃ номинального хода при скачкообразном изменении значения температуры регулируемой среды на величину зоны пропорциональности.

Смотри также родственные термины:

постоянная времени апериодической составляющей тока короткого замыкания в электроустановке: Электромагнитная постоянная времени, характеризующая скорость затухания апериодической составляющей тока короткого замыкания.

[ГОСТ 26522-85, статья 80]

постоянная времени газоанализатора : Время от впуска газа в газоанализатор до получения результата.

СНГ — сжиженный углеводородный (нефтяной) газ;

СПГ — компримированный (сжатый) природный газ;

СО — оксид углерода;

СН — углеводороды.

156 постоянная времени записи:

Постоянная времени RC-цепи, у которой частотная зависимость сопротивления или проводимости совпадает с амплитудно-частотной характеристикой канала записи или с одной из слагаемых этой характеристики

17б. Постоянная времени заряда детектора измерителя индустриальных радиопомех

D. Aufladezeitkonstante des Gleichrichters eines Funkstörmessgerätes

E. Electric charge time constant (of a detector)

F. Constante de temps électrique à la charge (d’un détecteur)

Время, необходимое для того, чтобы после подачи на вход детектора измерителя индустриальных радиопомех синусоидального напряжения постоянной амплитуды напряжение на его емкостной нагрузке достигло 63 % установившегося значения

3.4 постоянная времени заряда детектора Т_с : Время, необходимое для того, чтобы после подачи синусоидального напряжения постоянной амплитуды на вход каскада, предшествующего детектору, напряжение на выходе детектора достигло 63 % установившегося значения.

Примечание — Постоянную времени детектора определяют следующим образом: синусоидальный сигнал постоянной амплитуды, имеющий частоту, равную центральной частоте полосы усилителя промежуточной частоты (ПЧ), подают на вход каскада, непосредственно предшествующего детектору. К усилителю постоянного тока подключают безинерционный прибор (например осциллограф) и отмечают показание

D, соответствующее установившемуся значению.

Для предотвращения перегрузки используемых каскадов устанавливают такой уровень входного сигнала, при котором выходной сигнал тракта остается в пределах линейного рабочего динамического диапазона. Затем синусоидальный сигнал такого же уровня с прямоугольной огибающей подают только на ограниченное время, устанавливаемое так, чтобы зарегистрированное показание измерительного прибора было 0,63D. Длительность такого сигнала равна постоянной времени заряда детектора.

Определения термина из разных документов: постоянная времени заряда детектора Т

с

62. Постоянная времени конденсатора

D. Zeitkonstante

E. Time constant

F. Constante de temps

Величина, равная произведению сопротивления изоляции конденсатора на его емкость

54. Постоянная времени магнитного усилителя

Time constant of transductor

Время переходного процесса магнитного усилителя, за которое изменение выходной величины в нагрузке магнитного усилителя достигает 63 % установившегося значения при скачкообразном изменении входной величины

78. Постоянная времени нагруженного трансформатора малой мощности

D. Zeitkonstante des Übertragers unter last

E. Time constant of a transformer under load

F. Constante de temps du transformateur charge

Постоянная времени электрической цепи нагруженного трансформатора, определяемая отношением индуктивности намагничивания к эквивалентному сопротивлению трансформатора

76. Постоянная времени первичной обмотки трансформатора малой мощности

D. Zeitkonstante der Primarwicklung des Ubertragers

E. Time constant of a transformer primary winding

F. Constante de temps denroulement primaire

Схемная функция

25. Постоянная времени радиоэлектронной схемы

Обратная величина модуля собственного значения матрицы Якоби в системе дифференциальных уравнений, являющейся математической моделью радиоэлектронной схемы

25. Постоянная времени радиоэлектронной схемы

3.5 постоянная времени разряда детектора T_D : Время, необходимое для того, чтобы после прекращения подачи синусоидального напряжения постоянной амплитуды на вход устройства, непосредственно предшествующего детектору, напряжение на выходе детектора уменьшилось до 37 % его первоначального значения.

Примечание — Метод измерения аналогичен методу для измерения постоянной времени заряда детектора, но вместо сигнала, подаваемого в течение ограниченного времени, этот сигнал прерывается на ограниченное время. Время, необходимое для того, чтобы показание прибора уменьшилось до 0,37

D, является постоянной времени разряда детектора.

Определения термина из разных документов: постоянная времени разряда детектора T_D

17в. Постоянная времени разряда детектора измерителя индустриальных радиопомех

D. Entladezeitkonstante des Gleichrichters eines Funkstörmessgerätes

E. Electric discharge time constant (of a detector)

F. Constante de temps électrique à la décharge (d’un détecteur)

Время, необходимое для того, чтобы после снятия со входа детектора измерителя индустриальных радиопомех синусоидального напряжения постоянной амплитуды напряжение на его емкостной нагрузке уменьшилось до 37 % первичного значения

Постоянная времени релаксации

Время, в течение которого электрический заряд объекта при свободной утечке уменьшается в е раз

124. Постоянная времени СВЧ диода

τ

Произведение емкости перехода на последовательное сопротивление потерь СВЧ диода

3.29 постоянная времени синхронной машины по продольной оси при разомкнутой обмотке якоря переходная: Электромагнитная постоянная времени, определяемая параметрами обмотки возбуждения синхронной машины по поперечной оси.

6. Постоянная времени тепловой инерции авиационного датчика температуры

Постоянная времени датчика температуры

Время, необходимое для того, чтобы при внесении авиационного датчика температуры в среду с постоянной температурой разность между температурами среды и авиационного датчика температуры в области регулярного режима, определяемая по величине сигнала авиационного датчика температуры, стала равной 0,37 значения разности температуры установившегося теплового равновесия и начальной температуры авиационного датчика

77. Постоянная времени трансформатора малой мощности

D. Zeitkonstante des Übertragers

E. Transformer time constant

F. Constante de temps du transformateur

Постоянная времени электрической цепи трансформатора, определяемая суммой постоянных времен и всех обмоток трансформатора с учетом режимов работы

45. Постоянная времени цепи обратной связи на высокой частоте биполярного транзистора

D. HF-Rückwirkungszeitkonstante

E. Collector-base time constant

t_s

Произведение сопротивления базы на активную емкость коллекторного перехода

57. Постоянная времени цепи управления магнитного усилителя

Input time constant of transductor

Разность суммарной и добавочной постоянных времени

75. Постоянная времени электрической цепи

По ГОСТ 19880-74*

274 постоянная времени электрической цепи

Величина, характеризующая электрическую цепь, в которой преходящий электрический ток является экспоненциальной функцией времени, равная интервалу времени, в течение которого преходящий электрический ток в этой цепи убывает в

е раз.

Примечание — е — основание натурального логарифма

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

ПОСТОЯННАЯ ВРЕМЕНИ это что такое ПОСТОЯННАЯ ВРЕМЕНИ: определение — Философия.НЭС

ПОСТОЯННАЯ ВРЕМЕНИ

временной параметр, характеризующий динамические свойства (инерционность) объекта исследования и служащий мерой времени установления стационарного состояния (или стационарного режима функционирования). Это определение П. в., ставшее традиционным, обычно конкретизируется как интервал длительности, в течение которого параметр, характеризующий переходный процесс, изменяется в определенное число (как правило, в е) раз (е ? 2,72). На сегодняшний день известно множество временных параметров материальных процессов становления и закономерной эволюции материальных тел и систем, которые хотя и не удовлетворяют традиционному определению П. в., тем не менее заслуживают квалификации как П. в. Разные временные параметры, являющиеся, фактически, П. в., имеют специфические наименования и не всегда осознаются как П. в. Вместе с тем системное изучение П. в. позволило бы многое прояснить в механизмах и закономерностях течения материальных процессов становления и эволюции материальных тел и систем. Четкое уяснение природы П. в. должно, с одной стороны, расширить круг временных показателей, являющихся фактически П. в. соответствующих процессов, во-вторых, подготовить исследователей к выявлению П. в., измеренной в единицах разных типов времени. I. Постоянные времени материальных процессов. Причины возникновения П. в. материальных процессов различны. В одних случаях П. в. возникают в силу наличия энергетических барьеров на пути превращения количественных изменений в качественные; в других — в силу необходимости реализации определенных процессов на более фундаментальных уровнях организации материального мира для возникновения доступных наблюдению изменений в макромире. Возможны и иные причины. Традиционное определение П. в. обусловлено тем, что особым объектом изучения П. в. стали в тех разделах физики, в которых течение материальных процессов описывается дифференциальными и интегральными уравнениями. В структуре уравнений исследуемых процессов и появляется обычно некоторый параметр, названный «постоянным времени», от величины которого зависит скорость течения процесса. В связи с быстрым развитием за последнее полстолетие вычислительной техники огромное значение приобрели П. в. электромагнитных процессов. Зная характер зависимости П. в. различных узлов электронных систем от физических характеристик электронных схем и каналов связи, можно точно рассчитать и отрегулировать все П. в. таким образом, чтобы сигналы своевременно поступали в соответствующие узлы электронной системы. Многие П. в. получили особые названия как «времена» тех или иных процессов: «время абсорбции», «время реверберации», «время релаксации» и др. I. 1. Время абсорбции (от лат. absorptio — поглощение) интервал длительности, на протяжении которого из раствора или смеси газов твердым телом, жидкостью или тканями живого организма поглощается определенный объем конкретного вещества. В. а. играет важную роль в технологических процессах химической промышленности, системах жизнеобеспечения космических кораблей и в физиологических процессах живых организмов, в основе которых лежат процессы абсорбции. Например, в медицине режимы медикаментозного лечения определяются с учетом времени абсорбции тканями разных органов тех или иных компонентов лекарств. I. 2. Время адсорбции (от лат. ad — на, при и sorbeo поглощаю) — интервал длительности, на протяжении которого адсорбированная молекула находится на адсорбирующей поверхности жидкости или твердого тела, входя в состав покрывающего эту поверхность тонкого слоя адсорбированных молекул. В. а. может колебаться в широких пределах. Скоростью адсорбции (соответственно скоростью десорбции) называется количество молекул, «прилипающих» к адсорбирующей поверхности и освобождающихся от связи с этой поверхностью за единицу времени. Различаются физическая и химическая адсорбции. При физической адсорбции связями, удерживающими молекулы адсорбента, являются Вандерваальсовы связи (взаимодействия наведенных диполей), поляризационные связи (ион-дипольные взаимодействия), водородные, координационные (взаимодействия донор — акцептор). При возникновении между молекулами адсорбента и адсорбата химических связей говорят о хемосорбции. Скорость хемосорбции, как и любого химического процесса, увеличивается с повышением температуры. Адсорбированные молекулы не только совершают движение вдоль поверхности адсорбента, но и колеблются, то приближаясь, то удаляясь от нее. Чем выше температура, тем интенсивнее колебательное движение, а следовательно больше вероятность того, что связь молекулы с поверхностью будет разорвана и молекула десорбируется. Поэтому с ростом температуры уменьшается В. а. и снижается равновесное количество адсорбированных молекул. I. 3. Время задержки — интервал длительности, на который задерживается: а) сигнал в электронных технических системах или их блоках. В электронной технике каждый составной элемент обладает своим временем задержки, в силу чего слаженная работа всей системы возможна только в том случае, если сеть элементов, через которые проходят сигналы, точно согласована по своим временным характеристикам. Для достижения такой согласованности, помимо регулирования (в пределах возможности) времен задержки элементов системы, приходится вводить в ее структуру специально отрегулированные или саморегулирующиеся линии задержки; b) прохождение документа через систему организации и управления производством и другими сферами деятельности людей; c) воздействие тех или иных событий, результатов развития живого организма, биоценоза, человеческого общества и других развивающихся систем на дальнейшую их эволюцию. I. 4. Время запаздывания — термин, обозначающий: 1) при радио- и звуколокации, а также при измерении высоты полета летательных аппаратов (самолетов, искусственных спутников и т.п.) с помощью радиовысотомеров интервал длительности, на который отстает отраженный от объекта или от поверхности Земли сигнал по отношению к сигналу, поступившему в приемник непосредственно от передатчика. По времени запаздывания определяется расстоя

Постоянная времени — Time constant

В физике и технике , то постоянная времени , обычно обозначается греческой буквой т (тау), является параметр , характеризующий реакцию на стадии ввода первого порядка, линейного стационарна системы (LTI). Постоянное время является основной характеристикой блоком из первого порядка системы LTI.

Во временной области, обычный выбор , чтобы исследовать ответ времени через шаг ответ на ступенчатый входной сигнал , или импульсный отклик на дельта — функции Дирака ввода. В частотной области (например, глядя на преобразование Фурье от стадии реакции, или используя входной сигнал , который является простой синусоидальной функцией времени) постоянное время также определяет пропускную способность по времени-инвариантной системы первого порядка, то есть частота , при которой мощность выходного сигнала падает до половины значения , которое он имеет на низких частотах.

Постоянное время также используются для характеристики частотной характеристики различных обработки сигналов системов — магнитных лент , радиопередатчиков и приемников , запись и воспроизведение резки оборудования, а также цифровые фильтры — которые могут быть смоделированы или аппроксимированы первыми порядка системами LTI. Другие примеры включают в себя постоянное время , используемые в системах управления для интегральных и производных контроллеров действий, которые часто являются пневматическими , а не электрическими.

Временные константы особенность сосредоточенного системного анализа (сосредоточенный метод анализа мощности) для тепловых систем, используемого , когда объекты охлаждения или теплого равномерно под действием конвективного охлаждения или потепления.

Физически, постоянное время представляет истекшее время , необходимое для реакции системы на распад к нулю , если система продолжала распад на начальной скорости, из — за постепенное изменение скорости распада реакция будет иметь фактически снизилось по стоимости в на этот раз (скажем , от стадии снижения). В возрастающей системе, постоянное время этого время для системы шага ответа , чтобы достичь ее окончательного (асимптотического) значения (скажем , от шага увеличения). При радиоактивном распаде постоянного времени называются постоянная затухание ( Л ), и оно представляет собой как среднее время жизни распадающейся системы (такие как атом) , прежде чем он распадается, или время, которое требуется для всех , кроме 36,8% из атомов распад. По этой причине, постоянное время длиннее , чем период полураспада , который является временем только 50% атомов к распаду. 1/е≈36,8%{\ Displaystyle 1 / е \ примерно 36,8 \, \%}1-1/е≈63,2%{\ Displaystyle 1-1 / е \ примерно 63,2 \, \%}

Дифференциальное уравнение

Первого порядка системы LTI характеризуются дифференциальным уравнением

τdВdT+Взнак равное(T){\ Displaystyle {\ тау} {дУ \ над DT} + V = F (T)}

где τ представляет собой экспоненциальное затухание постоянная и V является функцией времени т

Взнак равноВ(T),{\ Displaystyle V = V (т).}

Правое это вынуждает функцию F (T) , описывающая внешние вождения функцию времени, которую можно рассматривать в качестве системного входа , к которой V (T) является ответом или выхода системы. Классические примеры для F (т) являются:

Функция Хевисайда , часто обозначается и (Т) :

U(T)знак равно{0,T<01,T≥0{\ Displaystyle и (г) = {\ BEGIN {случаи} 0, & т <0 \\ 1, & т \ GEQ 0 \ конец {случаи}}}

импульсная функция , часто обозначается d (T) , а также функция синусоидальной входного сигнала:

е(T)знак равноAгрех⁡(2πеT){\ Displaystyle F (T) = A \ sin (2 \ пи фут)}

или же

е(T)знак равноAеJωT,{\ Displaystyle е (т) = Ае ^ {J \ омега т},}

где является амплитуда функции форсирования, F является частота в Герцах, и ω = 2π F является частота в радианах в секунду.

Пример решения

Пример решение дифференциального уравнения с начальным значением V ₀ и не заставляя функции

В(T)знак равноВое-T/τ{\ Displaystyle V (T) = V_ {о} е ^ {- т / \ тау}}

где

Вознак равноВ(Tзнак равно0){\ Displaystyle V_ {O} = В (Т = 0)}

это начальное значение V . Таким образом, реакция является экспоненциальный спад с постоянной времени т .

обсуждение

предполагать

В(T)знак равноВ0е-T/τ{\ Displaystyle V (T) = V_ {0} {е ^ — т / \ тау}},

Такое поведение называется «затухающей» показательной функции. Время (тау) упоминаются как «постоянное время» и может быть использован (как в данном случае) , чтобы указать , как быстро экспоненциальная функция затухает. τ{\ Displaystyle \ тау}

Вот:

т = время ( как правило , в контрольной инженерии)T>0{\ Displaystyle т> 0}

V ₀ = начальное значение (см «конкретные случаи» ниже).

Особые случаи

1) Пусть ; то , и такTзнак равно0{\ Displaystyle т = 0}Взнак равноВ0е0{\ Displaystyle V = V_ {0} е ^ {0}}Взнак равноВ0{\ Displaystyle V = V_ {0}}

2) Пусть ; затемTзнак равноτ{\ Displaystyle т = \ тау}Взнак равноВ0е-1≈0,37В0{\ Displaystyle V = V_ {0} е ^ {- 1} \ около 0.37V_ {0}}

3) Пусть и такВзнак равное(T)знак равноВ0е-Tτ{\ Displaystyle V = F (T) = V_ {0} е ^ {- {т \ над \ тау}}}ИтT→∞е(T)знак равно0{\ Displaystyle \ Нт _ {т \ к \ infty} F (T) = 0}

4) Пусть ; затемTзнак равно5τ{\ Displaystyle т = 5 \ тау}Взнак равноВ0е-5≈0,0067В0{\ Displaystyle V = V_ {0} е ^ {- 5} \ около 0.0067V_ {0}}

После того, как в течение одного постоянная времени функция достигает й ^-1 = примерно 37% от ее исходного значения. В случае 4, после того, как пять постоянных времени функции достигает значения менее чем 1% от его первоначальной. В большинстве случаев этот порог 1% считается достаточно предположить , что функция заглохла к нулю — как правило, в контроле инженерных стабильную системы является тот , который имеет такое общее затухающего поведения.

Связь постоянная времени с пропускной способностью

Пример отклика системы с функцией форсирования синусоидальной волны. Ось времени в единицах постоянная времени . Ответ затухает стать простой синусоидой.τ{\ Displaystyle \ тау} Частотный отклик системы в зависимости от частоты в единицах ширины полосы ф _3dB . Ответ нормирован на нулевое значение частоты единицы, и падает до 1 / √2 в полосе пропускания.

Предположим, что функция форсирование выбрана в качестве синусоидальной так:

τdВdT+Взнак равное(T)знак равноAеJωT,{\ Displaystyle \ тау {дУ \ над DT} + V = F (T) = Ае ^ {J \ омега T}.}

(Ответ на реальный косинус или синусоидальный входной сигнал можно получить, взяв действительную или мнимую часть конечного результата, в силе формулы Эйлера .) Общее решение этого уравнения для времен т ≥ 0 с, предполагая , V (т = 0 ) = V ₀ является:

В(T)знак равноВ0е-T/τ+Aе-T/τ∫0TdT’ еT’/τеJωT'{\ Displaystyle V (T) = V_ {0} е ^ {- т / \ тау} + Ае ^ {- т / \ тау} \ Int _ {0} ^ {т} \, дт ‘\ е ^ {т ‘/ \ тау} е ^ {j \ омега т’}}

знак равноВ0е-T/τ+A1Jω+1/τ(еJωT-е-T/τ),{\ Displaystyle = V_ {0} {е ^ — т / \ тау} + А {\ гидроразрыва {1} {J \ омега + 1 / \ тау}} \ влево (е ^ {J \ омега т} -e ^ {-t / \ тау} \ справа).}

При больших времен распадающегося экспонент становится пренебрежимо малым и стационарным решение или длительное время решение:

В∞(T)знак равно1/τJω+1/τAеJωT,{\ Displaystyle V _ {\ infty} (т) = {\ гидроразрыва {1 / \ тау} {J \ омега + 1 / \ тау}} Ае ^ {J \ омега т}.}

Величина этого ответа является:

|В∞(T)|знак равноA1τ(ω2+(1/τ)2)1/2знак равноA11+(ωτ)2,{\ Displaystyle | V _ {\ infty} (т) | = А {\ гидроразрыва {1} {\ тау \ слева (\ Omega ^ {2} + (1 / \ тау) ^ {2} \ справа) ^ {1 / 2}}} = A {\ гидроразрыва {1} {\ SQRT {1 + (\ Omega \ тау) ^ {2}}}}.}

По соглашению, пропускная способность этой системы является частота , где | V _∞ | ² падает до половины стоимости, или где ωτ = 1. Это обычная пропускная способность конвенции, определяется как диапазон частот , где мощность падает менее чем на половину (не более -3 дБ). Используя частоту в герцах, а не радиан / с (ω = 2π F ):

е3dВзнак равно12πτ,{\ Displaystyle F_ {3dB} = {\ гидроразрыва {1} {2 \ пи \ тау}}.}

Обозначения е _3dB проистекает из выражения власти в децибелах и наблюдения , что половинная мощность соответствует падению величины | V _∞ | на коэффициент 1 / √2 , или на 3 дБ.

Таким образом, постоянное время определяет пропускную способность этой системы.

Переходный с произвольными начальными условиями

Шаг отклика системы для двух различных начальных значений V ₀ , один выше конечного значения и один в нуле. Ответ Давний является константой, V _∞ . Ось времени в единицах постоянная времени .τ{\ Displaystyle \ тау}

Предположим, что функция заставляя выбрана в качестве пошагового ввода так:

dВdT+1τВзнак равное(T)знак равноAU(T),{\ Displaystyle {дУ \ над DT} + {\ гидроразрыва {1} {\ тау}} В = F (T) = Аи (т),}

с и (Т) функции Хевисайда. Общее решение этого уравнения для времен т ≥ 0 с, предполагая , V (т = 0) = V ₀ является:

В(T)знак равноВ0е-T/τ+Aτ(1-е-T/τ),{\ Displaystyle V (T) = V_ {0} {е ^ — т / \ тау} + А \ тау \ слева (1-е ^ {- т / \ тау} \ справа).}

(Можно отметить, что эта реакция является ω → 0 предел выше ответ на синусоидальный вход.)

Долгое время решение не зависит от времени и не зависит от начальных условий:

В∞знак равноAτ,{\ Displaystyle V _ {\ infty} = A \ тау.}

Постоянное время остается одинаковой для одной и той же системы, независимо от начальных условий. Проще говоря, система приближается к его конечному, стационарное положению с постоянной скоростью, независимо от того, насколько близко она к этому значению в любой произвольной начальной точке.

Например, рассмотрим электрический двигатель которого стартап хорошо моделируется первого порядка системы LTI. Предположим, что при запуске из состояния покоя, двигатель занимает ⅛ секунды, чтобы достигнуть 63% от его номинальной скорости 100 оборотов в минуту, или 63 RPM-дефициту 37 оборотов в минуту. Тогда это будет обнаружено, что после следующего ⅛ секунды, двигатель ускорило дополнительно 23 оборотов в минуту, что равно 63% от той разницей, 37 оборотов в минуту. Это приводит его к 86 RPM-прежнему 14 оборотов в минуту низкого уровня. После третьего ⅛ секунды, двигатель будет получили дополнительный 9 RPM (63% от той разницей, 14 оборотов в минуту), положив ее на 95 оборотов в минуту.

На самом деле, учитывая любую начальную скорость с ≤ 100 оборотов в минуте, ⅛ секунды позже этот конкретный двигатель получил дополнительную 0,63 × (100 — с ) RPM.

Примеры временных констант

Временные константы в электрических цепях

Конденсатор напряжение шага отклик. 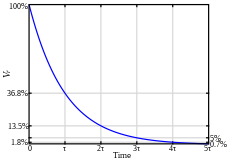Индуктор напряжение шага ответ.

В цепи RL , состоящей из одного резистора и катушки индуктивности, постоянное время (в секундах ) является τ{\ Displaystyle \ тау}

τзнак равноLр{\ Displaystyle \ тау = {Ь \ над R}}

где R представляет собой сопротивление (в омах ) , и L является индуктивность (в генри ).

Аналогичным образом , в цепи RC , состоящей из одного резистора и конденсатора, постоянное время (в секундах): τ{\ Displaystyle \ тау}

τзнак равнорС{\ Displaystyle \ тау = RC}

где R представляет собой сопротивление (в омах ) , и С представляет собой емкость (в фарадах ).

Электрические цепи часто являются более сложными , чем этими примеры, и могут проявлять различные постоянное время (См ответа Шага и полюс расщепление для некоторых примеров.) В случае , когда обратная связь присутствует, система может демонстрировать нестабильные, возрастающие колебания. Кроме того, физические электрические цепи редко действительно линейные системы для очень низких возбуждений амплитуды , за исключением; Однако приближение линейности широко используется.

В цифровых электронных схемах еще одна меры, то FO4 часто используются. Это может быть преобразовано в постоянная время единицы с помощью уравнения . 5τзнак равноFO4{\ Displaystyle 5 \ тау = {\ текст {FO4}}}

Тепловое постоянное время

Временные константы особенность сосредоточенного системного анализа (сосредоточенный метод анализа мощности) для тепловых систем, используемого , когда объекты охлаждения или теплого равномерно под действием конвективного охлаждения или потепления . В этом случае передача тепла от тела до температуры окружающей среды в данный момент времени, пропорциональна разности температур между телом и окружающей средой:

Fзнак равночасAs(T(T)-Ta),{\ Displaystyle F = ha_ {s} \ влево (Т (т) -T_ {а} \ справа),}

где ч есть коэффициент теплопередачи , а _с собой площадь поверхности, Т (т) = температура тела в момент времени Т , и Т постоянная температура окружающей среды. Положительный знак указывает на то соглашение , что F является положительным , когда тепло оставляя тело , поскольку его температура выше , чем температура окружающей среды ( F является внешним потоком). Если потери тепла в окружающую среду, это передача тепла приводит к снижению температуры тела , заданное:

ρспВdTdTзнак равно-F,{\ Displaystyle \ Rho C_ {р} V {\ гидроразрыва {дТ} {дт}} = — F,}

где ρ = плотность, с _р = удельная теплоемкость и V представляет собой объем тела. Отрицательный знак указывает температура падает , когда передача тепла наружу от тела (то есть, когда Р > 0). Приравнивая эти два выражения для передачи тепла,

ρспВdTdTзнак равно-часAs(T(T)-Ta),{\ Displaystyle \ Rho C_ {р} V {\ гидроразрыва {дТ} {дт}} = -. Ha_ {s} \ влево (Т (т) -T_ {а} \ справа)}

По-видимому, это первый заказ ЛТИТЕ систему, которая может быть отлита в виде:

dTdT+1τTзнак равно1τTa,{\ Displaystyle {\ гидроразрыва {дТ} {дт}} + {\ гидроразрыва {1} {\ тау}} Т = {\ гидроразрыва {1} {\ тау}} T_ {а},}

с

τзнак равноρспВчасAs,{\ Displaystyle \ тау = {\ гидроразрыва {\ Rho C_ {р} V}, {ha_ {s}}}.}

Другими слова, говорит постоянное время , что большие массы ρV и больше теплоемкость с _р привести к замедлению изменений температуры, а более крупные площади поверхности _сек и лучше перенос тепла ч приводят к более быстрым изменениям температуры.

Сравнение с вводным дифференциальным уравнением предполагает возможное обобщение на температуры , изменяющиеся во время окружающей среды Т _{течения} . Тем не менее, сохраняя при этом простой постоянный окружающий пример, путем замены переменной & Delta ; t ≡ ( Т — Т ), находим:

dΔTdT+1τΔTзнак равно0.{\ Displaystyle {\ гидроразрыва {d \ Delta T}, {дт}} + {\ гидроразрыва {1} {\ тау}} \ Дельта Т = 0.}

Системы , для которых охлаждения удовлетворяет указанное выше показательного уравнения называются удовлетворяют закон Ньютона охлаждения . Решение этого уравнения показывает , что, в таких системах, разница между температурой системы и ее окружением & Delta ; t как функцию времени т , определяется по формуле:

ΔT(T)знак равноΔT0е-T/τ,{\ Displaystyle \ Delta T (T) = \ Delta T_ {0} {е ^ — т / \ тау}}

где & Delta ; t ₀ является начальной разностью температур, в момент время T = 0. В словах, тело принимает ту же температуру, что и температуры окружающей среды при экспоненциально медленной скорости , определяемой постоянная времени.

Временные константы в нейробиологии

В потенциале действия (или даже в пассивном распространении сигнала) в нейроне , постоянное время является τ{\ Displaystyle \ тау}

τзнак равнормсм{\ Displaystyle \ тау = R_ {т} C_ {т}}

где г _м является сопротивление поперек мембраны и гр _м представляет собой емкость мембраны.

Сопротивление через мембрану , является функцией числа открытых ионных каналов и емкостью является функцией свойств липидного бислой .

Постоянное время используются для описания подъема и падения напряжения мембраны, где рост описываются

В(T)знак равноВМаксимум(1-е-T/τ){\ Displaystyle V (T) = V _ {\ textrm {макс}} (1-е ^ {- т / \ тау})}

и падение описывается

В(T)знак равноВМаксимуме-T/τ{\ Displaystyle V (T) = V _ {\ textrm {макс}} {е ^ — т / \ тау}}

где напряжение в милливольтах, время в секундах, а в секундах. τ{\ Displaystyle \ тау}

V _макс определяются как максимальное напряжение , полученным в потенциале действия, где

ВМаксимумзнак равнормя{\ Displaystyle V _ {\ textrm {макс}} = R_ {т} I}

где г _м этого сопротивления через мембрану , и я являюсь текущим.

Установка для т = для подъема устанавливает V ( т ) , равное 0,63 В _макс . Это означает , что постоянное время этого время , прошедшее после того, как 63% от V _макса был достигнуто τ{\ Displaystyle \ тау}

Установка для т = для падения устанавливает V ( т ) , равное 0,37 V _макс , а это означает , что постоянное время этого время , прошедшее после того, как она упала до 37% от V _макса . τ{\ Displaystyle \ тау}

Чем больше постоянная времени, тем медленнее рост или падение потенциала нейрона. Длинное постоянное время может привести к временной суммации , или алгебраическому суммированию повторных потенциалов. Короткое постоянное время , а производит детектор совпадений путем пространственного суммирования .

Экспоненциальный распад

В экспоненциальном распаде , такие как из радиоактивного изотопа, постоянное время может быть интерпретирована как среднее время жизни . Полураспад Т _HL связан с экспоненциальным постоянная временем с помощью τ{\ Displaystyle \ тау}

TЧАСLзнак равноτ⋅LN2.{\ Displaystyle T_ {HL} = \ тау \ CD \ mathrm {пер} \ 2.}

Взаимные постоянная время называются постоянной распада , и обозначаютсяλзнак равно1/τ,{\ Displaystyle \ лямбда = 1 / \ тау.}

Метеорологические датчики

Постоянное время этого количество времени, которое требуется для метеорологического датчика реагировать на быстрое изменение измеряемой величины , пока он не измеряет значения в пределах допуска точности , как правило , ожидаемом от датчика.

Чаще всего это относится к измерению температуры, температуры точки росы, влажность и давление воздуха. Радиозонды особенно страдает из — за их быстрое увеличение высоты.

Смотрите также

Заметки

Рекомендации

внешняя ссылка

Постоянная времени — Карта знаний

• Постоянная времени — характеристика экспоненциального процесса, определяющая время, через которое амплитуда процесса упадёт в «е» раз (е≈2,718).

Источник: Википедия

Связанные понятия

Переходный процесс — в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося состояния. Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы. Примерами внешнего воздействия могут быть дельта-импульс, скачок или синусоида. Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку. Коэффициент фазовой синхронизации (средняя фазовая когерентность) — численный показатель, количественно характеризующий синхронизованность фаз двух осцилляторов и отражающий стабильность разности этих фаз. При точном совпадении фаз коэффициент равен единице, при отсутствии синхронизации — нулю. Понятие коэффициента фазовой синхронизации широко используется в теории динамических систем и теории хаоса. Волна́ — изменение некоторой совокупности физических величин (характеристик некоторого физического поля или материальной среды), которое способно перемещаться, удаляясь от места его возникновения, или колебаться внутри ограниченных областей пространства. Быстро-медленная система в математике — это динамическая система, в которой присутствуют процессы, происходящие в разных масштабах времени. Фазовые переменные такой системы делятся на два класса: «быстрые» и «медленные» переменные. Скорость изменения «быстрых» переменных почти во всех точках фазового пространства много быстрее скорости изменения «медленных» переменных. Траектории таких систем состоят из чередующихся участков медленного «дрейфа» и быстрых «срывов». Быстро-медленные системы описывают…

Упоминания в литературе

где T=T2 – постоянная времени. x=Т1/2Т – относительный коэффициент демпфирования. Полагая обратную связь равной 1, структурную схему системы можно представить на рисунке 1.9. В этом случае передаточная функция всей системы Фрагмент нативной ЭЭГ ребенка группы риска – незрелый высокоамплитудный тип (50–100 мкВ) с несформированными регионарными различиями и замедлением корковой ритмики (4–4,5 Гц). Нижняя граница частот – постоянная времени 0,1 с Снижение положительного напряжения вызывает постепенное закрывание транзистора Q2. Постоянная времени разряда конденсатора определяется номиналами элементов С5 и R4 и параллельного соединения открытого перехода база-эмиттер транзистора Q2 и резистора R5. Параметры пассивных элементов должны выбираться таким образом, чтобы закрывание транзистора происходило после появления отрицательных напряжений вторичных каналов на резисторе R2 и диоде D2. Если это условие соблюдается, то после закрывания транзистора Q2 напряжение на аноде D4 не примет положительного значения и сбоя в работе источника питания не произойдет.

Связанные понятия (продолжение)

Ци́кл и́ндекса (васцилля́ция) — явление гидродинамической неустойчивости вращения неравномерно нагретой жидкости или газа, первоначально обнаруженное как квазипериодическое изменение индекса зональной циркуляции атмосферы… Электрический импульс — кратковременный всплеск электрического напряжения или силы тока в определённом, конечном временном промежутке. Различают видеоимпульсы — единичные колебания какой-либо формы и радиоимпульсы — всплески высокочастотных колебаний. Видеоимпульсы бывают однополярные (отклонение только в одну сторону от нулевого потенциала) и двухполярные. Перерегулирование — в теории управления, электронике и математике ограниченный по времени выброс сигнала или функции над целевым значением. Чаще всего рассматривается в качестве динамической характеристики динамической системы (например фильтра низких частот) при рассмотрении переходной функции. Перерегулирование зачастую сопровождается затухающими колебаниями. Модель сейсмического воздействия «СА-482» — совокупность универсальных характеристик, предназначенных для расчётов сейсмостойкости наземных объектов, состоящая из обобщённых спектров коэффициента динамичности (СКД) и синтезированной акселерограммы (СА-482). Цепь Чуа или схема Чуа — простейшая электрическая цепь, демонстрирующая режимы хаотических колебаний. Была предложена профессором Калифорнийского университета Леоном Чуа в 1983 году. Цепь состоит из двух конденсаторов, одной катушки индуктивности, линейного резистора и нелинейного резистора с отрицательным сопротивлением (обычно называемого диодом Чуа). Це́лостность сигна́лов (англ. Signal Integrity) — наличие достаточных для безошибочной передачи качественных характеристик электрического сигнала. Стационарность или постоянство — свойство процесса не менять свои характеристики со временем. Понятие используется в нескольких разделах науки. Внẏтренние гравитациỏнные вỏлны (ВГВ) или инерциóнно-гравитациóнные вóлны (ИГВ) — одна из форм колебательных движений, которые существуют в атмосфере как упругой среде. Термин «гравитационные» в названии данного типа волн указывает на то, что сила тяжести является одним из факторов, определяющих существование ВГВ.

Подробнее: Внутренние гравитационные волны

Моде́ль биологи́ческого нейро́на — математическое описание свойств нейронов, целью которого является точное моделирование процессов, протекающих в таких нервных клетках. В отличие от подобного точного моделирования, при создании сетей из искусственных нейронов обычно преследуются цели повышения эффективности вычислений. Гистере́зис (греч. ὑστέρησις — отставание, запаздывание) — свойство систем (физических, биологических и т. д.), мгновенный отклик которых на приложенные к ним воздействия зависит в том числе и от их текущего состояния, а поведение системы на интервале времени во многом определяется её предысторией. Для гистерезиса характерно явление «насыщения», а также неодинаковость траекторий между крайними состояниями (отсюда наличие остроугольной петли на графиках). Не следует путать это понятие с инерционностью… Фа́зовый перехо́д (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий. С точки зрения движения системы по фазовой диаграмме при изменении её интенсивных параметров (температуры, давления и т. п.), фазовый переход происходит, когда система пересекает линию, разделяющую две фазы. Поскольку разные термодинамические фазы описываются различными уравнениями состояния, всегда можно найти величину, которая скачкообразно меняется… Цифровой вычислительный синтезатор (ЦВС), известный еще как схема прямого цифрового синтеза (DDS) — электронный прибор, предназначенный для синтеза сигналов произвольной формы и частоты из единственной опорной частоты, поставляемой генератором тактовых импульсов. Характерной особенностью ЦВС является то, что отсчеты синтезируемого сигнала вычисляются цифровыми методами, после чего передаются на цифро-аналоговый преобразователь (ЦАП), где и происходит их преобразование в аналоговую форму (напряжение… Задача характеризации элементов микросхем заключается в получении зависимостей функциональных параметров библиотечного элемента или блока от длительности фронтов сигналов на входе и от величины нагрузочных емкостей для заданных наборов этих величин. В коммерческих системах характеризации (SiliconSmart , Virtuoso Liberate Characterization Solution , Virtuoso Variety Statistical Characterization Solution , Virtuoso Liberate MX Memory Characterization Solution , Kronos Characterizer Plus ) такие зависимости… Коэффициент стоячей волны (КСВ, от англ. standing wave ratio, SWR) — отношение наибольшего значения амплитуды напряжённости электрического или магнитного поля стоячей волны в линии передачи к наименьшему. Блочно-ориентированные модели — это представление нелинейных систем в виде различных комбинаций инерционных звеньев и нелинейных безынерционных математических элементов. Такое представление моделей позволяет связать в явном виде входные и выходные переменные объектов с различной структурой и степенью нелинейности. К таким системам относятся системы типа Гаммерштейна, Винера, Винера-Гаммерштейна, фильтра Заде, обобщенной модели Винера и Sm-системы. Фронт сигнала — одно из ключевых понятий в теории триггеров в электронике. Например, триггеры со счетным входом, D-триггеры, JK-триггеры изменяют своё состояние, в зависимости от реализации, по фронту или спаду входных сигналов, которые обычно называют тактирующими сигналами, но эти сигналы не обязательно, и даже редко, являются периодическими тактирущими импульсами. Время распада метастабильного состояния — это физическая величина определяемая временем жизни метастабильного состояния. Также часто обозначается как время первого достижения. Автоволны (англ. autowaves) — это самоподдерживающиеся нелинейные волны в активных средах (то есть содержащих распределённые источники энергии). Термин в основном применяется к процессам, где волной переносится относительно малая энергия, которая необходима для синхронизации или переключения активной среды. Коэффициент формы — это отношение среднеквадратичного значения какой-то величины к среднему модулю (среднему абсолютному значению) той же величины. Если зависимость этой величины от другой переменной изобразить в виде графика, то коэффициент формы покажет, насколько форма этой линии отличается от горизонтальной прямой. Коэффициент формы постоянной функции равен единице. Теория массового обслуживания, или очередей (англ. queueing theory), — раздел теории вероятностей, целью исследований которого является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящих из неё, длительности ожидания и длины очередей. В теории массового обслуживания используются методы теории вероятностей и математической статистики. Неустойчивость Рихтмайера — Мешкова возникает между двумя контактирующими сплошными средами различной плотности, когда поверхность раздела испытывает импульс ускорения, например при прохождении ударной волны. Развитие нестабильности начинается с возмущения малой амплитуды, которая первоначально возрастает линейно со временем. Далее неустойчивость приобретает нелинейный характер со смешиванием веществ. Косинор или косинор-анализ — метод обработки коротких временных, основанный на приближении временного ряда косинусоидой. В физике и химии явлением перколяции (от лат. percōlāre — просачиваться, протекать) называется явление протекания или непротекания жидкостей через пористые материалы, электричества через смесь проводящих и непроводящих частиц и другие подобные процессы. Теория перколяции находит применение в описании разнообразных систем и явлений, в том числе таких, как распространение эпидемий и надежность компьютерных сетей.

Подробнее: Перколяция

Частота́ — физическая величина, характеристика периодического процесса, равна количеству повторений или возникновения событий (процессов) в единицу времени. Рассчитывается, как отношение количества повторений или возникновения событий (процессов) к промежутку времени, за которое они совершены. Стандартные обозначения в формулах — ν, f или F. Задача Стефана представляет собой особый вид краевой задачи для дифференциального уравнения в частных производных, описывающая изменение фазового состояния вещества, при котором положение границы раздела фаз изменяется со временем. Наличие границ раздела между фазами, которые не задаются явно и могут смещаться со временем, является характерной особенностью таких задач. Скорость смещения межфазных границ определяется дополнительным условием на границе раздела фаз, что приводит задачу к нелинейному… Ревербератор (autowave reverberator) — автоволновой вихрь в двумерной активной среде.Ревербератор возникает в результате эволюции обрыва фронта плоской автоволны. Обрыв фронта автоволны может появляться, например, при столкновении фронта с невозбудимым препятствием — и в этом случае в зависимости от условий возможно возникновение либо спиральной волны, вращающейся вокруг этого препятствия, либо же автоволнового вихря со свободным концом, т.е. ревербератора. Временная область — анализ математических функций, физических сигналов или временных рядов в экономике или статистике охраны окружающей среды относительно времени. Во временной области значения сигнала или функции известное для всех действительных чисел в случае непрерывного времени, или в разные отдельные моменты в случае дискретного времени.. Инструментом, который обычно используется для визуализации реальных сигналов во временной области, является осциллограф. График временной области показывает… Переход Костерлица — Таулеса или переход Березинского — Костерлица — Таулеса (БКТ-переход) или топологический фазовый переход — фазовый переход в двумерной XY-модели. Это переход из состояния связанных пар вихрь-антивихрь при низких температурах в состояние с неспаренными вихрями и антивихрями при некоторой критической температуре. Переход назван в честь занимающихся конденсированными средами физиков Вадима Львовича Березинского, Джона М. Костерлица и Дэвида Дж. Таулеса. БКТ-переходы можно наблюдать… Всеми́рное координи́рованное вре́мя (англ. Coordinated Universal Time, фр. Temps Universel Coordonné; UTC) — стандарт, по которому общество регулирует часы и время. Отличается на целое количество секунд от атомного времени и на дробное количество секунд от всемирного времени UT1. Физика колебаний и волн — раздел общей физики, изучающий физические явления, характеризующиеся циклическим изменением физических величин во времени и в пространстве. Это — одна большая часть школьного курса физики, изучается после электромагнетизма ( рассматривая механические и электромагнитные процессы вместе ) или сразу с механикой ( в связи с тем, что теория колебаний и волн развивается на основе кинематики и динамики, что охватывает механика ). Период повторяемости, интервал повторения — оценка интервала времени между такими событиями, как землетрясение, наводнение или изменение расхода воды, сходной интенсивности или силы. Это статистическая величина, обозначающая средний интервал повторения в течение длительного периода времени. Как правило, её вычисление требуется для анализа риска (в том числе для оценки проектов в зонах с определенным риском), а также измерения сейсмостойкости сооружений в случае повторения землетрясений (с соответствующей… Время Ляпунова — время, за которое система приводится к полному хаосу. Определяется как число, обратное к наибольшей из экспонент Ляпунова системы. Названо в честь математика А. М. Ляпунова. Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число компонентов, фаз и термодинамических степеней свободы в равновесной термодинамической системе. Роль правила фаз особенно велика при рассмотрении гетерогенных равновесий в многофазных многокомпонентных системах. Одноро́дность времени — означает, что все моменты времени равноправны, то есть что если в два любые момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то начиная с этих моментов все явления в ней будут проходить совершенно одинаково. Однородность — одно из ключевых свойств времени в классической механике. Является фундаментальным обобщением опытных фактов.Все известные законы природы, в том числе для живой материи, подтверждают равномерность хода времени. Например… Амплиту́дно-часто́тная характери́стика (АЧХ) — зависимость амплитуды выходного сигнала некоторой системы от частоты её входного гармонического сигнала. Иногда эту характеристику называют «частотным откликом системы» (frequency response). Источник света — любой объект, излучающий электромагнитную энергию в видимой области спектра. По своей природе подразделяются на искусственные и естественные. Кардиовизор — прибор и одноименная оригинальная технология измерения электрических микроальтернаций сигнала ЭКГ. Пара́метр (от др.-греч. παραμετρέω — «отмеривающий»; где παρά: «рядом», «второстепенный», «вспомогательный», «подчинённый»; и μέτρον: «измерение») — величина, значения которой служат для различения элементов некоторого множества между собой.. Параметр — величина, постоянная в пределах данного явления или задачи, но при переходе к другому явлению или задаче могущая изменить своё значение. Иногда параметрами называют также величины, очень медленно изменяющиеся по сравнению с другими величинами (переменными… Синхро́нный усили́тель — тип электронного усилителя, в котором применён принцип синхронного детектирования сигнала. Фаза Берри — фаза, набегающая при прохождении квантовомеханической системой замкнутой траектории в пространстве параметров, когда система подвержена циклическому адиабатическому возмущению. Также называется геометрической фазой, топологической фазой, или фазой Панчаратнама — Берри в честь С. Панчаратнама и сэра Майкла Берри. Явление было сначала обнаружено в 1956 году и открыто вновь в 1984 году. Фаза Берри может наблюдаться в эффекте Ааронова — Бома и при коническом пересечении поверхностей потенциальной… Фильтр Чебышёва — один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад амплитудно-частотной характеристики (АЧХ) и существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания (фильтр Чебышёва I рода) и подавления (фильтр Чебышёва II рода), чем у фильтров других типов. Фильтр получил название в честь известного русского математика XIX века Пафнутия Львовича Чебышёва, так как характеристики этого фильтра…

ПОСТОЯННАЯ ВРЕМЕНИ — что такое в Большой советской энциклопедии

Смотреть что такое ПОСТОЯННАЯ ВРЕМЕНИ в других словарях:

ПОСТОЯННАЯ ВРЕМЕНИ

ПОСТОЯННАЯ ВРЕМЕНИ , величина, характеризующая инерционность динамической системы; имеет размерность времени. Напр., постоянная времени электрической ц

ПОСТОЯННАЯ ВРЕМЕНИ

ПОСТОЯННАЯ ВРЕМЕНИ, величина, характеризующая инерционность динамической системы; имеет размерность времени. Напр., постоянная времени электрической це

ПОСТОЯННАЯ ВРЕМЕНИ

«…120) постоянная времени — время, отсчитываемое с момента приложения светового воздействия, которое требуется току, чтобы достигнуть уровня (1 — 1/е

ПОСТОЯННАЯ ВРЕМЕНИ

        обобщённый параметр, характеризующий динамические свойства (инерционность) объекта исследования и имеющий размерность времени. Любой сложный фи

ПОСТОЯННАЯ ВРЕМЕНИ

(временной параметр, характеризующий динамические свойства (инерционность) объекта исследования и служащий мерой времени установления стационарного сос

ПОСТОЯННАЯ ВРЕМЕНИ

время, которое требуется световому стимулу при увеличении тока, чтобы достигнуть уровня (1 — 1/е) от конечного значения (т.е.63% от конечного значения)

ПОСТОЯННАЯ ВРЕМЕНИ

— величина, характеризующая инерционность динамическойсистемы; имеет размерность времени. Напр., постоянная времениэлектрической цепи характеризует ско

ПОСТОЯННАЯ ВРЕМЕНИ

величина, характеризующая инерционность динамич. системы; имеет размерность времени. Напр., П. в. элект-рич. цепи характеризует скорость изменения тока

ПОСТОЯННАЯ ВРЕМЕНИ

ПОСТОЯННАЯ ВРЕМЕНИ, величина, характеризующая инерционность динамической системы; имеет размерность времени. Напр., постоянная времени электрической це

ПОСТОЯННАЯ ВРЕМЕНИ

ПОСТОЯННАЯ ВРЕМЕНИ — величина, характеризующая инерционность динамической системы; имеет размерность времени. Напр., постоянная времени электрической ц

ПОСТОЯННАЯ ВРЕМЕНИ

[time constant] — обобщенный параметр, характеризующий динамические свойства (инерционность) объекта исследования и имеющий размерность времени. Ппосто

ПОСТОЯННАЯ ВРЕМЕНИ

промежуток времени т, в течение к-poro параметр, характеризующий переходный процесс, изменяется не раз (е ~ 2,718). Напр., при разрядке конденсатора ём

Переходный процесс — Википедия

Переходный процесс — в теории систем представляет изменения во времени координат динамической системы, до некоторого установившегося состояния; возникает под влиянием возмущающих воздействий, изменяющих её состояние, структуру или параметры, а также вследствие ненулевых начальных условий.^{[B: 1]}

Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы. Широкое применение нашло экспериментальное и аналитическое определение и построение переходных процессов для наиболее неблагоприятных условий работы динамической системы при внешних возмущениях типа дельта-функции, ступенчатом или синусоидальных воздействиях.^{[B: 1][B: 2]}

Оценка качества САУ по виду кривой переходного процесса производится при помощи так называемых прямых показателей качества — перерегулирования, допустимого числа колебаний и времени переходного процесса. Обычно рассматривают переходный процесс, возникающий в системе при воздействии единичной ступенчатой функции, т. е. переходная функция замкнутой системы.^[1]

Время переходного процесса[править | править код]

Длительность переходного процесса в системе характеризует её быстродействие, а его характер определяет качество системы. За количественную характеристику длительности переходного процесса принимают время, необходимое выходному сигналу системы для того, чтобы приблизиться к своему установившемуся значению, т. е. время, по истечению которого выполняется равенство:

|h(t)−hst|⩽ϵ{\displaystyle |h(t)-h_{st}|\leqslant \epsilon }

где hst{\displaystyle h_{st}} — установившееся значение и ϵ{\displaystyle \epsilon } — наперёд заданное положительное число.^[1]

Иллюстрация понятия «переходный процесс»; построена на основе «Энциклопедия кибернетики» ^{[B: 1]}

В линейных непрерывных динамических системах принято рассматривать П. п., вызванный единичным ступенчатым возмущением; но в этом случае установившееся значение достигается за бесконечно большое время. Если же ограничить точность достижения установившегося значения некоторой малой величиной ϵ{\displaystyle \epsilon }, то тогда длительность П. п. t{\displaystyle t} будет конечной величиной.^{[B: 1]}

В приложениях теории управления обычно в САУ принимают ϵ{\displaystyle \epsilon } равной 0,01–0,05 от hst{\displaystyle h_{st}}, т. е. переходный процесс считают закончившимся, когда переходная функция отличается не более, чем на 1–5 % от своего установившегося (стационарного) значения.^[1]

Перерегулирование[править | править код]

Перерегулирование (определяется величиной первого выброса) — отношение разности максимального значения переходной характеристики и её установившегося значения к величине установившегося значения. Измеряется обычно в процентах.

Степень затухания переходного процесса[править | править код]

Степень затухания переходного процесса определяется относительным уменьшением соседних амплитуд переходной характеристики.^{[B: 3]} Числителем является амплитуда первого колебания. Степень затухания показывает во сколько раз уменьшается амплитуда второго колебания по сравнению с первым.

Степень затухания системы зависит от показателя колебательности M{\displaystyle M} (см. ниже).

Логарифмический декремент колебания[править | править код]

Логарифмический декремент колебания — натуральный логарифм отношения амплитуд двух соседних перерегулирований. Обратная ему величина показывает, за какое число колебаний их амплитуда уменьшается в e{\displaystyle e} раз (e{\displaystyle e} — основание натуральных логарифмов). Уместен лишь для характеристики линейных систем.^{[B: 4]}

Колебательность[править | править код]

Характеризует склонность системы к колебаниям и определяется как модуль отношения амплитуд второго колебания к амплитудам первого колебания. Колебательность системы характеризуют при помощи показателя колебательности M{\displaystyle M}, который представляет собой отношение резонансного пика при резонансной частоте к значению АЧХ при нулевой частоте.^[2] Показатель колебательности связан со степенью колебательности формулой:

M=1+m22m{\displaystyle M={\frac {1+m^{2}}{2m}}}.

При увеличении М, уменьшается показатель колебательности m и соответственно происходит уменьшение степени колебательности.

Установившаяся ошибка[править | править код]

Установившаяся ошибка системы — разница между предполагаемым и реальным значением выходного сигнала при времени, стремящемся к бесконечности. В идеальных астатических системах установившаяся ошибка равна нулю.

Электрические цепи[править | править код]

В электрической цепи переходный процесс характеризуется плавным инерционным изменением тока и напряжения в цепи в ответ на приложенное внешнее воздействие.^{[B: 5]}

Формулы, описывающие протекание простейших переходных процессов (разряд конденсатора через резистор):

U(t)=U0e(−t/τ){\displaystyle U(t)=U_{0}e^{(-t/\tau )}}

τ=RC{\displaystyle \tau =RC}

Где U0{\displaystyle U_{0}} — значение напряжения на конденсаторе в момент перед началом переходного процесса, τ{\displaystyle \tau } — постоянная времени переходного процесса, С — ёмкость, R — сопротивление элементов цепей.

Для цепей, содержащих индуктивность, постоянная времени равна τ=L/R{\displaystyle \tau =L/R}

1. ↑ ^{1 2 3} Пономарёв, 1974, § 5.7. Оценка запаса устойчивости и быстродействия по кривой процесса регулирования, с. 201-202.
2. ↑ МЭИ, 2011, 2.3. Решение линейных дифференциальных уравнений во временной области, с. 44-48.

1. ↑ ^{1 2 3 4} Энциклопедия кибернетики / Глушков В. М.. — Киев: Глав. ред. УСЭ, 1974. — 624 с.
2. ↑ Основы автоматического регулирования и управления / Пономарев В. М. и Литвинов А. П.. — М.: Высшая школа, 1974. — 439 с.
3. ↑ Управление и инноватика в теплоэнергетике / Андрюшин А. В., Сабанин В. Р., Смирнов. Н. И.. — М.: МЭИ, 2011. — 392 с. — ISBN 978-5-38300539-2.
4. ↑ Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. — 2-е изд., перераб. и испр.. — М.: Наука, 1981. — 918 с.
5. ↑ Веников В. А. Переходные электромеханические процессы в электрических системах. — М.: Высшая школа, 1978. — 415 с.