Переходные процессы в RC и LC цепях
Переходными процессами, возникающими в электрических цепях, называют явления (процессы), которые происходят в них после того как один из параметров испытал быстрое изменение. Например, включение и выключение ЭДС в цепи с сопротивлением и индуктивностью.
RC цепь
RC цепью называется электрическая цепь, которая состоит из конденсатора (конденсаторов) (емкость C), сопротивления (сопротивлений) (R) и источника ЭДС (рис.1). В такой цепи могут происходить только релаксационные непериодические процессы.

Рисунок 1.
Присутствие в цепи конденсатора исключает возможность существования в ней постоянного тока. Разность потенциалов между обкладками конденсатора полностью компенсирует действие сторонней ЭДС (источника). Переменный же ток в такой сети возможен благодаря переменному заряду на конденсаторе. Разность потенциалов на обкладках не компенсирует действия сторонней ЭДС, в результате чего поддерживается некоторая сила тока.
Закон Ома для RC цепи имеет вид:
где $q$ — заряд на обкладке конденсатора, $\frac{q}{C}$ — разность потенциалов между обкладками конденсатора, $U_0$- постоянное напряжение. Иногда уравнение (1) используют в виде:
Включение (выключение) постоянной ЭДС в RC цепи
Допустим, что постоянное напряжение ($U_0$) включают в момент времени, который мы принимаем за начальный ($t=0$). Из уравнения (1) следует, что:
Уравнение (2) при $t>0\ $запишем как:
Решением уравнения (4) при заданном начальном условии (3) является функция:
Из формулы (5) следует, что при $t\to \infty ,\ I\to 0.\ $ $I_{max}=\frac{U_0}{R}$. Время убывания силы тока ($\tau $) равно:
График функции $I\left(t\right)$ представлен на рис.2.

Рисунок 2.
Если в RC цепи емкость конденсатора велика, то ток после того как выключили источник постоянного напряжения может течь в цепи продолжительное время. Если в цепь включить лампу, то она сначала вспыхнет, за тем постепенно погаснет.
В момент времени, когда в RC цепи ток упал до нулевого значения, конденсатор зарядился максимально, разность потенциалов его обкладок равна величине сторонней ЭДС с противоположным знаком. Эти две величины компенсируют друг друга. Если каким-либо образом в этот момент выключить стороннюю ЭДС, то в цепи начнет течь ток, который возникает за счет некомпенсированной разности потенциалов на обкладках конденсатора. Начальная сила такого тока будет равна $\frac{U_0}{R}$, закон изменения тока. При этом закон изменения тока совпадет с функцией (5).
LC цепь
$LC$ цепью называют цепь, которая состоит из катушки индуктивности и емкости (рис.3).

Рисунок 3.
В подобной цепи, не имеющей активного сопротивления, можно создать электрические колебания. Для этого сообщают обкладкам конденсатора начальный заряд или возбуждают ток в индуктивности (например, включая внешнее магнитное поле, которое пронизывает витки катушки). Допустим, что мы зарядили конденсатор. На обкладках конденсатора имеются заряды $q$ и $-q$. Между обкладками конденсатора появляется электрическое поле, энергия ($W_q$) которого равна:
Составили цепь из катушки и заряженного конденсатора. Конденсатор начнет разряжаться, в контуре возникнет ток. При этом энергия электрического поля уменьшается, энергия магнитного поля, которое порождается током, который течет через индуктивность, растет. Энергия магнитного поля ($W_m$) равна:
Так как активное сопротивление контура считается равным нулю, потерь энергии нет, то электрическая энергия постепенно переходит в магнитную, за тем магнитная переходит в электрическую. В момент, когда напряжение на конденсаторе равно нулю (следовательно, $W_q=0$), магнитная энергия максимальна, следовательно, ток в цепи максимален. Ток уменьшается, заряд растет. Весь цикл повторяется бесконечно.
Уравнение колебаний в контуре без активного сопротивления
Уравнение, которое описывает процесс изменения заряда в $LC$ контуре, имеет вид:
где $\frac{1}{LC}={\omega }_0$ — собственная частота $LC$ — контура. Решением уравнения (9) служит функция:
Из (10) видно, что заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ${\omega }_0$.
Пример 1
Задание: Запишите функцию зависимости напряжения на конденсаторе от времени ($U(t)$) после замыкания ключа на рис. 4. Считать, что конденсатор был заряжен до напряжения $U_0$.

Рисунок 4.
Решение:
Используем второе правило Кирхгофа, запишем, что после того как ключ в цепи замкнули, выполняется равенство:
где $U_R$ — напряжение на сопротивлении, $U_C$ — напряжение на конденсаторе. При этом можно положить, что:
\[U_R=RI_R,\ I_C=C\frac{dU_C}{dt},\ I\left(t\right)=I_C=I_R\left(1.2\right),\]где $I_C,I_R$ токи, текущие через конденсатор и сопротивление. Используем выражения (1.2) преобразуем уравнение (1.1), получим:
\[\frac{dU_C}{dt}+\frac{1}{RC}U_C=0\left(1.3\right).\]Решение уравнения (1.3) запишем в виде:
\[U_C\left(t\right)=Aexp\left(-\frac{t}{RC}\right)\left(1.4\right).\]Постоянную А найден их начального условия задачи ($U_C\left(0\right)=U_0$), следовательно А=$U_0$.
Ответ: $U_C\left(t\right)=U_0exp\left(-\frac{t}{RC}\right).$
Пример 2
Задание: Приведите пример, как получить в примере 1 режим зарядки и разрядки конденсатора?
Решение:
Заданный режим можно получить, если в качестве источника постоянного напряжения использовать генератор прямоугольных импульсов (поставить его на место ключа рис. 4). При этом ЭДС источника ($\varepsilon (t$)) должна выглядеть как:

Рисунок 5.
где $T_i$ — длительность импульса, причем это время должно быть существенно больше, чем время релаксации для того, чтобы напряжение на конденсаторе успело стать равным ${{\mathcal E}}_0$.
Расчёт постоянной времени RC-цепочки. Переходные процессы в электрических цепях
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Для логического завершения этой схемы нужно подключить резистор и конденсатор к какому-либо активному электронному компоненту, как на рис. 17.2: например, к логическому элементу или транзистору.
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили табл. 17.2.
Таблица 17.2. Соотношения закона Ома
Расчёты частоты и длины волны
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Рассмотрим RC-цепь, изображенную на рис. 3.20,а. Пусть на входе этой цепи действует напряжение u1(t).
Рис. 3.20. Дифференцирующие RC-(а) и RL-(б) цепи.
Тогда для этой цепи справедливо соотношение
и с учетом преобразований будем иметь
(3.114)
Если для данного сигнала выбрать постоянную времени цепи τ=RC настолько большим, что вкладом второго члена правой части (3.114) можно пренебречь, то переменная составляющая напряжения uR≈u1. Это значит, что при больших постоянных времени напряжение на сопротивлении R повторяет входное напряжение. Такую цепь применяют тогда, когда необходимо передать изменения сигнала без передачи постоянной составляющей.
При очень малых значениях τ в (3.114) можно пренебречь первым слагаемым. Тогда
(3.115)
т. е. при малых постоянных времени τ RC-цепь (рис. 3.20,а) осуществляет дифференцирование входного сигнала, поэтому такую цепь называют дифференцирующей RC-цепью.
Аналогичными свойствами обладает и RL-цепь (рис. 3.20,б).
Рис. 3.21. Частотные (а) и переходная (б) характеристики дифференцирующих цепей.
Сигналы при прохождении через RС- и RL-цепи называют быстрыми, если
или медленными, если
Отсюда следует, что рассмотренная RC-цепь дифференцирует медленные и пропускает без искажения быстрые сигналы.
Для гармонической э. д. с. аналогичный результат легко получить, вычисляя коэффициент передачи цепи (рис. 3.20,а) как коэффициент передачи делителя напряжения со стационарными сопротивлениямиR и XC=1/ωC:
(3.116)
При малых τ, а именно когда τ
При этом фаза выходного напряжения (аргумент K) равна π/2. Сдвиг гармонического сигнала по фазе на π/2 эквивалентен его дифференцированию. При τ>>1/ω коэффициент передачи K≈1.
В общем случае модуль коэффициента передачи (3.116), или частотная характеристика цепи (рис. 3.20,а):
(3.118)
а аргумент K, или фазовая характеристика этой цепи:
Эти зависимости показаны на рис. 3.21,а.
Такими же характеристиками обладает RL-цепь на рис. 3.20,б с постоянной времени τ=L/R.
Если в качестве выходного сигнала взять единичный скачок напряжения , то интегрированием уравнения (3.114) можно получить переходную характеристику дифференцирующей цепи, или временную зависимость выходного сигнала при единичном скачке напряжения на входе:
График переходной характеристики показан на рис. 3.21,б.
Рис. 3.22. Интегрииующие RC-(а) и LC-(б) цепи.
Рассмотрим RC-цепь, изображенную на рис. 3.22,а. Она описывается уравнением
(3.121)
При малых τ=RC (для «медленных» сигналов) uC≈u1. Для «быстрых» сигналов напряжение u1 интегрируется:
Поэтому RC-цепь, выходное напряжение которого снимается с емкости C называют интегрирующей цепью.
Коэффициент передачи интегрирующей цепи определяется выражением
(3.123)
При ω
Частотная и фазовая характеристики описываются соответственно выражениями
(3.124)
Рис. 3.23. Частотные (а) и переходная (б) характеристики интегрирующих цепей.
и изображены на рис. 3.23,а. Переходная характеристика (рис. 3.23,б) получается интегрированием (3.121) при :
При равных постоянных времени такими же свойствами обладает RL-цепь, изображенная на рис. 3.22,б.
Электрическая цепь, в к-рой выходное напряжение U вых (t)(или ток) пропорционально интегралу по времени от входного напряжения U вх (t) (или тока):
Рис. 1. Интегратор на операционном усилителе. С
под действием приложенного тока или накопление магн. потока в катушке с индуктивностью L под действием приложенного напряжения Преимущественно используются И. ц. с конденсатором. R,
равен току заряда
конденсатора С, а напряжение в точке их соединения равно нулю. В результате Произведение RС=t, характеризующее скорость заряда конденсатора, наз. постоянной времени И. ц. RC-И.
ц. (рис. 2, а). В этой схеме ток заряда конденсатора определяется разностью входного и выходного напряжений поэтому интегрирование входного напряжения выполняется приближённо и тем точнее, чем меньше выходное напряжение по сравнению с входным. Последнее условие выполняется, если постоянная времени t много больше интервала времени, по к-рому происходит интегрирование. Для правильного интегрирования импульсного входного сигнала необходимо, чтобы t была много больше длительности импульса Т(рис. 3). Аналогичными свойствами обладает RL-И. ц., показанная на рис. 2, б, для к-рой постоянная времени равна L/R.
Рис. 3. 1 — входной прямоугольный импульс; 2 — выходное напряжение интегрирующей цепи при tдT.
И. ц. применяются для преобразования импульсов, модулированных по длительности, в импульсы, модулированные по амплитуде, для удлинения импульсов, получения пилообразного напряжения, выделения низкочастотных составляющих сигнала и т. п. И. ц. на операц. усилителях
Постоянная времени — Википедия
Материал из Википедии — свободной энциклопедии
Постоя́нная вре́мени — характеристика экспоненциального процесса, определяющая время, через которое некоторый параметр процесса изменится в «е» раз (е≈2,718).
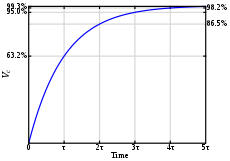
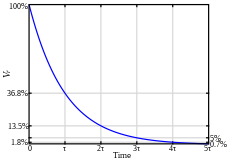
В радиотехнике постоянная времени τ{\displaystyle \tau } характеризует длительность протекания переходного процесса, обычно это тот промежуток времени, в течение которого реакция схемы на единичный скачок (функция Хевисайда) достигает 1−1/e≈63,2%{\displaystyle 1-1/e\approx 63,2\,\%} от своего конечного значения. Также постоянная времени характеризует время убывания реакции до уровня 1/e≈36,8%{\displaystyle 1/e\approx 36,8\,\%} от своего первоначального значения.
Фильтры[править | править код]
Постоянная времени связана с граничной частотой, либо с частотой пропускания фильтра нижних частот:
- fgr=12πτ.{\displaystyle f_{gr}={1 \over 2\pi \tau }.}
Определение постоянной времени. Переходные процессы в R-L-C-цепи (Лекция №26)
Переходные процессы в цепи с одним накопителем энергии и произвольным числом резисторов
Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение.
Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис.1, а) со схемой замещения на рис. 1,б.
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как:
,
и с емкостным, как:
,
где — входное сопротивление цепи по отношению к зажимам 1-2 подключения ветви, содержащей накопитель энергии.
Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать
,
где в соответствии с вышесказанным
.
Переходные процессы при подключении последовательной
R-L-C-цепи к источнику напряжения
Рассмотрим два случая:
а) ;
б) .
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
| . | (1) |
Тогда для первого случая принужденная составляющая этого напряжения
| . | (2) |
Характеристическое уравнение цепи
,
решая которое, получаем
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1. или , где — критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.
В этом случае
| . | (3) |
2. — предельный случай апериодического режима.
В этом случае и
| . | (4) |
3. — периодический (колебательный) характер переходного процесса.
В этом случае и
| , | (5) |
где — коэффициент затухания; — угловая частота собственных колебаний; — период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
.
Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации , запишем для t=0 два уравнения:
решая которые, получим
; .
Таким образом,
.
Тогда ток в цепи
и напряжение на катушке индуктивности
.
На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .
Для критического режима на основании (2) и (4) можно записать
.
При
Таким образом
и
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
.
Для нахождения постоянных интегрирования запишем
откуда и .
Тогда
.
На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
и
,
где ; ; .
Таким образом,
и .
Здесь также возможны три режима:
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 — ; 2 — ; 3 — , — которые представлены на рис. 6,а…6,в соответственно.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- Как можно определить постоянную времени в цепи с одним накопителем энергии по осциллограмме тока или напряжения в какой-либо ветви?
- Определить, какой процесс: заряд или разряд конденсатора в цепи на рис. 2 – будет происходить быстрее?
- Влияет ли на постоянную времени цепи тип питающего устройства: источник напряжения или источник тока?
- В цепи на рис. 2 , С=10 мкФ. Чему должна быть равна индуктивность L катушки, устанавливаемой на место конденсатора, чтобы постоянная времени не изменилась?
- Как влияет на характер переходного процесса в R-L-C-контуре величина сопротивления R и почему?
- Определить ток через катушку индуктивности в цепи на рис. 7, если ; ; ; ; .
- Определить ток в ветви с конденсатором в цепи на рис. 8, если ; ; ; .
Ответ: заряд.
Ответ: L=0,225 Гн.
Ответ: .
Ответ: .
40 Постоянная времени.
В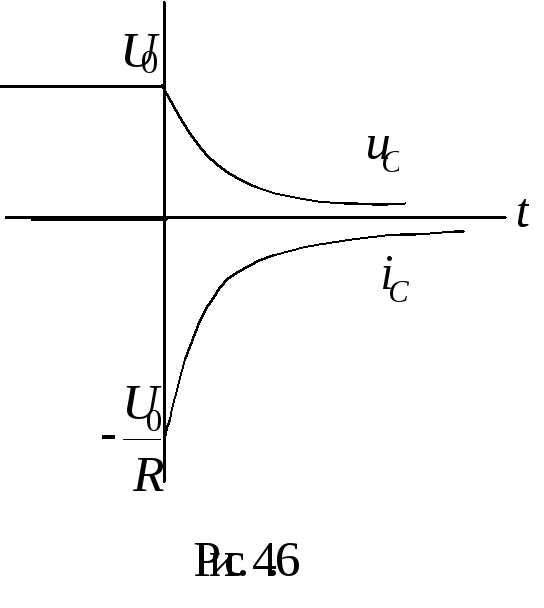 еличин,
характеризующая скорость изменения
электрической величины в переходном
режиме, называетсяпостоянная времени
().
еличин,
характеризующая скорость изменения
электрической величины в переходном
режиме, называетсяпостоянная времени
().
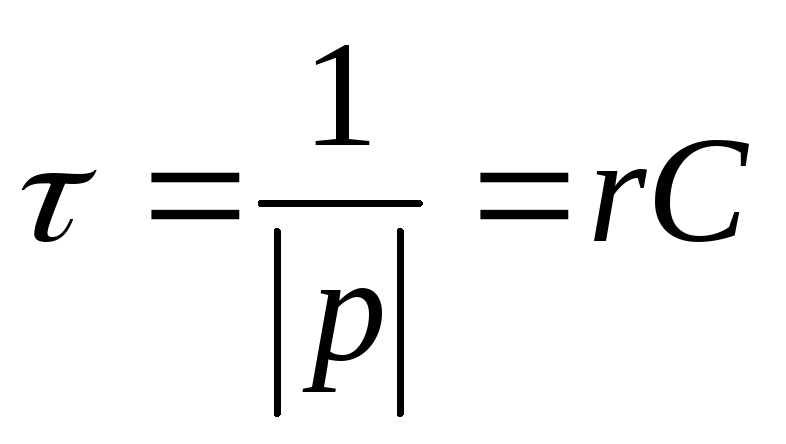
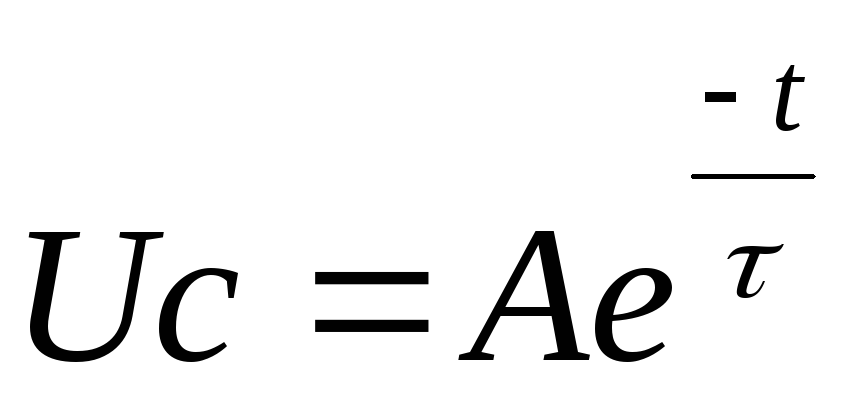
t=0- нач. усл.
Uc(0+)=А
Воспользуемся 2 правилом коммутации:
Uc(-0)=U0=A=Uc(+0)
Uc=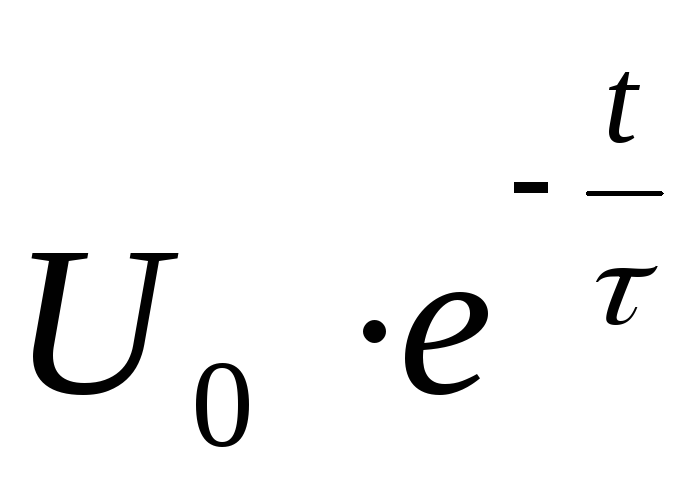 -закон
из-ияUна С
-закон
из-ияUна С
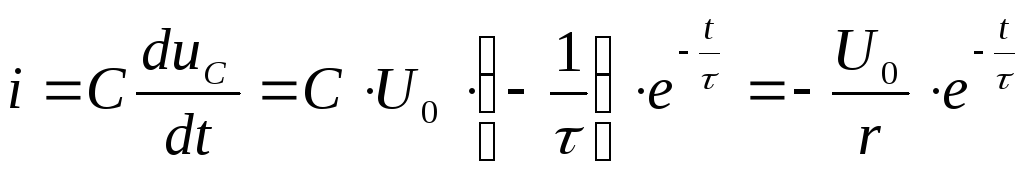 —
закон изм — ия тока
—
закон изм — ия тока
Чем больше  ,
тем медленнее переходный процесс, тем
больше
,
тем медленнее переходный процесс, тем
больше .
Хотя полученные выше выражения определяют
бесконечную длительность переходного
процесса – свободные составляющие лишь
асимптотически стремятся к нулю –
практически можно считать, что переходный
процесс заканчивается за время, равное
.
Хотя полученные выше выражения определяют
бесконечную длительность переходного
процесса – свободные составляющие лишь
асимптотически стремятся к нулю –
практически можно считать, что переходный
процесс заканчивается за время, равное  .
.
П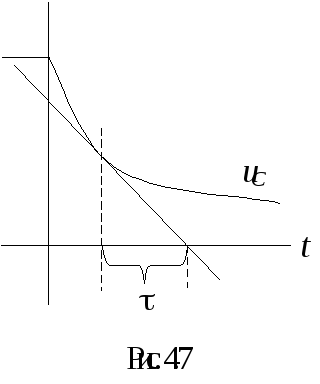 остоянную
времени можно графически определить
по длине подкасательной, проведённой
в любой точке свободной составляющей
переходного процесса (рис. 4.7).
остоянную
времени можно графически определить
по длине подкасательной, проведённой
в любой точке свободной составляющей
переходного процесса (рис. 4.7).
Постоянная времени измеряется в секундах и для цепей первого порядка связана с корнем характеристического уравнения
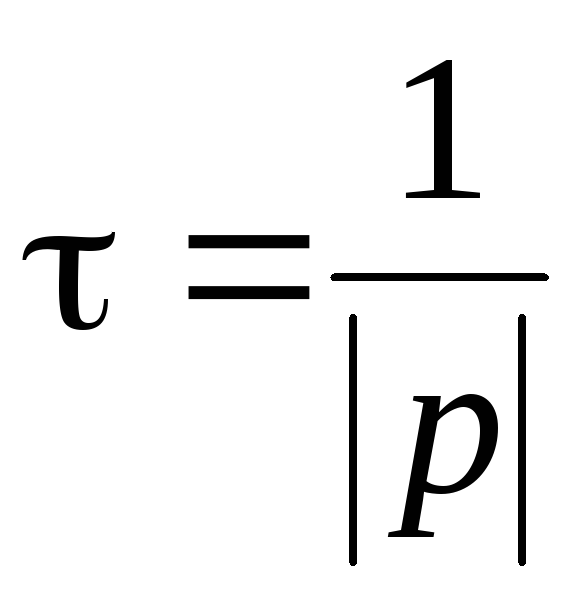 . (4.10)
. (4.10)
Рассмотрим энергетические соотношения, описывающие работу цепи после коммутации.
41 Подключение rc-цепи к источнику постоянного напряжения
1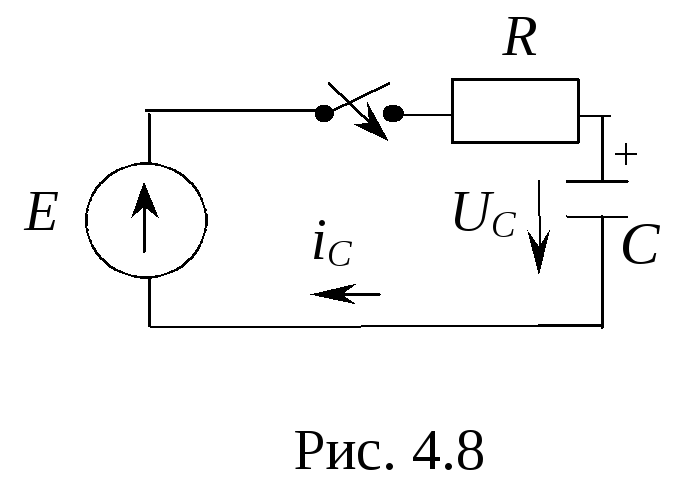 .
Запишем правило коммутации для цепи на
рис. 4.8
.
Запишем правило коммутации для цепи на
рис. 4.8
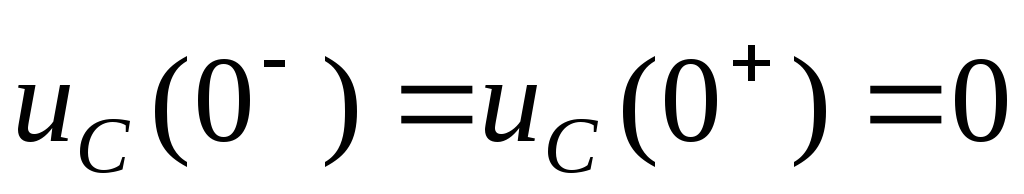 .
.
2. Получим дифференциальное уравнение цепи
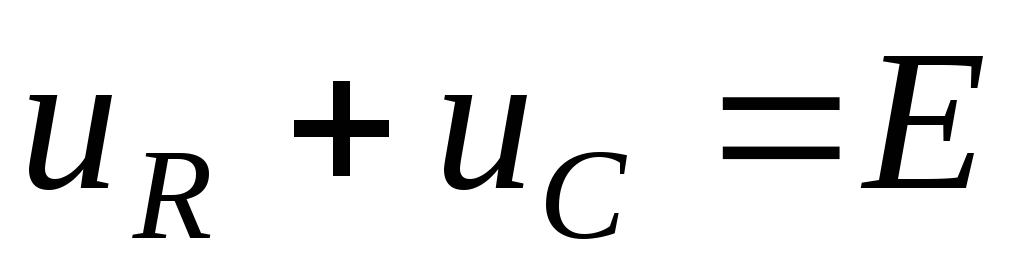 ,
,
+
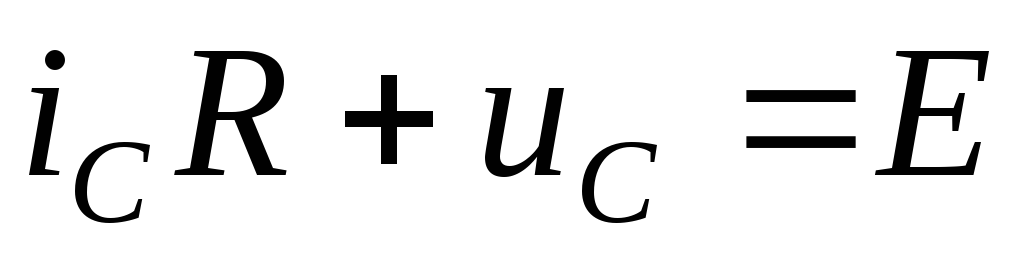 ,
, 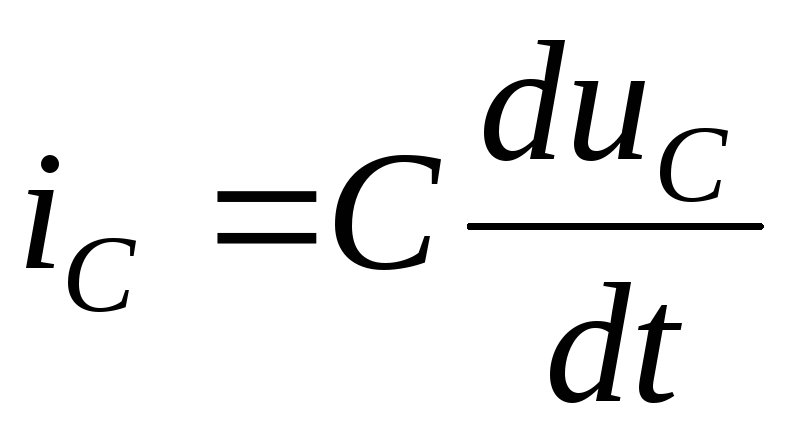 ,
, 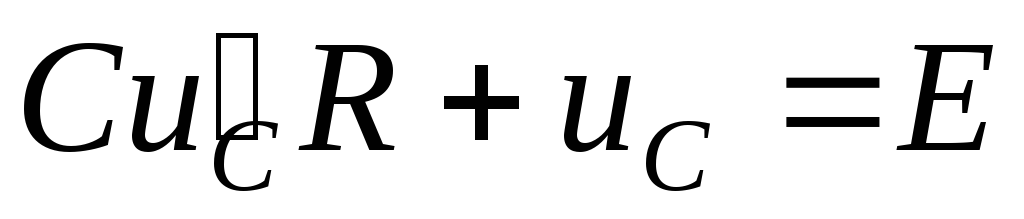 .
.
Характеристическое уравнение цепи
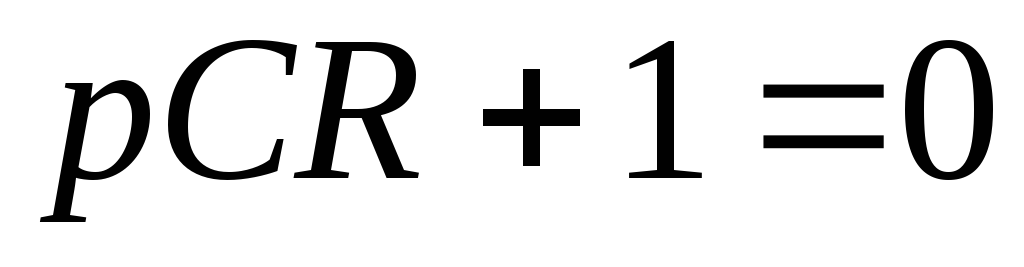 ,
,
корень которого
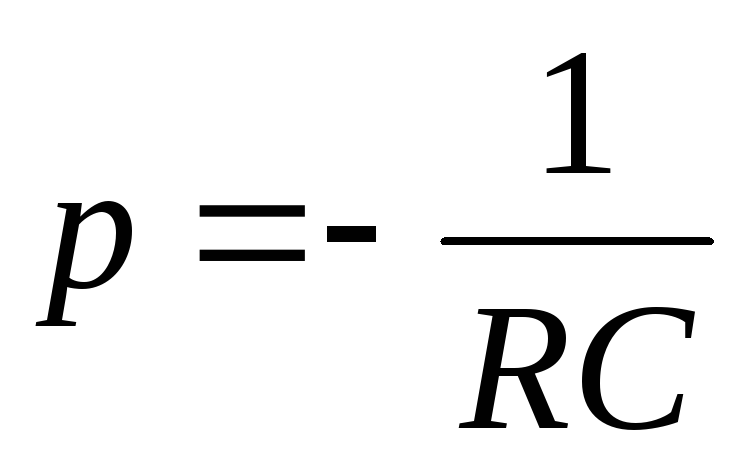 .
.
Постоянная времени 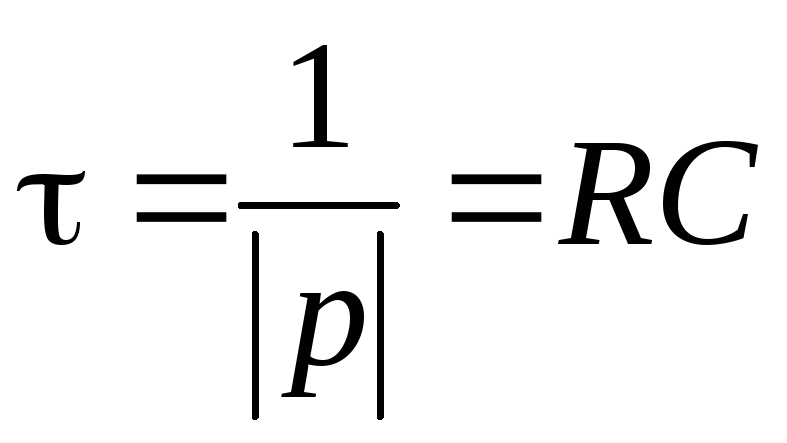 .
.
3. Запишем полное решение
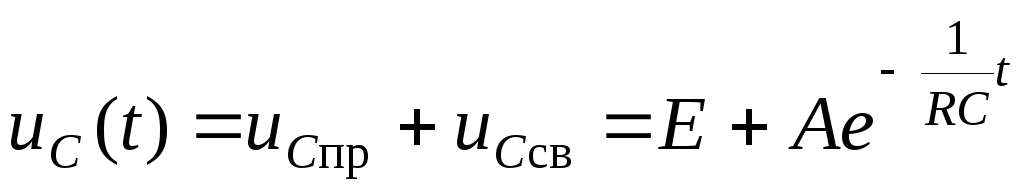 .
.
Здесь свободная составляющая также включает только одну экспоненту, поскольку цепь имеет первый порядок.
4 . Подставив
в полное решениеt= 0+,
определим постоянную интегрирования
на основании правил коммутации
. Подставив
в полное решениеt= 0+,
определим постоянную интегрирования
на основании правил коммутации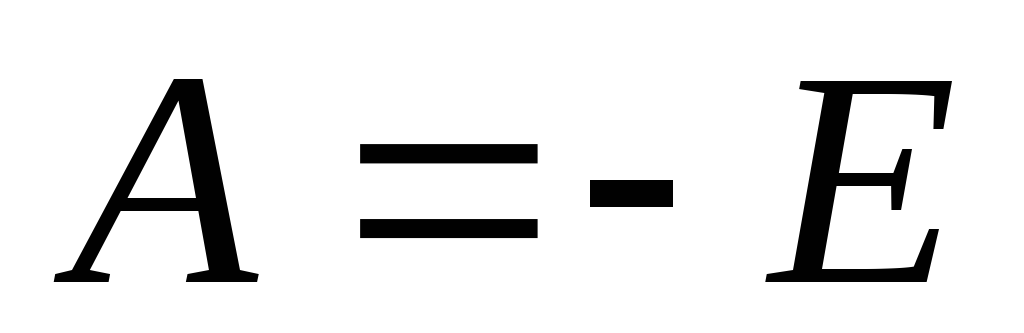 .
.
Таким образом, окончательный результат имеет вид
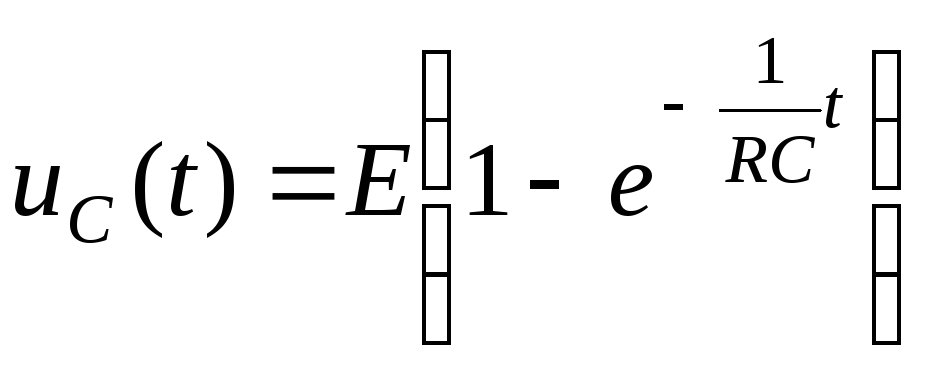 .
.
Ток в цепи
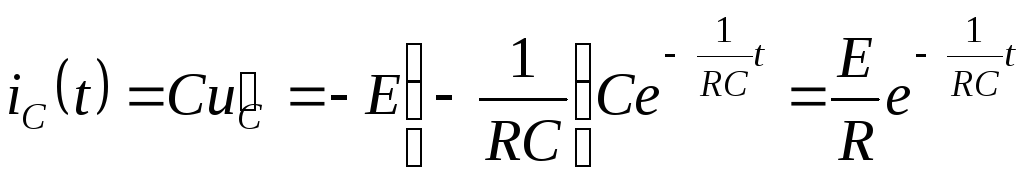 .
.
Графики изменения 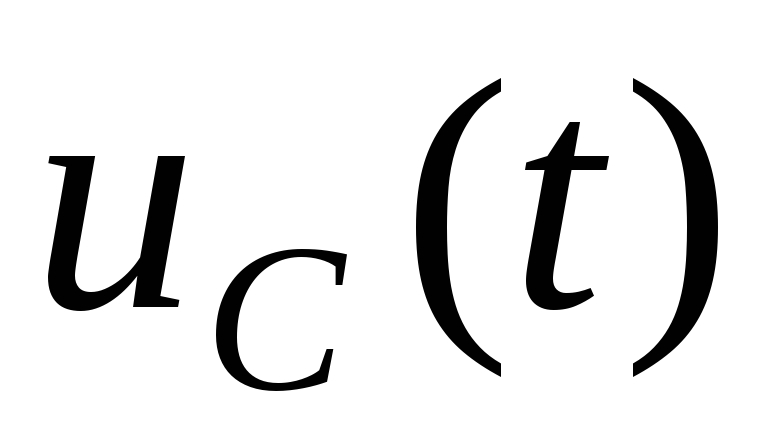 и
и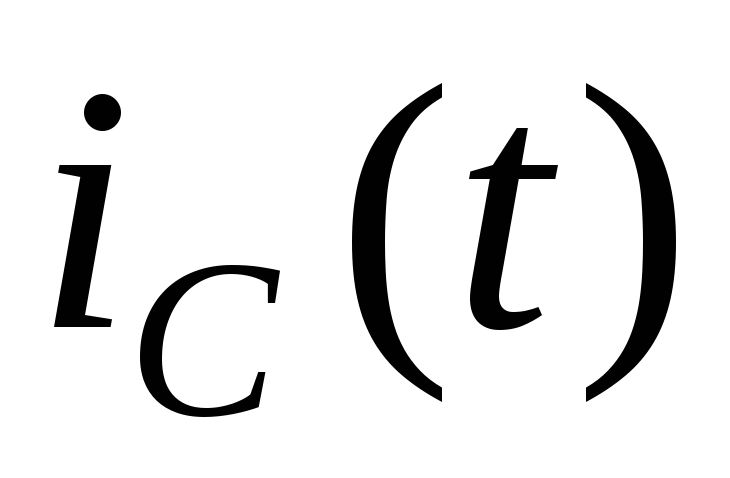 представлены на рис. 4.9. Значение тока,
содержащее лишь свободную составляющую,
максимально в начальный момент времени,
когда оно скачком достигает значение
представлены на рис. 4.9. Значение тока,
содержащее лишь свободную составляющую,
максимально в начальный момент времени,
когда оно скачком достигает значение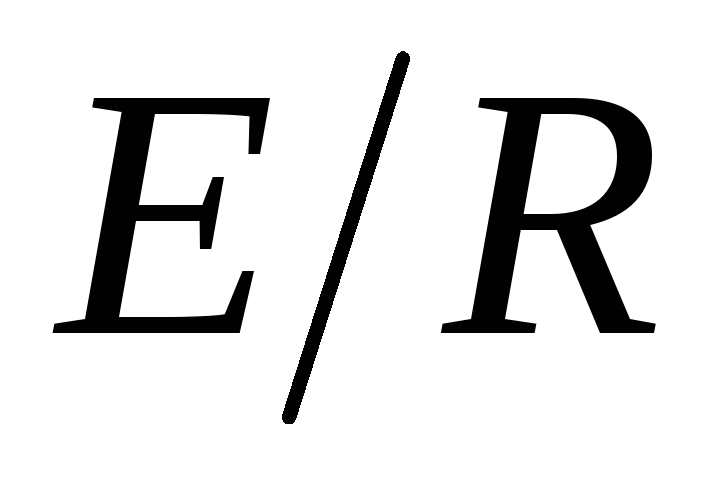 ,
и все напряжение источника приложено
к резистору. По мере зарядки конденсатора
напряжение на нем повышается, что ведет
к соответственному уменьшению тока в
цепи.
,
и все напряжение источника приложено
к резистору. По мере зарядки конденсатора
напряжение на нем повышается, что ведет
к соответственному уменьшению тока в
цепи.
42 Подключение индуктивности l к источнику постоянной эдс.
Подключение R -цепи
к источнику постоянного напряжения
-цепи
к источнику постоянного напряжения
1 .
Запишем правило коммутации для цепи на
рис. 4.10
.
Запишем правило коммутации для цепи на
рис. 4.10
 .
.
2. Получим дифференциальное уравнение цепи
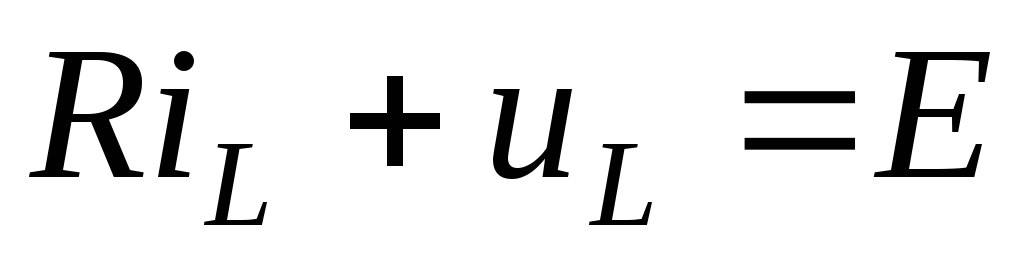 ,
,
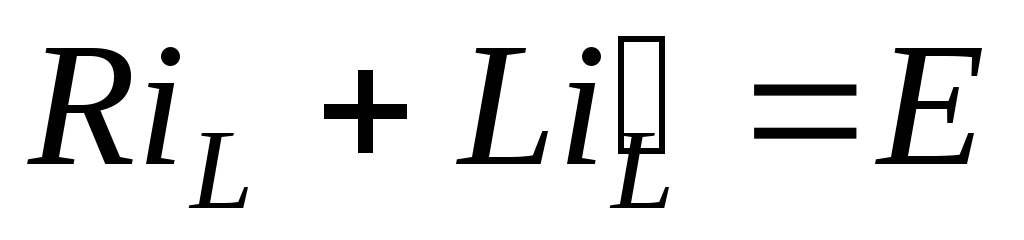 ,
,
характеристическое уравнение
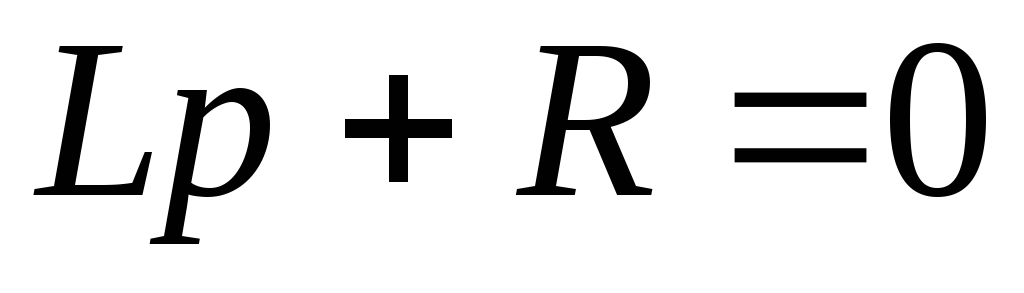 .
.
Корень характеристического уравнения и постоянная времени соответственно
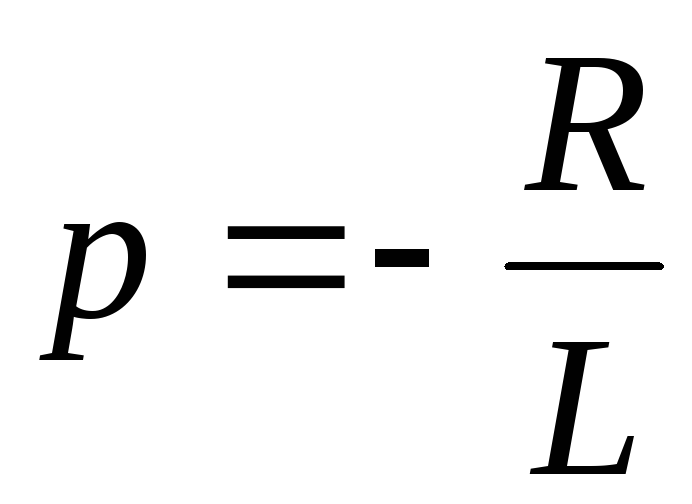 ,
,  .
.
3. Полное решение имеет вид:
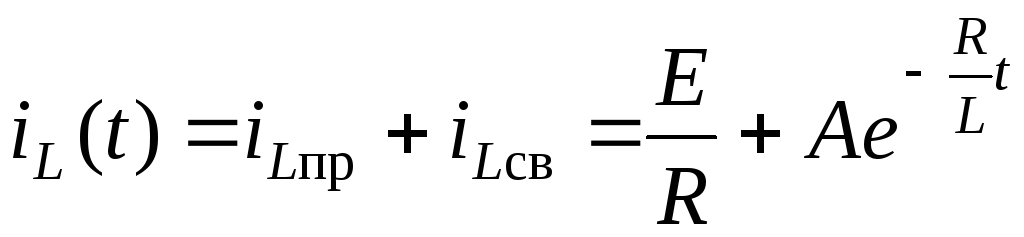 .
.
4. Подставив в iL(t) t = 0+ на основании правила коммутации определим постоянную интегрирования
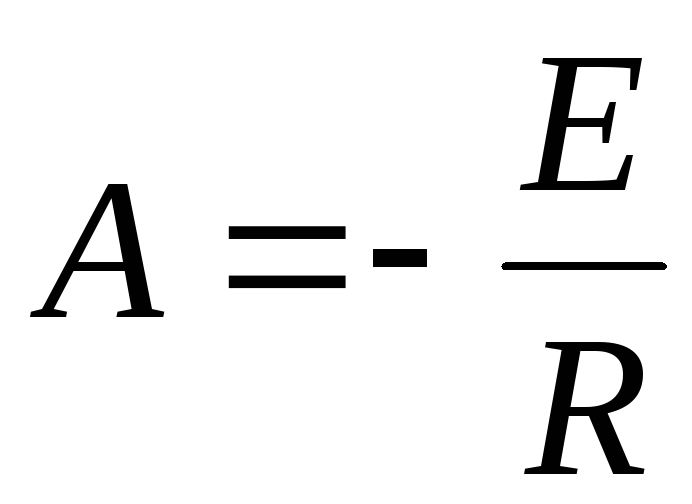 .
.
Т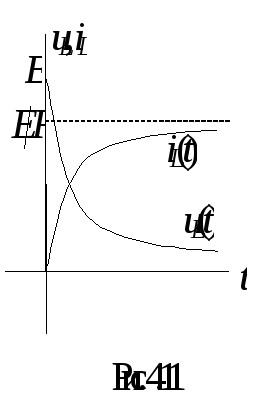 аким
образом,
аким
образом,
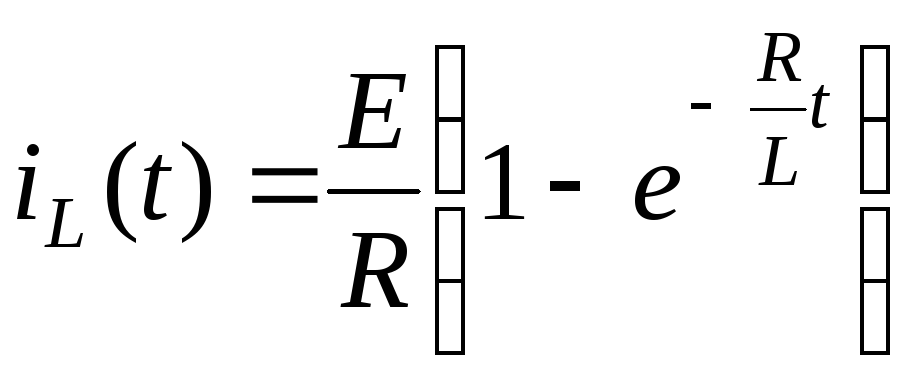 .
.
Напряжение на индуктивности
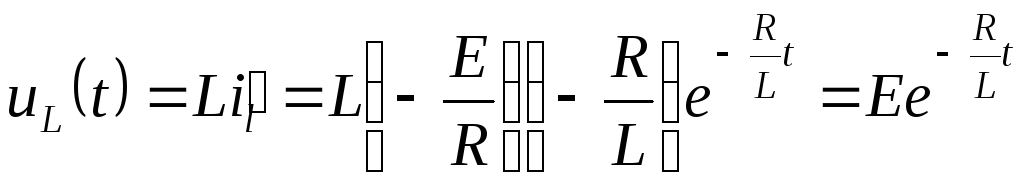 .
Графики изменения uL(t), iL(t)
приведены на рис. 4.11.
.
Графики изменения uL(t), iL(t)
приведены на рис. 4.11.
44 Подключение rc-цепи к источнику гармонического напряжения.
Рассмотрим случай, когда в цепи (рис. 4.12) действует источник синусоидальной ЭДС
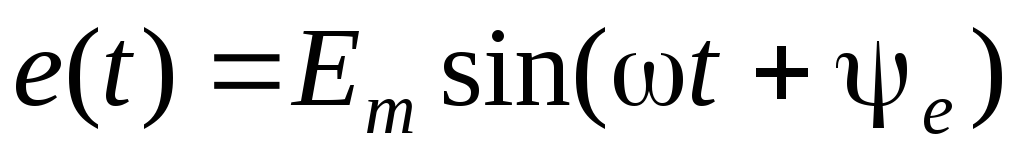 .
.
Здесь 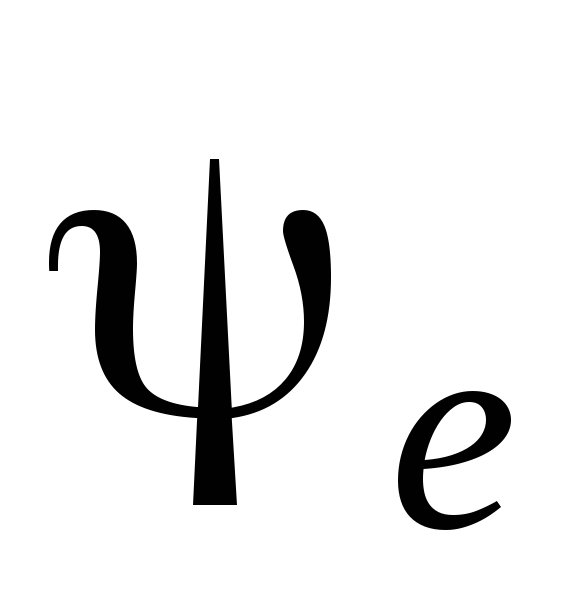 – фаза включения, т.к. она определяется
моментом срабатывания коммутатора.
Интуитивно следует ожидать влияние
– фаза включения, т.к. она определяется
моментом срабатывания коммутатора.
Интуитивно следует ожидать влияние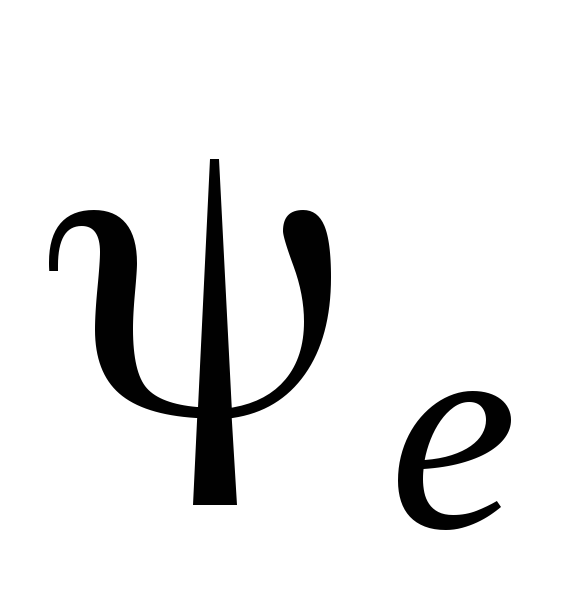 на качественную и количественную картину
протекания переходного процесса.
на качественную и количественную картину
протекания переходного процесса.
Порядок расчета переходных процессов, описанный выше, не претерпевает никаких изменений.
1. Запишем правило коммутации
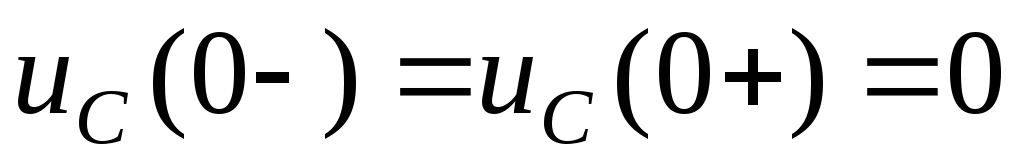 .
.
2. Дифференциальное уравнение и соответствующее ему характеристическое уравнение:
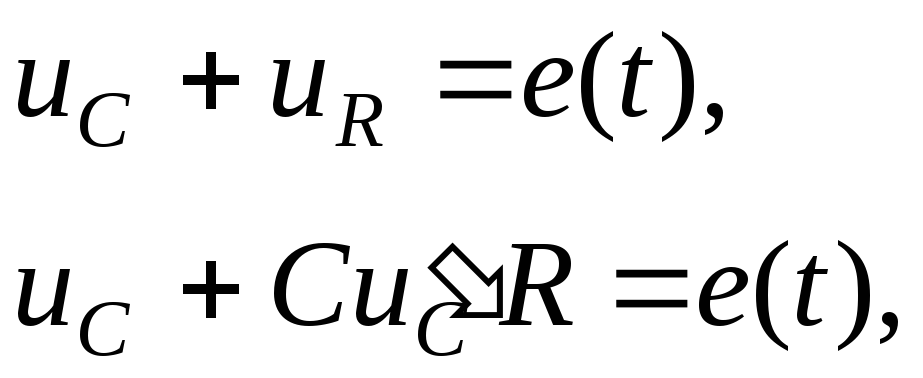
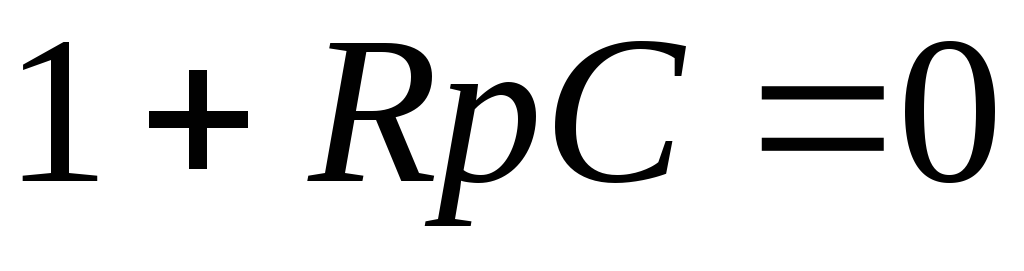 .
.
Корень характеристического уравнения
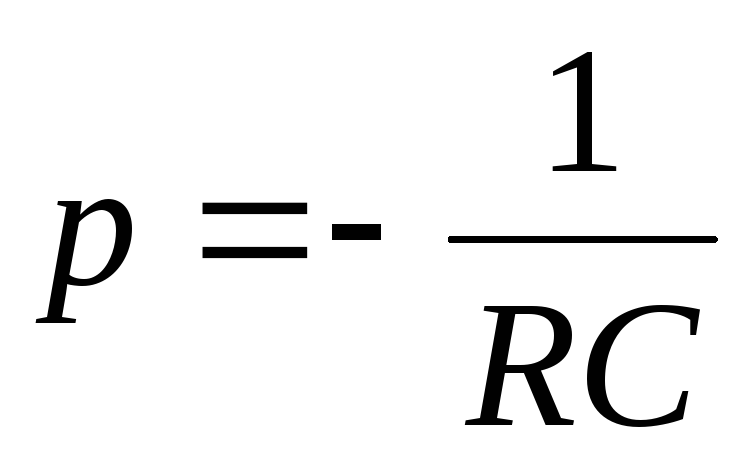 .
.
3. Полное решение для рассматриваемой цепи первого порядка
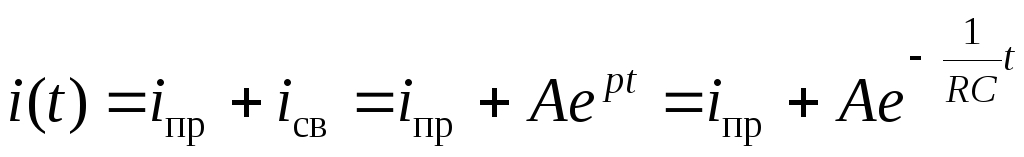 .
.
4. Расчет принужденной составляющей произведем символическим методом
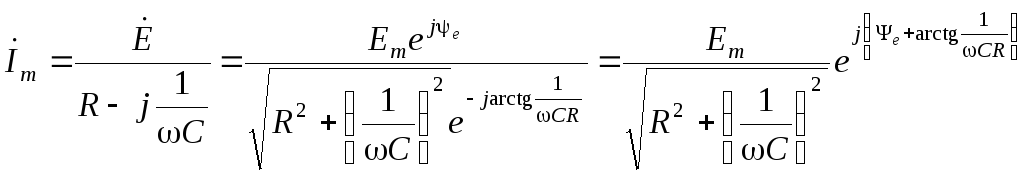 ;
;
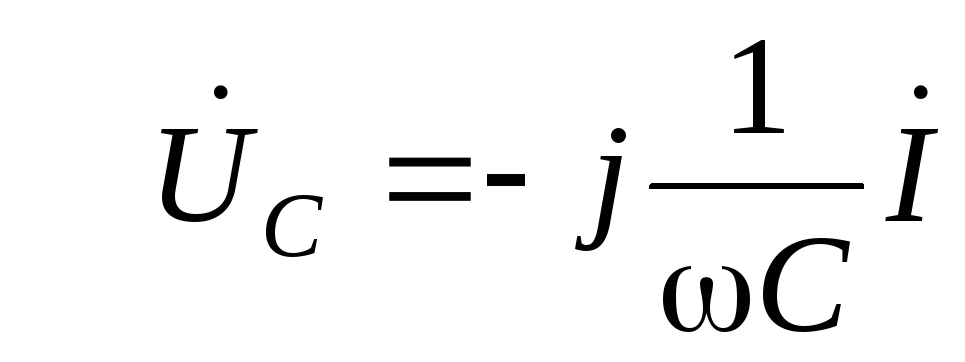 ;
;
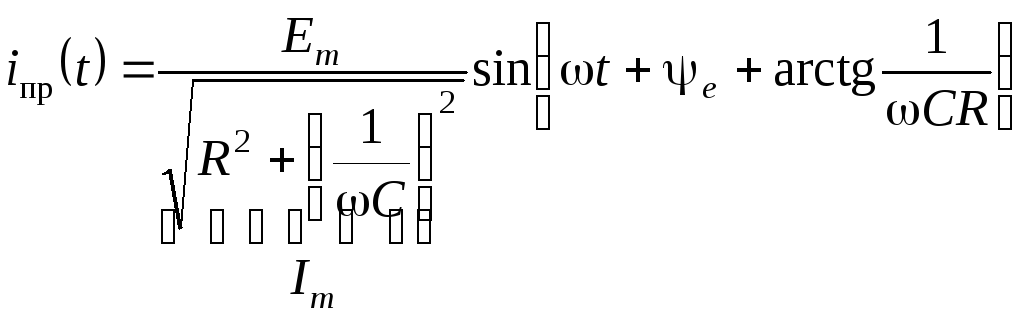 ;
;

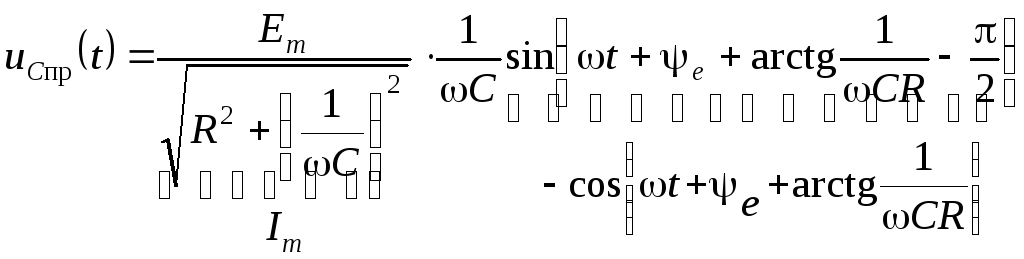 .
.
5. Для расчета постоянной интегрирования запишем полное решение для момента t = 0+
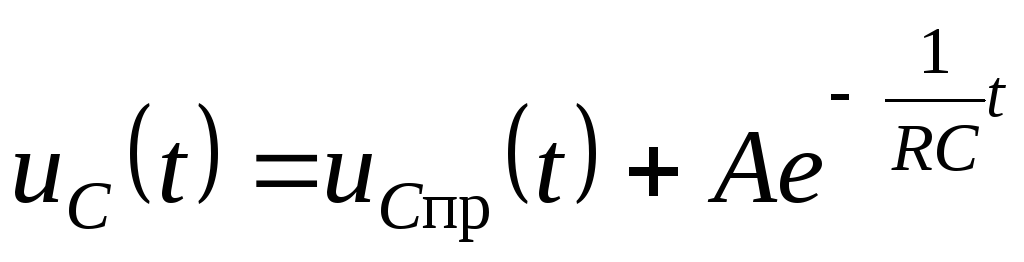 ;
;
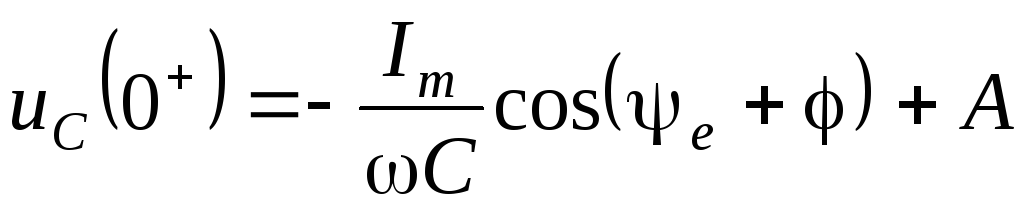 .
.
В соответствии с правилом коммутации
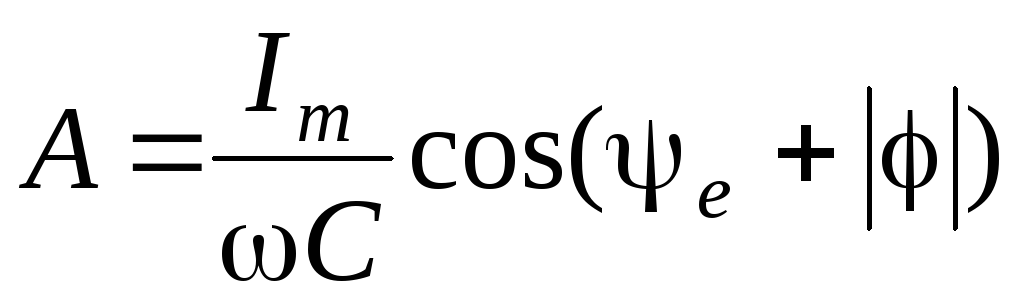 ;
;
Таким образом,
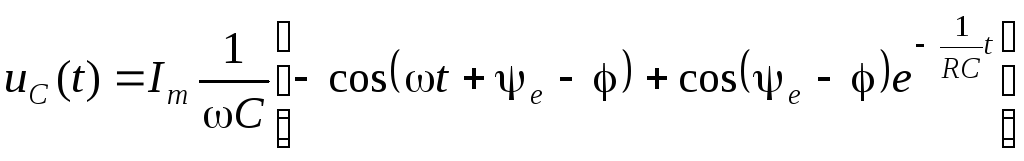
или
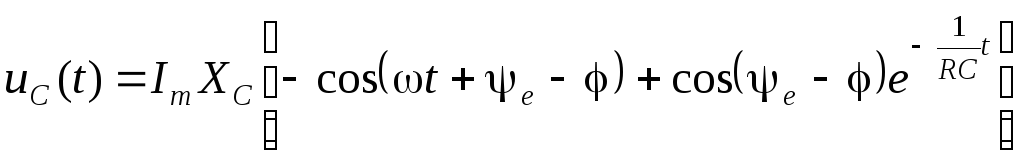 .
.
Определим
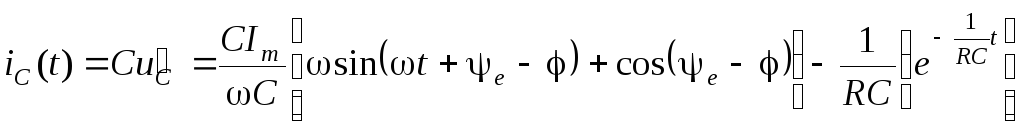 ;
;
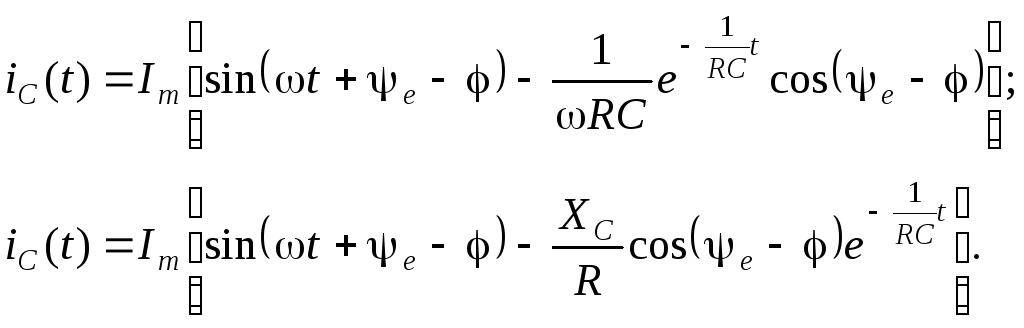
Оба выражения для uCиiCв общем случае имеют периодическую
принужденную и апериодическую свободную
составляющие. При этом характер
переходного процесса существенно
зависит от двух факторов – начальной
фазы напряжения источника в момент
включения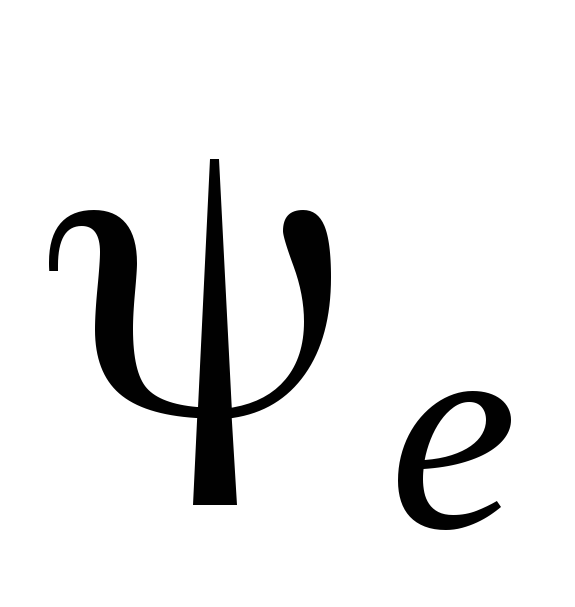 и соотношения параметров цепи
и соотношения параметров цепи иR.
иR.
Исследуем ожидаемое
влияние фазы включения 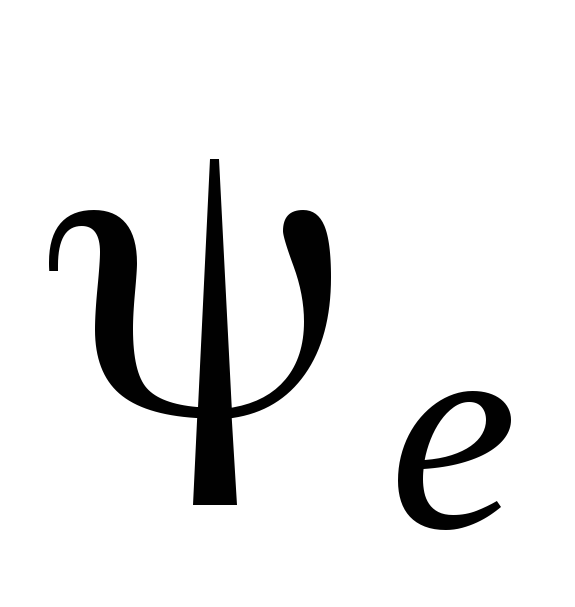 источника на переходный режим
источника на переходный режим
1) Пусть 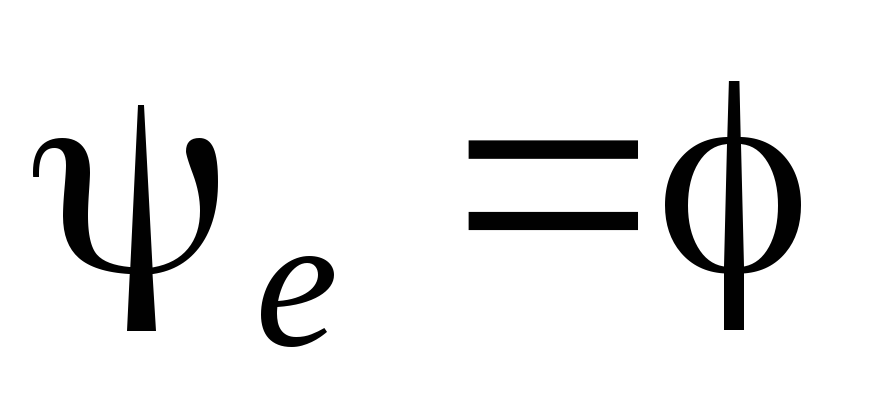 ,
тогда
,
тогда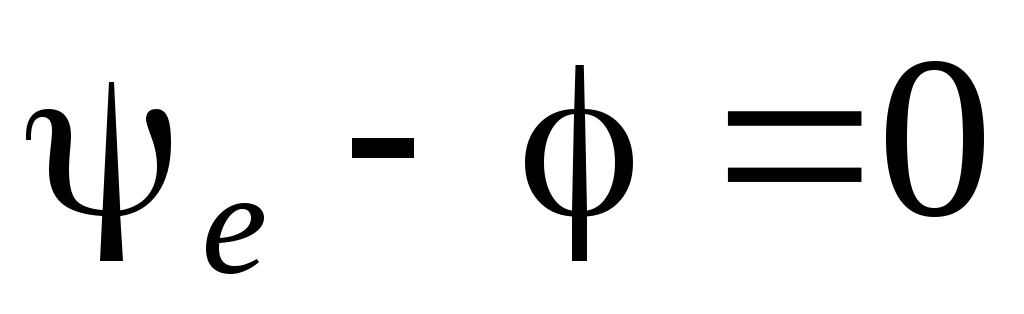 .
Посколькуcos 0 = 1,
получим
.
Посколькуcos 0 = 1,
получим
.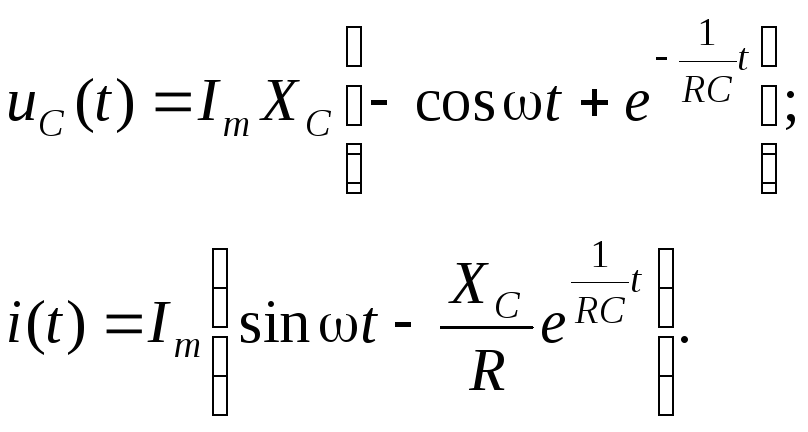
а) исследование
кривой напряжения (рис. 4.13) наглядно
демонстрирует, что максимальное
напряжение в переходном режиме ограничено 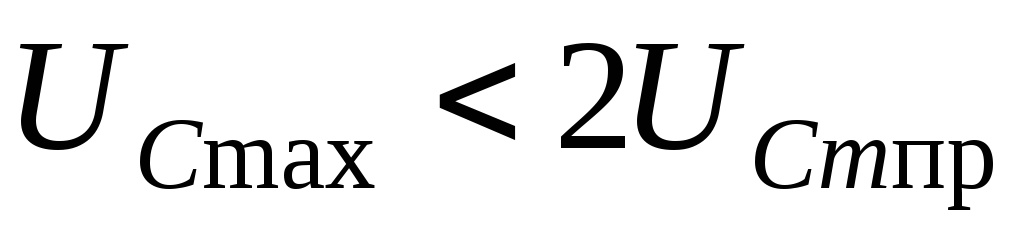 .
.
б) исследование кривой тока (рис. 4.14).
Максимальное
значение тока в переходном режиме
зависит от соотношения 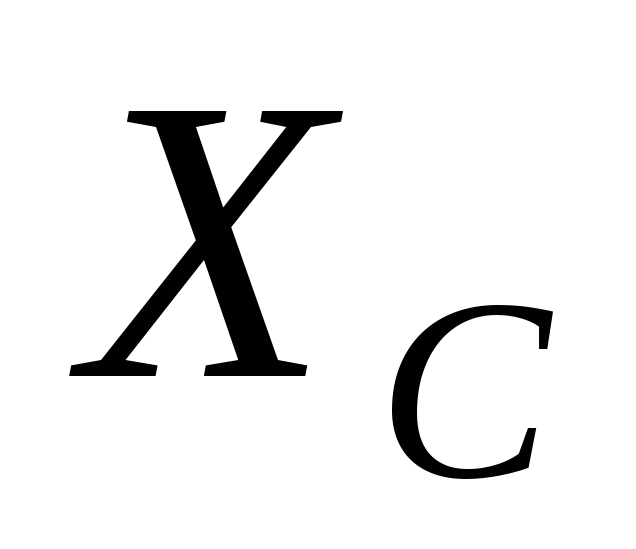 иR и может превышатьImпр в несколько раз. Однако этот начальный
всплеск тока является кратковременным.
иR и может превышатьImпр в несколько раз. Однако этот начальный
всплеск тока является кратковременным.
2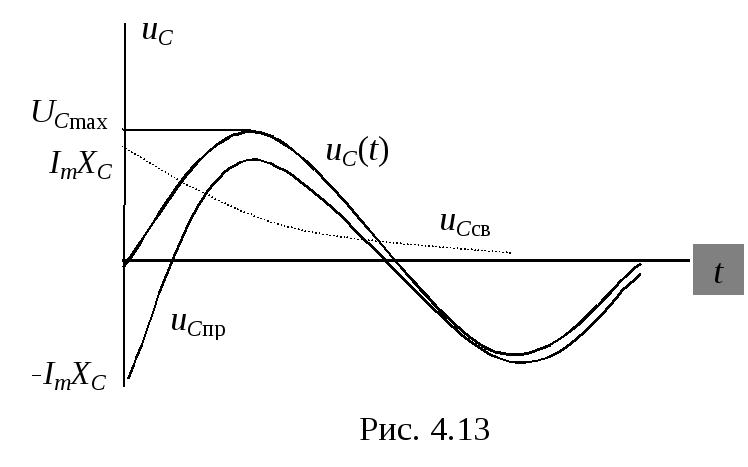 )
В случае, если
)
В случае, если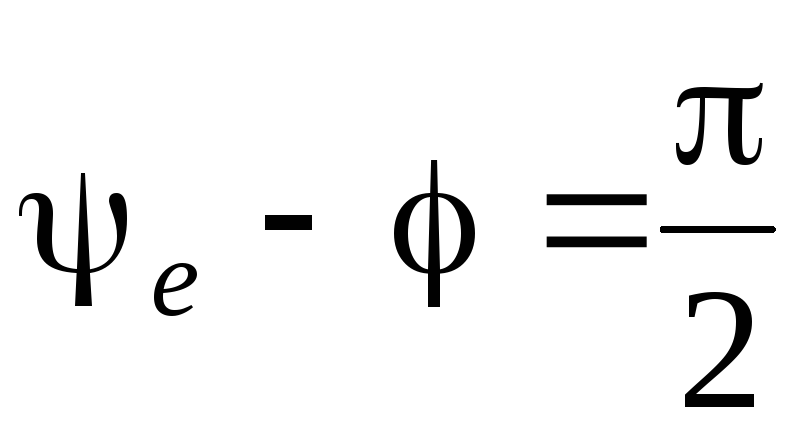 ,
поскольку
,
поскольку 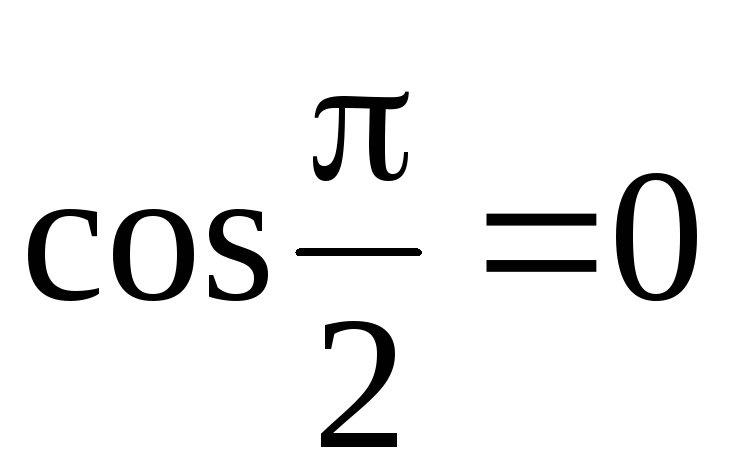 ,
получим
,
получим
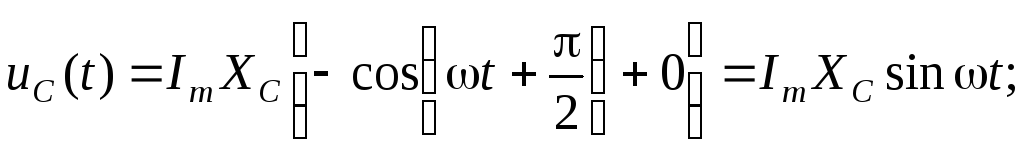
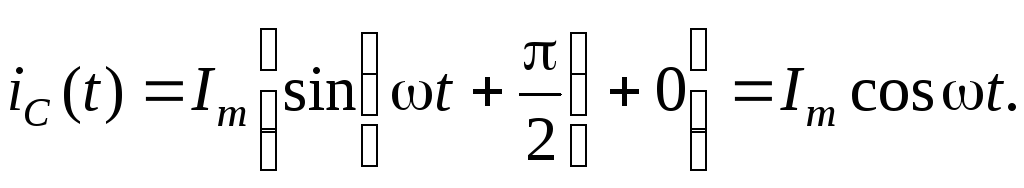
Т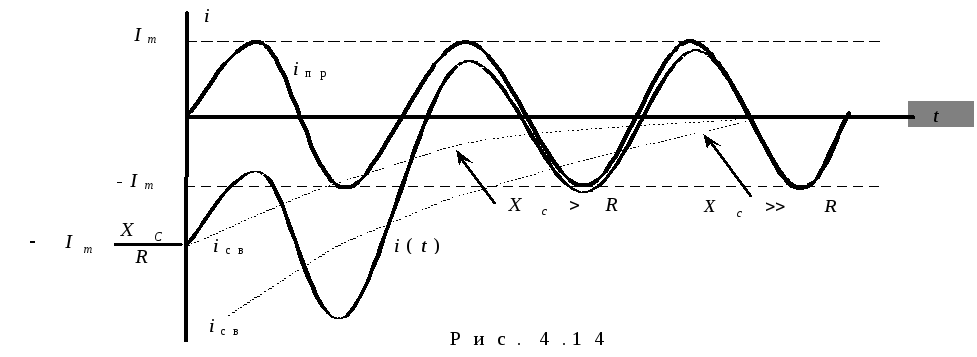 аким
образом, в данном случае в цепи переходный
процесс не наблюдается.
аким
образом, в данном случае в цепи переходный
процесс не наблюдается.
1.5 Постоянная времени цепи и ее физический смысл
Закон
изменения множителя 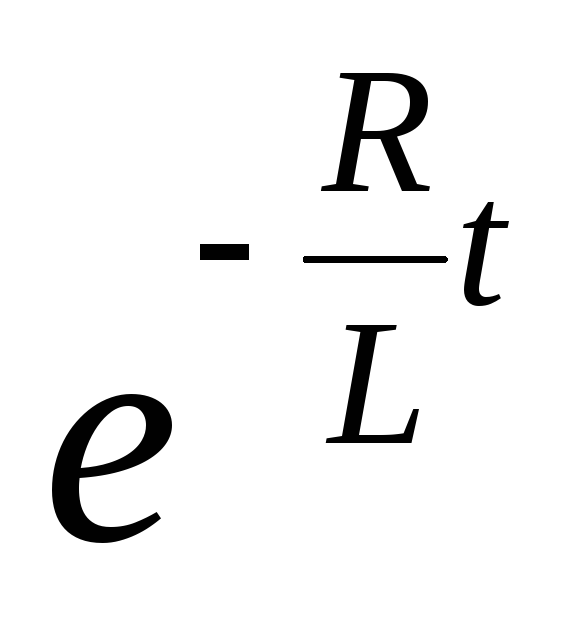 зависит от величины
зависит от величины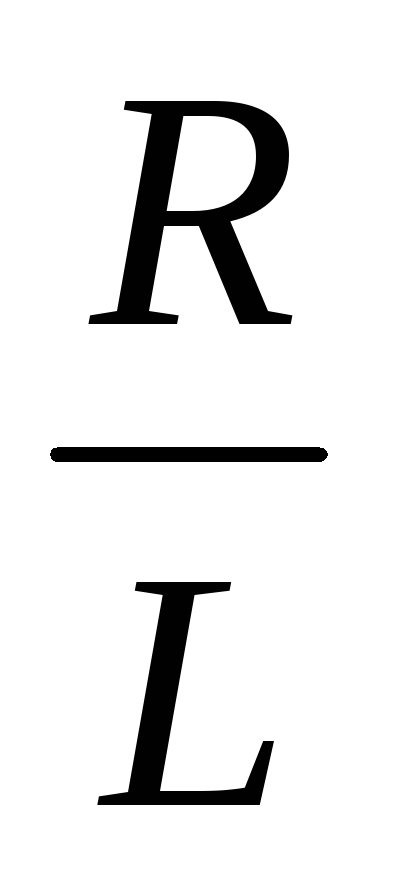 .
Эта величина имеет размерность времени
и называется постоянной времени цепи.
Обозначается постоянная времени
греческой буквой .
.
Эта величина имеет размерность времени
и называется постоянной времени цепи.
Обозначается постоянная времени
греческой буквой .
Через 5 после коммутации любой ток или напряжение цепи достигает 99,3% от своего предельного значения (при t ). В неразветвленной RL- цепи (рис.1.2):
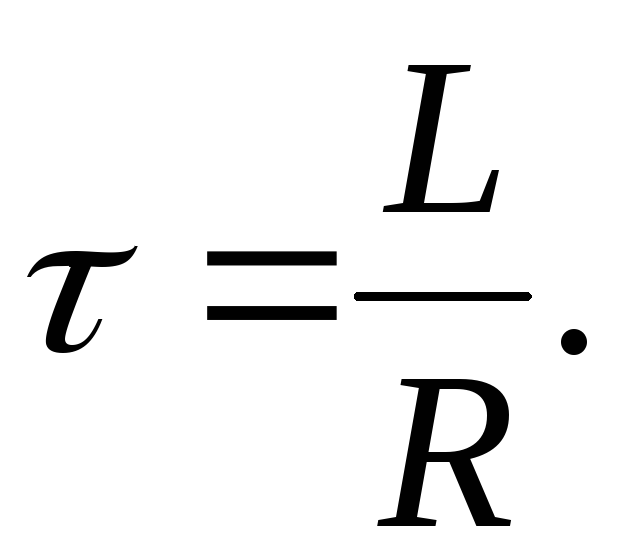 (1.15)
(1.15)
Таким
образом, имеем решение для iL(t) при  0+,
т.е. при всех t переходного процесса:
0+,
т.е. при всех t переходного процесса:
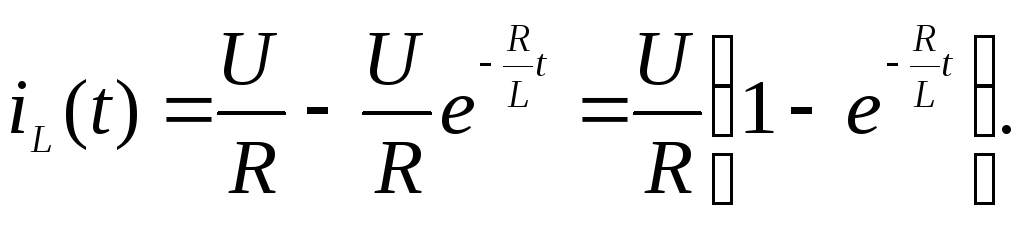 . (1.16)
. (1.16)
Определяем напряжение на резисторе R и индуктивности L в переходном режиме:
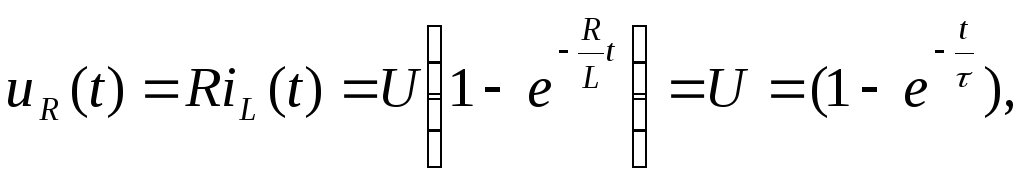 (1.17)
(1.17)
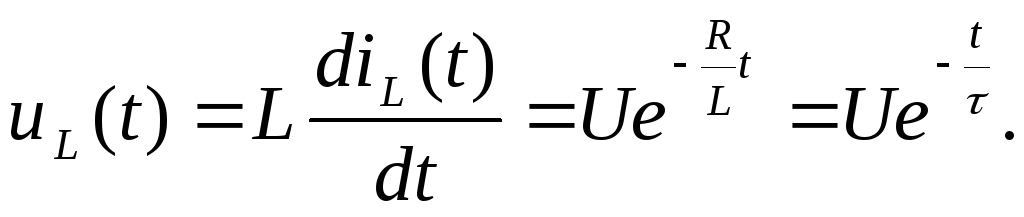 (1.18)
(1.18)
 По
формулам (1.17),
(1.18) построим
графики изменения напряжений от времени t.
По
формулам (1.17),
(1.18) построим
графики изменения напряжений от времени t.
1
2
3
4
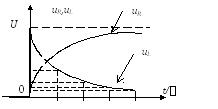
Рис. 1.4
Из рис. 1.4 видно, что при любом значении t сумма напряжений uR и uL составляет величину входного напряжения U, что подтверждает второй закон Кирхгофа.
Анализ
полученных результатов показывает, что
при нулевых начальных условиях в момент t=0+ индуктивность ведет себя как бесконечно
большое сопротивление (разрыв цепи), а
при t ,
как бесконечно малое сопротивление
(короткое замыкание цепи).
,
как бесконечно малое сопротивление
(короткое замыкание цепи).
Постоянная
времени τ – это время, в течение которого свободная
составляющая iсв изменяется ровно в “e”
раз. Покажем это. Для этого сравним два
значения iсв при
произвольном времени t,
взятых через время τ: 


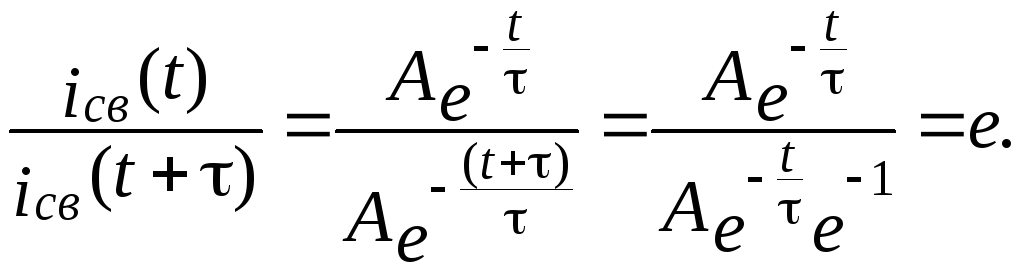
Таким
образом, величина τ определяет скорость протекания
переходного процесса в цепи, т.к. через
(4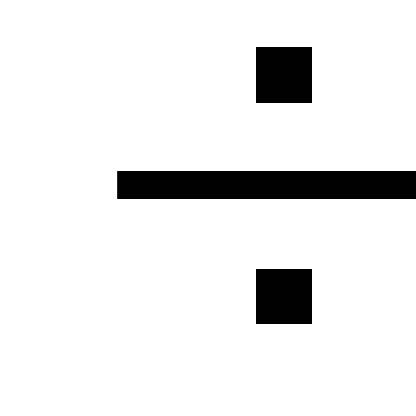 5)τ он обычно практически заканчивается.
5)τ он обычно практически заканчивается.
2.Расчет прохождения сигнала через линейные электрические цепи
Параметры сигнала:
длительность импульса: 0,4 мс; период сигнала: 1,5 мс; середина импульса: 0,014 мс; максимальное и минимальное значение сигнала: 0,5 и 0 В.
2.1Разложение импульсных колебаний на гармонические составляющие
Результат воздействия на электрическую цепь синусоидального напряжения и тока можно найти при помощи символического метода решения уравнений Кирхгофа. Форма синусоидального напряжения (или тока) на выходе любой линейной электрической цепи остается синусоидальной, а амплитуда напряжений и его начальная фаза изменяются. Поэтому при рассмотрении воздействия на электрические цепи несинусоидальных напряжений (токов) во многих случаях целесообразно представить их в виде некоторой суммы синусоидальных колебаний.
Любое периодическое несинусоидальное колебание можно разложить в бесконечный тригонометрический ряд, состоящий из постоянной составляющей и синусоидальных составляющих различной частоты, амплитуды и фазы. Совокупность этих синусоидальных или гармонических составляющих называется частотным спектром.
Тригонометрический ряд, получающийся при разложении периодических несинусоидальных колебаний, называется рядом Фурье [7, с.7]:
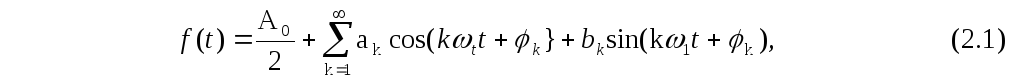
Коэффициенты ряда Фурье ( А0, ak, bk и φk ) рассчитываем по формулам [7, c.7]:



Где
f(t) – несинусоидальная периодическая функция;
Т – период колебаний, т.е. наименьшее время, по истечении которого колебания полностью повторяются, 1/с;
ω1 – скорость изменения фазы (угловая частота) первой или основной гармоники, рад/с;
k – порядковый номер гармоники.
В радиотехнике для определения отклика цепи на негармоническое воздействие f(t) используют косинусную форму ряда Фурье [1, с.276]:
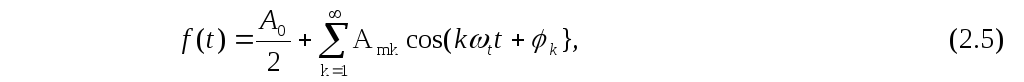
которая связана с рядом Фурье (2.1) следующими соотношениями [1, с.276]:

где Amk –это амплитуда «k»-ой гармоники, функция четная относительно частоты;
φk – начальная фаза «k»-ой гармоники, функция нечетная относительно частоты и поэтому может принимать как положительные значения, так и отрицательные;
А0 – постоянная составляющая воздействия f(t).
Амплитуды всех гармоник разложения (Amk) вместе с постоянной составляющей разложения (А0) образуют амплитудно-частотный спектр (АЧС) воздействия f(t).
Начальные фазы всех гармоник разложения (ψk) образуют фазо-частотный спектр (ФЧС) воздействия f(t).
Заданный импульс напряжения выражается в пределах одного периода функцией
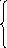 0,5,
0,5,
f(t)=
0, 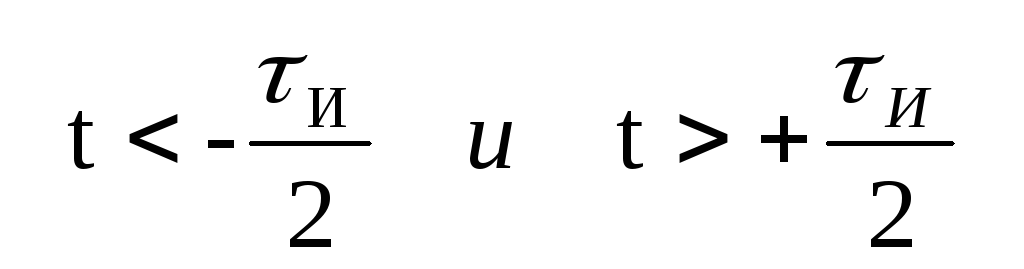
т.е. мы имеем импульсное напряжение прямоугольной формы с периодом повторения Т и длительностью импульса τИ со смещением середины импульса относительно оси ординат.
Интегрирование
проводим в пределах от 0 до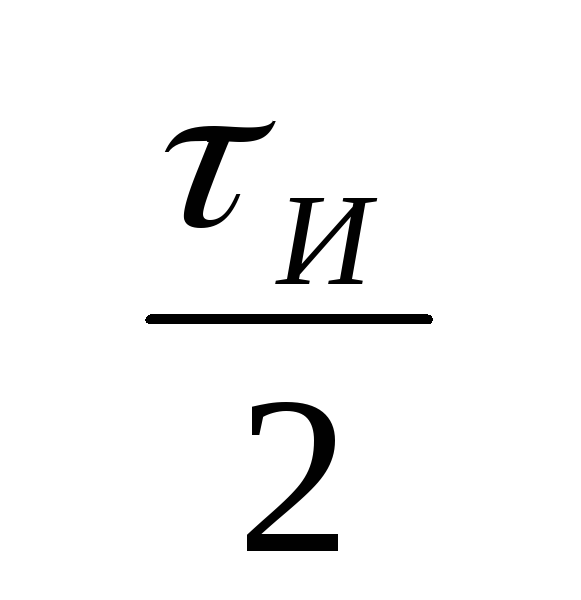 ,
введя перед интегралом множитель 2.
,
введя перед интегралом множитель 2.
Постоянная составляющая ряда на основании формулы (2.2) будет равна
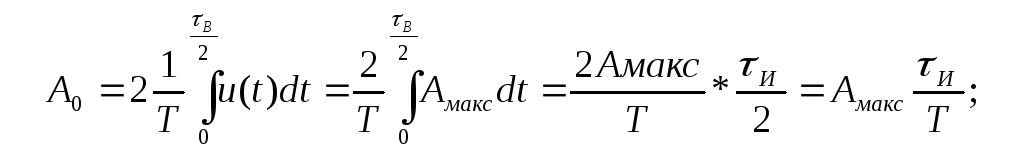
Коэффициенты аk, bk (формулы (2.3) и (2.4)) :
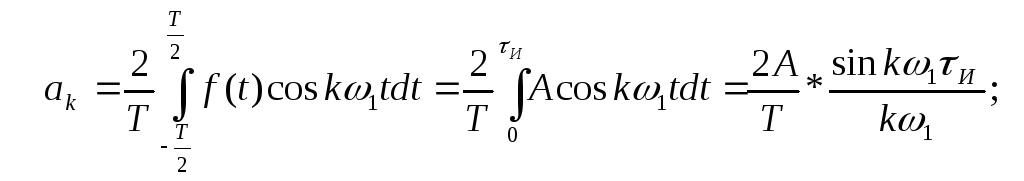
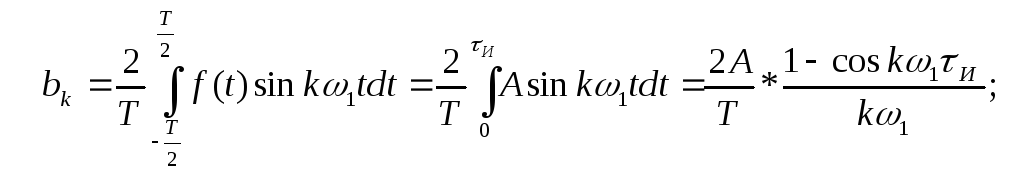
Рассчитываем коэффициенты (амплитуды гармоник) при косинусных составляющих ряда Фурье, а также начальные фазы гармоник:
Тогда
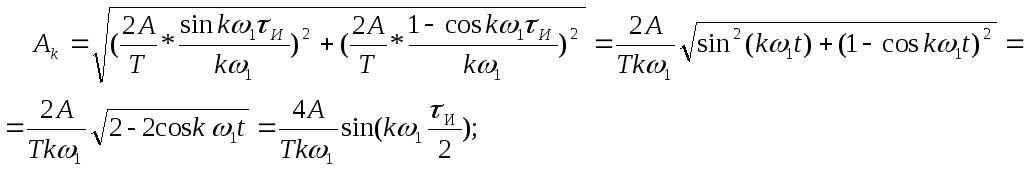
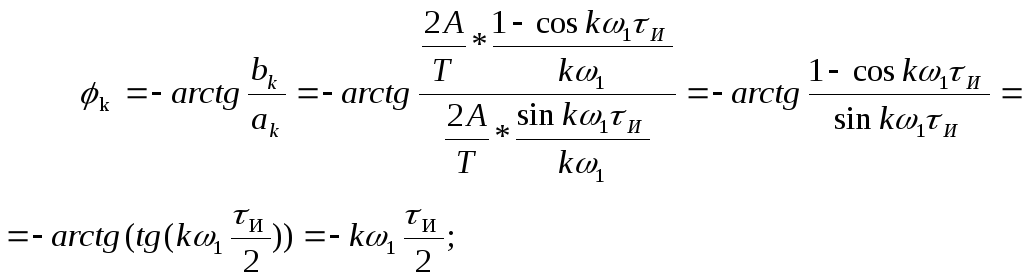
Учитывая
то, что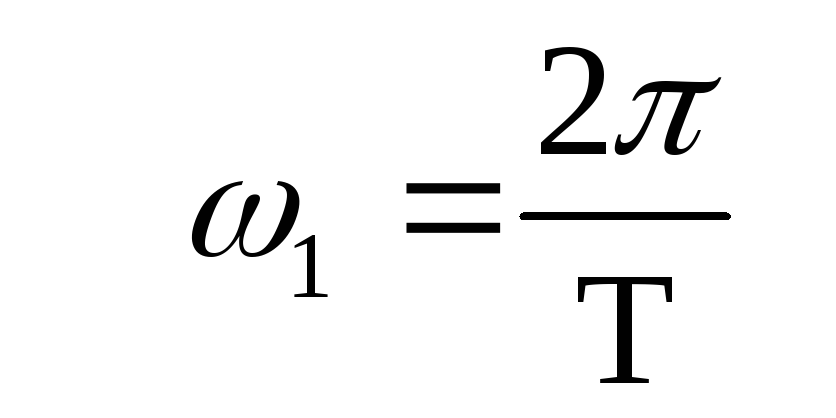 [2,
c.98],
[2,
c.98],
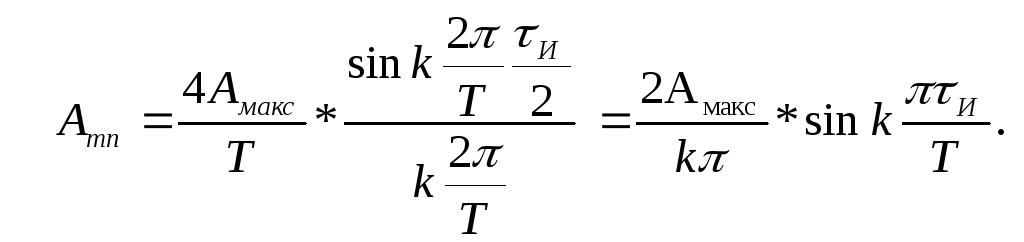
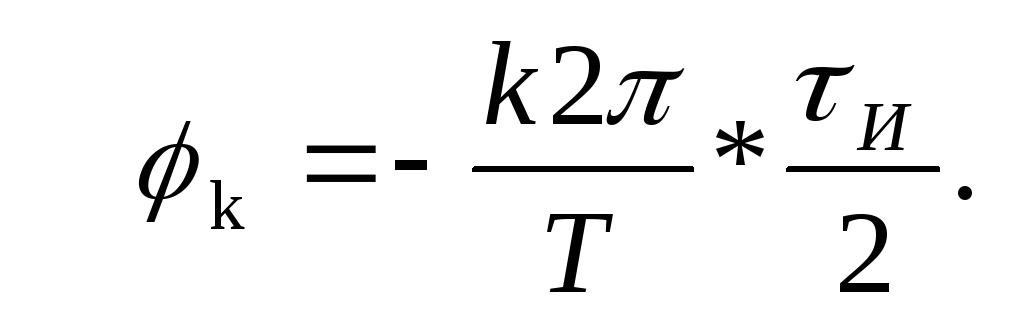

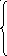
Подставляя численные значения в формулы, получим амплитуды и начальные фазы гармонических составляющих ряда Фурье.
Таким
образом рассчитывают периодические
колебания функций четных относительно
частоты. При смещении момента отсчета
времени на любую величину, т.е. при
запаздывании или опережении процесса
на время t0,
учитываем смещение середины импульса
относительно оси ординат. Смещение
периодической функции не изменяет
значений амплитуд гармоник. Начальные
фазы гармоник изменяются на угол 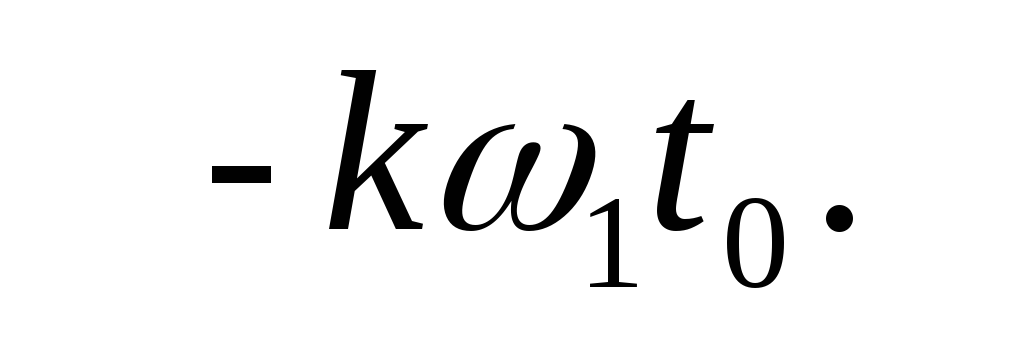 [2,с.276],
[2,с.276],
где t0 – время начала переднего фронта импульса.
t0=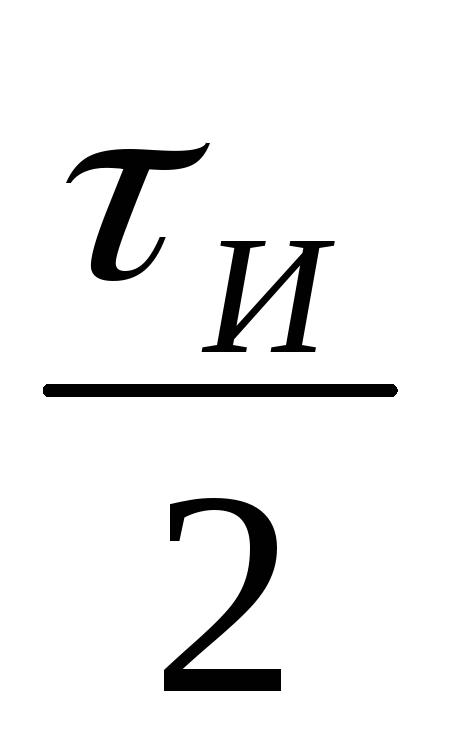 —tсмещения=
— 0,2+0,014= — 0,186,
—tсмещения=
— 0,2+0,014= — 0,186,
т.е. начальные фазы гармонических составляющих сигнала воздействия рассчитываются по формуле:
. 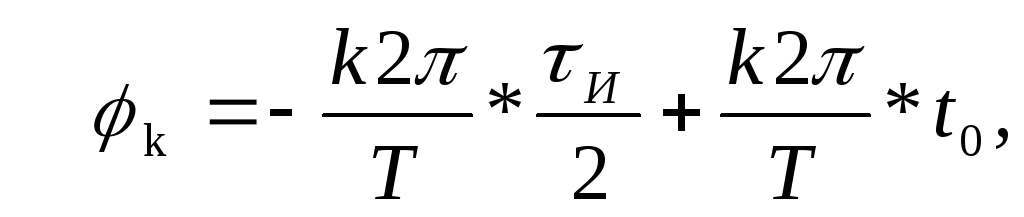
Рассчитаем постоянную составляющую
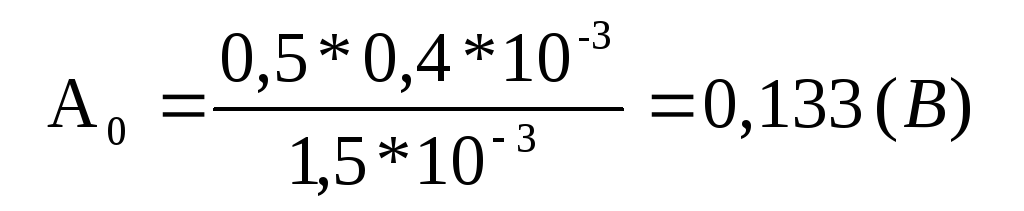 ,
,
и амплитуды и начальные фазы гармонических составляющих:
для первой гармоники (k=1)
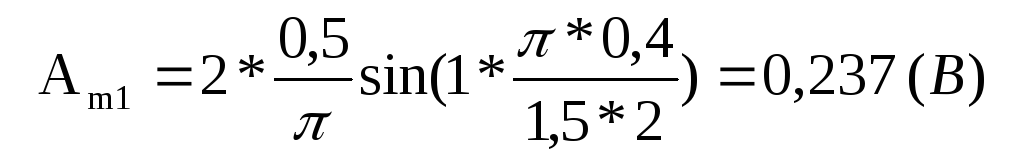
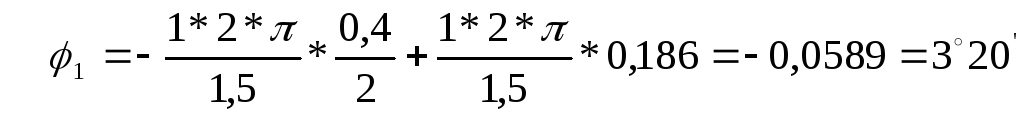
для второй гармоники (k =2)
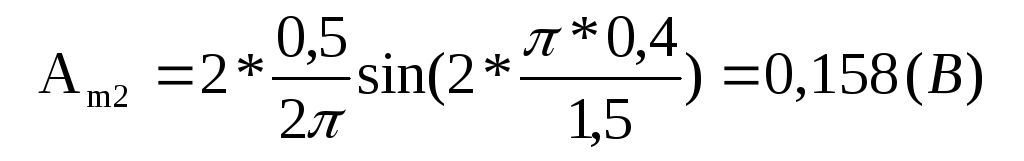
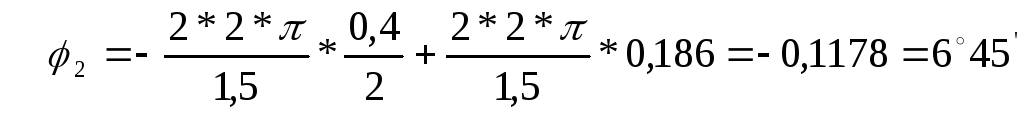
для третьей гармоники (k =3)

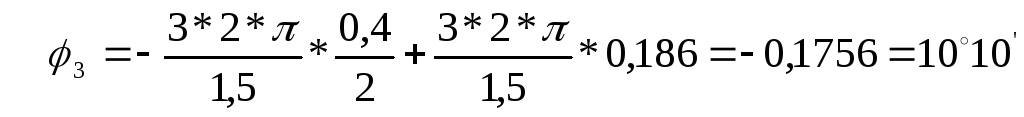
для четвертой гармоники (k =4)
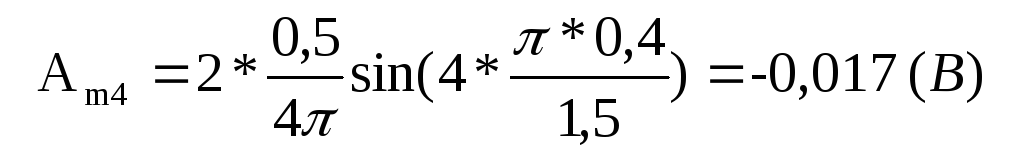
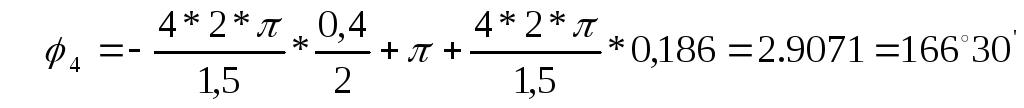
для пятой гармоники (k =5)
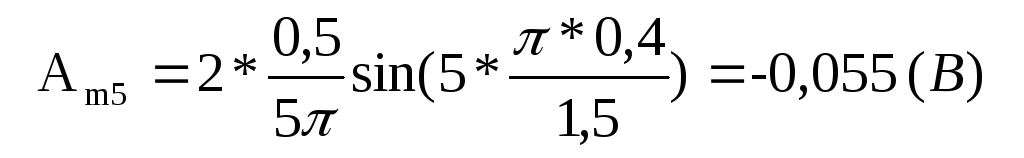
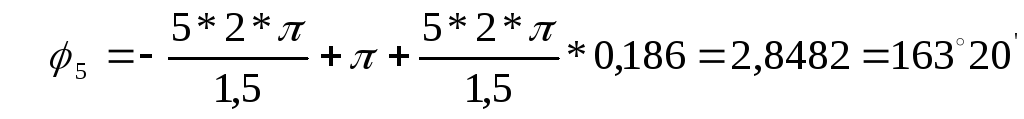
для шестой гармоники (k =6)
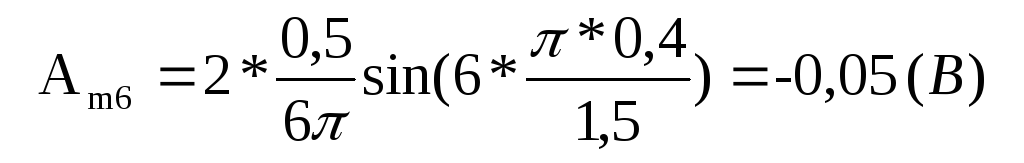
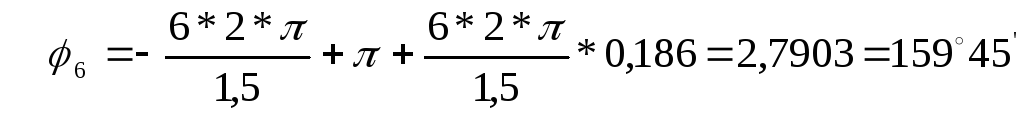
для седьмой гармоники (k =7)
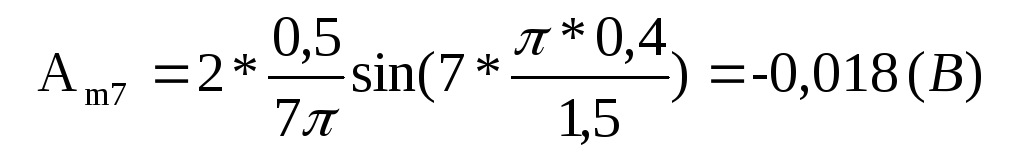
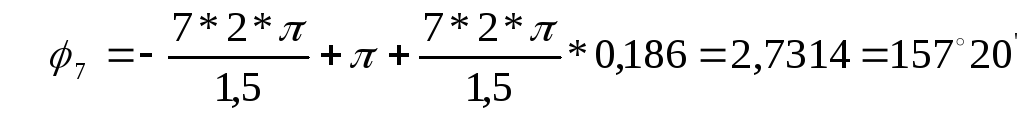
для восьмой гармоники (k =8)
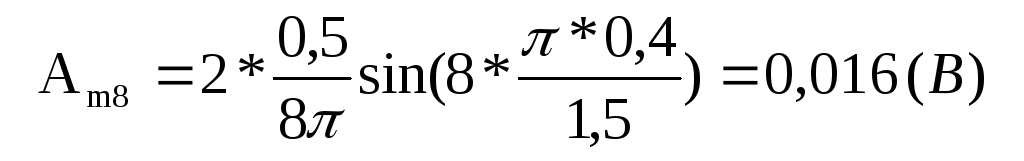
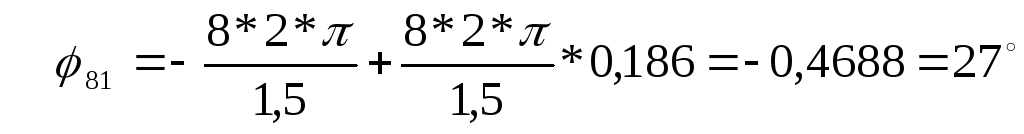
для девятой гармоники (k =9)
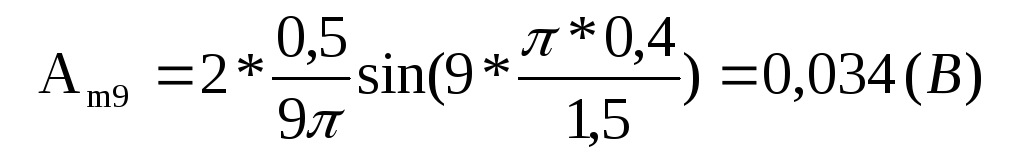
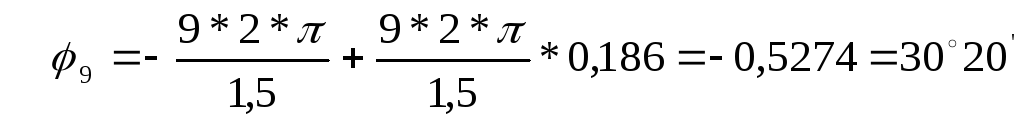
для десятой гармоники (k =10)
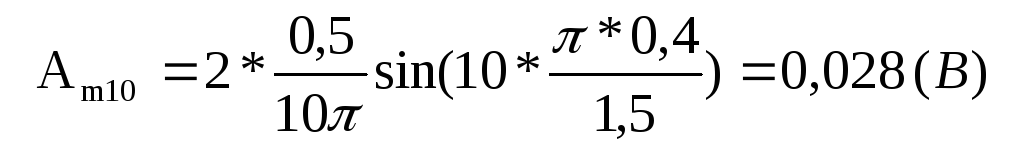
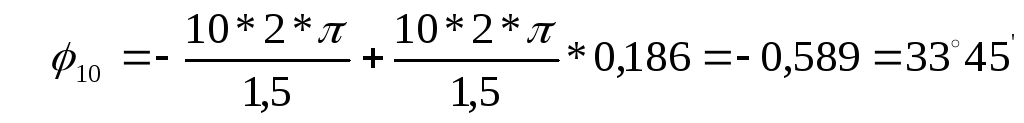
Амплитудный и фазовый спектр сигнала воздействия изображен на рис. 2.1
5. Резонанс в последовательно параллельных цепях | 6. Резонанс | Часть2
5. Резонанс в последовательно параллельных цепях
Резонанс в последовательно параллельных цепях
В простых реактивных схемах с небольшим сопротивлением или отсутствием такового, на резонансной частоте проявляются эффекты радикального изменения импеданса. Импеданс параллельной LC цепи (колебательного контура) в состоянии резонанса достигает бесконечного значения. Импеданс последовательной LC цепи в состоянии резонанса достигает нулевого значения. Формула расчета резонансной частоты, как вы помните, имеет следующий вид:
Однако, как только в большинство LC цепей вводятся значимые значения сопротивлений, этот простой расчет резонанса становится недействительным. Мы с вами рассмотрим несколько LC цепей, с включенными в их состав резисторами, используя прежние значения емкости и индуктивности: 10 мкФ и 100 мГн соответственно. Согласно приведенной выше формуле, резонансная частота этих цепей должна быть равна 159,155 Гц. Давайте при помощи ниже приведенных SPICE анализов посмотрим, в каких точках значения тока будут иметь максимальные или минимальные значения:
resonant circuit v1 1 0 ac 1 sin с1 1 0 10u r1 1 2 100 l1 2 0 100m .ac lin 20 100 400 .plot ac i(v1) .end
Как видите, ток достигает своего минимального значения на частоте 136,8 Гц (вместо рассчитанной по формуле частоты 159,2 Гц).
Фиктивный резистор в ветвь с катушкой индуктивности мы включили для того, чтобы предотвратить прямую связь «катушка индуктивности — источник напряжения», которую так не может терпеть SPICE. Этот резистор должен иметь очень низкое значение для минимального воздействия на поведение схемы.
resonant circuit v1 1 0 ac 1 sin r1 1 2 100 c1 2 0 10u rbogus 1 3 1e-12 l1 3 0 100m .ac lin 20 100 400 .plot ac i(v1) .end
Минимальный ток будет на частоте близкой к 180 Гц вместо 159,2 Гц!
Теперь давайте переключим наше внимание на последовательные LC цепи. Здесь мы поэкспериментируем с подключением значимых сопротивлений параллельно катушке индуктивности или конденсатору (помимо этих сопротивлений нам нужно последовательно с катушкой индуктивности и конденсатором включить резистор (R1) сопротивлением 1 Ом, который будет ограничивать общий ток при резонансе). Если мы подключим резистор (R2) сопротивлением 100 Ом параллельно катушке индуктивности, то результат будет следующим:
resonant circuit v1 1 0 ac 1 sin r1 1 2 1 c1 2 3 10u l1 3 0 100m r2 3 0 100 .ac lin 20 100 400 .plot ac i(v1) .end
Максимальный ток будет на частоте близкой к 178,9 Гц вместо 159,2 Гц!
И наконец, рассмотрим последовательную LC цепь, в которой сопротивление включено параллельно с конденсатором:
resonant circuit v1 1 0 ac 1 sin r1 1 2 1 c1 2 3 10u r2 2 3 100 l1 3 0 100m .ac lin 20 100 200 .plot ac i(v1) .end
Максимальный ток будет на частоте 136,8 Гц вместо 159,2 Гц!
Способность добавочного сопротивления смещать точку, в которой импеданс LC цепи достигает максимума или минимума, называется антирезонансом. Разобрав вышеприведенные примеры вы наверное заметили как сопротивление влияет на резонансную частоту схемы:
Параллельная LC цепь (колебательный контур):
- R последовательно с L: резонансная частота смещается вниз
- R последовательно с C: резонансная частота смещается вверх
Последовательная LC цепь:
- R параллельно с L: резонансная частота смещается вверх
- R параллельно с C: резонансная частота смещается вниз
Все вышесказанное показывает нам взаимодополняющую природу конденсаторов и катушек индуктивности: последовательное соединение сопротивления с одним из этих компонентов (например с конденсатором) создает эффект антирезонанса, эквивалентный параллельному соединению этого же сопротивления с другим компонентом (катушкой индуктивности). Если вы еще внимательнее посмотрите на SPICE примеры, то увидите, что частоты смещаются на одинаковую величину, а графики представляют собой зеркальное отображение друг друга.
Антирезонанс — это эффект, о котором должны знать все проектировщики резонансных схем. Уравнения для определения «смещения» антирезонанса довольно сложны, и не будут рассматриваться в рамках данной статьи. Для начинающих радиолюбителей изложенного материала вполне достаточно, чтобы понять, что такой эффект существует и каковы его последствия.
Дополнительное сопротивление может возникнуть практически во всех LC цепях. Если при производстве конденсаторов существует возможность минимизировать паразитные сопротивления, то практически все катушки индуктивности имеют значимые величины таких сопротивлений благодаря длинным проводам, используемым при их изготовлении. Более того, благодаря скин-эффекту сопротивление провода будет увеличиваться вместе с увеличением частоты. Таким образом, катушки индуктивности обладают не просто сопротивлением, а частотно-зависимым сопротивлением.
Помимо борьбы с сопротивлением проводов, мы также должны бороться с потерями в железных сердечниках катушек индуктивности (которые проявляются в виде дополнительных сопротивлений в цепи). Нам известно, что железо является проводником как электричества, так и магнитного потока. Исходя из этого можно прийти к выводу, что изменение магнитного потока, произведенное прохождением переменного тока через катушку индуктивности, индуцирует электрические токи в самом сердечнике (вихревые токи). Этот эффект можно минимизировать путем применения пластинчатых сердечников, высококачественных материалов и правильными расчетами самих сердечников. Полностью устранить данный эффект практически невозможно.
Заметным исключением из правила смещения резонансной частоты при добавлении значимого сопротивления являются схемы с последовательным включением резистора, катушки индуктивности и конденсатора («RLC»). До тех пор, пока все компоненты будут соединены последовательно друг с другом, резонансная частота не будет зависеть от сопротивления.
series rlc circuit v1 1 0 ac 1 sin r1 1 2 100 c1 2 3 10u l1 3 0 100m .ac lin 20 100 200 .plot ac i(v1) .end
Максимальный ток на частоте 159,2 Гц!
Обратите внимание, что пиковое значение тока на этом графике не изменилось по сравнению с рассмотренной в одной из предыдущих статей последовательной LC цепью (с символическим сопротивлением 1 Ом), хотя величина сопротивления теперь в 100 раз больше. Единственной вещью, которая подверглась изменению, является «острота» кривой. Очевидно, эта цепь резонирует не так сильно, как цепь с меньшим последовательным сопротивлением (как говорят, она «менее избирательна»), но, по крайней мере, она обладает той же самой собственной частотой.
Стоит отметить, что антирезонанс создает эффект демпфирования (успокоения) колебаний в таких LC цепях, как колебательные контуры. В начале этого раздела мы с вами видели, как подключенные друг к другу конденсатор и катушка индуктивности действуют подобно маятнику. Если при раскачивании маятника происходит превращение кинетической энергии (движение) в потенциальную (высота), то в электрической цепи происходит передача энергии от конденсатора к катушке индуктивности и обратно посредством чередующихся форм тока (кинетическое движение электронов) и напряжения (потенциал электрической энергии). В идеальном колебательном контуре (с нулевым сопротивлением) такие колебания будут продолжаться вечно, точно так же как лишенный трения маятник будет вечно раскачиваться на своей резонансной частоте. Но, в реальном мире такие электрические цепи и механизмы найти практически невозможно. Потери энергии через сопротивление (или потери в сердечнике катушки индуктивности и т.п) приводят к тому, что амплитуда колебаний постепенно снижается, и в конце концов сходит на нет. Если в колебательном контуре будут достаточно большие потери энергии, то он вообще не будет резонировать.
Демпфирующее свойство антирезонанса рассмотрено нами не только ради праздного любопытства. Оно весьма эффективно может использоваться для устранения нежелательных колебаний в цепях, содержащих паразитные индуктивности или емкости (а ими обладают практически все цепи). В качестве примера давайте рассмотрим следующую L/R цепь:
Идея этой схемы проста: она «заряжает» катушку индуктивности, когда выключатель замкнут. Скорость зарядки катушки устанавливается отношением L/R, представляющим собой постоянную времени цепи (измеряемую в секундах). Однако, если вы сами соберете такую схему, то столкнетесь с неожиданными колебаниями напряжения на катушке индуктивности при замкнутом выключателе (см. рисунок ниже). Почему это происходит? Как мы можем иметь резонансное колебание в цепи, в которой нет конденсатора, а есть только катушка индуктивности, резистор и батарея?
Все катушки индуктивности обладают определенной величиной паразитной емкости. Эта емкость возникает между отдельными витками катушки, между витками и сердечником, витками и экраном, витками и другими элементами конструкции. Кроме того, паразитную емкость может создать размещение дорожек на печатных платах. Устранить полностью такую емкость практически невозможно. Если паразитная емкость приводит к появлению ненужного резонанса (нежелательным колебаниям переменного напряжения), то на помощь может прийти дополнительное сопротивление. Высокая величина сопротивления R вызовет состояние антирезонанса, рассеивая достаточно энергии, чтобы помешать индуктивности и паразитной емкости поддерживать колебания в течении длительного времени.
Интересно, что принцип применения сопротивления для устранения нежелательного резонанса очень часто используется при проектировании механических систем, где любой движущийся объект (обладающий определенной массой) является потенциальным резонатором. Одним из таких примеров являются амортизаторы в автомобиле. Без амортизаторов автомобиль будет долго прыгать на резонирующей частоте после любой неровности на дороге. Роль амортизаторов заключается во введении антирезонирущего эффекта путем гидравлического рассеивания энергии (точно так же, как резистор рассеивает энергию электрически).

